ABSTRACT
The sensitivity of radar systems to detect different velocity populations of the incoming micrometeoroid flux is often the first argument considered to explain disagreements between models of the Near-Earth dust environment and observations. Recently, this was argued by Nesvorný et al. to support the main conclusions of a Zodiacal Dust Cloud (ZDC) model which predicts a flux of meteoric material into the Earth's upper atmosphere mostly composed of small and very slow particles. In this paper, we expand on a new methodology developed by Janches et al. to test the ability of powerful radars to detect the meteoroid populations in question. In our previous work, we focused on Arecibo 430 MHz observations since it is the most sensitive radar that has been used for this type of observation to date. In this paper, we apply our methodology to two other systems, the 440 MHz Poker Flat Incoherent Scatter Radar and the 46.5 Middle and Upper Atmosphere radar. We show that even with the less sensitive radars, the current ZDC model over-predicts radar observations. We discuss our results in light of new measurements by the Planck satellite which suggest that the ZDC particle population may be characterized by smaller sizes than previously believed. We conclude that the solution to finding agreement between the ZDC model and sensitive high power and large aperture meteor observations must be a combination of a re-examination not only of our knowledge of radar detection biases, but also the physical assumptions of the ZDC model itself.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The new Zodiacal Dust Cloud (ZDC) model reported by Nesvorný et al. (2010, 2011b), hereafter referred to as ZoDy, follows the dynamical evolution of dust particles after ejection utilizing the orbital properties and lifetimes of comets and asteroids. Among the main results, the model, which is primarily constrained by the latitudinal (ecliptic) distribution of the IR spectrum obtained with the Infrared Astronomical Satellite (IRAS), predicts that (1) 85%–95% of the IR emission of the ZDC is produced by dust in the inner solar system with masses ranging from 1 to 10 μg which originates from Jupiter family comets (JFCs); (2) the dust has near-prograde orbits and thus impact Earth at a mean geocentric speed of about 14 km s−1 with an absence of significant orbital eccentricities; and (3) the dust cloud produces a global meteoric mass input into the Earth's atmosphere of around 32 t/d (±50%), representing 50%–70% of the total input. Some of these results are in general disagreement with decades of observations using ground-based radars and a qualitative explanation for this discord reported by Nesvorný et al. (2011a) argues that this is due to the fact that radars cannot detect small particles entering the atmosphere at low velocities due to the relatively low production of electrons. However, that work utilized results derived from the detection of specular trail reflections by two meteor radars whose sensitivity is too low to test this hypothesis rigorously.
Motivated by these findings, we reported in Janches et al. (2014b, hereafter referred as Paper I), a new probabilistic approach to estimate the sensitivity of the Arecibo Observatory (AO) 430 MHz radar to detect such particles in the form of meteor head echoes as a function of particle mass (m), incoming velocity (V) and entry angle (α). High Power and Large Aperture (HPLA) radars have the sensitivity to test this hypothesis and in particular AO is the most sensitive radar used for meteor observations to date. Thus, we focused in Paper I on this system where we integrated and employed existing comprehensive models of meteoroid ablation, ionization, and radar detection to enable accurate interpretation of radar observations and show that some agreement in the hourly rates is found between model predictions and Arecibo observations only when (1) we invoke the lower limit of the model predicted flux (∼16 t/d) and (2) we revise the extensively used ionization probability of ablating metal atoms reported by Jones (1997) by using laboratory measurements of the ionization cross sections of high speed metal atom beams. These revisions resulted in ionization probabilities that are up to two orders of magnitude smaller for low-speed meteors, and are probably lower limits. Nevertheless, the model over predicts the slow portion of the Arecibo radial velocity distributions by a factor of three, suggesting the model requires some revision. It is important to note, however, that the the results reported in Paper I do support ZoDy's main hypothesis that most of the 12–14 km s−1 particles with mass equal to 1–10 μg could remain undetected, even by the Arecibo radar, and the disagreement actually originates from the number of particles with higher velocities ( km s−1) entering the beam at larger zenith angles, which is too high and thus continues to dominate the predicted distributions.
km s−1) entering the beam at larger zenith angles, which is too high and thus continues to dominate the predicted distributions.
Our approach utilized the Chemical Ablation Model (CABMOD) developed by Vondrak et al. (2008) to calculate the electron production profiles as a function of altitude of a given particle, and the radar antenna Gain pattern, G, to estimate the meteor signal-to-noise ratio (S/N) as a function of the physical location of the particle's path through the radar beam. This approach results in the calculation of the probability that a particle would be detected by the radar as a function of its dynamical parameters, based on the specification of what portion of the illuminated radar volume in the Earth's mesosphere, where ablation occurs and meteors are produced, will have the sensitivity required to detect the given particle.
In this work, we extend our detectability treatment to two other HPLA radars and compare them with the results reported in Paper I, thus generalizing the methodology to other systems utilized extensively for meteor head echo observations for which we have data. In particular, we utilize the 440 MHz Poker Flat Incoherent Scatter Radar (PFISR) operating in Poker Flat, Alaska and the 46.5 MHz Middle and Upper (MU) Atmosphere Radar in Shigaraki, Japan. The study of the Sporadic Meteor Complex resulting from the ZDC with these systems provides two important contrasts to the AO observations which can be used to constrain further ZoDy and any other model of the meteoroid environment (e.g., Fentzke et al. 2009). First, the observations are characterized by significant differences in the geographical and seasonal variability of the detected meteors due to the large differences in the latitudes at which the radars operate (18 3N for AO, 34
3N for AO, 34 9N for MU, and 65
9N for MU, and 65 1N for PFISR). These differences have been demonstrated to be caused, at least in part, by the visibility of the different apparent sporadic meteor sources at each location and season (Janches et al. 2006; Fentzke & Janches 2008; Fentzke et al. 2009; Pifko et al. 2013). Second, each system has significant differences in detection sensitivity, and thus they enable the detection of somewhat different portions of the incoming flux (Janches et al. 2008, 2014a; Fentzke et al. 2009; Pifko et al. 2013). Any accurate model of the meteoroid influx and its detection should reproduce the observed differences due to these two factors.
1N for PFISR). These differences have been demonstrated to be caused, at least in part, by the visibility of the different apparent sporadic meteor sources at each location and season (Janches et al. 2006; Fentzke & Janches 2008; Fentzke et al. 2009; Pifko et al. 2013). Second, each system has significant differences in detection sensitivity, and thus they enable the detection of somewhat different portions of the incoming flux (Janches et al. 2008, 2014a; Fentzke et al. 2009; Pifko et al. 2013). Any accurate model of the meteoroid influx and its detection should reproduce the observed differences due to these two factors.
We will describe the extension of the detection probability calculation and compare the results among the different systems in Section 2. In Section 3 we will combine ZoDy with our probability calculations to predict the manner in which the different radar systems should observe this flux and compare the results with our observations. Finally we present a discussion of our results in Section 4 and conclusions in Section 5.
2. DETECTION PROBABILITY ESTIMATION
The treatment to estimate the detection probability of a meteor head echo given a set of meteoroid dynamical parameters 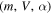 is described in detail in Paper I. In this work we will limit only to describing in detail the modifications required to extend the model to the additional radars. Figure 1 summarizes our approach reported in Paper I: given a flux of particles (F) characterized by (m, V), and originating from a particular radiant characterized by the ecliptic longitude (λ) and ecliptic latitude (β), the probability of detecting head echoes produced by such flux at a given time t is characterized by two areas described by
is described in detail in Paper I. In this work we will limit only to describing in detail the modifications required to extend the model to the additional radars. Figure 1 summarizes our approach reported in Paper I: given a flux of particles (F) characterized by (m, V), and originating from a particular radiant characterized by the ecliptic longitude (λ) and ecliptic latitude (β), the probability of detecting head echoes produced by such flux at a given time t is characterized by two areas described by
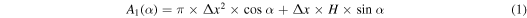
and
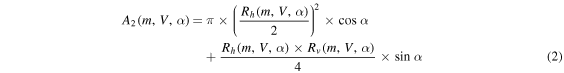
where 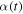 is the instantaneous zenith angle in the local horizon coordinate system of the pair (λ, β), H is the altitude range where the atmosphere is dense enough to produce ablation, and hence meteors,
is the instantaneous zenith angle in the local horizon coordinate system of the pair (λ, β), H is the altitude range where the atmosphere is dense enough to produce ablation, and hence meteors, 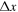 is the horizontal distance of the radar illuminated region, and A2, is the cross-sectional area of the radar volume where the amount of electrons produced by the meteoroids will be optimal for detection.7
This area is characterized by the vertical range
is the horizontal distance of the radar illuminated region, and A2, is the cross-sectional area of the radar volume where the amount of electrons produced by the meteoroids will be optimal for detection.7
This area is characterized by the vertical range  and horizontal distance
and horizontal distance 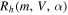 , which define the region within the radar beam where enough electrons are produced by the ablating particle to result in detection (see discussion surrounding Figure 11 in Paper I). Note that A1 is only dependent on the zenith angle while A2 depends on the particle's characteristics. Given these two areas we can define the probability of detection of a particle with a given mass, velocity and entry angle as:
, which define the region within the radar beam where enough electrons are produced by the ablating particle to result in detection (see discussion surrounding Figure 11 in Paper I). Note that A1 is only dependent on the zenith angle while A2 depends on the particle's characteristics. Given these two areas we can define the probability of detection of a particle with a given mass, velocity and entry angle as:
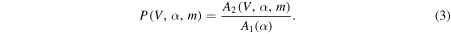
Figure 1. Schematic of our probabilistic approach described in detail in Janches et al. (2014b).
Download figure:
Standard image High-resolution imageThe three quantities in this calculation that will be unique to a given radar system will be H, the minimum S/N detectable by the system and the radar gain, G. The minimum S/N and G are required to determine  and
and  .
.
2.1. Altitude Range and S/N Threshold Determination
As in Paper I, the altitude range, H, is derived from the detected altitude distribution resulting from the observations from each radar system while the detection threshold is the minimum measured S/N. The AO observations were obtained during a monthly campaign performed in 2002 (Janches et al. 2003) and currently covered January to July. We have observations during the latter part of the year but those data have not yet been fully analyzed. The PFISR and MU observations utilized here were obtained in two separate campaigns that were aimed at measuring the seasonal variability of the meteor rates at different latitudes. Details of the observations are reported by Sparks et al. (2009) for the case of PFISR and by Pifko et al. (2013) for the case of MU. Both sets of observations covered a period of 24 hr near the equinoxes and solstices. For the case of PFISR the observing dates were taken on 2007 March 6, June 18, September 98
and December 1. The MU data were taken on 2008 December 19 and 2009 March 21, June 19 and September 25. Figure 2 displays the measured altitude and S/N distributions by the three radars. Each distribution in this figure combines all the available data for the particular radar system. As in Paper I, the altitude range for AO (HAO) is considered to be 55 km. For the case of PFISR and MU we determine from Figure 2 that  40 km and
40 km and  km.
km.
Figure 2. Altitude (left panels) and S/N (right panels) distributions resulted from the observations of AO (top), PFISR (middle), and MU (bottom) utilized in this work. The solid lines on left panels represent fits to the S/N using Equation (4).
Download figure:
Standard image High-resolution imageFor the case of the detection threshold, in Paper I we investigated two values for AO, −20 and −10 dB, even though the system can detect meteors with S/N values as low as −30 dB (see upper right panel in Figure 2). We found that the closest agreement between observations and ZoDy predictions was obtained when we utilized a threshold of −10 dB and we will adopt this value for the rest of this work. We note, however, that this is a conservative value because, as is clear in Figure 2, AO detects much lower S/N. For the case of PFISR and MU the values are again obtained from their detected S/N distributions (Figure 2) and determined to be −7 and −5 dB, respectively. It is interesting to note that the threshold cut off in these less sensitive systems is sharper than that from AO, emphasizing the ability of AO to detect weaker signals. This is likely a result of AO's ability to observe smaller particles (see Section 4). In addition, for larger S/N (i.e., S/N values larger than the peak of the distribution) the dependence of the number of detections as a function of S/N appears to be similar for the three systems. If we consider that the meteor S/N is somewhat proportional to the meteoroid mass, then we can assume that
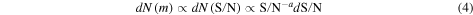
where a is a proxy for the mass index distribution. The thick line in the left panels of Figure 2 show a fit of Equation (4) resulting in 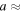 0.07, 0.08, and 0.1 for AO, PFISR, and MU, respectively, indicating that these systems detect similar populations at the larger end of the mass distribution.
0.07, 0.08, and 0.1 for AO, PFISR, and MU, respectively, indicating that these systems detect similar populations at the larger end of the mass distribution.
2.2. Modeling the Meteor S/N
In order to determine the probability of detection of a meteor produced by a particle with a given set of dynamical parameters  we need to calculate
we need to calculate 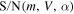 as a function of position within the radar beam. To accomplish this task we calculate first the meteor Radar Cross Section (RCS) using electron profiles derived from CABMOD and assuming that the head echo is an ensemble of electrons, Ne, within a spherical cloud with diameter equal to the atmospheric Mean Free Path. We then consider all the possible paths through the radar beam that the particle can follow that fall within the altitude range for which ablation is produced, and use the radar gain pattern and the radar equation to estimate the meteor S/N (see Equations (2)–(7) in Paper I for a detail description of the methodology).
as a function of position within the radar beam. To accomplish this task we calculate first the meteor Radar Cross Section (RCS) using electron profiles derived from CABMOD and assuming that the head echo is an ensemble of electrons, Ne, within a spherical cloud with diameter equal to the atmospheric Mean Free Path. We then consider all the possible paths through the radar beam that the particle can follow that fall within the altitude range for which ablation is produced, and use the radar gain pattern and the radar equation to estimate the meteor S/N (see Equations (2)–(7) in Paper I for a detail description of the methodology).
It is important to emphasize that, CABMOD must assume a parameterization of the ionization probability (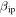 ). Originally, Vondrak et al. (2008) utilized the function derived by Jones (1997). In Paper I, we have found, however, that using this
). Originally, Vondrak et al. (2008) utilized the function derived by Jones (1997). In Paper I, we have found, however, that using this 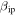 , which is universally utilized in radar meteor research (Close et al. 2002; Janches et al. 2009; Nesvorný et al. 2011a; Weryk & Brown 2013, among some assorted type of investigations), ZoDy over-predicts the Arecibo observed rates by 10 to 20 times and the peak of the slow portion of the line of sight velocity distribution by 2 to 3 orders of magnitude. We proposed then that this strong disagreement, could be due, at least in part, to the accuracy of the determination of
, which is universally utilized in radar meteor research (Close et al. 2002; Janches et al. 2009; Nesvorný et al. 2011a; Weryk & Brown 2013, among some assorted type of investigations), ZoDy over-predicts the Arecibo observed rates by 10 to 20 times and the peak of the slow portion of the line of sight velocity distribution by 2 to 3 orders of magnitude. We proposed then that this strong disagreement, could be due, at least in part, to the accuracy of the determination of 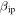 which, as argued by Jones (1997), is likely overpredicted by at least an order of magnitude. Further exploration on this issue lead to a re-estimation of
which, as argued by Jones (1997), is likely overpredicted by at least an order of magnitude. Further exploration on this issue lead to a re-estimation of 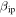 as a function of collision energy, utilizing earlier measurements of the ionization cross section of K atoms over the full range of collision energies (Cuderman 1972) and demonstrated that,
as a function of collision energy, utilizing earlier measurements of the ionization cross section of K atoms over the full range of collision energies (Cuderman 1972) and demonstrated that, 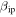 is potentially about 2 orders of magnitude lower than the values reproduced by Jones (1997) for the case of Na and K at speeds below 20 km s−1, and slightly less than 1 order of magnitude lower for the main elements (Fe, Mg, Si, and O) at higher speeds. Utilizing this revision in CABMOD resulted in better agreement between ZoDy predictions and Arecibo observations. In this work we will present results using two values of
is potentially about 2 orders of magnitude lower than the values reproduced by Jones (1997) for the case of Na and K at speeds below 20 km s−1, and slightly less than 1 order of magnitude lower for the main elements (Fe, Mg, Si, and O) at higher speeds. Utilizing this revision in CABMOD resulted in better agreement between ZoDy predictions and Arecibo observations. In this work we will present results using two values of 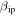 ,
, 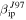 which refers to the original CABMOD electron profile values utilizing the results reported in Jones (1997), and
which refers to the original CABMOD electron profile values utilizing the results reported in Jones (1997), and 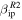 , which corresponds to the Revision 2 values in Paper I, for which the best agreement was found.
, which corresponds to the Revision 2 values in Paper I, for which the best agreement was found.
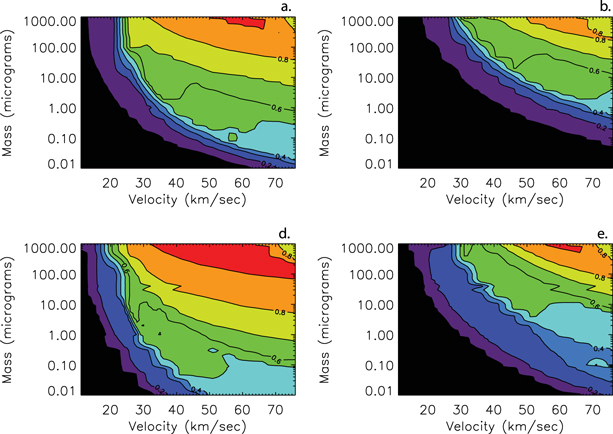
The radar Gain (G) pattern is particular of each system, as seen in Figure 3, and thus the detection model needs to be adapted to each case separately. For the case of AO, in Paper I we described the main beam radiation pattern and the first side lobe as a combination of two Gaussians. In this work, we improve this description by introducing a parameterization of the more accurate calculation reported by Breakall & Mathews (1982), which results in the pattern displayed in the top panel of Figure 3. Figure 4 shows the detection probabilities as a function of particle mass and velocity for an assumed entry angle of 45° and detection threshold of −10 dB. The top panels of Figure 4 represent the results reported in Paper I while the bottom panels are those derived from the improved AO's radiation pattern description. The left panels are the results considering 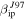 while the right panels are the results derived using
while the right panels are the results derived using 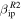 . As seen in this figure, this new treatment results in an increase of the detection probability for small masses (
. As seen in this figure, this new treatment results in an increase of the detection probability for small masses (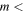 1 μg) and velocities greater than 20 km s−1. This will increase somewhat the disagreement between the observed and model fluxes (Section 3).
1 μg) and velocities greater than 20 km s−1. This will increase somewhat the disagreement between the observed and model fluxes (Section 3).
Figure 3. Radiation patterns of AO (top), PFISR (middle), and MU (bottom). Note the significantly different scales on the x-axis for each radar.
Download figure:
Standard image High-resolution imageFigure 4. Contour plots of the probability as a function of meteoroid mass and velocity assuming α = 45° for AO utilizing a Gaussian parameterization of the radiation pattern as in Paper I (top) and the more accurate description introduced in this work (bottom). Panels on the left assume 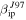 while panels on the right utilize
while panels on the right utilize  .
.
Download figure:
Standard image High-resolution imagePFISR's gain is displayed in the middle panel of Figure 3 which results from calculating the radiation pattern, following standard antenna theory (see for example Stutzman & Thiele 1981), of phased antenna array consisting of 4096 crossed-dipoles arranged in a rectangle of dimensions of 31.3 × 27.4 m (64 × 64 dipoles). Similarly, MU's gain is calculated as a phased array of 475 cross dipoles arranged in an ellipse of 99 × 101.3 m (a circle of 50 m in radius for practical purposes, bottom panel of Figure 3). In a similar manner than for AO in Paper I, we only considered the first side lobes in this work. Observational evidence shows that detection outside of the region comprised by the main beam and the first side lobe are less than a fraction of a percent (see for example Janches et al. 2004; Kero et al. 2011). Table 1 provides additional system parameters of each radar that are also required for this calculation. Finally, it is important to note that, unlike the radiation patterns of the AO and MU radars, PFISR's is not circular (Figure 3), which adds an additional azimuthal dependence on the calculation of the detection probability. We performed tests to examine the effect that different azimuth entry angle would have in the probability calculation, which resulted in mostly negligible differences except for particles with  10 μg and
10 μg and 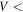 20 km s−1. As it will be discussed next, PFISR's detection probability for these ranges of masses and velocity are low, so the differences due to the azimuthal dependence will not significantly impact the overall results.
20 km s−1. As it will be discussed next, PFISR's detection probability for these ranges of masses and velocity are low, so the differences due to the azimuthal dependence will not significantly impact the overall results.
Table 1. System Parameters
| Parameter | AO | PFISR | MU |
|---|---|---|---|
| Wavelength (m) | 0.69 | 0.68 | 6.45 |
| Tsys (K) | 120 | 120 | 12000 |
| Bandwidth (MHz) | 1 | 1 | 3.5 |
| GMax (dB) | 61 | 40.5 | 34 dB |
Download table as: ASCIITypeset image
Figure 5 shows the probability of detection as a function of velocity for the case of a particle with mass equal to 10 μg and three different entry zenith angle (15°, 45° and 75°) for the three radar systems considered in this work. The black lines correspond to the use of 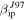 , while the red lines correspond to
, while the red lines correspond to 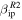 . As in Paper I, we focus on this particle mass first because this is the main contributor in ZoDy's flux (Nesvorný et al. 2010, 2011b). The first result which becomes evident from this figure is that for the given particle parameters and when considering the original results using
. As in Paper I, we focus on this particle mass first because this is the main contributor in ZoDy's flux (Nesvorný et al. 2010, 2011b). The first result which becomes evident from this figure is that for the given particle parameters and when considering the original results using 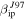 , AO is the only system that can detect particles of this mass when
, AO is the only system that can detect particles of this mass when  15 km s−1, although as the angle increases to shallower entries, these particles become undetectable (bottom panel). PFISR's probability of detection will be higher than 0 only when
15 km s−1, although as the angle increases to shallower entries, these particles become undetectable (bottom panel). PFISR's probability of detection will be higher than 0 only when 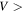 15 km s−1 and MU when
15 km s−1 and MU when 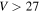 km s−1, even at the higher zenith angles. It is important to note that even though the probabilities for PFISR and MU are greater than 0 for these small velocities they are over an order of magnitude smaller than AO's. This is in strong agreement with the minimum detectable values that were previously reported utilizing a significantly less comprehensive treatment for which only the meteor RCS and maximum radar gain were considered (see Table 3 and corresponding discussion in Janches et al. 2014a). These results shows once again that AO is a unique instrument to fully test the hypothesis that most of the flux predicted by ZoDy is undetected. This is because even though the probability of detection is small (2%–5%), ZoDy predicts such a large number of these particles that they should still contribute significantly to the AO observed distributions. When considering
km s−1, even at the higher zenith angles. It is important to note that even though the probabilities for PFISR and MU are greater than 0 for these small velocities they are over an order of magnitude smaller than AO's. This is in strong agreement with the minimum detectable values that were previously reported utilizing a significantly less comprehensive treatment for which only the meteor RCS and maximum radar gain were considered (see Table 3 and corresponding discussion in Janches et al. 2014a). These results shows once again that AO is a unique instrument to fully test the hypothesis that most of the flux predicted by ZoDy is undetected. This is because even though the probability of detection is small (2%–5%), ZoDy predicts such a large number of these particles that they should still contribute significantly to the AO observed distributions. When considering 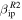 , however, the estimation shows that AO, PFISR and MU will detect meteors produced by 10 μg particles only when the
, however, the estimation shows that AO, PFISR and MU will detect meteors produced by 10 μg particles only when the 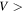 17, 35, and 60 km s−1, respectively. In particular for MU, even at the highest velocities the probability of detecting a 10 μg particle never exceeds 10% when the revised ionization probability values are utilized.
17, 35, and 60 km s−1, respectively. In particular for MU, even at the highest velocities the probability of detecting a 10 μg particle never exceeds 10% when the revised ionization probability values are utilized.
Figure 5. Detection probability as a function of meteor velocity for a particle with m = 10 μg for four different entry angles for the three radar system utilized in this work. Black lines assumes 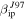 while red lines are the results derived using
while red lines are the results derived using 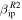 .
.
Download figure:
Standard image High-resolution imageA more general view of these results is presented in Figure 6 where contour plots of the probability as a function of meteoroid mass and velocity are shown for a zenith entry angle equal to 45°. The panels on the left side of this figure are the results obtained utilizing 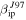 while the right side panels show the results utilizing
while the right side panels show the results utilizing 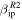 . It can be seen from the bottom panels of this figure that for either adopted β value, the MU radar will not be able to detect particles smaller than 1 μg irrespective of entry speed. In addition, if
. It can be seen from the bottom panels of this figure that for either adopted β value, the MU radar will not be able to detect particles smaller than 1 μg irrespective of entry speed. In addition, if 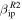 is utilized, the probability of detecting particles with
is utilized, the probability of detecting particles with 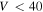 km s−1 is practically 0 and this radar will only detect particles at these speeds if the masses are almost 1 mg (bottom right panel). This is likely an indication that Revision 2 of
km s−1 is practically 0 and this radar will only detect particles at these speeds if the masses are almost 1 mg (bottom right panel). This is likely an indication that Revision 2 of 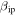 presented in Paper I is too extreme since MU's velocity distributions show a significant number, although a minority, of detections of meteors with velocities smaller than 30 km s−1 (Kero et al. 2011; Pifko et al. 2013). An alternative explanation is that MU detects a significant number of particles with masses greater than a milligram. For the case of PFISR (middle panels), the system appears to be sensitive to particles smaller than 1 μg only if
presented in Paper I is too extreme since MU's velocity distributions show a significant number, although a minority, of detections of meteors with velocities smaller than 30 km s−1 (Kero et al. 2011; Pifko et al. 2013). An alternative explanation is that MU detects a significant number of particles with masses greater than a milligram. For the case of PFISR (middle panels), the system appears to be sensitive to particles smaller than 1 μg only if 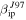 is assumed and the particle entry velocity are greater than 40 km s−1. For the case of
is assumed and the particle entry velocity are greater than 40 km s−1. For the case of 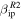 , the model predicts that PFISR will not detect particles slower than 25 km s−1 irrespective of mass. This is roughly in agreement with absolute velocities measured using interferometry at PFISR (Sparks et al. 2010). This requires the use of smaller sections of the antenna array as receivers and thus results in even much lower sensitivity that the observations presented in this work. Finally, the top panel shows the greater predicted sensitivity of AO which will detect sub-microgram particle for both
, the model predicts that PFISR will not detect particles slower than 25 km s−1 irrespective of mass. This is roughly in agreement with absolute velocities measured using interferometry at PFISR (Sparks et al. 2010). This requires the use of smaller sections of the antenna array as receivers and thus results in even much lower sensitivity that the observations presented in this work. Finally, the top panel shows the greater predicted sensitivity of AO which will detect sub-microgram particle for both 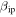 values considered, although over different velocity ranges.
values considered, although over different velocity ranges.
Figure 6. Contour plots of the probability as a function of meteoroid mass and velocity assuming α = 45° for AO (top), PFISR (middle), and MU (bottom). Panels on the left assume 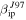 while panels on the right utilize
while panels on the right utilize 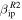 .
.
Download figure:
Standard image High-resolution image3. IMPLEMENTATION TO THE ZODIACAL DUST MODEL
As discussed earlier and in Paper I, the work presented here is motivated by the findings reported in Nesvorný et al. (2010) which predict JFC particles with masses of the order of 1–10 μg represent 90% of the total IR emission in the ZDC. The model also predicts that these particles will have low speeds when impacting the Earth (∼11–20 km s−1). Furthermore, these particles, which would originate mostly from the Helion and Antihelion sporadic meteoroid apparent sources, should represent about 50%–70% of the incoming meteoroid mass flux into the Earth's atmosphere, amounting to approximately 32 daily tons of material. In Paper I, we utilized the methodology summarized in the previous section to determine what portion of this flux, if any, can be detected by the much more sensitive AO radar and its head echo observing technique in order to further quantitatively constrain ZoDy with ground-based observations. We showed that some level of agreement was achieved when the ionization probability of ablating meteoroids was substantially revised and conservative detection thresholds were adopted. In this section we will expand our probabilistic treatment to the case of the less sensitive PFISR and MU radars.
As in Paper I, we will compare ZoDy's results with two quantities observed by the radars: the daily rates and the meteor velocity distributions. Both quantities are strongly dependent on the time-of-day, day-of-year and location of the observations (Janches et al. 2006; Fentzke & Janches 2008). We note that for the case of AO and PFISR, the observations utilized in this work were obtained without the use of interferometry, and thus the results do not have information regarding direction. This implies that for the comparison with the model predictions we consider the line of sight (vertical in this case, Janches et al. 2003; Sparks et al. 2009) velocity information. For the case of the MU radar observations however, interferometry was available (Pifko et al. 2013) and thus we use the absolute geocentric speeds for the comparisons. To perform these tasks we first calculate what portion of ZoDy's flux (i.e., particles per unit area and per day; 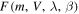 ) occurs over each radar during a relatively short (
) occurs over each radar during a relatively short (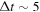 minutes) period of time. In addition, for the case of AO and PFISR, we calculate the instantaneous local zenith angle,
minutes) period of time. In addition, for the case of AO and PFISR, we calculate the instantaneous local zenith angle, 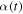 , of the ecliptic radiant pair (λ, β) during this short period, in order to estimate the meteoroid entry angle and thus obtain the radial velocity. Once these variables are calculated they need to be "biased" by their probability-of-observation using the methodology derived in Paper I and summarized in Section 2. This calculation results in
, of the ecliptic radiant pair (λ, β) during this short period, in order to estimate the meteoroid entry angle and thus obtain the radial velocity. Once these variables are calculated they need to be "biased" by their probability-of-observation using the methodology derived in Paper I and summarized in Section 2. This calculation results in
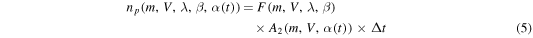
where 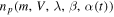 is the number of particles with ecliptic coordinate radiant
is the number of particles with ecliptic coordinate radiant 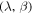 , mass m, and velocity V detected by the radar at a give time t.
, mass m, and velocity V detected by the radar at a give time t.
In Paper I we explored observations performed in 2002 January 21 with AO and determined that the best agreements with ZoDy predictions were found when we utilized 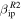 and a detection threshold of −10 dB. However, considering the differences in the probability calculation using the new AO beam parameterization illustrated in Figure 4, we re-examine those results first. Figures 7 and 8 display the comparison between the detected rates and radial velocity distribution, respectively, by AO, with the predicted quantities from ZoDy for representative days in the first 7 months of 2002. The dotted lines are the predictions using the Gaussian parameterization of the AO beam pattern, while the solid lines are those obtained with the new treatment presented in the top panel of Figure 3. It can be seen from Figure 7 that even though the increase in detection probability for small and fast particles resulting from the new pattern treatment (Figure 4) was small relative to the results presented in Paper I, these particles are so numerous according to ZoDy that this results in an over-prediction of the detected rate by up to a factor of two at the peak of detection (∼06:00 LT) and a factor of 200 at the minimum (∼18:00 LT). For the case of the radial velocity distributions, using the Gaussian pattern resulted in an over-prediction by ZoDy of a factor of 3. With the new radar pattern description the peak of the radial velocity distribution is 25 times larger than those actually detected by the radar. In addition, the model does not seem to show a significant seasonal variability which is clear in the observations. This suggests that the variability at tropical latitudes, such as AO's, may be driven by the detection of Apex particles since they should represent the majority of the observations according to previous models (Fentzke & Janches 2008). It is important to note once again, that currently, ZoDy does not include Oort Cloud Comets (OCCs) or Halley Type Comets (HTCs). These orbital families contribute to the faster Apex (OCCs; Nesvorný et al. 2011b) and Toroidal (HTCs; Pokorný et al. 2014) apparent sporadic meteor sources. Thus the disagreement in the velocity distribution for high speeds is expected.
and a detection threshold of −10 dB. However, considering the differences in the probability calculation using the new AO beam parameterization illustrated in Figure 4, we re-examine those results first. Figures 7 and 8 display the comparison between the detected rates and radial velocity distribution, respectively, by AO, with the predicted quantities from ZoDy for representative days in the first 7 months of 2002. The dotted lines are the predictions using the Gaussian parameterization of the AO beam pattern, while the solid lines are those obtained with the new treatment presented in the top panel of Figure 3. It can be seen from Figure 7 that even though the increase in detection probability for small and fast particles resulting from the new pattern treatment (Figure 4) was small relative to the results presented in Paper I, these particles are so numerous according to ZoDy that this results in an over-prediction of the detected rate by up to a factor of two at the peak of detection (∼06:00 LT) and a factor of 200 at the minimum (∼18:00 LT). For the case of the radial velocity distributions, using the Gaussian pattern resulted in an over-prediction by ZoDy of a factor of 3. With the new radar pattern description the peak of the radial velocity distribution is 25 times larger than those actually detected by the radar. In addition, the model does not seem to show a significant seasonal variability which is clear in the observations. This suggests that the variability at tropical latitudes, such as AO's, may be driven by the detection of Apex particles since they should represent the majority of the observations according to previous models (Fentzke & Janches 2008). It is important to note once again, that currently, ZoDy does not include Oort Cloud Comets (OCCs) or Halley Type Comets (HTCs). These orbital families contribute to the faster Apex (OCCs; Nesvorný et al. 2011b) and Toroidal (HTCs; Pokorný et al. 2014) apparent sporadic meteor sources. Thus the disagreement in the velocity distribution for high speeds is expected.
Figure 7. Comparison between predicted detected meteor rates assuming ZoDy to be the incoming flux and those observed by AO during selected days in seven months time interval. Dashed lines are the results reported in Paper I utilizing the Gaussian parameterization of AO radiation pattern while the solid lines are the results with the improved beam description. The thick line histograms correspond to the observed results.
Download figure:
Standard image High-resolution imageFigure 8. Comparison between predicted detected meteor radial velocity distributions assuming ZoDy to be the incoming flux and those observed by AO during selected days in seven months time interval. Dashed lines are the results reported in Paper I utilizing the Gaussian parameterization of AO radiation pattern while the solid lines are the results with the improved beam description. The thick line histograms correspond to the observed results.
Download figure:
Standard image High-resolution imageFigures 9 and 10 display the comparison between observations and model predictions of the daily rates and radial velocity distribution, respectively, for the case of PFISR. The solid lines corresponds to the use of 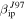 value in CABMOD while the dotted line uses its revised value
value in CABMOD while the dotted line uses its revised value 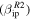 . Note that due to the detected rates at PFISR, which are significantly smaller than for AO, the data are organized in 20 minutes bins rather than the 5 minutes bins used in the case of AO observations (Figure 4). It can be seen that for the case of the daily rates (Figure 9) the model over-predicts the daily detection by a factor of 10 to 40 during the intervals of maximum detection and 50 to 100 during the minima, strongly depending on season. For the case of
. Note that due to the detected rates at PFISR, which are significantly smaller than for AO, the data are organized in 20 minutes bins rather than the 5 minutes bins used in the case of AO observations (Figure 4). It can be seen that for the case of the daily rates (Figure 9) the model over-predicts the daily detection by a factor of 10 to 40 during the intervals of maximum detection and 50 to 100 during the minima, strongly depending on season. For the case of 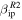 , ZoDy continues to predict larger rates than those detected, however, during the peak of the detections the disagreement is only less than a factor of 2, and a factor of 5–10 during the minima. At these high latitudes, ZoDy does reproduce some level of seasonality, especially in the shape of daily variability. However, while the data show a difference between September (highest detection rate) and March (lowest detection rate) by a factor of 5, the model varies by a significantly smaller factor. For the case of the radial velocity distributions displayed in Figure 10, however, the disagreement is even greater than for the case of AO where ZoDy predicts 400 to 500 times more particles at the peak of the distribution than those detected by the radar if
, ZoDy continues to predict larger rates than those detected, however, during the peak of the detections the disagreement is only less than a factor of 2, and a factor of 5–10 during the minima. At these high latitudes, ZoDy does reproduce some level of seasonality, especially in the shape of daily variability. However, while the data show a difference between September (highest detection rate) and March (lowest detection rate) by a factor of 5, the model varies by a significantly smaller factor. For the case of the radial velocity distributions displayed in Figure 10, however, the disagreement is even greater than for the case of AO where ZoDy predicts 400 to 500 times more particles at the peak of the distribution than those detected by the radar if 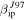 and one order of magnitude more for the case of
and one order of magnitude more for the case of 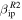 . The reason for this is partly due to the fact that PFISR will observe the incoming flux, on average, at a shallower entry angle than AO due to its higher latitude location (Janches et al. 2006; Fentzke et al. 2009; Sparks et al. 2009), which results in an increase of lower radial velocities, specially by the faster and larger particles that PFISR is able to detect. This once again shows that the hypothesis that the small and slow flux is undetected is supported by this work, and that the large disagreement between observations and ZoDy originates from the high quantity of predicted particles with relatively larger masses and faster velocities.
. The reason for this is partly due to the fact that PFISR will observe the incoming flux, on average, at a shallower entry angle than AO due to its higher latitude location (Janches et al. 2006; Fentzke et al. 2009; Sparks et al. 2009), which results in an increase of lower radial velocities, specially by the faster and larger particles that PFISR is able to detect. This once again shows that the hypothesis that the small and slow flux is undetected is supported by this work, and that the large disagreement between observations and ZoDy originates from the high quantity of predicted particles with relatively larger masses and faster velocities.
Figure 9. Comparison between predicted detected meteor rates assuming ZoDy to be the incoming flux and those observed by PFISR for four months representative of each season. Solid lines corresponds to the use  while dashed lines correspond to
while dashed lines correspond to  . The thick line histograms correspond to the observed results. Note that the bin size in the data histograms is 20 minutes in comparison to the 5 minutes bin size for the case of AO (Figure 7) and MU (Figure 11) rates.
. The thick line histograms correspond to the observed results. Note that the bin size in the data histograms is 20 minutes in comparison to the 5 minutes bin size for the case of AO (Figure 7) and MU (Figure 11) rates.
Download figure:
Standard image High-resolution imageFigure 10. Comparison between predicted detected meteor radial velocity distributions assuming ZoDy to be the incoming flux and those observed by PFISR for four months representative of each season. Solid lines corresponds to the use 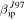 while dashed lines correspond to
while dashed lines correspond to 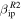 . The thick line histograms correspond to the observed results.
. The thick line histograms correspond to the observed results.
Download figure:
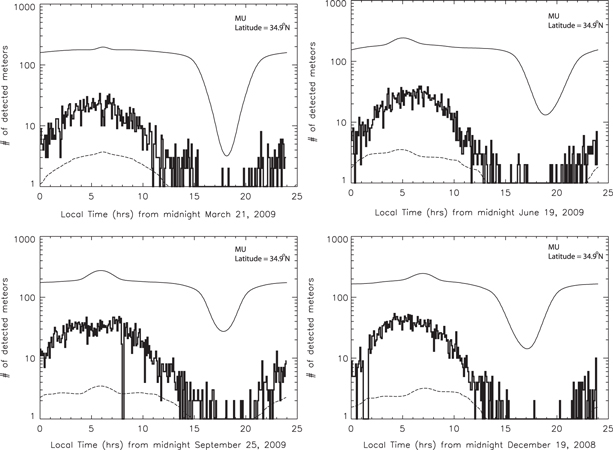
Standard image High-resolution imageFinally, the comparison between MU observations and ZoDy are shown in Figures 11 and 12 for the daily rates and absolute velocity distributions, respectively. Once again the solid lines correspond to using the original value of the ionization coefficient 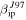 reported by Jones (1997), while the dotted lines use the revised value
reported by Jones (1997), while the dotted lines use the revised value 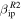 reported in Paper I. As expected, using the original value of the ionization coefficient, ZoDy predicts larger rates than those observed by the radar as shown in Figure 11. However, for the case of MU, this overprediction is only a factor of three, which represents a discrepancy of about an order of magnitude smaller than for the cases of AO (Paper I) and PFISR (Figure 9). For the case of the revised ionization probability, for the first time ZoDy predicts a daily rate that is lower than those detected by the radar by almost an order of magnitude for the entire daily period. For the case of the absolute velocity, the model predicts, when
reported in Paper I. As expected, using the original value of the ionization coefficient, ZoDy predicts larger rates than those observed by the radar as shown in Figure 11. However, for the case of MU, this overprediction is only a factor of three, which represents a discrepancy of about an order of magnitude smaller than for the cases of AO (Paper I) and PFISR (Figure 9). For the case of the revised ionization probability, for the first time ZoDy predicts a daily rate that is lower than those detected by the radar by almost an order of magnitude for the entire daily period. For the case of the absolute velocity, the model predicts, when 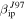 is utilized, a distribution where most of the particles with V < 15 km s−1 have been removed (i.e., undetected). It also predicts a dominant peak centered at 30 km s−1 which is 2 orders of magnitude larger than the detected peak and a faster population centered at ∼60 km s−1, which is somewhat in agreement with the MU observations. However, since MU interferometry allows for the determination of orbital information (Pifko et al. 2013), we know that the majority of the fast population of the MU's observations corresponds to particles originating in the Apex source, rather than the Helion and Antihelion. Thus in order for ZoDy to agree with the observations, this peak should be significantly smaller in magnitude, since currently ZoDy does not include meteoroids originating from this source. This scenario occurs when we use
is utilized, a distribution where most of the particles with V < 15 km s−1 have been removed (i.e., undetected). It also predicts a dominant peak centered at 30 km s−1 which is 2 orders of magnitude larger than the detected peak and a faster population centered at ∼60 km s−1, which is somewhat in agreement with the MU observations. However, since MU interferometry allows for the determination of orbital information (Pifko et al. 2013), we know that the majority of the fast population of the MU's observations corresponds to particles originating in the Apex source, rather than the Helion and Antihelion. Thus in order for ZoDy to agree with the observations, this peak should be significantly smaller in magnitude, since currently ZoDy does not include meteoroids originating from this source. This scenario occurs when we use 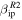 , where the predicted distributions are smaller by a factor of 2 to 3. It is also interesting that according to these results, the revision of β for the case of the MU observations results in a complete removal of particles with
, where the predicted distributions are smaller by a factor of 2 to 3. It is also interesting that according to these results, the revision of β for the case of the MU observations results in a complete removal of particles with 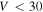 km s−1, which is expected given the results shown in Figure 6, indicating once again that this revision may be too extreme.
km s−1, which is expected given the results shown in Figure 6, indicating once again that this revision may be too extreme.
Figure 11. Comparison between predicted detected meteor rates assuming ZoDy to be the incoming flux and those observed by MU for four months representative of each season. Solid lines corresponds to the use  while dashed lines correspond to
while dashed lines correspond to 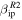 . The thick line histograms correspond to the observed results.
. The thick line histograms correspond to the observed results.
Download figure:
Standard image High-resolution imageFigure 12. Comparison between predicted detected meteor geocentric absolute velocity distributions assuming ZoDy to be the incoming flux and those observed by MU for four months representative of each season. Solid lines corresponds to the use 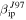 while dashed lines correspond to
while dashed lines correspond to  . The thick line histograms correspond to the observed results.
. The thick line histograms correspond to the observed results.
Download figure:
Standard image High-resolution imageA final note about the comparisons presented in this section is that, when looking at the three radars, it is evident that MU sensitivity appears to be the limit for which studies like the one presented in this work and Paper I can be useful. Radars less sensitive than MU, as is the case of AMOR and CMOR (Nesvorný et al. 2011a), do not provide useful constraints to a model like ZoDy, because independently of the 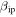 utilized, those systems will not have the sensitivity to detect any portion of the population of interest to this work.
utilized, those systems will not have the sensitivity to detect any portion of the population of interest to this work.
4. DISCUSSION
In order to understand the implication of our results we show in Figure 13, a comparison between the characteristics of the ZoDy flux that travels through the three different radar beams utilized in this work, which we refer to here as the input distributions, and the portion that is predicted to be detected by the systems. The top panels in Figure 13 show the absolute velocity distributions while the bottom panels show the mass distributions. The left columns are the results when 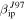 is utilized while the right are those derived with
is utilized while the right are those derived with  . The solid lines in the four panels represent the input distributions and as expected, they reflect ZoDy's main characteristics with a velocity distribution heavily weighted toward meteors with absolute speeds of 12–14 km s−1 (panels (a) and (b)). The difference in the input distributions of the three radars results from their different beam sizes. MU's pattern is the widest (Figure 3) of the three systems and thus has a potential collecting volume which results in 2 and 1 order of magnitude more particles occurring over MU's collecting area than over AO and PFISR, respectively. However, when we look at the predicted detections (dashed lines), the scenario reverses with AO, as a result of its greater sensitivity, detecting more particles that PFISR and MU. For the case of the distributions derived using
. The solid lines in the four panels represent the input distributions and as expected, they reflect ZoDy's main characteristics with a velocity distribution heavily weighted toward meteors with absolute speeds of 12–14 km s−1 (panels (a) and (b)). The difference in the input distributions of the three radars results from their different beam sizes. MU's pattern is the widest (Figure 3) of the three systems and thus has a potential collecting volume which results in 2 and 1 order of magnitude more particles occurring over MU's collecting area than over AO and PFISR, respectively. However, when we look at the predicted detections (dashed lines), the scenario reverses with AO, as a result of its greater sensitivity, detecting more particles that PFISR and MU. For the case of the distributions derived using 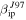 , both AO and PFISR have predicted velocity distributions with dominant peaks at ∼30 km s−1, while MU is only 5 km s−1 larger. However, for the revised ionization probability, AO maintains the dominant peak at 30 km s−1, while PFISR and MU shift to 35 and 40 km s−1, respectively. This shows that these less sensitive systems are more susceptible to the revision of this parameter. Finally, only for the least sensitive MU radar results and utilizing an extreme revision of the widely used ionization probability, the high velocity meteors become the dominant population in the distribution even though they are the minority of the incoming flux. It is important to note that the only atmospheric parameter affecting the ablation is the atmospheric density profile experienced by the incoming meteoroid as shown in Vondrak et al. (2008). While the ambient plasma density may have an impact on the formation of meteor trails, in particular the non-specular ones (Dyrud et al. 2002), it does not affect the head echo. So the fact that the measurements presented in this manuscript were performed at sites with different ionospheric conditions it does not impact our results. One other parameter that may differ between radars and influences the S/N calculation is the sky noise, which can be particularly strong at the lower frequencies. For example, Kero et al. (2011) shows that the diurnal cycle of the sky noise background in zenith at Shigaraki varies from its lowest values around 5000 K to almost 15,000 K when Cygnus-A is near the beam. At the AO and PFISR's transmitted higher frequencies, however, the sky noise will decrease dramatically. This effect is included in the Tsys of each radar used for the S/N calculation (Table 1 and Paper I).
, both AO and PFISR have predicted velocity distributions with dominant peaks at ∼30 km s−1, while MU is only 5 km s−1 larger. However, for the revised ionization probability, AO maintains the dominant peak at 30 km s−1, while PFISR and MU shift to 35 and 40 km s−1, respectively. This shows that these less sensitive systems are more susceptible to the revision of this parameter. Finally, only for the least sensitive MU radar results and utilizing an extreme revision of the widely used ionization probability, the high velocity meteors become the dominant population in the distribution even though they are the minority of the incoming flux. It is important to note that the only atmospheric parameter affecting the ablation is the atmospheric density profile experienced by the incoming meteoroid as shown in Vondrak et al. (2008). While the ambient plasma density may have an impact on the formation of meteor trails, in particular the non-specular ones (Dyrud et al. 2002), it does not affect the head echo. So the fact that the measurements presented in this manuscript were performed at sites with different ionospheric conditions it does not impact our results. One other parameter that may differ between radars and influences the S/N calculation is the sky noise, which can be particularly strong at the lower frequencies. For example, Kero et al. (2011) shows that the diurnal cycle of the sky noise background in zenith at Shigaraki varies from its lowest values around 5000 K to almost 15,000 K when Cygnus-A is near the beam. At the AO and PFISR's transmitted higher frequencies, however, the sky noise will decrease dramatically. This effect is included in the Tsys of each radar used for the S/N calculation (Table 1 and Paper I).
Figure 13. Top: comparison between the distribution of absolute velocities of meteors traveling through the radar beam predicted by ZoDy and those predicted to be detected by the three radars using our approach. Bottom: comparison between the distribution of meteors masses input by ZoDy and those predicted to be detected by the three radars using our approach. Left panels utilize 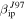 while right panels utilize
while right panels utilize 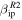 .
.
Download figure:
Standard image High-resolution imageRegarding the comparison of the predicted incoming and detected mass distributions (solid and dashed lines, respectively, in panels (c) and (d)), it can be seen that the new parameterization of the AO radiation pattern increases by an order of magnitude the expected detection of small particles (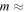 1 × 10
1 × 10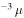 g) with respect to the results presented in Paper I. That is, if ZoDy correctly predicts the incoming meteoroid flux, AO should detect 1 in 104 of these particles for the case of
g) with respect to the results presented in Paper I. That is, if ZoDy correctly predicts the incoming meteoroid flux, AO should detect 1 in 104 of these particles for the case of 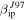 . Furthermore, not only the minimum mass detected by PFISR and MU are 1 and 2 order of magnitude larger than AO's, irrespective of the value of
. Furthermore, not only the minimum mass detected by PFISR and MU are 1 and 2 order of magnitude larger than AO's, irrespective of the value of 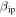 , but also the number of detections by these less sensitive radars toward the smaller end of their respective distributions decreases much more rapidly than for AO. This implies that the differences noted earlier in the S/N distributions (discussion surrounding Figure 2 in Section 2.1) are most likely real physical results. That is, the decrease in the numbers of detections toward smaller S/N values is less sharp for AO than for PFISR and MU which show a sudden cutoff. Finally, we note that for masses larger than a given mass, the less sensitive system is predicted to detect more particles than the more sensitive ones. For example, for masses greater than 10 μg for the case of
, but also the number of detections by these less sensitive radars toward the smaller end of their respective distributions decreases much more rapidly than for AO. This implies that the differences noted earlier in the S/N distributions (discussion surrounding Figure 2 in Section 2.1) are most likely real physical results. That is, the decrease in the numbers of detections toward smaller S/N values is less sharp for AO than for PFISR and MU which show a sudden cutoff. Finally, we note that for masses larger than a given mass, the less sensitive system is predicted to detect more particles than the more sensitive ones. For example, for masses greater than 10 μg for the case of 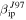 the number of detections by MU is larger than PFISR, and both are larger than AO, following the characteristics of the incoming flux. This is because, once the particles are large enough to be detected by any of the systems, the size of the collecting area becomes the more crucial factor in determining the number of detections (Janches et al. 2014a). However, for the case of
the number of detections by MU is larger than PFISR, and both are larger than AO, following the characteristics of the incoming flux. This is because, once the particles are large enough to be detected by any of the systems, the size of the collecting area becomes the more crucial factor in determining the number of detections (Janches et al. 2014a). However, for the case of 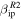 , MU detections for particles larger than 100 μg becomes equal to those predicted to be detected by PFISR. This is because, as shown in the previous section, the revised values of
, MU detections for particles larger than 100 μg becomes equal to those predicted to be detected by PFISR. This is because, as shown in the previous section, the revised values of 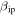 result in very small detection probabilities for MU for all velocities and mass ranges (Figures 5 and 6). These results continue to suggest that this revision may be too extreme as it is evident that the daily rates at MU are significantly larger than those detected by PFISR (Figures 9 and 11). As discussed in Paper 1, the revised β values were determined from laboratory measurements of the ionization probability of a beam of fast K atoms colliding with N2 or O2 (Cuderman 1972). However, there is more recent experimental data available for Na + O2 and N2 collisions (Kleyn et al. 1978) which, although not focused on measuring absolute values, indicates that the cross sections for Na (and K) could be somewhat larger than implied by the Cuderman study. This would be consistent with the MU and PFISR radar detections. Na and K are particularly of interest because, as volatiles, they are the elements that will ablate more easily off the meteoroid's body according to differential ablation (Vondrak et al. 2008; Janches et al. 2009), and the most likely candidates to produce enough electrons when particles are small and slow to make the meteors visible by a radar (see Paper I).
result in very small detection probabilities for MU for all velocities and mass ranges (Figures 5 and 6). These results continue to suggest that this revision may be too extreme as it is evident that the daily rates at MU are significantly larger than those detected by PFISR (Figures 9 and 11). As discussed in Paper 1, the revised β values were determined from laboratory measurements of the ionization probability of a beam of fast K atoms colliding with N2 or O2 (Cuderman 1972). However, there is more recent experimental data available for Na + O2 and N2 collisions (Kleyn et al. 1978) which, although not focused on measuring absolute values, indicates that the cross sections for Na (and K) could be somewhat larger than implied by the Cuderman study. This would be consistent with the MU and PFISR radar detections. Na and K are particularly of interest because, as volatiles, they are the elements that will ablate more easily off the meteoroid's body according to differential ablation (Vondrak et al. 2008; Janches et al. 2009), and the most likely candidates to produce enough electrons when particles are small and slow to make the meteors visible by a radar (see Paper I).
As in Paper I, these results show that even by extensively revising the widely used ionization coefficient of ablating meteors reported by Jones (1997), the fluxes predicted by ZoDy are significantly larger than those actually observed. The analysis presented here indicates that ZoDy is in need of revision. Recently, Ade et al. (2014) reported results obtained with the Planck satellite, which provides a set of all-sky maps at nine frequencies from 30 to 857 GHz in which diffuse interplanetary dust emission was observed. The authors used these measurements to investigate the behavior of zodiacal emission over the whole sky at sub-millimetre and millimetre wavelengths and found that the fall-off in emissivity of the Diffuse Cloud with increasing wavelength was characteristic of 30 μm particles, as oppose to the 100 μm particles dominating ZoDy distribution. If this is the case, then it would imply that the characteristic particle mass of the incoming flux is about a factor of 27 smaller than ZoDy's. This could improve our results significantly, since even AO's probability to detect particles lighter than 1 μg traveling at 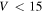 km s−1 is very small, even when using
km s−1 is very small, even when using 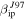 . To explore this hypothesis as a potential source of reconciling the model with radar observations we modified ZoDy's Size Distribution Frequency to break at D = 30 μm. When the new distribution is calibrated against IRAS, it gives the total Earth accretion of ∼30 tons/day, similar to that of the original model. Note that this treatment uses a collisional lifetime independent of size (τ = 3 × 105 year), as oppose to the original model that uses the values reported by Grün et al. (1985). The results of this test are displayed in Figure 14, where the panels to the right are the daily rates and the panels to the left are the velocity distributions for each system for the observations performed in March. The red lines corresponds to the observations, the solid line to the model predictions using
. To explore this hypothesis as a potential source of reconciling the model with radar observations we modified ZoDy's Size Distribution Frequency to break at D = 30 μm. When the new distribution is calibrated against IRAS, it gives the total Earth accretion of ∼30 tons/day, similar to that of the original model. Note that this treatment uses a collisional lifetime independent of size (τ = 3 × 105 year), as oppose to the original model that uses the values reported by Grün et al. (1985). The results of this test are displayed in Figure 14, where the panels to the right are the daily rates and the panels to the left are the velocity distributions for each system for the observations performed in March. The red lines corresponds to the observations, the solid line to the model predictions using 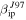 and the dotted line using
and the dotted line using 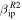 . The first result that become apparent is that the predicted distributions detected by AO when
. The first result that become apparent is that the predicted distributions detected by AO when 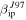 is utilized, do not significantly change. This is because, as seen from Figure 13, AO is already sensitive to the smaller distributions suggested by the Planck measurements. It can also be seen from the results in the panels of Figure 14 that, although some improvement is achieved for the rest of the cases, even when reducing the characteristic mass of ZoDy by a factor of 27, the model over-predicts by one to two orders of magnitude the observed distributions for the case of AO and PFISR when the original value of
is utilized, do not significantly change. This is because, as seen from Figure 13, AO is already sensitive to the smaller distributions suggested by the Planck measurements. It can also be seen from the results in the panels of Figure 14 that, although some improvement is achieved for the rest of the cases, even when reducing the characteristic mass of ZoDy by a factor of 27, the model over-predicts by one to two orders of magnitude the observed distributions for the case of AO and PFISR when the original value of 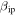 is considered. Only for the MU results the predictions are approximately the same values than the observations, which would disagree with the fact that the majority of the detections from these systems should be from meteors originating from the Apex source (currently not included in ZoDy). Since ZoDy particles are mostly originating from the Helion and Antihelion directions, their detections should represent about 30% of the observations (Fentzke & Janches 2008; Fentzke et al. 2009; Pifko et al. 2013). For the case of
is considered. Only for the MU results the predictions are approximately the same values than the observations, which would disagree with the fact that the majority of the detections from these systems should be from meteors originating from the Apex source (currently not included in ZoDy). Since ZoDy particles are mostly originating from the Helion and Antihelion directions, their detections should represent about 30% of the observations (Fentzke & Janches 2008; Fentzke et al. 2009; Pifko et al. 2013). For the case of 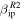 , only the predicted distributions for PFISR and MU fall below the observed ones as it would be expected if ZoDy's flux would be mostly undetected and would represent less than a half of the detections. Looking at the PFISR and MU results in particular, the predicted occurrence rate at the peak when using the revised value of the ionization probability is less than 6 meteors per 20 minutes and 1 meteor in a 5 minutes bin, respectively. Because of the interferometry capabilities of MU, we know that it observes more meteors originating from these sources (Kero et al. 2011; Pifko et al. 2013), which shows that the revision of
, only the predicted distributions for PFISR and MU fall below the observed ones as it would be expected if ZoDy's flux would be mostly undetected and would represent less than a half of the detections. Looking at the PFISR and MU results in particular, the predicted occurrence rate at the peak when using the revised value of the ionization probability is less than 6 meteors per 20 minutes and 1 meteor in a 5 minutes bin, respectively. Because of the interferometry capabilities of MU, we know that it observes more meteors originating from these sources (Kero et al. 2011; Pifko et al. 2013), which shows that the revision of 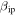 is clearly too extreme. Once again, the disagreement at the higher end of the velocity distributions is mostly due to the fact that ZoDy does not include the populations of particles that would produce meteoroids with high geocentric speeds. However, this test is a clear indication that the solution to finding agreement between ZoDy and sensitive HPLA meteor observations requires a re-examination not only of our knowledge on the ablation, ionization and radar detection processes but also the physical assumptions in the ZDC model itself.
is clearly too extreme. Once again, the disagreement at the higher end of the velocity distributions is mostly due to the fact that ZoDy does not include the populations of particles that would produce meteoroids with high geocentric speeds. However, this test is a clear indication that the solution to finding agreement between ZoDy and sensitive HPLA meteor observations requires a re-examination not only of our knowledge on the ablation, ionization and radar detection processes but also the physical assumptions in the ZDC model itself.
Figure 14. Comparison between predicted detected meteor rates (left panels) and geocentric radial or absolute velocity distributions (right panels) assuming ZoDy to be the incoming flux and those observed by AO (top), PFISR (middle), and MU (bottom) for the month of march assuming ZoDy's particle size distribution is characterize by 30 μm diameter dust. Red lines are the observations. Solid lines corresponds to the use 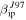 while dashed lines correspond to
while dashed lines correspond to 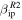 .
.
Download figure:
Standard image High-resolution image5. CONCLUSIONS
In this manuscript we applied our new approach for estimating the detection probability of meteors by HPLA radars reported in Janches et al. (2014b) to three different radar systems with significant different characteristics. We utilized this methodology to address the meteoric mass flux into planetary atmospheres in a comprehensive manner by combining models of dust release from celestial bodies, orbital evolution, ablation, and ionization processes when dust particles encounter planetary atmospheres. The focus in this study was to constrain a recently developed physical model of the ZDC reported by Nesvorný et al. (2010) in order to predict the daily rates and velocity distributions that should be detected by the HPLA systems utilized in this study. In particular, we have compared these model results with head echo meteor observations obtained with the 430 MHz Arecibo Observatory radar, the 440 MHz Poker Flat Incoherent Scatter Radar, and the 46.5 MHz Middle and Upper Atmosphere radar. We showed how the different systems detect different parts of the incoming populations and discussed the implications. The main result is that even with the least sensitive MU radar system, the current ZDC model over-predicts the radar observations of detected rates and velocity distributions. We finally discussed our results in the light of new measurements by the Planck satellite which suggest the ZDC particle population may be characterized by smaller sizes than those assumed in ZoDy, which was constrained by observations from the InfraRed Astronomy Satellite. We conclude that the solution to finding agreement between ZoDy and sensitive HPLA radar meteor observations must involve both, a re-examination of radar detection biases and also the physical assumptions behind the ZDC model.
D.J. is supported by NASA awards 12-PAST12-0007 and 12-PATM12-0006. D.N. has been supported through NASA's Solar System Works. J.M.C.P. and W.F. are supported by the European Research Council (project number 291332-CODITA) and the work of D.V. was partly supported by the Czech Grant Agency (grant P209-13-01308S). The Arecibo Observatory is operated by SRI International under a cooperative agreement with the National Science Foundation. The Poker Flat Incoherent Scatter Radar (PFISR) is operated by SRI International on behalf of the US National Science Foundation under NSF Cooperative Agreement AGS-1133009. The MU radar system belongs to and is operated by the Research Institute of Sustainable Humanosphere (RISH), Kyoto University, Uji, Kyoto, Japan. D.J. is grateful to the Japanese Society for the Promotion of Science (JSPS) who supported his visit to the University of Kyoto, Japan, in 2009 under a short term fellowship, making the observations presented here and this study possible. The authors wish to thank Prof. T. Nakamura and Dr. J. Kero for useful discussion regarding the MU radar system.
Footnotes
- 7
- 8
The September data was taken in intervals over the course of three days: 2007 September 9, 10, and 14; (Sparks et al. 2009) however, for the purpose of this work we will assume they were taken all over a period of one day.