ジャクソン・ポロックが描いた「ドリップ・ペインティング」は、一見、子供が描き散らかした絵のようにも見えます。無秩序に絵具がちりばめられたかのようなこの作品は、実際、絵具を垂らしたり、流したり、投げつけたりといった独特の手法により制作されています。「私にだってこれくらいの絵は描ける」、そんな感想を持つ方もいらっしゃるのではないでしょうか?
物理学者のリチャード・テイラーは、今から10年ほど前に、こうした感想とはまったく正反対の考えを科学的な視点から引き出しました。
彼によれば、ポロックのドリッピングの技術は非常に卓越したものであり、だれにでも簡単にまね出来るようなものではないそうなんです。
ポロックの絵に見る、無秩序の中の秩序
テイラーは、「ポロックの絵はフラクタルである」と言いました。
「フラクタル」とはもともと、数学者のブノワ・マンデルブロが考え出した幾何学の概念で、図形の「部分」と「全体」が自己相似、つまり互いに似通っているもののことを指します。面白いことに、この性質は、自然界を大小様々なスケールで見た時にも確認されます。
例えば、下の写真をごらんください。「フラクタル」を説明するのによく使われるロマネスコ・ブロッコリです。

最美的蔬菜–Romanesco Cauliflower by IsaacMao is licensed under CC BY 2.0 Deed
このブロッコリを観察すると、小さな房がいくつも集まって形作られていることが分かります。そして興味深いことに、それら小さな房と、このブロッコリ全体はとても良く似た形状をしています。さらにその小さな房も、実は、より小さな房の集合体なのです。
「フラクタル」とは、このブロッコリのように、部分を拡大した時にも、そのもの全体の構造を見出せるようなものを指します。
テイラーは、このブロッコリに見られるようなフラクタル構造を、ポロックの作品に見出したのです。
ポロックの「ドリップペイント」に潜むフラクタル
下の図をご覧ください。2次元空間内にあるフラクタルは、1から2までの「D値」を使って表すことができます。左端のD=1は単なる直線をあらわしています。また、右端のD=2は、完全な面をあらわします。D=1はとてもシンプルな状態であり、D値が2に近づけば近づくほど、そのフラクタル構造は複雑になっていきます。
テイラーによれば、人間が心地よいと感じるD値があるそうです。それは1.3から1.5。この値は、自然界から得られたフラクタルであっても、あるいはポロックの絵のように人がつくったものであっても、同様の範囲を示すそうです。
さらに興味深いのは、自然界から得られるD値は、おおむねこの範囲内に収まるとのことです。雲は、1.3。海岸線は、1.1から1.4を示します。
では、ポロックのドリップ・ペインティングのD値は、どれくらいなのでしょうか?
ポロックがドリッピングによって絵を描いたのは、自殺に至るまでのほんの10年ほどの間でしかありません。
しかしテイラーによれば、ポロックはその間に、驚くほどドリッピングの技術に磨きをかけ続けたそうです。その10年間、D値は上昇し続けます。
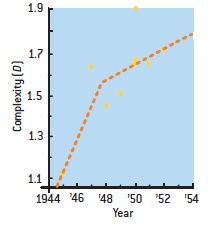
ポロックが1945年に描いた絵のD値は、1.12。それが、1952年には、1.7に上がっています。さらにポロックは同じ年に、1.9という非常に高いD値を示す絵も描いています。しかし、大変興味深いことに、ポロックはこの絵を自ら破棄してしまいます。おそらくポロックは、直観で、この絵は複雑すぎると判断したのでしょう。
ポロックの絵に、不思議と親しみを感じるのは、彼が自然界の秩序を表現したかったからかもしれません。
ジャクソン・ポロックの絵は、だれにでも描けるようなものか?
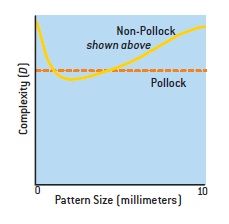
さて、テイラーは、フラクタルであることがポロックのドリップ・ペイントの特徴であると示すために、あえてポロック以外の人が描いたドリップ・ペイントを、同様に調査しています。下の絵をご覧ください。
このような本当に無作為な絵を前にすると、一見無造作につくられているように見えるポロックの絵は、実際は意図的につくられていると理解できるように思います。
テイラーが分析した結果、この絵からはフラクタルを見出すことができませんでした。フラクタル構造を持つ絵からは、どの部分をとっても、常に一定のD値が得られるのだそうです。ポロックの絵は、どこをとっても同じD値を示すのに対し、ポロック以外の人が描いた絵は、下のような曲線を示しました。
絵の中に複雑なフラクタル構造をつくりあげるには、ドリッピングの技術を洗練させる必要があります。ですから、ポロックの絵は、だれでも描けるような絵ではないのです。
テイラーは、フラクタルであることがポロックのドリップペイントの大きな特徴であり、そこから作品の真贋までも判断できると言っています。
テイラーが、ポロックの研究を始めたきっかけ
ところで、テイラーがポロックの研究を始めたきっかけもまた、私は大変面白いと思います。最後に少し触れてみたいと思います。
ポロックの研究をする以前、まだ物理学者として大学で教鞭をとっていた頃のテイラーの趣味は、抽象絵画を描くことだったそうです。そのため、ポロックにも興味を持っていたのだとか。しかし彼は、絵描きを単なる趣味に止めておくことができませんでした。そしてついに彼は、大学の先生を辞め、美術学校の生徒になって、終日アートに時間を費やすことを決意しました。
ある時、その美術学校で1週間を費やす屋外制作が行われました。ところが、あいにくの吹雪で生徒たちは連日室内に閉じ込められてしまい、思うように制作をすすめることができなくなりました。そこで、悪天候の中でも、「自然画」を描く方法はないかと皆で模索したそうです。
話し合いの結果、生徒たちは、自らが外に出て絵を描くのではなく、強風で吹き飛ばされた木の枝を使って、絵を描くための仕組みをつくり出しました。彼らがつくった構造物には、塗料が入った容器が固定されており、風の勢いによって塗料が飛び散る仕掛けが施されています。そして、その構造物の下には、キャンバスが敷かれています。生徒たちは、嵐の中、それを一晩放置しました。
次の日の朝、外に出てキャンバスを見た時、テイラーは、「ポロックの絵が出来た」と感じたそうです。
彼はこの体験から、「ポロックは、自然のリズムを取り入れながら絵を描いていたに違いない」と推考しました。
この憶測を実証すべく、テイラーは、このあと再び科学者に戻ります。そして、ポロックの研究に没頭することになるのです。
ポロックが用いたドリッピングという技法は、小さな子供にも、たやすく使うことができます。ですから、「ポロックの絵のようなもの」は、子供でも簡単に描けるのです。
しかしテイラーは、先の嵐の夜につくられた絵を、非常に表面的な図像から、安易に「ポロックの絵だ」と言ったわけではなかったのです。ドリッピングは「だれにでも簡単に使える技法」であるにも関わらず、テイラーは、人間ではなく強風によってつくられた塗料の軌跡に、「ポロックの絵のようなもの」を見出しています。ここに、科学者としてのテイラーの鋭い洞察力を感じることができます。この時すでにテイラーは、ポロックの絵に、どこか超人的な雰囲気を感じ取っていたのだと思います。