■交互作用が出たとき
2002.01.22. 作成
| う~んと,この記述は,きちんとした統計的な知識にもとづいて書いているわけではなく,今まで自分が教わってきたことや,いろいろな論文を読んだ経験から書いています。ですので,絶対正しい!と自信をもって言えない弱みがあります。そこで,「文章講座」にではなく,こちらのほうにひっそりと書いておきます。 |
1.分散分析はむずかしい
毎年論文を読んでいて,みんな苦労しているなあとつくづく思うのが,分散分析の結果の記述。たしかに,いろんな数字がゴチャゴチャと出てきて,何をどう書いたらいいのかわからないのも無理はありません。特に,交互作用が出てしまうとたいへん。だから,統計の本を見て,そこに示されている書き方をそのまま使おうとするのもよくわかります。だけど。
読んでいて,どうも違和感を抱くのです。ほんとにこの書き方でいいの? データの傾向をちゃんと読みとれているの? そこで,分散分析の結果の書き方について,私の考え方を書いておきたいと思います。
2.基本的な考え方
まず,はじめに基本的な考え方を示します。
A.分散分析表は,データの分散が各要因にどのように分割されるかを示している。したがってここでは,どの要因が有意だったか,どの要因が有意でなかったかという「分布状態」を示すことが重要になる。つまり,有意だった要因は原則としてすべて記述しておくべきである。
B.分散分析の下位検定(単純主効果検定や多重比較)は,「a群とb群の間に差がある」と個別に言いたいときの有意性を保証する役割を果たす。したがって,すべての検定結果を記述する必要はなく,差を見たい比較に関してだけ記述すればよい。
この2つが基本です。
3.交互作用があっても主効果を書く
「交互作用が出てきたら,主効果には意味がない」というのは,どの統計本にも書いてあることであり,統計的に正しい指摘です。しかしそれは,「主効果はない」ということではなく,結論を一時保留して,単純主効果分析で細かく分析しなさい,という意味です。単純主効果分析でどの水準でも有意差が得られれば,やはりそこには全体的な効果があると言えるわけです。
だから「交互作用が出たら主効果には言及するな」というのは違和感があります。A.の基準から見ても,交互作用しか得られなかった場合と,主効果もあって交互作用も出てきた場合とをきちんと区別するために,主効果にも交互作用にも言及しておくのが望ましいと思います。ちなみに,外国の論文ではこのような場合,主効果について記述した後に,「しかしこの主効果は,有意な交互作用によって限定される(qualified)」などと書いて,交互作用の説明に入っていきます。(といっても,私が読んだ範囲では,ということですが)
具体的に見てみましょう。たとえば,実験条件(実験群・統制群)×性別の分散分析を行い,条件の主効果が0.1%水準で有意,交互作用が10%水準の有意傾向,という場合を想像してみてください。おそらくこの結果は,男でも女でも条件の差は明確に見られるが,男女で差の大きさがいくぶん異なっている,ということを示しています。主効果がなく,交互作用だけだったら,この実験条件は男または女にしか効果を示さなかった,あるいは男と女で逆の傾向を示した(しかも有意傾向)ということになりますから,だいぶイメージが変わります。だから,先のような結果を「分散分析の結果,交互作用が得られた」と一言でまとめてしまったら,誤解されそうじゃありませんか。読者が誤解するだけでなく,書いている本人も,交互作用的にしか結果を解釈しちゃいけないと思い込んでしまいませんか。
私は,交互作用の有無にかかわらず,有意差が得られた要因についてはすべて記述すべきだと思います。それによって,読者はデータの性質についておおよそのイメージを持つことができます。そのイメージを持ちながら,下位分析の結果を読むことができます。これはだいじ。「交互作用が有意だった」だけだと,単純主効果検定と多重比較のゴチャゴチャした結果から,イメージを作り上げないといけなくなります。これは,「交互作用が出れば主効果は無意味」という統計学上の議論とは,別の問題です。
4.下位検定は必要な部分だけ用いる
これも統計の本によれば,分散分析で有意差が得られたとき,どの群とどの群の間に有意差があるかを示すために,t検定を繰り返してはいけません。推測統計というのは,「偶然に起こりうる可能性がどれだけあるか」を基盤にしていますので,ランダムに2群を取り出して比較しても,20回に1回は有意差が得られてしまうからです。比較を繰り返すほど,偶然誤差を有意な差と誤解して検出してしまう危険性が増えるのです。そこで,統計的に有意水準を操作して,各群間の差の有無を「安全に」見積もろうというのが,下位検定の基本的役割だと思います。
言いかえると,下位検定というのは,「a群とb群との間に差がある」という結論を裏づけるために用いるものです。だいじなのは,「どの群間に差があったか」という説明で,統計値はそれを裏づけるために,書き手が知っていればよい数値なのです。
たとえば,先のような条件×性別の分散分析で交互作用が見られたら,それが「条件の効果が男子にしか見られなかった」という交互作用なのか,「条件の効果が男女で逆に出ている」という交互作用なのか,あるいは「男女とも同じ傾向なのだが,女子のほうがより強い影響を受けている」という交互作用なのかを,説明しないといけません。そのときに,下位検定の有意差の結果と矛盾しないよう,妥当な説明を導き出せばよいのです。
単純主効果検定では,実験群/統制群の中の男女差と,男子/女子の中の条件差というように,2つの方向からの分析を順に書き出してくれますが,この結果は必ずしも全部記述する必要はありません。上に書いたような結論を導きたければ男女別の条件差に関する統計値を書いて結論を書けばいいのですし,「条件1は女子にしか効果のない勉強法だが,条件2は男女同様に役立っている」というような結論を導き出したければ,条件ごとの男女差の統計値を示せばいいことになります。
pre-postデザインで実験群と統制群を比較するのであれば,実験群におけるpre-postの差,postにおける実験群と統制群との差の両方が重要な意味を持っていますので,これは両方言及したほうがいいでしょう。ただし,この場合2つそれぞれ意味のちがう比較をしていることに注意。1つの比較をするためには1つの方向から見ればいいのです。
ま,実際にはねらい通りの差が出てくるとは限らないので,両方向の統計値に言及しないといけない場合が多いのですが,考え方としては,必ずしも両方向から記述しなくてもいい,ということです。
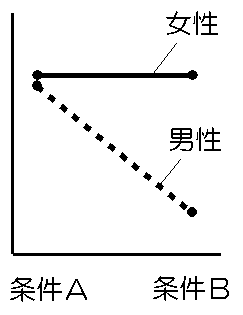 ただし,注意してほしいのは,図のような結果になったときです。男女別の条件差という観点から単純主効果検定の結果を見ると,女性ではn.s.,男性で有意差が見られます。じゃあ,それにもとづいて,「男性では条件Aの方が効果が高かったが,女性では条件間の差が認められなかった」とまとめていいでしょうか?
ただし,注意してほしいのは,図のような結果になったときです。男女別の条件差という観点から単純主効果検定の結果を見ると,女性ではn.s.,男性で有意差が見られます。じゃあ,それにもとづいて,「男性では条件Aの方が効果が高かったが,女性では条件間の差が認められなかった」とまとめていいでしょうか?
また,条件ごとの性差という観点から見て,「条件Bでは女性に大きな効果が認められたが,条件Aでは差が見られなかった」とまとめたらどうでしょう? どちらのまとめも,図から読みとれるデータの傾向をちゃんと言い表せていないように思えませんか?
図を見ると,どうやら条件Bの男性<だけ>が,他の群と比べて効果が低いようです。このような場合は,両方向からの検定結果をふまえたうえで(男性の中の条件A>条件B,条件Bの中の女性>男性,さらに条件Aの女性=条件Bの女性=条件Aの男性),「他の3群と比較して,この群だけが効果が低いことが認められた。」と書くのが,いちばんデータをうまく説明していると思います。
多重比較もそうです。こういうのはあまりないと思いますが,全部の群を比較しなくても,条件A群と統制群,条件B群と統制群,というように選択した一部の群間だけ比較してもいいのです。
つまり,下位検定でだいじなのは,データのどこに差があるかをうまくコトバで説明することなのです。で,その説明が妥当であることを裏づけるために,いろいろな統計値があるのだと考えていいと思います。だから,統計値をもれなく示すのではなくて,必要な統計値に絞って書いていいのです。またその書き方も,統計本の書き方に忠実に沿って書くのがいいわけではなく,きちんとデータを見て,その傾向をうまく言い表せるように工夫すべきだと思います。
以上