科学技術計算関連Pythonパッケージの概要

科学技術計算関連
Pythonパッケージの概要
神嶌敏弘（産業技術総合研究所） http://www.kamishima.net/
2016.9.9 第15回情報科学技術フォーラム (FIT2016)
Python によるデータ分析 ̶ 分析の基本とデータ分析コンペでの実践
1開始

このチュートリアルについて
2
プログラミング言語 Python
Perl，Ruby，PHP と同様のスクリプト言語
1991年2月に Guido van Rossum（現 DropBox）が0.9.0を発表
数値関連パッケージが充実しており，データ分析でよく使われている
チュートリアルの前提と目的
「 Pythonの文法」と「統計・機械学習」の知識を前提
ライブラリを用いたデータ分析用アルゴリズム実装の概要
チュートリアルのトピック
主要パッケージと実行環境
機械学習アルゴリズムの実装
関連パッケージと情報源

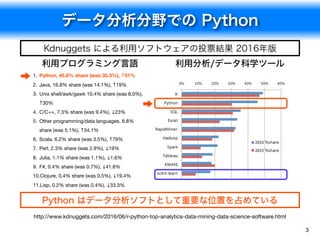
データ分析分野での Python
3
Kdnuggets による利用ソフトウェアの投票結果 2016年版
http://www.kdnuggets.com/2016/06/r-python-top-analytics-data-mining-data-science-software.html
利用分析/データ科学ツール利用プログラミング言語
1. Python, 45.8% share (was 30.3%), ↑51%
2. Java, 16.8% share (was 14.1%), ↑19%

3. Unix shell/awk/gawk 10.4% share (was 8.0%),
↑30%

4. C/C++, 7.3% share (was 9.4%), ↓23%

5. Other programming/data languages, 6.8%
share (was 5.1%), ↑34.1%

6. Scala, 6.2% share (was 3.5%), ↑79%

7. Perl, 2.3% share (was 2.9%), ↓19%

8. Julia, 1.1% share (was 1.1%), ↓1.6%

9. F#, 0.4% share (was 0.7%), ↓41.8%

10.Clojure, 0.4% share (was 0.5%), ↓19.4%

11.Lisp, 0.2% share (was 0.4%), ↓33.3%
Python はデータ分析ソフトとして重要な位置を占めている

データ分析における Python
4
他のデータ分析ツールと比較したときの長所と短所
長所
インタープリタだが主要な計算はネイティブで高速に実行
普通のプログラミング言語 → データ分析以外のAPIとの連携が容易，
データ構造やメモリ管理の自由度が大きい，デバッガ・テストなどの
機能が利用できる
数値計算系のライブラリや，他の数値計算ソフトへのライブラリが
充実している
短所
普通のプログラミング言語 → クラスなどプログラミングに関わる宣
言の記述などが必要になる
ライブラリは充実しているが R には及ばない

目次
5
第Ⅰ部：主要パッケージと実行環境
主要パッケージ：NumPy/SciPy と scikit-learn
実行環境：環境構築とクラウド
第Ⅱ部：機械学習アルゴリズムの実装
クラスの実装：scikit-learn形式のクラスと unittest など
数値計算tips：NumPyの基本と便利な機能
第Ⅲ部：関連パッケージと情報源
関連パッケージ：IPython，scikit-statmodels，最適化，ベイズ推
定，数式処理，高速化など
情報源：Pythonによるデータ分析についての資料や勉強会

6
主要パッケージ
NumPy/SciPy と scikit-learn

NumPy
7
NumPy：多次元配列を効率よく，簡単に扱うためのライブラリ
ホームページ： http://www.numpy.org/
内部的にはネイティブコードで実行されるので演算は高速
柔軟な要素の参照（fancy indexing）
データの一括処理（ユニバーサル関数，ブロードキャスティング）
数値・論理演算，線形代数，初等関数，集約演算，乱数生成など
フーリエ変換や関数あてはめなどのやや高度な演算も可能
歴史：Matrix Object (1994)，Numeric (1995)，Numarray
(2001) などのプロジェクトを2005年に Travis Oliphant（現
Continuum Analytics）が統合して誕生
詳しい歴史： http://www.slideshare.net/shoheihido/sci-
pyhistory

SciPy
8
SciPy：NumPy より高度な数値演算処理
ビルドに Fortran も用いているので，SciPy がインストールされて
いれば，NumPy のフーリエ変換なども高速になる
低次の演算：物理定数，疎行列，特殊関数，確率分布など
高次の計算：非線形最適化，補間，数値積分，計算幾何など
歴史：2001年に複数のライブラリを統合して誕生
import numpy as np
import scipy as sp
NumPy / SciPy を読み込むときの一般的な省略名

scikit-learn
9
scikit-learn：非深層学習系の機械学習ライブラリの代表
ホームページ： http://scikit-learn.org/stable/
多くのアルゴリズムを統一された API で利用可能
歴史：2007に Google Summer of Code のプロジェクトとして始
まり，2010年以降 INRIA のメンバーが加わって発展した
主要な機能
教師あり学習：一般化線形モデル，SVM，アンサンブル学習など
教師なし学習：クラスタリング，異常検出，密度推定など
モデル選択と評価：交差確認，評価指標，超パラメータ探索など
データ変換：次元削減，標準化など
その他：ベンチマークデータ読み込み，テストデータ生成など

scikit-learn：線形回帰の例
10
サンプルファイル：linear_regression.ipynb
線形回帰の利用例
パッケージの読み込み
In [1]: import numpy as np
from sklearn import linear_model
区間 [0, 10] と [0, 5] 上の一様分布に従う，2次元の独立変数のサンプルを100個生成
In [2]: X = np.array([np.random.uniform(0, 10, 100), np.random.uniform(0, 5, 100)]).T
回帰式で従属変数を生成
In [3]: y = np.dot(np.array([[1, 3]]), X.T).ravel() + 10.0 + np.random.normal(0, 0.1, 100)
線形回帰用のクラスを生成する；データに依存しないパラメータを指定
ここでは切片項を使う指定を行う
In [4]: clr = linear_model.LinearRegression(fit_intercept=True)
y = 1 + 3 + 10x1 x2

scikit-learn：線形回帰の例
11
http://scikit-learn.org/stable/documentation.html
の Tutorial や User Guide に多数のサンプル
ﬁtメソッドでデータをあてはめ
In [5]: clr.fit(X, y)
従属変数の係数を調べると，ほぼ元の回帰式のとになっている
In [6]: clr.coef_
predictメソッドで推定したモデルに基づく予測
入力に対する予測値は，ほぼ元の回帰式から得られる値になっている
In [7]: clr.predict([1, 2])
Out[5]: LinearRegression(copy_X=True, fit_intercept=True, normalize=False)
1 3
Out[6]: array([ 0.99926392, 3.00026426])
x = (1, 2) 17
Out[7]: 17.00185966342633

12
実行環境
環境構築とクラウド

実行環境の構築
13
Python バージョン 2 と 3 の選択
一部の後方互換性がないバージョン 2 から 3 への過渡期
Python 2 の資産がある場合 
→ import __future__ や six ライブラリなどを用いつつ移行
これから始める場合 
→ Python 3 で始めても科学技術計算系のパッケージは対応済み
3.4 の統計量パッケージの標準化，3.5 の行列演算子導入などの
新機能の恩恵がある
Python による科学技術計算の実行環境構築
Python では pip コマンドを使ってパッケージをインストールする
のが標準的だが，SciPy などのビルドは難しい 
→ 各種のパッケージをまとめたインストーラを利用することを強
く薦める

インストーラ
14
フリーのものと商用のものがあるが，商用でもパッケージ数やサポー
トに制限のある無料版が提供されている
PyMC や Theano などインストーラによっては含まれないものも
フリー
apt / yum / port / brew（Linux / Mac / BSD などUNIX系）
商用
Continuum Analytics Anaconda
https://store.continuum.io/cshop/anaconda/
Enthought Canopy
https://www.enthought.com/
その他 http://ibisforest.org/index.php?python%2Fnumpy を参照

クラウドサービス
15
クラウド上で動作する Python の科学技術計算環境
サービスによって利用できるパッケージは異なる
SageMathCloud：ワシントン大が運営するフリーサービス
https://cloud.sagemath.com

StarCluster：MITによるクラウド上に計算環境を構築するソフト
http://star.mit.edu/cluster/

商用サービス：制限付きの無料版があり，Python での科学技術計算
を試してみるには便利
IPython Notebook on Azure，Python Anywhere，Wakari.IO など

16
クラスの実装
scikit-learn形式のクラスと unittest

アルゴリズムのクラスによる実装
17
機械学習のアルゴリズムは，関数でも実装できるが，クラスを定義し
て実装すると以下の利点がある
Pythonの適性：Python はオブジェクト指向型言語なので，クラス
による実装に適している
クラスの継承や Mixin の利用：一部だけが異なる学習アルゴリズム
を容易に実装できる
学習結果の保存：cPickle といったオブジェクトのシリアライズを利
用して，学習したモデルのオブジェクトを保存可能
scikit-learnとの連携：scikit-learn のクラスの作成規則に沿って実
装することで，その機能を利用できる

scikit-learnのAPI仕様
18
scikit-learn のクラス設計の基本仕様
Coding Guidelines：http://scikit-learn.org/stable/developers/
コンストラクタ：クラスの初期化
引数：データに依存しないアルゴリズムのパラメータ
ﬁt()メソッド：あてはめ・学習
引数：訓練データと，データに依存したパラメータ
predict()メソッド：学習済みデータを用いた予測
引数：予測対象の新規の入力データ
score()メソッド：モデルのデータへのあてはめの良さの評価
評価対象のデータを，このメソッドの引数で指定する．
transform()メソッド：次元削減などのデータ変換

MixIn を用いたクラス
19
LogFuncMixin
object
funcメソッドは
対数関数
LinearFuncMixin
object
funcメソッドは
線形関数
FuncFitMixin
object
funcメソッドで，あてはめを
するﬁtと予測をするpredict
Mixin（メソッドのみのクラス）による一部だけが異なる手法の実装
LogFit
BaseEstimator, RegressorMixin,
LogFuncMixin, FuncFitMixin
対数関数でのあてはめ
LinearFit
BaseEstimator, RegressorMixin,
LinerFuncMixin, FuncFitMixin
線形関数でのあてはめ
緑色は親クラス
BaseEstimator と RegressorMixin は scikit-learnのクラス
必要な機能を組み合わせて部分的に異なるクラスを容易に実装可能

class LinearFit(BaseEstimator, RegressorMixin,
LinearFuncMixin, FuncFitMixin):
pass
class LogFit(BaseEstimator, RegressorMixin,
LogFuncMixin, FuncFitMixin):
pass
Mixin を用いたクラス
20
サンプルファイル：class_mixin.ipynb
対数関数のMixin
線形関数のMixin
あてはめと予測のMixin
対数関数へのあてはめ
class LogFuncMixin(object):
def func(self, x, a, b):
return a * np.log(x) + b
class LinearFuncMixin(object):
def func(self, x, a, b):
return a * x + b
class FuncFitMixin(object):
def fit(self, x, y):
popt, pcov = curve_fit(self.func, x, y)
self.coef_ = popt
def predict(self, x):
return self.func(x, *self.coef_)
線形関数へのあてはめ

scikit-learnとの連携
21
scikit-learn のクラスの規則に従うことで，その機能を利用する
ﬁt() や predict() などのメソッドの規則を踏襲する
sklearn.base.BaseEstimator クラスを親とし，score() メソッドを
含む sklearn.base.ClassiﬁerMixin なども継承する
交差確認による評価や，グリッド探索による超パラメータ設定が容易
になる
サンプルファイル：cross_validation.ipynb
IRISデータのロードと SVM 分類器の作成
In [5]: iris = datasets.load_iris()
clf = svm.SVC(kernel='linear', C=1)
交差確認による汎化誤差の評価．n_jobs=-1 とすると全CPUを使って並列計算
In [9]: scores = cross_validation.cross_val_score(clf, iris.data, iris.target, cv=5, n_jobs=5)
np.mean(scores)
Out[9]: 0.98000000000000009

unittestのすすめ
22
unittest：プログラムの最小単位ごとに，その入出力を検証する
厳密に最小単位でなくても，リファクタリングや効率化で書き換え
たときに自動で検証できるようになる
一度信頼できる結果を得たときに，その結果と一致するかどうかだ
けの簡単なものでも有用なので，テストを書くことを薦める
Python の場合は nosetests というコマンドによりテストを実行でき
る
パッケージ全体について，全てのテストをまとめて実行できる
% nosetests -v test_svc.py
test_ﬁt (test_svc.Test_SVC) ... ok
----------------------------------------------------------------------
Ran 1 test in 0.742s
OK

unittestのファイル
23
class Test_SVC(unittest.TestCase):
def test_fit(self):
# 小さなテストデータから，テストする分類器でモデルを学習
from sklearn import svm
from sklearn import datasets
iris = datasets.load_iris()
clf = svm.SVC(kernel='linear', C=1)
clf.fit(iris.data[50:150, :], iris.target[50:150])
# 係数が一致しているかを検証
# 実数値は厳密な一致ではなく3桁か5桁ぐらいの精度で一致を検証
np.testing.assert_allclose(clf.coef_,
[[-0.59549776, -0.9739003 , 2.03099958, 2.00630267]],
rtol=1e-5)
# 分類結果が一致しているかを検証
# クラスのような離散値は厳密な一致を検証
classes = clf.predict(iris.data[[50, 51, 100, 101], :])
np.testing.assert_array_equal(classes, [1, 1, 2, 2])
サンプルファイル：test_svc.py

unittestと乱数
24
乱数で初期化するアルゴリズムでは，実行するたびに結果が変わる
ため結果が一致するかどうかを検証できない
乱数のシードを与え，クラス専用の疑似乱数生成器を作成する
scikit-learn のユーティリティ関数 check_random_state() が便利
サンプルファイル：random_state.py
class RandomStateSample(BaseEstimator, TransformerMixin):
# シードの初期化を行わない None が random_state のデフォルト値
# unittest や再現性が必要な実験では適当な整数値を与える
def __init__(self, random_state=None):
self.random_state = random_state
# fit メソッドにも random_state を追加しておくと便利
def fit(self, X=None, y=None, random_state=None):
if random_state is None:
random_state = self.random_state
self._rng = check_random_state(random_state)
return self._rng.randn(10)

25
数値計算tips
NumPyの基本と便利な機能

NumPy 配列の基礎
26
np.ndarray：N-d Array すなわち，N次元配列を扱うためのクラス
Python 本体の多重リストによる多次元配列とは次の点が異なる
1. メモリ上での保持：メモリの連続領域上に保持
形状変更には全体の削除・再生成が必要．
2. 要素の型：基本的に全て同じ型の要素
3. 配列の形状：各次元ごとの要素数が等しい
4. 高度で高速な演算操作
行や列を対象とした多くの高度な数学的操作を，多重リストより容
易かつ高速に適用可能 (fancy indexing)
配列中の全要素，もしくは一部の要素に対し，一括して演算や関数
を適用することで，高速な処理が可能 (ブロードキャスト，ユニ
バーサル関数)

NumPy 配列の生成
27
np.array を使った生成
要素が 1, 2, 3 である長さ 3 のベクトルの例
2重にネストしたリストで表した配列の例
np.empty：初期化なしの配列生成，メモリだけの確保
np.eye / np.identity：単位行列
np.ones, np.zeros：1行列，0行列
In [10]: a = np.array([1, 2, 3])
In [11]: a
Out[11]: array([1, 2, 3])
In [12]: a = np.array([[1.5, 0], [0, 3.0]])
In [13]: a
Out[13]:
array([[ 1.5, 0. ],
[ 0. , 3. ]])

NumPy 配列の属性と要素の参照
28
np.ndarray クラスの主な属性
class np.ndarray
dtype：配列要素の型
後ほど，詳細を述べる
ndim：配列の次元数
ベクトルでは 1 に，配列では 2
shape：配列の各次元の大きさ＝配列の形状
各次元ごとの配列の大きさをまとめたタプルで指定
例：長さが 5 のベクトルは (5,)
※ Python のタプルは1要素のときは “,” が必要
例：2×3行列では (2, 3)

dtype 属性
29
Python のビルトイン型に対応する型：np. を前に付けるだけ
真理値型＝ np.bool，整数型＝ np.int，浮動小数点型＝ np.ﬂoat，
複素数型＝ np.complex
※ メモリのビット数を明示的に表す np.int32 や np.ﬂoat64 なども，
メモリの節約や，C などのライブラリとの連携のために存在
ビルトイン型の str / unicode と NumPy のdtype の相違点
np.ndarray の要素の大きさが同じである必要 → 文字列は固定長
np.dtype('S<文字数>') や np.dtype('U<文字数>') で定義
配列生成関数の dtype 引数で指定するか，astype() メソッドを使っ
て指定する

np.ndarrayの要素の参照
30
各次元ごとに何番目の要素を参照するかを指定する方法
例：1次元配列なら a[3]，2次元配列なら a[1, 2] のように
※ 添え字の範囲は，1 からではなく 0 から，a.shape が返す値より
も一つ前の値まで（例：a.shape が (5,) なら 0 から 4 の範囲）
スライス：リストのスライスと同様の記法で配列の一部分を参照する
1次元配列：リストのスライス表記と同様の開始:終了:増分の形式
“:” のみを使って，行や列全体を取り出す操作は頻繁に利用
In [1]: x = np.array([0, 1, 2, 3, 4])
In [2]: x[1:3]
Out[2]: array([1, 2])
In [3]: x = np.array([[11, 12, 13], [21, 22, 23]])
In [4]: x[0, :]
Out[4]: array([11, 12, 13])
In [5]: x[:, 1]
Out[5]: array([12, 22])

np.ndarrayと数学の行列
31
1次元の np.ndarray 配列には，線形代数でいう縦ベクトルや横ベ
クトルという区別はなく，1次元配列は転置できない
縦ベクトルや横ベクトルを区別して表現するには，それぞれ列数が1
である2次元の配列と，行数が1である2次元配列を利用
ベクトルを行列にするには np.newaxis や reshape メソッドを利用
※ reshpe で -1 は，全体の要素数を考慮して適宜選択の指定
In [1]: np.array([[1], [2], [3]])
Out[1]:
array([[1],
[2],
[3]])
In [1]: a = np.array([1, 2, 3])
In [2]: a[:, np.newaxis]
Out[2]:
array([[1],
[2],
[3]])
In [3]: a[np.newaxis, :]
Out[3]: array([[1, 2, 3]])
In [1]: a = np.array([1, 2, 3])
In [2]: a.reshape(-1, 1)
Out[2]:
array([[1],
[2],
[3]])
In [3]: a.reshape(1, -1)
Out[3]: array([[1, 2, 3]])

ユニバーサル関数
32
ユニバーサル関数：入力した配列の各要素に関数を適用し，その結
果を入力と同じ形の配列して返す
ユニバーサル関数の機能を利用するには，mathパッケージの
math.log() などではなく，NumPy の np.log() を用いる
論理関数のユニバーサル関数は np.logical_and() など
ユーザ関数をユニバーサル化する np.vectorize() や np.frompyfunc()

np.vectorize() をデコレータとして使った例
In [10]: a
Out[10]: array([1, 2, 3])
In [11]: np.log(a)
Out[11]: array([ 0. , 0.69314718, 1.09861229])
In [1]: @np.vectorize
...: def squre_plus_one(x):
...: return x**2 + 1.0
In [2]: squre_plus_one(np.arange(3))
Out[2]: array([ 1., 2., 5.])

ブロードキャスト
33
ブロードキャスト：要素ごとの演算を行うときに，配列の大きさが
異なっていれば自動的に要素をコピーして大きさを揃える機能
例：大きさがそれぞれ 0次元配列 a，長さ3の1次元ベクトル b，
2×3 の行列 c の要素積を求める
大きさが1の次元は，必要に応じて要素の値を自動的にコピーする
np.newaxis により次元数を合わせてから利用することを薦める
多重 for ループの各変数が，各次元に対応していると考えて実装する
とよいだろう
※ http://www.kamishima.net/mlmpyja/nbayes2/distclass.html
a b c
0 0
0 0 0 00 0
0 00 0
0 1 0 2
0 1 0 20 0
0 0 1 0 1 1 1 2
0 1 0 20 0
0 1 2
0
1
0 1 2
0
1
0 1 2
0
1
a[np.newaxis, np.newaxis] * b[np.newaxis, :] * c[:, :]

行列演算の関数プログラミング的実装
34
map() と reduce() を使った関数プログラミング的な実装に基づく
と，NumPy による計算は理解しやすいだろう
リストではなく，共通の配列に map() して要素ごとの計算をしたあ
と，sum() や max() などの集約演算で reduce() すると考える
例：pLSAモデル
Pr[X, Y ] =
P
Z Pr[X|Z] Pr[Z|Y ] Pr[Y ]
Pr[X | Z ]
pXgZ[x, z]
Pr[Z | Y ]
pZgY[z, y]
Pr[Y ]
pY[y]
y
z
z
x
y

行列演算の関数プログラミング的実装
35
pXgZ[x,z,np.newaxis]
z
x
np.newaxisやブロードキャストで共通の配列に揃える
pZgY[np.newaxis,z,y] pY[np.newaxis,np.newaxis,y]
z
y y
要素ごとの計算（map のイメージ）
pXgZ[x,z,np.newaxis] * pZgY[np.newaxis,z,y] * pY[np.newaxis,np.newaxis,y]
np.sum(pXgZ[x,z,np.newaxis] * pZgY[np.newaxis,z,y]
* pY[np.newaxis,np.newaxis,y], axis=1)
集約演算（reduceのイメージ）
z
y
x
newaxis
newaxis
newaxis
newaxis
sum()
x
y

欠損値や無限値
36
欠損値 np.nan や無限大・無限小 np.inf などを含むデータの処理
配列の要素が全て有限値かどうかを検査する
np.all(np.isﬁnite(x)) の代わりに np.isﬁnite(x.sum())
np.nan を除外した集約演算
総和 np.nansum() や最大値 np.nanargmax() などがある
この場合に特化した bottleneck というパッケージも存在
欠損値を他の値で置き換える
ユニバーサルな3項演算子にあたる np.where() が便利
In [10]: a
Out[10]: array([ 0., nan, 1., inf, 2.])
In [11]: np.where(np.isfinite(a), a, -1.0)
Out[11]: array([ 0., -1., 1., -1., 2.])

欠損値や無限値
37
scikit-learn で開発者用に提供されている欠損値などの検査関数
http://scikit-learn.org/stable/developers/utilities.html

sklern.utils には下記の関数の他，数値演算やテスト用のものが

assert_all_ﬁnite

配列に無限値や欠損値が含まれていると ValueError を発生
check_array

配列の要素の型の変換，次元数や大きさの検査，無限値・欠損値の
有無などをまとめて実行できる
check_X_y

check_array に加え，特徴用配列 X と教示情報用配列 y の大きさ
の一致を検査

scipy.optimize
38
scipy.optimize：非線形最適化のパッケージ，機械学習ではよく利用
minimize_scolar()：有限区間上のスカラー関数の最適化
brent brent法，golden 黄金分割法

minimize()：多次元の非線形最小化
勾配を使わない最適化：勾配を求める必要はないが，代わりに目的
関数の評価回数が増えるので非常に遅い
Nelder-Mead ネルダー・ミード法，Powell パウエル法
勾配を使う最適化：収束は早いが，勾配やヘシアンも与える必要
CG 共役勾配法，BFGS BFGS法，Newton-CG ニュートン法
※ BFGSやニュートンは収束は早いがヘシアン計算で遅くなることも
制約付きの最適化：パラメータが有限区間にある多次元最適化
L-BFGS-B，TNC 切断ニュートン法，COBYLA

演算エラー処理
39
np.log(0) など有限にならない値を求めると，警告メッセージが表示
される
このような演算例外に対する挙動を変更するのが np.seterr()
状況の指定：全般 all，割り算 divde，オーバーフロー over，アン
ダーフロー under，不正演算 invalid
動作の指定：無視 ignore，警告表示 warn/print，例外送出 raise，
関数呼び出し call，ログの記録 log
np.seterr(all=‘ignore’) とすると警告メッセージを全て抑制できる

40
関連パッケージ
IPython，scikit-statmodels，最適化など

IPython
41
便利な対話的な実行環境
コマンドの補完（tabキー），ヒストリの管理など
notebook は，計算結果をそのままメモとして残すことができる
ipypararrel で複数のマシン上でのジョブ管理ができる
ドキュメントの参照
オブジェクト名 + “?” で，そのオブジェクトの説明を参照できる
マジックコマンド：% (単一行)や %% (複数行) で始まるコマンド群
%quickref：コマンドのリファレンス
%cd，%ls：shell としてのコマンド
%timeit：関数の実行時間の計測
%run：ファイルの実行
%pycat：カラーリング付きのソース表示

Jupyter notebook
42
分析コードとメモを一つにまとめておける
Jupyter は ipython と独立して，Python の他，R / Julia など
様々なスクリプト言語が利用できるようになった．
起動：コマンドラインでは “jupyter-notebook”
ヘルプの keyboard shortcuts を最初に読むとよい
メモの記述：Markdown 記法と，LaTeX の数式記法が利用可能
カスタマイズ：“ipython proﬁle create” を実行すると，“ipython
proﬁle locate” で表示される場所に“ipython_default” が作成され，カ
スタマイズ可能に
その中の startup ディレクトリに起動ファイル .ipy を設置できる
分析結果の保存：notebook は .ipynb ファイルに保存できる
ノートブックの公開：nbviewer http://nbviewer.ipython.org や
GitHubで公開できる

SymPy
43
数式処理を行うためのパッケージ
最初に sympy.init_session() を実行
しておくと便利
x, y, z, t を実数変数，k, m, n を
整数変数と認識するようになる
主な機能
微分：diﬀ，積分：integrate，
極限：limit
展開：expand，単純化：
simplify，テイラー展開：series
方程式の解：solve
サンプルファイル：sympy_demo.ipynb

sympy.init_session() 実行後に行う
微分
In [2]:
diff((x ** 2 + log(x)) / x, x)
積分
In [3]:
integrate(x ** 3 + sin(x) ** 2, x)
展開
In [4]:
expand((x + 1)**2)
Out[2]:
(2x + ) − ( + log (x))
1
x
1
x
1
x2
x2
Out[3]:
+ − sin (x) cos (x)
x4
4
x
2
1
2
Out[4]:
+ 2x + 1x2

scikit-statmodels
44
scikit-learn と同様に使える，scikit-learn に対する特色は
ARMA などの時系列分析モデル
R言語のように線形モデルを記述する記法を備える
多重検定など検定周辺の機能
パッケージの読み込み
In [1]: import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
データの読み込み
In [2]: url = 'http://vincentarelbundock.github.io/Rdatasets/csv/HistData/Guerry.csv'
dat = pd.read_csv(url)
回帰モデルのあてはめ
In [3]: results = smf.ols('Lottery ~ Literacy + np.log(Pop1831)', data=dat).fit()
結果の表示
In [4]: print results.summary()
サンプルファイル：statsmodels_demo.ipynb

ベイズ推定
45
Python でのベイズ推定では PyMC と PyStan が著名
どちらも，生成モデルを定義すると MCMC により，データを与
えたときの変数の事後分布を推定する
PyMC http://pymc-devs.github.io/pymc/
Python でのベイズ推定パッケージとしては開発が長く続いている
Python のオブジェクトを使ってモデルを構築できる
PyStan https://pystan.readthedocs.org
後発のパッケージで注目されている
専用の記述言語でモデルを構築し，Python や R から呼び出す

PyMC
46
1. μ ～ Normal(0.0, 0.12
)
2. For i in 1 … N
(a) xi ～ Normal(μ, 1.02
)
μ x
N
仮想コードグラフィカルモデル
モデルの構築
生成モデルは，非常に単純：
※ NumPy の np.random.normal は平均と標準偏差で指定するが，PyMC の正規分布は，標準偏差ではなく精度（分散の逆数・逆行列）で指定す
る．
は，平均がで，分散がとしておく．このについては標本が観測される（グラフィカルモデルでいえば黒丸）ので，
value=x_sample と observed=True を指定しておく．
In [4]: mu = Normal('mu', 0, 1 / (0.1 ** 2))
x = Normal('x', mu=mu, tau=1/(1.0**2), value=x_sample, observed=True)
MCMCによる事後確率の推定
マルコフ連鎖のモデルを指定． input で関連する変数を指定し，適当な回数だけ反復する．
In [5]: M = MCMC(input=[mu, x])
M.sample(iter=10000)
μ ∼ Normal(0, )0.12
x ∼ Normal(μ, )1.02
x μ 1/0.01 x
[-----------------100%-----------------] 10000 of 10000 complete in 0.5 sec
サンプルファイル：pymc_demo.ipynb

PyMC
47
左上はのサンプル値の反復中の変化，左下は自己相関で収束してるかどうかを確認できる．右がのデータを観測したあとのパラメータの事後
分布
In [6]: Matplot.plot(mu)
μ μ
Plotting mu

自動微分
48
Theano や多くの深層
学習関連パッケージが
提供する機能
数値微分とは異なり，
解析的に微分し，数値
を代入した結果を得る
他にも数式を直接的に
定義可能
非線形最適化など各種
の数理計画法で結果を
利用できる
サンプルファイル：theano_auto_diﬀ.ipynb
Theano 関連パッケージの読み込み
In [2]: import theano
import theano.tensor as T
スカラー変数のシンボルの定義
In [4]: x = T.dscalar('x') # double scalar
関数を定義
In [5]: f = T.sin(x)
変数に，値を代入して関数評価する：
In [10]: func_f = theano.function(inputs=[x], outputs=f)
func_f(np.pi)
関数を微分して，値で評価する：
In [12]: diff_f = theano.function(inputs=[x], outputs=T.grad(f, x))
diff_f(np.pi)
f(x) = sin(x)
x π f(x) sin(π) = 0
f(x) π (π) = cos(π) = −1.0sin′
Out[10]: array(1.2246467991473532e-16)
Out[12]: array(-1.0)

Theano：シンボル変数の定義
49
In [1]: import theano
In [2]: import theano.tensor as T
In [3]: x = T.scalar('x')
In [4]: a = T.dmatrix('A')
In [5]: y = T.drow('y')
パッケージのインポート
シンボルの定義
dscalar は倍精度のスカラー，dmatrix は倍精度の行列など
引数はシンボルの名前．pprint などの表示に用いる
複数のシンボルをまとめて定義する scalars や matrices なども
b：バイトｗ：16bit整数 i：32bit整数 l：64bit整数
f：単精度 d：倍精度 c：複素数
scalar：スカラー vector：ベクトル
matrix：行列
row：行数1の行列 col：列数1の行列
tensor3：3次元テンソル tensor4：4次元テンソル

Theano：関数の定義と評価
50
In [6]: f = theano.function([x, y], x + y)
In [7]: f(3, [[1, 2]])
Out[8]: array([[ 4., 5.]])
関数の定義と評価
theano.function( inputs=〈入力変数〉, outputs=〈出力式〉)
入力変数と出力式を指定して関数を定義
入力変数には定義したシンボルを与える
関数に入力を与えれば，関数をその入力値で評価して結果を返す
6行：入力はスカラー x と，行ベクトル y であることを，出力式は 
出力式は x + y であることを指定して，関数 f を定義
7行：x=3，y=[[1, 2]] を与えると，x + y の式を評価して 
[[4, 5]] の行ベクトルを得る

Theano：関数の定義と評価
51
自動微分
In [9]: f = x**2 + T.log(x)
In [10]: grad_f = theano.function([x], T.grad(f, x))
In [11]: grad_f(1.0)
Out[11]: array(3.0)
T.grad(〈微分する式〉，〈微分する変数〉)
式や変数の指定には定義したシンボルを用いて記述する
9行：関数 f(x) = x2
+ log x を定義
10行：T.grad(f, x) で関数 f を変数 x
11行：f(x) を x で微分した f’(x) = 2x + 1/x を x=1.0 で評価して 3.0
の解を得る

最適化関連パッケージ
52
scipy その他の最適化関連

scipy.optimize.root 関数値を0にする入力値である根を求める
scipy.optimize.linprog 線形プログラミング
cvxopt http://cvxopt.org
機械学習では必要になる凸最適化に特化
凸最適化で著名な Stephen Boyd のチームが作成
autograd https://github.com/HIPS/autograd
Theano のようにシンボルを定義せず，Python 関数そのままで自
動微分ができる
OpenOpt http://openopt.org
自動微分をサポート
線形計画，非線形計画，整数計画など多くのソルバーのラッパー

機械学習の総合パッケージ
53
MLlib http://spark.apache.org/mllib/
大規模並列データ処理環境Spark上で動作する
分類・相関・クラスタリングに加え，頻出パターンマイニングも
Orange http://orange.biolab.si
分析モデルを GUI を用いて対話的に構築できる統合環境
頻出パターンマイニングなどの拡張プラグインも
Shogun http://www.shogun-toolbox.org
カーネル法，マルチタスク学習重視
Vowpal Wabbit https://github.com/JohnLangford/vowpal_wabbit/wiki
オンライン最適化を用いた大規模・高速対応

深層学習
54
Pythonから利用できる深層学習フレームワークは多数
TensorFlow https://www.tensorflow.org/
計算モデルの可視化，分散環境，ユーザコミュニティが大規模
Keras https://keras.io/
Theano や TensorFlow を演算基盤に，モデルを簡易に定義可能
MXNet https://mxnet.readthedocs.io/
対象スクリプト言語数，命令・記号の両方による記述，分散環境
Caffe http://caffe.berkeleyvision.org/
画像認識が中心で，配布されている学習済みモデルが多い
Chainer http://chainer.org/
回帰結合などで依存関係を動的に構築，親切なエラーメッセージ

高速化
55
dask http://dask.pydata.org/en/latest/
NumPy や Pandas の一部のAPIを並列化
numexpr https://github.com/pydata/numexpr
要素ごとの演算をキャッシュミスが起きないようにする
bottleneck http://berkeleyanalytics.com/bottleneck/
欠損値 np.nan がある場合に高速化
Cython http://cython.org
制限はあるが Python をネイティブコードに変換できる
型宣言をコードに追加するとさらに高速化できる
高速な実行環境
PyPy：文法を制限した Python を実行
Numba：NumPy用のコンパイラ
PySton：clang などの仮想マシン LLVM 上で実行

その他のパッケージ
56
matplotlib http://matplotlib.org
グラフの描画
Pandas http://pandas.pydata.org
R言語のデータフレームのような表データに対する多様な操作
csvkit http://csvkit.readthedocs.org
csvファイルを操作する便利なコマンド群
Sphinx http://sphinx-doc.org
ReStructuredText 形式で記述するドキュメント作成ソフト
OpenCV http://opencv.org
画像処理で著名なライブラリ．Pythonインタフェースあり
NLTK http://www.nltk.org
自然言語処理のPythonパッケージ

57
情報源
Pythonによるデータ分析についての資料や勉強会

資料
58
Python Scientiﬁc Lecture Notes http://scipy-lectures.github.io/
一部邦訳 http://turbare.net/transl/scipy-lecture-notes/

科学技術計算に関連する話題を広くカバーした資料
Numpy Example List http://wiki.scipy.org/Numpy_Example_List
少し慣れてから一通り目を通すといろいろ発見がある
NumPy for Matlab Users http://wiki.scipy.org/NumPy_for_Matlab_Users
Matlab を知っている人向けの対応表
機械学習のPythonとの出会い http://www.kamishima.net/mlmpyja/
拙著の機械学習手法の実装を例にしたチュートリアル
朱鷺の杜Wiki http://ibisforest.org/index.php?python
関連情報をいろいろ集めてまとめています

国際会議・勉強会
59
SciPy Conferences http://conference.scipy.org
科学技術計算での Python 利用に関する国際会議
US，欧州，各国の会議情報があり，スライド・ビデオを公開
PyCon JP http://www.pycon.jp
毎年9月に開催．アジア太平洋の PyCon APAC として開催される
ことも
Python全般の国内会議．科学技術計算系の講演が，ここ数年急激
に増えた
PyData Tokyo http://pydatatokyo.connpass.com
データ分析でのPython利用の勉強会

サンプルファイル
60
小嵜耕平さんの資料
Python とデータ分析コンテストの実践
https://speakerdeck.com/smly/python-todetafen-xi-
kontesutofalseshi-jian

本チュートリアルのサンプルファイル
https://github.com/tkamishima/ﬁt2016tutorial

科学技術計算関連Pythonパッケージの概要

More Related Content

科学技術計算関連Pythonパッケージの概要