Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
SlideShare a Scribd company logo

関数プログラミング入門

•
•
Hideyuki Tanaka
Hideyuki Tanaka

Introduction to Functional Programming

1 of 101
関数プログラミング入門 情報オリンピック春季トレーニング合宿 2010/03/22 田中英行
自己紹介 • 田中英行 (@tanakh, id:tanakh) • TopCoder (id:haskell-master) • Haskell Lover（not master!） • ICPC2004-5 世界大会 • Preferred Infrastructure勤務 – ICPC OB多数在籍 – アルバイト・インターン等、 興味のある方はご連絡を！
本日の内容 • 関数プログラミング入門 – 参照透明 – クロージャ – 遅延評価 – リスト処理 – etc… • 関数プログラミングにまつわる話題 – 永続データ構造 – 並行計算 – ソフトウェアトランザクショナルメモリ（STM）
関数（関数型）プログラミングとは • 関数を評価することによって 計算を行おうとする プログラミングパラダイム • 手続き型プログラミングと相対する概念 – ※宗教です
手続き型プログラミング • 状態を書き換えて計算を進める – 変数代入 – ループ – 手続き呼び出し • 手続き型プログラミング言語 – C/C++, Java, Perl, Pythonなど – 現在のメインストリーム – 競技プログラミングで使えるのも大体これ
（オブジェクト指向プログラミング） • 手続きを抽象化する一手法 • オブジェクト＝データ＋手続き • 最近の手続き型言語の主流 – C++, Java, Python, …
関数プログラミング • 関数プログラミングを行うための機能を有したプ ログラミング言語 • 研究分野での利用が多い – 実アプリではあまり使われておらず – もっと普及するべき…（そのために来ました） • 関数型プログラミング言語 – 純粋関数型 • Haskell, Clean – 非純粋関数型 • Lisp, Scheme, Objective Caml, Clojure
マルチパラダイム • 関数型とオブジェクト指向の融合を目指す – Scala • 関数型言語へのオブジェクト指向の導入 – Objective Caml – （Objectiveの部分は蛇足との声も多数） • オブジェクト指向言語への関数型の導入 – 最近のオブジェクト指向言語いろいろ – 関数型言語の機能を取り込むのがトレンド
関数プログラミングの特徴 • 関数を第一級（ファーストクラス）の値として扱う • 値を関数に渡し、別の値を返す • 参照透明である – 変数の値を書き変えない ⇔ 手続き型 – 変数の値を書きかえることにより計算
参照透明 • 状態を持たない • 変数への再代入なし { { int x = foo(123); int x = 10; … x++; int y = foo(123); } assert(x==y); } 変数の書き換えなし 同じ関数の評価は必ず同じ値になる
参照透明でない例(1) • 呼び出す度に状態が変化する – 値を返す以外の状態変化 – 副作用という int count(int inc){ static int cur = 0; cur += inc; return cur; }
参照透明でない例(2) • 入出力を伴う場合 char getchar(); // 呼び出す度に値が変わる FILE *f=fopen(“hoge.txt”, “r”); fread(buf, 1, size, f); // 環境によって値が変わる
制御構造 • ループなどはない – 副作用を前提としているので書けない int acc = 0; for (int i=0; i<100; i++){ acc += i; }
「ない」ことの力？ • 関数型言語では – ○○をしません – ○○はありません • 機能を制限することが記述力を与えることは あるのか？ ⇒ もちろんそんなことはない ⇒ (そんなことはないこともない)
「ない」ことの力？ • 「関数プログラマは大きな物質的利益があると 主張する。関数プログラマは従来のプログラマよ り桁違いに生産的である。関数プログラムは桁 違いに短かいから」 – “なぜ関数プログラミングは重要か” • 変数の代入がない ⇒ 手続き型プログラムの90%は代入 ⇒ 90%のコードがなくなる • （な…何をいっているのか…） – もちろんジョークですけど
参照透明のメリット • いくつかの現実的なメリット • デバッグがやりやすい – オブジェクトの状態など考えなくてもよい • 動作がわかりやすい – オブジェクトの状態など考えなくてもよい
それでプログラム出来るの？ • 副作用なしでプログラム出来るの？ • 状態なしでプログラム出来るの？ • 値書き変えずにプログラム出来るの？ ⇒ そのための関数型言語です
しかし、実際の関数型言語では • 副作用を認めているものもある ⇒ 非純粋関数型言語 （Lisp, Scheme, Objective Caml） • 完全に参照透明 ⇒純粋関数型言語 （Haskell, Clean） – しかし、副作用を扱う必要はあるので、 なんとかして副作用を扱う術を提供（後述）
ちなみに… • こっちも宗教です
関数型プログラミング言語の機能 • ファーストクラスクロージャ • 末尾再帰最適化 • カリー化 • 遅延評価 • リスト操作 ハスケル・カレー
Haskell文法紹介 f x = x + 1 -- 関数定義 f = ¥x -> x + 1 -- ラムダ式（関数リテラル） (1, “hoge”) -- タプル [1, 2, 3] -- リスト f (a, b) = a+b -- タプルを引数にとる関数 f a b = a+b -- 2引数関数 f n = if n<0 then –n else n -- 条件分岐 f x = let y = x+1 in y*y -- ローカル変数 f x = g x + h x (x+1) -- 関数適用 1ページに収めるのは無理がありましたね…
ファーストクラスクロージャ • 関数を第一級の値として扱える – 関数を値として関数に渡せる – 関数を関数の返り値として返せる
関数ポインタとは違うのか？ • 関数の使用に変な制限がつかない – 関数をどこでも定義できる • 関数をネストできる • 関数をリテラルとして書ける – 関数からネストした変数が参照できる
例 • ネストした関数 • 外側の変数の参照 • (gcc拡張で出来るという話も) int foo(int x){ int bar(int y){ foo x = return x+y; let bar y = x + y in } bar (x+1) return bar(x+1); }
クロージャとは • 関数とそれを評価する環境のペア – 外側のスコープの変数を束縛できる plus x = plus(int x){ let f = ¥y -> x+y in int f(int y){ f return x+y; } plus1 = plus 1 return f; plus2 = plus 2 } plus1 10 => 11 plus1=plus(1); plus2 10 => 12 plus1(10); => 11 こういうのはCではできない
レキシカルクロージャ • 字面上（レキシカル）のスコープでローカル変 数を束縛できるクロージャ • ローカル変数は通常スタック上にあるので – スタックをコピーする – スタックをヒープに取る plus(int x){ – （そもそもサポートしない） int f(int y){ return x+y; – 等が必要 } return f; }
関数オブジェクトでは駄目なのか？ • 関数オブジェクトは状態（環境）を持てる struct plus{ int x; plus(int x):x(x) {} int operator(int y){ return x+y; } }; … plus1=plus(1); plus2=plus(2); plus1(10); => 11 plus2(10); => 12
クロージャ＝オブジェクト • 両者は等価 – 片方でもう片方を実現できる • ただし、オブジェクトを関数として扱うのは – 記法 （いちいちクラスを定義しないといけない） • boost::lambdaとかもあるけど… – 変数のスコープ （レキシカルスコープ便利） – 生成コスト – などの点で不利
カリー化 • クロージャを用いて、二引数関数を 一引数関数に変換できる – 任意の関数を１引数関数に変換できる – カリー化という • カリー化された関数は、部分適用できるよう になる f (x,y) = x+y f 1 2 // => 3 ↓ カリー化 f = ¥x -> (¥y -> x+y) plus1 = f 1 // 部分適用 ↓ 略記法 plus1 2 // => 3 f x y = x + y
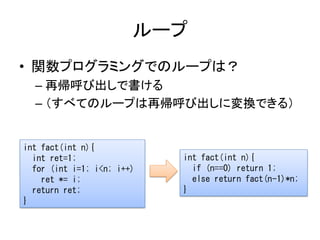
ループ • 関数プログラミングでのループは？ – 再帰呼び出しで書ける – （すべてのループは再帰呼び出しに変換できる） int fact(int n){ int ret=1; int fact(int n){ for (int i=1; i<n; i++) if (n==0) return 1; ret *= i; else return fact(n-1)*n; return ret; } }
再帰呼び出しの問題 • ループ回数が多くなった時 – スタックオーバーフローする fact(100000); => Segmentation fault • パフォーマンスの問題 – 毎度スタックに引数とリターンアドレス積んで 関数呼び出し – 重い
末尾再帰（tail recursion） • 関数の最後にあるような再帰呼び出し – 再帰呼び出しをジャンプに最適化できる • ループはすべて末尾再帰呼び出しに 変換できる – ループと同じ効率で実行できる int fact(int n){ int fact(int n, int acc){ if (n==0) return 1; if (n==0) return acc; else return fact(n-1)*n; else return fact(n-1, acc*n); } }
末尾呼び出し(tail call)最適化 • 末尾の関数呼び出しは再帰でなくともジャン プに書き換えられる • 二つ以上の関数が相互に再帰しているケー スなど • サポートしていない bool even(int n){ if (n==0) return true; 関数型言語もある return odd(n-1); } – JVM上の言語 bool odd(int n){ – Scala, Clojureなど if (n==0) return false; return even(n-1); }
リスト • 関数プログラミングではリストがよく用いられる – 再帰的データ構造なので • 特徴 – 単方向リンクリスト – 先頭に追加がO(1) – 先頭からの削除がO(1) 1 2 3
Haskellのリスト • リスト例 a = [] -- 空リスト b = 1 : (2 : (3 : []))) c = 1 : 2 : 3 : [] --上の略記 d = [1, 2, 3] --上の略記 e = 5 : d -- [5, 1, 2, 3] f = head d -- 1 g = tail d -- [2, 3]
リストと再帰 • リストの処理が再帰で自然に書ける doubleList [] = [] doubleList (x:xs) = (x*2) : doubleList xs incrementList [] = [] incrementList (x:xs) = (x+1) : incrementList xs sum [] = 0 sum (x:xs) = x + sum xs 似た処理 →抽象化できない？ product [] = 1 product (x:xs) = x * reverse xs
map • リストの変換を高階関数を用いて抽象化 – 関数を引数としてとる関数 map f [] = [] map f (x:xs) = f x : map f xs doubleList ls = map (¥x -> x * 2) ls incrementList ls = map (¥x -> x +1) ls
fold • リストの畳込み fold f v [] = v fold f v (x:xs) = f x (fold f v xs) sum ls = fold (¥x y -> x+y) 0 ls 1 : (2 : (3 : []))) 1 + (2 + (3 + 0))) product ls = fold (¥x y -> x*y) 1 ls 1 : (2 : (3 : []))) 1 * (2 * (3 * 1)))
filter • 条件を満たす要素のみ取り出す filter p [] = [] filter p (x:xs) = if p x then x : filter p xs else filter p xs filter isEven [1, 2, 3, 4, 5] => [2, 4] filter isPrime [1, 2, 3, 4, 5] => [2, 3, 5]
応用例 • 100以下の素数の二乗の和を求めよ fold (+) 0 (map (¥x -> x*x) (filter isPrime [1..100])) • リストに関するかなりの操作を この三つの関数の組み合わせで行える – リスト内包表記というのもある • Haskell, Pythonなど sum [ i*i | i <- [1..100], isPrime i] こう書ける
遅延評価 • 必要になるまで式の評価を遅らせる – 参照透明なら、式をいつ評価してもいい • Haskellはデフォルトで遅延評価する • Lisp, Objective Camlなどは正格評価 square x = x*x square x = x*x square(1+2) square(1+2) => square(3) => (1+2)*(1+2) => 3*3 => 3*3 => 9 => 9 正格評価 遅延評価
遅延評価の利点(1) • 正格評価ではエラーになるものでも、遅延評 価ではエラーにならないケースがある – 遅延評価の方が正しく動くプログラムの範囲が 大きい fst (a, b) = a fst (a, b) = let c = a/b in fst (123, 1/0) if b==0 => 123 then -1 else c fst (1, 0) => -1
遅延評価の利点(2) • 正格評価では停止しないプログラムでも、遅 延評価では停止することがある – 遅延評価のほうが停止するプログラムが多い loop i = loop (i+1) + 1 f (a, b) = a f (1, loop 0) => 1
遅延評価の利点(3) • 遅延評価だと不要な計算が省略され 計算量が減る場合がある • たらいまわし関数 tarai x y z = if x <= y then y else tarai (tarai (x-1) y z) (tarai (y-1) z x) (tarai (z-1) x y)
例：無限リスト • 無限の長さを持つリストを定義できる ones = 1 : ones nums = 1 : map (¥x -> x+1) nums • 必要な部分だけ取り出せる take 10 ones => [1,1,1,1,1,1,1,1,1,1] take 10 nums => [1,2,3,4,5,6,7,8,9,10]
例：フィボナッチ数列 • フィボナッチ数列が無限に入ったリスト fibs = 1 : 1 : zipWith (¥x y -> x+y) fibs (tail fib) zipWith f (x:xs) (y:ys) = f x y : zipWith f xs ys fibs: 1 1 2 3 5 8 13 21 … tail fibs: 1 2 3 5 8 13 21 …
例：ソート、最小要素 • 必要な要素だけソートされる – 最小k要素なども自明な実装で尐ない計算量 sort [] = [] sort (x:xs) = let a = filter (¥v -> v<x) xs in let b = filter (¥v -> v>=x) xs in sort a ++ [x] ++ sort b let a = [3,1,4,2,5] sort a => [1,2,3,4,5] head (sort a) => 1 take 3 (sort a) => [1,2,3]
副作用 • 副作用のないプログラムはない – 端末からの入力 – ファイル入出力 – GUI操作 – などなど ⇒ 関数プログラミングでも副作用を 何とかして扱う必要がある
関数型言語での副作用の取り扱い • 副作用を許す(非純粋) – Lisp, Scheme, Objective Caml など • 一意型(Linear Type) – Clean • 遅延ストリーム – Miranda, 昔のHaskell • モナド（Monad） – Haskell ↑類似品に注意
一意型を用いる方法(1) • プログラム＝世界→新しい世界への関数 • 一意型＝ただ1度のみ参照される変数 • 各副作用は、一意型である世界を引数にとり、 変更された世界を返す main :: *World -> *World main w1 = let (w2, line) = getLine w1 in let w3 = putStrLn w2 line in w3
一意型を用いる方法(2) • 2回参照されてはいけない – 世界は保存されないしロールバックもされない 二回参照 main :: *World -> *World main w1 = let (w2, line1) = getLine w1 in let (w3, line2) = getLine w1 in let w4 = putStr w3 (line1++line2) in w4
遅延ストリームを用いた方法 • プログラム＝入力例→出力列への関数 • 入力は遅延リスト – 入力が揃った時点で生成される • 概念は分かりやすい – しかしプログラムとしては扱い難い main :: [Request] -> [Response] main reqs = process reqs process (Input line : rest) = Output line : process rest
モナドを用いた方法 • プログラム＝アクションを組み立てる関数 – アクションを組み立てるのは参照透明 • （副作用のある）アクションを実行するのは処 理系の役目 main :: IO () main = do main = line1 <- getLine getLine >>= (¥line1 -> line2 <- getLine getLine >>= (¥line2 -> putStr (line1 ++ line2) putStr (line1 ++ line2) )) 略記
モナドについて • 現在純粋関数型言語での主流 • 組み合わせがやりやすい – モジュラリティが高い • 詳しい説明は今回は割愛 – ちゃんと説明しようとするとすごい分量になっちゃ いそうなので – 興味のある方は、「モナドのすべて」というWeb上 の文章がおすすめ
参照透明であることの利点 • なぜそうまでして参照透明である必要がある のか？ – バグが出にくい・バグが直しやすい – 遅延評価を利用できる – 並列・並行計算と相性が良い
mutable, immutable • 変更可能なデータをmutable、 変更不可能なデータをimmutableと呼ぶ • 例えば・・・ – C++の配列はmutable – Javaの文字列はimmutable • 参照透明で扱えるのはimmutableなもののみ – 当然副作用を扱えないので – （一意型を用いた例外はあります）
関数プログラミングとimmutable • immutableなデータに関する操作は参照透明 • ゆえに、関数プログラミングにおいては immutableなデータが重要 • 配列、キュー、マップその他もろもろのデータ 構造についてimmutableなものが必要 • しかしimmutableはオーバーヘッドになるので、 なるべく効率の良いデータ構造が必要 – 永続データ構造というものが考えられている
永続(Persistent)データ構造 • 更新される際に、変更前の値を常に保持する データ構造 – immutableなデータ構造の構築に利用できる • 例えば・・・ – 配列を更新しても、前の配列は残しておかなけれ ばならない let a = some array … let b = a[0] <- 1 print b[0] ; => 1 print a[0] ; => 前の値
リスト • 最も単純な永続データ構造 • スタックとしても使える b a let a = [1, 2] let b = 9 : a ９ １ ２
配列(1) • Persistentでかつ読み書きともにO(1)でできる データ構造は（今のところは）ない • もっとも単純な実装 – 更新時に完全な複製を作る – 参照O(1) – 更新O(n) a 1 2 3 4 5 – 読み込み専用なら 現実的 b 1 2 9 4 5
配列(2) • 更新したところだけ覚えておく – 参照O(update) – 更新O(1) – 更新に比例するメモリが必要 – 更新回数に比べて参照回数が尐ない場合 a 1 2 3 4 5 b 2=>9
配列(3) • バランスツリーで保持 – 参照O(logn) – 更新O(logn) b a • Clojureでのimmutable array – 小さい配列のhackなど 9 1 2 3
キュー • 次の二つの操作をサポートするデータ構造 – push : データを挿入 – pop : データを挿入した順に取り出す • 両方O(1)でできる 6 5 4 3 2 1 push キュー pop
キュー実装 • リスト2個でキューを表す – 前半を表すリストと、後半を表すリスト • push – 後半を表すリストにデータ追加 • pop – 前半を表すリストからデータ取り出し – 前半のリストが空なら、後半のリストを反転して 前半のリストにする
キュー動作例 • 例 F F F F 1 2 R R 1 R 2 1 R push 1 push 2 pop F 2 F 2 …… R 3 R push 3 1
キュー計算量 • 計算量 – push • O(1) (リストの先頭にデータ付け加えるだけ) – pop • ワーストケース : O(n) • ならし(amortized)計算量： O(1) • ※ならし計算量 – 一回あたりの平均計算量
興味のある方は… • より詳しくは Purely Functional Data Structure (Chris Okasaki) を読まれるべし – 各種データ構造 – 遅延評価における計算量解析手法 – （全人類が読むべき書籍第2位だそうです）
並行（Concurrent）プログラミング • 複数の処理（タスク）を同時に動かすプログラム – e.g. マルチスレッド • CPUのシングルスレッド性能の頭打ち – フリーランチは終わった – （いいCPUを買って来れば勝手にプログラムが 速くなる時代は終わった） • これからの時代、否が応にも マルチスレッドプログラミングを しなければならない
並行プログラムは難しい • 「Javaのプログラムの殆どに並行処理のバグ があるので、プログラムが無事に動いていて もそれは”偶然”動くに過ぎない」 – “Java Concurrency in Practice” • なぜ難しいのか？ – バグが発生しそうな箇所が逐次プログラムよりも 多いから
スレッドセーフ • 複数のスレッドから呼び出される・アクセスさ れても大丈夫なこと • これを確保するのはとても難しい – 並行プログラムのバグは再現するのがとても難し い（タイミングがシビアなど）ケースも多い
スレッドセーフでない例 • 何の変哲もないカウンタ – 複数スレッドから同時に呼ばれると破綻 class Counter{ private int cnt=0; public int increment(){ return cnt++; } }
スレッドセーフでない例 • インクリメントはアトミック（不可分）ではない – 変数から読み込み – インクリメント – 変数へ書き込み • 競合状態（Race Condition） スレッドA 9+1=10 値9読み出し 書き込み 9+1=10 スレッドB 値9読み出し 書き込み ・同じ値が二度返る ・2回呼ばれたのにカウンタが1しか増えない
修正例 • ロックを取ってやる class Counter{ private int cnt=0; synchronized public int increment(){ return cnt++; } } – ※いつも簡単に直せるとは限らない
関数プログラミングと並行計算(1) • なんと！！immutableなオブジェクトは 必ずスレッドセーフになっている！ – 自明ですが… • immutableは最も強力な並行計算の 構成要素 – 参照透明を基本とし、immutableをよしとする 関数プログラミングはこの意味において 並行計算と相性が良い
関数プログラミングと並行計算（2） • immutableのみでは、スレッド間で通信ができ ない • 関数プログラムにおいても、尐なからず mutableの部分が必要 – そこにバグの入り込む余地がある
関数プログラミングと”並列”計算 • 並列(Parallel)計算⇔並行(Concurrent)計算 • 1つのタスクを複数のプロセッサを用いて高速 に実行する • 参照透明が利用できる – 式が常に同じ値に評価される – → いつ評価しても良い – → 並列に評価しても良い f x = g x + h x • 今回は並行の話 これら二つを、それぞれの定義に依らず、 いつでも自由に並列に評価して良い
排他制御 • 複数のプロセスがアクセスできる共有資源に 対し、同時アクセスされても整合性を保てるよ うにするための処理 • 複数のプロセスがアクセスするところには基 本的に排他制御が必要 – さっきのカウンタの例など • いろいろ方法がある
排他制御の方法 • ロック – 広く使われている、原始的な方法 – 共有資源にアクセスする際にロック・アンロック • メールボックス – Erlang, Scalaなどで利用される – 各プロセスがメッセージキューを持つ • トランザクショナルメモリ – Haskell, Clojureなどで利用される – メモリ操作をトランザクションとして実行
ロック • 最も基本的な並列プリミティブ – mutexとか、Critical Sectionとか – 大抵はOSが何らかの手段を用意している • ライブラリという形で利用 – C言語など • 言語使用に組み込み – Java(synchronized)など • 扱いが難しい
クリティカルセクション • プログラム中で、複数の処理が同時に実行さ れると異常をきたす箇所 – 同時に1つのスレッドしか実行してはいけない箇所 • クリティカルセクションへの進入時にロックを 獲得 private Hoge h; • 脱出時に開放 public void foo(){ synchronized(h){ // ロック獲得 … // クリティカルセクション } // ロック開放 }
ロックの問題点 • ロックの過剰 – 性能低下 • ロックの不足 – 競合状態（バグ） • ロックの間違い – デッドロック（バグ）
ロックの過剰 • 余計なメソッドにsynchronizedをつける、配列 を全体でロックするなど – 本来クリティカルセクションでない部分が 排他制御されてしまう – 性能の低下を招く • 細かくロックを制御しなければならない – ロックの粒度 （粗粒度→細粒度） – 配列全体→要素ごとにロックなど
ロックの不足 • ロックすべき箇所でロックをし忘れる • 競合状態を招く • バグになる – 再現しにくく、嫌なタイミングで 見計らったかのように発現する 最悪のバグになりがち
ロックの間違い • スレッド1ではオブジェクトA、Bの順でロック • スレッド2ではオブジェクトB、Aの順でロック – デッドロックする可能性 スレッド１ Aロック Bロック待ち スレッド２ Bロック Aロック待ち • 複数のオブジェクトをロックする場合、 ロックする順番を必ず守るようにする
ロックを正確に使うのはとても難しい • これらをすべて守らねばならない • 大規模アプリで、一箇所でも漏れがあっては ならない – カウンタの例のようなコードがあってはならない • しかし並行プログラムは… – テストが難しい（事前にバグを見つけるのが難しい） – バグの再現が難しい – バグを取るのが難しい – 三重苦
ロックの本質的問題 • ここまででも十分面倒なのだが… • ロックを用いたプログラムは自由に組み合わ せることができない、という問題がある • 組み合わせられない？
例：銀行アプリ • 預け入れ・引き出しができる銀行クラス – これだけだと何の問題もないけど… class Bank{ int balance; synchronized public void deposit(int amount){ balance += amount; } synchronized public boolean withdraw(int amount){ if (balance >= amount){ balance -= amount; return true; } return false; } }
例(2) • 銀行Aから銀行Bに送金したい public void send(Bank a, Bank b, int amount){ if (a->withdraw(amount)) b->deposit(amount); } • これはダメ – 送金はアトミックに行われる必要がある – aから引き出した瞬間の状態が他のスレッドに見 える可能性がある
例(3) • ロックを取ってみる public void send(Bank a, Bank b, int amount){ synchronized(a){ synchronized(b){ if (a->withdraw(amount)) b->deposit(amount); } } } • これでもダメ！ Bank a, b; – デッドロックするかも send(a, b); // thread-1 – bのロックは要らない場合も send(b, a); // thread-2
例(4) • 処理が必要とするロックをすべて確認して、 決まった順序でロックをとらなければならない public void send(Bank a, Bank b, int amount){ Bank la = a<b?a:b; Bank lb = a<b?b:a; synchronized(la){ synchronized(lb){ if (a->withdraw(amount)) b->deposit(amount); } } }
問題点 • あるメソッドが獲得するロックを知らなければ ならない • 呼び出し元でロックしなければならない – モジュラリティの崩壊 • 条件に応じてロックするオブジェクトが変わる 場合にうまく対処できない • これは、ロックが抱える本質的問題
トランザクショナルメモリ • 共有資源へのアクセスをトランザクションとし て表現する – トランザクションは“他に動作しているスレッドがな い”状況での動作と同じ動作をする保証がされる – （データベーストランザクションとの類似） • ソフトウェアのみで実現するものを特にソフト ウェアトランザクショナルメモリ（STM）と呼ぶ – （ハードウェアを利用する実装もある）
データベーストランザクションとの関連 • ACID（データベース）ACI（STM） – Atomicity • 中途半端に実行されることがない – Consistency • 整合性が保たれる – Isolation • 途中の状態が外から見えない – (Durability) • 永続性
例 class Bank{ int balance; public void deposit(int amount){ atomic{ balance += amount; } } public bool withdraw(int amount){ atomic{ if (balance >= amount){ balance -= amount; return true; } return false; } } } ※擬似的なコードです
説明 • atomic – 中の処理をトランザクションとして実行 – メモリの操作がACIを満たす • 実装方法例 – とりあえず並行に実行する • メモリへの書き込みはスレッドローカルに保持 – 最後まで実行したら、書き込みを試みる • 競合してたらロールバック(最初から再度実行し直し) • 競合していなかったらコミット
STMの利点 • デッドロックしない – そもそもロックしないので • 粒度の制御がいらない – 処理系が勝手にやる • 自由に組み合わせが可能 – 一番大きな利点
STMの組み合わせ • 自由に組み合わせが可能 – atomicで囲うだけ – メモリ操作がトランザクションとして実行されるだ けなので public void send(Bank a, Bank b, int amount){ atomic{ if (a->withdraw(amount)) b->deposit(amount); } }
Clojureでの例 • プログラムの大部分はimmutable • 値の更新は次のいずれか – スレッドローカル変数 – STM経由 • スレッドセーフで、デッドロックフリーなコード しか書けない – 先に挙げたロックの問題点をほぼ解消
STMの欠点 • ロールバックがいつ起こるかわからないので、 パフォーマンスの予測がしづらい • 極めて慎重に書かれたロックプログラムより 性能的には劣る • トランザクション中にIOなどしてはいけない – 再実行される可能性があるので
STMとIOの取り扱い • トランザクション中にIOをやらないのは プログラマの努力目標 – Clojureとか – やったら実行時にバグる • 型システムでトランザクション中にIOがないこ とを保証 – Haskell – やったらコンパイラに怒られる
まとめ • …と、いうわけで • 関数プログラミングのお話をしました • 三行まとめ – コードがすっきり – バグに悩まされない – 並行プログラミングと相性がいい • ご清聴ありがとうございました

More Related Content

関数プログラミング入門