algorithmに関するnobu-qのブックマーク (17)
-
nobu-q 2010/03/19
-
Data Compression Programs
Data Compression Programs by Matt Mahoney As of July 23, 2009, this page is no longer maintained. The newest version can be found at http://mattmahoney.net/dc/ All software on this page is open source licensed under GPL and believed to be unencumbered by patents. All downloads include Windows executables and C++ source code for Windows or Linux/UNIX. The source code comments explain how the prog
-
-
-
SR-Tree
SR-Tree (Sphere/Rectangle-Tree) [ Japanese / English ] 概要 発表文献 ライブラリ <2002/09/14> ビデオ <1998/11/18> オンラインデモ 関連研究 概要 SR-Tree とは？ SR-Tree は高次元点データに対する最近接検索を高速化するためのインデッ クス構造です。 用途は？ 特徴ベクトルに対する類似検索が代表例です。画像データに対する内容検索の 実現法として、特徴ベクトルを類似検索する方法が広く使われていますが [FSN+95,WKS+96]、そ の際に必要となる高次元空間での最近接検索を高速化できます。 特徴は？ 最近接検索の高速化法としては、R*-tree [BKS+90] を用いる方法や SS-tree [WJ96] を用いる方法が提案 されていますが、SR-tree はこれらよりも更に高速です。
-
MapReduce on Tyrant - mixi engineer blog
先日、隅田川の屋形船で花見と洒落込んだのですが、その日はまだ一分咲きも行ってなくて悲しい思いをしたmikioです。今回はTokyo Tyrant（TT）に格納したデータを対象としてMapReduceのモデルに基づく計算をする方法について述べます。 MapReduceとは Googleが使っているという分散処理の計算モデルおよびその実装のことだそうですが、詳しいことはググってください。Googleによる出自の論文やApacheプロジェクトによるHadoopなどのオープンソース実装にあたるのもよいでしょう（私は両者とも詳しく見ていませんが）。 今回の趣旨は、CouchDBがMapReduceと称してJavaScriptで実現しているデータ集計方法をTTとTCとLuaでやってみようじゃないかということです。簡単に言えば、以下の処理を実装します。 ユーザから計算開始が指示されると、TTは、DB内の
-
References on Nearest Neighbors and Similarity Search
The Homepage of Nearest Neighbors and Similarity Search Maintained by Yury Lifshits Update: this page is frozen. Please visit the successor page by Arnoldo Muller I am now trying to sort all papers by topic. This work is in progress. Please email me all papers I missed so far. Subareas: Nearest neighbors in general metric space Branch and bound for Euclidean space Mapping-based techniques: localit
-
UB-tree - Wikipedia
The UB-tree as proposed by Rudolf Bayer and Volker Markl is a balanced tree for storing and efficiently retrieving multidimensional data. It is basically a B+ tree (information only in the leaves) with records stored according to Z-order, also called Morton order. Z-order is simply calculated by bitwise interlacing the keys. Insertion, deletion, and point query are done as with ordinary B+ trees.
-
-
Aho Corasick 法 - naoyaのはてなダイアリー
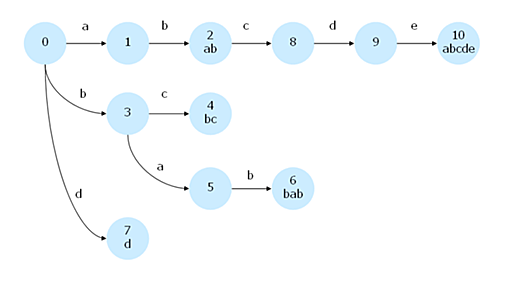
適当な単語群を含む辞書があったとします。「京都の高倉二条に美味しいつけ麺のお店がある」*1という文章が入力として与えられたとき、この文章中に含まれる辞書中のキーワードを抽出したい、ということがあります。例えば辞書に「京都」「高倉二条」「つけ麺」「店」という単語が含まれていた場合には、これらの単語(と出現位置)が入力に対しての出力になります。 この類の処理は、任意の開始位置から部分一致する辞書中のキーワードをすべて取り出す処理、ということで「共通接頭辞検索 (Common Prefix Search)」などと呼ばれるそうです。形態素解析、Wikipedia やはてなキーワードのキーワードリンク処理などが代表的な応用例です。 Aho Corasick 法 任意のテキストから辞書に含まれるキーワードをすべて抽出するという処理の実現方法は色々とあります。Aho Corasick 法はその方法のひと
-
スペル修正プログラムはどう書くか
Peter Norvig / 青木靖 訳 先週、2人の友人(ディーンとビル)がそれぞれ別個にGoogleが極めて早く正確にスペル修正できるのには驚くばかりだと私に言った。たとえば speling のような語でGoogleを検索すると、0.1秒くらいで答えが返ってきて、もしかして: spelling じゃないかと言ってくる(YahooやMicrosoftのものにも同様の機能がある)。ディーンとビルが高い実績を持ったエンジニアであり数学者であることを思えば、スペル修正のような統計的言語処理についてもっと知っていて良さそうなものなのにと私は驚いた。しかし彼らは知らなかった。よく考えてみれば、 別に彼らが知っているべき理由はないのだった。 間違っていたのは彼らの知識ではなく、私の仮定の方だ。 このことについてちゃんとした説明を書いておけば、彼らばかりでなく多くの人に有益かもしれない。Googleの
-
An Implementation of Double-Array Trie
Contents What is Trie? What Does It Take to Implement a Trie? Tripple-Array Trie Double-Array Trie Suffix Compression Key Insertion Key Deletion Double-Array Pool Allocation An Implementation Download Other Implementations References What is Trie? Trie is a kind of digital search tree. (See [Knuth1972] for the detail of digital search tree.) [Fredkin1960] introduced the trie terminology, which is
-
大規模データ処理のための行列の低ランク近似 -- SVD から用例ベースの行列分解まで -- - 武蔵野日記
id:naoya さんのLatent Semantic Indexing の記事に触発されて、ここ1週間ほどちょくちょく見ている行列の近似計算手法について書いてみる。ここでやりたいのは単語-文書行列(どの単語がどの文書に出てきたかの共起行列)や購入者-アイテム行列(どの人がどの本を買ったかとか、推薦エンジンで使う行列)、ページ-リンク行列(どのページからどのページにリンクが出ているか、もしくはリンクをもらっているか。PageRank などページのランキングの計算に使う)、といったような行列を計算するとき、大規模行列だと計算量・記憶スペースともに膨大なので、事前にある程度計算しておけるのであれば、できるだけ小さくしておきたい(そして可能ならば精度も上げたい)、という手法である。 行列の圧縮には元の行列を A (m行n列)とすると A = USV^T というように3つに分解することが多いが、も
-
-
最長片道きっぷの経路を求める
最長片道きっぷの経路を求める Index & Overview あらまし この文書は、ＪＲの最長片道きっぷの経路を、 整数計画法と全探索の２つの方法で求めた過程をまとめたものです。 前者では厳密に、後者ではややイイカゲンに、その経路を求めることに成功し、 ２つの方法で求めた経路は一致しました。 トピックス NHK の紀行番組「列島縦断 鉄道12000kmの旅」をきっかけにこの Web ページを探し当てた方は、まず「付録２（2004年３月版）」をご覧ください。 現状の最長片道きっぷの経路や、ありそうな質問をまとめてあります。 ふと思い立って、2006年５月版の最長片道きっぷ経路図（PDF 形式、35,414 bytes）を作りました。 2004年３月版の地図との相違点はただ１点、 「富山港線を削除した」ことです（2006年２月28日廃止）。 もともと最長経路に含まれていなかった路線が廃止にな
-
Winter School on Graphs and Algorithms, RIMS 2008
Lecturers (>> Abstracts) Bojan Mohar (Simon Fraser University, Canada ) Coloring-flow Duality for Graphs on Surfaces Finding Shortest Cycles with Restricted Homotopy Bruce Reed (McGill University, Canada), Algorithms for Minor Containment (Two sessions) Robin Thomas (Georgia Institute of Technology, USA) Pfaffian Orientations of Graphs (Two sessions) Carsten Thomassen (Technical University
-
-
1
Algorithmic graph theory book 0.3 released公式Twitter
- @HatenaBookmark
リリース、障害情報などのサービスのお知らせ
- @hatebu
最新の人気エントリーの配信
キーボードショートカット一覧
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
