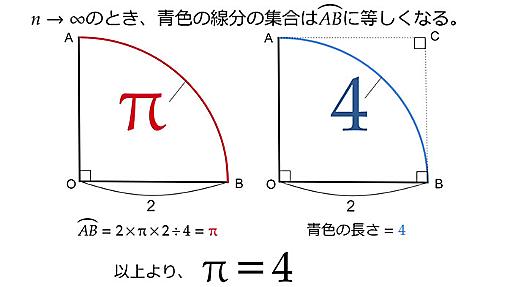
文章で人にアイディアを伝えるのって難しいんですね。 めげずにやっていきたい。 別の書き方で 2/3 派に反論していきたい。 まず問題と 2/3 派の模範解答を再掲する。 問題 2人きょうだいの子供のうち、1人が男の子の場合、もう1人が女の子である確率はいくらか? 解答 すべてのパターンはこう。 j k l m older older older older 男 男 女 女 男 女 男 女 younger younger younger younger *1 問題の条件からどちらも女性のペアである m は除外できる。 全パターンは j と k と l の3パターン。 そのうちもう一人が女の子のパターンは k と l の2パターン。 ゆえに 2/3 。 ここから反論 この問題を見て素直に表を書くならこうだろう。 g h i 男 男 女 男 女 女 *2 表(2)は、表(1)の中の h(男, 女