A Geometric Perspective on Structured Light Coding

Abstract

We present a mathematical framework for analysis and design of high-performance structured light (SL) coding schemes. Using this framework, we design Hamiltonian SL coding, a novel family of SL coding schemes that can recover 3D shape with high precision, with only a small number (as few as three) of images. We establish structural similarity between popular discrete (binary) SL coding methods, and Hamiltonian coding, which is a continuous coding approach. Based on this similarity, and by leveraging design principles from several different SL coding families, we propose a general recipe for designing Hamiltonian coding patterns with specific desirable properties, such as patterns with high spatial frequencies for dealing with global illumination. We perform several experiments to evaluate the proposed approach, and demonstrate that Hamiltonian coding based SL approaches outperform existing methods in challenging scenarios, including scenes with dark albedos, strong ambient light, and interreflections.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Structured light (SL) is a widely used 3D imaging technique in several applications, including industrial automation, augmented reality, and robot navigation. Laser scanning [9] based SL systems can recover 3D shape with extreme precision (10–100 $\upmu$m), albeit at the cost of a large acquisition time. Applications such as industrial inspection require high precision, but with a limited acquisition time budget. While single-shot SL approaches [33] can recover depths with only a single image, the depths are spatially smoothed, resulting in loss of detail. Multi-pattern SL approaches project a series of patterns so that each projector pixel is assigned a unique temporal intensity code. These codes are used to establish per-pixel correspondence for each camera pixel, thereby achieving high spatial resolution. However, unfortunately, their depth precision in demanding scenarios (small time budget, low signal-to-noise ratio) remains low, and is often the bottleneck in widespread adoption of SL 3D imaging in key applications.

The depth precision of a multi-pattern SL system is determined by the coding scheme, i.e., the set of patterns that the light source projects. The problem of designing optimal patterns that achieve high depth precision was first formulated by Horn and Kiryati [18]. However, finding a closed form (or even a numerical) solution was considered infeasible. Instead, a family of patterns based on intuitions from digital communications literature was proposed. These patterns, designed using Hilbert space filling curves, belonged to the class of discrete coding schemes (intensities of the patterns are from a discrete set). While these patterns perform well in high signal-to-noise ratio (SNR) settings, their performance degrades as noise increases. In general, designing optimal SL patterns, especially for low SNR scenarios, as well as developing formal tools for analyzing the performance of different methods, remains an open problem.

In this paper, we propose a theoretical framework for analysis and design of novel, high-performance SL coding methods. We consider continuous coding, which achieves sub-pixel correspondence mapping, and require fewer images as compared to discrete coding approaches [18, 20]. We analyze the geometry of SL coding (image formation) and decoding to derive a general performance metric of SL coding schemes. While this metric can be used to predict the performance of a given scheme, it is expensive to compute, and thus, unsuitable as an objective function in code optimization. We take inspiration from recent work in time-of-flight code design [15], and derive a surrogate metric based on first order differential analysis of the image formation equation. The surrogate is easy to compute, and lends itself to an intuitive geometric interpretation.

Based on this metric, we propose a new family of SL codes, called Hamiltonian patterns. Hamiltonian coding achieves up to an order of magnitude higher precision as compared to existing approaches, especially in low SNR scenarios, while requiring a small number of images (as few as three).¹ Despite being a continuous coding scheme, the construction of Hamiltonian patterns shares structural similarities with that of the widely used binary Gray coding [20]. Our key observation is that, due to this similarity, the techniques developed for Gray coding can be easily adapted to design Hamiltonian patterns. By drawing upon design principles for Gray codes [13], we develop Hamiltonian patterns with desired properties, for example, high frequency patterns that are robust to a broad range of global illumination.

Practical implications: Conceptually, Hamiltonian coding forms a bridge between binary and continuous SL coding approaches. This provides a general recipe for design of high-performance SL patterns, even in challenging scenarios with low SNR and global illumination. We evaluate the performance of the proposed coding approaches on challenging scenes with low albedo, interreflections and scattering. Our results demonstrate that Hamiltonian codes outperform several conventional approaches, as well as recent coding schemes specifically designed for dealing with global illumination [14]. Due to the SNR benefits, and a single, universal, design and decoding algorithm, Hamiltonian patterns could become an alternate building-block (instead of sinusoid functions) in continuous SL based 3D imaging systems.

Fig. 1.

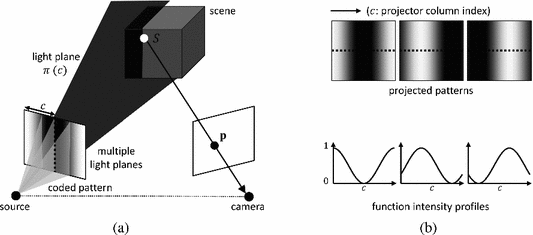
Structured light (SL) 3D imaging. (a) A continuous SL coding system consists of a projector that projects patterns with a continuous range of intensities. A unique intensity code is assigned to every projector column, which is used to determine correspondence with camera pixels. (b) In sinusoid phase-shifting, the projected patterns have sinusoid intensity profiles.

2 Related Work

Structured light coding design: Several different structured light coding strategies have been proposed over the last three decades. These include binary Gray coded patterns [20], color coding [1], ramp coding [2], sinusoid coding [35], trapezoid coding [19], and edge coding [38]. For a comprehensive survey on structured light code design, please see [34]. Surprisingly, there is little work on analyzing the relative performance of different coding schemes. Horn et al. [18] considered the problem of designing optimal structured light patterns for discrete coding schemes, where the intensity of each projected column can take a discrete number of intensity values. In contrast, our goal is to develop a theoretical framework for design and analysis of continuous coding schemes, where the projected intensities can emit a continuous range of values.

Structured light in the presence of global illumination: Several SL techniques have been proposed for mitigating errors due to interreflections and scattering. These can be broadly categorized into two classes: (a) Optical approaches, such as those based on polarization [7] and epipolar scanning [27], which require specialized hardware, and (b) Pattern coding approaches which involve designing patterns that are robust to global illumination. These include discrete binary patterns [13, 39], or continuous sinusoid patterns [6, 8, 14, 25]. We propose a general family of continuous patterns that outperform existing coding strategies for dealing with global illumination, without requiring additional hardware. Note that the proposed coding schemes are orthogonal to, and can be used in a complementary manner with, the optical approaches [27].

3 Image Formation Model

A SL system consists of a projector and a camera, as shown in Fig. 1 (a). The projector projects one or more intensity patterns on the scene. For each pattern, the camera captures an image. Single-shot methods [29, 30, 33, 37] need only a single image, but assume that scene depths are locally smooth, resulting in loss of fine geometric details. In this paper, we consider multi-shot methods where several patterns are projected, and depths are computed on a per-pixel basis. Most multi-shot structured light systems use patterns which can be expressed as a 1D coding function, so that all the pixels within each column (or row) have the same intensity. The projector can be modeled as emitting several light planes, one from each column, as shown in Fig. 1 (a). In order to compute depth at a camera pixel, we need to determine its corresponding light plane (the light plane that illuminates the scene point imaged at the pixel). This is achieved by assigning a unique intensity code to every column; the length of the code is the number of projected patterns. For instance, the intensity code could be binary [28] or N-ary [3, 18] where each columns could have 2, or N discrete intensity values.

Binary and K-ary coding belong to the class of discrete coding methods, where the coding function takes only discrete values. These methods assume that the light source emits a discrete set of light planes. The number of possible depth values at a camera pixel is bounded by the number of light planes. Thus, the depth resolution achieved by a discrete coding method is limited. Our focus is on continuous coding methods, where the coding functions are continuous and piece-wise differentiable functions. For example, sinusoid phase-shifting [35], one of the most widely used structured light techniques, is a continuous coding method in which the 1D coding functions are sinusoids (Fig. 1 (b)). Due to a continuum of light planes, continuous techniques are capable of achieving significantly higher depth resolution as compared to discrete methods².

Let the number of projected patterns (and captured images) be K. Each projected pattern is represented by a 1D coding function $P_i (c), \,\, 1 \le i \le K$, where $c \left( 1 \le c \le N_c\right)$ is the projector column index, and $N_c$ is the total number of columns in the projector. The functions are assumed to be normalized so that $0 \le P_i (c) \le 1$. Consider a scene point S that is illuminated by column number c and imaged at camera pixel $\mathbf {p}$. The intensities received at $\mathbf {p}$ are given by:

$$\begin{aligned} I_i (\mathbf {p}) = \alpha (\mathbf {p}, c) P_i (c) + A (\mathbf {p})\,, \end{aligned}$$

(1)

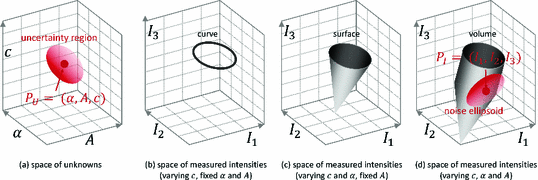
where $\alpha (\mathbf {p}, c)$ is albedo term; it is defined as the image brightness received at $\mathbf {p}$ if column c emits unit intensity. $A (\mathbf {p})$ is the ambient illumination term; it is the image brightness at $\mathbf {p}$ due to light sources other than the projector. In general, both $\alpha (\mathbf {p}, c)$ and $A (\mathbf {p})$ are unknown, along with the column correspondence c. Thus, the space of unknowns can be represented as a 3D space, as shown in Fig. 2 (a).

Fig. 2.

Geometry of Structured Light Patterns. A structured light coding scheme can be modeled as a mapping from (a) the space of unknowns to (b, c, d) the space of measured intensities. Given an intensity measurement, projector correspondence is estimated via an inverse mapping (decoding function) from the measurement space to the unknown space. (d) Noise in the measurement space leads to uncertainty in the recovered unknowns, resulting in low depth resolution

4 Geometry of Structured Light Coding

What is the space of measured intensities for a structured light coding scheme? A structured light coding scheme, defined by the coding functions $[P_1, \ldots , P_K]$, maps a point $P_U = [\alpha , A, c]$ in the unknown space to a point $P_I = [I_1, \ldots , I_K]$ in the K-dimensional space of measured intensities. For example, consider the 1D set of unknown points, for fixed values of $\alpha$ and A, but varying correspondence c. Sinusoid coding scheme for $K=3$ maps this set of unknown points to a 1D set of points which form a circle in the measurement space. This is illustrated in Fig. 2 (b). A 2D set of unknowns where both c and $\alpha$ are varied are mapped to a 2D set of points forming a hollow cone (Fig. 2 (c)). The entire 3D set of unknowns is mapped to a 3D volume of points, formed by extruding the cone along a line segment, as shown in Fig. 2 (d).

Given a camera pixel, let $I_i$ be the true intensity measurement for pattern $P_i$. The actual measured intensity $I'_i$, including noise, is given as:

$$\begin{aligned} \widehat{I_i} = I_i + \nu _i \,, \end{aligned}$$

(2)

where $\nu _i$ is the noise in the intensity measurement $I_i$, including both read noise and photon noise [17]. Note that the point $P_{I'} = [I'_1, \ldots , I'_K ]$ representing the vector of actual measured intensities may lie outside the space of possible true intensities.

4.1 Decoding and Effect of Noise

Given the actual intensities $P_{I'} = [I'_1, \ldots , I'_K ]$ measured at a camera pixel, projector correspondence is computed by a decoding function, which is an inverse mapping from the measurement space to the unknown space. Due to the randomness associated with the measurements $P_{I'}$, the decoded unknown point is a random variable, whose distribution is denoted with an uncertainty region, as shown in Fig. 2 (a) ³. Due to this uncertainty, the decoding algorithm may compute an inaccurate correspondence $c'$. This uncertainty places fundamental limits on the achievable depth resolution.

Let the error in the computed correspondence be $\triangle {c} = |c' - c|$. Given a coding scheme and a decoding function, the expected correspondence error $\mathbb {E}(\triangle {c})$, averaged over the entire space of unknowns, is given as:

(3)

where $c'$ and c are the estimated and true projector correspondence values for measured intensities $P_{I'}$. $p\left( P_{I'}\right) \sim \mathcal {N} \left( P_{I}, \varSigma \right)$ is the Gaussian probability distribution function (illustrated as noise ellipsoid in Fig. 2 (d)) of $P_{I'}$, with the true intensity point $P_I$ as the mean, and noise covariance $\varSigma _{I}$. The double integral is taken over the unknown space and the measurement space.

Fig. 3.

Coding curves of various structured light coding methods. (a) Coding functions (1 out of 3) for different SL coding schemes. (b) Coding curves and curve lengths for $K=3$.

4.2 Optimizing Structured Light Coding

Since depth error is proportional to correspondence error, the optimal structured light coding scheme can be defined as the one that minimizes the expected correspondence error $\mathbb {E}(\triangle {c})$, as derived in Eq. 3. Unfortunately, $\mathbb {E}(\triangle {c})$ is difficult to optimize analytically, and expensive to even compute numerically. The optimization must be performed in the high-dimensional space of coding functions, making it further intractable.

In order to perform the optimization, we propose a surrogate objective function based on a first order differential analysis of the image formation equation (Eq. 1). This metric is inspired by recent work in coding design for time-of-flight (ToF) imaging [15], where a similar analysis was performed in the temporal domain. The surrogate metric is defined in terms of the coding curve, which is a geometric representation of a structured light coding scheme. Specifically, consider a structured light coding scheme represented by patterns $P_i, \, 1 \le i \le K$. The coding curve for this scheme is the set of points $\left[ P_1 (c), \ldots , P_K (c) \right]$ in the K-dimensional space, as the projector column index c is varied. For example, the coding curve of sinusoid coding is a circle in K-dimensional space, as shown in Fig. 3 (b). Given a coding scheme, let $\varLambda$ be the length of the corresponding coding curve. Then, the surrogate metric $\varUpsilon$ is given as:

$$\begin{aligned} \varUpsilon \propto \frac{ \varsigma }{\alpha _{mean} \,\, \varLambda }\,, \end{aligned}$$

(4)

where $\varsigma$ is the standard deviation of measurement noise, and $\alpha _{mean}$ is the mean $\alpha$ over the space of unknowns. See supplementary technical report for a derivation.

Intuitively, a longer coding curve spreads the measurement points further apart in the measurement space, resulting in lower decoding errors due to noise. A similar intuition, inspired by design of communication codes, was used in [18] for design of discrete structured light patterns. Equation 4 formalizes this intuition, and provides an approximate, but analytical expression for the performance of a SL coding scheme in terms of its coding curve length. Given a structured light coding scheme, its coding curve length $\varLambda$ is an intuitive and fast to compute geometric property. Furthermore, given system dependent constant $\varsigma$, and a mean scene albedo $\alpha _{mean}$, $\varUpsilon$ is, in general, approximately proportional to the expected correspondence error $\mathbb {E}(\triangle {c})$ (an exception is if the coding curve is not distance preserving, as discussed in the next section). This suggests that the coding curve length $\varLambda$ can be used as an approximate metric for designing high-performance structured light coding methods: larger the coding curve length, lower the expected correspondence error, and hence, higher the expected depth resolution.

The coding curves of some of the commonly used structured light coding schemes (ramp [2], sinusoid [35], triangle [5]) are shown in Fig. 3. For example, the coding curve of the ramp coding scheme [2] (the three projected patterns are a constant 1, a constant 0, and an intensity ramp) is a line segment of length 1, whereas the coding curve of the widely used sinusoid coding [35] is a circle of radius $\frac{\sqrt{K}}{2 \sqrt{2}}$, where $K \ge 3$ is the number of phase-shifts (number of measurements). For $K=3$, the coding curve length of sinusoid coding is ${\approx }3.84$ times that of ramp coding. Thus, given the same scene and imaging system, sinusoid coding should achieve approximately 3.84 times high precision (lower error) as compared to ramp coding, as shown later in Sect. 7.

5 Hamiltonian Coded Structured Light

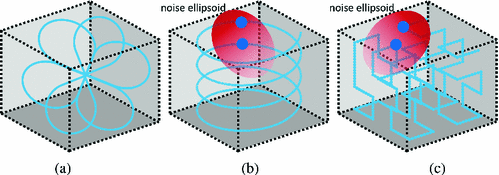
As described in the previous section, structured light coding schemes with long coding curves can achieve high depth resolution. Can we use this design principle to design high performance structured light coding schemes? Figure 4 shows three potential coding curves. The first curve is long, but self-intersecting. Therefore, it does not define a unique mapping from projector correspondences to captured intensities, and thus, does not represent a valid coding scheme. The second and third curves (a helix, and a Hilbert-space filling curve [18]), are long, and non self-intersecting. However, these curves are not distance preserving, i.e., there are points on the curve that are distant along the curve, but close in the Euclidean distance sense. While coding schemes based on these curves can achieve high performance in low noise settings, their performance can deteriorate rapidly for moderate to high amounts of noise, resulting in large decoding errors.

Fig. 4.

Examples of long but low-performance coding curves. (a) A self-intersecting coding curve does not define a unique mapping from projector correspondences to intensities, and does not represent a valid coding scheme. (b-c) A helix, and a Hilbert-space filling curve. These curves are not distance preserving, and may result in large errors even for small noise.

Thus, we aim to design coding curves that, in addition to being long, are non self-intersecting and distance preserving. One family of curves with these properties is Hamiltonian cycles on hypercube graphs, formed by the vertices and edges of the K-dimensional unit hypercube [15]. A Hamiltonian cycle on the hypercube graph is a path that visits all the vertices of the cube exactly once.

5.1 Designing Hamiltonian SL Patterns

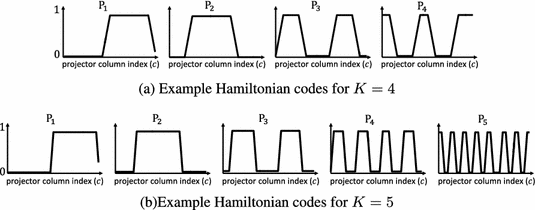
The coding curve is a geometric representation of the SL patterns; there is a one-to-one correspondence between a set of SL coding functions, and a coding curve. Given a coding curve in K dimensions, we can create the corresponding set of K SL coding functions, and vice versa. Consider a Hamiltonian cycle on the K-dimensional unit cube as the coding curve. Then, the $i^{th}$ coding function $P_i$ for the Hamiltonian coding scheme is defined as the set of value of the $i^{th}$ coordinate of points on the Hamiltonian cycle. The resulting Hamiltonian coding functions are trapezoidal-shaped, as shown in Fig. 3, top-right. For $K=3$, the three trapezoidal functions are evenly shifted copies of each other. Incidentally, three phase-shifted trapezoidal functions have been proposed in previous work [19, 38], and can be considered a special case of the family of Hamiltonian coding schemes. In contrast, higher order Hamiltonian coding functions ($K>3$) are not necessarily shifted versions of each other, as illustrated in Fig. 5.

Coding curve length: While constructing the Hamiltonian cycle, we exclude the origin and the diagonally opposite vertex. This is done so that for every projector column c, at least one (out of K) projected value is 0, and at least one projected value is 1. Finding a Hamiltonian cycle on this reduced set of vertices is an NP-complete problem, with no known polynomial time algorithms. Fortunately, for relatively small K, it is possible to find cycles using search-based algorithms. The length of the cycle is $2^K - 2$, if K is odd, and $2^K - 4$, if K is even [15]. Since the length of the curve increases exponentially with K, it can be more than an order of magnitude longer than the curve of sinusoid coding, whose length increases only as $\sqrt{K}$ (Fig. 3). Furthermore, Hamiltonian cycles have good locality preserving properties [10], i.e., given any two points on the curve, the ratio between their Euclidean distance and distance along the curve is bounded.

5.2 Depth Recovery Algorithm for Hamiltonian Coding

The coding functions $P_i \,\, \left( 1 \le i \le K \right)$ for Hamiltonian SL coding can be sub-divided into $2^K-2$ (or $2^K-4$) sub-intervals. In each sub-interval, one (out of K) function increases (or decreases) linearly from 0 to 1 (1 to 0). The remaining $K-1$ functions are constant 0 or 1. Let the sub-intervals be indexed by $\lambda , \,\, 1 \le \lambda \le K-2 \,\, (\text {or} \,\, K-4)$. Given a set of measured intensities $I = [I_1, I_2, \ldots , I_K]$, the decoding algorithm, i.e., finding the projector correspondence c, involves two steps:

1. Estimating the index $\lambda$ of the sub-interval thatclies in: The key observation is that for each sub-interval, the identities (indices) and values of the $K-1$ coding functions that are constant within the sub-interval, are unique. Therefore, $\lambda$ can be computed by identifying the indices and values of the measured intensities that correspond to the $K-1$ constant functions. This is achieved by clustering the K measured intensities (at every pixel) into three clusters: one cluster corresponds to the coding functions being 0 (low intensities), one cluster corresponds to the coding functions being 1 (high intensities), and the third cluster corresponds to the linearly increasing (or decreasing) function (median intensity).⁴ These clusters give the identities and the values of the intensity measurements corresponding to the $K-1$ constant functions.

2. Estimating the correspondence c within the sub-interval: The second step is to determine the location of the correspondence c within the sub-interval $\lambda$. Consider the set of projected intensities $\mathbf {P} (c) = [P_1 (c), P_2 (c), \ldots , P_K (c)]$ for the projector column c. As discussed above, the correspondence c lies in a sub-interval of the coding functions, which corresponds to an edge of the Hamiltonian cycle. Suppose the edge is between cube vertices $\mathbf {P_{left}}$ and $\mathbf {P_{right}}$. Then, the coding curve point $\mathbf {P_c}$ is given as a linear combination of $\mathbf {P_{left}}$ and $\mathbf {P_{right}}$: $\mathbf {P} (c) = \kappa \mathbf {P_{left}} + (1 - \kappa ) \mathbf {P_{right}}$, where $0 \le \kappa \le 1$ is the location of the correspondence c within the sub-interval $\lambda$.

Let $\mathbf {I_{low}}$ be the set of intensities in the cluster corresponding to low intensities, as discussed above in Step 1. Let the mean of these intensities be $I_{min} = mean (\mathbf {I_{low}})$. Similarly, let the mean of the intensities in the high intensities cluster be $I_{max} = mean (\mathbf {I_{high}})$. Then, the sub-interval location $\kappa$ is given as: $\frac{I - I_{min}}{I_{max} - I_{min}}$, where $I = [I_1, I_2, \ldots , I_K]$ is the set of measured intensities. Then, the sub-interval index $\lambda$ and the location within the sub-interval $\kappa$ can be used to determine the correspondence c.

Fig. 5.

Higher order Hamiltonian patterns ($K>3$) are not shifted versions of each other. In contrast, Hamiltonian patterns for $K=3$ (Fig. 3) are shifted versions of each other

6 Dealing with Global Illumination and Defocus

The image formation model considered in Eq. 1 assumes that scene points are illuminated only directly by the projector, so that each camera pixel receives light only from a single projector column. But, in general, scene points may receive light from other scene points as well, due to interreflections and scattering. Such effects, collectively called indirect or global illumination, can lead to significant errors in the recovered shape [14, 26]. One strategy to achieve robustness to global illumination is to design coding methods which use patterns with only high spatial frequencies [6, 8, 13, 14, 25]. However, the Hamiltonian patterns designed in the previous section have a combination of high and low frequencies, as shown in Fig. 5. Can we design Hamiltonian patterns with only high spatial frequencies? We propose two approaches for developing high frequency Hamiltonian patterns, based on design principles used in discrete Gray coding and continuous sinusoid coding.

6.1 Designing High-Frequency Hamiltonian Patterns Using Gray Codes

A Hamiltonian cycle corresponds to the order in which the hypercube vertices are visited. Our key observation is that for $K>3$, the Hamiltonian cycle on a hypercube graph is not unique (modulo isomorphic cycles). For $K>3$, there exists multiple (exponential in K) orderings of the vertices of the hypercubes, corresponding to different Hamiltonian cycles. Each cycle corresponds to a different set of pattern coding functions. For example, Fig. 6 (top two rows) shows two different sets of Hamiltonian patterns for $K=8$. The second key observation is that different coding functions have different properties in terms of the set of constituent spatial frequencies. For instance, in the first set (top row), different patterns have a broad range of spatial frequencies (from low to high). On the other hand, in the second set of patterns (second row), all the patterns have relatively high, and similar frequencies.

Relationship between Hamiltonian functions and Gray codes: Gray codes [11] are a sequence of binary codes so that consecutive codes differ only in 1 bit. A K-bit Gray code sequence can be constructed by traversing the vertices of a K-D hypercube along a Hamiltonian cycle. Each cube vertex is assigned a binary code, given by its coordinates. For example, origin is assigned a binary code $[0,\ldots ,0]$. The Gray code sequence is then given by the sequence in which the cube vertices are visited. Therefore, a Hamiltonian cycle on a hypercube graph induces both a Gray codes sequence, as well as a set of Hamiltonian functions: the Hamiltonian functions can be considered as the continuous versions of the binary Gray codes. Different Hamiltonian cycles induce Gray codes and Hamiltonian functions with different characteristics. For instance, the Hamiltonian patterns shown in Fig. 6 (a) are designed based on conventional, reflected Gray codes [20, 31]. These codes have a broad range of frequencies (including low frequencies) and are unsuitable for dealing with global illumination.

In order to scan scenes with global illumination, Gray codes with only high spatial frequencies have been proposed [13]. We leverage the one-to-one relationship between a Gray code sequence and Hamiltonian functions to design Hamiltonian patterns with high frequencies. Figure 6 (middle row) shows Hamiltonian patterns using a sequence of antipodal Gray codes [4, 21, 22], which have the property that the binary complement of a string appears a fixed distance from it in the ordering. Antipodal Gray codes, and the corresponding Hamiltonian functions have a narrow set of high frequencies, thus resulting in robustness to global illumination effects. Note that the Hamiltonian patterns may appear binary at first glance; please zoom in to the images to observe the continuous intensity gradations near the edges.

6.2 Micro Hamiltonian Coding

In addition to binary coding, continuous coding schemes based on sinusoid patterns [6, 14, 25] have been proposed for dealing with global illumination. For example, the micro phase shifting approach [14] uses sinusoid patterns with frequencies within a narrow, high-frequency band. Phase unwrapping is performed by combining phase information from several high-frequencies. We leverage this principle to design a family of high-frequency Hamiltonian coding schemes. The key idea is to use multiple sets of Hamiltonian functions, with small, co-prime periods (high frequencies). We call this approach micro Hamiltonian coding, due to the use of small (micro) periods for every pattern. For example, Fig. 6 (c) shows a micro Hamiltonian coding scheme with $K=8$ patterns created by combining two sets of Hamiltonian patterns: K3 and K5 Hamiltonian codes (Figs. 3 (right), and 5 (b)), with periods 203 pixels and 97 pixels, respectively. The number of projector columns is $N_c = 1920$. While each set recovers the correspondence modulo its respective period, the ambiguous correspondences can be combined via phase-unwrapping techniques [14, 16] to recover unambiguous depths.

Fig. 6.

Hamiltonian patterns for dealing with global illumination and defocus. (a) Hamiltonian patterns for $K=8$ based on the reflected Gray codes. These patterns have a broad range of frequencies (including low frequencies) and are unsuitable for dealing with global illumination. (b) Hamiltonian patterns based on antipodal Gray codes. (c) Micro Hamiltonian coding created by combining K3 and K5 Hamiltonian patterns, with small periods. Patterns in (b) and (c) have high frequencies, and are robust to a range of global illumination effects. (color figure online)

Design space of micro Hamiltonian coding: Micro Hamiltonian coding offers a rich design space, and enables a fine control of the properties (e.g., spatial frequencies) of the projected patterns. Several base Hamiltonian pattern sets, with different periods, can be combined into a single micro Hamiltonian coding scheme. For instance, a micro Hamiltonian scheme with $K=8$ patterns can be designed by combining K3 and K5 base Hamiltonian sets, or two K4 base Hamiltonian sets with different periods. Given the rich design space, a natural question to ask is: Which base patterns should be combined, and how should the individual periods be determined? Given system parameters (e.g., the number of projector columns, number of projected patterns), and scene characteristics (e.g., amount and nature of global illumination), we use a simple, search-based procedure to compute the best combination of base patterns and periods (from a set of available combinations) of a micro Hamiltonian coding scheme. Our algorithm is similar in spirit to frequency selection algorithms used for optimizing sinusoid coding [14]. Patterns shown in Fig. 6 (c) were designed using this optimization procedure.

Antipodal Hamiltonian coding vs. Micro Hamiltonian coding: Both micro Hamiltonian coding and Gray code based Hamiltonian coding (e.g., antipodal Hamiltonian patterns) are designed to achieve robustness to global illumination. Gray code based Hamiltonian schemes have a restricted design space, and allow limited control over the spatial frequencies of the projected patterns. In contrast, micro Hamiltonian coding provides greater control over the spatial frequencies. On the other hand, micro Hamiltonian codes require phase unwrapping for decoding, and thus, may suffer from errors in low SNR scenarios due to incorrect unwrapping. In contrast, antipodal Hamiltonian codes achieve high precision even in low SNR, as shown in Figs. 9 and 10.

7 Experiments and Results

For our experiments, we used a structured light system consisting of a Canon T5i DSLR camera, and an Epson 3LCD projector. First, we evaluate the proposed Hamiltonian coding schemes under different signal-to-noise ratio (SNR) settings. The scene was a diffuse, white planar surface, with known ground truth depths, approximately in the range [1100,1600] millimeters. A broad range of SNR scenarios were emulated by using different brightness values of the source projector (that projected the structured light patterns), and another projector that acted as an ambient illumination source.

Fig. 7.

Comparison of various coding schemes for a planar scene. Hamiltonian coding outperforms existing schemes over a broad range of SNR scenarios. At high SNR (high source strength, low ambient light), multi-frequency sinusoid scheme achieve similar performance as Hamiltonian coding. However, at low SNR, multi-frequency sinusoid schemes suffer from large depth errors. In contrast, the performance of Hamiltonian coding degrades gracefully as the SNR decreases.

Fig. 8.

Comparison for $K=5$. Multi-frequency sinusoid coding can recover the fine geometric details in high SNR conditions. However, its performance degrades considerably in low SNR settings, resulting in large errors for the black lava rock. In contrast, Hamiltonian coding can recover fine details such as the pores on the rock, despite extremely low albedo.

Fig. 9.

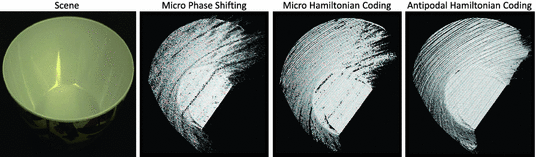
Scene with interreflections. All three coding schemes have high frequencies, and are relatively robust to global illumination. Micro PS performs reliably in moderate to high SNR scenarios (base of the bowl). However, its performance degrades at low SNR (at the edges of the bowl) due to low signal strength, resulting in large depth errors. Please zoom in for details.

Fig. 10.

Scenes with scattering and defocus. Hamiltonian coding outperforms MPS at low SNR, while mitigating errors due to scattering and defocus.

Figure 7 shows the depth errors for several coding schemes, at different source and ambient light strengths, and different number of patterns (K). We kept the capture time and the unambiguous depth range the same for all coding schemes. To achieve the latter, the period of the coding functions for all the schemes was fixed to 1920 columns. For $K=3$, ramp coding [2] results in large errors, due to a small coding curve length (Fig. 3). For $K=4, 5$, Hamiltonian coding significantly outperforms existing approaches such as sinusoid coding. The coding curves for edge patterns [38] and Hilbert patterns [18] are not distance preserving, which results in large depth errors at low SNR (low source brightness, high ambient brightness) settings.

For $K=5$, we compare Hamiltonian coding with a multi-frequency sinusoid scheme, which uses sinusoid patterns of multiple frequencies, for example, one high frequency and one low (unit) frequency [36]. Specifically, we used 3 patterns with a period of 1920 columns (unit frequency), and 2 patterns (separated by $\frac{\pi }{2}$ shifts) with a period of 160 pixels (high frequency). The high frequency phase provides accurate but ambiguous projector correspondence. The low frequency phase is then used to resolve the ambiguities (phase unwrapping). At high SNR, multi-frequency sinusoid scheme achieves similar performance as Hamiltonian coding. However, at low SNR, it suffers from inaccurate unwrapping, and thus, large depth errors. In contrast, the performance of Hamiltonian coding degrades gracefully as the SNR decreases.

Visual comparisons: Figure 8 shows visual comparisons between different coding schemes. Single-frequency sinusoid, in general, achieves a low depth resolution, resulting in loss of surface detail. With the same source power and capture time, Hamiltonian coding recovers subtle details such as the facial features of the statue (Fig. 8). Multi-frequency sinusoid coding can recover fine geometric details in high SNR conditions. However, its performance degrades considerably in low SNR, resulting in large errors for the black lava rock (Fig. 8). In contrast, Hamiltonian coding can recover fine details such as the pores on the rock, despite the scene having extremely low albedo. Please see the supplementary technical report for more results, including comparisons for a 3D time lapse sequence captured under varying ambient light.

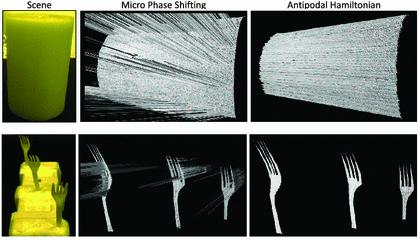
Scenes with global illumination and defocus: Figures 9 and 10 show depth recovery results for scenes with global illumination and defocus. The bowl is made of white, glossy material, resulting in strong interreflections. The candle has subsurface scattering. The depth-range for the forks scene is large, resulting in projector defocus. We used the antipodal Hamiltonian coding and micro Hamiltonian coding, as shown in Fig. 6 (b,c). We compared these schemes with micro phase shifting [14] (MPS) with $K=8$ patterns. While MPS performs reliably in moderate to high SNR scenarios, its performance degrades at low SNR due to unwrapping errors, resulting in large depth errors. Micro Hamiltonian coding also suffers from depth errors in low SNR due to incorrect unwrapping. However, it outperforms MPS by virtue of using high frequency Hamiltonian patterns, instead of sinusoids. Antipodal Hamiltonian method performs well even at low SNR, while mitigating errors due to global illumination effects.

8 Limitations and Future Outlook

Optimality of coding schemes: The coding schemes designed in this paper, although substantially better than current state-of-the-art, are not provably optimal. It may be possible to design schemes with further improved performance by using advanced optimization algorithms [24], based on the geometric concepts proposed in the paper. Another interesting future research direction is to design coding schemes that incorporate imaging system characteristics [24] and scene priors [23, 32].

Dealing with extreme global and ambient illumination: The Hamiltonian patterns designed for dealing with global illumination can only handle relatively low frequency interreflections. For scenes with strong, specular interreflections (e.g., mirrors), the proposed techniques can be used in conjunction with optical approaches for mitigating errors due to high-frequency interreflections [27]. Similarly, for scenes with strong ambient illumination, the proposed coding approaches can be used in a complementary manner with optical methods for suppressing ambient illumination [12, 27].