Keywords

1 Introduction

Predicting hydrological phenomena is of great importance for various fields such as climate change impact studies and flood prediction. An outline of the principles and structure of physically-based hydrological models is given in [8]. Experimental hydrology often provides the scientific basis for hydrological catchment models. However, the great complexity, size and uniqueness of hydrological catchmentsFootnote 1 makes a methodology involving physical experiments unfeasible if not impossible for catchments exceeding a few hectars. Hydrologists remedy by performing in silico experiments, simulating the hydrological processes in the basins.

Different classes of hydrological models exist. In this study, we focus on distributed land-surface models (dLSMs). dLSMs focus on detailed modelling of vertical processes and the correct simulation of mass and energy balance at the land-surface. To this end, they solve the hydrological water balance equation globally for the entire domain and locally for the subdomains dictated by the discretization.

A key characteristic of dLSMs is their focus on vertical surface-processes, such as evapotranspiration, snow processes, infiltration and plant growth. Lateral processes such as discharge concentration and lateral subsurface flow are simulated in a simplified way, if they are simulated at all. For this investigation we will consider vertical and lateral processes in a de-coupled way. The reason for this is the fact that vertical processes can, in general, be computed concurrently for all points in the domain. Lateral processes, in contrast, require information from the surrounding area and can therefore not be computed concurrently. They consist mainly of simple fluid dynamics simulations, and are computationally less demanding than the vertical processes. However, the structure of communication is dictated by the lateral processes, so for a scalable, parallel dLSM, an integrated approach that considers both aspects is required.

Various computer codes exist that implement different aspects of the hydrological theory behind dLSMs. WaSiM [22] for example is a hydrological model that solves the one-dimensional Richards’s equation to simulate vertical soil water movement. PROMET [16] features a detailed simulation of plant growth. The open-source code WRF-Hydro [9] was designed to link multi-scale process models of the atmosphere and terrestrial hydrology. These models are the basis for a number of different applications ranging from flood prediction [10], climate change impact studies [17] to land use scenario evaluation [19].

In contrast to dLSMs, which focus on surface processes, integrated hydrological models such as Parflow [18] or HydroGeoSphere [6] focus on the simulation of subsurface flow. They solve the three-dimensional Richards’s equation fully coupled to the surface runoff. Parallel implementations of integrated hydrological models, scaling to supercomputer capabilities are already available [7]. However, for a number of reasons integrated hydrological models can not be used substitutively for dLSMs.

The hydrological modelling community using dLSMs is currently moving from desktop models to small-size distributed clusters. Currently, dLSMs do not scale well beyond 64 processors [24]. The authors of [4] list four examples related to global environmental change that require high-resolution models of terrestrial water on a global scale.

Advanced methods for Bayesian inference and uncertainty quantification such as e.g. [3] are often based on Markov-Chain Monte Carlo methods, which require a great amount of sequential model evaluations. In order to obtain results for dLSM-based hydrology analyses in a reasonable amount of time, the execution time of a single model evaluation needs to be reduced. Parallelization and deployment on supercomputers is one possibility to achieve this. In summary, better parallelization schemes and dLSMs scaling to the abilities of modern supercomputers would greatly advance the capabilities of hydrologists.

Parallelization efforts have been undertaken for a number of hydrological models. However, the employed strategies rarely aim for an ideal load balancing and minimized communication efforts. In [14], a hydrological model is parallelized under the assumption that downstream cells require information of upstream cells. The catchment is interpreted as a binary tree, which is partitioned and distributed among processors, using a master-slave approach. With this approach, the authors decrease the execution time of the serial algorithm by a factor of five on multiple processors. WRF-Hydro partitions the domain into rectangular blocks [9], yet we are not aware of any scaling experiments for this implementation. In WaSiM [22], the domain is partitioned by distributing different rows to different processors. The parallelization strategies of WRF-Hydro and WaSiM both do not take the communication structure into account that is necessary to compute the flow-equations in parallel. It is likely that this limits the scaling potential to a limited amount of processors. In [24], the TIN-based hydrological model tRIBS is parallelized. A graph-based domain decomposition method is employed to produce a communication efficient partitioning. Scaling experiments indicate scalability up to about 64 processors. No contribution except [24] attempts to minimize the required point-to-point communication. Therefore, the hydrological community still lacks a parallelized dLSM which efficiently scales to the capabilities of modern supercomputers.

In this paper, we re-visit some of the graph-based domain decomposition methods suggested by [24], adapt it for a regular grid and conduct a more thorough analysis of its communication patterns. We compare different coordinate-based domain decomposition methods with a graph-based method, and investigate the impact on the necessary point-to-point communication. Furthermore, we perform an artificial strong scaling experiment and compute theoretical peak values for parallel speed-up for an example application on up to 8, 192 processors. As we want to conduct a methodological study of the suitability of different domain-decomposition methods for dLSMs we limit the evaluation to a simplified communication and work-balance model and do not measure performance of an actual application.

We will start by giving an overview over the functionality of dLSMs. Subsequently, we introduce the governing equations of the lateral processes and show how they dictate a specific communication structure. We then introduce the different domain decomposition methods. Finally, we present theoretical peak values of speed-up and efficiency and evaluate the potential for the minimization of point-to-point communication.

2 Theory

2.1 The Computational Domain of dLSMs

The focus of this study lies on the efficient decomposition of the computational domain of dLSMs. The computational domain commonly comprises one hydrological catchment as defined in the introduction, is denoted by \(\varOmega \in \mathbb {R}^2\) and fulfills the following assumptions:

  1. 1.

    Any point \(x \in \varOmega \) has an elevation h(x).

  2. 2.

    There is exactly one outlet \(O_{\varOmega }\) located on the boundary \(\partial \varOmega \) of the domain \(\varOmega \), where the minimum \(h_{0}\) of h is located.

  3. 3.

    \(\varOmega \) does not contain any sinks, i.e., there is a monotonously decreasing path from any point \(x \in \varOmega \) to the outlet \(O_{\varOmega }\).

In practice, the domain is commonly derived from a digital elevation model of the basin and a given outlet \(O_{\varOmega }\) with a gauging station where discharge measurements are taken.

For \(\varOmega \) as well as for any subdomain \(\omega \) of \(\varOmega \), the hydrological water balance equation holds. Commonly the domain is discretized into a regular grid. However, other discretization methods also exist. The water budget equation is then solved for any cell of the grid individually. This step usually requires the greatest computational effort. The structure of point-to-point communication is dictated by the lateral processes. In dLSMs these processes are commonly simulated under the following assumptions:

  1. 1.

    The flow direction is dependent on the topography given by h.

  2. 2.

    Flow follows the steepest gradient of h on the domain \(\varOmega \).

  3. 3.

    Flow is one-dimensional along the deterministic flow paths derived under the previous two assumptions.

The exact drainage network is commonly derived from the digital elevation model of the domain by the D8-Algorithm [20]. This algorithm assigns a flow direction to each cell under the consideration of the altitude h(x) of all eight neighbouring cells. The flow is always directed towards the neighbouring cell with the smallest altitude. In Fig. 1, a simple example of a domain for a dLSM is given.

Fig. 1.
figure 1

Typical domain for the solution of the Saint-Venant Equations in hydrological land surface models. White cells show cells for which the hydrological water balance equation is solved. Black lines indicate the flow structure, derived by the D8-Algorithm, on which the Saint Venant equations are solved. Grey cells are not part of the catchment to be simulated and thus not part of the domain \(\varOmega \).

Full size image

2.2 Governing Equations

In hydrological catchments, a number of lateral processes occur physically. These include, but are not limited to, channel flow, surface runoff and subsurface flow. In this paper, we focus on channel flow, but the method can be extended to include other lateral processes. Given the assumption of one-dimensional flow, the governing equations of the channel flow are the Saint-Venant equations, with spatial dimension x and time t:

$$\begin{aligned} \frac{ \delta Q(x, t) }{\delta t} + \frac{\delta A(x,t)}{\delta t}&= f (x, t) \end{aligned}$$
(1)
$$\begin{aligned} \frac{1}{A(x, t)} \frac{\delta Q(x, t)}{\delta t} + \frac{1}{A(x, t)} \frac{\delta }{\delta x} \left( \frac{Q(x, t)^{2}}{A(x, t)}\right) + g\frac{\delta y}{\delta x} - g(S_{0} - S_{f})&= 0 \end{aligned}$$
(2)

Here, Q is the discharge measured in \([m^{3}/s]\), A represents the cross-sectional area given in \([m^{2}]\), g is gravitational acceleration and y is the water level in [m]. Finally, \(S_{0}\) represents the slope of the channel, \(S_{f}\) is the friction slope and f(x, t) is a source term describing the runoff generated on every point x for every time step t. The source term f(x, t) represents the result of the hydrological water budget equation, and as such its computation comprises the simulation of all vertical processes. The one-dimensional Saint-Venant equations are solved on the flow structure derived by the D8-Algorithm. For the flow structure graph, the following holds:

  1. 1.

    All cells of the discretized domain \(\varOmega _{h}\) are nodes of the graph.

  2. 2.

    A cell can only be connected by an edge to its neighbouring cells.

  3. 3.

    The root of the flow structure is located at the outlet \(O_{\varOmega }\).

Note that whenever the flow structure (i.e. the graph) is cut during domain decomposition, point-to-point communication is induced. Hence, for an efficient communication the graph should be cut as little as possible.

Solutions of the Saint-Venant equations in dLSMs are commonly obtained by kinematic or diffusive wave approximations. Solution methods for the kinematic wave usually involve looping over the cells in an upstream to downstream order to compute a discharge for each cell. For these kinematic wave methods, only the discharge of upstream cells is required, as backwater effects cannot be simulated with this method [23]. Diffusive wave methods can be used to simulate backwater effect. Thus, they also require additional information from downstream cells, which induces additional communication. The exact parallel implementation of these methods is not part of this study, but a rough overview is necessary in order to comprehend the method proposed in the following section.

2.3 Domain Decomposition

At the core of most parallelization strategies lies the division of computational work among computational resources. We investigate an approach which involves the decomposition of the domain \(\varOmega \) into subdomains \(\omega \) to be computed on different processors. For the domain decomposition, we consider four different algorithms, three coordinate-based and one graph-based. For all algorithms we use the implementation provided by the Zoltan library [5].

The first algorithm considered is called “Block-Partitioning”. The algorithm considers the unique ID of each cell and assigns each processor a block of ids. Therefore, this algorithm is heavily dependent on the cell-ID, which is application dependent. We include this algorithm in the analysis, as it is the most commonly used domain decomposition method included in current parallel implementations of dLSMs. WaSiM [22], for example, uses an altered version of this algorithm.

Secondly, we consider Recursive Coordinate Bisection [2]. This algorithm determines partitions by recursively dividing the domain along its longest dimension. This method reduces communication by minimizing the length of partition borders.

Additionally, a method employing the Hilbert curve was considered. Here, discrete iterates of the space-filling Hilbert curveFootnote 2 are constructed. Partitioning is done by cutting the preimage of the discrete iterates of the Hilbert curve into parts of equal size and assigning the resulting 2D subdomains to different processors [5].

Finally, we investigate the method also used by [24]. Here, the flow direction graph is considered in order to minimize the necessary communication. We employ graph-partitioning methods, which attempt to partition the given graph into sub-graphs of almost equal size, while minimizing the amount of edges cut. We use the parallel graph-partitioning algorithm described in [11, 13] and parallelized in [12, 21].

3 Application Example

In order to avoid the overhead of the parallelization of an entire dLSM, we first measured the execution time per cell and time step of a PROMET model of the Upper-Danube catchment with 76, 215 cells. These measurements were then used to perform an artificial strong scaling experiment from one processor to 8, 192 processors. The outlet of this model is located at the gauging station in Passau, Germany. A more detailed description of the catchment, the model and its validation is given in [15]. The catchment was chosen for its heterogeneous domain, which includes cells in alpine regions as well as cells with agricultural use in the Alpine Foreland. These characteristics suggest a heterogenous load behaviour. Furthermore, it represents a typical model size of current dLSMs.

Fig. 2.
figure 2

Measured execution times for individual cells for one time step (left) and mean execution time over one year (right) of the hydrological Model PROMET [16]. The individual time step demonstrates the heterogeneity of computational load in one time step. The one-year mean shows the homogeneity of the total computational effort over the entire simulation period.

Full size image

The measured cell executions times of the Upper-Danube model are displayed in Fig. 2. While the total computational effort is homogeneously distributed, the computational effort for individual time steps can be quite heterogeneous.

The results of the domain decomposition algorithms introduced in the previous section for a small, overseeable head catchment are displayed in Fig. 3.

Fig. 3.
figure 3

Resulting partitioning of the different algorithms applied to a small head-catchment. Cells with identical colour are computed on the same processor. Flow paths in red correspond to cut edges in the graph.

Full size image

The illustration of the block-wise domain decomposition (top-left) shows PROMET’s scheme to determine the cell-ID by sequential assignment from the top left to the bottom right corner of the domain.

The scaling experiments in Sect. 4 were performed using the measured cell execution times. Rather than performing dummy-calculations to simulate the load generated by the source-term f(x, t) of Eq. (1), we decided to estimate the runtime by computing the sum of execution times on each processor. So with exception of the single cell measures, no real application code is executed. This allowed us to consider more methods without the overhead of implementing them into a dLSM and wasting CPU-hours on dummy calculations. Consequently, the reported metrics are theoretical peak values, which only take into account the load balance.

In order to evaluate the scaling experiments, we computed theoretical peak values of parallel speed-up \(S_{p}\) and the parallel efficiency \(E_{p}\) based on the estimated runtimes. These are:

$$\begin{aligned} S_{p} = \frac{T_{1}}{T_{p}} \end{aligned}$$
(3)
$$\begin{aligned} E_{p} = \frac{S_{p}}{p}, \end{aligned}$$
(4)

where \(T_{1}\) is the total runtime on a single processor, and \(T_{p}\) is the runtime on p processors. Furthermore, the edge-cut count \(E_C\) was computed, which is the sum of all edges spanning over two processors. We use the edge-cut count as an estimate for the communication overhead introduced by a parallel implementation of the lateral processes.

We considered two synchronization scenarios, which should represent the lower and upper boundary in terms of synchronization requirements. The first scenario (unsynchronized) assumes no synchronization during the simulation and represents the lower boundary. The second scenario (synchronized) assumes that all cells need to be synchronized at the end of every time step and therefore represents the upper boundary, and would be required for a diffusive wave model for the lateral processes.

4 Results

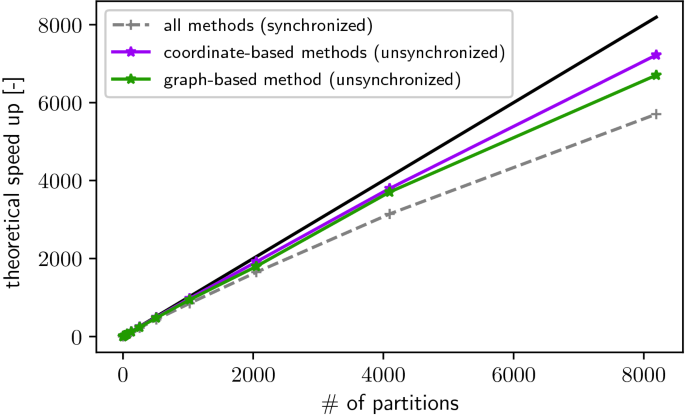
The theoretical speed-up values computed during the strong scaling experiment are displayed in Fig. 4.

Fig. 4.
figure 4

Theoretical peak values of parallel speed-up computed for the four different domain decomposition algorithms for the synchronized and unsynchronized scenario. Runtime was estimated by summing the execution times of all cells on given processor. At 8, 192 processors, each partition contains approximately nine cells.

Full size image

Figure 4 shows that, for synchronized simulations, all methods solve the load-balancing task equally well, and produce a partitioning which yields a theoretical speed up of  5, 740. This corresponds to a parallel efficiency of 0.7. For unsynchronized simulations, the coordinate-based methods outperform the graph-based method by \(6\%\), with theoretical speed up values of  7, 200 and 6, 722 respectively. This can be explained by the more constant partition size produced by the coordinate-based methods. Without a synchronization barrier at the end of each time step, the total computational load over the whole simulation time needs to be balanced, rather than the more heterogeneous load at each individual time step. The distribution of partition sizes is less relevant for the synchronized case, because load-imbalances are realized at the end of every time step without the possibility to be damped over the remaining simulation.

Fig. 5.
figure 5

Total number of flow paths cut and number of paths cut per partition for four different domain decomposition algorithms on different numbers of processors. The edge-cut count is determined by counting the edges that connect nodes on different partitions. It serves as a proxy for the necessary point-to-point communication. At 8, 192 processors, each subdomain contains approximately 9 cells.

Full size image

Much more severe differences between the methods can be found in the communication overhead potentially introduced by a parallel implementation of lateral processes. In Fig. 5, the total amount of flow paths cut is displayed. Here, the graph-based method shows significant advantages over the coordinate-based methods. The superiority of graph-partitioning becomes even more apparent if the flow paths cut per partition are considered. Here, the graph-based method is capable of producing partitionings with approximately 2.1 flow path cuts per partition, which mostly corresponds to one inlet and one outlet per partition. This holds true over the entire range of processors considered. For coordinate-based methods the number of flow paths cut is strongly dependant on the length of the partition border. Thus, for decreasing partition sizes the methods approach again. However, for future problems with significantly more than 76, 000 cells and therefore bigger partitions the superiority of the graph-based method will be even more severe.

5 Discussion

For unsynchronized simulations, there is a strong connection between the number of cells computed on a processor and the workload of this processor. This is caused by the homogeneous distribution of the total computational effort of the simulation (see Fig. 2 (right)). For synchronized simulations, this connection is significantly weaker, because load-imbalances that are present in a given time step are realized immediately. In unsynchronized simulations, these imbalances can dissipate over the remaining simulation. Therefore, the disadvantage of the graph-based method seen for unsynchronized simulations is not relevant for synchronized simulations.

Furthermore, the great drop between unsynchronized and synchronized simulations indicates that speed-up could be further improved by relaxing the synchronization requirements of the different algorithms for the simulation of the lateral processes. Of course, this has to be done under the consideration of the underlying physical processes.

Subsequently, the superiority of the of the graph-based domain decomposition in terms of the number of flow paths cut per partition over the entire range of processors needs to be noted. This result emphasizes the advantages of using graph-based domain decomposition for parallel implementations of the lateral processes in dLSMs most convincingly.

The artificial strong scaling experiment was conducted up to 8, 192 processors and yielded parallel efficiences between 0.70 and 0.88. These are, in comparison to integrated hydrological model such as Parflow, rather poor efficiencies on a small amount of processors. The catchment model of the Upper-Danube in the considered resolution simply is not big enough to be scaled to more processors. Models with more cells need to considered for scaling experiments with more processors. It is assumed that hydrologists will want to compute such models in the near future. Therefore, larger test scenarios with the possibility to be scaled up to the capabilities of current supercomputers will become available soon.

Furthermore, these results have to be seen in the context of current parallel dLSMs. The implementation of [24] reaches a parallel efficiency of approximately 0.3 on 64 processors.

Other codes scale even worse. For hyper-resolution global modelling as described in [4] this will not suffice. Also, for catchment studies at higher spatial resolutions, scalability beyond 64 processors is advantageous and would support scientific progress in hydrology.

6 Conclusion

We investigated several domain decomposition strategies for dLSMs. Strategies based purely on the coordinates of cells as well as a strategy acknowledging the special nature of the domain of the lateral processes were considered. We performed simplified scaling experiments to evaluate the suitability of these methods, and computed theoretical peak values for speed-up and parallel efficiency. For synchronized simulations, graph-based and coordinate-based domain decomposition yield similar speed-up values, which suggests that the advantageous communication structure of the graph-based methods would lead to a more scalable solution. For unsynchronized simulations, coordinate-based methods scale about \(6\%\) better. It remains to be demonstrated that the advantageous communication structure makes up for this gap.

One of the shortcomings of this study, the disregard of the induced communication effort, will be addressed by a parallel implementation of the methods used to solve the Saint-Venant equations in dLSMs. Furthermore, for dLSMs inducing greater and more heterogenous computational effort dynamic load-balancing strategies should be researched. Examples for such dLSMs include WaSiM, where the vertical soil water movement is simulated by the 1D-Richards’s equation.