Handling Mixture Optimisation Problem Using Cautious Predictions and Belief Functions

Abstract

Predictions from classification models are most often used as final decisions. Yet, there are situations where the prediction serves as an input for another constrained decision problem. In this paper, we consider such an issue where the classifier provides imprecise and/or uncertain predictions that need to be managed within the decision problem. More precisely, we consider the optimisation of a mix of material pieces of different types in different containers. Information about those pieces is modelled by a mass function provided by a cautious classifier. Our proposal concerns the statement of the optimisation problem within the framework of belief function. Finally, we give an illustration of this problem in the case of plastic sorting for recycling purposes.

1 Introduction

Mixing materials in the right amount is a common problem in many industries. Depending on the desired properties, the mixture must meet certain constraints on the proportions of each material. In the case where the mixing is done progressively, one must know, at each step, the materials present in the piece to be added and the materials present in the existing mixture in order to check if the new mixture respects the proportion constraints. This problem can be encountered in several applications; when refining crude-oil into useful petroleum products, one has to manage the mixture of different hydrocarbon products; when recycling plastic, the portion of some material type should not exceed some thresholds; when producing different types of wood paneling, each type of paneling is made by gluing and pressing together a different mixture of pine and oak chips; etc. The work presented in this paper is motivated by the problem of plastic sorting for recycling purposes, that will serve as a running and illustrative example of our proposal. More precisely, we have to assign plastic pieces issued from a deposit to various containers, knowing that pieces can be of different materials, and that each container should satisfy some constraints w.r.t. the proportion of materials it contains. Our goal is then to find the sorting optimizing the recycling process.

As sorting plastic manually is time and cost-consuming, automatic processing machines are now put in place, with several sensors (e.g., infra-red cameras) installed to recognize the material of a plastic piece. The obtained signal is then processed by automatic model learned from pieces labelled in favourable conditions (see [8] for more details). Of course, as real conditions are much less favourable, there may be a lot of uncertainties regarding the actual material of on-line processed pieces, which explains the need for reliable yet precise enough classifiers [2, 8, 11, 15]. In our setting, we consider that such classifiers returns mass functions modelling our knowledge about the material type.

A classical tool to perform optimization under uncertainty is stochastic optimization. We will extend such a setting to belief functions, first by considering the Choquet integral instead of the classical expectation as an objective function, and second by replacing the probability measure by the pair belief/plausibility measures. As we add pieces to a given container, we will also have to compute the global uncertainty of a container by adding mass functions of different weights. To do so, we will adapt the technique proposed in [7] for general intervals to the case of discrete proportions.

The paper is organised as follows. The problem is formalized as a stochastic optimisation problem in Sect. 2. Section 3 gives some reminders about belief functions, summing operation of mass functions, cautious prediction, and Choquet integral. In Sect. 4, the optimisation problem of pieces sorting is formalized in the framework of belief functions. The illustration concerning plastic sorting is presented in Sect. 5.

2 Stochastic Optimisation Problem Formalisation

We consider a deposit of scrap plastic, crude-oil, wood, etc., with a total physical weight W. This weight represent a set of pieces that will be put in C containers depending on the composition of each piece. In the end, each container c will contain a weight of material $w^{end}_c$, with $\sum \limits _{c =1}^{C} w^{end}_c = W$. The n types of materials are represented by the set $S=\{s_1,\ldots ,s_n\}$, and we denote by $\theta ^{c,end}_i$ the proportion of material $s_i$ present in the container at the end of the sorting.

Since pieces are supposed to be on conveyor belts, the optimisation process will be performed step-wisely, deciding for each new piece in which container it should go. Doing so, the final step, i.e., end, gives the proportions $\theta ^{c,end}_1$, $\theta ^{c,end}_2,\ldots ,\theta ^{c,end}_n$ in each container and the weights $w^{end}_1,\ldots ,w^{end}_n$ can be deduced by weighting each container. To avoid complicating notations, we omit the time or step reference in the optimisation problem. The optimisation problem can be set as follows:

$$\begin{aligned}&\!\max _{c \in \{1,\ldots , C\}}&\qquad&g_c(s_f) \end{aligned}$$

(1a)

$$\begin{aligned}&\text {subject to}&h_{c}(\theta ^c_1,\ldots ,\theta ^c_n) \le 0, \; c=1,\ldots , C, \end{aligned}$$

(1b)

$$\begin{aligned}&&\sum \limits _{i=1}^{n} \theta ^c_i = 1, \; c=1,\ldots , C \end{aligned}$$

(1c)

where:

• The objective function (1a) is such that $g: S \rightarrow \mathbb {R}^+$, with $g_c(s_i)$ the gain obtained if a material of type $s_i$ is added to container c;

• $\theta ^c_i$ is the proportion of material type $s_i$ in the container c after adding the new piece to it,

• The constraints (1b) are expressed using function $h_{c}: [0,1]^n \rightarrow [-1,1]$. They are of the form $h_{c,A}(\theta _1,\ldots ,\theta _n) =\sum \limits _{i \in A} \theta _i - \alpha _c \le 0$ with $A \subseteq S$, meaning that the proportion of materials of types A should not exceed $\alpha _c$ in container c;

• The constraint (1c) means simply that proportions sum up to 1.

The deterministic version of this problem is easy to solve, but becomes more complicated if the piece f composition is uncertain, for instance given by a probability mass function (pmf) p(.|f) over S. The optimisation becomes then stochastic, and (1a) is replaced by

$$\begin{aligned} \max _{c \in \{1,\ldots , C\}} \,\,\,\, \mathbb {E}_{p(.|f)}[g_c] \end{aligned}$$

(2)

where $\mathbb {E}_{p(.|f)}$ is the expectation w.r.t. p(.|f). Remark then that p(.|f) can be converted to a pmf over the discrete subset of proportions $\{(1,0,\ldots ,0),\ldots , (0,\ldots ,1)\}$ of $[0,1]^n$. Indeed, to check to which extent constraints are satisfied, we will need to compute probabilities over proportions. We denote by $p_c \oplus p(.|f)$ the result of adding the current probabilistic proportions $p_c$ of the container with p(.|f), accounting for the current weight of the container and the weight of f.

The constraints (1b) are then replaced by chance constraints

$$\begin{aligned} \mathbb {P}_{f,c} (h_{c,A}(\theta ^c_1,\ldots ,\theta ^c_n) \le 0) \ge \eta , c=1,\ldots ,C. \end{aligned}$$

(3)

where $\mathbb {P}_{f,c}$ is the measure induced from $p_c \oplus p(.|f)$, and $\eta$ is typically close to 1. Finally the stochastic optimisation problem is the following

$$\begin{aligned}&\!\max _{c \in \{1,\ldots , C\}}&\qquad&\mathbb {E}_{p(.|f)}[g_c] \end{aligned}$$

(4a)

$$\begin{aligned}&\text {subject to}&\mathbb {P}_{f,c} (h_{c,A}(\theta ^c_1,\ldots ,\theta ^c_n) \le 0) \ge \eta , \; c=1,\ldots , C, \end{aligned}$$

(4b)

$$\begin{aligned}&&\sum \limits _{i=1}^{n} \theta ^c_i = 1, \; c=1,\ldots , C. \end{aligned}$$

(4c)

However, it may be the case that pieces uncertainty is too severe to be modelled by probabilities, in which case more general models, such as belief functions, should be used. In the next sections, we discuss an extension of Eqs. (2)–(3) for such uncertainty models.

3 Reminders

3.1 Belief Functions

Belief functions [12, 14] are uncertainty models that combine probabilistic and set-valued uncertainty representations, therefore providing an expressive and flexible framework to represent different kinds of uncertainty. Beyond probabilities and sets, they also extend possibility theory [5].

Given a space $\mathcal {X}$ with elements x, the basic tools used within belief function theory is the mass function, also called basic belief assignment (bba), is a set function $m : 2^{\mathcal {X}} \rightarrow [0,1]$ satisfying

$$m(\emptyset )=0 \text { and } \sum \limits _{A \subseteq \mathcal {X}} m(A) = 1.$$

The elements $A \in 2^{\mathcal {X}}$ such that $m(A)>0$ are called focal elements and they form a set denoted $\mathbb {F}$. $(m, \mathbb {F})$ is called body of evidence.

The belief function $Bel:2^{\mathcal {X}} \rightarrow \left[ 0,1 \right]$ is a set function that measures how much an event A is implied by our information such that

$$Bel(A) = \sum \limits _{B \subseteq \mathcal {X}, B \subseteq A} m(B).$$

The plausibility function $Pl : 2^{\mathcal {X}} \rightarrow \left[ 0,1 \right]$ is a set function that measures how much an event A is consistent with our information such that

$$Pl(A) = \sum \limits _{B \subseteq \mathcal {X}, B \cap A \ne \emptyset } m(B).$$

Note that when focal elements are singletons x, we have $Bel=Pl$ and retrieve probabilities.

3.2 Sum Operation on Imprecise Proportion

Let us denote the unit simplex by $\mathbb {U}=\{(\theta _1,\ldots ,\theta _n) \in [0,1]^n: \sum \limits _{i=1}^{n} \theta _i=1\}$. Let us consider two sets of pieces $sf^1$ and $sf^2$ made of materials among $S=\{s_1,\ldots ,s_n\}$ with physical masses $w^1$ and $w^2$. The information about the material type proportions in $sf^1$ and $sf^2$ are given respectively by the bodies of evidence $(m^1, \mathbb {F}^1)$ and $(m^2, \mathbb {F}^2)$ defined over $\mathbb {U}$, with discrete focal elements in a finite number. A focal element in $\mathbb {F}^1$ (resp. $\mathbb {F}^2$) is in the form $J = J_1 \times \ldots \times J_n$ (resp. $K = K_1 \times \ldots \times K_n$) where $J_i$ (resp. $K_i$), $i \in \{1,\ldots ,n\}$ is an imprecise information about the proportion of $s_i$ in $sf^1$ (resp. $sf^2$).

The information resulting from adding $sf^2$ with $sf^1$ is a mass function denoted $m^{1 \oplus 2}$ and defined as follows for $I \subset \mathbb {U}$ [7]:

$$\begin{aligned} m^{1 \oplus 2}(I)=\sum _{\begin{array}{c} J \in \mathbb {F}^1, K \in \mathbb {F}^2\\ I=J \boxplus K \end{array}} m^1(J )\,\,.\,\,m^2(K). \end{aligned}$$

(5)

where $\mathbb {F}^{1 \oplus 2}$ is a finite set made of discrete subsets of $\mathbb {U}$ resulting from summing proportion in $\mathbb {F}^{1}$ and $\mathbb {F}^{2}$; the total weight associated to the mixture is $w^1 + w^2$ and $\boxplus$ is defined for two focal elements $J \in \mathbb {F}^1$ and $K \in \mathbb {F}^2$ as follows:

$$J \boxplus K=I_1 \times \ldots \times I_n, \text { with } I_i=\{\frac{w^1 \,\, x + w^2 \,\, y}{w^1 + w^2}, x \in J_i , y \in K_i \}.$$

Note that in case where imprecise information are convex sets, e.g. intervals, only the lower and the upper bounds of the intervals are involved in the determination of $J \boxplus K$ [7].

Example 1

Let us consider the case where $S = \{ s_1, s_2, s_3, s_4\}$ and $sf^1$ and $sf^2$ are both composed of a single piece each with weight 1 kg. In Table 1, we give an example of two bodies of evidence for these two sets of pieces. The focal elements presented in Table 1 have the following meaning: $J_1$ means that $sf^1$ is a pure material of type $s_1$ or $s_2$, and $J_2$ means that $sf^1$ is a pure material of type $s_2$, and similarly for $K_1,K_2$.

Table 1. Bodies of evidence.

The obtained mass function when mixing $sf^1$ and $sf^2$ is given by its body of evidence $(\{I_1,I_2,I_3,I_4\},m^{1 \oplus 2})$ as follows:

$$\begin{aligned} \begin{array}{ll} I_1=J_1 \boxplus K_1=\{0,\dfrac{1}{2},1\} \times \{0,\dfrac{1}{2},1\} \times \{0\} \times \{0\}, &{} m^{1 \oplus 2}(I_1)=0.3,\\ I_2=J_1 \boxplus K_2=\{\dfrac{1}{2},1\} \times \{0,\dfrac{1}{2}\} \times \{0\} \times \{0\}, &{} m^{1 \oplus 2}(I_2)=0.2, \\ I_3=J_2 \boxplus K_1=\{0,\dfrac{1}{2}\} \times \{\dfrac{1}{2},1\} \times \{0\} \times \{0\}, &{} m^{1 \oplus 2}(I_3)=0.3, \\ I_4=J_2 \boxplus K_2=\{\dfrac{1}{2}\} \times \{\dfrac{1}{2}\} \times \{0\} \times \{0\}, &{} m^{1 \oplus 2}(I_4)=0.2.\\ \end{array} \end{aligned}$$

3.3 Inference from Imprecise Proportions

The set $A_{\alpha }$ of vector proportions that satisfy $\sum \limits _{i \in A} \theta _i \le \alpha$ is of interest in our problem because it allows expressing constraints containers must respect, as indicate Eq. (1b). Thus we need to make inferences over such event. Given focal elements $I=I_1 \times ... \times I_n$, in case where $I_i=[\ell _i,u_i]$ are intervals it was shown [7] that

$$I \subseteq A_{\alpha } \Leftrightarrow \min (\sum \limits _{s_i \in A} u_i,1-\sum \limits _{s_i \not \in A} \ell _i,) \le \alpha $$

$$\mathcal {I} \cap A_{\alpha } \ne \emptyset \Leftrightarrow \max (\sum _{s_i \in A} \ell _i,1-\sum _{s_i \not \in A} u_i) \le \alpha $$

In the discrete case where $I_i=\{ \tau _1, \tau _2, \ldots , \tau _{|I_i|}\}$, $\tau _i \in [0,1]$, the two previous formulae remain valid when considering $u_i=\max \limits _{t=1,\ldots ,|I_i|} \tau _t$ and $\ell _i=\min \limits _{t=1,\ldots ,|I_i|} \tau _t$.

3.4 Cautious Predictions

In our case, belief functions will be produced by classifiers that will be learned from a set of examples/pieces $f_1, \ldots , f_l$ having m features $X_1, \ldots , X_m$ having received a label in S. Given a new object f, this classifier will output a mass m(.|f) as a prediction.

Such classifiers are indeed useful in our application, as they provide more reliable information, and can account for many defects, such as the missingness of some feature $X_j$ for f (due to a broken sensor), or the fact that measurements are done by industrial on line machine device instead of laboratory measurements, meaning that variability in measurement due to atmospheric disturbances, ageing of plastics, black or dark-coloured materials, etc. lead to reducing the quality of the spectrum obtained from plastic pieces. In this situation, classifier producing point prediction, i.e., single element from S as prediction, will make to many errors to provide a reliable sorting. Instead of point prediction classifiers, we will use classifiers providing cautious predictions in form of a posterior mass function over S [8], but the approach could apply to other such classifiers [3, 4, 11]. It should be stressed that in our case, one could prefer to put a good plastic in a low price container rather than ruining a high price container by violating constraints (1b), so being cautious by accounting for imperfectness of information is essential.

3.5 Choquet Integral

The Choquet integral [9] is an integral that applies to non-additive measures, often referred as fuzzy measures [10]. Since a Belief function defined over a space S is such a fuzzy measure¹, we can apply the Choquet integral to it in the following way: given a vector of real positive values $y=(y_1,...,y_n) \in \mathbb {R}^{+n}$, its Choquet integral w.r.t. Bel is defined as

$$\begin{aligned} C_{Bel} (y)=\sum \limits _{i=1}^{n} (y_{\sigma (i)}-y_{\sigma (i-1)}) Bel(\{s_{\sigma (i)},s_{\sigma (i+1)},...,s_{\sigma (n)}\}) \end{aligned}$$

(6)

where $0=y_{\sigma (0)} \le y_{\sigma (1)} \le y_{\sigma (2)} \le ... \le y_{\sigma (n)}$ ($\sigma$ is a permutation over $\{1,\ldots ,n\}$).

If $Bel=Pl$, then Eq. (6) is simply the standard expectation operator. Otherwise, it can be interpreted as the lower expectation taken over all probabilities $Bel \le P \le Pl$, i.e., all probabilities bounded by our imprecise knowledge.

4 Optimisation Problem Statement in the Framework of Belief Function

We now provide an equivalent of the optimisation problem ingredients (4a)–(4c) in the framework of belief function. We consider all the previous ingredients, except that now the information about a new piece to add to a container is given by a mass function m(.|f) defined over $S=\{s_1, \ldots ,s_n\}$, and our information about the proportions of materials in a given container c is also given by a mass function $m^c$ bearing on $\mathbb {U}$. As before, one can easily go from a mass m(.|f) on S to a mass on $\mathbb {U}$ (see Example 1 for an illustration).

4.1 The Objective Function

The expected value in the objective function (2) can be replaced by the Choquet integral based on the belief function Bel(.|f). As in Sect. 2, we will only be interested to model in the objective function the potential gain of adding the new piece f to one of the container, without bothering about the container current proportions, as those will be treated in the constraints. If g is the overall gain of a container containing materials of a specified kind $\overline{A}$, where elements $A \subset S$ are considered as impurities whose percentage should not exceed $\alpha _c$, we simply consider the function $g_c(s)=g(s)$ for $s \in \overline{A}$, and $g_c(s)=\alpha _c\cdot g(s)$.

Example 2

Consider four material types $S=\{s_1,\ldots ,s_4\}$ and three containers. Table 2 presents an example of gains obtained when adding piece f to each container. We consider that container 1 is dedicated to $s_1$ and other type proportions should not exceed $\alpha _{1}$; container 2 is dedicated to $s_2$ and $s_3$ (deemed compatible for recycling) and other type proportions should not exceed $\alpha _{2}$; container 3 is the garbage bin, so $\alpha _3=1$.

Table 2. Container gains.

The example of Table 2 shows that the larger the threshold, the higher the gain when adding impurities to a container.

Still denoting by $g_c(s_i)$ the gain obtained if the real type of the added piece to the container c is $s_i$, Eq. (2) becomes:

$$\begin{aligned} \max _{c \in \{1,\ldots ,C\}} \,\,\,\, C_{Bel(.|f)}(g_c(s_1),\ldots ,g_c(s_n)) \end{aligned}$$

(7)

The objective function (7) is an expected value based on Choquet integral where gains are weighted related to our belief on the material type of the new piece including imprecise information. Let denotes $x_{(1)}=\min \limits _{i=1,n} g_c(s_i)$, $\ldots$, $x_{(n)}=\max \limits _{i=1,n} g_c(s_i)$ such as $x_{(1)} \le x_{(2)} \le \ldots \le x_{(n)}$, then this expected value guarantee $x_{(1)}$ surely and adds to it the gaps $x_{(i)}-x_{(i-1)}$ weighted by  $Bel(\{s_{(i)},\ldots ,s_{(n)}\}|f)$.

Example 3

Let us consider a mass function m(.|f) with the following body of evidence $(\{\{s_1\},\{s_1,s_2\}\},(0.2,0.8))$. The resulting Bel(.|f) is given in Table 3.

Table 3. Belief function.

If we consider $\alpha _1=0.25$ and $\alpha _2=0.3$ in Table 2, we obtain the gains in Table 4.

Table 4. Container gains.

In this case, without considering constraints, f should go in container 1.

4.2 The Constraints

Let us consider that the physical weight of f is $w^f$ and the physical weight of the current pieces in the container c is $w^c$. The formula (5) gives us the new mass function $m^{f\oplus c}$ when adding the piece f to the container c. The constraints in (3) check whether impurities in containers are not too high. However, we must now replace he probability measure $\mathbb {P}^{f\oplus c}$ in this constraint is by the pair $(Bel^{f\oplus c}, Pl^{f\oplus c})$. One may reasonably requires the degree of certainty that a constraint is satisfied to be very high, and the degree of plausibility of this same constraint to be satisfied to be close to 1. Such a reasoning can be applied by replacing the constraint (3) by two constraints:

$$\begin{aligned} Bel^{f\oplus c} (h_{c}(\theta _1,\ldots ,\theta _n) \le 0) > \eta _c, \,\, c=1,\ldots ,C, \end{aligned}$$

(8a)

$$\begin{aligned} Pl^{f\oplus c} (h_{c}(\theta _1,\ldots ,\theta _n) \le 0) \sim 1, \,\, c=1,\ldots ,C. \end{aligned}$$

(8b)

where $\eta _c \in ]0,1]$ are enough large. Note that such ideas are not new, and have been for instance recently applied to the travelling salesman problem [6].

Example 4

If we go back to the Example 2, the considered constraints for each container can be given as follows:

Container 1:

$$Bel^{f\oplus c} (\sum \limits _{i \ne 1} \theta _i \le \alpha _1) > \eta _1, \,\,\, Pl^{f\oplus c} (\sum \limits _{i \ne 1} \theta _i \le \alpha _1) \sim 1,$$

Container 2:

$$Bel^{f\oplus c} (\sum \limits _{i \ne 2,3} \theta _i \le \alpha _2) > \eta _2, \,\,\, Pl^{f\oplus c} (\sum \limits _{i \ne 2,3} \theta _i \le \alpha _2) \sim 1,$$

Container 3:

$$Bel^{f\oplus c} (\sum \limits _{i \ne 4} \theta _i \le \alpha _3) > \eta _3,\,\,\, Pl^{f\oplus c} (\sum \limits _{i \ne 4} \theta _i \le \alpha _3) \sim 1.$$

Let us denote $A_{\alpha }$ the set of vector proportions that satisfy $\sum \limits _{i \in A} \theta _i \le \alpha$. In Sect. 3.3 we give the way to determine $Bel(A_{\alpha })$ and $Pl(A_{\alpha })$ that are required to check the constraints (8a) and (8b).

Finally, we have the following optimisation problem to decide in each container a piece f should be added:

$$\begin{aligned}&\!\max _{c \in \{1,\ldots ,C\}}&\qquad&C_{Bel(.|f)}(g_c(s_1),\ldots ,g_c(s_n)) \end{aligned}$$

(9a)

$$\begin{aligned}&\text {subject to}&Bel^{f\oplus c} (h_{c}(\theta ^c_1,\ldots ,\theta ^c_n) \le 0) > \eta _c, \,\, c=1,\ldots ,C, \end{aligned}$$

(9b)

$$\begin{aligned}&&Pl^{f\oplus c} (h_{c}(\theta ^c_1,\ldots ,\theta ^c_n) \le 0) \sim 1, \,\, c=1,\ldots ,C, \end{aligned}$$

(9c)

$$\begin{aligned}&&\sum \limits _{i=1}^{n} \theta ^c_i = 1, c=1,\ldots ,C. \end{aligned}$$

(9d)

To solve the optimisation problem (9a)–(9d) one needs to assess (9a) for each container for the finite number of pieces in the deposit. Complexity issues arise when the number of pieces is very large. Indeed, the number of focal elements involved when determining $Bel^{f\oplus c}$ (9b) and $Pl^{f\oplus c}$ (9c) become exponential, yet one can easily solve this issue by considering approximations (e.g., deleting focal elements of very small mass).

5 Illustration

In this section we present an application concerning plastic sorting where the pieces of a deposit should be separated by types of materials in different containers prior to recycling due to some physico-chemical reasons related to non-miscibility. Optical sorting devices are used to automatically sort the pieces. As it is shown in Fig. 1 borrowed from [1], pieces of plastics arrive continuously on a conveyor belt before being recorded by an infra-red camera. However, the on line acquired information is subject to several issues inducing the presence of imprecision on one hand, i.e. some features information are not precise enough to draw clear distinctions between the materials type, and uncertainty on the other hand, i.e. due to the reliability of information caused by atmospheric disturbance, etc (please refer to [8] for more details). Two sources of information are used to collect data. The first source of data is the Attenuated Total Reflection (ATR) which gives excellent quality of spectra that allows experts to label pieces easily. The second source is the optical device which provides spectra of lesser quality. Since small quantity of badly sorted plastics can lead to high decreases of impact resistance [13] and of monetary value, impurities should be limited. Thus, experts have defined tolerance threshold on the proportions of impurities.

Fig. 1.

Example of sorting device

In this illustration we propose a sorting procedure based on the optimisation problem in (9a)–(9d). The cautious classification is provided using the evidential classifier proposed in [8].

Let us recap the procedure performed to sort each fragment f:

• Estimate the resulting composition of each container c if we add f to it as a mass function $m^{f \oplus c}$ using the sum operation defined in Sect. 3.2.

• Select the containers verifying the constraints (9b) and (9c).

• Compare the objective function (9a) for the selected container.

• Update the evidence about the chosen container.

5.1 Data Presentation

Let us consider a plastic waste deposit composed of 25 pieces of four material types $s_1, s_2, s_3, s_4$. All the pieces have the weight $w = 1$. Each piece should be sent to one of the three containers dedicated for specific material types. The first container is dedicated to plastic types $s_1$, $s_2$ and the proportions of impurities, i.e $s_3, s_4$, should not exceed $\alpha _1= 0.05$. The second container is dedicated to plastic types $s_3$, $s_4$, and the proportions of impurities, i.e $s_1, s_2$, should not exceed $\alpha _2= 0.05$. The third container is actually the reject option, thus all types of plastics are considered as impurities (or considered as valid materials), but there is no need to control them, thereby $\alpha _3 = 1$. Table 5 gives the gains considered for the containers.

Table 5. Container gains for plastic sorting.

The database used for the experimentation are 23365 industrially acquired spectra. Each example of the database is composed of its 154-dimension features and its ATR label.

5.2 Simulations

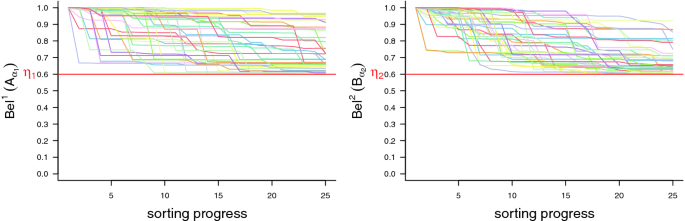
The evidential classifier proposed in [8] has been trained on the 11747 examples and applied on the testing set, i.e., 11618 other examples. We obtained 11618 mass functions $m(.|f_1), \dots , m(.|f_{11618})$. In order to evaluate the sorting procedure, we tested the performances on 40 simulations of fragment streams. The simulation of a stream was done by selecting randomly indexes orders of testing fragments $f_1, \dots , f_{11618}$. For computational reasons, we stopped the sorting procedure at the 25th fragment for each simulation. Note that the complexity of the sorting procedure is exponential, i.e., $\mathcal {O}((2^{|S|}){^{nb \,\,of \,\,pieces}})$ [7]. Figure 2, 3 and 4 show respectively the evolution of the weight of materials in the two first containers, the belief that the constraints are respected and the real proportions of impurities. Each curves represents one simulation and we keep the same color in all the figures. The thresholds are set to $\eta _1 = \eta _2=0.6$.

Fig. 2.

Evolution of the weight of materials in container 1 and 2.

In Fig. 2 we observe that the choice between the two first containers is balanced. As we can see in Fig. 3, the constraints defined in (9b) are always respected. Using the testing labels we can evaluate the real proportions of impurities.

Fig. 3.

Evolution of the belief that the constraints are respected in containers 1 and 2.

Fig. 4.

Evolution of real proportions of impurities in containers 1 and 2.

In Fig. 4, we observe that the proportion of impurities are most of the times below the required threshold except for a few simulations where mistakes are made for the first pieces added in container 1 and 2. Since at the beginning of the sorting, there are only few pieces, the mistakes have a high impact on the proportions. After checking, it turned out that the mass functions provided for these examples were not accurate. In order to evaluate the quality of the resulting sorted material, we introduce the score $q_c$ as the percentage of simulations respecting impurities proportions constraints at the end of the sorting in the container c. With the proposed approach we obtain $q_{1} = 77.5 \%$ and $q_{2} = 62.5 \%$. This is significantly higher than the required levels $60 \%$, which is in-line with the fact that we are acting cautiously. In terms of gains, the average gain obtained in the simulations is 1901.475$ while the optimal would have been 2500$, in the ideal case where all pieces are sorted in the correct container. However, this would only have been possible if we had perfect classification results, something that is unlikely.

5.3 Discussion

In order to verify the benefit of the proposed sorting procedure based on the optimisation problem (9a)–(9d), named here evidential procedure, we compare it to the stochastic procedure based on the stochastic optimisation problem (4a)–(4c) and to the deterministic procedure based on optimisation problem (1a)–(1c). We consider stochastic procedure based on the Pignistic probability derived from m(.|f) while the deterministic procedure is based on a classifier producing point prediction. The simulations whose results are in the Table 6 are made in the same settings and numbers as in Sect. 5.2. Two criteria are used to perform this comparison: the quality of the resulting materials in the two containers $q_1$, $q_2$; the rate of average gain obtained on all simulations, denoted Rag.

What we see here is that not accounting for uncertainty, or considering a less expressive model (i.e., probabilities) do indeed bring a better average gain, but fails to meet the constraints imposed to the containers for them to be usable at all. Indeed, the evidential procedure achieves high quality of the sorting material while the two other procedures do not respect the required constraints on the containers composition. This could be solved by considering more penalizing gains in case of bad sorting for the deterministic procedure and stochastic procedure, yet this would complexify the procedure. Thus the evidential procedure seems preferable for applications where constraints on impurities are strong, i.e. very small $\alpha$ or when the confidence level required for the application is high, i.e., $\eta$ closer to 1. When such requirements are not necessary, we would advice the use of an alternative procedure less computationally demanding.

Table 6. Comparison with alternative procedures

6 Conclusion

We proposed in this paper a formulation of the mixture problem of material types in the framework of belief functions. The usefulness of this work is illustrated using the sorting procedure of plastic material. A stepwise approach is proposed to avoid the complicated complete resolution. As perspectives for this work, one should optimise the stepwise summing of mass functions in on line sorting procedure by controlling the focal elements generated at each step in order to overcome the exponential complexity. Furthermore, one may relax the constraints on impurities at each step by requiring them only at the end of the sorting procedure.