Proof-of-Burn

Abstract

Proof-of-burn has been used as a mechanism to destroy cryptocurrency in a verifiable manner. Despite its well known use, the mechanism has not been previously formally studied as a primitive. In this paper, we put forth the first cryptographic definition of what a proof-of-burn protocol is. It consists of two functions: First, a function which generates a cryptocurrency address. When a user sends money to this address, the money is irrevocably destroyed. Second, a verification function which checks that an address is really unspendable. We propose the following properties for burn protocols. Unspendability, which mandates that an address which verifies correctly as a burn address cannot be used for spending; binding, which allows associating metadata with a particular burn; and uncensorability, which mandates that a burn address is indistinguishable from a regular cryptocurrency address. Our definition captures all previously known proof-of-burn protocols. Next, we design a novel construction for burning which is simple and flexible, making it compatible with all existing popular cryptocurrencies. We prove our scheme is secure in the Random Oracle model. We explore the application of destroying value in a legacy cryptocurrency to bootstrap a new one. The user burns coins in the source blockchain and subsequently creates a proof-of-burn, a short string proving that the burn took place, which she then submits to the destination blockchain to be rewarded with a corresponding amount. The user can use a standard wallet to conduct the burn without requiring specialized software, making our scheme user friendly. We propose burn verification mechanisms with different security guarantees, noting that the target blockchain miners do not necessarily need to monitor the source blockchain. Finally, we implement the verification of Bitcoin burns as an Ethereum smart contract and experimentally measure that the gas costs needed for verification are as low as standard Bitcoin transaction fees, illustrating that our scheme is practical.

Appendix: Full Proofs

Applying an efficiently computable function to indistinguishable distributions preserves indistinguishability.

Lemma 4

(Indistinguishability preservation). Given two computationally indistinguishable distribution ensembles $\{X_\kappa \}_{\kappa \in \mathbb {N}}$ and $\{Y_\kappa \}_{\kappa \in \mathbb {N}}$, let $\{f_\kappa \}_{\kappa \in \mathbb {N}}$ be a family of efficiently computable functions. Then the distribution ensembles $X' = \{f_\kappa (X_\kappa )\}_{\kappa \in \mathbb {N}}$ and $Y' = \{f_\kappa (Y_\kappa )\}_{\kappa \in \mathbb {N}}$ are computationally indistinguishable.

We call a distribution ensemble unpredictable if no polynomial-time adversary can guess its output. We observe that, if each element of a distribution appears with negligible probability, then the distribution must be unpredictable. Public keys generated from secure signature schemes must be unpredictable.

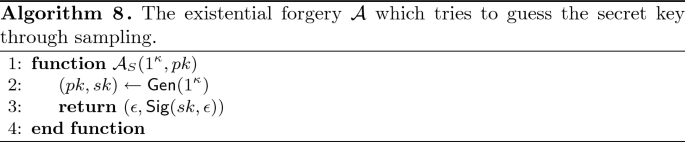
Lemma 2

(Public key unpredictability). Let $S = (\textsf {Gen}, \textsf {Sig}, \textsf {Ver})$ be a secure signature scheme. Then the distribution ensemble $X_\kappa = \{(sk, pk) \leftarrow \textsf {Gen}(1^\kappa ); pk\}$ is unpredictable.

Proof

Let $p = \max _{\widehat{pk} \in [X_\kappa ]}\Pr _{pk \leftarrow X_\kappa }[pk = \widehat{pk}]$. Consider the existential forgery adversary $\mathcal {A}$ illustrated in Algorithm 8 which works as follows. It receives pk as its input from the challenger, but ignores it and generates a new key pair $(pk', sk') \leftarrow \textsf {Gen}(1^\kappa )$. Since the two invocations of $\textsf {Gen}$ are independent,

$$\begin{aligned} \Pr [pk = pk'] \ge \max _{\widehat{pk} \in [X_\kappa ]}\Pr [pk = \widehat{pk} \wedge pk' = \widehat{pk}]\\ = \max _{\widehat{pk} \in [X_\kappa ]}\Pr [pk = \widehat{pk}]\Pr [pk' = \widehat{pk}]\\ = \max _{\widehat{pk} \in [X_\kappa ]}\left( \Pr [pk = \widehat{pk}]\right) ^2 = p^2 \,. \end{aligned}$$

The adversary checks whether $pk = pk'$. If not, it aborts. Otherwise, it uses $sk'$ to sign the message $m = \epsilon$ and returns the forgery $\sigma = \textsf {Sig}(sk, m)$. From the correctness of the signature scheme, if $pk = pk'$, then $\textsf {Ver}(pk, \textsf {Sig}(sk, m)) = \mathsf {true}$ and the adversary is successful. Since the signature scheme is secure, $\Pr [\textsf {Sig-forge}^{cma}_{\mathcal {A},S}] = \textsf {negl}(\kappa )$. But $\Pr [pk = pk'] \le \Pr [\textsf {Sig-forge}^{cma}_{\mathcal {A},S}]$ and therefore $p \le \sqrt{\Pr [pk = pk']} \le \textsf {negl}(\kappa )$. From this, we deduce that the distribution ensemble $X_\kappa$ is unpredictable.    $\square$

Lemma 3

(Random Oracle unpredictability). Let $\mathcal {T}$ be an unpredictable distribution ensemble and H be a Random Oracle. The distribution ensemble $X = \{t \leftarrow \mathcal {T}; H(t)\}$ is indistinguishable from the uniform distribution ensemble $\mathcal {U}(\{0,1\}^\kappa )$.

Proof

Let $\mathcal {A}$ be an arbitrary polynomial distinguisher between X and $\mathcal {U}(\{0, 1\}^\kappa )$. We construct an adversary $\mathcal {A}^*$ against $\textsc {predict}_{\mathcal {T}}$. Let r denote the (polynomial) maximum number of random oracle queries of $\mathcal {A}$. The adversary $\mathcal {A}^*$ is illustrated in Algorithm 9 and works as follows. Initially, it chooses a random bit $b {\mathop {\leftarrow }\limits ^{\$}} \{0, 1\}$ and sets $Z = X$ if $b = 0$, otherwise sets $Z = \mathcal {U}(\{0,1\}^\kappa )$. It samples $z \leftarrow Z$. If $b = 0$, then z is chosen by applying $\mathsf {GenAddr}$ which involves calling the random oracle H with some input pk. It then chooses one of $\mathcal {A}$’s queries $j {\mathop {\leftarrow }\limits ^{\$}} [r]$ uniformly at random. Finally, it outputs the input received by the random oracle during the $j^\text {th}$ query of $\mathcal {A}$.

We will consider two cases. Either $\mathcal {A}$ makes a random oracle query containing pk, or it does not. We will argue that, if $\mathcal {A}$ makes a random oracle query containing pk with non-negligible probability, then $\mathcal {A}^*$ will be successful with non-negligible probability. However, we will argue that, if $\mathcal {A}$ does not make the particular random oracle query, it will be unable to distinguish X from $\mathcal {U}(\{0,1\}^\kappa )$.

Let $\textsc {qry}$ denote the event that $b = 0$ and $\mathcal {A}$ asks a random oracle query with input pk. Let x denote the random variable sampled by the challenger in the predictability game of $\mathcal {A}^*$. Let $\textsc {exqry}$ denote the event that $b = 0$ and $\mathcal {A}$ asks a random oracle query with input equal to x. Observe that, since the input to $\mathcal {A}$ does not depend on x, we have that $\Pr [\textsc {exqry}] = \Pr [\textsc {qry}]$. As j is chosen independently of the execution of $\mathcal {A}$, conditioned on $\textsc {exqry}$ the probability that $\mathcal {A}^*$ is able to correctly guess which query caused $\textsc {exqry}$ will be $\frac{1}{r}$. Therefore we obtain that $\Pr [\textsc {predict}_{\mathcal {A}^*,\mathcal {T}}(\kappa ) = \mathsf {true}] = \frac{1}{r}\Pr [\textsc {exqry}] = \frac{1}{r}\Pr [\textsc {qry}]$. As $\Pr [\textsc {predict}_{\mathcal {A}^*,\mathcal {T}}(\kappa ) = \mathsf {true}] \le \textsf {negl}(\kappa )$ and r is polynomial in $\kappa$, we deduce that $\Pr [\textsc {qry}] \le \textsf {negl}(\kappa )$.

Consider the computational indistinguishability game in which the distinguisher gives a guess $b^*$ attempting to identify the origin b of its input (with $b = 0$ indicating that the first distribution was sampled, and $b = 1$ indicating that the second distribution was sampled). If $b = 0$, then the distinguisher $\mathcal {A}$ receives a truly random input $pkh = H(pk)$. If the distinguisher does not query the random oracle with input pk, the input of the distinguisher is truly random and therefore $\Pr [b^* = 0|b = 0|\lnot \textsc {qry}] = \Pr [b^* = 0|b = 1]$.

Consider the case where $b = 0$ and apply total probability to obtain

$$\begin{aligned}&\Pr [b^* = 0|b = 0] =\\&\Pr [b^* = 0|\textsc {qry}]\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 0|\lnot \textsc {qry}]\Pr [\lnot \textsc {qry}]\\ \le&\Pr [b^* = 0|\textsc {qry}]\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 0|\lnot \textsc {qry}]\\ \le&\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 0|\lnot \textsc {qry}] \end{aligned}$$

Then $\Pr [\textsc {dist}\text {-}\textsc {game}_{\mathcal {A},X,\mathcal {U}(\{0,1\}^\kappa )} = \mathsf {true}] = \Pr [b = b^*]$ is the probability of success of the distinguisher. Applying total probability we obtain

$$\begin{aligned} \Pr [b = b^*]&= \Pr [b = b^*|b = 0]\Pr [b = 0] + \Pr [b = b^*|b = 1]\Pr [b = 1]\\&= \frac{1}{2}(\Pr [b^* = 0|b = 0] + \Pr [b^* = 1|b = 1])\\&\le \frac{1}{2}(\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 0|\lnot \textsc {qry}] + \Pr [b^* = 1|b = 1])\\&= \frac{1}{2}(\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 1] + \Pr [b^* = 1|b = 1])\\&= \frac{1}{2}(\Pr [\textsc {qry}] + \Pr [b^* = 0|b = 1] + (1 - \Pr [b^* = 0|b = 1]))\\&= \frac{1}{2}(1 + \Pr [\textsc {qry}]) \le \frac{1}{2} + \textsf {negl}(\kappa )\end{aligned}$$

   $\square$