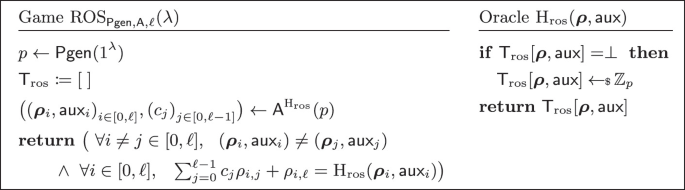On the (in)security of ROS

Abstract

We present an algorithm solving the ROS (Random inhomogeneities in a Overdetermined Solvable system of linear equations) problem mod p in polynomial time for $\ell > \log p$ dimensions. Our algorithm can be combined with Wagner’s attack, and leads to a sub-exponential solution for any dimension $\ell$ with best complexity known so far.

When concurrent executions are allowed, our algorithm leads to practical attacks against unforgeability of blind signature schemes such as Schnorr and Okamoto–Schnorr blind signatures, threshold signatures such as GJKR and the original version of FROST, multisignatures such as CoSI and the two-round version of MuSig, partially blind signatures such as Abe–Okamoto, and conditional blind signatures such as ZGP17. Schemes for e-cash and anonymous credentials (such as Anonymous Credentials Light) inspired from the above are also affected.

1 Introduction

One of the most fundamental concepts in cryptanalysis is the birthday paradox. Roughly, it states that among $O(\sqrt{p})$ random elements from the range ${\left[ 0,p-1\right] }$ (where p is a prime), there exist two elements a and b such that $a=b$, with high probability. In a seminal work, Wagner gave a generalization of the birthday paradox to $\ell$ dimensions which asks to find $x_i\in L_i, i\in {\left[ 0,\ell -1\right] }$ such that $x_0+ \cdots + x_{\ell -1}=0 \pmod p$, where $L_i$ are lists of random elements.

His work also showed a simple and elegant algorithm to solve the problem in subexponential time $O((\ell +1) \cdot 2^{\left\lceil \log p\right\rceil /(1 + \left\lfloor \log (\ell + 1)\right\rfloor )})$ and explained how it could be applied to perform cryptanalysis on various schemes. Among the most important applications of Wagner’s technique is a subexponential solution to the ROS (Random inhomogeneities in a Overdetermined Solvable system of linear equations) problem [Sch01, FPS20], which is defined as follows. Given a prime number p and access to a random oracle ${\textsc {H}_{{\text {ros}}}}$ with range in $\mathbb {Z}_p$, the ROS problem (in dimension $\ell$) asks to find $(\ell +1)$ affine functions $\boldsymbol{\rho }_i$ for $i=0, \dots , \ell$, $(\ell +1)$ bit strings $\textsf {aux}_i \in {\{0,1\}}^*$ (with $i \in {\left[ 0,\ell \right] }$), and a vector $\mathbf {c} = (c_0, \dots , c_{\ell -1})$ such that:

$$\begin{aligned} {\textsc {H}_{{\text {ros}}}}{(\boldsymbol{\rho }_i, \textsf {aux}_i)} = \boldsymbol{\rho }_i(\mathbf {c}) \qquad \text {for all } i \in {\left[ 0,\ell \right] }. \end{aligned}$$

This problem was originally studied by Schnorr [Sch01] in the context of blind signature schemes. Using a solver for the ROS problem, Wagner showed that the unforgeability of the Schnorr and Okamoto-Schnorr blind signature schemes can be attacked in subexponential time whenever more than $O(\log p)$ signatures are issued concurrently. In this work, we revisit the ROS problem and its applications. We make the following contributions.

• We give the first polynomial time solution to the ROS problem for $\ell > \log p$ dimensions.

• We show how the above solution can be combined with Wagner’s techniques to yield an improved subexponential algorithm for dimensions lower than $\log p$. The resulting construction offers a smooth trade-off between the work and the dimension needed to solve the ROS problem. It outperforms the runtime of Wagner’s algorithm for a broad range of dimensions.

• Finally, we describe how to apply our new attack to an extensive list of schemes. These include: blind signatures [PS00, Sch01], threshold signatures [GJKR07, KG20a], multisignatures [STV+16, MPSW18a], partially blind signatures [AO00], conditionally blind signatures [ZGP17, GPZZ19], and anonymous credentials [BL13, Bra94] in a concurrent setting with $\ell > \log p$ parallel executions. While our attacks do not contradict the security arguments of those schemes (which are restricted only to sequential or bounded number of executions), it proves that these schemes are unpractical for some real-world applications (cf. Sect. 7).

1.1 Technical Overview

Let $\mathsf {Pgen}(1^\lambda )$ be a parameter generation algorithm that given as input the security parameter $\lambda$ in unary form, outputs a prime p of length $\lambda = \lceil \log p \rceil$. In this work, we prove the following main theorem:

Theorem 1

(ROS attack). If $\ell > \lambda$, then there exists a (probabilistic) adversary that runs in expected polynomial time and solves the ROS problem relative to $\mathsf {Pgen}$ with dimension $\ell$ with probability 1.

Let $B(\mathbf {x}):=\sum _{i=0}^{\lambda -1} 2^i \boldsymbol{\rho }_i(x_i)$ for functions $\rho _i$ where $i\in [0,\lambda -1]$. If we can set $\rho _i(x_i)$ to be the multivariate polynomials that evaluate to 0 at the point $c_i^0$ and to 1 at the point $c_i^1$ (for $i \in {\left[ 0,\ell -1\right] }$), then we can write any value $y\in [0,p-1]$ as $y=B(c_0^{b_0},\dots ,c_{\ell -1}^{b_{\ell -1}})$, where the $b_i$ values are such that $y=\sum _{i=0}^{\lambda -1} 2^i b_i$. Using this idea, we first define all the functions $\boldsymbol{\rho }_0,\dots ,\boldsymbol{\rho }_{\ell -1}$ along with the corresponding pairs of points $c_i^0,c_i^1$ that are obtained as $c^b_i:={\textsc {H}_{{\text {ros}}}}{(\boldsymbol{\rho }_i, b)}$. In a second step, we choose $\boldsymbol{\rho }_\ell (\mathbf {x}):=B(\mathbf {x})$, and query $y:={\textsc {H}_{{\text {ros}}}}{(\boldsymbol{\rho }_\ell , \textsf {aux}_\ell )}$. Now, we can write $y=\sum _{i=0}^{\lambda -1} 2^i b_i$ which determines a point $c_i^{b_i}$ from every pair. We can output the chosen points in $\mathbf {c}$ along with the vector of affine functions $(\boldsymbol{\rho }_0, \dots , \boldsymbol{\rho }_\ell )$ as a solution to the ROS problem. (Note that $\boldsymbol{\rho }_{\ell }=B(\mathbf {x})$ is also affine.) This attack runs in expected polynomial time (since with small probability, ${\textsc {H}_{{\text {ros}}}}$ produces collisions, in which case steps need to be repeated) and works whenever $\ell >\log p$. This requirement ensures that it is always possible to write any value with $\ell$ terms in binary representation. To circumvent the restriction $\ell > \log p$, we prove a second theorem:

Theorem 2

(Generalized ROS attack). Let $L \ge 0$ be an integer and $w \ge 0$ be a real number. If $\ell \ge \max \{2^w-1,\lceil 2^w-1+\lambda -(w+1)\cdot L\rceil \}$, then there exists a (probabilistic) adversary that runs in expected time $O(2^{w+L})$ and solves the ROS problem relative to $\mathsf {Pgen}$ and dimension $\ell$ with probability 1.

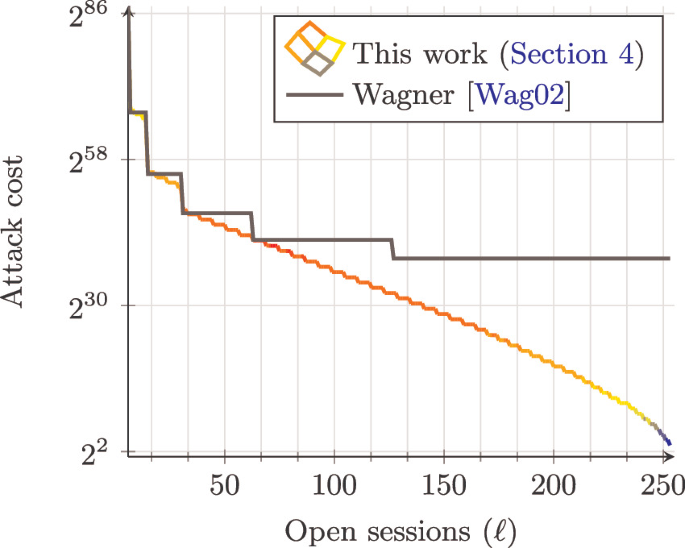
The idea of this attack is to combine the technique from the first attack with the basic subexponential attack of Wagner. Instead of writing y entirely in binary as above, which requires $\ell$ dimensions, we first find a sum s of $2^w$ values which include y, but satisfies $\left|s \right|\in [0,\frac{p}{2^{(w+1)\cdot L}}-1] \pmod p$. Note that s can be represented with $\lambda -(w+1)\cdot L$ many bits in binary representation. This approach requires, in total, $\lceil 2^w+\lambda -(w+1)\cdot L-1\rceil$ dimensions and $2^{w+L}$ overall work. As illustrated in Fig. 4, this leads to improvements over Wagner’s attack relatively quickly as the dimension $\ell$ of the ROS problem increases. We remark that, while in our first attack we give a concrete probability of failure, our second attack is based on the conjecture that Wagner’s algorithm for $\mathbb {Z}_p$ succeeds with constant probability. While we are not aware of any formal analysis of Wagner’s algorithm over $\mathbb {Z}_p$, we remark that it is considered a standard cryptanalytic tool [DEF+19]. Our attack can be seen as strictly improving over its (conjectured) performance when applied to solve the ROS problem.

1.2 Impact of the Attacks

Any cryptographic construction that bases its security guarantees on the hardness of the ROS problem is affected by our attacks.

Blind Signatures. An immediate consequence of our findings is the first polynomial-time attack against Schnorr blind signatures [Sch01] and Okamoto–Schnorr blind signatures [PS00] in the concurrent setting with $\ell > \log p$ parallel executions.¹ Structurally, our attack builds on the one shown by Schnorr [Sch01], who showed that a solver to the ROS problem can be turned into an attacker against one-more unforgeability of blind Schnorr and Okamoto-Schnorr signatures. As a concrete example, the attack in Sect. 5 breaks one-more unforgeability of blind Schnorr signatures over 256-bit elliptic curves in a few seconds (when implemented in Sage [S+20]), provided that the attacker can open 256 concurrent sessions.

Other Affected Constructions. Our attack can be adapted to an extensive list of schemes which include threshold signatures [GJKR07, KG20a], multisignatures [STV+16, MPSW18a], partially blind signatures [AO00], conditionally blind signatures [ZGP17, GPZZ19], blind anonymous group signatures [CFLW04], blind identity-based signcryption [YW05], and blind signature schemes from bilinear pairings [CHYC05]. We note that some of the previous works claim security only for non-concurrent executions or with a bounded number of executions; therefore, our attacks do not contradict their security claims but render these schemes unsuitable for a broad range of real-world use cases.

Scope of Our Attacks and Countermeasures. Our attacks do not extend to the modified-ROS [FPS20] and the generalized-ROS [HKLN20] problems. The concrete hardness of both problems remains an intriguing open question.

2 Preliminaries

In this work, we assume that logarithm is always base 2. Let again $\mathsf {Pgen}(1^\lambda )$ be a parameter generation algorithm that given as input the security parameter $\lambda$ in unary outputs a prime p of length $\lambda = \lceil \log p \rceil$. The ROS problem for $\ell$ dimensions, displayed in Fig. 1, is hard if no adversary can solve the ROS problem in time polynomial in the security parameter $\lambda$. i.e.:

Fig. 1.

The ${\text {ROS}}^{}_{\mathsf {Pgen}, \mathcal {A}, \ell }(\lambda )$ game. Above, $\rho _{i,j}$ is the j-th coefficient of the polynomial $\boldsymbol{\rho }_i$, i.e., $\boldsymbol{\rho }_i(\mathbf {x}) = \sum _{j=0}^{\ell -1} \rho _{i,j} x_i + \rho _{i,\ell }$.

Alternative Formulations of ROS. Fuchsbauer et al. [FPS20, Fig. 7] present a variant of ${\text {ROS}}^{}_{\mathsf {Pgen}, \mathcal {A}, \ell }(\lambda )$ the gamewith linear instead of affine functions $\boldsymbol{\rho }_i$ (i.e., where $\rho _{i,\ell } = 0$). Hauck et al. [HKL19, Fig. 3] allow only for linear functions, and do not allow for auxiliary information $\textsf {aux}$ within ${\textsc {H}_{{\text {ros}}}}$ (i.e., where $\textsf {aux}_i = \bot$).² These formulations are all equivalent.

First, any adversary $\mathcal {A}$ for ROS with affine functions as per Fig. 1 can be reduced to an adversary $\mathcal {B}$ for ROS with linear functions as per [FPS20]: $\mathcal {B}$ runs $\mathcal {A}$ and for every query of the form $((\rho _{i, 0}, \dots , \rho _{i, \ell }), \textsf {aux}_i)$ to the oracle ${\textsc {H}_{{\text {ros}}}}$ (made by $\mathcal {A}$), it returns ${\textsc {H}_{{\text {ros}}}}((\rho _{i, 0}, \dots , \rho _{i, \ell -1}), (\rho _{i, \ell } \Vert \textsf {aux}_i)) - \rho _{i, \ell }$. Finally, $\mathcal {B}$ modifies accordingly the solution output by $\mathcal {A}$ by concatenating $\rho _{i,\ell }$ to the corresponding $\textsf {aux}_i$.

Second, any adversary $\mathcal {A}$ for ROS with linear functions can be reduced to an adversary $\mathcal {B}$ for ROS with linear functions and without auxiliary information as per [HKL19]. We assume without loss of generality that $\mathcal {A}$ never makes twice the same query. Then $\mathcal {B}$ runs $\mathcal {A}$ and for every query of the form $((\rho _{i, 0}, \dots , \rho _{i, \ell -1},0), \textsf {aux}_i)$ to the oracle (made by $\mathcal {A}$), it picks a random scalar $r \in \mathbb {Z}_p^*$ and returns ${\textsc {H}_{{\text {ros}}}}((r \cdot \rho _{i, 0}, \dots , r \cdot \rho _{i, \ell -1}), \perp ) \cdot r^{-1} \bmod p$. When $\mathcal {A}$ outputs a solution ${(\boldsymbol{\rho }_i, \textsf {aux}_i)}_{i \in {\left[ 0,\ell \right] }}, {(c_j)}_{j \in {\left[ 0,\ell -1\right] }}$, $\mathcal {B}$ outputs $(r \cdot \boldsymbol{\rho }_i)_{i \in {\left[ 0,\ell \right] }}, (c_j)_{j \in {\left[ 0,\ell -1\right] }}$. The simulation of the oracle ${\textsc {H}_{{\text {ros}}}}$ is perfect unless there is a collision in the scalar r, which happens with negligible probability in $\lambda$.

3 Attack

In this section, we prove Theorem 1. We abuse notation and $\boldsymbol{\rho }_i$ denotes both the vector $\boldsymbol{\rho }_i = (\rho _{i,0},\dots ,\rho _{i,\ell }) \in \mathbb {Z}_p^{\ell +1}$ and the corresponding affine function $\boldsymbol{\rho }_i(\mathbf {x}) = \sum _{j=0}^{\ell -1} \rho _{i,j} \cdot x_j + \rho _{i,\ell }$ (where $\mathbf {x} = (x_0,\dots ,x_{\ell -1})$).

Proof

(of Theorem 1). We construct an adversary for ${\text {ROS}}^{}_{\mathsf {Pgen}, \mathcal {A}, \ell }(\lambda )$, where $\ell > \log p$. Recall that to simplify the description of the attack, we use a polynomial formulation of ROS, i.e., we represent vectors $\boldsymbol{\rho }_{i} = (\rho _{i,0}, \dots , \rho _{i, \ell })$ as linear multivariate polynomials in $\mathbb {Z}_p[x_0, \dots , x_{\ell -1}]$:

$$\begin{aligned} \boldsymbol{\rho }_i(x_0,\dots ,x_{\ell -1}) = \rho _{i, 0}x_0 + \dots + \rho _{i,\ell -1} x_{\ell -1} + \rho _{i, \ell } . \end{aligned}$$

(1)

The goal for the adversary $\mathcal {A}$ is to output $(\boldsymbol{\rho }_i,\textsf {aux}_i)_{i\in {\left[ 0,\ell \right] }}$ and $\mathbf {c} = (c_0, \dots , c_{\ell -1})$ such that:

$$\begin{aligned} \boldsymbol{\rho }_i(\mathbf {c}) = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}_i) \qquad \text {for all } i \in {\left[ 0,\ell \right] }. \end{aligned}$$

Define:

and find two strings $\textsf {aux}_i^0$ and $\textsf {aux}_i^1$ such that are different for $b=0$ and $b=1$.³ Then, let:

for all $i =0, \dots , \ell -1$. We remark that, if $x_i = c^b_i$, then $x_i' = b$ (for $b =0,1$). Define and query .Finally, write y in binary as:

$$\begin{aligned} y = \sum _{i=0}^{\ell -1}2^{i}b_i \pmod p. \end{aligned}$$

(As $2^\ell > p$, it is possible to write y this way, and this implicitly defines the $b_i$’s.) The adversary $\mathcal {A}$ outputs the solution $(\boldsymbol{\rho }_0,\textsf {aux}_0^{b_0}), \dots ,(\boldsymbol{\rho }_{\ell -1}, \textsf {aux}_{\ell -1}^{b_{\ell -1}}),(\boldsymbol{\rho }_{\ell },\perp )$ and . We have indeed that, for $i \in {\left[ 0,\ell -1\right] }$, $\boldsymbol{\rho }_i(\mathbf {c}) = c_i^{b_i} ={\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}_i^{b_i})$ and:

$$\begin{aligned} \boldsymbol{\rho }_{\ell }(\mathbf {c}) = \sum _{i=0}^{\ell -1} 2^ix'_i(\mathbf {c}) = \sum _{i=0}^{\ell -1} 2^ib_i = y = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_{\ell },\perp ) . \end{aligned}$$

   $\square$

Remark 1

In [FPS20, Sec. 5], Fuchsbauer, Plouviez, and Seurin proposed a variant of ROS, called modified ROS. The attack above does not apply to modified ROS.

4 Generalized Attack

We present a combination of Wagner’s subexponential k-list attack and the polynomial time attack from Sect. 3. This combined attack yields a subexponentially efficient algorithm against ROS which requires fewer dimensions than the attack in the previous section (i.e., less than $\lambda = \lceil \log p \rceil$). However, for some practical cases, the attack significantly outperforms Wagner’s attack in terms of work, for the same number of dimensions. At a very high level, our attack works as follows. We set $k_1=2^w-1$, $k_2=\max (0,\,\lceil \lambda -(w+1)\cdot L \rceil )$, and the dimension $\ell = k_1+k_2$, for some integer w and some real number $L>0$.

First, we use a generalization of Wagner’s algorithm to find a “small” sum $s = y_{k_2}^* + \dots + y_{\ell }^*$ of $k_1$ values $y^*_{i}:=-{\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_{i},\textsf {aux}_i)$, where the polynomials $\boldsymbol{\rho }_i(\mathbf {x})$ are chosen to make the second step of the attack work.⁴ As we describe below, we can obtain that $|s| < 2^{k_2-1}$ using $O(2^{w+L})$ hash queries and space $O(w 2^{L})$. Then, we use the technique from the previous section in order to represent the sum s as a binary sum of at most $k_2$ terms. Finally, we subtract the $k_1-1$ terms $y_{k_2}^*,...,y_{k_2+k_1-1}^*=y_{\ell -1}^*$ to extract the term $y_{\ell }^*$. This solves the ROS problem. The attack runs in overall time $O(2^{w+L})$, space $O(w 2^{L})$, and requires $\ell =\max (2^w-1,\, \lceil 2^w-1+\lambda - (w+1)\cdot L \rceil )$ dimensions.

We remark that the attack is a generalization of both Wagner’s attack and our polynomial-time attack from Sect. 3. Wagner’s attack corresponds to the case where $L = \lambda / (w+1)$ and $\ell = 2^w-1$. Our polynomial-time attack corresponds to the case $w=0$, $L=0$, $\ell = \lambda$.

Examples. For a prime p of $\lambda = 256$ bits, a concrete example yields $w=5,L=15$, i.e., $\ell =32+256-6\cdot 15-1=197$ dimensions and time roughly $2^{20}$ and space roughly $5 \cdot 2^{15}$ (elements of $\mathbb {Z}_p$). On the other hand, Wagner’s algorithm for 197 dimensions requires time roughly $2^{\lfloor \log 197\rfloor }\cdot 2^{\frac{256}{\lfloor \log 197\rfloor +1}}=2^7\cdot 2^{32}=2^{39}$ and space roughly $\lfloor \log 197\rfloor \cdot 2^{{\frac{256}{\lfloor \log 197\rfloor +1}}} = 7 \cdot 2^{32}$.

For a 512 bit modulus, a concrete example yields $w=6,L=46$, i.e., $\ell =64+512-7\cdot 46-1=253$ dimensions and time roughly $2^{53}$ and space roughly $6 \cdot 2^{46}$. Wagner’s algorithm for 254 dimensions requires time roughly $2^{\lfloor \log 254\rfloor }\cdot 2^{\frac{512}{\lfloor \log 255\rfloor +1}}=2^7\cdot 2^{64}=2^{71}$ and space roughly $\lfloor \log 254\rfloor \cdot 2^{\frac{512}{\lfloor \log 255\rfloor +1}} = 7 \cdot 2^{64}$.⁵

4.1 Generalized k-List Algorithm

In this section, we write elements $\mathbb {Z}_p$ as signed integers in $[-\frac{p-1}{2},\frac{p-1}{2}]$. Let w and L be two positive integers. We define the following integer intervals:

Remark that $\mathbb {Z}_p = I_w$.

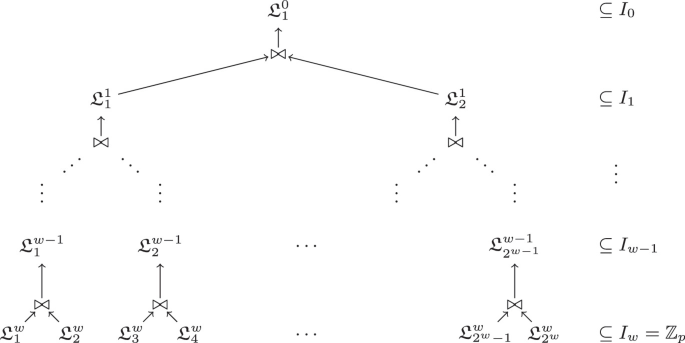
We now describe the k-list algorithm, which is the core of the Wagner’s algorithm. We generalize it to match our needs and to output elements that sum to something in $I_{-1}$ rather than to exactly 0. (This essentially corresponds to executing Wagner’s attack as usual, but stopping earlier.) The algorithm is defined relative to random oracle ${\textsc {H}_{{\text {ros}}}}$. It takes as input $(w,L,\boldsymbol{\rho }_1,\dots ,\boldsymbol{\rho }_{k})$ and outputs $(\textsf {aux}^*_1,\dots ,\textsf {aux}^*_k)$ with $k=2^w$ such that:

The high-level idea of the algorithm is to use $2^{w+1}-1$ lists of about $2^L$ values organized as a tree, as depicted in Fig. 2, and to ensure that lists $\mathfrak {L}_i^w$ at level i contains elements from the set $I_i$.

• Setup/Leaves: fills the lists $\mathfrak {L}^w_i$ in the leaves with $2^L$ points of the form ${\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}) \in \mathbb {Z}_p = I_w$, for $\textsf {aux}\in {[1,2^L]}$.

• Collisions/Join: The algorithm now proceeds to find collisions in levels from w to 1. At level i, process the $2^{i-1}$ pairs of lists $(\mathfrak {L}^i_1,\mathfrak {L}^i_2),\dots ,(\mathfrak {L}_{2^i-1},\mathfrak {L}_{2^i})$ into $2^{i-1}$ lists $\mathfrak {L}^{i-1}_1,\dots ,\mathfrak {L}^{i-1}_{2^{w-1}}$ as follows:

  

  (Remember that $a,b \in \mathbb {Z}_p$ and $a+b$ is computed modulo p.) Moreover, we implicitly assume that the algorithm stores back pointers to a and b s.t. they can efficiently be recovered at a later point.

• Output: Let $\mathfrak {L}^0 = \mathfrak {L}^0_1$ denote the (only) list created at level 1. The algorithm finds an element $s \in \mathfrak {L}^0$ such that $s \in I_{-1}$. If no such element exists, it returns $\perp$. Otherwise, it recovers $k=2^w$ strings $\textsf {aux}^*_1, \dots , \textsf {aux}^*_k$ such that $y_i^*={\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}_i^*) \in \mathfrak {L}^w_i$ and $s = y_1^*+\dots +y_k^*$. It returns $(\textsf {aux}_1^*,\dots , \textsf {aux}_k^*)$.

We formally write the algorithm in Fig. 3.

Fig. 2.

Tree of lists for the k-list algorithm ($\bowtie$ represents the join operation in the algorithm; the sets in the right handside are the sets to which the elements of the lists of a given level belong).

Correctness. We do not prove correctness of in this work, since our algorithm’s correctness is implied by the correctness of Wagner’s original algorithm. More precisely, our algorithm performs identical steps as Wagner’s, but stops upon finding a sum of values with a suitably small absolute value, i.e., one that falls into $I_0$. On the other hand, Wagner’s algorithm keeps continuing with more levels until it finds values who sum to 0. However, we remark that we are not aware of a formal analysis of Wagner’s algorithm for values in $\mathbb {Z}_p$. The work of Minder and Sinclair [MS09] analyses the case of finding a weighted sum of vectors of $\mathbb {Z}_p$ values that sum to zero in each component, but uses a different technique from the one presented in Wagner’s paper (and used here). Our attack can be seen as working under the assumption that Wagner’s algorithm works correctly, i.e., has constant failure probability (see below). We can repeat the attack until it succeeds, which makes the resulting algorithm expected polynomial time. Formally analyzing the failure probability of Wagner’s algorithm over $\mathbb {Z}_p$ remains an important open problem.

Complexity. Overall, the algorithm runs in time $O(2^{w+L})$ and is conjectured to succeed with constant probability. (As described [Wag02], this running time is made possible using an optimized join operation such as Hash Join or Merge Join). The algorithm uses space $O(2^{w+L})$, but by evaluating the collisions/joins in postfix order (in the tree), this can be reduced to $O(w 2^L)$.

Fig. 3.

The k-list algorithm.

4.2 Combined Attack

We now prove Theorem 2.

Proof

Recall that $k_1 = 2^w-1$ and $k_2 = \max (0, \lceil \lambda -(w+1)\cdot L \rceil )$. Set $\ell =k_1+k_2$. For all $i \in {\left[ 0,\ell -1\right] }$, define:

and find two strings $\textsf {aux}_i^0$ and $\textsf {aux}_i^1$ with different hash values $c^{0}_i = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}^0_i)$ and $c^{1}_i = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}^1_i)$. Then, let:

for all $i \in {\left[ 0,k_2-1\right] }$. We remark that, if $x_i = c^b_i$, then $x_i' = b$ (for $b =0,1$). Define:

Run (where $k = k_1+1 = 2^w$) and define for $i \in [k_2,\ell ]$:

and for $i \in [k_2,\ell -1]$. Set:

(2)

Write $s + \lfloor (p-1)/2^{(w+1)\cdot L +1} \rfloor$ in binary as:

$$\begin{aligned} s + \left\lfloor \frac{p-1}{2^{(w+1)\cdot L +1}}\right\rfloor = \sum _{i=0}^{k_2-1} 2^{i}b_i \quad \in {\left[ 0,\left\lfloor \frac{p-1}{2^{(w+1)\cdot L }}\right\rfloor \right] } , \end{aligned}$$

(3)

which is possible since $p < 2^{\lambda }$, $k_2 = \lambda - (w+1)\cdot L$, hence $(p-1) / 2^{(w+1)\cdot L} < 2^{k_2}$. Define:

$\mathcal {A}$ outputs: $(\boldsymbol{\rho }_0,\textsf {aux}_0), \dots ,(\boldsymbol{\rho }_{\ell }, \textsf {aux}_{\ell })$ and:

Fig. 4.

Concrete cost of our combined attack compared to Wagner’s [Wag02] for $\lambda = 256$ and $\ell < 256$. The color key indicates the different values of w used to estimate the cost. For $\ell \ge 256$, the attack of Sect. 3 applies.

We have indeed that:

$$ \boldsymbol{\rho }_i(\mathbf {c}) = c_i = {\left\{ \begin{array}{ll} c_i^{b_i} = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}^{b_i}_i) &{}\text {for } i \in [0,k_2-1] ,\\ y_i^* = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_i,\textsf {aux}^*_i) &{}\text {for } i \in [k_2,k_1+k_2-1] . \end{array}\right. } $$

and:

$$\begin{aligned} \boldsymbol{\rho }_{\ell }(\mathbf {c})&= \sum _{i=0}^{k_2-1} 2^ix'_i(\mathbf {c}) - \left\lfloor \frac{p-1}{2^{(w+1)\cdot L + 1}} \right\rfloor - \sum _{i=k_2}^{k_1+k_2-1} x_i(\mathbf {c}) \\&= \sum _{i=0}^{k_2-1} 2^ib_i - \left\lfloor \frac{p-1}{2^{(w+1)\cdot L + 1}} \right\rfloor - \sum _{i=k_2}^{k_1+k_2-1} y^*_i\\&= s - \sum _{i=k_2}^{k_1+k_2-1} y^*_i= y^*_{k_2+k_1} = {\textsc {H}_{{\text {ros}}}}(\boldsymbol{\rho }_\ell ,\textsf {aux}^*_\ell ) , \end{aligned}$$

where the third equality comes from Eq. 2 while the fourth equality comes from Eq. 3. The attack requires $k_1+k_2=\max \{2^w-1,\lceil 2^w-1+\lambda -(w+1)\cdot L \rceil \}$ dimensions, runs in time $O(2^{w+L})$, and in space $O(w 2^L)$.    $\square$

5 Affected Blind Signatures

For simplicity and clarity of exposition, we implement only the attack presented in Sect. 3. Our attack can be easily adapted for the one presented in Sect. 4.

Throughout the remaining of this manuscript, we will assume the existence of a group generator algorithm $\mathsf {GrGen}(1^\lambda )$ that, given as input the security parameter in unary form outputs the description $\varGamma = (\mathbb {G}, p, G)$ of a group $\mathbb {G}$ of prime order p generated by G. Similarly to Sect. 2, we assume that the prime p is of length $\lambda$. We use additive notation for the group law.

5.1 Schnorr Blind Signatures

A Schnorr blind signature [Sch01, FPS20] for a message $m \in \{0,1\}^*$ consists of a pair $(R, s) \in \mathbb {G}\times \mathbb {Z}_p$ such that $sG - cX = R$, where and $X \in \mathbb {G}$ is the verification key. A formal description of the protocol can be found in [FPS20, Fig. 6], using the same notation employed here.

We construct a probabilistic (expected) polynomial-time adversary $\mathcal {A}$ that is able to produce $\ell +1$ signatures after opening $\ell \ge \left\lceil \log p\right\rceil = \lambda$ parallel sessions. $\mathcal {A}$ selects a message $m_\ell \in \{0,1\}^*$ for which a signature will be forged. It opens $\ell$ parallel sessions, querying $\textsc {Sign}_0()$ and receiving $\mathbf {R} = (R_0, \dots , R_{\ell -1}) \in \mathbb {G}^\ell$. Let $m_i^b$ be a random message and for $i \in {\left[ 0,\ell -1\right] }$ and $b \in \{0,1\}$. If $c_i^0 = c_i^1$, two different messages $m_i^0$ and $m_i^1$ are chosen until $c_i^0 \ne c_i^1$. Define as per Sect. 3, that is:

(4)

Let , where $\boldsymbol{\rho }_\ell (\mathbf {R})$ denotes the evaluation of the affine function $\boldsymbol{\rho }_\ell$ over $(R_0, \dots R_{\ell -1})$. Define and let $\mathbf {c} = (c_0^{b_0}, \dots , c_{\ell -1}^{b_{\ell -1}})$. Complete the $\ell$ opened sessions querying $\textsc {Sign}_1(i, c_i^{b_i})$, for $i \in {\left[ 0,\ell -1\right] }$. The adversary thus obtains responses satisfying:

$$ s_i G - c_i^{b_i} X = R_i,\qquad \text {for } i \in {\left[ 0,\ell -1\right] }. $$

Let . Then $(m_\ell , (R_\ell , s_\ell ))$ is a valid forgery. In fact, by perfect correctness of Schnorr blind signatures, we have:

$$\begin{aligned} R_\ell = \boldsymbol{\rho }_\ell (\mathbf {R}) - \rho _{\ell , \ell } X&= \sum ^{\ell -1}_{i=0} \rho _{\ell , i} \cdot R_i + \rho _{\ell , \ell } \cdot (G-X) \\&= \sum ^{\ell -1}_{i=0} \rho _{\ell , i} \cdot (s_iG - c_i^{b_i}X) + \rho _{\ell , \ell } \cdot (G-X) \\&= \boldsymbol{\rho }_\ell (\mathbf {s}) \cdot G - \boldsymbol{\rho }_{\ell }(\mathbf {c}) \cdot X\\&= s_\ell G - c_\ell X, \end{aligned}$$

where $c_\ell = \mathsf {H}(R_\ell , m_\ell ) = \boldsymbol{\rho }_\ell (\mathbf {c})$ by Eq. 4. Let for $i \in {\left[ 0,\ell -1\right] }$. The adversary outputs $(m_i, (R_i, s_i))$ for $i \in {\left[ 0,\ell \right] }$.

Remark 2

The attack does not apply to the clause blind Schnorr signature scheme [FPS20, Sec. 5], which relies on the modified ROS problem.

5.2 Okamoto–Schnorr Blind Signatures

An Okamoto–Schnorr blind signature [PS00] for a message m consists of a tuple $(R, s, t) \in \mathbb {G}\times \mathbb {Z}_p^2$ such that $sG + tH - cX = R$, where , and (G, H) are two nothing-up-my-sleeve generators of $\mathbb {G}$. The attack of the previous section directly extends to Okamoto–Schnorr signatures: $\mathcal {A}$ operates exactly as before until Eq. 4. Then, the forgery is constructed as:

We stress again that this does not contradict the security analysis of Stern and Pointcheval [PS00], whose security was reduced to ${\text {DLOG}}^{}_{\mathsf {GrGen},\mathcal {A}}(\lambda )$ for a $\mathsf {polylog}(\lambda )$ number of queries.

6 Other Constructions Affected

In this section, we overview how the attacks presented in Sects. 3 and 4 apply to a number of other cryptographic primitives. To simplify exposition, we focus on adapting the attack of Sect. 3. We note that, in some cases (e.g., multi-signatures), we break the security claims of the papers, while for other primitives (e.g., threshold signatures), our attack illustrates the tightness of the security theorems, which assume either non-concurrent setting, or up to a logarithmic number of concurrent executions.

6.1 Multi-signatures

A multi-signature scheme allows a group of signers $S_1, \ldots , S_n$, each having their own key pair $(\mathsf {pk}_j, \mathsf {sk}_j)$, to collaboratively sign a message m. The resulting signature can be verified given the message and the set of public keys of all signers.

CoSi. CoSi is a multi-signature scheme introduced by Syta et al. [STV+16], that features a two-round signing protocol. The signers are organized in a tree structure, where $S_1$ is the root of the tree. A signature for a message $m \in \{0,1\}^*$ consists of a pair $(c, s) \in \mathbb {Z}_p^2$ such that $c=\mathsf {H}(sG-c\cdot \mathsf {pk}, m)$, where $\mathsf {pk}= \sum _{j=1}^{n} \mathsf {pk}_j \in \mathbb {G}$ is the aggregated verification key. A formal description of the protocol can be found in [DEF+19, Sec. 2.5]; we use the same notation, except that we employ additive notation xG instead of multiplicative notation $g^x$.

Attack. We present an attack for a two-node tree where the attacker controls the root $S_1$. The attack can easily be extended to other settings, similarly to [DEF+19, Sec. 4.2]. Our attack allows the signer $S_1$ to forge one signature, for an arbitrary message $m_\ell \in \{0,1\}^*$, after performing $\ell \ge \left\lceil \log p\right\rceil = \lambda$ interactions with the honest signer $S_2$. Recall that $\mathsf {pk}= \mathsf {pk}_1 + \mathsf {pk}_2$ where $\mathsf {pk}_i = \mathsf {sk}_i G$. The signing protocol proceeds as follows. First, $S_1$ obtains a commitment $t_2 = r_2 G$ from $S_2$, and computes ${\bar{t}} = t_1 = r_1G + t_2$ for a random $r_1$. Then, $S_1$ computes the challenge $c = \mathsf {H}({\bar{t}}, m)$, and sends $({\bar{t}}, c)$ to $S_2$. Next, $S_2$ returns . Finally, $S_1$ computes and outputs the signature (c, s) for the message m.

The attack proceeds as follows. $S_1$ opens $\ell$ parallel sessions with $\ell$ arbitrary distinct messages $m_0, \ldots ,m_{\ell -1}\in \{0,1\}^*$. For each session, $S_1$ gets the commitments $t_i=r_iG$ from $S_2$ at the end of the first round of signing. Now, it samples two random values $r_{i,0}, r_{i,1}$ for each $i\in {\left[ 0,\ell -1\right] }$, defines $\bar{t}_i^0=r_{i,0}G+t_i$ and $\bar{t}_i^1=r_{i,1}G+t_i$, and computes $c_i^b = \mathsf {H}(\bar{t}_i^b, m_i)$. (As usual, if $c_i^0 = c_i^1$, $S_1$ samples again $r_{i,0}$ and $r_{i,1}$ until $c_i^0 \ne c_i^1$.) $S_1$ then defines the polynomial , computes and . $S_1$ computes $d_\ell = c_\ell - \boldsymbol{\rho }(c_0^0, \ldots , c_{\ell -1}^0)$ and writes this value in binary as $d_\ell = \sum _{i=0}^{\ell -1}2^ib_i$. It then closes the $\ell$ sessions by using $\bar{t}_i= \bar{t}_i^{b_i}$ and $c_i = c_i^{b_i}$. At the last step of the signing sessions, $S_1$ obtains values $s_i=r_i+c_i\cdot \mathsf {sk}_2$ from $S_2$, and closes the sessions honestly using $r_{i, b_i}$. Finally, $S_1$ concludes its forgery by defining : the pair $(c_\ell , s_\ell )$ is a valid signature for $m_\ell$. In fact:

$$\begin{aligned} s_\ell G-c_\ell \cdot \mathsf {pk}&= (\boldsymbol{\rho }(\mathbf {s}) + c_\ell \cdot \mathsf {sk}_1)G -c_\ell \cdot \mathsf {pk}\\&= \sum _{i=0}^{\ell -1} \frac{2^i s_i}{c_i^1 - c_i^0} G -c_\ell \cdot \mathsf {pk}_2 \\&= \sum _{i=0}^{\ell -1} \frac{2^i (r_i + c_i^{b_i}\cdot \mathsf {sk}_2)}{c_i^1 - c_i^0} G-c_\ell \cdot \mathsf {pk}_2 \\&= \sum _{i=0}^{\ell -1} \frac{2^i r_i}{c_i^1 - c_i^0} G + \left( \sum _{i=0}^{\ell -1} \frac{2^i c_i^{b_i}}{c_i^1 - c_i^0} -c_\ell \right) \cdot \mathsf {pk}_2 \\&= \sum _{i=0}^{\ell -1} \frac{2^i t_i}{c_i^1 - c_i^0} + \left( \sum _{i=0}^{\ell -1} 2^i b_i + \sum _{i=0}^{\ell -1} \frac{2^i c_i^0}{c_i^1 - c_i^0} -c_\ell \right) \cdot \mathsf {pk}_2 \\&= \sum _{i=0}^{\ell -1} \frac{2^i t_i}{c_i^1 - c_i^0} + \underbrace{\left( \sum _{i=0}^{\ell -1} 2^i b_i + \boldsymbol{\rho }(c_0^0, \ldots , c_{\ell -1}^0) - c_\ell \right) }_{=d_\ell -d_\ell =0}\cdot \mathsf {pk}_2 \\&= \boldsymbol{\rho }(t_0, \ldots , t_{\ell -1}) = t_\ell \,, \end{aligned}$$

and $c_\ell = \mathsf {H}(t_\ell , m_\ell )$ by definition.

Two-Round MuSig. As in [DEF+19], the above technique (with some minor modifications) can be applied to the two-round MuSig as initially proposed by Maxwell et al. [MPSW18a], as the main difference between CoSi and two-round MuSig is in how the public key is aggregated in order to avoid rogue-key attacks. Our attack does not apply to the updated MuSig that uses a 3-round signing algorithm [MPSW18b].

6.2 Threshold Signatures

A (t, n)-threshold signature scheme assumes that the secret signing key is split among n parties $\mathsf {P}_1,\ldots ,\mathsf {P}_n$ in a way that allows any subset of at least t out of the n parties to produce a valid signature. As long as the adversary corrupts less than the threshold number of parties, it is not possible to forge signatures or learn any information about the signing key.

GJKR07. Gennaro, Jarecki, Krawczyk, Rabin proposed a threshold signature scheme based on Pedersen’s distributed key generation (DKG) protocol in [GJKR07, Section 5.2]. At a very high level, Pedersen’s DKG protocol allows to generate a random group element $X = \chi G$ so that its discrete logarithm $\chi$ is shared both additively and according to Feldman secret sharing [Fel87] scheme, between a set of “qualified” parties. For the attack we present below, all parties $\mathsf {P}_1,\dots ,\mathsf {P}_n$ (included the ones that are controlled by the adversary) will remain qualified.⁶ We denote by $\chi _j$ the additive share of party $\mathsf {P}_j$. We have $\chi = \sum _{j=1}^n \chi _j$. Importantly for the attack, the adversary controlling for example $\mathsf {P}_1$, can see all the group elements $\chi _2 G, \dots , \chi _n G$ and then can choose its value $\chi _1$. This is due to the way the Feldman secret sharing is performed.

In the threshold signature scheme of Gennaro et al. [GJKR07], the parties execute a distributed key generation procedure to produce a verification key , where the secret key $\mathsf {sk}$ is additively shared between the parties: each party $\mathsf {P}_j$ has an additive share $\mathsf {sk}_j$, so that $\mathsf {sk}= \sum _{j=1}^n \mathsf {sk}_j$. A signature (R, s) for a message $m \in \{0,1\}^*$ is generated as follows. The participants run once again the distributed key generation protocol to produce a commitment $t = r G \in \mathbb {G}$, where r is additively shared between the parties: each party $\mathsf {P}_j$ has a share $r_j$, so that $r = \sum _{j=1}^n r_j$. Then, each party computes a share of the response:

(5)

Let . Then (c, s) is a valid signature on m. In fact:

$$\begin{aligned} s G = \sum _{j=1}^{n} r_j G + c \cdot \sum _{j=1}^{n} \mathsf {sk}_j \cdot G = t + c \cdot \mathsf {pk}, \end{aligned}$$

(6)

where $c= \mathsf {H}(t, m)$.

Concurrent Setting Insecurity. Gennaro et al. [GJKR07] proved the security of the scheme in a standalone sequential setting, where no two instances of the protocol can be run in parallel. We remark that if an adversary is allowed to start $\ell \ge \lceil \log p \rceil$ sessions in parallel, the attack against CoSi in Sect. 6.1 can be directly adapted to attack this threshold signature scheme for $n=2$. The attack of both schemes use the fact that the adversary $\mathsf {P}_1$ (or signer $S_1$ in CoSi) can see the commitment $t_2 = r_2 G$ of the honest party $\mathsf {P}_2$ (or honest signed $S_2$) and only then choose $r_1$ that defines the commitment $t = r_1 G + t_2$. The generalization to any $n \ge 2$ is straightforward.

Scope of the Attack. Our attack is an attack against the proposed threshold signature scheme when instantiated with Pedersen’s DKG, but not an attack against Perdersen’s DKG itself (i.e., JF-DKG from [GJKR07, Fig. 1]). Furthermore, the attack does not work when Perdersen’s DKG is replaced by the new DKG protocol from [GJKR07, Fig. 2].

Original Version of FROST. Komlo and Goldberg FROST [KG20a] proposed an extension of the above threshold signature scheme that was similarly affected by the above concurrent attack. On 19 July 2020, they updated the signing algorithm [KG20b] in a way that is no more susceptible to the above issue: each party now shares $(D_j, E_j)$ and the commitment is computed as $R = \sum _j D_j + h_j E_j$, where . We direct the reader to [KG20b, Fig. 3] for a more detailed illustration of the problem and the fix.

6.3 Partially Blind Signatures

Partially blind signatures [AO00] are an extension of blind signature schemes that allow the signer to include some public metadata (e.g., expiration date, collateral conditions, server name, etc.) in the resulting signature. The original construction [AO00], as well as schemes inspired from it, such as Anonymous Credentials Light [BL13] and restrictive partially-blind signatures from bilinear pairings [CZMS06], might not provide the desired security properties.

Abe–Okamoto. Abe and Okamoto [AO00, Fig. 1] propose a partially blind signature scheme inspired from Schnorr blind signatures. Given a verification key and some public information $\textsf {info}$ that is hashed into the group , a partially blind signature for the message $m \in \{0,1\}^*$ is a tuple $(r, c, s, d) \in \mathbb {Z}_p$ where $c + d = \mathsf {H}(rG + cX,\,\, sG + dZ,\, Z,\, m)$.

Attack. The security of the above partially blind signature is proved up to a poly-logarithmic number of parallel open sessions in the security parameter [AO00]. We show that the security claim is tight by showing that there exists a poly-time attacker against one-more unforgeability in the setting where the adversary can have $\ell = O(\lambda )$ open sessions using the same metadata $\textsf {info}$. The attack follows essentially the same strategy of Sect. 5.1. First, the attacker opens $\ell$ parallel sessions and obtains the commitments $(A_i, B_i) \in \mathbb {G}^2$ for $i \in {\left[ 0,\ell -1\right] }$. It then constructs the polynomial $\boldsymbol{\rho }_\ell$ as per Eq. 4. The forged signature for an arbitrary message $m^*$ is computed using the challenge:

and closing the $\ell$ sessions as in Sect. 5.1, i.e., by using the challenges $e_i^{b_i}$ where $b_i$ is the i-th bit of the canonical representation of $e_\ell$. Given the signatures $(r_i, c_i^{b_i}, s_i, d_i)$ for $i \in {\left[ 0,\ell -1\right] }$, the attacker can finally create its forgery $(\boldsymbol{\rho }(\mathbf {r}), \boldsymbol{\rho }(\mathbf {c}), \boldsymbol{\rho }(\mathbf {s}), \boldsymbol{\rho }(\mathbf {d}))$. The forgery is indeed correct because:

$$\begin{aligned} \boldsymbol{\rho }(\mathbf {c}) + \boldsymbol{\rho }(\mathbf {d})&= \sum _i \rho _i (c_i^{b_i} + d_i) + \rho _{\ell , \ell } + \rho _{\ell , \ell } \\&= \boldsymbol{\rho }(e_0^{b_0}, \dots , e_{\ell -1}^{b_\ell -1}) + \rho _{\ell , \ell }\\&= \mathsf {H}(\boldsymbol{\rho }_\ell (\mathbf {r}) G + \boldsymbol{\rho }_\ell (\mathbf {c})X,\, \boldsymbol{\rho }_\ell (\mathbf {s})G + \boldsymbol{\rho }_\ell (\mathbf {d})Z,\, Z,\, m^*)\,. \end{aligned}$$

Anonymous Credentials Light. Inspired from Abe’s blind signature [Abe01], Baldimitsi and Lysyanskaya [BL13] developed anonymous credentials light (ACL). The security proof of their scheme is under standard assumptions in the sequential settings. The public parameters are a so-called real public key $Y = xG$ and a tag public key $Z = wG$ (using the paper’s notation). During the signing protocol, the signer produces two shares $Z_1, Z_2$ of Z such that $Z_1 + Z_2 = Z$, and proves either knowledge of Y (referred to as y-side), or of $Z_1, Z_2$ (so-called z-side). The discrete log of $Z_1, Z_2$ is never known by the signer, and the z-branch is inherited by Abe’s blind signature and is necessary for the proof of security.

The essential difference between ACL and Abe’s blind signature is the computation of $Z_1$: while in Abe’s scheme it is computed invoking the random oracle over a random string (so that neither the user nor the signer know its discrete logarithm), in ACL it is computed starting from the user’s commitment $C = \sum _{i=0}^n l_iH_i + rH$ (where $l_0, \dots , l_n)$ is the list of attributes) and the user could know a discrete-log relation across multiple sessions. This difference is fatal in the concurrent settings.

Attack. The attacker $\mathcal {A}$ opens $\ell$ parallel sessions, all with the same commitment C, and will provide a one-more forgery for an arbitrary message $m^*$ on the same commitment C.

After opening the $\ell$ concurrent sessions, the attacker proves in zero-knowledge (as per protocol issuance) that the attributes required are valid, following the reigistration phase as prescribed in the protocol. Let $d_0, \dots , d_{\ell -1}$ denote the randomization key used by the server to re-randomize the commitment C (displayed in [BL13, Fig. 1] as rnd) and sent to the user at the end of the registration phase. Upon receiving $A_i \in \mathbb {G}$ (the commitment of the y-side) and $A'_{1, i}, A'_{2, i}$ (the commitment of the z-side), for $i \in {\left[ 0,\ell \right] }$, the attacker computes the polynomial $\boldsymbol{\rho }_\ell$ defined in Sect. 3 (using the commitments and the message of the previous sessions), and computes the commitment forgeries:

For simplicity, we assume that the re-randomization of Z is not performed by the attacker, i.e. $\tau = 1$, and that no blinding is performed: the attacker simply hashes the values, as they are received from the adversary. $\mathcal {A}$ sends the challenges according to the bits of $\mathsf {H}(Z, C, A_\ell , A_{1, \ell }, A_{2,\ell })$, similarly to Sect. 5, and receives the responses $(c_i, r_i, c'_i,r_{1, i}', r_{2, i}') \in \mathbb {Z}_p^5$, for $i \in {\left[ 0,\ell \right] }$. The adversary $\mathcal {A}$ computes the forged responses for the y-side:

In fact, it holds that:

$$\begin{aligned} r_\ell G + c_\ell Y&= \sum _{i=0}^{\ell } \rho _{i, \ell } \big (r_iG + c_i Y\big ) + \rho _{\ell , \ell } (Y+G) = A_\ell \\ r_{1, \ell }'G + c'_{\ell } C&= \sum _{i=0}^{\ell -1} \rho _{i, \ell } \big (r_{1, i}' G + c'_i (C + d_i G)\big ) + \rho _{\ell , \ell } (C + G) = A_{1, \ell } \\ r_{2, \ell }'G + c'_{\ell }(Z-C)&= \sum _{i=0}^{\ell -1} \rho _{i, \ell } \big (r_{2, i}' G + c'_i (Z - C - d_i G)) + \rho _{\ell , \ell } (Z-C) = A_{2, \ell } \\ \end{aligned}$$

And the verification of the re-randomization $\tau$ is trivially satisfied.

6.4 Conditional Blind Signatures

Conditional blind signatures (CBS), introduced by Grontas et al. [ZGP17], allow a user to request a blind signature on messages of their choice, and the server has a secret boolean input which determines if it will issue a valid signature or not. CBS only allow a designated verifier to check the validity of the signature; the user will not able to distinguish between valid and invalid signatures. Conditional blind signature have application in e-voting schemes [GPZZ19].

ZGP17. Zacharakis et al. [ZGP17] propose an instantiation of CBS as an extension of Okamoto–Schnorr blind signatures, where the (designated) verifier holds a secret verification key $k \in \mathbb {Z}_p$ and publishes $K = kG$ as public information. During the execution of Okamoto–Schnorr, one of the two responses (s, t) will be computed in $\mathbb {G}$ rather than $\mathbb {Z}_p$, using K as a generator. Only the designated verifier, who knows the discrete log of K can now check the verification equation.

The attack from Sect. 5.2 directly applies also to their scheme, and leads to a poly-time adversary that with $\lambda$ queries to the signing oracle for the same bit $b=1$ can produce one-more forgery with overwhelming probability. This attack does not invalidate the security claims of [ZGP17], which are argued only for a poly-logarithmic number of parallel open sessions.

6.5 Other Schemes

The following papers prove rely on the hardness of the ROS problem for their security proofs, and henceforth may not provide the expected security guarantees: blind anonymous group signatures [CFLW04]; blind identity-based signcryption [YW05]; blind signature schemes from bilinear pairings [CHYC05].

7 Conclusions

Our work provides a polynomial attack against ${\text {ROS}}^{}_{\ell }(\lambda )$ when $\ell > \log p$, and a sub-exponential attack for $\ell < \log p$. This impacts the one-more unforgeability property of Schnorr and Okamoto–Schnorr blind signatures, plus a number of cryptographic schemes derived from them. Our attacks run in polynomial time only in the concurrent setting, and only for $\ell > \log p$ parallel signing sessions.

Concretely, the cost of the attack and the number of sessions required are rather small: for today’s security parameters, the attack could be already mounted with $\ell = 9$ parallel open sessions. As already pointed out by [FPS20], even just $\ell = 16$ open sessions could lead to a forgery in time $O(2^{55})$. For $\ell =128$, our attack of Sect. 4 leads to a forgery in time $O(2^{32})$. For $\ell = 256$, our attack of Sect. 3 produces a forgery in a matter of seconds on commodity hardware. Although 256 parallel signing sessions might seem at first unrealistic, modern large-scale web servers must handle more than 10 million concurrent sessions⁷. Given our attack, the main takeaway of our work is that blind Schnorr signatures are unsuitable for wide-scale deployments.

The easiest countermeasure to our attack could be to allow only for sequential signing sessions, as Schnorr blind signatures are unforgeable in the algebraic group model for polynomially many sessions [KLRX]. Another countermeasure to our attack could be to employ (much) larger security parameters, require the signer to enforce strong ratio limits, and perform frequent key rotations, accepting the tradeoffs given by our attacks. Finally, Fuchsbauer et al. [FPS20] recently introduced a variant of blind Schnorr signatures (the clause version) which is unaffected by our attack. Unfortunately, it relies on the conjectured hardness of the so-called modified ROS problem, which is still relatively new and has not been subject to any significant cryptanalysis.

To conclude, other blind signature schemes are to this day considered secure and should be considered as alternatives: blind RSA [Cha82], blind BLS [Bol03], and Abe’s blind signature scheme [Abe01, KLRX].