Efficient Proofs of Knowledge for Threshold Relations

Abstract

Recently, there has been great interest towards constructing efficient zero-knowledge proofs for practical languages. In this work, we focus on proofs for threshold relations, in which the prover is required to prove knowledge of witnesses for k out of $\ell$ statements.

The main contribution of our work is an efficient and modular transformation that starting from a large class of $\varSigma$-protocols and a corresponding threshold relation $\mathcal {R}_\mathsf {k,\ell }$, provides an efficient $\varSigma$-protocol for $\mathcal {R}_\mathsf {k,\ell }$ with improved communication complexity w.r.t. prior results. Our transformation preserves statistical/perfect honest-verifier zero knowledge.

A A \(\varSigma \)-Protocols

We consider a 3-round public-coin protocol $\varPi$ for an NP language $\mathcal {L}$ with a poly-time relation $\mathcal {R}_\mathcal {L}$. $\varPi =(\textsf{P}_0,\textsf{P}_1,\textsf{V})$ is run by a prover running auxiliary algorithms $\textsf{P}_0,\textsf{P}_1$ and a verifier running an auxiliary algorithm $\textsf{V}$. The prover and the verifier receive common input $x$ and the security parameter $1^\lambda$. The prover receives as an additional private input a witness $w$ for $x$. Prover and verifier use the auxiliary algorithms $\textsf{P}_0, \textsf{P}_1,\textsf{V}$¹³ in the following way:

• 1. The prover runs $\textsf{P}_0$ on common input $x$, private input $w$, randomness R, and outputs a message a. The prover sends a to the verifier;

• 2. The verifier samples a random challenge and sends c to the prover;

• 3. The prover runs $\textsf{P}_1$ on common input $x$, private input $w$, first-round message a, randomness R, and challenge c, and outputs the third-round message z, which is then sent to the verifier;

• 4. The verifier outputs 1 if $\textsf{V}(x,a,c,z)=1$, and rejects otherwise.

The transcript (a, c, z) for the protocol $\varPi =(\textsf{P}_0,\textsf{P}_1,\textsf{V})$, and common statement $x$ is called accepting if $\textsf{V}(x,a,c,z)=1$.

Definition 1

A 3-round public-coin protocol $\varPi =(\textsf{P}_0,\textsf{P}_1,\textsf{V})$, is a $\varSigma$-protocol for an NP language $\mathcal {L}$ with a poly-time relation $\mathcal {R}_\mathcal {L}$ iff the following holds

• Completeness: For all $x\in \mathcal {L}$ and $w$ such that $(x,w)\in \mathcal {R}_\mathcal {L}$ it holds that:

  

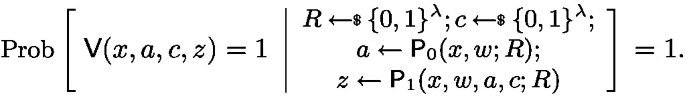
• Special Soundness: $\exists \;PPT\;\textsf{Extract}$, such that on input $x$ and two accepting transcripts $(a,c_0,z_0)$ and $(a,c_1,z_1)$ for $x$, where $c_0\ne c_1$, it holds that

  $$ \text{ Prob }\left[ \;(x,w)\in \mathcal {R}_\mathcal {L}|w\leftarrow \textsf{Extract}(x,a,c_0,c_1,z_0,z_1)\;\right] =1. $$

• Special HVZK (SHVZK): There exists a PPT simulator $\mathcal {S}$ that, on input an instance $x\in \mathcal {L}$ and challenge c, outputs (a, z) such that (a, c, z) is an accepting transcript for $x$. Moreover, the distribution of the output of $\mathcal {S}$ on input $(x,c)$ is computationally/statistically/perfectly indistinguishable from the distribution obtained when the verifier sends c as challenge and the prover runs on common input $x$ and any private input $w$ such that $(x,w) \in \mathcal {R}_\mathcal {L}$.

• Computational Special Soundness: $\exists \; PPT\;\textsf{Extract}\ s.t.\; \forall \;PPT\;\textsf{P}^*\;\exists$ a negl. function $\nu (\cdot )$ such that $\forall x\in \mathcal {L}$, $\text{ Prob }\left[ \;\textsf{ExpExt}_{\textsf{P}^*,\textsf{Extract}}(x)=1\;\right] \le \nu (|x|).$

  

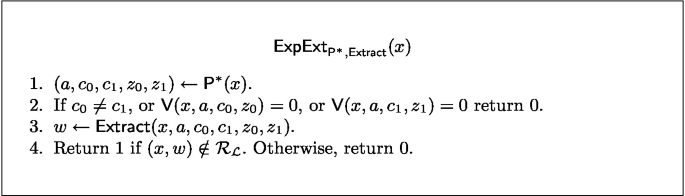
1.1 A.1 A.1 Stackable $\varSigma$-protocols

Definition 2

(Computational/Statistical EHVZK). Let $\varSigma = (\textsf{P}_0,\textsf{P}_1, \textsf{V})$, be a $\varSigma$-protocol for an NP language $\mathcal {L}$. $\varSigma$ is EHVZK if there exists a PPT algorithm $\mathcal {S}^\textsf{EHVZK}$ such that for all PPT/unbounded ${\mathcal {D}}$, and $c\in \{0,1\}^\lambda$, there exists an efficiently samplable distribution $D^{(z)}_{x,c}$ and a negligible function $\nu (\cdot )$ such that for all $x\in \mathcal {L}$

$$ \Big |\text{ Prob }\left[ \;\textsf{ExpEHVZK}_{(\textsf{P}_0,\textsf{P}_1),{\mathcal {D}}}(c)=1\;\right] - \text{ Prob }\left[ \;\textsf{ExpEHVZK}_{\mathcal {S}^\textsf{EHVZK},{\mathcal {D}}}(c)=1\;\right] \Big |\le \nu (|x|). $$

We say instead that a $\varSigma$-protocol is perfect EHVZK if the difference between the probabilities is exactly 0. The experiment $\textsf{ExpEHVZK}$ for EHVZK follows.

Definition 3

($\varSigma$-protocol with recyclable third messages). Let $\varSigma =(\textsf{P}_0,\textsf{P}_1,\textsf{V})$ be a $\varSigma$-protocol for an NP language $\mathcal {L}$, $\varSigma$ has recyclable third messages if for every $c\in \{0,1\}^\lambda$, there exists an efficiently samplable distribution $D^{(z)}_c$, such that for all $(x, w)\in \mathcal {R}_\mathcal {L}$, it holds that

Definition 4

(Stackable $\varSigma$-protocol). We say that a $\varSigma$-protocol $\varSigma =(\textsf{P}_0,\textsf{P}_1,\textsf{V})$, is stackable, if it is a EHVZK $\varSigma$-protocol and has recyclable third messages.