Topological Comparisons of Fluvial Reservoir Rock Volumes Using Betti Numbers: Application to CO$_{2}$ Storage Uncertainty Analysis

Abstract

To prevent the release of large quantities of CO$_{2}$ into the atmosphere, carbon capture and storage (CCS) represents a potential means of mitigating the contribution of fossil fuel emissions to global warming and ocean acidification. Fluvial saline aquifers are favourite targeted reservoirs for CO$_{2}$ storage. These reservoirs are very heterogeneous but their heterogeneities were rarely integrated into CO$_{2}$ reservoir models. Moreover, contrary to petroleum reservoirs, the available dataset is very limited and not supposed to be enriched. This leads to wide uncertainties on reservoir characteristics required for CSS management (injection location, CO$_{2}$ plume migration, etc.). Stochastic simulations are classical strategies in such under-constrained context. They aim at generating a wide number of models that all fit the available dataset. The generated models serve as support for computing the required reservoir characteristics and their uncertainties. A challenge is to optimize the uncertainty computations by selecting stochastic models that should have a priori very different flow behaviours. Fluid flows depend on the connectivity of reservoir rocks (channel deposits). In this paper, it is proposed to study the variability of the Betti numbers in function of different fluvial architectures. The aim is to quantify the impact of fluvial heterogeneities and their spatial distribution on reservoir rock topology and then on CO$_{2}$ storage capacities. Representative models of different scenarios of channel stacking and their internal heterogeneities are generated using geostatistical simulation approaches. The Betti numbers are computed on each generated models and statistically analysed to exhibit if fluvial architecture controls reservoir topology.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The impact of the heterogeneities on the reservoir performances has always been a key topic in geosciences, especially in the case of fluvial reservoirs. They consist of sediments deposited along rivers. They are very heterogeneous and characterized by a complex spatial organization of sedimentary entities.

Many studies have been developed for analyzing uncertainty of hydrocarbon fluvial reservoirs [1]. For instance, stochastic simulation methods have been proposed to generate plausible 3D models of fluvial sedimentary architectures, conditioned to available subsurface data (e.g., seismic, well). These sets of 3D models serve as support for risk assessments. An important issue is to characterize the uncertainties on dynamic reservoir characteristics because flow simulators are highly time and power consuming. As a consequence, only few 3D models of reservoir heterogeneity are used to perform flow simulations. For several years, optimization techniques [2] have been proposed to scan more rapidly the uncertainty space. It is based on the determination of distances between the generated stochastic simulations. Descriptors, i.e. variables estimated on the reservoir, are used to define distances between models and multivariate statistics are used to guide the selection of a limited subset of 3D reservoir models that are very different and that correspond to a representative subsampling of the generated plausible models.

In the CO$_{2}$ geological storage context, taking into account high resolution heterogeneity is still at the beginning even though some studies have shown the impact of heterogeneities on CO$_{2}$ reservoir performances and capacities [3, 4]. Techniques proposed for petroleum reservoir analysis [1, 2, 5] may be used as basis for CO$_{2}$ applications. Several descriptors have been proposed to describe the geometry and the topology (i.e. connectivity) of reservoir rocks. However, differences exist between the problematics of petroleum and CO$_{2}$-storage reservoirs. First, the involved space and time scales are greater in the CO$_{2}$-storage domain than in the hydrocarbon industry. Second, the amount and availability of data are generally much more limited in CO$_{2}$ context. Finally, the use of flow simulation in CCS studies is not for predicting the flow path from an injection well to a producing one, but mainly for estimating the reservoir capacity and overpressure. This means that specific descriptors are needed.

In this paper, we focus on searching formal frameworks to define topological descriptors. Indeed, several geometrical characteristics have been already proposed [2, 5, 6], while only descriptors based on degraded flow simulations have been proposed for describing the reservoir connectivity. Even if these descriptors provide insights on rough flow behavior, they remain time consumming. The question is then to determine if the “static” topology of the reservoir rocks can also provide information about fluid flow behaviors. In this paper, we propose to use the formal framework of the Betti number to study the topology of the reservoir rock volume. However, we focus on determining if different fluvial architectures lead to significant differences of Betti number averages.

In a first section, basics on fluvial sediment architecture and the main modelling issues are presented. To compare the Betti numbers on different fluvial architectures, we propose to generate a synthetic data set of different 3D fluvial reservoirs. It is then possible to master the explanatory parameters of the models. Thus, the method used for generating the synthetic dataset and the explanatory parameters are described in a second section. In a third part, the mathematical background of the Betti numbers is briefly presented. The proposed approach for using the Betti numbers as descriptors is then described in a fourth section. The statistical approaches proposed to analyse the connectivity of these different reservoir models are also explained. Finally, the results are shown and discussed.

2 Fluvial Reservoir Modelling and Problematics

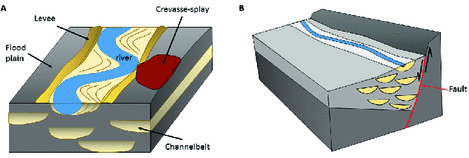
Rivers bring and deposit coarse sediments along their path (Fig. 1(A)) in a flood plain consisting in fine sediments. If the river becomes unstable due to internal or external (e.g. tectonics) factors, an avulsion occurs and the river path changes its location, potentially its orientation, in the flood plain. Coarse sediments are then deposited at the new river location. The sedimentary bodies deposited between two avulsions are often termed as channels even if the more convenient terminology is channelbelts [7, 8]. Thus, fluvial reservoirs consist in the stackings of elongated tabular permeable bodies, the channelbelts, in an impermeable background. The fluvial architecture follows sedimentological laws such as: the channelbelt bodies pass entirely through the volume and their positions are correlated, in most cases [4, 9] (Fig. 1(B)). The fluvial reservoirs are highly compartmentalized: the channelbelt bodies may be amalgamated in certain places and the connectivity between these bodies has then a major impact on the final reservoir rock organization, hence fluid flows.

Fig. 1.

Fluvial architecture: (A) channelbelt stackings and associated overbank deposits (levees, crevasse-splays, flood plain fines); (B) Conceptual model of a channelbelt stacking influenced by a fault activity (modified from [9]).

For modelling purpose, it is common to only consider two lithologies ([4], Fig. 1(A)): the overbank deposits (mainly impermeable) and the channelbelts (reservoir rocks). Several algorithms have been proposed to stochastically reproduce the channelbelt stackings of fluvial architecture. Poisson point processes and simulated annealing are the most known techniques [1, 10]. However, even if they assert to provide equiprobable models conditioned to subsurface data, both techniques consider channel positions as independent and do not assert that the generated objects totally pass through the volume. These drawbacks have been noticed by several authors [4, 11, 12]. In [4], the authors propose an algorithm to stochastically reproduce channel stackings that fit sedimentological laws. However, this technique is unconditional and can not then account for subsurface data. The integration of geological laws into stochastic conditioned models is still a sensitive issue in reservoir modelling [12] and a question is to determine which sedimentological laws really influence reservoir behaviors [5].

In this work, the objective is to determine if the connectivity of the reservoir rocks is in average influenced by different scenarios of channel stacking. An algorithm inspired from [4] was used to generate different families of stochastic models. The Betti numbers are proposed as descriptors for formelly compare the final topology, i.e. connectivity, of the reservoir rocks.

3 Synthetic Data Set

A grid of $100\times 100\times 100$ cells and $50\times 50\times 25$ scale was built. A channelbelt template is also constructed as a median polygonal line with perpendicular demi-ellipse cross-sections. Its length is twice the grid one to ensure that simulated objects totally pass through the volume. At a first glance, the object sizes have no importance as we only deal with topology. However, the channel sizes are chosen small enough compared to the grid in order to assert that the stochastic simulation is an ergodic process (i.e. statistics are reproduced on a realization [1]).

The principle of the algorithm is to simulate N channelbelt parametric objects within the volume. At each step, a channelbelt object is randomly generated and located in the volume using translation and rotation operations. Many parameters are required to define the dimensions, the sinuosity, the orientation and the location of a simulated channelbelt object. In this work, only two aspects have been considered as variable: the style of stacking and the orientations of the channelbelts. Indeed, the more parameters are variable, the more models are required for cross comparisons. Except the width and height of the channel sections, all the parameters are simulated using a Monte Carlo sampling on a density probability law. For a sake of simplicity, the probability laws are always considered as uniform and noticed U(min, max) in the following. The minimum and maximum values are chosen so that it reproduces “realistic” shapes of channelbelts.

The sinuosity of the channel middle lines is simulated using a cosine equation as follows:

$$\begin{aligned} \left. \begin{array} {l} X = a \cdot cos(\phi +\tau \cdot \frac{Y + 40}{280} \\ \phi = \frac{b \cdot \pi }{180} \\ \tau = c \cdot \pi \end{array} \right. \end{aligned}$$

(1)

where $a \sim U(5,20)$, $b \sim U(5,30)$ and $c \sim U(1,5)$. The width and height of the channel sections are constant and equal, respectively, to 10 and 3.

On one hand, two different styles of channel stacking were simulated (Fig. 2):

• 1. unstructured: the $i^{th}$ simulated object is randomly located in the volume, independently from the $i-1$ already simulated objects. This is similar to Poisson point process as the events are considered as independent.

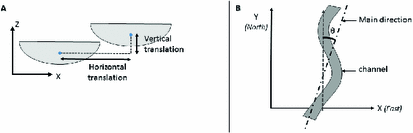
• 2. structured: the location of the $i^{th}$ object depends on the location of the $i-1^{th}$ object. Vertical and lateral translations are defined between them (Fig. 2(A)). These values are simulated using a Monte Carlo sampling on, respectively, U(0, 3) and $U(-10,10)$, except for the first simulated object for which the lateral translation is randomly chosen in the volume. The vertical translation asserts that there is no vertical gap between the $i-1^{th}$ and the $i^{th}$ objects. The values follow the sedimentological laws detailed in [4].

On the other hand, the orientations of the channel bodies are modified. In two model series, the channelbelt orientation $\theta$ varies from $-10^\circ$ to $10^\circ$, and in the two others from $-90^\circ$ to $90^\circ$ (Fig. 2(B)). In other words, the channelbelts are roughly oriented in the same directions (North-South) for the first two series, and in any orientations for the two others.

This leads to four series of models: (A) unstructured, orientations simulated on $U(-10^\circ ,10^\circ$); (B) unstructured, $U(-90^\circ ,90^\circ$); (C) structured, $U(-10^\circ ,10^\circ$); and (D) structured, $U(-90^\circ ,90^\circ$). Figure 3 shows top and cross-section views of two models corresponding to, respectively, A and D type.

Fig. 2.

Parameters for location simulation: (A) vertical and horizontal translations between objects $i-1$ and i; (B) Definition of the angle $\theta$ for simulating the main channel orientations.

Moreover, it may be easy to imagine that proportions can also control the Betti numbers, even if no specific study has been dedicated to that problem, to our knowledge. To illustrate this phenomenon, a purely random white noise of a binary variable was simulated for a proportion of black pixels from 0 to $100\,\%$. It may be seen in Fig. 4 that the Betti numbers are influenced in average by the proportion. For this reason, we choose to generate 3D models of channel stacking for which the poportion of the reservoir rock (channel) ranges over [0.35, 0.4] (in average, 20 objects are simulated in the volume). This proportion range is realistic and for a first study, corresponds to a balance between a too small reservoir rock proportion leading to isolated small bodies (unexploitable) and a high proportion (e.g. $80\,\%$), for which it has been shown that the geometry and the organization of the channels have no more impact on reservoir behavior [5, 13].

Fifty simulations were provided for each model type (A, B, C and D) to have a sufficient sampling of models. Simulations were performed using a Gopy research plugin of the Gocad® software. The generated 3D models are firstly represented as a set of parametric objects (Fig. 3, top view). These models are secondly rasterized in the grid by storing the value 1 when a cell is intersected by a channel and 0, else. At the end, the 3D models represent binary volumes (3D grids), for which the value 1 corresponds to the reservoir rocks (channels) and 0 the background (impermeable).

Fig. 3.

Examples of 3D models: (left) the 8$^{th}$ simulation in the model A, section of the 3D grid and top view of the corresponding simulated parametric objects; (right) the 7$^{th}$ simulation in the model D, section of the 3D grid and top view of the corresponding simulated parametric objects.

Fig. 4.

Betti numbers ($\beta _0$ in blue, $\beta _1$ in green and $\beta _2$ in red) computed for each proportion of black pixels, over 10000 experiments on a $7\times 7\times 7$ grid. (Color figure online)

3.1 3D Cubical Complexes and Homology

The following section defines the Betti numbers for binary volumes. Let us first point out that these numbers cannot be directly obtained from the volume, so an intermediate structure, called cubical complex, must be considered.

An elementary interval is an interval of the form $[k, k+1]$ or a degenerate interval [k, k], where $k \in \mathbb {Z}$. An elementary cube is the Cartesian product of n elementary intervals, and the number of non-degenerate intervals in this product is its dimension. An elementary cube of dimension q will be called q-cube for short. Given two elementary cubes P and Q, we say that P is a face of Q if $P \subset Q$. A 3D cubical complex is a set of elementary cubes. The boundary of a q-cube is the collection of its $(q-1)$-dimensional faces.

Given a binary volume X, we can define a topologically equivalent 3D cubical complex K(X) which contains a 3-cube $\left[ x_1, x_1+1 \right] \times \left[ x_2, x_2+1 \right] \times \left[ x_3, x_3+1 \right]$ for every voxel $(x_1, x_2, x_3)$ of X.

A chain complex (C, d) is a sequence of $\mathfrak {R}$-modules $C_0, C_1, \ldots$ (called chain groups and homomorphisms $d_1 : C_1 \rightarrow C_0, d_2 : C_2 \rightarrow C_1, \ldots$ (called differential or boundary operators) such that $d_{q-1} d_q = 0$, for all $q > 0$, where $\mathfrak {R}$ is some ring, called the ground ring or ring of coefficients. In this paper we fix $\mathfrak {R} = \mathbb {Z}_2$ since we work in a three-dimensional space. The group chains are thus $\mathbb {Z}_2$-vector spaces.

A 3D cubical complex K induces a chain complex. $C_q(K)$ is the $\mathbb {Z}_2$-vector space of dimension $f_q(K)$, the number of q-cubes in K. Its elements (called q-chains) are formal sums of q-cubes with coefficients in $\mathbb {Z}_2$, so they can be interpreted as sets of q-cubes. The linear operator $d_q$ maps each q-cube to the sum of its $(q-1)$-dimensional faces.

A q-chain x is a cycle if $d_q(x) = 0$, and a boundary if $x = d_{q+1}(y)$ for some $(q+1)$-chain y. By the property $d_{q-1} d_q = 0$, every boundary is a cycle, so we can define the q-th homology group of the chain complex (C, d):

$$\begin{aligned} H(C)_q = \ker (d_q) / \mathrm {im}(d_{q+1}). \end{aligned}$$

(2)

This set is a group isomorphic to $(\mathbb {Z}_2)^b$ for some $b \ge 0$. The ranks of the homology groups are called the Betti numbers.

In the present work, the Betti numbers are scrutinized to determine if they can be used for describing differences on reservoir geobody network or connectivity.

4 Betti Numbers Used as Descriptor

4.1 Computations and Geological Meanings

This section aims at defining the “physical” meaning of each Betti number in the case where the targeted object is a reservoir 3D model. Indeed, we may consider two kinds of volume: the volume of reservoir rock (channelbelt sediments), which corresponds to fluid storage and drainage, and the volume of impermeable rocks (overbank deposits), which corresponds to flow barrier. We can then consider not only the Betti numbers $\beta _0$, $\beta _1$ and $\beta _2$ of the reservoir rock volumes but also the Betti numbers of the impermeable background, that we refer to as $\beta _0^{-}$, $\beta _1^{-}$ and $\beta _2^{-}$ in the following.

The Betti number of dimension $\beta _0$ represents the number of reservoirs contained in the background. By “reservoir”, we mean the amalgamated channelbelt bodies that lead to a connected volume of reservoir rock. The Betti numbers $\beta _1$ and $\beta _2$ represent, respectively, the number of impermeable tunnels and cavities contained in the reservoir rock. These two parameters may have importance for CO$_{2}$ storage application, as it has been shown that the presence of impermeable lenses in a reservoir rock volume increases the capacity of CO$_{2}$ storage [14], because of the CO$_{2}$ accumulation under the lenses.

Concerning the complementary volume (i.e. the impermeable background), $\beta _0^{-}$ is the number of the barriers that compartmentalize the reservoir. Obviously, $\beta _1^{-}$ and $\beta _2^{-}$ are the number of tunnels and cavities in the background, respectively. The tunnels may have importance as they represent potential leaks for CO$_{2}$ in the impermeable covers. It is of paramount importance for storage efficiency and reliability that the CO$_{2}$ does not migrate inside the impermeable covers. Several studies have been conducted on the impact of thin permeable tunnels (e.g. faults) in impermeable sediments [15].

The Betti numbers were calculated using an add hoc C++/python code and the RedHom software [16]. The ad hoc code was developed to automate the model import into the RedHom software and to extract a convenient output format (i.e. column based file) from RedHom outputs for the statistical analysis over the 200 models.

4.2 Statistical Tests

As previously mentioned, the final objective is to determine if significant differences in Betti number values can be observed between the four series of models. A common way to achieve this is the use of hypothesis testing. In this study, we propose to use the non-parametric Kruskal-Wallis test, whose purpose is to compare the mean of a random variable V between different samplings, that are assumed to be independent but that can have different sizes. This test does not require that V follows a particular parametric distribution law.

Let us consider N samplings on which a random variable V has been measured and $m_i$ the means of V on the $i^{th}$ sampling. The Kruskal-Wallis test is presented as follows:

$$\begin{aligned} \left\{ \begin{array} {lll} \text{ The } \text{ null } \text{ hypothesis, } &{} H_0: &{} m_1 = m_2 = ... = m_N \\ \text{ The } \text{ alternative } \text{ hypothesis, } &{} H_1: &{} \exists i,j / m_i \ne m_j \end{array} \right. \end{aligned}$$

(3)

The underlying objective is to determine if the samplings are stemming from the same statistical population (the null hypothesis). Thus, the question is to reject or not $H_0$. As any hypothesis testing, it relies on the computation of a statistics t that should follow a given hypothetic law under $H_0$. Then, an observed value $t_{obs}$ is computed from the samplings and compared to a critical value $t_{c}$. This critical value is defined by assuming a given risk $\alpha$, which corresponds to the probability to reject $H_0$ although it is true. If $t_{obs}$ is greater than $t_c$, $H_0$ is rejected, else it is accepted. Another way to interpret results is to compute the p-value, which corresponds to the probability of rejecting $H_0$ although it is true, computed from the samplings. If it is greater than $\alpha$ then $H_0$ is accepted, otherwise rejected.

In the case of $H_0$ rejection, it is a common practice to use post hoc tests that allows the determination of which means are different from the others. In this study, the post hoc test “Kruskalmc” (multiple comparison) was chosen in order to evaluate differences in medians among the four models. It is important to notice that this test is less powerful than the Kruskal-Wallis test. This can lead to unconsitent results between the two tests. The power of an hypothesis testing corresponds to the probability to reject $H_0$ when $H_1$ is true. It characterizes its robustness.

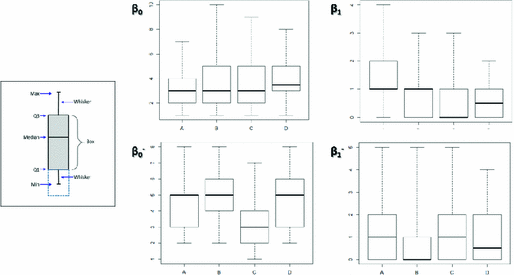
Moreover, in order to scrutinize the values of the Betti numbers, we propose to use the boxplot (Fig. 5). The box plot displays the full range of variation (from min to max), the likely range of variation (the IQR), and a typical value (the median). They have also lines extending vertically from the boxes (whiskers) indicating variability outside the upper and lower quartiles. Outliers may be plotted as individual points. The spacing between the different parts of the box indicate the degree of dispersion (spread) and skewness in the data, and show outliers.

The statistical analysis was performed using the R software.

Fig. 5.

Boxplots: left, diagram of the boxplot parameters; right, the four boxplots for each Betti number.

5 Results and Discussion

5.1 Kruskal-Wallis Tests

For the 200 generated simulations, no cavity was found: $\beta _2=0$ and $\beta _2^{-}=0$. They are then not studied. Concerning the four other numbers, Table 1 summarizes the results found for the Kruskal-Wallis test. Except for $\beta _0$, all the p-values are under $5\,\%$. Thus, it can be concluded that the mean of $\beta _0$ is not significantly different between the different series. On the contrary, for $\beta _1$, $\beta _0^-$ and $\beta _1^{-}$, there is at least one mean that is significantly different from the others. The post hoc test “Kruskalmc” was applied to evaluate differences among the four models for these three variables. Table 2 summarizes the results. For $\beta _1$, the models are all different. In terms of $\beta _0^{-}$, the models C is significantly different from the others. Finally, all the models are considered as similar in terms of $\beta _1^{-}$. This is unconsistent with previous results. However, as previously mentioned, the “kruskalmc” test is less powerful and “more easily accepts” $H_0$, which can explain these results. Moreover, the found p-values (0.03774) is very close to $5\,\%$. Similarly, the $t_{obs}$ of the comparison between $A-B$ (27.3) is very close to the critical value (27.7123). This means that using a higher risk than $5\,\%$, the means could be considered as different and that the models B would be considered as different from A, C and D. In order to depict graphically the four groups of numerical data through their quartiles, boxplots were used (see Fig. 5). These plots confirm previous interpretations.

Table 1. Results of the Kruskal-Wallis test, p-values are always under $5\,\%$, except for $\beta _0$ (in bold). It may be noticed that the p-value of $\beta _1^{-}$ (in italic) is close to $5\,\%$.

Table 2. Results of the Kruskal-Wallis post hoc test, applied for $\beta _1$, $\beta _0^-$, and $\beta _1^-$.

5.2 Interpretations and Discussions

Considering a proportion of reservoir rock between [0.35; 0.4], it could be said that the number of reservoir geobodies does not depend on the stacking law and the channel orientation variability. On the contrary, both stacking and orientations modify significantly the number of impermeable tunnels in the reservoir rocks. Regarding Fig. 5, the unstructured models seem to increase the occurence of tunnels, in average. This means that this type of reservoir architecture is more tortuous and may facilitate dissolutions if these impermeable tunnels are preferentially horizontal [14]. Concerning the number of impermeable compartmentalization ($\beta _0^{-}$), it seems that unstructured models with sub-parallel channel orientation present smaller occurences of these features. Regarding Fig. 5, higher orientation variability leads to higher compartmentalization. On the contrary, the stacking correlation tends to decrease it. Both trends explain that the models C are different from the others, with a smallest mean. This result is suprising as we could imagine at a first glance that the stacking correlation tends to create vertical chimneys of reservoir geobodies that separate the background in different components. Finally, the number of permeable tunnel in background ($\beta _1^{-}$) seems to be positively influenced by the stacking correlation but negatively impacted by the channel orientation variability. This leads to differentiate models B from the others. However, the difference is not clearly significant as $p-value$ and observed statistics are close to the cutoffs.

6 Conclusion

This preliminary study allowed us to define a “physical meaning” to the Betti numbers computed on both permeable and impermeable volumes for reservoir characterizations. Six variables were defined, but only four were really used in the study because no cavity was found. This study also highlights that the type of channelbelt stackings influence the reservoir topology. These results have been only performed for a proportion of reservoir rocks ranged over [0.35; 0.4]. It could be interesting to test if the trends observed in this study remain similar for different proportions. It may be noticed that some Betti numbers correspond to entities that can be computed using more classical algorithms, such as $\beta _0$ and $\beta ^-_0$. However, Betti numbers are known as powerful to characterize the number of tunnels, which generally remains the most difficult task. The presence of permeable tunnels in impermeable background caused by faults or lithologies have major impacts on CO$_{2}$ storage risks. Thus, the use of Betti numbers helps computing relevant topological indices for reservoir compactness characterization. In further studies, we will study the impact on proportions on the observed trends but also we will analyze more complex models having more than two lithologies. Finally, hydraulic behavior will be also studied to check if relationships exist between static (reservoir rock network) and dynamic (flow path) topology.