Keywords

1 Introduction

Physics-based analogies have found widespread use in the analysis and understanding of network structure. Examples include the use of ideas from statistical mechanics [1, 2], thermodynamics [3, 4] and quantum information [5, 6]. For instance, statistical mechanics has been used to characterize the degree distribution of different types of complex networks [1]. Using a thermodynamic heat-bath analogy, the concepts of network communicability and balance have been defined [3]. By using quantum walks the process of preferential attachment has been shown to lead to the intriguing phenomenon of super-cluster condensation in growing networks [7]. Both Bose-Einstein and Fermi-Dirac statistics have been used to describe quantum geometries in networks [5].

One particularly interesting and widely studied approach is to use thermodynamic analogies as a means of characterizing networks [4]. Here the Laplacian matrix plays the role of network Hamiltonian, and the energy states of a network are the eigenvalues of the Laplacian. By modeling the network as a set of energy states occupied by a system of particles, thermodynamic properties such as total energy and entropy can be computed, and used as network characterizations. The energy states are populated by particles in thermal equilibrium with a heat bath. A key element in this thermalisation approach is to model how the energy states are occupied at a particular temperature. Normally this is assumed to be follow the classical Maxwell-Boltzmann distribution, where the particles are distinguishable and weakly interacting.

In this paper, on the other hand, we explore the case where the particles are quantum mechanical in nature and obey spin statistics. In other words, they are indistinguishable, and are either fermions (half integer spin) or bosons (integer spin). Particles with integer spin are subject to Bose-Einstein statistics and do not obey the Pauli exclusion principle. They can aggregate in the same energy state. At low temperature this leads to the phenomenon of Bose-Einstein condensation. There has been work aimed at extending this model to networks. For instance, by mapping the network model to a Bose gas, phase transitions have been studied in network evolution associated with Bose-Einstein condensation [7]. This model has also been extended to understand processes such as supersymmetry in networks [3]. In the meanwhile, particles with half integer spin are subject to Fermi-Dirac statistics and obey the Pauli exclusion principle. They give rise to models of network structures constrained by the occupancy of the nodes and edges. Examples include traffic flow and also the modelling of certain types of geometric networks such as the Cayley tree [8]. Formally, these physical systems can be described by partition functions with the microscopic energy states, which are represented by a suitable chosen Hamiltonian. In the network theory, the Hamiltonian is computed from the adjacency or Laplacian matrix, but recently, Ye et al. [4], have shown how the partition function can be derived from a characteristic polynomial instead.

Despite this interest in alternative models of the thermalised distribution of energy states under different spin statistics, there has been little systematic study of the resulting thermodynamic characterizations of network structure. Here we consider the effects of occupation statistics on the populations of the energy states where the Hamiltonian operator is the normalized Laplacian matrix and the energy states are given by the network spectrum. We characterize the thermalised system of energy states using partition functions relevant to Bose-Einstein and Fermi-Dirac occupation statistics. From the partition functions we compute average energy and entropy of the system of particles. Because Bose-Einstein particles coalescence in low energy states, and Fermi-Dirac particles have a greater tendency to occupy high energy states because of the Puli exclusion principle, these types of spin statistics lead to very different distributions of energy and entropy for a network with a given structure (i.e. set of normalised Laplacian eigenvalues). Moreover, at low temperature the distributions are also different from the classical Maxwell-Boltzmann case. It is these low-temperature differences in energy and entropy that we wish to investigate as a means of characterizing differences in network structure.

This paper is organised as follows. Section 2 briefly reviews the basic concepts in network representation, especially with density matrix and Hamiltonian operator on graphs. Section 3 reviews the thermodynamic quantities i.e. entropy and energy, and also illustrates Bose-Einstein and Fermi-Dirac statistics. Section 4 provides our experimental evaluation. Finally, Sect. 5 provides the conclusion and direction for future work.

2 Graph Representation

In this section, we provide details of graph representation in quantum theory. We briefly introduce the concept of density matrix for a graph and then give the definition of Hamiltonian operator with the normalized Laplacian matrix.

2.1 Density Matrix

In quantum mechanics the density matrix is used to describe a system whose state is an ensemble of pure quantum states \(| \psi _i \rangle \), each with probability \( p_i \). The density matrix is defined as

$$\begin{aligned} \varvec{\rho }= & {} \sum _{i=1}^{|V|} p_i | \psi _i \rangle \langle \psi _i | \end{aligned}$$
(1)

In the graph domain, the normalised Laplacian matrix has been used to model the density of states for a network [6, 9]. Let G(V, E) be an undirected graph with node set V and edge set \(E \subseteq V \times V\), and let |V| represent the total number of nodes on graph G(V, E). The adjacency matrix A of a graph is defined as

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0&{} \text {if }(u,v)\in E\\ 1&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(2)

Then the degree of node u is \(d_u = \sum _{v \in V} A_{uv}\).

The normalized Laplacian matrix \(\tilde{L}\) of the graph G is defined as \( \tilde{L} = D^{-\frac{1}{2}}LD^{\frac{1}{2}} \), where \(L = D - A\) is the Laplacian matrix and D denotes the degree diagonal matrix whose elements are given by \(D(u,u) = d_u\) and zeros elsewhere. The element-wise expression of \(\tilde{L}\) is

$$\begin{aligned} \tilde{L}_{uv} = {\left\{ \begin{array}{ll} 1&{} \text {if } u = v \text { and } d_u\ne 0\\ -\frac{1}{\sqrt{d_u d_v}}&{} \text {if } u \ne v\text { and } (u,v) \in E\\ 0&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(3)

With this notation, Severini et al. [6, 9] specify the density matrix to be \( \varvec{\rho } = \frac{\tilde{L}}{|V|} \). When defined in this was way the density matrix is Hermitian i.e. \(\varvec{\rho } = \varvec{\rho ^\dagger }\) and \( \varvec{\rho } \ge 0, \text {Tr} \varvec{\rho } = 1\). It plays an important role in the quantum observation process, which can be used to calculate the expectation value of measurable quantity.

2.2 Hamiltonian Operator of a Graph

In quantum mechanics, the Hamiltonian operator is the sum of the kinetic energy and potential energy of all the particles in the system. It is the energy operator of the system and the standard formulation on a manifold is \(\hat{H} = -\nabla ^2 + U(r,t)\).

In our case, we assume the graph to be in contact with a heat reservoir. The eigenvalues of the Laplacian matrix can be viewed as the energy eigenstates, and these determine the Hamiltonian and hence the relevant Schrödinger equation which govern the particles in the system. The particles occupy the energy states of the Hamiltonian subject to thermal agitation by the heat bath. The number of particles in each energy state is determined by the temperature, the assumed model of occupation statistics and the relevant chemical potential.

If we take the kinetic energy operator \(-\nabla ^2\) to be the negative of the adjacency matrix, i.e. \(-A\), and the potential energy U(r, t) to be the degree matrix D, then the Hamiltonian operator is the Laplacian matrix on graph. Similarly, the normalized form of the graph Laplacian can be viewed as the Hamiltonian operator \( \hat{H} = \tilde{L} \).

In this case, the energy states of the network \(\lbrace \varepsilon _i \rbrace \) are then the eigenvalues of the Hamiltonian \( \hat{H} | \psi _i \rangle = \tilde{L} | \psi _i \rangle = E_i | \psi _i \rangle \).

The eigenvalues are all greater than or equal to zero, and the multiplicity of the zero eigenvalue is the number of connected components in the network. Furthermore, the density matrix commutes with the Hamiltonian, i.e. the associated Poisson bracket is zero,

$$\begin{aligned}{}[ \hat{H}, \rho ] = [ \tilde{L}, \frac{\tilde{L}}{|V|} ] = 0 \end{aligned}$$
(4)

which means that the network is in equilibrium when there are no changes in the density matrix which describes the system.

3 Quantum Statistics in Networks

Quantum statistics can be combined with network theory to characterize network properties. The network can be viewed as a grand canonical ensemble, and the thermal quantities, such as energy and entropy, depend on the assumptions concerning the Hamiltonian for the system and the corresponding partition function.

3.1 Thermodynamic Quantities

We consider the network as a thermodynamic system specified by N particles with energy states given by the Hamiltonian operator, and it is immersed in a heat bath with temperature T. The ensemble is represented by a partition function \(Z(\beta , N)\), where \(\beta \) is inverse of temperature. When specified in this way the various thermodynamic characterizations can be computed for the networks. For instance, the average energy is given by

$$\begin{aligned} U = \left[ - \frac{\partial }{\partial \beta } \log Z(\beta , N) \right] _N = \mathrm{Tr} \left( \rho H \right) = k_B T^2 \left[ \frac{\partial }{\partial T} \log Z \right] _N \end{aligned}$$
(5)

the thermodynamic entropy by

$$\begin{aligned} S = k_B \left[ \frac{\partial }{\partial T} T \log Z \right] _N \end{aligned}$$
(6)

and the chemical potential by

$$\begin{aligned} \mu = -k_B T \left[ \frac{\partial }{\partial N} \log Z \right] _\beta \end{aligned}$$
(7)

For each distribution we capture the statistical mechanical properties of particles in the system using the partition function associated with the different occupation statistics. The network can then be characterized using thermodynamic quantities computed from the partition function, and these include the entropy, energy and temperature.

3.2 Bose-Einstein Statistics

The Bose-Einstein distribution applies to indistinguishable bosons. Each energy state specified by the network Hamiltonian can accommodate an unlimited number of particles. Without obeying the Pauli exclusion principle, Bosons subject to Bose-Einstein statistics can aggregate in the same energy state.

For a system of the network, as the grand-canonical ensemble with a varying number of particles N and a chemical potential \(\mu \), the Bose-Einstein partition function is

$$\begin{aligned} Z_{_{BE}} = \det \left( I - e^{\beta \mu } \exp [-\beta \tilde{L}] \right) ^{-1} = \prod _{i=1}^{|V|} \left( \frac{1}{1 - e^{\beta (\mu -\varepsilon _i)}} \right) \end{aligned}$$
(8)

From Eqs. (5) and (6), the average energy is

$$\begin{aligned} \left\langle U \right\rangle _{_{BE}}&= - \frac{\partial \log Z}{\partial \beta } = -\sum _{i=1}^{|V|} {\frac{(\mu -\varepsilon _i)e^{\beta (\mu -\varepsilon _i)}}{1-e^{\beta (\mu -\varepsilon _i)}}} \end{aligned}$$
(9)

while the corresponding entropy is

$$\begin{aligned} S_{_{BE}}&= \log Z + \beta \langle U \rangle&= -\sum _{i=1}^{|V|} {\log {\left( 1-e^{\beta (\mu -\varepsilon _i)}\right) }} - \beta \sum _{i=1}^{|V|} { \frac{(\mu -\varepsilon _i)e^{\beta (\mu -\varepsilon _i)}}{1-e^{\beta (\mu -\varepsilon _i)}}} \end{aligned}$$
(10)

Both the average energy and entropy depend on the chemical potential for the partition function and hence they are determined by the number of particles in the system. At the temperature \(\beta \), the corresponding number of particles in the level i with energy \(\varepsilon _i\) is

$$\begin{aligned} n_i = {{1} \over {\exp [ \beta (\varepsilon _i - \mu )]-1}} \end{aligned}$$
(11)

As a result, the total number of particles in the system is

$$\begin{aligned} N = \sum _{i=1}^{|V|} n_i = \sum _{i=1}^{|V|} {{1} \over {\exp [\beta (\varepsilon _i - \mu )]-1}} = \mathrm{Tr} \biggl [ {{1}\over {\exp (-\beta \mu ) \exp [\beta \tilde{L}]- I}} \biggr ] \end{aligned}$$
(12)

In order for the number of particles in each energy state to be non-negative, the chemical potential must be less than the minimum energy level, i.e. \(\mu < \min \varepsilon _i\).

The equivalent function of density matrix in this case is given by

$$\begin{aligned} \varvec{\rho }_{_{BE}}=\frac{1}{\mathrm{Tr}(\varvec{\rho }_1)+ \mathrm{Tr}(\varvec{\rho }_2)} \left( \begin{array}{cc} \varvec{\rho }_1 &{} 0 \\ 0 &{} \varvec{\rho }_2 \end{array}\right) \end{aligned}$$
(13)

where \( \varvec{\rho }_1=-\left( \exp [\beta ( \tilde{L}-\mu I)]- I \right) ^{-1} \) and \( \varvec{\rho }_2=\left( I - \exp [-\beta ( \tilde{L}-\mu I)]\right) ^{-1} \).

Since Bose-Einstein statistics allow particles to coalesce in the lower energy levels, the corresponding energy and entropy reflect the smaller Laplacian eigenvalues most strongly. As a result the number of connected components (the multiplicity of the zero eigenvalue), and spectral gap (the degree of bi-partiality in a graph) are most strongly reflected.

3.3 Fermi-Dirac Statistics

The Fermi-Dirac distribution applies to indistinguishable fermions with a maximum occupancy of one particle in each energy state. Particles cannot be added to states that are already occupied, and hence obey the Pauli exclusion principle.

These particles behave like a set of free fermions in the complex network with energy states given by the network Hamiltonian. The statistical properties of the networks are thus given by the Fermi-Dirac statistics of the equivalent quantum system, and the corresponding partition function is

$$\begin{aligned} Z_{_{FD}} = \det \left( I + e^{\beta \mu } \exp [-\beta \tilde{L}] \right) = \prod _{i=1}^{|V|} \left( 1 + e^{\beta (\mu -\varepsilon _i)} \right) \end{aligned}$$
(14)

From Eq.(5) the average energy of the Fermi-Dirac system is

$$\begin{aligned} \left\langle U \right\rangle _{_{FD}}&= - \frac{\partial \log Z}{\partial \beta } = -\sum _{i=1}^{|V|} {\frac{ (\mu -\varepsilon _i)e^{\beta (\mu -\varepsilon _i)}}{1+e^{\beta (\mu -\varepsilon _i)}}} \end{aligned}$$
(15)

And the associated entropy is given by

$$\begin{aligned} S_{_{FD}}&= \log Z + \beta \langle U \rangle&= \sum _{i=1}^{|V|} {\log {\left( 1+e^{\beta (\mu -\varepsilon _i)}\right) }} - \beta \sum _{i=1}^{|V|} { \frac{(\mu -\varepsilon _i)e^{\beta (\mu -\varepsilon _i)}}{1+e^{\beta (\mu -\varepsilon _i)}}} \end{aligned}$$
(16)

Under Fermi-Dirac statistics, on the other hand, the number of particles occupying the ith energy state is

$$\begin{aligned} n_i = {{1} \over {\exp [ \beta (\varepsilon _i - \mu )]+1}} \end{aligned}$$
(17)

and the total number of particles in the network system is

$$\begin{aligned} N = \sum _{i=1}^{|V|} n_i = \sum _{i=1}^{|V|} {{1} \over {\exp [\beta (\varepsilon _i - \mu )]+1}} = \mathrm{Tr} \biggl [ {{1}\over {\exp (-\beta \mu ) \exp [\beta \tilde{L}]+ I}} \biggr ] \end{aligned}$$
(18)

With a single particle per energy state, the chemical potential is hence just the nth energy level, and so \(\mu = \varepsilon _n\).

Similarly, we find that the equivalent density matrix function

$$\begin{aligned} \varvec{\rho }_{_{FD}}=\frac{1}{\mathrm{Tr}(\varvec{\rho }_3)+\mathrm{Tr}(\varvec{\rho }_4)}\left( \begin{array}{cc} \varvec{\rho }_3 &{} 0 \\ 0 &{} \varvec{\rho }_4 \end{array}\right) \end{aligned}$$
(19)

where \( \varvec{\rho }_3=\left( I +e^{-\beta \mu }\exp [\beta \tilde{L}]\right) ^{-1} \) and \( \varvec{\rho }_4=\left( I +e^{\beta \mu }\exp [-\beta \tilde{L}]\right) ^{-1} \).

Since Fermi-Dirac statistics exclude multiple particles from the same energy level, the corresponding energy and entropy do not just reflect the lower part of the Laplacian spectrum, and are sensitive to a greater portion of the distribution of Laplacian eigenvalues. As a result, we might expect them to be more sensitive to subtle differences in network structure.

4 Experiments and Evaluations

In this section, we provide experiments to evaluate the proposed spin statistical models. We commence by assessing the performance on synthetic data using the entropy for network classification problems. We then apply on the real-world financial networks to distinguish significant structural variance.

4.1 Numerical Results

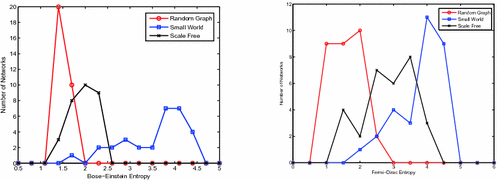
At first, we investigate how well the different spin statistic models can be used to distinguish synthetic networks generated from the Erdős-Rényi random graphs, Watts-Strogatz small-world networks [10] and Barabási-Albert scale-free network models [11]. We conduct numerical experiments to evaluate whether the thermodynamic quantity, i.e. entropy, can represent differences in the networks.

These synthetic graphs are created using a variety of model parameters with the number of nodes varying between 100 to 1,000. For small world networks, the rewiring probability is \(p = 0.2\) and average node degree is \( n = 20\). The scale free networks are derived from Barabási-Albert model [11] with preferential attachment \(m = 10\) at each growing step. To simplify the calculation, we set the Boltzmann constant to unity and particle number to one throughout the experiments.

Fig. 1.
figure 1

Histogram of entropy for three classes of synthetic networks in Bose-Einstein statistics and Fermi-Dirac statistics. Temperature \(\beta = 10\) and particle number \(N = 1\).

Full size image

We compare the entropy resulting from the twos spin statistics models. Figure 1 shows the resulting histogram of entropy derived from Bose-Einstein and Fermi-Dirac statistics respectively. In each case the different networks are well separated by the thermodynamic entropy. In the case of Fermi-Dirac statistics, the three clusters of networks are a slightly better clustered than those obtained with Bose-Einstein statistics.

4.2 Experimental Results

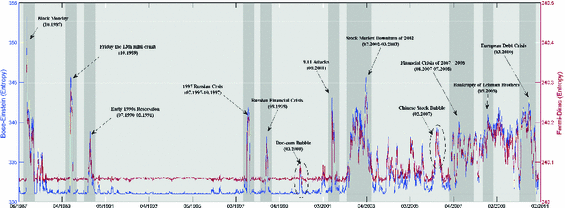
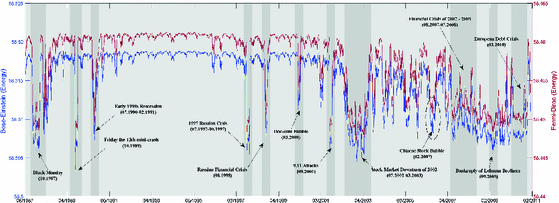
The real-world data is extracted from the daily prices of 3,799 stocks traded on the New York Stock Exchange (NYSE). These data provided an empirical investigation in studying the role of communities in the structure of the stock market. We use the correlations of the times-serial stock price to establish networks for the trading days. For each day of trading the correlation is computed between each pair of stock being traded using a time window of 28 days. Edges are created between those pairs of stock whose cross correlation coefficients are in the highest 5 %. In this way we obtain a sequence of networks representing the topological structure of the New York stock market from January 1986 to February 2011. This yields a sequence of time-varying networks with a fixed number of 347 nodes and varying edge structure for 5,976 trading days.

Fig. 2.
figure 2

Entropy in NYSE (1987–2011) derived from Bose-Einstein and Fermi-Dirac statistics. Critical financial events, i.e., Black Monday, Friday the 13th mini-crash, Early 1990s Recession, 1997 Asian Crisis, 9.11 Attacks, Downturn of 2002–2003, 2007 Financial Crisis, the Bankruptcy of Lehman Brothers and the European Debt Crisis, can be represented in thermodynamic entropy with Maxwell-Boltzmann statistic. It is efficient to use partition function associating with entropy to identify events in NYSE. (Color figure online)

Full size image
Fig. 3.
figure 3

Thermodynamic energy from Bose-Einstein and Fermi-Dirac statistics occupation statistics for NYSE (1987–2011). Critical financial events, i.e., Black Monday, Friday the 13th mini-crash, Early 1990s Recession, 1997 Asian Crisis, 9.11 Attacks, Downturn of 2002–2003, 2007 Financial Crisis, the Bankruptcy of Lehman Brothers and the European Debt Crisis, all appear as distinct events. (Color figure online)

Full size image

We plot the entropy and energy for both Bose-Einstein (blue) and Fermi-Dirac (red) statistics. In order to avoid the thermal disruption in quantum statistics at high temperature, we investigate the spin statistical differences in entropy and energy at low temperature region. Here, to compare the performance, we set the same temperature \(\beta = 10\) and particle number \(N = 1\) for both two cases.

Figure 2 shows both entropies with various financial events annotated, including Black Monday, Friday the 13th mini-crash, Early 1990s Recession, 1997 Asian Crisis, 9.11 Attacks, Downturn of 2002–2003, 2007 Financial Crisis, the Bankruptcy of Lehman Brothers and the European Debt Crisis. In each case the entropy undergoes sharp increase corresponding to the financial crises, which are associated with dramatic structural changes in the networks. Similarly in Fig. 3, the energy is also effective in indicating the critical events. The different feature is that energy undergoes a sharp decrease during the financial crises. Moreover, the Bose-Einstein quantities show the greatest variation during the crises, suggesting that changes in cluster-structure (modularity) are important during these episodes.

5 Conclusion

In this paper, we explore the thermodynamic characterizations resulting from different choices of quantum spin statistics, i.e. Bose-Einstein statistics and Fermi-Dirac statistics, in a heat-bath analogy. The method is based on uses the normalized Laplacian matrix as the Hamiltonian operator of the network. The thermodynamic entropy and energy are then computed from the partition functions for Bose-Einstein and Fermi-Dirac energy level occupation statistics.

We have undertaken experiments on both synthetic and real-world network data to evaluate these two spin statistical methods and have analyzed their properties. The results reveal that both entropies are effective in characterizing dynamic network structure, and distinguish different types of network models (random graphs, small world networks, and scale free networks).

Finally, future work will explore the use of the thermodynamic variables in detecting network anomalies and disturbances. Additionally, we will explore the role of the framework for characterizing phase transitions in network structure.