Delayed-Input Non-Malleable Zero Knowledge and Multi-Party Coin Tossing in Four Rounds

Abstract

In this work we start from the following two results in the state-of-the art:

• 1. 4-round non-malleable zero knowledge (NMZK): Goyal et al. in FOCS 2014 showed the first 4-round one-one NMZK argument from one-way functions (OWFs). Their construction requires the prover to know the instance and the witness already at the 2nd round.

• 2. 4-round multi-party coin tossing (MPCT): Garg et al. in Eurocrypt 2016 showed the first 4-round protocol for MPCT. Their result crucially relies on 3-round 3-robust parallel non-malleable commitments. So far there is no candidate construction for such a commitment scheme under standard polynomial-time hardness assumptions.

We improve the state-of-the art on NMZK and MPCT by presenting the following two results:

• 1. a delayed-input 4-round one-many NMZK argument $\varPi _{\mathsf {NMZK}}$ from OWFs; moreover $\varPi _{\mathsf {NMZK}}$ is also a delayed-input many-many synchronous NMZK argument.

• 2. a 4-round MPCT protocol $\varPi _{\mathsf {MPCT}}$ from one-to-one OWFs; $\varPi _{\mathsf {MPCT}}$ uses $\varPi _{\mathsf {NMZK}}$ as subprotocol and exploits the special properties (e.g., delayed input, many-many synchronous) of $\varPi _{\mathsf {NMZK}}$.

Both $\varPi _{\mathsf {NMZK}}$ and $\varPi _{\mathsf {MPCT}}$ make use of a special proof of knowledge that offers additional security guarantees when played in parallel with other protocols. The new technique behind such a proof of knowledge is an additional contribution of this work and is of independent interest.

1 Introduction

Non-malleable zero-knowledge (NMZK) and secure multi-party computation (MPC) are fundamental primitives in Cryptography. In this work we will study these two primitives and for the case of MPC we will focus on the coin-tossing functionality that is among the most studied functionalities.

NMZK. The first construction of NMZK was given by Dolev et al. in [15]. Later on, Barak in [2] showed the first constant-round construction. An improved construction was then given by Pass and Rosen in [35, 36]. The work of Goyal et al. [23] obtained the first round-optimal construction requiring only 4 rounds and one-way functions (OWFs). Their construction requires the instance and the witness to be known already when the prover plays his first round. Their definition is the standard one-one definition where the adversary opens two sessions, one with a prover and one with a verifier.

The fact that the instance and the witness need to be known already at the second round is an important limitation when NMZK is used as subprotocol to prove statements about another subprotocol played in parallel. Moreover the one-one security is an important limitation when NMZK is used in a multi-party scenario where several of such argument systems are played in parallel.

The above two limitations clearly raise the following natural and interesting open questions:

• Open Question 1: is there a 4-round delayed-input NMZK argument system?

• Open Question 2: is there a 4-round many-many synchronous NMZK argument system?

Multi-party coin-flipping (MPCT). In [24], Katz et al. obtained a constant-round secure MPC protocol using sub-exponential hardness assumptions. This results was then improved by Pass in [34] that showed how to get bounded-concurrent secure MPC for any functionality with standard assumptions. Further results of Goyal [19] and Goyal et al. [21] relied on better assumptions but with a round complexity still far from optimal.

A very recent work of Garg et al. [18] makes a long jump ahead towards fully understanding the round complexity of secure MPCT. They show that the existence of a 3-round 3-robust parallel non-malleable commitment scheme implies a 4-round protocol for secure MPCT for polynomially many coins with black-box simulation. Some candidate instantiations of such special commitment scheme [17, 38] are the one of Pass et al. [33] based on non-falsifiable assumptions, or the one of Ciampi et al. [6] based on sub-exponentially strong one-to-one one-way functions. The achieved round complexity (i.e., 4 rounds) is proven optimal in [18] when simulation is black box and the number of bits in the output of the functionality is superlogarithmic.

A very recent result of Ananth et al. [1] constructs a 4-round MPC protocol for any functionality assuming DDH w.r.t. superpolynomial-time adversaries. The above state-of-the art leaves open the following question.

Open Question 3: is there a 4-round secure MPCT protocol under standard assumptions?

1.1 Our Contribution

In this paper we solve the above 3 open problems. More precisely we present the following results:

• 1. a delayed-input 4-round one-many NMZK argument $\varPi _{\mathsf {NMZK}}$ from OWFs, therefore solving Open Question 1; moreover $\varPi _{\mathsf {NMZK}}$ is also a delayed-input many-many synchronous NMZK argument, therefore solving Open Question 2;

• 2. a 4-round MPCT protocol $\varPi _{\mathsf {MPCT}}$ from one-to-one OWFs, therefore solving Open Question 3¹.

The two constructions are not uncorrelated. Indeed $\varPi _{\mathsf {MPCT}}$ uses $\varPi _{\mathsf {NMZK}}$ as subprotocol and exploits the special properties (e.g., delayed input, many-many synchronous) of $\varPi _{\mathsf {NMZK}}$. Moreover both $\varPi _{\mathsf {NMZK}}$ and $\varPi _{\mathsf {MPCT}}$ make use of a special proof of knowledge that offers additional security guarantees when played in parallel with other protocols. Designing such a proof of knowledge is an additional contribution of this work and is of independent interest.

Interestingly, several years after the 4-round zero knowledge argument system from OWFs of [3], the same optimal round complexity and optimal complexity assumptions have been shown sufficient in this work for delayed-input NMZK and in [5] for resettably sound zero knowledge.

More details on our two new constructions follow below.

MPCT from NMZK. A first main idea that allows us to bypass the strong requirements of the construction of [18] is that we avoid robust/non-malleable commitments and instead focus on non-malleable zero knowledge. Since we want a 4-round MPCT protocol, we need to rely on 4-round NMZK. The only known construction is the one of [23]. Unfortunately their NMZK argument system seems to be problematic to use in our design of a 4-round MPCT protocol. There are two main reasons. The first reason is that the construction of [23] uses the technique of secure computation in the head and therefore requires the instance already in the second round. This is often a problem when the NMZK argument is played in parallel with other subprotocols as in our construction. Indeed these additional subprotocols end in the 3rd or 4th round and typically² need to be strengthened by a zero-knowledge proof of correctness. The second reason is that in the setting of 4-round MPCT the adversary can play as a many-many synchronous man-in-the-middle (MiM), while the construction of [23] is proved one-one non-malleable only.

We therefore improve the state-of-the-art on NMZK constructing a delayed-input NMZK argument system. Our construction only needs one-way functions and is secure even when (a) there are polynomially many verifiers (i.e., it is a one-many NMZK argument), and (b) there are polynomially many provers and they are in parallel. We will crucially use both the delayed-input property and security with parallelized many provers and verifiers in our secure MPCT construction. Moreover our NMZK is also crucially used in [8].

1.2 Technical Overview on Our NMZK

Issues in natural constructions of NMZK. A natural construction of a NMZK argument from OWFs consists of having: (1) a 3-round sub-protocol useful to extract a trapdoor from the verifier of NMZK; (2) a 4-round non-malleable commitment of the witness for the statement to be proved; (3) a 4-round witness-indistinguishable proof of knowledge (WIPoK) to prove that either the committed message is a witness or the trapdoor is known. By combining instantiations from OWFs of the above 3 tools in parallel we could obtain 4-round NMZK from OWFs. The simulator-extractor for such a scheme would (1) extract the trapdoor from the verifier; (2) commit to 0 in the non-malleable commitment; (3) use the trapdoor as witness in the WIPoK; (4) extract the witness from the arguments given by the MiM by extracting from the WIPoK or from the non-malleable commitment.

Unfortunately it is not clear how to prove the security of this scheme when all sub-protocols are squeezed into 4 rounds. The problem arises from the interactive nature of the involved primitives. Indeed notice that the 4-round non-malleable commitment is executed in parallel with the 4-round WIPoK. When in a hybrid of the security proof the trapdoor is used as witness in the 4-round WIPoK played on the left, the MiM could do the same and also commits to the message 0 in the non-malleable commitment. To detect this behavior, in order to break the WI, the reduction should extract the message committed in the non-malleable commitment by rewinding the MiM. This implies that also the 4-round WIPoK involved in the reduction must be rewound (we recall that these two sub-protocols are executed in parallel). It is important to observe that if in some hybrid we allow the MiM to commit to the message 0 when the witness of the WIPoK given on the left is switched to the trapdoor, then the simulator-extractor (that corresponds to the final hybrid) will have no way to extract a witness from the MiM (and this is required by the definition of NMZK). Indeed from a successful MiM that commits to 0 the extraction from the WIPoK can only give in output the trapdoor. Therefore the simulator-extractor would fail.

A special delayed-input WIPoK $\varPi ^\mathsf {OR}$ . In order to overcome the above problem we follow a recent idea proposed in [7] where non-interactive primitives instead of 3-rounds WIPoKs are used in order to construct a concurrent non-malleable commitment in four rounds. In this way, in every security reduction to such primitives, it will be always possible to extract the message committed in the non-malleable commitment without interfering with the challenger involved in the reduction.

In [7] the authors propose an ad-hoc technique that avoids such a rewinding issue by using a combination of instance-dependent trapdoor commitments (IDTCom) and special honest-verifier zero knowledge (Special HVZK) proofs of knowledge. In this paper we propose a generic approach to construct a special delayed-input WIPoK $\varPi ^\mathsf {OR}$ that can be nicely composed with other protocols in parallel. We construct $\varPi ^\mathsf {OR}$ in two steps.

In 1st step we consider the construction of 3-round WIPoK for $\mathcal {N}\mathcal {P}$ of Lapidot and Shamir (LS) [25]³ that enjoys adaptive-input Special HVZK⁴ and observe that LS does not enjoy adaptive-input special soundness. That is, given and accepting transcript $(a,0,z_0)$ for the statement $x_0$ and an accepting transcript $(a,1,z_1)$ for the statement $x_1$, then only the witness $x_1$ can be efficiently extracted. More precisely, only the witness for the statement where the challenge-bit was equal to 1⁵ (see Definition 5 for a formal definition of adaptive-input special soundness) can be extracted. Therefore we propose a compiler that using ${\mathsf {LS}}=(\mathcal {P}, \mathcal {V})$ in a black-box way outputs a 3-round protocol ${\mathsf {LS}}'=(\mathcal {P}', \mathcal {V}')$ that maintains the adaptive-input Special HVZK and moreover enjoys adaptive-input special soundness.

In the second step we show how to combine the OR composition of statements proposed in [12] with ${\mathsf {LS}}'$ in oder to obtain a WIPoK $\varPi ^\mathsf {OR}$ such that: (a) a reduction can be successfully completed even when there are rewinds due to another protocol played in parallel; (b) the statement (and the corresponding witness) are required to be known only in the last round. Both properties are extremely helpful when a WIPoK is played with other protocols in parallel.

We now give more details about the two steps mentioned above.

– First step: ${\mathsf {LS}}'=(\mathcal {P}', \mathcal {V}')$. Our construction of ${\mathsf {LS}}'$ works as follows. The prover $\mathcal {P}'$ runs two times $\mathcal {P}$ using different randomnesses thus obtaining two first rounds of LS $a_0$ and $a_1$. Upon receiving the challenge-bit b from the verifier $\mathcal {V}$, the statement x to be proved and the corresponding witness w, $\mathcal {P}'$ runs $\mathcal {P}$ in order to compute the answer $z_0$ with respect to the challenge b for $a_0$ and the answer $z_1$ with respect to the challenge $1-b$ for $a_1$. $\mathcal {V}'$ accepts if both $(a_0, b, z_0, x)$ and $(a_1, 1-b, z_1, x)$ are accepting for $\mathcal {V}$. We now observe that every accepting transcript for ${\mathsf {LS}}'$ contains a sub-transcript that is accepting for $\mathcal {V}$ where the bit 1 has been used as a challenge. From what we have discussed above, it is easy to see that ${\mathsf {LS}}'$ enjoys adaptive-input special soundness.

– Second step: adaptive-input PoK for the OR of compound statements. We combine together two executions of ${\mathsf {LS}}'$ by using the trick for composing two $\varSigma$-protocols $\varSigma _0, \varSigma _1$ to construct a $\varSigma$-protocol for the $\mathcal {N}\mathcal {P}$-language $L_0\ \text {OR}\ L_1$ [12]. Let the compound statement to be proved be $(x_0, x_1)$, with $x_0\in L_0$ and $x_1\in L_1$, and let $w_b$ be the witness for $x_b$. The protocol $\varPi ^\mathsf {OR}$ proposed in [12] considers two $\varSigma$-protocols $\varSigma _0$ and $\varSigma _1$ (respectively for $L_0$ and $L_1$) executed in parallel, but after receiving the challenge c form the verifier, the prover can use as challenges for $\varSigma _0$ and $\varSigma _1$ every pair $(c_0,c_1)$ s.t. $c_0\oplus c_1=c$. Therefore the prover could choose in advance one of the challenge to be used, (e.g., $c_{1-b}$), and compute the other one by setting $c_b=c\oplus c_{1-b}$. In this way the transcript for $\varSigma _{1-b}$ can be computed using the Special HVZK simulator while the transcript for $\varSigma _b$ is computed using the witness $w_b$. Thus the prover has the “freedom” of picking one out of two of the challenge before seeing c, but still being able to complete the execution of both $\varSigma _0$ and $\varSigma _1$ for every c. We will show that this “freedom” is sufficient to switch between using $w_0$ and $w_1$ (in order to prove WI) even when it is required to answer to additional (and different) challenges $c^1,\dots ,c^{\mathsf{poly}(\lambda )}$ (i.e., when some rewinds occur). Indeed it is possible to change the witness used (from $w_0$ to $w_1$) in two steps relying first on the Special HVZK of $\varSigma _1$, and then on the Special HVZK of $\varSigma _0$. More precisely we consider the hybrid experiment $H^{w_0}$ as the experiment where in $\varPi ^\mathsf {OR}$ the witness $w_0$ is used (analogously we define $H^{w_1}$). We now consider $H^{w_0,w_1}$ that differs from $H^{w_0}$ because both the witnesses $w_0$ and $w_1$ are used. We prove that $H^{w_0}$ and $H^{w_0,w_1}$ are indistinguishable due to the Special HVZK of $\varSigma _1$ even tough $\varPi ^\mathsf {OR}$ is rewound polynomially many times. The reduction works as follows. A challenge $c_1$ is chosen before the protocol $\varPi ^\mathsf {OR}$ starts and the Special HVZK challenger is invoked thus obtaining $(a_1, z_1)$. The transcript for $\varSigma _0$ is computed by the reduction using the witness $w_0$ in order to answer to the challenge $c_0^i = c^i \oplus c_1$ for $i=1,\dots ,\mathsf{poly}(\lambda )$. We recall the we are in a setting where $\varPi ^\mathsf {OR}$ could be rewound, and therefore the reduction needs to answer to multiple challenges. We observe that the reduction to the Special HVZK is not disturbed by these rewinds because $c_1$ can be kept fixed. The same arguments can be used to prove that $H^{w_0,w_1}$ is computationally indistinguishable from $H^{w_1}$.

We then show that as $\varPi ^\mathsf {OR}$ preserves the special-soundness of the input $\varSigma$-protocols, as well as preserves the adaptive-input special soundness when two instantiations of ${\mathsf {LS}}'$ are used. Moreover the above reductions to Special HVZK can be done relying on adaptive-input Special HVZK. Finally $\varPi ^\mathsf {OR}$ can be upgrade from adaptive-input special soundness to adaptive-input PoK using a theorem of [11].

Our NMZK argument system $\mathsf {NMZK}$ . We run $\varPi ^\mathsf {OR}$ in parallel with a 4-round public-coin one-one honest-extractable synchronous non-malleable commitment scheme $\varPi _{\mathsf {nm}}$ ⁶. A construction for such a scheme in 4 rounds was given by [22]. The prover of the NMZK argument runs $\varPi ^\mathsf {OR}$ in order to prove either the validity of some $\mathcal {N}\mathcal {P}$-statement, or that the non-malleable commitment computed using $\varPi _{\mathsf {nm}}$ contains a trapdoor. The simulator for NMZK works by extracting the trapdoor, committing to it using the non-malleable commitment, and using knowledge of both the trapdoor and the opening information used to compute the non-malleable commitment as a witness for $\varPi ^\mathsf {OR}$. The 3-round subprotocol from OWFs for the trapdoor extraction follows the one of [7]. More precisely the trapdoor is represented by the knowledge of two signatures under a verification key sent by the verifier in the 1st round. In order to allow the extraction of the trapdoor, the verifier of NMZK sends a signature of a message randomly chosen in the 3rd round by the prover.

The security proof of one-many NMZK. The simulator of NMZK extracts the trapdoor⁷, and commits to it using $\varPi _{\mathsf {nm}}$. Following the proof approach provided in [6], we need to prove that the MiM adversary does not do the same. More precisely we want to guarantee that there is no right session where the MiM commits to two signatures of two different messages. The reduction to the non-malleability of the underlying commitment scheme isolates one right session guessing that the MiM has committed there to the trapdoor. The distinguisher for the non-malleable commitment takes as input the committed message an checks if it corresponds to two signatures of two different messages for a given signature key. The above proof approach works only with synchronous sessions (i.e., for synchronous one-many NMZK). Indeed $\varPi _{\mathsf {nm}}$ is secure only in the synchronous case. In order to deal with the asynchronous case we rely on the honest-extractability of $\varPi _{\mathsf {nm}}$.

We recall that $\varPi ^\mathsf {OR}$ is run in parallel with $\varPi _{\mathsf {nm}}$ in order to ensure that either the witness for an $\mathcal {N}\mathcal {P}$-statement x is known or the trapdoor has been correctly committed using $\varPi _{\mathsf {nm}}$. For our propose we only need to ensure that the MiM never commits to the trapdoor. If this is not the case than there exists a right session where the MiM is committing correctly to the trapdoor using $\varPi _{\mathsf {nm}}$ with non-negligible probability. This means that we can extract the message committed by the MiM by just relying on the honest-extractability of $\varPi _{\mathsf {nm}}$. Therefore we can make a reduction to the hiding of $\varPi _{\mathsf {nm}}$ ⁸.

In order to prove that also in the reductions to adaptive-input Special HVZK the MiM still does not commit to the trapdoor we can uses the same approach explained above. Note that in these reductions it is crucial that the rewinds needed to extract the committed message in $\varPi _{\mathsf {nm}}$ do not disturb the challengers involved in the reductions.

From one-many NMZK to synchronous many-many NMZK. Our one-many NMZK is also synchronous many-many NMZK. Indeed, the simulator can extract (simultaneously) the trapdoor from the right sessions, playing as described above. The only substantial difference is that we need to use a many-one non-malleable commitment with all the properties listed above. Following the approach proposed in the security proof of Proposition 1 provided in [28], it is possible to claim that a synchronous (one-one) non-malleable commitment is also synchronous many-one non-malleable.

1.3 4-Round Secure Multi-Party Coin Tossing

Our MPCT protocol will critically make use of our delayed-input synchronous many-many NMZK from OWFs, and of an instantiation of $\varPi ^\mathsf {OR}$. However, similarly to [18] our protocol consists of each party committing to a random string r, that is then sent in the clear in the last round. Moreover there will be a simulatable proof of correctness of the above commitment w.r.t. r, that is given to all parties independently. The output consists of the $\bigoplus$ of all opened strings. We now discuss in more details the messages exchanged by a pair of parties $P_1$ and $P_2$ in our multi-party coin tossing protocol $\varPi _\mathsf {MPCT}$. The generalization to n players is straight-forward and discussed in Sect. 4.1.

Informal description of the protocol. $P_1$, using a perfectly binding computationally hiding commitment scheme, commits in the first round to a random string $r_1$ two times thus obtaining $\mathtt {com}_0, \mathtt {com}_1$. Moreover $P_1$ runs $\varPi ^\mathsf {OR}$ in order to prove knowledge of either the message committed in $\mathtt {com}_0$ or the message committed in $\mathtt {com}_1$. In the last (fourth) round $P_1$ sends $r_1$. In parallel, an execution of a NMZK ensures that both $\mathtt {com}_0$ and $\mathtt {com}_1$ contain the same message $r_1$ (that is sent in the fourth round)⁹. When $P_1$ receives the last round that contains $r_2$, $P_1$ computes and outputs $r_1\oplus r_2$. $P_2$ symmetrically executes the same steps using as input $r_2$.

The simulator for $\varPi _\mathsf {MPCT}$ runs the simulator of NMZK and extracts the input $r^\star$ from the malicious party using the PoK extractor of $\varPi ^\mathsf {OR}$. At this point the simulator invokes the functionality thus obtaining r and plays in the last round $r_s=r \oplus r^\star$. Note that the values that the simulator commits in $\mathtt {com}_0$ and $\mathtt {com}_1$ are unrelated to $r_s$ and this is possible because the NMZK is simulated. The extraction of the input from the adversary made by the simulator needs more attention. Indeed the security of NMZK will ensure that, even though the simulator cheats (he commits to a random string in both $\mathtt {com}_0$ and $\mathtt {com}_1$) the adversary can not do the same. Therefore the only way he can complete an execution of $\varPi _\mathsf {MPCT}$ consists of committing two times to $r^\star$ in the first round, and send the same value in the fourth round. This means that the value extracted (in the third round) from the PoK extractor of $\varPi ^\mathsf {OR}$ is the input of the malicious party.

Our security proof consists of showing the indistinguishability of the following hybrid experiments. The first hybrid experiment differs from the real game by using the simulator of NMZK. The simulator, in order to extract the trapdoor from the adversary, rewinds from the third to the second round, thus rewinding also $\varPi ^\mathsf {OR}$. Indeed the adversary, for every different second round of the NMZK could sent a different second round for $\varPi ^\mathsf {OR}$. This becomes a problem when we consider the hybrid experiment $H_i$ where the witness for $\varPi ^\mathsf {OR}$ changes. Due to the rewinds made by the simulator of the NMZK it is not clear how to rely on the security of the WI property of $\varPi ^\mathsf {OR}$ (the challenger of WI would be rewound). This is the reason why, also in this case, we need to consider an intermediate hybrid experiment $H^{w_0,w_1}$ where both witnesses of $\varPi ^\mathsf {OR}$ can be used. Then we can prove the indistinguishability between $H^{w_0,w_1}$ and $H_i$ still relying on the Special HVZK of the sub-protocol used in $\varPi ^\mathsf {OR}$ (Blum’s protocol suffices in this case).

2 Definitions and Tools

Preliminaries. We denote the security parameter by $\lambda$ and use “||” as concatenation operator (i.e., if a and b are two strings then by a||b we denote the concatenation of a and b). For a finite set Q, $x\leftarrow Q$ sampling of x from Q with uniform distribution. We use the abbreviation ppt that stays for probabilistic polynomial time. We use $\mathsf{poly}(\cdot )$ to indicate a generic polynomial function. A polynomial-time relation ${\mathsf {Rel}}$ (or polynomial relation, in short) is a subset of $\{0, 1\}^*\times \{0,1\}^*$ such that membership of (x, w) in ${\mathsf {Rel}}$ can be decided in time polynomial in |x|. For $(x,w)\in {\mathsf {Rel}}$, we call x the instance and w a witness for x. For a polynomial-time relation ${\mathsf {Rel}}$, we define the $\mathcal {N}\mathcal {P}$-language $L_{{\mathsf {Rel}}}$ as $L_{{\mathsf {Rel}}}=\{x|\exists \ w: (x, w)\in {\mathsf {Rel}}\}$. Analogously, unless otherwise specified, for an $\mathcal {N}\mathcal {P}$-language L we denote by ${\mathsf {Rel}}_\mathsf {L}$ the corresponding polynomial-time relation (that is, ${\mathsf {Rel}}_\mathsf {L}$ is such that $L=L_{{\mathsf {Rel}}_\mathsf {L}}$). We also use $\hat{L}$ to denotes the language that includes L and all well formed instances that are not in L. Let A and B be two interactive probabilistic algorithms. We denote by $\langle A(\alpha ),B(\beta )\rangle (\gamma )$ the distribution of B’s output after running on private input $\beta$ with A using private input $\alpha$, both running on common input $\gamma$. A transcript of $\langle A(\alpha ),B(\beta )\rangle (\gamma )$ consists of the messages exchanged during an execution where A receives a private input $\alpha$, B receives a private input $\beta$ and both A and B receive a common input $\gamma$. Moreover, we will refer to the view of A (resp. B) as the messages it received during the execution of $\langle A(\alpha ),B(\beta )\rangle (\gamma )$, along with its randomness and its input. We denote by $A_r$ an algorithm A that receives as randomness r. In Appendix A we recall some useful definitions. We assume familiarity with the well-known formal definitions for secure multi-party computation.

3 4-Round Delayed-Input NMZK from OWFs

Delayed-Input non-malleable zero knowledge. Following [26] we use a definition that gives to the adversary the power of adaptive-input selection. More precisely, in [26] the adversary selects the instance and then a Turing machine outputs the witness in exponential time. Here we slightly deviate (similarly to [14]) by (1) requiring the adversary to output also the witness and (2) allowing the adversary to make this choice at the last round. This choice is due to our application where delayed-input non-malleable zero knowledge is used. Indeed we will show that this definition is enough for our propose. More precisely our definition (similarly to [7]) we will allow the adversary to explicitly select the statement, and as such the adversary will provide also the witness for the prover. The simulated game however will filter out the witness so that the simulator will receive only the instance. This approach strictly follows the one of [14] where adaptive-input selection is explicitly allowed and managed in a similar way. As final remark, our definition will require the existence of a black-box simulator since a non-black-box simulator could retrieve from the code of the adversary the witness for the adaptively generated statement. The non-black-box simulator could then run the honest prover procedure, therefore canceling completely the security flavor of the simulation paradigm.

Let $\varPi =(\mathcal {P}, \mathcal {V})$ be a delayed-input interactive argument system for a $\mathcal {N}\mathcal {P}$-language L with witness relation ${\mathsf {Rel}}_\mathsf {L}$. Consider a ppt MiM adversary $\mathcal {A}$ that is simultaneously participating in one left session and $\mathsf{poly}(\lambda )$ right sessions. Before the execution starts, $\mathcal {P}, \mathcal {V}$ and $\mathcal {A}$ receive as a common input the security parameter in unary $1^\lambda$. Additionally $\mathcal {A}$ receives as auxiliary input $z\in \{0,1\}^\star$. In the left session $\mathcal {A}$ verifies the validity of a statement x (chosen adaptively in the last round of $\varPi$) by interacting with $\mathcal {P}$ using identity ${\mathtt {id}}$ of $\mathcal {A}$’s choice. In the right sessions $\mathcal {A}$ proves the validity of the statements $\tilde{x}_1\dots , \tilde{x}_{\mathsf{poly}(\lambda )}$ ¹⁰ (chosen adaptively in the last round of $\varPi$) to the honest verifiers $\mathcal {V}_1,\dots , \mathcal {V}_{\mathsf{poly}(\lambda )}$, using identities $\tilde{{\mathtt {id}}}_1, \dots , \tilde{{\mathtt {id}}}_{\mathsf{poly}(\lambda )}$ of $\mathcal {A}$’s choice.

More precisely in the left session $\mathcal {A}$, before the last round of $\varPi$ is executed, adaptively selects the statement x to be proved and the witness w, s.t. $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$, and sends them to $\mathcal {P}$ ¹¹.

Let $\mathsf{{View}}^\mathcal {A}(1^\lambda , z)$ denote a random variable that describes the view of $\mathcal {A}$ in the above experiment.

Definition 1 (Delayed-input NMZK)

A delayed-input argument system $\varPi =(\mathcal {P}, \mathcal {V})$ for an $\mathcal {N}\mathcal {P}$-language L with witness relation ${\mathsf {Rel}}_\mathsf {L}$ is delayed-input non-malleable zero knowledge (NMZK) if for any MiM adversary $\mathcal {A}$ that participates in one left session and $\mathsf{poly}(\lambda )$ right sessions, there exists a expected ppt machine $S(1^\lambda , z)$ such that:

• 1. The probability ensembles $\{ S^1(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }$ and $\{ \mathsf{{View}}^\mathcal {A}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }$ are computationally indistinguishable over $\lambda$, where $S^1(1^\lambda , z)$ denotes the first output of $S(1^\lambda , z)$.

• 2. Let $(\mathsf{{View}}, w_1,\dots ,w_{\mathsf{poly}(\lambda )})$ denote the output of $S(1^\lambda , z)$, for some $z \in \{0,1\}^\star$. Let $\tilde{x}_1, \dots , \tilde{x}_{\mathsf{poly}(\lambda )}$ be the right-session statements appearing in $\mathsf{{View}}$ and let ${\mathtt {id}}$ and $\tilde{{\mathtt {id}}}_1, \dots , \tilde{{\mathtt {id}}}_{\mathsf{poly}(\lambda )}$ be respectively the identities used in the left and right sessions appearing in $\mathsf{{View}}$. Then for every $i \in \{1,\dots , \mathsf{poly}(\lambda )\}$, if the i-th right session is accepting and ${\mathtt {id}}\ne \tilde{{\mathtt {id}}}_i$, then $\tilde{w}_i$ is s.t. $( \tilde{x}_i, \tilde{w}_i) \in {\mathsf {Rel}}_\mathsf {L}$.

The above definition of NMZK allows the adversary to select statements adaptively in the last round both in left and in the right sessions. Therefore any argument system that is NMZK according to the above definition enjoys also adaptive-input argument of knowledge. Following [27] we say that a MiM is synchronous if it “aligns” the left and the right sessions; that is, whenever it receives message i on the left, it directly sends message i on the right, and vice versa. In our paper we also consider the notion of delayed-input many-many synchronous NMZK, that is equal to the notion of delayed-input NMZK except that polynomially many left and right sessions are played in synchronously.

In the rest of the paper, following [23], we assume that identities are known before the protocol begins, though strictly speaking this is not necessary, as the identities do not appear in the protocol until after the first prover message. The MiM can choose his identity adversarially as long as it differs from the identities used by honest senders. As already observed in previous works, when the identity is selected by the sender the id-based definitions guarantee non-malleability as long as the MiM does not behave like a proxy (an unavoidable attack). Indeed the sender can pick as ${\mathtt {id}}$ the public key of a signature scheme signing the transcript. The MiM will have to use a different ${\mathtt {id}}$ or to break the signature scheme.

3.1 Our Protocol: $\mathsf {NMZK}$

For our construction of a 4-round delayed-input non-malleable zero knowledge $\mathsf {NMZK}=(\mathcal {P}_\mathsf {NMZK}, \mathcal {V}_\mathsf {NMZK})$ for the $\mathcal {N}\mathcal {P}$-language L we use the following tools.

• 1. A signature scheme $\mathsf {\Sigma }=(\mathsf {Gen},\mathsf {Sign},\mathsf {Ver})$.

• 2. A 4-round public-coin synchronous honest-extractable non-malleable commitment scheme $\mathsf {NM}=(\mathcal {S},\mathcal {R})$ (See Appendix A.3 for a formal definition).

• 3. Two instantiations of the adaptive-input special sound LS protocol described in Appendix B in order to construct a 4-round delayed-input public-coin proof system for the OR of compound statement $\varPi _{\mathsf {OR}}=(\mathcal {P}_{\mathsf {OR}}, \mathcal {V}_{\mathsf {OR}})$ as described in Appendix B.2. More in details we use the following proof systems.

  • 3.1 A 4-round delayed-input public coin $\mathsf {LS} _L=(\mathcal {P}_L,\mathcal {V}_L)$ for the $\mathcal {N}\mathcal {P}$-language L with adaptive-input Special HVZK simulator $S_L$. $\mathsf {LS} _L=(\mathcal {P}_L,\mathcal {V}_L)$ is adaptive-input special sound for the corresponding relation ${\mathsf {Rel}}_L$ with instance length $\ell _L$.

  • 3.2 A 4-round delayed-input public coin $\mathsf {LS} _{\mathsf {nm}}=(\mathcal {P}_{\mathsf {nm}},\mathcal {V}_{\mathsf {nm}})$ with adaptive-input Special HVZK simulator $S_{\mathsf {nm}}$. $\mathsf {LS} _{\mathsf {nm}}=(\mathcal {P}_{\mathsf {nm}},\mathcal {V}_{\mathsf {nm}})$ is adaptive-input special sound for the $\mathcal {N}\mathcal {P}$-relation ${\mathsf {Rel}}_\mathsf {L_{\mathsf {nm}}}$ where

    $$\begin{aligned} \begin{aligned}&L_{\mathsf {nm}}= \{(\mathsf {vk}, \tau =({\mathtt {id}}, {\mathsf {nm}}_1,{\mathsf {nm}}_2,{\mathsf {nm}}_3, {\mathsf {nm}}_4), s_1: \exists (\mathtt {dec}_{\mathsf {nm}}, s_0, \sigma _1, \mathtt {msg}_1, \sigma _2,\mathtt {msg}_2)\\&\text { s.t. }\ \mathsf {Ver}(\mathsf {vk}, \mathtt {msg}_1, \sigma _1)=1\ \text {AND}\ \mathsf {Ver}(\mathsf {vk}, \mathtt {msg}_2, \sigma _2)=1\ \text {AND}\ \mathtt {msg}_1\ne \mathtt {msg}_2\ \text {AND}\\&\mathcal {R}\ \text {accepts } ({\mathtt {id}}, s_1,\mathtt {dec}_{\mathsf {nm}}) \text { as a valid decommitment of } \tau \ \text {AND}\ s_0\oplus s_1=\sigma _1||\sigma _2 \}. \end{aligned} \end{aligned}$$

    We denote with $\ell _{\mathsf {nm}}$ the dimension of the instances belonging to $L_{\mathsf {nm}}$. Informally by running $\mathsf {LS} _{\mathsf {nm}}$ one can prove that the message committed using a non-malleable commitment XORed with the value $s_1$ represents two signatures for two different messages w.r.t. the verification key $\mathsf {vk}$.

  Moreover $\varPi ^\mathsf {OR}$ is also adaptive-input PoK for the relation ${\mathsf {Rel}}_\mathsf {L_{\mathsf {OR}}}=\{((x_L, x_{\mathsf {nm}}), w) : ((x_L,w)\in {\mathsf {Rel}}_L) \ \text {OR} \ ((x_{\mathsf {nm}},w)\in {\mathsf {Rel}}_\mathsf {L_{\mathsf {nm}}})\}$ (see Theorem 10 in Appendix B.2 for more details).

Overview of our protocol. We now give an high-level description of our delayed-input NMZK of Fig. 1. For a formal description see Fig. 2.

In the first round $\mathcal {V}_\mathsf {NMZK}$ computes a pair of signature-verification keys $(\mathsf{sk},\mathsf {vk})$ sending $\mathsf {vk}$ to $\mathcal {P}_\mathsf {NMZK}$. Also $\mathcal {V}_\mathsf {NMZK}$ computes the (public coin) first rounds ${\mathsf {nm}}_1$ of $\mathsf {NM}$, $\mathsf {ls}^1_L \leftarrow \mathcal {V}_L(1^\lambda , \ell _L)$ and $\mathsf {ls}^1_{\mathsf {nm}}\leftarrow \mathcal {V}_L(1^\lambda , \ell _{\mathsf {nm}})$. $\mathcal {V}_\mathsf {NMZK}$ completes the first round by sending $(\mathsf {vk}, \mathsf {ls}^1_L, \mathsf {ls}^1_{\mathsf {nm}}, {\mathsf {nm}}^1)$ to $\mathcal {P}_\mathsf {NMZK}$.

In the second round $\mathcal {P}_\mathsf {NMZK}$ computes $\mathsf {ls}^2_L\leftarrow \mathcal {P}_L(1^\lambda , \mathsf {ls}^1_L,\ell _L)$ and sends $\mathsf {ls}^2_L$. Furthermore picks $\mathsf {ls}^3_{\mathsf {nm}}\leftarrow \{0, 1\}^\lambda$ and runs $\mathsf {ls}^2_{\mathsf {nm}}\leftarrow S_{\mathsf {nm}}(1^\lambda , \mathsf {ls}^1_{\mathsf {nm}}, \mathsf {ls}^3_{\mathsf {nm}}, \ell _{\mathsf {nm}})$ in order to send $\mathsf {ls}^2_{\mathsf {nm}}$. $\mathcal {P}_\mathsf {NMZK}$ now commits to a random message $s_0$ using the non-malleable commitment $\mathsf {NM}$ by running $\mathcal {S}$ on input $1^\lambda , s_0, {\mathsf {nm}}_1$ and the identity ${\mathtt {id}}$ thus obtaining and sending ${\mathsf {nm}}_2$. Also $\mathcal {P}_\mathsf {NMZK}$ sends a random message $\mathtt {msg}$.

In the third round of the protocol, upon receiving $\mathtt {msg}$, $\mathcal {V}_\mathsf {NMZK}$ computes and sends a signature $\sigma$ of $\mathtt {msg}$ by running $\mathsf {Sign}(\mathsf{sk}, \mathtt {msg})$. $\mathcal {V}_\mathsf {NMZK}$ picks and sends $\mathsf {c}\leftarrow \{0, 1\}^\lambda$. Also he computes and sends the (public coin) third rounds ${\mathsf {nm}}_3$ of $\mathsf {NM}$.

Fig. 1.

Our 4-round delayed-input NMZK

In the fourth round $\mathcal {P}_\mathsf {NMZK}$ checks whether or not $\sigma$ is a valid signature for $\mathtt {msg}$ w.r.t. the verification key $\mathsf {vk}$. In the negative case $\mathcal {P}_\mathsf {NMZK}$ aborts, otherwise he continues with the following steps. $\mathcal {P}_\mathsf {NMZK}$ computes $\mathsf {ls}^3_L=\mathsf {ls}^3_{\mathsf {nm}}\oplus \mathsf {c}$. Upon receiving the instance x to be proved and the witness w s.t. $(x,w)\in {\mathsf {Rel}}_L$, $\mathcal {P}_\mathsf {NMZK}$ completes the transcript for $\mathsf {LS} _L$ running $\mathsf {ls}^4_L\leftarrow \mathcal {P}_L(x, w, \mathsf {ls}^3_L)$. At this point $\mathcal {P}_\mathsf {NMZK}$ completes the commitment of $s_0$ by running $\mathcal {S}$ on input ${\mathsf {nm}}_3$ thus obtaining $({\mathsf {nm}}_4,\mathtt {dec}_{\mathsf {nm}})$. $\mathcal {P}_\mathsf {NMZK}$ picks a random string $s_1$, sets $x_{\mathsf {nm}}=(\mathsf {vk}, {\mathtt {id}}, {\mathsf {nm}}_1,{\mathsf {nm}}_2,{\mathsf {nm}}_3, {\mathsf {nm}}_4, s_1)$ and runs $\mathsf {ls}^4_{\mathsf {nm}}\leftarrow S_{\mathsf {nm}}(x_{\mathsf {nm}})$. $\mathcal {P}_\mathsf {NMZK}$ completes the fourth round by sending ($\mathsf {ls}^3_L, \mathsf {ls}^4_L, {\mathsf {nm}}_4, s_1, \mathsf {ls}^3_{\mathsf {nm}}, \mathsf {ls}^4_{\mathsf {nm}}, x, x_{\mathsf {nm}})$.

The verifier $\mathcal {V}_\mathsf {NMZK}$ accepts x iff the following conditions are satisfied: (1) $\mathsf {c}$ is equal to $\mathsf {ls}^3_L \oplus \mathsf {ls}^3_{\mathsf {nm}}$; (2) $\mathcal {V}_L(x,\mathsf {ls}^1_L,\mathsf {ls}^2_L,\mathsf {ls}^3_L, \mathsf {ls}^4_L)=1$; (3) $\mathcal {V}_{\mathsf {nm}}(x_{\mathsf {nm}}, \mathsf {ls}^1_{\mathsf {nm}},\mathsf {ls}^2_{\mathsf {nm}},\mathsf {ls}^3_{\mathsf {nm}}, \mathsf {ls}^4_{\mathsf {nm}})=1$.

Fig. 2.

Formal construction of our delayed-input NMZK.

The simulator extractor. Informally, the simulator ${\mathsf {Sim}_\mathsf {NMZK}}$ of our protocol interacts with the adversary $\mathcal {A}_\mathsf {NMZK}$ emulating both the prover in the left session and polynomially many verifiers in the right sessions. In the right sessions ${\mathsf {Sim}_\mathsf {NMZK}}$ interacts with $\mathcal {A}_\mathsf {NMZK}$ as the honest verifiers do. While, in the left session for an instance $x\in L$ chosen adaptively by $\mathcal {A}_\mathsf {NMZK}$, ${\mathsf {Sim}_\mathsf {NMZK}}$ proves, using $\varPi _\mathsf {OR}$, that the message committed in $\mathsf {NM}$ contains two signatures of two different messages w.r.t. the verification key $\mathsf {vk}$. In more details ${\mathsf {Sim}_\mathsf {NMZK}}$ runs the adaptive-input Special HVZK simulator of $\mathsf {LS} _L$ to complete the transcript for $\mathsf {LS} _L$ w.r.t. the instance x. In order to use the honest prover procedure to compute the transcript of $\mathsf {LS} _{\mathsf {nm}}$, $\mathsf {Sim}_\mathsf {NMZK}$ extracts two signatures for two different messages by rewinding $\mathcal {A}_\mathsf {NMZK}$ from the third to the second round and by committing to them using $\mathsf {NM}$ ¹². More precisely the simulator commits to a random string $s_0$, but computes $s_1$ s.t. $s_1=(\sigma _1||\sigma _2)\oplus s_0$ ¹³. Therefore the execution of $\varPi _{\mathsf {OR}}$ can be completed by using the knowledge of the two signatures committed using $\mathsf {NM}$. We use the xor trick originally provided in [6] in order to avoid any additional requirement w.r.t. the underlying non-malleable commitment scheme $\mathsf {NM}$. Indeed if the sender of $\mathsf {NM}$ could decide the message to commit in the last round, then $\mathsf {Sim}_\mathsf {NMZK}$ can simply compute the first round of $\mathsf {NM}$, extract the signature, and compute the last round of $\mathsf {NM}$ by committing to $\sigma _1||\sigma _2$. It is important to observe that even though the non-malleable commitment scheme of [22] fixes the message to be committed in the third round, there is in general no guarantee that such a scheme is secure against an adversary that adaptively chooses the challenge messages in the last round of the non-malleability security game. Therefore, even though the completeness of our scheme would work without using the trick of [6], it would be unclear, in general, how to prove the security of our final scheme. A formal description of ${\mathsf {Sim}_\mathsf {NMZK}}$ can be found in the proof of Theorem 1.

The formal construction of our delayed-input NMZK $\mathsf {NMZK}=(\mathcal {P}_\mathsf {NMZK},\mathcal {V}_\mathsf {NMZK})$ for the $\mathcal {N}\mathcal {P}$-language L can be found in Fig. 2.

Theorem 1

If OWFs exist, then $\mathsf {NMZK}$ is a 4-round delayed-input NMZK AoK for $\mathcal {N}\mathcal {P}$.

Proof

We divide the security proof in two parts, proving that $\mathsf {NMZK}$ enjoys delayed-input completeness and NMZK. The proof of NMZK is divided also in two lemmas, one for each of the two properties of Definition 1. Before that, we recall that $\mathsf {LS} _{\mathsf {nm}}$ and $\mathsf {LS} _L$ can be constructed from OWFs (see Appendix A) as well as $\mathsf {\Sigma }$ (using [39]) and the 4-round public-coin synchronous honest-extractable non-malleable commitment scheme $\mathsf {NM}$ (see Appendix A.3).

(Delayed-Input) Completeness. The completeness follows directly from the delayed-input completeness of $\mathsf {LS} _{\mathsf {nm}}$ and $\mathsf {LS} _L$, the correctness of $\mathsf {NM}$ and the validity of $\mathsf {\Sigma }$. We observe that, due to the delayed-input property of $\mathsf {LS} _L$, the statement x (and the respective witness w) are used by $\mathcal {P}_\mathsf {NMZK}$ only to compute the last round. Therefore also $\mathsf {NMZK}$ enjoys delayed-input completeness.

(Delayed-Input) NMZK. Following Definition 1 we start by describing how the simulator ${\mathsf {Sim}_\mathsf {NMZK}}$ for $\mathsf {NMZK}$ works. In the left session ${\mathsf {Sim}_\mathsf {NMZK}}$ interacts with the MiM adversary $\mathcal {A}_\mathsf {NMZK}$ in the following way. Upon receiving the first round, $\mathsf {vk}$, $\mathsf {ls}^1_L$, $\mathsf {ls}^1_{\mathsf {nm}}$, ${\mathsf {nm}}_1$, from $\mathcal {A}_\mathsf {NMZK}$, ${\mathsf {Sim}_\mathsf {NMZK}}$ on input $\mathsf {ls}^1_{\mathsf {nm}}$ computes $\mathsf {ls}^2_{\mathsf {nm}}$ by running $\mathcal {P}_{\mathsf {nm}}$. ${\mathsf {Sim}_\mathsf {NMZK}}$ picks $\mathsf {ls}^3_L\leftarrow \{0,1\}^\lambda$ and runs $S_L$ on input $1^\lambda$, $\ell _L$, $\mathsf {ls}^1_L$, $\mathsf {ls}^3_L$ thus obtaining $\mathsf {ls}^2_L$. ${\mathsf {Sim}_\mathsf {NMZK}}$, in order to commit to a random message $s_0$ runs $\mathcal {S}$ on input ${\mathsf {nm}}_1$, the identity ${\mathtt {id}}$ and $s_0$ thus obtaining ${\mathsf {nm}}_2$. ${\mathsf {Sim}_\mathsf {NMZK}}$ sends $\mathsf {ls}^2_L, \mathsf {ls}^2_{\mathsf {nm}}, {\mathsf {nm}}_2$ and a random message $\mathtt {msg}_1$ to $\mathcal {A}_\mathsf {NMZK}$. Upon receiving the third round, $\mathsf {c}$, ${\mathsf {nm}}_3$, $\sigma _1$, and instance x to be proved from $\mathcal {A}_\mathsf {NMZK}$, the simulator checks whether or not $\sigma _1$ is a valid signature for $\mathtt {msg}_1$ w.r.t. the verification key $\mathsf {vk}$. In the negative case ${\mathsf {Sim}_\mathsf {NMZK}}$ aborts, otherwise $\mathsf {Sim}_\mathsf {NMZK}$ rewinds $\mathcal {A}_\mathsf {NMZK}$ from the third to the second round in order to obtain a second signature $\sigma _2$ for a different message $\mathtt {msg}_2$. After the extraction of the signatures $\mathsf {Sim}_\mathsf {NMZK}$ returns to the main thread and computes the fourth round as follows¹⁴.

${\mathsf {Sim}_\mathsf {NMZK}}$ completes the commitment of $s_0$ by running $\mathcal {S}$ on input ${\mathsf {nm}}_3$ thus obtaining $({\mathsf {nm}}_4,\mathtt {dec}_{\mathsf {nm}})$ and sending ${\mathsf {nm}}_4$. Furthermore $\mathsf {Sim}_\mathsf {NMZK}$ sets $s_1$ s.t. $s_1= (\sigma _1|| \sigma _2)\oplus s_0$, $x_{\mathsf {nm}}=(\mathsf {vk}, {\mathtt {id}}, {\mathsf {nm}}_1,{\mathsf {nm}}_2,{\mathsf {nm}}_3,{\mathsf {nm}}_4, s_1)$, $w_{\mathsf {nm}}=(\mathtt {dec}_{\mathsf {nm}}, s_0, \sigma _1, \mathtt {msg}_1, \sigma _2,\mathtt {msg}_2)$ and completes the transcript for $\mathsf {LS} _{\mathsf {nm}}$ obtaining $\mathsf {ls}^4_{\mathsf {nm}}$ by running the prover procedure $\mathcal {P}_{\mathsf {nm}}$ on input $x_{\mathsf {nm}}$, $w_{\mathsf {nm}}$ and $\mathsf {ls}^3_L \oplus \mathsf {c}$. At this point ${\mathsf {Sim}_\mathsf {NMZK}}$ runs the adaptive-input Special HVZK simulator $S_L$ on input x thus obtaining $\mathsf {ls}^4_L$. Then the values $(\mathsf {ls}^3_L, \mathsf {ls}^4_L,{\mathsf {nm}}_4, s_1, \mathsf {ls}^3_{\mathsf {nm}}, \mathsf {ls}^4_{\mathsf {nm}}, x, x_{\mathsf {nm}})$ are sent to $\mathcal {A}_\mathsf {NMZK}$. At the end of the execution ${\mathsf {Sim}_\mathsf {NMZK}}$ outputs $\mathcal {A}_\mathsf {NMZK}$’s view in the main thread. Furthermore, he uses the extractor of $\mathsf {LS} _L$ to extract and output, from the $\mathsf{poly}(\lambda )$ right sessions, the witnesses $\tilde{w}_1, \dots , \tilde{w}_{\mathsf{poly}(\lambda )}$ used by $\mathcal {A}_\mathsf {NMZK}$ to compute the transcript of $\varPi ^\mathsf {OR}$ (the witnesses correspond to statements $\tilde{x}_i$ proved by $\mathcal {A}_\mathsf {NMZK}$ in the i-th right session, for $i=1,\dots , \mathsf{poly}(\lambda )$).

Lemma 1

$\{ {\mathsf {Sim}_\mathsf {NMZK}}^1(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*} \approx \{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*},$ where ${\mathsf {Sim}_\mathsf {NMZK}}^1(1^\lambda , z)$ denotes the 1st output of ${\mathsf {Sim}_\mathsf {NMZK}}$.

In order to prove the above lemma we consider the series of hybrid experiments described below. In the proof we denote with $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_i}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ the random variable that describes the view of ${\mathcal {A}_\mathsf {NMZK}}$ in the hybrid $\mathcal {H}_i(1^\lambda ,z)$. Let p the probability that in the real execution $\mathcal {A}_\mathsf {NMZK}$ completes the left session.

• We start considering the hybrid experiment $\mathcal {H}_0(1^\lambda , z)$ in which in the left session $\mathcal {P}_\mathsf {NMZK}$ interacts with $\mathcal {A}_\mathsf {NMZK}$ and in the i-th right session ${\mathcal {V}_\mathsf {NMZK}}_i$ interacts with $\mathcal {A}_\mathsf {NMZK}$, for $i =1,\dots , \mathsf{poly}(\lambda )$. Note that $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_0}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*} = \{ \mathsf{{View}}^\mathcal {A}_\mathsf {NMZK}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$. The hybrid experiment $\mathcal {H}_1(1^\lambda , z)$ differs from $\mathcal {H}_0(1^\lambda , z)$ only in the fact that in the left session of $\mathcal {H}_1(1^\lambda , z)$ $\mathcal {A}_\mathsf {NMZK}$ is rewound from the third to the second round, in order to extract two signatures $\sigma _1,\sigma _2$ for two distinct messages $(\mathtt {msg}_1, \mathtt {msg}_2)$ w.r.t. a verification key $\mathsf {vk}$. Note that after p rewinds the probability of not obtaining a valid new signature is less than 1 / 2. Therefore the probability that $\mathcal {A}_\mathsf {NMZK}$ does not give a second valid signature for a randomly chosen message after $\lambda /p$ rewinds is negligible in $\lambda$. For the above reason the procedure of extraction of signatures for different messages in $\mathcal {H}_1(1^\lambda , z)$ succeeds except with negligible probability. Observe that the above deviation increases the abort probability of the experiment only by a negligible amount, therefore $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_0}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*} \equiv _s \{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_1}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$.

• The hybrid experiment $\mathcal {H}_2(1^\lambda , z)$ differs from $\mathcal {H}_1(1^\lambda , z)$ only in the message committed using $\mathsf {NM}$. Indeed $\mathcal {P}_\mathsf {NMZK}$ commits using $\mathsf {NM}$ to two signatures $\sigma _1,\sigma _2$ of two distinct messages $(\mathtt {msg}_1, \mathtt {msg}_2)$ instead of a random message. In more details, $\mathcal {P}_\mathsf {NMZK}$ commits to a random string $s_0$ using $\mathsf {NM}$ and in 4th round sets and sends $s_1=(\sigma _1||\sigma _2)\oplus s_0$, instead of sending $s_1$ as a random string. Observe that the procedure of extraction of the signatures succeeds in $\mathcal {H}_2(1^\lambda , z)$ with non-negligible probability, because the first three rounds are played exactly as in $\mathcal {H}_1(1^\lambda , z)$. Now we can claim that $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_2}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ and $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_1}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ are computationally indistinguishable by using the computationally-hiding property of $\mathsf {NM}$. Suppose by contradiction that there exist an adversary ${\mathcal {A}_\mathsf {NMZK}}$ and a distinguisher $\mathcal {D}_\mathsf {NMZK}$ such that $\mathcal {D}_\mathsf {NMZK}$ distinguishes $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_1}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ from $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_2}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$. Then we can construct an adversary $\mathcal {A}_\mathsf {Hiding}$ that breaks the computationally hiding of $\mathsf {NM}$ in the following way. $\mathcal {A}_\mathsf {Hiding}$ sends to the challenger of the hiding game $\mathcal {C}_\mathsf {Hiding}$ two random messages $(m_0, m_1$). Then, in the left session $\mathcal {A}_\mathsf {Hiding}$ acts as $\mathcal {P}_\mathsf {NMZK}$ except for messages of $\mathsf {NM}$ for which he acts as proxy between $\mathcal {C}_\mathsf {Hiding}$ and ${\mathcal {A}_\mathsf {NMZK}}$. When $\mathcal {A}_\mathsf {Hiding}$ computes the last round of the left session $\mathcal {A}_\mathsf {Hiding}$ sets and sends $s_1=\sigma _1||\sigma _2\oplus m_0$. In the right sessions $\mathcal {A}_\mathsf {Hiding}$ interacts with $\mathcal {A}_{\mathsf {ZK}}$ acting as $\mathcal {V}_\mathsf {NMZK}$ does. At the end of the execution $\mathcal {A}_\mathsf {Hiding}$ runs $\mathcal {D}_\mathsf {NMZK}$ and outputs what $\mathcal {D}_\mathsf {NMZK}$ outputs. It is easy to see that if $\mathcal {C}_\mathsf {Hiding}$ commits to $m_1$ then, $\mathcal {A}_{\mathsf {ZK}}$ acts as in $\mathcal {H}_1(1^\lambda , z)$, otherwise he acts as in $\mathcal {H}_2(1^\lambda , z)$. Note that the reduction to the hiding property of $\mathsf {NM}$ is possible because the rewinds to extract a second signature do not affect the execution with the challenger of $\mathsf {NM}$ that remains straight-line.

• The hybrid experiment $\mathcal {H}_3(1^\lambda , z)$ differs from $\mathcal {H}_2(1^\lambda , z)$ in the way the transcript of $\mathsf {LS} _{\mathsf {nm}}$ is computed. More precisely, the prover $\mathcal {P}_{\mathsf {nm}}$ of $\mathsf {LS} _{\mathsf {nm}}$ is used to compute the messages $\mathsf {ls}^2_{\mathsf {nm}}$ and $\mathsf {ls}^4_{\mathsf {nm}}$ instead of using the adaptive-input Special HVZK simulator. Note that due to the delayed-input property of $\mathsf {LS} _{\mathsf {nm}}$ the statement $x_{\mathsf {nm}}=(\mathsf {vk}, {\mathsf {nm}}_1,{\mathsf {nm}}_2,{\mathsf {nm}}_3,{\mathsf {nm}}_4, s_1)$ and the witness $w_{\mathsf {nm}}=(\mathtt {dec}_{\mathsf {nm}}, s_0, \sigma _1, \mathtt {msg}_1, \sigma _2,\mathtt {msg}_2)$ are required by $\mathcal {P}_{\mathsf {nm}}$ only to compute $\mathsf {ls}^4_{\mathsf {nm}}$ and are not needed to compute $\mathsf {ls}^2_{\mathsf {nm}}$. Observe that the procedure of extraction of the signatures succeeds in $\mathcal {H}_3(1^\lambda , z)$ with non-negligible probability due to the adaptive-input Special HVZK of $\mathsf {LS} _{\mathsf {nm}}$. From the adaptive-input Special HVZK of $\mathsf {LS} _{\mathsf {nm}}$ it follows that $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_2}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ and $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_3}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$ are computationally indistinguishable.

• The hybrid $\mathcal {H}_4(1^\lambda , z)$ differs from $\mathcal {H}_3(1^\lambda , z)$ in the way the transcript of $\mathsf {LS} _L$ is computed. More precisely, the adaptive-input Special HVZK simulator of $\mathsf {LS} _L$ is used to compute the messages $\mathsf {ls}^2_L$ and $\mathsf {ls}^4_L$ using as input $\mathsf {ls}^1_L$ received by $\mathcal {A}_\mathsf {NMZK}$, the statement x and a random string $\mathsf {ls}^3_L$ chosen by the hybrid experiment. We observe that in order to complete the execution of $\varPi _\mathsf {OR}$ the honest prover procedure $\mathcal {P}_{\mathsf {nm}}$ can be used on input $x_{\mathsf {nm}}$, $w_{\mathsf {nm}}$ and $\mathsf {ls}^3_{\mathsf {nm}}= \mathsf {ls}^3_L \oplus \mathsf {c}$. Moreover adaptive-input Special HVZK of $\mathsf {LS} _L$ ensures that the extraction procedure of the signatures succeeds in $\mathcal {H}_4(1^\lambda , z)$ with non-negligible probability and that $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_4}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}\approx \{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_3}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*}$. Note that $\mathcal {H}_4(1^\lambda , z)$ corresponds to the simulated experiment, that is the experiment where ${\mathsf {Sim}_\mathsf {NMZK}}$ interacts with the adversary $\mathcal {A}_\mathsf {NMZK}$ emulating both a prover in the left session and polynomially many verifiers in the right sessions. This implies that $\{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_4}(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^*} = \{ S^1(1^\lambda , z) \}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }$.

The proof ends with the observation that for all $\lambda \in \mathbb {N}, z\in \{0,1\}^*$ it holds that: $\{ \mathsf{{View}}^\mathcal {A}_\mathsf {NMZK}(1^\lambda , z) \}_{\lambda ,z} = \{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_0}(1^\lambda , z) \}_{\lambda ,z} \approx \dots \approx \{ \mathsf{{View}}^{\mathcal {A}_\mathsf {NMZK}}_{\mathcal {H}_4}(1^\lambda , z) \}_{\lambda ,z}$ $= \{ S^1(1^\lambda , z) \}_{\lambda ,z}$

Lemma 2

Let $\tilde{x}_1,\dots ,\tilde{x}_{\mathsf{poly}(\lambda )}$ be the right-session statements appearing in $\mathsf{{View}}={\mathsf {Sim}_\mathsf {NMZK}}^1(1^\lambda , z)$ and let ${\mathtt {id}}$ be the identity of the left session and $\tilde{{\mathtt {id}}}_1,\dots ,\tilde{{\mathtt {id}}}_{\mathsf{poly}(\lambda )}$ be the identities of right sessions appearing in $\mathsf{{View}}$. If the i-th right session is accepting and ${\mathtt {id}}\ne \tilde{{\mathtt {id}}}_i$ for $i =1,\dots ,{\mathsf{poly}(\lambda )}$, then except with negligible probability, the second output of ${\mathsf {Sim}_\mathsf {NMZK}}(1^\lambda ,z)$ is $\tilde{w}_i$ such that $( \tilde{x}_i, \tilde{w}_i) \in {\mathsf {Rel}}_\mathsf {L}$ for $i =1,\dots ,{\mathsf{poly}(\lambda )}$.

We now reconsider the hybrid experiments $\mathcal {H}_k$ for $k=0,\dots , 4$ described in the security proof of Lemma 1, and prove that they all enjoys an additional property. That is, in the right sessions $\mathcal {A}_\mathsf {NMZK}$ never commits, using $\mathsf {NM}$, to a message $\tilde{s}_0$ and sends a value $\tilde{s}_1$ s.t. $\tilde{s}_0\oplus \tilde{s}_1= \tilde{\sigma }_1||\tilde{\sigma }_2$ where $\tilde{\sigma }_1,\tilde{\sigma }_2$ are two signatures for to different messages. Since $\mathcal {A}_\mathsf {NMZK}$ does not commit to the signatures then the transcript computed using $\mathsf {LS} _{\mathsf {nm}}$ correspond to a false instance, therefore for the adaptive-input PoK property of $\varPi _\mathsf {OR}$, $\mathcal {A}_\mathsf {NMZK}$ in the i-th right session chooses a statement $\tilde{x}_i$ and essentially completes the corresponding transcript of $\mathsf {LS} _L$ using the witness $\tilde{w}_i$ s.t. $( \tilde{x}_i, \tilde{w}_i) \in {\mathsf {Rel}}_\mathsf {L}$ for $i \in \{1,\dots ,{\mathsf{poly}(\lambda )}\}$. For the above chain of implications we are ensured that in all hybrids $\mathcal {A}_\mathsf {NMZK}$ uses the witnesses to complete the transcripts of $\varPi ^\mathsf {OR}$ in the right sessions. Therefore also in the simulated experiment, that corresponds to the last hybrid experiment, the $\mathcal {A}_\mathsf {NMZK}$ behavior allows $\mathsf {Sim}_\mathsf {NMZK}$ to extract the witness used by $\mathcal {A}_\mathsf {NMZK}$ (that is internally executed by ${\mathsf {Sim}_\mathsf {NMZK}}$) using the extractor of $\varPi ^\mathsf {OR}$ (that exists from the adaptive-PoK property enjoyed by $\varPi ^\mathsf {OR}$).

In order to prove that in $\mathcal {H}_0,\dots ,\mathcal {H}_4$ $\mathcal {A}_\mathsf {NMZK}$ does not commit to two signatures in any of the right sessions we rely on the “mild” non-malleability and the honest-extraction property enjoyed by $\mathsf {NM}$. More precisely, in each hybrid experiment, we use the honest-extraction¹⁵ property to extract the signatures from the right sessions (that by contradiction are committed using $\mathsf {NM}$). During the proof we need to show that the rewinds made by the honest-extractor do not interfere with the various reductions. Roughly speaking our security proof works because only non-interactive primitives are used, therefore the rewinds made by the extractor of $\mathsf {NM}$ do not rewind the challenger involved in the reduction. In particular, consider the hybrid $\mathcal {H}_3$ where we switch from the adaptive-input Special HVZK simulator of $\mathsf {LS} _{\mathsf {nm}}$ to the honest prover procedure and $\mathcal {H}_4$ where we start to use adaptive-input Special HVZK simulator of $\mathsf {LS} _L$. In this two hybrid experiments in order to prove that $\mathcal {A}_\mathsf {NMZK}$ does not commit to the signatures we rely on the adaptive-input Special HVZK and the rewinds do not affect the reduction. Indeed when we rely on adaptive-input Special HVZK of $\mathsf {LS} _L$ ($\mathsf {LS} _{\mathsf {nm}}$) the honest prover procedure of $\mathsf {LS} _{\mathsf {nm}}$ ($\mathsf {LS} _L$) can be used in order to complete the execution of $\varPi _\mathsf {OR}$. In this way the third round $\mathsf {ls}^3_L$ ($\mathsf {ls}^3_{\mathsf {nm}}$) can be kept fixed thus computing $\mathsf {ls}^3_{\mathsf {nm}}= \mathsf {c}^i \oplus \mathsf {ls}^3_L$ ($\mathsf {ls}^3_L = \mathsf {c}^i \oplus \mathsf {ls}^3_{\mathsf {nm}}$) for every $c^i$ that could be sent by $\mathcal {A}_\mathsf {NMZK}$ during the rewinds. It is not clear how to do such a security proof by directly relying on the WI property of $\varPi _\mathsf {OR}$. The formal proof for this lemma can be found in the full version (see [9]).

Theorem 2

If OWFs exists, then $\mathsf {NMZK}$ is a delayed-input synchronous many-many NMZK AoK for $\mathcal {N}\mathcal {P}$.

Proof

The proof proceeds very similarly to the one showed for Theorem 1. The main difference between these two proofs is that we now have to consider also polynomially many synchronous left sessions played in parallel. Therefore the only difference between this proof and the one of Theorem 1 is that in the reductions we need to rely on the security of a many-one non-malleable commitment scheme and on the adaptive-input SHVZK (that is closed under parallel composition). Therefore, when we make a reduction on the adaptive-input SHVZK, we can simply use the parallel version of the primitives. Regarding a many-one non-malleable commitment, we notice that using the same arguments of the security proof of Proposition 1 provided in [28], it is possible to claim that a synchronous (one-one) non-malleable commitment is also synchronous many-one non-malleable. Therefore no additional assumptions are required in order to prove that $\mathsf {NMZK}$ is also delayed-input synchronous many-many NMZK. Note also that, the simulator needs to extract the trapdoor (the signatures of two different messages) in all the left (synchronous) sessions completed in the main thread. We can show that the extraction succeeds except with negligible probability using the same arguments used in the security proof of Theorem 1.

4 Multi-Party Coin-Tossing Protocol

4.1 4-Round Secure Multi-Party Coin Tossing: $\varPi _\mathsf {MPCT}$

The high-level idea of our protocol $\varPi _\mathsf {MPCT}$ significantly differs from the one of [18] (e.g., we use our 4-round delayed-input synchronous many-many NMZK instead of 3-round 3-robust parallel non-malleable commitment scheme). However, similarly to [18] our protocol simply consists of each party committing to a random string r, which is opened in the last round along with a simulatable proof of correct opening given to all parties independently. The output consists of the $\oplus$ of all opened strings. Let’s see in more details how our $\varPi _\mathsf {MPCT}$ works. For our construction we use the following tools.

• 1. A non-interactive perfectly binding computationally hiding commitment scheme $\mathsf {PBCOM}=(\mathsf{{Com}}, \mathsf{{Dec}})$.

• 2. A $\varSigma$-protocol $\mathsf {BL}_{L}=(\mathcal {P}_{L},\mathcal {V}_{L})$ for the $\mathcal {N}\mathcal {P}$-language $L=\{\mathtt {com}: \exists \ (\mathtt {dec}, m) \text { s.t. }\ \mathsf{{Dec}}(\mathtt {com}, \mathtt {dec}, m)=1\}$ with Special HVZK simulator $\mathsf {Sim}_{L}$. We uses two instantiations of $\mathsf {BL}_{L}$ in order to construct the protocol for the OR of two statements $\varPi _{\mathsf {OR}}$ as described earlier (Appendix B.2 for more details). $\varPi _{\mathsf {OR}}$ is a proof system for the $\mathcal {N}\mathcal {P}$-language $L_{\mathtt {com}}=\{(\mathtt {com}_0, \mathtt {com}_1): \exists \ (\mathtt {dec}, m) \text {s.t.}\ \mathsf{{Dec}}(\mathtt {com}_0, \mathtt {dec}, m)=1 \ \text {OR} \ \mathsf{{Dec}}(\mathtt {com}_1, \mathtt {dec}, m)=1 \}$ ¹⁶. Informally, by running $\varPi _{\mathsf {OR}}$, one can prove the knowledge of the message committed in $\mathtt {com}_0$ or in $\mathtt {com}_1$.

• 4. A 4-round delayed-input synchronous many-many NMZK $\mathsf {NMZK}=(\mathcal {P}_\mathsf {NMZK},\mathcal {V}_\mathsf {NMZK})$ for the following $\mathcal {N}\mathcal {P}$-language

  $$\begin{aligned} \begin{aligned} L_\mathsf {NMZK}=\{((\mathtt {com}_0, \mathtt {com}_1), m):\ \forall i\in \{0, 1\}\ \exists \ \mathtt {dec}_i\ \text {s.t.}\ \mathsf{{Dec}}(\mathtt {com}_i, \mathtt {dec}_i, m)=1\}. \end{aligned} \end{aligned}$$

  Informally, by running $\mathsf {NMZK}$, one can prove that 2 commitments contain the same message m.

4.2 $\varPi _\mathsf {MPCT}$: Informal Description and Security Intuition

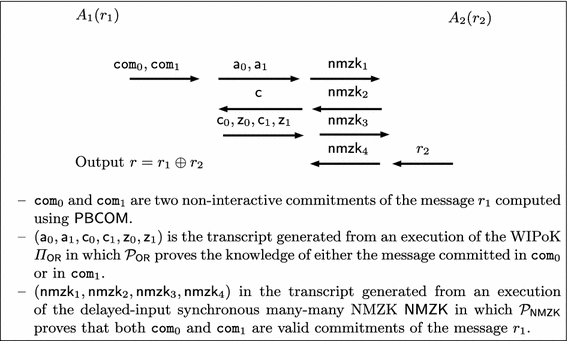
The high level description of our protocol between just two parties $(A_1, A_2)$ is given in Fig. 3. For a formal description of $\varPi _\mathsf {MPCT}$ we refer the reader to Sect. 4.3. In Fig. 3 we consider an execution of $\varPi _\mathsf {MPCT}$ that goes from $A_1$ to $A_2$ (the execution from $A_2$ to $A_1$ is symmetric). We recall that the protocol is executed simultaneously by both $A_1$ and $A_2$. The main idea is the following. Each party commits to his input using two instantiations of a non-interactive commitment. More precisely we have that $A_1$ computes two non-interactive commitments $\mathtt {com}_0$ and $\mathtt {com}_1$ (along with their decommitment information $\mathtt {dec}_0$ and $\mathtt {dec}_1$) of the message $r_1$. Each party also runs $\varPi _{\mathsf {OR}}$ for the $\mathcal {N}\mathcal {P}$-language $L_\mathtt {com}$, from the first to the third round, in order to prove knowledge of the message committed in $\mathtt {com}_0$ or in $\mathtt {com}_1$. In the last round each party sends his own input (i.e. $r_1$ for $A_1$ and $r_2$ for $A_2$) and proves, using a delayed-input synchronous many-many non-malleable ZK for the $\mathcal {N}\mathcal {P}$-language $L_\mathsf {NMZK}$, that messages committed using $\mathsf {PBCOM}$ were actually equal to that input (i.e. $r_1$ for $A_1$ and $r_2$ for $A_2$). That is, $A_1$ sends $r_1$ and proves that $\mathtt {com}_0$ and $\mathtt {com}_1$ are valid commitments of the message $r_1$.

Fig. 3.

$\varPi _\mathsf {MPCT}$: Informal description of the execution from $A_1$ to $A_2$. The execution from $A_2$ to $A_1$ is symmetric.

Intuition about the security of $\varPi _\mathsf {MPCT}$ . Let $A_1^*$ be the corrupted party. Informally the simulator $\mathsf {Sim}$ works as follows. $\mathsf {Sim}$ starts an interaction against $A_1^*$ using as input a random string y until the third round of $\varPi _\mathsf {MPCT}$ is received by $A_1^*$. More precisely, in the first round he computes two commitments $\mathtt {com}_0$ and $\mathtt {com}_1$ (along with their decommitment information $\mathtt {dec}_0$ and $\mathtt {dec}_1$) of y, and runs $\mathcal {P}_\mathsf {OR}$ using as a witness ($\mathtt {dec}_1, y$). After the 3rd round $\mathsf {Sim}$ extracts the input $r_1^*$ of the corrupted party $A_1^*$ using the extractor $E_\mathsf {OR}$ of $\varPi _\mathsf {OR}$ (that exists from the PoK property of $\varPi _\mathsf {OR}$) and sends $r_1^*$ to the ideal world functionality. At this point $\mathsf {Sim}$ receives r from the ideal-world functionality, and completes the execution of the 4th round by sending $r_2=r\oplus r_1^*$. We observe that $\mathsf {Sim}$, in order to send a string $r_2$ that differs from y in the 4th round, has to cheat in $\mathsf {NMZK}$. This is done by simply running the simulator of $\mathsf {NMZK}$. To prove the security of our scheme we will go through a sequence of hybrid experiments in order to show that the output view of the adversary in the real world can be simulated in the ideal world by $\mathsf {Sim}$. The security proof strongly relies on the non-malleable zero knowledge property of $\mathsf {NMZK}$. Indeed the aim of $\mathsf {NMZK}$ is to ensure that the adversary does not maul the messages received from $\mathsf {Sim}$. That is, the behavior of $A_1^*$ allows to extract, in every hybrid experiments that we will consider, the correct input of $A_1^*$. This holds even in case the commitments sent by $\mathsf {Sim}$ to $A_1^*$ are commitments of a random string y, and the value sent in the 4th round is inconsistent with the value committed in the first round.

4.3 Formal Description

Let $P = \{P_1,\dots ,P_n\}$ be the set of parties. Furthermore, denote by $({\mathtt {id}}_1,\dots , {\mathtt {id}}_n)$ ¹⁷ the unique identities of parties $\{P_1,\dots ,P_n\}$, respectively. Let us denote by $\mathsf {F_{MPCT}}:(1^{\lambda })^n \rightarrow \{0,1\}^{\lambda }$ the function $\mathsf {F_{MPCT}}(r_1,\dots ,r_n)=r_1\oplus \dots \oplus r_n$. The protocol starts with each party $P_i$ choosing a random string $r_i$ for $i=1,\dots ,n$. It consists of four rounds, i.e., all parties send messages in each round and the messages of all executions are seen by every party. Following [18] we describe the protocol between two parties $(A_1, A_2)$ observing that the real protocol actually consists of n simultaneous executions of a two-party coin-tossing protocol $\varPi _\mathsf {MPCT}=(A_1,A_2)$ between parties $(P_i, P_j)$ where $P_i$ acts as $A_1$ with input $r_i$ and $P_j$ acts as $A_2$ with input $r_j$ (both are symmetric). Let the input of $A_1$ be $r_1$, and the input of $A_2$ be $r_2$. The set of messages enabling $A_1$ to learn the output are denoted by $(m_1,m_2,m_3,m_4)$ where $(m_1,m_3)$ are sent by $A_1$ and $(m_2,m_4)$ are sent by $A_2$. Likewise, the set of messages enabling $A_2$ to learn the output are denoted by $(\tilde{m}_1,\tilde{m}_2,\tilde{m}_3,\tilde{m}_4)$ where $(\tilde{m}_1,\tilde{m}_3)$ are sent by $A_2$ and $(\tilde{m}_2,\tilde{m}_4)$ are sent by $A_1$. Therefore, messages $(m_l, \tilde{m}_l)$ are simultaneously exchanged in the l-th round for $l=1,\dots ,4$.

Protocol $\varPi _\mathsf {MPCT}$ . Common input: security parameter $\lambda$, instances length: $\ell _\mathsf {NMZK}$, $\ell _\mathtt {com}$.

• Round 1. We first describe how $A_1$ constructs $m_1$.

  • 1. Compute $(\mathtt {com}_0, \mathtt {dec}_0) \leftarrow \mathsf{{Com}}(r_1)$ and $(\mathtt {com}_1, \mathtt {dec}_1) \leftarrow \mathsf{{Com}}(r_1)$.

  • 2. Compute $\mathsf {a}_0\leftarrow \mathcal {P}_{L}(1^\lambda , \mathtt {com}_0, (\mathtt {dec}_0, r_1))$.

  • 3. Pick $\mathsf {c}_{1} \leftarrow \{0,1\}^\lambda$ and compute $(\mathsf {a}_{1}, \mathsf {z}_{1})\leftarrow \mathsf {Sim}_{L}(1^\lambda , \mathtt {com}_1, \mathsf {c}_{1})$.

  • 4. Run $\mathcal {V}_\mathsf {NMZK}$ on input $1^{\lambda }$ and $\ell _\mathsf {NMZK}$ thus obtaining the 1st round $\mathsf {nmzk}_1$ of $\mathsf {NMZK}$.

  • 5. Message $m_1$ is defined to be $(\mathtt {com}_0, \mathtt {com}_1,\mathsf {a}_0, \mathsf {a}_1, \mathsf {nmzk}_1)$.

  Likewise, $A_2$ performs the same action as $A_1$ in order to construct $\tilde{m}_1=(\tilde{\mathtt {com}}_0, \tilde{\mathtt {com}}_1,$ $\tilde{\mathsf {a}}_0, \tilde{\mathsf {a}}_1, \tilde{\mathsf {nmzk}}_1)$.

• Round 2. In this round $A_2$ sends message $m_2$ and $A_1$ sends $\tilde{m}_2$. We first describe how $A_2$ constructs $m_2$.

  • 1. Run $\mathcal {P}_\mathsf {NMZK}$ on input $1^{\lambda }$, ${\mathtt {id}}_2$, $\ell _\mathsf {NMZK}$ and $\mathsf {nmzk}_1$ thus obtaining the 2nd round $\mathsf {nmzk}_2$ of $\mathsf {NMZK}$.

  • 2. Pick $\mathsf {c} \leftarrow \{0,1\}^\lambda$.

  • 3. Define message $m_2=( \mathsf {c}, \mathsf {nmzk}_2)$.

  Likewise, $A_1$ performs the same actions as $A_2$ in the previous step to construct the message $\tilde{m}_2=(\tilde{\mathsf {c}},\tilde{\mathsf {nmzk}}_2)$.

• Round 3. In this round $A_1$ sends message $m_3$ and $A_2$ sends $\tilde{m}_3$. $A_1$ prepares $m_3$ as follows.

  • 1. Compute $\mathsf {c}_0 = \mathsf {c} \oplus \mathsf {c}_1$ and $\mathsf {z}_0 \leftarrow \mathcal {P}_{L}(\mathsf {c}_0)$.

  • 2. Run $\mathcal {V}_\mathsf {NMZK}$ on input $\mathsf {nmzk}_2$ thus obtaining the 3rd round $\mathsf {nmzk}_3$ of $\mathsf {NMZK}$.

  • 3. Define $m_3=(\mathsf {nmzk}_3, \mathsf {c}_0, \mathsf {c}_1, \mathsf {z}_0, \mathsf {z}_1\big )$.

  Likewise, $A_2$ performs the same actions as $A_1$ in the previous step to construct the message $\tilde{m}_3=(\tilde{\mathsf {nmzk}}_3, \tilde{\mathsf {c}}_0, \tilde{\mathsf {c}}_1, \tilde{\mathsf {z}}_0,\tilde{\mathsf {z}}_1)$.

• Round 4. In this round $A_2$ sends message $m_4$ and $A_1$ sends $\tilde{m}_4$. $A_2$ prepares $m_4$ as follows.

  • 1. Check that the following conditions are satisfied: (a) $\mathsf {c}=\mathsf {c}_0\oplus \mathsf {c}_1$; (b) the transcript $\mathsf {a}_0,\mathsf {c}_0, \mathsf {z}_0$ is accepting w.r.t. the instance $\mathtt {com}_0$; (c) the transcript $\mathsf {a}_1,\mathsf {c}_1, \mathsf {z}_{1}$ is accepting w.r.t. the instance $\mathtt {com}_1$. If one of the check fails then output $\perp$, otherwise continue with the following steps.

  • 2. Set $x_\mathsf {NMZK}=(\tilde{\mathtt {com}}_0, \tilde{\mathtt {com}}_1, r_2)$ and $w_\mathsf {NMZK}=(\tilde{\mathtt {dec}}_0, \tilde{\mathtt {dec}}_1)$.

  • 3. Run $\mathcal {P}_\mathsf {NMZK}$ on input $\mathsf {nmzk}_3$, the statement to be proved $x_\mathsf {NMZK}$ and the witness $w_\mathsf {NMZK}$ s.t. $(x_\mathsf {NMZK},w_\mathsf {NMZK})\in {\mathsf {Rel}}_{L_\mathsf {NMZK}}$, thus obtaining the 4th round $\mathsf {nmzk}_4$ of $\mathsf {NMZK}$.

  • 4. Define $m_4=(r_2, x_\mathsf {NMZK}, \mathsf {nmzk}_4)$.

  Likewise, $A_1$ performs the same actions as $A_2$ in the previous step to construct the message $\tilde{m}_4=(r_1, \tilde{x}_\mathsf {NMZK}, \tilde{\mathsf {nmzk}}_4)$.

Output computation of $\varPi _\mathsf {MPCT}$ . Check, for each party, if $(\mathsf {nmzk}^i_1, \mathsf {nmzk}^i_2,$ $\mathsf {nmzk}^i_3, \mathsf {nmzk}^i_4)$ is accepting for $\mathcal {V}_\mathsf {NMZK}$ with respect to the instance $x^i_\mathsf {NMZK}$ ($i=1, \dots , n$) and that all pairs of parties used the same inputs $(r_1,\dots ,r_n)$. If so, output $r=r_1\oplus \dots \oplus r_n$.

Theorem 3

If one-to-one OWFs exist, then the multi-party protocol $\varPi _\mathsf {MPCT}$ securely computes the multi-party coin-tossing functionality with black-box simulation.

The formal security proof can be found in the full version (see [9]).

Appendices

A Standard Definitions

Definition 2 (Proof/argument system)

A pair of ppt interactive algorithms $\varPi =(\mathcal {P},\mathcal {V})$ constitute a proof system (resp., an argument system) for an $\mathcal {N}\mathcal {P}$-language L, if the following conditions hold:

• Completeness: For every $x\in L$ and w such that $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$, it holds that: $\mathrm{Prob}\left[ \langle \mathcal {P}(w), \mathcal {V}\rangle (x) =1\right] =1.$

• Soundness: For every interactive (resp., ppt interactive) algorithm $\mathcal {P}^{\star }$, there exists a negligible function $\nu$ such that for every $x \notin L$ and every z: $\mathrm{Prob}\left[ \langle \mathcal {P}^{\star }(z), \mathcal {V}\rangle (x) =1\right] < \nu (|x|).$

A proof/argument system $\varPi =(\mathcal {P},\mathcal {V})$ for an $\mathcal {N}\mathcal {P}$-language L, enjoys delayed-input completeness if $\mathcal {P}$ needs x and w only to compute the last round and $\mathcal {V}$ needs x only to compute the output. Before that, $\mathcal {P}$ and $\mathcal {V}$ run having as input only the size of x. The notion of delayed-input completeness was defined in [10]. An interactive protocol $\varPi =(\mathcal {P},\mathcal {V})$ is public coin if, at every round, $\mathcal {V}$ simply tosses a predetermined number of coins (i.e. a random challenge) and sends the outcome to the prover. Moreover we say that the transcript $\tau$ of an execution $b=\langle \mathcal {P}(z), \mathcal {V}\rangle (x)$ is accepting if $b=1$.

Definition 3

(Proof of Knowledge [27]). A protocol $\varPi =(\mathcal {P}, \mathcal {V})$ that enjoys completeness is a proof of knowledge (PoK) for the relation ${\mathsf {Rel}}_\mathsf {L}$ if there exists a probabilistic expected polynomial-time machine $\mathsf {E}$, called the extractor, such that for every algorithm $\mathcal {P}^\star$, there exists a negligible function $\nu$, every statement $x\in \{0,1\}^\lambda$, every randomness $r\in \{0,1\}^\star$ and every auxiliary input $z\in \{0,1\}^\star$,

$\mathrm{Prob}\left[ \langle \mathcal {P}_{r}^{\star }(z), \mathcal {V}\rangle (x)=1\right] \le \mathrm{Prob}\left[ w \leftarrow \mathsf {E}^{\mathcal {P}_{r}^{\star }(z)} (x) :(x,w) \in {\mathsf {Rel}}_\mathsf {L}\right] +\nu (\lambda ).$

We also say that an argument system $\varPi$ is a argument of knowledge (AoK) if the above condition holds w.r.t. any ppt $\mathcal {P}^\star$.

In our security proofs we make use of the following observation. An interactive protocol $\varPi$ that enjoys the property of completeness and PoK (AoK) is a proof (an argument) system. Indeed suppose by contradiction that is not. By the definition of PoK (AoK) it is possible to extract the witness for every theorem $x\in \{0,1\}^\lambda$ proved by $\mathcal {P}^\star _r$ with probability greater than $\mathrm{Prob}\left[ \langle \mathcal {P}_{r}^{\star }(z), \mathcal {V}\rangle (x)=1\right]$; contradiction. In this paper we also consider the adaptive-input PoK/AoK property for all the protocols that enjoy delayed-input completeness. Adaptive-input PoK/AoK ensures that the PoK/AoK property still holds when a malicious prover can choose the statement adaptively at the last round.

A 3-round protocol $\varPi =(\mathcal {P}, \mathcal {V})$ for a relation ${\mathsf {Rel}}_\mathsf {L}$ is an interactive protocol played between a prover $\mathcal {P}$ and a verifier $\mathcal {V}$ on common input x and private input w of $\mathcal {P}$ s.t. $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$. In a 3-round protocol the first message $\mathsf {a}$ and the third message $\mathsf {z}$ are sent by $\mathcal {P}$ and the second messages $\mathsf {c}$ is played by $\mathcal {V}$. At the end of the protocol $\mathcal {V}$ decides to accept or reject based on the data that he has seen, i.e. $x, \mathsf {a}, \mathsf {c}, \mathsf {z}$. We usually denote the message $\mathsf {c}$ sent by $\mathcal {V}$ as a challenge, and as challenge length the number of bit of $\mathsf {c}$.

Definition 4

( $\varSigma$ -Protocol). A 3-round public-coin protocol $\varPi =(\mathcal {P}, \mathcal {V})$ for a relation ${\mathsf {Rel}}_\mathsf {L}$ is a $\varSigma$-Protocol if the following properties hold:

• Completeness: if $(\mathcal {P}, \mathcal {V})$ follow the protocol on input x and private input w to $\mathcal {P}$ s.t. $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$, $\mathcal {V}$ always accepts.

• Special soundness: if there exists a polynomial time algorithm such that, for any pair of accepting transcripts on input x, $(\mathsf {a}, \mathsf {c}_1, \mathsf {z}_1), (\mathsf {a}, \mathsf {c}_2, \mathsf {z}_2)$ where $\mathsf {c}_1 \ne \mathsf {c}_2$, outputs witness w such that $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$.

• Special Honest Verifier Zero-knowledge (Special HVZK): there exists a ppt simulator algorithm $\mathsf {Sim}$ that for any $x\in L$, security parameter $\lambda$ and any challenge $\mathsf {c}$ works as follow: $(\mathsf {a}, \mathsf {z}) \leftarrow \mathsf {Sim}(1^\lambda , x, \mathsf {c})$. Furthermore, the distribution of the output of $\mathsf {Sim}$ is computationally indistinguishable from the distribution of a transcript obtained when $\mathcal {V}$ sends $\mathsf {c}$ as challenge and $\mathcal {P}$ runs on common input x and any w such that $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$ ¹⁸.

Definition 5

A delayed-input 3-round protocol $\varPi =(\mathcal {P}, \mathcal {V})$ for relation ${\mathsf {Rel}}_\mathsf {L}$ enjoys adaptive-input special soundness if there exists a polynomial time algorithm such that, for any pair of accepting transcripts $(\mathsf {a}, \mathsf {c}_1, \mathsf {z}_1)$ for input $x_1$ and $(\mathsf {a}, \mathsf {c}_2, \mathsf {z}_2)$ for input $x_2$ with $\mathsf {c}_1\ne \mathsf {c}_2$, outputs witnesses $w_1$ and $w_2$ such that $(x_1,w_1)\in {\mathsf {Rel}}_\mathsf {L}$ and $(x_2,w_2)\in {\mathsf {Rel}}_\mathsf {L}$.

Definition 6

A delayed-input 3-round protocol $\varPi =(\mathcal {P}, \mathcal {V})$ for relation ${\mathsf {Rel}}_\mathsf {L}$ enjoys adaptive-input Special Honest Verifier Zero-knowledge (adaptive-input Special HVZK) if there exists a two phases ppt simulator algorithm $\mathsf {Sim}$ that works as follow:

• 1. $\mathsf {a}\leftarrow \mathsf {Sim}(1^\lambda , \mathsf {c}, \kappa ; \rho )$, where $1^\lambda$ is the security parameter, $\mathsf {c}$ is the challenge $\kappa$ is the size of the instance to be proved and the randomness $\rho$;

• 2. $\mathsf {z}\leftarrow \mathsf {Sim}(x, \rho )$ ¹⁹, where x is the instance to be proved.

$\varPi$ is adaptive-input Special HVZK if any $x\in L$ and for any $\mathsf {c}\in \{0,1\}^\lambda$, the distribution of the transcripts $(\mathsf {a}, \mathsf {c}, \mathsf {z})$, computed by $\mathsf {Sim}$, is computationally indistinguishable from the distribution of a transcript obtained when $\mathcal {V}$ sends $\mathsf {c}$ as challenge and $\mathcal {P}$ runs on common input x and any w (available only in the third round) such that $(x,w)\in {\mathsf {Rel}}_\mathsf {L}$.

1.1 A.1 Commitment Schemes

Definition 7 (Commitment Scheme)

Given a security parameter $1^\lambda$, a commitment scheme $\mathtt{CS}=(\mathsf {Sen}, \mathsf {Rec})$ is a two-phase protocol between two ppt interactive algorithms, a sender $\mathsf {Sen}$ and a receiver $\mathsf {Rec}$. In the commitment phase $\mathsf {Sen}$ on input a message m interacts with $\mathsf {Rec}$ to produce a commitment ${\mathtt {com}}$, and the private output ${\mathtt {d}}$ of $\mathsf {Sen}$.

In the decommitment phase, $\mathsf {Sen}$ sends to $\mathsf {Rec}$ a decommitment information $(m,{\mathtt {d}})$ such that $\mathsf {Rec}$ accepts m as the decommitment of $\mathtt {com}$.

We consider the classic notions of correctness, perfect and statistical binding, computation and statistical hiding.

1.2 A.2 3-Round Honest-Extractable Commitment Schemes

Informally, a 3-round commitment scheme is honest-extractable if there exists an efficient extractor that having black-box access to any efficient honest sender that successfully performs the commitment phase, outputs the only committed string that can be successfully decommitted. We give now a definition that follows the one of [37].

Definition 8 (Honest-Extractable Commitment Scheme)

A perfectly (resp. statistically) binding commitment scheme $\mathtt{ExCS}= (\mathrm {ExSen}, \mathrm {ExRec})$ is an honest-extractable commitment scheme if there exists an expected ppt extractor ExtCom that given oracle access to any honest sender $\mathrm {ExSen}$, outputs a pair $(\tau , m)$ such that the following two properties hold:

• Simulatability: $\tau$ is identically distributed to the view of $\mathrm {ExSen}$ (when interacting with an honest $\mathrm {ExRec}$) in the commitment phase.

• Extractability: The probability that there exists a decommitment of $\tau$ to a message $m'$, where $m' \ne m$ is 0 (resp. negligible).

1.3 A.3 Non-malleable Commitments

In order to define a non-malleable commitment we follow [28, 29]. Let $\mathsf {\varPi }=(\mathsf {Sen},\mathsf {Rec})$ be a statistically binding commitment scheme. And let $\lambda$ be the security parameter. Consider a MiM adversary $\mathcal {A}$ that, on auxiliary input z participates in a left and a right session. In the left sessions the MiM adversary $\mathcal {A}$ interacts with $\mathsf {Sen}$ receiving commitment to value m using an identity ${\mathtt {id}}$ of its choice. In the right session $\mathcal {A}$ interacts with $\mathsf {Rec}$ attempting to commit to a related value $\tilde{m}$ again using identity of its choice $\tilde{{\mathtt {id}}}$. If the right commitment is invalid, or undefined, its value is set to $\perp$. Furthermore, if $\tilde{{\mathtt {id}}} = {\mathtt {id}}$ then $\tilde{m}$ is also set to $\perp$ (i.e., a commitment where the adversary uses the same identity of the honest senders is considered invalid). Let ${\mathsf {\mathsf{{mim}}}}^{\mathcal {A},m}_\mathsf {\varPi }(z)$ denote a random variable that describes the values $\tilde{m}$ and the view of $\mathcal {A}$ in the above experiment.

Definition 9

(Non-malleable commitment scheme [28, 29]). A commitment scheme is non-malleable with respect to commitment if, for every ppt MiM adversary $\mathcal {A}$, for every $m_0\in \{0,1\}^{\mathsf{poly}(\lambda )}$ and $m_1\in \{0,1\}^{\mathsf{poly}(\lambda )}$ the following holds

$$\{{\mathsf {\mathsf{{mim}}}}_\mathsf {\varPi }^{\mathcal {A},m_0} (z)\}_{z\in \{0,1\}^\star } \,{ \approx }\, \{{\mathsf {\mathsf{{mim}}}}_\mathsf {\varPi }^{\mathcal {A},m_1} (z)\}_{z\in \{0,1\}^\star }.$$

We say that a commitment is valid or well formed if it admits a decommitment to a message $m\ne \bot$.

For our propose we use a 4-round synchronous honest-extractable non-malleable commitment. That is, a commitment scheme that enjoys (1) non-malleability only against synchronous adversaries, (2) is extractable w.r.t. honest sender (honest-extractable) and (3) is public-coin. The non-malleable commitment $\varPi$ provided in Fig. 2 of [22] enjoys non-malleability against synchronous adversary (as proved in Theorem 1 of [22]), is public coin and can be instantiated in 4 rounds relying on OWFs (the protocol can be squeezed to 3 rounds using one-to-one OWFs).

Also, as stated in Sect. 5 of [22], given a commitment computed by the sender of $\varPi$ one can rewind the sender in order to obtain a new accepting transcript with the same first round (resp., first two rounds if we consider the instantiation that relies on OWFs) in order to extract a message m. Moreover, if the sender is honest, then it is possible to claim that m is the actual message committed by the sender. We remark that we do not require any form of extractability against malicious senders.

B Special WIPoK

1.1 B.1 Improving the Soundness of LS

In this section we consider the 3-round WIPoK for the $\mathcal {N}\mathcal {P}$-complete language of graph Hamiltonicity (HC), provided in [25], and we will refer to this construction as the LS protocol. An interesting property of this WIPoK is that only the size of the statement need to be known before the last round by both the prover and the verifier. We show that the LS protocol does not enjoys special soundness when the statement to be proved is adaptively chosen by the prover in the last round. That is, if two accepting transcripts (that share the first round) are provided w.r.t. to two different instances $x_0$ and $x_1$, then only the witness w for $x_b$ is extracted (with $b\in \{0,1\}$). More precisely, given the accepting transcript $(\mathsf {ls}^1, \mathsf {ls}_0^2, \mathsf {ls}_0^3)$ for the statement $x_0$ and $(\mathsf {ls}^1, \mathsf {ls}_1^2, \mathsf {ls}_1^3)$ for the statement $x_1$ (with $\mathsf {ls}_0^2\ne \mathsf {ls}_1^2$) then it could be that only $w_b$ can be extracted. We provide a construction that overcomes this issue, allowing the extraction of the witnesses for both $x_0$ and $x_1$ thus obtaining a $\varSigma$-protocol where the special soundness holds even when the two accepting transcripts refer to different theorems adaptively chosen in the last round. Following [11] we refer to this property as adaptive-input special soundness (see Definition 5).

Before showing why LS is not already adaptive-input special sound and how our construction works, we briefly describe the LS protocol with one-bit challenge following [32]. Let $\mathcal {P}$ be prover and $\mathcal {V}$ the verifier. The common input of $\mathcal {P}$ and $\mathcal {V}$ is $\kappa$, that represents the number of vertexes of the instance G to be proved. The graph G is represented by a $\kappa \times \kappa$ adjacency matrix $\mathsf {MG}$ where $\mathsf {MG}[i][j]=1$ if there exists an edge between vertexes i and j in G. A non-edge position i, j is a pair of vertexes that are not connected in G and for which $\mathsf {MG}[i][j] = 0$.

• $\mathcal {P}$ picks a random $\kappa$-vertex cycle graph C and commits bit-by-bit to the corresponding adjacency matrix using a statistically binding commitment scheme.

• $\mathcal {V}$ responds with a randomly chosen bit b.

• $\mathcal {P}$ on input the graph G and the Hamiltonian cycle w executes the following steps. If $b = 0$, $\mathcal {P}$ opens all the commitments, showing that the matrix committed in the first round is actually an $\kappa$-vertex cycle. If $b = 1$, $\mathcal {P}$ sends a permutation $\pi$ mapping the vertex of C in G. Then it opens the commitment of the adjacency matrix of C corresponding to the non-edges of G.

• $\mathcal {V}$ accepts (outputs 1) if what he receives in the third round is consistent with the bit b that he was sent in the second round.

Getting the answer for both $b = 0$ and $b = 1$ (w.r.t. to the same graph G) allows the extraction of the cycle for G. The reason is the following. For $b = 0$ one gets the random cycle C. Then for $b = 1$ one gets the permutation mapping the random cycle in the actual cycle that is given to $\mathcal {P}$ before the last message of the protocol.

We now observe that a malicious prover $\mathcal {P}^\star$ could gives the answer for $b=0$ w.r.t. to the graph $G_0$ and the answer for $b=1$ w.r.t. the graph $G_1$ (due to the delayed-input nature of LS). This means that even knowing two accepting transcripts that share the first round, the permutation that maps the vertexes of C in $G_0$ it is not known. Therefore an efficient algorithm can only compute the cycle $w_1$ of $G_1$ and gets no information about the Hamiltonian cycle of $G_0$. Summing up, given the accepting transcripts $(\mathsf {ls}^1, 0, \mathsf {ls}_0^3)$ for the graph $G_0$ and $(\mathsf {ls}^1, 1, \mathsf {ls}_1^3)$ for the graph $G_1$, only the Hamiltonian cycle for $G_1$ can be computed. That is, only the cycle for the graph proved by $\mathcal {P}^\star$ to be Hamiltonian using as a second round the challenge 1 can be efficiently computed. Starting from this observation, in order to allow an efficient algorithm to compute cycles for both $G_0$ and $G_1$, we construct an improved version of LS that we denoted with ${\mathsf {LS}}^\mathsf {imp}=(\mathcal {P}^\mathsf {imp}, \mathcal {V}^\mathsf {imp})$. ${\mathsf {LS}}^\mathsf {imp}$ uses LS in a black-box way. For ease of exposition we use the following notation. $\mathsf {ls}^1\leftarrow \mathcal {P}(1^\lambda , \kappa ;\rho )$ denotes that $\mathcal {P}$ is executed on input the security parameter (in unary) $1^\lambda$, $\kappa$ and the randomness $\rho$ and gives in output the first round of LS $\mathsf {ls}^1$. $\mathsf {ls}^3\leftarrow \mathcal {P}(G,w,\mathsf {ls}^2, \rho )$ denotes that $\mathcal {P}$ has computed the third round of LS by running on input the graph G, the cycle w for the graph G, the bit $\mathsf {ls}^2$ and the randomness used to compute $\mathsf {ls}^1$. $\mathcal {V}(\mathsf {ls}^1, \mathsf {ls}^2, \mathsf {ls}^3, G)$ denotes the output of $\mathcal {V}$ on input $\mathsf {ls}^1, \mathsf {ls}^2, \mathsf {ls}^3$ and the graph G. Let $\kappa$ be the number of vertexes of the graph G to be proved, our ${\mathsf {LS}}^\mathsf {imp}=(\mathcal {P}^\mathsf {imp}, \mathcal {V}^\mathsf {imp})$ works as follows.

• 1. $\mathcal {P}^\mathsf {imp}$ on input the security parameter $\lambda$, $\kappa$ and the randomness $\rho _0||\rho _1$ computes and sends $\mathsf {ls}_0^1\leftarrow \mathcal {P}(1^\lambda , \kappa ; \rho _0)$, $\mathsf {ls}_1^1\leftarrow \mathcal {P}(1^\lambda , \kappa ; \rho _1)$.

• 2. $\mathcal {V}^\mathsf {imp}$ picks and sends a random bit b.

• 3. $\mathcal {P}^\mathsf {imp}$, upon receiving b, on input the graph G and the Hamiltonian cycle w for G computes and sends $\mathsf {ls}_0^3\leftarrow \mathcal {P}(G,w,b,\rho _0)$, $\mathsf {ls}_1^3\leftarrow \mathcal {P}(G,w,1-b,\rho _1)$.

• 4. $\mathcal {V}^\mathsf {imp}$ accepts iff $\mathcal {V}(G, \mathsf {ls}_0^1, b, \mathsf {ls}_0^3)=1$ and $\mathcal {V}(G, \mathsf {ls}_1^1, 1-b, \mathsf {ls}_1^3)=1$.

Theorem 4

Assuming one-to-one OWFs, ${\mathsf {LS}}^\mathsf {imp}$ is a $\varSigma$-protocol with adaptive-input Special HVZK and adaptive-input special soundness. Moreover ${\mathsf {LS}}^\mathsf {imp}$ is Zero Knowledge.

Proof

(Delayed-input) Completeness. The (delayed-input) completeness of ${\mathsf {LS}}^\mathsf {imp}$ comes from the (delayed-input) completeness of LS.

Adaptive-input special soundness. Let us consider two accepting transcripts that share the first round for ${\mathsf {LS}}^\mathsf {imp}$: $\big ((\mathsf {ls}_0, \mathsf {ls}_1), 0, (\mathsf {ls}^3_0, \mathsf {ls}^3_1)\big )$ for the statement G and $\big ((\mathsf {ls}_0, \mathsf {ls}_1), 1, ({\mathsf {ls}^3_1}', {\mathsf {ls}^3_1}')\big )$ for the statement $G'$. We can isolate the sub-transcripts $(\mathsf {ls}_0, 0, \mathsf {ls}_0^3)$ and $(\mathsf {ls}_0, 1, {\mathsf {ls}_0^3}')$ and observe that $\mathcal {V}(G, \mathsf {ls}_0^1, 0, \mathsf {ls}_0^3)=1=\mathcal {V}(G' \mathsf {ls}_0^1, 1, {\mathsf {ls}_0^3}')$. From what we discuss before about LS we know that in this case the witness w for $G'$ can be extracted. Also let us now consider the two sub-transcripts $(\mathsf {ls}_1, 1, \mathsf {ls}_1^3)$ and $(\mathsf {ls}_1, 0, {\mathsf {ls}_1^3}')$. Also in this case, by observing that $\mathcal {V}(G, \mathsf {ls}_1, 1, \mathsf {ls}_1^3)=1=\mathcal {V}(G', \mathsf {ls}_1, 0, {\mathsf {ls}_1^3}')$, the cycle for G can be efficiently computed.

Adaptive-input Special HVZK. Following [30], we consider an adaptive-input Special HVZK simulator S associated to the LS’s protocol. This is equal to a Special HVZK simulator with the additional property that the first round can be simulated without knowing the instance to be proved (see Definition 6). In more details S works in two phases. In the first phase just $1^\lambda$, the challenge $\mathsf {ls}^2$, the number of vertexes $\kappa$ is used to output the first round $\mathsf {ls}^1$. We denote this phase using: $\mathsf {ls}^1\leftarrow S(1^\lambda , \mathsf {ls}^2, \kappa )$. In the second phase S takes as input the instance and output the third round $\mathsf {ls}^3$. We denote this phase using $\mathsf {ls}^3\leftarrow S(G)$. The adaptive-input Special HVZK simulator $S^\mathsf {imp}$ for ${\mathsf {LS}}^\mathsf {imp}$ just internally runs S two times, once using b and once using $1-b$ as a challenge. In more details the two phase of $S^\mathsf {imp}$ are the following.

• 1. $S^\mathsf {imp}$, on input $1^\lambda$, the challenge b, $\kappa$ and the randomness $\rho _b||\rho _{1-b}$, computes $\mathsf {ls}_b^1\leftarrow S(1^\lambda , b, \kappa ;\rho _b)$, $\mathsf {ls}_{1-b}^1\leftarrow S(1^\lambda , 1-b, \kappa ; \rho _{1-b})$ and outputs $(\mathsf {ls}_b^1, \mathsf {ls}_{1-b}^1)$.

• 2. $S^\mathsf {imp}$, on input the graph G, $\rho _0$ and $\rho _1$ computes $\mathsf {ls}_b^3 \leftarrow S(G, \rho _b)$, $\mathsf {ls}_{1-b}^3 \leftarrow S(G, \rho _{1-b})$ and outputs $(\mathsf {ls}_b^3, \mathsf {ls}_{1-b}^3)$.

The transcript $\big ((\mathsf {ls}_b^1, \mathsf {ls}_{1-b}^1), b, (\mathsf {ls}^3_{b}, \mathsf {ls}^3_{1-b})\big )$ output by $S^\mathsf {imp}$ is computationally indistinguishable from a transcript computed by $\mathcal {P}^\mathsf {imp}$ (that uses as input an Hamiltonian cycle w of G) due to the security of the underlying adaptive-input Special HVZK simulator S.

Zero-Knowledge. The ZK simulator of ${\mathsf {LS}}^\mathsf {imp}$ just needs to guess the bit b chosen by the adversarial verifier and runs the adaptive-input Special HVZK simulator.

It is easy to see that (as for LS) if we consider $\lambda$ parallel executions of ${\mathsf {LS}}^\mathsf {imp}$ then we obtain a protocol ${\mathsf {LS}}^\lambda$ that still enjoys adaptive-input completeness, adaptive-input special soundness, adaptive-input Special HVZK. Moreover ${\mathsf {LS}}^\lambda$ is WI. Formally, we can claim the following theorems.

Theorem 5

Assuming one-to-one OWFs, ${\mathsf {LS}}^\lambda$ is a $\varSigma$-protocol with adaptive-input Special HVZK, and adaptive-input special soundness. Moreover ${\mathsf {LS}}^\lambda$ is witness indistinguishable (WI).

Proof

Completeness, adaptive-input special soundness and adaptive-input Special HVZK come immediately from the adaptive-input special soundness and adaptive-input Special HVZK of ${\mathsf {LS}}^\mathsf {imp}$. The WI comes from the observation that ${\mathsf {LS}}^\mathsf {imp}$ is WI (due to the zero knowledge property), and that WI is preserved under parallel (and concurrent) composition.

Theorem 6

Assuming OWFs, ${\mathsf {LS}}^\lambda$ is a 4-round public-coin proof system with adaptive-input Special HVZK, adaptive-input special soundness and WI.

Proof

The proof of this theorem just relies on the observation that in order to instantiate a statistically binding commitment scheme using OWFs an additional round is required to compute the first round of Naor’s commitment scheme [31].

Observe that since Hamiltonicity is an $\mathcal {N}\mathcal {P}$-complete language, the above constructions work for any $\mathcal {N}\mathcal {P}$ language through $\mathcal {N}\mathcal {P}$ reductions. For simplicity in the rest of the paper we will omit the $\mathcal {N}\mathcal {P}$ reduction therefore assuming that the above scheme works directly on a given $\mathcal {N}\mathcal {P}$-language L.

1.2 B.2 Combining (Adaptive-Input) Special HVZK PoK Through [12]

In our paper we use the well known technique for composing two $\varSigma$-protocols to compute the OR for compound statement [12, 16]. In more details, let $\varPi _0=(\mathcal {P}_0, \mathcal {V}_0)$ and $\varPi _1=(\mathcal {P}_1, \mathcal {V}_1)$ be $\varSigma$-protocols for the respective $\mathcal {N}\mathcal {P}$-relation ${\mathsf {Rel}}_\mathsf {L_0}$ (with Special HVZK simulator $\mathsf {Sim}_0$) and ${\mathsf {Rel}}_\mathsf {L_1}$ (with Special HVZK simulator $\mathsf {Sim}_1$). Then it is possible to use $\varPi _0$ and $\varPi _1$ to construct $\varPi ^\mathsf {OR}=(\mathcal {P}_{\mathsf {OR}}, \mathcal {V}_{\mathsf {OR}})$ for relation ${\mathsf {Rel}}_\mathsf {_{\mathsf {OR}}}=\{((x_0,x_1),w): ((x_0,w)\in {\mathsf {Rel}}_\mathsf {L_0}) \ \text {OR} \ ((x_1,w)\in {\mathsf {Rel}}_\mathsf {L_1})\}$ that works as follows.

Protocol $\varPi ^\mathsf {OR}=(\mathcal {P}_{\mathsf {OR}}, \mathcal {V}_{\mathsf {OR}})$ : Let $w_b$ with $b\in \{0,1\}$ be s.t. $(x_b,w_b)\in {\mathsf {Rel}}_\mathsf {L_b}$. $\mathcal {P}_{\mathsf {OR}}$ and $\mathcal {V}_{\mathsf {OR}}$ on common input $(x_0, x_1)$ and private input $w_b$ compute the following steps.

• $\mathcal {P}_{\mathsf {OR}}$ computes $\mathsf {a}_b\leftarrow \mathcal {P}_b(1^\lambda ,x_b,w_b)$. Furthermore he picks $\mathsf {c}_{1-b}\leftarrow \{0,1\}^\lambda$ and computes $(\mathsf {a}_{1-b}, \mathsf {z}_{1-b})\leftarrow \mathsf {Sim}_{1-b}(1^\lambda , x_{1-b}, \mathsf {c}_{1-b})$. $\mathcal {P}_{\mathsf {OR}}$ sends $\mathsf {a}_0, \mathsf {a}_1$ to $\mathcal {V}_{\mathsf {OR}}$.

• $\mathcal {V}_{\mathsf {OR}}$, upon receiving $\mathsf {a}_0,\mathsf {a}_1$ picks $\mathsf {c}\leftarrow \{0,1\}^\lambda$ and sends $\mathsf {c}$ to $\mathcal {P}_{\mathsf {OR}}$.

• $\mathcal {P}_{\mathsf {OR}}$, upon receiving $\mathsf {c}$ computes $\mathsf {c}_b=\mathsf {c}_{1-b} \oplus \mathsf {c}$ and computes $\mathsf {z}_b \leftarrow \mathcal {P}_b(\mathsf {c}_b)$. $\mathcal {P}_{\mathsf {OR}}$ sends $\mathsf {c}_0, \mathsf {c}_1, \mathsf {z}_0$ $\mathsf {z}_1$ to $\mathcal {V}_{\mathsf {OR}}$.

• $\mathcal {V}_{\mathsf {OR}}$ checks that the following conditions holds: $\mathsf {c}=\mathsf {c}_0 \oplus \mathsf {c}_1$, $\mathcal {V}_0(x_0, \mathsf {a}_0, \mathsf {c}_0, \mathsf {z}_0)=1$ and $\mathcal {V}_1(x_1, \mathsf {a}_1, \mathsf {c}_1, \mathsf {z}_1)=1$. If all the checks succeed then outputs 1, otherwise outputs 0.

Theorem 7

([12]). Let $\varSigma _0$ and $\varSigma _1$ be two $\varSigma$-protocols, then $\varPi ^\mathsf {OR}=(\mathcal {P}_{\mathsf {OR}}, \mathcal {V}_{\mathsf {OR}})$ is a $\varSigma$-protocol for ${\mathsf {Rel}}_\mathsf {L_\mathsf {OR}}$.

Theorem 8

([13]). Let $\varPi =(\mathcal {P}, \mathcal {V})$ be a $\varSigma$-protocol for relation ${\mathsf {Rel}}_\mathsf {L}$ with negligible soundness error²⁰, then $\varPi$ is a proof of knowledge for ${\mathsf {Rel}}_\mathsf {L}$.

In our work we instantiate $\varPi ^\mathsf {OR}$ using as $\varPi _0$ and $\varPi _1$ the Blum’s protocol [4] for the $\mathcal {N}\mathcal {P}$-complete language for graph Hamiltonicity (that also is a $\varSigma$-Protocol). Therefore Theorem 7 (and Theorem 8) can be applied.

We also consider an instantiation of $\varPi ^\mathsf {OR}$ using as $\varPi =(\mathcal {P}, \mathcal {V})$ our ${\mathsf {LS}}^\lambda$. If we instantiate $\varPi ^\mathsf {OR}$ using ${\mathsf {LS}}^\lambda$ and the corresponding adaptive-input Special HVZK simulator ${\mathsf {LS}}^\lambda$, then $\varPi ^\mathsf {OR}$ is adaptive-input special soundness. More formally we can claim the following theorem.

Theorem 9

If $\varPi ^\mathsf {OR}$ is instantiated using ${\mathsf {LS}}^\lambda$ (and the corresponding adaptive-input Special HVZK simulator $S^\lambda$), then $\varPi ^\mathsf {OR}$ enjoys the delayed-input completeness and adaptive-input special soundness for the $\mathcal {N}\mathcal {P}$-relation ${\mathsf {Rel}}_\mathsf {L_\mathsf {OR}}$.

Proof

The delayed-input completeness follows from the delayed-input completeness of ${\mathsf {LS}}^\lambda$.

Adaptive-input special soundness. Let us consider two accepting transcripts that share the first round for $\varPi ^\mathsf {OR}$: $\big ((\mathsf {\pi }_0, \mathsf {\pi }_1), \mathsf {\pi }^2, (\mathsf {\pi }_0^2, \mathsf {\pi }_0^3, \mathsf {\pi }_1^2, \mathsf {\pi }_1^3)\big )$ for the statement $(x_0, x_1)$ and $\big ((\mathsf {\pi }_0, \mathsf {\pi }_1), {\mathsf {\pi }^2}', ({\mathsf {\pi }_0^2}', {\mathsf {\pi }_0^3}', {\mathsf {\pi }_1^2}'{\mathsf {\pi }_1^3}')\big )$ for the statement $(x'_0, x'_1)$, where $\mathsf {\pi }^2 \ne {\mathsf {\pi }^2}'$. We observe that since $\mathsf {\pi }^2 \ne {\mathsf {\pi }^2}'$, $\mathsf {\pi }^2= \mathsf {\pi }_0^2 \oplus {\mathsf {\pi }_1^2}$ and ${\mathsf {\pi }^2}'= {\mathsf {\pi }_0^2}' \oplus {\mathsf {\pi }_1^2}'$ it holds that either $\mathsf {\pi }_0^2 \ne {\mathsf {\pi }_0^2}'$ or $\mathsf {\pi }_1^2 \ne {\mathsf {\pi }_1^2}'$. Suppose w.l.o.g. that $\mathsf {\pi }_0^2 \ne {\mathsf {\pi }_0^2}'$. Then we are guaranteed from the adaptive-input special soundness of ${\mathsf {LS}}^\lambda$ that using the transcripts $(\mathsf {\pi }_0, {\mathsf {\pi }_0^2}, {\mathsf {\pi }_0^3})$ and $(\mathsf {\pi }_0, {\mathsf {\pi }_0^2}', {\mathsf {\pi }_0^3}')$ the values $(w_a, w_b)$ s.t. $(x_0,w_a)\in {\mathsf {Rel}}_\mathsf {L_0}$ and $(x_0',w_b)\in {\mathsf {Rel}}_\mathsf {L_0}$ can be extracted in polynomial-time. The same arguments can be used when $\mathsf {\pi }_1^2 \ne {\mathsf {\pi }_1^2}'$.

Using a result of [11] we can claim the following theorem.

Theorem 10

$\varPi ^\mathsf {OR}$ instantiated using ${\mathsf {LS}}^\lambda$ is an adaptive-input PoK for the $\mathcal {N}\mathcal {P}$-relation ${\mathsf {Rel}}_\mathsf {{L}_\mathsf {OR}}$.

It would be easy to prove that $\varPi ^\mathsf {OR}$ is also WI, however in this paper we are not going to rely directly on the WI property of $\varPi ^\mathsf {OR}$, in order to deal with the rewinding issue that we have described earlier. More precisely, in the two main contributions of this paper we will use $\varPi ^\mathsf {OR}$ (the one instantiated from Blum’s protocol and the one instantiated using ${\mathsf {LS}}^\lambda$) in a non-black box way in order to prove the security of our protocols. It will be crucial for our reduction to rely on the (adaptive-input) Special HVZK of $\varPi _0$ and $\varPi _1$ instead of using directly the WI property of $\varPi ^\mathsf {OR}$. The intuitively reason is that it is often easier in a reduction to rely on the security of a non-interactive primitive (like Special HVZK is) instead of an interactive primitive (like WI). This is the reason why we use the OR composition of [12, 16] combined with the Blum’s protocol (or the LS protocol) instead of relying on the (adaptive-input) WI provided by a Blum’s protocol (LS protocol). In the rest of the paper, in order to rely on OWFs only, we sometimes use a four round version of Blum’s and LS protocols. In this case there is an additional initial round that goes from the verifier to the prover and corresponds to the first round of Naor’s commitment scheme [31].