More Efficient Universal Circuit Constructions

Abstract

A universal circuit (UC) can be programmed to simulate any circuit up to a given size n by specifying its program bits. UCs have several applications, including private function evaluation (PFE). The asymptotical lower bound for the size of a UC is proven to be $\varOmega (n\log n)$. In fact, Valiant (STOC’76) provided two theoretical UC constructions using so-called 2-way and 4-way constructions, with sizes$~5n\log _2n$ and $4.75n\log _2n$, respectively. The 2-way UC has recently been brought into practice in concurrent and independent results by Kiss and Schneider (EUROCRYPT’16) and Lipmaa et al. (Eprint 2016/017). Moreover, the latter work generalized Valiant’s construction to any k-way UC.

In this paper, we revisit Valiant’s UC constructions and the recent results, and provide a modular and generic embedding algorithm for any k-way UC. Furthermore, we discuss the possibility for a more efficient UC based on a 3-way recursive strategy. We show with a counterexample that even though it is a promising approach, the 3-way UC does not yield an asymptotically better result than the 4-way UC. We propose a hybrid approach that combines the 2-way with the 4-way UC in order to minimize the size of the resulting UC. We elaborate on the concrete size of all discussed UC constructions and show that our hybrid UC yields on average 3.65% improvement in size over the 2-way UC. We implement the 4-way UC in a modular manner based on our proposed embedding algorithm, and show that our methods for programming the UC can be generalized for any k-way construction.

1 Introduction

Universal circuits (UCs) are Boolean circuits that can be programmed to simulate any Boolean function f(x) up to a given size by specifying a set of program bits $p_f$. The UC then receives these program bits as input besides the input x to the functionality, and computes the result as $UC(x, p_f) = f(x)$. This means that the same UC can evaluate multiple Boolean circuits, only the different program bits are to be specified.

Valiant proposed an asymptotically size-optimal construction in [Val76] with size $\varTheta (n\log n)$ and depth $\mathcal {O}(n)$, where n is the size of the simulated Boolean circuit description of f(x). He provides two constructions, based on 2-way and 4-way recursive structures. Recently, optimizations of Valiant’s size-optimized construction appeared in concurrent and independent works of [KS16] and [LMS16]. Both works implement Valiant’s 2-way recursive construction.

1.1 Applications of Universal Circuits

Size-optimized universal circuits have many applications. We review some of them here and refer to [KS16, LMS16] for further details.

Private Function Evaluation (PFE). Secure two-party computation or secure function evaluation (SFE) provides interactive protocols for evaluating a public function f(x, y) on two parties’ private inputs x and y. However, in some scenarios, the function f is a secret input of one of the parties. This setting is called private function evaluation (PFE). PFE of f(x) can be achieved by running SFE of $UC(x, p_f)$, where the UC is a public function and the program bits $p_f$ – and therefore f – are kept private due to the properties of SFE. Protocols designed especially for PFE such as [MS13, BBKL17] achieve the same asymptotic complexity $\mathcal {O}(n\log n)$ as PFE using UCs, where n is the size of the function f.¹ However, to the best of our knowledge, they have not yet been implemented, and they are not as generally applicable as PFE with UCs.

UC-based PFE can be easily integrated into any SFE framework and can directly benefit from recent optimizations. For instance, outsourcing UC-based PFE is directly possible with outsourced SFE [KR11]. The non-interactive secure computation protocol of [AMPR14] can also be generalized to obtain a non-interactive PFE protocol [LMS16].

One of the first applications for PFE was privacy-preserving checking for credit worthiness [FAZ05], where not only the loanee’s data, but also the loaner’s function needs to be kept private. PFE allows for running proprietary software on private data, such as privacy-preserving software diagnosis [BPSW07], medical programs [BFK+09], or privacy-preserving intrusion detection [NSMS14]. UCs can be applied to obliviously filter remote streaming data [OI05] and for hiding queries in private database management systems such as Blind Seer [PKV+14, FVK+15].

Applications Beyond PFE. Universal circuits can be applied for program obfuscation. Candidates for indistinguishability obfuscation are constructed using a UC as a building block in [GGH+13a, BOKP15], which can be improved using Valiant’s UC implementation [KS16]. Direct program obfuscation was proposed in [Zim15], where the circuit is a secret key to a UC. [LMS16] mentions that UCs can be applied for secure two-party computation in the batch execution setting [HKK+14, LR15]. It can be applied for verifiable computation [FGP14], and for multi-hop homomorphic encryption [GHV10]. Ciphertext-policy Attribute-Based Encryption was proposed in [Att14], where the policy circuit is hidden [GGH+13b].

1.2 Related Work on Universal Circuits

Valiant defined universal circuits in [Val76] and gave two size-optimized constructions. The constructions are based on so-called edge-universal graphs (EUGs) and utilize either a 2-way or a 4-way recursive structure, also called 2-way or 4-way UCs. Both achieve the asymptotically optimal size $\varTheta (n\log n)$ [Val76, Weg87], where n is the size of the simulated circuit. The concrete complexity of the 4-way UC is ${\sim } 4.75 n\log _2 n$ which is smaller than that of the 2-way UC of ${\sim } 5 n \log _2 n$ [Val76].

The first modular UC construction was proposed by Kolesnikov and Schneider in [KS08b]. This construction achieves a non-optimal asymptotic complexity of $\mathcal {O}(n\log ^2 n)$, and was the first implementation of UCs. A generalization of UCs for n-input gates was given in [SS08].

Recently, two independent works have optimized and implemented Valiant’s 2-way UC [KS16, LMS16]. Kiss and Schneider in [KS16] mainly focus on the most prominent application of UCs, i.e., private function evaluation (PFE). Due to the free-XOR optimization of [KS08a] in the SFE setting, they optimize the size of the UC for the number of AND gates in the resulting UC implementation and provide a framework for PFE using UCs as public function. They also propose hybrid constructions for circuits with a large number of inputs and outputs, utilizing efficient building blocks from [KS08b]. Lipmaa et al. in [LMS16] also provide an (unpublished) implementation of the 2-way UC. While keeping the number of AND gates minimal, they additionally optimize for the total number of gates, i.e., include optimizations to also reduce the number of XOR gates. They adapt the construction to arithmetic circuits and generalize the design to a k-way construction in a modular manner, for $k\ge 2$.

Both papers utilize 2-coloring of the underlying graphs for defining the program bits $p_f$ for any given functionality f. Generally, 2-coloring can be utilized for any $2^i$-way construction. [LMS16] calculate the optimal value for k to be 3.147, and conclude that the two candidates for the most efficient $2^i$-way constructions are the 2-way and 4-way UCs, of which the 4-way construction results in an asymptotically smaller size.

So far only Valiant’s 2-way UC has been implemented and the not yet implemented 4-way UC was postulated to be the most efficient one.

1.3 Outline and Our Contributions

In summary, we provide the first implementation and detailed evaluation of Valiant’s 4-way UC and propose an even more efficient hybrid UC. We elaborate on the size of the generalized k-way UCs for $k \ne 2$ and $k \ne 4$.

After revisiting Valiant’s UC construction [Val76, KS16] and its k-way generalization [LMS16] in Sect. 2, we provide the following contributions:

Our modular programming algorithm (Sect. 3 ): We detail a modular algorithm that provides the description of the input function f as program bits $p_f$ to the UC, both for Valiant’s 4-way UC as well as for the k-way UC of Lipmaa et al. [LMS16].

New universal circuit constructions (Sect. 4 ): We start with a new 3-way UC. After providing modular building blocks for this UC, we show that it is asymptotically larger than Valiant’s UCs. Then, we propose a hybrid UC construction that can efficiently combine k-way constructions for multiple values of k.² With this, we combine Valiant’s 2-way and 4-way UCs to achieve the smallest UC known so far.

Size of UCs (Sect. 5 ): We compare the asymptotic and concrete sizes of Valiant’s (2-way and 4-way) UCs and that of different k-way UCs. We show that of all k-way UCs, Valiant’s 4-way UC provides the best results for large circuits. Moreover, our hybrid UC in most cases improves over the 2-way UC by up to around 4.5% in its size, and over the 4-way UC by up to 2% (for large input circuits). In Table 1 we compare the concrete communication of PFE using SFE and our new UC implementation to the previous works on special-purpose OT-based PFE protocols.

Implementation of Valiant’s 4-way UC and experiments (Sect. 6 ): We implement Valiant’s 4-way UC and describe how our implementation can directly be used in the PFE framework of [KS16]. We experimentally evaluate the performance of our UC generation and programming algorithm with a set of example circuits and compare it on the same platform with the 2-way UC compiler of [KS16].

Table 1. Comparison of overall communication between special-purpose PFE protocols and UC-based ones for simulated circuits of size n. The numbers are for 128 bit symmetric security. The underlying SFE protocol for UC-based PFE is Yao’s protocol [Yao86] with the garbled row reduction optimization [NPS99] and X- and Y-switching blocks are instantiated using free XORs as described in [KS08a]. This yields one ciphertext per X- and Y-switching block, and three ciphertexts per universal gate.

2 Preliminaries

In this section, we summarize the existing UC constructions. We provide necessary background information in Sect. 2.1, explain Valiant’s construction [Val76] in Sect. 2.2 and the improvements of [KS16, LMS16] on the 2-way, 4-way and k-way UCs in Sects. 2.3, 2.4 and 2.5, respectively.

2.1 Preliminaries to Valiant’s UC Constructions

Let $G=(V, E)$ be a directed graph with set of nodes V and edges $E \subseteq V \times V$. The number of incoming [outgoing] edges of a node is called its indegree [outdegree]. A graph has fanin [fanout] d if the indegree [outdegree] of all its nodes is at most d. In the following, we denote by $\varGamma _d(n)$ the set of all acyclic graphs with fanin and fanout d having n nodes. Similarly, the fanin [fanout] of a circuit can be defined based on the maximal number of incoming [outgoing] wires of all its gates, inputs and outputs.

Let $G = (V, E) \in \varGamma _d(n)$. A mapping $\eta ^G:V \rightarrow \{1, \ldots , n\}$ is called topological order if $(a_i, a_j) \in E \Rightarrow \eta ^G(a_i) < \eta ^G(a_j)$ and $\forall a_1, a_2 \in V: \eta ^G(a_1) = \eta ^G(a_2) \Rightarrow a_1 = a_2$. A topological order in $G\in \varGamma _d(n)$ can be found with computational complexity $\mathcal {O}(dn)$.

A circuit $C_{u, v}^{k^*}$ with u inputs, $k^*$ gates and v outputs and fanin or fanout $d >~2$ can be reduced to a circuit with fanin and fanout 2. Shannon’s expansion theorem [Sha49, Sch08] describes how gates with larger fanin can be reduced to gates with two inputs by adding additional gates. [Val76, KS16] describe adding copy gates in order to eliminate larger fanout and elaborate on the implied overhead ($k\le 2k^*+v$). [KS08b, KS16] implement these methods and we thus assume that our input Boolean circuit $C_{u, v}^k$ has fanin and fanout 2 for all its u inputs, k gates and v outputs. We transform $C_{u, v}^k$ into a $\varGamma _2(n)$ graph G with $n=u + v+ k$ by creating a node for each input, gate and output, and an edge for each wire in $C_{u, v}^k$.

Edge-embedding is a mapping from graph $G=(V, E)$ into $G^\prime =(V^\prime , E^\prime )$ with $V \subseteq V^\prime$ and $E^\prime$ containing a path for each $e \in E$, such that the paths are pairwise edge-disjoint. A graph $U_n(\varGamma _d)=(V_U, E_U)$ is an Edge-Universal Graph (EUG) for $\varGamma _d(n)$ if every graph $G \in \varGamma _d(n)$ can be edge-embedded into $U_n(\varGamma _d)$.³ $U_n(\varGamma _d)$ has distinguished nodes called poles $\{p_1, \ldots , p_n\} \subseteq V_U$ where each node $a \in V$ is mapped to exactly one pole with a mapping $\varphi$, such that every node in G has a corresponding pole in $U_n(\varGamma _d)$. This mapping is defined by a concrete topological order $\eta ^G$ of the original graph G, i.e., $\varphi : V \rightarrow V_U$ with $\varphi (a) = p_{\eta ^G(a)}$. Besides the poles, $U_n(\varGamma _d)$ might have additional nodes that enable the edge-embedding. For each edge $(a_i, a_j) \in E$ we then define a disjoint path between the corresponding poles $(\varphi (a_i), \ldots , \varphi (a_j)) = (p_{\eta ^G(a_i)}, \ldots , p_{\eta ^G(a_j)})$ in $U_n(\varGamma _d)$, i.e., without using any edge in $U_n(\varGamma _d)$ in more than one path.

Fig. 1.

(a) shows an example $\varGamma _2(5)$ graph G. (b)–(c) show the edge-embedding of G into two $U_5(\varGamma _1)$ instances with poles $(p_1, \dots , p_5)$. (d) shows the edge-embedding of G into one $U_5(\varGamma _2)$ graph.

Let $U_n(\varGamma _1)$ be an EUG for graphs in $\varGamma _1(n)$ with poles $P = \{p_1, \ldots , p_n\}$. The poles have fanin and fanout 1, while all other nodes have fanin and fanout 2. An EUG $U_n(\varGamma _d)$ for $d \ge 2$ can be created by taking d instances of $U_n(\varGamma _1)$ EUGs, and merging each pole $p_i$ with its multiple instances, allowing the poles to have fanin-fanout d. Let $U_n(\varGamma _d) = (V_U^{\prime }, E_U^{\prime })$ be an EUG with fanin and fanout d, with $U_n(\varGamma _1)_1 = (V_1, E_1), \ldots , U_n(\varGamma _1)_d = (V_d, E_d)$. P contains the merged poles and $V_U^{\prime } = P \cup _{i=1}^{d} V_i \backslash P_i$ and $E_U^{\prime } = \cup _{i=1}^{d} E_i$.

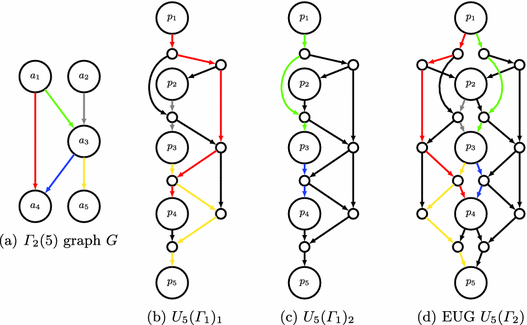
We give an example for better understanding. Let $G=(V, E)$ be the graph with 5 nodes in Fig. 1a. Our aim is to edge-embed G into EUG $U_5(\varGamma _2)$. Therefore, we use two instances of $U_5(\varGamma _1)$: $U_5(\varGamma _1)_1$ in Fig. 1b and $U_5(\varGamma _1)_2$ in Fig. 1c. The edges  and  are embedded in $U_5(\varGamma _1)_1$, and the edges and in $U_5(\varGamma _1)_2$. Merging the poles of $U_5(\varGamma _1)_1$ and $U_5(\varGamma _1)_2$ produces $U_5(\varGamma _2)$ shown in Fig. 1d.

2.2 Valiant’s UC Constructions

The size of a function f represented by a circuit $C_{u, v}^k$ with fanin and fanout 2 is $n = u + v + k$. In the following, we describe Valiant’s UC construction [Val76, Weg87] that can be programmed to evaluate any function of size n. Circuit $C_{u, v}^k$ is represented as a graph $G \in \varGamma _2(n)$ (cf. Sect. 2.1).

Valiant’s UC is based on an EUG $U_n(\varGamma _2) = (V_U, E_U)$ with fanin and fanout 2, which can be transformed to a Boolean circuit. $P\subseteq V_U$ contains the poles of $U_n(\varGamma _2)$ (cf. Sect. 2.1). Poles $\{1, \ldots , u\}$ correspond to the inputs, $\{(u + 1), \ldots , (u + k)\}$ to the gates, $\{(u + k + 1), \ldots , n\}$ to the outputs of $C_{u, v}^k$. The edges of the graph of the circuit $G = (V, E)$ have to be embedded into $U_n(\varGamma _2)$. After the transformations described in Sect. 2.1, every node in G has fanin and fanout 2, and we denote a topological order on V by $\eta ^G$. We briefly describe the edge-embedding process in Sects. 2.3 and 3.

Translating a $\varvec{U_n(\varGamma _2)}$ into a Universal Circuit. Every node $w \in V_U$ fulfills a task when $U_n(\varGamma _2)$ is translated to a UC. Programming the UC means specifying its control bits along the paths defined by the edge-embedding and by the gates of circuit $C_{u,v}^k$. Depending on the number of incoming and outgoing edges and its type, a node is translated to:  

G1.:

If w is a pole and corresponds to an input or output in G, then w is an input or output in $U_n(\varGamma _2)$ as well.

G2.:

If w is a pole and corresponds to a gate in G, w is programmed as a universal gate (UG). A 2-input UG supports any of the 16 possible gate types represented by the 4 control bits of the gate table $(c_1, c_2, c_3, c_4)$. It implements function ug: $\{0, 1\}^2 \times \{0, 1\}^4 \rightarrow \{0, 1\}$ that computes:

$$\begin{aligned} ug(x_1, x_2, c_1, c_2, c_3, c_4) = \overline{x_1}\overline{x_2}c_1 + \overline{x_1}x_2c_2 + x_1 \overline{x_2} c_3 + x_1 x_2 c_4. \end{aligned}$$

(1)

Generally, a UG can be implemented with 3 AND and 6 XOR gates (resp. with a two-input gate when using Yao’s protocol for SFE) [KS16].

G3.:

If w is no pole and has indegree and outdegree 2, w is programmed as an X-switching block, that computes $f_X: \{0, 1\}^2 \times \{0, 1\} \rightarrow \{0, 1\}^2$ with $f_X((x_1, x_2), c) = (x_{1+c}, x_{2-c})$. This block can be implemented with 1 AND and 3 XORs (resp. a one-input gate with Yao) [KS08a].

G4.:

If w is no pole and has indegree 2 and outdegree 1, w is programmed as a Y-switching block that computes $f_Y: \{0, 1\}^2 \times \{0, 1\} \rightarrow \{0, 1\}$ with $f_Y((x_1, x_2), c) = x_{1+c}$. This block can be implemented with 1 AND and 2 XORs (resp. a one-input gate with Yao) [KS08a].

G5.:

If w is no pole and has indegree 1 and outdegree 2, it has been placed to copy its input to its two outputs. Therefore, when translated to a UC, w is replaced by multiple outgoing wires in the parent node [KS16], since the UC itself does not have the fanout 2 restriction. In $U_n(\varGamma _2)$, w is added due to the fanout 2 restriction in the EUG.

G6.:

If w is no pole and has indegree and outdegree 1, w is removed and replaced by a wire between its parent and child nodes.

 

The nodes programmed as UG (G2), X-switching block (G3) or Y-switching block (G4) are so-called programmable blocks. This means that a programming bit or vector is necessary besides the two inputs to define their behavior as described above. These programming bits and vectors that build up the programming of the UC $p_f$ are defined by the paths in the edge-embedding of G (the graph of circuit $C_{u, v}^k$ describing f) into $U_n(\varGamma _2)$.

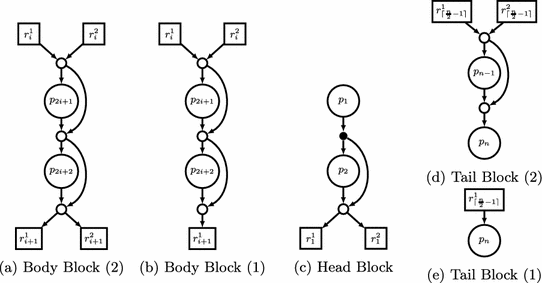
Recursion Base. Valiant’s construction is recursive, and the recursion base is reached when the number of poles is between 1 and 6. These recursion base graphs are shown in [Val76, KS16]. $U_1(\varGamma _1)$ is a single pole, $U_2(\varGamma _1)$ and $U_3(\varGamma _1)$ are two and three connected poles, respectively. $U_4(\varGamma _1)$, $U_5(\varGamma _1)$ and $U_6(\varGamma _1)$ are constructed with 3, 7 and 9 additional nodes, respectively.

Fig. 2.

(a) shows Valiant’s 2-way EUG $U_n^{(2)}(\varGamma _1)$ [Val76]. (c) shows the corresponding head block, (b) and (d)–(e) show body and tail blocks, respectively, for different numbers of poles.

2.3 Valiant’s 2-Way UC Construction

We described in Sect. 2.1 that a $U_n(\varGamma _d)$ EUG can be constructed of d instances of $U_n(\varGamma _1)$ EUGs. Therefore, Valiant provides an EUG for $\varGamma _1(n)$ graphs, two of which can build an EUG for $\varGamma _2(n)$ graphs. Let $P = \{p_1, \ldots , p_n\}$ be the set of poles in $U_n^{(2)}(\varGamma _1)$ that have indegree and outdegree 1. Valiant’s 2-way EUG construction for $\varGamma _1(n)$ graphs of size ${\sim } 2.5n\log _2 n$ is shown in Fig. 2, where we emphasize the poles as large circles and the additional nodes as small circles or rectangles. The corresponding UC has twice the size ${\sim } 5n\log _2 n$, since it corresponds to the EUG for $\varGamma _2(n)$ graphs.

The rectangles are special nodes that build the set of poles in the next recursion step, i.e., $R^1_{\lceil {\frac{n}{2}-1}\rceil } = \{r^1_1, \ldots , r^1_{\lceil {\frac{n}{2}-1}\rceil }\}$, $R^2_{\lceil {\frac{n}{2}-1}\rceil } = \{r^2_1, \ldots \, r^2_{\lceil {\frac{n}{2}-1}\rceil }\}$. Another EUG is built with these poles which produces new subgraphs with size $\lceil {\frac{\lceil {\frac{n}{2}-1}\rceil }{2}-1}\rceil$, s.t. we have four subgraphs at this level.

This construction is called the 2-way EUG or UC construction. An open-source implementation of this construction optimized for PFE is provided in [KS16]. Independently, [LMS16] also implemented this 2-way UC, additionally optimizing for the total number of gates.

2.4 Valiant’s 4-Way UC Construction

Valiant provides another, so-called 4-way EUG or UC construction [Val76]. $U_n^{(4)}(\varGamma _1)$ has a 4-way recursive structure, i.e., nodes in special sets $R^1_{\lceil {\frac{n}{4}-1}\rceil }$, $R^2_{\lceil {\frac{n}{4}-1}\rceil }$, $R^3_{\lceil {\frac{n}{4}-1}\rceil }$ and $R^4_{\lceil {\frac{n}{4}-1}\rceil }$ are the poles in the next recursion step (cf. Fig. 4a). The recursion base is the same as in Sect. 2.2. This construction results in UCs of smaller size ${\sim }4.75 n\log _2n$ but has not been implemented before due to its more complicated structure.

2.5 Lipmaa et al.’s Generalized k-Way UC Construction

In [LMS16], Lipmaa et al. generalize Valiant’s approach by providing a UC with any number of recursion points k, the so-called k-way EUG or UC construction. We note that their construction slightly differs from Valiant’s EUG construction, since they do not consider the restriction on the fanout of the poles, i.e., the nodes in the EUG that correspond to universal gates or inputs (cf. Sect. 2.2). This optimization has also been included in [KS16] when translating an EUG to a UC, but including it in the block design leads to better sizes for the number of XOR gates.

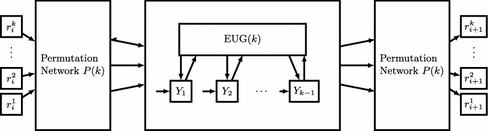
The idea is to split $n = u\,+\,v\,+\,k$ in $m = \lceil {\frac{n}{k}}\rceil$ blocks as shown in Fig. 3. Every block i consists of k inputs $r_{i}^1, r_{i}^2, \ldots , r_{i}^k$ and k outputs $r_{i+1}^1, r_{i+1}^2, \ldots , r_{i+1}^k$ as well as k poles, except for the last block which has a number of poles depending on n mod k. For every $j \le k$, the list of all $r_i^j$ builds the poles of the $\text {j}^{\text {th}}$ subgraph of the next recursion step, i.e. we have k subgraphs. Additionally, every block begins and ends with a Waksman permutation network [Wak68] such that the inputs and outputs can be permuted to every pole. A Y-switching block is placed in front of every pole $p_i$ which is connected to the $\text {i}^{\text {th}}$ output of the permutation network as well as the $\text {i}^{\text {th}}$ output of a block-intern EUG $U_k(\varGamma _1)$. Thus, [LMS16] reduce the problem of finding an efficient k-way EUG $U_n^{(k)}(\varGamma _2)$ to the problem of finding the smallest EUG $U_k(\varGamma _1)$. Their solution is to build the block-intern EUG with the UC construction of [KS08b], which was claimed to be more efficient for smaller circuits than [Val76]. However, they calculate the optimal k value to be around 3.147, which implies that the best solutions are found using small EUGs, for which Valiant provides hand-optimized solutions (i.e., for $k=2, 3, 4, 5, 6$) [Val76].

Fig. 3.

k-way EUG construction $U_n^{(k)}(\varGamma _1)$ [LMS16].

3 Our Modular Edge-Embedding Algorithm

The detailed embedding algorithm and the open-source UC implementation of [KS16] was specifically built for the 2-way UC, dealing with the whole UC skeleton as one block. In contrast, based on the modular design of [LMS16], we modularize the edge-embedding task into multiple sub-tasks and describe how they can be performed separately. In this section, we detail this modular approach for edge-embedding a graph into Valiant’s 4-way EUG: the edge-embedding can be split into two parts, which are then combined. In Sect. 3.1, we describe our modular approach based on the edge-embedding algorithm of [KS16] for Valiant’s 2-way EUG. This can be generalized to any $2^i$-way EUG construction. Moreover, the same algorithm can be applied with a few modifications for Lipmaa et al.’s k-way recursive generalization [LMS16], which we describe in Sect. 3.2.

3.1 Edge-Embedding in Valiant’s 4-Way UC

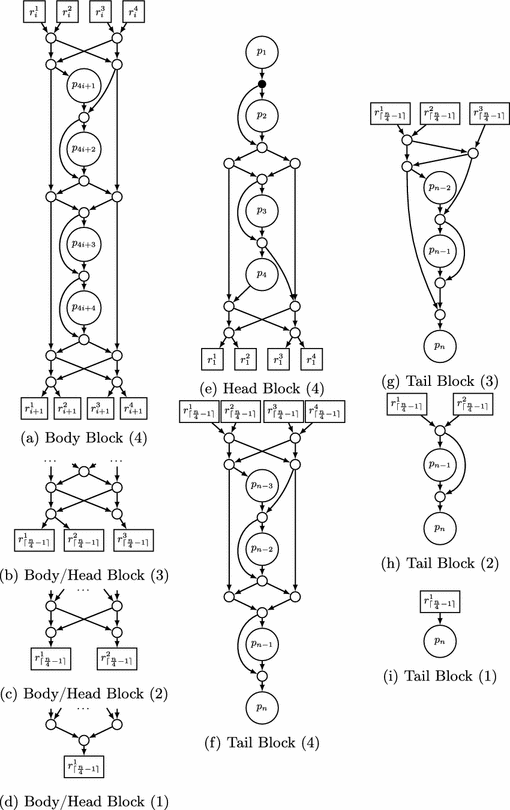
Similar to the 2-way EUG construction (cf. Sect. 2.3), Valiant provides a 4-way EUG construction for $\varGamma _1(n)$ graphs which can be extended to an EUG for $\varGamma _2(n)$ graphs by utilizing two instances $U_n^{(4)}(\varGamma _1)_1$ and $U_n^{(4)}(\varGamma _1)_2$ as described in Sect. 2.1. The construction with our optimizations is visualized in Fig. 4. Valiant offers the main, so-called Body Block (Fig. 4a) consisting of 4 poles (large circles), 15 nodes (small circles) as well as 8 recursion points (squares). These body blocks are connected such that the 4 top [bottom] recursion points of one block are the 4 bottom [top] recursion points of the next block. Similarly to the 2-way EUG, 4 sets are created for n nodes, i.e., $R^1_{\lceil {\frac{n}{4}-1}\rceil } = \{r^1_1, \ldots , r^1_{\lceil {\frac{n}{4}-1}\rceil }\}$, $R^2_{\lceil {\frac{n}{4}-1}\rceil } = \{r^2_1, \ldots , r^2_{\lceil {\frac{n}{4}-1}\rceil }\}$, $R^3_{\lceil {\frac{n}{4}-1}\rceil } = \{r^3_1, \ldots , r^3_{\lceil {\frac{n}{4}-1}\rceil }\}$, and $R^4_{\lceil {\frac{n}{4}-1}\rceil } = \{r^4_1, \ldots , r^4_{\lceil {\frac{n}{4}-1}\rceil }\}$ which are the poles of 4 $U_{\lceil {\frac{n}{2}}\rceil -1}(\varGamma _1)$ EUGs in the next recursion step. Then, these also create 4 subgraphs until the recursion base is reached, cf. Sect. 2.2.

Fig. 4.

(a) shows Valiant’s 4-way EUG $U_n^{(4)}(\varGamma _1)$ [Val76]. (e) shows our head block construction, (a)–(d) and (f)–(i) show our body and tail block constructions, respectively, for different numbers of poles.

We note that the top [bottom] block does not need the upper [lower] recursion points since its poles are the inputs [outputs] in the block. Therefore, we provide so-called Head and Tail Blocks. A Head Block occurs at the top of a chain of blocks (cf. Fig. 4e), it has 4 poles, no inputs, 4 output recursion points and 10 nodes, of which the first one (denoted by a filled circle) has one input and therefore translates to wires in the UC.

As a counterpart, Tail Blocks occur at the bottom of a chain of blocks, have at most 4 poles, 4 input recursion points, no outputs and at most 10 nodes depending on the number of poles. The 4 tail block constructions are depicted in Figs. 4f–i and are used, based on the remainder of n modulo 4, with the respective body or head blocks when $n\in \{5, 6, 7\}$, the lower parts of which are shown in Figs. 4a–d.

Block Edge-Embedding. In this first part of the edge-embedding process, we consider the 4 top [bottom] recursion points of the block as intermediate nodes where the inputs [outputs] of the block enter [leave]. The blocks are built s.t. any of these inputs can be forwarded to exactly one of the 4 poles of the block and the output of any pole can be forwarded to exactly one output or another pole having a higher topological order.

We formalize this behaviour as follows: In $U_n^{(4)}(\varGamma _1)=(V_U, E_U)$, let B be the block visualized in Fig. 4a with poles $p_{4i+1}, \ldots , p_{4i+4}$. Let mapping $\eta ^U: V_U\rightarrow \mathbb {N}^+$ denote a topological order of $V_U$. Then, the nodes $r_i^1, \ldots , r_i^4$ and $r_{i+1}^1, \ldots , r_{i+1}^4$ denote the input and output recursion points of block B. Additionally, let ${in} = (in_1, \ldots , in_4) \in \{0, \ldots , 4\}^4$ and ${out}=(out_1, \ldots , out_4) \in \{0, \ldots , 7\}^4$ denote the input and output vectors of B. The value 0 of the input and output vectors is a dummy value which is used if an input [a pole] is not forwarded to any pole [output] of B. The output vector has a larger value range, since a pole can be forwarded to another pole or an output recursion point. Therefore, we use values 1, 2 and 3 for poles $p_2, p_3$ and $p_4$ and values 4, 5, 6 and 7 for the output recursion points. Pole $p_1$ cannot be a destination for a path in B, since $\eta ^U(p_1)$ is less than the topological order of any other pole in B. Additionally, the values of in and out need to be pairwise different or 0. Every combination of input and output vector covering the conditions formalized below in Eqs. 2–6 are valid for B. A pair $(r_i^l, p_j) \in \mathcal {P}$ or $(p_j, r_{i+1}^l) \in \mathcal {P}$ is a path from $r_i^l$ to $p_j$ or $p_j$ to $r_i^l$ in the set of all paths $\mathcal {P}$ in B. Then, $\mathcal {P}_B \subseteq \mathcal {P}$ denote the paths that are to be edge-embedded (cf. Sect. 6.1).

$$\begin{aligned} \forall l \in \{1, \ldots , 4\}: in_l \ne 0 \rightarrow&(r_i^l, p_{in_l}) \in \mathcal {P}_B,\end{aligned}$$

(2)

$$\begin{aligned} out_l \ne 0 \wedge out_l< 4 \rightarrow&(p_j, p_{1 + out_l}) \in \mathcal {P}_B \wedge \eta ^U(p_j) < \eta ^U(p_{1 + out_l}) \end{aligned}$$

(3)

$$\begin{aligned} out_l > 3 \rightarrow&(p_j, r_{i+1}^{l - 3}) \in \mathcal {P}_B.\end{aligned}$$

(4)

$$\begin{aligned} \forall in_i, in_j \in in: i \ne j \rightarrow&in_i = 0 \vee in_i \ne in_j.\end{aligned}$$

(5)

$$\begin{aligned} \forall out_i, out_j \in out: i \ne j \rightarrow&out_i = 0 \vee out_i \ne out_j. \end{aligned}$$

(6)

Recursion Point Edge-Embedding. The block edge-embedding covers only the programming of the nodes within a block. Another task left is to program the recursion points. We use the supergraph construction of [KS16] which, in every step, splits a $\varGamma _2(n)$ graph in two $\varGamma _1(n)$ graphs, which are merged to two $\varGamma _2(\lceil {\frac{n}{2}-1}\rceil )$ graphs. [KS16] use this for defining the paths in Valiant’s 2-way EUG. For Valiant’s 4-way EUG, we use every second step of their algorithm with a minor modification.

Let $C_{u, v}^k$ be the Boolean circuit computing function f that our UC needs to compute, and $G \in \varGamma _2(n)$ its graph representation (cf. Sect. 2.2).

• 1. Splitting G $\in \varGamma _2(n)$ in two $\varGamma _1(n)$ graphs $G_1$ and $G_2$: As described in Sect. 2.1, Valiant’s UC is derived from an EUG for $\varGamma _2(n)$ graphs, which consists of two EUGs for $\varGamma _1(n)$ graphs merged by their poles. Therefore, G is split into two $\varGamma _1(n)$ graphs $G_1$ and $G_2$. $G_1$ and $G_2$ then need to be edge-embedded into EUGs $(U_n^{(4)}(\varGamma _1))_1$ and $(U_n^{(4)}(\varGamma _1))_2$, respectively. $G=(V, E)\in \varGamma _2(n)$ is split by 2-coloring its edges as described in [Val76, KS16], which can always be done due to Kőnig’s theorem [Kő31, LP09]. After 2-coloring, E is divided to sets $E_1$ and $E_2$, using which we build $G_1 = (V, E_1)$ and $G_2 = (V, E_2)$, with the following conditions:

  $$\begin{aligned} \forall e \in E:&(e \in E_1 \vee e \in E_2) \wedge \lnot (e \in E_1 \wedge e \in E_2). \end{aligned}$$

  (7)
  $$\begin{aligned} \forall e = (v_1, v_2) \in E_1:&\lnot \exists e' = (v_3, v_4) \in E_1: v_2 = v_4 \vee v_1 = v_3.\end{aligned}$$

  (8)
  $$\begin{aligned} \forall e = (v_1, v_2) \in E_2:&\lnot \exists e' = (v_3, v_4) \in E_2: v_2 = v_4 \vee v_1 = v_3. \end{aligned}$$

  (9)

• 2. Merging a $\varGamma _1(n)$ graph into a $\varGamma _2(\lceil {\frac{n}{2}-1}\rceil )$ graph: In an EUG, the number of poles decreases in each recursion step and therefore, merging a $\varGamma _1(n)$ graph into a $\varGamma _2(\lceil {\frac{n}{2}-1}\rceil )$ graph provides information about the paths to be taken. Let $G_1 = (V, E) \in \varGamma _1(n)$ be a topologically ordered graph and $G_m = (V^\prime , E^ \prime ) \in \varGamma _2(\lceil {\frac{n}{2}}\rceil )$ be a graph with nodes $v^\prime _1, \ldots , v^\prime _{\lceil {\frac{n}{2}}\rceil }$. We define two labellings $\eta _{\text {in}}$ and $\eta _{\text {out}}$ on $G_m$ with $\eta _{\text {in}}(v_i) = i$ and $\eta _{\text {out}}(v_i) = \eta _{\text {in}}(v_i)\,-\,1 = i\,-\,1$. Additionally, we define a mapping $\theta _V$ that maps a node $v_i \in V$ to a node $v_j \in V^\prime$ with $\theta _V(v_i) = v^\prime _{\lceil {\frac{i}{2}}\rceil }$. That means two nodes in $G_1$ are mapped to one node in $G_m$. At last, we define a mapping $\theta _E$ that maps an edge $e_i = (v_i, v_j) \in E$ to an edge $e_j \in E^\prime$ with $\theta _E((v_i, v_j)) = (v_{\eta _{\text {in}}(\theta _V(v_i))}, v_{\eta _{\text {out}}(\theta _V(v_j))})$. That means every edge in $G_1$ is mapped to an edge in $G_m$ as follows: $e = (v_i, v_j) \in E$ is mapped to $e^\prime = (v_k^\prime , v_l^\prime ) \in E^\prime$, s.t. $v_k^\prime = \theta _V(v_i)$, but $v_l^\prime$ is not the new node of $v_j$ in $G_m$ but $v_{l+1}^\prime$. $G_m$ is built as follows: $V' = \{v_1^\prime , \ldots , v_{\lceil {\frac{n}{2}}\rceil }^\prime \}$ and $E^\prime =\bigcup _{e \in E}\theta _E(e)$. Then for all $e = (v_i^\prime , v_j^\prime ) \in E^\prime$ and $j < i$, e is removed from $E^\prime$, along with the last node $v_{\lceil {\frac{n}{2}}\rceil }$ (due to the definition of $\theta _E$, it does not have any incoming edges). The resulting $G_m$ is a topologically ordered graph in $\varGamma _2(\lceil {\frac{n}{2}-1}\rceil )$.

• 3. The supergraph for Valiant’s 4-way EUG construction: In the first step, G is split to two $\varGamma _1(n)$ graphs $G_1$ and $G_2$. $G_1$ and $G_2$ contain all the edges that should be embedded as paths between poles in the first and second EUGs for $\varGamma _1(n)$, respectively. We now explain how to edge-embed the $\varGamma _1(n)$ graph $G_1$ into an EUG $U_n^{(4)}(\varGamma _1)$ (for $G_2$ it is the same).

For embedding in a 2-way UC, $G_1$ is firstly merged to a $\varGamma _2(\lceil {\frac{n}{2}}\rceil )$ graph $G_{m}$. $G_{m}$ is then 2-colored and split into two $\varGamma _1(\lceil {\frac{n}{2}}\rceil )$ graphs $G_1^{\text {1}}$ and $G_1^{\text {2}}$ [KS16]. These get merged to two $\varGamma _2(\lceil {\frac{\lceil {\frac{n}{2}-1}\rceil }{2}-1}\rceil )$ graphs $G_{m}^{\text {1}}$ and $G_{m}^{\text {2}}$. $G_1^{\text {1}}$ is the first and $G_1^{\text {2}}$ is the second subgraph of $G_1$. Then $G_1^{\psi \circ \text {1}}$ and $G_1^{\psi \circ \text {2}}$ denote the first and second subgraph of $G_1^{\psi }$, respectively. These steps are repeated until the $\varGamma _1$ subgraphs have at most 4 nodes.

In Valiant’s 4-way EUG construction [Val76], a supergraph that creates 4 subgraphs in each step is necessary. We require a merging method where a $\varGamma _1(n)$ graph is merged to a $\varGamma _4(\lceil {\frac{n}{4}-1}\rceil )$ graph where 4 nodes build a new node, and 4-color this graph to retrieve 4 subgraphs. However, this can directly be solved by using the method described above from [KS16]: after repeating the 2-coloring and the merging twice, we gain 4 subgraphs ($G_1^{\text {11}}$, $G_1^{\text {12}}$, $G_1^{\text {21}}$ and $G_1^{\text {22}}$). These can be used as if they were the result of 4-coloring the graph obtained by merging every 4 nodes into one.

However, there is a modification in this case: the first 2-coloring is a preprocessing step, which does not map to an EUG recursion step. Therefore, we have to define another labelling $\eta _{\text {out}_P}(v) = \eta _{\text {in}}(v)$, since in this preprocessing step we need to keep node $v_{\lceil {\frac{n}{2}}\rceil }$. Then the creation of the supergraph for the 4-way EUG construction works as follows: We merge $G_1$ to a $\varGamma _2(\lceil {\frac{n}{2}}\rceil )$ graph with labelling $\eta _{\text {in}}$ and $\eta _{\text {out}_P}$ and get $G_{m}$. After that, we split $G_{m}$ into two $\varGamma _1(\lceil {\frac{n}{2}}\rceil )$ graphs $G_1^{\text {1}}$ and $G_1^{\text {2}}$. These get merged to $\varGamma _2(\lceil {\frac{n}{4}}\rceil -1)$ graphs $G_{m}^{\text {1}}$ and $G_{m}^{\text {2}}$ using the $\eta _{\text {in}}$ and $\eta _{\text {out}}$ labellings. Finally, these two graphs get splitted into 4 $\varGamma _1(\lceil {\frac{n}{4}-1}\rceil )$ graphs $G_1^{\text {11}}$, $G_1^{\text {12}}$, $G_1^{\text {21}}$ and $G_1^{\text {22}}$. These are the relevant graphs for the first recursion step in Valiant’s 4-way EUG construction. Now we continue for all 4 subgraphs until we reach the recursion base with 4 or less nodes.

4-Way Edge-Embedding Algorithm. In Listing 1, we combine block edge-embedding and recursion point edge-embedding:

Let U denote the part of $U_n^{(4)}(\varGamma _1)$ without recursion steps (the main chain of blocks) and $G_1 = (V, E)$ be the $\varGamma _1(n)$ graph which is to be edge-embedded in $U_n^{(4)}(\varGamma _1)$. S denotes the set of the 4 subgraphs of $G_1$ in the supergraph, i.e. $S=\{G_1^{\text {11}}, G_1^{\text {12}}, G_1^{\text {21}}, G_1^{\text {22}}\}$. A recursion step graph of U is one of the graphs having one of the 4 sets of recursion points as poles (e.g. $r^1_1, \ldots , r^1_{\lceil {\frac{n}{4}-1}\rceil }$) without the recursion steps. R denotes the set of all 4 recursion step graphs of U, and B denotes the set of all blocks in U.

We give a brief explanation of Listing 1 that describes the edge-embedding process. For any edge $e = (v_i, v_j) \in E$ in $G_1$, $b_i$ and $b_j$ denote the block numbers in which $v_i$ and $v_j$ are. There are 2 cases:

• 1. $v_i$ and $v_j$ are in the same block: $b_i = b_j$ . The edge-embedding can be solved within the block and no recursion points have to be programmed for this path. Therefore, vector out of block $B_{b_i}$ is set accordingly.

• 2. $v_i$ and $v_j$ are in different blocks: $b_i \ne b_j$ . There exists an edge $e^\prime = ({b_i}, {b_{j - 1}})$ in one of the four $\varGamma _1(\lceil {\frac{n}{4}-1}\rceil )$ subgraphs of $G_1$ that is not yet used for an edge-embedding. This determines that the path in the next recursion step has to be between poles $p_{b_i}$ and $p_{b_{j - 1}}$. We denote with $s \in S$ the subgraph of $G_1$ which contains $e^\prime$, and x denotes its number in S, i.e. $S_x = s$. This implies in which of the 4 recursion step graphs we need to edge-embed the path from $p_{b_i}$ to $p_{b_{j - 1}}$, and so which recursion points we need to program. We first set the programming bit of the x-th input [output] recursion points to 1 since the path between the poles with labelling i and j enters [leaves] the next recursion step over this recursion point. A special case to be considered here is when blocks $B_{b_i}$ and $B_{b_j}$ are neighbours (i.e. $b_j = b_i + 1$). Then, the path enters and leaves the next recursion step graph at the same node, whose programming bit thus has to be 0. The output vector of block $B_{b_i}$ is the $i^\prime$ ^th value to the x ^th recursion point and the input vector of block $B_{b_j}$ is the x ^th value to the $j^\prime$ ^th pole in this block.

We repeat these steps for all edges $e \in E$. Since all in- and output vectors of all blocks in B are set, they can be embedded with the block edge-embedding. For all 4 subgraphs of $G_1$ in the supergraph and in the EUG, we call the same procedure with $S_i \in S$, $R_i \in R$, $1 \le i \le 4$.

3.2 Edge-Embedding in Lipmaa et al.’s k-Way UC

In this section, we extend the recent work of [LMS16] by providing a detailed and modular embedding mechanism for any k-way EUG construction described in Sect. 2.5. We provide the main differences to the edge-embedding of the 4-way EUG construction detailed in Sect. 3.1.

k -Way Block Edge-Embedding. In this setting, our main block is a programmable block B of size x with k poles $p_1, \ldots , p_k$, and k input [output] recursion points $r_0^1, \ldots , r_0^k$ [$r_1^1, \ldots , r_1^k$]. B is topologically ordered with mapping $\eta ^U$ as defined in Sect. 2.1. Vectors $in =(in_1, \ldots , in_k) \in \{0, \ldots , k\}^k$, and $out = (out_1, \ldots , out_k) \in \{0, \ldots , 2k - 1\}^k$ denote the input and output vectors of B, respectively. Values $k, \ldots , 2k-1$ in out denote the recursion point targets $r_1^1, \ldots , r_1^k$ (cf. Sect. 3.1). We formalize the setting of in and out in Eqs. 10–14. We denote with $\mathcal {P}$ the set of all paths in B, and the $\mathcal {P}_B \subseteq P$ the paths that get edge-embedded in B.

$$\begin{aligned} \forall i \in \{1, \ldots , k\}: in_i \ne 0 \rightarrow&(r_0^i, p_{in_i}) \in \mathcal {P}_B,\end{aligned}$$

(10)

$$\begin{aligned} out_i \ne 0 \wedge out_i< k \rightarrow&(p_i, p_{1 + out_i}) \in \mathcal {P}_B \wedge \eta ^U(p_i) < \eta ^U(p_{1 + out_i}) \end{aligned}$$

(11)

$$\begin{aligned} out_i > k - 1 \rightarrow&(p_i, r_1^{i - k + 1}) \in \mathcal {P}_B.\end{aligned}$$

(12)

$$\begin{aligned} \forall in_i, in_j \in in: i \ne j \rightarrow&in_i = 0 \vee in_i \ne in_j.\end{aligned}$$

(13)

$$\begin{aligned} \forall out_i, out_j \in out: i \ne j \rightarrow&out_i = 0 \vee out_i \ne out_j. \end{aligned}$$

(14)

k -Way Recursion Point Edge-Embedding. $G \in \varGamma _2(n)$ denotes the transformed graph of a Boolean circuit $C_{u, v}^k$, where $n=u+k+v$.

• 1. Splitting $G \in \varGamma _2(n)$ in two $\varGamma _1(n)$ graphs $G_1$ and $G_2$ : Similarly as in Sect. 3.1, we first split G into two $\varGamma _1(n)$ graphs $G_1$ and $G_2$ with 2-coloring.

• 2. Merging a $\varGamma _1(n)$ graph into a $\varGamma _k(\lceil {\frac{n}{k}-1}\rceil )$ graph: $G_1 = (V, E) \in \varGamma _1(n)$ is merged into a $\varGamma _k(\lceil {\frac{n}{k}-1}\rceil )$ graph $G_{m} = (V^\prime , E^\prime )$ (same for $G_2$). Therefore, we redefine mapping $\theta _V$ (cf. Sect. 3.1) that maps node $v_i \in V$ to node $v_j \in V^\prime$. In this scenario, k nodes in V build one node in $V^\prime$, so $\theta _V(v_i) = v_{\lceil {\frac{i}{k}}\rceil }$. The mapping of the edges $\theta _E$ is the same as in the 4-way EUG construction, and $(v_i', v_j')\in E'$ where $j<i$ edges are removed along with $v_{\lceil {\frac{n}{k}}\rceil }$ in the end. $G_m$ is then a topologically ordered graph in $\varGamma _1(\lceil {\frac{n}{k}-1}\rceil )$.

• 3. The supergraph for Lipmaa et al.’s k-way EUG construction: The next step is to split $G_{m} \in \varGamma _1(\lceil {\frac{n}{k}-1}\rceil )$ into k $\varGamma _1(\lceil {\frac{n}{k}-1}\rceil )$ graphs. This is done with k-coloring: a directed graph $K=(V, E)$ can be k-colored, if k sets $E_1, \ldots , E_k\subseteq E$ cover the following conditions:

  $$\begin{aligned} \forall i, j \in&\{1, \ldots , k\}: i \ne j \rightarrow E_i \cap E_j = \emptyset . \end{aligned}$$

  (15)
  $$\begin{aligned} \forall e \in&E: \exists i \in \{1, \ldots , k\}: e \in E_i.\end{aligned}$$

  (16)
  $$\begin{aligned} \forall i \in&\{1, \ldots , k\}: \forall e = (v_1, v_2) \in E_i: \nonumber \\&\lnot \exists e^\prime = (v_3, v_4)\in E_i: v_2 = v_4 \vee v_1 = v_3. \end{aligned}$$

  (17)

  According to Kőnig’s theorem [Kő31, LP09], $\varGamma _k(n)$ graphs can always be k-colored efficiently (cf. full version [GKS17, Appendix A] for details). The rest of the supergraph construction and the way it is used for edge-embedding is the same as for the 4-way EUG construction as described in Sect. 3.1.

k -Way Edge Embedding Algorithm. The edge-embedding algorithm is the same as shown in Listing 1, after replacing every 4 with k.

4 New Universal Circuit Constructions

Here, we describe our ideas for novel, potentially more efficient, UC constructions. Firstly, in Sect. 4.1, we describe modular building blocks for a 3-way UC. We show that Valiant’s optimized $U_3(\varGamma _1)$ cannot directly be applied as a building block in the construction due to the fact that it must have an additional node to be a generic EUG. We prove that the EUG without this node is not a valid EUG by showing a counterexample. Therefore, it actually results in a worse asymptotic size than Valiant’s 2-way and 4-way UC constructions. Secondly, in Sect. 4.2, we propose a hybrid UC construction, utilizing both Valiant’s 2-way and 4-way UC constructions so that the overall size of the resulting hybrid UC is minimized, and is at least as efficient as the better construction for the given size.

4.1 3-Way Universal Circuit Construction

The optimal k value for minimizing the size of the k-way UC was calculated to be 3.147 in [LMS16]. We describe our idea of a 3-way UC construction. Intuitively, based on an optimization by Valiant [Val76], this UC should result in the best asymptotic size. The asymptotic size of any k-way UC depends on the size of its modular body block $B_k$ (e.g., Fig. 4a for the 4-way UC). Once it is determined, the size of the UC is $\text {size}(U^{(k)}_n(\varGamma _2))=2\cdot \text {size}(U^{(k)}_n(\varGamma _1))$ $\approx$ $2\cdot \frac{\text {size}(B_k)}{k} n\log _k n = 2\cdot \frac{\text {size}(B_k)}{k \log _2(k)} n\log _2 n$. The modular block consists of two permutation networks P(k), an EUG $U_k(\varGamma _1)$, and $(k-1)$ Y-switching blocks (cf. Sect. 2.5, [LMS16]).

Size of Body Block $\varvec{B_3}$ with Valiant’s Optimized $\varvec{U_3(\varGamma _1)}$ . According to Valiant [Val76], an EUG $U_3(\varGamma _1)$ with 3 poles contains only 3 connected poles (used as recursion base in Sect. 2.2). An optimal permutation network P(3) that achieves the lower bound has 3 nodes as well. This implies that size$(B_3)=2\cdot P(3)+\text {size}(U_3(\varGamma _1))+(3-1) = 11$. Then, the size of the UC becomes $\approx 2\cdot \frac{11}{3\log _2 3} n\log _2 n\approx 4.627 n \log _2 n$, which means an asymptotically by around 2.5% smaller size than that of the 4-way UC.

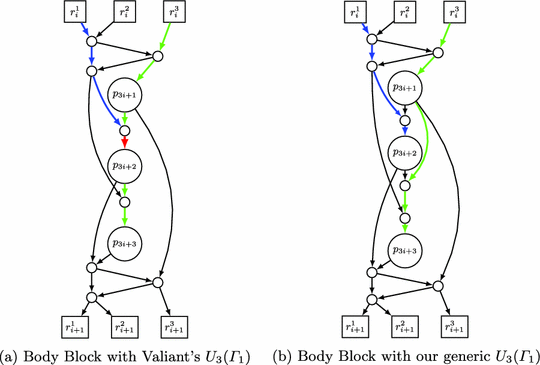
However, there is a flaw in this initial design. Valiant’s $U_3(\varGamma _1)$ only works as an EUG for 3 nodes under special conditions, e.g., when it is a subgraph within a larger EUG construction. There are 3 possible edges in a topologically ordered graph $G=(V, E)$ in $\varGamma _1(3)$: (1, 2), (2, 3) and (1, 3). (1, 2) and (2, 3) can be directly embedded in $U_3(\varGamma _1)$ using $(p_1, p_2)$ and $(p_2, p_3)$, respectively. (1, 3), however, has to be embedded as a path through node 2, i.e., as a path $((p_1, p_2), (p_2, p_3))$. When $U_3(\varGamma _1)$ is a subgraph of a bigger EUG, this is possible by programming $p_2$ accordingly. However, when we use this $U_3(\varGamma _1)$ as a building block in our EUG construction, it cannot directly be applied. A generic $U_3(\varGamma _1)$ that can embed (1, 3) without going through $p_2$ as before has an additional Y-switching block.

We depict in Fig. 5a the 3-way body block that uses Valiant’s optimized $U_3(\varGamma _1)$ in the k-way block design of [LMS16]. Assume that the output of pole $p_{3i+1}$ has to be directed to pole $p_{3i+3}$. Then, it needs to go through pole $p_{3i + 2}$, which means that the edge going in to $p_{3i + 2}$ is used by this path. However, there might be an other edge coming from the permutation network as an input to $p_{3i + 2}$, e.g., from $p_{3i}$ from the preceding block. This cannot be directed to $p_{3i+2}$ anymore as shown in Fig. 5a. Therefore, in the 3-way body block construction, it does not suffice to use Valiant’s optimized $U_3(\varGamma _1)$ [Val76].

Fig. 5.

Body block construction for our 3-way EUG $U_n^{(3)}(\varGamma _1)$.

Size of Body Block $\varvec{B_3}$ with Our Generic $\varvec{U_3(\varGamma _1)}$ . In Fig. 5b, we show the 3-way body block with the generic $U_3(\varGamma _1)$ that allows the output from $p_{3i+1}$ to be directed to $p_{3i+3}$ without having to go through $p_{3i+2}$. This results in size$(B_3) = 2\cdot P(3) + \text {size}(U_3(\varGamma _1)) + (3-1) = 12$, which implies that the asymptotic size of the UC is ${\approx } 2\cdot \frac{12}{3\log _2 3} n \log _2 n \approx 5.047n\log _2 n$. Unfortunately, this is worse than the asymptotic size of the 2-way construction, and we therefore conclude that the asymptotically most efficient known UC construction is Valiant’s 4-way UC construction.

4.2 Hybrid Universal Circuit Construction

In this section, we detail our hybrid UC that minimizes its size based on Valiant’s 2-way and 4-way UCs, which are asymptotically the smallest UCs to date. Given the size of the input circuit $C_{u,v}^k$, i.e., $n=u+k+v$, we can calculate at each recursion step if it is better to create 2 subgraphs of size $\lceil {\frac{n}{2}-1}\rceil$ and utilize the 2-way recursive skeleton, or it is more beneficial to create a 4-way recursive skeleton with 4 subgraphs of size $\lceil {\frac{n}{4}-1}\rceil$.

We assume that for every n, we have an algorithm that computes the size (size$(U_n^\text {hybrid}(\varGamma _1))$) of the hybrid construction for sizes smaller than n. We give details on how it is computed in Sect. 5. Then, Listing 2 describes the algorithm for constructing a hybrid UC, at each step based on which strategy is more efficient. We note that our hybrid construction is generic, and given multiple k-way UC constructions as parameter K ($K=\{2, 4\}$ in our example), it minimizes the concrete size of the resulting UC.

5 Size of UC Constructions

Lipmaa et al.’s k-way UC construction is depicted in a modular manner in [LMS16, Fig. 12] and discussed briefly in Sect. 2.5 and Fig. 3. They show that a k-way body block consists of two permutation networks P(k), an EUG for k nodes, i.e., $U_k(\varGamma _1)$, and additionally, $(k-1)$ Y-switching blocks. In this section, we recapitulate the sizes (Table 2) of the k-way EUG and give an estimate for the leading constant for Lipmaa et al.’s EUG construction with size $\mathcal {O}(n\log _2n)$, for $k\in \{2, \ldots , 8\}$. For a detailed discussion on the depth of the UCs, the reader is referred to the full version of this paper [GKS17, Sect. 5]. We conclude that the best asymptotic size is achieved by Valiant’s 4-way UC. This result does not exclude the possibility for a more efficient UC in general, but it shows that the most efficient UC using Lipmaa et al.’s k-way UC from [LMS16] is the 4-way UC. Two k-way EUGs for $\varGamma _1(n)$ graphs build up an EUG for $\varGamma _2(n)$ graphs as described in Sect. 2.1. Therefore, the leading constant for the size of the UC is twice that of the EUG $U_n^{(k)}(\varGamma _1)$, which is summarized in the same table.

5.1 Asymptotic Size of k-Way UC Constructions

We review the sizes of the building blocks of a k-way body block, i.e., the size of an EUG $U_k(\varGamma _1)$ for k, and the size of a permutation network P(k) with k inputs and outputs, as well as the size of the resulting UCs.

Table 2. The leading factors of the asymptotic $\mathcal {O}(n \log _2 n)$ size for k-way edge-universal graphs $(U_n^{(k)}(\varGamma _1))$ and universal circuits (UC) for $k\in \{2, \ldots , 8\}$. n denotes the size of the input $\varGamma _2(n)$ circuit, $U_k(\varGamma _1)$ the size of Valiant’s edge-universal graph with k poles, $U^{\text {KS08}}(k)$ the size of the UC of [KS08b], $P^\text {l}(k)$ the lower bound for the size of a permutation network for k nodes, and $P^\text {W}(k)$ the size of Waksman’s permutation network [Wak68]. $B^W_k$ is the size of the body block.

Edge-Universal Graph with k Poles. Valiant optimized EUGs up to size 6 by hand in [Val76]: for $k=2$, $U_2(\varGamma _1)$ has two poles, for $k=3$ we discussed in Sect. 4.1 that an additional node is necessary. For $k\in \{4, 5, 6\}$ the sizes are $\{6, 10, 13\}$, as shown in [KS16, Fig. 1] (note that the nodes noted as empty circles disappear in the UC ). For $k=7$ and $k=8$, we observe that Valiant’s 2-way UC results in a better size than that of the 4-way UC due to the smaller permutation network and less recursion nodes. Therefore, we use these constructions to compute the size of $U_7(\varGamma _1)$ and $U_8(\varGamma _1)$. As mentioned in [LMS16], another possibility is to use the UC of [KS08b] instead of these EUGs since they have better sizes for small circuits. These UCs $U^{\text {KS08}}(k)$ are built from two smaller $U^{\text {KS08}}({\frac{k}{2}})$, a $P(\frac{k}{2})$ and $\frac{k}{2}$ Y switches. It results in a smaller size of 21 for $k=8$.

Permutation Networks. Waksman in [Wak68] showed that the lower bound for the size of a permutation network is $\lceil \log _2(k!) \rceil$ for k elements. We present this lower bound in Table 2 as $P^\text {l}(k)$. The permutation network with the smallest size is Waksman’s permutation network $P^\text {W}(k)$ [Wak68, BD02]. For $k\in \{2, 3, 4\}$ its size reaches the lower bound, but for larger k values, his permutation network utilizes additional nodes. Since these are the smallest existing permutation networks, we use these when calculating the size of the UC. Even with the lower bound $P^\text {l}(k)$, for $k\in \{5, 6, 7, 8\}$ we would have the respective leading terms $\{4.824, 4.900, 5.190, 5\}$, which are larger than 4.75 for $k=4$.

Body Blocks. A body block $B_k^W$ is built of $(k-1)$ Y-switching blocks, an EUG for k nodes, and two permutation networks [LMS16] (cf. Fig. 3). The size of $B_k^W$ is the sum of the sizes of its building blocks, i.e., $\text {size}(B_k^W)=\min \left( \text {size}(U_k(\varGamma _1)), \text {size}(U^\text {KS08}(k))\right) +2\cdot \text {size}(P^W(k)) + k-1.$

Edge-Universal Graphs and Universal Circuits with n Poles. The asymptotic size of EUG $U_n^{(k)}(\varGamma _1)$ is determined as $\text {size}(U_n^{(k)}(\varGamma _1))=\frac{\text {size}(B^W_k)}{k\log _2 k}n\log _2 n$ and the leading factor for a UC is twice this number.

5.2 Concrete Size of UC Constructions

The size of Lipmaa et al.’s k-way universal circuits depends on the size of their building blocks [LMS16]. More concretely, finding either better edge-universal graphs for small number of nodes or optimal permutation networks could improve the sizes of these UCs. Lipmaa et al. calculated the optimal k value for minimizing the size of a k-way UC to be 3.147 [LMS16].

Table 2 shows that the smallest sizes are achieved by the 4-way, followed by the 2-way UCs. The 3-way UC, as mentioned in Sect. 4.1, is less efficient due to the additional node in $U_3(\varGamma _1)$. We observe that the sizes grow with increasing k values due to the permutation networks and EUGs.

Concrete Sizes of 4-Way and 2-Way UCs. Based on the parity (2-way UC) and the remainder modulo 4 (4-way UC), not only the size of the outest skeleton, but also that of the smaller subgraphs can be optimized. It was considered in [KS16] for the 2-way UC, and we now generalize the approach for k-way UCs. We provide a recursive formula for the concrete size of the optimized k-way EUG as follows. Let $m_k$ be defined as

$$\begin{aligned} m_k := {\left\{ \begin{array}{ll} n \mod k &{} \text {if } k \not \mid n,\\ k &{} \text {if } k \mid n. \end{array}\right. } \end{aligned}$$

(18)

Then, given the designed Head, Body and Tail blocks with sizes shown in Table 3, we can compute the size by calculating the size of all the components of the outest skeleton, and the sizes of the smaller subgraphs with the recursive formula shown in Eq. 19.⁴

(19)

Table 3. The sizes of building blocks of the 2-way and 4-way UCs (cf. Figs. 2 and 4).

Concrete Size of Our Hybrid UC. We provide a hybrid UC in Sect. 4.2 for minimizing the size of the resulting UC. This construction chooses at each step the skeleton that results in the smallest size and therefore, we provide the recursive algorithm for determining its size in Eq. 20. size(Head$_k{(i)}$), size(Tail$_k(i)$) and size(Body$_k(i)$) are the values from Table 3 for $k = 2$ and $k = 4$. The size of the hybrid UC is minimized as

(20)

which can be computed using a dynamic programming algorithm.

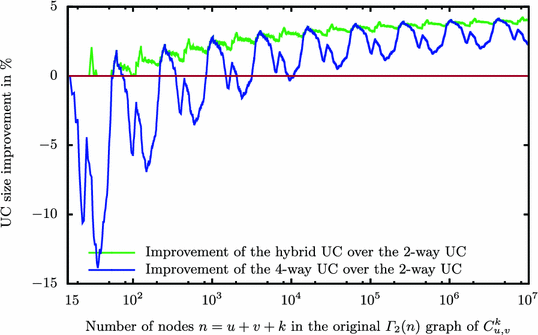
Improvement of 4-Way Construction. The bottom (blue) line in Fig. 6 shows the concrete improvement in percentage of the 4-way UC construction over the 2-way UC construction up to ten million nodes in the simulated input circuit. From the asymptotic leading factors in Table 2, we expect an improvement of up to $1-\frac{4.75}{5}=5\%$. For the smallest n values ($n\le 15$), the 2-way UC is up to 33.3% better than the 4-way UC. However, from $n=212$ on, the 4-way UC construction is better, except for some short intervals as shown in Fig. 6 (the difference in these intervals, however, is at most 3.45%). From here on, the 4-way UC is on average 3.12% better in our experiments, where the biggest improvement is 4.48%. Moreover, from $n=10885$ on, the 4-way UC always outperforms the 2-way UC.

Fig. 6.

Improvement of our hybrid and Valiant’s 4-way UC over Valiant’s 2-way UC for $15 \le n\le 10^7$ with logarithmic x axis. (Color figure online)

Improvement of Hybrid Construction. The improvement achieved by our hybrid construction (cf. Sect. 4.2) is depicted in the same Fig. 6, as the top (green) line. For some n values the hybrid UC achieves the same size as the 2- or 4-way UCs, but due to its nature, it is never worse. This means that the improvement of our hybrid UC is always nonnegative, and greater than or equal to the improvement achieved by the 4-way UC. Moreover, in most cases the hybrid UC results in better sizes than any of the other two constructions: this means that some subgraphs are created for an n for which the 2-way UC is smaller, and therefore the 2-way recursive structure is utilized. The overall improvement for all n values is on average 3.65% and at most 4.48% over the 2-way UC construction.

6 Implementation and Evaluation

The first implementation of Valiant’s 2-way UC, along with a toolchain for PFE (cf. Sect. 1.1) was given in [KS16]. The 4-way UC has smaller asymptotic size ${\sim } 4.75 n\log _2n$, but has not been implemented before due to its more complicated structure and embedding algorithm.

In this work, we improve the implementation of the open-source framework of [KS16] by using the 4-way UC construction that can directly be applied in the PFE framework. Our improved implementation is available at http://encrypto.de/code/UC. Firstly, the functionality is translated to a Boolean circuit using the Fairplay compiler [MNPS04, BNP08]. This is then transformed into a circuit in $\varGamma _2(n)$, i.e., with at most two incoming and outgoing wires for each gate, input and output. This is done in a preprocessing step of the framework in [KS16]. The input circuit description of our UC implementation is the same as that of the UC compiler of [KS16], and we also adapt our output UC format to that of [KS16] that includes the gate types described in Sect. 2.2. This format is compatible with the ABY framework [DSZ15] for secure function evaluation.

We discuss our implementation of Valiant’s 4-way UC in Sect. 6.1 and give experimental results in Sect. 6.2. For a description on how the hybrid UC can be implemented, the reader is referred to the full version [GKS17, Sect. 6.3].

6.1 Our 4-Way Universal Circuit Implementation

The architecture of our UC implementation is the same as that of [KS16], and therefore, we describe our UC design based on the steps described in [KS16, Fig. 6]. Our implementation gets as input a circuit with u inputs, v outputs and k gates, and outputs a 4-way UC with size $n=u+k+v$, as well as the programming $p_f$ corresponding to the input circuit (cf. Sect. 1).

Transforming Circuit $C_{u, v}^k$ into $\varGamma _2(u+k+v)$ Graph G . As a first step, we transform the circuit $C_{u, v}^k$ into a $\varGamma _2(n)$ graph $G = (V, E)$ with $n=u+k+v$ (cf. Sect. 2.1). Then, we define a topological order $\eta ^G$ on the nodes of G s.t. every input node $v_i$ has a topological order of $1 \le \eta ^G(v_i) \le u$ and every output node $v_j$ is labelled with $u+k+1\le \eta ^G(v_j) \le u + k + v$.

Creating an EUG $U_n^{(4)}(\varGamma _2)$ for $\varGamma _2(n)$ Graphs. An EUG $U_n^{(4)}(\varGamma _2)$ is constructed by creating two instances of $U_n^{(4)}(\varGamma _1)$ as shown in Sect. 2.2. The two instances get merged to $U_n^{(4)}(\varGamma _2)$ so that one builds the left inputs and outputs and the other builds the right inputs and outputs of the gates (based on the two-coloring of G). We create the EUGs with Valiant’s 4-way EUG [Val76] with our optimized blocks from Sect. 3.1 (cf. Fig. 4).

Table 4. Comparison of the sizes of the UCs (2-way, 4-way, and hybrid) for sample circuits from [TS15]. Bold numbers denote if the 2-way or the 4-way UC is smaller; the smallest size is always achieved by our hybrid UC. The UC generation time is given for both implemented UCs.

Programming $U_n^{(4)}(\varGamma _2)$ to Compute $C_{u, v}^k$ . We edge-embed graph G into $U_n^{(4)}(\varGamma _2)$ as described in Sect. 3.1. [KS16] use their supergraph construction to define the paths between the poles uniquely for Valiant’s 2-way EUG. We modify this supergraph as described in Sect. 3.1 for Valiant’s 4-way EUG and perform the edge-embedding as described in Listing 1. The programming bits of the nodes are set during the edge-embedding process along the paths between the poles. The block edge-embedding is done by analyzing the possible input values and defining the valid paths as described in Sect. 3.1.

Outputting a Universal Circuit with Its Programming. As a final step, EUG $U_n^{(4)}(\varGamma _2)$ is topologically ordered and output in the UC format of [KS16]. The programming bits $p_f$ defined by the embedding are also output in a separate file based on the topological order.

6.2 Our Experimental Results

In order to show the improvement of our method, we ran experiments on a Desktop PC, equipped with an Intel Haswell i7-4770K CPU with 3.5 GHz and 16 GB RAM, and provide our results in Table 4. To compare with the runtime of the UC compiler of [KS16], we ran the same experiments on the same platform using their 2-way UC implementation.

As [KS16], we use a set of real-life circuits from [TS15] for our benchmarks, and compare the sizes of the resulting circuits and the generation and embedding runtimes. We can see that from the 2-way and 4-way UC constructions, the 4-way UC, as expected, is always smaller for large circuits than the 2-way UC. However, it is sometimes better even for small circuits, e.g., for 32-bit addition with $n=342$. The hybrid construction always provides the smallest UC for our example circuits.

In the last two columns, we report the runtime of the UC compiler of [KS16] and our 4-way UC implementation for generating and programming the universal circuit corresponding to the example circuits. Table 4 shows that the differences in runtime are not significant, and due to its more complicated structure, the 4-way UC takes more time to generate and program in general. However, we can see from the largest example with more than 200000 nodes that asymptotically, the 4-way UC results in a runtime improvement as well, as less nodes need to be programmed.