Keywords

1 Introduction

Graphs are an important data structure that are used to represent relationships between entities in a wide range of domains. An interesting aspect in graph analysis is the notion of (structural) centrality, which pertains to quantifying importance of entities (or vertices, nodes) within the context of the graph structure as defined by it’s relationships (or edges). The need to compute centrality and convey it through visualization is seen in many areas, for example, in biology [27], transportation [6] and social sciences [5]. In this work, we propose a method to visualize node centrality information in the context of overall graph structure, which we capture through intervertex (graph theoretical) distances. The proposed method determines a layout (positions of nodes on a 2D drawing) that meet the following two, often competing, criteria:

  • Preservation of distances: The Euclidean (geometrical) distances in the layout should approximate, to the extent possible, the graph theoretical distances between the respective nodes.

  • Anisotropic radial monotonicity: Along any ray traveling away from the position of the most central node, nodes with a lower centrality should be placed geometrically further along the ray.

We also introduce a visualization strategy for the proposed layout that further highlights the centrality and structure in the graph by using additional encoding channels, and demonstrate the benefits of our approach with real datasets (see Fig. 1 as an example).

Visualization methods for gaining insights from graph structured data are an important and active area of research. Significant efforts in this area are targeted toward developing effective layouts. Layout methods can have various goals that range from trying to reduce clutter and edge crossings [7] to faithfully representing the structure by preserving the distances between nodes and topological features [15]. As positions are the best way to graphically convey numbers [8], layouts are also used to convey numerically encoded measures of hierarchy or importance associated with nodes [5, 11].

Fig. 1.
figure 1

Visualization of Zachary’s karate club social network using (a) MDS, (b) radial layout, and (c) anisotropic radial layout. Node sizes encode betweenness centrality.

Full size image

Radial layouts have been shown to be an effective method to visually convey the relative importance of nodes, where importance may be defined, for instance, by a node’s centrality [5]. The centrality of a node is a quantification of its importance in a graph by considering its various structural properties, such as, connectedness, closeness to others, and role as an intermediary [14, 34]. In conventional radial layouts, the distance of nodes from the geometric center (origin) of the layout depends only on the node’s centrality, and nodes with a higher centrality value are placed closer to the origin in the layout, often times forming rings or concentric circles.

Given a graph and centrality values associated with its nodes, several approaches have been proposed to determine a radial layout. One line of work, which deals with discrete centrality values, attempts to minimize edge crossings [1]. Another approach, which also tackles continuous centrality values, involves optimizing a stress energy (Sect. 2.2) by including a penalty for representation error (of graph distances) as well as deviation from radial constraints [5, 6]. The penalty acts a soft constraint wherein the solution is allowed to deviate from the constraint at the expense of increased local stress. The literature shows that radial constraints may also be included as a hard constraint by only allowing those solutions that satisfy the constraints [2, 12, 13].

While state-of-the-art methods for radial graph layout do effectively convey node centrality, the associate circular centrality constraints make it difficult to preserve other important, structural graph characteristics such as distances, which, in turn, makes it difficult to preserve the holistic structure of the graph. On the other hand, despite being effective in preserving the overall structure, general layout methods such as multidimensional scaling are often fail to readily convey centrality (e.g. by failing to ensure that structurally central nodes in the graph-theoretical sense appear near the center of the layout and vice versa). In this manuscript, we propose a method that simultaneously tackles both the above issues.

The underlying idea for the proposed layout algorithm is that we can relax the constraint that requires nodes with similar centrality to lie on a circle, and instead, allow for such nodes to be constrained by a more general shape: a simple closed curve or centrality contour. Centrality contours are nested isolevel curves on a smooth, radially decreasing estimate of node centrality values over a 2D field. We demonstrate that the additional flexibility in placing the nodes afforded by the centrality contours over circles, in conjunction with some additional visual cues in the background, lets us achieve a better trade off than existing methods in conveying centrality and general structure together.

2 Background

In this section, we describe the various underlying technicalities that are relevant to the proposed method, and begin with some notation/definitions.

We define a weighted, undirected graph G(V, E, W) as a set of vertices (or nodes) V, a set of edges \(E \subseteq V \times V\) and a set of edge weights, \(W:E \mapsto \mathbb {R}^+\), assigned to each edge. We define n to be cardinality of node set; i.e., \(n=|V|\). The graph-theoretical distance (shortest-path along edges) between two nodes u and v is denoted by \(d_{uv}\). We denote a general position in a 2D layout as \({\bar{x}=(x,y)}\) and the Euclidean distance between two nodes u and v as \({\delta (\bar{x}_i,\bar{x}_j) =|| \bar{x}_u - \bar{y}_v ||_2}\).

2.1 Centrality and Depth

The need to measure, and quantify, the importance of individual entities within the context of a group occurs in many domains. In graph analytics, this need is addressed by centrality indices, which are typically real-valued functions over the nodes of a graph [34]. The specific properties that qualify the importance of nodes may depend on the application or data type, and several methods to compute centrality have been proposed, such as degree centrality [14], closeness centrality [26], and betweenness centrality [14]. While the emphasis of the various centrality definitions can be different, they all share a common characteristic of depending only on the structure of the graph rather than parameters associated with the nodes [34]. For the examples in this paper we use betweenness centrality due to its relevance to the datasets (Sect. 4).

The betweenness centrality of a node, \(v\in G\), is defined as the percentage (or number) of shortest paths in the entire graph G that pass through the node v. As shown in work of Raj et al. [23], barring instances of multiple geodesics, betweenness centrality is a special case of a more general notion of vertex depth on graphs—a generalization of data depth to vertices on graphs. Data depth is a family of methods from descriptive statistics that attempts to quantify the idea of centrality for ensemble data without any assumption of the underlying distribution. Data depth methods often rely on the formation of bands from convex sets and the probability of a point lying within a randomly chosen band. The extension of band depth to graphs [23] relies on the convex closure of a set of points (via shortest paths), and thereby generalizes betweenness centrality by considering bands formed by sets of nodes, rather than only the shortest paths between pairs of nodes, and allows for a nonuniform probability distribution over the nodes of the graph.

Fig. 2.
figure 2

An (a) interpolation field for node centrality values, and (b) the associated (radially) monotonic field for a 30 node random graph generated using the Barabasi-Albert model. Node positions are determined using MDS and node sizes encode betweenness centrality.

Full size image

In addition to graphs, data depth methods have been proposed for several other data types such as points in Euclidean space [29], functions [19], and curves [20, 22]. Despite their distinct formulations, data depth methods are expected to share a few common desirable properties [33] such as: 1. maximum at geometric center 2. zero at infinity 3. radial monotonicity; which make data depth an attractive basis for ensemble visualization methods [22, 25, 28]. Graph centrality is a type of data depth on the nodes of a graph, and here we pursue layout methods that convey these depth properties.

2.2 Stress and Multidimensional Scaling (MDS)

Our proposed method is based on a modification to the MDS objective function, and therefore we give a brief summary of MDS. MDS is family of methods that help visualize the similarity (or dissimilarity) between members in a data set [4]. Over the years, MDS has been the foundation for a range of graph drawing algorithms that aim to achieve an isometry between graph theoritical- and Euclidian distances between nodes [6, 17]. From among various types of MDS methods that exist, here we consider metric MDS with distance scaling, which is popular in the graph drawing literature [15] (see Fig. 2 for an example).

In the context of graph drawing, given a distance matrix based on graph-theoretical distance, the goal is to find node positions \({X = \{\bar{x}_i:1 \le i \le n\}}\) that minimize the following sum of squared residuals—also known as stress:

$$\begin{aligned} \sigma (X) = \sum _{u,v} w_{uv}\big ( d_{uv} - ||\bar{x}_u - \bar{x}_v||_2 \big )^2, \end{aligned}$$
(1)

where \(w_{uv} \ge 0\) is the weighting term for residual associated with pair u, v. In the proposed work we employ a standard weighting scheme for graphs, known as elastic scaling [21], by setting \(w_{uv}=d^{-2}_{uv}\). This gives preference to local distances by minimizing relative error rather than absolute error during the optimization.

Node positions that minimize the objective (Eq. (1)) have been shown to be visually pleasing and convey general structure of the graph [17]. Although, the state-of-the-art approach for optimizing the objective function is stress majorization [15], we employ standard gradient descent because of its compatibility with the proposed modification to the objective (Sect. 3). The gradient of the standard MDS objective is as follows [4]:

$$\begin{aligned} \nabla \sigma (X) = 2VX - B(X)X \end{aligned}$$
(2)

where matrices \(V=(v_{ij})\) and \(B=(b_{ij})\), with \(1 \le i, j \le n\), can be compactly represented as:

2.3 Strictly Monotone and Smooth Regression

The proposed method also relies on the construction of a smooth and radially decreasing approximation of centrality values over a 2D field, which we call the monotonic field (Fig. 2). The first part of this construction is an interpolation of centrality values of sparsely located nodes on the layout to obtain a dense 2D field, which we call the interpolation field (Fig. 2a). For this we use thin plate splines [3] interpolation, a standard technique for interpolating unstructured data which produces optimally smooth fields.

The next part is to construct a radially monotonic approximation of the interpolation field. We devote the rest of this section to a brief description of the method that we use for constructing this approximation (monotonic field), which is adapted from Dette et al. [9, 10].

For a 1D function [9], \(m(t):[0,1] \rightarrow \mathbb {R}\), an elegant algorithm for computing its monotonic approximation \(\hat{m}_A(t)\) proceeds as follows in two steps [9]:

  • Step 1 (Monotonization): Construct a density estimate from sampled values of input function m and use it as input to compute an estimate of the inverse of the regression function \(\hat{m}_A^{-1}\).

    $$\begin{aligned} \hat{m}_A^{-1}(t) = \frac{1}{Q \omega } \sum _{i=1}^Q \int _{\infty }^t K \Bigg (\frac{m\big (\frac{i}{Q}\big )-u}{\omega } \Bigg ) du, \end{aligned}$$
    (3)

    where Q is the parameter controlling the sampling density, K is a continuously differentiable and symmetric kernel, and \(\omega \) is the bandwidth. Here, \(\hat{m}_A^{-1}\) is a strictly increasing estimate of \(m^{-1}\), however, we can easily obtain a strictly decreasing estimate by reversing the limits on the integral in Eq. (3).

  • Step 2 (Inversion): Obtain the final estimate of \(\hat{m}_A\) by numerically inverting \(\hat{m}_A^{-1}\).

In order to obtain an approximation to a 2D function that is monotonic along radial lines emanating from the deepest or most central node, we use a polar coordinate representation of the field. We build the polar representation by sampling the interpolation field along 360 evenly spaced, center outward rays. The idea is to repeatedly monotonize the interpolation field with respect to a single variable i.e., for a fixed value of the angular coordinate, obtain a (1D) estimate that is strictly decreasing along the radial coordinate. We then repeat this process, successively monotonizing 1D functions that correspond to each value of angular coordinate in its (discrete) domain; see Fig. 2b for an example of the resulting monotonic field. The spline interpolation is smooth, and by the properties of the monotonic approximation (see [10]), the resulting monotonic field is smooth (except at origin, where polar the coordinates maybe nonsmooth).

3 Method

Here we describe our method in two parts. First is the layout algorithm (Sect. 3.1), and second is a visualization strategy (Sect. 3.2) that complements the layout to simultaneously convey graph structure and node centrality.

Fig. 3.
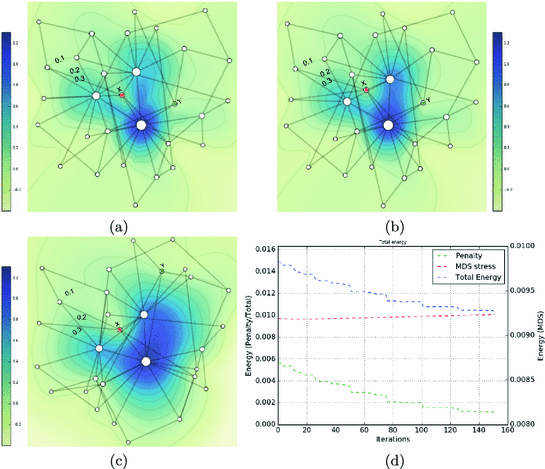
figure 3

Sensitivity of anisotropic radial layout to penalty weights for the graph in Fig. 2: (a) \(w_{\rho }=0.1\), (b) \(w_{\rho }=1\), (c) \(w_{\rho }=10\); centrality contours with isovalues 0.1, 0.2 and 0.3 as well as nodes X (red) and Y (green) with centrality values 0.2 and 0.1 are identified, and (d) a typical plot of objective energy during the optimization process (\(w_{\rho }=1\)). (Color figure online)

Full size image

3.1 Anisotropic Radial Layout

In addition to preserving the graph-theoretical distances, we also aim to place every node on a radially monotonic approximation of a centrality field—called the monotonic field (Sect. 2.3)—such that the value of the field at the location of the node is equal to the centrality value of the node. We accomplish this by modifying the (distance preserving) MDS objective or stress (Sect. 2.2) to incorporate the following penalty term, which penalizes the deviation of monotonic field values from the node centrality values:

$$\begin{aligned} \rho (X) = \big (M_{X,\bar{c}}(X) - \bar{c}\big )^2 \end{aligned}$$
(4)

where \(\bar{c} \in \mathbb {R}^n\) is a vector of node centrality values and \(X \in \mathbb {R}^{n \times 2} =\) \(\{\bar{x}_i:1 \le i \le n\}\) denotes associated node positions. \(M_{X,\bar{c}}(X) \in \mathbb {R}^n\) denotes a vector of values of the 2D monotonic field at locations X. The symbols in the subscript (X and \(\bar{c}\)) denote the use of node positions and centrality values in the construction of the monotonic field. In the limiting case where the interpolation field (Sect. 2.3) itself is monotonic, the value of this penalty term drops to zero. Our final objective is a sum of the MDS stress and the above penalty term, and can be stated as follows:

$$\begin{aligned} \gamma \big (X\big ) = \underbrace{\sigma (X)}_{\text {MDS stress}} + \quad w_{\rho } \; \rho (X) \end{aligned}$$
(5)

where \(w_{\rho }\) is a weighting factor that controls the influence of the penalty, with respect to the MDS stress. The gradient of the modified objective above is obtained as:

$$\begin{aligned} \nabla \gamma \big (X \big ) = \nabla \sigma (X) + w_{\rho } \times \underbrace{2 \big (M_{X,\bar{c}}(X) - \bar{c}\big ) \odot \nabla M_{X,\bar{c}}(X)}_{\nabla \rho (X)}, \end{aligned}$$
(6)

where \(\odot \) denotes element wise product. It is difficult to compute the gradient of \( M_{X,\bar{c}}(X)\) because of dependence of M on X and the associated process for monotonic approximation. Therefore, we let the field lag, and treat X (in subscript) as a constant when numerically approximating the gradient of M. We deal with the resulting accumulation of error by recomputing the depth field after a fixed number of iterations, or lag, denoted by \(\ell \).

The parameters \(w_{\rho }\) and \(\ell \) need to be chosen carefully. \(w_{\rho }\) needs to be set to find a balance between preserving the intrinsic graph structure and ensuring that the centrality of nodes match the field value at their position. Figure 3a-c show, respectively, results of a small \(w_{\rho }\) unable to move nodes to appropriate positions with regard to the field (observe nodes X, Y), an intermediate \(w_{\rho }\), and a large \(w_{\rho }\) resulting in unnecessary structural distortion with regard to initial positions (observe node Y). The parameter \(\ell \) controls the lag of the monotonic field; if \(\ell \) is too small, the frequent updates can lead to instabilities, while values that are too large can cause slow convergence. A typical energy profile during optimization is shown in Fig. 3d; where the sharp changes in the total energy correspond to the updates of the monotonic field. We encourage the layout to be as similar as possible to the MDS layout by initializing the node positions as determined by an unmodified MDS objective [15]. The entire process, as summarized in Algorithm 1, iterates until updates no longer result in significant changes to node positions.

The computational complexity of a single iteration is \(\mathcal {O}(n^3)\) due to the step of computing the monotonic field which involves interpolation using thin plate spline. However, we only update the field once every \(\ell \) iterations. This leads to a complexity of \(\mathcal {O}(n^2)\) (same as MDS) for a large majority of iterations.

figure a

3.2 Visualization

In this layout, nodes are constrained to lie on level sets of centrality, which are general closed curves, rather than circles, and the shapes of these curves depend on the structure of the graph. Therefore, we can help interpretability of the layout and reduce cognitive load for the user by providing additional cues for shapes of these curves. We provide cues in the form of faded renderings of centrality contours (isolines on the monotonic field) and a monotonic field colormap in the background. The radial monotonicity described in Sect. 3.1 ensures that the contours are nested curves that enclose a common maxima (at origin); leading to a bijective mapping between contours and centrality values, and pushing nodes to lie on the unique contour that corresponds to their centrality. In this paper, we normalize node centrality to fall between 0 and 1; and show 10 contour curves that evenly span this range. We also use node size as an extra encoding channel for centrality—in addition to location—to further highlight the centrality structure. We can, of course, use the size channel to encode centrality even with the standard MDS layout, however, that approach can lead to the issue of conflicting centrality cues from size and location channels (see image (a) in Figs. 1, 4 and 5).

Fig. 4.
figure 4

Network of terrorists and affiliates connected to the 2004 Madrid train bombing using (a) MDS, (b) radial layout, (c) anisotropic radial layout. (Color figure online)

Full size image

4 Results

4.1 Zachary’s Karate Club

The Zachary’s karate club graph is a well known data set that is a social network of friendships in a karate club at a US university, as recorded during a study [32]. This graph contains 34 nodes, each representing an individual, and 78 unweighted edges that represent a friendship between the associated individuals (Fig. 1). During the period of observation, a conflict between two key members, identified as the “administrator” and “instructor”, leads to a split in the club, giving it an interesting two cluster structure. In Fig. 1, nodes representing members who are part of the instructor’s and administrator’s groups are drawn in green and blue, respectively.

Figure 1 shows three different visualizations of the karate club network: MDS, radial layout (from [6]), and anisotropic radial layout (ARL). We can make a few observations from the visualizations. While MDS does a good job of preserving the two clusters, it is does not unambiguously convey centrality. On the other hand, radial layout clearly showcases the centrality at the expense of dispersing the clusters by distorting distances among their nodes, thereby obscuring their internal structure. We see that ARL is able to largely preserve the structure seen in MDS with clearly distinguishable clusters, and also clearly convey the centrality information. While radial layout pushes the instructor’s group far away due to low betweenness centrality, ARL lets them remain close by bringing in the outermost contour toward to the group instead. Similarly, the administrator is also allowed to remain closer to their group by the protrusion of the inner contours, which enclose the most central nodes, toward the administrator.

4.2 Terrorist Network from 2004 Madrid Train Bombing

Figure 4 shows visualizations of a network of individuals connected to the bombing of trains in Madrid on March 11, 2004. This data was originally compiled by Rodriguez [24] from newspaper articles that reported on the subsequent police investigation. There are 64 nodes that represent suspects and their relatives, and 243 edges that have weights ranging from 1 to 4 which represent an aggregated strength of connection based on various parameters such as contact, kinship, ties to Al Qaeda, etc [16]. In Fig. 4, (as well as Fig. 5), distances between nodes are related inversely to edge weights. In the visualization, we identify nodes using numbers to avoid text clutter, however, we include a mapping to names of individuals represented by the nodes in the Appendix.

Fig. 5.
figure 5

Coappearance network for characters in the novel Les Miserables using (a) MDS, (b) radial layout, (c) anisotropic radial layout. (Color figure online)

Full size image

Rodriguez [24] identifies several key suspects as follows: ring leaders (marked in blue in Fig. 4), members of a field operating group who were closely involved with the actual carrying out the attack (green), intermediaries (red), as well as suspects with local roots, ties to foreign Al Queda, and those who supplied explosives. On comparing the visualizations in Fig. 4 we see that ARL (Fig. 4c) is able to better preserve the structure and cohesiveness of the core members of the field operating group in comparison to the radial layout (Fig. 4b). Critically, a key mastermind in this event, despite having a low centrality (due to communicating often through an intermediary), is allowed to be close to the center in the ARL. This arrangement, possible due to the ability of centrality contours to adapt to the circumstance, preserves the close association between the masterminds that is lost in the radial layout. We also see that the flexibility of contours in ARL preserves the locality of various groups, which allows us to see the role of intermediaries with high centrality in acting as a bridge between various groups.

4.3 Coappearance Network for Characters in Les Miserables

The third dataset is a graph of character associations in the famous French novel Les Miserables (Fig. 5) [18]. This graph consists of 77 nodes, each representing a character in the novel, and 254 weighted edges where the weights represent the number of chapters that feature both characters associated with an edge.

We see the that the main protagonist Valjean (marked in red) is placed prominently in all three visualizations (Fig. 5). However, other key characters in the plot such as Inspector Javert (blue) and Cosett (orange), who do not appear often with characters other than the protagonist (and thus have low betweenness centrality) are treated differently. While the radial layout relegates them to the periphery (far from Valjean) (Fig. 5b), MDS (Fig. 5a) paints a conflicting picture with regard to their centrality, e.g., Cosett’s node almost overlaps with Valjean despite its low centrality. In contrast, the proposed ARL (Fig. 5c) is able to coherently convey the low centrality of the Inspector Javert and Cosett, as well as, their closeness to Valjean. The above issue of distance distortion appears to be a frequent occurrence in the radial layout due to many characters who have a low centrality value causing them to end up being packed in the outer periphery. A case of contrast is that of the character Bishop Myriel (green) who despite being associated with several characters, is only seen with Valjean once.

5 Discussion

This paper describes an energy-based layout algorithm for graphs, called anisotropic radial layout, which conveys structural centrality using anisotropic, radial constraints, while also preserving approximate distances (or structure) in the graph. In contrast to existing methods for conveying node centrality which employ an isotropic centrality field [2, 6], the proposed method determines an anisotropic centrality field on which to project nodes. While the energy minimization strategy described in this paper allows the solution to deviate from constraints, one can enforce hard constraints by adding a post processing step that projects nodes onto the closest position on their associated isocontour.

The key implication of the anisotropic centrality field in our method is that more central nodes are allowed to be placed further from origin than less central nodes—without an energy penalty—if they do not lie on a common ray; which aids our objective of achieving a better balance between visual representations of centrality and structure than possible with existing methods. Our objective differs from other prior work that use centrality or continuous fields to visualize structure of dense graphs [30, 31].