Abstract
We construct the first UC commitment scheme for binary strings with the optimal properties of rate approaching 1 and linear time complexity (in the amortised sense, using a small number of seed OTs). On top of this, the scheme is additively homomorphic, which allows for applications to maliciously secure 2-party computation. As tools for obtaining this, we make three contributions of independent interest: we construct the first (binary) linear time encodable codes with non-trivial distance and rate approaching 1, we construct the first almost universal hash function with small seed that can be computed in linear time, and we introduce a new primitive called interactive proximity testing that can be used to verify whether a string is close to a given linear code.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Additive Homomorphism
- Universal Composability (UC)
- Commitment Scheme
- Universal Hash Function
- Commitment Protocol
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Commitment schemes are one of the fundamental building blocks of cryptographic protocols. In a nutshell, a commitment scheme is a two party protocol that allows a prover P to commit to a secret without revealing it to the verifier V. Later on, in an unveil phase P can convince V that the commitment contains a specific secret. Classically, two security properties are required of commitment schemes: The hiding property requires that the verifier V does not learn anything about the committed secret before the unveil and the binding property requires that the prover P cannot change the committed secret after the commit phase.
A stronger security requirement is (stand-alone) simulation-based security, where we require that any interaction with a commitment protocol is indistinguishable from a perfectly secure ideal commitment. Commitment schemes that satisfy these security notions can be realized stand-alone (i.e. no trusted setup required) from basic and highly efficient cryptographic primitives such as pseudorandom generators [Nao91].
However, commitment schemes are rarely used just by themselves; they are used as components in complex protocols. In such a situation, the stand-alone simulation-based security guarantee breaks down as several (nested) instances of a commitment protocol might be executed with correlated secrets.
The most prominent security framework that captures this scenario of protocols running in a larger context is Canetti’s UC framework [Can01]. UC security offers very strong composability guarantees; in particular UC secure protocols can be used in arbitrary contexts retaining their security properties. This however comes at a price, as UC commitments cannot be realized without trusted setup assumptions such as common reference strings [CF01]. On the positive side, it is well known that realizing UC secure commitments is sufficient for general UC secure two-party and multiparty computation [CLOS02].
Any commitment scheme that is UC secure must be both straight-line extractable and equivocal, meaning a simulator must have means to efficiently obtain the message in a commitment sent by a malicious prover and also change the contents of a commitment sent to a malicious verifier without having (non-black-box) access to these machines. To obtain these strong properties, earlier constructions of UC commitments (e.g. [CF01, Lin11, BCPV13]) relied on expensive public key primitives for every single instance of the protocol, which makes them considerably less efficient than stand-alone secure commitments (which, as mentioned above, can be realized from minimal cryptographic primitives). The most efficient UC commitment protocols based directly on public key assumptions [Lin11, BCPV13] require exponentiations in groups of larger order and have therefore a typical computational complexity of \(\varOmega (n^3)\) for commitments to n-bit messages.
A recent line of research [GIKW14, DDGN14, CDD+15, FJNT16, Bra16] is concerned with the construction of UC secure commitments schemes for which the use of public key primitives is confined to a once-and-for-all setup phase, the cost of which can be amortized over many sessions later on.
This gives us the possibility to build extremely efficient commitment schemes. Let us therefore consider what we can hope to achieve: Clearly, the best running time we can have is O(n) for committing and opening n bits, since one must look at the entire committed string. As for communication, let us define the rate of a commitment scheme to be the size of the committed string divided by the size of a commitment. Now, a UC commitment must be of size at least the string committed to, because the simulator we need for the proof of UC security must be able to extract the committed string from the commitment. Therefore the rate of a UC commitment scheme must be at most 1.Footnote 1 If a commitment to n bits has size \(n + o(n)\) bits, we will say it has rate approaching 1.
Another desirable property for commitment schemes is the additively homomorphic property: we interpret the committed strings as vectors over some finite field, and V can add any two commitments, to vectors \(\mathbf {a},\mathbf {b}\). The result will be a commitment that can be opened to (only) \(\mathbf {a} + \mathbf {b}\) while revealing nothing else about \(\mathbf {a}\) and \(\mathbf {b}\). Note that this additive property is crucial in applications of string commitments to secure computation: In [FJN+13], it was shown how to do maliciously secure 2-party computation by doing cut-and-choose on garbled gates rather than on garbled circuits. This performs asymptotically better than conventional cut-and-choose but requires an additive commitment scheme to “glue” the garbled gates together to a circuit. In [AHMR15], additive commitments were used in a similar way for secure RAM computation. Any efficiency improvements for commitments are directly inherited by these applications.
1.1 Previous Work
In [GIKW14, Bra16] rate 1 was achieved. On the other hand, [DDGN14] achieved constant rate and additively homomorphic commitments. In follow-up work, linear time and additive homomorphism were achieved in [CDD+15], and shortly after, in [FJNT16], rate 1 and additively homomorphic commitments were achieved.
Now, the obvious question is of course: can this line of research be closed, by constructing a commitment scheme with the optimal properties of rate 1 and linear time – and also with the additive property?
To see why the answer is not clear from previous works in this line of research [GIKW14, DDGN14, CDD+15, FJNT16], let us briefly describe the basic ideas in those constructions:
P will encode the vector \(\mathbf {s}\) to commit to using a linear error correcting code \(\mathsf {C}\), to get an encoding \(\mathsf {C}(\mathbf {s})\). Now he additively secret-shares each entry in \(\mathsf {C}(\mathbf {s})\) and a protocol is executed in which V learns one share of each entry while P does not know which shares are given to V. This phase uses a small number of seed OT’s that are done in a once-and-for-all set-up phase analogous to the set-up of “watchlists” in the MPC-in-the-head and IPS compiler constructions [IPS09, IPS08]. To open, P reveals the codeword and both shares of each entry. V checks that the shares are consistent with those he already knew, reconstructs \(\mathsf {C}(\mathbf {s})\) and checks that it is indeed a codeword. This is clearly hiding because V has no information on \(\mathsf {C}(\mathbf {s})\) at commit time. Binding also seems to follow easily: if P wants to change his mind to another codeword, he has to change many entries and hence at least one share of each modified entry. We can expect that V will notice this with high probability since P does not know which share he can change without being caught. There is a problem, however: a corrupt P does not have to send shares of a codeword at commitment time, so he does not have to move all the way from a codeword to the next one, and it may not be clear (to the simulator) which string is being committed.
Three solutions to this have been proposed in earlier work: in [CDD+15] the minimum distance of \(\mathsf {C}\) is chosen so large that P’s only chance is to move to the closest codeword. This has a cost in efficiency and also means we cannot have the additive property: if we add codewords with errors, the errors may accumulate and binding no longer holds. In [DDGN14], a verifiable secret-sharing scheme was used on top of the coding, this allows V to do some consistency checks that forces P to use codewords, except with negligible probability. But it also introduces a constant factor overhead which means there is no hope to get rate 1. Finally, in [FJNT16], the idea was to force P to open some random linear combinations of the codewords. In the case of binary strings, k linear combinations must be opened, where k is the security parameter. This indeed forces P to use codewords and gives us the additive property. Also, a couple of tricks were proposed in [FJNT16] which gives commitments with rate 1, if the code \(\mathsf {C}\) has rate 1. On the other hand, they could not get linear time this way, first because no linear time encodable codes with rate approaching 1 were knownFootnote 2, and second because one needs to visit each of prover’s codewords \(\varOmega (k)\) times to compute the linear combinations.
1.2 Our Contribution
In this paper, we show that we can indeed have UC commitments that have simultaneously rate approaching 1, linear time and additive homomorphism. A comparison between our results and previous works can be seen in Table 1. While we follow the same blue-print as in previous work, we overcome the obstacles outlined above via three technical contributions that are of independent interest:
-
1.
We introduce a primitive we call interactive proximity testing that can be used to verify whether a given string s is in an interleaved linear code \(\mathsf {C}^{\odot m}\), or at least close to \(\mathsf {C}^{\odot m}\).Footnote 3 The idea is to choose a random almost universal and linear hash function h and test whether \(h(s)\in h(\mathsf {C}^{\odot m})\). We show that if s is “too far” away from \(\mathsf {C}^{\odot m}\), then this test will fail with high probability. Intuitively, this makes sense to use in a 2-party protocol because the party holding s can allow the other party to do the test while only revealing a small amount of information on s, namely h(s). Of course, this assumes that the verifying party has a way to verify that the hash value is correct, more details on this are given later.
-
2.
In order to be able to use interactive proximity testing efficiently in our protocol, we construct the first family of (linear) almost universal hash functions that can be computed in linear time, where for a fixed desired collision probability, the size of the seed only depends logarithmically on the input size. We note that the verification method from [FJNT16] is a special case of our proximity testing, where the hash function is a random linear function (which cannot be computed in linear time)Footnote 4.
-
3.
We present the first explicit construction of linear time encodable (binary) codes with rate approaching 1. The construction is basically a family of iterated Sipser-Spielman codes [Spi96] and uses a family of explicit expander graphs constructed by Capalbo et al. [CRVW02]. Previous linear time encodable codes [Spi96, GI02, GI03, GI05, DI14] did not approach rate 1, which was a clear obstacle to our results.
2 Preliminaries
In the sections we establish notation and introduce notions that will be used throughout the paper. We borrow much of the notation from [CDD+15].
2.1 Notation
The set of the n first positive integers is denoted \([n] = \{ 1,2,\ldots ,n \}\). Given a finite set D, sampling a uniformly random element from D is denoted  and sampling a uniformly random subset of n elements from D is denoted
and sampling a uniformly random subset of n elements from D is denoted  . Vectors of elements of some field are denoted by bold lower-case letters, while matrices are denoted by bold upper-case letters. Concatenation of vectors is represented by \(\mathbin {\Vert }\). For \(\mathbf {z} \in \mathbb {F}^k\), \(\mathbf {z}[i]\) denotes the i’th entry of the vector, where \(\mathbf {z}[1]\) is the first element of \(\mathbf {z}\). For a matrix \(\mathbf {M}\in \mathbb {F}^{n \times k}\), we let \(\mathbf {M}[\cdot , j]\) denote the j’th column of \(\mathbf {M}\) and \(\mathbf {M}[i,\cdot ]\) denote the i’th row. The column span of \(\mathbf {M}\), denoted by \(\langle \mathbf {M} \rangle _{\mathrm {col}}\) is the vector subspace of \(\mathbb {F}^n\) spanned over \(\mathbb {F}\) by the columns \(\mathbf {M}[\cdot , 1], \dots , \mathbf {M}[\cdot , k]\) of \(\mathbf {M}\). The row support of \(\mathbf {M}\) is the set of indices \(I\subseteq \{1,\dots ,n\}\) such that \(\mathbf {M}[i,\cdot ]\ne \mathbf{0}\).
. Vectors of elements of some field are denoted by bold lower-case letters, while matrices are denoted by bold upper-case letters. Concatenation of vectors is represented by \(\mathbin {\Vert }\). For \(\mathbf {z} \in \mathbb {F}^k\), \(\mathbf {z}[i]\) denotes the i’th entry of the vector, where \(\mathbf {z}[1]\) is the first element of \(\mathbf {z}\). For a matrix \(\mathbf {M}\in \mathbb {F}^{n \times k}\), we let \(\mathbf {M}[\cdot , j]\) denote the j’th column of \(\mathbf {M}\) and \(\mathbf {M}[i,\cdot ]\) denote the i’th row. The column span of \(\mathbf {M}\), denoted by \(\langle \mathbf {M} \rangle _{\mathrm {col}}\) is the vector subspace of \(\mathbb {F}^n\) spanned over \(\mathbb {F}\) by the columns \(\mathbf {M}[\cdot , 1], \dots , \mathbf {M}[\cdot , k]\) of \(\mathbf {M}\). The row support of \(\mathbf {M}\) is the set of indices \(I\subseteq \{1,\dots ,n\}\) such that \(\mathbf {M}[i,\cdot ]\ne \mathbf{0}\).
We say that a function \(\epsilon \) is negligible in n if for every positive polynomial p there exists a constant c such that \(\epsilon (n) < \frac{1}{p(n)}\) when \(n > c\). Two ensembles \(X=\{X_{\kappa ,z}\}_{\kappa \in \mathbb {N}, z\in \{0,1\}^*}\) and \(Y=\{Y_{\kappa ,z}\}_{\kappa \in \mathbb {N}, z\in \{0,1\}^*}\) of binary random variables are said to be statistically indistinguishable, denoted by \(X \approx _s Y\), if for all z it holds that \(\mid \Pr [\mathcal {D}(X_{\kappa ,z})=1]-\Pr [\mathcal {D}(Y_{\kappa ,z})=1]\mid \) is negligible in \(\kappa \) for every probabilistic algorithm (distinguisher) \(\mathcal {D}\). In case this only holds for computationally bounded (non-uniform probabilistic polynomial-time (PPT)) distinguishers we say that X and Y are computationally indistinguishable and denote it by \(\approx _c\).
2.2 Coding Theory
We denote finite fields by \(\mathbb {F}\) and write \(\mathbb {F}_q\) for the finite field of size q. For a vector \(\mathbf {x} \in \mathbb {F}^n\), we denote the Hamming-weight of \(\mathbf {x}\) by \(\Vert \mathbf {x} \Vert _0 = | \{ i \in [n]: \mathbf {x}[i] \ne 0 \}|\). Let \(\mathsf {C} \subset \mathbb {F}^n\) be a linear subspace of \(\mathbb {F}^n\). We say that \(\mathsf {C}\) is an \(\mathbb {F}\)-linear [n, k, s] code, if \(\mathsf {C}\) has dimension k and it holds for every nonzero \(\mathbf {x} \in \mathsf {C}\) that \(\Vert \mathbf {x} \Vert _0 \ge s\), i.e., the minimum distance of \(\mathsf {C}\) is at least s. The distance \(\mathsf {dist}(\mathsf {C},\mathbf {x})\) between \(\mathsf {C}\) and a vector \(\mathbf {x}\in \mathbb {F}^n\) is the minimum of \(\Vert \mathbf {c-x} \Vert _0\) when \(\mathbf {c}\in \mathsf {C}\). The rate of an \(\mathbb {F}\)-linear [n, k, s] code is \(\frac{k}{n}\) and its relative minimum distance is \(\frac{s}{n}\).
A matrix \(\mathbf {G}\in \mathbb {F}^{n \times k}\) is a generator matrix of \(\mathsf {C}\) if \(\mathsf {C}=\{\mathbf {G}\mathbf {x}:\mathbf {x}\in \mathbb {F}^k\}\). The code \(\mathsf {C}\) is systematic if it has a generator matrix \(\mathbf {G}\) such that the submatrix given by the top k rows of \(\mathbf {G}\) is the identity matrix \(\mathbf {I}\in \mathbb {F}^{k \times k}\). A matrix \(\mathbf{P}\in \mathbb {F}^{(n-k) \times n}\) of maximal rank \(n-k\) is a parity check matrix of \(\mathsf {C}\) if \(\mathbf{P}\mathbf {c}=0\) for all \(\mathbf {c}\in \mathsf {C}\). When we have fixed a parity check matrix \(\mathbf{P}\) of \(\mathsf {C}\) we say that the syndrome of an element \(\mathbf {v}\in \mathbb {F}^n\) is \(\mathbf{P}\mathbf {v}\).
For an \(\mathbb {F}\)-linear [n, k, s] code \(\mathsf {C}\), we denote by \(\mathsf {C}^{\odot m}\) the m-interleaved product of \(\mathsf {C}\), which is defined by
In other words, \(\mathsf {C}^{\odot m}\) consists of all \(\mathbb {F}^{n \times m}\) matrices for which all columns are in \(\mathsf {C}\). We can think of \(\mathsf {C}^{\odot m}\) as a linear code with symbol alphabet \(\mathbb {F}^m\), where we obtain codewords by taking m arbitrary codewords of \(\mathsf {C}\) and bundling together the components of these codewords into symbols from \(\mathbb {F}^m\). For a matrix \(\mathbf{E}\in \mathbb {F}^{n \times m}\), \(\Vert \mathbf{E} \Vert _0\) is the number of nonzero rows of \(\mathbf{E}\), and the code \(\mathsf {C}^{\odot m}\) has minimum distance at least \(s'\) if all nonzero \(\mathbf{C}\in \mathsf {C}^{\odot m}\) satisfy \(\Vert \mathbf{C} \Vert _0\ge s'\). Furthermore, \(\mathbf{P}\) is a parity-check matrix of \(\mathsf {C}\) if and only if \(\mathbf{P}{} \mathbf{C}=\mathbf{0}\) for all \(\mathbf{C}\in \mathsf {C}^{\odot m}\).
2.3 Universal Composability
The results presented in this paper are proven secure in the Universal Composability (UC) framework introduced by Canetti in [Can01]. We refer the reader to Appendix A and [Can01] for further details.
Adversarial Model: Our protocols will be proved secure against static and active adversaries. This means that corruption is assumed to take place before the protocols starts execution and that the adversary may deviate from the protocol in any arbitrary way.
Setup Assumption: Since UC commitment protocols cannot be obtained in the plain model [CF01], they need a setup assumption, i.e., some resource available to all parties before the protocol starts. In the case of our protocol, our goal is to prove security in the \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model [Can01, CLOS02], where the parties have access to an ideal 1-out-of-2 OT functionality. In order to attain this, we first prove our protocol secure in the \(\mathcal {F}_{\mathrm {ROT}} \)-hybrid model, where the resource that the parties have access to is an 1-out-of-2 random OT functionality, which we describe below. Since we can implement \(\mathcal {F}_{\mathrm {ROT}} \) in the \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model, as shown in Appendix B, the composability guarantees of the UC framework imply that we can achieve security for our commitment scheme in the \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model too.
Ideal Functionalities: In Sect. 5, we construct an additively homomorphic string commitment protocol that UC-realizes the functionality \(\mathcal {F}_\mathrm {HCOM} \), which is described in Fig. 1. This functionality basically augments the standard multiple commitments functionality \(\mathcal {F}_\mathrm {MCOM} \) from [CLOS02] by introducing a command for adding two previously stored commitments and an abort command in the Commit Phase. \(\mathcal {F}_\mathrm {HCOM} \) differs from a similar functionality of [CDD+15] in that it gives an honest sender commitments to random messages instead of letting it submit a message as input. In order to model corruptions, functionality \(\mathcal {F}_\mathrm {HCOM} \) lets a corrupted sender choose the messages it wants to commit to. The abort is necessary to deal with inconsistent commitments that could be sent by a corrupted party.
In fact, our additively homomorphic commitment protocol is constructed in the \(\mathcal {F}_{\mathrm {ROT}} \)-hybrid model. Functionality \(\mathcal {F}_{\mathrm {ROT}} \) models a random oblivious transfer of \(n \times m\) matrices \(\mathbf {R}_0,\mathbf {R}_1\) where the receiver learns a matrix \(\mathbf {S}\) where each row is selected from either \(\mathbf {R}_0\) or \(\mathbf {R}_1\). Notice that this functionality can be trivially realized in the standard \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model as shown in Appendix B. We define \(\mathcal {F}_{\mathrm {OT}} \) in Appendix B and \(\mathcal {F}_{\mathrm {ROT}} \) in Fig. 2 following the syntax of [CLOS02]. Notice that \(\mathcal {F}_{\mathrm {OT}} \) can be efficiently UC-realized by the protocol in [PVW08], which can be used to instantiate the setup phase of our commitment protocols.
3 Interactive Proximity Testing
In this section, we will introduce our interactive proximity testing technique. It consists in the following argument: suppose we sample a function \(\mathbf {H}\) from an almost universal family of linear hash functions (from \(\mathbb {F}^m\) to \(\mathbb {F}^\ell \)), and we apply this to each of the rows of a matrix \(\mathbf {X}\in \mathbb {F}^{n \times m}\), obtaining another matrix \(\mathbf {X'}\in \mathbb {F}^{n \times \ell }\); because of linearity, if \(\mathbf {X}\) belonged to an interleaved code \(\mathsf {C}^{\odot m}\), then \(\mathbf {X'}\) belongs to the interleaved code \(\mathsf {C}^{\odot \ell }\). This suggests that we can test whether \(\mathbf {X}\) is close to \(\mathsf {C}^{\odot m}\) by testing instead if \(\mathbf {X'}\) is close to \(\mathsf {C}^{\odot \ell }\). Theorem 1 states that indeed the test gives such guarantee (with high probability over the choice of the hash function) and moreover, if these elements are close to the respective codes, the “error patterns” (the set of rows that have to be modified in each of the matrices in order to correct them to codewords) are the same.
Definition 1
(Almost Universal Linear Hashing). We say that a family \(\mathcal {H}\) of linear functions \(\mathbb {F}^n \rightarrow \mathbb {F}^s\) is \(\epsilon \)-almost universal, if it holds for every non-zero \(\mathbf{x} \in \mathbb {F}^n\) that

where \(\mathbf{H}\) is chosen uniformly at random from the family \(\mathcal {H}\). We say that \(\mathcal {H}\) is universal, if it is \(|\mathbb {F}^{-s}|\)-almost universal. We will identify functions \(H \in \mathcal {H}\) with their transformation matrix and write \(\mathbf{H}(\mathbf{x}) = \mathbf{H} \cdot \mathbf{x}\).
We will first establish a property of almost universal hash functions that can be summarized as follows. Applying a randomly chosen linear hash function \(\mathbf{H}\) from a suitable family \(\mathcal {H}\) to a matrix \(\mathbf{M}\) will preserve its rank, unless the rank of \(\mathbf{M}\) exceeds a certain threshold r. If the rank of \(\mathbf{M}\) is bigger than r, we still have the guarantee that the rank of \(\mathbf{H} \cdot \mathbf{M}\) does not drop below r.
Lemma 1
Let \(\mathcal {H}: \mathbb {F}^m \rightarrow \mathbb {F}^{r + s + t}\) be a family of \({|\mathbb {F}|}^{-(r + s)}\)-almost universal linear functions. Fix a matrix \(\mathbf{M} \in \mathbb {F}^{m \times n}\). Then it holds for  that
that
Remark 1
Since rank is preserved by transposition, we can state the consequence of the Lemma equivalently as
Proof
If \(\mathsf {rank}(\mathbf{M}) = 0\) the statement is trivial. Thus assume \(\mathsf {rank}(\mathbf{M}) > 0\). Let \(V = \langle \mathbf{M} \rangle _{\mathrm {col}}\) be the column-span of \(\mathbf{M}\). We will first compute \(\mathbb {E}[ | \ker (\mathbf{H}) \cap V| - 1]\). By linearity of expectation we have that
As \(| \ker (\mathbf{H}) \cap V| - 1\) is non-negative, it follows by the Markov inequality that
Thus it follows that
-
If \(\mathsf {rank}(\mathbf{M}) = \dim (V) \le r\), then it holds that
$$ |V| \cdot {|\mathbb {F}|}^{- r} \le 1 $$and (1) implies
$$ \Pr [ | \ker (\mathbf{H}) \cap V| > 1 ] \le {|\mathbb {F}|}^{- s}. $$But since \(\dim ( \ker (\mathbf{H}) \cap V) = \mathsf {rank}(\mathbf{M}) - \mathsf {rank}(\mathbf{H} \mathbf{M})\), this means that
$$ \Pr [ \mathsf {rank}(\mathbf{H} \mathbf{M}) < \mathsf {rank}(\mathbf{M}) ] \le {|\mathbb {F}|}^{- s}. $$ -
On the other hand, if \(\mathsf {rank}(\mathbf{M}) = \dim (V) \ge r\), then we can restate (1) as
$$ \Pr [ \dim ( \ker (\mathbf{H}) \cap V) > \mathsf {rank}(\mathbf{M}) - r] \le {|\mathbb {F}|}^{- s}. $$Again using \(\dim ( \ker (\mathbf{H}) \cap V) = \mathsf {rank}(\mathbf{M}) - \mathsf {rank}(\mathbf{H} \mathbf{M})\) we obtain
$$ \Pr [ \mathsf {rank}(\mathbf{H} \mathbf{M}) < r] \le {|\mathbb {F}|}^{- s}. $$
All together, we obtain
which concludes the proof.
The next lemma states that we obtain a lower bound the distance of a matrix \(\mathbf{X}\) from an interleaved code \(\mathsf {C}^{\odot m}\) by the rank of \(\mathbf{P} \mathbf{X}\).
Lemma 2
Let \(\mathsf {C}\) be a \(\mathbb {F}\)-linear [n, k, s] code with a parity check matrix \(\mathbf{P}\). It holds for every \(\mathbf{X} \in \mathbb {F}^{n \times m}\) that \(\mathsf {dist}(\mathsf {C}^{\odot m},\mathbf{X}) \ge \mathsf {rank}(\mathbf{P} \mathbf{X})\).
Proof
Let \(\mathbf{E} \in \mathbb {F}^{n \times m}\) be a matrix of minimal row support such that \(\mathbf{X} - \mathbf{E} \in \mathsf {C}^{\odot m}\), i.e., \(\Vert \mathbf{E}\Vert _0 = \mathsf {dist}(\mathsf {C}^{\odot m},\mathbf{X})\). Clearly \(\mathbf{P}{} \mathbf{X} = \mathbf{P}{} \mathbf{E}\). It follows that
Lemma 3
Let \(\mathsf {C}\) be a \(\mathbb {F}\)-linear [n, k, s] code with a parity check matrix \(\mathbf{P}\). Let \(\mathbf{X} \in \mathbb {F}^{n \times m}\) and \(\mathbf{X}' \in \mathbb {F}^{n \times m'}\). If it holds that
then for any \(\mathbf{C}' \in \mathsf {C}^{\odot m'}\) there exists a \(\mathbf{C} \in \mathsf {C}^{\odot m}\) such that the row support of \(\mathbf{X} - \mathbf{C}\) is contained in the row support of \(\mathbf{X}' - \mathbf{C}'\). As a consequence, it also holds that
Proof
As \(\langle \mathbf{P} \mathbf{X} \rangle _{\mathrm {col}} \subseteq \langle \mathbf{P} \mathbf{X}' \rangle _{\mathrm {col}}\), we can express \(\mathbf{P} \mathbf{X}\) as
for a matrix \(\mathbf{T} \in \mathbb {F}^{m' \times m}\). This implies that \(\mathbf{P}(\mathbf{X} - \mathbf{X}'{} \mathbf{T}) = 0\), from which it follows that \(\mathbf{X} - \mathbf{X}'{} \mathbf{T} \in \mathsf {C}^{\odot m}\). Thus there exists a \(\hat{\mathbf {C}} \in \mathsf {C}^{\odot m}\) with
Now fix an arbitrary \(\mathbf{C}' \in \mathsf {C}^{\odot m'}\). Rearranging Eq. (2), we obtain
Setting \(\mathbf{C} = \hat{\mathbf {C}} + \mathbf{C}' \mathbf{T}\) it follows directly that the row support of \(\mathbf{X} - \mathbf{C}\) is contained in the row support of \(\mathbf{X}' - \mathbf{C}'\), as \(\mathbf{X} - \mathbf{C} = (\mathbf{X}' - \mathbf{C}') \mathbf{T}\).
Theorem 1
Let \(\mathcal {H}: \mathbb {F}^m \rightarrow \mathbb {F}^{2s + t}\) be a family of \({|\mathbb {F}|}^{-2s}\)-almost universal \(\mathbb {F}\)-linear hash functions. Further let \(\mathsf {C}\) be an \(\mathbb {F}\)-linear [n, k, s] code. Then for every \(\mathbf{X} \in \mathbb {F}^{n \times m}\) at least one of the following statements holds, except with probability \({|\mathbb {F}|}^{-s}\) over the choice of  :
:
-
1.
\(\mathbf{X} \mathbf{H}^\top \) has distance at least s from \(\mathsf {C}^{\odot (2s + t)}\)
-
2.
For every \(\mathbf{C}' \in \mathsf {C}^{\odot (2s + t)}\) there exists a \(\mathbf{C} \in \mathsf {C}^{\odot m}\) such that \(\mathbf{X} \mathbf{H}^\top - \mathbf{C}'\) and \(\mathbf{X} - \mathbf{C}\) have the same row support
Remark 2
If the first item in the statement of the Theorem does not hold, the second one must hold. Then we can efficiently recover a codeword \(\mathbf{C}\) with distance at most \(s-1\) from \(\mathbf{X}\) using erasure correction, given a codeword \(\mathbf{C}' \in \mathsf {C}^{\odot (2s + t)}\) with distance at most \(s-1\) from \(\mathbf{X} \mathbf{H}^\top \). More specifically, we compute the row support of \(\mathbf{X} \mathbf{H}^\top - \mathbf{C}'\), erase the corresponding rows of \(\mathbf{X}\) and recover \(\mathbf{C}\) from \(\mathbf{X}\) using erasure correctionFootnote 5. The last step is possible as the distance between \(\mathbf{X}\) and \(\mathbf{C}\) is at most \(s-1\).
Proof
We will distinguish two cases, depending on whether \(\mathsf {rank}(\mathbf{P}{} \mathbf{X}) \ge s\) or \(\mathsf {rank}(\mathbf{P}{} \mathbf{X}) < s\).
-
Case 1: \(\mathsf {rank}(\mathbf{P}{} \mathbf{X}) \ge s\). It follows by Lemma 1 that \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top )\) is at least s, except with probability \({|\mathbb {F}|}^{-s}\) over the choice of
 . Thus fix a \(\mathbf{H} \in \mathcal {H}\) with \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) \ge s\). It follows by Lemma 2 that \(\mathsf {dist}(\mathsf {C}^{\odot m},\mathbf{X} \mathbf{H}^\top ) \ge s\), i.e., the first item holds.
. Thus fix a \(\mathbf{H} \in \mathcal {H}\) with \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) \ge s\). It follows by Lemma 2 that \(\mathsf {dist}(\mathsf {C}^{\odot m},\mathbf{X} \mathbf{H}^\top ) \ge s\), i.e., the first item holds. -
Case 2: \(\mathsf {rank}(\mathbf{P}{} \mathbf{X}) < s\). It follows from Lemma 1 that \(\mathsf {rank}(\mathbf{P}{} \mathbf{X} \mathbf{H}^\top ) = \mathsf {rank}(\mathbf{P} \mathbf{X})\), except with probability \({|\mathbb {F}|}^{-s}\) over the choice of
 . Thus fix a \(\mathbf{H} \in \mathcal {H}\) with \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) = \mathsf {rank}(\mathbf{P} \mathbf{X})\). Since \(\langle \mathbf{P} \mathbf{X} \mathbf{H}^\top \rangle _{\mathrm {col}} \subseteq \langle \mathbf{P} \mathbf{X} \rangle _{\mathrm {col}}\) and \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) = \mathsf {rank}(\mathbf{P} \mathbf{X})\), it holds that \(\langle \mathbf{P} \mathbf{X} \mathbf{H}^\top \rangle _{\mathrm {col}} = \langle \mathbf{P} \mathbf{X} \rangle _{\mathrm {col}}\). It follows from Lemma 3 that for every \(\mathbf{C}' \in \mathsf {C}^{\odot (2s + t)}\) there exists a \(\mathbf{C} \in \mathsf {C}^{\odot m}\) such that \(\mathbf{X} \mathbf{H}^\top - \mathbf{C}'\) and \(\mathbf{X} - \mathbf{C}\) have the same row support, i.e., the second item holds.
. Thus fix a \(\mathbf{H} \in \mathcal {H}\) with \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) = \mathsf {rank}(\mathbf{P} \mathbf{X})\). Since \(\langle \mathbf{P} \mathbf{X} \mathbf{H}^\top \rangle _{\mathrm {col}} \subseteq \langle \mathbf{P} \mathbf{X} \rangle _{\mathrm {col}}\) and \(\mathsf {rank}(\mathbf{P} \mathbf{X} \mathbf{H}^\top ) = \mathsf {rank}(\mathbf{P} \mathbf{X})\), it holds that \(\langle \mathbf{P} \mathbf{X} \mathbf{H}^\top \rangle _{\mathrm {col}} = \langle \mathbf{P} \mathbf{X} \rangle _{\mathrm {col}}\). It follows from Lemma 3 that for every \(\mathbf{C}' \in \mathsf {C}^{\odot (2s + t)}\) there exists a \(\mathbf{C} \in \mathsf {C}^{\odot m}\) such that \(\mathbf{X} \mathbf{H}^\top - \mathbf{C}'\) and \(\mathbf{X} - \mathbf{C}\) have the same row support, i.e., the second item holds.
4 Linear Time Primitives
In this section, we will provide constructions of almost universal hash functions and rate-1 codes with linear time complexity.
4.1 Linear Time Almost Universal Hashing with Short Seeds
Theorem 2
[IKOS08, DI14]. Fix a finite field \(\mathbb {F}\) of constant size. For all integers n, m with \(m \le n\) there exists a family of linear universal hash functions \(\mathcal {G}: \mathbb {F}^n \rightarrow \mathbb {F}^m\) such that each function \(G \in \mathcal {G}\) can be described by O(n) bits and computed in time O(n).
It is well know that evaluating a polynomial of degree at most d over a field \(\mathbb {F}\) is a \((d-1)/|\mathbb {F}|\)-almost universal hash function. We will use the family provided in Theorem 2 to pre-hash the input in a block-wise manner, such that the computation time of the polynomial hash function becomes linear in the size of the original input. A similar speed-up trick was used in [IKOS08] to construct several cryptographic primitives, for instance pseudorandom functions, that can be computed in linear time.
Lemma 4
Let \(d = d(s)\) be a positive integer. Let \(\mathbb {F}\) be a finite field of constant size and \(\mathbb {F}'\) be an extension field of \(\mathbb {F}\) of degree \(\lceil s + \log _{|\mathbb {F}|}(d) \rceil \). Let \(n = n(s,d)\) be such that a multiplication in \(\mathbb {F}'\) can be performed in time O(n). Let \(\mathcal {G}: \mathbb {F}^n \rightarrow \mathbb {F}'\) be a family of \(\mathbb {F}\)-linear universal hash functions which can be computed in time O(n) and has seed length O(n). For a function \(G \in \mathcal {G}\) and an element \(\alpha \in \mathbb {F}'\), define the function \(H_{G,\alpha }: \mathbb {F}^{d \cdot n} \rightarrow \mathbb {F}' \cong \mathbb {F}^{s + \log _{|\mathbb {F}|}(d)}\) by
where \(\mathbf{x} = (\mathbf{x}_0,\dots ,\mathbf{x}_{d-1}) \in (\mathbb {F}^n)^d\). Define the family \(\mathcal {H}\) by \(\mathcal {H} = \{ H_{G,\alpha } : G \in \mathcal {G}, \alpha \in \mathbb {F}' \}\). Then the family \(\mathcal {H}\) is \(2^{-s}\)-almost universal, has sub-linear seed-length O(n) and can be computed in linear time \(O(d \cdot n)\).
Remark 3
We can choose the function n(s, d) as small as \(O((s + \log _{|\mathbb {F}|}(d)) \cdot \text {polylog}(s + \log _{|\mathbb {F}|}(d)))\), if a fast multiplication algorithm for \(\mathbb {F}'\) is used.
Proof
We will first show that \(\mathcal {H}\) is \(2^{-s}\) almost universal. Let \(\mathbf{x} = (\mathbf{x}_0,\dots ,\mathbf{x}_{d-1}) \ne 0\). Thus there exists an \(i \in \{0,\dots ,d-1\}\) such that \(\mathbf{x}_i \ne 0\). Consequently, it holds for a randomly chosen  that \(G(\mathbf{x}_i) \ne 0\), except with probability \(1 / |\mathbb {F}'|\). Suppose now that \(0 \ne (G(\mathbf{x}_0),\dots ,G(\mathbf{x}_{d-1})) \in {\mathbb {F}'}^d\).
that \(G(\mathbf{x}_i) \ne 0\), except with probability \(1 / |\mathbb {F}'|\). Suppose now that \(0 \ne (G(\mathbf{x}_0),\dots ,G(\mathbf{x}_{d-1})) \in {\mathbb {F}'}^d\).
is a non-zero polynomial of degree at most \(d-1\), and consequently P(X) has at most \(d-1\) zeros. It follows that for a random  that
that
except with probability \((d-1)\ | \mathbb {F}' |\). All together, we can conclude that \(H_{G,\alpha }(\mathbf{x}) \ne 0\), except with probability
over the choice of 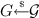 and
and  , as \(|\mathbb {F}'| = |\mathbb {F}|^{s + \log _{|\mathbb {F}|}(d)}\).
, as \(|\mathbb {F}'| = |\mathbb {F}|^{s + \log _{|\mathbb {F}|}(d)}\).
Notice that the seed size of \(H_{G,\alpha }\) is
We will finally show that for any choice of \(G \in \mathcal {G}\) and \(\alpha \in \mathbb {F}'\) the function \(H_{G,\alpha }\) can be computed in linear time in the size of its input \(\mathbf{x}\). Computing \(G(\mathbf{x}_1),\dots ,G(\mathbf{x}_d)\) takes time \(O(d \cdot n)\), as computing each \(G(\mathbf{x}_i)\) takes time O(n). Next, evaluating the polynomial \(P(X) = \sum _{i = 0}^{d-1} G(\mathbf{x}_i) X^i\) at \(\alpha \) naively costs \(d-1\) additions and \(2(d-1)\) multiplications. Since both additions and multiplications in \(\mathbb {F}'\) can be performed in time O(n), the overall cost of evaluating P(X) at \(\alpha \) can be bounded by \(O(d \cdot n)\). All together, we can compute \(H_{G,\alpha }\) in time \(O(d \cdot n)\), which is linear in the size of the input.
Instantiating the family \(\mathcal {G}\) in Lemma 4 with the family provided in Theorem 2, we obtain the following theorem.
Theorem 3
Fix a finite field \(\mathbb {F}\) of constant size. There exists an explicit family \(\mathcal {H}: \mathbb {F}^n \rightarrow \mathbb {F}^{s + O(\log (n))}\) of \(|\mathbb {F}|^{-s}\)-universal hash functions that can be represented by \(O(s^2)\) bits and computed in time O(n).
4.2 Linear Time Rate-1 Codes
For the construction in this section we will need a certain kind of expander graph, called unique-neighbor expander.
Definition 2
Let \(\varGamma = (L,R,E)\) be a bipartite graph of left-degree d with \(|L| = n\) and \(|R| = m\). We say that \(\varGamma \) is a (n, m, d, w)-unique neighbor expander, if for every non-empty subset \(S \subseteq L\) of size at most w, there exists at least one vertex \(r \in R\) such that \(|\varGamma (r) \cap S| = 1\), where \(\varGamma (r) = \{ l \in L : (l,r) \in E \}\) is the neighborhood of r.
Lemma 5
Fix a finite field \(\mathbb {F}\) of constant size. Let \(\mathsf {C}\) be an \(\mathbb {F}\)-linear [m, k, s] code. Further let \(\varGamma \) be a (n, m, d, w)-unique-neighbor expander such that \(w \cdot d < s\). Let \(\mathbf{H}_\varGamma \) be the adjacency matrix of \(\varGamma \). Then the code \(\mathsf {C}' = \{\mathbf{c} \in \mathbb {F}^n | \mathbf{H}_\varGamma \cdot \mathbf{c} \in \mathsf {C} \}\) is an \(\mathbb {F}\)-linear \([n,n - m + k,w]\) code.
Proof
Clearly, \(\mathsf {C}'\) has length n. If \({\mathbf{H}}_{\mathsf {C}}\) is a parity check matrix of \(\mathsf {C}\), then \(\mathbf{H}_\mathsf {C} \cdot \mathbf{H}_\varGamma \in \mathbb {F}^{(m - k) \times n}\) is a parity check matrix of \(\mathsf {C}'\). Thus, the dimension of \(\mathsf {C}'\) is at least \(n - m + k\). Now, let \(\mathbf{e} \in \mathbb {F}^n\) be a non-zero vector of weight less than w. Then, by the unique neighbor expansion property of \(\varGamma \), \(\mathbf{H}_\varGamma \cdot \mathbf{e}\) is a non-zero vector of weight at most \(d \cdot w\). But now it immediately holds that \(\mathbf{H}_\varGamma \cdot \mathbf{e} \notin \mathsf {C}\), as \(\mathsf {C}\) has distance at least \(s > d \cdot w\). Thus, \(\mathsf {C}'\) has minimum distance at least w.
Remark 4
The same arguments show that if \(\varGamma \) is a (n, m, d, w)-unique-neighbor expander (with no additional conditions on the parameters), the code \(\mathsf {C}'' = \{\mathbf{c} \in \mathbb {F}^n | \mathbf{H}_\varGamma \cdot \mathbf{c}= \mathbf{0}\}\) is an \(\mathbb {F}\)-linear \([n,n - m,w]\) code.
We will now use the statement of Lemma 5 on a suitable chain of expander graphs to obtain codes with rate 1 and a linear time parity check operation. We will use the following families of explicit expander graphs due to Capalbo et al. [CRVW02].
Theorem 4
[CRVW02]. For all integers n, \(m < n\) there exists an explicit (n, m, d, w)-unique-neighbor expander \(\varGamma \) with
Moreover, if \(n = O(m)\), then \(\varGamma \) can be constructed efficiently.
Lemma 6
Fix a finite field \(\mathbb {F}\) of constant size. There exists a constant \(\gamma > 0\) and an explicit family \((\mathsf {C}_s)_s\) of \(\mathbb {F}\)-linear codes, where \(\mathsf {C}_s\) has length \(O(s^2)\), minimum distance s and rate \(1 - s^{-\gamma }\), i.e. the rate of \(\mathsf {C}_s\) approaches 1. Moreover, the parity check operation of \(\mathsf {C}\) can be performed in \(O(s^2)\), which is linear in the codeword length.
Proof
By Theorem 4, there exists a constant d and a constant \(\alpha \), such that for all choices of m there exists a (2m, m, d, w)-unique-neighbor expander \(\varGamma \) with \(w \ge \alpha m / d\). Now let t be a constant such that \(t \cdot \alpha \ge 1\) and let \(\ell > 0\) be an integer. Choosing \(m_i = t \cdot 2^{i-1} d^\ell s\), we obtain a chain of \((2 m_i,m_i,d,w_i)\)-unique-neighbor expanders \(\varGamma _i\) with \(w_i \ge \alpha m_i / d\). For \(1 \le i \le \ell \) we can get a lower bound for \(w_i\) by
as \(\alpha t \ge 1\) and \(i \ge 1\). We thus obtain that \(\varGamma _i\) is also a \((t \cdot 2^i d^\ell s, t \cdot 2^{i-1} d^\ell s,d,d^{\ell -i}s)\)-unique neighbor expander.
We will choose \(\mathsf {C}_1 = \{ \mathbf{c} \in \mathbb {F}^{} : \mathbf{H}_{\varGamma _1} \mathbf{c} = 0\}\), which is a code of length \(t 2 d^\ell s\) and distance at least \(d^{\ell -1} s\) by Remark 4. Applying Lemma 5 on \(\mathsf {C}_1\) with the expander \(\varGamma _2\), we obtain a code \(\mathsf {C}_2\) of length \(t 2^2 d^\ell s\) and distance \(d^{\ell -2} s\). Iterating this procedure for \(i \le \ell \), applying Lemma 5 on \(\mathsf {C}_i\) with expander \(\varGamma _{i+1}\), we obtain codes \(\mathsf {C}_i\) of length \(t 2^i d^\ell s\) and distance \(d^{\ell - i} s\). Thus, \(\mathsf {C}_\ell \) is a code of length \(t (2d)^\ell s\) and minimum distance s. By construction, the matrix
is its parity check matrix. Notice that multiplication \(\mathbf{H}_\ell \) can be performed in linear time \(O(t (2d)^\ell s)\) in the codeword length. This can be seen as multiplication with \(\mathbf{H}_{\varGamma _i}\) can be performed it time \(O(d \cdot t 2^i d^\ell s)\) and thus multiplication with \(\mathbf{H}_\ell \) can be performed in time
We can also see from \(\mathbf{H}_\ell \) that the dimension of \(\mathsf {C}_\ell \) is at least \(t (2d)^\ell s - t d^\ell s\), i.e. \(\mathsf {C}_\ell \) has rate \(1 - 2^{-\ell }\). Now, choosing \(\ell = \lceil \log (s) / \log (2d) \rceil \) we obtain a code \(\mathsf {C}\) of length \(O(s^2)\), minimum distance s and rate \(1 - s^{- \gamma }\), where \(\gamma \ge 1 / \log (2d)\) is a constant. This concludes the proof.
We will now convert the codes constructed in Lemma 6 into codes with linear time encoding operation. The idea is simple: compute a syndrome of a message with respect to the parity check matrix promised in Lemma 6, encode this syndrome using a good code \(\mathsf {C}_2\) and append the encoded syndrome to the message. This systematic code has a linear time encoding operation, and the next Lemma shows that it has also good distance and rate.
Lemma 7
Fix a finite field \(\mathbb {F}\) of constant size. Let \(\mathsf {C}_1\) be an \(\mathbb {F}\)-linear \([n,n - m,d]\) code with linear time computable parity check operation with respect to a parity check matrix \(\mathbf{H}_1\). Further let \(\mathsf {C}_2\) be an \(\mathbb {F}\)-linear [l, m, d] code with a linear time encoding operation with respect to a generator matrix \(\mathbf{G}_2\). Then the code \(\mathsf {C}_3\), defined via the encoding operation \(\mathbf{x} \mapsto (\mathbf{x},\mathbf{G}_2 \cdot \mathbf{H}_1 \cdot \mathbf{x})\) is an \(\mathbb {F}\)-linear \([n + l,n,d]\) code with linear time encoding operation.
Proof
The fact that \(\mathsf {C}_3\) is linear time encodable follows immediately, as multiplication with both \(\mathbf{H}_1\) and \(\mathbf{G}_2\) are linear time computable. Moreover, it also follows directly from the definition of \(\mathsf {C}_3\) that \(\mathsf {C}_3\) has length \(n + l\) and dimension n. We will now show that \(\mathsf {C}_3\) has minimum distance at least d. Let \(\mathbf{e} = (\mathbf{e}_1,\mathbf{e}_2) \in \mathbb {F}^{n + l}\) be a non-zero vector of weight less than d. Clearly it holds that both \(\mathbf{e}_1\) and \(\mathbf{e}_2\) have weight less than d. If \(\mathbf{e}_2\) is non-zero, then \(\mathbf{e}_2 \notin \mathsf {C}_2\), as \(\mathsf {C}_2\) has minimum distance d. On the other hand, if \(\mathbf{e}_1\) is non-zero, then \(\mathbf{H}_1 \cdot \mathbf{e}_1\) is non-zero as \(\mathsf {C}_1\) has distance d. But then, \(\mathbf{G}_2 \cdot \mathbf{H}_1 \mathbf{e}_1\) has weight at least d, as \(C_2\) has minimum distance d and \(\mathbf{H}_1 \cdot \mathbf{e}_1\) is non-zero. Consequently, \(\mathbf{G}\cdot \mathbf{H}_1 \cdot \mathbf{e}_1 \ne \mathbf{e}_2\), as \(\mathbf{e}_2\) has weight less than d. We conclude that \((\mathbf{e}_1,\mathbf{e}_2) \notin \mathsf {C}_3\).
To use Lemma 7, we need a family of linear time encodable codes with constant rate and constant relative minimum distance. Such codes were first constructed by Spielman [Spi96].
Theorem 5
[Spi96, GI05]. Fix a finite field \(\mathbb {F}\) of constant size. Then there exists a family \(\{ C_n \}\) of \(\mathbb {F}\)-linear codes with constant rate and constant relative minimum distance which supports linear time encoding.
We can now bootstrap the statement of Lemma 6 into a linear time encodable code of rate 1 using Lemma 7 and Theorem 5.
Theorem 6
Fix a finite field \(\mathbb {F}\) of constant size. There exists a constant \(\gamma > 0\) and an explicit family of \(\mathbb {F}\)-linear codes \((\mathsf {C}_s)_s\) of length \(O(s^2)\), minimum distance s and rate \(1 - s^{-\gamma }\), which approaches 1. Moreover, \(\mathsf {C}\) has an encoding algorithm \(\mathsf {Enc}\) that runs in time \(O(s^2)\), which is linear in the codeword length.
5 Linear Time and Rate 1 Additive Commitments
In this section we construct a protocol for additively homomorphic commitments that UC realizes functionality \(\mathcal {F}_\mathrm {HCOM} \). This protocol achieves (amortized) linear computational complexity for both parties and rate 1, meaning that the ratio between the size of the committed messages and the size of the data exchanged by the parties in the protocol approaches one. We will show how to make commitments to random strings, which allows the protocol to achieve sublinear communication complexity in the commitment phase while keeping rate 1 in the opening phase, a property that finds applications in different scenarios of multiparty computation [FJN+13]. This protocol can be trivially extended to standard commitments by having the sender also send the difference between the random and the desired strings. The resulting protocol maintains rate 1 and linear computational complexity.
The construction in this section will be based on a systematic binary linear code \(\mathsf {C}\), an [n, k, s] code, where s is the statistical security parameter and n is \(k+ O(s)\). It follows from the construction in Sect. 4.2 that for any desired value of s, we can make such a code for any k, that is, the rate tends to 1 as k grows, and furthermore that encoding in \(\mathsf {C}\) takes linear time. We also need a family of linear time computable almost universal hash functions \(\mathcal H\). Furthermore the functions in \(\mathcal H\) must be linear. The functions will map m-bit strings to l-bit strings, where m is a parameter that can be chosen arbitrarily large (but polynomially related to n, k and l). We use the construction from Theorem 3, and hence, since we will need collision probability \(2^{-2s}\), we set \(l= 2s + \log (m)\).
We will build commitments to k-bit random strings, and the protocol will produce \(m-l\) such commitments. In Appendix C we show how our protocol can be used to commit to arbitrary messages achieving still preserving linear computational complexity and rate-1. In fact, in Sect. 5.1 we show that we can get even higher rate when committing to random messages. In the following, all vectors and matrices will be assumed to have binary entries. The construction can easily be generalized to other finite fields. The Commitment Phase is described in Fig. 3 and the Addition procedure and Opening Phase are described in Fig. 4. Notice that the Opening Phase presented in Fig. 4 does not achieve rate-1 but we show how to do so in Sect. 5.1. The security of our protocols is formally stated in Theorem 7.
As shown in Appendix B, we can implement \(\mathcal {F}_{\mathrm {ROT}} \) based on n one-out-of-two OT’s on short strings (of length equal to a computational security parameter) using a pseudo-random generator and standard techniques. This will give the result mentioned in the introduction: we can amortize the cost of the OT’s over many commitments.
Theorem 7
\(\varPi _\mathrm {HCOM} \) UC-realizes \(\mathcal {F}_\mathrm {HCOM} \) in the \(\mathcal {F}_{\mathrm {ROT}} \)-hybrid model with statistical security against a static adversary. Formally, there exists a simulator \({\mathcal S}\) such that for every static adversary \(\mathcal A\), and any environment \(\mathcal Z\), the environment cannot distinguish \(\varPi _\mathrm {HCOM} \) composed with \(\mathcal {F}_{\mathrm {ROT}} \) and \(\mathcal A\) from \({\mathcal S}\) composed with \(\mathcal {F}_\mathrm {HCOM} \). That is, we have
Proof
Simulation when both players are honest is trivial, so the theorem follows from the Lemmas 8 and 9 below, which establish security against a corrupt \(P \) and a corrupt \(V \), respectively.
Lemma 8
There exists a simulator \({\mathcal S}_P\) such that for every static adversary \(\mathcal A\) who corrupts \(P \), and any environment \(\mathcal Z\), the environment cannot distinguish \(\varPi _\mathrm {HCOM} \) composed with \(\mathcal {F}_{\mathrm {ROT}} \) and \(\mathcal A\) from \({\mathcal S}_P\) composed with \(\mathcal {F}_\mathrm {HCOM} \). That is, we have
Proof
Assume that the sender \(P \) is corrupted. We use \(\hat{P}\) to denote the corrupted sender. In the UC framework, this is actually the adversary, which might in turn be controlled by the environment. We describe the simulator \(\mathcal {S}_{P}\) in Fig. 5. The simulator \(\mathcal {S}_{P}\) will run protocol \(\varPi _\mathrm {HCOM} \) with an internal copy of \(\hat{P}\) exactly as the honest V would have done. First, \(\mathcal {S}_{P}\) runs the instance of \(\mathcal {F}_{\mathrm {ROT}} \) used by \(\hat{P}\) and V exactly as in the real execution. In the commitment phase, if V aborts, then the simulator aborts. If V does not abort, then the simulator inspects \(\mathcal {F}_{\mathrm {ROT}} \) and reads off the matrices \(\mathbf {R}_0\) and \(\mathbf {R}_1\) that \(\hat{P}\) gave as input. Now let \({\mathbf {W}}\) be the correction matrix sent by \(\hat{P}\) and define \(\mathbf {A}_0 = \mathbf {R}_0\) and \(\mathbf {A}_1 = \mathbf {R}_1 + {\mathbf {W}}\). Let \(\mathbf {A} = \mathbf {A}_0 + \mathbf {A}_1\). Notice that because \(\hat{P}\) is malicious, it might be the case that \(\mathbf {A} \not \in \mathsf {C}^{\odot m}\).
We now describe how the simulator decodes the columns of \(\mathbf {A}\). The simulator will identify \(< s\) rows such that \(\mathbf {A}\) is in \(\mathsf {C}^{\odot m}\) except for the identified rows. As the code has distance s, this allows to erasure decode each column j of \(\mathbf {A}\) to \(\mathsf {C}\) and the corresponding decoded message will be the extracted message \(\mathbf {m}_j\) that the simulator will input to \(\mathcal {F}_\mathrm {HCOM} \). We now give the details.
Let \(R \subset [n]\) be a set of indices specifying rows of \(\mathbf {A}\). For a column vector \(\mathbf {c} \in \mathbb {F}^n\) we let \(\pi _R(\mathbf {c}) = ( \mathbf {c}[i] )_{i \in [n]\setminus R}\) be the vector punctured at the indices \(i \in R\). For a matrix \(\mathbf {M}\) we let \(\mathbf {M}_R = \pi _R(\mathbf {M})\) be the matrix with each column punctured using \(\pi _R\) and for a set S we let \(S_R = \{ \pi _R(s) \vert s \in S \}\). The simulator will need to find \(R \subset [n]\) with \(\vert R \vert < s\) such that
It should furthermore hold that
where \(\hat{P}\) here denotes the view of \(\hat{P}\) in the simulator so far, i.e., the adversary can guess R and each choice bit \(b_i\) for \(i \in R\) with certainty at this point in the simulation and has no extra information on \(b_i\) for \(i \not \in R\).
Define \(\mathbf {T} := \mathbf {A} \mathbf {H}\). Let \(\hat{\mathbf {T}}_0\) and \(\hat{\mathbf {T}}_1\) be the values sent by P and let \(\hat{\mathbf {T}} = \hat{\mathbf {T}}_0 + \hat{\mathbf {T}}_1\). Let \({\mathbf {T}}_0 = \mathbf {R}_0 \mathbf {H}\) and \({\mathbf {T}}_1 = (\mathbf {R}_1 + \mathbf {W})\mathbf {H}\) be the values that \(\hat{P}\) should have sent. Let \({\mathbf {T}} = {\mathbf {T}}_0 + {\mathbf {T}}_1\). Let R be the smallest set such that \(\hat{\mathbf {T}}_R = \mathbf {T}_R\). We claim that this set fulfills (3), (4) and (5).
We know that the receiver did not abort, which implies that \(\mathbf {\Delta } \hat{\mathbf {T}}_0 + (\mathbf {I}-\mathbf {\Delta })\hat{\mathbf {T}}_1 = \mathbf {B}\mathbf {H}\). The i’th row of \(\mathbf {\Delta } \hat{\mathbf {T}}_0 + (\mathbf {I}-\mathbf {\Delta })\hat{\mathbf {T}}_1\) can be seen to be \(\hat{\mathbf {T}}_{b_i}[i,\cdot ]\). The i’th row of \(\mathbf {B}\) can be seen to be \(b_i \mathbf {W}[i,\cdot ] + \mathbf {R}_{b_i}\), so the i’th row of \(\mathbf {B}\mathbf {H}\) is \(\mathbf {T}_{b_i}[i,\cdot ]\). We thus have for all i that
For each \(i \in R\) we have that \(\hat{\mathbf {T}}[i,\cdot ] \ne \mathbf {T}[i,\cdot ]\), so we must therefore have for all \(i \in R\) that
It follows that if V for position i had chosen the choice bit \(1-b_i\) instead of \(b_i\), then the protocol would have aborted. Since \(\hat{P}\) can compute the correct values \(\mathbf {T}_{b_i}[i,\cdot ]\) and \(\mathbf {T}_{1-b_i}[i,\cdot ]\) it also knows which value of \(b_i\) will make the test pass. By assumption the protocol did not abort. This proves (4). It also proves that the probability of the protocol not aborting and R having size \(\vert R \vert \) is at most \(2^{-\vert R \vert }\) as \(\hat{P}\) has no information on \(b_1, \ldots , b_n\) prior to sending \(\hat{\mathbf {T}}_0\) and \(\hat{\mathbf {T}}_1\) so \(\hat{P}\) can guess \(( b_i )_{i \in R}\) with probability at most \(2^{-\vert R\vert }\). It is easy to see that the value of the bits \(b_i\) for \(i \not \in R\) do not affect whether or not the test succeeds. Therefore these bits are still uniform in the view of \(\hat{P}\) at this point.
In particular, we can therefore continue under the assumption that \(\vert R \vert < s\). We can then apply Theorem 1 where we set \(\mathbf {X} = \mathbf {A}\). From \(\vert R \vert < s\) it follows that \(\mathbf {X} \mathbf {H}\) has distance less than s to \(\mathsf {C}^{\odot m}\), so we must be in case 2 in Theorem 1. Now, since the receiver checks that \(\hat{\mathbf {T}} \in \mathsf {C}^{\odot l}\) and the protocol did not abort, we in particular have that \(\hat{\mathbf {T}}_R \in \mathsf {C}^{\odot l}_R\) from which it follows that \(\mathbf {T}_R \in \mathsf {C}^{\odot l}_R\), which in turn implies that \(\mathbf {A}_R\mathbf {H} \in \mathsf {C}^{\odot l}_R\) and thus \(\mathbf {X}_R\mathbf {H} \in \mathsf {C}^{\odot l}_R\). We can therefore pick a codeword \(\mathbf {C}' \in \mathsf {C}^{\odot l}\) such that the row support of \(\mathbf {X}\mathbf {H} - \mathbf {C}'\) is R. From Theorem 1 we then get that there exists \(\mathbf {C} \in \mathsf {C}^{\odot m}\) such that the row support of \(\mathbf {A} - \mathbf {C}\) is R. From this it follows that \(\mathbf {A}_R = \mathbf {C}_R\), which implies (3).
Now notice that since \(\mathsf {C}\) has distance s and \(\vert R \vert < s\) the punctured code \(\mathsf {C}_R\) will have distance at least 1. Therefore the simulator can from each column \(\mathbf {A}[i,\cdot ]_R \in \mathsf {C}_R\) decode the corresponding message \(\mathbf {m}_j \in \{0,1\}^k\). This the message that the simulator will input to \(\mathcal {F}_\mathrm {HCOM} \) on behalf of \(\hat{P}\).
In order to fool \(\mathcal {S}_{P}\) and open a commitment to a different message than the one that has been extracted from \(\mathbf {A}[\cdot ,j]\), \(\hat{P}\) would have to provide \(\mathbf {A}^{\prime }_0[\cdot ,j],\mathbf {A}^{\prime }_1[\cdot ,j]\) such that \(\mathbf {A}^{\prime }[\cdot ,j]=\mathbf {A}^{\prime }_0[\cdot ,j]+\mathbf {A}^{\prime }_1[\cdot ,j]\) is a valid codeword of \(\mathsf {C}\) corresponding to a different message \(\mathbf {m}'\). However, notice that since \(\mathsf {C}_R\) has distance \(s - \vert R \vert \), that would require \(\hat{P}\) to modify an additional \(s - \vert R \vert \) positions of \(\mathbf {A}\) that are not contained in \(\mathbf {B}\) so that it does not get caught in the checks performed by a honest \(V \) in the opening phase. That means that \(\hat{P}\) would have to guess \(s - \vert R \vert \) of the choice bits \(b_i\) for \(i \not \in R\). It follows from (5) that this will succeed with probability at most \(2^{s-\vert R \vert }\).
Lemma 9
There exists a simulator \({\mathcal S}_V\) such that for every static adversary \(\mathcal A\) who corrupts \(V \), and any environment \(\mathcal Z\), the environment cannot distinguish \(\varPi _\mathrm {HCOM} \) composed with \(\mathcal {F}_{\mathrm {ROT}} \) and \(\mathcal A\) from \({\mathcal S}_V\) composed with \(\mathcal {F}_\mathrm {HCOM} \). That is, we have
Proof
In case \(V \) is corrupted, the simulator \(\mathcal {S}_{V}\) has to run \(\varPi _\mathrm {HCOM} \) with an internal copy of \(\hat{V}\), commit to a dummy string and then be able to equivocate this commitment (i.e. open it to an arbitrary message) when it gets the actual message from \(\mathcal {F}_\mathrm {HCOM} \). In order to achieve this, we can construct a \(\mathcal {S}_{V}\) that executes the commitment phase exactly as in \(\varPi _\mathrm {HCOM} \) only deviating in the opening phase. Note that after the commit phase \(\hat{V}\) has no information at all about the committed strings. This holds because the additive shares in \(\mathbf{S}\) trivially contain no information and furthermore because the columns in sacrificed positions a(j) contain uniformly random data and are never opened. This completely randomizes the data seen by \(\hat{V}\) in the verification stage (\(\mathbf{T_0, T_1}\)).
Therefore, \(\mathcal {S}_{V}\) can use its knowledge of \(b_1,\ldots ,b_n\) to open a commitment to an arbitrary message without being caught, by modifying position of the matrices that are unknown to \(\hat{V}\) (i.e. unknown to \(V \) in the real world). We describe \(\mathcal {S}_{V}\) in Fig. 6. Note that \(\mathcal {S}_{V}\) exactly follows all the steps of \(\varPi _\mathrm {HCOM} \) (and \(\mathcal {F}_{\mathrm {ROT}} \)) except for when it opens commitments. Instead, in the opening phase, \(\mathcal {S}_{V}\) sends \(\mathbf {A_0}^{\prime }[\cdot , j], \mathbf {A_1}^{\prime }[\cdot , j]\), which differ from \(\mathbf {A_0}[\cdot , j], \mathbf {A_1}[\cdot , j]\) that was set in the commitment phase and that would be sent in a real execution of \(\varPi _\mathrm {HCOM} \). However, \(\mathbf {A_0}^{\prime }[\cdot , j], \mathbf {A_1}^{\prime }[\cdot , j]\), only differ from \(\mathbf {A_0}[\cdot , j], \mathbf {A_1}[\cdot , j]\) in positions that are unknown by \(\hat{V}\). Hence, the joint distribution of the ideal execution with simulator \(\mathcal {S}_{V}\) is statistically indistinguishable from the real execution of \(\varPi _\mathrm {HCOM} \) with a corrupted receiver.
5.1 Computational Complexity and Rate
It is straightforward to verify that the Commitment, Addition and Opening protocols run in linear time, or more precisely, that the computational cost per bit committed to is constant. Indeed, it follows easily from the fact that \(\mathsf {C}\) is linear time encodable and that H can be computed in linear time. This holds, even if we consider the cost of implementing \(\mathcal {F}_{\mathrm {ROT}} \) and \(\mathcal {F}_{\mathrm {OT}} \): the first cost is linear if we use a PRG that costs only a constant number of operations per output bit. The cost of the OT operations is amortized away if we consider a sufficiently large number of commitments.
Furthermore, the commitment protocol achieves rate 1, i.e., the amortized communication overhead per committed bit is o(1) as we increase the number of bits committed in one commitment. This follows from the fact that \(\mathsf {C}\) is rate-1 and that the communication cost of the verification in the final steps of the protocol only depends on the security parameter, and hence is “amortized away”. Note that in the case where the sender only wants to be committed to random messages, it is possible to achieve rate higher than 1 in the commitment phase. This happens if we plug in the implementation of \(\mathcal {F}_{\mathrm {ROT}} \) based on \(\mathcal {F}_{\mathrm {OT}} \), since then the random strings output from \(\mathcal {F}_{\mathrm {ROT}} \) are generated locally from a short seed using a PRG, and later the sender is only required to send the bottom \(n-k\) rows of \(\mathbf {W}\) and the matrices \(\mathbf {T_0},\mathbf {T_1}\), which are both of the order of O(s).
The opening protocol does not achieve rate 1 as it stands because the communication is about twice the size of the committed string (both \(\mathbf {A_0}[\cdot , j]\) and \(\mathbf {A_1}[\cdot , j]\) are sent). However, for sufficiently long messages, we can get rate-1 by using the same verification method as used in the commitment protocol, namely we open many commitments at once. We can think of this as opening an entire matrix \(\mathbf {A}\) instead of its columns one by one. The idea is then that \(V \) selects a hash function \(\mathbf {H}\) and \(P \) sends \(\mathbf {A}\) as well as \(\mathbf {T_0}= \mathbf {A_0}\mathbf {H}\) and \(\mathbf {T_1}= \mathbf {A_1}\mathbf {H}\). The receiver checks that \(\mathbf {A}\mathbf {H} = \mathbf {T_0} + \mathbf {T_1}\), that all columns in \(\mathbf {A}\) are in \(\mathsf {C}\) and that \(\mathbf {\Delta } \mathbf {T_0} + (\mathbf {I}-\mathbf {\Delta })\mathbf {T_1} = \mathbf {B}\mathbf {H}\). This can be shown secure by essentially the same proof as we used to show the commitment protocol secure against a corrupt sender. Now the communication overhead for verification is insignificant for large enough matrices \(\mathbf {A}\).
Notes
- 1.
However, as we shall see, if one only needs to commit to random bit strings, one can hope to generate these pseudorandomly from a short seed, and have rate higher than 1 for commitment (but of course not for opening).
- 2.
Of course, rate 1 and linear time is trivial if there are no demands to the distance: just use the identity as encoding. What we mean here is that the code has length \(n+o(n)\) and yet, as n grows, the distance remains larger than some parameter k.
- 3.
A codeword in an interleaved code is a matrix in which all m columns are in some underlying code \(\mathsf {C}\).
- 4.
On the other hand, we pay a small price for having a non-random function, namely the output size for the hash function needs to be \(\varTheta (s) + \log (m)\) rather than \(\varTheta (s)\), where s is the security parameter and m is the number of commitments.
- 5.
Recall that erasure correction for linear codes can be performed efficiently via gaussian elimination.
- 6.
Apart from \(\mathbf {T}_0,\mathbf {T}_1\), which only depend on the security parameter and are amortized over many commitments.
References
Afshar, A., Hu, Z., Mohassel, P., Rosulek, M.: How to efficiently evaluate RAM programs with malicious security. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 702–729. Springer, Heidelberg (2015)
Blazy, O., Chevalier, C., Pointcheval, D., Vergnaud, D.: Analysis and improvement of Lindell’s UC-secure commitment schemes. In: Jacobson Jr., M.J., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 534–551. Springer, Heidelberg (2013)
Brandão, L.T.A.N.: Very-efficient simulatable flipping of many coins into a well. In: Cheng, C.M., et al. (eds.) PKC 2016. LNCS, vol. 9615, pp. 297–326. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49387-8_12
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS, pp. 136–145. IEEE Computer Society (2001)
Cascudo, I., Damgård, I., David, B.M., Giacomelli, I., Nielsen, J.B., Trifiletti, R.: Additively homomorphic UC commitments with optimal amortized overhead. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 495–515. Springer, Heidelberg (2015)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, p. 19. Springer, Heidelberg (2001)
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: STOC, pp. 494–503 (2002)
Capalbo, M.R., Reingold, O., Vadhan, S.P., Wigderson, A.: Randomness conductors and constant-degree lossless expanders. In: Proceedings on 34th Annual ACM Symposium on Theory of Computing, 19–21 May 2002, Montréal, Québec, Canada, pp. 659–668 (2002)
Damgård, I., David, B., Giacomelli, I., Nielsen, J.B.: Compact VSS and efficient homomorphic UC commitments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 213–232. Springer, Heidelberg (2014)
Druk, E., Ishai, Y.: Linear-time encodable codes meeting the gilbert-varshamov bound and their cryptographic applications. In: Naor, M. (ed.) Innovations in Theoretical Computer Science, ITCS 2014, Princeton, NJ, USA, 12–14 January 2014, pp. 169–182. ACM (2014)
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Nordholt, P.S., Orlandi, C.: MiniLEGO: efficient secure two-party computation from general assumptions. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 537–556. Springer, Heidelberg (2013)
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Trifiletti, R.: On the complexity of additively homomorphic uc commitments. In: Kushilevitz, E., et al. (eds.) TCC 2016-A. LNCS, vol. 9562, pp. 542–565. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_23
Guruswami, V., Indyk, P.: Near-optimal linear-time codes for unique decoding and new list-decodable codes over smaller alphabets. In: Reif, J.H. (ed.) Proceedings on 34th Annual ACM Symposium on Theory of Computing, 19–21 May 2002, Montréal, Québec, Canada, pp. 812–821. ACM (2002)
Guruswami, V., Indyk, P.: Linear time encodable and list decodable codes. In: Larmore and Goemans [LG03], pp. 126–135
Guruswami, V., Indyk, P.: Linear-time encodable/decodable codes with near-optimal rate. IEEE Trans. Inf. Theor. 51(10), 3393–3400 (2005)
Garay, J.A., Ishai, Y., Kumaresan, R., Wee, H.: On the complexity of UC commitments. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 677–694. Springer, Heidelberg (2014)
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Cryptography with constant computational overhead. In: Dwork, C. (ed.) STOC, pp. 433–442. ACM (2008)
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008)
Ishai, Y., Prabhakaran, M., Sahai, A.: Secure arithmetic computation with no honest majority. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 294–314. Springer, Heidelberg (2009)
Larmore, L.L., Goemans, M.X. (eds.) Proceedings of the 35th Annual ACM Symposium on Theory of Computing, 9–11 June 2003, San Diego, CA, USA. ACM (2003)
Lindell, Y.: Highly-efficient universally-composable commitments based on the DDH assumption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 446–466. Springer, Heidelberg (2011)
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008)
Spielman, D.A.: Linear-time encodable and decodable error-correcting codes. IEEE Trans. Inf. Theor. 42(6), 1723–1731 (1996)
Vadhan, S., Zheng, C.J.: Characterizing pseudoentropy and simplifying pseudorandom generator constructions. In: Proceedings of the 44th Symposium on Theory of Computing, pp. 817–836. ACM (2012)
Acknowledgements
A major part of this work was done while Ignacio Cascudo and Nico Döttling were also with Aarhus University.
The authors acknowledge support from the Danish National Research Foundation and The National Science Foundation of China (under the grant 61361136003) for the Sino-Danish Center for the Theory of Interactive Computation and from the Center for Research in Foundations of Electronic Markets (CFEM), supported by the Danish Strategic Research Council.
In addition, Ignacio Cascudo acknowledges support from the Danish Council for Independent Research, grant no. DFF-4002-00367.
Nico Döttling gratefully acknowledges support by the DAAD (German Academic Exchange Service) under the postdoctoral program (57243032). While at Aarhus University, he was supported by European Research Council Starting Grant 279447. His research is also supported in part from a DARPA/ARL SAFEWARE award, AFOSR Award FA9550-15-1-0274, and NSF CRII Award 1464397. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
Jesper Buus Nielsen was supported by European Research Council Starting Grant 279447.
The authors thank the anonymous reviewers of CRYPTO 2016 for their comments, which contributed to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Universal Composability
We adopt description of the Universal Composability (UC) framework given in [CDD+15]. In this framework, protocol security is analyzed under the real-world/ideal-world paradigm, i.e. by comparing the real world execution of a protocol with an ideal world interaction with the primitive that it implements. The model has a composition theorem, that basically states that UC secure protocols can be arbitrarily composed with each other without any security compromises. This desirable property not only allows UC secure protocols to effectively serve as building blocks for complex applications but also guarantees security in practical environments where several protocols (or individual instances of protocols) are executed in parallel, such as the Internet.
In the UC framework, the entities involved in both the real and ideal world executions are modeled as probabilistic polynomial-time Interactive Turing Machines (ITM) that receive and deliver messages through their input and output tapes, respectively. In the ideal world execution, dummy parties (possibly controlled by an ideal adversary \(\mathcal {S}\) referred to as the simulator) interact directly with the ideal functionality \(\mathcal {F}\), which works as a trusted third party that computes the desired primitive. In the real world execution, several parties (possibly corrupted by a real world adversary \(\mathcal {A}\)) interact with each other by means of a protocol \(\pi \) that realizes the ideal functionality. The real and ideal executions are controlled by the environment \(\mathcal {Z} \), an entity that delivers inputs and reads the outputs of the individual parties, the adversary \(\mathcal {A}\) and the simulator \(\mathcal {S}\). After a real or ideal execution, \(\mathcal {Z} \) outputs a bit, which is considered as the output of the execution. The rationale behind this framework lies in showing that the environment \(\mathcal {Z} \) (that represents all the things that happen outside of the protocol execution) is not able to efficiently distinguish between the real and ideal executions, thus implying that the real world protocol is as secure as the ideal functionality.
We denote by \(\mathsf {REAL}_{\pi , \mathcal {A}, \mathcal {Z}}(\kappa ,z,\bar{r})\) the output of the environment \(\mathcal {Z} \) in the real-world execution of protocol \(\pi \) between n parties with an adversary \(\mathcal {A}\) under security parameter \(\kappa \), input z and randomness \(\bar{r}=(r_{\mathcal {Z}},r_{\mathcal {A}},r_{P_1},\ldots ,r_{P_n})\), where \((z,r_{\mathcal {Z}})\), \(r_{\mathcal {A}}\) and \(r_{P_i}\) are respectively related to \(\mathcal {Z} \), \(\mathcal {A}\) and party i. Analogously, we denote by \(\mathsf {IDEAL}_{\mathcal {F}, \mathcal {S}, \mathcal {Z}}(\kappa ,z,\bar{r})\) the output of the environment in the ideal interaction between the simulator \(\mathcal {S}\) and the ideal functionality \(\mathcal {F}\) under security parameter \(\kappa \), input z and randomness \(\bar{r}=(r_{\mathcal {Z}},r_{\mathcal {S}},r_{\mathcal {F}})\), where \((z,r_{\mathcal {Z}})\), \(r_{\mathcal {S}}\) and \(r_{\mathcal {F}}\) are respectively related to \(\mathcal {Z} \), \(\mathcal {S}\) and \(\mathcal {F}\). The real world execution and the ideal executions are respectively represented by the ensembles \(\mathsf {REAL}_{\pi , \mathcal {A}, \mathcal {Z}}=\{\mathsf {REAL}_{\pi , \mathcal {A}, \mathcal {Z}}(\kappa ,z,\bar{r})\}_{\kappa \in \mathbb N}\) and \(\mathsf {IDEAL}_{\mathcal {F}, \mathcal {S}, \mathcal {Z}}=\{\mathsf {IDEAL}_{\mathcal {F}, \mathcal {S}, \mathcal {Z}}(\kappa ,z,\bar{r})\}_{\kappa \in \mathbb N}\) with \(z \in \{0,1\}^{*}\) and a uniformly chosen \(\bar{r}\).
In addition to these two models of computation, the UC framework also considers the \(\mathcal {G}\)-hybrid world, where the computation proceeds as in the real-world with the additional assumption that the parties have access to an auxiliary ideal functionality \(\mathcal {G}\). In this model, honest parties do not communicate with the ideal functionality directly, but instead the adversary delivers all the messages to and from the ideal functionality. We consider the communication channels to be ideally authenticated, so that the adversary may read but not modify these messages. Unlike messages exchanged between parties, which can be read by the adversary, the messages exchanged between parties and the ideal functionality are divided into a public header and a private header. The public header can be read by the adversary and contains non-sensitive information (such as session identifiers, type of message, sender and receiver). On the other hand, the private header cannot be read by the adversary and contains information such as the parties’ private inputs. We denote the ensemble of environment outputs that represents the execution of a protocol \(\pi \) in a \(\mathcal {G}\)-hybrid model as \(\mathsf {HYBRID}^{\mathcal {G}}_{\pi , \mathcal {A}, \mathcal {Z}}\) (defined analogously to \(\mathsf {REAL}_{\pi , \mathcal {A}, \mathcal {Z}}\)). UC security is then formally defined as:
Definition 3
A n-party (\(n \in \mathbb N\)) protocol \(\pi \) is said to UC-realize an ideal functionality \(\mathcal {F}\) in the \(\mathcal {G}\)-hybrid model if, for every adversary \(\mathcal {A}\), there exists a simulator \(\mathcal {S}\) such that, for every environment \(\mathcal {Z}\), the following relation holds:
We say that the protocol is statistically secure if the same holds for all \(\mathcal {Z} \) with unbounded computing power.
B Implementing \(\mathcal {F}_{\mathrm {ROT}}\)
For the sake of simplicity we construct our commitment protocol in the \(\mathcal {F}_{\mathrm {ROT}} \)-hybrid model. Here we show that \(\mathcal {F}_{\mathrm {ROT}} \) can be realized in the \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model in a straightforward manner. Intuitively, we have \(P_s \) sample two random matrices \(\mathbf {R_0},\mathbf {R_1}\) and do an OT for each row, where it inputs a row from each matrix (i.e. \(\mathbf {R_0}[i,\cdot ],\mathbf {R_1}[i,\cdot ]\)) and \(P_r \) inputs a random choice bit. However, this naïve construction has communication complexity that depends on the size of the matrices, since it needs n OTs of m-bit strings.
Using both a pseudorandom number generator \(\mathsf {prg}\) and access to \(\mathcal {F}_{\mathrm {OT}} \) (Fig. 7), it is possible to realize \(\mathcal {F}_{\mathrm {ROT}} \) in a way that its communication complexity only depends on the number of rows of the matrices and a computational security parameter (Fig. 8). This is a key fact in achieving rate 1 for our commitment scheme, since the number of rows required in our protocol is independent from the number of commitments to be executed, allowing the communication cost to be amortized over many commitments. On the other hand, (amortized) linear time can be obtained by employing a pseudorandom number generator that only requires a constant number of operations per output bit (e.g. [VZ12]). As shown in the protocol description, expensive OT operations are only used n (the number of rows) times while the number of calls to the \(\mathsf {prg}\) is a fraction of the number of commitments (the number of columns). This allows us to obtain an arbitrary number of commitments from a fixed number of OTs and a small number of calls to \(\mathsf {prg}\).
Let \(\mathsf {prg}:\{0,1\}^{\kappa } \rightarrow \{0,1\}^{\ell }\) be a pseudorandom number generator that stretches a seed  into a pseudorandom string \(r \in \{0,1\}^{\ell }\). Intuitively, for \(i=1,\ldots ,n\), we call \(\mathcal {F}_{\mathrm {OT}} \) with \(P_s \)’s input equal to
into a pseudorandom string \(r \in \{0,1\}^{\ell }\). Intuitively, for \(i=1,\ldots ,n\), we call \(\mathcal {F}_{\mathrm {OT}} \) with \(P_s \)’s input equal to  and \(P_r \)’s input equal to
and \(P_r \)’s input equal to  . After all the OTs are done, \(P_s \) sets \(\mathbf {R_0}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{0,i}})\) and \(\mathbf {R_1}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{1,i}})\), while \(P_r \) sets \(\mathbf {S}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{b_i,i}})\). The output matrices have n rows and \(\ell \) columns. However, an arbitrary number of columns m can be obtained by saving the last \(\kappa \) bits of every output of \(\mathsf {prg}\), repeatedly running \(\mathsf {prg}\) using these bits as seeds and concatenating the outputs (minus the last \(\kappa \) bits) until m bits are obtained.
. After all the OTs are done, \(P_s \) sets \(\mathbf {R_0}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{0,i}})\) and \(\mathbf {R_1}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{1,i}})\), while \(P_r \) sets \(\mathbf {S}[i,\cdot ]=\mathsf {prg}(\mathbf {r_{b_i,i}})\). The output matrices have n rows and \(\ell \) columns. However, an arbitrary number of columns m can be obtained by saving the last \(\kappa \) bits of every output of \(\mathsf {prg}\), repeatedly running \(\mathsf {prg}\) using these bits as seeds and concatenating the outputs (minus the last \(\kappa \) bits) until m bits are obtained.
Lemma 10
\(\varPi _{\mathrm {ROT}} \) UC-realizes \(\mathcal {F}_{\mathrm {ROT}} \) in the \(\mathcal {F}_{\mathrm {OT}} \)-hybrid model with computational security against a static adversary. Formally, there exists a simulator \(\mathcal {S}\) such that for every static adversary \(\mathcal {A}\) and any environment \(\mathcal Z\):
Proof
(Sketch). The simulator \(\mathcal {S}\) acts as \(\mathcal {F}_{\mathrm {OT}} \) when running \(\varPi _{\mathrm {ROT}} \) with an internal copy of \(\mathcal {A}\). In case \(P_s \) is corrupted, \(\mathcal {S}\) extracts the inputs \((\mathbf {r_{0,1}},\mathbf {r_{1,1}}),\ldots ,(\mathbf {r_{0,n}},\mathbf {r_{1,n}})\) given by \(\mathcal {A}\) to \(\mathcal {F}_{\mathrm {OT}} \), constructs \(\mathbf {R_0},\mathbf {R_1}\) according to the protocol and sends them to \(\mathcal {F}_{\mathrm {ROT}} \). In case \(P_r \) is corrupted, \(\mathcal {S}\) extracts the inputs \(b_1,\ldots ,b_n\), samples random matrices  , constructs \(\mathbf {S}\) according to the protocol and sends \((b_1,\ldots ,b_n),\mathbf {S}\) to \(\mathcal {F}_{\mathrm {ROT}} \). Basically, the ideal and the real distributions are computationally indistinguishable due to \(\mathsf {prg}\)’s pseudorandomness, i.e. an environment \(\mathcal {Z} \) that distinguishes between the ideal and real distributions could be used to distinguish a pseudorandom string output by \(\mathsf {prg}\) from a uniformly random string of same size.
, constructs \(\mathbf {S}\) according to the protocol and sends \((b_1,\ldots ,b_n),\mathbf {S}\) to \(\mathcal {F}_{\mathrm {ROT}} \). Basically, the ideal and the real distributions are computationally indistinguishable due to \(\mathsf {prg}\)’s pseudorandomness, i.e. an environment \(\mathcal {Z} \) that distinguishes between the ideal and real distributions could be used to distinguish a pseudorandom string output by \(\mathsf {prg}\) from a uniformly random string of same size.
C Committing to Arbitrary Messages
Protocol \(\varPi _\mathrm {HCOM} \) described in Sect. 5 realizes \(\mathcal {F}_\mathrm {HCOM} \) and thus only allows the sender to commit to random messages. However, this can be trivially used to commit to arbitrary messages while preserving all properties of our scheme, namely, additive homomorphism, linear computational complexity and rate 1. This is achieved by having the sender also give the receiver the difference between the random string that it is committed to through \(\varPi _\mathrm {HCOM} \) and the arbitrary string that he wishes to commit to. First, \(P \) runs the commitment phase of \(\varPi _\mathrm {HCOM} \) and becomes committed to a string \(\mathbf {m}\), then it computes \(\mathbf {c}=\mathbf {m}^{\prime }-\mathbf {m}\) and sends \(\mathbf {c}\) to \(V \) (where \(\mathbf {m}^{\prime }\) is the message that \(P \) wishes to commit to). The addition of two commitments can proceed the same way as in \(\varPi _\mathrm {HCOM} \) with an extra step of setting \(\mathbf {c}_3=\mathbf {c}_1+\mathbf {c}_2=\mathbf {m}^{\prime }_1+\mathbf {m}^{\prime }_2-\mathbf {m}_1-\mathbf {m}_2\). In the opening phase, \(P \) proceeds exactly like in \(\varPi _\mathrm {HCOM} \) and \(V \) obtains the intended message by computing \(\mathbf {m}^{\prime }=\mathbf {c}+\mathbf {m}\). We call this protocol \(\varPi _\mathrm {AHCOM} \) and described it in the \(\mathcal {F}_\mathrm {HCOM} \)-hybrid model in Fig. 9.
The security of \(\varPi _\mathrm {AHCOM} \) can be trivially observed since all we do is sending the difference between a random string that the sender is already committed to and the arbitrary string he wishes to commit to. The random string acts as a one-time pad hiding all information and binding is guaranteed by \(\mathcal {F}_\mathrm {HCOM} \), hence we obtain statistical security in the \(\mathcal {F}_\mathrm {HCOM} \)-hybrid model (which is realized by \(\varPi _\mathrm {HCOM} \)). Notice that the extra communication does not reduce the rate of the resuting commitment scheme, since in \(\varPi _\mathrm {HCOM} \)’s commitment phase only the \(n-k\) bottom rows of \(\mathbf {W}\) are sentFootnote 6 and here we send the remaining k bits that define \(\mathbf {m}^{\prime }\). Moreover, it is possible to embed the difference \(\mathbf {c}\) in \(\mathbf {W}\) so that no extra rounds are required.
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Cascudo, I., Damgård, I., David, B., Döttling, N., Nielsen, J.B. (2016). Rate-1, Linear Time and Additively Homomorphic UC Commitments. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9816. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53015-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-662-53015-3_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53014-6
Online ISBN: 978-3-662-53015-3
eBook Packages: Computer ScienceComputer Science (R0)










