Compatible Spanning Circuits and Forbidden Induced Subgraphs

Abstract

A compatible spanning circuit in an edge-colored graph G (not necessarily properly) is defined as a closed trail containing all vertices of G in which any two consecutively traversed edges have distinct colors. The existence of extremal compatible spanning circuits (i.e., compatible Hamilton cycles and compatible Euler tours) has been studied extensively. Recently, sufficient conditions for the existence of compatible spanning circuits visiting each vertex at least a specified number of times in specific edge-colored graphs satisfying certain degree conditions have been established. In this paper, we continue the research on sufficient conditions for the existence of such compatible s-panning circuits. We consider edge-colored graphs containing no certain forbidden induced subgraphs. As applications, we also consider the existence of such compatible spanning circuits in edge-colored graphs G with κ(G) ≥ α(G), κ(G) ≥ α(G) − 1 and κ (G) ≥ α(G), respectively. In this context, κ(G), α(G) and κ (G) denote the connectivity, the independence number and the edge connectivity of a graph G, respectively.

1 Introduction

Throughout this paper, all graphs considered are finite undirected and simple. For terminology and notations not defined here, we refer the reader to the textbook of Bondy and Murty [5].

Let G be a graph. We use V (G) and E(G) to denote the set of vertices of G and the set of edges of G, respectively. For a vertex v ∈ V (G), we denote the set of edges of G incident with v by E_G(v), and we denote the set of neighbors of v in G by N_G(v). The degree of a vertex v in a graph G, denoted by d_G(v), is defined to be the cardinality of E_G(v). In particular, we write δ(G) = min{d_G(v) | v ∈ V (G)} and $\sigma_{3} (G) = \min \{ d_{G} (u) + d_{G} (v) + d_{G} (w)|u,v,w \in V(G) \, and \, uv,uw,vw \notin E(G)\} ,$ where the vertices u, v and w of G are pairwise distinct. If no ambiguity can arise, we will use E(v), N (v) and d(v) instead of E_G(v), N_G(v) and d_G(v), respectively.

Let H be a set of connected graphs. If |H|≥ 2, then for any two graphs of H, we always assume that each of them is not an induced subgraph of the other. A graph G is said to be H-free if G contains no graph H ∈ H as an induced subgraph, and each graph H ∈ H is called a forbidden induced subgraph of G. If G is {H}-free, then we simply say that G is H-free, and G is claw-free if H = K_1,3. Throughout this paper, when we mention a H-free graph, we always assume that any member of H is not a path P₂ or P₃, because a P₂-free graph is empty (edgeless) and a connected P₃-free graph is complete (the problem we consider in this paper has been solved for complete graphs in [16]). Let H₁ and H₂ be two sets of connected graphs. We write H₁ $\preceq$ H₂ if there exists a graph H₁ ∈ H₁ such that H₁ is an induced subgraph of H₂ for each graph H₂ ∈ H₂. Clearly, if H₁ $\preceq$ H₂, then every H₁-free graph is also H₂-free.

Following [16], a closed trail (no edge is traversed more than once) in a graph G visiting (containing) each vertex of G is defined as a spanning circuit of G. A Hamilton cycle of a graph G is a spanning circuit that visits each vertex of G exactly once; an Euler tour of G is a spanning circuit that traverses each edge of G. Hence, a spanning circuit can be viewed as a common relaxation of a Hamilton cycle and an Euler tour. A graph is called hamiltonian if it contains a Hamilton cycle, and a graph is called eulerian if it admits an Euler tour. It is well-known that determining whether a graph is hamiltonian is NP-complete. A well-known characterization of eulerian graphs states that a connected graph G is eulerian if and only if the degree of each vertex of G is even (see [5]).

There are polynomial-time algorithms for finding an Euler tour in an arbitrary eulerian graph, one of them is due to Fleury (see [5]). It is not difficult to see that each spanning circuit (if it exists) of a graph G corresponds to a spanning eulerian subgraph of G. A graph is called supereulerian if it contains a spanning eulerian subgraph (spanning circuit). Pulleyblank [28] proved that it is NP-complete to determine whether a graph is supereulerian. For more details on the topic of supereulerian graphs, we refer the reader to Catlin’s excellent survey [9] and its supplement [23].

Following [16], an edge-coloring of a graph G is defined as a mapping c : E(G) → N, where N is the set of natural numbers. An edge-colored graph refers to a graph with a fixed edge-coloring. Two edges of a graph are called consecutive with respect to a trail (with a fixed orientation) if they are traversed consecutively along the trail. A compatible spanning circuit in an edge-colored graph is a spanning circuit in which any two consecutive edges have distinct colors. An edge-colored graph is called properly colored if each pair of adjacent edges of the graph has distinct colors. Thus, a compatible Hamilton cycle is properly colored, and a properly colored spanning circuit is also compatible. Conversely, a compatible spanning circuit is obviously not necessarily properly colored. Therefore, a compatible spanning circuit can be viewed as a generalization of a properly colored spanning circuit. Compatible spanning circuits are quite useful in applications of graph theory, for example, in genetic and molecular biology [27, 31, 32], in the design of printed circuit and wiring boards [33], and in channel assignment of wireless networks [1, 30].

Let G be an edge-colored graph. We use c(e) to denote the color appearing on the edge e of G, and we write C(G) = {c(e) | e ∈ E(G)}. Let $d_{G}^{i} (v)$ be the cardinality of the set {e ∈ E_G(v) | c(e) = i} for a vertex v ∈ V (G) and a color i ∈ C(G). We define the maximum monochromatic degree of a vertex v of G as $\Delta_{G}^{mon} (v) = {\text{max}}\{ d_{G}^{i} (v)|i \in C(G)\}$. When no confusion can occur, we will denote $\Delta_{G}^{mon} (v)$ by ∆^mon(v).

The existence of extremal compatible spanning circuits, i.e., compatible Hamilton cycles and compatible Euler tours in specific edge-colored graphs has been extensively studied in previous literature. The research on the existence of compatible Hamilton cycles in edge-colored graphs can date back to the 1970s, and this topic has also attracted new attention recently (see [24] and some related references cited by it). On the other hand, Kotzig [22] established a necessary and sufficient condition for the existence of compatible Euler tours in edge-colored eulerian graphs. We refer the reader to [4, 13] for more results on the existence of compatible Euler tours.

Recently, the existence of more general compatible spanning circuits (i.e., not necessarily a compatible Hamilton cycle or Euler tour) in specific edge-colored graphs has been considered in [14,15,16]. In particular, sufficient conditions for the existence of compatible spanning circuits visiting each vertex at least a specified number of times in specific edge-colored graphs satisfying certain degree conditions have been established in [14, 16]. In this paper, we continue the research on sufficient conditions for the existence of compatible spanning circuits visiting each vertex at least a specified number of times. We establish sufficient conditions for the existence of such compatible spanning circuits in edge- colored graphs that do not contain certain forbidden induced subgraphs. As applications, we also consider the existence of such compatible spanning circuits in edge-colored graphs G with κ(G) ≥ α(G), κ(G) ≥ α(G) − 1 and κ^t(G) ≥ α(G), respectively. In this context, κ(G), κ^t(G) and α(G) denote the connectivity, the edge connectivity and the independence number of a graph G, respectively.

2 Main Results

In this section, we list our main results included in this paper. We postpone the proofs of these results to Sect. 4 in order not to interrupt the flow of the narrative.

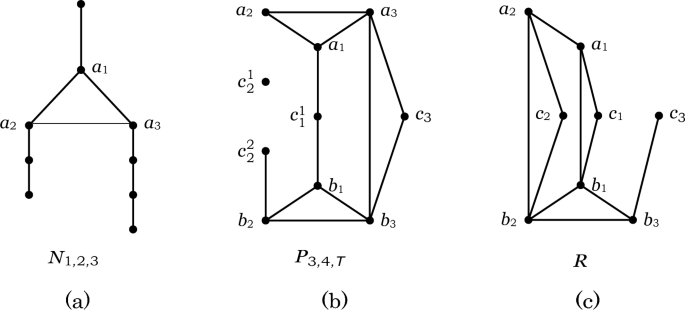
Before proceeding, we first introduce some essential graphs that are used as forbidden induced subgraphs in our results. For integers i, j, k with 0 ≤ i ≤ j ≤ k, let N_i,j,k be a graph obtained from a triangle and three disjoint paths of lengths i, j, k, respectively by identifying three vertices of the triangle with three end vertices of the paths, one for each of the paths. (As an example, the graph N_1,2,3 is depicted in Fig. 1a.) Let P_n be a path on n vertices, and let P denote the class of all graphs obtained from two disjoint triangles a₁a₂a₃a₁, b₁b₂b₃b₁ by joining each pair of vertices a_i, b_i by a path $P_{{k_{i} }} = a_{i} c_{i}^{1} c_{i}^{2} \cdots c_{i}^{{k_{i} - 2}} b_{i}$ with k_i ≥ 3 or by a triangle a_ib_ic_ia_i for i ∈ {1, 2, 3}. We denote a graph from P by $P_{{x_{1} ,x_{2} ,x_{3} }}$, where x_i = k_i if the two vertices a_i and b_i are joined by a path $P_{{k_{i} }}$, and x_i = T if the two vertices a_i and b_i are joined by a triangle a_ib_ic_ia_i for i ∈ {1, 2, 3}. (As an example, the graph P_3,4,T is depicted in Fig. 1b.) Let R be a graph obtained by removing one vertex of degree 4 from P_T,T,T (see Fig. 1c). Note that the labels in these graphs are only used to illustrate how these graphs are constructed from triangles and paths, but that we do consider them as unlabeled graphs, so R is the unique unlabeled graph isomorphic to the labeled graph of Fig. 1c.

Fig. 1

The graphs N_1,2,3, P_3,4,T and R

We first consider the existence of compatible spanning circuits visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times in edge-colored 2-connected claw-free graphs, as follows.

Theorem 2.1

Let G be an edge-colored 2-connected claw-free graph on n (n ≥ 3) vertices such that ∆^mon(v) ≤ (d(v) − 1)/2 for each vertex v with d(v) ≥ 3, and ∆^mon(v) = 1 otherwise. Then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times, if one of the following holds:

• (1) δ(G) ≥ (n − 2)/3;

• (2) σ₃(G) ≥ n − 2;

• (3) G is 3-connected and δ(G) ≥ (n + 38)/10;

• (4) G is 5-connected and δ(G) ≥ 6;

• (5) G is 7-connected;

• (6) G is H-free, where H is an induced subgraph of P₆, N_0,1,2 or N_1,1,1;

• (7) G is H-free, where H is an induced subgraph of N_0,0,3, and n ≥ 10;

• (8) G is H-free, where H {P₇, P_T,T,T}, H {N_1,1,2, P_T,T,T}, H {N_0,1,2, P_3,3,3} or H {N_0,1,3, R}.

Remark 2.1

In Theorem 2.1, it is worth noting that Condition (1) implies Condition (2), and Condition (5) implies Condition (4).

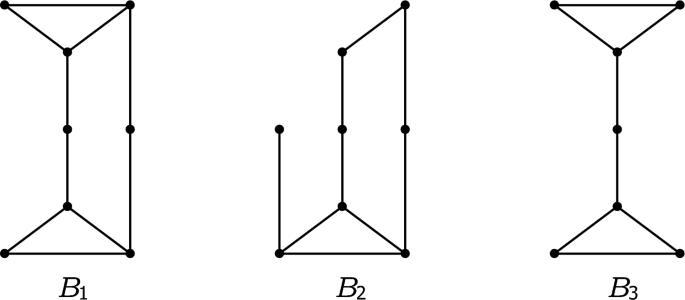
By replacing the conditions of Theorem 2.1 by some other conditions, we can still guarantee the existence of compatible spanning circuits visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times in edge-colored 2-connected claw-free graphs, as shown in the following theorem. In order to state our result, we introduce three induced subgraphs B_i (i ∈ {1, 2, 3}) of the graph P_3,3,3, which are depicted in Fig. 2. We further define three families of pairs of graphs serving as forbidden induced subgraphs in the following result. Set H₁ = {{P_3,3,3, Y} | Y ∈ {P₈, N_0,1,4, N_1,1,3, N_1,2,2}}, H₂ = {{X, Y} | X ∈ {B₁, B₂}, Y ∈ {P₉, N_0,1,5, N_1,1,4, N_1,2,3, N_2,2,2}} and H₃ = {{B₃, Y} | Y ∈ {P₁₀, N_0,2,5, N_1,2,4, N_2,2,3}}.

Fig. 2

Three induced subgraphs of P_3,3,3

Theorem 2.2

Let G be an edge-colored 2-connected claw-free graph such that ∆^mon(v) ≤ (d(v) − 1)/2 for each vertex v with d(v) ≥ 3, and ∆^mon(v) = 1 otherwise. Then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times, if one of the following holds:

• (1) G is 4-edge-connected;

• (2) G is H-free, where H is an induced subgraph of P₇, N_0,1,3 or N_1,1,2;

• (3) G is H-free, where H H_i and H_i ∈ H₁ ∪ H₂ ∪ H₃;

• (4) G is $P^{*}$-free, where $P^{ * } = \{ P_{{x_{1} ,x_{2} ,x_{3} }} \in P|x_{1} ,x_{2} ,x_{3} = T \, and \, 3 \le x_{1} \le x_{2} \le x_{3} \} ;$

• (5) G is a graph with the longest induced cycle of length at most 5.

We also show that the sufficient conditions of Theorem 2.2 can still guarantee the existence of compatible spanning circuits visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times in edge-colored 2-edge-connected claw-free graphs, as follows. So we can relax 2-connectivity to 2-edge-connectivity.

Theorem 2.3

Let G be an edge-colored 2-edge-connected claw-free graph satisfying one of Conditions (1)–(5) of Theorem 2.2. If ∆^mon(v) ≤ (d(v) − 1)/2 for each vertex v with d(v) ≥ 3, and ∆^mon(v) = 1 otherwise, then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v)\, - \,{1})/{2}} \right\rfloor$ times.

We can also confirm the existence of compatible spanning circuits visiting each vertex at least a specified number of times in edge-colored connected (2-connected, respectively) graphs G with κ(G) ≥ α(G) (κ(G) ≥ α(G) − 1, respectively), as shown in the following two theorems.

Theorem 2.4

Let G be an edge-colored connected graph on n (n ≥ 3) vertices such that κ(G) ≥ α(G). If ∆^mon(v) ≤ (d(v) − κ(G))/2 for each vertex v with d(v) ≥ κ(G) + 2, and ∆^mon(v) = 1 otherwise, then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v) - \kappa (G))/{2}} \right\rfloor$ times.

Before stating the next result, we first introduce the graphs K_2,3, K_2,3(1), K_2,3(2) and $K_{{{2},{3}}}^{t}$ that are used as exceptional graphs in our result, and that are depicted in Fig. 3. In the following theorem, when we say that a graph G^t is obtained from a graph G by replacing a vertex v of G by a graph H disjoint with G, we mean that the number of edges in G^t joining H to G − v exactly equals d_G(v) (we do not need to care which vertices of H are incident with the edges of G^t joining H to G − v).

Fig. 3

The graphs K_2,3, K_2,3(1), K_2,3(2) and $K_{{{2},{3}}}^{t}$

Theorem 2.5

Let G be an edge-colored 2-connected graph such that κ(G) ≥ α(G) − 1. If ∆^mon(v) ≤ (d(v) − κ(G) − 1)/2 for each vertex v with d(v) ≥ κ(G) + 3, and ∆^mon(v) = 1 otherwise, then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v) - \kappa (G) - 1)/{2}} \right\rfloor$ times, unless

• (1) $G \in \{ P,K_{2,3} ,K_{2,3} \left( 1 \right),K_{2,3} \left( 2 \right),K_{2,3}^{t} \} ,$ where P is the Petersen graph; or

• (2) G is one of 2-connected graphs obtained from K_2,3 or K_2,3(1) by replacing a vertex whose all neighbors have degree 3 in K_2,3 or K_2,3(1) by a complete graph on at least three vertices.

Inspired by the proof of Theorem 2.5, we further confirm the existence of compatible spanning circuits visiting each vertex at least a specified number of times in edge-colored connected graphs G with κ^t(G) ≥ α(G), as follows.

Theorem 2.6

Let G be an edge-colored connected graph on n (n ≥ 3) vertices such that κ^t(G) ≥ α(G). If ∆^mon(v) ≤ (d(v) − κ^t(G))/2 for each vertex v with d(v) ≥ κ^t(G) + 2, and ∆^mon(v) = 1 otherwise, then G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d(v) - \kappa^{t} (G))/{2}} \right\rfloor$ times.

In the next section, we present the key ingredients for our proofs of the above results that are postponed to Sect. 4.

3 Preliminaries

In this section, we give some basic results which will be used in the proofs of the main results in Sect. 4. All the results that are listed below are from existing literature and due to different (groups of) researchers, except for the next key theorem and its corollaries.

Theorem 3.1

Let G be a claw-free hamiltonian graph. Then G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − 2 for each vertex v of H.

Proof

Let H be a given Hamilton cycle of the graph G. Note that the Hamilton cycle H itself is a spanning eulerian subgraph of G. We start with the Hamilton cycle H. Using a greedy idea, we extend the Hamilton cycle H to become a desired spanning eulerian subgraph of G by repeatedly performing the following two operations (in any order) as long as possible:

Operation 1. If there exists a triangle in the subgraph G^t = G − E(H), then add the edges of the triangle to H;

Operation 2. If there exists a 2-path uwv in the subgraph G^t = G − E(H) for an edge uv of H, then replace the edge uv of H by the edges uw and wv.

For simplicity of the notation, we still use the notation H to denote the resulting spanning eulerian subgraph of G after each of the above operations.

Next, we prove by contradiction that the eventual resulting spanning eulerian subgraph H of G satisfies d_H (v) ≥ d_G(v) − 2 for each vertex v of H. Suppose, to the contrary, that there exists a vertex x of H such that d_H (x) ≤ d_G(x) − 3. It follows that there exist three neighbors x₁, x₂ and x₃ of x in G such that $xx_{i} \notin E(H)$ for i ∈ {1, 2, 3}. Since the graph G is claw-free, we have α(G[{x₁, x₂, x₃}]) ≤ 2. Without loss of generality, we suppose that x₁x₂ ∈ E(G). If $x_{1} x_{2} \notin E(H),$ then we can continue to perform Operation 1 (i.e., add these edges xx₁, x₁x₂ and xx₂ to H). If x₁x₂ ∈ E(H), then we can continue to perform Operation 2 (i.e., replace the edge x₁x₂ of H by the two edges x₁x and xx₂). In both cases we obtain a contradiction with the assumption that H is the resulting graph. This completes the proof. □

Using similar arguments as in the proof of Theorem 3.1, we can obtain the following more general result in a straightforward way.

Corollary 3.1

Let k be an integer such that k ≥ 3, and let G be a K_1,k-free hamiltonian graph. Then G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − k + 1 for each vertex v of H.

Remark 3.1

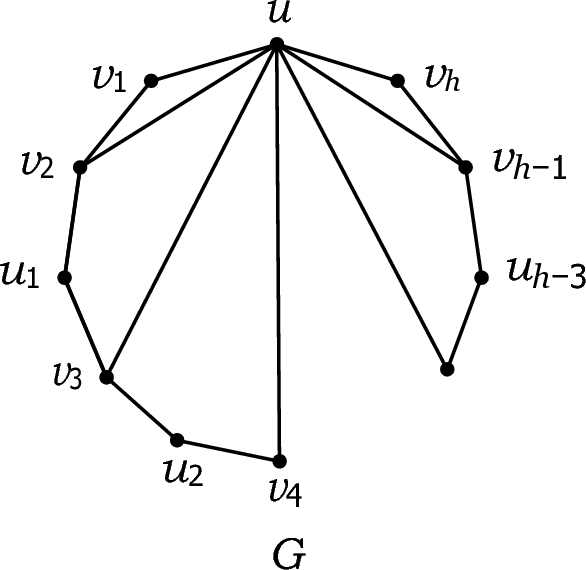
The following example shows that the bound on d_H (v) in Corollary 3.1 is tight. In particular, the case with h = 4 in the example also shows that the bound on d_H (v) in Theorem 3.1 is tight.

Example 3.1

Let h be an integer such that h ≥ 4, and let G be a graph obtained from a Hamilton cycle $H = uv_{1} v_{2} u_{1} v_{3} u_{2} v_{4} \cdots u_{h - 3} v_{h - 1} v_{h} u$ on 2h − 2 vertices by joining vertices u and v_i by an edge for each integer i with 2 ≤ i ≤ h − 1 (see Fig. 4).

Fig. 4

The graph illustrating Example 3.1

One can check that d_G(u) = h and α(G[N (u)]) = h − 2 for the graph G of Example 3.1. Hence, for h ≥ 5 it follows that the graph G is K_1,h−1-free, since all other vertices (= u) have degree at most 3 in G. For h = 4, it is straightforward to check that G is claw-free. Observing the vertices with degree 2, it is easy to check that for all h ≥ 4 the graph G has a unique spanning eulerian subgraph, namely the Hamilton cycle H of G. We have d_H (u) = 2 = h − (h − 1) + 1 = d_G(u) − (h − 1) + 1 = d_G(u) − k + 1, where k = h − 1.

Using similar arguments as in the proof of Theorem 3.1, we immediately obtain the following counterpart for supereulerian graphs, by starting with a spanning eulerian subgraph of the supereulerian graph, which is not necessarily a Hamilton cycle.

Corollary 3.2

Let k be an integer such that k ≥ 3, and let G be a K_1,k-free supereulerian graph. Then G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − k + 1 for each vertex v of H.

Now, we list some known results on hamiltonian graphs which will be used in the proof of Theorem 2.1 in Sect. 4. The forbidden induced subgraphs involved in the following theorem have been introduced in Sect. 2.

Theorem 3.2

Let G be a 2-connected claw-free graph on n (n ≥ 3) vertices. Then G is hamiltonian if one of the following holds:

• (1) (Matthews and Sumner [26]) δ(G) ≥ (n − 2)/3;

• (2) (Broersma [6], and Zhang [35]) σ₃(G) ≥ n − 2;

• (3) (Favaron and Fraisse [12]) G is 3-connected and δ(G) ≥ (n + 38)/10;

• (4) (Kaiser and Vr´ana [21]) G is 5-connected and δ(G) ≥ 6;

• (5) (Ryj´aˇcek [29]) G is 7-connected;

• (6) (Bedrossian [3]) G is H-free, where H is an induced subgraph of P₆, N_0,1,2 or N_1,1,1;

• (7) (Faudree et al. [11]) G is H-free, where H is an induced subgraph of N_0,0,3, and n ≥ 10;

• (8) (Brousek [7]) G is H-free, where H {P₇, P_T,T,T}, H {N_1,1,2, P_T,T,T}, H {N_0,1,2, P_3,3,3} or H {N_0,1,3, R}.

We will also use the following well-known sufficient condition for a graph to be hamiltonian in the proof of Theorem 2.4 in Sect. 4.

Theorem 3.3

(Chvátal and Erdös [10]) Let G be a connected graph on n (n ≥ 3) vertices. If κ(G) ≥ α(G), then G is hamiltonian.

Next, we list some known results on supereulerian graphs which will be used in the proofs of Theorems 2.2 and 2.3 in Sect. 4. The forbidden induced subgraphs involved in the following theorem have been introduced in Sect. 2.

Theorem 3.4

Let G be a 2-connected claw-free graph. Then G is supereulerian if one of the following holds:

• (1) (Catlin [8], and Jaeger [20]) G is 4-edge-connected;

• (2) (Lv and Xiong [25]) G is H-free, where H is an induced subgraph of P₇, N_0,1,3 or N_1,1,2;

• (3) (Wang and Xiong [34]) G is H-free, where H H_i and H_i ∈ H₁ ∪ H₂ ∪ H₃;

• (4) (Wang and Xiong [34]) G is $P^{*}$-free, where $P^{ * } = \{ P_{{x_{1} ,x_{2} ,x_{3} }} \in P | x_{1} ,x_{2} ,x_{3} = T \, and \, 3 \le x_{1} \le x_{2} \le x_{3} \} ;$

• (5) (Wang and Xiong [34]) G is a graph with the longest induced cycle of length at most 5.

We will also use the following result on supereulerian graphs in the proof of Theorem 2.5 in Sect. 4. The exceptional graphs involved in the following theorem have been introduced in Sect. 2.

Theorem 3.5

(Han et al. [18]) Let G be a 2-connected graph. If κ(G) ≥ α(G) − 1, then G is supereulerian, unless

• (1) $G \in \{ P,K_{2,3} ,K_{2,3} \left( 1 \right),K_{2,3} (2),K_{2,3}^{t} \} ,$ where P is the Petersen graph; or

• (2) G is one of 2-connected graphs obtained from K_2,3 or K_2,3(1) by replacing a vertex whose all neighbors have degree 3 in K_2,3 or K_2,3(1) by a complete graph on at least three vertices.

We will also use the following sufficient condition for a graph to be supereulerian in the proof of Theorem 2.6 in Sect. 4.

Theorem 3.6

(Bang-Jensen and Maddaloni [2]). Let G be a connected graph on n (n ≥ 3) vertices. If κ^t(G) ≥ α(G), then G is supereulerian.

Finally, we list the following theorem on the existence of compatible Euler tours that will be frequently used in the proofs of the main results in Sect. 4.

Theorem 3.7

(Kotzig [22]). Let G be an edge-colored eulerian graph. Then a compatible Euler tour exists if and only if ∆^mon(v) ≤ d(v)/2 for each vertex v of G.

4 Proofs of the Main Results

Proof of Theorem 2.1

Let G be an edge-colored 2-connected claw-free graph on n (n ≥ 3) vertices satisfying one of Conditions (1)–(8) of Theorem 2.1. It follows that G is a claw-free hamiltonian graph by Theorem 3.2. By Theorem 3.1, G contains a spanning eulerian subgraph H such that d_H (v) = d_G(v) − 1 for each vertex v of G of odd degree and d_H (v) ≥ d_G(v) − 2 for each vertex v of G of even degree. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - 1)/2$ for each vertex v of G with d_G(v) ≥ 3, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le \left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor \le d_{H} (v)/2$ for each vertex v of G with d_G(v) ≥ 3. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = 1 \le d_{H} (v)/2$ for each vertex v of G with d_G(v) = 2. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor$ times. This completes the proof. □

Proof of Theorem 2.2

Let G be an edge-colored 2-connected claw-free graph satisfying one of Conditions (1)–(5) of Theorem 2.2. It follows that G is a claw-free supereulerian graph by Theorem 3.4. By Corollary 3.2, G contains a spanning eulerian subgraph H such that d_H (v) = d_G(v) − 1 for each vertex v of G of odd degree and d_H (v) ≥ d_G(v) − 2 for each vertex v of G of even degree. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - 1)/2$ for each vertex v of G with d_G(v) ≥ 3, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le \left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor \le d_{H} (v)/2$ for each vertex v of G with d_G(v) ≥ 3. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = 1 \le d_{H} (v)/2$ for each vertex v of G with d_G(v) = 2. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor$ times. This completes the proof. □

Proof of Theorem 2.3

Let G be an edge-colored 2-edge-connected claw-free graph satisfying one of Conditions (1)–(5) of Theorem 2.2. If G is 2-connected, then it is a claw-free supereulerian graph by Theorem 3.4. Next, we assume that G is a graph with connectivity 1. Now, we consider the nontrivial blocks of G. Note that every nontrivial block of G is 2-connected. Moreover, we conclude that every nontrivial block of G satisfies one of Conditions (1)–(5) of Theorem 2.2; otherwise, G would not satisfy any one of Conditions (1)–(5) of Theorem 2.2. It follows that every nontrivial block of G is a supereulerian graph by Theorem 3.4. We can show that G is supereulerian by taking one spanning eulerian subgraph from every nontrivial block of G and then combining these spanning eulerian subgraphs to obtain a spanning eulerian subgraph of G. Recall that G is a claw-free graph. By Corollary 3.2, G contains a spanning eulerian subgraph H such that d_H (v) = d_G(v) − 1 for each vertex v of G of odd degree and d_H (v) ≥ d_G(v) − 2 for each vertex v of G of even degree. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - {1})/{2}$ for each vertex v of G with d_G(v) ≥ 3, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le \left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor \le d_{H} (v)/2$ for each vertex v of G with d_G(v) ≥ 3. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = 1 \le d_{H} (v)/2$ for each vertex v of G with d_G(v) = 2. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - 1)/2} \right\rfloor$ times. This completes the proof. □

Proof of Theorem 2.4

Let G be an edge-colored connected graph on n (n ≥ 3) vertices such that κ(G) ≥ α(G). It follows that G is a hamiltonian graph by Theorem 3.3. Since we have α(G) ≤ κ(G), G is a K_1,κ(G)+1-free graph. If κ(G) = 1, then we have α(G) = 1, implying that G is a complete graph. It is not difficult to check that the complete graph G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − κ(G) for each vertex v of H (in fact H = G, if n is odd; otherwise, H = G − M, where M is an arbitrary prefect matching of G). Now, we consider the case that κ(G) ≥ 2. By Corollary 3.1, G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − κ(G) for each vertex v of H. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa (G))/{2}$ for each vertex v of G with d_G(v) ≥ κ(G) + 2, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa (G))/{2} \le d_{H} (v)/{2}$ for each vertex v of G with d_G(v) ≥ κ(G) + 2. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = 1 \le d_{H} (v)/2$ for each vertex v of G with d_G(v) ≤ κ(G) + 1. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - \kappa (G))/{2}} \right\rfloor$ times. This completes the proof. □

Proof of Theorem 2.5

Let G be an edge-colored 2-connected graph such that κ(G) ≥ α(G) − 1 and $G \notin \{ P,K_{2,3} ,K_{2,3} \left( 1 \right),K_{2,3} (2),K_{2,3}^{t} \} ,$ where P is the Petersen graph and the other graphs have been depicted in Fig. 3. We further assume that G is not any one of 2-connected graphs obtained from K_2,3 or K_2,3(1) by replacing a vertex whose all neighbors have degree 3 in K_2,3 or K_2,3(1) by a complete graph on at least three vertices. It follows that G is a supereulerian graph by Theorem 3.5. Since we have α(G) ≤ κ(G) + 1, G is a K_1,κ(G)+2-free graph. By Corollary 3.2, G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − κ(G) − 1 for each vertex v of H. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa (G) - {1})/{2}$ for each vertex v of G with d_G(v) ≥ κ(G) + 3, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa (G) - {1})/{2} \le d_{H} (v)/{2}$ for each vertex v of G with d_G(v) ≥ κ(G) + 3. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = {1} \le d_{H} (v)/{2}$ for each vertex v of G with d_G(v) ≤ κ(G) + 2. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - \kappa (G) - {1})/{2}} \right\rfloor$ times. This completes the proof. □

Proof of Theorem 2.6

Let G be an edge-colored connected graph on n (n ≥ 3) vertices such that κ^t(G) ≥ α(G). It follows that G is a supereulerian graph by Theorem 3.6. Since we have α(G) ≤ κ^t(G), G is a K_{1,κ (G)+1}-free graph. If κ^t(G) = 1, then we have α(G) = 1, implying that G is a complete graph. It is not difficult to check that the complete graph G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − κ^t(G) for each vertex v of H (in fact H = G, if n is odd; otherwise, H = G − M, where M is an arbitrary prefect matching of G). Now, we consider the case that κ^t(G) ≥ 2. By Corollary 3.2, G contains a spanning eulerian subgraph H such that d_H (v) ≥ d_G(v) − κ^t(G) for each vertex v of H. If $\Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa^{t} (G))/2$ for each vertex v of G with d_G(v) ≥ κ^t(G) + 2, then we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) \le (d_{G} (v) - \kappa^{t} (G))/2 \le d_{H} (v)/2$ for each vertex v of G with d_G(v) ≥ κ^t(G) + 2. Since H is a spanning eulerian subgraph of G, we have d_H (v) ≥ 2 for each vertex v of G. Thus, we have $\Delta_{H}^{mon} (v) \le \Delta_{G}^{mon} (v) = {1} \le d_{H} (v)/{2}$ for each vertex v of G with d_G(v) ≤ κ^t(G) + 1. Based on the above argument, there exists a compatible Euler tour in H by Theorem 3.7. Therefore, G contains a compatible spanning circuit visiting each vertex v at least $\left\lfloor {(d_{G} (v) - \kappa^{t} (G))/{2}} \right\rfloor$ times. This completes the proof. □

5 Concluding Remarks

In this work, we first proved a key theorem (i.e., Theorem 3.1) that deals with the existence of spanning eulerian subgraphs H of G satisfying d_H (v) ≥ d_G(v) − 2 for each vertex v of G, and we obtained some related corollaries. We then established sufficient conditions for the existence of compatible spanning circuits visiting each vertex at least a specified number of times in specific edge-colored graphs that do not contain certain forbidden induced subgraphs, by combining the conditions of Theorem 3.1 (or its corollaries) with the conditions of Theorem 3.7. As applications, we also considered the existence of such compatible spanning circuits in edge-colored graphs G with κ(G) ≥ α(G), κ(G) ≥ α(G)−1 and κ^t(G) ≥ α(G), respectively.

Although we did not consider any counterparts of our results for digraphs, we realize that counterparts for digraphs analogous to Theorem 3.7 have been discussed (see [13, 17, 19]). Motivated by the ideas we explored in this paper, it is natural to consider the existence of compatible spanning circuits visiting each vertex at least a specified number of times in arc-colored digraphs. However, it looks difficult or even impossible to obtain a straightforward analogue of Theorem 3.1 for digraphs, indicating that it is very likely that different approaches are necessary. We leave this as an open problem.

Problem 5.1.

Let D be an arc-colored digraph. Can D contain a compatible spanning circuit visiting each vertex at least a specified number of times? If so, under what conditions does D contain such a compatible spanning circuit?