Some Properties of Gromov–Hausdorff Distances

Abstract

The Gromov–Hausdorff distance between metric spaces appears to be a useful tool for modeling some object matching procedures. Since its conception it has been mainly used by pure mathematicians who are interested in the topology generated by this distance, and quantitative consequences of the definition are not very common. As a result, only few lower bounds for the distance are known, and the stability of many metric invariants is not understood. This paper aims at clarifying some of these points by proving several results dealing with explicit lower bounds for the Gromov–Hausdorff distance which involve different standard metric invariants. We also study a modified version of the Gromov–Hausdorff distance which is motivated by practical applications and both prove a structural theorem for it and study its topological equivalence to the usual notion. This structural theorem provides a decomposition of the modified Gromov–Hausdorff distance as the supremum over a family of pseudo-metrics, each of which involves the comparison of certain discrete analogues of curvature. This modified version relates the standard Gromov–Hausdorff distance to the work of Boutin and Kemper, and Olver.

1 Introduction

The Gromov–Hausdorff distance is a useful tool for studying topological properties of families of metric spaces. According to Berger [2], Gromov first introduced the notion of Gromov–Hausdorff distance in his ICM 1979 address in Helsinki on synthetic Riemannian geometry. The goal of the program he put forward was the study of all (Riemannian) metric structures: to give some structure to this space and to study completeness, possible convergences, compact families, and related concepts. Gromov made use of the Gromov–Hausdorff distance as a tool for attacking the proof of his theorem on groups of polynomial growth [12].

For a map ϕ:X→Y between metric spaces (X,d _X ) and (Y,d _Y ), its distortion is given by

$$ \mathrm {dis} ({\phi} ):=\sup_{x,x'\in X}\bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(\phi(x),\phi \bigl(x'\bigr)\bigr)\bigr|.$$

(1)

The Gromov–Hausdorff distance between (compact) metric spaces X and Y can be proved [18] to be equal to

$$ d_{\mathcal{G}\mathcal{H}}({X},{Y}) = \inf_{\tiny \begin{array}{ll} \phi:X\rightarrow Y\\\psi:Y\rightarrow X\end{array}} \frac{1}{2}\max\bigl(\mathrm {dis} ({\phi} ),\mathrm {dis} ({\psi} ),C(\phi,\psi )\bigr),$$

(2)

where, for maps ϕ:X→Y and ψ:Y→X,

$$ C(\phi,\psi) := \sup_{\tiny x\in X,\,y\in Y}\bigl|d_X\bigl(x,\psi(y)\bigr)-d_Y\bigl(\phi(x),y\bigr)\bigr|.$$

(3)

See Definition 3.2 for the standard form of the GH distance. Note that the condition that C(ϕ,ψ)<δ implies that d _X (x,ψ∘ϕ(x))<δ for all x∈X and d _Y (y,ϕ∘ψ(y))<δ for all y∈Y which is a relaxation of the condition that ϕ and ψ be inverses of each other.

The Gromov–Hausdorff distance has received attention in the applied literature, where the motivation for its use originated in the area of object matching under invariances [24, 25]. The idea is to regard objects as metric spaces in a manner such that the choice of metric with which these objects are endowed dictates the type of invariance that is desired. A standard example is that of comparing objects in Euclidean space under invariance to rigid isometries: in that case objects are given the (restriction of the) Euclidean metric.

It is known that solving for the GH distance between finite metric spaces leads to NP-hard problems [20]. Applied researchers have tackled the numerical computation of the GH distance using ad hoc optimization techniques [6, 24, 25] and not many inroads have been made into producing lower bounds for the GH distance, see [10, 20, 21]. See [23] for properties of the related Gromov–Wasserstein distance in the context of metric spaces endowed with probability measures.

In this paper we identify a number of new lower bounds for the Gromov–Hausdorff distance, all of which can be computed in polynomial time. We also study a certain modified version of the Gromov–Hausdorff distance which is in turn related to a family of isometry invariants of metric spaces that provides full classification of compact metric spaces up to isometry. We believe that the material in this paper will provide more understanding about the use of the Gromov–Hausdorff distance in applications, as well as about its relationship with pre-existing work.

1.1 Organization of the Paper

In Sect. 1.2 we set up basic terminology. In Sect. 2 we first introduce the definition of several isometry invariants of compact metric spaces and discuss their ability to discriminate between certain metric spaces. In Sect. 3 we recall the main properties of the standard Gromov–Hausdorff distance and the topology it generates. Then, in Sect. 3.1, we state Theorem 3.4: this theorem establishes a hierarchy of lower bounds for the GH distance between two given compact metric spaces, which involves, in a precise sense, the comparison of all the invariants defined in Sect. 2. In Sect. 3.1 we also look into the numerical implementation and computational complexity of the lower bounds stated in Theorem 3.4.

In Sect. 4, we explain how, with a small change to expression (2), we obtain another possible distance between compact metric spaces, which we call the modified Gromov–Hausdorff distance. The definition of this distance is motivated by computational considerations [6, 24, 25], and it leads to solving two independent or decoupled matching problems. In that section we give several examples, and by an explicit construction, we also prove that this new definition gives us a distance which is different from the standard GH distance. In Theorem 4.1 we prove that this modified Gromov–Hausdorff does provide a legitimate distance on the collection of all compact metric spaces, and in Theorem 4.2 we prove that both the standard GH distance and the modified GH distance are topologically equivalent within Gromov–Hausdorff precompact classes of compact metric spaces. The modified GH distance turns out to be a lower bound for the standard GH distance.

In Sect. 5 we discuss another family of isometry invariant of metric spaces, called curvature sets, which were first considered by Gromov in [13]. We discuss how these invariants absorb useful information from compact metric spaces, in a manner that suggests that they may be of interest in practical applications. In addition, we also show how curvature sets are intimately related to the constructions of Boutin and Kemper [4], and Olver [26]. Theorem 5.1 provides a decomposition of the modified GH distance as the supremum over a family of pseudo-metrics on the collection of all compact metric spaces, where each of these pseudo-metrics involves the comparison of curvature sets of the intervening spaces.

Finally, in Sect. 6 we give some remarks about possible extensions.

With the goal of providing a reference for some aspects of the Gromov–Hausdorff distance that are not covered elsewhere, we provide proofs for all our results, and in order to maximize readability, we give all proofs of our mathematical statements at the end of the section where they are stated.

1.2 Background and Notation

Recall that a metric space is a pair (X,d _X ) where X is a set and d _X :X×X→ℝ⁺ with the properties (I) d _X (x,x′)=d _X (x′,x) for all x,x′∈X; (II) d _X (x,x″)≤d _X (x,x′)+d _X (x′,x″) for all x,x′,x″∈X; and (III) d _X (x,x′)=0 if and only if x=x′.

By ${{\mathcal{B}}}({X})$ we denote all Borel sets of X. Recall that a set S⊂X is called an ε-net of X if for all x∈X there exists s∈S with d _X (x,s)≤ε. If λ≥0 and (X,d _X ) is any metric space, then λ⋅X will denote the metric space (X,λ⋅d _X ). We denote by $\mathcal{G}$ the collection of all compact metric spaces. Given (X,d _X ) and (Y,d _Y ) in $\mathcal{G}$, a map φ:X→Y is called an isometry if d _X (x,x′)=d _Y (φ(x),φ(x′)) for x,x′∈X and φ is surjective. When this happens, one says that X and Y are isometric. Given a fixed set ℑ, we say that a function $\iota:\mathcal{G}\rightarrow\mathfrak{I}$ is an isometry invariant of metric spaces, if ι(X)=ι(Y) whenever X and Y are isometric.

For a Riemannian manifold (X,g _X ) we denote by vol _X (⋅) the Riemannian volume measure on X; its total volume by Vol(X)=vol _X (X); and its geodesic distance function by d _X .

For n∈ℕ, let Δ _n denote the (n−1)-simplex: a metric space with n points all at unit distance from each other. For a,b,c>0 satisfying all triangle inequalities, T(a,b,c) denotes the three point metric space

For k∈ℕ let Π _k denote the set of all permutation matrices of size k×k. It will be useful to consider the following notation: D _X is the map that assigns each finite subset $\mathbb{X}$ of the metric space (X,d _X ) with its distance matrix, that is, $\mathbf{D}_{X}(\mathbb{X}) =({\!}({d_{X}(x,x')})\!)_{x,x'\in\mathbb{X}}$.

Recall that a subset A of a topological space Z is precompact whenever its closure $\overline{A}$ is a compact subset of Z.

2 Isometry Invariants of Metric Spaces

The theoretical literature is mainly concerned with properties of the topology generated by the GH distance on $\mathcal{G}$, and whenever $\iota:\mathcal{G}\rightarrow \mathbb{R}$ is an isometry invariant of metric spaces, available results about the stability of ι are of qualitative nature, namely that $\iota(X_{n})\stackrel {n}{\longrightarrow } \iota(X)$ whenever {X _n } _n∈ℕ is a sequence of compact metric spaces converging to X in the GH sense. Examples of this are contained in [14–16, 19]. In contrast, in applications, one is mostly concerned with problems that require a quantitative type of stability of the invariants, namely that

$$ \bigl|\iota(X)-\iota(Y)\bigr|\leq \varPsi \bigl(d_{\mathcal{G}\mathcal{H}}({X},{Y})\bigr)\quad \mbox{for all}\ X,Y\in\mathcal{G},$$

(4)

for some non-decreasing function Ψ:ℝ⁺→ℝ⁺ with Ψ(0)=0. One reason why identifying quantitatively stable metric invariants is important is because inequalities such as (4) provide lower bounds for the GH distance that can be used for discriminating objects or datasets in practical applications, without incurring the potentially high computational cost of estimating the full GH distance.

In Theorem 3.4 we prove the quantitative stability of several isometry invariants of metric spaces that we now define.

Definition 2.1

For a given compact metric space (X,d _X ) we define the following invariants:

• Diameter: diam(X):=max _x,x′ d _X (x,x′).

• Separation: sep(X):=inf _x≠x′ d _X (x,x′).

• Circum-radius: rad(X):=min _x max _x′ d _X (x,x′).

• Eccentricity Function: ecc _X :X→ℝ⁺ given by x↦max _x′ d _X (x,x′).

• Distance set: $\boldsymbol{\mathcal{D}}_{X}:=\{d_{X}(x,x'),\,x,x'\in X\}$.

• Local distance sets: $\boldsymbol{\mathcal {L}}_{X}:X\rightarrow {{\mathcal{B}}}({\mathbb{R}^{+}})$ given by x↦{d _X (x,x′), x′∈X}.

In the applied literature, local distance sets have been considered by Grigorescu and Petkov [11], eccentricities by Hilaga et al. [17] and Hamza and Krim [1], global distance sets by Osada et al. [27] and Boutin and Kemper [4].

Example 2.1

(Two non-isometric metric spaces with the same distance set)

A strikingly simple example is the following one [3], which provides two non-isometric finite sets of points on the real line which have the same distribution of distances: let X={0,1,4,10,12,17}⊂ℝ and Y={0,1,8,11,13,17}⊂ℝ. Then

$$\boldsymbol {\mathcal {D}}_{X}=\boldsymbol {\mathcal {D}}_{Y} =\{0,1,2,3,4,5,6,7,8,9,10,11,12,13,16,17\}.$$

Note, however, that ecc _X (X)={10,12,13,16,17} whereas ecc _Y (Y)={9,11,13,16,17}. The case of perfect discrimination of finite Euclidean metric spaces using distance sets has been carefully analyzed in [4].

Example 2.2

(Two non-isometric spaces with matching eccentricities)

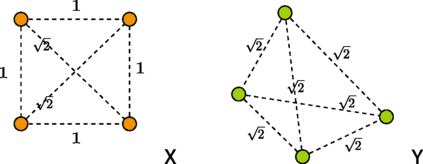
Consider the two metric spaces X and Y of Fig. 1. Note that they have matching eccentricities (i.e. there exists a bijection from one space into the other that preserves the values of the eccentricities). Note, however, that $\boldsymbol {\mathcal {D}}_{X}=\{0,1,\sqrt{2}\}$ whereas $\boldsymbol {\mathcal {D}}_{Y}=\{0,\sqrt{2}\}$.

Fig. 1

Two non-isometric metric spaces with matching eccentricities but different distance sets, see Example 2.2

Remark 2.1

Note that by the preceding examples, the lower bounds given by (11) and (14) in Theorem 3.4 are independent.

Remark 2.2

Distance sets and local distance sets are useful mostly for discriminating between finite metric spaces. Note that for a connected metric space X, sep(X)=0 and $\boldsymbol{\mathcal{D}}_{X}=[0,{\mathbf {diam}}({X})]$. Also, note that for any compact metric space X,

• $\boldsymbol{\mathcal{L}}_{X}(x) \subseteq[0,\mathbf {ecc}_{X}(x)]$ for all x∈X. There is equality for connected metric spaces.

• rad(X)=min _p ecc _X (p)≤ecc _X (x)≤max _p ecc _X (p)=diam(X), for all x∈X.

Finally, notice that for spheres $\mathbb{S}^{n}$ (regarded as metric spaces by endowing them with the geodesic distance), ${\mathbf {rad}}({\mathbb{S}^{n}})={\mathbf {diam}}({\mathbb{S}^{n}})=\mathbf {ecc}_{\mathbb{S}^{n}}(\cdot)=\pi$, for all n∈ℕ and hence these invariants fail to discriminate spheres of different dimensions.

Example 2.3

One has rad(T(a,b,c))=min(max(a,b),max(b,c),max(c,a)).

3 The Gromov–Hausdorff Distance and Lower Bounds

In this section we recall the main properties of the GH distance and then in Sect. 3.1 we state and prove a theorem about the quantitative stability of the invariants introduced in Definition 2.1.

Definition 3.1

Let (Z,d) be a metric space and A,B⊂Z. Then, the Hausdorff distance between A and B is given by

$$ d_{\mathcal{H}}^{Z} ({A},{B} ):=\max\Bigl(\sup_{a\in A}\inf_{b\in B}d(a,b),\sup_{b\in B}\inf_{a\in A} d(a,b)\Bigr).$$

(5)

The Hausdorff distance is indeed a metric on the collection of closed subsets of a compact metric space (Z,d) [7, Proposition 7.3.3].

Definition 3.2

(Chap. 3 of [13])

The Gromov–Hausdorff distance $d_{\mathcal{G}\mathcal{H}}({X},{Y})$ between compact metric spaces (X,d _X ) and (Y,d _Y ) is defined to be the infimal ε>0 s.t. there exists a metric d on X⊔Y with $d_{|_{X\times X}}=d_{X}$ and $d_{|_{Y\times Y}} = d_{Y}$ for which the Hausdorff distance between X and Y (as subsets of (X⊔Y,d)) is less than ε. From now on let $\mathcal{G}$ denote the collection of all compact metric spaces.

Definition 3.3

(The Gromov–Hausdorff topology)

One says that $\{(X_{n},d_{X_{n}})\}_{n\in \mathbb{N}}\subset\mathcal{G}$ Gromov–Hausdorff converges to $X\in\mathcal{G}$ if and only if $d_{\mathcal{G}\mathcal{H}}({X_{n}},{X})\rightarrow0$ as n↑∞.

Theorem 3.1

(Chap. 10 [29])

The space $(\mathcal{G},d_{\mathcal{G}\mathcal{H}})$ is separable and complete.

Definition 3.4

(Covering number)

For each ρ≥0 let cov _X (ρ) denote the minimal number of open balls of radius ρ with which one can cover the compact metric space X.

The topology generated by the GH distance (see Definition 3.3) is rather coarse and this allows the existence of rich families of precompact sets.

Theorem 3.2

(Gromov’s precompactness theorem, [7])

For a bounded function N:ℝ⁺→ℕ and D>0 let $\mathcal {F}(N;D)\subset\mathcal{G}$ denote the collection of all compact metric spaces X with diam(X)≤D and s.t. cov _X (ρ)≤N(ρ) for each ρ>0. Then, $\mathcal{F}(N;D)$ is precompact for the Gromov–Hausdorff topology.

Example 3.1

(Simplices)

Consider the family {Δ _n , n∈ℕ} of compact metric spaces. One has diam(Δ _n )=1 for all n∈ℕ but clearly there exists no function N:ℝ⁺→ℕ as in Theorem 3.2. We see in Example 4.1 below that $d_{\mathcal{G}\mathcal{H}}({\varDelta_{n}},{\varDelta_{m}})=\frac{1}{2}$ for all n≠m; hence {Δ _n } _n∈ℕ cannot have a converging sub-sequence.

Remark 3.1

(Precompact families of Riemannian manifolds)

In the Riemannian context, the collection $\mathcal{R}(n,\kappa,D)$ of n-dimensional Riemannian closed connected manifolds (seen as metric spaces when endowed with geodesic distances) with uniform upper bound D on their diameters and uniform lower bound (n−1)κ on their Ricci curvatures is precompact for the GH topology [29, Corollary 31]. Indeed, from the Bishop–Gromov relative volume comparison theorem [30, Theorem 3.3] one sees that for any $X\in \mathcal{R}(n,\kappa,D)$

$${\mathbf {cov}}_{X} ({\rho} )\leq C\cdot\rho^{-n},\quad \mbox{for all}\ \varepsilon\in[0,D],$$

where C=C(n,κ,D) is a constant that only depends on n, κ, and D. Hence, Theorem 3.2 applies.

Theorem 3.3 item 5 below provides an alternative expression for the GH distance.

Definition 3.5

(Correspondence)

For sets A and B, a subset R⊂A×B is a correspondence (between A and B) if and only if

• ∀a∈A, there exists b∈B s.t. (a,b)∈R.

• ∀b∈B, there exists a∈X s.t. (a,b)∈R.

Let ${\mathcal{R}}({A},{B})$ denote the set of all possible correspondences between sets A and B.

Example 3.2

Let ϕ:X→Y and ψ:Y→X be given maps. Then, one can induce a correspondence R(ϕ,ψ) out of these maps, given by

$$R(\phi,\psi):=\bigl\{\bigl(x,\phi(x)\bigr),\,x\in X \bigr\}\cup\bigl\{\bigl(\psi (y),y\bigr),\,\,y\in Y\bigr\}.$$

Theorem 3.3

[7]

• (1) Let (X,d _X ), (Y,d _Y ) and (Z,d _Z ) be metric spaces then

  $$d_{\mathcal{G}\mathcal{H}}({X},{Y})\leq d_{\mathcal{G}\mathcal{H}}({X},{Z}) + d_{\mathcal{G}\mathcal{H}}({Y},{Z}).$$

• (2) Assume that (X,d _X ) and (Y,d _Y ) are compact metric spaces. Then $d_{\mathcal{G}\mathcal{H}}({X},{Y})=0$ if and only if (X,d _X ) and (Y,d _Y ) are isometric.

• (3) Let $\mathbb{X}$ be a subset of the compact metric space (X,d _X ). Then

  $$d_{\mathcal{G}\mathcal{H}}\bigl ({(X,d_X)},{(\mathbb{X},{d_X}_{|_{\mathbb{X}\times\mathbb {X}}})}\bigr )\leq d_{\mathcal{H}}^{X} ({\mathbb{X}},{X} ).$$

• (4) For compact metric spaces (X,d _X ) and (Y,d _Y ):

  $$d_{\mathcal{G}\mathcal{H}}({X},{Y}) \leq \frac{1}{2}\max\bigl({\mathbf {diam}} ({X} ),{\mathbf {diam}} ({Y} )\bigr).$$

  (6)

• (5) For compact metric spaces (X,d _X ) and (Y,d _Y ),

  $$ d_{\mathcal{G}\mathcal{H}}({X},{Y})=\frac{1}{2}\inf_{R\in {\mathcal{R}}({X},{Y})}\sup_{\tiny \begin{array}{ccc}x_1,x_2\in X\\ y_1,y_2\in Y\\ s.t.\,(x_i,y_i)\in R\\\end{array}} \bigl|d_X(x_1,x_2)-d_Y(y_1,y_2)\bigr|.$$

  (7)

Remark 3.2

Note that items 1 and 2 of the theorem encode the symmetry of the GH distance: let Z=X; then $d_{\mathcal{G}\mathcal{H}}({X},{Y})\leq d_{\mathcal{G}\mathcal{H}}({X},{X})+d_{\mathcal{G}\mathcal{H}}({Y},{Z})=d_{\mathcal{G}\mathcal{H}}({Y},{X})$ for all $X,Y\in\mathcal{G}$. Hence, by exchanging the roles of X and Y, one sees that $d_{\mathcal{G}\mathcal{H}}({X},{Y})=d_{\mathcal{G}\mathcal{H}}({Y},{X})$.

Remark 3.3

Note that (2) asserts that the infimum over all correspondences $R\in {\mathcal{R}}({X},{Y})$ in (7) can be restricted to all those correspondences with the form described in Example 3.2.

Example 3.3

(Distance between homothetic spaces)

Let $(X,d_{X})\in\mathcal{G}$ and λ≥0. Then,

$$d_{\mathcal{G}\mathcal{H}}\bigl ({(X,d_X)},{(X,\lambda\cdot d_X)}\bigr )=\frac{|\lambda-1|}{2}\cdot {\mathbf {diam}} ({X} ).$$

Indeed, since diam((X,λ⋅d _X ))=λ⋅diam(X), by (13) we see that $d_{\mathcal{G}\mathcal{H}} ((X,d_{X}), (X,\lambda\cdot d_{X}))\geq\frac{|\lambda -1|}{2}\cdot {\mathbf {diam}}({X})$. For the reverse inequality, consider the correspondence R=diag(X×X). Then by (7),

$$d_{\mathcal{G}\mathcal{H}}\bigl ({(X,d_X)},{(X,\lambda\cdot d_X)}\bigr )\leq \frac{1}{2}\max_{x,x'\in X}\bigl|d_X\bigl(x,x'\bigr)-\lambda\cdot d_X\bigl(x,x'\bigr)\bigr|=\frac{|\lambda-1|}{2}\cdot {\mathbf {diam}} ({X} ).$$

Example 3.4

Fix $(X,d_{X})\in\mathcal{G}$. Consider the sequence $\{(X,\frac{1}{n}\cdot d_{X})\}_{n\in \mathbb{N}}\subset\mathcal{G}$. Then, this sequence Gromov–Hausdorff converges to the metric space consisting of a single point.

Remark 3.4

(Gromov–Hausdorff distance and the BQAP)

We want to argue that expression (7) is very similar to the BQAP (Bottleneck Quadratic Assignment Problem). Let us restrict ourselves to the case of finite metric spaces, $\mathbb{X}=\{x_{1},\ldots,x_{n}\}$ and $\mathbb{Y}=\{y_{1},\ldots,y_{m}\}$. For $R\in{\mathcal{R}}(\mathbb{X},\mathbb{Y})$ let $\delta_{ij}^{R}$ equal 1 if (i,j)∈R and 0 otherwise. Then we have

$$d_{\mathcal{G}\mathcal{H}}({\mathbb{X}},{\mathbb{Y}}) = \frac{1}{2}\min_R\,\max_{i,k,j,l}\varGamma_{ikjl}\,\,\delta_{ij}^R\delta_{kl}^R,$$

where Γ _ikjl :=|d _X (x _i ,x _k )−d _Y (y _j ,y _l )|.

Note that one can recast the above problem as follows. Let D denote the set of matrices defined by the following constraints:

• (1) δ _ij ∈{0,1} for all i,j;

• (2) ∑ _i δ _ij ≥1 for all j;

• (3) ∑ _j δ _ij ≥1 for all i;

and let L(δ):=max _ijkl Γ _ikjl δ _ij δ _kl . Then the computation of $d_{\mathcal{G}\mathcal{H}}({\mathbb{X}},{\mathbb{Y}})$ is equivalent to min _δ∈D L(δ) which can be regarded as a generalized version of the BQAP. In the standard BQAP [9, 28] n=m and the inequalities (2) and (3) defining D above are actually equalities, what forces each δ to be a permutation matrix.

Actually, we prove next that, when n=m, min _δ∈D L(δ) reduces to a BQAP. It is known that, as an instance of binary integer quadratic programming, the BQAP is an NP-hard problem [28]. Indeed, it is clear that for any δ∈D there exist P∈Π _n (n×n permutations matrices) such that δ _ij ≥P _ij for all 1≤i,j≤n. Then, since Γ _ikjl is non-negative for all 1≤i,j,k,l≤n, it follows that L(δ)≥L(P). Therefore the minimal value of L(δ) is attained at some δ∈Π _n .

3.1 Gromov–Hausdorff Stability of Metric Invariants

Theorem 3.4 below makes precise a sense in which the metric invariants of Sect. 2 are organized into a hierarchy of lower bounds for the GH distance.

Theorem 3.4

Let X,Y be two compact metric spaces and F _X,Y :X×Y→ℝ⁺ be given by

$$(x,y)\mapsto\inf_{R}\sup_{(x',y')\in R} \bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(y,y'\bigr) \bigr|,$$

where here and below all infima are over $R\in {\mathcal{R}}({X},{Y})$. Then,

(8)

(9)

(10)

Then, in turn

(11)

(12)

(13)

and

(14)

(15)

Remark 3.5

Similar hierarchies of lower bounds are possible in contexts when one assumes that more structure is given to the spaces. One concrete example of this is the case of metric measure spaces: compact metric spaces enriched with probability measures, where instead of the GH distance one constructs a mass transportation variant called the Gromov–Wasserstein distance [23]. In the more extreme case when one assumes that the spaces are restricted to a subclass of $\mathcal{G}$ given by the collection of all compact Riemannian manifolds without boundary, then another similar hierarchy is possible, where now the GH distance is supplanted by a certain spectral version of the Gromov–Wasserstein distance, and the intervening lower bounds involve invariants that absorb spectral information of the underlying spaces [22].

Remark 3.6

Notice that for all n,m∈ℕ, $F_{\mathbb{S}^{n},\mathbb{S}^{m}}(x,y)=0$ for all $x\in \mathbb{S}^{n}$ and $y\in \mathbb{S}^{m}$. Hence, all lower bounds in Theorem 3.4 are unable to discriminate between spheres of different dimension, see, however, Example 5.3.

Remark 3.7

(About the complexity associated to computing the lower bounds)

Notice that in the case both X and Y are finite, and given F _X,Y , lower bound (8) above can be computed by solving |X|⋅|Y| bottleneck assignment problems [9, Chap. 6], each of which can be solved using the thresholding algorithm of [8, Sect. 5], with running time θ _N :=O(N ^2.5logN), where N=max(|X|,|Y|). This lower bound is structurally the same as Lawler’s lower bound [28] in the context of the QAP. Now, the computation of F _X,Y incurs cost N ²⋅θ _N as well and hence the total cost of computing (8) is 2⋅N ²⋅θ _N .

Similarly, the computation of $\mathcal{A}(X,Y)$ incurs a running time θ _N +N ²⋅c _N where c _N is the cost of computing $d_{\mathcal{H}}^{\mathbb{R}^{+}}({\boldsymbol {\mathcal {L}}_{X}(x_{0})},{\boldsymbol {\mathcal {L}}_{Y}(y_{0})})$ for a given pair (x ₀,y ₀)∈X×Y, which can be bounded by N ².

Finally, computing the RHS of (11) incurs cost θ _N +2⋅N ².

We now turn our attention to the proof of Theorem 3.4. The proofs of the following three lemmas are given at the end of this section.

Lemma 3.1

Let (Z,d _Z ) be a metric space. Then, for all A,B⊂Z

$$d_{\mathcal{H}}^{Z} ({A},{B} ) = \inf_{R\in {\mathcal{R}}({A},{B})}\sup_{(a,b)\in R}d_Z(a,b).$$

Lemma 3.2

Let A,B⊂ℝ, then

$$d_{\mathcal{H}}^{\mathbb{R}} ({A},{B} )\geq\max\bigl(|\inf A - \inf B|,|\sup A - \sup B|\bigr).$$

Lemma 3.3

Let A,B be sets and G _A :A→ℝ and G _B :B→ℝ be any two given real valued functions. Then,

$$\inf_{R\in {\mathcal{R}}({A},{B})}\sup_{(a,b)\in R} \bigl|G_A(a)-G_B(b)\bigr|\geq d_{\mathcal{H}}^{\mathbb{R}}\bigl ({G_A(A)},{G_B(B)}\bigr ).$$

Proof of Theorem 3.4

Let us first prove (8). Pick any $R\in {\mathcal{R}}({X},{Y})$ and notice that for all (x,y)∈R

Thus,

$$\sup_{(x,y),(x',y')\in R}\bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(y,y'\bigr)\bigr|\geq\sup_{(x,y)\in R}F_{X,Y}(x,y)\geq\inf_R \sup_{(x,y)\in R}F_{X,Y}(x,y),$$

from which it follows that

$$\inf_R \sup_{(x,y),(x',y')\in R}\bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(y,y'\bigr)\bigr|\geq\inf_R\sup_{(x,y)\in R} F_{X,Y}(x,y).$$

This concludes the proof of (8) since by Theorem 3.3 item 5 the LHS equals $2\cdot d_{\mathcal{G}\mathcal{H}}({X},{Y})$.

For the proof of (9), assume that η>0 and $R\in {\mathcal{R}}({X},{Y})$ are s.t. F _X,Y (x,y)<2η for all (x,y)∈R. This in turn implies that for each (x,y)∈R can find $R_{(x,y)}\in {\mathcal{R}}({X},{Y})$ with |d _X (x,x′)−d _Y (y,y′)|<2η for all (x′,y′)∈R _(x,y). Fix any (x,y)∈R and pick $a\in \boldsymbol {\mathcal {L}}_{X}(x)$. Then, there exists x′∈X s.t. a=d _X (x,x′). Let y′∈Y be s.t. (x′,y′)∈R _(x,y) and let $b=d_{Y}(y,y')\in \boldsymbol {\mathcal {L}}_{Y}(y)$. Now,

$$|a-b|=\bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(y,y'\bigr)\bigr|\leq\sup_{(x',y')\in R_{(x,y)}} \bigl|d_X\bigl(x,x'\bigr)-d_Y\bigl(y,y'\bigr)\bigr|<2\eta.$$

Similarly, for any $b\in \boldsymbol {\mathcal {L}}_{Y}(y)$ one can find $a\in \boldsymbol {\mathcal {L}}_{X}(x)$ with |a−b|<2η. Thus,

$$d_{\mathcal{H}}^{\mathbb{R}^+}\bigl ({\boldsymbol {\mathcal {L}}_{X}(x)},{\boldsymbol {\mathcal {L}}_{Y}(y)}\bigr )<2\eta,\quad \mbox{for any}\ (x,y)\in R.$$

This implies that $\mathcal{A}(X,Y)<\eta$ and the conclusion follows since $\eta> \frac{1}{2}\inf_{R}\sup_{(x,y)\in R}F_{X,Y}(x,y)$ was arbitrary.

For (11) note that since for any x∈X and y∈Y, $\max\{t\in \boldsymbol {\mathcal {L}}_{X}(x)\}=\mathbf {ecc}_{X}(x)$, and similarly $\max\{t\in \boldsymbol {\mathcal {L}}_{Y}(y)\}=\mathbf {ecc}_{Y}(y)$, then by Lemma 3.2, $d_{\mathcal{H}}^{\mathbb{R}} ({\boldsymbol {\mathcal {L}}_{X}(x)},{\boldsymbol {\mathcal {L}}_{Y}(y)} )\geq|\mathbf {ecc}_{X}(x)-\mathbf {ecc}_{Y}(y)|$ for all (x,y)∈X×Y. Pick any $R\in {\mathcal{R}}({X},{Y})$ and notice that then

from which (11) follows.

The validity of (12) follows directly from Lemma 3.3.

Note that as we saw in Remark 2.2, for any compact metric space X, min _x∈X ecc _X (x)=rad(X) and max _x∈X ecc _X (x)=diam(X), applying Lemma 3.2, one readily obtains (13).

For (14) notice that $\boldsymbol {\mathcal {L}}_{X}(X)=\boldsymbol {\mathcal {D}}_{X}$, $\boldsymbol {\mathcal {L}}_{Y}(Y)=\boldsymbol {\mathcal {D}}_{Y}$, and apply Lemma 3.3. The proof of (15) follows directly from Lemma 3.2 and the observation that $\max\{\boldsymbol {\mathcal{D}}_{X}\}={\mathbf {diam}}({X})$. □

Proof of Lemma 3.1

Let ε>0 and $R\in\mathcal{R}(A,B)$ be s.t. d(a,b)<ε for all (a,b)∈R. Since R is a correspondence between A and B it follows that inf _b∈B d(a,b)<ε for all a∈A and inf _a∈A d(a,b)<ε for all b∈B. Recalling (5) it follows that $d_{\mathcal{H}}^{Z}(A,B)\leq\varepsilon$.

Assume now that $d_{\mathcal{H}}^{Z}(A,B)<\varepsilon$. Then, for each a∈A there exist b∈B s.t. d(a,b)<ε. Then, we may define ϕ:A→B s.t. d(a,ϕ(a))<ε for all a∈A. Similarly, define ψ:B→A s.t. d(ψ(b),b)<ε for all b∈B. Consider $R(\phi,\psi)\in {\mathcal{R}}({A},{B})$ as in Example 3.2. By construction d(a,b)<ε for all (a,b)∈R and hence we are done. □

Proof of Lemma 3.2

Assume that $\varepsilon> d_{\mathcal{H}}^{\mathbb{R}} ({A},{B} )$. Then, for any a∈A there exists b∈B with |a−b|<ε. In particular, ε+b>a≥infA, and hence ε+b>infA for all b∈B. It follows that ε+infB>infA and similarly, ε+infA>infB. Thus, ε>|infA−infB|. The inequality for the difference of suprema is similar. □

Proof of Lemma 3.3

Let ε>0 and $R\in {\mathcal{R}}({A},{B})$ be s.t. ε>|G _A (a)−G _B (b)| for all (a,b)∈R. Consider S _R ⊂G _A (A)×G _B (B) defined by

$$S_R=\bigl\{(s,t)|\,\exists(a,b)\in R\,\,\mbox{s.t.}\,\,t=G_A(a),\, s=G_B(b)\bigr\}.$$

Now, S _R is a correspondence between G _A (A) and G _B (B). Indeed, pick any t∈G _A (A) and let a∈A be s.t. t=G _A (a). Then, there exists b∈B with (a,b)∈R and hence s=G _B (b) is s.t. (t,s)∈S _R . Similarly, for any s∈G _B (B) one can find t∈G _A (A) with (t,s)∈S _R .

Finally, note that |t−s|<ε for all (t,s)∈S _R . The conclusion now follows from Lemma 3.1. □

4 The Modified Gromov–Hausdorff Distance

We now consider a variant of the Gromov–Hausdorff distance, which we refer to as the modified Gromov–Hausdorff distance. The definition of this new distance is motivated by computational considerations [6, 24, 25].

Recall that according to (2), the GH distance between $X,Y\in\mathcal{G}$ is given by

$$\inf_{\tiny \begin{array}{ll} \phi:X\rightarrow Y\\\psi:Y\rightarrow X\end{array}} \frac{1}{2}\max\bigl(\mathrm {dis} ({\phi} ),\mathrm {dis} ({\psi} ),C(\phi,\psi )\bigr),$$

where C(ϕ,ψ) is a coupling term given by (3). Notice that if we drop C(⋅,⋅) inside the max(⋯) above, then the minimization over ϕ and ψ yields two decoupled problems, that is,

$$\inf_{\tiny \begin{array}{ll} \phi:X\rightarrow Y\\\psi:Y\rightarrow X\end{array}} \frac{1}{2}\max\bigl(\mathrm {dis} ({\phi} ),\mathrm {dis} ({\psi} )\bigr) =\frac {1}{2}\max \bigl(\operatorname{infdis}(X\rightarrow Y),\operatorname{infdis}(Y\rightarrow X)\bigr),$$

where

$$ \operatorname{infdis}(X\rightarrow Y):=\inf\bigl\{ \mathrm {dis} ({\phi} );\,\phi:X\rightarrow Y\bigr\}.$$

(16)

This leads to the following definition:

Definition 4.1

(Modified Gromov–Hausdorff distance)

Define the modified Gromov–Hausdorff distance between $X,Y\in\mathcal {G}$ by

$$ \widehat {d}_{\mathcal{G}\mathcal{H}} ({X},{Y} ):= \frac{1}{2}\max \bigl(\operatorname{infdis}(X\rightarrow Y),\operatorname{infdis}(Y\rightarrow X)\bigr).$$

(17)

For brevity we will sometimes refer to the modified Gromov–Hausdorff distance by $\widehat {\mbox {GH}}$ .

The definition of $\widehat {\mbox {GH}}$ above expresses the fact that this distance can be computed by solving two decoupled or independent sub-matching problems: (I) finding the best map from X to Y, and (II) finding the best map in the opposite direction. This type of problem admits a binary integer programming formulation similar to the one in Remark 3.4 and is therefore still NP-hard, but, for global optimization strategies such as those of [6, 25], having two decoupled problems is an important property that reduces the overall size of the optimization problem that one needs to solve in practice.

4.1 Properties of the Modified Gromov–Hausdorff Distance

We now prove that $\widehat {\mbox {GH}}$ does indeed define a legitimate distance on collection the isometry classes of $\mathcal{G}$. In addition, in this section we prove that these two distance are in general not equal, establish their topological equivalence, and also present several examples.

Theorem 4.1

We have

• (1) For all $X,Y\in\mathcal{G}$, $d_{\mathcal{G}\mathcal{H}}({X},{Y})\geq \widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})$.

• (2) $\widehat {d}_{\mathcal{G}\mathcal{H}}({},{})$ is a strict metric on the isometry classes of spaces in $\mathcal{G}$:

  • For $X,Y\in\mathcal{G}$, $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})=0$ if and only if X and Y are isometric.

  • For $X,Y,Z\in\mathcal{G}$, $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})\leq \widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Z})+\widehat {d}_{\mathcal{G}\mathcal{H}}({Z},{Y})$.

In Remark 4.1 below, by an explicit construction we prove that the GH and $\widehat {\mbox {GH}}$ distances turn out to be not equal in general, see Fig. 2. Interestingly, however, the GH distance and the modified GH distance are topologically equivalent within GH-precompact families of metric spaces.

Fig. 2

In the figure, 1+β>α>2>β>1. Top: the two metric spaces that we use for constructing a family of counterexamples which show that the GH and $\widehat {\mbox {GH}}$ distances do not always agree. On the right, the interior of the triangle in the α–β plane represents the set of pairs (α,β) for which the construction is possible. Notice that rad(X _α )=α and rad(Y _β )=1, and hence by (13), $d_{\mathcal{G}\mathcal{H}}({X_{\alpha}},{Y_{\beta}})\geq\frac{\alpha-1}{2}>\frac{1}{2}$. Bottom: two maps with distortion 1, which proves that $\widehat {d}_{\mathcal{G}\mathcal{H}}({X_{\alpha}},{Y_{\beta}})\leq\frac{1}{2}$

Theorem 4.2

Let $\mathcal{F}$ be a GH-precompact family of compact metric spaces. Then, for any ε>0 there exists $\delta=\delta(\mathcal {F},\varepsilon)>0$ s.t. whenever $X,Y\in\mathcal{F}$ satisfy $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})<\delta$, then $d_{\mathcal{G}\mathcal{H}}({X},{Y})<\varepsilon$.

Example 4.1

(GH and $\widehat {\mbox {GH}}$ distances between simplices)

We claim that

$$d_{\mathcal{G}\mathcal{H}}({\varDelta_n},{\varDelta_m})=\widehat {d}_{\mathcal{G}\mathcal{H}} ({\varDelta_n},{\varDelta_m} )=\frac{1}{2},\quad \mbox{for all}\ n\neq m.$$

Indeed, since diam(Δ _n )=diam(Δ _m )=1, by Theorem 3.3 item 4, $d_{\mathcal{G}\mathcal{H}}({\varDelta_{n}},{\varDelta_{m}}) \leq\frac{1}{2}$. Now, we estimate $\widehat {d}_{\mathcal{G}\mathcal{H}}({\varDelta_{n}},{\varDelta_{m}})$ from below and prove that $\widehat {d}_{\mathcal{G}\mathcal{H}}({\varDelta_{n}},{\varDelta_{m}})\geq\frac{1}{2}$ which by Theorem 4.1 item 1 will finish the proof. Assume that n>m, then, we claim that

• (a) dis(ϕ)≥1 for all ϕ:Δ _n →Δ _m , and

• (b) $\operatorname{infdis}(\varDelta_{m}\rightarrow\varDelta_{n})=0$.

Thus, by definition of $\widehat {\mbox {GH}}$ (17), $\widehat {d}_{\mathcal{G}\mathcal{H}}({\varDelta_{n}},{\varDelta_{m}})\geq\frac{1}{2}$. Item (b) is clear as Δ _m ↪Δ _n isometrically. For (a) notice that since n>m, for all ϕ:Δ _n →Δ _m , there exist x,x′∈Δ _n with x≠x′ s.t. ϕ(x)=ϕ(x′). Hence $\mathrm {dis} ({\phi} )\geq|d_{\varDelta _{n}}(x,x')-d_{\varDelta _{m}}(\phi(x),\phi(x'))| =1$.

Example 4.2

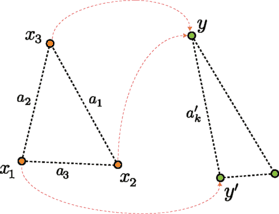
(Explicit formula for the modified Gromov–Hausdorff distance between metric spaces with three points)

Fix a ₁,a ₂,a ₃>0 and $a_{1}', a_{2}', a_{3}'>0$ that verify all triangle inequalities and denote T=T(a ₁,a ₂,a ₃) and $\mathrm {T}' =\mathrm {T}(a_{1}',a_{2}',a_{3}')$. Let {x ₁,x ₂,x ₃} and {y ₁,y ₂,y ₃} be the underlying sets of T and T′, respectively. We also introduce the convention that a ₁=d _T(x ₂,x ₃), a ₂=d _T(x ₁,x ₃), a ₃=d _T(x ₁,x ₂), and $a_{1}' = d_{\mathrm {T}'}(y_{2},y_{3})$, $a_{2}' = d_{\mathrm {T}'}(y_{1},y_{3})$, $a_{3}' = d_{\mathrm {T}'}(y_{1},y_{2})$.

A map ϕ:T→T′:

• (A) Can be a bijection;

• (B) Can map two points in T to one point in T′, and the remaining point in T to a different point in T′; or

• (C) Can map all three points to one point.

In case (A), the minimal distortion over all such maps is

$$\delta\bigl(\mathrm {T}\leftrightarrow \mathrm {T}'\bigr):=\min_\xi\max_i\bigl|a_i-a_{\xi_i}'\bigr|,$$

where ξ ranges over all permutations of {1,2,3}.

In case (C), the distortion of any map is max _i a _i =diam(T).

Finally, for case (B), we see that the minimal distortion is

$$\gamma\bigl(\mathrm {T}\rightarrow \mathrm {T}'\bigr):=\min_{i}\max\Bigl(a_i,\min_k\max_{j\neq i}\bigl|a_j-a_k'\bigr|\Bigr).$$

This can be seen as follows: one fixes i∈{1,2,3}, which for the moment we assume to be 1. Then, consider ϕ:T→T′ that maps points x ₂ and x ₃ to the same point y in Y, and point x ₁ to point y′≠y. Write $d_{\mathrm {T}'}(y,y')=a_{k}'$ for some k∈{1,2,3}. See Fig. 3. Then, the distortion incurred by the map ϕ is

Fig. 3

A map ϕ as in case (B) of Example 4.2. Note that for this map, $\mathrm {dis} ({\phi} )= \max(a_{1},|a_{2}-a_{k}'|,|a_{3}-a_{k}'| )$

The bound dis(ϕ)≥γ(T→T′) applies to any ϕ satisfying condition (B). Since all equalities above can be attained, one obtains

$$\operatorname{infdis}\bigl(\mathrm {T}\rightarrow \mathrm {T}'\bigr) = \min\bigl(\delta \bigl(\mathrm {T}\leftrightarrow \mathrm {T}'\bigr),{\mathbf {diam}} ({\mathrm {T}} ),\gamma\bigl(\mathrm {T}\rightarrow \mathrm {T}'\bigr)\bigr).$$

By exchanging the roles of T and T′ we then find an explicit formula for the $\widehat {\mbox {GH}}$ distance between T and T′:

$$ \widehat {d}_{\mathcal{G}\mathcal{H}} ({\mathrm {T}},{\mathrm {T}'} ) =\frac{1}{2}\max\bigl(\min \bigl(\delta,{\mathbf {diam}} ({\mathrm {T}} ),\gamma\bigl(\mathrm {T}\rightarrow \mathrm {T}'\bigr)\bigr), \min\bigl(\delta,{\mathbf {diam}} ({\mathrm {T}'} ),\gamma\bigl(\mathrm {T}'\rightarrow \mathrm {T}\bigr)\bigr)\bigr),$$

(18)

where we have abbreviated δ=δ(T↔T′).

It is of interest to ascertain whether the GH and $\widehat {\mbox {GH}}$ distances are in some sense comparable (recall Theorem 4.1 item 1). A first question is whether GH and $\widehat {\mbox {GH}}$ could be equal in general.

Remark 4.1

(The GH and $\widehat {\mbox {GH}}$ distances are not equal in general)

We construct a two-parameter family of counterexamples as follows. Pick α,β>0 s.t. 1+β>α>2>β>1 and consider the 3-point metric spaces X _α and Y _β shown in Fig. 2. Then, by Example 2.3, rad(X _α )=α and rad(Y _β )=1. Hence, invoking the lower bound for the GH distance given by (13) one finds that

$$d_{\mathcal{G}\mathcal{H}}({X_\alpha},{Y_\beta})\geq\frac{\alpha-1}{2}>\frac{1}{2}.$$

On the other hand, from Example 4.2 and simple algebraic manipulations one sees that

$$\widehat {d}_{\mathcal{G}\mathcal{H}} ({X_\alpha},{Y_\beta} )=\frac{1}{2}.$$

Indeed, using the notation of Example 4.2, δ(X _α ↔Y _β )=max(α−β,α−1)=α−1>1, diam(X _α )=α, diam(Y _β )=β, γ(X _α →Y _β )=γ(Y _β →Y _α )=1. Thus, $\widehat {d}_{\mathcal{G}\mathcal{H}}({X_{\alpha}},{Y_{\beta}})=\frac{1}{2}$ by (18).

Alternatively, it is easy to construct maps ϕ:X _α →Y _β and ψ:Y _β →X _α with $\max (\mathrm {dis} ({\phi} ),\mathrm {dis} ({\psi} ))=\frac{1}{2}$, see Fig. 2.

4.2 Proofs of Theorems 4.1 and 4.2

Lemma 4.1

Let $X,Y,Z\in\mathcal{G}$, ϕ:X→Y and ϕ′:Y→Z. Then,

$$\mathrm {dis} ({\phi} )+\mathrm {dis} \bigl ({\phi'} \bigr )\geq \mathrm {dis} \bigl ({\phi'\circ \phi} \bigr ).$$

In particular,

$$\operatorname{infdis}(X\rightarrow Y) + \operatorname{infdis}(Y\rightarrow Z)\geq\operatorname{infdis} (X\rightarrow Z).$$

Proof

Let ϕ:X→Y and ϕ′:Y→Z. Pick x,x′∈X and write

Hence,

$$ \mathrm {dis} ({\phi} ) + \sup_{x,x'\in X} \bigl|d_Y\bigl(\phi(x),\phi\bigl(x'\bigr)\bigr)-d_Z\bigl(\phi'\circ\phi(x),\phi'\circ \phi (x)\bigr) \bigr|\geq \mathrm {dis} \bigl ({\phi'\circ\phi} \bigr ).$$

(19)

Since

then, from (19) it follows that

$$\mathrm {dis} ({\phi} )+\mathrm {dis} \bigl ({\phi'} \bigr )\geq \mathrm {dis} \bigl ({\phi'\circ \phi} \bigr ).$$

But the RHS of the above inequality is never smaller than $\operatorname{infdis}(X\rightarrow Z)$, thus

$$\mathrm {dis} ({\phi} )+\mathrm {dis} \bigl ({\phi'} \bigr )\geq\operatorname{infdis}(X\rightarrow Z),$$

from which the second claim follows. □

Proof of Theorem 4.1

Item 1 is true by the definition of $\widehat {\mbox {GH}}$ and (2).

In order to prove item 2 we need to prove symmetry, the triangle inequality, and the fact that $d_{\mathcal{G}\mathcal{H}}({X},{Y})=0$ if and only if X and Y are isometric. Symmetry is clear, and the triangle inequality can be proved as follows: let $X,Y,Z\in\mathcal{G}$ and δ ₁,δ ₂>0 be s.t. $\delta_{1}>\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Z})$ and $\delta_{2}>\widehat {d}_{\mathcal{G}\mathcal{H}}({Y},{Z})$. Further, let ϕ ₁:X→Z, ϕ ₂:Y→Z, ψ ₁:Z→X, ψ ₂:Z→Y s.t. max(dis(ϕ ₁),dis(ψ ₁))<2δ ₁ and max(dis(ϕ ₂),dis(ψ ₂))<2δ ₂. Let ϕ:X→Y be given by ψ ₂∘ϕ ₁ and ψ:Y→X by ψ ₁∘ϕ ₂. From Lemma 4.1 one then sees that max(dis(ϕ),dis(ψ))<2(δ ₁+δ ₂), and hence $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})<\delta_{1}+\delta_{2}$, from which the triangle inequality follows.

That $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})=0$ when X and Y are isometric follows from item 1 and the similar claim for the standard GH distance (Theorem 3.3). Assume now that $X,Y\in\mathcal{G}$ are s.t. $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})=0$. Then, this implies the existence of a sequence {ϕ _n } _n∈ℕ of maps ϕ _n :X→Y with dis(ϕ _n )→0 as n↑∞. From now on the proof follows standard steps which we only sketch, see [7, Sect. 7.3]. Since X is compact, there is a countable dense S⊂X which we henceforth fix. By a diagonal procedure one can choose a sub-sequence {n _k } _k ⊂ℕ s.t. for every x∈S, $\{\phi_{n_{k}}(x)\}_{k}$ converges in Y. Define a map ϕ:S→Y as the point-wise limit of $\{\phi_{n_{k}}\}_{k}$: $\phi(x)=\lim_{k}\phi_{n_{k}}(x)$ for x∈S. Since $\mathrm {dis} ({\phi_{n_{k}}} )\rightarrow0$ as k↑∞, one has $d_{X}(x,x')=\lim_{k}d_{Y}(\phi_{n_{k}}(x),\phi_{n_{k}}(x'))=d_{Y}(\phi (x),\phi (x'))$ for all x,x′∈S. Thus, ϕ:S→X is distance preserving, and since S is dense, it can be extended to a distance preserving map from X to Y. Similarly, there exists ψ:Y→X distance preserving, and hence ψ∘ϕ is distance preserving from X into itself, and since X is compact, ψ∘ϕ must be surjective. It follows that ψ must be surjective and therefore an isometry. □

Proof of Theorem 4.2

Assume to the contrary that there exists ε ₀>0 s.t. for all n∈ℕ, one can find $X_{n},Y_{n}\in\mathcal{F}$ for which $d_{\mathcal{G}\mathcal{H}}({X_{n}},{Y_{n}})\geq\varepsilon_{0}$ and $\widehat {d}_{\mathcal{G}\mathcal{H}}({X_{n}},{Y_{n}})<\frac{1}{n}$. Consider the sequences $\{X_{n}\}_{n\in \mathbb{N}},\{Y_{n}\}_{n\in \mathbb{N}}\subset \mathcal {F}$. By hypothesis, one can assume that up to extraction of a sub-sequence, {X _n } _n and {Y _n } _n converge in the GH distance to some $X_{0},Y_{0}\in\overline{\mathcal{F}}$ (here $\overline {\mathcal {F}}$ is the closure of $\mathcal{F}$ in the GH topology), respectively. We will still denote these sub-sequences by {X _n } _n and {Y _n } _n , respectively. By the triangle inequality for the modified GH distance we have

$$\widehat {d}_{\mathcal{G}\mathcal{H}} ({X_0},{Y_0} )\leq \widehat {d}_{\mathcal{G}\mathcal{H}} ({X_n},{X_0} ) + \widehat {d}_{\mathcal{G}\mathcal{H}} ({Y_n},{Y_0} ) +\widehat {d}_{\mathcal{G}\mathcal{H}} ({X_n},{Y_n} ).$$

By construction of {X _n } _n and {Y _n } _n , $\widehat {d}_{\mathcal{G}\mathcal{H}}({X_{n}},{Y_{n}})<\frac {1}{n}$, and by Theorem 4.1 item 1 the GH distance is not less than the modified GH distance, thus

$$\widehat {d}_{\mathcal{G}\mathcal{H}} ({X_0},{Y_0} )\leq d_{\mathcal{G}\mathcal{H}}({X_n},{X_0}) + d_{\mathcal{G}\mathcal{H}}({Y_n},{Y_0}) +\frac{1}{n}.$$

Taking limit as n↑∞ we find that $\widehat {d}_{\mathcal{G}\mathcal{H}}({X_{0}},{Y_{0}})=0$ and since X ₀ and Y ₀ are compact, Theorem 4.1 guarantees that X ₀ and Y ₀ are isometric. On the other hand, we have

by the triangle inequality for the GH distance. Taking the limit as n↑∞ we see that

$$0<\varepsilon_0\leq d_{\mathcal{G}\mathcal{H}}({X_0},{Y_0})$$

which by Theorem 3.3 item 2 contradicts the fact that X ₀ and Y ₀ are compact and isometric. □

5 Curvature Sets and a Structural Theorem for the Modified Gromov–Hausdorff Distance

We now establish a connection between the Gromov–Hausdorff distance and the work of Boutin and Kemper [4, 5] and Olver [26].

Boutin and Kemper have studied the characterization of certain metric spaces by their distribution of distances and distribution of triangles. Roughly, to a finite metric space $(\mathbb {X},d_{\mathbb {X}})$ one attaches $D_{2}(\mathbb{X})=\{d_{\mathbb{X}}(x,x');\,x,x'\in \mathbb{X}\}$ and $D_{3}(\mathbb{X})=\{T(x,x',x'');\,x,x',x''\in \mathbb {X}\}$, where T(x,x′,x″) is the three point pseudo-metric space with metric given by restriction of $d_{\mathbb{X}}$ to {x,x′,x″}. Notice that one can regard $D_{2}(\mathbb{X})$ as the set of all 2-point pseudo-metric spaces arising from $\mathbb{X}$. The ensuing question is whether these metric invariants are able to characterize finite metric spaces in a certain restricted class up to isometry.

One of the motivations that Boutin and Kemper cite is

Open Problem 1

In [31, p. 29] Ulam asked the question:

Suppose A and B are sets with n elements each (n≥3). A metric d is given on A s.t. d(x,y)∈{0,1,2} for all x,y∈A. A similar metric is given on B. Now suppose that the n−1 element subsets of A and B can be labeled A ₁,…,A _n and B ₁,…,B _n in a way such that each A _i is isometric to B _i . Does this force A to be isometric to B?

In this paper we point out that Gromov [13] has made use of similar constructions in his considerations, where for a compact metric space (X,d _X ) and k∈ℕ, he defines K _k (X), the kth curvature set of X, as the collection of all the k-points pseudo-metric spaces arising from X by restriction of the metric d _X :

Definition 5.1

(Curvature sets, [13])

For a metric space X and k∈ℕ, let

$$\mathbf {K}_{k}({X})=\bigl\{\mathbf {D}_{X} (\mathbb{X} ),\,\mathbb{X}\subset X\,\mbox {and}\, |\mathbb{X}|=k\bigr\},$$

denote the curvature set of X of order k. Note that $\mathbf {K}_{k}({X})\subset {\mathbf {Sym}}_{k}^{+}$.

Gromov goes on to define a topology on the collection of all isometry classes of compact metric spaces where {X _n } _n∈ℕ is said to converge to X whenever

$$ \mathbf {K}_{k}({X_n})\ \mbox{converges to}\ \mathbf {K}_{k}({X})\ \mbox{as}\ n\uparrow\infty\quad \mbox{for all}\ k\in \mathbb{N}.$$

(20)

Remark 5.1

In a completely different language, the pioneering work of Olver on joint invariants [26] has established that smooth planar curves X and Y are rigidly isometric if and only if K ₄(X)=K ₄(Y). In a similar manner, Olver proved that two smooth surfaces X and Y embedded in ℝ³ are rigidly isometric if and only if K ₇(X)=K ₇(Y). Curves and surfaces are regarded as metric spaces once endowed with the restriction of the Euclidean metric. Olver’s motivation for considering these joint invariants comes from the desire to avoid directly estimating curvatures of, say curves, from discrete data sampled from the curve—an inherently noisy process.

The works of Boutin and Kemper, and Olver therefore suggest that one defines a distance between certain classes of objects based on quantifying the dissimilarity between their corresponding curvature sets. We show next that this idea is actually realized by the $\widehat {\mbox {GH}}$ distance.

5.1 The Structural Theorem

We prove the following structural theorem for the $\widehat {\mbox {GH}}$ distance which decomposes the computation of $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})$ into a direct comparison of the curvature sets of X and Y of successively higher order. This theorem implies in particular that $\widehat {\mbox {GH}}$ metrizes the topology (20) defined by Gromov.

Theorem 5.1

(Structural theorem)

For all compact metric spaces X and Y,

$$ \widehat {d}_{\mathcal{G}\mathcal{H}} ({X},{Y} )=\frac{1}{2}\sup_{k\in \mathbb{N}}d_{\mathcal{H}}^{{\mathbf {Sym}}_{k}^{+}}\bigl ({\mathbf {K}_{k}({X})},{\mathbf {K}_{k}({Y})}\bigr ).$$

(21)

In the statement, $d_{\mathcal{H}}^{{\mathbf {Sym}}_{k}^{+}}$ is the Hausdorff distance in ${\mathbf {Sym}}_{k}^{+}$: the set of all symmetric matrices with non-negative entries and zero diagonal, which we view as a metric space with metric $d_{{\mathbf {Sym}}_{k}^{+}}(A,B):=\max_{ij}|a_{ij}-b_{ij}|$, for A=((a _ij )) and B=((b _ij )) in ${\mathbf {Sym}}_{k}^{+}$.

As an application of Theorem 5.1 and an explicit computation of $\mathbf {K}_{3}({\mathbb{S}^{1}})$ and $\mathbf {K}_{3}({\mathbb{S}^{2}})$, in Example 5.3 we lower bound the GH distance between $\mathbb{S}^{1}$ and $\mathbb{S}^{2}$ by $\frac{\pi}{12}$.

5.2 Remarks About Curvature Sets

Remark 5.2

Note that $\boldsymbol {\mathcal {D}}_{X}\simeq \mathbf {K}_{2}({X})$ where the isomorphism notion ≃ is ${\mathbf {Sym}}_{2}^{+}\simeq \mathbb{R}_{+}$.

Example 5.1

Let a ₁,a ₂,a ₃∈ℝ⁺ be the sides of a (possibly degenerate) triangle. Consider the (possibly degenerate) three point metric space T=T(a ₁,a ₂,a ₃). Then,

• K ₁(T)={0}.

• .

• 

  Since ${\mathbf {Sym}}_{3}^{+}\simeq \mathbb{R}_{+}^{3}$, we see that

  $$\mathbf {K}_{3}({\mathrm {T}})\simeq\Biggl\{ \left ( \begin{array}{c}0 \\0 \\0 \end{array} \right )\Biggr\}\cup \bigcup _{P\in\varPi_3} \Biggl\{P \left ( \begin{array}{c}a_1 \\a_2 \\a_3 \end{array} \right )\Biggr\} \cup \bigcup_i\bigcup _{P\in\varPi_3} \Biggl\{P \left ( \begin{array}{c}a_i \\a_i \\0 \end{array} \right )\Biggr\}.$$

Example 5.2

(Computation of $\mathbf {K}_{3}({\mathbb{S}^{1}})$ and $\mathbf {K}_{3}({\mathbb{S}^{2}})$)

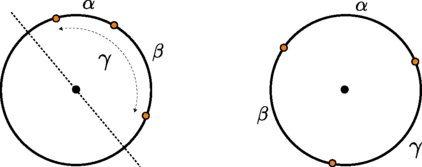
Notice that, whenever picking three points on $\mathbb{S}^{1}$, either they all fall on the same semi-circle, in which case one of the distances is the sum of the other two, or the three points are such that no line passing by the center of the circle can leave the points in the same semi-circle, see Fig. 4.

Fig. 4

Two possibilities for three points on $\mathbb{S}^{1}$. On the left figure: γ=α+β, and on the right figure: α+β+γ=2π

Thus, one has

Since ${\mathbf {Sym}}_{3}^{+}\simeq \mathbb{R}_{+}^{3}$, we see that $\mathbf {K}_{3}({\mathbb{S}^{1}})$ is isomorphic to the (hollow) regular tetrahedron in $\mathbb{R}^{3}_{+}$ with vertexes (0,0,0), (0,π,π), (π,0,π), and (π,π,0).

Now, consider three generic points s ₁,s ₂,s ₃ on $\mathbb{S}^{2}\subset \mathbb{R}^{3}$ and let Γ be the plane determined by them. Then, $s_{i}\in \varGamma \cap \mathbb{S}^{2}$, i=1,2,3, and there exists α∈[0,1] s.t. $\varGamma \cap \mathbb{S}^{2}$ is isometric to $\alpha\cdot \mathbb{S}^{1}$. Hence, the distance matrix $({\!}({d_{\mathbb{S}^{2}}(s_{i},s_{j})})\!)_{i,j=1}^{3}$ belongs to $\mathbf {K}_{3}({\alpha\cdot \mathbb{S}^{1}})=\alpha\cdot \mathbf {K}_{3}({\mathbb{S}^{1}})$. Thus, $\mathbf {K}_{3}({\mathbb{S}^{2}})\subseteq\bigcup_{\alpha\in[0,1]}\alpha\cdot \mathbf {K}_{3}({\mathbb{S}^{1}})$. Conversely, for any $M\in \mathbf {K}_{3}({\mathbb{S}^{1}})$ and α∈[0,1] there exist $s_{1},s_{2},s_{3}\in \mathbb{S}^{2}$ s.t. $\alpha\cdot M = ({\!}({d_{\mathbb{S}^{2}}(s_{i},s_{j})})\!)_{i,j=1}^{3}$. Thus, $\mathbf {K}_{3}({\mathbb{S}^{2}})$ is the cone over $\mathbf {K}_{3}({\mathbb{S}^{1}})$ given by

$$\mathbf {K}_{3}\bigl ({\mathbb{S}^2}\bigr )=\bigl\{\alpha\cdot M;\,\alpha\in[0,1],\,M\in \mathbf {K}_{3}\bigl ({\mathbb{S}^1}\bigr ) \bigr\}.$$

Finally, one sees that $\mathbf {K}_{3}({\mathbb{S}^{2}})$ is isomorphic to the (full) regular tetrahedron with vertices (0,0,0), (0,π,π), (π,0,π) and (π,π,0).

Example 5.3

(Lower bound for the Gromov–Hausdorff distance between $\mathbb{S}^{1}$ and $\mathbb{S}^{2}$)

We claim that $\widehat {d}_{\mathcal{G}\mathcal{H}}({\mathbb{S}^{1}},{\mathbb{S}^{2}})\geq\frac{\pi}{12}$.

From Theorem 5.1 we see that $\widehat {d}_{\mathcal{G}\mathcal{H}}({\mathbb{S}^{1}},{\mathbb{S}^{2}})\geq\frac{1}{2}d_{\mathcal{H}}^{{\mathbf {Sym}}_{3}^{+}} ({\mathbf {K}_{3}({\mathbb{S}^{1}})},{\mathbf {K}_{3}({\mathbb{S}^{2}})} )$. From Example 5.2, the circumcenter of $\mathbf {K}_{3}({\mathbb{S}^{2}})$ is

thus

$$d_{\mathcal{H}}^{{\mathbf {Sym}}_{3}^{+}}\bigl ({\mathbf {K}_{3}\bigl ({\mathbb{S}^1}\bigr )},{\mathbf {K}_{3}\bigl ({\mathbb{S}^2}\bigr )}\bigr )= \min_{M\in \mathbf {K}_{3}({\mathbb{S}^1})}d_{{\mathbf {Sym}}_{3}^{+}}(M,G)=\min_{q\in Q} \|q-g\|_{\ell^\infty},$$

where Q is the hollow regular tetrahedron with vertexes (π,π,0), (π,0,π), (0,π,π) and (0,0,0), and $g=\frac{\pi }{2}(1,1,1)$. The minimum above is attained at any of the centers of the equilateral triangles formed by any three of the vertexes of Q. Note that the circumcenter of the face of Q with vertexes (π,π,0), (π,0,π) and (0,π,π) is $\frac{2\pi}{3}(1,1,1)$, hence, the value of the minimum is $\|\frac{2\pi}{3}(1,1,1)-\frac {\pi}{2}(1,1,1) \|_{\ell^{\infty}} = \frac{\pi}{6}$. The claim follows.

Compare with Remark 3.6, which tells us that none of the isometry invariants playing a role in the bounds of Theorem 3.4 is able to distinguish between spheres of different dimension.

Example 5.4

(A counterexample)

For any ℓ∈ℕ there exist two non-isometric metric spaces X and Y such that K _k (X)=K _k (Y) for all k≤ℓ. Indeed, pick n,m∈ℕ with n>m≥ℓ and let X=Δ _n and Y=Δ _m . Since their cardinality is different, X and Y are not isometric; but any subset $\mathbb{X}$ of X with at most k≤ℓ points embeds isometrically into Y and viceversa. Then, given any k≤ℓ, K _k (Δ _n )=K _k (Δ _m ).

Nonetheless, note that since by Theorem 4.1 $\widehat {\mbox {GH}}$ is a distance on $\mathcal{G}$, then Theorem 5.1 implies that, for given compact metric spaces X and Y, the totality of all curvature sets are able to discriminate whether X and Y are isometric.

Remark 5.3

One can interpret (21) as providing a decomposition of $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})$ into different terms indexed by k∈ℕ which provide increasingly more information about the similarity of X and Y. Note in particular that since $d_{\mathcal{H}}^{{\mathbf {Sym}}_{2}^{+}} ({\mathbf {K}_{2}({X})},{\mathbf {K}_{2}({X})} )=d_{\mathcal{H}}^{\mathbb{R}^{+}} ({\boldsymbol {\mathcal {D}}_{X}},{\boldsymbol {\mathcal {D}}_{Y}} )$, the first term in this decomposition is given by a comparison of the distance sets of X and Y, cf. Remark 5.2. This observation provides an alternative way of proving that $d_{\mathcal{G}\mathcal{H}}({X},{Y})\geq\frac{1}{2}d_{\mathcal{H}}^{\mathbb{R}^{+}} ({\boldsymbol {\mathcal {D}}_{X}},{\boldsymbol {\mathcal {D}}_{Y}} )$, compare with Theorem 3.4.

5.3 The proof of Theorem 5.1

Lemma 5.1

Let X be a compact metric space and let {x ₁,…,x _n }⊂X be an ε-net for X. For each i=1,…,r let V _i be the Voronoi cell corresponding to x _i , i.e. V _i ={x | d _X (x,x _i )<min _j≠i d _X (x,x _j )}. Then, for each i, V _i ⊆B(x _i ,ε).

Proof of Lemma 5.1

Let z∈V _i for some i∈{1,2,…,n}. Assume that z∉B(x _i ,ε), that is, d _X (z,x _i )≥ε. By hypothesis there exists j∈{1,2,…,n} with z∈B(x _j ,ε), which implies d _X (z,x _j )<ε≤d _X (z,x _i ), a contradiction. □

Proof of Theorem 5.1

First we prove that $d_{\mathcal{H}}^{{\mathbf {Sym}}_{k}^{+}} ({\mathbf {K}_{k}({X})},{\mathbf {K}_{k}({Y})} )\leq \widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})$ for all k∈ℕ. Assume that for some η>0, $\widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})<\eta$ and let ϕ:X→Y, ψ:Y→X be s.t. max(dis(ϕ),dis(ψ))<2η. Fix k∈ℕ and let $\mathbb{X}=\{x_{1},\ldots,x_{k}\}$ be any collection of k points in X. Then, recalling the definition of $d_{{\mathbf {Sym}}_{k}^{+}}$ on p. 20:

$$d_{{\mathbf {Sym}}_{k}^{+}}\bigl(\mathbf{D}_X(\mathbb{X}),\mathbf{D}_Y\bigl(\phi(\mathbb {X})\bigr)\bigr)=\max_{i,j}\bigl|d_X(x_i,x_j)-d_Y\bigl(\phi(x_i),\phi(x_j)\bigr)\bigr|\leq \mathrm {dis} ({\phi } ) < 2\eta.$$

Similarly, for any collection of k points $\mathbb{Y}=\{y_{1},\ldots ,y_{k}\}\subset Y$,

$$d_{{\mathbf {Sym}}_{k}^{+}}\bigl(\mathbf{D}_Y\bigl(\psi(\mathbb{Y})\bigr),\mathbf{D}_Y(\mathbb{Y})\bigr) < 2\eta.$$

Hence, $d_{\mathcal{H}}^{{\mathbf {Sym}}_{k}^{+}} ({\mathbf {K}_{k}({X})},{\mathbf {K}_{k}({Y})} )<2\eta$ and the claim follows by letting $\eta\rightarrow \widehat {d}_{\mathcal{G}\mathcal{H}}({X},{Y})$ and noticing that k∈ℕ was arbitrary.

Assume now that for all k∈ℕ, $d_{\mathcal{H}}^{{\mathbf {Sym}}_{k}^{+}} ({\mathbf {K}_{k}({X})},{\mathbf {K}_{k}({Y})} )<2\eta$. Fix ε>0 and let $\mathbb{X}_{\varepsilon}=\{x_{1},\ldots,x_{n}\}\subset X$ be an ε/2-net for X. Then, there exists M∈K _n (Y) and $\mathbb{Y}_{\varepsilon}'=\{y_{1}',\ldots,y_{n}'\}\in Y$ s.t. $M=\mathbf{D}_{Y}(\mathbb{Y}_{\varepsilon}')$ and $d_{{\mathbf {Sym}}_{n}^{+}}(\mathbf {D}_{X}(\mathbb{X}_{\varepsilon}),M)<2\eta$. Let $\phi_{\varepsilon}:\mathbb{X}_{\varepsilon}\rightarrow Y$ be given by $x_{i}\mapsto y_{i}'$ for i=1,2,…,n. Then, by construction, dis(ϕ _ε )<2η. Similarly, construct $\mathbb{Y}_{\varepsilon}$, an ε/2-net for Y and $\psi_{\varepsilon}:\mathbb{Y}_{\varepsilon}\rightarrow X$ s.t. dis(ψ _ε )<2η.

Consider the Voronoi tessellation of X induced by $\mathbb {X}_{\varepsilon}$, and for each i=1,…,n, let V _i be the Voronoi cell corresponding to $x_{i}\in\mathbb{X}_{\varepsilon}$. Now, let the map ϕ:X→Y be given for all i by V _i ∋x↦ϕ _ε (x _i ), i.e. we map all points inside the Voronoi cell corresponding to x _i to the image of x _i under ϕ _ε . For x∈X\⋃ _i V _i , there exists I⊂{1,…,n} with |I|≥2 s.t. d _X (x,x _i )=d _X (x,x _j ) for all i,j∈I. For those x then define ϕ(x) to be any element of the (finite) set {ϕ _ε (x _i ),  i∈I}. It follows that dis(ϕ)≤ε+2η. Indeed, notice that for any x,x′∈X there exist i,j∈{1,2,…,n} such that $x\in\overline{V_{i}}$, ϕ(x)=ϕ _ε (x _i ), and $x'\in\overline{V_{j}}$, ϕ(x′)=ϕ _ε (x _j ), and hence

where the last inequality follows from Lemma 5.1 and the fact the fact that $\mathbb{X}_{\varepsilon}$ is an ε/2-net for X. Since x,x′∈X are arbitrary we see that dis(ϕ)<2η+ε.

Similarly, we can construct a map ψ:Y→X with dis(ψ)≤2η+ε/2. We then see that

$$\widehat {d}_{\mathcal{G}\mathcal{H}} ({X},{Y} )\leq\frac{1}{2}\max\bigl(\mathrm {dis} ({\phi} ),\mathrm {dis} ({\psi } )\bigr)\leq \eta+\frac{\varepsilon}{2},$$

from which the claim follows by letting ε→0 and $\eta\rightarrow\frac{1}{2}\sup_{k}d_{\mathcal{H}}^{\mathbf{Sym}_{k}^{+}}(\mathbf{K}_{k}(X), \mathbf{K}_{k} (Y))$. □

6 Discussion

Several aspects remain to be explored, most interestingly perhaps the numerical estimation of $\widehat {\mbox {GH}}$ using the structural theorem (Theorem 5.1). Strengthening the claim of Theorem 4.2 for specific subfamilies of $\mathcal{G}$ also appears to be of interest.