Symmetries of Equivelar 4-Toroids

Abstract

We derive some general results on the symmetries of equivelar toroids and provide detailed analysis of the subgroup lattice structure of the dihedral group D ₄ and of the octahedral group to complete classification by symmetry type of those in ranks 3 and 4.

1 Introduction

Over the last few decades numerous papers dealt with polytopes and maps that have large automorphism groups but are not necessarily regular (see for example [4, 6, 8, 14, 15]). In particular, a lot of research has been done on chiral polytopes which are now better understood. Among the major achievements are the complete characterisation of their automorphism groups and the proof of their existence in each rank (see [15, 16]). Chiral polytopes are particular examples of polytopes whose automorphism group has only two orbits on the flags. The characterisation of the automorphism groups of polytopes in rank 3 with exactly two flag orbits was completed in [8] and is expected to be completed in [9] for any rank n. Relaxing symmetry further, we consider equivelar polytopes (first defined and considered in [12]), which are essentially polytopes that can be assigned a Schläfli type. Such polytopes admit local isomorphisms that need not extend to global symmetries.

The classification of regular and chiral maps on the 2-torus (3-toroids) is well known. It was initially published in 1948 by Coxeter [2] and beautifully exposed in [3]. Recently, Duarte [5] extended the classification to all 2-orbit maps on the torus. Equivelar polyhedral maps on the torus, which are essentially equivelar rank 3 polytopes, were classified by Brehm and Kühnel [1].

The complete classification of regular and chiral toroids of all ranks (which can be viewed as tessellations of higher dimensional torii) was completed by McMullen and Schulte in [10] (see also [11, Sect. 6]). In particular, they show that there exist no chiral toroids of rank greater than 3. Furthermore, Hartley, McMullen and Schulte (see [7]) showed that for n≥2, the n-torus is the only n-dimensional compact euclidean space-form which can admit a regular or chiral tessellation; moreover, chirality can only occur if n=2.

In this paper we study properties of the automorphism groups of equivelar toroids and classify all equivelar toroids of ranks 3 and 4 into families according to their symmetry types. Sects. 2 and 3 of the paper give the necessary background on integer lattices and their symmetries, regular tessellations and toroids of rank n. In Sect. 4 we classify equivelar 3-toroids. In Sect. 5, we determine the conjugacy classes of the symmetry group of the cubical tessellation that project to automorphisms of 4-toroids. Finally, in Sects. 6 and 7 we classify equivelar 4-toroids. In particular, we show that there exist no toroids with two flag orbits, but that there are equivelar toroids with k orbits of flags for every divisor k of 24 distinct from 2.

2 Symmetries of Integer Lattices

An integer lattice of rank n is a set Λ(A)={Ax | x∈ℤⁿ}, where A is an n by n integer matrix of non zero determinant |A|. The set of columns of A, called a basis of Λ(A), is linearly independent. In this section we develop tools that will enable us to understand symmetries of integer lattices.

We start by determining when two given bases generate the same lattice. The necessary and sufficient conditions for this are in Corollary 2, which follows directly from the next lemma.

Lemma 1

Let A,B∈ℤ^n×n where |A|≠0≠|B|. Then Λ(A)⊆Λ(B) if and only if |B| divides all elements of adj(B)A. In this case, |B| divides |A|.

Proof

Note that Λ(A)⊆Λ(B) if and only if for each x∈ℤⁿ there exists y∈ℤⁿ, such that Ax=By. Recall that adj(B)=|B|B ⁻¹, where adj(B) is the adjoint matrix of B. It then follows that adj(B)Ax=|B|y. Clearly, there is a solution y∈ℤⁿ for very x∈ℤⁿ if and only if every entry of adj(B)A is divisible by |B|. This implies that |B|ⁿ divides |adj(B)A|. Furthermore, for any matrix M with |M|≠0, we have |adj(M)|=|M|ⁿ⁻¹ and

$$\big|\mathrm {adj}(B)A\big| = \big|\mathrm {adj}(B)\big|\cdot|A| = |B|^n\frac{|A|}{|B|}, $$

implying that |B| divides |A|. □

Corollary 2

Let A,B∈ℤ^n×n, |A|≠0 and |B|≠0. Then Λ(A)=Λ(B) if and only if |A|=±|B| and |A| divides each element of adj(B)A and adj(A)B.

In the remainder of the paper we interpret the elements of Λ(A) as a set of points in $\mathbb{E}^{n}$ with integer coordinates with respect to certain basis. In this context, the following proposition specifies conditions under which a given linear transformation preserves Λ(A).

Proposition 3

Let Λ(A) be an integer lattice and μ be a linear transformation given by the matrix M with |M|≠0. Then μ preserves the lattice if and only if |A| divides all entries of adj(MA)A and all entries of adj(A)MA. In this case |M|=±1. In particular, if M ²=I the above condition reduces to |A| divides all entries of adj(MA)A.

Proof

The matrix M preserves the lattice if and only if Λ(MA)=Λ(A), which by Corollary 2 is true if and only if |MA|=±|A| divides all entries of adj(MA)A and all entries of adj(A)MA. In particular, this implies |M|=±1. If M ²=I, then adj(M)=±M. Therefore adj(MA)A=adj(A)adj(M)A=±adj(A)MA. □

An important class of integer lattices are lattices invariant under a linear hyperplane reflection. Let Λ:=Λ(A) be a rank n integer lattice in $\mathbb{E}^{n}$ which is symmetric by a reflection R in a hyperplane Π (hence the origin o is a lattice point invariant under R). Since for any vector v∈Λ, Rv+v∈Π, the set of orthogonal projections of {2v∣v∈Λ} is a rank n−1 sublattice contained in the lattice Λ _Π :=Π∩Λ.

Let v∈Λ∖Λ _Π be such that d(v,Π)≤d(y,Π) for every y∈Λ∖Λ _Π and let d:=d(v,Π). As kv is in Λ for any k∈ℤ we note that ⋃ _k∈ℤ(Λ _Π +kv)⊆Λ. Furthermore, the minimality of d clearly implies that every lattice point must be contained in Λ _Π +kv, for some k∈ℤ, and hence Λ=⋃ _k∈ℤ(Λ _Π +kv). It follows that any point of the lattice Λ can be written as a point in Λ _Π +kv, for some k∈ℤ (and 2v projects orthogonally to Π onto a point in Λ _Π ).

To conclude this section, we state some properties about integer lattices in $\mathbb{E}^{2}$ that will be used later in Sect. 4.

Lemma 4

Let Λ(A) be an integer lattice of $\mathbb{E}^{2}$. Then there exist integers a,b and c such that Λ(A)=Λ(B), with Λ(B) the integer lattice with basis {(a,b),(c,0)}.

Proof

Let A ₁=(x ₁,y ₁) and A ₂=(x ₂,y ₂) be the columns of A. If y ₁ y ₂=0 the lemma follows trivially. Otherwise, let r:=gcd(y ₁,y ₂) and let p,q∈ℤ be such that r=py ₁+qy ₂. The lemma follows by Corollary 2, since Λ(A)=Λ(B), for a=px ₁+qx ₂,b=r and $c=\frac{x_{1}y_{2}-x_{2}y_{1}}{r}$. □

The next proposition now follows directly from Proposition 3.

Proposition 5

Let R ₁:(x,y)↦(y,x), R ₂:(x,y)↦(x,−y) and $R_{2}':(x,y) \mapsto (x+y,-y)$. Let Λ be an integer lattice of $\mathbb{E}^{2}$ with basis (a,b) and (c,0). Then:

• 1. R ₁ preserves Λ if and only if b|a, b|c and $\frac{c}{b} | 1-\frac{a^{2}}{b^{2}}$.

• 2. R ₂ preserves Λ if and only if c|2a.

• 3. $R_{2}'$ preserves Λ if and only if c|2a+b.

• 4. R ₁ R ₂ preserves Λ if and only if b|a, b|c and $\frac{c}{b} | 1+\frac{a^{2}}{b^{2}}$.

• 5. $R_{1} R_{2}'$ preserves Λ if and only if b|a, b|c and $\frac{c}{b} |1+\frac{a}{b}+\frac{a^{2}}{b^{2}}$.

3 Toroids of Rank n

We define a tessellation of Euclidean n-space $\mathbb{E}^{n}$ as a locally finite collection $\mathcal {U}$ of n-dimensional convex polytopes (n-polytopes), called cells, which cover $\mathbb{E}^{n}$ and tile it in a face-to-face manner. That is, the cells of $\mathcal {U}$ cover $\mathbb{E}^{n}$ and if two cells have non-empty intersection, then they have disjoint interiors and meet in a common i-face of each for some i. We shall only consider Euclidean tessellations with isomorphic regular convex polytopes as cells.

A flag of an n-polytope is a maximal subset of pairwise incident faces of the polytope, including the polytope itself. A flag of a tessellation is defined to be a flag of any of its cells. We say that two flags of $\mathcal {U}$ are i-adjacent if they differ only in a face of dimension i. Note that for each flag Ψ and each i∈{0,…,n} there is a unique i-adjacent flag to Ψ; we denote that flag by Ψ ⁱ, and extend this notation recursively $(\varPsi^{i_{k}, \dots, i_{1}})^{i_{0}}=: \varPsi^{i_{k}, \dots, i_{1}, i_{0}}$. A tessellation $\mathcal {U}$ is said to be regular if its group of symmetries $\mathrm {Aut}(\mathcal {U})$ (that is, the group of isometries of $\mathbb{E}^{n}$ which preserve $\mathcal {U}$) is transitive on the flags of $\mathcal {U}$. The symmetry group of a regular tessellation is a Coxeter group generated by reflections R ₀,…,R _n , where R _i maps a fixed (base) flag Φ to its i-adjacent flag Φ ⁱ. Note that, given a base flag, the reflections R ₀,…,R _n are unique. Regular tessellations are equivelar in the sense that they have a (Schläfli) type {p ₁,…,p _n−1}, where p _i is the order of R _i−1 R _i . In other words, for each i≥2, the number p _i of i faces between a (i−2)-face and a (i+1)-face depends only on i and not on the chosen faces. Similarly, the number p ₁ of edges in a 2-face F, does not depend on the choice of F.

For each n≥2, there is a regular tessellation by n-cubes with type {4,3ⁿ⁻²,4}. In the plane, there are also triangular and hexagonal tessellations with types {3,6} and {6,3}, respectively. For n=4, there are also two exceptional tessellations, one of type {3,3,4,3} and its dual of type {3,4,3,3}, having 4-cross-polytopes and 24-cells as cells, respectively.

Table 1 gives a complete list, up to similarity and duality, of all regular Euclidean tessellations. For each tessellation, the second column of the table gives a set of generators R ₀,…,R _n for its symmetry group (here, the points of $\mathbb{E}^{n}$ are given by coordinates (x ₁,…,x _n )). The third column of the table gives the central element of the symmetry group of the tessellation, in terms of the generators R ₀,…,R _n . We shall make use of such element is Sects. 4 and 5, when we classify the possible symmetry types that rank 3 and 4 equivelar toroids may have.

Table 1 Symmetries of the regular Euclidean tessellations

We denote by $\mathbf{T} \leq \mathrm {Aut}(\mathcal {U})$ the group of all translations fixing the Euclidean tessellation $\mathcal {U}$. We identify this group with the orbit of the origin o of $\mathbb{E}^{n}$ under T and note that the set of points o T can be interpreted as an integer lattice. Each subgroup Λ of T generated by n linearly independent translations t ₁,…,t _n yields a lattice Λ:=o Λ of rank n, and the corresponding translation vectors v ₁,…,v _n determine a fundamental region for Λ (which is the parallelepiped spanned by {v ₁,…,v _n }).

A toroid of rank n+1 or an (n+1)-toroid is the quotient of a tessellation $\mathcal {U}$ of $\mathbb{E}^{n}$ by a rank n subgroup Λ≤T, or using the identification presented above, by a lattice Λ. We say that Λ induces the toroid, and denote the latter by $\mathcal {U}/ \varLambda$. It is natural to define an i-face of a toroid $\mathcal {U}/ \varLambda$ to be an orbit of an i-face of $\mathcal {U}$ and a flag of $\mathcal {U}/ \varLambda$ as an orbit of a flag of $\mathcal {U}$. If the tessellation $\mathcal {U}$ is equivelar of Schläfli type {p ₁,…,p _n−1} we say that any toroid $\mathcal {U}/ \varLambda$ is also equivelar with Schläfli type {p ₁,…,p _n−1}. Note that the toroids for which all the vertices of each cell of $\mathcal {U}$ are different under Λ, with the induced partial order are abstract (n+1)-polytopes, in the sense of [11].

We now make use of the fact that with any toroid, just as is the case with abstract polytopes, we can associate a monodromy group (see for example [14]) induced by a flag action. In fact, abstract polytopes are special cases of F-actions [13], where $F = \mathcal{C}$, the corresponding Coxeter group. Generally F-actions can be used to study structures like maps, hypermaps or polytopes where the chosen base flags act as a reference point for dealing with different kinds of morphism, including automorphisms, projections and lifts of automorphisms. Furthermore, F-actions can be used to find the relationships between the monodromy group and the automorphism group, through the stabiliser of a base flag and its normaliser in the monodromy group.

Except for the tessellations with type {6,3} and {3,4,3,3}, the symmetry group $\mathrm {Aut}(\mathcal {U})$ of a regular tessellation $\mathcal {U}$ of the Euclidean space $\mathbb{E}^{n}$ is of the form T⋊S, where S denotes the stabiliser of a vertex of $\mathcal {U}$ (see for example [11, Sect. 6]). Without loss of generality, we assume that S is the stabiliser of the origin o. Whenever the vertex set of $\mathcal {U}$ is the vertex set of a lattice (that is, whenever $\mathcal {U}$ is not of type {6,3} nor {3,4,3,3}), we denote it by $\varLambda_{\mathcal {U}}$.

Note that for a translation t _a by a vector a and an isometry s fixing the origin, s ⁻¹ t _a s=t _as , where t _as is the translation by the image of a under s. This implies that the action by conjugation by an isometry fixing the origin of a translation group is equivalent to the action of the isometry on the corresponding translation vectors.

For a given tessellation $\mathcal {U}$ the toroids $\mathcal {U}/ \varLambda$ and $\mathcal {U}/ \varLambda'$ are isomorphic if Λ and Λ′ are conjugate in $\mathrm {Aut}(\mathcal {U})$. It now follows that the toroids are isomorphic if and only if there is a symmetry in $\mathrm {Aut}(\mathcal {U})$ sending Λ to Λ′. A symmetry $\gamma \in \mathrm {Aut}(\mathcal {U})$ induces (projects to) an automorphism of a toroid $\mathcal {U}/ \varLambda$ if it normalises Λ, that is, if and only if the lattice Λ is invariant under γ. Geometrically, this is equivalent to mapping fundamental regions of Λ to fundamental regions of Λ. Clearly, different symmetries of $\mathcal {U}$ may induce the same automorphism of $\mathcal {U}/ \varLambda$. The automorphism group of the toroid $\mathcal {U}/\varLambda$ is therefore the group induced by the normaliser $\mathrm {Norm}_{\mathrm {Aut}(\mathcal {U})}(\boldsymbol{\Lambda})$, that is, $\mathrm {Aut}(\mathcal {U}/ \varLambda) \cong \mathrm {Norm}_{\mathrm {Aut}(\mathcal {U})}(\boldsymbol{\Lambda})/\boldsymbol{\Lambda}$.

The automorphism group of $\mathcal {U}/ \varLambda$ acts on the set of flags of $\mathcal {U}/ \varLambda$ in a natural way. That is, given a flag Φ of $\mathcal {U}/ \varLambda$, there is a flag $\hat{\varPhi}$ of $\mathcal {U}$ such that $\varPhi= \hat{\varPhi}\boldsymbol{\Lambda}$ and hence for each $\gamma \in \mathrm {Aut}(\mathcal {U}/ \varLambda)$, $\varPhi \gamma =( \hat{\varPhi} \boldsymbol{\Lambda}) \gamma = (\hat{\varPhi} \hat{\gamma}) \boldsymbol{\Lambda}$, where $\hat{\gamma} \in \gamma \boldsymbol{\Lambda}$.

Clearly, every translation fixing $\mathcal {U}$ induces an automorphism of $\mathcal {U}/ \varLambda$, and the translations in Λ induce (project to) the trivial automorphism of $\mathcal {U}/ \varLambda$. The automorphism χ of $\mathcal {U}/ \varLambda$ induced by the isometry of $\mathbb{E}^{n}$ that sends each vector x to −x (the central inversion of $\mathbb{E}^{n}$) plays an important role in our classification of toroids. For each tessellation $\mathcal {U}$ of $\mathbb{E}^{n}$ the last column in Table 1 gives χ in terms of the generators R ₁,…,R _n . Since χ normalises any subgroup of T and 〈χ〉∩T={ε}, it follows that 〈T,χ〉=T⋊〈χ〉. This implies that any automorphism group of a toroid $\mathcal {U}/ \varLambda$ is induced by a subgroup K such that $\mathbf{T} \rtimes \langle \chi\rangle \le {\mathbf{K}} \le \mathrm {Aut}(\mathcal {U})$.

By the correspondence theorem on group morphisms, the subgroups K with $\mathbf{T} \rtimes \langle \chi\rangle \le {\mathbf{K}} \le \mathrm {Aut}(\mathcal {U})$ are in one-to-one correspondence with subgroups K′ of S containing χ, where K′ corresponds to the subgroup T⋊K′. Therefore, to classify toroids we need to determine which symmetries in S normalise Λ.

Note that a translation subgroup Λ and its conjugate Λ′:=γ ⁻¹ Λ γ, with γ∈S represent isomorphic toroids. (For example, a chiral map and its enantiomorphic form, that is, the left- and right-handed versions of the same map, are isomorphic in this sense.) Then, given a subgroup K ₁ and its conjugate K ₂=γ ⁻¹ K ₁ γ, where T⋊〈χ〉≤K ₁,K ₂≤T⋊S, it follows that K ₁/Λ≅K ₂/Λ′. Hence, for our classification only one conjugacy class of K with $\mathbf{T} \rtimes \langle \chi\rangle \le {\mathbf{K}} \le \mathrm {Aut}(\mathcal {U})$ need be considered; or equivalently, we need to consider only one conjugacy class of K′, with 〈χ〉≤K′≤S.

According to [14], the number of different orbits of flags of a toroid $\mathcal {U}/ \varLambda$ under $\mathrm {Aut}(\mathcal {U}/ \varLambda)$ equals the index of $\mathrm {Norm}_{\mathrm {Aut}(\mathcal {U})}(\boldsymbol{\Lambda})$ in $\mathrm {Aut}(\mathcal {U})$, which is the same as the index of K′ in S.

We now summarise the above in the following lemma.

Lemma 6

With the notation as above the following statements hold.

• (a) An automorphism γ∈S projects to an automorphism of $\mathcal {U}/\varLambda$ if and only if γ normalises Λ. This is, if and only if γ(Λ)=Λ.

• (b) Since all sublattices Λ are centrally symmetric, χ always projects to $\mathrm {Aut}(\mathcal {U}/\varLambda)$.

• (c) The automorphism group $\mathrm {Aut}(\mathcal {U}/ \varLambda)$ of $\mathcal {U}/ \varLambda$ is isomorphic to

  $$({\mathbf{K}'} \ltimes \mathbf{T})/ \boldsymbol{\Lambda} \cong {\mathbf{K}'} \ltimes (\mathbf{T}/\boldsymbol{\Lambda}), $$

  where K′={γ∈S | γ ⁻¹ Λ γ=Λ}={γ∈S | γ(Λ)=Λ}. In particular, 〈χ〉≤K′≤S. The group $\mathrm {Aut}(\mathcal {U}/ \varLambda)$ has k orbits on the set of flags of $\mathcal {U}/ \varLambda$ if and only if the index of K in S is k.

• (d) The toroids $\mathcal {U}/\varLambda$ and $\mathcal {U}/\varLambda'$ are isomorphic if and only if Λ and Λ′ are conjugate in $\mathrm {Aut}(\mathcal {U})$. This in turn is true if and only if there exists γ∈S, such that Λ=γ(Λ′).

It is natural to define a regular toroid $\mathcal {U}/ \varLambda$ as a toroid whose group of automorphisms acts transitively on the set of its flags, or equivalently, a toroid $\mathcal {U}/ \varLambda$ is regular if all symmetries in the stabiliser $\mathbf{S} \leq \mathrm {Aut}(\mathcal {U})$ of the origin o project to an automorphism of $\mathcal {U}/ \varLambda$. A toroid is said to be k orbit if its automorphism group has exactly k orbits on flags. Chiral toroids are defined to be 2-orbit toroids that have adjacent flags in different orbits.

If the tessellation $\mathcal {U}$ is regular, the associated toroid $\mathcal {U}/ \varLambda$ can be assigned the Schläfli type of $\mathcal {U}$ and in this case we say that the toroid is equivelar. Clearly, any regular toroid is equivelar, but the converse is not necessarily true. For example, chiral 3-toroids on the torus are equivelar but not regular.

4 Equivelar 3-Toroids

The classification of regular and chiral toroidal maps was given in 1948 by Coxeter [2] (see also [3]). The classification of equivelar polyhedral toroidal maps (that is, toroids in which the intersection of two distinct faces is either empty, a common vertex or a common edge) was recently completed by Brehm and Kühnel in [1]. In this section, using a new approach, we also classify such toroids. Our methodology extends to enable the classification in any rank, and shall be used in subsequent sections for the classification in rank 4.

By definition, equivelar 3-toroids have Schläfli type {4,4}, {3,6} or {6,3}. Our approach makes use of the fact that vertices of the tessellations of type {4,4} and {3,6} form an integer lattice. Using duality, one can then describe those toroids with type {6,3} as well.

4.1 Equivelar Toroids of Type {4,4}

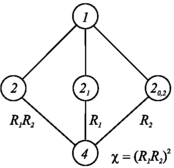
Let $\mathcal {U}$ be the regular tessellation with type {4,4}. Using the notation of the previous section, we note that S=〈R ₁,R ₂〉 and χ∈S, where R ₁,R ₂ and χ are as in Table 1. To make use of Lemma 6 we note that in this case there are only three conjugacy classes of proper subgroups of S distinct from 〈χ〉 containing 〈χ〉, namely 〈χ,R ₁〉, 〈χ,R ₂〉 and 〈χ,R ₁ R ₂〉.

In Fig. 1 we give all five possible conjugacy classes of subgroups K′ with the property that 〈χ〉≤K′≤S. The class corresponding to the stabiliser S and representing all regular (1-orbit) toroids of type {4,4} is labelled ‘1’. The label ‘4’ represents all 4-orbit toroids of type {4,4} and corresponds to the subgroup 〈χ〉 of the stabiliser S. The three classes corresponding to the subgroups 〈χ,R ₁ R ₂〉, 〈χ,R ₁〉 and 〈χ,R ₂〉 are labelled 2, 2₁ and 2_0,2, respectively, and represent three different classes of 2-orbit toroids of type {4,4}. The labels used are the same as in [14]. Henceforth, in this subsection we name the classes by these labels.

Fig. 1

Conjugacy classes of vertex stabilisers for toroids of type {4,4}

The vertex set of the regular tessellation $\mathcal {U}= \{4,4\}$ may be taken to be ℤ², the set of points in $\mathbb{E}^{2}$ with integer coordinates. Let the base of the corresponding lattice Λ _{4,4} be the standard orthonormal basis {e ₁,e ₂}. Every sublattice Λ of Λ _{4,4} can be described by two generating translations t ₁ and t ₂ with vectors v ₁ and v ₂, respectively. The induced toroid $\mathcal {U}/ \varLambda$ is denoted by $\{4,4\}_{v_{1}, v_{2}}$.

First we consider the class 1, that is, the case where the toroid $\mathcal {U}/\varLambda$ is regular and the corresponding vertex stabiliser of o in $\mathcal {U}$ is S=〈R ₁,R ₂〉. Then, R ₁ R ₂∈S is the rotation by $\frac{\pi}{2}$ around o. Assuming v∈Λ∖{o} is such that d(v,o)≤d(v′,o) for any v′∈Λ∖{o}, the orbit of v under 〈R ₁ R ₂〉 is a set of four points forming the vertices of a square. Clearly, there cannot be other points in Λ at distance d(v,o) from o as the distance between any such point and v〈R ₁ R ₂〉 would be smaller than d(v,o). In addition, since R ₁,R ₂∈S, these four points must be either on the coordinate axes x and y or on the lines y=x and y=−x, yielding the two well-known possible families of regular toroids {4,4}_(a,0),(0,a) and {4,4}_{(a,a),(a,−a)}, respectively. (In the notation of [3], these two toroids are denoted by {4,4}_(a,0) and {4,4}_(a,a), respectively, but in order to specify classes of equivelar 3-toroids in general we need to use two vectors.)

Let us now consider the conjugacy class 2, that is, the class consisting of chiral toroids. The corresponding vertex stabiliser of o is K′=〈R ₁ R ₂〉. As above, using the rotation R ₁ R ₂∈K′ we see that the four points in Λ closest to o form a square. If none of these four points are on a coordinate axis or the lines y=±x, the toroid is chiral, otherwise it is regular. Such toroids are the well-known {4,4}_{(b,c),(−c,b)}, where bc(b−c)≠0 (note that in [3], these are denoted by {4,4}_(b,c)).

For the conjugacy class 2_0,2 the reflection R ₂ in the x-axis belongs to K′. Following Sect. 2, we let Λ=⋃ _k∈ℤ(Λ _Π +kv), where Π is the x-axis and v∉Π can be chosen to be a lattice point closest to the origin among the ones closest to Π. Let c∈ℤ be such that (c,0) is a generating vector of Λ _Π . Then either $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$ or $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$ giving us the two possible families for toroids in this class. If $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$, then v=(0,b) for some b∈ℤ, giving us the toroid {4,4}_(c,0),(0,b) that is in class 2_0,2 whenever c≠b, and regular otherwise. If $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$, then c∈ℤ is even and $v=(\frac{c}{2}, b)$, giving us the toroid {4,4}_{(c,0),(c/2,b)}={4,4}_{(c/2,b),(c/2,−b)} that is in class 2_0,2 whenever $b\neq\frac{c}{2}$ and regular otherwise. The maps in this class were also described in [5] within the theory of 2-orbit hypermaps.

Similar arguments can now be used for the conjugacy class 2₁ and the reflection R ₁∈K′ in the line y=x. Now Λ=⋃ _k∈ℤ(Λ _Π +kv), where Π is the line y=x and v∉Π a lattice point closest to the origin among the ones closest to Π. Let c∈ℤ be such that (c,c) is a generating vector of Λ _Π . Then either $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$ or $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$ giving us the two possible families for toroids in this class. If $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$, then v=(−b,b) for some b∈ℤ, giving us the toroid {4,4}_{(c,c),(−b,b)} that is in class 2₁ whenever c≠b and regular otherwise. If $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$, then v=(b,c−b) with b∈ℤ, giving us the toroid {4,4}_{(c,c),(b,c−b)}={4,4}_{(c−b,b),(b,c−b)} that is in class 2₁ whenever b≠0,c and regular otherwise. The maps in this class were also described in [17], within the theory edge-transitive maps.

Any other lattice not symmetrical by any conjugate of R ₁, R ₂ or R ₁ R ₂ is a lattice in class 4. We can now prove the following theorem that classifies, up to isomorphism, all toroids of type {4,4}.

Theorem 7

Equivelar toroids with Schläfli type {4,4} can be described as $\{4,4\}_{v_{1},v_{2}}$, where v ₁ and v ₂ are two linearly independent vectors. Furthermore, given integers a>b>0 the classes of toroids are as follows.

• Class 1 contains the two families of regular toroids

  $$\{4,4\}_{(a,0),(0,a)} \quad \mathrm{and} \quad \{4,4\}_{(a,a),(a,-a)}. $$

• Class 2 contains the family of chiral toroids

  $$\{4,4\}_{(a,b),(-b,a)}. $$

• Class 2_0,2 contains the two families of toroids

  $$\{4,4\}_{(a,0),(0,b)}\quad \mathrm{and} \quad \{4,4\}_{(a,b),(a,-b)}. $$

• Class 2₁ contains the two families of toroids

  $$\{4,4\}_{(a,a),(-b,b)}\quad \mathrm{and} \quad \{4,4\}_{(a,b),(b,a)}. $$

• Class 4 contains the family of toroids

  $$\{4,4\}_{(a,b),(c,0)}, $$

  where c≥a−b, c≠2a≠4c and if b∣a,c, then $\frac{c}{b} \nmid 1 \pm \frac{a^{2}}{b^{2}}$.

Proof

First note that for any integer a, {4,4}_(a,0),(0,a) and {4,4}_{(−a,0),(0,−a)} are isomorphic toroids. For class 1, the condition a>0 guaranties that any two members in each family are different. For classes 2, 2_0,2 and 2₁, interchanging a and b produces an isomorphic copy of the toroid (which for class 2 is in fact its enantiomorphic toroid). The condition a>b>0 guaranties that any two members in each family are non-isomorphic.

For class 4, we use Lemma 4 to find the generating vectors (a,b) and (c,0). To guaranty that two toroids of the family are non-isomorphic, in addition to the condition a>b>0, we now need the extra condition c≥a−b. Furthermore, by Proposition 5, if either c=2a, a=2c or b∣a,c and $\frac{c}{b} \mid 1 \pm \frac{a^{2}}{b^{2}}$, the toroid would have additional symmetries by R ₁, R ₂ or R ₁ R ₂ and hence would have at most two orbits of flags, thus not belonging to class 4. □

4.2 Equivelar Toroids of Type {3,6}

Let $\mathcal {U}$ be the regular tessellation of type {3,6} of the Euclidean plane. It is convenient (and common) to use $\{ e_{1}, \frac{1}{2}e_{1} + \frac{\sqrt{3}}{2}e_{2}\}$ as the basis of the corresponding lattice Λ _{3,6}.

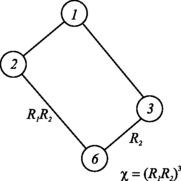
Again, using the notation introduced in Sect. 3, we note that S=〈R ₁,R ₂〉 and χ∈S (see Table 1). Making use of Lemma 6 we note that there are, up to conjugation, only two proper subgroups of S distinct from 〈χ〉 containing 〈χ〉, namely 〈χ,R ₁ R ₂〉 and 〈χ,R ₂〉.

In Fig. 2 we give all four possible conjugacy classes of subgroups K′ with 〈χ〉≤K′≤S. As before, the class corresponding to the stabiliser S and representing all regular (1-orbit) toroids now of type {3,6} is labelled ‘1’. The label ‘6’ represents all 6-orbit toroids of type {3,6} and corresponds to the subgroup 〈χ〉 of the stabiliser S. The class corresponds to the subgroup 〈χ,R ₁ R ₂〉, labelled ‘2’, represents all chiral (2-orbit) toroids of type {3,6}. Finally, label ‘3’ represents 3-orbit toroids of type {3,6} and corresponds to the subgroup 〈χ,R ₂〉. Henceforth, in this subsection we name the classes by these labels.

Fig. 2

Conjugacy classes of vertex stabilisers for toroids of type {3,6}

First we consider the class 1, that is, the case where the toroid $\mathcal {U}/\varLambda$ is regular and the corresponding vertex stabiliser of o in $\mathcal {U}$ is K′=〈R ₁,R ₂〉. Then, R ₁ R ₂∈K′ is the rotation by $\frac{\pi}{3}$ around o.

Assuming v∈Λ∖{o} is such that d(v,o)≤d(v′,o) for any v′∈Λ∖{o}, the orbit of v under 〈R ₁ R ₂〉 is a set of six points forming the vertices of a regular hexagon. Clearly, there can be no other point in Λ at distance d(v,o) from o as the distance between any such point and v〈R ₁ R ₂〉 would be smaller than d(v,o). In addition, as R ₁,R ₂∈K′, these six points must be either on the lines y=0, x=0 and y=−x or on the lines y=x, 2y=−x and y=−2x, yielding the two well-known families of regular toroids {3,6}_(a,0),(0,a) and {3,6}_{(a,a),(2a,−a)}, respectively. (In the notation of [3], these two toroids are denoted by {3,6}_(a,0) and {3,6}_(a,a), respectively.)

Let us now consider the conjugacy class 2, that is, the class consisting of chiral toroids. The corresponding subgroup of the vertex stabiliser of o is K′=〈R ₁ R ₂〉. As in the regular case, the rotation R ₁ R ₂∈K′, and the six points in Λ∖{o} closest to o form a regular hexagon. If these six points are not on the lines described above, the toroid is chiral, otherwise it is regular. Such toroids are the well-known {3,6}_{(a,b),(−b,a+b)}, where ab(a−b)≠0 (in [3] these are denoted {3,6}_(a,b)). By choosing a>b>0, we guarantee that only one of the two isomorphic (enantiomorphic) toroids is considered.

It remains to analyse the class 3. For this class the reflection R ₂ in the x-axis, sending a point (x,y) to (x+y,−y), is an element of K′. Following Sect. 2, Λ=⋃ _k∈ℤ(Λ _Π +kv), where Π is the x-axis and v∉Π is the lattice point closest to the origin among the ones closest to Π. Let c∈ℤ be such that (c,0) is a generating vector of Λ _Π . Then, either $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$ or $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$, giving us the two possible families for toroids in this class. If $\frac{1}{2}(v + vR_{2}) \in \varLambda_{\varPi}$, then the closest point to o, not in Λ _Π , is on the line through o perpendicular to the x-axis, so that v=(−d,2d) for some integer d, giving us the toroid {3,6}_{(c,0),(−d,2d)} in class 3. If $\frac{1}{2}(v + vR_{2}) \notin \varLambda_{\varPi}$, then v=(a,c−2a), giving us the toroid {3,6}_{(c,0),(a,c−2a)}={3,6}_{(a,c−2a),(c−a,2a−c)} that is in class 3 whenever a≠c and regular otherwise. The maps in this class were also described in [14] within the theory of k orbit maps.

Any other lattice not symmetrical by a conjugate of R ₂ or R ₁ R ₂ is a lattice in class 6. The proof of the following theorem now follows from Lemma 4 and Proposition 5, using similar arguments to those we used in the proof of Theorem 7.

Theorem 8

Equivelar toroids with Schläfli type {3,6} can be described as $\{3,6\}_{v_{1},v_{2}}$, where v ₁ and v ₂ are two linearly independent vectors. Furthermore, given integers a>b>0, c>0 and d>0 the classes of toroids are as follows.

• Class 1 contains the two families of regular toroids

  $$\{3,6\}_{(a,0),(0,a)} \quad \mathrm{and} \quad \{3,6\}_{(a,a),(2a,-a)}. $$

• Class 2 contains the family of chiral toroids

  $$\{3,6\}_{(a,b),(-b,a+b)}. $$

• Class 3 contains the two families of toroids

  $$\{3,6\}_{(a,0),(-c,2c)}\quad \mathrm{and} \quad \{3,6\}_{(a,d),(a+d,-d)}. $$

• Class 6 contains the family of toroids

  $$\{3,6\}_{(a,b),(c,0)}, $$

  where c≥a−b, c∤2a+b and if b∣a,c, then $\frac{c}{b} \nmid 1 - \frac{a^{2}}{b^{2}}$ and $\frac{c}{b} \nmid 1 + \frac{a}{b}+ \frac{a^{2}}{b^{2}}$.

The above theorem gives the classification of 3-toroids of type {3,6} and using duality one derives the classification of 3-toroids of type {6,3}.

5 Conjugacy Classes of Equivelar 4-Toroids

In this section we determine all classes of equivelar 4-toroids. The toroids are obtained as quotients of the tessellation $\mathcal {U}$ of type {4,3,4} of the Euclidean 3-space according to the conjugacy classes of subgroups of the vertex stabiliser in $\mathrm {Aut}(\mathcal {U})$. Let {e ₁,e ₂,e ₃} be the standard orthonormal basis of the corresponding lattice Λ _{4,3,4}. Every rank 3 sublattice Λ⊆Λ _{4,3,4} can be described by three generating translations t ₁, t ₂ and t ₃ with respect to three linearly independent vectors v ₁, v ₂ and v ₃, respectively. The corresponding 4-toroid $\mathcal {P}=\mathcal {P}(\varLambda)=\mathcal {U}/ \varLambda$ is denoted by $\{4,3,4\}_{v_{1}, v_{2}, v_{3}}$.

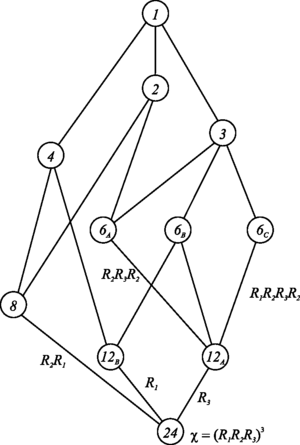
The symmetry group of a vertex-figure of the tessellation {4,3,4} is the octahedral group. Taking the vertex-figure at the origin and specifying its base flag Φ, the octahedral group S is generated by the reflections R ₁,R ₂,R ₃ given in Table 1. Using simple geometric arguments, the relationship between conjugacy classes of subgroups of S containing the central symmetry χ can be seen to be as in Fig. 3. (In fact, one can see that this is the subgroup lattice of the automorphism group of the hemi-octahedron.) Each class labelled k, represents a conjugacy class of subgroups of index k in S. The index of each subgroup determines the number of orbits of the toroids in that class. It follows that there are at most 11 different classes of toroids ranging from regular, that is in class 1, to 24-orbit toroids. As we shall see, some conjugacy classes contain no toroids. For example, since χ is a word of odd length, there can be no chiral toroids of rank 4. In Sect. 6 we shall prove that class 2 is in fact empty. An alternative proof of the nonexistence can be derived from the fact that any toroid admitting all symmetries required for the class 2 must be regular.

Fig. 3

Lattice of conjugacy classes of vertex-stabilisers for toroids of type {4,3,4}

In Fig. 3 certain edges connecting two conjugacy classes of subgroups are labelled by automorphisms in S, which indicate, just as in Fig. 1 and 2, that a group in the conjugacy class of smaller index can be generated by adjoining that automorphism to the group in the class of larger index.

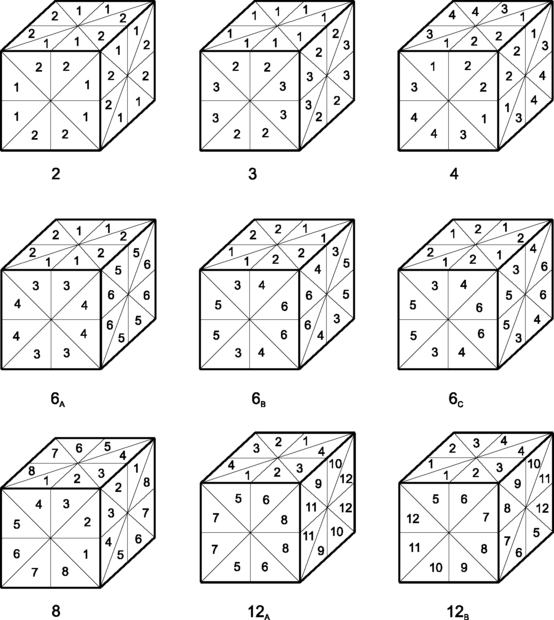
Each class of equivelar 4-toroids in Fig. 3 is uniquely determined by the flag arrangement on a vertex-figure of a toroid in that class. For any toroid $\mathcal {P}=\mathcal {U}/ \varLambda$, the subgroup T/Λ, whose elements we refer to as the translations of $\mathcal {P}$, is a normal subgroup of $\mathrm {Aut}(\mathcal{P})$. Hence, the translations of the toroid act vertex-transitively and the flag arrangement extends to the entire toroid. In particular, the flag arrangement in a vertex-figure completely determines the flag arrangement in any facet. As the automorphism group of an equivelar 4-toroid $\mathcal{P}$ is also facet-transitive, it follows that the flag arrangement of each facet can be extended to the entire toroid by translations. In addition, because of the invariance under the central symmetry χ as well as the translations of $\mathcal {P}$, one can specify the flag arrangement by considering only three 2-faces of a facet sharing a vertex. The flag arrangement on a facet of 4-toroids in the classes given in Fig. 3 can be derived from the labels of the edges in the figure and are shown in Fig. 4.

Fig. 4

Flag arrangements on facets of equivelar rank 4 toroids

6 Lattices Invariant Under R ₃

In this section we describe toroids $\mathcal {U}/ \varLambda$, where Λ is a lattice invariant under R ₃. Our technique consists of showing how each family of equivelar 3-toroids listed in Theorem 7 can be extended to a family of equivelar 4-toroid invariant under R ₃. Throughout, Π denotes the plane z=0 fixed by R ₃. As before we let $\mathcal {P}=\mathcal {P}(\varLambda)$ be the 4-toroid induced by Λ. As noted in Sect. 2, Λ _Π =Λ∩Π is a 2-dimensional sublattice of Λ inducing an equivelar toroid $\mathcal{K}=\mathcal{K}(\varLambda)$ of type {4,4}.

The classification of regular and chiral toroids of any rank was completed by McMullen and Schulte in [10]. Since regular and 2-orbit 4-toroids are all invariant under R ₃ (see Fig. 3), in this section we obtain this classification, for rank 4, using methods similar to the ones we used for rank 3 in Sect. 4. In fact, we conclude that there are no 2-orbit equivelar toroids of rank 4.

6.1 Extensions of 3-Toroids

Since R ₃ and the translations preserving $\mathcal {U}$ project to symmetries of the 4-toroid $\mathcal {P}$, a flag containing an edge in the direction of the z-axis and its 0-adjacent flag are in the same orbit. We consider all possible ways in which the 3-toroid $\mathcal{K}$ induced by Λ _Π can be extended to a 4-toroid. Note that, since χ is the product of the reflections about the three coordinates planes, the half-turn χR ₃ about the z-axis leaves Λ invariant. In other words, the restriction of χ to Π extends to a half-turn in $\mathbb{E}^{3}$ that preserves Λ. The other symmetries of $\mathcal{K}$ that have to be considered (see Fig. 1) are the reflections denoted r ₁ and r ₂, about the lines x=y and y=0, respectively, as well as the rotation r ₁ r ₂. These symmetries of $\mathcal{K}$ need not always extend to symmetries of $\mathcal {P}$. In what follows we shall make use of the following straight-forward lemma.

Lemma 9

Let $\mathcal {P}$, $\mathcal{K}$, r ₁ and r ₂ be as above. If r ₁, r ₂ or r ₁ r ₂ are symmetries of $\mathcal{K}$ that extend to symmetries of $\mathcal {P}$, then they extend to R ₁, R ₂ R ₃ R ₂ or R ₁ R ₂ R ₃ R ₂, respectively.

We note that not every symmetry of a 4-toroid $\mathcal {P}$ can be obtained by the extensions given in Lemma 9. In fact, if $\mathcal {P}$ is also symmetric under R ₂ R ₁, then $\mathcal {P}$ must be in class 1 or 2, according to Fig. 3.

The non trivial conjugates of R ₂ R ₁ in S are R ₃ R ₂ R ₁ R ₃, R ₂ R ₃ R ₁ R ₂ R ₃ R ₂ and R ₃ R ₂ R ₁ R ₂ R ₃ R ₂. However, since $\mathcal {P}$ is invariant under R ₃ it is invariant under any of the conjugates of R ₂ R ₁ if and only if it is invariant under all of them (see Fig. 3). Hence, to determine the symmetries of $\mathcal {P}$ one has to consider which symmetries of $\mathcal{K}$ extend, as well as whether $\mathcal {P}$ is invariant under R ₂ R ₁.

Following the relationships between classes in Fig. 3 we note that if $\mathcal{K}$ is in class 1, $\mathcal {P}$ can be in class 1, 2, 3, 6 _A , 6 _B , 6 _C or 12 _A , depending on which symmetries of $\mathcal{K}$ extend to $\mathcal {P}$ and whether R ₂ R ₁ is a symmetry of $\mathcal {P}$.

If $\mathcal{K}$ is in class 2, 2₁ or 4, the flags in a facet of $\mathcal {P}$ may be labelled as the flags of 12 _A (see Fig. 4) in such a way that the flags labelled 1,2,3 and 4 contain the 2-faces parallel to Π. In addition, if $\mathcal{K}$ is in class 2 or 2₁, the flags in a facet of $\mathcal {P}$ may also be labelled as the flags of 6 _C or 6 _B , respectively, in such a way that the flags labelled 1 and 2 contain the 2-faces parallel to Π. However, in the labelling of cubes in Fig. 4, two flags with different labels when restricted to Π, may belong to the same flag orbit of $\mathcal{K}$. We now deduce the following lemma.

Lemma 10

Let $\mathcal {P}=\mathcal {P}(\varLambda)$ be an equivelar 4-toroid invariant under R ₃, the reflection in the plane Π (the plane z=0). If the 3-toroid $\mathcal{K}$ induced by Λ∩Π is in class 2, 2₁ or 4 then $\mathcal {P}$ has at least 6, 6 or 12 flag orbits, respectively. In particular, $\mathcal {P}$ is not invariant under R ₂ R ₁.

Finally, if $\mathcal{K}$ is in class 2_0,2, using similar arguments we note that $\mathcal {P}$ can be in class 2, 6 _A or 12 _A . Furthermore, the restrictions of 4-toroids in class 3 to the planes x=0 and y=0 are 3-toroids in class 2_0,2 (see Fig. 4). Moreover, in this case, $\mathcal {P}$ is also invariant under the reflections in the planes x=0 and y=0. Therefore, an extension of a 3-toroid $\mathcal{K}$ in class 2_0,2 can happen to be in class 3. If this case $\mathcal {P}$ has to be invariant under the 4-fold rotation about the x- or y-axis. However, the restriction of $\mathcal {P}$ to the plane x=0 or y=0 yields a 3-toroid in class 1. Therefore a 4-toroid in class 3 can be considered as one arising from $\mathcal{K}$ in class 1, as we shall do.

Among different ways of extending $\mathcal{K}$ to a 4-toroid, the most natural extension is the one for which all the points of Λ project orthogonally to the points of Λ _Π . In this case, we say that Λ is a vertical translation lattice with respect to Π, that is, Λ=⋃ _k∈ℤ(Λ _Π +kv) where v=(0,0,d) for some d∈ℤ as defined in Sect. 2. Throughout this section we shall refer to a vertical translation lattice with respect to Π simply as a vertical translation lattice.

The following lemma describes the location of the translates of Λ _Π whenever Λ is not a vertical translation lattice.

Lemma 11

Let Π be the plane z=0 and Λ a lattice invariant under the reflection in Π. Assume also that Λ is not a vertical translation lattice. Then Λ=⋃ _k∈ℤ(Λ _Π +kv) for some v=(x,y,d), where x, y are integers, d a positive integer, (2x,2y,0)∈Λ and (x,y,0)∉Λ.

Proof

As in Sect. 2, we recall that Λ=⋃ _z∈ℤ(Λ _Π +kv) for some v=(x,y,d)∉Π where d:=d(v,Π)≤d(w,Π) for every w∈Λ∖Λ _Π . Note that v does not project orthogonally to Π into a point of Λ since otherwise Λ would be a vertical translation lattice.

Observe that v+vR ₃∈Λ _Π , and that this point is (2x,2y,0), the orthogonal projection of 2v in Π. □

The points of Λ, whenever Λ is not a vertical translation lattice, belong to planes Π+k(0,0,d) for k∈ℤ. If k is even the points of Λ in Π+k(0,0,d) all project orthogonally to Λ _Π . On the other hand, if k is odd the points of Λ in Π+k(0,0,d) project orthogonally to a translate Λ _Π +w of Λ _Π where w∉Λ _Π and 2w∈Λ _Π .

Recall that since Λ _Π induces an equivelar 3-toroid of type {4,4}, it is determined by two independent vectors v ₁ and v ₂. Whenever Λ is not a vertical translation lattice, without loss of generality, by using the translation subgroup we may choose v to project to either $\frac{v_{1}}{2}$, $\frac{v_{2}}{2}$ or $\frac{v_{1}+v_{2}}{2}$. In the remainder of this section, for each family of equivelar 3-toroids listed in Theorem 7 we shall analyse the toroid $\mathcal {P}= \mathcal {U}/ \varLambda$ when Λ is a vertical translation lattice (so that v projects to a point of Λ _Π ), when v projects to $\frac{v_{1}+v_{2}}{2}$ (that is, the centre of a fundamental region of Λ _Π ) and when v projects to $\frac{v_{1}}{2}$ or $\frac{v_{2}}{2}$ (the mid-point of an edge of a fundamental region of Λ _Π ). This will lead to a classification of equivelar 4-toroids in classes 1, 2, 3, 6 _A , 6 _B , 6 _C and 12 _A . To achieve this classification we shall make use of the flag arrangements on facets of the toroids in these classes given in Fig. 4.

6.2 Vertical Translation Lattice

We start by assuming that Λ _Π induces a regular 3-toroid $\mathcal{K}$ in one of the two families {4,4}_(a,0),(0,a) or {4,4}_{(a,a),(a,−a)} for a positive integer a. In both cases, the symmetries r ₁ and r ₂ of $\mathcal{K}$ defined above extend to symmetries of $\mathcal {P}$. As discussed in the previous subsection, it follows that $\mathcal {P}$ is either in class 3 or regular.

In the case of the first family, if $\mathcal {P}$ is regular, then $\mathcal {P}$ is also invariant under R ₂. In this case, since (0,0,d)∈Λ, it follows that (0,0,d)R ₂=(0,d,0)∈Λ _Π implying that d≥a. On the other hand (0,a,0)R ₂=(0,0,a) implying that a≥d by the minimality of d. Hence d=a and Λ=〈(a,0,0),(0,a,0),(0,0,a)〉, inducing the regular toroid {4,3,4}_{(a,0,0),(0,a,0),(0,0,a)} (denoted by {4,3,4}_(a,0,0) in [11]). The set of points of Λ forms a cubic lattice. If d≠a, then Λ is not invariant under R ₂ and the toroid $\mathcal {P}=\{4,3,4\}_{(a,0,0), (0,a,0), (0,0,d)}$ is in class 3.

In the case of the second family (that is, $\mathcal{K}$ is the regular toroid {4,4}_{(a,a),(a,−a)}, for some integer a) we obtain a toroid {4,3,4}_{(a,a,0),(a,−a,0),(0,0,d)} in class 3. In fact, assuming that $\mathcal {P}$ is regular, implies that (a,a,0)R ₂ R ₁=(0,a,a) is in Λ not projecting to a point in Λ _Π , contradicting the fact that Λ is a vertical translation lattice.

For the case where Λ is a vertical translation lattice and Λ _Π induces a chiral 3-toroid $\mathcal{K}$, $\mathcal {P}$ is the 4-toroid {4,3,4}_{(a,b,0),(−b,a,0),(0,0,d)}. The symmetry r ₁ r ₂ of $\mathcal{K}$ extends to a symmetry of $\mathcal {P}$ implying that the latter belongs to either class 6 _C , 3 or 1. Lemma 10 then implies that the toroid is in class 6 _C .

We now analyse the case where Λ is a vertical translation lattice and Λ _Π induces a 3-toroid $\mathcal{K}$ in class 2_0,2. In this case $\mathcal {P}$ is the 4-toroid {4,3,4}_{(a,0,0),(0,b,0),(0,0,d)} or the toroid {4,3,4}_{(a,b,0),(a,−b,0),(0,0,d)} where a>b>0. The symmetry r ₂ of $\mathcal{K}$ extends to a symmetry of $\mathcal {P}$. Hence $\mathcal {P}$ belongs to either class 6 _A , 3 or 2 and since a≠b, clearly $\mathcal {P}$ does not belong to class 1. In what follows we shall consider each of these cases.

We first show that if $\mathcal{K}$ is in class 2_0,2, then $\mathcal {P}$ cannot be a 2-orbit toroid. Suppose otherwise, that is, $\mathcal {P}$ is in class 2. Then Λ must be invariant under R ₂ R ₁ which cyclically permutes the three coordinate axes. However, the translations along the x- and y-axes fixing Λ are with respect to the vectors k(a,0,0) and k(0,b,0) for {4,3,4}_{(a,0,0),(0,b,0),(0,0,d)}, and k(2a,0,0) and k(0,2b,0) for {4,3,4}_{(a,b,0),(a,−b,0),(0,0,d)}. In both cases, it follows that a=b, contradicting our hypothesis. Therefore $\mathcal {P}$ is not a 2-orbit toroid.

We recall from Sect. 6.1 that if $\mathcal {P}$ is in class 3, then we consider it as a 4-toroid arising from class 1 and therefore it is not necessary to derive details of such toroids here.

Assuming $\mathcal {P}$ is in class 6 _A , either $\mathcal {P}= \{4,3,4\}_{(a, 0, 0),(0, b,0),(0,0,d)}$ or $\mathcal {P}=\{4,3, 4\}_{(a, b, 0),(a,-b,0),(0,0,d)}$, with a≠b in both cases. If $\mathcal {P}= \{4,3,4\}_{(a, 0, 0),(0, b,0),(0,0,d)}$ and a=d or b=d, then Λ is invariant under the 4-fold rotation about y- or x-axis, respectively, which would imply that $\mathcal {P}$ has 3 orbits of flags and therefore cannot be in class 6 _A . On the other hand, it is easy to see that if $\mathcal {P}=\{4,3,4\}_{(a, b, 0),(a,-b,0),(0,0,d)}$, no extra symmetry can be obtained as Λ is not invariant under a 3-fold or a 4-fold rotation.

In the case where Λ is a vertical translation lattice and Λ _Π induces a 3-toroid $\mathcal{K}$ in class 2₁, $\mathcal {P}$ is the 4-toroid {4,3,4}_{(a,a,0),(b,−b,0),(0,0,d)} or the toroid {4,3,4}_{(a,b,0),(b,a,0),(0,0,d)} where a>b>0. By Lemma 10, the toroid must belong to class 6 _B , since the symmetry r ₁ of $\mathcal{K}$ extends to a symmetry of $\mathcal {P}$.

Finally, when Λ is a vertical translation lattice and Λ _Π induces a 3-toroid $\mathcal{K}$ in class 4, $\mathcal {P}$ is the 4-toroid {4,3,4}_{(a,b,0),(c,0,0),(0,0,d)} with the conditions given in Theorem 7 for class 4. In this case $\mathcal {P}$ is in fact in class 12 _A as follows from Lemma 10.

The above classification of equivelar 4-toroids arising from vertical translation lattices invariant under R ₃ is summarised in Table 2, where “∗” stands for d>0, c≥a−b, c≠2a≠4c, and if b∣a and b∣c then c/b∤1±a ²/b ².

Table 2 Classes of equivelar 4-toroids with vertical translation lattices invariant under the reflection R ₃ in the xy-plane

6.3 Non-Vertical Translation Lattices

We shall now assume that Λ is not a vertical translation lattice and in the first instance consider the case in which a point of Λ projects to $\frac{v_{1}+v_{2}}{2}$.

Let us start by assuming that the 3-toroid $\mathcal{K}$ induced by Λ _Π is regular. As before, the symmetries r ₁ and r ₂ of $\mathcal{K}$ extend to symmetries of $\mathcal {P}$. Hence $\mathcal {P}$ is either regular or in class 3. Since v∈Λ projects to the centre of the fundamental region of Λ _Π , $\mathcal {P}$ is either $\{4,3,4\}_{(a,0,0),(0,a,0),(\frac{a}{2},\frac{a}{2},d)}$ or {4,3,4}_{(a,a,0),(a,−a,0),(a,0,d)}, depending on which of the two regular toroids of type {4,4} is induced by Λ _Π . In the former case, $\mathcal {P}$ is regular whenever $d=\frac{a}{2}$, implying that $\varLambda = \langle (a,0,0), (0,a,0), (\frac{a}{2},\frac{a}{2},\frac{a}{2}) \rangle$, giving us the regular toroid $\{4,3,4\}_{(\frac{a}{2},\frac{a}{2},-\frac{a}{2}),(\frac{a}{2},-\frac{a}{2},\frac{a}{2}),(-\frac{a}{2},\frac{a}{2},\frac{a}{2})}$ (denoted by $\{4,3,4\}_{(\frac{a}{2},\frac{a}{2},\frac{a}{2})}$ in [11]). In this case the set of points of Λ is a body-centred cubic lattice. In the latter case $\mathcal {P}$ is regular whenever d=a. In fact we have Λ=〈(a,a,0),(a,−a,0),(a,0,a)〉, giving us the regular toroid {4,3,4}_{(a,a,0),(a,−a,0),(a,0,a)} (denoted by {4,3,4}_(a,a,0) in [11]). The set of points of Λ in this case is a face-centred cubic lattice. In either case, if $\mathcal {P}$ is not regular, then it is in class 3.

If the 3-toroid $\mathcal{K}$ induced by Λ _Π is either in class 2 or 2₁, the corresponding symmetry r ₁ r ₂ or r ₁ extends to a symmetry of $\mathcal {P}$. By Lemma 10 we see that $\mathcal {P}$ is, respectively in class 6 _C or 6 _B .

We now turn our attention to the case when the 3-toroid $\mathcal{K}$ induced by Λ _Π is in class 2_0,2. Then, Λ is either

$$\{4,3,4\}_{(a,0,0),(0,b,0),(\frac{a}{2},\frac{b}{2},d)}\quad \mbox{or}\quad \{4,3,4\}_{(a,b,0),(a,-b,0),(a,0,d)}. $$

Note that the toroid $\{4,3,4\}_{(a,0,0),(0,b,0),(\frac{a}{2},\frac{b}{2},\frac{a}{2})}$ is isomorphic to

$$\{4,3,4\}_{(a,0,0),(0,a,0),(\frac{a}{2},\frac{a}{2},\frac{b}{2})}, $$

which is in class 3. Similarly, $\{4,3,4\}_{(a,0,0),(0,b,0),(\frac{a}{2},\frac{b}{2},\frac{b}{2})}$ is isomorphic to

$$\{4,3,4\}_{(b,0,0),(0,b,0),(\frac{b}{2},\frac{b}{2},\frac{a}{2})}, $$

which is again in class 3. On the other hand, the toroids {4,3,4}_{(a,b,0),(a,−b,0),(a,0,a)} and {4,3,4}_{(a,b,0),(a,−b,0),(a,0,b)} are isomorphic to {4,3,4}_{(a,a,0),(a,−a,0),(a,0,b)} and {4,3,4}_{(b,b,0),(b,−b,0),(b,0,a)} respectively, which are again in class 3. But all these toroids in class 3 have been considered before. Similar arguments as we used for the vertical translation lattices now imply that in both families any other choice of d yields a toroid in class 6 _A .

We finally note that if the toroid induced by Λ _Π is in class 4, Lemma 10 implies that $\mathcal {P}$ is in class 12 _A .

Table 3 contains all the equivelar toroids induced by non-vertical translation lattices Λ such that a point v∈Λ projects to $\frac{v_{1}+v_{2}}{2}$. In this table, “∗” stands for d>0, c≥a−b, c≠2a≠4c, and if b∣a and b∣c then $\frac{c}{b} \nmid 1 \pm \frac{a^{2}}{b^{2}}$.

Table 3 Classes of equivelar 4-toroids induced by non-vertical translation lattices Λ invariant under the reflection on the xy-plane such that a point v∈Λ∖Λ _Π projects to the centre of a fundamental region of Λ _Π , the sublattice of Λ contained in the xy-plane

We finish the analysis of lattices invariant under R ₃ by considering the case when Λ is not a vertical translation lattice and has a generating vector projecting to the mid-point of an edge of the fundamental region of the 3-toroid $\mathcal{K}$ induced by Λ _Π . That is, it only remains to consider the possibilities of a point of Λ projecting into $\frac{v_{1}}{2}$ or to $\frac{v_{2}}{2}$.

We start by considering the case when $\mathcal{K}$ is of type {4,4}_(a,0),(0,b) (here b might be equal to a). Hence, depending on whether a generating vector v∈Λ projects to $\frac{v_{1}}{2}$ or to $\frac{v_{2}}{2}$, $\mathcal {P}$ is either $\{4,3,4\}_{(a,0,0), (0,b,0), (\frac{a}{2}, 0, d)}$ or $\{4,3,4\}_{(a,0,0), (0,b,0), (0, \frac{b}{2}, d)}$. These toroids cannot have R ₁ R ₂ as a symmetry since such rotation permutes the coordinate axes and this is clearly not possible. Note furthermore that in both cases the symmetry r ₂ of $\mathcal{K}$ extends to $\mathcal {P}$, and that the symmetry r ₁ of $\mathcal{K}$ does not extend even when a=b. If $d=\frac{a}{2}$ ($d=\frac{b}{2}$, respectively), then Λ is invariant under a 4-fold rotation about the x-axis (y-axis, respectively) and that toroid can be considered as one arising from a 3-toroid in class 1. Otherwise $\mathcal {P}$ is in class 6 _A .

If the toroid $\mathcal{K}$ is regular of type {4,4}_{(a,a),(a,−a)} then without loss of generality we assume that Λ is $\{4,3,4\}_{(a,a,0),(a,-a,0),(\frac{a}{2},\frac{a}{2},d)}$, as the choice of $\frac{v_{1}}{2}$ or $\frac{v_{2}}{2}$ leads to isomorphic toroids. It is now not difficult to see that Λ is invariant under R ₁, and therefore $\mathcal {P}$ belongs to class 1, 3 or 6 _B . Note, however, that the symmetry r ₂ of $\mathcal{K}$ does not extend, implying in fact that $\mathcal {P}$ is in class 6 _B .

If the toroid $\mathcal{K}$ is in the family {4,4}_{(a,b),(a,−b)} then without loss of generality we can choose Λ to be $\{4,3,4\}_{(a,b,0),(a,-b,0),(\frac{a}{2},\frac{b}{2},d)}$. In this case none of the symmetries of $\mathcal{K}$ extend, and hence these toroids are in class 12 _A .

In the case where the toroid $\mathcal{K}$ is in class 2₁, the only symmetry of $\mathcal{K}$ that can extend is r ₁. However, this only happens whenever $\mathcal{K}$ belongs to the family {4,4}_{(a,a),(b,−b)}. Therefore, by Lemma 10 the toroids $\{4,3,4\}_{(a,a,0),(b,-b,0),(\frac{a}{2},\frac{a}{2}, d)}$ and $\{4,3,4\}_{(a,a,0),(b,-b,0),(\frac{b}{2},\frac{b}{2}, d)}$ are in class 6 _B , while the toroids

$$\{4,3,4\}_{(a,b,0),(b,a,0),(\frac{a}{2},\frac{b}{2}, d)} $$

and its isomorphic toroid $\{4,3,4\}_{(a,b,0),(b,a,0),(\frac{b}{2},\frac{a}{2}, d)}$ belong to class 12 _A .

Finally, none of the symmetries of a toroid $\mathcal{K}$ in class 2 or 4 extend. By Lemma 10 such toroids also belong to class 12 _A .

In Table 4, “∗” stands for d>0, c≥a−b, c≠2a≠4c, and if b∣a and b∣c then $\frac{c}{b} \nmid 1 \pm \frac{a^{2}}{b^{2}}$.

Table 4 Classes of equivelar 4-toroids induced by non-vertical translation lattices Λ invariant under the reflection in the xy-plane such that a point v∈Λ∖Λ _Π projects to the middle point of an edge of the sublattice of Λ contained in the xy-plane

In particular, the above analysis implies the following theorem.

Theorem 12

There are no 2-orbit equivelar 4-toroids.

7 Lattices Not Invariant Under R ₃

Throughout this section we let $\mathcal {P}= \mathcal {U}/ \varLambda$ be a 4-toroid such that Λ is not invariant under R ₃. If $\mathcal {P}$ is in class 4, then Λ is invariant under the 3-fold rotation R ₂ R ₁, as well as under the plane reflection R ₁, whose mirror contains the axis of rotation of R ₂ R ₁. If $\mathcal {P}$ is in class 8, then Λ is invariant under R ₂ R ₁, but not under R ₁ (see Fig. 3). These two classes are described in Sect. 7.1. If $\mathcal {P}$ is in class 12 _B , then Λ is invariant under R ₁ but not under R ₂ R ₁. This class is described in Sect. 7.2. Finally, if Λ is not invariant under R ₁ or R ₂ R ₁, then $\mathcal {P}$ must be in class 24.

7.1 Lattices Invariant Under R ₂ R ₁

The 3-fold rotation R ₂ R ₁ fixes the line generated by the vector e=(1,1,1). Let Π _e be the plane x+y+z=0, invariant under R ₂ R ₁ and let Λ be a rank 3 sublattice of Λ _{4,3,4} invariant under R ₂ R ₁. Note that Λ _{4,3,4}∩Π _e is a lattice isomorphic to the lattice Λ _{3,6}, generated by the vectors u ₁=(1,0,−1) and u ₂=(0,1,−1). For any v∈Λ, v+v(R ₂ R ₁)+v(R ₂ R ₁)² must project into o. This implies that 3v projects orthogonally to Π _e into a point of Λ since its distance to Π _e coincides with that of v+v(R ₂ R ₁)+v(R ₂ R ₁)². Hence $\varLambda_{\varPi_{e}} := \varLambda \cap \varPi_{e}$ is a rank 2 sublattice of Λ _{4,3,4}∩Π _e invariant under R ₂ R ₁. It follows from the structure of the conjugacy classes of 3-toroids with type {3,6} (see Fig. 2) that $\varLambda_{\varPi_{e}}$ induces either a regular or a chiral 3-toroid $\mathcal{K}$, and therefore we may choose a generating set {v ₁,v ₂} of $\varLambda_{\varPi_{e}}$, where v ₁ and v ₂ have the same length and the angle between them is $\frac{\pi}{3}$. We shall consider the vectors v ₁ and v ₂ in terms of the basis {u ₁,u ₂}. Since χ is the central inversion at the origin, the composition R ₂ R ₁ χ is a rotatory reflection of order 6, whose restriction to the plane Π _e is a 6-fold rotation.

Since R ₁ preserves Π _e , if Λ is invariant under R ₁ then so is $\varLambda_{\varPi_{e}}$. This implies that the 3-toroid $\mathcal{K}$ is regular. However, even if Λ is not invariant under R ₁, $\mathcal{K}$ may still be regular, as we shall see below.

We say that Λ is a vertical translation lattice with respect to $\varLambda_{\varPi_{e}}$ whenever $\varLambda = \bigcup_{k\in \mathbb{Z}} (\varLambda_{\varPi_{e}} +kv)$ where v=(l,l,l) for some l∈ℤ as in Sect. 2. In this case, the distance between Π _e and Π _e +v (the first translate of Λ _Π in the direction of e intersecting Λ) is a multiple of $\sqrt{3}$.

The following lemma describes the location of the translates of $\varLambda_{\varPi_{e}}$, including the case when Λ is not a vertical translation lattice.

Lemma 13

Let Λ be an integer lattice invariant under R ₂ R ₁, and let Π _e and $\varLambda_{\varPi_{e}}$ as above. Let {v ₁,v ₂} be a generating set for $\varLambda_{\varPi_{e}}$ consisting of vectors with the same length and an angle of $\frac{\pi}{3}$ between them. Then $\varLambda = \bigcup_{k\in \mathbb{Z}} (\varLambda_{\varPi_{e}} + kv)$ where v is a point in Λ∖Π _e closest to Π _e that projects to either the origin o, to $\frac{v_{1}+v_{2}}{3}$ or to $2\frac{v_{1}+v_{2}}{3}$.

Proof

Without loss of generality assume that v projects orthogonally to Π _e to a point in the parallelogram determined by v ₁ and v ₂, since otherwise we could instead consider the appropriate translate of v.

If Λ is a vertical translation lattice with respect to Π _e , then v projects to o.

Recall that 3v projects orthogonally to Π _e into a point of Λ. An easy calculation shows that v projects to one of the nine points iv ₁+jv ₂ where $i, j \in \{0, \frac{1}{3}, \frac{2}{3}\}$. If Λ is not a vertical translation lattice, then i and j are not both 0, giving us eight possible points for the projection of v. Note that these eight points are equivalent in pairs under χ and translations preserving Λ, hence without loss of generality we may assume that v projects to $\frac{v_{1}}{3}$, $\frac{v_{2}}{3}$, $\frac{v_{1}+v_{2}}{3}$ or $\frac{v_{1}+2v_{2}}{3}$.

If v projects to $\frac{v_{1}}{3}$, then it is easy to verify that $v - v R_{2}R_{1} = \frac{v_{1}}{3} - \frac{v_{1}}{3} (R_{2}R_{1}) \notin \varLambda$, which is a contradiction. Similarly, v cannot project to $\frac{v_{2}}{3}$ or to $\frac{v_{1}+2v_{2}}{3}$. Hence we need only consider $\frac{v_{1}+v_{2}}{3}$ and $2\frac{v_{1}+v_{2}}{3}$ as projections of v. □

We note that if Λ is a vertical translation lattice, R ₁ preserves Λ whenever $\mathcal{K}$ is a regular 3-toroid. When Λ is not a vertical translation lattice and $\mathcal{K}=\{3,6\}_{(a,0),(0,a)}$ for some integer a (where we take (a,0) and (0,a) in terms of the basis {u ₁,u ₂}), R ₁ is still a symmetry of Λ. However, this is not the case if Λ is not a vertical translation lattice and $\mathcal{K}=\{3,6\}_{(a,a),(2a,-a)}$, for some integer a.

In conclusion, the classification of toroids in classes 4 and 8 is as in Table 5. Recall that here we consider toroids induced by lattices invariant under R ₂ R ₁. As mentioned above, v is a point in $\varLambda \setminus \varLambda_{\varPi_{e}}$ closest to $\varLambda_{\varPi_{e}}$. We note that in the table the generating vectors of the toroids are given in terms of the canonical basis {e ₁,e ₂,e ₃} (as opposed to in terms of {u ₁,u ₂} as it was the case for $\mathcal{K}$). The conditions on the parameters required in the second row of the table ensure that the obtained toroid in indeed in class 4.

Table 5 Classes of non-regular toroids induced by lattices invariant under the rotation R ₂ R ₁ by $\frac{\pi}{3}$ about the line generated by the vector (1,1,1)

7.2 Class 12 _B

Toroids in class 12 _B are invariant under R ₁, which is the reflection with respect to the plane x=y, denoted by Π ₁. Note that the set of points of Λ _{4,3,4} in the plane Π ₁, generated by the vectors (1,1,0) and (0,0,1), coincides with the point set of a lattice of rectangles with sides of lengths 1 and $\sqrt{2}$. The only possible symmetries of this rectangular lattice stabilising the origin are the half-turn induced by χ and the reflections with respect to the lines in the directions (1,1,0) and (0,0,1). Consequently, a toroid induced by a sublattice of the rectangular lattice is of type {4,4} in class 2_0,2 or in class 4.

Assume that Λ is a sublattice of Λ _{4,3,4} invariant under R ₁, and let $\varLambda_{\varPi_{1}}:=\varLambda \cap \varPi_{1}$. We say that Λ is a vertical translation lattice whenever $\varLambda = \bigcup_{k \in \mathbb{Z}} (\varLambda_{\varPi_{1}} +kv)$ where v=(d,−d,0) for some d∈ℤ. The following lemma describes the location of the translates of $\varLambda_{\varPi_{1}}$ whenever Λ is not a vertical translation lattice. Its proof is analogous to that of Lemma 11.

Lemma 14

Let Π ₁ be the plane x=y and Λ a lattice invariant under the reflection in Π ₁. If Λ is not a vertical translation lattice, then $\varLambda = \bigcup_{k \in \mathbb{Z}} (\varLambda_{\varPi_{1}} +kv)$ for v=(x+d,x−d,z)∈Λ, such that (2x,2x,2z)∈Λ and (x,x,z)∉Λ.

Assume that $\varLambda_{\varPi_{1}}$ is not a vertical translation lattice, and that it is generated by vectors v ₁ and v ₂. Lemma 14 implies that the points of Λ project orthogonally to Π ₁ into translates of either $\frac{v_{1}}{2}$, $\frac{v_{2}}{2}$ or $\frac{v_{1}+v_{2}}{2}$.

To determine all toroids in class 12 _B we shall consider sublattices of Λ _{4,3,4}∩Π ₁ and determine all possible ways to extend them to sublattices of Λ _{4,3,4}. In doing so, we need to eliminate those extended lattices that gain extra symmetries. According to Fig. 3 the extra symmetries we need to consider are R ₃ and R ₂ R ₁.

We start by analysing the case where $\varLambda_{\varPi_{1}}$ induces a toroid $\mathcal{K}$ in class 2_0,2.

The generating set of vectors {v ₁,v ₂} of $\varLambda_{\varPi_{1}}$ can be chosen to be either {(a,a,0),(0,0,b)} or {(a,a,b),(a,a,−b)}. In the first case, the fundamental region is a rectangle, whereas in the second case it is a rhombus.

We first consider the case where fundamental region of $\varLambda_{\varPi_{1}}$ is a rectangle. If Λ is a vertical translation lattice, then v=(d,−d,0) and

$$\mathcal {P}= \{4,3,4\}_{(a,a,0), (0,0,b), (d,-d,0)}= \{4,3,4\}_{(a,a,0), (d,-d,0), (0,0,b)} $$

is in class 3 or 6 _B , as in Table 2. If v projects to $\frac{v_{1}}{2}$, then

$$\mathcal {P}= \{4,3,4\}_{(a,a,0), (0,0,b), (\frac{a+d}{2},\frac{a-d}{2},0)}= \{4,3,4\}_{(\frac{a+d}{2},\frac{a-d}{2},0),(\frac{a-d}{2},\frac{a+d}{2},0), (0,0,b)} $$

is in class 1, 3 or 6 _B as in Table 2. If v projects to $\frac{v_{2}}{2}$, then

$$\mathcal {P}= \{4,3,4\}_{(a,a,0), (0,0,b), (d,-d,\frac{b}{2})}= \{4,3,4\}_{(a,a,0),(2d,-2d,0), (d,-d,\frac{b}{2})} $$

is in class 6 _B as in Table 4. Finally, if v projects to $\frac{v_{1}+v_{2}}{2}$, then

$$\mathcal {P}= \{4,3,4\}_{(a,a,0), (0,0,b), (\frac{a+d}{2},\frac{a-d}{2},\frac{b}{2})}= \{4,3,4\}_{(a,a,0),(d,-d,0), (\frac{a+d}{2},\frac{a-d}{2},\frac{b}{2})} $$

is in class 1, 3 or 6 _B as in Table 3. It follows that for all possible choices for projection of v, Λ is invariant under R ₃ and hence $\mathcal {P}$ is not in class 12 _B .

We now examine the case when the fundamental region of $\varLambda_{\varPi_{1}}$ is a rhombus. If v projects to o, then

$$\mathcal {P}= \{4,3,4\}_{(a,a,b), (a,a,-b), (d,-d,0)}= \{4,3,4\}_{(2a,2a,0),(d,-d,0), (a,a,b)} $$

is in class 6 _B (see Table 4). If v projects to $\frac{v_{1}+v_{2}}{2}$, then

$$\mathcal {P}= \{4,3,4\}_{(a,a,b), (a,a,-b), (a+d,a-d,0)}= \{4,3,4\}_{(a-d,a+d,0),(a+d,a-d,0), (a,a,b)} $$

is in class 1, 3 or 6 _B (see Table 3). Now assume that v projects to $\frac{v_{1}}{2}$. (Note that the case v projects to $\frac{v_{2}}{2}$ leads to an isomorphic toroid, so it is not necessary to consider it.) It is an easy calculation to verify that vR ₃∉Λ and so that in this case Λ is not invariant under R ₃. Since v projects to $\frac{v_{1}}{2}$, the generating vectors of Λ can be taken to be (a,a,b),(a,a,−b) and $(\frac{a+d}{2}, \frac{a-d}{2}, \frac{b}{2})$. The lattice Λ is now invariant under R ₁ but not under R ₃, implying that the induced toroid is either in class 4 or 12 _B . By choosing a different generating set, with two generators in Π ₁, the toroids in class 4 (listed in Table 5) can also be expressed as indicated below.

(1)

Proposition 3 implies that these toroids do not arise from the lattice Λ. Hence the toroid $\mathcal {P}= \{4,3,4\}_{(a,a,b), (a,a,-b),(\frac{a+d}{2}, \frac{a-d}{2}, \frac{b}{2})}$ is in class 12 _B .

We finally analyse the case when $\mathcal{K}$ is in class 4. In this case Λ is not invariant under R ₃, implying that the induced toroid is either in class 4 or 12 _B , depending on whether Λ is invariant under R ₂ R ₁ or not. As before, let v ₁ and v ₂ be the generators of $\varLambda_{\varPi_{1}}$. Recall that the generating vectors of the restriction of the lattice Λ _{4,3,4} to the plane Π ₁ are (1,1,0) and (0,0,1). By Lemma 4 and Proposition 5, v ₁ and v ₂ can be chosen to be v ₁=a(1,1,0)+b(0,0,1)=(a,a,b), v ₂=c(1,1,0)+0(0,0,1)=(c,c,0) such that c∤2a. Since Λ is invariant under R ₁, the toroid $\mathcal {P}$ is {4,3,4}_{(a,a,b),(c,c,0),v} , where v is one of the following vectors: (d,−d,0), $(\frac{a+d}{2}, \frac{a-d}{2}, \frac{b}{2})$, $(\frac{c+d}{2}+d, \frac{c-d}{2}, 0)$ or $(\frac{a+c+d}{2}, \frac{a+c-d}{2}, \frac{b}{2})$, with c∤2a. Furthermore, for $\mathcal {P}$ to be in class 12 _B , Λ cannot be invariant under R ₂ R ₁. We shall use Proposition 3 to determine conditions on a,b,c and d under which this happens.

Let A be the matrix whose columns are the generating vectors of Λ. Let

$$M= \left( \begin{array}{c@{\quad}c@{\quad}c} 0&1&0\\ 0&0&1\\ 1&0&0 \end{array} \right) $$

be the matrix corresponding to the isometry R ₂ R ₁. Then, for v=(d,−d,0) we have |A|=−2bcd whereas |A|=−bcd for the remaining 3 possible choices of v.

We first note that if v=(d,−d,0), that is, v projects to o, then the entry (adj(MA)A)₃₃=bcd, implying that the determinant of A divides it only when bcd=0. But bcd≠0 since (a,a,b),(c,c,0),(d,−d,0) generate the lattice Λ, implying that $\mathcal {P}= \{4,3,4\}_{(a,a,b), (c,c,0), (d,-d,0)}$ is in class 12 _B whenever c∤2a.

If $v=(\frac{a+d}{2}, \frac{a-d}{2}, \frac{b}{2})$, that is, if v projects into $\frac{v_{1}}{2}$, then the toroid $\mathcal {P}$ is in class 12 _B whenever |A| does not divide all the entries of the matrices adj(MA)A and adj(A)MA. That is,

• (*) 4bcd does not divide all the entries of

  $$\left( \begin{array}{c@{\quad}c@{\quad}c} 2c(-ab+b^2-2ad) & -2c^2(b+2d) & c(-ab-bd - 2ad +2d^2 +b^2) \\ 2d(a-b)(2a+b) & 2cd(2a-b) & 2d(2a+b)(a-b-d) \\ 4bc(a-b) & 4bc^2 & 2bc(a+d-b) \end{array} \right) $$

  and

  $$\left( \begin{array}{c@{\quad}c@{\quad}c} 2c(ab-b^2-2ad) & 2c^2(b-2d) & c(ab-bd-b^2-2ad-2d^2) \\ 2d(2a+b)(a-b) & 2cd(2a-b) & 2(2a+b)(a-b+d) \\ 4bc(b-a) & -4bc^2 & 2bc(b+d-a) \end{array} \right). $$

When $v = (\frac{a+c+d}{2}, \frac{a+c-d}{2}, \frac{b}{2})$ projects to $\frac{v_{1} + v_{2}}{2}$ no new toroids are derived (since we may instead take a new fundamental region for $\varLambda_{\varPi_{1}}$ determined by $v_{1}' := (a+c, a+c, b)$ and v ₂=(c,c,0) and so v projects to $\frac{v_{1}'}{2}$).

Finally, if $v=(\frac{c+d}{2},\frac{c-d}{2}, 0)$, that is, if v projects to $\frac{v_{2}}{2}$, then again the toroid $\mathcal {P}$ is in class 12 _B whenever |A| does not divide all the entries of the matrices adj(MA)A and adj(A)MA. That is,

• (**) 4bcd does not divide all the entries of

  $$\left( \begin{array}{c@{\quad}c@{\quad}c} -4acd & -4c^2d & -2cd(c-d) \\ 2(a-b)(-bc+2ad+bd) & 2c(2ad-bc-bd) & -bc^2+2acd-2bcd-2ad^2-2bd^2 \\ 4bc(a-b) & 4bc^2& 2bc(c+d) \end{array} \right) $$

  and

  $$\left( \begin{array}{c@{\quad}c@{\quad}c} -4acd & -4c^2d & -2cd(c+d) \\ 2(a-b)(bc+2ad+bd) & 2c(bc+2ad-bd) & bc^2+2acd-2bcd+2ad^2+2bd^2\\ 4bc(b-a) & -4bc^2 & -2bc(c-d) \end{array} \right). $$

In summary we have Table 6, where the divisibility conditions ∗ and ∗∗ are given above.

Table 6 Toroids in class 12 _B

8 Conclusions

In Sects. 6 and 7 we classified equivelar 4-toroids. We summarise our analysis in the following theorem.

Theorem 15

Toroids with Schläfli type {4,3,4} can be described as $\{4,3,4\}_{v_{1},v_{2},v_{3}}$, where v ₁,v ₂ and v ₃ are three linearly independent vectors. Furthermore, the classes of toroids are as follow.

• Class 1 contains three families of toroids, given in Tables  2 and 3.

• Class 3 contains four families of toroids, given in Tables  2 and 3.

• Class 4 contains three families of toroids, given in Table  5.

• Class 6 _A contains seven families of toroids, given in Tables  2, 3 and 4.

• Class 6 _B contains seven families of toroids, given in Tables  2, 3 and 4.

• Class 6 _C contains two families of toroids, given in Tables  2 and 3.

• Class 8 contains three families of toroids, given in Table  5.

• Class 12 _A contains seven families of toroids, given in Tables  2, 3 and 4.

• Class 12 _B contains five families of toroids, given in Table  6.

• Class 24 contains all equivelar toroids not isomorphic to toroids in any of the previous classes.

To determine the class of a 4-toroid $\{4,3,4\}_{v_{1},v_{2},v_{3}}$, one needs to repeatedly apply Proposition 3 where the matrix A is given by the generating vectors v ₁,v ₂,v ₃ and the matrices M are determined by the symmetries which label the edges of Fig. 3 and their conjugates in the stabiliser S of the origin. One can also use some geometric arguments to simplify this verification. For example, the toroid $\mathcal {P}:=\{4,3,4\}_{(3,0,0), (1,3,0), (1,1,4)}$ can be seen to be in class 24 as follows. The smallest vectors in the lattice Λ inducing this toroid that lie on the x-, y- and z-axis are (3,0,0), (0,9,0) and (0,0,36), respectively. This immediately implies that Λ is not invariant under R ₁, R ₂ R ₁ or any of their conjugates, as any of these symmetries permute the coordinate axes. Furthermore, to see that Λ is not invariant under R ₃ or under any of its conjugates (that is, R ₂ R ₃ R ₂ and R ₁ R ₂ R ₃ R ₂ R ₁) we use Proposition 3 and note that det(A)=36 does not divide all the entries of the corresponding matrices adj(MA)A.

While in rank 3 each toroid is described by a unique set of parameters given in Theorems 7 and 8, two different sets of parameters in Tables 2 to 6 may determine the same 4-toroid. The necessary, but not sufficient, condition is that the determinants of the matrices determined by the two sets of generators are equal. Further calculations to eliminate duplications lead to lengthy conditions and complicated analysis, while not substantially contributing to the findings of the paper and we have chosen to omit it.

In rank n, for n>4, the number of possible classes of symmetries of equivelar n-toroids grows fast. This makes the analysis we present here unfeasible for higher ranks. However, the ideas on this paper can be used to classify toroids of rank n for any symmetry type. Of particular interest would be to classify 2-orbit toroids of any rank n>4, or to determine that there are none.