Reducing noise impact on MLP training

Abstract

In this paper we propose and discuss several new approaches to noise-resistant training of multilayer perceptron neural networks. Two groups of approaches: input ones, based on instance selection and outlier detection, and output ones, based on modified robust error objective functions, are presented and compared. In addition we compare them to some known methods. The experimental evaluation of the methods on classification and regression tasks and comparison of their performances for different amounts of noise in the training data, proves the effectiveness of the proposed approaches.

1 Introduction

Artificial neural networks are one of the most popular models applied to predictive analysis. Especially multilayer perceptrons (MLP) have been successively used in various applications, such as function approximation, classification, pattern recognition or signal and image processing. MLPs do not require any prior knowledge about input-output dependencies and are able to learn and build the data models based on training examples. This is why they are popular and often considered easy-to-use tools. However, the performance of such networks, trained by minimizing an error function on the training set, strongly depends on the quality of the data (Chen and Jain 1994; Liano 1996). For the contaminated, noisy datasets with many outlying and erroneous patterns, the desired mapping from the input to output space cannot be properly achieved. In this case, also neural networks trained on that data do not build the desired model, instead trying to fit to the noisy training examples.

We developed two groups of approaches designed to deal with the problem of outliers in the training data. The first group, so-called robust learning algorithms, is based mainly on novel error performance measures, derived from robust statistical estimators. In these approaches the training data is left in its original, potentially contaminated, state, but the network training process is modified. From that group we presented in Kordos and Rusiecki (2013) the LMLS (Least Mean Log Squares), MAE (Median of Absolute Errors), MIF (Median Neuron Input) and MedSum performance measures. In this work we discuss three others methods: ILMedS (Iterative Least Median of Squares) Rusiecki (2012), LTA (Least Trimmed Absolute Deviations) Rusiecki (2013) and TEF (Trapezoid Error Function) in Sect. 3. The second group is based on instance selection and outlier detection methods. In this case, the training data are reduced or corrected, to remove the impact of outliers. This is discussed in Sect. 4. We also describe hybrid methods, joining the aforementioned approaches. Next section presents broad experimental comparison of different methods on several regression and classification tasks. In this work we use not only the real datasets, but also add different levels of noise to input attributes, to output values and to both, and analyze how the performance of particular methods depends on noise level and location. We perform experimental comparison of the new methods proposed and some other methods known from the literature. For that purpose we conducted 1440 different experiments. Finally, in the last section, we conclude the work and discuss in which cases each method should be used and in which conditions the methods proposed by us display their superiority.

2 Robust learning and outliers

An outlier can be defined as an observation numerically distant from the majority of the data. Such a pattern can be a point that is close to its neighbors in the input space, but far from them in the output space (different class or much different value in the case of regression) or that is far from any points as well in the input as in the output space. Outliers may be generated as measurement artifacts, rounding errors, human mistakes, long-tailed noise distribution, etc. According to Hampel et al. (2005), the quantity of outliers ranges from 1 to 10 % in typical raw data, however it is hard to predict how much outliers the real data contain. Detecting such points is not trivial, moreover, sometimes it cannot be clearly stated if a given point is an outlier or not and rather some degree of outlierness than a crisp decision is preferred. In general, while building a data-driven model we do not intend to disregard such a point but only weaken its influence on the model parameters.

Multilayer perceptron neural networks (MLP) are trained by minimizing an error function on the training set. This supervised training scheme strongly depends on the training data quality. The training procedure builds a model trying to fit the data points as close as possible. This is clearly evident that outliers and erroneous training patterns may affect final network performance by leading to improper mapping from the input to the output space. Obviously, the most frequently used error measure, mean squared error (MSE), can be considered as optimal only for clean training data or data contaminated by at most errors generated from zero-mean Gaussian distribution (Hampel et al. 2005; Huber 1981; Olive and Hawkins 2007). When the data contains gross errors or outliers the method becomes unreliable (Chen and Jain 1994; Liano 1996; Pernia-Espinoza et al. 2005). To overcome this problem several methods, mainly based on modified error measures, have been proposed Chen and Jain (1994), Chuang et al. (2000), El-Melegy et al. (2009), Liano (1996) and Rusiecki (2012)).

2.1 Modified error measures

Replacing the MSE criterion with a new error function, based on the idea of so-called robust statistical methods, is the most common approach to make the MLP training more robust to the presence of outliers in the training data. The typical MSE function, derived from the least mean squares method is therefore strongly influenced by large errors. To demonstrate this phenomenon let us introduce a network performance function. We consider, without loss of generality, a simple feed-forward neural network with one hidden layer. We assume that the training set consists of $n$ pairs:

$\{(\mathbf {x}_1,\mathbf {t}_1), (\mathbf {x}_2,\mathbf {t}_2), \dots , (\mathbf {x}_n,\mathbf {t}_n)\}$, where $\mathbf {x}_i \in R^p$ denotes the $p$-dimensional $i$th input vector and $\mathbf {t}_i \in R^q$ the corresponding $q$-dimensional network target. For the given input vector $\mathbf {x}_i=(x_{i1}, x_{i2}, \ldots , x_{ip})^T$, the output of the $j$th neuron of the hidden layer is given as:

$$\begin{aligned} z_{ij}= f_1 \left( \sum _{k=1}^\gamma w_{jk}x_{ik}-b_j \right) =f_1(u_{ij}),\quad \text{ for } j=1, 2,\ldots ,l, \end{aligned}$$

(1)

where $f_1(\cdot )$ is the activation function of the hidden layer, $w_{jk}$ is the weight between the $k$th net input and $j$th neuron, and $b_j$ is the bias of the $j$th neuron.

The output of such network ${\varvec{y}}_{i}=(y_{i1}, y_{i2}, \ldots , y_{iq})^T$ is given as:

$$\begin{aligned} y_{iv}=f_2 \left( \sum _{j=1}^l w'_{vj}z_{ij}-b'_v \right) =f_2(u_{iv}),\quad \text{ for } v=1, 2, \ldots , q. \end{aligned}$$

(2)

Here $f_2(\cdot )$ is the output layer activation function, $w'_{vj}$ denotes the weight between the $v$th neuron of the output layer and the $j$th neuron of the hidden layer, and $b'_v$ is the bias of the $v$th neuron of the output layer.

If we define the residuals $r_i$ as:

$$\begin{aligned} r_i=\sum _{v=1}^q |(y_{iv}-t_{iv})|, \end{aligned}$$

(3)

the performance function may be written as:

$$\begin{aligned} E=\frac{1}{n}\sum \limits _{i=1}^n {\rho \left( {r_i } \right) } , \end{aligned}$$

(4)

where $\rho (r_{i})$ is a loss function (Hampel et al. 2005), $r_{i}$ is an error for the $i$-th training pattern (3), and $n$ is the size of the training set.

Applying a quadratic loss function:

$$\begin{aligned} \rho (r_i) = \frac{{r_i}^2}{2}, \end{aligned}$$

(5)

leads us directly to the minimized network performance equal to the mean squared error (MSE):

$$\begin{aligned} E_{mse}=\frac{1}{n}\sum \limits _{i=1}^n {{r_i }^2} . \end{aligned}$$

(6)

To measure the influence of residuals to the training process, the influence function was introduced Hampel et al. (2005); Liano (1996) as a derivative of the loss function:

$$\begin{aligned} \psi (r_i)=\frac{\partial \rho (r_i)}{\partial r_i}. \end{aligned}$$

(7)

Hence, for the MSE performance function, the influence is linear:

$$\begin{aligned} \psi (r_i) = r_i, \end{aligned}$$

(8)

which means the larger the error, the larger its impact on the network training process. This is why the model built by a network becomes unpredictable, when the training procedure minimizing MSE is applied on the contaminated data.

To cope with the problem of outliers in the training set, robust learning algorithms have been proposed (Chen and Jain (1994); Chuang et al. (2000); El-Melegy et al. (2009); Liano (1996); Rusiecki (2012). These methods very often make use of modified error function, achieving the robustness to outliers by reducing the impact of large training residuals, potentially caused by outlying data points.

First approaches to modify error function were based on robust M-estimators well known in the field of robust statistics (Hampel et al. 2005; Huber 1981). In Liano (1996) Liano proposed a new LMLS (Least Mean Log Squares) error function based on the idea of M-estimator, which should be optimal for the Cauchy distribution but performs well also for other long-tailed error distributions. This seems to be simultaneously the most cited technique (Chen and Jain 1994; Chuang et al. 2000; El-Melegy et al. 2009; El-Melegy 2013), and the most popular robust error measure, mainly because of its simplicity. The LMLS error can be defined as:

$$\begin{aligned} E_{\textit{LMLS}} = \frac{1}{n} \sum _{i=1}^n \log \left( 1+\frac{1}{2}{r_{i}}^2 \right) . \end{aligned}$$

(9)

One may notice that for the error defined by Eq. (9), the impact of large residuals is gradually decreased. Similar approach, the Hampel’s hyperbolic tangent with additional scale estimator $\beta$, was used by Chen and Jain (1994). The scale estimator helped in determining the range of residuals believed to be outliers: all the residuals larger than $\beta$ were partially excluded from the training procedure. Chuang and Su (2000) proposed a similar error performance function using the annealing scheme to decrease $\beta$ with the training progress. In Pernia-Espinoza et al. (2005) a more sophisticated approach, using tau-estimators, was described. Also quantile-based estimators were applied by Rusiecki as the error function in the LTS (Least Trimmed Squares) Rusiecki (2007) and LTA (Least Trimmed Absolute Values) Rusiecki (2013) algorithms, and in El-Melegy et al. (2009), where El-Melegy et al. presented the Simulated Annealing for Least Median of Squares (SA-LMedS) algorithm. Similar median error function was described in Rusiecki (2012). A combination of the error measure based on robust estimators and approaches known from image processing, as random sample consensus algorithm, was applied by El-Melegy in El-Melegy (2011a, (2011b) and El-Melegy (2013).

In this work we discuss mainly two algorithms: LTA and LMedS methods, because previous studies revealed that they perform better than other aforementioned solutions (El-Melegy et al. 2009; Rusiecki 2012, 2013).

3 LTA, ILMedS and TFE

3.1 Trimmed and median-based error measures

Between many modified error functions described in the previous section, the most effective are those based on quantile and trimmed performance measures (El-Melegy et al. 2009; Rusiecki 2012, 2013). It is not surprising when we consider their theoretical derivation. A breakdown point of a robust statistical estimator is defined as the smallest percentage $\epsilon ^*$ of contaminated data that can cause the estimator to take on aberrant values Hampel et al. (2005). Obviously, the most robust estimators possess the highest breakdown points, however, the best that can be expected is $\epsilon ^* = 0.5$ (Rousseeuw 1984). For the least squares method we have $\epsilon ^* = 0$, while for the least trimmed absolute value (LTA) and the least median of squares (LMed) the breakdown point close is to $\epsilon ^* = 0.5$.

3.2 Least trimmed absolute values

The least trimmed absolute value estimator (LTA) is one of the classical high breakdown point robust location estimators. It uses absolute values of residuals as $L_1$ norm, but the summation is replaced with a trimmed sum.

For the general nonlinear regression model:

$$\begin{aligned} y_{i}=\eta (x_{i},\theta )+\epsilon _{i},\quad i=1,\ldots ,n, \end{aligned}$$

(10)

where $y_{i}$ is the dependent variable, $x_{i}=(x_{i1},\ldots ,x_{ik})$ the independent input vector, $\theta \in R^{p}$ denotes the underlying parameter vector, and $\epsilon _{i}$ independent and identically distributed (iid) random errors with a continuous distribution function, we define the least trimmed absolute value estimator as:

$$\begin{aligned} \hat{\theta }=\arg \min _{\theta \in R^{p}}\sum _{i=1}^{h}(|r|)_{i:n}, \end{aligned}$$

(11)

where $(|r|)_{1:n}\le \cdots \le (|r|)_{n:n}$ are the absolute residuals $|r_i(\theta )|=|y_i-\eta (x_i, \theta )|$ sorted in ascending order, so in the sum only $h$ smallest absolute values are used. Choosing the trimming constant $h$ in the range $n/2 < h\le n$ we can decide what percentage of largest residuals will not affect the estimator.

3.2.1 LTA error criterion

Based on the LTA estimator we can define new robust LTA error criterion (Rusiecki 2013) as:

$$\begin{aligned} E_{LTA}=\sum _{i=1}^h (|r|)_{i:n}, \end{aligned}$$

(12)

where $(|r|)_{1:n}\le \dots \le (|r|)_{n:n}$ are ordered absolute network output residuals. As one may notice, the error function given by Eq. (12) excludes from the training process patterns causing largest errors in a given epoch simply assuming that they were caused by outliers in the training set. In Rusiecki (2013) a simple approach to estimate the scaling factor $h$, based on he median of all absolute deviations from the median (MAD) (Huber 1981), was presented. The MAD is defined as:

$$\begin{aligned} \text{ MAD } (r_i) = 1.483 \text{ median }|r_i - median(r_i)|, \end{aligned}$$

(13)

and the trimming parameter can be calculated as:

$$\begin{aligned} h = \Vert \{r_i: |r_i|<3 \times \text{ MAD }(|r_i|), i=1\dots n\}\Vert . \end{aligned}$$

(14)

If the estimated amount of outliers in the training data is known, then $h$ can be set empirically and Eq. (14) is not needed. However, in our tests it was calculated with Eq. (14), to make the whole algorithm less parameter-dependent.

3.3 Iterative least median of squares

3.3.1 LMedS estimator

Similarly to the LTA estimator, the least median of squares (LMedS) is a high-breakdown robust estimator. It was originally proposed by Rousseeuw (1984) but informally used even earlier (Huber 1981). In the LMedS estimator squared residuals are not summed but their median is minimized:

$$\begin{aligned} \hat{\theta } = \arg \min _{i}\text{ med } {r_i}^2. \end{aligned}$$

(15)

3.3.2 Iterative LMedS

The LMedS error criterion was proposed in El-Melegy et al. (2009), where simulated annealing was employed to minimize the median error. The LMedS is given as:

$$\begin{aligned} E_{med}=\text{ med } {r_i}^2. \end{aligned}$$

(16)

Additional training procedure making the algorithm more effective in minimizing the error criterion given by Eq. (16) was described in El-Melegy et al. (2009), Rusiecki (2012). In this method, after an initial training phase, the robust standard deviation (RSD) (Rousseeuw and Leroy 1987) is calculated as:

$$\begin{aligned} \sigma _r = 1.4826 \times \left( 1+ \frac{5}{(n-p)}\right) \sqrt{E_{med}^*}, \end{aligned}$$

(17)

where $E_{med}^*$ is the best achieved LMedS error ($n$ and $p$ are the size of the training set and the dimension of the input). Based on the RSD, all the training patterns associated with residuals exceeding a threshold:

$$\begin{aligned} r_i^2 \ge 2.5 \times \sigma _r^2 \end{aligned}$$

(18)

are then removed from the training set, and the whole procedure is repeated iteratively several times. For the detailed explanation of the chosen threshold and methodology a reader is referred to El-Melegy et al. (2009); Rousseeuw and Leroy (1987); Rusiecki (2012).

3.4 Trapezoid error function

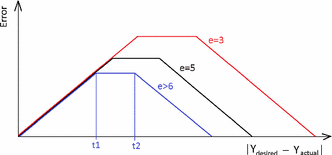
The idea of trapezoid error function (TEF) is to smoothly reduce the outliers influence on the network training. Thus, if the distance $d$ between the actual and the desired network output is small, the TEF grows with $d$. When $d$ further grows, TEF levels out for a while, and finally TEF begins decreasing with further growth of $d$, as very high $d$ is supposedly connected with an outlier. Not only trapezoid function satisfies these criteria and also other “bump” functions of similar properties (first increasing and then decreasing with the growth of $d$) could be used. However, the function must be introduced gradually, because at the beginning of the training the network weights are random and high $d$ value does not necessarily point to an outlier. The trapezoid error function is presented in Fig. 1 and in the pseudo-code:

Fig. 1

Trapezoid error function for epoch $e=3$, $e=5$ and $e>6$

The problem that appears when applying LTA, LMedS or bump error functions is that they are not continuous and non-differentiable, so some approximations of their derivatives in gradient-based learning are required. We decided to use an alternative approach, training the networks with our own non-gradient method called Variable Step Search (VSS) Algorithm (Kordos and Duch 2008). The VSS algorithm estimates the optimal modifications of single weights at each iteration, based on their changes in previous iterations, and then adjusts the changes. The signals (unlike in gradient-based methods) are propagated each time only through the recently changed fragments of the network, because change of a single weight does not change signal propagations in the entire network. This makes the training process fast. To limit the number of compared variables we use VSS with the same default parameters for all the tests.

4 Outlier reduction

So far we discussed how to reduce the noise influence on network learning by modifying the network properties. Another possibility is to modify the data by detecting the instances which differ much from their neighbors and either remove them from the training sets or mark them as outliers to be processed by the network training differently. In the first case we developed a generalized version of the ENN algorithm (Blachnik and Kordos 2014) for instance selection and in the second case we developed the Modified k-NN Global Anomaly Score (k-NN GAS) (Kordos and Rusiecki 2013) for outlier reduction.

5 Instance selection

Instance selection algorithms in general fall into two categories: compression methods and noise filters. The purpose of compression (condensation) methods is to remove an instance if it is too similar to its neighbors. That allows for reducing the data size and frequently also for improving generalization. An example of compression methods is the CNN (Condensed Nearest Neighbor) algorithm (Wilson 1972). Although we could have used the compression methods, we do not use them in this work for the sake of simplicity. The aim of noise filters is to remove an instance if it differs too much from its neighbors. This is the opposite of compression methods. An example of noise filters is the ENN (Edited Nearest Neighbor) algorithm (Wilson 1972).

If an instance is too different it can be considered as some error in the data and thus it gets removed. We can also use methods from both groups on the same data. However, the order of applying them is crucial. First the noise filters must be applied and then the compression methods. In the case of classification the instances that are really needed to determine the decision boundaries between classes are those situated close to the decision boundaries. As in classification the definition of “similarity to $k$ nearest neighbors” can be in practice reduced to “being of the same class as $k$ nearest neighbors”, almost all the instances situated far from the decision boundaries will have the same class as their neighbors and thus will be removed by the condensation methods. The only instances that will remain will be those close to the boundaries and the outliers. However, the distribution of the classes of the $k$ nearest neighbors of the outliers will be the same as before the selection. But the distribution of the classes of the $k$ nearest neighbors of the boundary instances will be quite different, because a lot of the same class neighbors have already been removed. If we apply a noise filter at this moment, the filter can remove as well the outliers as the boundary instances, which would lead to a very strange situation. If the noise filter is applied before the condensation method it will perform as expected removing only the outliers.

A large surveys of instance selection algorithms for classification tasks appeared in Salvador et al. (2012) and Jankowski. On the other hand, there only very few approaches to instance selection for regression tasks can be found in the literature and in the the publications we were able to find the experiments were conducted only on artificial datasets, which were generated especially for the purpose of the experiments. Tolvi (2004) presented a genetic algorithm to perform feature and instance selection for linear regression models. In their works Guillen (2009) discussed the concept of mutual information used for selection of prototypes in regression problems. Zhang 1997 presented a method to select the input vectors while calculating the output with k-NN.

In regression the problem is more complex. First of all the concept of “the same class” is not defined and consequently it cannot be used as a similarity measure. Therefore we introduced some arbitrary threshold $\theta$. If the output value of on instance differs no more than $\theta$ from the average values of its $k$ nearest neighbors outputs, we assume that the similarity condition is satisfied. However, as our experiments showed the $\theta$ parameter should not be constant in the entire data space. In the area of high data density $\theta$ should be smaller, because even a relatively low difference indicate an incorrect value. While in the sparse areas the threshold $\theta$ should be set to a higher values. For that reason, for each instance we use $\theta$ proportional to the standard deviation of its $k$ nearest neighbors. As the experiments showed, $\theta$ proportional to the standard deviation of $k$ nearest neighbors of the instance rather than of the whole dataset allows for obtaining higher compression while maintaining the same prediction accuracy. In general the threshold should be determined experimentally, but our experiments showed that in the GenENN algorithm (Kordos et al. 2013), the rejection threshold $\theta$ can be set to 2–8 standard deviations of the data for a broad range of regression problems. The higher value can be used for a better quality data and the lower for highly contaminated data. The reason for this is that in more contaminated data there are more outliers that should be removed and there is a higher probability that the some of the neighbors of the considered instance are also outliers. While in a better quality data even the points that are far from their neighbors do not necessary require rejection, as they may not contain any wrong values. The best results can be obtained if $\theta$ is experimentally determined for each dataset. However, in the experiments we used a simplified rule of thumb, as described in the experimental section, which on one hand produces not so accurate results, but on the other hand the topic of instance selection algorithm optimization is out of scope of this paper.

The instance selection algorithm we used is Generalized Edited Nearest Neighbor (GenENN) (Kordos et al. 2013), which we developed from the ENN algorithm (Wilson 1972). In the implementation used in our tests, GenENN rejects the instances if their output differs more than $\theta$ from a value predicted by the weighted k-NN with $k=9$, where the weight $w_i$ exponentially decreases with the distance $d_i$ between the given instance and its $i$-th neighbor $x_i$. The predicted output $y$ is expressed as:

$$\begin{aligned} y = \frac{\sum _{i=1}^{k}w_i y_i}{\sum _{i=1}^{k}w_i} \end{aligned}$$

(19)

where $w_i=2^{-0.2d_i}$. As the regression model to predict the output $Y(x_i)$ we use k-NN with $k=9$ and the Model(T,$x_i$) can be any learner, as neural network, decision tree, etc. However, in the experiments in this work we also use k-NN with $k=9$ as the model. The number of nearest neighbors $k$ was evaluated experimentally and $k=9$ appears to be a good choice for a broad range of problems (Kordos and Rusiecki 2013).

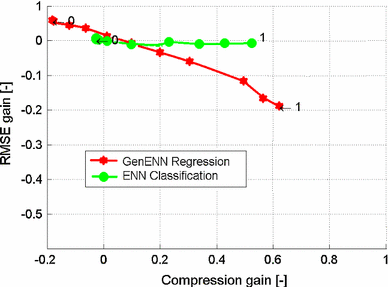
In Blachnik and Kordos (2014) we evaluated the possible gains of bagging of six different instance selection algorithms. Figure 2 presents the results obtained by averaging the results of ENN for classification and GenENN for regression problems on several different datasets. The bagging ensemble selected a final training set, on which a single k-NN was used to predict the output. The results show how much the bagging improved the results in terms of prediction accuracy of the k-NN learner in tenfold crossvalidation compared to a single instance selection algorithm (point 0,0). Positive values on both axes are desired, because they indicate gain in better data compression and in higher prediction accuracy. The parameters of the bagging is the acceptance threshold, that is a number between 0 and 1, which indicates what percentage of the instance selection algorithms within the bagging ensemble must select an instance to finally decide that the instance is selected. We present the example to show that the results presented in the tables in the experimental section can still be improved on average by up to 5 % in case of regression and due to smaller dataset size the network training can be about twice faster in classification. However, in the current work we do not use the bagging instance selection ensembles in the tests, because it would introduce another parameter to optimize and the number of experiments to be performed would grow from the 1440 that we conducted to several thousands.

5.1 Anomaly detection

The problem with instance selection algorithms is that the decision made by them about each instance must be crisp: either preserve or reject. In practice it is frequently difficult to set a good rejection threshold $\theta$ and therefore it can be desired to replace the crisp decision with a fuzzy one. That is we do not reject any instances, but evaluate the probability of each instance being an outlier and then we assign a weight denoted as $c_{out,n}$ to each instance. The instances with higher weights are more likely to be outliers and thus their influence on the MLP training should be limited. We obtain this by calculating the root mean square error RMSE that we minimize in the network training with the following formula:

$$\begin{aligned} { RMSE} = \sqrt{\frac{\displaystyle \sum _{n=0}^{N}{((y_{r,n}-y_{p,n})^2}/c_{out,n})}{N}} \end{aligned}$$

(20)

where $N$ is the number of instances, $y_{r,n}$ is the real value of the $n$-th instance output, $y_{p,n}$ is the predicted value of the $n$-th instance output and $c_{out,n}$ is the outlier coefficient of the $n$-th instance.

There are a lot of anomaly detection methods and a survey of them can be found in Ben-Gal (2005). We decided to adjust the k-NN Global Anomaly Score algorithm (k-NN GAS) to labeled data. The original k-NN GAS calculates the anomaly score using the k-NN algorithm. The outlier score of an $n$-th instance $d_{x,n}$ is the average distance between the instance and its $k$ nearest neighbors. In case of labeled data we need both distances: in the input space $d_{x,n}$ and in the output space $d_{y,n}$, in a similar way as we needed to determine $\theta$ in GenENN. And the purpose is also the same: to make more outstanding instances less influence the network training and we also need to adjust the coefficient to local data density for the same reason we needed to adjust $\theta$. We use Euclidean distance measure to calculate the distances $d_{y,n}$ and $d_{x,n}$ and as the number of neighbors we again use $k=9$. Thus the modified global anomaly score of the $n$-th instance is defined as:

$$\begin{aligned} c_{out,n}= d_{y,n} / d_{x,n} \end{aligned}$$

(21)

6 Experimental evaluation

Before the experiments, all the datasets were standardized so that the mean value of each numerical variable is 0 and the standard deviation is one. That enabled easy adding of the desired noise values, made direct comparison of the results more straightforward and enabled the neural network to work in the middle area of the hyperbolic tangent transfer function. All the datasets in the version we used for the tests and the source code of our program can be downloaded at Software and datasets (2014).

6.1 Regression datasets

6.1.1 Yacht hydrodynamics

The dataset contains 308 experiments, which were performed at the Delft Ship Hydromechanics Laboratory. There are 6 input variables describing the ships: position of the center of buoyancy, prismatic coefficient, length-displacement ratio, beam-draught ratio, length-beam ratio and Froude number (Merz and Murphy 2015). The purpose is to predict the residuary resistance per unit weight of displacement.

6.1.2 Building

One real-world training task was taken from the PROBEN 1 benchmark collection (Prechelt 1994). The task was to predict building energy consumption based on 14 input variables, such as the date, time, and weather conditions. There are 1052 instances in the dataset.

6.1.3 Concrete compression strength

There are 1030 instances with 7 input attributes in the dataset reflecting the amount of particular substances in the concrete mixture, such as cement, slag, water, etc. (Merz and Murphy 2015). The task is to predict the concrete compressive strength. There are 1030 instances in the database.

6.1.4 Crime and communities

There are 318 instances with originally 120 input attributes in the data set, describing various social, economic and criminal factors (Merz and Murphy 2015). However, after preliminary feature selection we used only 7 attributes to predict is per capita violent crime.

6.1.5 Steel

The dataset contains 960 instances with 12 input attributes. The task is to predict the amount of carbon that must be added in the steel-making process, given various chemical and physical properties of the liquid steel in the furnace. The data comes from one of the steelworks we were working for in the past (Software and datasets 2014).

6.2 Classification datasets

6.2.1 Image segmentation

The original dataset at Merz and Murphy (2015) were divided into 210 training and 2100 test examples. We merged the two sets and randomly chosen 1000 instances. The instances were drawn from a database of 7 outdoor images segmented to create a classification for every pixel. Each instance is a 3 $\times$ 3 pixel region. There are 19 continuous attributes depicting various aspects of color and geometry of that region. The purpose is to predict the object in the region. There are 7 classes, as: brickface, sky, foliage, cement, window, path, grass.

6.2.2 Banknote authentication

The data were extracted from photos of genuine and forged banknote-like specimens. The final images have 400x 400 pixels. Then a wavelet transform was performed to extract four features from images: variance, skewness, curtosis, and entropy of image. The two classes are: genuine and forged. There are 1372 instances (Merz and Murphy 2015).

6.2.3 Climate simulation model crashes

There are 540 instances and 18 attributes, which describe 18 climate model input parameters. The purpose is to predict climate model simulation crashes. There are two classes: crash and no-crash (Merz and Murphy 2015).

6.2.4 Seeds

The 210 instances depict measurements of 7 geometrical properties of kernels belonging to three different kinds of wheat. The purpose is to predict the wheat kind (Merz and Murphy 2015).

6.2.5 Iris

Iris Merz and Murphy (2015) with 150 attributes and 3 classes is one of the simplest and best known datasets and we decided to use it to have a good reference point.

6.3 Testing methodology

We performed the experiments in software created by us in C# language. The source code can be downloaded from Software and datasets (2014). The testing process consists of the following blocks:

• 1. Obtaining from the original dataset the 10 training and 10 test subsets used in each crossvalidation iteration.

• 2. On each training subset two operations are performed (if needed): instance selection with generalized ENN algorithm and outlier detection with modified k-NN Global Anomaly Score method.

• 3. The MLP neural network is trained on the test subsets using the VSS algorithm with one a an appropriate error function (MSE, ILMedS, LTA, TEF) and a possible error weighting if k-NN Global Anomaly Score was used in the preceding step or discarding some of the instances if the generalized ENN was used in the preceding step.

• 4. The network error on the corresponding test subset is evaluated always using RMSE for regression tasks and classification accuracy for classification tasks, even if a different error measure was used in the training. That allows us to directly compare the results obtained with different methods.

• 5. The mean RMSE (for regression) or classification accuracy (for classification) and the standard deviation are calculated over the 10 test sets within the crossvalidation and these values are reported in the tables.

We used a standard MLP network architecture with one hidden layer and 5 neurons in the hidden layer for all datasets, except image segmentation and climate simulation model crashes, where we used 9 neurons in the hidden layer. We trained all the networks for 12 epochs with the VSS algorithm. Since the purpose of the experiments was not to select the optimal network architecture and the optimal stopping criteria, but to evaluate the noise-robust methods, we did not perform any optimization of the network structure and number of training epochs. That would obviously improve the results; however we were rather more interested in the performance ratio between particular methods than in the absolute values of the network performance. We used hyperbolic tangent transfer function in the hidden and output layer for classification and hyperbolic tangent transfer function in the hidden and linear transfer function in the output layer for regression. The number of output neurons for classification was equal to the number of classes.

Also in case of classification, a term preventing too high weight growth was added to the error function: the classification was considered correct if the signal generated by the output neuron associated with the class of the current vector (and when it was $\ge$ 0.997, the error for that neuron was set to zero) was higher than the signals of all other output neurons (and when any of that signals was $\le -0.997$, the error for that neuron was set to zero).

In our software it is possible to train the networks with any number of hidden layers and also with additional direct connections between input and output layer, but trying to optimize the network architectures would first require thousands of tests, and second it would make more difficult comparison of the learning methods.

We performed experiments with the original datasets and with 15 levels of added noise. For inputs and outputs in regression and for inputs in classification the noise levels were:

• 0. $a=0$, $f=0$;

• 1. $a=0.5$, $f=0.20$;

• 2. $a=0.8$5, $f=0.25$;

• 3. $a=1.5$, $f=0.30$;

• 4. $a=2.5$, $f=0.35$;

• 5. $a=4.0$, $f=0.40$;

where $a$ (amplitude) is the standard deviation of the Gaussian distribution from which the random noise was added and $f$ (frequency) is the probability of the noise being added to the data (uniform distribution). For outputs in classification the following values of $f$ were used:

• 0. $f=0$;

• 1. $f=0.12$;

• 2. $f=0.24$;

• 3. $f=0.36$;

• 4. $f=0.48$;

• 5. $f=0.60$;

where $f$ is the probability of the noise being added to the data (uniform distribution); with probability $f$ the class of a given instance was substituted with a class of a random instance (thus in some cases the class could remain unchanged).

In the header lines of the tables the two digits x/y mean: input noise level/output noise level. Thus 0/0 means no noise added, and e.g. 2/0 means: input level noise $=$ 2, output level noise $=$ 0, 0/2 means: input level noise $=$ 0, output level noise $=$ 2, 2/2 means: input level noise $=$ 2, output level noise $=$ 2.

Fig. 2

Compression-accuracy gain plots of ENN and GenENN bagging ensembles

6.4 Results

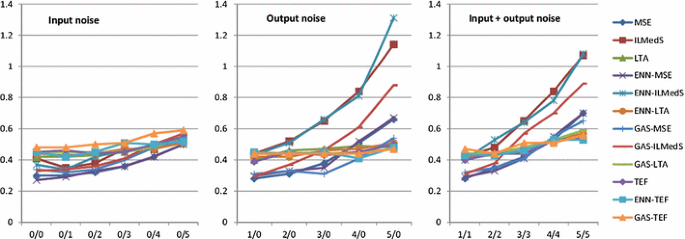
Analyzing results obtained for the regression problems, we can see some general tendencies, which are best visible in Fig. 3. For low levels of noise, networks trained with the MSE objective function perform quite well, much better than trained with LTA. As the noise level increases, LTA is gaining advantage over MSE. Also ENN and k-NN GAS methods added to MSE display their advantages. However, none of the methods is as universal to be superior in each condition, when their performance for different levels of noise is compared. Although for the data without artificial contamination we could expect traditional MSE method to perform relatively well, for some datasets, there exist methods that outperform MSE even for the clean data. This may be due to the fact that the methods were tested on real data that could already contain some noise (Fig. 4).

Fig. 3

Experimental results (RMSE) for Steel dataset. Note that for some other datasets TEF gives much better results

Fig. 4

Experimental results (classification accuracy) for climate simulation model crashes dataset

As it might be expected, combining input and output noise in the training data, had the largest impact on network learning. Robust learning algorithms (LTA and ILMedS), dedicated to regression tasks, often presented good performance, especially for higher levels of contamination. Unfortunately, results for these methods observed in our previous research, reported in Rusiecki (2012, (2013), for experiments performed on different datasets with different methodology, were much better. Looking at the Fig. 3 for exemplary dataset, one may notice an interesting phenomenon. The ENN and GAS methods, combined with different learning algorithms, usually keep their general direction: if an algorithm is stable with increasing noise, the hybrid version of the method is also stable, whereas when the error grows rapidly for the basic algorithm, when the noise increases, it grows also for the modified method.

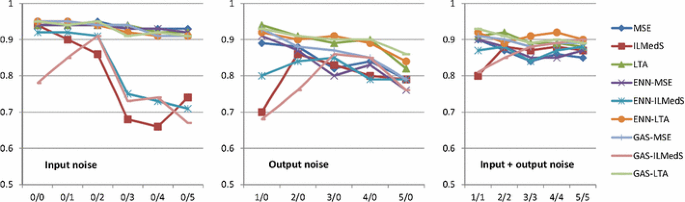
The ILMedS method was designed especially for regression tasks and therefore it is expected that its performance for classification problems can be poor.

When we analyze the tests performed for classification tasks, it is not hard to notice that increasing noise level in the input, as well as in the output data, makes the classification accuracy deteriorate. What may be surprising is that LTA method, though designed for regression tasks, performs well for many tested datasets. Interesting results were obtained for Banknote Authentication dataset: the accuracy for this task was almost perfect for many input and output noise levels. This may suggest that the classes for this dataset are easily separable. In many cases (e.g. for Seeds dataset) LTA, ILMedS and the hybrid solutions are definitely better than traditional approach, especially for the joined input/output noise.

7 Conclusions

In this paper we discussed the problem of training MLP networks on noisy data. Several state-of-the-art methods were described and implemented in our testing environment. These include methods created by us, as TEF, GenENN and modified GAS. One group of methods, which works at the network output, was based on robust learning algorithms, while another one, which works at the network input, uses instance selection and outlier detection methods. Hybrid approaches, combining one input with one output method were also proposed and examined. We performed many simulations and experiments to determine the quality of neural networks trained with the tested algorithms for different levels of noise and outliers added to the training sets. In the training data we considered corrupted outputs, inputs, and noise in both of them. Only real-life training data were used in order to allow reliable examination of the methods (Tables 1, 2, 3, 4, 5, 6 , 7, 8, 9, 10).

Table 1 RMSE in tenfold crossvalisation for Yacht Hydrodynamics dataset. In each table the upper row contains mean values and the lower row standard deviations. Note that the standard deviation always comes from two sources: method dependant (random initial weights in the neural network) and data dependant (differences in particular sets of training-test datasets)

Table 2 RMSE in tenfold crossvalidation for Building dataset

Table 3 RMSE in tenfold crossvalidation for Concrete dataset

Table 4 RMSE in tenfold crossvalidation for Crime dataset

Table 5 RMSE in tenfold crossvalidation for Steel dataset

Table 6 Classification accuracy in tenfold crossvalidation for Image Segmentation dataset

Table 7 Classification accuracy in tenfold crossvalidation for Banknote Authentication dataset

Table 8 Classification accuracy in tenfold crossvalidation for climate simulation model crashes dataset

Table 9 Classification accuracy in tenfold crossvalidation for Seeds dataset

Table 10 Classification accuracy in tenfold crossvalidation for Iris dataset

The general conclusions from the work are that the network training method should be adjusted to the amount of noise in the data. In regression tasks, MSE can be used for low noise level, LTA and TEF for high. Because prior to the network training, the noise level may be unknown, it is worth trying first both methods: MSE and LTA and then trying to add GenENN or k-NN GAS to the better performing one. When the results for both types of problems, regression and classification, are considered, combination of ENN and LTA algorithm presents the best performance, which can probably be further improved if we use the bagging ensemble of ENN algorithms. However, in most regression datasets, the TEF methods performed especially good, in some cases allowing to obtain RMSE on the test set up to 40 % lower than any other method. For that reason, in our future work, we want to examine the use of various “bump” functions as robust learning methods and application of the robust methods to deep learning neural architectures. The regular MSE algorithm, even for not contaminated data, in most classification tasks was outperformed by robust methods.