Sharp MSE Bounds for Proximal Denoising

Abstract

Denoising has to do with estimating a signal $\mathbf {x}_0$ from its noisy observations $\mathbf {y}=\mathbf {x}_0+\mathbf {z}$. In this paper, we focus on the “structured denoising problem,” where the signal $\mathbf {x}_0$ possesses a certain structure and $\mathbf {z}$ has independent normally distributed entries with mean zero and variance $\sigma ^2$. We employ a structure-inducing convex function $f(\cdot )$ and solve $\min _\mathbf {x}\{\frac{1}{2}\Vert \mathbf {y}-\mathbf {x}\Vert _2^2+\sigma {\lambda }f(\mathbf {x})\}$ to estimate $\mathbf {x}_0$, for some $\lambda >0$. Common choices for $f(\cdot )$ include the $\ell _1$ norm for sparse vectors, the $\ell _1-\ell _2$ norm for block-sparse signals and the nuclear norm for low-rank matrices. The metric we use to evaluate the performance of an estimate $\mathbf {x}^*$ is the normalized mean-squared error $\text {NMSE}(\sigma )=\frac{{\mathbb {E}}\Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2}{\sigma ^2}$. We show that NMSE is maximized as $\sigma \rightarrow 0$ and we find the exact worst-case NMSE, which has a simple geometric interpretation: the mean-squared distance of a standard normal vector to the ${\lambda }$-scaled subdifferential ${\lambda }\partial f(\mathbf {x}_0)$. When ${\lambda }$ is optimally tuned to minimize the worst-case NMSE, our results can be related to the constrained denoising problem $\min _{f(\mathbf {x})\le f(\mathbf {x}_0)}\{\Vert \mathbf {y}-\mathbf {x}\Vert _2\}$. The paper also connects these results to the generalized LASSO problem, in which one solves $\min _{f(\mathbf {x})\le f(\mathbf {x}_0)}\{\Vert \mathbf {y}-{\mathbf {A}}\mathbf {x}\Vert _2\}$ to estimate $\mathbf {x}_0$ from noisy linear observations $\mathbf {y}={\mathbf {A}}\mathbf {x}_0+\mathbf {z}$. We show that certain properties of the LASSO problem are closely related to the denoising problem. In particular, we characterize the normalized LASSO cost and show that it exhibits a “phase transition” as a function of number of observations. We also provide an order-optimal bound for the LASSO error in terms of the mean-squared distance. Our results are significant in two ways. First, we find a simple formula for the performance of a general convex estimator. Secondly, we establish a connection between the denoising and linear inverse problems.

Appendices

Auxiliary Results

Fact 10.1

(Hyperplane separation theorem [10]) Assume ${\mathcal {C}}_1,{\mathcal {C}}_2\subseteq {\mathbb {R}}^n$ are disjoint closed sets at least one of which is compact. Then, there exists a hyperplane H such that ${\mathcal {C}}_1,{\mathcal {C}}_2$ lies on different open half planes induced by H.

Fact 10.2

(Properties of the projection [10, 14]) Assume ${\mathcal {C}}\subseteq {\mathbb {R}}^n$ is a nonempty, closed and convex set and $\mathbf {a},\mathbf {b}\in {\mathbb {R}}^n$ are arbitrary points. Then,

$$\begin{aligned} \Vert \text {Proj}(\mathbf {a})-\text {Proj}(\mathbf {b})\Vert _2\le \Vert \mathbf {a}-\mathbf {b}\Vert _2. \end{aligned}$$

The projection $\text {Proj}(\mathbf {a},{\mathcal {C}})$ is the unique vector satisfying,

$$\begin{aligned} \text {Proj}(\mathbf {a},{\mathcal {C}})=\arg \min _{\mathbf {v}\in {\mathcal {C}}}\Vert \mathbf {a}-\mathbf {v}\Vert _2. \end{aligned}$$

(86)

The projection $\text {Proj}(\mathbf {a},{\mathcal {C}})$ is also the unique vector $\mathbf {s}_0$ that satisfies,

$$\begin{aligned} \left<\mathbf {s}_0,\mathbf {a}-\mathbf {s}_0\right>=\sup _{\mathbf {s}\in {\mathcal {C}}} \left<\mathbf {s},\mathbf {a}-\mathbf {s}_0\right>. \end{aligned}$$

(87)

In other words, $\mathbf {a}$ and ${\mathcal {C}}$ lie on different half planes induced by the hyperplane that goes through $\text {Proj}(\mathbf {a},{\mathcal {C}})$ and that is orthogonal to $\mathbf {a}-\text {Proj}(\mathbf {a},{\mathcal {C}})$.

Fact 10.3

(Moreau’s decomposition theorem [55]) Let ${\mathcal {C}}$ be a closed and convex cone in ${\mathbb {R}}^n$. For any $\mathbf {v}\in {\mathbb {R}}^n$, the followings are equivalent:

• $\mathbf {v}=\mathbf {a}+\mathbf {b}$, $\mathbf {a}\in {\mathcal {C}},\mathbf {b}\in {\mathcal {C}}^*$ and $\mathbf {a}^T\mathbf {b}=0$.

• $\mathbf {a}=\text {Proj}(\mathbf {v},{\mathcal {C}}),\mathbf {b}=\text {Proj}(\mathbf {v},{\mathcal {C}}^*)$.

Definition 10.1

(Lipschitz function) $h(\cdot ):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is called L-Lipschitz if for all $\mathbf {x},\mathbf {y}\in {\mathbb {R}}^n$, $|h(\mathbf {x})-h(\mathbf {y})|\le L\Vert \mathbf {x}-\mathbf {y}\Vert _2$.

The next lemma provides a concentration inequality for Lipschitz functions of Gaussian vectors [54].

Fact 10.4

Let $\mathbf {g}\sim {\mathcal {N}}(0,I)$ and $h(\cdot ):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be an L-Lipschitz function. Then for all $t\ge 0$:

$$\begin{aligned} {\mathbb {P}}(|h(\mathbf {g})-{\mathbb {E}}[h(\mathbf {g})]|\ge t)\le 2\exp \left( -\frac{t^2}{2L^2}\right) . \end{aligned}$$

Lemma 10.1

For any $\mathbf {g}\sim {\mathcal {N}}(0,I)$, $c>1$, we have that

$$\begin{aligned} {\mathbb {P}}(\Vert \mathbf {g}\Vert _2\ge c\sqrt{n})\le 2\exp \left( -\frac{(c-1)^2n}{2}\right) . \end{aligned}$$

Proof

${\mathbb {E}}[\Vert \mathbf {g}\Vert _2]\le \sqrt{{\mathbb {E}}[\Vert \mathbf {g}\Vert _2^2]}=\sqrt{n}$. Secondly $\ell _2$ norm is a 1-Lipschitz function due to the triangle inequality. Hence

$$\begin{aligned} {\mathbb {P}}(\Vert \mathbf {g}\Vert _2\ge c\sqrt{n})\le {\mathbb {P}}(\Vert \mathbf {g}\Vert _2\ge (c-1)\sqrt{n}+{\mathbb {E}}[\Vert \mathbf {g}\Vert _2])\le 2\exp \left( -\frac{(c-1)^2n}{2}\right) . \end{aligned}$$

$\square$

Lemma 10.2

Let ${\mathcal {C}}$ be a closed and convex cone in ${\mathbb {R}}^n$. Then, ${\mathbf{D}}({\mathcal {C}})+{\mathbf{D}}({\mathcal {C}}^*)=n$.

Proof

Using Fact 10.3, any $\mathbf {v}\in {\mathbb {R}}^n$ can be written as $\text {Proj}(\mathbf {v},{\mathcal {C}})+\text {Proj}(\mathbf {v},{\mathcal {C}}^*)=\mathbf {v}$ and $\left<\text {Proj}(\mathbf {v},{\mathcal {C}}),\text {Proj}(\mathbf {v},{\mathcal {C}}^*)\right>=0$. Hence,

$$\begin{aligned} \Vert \mathbf {v}\Vert ^2=\Vert \text {Proj}(\mathbf {v},{\mathcal {C}}^*)\Vert ^2+\Vert \text {Proj}(\mathbf {v},{\mathcal {C}})\Vert ^2=\text {dist}(\mathbf {v},{\mathcal {C}})^2+\text {dist}(\mathbf {v},{\mathcal {C}}^*)^2. \end{aligned}$$

Letting $\mathbf {v}\sim {\mathcal {N}}(0,{\mathbf{I}})$ and taking the expectations, we can conclude. $\square$

Subdifferential of the Approximation

Proof (Proof of Lemma 3.3)

Recall that $\hat{f}_{\mathbf {x}_0}(\mathbf {x}_0+\mathbf {v})-f(\mathbf {x}_0)$ is equal to the directional derivative $f'({\mathbf {x}_0},\mathbf {v})=\sup _{\mathbf {s}\in \partial f(\mathbf {x}_0)} \left<\mathbf {s},\mathbf {v}\right>$. Also recall the “set of maximizing subgradients” from (34). Clearly, $\partial f'({\mathbf {x}_0},\mathbf {v})=\partial \hat{f}_{\mathbf {x}_0}(\mathbf {x}_0+\mathbf {v})$. We will let $\mathbf {x}={\mathbf {w}}+\mathbf {x}_0$ and investigate $\partial f'({\mathbf {x}_0},{\mathbf {w}})$ as a function of ${\mathbf {w}}$.

If ${\mathbf {w}}=0:$ For any $\mathbf {s}\in \partial f(\mathbf {x}_0)$ and any $\mathbf {v}$ by definition, we have:

$$\begin{aligned} f'({\mathbf {x}_0},\mathbf {v})-f'({\mathbf {x}_0},0)=f'({\mathbf {x}_0},\mathbf {v})=\sup _{\mathbf {s}'\in \partial f(\mathbf {x}_0)} \left<\mathbf {v},\mathbf {s}'\right>\ge \left<\mathbf {v},\mathbf {s}\right>\end{aligned}$$

hence $\mathbf {s}\in \partial f'({\mathbf {x}_0},0)$. Conversely, assume $\mathbf {s}\not \in \partial f(\mathbf {x}_0)$, then there exists $\mathbf {v}$ such that:

$$\begin{aligned} f(\mathbf {v}+\mathbf {x}_0)<f(\mathbf {x}_0)+\left<\mathbf {v},\mathbf {s}\right>. \end{aligned}$$

By convexity for any $\epsilon >0$:

$$\begin{aligned} \frac{f(\epsilon \mathbf {v}+\mathbf {x}_0)-f(\mathbf {x}_0)}{\epsilon }\le f(\mathbf {v}+\mathbf {x}_0)-f(\mathbf {x}_0)<\left<\mathbf {v},\mathbf {s}\right>. \end{aligned}$$

Taking $\epsilon \rightarrow 0$ on the left-hand side, we find:

$$\begin{aligned} f'({\mathbf {x}_0},\mathbf {v})-f'({\mathbf {x}_0},0)=f'({\mathbf {x}_0},\mathbf {v})<\left<\mathbf {v},\mathbf {s}\right>\end{aligned}$$

which implies $\mathbf {s}\not \in \partial f'({\mathbf {x}_0},0)$.

If ${\mathbf {w}}\ne 0$: Now, consider the case ${\mathbf {w}}\ne 0$. Assume $\mathbf {s}\in \partial f(\mathbf {x}_0,{\mathbf {w}})$. Then, for any $\mathbf {v}$, we have:

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\mathbf {v})-f'({\mathbf {x}_0},{\mathbf {w}})&=\sup _{\mathbf {s}_1\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}}+\mathbf {v},\mathbf {s}_1\right>-\sup _{\mathbf {s}_2\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}},\mathbf {s}_2\right>\\&=\sup _{\mathbf {s}_1\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}}+\mathbf {v},\mathbf {s}_1\right>- \left<{\mathbf {w}},\mathbf {s}\right>\ge \left<\mathbf {v},\mathbf {s}\right>. \end{aligned}$$

Hence, $\mathbf {s}\in \partial f'({\mathbf {x}_0},{\mathbf {w}})$. Conversely, assume $\mathbf {s}\not \in \partial f(\mathbf {x}_0,{\mathbf {w}})$. Then, we will argue that $\mathbf {s}\not \in \partial f'({\mathbf {x}_0},{\mathbf {w}})$.

Assume $f'({\mathbf {x}_0},{\mathbf {w}})=c\Vert {\mathbf {w}}\Vert _2^2$ for some scalar $c=c({\mathbf {w}})$. We can write $\mathbf {s}=a{\mathbf {w}}+\mathbf {u}$ where $\mathbf {u}^T{\mathbf {w}}=0$. Choose $\mathbf {v}=\epsilon {\mathbf {w}}$ with $|\epsilon |<1$. We end up with:

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\mathbf {v})-f'({\mathbf {x}_0},{\mathbf {w}})=\epsilon \sup _{\mathbf {s}_1\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}},\mathbf {s}_1\right>=c\epsilon \Vert {\mathbf {w}}\Vert _2^2\ge \left<\mathbf {s},\mathbf {v}\right>=a\epsilon \Vert {\mathbf {w}}\Vert _2^2. \end{aligned}$$

Consequently, we have $c\epsilon \ge a\epsilon$ for all $|\epsilon |<1$ which implies $a=c$. Hence, $\mathbf {s}$ can be written as $c{\mathbf {w}}+\mathbf {u}$. Now, if $\mathbf {s}\in \partial f(\mathbf {x}_0)$, then $\mathbf {s}\in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)$ as it maximizes $\left<\mathbf {s}',{\mathbf {w}}\right>$ over $\mathbf {s}'\in \partial f(\mathbf {x}_0)$. However, we assumed $\mathbf {s}\not \in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)$. Observe that $\mathbf {u}=\mathbf {s}-c{\mathbf {w}}$ and $\partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}$ lies on $n-1$-dimensional subspace H that is perpendicular to ${\mathbf {w}}$. By assumption $\mathbf {u}\not \in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}$. We will argue that this leads to a contradiction. By making use of convexity of $\partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}$ and invoking hyperplane separation theorem (Fact 10.1), we can find a direction $\mathbf {h}\in H$ such that:

$$\begin{aligned} \left<\mathbf {h},\mathbf {u}\right>>\sup _{\mathbf {s}'\in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}}\left<\mathbf {h},\mathbf {s}'\right>. \end{aligned}$$

(88)

Next, considering $\epsilon \mathbf {h}$ perturbation, we have:

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\epsilon \mathbf {h})-f'({\mathbf {x}_0},{\mathbf {w}})=\sup _{\mathbf {s}_1\in \partial f(\mathbf {x}_0)}( \epsilon \left<\mathbf {h},\mathbf {s}_1\right>-\sup _{\mathbf {s}_2\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}},\mathbf {s}_2-\mathbf {s}_1\right>). \end{aligned}$$

Denote the $\mathbf {s}_1$ that establish equality by $\mathbf {s}_1^*$.

Claim As $\epsilon \rightarrow 0$, $\left<\mathbf {s}_1^*,{\mathbf {w}}\right>\rightarrow c\Vert {\mathbf {w}}\Vert _2^2$. $\square$

Proof

Recall that $\partial f(\mathbf {x}_0)$ is bounded. Let $R=\sup _{\mathbf {s}'\in \partial f(\mathbf {x}_0)}\Vert \mathbf {s}'\Vert _2$. Choosing $\mathbf {s}_1\in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)$, we always have:

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\epsilon \mathbf {h})-f'({\mathbf {x}_0},{\mathbf {w}})\ge \epsilon \left<\mathbf {s}_1,\mathbf {h}\right>\ge -\epsilon R\Vert \mathbf {h}\Vert _2. \end{aligned}$$

On the other hand, for any $\mathbf {s}_1$ we may write:

$$\begin{aligned} \epsilon \left<\mathbf {h},\mathbf {s}_1\right>-\sup _{\mathbf {s}_2\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}},\mathbf {s}_2-\mathbf {s}_1\right>\le \epsilon R\Vert \mathbf {h}\Vert _2+\left<\mathbf {s}_1,{\mathbf {w}}\right>-c\Vert {\mathbf {w}}\Vert _2^2. \end{aligned}$$

Hence, for $\mathbf {s}_1^*$, we obtain:

$$\begin{aligned} \epsilon R\Vert \mathbf {h}\Vert _2+\left<\mathbf {s}_1^*,{\mathbf {w}}\right>-c\Vert {\mathbf {w}}\Vert _2^2\ge -\epsilon R\Vert \mathbf {h}\Vert _2\implies \left<\mathbf {s}_1^*,{\mathbf {w}}\right>\ge c\Vert {\mathbf {w}}\Vert _2^2-2\epsilon R\Vert \mathbf {h}\Vert _2. \end{aligned}$$

Letting $\epsilon \rightarrow 0$, we obtain the desired result. $\square$

Claim Given $\partial f(\mathbf {x}_0)$, for any $\epsilon '>0$ there exists a $\delta >0$ such that for all $\mathbf {s}_1\in \partial f(\mathbf {x}_0)$ satisfying $\left<\mathbf {s}_1,{\mathbf {w}}\right>>c\Vert {\mathbf {w}}\Vert _2^2-\delta$ we have $\text {dist}(\mathbf {s}_1,\partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0))<\epsilon '$.

Proof

Assume for some $\epsilon '>0$, claim is false. Then, we can construct a sequence $\mathbf {s}(i)$ such that $\text {dist}(\mathbf {s}(i),\partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0))\ge \epsilon '$ but $\left<\mathbf {s}(i),{\mathbf {w}}\right>\rightarrow c\Vert {\mathbf {w}}\Vert _2^2$. From the well-known Bolzano–Weierstrass Theorem and the compactness of $\partial f(\mathbf {x}_0)\subseteq {\mathbb {R}}^n$, $\mathbf {s}(i)$ will have a convergent subsequence whose limit $\mathbf {s}(\infty )$ will be inside $\partial f(\mathbf {x}_0)$ and will satisfy $\left<\mathbf {s}_\infty ,{\mathbf {w}}\right>=c\Vert {\mathbf {w}}\Vert _2^2=f'({\mathbf {x}_0},{\mathbf {w}})$. On the other hand, $\text {dist}(\mathbf {s}(\infty ),\partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0))\ge \epsilon '\implies \mathbf {s}(\infty )\not \in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)$ which is a contradiction.

Going back to what we have, using the first claim, as $\epsilon \mathbf {h}\rightarrow 0$, $\left<\mathbf {s}_1^*,{\mathbf {w}}\right>\rightarrow c\Vert {\mathbf {w}}\Vert _2^2$. Using the second claim, this implies for some $\delta$ which approaches to 0 as $\epsilon \rightarrow 0$, we have:

$$\begin{aligned} \sup _{\mathbf {s}_1\in \partial f(\mathbf {x}_0)}( \epsilon \left<\mathbf {h},\mathbf {s}_1\right>-\sup _{\mathbf {s}_2\in \partial f(\mathbf {x}_0)} \left<{\mathbf {w}},\mathbf {s}_2-\mathbf {s}_1\right>)\le \epsilon (\delta \Vert \mathbf {h}\Vert _2+\sup _{\mathbf {s}'\in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}}\left<\mathbf {s}',\mathbf {h}\right>). \end{aligned}$$

Finally, based on (88), whenever $\epsilon$ is chosen to ensure $\delta \Vert \mathbf {h}\Vert _2<\left<\mathbf {h},\mathbf {u}\right>-\sup _{\mathbf {s}'\in \partial f(\mathbf {x}_0,\mathbf {x}-\mathbf {x}_0)-c{\mathbf {w}}}\left<\mathbf {s}',\mathbf {h}\right>$ we have,

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\epsilon \mathbf {h})-f'({\mathbf {x}_0},{\mathbf {w}})<\epsilon \left<\mathbf {h},\mathbf {u}\right>, \end{aligned}$$

which contradicts with the initial assumption that $\mathbf {s}$ is a subgradient of $f'({\mathbf {x}_0},\cdot )$ at ${\mathbf {w}}$, since,

$$\begin{aligned} f'({\mathbf {x}_0},{\mathbf {w}}+\epsilon \mathbf {h})-f'({\mathbf {x}_0},{\mathbf {w}})\ge \left<\mathbf {s},\epsilon \mathbf {h}\right>=\epsilon \left<\mathbf {u},\mathbf {h}\right>. \end{aligned}$$

$\square$

Lemma 11.1

$\hat{f}_{\mathbf {x}_0}(\mathbf {x})$ is a convex function of $\mathbf {x}$.

Proof

To show convexity, we need to argue that the function $f'({\mathbf {x}_0},{\mathbf {w}})$ is a convex function of ${\mathbf {w}}=\mathbf {x}-\mathbf {x}_0$.

Observe that $g({\mathbf {w}})=f(\mathbf {x}_0+{\mathbf {w}})-f(\mathbf {x}_0)$ is a convex function of ${\mathbf {w}}$ and behaves same as the directional derivative $f'({\mathbf {x}_0},{\mathbf {w}})$ for sufficiently small ${\mathbf {w}}$. More rigorously, from (32), for any ${\mathbf {w}}_1,{\mathbf {w}}_2\in {\mathbb {R}}^n$ and $\delta >0$ there exists $\epsilon >0$ such that, we have:

$$\begin{aligned} g(\epsilon {\mathbf {w}}_1)\le f'({\mathbf {x}_0},\epsilon {\mathbf {w}}_1)+\delta \epsilon , ~g(\epsilon {\mathbf {w}}_2)\le f'({\mathbf {x}_0},\epsilon {\mathbf {w}}_2)+\delta \epsilon . \end{aligned}$$

Hence, for any $0\le c\le 1$:

$$\begin{aligned} f'({\mathbf {x}_0},\epsilon (c{\mathbf {w}}_1+(1-c){\mathbf {w}}_2))&\le g(\epsilon (c{\mathbf {w}}_1+(1-c){\mathbf {w}}_2))\\&\le cg(\epsilon {\mathbf {w}}_1)+(1-c)g(\epsilon {\mathbf {w}}_2)\\&\le cf'({\mathbf {x}_0},\epsilon {\mathbf {w}}_1)+(1-c)f'({\mathbf {x}_0},\epsilon {\mathbf {w}}_2)+\epsilon \delta \end{aligned}$$

Making use of the fact that $f'({\mathbf {x}_0},\epsilon \mathbf {s})=\epsilon f'({\mathbf {x}_0},\mathbf {s})$ for any direction $\mathbf {s}$, we obtain:

$$\begin{aligned} f'({\mathbf {x}_0},c{\mathbf {w}}_1+(1-c){\mathbf {w}}_2)\le cf'({\mathbf {x}_0},{\mathbf {w}}_1)+(1-c)f'({\mathbf {x}_0},{\mathbf {w}}_2)+ \delta . \end{aligned}$$

Letting $\delta \rightarrow 0$, we may conclude with the convexity of $f'({\mathbf {x}_0},\cdot )$ and problem (37). $\square$

Swapping the Minimization over $\tau$ and the Expectation

Lemma 12.1

([13, 53]) Assume $\mathbf {g}\sim {\mathcal {N}}(0,{\mathbf{I}}_n)$ and let $h(\cdot ):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be an L-Lipschitz function. Then, we have:

$$\begin{aligned} \text {Var}(h(\mathbf {g}))\le L^2 \end{aligned}$$

We next show a closely related result.

Lemma 12.2

Assume $\mathbf {g}\sim {\mathcal {N}}(0,{\mathbf{I}}_n)$ and let $h(\cdot ):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be an L-Lipschitz function. Then, we have:

$$\begin{aligned} |h(\mathbf {g})-{\mathbb {E}}[h(\mathbf {g})]|\le \sqrt{2\pi }L \end{aligned}$$

Proof

From Lipschitzness of $h(\cdot )$, letting $\mathbf {a}=h(\mathbf {g})-{\mathbb {E}}[h(\mathbf {g})]$ and invoking Lemma 10.4 for all $t\ge 0$, we have:

$$\begin{aligned} {\mathbb {P}}(|\mathbf {a}-{\mathbb {E}}[\mathbf {a}]|\ge t)= {\mathbb {P}}(|\mathbf {a}|\ge t)\le 2\exp \left( -\frac{t^2}{2L^2}\right) \end{aligned}$$

Denote the probability density function of $|\mathbf {a}|$ by $p(\cdot )$ and let $Q(u)={\mathbb {P}}(|\mathbf {a}|\ge u)$. We may write:

$$\begin{aligned} {\mathbb {E}}[|\mathbf {a}|]=\int _{0}^{\infty }u p(u)du=\int _{\infty }^{0}udQ(u)=[uQ(u)]_{\infty }^0+\int _{0}^{\infty }Q(u)du \end{aligned}$$

Using $Q(u)\le 2\exp \left( -\frac{u^2}{2L^2}\right)$ for $u\ge 0$, we have:

$$\begin{aligned}{}[uQ(u)]_{\infty }^0=\left[ 2u\exp \left( -\frac{u^2}{2L^2}\right) \right] _{\infty }^0=0 \end{aligned}$$

Next,

$$\begin{aligned} \int _{0}^{\infty }Q(u)du\le \int _{0}^{\infty }2\exp \left( -\frac{u^2}{2L^2}\right) du=\sqrt{2\pi }L \end{aligned}$$

$\square$

Lemma 12.3

Suppose Assumption 6.1 holds. Recall that $\tau (\mathbf {v})=\arg \min _{\tau \ge 0}\text {dist}(\mathbf {v},\tau \partial f(\mathbf {x}_0))$. Then, for all $\mathbf {v}_1,\mathbf {v}_2$,

$$\begin{aligned} |\tau (\mathbf {v}_1)-\tau (\mathbf {v}_2)|\le \frac{\Vert \mathbf {v}_1-\mathbf {v}_2\Vert _2}{\Vert \mathbf {e}\Vert _2} \end{aligned}$$

(89)

Hence, $\tau (\mathbf {v})$ is $\Vert \mathbf {e}\Vert _2^{-1}$-Lipschitz function of $\mathbf {v}$.

Proof

Let $\mathbf {a}_i=\text {Proj}(\mathbf {v}_i,\text {cone}(\partial f(\mathbf {x}_0)))$ for $1\le i\le 2$. Using Lemma 10.2, we have $\Vert \mathbf {a}_1-\mathbf {a}_2\Vert _2\le \Vert \mathbf {v}_1-\mathbf {v}_2\Vert _2$ as $\partial f(\mathbf {x}_0)$ is convex. Now, we will further lower bound $\Vert \mathbf {v}_1-\mathbf {v}_2\Vert _2$ as follows:

$$\begin{aligned} \Vert \text {Proj}(\mathbf {a}_1-\mathbf {a}_2,T)\Vert _2\le \Vert \mathbf {a}_1-\mathbf {a}_2\Vert _2\le \Vert \mathbf {v}_1-\mathbf {v}_2\Vert _2 \end{aligned}$$

Now, observe that $\Vert \text {Proj}(\mathbf {a}_1-\mathbf {a}_2,T)\Vert _2=\Vert \tau (\mathbf {v}_1)\mathbf {e}-\tau (\mathbf {v}_2)\mathbf {e}\Vert _2$. Hence, we may conclude with (89). $\square$

Lemma 12.4

Let ${\mathcal {C}}$ be a convex and closed set. Define the set of $\tau$ that minimizes $\text {dist}(\mathbf {v},\tau {\mathcal {C}})$,

$$\begin{aligned} {\mathbf{T}}(\mathbf {v})=\left\{ \tau \ge 0\big |\arg \min _{\tau \ge 0}\text {dist}(\mathbf {v},\tau {\mathcal {C}})\right\} \end{aligned}$$

and let $\tau (\mathbf {v})=\inf _{\tau \in {\mathbf{T}}(\mathbf {v})}\tau$. $\tau (\mathbf {v})$ is uniquely determined, given ${\mathcal {C}}$ and $\mathbf {v}$. Further, assume $\tau (\mathbf {v})$ is an L Lipschitz function of $\mathbf {v}$ and let $R:=R({\mathcal {C}})=\max _{\mathbf {u}\in {\mathcal {C}}}\Vert \mathbf {u}\Vert _2$. Then,

$$\begin{aligned} \min _{\tau \ge 0}{\mathbb {E}}[\text {dist}(\mathbf {g},\tau {\mathcal {C}})^2]\le {\mathbf {D}}(\text {cone}({\mathcal {C}}))+2\pi (R^2L^2+RL\sqrt{{\mathbf {D}}(\text {cone}({\mathcal {C}}))}+1) \end{aligned}$$

Proof

Let $\mathbf {g}\sim {\mathcal {N}}(0,{\mathbf{I}})$ and let $\tau ^*={\mathbb {E}}[\tau (\mathbf {g})]$. Now, from triangle inequality:

$$\begin{aligned} |\tau (\mathbf {v})-\tau ^*|\le t\implies \text {dist}(\mathbf {v},\tau ^* {\mathcal {C}})\le \text {dist}(\mathbf {v},\tau (\mathbf {v}) {\mathcal {C}})+Rt \end{aligned}$$

Consequently,

$$\begin{aligned} {\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})]\le & {} \min _{\tau \ge 0}{\mathbb {E}}[\text {dist}(\mathbf {g},\tau {\mathcal {C}})]\le {\mathbb {E}}[\text {dist}(\mathbf {g},\tau ^*{\mathcal {C}})]\\&\le {\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})+R|\tau (\mathbf {g})-\tau ^*|] \end{aligned}$$

This gives:

$$\begin{aligned} {\mathbb {E}}[\text {dist}(\mathbf {g},\tau ^*{\mathcal {C}})]-{\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})]\le R{\mathbb {E}}[|\tau (\mathbf {g})-\tau ^*|] \end{aligned}$$

Observing ${\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})]={\mathbb {E}}[\text {dist}(\mathbf {g},\text {cone}({\mathcal {C}}))]\le \sqrt{{\mathbf {D}}(\text {cone}({\mathcal {C}}))}$, and using Lemma 12.2 we find:

$$\begin{aligned} {\mathbb {E}}[\text {dist}(\mathbf {g},\tau ^*{\mathcal {C}})]-\sqrt{{\mathbf {D}}(\text {cone}({\mathcal {C}}))}\le \sqrt{2\pi }RL \end{aligned}$$

This yields:

$$\begin{aligned} {\mathbb {E}}[\text {dist}(\mathbf {g},\tau ^*{\mathcal {C}})]^2-{\mathbf {D}}(\text {cone}({\mathcal {C}}))\le \sqrt{2\pi }RL(2\sqrt{{\mathbf {D}}(\text {cone}({\mathcal {C}}))}+\sqrt{2\pi }RL) \end{aligned}$$

Using Lemma 12.1 we have ${\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})]^2\ge {\mathbb {E}}[\text {dist}(\mathbf {g},\tau (\mathbf {g}){\mathcal {C}})^2]-1$, which gives:

$$\begin{aligned} \min _{\tau \ge 0}{\mathbb {E}}[\text {dist}(\mathbf {g},\tau {\mathcal {C}})^2]-{\mathbf {D}}(\text {cone}({\mathcal {C}}))\le 2\pi R^2L^2+2\sqrt{2\pi }RL\sqrt{{\mathbf {D}}(\text {cone}({\mathcal {C}}))}+1 \end{aligned}$$

$\square$

Intersection of a Cone and a Subspace

1.1 Intersections of Randomly Oriented Cones

Based on Kinematic formula (Theorem 7.1), one may find the following result on the intersection of the two cones. We first consider the scenario in which one of the cones is a subspace.

Proposition 13.1

(Intersection with a subspace) Let A be a closed and convex cone and let B be a linear subspace. Denote $\delta (A)+\delta (B)-n$ by $\delta (A,B)$. Assume the unitary ${\mathbf {U}}$ is generated uniformly at random. Given $\epsilon >0$, we have the following:

• If $\delta (A)+\delta (B)+\epsilon \sqrt{n}>n$,

  $$\begin{aligned} {\mathbb {P}}(\delta (A\cap {\mathbf {U}}B)\ge \delta (A,B)+\epsilon \sqrt{n})\le 8\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

• ${\mathbb {P}}(\delta (A\cap {\mathbf {U}}B)\le \delta (A,B)-\epsilon \sqrt{n})\le 8\exp \left( -\frac{\epsilon ^2}{64}\right)$.

Proof

Denote $A\cap {\mathbf {U}}B$ by C. Let H be a subspace with dimension $n-d$ chosen uniformly at random independent of ${\mathbf {U}}$. Observe that ${\mathbf {U}}B\cap H$ is a $\delta (B)-d$-dimensional random subspace for $d<\delta (B)$. Hence, using Theorem 7.1 with A and ${\mathbf {U}}B\cap H$ yields:

$$\begin{aligned}&\delta (A)+\delta (B)-d\le n-t \sqrt{n}\implies {\mathbb {P}}(A\cap {\mathbf {U}}B\cap H=\{0\})\ge 1-4\exp \left( -\frac{t^2}{16}\right) \end{aligned}$$

(90)

$$\begin{aligned}&\delta (A)+\delta (B)-d\ge n+t \sqrt{n}\implies {\mathbb {P}}(A\cap {\mathbf {U}}B\cap H=\{0\})\le 4\exp \left( -\frac{t^2}{16}\right) . \end{aligned}$$

(91)

Observe that (90) is true even when $d\ge \delta (B)$ since if $d\ge \delta (B)$, ${\mathbf {U}}B\cap H=\{0\}$ with probability 1.

Proving the first statement: Let $\gamma =\delta (A)+\delta (B)-n$, $\gamma _{\epsilon }=\gamma +\epsilon \sqrt{n}$ and $\gamma _{\epsilon /2}=\gamma +\frac{\epsilon }{2}\sqrt{n}$. We assume $\gamma _{\epsilon }>0$. Observing $A\cap {\mathbf {U}}B\cap H=C\cap H$, we may write:

$$\begin{aligned}&{\mathbb {P}}(C\cap H=\{0\})\le {\mathbb {P}}(C\cap H=\{0\}\big |\delta (C)\ge \gamma _{\epsilon })+{\mathbb {P}}(\delta (C)\le \gamma _{\epsilon })\nonumber \\&\text {and}~~~{\mathbb {P}}(\delta (C)\le \gamma _{\epsilon })\ge {\mathbb {P}}(C\cap H=\{0\})- {\mathbb {P}}(C\cap H=\{0\}\big |\delta (C)\ge \gamma _{\epsilon }) \end{aligned}$$

(92)

If $\gamma _{\epsilon }>n$, ${\mathbb {P}}(\delta (C)\le \gamma _{\epsilon })=1$. Otherwise, choose $d=\max \{\gamma _{\epsilon /2},0\}$.

Case 1 If $d=0$, then $\gamma _{\epsilon /2}\le 0$ and $H={\mathbb {R}}^n$. This gives,

$$\begin{aligned} {\mathbb {P}}(C\cap H=\{0\}\big |\delta (C)\ge \gamma _{\epsilon })={\mathbb {P}}(C=\{0\}\big |\delta (C)\ge \gamma _{\epsilon })=0. \end{aligned}$$

(93)

Also, choosing $t=\frac{\epsilon }{2}\sqrt{n}$ in (90) and using $\gamma \le -\frac{\epsilon }{2}\sqrt{n}$, we obtain:

$$\begin{aligned} {\mathbb {P}}(C\cap H=\{0\})={\mathbb {P}}(C=\{0\})\ge 1-4\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

(94)

Case 2 Otherwise, $d=\gamma _{\epsilon /2}>0$. Applying Theorem 7.1, we find:

$$\begin{aligned} {\mathbb {P}}(C\cap H=\{0\}\big |\delta (C)\ge \gamma _{\epsilon })\le 4\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

(95)

Next, choosing $t=\frac{\epsilon }{2}\sqrt{n}$ in (90), we obtain:

$$\begin{aligned} {\mathbb {P}}(C\cap H=\{0\})\ge 1-4\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

(96)

Overall, combining (92), (93), (94), (95) and (96), we obtain:

$$\begin{aligned} {\mathbb {P}}(\delta (C)\le \gamma _{\epsilon })\ge 1-8\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

Proving the second statement: In the exact same manner, this time, let $\gamma _{-\epsilon }=\gamma -\epsilon \sqrt{n}$, $\gamma _{-\epsilon /2}=\gamma -\frac{\epsilon }{2}\sqrt{n}$. If $\gamma _{-\epsilon }<0$,

$$\begin{aligned} {\mathbb {P}}(\delta (C)\le \gamma _{-\epsilon })\le {\mathbb {P}}(\delta (C)<0)=0. \end{aligned}$$

Otherwise, let $d=\gamma _{-\epsilon /2}$, we may write,

$$\begin{aligned} {\mathbb {P}}(\delta (C)\ge \gamma _{-\epsilon })\ge {\mathbb {P}}(C\cap H\ne \{0\})- {\mathbb {P}}(C\cap H\ne \{0\}\big |\delta (C)\le \gamma _{-\epsilon }) \end{aligned}$$

(97)

in an identical way to (92). Repeating the previous argument and using (91), we may first obtain,

$$\begin{aligned} {\mathbb {P}}(C\cap H\ne \{0\})\ge 1-4\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

and using Theorem 7.1,

$$\begin{aligned} {\mathbb {P}}(C\cap H\ne \{0\}\big |\delta (C)\le \gamma _{-\epsilon })\le 4\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

Combining these gives the desired result.

$$\begin{aligned} {\mathbb {P}}(\delta (C)\ge \gamma _{-\epsilon })\ge 1-8\exp \left( -\frac{\epsilon ^2}{64}\right) . \end{aligned}$$

$\square$

Proof of Theorem 2.1: Lower Bound

Theorem 14.1

Let ${\mathcal {C}}$ be a closed and convex set, $\mathbf {v}\sim {\mathcal {N}}(0,{\mathbf{I}})$ and let $\mathbf {x}^*(\sigma \mathbf {v})=\arg \min _{\mathbf {x}\in {\mathcal {C}}} \Vert \mathbf {x}_0+\sigma \mathbf {v}-\mathbf {x}\Vert _2$. Then, we have,

$$\begin{aligned} \lim _{\sigma \rightarrow 0}\frac{{\mathbb {E}}\left[ \Vert \mathbf {x}^*(\sigma \mathbf {v})-\mathbf {x}_0\Vert _2^2\right] }{\sigma ^2}={\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*). \end{aligned}$$

Proof

Let $1\ge \alpha ,\epsilon > 0$ be numbers to be determined. Denote probability density function of a ${\mathcal {N}}(0,c{\mathbf{I}})$ distributed vector by $p_c(\cdot )$. From Lemma 15.1, the expected error ${\mathbb {E}}[\Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2]$ is simply,

$$\begin{aligned} \int _{\mathbf {v}\in {\mathbb {R}}^n}\Vert \text {Proj}(\sigma \mathbf {v},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_1(\mathbf {v})d\mathbf {v}. \end{aligned}$$

Let $S_{\alpha }$ be the set satisfying:

$$\begin{aligned} S_{\alpha }=\left\{ \mathbf {u}\in {\mathbb {R}}^n|\frac{\Vert \text {Proj}(\mathbf {u},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{\Vert \mathbf {u}\Vert _2}\ge \alpha \right\} . \end{aligned}$$

Let $\bar{S}_\alpha ={\mathbb {R}}^n-S_\alpha$. Using Proposition 15.1, given $\epsilon >0$, choose $\epsilon _0>0$ such that for all $\Vert \mathbf {u}\Vert _2\le \epsilon _0$ and $\mathbf {u}\in S_{\alpha }$, we have,

$$\begin{aligned} \Vert \text {Proj}(\mathbf {u},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2\ge (1-\epsilon )\Vert \text {Proj}(\mathbf {u},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2. \end{aligned}$$

(98)

Now, let $\mathbf {z}=\sigma \mathbf {v}$. Split the error into three groups, namely

• $F_1=\int _{\Vert \mathbf {z}\Vert _2\le \epsilon _0,\mathbf {z}\in S_{\alpha }}\Vert \text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_\sigma (\mathbf {z})d\mathbf {z}$,   $T_1=\int _{\Vert \mathbf {v}\Vert _2\le \frac{\epsilon _0}{\sigma },\mathbf {v}\in S_{\alpha }}\Vert \text {Proj}(\mathbf {v},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_1(\mathbf {v})d\mathbf {v}$.

• $F_2=\int _{\Vert \mathbf {z}\Vert _2\ge \epsilon _0,\mathbf {z}\in S_{\alpha }}\Vert \text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_\sigma (\mathbf {z})d\mathbf {z}$,   $T_2=\int _{\Vert \mathbf {v}\Vert _2\ge \frac{\epsilon _0}{\sigma },\mathbf {v}\in S_{\alpha }}\Vert \text {Proj}(\mathbf {v},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_1(\mathbf {v})d\mathbf {v}$.

• $F_3=\int _{\mathbf {z}\in \bar{S}_{\alpha }}\Vert \text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_\sigma (\mathbf {z})d\mathbf {z}$,            $T_3=\int _{\mathbf {v}\in \bar{S}_{\alpha }}\Vert \text {Proj}(\mathbf {v},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2^2p_1(\mathbf {g})d\mathbf {v}$.

The rest of the argument will be very similar to the proof of Proposition 4.2. We know the following from Proposition 3.1:

$$\begin{aligned}&T_1+T_2+T_3={\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)\\&F_1+F_2+F_3={\mathbb {E}}[\Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2]\le \sigma ^2(T_1+T_2+T_3). \end{aligned}$$

To proceed, we will argue that the contributions of the second and third terms are small for sufficiently small $\sigma ,\alpha ,\epsilon >0$. Observe that:

$$\begin{aligned} T_3\le \int _{\mathbf {v}\in \bar{S}_{\alpha }}\alpha ^2\Vert \mathbf {v}\Vert _2^2p_1(\mathbf {v})d\mathbf {v}\le \alpha ^2n. \end{aligned}$$

For $T_2$, we have:

$$\begin{aligned} T_2\le \int _{\Vert \mathbf {v}\Vert _2\ge \frac{\epsilon _0}{\sigma }}\Vert \mathbf {v}\Vert _2^2p_1(\mathbf {g})d\mathbf {v}=C\left( \frac{\epsilon _0}{\sigma }\right) . \end{aligned}$$

Since $\Vert \mathbf {g}\Vert _2$ has finite second moment, fixing $\epsilon _0>0$ and letting $\sigma \rightarrow 0$, we have $C\left( \frac{\epsilon _0}{\sigma }\right) \rightarrow 0$. For $T_1$, from (98), we have:

$$\begin{aligned} F_1\ge (1-\epsilon )^2\sigma ^2T_1. \end{aligned}$$

Overall, we found:

$$\begin{aligned} \frac{{\mathbb {E}}\left[ \Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2\right] }{\sigma ^2}\ge \frac{F_1}{\sigma ^2}\ge (1-\epsilon )^2\frac{T_1}{T_1+T_2+T_3}{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*). \end{aligned}$$

Writing $T_1={\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)-T_2-T_3\ge {\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)-\alpha ^2n-C\left( \frac{\epsilon _0}{\sigma }\right)$, we have:

$$\begin{aligned} \frac{T_1}{T_1+T_2+T_3}\ge \frac{{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)-\alpha ^2n-C\left( \frac{\epsilon _0}{\sigma }\right) }{{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)}. \end{aligned}$$

Letting $\sigma \rightarrow 0$ for fixed $\alpha ,\epsilon _0,\epsilon$, we obtain

$$\begin{aligned} \lim _{\sigma \rightarrow 0}\frac{{\mathbb {E}}\left[ \Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2\right] }{\sigma ^2{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)}\ge (1-\epsilon )^2\frac{{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)-\alpha ^2n}{{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)}. \end{aligned}$$

Since $\alpha ,\epsilon$ can be made arbitrarily small, we obtain $\lim _{\sigma \rightarrow 0}\frac{{\mathbb {E}}[\Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2^2]}{\sigma ^2{\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)}=1$. $\square$

The next result shows that, as $\sigma \rightarrow 0$, we can exactly predict the cost of the constrained problem.

Proposition 14.1

Consider the setup in Theorem 14.1. Let ${\mathbf {w}}^*(\sigma \mathbf {v})=\mathbf {x}^*(\sigma \mathbf {v})-\mathbf {x}_0$. Then,

$$\begin{aligned} \lim _{\sigma \rightarrow 0}\frac{{\mathbb {E}}\left[ \Vert \sigma \mathbf {v}-{\mathbf {w}}^*(\sigma \mathbf {v})\Vert _2^2\right] }{\sigma ^2}={\mathbf{D}}(T_{\mathcal {C}}(\mathbf {x}_0)). \end{aligned}$$

Proof

Let ${\mathbf {w}}^*={\mathbf {w}}^*(\sigma \mathbf {v})$ and $\mathbf {z}=\sigma \mathbf {v}$. $\mathbf {z}-{\mathbf {w}}^*$ satisfies two conditions.

• From Lemma 15.1, $\Vert \mathbf {z}-{\mathbf {w}}^*\Vert _2=\text {dist}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\ge \text {dist}(\mathbf {z},T_{\mathcal {C}}(\mathbf {x}_0))$.

• Using Lemma 15.4, $\Vert \mathbf {z}-{\mathbf {w}}^*\Vert _2^2+\Vert {\mathbf {w}}^*\Vert _2^2\le \Vert \mathbf {z}\Vert _2^2$.

Consequently, when $\mathbf {v}\sim {\mathcal {N}}(0,{\mathbf{I}})$, we find:

$$\begin{aligned} n\sigma ^2= & {} {\mathbb {E}}\left[ \Vert \mathbf {z}\Vert _2^2\right] \ge {\mathbb {E}}\left[ \Vert \mathbf {z}-{\mathbf {w}}^*\Vert _2^2\right] +{\mathbb {E}}\left[ \Vert {\mathbf {w}}^*\Vert _2^2\right] \\&\ge \sigma ^2{\mathbb {E}}\left[ \text {Proj}(\mathbf {v},T_{\mathcal {C}}(\mathbf {x}_0)^*)^2\right] +{\mathbb {E}}\left[ \Vert {\mathbf {w}}^*\Vert _2^2\right] . \end{aligned}$$

Normalizing both sides by $\sigma ^2$ and subtracting ${\mathbf{D}}(T_{\mathcal {C}}(\mathbf {x}_0))={\mathbb {E}}[\text {Proj}(\mathbf {v},T_{\mathcal {C}}(\mathbf {x}_0)^*)^2]$ and ${\mathbb {E}}[\Vert {\mathbf {w}}^*\Vert _2^2]$, we find:

$$\begin{aligned} {\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)-\frac{{\mathbb {E}}\left[ \Vert {\mathbf {w}}^*\Vert _2^2\right] }{\sigma ^2}\ge \frac{{\mathbb {E}}\left[ \Vert \mathbf {z}-{\mathbf {w}}^*\Vert _2^2\right] }{\sigma ^2}-{\mathbf{D}}(T_{\mathcal {C}}(\mathbf {x}_0))\ge 0 \end{aligned}$$

where we used Lemma 10.2. Now, letting $\sigma \rightarrow 0$ and using the fact that $\lim _{\sigma \rightarrow 0}\frac{{\mathbb {E}}[\Vert {\mathbf {w}}^*\Vert _2^2]}{\sigma ^2}={\mathbf {D}}(T_{\mathcal {C}}(\mathbf {x}_0)^*)$, we find the desired result. $\square$

Approximation Results on Convex Cones

Remark

Throughout the section, ${\mathcal {C}}$ is assumed to be a nonempty, closed and convex set in ${\mathbb {R}}^n$.

1.1 Standard Observations

Property 15.1

Let $\mathbf {x}_0\in {\mathcal {C}}$ and $\mathbf {y}=\mathbf {x}_0+\mathbf {z}\in {\mathbb {R}}^n$. From Lemma 86, recall that $\text {Proj}(\mathbf {y},{\mathcal {C}})$ is the unique vector that is equal to $\arg \min _{\mathbf {u}\in {\mathcal {C}}}\Vert \mathbf {y}-\mathbf {u}\Vert _2$. By definition of feasible set $F_{\mathcal {C}}(\mathbf {x}_0)$, we also have, $\text {Proj}(\mathbf {y},{\mathcal {C}})=\text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))$.

Lemma 15.1

For all $\mathbf {z}\in {\mathbb {R}}^n$ and $\mathbf {x}_0\in {\mathcal {C}}$, we have

$$\begin{aligned} \Vert \text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2\le \Vert \text {Proj}(\mathbf {z},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2. \end{aligned}$$

Proof

Setting $f(\cdot )=0$ and $\mathbf {y}=\mathbf {x}_0+\mathbf {z}$ in Lemma 3.2, we have

$$\begin{aligned} \Vert \text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2=\Vert \mathbf {x}^*-\mathbf {x}_0\Vert _2\le \text {dist}(\mathbf {z},T_{\mathcal {C}}(\mathbf {x}_0)^*)=\Vert \text {Proj}(\mathbf {z},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2. \end{aligned}$$

$\square$

The following lemma shows that projection onto the feasible cone is arbitrarily close to the projection onto the tangent cone as we scale down the vector. This is due to Proposition 5.3.5 of Chapter III of [48].

Lemma 15.2

Assume $\mathbf {x}_0\in {\mathcal {C}}$. Then, for any $\mathbf {z}\in {\mathcal {C}}$,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \frac{\text {Proj}(\epsilon {\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))}{\epsilon }\rightarrow \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0)). \end{aligned}$$

Hence,

• If $\text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))=0$, using Lemma 15.1, $\text {Proj}(\mathbf {z},F_{\mathcal {C}}(\mathbf {x}_0))=0$.

• If $\text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\ne 0$,

  $$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{\Vert \text {Proj}(\epsilon {\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{\Vert \text {Proj}(\epsilon {\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}=1. \end{aligned}$$

1.2 Uniform Approximation to the Tangent Cone

Proposition 15.1

Let ${\mathcal {C}}$ be a closed and convex set including $\mathbf {x}_0$. Denote the unit $\ell _2$-sphere in ${\mathbb {R}}^n$ by ${\mathcal {S}}^{n-1}$ and let $1\ge \alpha >0$ be arbitrary. Given $\alpha ,\epsilon >0$, there exists an $\epsilon _0>0$ such that for all ${\mathbf {w}}\in {\mathcal {S}}^{n-1}$, $\Vert \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2\ge \alpha$ and for all $0<t\le \epsilon _0$, we have:

$$\begin{aligned} \frac{\Vert \text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{t\Vert \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}\ge 1-\epsilon . \end{aligned}$$

(99)

In particular, setting $\alpha =1$, given $\epsilon >0$, there exists $\epsilon _0>0$ such that, for all $t\le \epsilon _0$ and all ${\mathbf {w}}\in T_{\mathcal {C}}(\mathbf {x}_0)\cap {\mathcal {S}}^{n-1}$, $\Vert \text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2\ge (1-\epsilon )t$.

Remark

Note that statements of Propositions 15.1 and 4.1 are quite similar.

Proof

Given $\alpha >0$, consider the following set:

$$\begin{aligned} S=\left\{ {\mathbf {w}}\in {\mathcal {S}}^{n-1}\Big |\Vert \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2\ge \alpha \right\} . \end{aligned}$$

This set is closed and bounded and hence compact. Define the following function on this set

$$\begin{aligned} c({\mathbf {w}})=\max \left\{ c>0 \left| \frac{\Vert \text {Proj}(c{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}\ge 1-\epsilon \right. \right\} . \end{aligned}$$

$c({\mathbf {w}})$ is strictly positive due to Lemma 15.2 and it can be as high as infinity. Furthermore, from Lemma 15.3, we know that whenever $c<c({\mathbf {w}})$

$$\begin{aligned} \frac{\Vert \text {Proj}(c{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}\ge 1-\epsilon \end{aligned}$$

as well. Let $s({\mathbf {w}})=\min \{1,c({\mathbf {w}})\}$. If $s({\mathbf {w}})$ is continuous, since ${\mathcal {S}}^{n-1}$ is compact $s({\mathbf {w}})$ will attain its minimum which implies $c({\mathbf {w}})\ge s({\mathbf {w}})\ge \epsilon _0>0$ for some $\epsilon _0$. Again, this also implies, for all ${\mathbf {w}}\in {\mathcal {S}}^{n-1}$, and $0<t\le \epsilon _0$,

$$\begin{aligned} \frac{\Vert \text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert t\text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}\ge 1-\epsilon . \end{aligned}$$

To end the proof, we will show continuity of $s({\mathbf {w}})$.

Claim $s({\mathbf {w}})$ is continuous. $\square$

Proof

We will show that $\lim _{{\mathbf {w}}_2\rightarrow {\mathbf {w}}_1}s({\mathbf {w}}_2)=s({\mathbf {w}}_1)$. To do this, we will make use of the continuity of the functions $\Vert \text {Proj}(c_1{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2$, $\Vert \text {Proj}(c_1{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0)\Vert _2$ and $\frac{\Vert \text {Proj}(c_1{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c_1{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}$ when the denominator is nonzero. Given ${\mathbf {w}}_1$, let $c_1=\min \{2,c({\mathbf {w}}_1)\}$.

Case 1 If $\frac{\Vert \text {Proj}(c_1{\mathbf {w}}_1,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c_1{\mathbf {w}}_1,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}>1-\epsilon$, then $c({\mathbf {w}}_1)>2$ and for all ${\mathbf {w}}_2$ sufficiently close to ${\mathbf {w}}_1$, $\frac{\Vert \text {Proj}(c_1{\mathbf {w}}_2,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c_1{\mathbf {w}}_2,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}$ is more than $1-\epsilon$ and hence $c({\mathbf {w}}_2)\ge 2>1$. Hence, $s({\mathbf {w}}_1)=s({\mathbf {w}}_2)$.

Case 2 Now, assume $\frac{\Vert \text {Proj}(c_1{\mathbf {w}}_1,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c_1{\mathbf {w}}_1,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}=1-\epsilon$ which implies $c_1=c({\mathbf {w}}_1)$. Using the “strict decrease” part of Lemma 15.3, for any $\epsilon '>0$ and $c'=c_1-\epsilon '$, $\frac{\Vert \text {Proj}(c'{\mathbf {w}}_1,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c'{\mathbf {w}}_1,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}>1-\epsilon$. Then, for ${\mathbf {w}}_2$ sufficiently close to ${\mathbf {w}}_1$, $\frac{\Vert \text {Proj}(c'{\mathbf {w}}_2,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c'{\mathbf {w}}_2,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}>1-\epsilon$ which implies $c({\mathbf {w}}_2)\ge c'$. Hence, $c({\mathbf {w}}_2)\ge c_1-\epsilon '$ for arbitrarily small $\epsilon '>0$. Conversely, for any $\epsilon '>0$ and $c'=c_1+\epsilon '$, $\frac{\Vert \text {Proj}(c'{\mathbf {w}}_1,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c'{\mathbf {w}}_1,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}<1-\epsilon$. Then, for ${\mathbf {w}}_2$ sufficiently close to ${\mathbf {w}}_1$, $\frac{\Vert \text {Proj}(c'{\mathbf {w}}_2,F_{\mathcal {C}}(\mathbf {x}_0)\Vert _2}{\Vert \text {Proj}(c'{\mathbf {w}}_2,T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}<1-\epsilon$ which implies $c({\mathbf {w}}_2)\le c'$. Hence, $c({\mathbf {w}}_2)\le c_1+\epsilon '$ for arbitrarily small $\epsilon '>0$. Combining these, we obtain $c({\mathbf {w}}_2)\rightarrow c({\mathbf {w}}_1)$ as ${\mathbf {w}}_2\rightarrow {\mathbf {w}}_1$. This also implies $s({\mathbf {w}}_2)\rightarrow s({\mathbf {w}}_1)$. $\square$

This finishes the proof of the main statement (99). For the $\alpha =1$ case, observe that $\Vert {\mathbf {w}}\Vert _2=1$ and $\Vert \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2=1$ implies ${\mathbf {w}}\in T_{\mathcal {C}}(\mathbf {x}_0)$.

Lemma 15.3

Let $\mathbf {x}_0{\in }{\mathbb {R}}^n$ and let ${\mathbf {w}}$ have unit $\ell _2$-norm and set $l_T{=}\Vert \text {Proj}({\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\Vert _2$. Define the function,

$$\begin{aligned} g(t)={\left\{ \begin{array}{ll} \frac{\Vert \text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{t}~\text {for}~t>0\\ l_T~\text {for}~t=0\end{array}\right. }. \end{aligned}$$

Then, $g(\cdot )$ is continuous and nonincreasing on $[0,\infty )$. Furthermore, it is strictly decreasing on the interval $[t_0,\infty )$ where $t_0=\sup _{t} \{t>0\big |g(t)=l_T\}$.

Proof

Due to Lemma 15.1, $g(t)\le l_T$ and from Lemma 15.2, the function is continuous at 0. Continuity at $t\ne 0$ follows from the continuity of the projection (see Fact 10.2). Next, if $g(t)=l_T$, using the fact that $F_{\mathcal {C}}(\mathbf {x}_0)$ contains 0, the second statement of Lemma 15.4 gives,

$$\begin{aligned} \text {Proj}(t{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))=\text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\in F_{\mathcal {C}}(\mathbf {x}_0). \end{aligned}$$

From convexity, $\text {Proj}(t'{\mathbf {w}},T_{\mathcal {C}}(\mathbf {x}_0))\in F_{\mathcal {C}}(\mathbf {x}_0)$ for all $0\le t'\le t$. Hence, $g(t')=l_T$. This implies $g(t)=l_T$ for $t\le t_0$.

Now, assume $t_1>t_0$ and $t_1>t_2>0$ for some $t_1,t_2>0$. Then, $g(t_1)<l_T$, and hence, the third statement of Lemma 15.4 applies. Setting $\alpha =\frac{t_2}{t_1}$ in Lemma 15.4, we find,

$$\begin{aligned} \Vert \text {Proj}(t_1{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2<\frac{\Vert \text {Proj}(t_2{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{\frac{t_2}{t_1}}, \end{aligned}$$

which implies the strict decrease of $\frac{\Vert \text {Proj}(t{\mathbf {w}},F_{\mathcal {C}}(\mathbf {x}_0))\Vert _2}{t}$ over $t\ge t_0$. $\square$

For the rest of the discussion, given three points A, B, C in ${\mathbb {R}}^n$, the angle induced by the lines AB and BC will be denoted by $A\hat{B}C$.

Lemma 15.4

Let ${\mathcal {K}}$ be a convex and closed set in ${\mathbb {R}}^n$ that includes 0. Let $\mathbf {z}\in {\mathbb {R}}^n$ and $0<\alpha <1$ be arbitrary, let $\mathbf {p}_1=\text {Proj}(\mathbf {z},{\mathcal {K}})$, $\mathbf {p}_2=\text {Proj}(\alpha \mathbf {z},{\mathcal {K}})$. Denote the points whose coordinates are determined by $0,\mathbf {p}_1,\mathbf {p}_2,\mathbf {z}$ by $O, P_1,P_2$ and Z, respectively. Then,

• $Z\hat{P_1}O$ is either wide or right angle.

• If $Z\hat{P_1}O$ is right angle, then $\mathbf {p}_1=\frac{\mathbf {p}_2}{\alpha }=\text {Proj}(\mathbf {z},T_{\mathcal {K}}(0))$.

• If $Z\hat{P_1}O$ is wide angle, then $\Vert \mathbf {p}_1\Vert _2<\frac{\Vert \mathbf {p}_2\Vert _2}{\alpha }\le \Vert \text {Proj}(\mathbf {z},T_{\mathcal {K}}(0))\Vert _2$.

Proof

Acute angle: Assume $Z\hat{P_1}O$ is acute angle. If $Z\hat{O}P_1$ is right or wide angle, then 0 is closer to $\mathbf {z}$ than $\mathbf {p}_1$ which is a contradiction. If $Z\hat{O}P_1$ is acute angle, then draw the perpendicular from Z to the line $OP_1$. The intersection is in ${\mathcal {K}}$ due to convexity and it is closer to $\mathbf {z}$ than $\mathbf {p}_1$, which again is a contradiction.

Right angle: Now, assume $Z\hat{P_1}O$ is right angle. Using Fact 10.2, there exists a hyperplane H that separates $\mathbf {z}$ and ${\mathcal {K}}$ passing through $P_1$ which is perpendicular to $\mathbf {z}-\mathbf {p}_1$. The line $P_1O$ lies on H. Consequently, for any $\alpha \in [0,1]$, the closest point to $\alpha \mathbf {z}$ over ${\mathcal {K}}$ is simply $\alpha \mathbf {p}_1$. Hence, $\mathbf {p}_2=\alpha \mathbf {p}_1$. Now, let $\mathbf {q}_1:=\text {Proj}(\mathbf {z},T_{\mathcal {K}}(0))$. Then, $\text {Proj}(\alpha \mathbf {z},T_{\mathcal {K}}(0))=\alpha \mathbf {q}_1$. If $\mathbf {q}_1\ne \mathbf {p}_1$, then $\Vert \mathbf {q}_1\Vert _2>\Vert \mathbf {p}_1\Vert _2$ since $\Vert \mathbf {z}-\mathbf {q}_1\Vert _2<\Vert \mathbf {z}-\mathbf {p}_1\Vert _2$ and:

$$\begin{aligned} \Vert \mathbf {q}_1\Vert _2^2=\Vert \mathbf {z}\Vert _2^2-\Vert \mathbf {z}-\mathbf {q}_1\Vert _2^2> \Vert \mathbf {z}\Vert _2^2-\Vert \mathbf {z}-\mathbf {p}_1\Vert _2^2\ge \Vert \mathbf {p}_1\Vert _2^2 \end{aligned}$$

where the last inequality follows from the fact that $Z\hat{P_1}O$ is not acute. Then,

$$\begin{aligned} \lim _{\alpha \rightarrow 0}\frac{\Vert \text {Proj}(\mathbf {z},T_{\mathcal {K}}(0))\Vert _2}{\Vert \text {Proj}(\mathbf {z},{\mathcal {K}})\Vert _2}=\frac{\Vert \mathbf {q}_1\Vert _2}{\Vert \mathbf {p}_1\Vert _2}>1 \end{aligned}$$

which contradicts with Lemma 15.2.

Wide angle: Finally, assume $Z\hat{P_1}O$ is wide angle. We start by reducing the problem to a two-dimensional one. Obtain ${\mathcal {K}}'$ by projecting the set ${\mathcal {K}}$ to the 2D plane induced by the points $Z,P_1$ and O. Now, let $\mathbf {p}_2'=\text {Proj}(\alpha \mathbf {z},{\mathcal {K}}')$. Due to the projection, we still have

$$\begin{aligned} \Vert \mathbf {z}-\mathbf {p}_2'\Vert _2\le \Vert \mathbf {z}-\mathbf {p}_2\Vert _2\le \Vert \mathbf {z}-\alpha \mathbf {p}_1\Vert _2 \end{aligned}$$

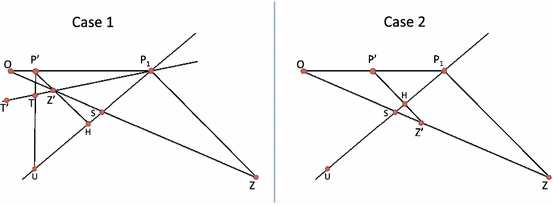
and $\Vert \mathbf {p}_2'\Vert _2\le \Vert \mathbf {p}_2\Vert _2$. Next, we will prove that $\Vert \mathbf {p}_2'\Vert _2>\Vert \alpha \mathbf {p}_1\Vert _2$ to conclude. Figure 7 will help us explain our approach. Let the line $UP_1$ be perpendicular to $ZP_1$. Assume, it crosses ZO at S. Let $P'Z'$ be parallel to $P_1Z_1$. Observe that $P'$ corresponds to $\alpha \mathbf {p}_1$. H is the intersection of $P'Z'$ and $P_1U$. Denote the point corresponding to $\mathbf {p}_2'$ by $P_2'$. Observe that $P_2'$ satisfies the following:

• $P_1$ is the closest point to Z in ${\mathcal {K}}$ and hence $P_2'$ lies on the left of $P_1U$ (same side as O).

• $P_2$ is the closest point to $Z'$. Hence, $Z'\hat{P_2}P_1$ is not acute angle. Otherwise, we can draw a perpendicular to $P_2P_1$ from $Z'$ and end up with a shorted distance. This would also imply that $Z'\hat{P_2'}P_1$ is not acute as well. The reason is, due to projection, $|Z'P_2'|\le |Z'P_2|$ and $|P_2'P_1|\le |P_2P_1|$ and hence,

  $$\begin{aligned} |Z'P_1|\ge |Z'P_2|^2+|P_2P_1|^2\ge |Z'P_2'|^2+|P_2'P_1|^2. \end{aligned}$$

  (100)

• $P_2'$ has to lie below or on the line $OP_1$ otherwise, perpendicular to $OP_1$ from $Z'$ would yield a shorter distance than $|P_2'Z'|$.

• $\mathbf {p}_2\ne \alpha \mathbf {p}_1$. To see this, note that $Z'\hat{P'}O$ is wide angle. Let $\mathbf {q}\in {\mathbb {R}}^n$ be the projection of $\alpha \mathbf {z}$ on the line $\{c\mathbf {p}_1\big |c\in {\mathbb {R}}\}$ and point Q denote the vector $\mathbf {q}$. If Q lies between O and $P_1$, $\mathbf {q}\in {\mathcal {K}}$ and $|QZ'|<|P'Z'|$. Otherwise, $P_1$ lies between Q and $P'$ and hence $|P_1Z'|<|P'Z'|$ and $\mathbf {p}\in {\mathcal {K}}$. This implies $P_2,P_2'\ne P'$.

Based on these observations, we investigate the problem in two cases illustrated in Fig. 7.

Fig. 7

Possible configurations of the points in Lemma 15.4

Case 1 (S lies on $Z'Z$): Consider the left-hand side of Fig. 7. If $P_2'$ lies on the right-hand side of $P'U$, this implies $|P_2'O|> |P'O|$ which is what we wanted.

If $P_2'$ lies on the region induced by $OP'TT'$, then $P_1\hat{P}_2'Z'$ is acute angle as $P_1\hat{Z}'P_2'>P_1\hat{Z}'P'$ is wide, which contradicts with (100).

If $P_2'$ lies on the remaining region $T'TU$, then $Z'\hat{P}_2'P_1$ is acute. The reason is that $P'_2\hat{Z}'P_1$ is wide as follows

$$\begin{aligned} P'_2\hat{Z}'P_1\ge P'_2\hat{T}P_1\ge U\hat{T}P_1>U\hat{P}'P_1=\frac{\pi }{2}. \end{aligned}$$

Case 2 (S lies on $OZ'$): Consider the right-hand side of Fig. 7. Due to location restrictions, $P_2'$ lies on either $P_1P'H$ triangle or the region induced by $OP'HU$. If it lies on $P_1P'H$, then $O\hat{P'}P_2'\ge O\hat{P'}H$ (thus wide), which implies $|OP_2'|>|OP'|$ as $O\hat{P}'P_2'$ is wide angle and $P'\ne P_2'$.

If $P_2'$ lies on $OP'HU$, then $P_1\hat{P}_2'Z'<P_1\hat{H}Z'=\frac{\pi }{2}$ hence $P_1\hat{P}'_2Z'$ is acute angle which contradicts with (100).

In all cases, we end up with $|OP_2'|>|OP'|$ which implies $\Vert \mathbf {p}_2\Vert _2\ge \Vert \mathbf {p}_2'\Vert _2>\alpha \Vert \mathbf {p}_1\Vert _2$ as desired.

Finally, apply Lemma 15.1 on $\alpha \mathbf {z}$ to upper bound $\Vert \mathbf {p}_2\Vert _2$ by $\alpha \Vert \text {Proj}(\mathbf {z},T_{\mathcal {K}}(0))\Vert _2$. $\square$