Abstract
A simplified procedure is proposed to predict the largest peak seismic response of an asymmetric building to horizontal bi-directional ground motion, acting at an arbitrary angle of incidence. The main characteristics of the proposed procedure is as follows. (1) The properties of two independent equivalent single-degree-of-freedom models are determined according to the principal direction of the first modal response in each nonlinear stage, rather than according to the fixed axis based on the mode shape in the elastic stage; the principal direction of the first modal response in each nonlinear stage is determined based on pushover analysis results. (2) The bi-directional horizontal seismic input is simulated as identical spectra of the two horizontal components, and the contribution of each modal response is directly estimated based on the unidirectional response in the principal direction of each. (3) The drift demand at each frame is determined based on four pushover analyses considering the combination of bi-directional excitations. In the numerical example, nonlinear time-history analyses of six four-story torsionally stiff (TS) asymmetric buildings are carried out considering various directions of seismic inputs, and these results are compared with the predicted results. The results show that the proposed procedure satisfactorily predicts the largest peak response displacement at the flexible-side frame of a TS asymmetric building.

















Similar content being viewed by others
References
AIJ (1999) Design guidelines for earthquake resistant reinforced concrete buildings based on inelastic displacement concept. Architectural Institute of Japan, Tokyo (Japanese)
Antoniou S, Pinho R (2004) Development and verification of a displacement-based adaptive pushover procedure. J Earthq Eng 8:643–661
ATC-40 (1996) Seismic evaluation and retrofit of concrete buildings, vol 1. Applied Technology Council, Redwood City, CA
ASCE (2007) Seismic rehabilitation of existing buildings. American Society of Civil Engineering, Reston, VA
BCJ (2010) The building standard law of Japan on CD-ROM. The Building Center of Japan, Tokyo
Bhatt C, Bento R (2011) Assessing the seismic response of existing RC buildings using the extended N2 method. Bull Earthq Eng 9:1183–1201
Beyer K, Boomer JJ (2007) Selection and scaling of real accelerograms for bi-directional loading: a review of current practice and code provisions. J Earthq Eng 11(S1):13–45
Bosco M, Ghersi A, Marino EM (2012) Corrective eccentricities for assessment by nonlinear static method of 3D structures subjected to bidrectional ground motion. Earthq Eng Struct Dyn 41:1751–1773
Bosco M, Marino EM, Ghersi A (2013) An analytical method for evaluation of the in-plan irregularity of non-regularly asymmetric buildings. Bull Earthq Eng. doi:10.1007/s10518-013-9438-3
CEN (2004) Eurocode 8—design of structures for earthquake resistance. Part 1: general rules, seismic actions and rules for buildings. European standard EN 1998–1, European Committee for Standardization, Brussels
Chopra AK, Goel RK (2002) A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq Eng Struct Dyn 31:561–582
Chopra AK, Goel RK (2004) A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings. Earthq Eng Struct Dyn 33:903–927
D’Ambrisi A, De Stefano M, Tanganelli M (2009) Use of pushover analysis of predicting seismic response of irregular buildings: a case study. J Earthq Eng 13:1089–1100
De Stefano M, Pintucchi B (2008) A review on seismic behaviour of irregular building structure since 2002. Bull Earthq Eng 6:285–308
De Stefano M, Pintucchi B (2010) Predicting torsion-induced lateral displacements for pushover analysis: influence of torsion system characteristics. Earthq Eng Struct Dyn 39:1369–1394
Fajfar P, Fischinger M (1988) N2-a method for non-linear seismic analysis of regular buildings. In: Proceedings of ninth world conference on earthquake engineering, vol 5, pp 111–116. Tokyo-Kyoto, Japan
Fajfar P, Maruŝić D, Peruŝ I (2005) Torsional effects in the pushover-based seismic analysis of buildings. J Earthq Eng 9:831–854
FEMA (1997) NEHRP guidelines for the seismic rehabilitation of buildings, FEMA Publication 273. Federal Emergency Management Agency, Washington, DC
Fujii K (2007) Prediction of seismic response of multi-story unsymmetric frame buildings. In: Proceedings of 8th pacific conference on earthquake engineering, paper no. 017, Singapore
Fujii K (2010) Seismic assessment of asymmetric buildings considering the critical direction of seismic input. In: Proceedings of 14th European conference on earthquake engineering, paper no. 623, Ohrid, Macedonia
Fujii K (2011) Nonlinear static procedure for multi-story asymmetric frame buildings considering bi-directional excitation. J Earthq Eng 15:245–273
Fujii K (2012) Prediction of largest peak seismic response at flexible-side frame of asymmetric buildings. In: Proceedings of 15th world conference on earthquake engineering, paper no. 0457, Lisbon, Portugal
Fujii K, Ikeda T (2012) Shaking table test of irregular buildings under horizontal excitation acting in an arbitrary direction. In: Proceedings of 15th world conference on earthquake engineering, paper no. 0439, Lisbon, Portugal
Fujii K, Nakano Y, Sakata H (2006) Nonlinear analysis of single-story unsymmetric buildings with elasto-plastic seismic control devices. In: Proceedings of eighth U.S. national conference on earthquake engineering, paper no. 217, San Francisco, USA
González P (1992) Considering earthquake direction on seismic analysis. In: Proceedings of the tenth world conference on earthquake engineering, vol 7, pp 3809–3913. Madrid, Spain
Hejal R, Chopra AK (1987) Earthquake response of torsionally-coupled buildings. Earthquake Engineering Research Center, report no. UCB/EERC-87/20, College of Engineering, University of California at Berkeley
Isakovic T, Fischinger M (2011) Applicability of pushover methods to the seismic analysis of an RC bridge, experimentally tested on three shake tables. J Earthq Eng 15:303–320
Kostinakis KG, Athanatopoulou AM, Avramidis IE (2013) Evaluation of inelastic response of 3D single-story R/C frames under bi-directional excitation using different orientation schemes. Bull Earthq Eng 11:637–661
Kreslin M, Fajfar P (2010) Seismic evaluation of an existing complex RC building. Bull Earthq Eng 8:363–385
Kreslin M, Fajfar P (2012) The extended N2 method considering higher mode effects in both plan and elevation. Bull Earthq Eng 10:695–715
López A, Torres R (1997) The critical angle of seismic incidence and the maximum structural response. Earthq Eng Struct Dyn 26:881–894
López A, Hernández JJ, Bonilla R, Fernández A (2006) Response spectra for multicomponent structural analysis. Earthq Spectra 22:85–113
Moghadam AS, Tso WK (1996) Damage assessment of eccentric multistorey buildings using 3-D pushover analysis. In: Proceedings of 11th world conference on earthquake engineering, paper No. 997, Acapulco, Mexico
Muto K, Hisada T, Tsugawa T, Bessho S (1974) Earthquake resistant design of a 20 story reinforced concrete buildings. In: Proceedings of the 5th world conference on earthquake engineering, 1960–1969, Rome, Italy
Otani S (1981) Hysteresis models of reinforced concrete for earthquake response analysis. J Faculty Eng Univ Tokyo 36(2):125–156
Otani S (2000) New seismic design provision in Japan. In: Proceeding of the second U.S.-Japan workshop on performance-based earthquake engineering methodology for reinforced concrete structures. PEER report vol 10, pp 3–14
Penzien J, Watabe M (1975) Characteristics of 3-dimensional earthquake ground motions. Earthq Eng Struct Dyn 3:365–373
Peruŝ I, Fajfar P (2005) On the inelastic torsional response of single-storey structures under bi-axial excitation. Earthq Eng Struct Dyn 34:931–941
Saiidi M, Sozen MA (1981) Simple nonlinear seismic analysis of R/C structures. J Struct Div, ASCE 107:937–952
Sudo S, Sera K, Nishikawa, T. (1996) Torsional response analysis of buildings subjected to bi-directional ground motions. In: Proceedings of the eleventh world conference on earthquake engineering, paper no. 865, Acapulco, Mexico
Acknowledgments
The author thanks the two anonymous reviewers who provided considerable help in improving the content and text of the original manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Formulation of the equivalent SDOF model considering bi-directional excitations
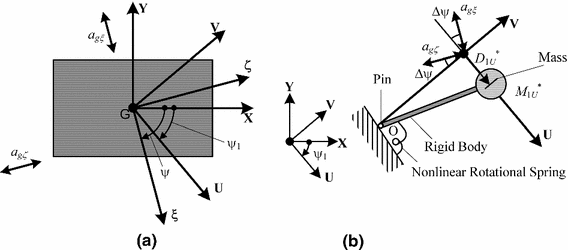
Considering a set of orthogonal \(\xi \)- and \(\zeta \)-axes in the X–Y plane with an angle \(\psi \) as shown in Fig. 18, the equation of motion for an \(N\)-story asymmetric frame building model can be written as Eq. (25).
where
In Eq. (25), C is the damping matrix, and \(a_{g\xi }(\hbox {t})\) and \(a_{g\zeta }(\hbox {t})\) are the ground accelerations of the \(\xi \)- and \(\zeta \)-axis components, respectively. Let the U-axis be the principal axis of the first modal response, while the V-axis is orthogonal to the U-axis. The tangent of \(\psi _{1}\), the angle of incidence of the U-axis with respect to the X-axis, is determined from Eq. (28).
Assume that the building oscillates predominantly in the first mode under U-directional (unidirectional) excitation, and predominantly in the second mode under V-directional excitation. Under bi-directional excitation, it is assumed that displacement \(\mathbf{d}(t)\) and the restoring force \(\mathbf{f}_\mathbf{R } (t)\) can be written in the form of Eqs. (29) and (30), respectively, even if the building oscillates beyond the elastic range.
where
It is also assumed that Eqs. (29) and (30) are still valid in the nonlinear stage if the change in mode shape is properly taken into account, and the U-axis is determined based on the first mode vector in the nonlinear stage. By substituting Eqs. (29) and (30) into Eqs. (25) and (34) is obtained:
By multiplying \(\Gamma _{1U} \varvec{\upvarphi }_\mathbf{1}^{\mathbf{T}}\) from the left side of Eq. (34) and considering Eqs. (35) through (38), the equation of motion for the equivalent SDOF model representing the first modal response is obtained as Eq. (39).
In Eq. (35), \(M_{1U}^{*}\) and \(C_{1U}^{*}\) are the first modal mass and the first modal damping coefficient, respectively. The ground acceleration component in the U-axis, \(a_{gU}(t)\), is defined as:
Therefore, Eq. (39) can be rewritten in a simplified form as:
To derive the equation of motion for the equivalent SDOF model representing the second modal response, the tangent of \(\psi _{2}\), the angle of incidence for the principal direction of the second modal response with respect to the X-axis, is formulated as:
By multiplying \(\Gamma _{2V} \varvec{\upvarphi }_\mathbf{2}^{\mathbf{T}}\) from the left side of Eq. (34) and considering Eqs. (36) and (43), Eq. (44) is obtained.
In Eq. (43), \(M_{2V}^{*}\) and \(C_{2V}^{*}\) are the second modal mass and the second modal damping coefficient, respectively. It is assumed that the principal directions of the first and second modal responses are mutually close to orthogonal. This assumption can be expressed as:
In other words, the principal axis of the second modal response is close to the V-axis. From Eqs. () and (45), Eq. (46) is obtained.
Therefore, considering Eq. (47), Eqs. (48) and (49) can be derived.
Substituting Eqs. (47) and (48) into Eq. (44) and considering Eq. (49), the equation of motion of the equivalent SDOF model representing the second modal response is obtained as Eq. (50).
In Eq. (49), \(a_{gV}(t)\) is the ground acceleration component along the V-axis.
As described in Sect. 2, it is assumed that the spectra of the two horizontal ground motion components are identical. From this assumption, the relationship for the response acceleration spectra of the U- and V-components \(S_{AU}(T)\) and \(S_{AV}(T)\) is expressed as:
In Eq. (51), \(S_{A\xi }(T)\) and \(S_{A\zeta }(T)\) are the response acceleration spectra of the \(\xi \)- and \(\zeta \)- components, respectively. Therefore, the same response spectra are used to predict the peak response of the first and second mode.
Appendix 2: The flow of “the displacement-based mode-adaptive pushover analysis”
In the pushover analysis, which is referred to as the “displacement-based mode-adaptive pushover analysis”, the following assumptions are made.
-
(1)
One-component model, with two nonlinear flexural springs at both ends and one nonlinear shear spring in the middle of the line element, is applied to all members. The envelope curve for each nonlinear spring of all members is symmetric over the positive and negative ranges.
-
(2)
The equivalent stiffness of each nonlinear spring can be defined by its secant stiffness at the peak deformation previously derived in the calculation.
-
(3)
The first mode shape at each loading stage \({}_\mathbf{n}\varvec{\upvarphi }_\mathbf{1}\) can be determined based on the equivalent stiffness.
-
(4)
The deformation shape imposed on a model is similar to the first mode shape obtained in (2) and (3).
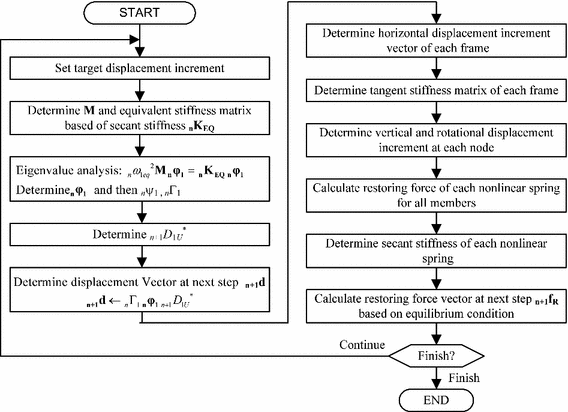
Figure 19 shows a flow chart of the displacement-based mode-adaptive pushover analysis procedure applied in this paper. The main difference between the present analysis and the pushover analysis proposed by Antoniou and Pinho (2004) is that in the present analysis the secant stiffness of each element is used to determine the mode shape and the displacement shape (not the displacement increment) at each nonlinear stage. Antoniou and Pinho use the tangent stiffness of each element to determine the mode shape and the displacement increment in their analysis.
Appendix 3: Formulation of the torsional index based on mode shape
The \(k\)th equivalent modal mass with respect to the \(k\)th principal direction of the modal response \(M_{k}^{*}\) is expressed as Eq. (52). Assuming from Eq. (51) that the \(k\)th mode is purely translational \((\phi _{\Theta jk} = 0),\) the \(k\)th equivalent modal mass ignoring the rotational component \(M_{kT}^{*}\) can be expressed as Eq. (53).
From Eqs. (52) and (53), the ratio \((M_{kT}^{*}/M_{k}^{*})\) is obtained as:
In Eq. (54), the ratio \((M_{kT}^{*}/M_{k}^{*})\) is the reduction ratio of the \(k\)th equivalent modal mass resulting from the rotational component; if the \(k\)th mode is purely translational, the ratio \((M_{kT}^{*}/M_{k}^{*})\) is unity, while if it is a purely torsional mode, the ratio \((M_{kT}^{*}/M_{k}^{*})\) is zero. Equation (54) can be rewritten as Eq. (55), considering the torsional index of the \(k\)th mode, \(R_{\rho k}\), defined by Eq. (56), which is identical to Eq. (22).
From Eq. (55), it can be seen that the ratio \((M_{kT}^{*}/M_{k}^{*})\) is unity when \(R_{\rho k}\) is zero (purely translational), while \((M_{kT}^{*}/ M_{k}^{*})\) is close to zero when \(R_{\rho k}\) is significantly large. Therefore, the terms “predominantly translational” and “predominantly torsional” can be defined by the value of \(R_{\rho k}\); when \(R_{\rho k} < 1,\) the mode is “predominantly translational” and when \(R_{\rho k}> 1,\) the mode is “predominantly torsional”. Note that the index \(R_{\rho k}\) can be used for both single-story and multi-story irregular buildings.
Appendix 4: Classification of structural systems as torsionally stiff (TS) or torsionally flexible (TF)
In general, the classification of structural systems as TS or TF systems is based on the ratio of uncoupled torsional to lateral frequencies \(\Omega _{\theta }\) of the corresponding torsionally balanced system (e.g., Hejal and Chopra 1987). However, here the classification is made based on the first and the second modes because the ratio \(\Omega _{\theta }\) can be rigorously evaluated only for one-story asymmetric buildings (and multi-story asymmetric buildings that satisfy certain conditions). In other words, the classification is made using the torsional indices of the first and second modes, \(R_{\rho 1}\) and \(R_{\rho 2}\).
Bosco et al. (2013) proposed a method to evaluate the static eccentricity and the ratio \(\Omega _{\theta }\) of multi-story asymmetric buildings from static analyses. In this appendix, their method is applied to the six four-story building models investigated in this article and the ratio \(\Omega _{\theta }\) in each story is evaluated.
The evaluated results are shown in Table 4. The ratio of uncoupled torsional to lateral frequencies in the X- and Y-direction, \(\Omega _{\theta X}\) and \(\Omega _{\theta Y}\), respectively, are larger than 1 for all the stories in the four building models (Models A1, A2, B2, and B3). Therefore, from the classification based on \(\Omega _{\theta }\), these four building models are classified as TS systems in both directions. However, in the case of Models B1 and B4, the classification based on \(\Omega _{\theta }\) is difficult because in the first story \(\Omega _{\theta X}\) and \(\Omega _{\theta Y}\) are smaller than 1, while in the upper two stories \(\Omega _{\theta X}\) and \(\Omega _{\theta Y}\) are larger than 1. Conversely, the classification based on \(R_{\rho 1}\) and \(R_{\rho 2}\) is quite clear, as shown in Fig. 8; for all building models,\(R_{\rho 1}\) and \(R_{\rho 2}\) are smaller than 1. Therefore, the author believes that for a multi-story building the classification of the structural system as a TS or TF system should be made based on the mode shape of the first and second modes.
Rights and permissions
About this article
Cite this article
Fujii, K. Prediction of the largest peak nonlinear seismic response of asymmetric buildings under bi-directional excitation using pushover analyses. Bull Earthquake Eng 12, 909–938 (2014). https://doi.org/10.1007/s10518-013-9557-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-013-9557-x