Explainable decomposition of nested dense subgraphs

Abstract

Discovering dense regions in a graph is a popular tool for analyzing graphs. While useful, analyzing such decompositions may be difficult without additional information. Fortunately, many real-world networks have additional information, namely node labels. In this paper we focus on finding decompositions that have dense inner subgraphs and that can be explained using labels. More formally, we construct a binary tree T with labels on non-leaves that we use to partition the nodes in the input graph. To measure the quality of the tree, we model the edges in the shell and the cross edges to the inner shells as a Bernoulli variable. We reward the decompositions with the dense regions by requiring that the model parameters are non-increasing. We show that our problem is NP-hard, even inapproximable if we constrain the size of the tree. Consequently, we propose a greedy algorithm that iteratively finds the best split and applies it to the current tree. We demonstrate how we can efficiently compute the best split by maintaining certain counters. Our experiments show that our algorithm can process networks with over million edges in few minutes. Moreover, we show that the algorithm can find the ground truth in synthetic data and produces interpretable decompositions when applied to real world networks.

1 Introduction

Discovering dense regions in a graph is a popular tool for analyzing graphs, with applications such as modeling (Bollobás 1984; Carmi et al. 2007), social network and influence analysis (Seidman 1983; Kitsak et al. 2010; Ugander et al. 2012), visualization (Alvarez-Hamelin et al. 2006), bioinformatics (Bader and Hogue 2003; Hagmann et al. 2008), and team formation (Bonchi et al. 2014).

While useful, analyzing such decompositions may be difficult without additional information. Fortunately, many real-world networks have additional information besides the edges. We focus on networks with node labels. Our goal is two-fold. First, we aim to decompose the given graph such that the inner regions are more dense. Secondly, the decomposition must come with a summary based on the node labels. We can then use the obtained summary to study the network structure and which labels correspond to the relatively dense regions of the graph.

We can tackle this task in two different ways. The first approach is to ignore labels at first and find a good decomposition. Once the decomposition is discovered we then use labels to find a good explanation for the decomposition. Methods of this nature have been proposed for explaining clusters and communities (Davidson et al. 2018; Bai et al. 2020; Li et al. 2010). The second approach is to design a problem that simultaneously optimizes the given score while requiring that the decomposition is explanaible with labels. Such approaches have been proposed for discovering communities (Galbrun et al. 2014; Pool et al. 2014; Atzmueller et al. 2016) and conceptual clusterings (Fisher 1987; Gennari et al. 1989; Ouali et al. 2016; Guns et al. 2011).

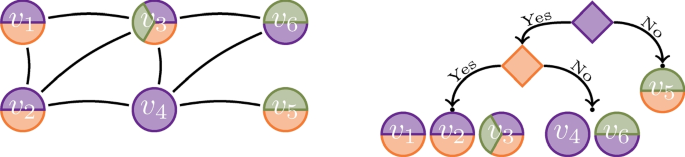
We will focus on the second approach, primarily because we can require that the discovered structured has to be explainable by labels. More specifically, we construct a binary tree T that we use to partition the nodes in the input graph. Each leaf represents a single shell, that is, a set of nodes, and each non-leaf in T will contain a label that we use to partition the nodes. Such trees can be visualized in order to study the corresponding decomposition, as demonstrated in Fig. 4 in Sect. 7.

To measure the quality of the tree, we model the edges in the ith shell and the cross edges to the inner shells as a Bernoulli variable parameterized with $\lambda _i$. We use the log-likelihood of this model as the score for tree. To reward the decompositions, where the inner regions are more dense, we require that $\lambda _{i} \ge \lambda _{i + 1}$.

We need to restrict the size of the tree as otherwise a label tree using every possible label is always optimal. To this end, we consider two variants. In the first variant, we restrict the number of leaves with a constraint k. In the second variant we penalize large trees with a BIC criterion. We show that both problems are NP-hard and that the first problem is inapproximable.

We should stress that we cannot use the aforementioned works directly as our goal is substanially different than the goals considered previously. Therefore, in order to find good trees we propose a straightforward greedy algorithm. We start with the empty tree, find the optimal split, augment the tree with the found split, and repeat until we have k leaves or the BIC score no longer improves.

The computational bottleneck of this algorithm is searching for a new candidate. A naive implementation requires enumerating over the edges every time a split needs to be evaluated. We sidestep this issue by showing that we can compute the score by maintaining certain counters. An additional challenge comes from the need to find optimal parameters $\Lambda$ for the edge probabilities. Especially, the monotonicity constraint requires additional steps. In summary, we show that the running time is $\mathcal {O} \mathopen {}\left( m + (R + S) \log (R + S) + \min (R, kL) k\log ^2 k\right)$, where m is the number of edges, k is the number of the leaves in the resulting tree, L is the number of labels R is the number of node-label pairs, and $S = \sum \deg (v) {\left| lab \mathopen {}\left( v\right) \right| }$.

Our experiments show that the algorithm is fast: we can process networks with over million edges in few minutes. Moreover, we show that the algorithm can find the ground truth in synthetic networks and produces interpretable decompositions when applied to real-world networks.

The rest of the paper is organized as follows. In Sect. 2 we introduce preliminary notation and provide formal problem definition. We introduce the algorithm in Sects. 3–5. We present related work in Sect. 6 and experimental evaluation in Sect. 7. We conclude with discussion in Sect. 8. The proofs are given in “Appendix”.

2 Problem definition

We will first establish preliminary notation and define our problem.

Assume an undirected graph $G = (V, E, lab )$ with n nodes V and m edges E, and a function $lab$ that maps each node $v \in V$ to a set of labels $lab \mathopen {}\left( v\right)$. Given two sets of nodes U and W, we write E(U) to be the edges that have both end points in U and E(U, W) to be the edges between U and W.

Our goal is to produce a decomposition that can be explained with a label tree. Formally, a label tree T is a binary ordered tree where each non-leaf node is associated with a label $\ell$ and a binary value $b \in \left\{ 0, 1\right\}$.

Given a set of labels L we can traverse T from the root to a leaf: Assume that we are at node $\alpha \in T$ with a label $\ell$ and a binary value b. If $\ell \in L$ and $b = 1$, or $\ell \notin L$ and $b = 0$ we traverse to the right branch, otherwise we traverse to the left branch. We repeat this procedure until we reach a leaf.

Given a graph $G = (V, E, lab )$ we traverse every node $v \in V$ using a label set $lab \mathopen {}\left( v\right)$, and obtain a partition ${\mathcal {S}} = (S_1, \ldots , S_k)$ of V, where k is the number of leaves in T. We will write $shells \mathopen {}\left( T, G\right)$ to denote ${\mathcal {S}}$.

Example 2.1

Consider a toy graph and and a label tree given in Fig. 1. The given tree defines 3 shells: $S_1 = \left\{ v_1, v_2, v_3\right\}$ contains the nodes with purple and orange labels, $S_2 = \left\{ v_4, v_6\right\}$ contains the nodes with purple but no orange label, and $S_3 = \left\{ v_5\right\}$ contain the node with no purple label.

Fig. 1

Toy example of a graph and a label tree. Optimal parameters for the label tree are $\lambda _1 = 3/3$, $\lambda _2 = 4/7$, and $\lambda _3 = 1/5$

We will measure the quality of a partition ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$ by modeling the edges using a simple Bernoulli model. More formally, let us write $C_i = S_1 \cup \cdots \cup S_i$ to be the union of all shells up to i. For convenience, let us also write $C_0 = \emptyset$.

We will model the edges in G using k Bernoulli variables, where k is the number of partitions. Let $\Lambda = (\lambda _1, \ldots , \lambda _k)$ be the parameters for the Bernoulli variables. We model the edges in $F_i = E(C_i) \setminus E(C_{i - 1})$ using a Bernoulli variable parameterized with $\lambda _i$. Note that the set of edges $F_i$ includes all the edges in $S_i$ as well as all the cross edges between $S_i$ and $S_j$, where $j < i$. The maximum number of such edges is $d_i = {{\left| C_i\right| } \atopwithdelims ()2} - {{\left| C_{i - 1}\right| } \atopwithdelims ()2}$. The negative log-likelihood of the model for $F_i$ is equal to $q \mathopen {}\left( {\left| F_i\right| }, d_i, \lambda _i\right)$, where

$$\begin{aligned} q \mathopen {}\left( a, b, \lambda \right) = -a\log \lambda - (b - a) \log (1 - \lambda ), \end{aligned}$$

(1)

where the convention $0 \times \log 0 = 0$ is used. The final score is the negative log-likelihood of each $F_i$ combined,

$$\begin{aligned} q \mathopen {}\left( T, G, \Lambda \right) = \sum _{i = 1}^k q \mathopen {}\left( {\left| F_i\right| }, d_i, \lambda _i\right) . \end{aligned}$$

(2)

Note that smaller values indicate better partition. We use the negative log-likelihood as this will be more notationally convenient.

Our goal is to find T and $\Lambda$ minimizing $q \mathopen {}\left( T, G, \Lambda \right)$.

Several remarks are in order. First, we prefer partitions whose inner shells, that is, shells with smaller indices, are more dense than the outer shells, that is, shells with larger indices. We take this preference into account by requiring that the parameters in $\Lambda$ are non-increasing, that is, $\lambda _1 \ge \cdots \ge \lambda _k$. Such constraint will favor partitions with more dense inner shells. Given a tree T and input graph G, if $\Lambda$ is optimal, we will write $q \mathopen {}\left( T, G\right)$ to mean $q \mathopen {}\left( T, G, \Lambda \right)$.

Note that $q \mathopen {}\left( T, G, \Lambda \right)$ is a negative log-likelihood of a stochastic block model, where the shells are the blocks and the edge probability between ith and jth block is $\lambda _{\max (i, j)}$, and that we also require that $\lambda _1 \ge \cdots \ge \lambda _k$.

Example 2.2

Consider Fig. 1. The optimal parameters without the monotonicity constraints are the edge proportions. There are 3 edges between 3 nodes in $S_1$, implying that $\lambda _1 = 3/d_1 = 1$, where $d_1 = {{\left| S_1\right| } \atopwithdelims ()2} = 3$ is optimal. Similarly, there are 4 edges within $S_2$ and between $S_2$ and $S_1$, consequently $\lambda _2 = 4 / d_2 = 4/7$, where $d_2 = {{\left| S_2\right| } \atopwithdelims ()2} + {\left| S_1\right| }{\left| S_2\right| } = 7$. Lastly, $\lambda _3 = 1 / d_3 = 1/5$ is optimal, where $d_3 = ({\left| S_1\right| } + {\left| S_2\right| }){\left| S_3\right| } = 5$. Note that the monotonicity constraints in this case are satisfied. The score is equal to $q \mathopen {}\left( T, G\right) = q \mathopen {}\left( 3, 3, 1\right) + q \mathopen {}\left( 4, 7, 4/7\right) + q \mathopen {}\left( 1, 5, 1/5\right) \approx 0 + 4.8 + 2.7 = 7.5$.

Lastly, adding a new node in T will never increase the score: Assume a graph G, a label tree T, and set of parameters $\Lambda$. Construct a new tree $T'$ by replacing a leaf with a non-leaf node (and two leaves). Create new set of parameters $\Lambda '$ where the parameter, say $\lambda$, corresponding to the leaf is replaced by the two parameters (corresponding to the new two leaves), both equal to the value of $\lambda$. Then $q \mathopen {}\left( T, G, \Lambda \right) = q \mathopen {}\left( T', G, \Lambda '\right)$.

Example 2.3

Consider Fig. 1. Define a new tree $T'$ by splitting the left-most leaf such that nodes with green label are placed in the new right leaf, do the same split for the middle leaf as well. The new shells are $S'_1 = \left\{ v_1, v_2\right\}$, $S'_2 = \left\{ v_3\right\}$, $S'_3 = \left\{ v_4\right\}$, $S'_4 = \left\{ v_6\right\}$, and $S'_5 = \left\{ v_5\right\}$. The new parameters are $\lambda '_1 = \lambda '_2 = 1$, $\lambda '_3 = \lambda '_4 = 4/7$, and $\lambda '_5 = 1/5$. Note that these new parameters are not optimal. Nevertheless, the score is $q \mathopen {}\left( T', G, \Lambda '\right) = q \mathopen {}\left( 1, 1, 1\right) + q \mathopen {}\left( 2, 2, 1\right) + q \mathopen {}\left( 2, 3, 4/7\right) + q \mathopen {}\left( 2, 4, 4/7\right) + q \mathopen {}\left( 1, 5, 1/5\right) \approx 7.5.$

Consequently, there is a tree that uses every label while minimizing the score. Such trees may be counter-productive if the number of labels is large or if there are irrelevant labels. Hence, we would like to constraint the size of T. We consider two different approaches which leads to the two following problem statements. First, we can limit the number of leaves directly.

Problem 2.1

(CTree) Given a graph G, and an integer k, find a label tree T with at most k leaves and a set $\Lambda$ of non-increasing parameters $\Lambda$ minimizing $q \mathopen {}\left( T, G, \Lambda \right)$.

Secondly, we penalize the new nodes with Bayesian Information Criterion (BIC).

Problem 2.2

(CTreeBIC) Given a graph $G = (V, E, lab )$, find a label tree T and a set $\Lambda$ of non-increasing parameters $\Lambda$ minimizing

$$\begin{aligned} q_{ BIC } \mathopen {}\left( T, G, \Lambda \right) = q \mathopen {}\left( T, G, \Lambda \right) + \frac{1}{2} k \log {{\left| V\right| } \atopwithdelims ()2}, \end{aligned}$$

where k is the number of leaves in T.

Without the monotonicity constraint $\lambda _1 \ge \cdots \ge \lambda _k$, finding the optimal parameters $\Lambda$ for a fixed tree T is trivial, that is, they are $\lambda _i = {\left| F_i\right| } / d_i$, where $F_i$ and $d_i$ are the same as in Eq. 2.

The monotonicity constraint complicates the solution as we cannot longer consider each $\lambda$ separately. Luckily, we can still find the optimal parameters quickly using isotonic regression. We will discuss the parameter optimization in Sect. 5 after we have described the search algorithm for the tree T in the next two sections.

3 Finding good label trees

In this section we prove that both problems are NP-hard. Therefore, we then propose a strategy where the label tree is grown greedily by finding the best leaf split. We discuss the details of the algorithm in the next two sections.

Our first step is to state that both problems cannot be solved in polynomial time.

Proposition 3.1

CTree is NP-hard.

Proposition 3.2

CTreeBIC is NP-hard.

The proofs of Propositions 3.1–3.2 are given in “Appendix A”. The proof of Proposition 3.1 reveals a stronger result: there is no polynomial-time algorithm with approximation guarantee for CTree.

Corollary 3.1

If ${\textbf {P}}\ne {\textbf {NP}}$, then CTree is inapproximable.

In order to find trees with a good score, we propose a greedy algorithm by iteratively changing a leaf $\alpha$ in the current tree T with a new non-leaf node with label $\ell$ and a boolean variable b. We will denote this new tree with $T + (\alpha , \ell , b)$.

The algorithm proceeds as follows: We start with an empty tree T. We find the best split $(\alpha , \ell , b)$ and replace T with $T + (\alpha , \ell , b)$. We continue the iteration until we have have k leaves (CTree) or the BIC score will no longer improve (CTreeBIC). The high-level pseudo-code is given in Algorithm 1.

Algorithm 1

$\textsc {Greedy} (G)$, finds label tree greedily.

We will discuss the details in the next two sections. We will first focus on maintaining the counters that allow us to compute the score for a set of parameters $\Lambda$, and then we describe how to select the optimal parameters.

Propositions 4.2 and 5.2 show that the algorithm runs in

$$\begin{aligned} \mathcal {O} \mathopen {}\left( m + (R + S) \log (R + S) + \min (R, kL) k\log ^2 k\right) \end{aligned}$$

time, where k is the number of the leaves in the resulting tree, L is the number of labels R is the number of node-label pairs, and $S = \sum \deg (v) {\left| lab \mathopen {}\left( v\right) \right| }$.

4 Computing score quickly

The computational bottleneck of Greedy is looking for the optimal split. In order to avoid sorting nodes and enumerating over all edges every time a split is tested, we maintain several counters that speed up the process significantly.

In this section we describe the counters and the procedures required to maintain them. In the next section we describe how these counters are then used to find the optimal $\Lambda$ and consequently compute the score.

4.1 Counters needed for computing the score

Assume a label tree T. Let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$ and write $C_i = S_1 \cup \cdots \cup S_i$. Let $\alpha$ be the ith leaf. We maintain the following counters:

• 1. $n[\alpha ] = {\left| S_i\right| }$, the number of nodes in the leaf,

• 2. $c[\alpha ] = {\left| C_{i - 1}\right| }$, the number of nodes in the previous leaves,

• 3. $m[\alpha ] = {\left| E(S_i)\right| } + {\left| E(C_{i - 1}, S_i)\right| }$, the number of edges in $S_i$ plus the number of cross-edges to the inner leaves.

We can compute the score using these counters since

$$\begin{aligned} q \mathopen {}\left( T, G, \Lambda \right) = \sum _{\begin{array}{c} {\alpha \text { is} }\\ {\text {the } i \text {th leaf}} \end{array}} q \mathopen {}\left( m[\alpha ], n[\alpha ]c[\alpha ] + {n[\alpha ] \atopwithdelims ()2}, \lambda _i\right) \ . \end{aligned}$$

(3)

These counters are not enough since during Greedy, we want to compute the score of $T + (\alpha , \ell , b)$ efficiently. In order to do that, for each leaf $\alpha$ and a label $\ell$, we maintain the following additional counters,

• 1. $n[\alpha , \ell ] = {\left| U\right| }$, where U are the nodes in $\alpha$ with label $\ell$,

• 2. $m[\alpha , \ell ] = {\left| E(U)\right| } + {\left| E(C_{i - 1}, U)\right| }$, the number of edges in U plus the number of cross-edges to the inner leaves,

• 3. $r[\alpha , \ell ] = {\left| E(S_i \setminus U, U)\right| }$, the number of cross-edges between U and $S_i \setminus U$.

We can use these counters as follows. Assume a tree T, and let $T' = T + (\alpha , \ell , b)$. Let $\beta$ and $\gamma$ be the new leaves. Then the counters of other leaves remain unchanged. If $b = 1$, then the counters for $\beta$ and $\gamma$ are

$$\begin{aligned} n[\beta ] = n[\alpha , \ell ], \quad m[\beta ] = m[\alpha , \ell ],\quad n[\gamma ] = n[\alpha ] - n[\beta ], \quad m[\gamma ] = m[\alpha ] - m[\beta ]. \end{aligned}$$

(4)

If $b = 0$, then the counters are

$$\begin{aligned} n[\gamma ] = n[\alpha , \ell ], \ m[\gamma ] = m[\alpha , \ell ] + r[\alpha , \ell ],\ n[\beta ] = n[\alpha ] - n[\gamma ], \ m[\beta ] = m[\alpha ] - m[\gamma ] \ . \end{aligned}$$

(5)

Finally, $c[\beta ] = c[\alpha ]$ and $c[\gamma ] = c[\alpha ] + n[\beta ]$.

Using these counters and Eq. 3 we can compute $q \mathopen {}\left( T', G, \Lambda \right)$.

4.2 Maintaining counters

In order to maintain the counters, we maintain the following lists: Let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$, and let $\alpha$ be the ith leaf. We will store the nodes $S_i$ as a linked list $V[\alpha ]$. Similarly, we maintain a linked list of $V[\alpha , \ell ]$ of nodes in $S_i$ with label $\ell$.

Once we have found a leaf that we want to split, say $\alpha$, we need to compute the counters for the two new leaves $\beta$ and $\gamma$. Computing the leaf counters $n[\cdot ]$, $c[\cdot ]$, and $m[\cdot ]$ is trivial with Eqs. 4–5. We can compute the new label counters from scratch, however, it is faster to compute the labels for one new leaf and use the following proposition to compute the counters for the other leaf.

Proposition 4.1

Let $\beta$ and $\gamma$ be the two new leaves in $T + (\alpha , \ell , b)$. Then for any label o,

$$\begin{aligned} n[\alpha , o]= & {} n[\beta , o] + n[\gamma , o], \quad m[\alpha , o] = m[\beta , o] + m[\gamma , o],\\ r[\alpha , o]= & {} r[\beta , o] + r[\gamma , o] + C_{o}, \end{aligned}$$

where $C_{o} = {\left| \left\{ (u, v) \in E(V[\beta ], V[\gamma ]) \mid o \in lab \mathopen {}\left( u\right) \triangle lab \mathopen {}\left( v\right) \right\} \right| }$ is the number of cross-edges disagreeing on label o.¹

We omit the proof of this proposition due to its triviality.

We can use Proposition 4.1 as follows. For a selected label $\ell '$, we first compute $n[\beta , \ell ']$, $m[\beta , \ell ']$, and $r[\beta , \ell ']$ and $C_{\ell '}$ by enumerating over $V[\beta$] and the adjacent edges, and then use Prop. 4.1 to obtain the corresponding counters for $\gamma$. Alternatively, we can first compute the counters for $\gamma$ and then use them to compute the counters for $\beta$.

Of these two approaches, we choose the one which is faster. In order to select which approach to use, we compute and use the following counter,

$$\begin{aligned} t[\alpha ] = \sum _{v \in V[\alpha ]} (1 + \deg v){\left| lab \mathopen {}\left( v\right) \right| }. \end{aligned}$$

The algorithm Split, given in Algorithm 2, for splitting proceeds as follows. We first compute the counters $n[\cdot ]$, $c[\cdot ]$, $m[\cdot ]$, $t[\cdot ]$, and the lists $V[\cdot ]$. Assume $t[\beta ] < t[\gamma ]$. We visit every $v \in V[\beta ]$ and $\ell ' \in lab \mathopen {}\left( v\right)$ and move v from $V[\alpha , \ell ']$ to form $V[\beta , \ell ']$; the remaining nodes form $V[\gamma , \ell ']$. We then compute the label counters for $\beta$ and label $\ell '$ by enumerating $V[\beta , \ell ']$ and the adjacent edges, and use Proposition 4.1 to obtain the corresponding counters for $\gamma$. If $t[\beta ] \ge t[\gamma ]$ we do the same procedure except that we swap the roles of $\beta$ and $\gamma$.

Finally, we do the following speed-ups. We do not store any edges between the leaves. Instead, for each $v \in S_i$, we store a counter s[v] which is the number of edges from v to $S_1, \ldots , S_{i - 1}$. Moreover, if a label $\ell$ was used to split a node $\alpha$, we do not consider using $\ell$ for splitting descendants of $\alpha$ as there is no gain in using $\ell$.

Algorithm 2

$\textsc {Split} (\alpha , \ell , b)$, computes $T + (\alpha , \ell , b)$

Finally, we will bound the total running time of all calls of Split during Greedy.

Proposition 4.2

Maintaining label tree can be done in $\mathcal {O} \mathopen {}\left( m + (R + S) \log (R + S) \right)$ time, where R is the number of node-label pairs, and $S = \sum \deg (v) {\left| lab \mathopen {}\left( v\right) \right| }$.

5 Finding optimal $\Lambda$

Next we discuss finding optimal $\Lambda$ and consequently computing the score. More specifically, we argue that optimal $\Lambda$ can be obtained in $\mathcal {O} \mathopen {}\left( k\right)$ time, if computed from scratch, or optimal $\Lambda$ can be maintained in $\mathcal {O} \mathopen {}\left( \log ^2 k\right)$ time, where k is the number of leaves.

5.1 Computing $\Lambda$ from scratch

Our next step is to find $\Lambda$ minimizing $q \mathopen {}\left( T, G, \Lambda \right)$. Let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$ be the partition induced by the tree, and let $C_i = S_1, \ldots , S_i$ be the set of of all shells up to i.

To simplify the notation in this section, assume that we are given two sequences A and B of k integers with $a_i \le b_i$, and let us extend the definition of a score by defining

$$\begin{aligned} q \mathopen {}\left( A, B, \Lambda \right) = \sum _{i = 1}^k q \mathopen {}\left( a_i, b_i, \lambda _i\right) . \end{aligned}$$

Equation 3 states that we can obtain the sequences A and B from the maintained counters such that $q \mathopen {}\left( T, G, \Lambda \right) = q \mathopen {}\left( A, B, \Lambda \right)$.

Given the sequences A and B, the optimal $\Lambda$ without any constraints is given by $\lambda _i = a_i / b_i$. However, we require that $\Lambda$ is non-increasing. Fortunately, we can use a classic method known as Pool Adjacent Violators Algorithm (Pava) (Ayer et al. 1955). The algorithm proceeds as follows: We search for $a_i / b_i < a_{i + 1} / b_{i + 1}$. If one is found, then the entries are replaced with their sums $a_i + a_{i + 1}$ and $b_i + b_{i + 1}$, respectively. This process is continued until no violations are left. We will denote the resulting sequences as $A', B' = \textsc {Pava} (A, B)$. We can use $A', B'$ to find optimal $\Lambda$ as follows.

Proposition 5.1

(Ayer et al. 1955) Let $A', B' = \textsc {Pava} (A, B)$. Let $j_i$ be the index of the entry in $(A', B')$ that contains the ith entry of (A, B). Write $\lambda _i = a_{j_i} / b_{j_i}$. Then $\Lambda$ is non-increasing and minimizes $q \mathopen {}\left( A, B, \cdot \right)$.

The running time of Pava is in $\mathcal {O} \mathopen {}\left( k\right)$, see e.g., Calders et al. (2014), which leads to the next result.

Proposition 5.2

Let G be a graph with n nodes, L labels, and R node-label pairs. If we recompute $\Lambda$ from scratch every time we test a split, then the total time needed for tests is in $\mathcal {O} \mathopen {}\left( \min (R, kL) k^2\right)$, where k is the number of leaves in the final tree.

5.2 Maintaining $\Lambda$

We can further speedup the algorithm by not computing $\Lambda$ from scratch but instead updating it (and reversing it back) as we test different splits. To this end, note that as we look for the best split $(\alpha , \ell , b)$, only one entry is replaced by two entries in the sequences A and B. We can use this fact by first arguing that Pava is equivalent to finding convex hull of a certain set of points in a plane. We can then use a classic convex hull maintenance algorithm to maintain the score in $\mathcal {O} \mathopen {}\left( \log ^2 k\right)$ time.

Let us first establish the connection between Pava and the convex hull. Given a set of points $P = (X, Y)$, a subset $P^* \subseteq P$ is the lower convex hull of P if the segments between adjacent points in $P^*$ form a convex curve such that every point in P is above or at that curve. The following proposition shows the connection.

Proposition 5.3

Assume two sequences A and B of k numbers with $0 \le a_i \le b_i$. Let $A^*, B^* = \textsc {Pava} (A, B)$. Define

$$\begin{aligned} x_i = \sum _{j = 1}^i a_j,\quad y_i = \sum _{j = 1}^i b_j,\quad x_i^* = \sum _{j = 1}^i a_j^*,\quad y_i^* = \sum _{j = 1}^i b_j^*,\quad \end{aligned}$$

and $x_0 = y_0 = x_0^* = y_0^* = 0$. Then $X^*, Y^*$ is the lower convex hull of X, Y.

We can use this result as follows: Assume that the current label tree is T and let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$ be its shells. Assume that we want to replace the ith leaf $\alpha$ with a non-leaf and let $T' = T + (\alpha , \ell , b)$ be the corresponding tree.

Write ${\mathcal {S}}' = shells \mathopen {}\left( T', G\right)$. Then $S_j' = S_j$ for $j < i$, and $S_{j + 1}' = S_j$ for $j > i$. Moreover, $S_i = S_{i}' \cup S_{i + 1}'$.

Let A and B such that $q \mathopen {}\left( A, B, \Lambda \right) = q \mathopen {}\left( T, G, \Lambda \right)$. Let X, Y be the corresponding points in a plane as defined in Proposition 5.3. Let $X', Y'$ be the points constructed similarly using $T'$. A straightforward argument shows that $X', Y'$ is equal to X, Y with one additional point, namely $x'_i, y'_i$.

An algorithm by Overmars and Van Leeuwen (1981) allows us to maintain convex hull under point addition and removal in $\mathcal {O} \mathopen {}\left( \log ^2 k\right)$ time, where k is the number of points. More importantly, the same algorithm can maintain any statistic of the form

$$\begin{aligned} \sum _i f(x^*_i - x^*_{i - 1}, y^*_i - y^*_{i - 1}), \end{aligned}$$

(6)

where $(x_i^*, y_i^*)$ is the ith point in the hull. Proposition 5.3 states that $x^*_i - x^*_{i - 1}$ and $y^*_i - y^*_{i - 1}$ are $a^*_i$ and $b^*_i$ returned by Pava. Consequently, if we select

$$\begin{aligned} f(a, b) = -a\log (a/b) - (b - a)\log (1 - a/b), \end{aligned}$$

the sum in Eq. 6 is equal to the score $q \mathopen {}\left( A, B, \Lambda \right)$ with the optimal $\Lambda$.

In summary, to test a new split for T, we use an algorithm by Overmars and Van Leeuwen (1981) to obtain $q \mathopen {}\left( T', G, \Lambda \right)$ with optimal $\Lambda$ in $\mathcal {O} \mathopen {}\left( \log ^2 k\right)$ time. We also use the same algorithm to revert back to T once we have tested the split.

The algorithm by Overmars and Van Leeuwen (1981) is not the fastest algorithm to maintain a hull. An algorithm by Brodal and Jacob (2002) maintains a structure describing a hull in $\mathcal {O} \mathopen {}\left( \log k\right)$ time. The issue here is that the method does not provide a straightforward way to maintain a sum given in Eq. 6, and cannot be used directly.

Finally, let us look at the total time needed to test the splits.

Proposition 5.4

Let G be a graph with n nodes, L labels, and R node-label pairs. Then the total time needed to test the split candidates is $\mathcal {O} \mathopen {}\left( \min (R, kL) k\log ^2 k\right)$, where k is the number of leaves in the final tree.

6 Related work

Core decomposition is a popular method for finding nested structure with increasingly dense inner regions. Core decomposition has been extended to directed (Giatsidis et al. 2013), weighted (Serrano et al. 2009), temporal (Galimberti et al. 2018), and multi-layer (Galimberti et al. 2017) networks. Similar extensions for the methods presented in this paper provide potential future line of work.

An alternative decomposition is a notion k-truss, where each edge is required to be in at least k triangles (Huang et al. 2014; Zhao and Tung 2012; Zhang and Parthasarathy 2012; Wang and Cheng 2012; Cohen 2008). An extension of k-cores called (r, s) nucleus decomposition was proposed by Sariyuce et al. (2015) and Sarıyüce and Pinar (2016), where nodes are replaced with r-cliques and edges are replaced with s-cliques.

We can view the model that we use to evaluate the label trees as a special case of a stochastic block model (see, for example, Holland et al. 1983; Anderson et al. 1992), where edges between block i and block j are modeled with a Bernoulli variable, parameterized with $\lambda _{ij}$. The model that we use comes from requiring that $\lambda _{ij} = \lambda _{\max (i, j)}$ and that $\lambda _{i} \ge \lambda _{i + 1}$. We use this model to specifically favor a nested structure of increasingly more dense shells.

A related notion for discovering dense regions in graphs is searching for a dense subgraph, that is, finding a subgraph W maximizing ${\left| E(W)\right| } / {\left| W\right| }$. Dense subgraph can be found exactly in polynomial time (Goldberg 1984) but also 2-approximate with a simple linear-time algorithm (Charikar 2000). In fact, the algorithm is almost the same algorithm than discovering core decomposition: iteratively remove the vertex with the lowest degree, and among the subgraphs select the best. The fact that we are able to discover the optimal subgraph in polynomial time is in a stark contrast when compared for searching for largest cliques: an NP-hard and inapproximable problem (Zuckerman 2006).

Several variants have been proposed for dense subgraphs, such as, triangle-dense subgraphs (Tsourakakis 2015), where triangles are counted instead of edges, and distance-generalized subgraphs (Bonchi et al. 2019), where paths are counted instead of edges.

Galbrun et al. (2014) proposed discovering dense subgraphs that can be explained with conjunction of labels. Similarly, Pool et al. (2014) proposed looking for communities induced by label queries that maximize certain score based on the within and cross-edges: ideally, these communities are cliques with no cross-edges. The main conceptual difference between these approaches and ours is that we model the whole network while the aforementioned works look for local structures.

7 Experimental evaluation

In this section we present our experiments.

Datasets: To test our algorithm we used a series of synthetic datasets and co-authorship networks.

We generated the synthetic datasets as follows: we used 200 nodes that we divided into 10 groups of 20 nodes. Each node in the ith block received a label $\ell _i$. Given two nodes u and v belonging to blocks i and j with $i \le j$, we generated an edge (u, v) with probability j/20. This yields a network where the blocks with larger indices are more dense. Finally, we added additional labels by sampling independently labels for each node from a set of 1000 labels with a probability of d/1000. Here, d is a parameter, and we refer to this dataset as Syn(d). The average number of noise labels per node in Syn(d) is equal to d. We varied d from 5 to 100. The characteristics of Syn(5) is given in Table 1.

Table 1 Characteristics of the datasets and statistics of the obtained label trees: number of nodes, edges, and labels L, and number of node-label pairs R, normalized scores c and $c_ BIC$, running times (in seconds), and the number of leaves when the BIC criterion was used

We used co-authorship networks (Tang et al. 2008)² to study our algorithms. Here, the authors are the vertices, and there is an edge if two authors have a paper in common. The labels are field-of-study terms, given in the dataset, which are generic descriptions of each paper. The author received a label if he has at least 2 papers with that label.

We considered several snapshots from the larger dataset. More specifically, we extracted papers published in selected prominent DM/ML conferences: ECMLPKDD, ICDM, KDD, NIPS, SDM, and WWW. This allowed us to look at the differences between the networks from different conferences. We also combined these papers together to form Conferences network. Finally, we form a dataset Year2018 by extracting all³ the papers from the year 2018. We used year 2018 as the later years in the original data were incomplete. The characteristics of these datasets are given in Table 1.

Algorithms: We implemented the algorithm using C++,⁴ and used a computer with Intel Core i5 (2.3GHz) to conduct our experiments. Since k was of moderate size in our experiments, we did not use the convex hull to maintain the score. Instead we computed $\Lambda$ from scratch.

In order to compare our algorithm against we need a baseline approach that yields k-partition with dense hierarchical structure based on the node labels. Note that standard methods, such as core decomposition, do not acheve this goal. Therefore, we propose the following pipeline for the baseline algorithm. First we applied the algorithm by Tatti (2019) to find dense hierarchical structure. We then applied PAVA and a dynamic program for segmentation, see Bellman (1961), in order to group the discovered subgraphs into at most k increasingly dense shells while optimizing the log-likelihood. Note that we have not yet used any label information. We report this intermediate score. We then train a decision tree with at most k leaves using the labels as the input and the shell index as the output variable. We report the training error. Finally, we construct a new decomposition by applying the decision tree on the nodes, and report the final score.

Fig. 2

Kendall’s $\tau$ for discovered decomposition from Syn(d) compared against the ground truth as function of d. For each d, the figure shows the average and the minimum coefficient for generated 100 datasets. We set $k = 10$

Results: First, let us study how well Greedy recovers the ground truth from Syn(d). We report Kendall’s $\tau$ in Fig. 2 as a function of d. Here, for each d, we generated 100 datasets and computed average and the minimum of Kendall’s $\tau$. We see that on average the recovered decomposition is very close to the ground truth, with rank values being close to 0.99. There is a moderate downward trend: finding the ground truth from Syn(d) for larger d is more difficult. This is expected as there are more noisy labels present, giving Greedy a better chance to select an incorrect label.

We report the scores and the sizes of the discovered trees (when using the BIC criterion) in Table 1. Here, we normalize the score by multiplying the score with $100 / q \mathopen {}\left( T_0, G\right)$, where $T_0$ is a tree with a single leaf. The normalized scores show how we perform against a baseline model that does not use labels nor partition the nodes in any way. For real-world data, the change in the score is relatively subtle. This is a natural result as we do not expect having large cliques or otherwise really dense regions when compared to the remaining nodes. The BIC criterion produces relatively compact trees, with larger graphs producing larger trees. This is also expected as for smaller graphs there is not enough statistical evidence for splits where the change in neighboring parameters $\lambda$ is minor, that is, the gain in the log-likelihood does not overcome the BIC penalty.

Next, let us compare the results against the baseline. The scores for the intermediate decomposition $c_{ PRE }$ are lower. This is expected since, at this stage, we do not require the decomposition to be induced by the labels. This is seen in the accuracy of the decision tree: only 30% of the nodes can be explained by the labels. Once we form the final decomposition using the tree we see that the baseline scores are close but worse than the scores by our algorithm. This is expected since the baseline consists of multiple stages that do not optimize the score directly. Interestingly, baseline yields worse score $c_{ PRE }$ for Syn(5). This is because the algorithm used to find the initial hierarchy does not optimize the score directly.

Next, let us look at the computational time of Greedy, reported in Table 1. Here we see that the algorithm is practical even for large graphs. Computing the core was done in seconds, with the exception of using BIC criterion for Year2018 network, where the Greedy required 5.5 minutes. The main reason for the slower time is because here Greedy produced a tree with 370 leaves.

Fig. 3

a–c Running times for Conferences as a function of k, number of edges ${\left| E\right| }$, number of node-label pairs R. b and c We sampled nodes from Conferences with varying probability, and applied Greedy with $k = 100$

To further demonstrate the effect of k we show the computational time as a function of k in Fig. 3a using Conferences. We see that the time grows faster than linear as k increases. This is expected since finding new splits for larger trees requires more time.

We also studied the computational time as a function of ${\left| E\right| }$ and R, the number of node-label pairs. To this end, we sampled independently nodes from Conferences with probability p. By varying p we obtain a sequence of subgraphs for which we applied Greedy with $k = 100$. Figure 3b shows the time as a function of ${\left| E\right| }$ and Fig. 3c shows the time as a function of R. Figure 3c suggests linear growth of time as a function of R while Fig. 3b shows sublinear growth for ${\left| E\right| }$. The sublinear trend can be explained by the sampling process. Due to sampling, the expected number of edges is $p^2m$, where m is the number of edges in the original Conferences. On the other hand, the expected number of node-label pairs is pR. That is, subgraphs for smaller values of p will have bigger reduction in edges than in node-label pairs. In summary, we see that R has a strong effect on the computational time, an expected result as this is implied by Propositions 4.2 and 5.2.

Fig. 4

Label trees obtained from KDD (left tree) and NIPS (right tree) datasets with $k=10$ leaves. Blue edges indicate the direction for the papers having the label ($b = 1$)

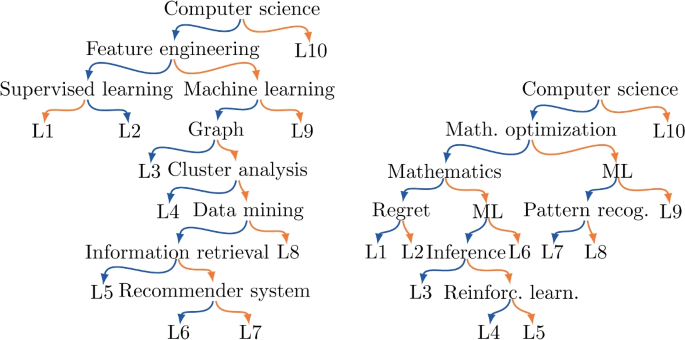
Finally, let us look at specific label trees. In Fig. 4 we show the tree obtained from KDD and NIPS. In both cases we use $k = 10$. We see some similarities in trees: both select Computer science as the initial term as there are more collaborations in papers with this term. However, there are differences as the labels reflect the typical topics in each conference.

8 Concluding remarks

In this paper we proposed mining explainable decompositions: more specifically, we propose finding label trees that yield decompositions with good log-likelihood and have dense inner regions.

We showed that the problem is NP-hard and we proposed a greedy heuristic. In order to make the algorithm fast, we maintain certain counters that allow us to search for the next best split efficiently. We confirmed this in our experiments by showing that we can process large graphs. Moreover, the method is able to find ground truth in synthetic data and find explainable decompositions in co-authorship networks.

Possible future lines of work is to extend the model for weighted and temporal networks, and consider other structures than trees for inducing the decompositions. Moreover, considering scores based on average/minimum degree of shells is also a potential line of work.

Proofs

Proof of Proposition 3.1

To prove the hardness we will provide a reduction from set cover (Cover). In Cover, we are given a universe U and a family of sets ${\mathcal {A}}$ and we are asked whether there are k sets in ${\mathcal {A}}$ covering U. We can safely assume that ${\left| U\right| } > 1$.

Given an instance of Cover, let us first construct the graph G. Given a universe $U = u_1, \ldots , u_n$, we define a set of nodes $V = v_0, v_1, \ldots , v_n$, where $v_i$ corresponds to $u_i$ for every $i = 1, \ldots , n$ and $v_0$ is one additional node. Let us write $V' = v_1, \ldots , v_n$.

We connect every node pair in $V'$. We leave $v_0$ as a singleton.

The labels $lab \mathopen {}\left( v_i\right)$ for each $v_i \in V'$ correspond to the sets in ${\mathcal {A}}$ containing $u_i$. The node $v_0$ has no labels, $lab \mathopen {}\left( v_0\right) = \emptyset$.

Let T, $\Lambda$ be a solution for CTree with T having at most $k + 1$ leaves. We claim that Cover has a solution if and only if $q \mathopen {}\left( G, T, \Lambda \right) = 0$.

Assume that $q \mathopen {}\left( T, G, \Lambda \right) = 0$. Let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$ Define $F_i$ and $d_i$ as they are used in Eq. 2.

First note that since the parameters for Bernoulli variable are between 0 and 1 the log-likelihood in Eq. 1 is non-positive. Consequently, $q \mathopen {}\left( \cdot \right) \ge 0$. Moreover, $q \mathopen {}\left( G, T, \Lambda \right) = 0$ is possible only if $d_i = 0$ or $d_i = {\left| F_i\right| }$ for every i.

Let $S_i$ be the shell containing $v_0$. We claim that $X = S_1 \cup \cdots \cup S_{i - 1} = V'$.

Assume that $X \ne V'$. Let j be the largest index with $S_j \cap V' \ne \emptyset$. Let $v_y \in V' \cap S_j$. Note that $j \ge i$ as otherwise $X = V'$. Select $v_x \in V' \setminus \left\{ v_y\right\}$. Then $(v_x, v_y) \in F_j$ but $(v_y, v_0) \notin F_j$, and consequently $0< {\left| F_j\right| } < d_j$, which is a contradiction. Thus, $X = V'$.

Let L be the labels used in T. Since T has at most $k + 1$ leaves, ${\left| L\right| } \le k$. Also, $lab \mathopen {}\left( v_x\right) \cap L \ne \emptyset$ for $v_x \in V'$ as otherwise $v_x \notin X$ which is a contradiction. Consequently, the subset in ${\mathcal {A}}$ corresponding to L solves Cover.

Assume now there is a cover and let L be the corresponding set of labels. Construct a label tree T by iteratively replacing the right-most leaf with unused label directing the nodes having that label to the left. This will result in a tree that partitions $v_0$ to the right-most leaf and the remaining nodes to other leaves. Set the parameters $\Lambda$ to be 0 for the right-most leaf and 1 for the remaining leaves. Now $q \mathopen {}\left( G, T, \Lambda \right) = 0$, and since the score cannot be negative this is also an optimal score, proving the proposition. $\square$

Proof of Corollary 3.1

The proof of Proposition 3.1 shows that Cover has a solution if and only if $q \mathopen {}\left( T, G, \Lambda \right) = 0$, where T and $\Lambda$ are the optimal solutions.

Let $T'$ and $\Lambda '$ be an approximate solution with an approximation guarantee $\alpha$. We claim that $q \mathopen {}\left( T, G, \Lambda \right) = 0$ if and only if $q \mathopen {}\left( T', G, \Lambda '\right) = 0$, which proves the corollary.

If $q \mathopen {}\left( T, G, \Lambda \right) = 0$, then $q \mathopen {}\left( T', G, \Lambda '\right) \le \alpha q \mathopen {}\left( T, G, \Lambda \right) = 0$. On the other hand, if $q \mathopen {}\left( T', G, \Lambda '\right) = 0$, then due to optimality $q \mathopen {}\left( T, G, \Lambda \right) \le q \mathopen {}\left( T', G, \Lambda '\right) = 0$. $\square$

Proof of Proposition 3.2

Assume an instance of Cover: a universe $U = u_1, \ldots u_n$, a family of sets ${\mathcal {A}}$, and an integer k. Let us first construct the graph G. Define $r = 2(k + 1)(n + 1)^2$. Define a set of nodes $V = V_0, V_1, \ldots , V_n$, where for each $i = 1, \ldots , n$, a set $V_i$ consists of r nodes, each node corresponding to $u_i$. The set $V_0$ is an additional set of r nodes. Let us write $V' = V_1 \cup \cdots \cup V_n$.

We connect every node in $V'$ to each other. We leave the nodes in $V_0$ as singletons.

The labels $lab \mathopen {}\left( v\right)$ for each $v \in V_i$ correspond to the sets in ${\mathcal {A}}$ containing $u_i$. The nodes in $V_0$ have no labels.

Let T, $\Lambda$ be a solution for CTreeBIC. We claim that Cover has a solution iff

$$\begin{aligned} q_{ BIC } \mathopen {}\left( T, G, \Lambda \right) \le \sigma , \quad \text {where}\quad \sigma = \frac{k + 1}{2} \log {r(n + 1) \atopwithdelims ()2}. \end{aligned}$$

Assume that $q_{ BIC } \mathopen {}\left( T, G, \Lambda \right) \le \sigma$.

Let ${\mathcal {S}} = shells \mathopen {}\left( T, G\right)$. Define $F_i$ and $d_i$ as they are used in Eq. 2. Define $\Lambda '$ with $\lambda '_i = {\left| F_i\right| } / d_i$. Since $\Lambda '$ are optimal parameters we have $q \mathopen {}\left( T, G, \Lambda '\right) \le q \mathopen {}\left( T, G, \Lambda \right)$.⁵ Let $C_i = S_1 \cup \cdots \cup S_i$.

We claim that the last non-empty shell contains only $V_0$. Assume otherwise: there is an index i such that $V_0 \subseteq C_i$ and $V_j \subseteq S_i$ where $j > 0$.

Since there are ${r(n + 1) \atopwithdelims ()2}$ node pairs in G, we have

$$\begin{aligned} d_i \le {r(n + 1) \atopwithdelims ()2} < \frac{1}{2} r^2\quad (n + 1)^2 . \end{aligned}$$

Moreover, there are ${r \atopwithdelims ()2}$ edges between the r nodes in $V_j$. Consequently, ${\left| F_i\right| } \ge {r \atopwithdelims ()2} \ge r^2 / 4$, and

$$\begin{aligned} \lambda _i' = \frac{{\left| F_i\right| }}{d_i} > \frac{1}{2(n + 1)^2}. \end{aligned}$$

There are $r^2$ node pairs between $V_0$ and $V_j$. None of these node pairs are in $F_i$, and they are modeled with a probability of $1 - \lambda _i'$. We can now lower bound the score with

$$\begin{aligned} q \mathopen {}\left( T, G, \Lambda '\right)\ge & {} - r^2 \log \left( 1 - \lambda _i'\right)> -r^2 \log \left( 1 - \frac{1}{2(n + 1)^2}\right)> \frac{r^2}{2(n + 1)^2} \\= & {} (k + 1)r = \frac{k + 1}{2}(r + r)> \frac{k + 1}{2}(2\log (n + 1) + 2\log r) > \sigma , \end{aligned}$$

where we have used the fact that $x < -\log (1 - x)$ and that $r> 2 \log r > 2\log (n + 1)$.

This is a contradiction, so there is no index i. Hence, the set $V_0$ appears alone in one of the shells, say $S_j$, and $C_{j - 1} = V'$. Moreover, $\lambda _j = 0$ and $\lambda _i = 1$ for $i < j$, and consequently $q \mathopen {}\left( T, G, \Lambda \right) = 0$. Since $q_{ BIC } \mathopen {}\left( T, G, \Lambda \right) \le \sigma$, T has at most $k + 1$ leaves.

Let L be the labels used in T. Since T has at most $k + 1$ leaves, ${\left| L\right| } \le k$. Also, $lab \mathopen {}\left( v\right) \cap L \ne \emptyset$ for $v \in V'$, as otherwise $v \in S_j$ which is a contradiction. Consequently, the subset in ${\mathcal {A}}$ corresponding to L solves Cover.

Assume now there is a cover and let L be the corresponding set of labels. Construct a label tree T and $\Lambda$ in the same manner as in the proof of Proposition 3.1. Then immediately $q \mathopen {}\left( T, G, \Lambda \right) = 0$ and

$$\begin{aligned} q_{ BIC } \mathopen {}\left( T, G, \Lambda \right) = \frac{{\left| L\right| } + 1}{2}\log {r(n + 1) \atopwithdelims ()2} \le \sigma , \end{aligned}$$

completing the proof. $\square$

To prove Proposition 4.2 we need the following lemma.

Lemma A.1

Let T be a binary tree. Assume a positive number $c_\alpha$ for each node $\alpha$. Assume that for each non-leaf node $\alpha$ with children $\beta$ and $\gamma$, it holds that $c_\alpha \ge c_\beta + c_\gamma$; define $d_\alpha = \min (c_\beta , c_\gamma )$. Let r be the root of T. Then $\sum _\alpha d_\alpha \le c_r(1 + \log _2 c_r)$.

Proof

We will prove the lemma by induction over the number of nodes in T. The claim is trivial for a tree with a single non-leaf.

To prove the general claim, let $\beta$ and $\gamma$ be the children of r. Assume that $c_\beta \le c_\gamma$. Then $d_r = c_\beta \le c_r / 2$ and the induction assumption applied to the subtrees rooted at $\beta$ and $\gamma$ implies

$$\begin{aligned} \begin{aligned} \sum _\alpha d_\alpha&\le d_r + c_\beta (1 + \log _2 c_\beta ) + c_\gamma (1 + \log _2 c_\gamma ) = c_\beta (1 + \log _2 2c_\beta ) + c_\gamma (1 + \log _2 c_\gamma ) \\&\le c_\beta (1 + \log _2 c_r) + c_\gamma (1 + \log _2 c_r) \le c_r(1 + \log _2 c_r) . \end{aligned} \end{aligned}$$

The $c_\beta \ge c_\gamma$ case is similar, proving the claim. $\square$

Proof of Proposition 4.2

Assume that we are splitting a leaf $\alpha$ using label $\ell$ into new leaves $\beta$ and $\gamma$. Let $W = V[\alpha , \ell ]$. Let $x_\alpha = {\left| W\right| }$ be the number of nodes in W, and let $y_\alpha = {\left| E(W, V)\right| }$ be the number of edges with at least one endpoint in W. Let $F_\alpha$ be the cross-edges between $\beta$ and $\gamma$, and let $z_\alpha = \sum _{(u, v) \in F_\alpha } (1 + {\left| lab \mathopen {}\left( u\right) \right| } + {\left| lab \mathopen {}\left( v\right) \right| })$.

In order to prove the result, we claim that $\textsc {Split} (\alpha , \ell , b)$ requires $\mathcal {O} \mathopen {}\left( x_\alpha + y_\alpha + z_\alpha + \min (t[\beta ], t[\gamma ])\right)$ time.

We compute the leaf counters in $\mathcal {O} \mathopen {}\left( 1\right)$ time using Eqs. 4–5.

Assume that $b = 1$ (the case for $b = 0$ is similar). We can compute $V[\beta ]$ and $V[\gamma ]$ in $\mathcal {O} \mathopen {}\left( x_\alpha \right)$ time by first moving $V[\alpha ]$ to $V[\gamma ]$ and then moving the vertices in W from $V[\gamma ]$ to $V[\beta ]$ in $\mathcal {O} \mathopen {}\left( x_\alpha \right)$ time. The first move is done by changing references, so we only need constant time.

Next, we compute $t[\beta ]$ by iterating over E(W, V) in $\mathcal {O} \mathopen {}\left( y_\alpha \right)$ time. Since $t[\gamma ] = t[\alpha ] - t[\beta ] - \sum _{(u, v) \in F_\alpha } ({\left| lab \mathopen {}\left( u\right) \right| } + {\left| lab \mathopen {}\left( v\right) \right| })$, we can compute $t[\gamma ]$ in $\mathcal {O} \mathopen {}\left( y_\alpha \right)$ time.

If $t[\beta ] < t[\gamma ]$, we compute $V[\beta , \ell ']$ and $V[\gamma , \ell ']$ by moving $V[\alpha , \ell ']$ to $V[\gamma , \ell ']$ and then moving the nodes that are in $V[\beta ]$ from $V[\gamma , \ell ']$ to $V[\beta , \ell ']$. The counters are then computed by enumerating the edges in $E(V[\beta , \ell '], V)$. By going over all labels $\ell '$, we can show that we can compute the counters, as well as the constants C in Proposition 4.1, in $\mathcal {O} \mathopen {}\left( t[\beta ] + z_\alpha \right)$ time. If $t[\beta ] \ge t[\gamma ]$, then the needed time is $\mathcal {O} \mathopen {}\left( t[\gamma ] + z_\alpha \right)$.

Deleting the edges in $F_\alpha$ can be done in $\mathcal {O} \mathopen {}\left( y_\alpha \right)$ time. Thus, $\textsc {Split} (\alpha , \ell , b)$ requires $\mathcal {O} \mathopen {}\left( x_\alpha + y_\alpha + z_\alpha + \min (t[\beta ], t[\gamma ])\right)$ time.

Next we sum over all splits.

A label cannot occur twice along a path in a label tree. Thus, the node-label pairs when counting $x_\alpha$ can occur only in one $\alpha$. Thus, $\sum _{\alpha } x_\alpha \le R$. Similarly, $\sum _{\alpha } y_\alpha \le S$.

Edges in $F_\alpha$ are deleted when processing $\alpha$ and will not occur during other calls of Split. Thus, $\sum _\alpha z_\alpha \le m + S$.

Let r be the root of the label tree. Lemma A.1 states that

$$\begin{aligned} \sum _{\alpha } \min (t[\beta ], t[\gamma ]) \in \mathcal {O} \mathopen {}\left( t[r] \log t[r]\right) , \end{aligned}$$

where the sum is taken over non-leaves $\alpha$ with leaves $\beta$ and $\gamma$. Since $t[r] = S + R$, this completes the proof. $\square$

Proof of Proposition 5.3

The claim follows immediately since Pava matches the convex hull algorithm by Graham (1972). $\square$

Proof of Proposition 5.2

In order to find the best split for a current tree T, we need to enumerate over all leaf-label pairs. There are at most kL of such pairs. Moreover, given a leaf $\alpha$, we only need to consider the labels that occur in a node that are in $\alpha$. Since a node can be in only one leaf, there are at most R leaf-label pairs needed to test.

Each split increases the size of T, so we test only $\mathcal {O} \mathopen {}\left( k\right)$ trees, and testing each candidate needs $\mathcal {O} \mathopen {}\left( k\right)$ time, proving the result. $\square$

Proof of Proposition 5.4

The proof follows the proof of Proposition 5.2, except testing each candidate needs $\mathcal {O} \mathopen {}\left( \log ^2 k\right)$ time. $\square$