A Reduced Basis Method for Radiative Transfer Equation

Abstract

Linear kinetic transport equations play a critical role in optical tomography, radiative transfer and neutron transport. The fundamental difficulty hampering their efficient and accurate numerical resolution lies in the high dimensionality of the physical and velocity/angular variables and the fact that the problem is multiscale in nature. Leveraging the existence of a hidden low-rank structure hinted by the diffusive limit, in this work, we design and test the angular-space reduced order model for the linear radiative transfer equation, the first such effort based on the celebrated reduced basis method (RBM). Our method is built upon a high-fidelity solver employing the discrete ordinates method in the angular space, an asymptotic preserving upwind discontinuous Galerkin method for the physical space, and an efficient synthetic accelerated source iteration for the resulting linear system. Addressing the challenge of the parameter values (or angular directions) being coupled through an integration operator, the first novel ingredient of our method is an iterative procedure where the macroscopic density is constructed from the RBM snapshots, treated explicitly and allowing a transport sweep, and then updated afterwards. A greedy algorithm can then proceed to adaptively select the representative samples in the angular space and form a surrogate solution space. The second novelty is a least squares density reconstruction strategy, at each of the relevant physical locations, enabling the robust and accurate integration over an arbitrarily unstructured set of angular samples toward the macroscopic density. Numerical experiments indicate that our method is effective for computational cost reduction in a variety of regimes.

Appendices

Appendix

1.1 Appendix A RB Method with the Diffusion Synthetic Acceleration

In this work, we apply the S2SA to speed up the convergence of the source iteration when algebraically solving the upwind DG discretization. One main advantage of the S2SA is that the same kind of kinetic solver as the full order one is applied. Another type widely used synthetic acceleration is the diffusion synthetic acceleration (DSA) [2, 3, 47]. Instead of using a low order $S_N$ model for a kinetic problem to approximate the correction Eq. (2.10) for $\delta f^{k+1}$ first and then to compute $\rho ^{k,c}=\langle \delta f^{k+1}\rangle$, the DSA method works with a discrete diffusion approximation, that is “consistent” (see [2] for the definition of the consistency), to approximate $\rho ^{k,c}$ directly. It is known that the source iteration with “inconsistent” DSA may converge slowly or even diverge in some regimes [2]. Compared with a straightforward S2SA method, the DSA will involve fewer degrees of freedom. Next we will use the 1D model on the slab geometry as an example to present a DSA method that is consistent to the upwind DG discretization, and then demonstrate and compare the performance of the RB method with both synthetic acceleration strategies.

1.2 A Consistent DSA Method

For the 1D slab geometry with $X=[0,1]$, by using an ansatz $\delta f(x,v)=\rho ^{k,c}(x)+3v g(x)$ and taking the zeroth, first moments of the correction equation (2.10) in the angular variable, we obtain an approximated diffusion model

$$\begin{aligned} \underbrace{\langle v^2\rangle }_{=\frac{1}{3}}&\partial _x\;({\sigma _t}^{-1}\partial _x \rho ^{k,c})+\sigma _a \rho ^{k,c}=\sigma _s(\rho ^{k,*}-\rho ^k), \quad \text {on}\; X \end{aligned}$$

(A.1a)

or, equivalently, in its first order form,

$$\begin{aligned} \partial _x g + \sigma _a \rho ^{k,c} = \sigma _s(\rho ^{k,*}-\rho ^k),\quad \underbrace{\langle v^2\rangle }_{=\frac{1}{3}} \partial _x \rho ^{k,c}+\sigma _t g = 0. \end{aligned}$$

(A.2a)

They will be complemented by the boundary conditions,

$$\begin{aligned}&\langle v(\rho ^{k,c}+3vg) \rangle ^{+}=\frac{1}{4}(\rho ^{k,c}+2g)=\frac{1}{4}(\rho ^{k,c}-\frac{2}{3\sigma _t}\partial _x \rho ^{k,c}) =0,\quad \text {at}\; x=0, \end{aligned}$$

(A.3a)

$$\begin{aligned}&\langle v(\rho ^{k,c}+3vg) \rangle ^{-}=-\frac{1}{4}(\rho ^{k,c}-2g)=- \frac{1}{4}(\rho ^{k,c}+\frac{2}{3\sigma _t}\partial _x \rho ^{k,c})=0,\quad \text {at}\; x=1. \end{aligned}$$

(A.3b)

Here $\langle \eta \rangle ^+=\frac{1}{2}\int _{v>0} \eta (v)dv$, $\langle \eta \rangle ^-=\frac{1}{2}\int _{v<0} \eta (v) dv$.

Let $\{T_i=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}], \; i=1\dots , N_x\}$ be a partion of the domain $X=[0,1]$, we then discretize (A.2) with a DG method: we seek $\rho ^{k,c}_h, g_h\in U_h^K$, such that $\forall \phi _h, \psi _h\in U_h^K$, $\forall i=1,\dots , N_x$,

$$\begin{aligned}&-\int _{I_i} g_h \partial _x \phi _h dx+ (\widehat{g_h} \phi ^-_{h})_{i+\frac{1}{2}}-(\widehat{g_h} \phi ^+_{h})_{i-\frac{1}{2}}+\int _{I_i} \sigma _a \rho _h^{k,c} \phi _h dx = \int _{I_i} \sigma _s(\rho ^{k,*}-\rho ^k) \phi _h dx, \end{aligned}$$

(A.4a)

$$\begin{aligned}&\frac{1}{3} \left( -\int _{I_i} \rho _h^{k,c} \partial _x \psi _h dx + (\widehat{\rho _h^{k,c}} \psi ^-_{h})_{i+\frac{1}{2}}-(\widehat{\rho _h^{k,c}} \psi ^+_{h})_{i-\frac{1}{2}}\right) +\int _{I_i} \sigma _t g_h \psi _h dx= 0. \end{aligned}$$

(A.4b)

The key to make the method (A.4) consistent to the upwind DG method for the transport sweep step lies in the numerical fluxes $(\widehat{g_h})_{i+\frac{1}{2}}$ and $(\widehat{\rho _h^{k,c}})_{i+\frac{1}{2}}$, that shall be based on the upwind flux for $\delta {f}$.² With this in mind, we take

$$\begin{aligned} (\widehat{g_h})_{i+\frac{1}{2}}&= \langle v\widehat{\delta f}^{\text {upwind}}\rangle _{i+\frac{1}{2}} = \langle v (\rho _h^{k,c}+3v g_h)\rangle ^+(x_{i+\frac{1}{2}}^-) + \langle v (\rho _h^{k,c}+3v g_h)\rangle ^-(x_{i+\frac{1}{2}}^+) \nonumber \\&=\{g_h\}_{i+\frac{1}{2}}-\frac{1}{4}[\rho _h^{k,c}]_{i+\frac{1}{2}}, \end{aligned}$$

(A.5a)

$$\begin{aligned} \frac{1}{3}(\widehat{\rho _h^{k,c}})_{i+\frac{1}{2}}&= \langle v^2\widehat{\delta f}^{\text {upwind}}\rangle _{i+\frac{1}{2}} =\langle v^2 (\rho _h^{k,c}+3v g_h)\rangle ^+(x_{i+\frac{1}{2}}^-) + \langle v^2 (\rho _h^{k,c}+3v g_h)\rangle ^-(x_{i+\frac{1}{2}}^+)\nonumber \\&= \frac{1}{3}\left( \{\rho _h^{k,c}\}_{i+\frac{1}{2}}-\frac{9}{8}[g_h]_{i+\frac{1}{2}}\right) . \end{aligned}$$

(A.5b)

Here $u(x_{i+\frac{1}{2}}^-)=u_{i+\frac{1}{2}}^-$ (resp. $u(x_{i+\frac{1}{2}}^+)=u_{i+\frac{1}{2}}^+$) stands for the left (resp. right) limit of u(x) at the cell interface $x_{i+\frac{1}{2}}$. And $\{u\}_{i+\frac{1}{2}}=\frac{1}{2}(u_{i+\frac{1}{2}}^++u_{i+\frac{1}{2}}^-), \;[u]_{i+\frac{1}{2}}=u_{i+\frac{1}{2}}^+-u_{i+\frac{1}{2}}^-$. At boundaries, the numerical fluxes are set as (A.5) with $\langle v^k (\rho _h^{k,c}+3v g_h)\rangle ^+(x_{\frac{1}{2}}^-)=0$, $\langle v^k (\rho _h^{k,c}+3v g_h)\rangle ^-(x_{N_x+\frac{1}{2}}^+)=0, \; k=1, 2$. In actual simulation, we eliminate $g_h$ in (A.4) at the algebraic level, leading to a smaller linear system for $\rho _h^{k,c}$ only, that is given in its matrix-vector form as follows,

$$\begin{aligned} \left( {\varvec{\Sigma }} _a -\frac{1}{4}\mathbf {D}_\mathrm{jump} -\frac{1}{3}\mathbf {D}_c({\varvec{\Sigma }} _t-\frac{3}{8}\mathbf {D}_{\text {jump}})^{-1}\mathbf {D}_c {\varvec{\rho }} ^{k,c}\right) {\varvec{\rho }} ^{k,c}={\varvec{\Sigma }} _S({\varvec{\rho }} ^{k,*}-{\varvec{\rho }} ^{k}), \end{aligned}$$

(A.6)

with $\mathbf {D}_c= \frac{1}{2}\left( \mathbf {D}^++\mathbf {D}^-\right)$, $\mathbf {D}_\text {jump} =\mathbf {D}^+-\mathbf {D}^-$, where

$$\begin{aligned} (\mathbf {D}^+)_{kl}&=-\sum _{i=1}^{N_x}\int _{T_i} \partial _x\phi _k(x) \phi _l(x) dx +\sum _{i=1}^{N_x-1}\phi _l(x^+_{i+\frac{1}{2}}) \phi _k(x^-_{i+\frac{1}{2}})-\sum _{i=1}^{N_x}\phi _l(x^+_{i-\frac{1}{2}}) \phi _k(x^+_{i-\frac{1}{2}}), \end{aligned}$$

(A.7a)

$$\begin{aligned} (\mathbf {D}^-)_{kl}&=-\sum _{i=1}^{N_x}\int _{T_i} \partial _x\phi _k(x) \phi _l(x) dx +\sum _{j=1}^{N_x}\phi _l(x^-_{i+\frac{1}{2}}) \phi _k(x^-_{i+\frac{1}{2}})-\sum _{i=2}^{N_x}\phi _l(x^-_{i-\frac{1}{2}}) \phi _k(x^+_{i-\frac{1}{2}}). \end{aligned}$$

(A.7b)

One example of “partially consistent” DSA methods is to use central fluxes as in [3]. Partially consistent DSA methods may result in slower convergence.

Table 4 Errors of the RB Method with the DSA and S2SA for 1D examples

Table 5 Relative computational time for 1D examples: (time with S2SA)/(time with DSA)

1.3 Comparison of the RB Method with the S2SA and the DSA

For the 1D examples, we replace the S2SA with the DSA in the source iteration, and compare the performance of the overall RB algorithm with the two different acceleration strategies. The stopping criteria is $r_\mathrm{tol}\le 10^{-4}$. For all examples, the full order solvers with the S2SA and the DSA in the source iteration always converge to the same result. The errors for the RB method with the S2SA and the DSA are reported in Table 4, and the relative computational time, defined as (time with S2SA)/(time with DSA), is summarized in Table 5. The full order model with the DSA is slightly more efficient in the diffusive regime, and it is comparable with the S2SA method in other regimes. For the diffusive and intermediate regimes (Examples 1-2), the RB method with the DSA is more efficient in both offline, but the errors are relatively larger. The angular samples picked by the greedy algorithm in the RB method are the same for both the DSA and S2SA, and hence the online computational costs of the RB method with the DSA and the S2SA are close to each other. For Example 4 (two-material problem) and Example 5 (transport regime), the RB method with the DSA fails to converge to the correct solution. It is known that reduced order methods can be more sensitive to the choice of preconditioners compared with full order solvers [12, 45, 48]. In summary, when combined with our RB method, the S2SA is more robust with various regimes and slightly more accurate. The RB method with the DSA is slightly more efficient if it converges, but it may fail to converge for problems with transport-dominant (sub)regions.

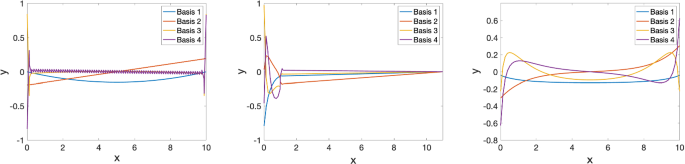
Appendix B Plots of Selected RB Functions

We here present some selected RB functions generated by the proposed algorithm. In Fig.  9, we plot the first four RB functions (after the SVD orthogonalization step) for 1D Examples 1, 4, 5 from Sect . 4.1. The most interesting example is the two-material problem in Example 4. Particularly, the presence of a material interface is captured by most RB functions. Moreover, all four RB functions behave fairly differently in the left subregion where the problem is transport dominant.

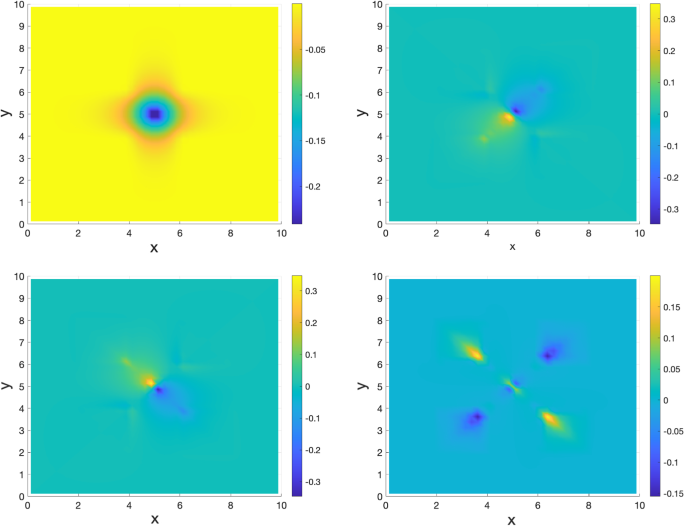
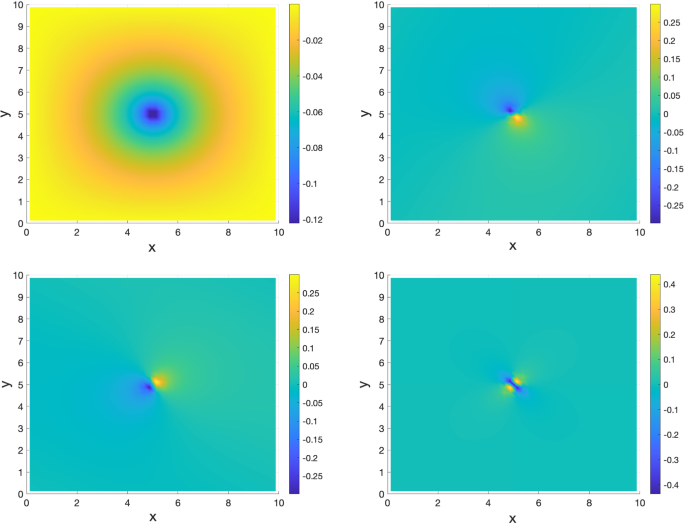
In Figs.  10, 11, we present the first four reduced basis functions of 2D Examples 1 and 2 from Sect.  4.2, again after the SVD orthogonalization step. The leading RB function captures the overall configuration of the density as in Fig.  7, while the remaining RB functions encode various multipole structures.

Fig. 9

First four reduced basis functions for 1D Examples 1 (left), 4 (middle), 5 (right)

Fig. 10

First four reduced basis functions, ordered from left to right and from top to bottom, for 2D Example 1 (checkerboard problem)

Fig. 11

First four reduced basis, ordered from left to right and from top to bottom, for 2D Example 2 (scattering dominant)