1 Introduction

We are concerned with the problem of learning with redundant models (or hypothesis classes). This setting is not uncommon in real-world machine learning and data mining problems. It is because the amount of available data is sometimes limited owing to the cost of data collection (e.g., in biomedical data analyses), while researchers can come up with an unbounded number of models for explaining the data that may contain a number of irrelevant features. For example, in sparse regression, one may consider a number of features that are much larger than that in the data, assuming that useful features are actually scarce (Rish and Grabarnik 2014). Another example is statistical conditional-dependency estimation, in which the number of the parameters to estimate is quadratic as compared to the number of random variables, while the number of nonzero coefficients are often expected to be sub-quadratic.

In the context of such a redundant model, there is a danger of overfitting, a situation in which the model fits the present data excessively well but does not generalize well. To address this, we introduce regularization and reduce the complexity of the models by taking the regularized empirical risk minimization (RERM) approach (Shalev-Shwartz and Ben-David 2014). In RERM, we minimize the sum of the loss and penalty functions to estimate parameters. However, the choice of the penalty function should be made cautiously as it controls the bias-variance trade-off of the estimates, and hence has a considerable effect on the generalization capability.

In conventional methods for selecting such hyperparameters, a two-step approach is usually followed. First, a candidate set of penalty functions is configured (possibly randomly). Then, a penalty selection criterion is computed for each candidate and the best one is chosen. Note that this method can be applied to any penalty selection criteria. Sophisticated approaches like Bayesian optimization (Mockus et al. 2013) and gradient-based methods (Larsen et al. 1996) also tend to leave the criterion as a black-box. Although leaving it as a black-box is advantageous in that it works for a wide range of penalty selection criteria, a drawback is that the full information of each specific criterion cannot be utilized. Hence, the computational costs can be unnecessarily large if the design space of the penalty function is high-dimensional.

In this paper, we propose a novel penalty selection method that utilizes information about the objective criterion efficiently on the basis of the minimum description length (MDL) principle (Rissanen 1978). We especially focus on the luckiness normalized maximum likelihood (LNML) code length (Grünwald 2007) because the LNML code length measures the complexity of regularized models without making any assumptions on the form of the penalty functions. Moreover, it places a tight bound on the generalization error (Grünwald and Mehta 2017). However, the actual use of LNML on large models is limited so far. This is owing to the following two issues.

  1. (I1)

    LNML contains a normalizing constant that is hard to compute especially for large models. This tends to make the evaluation of the code length intractable.

  2. (I2)

    Since the normalizing term is defined as a non-closed form of the penalty function, efficient optimization of LNML is non-trivial.

Next, solutions are described for the above issues. First, we derive an upper bound of the LNML code length, namely uLNML. The key idea is that, the normalizing constant of LNML, which is not analytic in general, is characterized by the smoothness of loss functions, which can often be upper-bounded by an analytic quantity. As such, uLNML exploits the smoothness information of the loss and penalty functions to approximate LNML with much smaller computational costs, which solves issue (I1). Moreover, within the framework of the concave–convex procedure (CCCP) (Yuille and Rangarajan 2003), we propose an efficient algorithm for finding a local minimima of uLNML, i.e., finding a good penalty function in terms of LNML. This algorithm only adds an extra analytic step to the iteration of the original algorithm for the RERM problem, regardless of the dimensionality of the penalty design. Thus, issue (I2) is addressed. We put together these two methods and propose a novel method of penalty selection named MDL regularization selection (MDL-RS).

We also validate the proposed method from theoretical and empirical perspectives. Specifically, as our method relies on the approximation of uLNML and the CCCP algorithm on uLNML, the following questions arise.

  1. (Q1)

    How well does uLNML approximate LNML?

  2. (Q2)

    Does the CCCP algorithm on uLNML perform well with respect to generalization as compared to the other methods for penalty selection?

For answering Question (Q1), we show that the gap between uLNML and LNML is uniformly bounded under smoothness and convexity conditions. As for Question (Q2), from our experiments on example models involving both synthetic and benchmark datasets, we found that MDL-RS is at least comparable to the other methods and even outperforms them when models are highly redundant as we expected. Therefore, the answer is affirmative.

The rest of the paper is organized as follows. In Sect. 2, we introduce a novel penalty selection criteria, uLNML, with uniform gap guarantees. Section 3 demonstrates some examples of the calculation of uLNML. Section 4 provides the minimization algorithm of uLNML and discusses its convergence property. Conventional methods for penalty selection are reviewed in Sect. 5. Experimental results are shown in Sect. 6. Finally, Sect. 7 concludes the paper and discusses the future work.

2 Method: analytic upper bound of LNMLs

In this section, we first briefly review the definition of RERM and the notion of penalty selection. Then, we introduce the LNML code length. Finally, as our main result, we show an upper bound of LNML (uLNML) with approximation error analyses and several examples.

2.1 Preliminary: regularized empirical risk minimization (RERM)

Let \(f_{X}:\mathbb {R}^p\rightarrow \overline{\mathbb {R}}(=\mathbb {R}\cup \left\{ \infty \right\} )\) be an extended-value loss function of parameter \(\theta \in \mathbb {R}^p\) with respect to data \(X=(x_1,\ldots ,x_n)\in {\mathcal {X}^n}\). We assume \(f_X(\theta )\) is a log-loss (but not limited to i.i.d. loss), i.e., it is normalized with respect to some base measure \(\nu \) over \({\mathcal {X}^n}\), where \(\int _{{\mathcal {X}^n}} \exp \left\{ -f_X(\theta )\right\} d\nu (X)= 1\) for all \(\theta \) in some closed subset \(\varOmega _0\subset \mathbb {R}^p\). Here, \(x_i\) can be a pair of a datum and label \((x_i, y_i)\) in the case of supervised learning. We drop the subscript X and just write \(f(\theta )=f_X(\theta )\) if there is no confusion.

The regularized empirical risk minimization (RERM) with convex domain \(\varOmega \subset \varOmega _0\) is defined as the following minimization

$$\begin{aligned} \mathrm {RERM}(\lambda ):\qquad \mathop {\mathrm {minimize}}\ f_X(\theta ) + g(\theta , \lambda )\quad \mathrm {s.t.}\quad \theta \in \varOmega , \end{aligned}$$
(1)

where \(g:\mathbb {R}^p\times \mathbb {A}\rightarrow \overline{\mathbb {R}}\) denotes the penalty function and \(\lambda \in \mathbb {A}\subset \mathbb {R}^d\) is the hyperparameter that parametrizes the shape of penalty on \(\theta \). We assume that at least one minimizer always exists in \(\varOmega \), and denote it as \(\hat{\theta }(X,\lambda )\). Here, we focus on a special case of RERM in which the penalty is linear to \(\lambda \),

$$\begin{aligned} g(\theta ,\lambda ) = \sum _{j=1}^d \lambda _j g_j(\theta ),\quad \lambda _j\ge 0\quad (j=1,\ldots , d), \end{aligned}$$
(2)

and \(\mathbb {A}\subset \mathbb {R}^d_+\) is a convex set of positive vectors. Finally, let us define \(D(\lambda )\overset{\mathrm{def}}{=}\{X\in {\mathcal {X}^n}\mid \hat{\theta }(X, \lambda )\in { \varOmega }^{\mathrm {o}}\}\), where \({ \varOmega }^{\mathrm {o}}\) is the interior of the set \(\varOmega \). Then, we assume that the following regularity condition holds:

Assumption 1

(Regular penalty)\(D(\lambda )\) is monotone increasing, i.e.,

$$\begin{aligned} \lambda \le \lambda '\Rightarrow D(\lambda ) \subset D(\lambda '), \end{aligned}$$

or equivalently,

$$\begin{aligned} \lambda \le \lambda ',\; \hat{\theta }(X,\lambda )\in { \varOmega }^{\mathrm {o}}\Rightarrow \hat{\theta }(X,\lambda ')\in { \varOmega }^{\mathrm {o}}. \end{aligned}$$

Regularization is beneficial from two perspectives. It improves the condition number of the optimization problem, and hence enhances the numerical stability of the estimates. It also prevents the estimate from overfitting to the training data X, and hence reduces generalization error.

However, these benefits come with an appropriate penalization. If the penalty is too large, the estimate will be biased. If the penalty is too small, the regularization no longer takes effect and the estimate is likely to overfit. Therefore, we are motivated to select a good \(\lambda \) as a function of data X.

2.2 Luckiness normalized maximum likelihood (LNML)

In order to select an appropriate hyperparameter \(\lambda \), we introduce the luckiness normalized maximum likelihood (LNML) code length as a criterion for the penalty selection. The LNML code length associated with \(\mathrm {RERM}(\lambda )\) is given by

$$\begin{aligned} \mathcal {L}(X\mid \lambda )&\overset{\mathrm{def}}{=}\min _{\theta \in \varOmega } f_X(\theta ) + g(\theta , \lambda ) + \log Z(\lambda ), \end{aligned}$$
(3)

where \(Z(\lambda )\overset{\mathrm{def}}{=}\int \max _{\theta \in \varOmega } \exp \left\{ -f_X(\theta )-g(\theta ,\lambda )\right\} d\nu (X)\) is the normalizing factor of LNML.

Note that LNML is originaly derived by generalization of the Shtarkov’s minimax coding strategy (Shtar’kov 1987; Grünwald 2007). The normalizing factor \(Z(\lambda )\) can be seen as a penalization of the complexity of \(\mathrm {RERM}(\lambda )\). It quantifies how much \(\mathrm {RERM}(\lambda )\) will overfit to random data. If the penalty g is small such that the minimum in (1) always takes a low value for all \(X\in {\mathcal {X}^n}\), \(Z(\lambda )\) becomes large. Specifically, any constant shift on the RERM objective, which does not change the RERM estimator \(\hat{\theta }\), does not change LNML since \(Z(\lambda )\) cancels it out. Moreover, recent advances in the analysis of LNML show that it bounds the generalization error of \(\hat{\theta }(X,\lambda )\) (Grünwald and Mehta 2017). Thus, our primary goal is to minimize the LNML code length (3).

2.3 Upper bound of LNML (uLNML)

The direct computation of the normalizing factor \(Z(\lambda )\) is often impossible because it requires integration of the RERM objective (1) over all possible data. To avoid the computational difficulty, we introduce an upper bound of \(Z(\lambda )\) that is analytic with respect to \(\lambda \). Then, adding the upper bound to the RERM objective, we have an upper bound of the LNML code length itself.

To derive the bound, let us define the following \({\overline{H}}\)-upper smoothness condition.

Definition 1

(\({\overline{H}}\)-upper smoothness) Let \({\overline{H}}\in \mathbb {S}_{++}^p\subset \mathbb {R}^{p\times p}\) be a symmetric positive definite matrix. A function \(f:\mathbb {R}^p\rightarrow \overline{\mathbb {R}}\) is called \({\overline{H}}\)-upper smooth, or \(({\overline{H}}, c, r)\)-upper smooth to avoid any ambiguity, if there exists a constant \(c\ge 0\), vector-valued function \(\xi :\mathbb {R}^p\rightarrow \mathbb {R}^p\), and monotone increasing function \(r:\mathbb {R}\rightarrow \overline{\mathbb {R}}_+\) such that

$$\begin{aligned} f(\psi )-f(\theta )\le c + \left\langle \xi (\theta ),\psi -\theta \right\rangle + \frac{1}{2}\left\| \psi -\theta \right\| _{{\overline{H}}}^2 + r(\left\| \theta -\psi \right\| ^2),\quad \forall \psi \in \mathbb {R}^p, \forall \theta \in \varOmega , \end{aligned}$$

where \(\left\| \psi -\theta \right\| _{{\overline{H}}}^2\overset{\mathrm{def}}{=}\left( \psi -\theta \right) ^\top {\overline{H}}(\psi -\theta )\) and \(r\left( t^2\right) =o\left( t^2\right) \).

A few remarks follow: The \({\overline{H}}\)-upper smoothness is a condition that is weaker than that of standard smoothness. In particular, \(\rho \)-smoothness implies \(\rho I_p\)-upper smoothness, and all the bounded functions are upper smooth with their respective triples \(({\overline{H}}, c, r)\). Moreover, the function r only describes the behavior of the function outside of \(\varOmega \). Thus, if the penalty \(g_j(\theta )\) is upper smooth, we can take the corresponding r zero without changing the solution of RERM.

Now, assume that \(f_X\) and \(g_j~(j=1,\ldots ,d)\) are upper-smooth:

Assumption 2

(Upper-smooth objective) Both of the following equivalent conditions are satisfied:

(i):

\(f_X\) is \(({\overline{H}}_0, c_0, r)\)-upper smooth for all \(X\in {\mathcal {X}^n}\) and \(g_j\) is \(({\overline{H}}_j, c_j, 0)\)-upper smooth (\(j=1,\ldots ,d\)).

(ii):

\(f_X(\cdot )+g(\cdot ,\lambda )\) is \(({\overline{H}}(\lambda ), c(\lambda ), r)\)-upper smooth for all \(X\in {\mathcal {X}^n}\) and all \(\lambda \ge \mathbf {0}\), where \({\overline{H}}(\lambda )\overset{\mathrm{def}}{=}{\overline{H}}_0+\sum _{j=1}^d\lambda _j {\overline{H}}_j\) and \(c(\lambda )\overset{\mathrm{def}}{=}c_0+\sum _{j=1}^d\lambda _j c_j\).

Then, the following theorem states that the upper bound depends on \(f_X\) and g only through their smoothness.

Theorem 1

(Upper bound of \(Z(\lambda )\)) Suppose that Assumption 2 holds. Let \(R(H;U) = \mathbb {E}_{z\sim \mathcal {N}_p[\mathbf {0}, H^{-1}]} \left[ \mathbb {1}_{U}(z) \exp \left\{ -r\left( \left\| z\right\| ^2\right) \right\} \right] \). Then, for all the symmetric neighbors of the origin \(U\subset \mathbb {R}^p\) satisfying \(\varOmega +U\subset \varOmega _0\), we have

$$\begin{aligned} Z(\lambda ) \le \bar{Z}(\lambda ) \overset{\mathrm{def}}{=}\frac{1}{R\left( {\overline{H}}_0;U\right) } \frac{e^{c(\lambda )}\det {{\overline{H}}(\lambda )}^{\frac{1}{2}}}{\sqrt{2\pi }^p} \int _{\varOmega + U} e^{-g(\theta , \lambda )} d\theta . \end{aligned}$$
(4)

Proof

Let \(q_\lambda (X)\overset{\mathrm{def}}{=}\int _{\varOmega +U} \exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\theta \). First, by Hölder’s inequality, we have

$$\begin{aligned} Z(\lambda )&= \int _{\mathcal {X}^n}\max _{\theta \in \varOmega }\exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\nu (X) \\ {}&\le \left\| \frac{\max _{\theta \in \varOmega } \exp \left\{ -f_{\cdot }(\theta )-g(\theta , \lambda )\right\} }{q_\lambda (\cdot )}\right\| _\infty \left\| q_\lambda (\cdot )\right\| _{L^1(\nu )} \\ {}&= \sup _{X\in {\mathcal {X}^n}}\max _{\theta \in \varOmega } \underbrace{\frac{\exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} }{q_\lambda (X)}}_{A} \underbrace{\int _{\mathcal {X}^n}q_\lambda (X)d\nu (X)}_{B}, \end{aligned}$$

where \(\left\| \cdot \right\| _\infty \) denotes the uniform norm and \(\left\| \cdot \right\| _{L^1(\nu )}\) denotes the \(L^1\)-norm with respect to measure \(\nu \). Then, we will bound \(A\) and \(B\) in the right-hand side, respectively. Since we assume that \(f_X(\theta )\) is a logarithmic loss if \(\theta \in \varOmega _0\), the second factor is simply evaluated using Fubini’s theorem,

$$ \begin{aligned} B&=\iint _{(\varOmega +U)\times {\mathcal {X}^n}} \exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\theta d\nu (X) \& = \int _{\varOmega +U} e^{-g(\theta , \lambda )}d\theta . \end{aligned}$$

On the other hand, by \({\overline{H}}(\lambda )\)-upper smoothness of \(f(\theta ) + g(\theta , \lambda )\), we have

$$\begin{aligned} A^{-1}&= q_\lambda (X)\exp \left\{ f_X(\theta )+g(\theta )\right\} \\&=\int _{\varOmega +U} \exp \left\{ f_X(\theta ) + g(\theta , \lambda )- f_X(\psi ) - g(\psi , \lambda )\right\} d\psi \\&\ge \int _{\varOmega +U} \exp \left\{ -c(\lambda ) - \left\langle \xi (\theta ),\psi -\theta \right\rangle - \frac{1}{2} \left\| \psi - \theta \right\| _{{\overline{H}}(\lambda )}^2-r(\left\| \psi -\theta \right\| ^2)\right\} d\psi \\&\ge e^{-c(\lambda )}\int _{U} \exp \left\{ -\left\langle \xi (\theta ),z \right\rangle - \frac{1}{2} \left\| z\right\| _{{\overline{H}}(\lambda )}^2-r(\left\| z\right\| ^2)\right\} dz\\&\ge e^{-c(\lambda )}\int _{U} \exp \left\{ - \frac{1}{2} \left\| z\right\| _{{\overline{H}}(\lambda )}^2-r(\left\| z\right\| ^2)\right\} dz\\&= e^{-c(\lambda )}\frac{\sqrt{2\pi }^p}{\det {\overline{H}}(\lambda ) ^{\frac{1}{2}}} R({\overline{H}}(\lambda );U)\\&\ge e^{-c(\lambda )}\frac{\sqrt{2\pi }^p}{\det {\overline{H}}(\lambda ) ^{\frac{1}{2}}} R({\overline{H}}_0;U). \end{aligned}$$

This concludes the proof. \(\square \)

The upper bound in Theorem 1 can be easily computed by ignoring the constant factor \(R({\overline{H}}_0, U)^{-1}\) given the upper smoothness of \(f_X\) and \(g(\cdot , \lambda )\). In particular, the integral \(\int _{\varOmega +U} e^{-g(\theta , \lambda )}d\theta \) can be evaluated in a closed form if one chooses a suitable class of penalty functions with a suitable neighbor U (e.g., quadratic penalty functions with \(U=\mathbb {R}^p\)). Therefore, we adopt this upper bound as an alternative of the LNML code length, namely uLNML,

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )&\overset{\mathrm{def}}{=}\min _{\theta \in \varOmega } f_X(\theta )+g(\theta ,\lambda ) + \log \bar{Z}(\lambda ), \end{aligned}$$
(5)

where \(\bar{Z}(\lambda )\) is defined in Theorem 1. Note that the symmetric set U should be fixed beforehand. In practice, we recommend just taking \(U=\mathbb {R}^p\) because uLNML with \(U=\mathbb {R}^p\) bounds uLNMLs with \(U\ne \mathbb {R}^p\) and then we have

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )&=\min _{\theta \in \varOmega } f_X(\theta )+g(\theta ,\lambda ) +c(\lambda ) + \frac{1}{2} \log \det {\overline{H}}(\lambda ) +\log \int _{\mathbb {R}^p} e^{-g(\psi ,\lambda )}d\psi + \mathrm {const.} \end{aligned}$$

However, for the sake of the later analysis, we leave U to be arbitrary.

We present two useful specializations of uLNML with respect to the penalty function \(g(\theta , \lambda )\). One is the Tikhonov regularization, known as \(\ell 2\)-regularization.

Corollary 1

(Bound for Tikhonov regularization) Suppose that Assumption 2 holds with \(f_X\). Suppose that \(g(\theta , \lambda )=\frac{1}{2} \sum _{j=1}^p \lambda _j \theta _j^2\) where \(\lambda _j> 0\) for all \(1\le j\le p\). Then, we have

$$\begin{aligned} Z(\lambda ) \le \frac{e^{c_0}}{R({\overline{H}}_0;\mathbb {R}^p)} \sqrt{\frac{\det ({\overline{H}}_0+\mathop {\mathrm {diag}}\lambda )}{\det \mathop {\mathrm {diag}}\lambda }}. \end{aligned}$$

Proof

The claim follows from setting \(U=\mathbb {R}^p\) in Theorem 1 and the fact that \(g(\cdot , \lambda )\) is \((\mathop {\mathrm {diag}}\lambda , 0, 0)\)-upper smooth. \(\square \)

The other one is that of lasso (Tibshirani 1996), known as \(\ell 1\)-regularization. It is useful if one needs sparse estimates \(\hat{\theta }(X,\lambda )\).

Corollary 2

(Bound for lasso) Suppose that Assumption 2 holds with \(f_X\). Suppose that \(g(\theta , \lambda )=\sum _{j=1}^p \lambda _j \left| \theta _j\right| \), where \(\lambda _j > 0\) for all \(1\le j\le p\). Then, we have

$$\begin{aligned} Z(\lambda ) \le \frac{e^{c_0}}{R({\overline{H}}_0;\mathbb {R}^p)}\sqrt{\frac{e}{2\pi }}^p \sqrt{\frac{\det ({\overline{H}}_0+(\mathop {\mathrm {diag}}\lambda )^2)}{\det (\mathop {\mathrm {diag}}\lambda )^2 }}. \end{aligned}$$

Proof

As in the proof of Corollary 1, it follows from Theorem 1 and the fact that \(g(\cdot , \lambda )\) is \(((\mathop {\mathrm {diag}}\lambda )^2, 1/2, 0)\)-upper smooth. \(\square \)

Finally, we present a useful extension for RERMs with Tikhonov regularization, which contains the inverse temperature parameter \(\beta \in [a, b]\ (0<a\le b)\) as a part of the parameter:

$$\begin{aligned} f_X(\beta , \theta )&=\beta \tilde{f}_X(\theta ) + \log C(\beta ), \end{aligned}$$
(6)
$$\begin{aligned} g(\beta , \theta , \lambda )&=\beta \tilde{g}(\theta , \lambda )=\beta \sum _{j=1}^d \frac{\lambda _j}{2} \theta _j^2, \end{aligned}$$
(7)

where \(C(\beta )\overset{\mathrm{def}}{=}\int e^{-\beta \tilde{f}_X(\theta )}d\nu (X)<\infty \) is the normalizing constant of the loss function. Here, we assume that \(C(\beta )\) is independent of the non-temperature parameter \(\theta \). Interestingly, the uLNML of variable temperature models (6), (7) coincides with that of the fixed temperature models given in Corollary 1 except with a constant.

Corollary 3

(Bound for variable temperature model) Let \((\beta , \theta )\in [a, b]\times \varOmega \) be the parameter of the model (6). Suppose that \(\tilde{f}_X(\theta )\) is \(({\overline{H}}_0, c_0, r)\)-upper smooth for all \(X\in {\mathcal {X}^n}\).

Then, there exists a constant \(C_{[a, b]}\) such that

$$\begin{aligned} Z(\lambda )\le \frac{C_{a,b}\; e^{(b+a/2)c_0}}{R(\frac{a}{2}{\overline{H}}_0;\mathbb {R}^p)} \sqrt{\frac{\det \left( {\overline{H}}_0 + \mathop {\mathrm {diag}}\lambda \right) }{\det \mathop {\mathrm {diag}}\lambda }}. \end{aligned}$$

Proof

Let \(\tilde{F}_X(\lambda )=\min _{\theta \in \varOmega } \tilde{f}_X(\theta )+\tilde{g}(\theta , \lambda )\). Let \(W=[a/2, b+a/2]\) and \(\tilde{q}_\lambda (X)=\int _W \exp \left\{ -\beta \tilde{F}_X(\lambda )-\log C(\beta )\right\} d\beta \). Note that \(\log C(\beta )\) is continuous and hence bounded over W, which implies that it is upper smooth. Let \((h_\beta , c_\beta , r_\beta )\) be the upper smoothness of \(\log C(\beta )\) over W. Then, using the same techniques as in Theorem 1, we have

$$\begin{aligned} Z(\lambda )&=\int \max _{\beta \in [a, b],\ \theta \in \varOmega } \exp \left\{ -\beta \left[ \tilde{f}_X(\theta )-\tilde{g}(\theta , \lambda )\right] -\log C(\beta )\right\} d\nu (X)\\&\le \max _{\beta \in [a, b]} \sup _{X\in {\mathcal {X}^n}} \exp \left\{ -\beta \tilde{F}_X(\lambda )-\log C(\beta )-\log \tilde{q}_\lambda (X)\right\} \int \tilde{q}_\lambda (X) d\nu (X)\\&\le C_{a,b} \int _W d\beta \int \max _{\theta \in \varOmega }\exp \left\{ -\beta \tilde{f}_X(\theta )-\beta \tilde{g}(\theta , \lambda )-\log C(\beta ) \right\} d\nu (X)\\&\le C_{a,b} \int _{W} d\beta \frac{e^{\beta c_0}}{R(\beta {\overline{H}}_0;\mathbb {R}^p)}\sqrt{\frac{\det \beta \left( {\overline{H}}_0 + \mathop {\mathrm {diag}}\lambda \right) }{\det \beta \mathop {\mathrm {diag}}\lambda }}\\&= \frac{C_{a,b}\;e^{(b+a/2) c_0}}{R(\frac{a}{2} {\overline{H}}_0;\mathbb {R}^p)} \sqrt{\frac{\det \left( {\overline{H}}_0 + \mathop {\mathrm {diag}}\lambda \right) }{\det \mathop {\mathrm {diag}}\lambda }}, \end{aligned}$$

where \(C_{a,b}\overset{\mathrm{def}}{=}\frac{e^{c_\beta }}{R_\beta (h_\beta ;[-a/2,a/2])} \sqrt{\frac{h_\beta }{2\pi }}\). \(\square \)

2.4 Gap between LNML and uLNML

In this section, we evaluate the tightness of uLNML. To this end, we now bound LNML from below. The lower bound is characterized with strong convexity of \(f_X\) and \(g(\cdot , \lambda )\).

Definition 2

(\({\underline{H}}\)-strong convexity) Let \({\underline{H}}\in \mathbb {S}_{++}^p\subset \mathbb {R}^{p \times p}\) be a symmetric positive definite matrix. A function \(f(\theta )\) is \({\underline{H}}\)-strongly convex if there exists a vector-valued function \(\xi :\mathbb {R}^p\rightarrow \mathbb {R}^p\) such that

$$\begin{aligned} f(\psi )-f(\theta )\ge \left\langle \xi (\theta ),\psi -\theta \right\rangle + \frac{1}{2}\left\| \psi -\theta \right\| _{\underline{H}}^2, \quad \forall \psi \in \mathbb {R}^p, \forall \theta \in \mathbb {R}^p. \end{aligned}$$

Note that \({\underline{H}}\)-strong convexity can be seen as the matrix-valued version of the standard strong convexity. Now, assume the strong convexity of \(f_X\) and \(g_j\):

Assumption 3

(Strongly convex objective) Both of the following equivalent conditions are satisfied:

(i):

\(f_X\) is \({\underline{H}}_0\)-strongly convex for all \(X\in {\mathcal {X}^n}\) and \(g_j\) is \({\underline{H}}_j\)-strongly convex (\(j=1,\ldots ,d\)).

(ii):

\(f_X(\cdot )+g(\cdot ,\lambda )\) is \({\underline{H}}(\lambda )\)-strongly convex for all \(X\in {\mathcal {X}^n}\) and all \(\lambda \ge \mathbf {0}\), where \({\underline{H}}(\lambda )\overset{\mathrm{def}}{=}{\underline{H}}_0+\sum _{j=1}^d \lambda _j {\underline{H}}_j\).

Then, we have the following lower bound on \(Z(\lambda )\).

Theorem 2

(Lower bound of \(Z(\lambda )\)) Suppose that Assumptions 1 and 3 hold. Let \(T(V)\overset{\mathrm{def}}{=}\inf _{\psi \in V} \int _{D(\mathbf {0})}\exp \left\{ -f_X(\psi )\right\} d\nu (X)\).

Then, for all \(V\subset \varOmega _0\), we have

$$\begin{aligned} Z(\lambda )\ge T(V) \frac{\det {\underline{H}}(\lambda )^{\frac{1}{2}}}{\sqrt{2\pi }^p} \int _{V} e^{-g(\theta ,\lambda )}d\theta . \end{aligned}$$
(8)

Proof

Let \(q_\lambda (X)\overset{\mathrm{def}}{=}\int _{V} \exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\theta \). First, from the positivity of \(q_\lambda \), we have

$$\begin{aligned} Z(\lambda )&= \int _{\mathcal {X}^n}\max _{\theta \in \varOmega }\exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\nu (X)\\&\ge \int _{D(\lambda )} \max _{\theta \in { \varOmega }^{\mathrm {o}}}\exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\nu (X)\\&\ge \inf _{X\in D(\lambda )}\underbrace{\max _{\theta \in {{ \varOmega }^{\mathrm {o}}}} \frac{\exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} }{q_\lambda (X)}}_{A} \underbrace{\int _{D(\lambda )} q_\lambda (X)d\nu (X)}_{B}. \end{aligned}$$

Then, we bound from below \(A\) and \(B\) in the right-hand side, respectively. Since we assumed that \(f_X(\theta )\) is a logarithmic loss, the second factor is simply evaluated using Fubini’s theorem,

$$\begin{aligned} B&\ge \iint _{V \times D(\mathbf {0})} \exp \left\{ -f_X(\theta )-g(\theta , \lambda )\right\} d\theta d\nu (X)\\&\ge T(V)\int _{V} e^{-g(\theta , \lambda )}d\theta , \end{aligned}$$

where the first inequality follows from Assumption 1.

On the other hand, by Lemma 1, we have

$$\begin{aligned} A^{-1}&= q_\lambda (X) \min _{\theta \in { \varOmega }^{\mathrm {o}}}\exp \left\{ f_X(\theta )+g(\theta )\right\} \\&=\int _{\varOmega } \exp \left\{ \min _{\theta \in { \varOmega }^{\mathrm {o}}}f_X(\theta ) + g(\theta , \lambda )- f_X(\psi ) - g(\psi , \lambda )\right\} d\psi \\&\le \int _{\varOmega } \exp \left\{ - \frac{1}{2} \left\| z\right\| _{{\underline{H}}(\lambda )}^2\right\} dz\\&\le \frac{\sqrt{2\pi }^p}{\det {\underline{H}}(\lambda ) ^{\frac{1}{2}}}. \end{aligned}$$

This concludes the proof. \(\square \)

The lower bound in Theorem 2 has a similar form with the upper bound \(\bar{Z}(\lambda )\). Therefore, combining Theorem 2 with Theorem 1, we have a uniform gap bound of uLNML.

Theorem 3

(Uniform gap bound of uLNML) Suppose that the assumptions made in Theorems 1 and 2 are satisfied. Suppose that the penalty function is quadratic, i.e., \({\overline{H}}_j={\underline{H}}_j\) and \(c_j=0\) for all \(j=1,\ldots ,d\). Then, the gap between LNML and uLNML is uniformly bounded as, for all \(X\in {\mathcal {X}^n}\) and \(\lambda \in \mathbb {A}\),

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )-\mathcal {L}(X|\lambda ) \le c_0 + \frac{1}{2} \log \frac{\det {\overline{H}}_0}{\det {\underline{H}}_0} - \log R({\overline{H}}_0;U) - \log T(\varOmega +U), \end{aligned}$$
(9)

where \(R({\overline{H}}_0;U)\) and T(V) is defined as in the preceding theorems.

Proof

From Theorems 1 and  2, we have

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )-\mathcal {L}(X|\lambda )&\le \log \bar{Z}(\lambda ) - \log Z(\lambda )\\&\le c(\lambda ) + \frac{1}{2} \log \frac{\det {\overline{H}}(\lambda )}{\det {\underline{H}}(\lambda )} -\log R({\overline{H}}_0;U)- \log T(V)\\&\qquad +\log \frac{\int _{\varOmega +U}e^{-g(\theta , \lambda )}d\theta }{\int _{V}e^{-g(\theta , \lambda )}d\theta }, \end{aligned}$$

where \(c(\lambda )=c_0\) from the assumption. Taking \(V=\varOmega +U\) to cancel out the last term,

we have

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )-\mathcal {L}(X|\lambda )&\le c_0 + \frac{1}{2} \log \frac{\det {\overline{H}}(\lambda )}{\det {\underline{H}}(\lambda )} - \log R({\overline{H}}_0;U) - \log T(\varOmega +U). \end{aligned}$$
(10)

Let \(\kappa (Q) \overset{\mathrm{def}}{=}\log \frac{\det ({\overline{H}}_0 + Q)}{\det ({\underline{H}}_0 + Q)}\) for \(Q\in \mathbb {S}_{+}^p\) and let \(\underline{Q}={\overline{H}}_0^{-\frac{1}{2}}Q{\overline{H}}_0^{-\frac{1}{2}}\) and \(\overline{Q}={\underline{H}}_0^{-\frac{1}{2}}Q{\underline{H}}_0^{-\frac{1}{2}}\). Then, we have

$$\begin{aligned} \frac{\partial }{\partial t}\kappa (tQ)&=\mathop {\mathrm {tr}}\left( ({\overline{H}}_0+tQ)^{-1}Q - ({\overline{H}}_0+tQ)^{-1}Q\right) \\&= \mathop {\mathrm {tr}}\left( (I+t\underline{Q})^{-1}\underline{Q} - (I+t\overline{Q})^{-1}\overline{Q}\right) \le 0, \end{aligned}$$

where the last inequality follows from \(\underline{Q}\preceq \overline{Q}\). This implies that

$$\begin{aligned} \log \frac{\det {\overline{H}}(\lambda )}{\det {\underline{H}}(\lambda )} = \kappa \left( \sum _{j=1}^d {\overline{H}}_j\right) \le \kappa (O) = \log \frac{\det {\overline{H}}_0}{\det {\underline{H}}_0}, \end{aligned}$$

which, combined with (10), completes the proof. \(\square \)

The theorem implies that uLNML is a constant-gap upper bound of the LNML code length if \(f_X\) is strongly convex. Moreover, the gap bound (9) can be utilized for choosing a good neighbor U. Suppose that there is no effective boundary in the parameter space, \(\varOmega ={ \varOmega }^{\mathrm {o}}\). Then, we can simplify the gap bound and the optimal neighbor U is explicitly given.

Corollary 4

(Uniform gap bound for no-boundary case) Suppose that the assumptions made in Theorem 3 is satisfied. Then, if \(\varOmega ={ \varOmega }^{\mathrm {o}}\), we have a uniform gap bound

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )-\mathcal {L}(X|\lambda ) \le c_0 + \frac{1}{2} \log \frac{\det {\overline{H}}_0}{\det {\underline{H}}_0} - \log R({\overline{H}}_0;U) \end{aligned}$$
(11)

for all \(X\in {\mathcal {X}^n}\) and all \(\lambda \in \mathbb {A}\). This bound is minimized with the largest U, i.e., \(U=\bigcap _{\theta \in \varOmega }\left[ \varOmega _0-\left\{ \theta \right\} \right] \).

Proof

According to Theorem 3, it suffices to show that \(T(V)\equiv 1\) for all \(V\subset \varOmega _0\). From the existence of the RERM estimate in \(\varOmega \), we have \(\hat{\theta }(X, \lambda )\in \varOmega ={ \varOmega }^{\mathrm {o}}\) for all \(X\in {\mathcal {X}^n}\) and all \(\lambda \in \mathbb {A}\). Therefore, we have \(D(\lambda )={\mathcal {X}^n}=D_\star \) and hence \(\int _{D_\star }e^{-f_X(\psi )}d\nu (X)\equiv 1\) for all \(\psi \in \varOmega _0\), which is followed by \(T(V)\equiv 1\). The second argument follows from the monotonicity of \(R(H;\cdot )\). \(\square \)

As a remark, if we assume in addition that \(f_X\) is a smooth i.i.d. loss, i.e., \(f_X=\sum _{i=1}^n f_{x_i}\) and \(c_0=0\), the gap bound is also uniformly bounded with respect to the sample size n. This is derived from the fact that the right-hand side of (11) turns out to be

$$\begin{aligned} \log \frac{\det n{\overline{H}}}{\det n{\underline{H}}}-\log \mathbb {E}_{z\sim \mathcal {N}_m[\mathbf {0}, \frac{1}{n}{\overline{H}}_0^{-1}]} \left[ \mathbb {1}_{U}(z)e^{-r(\Vert z\Vert ^2)}\right] \overset{n\rightarrow \infty }{\longrightarrow } \log \frac{\det {\overline{H}}}{\det {\underline{H}}}<\infty . \end{aligned}$$

2.5 Discussion

In previous sections, we derived an upper bound of the normalizing constant \(Z(\lambda )\) and defined an easy-to-compute alternative for the LNML code length, called uLNML. We also presented uniform gap bounds of uLNML for quadratic penalty functions. Note that uLNML characterizes \(Z(\lambda )\) with upper smoothness of the loss and penalty functions. This is both advantageous and disadvantageous. The upper smoothness can often be easily computed even for complex models like deep neural networks. This makes uLNML applicable to a wide range of loss functions. On the other hand, if the Hessian of the loss function drastically varies across \(\varOmega \), the gap can be considerably large. In this case, one may tighten the gap by reparametrizing \(\varOmega \) to make the Hessian as uniform as possible.

The derivation of uLNML relies on the upper smoothness of the loss and penalty functions. In particular, our current analysis on the uniform gap guarantee given by Theorem 3 holds only if the penalty function is smooth. This is violated if one employs the \(\ell 1\)-penalties.

We note that there exists an approximation of LNML called Rissanen’s asymptotic expansion (RAE), which was originally given by Rissanen (1996) for a special case and then generalized by Grünwald (2007). RAE approximates LNML except for the o(1) term with respect to n,

$$\begin{aligned} \mathcal {L}(X|\lambda )&= \min _{\theta \in \varOmega } f_X(\theta ) + g(\theta ,\lambda ) + \frac{p}{2}\log \frac{n}{2\pi } +\log \int _\varOmega \sqrt{\det I(\psi )} e^{-g(\psi , \lambda )}d\psi +o(1), \end{aligned}$$

where \(I(\psi )\overset{\mathrm{def}}{=}\int \left[ \nabla f_X(\theta ) \nabla f_X(\theta )^\top \right] e^{-f_X(\theta )} d\nu (X)\) denotes the Fisher information matrix. Differences between RAE and uLNML are seen from two perspectives: their approximation errors and tractability.

As for the approximation errors, one of the largest differences is in their boundedness. RAE’s o(1) term is not necessarily uniformly bounded with respect to \(\lambda \), and actually it can be unboundedly large for every fixed n as \(\left\| \lambda \right\| \rightarrow \infty \) in the case of, for example, the Tikhonov regularization. This is in contrast to uLNML in that the approximation gap is uniformly bounded with respect to \(\lambda \) according to Corollary 3, but it does not necessarily go to zero as \(n\rightarrow \infty \). This difference can be significant, especially in the scenario of penalty selection, where one compares different \(\lambda \) while n is fixed.

In terms of tractability, uLNML is usually easier to compute than RAE. One of the major obstacles when one compute RAE is that the integrand \(\sqrt{\det I(\psi )} e^{-g(\psi , \lambda )}\) depends on both of \(f_X\) and \(\lambda \). Unless the analytic value of the integral is known, which is unlikely especially for complex models, one may employ the Monte Carlo approximation to evaluate it, which is typically computationally demanding for high-dimensional models. On the other hand in uLNML, the unwieldy integral is replaced with the upper-smoothness term and the integral of the penalty. The upper smoothness can be computed with differentiation, which is often easier than integration, and the penalty integral does not depend on \(f_X\) anymore. Therefore, uLNML is often applicable to a wider class of models than that of RAE. See Sect. 3.2 for example.

3 Examples of uLNML

In the previous section, we have shown that the normalizing factor of LNML is bounded if the upper smoothness of \(f_X(\theta )\) is bounded. The upper smoothness can be easily characterized for a wide range of loss functions. Since we cannot cover all of it here, we present below a few examples that will be used in the experiments.

3.1 Linear regression

Let \(X\in \mathbb {R}^{n\times m}\) be a fixed design matrix and let \(y\in \mathbb {R}^n={\mathcal {X}^n}\) represent the corresponding response variables. Then, we want to find \(\beta \in \mathbb {R}^m\) such that \(y\approx X\beta \). We assume that the ‘useful’ predictors may be sparse, and hence, most of the coefficients of the best \(\beta \) for generalization may be close to zero. As such, we are motivated to solve the ridge regression problem:

$$\begin{aligned} \min _{\sigma ^2\in [a, b],\;\beta \in \mathbb {R}^d} -\log p\left( y|X,\beta ,\sigma ^2\right) + \frac{1}{2\sigma ^2} \sum _{j=1}^p \lambda _j \beta _j^2, \end{aligned}$$
(12)

where \(-\log p(y|X,\beta ,\sigma ^2)=\frac{1}{2\sigma ^2} \left\| y-X\beta \right\| ^2 + \frac{n}{2}\log 2\pi \sigma ^2\). According to Corollary 3, the uLNML of the ridge regression is given by

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )&= \min _{\sigma ^2\in [a, b],\;\beta \in \mathbb {R}^d}-\log p\left( y|X,\beta ,\sigma ^2\right) + \frac{1}{2\sigma ^2} \sum _{j=1}^p \lambda _j \beta _j^2\\&\quad +\frac{1}{2} \log \frac{\det (C + \mathop {\mathrm {diag}}\lambda )}{\det \mathop {\mathrm {diag}}\lambda }+\mathrm {const.}, \end{aligned}$$

where \(C\overset{\mathrm{def}}{=}X^\top X\). Note that the gap of the uLNML here is uniformly bounded, because the LNML of the variable temperature model (12) is bounded from below with that of fixed-variance models, which coincides with the above uLNML except with a constant.

3.2 Conditional dependence estimation

Let \(X=\left( x_1, x_2,\ldots , x_n\right) ^\top \in \mathbb {R}^{n\times m}={\mathcal {X}^n}\) be a sequence of n observations independently drawn from the m-dimensional Gaussian distribution \(\mathcal {N}_m[0, \varSigma ]\). We assume that the conditional dependence among the m variables in X is scarce, which means that most of the coefficients of precision \(\varTheta =\varSigma ^{-1}\in \mathbb {R}^{m\times m}\) are (close to) zero. Thus, to estimate the precision matrix \(\varTheta \), we penalize the nonzero coefficients and consider the following RERM

$$\begin{aligned} \min _{\varTheta \in \varOmega } -\log p(X|\varTheta ) + \frac{1}{2} \sum _{i\ne j} \lambda _{ij} \varTheta _{ij}^2, \end{aligned}$$
(13)

where \(-\log p(X|\varTheta )= \frac{1}{2}\left\{ \mathop {\mathrm {tr}}X^\top X \varTheta - n\log \det 2\pi \varTheta \right\} \) denotes the probability density function of the Gaussian distribution. Here, we take \(\varOmega =\left\{ \varTheta \in \mathbb {S}_{++}^{m}\;\big |\;\varTheta \succeq R^{-1}I_m\right\} \) such that the Hessian is appropriately bounded, \(\nabla _\varTheta ^2f_X=\varTheta ^{-1}\otimes \varTheta ^{-1}\preceq {\overline{H}}_0=\frac{R^2}{2}I_{m\times m}\). As for the choice of R, we can use any upper-bound estimates of the largest eigenvalue of \(\varTheta ^{-1}\). Specifically, we employed \(R=\left\| X^\top X/n\right\| _\infty \) in the experiments. As it is an instance of the Tikhonov regularization, from Corollary 1 with \({\overline{H}}_0=\frac{n}{2} R^{2}I_{m^2}\), the uLNML for the graphical model is given by

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda ) = \min _{\varTheta \in \varOmega } -\log p(X|\varTheta ) + \frac{1}{2} \sum _{i\ne j} \left[ \lambda _{ij} \varTheta _{ij}^2 + \log \left( 1+\frac{nR^2}{2\lambda _{ij}}\right) \right] . \end{aligned}$$

4 Minimization of uLNML

Given data \(X\in {\mathcal {X}^n}\), we want to minimize uLNML (5) with respect to \(\lambda \in \mathbb {A}\) as it bounds the LNML code length, which is a measure of the goodness of the penalty with respect to the MDL principle (Rissanen 1978; Grünwald 2007). Furthermore, it bounds the risk of the RERM estimate \(\mathbb {E}_Y f_Y(\hat{\theta }(X, \lambda ))\) (Grünwald and Mehta 2017). The problem is that grid-search-like algorithms are inefficient since the dimensionality of the domain \(\mathbb {A}\subset \mathbb {R}^d\) is high.

In order to solve this problem, we derive a concave–convex procedure (CCCP) for uLNML minimization. The algorithm is justified with the convergence properties that result from the CCCP framework. Then, we also give concrete examples of the computation needed in the CCCP for typical RERMs.

4.1 Concave–convex procedure (CCCP) for uLNML minimization

In the forthcoming discussion, we assume that \(\mathbb {A}\) is closed, bounded, and convex for computational convenience. We also assume that the upper bound of the normalizing factor \(\log \bar{Z}(\lambda )\) is convex with respect to \(\lambda \). This is not a restrictive assumption as the true normalizing term \(\log Z(\lambda )=\log \int \exp \left\{ \max _{\theta \in \varOmega } -f_X(\theta ) - g(\theta ,\lambda )\right\} d\nu (X)\) is always convex if the penalty is linear as given in (2). In particular, it is actually convex for the Tikhonov regularization and lasso as in Corollarys 1 and 2, respectively.

Recall that the objective function, uLNML, is written as

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )&= \min _{\theta \in \varOmega } f_X(\theta )+g(\theta ,\lambda )+\log \bar{Z}(\lambda ). \end{aligned}$$

Therefore, the goal is to find \(\lambda ^\star \in \mathbb {A}\) that attains

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda ^\star ) = \min _{\theta \in \varOmega , \lambda \in \mathbb {A}} h_X(\theta ,\lambda ), \end{aligned}$$

where \(h_X(\theta ,\lambda )\overset{\mathrm{def}}{=}f_X(\theta )+g(\theta ,\lambda )+\log \bar{Z}(\lambda )\). Note that the existence of \(\lambda ^\star \) follows from the continuity of the objective function \({\bar{\mathcal {L}}}(X|\lambda )\) and the closed nature of the domain \(\mathbb {A}\).

The minimization problem can be solved by alternate minimization of \(h_X\) with respect to \(\theta \) and \(\lambda \) as in Algorithm 1, which we call MDL regularization selection (MDL-RS). In general, minimization with respect to \(\theta \) is the original RERM (1) itself. Thus, it can often be solved with existing software or libraries associated with the RERM problem. On the other hand, for minimization with respect to \(\lambda \), we can employ standard convex optimization techniques since \(h_X(\theta , \cdot )\) is convex as both \(g(\theta , \cdot )\) and \(\log \bar{Z}(\cdot )\) are convex. Specifically, for some types of penalty functions, we can derive closed-form formulae of the update of \(\lambda \). If one employs the Tikhonov regularization and \({\overline{H}}_0\) is diagonal, then

$$\begin{aligned} \frac{\partial }{\partial \lambda _j} \left[ g(\theta _t, \lambda ) + \bar{Z}(\lambda )\right] =0 \Leftrightarrow \lambda = \frac{{\overline{H}}_{0, jj}}{2} \left[ \sqrt{1 + \frac{4}{\theta _{t,j}^2 {\overline{H}}_{0, jj}}} - 1\right] \quad \left( = \tilde{\lambda }_{t,j}\right) . \end{aligned}$$

Therefore, if \(\mathbb {A}=[a_1, b_1]\times \cdots \times [a_d, b_d]\), the convex part is completed by \(\lambda _{t,j}=\varPi _{[a_j, b_j]}\tilde{\lambda }_{t,j}\), where \(\varPi _{[a_j, b_j]}\) is the projection of the j-th coordinate. Similarly, if one employs the lasso,

$$\begin{aligned} \tilde{\lambda }_{t, j} = \root 3 \of {\alpha + \sqrt{\alpha ^2 + \left( \frac{{\overline{H}}_{0, jj}}{3}\right) ^3}} + \root 3 \of {\alpha - \sqrt{\alpha ^2 + \left( \frac{{\overline{H}}_{0, jj}}{3}\right) ^3}}, \end{aligned}$$

where \(\alpha ={\overline{H}}_{0, jj}/\left| \theta _{t,j}\right| \). The projection procedure is the same as that for Tikhonov regularization.

figure a

The MDL-RS algorithm can be regarded as a special case of concave–convex procedure (CCCP) (Yuille and Rangarajan 2003). First, the RERM objective is concave as it is the minimum of linear functions, \(F_X(\lambda )=\min _{\theta \in \varOmega } f_X(\theta ) + g(\theta , \lambda )\). Hence, uLNML is decomposed into the sum of concave and convex functions,

$$\begin{aligned} {\bar{\mathcal {L}}}(X|\lambda )=F_X(\lambda )+\log \bar{Z}(\lambda ). \end{aligned}$$

Second, \(\tilde{F}^{(t)}_X(\lambda )\overset{\mathrm{def}}{=}f_X(\theta _t) + g(\theta _t, \lambda )\) is a linear majorization function of \(F_X(\lambda )\) at \(\lambda =\lambda _{t-1}\), i.e., \(\tilde{F}^{(t)}_X(\lambda )\ge F_X(\lambda )\) for all \(\lambda \in \mathbb {A}\) and \(\tilde{F}^{(t)}_X(\lambda _{t-1})=F_X(\lambda _{t-1})\). Therefore, as we can write \(\lambda _{t}=\mathop {\mathrm {argmin}}_{\lambda \in \mathbb {A}}\tilde{F}^{(t)}_X(\lambda ) + \log \bar{Z}(\lambda )\), MDL-RS is a concave–convex procedure for minimizing uLNML. The CCCP interpretation of MDL-RS immediately implies the following convergence arguments. Please refer to Yuille and Rangarajan (2003) for the proofs.

Theorem 4

(Monotonicity of MDL-RS) Let \(\left\{ \lambda _t\right\} _{t=0}^{\infty }\) be the sequence of solutions produced by Algorithm 1. Then, we have \({\bar{\mathcal {L}}}(X|\lambda _{t+1}) \le {\bar{\mathcal {L}}}(X|\lambda _{t})\) for all \(t\ge 0\).

Theorem 5

(Local convergence of MDL-RS) Algorithm 1 converges to one of the stationary points of uLNML \({\bar{\mathcal {L}}}(X|\lambda )\).

Even if the concave part, i.e., minimization with respect to \(\theta \), cannot be solved exactly, MDL-RS still monotonically decreases uLNML as long as the concave part monotonically decreases the objective value, \(f_X(\theta _{t})+g(\theta _{t}, \lambda _{t-1}) \le f_X(\theta _{t-1})+g(\theta _{t-1}, \lambda _{t-1})\) for all \(t\ge 1\). This can be confirmed by seeing that \({\bar{\mathcal {L}}}(X|\lambda _{t})=h_X(\theta _{t+1}, \lambda _{t})\le h_X(\theta _t, \lambda _t)\le h_X(\theta _t, \lambda _{t-1})={\bar{\mathcal {L}}}(X|\lambda _{t-1})\) where \(h_X(\theta ,\lambda )=f_X(\theta )+g(\theta ,\lambda )\). Moreover, if the subroutine of the concave part is iterative, early stopping may be even beneficial in terms of the computational cost.

4.2 Discussion

We previously introduced the CCCP algorithm for minimizing uLNML, namely, MDL-RS. The monotonicity and local convergence property follow from the CCCP framework. One of the most prominent features of the MDL-RS algorithm is that the concave part is left completely black-boxed. Thus, it can be easily applied to the existing RERM.

There exists another approach for minimization of LNMLs in which a stochastic minimization algorithm is proposed (Miyaguchi et al. 2017). Instead of approximating the value of LNML, this directly approximates the gradient of LNML with respect to \(\lambda \) in a stochastic manner. However, since the algorithm relies on the stochastic gradient, there is no trivial way of judging if it is converged or not. On the other hand, MDL-RS can exploit the information of the exact gradient of uLNML to stop the iteration.

Approximating LNML with uLNML benefits us more; We can combine MDL-RS with grid search. Since MDL-RS could be trapped at fake minima, i.e., local minima and saddle points, starting from multiple initial points may be helpful to avoid poor fake minima, and help it achieve lower uLNML.

5 Related work

In the literature of model selection based on the MDL principle, there exist a number of methods that are concerned with discrete sets of candidate models (for example, see Roos et al. 2009; Hirai and Yamanishi 2011 among others). Note that in the problem of regularization selection, the candidate models are infinite in general and hence typical methods of the MDL model selection cannot be straightforwardly applied. Nevertheless, some of the RERM problems are addressed utilizing such methods. For example, the \(\ell _0\)-norm RERM can be casted into the discrete model selection over all the subsets of features (e.g., see Dhillon et al. 2011; Miyaguchi et al. 2017). On the other hand, our method is applicable to arbitrary penalty functions as long as they are reasonably upper-smooth, although this is not the case with the \(\ell _0\)-penalty. Therefore, our method can be regarded as a complement of the conventional discrete model selection.

As compared to existing methods of regularization selection, MDL-RS is distinguished by its efficiency in searching for penalties and its ease of systematic computation. Conventional penalty selection methods for large-dimensional models are roughly classified into three categories. Below, we briefly describe each one emphasizing its relationship and difference to the MDL-RS algorithm.

5.1 Grid search with discrete model selection criteria

The first category is grid search with a discrete model selection criterion such as the cross validation score, Akaike’s information criterion (AIC) (Akaike 1974), and Bayesian information criterion (BIC) (Schwarz 1978; Chen and Chen 2008). In this method, we choose a model selection criterion and a candidate set of the hyperparameter \(\{\lambda ^{(k)}\}_{k=1}^K\in \mathbb {A}\subset \mathbb {R}^d\) in advance. Then, we calculate the RERM estimates for each candidate, \(\theta ^{(k)}=\hat{\theta }(X, \lambda ^{(k)})\). Finally, we pick the best estimate according to the pre-determined criterion. This method is simple and universally applicable for any model selection criteria. However, the time complexity grows linearly as the number of candidates increases, and an appropriate configuration of the candidate set can vary corresponding to the data. This is specifically problematic for high dimensional design spaces, i.e., \(d\gg 1\), where the combinatorial number of possible configurations is much larger than the feasible number of candidates.

On the other hand, the computational complexity of MDL-RS often scales better. Though it depends on the time complexity of the subroutine for the original RERM problem, the MDL-RS algorithm is not explicitly affected by the curse of dimensionality. However, it can be used for model selection in combination with the grid search. Although MDL-RS provides a more efficient way to seek a good \(\lambda \) in a (possibly) high-dimensional space as compared to simple grid search, it is useful to combine the two. Since uLNML is nonconvex in general, MDL-RS may converge to a fake minimum such as local minima and saddle points depending on the initial point \(\lambda _0\). In this case, starting MDL-RS with multiple initial points \(\lambda _0=\lambda ^{(k)}\) may improve the objective value.

5.2 Evidence maximization

The second category is evidence maximization. In this methodology, one interprets the RERM as a Bayesian learning problem. The approach involves converting loss functions and penalty functions into conditional probability density functions \(p(X|\theta )=e^{-f_X(\theta )}\) and prior density functions \(p(\theta ;\lambda )=e^{-g(\theta , \lambda )}(\int e^{-g(\psi , \lambda )}d\psi )^{-1}\), respectively. Then, the evidence is defined as \(p(X;\lambda )=\int p(X|\theta )p(\theta ;\lambda )d\theta \) and it is maximized with respect to \(\lambda \). A successful example of evidence maximization is the relevance vector machine (RVM) proposed by Tipping (2001). It is a Bayesian interpretation of the ridge regression with different penalty weights \(\lambda _j\) on different coefficients, as described in Corollary 1. This results in so-called automatic relevance determination, and makes the approach applicable to redundant models.

The maximization of the evidence can also be thought of as an instance of the MDL principle, as it is equivalent to minimizing \(-\log p(X;\lambda )\) with respect to \(\lambda \), which is a code-length function of X. Moreover, both LNML and the evidence have an intractable integral in it. A notable difference between the two is the computational cost to optimize them. Though LNML contains an intractable integral in its normalizing term \(\log Z(\lambda )\), it can be systematically approximated by uLNML and uLNML is efficiently minimized via CCCP. On the other hand, in the case of evidence, we do not know of any approximation that is as easy to optimize and as systematic as uLNML. Even though a number of approximations have been developed for evidence such as the Laplace approximation, variational Bayesian inference (VB), and Markov chain Monte Carlo sampling (MCMC), these tend to be combined with grid search (e.g., Yuan and Lin 2005) except for some special cases such as the RVM and Gaussian processes (Rasmussen and Williams 2006).

5.3 Error bound minimization

The last category is error bound minimization. The generalization capability of RERM has been extensively studied in bounding generalization errors specifically on the basis of the PAC learning theory (Valiant 1984) and PAC-Bayes theory (Shawe-Taylor and Williamson 1997; McAllester 1999). There also exist a considerable number of studies that relate error bounds with the MDL principle, including (but not limited to) Barron and Cover (1991), Yamanishi (1992) and Chatterjee and Barron (2014). One might determine the hyperparamter \(\lambda \) by minimizing the error bound. However, being used to prove the learnability of new models, such error bounds are often not used in practice more than the cross validation score. MDL-RS can be regarded as an instance of the minimization of an error bound. Actually, uLNML bounds the LNML code length, which was recently shown to be bounding the generalization error of the RERM estimate under some conditions including boundedness of the loss function and fidelity of hypothesis classes (Grünwald and Mehta 2017).

6 Experiments

In this section, we empirically investigate the performance of the MDL-RS algorithm in terms of generalization errors.Footnote 1 We compare MDL-RS with conventional methods applying the two models introduced in Sect. 3 on both synthetic and benchmark datasets. In particular, because we expect that the proposed method performs better than the other methods if the model is high-dimensional, we focus on the dependency of the performance on the dimensionality.

6.1 Linear regression

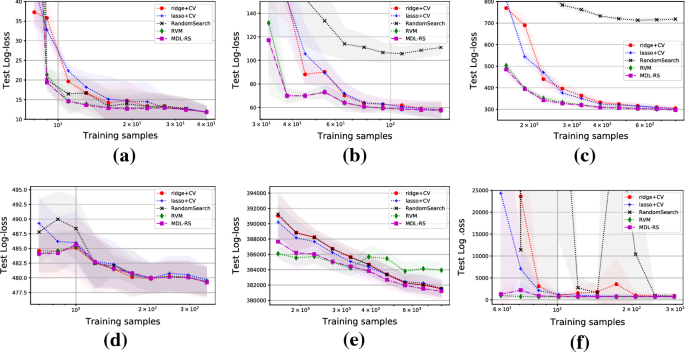
Setting For linear regression, we compared MDL-RS with the automatic relevance determination (ARD) regression with the relevance vector machine (RVM) (Tipping 2001) and deterministic and random grid search methods for the cross validation score. As for the deterministic cross validation, we employed the ridge regression and lasso while their penalty weights are configured as 20 points spread over \(\lambda _j=\lambda \in [10^{-4}, 10^0]\ (j=1,\ldots ,p)\) logarithmically evenly. As for the random cross validation, 100 random points are drawn from the log-uniform distribution over \([10^{-4}, 10^0]^p\). The performance metric is test logarithmic loss (log-loss) \(-\log p(y|X,\beta ,\sigma ^2)\) (see Sect. 3.1) on fivefold cross validation. Figure 1 shows the results of the comparison with six datasets, namely, three synthetic datasets and three real-world dataset. In the synthetic datasets, the number of design variables m varies from 5 to 100, and the true coefficients \(\beta \) are randomly chosen where some of them set to zero. The real-world examples are taken from the Diabetes dataset,Footnote 2 ResidentialBuilding dataset (Rafiei and Adeli 2015)Footnote 3 and YearPredictionMSD dataset.Footnote 4 We note that there is huge variety in the dimensionality of their parameter spaces: \(m=14\) for Diabetes, \(m=90\) for YearPredictionMSD and \(m=103\) for ResidentialBuilding dataset.

Result From the overall results, we can see that MDL-RS and RVM are comparable to one another and outperform the other three. Figure 1a–c suggest that the proposed method performs well in all the synthetic experiments. Figure 1d–f show the results of the real-world experiments. One can observe the same tendency as in the synthetic ones; Both MDL-RS and RVM outperform the rest in terms of generalization error (log-loss) and the difference is bigger when the sample size is smaller. However, note that in the YearPredictionMSD dataset, RVM converges to a poor local minima and hence fails to lower the log-loss well even with large training samples. It is also noteworthy that the performance of the random grid-search method becomes poor and unstable for the high-dimensional cases, which is due to the curse of dimensionality of the design space. These results emphasize the efficiency of MDL-RS in optimizing uLNML with high-dimensional models.

Fig. 1
figure 1

Convergence of log-loss in linear regression. The horizontal axes show the number of training samples in logarithmic scale, while the vertical axes show the test log-loss. Each shading area is showing ± 1 SD. a \(m=5\). b \(m=20\). c \(m=100\). d Diabetes. e YearPredictionMSD. f ResidentialBuilding

Full size image

6.2 Conditional dependence estimation

Setting For the estimation of conditional dependencies, we compared MDL-RS with the grid search of glasso (Friedman et al. 2008) with AIC, (extended) BIC and the cross validation score. We generated data \(X\in \mathbb {R}^{n\times m}\) from m-dimensional double-ring Gaussian graphical models (\(m=10, 20, 50, 100\)) in which each variable \(j\in [1, m]\) is conditionally dependent to its 2-neighbors \(j-2, j-1, j+1\) and \(j+2\;(\mathrm {mod}\ m)\) with a coefficient of 0.25. Note that MDL-RS can be applied to the graphical model just by computing the upper smoothness while RVM cannot be applied straightforwardly.

Result Figure 2 shows the results of the experiment. It is seen that all the estimators converge in the same rate, \(O(n^{-1})\), whereas MDL-RS gives the lowest Kullback–Leibler divergence by far specifically with large m. In particular, when \(m=100\), the proposed estimator outperforms the others by more than a factor of five. This supports our claim that penalty selection in high-dimensional design spaces has a considerable effect on the generalization capability when the model is redundant.

Fig. 2
figure 2

Convergence of Kullback–Leibler divergence for graphical models. The horizontal axes show the number of training samples in logarithmic scale, while the vertical axes show the divergence of estimates relative to true distributions. Each shading area is showing ±one-standard deviation. a \(m=10\). b \(m=20\). c \(m=50\). d \(m=100\)

Full size image

6.3 Discussion

Both results indicate that MDL-RS performs well specifically when the model is high-dimensional as expected. Note that the generalization error LNML and uLNML bound is the expected logarithmic loss \(\mathbb {E}_{X,Y} f_Y(\hat{\theta }(X, \lambda ))\), and the performance metric we employed in the experiments is (an unbiased estimator of) the logarithmic loss itself. Hence, if the metric is changed, then the result could be different.

7 Concluding remarks

In this paper, we proposed a new method for penalty selection on the basis of the MDL principle. Our main contribution was the introduction of uLNML, a tight upper bound of LNML for smooth RERM problems. This can be analytically computed, except for a constant, given the (upper) smoothness of the loss and penalty functions. We also presented the MDL-RS algorithm, a minimization algorithm of uLNML with convergence guarantees. Experimental results indicated that MDL-RS’s generalization capability was comparable to that of conventional methods. In the high-dimensional setting we are interested in, it even outperformed conventional methods.

In related future work, further applications to various models such as latent variable models and deep learning models must be analyzed. As the above models are not (strongly) convex, the extension of the lower bound of LNML to the non-convex case would also be an interesting topic of future study. While we bounded LNML with the language of Euclidean spaces, the only essential requirement of our analysis is upper smoothness of loss functions defined over parameter spaces. Therefore, we believe that it is possible to generalize uLNML to the Hilbert spaces to deal with infinite-dimensional models.