1 Introduction

In this work, we study the nonsmooth nonconvex finite-sum optimization problem

$$\begin{aligned} \begin{aligned} \text {min}_{x \in {\mathcal{X}}} F(x) := f(x) + h(x) \end{aligned} \end{aligned}$$

where \({\mathcal{X}} \subseteq {\mathbb{R}}^d\) is the parameter domain. \(f(x) = \frac{1}{n} \sum _{i=1}^n f_{i}(x)\) is the average of n functions, where each \(f_i\) is assumed to be a nonconvex function with a Lipchitz continuous gradient. h(x) is often taken to be a nonsmooth but convex function, for example, the \(L_1\) regularization. Recently, the smooth and unconstrained version of this problem has been thoroughly studied, i.e., when \(h(x) = 0\) and \({\mathcal{X}} = {\mathbb{R}}^d\). Since determining the global minimum of a nonconvex function is NP-hard, all prior convergence analyses have focused on the gradient complexity of different algorithms when finding the first-order stationary point of the loss F(x), i.e., \(\Vert \nabla F(x) \Vert _2^2 \le \epsilon\). To reduce the gradient complexity of the well-known gradient descent (GD) and stochastic gradient descent (SGD) algorithms, the famous Stochastic Variance Reduced Gradient method (SVRG) (Johnson & Zhang, 2013) and its variants have been proposed, including SAGA (Defazio et al., 2014), SCSG (Lei et al., 2017), SNVRG (Zhou et al., 2018b), SPIDER (Fang et al., 2018), stablized SVRG (Ge et al., 2019), and Natasha momentum variants (Allen-Zhu, 2017, 2018). Recently, Li et al. (2021) proposed a new algortihm named PAGE that uses a single loop structure but still achieves variance reduction. These algorithms are proven to accelerate the convergence of GD/SGD substantially.

When it comes to the nonsmooth constrained case, i.e., when \(h(x) \ne 0\) or \({\mathcal{X}} \subsetneq {\mathbb{R}}^{n}\), a few algorithms based on the idea of proximal gradient, which projects the updated parameter at each iteration to the space \({\mathcal{X}}\) by finding the closest point in \({\mathcal{X}}\) in terms of the h-regularized \(L_2\) distance, have been proposed. Given \(x_t \in {\mathcal{X}}\), the update rules of these algorithms share the form of

$$\begin{aligned} \begin{aligned} x_{t+1} :=&\text {argmin}_{x \in {\mathcal{X}}} \left\{ \alpha h(x)+ \frac{1}{2}\Vert x-(x_{t} - \alpha d_t)\Vert _2^2 \right\} \\ =&\text {argmin}_{x \in {\mathcal{X}}} \left\{ \alpha \langle d_{t}, x\rangle + \alpha h(x)+ \frac{1}{2}\Vert x-x_{t}\Vert _2^2 \right\} \end{aligned} \end{aligned}$$
(1)

where \(d_t\) is the descent direction and \(\alpha\) is the step size. For example, Ghadimi et al. (2016) provided the convergence rates of Proximal Gradient Descent (ProxGD), Proximal SGD(ProxSGD) when the dataset was sufficiently large. The gradient complexities of these algorithms are proven to match the original algorithms without the proximal operation, i.e., GD and SGD (Ghadimi et al., 2016). Reddi et al. (2016b) proposed ProxSVRG and ProxSAGA, which were the proximal gradient variants of SVRG and SAGA respectively, and analyzed their convergence rates. Li and Li (2018) proposed ProxSVRG+ and obtained even faster convergence than ProxSVRG with favorable constant minibatch sizes. Wang et al. (2019) proposed SpiderBoost based on SPIDER and further improved the gradient complexity of ProxSVRG+. Pham et al. (2020) proposed Prox-SARAH that could use dynamic step sizes and a large range of mini-batch sizes. A single-loop hybrid optimization algorithm was also proposed by Pham et al. (2021).

However, all the above extensions of GD/SGD and SVRG, both for the smooth unconstrained problem and the nonsmooth constrained optimization problem, cannot be easily extended to more general adaptive mirror descent algorithms on different parameter domains \({\mathcal{X}} \subsetneq {\mathbb{R}}^d\). Mirror descent algorithms are famous for using different divergence measures and non-Euclidean metrics to dynamically adapt to the landscape of different loss function (Duchi et al., 2011; Asi & Duchi, 2019). For example, when \({\mathcal{X}}\) is a subset of the \(L_p\) ball where \(1\le p < 2\), it is better to replace the Euclidean divergence term in Eq. 1 by the p-norm divergence for better robustness and stability of the algorithm (Gentile, 2003; Asi & Duchi, 2019). Also, adaptive step sizes, such as linear decay, warm up (Goyal et al., 2017), and restart (Loshchilov & Hutter, 2016) are frequently used in the training of neural networks in practice, which corresponds to using a time-varying step size \(\alpha\) in Eq. (1). However, recent papers of variance reduced algorithms use constant step sizes in their analyses, see e.g., Li and Li (2018); Zhou et al. (2018b). Moreover, self-adaptive algorithms such as Adam (Kingma & Ba, 2015) have become extremely popular in real-world applications, and these algorithms utilize self-adaptive Mahalanobis divergence to adapt to the geometry of different parameter space. All the aforementioned algorithms belong to the set of adaptive mirror descent algorithms, i.e., when the proximal function (defined in Sect. 3) is not fixed. However, no prior theoretical works have shown that variance reduction can accelerate different adaptive mirror descent algorithms.

Therefore, this work serves as the first step towards addressing a very important and interesting question: Can the variance reduction technique accelerate the convergence of all or most of the adaptive stochastic mirror descent algorithms that are specifically designed for different parameter domains? We give an affirmative answer to this question, with the only additional mild requirement that there is a lower bound for the strong convexity of the proximal functions in the mirror descent algorithms.

In particular, we highlight the following contributions:

  1. 1.

    A simple algorithmic framework for reducing variance in mirror descent algorithms. We propose an algorithmic framework, named SVRAMD, for variance reduction in adaptive mirror descent algorithms. The framework is simple and effective: it utilizes a double-loop structure and successfully reduces the variance of all mirror descent algorithms that satisfy our weak Assumption 1. We do not specify the form of the proximal functions or the parameter domain inside the algorithm and thus our framework is natural and adaptive.

  2. 2.

    General and optimal analysis of the proposed framework that is agnostic of form of the proximal function. We provide general analysis without specific forms of the proximal function that proves in both the nonsmooth nonconvex problems and the generalied P–L conditionded problems (see Sect. 4.4), the SVRAMD algorithm converges faster than the original stochastic adaptive mirror descent algorithms designed for different parameter domains. Moreover, the SFO complexity of SVRAMD matches those of popular algorithms in the nonsmooth problem and the state-of-the-art complexities in the generalized P–L conditioned problem.

  3. 3.

    Implications of our general theory. Our general theory implies several interesting results. For example, we claim that dynamic step sizes are allowed for different variance reduced algorithms. As long as the step sizes are upper bounded by the inverse of the smoothness constant 1/L, the proposed SVRAMD algorithm still converges faster than SAMD under the same step size schedule. Also, we claim that variance reduction can work well with self-adaptive algorithms, such as AdaGrad (Duchi et al., 2011) and RMSProp (Tieleman & Hinton, 2012) and make their convergence faster. Moreover, our choices of the hyper-parameters in the theoretical analysis provide a general intuition that larger batch sizes are suggested when using variance reduction on adaptive mirror descent algorithms with a smaller strong convexity parameter, which can be helpful when tuning the batch sizes in practice.

  4. 4.

    Experiments that validate our theoretical claims. To support the correctness of our theoretical claims, we run experiments on both synthetic data and on optimizing popular deep learning models on the MNIST (Schölkopf & Smola, 2002), the CIFAR-10 and the CIFAR-100 (Krizhevsky et al., 2009) datasets, which are known as extremely nonconvex and nonsmooth problems. All the experimental results are consistent with our theoretical findings.

2 Additional related work

Due to the huge amount of works in optimization algorithms and their analyses, we are not able to review all of them in this paper. Instead, we choose to review two additional lines of research that are closely related to this paper.

2.1 Self-adaptive algorithms and their analyses

Since the creation of AdaGrad (Duchi et al., 2011), self-adaptive algorithms have become popular choices for optimization, especially in recent deep learning research such as training language models in Natural Language Processing (NLP) and generative adversarial models in Computer Vision (CV) (Ghadimi et al., 2016). Kingma and Ba (2015) proposed Adam that combined momentum with RMSProp (Tieleman & Hinton, 2012) to further improve the convergence speed of AdaGrad, but Reddi et al. (2016b) proved that Adam could diverge even in convex problems, and proposed AMSGrad to resolve the convergence issue. Wilson et al. (2017) also showed that the generalization performance of Adam was worse than SGD. Therefore, several variants of Adam have been proposed to improve the convergence speed and the generalization performance of Adam, including AdaBound (Luo et al., 2019), NosAdam (Huang et al., 2019), Radam (Liu et al., 2019), AdaBelief (Zhuang et al., 2020) and AdaX (Li et al., 2020). However, many of the aforementioned literature only provided convergence analysis in convex problems. Recently, Zaheer et al. (2018), Chen et al. (2019), and Zhou et al. (2018a) showed the convergence rates of some self-adaptive algorithms, e.g., YOGI (Zaheer et al., 2018), AMSGrad, and AdaGrad, in the nonconvex smooth problem, but the provided rates of these algorithms were still asymptotically the same as that of SGD.

2.2 Variance reduction and general mirror descent

Utilizing the idea of variance reduction to boost the performance of general adaptive mirror descent algorithms is another heated research direction. Lei and Jordan (2020) extended SCSG to the general mirror descent form with some additional assumptions on the (fixed) proximal function, and they showed the advantage of the proposed extension in convex problems. Liu et al. (2020) proposed Adam+ and claimed that variance reduction could improve the convergence rate of a special variant of Adam. Dubois-Taine et al. (2021) proposed to use AdaGrad in the inner loop of SVRG to make the algorithm robust to different step size choices.

3 Problem setup and notations

In this section, we present the preliminary notations and the concepts used for the convergence analysis throughout this paper.

3.1 Notations

We first present the notations we use. For two matrices \(A, B \in {\mathbb{R}}^{d \times d}\), we use \(A\succeq B\) to denote that the matrix \(A - B\) is positive semi-definite. For two real numbers \(a,b \in {\mathbb{R}}\), we use \(a \wedge b, a \vee b\) as short-hands for \(\text {min}(a, b)\) and \(\text {max}(a, b)\). We use \(\lfloor a \rfloor\) to denote the largest integer that is smaller than a. We use \({\widetilde{O}}(\cdot )\) to hide logarithm factors in big-O notations, i.e., for two functions \(a_n\) and \(b_n\), \(a_n = {\widetilde{O}}(b_n)\) if \(a_n/b_n \le \left( \log n \right) ^{k}, \forall n > 0\) for some \(k>0\). Moreover, for an integer \(n\in {\mathbb{N}}\), we frequently use the notation [n] to represent the set \(\{1,2,\cdots , n\}\). For the loss function F(x), we denote the global minimum value of F(x) to be \(F^*\), and we frequently use the notation \(\varDelta _F = F (x_1) - F^*\), where \(x_1\) is the initialization point of the algorithm.

3.2 Assumptions and definitions for nonconvex nonsmooth analysis

The general update rule of the Stochastic Adaptive Mirror Descent (SAMD) algorithm with proximal functions \(\psi _{t}(x)\) is defined as follows

$$\begin{aligned} x_{t+1} = \text {argmin}_{x \in {\mathcal{X}}} \left\{ \alpha _t \langle g_{t}, x\rangle + \alpha _t h(x)+ B_{\psi _t}(x, x_{t}) \right\} \end{aligned}$$
(2)

where \(\alpha _t\) is the step size, \(g_t = \nabla f_{{\mathcal{I}}_j} (x_t)\) is the gradient from a random data batch \({\mathcal{I}}_j\), and h(x) is the regularization function on the dual space. \(B_{\psi _t}(x, x_t)\) is the Bregman divergence with respect to the proximal function \(\psi _t(x)\), defined as

$$\begin{aligned} B_{\psi _t}(x, y) = \psi _t(x) - \psi _t(y) - \langle \nabla \psi _t(y), x- y \rangle \end{aligned}$$

Different proximal functions \(\psi _t(x)\) would generate different Bregman divergences and thus different algorithms. For example, the update rule for ProxSGD is

$$\begin{aligned} x_{t+1} = \text {argmin}_{x \in {\mathcal{X}}} \left\{ \alpha _t \langle g_{t}, x\rangle + \alpha _t h(x)+ \frac{1}{2}\Vert x-x_t\Vert _2^2 \right\} \end{aligned}$$

In this case, \(B_{\psi _t}(x, y) = \frac{1}{2}\Vert x-y\Vert _2^2\) and it is generated by the (fixed) proximal function \(\psi _t(x) = \frac{1}{2}\Vert x\Vert _2^2\). In this work, we consider the general case where the proximal functions are not pre-determined and can change over time so that our analysis can not only be applied to ProxSGD but also other adaptive algorithms. However, we need to require that the proximal functions are all m-strongly convex on the domain \({\mathcal{X}}\) for some real constant \(m > 0\).

Assumption 1

The proximal functions \(\{\psi _{t}(x)\}_{t=1}^T\) are all m-strongly convex with respect to \(\Vert \cdot \Vert _2\) on the space \({\mathcal{X}}\), i.e., for any \(x, y \in {\mathcal{X}}\)

$$\begin{aligned} \begin{aligned} \psi _{t}(y) \ge \psi _{t}(x) + \langle \nabla \psi _{t}(x), y-x\rangle + \frac{m}{2}\Vert y-x\Vert _2^2, \forall t \in [T] \end{aligned} \end{aligned}$$

A very important property of Bregman divergence is that \(\psi _t(x)\) is m-strongly convex with respect to the \(L_2\) norm if and only if \(B_{\psi _t}(x, y) \ge \frac{m}{2}\Vert y-x\Vert _2^2\). The constant m can be viewed as a lower bound of the strong convexity of all the proximal functions \(\{\psi _{t}(x)\}_{t=1}^T\), where T is the total number of iterations. Therefore, Assumption 1 is actually a mild assumption. Here we provide a few examples of different proximal functions that satisfy Assumption 1, and the corresponding values of m to show the cases where our general theory can be applied.

Example 1

\(\psi _{t}(x) = \phi _{t}(x) + \frac{c}{2}\Vert x\Vert _2^2\), where \(c > 0\) is a real constant and each \(\phi _{t}(x)\) is an arbitrary convex differentiable function, then \(m = c\). It can be observed that this example reduces to the ProxSGD algorithm when \(\phi _t(x) = 0\) and \(c = 1\).

Example 2

\(\psi _{t}(x) = \frac{c_t}{2}\Vert x\Vert _2^2\), where \(c_t\) is a function of t that satisfies \(c_t \ge c, \forall t \in [T]\) for some constant \(c > 0\), then \(m = c\). This case is equivalent to using time-varying step sizes in ProxSGD even when \(\alpha _t\) is fixed, because \(B_{\psi _t}(x, y) = \frac{c_t}{2}\Vert x-y\Vert _2^2\) and we can divide all terms in Eq. (2) by the time-varying \(c_t\) simultaneously. In other words, we only require the actual step sizes (\(\alpha _t /c_t\)) to be upper bounded to satisfy Assumption 1, which is natural since an unbounded step size is never favorable during the optimization process.

Example 3

\(\psi _{t}(x) = \frac{1}{2}\Vert x\Vert _p^2\), where \(1<p\le 2\), then \(m = (p-1)\) because of the following sequence of inequalities

$$\begin{aligned} \begin{aligned} \frac{p-1}{2}\Vert x-y\Vert _2^2 \le \frac{p-1}{2}\Vert x-y\Vert _p^2 \le B_{\psi _t}(x,y), \end{aligned} \end{aligned}$$

These are standard results in convex analysis and the proof of them can be found in, e.g., Asi and Duchi (2019). As we have mentioned, such a case is especially useful when the domain \({\mathcal{X}}\) is the \(\ell _p\)-ball.

Example 4

\(\psi _{t}(x) = \frac{1}{2}\langle x, H_{t} x \rangle\), where \(H_t \in {\mathbb{R}}^{d\times d}\) and \(H_{t} \succeq c I, \forall t \in [T]\) for a constant \(c>0\), then \(m = c\). This case covers all the self-adaptive algorithms with a lower bound on the positive definiteness of the matrix \(H_t\). Such a lower bound can be guaranteed by simply adding cI to \(H_t\) when it is a non-negative diagonal matrix or by using some assumptions. More details will be discussed in Sect. 4.

Example 5

\(\psi _{t}(x) = \sum _{i=1}^d x_i \log x_i\). This case is useful when the domain is the simplex \({\mathcal{X}} = \{x \in {\mathbb{R}}^d \mid x \succeq 0, 1^Tx = 1\}\). Bregman divergence \(B_{\psi _t}(x,y)\) becomes the well-known KL divergence between x and y, and \(m = 1\).

Table 1 Comparisons of the SFO complexity (defined in Assumption 3) of different algorithms to reach the stationary point of the generalized gradient (Definition 1) in the nonconvex problems. Nonsmooth stands for the nonconvex nonsmooth problem and P–L represents the generalized P–L conditioned problem (Defition 2). n is the total number of samples and \(\epsilon\) is the bound on the norm of the generalized gradient, i.e., \({\mathbb{E}}[\Vert {g}_{X, t}\Vert ^2] \le \epsilon\). N.A. stands for not available because SpiderBoost and ProxSARAH did not provide convergence results for the P–L conditioned problem
Full size table

The convergence of different algorithms in the nonconvex smooth optimization problem (i.e., when \(h(x) = 0\)) is usually represented by the stationarity of the gradient \(\nabla F(x)\), i.e., given a point \({\hat{x}}\) chosen by a stochastic algorithm, we have \({\mathbb{E}}[\Vert \nabla F({\hat{x}}) \Vert ^2] \le \epsilon\)Footnote 1. However, because of the existence of h(x) in nonsmooth nonconvex problems, we need a special definition of the generalized gradient for adaptive mirror descent algorithms and the corresponding convergence criterion in order to analyze their convergence, as in Reddi et al. (2016b) and Li and Li (2018).

Definition 1

Given a point \(x_t \in {\mathcal{X}}\), the generalized gradient \({g}_{X,t}\) is defined as \({g}_{X,t} = \frac{1}{\alpha _t}(x_t - x_{t+1}^+)\), where \(x^{+}_{t+1}\) is defined as

$$\begin{aligned} \begin{aligned} x_{t+1}^+&= \text {argmin}_{x \in {\mathcal{X}}} \left\{ \alpha _t \langle \nabla f(x_t), x \rangle + \alpha _t h(x) + B_{\psi _t}(x, x_t) \right\} \end{aligned} \end{aligned}$$

We define the convergence criterion to be the stationarity of the generalized gradient \({\mathbb{E}}[\Vert {g}_{X, t}\Vert ^2] \le \epsilon\). In the definition of \(x^+_{t+1}\), we replace the stochastic gradient \(g_t\) in Eq. (2) by the accurate, full-batch gradient \(\nabla f(x_t)\). In other words, \(x_{t+1}^+\) is the next-step parameter if we use the full batch gradient \(\nabla f(x_t)\) for mirror descent at time t, and \(g_{X,t}\) is the difference between \(x_t\) and \(x_{t+1}^+\) scaled by the step size. Therefore, the generalized gradient is small when \(x_{t+1}^+\) and \(x_t\) are close enough and thus the algorithm converges. We emphasize that Definition 1 and the convergence criterion are commonly observed in the mirror descent algorithm literature such as Ghadimi et al. (2016); Li and Li (2018). We provide a few examples of \(g_{X,t}\) for further clarifications. If \(\psi _t(x) = \frac{1}{2}\Vert x\Vert ^2_2\), then the definition is equivalent to the gradient mapping in Li and Li (2018). If we further assume h(x) is a constant, then Definition 1 reduces to the original full batch gradient \(\nabla f(x)\). When h(x) is a constant and \(\psi _t(x) = \frac{1}{2}\langle x, H_t x\rangle\), the generalized gradient is equivalent to \(H_t^{-1} \nabla f(x)\), which is the update of self-adaptive algorithms.

Now, for the functions \(\{f_i\}_{i=1}^n\), we assume that they have L-Lipschitz continuous gradients, which is a standard assumption in the nonconvex optimization literature (Ghadimi et al., 2016; Reddi et al., 2016b; Li & Li, 2018).

Assumption 2

Each function \(f_i(x)\) has an L-Lipschitz continuous gradient, i.e., there exists a constant \(L > 0\) such that for any \(x, y \in {\mathcal{X}}\),

$$\begin{aligned} \begin{aligned} \Vert \nabla f_i(x) - \nabla f_i(y)\Vert _2 \le L\Vert x-y\Vert _2 \end{aligned} \end{aligned}$$

As in Li and Li (2018), we use the stochastic first-order oracle (SFO) complexity to compare the convergence rates of different algorithms.

Assumption 3

When given a parameter x, SFO returns one stochastic gradient \(\nabla f_j (x)\) that is unbiased with bounded variance \(\sigma ^2\), i.e., for any \(x \in {\mathcal{X}}\)

$$\begin{aligned} \begin{aligned}&{\mathbb{E}}_{j \sim [n]} \left[ \nabla f_j(x) \right] = \nabla f(x), {\mathbb{E}}_{j \sim [n]} \left[ \Vert \nabla f_j(x) - \nabla f(x)\Vert _2^2 \right] \le \sigma ^2 \end{aligned} \end{aligned}$$

In other words, the SFO complexity measures the number of gradient computations in the optimization process and thus how fast the algorithm converges. We summarize the SFO complexity of a few mirror descent algorithms in the nonconvex nonsmooth optimization problem in Table 1.

3.3 Assumptions and definitions for P–L condition

Next, we present the additional assumptions and definitions needed for the convergence analysis under the generalized Polyak–Lojasiewicz (P–L) condition (Polyak, 1963). The original P–L condition (in smooth problems, i.e., \(h(x) = 0\)), also known as the gradient dominant condition, is defined as

$$\begin{aligned} \begin{aligned} \exists \mu > 0, ~s.t.~ \Vert \nabla F(x)\Vert ^2 \ge 2\mu (F(x) - F^*), ~\forall x \in {\mathbb{R}}^d \end{aligned} \end{aligned}$$

which is weaker than restricted strong convexity and it has been studied in many nonconvex convergence analyses such as Reddi et al. (2016); Zhou et al. (2018b); Lei et al. (2017). However, because of the existence of h(x) in nonsmooth problems, the original P–L condition is no longer useful. Instead, we utilize the definition of the generalized gradient \(g_{X,t}\) to define the generalized P–L condition as follows.

Definition 2

The loss function F(x) satisfies the generalized P–L condition if

$$\begin{aligned} \begin{aligned} \exists \mu > 0, ~ s.t. ~\Vert g_{X,t}\Vert ^2 \ge 2\mu \left( F(x) - F^* \right) , ~ \forall x \in {\mathcal{X}} \end{aligned} \end{aligned}$$

where \(g_{X,t}\) is the generalized gradient defined in Definition 1.

Li and Li (2018) used a similar definition of the general P–L condition when \(\psi _t(x) = \frac{1}{2}\Vert x\Vert _2^2\), and ours is a natural extension since we consider general proximal functions in Eq. (2). The above definition reduces to the P–L condition by Li and Li (2018) when \(\psi _t(x) = \frac{1}{2}\Vert x\Vert _2^2\). If we further assume that h(x) is a constant, then Definition 2 is the same as the original P–L condition. For simplicity, we further assume that the constant \(\mu\) satisfies \(L/(m^2\mu ) \ge \sqrt{n}\), similar to what Li and Li (2018); Reddi et al. (2016b) assumed in their papers. The condition is similar to the “high condition number regime” for strongly convex optimization problems. It is noticeable that given the general P–L condition, the original convergence criterion \(({\mathbb{E}}[\Vert g_{X,t}\Vert ^2] \le \epsilon )\) is equivalent to

$$\begin{aligned} \begin{aligned} 2\mu \left[ {{\mathbb{E}}[F(x)] -F^*} \right] \le \epsilon \end{aligned} \end{aligned}$$

which means that the algorithm converges to the global minimum. The SFO complexity of a few mirror descent algorithms in the generalized P–L conditioned problem is also provided in Table 1.

4 Algorithm and convergence

In this section, we present our main theoretical results. In Sect. 4.1, we provide the convergence rate of the general stochastic adaptive mirror descent algorithm as a competitive baseline, which matches the best existing rates of non-adaptive mirror descent algorithms. In Sects. 4.2, 4.3, and 4.4, we present our generalized variance reduced mirror descent algorithm framework SVRAMD and provide its convergence analysis to show that variance reduction can accelerate the convergence of most adaptive mirror descent algorithms in both the nonconvex nonsmooth problem and the generalized P–L conditioned problem.

4.1 The adaptive mirror descent algorithm and its convergence

We first provide the the SFO complexities of the general Stochastic Adaptive Mirror Descent (SAMD) algorithm (Algorithm 1) in the nonconvex nonsmooth problem and the generalized P–L conditioned problem as the baseline, which are to the best of our knowledge, very important results but has not been established in literature. We prove that in both problems, the convergence rates of Algorithm 1 are similar to those of the non-adaptive mirror descent algorithm (Ghadimi et al., 2016), (Karimi et al., 2016). The proof of these important baseline SFO complexities are provided in Appendix A for the readers’ reference.

figure a

Theorem 1

Suppose that Assumption 1, 2, 3are satisfied. Set the learning rate and the mini-batch size in Algorithm 1 to be \(\alpha _t = m/L, b = n \wedge ({12\sigma ^2}/(m^2\epsilon ))\), then the output of Algorithm 1 converges with SFO complexity

$$\begin{aligned} O \left( \frac{n}{\epsilon } \wedge \frac{\sigma ^2}{\epsilon ^2} + n \wedge \frac{\sigma ^2}{\epsilon } \right) \end{aligned}$$

Remarks. The above complexity can be treated as \(O(n\epsilon ^{-1} \wedge \epsilon ^{-2})\) and it is the same as the complexity of non-adaptive mirror descent algorithms by Ghadimi et al. (2016). Algorithm 1 needs a relatively large mini-batch size (\(b = O(\epsilon ^{-1})\)) to obtain a convergence rate close to that of ProxGD (\(O(n\epsilon ^{-1})\)) and ProxSGD (\(O(\epsilon ^{-2})\)) (Reddi et al., 2016). However, it is still only asymptotically as fast as the faster one between ProxGD and ProxSGD, depending on whether \(\epsilon ^{-1}\) is larger than the sample size n. Next we provide the convergence rate of Algorithm 1 in the generalized P–L conditioned problem.

Theorem 2

Suppose that Assumption 1, 2, 3are satisfied. Further assume that the loss function F(x) satisfies the generalized P–L condition (Definition 2). Set the learning rate and the mini-batch sizes in Algorithm 1 to be \(\alpha _t = m/L, b_t = n~ \wedge ~({2(1+m^2)\sigma ^2}/(\epsilon m^2\mu ))\), then the output of Algorithm 1 converges with SFO complexity

$$\begin{aligned} O \left( \left( \frac{n}{\mu } \wedge \frac{\sigma ^2}{\mu ^2\epsilon }\right) \log \frac{1}{\epsilon } \right) \end{aligned}$$

Remarks

The above result is of order \(O \left( \left( n \wedge \frac{1}{\epsilon }\right) \log \frac{1}{\epsilon } \right)\). Similar to Theorem 1, the proved SFO complexity matches the smaller complexity of ProxSGD and ProxGD in the generalized P–L conditioned problem (Karimi et al., 2016). We emphasize that since the general Algorithm 1 covers ProxSGD (\(b=1\)) and ProxGD (\(b=n\)) with \(\psi _t(x) = \frac{1}{2}\Vert x\Vert _2^2\) as special cases, we believe that our convergence rates in Theorems 1 and 2 are the best rates achievable and serve as strong baselines.

4.2 The general variance reduced algorithm-SVRAMD

figure b

We now present the proposed Stochastic Variance Reduced Adaptive Mirror Descent (SVRAMD) algorithm, which is a simple and generalized variance reduction framework for different mirror descent algorithm designed for different parameter domains \({\mathcal{X}}\). We provide the pseudo-code in Algorithm 2. The input parameters \(B_t\) and \(b_t\) are called the batch sizes and the mini-batch sizes. The algorithm consists of two loops: the outer loop has T iterations while the inner loop has K iterations. At each iteration of the outer loop (line 4), we estimate a large batch gradient \(g_t = \nabla f_{{\mathcal{I}}_t}({x}_{t})\) with batch size \(B_t\) at the reference point \(x_t\), both of which will be stored during the inner loop. At each iteration of the inner loop (line 7), the large batch gradient is used to reduce the variance of the small batch gradient \(\nabla f_{\widetilde{{\mathcal{I}}}_t}(y_{k}^t)\) so that the convergence becomes more stable. Note that in line 8, the proximal function is an undetermined \(\psi _{tk}(x)\) which can change over time, therefore Algorithm 2 covers ProxSVRG+ and a lot more algorithms with different proximal functions. For example, if \(\psi _{tk}(x) = \frac{1}{2}\Vert x\Vert _2^2\), then \(B_{tk}(y, y_k^t) = \frac{1}{2}\Vert y - y_k^t\Vert _2^2\) and SVRAMD reduces to ProxSVRG+ (Li & Li, 2018). If \(\psi _{tk}(x) = \frac{1}{2} \langle x, H_{tk}x \rangle\), where \(H_{tk} \succeq mI\), then SVRAMD reduces to variance reduced self-adaptive algorithms for different matrices \(H_{tk}\), e.g., VR-AdaGrad in Sect. 4.5.

4.3 Nonconvex nonsmooth convergence

Now given the general form of Algorithm 2, we provide its SFO complexity in the nonconvex nonsmooth problem in the following theorem.

Theorem 3

Suppose that Assumption 1, 2, 3are satisfied. Set the learning rate, the batch sizes, the mini-batch sizes, and the number of inner-loop iterations in Algorithm 2 to be \(\alpha _t = m/L, ~ B_t = n \wedge ({20\sigma ^2}/m^2\epsilon ), ~b_t = b, ~K = \left\lfloor {\sqrt{b/20}}\right\rfloor \vee 1\), then the output of Algorithm 2 converges with SFO complexity

$$\begin{aligned} O \left( n + \frac{n}{\epsilon \sqrt{b}} \wedge \frac{\sigma ^2}{\epsilon ^2\sqrt{b}} + \frac{b}{\epsilon } \right) \end{aligned}$$

Remarks

The proof is relegated to Appendix B. Theorem 3 essentially claims that with Assumptions 1, 2, 3, we can guarantee the SFO complexity of Algorithm 2 is \(O \left( \frac{n}{\epsilon \sqrt{b}} \wedge \frac{\sigma ^2}{\epsilon ^2\sqrt{b}} + \frac{b}{\epsilon } \right)\), with an undetermined mini-batch size b to be tuned later.

Although \(\alpha _t\) is fixed in the theorem, \(\psi _{tk}\) can change over time and hence results in the adaptivity in the algorithm. For example, our theory indicates that using time-varying dynamic step sizes is allowed during the optimization process (Example 2 in Sect. 3). When we take the proximal function to be \(\psi _{tk}(x) = \frac{c_{tk}}{2}\Vert x\Vert _2^2, c_{tk} \ge m\), Algorithm 2 uses time-varying dynamic effective step size \(\alpha _t/c_{tk}\) (i.e., the same as \(\eta _t\) in Li and Li (2018)). As long as the effective step sizes \(\alpha _t/c_{tk}\) are upper bounded by the constant \((m/L)/m = 1/L\), Algorithm 2 still converges with the same complexity. Such a constraint is easy to satisfy for many step size schedules such as (linearly) decreasing step sizes, cyclic step sizes and warm up. Besides, \(\psi _{tk}\) can be even more complicated, such as Examples 1 and 4 we have mentioned in Sect. 3, which will be discussed later. Another interesting result observed in our theorem is that when m is small, we require a relatively larger batch size \(B_t\) to guarantee the fast convergence rate. We will later show that this intuition is actually supported by our experiments in Sect. 5.

While SCSG (Lei et al., 2017) and ProxSVRG (Reddi et al., 2016b) achieve their best convergence rate at either a too small or a too large mini-batch size, i.e., \(b =1\) or \(b=n^{2/3}\), our algorithm achieves its best performance using a moderate mini-batch size \(\epsilon ^{- 2/3}\). We provide the following corollary.

Corollary 1

Under all the assumptions and parameter settings in Theorem 3, further take \(b = \epsilon ^{- 2/3} \le n\), then the output of Algorithm 2 converges with SFO complexity

$$\begin{aligned} O \left( \frac{n}{\epsilon ^{2/3}} \wedge \frac{1}{\epsilon ^{5/3}} + \frac{1}{\epsilon ^{5/3}} \right) \end{aligned}$$

Remarks

The above SFO complexity is provably better than the SFO complexity of the SAMD algorithm in Theorem 1. Note that the number of samples is usually very large in modern datasets, such as \(n = 10^6\), thus \(b = \epsilon ^{- 2/3}\le n\) can be easily satisfied with a constant mini-batch size and a small enough \(\epsilon\), such as \(b=10^2, \epsilon = 10^{-3}\). If the above best complexity cannot be achieved, meaning that either n or \(\epsilon\) is too small, some sub-optimal solutions are still available for fast convergence. For example, setting \(b = n^{2/3}\) would generate \(O(n^{2/3}\epsilon ^{-1})\) SFO complexity, which is also smaller than the SFO complexity of Algorithm 1. Therefore, we conclude that if the parameters are carefully chosen, variance reduction can reduce the SFO complexity and accelerate the convergence of any adaptive mirror descent algorithm that satisfies Assumption 1 in the nonsmooth nonconvex problem. We summarize the SFO complexity generated by a few different choices of b in the nonconvex nonsmooth problem in Table 2.

As can be observed in Table 1 and 2, the SFO complexity of SVRAMD is the same as the best SFO complexity of ProxSVRG+ and SCSG in the nonsmooth problem. Although it is slightly worse than the-state-of-the-art SFO complexity of some optimization algorithms in \({\mathbb{R}}^d\) (e.g., the complexity of PAGE (Li et al., 2021)), we emphaisze that our paper is the first step towards proving that the simple variance reduction technique can accelerate most adaptive mirror descent algorithms. Whether it is possible to achieve the state-of-the-art complexity for different mirror descent algorithms on different domains \({\mathcal{X}}\) still remain interesting open questions. Moreover, we will show that our algorithm achieves the state-of-the-art complexity in the generalized P–L conditioned problem in the next subsection.

Table 2 Summary of the SFO complexity of SVRAMD given different choices mini-batch sizes b in both the nonsmooth problem and the generalized P–L conditioned problem (Theorem 3, 4). All notations follow Table 1. SVRAMD is much faster than the SAMD algorithm in the middle three cases, i.e., \(b = \epsilon ^{-2/3}\), \(b = \epsilon ^{-1}\) and \(b = n^{2/3}\). It is asymptotically at most as fast as SAMD when the mini-batch size is either too small or too big, i.e., \(b=1\) or \(b=n\)
Full size table

4.4 Convergence under the generalized P–L condition

Now we provide the convergence analysis of Algorithm 2 under the generalized P–L condition (Definition 2). Note that the only difference in Algorithm 2 for such problems is the final output, where we directly use the last \(x_{T+1}\) rather than randomly sample from the historical \(x_t\)s. Therefore, we preserve the simplicity of our algorithm in both the nonconvex nonsmooth problem and the generalized P–L conditioned problem. Now we present the SFO complexity of SVRAMD under the generalized P–L condition and show its linear convergence rate.

Theorem 4

Suppose that Assumption 1, 2, 3are satisfied. Further assume that F(x) satisfies the generalized P–L condition (Definition 2). Set the learning rate, the batch sizes, the mini-batch sizes, and the number of inner loop iterations in Algorithm 2 to be \(\alpha _t = m/L, ~B_t = n \wedge ({10\sigma ^2}/({\epsilon m^2\mu })), ~b_t = b, ~K = \lfloor {\sqrt{b/32}} \rfloor \vee 1\), then the output of Algorithm 2 converges with SFO complexity

$$\begin{aligned} O \left( (n \wedge \frac{\sigma ^2}{\mu \epsilon }){ \frac{1}{\mu \sqrt{b}}\log \frac{1}{\epsilon }} + { \frac{b}{\mu }\log \frac{1}{\epsilon }} \right) \end{aligned}$$

Remarks

The proof is provided in Appendix C. The above SFO complexity is of size \({\widetilde{O}}((n \wedge ( \epsilon )^{-1})b^{-1/2} + b)\) if we hide the logarithm terms. Compared with the SFO complexity of the SAMD algorithm, our complexity can be arguably smaller when we choose an appropriate mini-batch size b, which further proves our conclusion that variance reduction can be applied to most adaptive mirror descent algorithms to accelerate their convergence. We provide the following corollary for the best choice of b to show its effectiveness.

Corollary 2

Under all the assumptions and parameter settings in Theorem 4, further take \(b = (\mu \epsilon )^{- 2/3} \le n\). Then the output of Algorithm 2 converges with SFO complexity

$$\begin{aligned} O \left( (\frac{n\epsilon ^{1/3}}{\mu ^{2/3}} \wedge \frac{\epsilon ^{-2/3}}{\mu ^{5/3}} + \frac{\epsilon ^{-2/3}}{\mu ^{5/3}})\log \frac{1}{\epsilon } \right) \end{aligned}$$

Remarks

The above complexity is provably better than the SFO complexity of SAMD in Theorem 2. Moreover, our algorithm is so simple that it does need to perform any restart (as in ProxSVRG and ProxSAGA (Reddi et al., 2016b)) or use the stochastically controlled iterations or probability estimators tricks (as in SCSG and PAGE (Lei & Jordan, 2020; Li et al., 2021)). Therefore, Algorithm 2 automatically switches to fast convergence in regions satisfying the generalized P–L condition. We also provide the SFO complexity of some other choices of b in Table 2 for a clearer comparison. Similarly, if \(b = (\mu \epsilon )^{- 2/3}\) is impractical, using \(b = n^{2/3}\) also generates faster convergence than SAMD.

As can be observed in Tables 1 and 2, because in Corollary 2 we take \(b = (\mu \epsilon )^{-2/3} \le n\) and thus our \(O \left( \frac{1}{\epsilon ^{2/3}}\log \frac{1}{\epsilon } \right)\) complexity is better than the \(O \left( n \log \frac{1}{\epsilon } \right)\) complexity of PAGE (Li et al., 2021). Similar conclusions can be drawn for the case \(b = n^{2/3}\). The SFO complexity in Corollary 2 matches the complexity of ProxSVRG+, which is the state-of-the-art complexity in the generalized P–L conditioned problem. Therefore, we conclude that SVRAMD achieves comparable performances in both the nonsmooth problem and the P–L conditioned problem, and it accelerates SAMD.

4.5 Special case: self-adaptive algorithms

figure c

As we have mentioned in Sect. 3, self-adaptive algorithms such as AdaGrad are special cases of the general Algorithm 1 and thus we can use Algorithm 2 to accelerate them. The proximal functions of most adaptive algorithms have the form of \(\psi _t(x) = \frac{1}{2}\langle x, H_t x \rangle\), where \(H_t \in {\mathbb{R}}^{d\times d}\) is often designed to be a diagonal matrix.

Assumption 1 is satisfied if we consistently add a constant matrix mI to \(H_t\), with I being the identity matrix. We remark that such an operation is commonly used in self-adaptive algorithms to avoid division by zero or improper inverse operations (Duchi et al., 2010; Kingma & Ba, 2015), and thus variance reduction can be applied. Assumption 1 can also be satisfied for many special designs of \(H_t\) with some mild assumptions. For example, if \(H_{t,ii} = \sqrt{g_{1,i}^2 + g_{2,i}^2 + \cdots g_{t,i}^2}, \forall i \in [d]\) (the original AdaGrad algorithm), then \(H_{t} \succeq m I\) if there exists one \(\tau _i \in [t]\) on each dimension i such that \(g_{\tau _i, i} \ge m\), meaning that there is at least one derivative larger than m on each dimension in the whole optimization process. If such a mild condition holds, then the conclusions in Theorem 3, 4 and Corollary 1, 2 still hold.

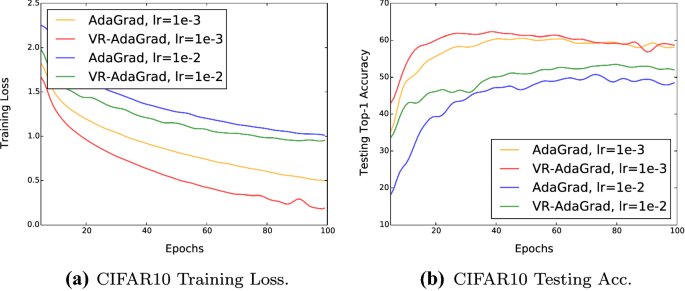
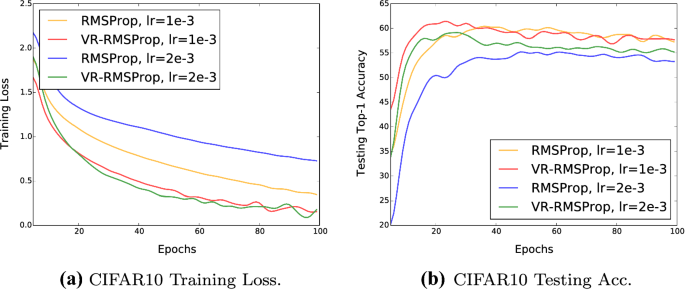
However, notice that the strong convexity lower bounds of these algorithms are relatively smaller (the constant m in the added matrix mI is often set as 1e-2 or even smaller in real experiments), Theorem 3 implies that the batch size \(B_t\) needs to be sufficiently large for these algorithm to converge fast. If variance reduction can work with such algorithms with small m, then we should expect good performances with the other algorithms that have large m’s. We provide the implementation for Variance Reduced AdaGrad (VR-AdaGrad) in Algorithm 3 and Variance Reduced RMSProp (VR-RMSProp) is similar.

One interesting question here is whether VR-AdaGrad and VR-RMSProp can converge even faster in nonconvex nonsmooth problems or generalied P–L conditioned problems, since AdaGrad and RMSProp are known to converge faster than SGD in convex problems. Our conjecture is that they cannot do so, at least not in the nonconvex case because their rapid convergence relies on not only the convexity of the problem, but also the sparsity of the gradients (Duchi et al., 2011). If neither of these two assumptions is assumed, we believe it would be difficult to prove any superiority of AdaGrad/RMSProp.

5 Experiments

In this section, experimental results are provided to validate our theoretical claims.

5.1 Synthetic data experiments

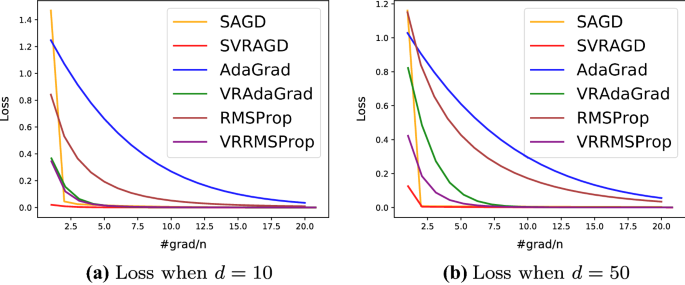
We first provide some preliminary experimental results on synthetic data to prove the correctness of our theory. We choose the task of regularized linear regression \(F(x) = \frac{1}{n}\Vert Ax-y\Vert _2^2 + c \Vert x\Vert _2^2\) with \(A \in {\mathbb{R}}^{n \times d}\) and \(x \in {\mathcal{X}} \subseteq {\mathbb{R}}^d\). We set the domain to be \({\mathcal{X}} = \{ x \in {\mathbb{R}}^d \mid \Vert x\Vert _{\infty } \le 1\}\). Each entry of the target \(x^*\) is generated from \({\mathcal{X}}\) uniform randomly. The rows of A are generated uniform randomly from the standard basis of \({\mathbb{R}}^{d}\) and the observation \(y \in {\mathbb{R}}^n\) is generated by \(y = Ax^* + v\), where \(v \sim {\mathcal{N}}(0, I_n)\). We examine our theoretical claims with different choices of the proximal functions, i.e., the case \(\frac{1}{2}\Vert x\Vert _2^2\), which we call SAGD and SVRAGD for Algorithm 1 and 2 respectively in Fig. 1 to avoid confusions, and the adaptive case \(\frac{1}{2}\langle x, H_t x \rangle\) where \(H_t\) is taken to be the diagonal matrices in AdaGrad, RMSProp, VR-AdaGrad, and VR-RMSProp (as discussed in Sect. 4.5). The hyper-parameters of aforementioned algorithms such as the learning rate, the batch sizes are chosen to be exactly the same as in Theorem 1 and 3. As shown in Fig. 1, variance-reduced algorithms converge much faster than the baseline algorithms in both the two cases \(d=10\) and \(d=50\), showing that our proposed method of variance reduction is effective. More details of our synthetic experiments can be found in Appendix D.2.

Fig. 1
figure 1

Performance of SAGD, SVRAGD, AdaGrad, RMSProp, VR-AdaGrad, and RMSProp on synthetic linear regression data. a training loss when \(d=10\) b training loss when \(d=50\)

Full size image

5.2 Deep learning experiments

We then present several experiments on training both shallow and deep neural networks on image datasets to further show the effectiveness of variance reduction in the SVRAMD algorithm, which are known to have highly nonconvex loss landscapes. Specifically, we train a two-layer fully connected network on the MNIST dataset, the LeNet (LeCun et al., 1998) on the CIFAR-10 dataset, and the ResNet-20 model on the CIFAR-100 dataset (He et al., 2016).

In general, we have followed the settings by Zhou et al. (2018b) on SNVRG for all our experiments. Except for normalization, we do not perform any additional data transformation or augmentation techniques such as rotation, flipping, and cropping on the images. Our code is based on publicly released PyTorch code.Footnote 2 All experiments here are conducted on one Nvidia V100 GPU. We have thoroughly tuned the hyper-parameters for all the algorithms. One important remark here is that for the batch sizes and mini batch sizes \(B_t\) and \(b_t\), we follow Zhou et al. (2018b) to use a slightly different but equivalent notation of batch size ratio \(r = B_t/b_t\). Increasing this ratio when \(b_t\) is fixed would be the same as increasing the batch size \(B_t\). More details of our deep learning experiments can be found in Appendix D.3.

Fig. 2
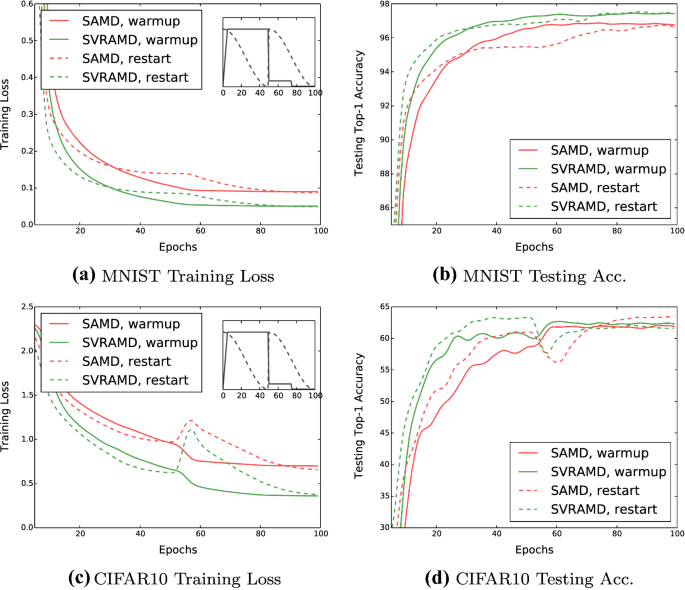
figure 2

Performance of SAMD and SVRAMD with different step size schedules. The solid lines are trained with the warmup schedule (warmup for 5 epochs then step decay) and the dashed lines are trained with the warm restart schedule. We plot the two schedules at the top-right corners of the training loss subfigures for the readers’ reference. a, b training loss and testing accuracy using fully connected network on MNIST. c, d training loss and testing accuracy using LeNet on CIFAR-10. The results were averaged over 5 runs

Full size image
Fig. 3
figure 3

a, d: training loss and testing accuracy on MNIST. b, e: training loss and testing accuracy on CIFAR-10. c and f: training loss and testing accuracy on CIFAR-100. The results are averaged over 5 runs

Full size image
Fig. 4
figure 4

a, d: training loss with different r on MNIST. b, e training loss with different r on CIFAR10 . c, f training loss with different ratio r on CIFAR100

Full size image

We first validate our claims in Sect. 4 by showing that variance reduction can work well with different step size schedules. We choose two special schedules that are both complicated enough and popular nowadays, warm up and warm restart. The proximal functions are set to be \(\frac{1}{2\alpha _t}\Vert x\Vert _2^2\), where \(\alpha _t\) is the step size. For warm up, we increase the step size from zero to the best step size of SAMD/SVRAMD linearly for the initial 5 epochs and then multiply the step size by 0.1 at the 50-th and the 75-th epoch. For warm restart, we decrease from the best step size to zero with cosine annealing in 50 epochs and then restart the decay. The training loss, the testing accuracy and the step size schedules on MNIST and CIFAR-10 are plotted in Fig. 2. As can be seen in the figures, converges faster than SAMD with both of the two special step size schedules, proving our claim that as long as the step sizes are bounded, variance reduction can still improve the convergence rate of SAMD with dynamic step sizes.

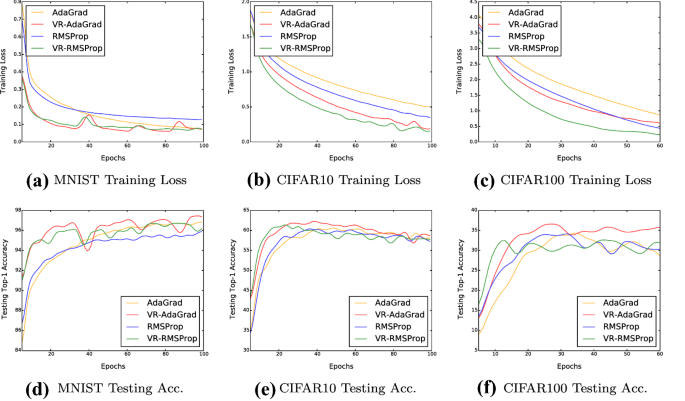
We then choose VR-AdaGrad and VR-RMSProp as the other two special examples of our general algorithm because they have relatively smaller lower bound of the strong convexity and their proximal functions are even more complicated. We use the constant step size schedule for these algorithms as they are self-adaptive. The training loss and the testing Top-1 accuracy of VR-AdaGrad, VR-RMSProp, and their original algorithms on all the three datasets are plotted in Fig. 3. As can be observed, the variance reduced algorithms converge faster than their original algorithms and their best testing Top-1 accuracy is also comparable or even higher, proving the effectiveness of variance reduction. We emphasize that the experiments are not designed to pursue the state-of-the-art performances, but to show that variance reduction can work well with any adaptive proximal functions and contribute to faster training, even if the proximal functions have very small strong convexity lower bound.

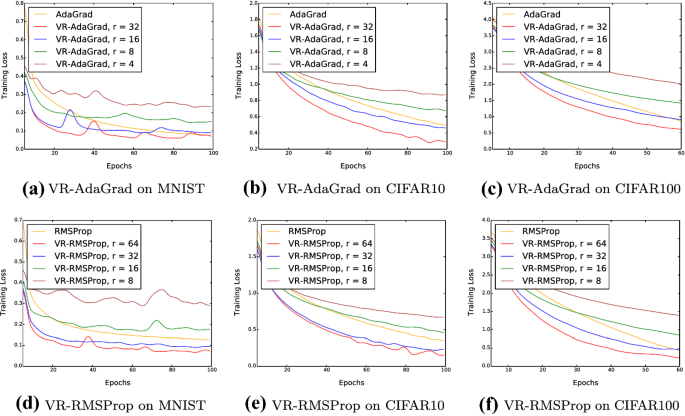
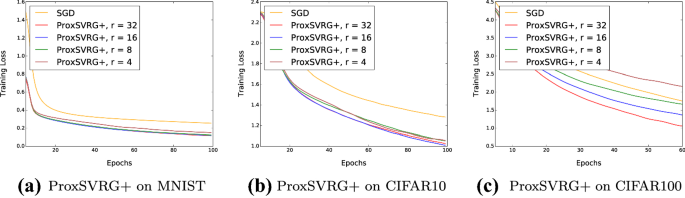
Finally, we also show that algorithms with weaker convexity need a larger batch size \(B_t\) to converge fast, which corresponds to our claims in Sects. 4.3 and 4.4. We fix the mini batch sizes \(b_t\) in VR-AdaGrad and VR-RMSProp to be the same as in the previous experiments and gradually increase the batch size ratio r. The baseline ratios of ProxSVRG+, which has a large strong convexity lower bound, are provided in Appendix D for the readers’ reference and the training performances of VR-AdaGrad and VR-RMSProp with different r are shown in Fig. 4. Note that ProxSVRG+ only needs a small ratio (\(r=4\) or \(r=8\)) to be faster than SGD (Li & Li, 2018), but for VR-RMSProp, even when \(r = 16\), the algorithms still do not converge faster than RMSProp, proving that algorithms with weaker convexity need larger batch sizes \(B_t\) to show the effectiveness of variance reduction.

6 Conclusions and future works

In this work, we provide the first algorithmic framework for accelerating adaptive mirror descent algorithms in different parameter domains using variance reduction. Theoretically, we prove that the proposed SVRAMD algorithm improves the convergence rates of adaptive mirror descent algorithms under a very mild assumption, both in the general nonsmooth nonconvex problems and the generalized P–L conditioned problems. Our theoretical results even match the state-of-the art results in the generalized P–L conditioned problems. Based on the generality of our algorithmic framework and the analysis, our theory can be applied to many different problems, such as (1). proving the soundness of using time-varying step sizes in the training process of SVRAMD, and (2). the effectiveness of applying variance reduction to adaptive algorithms such as AdaGrad and RMSProp. A potential future work direction is whether our Assumption 1 can still be replaced by weaker conditions, such as the CHEF conditions Lei and Jordan (2020) have mentioned in the convex case. Another interesting direction is whether the SFO complexity in the nonconvex nonsmooth problem can be further improved with the help of additional algorithmic components, for example, the nested variance reduction technique by Zhou et al. (2018b), momentum accelerations by Allen-Zhu (2017), or the probabilistic estimators by Li et al. (2021).