Abstract
Federated learning performed by a decentralized networks of agents is becoming increasingly important with the prevalence of embedded software on autonomous devices. Bayesian approaches to learning benefit from offering more information as to the uncertainty of a random quantity, and Langevin and Hamiltonian methods are effective at realizing sampling from an uncertain distribution with large parameter dimensions. Such methods have only recently appeared in the decentralized setting, and either exclusively use stochastic gradient Langevin and Hamiltonian Monte Carlo approaches that require a diminishing stepsize to asymptotically sample from the posterior and are known in practice to characterize uncertainty less faithfully than constant step-size methods with a Metropolis adjustment, or assume strong convexity properties of the potential function. We present the first approach to incorporating constant stepsize Metropolis-adjusted HMC in the decentralized sampling framework, show theoretical guarantees for consensus and probability distance to the posterior stationary distribution, and demonstrate their effectiveness numerically on standard real world problems, including decentralized learning of neural networks which is known to be highly non-convex.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Bayesian learning and inference have received a lot of attention in the literature as a principled way to avoid over-fitting and/or to quantify uncertainties in an integrated fashion by estimating the posterior distribution of the model parameters rather than a point-wise estimate. However, analytical solutions of exact posterior or sampling from the exact posterior is often impossible due to the intractability of the evidence. Therefore, Bayesian inference often relies on sampling methods broadly known as Markov Chain Monte Carlo (MCMC). To this effect, consider the following computation of a Bayesian posterior across a decentralized data set:
where \(i\in [m]\) indicates the index from a set of partitioned data, distributed across a set of agents connected on a communication graph. Each of the agents has access to data samples \(\{X_i,Y_i\}\) that are in general expected to have different distributions, and it is expected that during the process of finding the posterior, the labels are distributed in a heterogeneous way across agents, however, we wish for them all to be able to make inference on all types of samples.
When the likelihood function \(p(\{X_i,Y_i\}\vert \omega )\) arises from M-estimation for an exponential family and the prior is conjugate, the resulting distribution of \(\pi (\omega )\) is known to be of Gibbs form, \(\pi (\omega ) \propto {e^{-U(\omega )}}\), where U is referred to as a potential function for \(\omega\). This makes the process amenable to techniques arising in stochastic differential equations (SDEs), namely Langevin dynamics and Hamiltonian Monte Carlo, which implement a discretization of certain SDEs. The stationary distribution of these processes with a gradient term \(\nabla U(\omega )\) as the drift term in the SDE is precisely the Gibbs distribution above. For high dimensional parameter vectors, these approaches have been shown theoretically and numerically to scale better. Ergodicity of these methods was established in Roberts and Tweedie (1996) and Durmus et al. (2017). For these class of methods, asymptotic convergence to the stationary distribution, regardless of its form, has been established, as well as geometric convergence in measure for when the target distribution \(\pi (\omega ) \propto {e^{-U(\omega )}}\) is strongly log-concave, i.e. U is strongly convex and smooth. However, a Metropolis acceptance-rejection step is necessary to correct for the discretization bias.
Recently, the so-called “stochastic gradient" Langevin Monte Carlo (SGLD) and Hamiltonian Monte Carlo (SGHMC) approaches have become popular with the seminal work of Welling and Teh (2011) on SGLD. See Chen et al. (2014) for a popular work on SGHMC specifically. This was developed for “big-data" contexts wherein it is preferable to subsample from the dataset at each iteration, making these methods resemble stochastic gradient descent. By incorporating a diminishing stepsize akin to stochastic approximation methods in the implementation of the discretization, the Metropolis adjustment becomes no longer necessary. One favorable feature of this class of algorithms is their correspondence to simulated annealing, and with a carefully diminishing step-size and injected noise, non-asymptotic guarantees with respect to global optimality can be achieved, see for instance the recent works (Gao et al., 2021; Akyildiz & Sabanis, 2020; Chau & Rásonyi, 2022)). With respect to sampling, theoretical guarantees for SGHMC come in the form of 1) convergence to the stationary distribution with a diminishing stepsize and log concave distributions (or a moderate relaxation thereof to a log Sobolev or Poincaré inequality), e.g., Teh et al. (2016), Zhang et al. (2017), Chen et al. (2020) and Zou and Gu (2021) or, 2) with a constant step-size and dissipativity, guarantees of a bound on the bias that increases with the step-size, e.g., Gao et al. (2021) and Akyildiz and Sabanis (2020). This contrasts with the Metropolis adjusted variant which guarantees exact convergence to the desired distribution. Note that many contemporary problems of interest, such as Bayesian neural networks, are not expected to satisfy even a log-Sobolev inequality. However, although the geometric (for log Sobolev distributions) and general (otherwise) ergodicity of Metropolis adjusted HMC is a stronger result, beyond (Durmus et al., 2017) the convergence analyses in the literature are scant, suggesting that overall the method is not as readily amenable to thorough analysis. This is due to the heterogenous multi step kernel associated with the Metropolis adjusted HMC operation, as opposed to the simpler SGHMC, which can also draw on extensive convergence theory for stochastic gradient approaches to optimization. In this paper we consider the proof techniques introduced in Bou-Rabee et al. (2020) for inexact HMC to show ergodicity of the stochastic process generated by our algorithm.
In comparing the two empirically, broadly speaking it has been observed that HMC in general can perform better than SGHMC in terms of characterizing the uncertainty, which can be seen visually as mapping the posterior more faithfully far from the mode, and in performance metrics by considering statistical quality (log likelihood) as opposed to optimization criteria (RMSE) (Izmailov et al., 2021; Cobb & Jalaian, 2020). An intuitive argument based on first principles of HMC in regards to why subsampling is expected to degrade the performance is given in Betancourt (2015). Furthermore, SGHMC, like SG methods in general, suffer significant hyperparametric sensitivity– the learning rate schedule must often be frequently tuned for each problem in order to observe strong performance. Of course, on the other hand, in the high data volume regime, it becomes unclear as to how to scale HMC with Metropolis adjustment, as even the acceptance-rejection step requires evaluation of the posterior on all of the samples, and so guarantees without using the entire dataset at every iteration are scant.
Thus the constant stepsize Metropolis adjusted Langevin and HMC methods, as compared to their diminishing stepsize stochastic gradient variants stand as complementary techniques with distinct comparative advantages and disadvantages. Namely, for handling the computational load of large datasets and obtaining accurate point estimates, the stochastic gradient variants are to be preferred, however, when statistical accuracy of the entire posterior is prioritized or the potential exhibits nonconvexities, the constant stepsize Metropolis adjusted variants are the more appropriate choice. Overall, we wish to emphasize that in considering the various schemes for sampling, full-batch or stochastic, adjusted or unadjusted, all have devoted literature towards analyzing their performance in the centralized setting. Practitioners and researchers may prefer one, but there are variants of all that perform sampling at a high level of performance and efficiency, and we make no claim that one is inherently superior than the other. Instead, in order to endow a statistician with the most comprehensive toolbox available, with the most fine tuned theoretical understanding, all methods should be analyzed in detail in various settings. This work presents a scheme indicating how one can perform full (adjusted) Hamiltonian Monte Carlo in an environment of decentralized networks, complementing similar works studying SG schemes.
In this paper, we consider sampling in a decentralized architecture motivated by extensions of federated learning where the decentralized Bayesian extension (Lalitha et al., 2019)–with a variational inference approach–are shown to provide further robustness. We also mention (Shoham et al., 2019) as reviewing the difficulties associated with scaling federated learning. Note that we are considering specifically a decentralized architecture, i.e., one in which there is no central node that coordinates and distributes the work, and not the “hub-spoke"/“parameter-server"/“master-worker" node architecture framework of distributed computing. Thus, the recently popular “divide-and-conquer" approach (e.g., Hsieh et al. (2014) and Mesquita et al. (2020) for a contemporary Bayesian example) is incomparable. The agents never get to aggregate information and can only communicate with specific neighbors as indicated on the group, with the ultimate goal of ultimately sampling from the same global distribution.
By using a schema incorporating methods amenable to high parameter dimension, we hope to develop an algorithm with which every agent on the network successfully samples from high dimensional distributions. As such, our work is contextualized within a handful of studies focusing on SDE methods for decentralized sampling. In particular, Kungurtsev (2020) provided convergence and consensus guarantees for decentralized Langevin dynamics when the posterior is strongly convex. A diminishing stepsize is needed to ensure asymptotic consensus, placing this work conceptually within the stochastic gradient variants. Independently, Gürbüzbalaban et al. (2020) studied stochastic gradient Langevin dynamics, using different proof techniques, as well as stochastic gradient Hamiltonian Dynamics, again for the setting wherein U is strongly convex. Extension for non-log-concave potentials, but satisfying a Sobolev inequality, was given in Parayil et al. (2020). More recently, directed graphs are considered (Kolesov & Kungurtsev, 2021). The theoretical guarantees in these works take the optimization over measures approach to the analysis, and assumptions on the growth of the potentials (either strong convexity of the Sobolev inequality) are required, and in most cases a diminishing stepsize is used. Since a Metropolis adjustment step is not present in any of these methods, this is natural to be expected.
In this paper, we complete the program of extending SDE based sampling methods to the decentralized context by presenting the first algorithm, together with guarantees, for implementing sampling from the constant stepsize Metropolis-adjusted framework on a decentralized platform. This presents two significant methodological challenges: achieving consensus without a diminishing stepsize and performing a Metropolis acceptance-rejection procedure in a decentralized way. By carefully incorporating techniques inspired from the decentralized optimization literature along with developing a novel method for approximating the Metropolis acceptance ratio, we present an algorithm that performs HMC for decentralized data. Conceptually we seek to achieve that each agent, asymptotically, performs HMC, however, with gradient evaluations on the entire data set through gradually diffusing information. Theoretically we prove a bound in expected L2 error between our algorithm and the chain as generated by the classical HMC kernel, quantitatively bounding the discrepancy in terms of the step-size and the total number of sampling iterations. Thus, modulo some adjustable level of error relative to the number of samples, our algorithm approximates the probabilistic convergence properties of HMC, as for instance derived in Durmus et al. (2017), which showed ergodicity for general potentials and geometric ergodicity for strongly convex potentials.
The salient technical features of our proposed solution, specifically, consists of three methodological novelties. First, we integrate the concept of (gradient) tracking as appearing in decentralized optimization (Di Lorenzo & Scutari, 2016; Pu & Nedić 2020) for sampling, for the first time, and indicate its analogous benefit of allowing each agent to asymptotically perform, effectively, optimization on the same global function. This is in contrast to a repeated “zig-zag" pattern of local optimization and consensus pushing in disparate directions at each iterate, even more crucial for sampling since effectively each iterate is important, rather than some specific limit points. Secondly, we obtain guarantees of asymptotic consensus by incorporating multiple mixing rounds in each iteration (Berahas et al., 2018). Finally, we utilize a Metropolis adjustment step to correct for the discretization bias encountered in constant-step-size HMC. In order to compute an approximation to the full posterior in a decentralized context, we introduce a technique of tracking a decentralized second order Taylor approximation of the posterior, using only Hessian-vector products, and similarly tracking to communicate and aggregate local information across the network.
1.1 Graph structure
In this section we present the notation we use regarding the abstract graph that we use to model the communication structure of the network. The notation is standard in the literature for decentralized learning and distributed optimization, and presents a network of reasonable generality.
The communication network of the agents is modeled as a fixed undirected graph \({\mathcal {G}}\triangleq ({\mathcal {V}},{\mathcal {E}})\) with vertices \({\mathcal {V}}\triangleq \{1,..,m\}\) and \({\mathcal {E}}\triangleq \{(i,j)\vert i,j\in {\mathcal {V}}\}\) representing the agents and communication links, respectively. We assume that the graph \({\mathcal {G}}\) is strongly connected. We note by \({\mathcal {N}}_i\) the neighbors of i, i.e., \({\mathcal {N}}_i = \{j:(i,j)\in {\mathcal {E}}\}\). We define the graph Laplacian matrix \({\textbf{L}}={\textbf{I}}-{\textbf{W}}\), where \({\textbf{W}}={\textbf{A}}\otimes {\textbf{I}}\) with \({\textbf{A}}\) satisfying \({\textbf{A}}_{ij}\ne 0\) if \((i,j)\in {\mathcal {E}}\) and \({\textbf{A}}_{ij}=0\) otherwise. We assume that \({\textbf{W}}\) is double stochastic (and symmetric, since the graph is undirected). The eigenvalues of \({\textbf{L}}\) are real and can be sorted in a nonincreasing order \(1=\lambda _1({\textbf{L}})> \lambda _2({\textbf{L}})\ge ...\ge \lambda _n({\textbf{L}})\ge 0\). Defining, \(\beta := \lambda _2({\textbf{L}})\) we shall make the following assumption,
Assumption 1.1
It holds that,
This assumption holds for all but a small class of unusual graphs satisfying the standard requirements of a doubly-stochastic matrix as appearing classically in network consensus schemes. The large class of satisfactory graphs include the common lattice and ring structures that appear in pre-defined environments. For simplicity, however, we consider static graphs (i.e., the links do not change with time) that are undirected (communication occurs either both ways or not at all along a between any two agents).
We shall define \({\bar{\beta }}\) to be the smallest eigenvalue of \({\textbf{L}}\) that is nonzero.
2 Decentralized metropolis-adjusted Hamiltonian Monte Carlo
We are now ready to introduce our approach, which we present formally in Algorithm 1. As part of our approach we introduce two key concepts: gradient tracking, and a Taylor approximation to Metropolis adjustment. We will describe both components in the subsequent sections before describing how they combine in Algorithm 1.
2.1 Gradient tracking
Gradient tracking is a technique that enables every agent to obtain an estimate of the full gradient of the potential in a decentralized setting. While originally introduced and implemented for decentralized nonconvex optimization (Di Lorenzo & Scutari, 2016), here we use gradient tracking to enable gradient-based sampling of a potential, whereby each agent only has access to its own portion of the data. In our method, each agent tracks both first and second order information of the global potential, which we denote as \({\textbf{g}}^t_i\) and \(\aleph ^t_i\) respectively.
We index the individual agents by i and the iteration counter by t. Recall the notation in introduction, namely (1) and the subsequent discussion of the parameters to be statistically estimated, \(\varvec{\omega }\), the data samples \(\{X_i,Y_i\}\) and the potential function in the Gibbs form of the posterior, \(U(\varvec{\omega })\). To perform gradient tracking, a weighted average of communicating neighbors is balanced at each iteration to accumulate the gradient. This weighted average is determined by the mixing matrix, \(\varvec{W}\), of the network. As a result, each agent computes its local gradient of the potential, \(\nabla U(\varvec{\omega }^t; X_i,Y_i)=\nabla U_i(\varvec{\omega }^t)\), and updates its global estimation of the gradient using its current local gradient, its previous local gradient, and its current estimation of the global gradient. We display this update equation as follows:
We intend that as the parameter estimates reach consensus (agreement across agents) we expect that \(\varvec{g}\) to also reach consensus and in effect, every agent samples HMC on the entire dataset. Since in the context of sampling, each iteration is counted rather than just asymptotic limit points, we believe this should improve posterior characterization and avoid the characteristic zig-zagging of decentralized algorithms without gradient tracking. Tracking the Hessian of the potential is necessary to obtain a global estimate of the Hessian of the Hamiltonian with respect to the parameters, which will permit the principled use of a Metropolis step, at least approximately.
2.2 Taylor approximated Metropolis adjustment
A key challenge in performing Metropolis adjustment in the decentralized setting is the necessity of computing an evaluation of the potential over the entire data-set, which is in actuality distributed across nodes. In our algorithm, we calculate the acceptance probability as
i.e., using local quantities \(\aleph _i\) and \(\varvec{g}_i\) that stand as surrogates for the global information. In this Section we shall explain and justify this approach.
The second key component of our approach builds on gradient tracking by utilizing the tracked second order term, \(\aleph ^t_i\). One of the challenges in performing decentralized MCMC, is the requirement of a decentralized Metropolis-Hastings (MH) step. Since this involves evaluation of the posterior over the whole data set, it is unclear how this can be done with each agent only having access to its local data. Understandably, all previous approaches to decentralized sampling either use diminishing step-sizes (Kungurtsev, 2020) or accept the level of bias according to the discretization error (Gürbüzbalaban et al., 2020).
Recall the generic definition of the HMC Hamiltonian,
In order to perform a decentralized MH step, we first introduce the Metropolis adjustment step, which takes the difference between the Hamiltonian at the current time step, \(H(\varvec{\omega }^t,\varvec{p}^t)\) and the proposed Hamiltonian with new parameters, \(H(\varvec{\omega }^*,\varvec{p}^*)\), and accepts the new parameters according to the acceptance ratio \(\rho\), where \(\log \rho = \min \{0, - H(\varvec{\omega }^*,\varvec{p}^*) + H(\varvec{\omega },\varvec{p})\}\). In the decentralized setting each agent does not have access to the full Hamiltonian and therefore to overcome this problem, we can approximate the acceptance ratio using the tracked first and second order terms. As a result we perform a Taylor expansion to approximate our acceptance step.
To derive the approximated acceptance ratio, we first take a Taylor expansion of the Hamiltonian at the proposed time step \(\{\varvec{\omega }^*,\varvec{p}^*\}\) and define both \(\Delta \varvec{\omega } = \varvec{\omega }^* - \varvec{\omega }^t\) and \(\Delta {\textbf{p}} = {\textbf{p}}^* - {\textbf{p}}^t\). Then,
where the first and second order derivatives are evaluated at \(\{\varvec{\omega }^t,\varvec{p}^t\}\). As a result we can write the acceptance ratio as:
We are performing numerical integration with a single first order Euler update step, which gives \({\textbf{p}}^* = {\textbf{p}}^t + \epsilon {\textbf{g}}^t\), and \(\varvec{\omega }^* = \varvec{\omega }^t + \epsilon {\textbf{p}}^*\). Therefore, \(\Delta \varvec{\omega } = \epsilon {\textbf{p}}^*\) and \(\Delta {\textbf{p}}^* = \epsilon {\textbf{g}}^t\). As a result the first order terms cancel each other out leaving the quadratic terms. The second order derivative with respect to the momentum is a vector of ones (assuming the mass matrix is the identity) and the second order derivative with respect to the parameters is the Hessian of the unnormalized potential, \(\frac{\partial ^2 U}{\partial \varvec{\omega }^2}\). Rather than directly computing the full Hessian and using tracking in the same manner as Eq. (2), we can track the quadratic term directly and take advantage of the speed-up associated with the vector-Hessian product. As a result, each agent tracks this second order term using the equation
Thus we can set our our Metropolis acceptance to
We expect this to maintain, as in the gradient tracking, an asymptotic upper bound on the expected discrepancy between the second derivative of the potential at an average of the parameters across the agents, to their \(\aleph\) estimates thereof.
2.3 The algorithm
Algorithm 1 describes the decentralized Metropolis-adjusted Langevin algorithm, which combines the gradient tracking of first and second order terms as well as the Taylor approximated Metropolis step. Each agent starts by sampling its own momentum and then computes its own local gradient and quadratic second order term. Then each agent updates its estimated global gradient and quadratic terms using gradient tracking. Finally, each agent then makes a single step in the augmented parameter space (including both the model parameters and the momentum) and accepts with probability according to the approximated Metropolis acceptance ratio.


3 Convergence analysis
To analyze the convergence of Algorithm 1, we first write the vectorized expression for the iterate sequence generated by the Algorithm as follows. We shall denote \(\varvec{\omega }^t = \begin{pmatrix} \varvec{\omega }_1^T&...&\varvec{\omega }^T_m \end{pmatrix}^T\) as the set of parameter vectors \(\{\varvec{\omega }_i\}\) stacked together, and similarly for \(\varvec{p}^t\), \(\aleph ^t\) and \(\varvec{g}^t\).
where recall that \({\textbf{p}}^t\) be a normal random variable and \(u^t\) is uniformly distributed and by \({\mathcal {M}}\) we denote the approximate metropolis acceptance operator, defined to be,
3.1 Coupling to centralized HMC
We prepare a coupling argument for the convergence (see, for example, e.g., Durmus and Moulines (2019)). We bound the distance in probability measure of the the chain generated by (4) to the chain generated by m parallel centralized HMC chains all with access to the entire dataset, whose ergodicity properties are well established, for instance in Durmus et al. (2017). We show this by coupling (4) to centralized HMC, using the triangle inequality and intermediate quantities. Accordingly we consider that the exogenous random variables \({\textbf{p}}^t\) and \(u^t\) are the same across all of the intermediate constructed chains for all t.
We introduce the notation \({\bar{a}}\) to indicate the averaged and copied m times vector \(\{a_i\}\), e.g.,
and similarly for \(\bar{\varvec{g}}^t\) and \({{\bar{\aleph }}}^t\). The vector recursion for the averaged iterate satisfies,
Now we consider a hypothetical chain wherein there is a stack of m vectors undergoing the decentralized HMC iteration, and subsequently averaged and dispersed across the stack of m. In effect this is the chain wherein the evaluations are performed at the average parameter, and corresponds to exact HMC, however, with the approximate Metropolis operator using the second order approximation. We refer to this as Approximate HMC.
Finally, we write the centralized HMC iteration. Note that technically it is a stack of m copies of centralized HMC runs, for formal simplicity averaged together (in effect reducing the variance),
where now the Metropolis operator \(\hat{{\mathcal {M}}}\) uses the exact values of the pdf \(p(\varvec{\omega }^t)\) to calculate acceptance and rejection as opposed to an approximation associated with \(\aleph ^t\), and \({\bar{G}}\) is defined as,
Recall that \(\hat{\varvec{\omega }}^t\), being the update for standard centralized HMC (7), is an ergodic process as shown in the literature (Durmus et al., 2017). This implies that \({\mathbb {E}}\Vert \hat{\varvec{\omega }}^t\Vert\) and \({\mathbb {E}}\Vert {\bar{G}}(\hat{\varvec{\omega }}^t)\Vert\) are bounded. We denote these bounds by U and \(U_g\).
We make the following assumption on the potential function \(p(\varvec{\omega })\).
Assumption 3.1
It holds that \(U(\varvec{\omega })\) as a function of \(\varvec{\omega }\) has Lipschitz continuous first and second derivatives, with constants \(L_2=\sup _{\varvec{\omega }}\Vert \nabla ^2_{\varvec{\omega }\varvec{\omega }} U(\varvec{\omega })\Vert\) and \(L_3=\sup _{\varvec{\omega }}\Vert \nabla ^3_{\varvec{\omega }\varvec{\omega }\varvec{\omega }} U(\varvec{\omega })\Vert\).
For brevity we shall denote by \(M^{(k)}\) the k’th moment of \(\Vert {\textbf{p}}\Vert\), i.e., \({\mathbb {E}}\Vert {\textbf{p}}\Vert =M^{(1)}\), \({\mathbb {E}}\Vert {\textbf{p}}\Vert ^2=M^{(2)}\), etc.
The bound between the approximate and exact HMC is stated first, with the error accumulating from the Taylor remainder error of the Metropolis acceptance step. Note that the scale of the error is of order \(O(\epsilon ^{5})\) in the step-size.
Theorem 3.1
For any \(\epsilon\), if \(T_1(\epsilon )\) is sufficiently small such that,
we have that for \(t\le T_1(\epsilon )\), the expected L2 distance between \(\tilde{\varvec{\omega }}^t\) and \(\hat{\varvec{\omega }}^t\) is bounded up by the following expression,
Next we indicate the consensus error, the standard measure for the discrepancy between the parameter estimates across the agents. The consensus error does not accumulate, but rather stays upper bounded, with the mean-squared-error scaling with \(O(\epsilon ^2)\).
Theorem 3.2
Assume that \(\beta\) is small enough such that \(2\beta (3+2L_2+2 L_3)<1\). The consensus error is asymptotically bounded, specifically,
We note that there is a strict requirement on \(\beta\), it must be configured so as to encourage swift consensus to mitigate the drift from the Lipschitzianity of the updates. If the structure of the communication links in the graph is such that the bound is not satisfied, then one can simply run multiple consensus updates \(c\in {\mathbb {N}}\) for each round until \(\beta ^c\) satisfies the required bound.
Finally, the most involved derivation is the probabilistic mass error between approximate HMC and the evolution of the average of the iterates, with the discrepancy accumulating due to the evaluation of the gradient vectors at the parameter values taking place at individual agents’ parameter estimates rather than at the average. Formally,
Theorem 3.3
Let,
The L2 expected error accumulates as,
Considering Theorems 3.1, 3.2 and 3.3, we obtain an understanding of the degree to which the decentralized HMC Algorithm as presented in Algorithm 1 manages to recreate the behavior of centralized HMC up to some error. Given that HMC exhibits ergodicity towards the stationary distribution in the general case, and geometric ergodicity for strongly log-concave distributions (Durmus et al., 2017), our approach generates a sequence of samples with controlled approximate accuracy relative to one with these properties. This error, however, grows with the number of samples. Given the nested form of the guarantees, this can potentially grow quickly. Still, decreasing the step-size \(\epsilon\) will have the effect of decreasing all of the terms, and one run an arbitrary number of iterations with accuracy guarantees with ever decreasing \(\epsilon\), however at the expense of proportionally shorter trajectory times.
In considering the implications of the Theorem, at first glance it could appear that there is an exponentially increasing error, suggesting increasing bias, asymptotically. However, this result only shows the correspondence of the scheme to a centralized HMC. As in, for instance, an ODE integrator, we can only expect in the best case that the error will grow exponentially with time. In order to obtain mixing results for the algorithm, it will be necessary to consider it standalone, and introduce some additional assumptions on the landscape of the potential, which we do so in the next section.
Finally, to give a bit of a clearer picture of the results in this subsection, let us consider the simple case of all problem constants being equal to one. Then, the terms in Theorem 3.3 appear to be,
and thus clearly the required condition is satisfied for T if,
which yields a reasonably large number of samples. Now, subsequently, we have, for small enough \(\epsilon\) \(A_2(\epsilon ,t) \le 6\) and \(B_2(\epsilon ,t)\le 4 \epsilon\) and so the condition for Theorem 3.1 satisfied if,
which is roughly \(O(-\log \epsilon )\), indicating that the error is bounded by a small constant O(1) for a number of samples proportional to \(O(-\log \epsilon )\).
3.2 Inexact HMC under function growth assumptions
The result in the previous section indicates that the parameters sampled by the procedure outlined appears to follow a similar trajectory as centralized HMC, gradually diverging as the bias grows. Of course, in practice, we expect that the chain to converge, in some probabilistic sense, asymptotically. For that, however, we would need some assumptions about the potential function U, as is standard for analysis of gradient based sampling method. We present the following, along the lines of Bou-Rabee et al. (2020), and derive correspondingly similar results:
Assumption 3.2
The potential U satisfies,
-
1.
\(U\in C^4({\mathbb {R}}^d)\)
-
2.
U has a local minimum at \(\varvec{\omega }=0\) and \(U(0)=0\).
-
3.
U has bounded fourth derivatives, let \(L_4=\sup \limits _{\varvec{\omega }\in {\mathbb {R}}^d} \Vert \nabla ^4_{\varvec{\omega }^4} U(\varvec{\omega })\Vert\)
-
4.
U is strongly convex outside a Euclidean ball, i.e., \(\exists {\mathcal {R}},K>0\) such that for all \(\varvec{\omega },\varvec{\omega }'\in {\mathbb {R}}^d\) with \(\Vert \varvec{\omega }-\varvec{\omega }'\Vert \ge {\mathcal {R}}\),
$$\begin{aligned} \langle \varvec{\omega }-\varvec{\omega }',\nabla U(\varvec{\omega })-\nabla U(\varvec{\omega }')\rangle \ge K\Vert \varvec{\omega }-\varvec{\omega }'\Vert ^2 \end{aligned}$$
Remark 3.1
Note that we can suspect to also possibly be able to replace the last Assumption by the statement, appearing in Bou-Rabee et al. (2020): There exists a measurable function \(\Psi :{\mathbb {R}}^d\rightarrow [0,\infty )\) and constants \(\lambda ,\alpha \in (0,\infty )\) and \(R_2>0\) such that the level set \(\{\varvec{\omega }\in {\mathbb {R}}^d:\Psi (\varvec{\omega })\le 4\alpha /\lambda \}\) is compact and for all \(\varvec{\omega }\in {\mathbb {R}}^d\) with \(\Vert \varvec{\omega }\Vert \le R_2\),
We do not investigate this point in this paper, however.
We now develop a contraction argument based on the coupling appearing in Bou-Rabee et al. (2020) for \(\bar{\varvec{\omega }}\). For that, we denote a perturbed Metropolis operator,
with \(q^t\) a random variable representing \(\Vert \bar{\varvec{\aleph }}^{t+1}-\varvec{\aleph }^{t+1}\Vert\), \(\Vert \varvec{g}^{t+1}-\nabla U(\bar{\varvec{\omega }^t})\Vert\) and \(\Vert \nabla ^2_{\varvec{\omega }} U(\bar{\varvec{\omega }}^t)-\aleph ^{t+1}\Vert\) and thus bounded in expectation by \(K_T(\epsilon )=C_T K_c(\epsilon )\) with \(K_c(\epsilon )\) as defined in Theorem 3.2. This permits for the consideration of the transition as characterized by a Markov kernel.
Now we are ready to present the coupling representing one transition of \(\bar{\varvec{\omega }}^t\). Set a constant \(\gamma >0\) to satisfy \(\gamma {\mathcal {R}}\le 1/4\). We denote the other copy of the average parameter set by procedure as \(\bar{\varvec{\nu }}^t\) and the coupling transition as follows:
where,
where \({\bar{u}}\sim \text {Unif}(0,1)\) and \(p_{{\mathcal {N}}}\) is the pdf of a unit normal r.v.
Let the map \(\varvec{L}(\bar{\varvec{\omega }},\varvec{p},\varvec{q})\rightarrow (\bar{\varvec{\omega }}+\epsilon (\varvec{p}+\epsilon \nabla U(\bar{\varvec{\omega }})+\epsilon \varvec{q}),\varvec{p}+\epsilon \nabla U(\bar{\varvec{\omega }})+\epsilon \varvec{q})\) where \(\varvec{q}\) is a random variable representing the tracking error. Noting the relative simplicity of Euler integrator compared to the Verlet approach in Bou-Rabee et al. (2020), some of the bounds derived in Bou-Rabee (2020, Lemma 3.1 and 3.2) are immediate. We write them below without the need for a derivation:
Next we can obtain a contraction for the case of the initial parameter values being outside a Euclidean ball. This result is similar in statement and proof technique to Bou-Rabee (2020, Lemma 3.4 and Theorem 2.2).
Lemma 3.1
There exists a \(C>0\) depending only on \(L_2\) and \(L_3\), such that for \(\bar{\varvec{\omega }},\bar{\varvec{\nu }}\in {\mathbb {R}}^d\) satisfying \(\Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert \ge 2{\mathcal {R}}\) and \(\epsilon\) satisfying \(\epsilon ^2 L^2 < K\) and \((1+\Vert \bar{\varvec{\omega }}\Vert +\Vert \bar{\varvec{\omega }}\Vert )\epsilon \le K/C\) and,
it holds that,
where \(C_c\) depends on K, \(L_2\) and C
Proof
Indeed,
\(\square\)
Theorem 3.4
Fix some \(R_2>0\), there exists \({\bar{\epsilon }}>0\) depending only on K, \(L_2\), \(L_3\), \(L_4\), \(R_2\) and d such that for any \(\epsilon <{\bar{\epsilon }}\), and any \(\bar{\varvec{\omega }},\bar{\varvec{\nu }}\in {\mathbb {R}}^d\) with \(\Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert \ge 2 {\mathcal {R}}\) and \(\max (\Vert \bar{\varvec{\omega }}\Vert ,\Vert \bar{\varvec{\nu }}\Vert )\le R_2\),
Define a metric of the form,
with,
Furthermore, we require,
and set \(\gamma\) as appearing in (11) to be,
Finally we derive the ultimate result using the coupling introduced in this Section to obtain contractivity in the modified metric.
Theorem 3.5
For the constants satisfying the above equations, we obtain for sufficiently small \(\epsilon\) depending only on K, \(L_2\), \(L_3\), \(M^{(2)}\), \({\mathcal {R}}\), \(R_2\) and d that with \(\max (\Vert \bar{\varvec{\omega }},\bar{\varvec{\nu }}\Vert )\le R_2\) it holds that if \(\left\| \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\right\| > R_3(\epsilon )\) with \(R_3(\epsilon )\) depending linearly on \(\epsilon\) and otherwise on the same set of constants, we have,
with c given by,
Otherwise, for general \(\left\| \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\right\|\)
with \(K_e(\epsilon ) = O(\epsilon ^3)\).
The previous Theorem indicates that modulo a a ball corresponding to inexactness as associated with the consensus and tracking errors, proportional in size to \(\epsilon\), the stochastic process defined by the Algorithm exhibits quantitative contraction, and thus is almost ergodic. Inside such a ball, the contractivity or not depends on the relative values of the constants and the associated consensus error.
4 Examples
In this section we illustrate the performance of Algorithm 1, which we shall refer to as Decentralized HMC, comparing it to two baselines, Centralized HMC, which is performing HMC on the entire data set, and Decentralized ULA, which we implement as in Parayil et al. (2020).Footnote 1 We leave the discussion of the computing platform, problem dimensions, and hyperparameter selection to the appendix.
4.1 Gaussian mixture model
The purpose of this example is to illustrate pictorially the importance of the Metropolis adjustment step. Here we sample from a Gaussian mixture given by
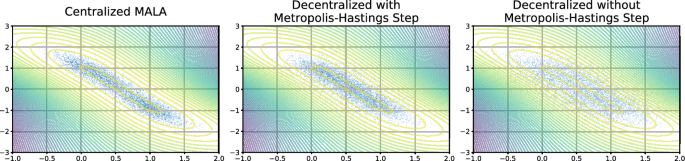
where \(\sigma _1^2 = 10, \sigma _2^2 = 1, \sigma _x^2 = 2\). For the centralized setting, 100 data samples are drawn from the model with \(\theta _1 = 0\) and \(\theta _2 = 1\), These are then split into 5 sets of 20 samples that are made available to each agent in the decentralised network. This is a similar setting to that of Parayil et al. (2020). Figure 1 compares sampling from the posterior distribution in both the centralized and decentralized settings. The contour plot corresponds to the true value of the log potential. The plot in the first column displays the samples from the centralized approach and can be thought of as the “ground truth". Columns two and three display the materialized samples for the decentralized setting, where column two applies the Taylor approximated Metropolis adjustment and column three does not. The discrepancy between these two schemes can be seen qualitatively via the spread of the samples. The Metropolis adjustment prevents the collection of samples in low probability regions and ensures that the samples stay in the high probability region in a similar manner to the centralized approach. Leaving out the Metropolis step means that samples that have low log probability are never rejected.
4.2 Linear regression
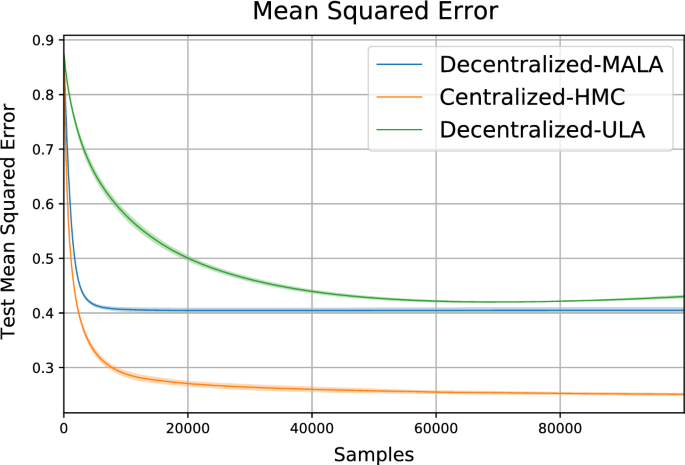
For our first example with real data, we investigate Bayesian linear regression with four agents applied to the Boston Housing data set (Harrison & Rubinfeld, 1978). In the decentralized setting, each agent is only given access to separate parts of the 13-dimensional feature space. Agents 1-3 have access to 3 input features (each a different set of 3) and agent 4 sees the remaining 4 features. We use a simple normal prior for each parameter of the model and compare the results in Fig. 2, which displays the cumulative mean squared error over samples. Our approach (in blue) converges and outperforms the baseline decentralized approach. The centralized approach, with access to all features achieves the best performance.
4.3 Logistic regression
For logistic regression we work with the MNIST data set (LeCun et al., 1998). We define two scenarios for decentralized learning. In scenario one, we only allow each agent partial observation of the total training set. In scenario two, we distribute the agents in a ring network such that each agent can only communicate with its two neighbors. Furthermore, for the ring network, each agent only has access to two classes of the training data.
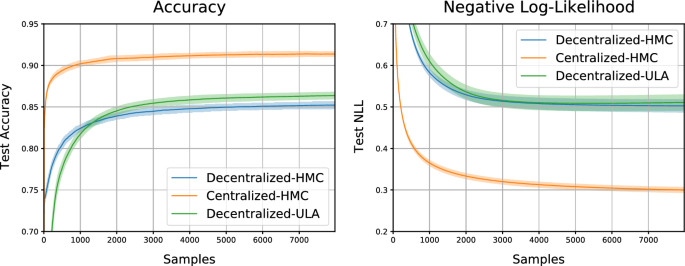
Partial observation For this experiment there are four agents where each only sees one quarter of the MNIST digit figure. The rest of the feature space is set to zeros. Figure 3 shows the results in statistical performance for the three schemes. The plots show cumulative performance averaged over all agents. The confidence intervals are one standard deviation and are calculated over 9 random seeds for all approaches.
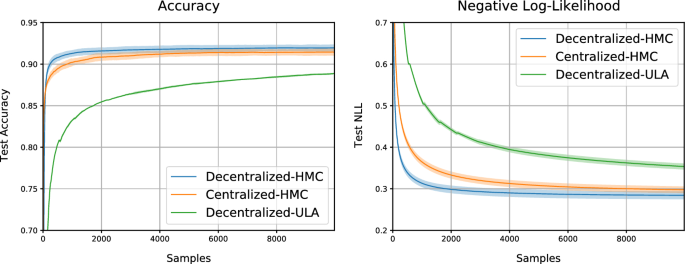
Ring network For this experiment there are five agents connected in a ring formation, such that each agent can only communicate with two other agents. Each agent only has access to two classes of digits in their training data, e.g. agent 0’s training data consists of digits 0–1. Figure 4 displays that in this setting, Decentralized HMC achieves similar performance to Centralized HMC, both of which in turn outperform Decentralized ULA.
4.4 Bayesian neural networks
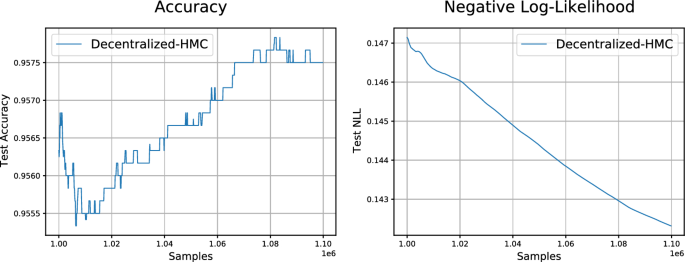
A unique contribution of our proposed algorithm is its treatment of nonconvex functions which has not been addressed in earlier work on decentralized sampling (Kungurtsev, 2020; Gürbüzbalaban et al., 2020; Parayil et al., 2020). To study this class of potentials, we ran our decentralized sampling scheme over two agents, each with their own neural network model and data. We provide each agent with half the classes available in the MNIST data set, i.e. one with access to digits 0–4 and the other with access to digits 5–9. Each network is fully fully connected with a single hidden layer of 100 units. Figure 5 displays the cumulative performance over the number of samples, averaged across the two agents for the test data. As is evident from the figure, our approach is able to learn in a decentralized fashion over nonconvex models. Without explicitly passing data between the two agents, each agent achieves good performance over classes it has never seen before.
5 Perspectives and conclusion
We presented an Algorithm that performs Metropolis-adjusted HMC sampling in a decentralized environment. Theoretically it appears to behave close in probability to exact HMC sampling, and numerically, appears to perform well on standard datasets. Theoretically, it would be interesting to establish ergodicity and convergence in probability of the chain generated by the Algorithm itself, rather than just a quantitative distance to the ergodic chain – whether this is possible is still an open question.
Availibility of data
Please see all the code in the repo: https://github.com/AdamCobb/dblmahmc.
Notes
However, unlike in Parayil et al. (2020), where they use stochastic gradients we apply their method without taking stochastic gradients.
References
Akyildiz, Ö.D., & Sabanis, S. (2020). Nonasymptotic analysis of stochastic gradient Hamiltonian Monte Carlo under local conditions for nonconvex optimization. arXiv preprint arXiv:2002.05465.
Berahas, A. S., Bollapragada, R., Keskar, N. S., & Wei, E. (2018). Balancing communication and computation in distributed optimization. IEEE Transactions on Automatic Control, 64(8), 3141–3155.
Betancourt, M. (2015). The fundamental incompatibility of Hamiltonian Monte Carlo and data subsampling. arXiv preprint arXiv:1502.01510.
Bou-Rabee, N., Eberle, A., & Zimmer, R. (2020). Coupling and convergence for Hamiltonian Monte Carlo. The Annals of applied probability, 30(3), 1209–1250.
Chau, H. N., & Rásonyi, M. (2022). Stochastic gradient Hamiltonian Monte Carlo for non-convex learning. Stochastic Processes and their Applications, 149, 341–368.
Chen, T., Fox, E., & Guestrin, C. (2014). Stochastic gradient Hamiltonian Monte Carlo. In: International Conference on Machine Learning, pp. 1683–1691. PMLR.
Chen, X., Du, S. S., & Tong, X. T. (2020). On stationary-point hitting time and ergodicity of stochastic gradient Langevin dynamics. Journal of Machine Learning Research, 21(68), 1–41.
Cobb, A.D., & Jalaian, B. (2020). Scaling Hamiltonian Monte Carlo inference for Bayesian neural networks with symmetric splitting. arXiv preprint arXiv:2010.06772.
Di Lorenzo, P., & Scutari, G. (2016). Next: In-network nonconvex optimization. IEEE Transactions on Signal and Information Processing over Networks, 2(2), 120–136.
Durmus, A., Moulines, E., & Saksman, E. (2017). On the convergence of Hamiltonian Mmonte Carlo. arXiv preprint arXiv:1705.00166.
Durmus, A., & Moulines, E. (2019). High-dimensional bayesian inference via the unadjusted langevin algorithm. Bernoulli, 25(4A), 2854–2882.
Gao, X., Gürbüzbalaban, M., & Zhu, L. (2021). Global convergence of stochastic gradient Hamiltonian Monte Carlo for nonconvex stochastic optimization: nonasymptotic performance bounds and momentum-based acceleration. Operations Research, 70, 2931–2947.
Gürbüzbalaban, M., Gao, X., Hu, Y., & Zhu, L. (2020). Decentralized stochastic gradient Langevin dynamics and Hamiltonian Monte Carlo. arXiv preprint arXiv:2007.00590.
Harrison, D., Jr., & Rubinfeld, D. L. (1978). Hedonic housing prices and the demand for clean air. Journal of Environmental Economics and Management, 5(1), 81–102.
Hsieh, C.-J., Si, S., & Dhillon, I. (2014). A divide-and-conquer solver for kernel support vector machines. In International Conference on Machine Learning, pp. 566–574. PMLR.
Izmailov, P., Vikram, S., Hoffman, M.D., & Wilson, A.G. (2021). What are Bayesian neural network posteriors really like? arXiv preprint arXiv:2104.14421
Kolesov, A., & Kungurtsev, V. (2021). Decentralized langevin dynamics over a directed graph. arXiv preprint arXiv:2103.05444.
Kungurtsev, V. (2020). Stochastic gradient langevin dynamics on a distributed network. arXiv preprint arXiv:2001.00665.
Lalitha, A., Wang, X., Kilinc, O., Lu, Y., Javidi, T., & Koushanfar, F. (2019). Decentralized Bayesian learning over graphs. arXiv preprint arXiv:1905.10466.
LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Mesquita, D., Blomstedt, P., & Kaski, S. (2020). Embarrassingly parallel MCMC using deep invertible transformations. In Uncertainty in Artificial Intelligence, pp. 1244–1252. PMLR.
Parayil, A., Bai, H., George, J., & Gurram, P. (2020). Decentralized Langevin dynamics for Bayesian learning. Advances in Neural Information Processing Systems, 33, 15978–15989.
Pu, S., & Nedić, A. (2020). Distributed stochastic gradient tracking methods. Mathematical Programming, 187, 409–457.
Roberts, G. O., Tweedie, R. L., et al. (1996). Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli, 2(4), 341–363.
Shoham, N., Avidor, T., Keren, A., Israel, N., Benditkis, D., Mor-Yosef, L., & Zeitak, I. (2019). Overcoming forgetting in federated learning on non-iid data. arXiv preprint arXiv:1910.07796.
Teh, Y. W., Thiery, A. H., & Vollmer, S. J. (2016). Consistency and fluctuations for stochastic gradient Langevin dynamics. Journal of Machine Learning Research, 17, 1–33.
Welling, M., & Teh, Y.W. (2011). Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), pp. 681–688. Citeseer.
Zhang, Y., Liang, P., & Charikar, M. (2017). A hitting time analysis of stochastic gradient Langevin dynamics. In Conference on Learning Theory, pp. 1980–2022. PMLR.
Zou, D., & Gu, Q. (2021). On the convergence of Hamiltonian Monte Carlo with stochastic gradients. In International Conference on Machine Learning, pp. 13012–13022. PMLR.
Funding
VK was supported by the OP VVV project CZ.02.1.01/0.0/0.0/16_019/0000765 “Research Center for Informatics”. AC and BJ were sponsored in part by the Army Research Laboratory under Cooperative Agreement W911NF-17-2-0196. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation here on.
Author information
Authors and Affiliations
Contributions
VK contributed to the theoretical analysis and algorithmic formulation. AC contributed to the numerical experiments and code. VK, AC, and TJ contributed equally to the discussions and writing of the manuscript. BJ contributed partially to editing and conceptual discussions in preparation of the manuscript.
Corresponding author
Ethics declarations
Conflicts
The authors have no relevant financial or non-financial interests to disclose.
Ethics approval
The authors believe there are no potential ethical considerations with this work.
Consent to participate and publish
All authors consent to the process of review and publication of the entire manuscript.
Additional information
Editor: Derek Greene
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1. Proofs of theoretical results
1.1 Appendix 1.1: Bounding approximate to centralized HMC
We first bound the distance in probability for the chain governing the update for \(\hat{\varvec{\omega }}^t\) in (7) and for \(\tilde{\varvec{\omega }}^t\) in (6).
Note that by construction, it always holds that,
Thus the only cause of a discrepancy between the chains for \(\tilde{\varvec{\omega }}^t\) and \(\hat{\varvec{\omega }}^t\) is the truncation of the potential at the second order to compute the acceptance probability. In particular we know that the error in this case is simply the Taylor expansion error, which is bounded by,
where \(L_3\) is given in Assumption 3.1.
Thus the discrepancy between \(\hat{\varvec{\omega }}\) and \(\tilde{\varvec{\omega }}\) amounts to the possibility of acceptance in one case and not the other, whose probability is bounded by (17) with the error being bounded by the change in the step, or \(\epsilon (\varvec{p}^t+\epsilon {\bar{G}}(\tilde{\varvec{\omega }}^t))\) (and \({\bar{G}}(\hat{\varvec{\omega }})\) in the other case). Let us now prove the main result of this Section. As by the notation of Algorithm 1 we refer to \(\tilde{\omega }^*\) and \({\hat{\omega }}^*\) as the proposed parameter samples following the Euler update for \(\tilde{\omega }^t\) and \({\hat{\omega }}^t\), respectively.
Proof
of Theorem 3.1
For notational brevity, we let,
Performing the recursion, we have that,
i.e., we partition the discrepancy as by probability of acceptance and rejection for each chain and the associated discrepancy with each form of iteration. Using the triangle inequality and the fact that the probabilities are mutually exclusive and exhaustive and so add to one, we have,
Now, let us bound the difference in the acceptance probabilities for the two chains as follows,
We also have the following norm bound on the expected update parameter update,
In the case of dual acceptance,
Combining these last three bounds with (18), we finally have
Thus, with \(\tilde{\varvec{\omega }}^0=\hat{\varvec{\omega }}^0\) we have that, for any \(\epsilon\), if \(T(\epsilon )\in {\mathbb {N}}\) is sufficiently small such that,
we have that for \(t\le T(\epsilon )\),
\(\square\)
1.2 Appendix 1.2: Consensus between decentralized and averaged HMC
Now we relate the process as generated by Algorithm 1 to the average dynamics as given by (5).
Proof
of Theorem 3.2 Consider the recursion in expected L2 error.
where we have used that \({\textbf{W}} \bar{\varvec{g}}^t = \frac{1}{m}\left( \varvec{I}\otimes \varvec{1} \varvec{1}^T\right) \varvec{g}^t= \frac{1}{m}\left( \varvec{I}\otimes \varvec{1} \varvec{1}^T\right) \bar{\varvec{g}}^t\), etc. throughout and, e.g., Di Lorenzo & Scutari (2016, Lemma 6) for the fact that \(\left\| \left( {\textbf{W}}-\frac{1}{m}(\varvec{I}\otimes \varvec{1} \varvec{1}^T)\right) \right\| \le \beta\). In the last inequality we subtracted \(\epsilon ^2\Vert {\textbf{g}}^{t+1}-\bar{{\textbf{g}}}^{t+1}\Vert\) from both sides and lower bounded the left hand side by half of its original.
Now the recursion implies that, using induction on the iterates,
\(\square\)
1.3 Appendix 1.3: Bounding averaged to approximate HMC
Proof
of Theorem 5.3 We have,
By the same argument we have,
Now we derive the difference in the parameters, noting in the first inequality below that we split the difference across the old parameter values, the update to the old parameter values, and exhaustively splitting the cases of one proposed parameter being accepted and the other not.
Clearly,
Now we must bound the discrepancy in probability of acceptance. We do this similarly as in the proof of Theorem 1. We use \({\mathcal {M}}_t\) and \(\tilde{{\mathcal {M}}}_t\) as shorthand for \({\mathcal {M}}(\varvec{\omega }^t-\epsilon (\varvec{p}^t+\epsilon \varvec{g}^{t+1}),\varvec{\omega }^t,\aleph ^{t+1},u^t)\) and \({\mathcal {M}}(\tilde{\varvec{\omega }}^t-\epsilon (\varvec{p}^t+\epsilon \tilde{\varvec{g}}^{t+1}),\tilde{\varvec{\omega }}^t,{\tilde{\aleph }}^{t+1},u^t)\), respectively. We compute the bounds,
Next, we see that we have already prepared the expression to bound the following term,
We see that in the parentheses the terms \({\mathbb {E}}\left\| \varvec{g}^{t+1}-\bar{\varvec{g}}^{t+1}\right\|\) and \({\mathbb {E}}\left\| \tilde{\varvec{g}}^{t+1}-\hat{\varvec{g}}^{t+1}\right\|\) already have a bound due to the previous two Theorems. Next,
Putting all of these expressions together we finally get,
Now, we consider that there exists a \(T_2(\epsilon )\) such that for \(t\le T_2(\epsilon )\), it holds that \(\max \left\{ {\mathbb {E}}\left\| \bar{\varvec{g}}^{t+1}-\tilde{\varvec{g}}^{t+1}\right\| ,\Vert \varvec{g}^t-\tilde{\varvec{g}}^t\Vert \right\} \le 1\). It is clear that such a \(T_2(\epsilon )\) exist for sufficiently small \(\epsilon\), as it holds trivially for \(t=0\). We derive the exact requirement on \(T_2(\epsilon )\) in the sequel. We have, however,
Finally, combining (21) with (22) and (24) we obtain,
Let \({\bar{K}}(\epsilon ,t)=\left( M^{(1)}+\epsilon \left( K_c+1+K_i(\epsilon ,t+1)+U_g\right) \right) +M^{(1)}+\epsilon U_g+\epsilon K_i(\epsilon ,t+1)\). Next, note that the inequality implies a monotonically increasing bound, so we can apply \(\left\| {\varvec{\omega }}^{t-1}-\bar{\varvec{\omega }}^{t-1}\right\| \le \left\| {\varvec{\omega }}^{t}-\bar{\varvec{\omega }}^{t}\right\|\). Then, subtracting \(\epsilon ^2{\mathbb {E}}\left\| \bar{\varvec{g}}^{t+1}-\tilde{\varvec{g}}^{t+1}\right\|\) from both sides and dividing by \(1-\epsilon ^2\) we get,
Now, defining,
We obtain the main result. \(\square\)
1.4 Appendix 1.4: Coupling and contraction outside a finite ball
In this Section we prove Theorem 3.4.
Proof
Let \({\mathcal {A}}_{\omega }\) and \({\mathcal {A}}_{\nu }\) be the acceptance probabilities corresponding to the updates of \(\varvec{\omega }\) and \(\varvec{\nu }\), respectively. Noting that the error q is unknown and cannot be coupled in the two chains, we compute,
From Lemma 3.1 we recall that that,
On the other hand, by Assumption,
but
Now we must bound \({\mathbb {P}}[{\mathcal {A}}_{\omega }^c\cup {\mathcal {A}}^c_{\nu }]\). We proceed,
where \(K_a(\epsilon )\) depends on \(L_2\) and \(K_T(\epsilon )\) and the last step follows similar reasoning as in the proof of Theorem 3.1. Putting these bounds together, we get,
which satisfies the conclusion for sufficiently small \(\epsilon\) relative to \({\mathcal {R}}^2\le \Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert ^2/4\). \(\square\)
1.5 Appendix 1.5: Global coupling and contraction
Here we prove Theorem 3.5. The proof is based on the original proof of Bou-Rabee (2020, Theorem 2.4)
Proof
For \(\Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert \ge 2{\mathcal {R}}\), there is the straightforward application of Theorem 3.4, where we write,
Define the event \({\mathcal {C}}:=\{\bar{\varvec{r}}-\bar{\varvec{p}}=\gamma (\bar{\varvec{\omega }}-\bar{\varvec{\nu }})\}\). Now for the case of \(\left\| \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\right\| <2{\mathcal {R}}\) we consider the exhaustive decomposition,
Now for the first expression, under the event \({\mathcal {A}}_{\omega }\cap {\mathcal {A}}_{\nu }\cap {\mathcal {C}}\) it holds that,
and thus by the concavity of \(\rho\),
Now as in the proof of Theorem 3.4, we have that \(\max ({\mathbb {P}}[{\mathcal {A}}_{\omega }^c],{\mathbb {P}}[{\mathcal {A}}_{\nu }^c])\le \epsilon ^2 K_a(\epsilon )\). Next, recall that by construction and Bou-Rabee (2020, Lemma 3.7) together with \(\gamma {\mathcal {R}}\le 1/4\) we have that \({\mathbb {P}}[{\mathcal {C}}^c]\le \frac{\gamma \Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert }{\sqrt{2\pi }}\le \frac{1}{4\sqrt{2\pi }}< \frac{1}{10}\). Thus, we can make \(\epsilon\) sufficiently small depending on \(\gamma\), \(L_2\) and the form of \(K_a(\epsilon )\) such that,
Next, it holds that for \(s\le R_1\), \(\rho (s)-\rho (r)\le \frac{1}{a}\rho '(r)\) and thus by Bou-Rabee (2020, Lemma 3.7) and the definition of \(a=1/\epsilon\), we have that,
Next, under \({\mathcal {A}}_{\omega }\cap {\mathcal {A}}_{\nu }\cap {\mathcal {C}}^c\), by the definition of \(\varvec{r}\),
Thus, with the fact that by construction \(R_1\ge \frac{5}{4}(1+\gamma \epsilon )\Vert \bar{\varvec{\omega }}-\bar{\varvec{\nu }}\Vert\) and by the properties of the coupling (see the proof of Bou-Rabee (2020, Theorem 2.4),
Finally,
and so, again by the convexity of \(\rho (\cdot )\),
Finally, putting all of these bounds together, we obtain,
Noting that,
and
we obtain the final result. \(\square\)
Appendix 2. Experiment hyperparameters
1.1 Linear regression
We set the doubly stochastic matrix, \({\textbf{W}} = \frac{1}{N_a}{\textbf{1}}_4\), where number of agents, \(N_a = 4\) and \({\textbf{1}}_4\) is a \(4\times 4\) matrix of ones. We run the experiment over 9 seeds for \(T = 10^5\) iterations. Hardware: MacBook Pro, Processor: 2.6 GHz 6-Core Intel Core i7, Memory: 16 GB.
-
Centralized HMC \(\epsilon = 4\times 10^{-4}\), \(L = 1\), prior precision \(= 1.0\).
-
Decentralized HMC \(\epsilon = 4\times 10^{-4}\), prior precision \(= 1.0\). We switch off the MH step for the first \(10^3\) steps to ensure that the Taylor approximation is only applied from a point closer to the target distribution.
-
Decentralized ULA \(\epsilon = 3\times 10^{-7}\). Following the same notation from Parayil et al. (2020): \(\beta _0 = 0.48,\delta _1 = 0.01, \delta _2 = 0.55, b_1 = 230, b_2 = 230\).
1.2 Logistic regression
Partial observation We set the doubly stochastic matrix, \({\textbf{W}} = \frac{1}{N_a}{\textbf{1}}_4\), where number of agents, \(N_a = 4\) and \({\textbf{1}}_4\) is a \(4\times 4\) matrix of ones. We run the experiment over 9 seeds for \(T = 8\times 10^3\) iterations. Hardware: GeForce RTX 2080 Ti.
-
Centralized HMC \(\epsilon = 0.001\), \(L = 1\), prior precision \(= 100.0\).
-
Decentralized HMC \(\epsilon = 5\times 10^{-4}\), prior precision \(= 100.0\). We switch off the MH step for the first \(2\times 10^3\) steps to ensure that the Taylor approximation is only applied from a point closer to the target distribution.
-
Decentralized ULA \(\epsilon = 1\times 10^{-5}\). Following the same notation from Parayil et al. (2020): \(\beta _0 = 0.48,\delta _1 = 0.01, \delta _2 = 0.55, b_1 = 230, b_2 = 230\).
Ring network We set the doubly stochastic matrix, \({\textbf{W}} = ({\textbf{I}} + {\textbf{A}})\frac{1}{N_a}\), where number of agents, \(N_a = 5\) and \({\textbf{I}}\) is the identity matrix, and \({\textbf{A}}\) is the adjacency matrix for a ring shaped graph. We run the experiment over 9 seeds for \(T = 1\times 10^4\) iterations. Hardware: GeForce RTX 2080 Ti.
-
Centralized HMC \(\epsilon = 0.001\), \(L = 1\), prior precision \(= 100.0\).
-
Decentralized HMC \(\epsilon = 0.003\), prior precision \(= 100.0\). We switch off the MH step for the first \(1\times 10^3\) steps to ensure that the Taylor approximation is only applied from a point closer to the target distribution.
-
Decentralized ULA \(\epsilon = 1\times 10^{-4}\). Following the same notation from Parayil et al. (2020): \(\beta _0 = 0.48,\delta _1 = 0.01, \delta _2 = 0.55, b_1 = 230, b_2 = 230\).
1.3 Bayesian neural network
We set the doubly stochastic matrix, \({\textbf{W}} = \frac{1}{N_a}{\textbf{1}}_2\), where number of agents, \(N_a = 2\) and \({\textbf{1}}_2\) is a \(2\times 2\) matrix of ones. We run the experiment for \(T = 5\times 10^5\) iterations. Decentralized HMC \(\epsilon = 7\times 10^{-5}\), prior precision \(= 10.0\). We switch off the MH step for the first \(2\times 10^3\) steps to ensure that the Taylor approximation is only applied from a point closer to the target distribution. Hardware: GeForce RTX 2080 Ti.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kungurtsev, V., Cobb, A., Javidi, T. et al. Decentralized Bayesian learning with Metropolis-adjusted Hamiltonian Monte Carlo. Mach Learn 112, 2791–2819 (2023). https://doi.org/10.1007/s10994-023-06345-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-023-06345-6