Introduction

In the past few decades, thermography nondestructive testing (NDT) methods have been widely applied to device assessment and component inspection in additive manufacturing, aerospace, transportation, electrical engineering and mechanical engineering [1, 2]. It is known that the thermography NDT methods have the advantages of fast detection speed, high detection accuracy and nondestructive evaluation [3,4,5]. It should be pointed out that the infrared thermography NDT methods can be divided into two types, namely the active infrared thermography (AIT) methods and the passive infrared thermography (PIT) methods. AIT methods employ an extra heating source to produce a temperature contrast between crack and normal areas. In PIT, the temperature difference of the crack and non-crack areas is measured without using extra heating sources. In general, the detection performance of the AIT methods outperforms the PIT ones due to the fact that various heating sources would lead to a large thermal contrast between crack and normal areas [6,7,8].

As a powerful AIT method, the eddy current pulsed thermography (ECPT) method has been successfully applied to various NDT tasks because of its simple operation and wide scanning range. In ECPT, an electromagnetic pulse with high current is applied to induce the eddy current in the specimen, and the heating distribution of the specimen is recorded by the infrared camera. Similar to other thermography methods, it is a challenging task in ECPT to build a physical model to accurately describe the NDT process because of complex thermal environment and various disturbances. In this context, a reasonable yet effective way is to deal with the acquired ECPT images for crack detection by using the data analysis techniques.

Thanks to their powerful capabilities in feature extraction, machine learning algorithms have been widely utilized in thermal image analysis [4, 5, 9,10,11,12,13]. A variety of image processing methods have been successfully applied for feature extraction of the thermal images such as the discrete wavelet transform method [14], the K-means clustering algorithm [15] and the thermal resistance effect model-based method [16]. The aforementioned image processing algorithms are normally applied to handle one specific thermal image through the ECPT-based NDT process [17]. It is worth mentioning that such a thermal image is manually selected according to experimental experience, where the image processing performance is largely affected by the expert knowledge.

To overcome the limitation of using one manually chosen image for crack detection, machine learning methods have been successfully applied for crack detection by using multiple NDT images (i.e., the NDT image sequences) during the past few years [18]. For instance, the frequency pattern extraction methods based on the Fourier transform have been adopted to enhance the image contrast through the phase map for detecting the cracks based on NDT image sequences [19, 20]. The principal component analysis (PCA) algorithms have been successfully adopted to extract the thermal features through the entire ECPT-based NDT process for crack detection [21, 22].

Unfortunately, the quality of the thermal images is influenced by the background noises and disturbances caused by experimental environment and material properties. To alleviate the influence of noises and disturbances, the powerful deep learning techniques have been widely adopted for image analysis [23,24,25,26]. For example, a two-stream convolutional neural network has been put forward in [24] for subsurface defect detection. A deep neural network-based subsurface damage detection approach has been developed in [23] for steel bridge defect detection. Among the popular deep learning techniques, the generative adversarial network (GAN) has been widely employed in computation vision thanks to its powerful abilities in data generation and pattern recognition [27, 28]. In fact, GANs have been successfully utilized to generate thermal images for thermographic data analysis [29]. Therefore, a seemingly natural idea is to employ the modified GAN to extract the features of a series of thermal images (which makes full use of the thermal information during the whole ECPT process), and the crack detection is then implemented based on the output of the GAN.

In this paper, a GAN-based crack detection approach is put forward where one designed penalty term is introduced into the loss function of the GAN, which not only enhances the feature extraction ability but also reduces the noises. To be specific, for each spatial point of the thermal image, the corresponding temperature values during the ECPT-based NDT process are fed to the GAN, and a pixel value of this spatial point is generated by the GAN. Then, an image is reconstructed based on these pixels derived by the GAN. Under the effect of the designed penalty term, the pixel difference between the crack area and non-crack area would be enlarged, which benefits the crack detection for the NDT process. In the developed crack detection strategy, the PCA algorithm is employed to alleviate the influence of the thermal transmission through the material. Data argumentation is applied to guarantee the effectiveness of the training data.

The main contributions of this paper can be outlined in the following three aspects:

  1. 1.

    A modified GAN is proposed where a penalty term is introduced in the loss function so as to enhance the feature extraction ability and restrain the effects induced by the noises.

  2. 2.

    The proposed GAN-based method is successfully employed for ECPT crack detection for the first time. With the utilization of the NDT image sequences, the reliability of the crack detection result can be guaranteed.

  3. 3.

    The performance of the developed GAN-based method is comprehensively evaluated for thermal image analysis. Experimental results verify the effectiveness of the developed modified GAN by comparing with that of the conventional GAN. The proposed GAN-based crack detection method is employed to solve a real-world ECPT-based NDT problem.

The rest of this paper is organized as follows. The background of the ECPT technique is provided in "Background", and the experimental setup of the ECPT detection system is also introduced. The methodology of the proposed GAN-based crack detection method is presented in "Methodology", where the basic knowledge of the conventional GAN and the details of the modified GAN are illustrated. Data preprocessing and data augmentation are shown in "Data Preprocessing". "ECPT Images" presents the ECPT images utilized in this paper. In "Experimental Results", experimental results and discussion are provided. The conclusions and the future work are summarized in "Conclusion".

Background

In this section, the basic knowledge of the ECPT technique is provided, and the hardware setup of an ECPT detection system is introduced.

Basic Knowledge of ECPT

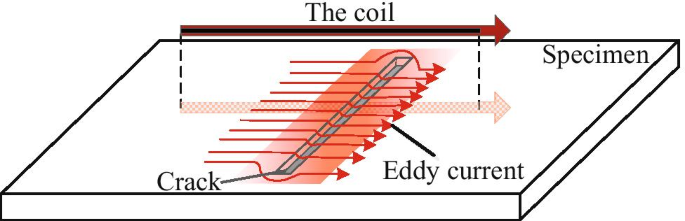
ECPT is an effective AIT method for detecting material degradations and failures. In ECPT, the eddy current is induced in the conductive material and generates the Joule heat, which leads to the temperature rise. In the crack area of the specimen, the conductive material influences the eddy current flow as well as the heat conduction, thereby increasing the temperature of the crack area. The thermal imaging system is employed to record the thermal contrast between the crack and non-crack area in the materials. The ECPT-based crack detection approach is displayed in Fig. 1.

Fig. 1
figure 1

The eddy current path through a conventional exciting coil

Full size image

The Joule heating of the eddy current in the material is expressed as follows:

$$\begin{aligned} Q = \frac{1}{\sigma }|J_{s}|^{2} = \frac{1}{\sigma }|\sigma E|^{2} \end{aligned}$$
(1)

where \(J_{s}\) is the eddy current density; Q indicates the sum of the Joule heating; \(\sigma\) indicates the conductivity of the material; and E represents the electric intensity.

In the ECPT, the heat in the crack area is accumulated as the electromagnetic energy continually injects. Furthermore, the heat diffusion causes that the temperature variation of the specimen is a dynamic process. The material heat conduction is given by:

$$\begin{aligned} \frac{\partial T}{\partial t} = \frac{\lambda }{\rho C_{p}}\left( \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}+\frac{\partial ^{2}T}{\partial z^{2}}\right) + \frac{1}{\rho C_{p}}q(x,y,z,t) \end{aligned}$$
(2)

where T represents the abbreviation of the temperature distribution (i.e., T(x, y, z, t)), where x, y, z are the Cartesian coordinates of the three-dimensional space and t is the time stamp; \(\lambda\), \(C_{p}\) and \(\rho\) indicate the thermal conductivity, the heat capacity and the density of the objective material, respectively; and q(x, y, z, t) is the internal heat generation function induced by the Joule heating process [30].

It is worth mentioning that the heat conduction process is slow compared with the thermographic sampling process. Hence, the thermal imaging system is capable of capturing the thermal features of the material (including the crack area). The time domain information of the thermal features is very important for crack detection.

ECPT Detection System

A typical ECPT detection system includes a thermal imager, a heating device (which is also known as an induction heating element), a heating coil and a specimen, which is shown in Fig. 2. A stainless steel specimen with several cracks (consisting of through-hole cracks and normal cracks) is displayed in Fig. 2. The heating coil is driven by the high-frequency and high-power alternating current generator device, which is the core component for energy injecting. By deploying a high-quality thermal imager, the NDT process of the ECPT detection system is recorded. It should be noticed that a computer is employed to control the heating device as well as the thermal imager.

Fig. 2
figure 2

The ECPT detection system and the specimen

Full size image

Methodology

Basic Knowledge of the GAN

As a popular generative model in deep learning, the GAN has been successfully applied to various practical applications, e.g., image translation, image synthesis, semantic segmentation and natural language processing. The original GAN consists of a generator and a discriminator. In the original GAN, the input of the generator is random noise. The input of the discriminator is the real data as well as the so-called fake data (produced by the generator). It should be mentioned that the purpose of the discriminator is to accurately identify the real data and the generated fake data. The output of the discriminator is a value in the range of (0, 1). The goal of the generator is to explore the distribution of the training data.

The loss function of the original GAN is shown as follows:

$$\begin{aligned} \begin{aligned} J(D,G) =&~\mathbb {E}_{x \sim \mathbb {P}_{r}(x)}[\log D(x)] \\&~+ \mathbb {E}_{{z} \sim \mathbb {P}_{f}(z)}[\log (1-D(G(z)))] \end{aligned} \end{aligned}$$
(3)

where \(D(\cdot )\) is the discriminator; \(G(\cdot )\) represents the generator; x is real data; z indicates the input of the generator; and \(\mathbb {P}_{r}\) and \(\mathbb {P}_{f}\) denote the distribution of real data and the distribution of the fake data (which is the output data of the generator), respectively.

Modified GAN

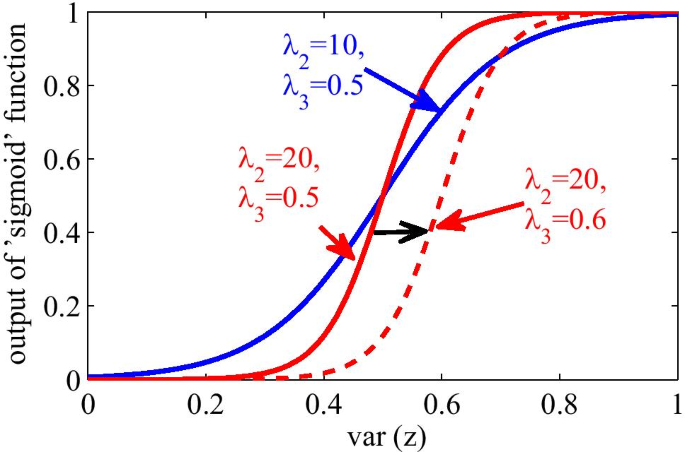
In this paper, a modified GAN is put forward to analyze the thermal images (which are obtained by using the ECPT technique) with the aim to identify the cracks. For crack detection, the input of the generator is the thermal signal (which indicates the temperature) of one individual point in the specimen, and the output of the generator is a value which identifies the individual point belonging to a crack or not. By reconstructing the output of the generator (which is trained by Eq. (3)), the obtained image is thus utilized for crack detection. In fact, the temperature of the non-crack area changes relatively slow and the temperature of the crack area changes relatively fast, which makes it difficult to analyze the obtained ECPT thermal images. It should be mentioned that the image contrast of the generated image is relatively small, which may lead to the overlapping of the crack area and the non-crack area. As such, the original loss function of the conventional GAN as shown in Eq. (3) is not suitable for crack detection by using the ECPT technique. In this paper, a modified GAN is put forward where a designed penalty term is introduced in the loss function so as to enhance the contrast ratio of the ECPT detection result. The sigmoid function is chosen as the penalty term in this paper according to its characteristics of 1) smooth; 2) differentiable; and 3) monotonic.

In this paper, a modified loss function is introduced where a penalty term is designed so as to enhance the feature extraction ability and improve the contrast ratio of the reconstructed image. The loss function of the modified GAN is given as follows:

$$\begin{aligned} \begin{aligned} V(D,G)= \lambda _{1}\frac{\Vert G(z) \Vert _2}{\frac{1}{1+e^{-\lambda _{2}[var(z)-\lambda _{3}]}} + P} + J(D,G) \end{aligned} \end{aligned}$$
(4)

where \(\lambda _{1}\) is the penalty parameter of the introduced penalty term; \(\lambda _{2}\) and \(\lambda _{3}\) are sigmoid function parameters; \(var(*)\) is the variance; P is a constant value; and \(\Vert G(z) \Vert _2\) is the Euclidean norm of G(z). In this paper, we aim to pursue

$$\min _{G} \max _{D}V(D,G).$$

To summarize, the modified loss function is designed to make G(z) as large as possible if the thermal signal z belongs to the crack area. It is challenging to identify whether the point belongs to the crack area or not when G(z) is around 0.5. In this situation, the penalty parameters \(\lambda _{2}\) and \(\lambda _{3}\) are employed to decrease the value of G(z) to a lower one, which contributes to the enhancement of the contrast ratio of the crack area. The influence of \(\lambda _{2}\) and \(\lambda _{3}\) on the sigmoid function is shown in Fig. 3. By selecting \(\lambda _{2}\) and \(\lambda _{3}\), the curve of the sigmoid function is fine-tuned for the training process, which is the nonlinear part of the neural networks.

Fig. 3
figure 3

The effect of \(\lambda _{2}\) and \(\lambda _{3}\) to the sigmoid function

Full size image

GAN-Based Crack Detection Method

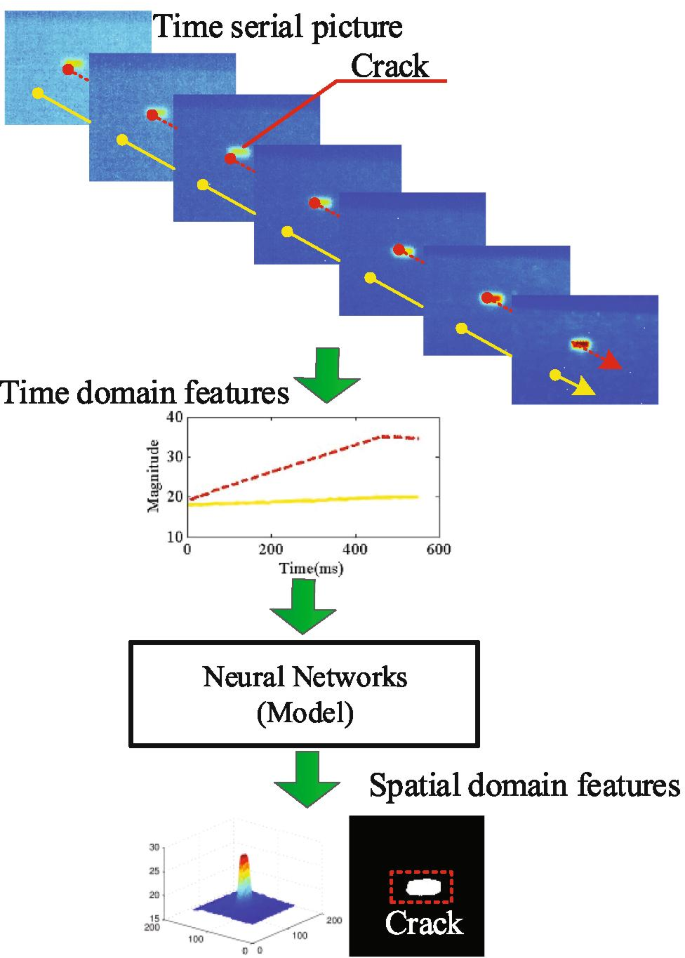
In this paper, the GAN is employed to analyze the thermal features of the ECPT images. The procedure of the GAN-based crack detection method is shown in Fig. 4.

Fig. 4
figure 4

Extracting the spatial features from time sequence signals

Full size image

The thermal signal of the spatial points reflects the heat conduction feature of the specimen. As mentioned previously, the temperature of the spatial point (that belongs to the crack) becomes higher within a relatively fast time period than that of the spatial point in the non-crack area. In this case, the temperature distribution of the crack points is different from that of the non-crack points. As shown in Fig. 4, the preprocessed thermal signal is utilized as the training data of the generator instead of random noise. The output of the generator is applied to reconstruct the detection image. Then, the detection image is post-processed by using a manually selected threshold for binarization so as to identify the crack. To summarize, a probability value is obtained to determine whether the corresponding spatial point belongs to the crack or not by extracting the features of the thermal signal by using the GAN.

Data Preprocessing

It is time-consuming and expensive to generate enough effective data for training a satisfactory deep learning model by using the ECPT technique. In the ECPT system, the thermal signal of the spatial points is easily influenced by the high-frequency noise during the NDT process. Therefore, it is of practical importance to preprocess the raw data for the further training process. In this paper, the thermal images captured through the ECPT-based NDT process are studied, and the thermal information of the spatial points in the specimen is investigated for all the selected image frames. In this section, the PCA-based feature selection of the thermal images and the data argumentation are discussed.

PCA-Based Feature Extraction

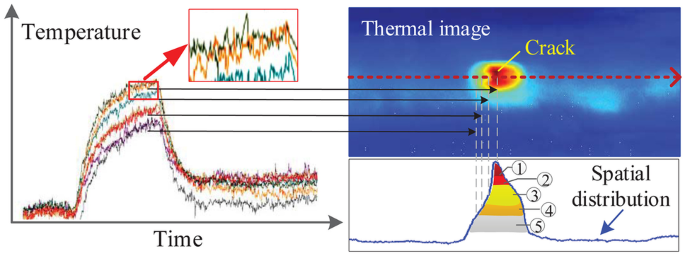
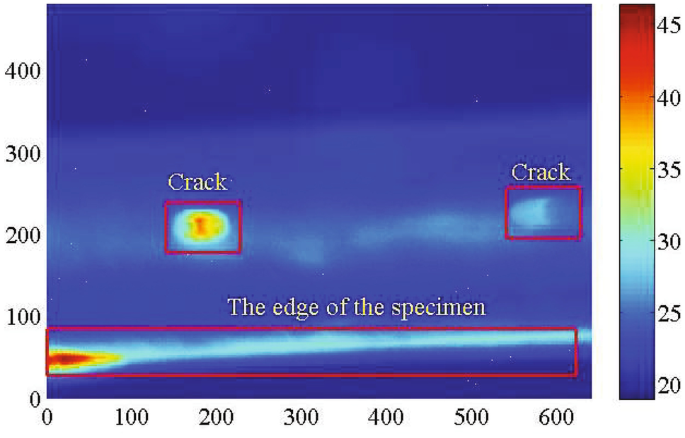
In the ECPT detection system, the thermal imager with high sampling rate captures the thermal images through the NDT process. It should be noted that the detection result of the thermal imaging systems is easily affected by external infrared radiation (produced by the external heating system) and surface radiation of the specimen, which leads to disturbances/noises in the images recorded by the thermal imager. The relationship between the temperature and the spatial information of the thermal signal during the NDT process is depicted in Fig. 5.

Fig. 5
figure 5

The spatial and temporal relationship of thermal signal

Full size image

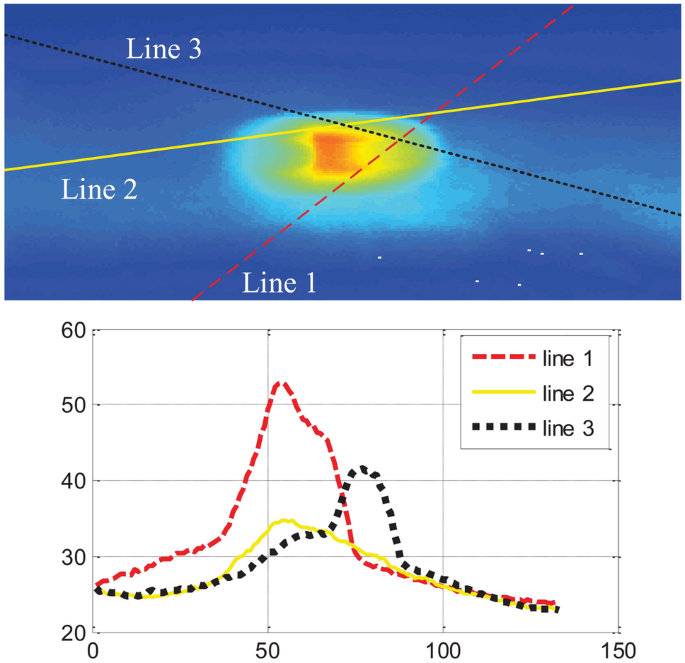
It can be seen in Fig. 5 that the temperature of the points inside/around the crack is much higher than that in other area. In addition, the temperature curve is not smooth due to the existence of noises. The NDT process is continuous, and the temperature of the spatial points around the crack area is also influenced, which makes it difficult to distinguish the crack and non-crack points based on the GAN trained by using the raw data. The temperature distribution of four randomly selected lines of the detected image is depicted in Fig. 6.

Fig. 6
figure 6

The temperature distribution of different continuous spatial point sets

Full size image

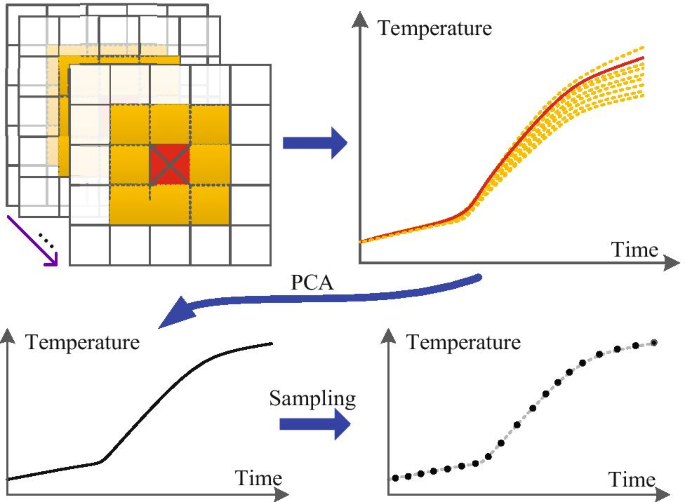
By using the PCA method, the first principal component is used as the generated signal. The procedure of the utilized signal processing method is shown in Fig. 7. The target object and its neighboring spatial points are 9 points in total. The corresponding thermal time series signals are processed by PCA, and then, a new signal is obtained with the main information of 9 signals.

Fig. 7
figure 7

The block diagram of time sequence signal fusion

Full size image

As mentioned previously, the thermal imager captures more than one thousand images in a short time because of its high sampling rate. To be specific, the sampling rate of the thermal imager is 1.5s and the excitation of the eddy current is 0.5s. As the heating process is slow, the temperature of the spatial points remains the same between several frames. It is therefore unnecessary to utilize all the image frames for the training process due to the computational cost. In this paper, the uniform sampling method is employed to select 201 image frames for training the GAN. The preprocessing of the thermal signal is depicted in Fig. 7, which fuses the thermal features extracted through the image sequences. In addition, the preprocessed thermal signals are normalized to improve the generalization ability of the GAN.

In signal processing, the sampling method is equivalent to adding a low pass filter. Through decreasing the sampling rate, the high-frequency components would be restrained. In order to get effective information and avoid the influences of the high-frequency noises, the sampling process is conducted after the PCA-based feature extraction process.

Data Augmentation

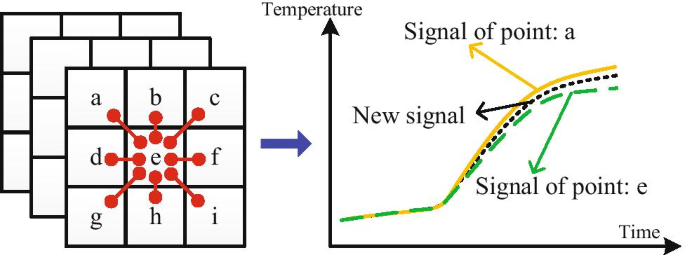
During the NDT crack detection process, a large amount of raw data is collected. Nevertheless, most of the obtained raw data include redundant information or noises, which requires data preprocessing. In this paper, data augmentation is employed to produce enough training data so as to guarantee the generalization ability of the modified GAN algorithm. In particular, an interpolation-based method is designed to generate new data, which is shown in Fig. 8. The value of the generated point is the mean value of the selected points. For example, a new data point m is generated by calculating the mean value of the e and its neighbor e.

The label of the generated new data point is given as follows:

$$\begin{aligned} L_{new} = L_{A} \& L_{B} \end{aligned}$$
(5)

where \(L_{a}\) and \(L_{e}\) represent the label of point A and point B, respectively; & denotes the logical conjunction “and.” It should be noted that the values of the thermal signals extracted by the image sequences are normalized to improve the generalization performance of the GAN.

Fig. 8
figure 8

The process of time sequence signal generating

Full size image

ECPT Images

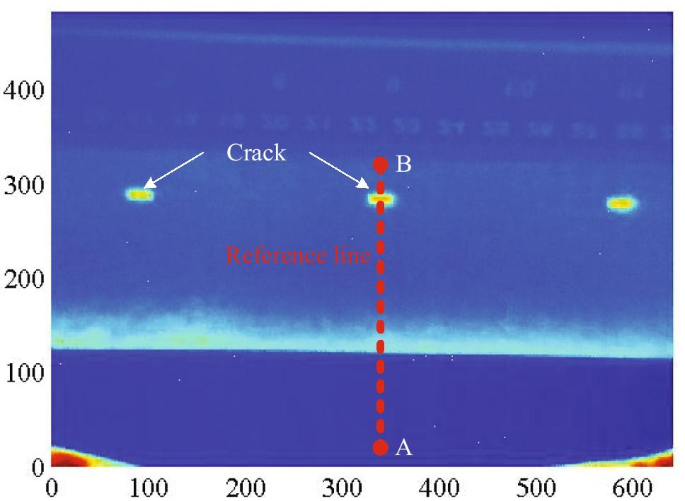
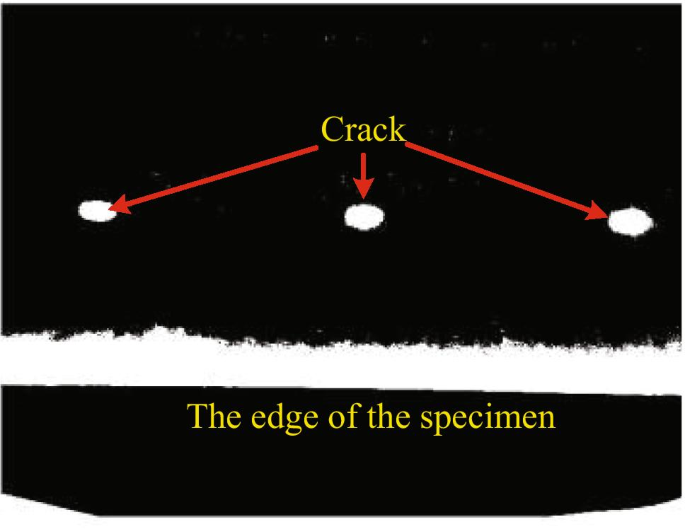
In this paper, the thermal images are preprocessed to extract the thermal signal as the input of the generator. An example of the thermal image captured through the infrared camera is depicted in Fig. 9. In Fig. 9, three cracks with different shapes are identified.

Fig. 9
figure 9

A typical thermal image captured through the NDT process

Full size image

The size of an acquired thermal image (as shown in Fig. 9) is \(480~\times ~640,\) and the total number of pixel points in this image is 307200. In order to enlarge the number of training data, there are more than 920480 data for GAN training by using the data generation method in this paper. The corresponding labeled image of Fig. 9 is shown in Fig. 10. Figure 10 is a binary image, which indicates that the class of the pixel points is only 0 or 1. To be specific, the pixel value of the crack points is 0 and the pixel value of the points in non-crack area is 1.

Fig. 10
figure 10

The labeled data

Full size image

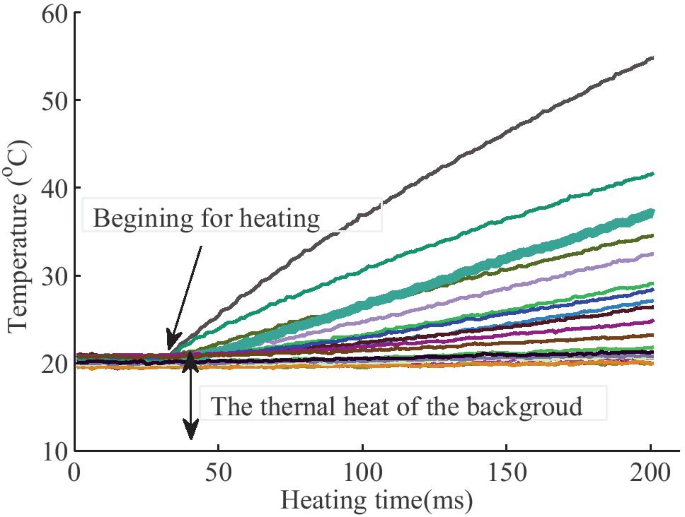
The temperature of the selected 15 pixel points in the reference line (as shown in Fig. 9) is displayed in Fig. 11. Note that the 15 pixel points are uniformly selected from position A to position B. In Fig. 11, the temperature value of the points in different positions starts to rise at different times, which indicates that the thermal energy transfers in the specimen in all directions. In this case, the size of the detected crack area is larger comparing with the size of the real crack area, which makes it difficult to use traditional image processing methods to detect the crack accurately.

Fig. 11
figure 11

The temperature of the selected points

Full size image

The testing data are the thermal images of the specimen with two cracks, where one crack is a through-hole crack and the other one is a normal crack with a small depth. One image frame of the testing thermal images is depicted in Fig. 12. In Fig. 12, the crack in the left side is the through-hole crack and the other one is the normal crack.

Fig. 12
figure 12

An example of the testing data: a thermal image with two cracks

Full size image

Experimental Results

Results and Discussion

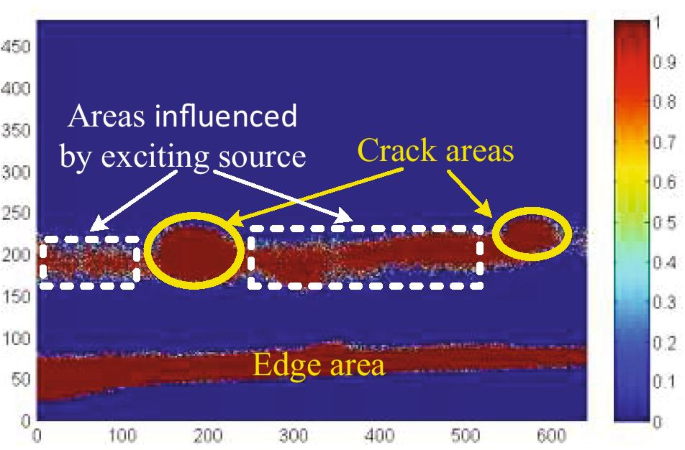
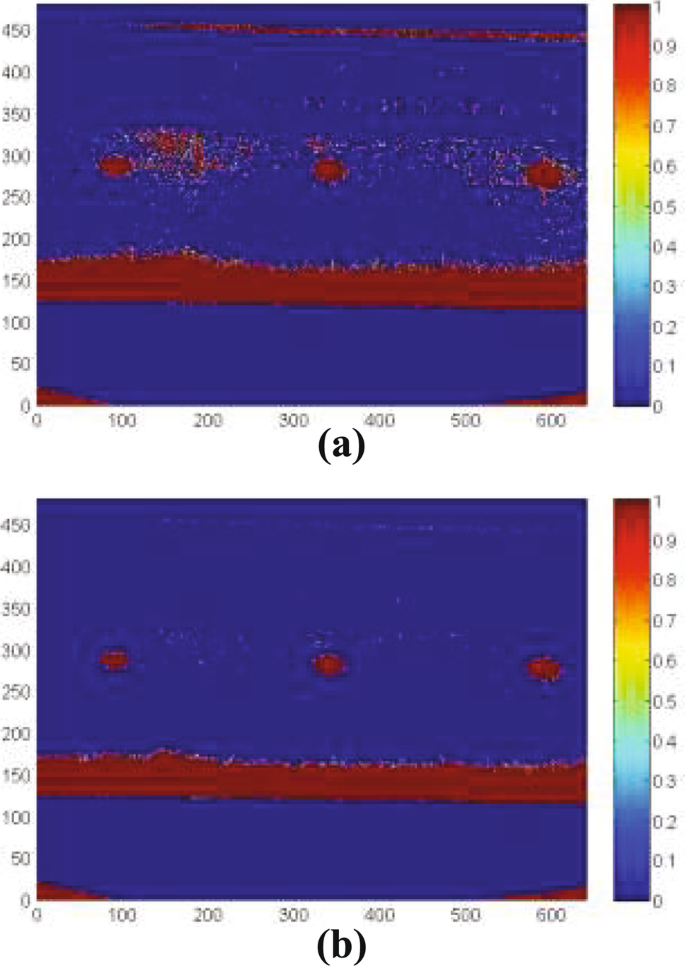
In this paper, the original GAN is employed for crack detection, and the corresponding experimental result is shown in Fig. 13. We can see that most of the background noises are reduced and the cracks are not identified successfully, which indicates that the contrast ratio of the obtained image is not large enough to distinguish the disturbances.

Fig. 13
figure 13

The result using the general GAN

Full size image

Experiment result of the modified GAN method is shown in Fig. 14. Results of the modified GAN trained by the original data and the PCA-based preprocessed data are depicted in Fig. 14a, b, respectively. Comparing with the result shown in Fig. 13, it can be seen that the contrast ratio of the generated image is relatively high and the background noises are reduced in Fig. 14, which indicates that the modified GAN outperforms the original GAN in dealing with thermal images. In addition, there are fewer noises between the cracks in Fig. 14b than that in Fig. 14a, which demonstrates the effectiveness of the PCA-based data preprocessing method.

Fig. 14
figure 14

(a) The result without PCA; (b) the result with PCA

Full size image

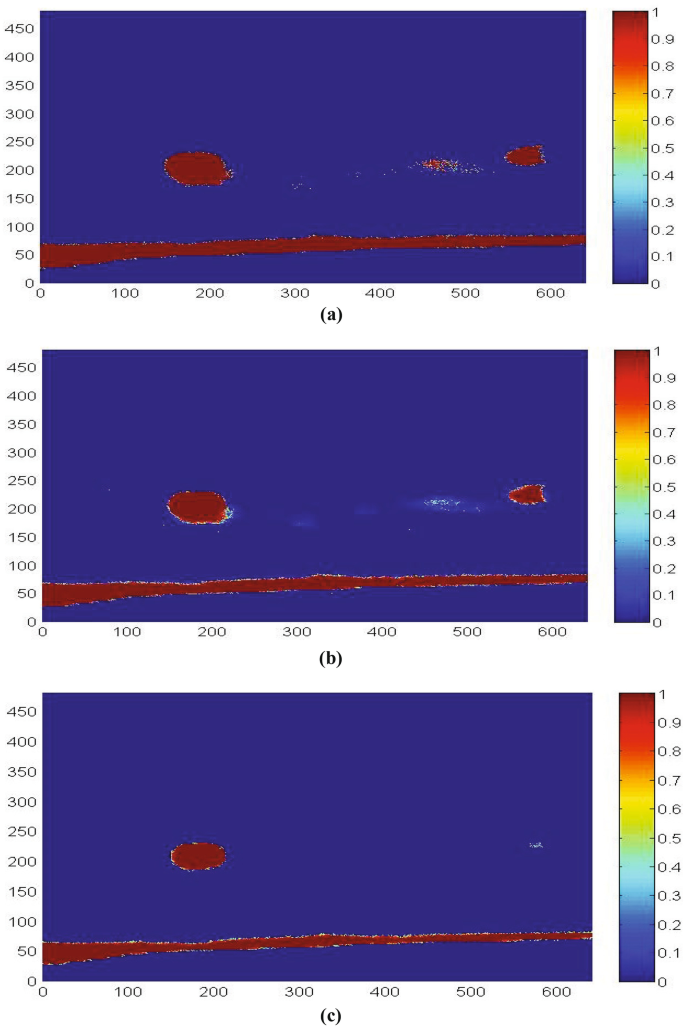
The testing results of the developed GAN-based crack detection method in Fig. 12 are displayed in Fig. 15. Different hyperparameters settings are tested as shown in Fig. 15. For the first experiment, the hyperparameters are set as \(\lambda _{1}=2, \lambda _{2}=0.1, \lambda _{3}=0.1\). In this experiment, \(\lambda _{3}\) is small which makes the thermal signal with small variance that cannot be reduced to a lower value. In this case, there are still some disturbances as shown in Fig. 15a. For the second experiment, the hyperparameters \(\lambda _{2}\) and \(\lambda _{3}\) are fine-tuned to make thermal signals with small variance to be reduced. It can be seen in Fig. 15b that most of the disturbances are alleviated. Figure 15c shows the size of the cracks is also reduced with relatively large hyperparameters. Furthermore, the crack areas are also reduced when enlarging the parameters. Based on results in Fig. 15, we can draw the conclusion that the hyperparameters of the penalty term have large influence on the generalization performance of the GAN.

Fig. 15
figure 15

(a) The result with \(\lambda _{1}=2, \lambda _{2}=0.1, \lambda _{3}=0.1\); (b) the result with \(\lambda _{1}=1.5, \lambda _{2}=0.7, \lambda _{3}=0.3\); and (c) the result with \(\lambda _{1}=0.7, \lambda _{2}=20, \lambda _{3}=0.5\)

Full size image

Conclusion

In this paper, a modified GAN algorithm has been put forward for the crack detection of an ECPT system by analyzing the captured thermal images. Motivated by the sigmoid function, a new penalty term has been designed and added in the loss function of the GAN, where the hyperparameters of the penalty term have been manually chosen according to experimental experience. The deployment of the penalty term has contributed to the feature extraction, and the background noises have been reduced. To extract the features of the thermal data, the PCA algorithm and the data augmentation method have been utilized in data preprocessing. Experimental results have demonstrated the effectiveness of the proposed GAN-based crack detection algorithm on the real-world ECPT dataset. In particular, the modified GAN has shown better performance than the conventional GAN. In our future work, we aim to: 1) develop an automatic hyperparameter selection scheme for GAN-based crack detection system based on evolutionary computation [31,32,33,34,35,36,37]; 2) apply our crack detection system to other thermography NDT tasks; 3) design a novel control strategy to enhance the detection performance of the crack detection system [38,39,40,41,42,43,44,45,46]; and 4) explore the dynamic behavior of the ECPT-based NDT process and study the thermography features based on signal processing and control theory [47,48,49,50,51,52,53,54,55,56].