Epidemic dynamics in census-calibrated modular contact network

Abstract

Network-based models are apt for understanding epidemic dynamics due to their inherent ability to model the heterogeneity of interactions in the contemporary world of intense human connectivity. We propose a framework to create a wire-frame that mimics the social contact network of the population in a geography by lacing it with demographic information. The framework results in a modular network with small-world topology that accommodates density variations and emulates human interactions in family, social, and work spaces. When loaded with suitable economic, social, and urban data shaping patterns of human connectance, the network emerges as a potent decision-making instrument for urban planners, demographers, and social scientists. We employ synthetic networks to experiment in a controlled environment and study the impact of zoning, density variations, and population mobility on the epidemic variables using a variant of the SEIR model. Our results reveal that these demographic factors have a characteristic influence on social contact patterns, manifesting as distinct epidemic dynamics. Subsequently, we present a real-world COVID-19 case study for three Indian states by creating corresponding surrogate social contact networks using available census data. The case study validates that the demography-laced modular contact network reduces errors in the estimates of epidemic variables.

1 Introduction

The study of infectious disease dynamics is known to be a challenging area of research. The dominant underlying reason is that, apart from the biology of contagion, the patterns of human connectance considerably influence the progression of infectious diseases. Since human connectivity plays a key role in the diffusion of contagion, two key factors, viz., density and demography of the population in a geography, have attracted serious attention from the research community. The definitive role played by these factors in spreading the COVID-19 pandemic is vindicated by recent studies (Balbo et al. 2020; Faziera et al. 2020; Jamshidi et al. 2020; Kang et al. 2020; Rahman et al. 2020; Arauzo-Carod 2021; Teller 2021; Von Seidlein et al. 2021).

1.1 Background and motivation

Since the onset of the COVID-19 pandemic, computer scientists, statisticians, and mathematical epidemiologists have riveted attention on accurate short- and long-term predictions for health care professionals and administrators (Agrawal et al. 2021, 2020; Ferretti et al. 2020; Giordano et al. 2020; Hamzah et al. 2020; Harsha et al. 2020; Ji et al. 2020; Li et al. 2020a; Liu et al. 2020; Mandal et al. 2020; Mao et al. 2020; Menon et al. 2020; Roy and Kar 2020; Schueller et al. 2020; Senapati et al. 2021; Shi et al. 2020; Small and Cavanagh 2020; Wynants et al. 2020). These works employ variants of compartmental models to forecast relevant epidemic variables, viz. peak day, peak cases, and epidemic span, to guide public health policy planners and epidemic management.

Taking stock of the performance of the COVID-19 models so far, eminent scientists have scrutinized and questioned the efficacy and accuracy of predictions of these models (Holmdahl and Buckee 2020; Ioannidis et al. 2020; Kuhl 2020; Saltelli et al. 2020). Despite their limitations, there is a general agreement that epidemic models are indispensable tools for public health policy planning. However, several measures are recommended for improving the quality of predictions. These include revisiting the forecasting methodology and models (Ioannidis et al. 2020; Kuhl 2020), prudently balancing the accuracy and complexity of models (Saltelli et al. 2020), advancing the theory of handling uncertainty (Ioannidis et al. 2020; Saltelli et al. 2020; Smith et al. 2020), and integrating individual behavior with disease dynamics (Jain et al. 2022).

Differential equation-based compartmental models, with the ambient assumption of a well-mixed and homogeneous population, are inadequate to model epidemic spread. Contagions often navigate through populations with heterogeneous social contacts, which are determined by their spatial distribution and demography. Network-based¹ approach is an alternative to equation-based modeling and is notably attractive for studying the spread of infectious diseases (Danon et al. 2011; Pellis et al. 2015; Small and Cavanagh 2020). Since it emulates direct contact between individuals in a population, network functions as an apposite apparatus to simulate the transmission of diseases and offers a platform to tune policies for mobility restrictions. Drawing substantially from the solid foundations of the compartmental models, the network-based approach is competent in modeling the social contact patterns of the population and estimating the size and span of an epidemic.

In a network-based approach, the structure of the underlying wire-frame for simulating the epidemic spread is a dominant factor influencing the quality of estimates. In this research, we study the role of a modular contact network² and its structure on the epidemic dynamics. We create the wire-frame to proxy the modular contact network of a population by considering the spatial structure and demography of a geography. Since these two aspects directly impact human interactions, running simulations on a density- and demography-aware social contact network has a strong potential to deliver realistic estimates of epidemic variables.

The current proposal for creating a demography-laced contact network for simulating the epidemic spread draws from two lines of research. The first one is related to the study of epidemic dynamics on interconnected networks aka network-of-networks (Hui and Zi-You 2007; Dickison et al. 2012; Saumell-Mendiola et al. 2012; Wang et al. 2013). Second is the set of studies that explore associations between epidemic dynamics, population density, and demography (Neiderud 2015; Faziera et al. 2020; Hamidi et al. 2020; Kang et al. 2020; Mueller and Papenhausen 2020; Rahman et al. 2020; Arauzo-Carod 2021; Bhadra et al. 2021; Von Seidlein et al. 2021).

Earlier works simulating epidemic spread over interconnected networks concur that these modular networks capture contagion dynamics realistically (Hui and Zi-You 2007; Saumell-Mendiola et al. 2012; Dickison et al. 2012; Li et al. 2014; Wang et al. 2014; Liu et al. 2015; Bhattacharyya and Vinay 2020). Most of these works study epidemic dynamics on a small-sized network consisting of a few modules (Hui and Zi-You 2007; Saumell-Mendiola et al. 2012; Wang et al. 2013). Studies also reveal that the strength and nature of the coupling between the constituent networks affect the epidemic dynamics (Dickison et al. 2012; Saumell-Mendiola et al. 2012). Ingraining the network with spatial information extends its ability to model population mobility and understand epidemic dynamics for different scenarios of mobility restrictions (Riley et al. 2015; Arauzo-Carod 2021).

The COVID-19 pandemic has spurred several location-based empirical investigations about the association of population density and demography with the evolution of the epidemic (Arauzo-Carod 2021; Bhadra et al. 2021; Faziera et al. 2020; Hamidi et al. 2020; Jamshidi et al. 2020; Kadi and Khelfaoui 2020; Kang et al. 2020; Rahman et al. 2020; Von Seidlein et al. 2021). Some studies related to localizing the spatial distribution of a region furnish evidence of a positive correlation between density and COVID-19-positive cases (Bhadra et al. 2021; Faziera et al. 2020; Kadi and Khelfaoui 2020). However, some findings that examine the association between population density and epidemic spread yield inconclusive signals (Hamidi et al. 2020; Jamshidi et al. 2020). A recent review of the pandemic-era literature that relates urban density and epidemic dynamics observes the lack of scientific consensus about the effect of density on epidemic spread (Teller 2021).

1.2 Contributions and organization

Our framework extends the small-sized city network proposed by Bhattacharyya and Vinay (2020) by fortifying the network with interaction patterns commensurate with the local demography of the population. Specific contributions to the research are listed below.

• i. We propose a framework for creating a census-calibrated modular contact network for a geography divided into zones (Sect. 2.1). The proposed framework is grounded in parsimony and uses basal demography data from the census. We estimate the interaction patterns by explicitly modeling family, social, and work contacts that arise due to population density variations and demography. The network thus created purports a wire-frame for simulating the epidemic spreading process.

• ii. Systematic study of synthetic modular network aka network-of-networks:

  • a. We affirm the small-world topology of the constructed network by quantifying its small-world-ness, and verify the Poisson degree distribution of the network (Sect. 4.1.1).

  • b. We experiment to understand the impact of zone structuring, density variations, and population mobility of a geography on the epidemic spread by constructing a synthetic modular network. Working with synthetic networks permits focused scrutiny of the factors being examined under the controlled environment (Sects. 4.1.2–4.1.4). Though these factors are decisive determinants of human connectance, to the best of the authors’ knowledge, this is the first systematic attempt to explicitly examine their relationship with the epidemic spread while dissociating from the complexities of other socio-economic factors.

  • c. We perform an ablation study by systematically adding demographic parameters in the network and observing epidemic variables. Our results reveal noticeable variations in epidemic dynamics as demographic parameters are gradually introduced into the network. The observations affirm our conjecture that incorporating demography in real-world epidemiology studies yields more realistic predictions (Sect. 4.1.5).

• iii. We present a real-world case study for three Indian states, viz., Delhi, Goa and Odisha, by creating their surrogate social network-of-networks using census data³ (Sect. 4.2).

  • a. We affirm the small-world topology of the networks constructed for three Indian states (Sect. 4.2.1).

  • b. We demonstrate that the demography-laced modular contact network improves the estimates of epidemic variables compared to synthetic network (Sect. 4.2.2).

Though we use SEIHRD⁴ epidemic model to study the COVID-19 pandemic as a backdrop, our framework for constructing a demography-laced modular network is generic, and the network is suitable for simulating any epidemic spread model.

2 Methods

2.1 Framing census-calibrated social contact network

The network of interconnected networks is a pertinent model for representing interconnections among individuals in the spatial structure of geography. We represent the contact patterns of the population in a geographical unit (state/city/town) as an interconnection of multiple networks (modules), each corresponding to a sub-unit (zone) of the geography. Nodes in a module denote individuals in the zone, and the edges denote interactions (contacts) between individuals.

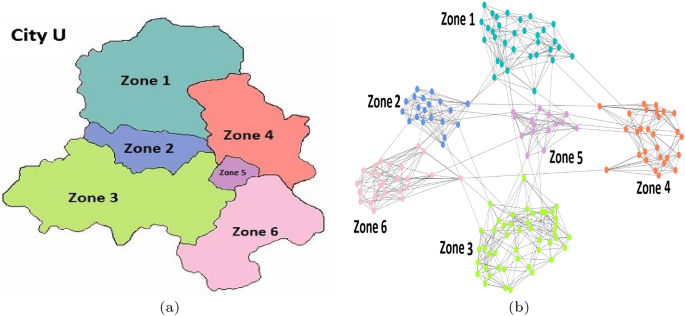
Example 1

Consider a geography of a toy city U comprising six zones as shown in Fig. 1a. The corresponding social contact network of U is modeled as an interconnection of six networks (Fig. 1b).

Fig. 1

a Illustration of a geography U with six zones, b Modular social contact network of geography U modeled as an interconnected network of six networks

Modules corresponding to zones are modeled as small-world networks with edges representing interactions between individuals in home space. Additional edges are added to each module, representing interactions outside the household in social space. The modules are then interconnected to model interactions in work space involving travel to (possibly) different zones.

Each module is impregnated with the corresponding demographic details of the zone, thereby capturing heterogeneity in the overall structure of the social contact network of the geography. Since family interactions represent contacts in the home space, the distribution of family size primarily dominates  the number of edges in the network module. The size of the working-age population in a zone determines the number of work edges in the module. Interactions outside the household to meet day-to-day social and shopping needs, medical assistance, etc., generate social contacts. Thus, diligent use of the demographic information of the zone approximates contact patterns akin to the real-world social contact network of the population.

2.1.1 Topology of a module

In a comprehensive account of networks and epidemiology of the infectious diseases, Danon et al. (2011) state that small-world-ness of the network has clear implications for disease spread and its control. Earlier, Shirley and Rushton (2005) empirically demonstrated that the dimension of the base lattice of a small-world network significantly affects the size and span of an epidemic. The dimension of the base lattice governs the topological properties of the network, which ultimately impacts the epidemic dynamics.

In this context, we make use of an important result given by Newman (2000), which relates clustering coefficient, average degree, and dimension of the lattice. In a small-world network with base lattice of dimension d and average degree k, the clustering coefficient (CC) is related to k and d as follows.

$$\begin{aligned} CC = \frac{3(k - 2d)}{4(k - d)}. \end{aligned}$$

(1)

The clustering coefficient of the network tends to zero when $k \longrightarrow 2d$, implying that the lattice loses its clustering property as the average degree approaches twice the dimension of the lattice. We, therefore, carefully choose the dimension of the base lattice while taking into account the population density, which influences the average degree and clustering coefficient of the curated network.

2.1.2 Embedding demography in modules

Consider a geography U divided into m zones $\{z_1, \ldots , z_m\}$ with compatible population vector $\vec {P}$, density vector $\vec {\Delta }$, household vector $\vec {H}$, and vector $\vec {K}$ denoting mean household size of zones. Element $p_i$ in $\vec {P}$ denotes the population of zone $z_i$, $\delta _i$ in $\vec {\Delta }$ denotes its population density, $h_i$ in $\vec {H}$ denotes its  number of households, and $k_i$ in $\vec {K}$ denotes its  mean household size.

We generate small-world networks $\{G_1, \ldots ,G_m\}$ corresponding to zones $\{z_1, \ldots , z_m\}$, with number of nodes equal to their respective populations. The degree of the regular base lattice for $G_i$ is set to $k_i$ (mean household size), and the dimension is decided based on the population density $\delta _i$ of $z_i$. According to the United Nations and Social Affairs (2017) global population survey, the average household size ranges from fewer than three persons per household to more than six in countries across the continents. Considering this range of household size, the dimension of the base lattice of a module is limited to $\{1, 2\}$, so that the average clustering coefficient and average path length are compatible with the small-world network.

Modeling interactions in family space: We define a function ${\mathcal {M}}: \vec {\Delta } \longrightarrow \vec {D}$ to map the population density of a zone to the dimension of the base lattice of the corresponding small-world network (module) as follows.

$$\begin{aligned} d_i = {\mathcal {M}}(\delta _i) ={\left\{ \begin{array}{ll} 1 &{} \text { if } \delta _i \le \Delta _{avg} \\ 2 &{} \text { otherwise,} \end{array}\right. } \end{aligned}$$

(2)

where $\Delta _{avg}$ denotes the average density of m zones in the geography. Small-world networks thus created corresponding to the m zones embody variation in the spatial density of the geography U. Notably, mapping ${\mathcal {M}}$ can be defined by the user to appropriately inlay family contacts in accordance with the social culture and ground realities of different zones of the geography. In geographies with no significant density variations, the dimensions for all modules  may be set uniformly.

The regular base lattice of dimension $d_i$ (using Eq. 2) is created with $p_i$ nodes of degree $k_i$, and is rewired with probability $\rho$ to yield a small-world module $G_i$. In this way, we obtain m networks, each infused with the basic demographic information of the corresponding zones in U, with edges ensconcing interactions in home space. The network is subsequently loaded with edges representing contacts in social and work spaces.

Modeling interactions in social space: Realistic depiction of social interactions in a network is an arduous task because of the gamut of complexities arising out of social and economic processes prevalent in the geography. Moreover, measuring and modeling social interactions poses formidable challenges because of their change with space and time.

We take an elemental view of the problem and consider social interactions as a function of the number of households in zone $z_i$. Element $h_i$ in vector $\vec {H}$ denotes the number of households in zone $z_i$. Since social interactions in geography are influenced by culture, demography, seasons, etc., sociability index $\tau$ provides the handle to capture these nuances in the wire-frame. Accordingly, $\tau$ is used as a multiplier to determine the number of social edges ($\tau \times h_i$) in $G_i$.

Modeling interactions in work space: Next, we connect the modules (corresponding to zones) to create a social contact network-of-networks for U. Following Liu et al. (2015), we use the coupling density vector $\vec {Q}$ of size m to interconnect modules. Demographically, $\vec {Q}$ denotes the size of the working population that mobilizes within and across zones for livelihood. Element $q_i$ denotes the fraction of individuals in $z_i$ traveling for work, thereby modeling contacts in work space. Hadamard product $\vec {P} \otimes \vec {Q}$ fixes the number of interconnecting edges for $G_i$ corresponding to zone $z_i$. The edges are added to $G_i$ such that they have one endpoint in $G_i$ and the other endpoint lies in any of the m modules (including $G_i$). The inter-and intra-modular edges thus created represent interactions in the work space.

The resulting network, with small-world topology, serves as the wire-frame for simulating the spread of an epidemic. Variation in the demography of the zones induces heterogeneity in connectance patterns in the modules. We designate this wire-frame as surrogate social contact network-of-networks (SSCN) of the geography U.

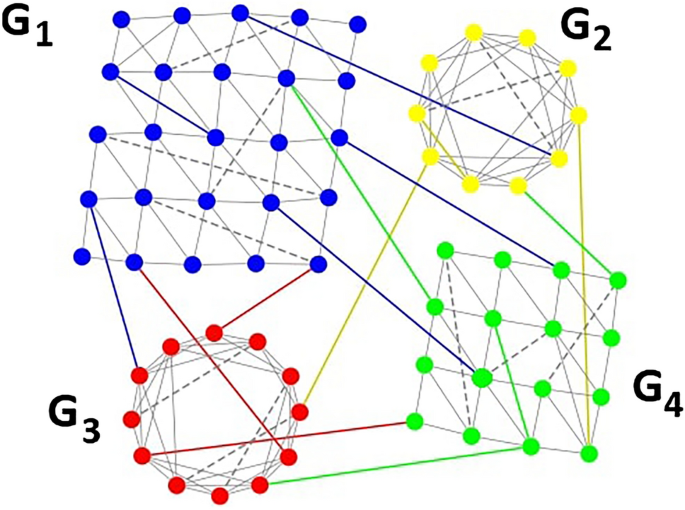
Example 2

Consider the following demographic information for a toy urban space U with four zones, mapping ${\mathcal {M}}$ as defined in Eq. 2 and sociability index $\tau = 1$.

• i. $\vec {P}=\{25,10,12,16\}$ - Population vector,

• ii. $\vec {\Delta }=\{5,2,3,4\}$ - Density vector,

• iii. $\vec {K}=\{6,6,6,6\}$ - Mean household size vector,

• iv. $\vec {H}=\{4,2,3,3\}$ - Household vector,

• v. $\vec {Q} = \{0.2, 0.3, 0.25, 0.25 \}$ - Coupling density vector

Average density ($\Delta _{avg}$) of U being 3.5, we obtain $\vec {D} = \{2,1,1,2\}$ as the resultant dimension vector. Modules created with the designated dimension of the base lattice and degree are rewired with probability $\rho =0.01$ to generate edges in home spaces (solid gray lines). Social edges are added using $\vec {H}$ and the sociability index $\tau$. Finally, the modules are interconnected by work edges using $\vec {P} \otimes \vec {Q}$. The final surrogate social contact network of U is shown in Fig. 2. Modules {$G_1,G_2,G_3,G_4$} correspond to zones {$z_1,z_2,z_3,z_4$}, with the number of nodes equal to their respective populations (shown in different colors). $G_2$ and $G_3$ have one-dimensional base lattice, and $G_1$ and $G_4$ have two-dimensional base lattice structure. Social contacts are shown with dash lines within the modules. Work contacts for a module are shown with the same color as that of the module. $\square$

Fig. 2

Illustration of a toy modular social contact network. The network has two 1D modules ( $G_2$, $G_3$) and two 2D modules ($G_1$, $G_4$). Solid gray edges within each module denote family contacts. Social contacts within each module are shown with gray dash lines. Work contacts (intra-and inter-module connections) are shown with the same color as that of the module

The methodology for constructing the wire-frame exploiting census data is inexpensive and generic compared to alternatives that infer contact patterns from human-mobility data obtained from smartphone-based GPS technology or by digital contact tracing (Ferretti et al. 2020; Huang et al. 2016; Ma and Lipsitch 2020).

2.1.3 Enriching the wire-frame

The framework described above induces a basic wire-frame to systematically study contagion dynamics in a geographical unit with varying demographic factors. The framework is versatile enough to accommodate employment, socio-economic, and behavioral data to simulate close-to-real social contact patterns. The prospects of enriching the wire-frame rise with the availability of quality demography data. We envisage possible enrichment of the wire-frame in one (or more) of the following ways, based on the data availability:

• i. The availability of detailed age distributions for the population allows for embedding more nuanced contact patterns in the network. Geographies with an aging population have fewer social contacts per household, while those with a younger population tend to have more social contacts. Sociability index $\tau$, which abstracts the extent of societal interactions in the population, can be set suitably to reflect the age distribution and regulate the number of edges in social space. Recent data collection exercise carried out by Koltai et al. (2022) to construct age-contact matrices with the high temporal and spatial resolution is a promising idea to obtain closer-to-representative contact networks.

• ii. Availability of land use data and employment-related data⁵ for zones admits mobility patterns closer to reality. Employment-related data for the population of the zones promote more realistic interconnections between modules. Detailed mobility data, if available, can be assimilated in the wire-frame by instantiating $m \times m$ interaction matrix to add interconnecting (work) edges between the modules. Zones with industrial and residential land use exhibit distinctly different patterns of social contacts compared to urban spaces with mixed land use. Thus, embedding land use data can refine the overall topology of the wire-frame by suitably grading the social and work contacts in a geography.

• iii. Zone-wise data for compliance with the recommended behavior and imposed restrictions can be incorporated into the network by appropriately altering contact patterns, thereby enabling empirical testing of behavioral and social conjectures that influence human interactions during the spread of epidemics. This accommodates the recent recommendations to align social and behavioral sciences with the epidemic spreading models (Van Bavel et al. 2020; Jain et al. 2022).

• iv. Network model of the social contacts in the population is potent to accommodate mobility restrictions like lockdown and curfew. Recently, Pung et al. (2022) collected high-resolution contact data among passengers and crew on cruise ships to examine the impact of combined interventions on the social contacts arising in different activity settings. Ingraining data for various interventions helps to study the effect of mobility restrictions between zones during the spread of an epidemic.

• v. The basic wire-frame considers all network modules at the same level. In case zones in the geography are divided further for administrative convenience (say, wards), the availability of the data for sub-units can extend the design of the network to two levels. The hierarchical network-of-networks provides a mechanism for examining several “what–if” scenarios at a micro-level and facilitates the focused study of the dynamics of local disease outbreaks.

It is important to note that temptation to introduce realism in the wire-frame to understand and explain epidemic dynamics in the real world may incur higher computational costs (Xia et al. 2015; Bhattacharyya and Vinay 2020). Such parameter-intensive models are more prone to errors and may produce results contrary to expectations.

2.2 Epidemic spread model

We simulate the spread of an epidemic in the population and study its dynamics to assess the effectiveness of the surrogate social contact network. Though any epidemic model viz., SI, SIR, and SIRS (Britton 2010) can be used for this purpose, we use a variant of the SEIR model to examine the role of demography in social contact networks using real data for the COVID-19 pandemic.

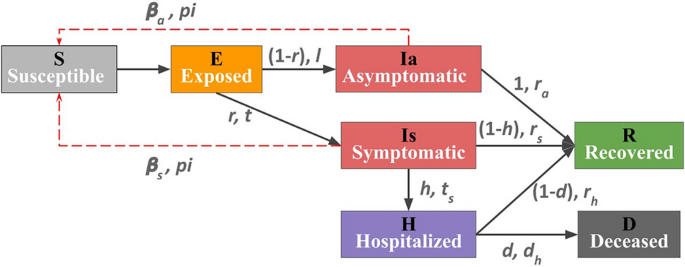
SEIR is a classical compartmental model consisting of four epidemiological classes, viz., S (susceptible), E (exposed), I (infected), and R (recovered). Several extensions of the classical SEIR epidemic process have been employed to study COVID-19 pandemic (Agrawal et al. 2020; Menon et al. 2020; Shi et al. 2020; Venkateswaran and Damani 2020; Wang et al. 2020; Senapati et al. 2021). We adopt a variant (SEIHRD) that splits class I into two compartments, viz., asymptomatic ($I_{a}$) and symptomatic ($I_{s}$). The model also compartmentalizes hospitalized (H) and deceased individuals (D), as shown in Fig. 3.

Fig. 3

SEIHRD Model: state transition pathways for an infected individual

Individuals in compartment E may develop symptoms and progress to the symptomatic infected ($I_s$) compartment with probability r in time period t. Due to their highly contagious state, these individuals are quarantined to curb the pathogen’s spread through direct contact. However, there is a small, finite probability $\beta _s$ that a symptomatic individual may pass the contagion to a susceptible individual through accidental contact. Even after the latency period (l), some exposed individuals do not exhibit symptoms and move to the asymptomatic infected ($I_a$) compartment. Unaware of their infected status, they intermix freely in the population, infecting susceptible contacts with a high transmission probability $\beta _{a}$ ($\gg \beta _s$). Asymptomatic individuals are unidentified and hence are instrumental in the spread of infection (Yu and Yang 2020; Agrawal et al. 2021).

Individuals in compartment $I_a$ who are asymptomatic recover naturally over time ($r_a$) and transit to the recovered compartment (R). Some symptomatic individuals may recover after a mild illness, while others get very sick and require hospitalization. The health of some symptomatic individuals worsens (in time $t_s$), and they move to the hospital compartment (H) with probability h. The remaining transit to compartment R after recovery within period $r_s$. Hospitalized individuals either recover from illness in period $r_h$ and move to compartment R or unfortunately die within period $d_h$ and move to compartment D. Isolation of symptomatic and hospitalized individuals connotes a quarantine state.

Initialization of the spreading process: We mark the seed node(s) as symptomatic infectious ($I_s$) and set all the neighbors as asymptomatic ($I_a$). We also expose (E) all the neighbors of nodes in $I_a$ compartment, assuming they exposed the susceptible contacts unknowingly. Finally, we simulate the spreading process and note the active cases to derive three epidemic variables: peak day, peak active cases, and span of the epidemic.

2.3 Implementation of non-pharmaceutical interventions

We implement non-pharmaceutical interventions (NPIs) by removing edges (contacts) from the network and restoring them when the intervention is rolled back. Assuming that public behavior is never perfect, the level of compliance required for lockdown is simulated by controlling the removal of edges. Since NPIs do not disrupt family contacts, the action of addition and removal of edges is restricted to work and social contacts only. Compliance parameters are set according to the derived notion of an appropriate NPI strategy. To implement lockdown observed with p% compliance, for example, (100 - p)% edges are kept in the network.

3 Materials

3.1 Parameters for synthetic modular network and epidemic simulation

Experiments use a synthetic modular social contact network that mimics a city with a population of size N = 100 K (N = $\Sigma _i p_i$), divided into m equi-sized zones (population of each zone $p_i=\frac{100\,K}{m}$). The demography for all zones is identical, i.e., all zones have the same household size ($k_i$  = 6), the same number of households ($h_i$ = 0.01*$p_i$). Since the population density of a zone determines the dimension of the base lattice for the corresponding module, we use a dimension vector $\vec {D}$ to model the connectance pattern arising due to population density, which is set as per the experimental objective. For simplicity, the sociability index $\tau$ is set to 1. Assuming the same working-age population for all zones, we use coupling density, $q_i$ = 0.01 for all modules unless specified explicitly. Each module is a small-world network rewired with probability $\rho$ = 0.01⁶. Table 1 summarizes the parameters for the construction of the demography-laced synthetic network. We initiate the SEIHRD spreading process with one random seed node. The parameters for the spreading model are given in Table 2.

Table 1 Parameters for creating a synthetic network for a geography with a population of size 100K (N) and m zones (modules). Each parameter vector is of size m and contains the specified demographic information, which is the same for all zones (modules). The number of modules m and dimension vector $\vec {D}$ for modules are set as per the experiment objective and value of x may be either 1 or 2

Table 2 Parameters used for simulation of SEIHRD epidemic spread process

3.2 Parameters for surrogate modular network and epidemic simulation

This section describes the demography data used to create a surrogate social contact network (SSCN) for the three Indian states (Delhi, Goa, and Odisha), the parameters of the spreading process, and simulation details. The selection of states is motivated by the diversity in the rural–urban agglomeration and population density. Delhi is the capital of India and the largest metropolitan city-state, with high urban agglomeration. Among small states, Goa has the largest urban population. Odisha has a predominantly rural population with lower wages and fewer job opportunities, primarily engaged in farming, fishing, and forestry, as per the report by Asian Development Bank (2017). We use demography estimates extrapolated from the 2011 Indian census for our study because the census scheduled for the year 2021 could not be held in India due to the COVID-19 pandemic. Actual active cases for Delhi, Goa, and Odisha are retrieved from COVID-19, India (2019).

3.2.1 Zones and demography

Delhi, the national capital of India, is a densely populated metropolis with an estimated population of 19.6 million, as per the census estimate for 2021. Since the basic demographic data for 2011 is available, we extrapolate the population of the nine zones and construct the SSCN of Delhi with nine modules. Each module is parametrized with the corresponding demographic data presented in Appendix A (Table 6).

Goa, an Indian coastal state, has an estimated current population of 1.528 million. There are two districts, North Goa and South Goa, which are further divided into six and five sub-districts, respectively. The SSCN of Goa is accordingly constructed with 11 modules, each parametrized with the corresponding demographic data shown in Table 7 of Appendix A.

Odisha, the $8^{th}$ largest state by area is the $11^{th}$ largest state with an estimated current population of 45.42 million. There are 30 districts, with 83% of the population living in rural areas. The SSCN of Odisha is constructed with 30 modules, each parametrized with the corresponding demographic data detailed in Appendix A (Table 8).

Table 3 summarizes the basal details of three states.

Table 3 Three Indian states and their demographic details as per Census 2011

3.2.2 Parameters for the spreading process

Epidemiologists strive to estimate $\beta$ (probability of transmission) from the epidemic statistics and use it to predict the course of an epidemic for a relatively short term, with automatic course correction when prediction error increases beyond a threshold. Techniques used to estimate $\beta$ span over the biological, statistical, and computational methods (Read et al. 2020; Mohamadou et al. 2020).

We simulate the epidemic spread in four phases, where parameters for the initial phase are the same as given in Table 2. We use estimates from the SUTRA model, which is hailed as a supermodel for India-specific predictions (Agrawal et al. 2021). SUTRA model estimates parameters for Indian states (from May 2020 to October 2021) in the next three phases as described in Appendix D. We draw the remaining parameters for simulation of the epidemic process from compatible India-specific studies⁷, the details of which are given in Table 2. The timeline of non-pharmaceutical interventions (NPIs) imposed by the Government of India is given in Appendix C (Table 10). The initiation process for simulation is explained below.

• i. Delhi simulation: We initiate simulation on SSCN of Delhi with real data of seven patients (reported on 14 March 2020 (COVID-19, India 2019)) as discussed in Sec. 2.2. We run epidemic spread simulations for Delhi, considering the initial phase of 14 March to 27 May 2020, using India-specific infectivity rate ($\beta _a$) drawn from early studies. We use the estimates from the SUTRA model for the next three phases. Thus, the transmission probabilities used for simulation are $\beta _a=(0.42,0.0978,0.1353,0.1182)$.

• ii. Goa simulation: Seven cases of COVID-19 were confirmed in Goa on 4 May 2020 (COVID-19, India 2019). We infect as many nodes in SSCN of Goa and initiate the spreading process as described in Sec. 2.2. We consider the initial phase for Goa epidemic spread simulations from 4 May 2020 till 27 May 2020 using India-specific infectivity rate ($\beta _a$). For the next three phases, we use the estimates from the SUTRA model. Thus the transmission probabilities used for simulating infection spread by the asymptomatic cases in four phases are $\beta _a=(0.42,0.1654,0.1953,0.1564)$.

• iii. Odisha simulation: Five cases of COVID-19 were confirmed in Odisha on 2 April 2020 (COVID-19, India 2019). We infect five nodes in SSCN of Odisha and initiate the spreading process as described in Sec.  2.2. We simulate epidemic spread in Odisha during the initial phase (2 April 2020 to 27 May 2020) using India-specific infectivity rate ($\beta _a$). For the next three phases, we use the estimates from the SUTRA model with the transmission probabilities in four phases as $\beta _a=(0.42,0.2014,0.2034,0.1496)$.

4 Results and discussion

We assess the merit of the basic wire-frame for understanding the role of demography on epidemic dynamics using synthetic networks. Though synthetic networks are antitheses of surrogate networks, their use accords options to scrutinize the impact of one control parameter while keeping others static. The COVID-19 case study for three Indian states indicates the validity of the conjecture that demography-laced networks realistically capture real-world epidemic dynamics.

We simulate the epidemic process and note the peak epidemic size, peak day, and span of the epidemic. Peak epidemic size is the maximum number of active cases (symptomatic and hospitalized) on a given day. The day when the active cases are maximum is the peak day. The span of an epidemic denotes the period between when the first and last cases were reported. All reported results are averaged over ten runs to mitigate the effect of randomness. In the plots, we show the epidemic curves with standard deviation as shaded regions. We use Python (64bits, v 3.7.2) to implement the SEIHRD model and create networks using the Igraph library. Programs are executed on Intel(R) Core(TM) i7, CPU @1.80GHz with 16GB RAM.

4.1 Epidemic dynamics in demography-laced synthetic modular networks

We confirm the small-world property of the wire-frame created by the proposed methodology in Sec. 4.1.1 before embarking on the detailed experimentation. We study the epidemic dynamics with variation in zone structure of a geographical unit in Sec. 4.1.2. Experiments reported in Sec. 4.1.3 demonstrate that high population density promotes the spread of infection. In Sec. 4.1.4, we validate that higher coupling density (population mobility) in the network expedites the epidemic spread, and network construction does not alter general principles of the epidemic spread.

4.1.1 Small-world-ness of wire-frame

Small-world networks are characterized by high clustering coefficients and small average path lengths. The clustering coefficient (CC) is the proxy for the quantitative assessment of locally dense regions, with high values typical of lattice-based regular networks. The average path length (APL) indicates the efficiency of transmission in the network, with shorter lengths typical of random networks. Thus, short APL accelerates the epidemic spread, while high CC retards it by limiting the ability of infected individuals to infect their local neighborhoods. Therefore, small-world-ness of social contact networks exhibits interesting epidemic dynamics because of the antithetical action of the two network properties.

Small-world-ness coefficient:Humphries and Gurney (2008) propose a metric to quantify the small-world-ness property based on APL and CC of the network. Let ${APL}_x$ and ${CC}_x$ be the average path length and average clustering coefficient of network x, where $x=R$ for the random network and $x=G$ for the network under investigation with the same size and order. Network G is considered to be small-world network iff $S(G) > 1$, where small-world-ness (S) of network G is quantified in Eq. 3 (Humphries and Gurney 2008).

$$\begin{aligned} S(G)=\frac{{CC}_G*{APL}_R}{{CC}_R*{APL}_G} \end{aligned}$$

(3)

We generate two sets of synthetic modular networks belonging to two categories. The first category of networks has all modules with a one-dimensional base lattice (M-1D), and the second category of networks has all modules with two-dimensional base lattice (M-2D). We consciously model networks (geographies) with the same population and uniform population densities in all zones to reduce two degrees of freedom. This gives us the opportunity to examine the effects of zoning (by varying the number of modules), population mobility (by varying coupling density), and topology on the epidemic dynamics for different population densities. We compute the average clustering coefficient and average path length for each network (Table 4). To allay the randomness of the generated networks, we report measurements averaged over ten runs along with standard deviations. It is observed that average clustering coefficients and average path lengths are higher for M-1D networks than M-2D networks due to the difference in the connectance patterns of the underlying base lattice. Further, the clustering coefficient remains nearly the same for each category despite increasing the number of modules. However, the average path length increases with increasing modules for both categories.

Table 4 Topological properties of M-1D and M-2D networks with population $N=100K$, average degree $\approx 6$. m: number of modules, CC: average clustering coefficient, APL: Average path length, S: small-world-ness coefficient

We present the value of the computed small-world-ness coefficient (S) for all networks using Eq. 3 in Table 4. The large positive values of S in the table affirm the small-world-ness of the wire-frames created by the proposed methodology. The value of coefficient S decreases noticeably due to increased path length for networks with the increase in the number of modules in both categories. The investigation positively indicates that the wire-frame displays small-world-ness property.

Degree distribution: Small-world networks approximately follow Poisson degree distribution (Zafarani et al. 2014). Consider a random variable $X \sim Poisson(\lambda )$ denoting the degree of a node. The probability mass function $P_X(x)$ and cumulative distribution function $F_X(x)$ of X are given as follows.

$$\begin{aligned} P_X(x)&= \frac{e^{-\lambda } \lambda ^x} {x!}; \quad x=0,1,2 ,\ldots \end{aligned}$$

(4)

$$\begin{aligned} F_X(x)&= \sum _{i=0}^{x} P(X=i);\quad x=0,1,2, \ldots \end{aligned}$$

(5)

A Poisson random variable Y is said to be doubly truncated if the extreme values of the variable are either missing or unobserved. The probability distribution of $Y (\alpha _l \le Y \le \alpha _r)$ is given in Eq. 6 (Zafarani et al. 2014).

$$\begin{aligned} P_Y(y) ={\left\{ \begin{array}{ll} 0 &{} y < \alpha _l \\ \dfrac{e^{-\lambda } \lambda ^y}{y!} [{F_X(\alpha _r)-F_X(\alpha _l - 1)}]^{-1} &{} \alpha _l \le Y \le \alpha _r \\ 0 &{} y > \alpha _r \end{array}\right. }. \end{aligned}$$

(6)

In the context of a social contact network of a population, it is realistic to assume that no individual is entirely isolated. Further, anthropology and sociology studies have confirmed a well-defined limit to the number of social contacts an average individual can retain in the physical world (De Ruiter et al. 2011). Ergo, the degree of nodes in the social contact network, is bounded at both ends $(\alpha _l \le X \le \alpha _r)$, and we expect the degree distribution of the constructed wire-frame to be doubly truncated Poisson distribution.

Let $x_1, \ldots . x_N$ denote the empirical degree distribution obtained from the network with N nodes and let $\bar{x}$ be the empirical mean. Considering it as a doubly truncated sample from Poison distribution, we estimate $\hat{\lambda }$, the mean degree of the network, using the maximum likelihood estimator (MLE) proposed by Cohen (1954). Note that the degree of the base lattice is the theoretical mean $\lambda$ of the small-world network, which is the same (six) for all networks. The likelihood function of a random sample of N observations from a Poisson population with a mean $\lambda$ may be written as Eq. 7.

$$\begin{aligned} P(x_1, \ldots , x_N)&= [{F_X(\alpha _r)-F_X(\alpha _l-1)}]^{-N}\nonumber \\&\quad e^{-N\lambda }{\lambda }^{\sum _{1}^{N}{x_i}} \left[ \prod _{1}^{N}{x_i!}\right] ^{-1}. \end{aligned}$$

(7)

The following estimated equation is obtained by differentiating the log-likelihood function ${\mathcal {L}}$ and equating it to zero (See Cohen (1954) for details).

$$\begin{aligned} \frac{d{\mathcal {L}}}{d\lambda } = \frac{\bar{x} }{\lambda } - 1 -\frac{P_X(\alpha _l - 1) - P_X(\alpha _r)}{F_X(\alpha _r) - F_X(\alpha _l-1)} = 0. \end{aligned}$$

(8)

Since there is no closed form, $\hat{\lambda }$ is computed by elementary iterative procedure to maximize $\frac{d{\mathcal {L}}}{d\lambda }$.

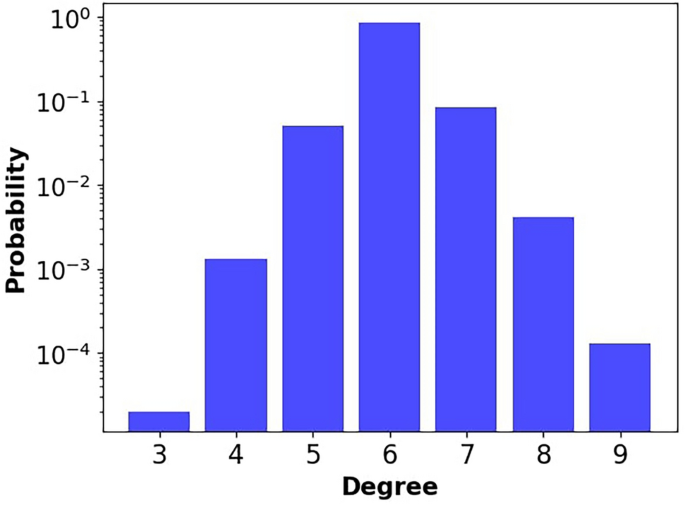
We compute the degree distributions of M-1D and M-2D networks. Since the average degree for the base lattice and other construction parameters for both categories of networks are the same, all networks display similar empirical degree distributions with N = 100K, an empirical mean $\bar{x} = 6.04$, $\alpha _l = 3$ and $\alpha _r = 9$ (Fig. 4). We estimate the mean degree using $\hat{\lambda } = 6$ as the first approximation and $\hat{\lambda } = 7$ as the next. Table 5 shows the iterative refinement of MLE, with $\hat{\lambda } = 6.2355$ as the estimated mean degree of the created wire-frames. This estimate is very close to the degree of the base lattice and the empirical average degree of 6.04 of the network.

Fig. 4

Empirical degree distribution of the generated networks as  doubly truncated Poisson distribution with $\alpha _l = 3$ and $\alpha _r=9$

Table 5 Iterative refinement of MLE of mean degree $\lambda$ for the synthetic network to determine the estimated value $\hat{\lambda }$, for which $\frac{d{\mathcal {L}}}{d\lambda } =0$

With two characteristics, viz., small-world-ness and Poisson degree distribution verified, it is reasonable to deduce that the generated M-1D and M-2D networks are small-world networks and mimic topological properties of real-world social contact networks.

4.1.2 Zoning of urban spaces and epidemic spread

With rapid urbanization in developing countries, adequate city planning and surveillance are potent tools to mitigate the spread of infectious diseases and improve public health (Neiderud 2015). Zoning of urban spaces, which is an important strategy for urban planning and governance, helps contain the epidemic and guides planners and administrators in imposing zone-wise travel restrictions in a graded fashion without shutting down the entire geography. We observe the effect of zoning on epidemic variables by focusing our attention on the number of zones and density for fixed population size. Keeping the population density uniform in all zones for both categories of networks insulates the spreading process from the effects of density variations. We simulate the epidemic spread over the networks generated earlier and note the active cases to derive the peak day, peak active cases ($I_s + H$), and span of the epidemic as three epidemic variables.

Fig. 5

Variation in peak day, peak active cases, and epidemic span in the M-1D and M-2D networks. The number of modules m varies from 1 to 100

Figure 5 shows the impact of variation in the number of modules (zones) in both categories M-1D and M-2D, on the epidemic variables. We observe that all three variables show similar trends for both categories with an increasing number of modules. Peak days arrive faster for smaller values of m, albeit comparatively earlier for M-2D networks. Peak active cases are higher for M-2D networks due to higher connectance in the underlying structure of the base lattice. Peak active cases, on the other hand, show a decreasing trend with an increase in modules in both categories. Fewer modules lead to biassed mobility between the modules, accelerating the spread of an epidemic, which results in higher peaks, earlier peak days, and a decreased span. Thus, despite the same average degree and average clustering coefficient in M-1D and M-2D networks, the difference in contagion dynamics is attributable to higher connectivity in M-2D networks.

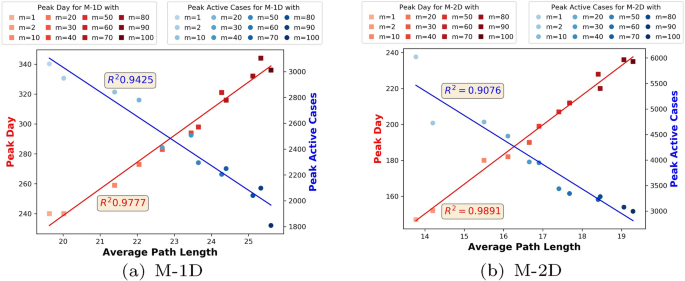
Figure 5 alludes to the negative relationship between peak day and peak active cases for networks in both categories, which is confirmed by high values of $R^2$ (0.9239 for M-1D and 0.892 for M-2D networks) as shown in Fig. 6. The color-coded data points and the regression line confirm that as the number of modules in the network (the number of zones in the geography) increases, peak active cases correlate negatively with the peak day for networks in both categories.

Fig. 6

Relationship between peak day and peak active cases with m in demography-laced synthetic modular networks. The number of modules (m) varies from 1 to 100 and is denoted by color-coded data points

Since the average path length (APL) in a social contact network is an important antecedent of the epidemic spread, we also investigate the relationship of APL with peak day and peak active cases for M-1D and M-2D networks for the different number of modules (Fig. 7). We plot APL on the X-axis, peak day values on the left Y-axis, and peak active cases on the right Y-axis. The average path length shows a strong linear relationship with both peak days and peak active cases, aligning with the theory. An increase in APL due to an increase in the number of modules (Table 4) negatively affects the transmission of contagion in the network, thereby causing the epidemic spread to slow down. This extends the peak day, resulting in a more restrained peak in both types of networks. On the other hand, a lower APL in networks with fewer modules induces rapid spread and higher peak active cases, matching the intuition that speedy transmission brings about a large-sized epidemic that quickly reaches its maximum size. This explains the rapid epidemic spread in M-2D networks compared to their M-1D counterparts.

Fig. 7

Relationship between average path length, and peak day and peak active cases in M-1D and M-2D networks of size 100K. The number of modules (m) varies from 1 to 100 and is denoted by color-coded data points

The stated observations are in tandem with earlier results showing that modular networks stagger the spread of epidemics (Dickison et al. 2012; Hui and Zi-You 2007; Saumell-Mendiola et al. 2012; Wang et al. 2014, 2013), thereby vindicating the proposed methodology for constructing the modular social contact network. Observations also indicate that if the urban space is divided into fewer zones (smaller m), peak cases are higher, and peak day arrives earlier in the event of an epidemic. Hence, the zoning of urban space is constructive not only for governance but also favorable for public health. Further, the choice of the dimension of the base lattice for creating a small-world network for a zone has a noticeable influence on the disease dynamics.

4.1.3 Density variations and epidemic spread

Demographic and socio-economic factors often override the role of population density in a geography on the spread of an epidemic. Higher-density regions in a geography are potential hot spots for the rapid spread of infection due to higher connectivity between inhabitants, thereby increasing the likelihood of transmission. Variations in population density and demography of zones in a city accord a unique heterogeneous structure, which manifests as distinct patterns of social contacts and are captured by the basic wire-frame. This motivates scrutiny of the impact of heterogeneity in population density on the epidemic spread.

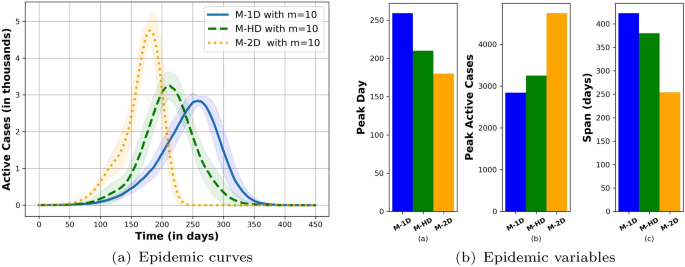
We create a hybrid network with 1D and 2D modules to model heterogeneous population densities. The network (M-HD) has $m=10$ modules (zones)⁸, with half of the zones with lower density and the rest with higher density. We use M-1D and M-2D with ten zones to model cities with uniform densities for all ten zones. All reported results are averaged over ten simulations, and the curves are shown with standard deviation as shaded regions in the plot. Figure 8 (a) shows the epidemic curves for three networks (M-1D, M-HD, and M-2D). The trajectory of the epidemic for the M-HD network lies in between those for the M-1D and M-2D networks. The comparison of peak day, peak active cases, and epidemic span shown in Fig. 8 (b) complies with the observation. Networks modeling the homogeneous density of zones either underestimate (in the case of M-1D) or overestimate (in the case of M-2D) the epidemic variables.

Fig. 8

Impact of density variations in demography-laced synthetic modular networks (M-1D, M-HD and M-2D) on epidemic dynamics

This result asserts that variations in connectivity patterns due to heterogeneous population density in geography perceptibly alters the course of the epidemic. Therefore, accommodating these variations is imperative for improving the quality of the prediction of epidemic trajectories. The proposed wire-frame thus facilitates the empirical study of the impact of density on epidemic dynamics by insulating the study from other environmental variables.

4.1.4 Population mobility and epidemic spread

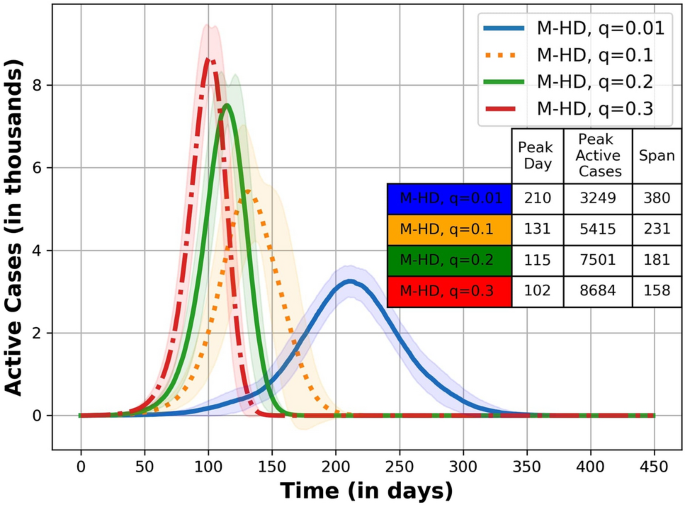
The work-related mobility of individuals between zones influences disease dynamics significantly. This experiment studies the impact of coupling density (population mobility) between zones in heterogeneous networks on disease dynamics. We create M-HD wire-frame with ten modules to model population density variations (as in Sec. 4.1.3). The wire-frame has uniform coupling density for all modules. We repeat the simulation of the epidemic spread over M-HD networks varying coupling density $q = \{0.01, 0.1, 0.2, 0.3\}$.

As expected, the epidemic spreads rapidly across the entire network in strongly coupled modules, resulting in a higher number of active cases and shorter epidemic spans (Fig. 9). The values of the epidemic variable are shown in the inset table in Fig. 9. Low coupling density confines the outbreak to the module and delays its spread. Since interconnecting edges are added randomly, networks with strongly coupled modules exhibit a higher degree of randomness and reshape epidemic dynamics.

Fig. 9

Epidemic curves for M-HD networks with varying coupling density q. Note that each network has a uniform coupling density for all modules

We find that epidemics in interconnected small-world networks spread with velocity in tandem with population mobility (coupling density) as observed in real-world populations, thereby vindicating the network construction methodology.

4.1.5 Demography and epidemic spread

This section compares the epidemic dynamics over two wire-frames of comparable size and order, but distinctly different connectance patterns. In the first one, social and work edges (contacts) are added systematically as per the demography. In contrast, the same number of edges are added randomly among the modules in the second network. Thus, the population size and the total number of social contacts are the same in both networks, yet the topology is different. Networks with random social and work edges have comparatively lower average path lengths.

We generate three pairs of modular networks with ten modules each: M-xD(Dem) and M-xD(Rand), for x = {1, 2, H}. Networks M-1D(.) and M-2D(.) represent geographies with uniform density zones, while M-HD(.) models an equal number of high- and low-density zones. The number of social and work edges is computed using demography data as described in Sect. 2.1.2. These edges are added randomly in M-xD(Rand) and as per the framework in M-xD(Dem). Thus, M-xD(Dem) networks are synthetic but laced with demography, while M-xD(Rand) networks are purely synthetic.

Fig. 10

Comparison of epidemic trajectories in M-xD(Dem) and M-xD(Rand) modular networks, size N=100K and number of modules m=10. The inset table in each sub-figure shows the values of epidemic variables

We run the simulation on all six networks and plot the epidemic curves in Fig. 10 (a-c). The shape of the curves for epidemic simulation over wire-frames laced with demography is distinctly different from those with random social contacts. When social and work edges are added randomly in the network (curves in dashed lines in the figure), the epidemic size is clearly overestimated; peak days arrive earlier, and spans are shorter.

Creating purely synthetic modular networks that depict populations with random contacts for simulating epidemic processes may not deliver reliable estimates, even though they may bear small-world properties. Demography data implanted in the wire-frame adds nuances that manifest as altered contagion dynamics.

4.2 COVID-19 case study for three Indian states

This section describes a case study for three Indian states, viz. Delhi, Goa and Odisha. Delhi is the city-state with nine⁹ zones and a high population density, while Goa has a lower population density. Odisha has a predominantly rural population with a lower population density. In this case study, we prove the validity of our conjecture that a demography-laced surrogate modular network delivers better estimates than one with random patterns of connectance. The generated wire-frames for states can be productively used as a tool for studying zonal outbreaks, mobility restrictions, vaccine administration, and other socio-economic and behavioral scenarios to aid policy planners and administrators in general.

4.2.1 Degree distribution

Before simulating the epidemic spread, we show that the wire-frames for the two states follow the degree distribution of small-world networks.

• i. Estimating mean degree for Delhi: The network has 19.6 million nodes, with mean degree $\bar{x} = 7.338$. The degree distribution of SSCN of Delhi is shown in Fig. 11a. Considering it as doubly truncated Poisson distribution at $\alpha _l = 3$, $\alpha _r = 24$, we estimate the mean degree $\hat{\lambda }$ (Eq. 8). Using $\hat{\lambda }=6$ and 8 as the first and next approximation, we estimate mean degree $\hat{\lambda } =7.2082$ for the Delhi network, which is very close to the empirical mean of 7.338.

• ii. Estimating the mean degree for Goa: SSCN of Goa has N=1.52 million nodes, $\alpha _l=3$, $\alpha _r=16$, and empirical mean degree $\bar{x} = 7.277$. The degree distribution of SSCN of Goa is shown in Fig. 11b. We estimate the mean degree $\hat{\lambda } = 7.1575$ of the Goa network, which is close to the observed mean degree of 7.277.

• iii. Estimating mean degree for Odisha: SSCN of Odisha has N=45.42 million nodes, $\alpha _l=1$, $\alpha _r=19$ and empirical mean degree $\bar{x} =6.958$. The degree distribution of SSCN of Odisha is shown in Fig. 11c. We estimate the mean degree $\hat{\lambda } = 6.9134$ of the Odisha network, which is close to the observed mean degree of 6.958.

Fig. 11

Doubly truncated poisson degree distribution of (a) Delhi SSCN with $\hbox {N}=19.6$ million, $\alpha _l=3$ and $\alpha _r=24$ (b) Goa SSCN with $\hbox {N}=1.52$ million, $\alpha _l=3$ and $\alpha _r=16$ and (c) Odisha SSCN with $\hbox {N}=45.41$ million, $\alpha _l=1$ and $\alpha _r=19$

Iterative refinements for the estimation of the mean degree of SSCN of Delhi, Goa, and Odisha are shown in Appendix B.

4.2.2 Epidemic simulations on SSCN

This experiment aims to demonstrate that epidemic simulation on a demography-based network and a comparable modular network with random connectivity reveals distinct contagion dynamics. We create three networks without embedding demography, one each for Delhi, Goa, and Odisha. Social and work edges are added randomly among the modules in these networks. These networks are denoted by SSCN(Rand). SSCN and SSCN(Rand) are comparable in the number of nodes and edges, but have different contact patterns.

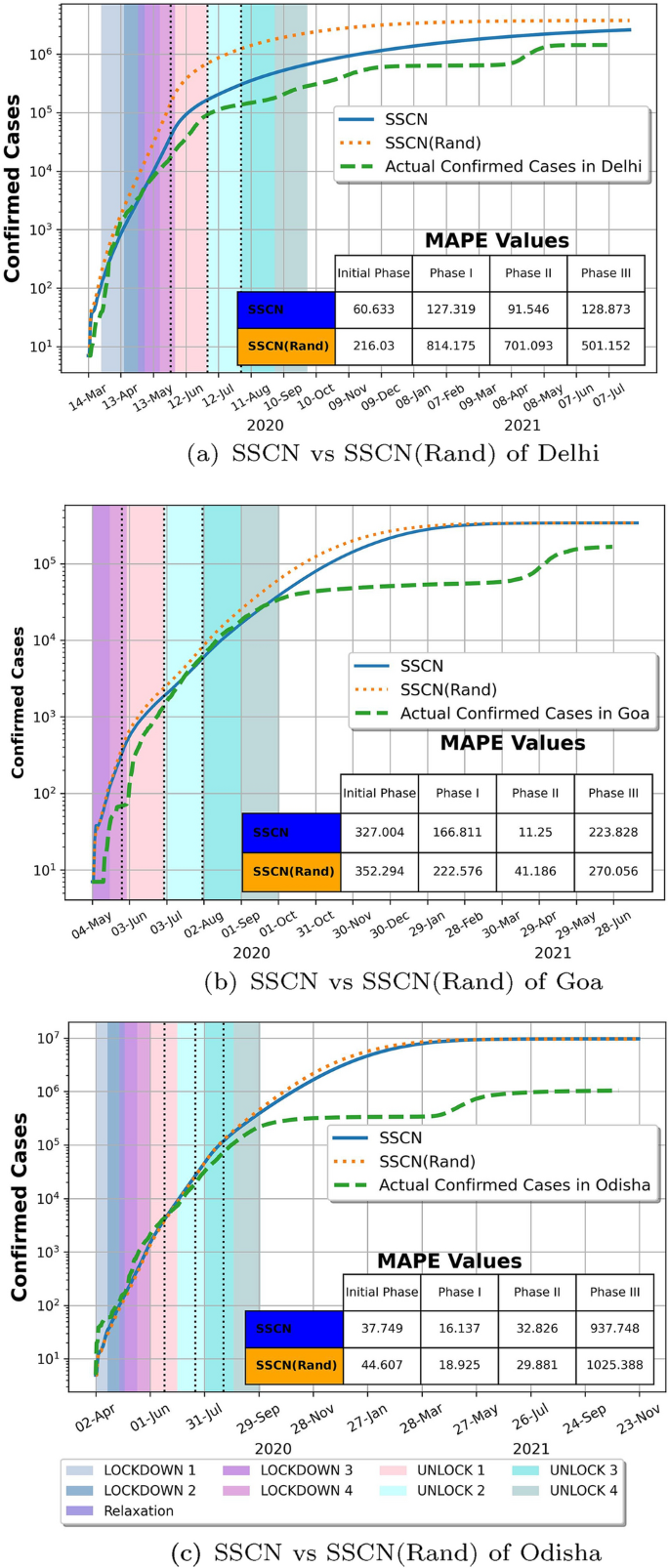
We simulate epidemic spread over six networks for three states, implementing non-pharmaceutical interventions (see Appendix C for the timeline), and noting confirmed cases ($I_s$+H+R+D)¹⁰. Cumulative confirmed cases predicted by the simulation are plotted against actual confirmed cases (COVID-19, India 2019) for the three states in Fig. 12 (a, b, and c). Events are marked with different colors in the figures to show NPIs imposed for the observed period (Table 10 in Appendix C). Black-dotted vertical lines in the figures mark the end of different phases (Table 11 in Appendix D).

Fig. 12

Epidemic curves for actual confirmed cases and those predicted by demography-based SSCN and SSCN(Rand) of Delhi, Goa, and Odisha. Values of mean absolute percentage error (MAPE) for the phases are shown in the inset tables

For all three states, the cumulative case curves for SSCN are closer to the actual curves than the SSCN (Rand) curves. This observation is in agreement with the results for demography-laced synthetic and purely synthetic networks presented in Sec. 4.1.5. This bolsters our confidence in the framework and strengthens our hypothesis that mimicking social contact patterns in the wire-frame is advantageous and gives better predictions.

We further strengthen the supposition by computing the errors for predicted variables by SSCN and SSCN(Rand) wire-frames. We compute mean absolute percentage error (MAPE) for the two sets of epidemic variables for SSCN and SSCN(Rand) and display values in the inset table in Fig. 12. We observe that error for the predicted epidemic spread in SSCN is lower in the initial phases, which are relatively short. The error for Phase III, which spans more than a year and represents a full-blown pandemic, is also lower than SSCN(Rand) for all three states.

Epidemic dynamics in the real world trigger multiple waves due to modulating public behavior (Funk et al. 2015; Li et al. 2020b; Van Bavel et al. 2020; Jain et al. 2022) and possibly changing biology of the contagion (Smith et al. 2020), both of which are not captured by compartmental models. Due to this characteristic of the epidemic spread process, we do not expect accurate predictions of epidemic variables for chosen states. Further, we emphasize that the objective of the experiment is not to flaunt the quality of predictions but to draw attention to the fact that demographic-infused wire-frame results in noticeable variation in the epidemic dynamics. Our observations motivate further investigation in this direction.

Comparison of the epidemic curves on SSCN and SSCN(Rand) wire-frames testifies that demography-laced surrogate social network for a geography delivers better estimates than the one with random patterns of connectance. SSCN(Rand) overestimates the confirmed cases and saturates faster in comparison to SSCN, as expected. The estimates of epidemic variables from the simulation over the demography-based SSCN display lower errors when compared with the actual data for the current COVID-19 pandemic. Consequently, differences in the shape of the two curves are attributable solely to the difference in the connectance patterns in the two networks.

5 Conclusions

In this paper, we show that epidemic dynamics in a census-calibrated modular contact network is distinctly different from those in a network with random connectance patterns. We propose a framework for creating a surrogate social contact network for a geography. The network embodies the social contact patterns arising from the variations in population density and demography of the constituent zones in a geography. Each zone is represented as a small-world network and is impregnated with interactions in family, social and work spaces. The resulting network is a manifestation of the patterns of connectance in the population of the geography and exhibits small-world properties. It also obeys the theoretical results for modular networks and the corresponding empirical observations.

We simulate the spread of the epidemic on the network and observe the epidemic dynamics as demography and density vary across a geography. We observe that increasing the number of zones in a geography retards the spread of an epidemic. We also demonstrate that synthetic networks, when ingrained with demographic information, alters the epidemic dynamics. Connectivity patterns arising due to heterogeneous population density and demography in a geography affect  the epidemic substantially. A case study using the geography and demography of three Indian states is presented to prove the efficacy of the proposed modular network for studying the epidemic dynamics.

The proposed wire-frame, which is a synthetic social contact network embedding the demography of a geography, is a potent tool for understanding the impact of density and demographic parameters on contagion dynamics. The wire-frame can be easily adapted for a variety of applications, including planning vaccination strategies and understanding the impact of mobility restrictions on epidemic dynamics. Behavioral and social conjectures that influence human interactions during the epidemic can also be empirically tested over the wire-frame.

The proposed framework has a few limitations, which warrant advanced investigation. The framework does not use location-based detailed data, which has a strong potential to improve the model resolution and its accuracy. Currently, the model assumes static population and fixed epidemic parameters over the course of the epidemic to keep the computational cost under control. Simulations using compute-intensive agent-based modeling techniques can further improve the quality of the result.

Appendices

Appendix A: Material for surrogate network of three Indian states

We extrapolate the demography data of Delhi, Goa, and Odisha for the current year using the ratio method. We compute the multiplier $\sigma = \frac{\text{2020 } \text{ census } \text{ estimate } \text{ population }}{\text{2011 } \text{ census } \text{ population }}$ to extrapolate demography parameter ${\mathcal {P}}$ as follows.

$$\begin{aligned} {\mathcal {P}}_{2020} = \sigma * {\mathcal {P}}_{2011}. \end{aligned}$$

(A1)

The demography data of Delhi, Goa, and Odisha for surrogate social network construction are shown in Tables 6, 7 and 8, respectively. It is noteworthy that $\vec {K}$ (mean household size) is not extrapolated. Its value is rounded off to the next higher even number and used as the degree of the base lattice in the module corresponding to the zone. Also, note that, for Delhi, we have extrapolated data for nine zones as per the 2011 census.

Table 6 District-wise demography data for nine districts in Delhi. $\dagger$ extrapolated parameter, $\ddagger$ computed as per Eq. 2

Table 7 Sub-district-wise demography data for Goa. $\dagger$ extrapolated parameter, $\ddagger$ computed as per Eq. 2

Table 8 District-wise demography data for Odisha. $\dagger$ extrapolated parameter, $\ddagger$ computed as per Eq. 2

Appendix B: Iterative refinement of MLE of the mean degree of SSCN

See Table 9.

Table 9 Iterative refinement of the MLE to estimate the required value $\hat{\lambda }$, the mean degree of SSCN of (a) Delhi, (b) Goa, and (c) Odisha

Appendix C: Timeline for non-pharmaceutical interventions

See Table 10.

Table 10 Timeline for Non-Pharmaceutical Interventions (NPIs) imposed by the Government of India along with % of edges retained in the network to observe the impact of interventions. W: Work contacts, S: Social contacts (as % of total contacts in each category)

Appendix D: Phases in SUTRA model

See Table 11.

Table 11 Estimated probability of infection $\beta _a$ for Delhi, Goa and Odisha in three phases of the SUTRA model starting from 28 May, 2020. *Extended to 31 October 2021 for Odisha