Evolutionary Symbolic Regression from a Probabilistic Perspective

Abstract

We examine the genetic evolution-based algorithm for symbolic regression from a probabilistic dynamical perspective. This approach permits us to follow the evolution of the search candidate functions from generation to generation as they improve their fitness and finally converge to the best function that matches a given data set. In particular, we use this statistical framework to explore the optimal external parameters that govern a special mutation operator, which can systematically improve the numerical value of constants contained in each candidate formula of the search space. We then apply symbolic regression to the chaotic logistic map and the Lorenz system.

Appendix

(A) $P_{m}(t)$ for a model system of M classes

To get some first insight into the time scales of the temporal evolution of the proportions $P_{m}(t)$ of each class under the tournament selection, we present in this appendix an oversimplified system of M classes, where the corresponding initial fitness densities $\rho _{m}(f,t=0)$ are so narrow that they do not overlap with each other. This permits us to derive a universal iteration scheme, where the proportions $P_{m}(t)$ can be computed directly from the set of $P_{m}(t=0)$ without specifying the shape of $\rho _{m}(f,t=0)$.

In general, the new set of proportions $P_{m}(t+1)$ after the application of all $N_\mathrm{pop}$ tournaments can be obtained via the expression

$$\begin{aligned} P_{m}(t+1)&=\int \limits _{0}^{\infty }\text {d}fP_{m}(t)\rho _{m}(f,t)n_{T}\nonumber \\&\quad \left[ 1-\sum _{m'=1}^{M}P_{m'}(t)\int \limits _{0}^{f}\text {d}f'\rho _{m'}(f',t)\right] ^{n_{T}-1} \end{aligned}$$

(14)

The assumption of non-overlapping densities means that we can assign each class a unique mean fitness value, defined as $\int _{0}^{\infty }\text {d}f'\ f'\rho _{m}(f',t)\equiv f_{m}$. This permits us to order the class labels such that their associated mean fitness increases with increasing label m, i.e., $f_{m}<f_{m+1}$. If we further assume that each $\rho _{m}(f,t)$ is basically non-zero only in the interval $[f_{m}-\varDelta f/2, f_{m}+\varDelta f/2]$, then the integration range of first integral $\int _{0}^{\infty }\text {d}f$ of Eq. (14) can be approximated by $\int _{f_{m}-\varDelta f/2}^{f_{m}+\varDelta f/2}\text {d}f$. This means that the largest upper integration value f of the second integral $\int _{0}^{f}\text {d}f'$ is at most $f=f_{m}+\varDelta f/2$. As a result, some of the integrals in $S(f,t)=n_{T}[1-\sum _{m'=1}^{M}P_{m'}(t)\int _{0}^{f}\text {d}f'\rho _{m'} (f',t)]^{n_{T}-1}$ can be partially evaluated and therefore simplify significantly. The densities $\rho _{m'}(f',t)$ with a fitness lower than $f_{m}$ are integrated over their entire extent and we can use $\int _{f_{m}-\varDelta f/2}^{f_{m}+\varDelta f/2}\text {d}f\rho _{m'}(f',t)=1$. As a result, we obtain $P_{m'}(t)\int _{0}^{f}\text {d}f'\rho _{m'}(f',t) =\sum _{m'=1}^{m-1}P_{m'}(t)+\int _{0}^{f}\text {d}f'\rho _{m'}(f,t)$. This permits us to represent the entire integrand in S(f, t) as a total derivative and we obtain

$$\begin{aligned} P_{m}(t+1)&=\int \limits _{f_{m}-\varDelta f/2}^{f_{m}-\varDelta f/2}\text {d}f\,P_{m}(t) \rho _{m}(f,t)n_{T}\nonumber \\&\quad \left[ 1-\sum _{m'=1}^{M}P_{m'}(t)-\int \limits _{0}^{f}\text {d}f'P_{m}(t) \rho _{m}(f',t)\right] ^{n_{T}-1} \nonumber \\&=\int \limits _{f_{m}-\varDelta f/2}^{f_{m}+\varDelta f/2}\text {d}f(-)\text {d}/\text {d}f\nonumber \\&\quad \left[ 1-\sum \limits _{m'=1}^{M}P_{m'}(t)-\int \limits _{0}^{f}\text {d}f'P_{m} (t)\rho _{m}(f',t)\right] ^{n_{T}}\nonumber \\&=(-)\left[ 1-\sum \limits _{m'=1}^{m-1}P_{m'}(t)-\int \limits _{0}^{f}\text {d}f'P_{m}(t) \rho _{m}(f',t)\right] ^{n_{T}}\nonumber \\&\qquad |_{f_{m} -\varDelta f/2}^{f_{m}+\varDelta f/2}\nonumber \\&=\left[ 1-\sum _{m'=1}^{m-1}P_{m'}(t)\right] ^{n_{T}} -\left[ 1-\sum _{m'=1}^{m}P_{m'}(t)\right] ^{n_{T}} \end{aligned}$$

(15)

If we expand this set of equations, we obtain the sequences of mutually coupled iterations

$$\begin{aligned} P_{1}(t+1)= & {} 1-[1-P_{1}(t)]^{n_{T}} \nonumber \\ P_{2}(t+1)= & {} [1-P_{1}(t)]^{n_{T}} -[1-P_{1}(t)-P_{2}(t)]^{n_{T}}\nonumber \\ P_{3}(t+1)= & {} [1-P_{1}(t)-P_{2}(t)]^{n_{T}} -[1-P_{1}(t)-P_{2}(t)-P_{3}(t)]^{n_{T}}\nonumber \\&\ldots \nonumber \\ P_{M}(t+1)= & {} [1-P_{1}(t)-P_{2}(t)-P_{3}(t) -\cdots -P_{M-1}(t)]^{n_{T}} \end{aligned}$$

(16)

This means that we have obtained an iteration scheme to calculate the class populations $P_{m}(t+1)$ of the next generation solely from the set of $P_{m}(t)$, which have a lesser (or equal fitness). One can easily convince oneself that the norm is preserved by this set of maps. i.e., $\sum _{m=1}^{M}P_{m}(t+1)=\sum _{m=1}^{M} P_{m}(t)=1$.

Fig. 5

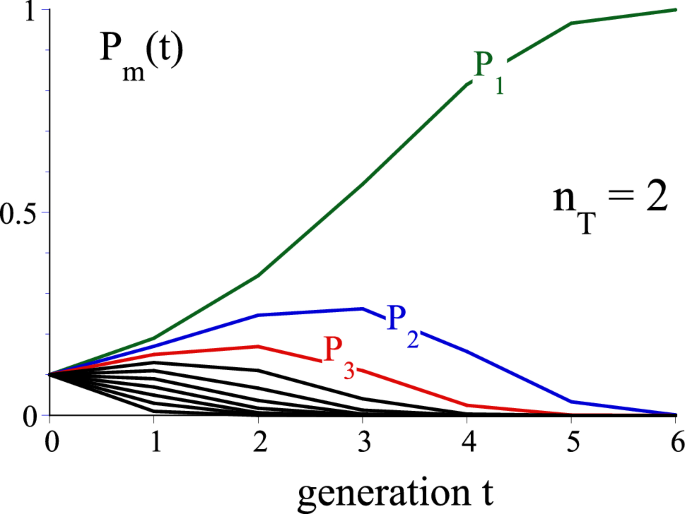
Evolution of the proportions $P_{m}(t)$ for ${M} =10$ classes for the first five generations according to the model given by Eq. (16). The initial proportion were chosen $P_{m}(t=0)=1/M$. We have only labeled the three proportions with the lowest three fitnesses

As an interesting side-note, we remark that despite the nonlinear feature of these iterative maps, for the class with the lowest fitness ${m}=1$, we have the simpler iterative scheme $P_{1}(t+1)=1-[1-P_{1}(t)]^{n_{T}}$, which converges consistently to $P_{1}(t\rightarrow \infty )\rightarrow 1$. If we introduce the complementary proportion $Q_{1}(t+1)\equiv 1-P_{1}(t+1)$, we have $1-P_{1}(t+1)=[1-P_{1}(t)]^{n_{T}}$ such that $Q_{1}(t+1)=Q_{1}(t)^{n_{T}}$. This has the solution $Q_{1}(t)=Q_{1}(0)^{tn_{T}}$ such that we have $P_{1}(t)=1-[1-P_{1}(0)]^{tn_{T}}$, so $P_{1}(t)$ grows monotonically on the time scale proportional to $n_{T}^{-1}$ and independent of the proportions $P_{m}$ of the other classes, as one might expect. While the decay is monotonic, its time scale depends not only on $n_{T}$, but also very sensitively on its initial value $P_{1}(0)$. If $P_{1}(0)\ll 1$, then for short times $P_{1}(t)$ grows linearly in time with a slope proportional to $n_{T}P_{1}(0)$, i.e., $P_{1}(t) = n_{T}P_{1}(0)t$.

On the opposite side, if m matches the total number of classes, i.e., m = M, then the iteration scheme for the class with the largest fitness $f_{M}$ simplifies to

$$\begin{aligned} P_{M}(t+1) =\left[ 1-\sum \limits _{m'=1}^{M-1}P_{m'}(t)\right] ^{n_{T}} =[1-\{1-P_{M}(t)\}]^{n_{T}}=P_{M}(t)^{n_{T}} \end{aligned}$$

(17)

This permits us to find the complete time evolution for $t=1,2,\ldots ,$ as $P_{M}(t)=P_{M}(0)^{tn_{T}}$ following a universal monotonic exponential decay with decay time proportional to $n_{T}^{-1}$.

The time evolution of all the other proportions $P_{M}(t)$ for $m\ne 1$ and $m\ne M$ can be non-momotonic. As an example, in Fig. 5 we show the evolution of $M=10$ classes and $P_{m}(t=0)=1/M$ for the first five generations with a tournament size $n_{T}=2$. We see that the low-fitness proportions, $P_{m}(t)$ (for ${m}=1$, ..., 5) increase first and then decay, except $P_{1}(t)$, which approaches monotonically 1.