Abstract
Dissipative phase transitions are a characteristic feature of open systems. One of the paradigmatic examples for a first order dissipative phase transition is the driven nonlinear single-mode optical resonator. In this work, we study a realization with an ultracold bosonic quantum gas, which generalizes the single-mode system to many modes and stronger interactions. We measure the effective Liouvillian gap of the system and find evidence for a first order dissipative phase transition. Due to the multi-mode nature of the system, the microscopic dynamics is much richer and allows us to identify a non-equilibrium condensation process.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Dissipative phase transitions [1–6] are characteristic of open systems, where the coupling to an external reservoir provides a source of dissipation which competes with an internal or external pumping process. Depending on the relative strength of the two processes, different steady states emerge or even coexist. Most notably, the steady-states can show properties which cannot be observed in equilibrium [7]. The generic properties of first and second order dissipative phase transitions can be derived from a spectral analysis of the system's Liouvillian [1, 2]. Critical behavior at the phase transition has been studied both, theoretically [2, 4, 8–12] and experimentally [6, 12–20]. One of the paradigmatic examples exhibiting a dissipative phase transition is a single-mode quantum system, realized, e.g., with a nonlinear optical medium in a cavity, which is coherently pumped by a laser and subject to cavity losses [6, 15–17, 21]. The Hamiltonian part of such a Kerr type system reads
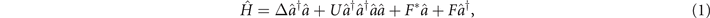
where Δ is the detuning between the mode energy and the photon energy of the pump laser, 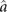 is the annihilation operator of the mode, F is the amplitude of the pumping laser and U denotes the interaction. The cavity losses are included via a master equation in Lindblad form,
is the annihilation operator of the mode, F is the amplitude of the pumping laser and U denotes the interaction. The cavity losses are included via a master equation in Lindblad form,
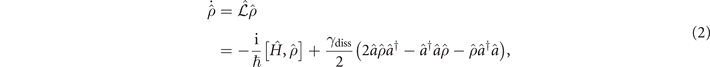
where γdiss is the loss rate and 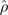 is the density operator. This model exhibits several prominent features: (i) there are two classes of states (with low and high occupation number) which are connected by a first order dissipative phase transition. (ii) While a mean-field treatment predicts optical bistability, the full quantum description (equations (1) and (2)) allows for tunneling between the steady states, thus erasing bistability and rendering the states metastable. (iii) As a consequence of (i) and (ii), single trajectories show a pronounced switching behavior between the two classes of states [6].
is the density operator. This model exhibits several prominent features: (i) there are two classes of states (with low and high occupation number) which are connected by a first order dissipative phase transition. (ii) While a mean-field treatment predicts optical bistability, the full quantum description (equations (1) and (2)) allows for tunneling between the steady states, thus erasing bistability and rendering the states metastable. (iii) As a consequence of (i) and (ii), single trajectories show a pronounced switching behavior between the two classes of states [6].
For multi-mode systems instead, much less is known. There exist only a few theoretical works [3, 4, 22–25], mostly on the driven-dissipative 2D Bose–Hubbard model. The extension to many modes in the interacting many-body regime poses many challenges to its theoretical description (see methods for an explicit form of the master equation). In practice, already a few tens of modes and particles make exact diagonalization intractable. Experimental studies of a dissipative phase transition in a multi-mode system therefore not only generalize the results of the single-mode Kerr oscillator, but also provide benchmarks for advanced theoretical methods to describe driven-dissipative systems.
In this work, we investigate the multi-mode version of the nonlinear Kerr resonator in an atomic quantum gas experiment. First results for the system under investigation have been reported previously by one of the authors [26, 27]. We present experimental indications that this system undergoes a first order dissipative phase transition when tuning the ratio between the coherent drive and the dissipation. We observe the same characteristic switching behavior as in the single-mode system and find signatures of a closing of the Liouvillian gap. On intermediate timescales, the system exhibits hysteresis and metastability. In particular, we identify and analyze a non-equilibrium condensation process. The system has triggered recent theoretical work using c-field methods [24] and a single-mode variational truncated Wigner approach [25].
The experimental system (figure 1(a)) consists of a Bose–Einstein condensate (BEC) loaded into a 1D optical lattice. This can be considered as an array of coupled two-dimensional BECs of neutral atoms. Each condensate occupies about 80 transverse harmonic oscillator modes. With a total of about 800 atoms in each condensate, the system is deep in the multi-mode regime with high mode occupation numbers. The central lattice site is subject to a homogeneous loss process with rate γdiss. The loss mechanism is realized by a focused electron beam, which is scanned across the central site and removes the atoms. A fraction of the atoms is converted into ions [28], which form the basis of our measurement signal. This way, we can measure the time-resolved atom number and the transverse extent of the atomic cloud in the central site. The lattice sites are connected via quantum mechanical tunneling with rate J, which constitutes the drive into the central site. The experimental sequence starts by initially preparing the system either with an 'empty' site (low occupation number in the central site) or with a 'full' site (same occupation number in all sites). We then record the temporal evolution of the site occupancy under the simultaneous influence of drive and dissipation.
Figure 1. (a) A Bose–Einstein condensate is loaded into a one-dimensional optical lattice. The individual sites of the condensate array are coupled via the coherent tunneling coupling J. The central site is subjected to particle loss, realized with an electron beam. The nonlinear interaction leads to an effective tunneling coupling Jeff to the neighboring sites (see text). The produced ions are guided towards a detector and provide a time-resolved measurement signal. (b) Single experimental trajectory (amber line, moving average is shown as dotted line) for an initial state with low atom number in the central site. After 200 ms evolution time, the trajectory switches to a high atom number, which is comparable to that of the neighboring sites. This jump is fitted with a sigmoid function (indigo dashed line). (c) Same as (b) for an initially high atom number in the central site. Time t = 0 is determined by the end of the initial state preparation procedure.
Download figure:
Standard image High-resolution imageIn figure 1, we show typical individual trajectories observed in the experiment for an initially empty (figure 1(b)) and full central site (figure 1(c)). The trajectories are characterized by a switching behavior, indicated by pronounced jumps in the site occupancy between the two states. The absolute magnitude of these jumps is large: about 700 atoms tunnel within a short time into or are removed from the central site. This switching behavior is reminiscent of that of the corresponding single-mode system [6] and hints at a dominant role of fluctuations. It has also been seen in a c-field treatment of this system [24].
The nature of the appearing states between which the system switches has been identified previously [27, 29]. For high occupation number, when the coherent drive dominates over the dissipation, there is a condensate in the central site, which is phase locked to the neighboring condensates. The whole system is in a superfluid state, all sites have similar atom numbers and the system exhibits steady-state transport known as coherent perfect absorption [29]. In the opposite limit of large loss rate, the central site features only a small occupation in each mode. The atomic ensemble is in a normal state and macroscopic phase coherence is absent. Hence, superfluid transport into that site is inhibited [27]. In the vicinity of the phase transition, where dissipation and drive are of similar strength, jumps are induced between the states.
To quantify the switching dynamics, we measure the time stamps of the jump for each trajectory. We then determine the time scales τnormal→superfluid = τns and τsuperfluid→normal = τsn for switching between the two configurations as well as the corresponding rates 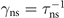 and
and 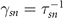 . The physical meaning of the switching rates becomes clear if one looks at the spectral decomposition of the Liouvillian
. The physical meaning of the switching rates becomes clear if one looks at the spectral decomposition of the Liouvillian
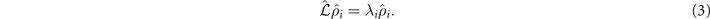
Here, λi
denotes the complex eigenvalue, and Re(λi
) ⩽ 0 is the damping rate of 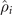 . Eigenvalues with Re(λi
) = 0 denote steady states. Note that for any non-zero Re(λi
), the
. Eigenvalues with Re(λi
) = 0 denote steady states. Note that for any non-zero Re(λi
), the 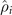 are not proper density matrices, as the trace is not preserved in time. A proper density matrix therefore always contains a contribution from at least one steady state. If two eigenvalues of equation (1) are zero, the system exhibits true bistability. If only one eigenvalue is zero, the spectrum of equation (3) shows a gap, the Liouvillian gap, which is defined by the smallest nonzero eigenvalue, min(−Re(λi
)). The Liouvillian gap therefore also defines the slowest relaxation rate of the system. This characteristic behaviour of the Liouvillian gap is sketched in the inset of figure 2.
are not proper density matrices, as the trace is not preserved in time. A proper density matrix therefore always contains a contribution from at least one steady state. If two eigenvalues of equation (1) are zero, the system exhibits true bistability. If only one eigenvalue is zero, the spectrum of equation (3) shows a gap, the Liouvillian gap, which is defined by the smallest nonzero eigenvalue, min(−Re(λi
)). The Liouvillian gap therefore also defines the slowest relaxation rate of the system. This characteristic behaviour of the Liouvillian gap is sketched in the inset of figure 2.
Figure 2. Effective Liouvillian gap. We plot γns + γsn for a dissipation rate of γdiss = 250 Hz as a function of tunneling coupling J/ℏ. (Inset) Paradigm of first-order dissipative phase transition. As the parameter ɛ reaches the critical value ɛc the Liouvillian gap λgap closes in the thermodynamic limit. Metastability is found in the vicinity of the critical point, giving rise to hysteresis.
Download figure:
Standard image High-resolution imageAs the full many-body problem is intractable, we adapt a simplified toy model, which was developed in [30] for the driven dissipative Bose–Hubbard model and applied in [16]. The toy model considers only two states between which the system can switch: the normal state and the superfluid state, represented by the density matrices 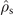 and
and  . The corresponding rate equation model features two steady states. One is a stable steady-state with eigenvalue λ = 0:
. The corresponding rate equation model features two steady states. One is a stable steady-state with eigenvalue λ = 0: 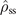 = (γns
= (γns
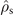 + γsn
+ γsn
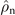 ). The second one is an exponentially decaying state, ρdec = (γns
). The second one is an exponentially decaying state, ρdec = (γns
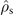 − γsn
− γsn
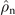 ), with eigenvalue λgap = −(γns + γsn). Hence, the toy model features an effective Liouvillian gap, given by λgap. Because the steady-state
), with eigenvalue λgap = −(γns + γsn). Hence, the toy model features an effective Liouvillian gap, given by λgap. Because the steady-state 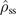 is a mixture of the normal and the superfluid state, a time resolved measurement of the site occupancy is characterized by jumps between the two states.
is a mixture of the normal and the superfluid state, a time resolved measurement of the site occupancy is characterized by jumps between the two states.
In the experiment, we can observe the system only for a finite time because of atom loss. As a consequence, we typically observe only one jump in a single trajectory (in very rare cases, we observe two). Therefore, we chose two different initial conditions to determine the rates γns and γsn individually, see also figure 1. In figure 2, we show the resulting effective Liouvillian gap, γns + γsn, as a function of the tunneling coupling for fixed dissipation strength. At the minimum, the gap is smaller than 1 Hz. This is two to three orders of magnitude smaller than the dissipation rate γdiss and the tunneling coupling J/ℏ, which are the intrinsic time scales of the system. The large difference in time scales is a strong indication of a dissipative phase transition and we take the minimum of the relaxation rate to be the position of the phase transition (see also the inset of figure 2, where the typical behaviour of a first order dissipative phase transition is sketched).
In the thermodynamic limit only at the critical point of the first order phase transition will the steady state be a mixture of the two phases. Right before and after the critical point the steady state is one of the two different phases of the system. For a finite size system a small region around the critical point is expected to be metastable, which may introduce hysterical behavior. This is typical of first-order phase transitions. In figure 3(a) we show that the normal (superfluid) state is the steady state of the system on the right (left) of the critical point. A region of metastability is found around this point. To explicitly show the emerging hysterical behavior, we measured the dynamic hysteresis by ramping the tunneling coupling up and back down (figure 3(b)).
Figure 3. (a) Metastability. We show the average filling after an evolution time of tmeas = 200 ms for the two different initial conditions (γdiss = 250 Hz). The black dashed lines indicate the phase transition extracted from figure 2. (b) Dynamic hysteresis. The amber and indigo line represent the measured ion signal when the tunneling coupling is ramped up and back down, respectively, while keeping the dissipation strength constant at γdiss = 250 Hz. The dynamic hysteresis curve shown is averaged over 130 realizations. Within the total ramp duration tramp = 650 ms the tunneling coupling is changed between J/ℏ = 30 Hz and J/ℏ = 1040 Hz and back.
Download figure:
Standard image High-resolution imageNote that only in the thermodynamic limit, which corresponds in our case to an infinite transverse extent of all lattice site, the Liouvillian gap is expected to close completely [1, 31], thus providing bistability at the critical point. The toy model introduced above neglects all density matrices except of ρs and ρn. Therefore, the effective Liouvillian gap is only an upper limit for the true Liouvillian gap. Strictly speaking, the large number of allowed density matrices makes it practically impossible to experimentally measure the true Liouvillian gap. Interestingly, experiment and theory encounter similar constraints in this respect.
So far, our findings are qualitatively similar to those for a single-mode nonlinear Kerr resonator. We now turn to the question, what genuine characteristics emerge from the multi-mode nature of our system and make it distinct from the single-mode system.
We start our discussion by analyzing the jumps in more detail. Because we are using interacting bosons, we expect to pass a condensation process during a jump from the normal to the superfluid state. Such a condensation process happens under non-equilibrium conditions, characterized by the competition between the coherent drive, atomic collisions/interactions and dissipation. Information on this non-equilibrium condensation process can be obtained from the time resolved site occupancy during the change and the transverse extent of the atom cloud. Figure 4 shows the averaged time-resolved detection signal as well as the transverse extent of the atomic cloud during state changes from the normal to superfluid state. We can identify three different stages. After an initial slow exponential growth of the atom number a sudden rise in the growth rate is apparent. An exponential fit to the initial part of the averaged trajectory is shown to highlight the speed-up in the filling rate above a critical atom number. In a final step, the filling of the central site eventually equals that of the neighboring sites and remains constant. The possibility of a change of the transverse extent of the cloud is a direct consequence of the multi-mode nature of the system and is therefore not expected to occur in single-mode systems.
Figure 4. Average jump. The average atom number (amber) and width of atomic cloud (indigo) during a state change are plotted. An initial exponential growth of the atom number (black dashed line) is abruptly sped up above a certain threshold filling. At the same time, the transverse extent shrinks. In order to average the individual jumps we overlay them at the center of the individual fitted sigmoid functions, which we take as t = 0. The threshold is given by the value of the exponential fit at the point where it deviates from the measured atom number by more than one standard deviation. We find a threshold value of 300(20) atoms. Tunneling couplings range from J/ℏ = 100 Hz to J/ℏ = 600 Hz and the dissipation strength amounts to γdiss = 250 Hz.
Download figure:
Standard image High-resolution imageThe average width shows an inverted behavior, however. The transverse extent of the cloud shrinks with increasing atom number. This is a consequence of the condensation process and the reduction of thermal fluctuations: all atoms tunneling from a neighboring reservoir into the central site have total energy equal to the chemical potential μ of the neighboring sites. In the beginning of the refilling process, when the central site contains barely any atoms, the interaction energy is converted into kinetic energy, leading to an effective finite temperature. From an approximation of the density distribution of the thermal part inside the central site by a Gaussian function the width of the cloud in the central site is calculated to be 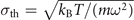 . Here ω denotes the radial trap frequency, kB the Boltzmann constant, m the mass of rubidium atoms, and T the temperature in the site. The condensate's radial extent in the central site is approximated by the Thomas–Fermi radius
. Here ω denotes the radial trap frequency, kB the Boltzmann constant, m the mass of rubidium atoms, and T the temperature in the site. The condensate's radial extent in the central site is approximated by the Thomas–Fermi radius 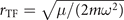 . The calculated widths for our system are 2.1(1) μm for the normal/thermal gas and 1.7(1) μm for the condensate. The experimental results (indigo line in figure 4) are in good agreement with these predictions.
. The calculated widths for our system are 2.1(1) μm for the normal/thermal gas and 1.7(1) μm for the condensate. The experimental results (indigo line in figure 4) are in good agreement with these predictions.
It is instructive to look at the timescale of this process by analyzing the duration of the state change in each trajectory individually. The duration of the individual state changes is taken to be the 2σ width of the fitted sigmoid function (see methods for details on the fitted function). We find that the shortest duration for a state change from the normal to the superfluid state is given by the tunneling time, τ ≈ ℏ/J (figure 5(a)). This can be explained as follows. For a small atom number in the central site we only expect an incoherent transport of particles into that site. However, when the density in the central site exceeds a critical value, high mode occupancy builds up. Fluctuations then trigger a condensation process, thus allowing for a coherent Josephson type of transport into the central site [32]. For fully established phase coherence across the central site, the maximum possible coherent transport is expected [29]. For scrambled and fluctuating phases, much longer durations are possible. We observe that the average duration of the state change is about four tunneling times and the longest duration for a state change can be even 20 times larger. In the other direction, from the superfluid to the normal state, the dissipation rate is the determining factor (figure 5(b)). No state change can be faster than the inverse of the dissipation rate and this is also our experimental observation. The average state change is again about two to five times longer and few trajectories show even longer durations. For small tunneling couplings and thus little coherent transport into the lattice site the dissipation is strong enough that even small fluctuations lead to an emptying of the site. With increasing tunneling coupling the coherent transport into the site becomes stronger thereby on average decreasing the rate at which the atom number in the site can be decreased. This leads to an increase of the average duration of jumps. For both types of jumps, such large variations hint at the dominant role of fluctuations for the system dynamics.
Figure 5. (a) Duration of the jumps from the normal to the superfluid state. We display the jump duration in units of the tunneling coupling J/ℏ, which corresponds to the fastest possible timescale (see text). Blue triangles denote the fastest jump for each measurement series, amber squares and error bars show the mean value together with the standard deviation. The mean duration is about four times longer than the shortest one. (b) Duration of the jumps from the superfluid to the normal state. In the case, we display the jump time in units of the dissipation rate γdiss, which corresponds to the fastest possible timescale (see text). Blue triangles denote the fastest jump for each measurement series, amber squares and error bars show the mean value together with the standard deviation. The mean duration can be significantly longer than the shortest one. The dashed lines are a guide to the eye for a normalized duration of 1.
Download figure:
Standard image High-resolution imageAnother important observation is that history appears to be relevant in our system. If the state changes were fully independent of the elapsed evolution time, the temporal distribution of the state changes would follow an exponential decay [33]. In our experiment, however, the temporal distribution of state changes is non-trivial (figure 6). We find small probabilities of a state change for early times, increasing probabilities as time elapses further followed by a final slow decay of probability. This supports our previous observation in figure 4, that a state change has preceding internal dynamics. To the best of our knowledge, such complex internal system dynamics has not been reported on single-mode systems.
Figure 6. Temporal distribution of jumps. We show a histogram of the normalized jump times for measurements with the system initialized in the normal state. The applied dissipation strength is γdiss = 250 Hz and tunneling couplings range from J/ℏ = 100 Hz to J/ℏ = 600 Hz. The histogram deviates strongly from an exponential behavior, which one would expect for independent jumps in a memoryless system.
Download figure:
Standard image High-resolution imageTo explain the above reported observations for state changes from the normal to the superfluid state, we have developed a simple stochastic rate model, which describes the microscopic system dynamics in the normal state. As indicated in figure 1, the mean-field energy (chemical potential) in the neighboring sites renders the direct tunneling process into the ground state of the central site off-resonant. In a single-mode Josephson array, this would lead to macroscopic quantum self-trapping, thus inhibiting any transport [34]. The multi-mode nature of our system changes this picture. Atoms are allowed to tunnel into higher orbital states of the central site, where they are subject to collisions between particles in different orbital states. Due to a Franck–Condon overlap between the condensate wave function in the neighboring site and the single particle states in the central site, the effective tunneling coupling is reduced and depends on the atom number in the central site [26]. Overall, we get an effective tunneling rate Γeff, which depends on the dissipation rate γdiss and the effective tunneling coupling Jeff(N), where N is the number of atoms in the central site. We thereby assume that the effective tunneling coupling depends linearly on the atom number and reaches the value of J for equal filling with the neighboring sites [26]. We find (see methods for further details):
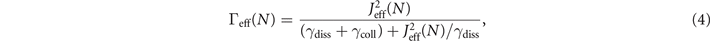
where γcoll is the collision rate in the lossy site in the normal state. The stochastic differential equation describing the population N in the lossy site then reads
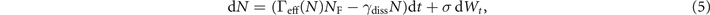
where NF is the atom number in the neighboring sites. The term σ dWt
with 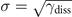 describes the fluctuations induced by the dissipation. The dynamics resemble those of geometric Brownian motions (for more details on the model see methods section). Note that due to the N-dependence of the effective tunneling rate, the rate equation is nonlinear.
describes the fluctuations induced by the dissipation. The dynamics resemble those of geometric Brownian motions (for more details on the model see methods section). Note that due to the N-dependence of the effective tunneling rate, the rate equation is nonlinear.
To simulate the system we time evolve many individual trajectories by Monte-Carlo simulations. When a trajectory reaches a threshold filling for the first time macroscopic phase coherence builds up and the jump occurs. In figure 7(a), we show a series of simulated trajectories. We take the time of the jump to be the time the threshold is reached. The introduction of a threshold filling followed by a condensation process gets backing from the measurement of the width of the atomic cloud within the central site during the jump (figure 4), as discussed above.
Figure 7. Simulation results. (a) 100 simulated trajectories initialized in the normal state. While the average trajectory (dashed line) shows an exponential decay, there are nevertheless trajectories (8 colored), that reach a threshold well above the initial number of atoms. We use the threshold filling as the only fitting parameter of the model. (b) The distribution of individual times of the jumps (shown for a tunneling coupling of J/ℏ = 380 Hz) is reproduced as well as (c) the fraction of trajectories that exhibit a jump.
Download figure:
Standard image High-resolution imageIn figure 7(b) we compare the temporal distribution of the simulated jumps with our measurement and in figure 7(c) we show the comparison for the fraction of trajectories exhibiting a jump. The only fitting parameter of our model is the threshold filling. We use it to match the experimentally measured temporal distribution of state changes and the fraction of trajectories that exhibit a jump (see figures 7(b) and (c) for a direct comparison). We find a critical value of 300 atoms, which is in good agreement with the value extracted from the measurement (figure 4).
This has to be compared to the critical atom number for Bose–Einstein condensation in thermal equilibrium. 2D BEC theory [35] gives a value of 100 atoms. This confirms that the fluctuations increase the critical atom number for condensation in the central site and underlines the qualitative difference between a dissipative phase transition and a phase transition in thermal equilibrium.
In summary, we have experimentally characterized a first-order dissipative phase transition in a multi-mode many-body quantum system. Our results extent the experimental studies on nonlinear optical Kerr resonators. While some features are qualitatively similar, the microscopic dynamics are much richer due to the multi-mode nature. For the future, we expect to see more experiments working on related systems, such as the driven dissipative 2D Bose–Hubbard model or corresponding fermionic counterparts. For the system at hand, a detailed study of the scaling of the Liouvillian gap with the system size would allow for a finite size scaling towards the thermodynamic limit. The measurement of critical exponents in the vicinity of the phase transition would allow for a deeper understanding of the classification of the phase transition [11].
1. Methods
1.1. The master equation
The master equation of our system is constructed in the following way. We first note that the atoms occupy the lowest band along the lattice direction. We are well within the tight binding approximation along this direction and introduce the discrete site index i. The central site corresponds to i = 0. The kinetic energy in the lattice direction results in the tunneling coupling J. In the two transverse directions (x, y) each site experiences a harmonic confinement with radial frequency ω⊥. The Hamiltonian of the central site in terms of bosonic field operators 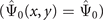 reads
reads
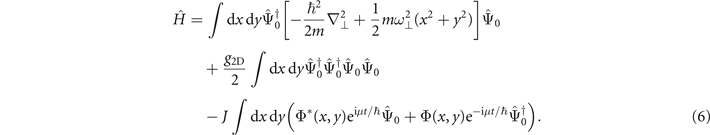
The effective interaction strength in the lattice site is given by g2D. The coherent drive is given by a mean-field wave function of the condensate in the two neighboring sites given by Φ(x, y)e−iμt/ℏ , where μ is the chemical potential. The large number of additional adjacent reservoir sites justifies to set Φ(x, y) constant in time.
The losses are included via a master equation,
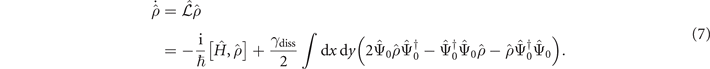
As outlined in the main text, an exact theoretical treatment is not possible. A stochastic mean-field description of this master equation has been developed and analyzed in detail in reference [24].
1.2. Fitting model
We fit a sigmoid function
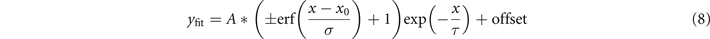
to the measured trajectories ymeas. Here, x0 gives the center of the error function (erf), which we take to be the time of the jump. The duration of the jump is defined as twice the width σ of the error function. The atom loss from the atomic cloud leads to a decline in signal strength over time, especially in the superfluid state. The exponential function takes this atom loss of the overall system into account. An offset is added in the model function to account for signal measured when probing an empty site.
1.3. Experimental setup
We use a BEC of 87Rb containing about 150 × 103 atoms. The atoms are trapped in a focused CO2-laser beam with a beam waist of 34 μm. The condensate is cigar-shaped with dimensions (115 × 6 × 6) μm in an approximately harmonic trap with frequencies 2π ⋅ (9.8, 197, 183) Hz. After its preparation the BEC is loaded into a one-dimensional blue detuned optical lattice created by two beams (λ = 774 nm, beam waist 500 μm) intersecting at 90°. The resulting lattice has a period of d = 547 nm. Each site contains a small 2D BEC with about 800 atoms at the center of the trap. The total number of lattice sites is about 200. In addition, an electron column implemented in the vacuum chamber provides a focused electron beam which is used to introduce a well-defined local particle loss as a dissipative process at one site of the lattice. In order to ensure a homogeneous loss process over the whole extent of this lattice site we rapidly scan the electron beam in the transverse direction (3 kHz scan frequency) with a sawtooth pattern. To adjust the dissipation strength γ, we vary the transverse extent of the scan pattern. In the experiments considered in this paper we start out with a BEC, load it into the 1D lattice at a depth of s = 30 (we give the values of the lattice depth V0 = s Erec in units of the recoil energy 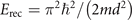 ) and—depending on the initial conditions—deplete one site. We then reduce the lattice depth to a value between s = 6 and s = 12 while keeping the electron beam scanning over the depleted site. Our measurement signal is the time-resolved ion signal from the scan at the lower lattice depth. Only in the case of the dynamical hysteresis measurement, the lattice depth is varied in time (for the measurement presented in figure 3(a) the lattice depth was varied at a constant rate from s = 4 to s = 20 and back).
) and—depending on the initial conditions—deplete one site. We then reduce the lattice depth to a value between s = 6 and s = 12 while keeping the electron beam scanning over the depleted site. Our measurement signal is the time-resolved ion signal from the scan at the lower lattice depth. Only in the case of the dynamical hysteresis measurement, the lattice depth is varied in time (for the measurement presented in figure 3(a) the lattice depth was varied at a constant rate from s = 4 to s = 20 and back).
1.4. Microscopic model
In order to develop a rate model for the dynamics in the central site in the normal state (low filling), we start out from a two-level system. The neighboring site corresponds to the ground state. Coherent coupling to a radially excited state in the central site is provided by an effective tunneling coupling Jeff, which takes into account the finite Franck–Condon overlap between the neighboring reservoir site and the radially excited state [27]. Atom loss from this radially excited state is described by the dissipation rate γdiss and dephasing caused by atomic collisions is included via γcoll. The rate equation for the central site is then given by
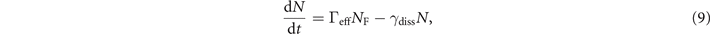
where N is the number of atoms in the central site and NF is that of the neighboring sites. Due to the large number of reservoir sites to which the neighboring site is coupled we set NF as constant. The effective tunneling rate Γeff in this effective two-level system is then given by
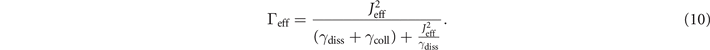
In our system atoms can tunnel between the full site (|ΦF⟩) and the resonant mode (|ΦE⟩) of the empty site with the effective tunnel rate Γeff. Introducing the overlap integral η = |⟨ΦF|ΦE⟩|, and assuming a linear dependence on the atom number for finite filling, we rewrite the effective tunnel rate as follows [26]:
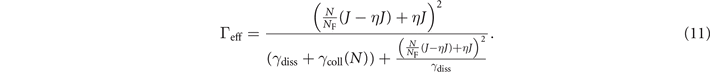
For low filling in the central site, as it is the case in the normal state, we linearize the above expression:
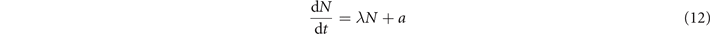
To model the fluctuations induced by the dissipation we introduce a stochastic term and obtain the stochastic differential equation
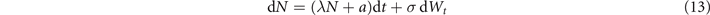
with a Wiener process Wt and
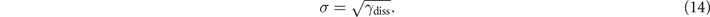
To solve equation (13) we use the Itô formula, a variant of the chain rule for stochastic multi-variable functions [36–38]. The solution to this SDE is then given by

with a standard normal variable x and c = a/λ.
Acknowledgments
We gratefully acknowledge fruitful discussions with M Davis, M Fleischhauer, C D Mink, A Pelster, and M Reeves. This project was funded by the DFG (German Science Foundation) within the CRC TR185 OSCAR Project Number 277625399. We thank A Gil Moreno for assistance in the early stage of the experiment.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Author contribution
JB, CB and MR performed the measurements. JB and MR evaluated and analyzed the data. HO has supervised the experiment. JB wrote the manuscript. All authors discussed the results and contributed to the manuscript.
Conflict of interest
The authors declare no competing interests.









