Abstract
The earlier analytical analysis (part A) of the susceptible–infectious–recovered (SIR) epidemics model for a constant ratio k of infection to recovery rates is extended here to the semi-time case which is particularly appropriate for modeling the temporal evolution of later (than the first) pandemic waves when a greater population fraction from the first wave has been infected. In the semi-time case the SIR model does not describe the quantities in the past; instead they only hold for times later than the initial time t = 0 of the newly occurring wave. Simple exact and approximative expressions are derived for the final and maximum values of the infected, susceptible and recovered/removed population fractions as well the daily rate and cumulative number of new infections. It is demonstrated that two types of temporal evolution of the daily rate of new infections j(τ) occur depending on the values of k and the initial value of the infected fraction I(0) = η: in the decay case for k ⩾ 1 − 2η the daily rate monotonically decreases at all positive times from its initial maximum value j(0) = η(1 − η). Alternatively, in the peak case for k < 1 − 2η the daily rate attains a maximum at a finite positive time. By comparing the approximated analytical solutions for j(τ) and J(τ) with the exact ones obtained by numerical integration, it is shown that the analytical approximations are accurate within at most only 2.5 percent. It is found that the initial fraction of infected persons sensitively influences the late time dependence of the epidemics, the maximum daily rate and its peak time. Such dependencies do not exist in the earlier investigated all-time case.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recently [1]—hereafter referred to as part A—new analytical solutions of the standard susceptible–infectious–recovered (SIR)-model without vital dynamics have been derived. The SIR model has been developed nearly 100 years ago [2, 3] to understand the time evolution of infectious diseases in human populations, but has also been applied to other societal phenomena such as the spread of rumors [4–6]. The new analytical solutions in part A allow for an arbitrary time dependence of the infection and recovery rates but assume that the ratio of the two rates is independent of time. Moreover, in part A we calculated explicitly the daily differential rate and the corresponding cumulative number of newly infected persons, quantities that regularly are monitored during outbreak of diseases such as the recent COVID-19 pandemic. These differential and cumulative numbers of infected persons are related with a typical delay time to the differential and cumulative death rates [7].
The SIR system is the simplest of the compartmental models used for the mathematical modeling of infectious diseases and had been solved numerically using various approaches, including Monte Carlo methods, wavelets, fuzzy control etc [8–27] and approximate solutions had been proposed [28, 29]. The considered population of N ≫ 1 initially unrecovered/unremoved persons is assigned to the three compartments S (susceptible), I (infectious), or R (recovered/removed). Persons from the population may progress between these compartments. Results from the SIR-system are fundamental as they can easily be generalized to more sophisticated models [30] such as (i) the susceptible–infected–recovered–deceased-model (SIRD-model), where R and D denote the group of people that have survived or died from the infection, respectively, and (ii) the susceptible–exposed–infectious–recovered-model (SEIR-model) [31], where E denotes the subgroup of people infected but not infectious and I the group of persons infected and infectious.
The basic equations of the SIR-model describe the time evolution of individuals in a fixed population of N initially unrecovered/unremoved persons. I(t), S(t) and R(t) denote the infected, susceptible and recovered/removed fractions of the N persons involved in the infection at time t subject to the sum constraint

Different to part A we adopt the initial conditions

with  denoting the initial seed infection fraction of the population, and where R(0) = 0 does not pose any restriction, as all quantities in this work describe fractions of the initially unrecovered/unremoved population, rather than a total population. The initial conditions (2) make the treatment here different from part A. This semi-time case is particularly useful and appropriate for modeling the temporal evolution of later (than the first) pandemic waves when a greater population fraction from the first wave has been infected. We do not assume here that the SIR model was describing the quantities in the past; instead they only hold for times later than the initial time t = 0 of the newly occurring wave. In the earlier all-time case the initial conditions (2) are incompatible within the SIR model as discussed in detail in part A. Still, the initial conditions (2) are useful to forecast the future dynamics of an epidemics. While negative times existed in part A, we consider only semipositive times t ⩾ 0.
denoting the initial seed infection fraction of the population, and where R(0) = 0 does not pose any restriction, as all quantities in this work describe fractions of the initially unrecovered/unremoved population, rather than a total population. The initial conditions (2) make the treatment here different from part A. This semi-time case is particularly useful and appropriate for modeling the temporal evolution of later (than the first) pandemic waves when a greater population fraction from the first wave has been infected. We do not assume here that the SIR model was describing the quantities in the past; instead they only hold for times later than the initial time t = 0 of the newly occurring wave. In the earlier all-time case the initial conditions (2) are incompatible within the SIR model as discussed in detail in part A. Still, the initial conditions (2) are useful to forecast the future dynamics of an epidemics. While negative times existed in part A, we consider only semipositive times t ⩾ 0.
Within the all-time case treated in part A the initial conditions for S, I, and R were proven to be interrelated, S(0) = e−ɛ was the only initial condition that had to be specified with no restriction on the value of ɛ ⩽ 1. Moreover, the initial conditions (2) are not compatible with part A where the assumption R(0) = 0 is forbidden.
Some but not all of the equations can be adopted from part A with the identification

Moreover, η and ɛ are basically identical for small values of η ≪ 1 considered in the semi-time case, since  , while the all-time case was not restricted to small ɛ. Although part A and B are qualitatively very different, in the limit of small η ≪ 1 the results are similar for small values of the inverse reproduction number.
, while the all-time case was not restricted to small ɛ. Although part A and B are qualitatively very different, in the limit of small η ≪ 1 the results are similar for small values of the inverse reproduction number.
We are applying the semi-time SIR model to real data as part of our supplementary information (https://stacks.iop.org/A/17/175601/mmedia).
2. General SIR-equations
If a(t) and μ(t) denote the time-dependent infection and recovery rates, respectively, the SIR-model is defined with the two dynamical equations [2, 3, 32]
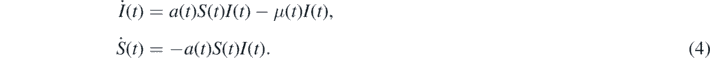
Here and in the following the dot stands for the derivative with respect to t. The third equation for the dynamics of R(t) follows from the sum constraint (1), i.e.

where we inserted equation (4). The second equation (4) can be written as
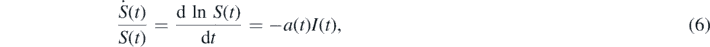
so that

implying that equation (5) becomes

with the ratio of infection and recovery rates

The first term on the right-hand side of the first dynamical equation (4) denotes the daily differential rate of newly infected persons from the desease, i.e.
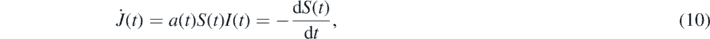
where the second equality results from the second equation (4). It is this rate  that is monitored during the outbreak of a pandemic wave.
that is monitored during the outbreak of a pandemic wave.
We emphasize that the half-time model here only considers semipositive times and adopts the two initial conditions (2) for S(0) and I(0). In contrast to part A it allows also for values of the ratio K(t) > 1 to investigate the temporal behavior of the pandemic wave.
2.1. Special case
As in part A we assume that the infection and recovery rates have the same time dependence, so that their positive ratio k, the inverse reproduction number, is time-independent and constant:
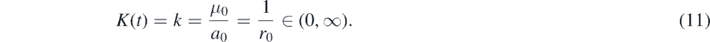
As indicated k = 1/r0 equals the inverse of the SIR-basic reproduction number r0. We emphasize that this special case includes the standard case used by most analysis before that both, the infection and recovery rates, are constants with respect to time.
The assumption (11) still allows us to take into account an arbitrary time-dependence of the infection rate a(t) which, of course, then is identical to the time dependence of the recovery due to assumption (11). Then it is convenient to introduce for arbitrary time dependence of the infection rate a(t) the new time variable

so that

Equations (4), (5) and (7) then read

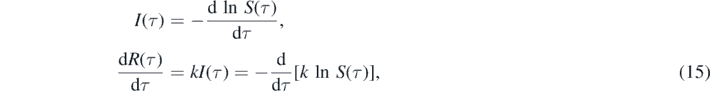
respectively. In equation (15) (dln S/dτ)τ=0 = −η in order to meet the initial condition (2) for I(0) = η. Equation (15) can be written as

or with the integration constant c0

Because of the initial conditions (2) for S(0) = 1 − η and R(0) = 0 the integration constant equals c0 = k ln(1 − η), so that
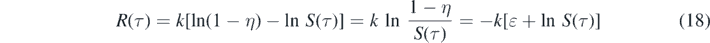
or

From the invariant  we obtain with equation (12) in the form dτ/dt = a(t) for differential rate of newly infected persons from the desease
we obtain with equation (12) in the form dτ/dt = a(t) for differential rate of newly infected persons from the desease
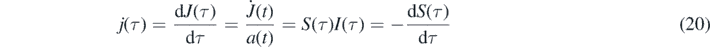
with the initial value j(0) = η(1 − η). The cumulative distribution corresponding to j(τ) is given by
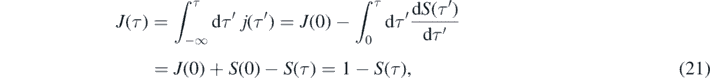
where the initial condition J(0) = I(0) = η had been used, in accord with equation (2).
2.2. Analytical solution
As in part A we introduce the quantity G(τ) by
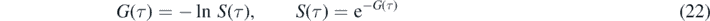
with the initial condition G(0) = −ln(1 − η) = ɛ. According to equations (15) and (18) then
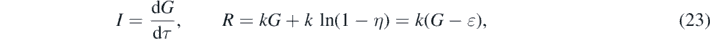
so that the sum constraint (1) provides the dynamical equation

or

Integrating equation (25) over τ then provides
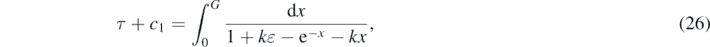
where the integration constant c1 has to be determined from the initial condition G(0) = ɛ, so that
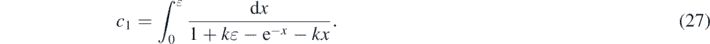
With equation (27) we obtain for equation (26) the formal solution

with  according to equation (12).
according to equation (12).
This solution (28) generalizes the known analytical solutions in the literature [2, 3, 29] as it holds for arbitrary time-dependence of the infection rate a(t). The mentioned known solutions can be reproduced with equation (28) by setting τ = a0 t on its left-hand side resulting from a constant injection rate a0. As non-pharmaceutical interventions (NPIs) during the pandemic wave generate a time-changing infection rate, the generalized solution (28) is highly valuable to assess quantitatively the effect of the NPIs on the time evolution of the disease. Substituting y = 1 − e−x and using equation (21) in the form

we obtain for the solution (28)

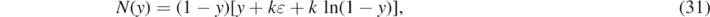
where we have introduced the inverse integrand N(y), that is parameterized by k and η. Taking the derivative with respect to τ highlights the fact that the inverse integrand in (30) is nothing but the differential rate of newly infected persons in terms of J(τ)
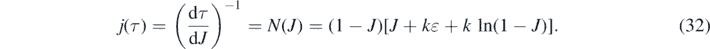
Once J(τ) and j(τ) are determined from equations (30) and (32), respectively, one obtains for the other interesting quantities according to equations (21), (20) and (18) that
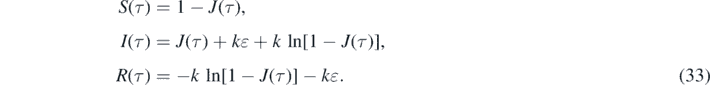
3. Exact results for final and maximum values
3.1. Maximum value G∞
The solution (28) indicates that the maximum value G∞ = G(τ = ∞) of the function G is attained when the denominator of the respective integrand vanishes, i.e.

Consequently,

where W0 is the principal solution of Lambert's equation and α given in terms of k and ɛ as
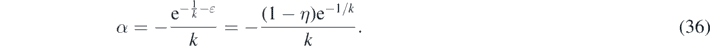
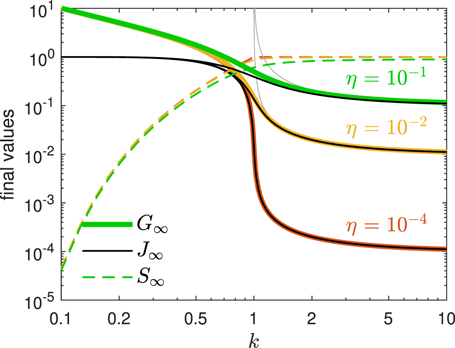
The argument α of the Lambert's W0 function in equation (35) is negative for all k and  . Accordingly, W0 ∈ [−1, 0] is negative as well, while G∞ ⩾ 0. As ɛ ≪ 1 the maximum G∞(k) is predominantly determined by the inverse basis reproduction number k. In figure 1 we show the maximum G∞ as a function of k and three different small values of η ≃ ɛ. It can be seen that G∞ has values significantly greater than unity for k ≪ 1, while it reaches
. Accordingly, W0 ∈ [−1, 0] is negative as well, while G∞ ⩾ 0. As ɛ ≪ 1 the maximum G∞(k) is predominantly determined by the inverse basis reproduction number k. In figure 1 we show the maximum G∞ as a function of k and three different small values of η ≃ ɛ. It can be seen that G∞ has values significantly greater than unity for k ≪ 1, while it reaches  at k = 1. The dashed black line shows the asymptotic behavior of G∞ ∼ 1/k at small k ≪ 1. Significant deviations from the asymptotic behavior set in at k ≈ 1/3. Note, that the α defined by equation (36) is just 1 − η = S(0) times the α that occurred in part A. This will have qualitative consequences for the asymptotic behaviors, to be discussed later below.
at k = 1. The dashed black line shows the asymptotic behavior of G∞ ∼ 1/k at small k ≪ 1. Significant deviations from the asymptotic behavior set in at k ≈ 1/3. Note, that the α defined by equation (36) is just 1 − η = S(0) times the α that occurred in part A. This will have qualitative consequences for the asymptotic behaviors, to be discussed later below.
Figure 1. Final τ → ∞ values G∞ (thick colored), J∞ = R∞ (solid black), and S∞ (dashed colored) vs k for three choices (different colors) of η ∈ {10−4, 0.01, 0.1}. Also shown is the asymptotic behavior of G∞, R∞, and J∞ (solid gray) according to equation (37). For large k ≫ 1 the three coincide.
Download figure:
Standard image High-resolution imageFor large values of k ≫ 1 the argument (36) is negative and |α(k ≫ 1)| ⩽ (1 − η)/k ≪ 1. With the asymptotic expansion (A-G10) of the Lambert function for small arguments W0(|z| ≪ 1) ≃ z we obtain in this limit
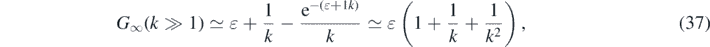
in excellent agreement with the numerical results for G∞ shown in figure 1 for values of k ⩾ 2.
3.2. Final values
The knowledge of G∞ from equation (35) and the solutions (28) and (30) allow us to derive a number of exact results. Equation (29) readily provides
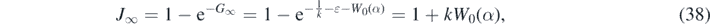
where we used the identity e−aW(z) = (W(z)/z)a . Likewise, according to equation (30) J∞ fulfills the transcendental equation

which is consistent with equation (38). Then according to equations (32) and (33)
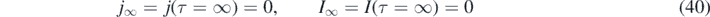
and
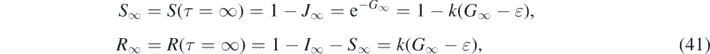
where we have used equation (34). In contrast to the all-time case in part A the final values J∞, R∞ and S∞ depend not only on the inverse basic reproduction number k but also on the fraction of initially infected persons ɛ = −ln(1 − η). Inserting G∞ from equation (35) we obtain with equation (38)

For large values of k ⩾ 5 we note

where we used equation (42). In figure 1 we plot the fractions R∞ and S∞ from (41) as a function of k ∈ [0, 10].
If the final values were known, one can calculate the corresponding k upon inverting the relationship between S∞ and k as

3.3. Differential rate of newly infected persons
Equation (32) can also be used, even without the explicit inversion of equation (30), to derive generally valid expressions for the time of maximum and the maximum level of the differential rate (20). The maximum of the differential rate (20) occurs when the derivative  vanishes. With equation (32) we find
vanishes. With equation (32) we find
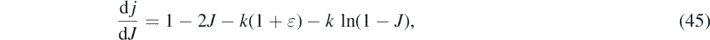
yielding for J0 the transcendental equation
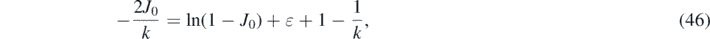
or

With the methods detailed in appendix G of part A the analytic solution of this equation can be expressed in terms of the non-principal solution W−1 of Lambert's equation
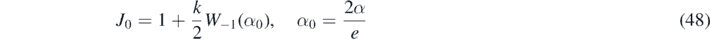
with α from (36).
Inserting equation (48) in equation (32) and making use of equation (46) yields for the maximum value in reduced time
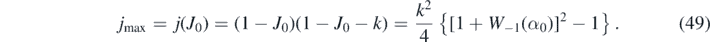
All these expressions for J0, jmax, and the J∞ etc are exact, as there are no approximations involved. Since W−1(α0) < − 2 for all k, the jmax is positive. But the time, at which jmax is reached, need not be at positive τ, i.e. it may have passed already. As the SIR model of the present part B is not valid for negative times, we have to simply ignore jmax for such cases, as opposed to part A where jmax was uniquely determined by any choice of initial conditions.
However, for a maximum to occur at finite positive times τ0 > 0, the derivative dj/dτ has to be positive at times 0 ⩽ τ < τ0. With equations (45) and (46) we readily find
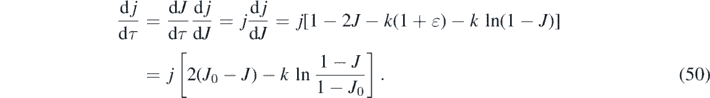
Since the requirement of a maximum jmax to exist at positive times is identical to the requirement of a positive dj/dτ at τ = 0, we can insert J(0) = η into the second line of equation (50) to find

where the relationship (3) between η and ɛ had been used. For inverse reproduction numbers k greater than 1 − 2η, the daily rate is monotonically decreasing at all times from its initial value j(0) = η(1 − η). Consequently, depending on the values of k and η we have two different cases:
- (a)The 'decay' case for large values of k ⩾ 1 − 2η, where the daily rate of newly injected persons monotonically decreases at all positive times from its initial maximum value j(0),
- (b)The 'peak case' if k < 1 − 2η where the daily rate of newly infected persons attains a maximum at a finite positive time.In table 1 we summarize the main relations between the various epidemical quantities as well as their minimum and maximum values.
Table 1. An attempt to help the reader to guide through this document. Peak time is meant to be the time where j reaches its maximum. Note that J0, equation (48), is very well approximated also by J*, equation (62). The coefficients a0,1,2 entering the quoted equations are given by equation (58), coefficients b0,1,2 are given by equation (63) (version I) and equation (65) (version II), remaining constants written down in equation (72). The exact τ in terms of J is given by equation (30). The peak time does not exist in the future when k < 1 − 2η, according to equation (51), or equivalently, when τ* < 0. The two versions I and II distinguish themselves only during decay times, and differ qualitatively mainly in their asymptotic behaviors at large times τ ≫ τ*. The reduced time τ is given in terms of physical time t via equation (12), which allows to model arbitrary time-dependent infection rates a(t).
| Quantity X = | S | I | R | J | j | G |
|---|---|---|---|---|---|---|
| In terms of J | 1 − J | Eq. (33) | Eq. (33) | id. | Eq. (32) | Eq. (22) |
| Initial value X(0) | 1 − η | η | 0 | η | η(1 − η) | ɛ |
| Minimum value Xmin | S∞ | η | 0 | η | 0 | ɛ |
| Maximum value Xmax | 1 − η | 1 − k[1 −ɛ + ln k] | R∞ | Eq. (41) | Eq. (49) | G∞ |
| Final value X∞ | Eq. (41) | 0 | Eq. (41) | Eq. (38) | 0 | Eq. (35) |
| Peak time τmax ≃ τ* | — | — | — | Eq. (73) | — | |
| Value at peak time | 1 − J0 | Eq. (33) | Eq. (33) | J0 | jmax | Eq. (22) |
| In terms of τ (τ ⩽ τ*) | Via J | Via J | Via J | Eq. (70) | Eq. (74) | Via J |
| In terms of τ (τ ⩾ τ*) | Via J | Via J | Via J | Eq. (71) | Eq. (74) | Via J |
| Asymptotic τ → ∞ behavior |
|
4. Approximate analytical solution
We are seeking for approximants for the time evolution of all SIR functions, including J(τ) and j(τ), that are compatible with the above solution (30)

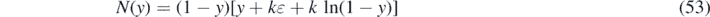
with ɛ = −ln(1 − η). We have already shown by equation (32) that the inverse integrand at y = J is the differential rate of newly infected persons j in terms of J.
In the following we are going to split this integral into two regimes (a) rise and (b) decay, corresponding to times τ characterized by a rising and decaying number of newly infected persons in the course of time. To this end we split the integral self-consistently at some J* so that the analytically known position J0 and height jmax = j(J0) of the maximum are exactly reproduced by the approximant. The rising part will thus be absent when J* < η. The two approximants of the inverse integrand will be denoted by ja (y) and jb (y) in regimes (a) and (b).
4.1. Requirements for an ideal approximant
An ideal approximant of the integrand must have several features:
- (a)The integral τ(J) must exist in analytic form,
- (b)The τ(J) function must exhibit an analytic inverse J(τ),
- (c)The exact and approximated reciprocal integrands must coincide at y = η to make sure the initial j(τ) is correctly captured,
- (d)The exact and approximated reciprocal integrands must coincide at y = J∞ to make sure J approaches the exact J∞ at large times,
- (e)The exact and approximated reciprocal integrands should have the same slope in the vicinity of the integral bounds, as these coefficients determine the asymptotic behavior of all SIR functions.If the integrand is approximated by two functions over disjunct regimes (a) and (b) separated by some y value (denoted by J*) there are further requirements:
- (f)The two approximants must possess identical values at y = J* to prevent a discontinuity in J(τ), and
- (g)They should have also the same first derivative at y = J* to prevent a discontinuity in j(τ) when calculated via J'(τ).Requirement (g) can be circumvented upon using the exact relation (32) or alternatively, and more conveniently, by just using j(τ) as given by the approximant, i.e., j(τ) = ja (J(τ)) within regime (a), and j(τ) = jb (J(τ)) within regime (b). We shall present below two approximants that both offer all but one of these ideal features. While the first approximant (referred to a version I) has (a)–(f), the second approximant (referred to as version II) has (a)–(d) and (f) and (g). The situation is depicted for both versions in figure 2.
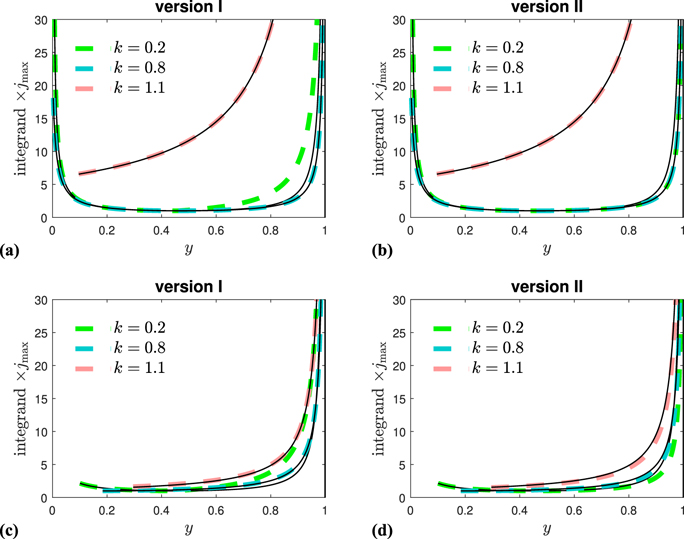
Figure 2. Detail concerning the development of the approximants. Exact (black solid) and approximated (colored) integrands 1/N(y) of equation (30) over their range of definition, y ∈ [η, J∞], multiplied by jmax for three different k and (a) and (b) η = 0.001 and (c) and (d) η = 0.1. While (a) and (c) depict the situation for version I (coefficients a0,1,2 from equation (58) and b1,2 from equation (63)), (b) and (d) show it for version II (same coefficients a0,1,2 and b1,2 from equation (65)). In this representation version II captures the integrand more precisely than version I, but version I has the advantage that the asymptotic behavior of τ(J) for J → J∞ is correctly captured. Note that a colored function is made of two parts that meet at y = J* where the integrand achieves its minimum.
Download figure:
Standard image High-resolution image4.2. Analytic inversion
To account for (a) and (b), with a side-view to the remaining requests, we note that the following indefinite integral, carrying a 2nd order polynomial in the denominator of the integrand (with the abbreviation  ),
),
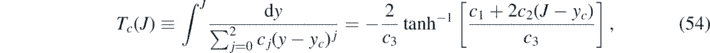
can be inverted analytically to yield
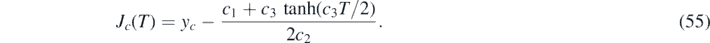
The derivative is thus
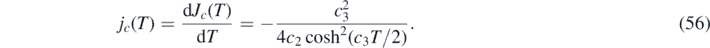
We will make use of these identities in the following section. Here, c is a placeholder for either (a) rise or (b) decay.
4.3. Expansion around ya = η
To account for the requirements (c) and (e) we use an optimized Taylor-expansion, i.e., Taylor expansion subject to a constraint [33], of the reciprocal integrand in equation (53) about y = ya = η. Up to 3rd order in y − η one has

where the coefficients follow from these requirements


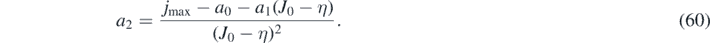
While a0 and a1 arise from the Taylor expansion, a2 ensures that equation (57) evaluated at y = J0 yields jmax, where both J0 and jmax are known from equations (48) and (49). This a2 is only slightly different from the a2 one obtains via the Taylor expansion. While a0 is positive, a2 is negative, and a1 may have either sign, depending on k. The abbreviation  will be used.
will be used.
4.4. Expansion around yb = J∞
To account for (d) and (e) we also expand the reciprocal integrand about y = yb = J∞ to write, again up to 3rd order,

where the sum does not involve b0 as the denominator N(y) vanishes at y = J∞. For the same reason b3 = |b1|. We could mention here the exact values for b1 and b2 resulting from Taylor expansion. But this would not help solving our problem. If we would go for using the approximant ja (y) within some range of y ∈ [η, J*] values, and jb (y) within the remaining range y ∈ [J*, J∞], the approximant would not share values and derivatives at y = J*, if the Taylor coefficients are used, and thus violate requirements (f) and (g).
Our solution to this discontinuity problem stems from the observation that ja (y) with coefficients given by equation (58) approximates the reciprocal integrand very well up to its extremum ja (J*) located at

In accord with our previous statements, a peak time occurs at positive times only when J* > η implying that a1 has to be positive (because a2 is negative), corresponding to k < 1 − 2η in light of (59). We note that this requirement agrees exactly with our earlier condition (51).
4.5. Coefficients b1 and b2 for version I
To fulfill condition (f) we need to require that jb (J*) = ja (J*). If we ignore the requirement (g) but take into account (e), then we arrive at our version I,

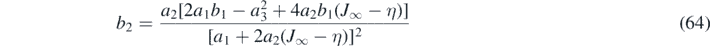
where b1 is a true Taylor coefficient. The abbreviation  has been used. Note that b1 ⩽ 0 while b2 may have either sign, depending on k and η. This version thus implies correct asymptotic behavior at large y at the expense of a jump in the derivative of J with respect to τ upon approaching J* from different sides, J > J* and J < J*. This jump does however not occur here, as we do not use a derivative to calculate j from J at J = J*, but two functions that meet at J*; the continuous j is already given by the approximants of the inverse integrand, ja
and jb
, which do not possess any jumps, and meet exactly where we split the integral, as this was the basic requirement leading to the coefficients in the present paragraph. Because this version I exhibits an exact Taylor coefficient b1, that determines the behavior in the vicinity of J∞, or equivalently, in the long time limit τ → ∞, we can deduce the asymptotic behavior of the exact solution of the semi-time SIR model in section 5.4.
has been used. Note that b1 ⩽ 0 while b2 may have either sign, depending on k and η. This version thus implies correct asymptotic behavior at large y at the expense of a jump in the derivative of J with respect to τ upon approaching J* from different sides, J > J* and J < J*. This jump does however not occur here, as we do not use a derivative to calculate j from J at J = J*, but two functions that meet at J*; the continuous j is already given by the approximants of the inverse integrand, ja
and jb
, which do not possess any jumps, and meet exactly where we split the integral, as this was the basic requirement leading to the coefficients in the present paragraph. Because this version I exhibits an exact Taylor coefficient b1, that determines the behavior in the vicinity of J∞, or equivalently, in the long time limit τ → ∞, we can deduce the asymptotic behavior of the exact solution of the semi-time SIR model in section 5.4.
4.6. Coefficients b1 and b2 for version II
The opposite case of fulfilling (g) while ignoring (e) yields version II


Also for this version, b1 ⩽ 0 and b2 may have either sign, depending on k and η. This version implies a continuously differentiable J, serves to reproduce the exact J up to times well beyond the peak time, but does not exhibit the correct asymptotic behavior at long times. This formal drawback is something that does not matter as long as k is not very small. We moreover know the asymptotic behavior  of the exact solution, that helps to rate when version II begins to fail.
of the exact solution, that helps to rate when version II begins to fail.
5. Results
5.1. Approximants for J(τ) and j(τ) (versions I and II)
Based on the considerations in the last section we are in the position to immediately write down the approximants for both versions. An approximant consists of two parts, Jrise(τ) to be used at τ ⩽ τ*, and Jdecay(τ) to be used at τ > τ*, where

according to equation (54). We will simplify this expression for τ* further below. To understand how we write down the approximant using the above equations, we recall that our approximation evaluates the integral τ in equation (52) via
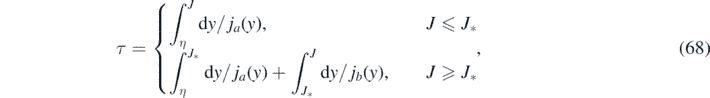
where the 2nd order polynomials ja (y) and jb (y) are characterized by coefficients a0,1,2 and b1,2, respectively, and where all these five coefficients as well as the J* were chosen to fulfill our criteria for an approximant, and explicitly expressed already in terms of k and η. Using equation (54) and τ* = τ(J*) we can write equation (68) as
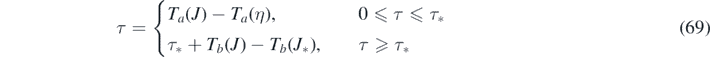
because c → a (and ya = η) has to be used for the rising J < J* (or equivalently, τ < τ*) regime, and c → b (and yb = J∞) afterwards. For the rising regime τ < τ* we can thus write τ + Ta (η) = Ta (J), where Ta (η) is a constant. According to equation (55) the inversion is
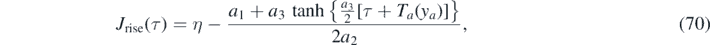
where ya = η has been used, and because the τ + Ta (η) has overtaken the role of T in equation (55).
Similarly, within the decay regime τ ⩾ τ*, equation (69) can be written as τ − τ* + Tb (J*) = Tb (J), where τ* and Tb (J*) are constants. According to equation (55) the inversion is
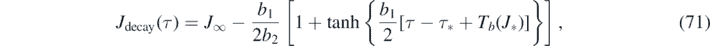
where yb = J∞ has been used, and because the τ − τ* + Tb (J*) has overtaken the role of T in equation (55).
It seems useful to explicitly write down the constants appearing in the above final expressions
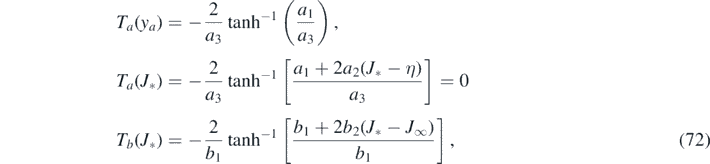
where we made use of equation (62) to simplify Ta (J*), and where J* was already expressed in terms of the coefficients in equation (62). As an aside we emphasize that by construction, more precisely, requirement (f), the two expressions Jrise(τ*) = Jdecay(τ*) agree. Inserting the coefficients from equation (72) we obtain for the maximum relative time (67) the simplified, still identical expression

so that Ta (ya ) in equations (72) and (70) turn out to be just identical to −τ*. These are final expressions for J(τ) in terms of the known coefficients, valid for both versions. If τ* lies in the past, or equivalently, if k < 1 − 2η, then J(τ) ≃ Jdecay(τ) is the only contribution to our approximant.
With this approximant for J(τ) at hand, the differential number of newly infected persons is simply given by jrise(τ) = ja [Jrise(τ)] with the 2nd order polynomial ja from equation (57), and jdecay(τ) = jb [Jdecay(τ)] with the 2nd order polynomial jb from equation (61). More explicitly,
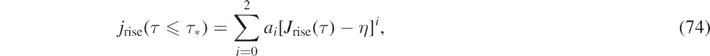
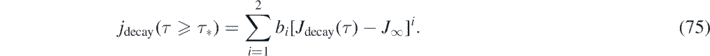
Because version II has the property (g), the differential number of cases is alternatively given by equation (56), i.e.,
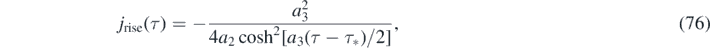
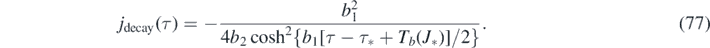
For version I, the daily new number of cases is not properly described by dJ/dτ, but instead is obtained from J via equation (74). For version II, equations (76) and (77) are just identical to equation (32) and also identical to equation (74) when J(τ) from equations (70) and (71) is used.
We recall that the remaining SIR quantities are directly obtained as well from J(τ) via S(τ) = 1 − J(τ), I(τ) = J(τ) + kɛ + k ln[1 − J(τ)], and R(τ) = 1 − S(τ) − I(τ).
5.2. Peak time and values at peak time
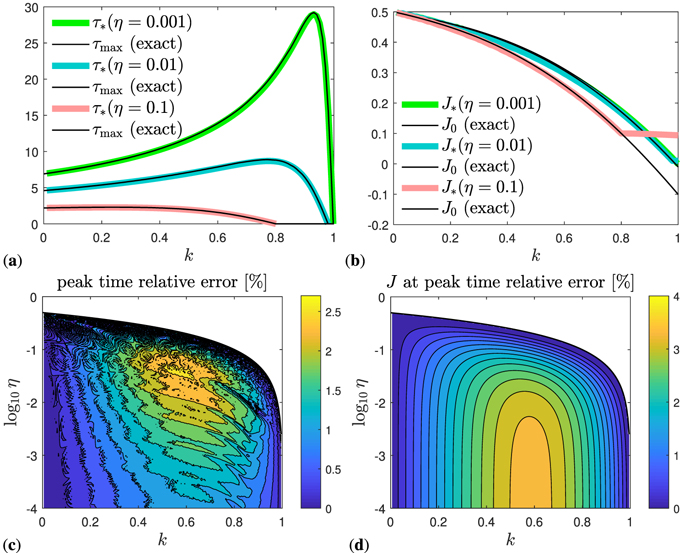
While the value jmax of the maximum of j(τ) at peak time τmax is captured exactly by construction of our approximants, the approximate peak time τ* given by equation (73) is compared with the numerically exact peak time τmax of the differential number of cases j(τ) in figure 3(a) for some selected values of η, to appreciate the dependency on k. The relative error for the selected parameter η values is well below 2% for all k. Such relative error of our approximant τ*, now as function of k and η, i.e., capturing the whole parameter space, is shown in figure 3(c). For these calculations and comparisons, the exact peak time τmax is obtained by solving equation (30), or alternatively, the SIR time evolution equations (14) and (15) numerically. As is visible from figure 3(c), the relative error of τ* does not exceed 2.5% in the worst case, which is located close to k = 0.6 and η = 10−1.5 ≈ 0.03. For both small and large k the relative error is extremely small, well below 0.1%. Our simple analytical approximant τ* for the peak time of daily newly infected persons can thus be considered precise for all practical purposes. As is obvious from figure 3(a), the peak time decreases with increasing η = I(0), for a given k.
Figure 3. (a) Peak time τmax versus k, compared with its approximant, τ* given by equation (73), for a few η values. The exact peak time τmax is obtained by solving equation (30), or alternatively, the SIR time evolution equations (14)–(15) numerically. (b) J at peak time, J0, compared with its approximant, J* stated by equation (62). Note that J* ⩾ η for the semi-time SIR, while J0 < η, or equivalently, k > 1 − 2η, marks the regime where the peak time does not lie in the future. Under such circumstances, there is only a regime of decay (J* = η). Note also, that J0 can get negative here, as opposed to part A, which corresponds to a choice of initial conditions that are incompatible with the all-time SIR model. (c) Relative error of the approximant τ* and (d) relative error of the approximant J*, now in the full k–η parameter space. The two shown quantities τ* and J* are identical for both versions I and II, and they only exist for k < 1 − 2η. Outside this regime, there is no peak in j.
Download figure:
Standard image High-resolution imageThe same holds true for the approximant J* of the cumulative number of infected persons at peak time, for which we know the exact analytic expression J0 as well. The two are compared with each other in figure 3(b) for some selected values of η, to appreciate the dependency on k. The relative error of our approximant J* over the whole parameter space is shown in figure 3(d). Note that J* ⩾ η for the semi-time SIR, while J0 < η, or equivalently, k > 1 − 2η, marks the regime where the peak time does not lie in the future. Under such circumstances, there is only a regime of decay (J* = η). Note also, that J0 can get negative here, as opposed to part A, which corresponds to a choice of initial conditions that are incompatible with the all-time SIR model. More specifically, J0 < 0 for k < 1 − 2η, which is just fine and irrelevant, while J* = η within this regime, which is characterized by a purely decaying J(τ). As shown by figure 3(b), the cumulative number of infected persons at peak time decreases with increasing η = I(0), for a given k.
5.3. Daily rate and cumulative number of infections
By our construction, the jrise(τ) achieves its maximum at time τ*, where jrise(τ*) = jmax is identical to the exact analytic result (49). The peak time τmax of the unapproximated j(τ) (if a peak time exists) is not exactly located at τ*, because J* is not exactly identical to J0 (figure 3(b)), as we discussed already. When there is no maximum in j at positive times, J* = η.
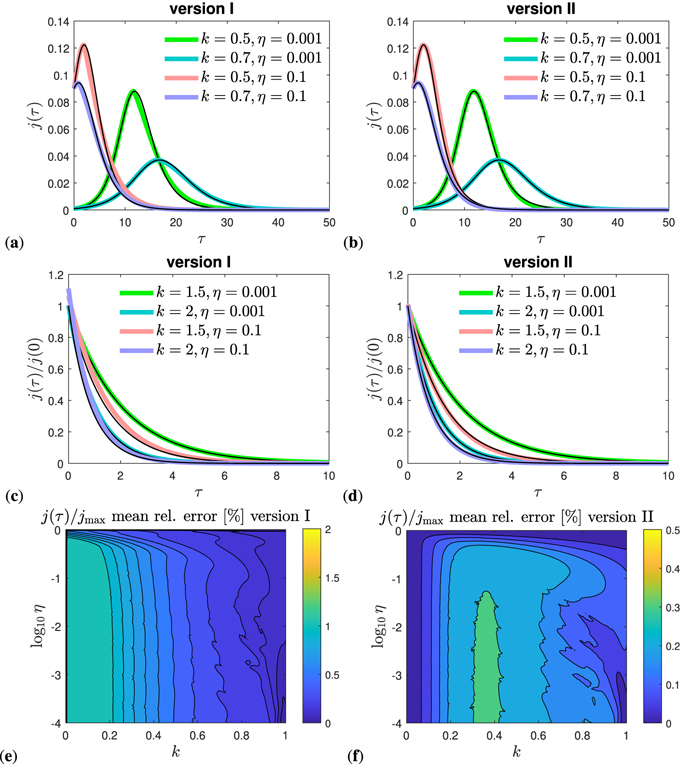
In figures 4(a) and (b) we plot the daily rate j(τ) of newly infected persons for the more relevant cases where a peak time is ahead in the future. These figures compare the time evolution of our approximants (version I and II) with the exact numerical solution of the SIR model. Decay cases are shown in figures 4(c) and (d), again for selected values of the parameters k and η. To make sure that we did not just pick suitable parameters here, the mean relative error of our approximant for j(τ) is evaluated as function of k and η in figures 4(e) and (f) for both versions, and over the whole range of parameter space. The relative errors of the approximant is below 0.3% everywhere for version II, and below 1% for all k > 0.02 for version I. As already known from figure 3(a) the peak time increases with increasing η and increasing k before dropping sharply when k approaches unity. There is no future peak time anymore for k > 1 − 2η, reflected by a negative τ* in that case.
Figure 4. (a)–(d) Differential number of cases j(τ) given by equation (74) (solid black) versus τ, compared with its approximant equation (74) (colored). (a) and (b) Representative cases k < 1 − 2η that exhibit a future peak time and (c) and (d) cases k > 1 − 2η where a peak time and rising regime is absent. While (a) and (c) show results for version I, (b) and (d) are for version II. The versions differ only at late times, beyond peak time. The peak time is given by τmax ≃ τ* in equation (73), the height jmax of the maximum of j(τ) given by equation (49). (e) and (f) Mean relative error of the reduced approximant j(τ)/jmax in the full k–η parameter space for both versions I and II. The exact reference j(τ) is obtained by solving equation (30), or alternatively, the SIR time evolution equations (14) and (15) numerically. The analytic approximant j(τ) is provided by equation (74), while jmax is given by equation (49). For the normalization we use the expression for jmax, even when the maximum does not lie in the future for k < 1 − 2η. The regime k > 1 is not shown in (e) and (f), but the agreement is excellent in this regime, more precisely, well below 0.2% for all η. We note that for version II the j(τ) approximant can alternatively be expressed by equation (77).
Download figure:
Standard image High-resolution imageSimilarly, in figure 5 we compare the approximations (70) and (71) for the cumulative number with the exact time dependence J(τ) obtained by the numerical integration of equation (30), for both versions I and II. While figures 5(a) and (b) focuses on the case where the peak times lies in the future, figures 5(c) and (d) is concerned with the decay cases. It is visible how the cumulative number at peak time, J0, approximated by J*, decreases with increasing k, in accord with figure 3(b), and is only weakly affected by the initial condition for η ≪ 1. The accuracy of the approximant is below 0.3% for any choice of parameters, if version II is used, while it exceeds 1% for version I but only for small k < 0.1.
Figure 5. Representative cases that exhibit a future peak time. (a) and (b) Cumulative number of infected persons J(τ) (solid black) versus reduced time τ, compared with its approximant equations (70) and (71) (colored). (c) and (d) Differential number of cases j(τ) given by equation (74) (solid black) versus τ, compared with its approximant equation (74) (colored). While (a) and (c) show results for version I, (b) and (d) are for version II. The versions differ only at late times. The peak time is given by τmax ≃ τ* in equation (73), the height of the maximum of j(τ) given by equation (49), and the value J0 = J(τmax) at peak time given by J0 ≃ J*, cf equations (48) and (62). Mean relative error of the reduced approximant J(τ)/J∞ in the full k–η parameter space for (c) version I and (d) version II. The exact reference J(τ) is obtained by solving equation (30), or alternatively, the SIR time evolution equations (14) and (15) numerically. The analytic approximant J(τ) is provided by equations (70) and (71). For the normalization we use the expression for J∞ given analytically by equation (38). The regime k > 1 is not shown here, but the agreement is excellent in this regime, more precisely, well below 0.2% for all k and η. While version I captures the asymptotic behavior correctly, it has an error slightly larger than 2% at very small k < 0.05, but otherwise it is competing very well with version II.
Download figure:
Standard image High-resolution imageRelative errors for all other SIR quantities are similarly small, and need not be discussed here, as all the S, I, R, G functions can be derived from J(τ), as table 1 mentioned already.
5.4. Asymptotic behavior
Overall, the difference between versions I and II is not easily appreciated from these figures, and therefore of minor relevance in practice. Both versions are in any case formally very similar as they only differ in the values of their polynomial coefficients b1 and b2, and thus in their behavior beyond the peak time. At early times the doubling time τ2 defined by j(τ + τ2) = 2j(τ) is given by τ2 = ln(2)/a3, according to equation (76). The difference between versions I and II is most pronounced if one focuses solely on j(τ) at very late times.
The differential rate of newly infected persons j(τ) exhibits an exponential decay

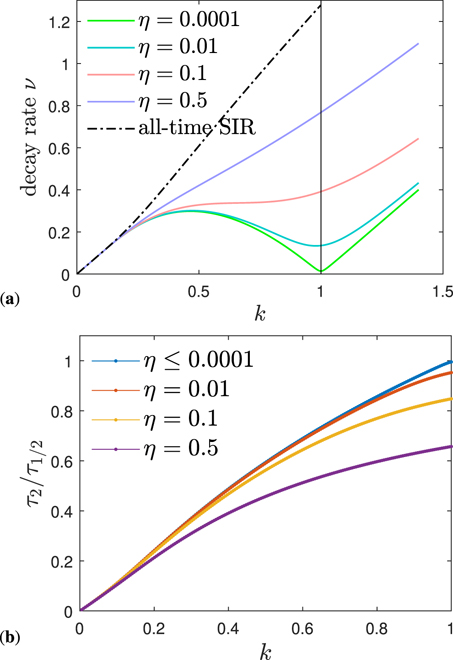
with some semipositive and constant, dimensionless decay rate ν at late times τ ≫ τmax under all conditions, that is obtained from equation (63). The decay rate is identical to ln(2)/τ1/2, if τ1/2 denotes the late half time, i.e., the time required for j to have dropped by a factor 2. Figure 6 shows the exact rate
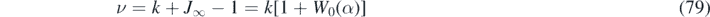
of the semi-time SIR as function of k, for various η, in perfect agreement with the decay rate featured by our approximant version I (ν = −b1 in that case). In equation (79) we have used equation (38) to replace J∞ by Lambert's function, with α defined by equation (36). This way the decay rate is formally identical to part A, recalling, that α for the present semi-time SIR model is S(0) times the α for the all-time SIR. The rate ν is positive, except for k = 0, and for k = 1 if η = 0. The decay rate generally increases with increasing initial fraction of infected persons, η. This means that the daily rate at late times decreases the faster the larger the initial fraction of infected persons is. Shown for comparison (dashed black) is the corresponding decay rate for the all-time SIR model from part A. We thus find that the exponential decrease is under all conditions faster for the all-time SIR, compared with the semi-time SIR. While for small η the exponent ν is almost symmetric about k = 1, it gets more and more asymmetric upon increasing η. We recall that the all-time SIR model is restricted to the regime k ∈ [0, kmax] with kmax = [S(0) − 1]/ln(S(0)) which is ![${k}_{\mathrm{max}}=\eta /\varepsilon \in \left(\right.\enspace 0,1\left. \right]$](https://content.cld.iop.org/journals/1751-8121/54/17/175601/revision6/aabed66ieqn13.gif) using our current notation.
using our current notation.
Figure 6. (a) The daily rate j(τ) exhibits an exponential decay at late times under all conditions. Here we show the exact prefactor ν = 1 − k − J∞ (in agreement with the prefactor produced by our approximant version I) in the exponent of limτ→∞ j(τ) ∝ e−ντ as function of k, for various η. Shown for comparison (dashed black) is the corresponding exponent for the all-time SIR model from part A. (b) Ratio between early doubling time τ2 and late half decay time τ1/2 of the differential rate of newly infected persons, j(τ), characterizing the asymmetry of the wave, as J0 − J∞/2 does. For η → 0, the semi-time SIR approaches the all-time SIR (part A) asymmetry given by τ2/τ1/2 = ν/(1 − k) with ν from equation (79). The asymmetry increases with decreasing k and with increasing η.
Download figure:
Standard image High-resolution image6. Summary and conclusions
The earlier analytical analysis [1] of the SIR epidemics model for a constant ratio k of infection to recovery rates is extended here to the semi-time case which is particularly appropriate for modeling the temporal evolution of later (than the first) pandemic waves when a greater population fraction from the first wave has been infected. In the semi-time case the SIR model does not describe the quantities in the past; instead they only hold for times later than the initial time t = 0 of the newly occurring wave. Simple exact and approximative expressions are derived for the final and maximum values of the infected, susceptible and recovered/removed population fractions as well the daily rate and cumulative number of new infections.
To arrive at these conclusions, we eliminated one of the time-dependent infection a(t) and recovery μ(t) rates—as in part A—by introducing the reduced time-variable τ defined by dτ/dt = a(t). For the special case of a constant ratio k = μ(t)/a(t) of the two rates the exact analytical solution (30) is derived providing

as an integral with the inverse integrand N(y) = (1 − y)[y + kɛ + k ln(1 − y)], where ɛ equals the negative logarithm of the initial susceptible fraction. All other epidemics quantities of interest can be deduced from the inversion J(τ) of the integral solution (80) according to equation (33) including the medically interesting daily rate of new infections j(τ) given in equation (32).
We noted that the inverse integrand itself N(J) = j(J) agrees with the daily rate j. Therefore whatever is adopted for the inverse integrand N(J), in order to perform the inversion of the integral solution, is identical to an assumption of the dependence j(J). As analytical approximation we suggested to use optimized Taylor-expansions of the inverse integrand N(J) up to second-order in either J − η or J∞ − J. Optimized refers to our approach of choosing the second order expansion coefficient a2 such that the first Taylor expansion evaluated at J0 yields jmax, where both the values of J0 and jmax can be inferred without solving the integral equation (80) explicitly. Both Taylor-expansions up to second order in J − η or J∞ − J, respectively, then allow us the analytical inversion of the integral (80) providing the temporal evolution J(τ) as well as j(τ) either from equation (32) or from j(τ) ≃ N(J(τ)) which agree exactly. We presented two variants of approximants, denoted as version I and II, which mainly differ in their asymptotic behavior at times large compared with the peak time, and their quality in the vicinity of the peak. Formally the two versions differ in their Taylor coefficients b1 and b2 characterizing N(y) within the regime past peak time, and they are therefore also identical for the case of a pure decay.
It is demonstrated that two qualitatively different types of temporal evolution of the daily rate of new infections j(τ) occur depending on the values of k and the initial value of the infected fraction I(0) = η: in the decay case for k ⩾ 1 − 2η the daily rate monotonically decreases at all positive times from its initial maximum value j(0) = η(1 − η). Alternatively, in the peak case for k < 1 − 2η the daily rate attains a maximum at a finite positive time. By comparing the approximated analytical solutions for j(τ) and J(τ) with the exact ones obtained by numerical integration of solution (80), it is shown that the analytical approximations are accurate within at most only 2.5 percent.
As opposed to the all-time SIR, we can apply this semi-time model to n different pandemic waves well separated in time, by resetting t = 0 at the begin of a new wave, and with the help of an recovered/removed fraction R∞, that is not anymore taken into account in a subsequent wave. The outcome of wave n, used as initial condition for wave n + 1, severely influences the temporal evolution of subsequent waves n + 1, n + 2, ...
The SIR model is often solved numerically using some initial condition η ≪ 1 that is incompatible with the all-time SIR model, and thus captured by the semi-time SIR model. Because η is so small, it is not obvious at first glance, or usually even not tested, if there is a problem with negative fractions of susceptible or infected persons at negative times. More importantly, we have shown here that the behavior at large times is dramatically affected by the choice of initial conditions. It is thus not true that some arbitrary small η is good enough to obtain a solution to the SIR model. It is just the opposite. The all-time SIR model, which is the SIR model that was originally developed to describe the time-evolution of the pandemic measures at all times, starting out with a vanishing number of infected persons at t → −∞, is not recovered as a special case of the semi-time SIR model. With this work we have clarified how the initial fraction of infected persons sensitively influences the late time dependence of the epidemics, the maximum daily rate and its peak time. Such dependencies do not exist in the earlier investigated all-time case.
Supplementary Information
We are applying the semi-time SIR model discussed here in real time to the first and second waves of the Covid-19 pandemics for more than 60 countries at https://www. complexfluids.ethz.ch/covid19-waveII. The fitting SIR parameters are tabulated there.
Acknowledgments
We thank both referees for very constructive reports.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).