Abstract
The physics of optical vortices, also known as twisted light, is now a well-established and a growing branch of optical physics with a number of important applications and significant inter-disciplinary connections. Optical vortex fields of widely varying forms and degrees of complexity can be realised in the laboratory by a host of different means. The interference between such beams with designated orbital angular momenta and optical spins (the latter is associated with wave polarisations) can be structured to conform to various geometrical arrangements. The focus of this review is on how such tailored forms of light can exert a controllable influence on atoms with which they interact. The main physical effects involve atoms in motion due to application of optical forces. The now mature area of atom optics has had notable successes both of fundamental nature and in applications such as atom lasers, atom guides and Bose–Einstein condensates. The concepts in atom optics encompass not only atomic beams interacting with light, but atomic motion in general as influenced by optical and other fields. Our primary concern in this review is on atoms in structured light where, in particular, the twisted nature of the light is made highly complex with additional features due to wave polarisation. These features bring to the fore a variety of physical phenomena not realisable in the context of atomic motion in more conventional forms of laser light. Atoms near resonance with such structured light fields become subject to electromagnetic fields with complex polarisation and phase distributions, as well as intricately structured intensity gradients and radiative forces. From the combined effect of optical spin and orbital angular momenta, atoms may also experience forces and torques involving an interplay between the internal and centre of mass degrees of freedom. Such interactions lead to new forms of processes including scattering, trapping and rotation and, as a result, they exhibit characteristic new features at the micro-scale and below. A number of distinctive properties involving angular momentum exchange between the light and the atoms are highlighted, and prospective applications are discussed. Comparison is made between the theoretical predictions in this area and the corresponding experiments that have been reported to date.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
List of symbols and abbreviations
| A⊥ | transverse electromagnetic vector potential |
| B | magnetic vector field; also represents artificial vector magnetic field |
 |
Laguerre–Gaussian mode normalisation constant |
| d | electric dipole moment |
| E⊥ | transverse electric vector field |

|
electric field vector |
| Erec | atom recoil energy |

|
average force |
| H | total Hamiltonian |
| Hint | interaction Hamiltonian |
| I | light intensity |
| IS | saturation intensity |
| J | current density |
| Jl(x) | Bessel function of the first kind of order l |
| k | wavevector |

|
Lagrangian density |
| L | total Lagrangian |
| L | orbital angular momentum density operator |
| l | winding number (azimuthal index) in a twisted beam |

|
linearly polarised light beams, with orthogonal polarisations |
 |
associated Laguerre polynomial |
 |
matrix element of interaction Hamiltonian Hint between quantum states i and f |
| M | mass of the two-particle atom |

|
magnetic dipole moment |
| pα=1,2 | momentum canonically conjugate to qα=1,2 |
| p | radial nodal index in a twisted beam |

|
electric polarisation vector |
 |
truncated electric polarisation vector (up to quarupole term) |
| qα=1,2 | particle position vector in the two-particle (hydrogenic) atom |
| Qij | (ij)th component of the electric quadrupole moment tensor |
| R | atomic centre of mass position vector variable |

|
optical spin angular momentum density |
| S | optical chirality flux |
| S | optical linear momentum density vector |
| s0 | saturation parameter |

|
torque on atomic centre of mass |

|
dipole potential |
 |
LG amplitude distribution function |

|
velocity vector of the atomic centre of mass |
| V(R) | artificial gauge scalar field of atom in an optical field |
| vD | the Doppler velocity |
| vrec | recoil velocity |
| vg | group velocity |
| w(z) | beam waist at position z in the beam |
| zR | Rayleigh range |
| αF | damping coefficient in Sisyphus cooling |
| αϕ | azimuthal damping coefficient in Sisyphus cooling |

|
atomic polarisability |
| Δ | detuning of light frequency from atomic transition frequency |
| Δ0 | static detuning |
| δ | doppler shift |

|
transverse Dirac delta function |
 ϕ ϕ |
two-level atom adiabaticity parameter |
 |
adiabaticity parameter |

|
non-adiabaticity parameter in Sisyphus effect |
| Φ | artificial magnetic flux |

|
optical chirality density |
| Γ | upper state de-excitation rate in a two-level atom |
| κ | scalar field helicity |
| λ | wavelength |
| Λ | generating function in a Power–Zienau–Woolley (PZW) gauge transformation |
 |
elastic modulus of LG donut dipole trap |
 |
momentum canonically conjugate to A⊥ |
 |
canonical momentum density of evanescent light |
 |
spin momentum density of evanescent light |
 |
wavepacket transverse spread |

|
evanescent wave helicity |
| Θklp | Laguerre–Gaussian phase function |
| σ± | left and right handed circular polrisation of light |
| Ω | rabi frequency |
| Ω0 |
rabi frequency associated with beam amplitude 
|
| Ψ | atomic state function on diffraction in atom vortices |
| AVB | atom vortex beam |
| HOT | helical optical tube |
| LG | Laguerre–Gaussian |
| OAM | orbital angular momentum |
| SOV | surface optical vortex |
| SPOV | surface plasmon optical vortices |
1. Introduction
The term 'twisted light' refers to various states of light which are endowed with the property of orbital angular momentum (OAM). These encompass a wide range, including twisted light in freely propagating beams such as Laguerre–Gaussian (LG) and Bessel beams [1] and other forms of twisted light inside optical fibres [2] and on fibres supporting twisted light [3], as well as wave guide arrays [4]. Twisted light modes have also featured in nonlinear waveguides [5] and as so-called surface optical vortices (SOVs) [6]. The reference to the twisted nature stems from the observation that the OAM property of the light makes the normal to its wave-fronts twist in a helical fashion with a degree of twisting depending on the OAM content. Freely propagating twisted beams are proto-typical twisted light and were the first to be explored; they are also referred to as optical vortex beams. It has been realised [7] that associated with the wave-front of such a state of light is a topological structure due to a singularity in phase. In cylindrical polar coordinates (ρ, ϕ, z) the phase of a pure vortex state takes the form  where l is the topological charge, also called the 'winding number' and the 'azimuthal quantum number'. The value of
where l is the topological charge, also called the 'winding number' and the 'azimuthal quantum number'. The value of  also quantifies, in terms of the reduced Planck constant ℏ the OAM conveyed per photon. Nye and Berry were the first to describe the topological features of the wave-front as a screw dislocation in a manner similar to that encountered in crystal defects [8].
also quantifies, in terms of the reduced Planck constant ℏ the OAM conveyed per photon. Nye and Berry were the first to describe the topological features of the wave-front as a screw dislocation in a manner similar to that encountered in crystal defects [8].
This review is concerned with the principles, recent developments and applications in the context where atoms interact with twisted light. Here we begin with the background theory of the interaction of atoms with electromagnetic fields in general, emphasising the division of the atom dynamics into gross motion associated with the centre of mass (which is dominated by the nuclear mass) and the internal motion involving the bound electrons, and the distinction between optical spin and optical OAM densities. This is followed by brief descriptions of conventional laser cooling and trapping of atoms, including Doppler and Sisyphus mechanisms. The essential formalism for twisted light fields is given next with emphasis on LG light as the most widely discussed form of twisted light. The inclusion of optical wave polarisation (photon spin) as one of the main sources of complexity of the twisted light is discussed with special emphasis on polarisation gradients arising in co- and counter-propagating twisted light beams with circular polarisations. This background sets the scene for the main aim of this review, namely the description arising when complex twisted light interacts with atoms.
One of the first issues to be addressed in the context of twisted light interaction with atoms is the possibility of exchange of OAM. Could the well known selection rules in the case of emission and absorption of ordinary (Gaussian) polarised light with atoms be modified with the involvement of the new ingredient in the form of OAM carried by twisted light? The theory of this process is based on the analysis of the transition matrix element for dipolar and quadrupolar active transitions and on the division between the centre of mass and the internal (electronic-type) motion of the atom. We highlight experiments carried out to date on this issue. The interaction also gives rise to modified optical forces that act on the centre of mass of the atom with additional characteristic features associated with the OAM content of the twisted light, including azimuthal Doppler shifts along with azimuthal forces and torques about the beam propagation direction and an azimuthal Sisyphus effect. Multiple beams are shown to lead to 'twisted molasses' and other novel forms of optical trapping, including the formation of 'Ferris wheels' and 'HOTs' which arise when co-propagating beams with opposite and identical winding numbers are formed.
Totally internally reflected twisted light can generate SOVs as evanescent waves carrying OAM and in the presence of a metallic film deposited on the surface, the evanescent modes acquire a plasmonic character. Such evanescent fields interact with atoms in the vicinity of the surface and the atoms may become trapped in the surface region.
LG twisted light beams have anomalous additional phase effects due to being focused beams with a well-defined waist plane at focus. The additional phase terms in the form of a Gouy phase and a curvature phase term are normally ignored but become significant for atoms localised the vicinity of the focus plane, particularly for LG light with large values of winding number l and/or radial number p. Under these circumstances the atoms experience enhanced anomalous phase effects in the form of modified gradient forces which can diminish the axial force component acting on the atom, or even reverse its direction.
Besides LG and Bessel beams where the dominant phase involves integer winding number l, light beams with fractional OAM have been considered. In particular, Götte et al [9] reported the generation of light carrying fractional OAM by limiting the number of Gouy phases in a superposition of LG light beams.
A well defined beam of atoms, like an optical beam, is essentially a de Broglie wave with a wavelength that depends on the atomic axial velocity. Diffraction through light masks, in techniques somewhat akin to, but rather different from, those used for the generation of twisted light, are expected to lead to the generation of twisted beams of atoms, so-called 'atom vortex beams'. Finally, we describe how the gross motion of atoms in twisted light gives rise to artificial gauge fields for atoms in donut modes and in Ferris wheel patterns.
In the conclusions section, we briefly identify a number of other treatments of atoms in twisted light that are beyond our scope in this review, including the trapping of ions in donut beams, the effects on cyclotron motion of ions in twisted light, spin–orbit coupling effects in this context and nonlinear effects.
2. Coupling light to atoms
The essential background physics describing the interaction of twisted light with atoms stems from conventional non-relativistic quantum electrodynamics [10] and considerable work has been carried out on this (see [11–18]). An atom subject to light typically exhibits two kinds of dynamics, namely the dynamics involving the gross motion of the atom as a whole, in terms of its centre of mass, and processes involving the internal dynamics in the form of transitions between quantum (electronic) states due to the emission and absorption of light quanta. These features play central roles in the context of twisted light interacting with atoms and it is helpful to tailor the formalism in a manner that highlights the roles of the internal and gross motions. It is common practice to explore interactions of atoms and molecules in terms of multipole moments, both electric and magnetic, coupled to the electromagnetic fields [13, 16]. The treatment becomes particularly simple, but perfectly adequate and transparent, when the atom comprises an outer electron and a nucleus surrounded by a closed-shell electron core. The corresponding particles have nett charges e1 =  (electron) and e2 =
(electron) and e2 =  (nucleus and core) and masses m1 = me (electronic mass), m2 = mc (nucleus and core). Any inner transitions of the core need not concern us. We must bear in mind that m2 ≫ m1, but it is important not to impose this condition from the outset, in order to fully take account of the centre of mass motion and its coupling to both the relative motions of the outer electron and core and the light fields. The two-particle atom coupled to the electromagnetic field has the following non-relativistic classical Lagrangian in the transverse (radiation) gauge [16]
(nucleus and core) and masses m1 = me (electronic mass), m2 = mc (nucleus and core). Any inner transitions of the core need not concern us. We must bear in mind that m2 ≫ m1, but it is important not to impose this condition from the outset, in order to fully take account of the centre of mass motion and its coupling to both the relative motions of the outer electron and core and the light fields. The two-particle atom coupled to the electromagnetic field has the following non-relativistic classical Lagrangian in the transverse (radiation) gauge [16]
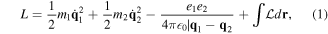
where
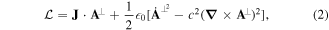
with  and
and  , the particle position variables and corresponding velocity vectors. In the radiation gauge
, the particle position variables and corresponding velocity vectors. In the radiation gauge  the Coulomb effects reside in the static inter-particle interaction and we only have A⊥ as the canonical field variable. Besides the Coulomb interaction, the coupling between the field and the particles occurs via the total current density
the Coulomb effects reside in the static inter-particle interaction and we only have A⊥ as the canonical field variable. Besides the Coulomb interaction, the coupling between the field and the particles occurs via the total current density
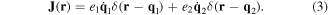
The dynamical variables in this canonical procedure are q1, q2 and  , and the corresponding canonical momenta are p1, p2 and
, and the corresponding canonical momenta are p1, p2 and  . These canonical momenta emerge from the Lagrangian as follows
. These canonical momenta emerge from the Lagrangian as follows
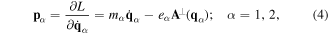
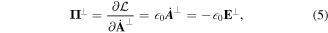
and we obtain the total Hamiltonian in the form
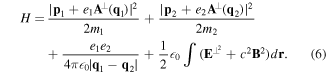
The transition to the corresponding quantum theory follows once we identify the canonical momentum and coordinate variables as operators obeying commutation rules
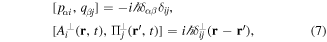
where  is the transverse delta function [10]. The above framework constitutes the non-relativistic QED theory for the two-particle atom interacting with light. However, so far the theory deals with two individual charged particles interacting with each other and with electromagnetic fields. We need to devise means of identifying features of the dynamics which recognise its division into types belonging to internal and gross motions. The most useful form occurs when we seek to express the Hamiltonian in equation (6) in a multipolar form. The complete theory can be generalised to a many-body system involving atoms and molecules with well defined centres. Such a theory is now known as the Power–Zienau–Woolley (PZW) theory, with numerous groups contributing to its development and analysis (see [11–29]). The key point is the observation that it is possible to take account of all multipoles, both electric and magnetic in closed forms and formally include inter- as well as intra-centre interactions [12]. As we emphasise above, the version of the theory in which we deal with a one-centre atom is both instructive and relatively simple. Our ultimate aim in the context of this model is to arrive at a Hamiltonian which is valid to all multipolar orders, but ultimately we shall need to highlight applications involving the leading electric dipole and quadrupole interactions, as these are the multipolar orders currently accessible to experimental work, including recent experiments on OAM exchange between atoms and twisted light.
is the transverse delta function [10]. The above framework constitutes the non-relativistic QED theory for the two-particle atom interacting with light. However, so far the theory deals with two individual charged particles interacting with each other and with electromagnetic fields. We need to devise means of identifying features of the dynamics which recognise its division into types belonging to internal and gross motions. The most useful form occurs when we seek to express the Hamiltonian in equation (6) in a multipolar form. The complete theory can be generalised to a many-body system involving atoms and molecules with well defined centres. Such a theory is now known as the Power–Zienau–Woolley (PZW) theory, with numerous groups contributing to its development and analysis (see [11–29]). The key point is the observation that it is possible to take account of all multipoles, both electric and magnetic in closed forms and formally include inter- as well as intra-centre interactions [12]. As we emphasise above, the version of the theory in which we deal with a one-centre atom is both instructive and relatively simple. Our ultimate aim in the context of this model is to arrive at a Hamiltonian which is valid to all multipolar orders, but ultimately we shall need to highlight applications involving the leading electric dipole and quadrupole interactions, as these are the multipolar orders currently accessible to experimental work, including recent experiments on OAM exchange between atoms and twisted light.
We begin by introducing the total electric polarisation vector field  for the two-particle system in the form
for the two-particle system in the form

in which λ is an integration parameter and R is the centre of mass position vector
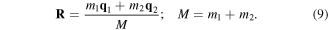
The above expression of the electric polarisation field of the two-particle system is a closed expression representing contributions from all electric multipoles excluding any net monopole (which can be included separately, e.g. in the case of an atomic ion). The multipoles manifest themselves on expanding the delta function appearing in  in powers of (qα − R), α = 1, 2. These two vectors are related to the internal coordinate of the two-particle system denoted by q
in powers of (qα − R), α = 1, 2. These two vectors are related to the internal coordinate of the two-particle system denoted by q

and it is easy to show that q1 − R = m2q/M and  . Making use of these relations, the polarisation vector field can be written entirely in terms of the internal coordinates q and the field position variable r. By expanding the delta functions in (8) in powers of q followed by integration over λ yields the ith Cartesian component of the expanded polarisation field vector
. Making use of these relations, the polarisation vector field can be written entirely in terms of the internal coordinates q and the field position variable r. By expanding the delta functions in (8) in powers of q followed by integration over λ yields the ith Cartesian component of the expanded polarisation field vector  . Up to the quadrupole moment, we have (using the Einstein convention that a repeated index is summed over a set of mutually orthogonal coordinates)
. Up to the quadrupole moment, we have (using the Einstein convention that a repeated index is summed over a set of mutually orthogonal coordinates)

where  is the electric dipole moment and
is the electric dipole moment and  is a (ij)th component of the electric quadrupole moment tensor. For electric dipole-active transitions, only the first term is applicable, while the second (quadrupole) term dominates in case of dipole forbidden transitions.
is a (ij)th component of the electric quadrupole moment tensor. For electric dipole-active transitions, only the first term is applicable, while the second (quadrupole) term dominates in case of dipole forbidden transitions.
In practice, one seldom goes beyond this truncated form of the electric polarisation as given in equation (11) and, unless otherwise stated, it is this form that we shall need when it comes to applications involving the coupling of the twisted light to atomic systems. Ultimately, it will prove convenient to use the notation  to refer to the truncated polarisation vector field, which we will subsequently define as follows
to refer to the truncated polarisation vector field, which we will subsequently define as follows

where D is a quadrupole-corrected dipole moment operator with components given by
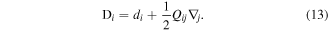
2.1. Canonical transformation
The coupling of the light to all the atomic multipoles is achievable via a PZW canonical transformation or, equivalently, a gauge transformation involving a characteristic generating function S in the form [13, 16]
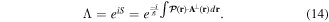
This unitary transformation gives rise to a new Hamiltonian Hnew which has the same form as the old Hamiltonian H, and to mark the distinction we now represent all transformed canonical variables with a prime. We have
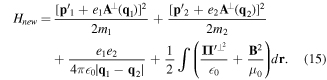
After transformation, the new momenta  and
and  are given by
are given by
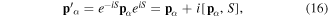
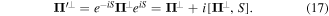
The evaluations of equations (16) and (17) both involve a commutator series, but it is easy to verify that both series terminate at the first commutator in each case due to the form of S in equation (14). We find
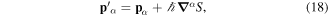
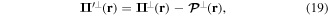
where  in equation (18) denotes differentiation with respect to the canonical coordinate qα. The vector field
in equation (18) denotes differentiation with respect to the canonical coordinate qα. The vector field  appearing in equation (19) stands for the transverse vector field part of the electric polarisation vector field given in equation (8), having made use of the commutation relations in equation (7).
appearing in equation (19) stands for the transverse vector field part of the electric polarisation vector field given in equation (8), having made use of the commutation relations in equation (7).
The formal multipolar Hamiltonian follows from equation (15) by direct use of equations (18) and (19). The next steps involve the division of the motion into the internal motion (which is characterised by the appearance of the relative coordinate q), and the gross motion involving the centre of mass coordinate R.
2.2. Decoupling of motions
Although we can continue the treatment without further recall of a multipolar expansion, it is instructive to focus again on the approximation in which the electric polarisation vector field takes its truncated form in equation (11) with leading contributions including only the electric dipole and the electric quadrupole terms We obtain for  after some algebra
after some algebra

Hence we can write for the transformed momenta, equations (18) and (19)
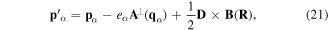
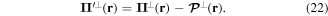
Note that the last term in equation (21) does not depend on α. Finally, substituting from equations (21) and (22) in equation (15), we obtain the transformed Hamiltonian in the following form
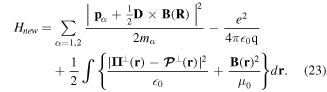
To arrive at a theory with explicit division of the motion into internal and gross motions, we have to define the centre of mass momentum P conjugate to the centre of mass position vector R, as defined in equation (9)

and the internal momentum p conjugate to the internal variable q by
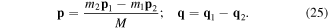
We can then express p1 and p2 in terms of P and p as follows

Equation (26) enables the explicit change from the particle canonical variables  and pα to internal variables (q, p) and gross motion variables (R, P). That the new pairs are independent canonical variables can easily be checked. We have
and pα to internal variables (q, p) and gross motion variables (R, P). That the new pairs are independent canonical variables can easily be checked. We have ![$[{{\rm{P}}}_{i},{{\rm{R}}}_{j}]=-i{\hslash }{\delta }_{{ij}};\,[{{\rm{p}}}_{i},{{\rm{q}}}_{j}]=-i{\hslash }{\delta }_{{ij}}$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn50.gif) and
and ![$[{{\rm{P}}}_{i},{{\rm{q}}}_{j}]=0\,=[{{\rm{p}}}_{i},{{\rm{R}}}_{j}]$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn51.gif) which follow by direct use of the commutator
which follow by direct use of the commutator ![$[{{\rm{p}}}_{\alpha i},{{\rm{q}}}_{\beta j}]=-i{\hslash }{\delta }_{\alpha \beta }{\delta }_{{ij}}.$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn52.gif) The above commutator relationships ensure that the new variables conform with the requirements for independent sets representing two independent motions in the absence of coupling. Substituting from equation (26) in equation (23), we get
The above commutator relationships ensure that the new variables conform with the requirements for independent sets representing two independent motions in the absence of coupling. Substituting from equation (26) in equation (23), we get
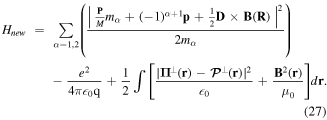
The Hamiltonian (27) simplifies considerably on expanding the square and we find
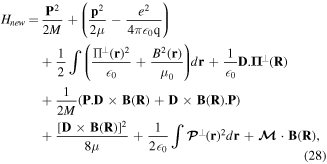
where μ is the reduced mass  and coupling terms are given in the truncated approximation. The ultimate term involves the magnetic moment
and coupling terms are given in the truncated approximation. The ultimate term involves the magnetic moment  coupling to the magnetic field also in the truncated approximation. This term arises from the product between p and D × B. In the dipole approximation where
coupling to the magnetic field also in the truncated approximation. This term arises from the product between p and D × B. In the dipole approximation where  , the leading contribution to the magnetic dipole moment is
, the leading contribution to the magnetic dipole moment is
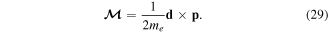
Equation (28) is the non-relativistic Hamiltonian for the electrically neutral two-particle atom in interaction with light. It is seen that the internal electronic-type motion is essentially separated from the gross motion, but these two subsystems of the atom are coupled by mutual interactions between charges and with the light fields. Amongst the various terms there are three that essentially represent unperturbed components of the system; these are the (zero-order) Hamiltonians representing the gross (centre of mass) motion, the internal (electronic-type) motion and the light fields—which appear as the first three terms of equation (28). Other terms represent couplings between the three subsystems; the fourth term represents the coupling of the atomic dipole as well as the quadrupole moments to the transverse part of the displacement field  (evaluated at the centre of mass coordinate R); the fifth constitutes the leading interaction involving the centre of mass with the truncated multipole moment and the magnetic field; the sixth is the diamagnetic field-type energy and the seventh term is an integral of the square of the polarisation field. The latter is a self energy contributing to the Lamb shift and may be absorbed in any renormalised energies pertaining to the internal motion. Finally, the last term is the leading interaction between the magnetic dipole of the atom and the magnetic field of the light, evaluated at the centre of mass R.
(evaluated at the centre of mass coordinate R); the fifth constitutes the leading interaction involving the centre of mass with the truncated multipole moment and the magnetic field; the sixth is the diamagnetic field-type energy and the seventh term is an integral of the square of the polarisation field. The latter is a self energy contributing to the Lamb shift and may be absorbed in any renormalised energies pertaining to the internal motion. Finally, the last term is the leading interaction between the magnetic dipole of the atom and the magnetic field of the light, evaluated at the centre of mass R.
2.3. Mechanical momentum and pressure force
A prominent feature of the Hamiltonian in equation (28), when taken in the truncated multipole approximation is the appearance of the term D × B. In the electric dipole approximation, this can be written as eAR where AR = q × B. Clearly AR plays the role of an electrodynamic vector potential. The significance of this can readily be seen by considering the particle canonical momenta. From equation (21), we can write
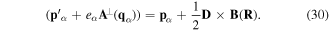
The left hand side is equal to  , so we can write
, so we can write
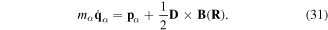
Summation over α = 1, 2 in all terms we get

Using equation (9), the left hand side of equation (32) is exactly  while the first term on the right hand side is just P. We therefore have
while the first term on the right hand side is just P. We therefore have
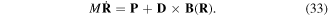
The relationship in (33) is between the canonical momentum P and the mechanical momentum  of the centre of mass in the truncated multipole approximation. The result also follows as a Heisenberg operator equation based on the Hamiltonian in equation (28). We have,
of the centre of mass in the truncated multipole approximation. The result also follows as a Heisenberg operator equation based on the Hamiltonian in equation (28). We have,

The radiation pressure force acting on the centre of mass in the dipole approximation follows from equation (33) by total time differentiation
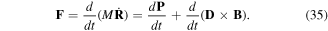
The force also follows from equation (34) as a Heisenberg operator equation in the form
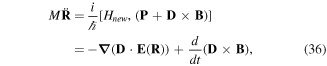
where  refers to differentiation with respect to the components of R. We have explicitly evaluated the first commutator
refers to differentiation with respect to the components of R. We have explicitly evaluated the first commutator ![$\tfrac{i}{{\hslash }}[{H}_{{new}},{\bf{P}}]={\boldsymbol{\nabla }}({\bf{D}}\cdot {\bf{E}})$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn61.gif) but left the second commutator as a time derivative. The last term is referred to as the Röntgen force, generalised here to include the quadrupole contribution. The so-called Röntgen effect arises when an electrically neutral system possessing a dipole moment is in motion in a magnetic field [19]. Here, we have shown that the corresponding interaction arises from a treatment incorporating the motion of the atomic centre of mass as a dynamical variable. Other effects that have been predicted to arise from the motion of neutral quantum systems include the rotational motion of a BEC with a form of distribution effectively associated with either a magnetic monopole distribution or an electric charge distribution [20]. We have therefore established that both dynamical attributes, namely the momentum and the corresponding pressure force, receive contributions directly attributable to the Röntgen interaction. The complete Hamiltonian in the truncated pole approximation is essential for studying processes involving the coupling of the atomic system to electromagnetic fields.
but left the second commutator as a time derivative. The last term is referred to as the Röntgen force, generalised here to include the quadrupole contribution. The so-called Röntgen effect arises when an electrically neutral system possessing a dipole moment is in motion in a magnetic field [19]. Here, we have shown that the corresponding interaction arises from a treatment incorporating the motion of the atomic centre of mass as a dynamical variable. Other effects that have been predicted to arise from the motion of neutral quantum systems include the rotational motion of a BEC with a form of distribution effectively associated with either a magnetic monopole distribution or an electric charge distribution [20]. We have therefore established that both dynamical attributes, namely the momentum and the corresponding pressure force, receive contributions directly attributable to the Röntgen interaction. The complete Hamiltonian in the truncated pole approximation is essential for studying processes involving the coupling of the atomic system to electromagnetic fields.
The multipolar theory of atom-field interactions, beginning with the seminal work by Power and Zienau [21] was subsequently developed and applied by several contributors. The reader is referred to the following sources for further information [22–29].
2.4. Quantum amplitudes and motion
Before proceeding further, it is helpful to recognise two quite distinct forms of mechanical response that arise in describing the evolution of a given atom + radiation state. As fully discussed elsewhere [30, 31], gradient forces are generally produced in response to interactions in which the initial and final states are identical, resulting in mechanical motion through response to a potential energy surface sculpted by the structure of a light-beam. Here, forces arise essentially as a secondary result from a position-dependent shift in the electronic energy, ΔE, which in the quantum framework is identifiable with the real part of a corresponding quantum amplitude. With no exchange of energy taking place between the radiation and the atom, the response has to be mediated by an isotropic property—one that has the full three-dimensional symmetry of the atom. Most commonly this is polarizability, denoted here by  , and when this engages with a radiation field with a locally variable strength there will be a resulting optical force given by;
, and when this engages with a radiation field with a locally variable strength there will be a resulting optical force given by;
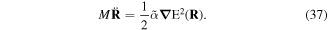
This expression of this form is commonly used to determine an optical trapping force.
In contrast are non-conservative interactions, in which radiation directly produces mechanical effect through quantum transitions that impart linear or angular momentum. Since the atomic and the radiation states both change, these interactions engage transition moments that are intrinsically non-isotropic. A further significant difference is that since the initial and final states differ, any observable will have a direct relation to the process rate—the latter normally associated with the modulus square of a quantum amplitude. In either case, in connection with imparted linear momentum the changes in matter state are generally associated with translational motion amenable to representation by classical physics; with angular momentum, however, internal changes in electronic state are necessarily quantum events and must be dealt with accordingly.
2.5. Optical momentum density and OAM density
A helical structure can be associated with two important and largely distinct aspects of light; most familiarly the sweep of the field vectors in circular polarization, and for twisted light the phase structure. Circular polarizations represent radiation states that are eigenfunctions of the operator for optical spin angular momentum (SAM), whose density operator is given by;

As such, each circularly polarized photon conveys a well-defined quantum spin, precisely σℏ, where σ = ±1 according to left/right helicity [32]. Photons of twisted or vortex forms of structured light in principle represent quantum eigenstates of an OAM density operator, expressible as follows;
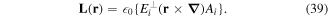
Both of the above results, equations (38) and (39), represent gauge-dependent quantities, cast in terms of the vector potential A(r). However, the separation of angular momentum into spin and orbital parts is a simplification that applies only in the paraxial approximation. More generally the separation is not absolute; there are transverse components and spin–orbit coupling in any significantly structured beam [33, 34] and there is indeed recent experimental proof of their interconversion in a cylindrically symmetric optical fibre [35]. For an objective perspective, it is therefore expedient to introduce more definitive, generalized measures of chirality for the radiation field. One suitable measure is the optical chirality density, defined as;
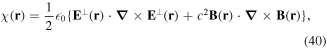
whose expectation value relative to the energy density in cognate units is bounded within the interval [−1, 1], the two limits signifying right- and left-handed circular polarizations [36]. We can also define a corresponding chirality flux;
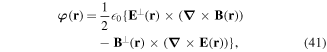
to satisfy the continuity equation
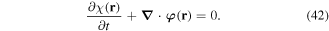
The volume integrals of both χ(r) and  are also directly related to the scalar field helicity [37]
are also directly related to the scalar field helicity [37]
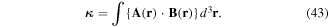
For plane waves, χ(r) and  effectively quantify a net SAM in terms of a difference in the number of left- and right-handed photons, for example [38]
effectively quantify a net SAM in terms of a difference in the number of left- and right-handed photons, for example [38]
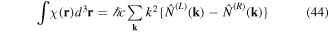
in which the right-hand side contains a difference between the corresponding photon number operators. When vortex modes are entertained, the key optomechanical parameter is represented by the OAM operator. In the paraxial approximation, for a mode with topological charge l this operator is expressible as;
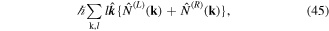
so that the spin and orbital parts of the total angular momentum effectively depend on the difference and sum, respectively, of the number operators for modes of opposite polarization helicity. From a different perspective this result is also consistent with the fact that fields whose mode expansions convey a phase factor  , are eigenfunctions of the angular momentum operator L [7]. The wide variety of other beams conveying OAM includes several other kinds of modified-Gaussian vortex beams [39], described as having a perfect optical vortex structure [40] and propagation-invariant Bessel beams [41]. For mode structures cast in a form that necessarily involves summation over an additional parameter (as is the case with perfect vortex beams, for example) the associated quanta are correspondingly associated with state superposition [40].
, are eigenfunctions of the angular momentum operator L [7]. The wide variety of other beams conveying OAM includes several other kinds of modified-Gaussian vortex beams [39], described as having a perfect optical vortex structure [40] and propagation-invariant Bessel beams [41]. For mode structures cast in a form that necessarily involves summation over an additional parameter (as is the case with perfect vortex beams, for example) the associated quanta are correspondingly associated with state superposition [40].
3. Laser cooling and trapping
3.1. Overview
The term 'laser cooling' refers to various methods in which an interaction of laser light is made to systematically cool atomic, molecular and condensed matter systems to lower temperatures. For general reviews (see [42–46]). The primary processes involve the exchange of laser photons leading to momentum and hence velocity changes. Doppler cooling is the simplest of a number of techniques leading to the systematic reduction of the temperature of atomic or molecular ensembles while Raman anti-Stokes techniques are used for cooling condensed matter systems. Besides Doppler cooling, the list of laser cooling schemes includes, among others: Sisyphus cooling [47]; Raman sideband cooling [48]; velocity-selective coherent population trapping; [49, 50] and electromagnetically induced transparency cooling [51]. In addition to laser cooling, the laser light can be made to trap atoms in the minima of optical potential wells set up by the laser light.
The atoms to be cooled are normally in the form of a dilute atomic gas and the Doppler mechanism is employed for cooling down to a microkelvin limit; for 85Rb the limit is commonly around 150 μK. The physical principles underlying Doppler cooling can be summarised succinctly as follows. When the frequency of the laser light is below a strong atomic transition frequency (a scenario referred to as red-detuning), then for an atom travelling in the direction of the laser source the light is blue-shifted in accordance with the Doppler effect. The atom absorbs a photon and so is slowed down on recoil. Consider now the effects of two counter-propagating laser beams of the same wavelength on a representative atom in a dilute atomic gas. Each atom absorbs more photons belonging to the laser beam opposite to its direction of motion in each event, thereby losing a linear momentum equal to the photon momentum. This atom is now in the excited state and so discharges its excitation by spontaneous emission in a random direction. The total effect of this basic cycle of photon absorption followed by emission is a reduction of the momentum of the atom, and so the atom loses speed. Repeated cycles then lead to a reduction of the centre of mass kinetic energy, which signifies cooling of the atom since (when compared with the case of molecules) they have no other centre of mass degrees of freedom.
Currently the most prominent use of laser cooling is in preparing samples of atomic ensembles with temperatures just above absolute zero, widely used for experiments that lead to a variety of effects, most notably Bose–Einstein condensation (BEC). Laser cooling has primarily been applied to atoms, but recently there has been progress leading to the cooling of more complex systems such as molecules [52, 53] and macro-scale objects [54, 55]. Depending on the size of the molecule, the problem of dissipating the energy from internal vibrational and rotational levels can present a considerable additional challenge [56].
When laser light is employed in the context of the laser cooling techniques mentioned above, it is commonly regarded as ordinary laser light in the sense that it is not endowed with OAM unless this feature is specifically introduced. The aim in the following is to highlight what has been achieved to date as regards the modifications to processes involving cooling and trapping of atoms when the laser light is twisted.
3.2. The Sisyphus effect
Soon after Doppler cooling appeared to be well-explained theoretically the experimental evidence showed that the existent theory was inadequate [57], as the measured kinetic temperatures achieved were significantly lower than those predicted by the Doppler mechanism. The failure of the Doppler mechanism to account solely for the lower temperatures achieved meant that a new theory was needed. This paved the way for the development of so-called sub-Doppler cooling mechanisms, most notably the mechanism based on the Sisyphus effect [58, 59]. As we discuss later, the Sisyphus effect is modified when the laser light is endowed with OAM, so it is helpful to first review the salient features of this effect.
There are two main differences between the Sisyphus cooling mechanism and Doppler cooling. In Sisyphus cooling, the main process involves the interaction of atoms with a light field characterised by spatial polarisation gradients. The specific polarisation gradients which have been utilised in the Sisyphus effect can be created by the superposition of two (for one-dimensional cooling) counter-propagating plane wave laser beams, with either mutually orthogonal linear polarisations [58], or with opposite circular polarisations [59]. The former is known in the literature as the lin ⊥ lin case, while the latter is represented as the σ+–σ−.
Consider now the first case where the two fields have mutually orthogonal polarisations. The electric field vectors of two identical, but counter-propagating laser beams, of frequency ω and axial wavevector  travelling in opposite directions along the z-axis, are given by
travelling in opposite directions along the z-axis, are given by  where
where  are the corresponding polarisation vectors and E0 is the amplitude or its quantum operator counterpart. We assume that the two beams have mutually orthogonal polarisations,
are the corresponding polarisation vectors and E0 is the amplitude or its quantum operator counterpart. We assume that the two beams have mutually orthogonal polarisations,  and
and  . The total the total electric field is the vector sum:
. The total the total electric field is the vector sum:
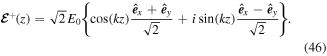
As depicted in figure 1, the interference of two counter-propagating laser beams with mutually orthogonal linear polarisations results in a total polarisation of left- and right-handed circularity alternately σ+ and σ− at planes separated by an axial distance of λ/4. Between planes the polarisation is linear with polarisation vector pointing at angles ±45°. This spatial variation of the wave polarisation along the common axis of the interfering beams constitutes a polarisation gradient, which—as will be explained—can lead to a spatially-dependent population differential.
Figure 1. Variations of the populations (spots) and energy level shifts of the ground state sub-levels along the z-axis. Reproduced with permission from [58].
Download figure:
Standard image High-resolution imageTo explain how Sisyphus cooling works, we consider an atom that possesses a Jg = 1/2 ground state which has only two Zeeman sub-levels g±1/2. Most laser cooling experiments use optical transitions  , the energy gap between the two states defined as ℏω0. We, therefore, consider a
, the energy gap between the two states defined as ℏω0. We, therefore, consider a  transition. As in Doppler cooling, we assume red-detuning Δ0 < 0 where Δ0 = (ω − ω0) [43]. The polarisation gradients created by the interfering counter-propagating beams affect the light shifts and the populations of the atomic levels which now become spatially dependent. This can be explained as follows. When the atom interacts with a non-resonant light field, then in the weak-field limit the ground state levels acquire light shifts U±. Similarly the populations of the Zeeman sub-levels (for an atom at rest) are now given by
transition. As in Doppler cooling, we assume red-detuning Δ0 < 0 where Δ0 = (ω − ω0) [43]. The polarisation gradients created by the interfering counter-propagating beams affect the light shifts and the populations of the atomic levels which now become spatially dependent. This can be explained as follows. When the atom interacts with a non-resonant light field, then in the weak-field limit the ground state levels acquire light shifts U±. Similarly the populations of the Zeeman sub-levels (for an atom at rest) are now given by  and
and  , so that these light shifts are spatially dependent and different for the Zeeman sub-levels g±1/2 as illustrated in figure 1. The optical potentials associated with the two Zeeman sub-level shifts are given by
, so that these light shifts are spatially dependent and different for the Zeeman sub-levels g±1/2 as illustrated in figure 1. The optical potentials associated with the two Zeeman sub-level shifts are given by
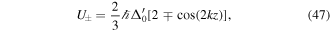
where Ω0 is the Rabi frequency. Also, Δ0 and  and the saturation parameter s0 are given by
and the saturation parameter s0 are given by
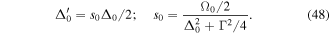
Note that U± are the optical potentials of the ground state sub-levels  . It is easy to see that the minima of U+ correspond to the maxima of U− and vice versa and the maxima and minima correspond to positions where the polarisation is
. It is easy to see that the minima of U+ correspond to the maxima of U− and vice versa and the maxima and minima correspond to positions where the polarisation is  (purely circular).
(purely circular).
Early theoretical works which sought to explain the Doppler cooling argued that the damping of the atomic gross motion arises from the fact that the atomic internal state does not follow adiabatically the variations of the laser field resulting from atomic motion [60]. Such an effect may be described by a non-adiabaticity parameter  = vτP/λ = v/(λΓ), defined as the ratio between the distance vτP covered by the atom with a velocity v during its internal relaxation time τP (τP = Γ−1), and the laser wavelength. For multi-level atoms, we can similarly define a non-adiabaticity parameter
= vτP/λ = v/(λΓ), defined as the ratio between the distance vτP covered by the atom with a velocity v during its internal relaxation time τP (τP = Γ−1), and the laser wavelength. For multi-level atoms, we can similarly define a non-adiabaticity parameter  . At low intensities, since
. At low intensities, since  it follows that
it follows that  . Thus non-adiabatic effects can appear at much lower velocities (
. Thus non-adiabatic effects can appear at much lower velocities ( ) than those required by Doppler cooling, and thus can ensure the presence of damping forces even at very low velocities.
) than those required by Doppler cooling, and thus can ensure the presence of damping forces even at very low velocities.
Dalibard and Cohen-Tannoudji [58] explained how the damping of the atomic motion is generated. The key point is that, as a condition, the atom must have internal states with energy sub-levels with a strong position-dependence, and which therefore experience large changes as the atom moves. The creation of polarisation gradients can ensure this condition. Let us assume that the atom moves along the z-axis, and it has a speed such that during the optical pumping time  it travels a distance of the order of the laser wavelength λ. If the atom starts from the bottom of a valley in a given Zeeman sub-level, then it has sufficient time to reach the top of the hill. At this position, it has a large probability to be optically pumped to the other sub-level and be shifted to the bottom of a valley, and so on: see figure 2. The atom is running uphill more frequently than downhill. This is called a low intensity Sisyphus effect, which arises from the correlations between the spatial modulations of light shifts and optical pumping rates. It is important to emphasise the term 'low intensity' as the Sisyphus effect we are discussing is valid in the low intensity regime. This is in contrast to another Sisyphus effect which is valid at high intensities, which we shall not discuss any further here [61].
it travels a distance of the order of the laser wavelength λ. If the atom starts from the bottom of a valley in a given Zeeman sub-level, then it has sufficient time to reach the top of the hill. At this position, it has a large probability to be optically pumped to the other sub-level and be shifted to the bottom of a valley, and so on: see figure 2. The atom is running uphill more frequently than downhill. This is called a low intensity Sisyphus effect, which arises from the correlations between the spatial modulations of light shifts and optical pumping rates. It is important to emphasise the term 'low intensity' as the Sisyphus effect we are discussing is valid in the low intensity regime. This is in contrast to another Sisyphus effect which is valid at high intensities, which we shall not discuss any further here [61].
Figure 2. When the optical pumping time is sufficiently long, an atom, initially in the g+1/2 Zeeman sub-level, has sufficient time to remain in the position-dependent sub-level which changes in energy (vertical scale) from its value at the bottom of the valley to its value at the top of the hill as the atom moves (from left to right in the figure). At this position, the atom has a large probability of being optically pumped into the higher state from which it then gets de-excited to the other sub-level g−1/2 at the bottom of the corresponding valley. This basic set of steps is repeated in each cycle. Reproduced with permission from [58].
Download figure:
Standard image High-resolution imageIn the process of Sisyphus cooling, an atomic sample eventually reaches an equilibrium temperature. In each optical pumping cycle, we have the emission of a fluorescence photon. Each such photon has an energy higher than the energy of the absorbed photon, by an amount in the order of the light shift  . The excess energy is transferred from the atom to the light field leading to a decrease of the atomic energy by the same amount. Repeated pumping cycles, thus, lead to a stepwise decrease of the atomic energy until its total energy is so low that the atom becomes trapped in the optical potential wells associated with the spatially modulated light shifts. The equilibrium temperature of sub-Doppler cooling is therefore expected to be given by:
. The excess energy is transferred from the atom to the light field leading to a decrease of the atomic energy by the same amount. Repeated pumping cycles, thus, lead to a stepwise decrease of the atomic energy until its total energy is so low that the atom becomes trapped in the optical potential wells associated with the spatially modulated light shifts. The equilibrium temperature of sub-Doppler cooling is therefore expected to be given by:
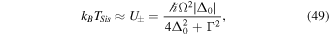
which for large detuning Δ0 ≫ Γ takes the form,
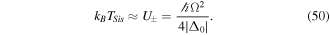
The detailed quantitative treatment of these predictions has been given in [58]. At low intensity, the magnitude of the light shift  of the ground state is much smaller than the natural width ℏΓ of the excited state. This explains why it is possible to attain temperatures about two orders of magnitude lower than the Doppler limit, which itself scales as ℏΓ. The Sisyphus cooling leads to a damping force which for large detuning is in the form,
of the ground state is much smaller than the natural width ℏΓ of the excited state. This explains why it is possible to attain temperatures about two orders of magnitude lower than the Doppler limit, which itself scales as ℏΓ. The Sisyphus cooling leads to a damping force which for large detuning is in the form,
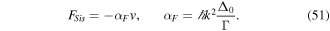
The friction coefficient αF which applies in the case of low intensity Sisyphus cooling, as given in equation (51), is much larger than the friction coefficient of Doppler cooling: the latter is of the order of  , where the saturation parameter s0 must be smaller than one. In typical experiments, both cooling mechanisms come into play. Although the friction force of the low intensity Sisyphus cooling acts within a much smaller velocity interval than the Doppler cooling, both mechanisms are useful. The Doppler cooling that acts over a relatively large velocity interval drags the atoms towards the velocity region where the Sisyphus cooling operates. Thus, use of the Doppler mechanism as a first step serves to increase dramatically the number of atoms affected by the sub-Doppler mechanism.
, where the saturation parameter s0 must be smaller than one. In typical experiments, both cooling mechanisms come into play. Although the friction force of the low intensity Sisyphus cooling acts within a much smaller velocity interval than the Doppler cooling, both mechanisms are useful. The Doppler cooling that acts over a relatively large velocity interval drags the atoms towards the velocity region where the Sisyphus cooling operates. Thus, use of the Doppler mechanism as a first step serves to increase dramatically the number of atoms affected by the sub-Doppler mechanism.
We have seen that the equilibrium temperature is proportional to the square of the Rabi frequency, which means that it is directly proportional to the laser intensity. This may incorrectly imply that lowering the intensity can lower the temperature indefinitely. But we must take into account the fact that the scheme is based on spontaneously emitted photons in each pumping cycle. Each photon imparts a recoil momentum ℏk to the atom which, according to its direction relative to the atomic motion, may either decrease or increase the atomic kinetic energy. The atomic motion continues to be cooled only so far as the decrease of the total atomic energy due to the Sisyphus effect, remains larger than the increase of the kinetic energy, of the order of Erec, due to recoil associated with the spontaneously emitted photon.
The qualitative description of low intensity Sisyphus cooling, as given above, is based on a classical description of the position of the atomic centre of mass. This means that the moving atom is treated as a classical point particle. This is a reasonable assumption only if the atomic wave packet, which describes quantum mechanically the centre of mass, is well localised in the laser wave. This assumption breaks down when the minimum temperature is achieved and this leads to the conclusion that we must then treat both internal and external variables quantum mechanically. In this case, we can take advantage of the fact that in the Sisyphus effect the motion of the atom occurs in spatially periodic potential wells. This is reminiscent of the electron motion in solid state lattices. Thus, the description of atomic motion could also be given in terms of Bloch states and energy bands [62–64]. In this regime, low intensity Sisyphus cooling is a result of optical pumping processes that accumulates the atoms into the lowest energy bands.
The above arguments may suggest that the photon recoil energy Erec should be the ultimate cooling limit. However, to cool the atomic motion to kinetic energies below the photon recoil energy, atoms with velocity v smaller than the recoil velocity vrec must be prevented from absorbing light [49, 50]. This condition can be satisfied by the creation of atomic dark states for which the fluorescence rate depends on the atomic velocity at the excitation, by a Raman process. When the velocity is zero, or close to zero, the atom does not absorb photons; it thus does not fluoresce, and so it does not experience recoil. We can also use selective Raman processes in which the excitation of the atoms is velocity-selective [65]. However, these mechanisms have basic physical differences from Doppler and Sisyphus cooling. First, the cooling with velocity-dependent dark states is not based on a force. It is rather the result of an inhomogeneous random walk in momentum space which vanishes as the atomic velocity tends to zero. Secondly, in Doppler and Sisyphus cooling the system reaches a steady state as a result of the competition between the cooling introduced by the friction, and the heating due to fluctuations associated with the random spontaneous emission processes. Such a competition does not exist in sub-recoil cooling.
As a corollary, it is interesting to note why the mechanism in question is called the Sisyphus effect. The name comes from Sisyphus, a hero of ancient Greek mythology who was punished by Zeus by being forced to transport a heavy rock to the top of a hill. Just before reaching the top, the rock slipped away and rolled downhill to the bottom. The Sisyphus effect is an allusion to his condemnation to repeat this eternally just as the atom loses kinetic energy through transitions involving the potential hills of its space modulated energy levels.
4. Twisted light
Light possessing optical SAM is well known, where optical spin is identified with the intrinsic property of wave polarisation. The much more recent discovery of twisted light began with the work in 1992 by Allen et al [7] who suggested that it should be possible to generate light beams possessing quantised OAM in the laboratory. The experimental confirmation followed soon after, with experiments carried out in a number of laboratories. Research on twisted light continues apace more than three decades later and it has led to fundamental advances in both concepts and applications (see [1, 66–69]). The most prominent mechanical applications of twisted light include the optical spanner as the rotational version of the optical tweezer which has also featured in a variety of other applications (see [70–75]). Other developments involving the application of twisted light include micro-manipulation [76]; quantum communications and cryptography [77–79] and phase contrast imaging (see [80–82]). Twisted light has been presented in some recent reviews which the reader is referred to, beginning with the 1999 review by Allen et al [1] followed by a number of edited books, reviews and theme issues (see [66–69, 83]). This topical review is concerned primarily with the interaction of twisted light with atoms and we feel it is helpful to begin by considering applications involving LG light as the prototypical form of twisted light. We shall also deal with complex twisted light, which we define as polarised twisted light arising in single or multiple beams and in various geometrical arrangements, including co-propagating or counter-propagating twisted beams with specified wave polarisations in one, two or three dimensional configurations. These sources of complexity gives rise to novel interactions with atoms in processes involving both the internal and gross atomic degrees of freedom.
4.1. LG light
It is a general feature of twisted light, exemplified by the LG beams, that different modes have helical wavefronts consisting of intertwined helices, as shown schematically in figure 3. Modes of the LG type, denoted LGklp, have a wavevector component k along the propagation direction and are characterised by the two integer indices: an azimuthal integer index l, representing the number of intertwined helices and a radial integer index p which arbitrates the number of radial nodes. These directly equate to the degree and order of the associated (generalised) Laguerre polynomial that modifies the Gaussian radial profile. The integer l can be positive or negative, representing two senses of helical wavefront rotation. When both l and p are zero, the mode (k, 0, 0) becomes simply a Gaussian distribution with no angular momentum.
Figure 3. Left: continuous phase ramps in transverse planes perpendicular to the beam axis for l = 1 (left, top) and l = 3 (left, bottom). Here, colours through the spectrum denote the optical phase, repeating on a 2π interval with an arbitrary zero. Right: the l = 3 three-part wavefront, a helical surface of constant phase.
Download figure:
Standard image High-resolution imageIn the paraxial approximation, the electric field associated with a LG mode, of wavelength λ = 2π/k and frequency ω propagating in the z-direction, and polarised in the x-direction is given by
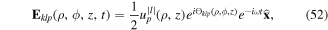
where  is the amplitude or mode distribution function
is the amplitude or mode distribution function
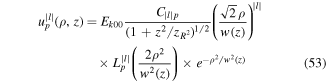
and Θklp is the phase function
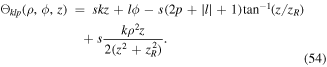
Here  is the associated Laguerre polynomial, w(z) is the beam waist at position z defined by
is the associated Laguerre polynomial, w(z) is the beam waist at position z defined by  , and zR is the Rayleigh range, which is related to w0, the waist at focus, by
, and zR is the Rayleigh range, which is related to w0, the waist at focus, by  where λ the wavelength of the light. In equation (54), the third term is the Gouy phase for the LG mode and the fourth term is referred to as the curvature phase term. The factor s = ±1 takes into account propagation in the opposite directions along the ±z-axes, while the factor
where λ the wavelength of the light. In equation (54), the third term is the Gouy phase for the LG mode and the fourth term is referred to as the curvature phase term. The factor s = ±1 takes into account propagation in the opposite directions along the ±z-axes, while the factor  is given by
is given by  .
.
An important feature of all twisted light fields is the existence of the phase factor eilϕ. However, the full phase Θklp(ρ, ϕ, z) is essential for describing the various effects including rotational effects when the light interacts with atoms and molecules. Figure 3 shows by way of an example the characteristic features of optical vortex beams concerning phase variations and helical wavefronts.
A LG beam characterised by the electric field Eklp(ρ, ϕ, z) has a linear momentum ℏk and carries an angular momentum equal to lℏ per photon. The quantum number l is called the winding number (or the topological charge) and we re-emphasise that l can take both negative and positive integer values, corresponding to right-hand and left-hand twisting of the wavefront. LG modes for which  but p = 0 are called donut modes, since the light intensity is ring-shaped as shown figure 4 for the cases l = 1 and l = 3. Figure 4 also shows the case of a double ring mode arising when l = 1, p = 1.
but p = 0 are called donut modes, since the light intensity is ring-shaped as shown figure 4 for the cases l = 1 and l = 3. Figure 4 also shows the case of a double ring mode arising when l = 1, p = 1.
Figure 4. The intensity distributions of modes, respectively, for LG1,0 (donut mode), LG3,0 (donut mode) and LG1,1 (two-ring). These radial intensity distributions are at the waist plane z = 0. The insets exhibit graphically the corresponding radial intensity distributions with radial distance in units of wavelength.
Download figure:
Standard image High-resolution imageFigure 5. In-plane field intensity distributions as for for the corresponding positive value of l of Bessel beams: l = 1 (left) and l = 2 (right). Here the colours denote an arbitrary intensity scale from a dark blue denoting zero through to bright yellow for the highest intensity regions. The corresponding Bessel modes with  have the same intensity distribution. However, the phase has the opposite sign. Reprinted figure with permission from [84], Copyright (2017) by the American Physical Society.
have the same intensity distribution. However, the phase has the opposite sign. Reprinted figure with permission from [84], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageIt is often sufficient to focus on the form of twisted light without explicit details of the LG form. An electromagnetic light mode of frequency ω and OAM lℏ possesses an electric field vector distribution which can be written in cylindrical polar coordinates  as follows
as follows
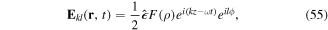
where  is a wave polarisation vector and F(ρ) is a scalar distribution function which depends only on the radial coordinate ρ. Note that, unless a paraxial approximation is deployed, the polarisation vector need not necessarily reside in the plane represented by
is a wave polarisation vector and F(ρ) is a scalar distribution function which depends only on the radial coordinate ρ. Note that, unless a paraxial approximation is deployed, the polarisation vector need not necessarily reside in the plane represented by  . The field in equation (55) emerges from the familiar LG light distribution in the limit of large Rayleigh range
. The field in equation (55) emerges from the familiar LG light distribution in the limit of large Rayleigh range  , a situation which is often encountered and is realisable in practice. This simplified form of field is advantageous for a number of reasons. It has the desired feature in being endowed with OAM, by virtue of the azimuthal phase factor, and is free from the curvature problems which often distract from the fundamental issues involving OAM of light in a real LG beam, i.e. with a finite Rayleigh range.
, a situation which is often encountered and is realisable in practice. This simplified form of field is advantageous for a number of reasons. It has the desired feature in being endowed with OAM, by virtue of the azimuthal phase factor, and is free from the curvature problems which often distract from the fundamental issues involving OAM of light in a real LG beam, i.e. with a finite Rayleigh range.
4.2. Other types of twisted light—Bessel beams
Besides the LG beam, a second, somewhat simpler, type of vortex beam is the Bessel beam [84]. This is characterised by a transverse electric field which is also a solution to the electromagnetic vector Helmholtz equation, with the modes characterised by only one integer number l, that can take either positive or negative values. We have in cylindrical polar coordinates r = (ρ, ϕ, z)
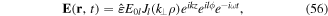
where E0l is the amplitude and the unit vector  designates a wave polarisation. The radial function Jl(k⊥ρ) is the Bessel function of order l where, as in LG beams, l is the winding number and the vortex beam carries lℏ OAM per photon. The wavevectors k⊥ and k stand for in-plane and axial wavevector variables. Figure 5 displays the field intensity distributions of two different Bessel beams characterised by different values of the winding number.
designates a wave polarisation. The radial function Jl(k⊥ρ) is the Bessel function of order l where, as in LG beams, l is the winding number and the vortex beam carries lℏ OAM per photon. The wavevectors k⊥ and k stand for in-plane and axial wavevector variables. Figure 5 displays the field intensity distributions of two different Bessel beams characterised by different values of the winding number.
5. Complexity due to wave polarisation
5.1. Multiple polarised beams
The superposition of multiple beams endowed with OAM can give rise to various field distributions and associated properties which become more complex when wave polarisation is included. The simplest cases are those in which two beams are involved and arranged to be co-axial identical or otherwise and may have different magnitudes and signs of winding numbers. They can be co-propagating or counter-propagating and may have the same polarisation. The influence of such states of twisted light on the near resonant optical forces and torques leading to the trapping and dynamics of the atoms immersed in them is discussed in section 7. It has been shown [85] how further complexity arises when the twisted light beams have circular wave polarisations (optical spins), giving rise to spatio-temporal polarisation gradients. We discuss below the simplest cases involving only two beams, as done in [85].
5.2. Co-propagating LG beams
Consider the case of two co-propagating LG beams, labelled 1 and 2 of the same frequency ω and axial wave vector k, with coinciding centres. The beams have the same magnitude of winding number l, but differ only in the sign of l. The total electric field vector distribution is then given by
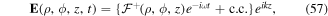
where c.c. denotes complex conjugation and  arises from the sum of the two electric fields. We have
arises from the sum of the two electric fields. We have
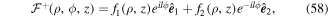
where f1,2 describe any LG light beam expressible through equations (52)–(54) with appropriate choice of quantum numbers and parameters. However, for the applications we consider here, the beams differ in the sign of l such that l1 = l and l2 = −l. The vectors  and
and  specify the wave polarisations of the beams, which in general involve any combination of linear polarisations, but more specifically we consider circular polarisation.
specify the wave polarisations of the beams, which in general involve any combination of linear polarisations, but more specifically we consider circular polarisation.
5.2.1. Co-propagating with σ+ − σ−
When the two co-propagating beams have opposite l, as well as opposite circular polarisations, we write
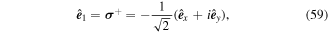
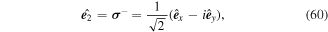
where  and
and  are the usual linear wave polarisation vectors along the x and y axes. Substituting for
are the usual linear wave polarisation vectors along the x and y axes. Substituting for  in equation (58), we have
in equation (58), we have
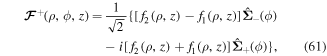
where  are polarisation vectors that depend on only the azimuthal angular position.
are polarisation vectors that depend on only the azimuthal angular position.
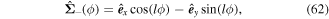
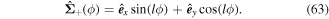
Thus, the polarisation of the interference fields is, in general, locally elliptical with an ellipticity given by
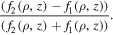
To illustrate the polarisation distribution in the resultant field of the above scenario involving co-propagating LG beams, we make use of the fact that the two beams are identical, except for the sign of l. This means that f1 = f2 = f. We then have from equation (61)
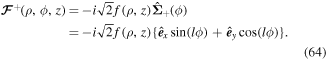
The polarisation is linear throughout, but its direction is independent of the axial position and depends only on the in-plane positions  . Figure 6 displays the polarisation distributions for two cases, l = ±1 and l = ±2. The dashed red circles coincide with the radial positions of maximum intensity.
. Figure 6 displays the polarisation distributions for two cases, l = ±1 and l = ±2. The dashed red circles coincide with the radial positions of maximum intensity.
Figure 6. Polarization distributions in the (x, y) plane for σ+–σ− co-propagating LG beams for two cases, l = ±1 (a) and l = ±2 (b). The dashed red circles show the radial position of maximum intensity. The distances are measured in units of the beam waist w0. The arrows represent polarisation directions.
Download figure:
Standard image High-resolution image5.2.2. Co-propagating with lin ⊥ lin polarisations
When the co-propagating beams have opposite winding numbers, but with wave polarizations that are linear and orthogonal, we have
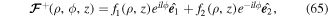
where now  and
and  . Substituting in equation (65), we get:
. Substituting in equation (65), we get:
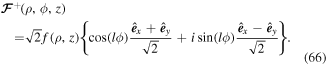
Clearly the polarization direction distribution does not depend on the axial position, but its form varies with angular position and is in general elliptical, displaying both linear and circular forms, as the azimuthal angle varies. This is illustrated in table 1. For a donut mode where p = 0 and a general value of l > 0, the region of maximum intensity occurs at a radial position,  , the polarisation changes from linear to circular along the arc of length
, the polarisation changes from linear to circular along the arc of length  . Thus, the spatial extent of the polarisation depends on the beam waist and the magnitude of the OAM.
. Thus, the spatial extent of the polarisation depends on the beam waist and the magnitude of the OAM.
Table 1.
Variation with azimuthal angle ϕ of the type of polarization for two co-propagating donut modes at fixed radial position  . It is seen that as ϕ changes from 0 to π/l, the type of polarization switches between linear and circular.
. It is seen that as ϕ changes from 0 to π/l, the type of polarization switches between linear and circular.
| ϕ | Polarization |
|---|---|
| 0 | Linear |
| π/4l | Circular σ− |
| π/2l | Linear |
| 3π/4l | Circular σ+ |
| π/l | Linear |
5.3. Counter-propagating LG beams
Now consider counter-propagating beams with opposite signs of winding numbers. The electric field distribution associated with an LG beam travelling along the negative z-axis can be found from the standard form by a simple transformation. This involves rotating the LG beam as a rigid body about the Cartesian y-axis by an angle π, which amounts to the substitution  and
and  . In terms of cylindrical polar coordinates, we have
. In terms of cylindrical polar coordinates, we have  and
and  . It is easy to see that this transformation affects only the phase factors but leaves the function f(ρ, z) unchanged. The polarisation of the light field in this case depends also on the axial position z.
. It is easy to see that this transformation affects only the phase factors but leaves the function f(ρ, z) unchanged. The polarisation of the light field in this case depends also on the axial position z.
5.3.1. Counter-propagating with 
Here, two counter-propagating beams have opposite circular polarisations, but the same winding number. The total electric field vector is now given by the analogue of equation (57)
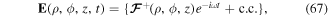
where now we have
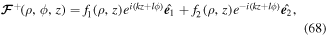
where  and
and  are given by equations (59) and (60), respectively. On substituting for these vectors in equation (68), we find
are given by equations (59) and (60), respectively. On substituting for these vectors in equation (68), we find
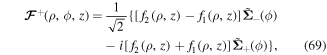
where  are polarisation vectors that now depend on both the azimuthal angular position ϕ and the axial position z.
are polarisation vectors that now depend on both the azimuthal angular position ϕ and the axial position z.
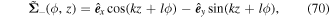
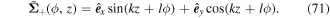
Once again we shall consider the case where the beams are similar, in which case, we have
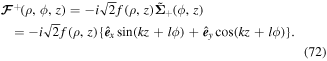
In this case, the polarisation distribution is z-dependent as well as angular dependent. The polarisation is linear and is constant in direction along spirals which result from the equation  . For example, the polarisation vector is
. For example, the polarisation vector is  along the spiral kz + lϕ = 0 and
along the spiral kz + lϕ = 0 and  along the spiral kz + lϕ = π/2, as shown in figure 7.
along the spiral kz + lϕ = π/2, as shown in figure 7.
Figure 7. Helices of constant linear polarisation. The red solid line corresponds to points where kz + lϕ = 0, where the polarisation is  , while the blue dashed line to points where kz + lϕ = π/2, where the polarisation is
, while the blue dashed line to points where kz + lϕ = π/2, where the polarisation is  . The helices correspond to points of maximum intensity.
. The helices correspond to points of maximum intensity.
Download figure:
Standard image High-resolution imageFigure 8 displays the polarisation distributions on the planes z = 0; λ/4; λ/2; 3λ/4 and λ in the case where l = 1. It is easy to see that the polarisation gradient distribution on the plane z = 0 for the counter-propagating fields is identical to that for the co-propagating LG beams for any z value.
Figure 8. Polarisation distributions on different z planes, but for σ+−σ− counter-propagating Laguerre–Gaussian (LG) beams with the same magnitude and sign of l. The distances are measured in units of the beam waist w0. Arrows represent polarisation direction. The red circles correspond to points of maximum intensity. The figures are labelled (a)–(d) corresponding to the axial positions z = 0, λ/4, λ/2, and 3λ/4, respectively.
Download figure:
Standard image High-resolution image5.3.2. Counter-propagation with lin  lin polarisations
lin polarisations
The second case is the one where the two beams have mutually orthogonal polarisations. The total electric field vector is now given by the analogue of equation (57)
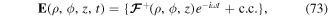
where now we have
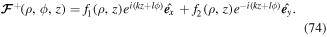
On substituting for these vectors in equation (74), we find

Now the polarisation is also in general elliptical, displaying both linear and circular forms, as the function kz + lϕ varies. This is illustrated in table 2.
Table 2.
Variation with axial and azimuthal position (z, ϕ) of the type of polarisation for two counter-propagating donut modes at fixed radial position  . As (kz + lϕ) changes from 0 to π, the type of polarisation switches between linear and circular.
. As (kz + lϕ) changes from 0 to π, the type of polarisation switches between linear and circular.
| kz + lϕ | Polarisation |
|---|---|
| 0 | Linear |
| π/4 | Circular
|
| π/2 | Linear |
| 3π/4 | Circular
|
| π | Linear |
As shown in table 2, the polarisation acquires certain forms along the spiral lines defined by kz + lϕ = constant. Figure 9 displays two sets of helices in separate plots, one set representing two helices of constant linear polarisation and the other set represents two of opposite circular polarisations. The helices correspond to points of maximum intensity.
Figure 9. (a) Helices of constant linear polarisation. The red solid line corresponds to points where kz + lϕ = 0 while the blue dashed line to points where kz + lϕ = π/2. (b) Helices of constant circular polarisation polarisation. The black solid line corresponds to points where kz + lϕ = π/4 while the red dashed line to points where kz + lϕ = 3π/4. The helices correspond to points of maximum intensity.
Download figure:
Standard image High-resolution image5.4. Rotating mode patterns
Finally, consider the case where the intensity pattern of the light fields rotates in time. This is achieved when the interfering beams have a slight difference in their frequencies. The selection of different values of beam winding numbers and polarizations gives rise to temporal polarization gradients. Here, we present two such schemes.
5.4.1. Circular polarisation 
Consider first two co-propagating LG beams, of opposite l but slightly different frequencies. Assume that beam 1 has frequency ω1 and a positive circular polarisation  and beam 2 has frequency ω2 and a negative circular polarisation
and beam 2 has frequency ω2 and a negative circular polarisation  . The electric field vector for the two co-propagating circularly polarised LG beams with different frequencies is given by the analogues of equations (57) and (58). We have
. The electric field vector for the two co-propagating circularly polarised LG beams with different frequencies is given by the analogues of equations (57) and (58). We have
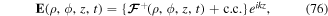
where
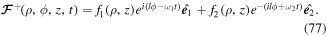
On following analogous steps to those in section 5.2.2, we have the analogue of equation (64)
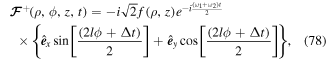
where Δ is the frequency difference Δ = ω2 − ω1. We now see the polarisation varying in both space and time. At a given axial plane, the polarisation pattern rotates at a rate which depends on the frequency difference Δ and the magnitude of the winding number l. Figure 10 displays a graphical illustration of the rotation of the polarisation vector in two different cases. The first is the case in which the beam 1 of frequency ω1 has l = 1 while beam 2 of frequency ω2 has l = −1, shown for different times t = 0 (left) and t = π/Δ (right). The second is the case in which beam 1 of frequency ω1 has l = −1 and beam 2 of frequency ω2 has l = 1 again shown for two different times t = 0 (left) and t = π/Δ (right). It is interesting to see that in the second case the polarisation changes from fully azimuthal to radial. Finally, we note that in the limit where the beams have the same frequency, i.e. when Δ ≡ ω2 − ω1 = 0, equation (78) reduces to equation (64), as it should.
Figure 10. The rotation of the polarisation vector, at z = 0, for the light field that is made up from the interference of two LG beams with opposite helicity, opposite circular polarisations and slightly different frequencies: (a) the case where the first beam of frequency ω1 has l = 1 and the second beam of frequency ω2 has l = −1 at two different times t = 0 (left) and t = π/Δ (right), (b) the case where the first beam of frequency ω1 has l = −1 and the second beam of frequency ω2 has l = 1 at two different times t = 0 (left) and t = π/Δ (right). The red circles correspond to points of maximum intensity.
Download figure:
Standard image High-resolution image5.4.2. The lin  lin case
lin case
Finally, we deal with the case where the two co-propagating LG beams, of opposite l but slightly different frequency have mutually orthogonal linear polarisations. Assume that beam 1 has frequency  and polarisation
and polarisation  and beam 2 has frequency ω2 and a polarisation
and beam 2 has frequency ω2 and a polarisation  . In this case, we have
. In this case, we have
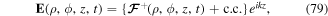
where
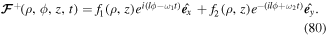
Since f1(ρ, z) = f2(ρ, z) = f(ρ, z), we find

Figure 11 displays the evolution of the polarisation vector, at z = 0, for the light field arising from the interference of two LG beams with mutually orthogonal polarisations, opposite winding numbers and slightly different frequencies. Two different cases involving two different time instants are shown. Note in particular how the polarisation changes from linear to circular and vice versa at different azimuthal angles.
Figure 11. The evolution of the polarisation vector, at z = 0, for a light field made up from the interference of two LG beams with mutually orthogonal polarizations, opposite helicity and slightly different frequencies: (a) the first beam of polarisation along the x-axis has frequency ω1 and l = 1 and the second beam of polarisation along the y-axis has frequency ω2 and l = −1 at two different times t = 0 (left) and t = π/Δ (right), (b) the first beam of polarisation along the x-axis has frequency ω1 and l = −1 and the second beam of polarisation along the y-axis has a frequency ω2 and l = 1 at times t = 0 (left) and t = π/Δ (right). The dashed circles correspond to points of maximum intensity.
Download figure:
Standard image High-resolution imageIn summary of this section, we have investigated the spatial and temporal polarisation of light fields created by the interference of either co-propagating, or counter-propagating LG beams when they have opposite winding number l and for the cases where they possess opposite circular polarisations,  and σ− and mutually orthogonal linear polarisations.
and σ− and mutually orthogonal linear polarisations.
When the LG beams are co-propagating and possess opposite circular polarisations we have found that for a fixed value of  , the polarisation is independent of the axial position z, so that within a normal beam cross-section, it is everywhere locally linear but the direction changes, depending on its polar position
, the polarisation is independent of the axial position z, so that within a normal beam cross-section, it is everywhere locally linear but the direction changes, depending on its polar position  . When the beams have mutually orthogonal polarisations the total polarisation again does not depend on the radial position, but now it can change from linear to σ− and then back to linear and σ+ as the azimuthal angle changes from 0 to 2π.
. When the beams have mutually orthogonal polarisations the total polarisation again does not depend on the radial position, but now it can change from linear to σ− and then back to linear and σ+ as the azimuthal angle changes from 0 to 2π.
When the LG beams are counter-propagating, the polarisation distribution depends on the axial position as well as the in-plane polar position (ρ, ϕ). Note the interesting symmetry in which the the distribution for z = λ/4 is the mirror reflection of that at z = 3λ/4. Similarly, the polarisation distribution for z = λ/2 is the mirror reflection of that for z = 0. The distributions at z = 0 and z = λ are identical.
A case in which the polarisation shows both temporal and spatial variations is that of interfering beams with slightly different frequency and opposite signs of winding number. We may again consider two different cases when the beams have opposite circular polarisations and mutually orthogonal polarisations. This difference in frequency has been shown to give rise to a rotation of the polarisation pattern. The temporal evolution is very similar to the sequence exhibited by the spatial dependence and so similar patterns will emerge, except that position-dependence is now replaced by a time-dependence.
6. Atom control and interactions
6.1. Overview
As an area of atomic and optical physics, atom optics is primarily concerned with the manipulation and control of the gross motion of atoms. The word 'optics' in 'atom optics' is in many respects an indication of realising and manipulating atoms in beam format, just as laser photons are realised in optical beam format. The analogy has led to the realisation in the laboratory of analogues of ordinary optical elements, such as atom mirrors, atom beam splitters and atom-guides [86], with the main control of atomic motion provided by optical forces.
The principal basis for the frequency-tuned optical confinement of atoms has its origin in forces associated with beam profile effects: equation (37) highlights the key role of the atomic polarizability. Resonance damping of the polarizability is attributable to several physically distinct processes responsible for the finite lifetimes of electronic excited states, which are not, in general, solely attributable to radiative decay. The accommodation of damping serves to represent dissipative and essentially stochastic effects, but it is impossible to fully accommodate the condition of time-reversal invariance—the Hamiltonian for an implicitly non-conservative system is necessarily non-Hermitian [87]. Accounting for the spherical symmetry of an ion or atom, the result is cast as:
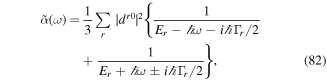
where the sum is taken over all excited electronic levels r of energy Er. The effect of the damping is primarily significant in the first, potentially resonant term in equation (82), and on approach to resonance with a specific excited state,  , it delivers signals with an approximately Lorentzian lineshape and full-width at half-maximum (FWHM) linewidth ΓX. Specifically, we have:
, it delivers signals with an approximately Lorentzian lineshape and full-width at half-maximum (FWHM) linewidth ΓX. Specifically, we have:
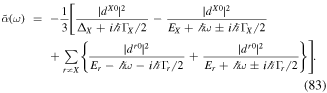
Different arguments support varying conclusions on the sign and magnitude of the damping in the anti-resonant terms the second and fourth in equation (83) (see [87–90]). However, the results for alternative signs cannot be experimentally discriminated, so these corrections can effectively be neglected.
In principle, red- and blue-detuning from a resonance leads to opposite signs for the dominant leading term—the principle is exploited in securing forces of opposite direction towards or away from regions of highest intensity, according to equation (37) and the first term in equation (83). However, it should be kept in mind that the presence of the third terms in equation (83) means that any switch in sign generally occurs at a frequency displaced from exact resonance.
Besides atom trapping as a useful property, optical forces can also lead to the transport of atoms in atom guides [91]. When Bessel beams are used as atom guides the atoms can be confined within the central region of the beam. The non-diffracting nature of the central region facilitates atom transport over long distances without transverse spreading as expected from the use of a non-vortex structured light beam. The width of the atom guide in the central region of the beam can be arranged to be as small as the order of the optical wavelength.
A LG-based dipole trap for atoms was first realized in 1997, in which approximately 108 Rb atoms were confined in the LG core region using a blue-detuned LG beam and two in-plane light beams [92]. A three-dimensional dark core region surrounded by bright light, referred to as a bottle beam, has subsequently been constructed using suitable combinations of LG beams [93]. Such beams have been used to trap samples of cold atoms [94, 95], including single Rb atoms [96] which could be trapped for several seconds. Theoretical work on atom trapping in bottle beams has been reported by Aldossary [97]. Furthermore, LG beams and their superpositions have been exploited in the construction of optical ring traps and ring lattices. A dark ring trap, generated at the focus of an LG10 mode, was shown to hold Rb atoms with a decay time of 1.5 s [98].
With suitable superpositions of co- or counter-propagating LG beams, ring lattices can be realized for trapping in bright or dark intensity regions. These may be used to simulate condensed matter effects: adjusting the phase twist can generate persistent currents [99, 100], and adjusting the boundary between the lattice sites should allow the realization of Mott insulator transitions. A large number of different trapping geometries is possible by combining LG modes of different OAM and radial mode number [101]. Single Rb atoms have been trapped at individual lattice sites of a bright rotating optical Ferris wheel [102]. The transfer of atoms between a bright and dark ring trap, simply by modifying the laser detuning, has also been observed [103]. OAM beams have also been used in the creation of dark spontaneous optical force traps [104].
6.2. OAM transfer
One of the issues that quickly arose in the context of the interaction of twisted light with atoms is whether OAM can be exchanged between the twisted light and the internal atomic degrees of freedom in a process involving transition between the energy levels in analogy with the photon SAM manifestation in a radiative transition. Electromagnetically driven transitions between atomic states occur whenever the exciting field properties match the redistribution of the atomic charge and the phase of the material wavefunction. As we have seen at the outset, atomic transitions are categorised as dipole-allowed, quadrupole-allowed and higher multipolar-allowed orders. The relatively clear-cut distinction between transitions allowed at different levels of multipolarity is one of the key simplifications, due to symmetry, that arise when dealing with atoms—in contrast to molecules where electronic transitions are frequently allowed by more than one form of multipole. In a dipole-allowed transition the atom engages with the optical field strength while in a quadrupole transition it engages only with the field gradient. The field gradients in atom-field interactions can lead to transitions for atoms localised in the dark regions of the light beam where there is weak light intensity but relatively strong field gradients.
6.3. Theory
Theoretical work has necessarily focused on the distinction between the internal motion and the gross motion of an atom (or molecule) due to interaction with fields possessing OAM, with due consideration of the selection rules involved in transitions [105, 106]. Initial forays into the theory were followed by some experimental work [107, 108] which confirmed the theoretical finding of [106] that no exchange of angular momentum arises between the light and the internal degrees of freedom in a dipole-allowed transition.
Here we outline the underlying theory of OAM transfer as given in reference [106]. We focus on the two-particle model of the neutral atom as a system consisting of a negatively charged electron of mass m1 and a positive atomic core of mass m2 as emphasised at the outset. The Hamiltonian of this system in interaction with the light field can be written as the following sum of four parts, to be discussed in turn
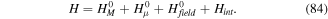
H0M is the centre of mass Hamiltonian, which is essentially the kinetic energy of the centre of mass
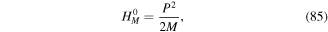
where P is the centre of mass momentum with M = m1 + m2 the total mass. The centre of mass momentum is conjugate to the centre of mass coordinate R, defined in terms of the particle position vectors qi; i = 1, 2, by
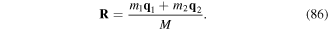
We are, however, interested in the possibility of the centre of mass rotating about a beam axis, so that the in-plane motion of the centre of mass kinetic energy is rotational. The appropriate form of the centre of mass Hamiltonian is then given by
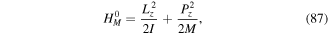
where Lz is the angular momentum operator. Here I stands for the moment of inertia of the atomic centre of mass about the z-axis and Pz is the centre of mass momentum axial vector component. The second term in equation (84), namely  , pertains to the internal 'electronic-type' motion
, pertains to the internal 'electronic-type' motion

where μ = m1m2/M is the reduced mass and p is the momentum conjugate to the internal coordinate q = q1 − q2. The second term in equation (88) is the Coulomb potential binding the two-particle system, with  . The third term in the total Hamiltonian is defined by
. The third term in the total Hamiltonian is defined by
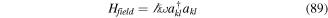
which is the field Hamiltonian in quantised form with akl the annihilation operator (its Hermitian conjugate being the corresponding creation operator) of the light mode in question of frequency ω, OAM lℏ and axial wavevector  . For present purposes, any radial index p can be suppressed; the assumption is a donut mode of the lowest order for any given value of l. Finally, the last Hamiltonian term is the interaction Hamiltonian describing the coupling between the light and the two-particle bound system, representing the molecule. In the PZW scheme this can be written as
. For present purposes, any radial index p can be suppressed; the assumption is a donut mode of the lowest order for any given value of l. Finally, the last Hamiltonian term is the interaction Hamiltonian describing the coupling between the light and the two-particle bound system, representing the molecule. In the PZW scheme this can be written as
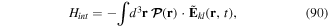
where  is the second quantised form of the electric field;
is the second quantised form of the electric field;  is the electric polarisation defined in a closed integral form as in equation (8).
is the electric polarisation defined in a closed integral form as in equation (8).
For simplicity, we have ignored all magnetic interactions. Note that, although the electric polarisation field defined in equation (8) appears to be a function of the individual particle coordinates q1 and q2, it can be written entirely in terms of the relative coordinate q using the relations
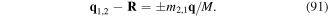
Any quantum-mechanical treatment of the interaction between the light and the atomic system must start by specifying the zero-order states of the overall motion, comprising the centre of mass motion (rotational and translational), the internal 'electronic-type' motion and the field state. The appropriate states are product states of the three-subsystem Hamiltonian  and can be written as
and can be written as
The unperturbed motion of the centre of mass in this product state is represented by an axial translational state with linear momentum Pz, together with a rotational eigenstate of the angular momentum operator Lz with corresponding eigenvalues ℏLz. The internal motion enters in terms of the hydrogenic excited discrete states  of energy Ee and a ground state
of energy Ee and a ground state  of energy Eg. The shorthand notation
of energy Eg. The shorthand notation  and
and  stand for
stand for  and
and  , respectively, where nj, lj, mj with j ≡ e, g are hydrogenic state quantum numbers. Finally, the ket
, respectively, where nj, lj, mj with j ≡ e, g are hydrogenic state quantum numbers. Finally, the ket  is the number state of the light field.
is the number state of the light field.
The evaluation of the coupling between matter and field involves working out the interaction matrix element  where
where
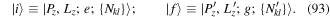
Specifically, we have
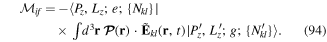
To evaluate this matrix element, we begin by expressing the interaction Hamiltonian in the following form
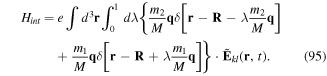
We cannot carry out the usual multipolar expansion, whereby the two delta functions are each expanded in powers of λm1,2/M, leading to a series of terms multiplied by  which ultimately gives rise to a dipole term, a quadrupole term and higher multipole terms The reason why the multipolar expansion is inappropriate at this stage is that the hydrogenic system has a centre of mass R which is significantly off-axis. To proceed, we now carry out the volume integral involving the full delta functions, but keeping the λ integral untouched for the time being. We have
which ultimately gives rise to a dipole term, a quadrupole term and higher multipole terms The reason why the multipolar expansion is inappropriate at this stage is that the hydrogenic system has a centre of mass R which is significantly off-axis. To proceed, we now carry out the volume integral involving the full delta functions, but keeping the λ integral untouched for the time being. We have
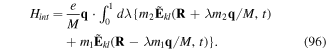
Note that the interaction is now such that the electric field of the twisted light is now evaluated at the r = R + λm2q/M in the first term and at r = R − λm1q/M in the second term.
The azimuthal dependence of the atomic internal motion is referred to the centre of mass coordinates, while the twisted beam has an axis coinciding with the z-axis of the laboratory coordinate system. The position vector variables of the centre of mass  and the atomic internal coordinate q in polar coordinates are written as follows:
and the atomic internal coordinate q in polar coordinates are written as follows:
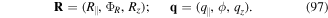
We need to incorporate the full azimuthal angular dependence which must be split into internal and centre of mass dependences. To be able to establish the azimuthal angular dependence, we consider projections of relevant vectors in a plane parallel to the (x, y) plane. The situation is shown in figure 12 for the vectors  and their sum
and their sum
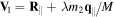
in the context of the first interaction term. Similarly, the vectors R∥ and (−λm1q∥/M) and their sum
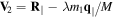
would apply in the context of the second interaction term.
Figure 12. The vector projections in the (x, y) plane and the corresponding azimuthal angles for the vectors  and their sum
and their sum  in the context of
in the context of  . Reproduced figure with permission from [106], Copyright (2002) by the American Physical Society.
. Reproduced figure with permission from [106], Copyright (2002) by the American Physical Society.
Download figure:
Standard image High-resolution imageIn pursuit of a multipolar expansion of the interaction Hamiltonian, the next step is to express the azimuthal dependence of the two vectors V1 and V2 in terms of the azimuthal angle ΦR of the centre of mass relative to the laboratory frame, and the azimuthal angle of the internal 'electronic' position vector ϕ relative to the centre of mass. This is followed by applying the approximations
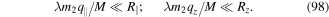
6.4. Transfer of OAM to centre of mass only—electric dipole interaction
We then find that the interaction Hamiltonian up to the quadrupole term consists of four contributions, which we can write as
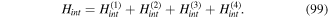
The leading term is identifiable as the electric dipole term, which emerges from the sum of the terms linear in the vector components of the internal coordinate q. We have
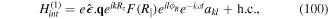
where F(R∥) is a function of the centre of mass coordinate R∥ only. We see that, besides the internal position operator  , this interaction Hamiltonian involves the centre of mass cylindrical coordinates (R∥, ΦR, Rz). Remember that the eigenstates of the internal dynamics are as for a hydrogen atom, with the position vector q expressible in spherical polar coordinates where ϕ is the azimuthal angle, as is the case in cylindrical coordinates. Substitution of this in the transition matrix element, equation (94), writing the explicit forms of the translational and rotational eigenstates of the centre of mass motion and performing the space integrals, we obtain
, this interaction Hamiltonian involves the centre of mass cylindrical coordinates (R∥, ΦR, Rz). Remember that the eigenstates of the internal dynamics are as for a hydrogen atom, with the position vector q expressible in spherical polar coordinates where ϕ is the azimuthal angle, as is the case in cylindrical coordinates. Substitution of this in the transition matrix element, equation (94), writing the explicit forms of the translational and rotational eigenstates of the centre of mass motion and performing the space integrals, we obtain
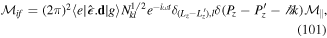
where d = eq is the electric dipole moment vector and  is the integral
is the integral
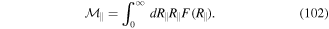
The Dirac delta function in equation (101) exhibits conservation of the centre of mass axial linear momentum with conventional linear momentum transfer between the light and the centre of mass. The Kronecker delta expresses conservation of OAM and there is clearly OAM transfer of magnitude lℏ between the light and the centre of mass rotational motion. This transfer is not to the internal motion, and it should be emphasised again that the internal motion does not participate in any exchange of momentum between the atom and the vortex light, neither linear momentum nor OAM. Only the centre of mass responds to the vortex. As we explain later, this is the process that leads to mechanical action involving the gross dynamics of the atom as a whole, through the motion of its centre of mass, and in which the atom experiences both rotational and translational forces.
6.5. Quadrupole interactions: OAM exchange
Consider next the terms  and
and  . These interaction terms are quadratic in the vector components of q and so correspond to quadrupole interactions. Explicitly, we have for the first type of quadrupole interaction
. These interaction terms are quadratic in the vector components of q and so correspond to quadrupole interactions. Explicitly, we have for the first type of quadrupole interaction
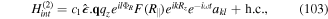
where c1 is a constant. The next type is of the form
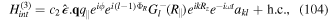
where c2 is a constant. The last is of the form
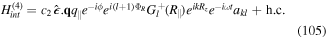
Once  , equation (103), is inserted in the matrix element in equation (94), we can readily deduce that this term cannot mediate any transfer of OAM between the light and the internal motion. However, transfer of OAM does occur between the light and the centre of mass motion, as in the electric dipole case. This is essentially the next order of the multipolar process, over and above that due to
, equation (103), is inserted in the matrix element in equation (94), we can readily deduce that this term cannot mediate any transfer of OAM between the light and the internal motion. However, transfer of OAM does occur between the light and the centre of mass motion, as in the electric dipole case. This is essentially the next order of the multipolar process, over and above that due to  . By contrast, we see in the expression for
. By contrast, we see in the expression for  in equation (104) that a factor
in equation (104) that a factor  now appears in the matrix element between the internal states
now appears in the matrix element between the internal states  and
and  , and the centre of mass azimuthal phase factor is now
, and the centre of mass azimuthal phase factor is now  . This is indicative of a transfer of OAM from the light beam to the internal motion, leaving only (l − 1)ℏ units to be transferred to the centre of mass rotation. Similarly when
. This is indicative of a transfer of OAM from the light beam to the internal motion, leaving only (l − 1)ℏ units to be transferred to the centre of mass rotation. Similarly when  , equation (105), is substituted in the matrix element, we can conclude that a transfer of OAM occurs between the internal motion and the light beam, with a balance of (l + 1)ℏ transferred to the centre of mass rotation. It is easy to check that the integrals over the azimuthal angle ϕ for the internal motion lead to the usual quadrupole selection rule
, equation (105), is substituted in the matrix element, we can conclude that a transfer of OAM occurs between the internal motion and the light beam, with a balance of (l + 1)ℏ transferred to the centre of mass rotation. It is easy to check that the integrals over the azimuthal angle ϕ for the internal motion lead to the usual quadrupole selection rule  where, as defined earlier, me and mg are the azimuthal quantum numbers of the respective internal states
where, as defined earlier, me and mg are the azimuthal quantum numbers of the respective internal states  and
and  involved in the transition.
involved in the transition.
We have thus demonstrated by explicit analysis that in the interaction of light possessing OAM with atoms (or molecules, by a directly similar mechanism) the major mechanism of exchange of OAM occurs in the electric dipole approximation and involves only the centre of mass motion and the light beam. The internal 'electronic-type' motion does not participate in any OAM exchange with the light beam to this leading order. It is only in the weaker electric quadrupole interaction that an exchange involving all three subsystems (the light, the atomic centre of mass and the internal motion) can take place. This involves one unit of OAM being exchanged between the light beam and the internal motion, with the remaining (l ± 1)ℏ units of OAM being transferred to the centre of mass motion. The quadrupole transitions thus involve participation of two units of OAM. These conclusions rule out any experiments which seek to observe OAM exchange involving light beams and the internal states of molecular systems via electric dipole transitions.
A different treatment of this problem was given by Lloyd et al [84] in the conventional QED framework using a coupling involving the vector potential A rather than the electric field as above. Lloyd et al confirmed theoretically that an optical vortex cannot transfer OAM to the internal atomic motion in a dipole active transition, although it could do so in a quadrupole transition.
6.6. Experimental work and other theoretical work on OAM exchange
Following the publication of the work in [106], experimental research began to test the validity of the main theoretical prediction, namely that OAM cannot be transferred between an optical vortex in a dipole active transition. There was need to experimentally find out whether the OAM can influence the internal electronic degrees of freedom of the atoms, a requirement at the core of the theoretical analysis, both in the electric dipole approximation and for higher order transitions. Mathevet et al [109] gave an intuitive argument for explaining the absence of magnetic orbital dichroism in an isotropic medium as a function of the sign of the OAM. They suggested that this effect cannot be observed in transitions essentially described by the electric dipole approximation, but only when considering (at least) the higher quadrupole order.
As noted earlier the compartmentalisation of optical angular momentum into spin and orbital parts cannot always be clear-cut, and when vortex radiation is associated with circular polarizations, spin–orbit coupling can arise [33]. Circular polarizations are, of course, widely associated with chiroptical phenomena, i.e. optical interactions exhibiting a quantitative difference in an observable such as rate of excitation, for molecules of opposite handedness engaging with a particular circular polarization or equally vice versa. It is therefore not surprising that the possibility of engaging twisted light with chiral matter has become a widely researched topic. Moreover, whilst the manifestations of spin–orbit interactions do not require engagement with chiral matter (see [33–35]) the latter offer additional scope for novel effects.
The first experimental report was by Araoka et al [107] who showed that LG light is not specific in interaction with chiral matter. This was followed by the work of Löffler et al [108] who concluded that they could not find any influence of the OAM on circular dichroism in cholesteric polymers. Despite the experimental evidence provided by the work of Aroaka et al [107] and Löffler et al [108], subsequent theoretical investigations continued on the issue of the transfer of OAM to the internal degrees of freedom of atoms and molecules with some regarding it as an unsettled matter (see [109–120]) and it appeared that the community was not entirely decided upon a matter which the theoretical analysis makes quite clear. As has recently been shown, it is only possible to break this embargo under conditions that thoroughly undermine the powerful spatial isotropy principles that otherwise generally apply. Specifically, they require a chiral molecule (which can support transitions simultaneously allowed by both electric dipole and quadrupole forms of coupling) held in a fixed orientation [121].
The most recent experimental work on OAM transfer in atoms is that by Giammanco et al [122] whose results we outline below. Giammanco et al's results confirmed the earliest theoretical finding and subsequent experimental evidence [106–108] regarding the lack of influence of the photon OAM on electric dipole transitions.
6.7. Giammanco et al experiment
In their experiment, Giammanco et al [122] aimed to find out whether or not the OAM of light has the same ability and manner of interacting with atoms as occurs for the SAM. They used laser light with different combinations of OAM and SAM to excite Rb atoms. The laser radiation was selected to inhibit or enhance the fluorescence according to the selection rules for the electric dipole transitions between the ground state and the first excited doublet states. Their experimental results showed that the OAM does not engage with the atomic internal (electronic) motion in dipole active transitions.
Figure 13 shows the absorption profiles in the case of left and right circularly polarized untwisted light (without OAM) and twisted light (with OAM). By sweeping the laser frequency in a range of 10 GHz across the Rb resonance profile, Giammanco et al were able observe the four minima in the transmission corresponding to the transitions from the ground state of 85Rb (F3, F2, inner minima) and 87Rb (F2, F1, outer minima). The Doppler width at their working temperature was about 529 MHz. This enabled the resolution of the hyperfine structure of the ground state (3.03 GHz and 6.83 GHz for 85Rb and 87Rb, respectively).
Figure 13. Transmitted radiation with modes OAM = 0 (black open squares) and OAM = 1 (grey full squares) for left circular polarization (top) and right circular polarization (bottom) of the laser beam transmitted radiation with modes OAM = 0 (black open squares) and OAM = 1 (grey full squares) for left circular polarization (top) and right circular polarization (bottom). The black squares are not clearly visible because they overlap with the grey squares. Reproduced with permission from [122].
Download figure:
Standard image High-resolution imageFigure 14 shows the fluorescence signals measured under the same experimental conditions as given in figure 13. As expected, the fluorescence exhibits a complementary behaviour with respect to the absorption. The profiles of the transition lines do not exhibit significant variations within the limits of the experimental error; and with both polarizations and OAM, no disappearance of the electric dipole transition effects was observed.
Figure 14. Rb fluorescence with modes OAM = 0 (black line) and OAM = 1 (grey line) for left circular polarization (top) and right circular polarization (bottom) of the laser beam. The black squares are not clearly visible because they overlap with the grey squares. Reproduced with permission from [122].
Download figure:
Standard image High-resolution imageAs pointed out, the experiment was an attempt to verify whether the total angular momentum of a light beam with an OAM component induces fluorescence excitation on alkali atoms or inhibits it, depending on the values of the OAM and of the SAM of the beam. Theoretical results [84, 106] suggested that this effect cannot be observed in transitions essentially described by the electric dipole approximation, but only when considering (at least) the higher quadrupole order. In short, these results corroborate the theoretical predictions [106].
The first experimental confirmation of quadrupole transitions involving twisted light interacting with a 40Ca+ ion was given in [123], in which Schmiegelow et al demonstrated that a transfer of OAM from the beam to the internal electronic degrees of freedom could be observed for a quadrupole transition of a single trapped ion. This paper is briefly summarised in the next section. More recent related work extended research by both theory and experiment involving 40Ca+ ion is that by Afansev et al [124] who also considered the effects of the position of the atom relative to the beam axis.
6.8. Schmiegelow et al experiment: OAM transfer in quadrupole transitions
In their experiment, Schmiegelow et al [123] excited an atomic transition with a vortex laser beam and demonstrated the transfer of optical OAM to the valence electron (i.e. to the internal degrees of freedom) of a single trapped ion. They observed strongly modified selection rules showing that an atom can absorb two quanta of angular momentum from a single photon: one from the spin and another from the spatial structure of the beam. Optical vortex beams possess both an axial field gradient and a transverse (i.e. in-plane) gradient both of which can drive quadrupole transitions. In particular, the core region of the LG1,0 beam possesses a strong field gradient, even though the intensity at the core vanishes. The interaction of such a gradient field with the quadrupole moment involves the transfer of OAM from the LG1,0 mode to the internal dynamics of the trapped ion.
The experiment by Schmiegelow et al involved a single laser-cooled 40Ca+ ion in a microstructured, segmented Paul trap. The positioning of the ion along the beam was achieved to a sub-micron accuracy by adjusting the voltages of the trapping electrodes. The key aspects of the experiment are the use of a quadrupole transition, the focusing of the probe beam close to the diffraction limit and the use of a well-localized atomic (ionic) system.
7. Radiation pressure forces and torques
As pointed out earlier, the Doppler effect has been exploited in laser cooling of atoms by a process called 'optical molasses' (see [42–46]). The principles of laser cooling have been explained in section 3.1. When two counter-propagating light beams are used, the atoms in both directions are slowed down. For atomic motion in directions transverse to the original axis one needs further pairs of orthogonal configurations, which act to slow the motions in an analogous manner, leading to the cooling of the motion in all three directions: this is essentially the optical molasses effect (see [125–128]).
The effects of structured light on atom dynamics, in both its forms, namely the gross motion and the internal motion have been thoroughly investigated (see references ([129–136]). These investigations have shown that the interaction of light carrying OAM with atoms introduces new significant features, namely that (i) there is, in addition to translational effects, a light-induced torque which causes a rotational motion of the atoms about the beam axis, and (ii) there are characteristic regions of maximum and minimum intensity in the beam cross-section. The forces and torque are, in general, time-dependent as well as position-dependent. As we discuss below, the full space- and time-dependence of the motion is, in general, characterised by a transient regime, followed by a steady state regime after a sufficiently large time has elapsed from the instant in which the beam is switched on (typically for elapsed times much larger than the characteristic time-scale of the problem).
7.1. Derivation of optical forces and torques
To derive the optical forces acting on a hydrogenic atom or molecule due to application of laser light we initially adopt a quantum mechanical approach based, once again, on the simple picture in which the atomic motion is described in terms of the gross dynamics of the centre of mass and the internal dynamics is in terms of a two-level system [131]. We shall see how the optical forces emerge naturally from the quantum-mechanical approach by appeal to the classical limit.
The total Hamiltonian of the light and atom and their interaction can be written as follows
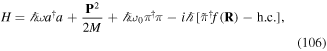
where  and f(R) are given by
and f(R) are given by
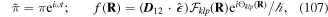
where π and π† are the ladder operators of the two-level atom; P is the momentum operator of the centre-of-mass with M the total mass and ω0 the transition frequency; a and a† are the annihilation and creation operators of the laser light of frequency ω.
Our goal is to derive expressions for the forces acting on the atomic centre of mass appropriate for the case of a coherent optical beam whose close approximation to classical wave means that the a and a† operators for the light become c-numbers involving a parameter b, such that
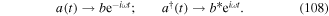
The interaction between the two-level atom and the laser light is given by the last term in equation (106). This is given above in the truncated multipole approximation as well as the rotating wave approximation and is evaluated at the centre of mass position vector  . The function f(R) in equation (107) involves
. The function f(R) in equation (107) involves  , the transition matrix element of the atom, including both dipole allowed and quadrupole allowed transitions. The atom is subject to a LG light mode characterised by the wave polarisation vector
, the transition matrix element of the atom, including both dipole allowed and quadrupole allowed transitions. The atom is subject to a LG light mode characterised by the wave polarisation vector  , the mode amplitude function,
, the mode amplitude function,  and phase Θklp(R), given by expressions of the forms in equations (52)–(54) with s = 1 (denoting forward propagation) in the latter case. Here, we have
and phase Θklp(R), given by expressions of the forms in equations (52)–(54) with s = 1 (denoting forward propagation) in the latter case. Here, we have

The mode indices l and p determine the field intensity distribution and are such that lℏ is the OAM content carried by each quantum.
The classical limit demands that the position R and the momentum operator P of the atomic centre of mass should take their average values r and P0 = MV, where V is the velocity vector of the centre of mass. This scheme treats the centre of mass motion classically while the internal atomic motion in terms of the two-level system continues to be treated quantum mechanically. This is a good approximation provided that the atomic wavepacket spread is much smaller than the laser wavelength, and that the centre of mass recoil energy in a transition is much smaller than the linewidth. The density matrix of the system can then be written as
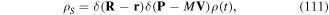
where ρ(t) is the density matrix of the internal two-level system. This follows the standard time evolution
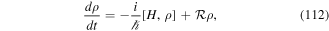
where  is an added term representing relaxation in the two-level system. The evolution of the density matrix is governed by the optical Bloch equations, which are as follows
is an added term representing relaxation in the two-level system. The evolution of the density matrix is governed by the optical Bloch equations, which are as follows

The relaxation processes in general involve two types of rates Γ1,2 and are assumed to include both elastic and inelastic collision rates Γcoll and such that
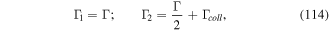
where Γ is the de-excitation rate of the upper state of the atomic transition. In the optical Bloch equations, Δ is the effective velocity-dependent detuning given by
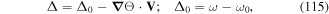
so that  is the static detuning. We have also set
is the static detuning. We have also set
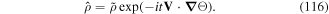
and applied the sum rule ρ11(t) + ρ22(t) = 1. The average force acting on the centre of mass is given by
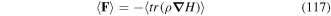
and this leads to a total force that is the sum of two different forces: a dissipative force  and a dipole force
and a dipole force  . The two radiation forces are related to the density matrix elements as follows
. The two radiation forces are related to the density matrix elements as follows
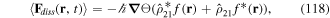
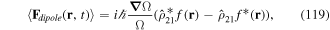
where Ω(R) is the position-dependent Rabi frequency
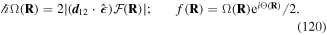
The gross motion is that of the centre of mass in response to the light fields. Once the total force  is known the atom dynamics can be determined by application of Newton's law, written in the form
is known the atom dynamics can be determined by application of Newton's law, written in the form
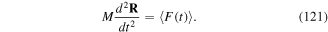
This, together with the initial conditions, namely the initial position vector components R(0) and initial velocity vector components V(0), are sufficient to determine the classical trajectory R(t) and the corresponding velocity  . The solution also provides information about the time-dependent torque acting on the atomic centre of mass.
. The solution also provides information about the time-dependent torque acting on the atomic centre of mass.
A kind of transient atom dynamics arises initially, just after the light is switched on, and depends on the characteristic time scale of the system. This type of dynamics becomes important when the excited state of the atom has a relatively long lifetime Γ−1 (Γ is the de-excitation rate of the upper state of the atomic transition) [136, 137]. An example of such a scenario was studied in detail by Carter et al [136] for the case of rare-earth ions such as Eu3+ ions whose transition  has a wavelength and transition rate λ = 614 nm and Γ = 1111 Hz, respectively [138]. Although transient dynamics is of interest, most of the attention has focused on the the steady state forces as in the case of laser cooling and trapping.
has a wavelength and transition rate λ = 614 nm and Γ = 1111 Hz, respectively [138]. Although transient dynamics is of interest, most of the attention has focused on the the steady state forces as in the case of laser cooling and trapping.
7.2. The steady state forces and torque
The steady state forces emerge on taking the limit  . This corresponds to setting time derivatives in the optical Bloch equations to zero. In the steady state, we have Γt ≪ 1, and we find that the steady state forces become position- and velocity-dependent and consist of two types. The force acting on a moving atom subject to a single LG beam propagating along the positive z-axis turns out to be in the form
. This corresponds to setting time derivatives in the optical Bloch equations to zero. In the steady state, we have Γt ≪ 1, and we find that the steady state forces become position- and velocity-dependent and consist of two types. The force acting on a moving atom subject to a single LG beam propagating along the positive z-axis turns out to be in the form
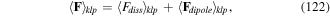
where  is the dissipative force
is the dissipative force
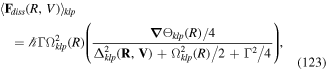
and  is the dipole force
is the dipole force
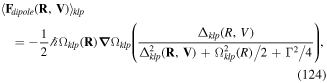
where  is the detuning which is both position- and velocity-dependent
is the detuning which is both position- and velocity-dependent
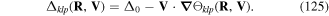
Both the dissipative and dipole forces involved in the context of non-vortex light are well known in atom cooling and trapping. The dissipative force is a net frictional force responsible for optical molasses, and the dipole force corresponds to a potential which traps the atom in regions of extremum light intensity.
A steady state light induced torque acts on the atomic centre of mass due to interaction with the twisted light as can be shown by examining the velocity-independent force terms Setting V = 0 and for motion near the beam waist, i.e. z ≪ zR we have
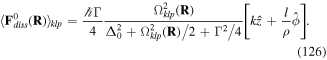
There are two vector components of this force: an axial component and an azimuthal one. Only the azimuthal component is responsible for the torque about the beam axis. Associated with the light induced force is a torque given by
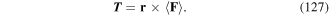
We find
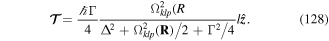
Berry and Shukla [139] referred to forces akin to the above azimuthal component as a curl force. In the saturation limit of high intensity corresponding to Ω ≫ Δ0 and Ω ≫ Γ, we obtain
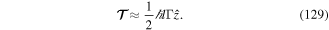
This relation of the light-induced torque acting on the atom was first derived by Babiker et al [129] and has a simple interpretation as follows. Since a torque is, by definition, angular momentum per unit time, the above saturation torque arises from an angular momentum lℏ delivered over a time period of  . The general form of the light-induced torque displays both velocity- and position-dependences, and so has well defined values along the atom trajectory.
. The general form of the light-induced torque displays both velocity- and position-dependences, and so has well defined values along the atom trajectory.
7.3. Atom trapping: dipole potential
The dipole force is the gradient of the dipole potential
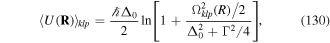
such that
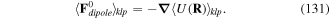
As in laser trapping with ordinary light, the dipole potential due to the LG beam traps atoms either in the high intensity regions of the LG beam for Δ0 < 0 (red-detuning), or in the case of blue detuning,  , in the low-intensity (i.e. dark) regions.
, in the low-intensity (i.e. dark) regions.
As an illustration we consider the LG donut mode propagating along the z-axis for which l = 1, p = 0. At focus, i.e. in the beam waist plane z = 0, the dipole potential has a minimum at radial position  . The locus of the minimum is therefore a circle in the (x, y) plane given by
. The locus of the minimum is therefore a circle in the (x, y) plane given by  and the atom is trapped for Δ0 < 0. Expanding the potential expression at focus, i.e.
and the atom is trapped for Δ0 < 0. Expanding the potential expression at focus, i.e.  to a harmonic approximation about ρ0, we have
to a harmonic approximation about ρ0, we have
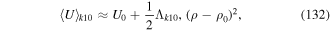
where  is the depth of the potential
is the depth of the potential
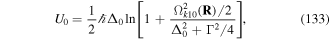
and  is the effective elastic modulus given by
is the effective elastic modulus given by
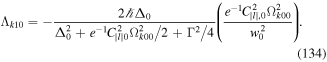
An atom of mass M, trapped in this potential would exhibit a vibrational motion about ρ = ρ0 of angular frequency approximately equal to  .
.
8. Doppler shifts and atom dynamics
8.1. Azimuthal and other Doppler shifts
The light-induced force and torque involve the effective velocity and position-dependent detuning Δklp given by
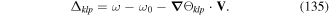
This can be written as follows
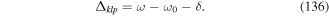
Because of its dependence on velocity the term δ is identified as a Doppler shift. On substituting for the LG phase function Θ(R), we obtain
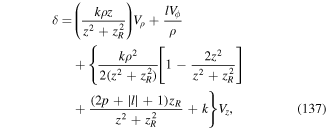
where Vρ, Vϕ and Vz are the velocity vector components in cylindrical polar coordinates. It is seen that δ consists of four terms: an axial term  , a term arising from the Gouy phase δGouy, a beam curvature term δcurve and an azimuthal term δazimuth, so that
, a term arising from the Gouy phase δGouy, a beam curvature term δcurve and an azimuthal term δazimuth, so that
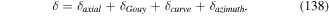
The axial term δaxial is identical to a Doppler shift due to a plane wave of wavenumber k travelling along the beam axis
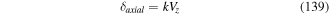
and the Gouy phase Doppler shift is
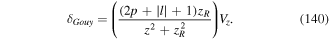
For LG beam with low integer values of l and p, the Gouy phase Doppler shift would be negligibly small since typically zR ≫ w0. As will be discussed later, this term becomes significant, for large values of l and/or p.
The curvature Doppler shift is given by
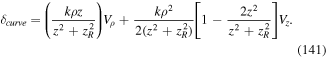
This Doppler shift is caused by the wavefront curvature spreading of the beam in the radial and axial directions and could be observable under appropriate conditions. Finally, a Doppler shift which arises directly from the vortex nature of the twisted light is the azimuthal Doppler shift, which is given by

This is directly proportional to the winding number l characterising the angular momentum property of the twisted light, but it is also inversely proportional to ρ the radial coordinate of the atom. Note that the dependence on l includes both the magnitude and the sign of the winding number.
Experimental work on the azimuthal Doppler shift was reported by Luo et al [140] and Aramaki et al [141]. Luo et al detected the Doppler effect associated with light beams carrying OAM in 'left-handed materials'. However, they reported that the azimuthal Doppler shift, proportional to the OAM of photons, was not reversed compared to conventional positive-index materials. They attributed this result to two joint contributions, one from the negative phase velocity and the other from the inverse screw of the wave-front. Aramaki et al performed a modified saturated absorption spectroscopy to separate the components. The optical vortex and a plane wave are used as a probe beam and pump beam, respectively. Although the plane-wave pump laser cancels the axial-direction Doppler shift, the azimuthal Doppler shift remained in the saturated dip. The spatial variation of the dip width provided information on the azimuthal Doppler shift.
8.2. Steady state atom trajectories
The dynamics of the atom is governed by Newton's second law, together with well defined initial conditions. The solutions leads to the trajectory R(t) as well as other dynamical properties of the system. However, the analytical form of the trajectory R(t) cannot be determined in general and there is, inevitably, a need to resort to computational analysis. One of the significant properties that can be verified directly is that the trajectories for two cases in which the atom is subject to single separate LG beams with opposite but equal signs of l, are identical except for a reversal of the direction of atom rotation. This is consistent with the dependence of the light-induced torque on the magnitude and sign of l.
8.3. Atoms in multiple twisted beams
It is well known that Doppler cooling leads to the optical molasses effect in multiple beams in one, two and three dimensions. We expect a form of optical molasses effect to occur for twisted beams, but the description of optical molasses in this context demands, as a first step, the specification of each of the multiple beam field distributions relative to the same (the laboratory) coordinate frame. This step requires the application of coordinate transformations. For relatively weak beams, the nett light-induced force due to all beams in the molasses configuration is the vector sum of individual light-induced forces and the atom trajectory in the multiple beams arises from the solution of the equation: mass times acceleration equals the vector sum of all forces entering Newton's law.
For illustration, we consider a basic twisted light beam of frequency ω, axial wavevector k and quantum numbers l and p coupled to an atom or an ion at a general position vector R = (ρ, ϕ, z). In cylindrical coordinates, the phase Θklp(R) and the Rabi frequency Ωklp(R) are taken as follows
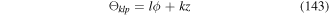
and
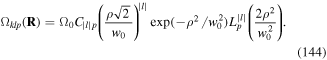
The above expressions apply for a LG beam in the large Rayleigh range limit z ≪ zR and also setting w(z) = w0, which also means disregarding beam curvature effects.
The steady state light-induced forces acting on the centre of mass are given above but with the approximate phase Θklp(R) and Rabi frequency Ωklp(R), as in equations (143) and (144). These expressions are in cylindrical polar coordinates with the direction of propagation along the positive z-axis. However, in order to derive the dynamics for multiple beams, we need to express the position dependence in Cartesian coordinates R = (x, y, z), using  and
and  . The expression for an LG beam whose axis of propagation is in an arbitrary direction is obtained by applying two successive transformations with the first transformation involving a rotation about the y-axis by an angle θ and the second is another rotation about the x-axis by an angle ψ.
. The expression for an LG beam whose axis of propagation is in an arbitrary direction is obtained by applying two successive transformations with the first transformation involving a rotation about the y-axis by an angle θ and the second is another rotation about the x-axis by an angle ψ.
An appropriate choice of θ and ψ leads to the force distribution due to a twisted light beam propagating in any desired direction. This procedure allows consideration of geometrical arrangements involving counter-propagating beams (especially those corresponding to one-, two- and three-dimensional optical molasses configurations).
As a specific application of the above scheme, we consider optical molasses of magnesium ions Mg+ in multiple beams. The requisite transition is of frequency ω0 corresponding to the wavelength λ = 280.1 nm and transition rate  s−1. The Mg+ mass is M = 4.0 × 10−26 kg. To have trapping in regions of high field intensities, we must choose red-detuned light such that Δ0 = −Γ/2 and we assume a value of the beam waist w0 = 35λ. The equation of motion for the Mg+ ion is written as
s−1. The Mg+ mass is M = 4.0 × 10−26 kg. To have trapping in regions of high field intensities, we must choose red-detuned light such that Δ0 = −Γ/2 and we assume a value of the beam waist w0 = 35λ. The equation of motion for the Mg+ ion is written as
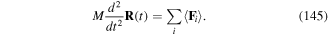
The sum is over all individual force vector contributions due to all beams present in the configuration. The simplest case is the one-dimensional molasses configuration, which involves a pair of identical counter-propagating twisted light beams arranged along the z-axis. Figure 15 (top left) shows the trajectory of the Mg+ ion with  and p1 = p2 = 0. The initial radial position is ρ = 10λ and the initial velocity is V(0) = 5 m s
and p1 = p2 = 0. The initial radial position is ρ = 10λ and the initial velocity is V(0) = 5 m s . The motion is for a time duration equal to 4 × 105 Γ−1.
. The motion is for a time duration equal to 4 × 105 Γ−1.
Figure 15. Top left: the path of a Mg+ ion in the one-dimensional twisted optical molasses created by two counter-propagating Laguerre–Gaussian beans with l1 = −l2 = 1 and p1 = p2 = 0 propagating along the z-axis. The initial velocity is  m s−1. Top right: trajectories of two Mg+ ions with different initial locations subject to a two-dimensional optical molasses formed by two pairs of counter-propagating twisted beams, with li = 1 and pi = 0 for i = 1–4. Each ion ends up motionless on the locus of lowest potential energy minima corresponding to two oblique orthogonal circles, as explained in the text. Bottom: trajectories of eight Mg+ ions in a three-dimensional twisted optical molasses formed by three pairs of counter-propagating LG beams with li = 1 and pi = 0 where i = 1–8. The initial velocity of each of the ions is
m s−1. Top right: trajectories of two Mg+ ions with different initial locations subject to a two-dimensional optical molasses formed by two pairs of counter-propagating twisted beams, with li = 1 and pi = 0 for i = 1–4. Each ion ends up motionless on the locus of lowest potential energy minima corresponding to two oblique orthogonal circles, as explained in the text. Bottom: trajectories of eight Mg+ ions in a three-dimensional twisted optical molasses formed by three pairs of counter-propagating LG beams with li = 1 and pi = 0 where i = 1–8. The initial velocity of each of the ions is  ms−1. The ions end up motionless at the corners of a cube of side w0.
ms−1. The ions end up motionless at the corners of a cube of side w0.
Download figure:
Standard image High-resolution imageOnce the Mg+ ion is trapped in the high intensity ring which is located at the fixed focus point z = 0, it rotates clockwise about the common axis. This rotation is due to the light-induced torque which, in the saturation limit, is given by  .
.
It is easy to see that the motion of the trapped ions at azimuthal speed vs gives rise to an electric current equal to  per rotating axially trapped particle. With vs of about 2 m s−1 and
per rotating axially trapped particle. With vs of about 2 m s−1 and  we have an ionic current of the order of a fA per particle. Note that the electric current scales with the number of trapped ions; if a million or so ions are involved they can produce an electric current on the nA scale.
we have an ionic current of the order of a fA per particle. Note that the electric current scales with the number of trapped ions; if a million or so ions are involved they can produce an electric current on the nA scale.
8.4. Twisted molasses in two- and three-dimensional configurations
The two-dimensional molasses configuration arises when we introduce in addition to the pair along the z-axis of waist w0 a second pair of counter-propagating beams along the x-axis of waist  , which can be equal or different from w0. The net force in this case is the vector sum of the individual forces from the four beams. The appropriate functional dependences of three of the beams are obtained from the expression of a beam along the z-direction using transformation equations for axis rotation. The trajectories in figure 15 (top right) are of two Mg+ ions initially located at different points with each having an initial velocity of
, which can be equal or different from w0. The net force in this case is the vector sum of the individual forces from the four beams. The appropriate functional dependences of three of the beams are obtained from the expression of a beam along the z-direction using transformation equations for axis rotation. The trajectories in figure 15 (top right) are of two Mg+ ions initially located at different points with each having an initial velocity of  . The ions are subject to the four beams where each beam of has a waist w0, an azimuthal index, l = 1, and radial index, p = 0.
. The ions are subject to the four beams where each beam of has a waist w0, an azimuthal index, l = 1, and radial index, p = 0.
The total torque about the common axis arising from each pair is zero. This is because the choice of l values produces identical torques of opposite senses which cancel in this case. Thus each ion ends up at a specific fixed point, depending on the initial conditions and it remains at that fixed point essentially motionless. To understand this, we should note that the deepest dipole potential well is four times the depth due to a single beam. The potential minima are situated on the locus of spatial points defined simultaneously by two equations  and
and  . For
. For  these two equations describe two orthogonal oblique circles representing the intersection curves of two cylinders of radii
these two equations describe two orthogonal oblique circles representing the intersection curves of two cylinders of radii  . Solving for x and y, we have
. Solving for x and y, we have  and
and  .
.
The locus of spatial points where the dipole potential is minimum can be described by the parametric equations
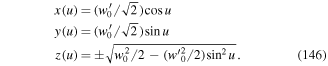
All Mg+ ions in the two-dimensional configuration of orthogonal counter-propagating pairs of twisted beams will be trapped at points lying on one of the two oblique circles, as determined by the initial conditions. An ensemble of Mg+ ions with a distribution of initial positions and velocities will populate the two circles, producing two orthogonal essentially static Mg+ ion loops. Associated with this system of charges would be a Coulomb field whose spatial distribution, for example, for ions uniformly distributed in the ring can easily be evaluated. When the values of l are such that each pair of beams generates a torque, the motion becomes more complicated, but the ions will seek to congregate in the region of potential minima, while responding to the combined effects of two orthogonal torques and orthogonal axial cooling forces.
When a third pair of counter-propagating beams is added to the two-dimensional configuration, orthogonal to the plane containing the original beams, we have a three-dimensional configuration. In this case, the deepest potential minima are located at eight discrete points defined by the coordinates:  . These coincide with the eight corners of a cube of side w0, centred at the origin of coordinates. Figure 15 (bottom) exhibits the trajectories of eight atoms which end up being trapped at the eight corners of the cube.
. These coincide with the eight corners of a cube of side w0, centred at the origin of coordinates. Figure 15 (bottom) exhibits the trajectories of eight atoms which end up being trapped at the eight corners of the cube.
8.5. The NIST-Gaithersburg experiments
A number of experiments by Anderson et al [142] and Clade' et al [144] showed that a BEC of sodium atoms can be trapped in the field of a donut beam and a Gaussian beam or a sheet beam and with the atomic ensemble exhibiting a quantised superfluid behaviour. The atoms were made to rotate in the donut ring by the light-induced torque [129] and constituted a relatively long-lived persistent current for a time more than twenty times the duration for the atoms confined in a spheroidal trap. A snap-shot image of the trapped atom is presented in figure 16. The flow was observed to persist even when there was a large (80%) thermal fraction present in the toroidal trap. These experiments open the possibility for investigations of the fundamental role of flow in superfluidity and of realizing the atomic equivalent of superconducting circuits and devices such as SQUIDs [145]. Atoms trapped in such ring-shaped traps could form the basis of quantum motors. Generally, such findings were hailed as paving the way towards the realisation of atom circuits in the field of atomtronics [145–147].
Figure 16. Time-of-flight image showing the donut shape characteristic of a atomic cloud with quantized rotation. Reproduced with permission from [143].
Download figure:
Standard image High-resolution image9. Azimuthal Sisyphus cooling
9.1. Sisyphus effect with twisted light
As described earlier the Sisyphus effect which uses ordinary plane wave laser light has been shown to provide an efficient cooling mechanism, which has succeeded in cooling atoms to temperatures well below the Doppler cooling limit [44, 58]. The point to emphasise here is that this cooling method is based on the creation of a standing wave exhibiting polarisation gradients using counter-propagating laser beams. The polarisation gradients are responsible for the generation of spatially dependent light shifts, which result in spatially modulated energy levels along the beam axis. This interaction landscape is characterised by potential hills which an atom has to climb more than it descends in the processes of stimulated and spontaneous emission cycles between the energy levels. The atom progressively loses its kinetic energy and slows down.
An analogue of the Sisyphus mechanism has been predicted by Lembessis et al [148] concerned with the case of the azimuthal atomic motion in the annular region of maximum intensity when the atom is irradiated by two LG beams with  polarizations, i.e. having orthogonal linear polarisations. The azimuthal motion arises in the context involving two co-centred, co propagating LG beams, labelled 1 and 2, of the same frequency ω and axial wave vector of magnitude k. The beams have the same magnitude of the winding number
polarizations, i.e. having orthogonal linear polarisations. The azimuthal motion arises in the context involving two co-centred, co propagating LG beams, labelled 1 and 2, of the same frequency ω and axial wave vector of magnitude k. The beams have the same magnitude of the winding number  but differ only in the sign of l.
but differ only in the sign of l.
In the focus plane z = 0, the electric field consists of two in quadrature fields with the amplitudes proportional to  and
and  . The wave polarisation form varies with angular position and is in general elliptical, displaying both linear and circular forms at certain angles, as ϕ varies. The situation is equivalent to the conventional polarisation gradient due to two counter-propagating plane wave light beams where the changes in polarisation are cyclic, with a spatial periodicity of the standing wave along the z-axis equal to the wavelength of the light λ = 2π/k. Here, the periodicity occurs in the azimuthal direction. However, the spatial extent of the polarisation gradient depends on the beam waist w0 as well as the winding number l.
. The wave polarisation form varies with angular position and is in general elliptical, displaying both linear and circular forms at certain angles, as ϕ varies. The situation is equivalent to the conventional polarisation gradient due to two counter-propagating plane wave light beams where the changes in polarisation are cyclic, with a spatial periodicity of the standing wave along the z-axis equal to the wavelength of the light λ = 2π/k. Here, the periodicity occurs in the azimuthal direction. However, the spatial extent of the polarisation gradient depends on the beam waist w0 as well as the winding number l.
We now consider the atom dynamics in such a light field and we focus on an atom with transitions between a hyperfine ground state Jg = 1/2 and an excited state Je = 3/2. The Clebsch–Gordan coefficients of the various possible transitions are indicated by the numbers in the inset of figure 17 with the squares of the numbers indicated representing the corresponding transition probabilities. We also make the assumption that the atomic motion is restricted in the annular region of radius  where the intensity of the beams is highest (when p = 0). The optical potentials associated with the two Zeeman sub-level shifts are given by
where the intensity of the beams is highest (when p = 0). The optical potentials associated with the two Zeeman sub-level shifts are given by
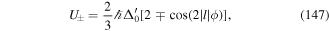
where s0 is the saturation parameter at  and
and  is given by
is given by
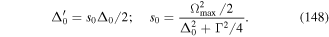
Here Ωmax is the Rabi frequency at ρ0 which, in the case where p = 0, is given by  . For large values of
. For large values of  , we may use Stirling's approximation and we have
, we may use Stirling's approximation and we have  . The potentials U± are the optical potentials for the
. The potentials U± are the optical potentials for the  sub-levels. It is easy to see that the minima of one potential correspond to the maxima of the other and vice versa, and the maxima and minima correspond to positions where the polarisation is
sub-levels. It is easy to see that the minima of one potential correspond to the maxima of the other and vice versa, and the maxima and minima correspond to positions where the polarisation is  (purely circular).
(purely circular).
Figure 17. Variations of the light-shifted energy levels with azimuthal position ϕ and the steady-state populations (full circles) for a Jg = 1/2 ground state interacting with two counter-propagating LG light beams in the lin ⊥ lin configuration and negative detuning. The ground state is light-shifted into the state g−1/2, which varies with ϕ as shown by the full curve, and g+1/2, whose variation with ϕ is shown by the dotted curve. The atom is trapped in the donut annular region and is assumed to be rotating with velocity vϕ. The most populated energy sublevel is the one with the largest negative light shift. The inset shows the processes of emission and absorption involved in the azimuthal Sisyphus effect between Je = 3/2 and Jg = 1/2 sublevels. The time lag τP associated with the optical pumping is responsible for the atom climbing on average more potential uphills than downhills as it rotates. Reproduced figure with permission from [148], Copyright (2011) by the American Physical Society.
Download figure:
Standard image High-resolution imageSuppose now that the angular position of the atom within the annular ring is  and that the light field has a circular polarisation
and that the light field has a circular polarisation  . If we assume that the atom is optically pumped to level
. If we assume that the atom is optically pumped to level  , the population of the level
, the population of the level  is then zero. Furthermore we consider that the detuning is negative so that both light shifts are negative. If the atom is shifted within the annular trap to an angular position at
is then zero. Furthermore we consider that the detuning is negative so that both light shifts are negative. If the atom is shifted within the annular trap to an angular position at  the level populations are reversed. Finally, if the atom is at angular positions where the polarization is linear, the two sublevels are equally populated. This scenario is summarized in figure 17.
the level populations are reversed. Finally, if the atom is at angular positions where the polarization is linear, the two sublevels are equally populated. This scenario is summarized in figure 17.
When the light intensity is sufficiently low so that the excited state population is negligible the cooling of the atomic azimuthal motion can be explained with reference to the inset of figure 17. This shows the energy levels for the  transition and the relevant transition probabilities. If the atom is located at
transition and the relevant transition probabilities. If the atom is located at  where the polarization is
where the polarization is  , the absorption of a σ− photon takes the atom from
, the absorption of a σ− photon takes the atom from  to
to  . This process is followed by a decay of the atom from the state
. This process is followed by a decay of the atom from the state  to the state
to the state  . If the decay is from
. If the decay is from  to
to  , the atom can absorb a σ− photon and have another chance to arrive at
, the atom can absorb a σ− photon and have another chance to arrive at  . By contrast, absorbing a σ− photon when in
. By contrast, absorbing a σ− photon when in  promotes the atom to
promotes the atom to  from which the atom can decay to
from which the atom can decay to  . It follows that in the steady state all the atomic population is optically pumped into
. It follows that in the steady state all the atomic population is optically pumped into  . If the atom is at
. If the atom is at  where the polarization is
where the polarization is  , the above scenario is reversed.
, the above scenario is reversed.
The damping of the atomic motion in the Sisyphus effect is characterised by a damping coefficient which can be calculated as follows. Let us assume that initially the atom performs circular motion at a radius  with an azimuthal speed vϕ. As explained in table 1 and with reference to figure 17, the atom in effect sees an azimuthal standing wave of an equivalent wavelength
with an azimuthal speed vϕ. As explained in table 1 and with reference to figure 17, the atom in effect sees an azimuthal standing wave of an equivalent wavelength  . We define the two-level relaxation time as τR = Γ−1 and an optical pumping time between sublevels
. We define the two-level relaxation time as τR = Γ−1 and an optical pumping time between sublevels  . In general the atomic internal state does not follow adiabatically the variations of the light field. To take into account this fact, we introduce two adiabaticity parameters: one is a two-level atom adiabaticity parameter
. In general the atomic internal state does not follow adiabatically the variations of the light field. To take into account this fact, we introduce two adiabaticity parameters: one is a two-level atom adiabaticity parameter  ϕ, defined as the ratio between the length of the arc travelled by the atom during its internal relaxation. The other is a characteristic length of the azimuthal spatial variations of the laser field (i.e. the wavelength λϕ). For
ϕ, defined as the ratio between the length of the arc travelled by the atom during its internal relaxation. The other is a characteristic length of the azimuthal spatial variations of the laser field (i.e. the wavelength λϕ). For  ϕ, we write
ϕ, we write
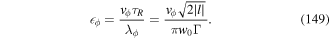
The corresponding multi-level parameter  is defined as
is defined as
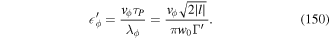
At low laser powers, we have  since
since  , i.e. τR ≪ τP. The condition for the non-adiabatic effects coming into play is then approximately given by
, i.e. τR ≪ τP. The condition for the non-adiabatic effects coming into play is then approximately given by  , which leads to
, which leads to
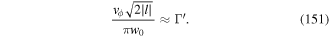
The resulting azimuthal damping force is then given by
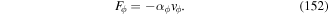
where αϕ is an azimuthal damping coefficient. This coefficient can be estimated qualitatively following Dalibard and Cohen-Tannoudji [58] and is given by
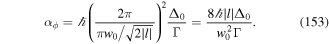
Associated with the friction force is a torque about the common beams' axis directed along  , operative at
, operative at  and given by
and given by
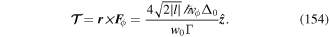
It is seen that the damping coefficient is proportional to the magnitude of the winding number l, while the torque is proportional to the square root of  through its dependence on the radius of the annular region. Hence the higher the value of
through its dependence on the radius of the annular region. Hence the higher the value of  the larger the annular radius, and consequently the larger the number of potential hills there are for the atoms to climb. Note that the damping coefficient and the torque are inversely proportional to the beam waist w0. The larger the beam waist, the further apart the potential hills are and this amounts to less effective damping and smaller torque due to the potential hill climbed by the atom.
the larger the annular radius, and consequently the larger the number of potential hills there are for the atoms to climb. Note that the damping coefficient and the torque are inversely proportional to the beam waist w0. The larger the beam waist, the further apart the potential hills are and this amounts to less effective damping and smaller torque due to the potential hill climbed by the atom.
As an illustration, we consider Cs atoms interacting with a light field of wavelength λ = 852.35 nm, which can thus excite the transition  , where the upper state
, where the upper state  has a spontaneous emission rate Γ = 3.25 × 107 s−1. We assume a detuning Δ0 = 2Γ and the Rabi frequency Ω is taken to be 0.1Γ. These atomic transitions and orders of parameter were used in the pioneering experiment that confirmed the validity of Sisyphus cooling mechanism [47]. Finally, for the LG beams we take
has a spontaneous emission rate Γ = 3.25 × 107 s−1. We assume a detuning Δ0 = 2Γ and the Rabi frequency Ω is taken to be 0.1Γ. These atomic transitions and orders of parameter were used in the pioneering experiment that confirmed the validity of Sisyphus cooling mechanism [47]. Finally, for the LG beams we take  and the beam waist w0 = 10λ. With these parameters equation (151) yields the azimuthal velocity at which Sisyphus effect commences as vϕ = 3.6 cm s−1. We have made use of the following relationship [58] giving the pumping rate
and the beam waist w0 = 10λ. With these parameters equation (151) yields the azimuthal velocity at which Sisyphus effect commences as vϕ = 3.6 cm s−1. We have made use of the following relationship [58] giving the pumping rate  in terms of Γ and the saturation parameter
in terms of Γ and the saturation parameter  . The value of the azimuthal damping coefficient corresponding to the above parameters turns out to be αϕ = 4.65 × 10−22 kg s−1. For the same parameters, the azimuthal velocity in the Doppler limit is vϕ = 8.82 cm s−1 approximately twice the azimuthal velocity at which the Sisyphus effect commences. Both are much larger than the recoil velocity of 0.35 cm s−1.
. The value of the azimuthal damping coefficient corresponding to the above parameters turns out to be αϕ = 4.65 × 10−22 kg s−1. For the same parameters, the azimuthal velocity in the Doppler limit is vϕ = 8.82 cm s−1 approximately twice the azimuthal velocity at which the Sisyphus effect commences. Both are much larger than the recoil velocity of 0.35 cm s−1.
9.2. Comparison with other azimuthal cooling mechanisms
It is instructive to compare the Sisyphus cooling mechanism with other azimuthal cooling mechanisms. The Doppler regime for a twisted single beam involves a torque acting on the two-level atom, which has a magnitude at the radial coordinate  (where the Rabi frequency maximises), is given by:
(where the Rabi frequency maximises), is given by:
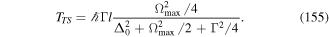
This torque is proportional to l and so can be positive or negative. It is easy to verify that it depends on the radial but not the angular position of the atom. In the saturation limit, achieved at high intensities, the torque becomes TTS ≈ lℏΓ/2, which is position-independent. In the twisted molasses (M) situation, which involves two counter-propagating donut beams, also within the Doppler regime, the atom experiences a torque of magnitude given by:
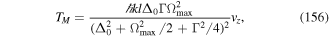
where vz is the axial component of the velocity. This torque is also proportional to l and in the high intensity limit, we have  . So this torque decreases with increasing intensity. By contrast, here the general torque in the azimuthal Sisyphus effect emerges as
. So this torque decreases with increasing intensity. By contrast, here the general torque in the azimuthal Sisyphus effect emerges as
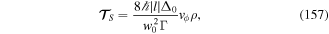
where  is the static detuning, applicable here as the Doppler effect is negligible at low velocities. This torque is proportional to the azimuthal velocity and the magnitude of l, and inversely proportional to the beam waist w0. It is a function of the radial coordinate ρ, but it does not depend on the light intensity. Significantly, this torque is proportional to the detuning Δ0, which can be positive, or negative. This suggests that the Sisyphus effect is a mechanism with which we can accelerate or decelerate the azimuthal atomic motion by simply changing the sign of the detuning, as in the twisted molasses case. This may be exploited for controlling the azimuthal motion in different types of atomic samples trapped in annular regions. We also see that the general torque in the azimuthal Sisyphus effect is inversely proportional to the relaxation rate Γ while in the case of Doppler cooling, it is directly proportional to Γ. This reflects the different physical processes that are behind the generation of the two cooling mechanisms.
is the static detuning, applicable here as the Doppler effect is negligible at low velocities. This torque is proportional to the azimuthal velocity and the magnitude of l, and inversely proportional to the beam waist w0. It is a function of the radial coordinate ρ, but it does not depend on the light intensity. Significantly, this torque is proportional to the detuning Δ0, which can be positive, or negative. This suggests that the Sisyphus effect is a mechanism with which we can accelerate or decelerate the azimuthal atomic motion by simply changing the sign of the detuning, as in the twisted molasses case. This may be exploited for controlling the azimuthal motion in different types of atomic samples trapped in annular regions. We also see that the general torque in the azimuthal Sisyphus effect is inversely proportional to the relaxation rate Γ while in the case of Doppler cooling, it is directly proportional to Γ. This reflects the different physical processes that are behind the generation of the two cooling mechanisms.
A crucial parameter in this context is the beam waist. In the case of the azimuthal Sisyphus effect the torque is inversely proportional to the square of the beam waist. In the annular region, where  , equation (157) yields
, equation (157) yields  . Thus twisted beams with large cross sections, i.e. weak focusing, will result in smaller torques. This is because as the beam waist increases the characteristic length of the azimuthal spatial variations of the laser field (i.e. the 'wavelength' λϕ) becomes larger. This is equivalent to a Sisyphus effect in a field with a larger wavelength and thus to a smaller Sisyphus torque. The torque created by the Doppler mechanism does not depend explicitly on the beam waist. This is clear in the case of irradiation by a single beam in the saturation limit; for the case of twisted molasses as given by equation (156), a larger beam waist (for a given power) results in a smaller Rabi frequency and thus to larger torques.
. Thus twisted beams with large cross sections, i.e. weak focusing, will result in smaller torques. This is because as the beam waist increases the characteristic length of the azimuthal spatial variations of the laser field (i.e. the 'wavelength' λϕ) becomes larger. This is equivalent to a Sisyphus effect in a field with a larger wavelength and thus to a smaller Sisyphus torque. The torque created by the Doppler mechanism does not depend explicitly on the beam waist. This is clear in the case of irradiation by a single beam in the saturation limit; for the case of twisted molasses as given by equation (156), a larger beam waist (for a given power) results in a smaller Rabi frequency and thus to larger torques.
Finally, we must emphasise the role of the dependence on the winding number l. In the Doppler mechanism, a larger winding number leads to larger torques and this is reasonable since it is associated with the angular momentum exchanged between the light and the atom. In the case of the azimuthal Sisyphus effect, again an increase in l leads to a larger damping. This is because the equivalent wavelength λϕ becomes smaller and thus leads to a more effective Sisyphus effect.
10. Ferris wheels
A Ferris wheel is a typical example of an optical lattice field with cylindrical symmetry. The term owes its origin to analogy with a rotating fairground ride. Ferris wheel light fields were proposed by Franke-Arnold et al in 2007 [100]. Since then there have been theoretical as well experimental works concerning the atom dynamics in the trapping sites of this light field. Using optical Ferris wheels it is possible to create both positive and negative optical potentials that are either static or can rotate around the beam axis at frequencies ranging from a few mHz to hundreds of MHz [100].
The generation of a Ferris wheel light field in its simplest form requires setting up two co-propagating LG beams with equal and opposite optical angular momenta, i.e. such that l1 = −l2. This type of light field is characterised by bright petal-like regions in a plane transverse to the propagation direction, and by using LG beams with different indices l and p it is possible to create dark lattices of different geometrical patterns [100, 101]. Furthermore, it has been shown that counter-propagating beams in three dimensions would lead to exotic light fields where the bright regions have the form of helical tubes twisted along the beams' propagation direction [149–154]. However, prior to the proposal of the optical Ferris wheel field, bright ring-shaped lattices had been used in optical tweezing experiments [155, 156].
A superfluid ensemble trapped in a rotating helical optical tube (HOT) has been shown to be associated with an artificial magnetic field [149]. The twisted tubes can be considered as a waveguide for atomic motion over distances significantly smaller than the Rayleigh range of the beam (z ≪ zR) [150], while connections between Gaussian lattices and HOTs have been also considered [150].
This scheme has been also proposed as an atomic guide along a helical path where the atom oscillates globally between two turning points [151]. However, a slight difference in the angular frequencies of the LG beams produces rotating HOTs, which have been used to study the flow of a cold bosonic ensemble (superfluid) trapped in the helical pattern [149]. The rotation of the reference frame (the helical pattern) can be used as laboratory equipment to demonstrate the difference between quantum and classical fluids [152]. The rotating helical pattern can also be used as a detector of the slow rotation of an interferometer [153]. The study of atom guiding inside a rotating HOT has shown that this mechanism can serve as an Archimedes spiral for elevating atoms [154].
Recently, such a cylindrical lattice has been proposed as a mechanism for exhibiting various realisations of a Hofstadter-Hubbard model with fermionic cold atoms, and it has been shown that this set up in the presence of interaction might allow the observation of fractional quantum Hall physics [157]. The Ferris wheel optical lattice has been used in an experiment where a trapped atom has been rotated and observed from its fluorescence [96]. In another recent work, the interaction of a two-level atom with a rotating Ferris wheel light field has been shown to create artificial gauge electromagnetic fields which propagate in closed paths [158]. Finally, besides lattices with cylindrical symmetry it is also possible to create other types of lattices by proper interference of LG beams. One such example is the stack of ring shaped traps which is created by the interference of counter-propagating beams with the same winding number [159].
10.1. Ferris wheel: co-propagating LG beams with 
Consider a Ferris wheel light field composed of two LG beams labelled 1, 2 co-propagating along the z-direction and both are polarised along the x-direction, but with opposite optical angular momenta l1 = −l2 = l. The electric fields of these LG beams are given by:
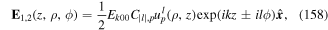
with
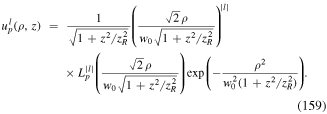
The total electric field of the optical Ferris wheel light field is the sum
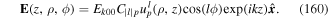
The intensity of the light field is then ![$I\propto {[{u}_{p}^{l}(\rho ,z)]}^{2}{\cos }^{2}(l\phi )$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn274.gif) . The presence of the factor
. The presence of the factor  leads to the appearance of
leads to the appearance of  petal-like high intensity regions. Figure 18 displays the spatial distribution of the Ferris wheel light field intensity (in arbitrary units) for the case where l = 2 and p = 0 and for the case where l = 2 and p = 1 together with the corresponding contour plots. These show the characteristic four petal-like intensity distribution. The Ferris wheel petal-like structure is richer when the radial index p is different from zero, in which case the intensity displays p + 1 petal-like regions.
petal-like high intensity regions. Figure 18 displays the spatial distribution of the Ferris wheel light field intensity (in arbitrary units) for the case where l = 2 and p = 0 and for the case where l = 2 and p = 1 together with the corresponding contour plots. These show the characteristic four petal-like intensity distribution. The Ferris wheel petal-like structure is richer when the radial index p is different from zero, in which case the intensity displays p + 1 petal-like regions.
Figure 18. (a), (b) The intensity (arbitrary units) of a Ferris wheel light field at z = 0. The field has been created from the superposition of two co-propagating LG beams with l1 = −l2 = 2. In the contour plot, we see the characteristic four petal-like regions of maximum intensity. (c), (d) The intensity (arbitrary units) of a Ferris wheel light field at z = 0. The field has been created from the superposition of two co-propagating LG beams with l1 = −l2 = 2 and p = 1. In the contour plot, we see the characteristic two zones of four petal-like regions of maximum intensity.
Download figure:
Standard image High-resolution imageThe above light fields are not the only ones that can be constructed. Other cylindrically symmetric optical lattices can be realised by interfering beams with opposite l but also different magnitudes. Such a scenario presents interesting features. The maximum of the at-focus intensity of the field of a donut beam occurs at the radial position  . Thus LG beams with different magnitudes of the azimuthal index l have their intensity maxima at different radial positions. The electric field of an LG beam has a FWHM equal to
. Thus LG beams with different magnitudes of the azimuthal index l have their intensity maxima at different radial positions. The electric field of an LG beam has a FWHM equal to  in the radial direction. The interference of such beams is such that
in the radial direction. The interference of such beams is such that  . The two LG fields have similar maximum amplitudes and are separated by one FWHM. This leads to a dark Ferris wheel lattice with an approximately uniform depth in the radial and azimuthal directions.
. The two LG fields have similar maximum amplitudes and are separated by one FWHM. This leads to a dark Ferris wheel lattice with an approximately uniform depth in the radial and azimuthal directions.
Furthermore, the optical Ferris wheel intensity patterns can be rotated in space when the two beams have a slight difference in frequency Δω = ω2 − ω1. There are various methods for the generation of precise laser frequency shifts, as for example by passing the light through an acousto-optical modulator, or when circularly polarized light is passed through a rotating half wave plate [160], which, due to an accumulated geometric or Berry phase [161], shifts the frequency by twice the rotational speed of the waveplate in the context of optical tweezers [162]. A rotating Ferris wheel due to a frequency difference Δω has an the electric field of the form:
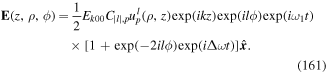
The corresponding intensity is such that ![$I\,\propto {[{u}_{p}^{l}(\rho ,z)]}^{2}{\cos }^{2}(l\phi -t{\rm{\Delta }}\omega /2)$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn280.gif) , indicating that the pattern rotates at a rate
, indicating that the pattern rotates at a rate  . This rotating pattern can be used as an azimuthal optical conveyor belt for trapped atoms as in the experiment by Xu et al [96]. It is important to note that for both bright and dark Ferris wheel lattices, the rotation is not subject to mechanical noise, which means that the pattern would be extremely stable over rotational frequencies ranging from mHz to tens of MHz.
. This rotating pattern can be used as an azimuthal optical conveyor belt for trapped atoms as in the experiment by Xu et al [96]. It is important to note that for both bright and dark Ferris wheel lattices, the rotation is not subject to mechanical noise, which means that the pattern would be extremely stable over rotational frequencies ranging from mHz to tens of MHz.
10.2. Trapping of atoms
Consider now the interaction of atoms with a Ferris wheel light field. Once more, we concentrate on a two-level atom with a transition frequency ω0 interacting with a static optical Ferris wheel light field. The interaction is characterised by a Rabi frequency given by:
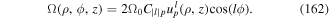
Assuming large detuning, the trapping optical dipole potential is given by:
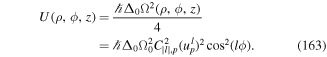
Here, Ω0 is the Rabi frequency associated with a Gaussian beam of the same power and beam waist as the two LG beams involved in setting up the optical Ferris wheel light field. The trapping potential (for Δ0 < 0) has minima at the radial positions  where
where  . An atom deeply trapped in such a rotationally symmetric potential is subject to the simple harmonic approximation about the potential minimum and irrespective of the value of l the potential has trapping regions on the common axis of the beams. In the trapping region located on the positive x-axis and for red detuning, the potential has a minimum at
. An atom deeply trapped in such a rotationally symmetric potential is subject to the simple harmonic approximation about the potential minimum and irrespective of the value of l the potential has trapping regions on the common axis of the beams. In the trapping region located on the positive x-axis and for red detuning, the potential has a minimum at  , so performing a Taylor expansion about this minimum, we find
, so performing a Taylor expansion about this minimum, we find
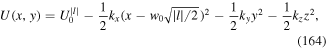
where the derived force constants kx, ky, kz and  are given by:
are given by:
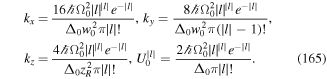
For large values of l, application of the Stirling's approximation gives  and we then have
and we then have
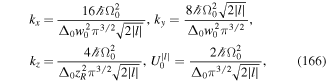
where we have taken the detuning  to be negative. The parameters kx, ky are larger than kz since in general zR ≫ w0. This means that in-plane trapping is much stronger than axial trapping. A complete three dimensional trapping would then require an additional trapping potential to be set up in the axial direction. In a Ferris wheel scheme, axial trapping can be considerable only for tightly focused beams. Moreover, equation (166) shows an interesting dependence on the index l, such that as l increases the potential
to be negative. The parameters kx, ky are larger than kz since in general zR ≫ w0. This means that in-plane trapping is much stronger than axial trapping. A complete three dimensional trapping would then require an additional trapping potential to be set up in the axial direction. In a Ferris wheel scheme, axial trapping can be considerable only for tightly focused beams. Moreover, equation (166) shows an interesting dependence on the index l, such that as l increases the potential  becomes shallower and a similar behaviour is shown by the axial potential. The in-plane potential depth decreases in the x-direction and increases in the y-direction. Furthermore, other features arise at other trapping positions such as the point
becomes shallower and a similar behaviour is shown by the axial potential. The in-plane potential depth decreases in the x-direction and increases in the y-direction. Furthermore, other features arise at other trapping positions such as the point  on the x-axis. At the corresponding trapping point
on the x-axis. At the corresponding trapping point  on the y-axis the force constant kx becomes ky and vice versa. Since the intensity pattern is rotationally symmetric, the potential at the different trapping sites can be cast in the form
on the y-axis the force constant kx becomes ky and vice versa. Since the intensity pattern is rotationally symmetric, the potential at the different trapping sites can be cast in the form
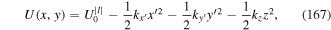
where the primed symbols are given by:
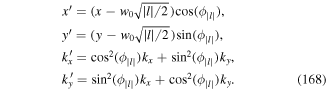
Thus, we have an anisotropic harmonic oscillator potential, and the harmonic approximation leads to oscillation frequencies given by  where M is the atomic mass.
where M is the atomic mass.
When two-level atoms are trapped in a dipole trap the trapping quality depends on two important factors, namely the depth of the optical dipole potential and the photon scattering rate. A numerical estimate of the trapping quality can be made as follows. Consider the D2  transition of 85Rb for which the de-excitation rate is Γ/2π = 5.98 MHz, the transition wavelength is λ = 780.9 nm, and the intensity is IS = 16.4 W m−2. We assume a ring lattice laser of total power of 0.12W, focused to a beam waist of w0 = 10 μm and a negative detuning of 1064 nm for trapping. The Rabi frequency associated with each beam is related to the saturation intensity IS by
transition of 85Rb for which the de-excitation rate is Γ/2π = 5.98 MHz, the transition wavelength is λ = 780.9 nm, and the intensity is IS = 16.4 W m−2. We assume a ring lattice laser of total power of 0.12W, focused to a beam waist of w0 = 10 μm and a negative detuning of 1064 nm for trapping. The Rabi frequency associated with each beam is related to the saturation intensity IS by  where
where  , with P the total available laser power (such that P/2 is provided by each of the interfering beams). Also, we have a scattering rate
, with P the total available laser power (such that P/2 is provided by each of the interfering beams). Also, we have a scattering rate  [163]. With these parameters, it is possible to construct a ring lattice of depth about 25 μK and a scattering rate S ≈ 0.013 s−1. The spatial distribution of the trapping potential is shown in figure 19.
[163]. With these parameters, it is possible to construct a ring lattice of depth about 25 μK and a scattering rate S ≈ 0.013 s−1. The spatial distribution of the trapping potential is shown in figure 19.
Figure 19. The trapping potential for a Ferris light field created from the superposition of two co-propagating LG beams with l1 = −l2 = 5. The potential is given in μK units.
Download figure:
Standard image High-resolution imageThe above analysis indicates that the Ferris wheel lattice could provide a potentially dynamic three-dimensional trap for atoms. The trapping is sufficient in the transverse direction, though the potential is shallower in the z-direction. For a lattice that traps in the intensity maxima (red lattice), we could use a tightly focused Ferris field (short Rayleigh range) but there is a trade-off between axial confinement and scattering rate. However, it has been suggested that an additional localisation field can be set up along the z-direction with a hybrid configuration of a Ferris light field and a quadrupole magnetic trap [164, 165]. Alternatively, it is possible to create an axial confinement in a ring lattice by using counter-propagating laser beams forming a standing wave. This leads to the generation of an axially separated stack of lattices similar to the ones in [99]. However, by introducing a frequency shift between the forward and backwards LG beams, the individual ring lattices will not only rotate but also translate along the z-axis.
10.3. Helical optical tubes (HOTs)
The twisted optical potential tubes or HOT are formed by the interference of two counter-propagating LG beams, with opposite winding numbers l and the same polarisation, which results in the generation of a three-dimensional twisted standing wave. When a two-level atom interacts with such a light field the optical dipole potential (in the far off-resonance case) is given by:
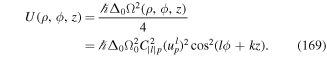
This HOT dipole potential is shown in figure 20 for the case where l = 1 and p = 0. This pattern has a left-handed helical shape with a pitch equal to 2πh ( ) and has two tubes where the maximum intensity is at the geometrical centre of each tube at z = 0 and decreases in the radial direction away from the centre of each tube, and away from the z = 0 plane along each tube.
) and has two tubes where the maximum intensity is at the geometrical centre of each tube at z = 0 and decreases in the radial direction away from the centre of each tube, and away from the z = 0 plane along each tube.
Figure 20. The HOT potential with mode l = 1 and p = 0. Reproduced from [151]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageThe motion of an atom in such a potential has been analysed in the semi-classical approximation which treats the external variables classically [151]. The atom is considered as subjected to both the optical dipole potential and the gravitational potential and depend on the helix orientation with respect to the lab frame. The equations of motion can be derived using the Lagrangian formalism in cylindrical coordinates, leading to three coupled nonlinear differential equations of the second order for which there is no exact general analytical solution. The atom trajectory can, however, be calculated numerically and analytically in special cases. The numerical solution is based on the fourth order Runge–Kutta method subject to initial conditions for the cold atom inside the HOT. For negative detuning, the atom is attracted towards the high intensity regions.
The initial position of the cold atom can be chosen at the maximum intensity point (which is the minimum value of the dipole potential), which, in cylindrical coordinates, is  , where n = 1, 2, ..., 2l is the index of the tubes of the helical optical potential. For example, for l = 1, the helical optical potential has two tubes: the first tube has index n = 1 while the second one has index n = 2, as in figure 20. For the initial velocity, we choose v = (vr, vϕ, vz) = (5 cm s−1, 5 cm s−1, 0). This is reasonable as the initial velocity of the cold atom should not be less than the recoil velocity vrec (in order to ensure the validity of the semi-classical approximation) and must be greater than the Doppler velocity vD (so as to keep the interaction resonant), i.e. vrec < v0 < vD.
, where n = 1, 2, ..., 2l is the index of the tubes of the helical optical potential. For example, for l = 1, the helical optical potential has two tubes: the first tube has index n = 1 while the second one has index n = 2, as in figure 20. For the initial velocity, we choose v = (vr, vϕ, vz) = (5 cm s−1, 5 cm s−1, 0). This is reasonable as the initial velocity of the cold atom should not be less than the recoil velocity vrec (in order to ensure the validity of the semi-classical approximation) and must be greater than the Doppler velocity vD (so as to keep the interaction resonant), i.e. vrec < v0 < vD.
For an atom in the region where  , assuming that the small radial 'wiggling' of the motion does not affect the global oscillations in the z-direction, it is possible to obtain an analytical solution of the equations of motion. We have
, assuming that the small radial 'wiggling' of the motion does not affect the global oscillations in the z-direction, it is possible to obtain an analytical solution of the equations of motion. We have
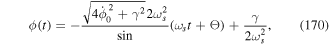
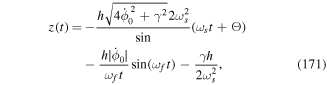
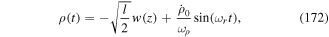
where  is the initial angular velocity,
is the initial angular velocity,  ,
,  ,
,  and
and  , where
, where  is the recoil energy,
is the recoil energy,  is the pitch angle with
is the pitch angle with  and
and  is the depth of the potential at the minimum point.
is the depth of the potential at the minimum point.
Figure 21 displays the trajectories, calculated both numerically and analytically, for the following set of parameters. The transition is taken as  in 85Rb for which λ = 780.2 nm, Is = 1.64 W m−2, and Γ/2π = 5.98 MHz. The recoil and Doppler velocities for laser cooling of an 85Rb atom are vrec = 0.602 cm s−1 and vD = 11.85 cm s−1, respectively [44]. The laser power is P = 80mW, detuning Δ = 2.57 × 1013 Hz and the beam waist w0 = 4 μm [96]. Figures 21(a) and (b) provide an excellent agreement between the numerical and analytical calculations. Both figures show the global oscillatory behaviour of the atom between two turning points along the z-axis and following a helical trajectory due to the helical geometry of the dipole potential.
in 85Rb for which λ = 780.2 nm, Is = 1.64 W m−2, and Γ/2π = 5.98 MHz. The recoil and Doppler velocities for laser cooling of an 85Rb atom are vrec = 0.602 cm s−1 and vD = 11.85 cm s−1, respectively [44]. The laser power is P = 80mW, detuning Δ = 2.57 × 1013 Hz and the beam waist w0 = 4 μm [96]. Figures 21(a) and (b) provide an excellent agreement between the numerical and analytical calculations. Both figures show the global oscillatory behaviour of the atom between two turning points along the z-axis and following a helical trajectory due to the helical geometry of the dipole potential.
Figure 21. The 3D trajectory of 85Rb atom along the helical tube with index n = 1 with a time duration of 8 μs calculated: (a) numerically (red line) and (b) analytically (blue line). Reproduced from [151]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageThe physical origin of this type of motion lies in the term  which is responsible for the formation of
which is responsible for the formation of  potential wells (each well corresponds to a tube in the potential depicted in figure 20 in the (z, ϕ) plane. Each of these wells has energy minima along the line lϕ + kz = (n − 1)π (n is the index of the tube of the potential). This topological feature of the dipole potential drives the atom to oscillate locally about the line lϕ + kz = (n − 1)π, which is the locus of the minima of the potential wells. Due to the coupling of the equations of motion the local oscillations induce an average motion along the line lϕ + kz = (n − 1)π, which guides the atom inside the tube of index n by keeping lϕ + kz = (n − 1)π and a radial distance
potential wells (each well corresponds to a tube in the potential depicted in figure 20 in the (z, ϕ) plane. Each of these wells has energy minima along the line lϕ + kz = (n − 1)π (n is the index of the tube of the potential). This topological feature of the dipole potential drives the atom to oscillate locally about the line lϕ + kz = (n − 1)π, which is the locus of the minima of the potential wells. Due to the coupling of the equations of motion the local oscillations induce an average motion along the line lϕ + kz = (n − 1)π, which guides the atom inside the tube of index n by keeping lϕ + kz = (n − 1)π and a radial distance  . This guiding elevates the atom along the z-direction.
. This guiding elevates the atom along the z-direction.
Another important parameter of the atomic motion is the beam width w(z) which depends on the position in the z-direction. This dependence, which is shown in figure 22, has normally been ignored in previous works concerning the atomic motion in twisted beams, being considered negligible. However, here it plays an important role. Due to the factor 1/w(z) the depth of the potential is modified in the z-direction. It is straightforward to understand that if the kinetic energy of the atom is less than the depth of the dipole potential on this larger scale, the atom will perform a global oscillation between two turning points. Thus, the motion inside the twisted optical potential tubes is made up of two component motions: a local atomic oscillation in the region 0 < z < λ and 0 < ϕ < 2π and a global oscillation in the region λ < z < zR. The two types of motion are due to the fact that the dipole potential has two different topological features with different spatial scales.
Figure 22. The scaled (in units of its maximum depth  ) twisted optical dipole potential as a function of z along the minima line
) twisted optical dipole potential as a function of z along the minima line  . Reproduced from [151]. © IOP Publishing Ltd. All rights reserved.
. Reproduced from [151]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageThe turning points of the atomic trajectory constitute one of the important features of the atomic motion inside the twisted optical tube. This feature defines the furthest point the atom can be guided along the HOT. Additionally, the turning points are a feature of the atomic gross motion that can be manipulated by changing the characteristic parameters of the LG beams, namely the power, the detuning and the beam waist. In general, the upper turning point of the atom can be higher when the dipole potential is weaker. This can be achieved by making the beam waist larger, the beam power smaller or the detuning larger. On the other hand, the lower turning point of the atom occurs at a lower position and farther than the upper turning point when the dipole potential becomes weaker.
The positions of the turning points are symmetric with respect to the origin when the dipole potential is strong and therefore the influence of gravity is negligible. When the dipole potential is dominant over the gravitational one, the trapped atom will oscillate between the symmetrical positions of the upper and lower turning points, a situation equivalent to an atom reflected between two mirrors of an atomic cavity. When the dipole potential is weaker an asymmetry between the positions of the lower and the upper turning points (where the lower turning point becomes more distant from the origin than the upper turning point) arises since the influence of gravity is then stronger. At the limit of very weak dipole potentials, the motion of the atom is governed almost entirely by gravity and thus has only one turning point. Its initial velocity allows the atom to move up and reach the upper turning point, then the atom starts to fall under the influence of gravity only and follows in its downward motion the helical path determined by the topology of the optical tubes.
10.4. An Archimedes screw for atoms
A HOT intensity pattern can also be rotated once we arrange for a slight frequency difference between the two interfering LG beams [166]. The most interesting effect on atomic motion is that for specific choices of the values and the sign of the rotating angular frequency the trapped atoms can be dragged in an upward or downward motion. In this case, the action of the rotating HOT on atoms is reminiscent of the operation of the Archimedes screw with which even today in several places of the world people elevate water from rivers and lakes. This Archimedes screw for atoms was proposed and presented in [154] and an experiment on this was reported by Hadad et al [168]. Here, we outline the essential elements of the treatment by Al Rsheed et al [154].
The potential in this scheme is given by
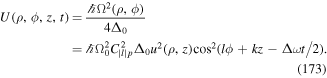
This potential rotates at an angular velocity  . The study of the atomic motion can be done in the rotating frame of reference, where the potential takes a form similar to the one in equation (169) but for new coordinates
. The study of the atomic motion can be done in the rotating frame of reference, where the potential takes a form similar to the one in equation (169) but for new coordinates  . The equations of motion for the new coordinates are as follows:
. The equations of motion for the new coordinates are as follows:
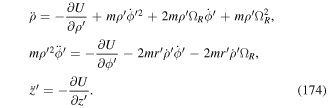
The third term on the right-hand side of the first equation in (174) and the last term in the second equation are Coriolis forces, while the last term in the first equation is a centrifugal force. These are well known forces that appear because of the rotation of the HOT. The above three equations of motion are coupled nonlinear differential equations of the second order for which there is no exact analytical solution, but a solution can be obtained numerically using the fourth-order Runge–Kutta method.
The motion of an atom that is trapped inside a rotating HOT can be explained in terms of inertial forces. Initially, an atom at rest inside a rotating HOT will experience a centrifugal force  and will then move along the radial direction. Once in motion it acquires a radial velocity and an associated Coriolis force
and will then move along the radial direction. Once in motion it acquires a radial velocity and an associated Coriolis force  along the azimuthal direction. This drives the rotating atom in a direction opposite to that of the angular velocity of the HOT. Finally, the atom will have a global motion along the HOT due to the coupling between the motions along the z- and the azimuthal directions. Consequently, the cold atom, which is initially at rest, will acquire a clockwise azimuthal velocity if it is trapped inside a counter-clockwise rotating HOT, while it will acquire a counter-clockwise azimuthal velocity if it is trapped inside a clockwise rotating HOT. In other words, the angular momentum that is transferred from the rotating HOT to the atom is directed opposite to the angular velocity of rotation of the HOT, in agreement with the prediction by Bekshaev et al [166].
along the azimuthal direction. This drives the rotating atom in a direction opposite to that of the angular velocity of the HOT. Finally, the atom will have a global motion along the HOT due to the coupling between the motions along the z- and the azimuthal directions. Consequently, the cold atom, which is initially at rest, will acquire a clockwise azimuthal velocity if it is trapped inside a counter-clockwise rotating HOT, while it will acquire a counter-clockwise azimuthal velocity if it is trapped inside a clockwise rotating HOT. In other words, the angular momentum that is transferred from the rotating HOT to the atom is directed opposite to the angular velocity of rotation of the HOT, in agreement with the prediction by Bekshaev et al [166].
We now demonstrate with a specific example that with a judicious choice of parameters the rotating HOT can be used for elevating atoms. To elevate an atom we must obey two conditions: first, the atom must be able to escape from the oscillations along the vertical z-direction and, second, it must simultaneously be kept trapped in the potential tube without escaping along the radial direction. Again the light field is assumed to excite the transition  , in 85Rb for which λ = 780.24 nm, Is = 16.4 W m−2, Γ/(2π) = 5.98 MHz, the laser power is P = 80 mW, the detuning is Δ0 = −2.57 × 1013 Hz and the beam waist is w0 = 5 μm. The initial velocity is taken as (vx = 5 cm s−1, vy = 5 cm s−1, vx = 0).
, in 85Rb for which λ = 780.24 nm, Is = 16.4 W m−2, Γ/(2π) = 5.98 MHz, the laser power is P = 80 mW, the detuning is Δ0 = −2.57 × 1013 Hz and the beam waist is w0 = 5 μm. The initial velocity is taken as (vx = 5 cm s−1, vy = 5 cm s−1, vx = 0).
Figure 23 shows the helical motion of the atom in the rotating frame of reference for two different angular velocities of the HOT:  ΩR = −70 kHz. In the first case, the atom is performing an oscillation in the upward z-direction and in the second case the atom is performing an oscillation in the downward z-direction. Note, however, that the atom oscillates between two vertical positions and it is not elevated or dragged downwards.
ΩR = −70 kHz. In the first case, the atom is performing an oscillation in the upward z-direction and in the second case the atom is performing an oscillation in the downward z-direction. Note, however, that the atom oscillates between two vertical positions and it is not elevated or dragged downwards.
Figure 23. The trajectory of a 85Rb atom with respect to the HOT frame of reference: (a) ΩR = 70 kHz, represented by the black line and (b) ΩR = −70 kHz, represented by the red line. Reproduced from [154]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageFigure 24 displays the time evolution of the vertical displacement of the atom. The atom can be elevated along the z-axis when the HOT rotates at angular velocities greater than 146 krad s−1 counter-clockwise. It can also move downwards when the HOT rotates at angular velocities greater than 150 krad s−1 clockwise. In these cases, the rotating HOT operates as an Archimedes screw for atoms. For other values of the rotational angular velocity, it clearly performs an oscillation along the z-axis, which means that it remains trapped in this direction.
Figure 24. The variation of a 85Rb atom elevation with initial velocity (vx = 5 cm s−1, vy = 5 cm s−1, vz = 0) for different angular rotation velocities of the HOT: 147 krad s−1 (black solid line), 146 krad s−1 (red dashed line), −151 krad s−1 (blue dashed–dotted line), and −150 krad s−1 (brown dotted line) (w0 = 5 m and l = 1). Reproduced from [154]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageThe operation of the rotating Ferris wheel as an Archimedes screw for atoms is possible for those angular velocities ΩR for which the atom during the elevation remains trapped in the radial direction. The angular frequency of the axial oscillations is given by:
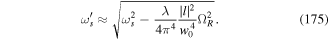
The angular frequency  in the radial direction can be computed numerically. Here ωs is the angular frequency of the axial oscillations in the static HOT case. Figure 25 displays the angular frequencies in the axial and radial directions and from the figure it can be seen that there are values of the HOT angular frequency
in the radial direction can be computed numerically. Here ωs is the angular frequency of the axial oscillations in the static HOT case. Figure 25 displays the angular frequencies in the axial and radial directions and from the figure it can be seen that there are values of the HOT angular frequency  for which the oscillation frequencies along the axial and radial direction,
for which the oscillation frequencies along the axial and radial direction,  and
and  respectively, become zero. We also see that the atomic radial frequency
respectively, become zero. We also see that the atomic radial frequency  is always larger than the atomic global frequency
is always larger than the atomic global frequency  and that there are rotation angular velocities for which these frequencies can be zero. In figure 25, these are denoted by
and that there are rotation angular velocities for which these frequencies can be zero. In figure 25, these are denoted by  and
and  , respectively. These are important since if the HOT rotates within the following range of angular velocities:
, respectively. These are important since if the HOT rotates within the following range of angular velocities:  then the atom can be elevated to any desired height along the z-axis while simultaneously remaining trapped in the radial direction. The atom can be transported upwards or downwards along the HOT by changing the direction of the rotation of the HOT. The values of
then the atom can be elevated to any desired height along the z-axis while simultaneously remaining trapped in the radial direction. The atom can be transported upwards or downwards along the HOT by changing the direction of the rotation of the HOT. The values of  and
and  can be controlled by changing the dipole potential parameters such as the winding number l, the beam waist w0, the beam power P, and the detuning Δ.
can be controlled by changing the dipole potential parameters such as the winding number l, the beam waist w0, the beam power P, and the detuning Δ.
Figure 25. The variation of  (red dashed line) and
(red dashed line) and  (black solid line) of a trapped 85Rb atom as a function of ΩR. The atom starts motion from rest, the beam waist of LG beams is w0 = 5 μm, and the orbital winding number is l = 1. Reproduced from [154]. © IOP Publishing Ltd. All rights reserved.
(black solid line) of a trapped 85Rb atom as a function of ΩR. The atom starts motion from rest, the beam waist of LG beams is w0 = 5 μm, and the orbital winding number is l = 1. Reproduced from [154]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageFigure 26. Total internal reflection of an LG beam at an angle greater than the critical angle (schematic). The incident beam is arranged such that at θ = 0 the beam waist coincides with the surface at z = 0. The evanescent light possesses angular momentum properties, but is confined near the surface, exponentially decaying in the direction normal to the surface. Reproduced with permission from [177].
Download figure:
Standard image High-resolution image11. Atomic interaction in evanescent waves
11.1. Goos–Hänschen and Imbert–Federov shifts
It is well established in elementary geometrical optics that when plane wave light is totally internally reflected at the interface between a dielectric material (like a glass prism) and vacuum then evanescent waves that propagate along the boundary are developed. An evanescent wave has an amplitude that decreases with distance away from the boundary so that its intensity falls away with a typical decay length of the order λ/2π where λ is the wavelength. The light fields associated with the evanescent wave have strong intensities and are localised within a small volume. There are thus strong spatial field gradients, which can influence atomic properties.
In addition to optical forces due to evanescent light atoms experience van der Waals attraction to the surface. Atoms can dwell in the vicinity of surfaces either as a result of chemisorption (producing bond formation) or physisorption. Here, we focus on physiosorbed atoms where binding energies are much smaller and the equilibrium distance to the surface is comparatively larger. Physisorbed atoms will respond to surface optical forces because they can represent a displacement from equilibrium, in a planar motion that leaves the distance to the surface unchanged. Undoubtedly, atomic-scale irregularity in the surface itself will modulate the atomic motions we describe, but these will be only minor perturbations to the main effects.
The physics of light at surfaces is in reality a little more involved when one is dealing with a light beam with finite spatial variations in the plane perpendicular to the axis of propagation. The first effect experienced by a light beam, such a Gaussian beam, on reflection is a Goos–Hänschen shift of the plane of incidence [169]. This is a lateral shift, which is distinct from a second, so-called, Imbert–Fedorov shift that is perpendicular to the plane of incidence [170, 171].
The reflection of a beam carrying OAM changes the vortex beam and creates additional modes of higher and lower orders. On reflection, a vortex beam has been shown to experience further shifts associated with the additional angular degrees of freedom. These are the angular Goos–Hänschen and Imbert–Federov shifts, both of which have been analysed and demonstrated [172, 173]. The angular shifts are in fact shifts in wavevector space (see [174, 175]). Merano et al [176] demonstrated both theoretically and experimentally that the spatial and angular shifts are in fact coupled.
However, the intensities of the additional modes responsible for the above shifts are typically small. A reasonable approximation is to ignore such effects and adopt a geometrical optics model in which the light beams are specularly reflected. When the totally internally reflected light is an LG beam that is assumed specularly reflected, the effect, as we explain shortly, is to produce SOVs [6]. These are evanescent waves endowed with angular momentum.
11.2. Atoms at surfaces
Electromagnetic surface modes can have strong interactions with two-level atoms in the vicinity of the interface, leading to considerable optical trapping potentials, forces and associated torques. We have seen that when the detuning of the laser light is positive, then the dipole force acts to repel the atoms away from the high intensity regions. With the potential barrier so created any incident atoms can be elastically reflected if their kinetic energy is smaller than the maximum of the optical dipole potential, and the system operates as an evanescent mode atom mirror (EWAM) [178]. A laser intensity of 1 W, focused on a surface area of the order of 1 mm2, creates an atom mirror on which an atom can be reflected if the component of its velocity normal to the mirror is lower than a few meters per second, which corresponds to kinetic temperatures on the order of few mK [43].
The evanescent wave atom mirror (EWAM) has been used in both the technological and fundamental research of atomic physics for many years [91, 178–205]. The EWAM allows one to reflect ultra-cold atoms [184] in order to probe quantum electrodynamic retardation effects [185]. It is also the basic component for the creation of gravito-optical traps [186, 187]. The first demonstration of an EWAM was in 1987, where it was used to reflect thermal atoms at grazing angles [188]. In 1990, it was used with cold atoms at normal incidence [189]. Since then, EWAM has been extensively studied by several groups, both experimentally [190–195] and theoretically [196–199]. The control of the effective potential barrier has been demonstrated in the case of a two-level atom interacting with surface plasmons [190–192], a dielectric waveguide structure [200] and a metallic film [201] deposited on the surface of the mirror. Multiple bounces of atoms have been observed when evanescent waves were created on concave surfaces [202]. The EWAM has also been used to investigate atom optics in the time domain [203]. One of the most spectacular properties of an EWAM is the quantum state-selective character of the atomic reflections which were demonstrated by Balykin et al [204]. An atom mirror of a three-level atom in the so-called Λ-configuration has also been proposed [205]. Finally, evanescent wave mirrors have been considered for small objects at surfaces [206–208], rather than for near-resonance atoms and molecules.
The intensity of the evanescent wave in an EWAM can be increased by a few orders of magnitude by introducing a thin metal layer into the dielectric-vacuum interface due to the excitation of surface plasmons produced, or by introducing a dielectric film of high refractive index, which essentially produces a dielectric optical fibre for the laser radiation. The repeated reflection of the laser light from the dielectric-vacuum and dielectric–dielectric interfaces substantially increases the intensity of the evanescent wave [209]. When an EWAM with a thin metal film is irradiated by an LG beam we have the so-called surface plasmon optical vortices (SPOVs). These specifically plasmonic modes which are once again features with an intrinsic angular momentum [210, 211].
11.3. Surface optical vortices (SOVs)
We now ignore the small beam effects in the forms of the Goos–Hänschen and Imbert–Federov shifts and adopt a geometrical optics model in which the twisted light beams are totally internally reflected at a planar interface between a dielectric material and vacuum. The result of the total internal reflection is the generation of an evanescent light which carries an in-plane distribution of the incident beam and its angular momentum properties. This is a surface optical vortex (SOV) endowed with the OAM of the incident light. Figure 26 schematically represents the process of total internal reflection leading to the generation of surface optical vortices, as surface modes with OAM.
The electric field of an LG beam travelling along the z-axis in a medium of a constant refractive index n, characterised by the integers l and p, frequency ω and axial wavevector k = nk0 where k0 = ω/c is the wavevector in vacuum. If the interface with the vacuum occupies the plane z = 0 and the angle of incidence, θ, exceeds the total internal reflection angle, an evanescent mode is created in the vacuum. The main requirements are the applicability of the standard phase matching condition of boundary reflection and the condition that the electric field vector component tangential to the surface is continuous across the boundary. Figure 27 displays the intensity distribution of an SOV due to an internally reflected LG mode on the planar surface of a dielectric. The assumed parameters are given in the caption of this figure.
Figure 27. The intensity distribution for the SOV created by the total internal reflection of a LG beam with l = 2; p = 1. The LG beam has a waist w0 = 200 μm and a power P = 1 mW. The beam has a wavelength  and is incident at angle θ = 30° at the interface of a piece of glass made of GaP with a refractive index n = 3.365. The glass is transparent at this wavelength which can excite the transition
and is incident at angle θ = 30° at the interface of a piece of glass made of GaP with a refractive index n = 3.365. The glass is transparent at this wavelength which can excite the transition  in 3Na. The beam has an intensity I0 = 25 kW m−2 = 390.25Isat, where Isat = 64 W m−2 is the saturation intensity for the sodium 32S1/2 − 32P3/2 transition. The intensity distribution is plotted in the (x, y) plane at z = 0.
in 3Na. The beam has an intensity I0 = 25 kW m−2 = 390.25Isat, where Isat = 64 W m−2 is the saturation intensity for the sodium 32S1/2 − 32P3/2 transition. The intensity distribution is plotted in the (x, y) plane at z = 0.
Download figure:
Standard image High-resolution imageThe evanescent light possesses well-defined intensity maxima and minima that can be used to trap adsorbed atoms or to reflect incident atoms with transition frequencies appropriately detuned from the frequency ω of the light. We also see that the spatial profile of the intensity distribution is, in fact, no longer circular, but elliptical, because the light strikes the surface at the angle of incidence θ and the ellipticity increases with increasing θ.
11.4. Surface plasmonic optical vortices (SPOVs)
Consider now the case of co-propagating incident beams of opposite winding number l creating an interference of two surface vortices, in a manner similar to that discussed in the previous section which leads to the generation of the optical Ferris wheel [100]. The total electric field in the vacuum region results from the interference of the two evanescent light beams in the azimuthal direction.
Twisted light can also lead to the generation of surface plasmonic optical vortices [212, 213]. An experimentally accessible scenario is the case where a thin metallic film is deposited on the surface of a glass prism and, as before, a LG beam is totally internally reflected on the inner interface as shown in figure 28.
Figure 28. Schematic total internal reflection of two LG beams at a planar dielectric interface with a metallic film, creating a surface plasmon from counter-propagating evanescent modes.
Download figure:
Standard image High-resolution imageThe metallic film enhances greatly the evanescent fields and the interaction with a two-level atom in the vicinity is stronger than in the absence of the metallic film, so the corresponding mechanical effects should be larger. From Maxwell's equations the electric field vector components emerge with in-plane polarisation in the three regions of the layered structure as shown in figure 28, namely a dielectric, occupying the region z < −d; a surface film occupying the region −d < z < 0, and the vacuum region occupying the space z > 0. These fields are then subject to boundary and phase-matching conditions. This procedure leads to the evanescent field in the vacuum region.
An atom in the vacuum region with position vector R(t) = (x(t), y(t), z(t)) interacts with the surface plasmon vortex and the interaction is characterised by the Rabi frequency Ω(R(t)) and the phase Θ(R(t)).
To confine the atom to an angular path in the plane parallel to the surface, it is necessary to use two internally reflected incident beams as shown in figure 28. Here, two LG beams, labelled 1 and 2, are incident at angles ϕ1 and ϕ2. The two beams, which are assumed as identical, are totally internally reflected and have field components within the film, and surface plasmonic components in the vacuum region. Once the forces acting on the centre of mass of the atom are specified, the motion of the atom in the vicinity of the surface can be determined. The dynamics again follows a Newtonian equation of motion, driven by a sum of the forces delivered by each beam.
To illustrate the results of the theory leading to typical trajectories, we consider a sodium atom in two confocal, counter-propagating LG beams as in figures 29 and 30 assuming the same magnitude of detuning, but one beam has positive detuning and the other negative detuning . It is seen that the trajectories of the sodium atom are very different in the two types of detuning. The confinement regions are now concentric elliptical valleys defined by the intensity distributions, radial confinement leading to vibrational motion in a radial direction and resulting in an overall zigzag trajectory.
Figure 29. Trajectory of the sodium atom in the evanescent fields generated by counter-propagating LG beams, with positive detuning, at a planar dielectric interface coated with a metallic film where  . The trajectory is superimposed on a rendering of the associated potential well. The parameters are as follows. The beam waist is taken as w0 = 35λ, with λ = 589.0 nm. The intensity is assumed to be I = 2.0 × 106 W m−2. The layer structure consists of a thin silver film of thickness d = 59 nm and electron density
. The trajectory is superimposed on a rendering of the associated potential well. The parameters are as follows. The beam waist is taken as w0 = 35λ, with λ = 589.0 nm. The intensity is assumed to be I = 2.0 × 106 W m−2. The layer structure consists of a thin silver film of thickness d = 59 nm and electron density  m−3, deposited on glass of dielectric constant
m−3, deposited on glass of dielectric constant  2 = 2.298. The magnitude of the detuning is
2 = 2.298. The magnitude of the detuning is  , where Γ = 6.13 × 107 s−1. The dipole moment is taken as
, where Γ = 6.13 × 107 s−1. The dipole moment is taken as  where aB is the Bohr radius.
where aB is the Bohr radius.
Download figure:
Standard image High-resolution imageFigure 30. Trajectory of the sodium atom in the evanescent fields generated by counter-propagating LG beams, with negative detuning, at a planar dielectric interface coated with a metallic film where l1 = l2 = 1; p = 0. The trajectory is superimposed on a rendering of the associated potential well.
Download figure:
Standard image High-resolution image11.5. Extraordinary spin in evanescent waves
In recent years, there has been a growing interest in extraordinary spin in evanescent light modes. The reference here is to spin directed transverse to the direction of propagation. Much of the work has been done for subwavelength optical fibres (see, for example, [214, 215]), but the phenomenon is general in this setting [216]. Note, however, that the twisting here is not in the phase of the optical field.
Bliokh et al [216] explored the local momentum and spin distributions of evanescent waves. The electric field of their evanescent wave emerges from that of an elliptically-polarised plane wave propagating along the z-axis carrying momentum and spin in the form  where k = ω/c. A rotation of the plane wave field by an imaginary angle iθ leads to the electric field Eevan of an evanescent mode in the half-space x > 0, occupied by vacuum
where k = ω/c. A rotation of the plane wave field by an imaginary angle iθ leads to the electric field Eevan of an evanescent mode in the half-space x > 0, occupied by vacuum
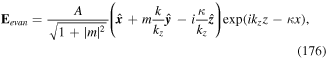
where  . In the above, A is the wave amplitude and caret denote unit vectors; m is a complex number that determines the polarisation state. The evanescent mode propagates along the z-axis and its field decays exponentially along the x-axis. It is characterised by the longitudinal wavenumbers kz and κ, the spatial decay rate. These combine to form the complex wavevector
. In the above, A is the wave amplitude and caret denote unit vectors; m is a complex number that determines the polarisation state. The evanescent mode propagates along the z-axis and its field decays exponentially along the x-axis. It is characterised by the longitudinal wavenumbers kz and κ, the spatial decay rate. These combine to form the complex wavevector  . The calculated density of each of the canonical momentum
. The calculated density of each of the canonical momentum  , spin momentum
, spin momentum  and SAM s of this evanescent wave are as follows
and SAM s of this evanescent wave are as follows

where (in Gaussian units)  is the spatially-inhomogeneous energy density of the wave and
is the spatially-inhomogeneous energy density of the wave and  is the helicity (ellipticity of polarisation).
is the helicity (ellipticity of polarisation).
The three expressions presented in equation (177) are the main findings of the work by Bliokh et al Bliokh2014 who emphasised the remarkable peculiarities of the momentum and spin. In particular:
- (1)Since kz > k, the evanescent wave possesses a longitudinal canonical momentum component
 which is greater than the plane wave momentum
which is greater than the plane wave momentum  that created it.
that created it. - (2)The group velocity in the evanescent wave is vgz = ckz/k > c which confirms that the evanescent wave is superluminal in the direction of propagation.
- (3)The theory predicts a super-momentum transfer per photon (i.e. larger than
 ) from the evanescent wave to a dipole particle via the radiation force
) from the evanescent wave to a dipole particle via the radiation force  . This is in conformity with the super-momentum transfer [217] which was observed earlier by Howard and Imbert [218] in the resonant interaction between a moving atom and an evanescent wave.
. This is in conformity with the super-momentum transfer [217] which was observed earlier by Howard and Imbert [218] in the resonant interaction between a moving atom and an evanescent wave. - (4)The results show that there are transverse y-components of the momentum and spin of the evanescent wave propagating in the (x, y) plane. The y-component of the momentum
 , which depends on the helicity
, which depends on the helicity  . The y-component of the spin is
. The y-component of the spin is  , which is helicity-independent.
, which is helicity-independent.
So far we have assumed that the evanescent wave exists in the vicinity of a planar surface. There are other contexts in which evanescent modes feature prominently, most notably in waveguides and in whispering galleries. Here too, it has been found that the polarisation of an allowed evanescent mode exhibits a longitudinal component along the direction of propagation. The work by Junge et al [214] investigated the interaction of a single atom with a whispering gallery mode in a microresonator, taking account of the effects of the non-transversal polarisation of the whispering gallery mode in the interaction.
12. Enhanced quadrupole effects with twisted light
12.1. Quadrupole transitions
The development of laser cooling and trapping has been based on the interaction of coherent light with atoms in the electric dipole approximation. Other higher multipolar effects have been ignored since they are considered to be too small [219]. The next in the multipolar order is the electric quadrupole. Electric quadrupole transition rates are typically smaller by a factor  in comparison with electric dipole transitions, where a0 is the Bohr radius and k is the wavenumber of the ordinary laser light. For processes involving transitions in the optical region, we have g ≈ 10−6.
in comparison with electric dipole transitions, where a0 is the Bohr radius and k is the wavenumber of the ordinary laser light. For processes involving transitions in the optical region, we have g ≈ 10−6.
Although usually weak, quadrupole effects become important at high intensities or when the light is tightly focused [220], or when the transition in question is driven between two long lived states, in which case the Rabi frequency may be larger than the linewidth, leading to coherent oscillations of the upper state population [221, 222]. Further advancements in optical techniques have allowed more quadrupole transitions to be observed and utilised. In particular, very weak quadrupole transitions have been detected in hydrogen molecules and these have been regarded as of particular interest in probing the atmospheres of various celestial objects [223]. Enhancements of optical absorption of an electric quadrupole transition in caesium atoms interacting with an evanescent field have also been observed [224]. Indeed, quadrupole transitions can be significantly enhanced in the vicinity of material surfaces, including microstructures where enhancements by two orders of magnitude are predicted and have been experimentally observed [225, 226].
12.2. Quadrupoles in twisted light
Here, we seek to explore what mechanical effects a LG beam would create on a two-level atom when the atomic transition is electric quadrupole allowed. The aim is to find out whether we can achieve mechanical effects of substantial strength when LG beams with high OAM content interact with atoms by quadrupole allowed transitions. Once more, we consider a two-level system with a ground state, denoted  of energy
of energy  and an excited state
and an excited state  of energy
of energy  , such that the resonance frequency is
, such that the resonance frequency is  . The atom interacts with an LG beam characterised by the quantum numbers l and p propagating along the z- axis with an axial wave-vector k.
. The atom interacts with an LG beam characterised by the quantum numbers l and p propagating along the z- axis with an axial wave-vector k.
The basic quantum mechanical Hamiltonian formalism in this case follows an analogous initial set of steps to those followed in the case of atoms interacting with light in the electric dipole approximation. The only difference here is that the interaction Hamiltonian is
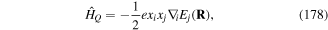
where the Einstein summation convention applies. Here xi are the components of the internal position vector x = (x, y, z) and ∇j are components of the gradient operator which act only on the spatial coordinates of the transverse electric field vector E as a function of the centre of mass variable R = (X, Y, Z).
We assume that the LG mode is linearly polarised along the x-direction and that its quantised electric field as a function of the centre of mass coordinate R now expressed in cylindrical coordinates R = (ρ, ϕ, Z) (with  ) has the familiar form of equations (52)–(54). Here, for simplicity, we shall ignore the Gouy phase such that the phase of the LG beam at position R is given by
) has the familiar form of equations (52)–(54). Here, for simplicity, we shall ignore the Gouy phase such that the phase of the LG beam at position R is given by  . With the electric field polarized along the x-direction, the quadrupole interaction Hamiltonian equation (178) now takes the form
. With the electric field polarized along the x-direction, the quadrupole interaction Hamiltonian equation (178) now takes the form
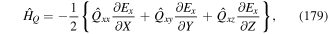
where  are the elements of the quadrupole tensor operator, which for the two-level atom can be written in terms of ladder operators as
are the elements of the quadrupole tensor operator, which for the two-level atom can be written in terms of ladder operators as
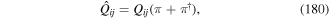
where  are quadrupole matrix elements between the two atomic levels.
are quadrupole matrix elements between the two atomic levels.
Substituting for the fields, we can write the quantised quadrupole interaction Hamiltonian in the form
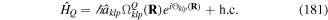
Here,  is the complex Rabi frequency defined as follows
is the complex Rabi frequency defined as follows
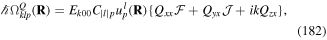
where, at z = 0,
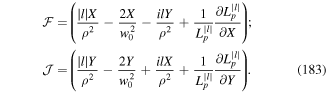
The form of the interaction Hamiltonian is similar to the one for the electric dipole transitions. The only difference is the way that the Rabi frequency has been defined. The theoretical and experimental justification of this model has been extensively discussed in [227]. With both the phase and the complex Rabi frequency defined, the steady state force on the moving atom due to the LG laser mode is written in a manner similar to case of electric dipole transitions. As in the case of electric dipole transitions, the dissipative force can now be understood as a result of quadrupole absorptions followed by spontaneous emissions of the light by the atom, while the quadrupole force, which is proportional to the gradient of the Rabi frequency, is responsible for confining the atom to the maximal or minimal intensity regions of the field, depending on the detuning Δklp. The quadrupole force is derivable from a quadrupole potential

In experimental situations where we have large detuning  , the quadrupole potential can be written to a good approximation as
, the quadrupole potential can be written to a good approximation as

It is clear from the above expressions that if we wish to compare the corresponding expressions for forces and potentials in the electric dipole and electric quadrupole transitions, we need to investigate the modulus squared Rabi frequency  , which is rather different from the corresponding case in electric dipole transitions.
, which is rather different from the corresponding case in electric dipole transitions.
For illustration, we now consider the case of an LG donut mode of winding number l, but for which p = 0. In this case, the derivative in  in equation (183) is equal to zero, since
in equation (183) is equal to zero, since  is a constant for all l. We also assume that the atom is constrained to move in the X–Y plane and the quadrupole transition is such that
is a constant for all l. We also assume that the atom is constrained to move in the X–Y plane and the quadrupole transition is such that  . this can occur for example in a
. this can occur for example in a  transition. In this case, the Rabi frequency equation (182) takes the following simpler form,
transition. In this case, the Rabi frequency equation (182) takes the following simpler form,
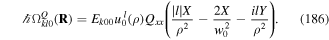
Expressing lengths in units of w0, so that  , etc, we find for the modulus square of the Rabi frequency entering the dissipative force
, etc, we find for the modulus square of the Rabi frequency entering the dissipative force

The topology of the Rabi frequency will be imprinted in the topology of the quadrupole potential in the case of large detuning. It is interesting to explore the relevant depth and the spatial structure of the trapping potential given by equation (185) and how these are affected by the choice of the vortex and atomic parameters. To be specific, we consider Cs as an atom recently explored for its quadrupolar transition  , specifying the de-excitation rate ΓQ and a quadrupolar matrix element Qxx. The optical vortex is such that the amplitude E000 is related to the intensity by
, specifying the de-excitation rate ΓQ and a quadrupolar matrix element Qxx. The optical vortex is such that the amplitude E000 is related to the intensity by  . We also need a suitable value for the detuning Δ and, since we wish to maximise the quadrupolar effects we take a large value of winding number l. The parameters are
. We also need a suitable value for the detuning Δ and, since we wish to maximise the quadrupolar effects we take a large value of winding number l. The parameters are 
 and
and 
 It is also convenient to define a scaling parameter Ω0 as follows
It is also convenient to define a scaling parameter Ω0 as follows
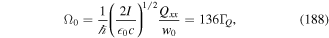
where the last equality emerges on substituting the relevant parameters defined above. Figure 31 displays the quadrupole potential and the corresponding contour plots in two different cases namely when l = 3 and l = 300. Experimentally, winding numbers as large as l = 300 can be achieved, as emphasised in [228]. The trapping potentials are given in absolute temperature units. It is obvious that the increase of the winding number l gives a deeper trapping potential. From the contour plots, we also see a different spatial structure of the potential. As l increases, we obtain two crescent-like trapping regions. This spatial structure can be explained by an analysis of equation (187) on substituting for  , expressed in terms of the dimensionless variables. In the large l case, we have a distribution with two regions of variation and there are high symmetry points. To identify the dependence on l, we consider the points
, expressed in terms of the dimensionless variables. In the large l case, we have a distribution with two regions of variation and there are high symmetry points. To identify the dependence on l, we consider the points  , the expression between the curly brackets in
, the expression between the curly brackets in  becomes equal to l2, while at the points
becomes equal to l2, while at the points  the curly bracket reduces to
the curly bracket reduces to  , both of these observations effectively scale as l2 for large l. We have also verified that the maxima and minima of
, both of these observations effectively scale as l2 for large l. We have also verified that the maxima and minima of  actually occur at the following
actually occur at the following  points
points

It is seen that the positions where the Rabi frequency maximises are different from those in the case where we have an electric dipole transition. In this case, the Rabi frequency maximises at points where  . The reason is that the strength of the electric quadrupole interaction depends on the gradient of the electric field. Thus, such an interaction can be maximum even at points where the electric field and thus the intensity are zero [229]. This counter-intuitive observation has been demonstrated in an experiment where a single ion was positioned at different locations inside an optical cavity [230].
. The reason is that the strength of the electric quadrupole interaction depends on the gradient of the electric field. Thus, such an interaction can be maximum even at points where the electric field and thus the intensity are zero [229]. This counter-intuitive observation has been demonstrated in an experiment where a single ion was positioned at different locations inside an optical cavity [230].
Figure 31. The quadrupole potential and the corresponding contour plots for two cases: (a) and (b) for l = 3, (c) and (d) for l = 300. Data as given in the text.
Download figure:
Standard image High-resolution imageThe depth of the quadrupole trap is sufficiently large to lead to the trapping of atoms. Moreover, as our analysis has shown the photon scattering rate is very low, so ensuring long trapping lifetimes. This means that the interaction of LG light with an atom in a quadrupole-allowed transition can lead to significant mechanical effects on the atoms. The facility to generate LG light in the laboratory with large values of l [228] indicates that the quadrupolar mechanical effects should be amenable to experimental verification.
It seems reasonable to suggest that a further enhancement of quadrupolar vortex interactions could be achieved by placing the atoms near the surface of plasmonic structures and arranging the generation of surface plasmonic modes endowed with the vortex properties. Dipole allowed transitions are subject to strong enhancement under these conditions.
13. Mechanical effects for large l and p
The study of the mechanical effects of LG beams with atoms has mostly been limited to cases of the lowest values of the winding number l. Furthermore, studies have ignored modes with non-zero values of the radial mode index p. As pointed out earlier, advances in technology and experimental techniques for the generation of twisted light have recently made possible the realisation of LG beams with very large values of both the winding number l and the radial index, p [231, 232]. The radial index p has in fact been dubbed as the 'ignored' quantum number, although its role in quantum communications has been emphasized in [228] and a quantum mechanical theory featuring the effects of p has been presented [233]. As the current experimental activity on the production of optical vortices with extremely large values of l and p continues [231, 232], we expect that more light will be shed on the physical role of the radial index p. For example, it has been suggested that LG beams with high values of p can be exploited in the creation of concentric cylindrical lattices which can offer a platform for the exhibition of quantum Hall physics with cold atoms [157].
It turns out that in the study of the mechanical effects of LG light on atoms the consideration of large l and p values brings to the fore optical phase terms, which have so far been discarded because for small l and p values they are justifiably negligible. We show here that considerable modifications arise in the physics involving atomic gross motion primarily because the radiation forces exerted by the light on the atoms are modified. The modifications stem from phase gradients originating from the beam curvature and the Gouy phase most prominently near the focus plane of the LG light mode. Both the Gouy and the curvature phase terms have so far been ignored in the analysis, with the Gouy phase strongly dependent on the values of l and p.
The Gouy phase is a basic property of all focused beams. Although frequently discussed with reference to focused light beams, it is also known to arise in the cases of focused acoustic and electron beams. It was first discovered over 11 decades ago by Gouy who made direct measurements in the case of optical beams [234, 235]. Over the years, the Gouy phase has been shown to play significant roles in a number of contexts as described in the interesting paper by Feng and Winful [236] who provided a physically transparent interpretation of the Gouy phase as originating from the in-plane spatial confinement of the focused beam. Hariharan and Robinson have given another explanation of the Gouy phase as a geometrical quantum effect which arises as a result of the uncertainty principle whenever there is a modification of the volume of space in which the light beam is transmitted [237]. One of the most prominent manifestations of the Gouy phase is in the context of optical tweezers, where it plays a role in the in-plane trapping of particles and leads to super-luminal phase velocities vϕ at focus. This suggests a sub-luminal group velocity vg of the light in vacuum which is in conformity with the product rule vϕvg = c2. Recent experiments suggest that light in vacuum travels at sub-luminal speeds for all beams, including Gaussian, Hermite-Gaussian and LG ones, which are endowed with lateral intensity spread. Of course, light only has its normal speed c in vacuum when propagating in the form of a plane wave [238].
13.1. Gouy phase and beam curvature effects
The mechanical effects of the Gouy and curvature phase terms on the gross motion of two-level atoms have been explored by Lembessis and Babiker [239]. The outlines of their arguments are as follows. In the paraxial approximation the electric field associated with a LG mode, of wavelength  propagating in the z-direction and polarised in the x−direction is given by equations (52)–(54). In equation (54), the third term is identified as the Gouy phase term, namely
propagating in the z-direction and polarised in the x−direction is given by equations (52)–(54). In equation (54), the third term is identified as the Gouy phase term, namely
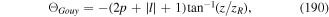
and the curvature term is the last term, namely

The beam is characterised by a wavevector given by  where the gradient of the phase function is given by:
where the gradient of the phase function is given by:
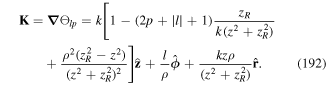
In fact not just the wavevector, but also the Poynting vector expressions are significantly modified compared with the expressions that are valid for low values of the indices l and p provided that we work with parameters that can make the contributions from the Gouy phase equation (190) and the curvature phase equation (191) of appreciable sizes. This conclusion, whilst it introduces additional complexity, suggests that when experimental results are assessed, it may be important to consider such effects if simpler formulations give imprecise agreement.
13.2. Modified radiation pressure forces
Recall that radiation pressure gives rise to two distinct forces, namely the dissipative force and the dipole force. In the saturation limit where  , the dissipative force can be approximated to
, the dissipative force can be approximated to
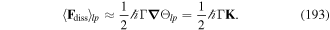
Consider the situation in which the atoms move near the focus plane of the LG mode such that z ≪ zR. In this case, the wave-vector of the beam K takes the following effective form

When the gradient terms originating from the Gouy phase and the curvature phase terms are considerable in size, they amount to an effective axial wavevector denoted by keff, so that the phase gradient in the vicinity of the focus plane can be written as
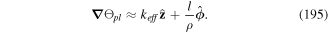
The above relations show clearly that the axial wavevector is modified from k to keff. In the specific case p = 0 and making use of the relation  we find that the winding number l should be close to (kw0)2 and since, kw0 ≫ 1, only LG beams with large value of l could exhibit a non-negligible effect, i.e. such that keff differs significantly from k.
we find that the winding number l should be close to (kw0)2 and since, kw0 ≫ 1, only LG beams with large value of l could exhibit a non-negligible effect, i.e. such that keff differs significantly from k.
To understand better the relevant size of the modifications we consider the following numerical estimations. Consider an LG mode of wavelength λ = 2π/k = 852.35 nm, with azimuthal and radial indices l = 300, p = 3, respectively. We focus on four different cases of beam waist with respective values  and 20λ , and seek to explore how the effective wavevector keff changes with the radial position r near the focus plane, i.e. in the region at z ≈ 0 of the beam. The plot of keff as a function of radius ρ, scaled in beam waist units, is shown in figure 32 in which we clearly see that keff becomes considerably different from that of k as the beam waist decreases in value. The effect is even more interesting since as we also see for w0 = 3λ the effective axial wavevector keff takes negative values at certain radial positions: the interpretation is that locally the atom 'sees' a beam travelling in the opposite direction. We must, however, be careful in interpreting this scenario since, as has recently been pointed out, when the focusing is very tight the generated LG beam is not a pure state as we have the production of modes with higher and lower winding numbers due to a small field component in the propagation direction, so the above ideal picture does not precisely apply [157, 240].
and 20λ , and seek to explore how the effective wavevector keff changes with the radial position r near the focus plane, i.e. in the region at z ≈ 0 of the beam. The plot of keff as a function of radius ρ, scaled in beam waist units, is shown in figure 32 in which we clearly see that keff becomes considerably different from that of k as the beam waist decreases in value. The effect is even more interesting since as we also see for w0 = 3λ the effective axial wavevector keff takes negative values at certain radial positions: the interpretation is that locally the atom 'sees' a beam travelling in the opposite direction. We must, however, be careful in interpreting this scenario since, as has recently been pointed out, when the focusing is very tight the generated LG beam is not a pure state as we have the production of modes with higher and lower winding numbers due to a small field component in the propagation direction, so the above ideal picture does not precisely apply [157, 240].
Figure 32. The ratio keff/k as a function of the radial position, scaled in beam waist units, for a LG mode of wavelength λ = 852.35 nm and indices l = 300, p = 3. The ratio is given for four different beam waists: w0 = 3λ (dotted), w0 = 5λ (dashed), w0 = 10λ (dotted–dashed) and w0 = 20λ (long dashed). The solid curve is a scaled plot of the intensity highlighting the regions where the beam intensity and thus its mechanical effects on atoms are considerable. The radial distance ρ is scaled in w0 units. Reprinted figure with permission from [239], Copyright (2016) by the American Physical Society.
Download figure:
Standard image High-resolution imageA direct consequence of the modification of the axial wavevector is that the dissipative force on a two-level atom is also modified. In the saturation limit, this force is now given by:
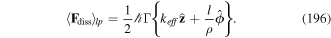
Note that the axial  dissipative force, which in the absence of the anomalous Gouy and curvature phases is known to be given simply by
dissipative force, which in the absence of the anomalous Gouy and curvature phases is known to be given simply by  , is now modified by the inclusion of the additional phase terms By contrast, these phase anomalies have no effect on the azimuthal
, is now modified by the inclusion of the additional phase terms By contrast, these phase anomalies have no effect on the azimuthal  force component. The analysis shows that, since the effective wavevector is nullified on critical radial distances and changes its sign from negative to positive around them, there may be novel ways to handle atoms via LG light beams. A light beam can decelerate the atomic motion even in the case where it propagates in the same direction with the atom.
force component. The analysis shows that, since the effective wavevector is nullified on critical radial distances and changes its sign from negative to positive around them, there may be novel ways to handle atoms via LG light beams. A light beam can decelerate the atomic motion even in the case where it propagates in the same direction with the atom.
The mechanical effects of light on atom are very sensitive to the Doppler shift experienced by a moving atom. If the atom has a velocity V then the Doppler shift is given by  . This topic has been investigated analytically by Allen, Babiker and Power, [130], so it now seems clear (in view of the discussion in section 8.1) that the Doppler shift too is subject to modifications due to Gouy and curvature phases for highly twisted light and there are also consequences in the context of the dynamics of the optical molasses in such LG beams [241].
. This topic has been investigated analytically by Allen, Babiker and Power, [130], so it now seems clear (in view of the discussion in section 8.1) that the Doppler shift too is subject to modifications due to Gouy and curvature phases for highly twisted light and there are also consequences in the context of the dynamics of the optical molasses in such LG beams [241].
14. Atom vortex beams
So far we have been dealing with optical vortex beams and their effects on atoms, and the key feature of the vortex nature is the angular momentum property. Vortex beams of a different nature have been contemplated, prompted by the creation in the laboratory of electron vortex beams [242, 243]. Electron vortex beams are also endowed with the property of OAM and they are characterized by a wavefunction bearing the phase factor  , as appears in the case of the optical vortex fields. However, there are marked differences in electron vortices (EVs) when compared to optical vortices in that EVs are characterized by the electron mass, electronic charge and electron spin, all of which introduce new effects that are absent in the optical vortex case. Studies of EVs and their interaction with matter are now progressing in both the theoretical and experimental fronts.
, as appears in the case of the optical vortex fields. However, there are marked differences in electron vortices (EVs) when compared to optical vortices in that EVs are characterized by the electron mass, electronic charge and electron spin, all of which introduce new effects that are absent in the optical vortex case. Studies of EVs and their interaction with matter are now progressing in both the theoretical and experimental fronts.
The concept of a vortex beam should apply to any de Broglie particles and this includes atoms, ions and molecules—provided that each can be produced in the form of an initial well defined ordinary beam—but it is unclear how one can generate the particle vortex in the case of a neutral atom beam. In both optical and EVs, the production relies on the generation of a material computer generated mask and diffraction is the physical process through which the vortex beams are realized.
To create atom vortex beams we need a suitable mask. The use of an optical mask suitably constructed from laser light as a diffracting agent appears at first sight as a reasonable choice. The proposal is that a beam of neutral atoms diffracted from a suitably constructed optical mask at near resonance with an atomic transition should lead to the generation of a discrete set of optical vortex states each endowed with the property of quantized OAM about the beam axis in units of ℏ. We analyse this suggestion and seek to define criteria for the selection of separate atom vortex beams and discuss prospects for potential applications.
When the atoms are cooled their speed is very small: consequently their de Broglie wavelength is large and could be comparable to the laser light wavelength. In this case, the atomic gross motion exhibits a quantum behaviour with a dominant wave-like character. One of the most important effects for the atomic motion where the wave-nature is exhibited is diffraction [43]. This effect occurs whenever the atomic wave-packet interacts with anything that shifts its phase or even its amplitude, through absorption. Diffraction can split the atomic wavefunction into a coherent superposition of momentum and/or angular momentum states. To achieve atomic diffraction atoms are normally sent through a light field with which they interact for a short time, normally smaller than Γ−1 which ensures that the probability of a spontaneous photon emission is negligible. In this case, when the detuning is large, the potential which corresponds to the atom-light interaction is real, acts as a pure phase object and the interaction potential operates as a thin diffraction grating. This is known as the Kapitza-Dirac scattering and occurs in the Raman-Nath limit [244]. Some experiments have shown that similar effects may arise when the interaction time is larger than Γ−1, but in addition we have far-detuning [245].
Over the years, diffraction of electromagnetic fields has played a key role for the generation of electromagnetic waves with a phase topological charge such as the optical LG beams [66]. But diffraction is a general wave effect and is not limited to light beams. It can also be present in matter waves. The production of EV is based on the diffraction of electron waves. The EVs are beams of electrons with a quantised angular momentum along the propagation axis [242, 243, 246]. The creation of such beams has been achieved by passing a plane electron wave through spiral phase plates [247] or holographic masks [248]. The quantised OAM constitutes a fundamentally new electron degree of freedom which could find application in a number of research areas and raises fundamental issues such as the transfer of electron angular momentum to matter [249].
As pointed out above, the proposal for the possible realisation of atom vortex (AV) beams using a diffracting element sprang from this background. Prior to this there were a few theoretical works dealing with atom diffraction. First it was shown that atom diffraction through a cylindrical optical lattice with a petal-like structure could give rise to AV beams with opposite winding numbers [250]. Subsequently, it was shown theoretically that the existence of atom Bessel beams was possible [251].
This was followed by the experimental creation of a Bessel beam of de Broglie matter waves [252]. The Bessel beam was produced by the free evolution of a thin toroidal atomic BEC which has been set into rotational motion.
The proposal of AV beams from free atoms involved similar ideas to those used in the generation of EV beams [253]. By free atoms we mean atoms in the form of a beam (thermal, BEC, etc) that propagates in free space and is diffracted by a properly tailored light field (a light mask). The short interaction time during the diffraction results in a phase imprint on the atomic wave function [254]. In a recent report, it has been shown that on using a light mask with a spiral like intensity pattern the diffraction gives rise to AV beams. These could be used as a mechanism for the generation of atomic Ferris wheel beams [255] whereby the diffraction involves a spiral-like light mask, which plays a role similar to that played by a spiral-like phase plate for the production of vortex light and electron beams [256]. The new element here is, as is the case with the OV and EV beams, that the generated AV beams are focused at different points along the beam propagation axis. By properly focusing these beams it is possible to make them interfere. The interference of two AV beams with opposite winding numbers leads to atom Ferris wheel beams. These are the atomic counterparts of the optical Ferris wheel beams with the characteristic petal-like transverse intensity patterns [100]. In what follows, we discuss the creation of atom vortex beams first by using fork-like light masks followed by the case of spiral light masks.
14.1. Diffraction through a fork-like light mask
The creation of a fork-like mask is achieved when we interfere a LG beam with a Gaussian (G) beam. The propagation direction of the G wave is considered to be slightly tilted at an angle β with respect to z-axis. Both beams are assumed to be polarised along the y-direction. The electric field of the G beam is given by
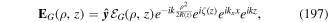
where  with EG,0 being the Gaussian wave amplitude. The total electric field of this configuration is:
with EG,0 being the Gaussian wave amplitude. The total electric field of this configuration is:
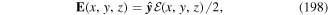
where  is the field distribution given by the sum
is the field distribution given by the sum
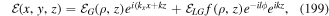
where  with l the winding number of the LG mode and the function
with l the winding number of the LG mode and the function ![$f(\rho ,z)\,={[1+{z}^{2}/{z}_{R}^{2}]}^{-1/2}{\left(\tfrac{\rho \sqrt{2}}{w(z)}\right)}^{| l| }{e}^{-{\rho }^{2}/w{(z)}^{2}}$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn397.gif) . The above field is characterised by an intensity I, which is proportional to
. The above field is characterised by an intensity I, which is proportional to  . Explicitly, at z = 0, we have:
. Explicitly, at z = 0, we have:
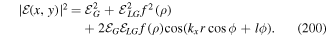
It is instructive at this stage to consider the following numerical example. We assume that the LG beam has a beam waist wLG,0 = 15 μm. The winding number of the LG beam is taken as l = 1 and its power is 81 μW. Both beams have wavelength λ = 589.16 nm. This is the wavelength which can excite the  transition in a Na atom which has a saturation intensity IS = 64 W m−2. The Gaussian beam has a beam waist equal to wG,0 = 200 μm and its power is 8.2 mW. The G beam propagation direction is tilted at an angle equal β = 50 with respect to the LG beam propagation direction. The spatial distribution of the total intensity is displayed in figure 33.
transition in a Na atom which has a saturation intensity IS = 64 W m−2. The Gaussian beam has a beam waist equal to wG,0 = 200 μm and its power is 8.2 mW. The G beam propagation direction is tilted at an angle equal β = 50 with respect to the LG beam propagation direction. The spatial distribution of the total intensity is displayed in figure 33.
Figure 33. Intensity of the total light field (at z = 0) made up by the interference of the LG beam with a tilted Gaussian wave. The LG beam has a beam waist wLG,0 = 15 μm. The winding number of the LG beam is taken as l = 1 and its power is 81 μW. Both beams have wavelength λ = 589.16 nm. This is the wavelength which can excite the  transition in a Na atom which has a saturation intensity IS = 64 W m−2. The Gaussian beam has a beam waist equal to wG,0 = 200 μm and its power is 8.2 mW. The G beam propagation direction is tilted at an angle equal β = 50 with respect to the LG beam propagation direction. The inset displays the corresponding contour plot.
transition in a Na atom which has a saturation intensity IS = 64 W m−2. The Gaussian beam has a beam waist equal to wG,0 = 200 μm and its power is 8.2 mW. The G beam propagation direction is tilted at an angle equal β = 50 with respect to the LG beam propagation direction. The inset displays the corresponding contour plot.
Download figure:
Standard image High-resolution imageA two-level atom interacting with the above field has a Rabi frequency  , which at z = 0 is given by,
, which at z = 0 is given by,
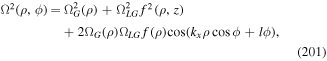
where  and
and  . On interacting with the mask field, the atom experiences an optical dipole potential. In the case of far detuning such that Ω/Δ ≪ 1, we have for the dipole potential
. On interacting with the mask field, the atom experiences an optical dipole potential. In the case of far detuning such that Ω/Δ ≪ 1, we have for the dipole potential
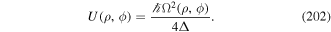
The dipole potential acts on the atom in its ground state and results in the diffraction of the atom over a short interaction time τ. We assume that the atom enters the potential at the time t = −τ and its state function at that instant is Ψ(ρ, ϕ, −τ). After the diffraction process, the atomic state function is at time t = 0 and is given by
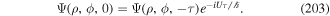
On substituting for U from equation (202), we have
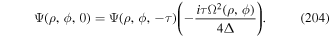
The physical interpretation of the above expression is that the diffraction process through the optical potential over the short period of time τ is in the form of a phase imprint on the initial wave function [256]. This is the basic principle of vortex sorting in BECs. Substituting for Ω from equation (201), we have
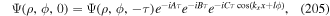
where A, B and C are functions of ρ only and are defined by
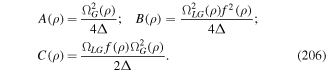
The last exponential factor involving dependence on kx and ϕ can be expressed as a sum over Bessel functions Jn(z) using the Jacobi–Anger identity, namely

We obtain
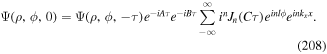
The initial state function of the atoms prior to entering the interaction region (i.e. at time t = −τ) is best discussed with reference to a practical scenario involving a cold atomic wavepacket. Such a wavepacket is considered to have a transverse Gaussian profile with a typical cross-section of dimensions of the order of tens of microns. Thus, we can write
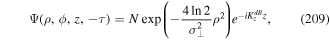
where  is the transverse size of the atomic wavepacket, KdBz is the atomic wavevector along the z-direction and N is a normalisation factor.
is the transverse size of the atomic wavepacket, KdBz is the atomic wavevector along the z-direction and N is a normalisation factor.
Equation (208) shows that the atomic state function is made up of a series of atom vortex states each labelled by the index n = 0, ±1, ±2, .... and each is endowed with angular momentum nlℏ propagating at an angle θn relative to the z-axis given by
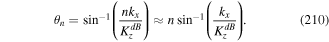
The central component is such that n = 0, which is an Airy-type state function and carries no angular momentum. Explicitly, we have

while the first order states are those for which n = ±1
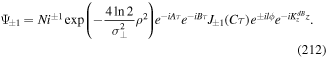
These state functions correspond to atomic beams carrying orbital angular momenta ±lℏ. Note that lℏ is the OAM of the LG beam which was required to construct the fork pattern. This angular momentum is seen here as having been transferred to the atomic beams to the lowest diffraction order. The situation is depicted schematically in figure 34. For practical purposes, it is desirable to be able to ensure that the atomic vortex beams are well separated, with minimum or no overlap. This requirement clearly depends on the parameters used to generate the diffraction pattern and the amplitude of a given component depends on the initial state and the corresponding Bessel function. The process described above is in fact a Raman-Nath diffraction and there are certain criteria in which the Raman-Nath regime applies, namely (i) that the width of the initial atomic beam must be large compared with the spatial extent of the diffracting potential and (ii) that the transverse kinetic energy of the atoms as they enter the diffraction region should be smaller than the maximum energy of the atom-light field interaction.
Figure 34. (a) Diffraction of the atoms through the light mask involving an LG donut beam of winding number l = 2. The LG beam travels along the z-axis and the tilted beam is in the (x, z) plane in a direction tilted with respect to the LG beam. (b) After the diffraction process different atom vortex states are shown separated in space and are labelled n = 0, ±1, ±2, ... with the nth vortex carrying orbital angular momentum nlℏ. Reprinted figure with permission from [253], Copyright (2014) by the American Physical Society.
Download figure:
Standard image High-resolution image14.2. Diffraction through a spiral light mask
The creation of a spiral mask is achieved when a Gaussian beam is passed through a thin lens of width d, refractive index n and focal length f. Then the electric field of the Gaussian beam is given by:
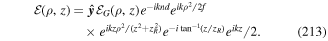
On interference of this beam with a LG donut beam l, p(=0), we have for the total electric field:
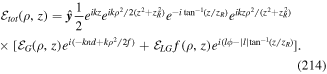
This field has an intensity proportional to the  , which at z = 0 is given by:
, which at z = 0 is given by:
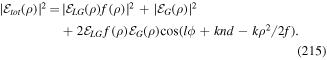
The intensity of this light field has a spiral profile in the transverse plane, as illustrated by the following numerical example. We assume that both beams have equal beam waists w0 = 15 μm, equal wavelengths λ = 1 083.33 nm. The Gaussian beam has a power of 0.3 μW while the LG beam has a power 1.4 μW. The wavelength corresponds to the transition  in the 4He atom. The winding number of the LG beam is l = 2, while the lens is characterised by the following parameter values: d = 0.5 mm and f = 100 μm. The intensity of the total light field with the characteristic spiral transverse profile is presented in figure 35.
in the 4He atom. The winding number of the LG beam is l = 2, while the lens is characterised by the following parameter values: d = 0.5 mm and f = 100 μm. The intensity of the total light field with the characteristic spiral transverse profile is presented in figure 35.
Figure 35. Intensity of the total light field (at z = 0) made up by the interference of the LG beam with the G beam. The inset to this figure shows the corresponding contour plot. The parameters used are as follows. Both beams have equal beam waists w0 = 15 μm, equal wavelengths λ = 1 083.33 nm. The Gaussian beam has a power of 0.3 μW while the LG beam has a power 1.4 μW. The wavelength corresponds to the transition  in the 4He atom. The winding number of the LG beam is l = 2, while the lens has d = 0.5 mm and f = 100 μm.
in the 4He atom. The winding number of the LG beam is l = 2, while the lens has d = 0.5 mm and f = 100 μm.
Download figure:
Standard image High-resolution imageThe atom interacting with the above field experiences a potential given in equation (202) with a Rabi frequency Ω(ρ, ϕ) whose square modulus is given by
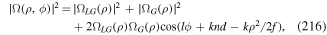
where  and ΩLG(ρ) = ΩLG,0f(ρ).
and ΩLG(ρ) = ΩLG,0f(ρ).
In the scheme shown in figure 36, a BEC which has been released from a trap moving in free space is directed towards the light mask and made to interact with it for a short time interval and gets diffracted by the optical dipole potential. We assume that the BEC initially occupying the ground state of the trap and immediately after its release enters the interaction region at time t = −τ. To a good approximation, the condensate wave-function can be considered as a Gaussian one as described in equation (209).
Figure 36. Scheme of the diffraction set up. (a) Schematic representation of the diffraction of the atoms through the light mask made up of a Laguerre–Gaussian beam interfering with a Gaussian beam; (b) after the diffraction process the different atom vortices are focused at different planes along the propagation axis and are labelled m = 0, ±1, ±2, ... with the mth vortex carrying an orbital angular momentum equal to lmℏ. Reprinted figure with permission from [253], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageAfter the diffraction, the atomic wave function acquires a phase imprint and so has the form,
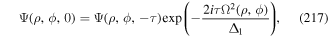
where Δ1 = ωL1 − ω0. Using equation (216) and the Jacobi–Anger equation, this becomes:
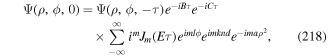
where  and
and  . The diffraction pattern consists of AV beams, with a quantised angular momentum along z-direction equal to mℏ. These AV beams are focused at the points mπ/λa = mf along the z-axis. This is a rather simpler diffraction pattern than that in the case of the fork-like mask described in the previous subsection. Here, the different AV beams are in focus in different planes along the propagation direction, while in the fork-like mask case they propagate in different directions. Equation (218) indicates that the diffraction pattern is made up of a term Ψ0 with no OAM content and different diffraction orders of opposite winding numbers Ψ±m which means there is a quantized OAM mℏ along the propagation axis.
. The diffraction pattern consists of AV beams, with a quantised angular momentum along z-direction equal to mℏ. These AV beams are focused at the points mπ/λa = mf along the z-axis. This is a rather simpler diffraction pattern than that in the case of the fork-like mask described in the previous subsection. Here, the different AV beams are in focus in different planes along the propagation direction, while in the fork-like mask case they propagate in different directions. Equation (218) indicates that the diffraction pattern is made up of a term Ψ0 with no OAM content and different diffraction orders of opposite winding numbers Ψ±m which means there is a quantized OAM mℏ along the propagation axis.
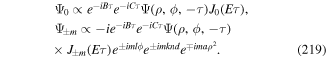
The two AVs with opposite angular momenta  are defocused over mf and
are defocused over mf and  respectively.
respectively.
The spiral diffraction scheme could be exploited for the generation of an atom Ferris wheel beam [255]. This is the atomic counterpart of the light Ferris wheel beam because the probability distribution at a plane transverse to the atomic propagation direction has a characteristic petal-like structure similar to the optical Ferris wheel transverse intensity pattern [100]. The fact that the generated AVBs are all focused on a straight line is the main advantage of the spiral diffraction scheme. If we can shift the focus of one AVB with winding number  , without disturbing the focus of all the other AVBs, then we can make it interfere with the AVB of winding number +m and generate the atom Ferris wheel. This can be achieved by the interaction of a suitably tailored vortex light field which can cause a second phase imprint on the AVB with winding number
, without disturbing the focus of all the other AVBs, then we can make it interfere with the AVB of winding number +m and generate the atom Ferris wheel. This can be achieved by the interaction of a suitably tailored vortex light field which can cause a second phase imprint on the AVB with winding number  . This imprint does not act on the other AVBs if we apply a spatially inhomogeneous magnetic field that makes all the rest of the AVBs very far detuned from the light field, so the associated phase shift is negligible.
. This imprint does not act on the other AVBs if we apply a spatially inhomogeneous magnetic field that makes all the rest of the AVBs very far detuned from the light field, so the associated phase shift is negligible.
The realization of atom vortex beams would open up a new area of atom optics in which atoms carrying OAM interact with each other, or with other forms of matter. Further theoretical studies and various applications should be anticipated including atom interferometry; the functioning of LG light mask as a dispersive prism for de Broglie wavelengths; the encoding and processing of quantum information in atom vortex states entangled with other states such as motional or spin atomic states; the interference of atomic vortices with opposite winding numbers and building quantum entanglement in the infinite dimensional Hilbert space of atom vortex states.
15. Artificial gauge fields and their origins
The significant advances made in the cooling and trapping of atomic motion have had impact on diverse branches of modern physics. In particular, there have been related activities in condensed matter physics [43]. This is mainly due to the possibility of engineering different forms of optical lattices which led to the creation of new synthetic condensed matter [257] paving the way to the demonstration of exotic topological phases of such systems [258]. Such applications involving light–matter interactions are a part of a broader area of investigation in modern physics, namely quantum simulations.
Quantum simulations are a striking vindication of Feynman's prophecy that instead of modelling quantum effects with the help of conventional computers we might use simple and controllable quantum systems as quantum simulators [259]. One area of physics where quantum simulations have found application is condensed matter physics. Many condensed matter effects are very hard to simulate on a classical computer, including high-temperature superconductivity and quantum magnetism. Computer simulations are specially hard in cases where electrons are strongly interacting.
Cold atoms interacting with coherent light fields are ideal quantum simulators for such cases since some of the parameters involved in the interaction can be engineered almost at will to suit a given model [260, 261]. The Hubbard model and the superfluid Mott-insulator transition are two famous examples of problems that can be simulated with cold atoms in optical lattices [262, 263]. One of the major problems of quantum simulations is the fact that atoms are electrically neutral. Therefore, it is, at first sight, quite difficult to simulate effects involving interactions with electric and magnetic fields. Over the last decade, schemes have been developed that can generate artificial Abelian and non-Abelian magnetic and electric fields when cold atoms interact with coherent light fields [264].
15.1. Two-level atoms
Currently there are different schemes which have been shown to lead to the generation of artificial magnetic and electric fields when atoms either in free space or when trapped in optical lattices interact with suitably structured light fields [257]. In the case of free atoms, their interaction with the light results in an atomic motion that mimics that of a charged particle subject to a magnetic field. This means that the atom is subject to a Lorentz-like force [264] causing the atom to move along a closed path. How does this type of motion arise? The physical origin of this force is the creation of a Berry phase acquired by a particle moving in a closed path [265]. The realisation of artificial magnetism requires the engineering of situations where a neutral particle is made to acquire a geometrical phase when it moves along a closed path C. Thus the focus turned to the Berry phase effect in atom-light interactions [266, 267]. In this case, the atom-light coupling gives rise to the so-called dressed states [268]. These states vary on a short spatial scale (typically the wavelength of light) and so the generated artificial gauge fields can be quite intense.
Consider an atom prepared in a dressed state  moving sufficiently slowly to follow adiabatically the local dressed state
moving sufficiently slowly to follow adiabatically the local dressed state  . On completing the trajectory C, it returns to the dressed state
. On completing the trajectory C, it returns to the dressed state  having acquired a phase factor that contains a geometric component. The quantum motion of the atom is formally equivalent to that of a charged particle in a static magnetic field. Such models have been studied for different beam configurations for two-level as well as three-level atoms [264]. It is important to note that the emergence of these artificial fields requires a coherent interaction between the light fields and the atoms. Thus, the interaction time must be limited in values t < Γ −1, with Γ being the spontaneous emission rate of the excited state.
having acquired a phase factor that contains a geometric component. The quantum motion of the atom is formally equivalent to that of a charged particle in a static magnetic field. Such models have been studied for different beam configurations for two-level as well as three-level atoms [264]. It is important to note that the emergence of these artificial fields requires a coherent interaction between the light fields and the atoms. Thus, the interaction time must be limited in values t < Γ −1, with Γ being the spontaneous emission rate of the excited state.
It is well established that if we make the assumption that the particle is initially prepared in the internal dressed state  and proceeds in an adiabatic elimination of the state
and proceeds in an adiabatic elimination of the state  then the interaction of the atom with the light field is formally equivalent to the motion of a charged particle in a vector field
then the interaction of the atom with the light field is formally equivalent to the motion of a charged particle in a vector field  and a scalar field V(R) given by [268]
and a scalar field V(R) given by [268]
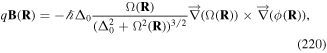
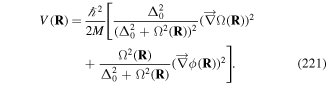
Here, Ω(R) is the Rabi frequency and ϕ(R) is the phase of the coherent light field. Note that the generation of an artificial vector field B demands that both the amplitude and the phase of the electric field have a spatial dependence and that a scenario where an atom is initially prepared in the state  instead of
instead of  will result in the same scalar potential energy V but opposite magnetic field B(R). The scalar potential V can be interpreted as the kinetic energy associated with the fast micromotion of the particle. This was first explained for a classical continuous internal degree of freedom by Aharonov and Stern [269]. The magnetic field is related to the Berry's phase that appears when a quantum system, here the two-state system associated with the internal degree of freedom of the particle, is slowly transported round a contour C, while remaining in one of the eigenstates of its Hamiltonian [265].
will result in the same scalar potential energy V but opposite magnetic field B(R). The scalar potential V can be interpreted as the kinetic energy associated with the fast micromotion of the particle. This was first explained for a classical continuous internal degree of freedom by Aharonov and Stern [269]. The magnetic field is related to the Berry's phase that appears when a quantum system, here the two-state system associated with the internal degree of freedom of the particle, is slowly transported round a contour C, while remaining in one of the eigenstates of its Hamiltonian [265].
The above theory is valid in the case where the light-atom coupling strength is far larger than the recoil energy associated with the exchange of a photon between the atom and the light field, i.e,  . However, when we consider the interaction of an atom with an optical vortex we need to take into account the fact that the processes of exchange between light and matter involve both linear and orbital-angular momentum. The recoil energy in this case is given by:
. However, when we consider the interaction of an atom with an optical vortex we need to take into account the fact that the processes of exchange between light and matter involve both linear and orbital-angular momentum. The recoil energy in this case is given by:

The second term in equation (222) is due to the angular momentum exchanged for an atom localised at a radial position ρ from the beam axis. At first sight, it seems that this angular momentum should be considerably large at small radial positions. However, an LG beam has a dark core at small radial positions and thus the probability of an interaction between the beam and the atom near the core is negligibly small. The interaction probability is considerable at regions where the vortex beam intensity is large. For a LG beam, with p = 0, the intensity is maximum at the radial coordinate  where the ratio of the values of the angular to the translational recoil kinetic energy terms is equal to
where the ratio of the values of the angular to the translational recoil kinetic energy terms is equal to  . It is easy to see that this ratio becomes larger as either the angular momentum lℏ carried by the vortex photon becomes larger, or the beam waist w0 becomes smaller. For the parameters and the particular atom interactions which we focus on here, the rotational recoil energy is negligible but it can be comparable to the translational recoil energy for smaller beam waists (tighter focusing) and high winding numbers.
. It is easy to see that this ratio becomes larger as either the angular momentum lℏ carried by the vortex photon becomes larger, or the beam waist w0 becomes smaller. For the parameters and the particular atom interactions which we focus on here, the rotational recoil energy is negligible but it can be comparable to the translational recoil energy for smaller beam waists (tighter focusing) and high winding numbers.
Consider next the case where the two-level atom is irradiated by a monochromatic LG beam propagating along the z-direction and plane-polarised, say, along the x-direction. In this case the atom, which is considered to be near the focus z = 0, experiences the following artificial vector field:
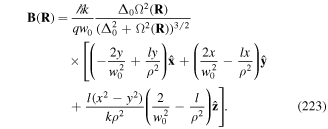
The above artificial magnetic field vector has three components which appear to have a complex position dependence. But the field expressions can fortunately be simplified further. The component Bz along the z-direction has a relatively small size compared to the other two components. This is easily seen because of the dependence on k in the denominator of the Bz expression. Thus, we can safely assume that the artificial magnetic field at focus lies on the (x, y) plane. We can have a more detailed picture of the properties of this field by plotting the magnitude of the magnetic field as well as the corresponding field lines on the (x, y) plane. Figure 37 displays the magnitude of the artificial magnetic field, and the inset to this figure is a vector plot which shows the direction of the generated artificial field. We have assumed that the LG beam has a winding number l = 1. In figure 38, we also display the artificial gauge magnetic field for a Gaussian (G) beam of the same power and beam waist. The light beams have a wavelength λ = 852 nm and so can excite the transition  in a 133Cs atom which has an excited state transition rate Γ = 2π × 5.15 MHz. We assume that both beams have the same power, and a beam waist equal to 150 μm. The interaction is characterised by a detuning Δ0 = 2.5Γ and a Rabi frequency Ω0 = 9Γ. All the plots shown below have been generated using the same parameters, where the magnetic field is in units of
in a 133Cs atom which has an excited state transition rate Γ = 2π × 5.15 MHz. We assume that both beams have the same power, and a beam waist equal to 150 μm. The interaction is characterised by a detuning Δ0 = 2.5Γ and a Rabi frequency Ω0 = 9Γ. All the plots shown below have been generated using the same parameters, where the magnetic field is in units of  .
.
Figure 37. Artificial magnetic field magnitude for a two-level atom (transition  in a 133Cs atom) irradiated by a LG beam with l = 1, while Ω0 = 9Γ and Δ = 2.5Γ. The magnetic field is in units of
in a 133Cs atom) irradiated by a LG beam with l = 1, while Ω0 = 9Γ and Δ = 2.5Γ. The magnetic field is in units of  .
.
Download figure:
Standard image High-resolution imageFigure 38. Artificial magnetic field magnitude for a two-level atom (transition  in a 133Cs atom). The atom is irradiated by a G beam while Ω0 = 9Γ and δ0 = 2.5Γ. The magnetic field is in units of
in a 133Cs atom). The atom is irradiated by a G beam while Ω0 = 9Γ and δ0 = 2.5Γ. The magnetic field is in units of  .
.
Download figure:
Standard image High-resolution imageFrom the comparison of the two figures, namely figure 37 and figure 38, it may be deduced that the magnitude of the artificial magnetic field for a LG is larger than that for a G beam. Note, however, that as the beam winding number l increases the magnitude of the generated artificial magnetic field decreases. The magnetic field in the case of the G beam has a cylindrical symmetry with a maximum ring area. In the case of LG beam the magnetic field has cylindrical symmetry but there are two concentric rings. Moreover, the direction of the field is opposite in the two rings and can be reversed with a change of the beam winding number from l to −l. It seems that the LG beams offer more possibilities for artificial magnetic field generation. There is thus the possibility of using artificial magnetic fields generated by LG beams for the creation of extended regions where the orbital magnetism can be be sufficiently strong to generate states of non-zero circulation. This is desirable in cases where a superfluid is placed in such regions in order that its ground state will exhibit a vortex lattice. In addition to the artificial magnetic vector field, there is also a scalar artificial potential V given by:
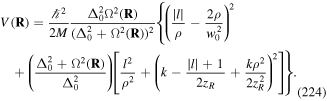
Figure 39 displays the artificial scalar potential in atomic recoil energy units while the inset represents the scalar potential when the same transition is excited by a Gaussian beam with the same power and beam waist. It can be seen that the magnitude of the scalar field generated by a LG beam is smaller than that generated by the interaction of the atom with a G beam. There is however a striking difference, namely the appearance of a donut like profile of the potential in the case of a LG beam, but not in the G case. This means that the potential will affect trapping in a LG beam as much as the artificial magnetic field in the inset affects the trapping in an ordinary Gaussian optical dipole trap.
Figure 39. Artificial scalar field magnitude for a two-level atom (transition  in a 133Cs atom) irradiated by a LG beam. Ω0 = 9Γ and Δ0 = 2.5Γ. The field values are given in recoil energy units.
in a 133Cs atom) irradiated by a LG beam. Ω0 = 9Γ and Δ0 = 2.5Γ. The field values are given in recoil energy units.
Download figure:
Standard image High-resolution image15.2. Three-level atoms
The use of two-level atoms for the creation of artificial gauge fields has a serious drawback arising from the fact the internal state of the atom is everywhere a linear combination of the ground and the excited state. The short lifetime of the excited state imposes a limit on the existence of such potentials. We may overcome this obstacle by considering the so called 'dark sates' which are possible when we consider atoms with a three-level lambda configuration [270–272].
In the lambda configuration, we have two ground states  and
and  , which can be two different hyperfine states of an atom, and an excited state
, which can be two different hyperfine states of an atom, and an excited state  . The atom interacts with two resonant coherent beams. The first one excites the transition
. The atom interacts with two resonant coherent beams. The first one excites the transition  while the second excites the transition
while the second excites the transition  . These excitations are characterized by Rabi frequencies
. These excitations are characterized by Rabi frequencies ![${{\rm{\Omega }}}_{1}({\bf{R}})\,=| {{\rm{\Omega }}}_{1}({\bf{R}})| \exp [{\phi }_{1}({\bf{R}})]$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn438.gif) and
and ![${{\rm{\Omega }}}_{2}({\bf{R}})=| {{\rm{\Omega }}}_{2}({\bf{R}})| \exp [{\phi }_{2}({\bf{R}})]$](https://content.cld.iop.org/journals/2040-8986/21/1/013001/revision2/joptaaed14ieqn439.gif) respectively. In the analysis of the artificial gauge fields with three-level atoms in the lambda-configuration, there are two factors that play important roles, namely the ratio of the two Rabi frequencies ζ and the phase difference of the two beams S. These factors are defined as follows
respectively. In the analysis of the artificial gauge fields with three-level atoms in the lambda-configuration, there are two factors that play important roles, namely the ratio of the two Rabi frequencies ζ and the phase difference of the two beams S. These factors are defined as follows
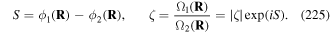
Assuming that the two ground states are at the same energy, we can neglect the two-photon detuning  . In this case the interaction Hamiltonian has two eigenstates—namely the dark one
. In this case the interaction Hamiltonian has two eigenstates—namely the dark one  and the bright one
and the bright one  which are given by:
which are given by:
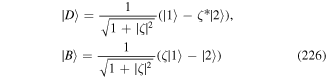
It has been shown that when the atom is in the dark state the artificial vector and scalar fields are given respectively by [271]:
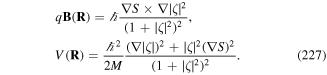
From this, we deduce that there is a non-vanishing artificial magnetic field only when there are non-zero gradients of the relative intensity and phase. This means that such a field cannot be created using plane waves interacting with the three-level atom.
There is a deeper physical meaning of the variables and parameters involved in equation (227). The gradient ∇S is proportional to the relative momentum of the two beams, while  is a vector associated with the centre of mass of the two beams. The suggestion is that to create an artificial magnetic field the two beams must have a relative OAM. This is the key feature of the scheme which has been proposed. Note that the above formalism is valid provided that the atoms move sufficiently slowly to remain in the dark state during their motion. This is the adiabaticity requirement which is formally given by the condition Ω ≫ F with
is a vector associated with the centre of mass of the two beams. The suggestion is that to create an artificial magnetic field the two beams must have a relative OAM. This is the key feature of the scheme which has been proposed. Note that the above formalism is valid provided that the atoms move sufficiently slowly to remain in the dark state during their motion. This is the adiabaticity requirement which is formally given by the condition Ω ≫ F with  the rms (root mean square) Rabi frequency, which characterizes the energy difference of the dark state with the remaining ones, and
the rms (root mean square) Rabi frequency, which characterizes the energy difference of the dark state with the remaining ones, and  , where v is the velocity vector. The adiabatic condition implies that Ω−1 should be much smaller than the time taken by an atom to travel a characteristic length over which the amplitude or the phase of the ratio ζ changes considerably. For atoms moving along the y-axis the relevant length is 1/k ≈ 10−7 m. On the other hand, the Rabi frequency can be of the order of 107 to 108 s−1. Therefore, the adiabatic condition should hold for atomic velocities up to meters per second. These estimations do not take into account the possible lifetime of the dark state due to adiabatic coupling [272].
, where v is the velocity vector. The adiabatic condition implies that Ω−1 should be much smaller than the time taken by an atom to travel a characteristic length over which the amplitude or the phase of the ratio ζ changes considerably. For atoms moving along the y-axis the relevant length is 1/k ≈ 10−7 m. On the other hand, the Rabi frequency can be of the order of 107 to 108 s−1. Therefore, the adiabatic condition should hold for atomic velocities up to meters per second. These estimations do not take into account the possible lifetime of the dark state due to adiabatic coupling [272].
Assume that the two beams are different and carry different orbital angular momenta so they are characterized by wavevectors  , winding numbers l1, l2 and Rabi frequencies Ω1(R), Ω2(R). We then have ζ = Ω1(R)/Ω2(R) and S = lϕ, where l = l1 − l2 is the difference of the beams winding numbers. This scheme generates an artificial magnetic field B given by:
, winding numbers l1, l2 and Rabi frequencies Ω1(R), Ω2(R). We then have ζ = Ω1(R)/Ω2(R) and S = lϕ, where l = l1 − l2 is the difference of the beams winding numbers. This scheme generates an artificial magnetic field B given by:
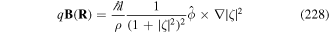
which for fields with a cylindrical symmetry as for LG beams has the final form:
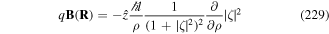
and there is also a scalar potential given by:
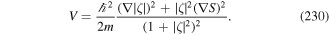
Unfortunately this scheme again suffers from a drawback: namely that the two LG beams are simultaneously zero at points where ρ = 0. Thus the adiabaticity condition is violated. However, the scheme can be adopted when one of the two beams is a LG beam while the other one is Gaussian as shown in figure 40. This then offers the advantage that the effective magnetic field can now be shaped by choosing proper beams.
Figure 40. (a) The energy level scheme for the Λ-type three-level atom interacting with the two beams. (b) Schematic representation of the experimental set-up with the two light beams incident on the cloud of atoms. The first field is of the form  , where each photon carry an orbital angular momentum lℏ along the propagation axis z. Reproduced from [271]. © IOP Publishing Ltd. All rights reserved.
, where each photon carry an orbital angular momentum lℏ along the propagation axis z. Reproduced from [271]. © IOP Publishing Ltd. All rights reserved.
Download figure:
Standard image High-resolution imageConsider an atom irradiated by a LG beam of winding number l and a G beam. In this case, we end up with the following artificial magnetic field:
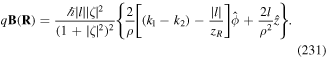
Equation (231) shows that the magnetic field is directed along the beam propagation axis, when the two beams are co-propagating with equal wave numbers so k1−k2 ≈ 0. By contrast, if the beams are counter-propagating then the field has an azimuthal component which dominates over the axial one. However, the azimuthal component comes mainly from the counter-propagating character of the two beams while the axial component comes from the optical angular momentum of the beam.
We now analyse the magnetic field in the case of co-propagating and counter-propagating beams when the two beams irradiate a Cs atom and excite a Λ-transition in the D2 line of the atom, where the common upper level is the 62P3/2 excited state while the two lower levels are the F = 3 and F = 4 hyperfine states of 62S1/2. As we see in figure 41, in the case of counter-propagating fields we obtain a stronger magnetic field which has a hole at the centre. This is not the case in the scenario involving co-propagating beams, but the magnetic field in that case is much weaker.
Figure 41. (Left) The magnetic field arising from the irradiation of a Cs atom by a LG beam and a Gaussian beam which are co-propagating. (Right) The magnetic field when the Cs atom is irradiated by a LG beam and a Gaussian beam which are counter-propagating. The magnetic field is in units of  . The Rabi frequency associated with the LG beam is ΩLG,0 = 9Γ, while the Rabi frequency associated with the Gaussian beam is ΩG,0 = 5Γ.
. The Rabi frequency associated with the LG beam is ΩLG,0 = 9Γ, while the Rabi frequency associated with the Gaussian beam is ΩG,0 = 5Γ.
Download figure:
Standard image High-resolution imageIt has been shown [272] that in this scheme, the effective magnetic flux through a circle of radius ρ0 is given by:
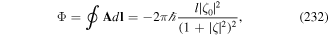
where 2πℏ is the Dirac flux quantum, and  is the intensity ratio at the radius ρ = ρ0. The flux Φ reaches its maximum of 2πℏl if the ratio
is the intensity ratio at the radius ρ = ρ0. The flux Φ reaches its maximum of 2πℏl if the ratio  , i.e. if the intensity of the probe field exceeds the control field at the selected radius ρ0. Since the winding number of the light beams can currently be as large as several hundreds, it is possible to induce a substantial flux Φ in the atomic cloud. This might enable us to study phenomena related to filled Landau levels with a large number of atoms in quantum gases.
, i.e. if the intensity of the probe field exceeds the control field at the selected radius ρ0. Since the winding number of the light beams can currently be as large as several hundreds, it is possible to induce a substantial flux Φ in the atomic cloud. This might enable us to study phenomena related to filled Landau levels with a large number of atoms in quantum gases.
15.3. SOVs
One case where it is possible to achieve the requirement of large gradients which is necessary for the creation of large magnitudes artificial fields is when a SOV interacts with an atom in the vicinity of a dielectric/vacuum interface [273]. As discussed earlier, it is reasonable to adopt a geometrical optics model in which the light beams involved in the total internal reflection, leading to the creation of evanescent light, are specularly reflected at the interface of a dielectric with vacuum—see figure 26. The SOVs are endowed with OAM; they are strongly localised and so have very large field gradients. These gradients depend crucially on the refractive index of the dielectric material and/or the angle of incidence of the laser beam. This gives us more control parameters with which we can monitor the properties of the artificial magnetic fields, specifically their strength and/or their spatial structure. Indeed we can choose a dielectric with a higher index of refraction, a larger angle of incidence as well as the parameters that determine the field magnitude in the free-space case like beam intensity, beam waist, Rabi frequency and detuning. There is also another parameter that will play an important role, namely the beam winding number l. It appears that as l increases the magnitude of the magnetic field increases. This point requires some detailed explanation. As the winding number increases the beam power is spread in a larger area. Thus, the intensity of the beam decreases and so does the Rabi frequency. Thus, the argument that the artificial magnetic fields become stronger as the winding number of the beam increases is true only provided that the Rabi frequency is properly adjusted, either by increasing the intensity or by decreasing the beam waist [274]. The strongest field is created if the incident angle of the plane wave is much greater than the critical angle for the total internal reflection θcr. Then, however, the magnetic field is considerable in a short range in vacuum [273]. This makes difficult to trap atomic clouds sufficiently far away from the surface of the prism-vacuum interface to avoid the influence of the van der Waals interaction between the atom and the dielectric material of the prism.
Artificial magnetic fields have been shown that can be used for creating atomic mirrors [273]. Typically, atom mirrors have been based on the optical dipole potential created by evanescent fields. However, in this context the atoms behave like charged particles inside an artificial magnetic field, thus they follow curved trajectories. If evanescent fields are properly tailored the atoms may be pushed away from the dielectric-vacuum interface due to a Lorentz-like force. Thus, in practice, we will have atom mirrors for three level atoms. In [273], the authors have shown that if a BEC trapped in a MOT is released and under the influence of the gravity is directed towards the prism-vacuum interface then the artificial magnetic field can act to reflect the falling atoms. Their scheme involves the interaction of a three-level atom with two coherent light fields: one an evanescent wave created by the total internal reflection of a Gaussian beam and the other is an ordinary Gaussian beam propagating in free space close to the surface. In the case of three-level atoms, very strong magnetic fields can be created when two Gaussian beams are laterally displaced. These fields can be even larger when the atoms interact with two laterally displaced evanescent fields [177]. It remains to be investigated if and how schemes involving different combinations of SOVs could lead to enhanced artificial gauge magnetic fields.
Artificial gauge fields with twisted beams have been realised in more complicated cases involving a tripod scheme of the light-atom coupling [275, 276]. This is a scheme where three laser beams drive transitions from three ground states to a common excited state. This scheme is interesting in the particular case where two of the beams are circularly polarised with opposite winding numbers l = ±1 propagating along the z-direction, while the third one is linearly polarised along the y-direction and propagates along the x-direction. In this case, the generated artificial magnetic field has a leading term which corresponds to the field of a magnetic monopole at the origin.
Finally, once again, we note that the schemes presented here concern the creation of artificial magnetic fields when twisted beams interact with atoms in free space. Such fields have also been generated for atoms trapped in optical lattices with the possibility of creating very strong artificial magnetic fields. The whole idea is based on the induction of a non-vanishing phase of atoms moving along a closed path on the lattice. This phase, proportional to the enclosed area, allows us to simulate a magnetic flux through the lattice [277]. A scheme with twisted beams based on this idea has been proposed to study realizations of a Hofstadter-Hubbard model on a cylinder geometry with fermionic cold atoms in optical lattices. The authors showed that the cylindrical optical lattices achieved with twisted beams can provide a landscape for the exhibition of fractional quantum Hall physics observed in this set-up [157].
16. Summary, conclusions and outlook
This review has focused on the interaction of atoms with structured light, most notably the case of light endowed with the property of the OAM. The analysis of a wide variety of phenomena has illustrated how interactions with this kind of light can give rise to novel features, entirely distinct from (and in addition to) the phenomena experienced when atoms interact with more conventional forms of laser light. This wide range of new effects includes the controllable transfer of OAM from the light to the centre of mass motion of individual atoms or, under certain circumstances, to internal (electronic-type) motions.
The prospect of engaging OAM with electronic transitions is a matter that has long been of sustained interest, with investigations continuing in both theory and experiment. The potential significance of this issue is brought to a sharp focus on recognizing that, in twisted light, the property of angular momentum is quantitatively different in individual photons. Nonetheless one of the first findings was that OAM cannot be transferred to the internal degrees of freedom of the atom in an electric dipole transitionthough this might occur in connection with the normally much weaker quadrupole transitions. This difference seems now to have been established unequivocally, through a range of experimental and theoretical studies, including the excitation of an electric quadrupole atomic transition involving OAM transfer to a valence electron in a trapped ion. However, the strong symmetry principles that play into the difference between dipole and quadrupole transitions are undermined in molecular systems, which are necessarily of lower symmetry than atoms.
One of the most prominent and striking features emphasised by this review is the optical response of atoms involving azimuthal motion with respect to the input beama response that can only arise due to the OAM of the light. It has been shown how dipole interactions between the light and the atomic centre of mass, with the participation of dipole transitions between energy levels near resonance, lead to optical forces and a light-induced torque. Moreover, the interaction leads to an optical dipole potential acting to trap the atom in well defined regions of maximal intensity, while the optical torque acts to keep them rotating in a ring at the high intensity regionsa phenomenon most readily observed in the simplest donut modes where quantised superfluid behaviour may be manifested.
In more intricate beam configurations, it has been shown that intriguing new effects can arise through the interplay of wave polarisation in multiple beams. The simplest casethe Sisyphus effect in which wave polarization provides a superior mechanism for cooling atoms (as compared to the Doppler mechanism) gains an additional capability when twisted light is deployed. When atomic motion is controlled in the azimuthal direction, co-propagating beams of slightly different frequency give rise to rotating petal-like patterns in a manner similar to a Ferris wheel. Such configurations prove to offer exotic field distributions that can act to trap and transport atoms. Nonetheless, our review has also highlighted some very useful experimental work on the azimuthal Doppler shift, a topic that appears to be worthy of further exploration.
In another range of developments, we have reported advances connected with the response of twisted light to media surfaces, which can lead to SOVs and plasmonic optical vortices and to extraordinary spin in evanescent waves. An OAM-endowed surface mode generated by total internal reflection, like other surface modes, has a small mode volume and can interact strongly with atoms localised in the vicinity of the surface. When ions are trapped in large numbers in such potential energy wells, which are of essentially elliptical shape when donut modes are deployed, the resulting circulation of charge can give rise to a significant current and an associated magnetic field.
Whilst the relatively simple phase property of twisted lightits linear dependence on azimuthal angleis well studied and widely characterized, there are other features of mode structure that we have shown also deserve attention. By analysing in detail the case of LG modesprototypical examples of twisted light, it has been shown that there are subtle and interesting features associated with beam curvature and Gouy phase. These are features that are enhanced for highly twisted modes, especially for atoms localised near the beam waist, where strong field gradients can lead to diminishing optical forcesconceivably even their annulment and/or reversal.
We have also discussed the concept of artificial gauge fields, exploring their application in the context of atom-field interactions whereby cold atoms interacting with coherent light fields constitute effective quantum simulators. Again, distinctive features arise when two- or three-level atoms interact with structured light, including SOVs. The optical engineering of such features is another promising and active area of current research.
On the basis that twisted light beams in many respects represent special forms of de Broglie waves, their concept is clearly generalisable to other de Broglie beams, including elementary particles such as electrons and neutronseven atomic and molecular beams. In the case of neutral atoms as de Broglie waves, it has been shown that generating an atom vortex beam requires the construction of a light mask to diffract atoms into vortex beam states. The predicted atom vortices are still to be realised in the laboratory, as indeed other types of de Broglie vortex beams. However, one can reasonably speculate that their realization would open up a new area of atom optics in which atoms carrying OAM interact with each other, or with other forms of matter.
Further theoretical studies and various applications may be anticipated, including atom interferometry; the functioning of an LG light mask as a dispersive prism for de Broglie wavelengths; the encoding and processing of quantum information in atom vortex states entangled with other states such as motional or spin atomic states; the interference of atomic vortices with opposite helicity, and building quantum entanglement in the infinite dimension Hilbert space of atom vortex states.
Although the main remit of this review has been to highlight the interaction of individual atoms with structured light, larger numbers of atoms can be trapped in ordered arrays known as optical lattices, ideally by the use of holographic optical traps. The possibility of controlled engagement with two or more particles introduces problems that are only readily addressed with particles significantly larger than atoms. For example, micron-sized particles or nanoparticles or groups of particles within groups can be individually and programmably steered by beam-dithering (time-sharing) techniques.
While the obvious problem with atoms is the need to overcome thermal motion, which is only feasible at very low temperatures, another quite different feature can then come into play. Groups of atoms, optically trapped at temperatures sufficiently low that their de Broglie wavelength is less than the mean atomic spacing, can undergo transition into a BEC, in which the whole assembly responds as a system with a single corporate wavefunction. A transnationally cold BEC assembly of atoms can exhibit a limited number of bulk motions [278], and Lembessis and Babiker have shown how the interference of counter-propagating LG beams, with opposite sign so that their torque effects add, can produce rotation [279]. Furthermore, a significant feature of rotating BECs is that they can exhibit vortices. Indeed, this is the most significant kind of bulk behaviour that an essentially localized, rotating assembly can exhibit. Here, the angular momentum conveyed by multiply-connected LG traps enables quantized vortex states to be identified, revealing the distinctive BEC character [280].
In addition to the production of such states through the combined action of several optical vortex beams [281–283], it has also been shown how a single non-paraxial LG beam can excite a superposition of such states [284]. Nonetheless, in most studies of this topic, atomic condensate vortices are engineered without the use of optical vortices, and the subject lies beyond the scope of the present review.
The outlook for the interaction of twisted light with matter seems set to extend in new work to explore different avenues in which either the form of structured light in other forms plays the key ingredient in the interaction, or the matter with which the light interacts is itself considered in different forms. There are rich possibilities to explore in connection with multiple beams in various configurations, especially inviting the development of both theory and experiment for the specific interaction of twisted light with twisted matter in bulk solid-state materials.
Acknowledgments
This review owes much to work with a number of colleagues and former research students and colleagues. The authors wish to acknowledge their valuable contributions. This project was supported by King Saud University, Deanship of Scientific Research, College of Sciences Research Centre.





















































