Abstract
We present the first measurements of the surface magnetic field of a late-M dwarf, LSR J1835+3259, with the help of the full-Stokes spectropolarimetry in the bands of diatomic molecules. Our measurements at different rotational phases of a dwarf yielded one 5σ and two 3σ magnetic field detections. The observational data have been obtained with the LRISp polarimeter at the Keck observatory on 2012 August 22 and 23. These data have been compared against synthetic full-Stokes spectra in the bands of the molecules CrH, FeH, and TiO, which have been calculated for a range of the stellar parameters and magnetic field strengths. Making use of χ2-minimization and maximum likelihood estimation, we determine the net magnetic field strength B (and not flux Bf) of LSR J1835+3259 to ∼5 kG with the help of the Paschen–Back effect in the CrH lines. Our measurements at different rotational phases suggest that the dwarf's surface might be covered with strong small-scale magnetic fields. In addition, recent findings of the dwarf's hydrogen emission and the Stokes V signal from the lower chromosphere indicate that its surface magnetic field might be changing rapidly giving rise to flare activity, similar to young dMe dwarfs. We substantiate the substellar origin of LSR J1835+3259 by making use of our own data as well as the photometric data from the all-sky surveys 2MASS and WISE.
Export citation and abstract BibTeX RIS
1. Introduction
Magnetic activity in fully convective low-mass stars ( ) and brown dwarfs (
) and brown dwarfs ( ) is predominantly inferred from their chromospheric (UV and Hα emission) and coronal (X-ray and radio emission) activity. For low-mass stars, which still have both radiative and convective zones a solar-like dynamo at work is assumed (Parker 1955, 1975). Thus, the magnetic flux tubes, which form at the bottom of the convection zone, rise to the stellar surface as a result of magnetic buoyancy. The convective motion "jostles" the rising magnetic flux tubes, leading to reconnection events and plasma heating. The former process gives rise to the chromospheric emission and the latter one leads to X-ray emission from the stellar coronae (see the review by Rosner et al. 1985). The boundary layer between the radiative and convective zones, called tachocline, is believed to play an important role in sustaining the solar-like dynamo (e.g., Charbonneau 2014). Others argue that the solar-like dynamo is distributed across the convective zone rather then confined to the tachocline (Brandenburg 2006; Guerrero & de Gouveia Dal Pino 2007). This becomes especially important in the context of fully convective dwarfs, for which the mechanism of generating their magnetic fields is not yet well studied. Several groups have performed magnetohydrodynamical simulations of fully convective objects, which predict different topologies of the surface magnetic fields (Dobler et al. 2006; Browning 2008; Yadav et al. 2015).
) is predominantly inferred from their chromospheric (UV and Hα emission) and coronal (X-ray and radio emission) activity. For low-mass stars, which still have both radiative and convective zones a solar-like dynamo at work is assumed (Parker 1955, 1975). Thus, the magnetic flux tubes, which form at the bottom of the convection zone, rise to the stellar surface as a result of magnetic buoyancy. The convective motion "jostles" the rising magnetic flux tubes, leading to reconnection events and plasma heating. The former process gives rise to the chromospheric emission and the latter one leads to X-ray emission from the stellar coronae (see the review by Rosner et al. 1985). The boundary layer between the radiative and convective zones, called tachocline, is believed to play an important role in sustaining the solar-like dynamo (e.g., Charbonneau 2014). Others argue that the solar-like dynamo is distributed across the convective zone rather then confined to the tachocline (Brandenburg 2006; Guerrero & de Gouveia Dal Pino 2007). This becomes especially important in the context of fully convective dwarfs, for which the mechanism of generating their magnetic fields is not yet well studied. Several groups have performed magnetohydrodynamical simulations of fully convective objects, which predict different topologies of the surface magnetic fields (Dobler et al. 2006; Browning 2008; Yadav et al. 2015).
Surface magnetic fields of low-mass stars can be studied with the help of spectroscopy and spectropolarimetry. High-resolution intensity spectra can provide information on magnetic flux Bf (f being the magnetic filling factor), and even field strength B. In particular, the Zeeman broadening has been employed to infer the magnetic properties of M dwarfs in atomic (Saar & Linsky 1985; Johns-Krull & Valenti 1996, 2000) and molecular (Reiners & Basri 2007, 2010; Afram et al. 2009) lines. Spectropolarimetry has also been used to reveal the magnetic signatures in M stars in atomic lines (Donati et al. 2006, 2008; Morin et al. 2008, 2010; Phan-Bao et al. 2009) as well as in TiO lines (Berdyugina et al. 2008). More details on magnetic field measurements in cool stars can be found in the reviews by Berdyugina (2005), Strassmeier (2009), Reiners (2012), and Linsky & Schöller (2015).
When applied to brown dwarfs, the above techniques for magnetic field measurements are mainly impeded by the following two facts. (1) High-resolution spectropolarimetry (or spectroscopy) of brown dwarfs is difficult because they are faint, and (2) modeling the spectropolarimetric signatures of molecules in the presence of a magnetic field is challenging (e.g., Berdyugina et al. 2003, 2005; Kuzmychov & Berdyugina 2013; Afram & Berdyugina 2015). In contrast to the early-M and hotter stars, where atomic lines dominate the absorption spectrum, molecules become an important absorber in the atmospheres of brown dwarfs (Kirkpatrick 2005).
There is growing evidence of chromospheric and coronal activity in fully convective dwarfs, presumably due to magnetic reconnection events (e.g., Gizis et al. 2000; Rutledge et al. 2000; Liebert et al. 2003; Fuhrmeister & Schmitt 2004; Stelzer 2004; Rockenfeller et al. 2006; Pineda et al. 2016). Moreover, radio surveys of cool dwarfs by Berger (2002) and Berger (2006) reveal that about 10% of the objects later than M7 show radio emission, which is associated with their magnetic activity. Both synchrotron and coherent emission mechanisms can give rise to radio emission in dwarf stars and brown dwarfs. While the synchrotron mechanism requires a rather weak magnetic field (∼10 G, Berger et al. 2008), the coherent emission arises from the regions with strong magnetic fields (≳1 kG, Hallinan et al. 2008).
Hallinan et al. (2008) argued the electron-cyclotron maser instability to be responsible for the coherent radio emission in the M8.5 dwarf LSR J1835+3259 (hereafter, LSR J1835). The authors estimated the magnetic field strength of the emitting region to ∼3 kG. Hallinan et al. (2015) have shown that this radio emission is also accompanied by the optical emission from the lower atmosphere, which is linked to a strong surface magnetic field (Berdyugina et al. 2017).
This study, which complements the analysis of the atomic Stokes profiles by Berdyugina et al. (2017), provides an independent measurement of the surface magnetic field of LSR J1835, which is free from assumptions made by Berger et al. (2008) and Hallinan et al. (2008, 2015). The novel approach for magnetic field measurements on cool dwarfs by Kuzmychov & Berdyugina (2013), which is based on the Paschen–Back effect in the CrH molecule, has been for the first time applied to a full-Stokes spectrum of a brown dwarf. It provides the net surface magnetic field strength B independently from the magnetic filling factor f, provided most of the CrH transitions enter the Paschen–Back regime. In the Zeeman regime, line profiles scale linearly with both magnetic field strength and magnetic filling factor. To the contrary, in the Paschen–Back regime, the shape of a line profile generally has a complicated dependence on the field strength, while it scales linearly with the magnetic filling factor.
The outline of the paper is as follows. Section 2 introduces the data acquisition and reduction process. Section 3 explains our models, which we compare to the observational data of LSR J1835 in Section 4. We assess the question of whether LSR J1835 is a low-mass star or a brown dwarf in Section 5. A discussion is included in Section 6 and conclusions follow in Section 7.
2. Observational Data
2.1. Data Acquisition
LSR J1835 was observed with the Low Resolution Imaging Spectropolarimeter (LRISp, Goodrich 1991) at the Keck observatory on two nights, 2012 August 22 and 23. In total, six full-Stokes measurements at different rotational phases with a signal-to-noise ratio (S/N) of about 700–900 were obtained (see Section 2.2.2 and Table 2). In addition, a G5Vv star HD 20630 was observed to calibrate the instrument throughput, which we use to determine the continuum level in the LSR J1835 spectra. Table 1 lists all scientific exposures analyzed along with supplemental information.
Table 1. Scientific Exposures
| Object | Date | MJD | Exposure | Retarder | Angle |
|---|---|---|---|---|---|
| (s) | (deg) | ||||
| LSR J1835 | 2012 Aug 22T11:15:54.99 | 56161.469387 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 22T11:28:29.50 | 56161.478119 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 22T11:40:59.63 | 56161.486801 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 22T11:53:27.73 | 56161.495460 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 22T12:06:28.71 | 56161.504499 | 600.0 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 22T12:19:06.83 | 56161.513274 | 600.0 | QWP+HWP | 38 |
| LSR J1835 | 2012 Aug 22T12:34:01.36 | 56161.523666 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 22T12:59:59.90 | 56161.541666 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 22T13:12:40.37 | 56161.550467 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 22T13:24:58.81 | 56161.559014 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 22T13:37:42.12 | 56161.567849 | 600.0 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 22T13:50:14.49 | 56161.576557 | 600.1 | QWP+HWP | 38 |
| LSR J1835 | 2012 Aug 22T14:04:25.16 | 56161.586402 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 22T14:17:00.03 | 56161.595139 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 22T14:29:30.14 | 56161.603821 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 22T14:41:57.75 | 56161.612474 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 22T14:54:52.33 | 56161.621440 | 600.0 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 22T15:07:26.74 | 56161.630171 | 600.0 | QWP+HWP | 38 |
| LSR J1835 | 2012 Aug 23T10:53:49.41 | 56162.454045 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 23T11:06:22.02 | 56162.462755 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 23T11:18:52.28 | 56162.471438 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 23T11:31:24.35 | 56162.480144 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 23T11:44:26.05 | 56162.489190 | 600.0 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 23T11:56:58.19 | 56162.497896 | 600.0 | QWP+HWP | 38 |
| LSR J1835 | 2012 Aug 23T12:10:22.70 | 56162.507207 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 23T12:22:55.16 | 56162.515916 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 23T12:35:24.41 | 56162.524588 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 23T12:47:57.12 | 56162.533300 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 23T13:08:21.42 | 56162.547470 | 599.6 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 23T13:20:53.42 | 56162.556174 | 600.0 | QWP+HWP | 38 |
| LSR J1835 | 2012 Aug 23T13:37:54.69 | 56162.567994 | 600.0 | HWP | −7 |
| LSR J1835 | 2012 Aug 23T13:50:28.69 | 56162.576721 | 600.0 | HWP | 38 |
| LSR J1835 | 2012 Aug 23T14:02:58.90 | 56162.585404 | 600.0 | HWP | 15.5 |
| LSR J1835 | 2012 Aug 23T14:15:27.01 | 56162.594063 | 600.0 | HWP | 60.5 |
| LSR J1835 | 2012 Aug 23T14:28:16.56 | 56162.602970 | 600.0 | QWP+HWP | −7 |
| LSR J1835 | 2012 Aug 23T14:40:51.74 | 56162.611710 | 600.0 | QWP+HWP | 38 |
| HD 20630 | 2012 Aug 22T15:25:05.78 | 56161.642467 | 1.2 | HWP | −7 |
| HD 20630 | 2012 Aug 22T15:28:16.73 | 56161.644638 | 1.2 | HWP | 38 |
| HD 20630 | 2012 Aug 22T15:30:44.18 | 56161.646384 | 1.2 | HWP | 15.5 |
| HD 20630 | 2012 Aug 22T15:33:16.43 | 56161.648107 | 1.2 | HWP | 60.5 |
| HD 20630 | 2012 Aug 22T15:35:29.83 | 56161.649651 | 1.2 | QWP+HWP | −7 |
| HD 20630 | 2012 Aug 22T15:37:42.73 | 56161.651189 | 1.2 | QWP+HWP | 38 |
Note. The LSR J1835 and HD 20630 scientific exposures. The columns include target name, date and UTC time at the begin of the observation, modified Julian date at the begin of the observation, exposure time, retarder used (HWP and QWP are half-wave and quarter-wave plates, respectively), and the position angle of the retarder.
Download table as: ASCIITypeset image
Table 2. Signal-to-noise Ratios
| Stokes | August 22nd | August 23rd |
|---|---|---|
| Q | 550 920 1060 | 840 620 1080 |
| U | 760 370 1080 | 610 930 780 |
| V | 610 950 1000 | 770 780 700 |
Note. Columns list the S/Ns (rounded to a tenth) for the LSR J1835 quv data sets in chronological order computed with the help of a low-pass filter.
Download table as: ASCIITypeset image
LRISp provides a dual-beam polarimetry mode and can measure both linear and circular polarization (Goodrich et al. 1995). The polarization is measured with the help of a half-wave plate only (linear) or a quarter-wave plate that precedes the half-wave plate (circular). To obtain a full-Stokes measurement, a standard modulation scheme is applied. Hence, the components of the Stokes vector are obtained as follows.
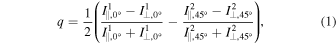
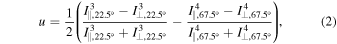
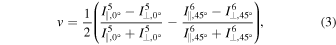
where I is a spectrum obtained during one exposure. The upper index denotes the exposure number; the first lower index, ∥ or ⊥, refer to the ordinary or extraordinary beam; the second lower index is the angular position of the half-wave plate according to the standard modulation scheme. The Stokes parameters are written in the lower case symbols when normalized to the total intensity.
The Stokes parameter I, or i when normalized to the continuum intensity Icont, can be obtained from any of the three single Stokes measurements in Equations (1)–(3) in the following way.
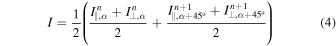
or
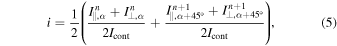
where n = 1, 3, 5 is the number of exposure, and α is the corresponding angular position of the half-wave plate. We will address the question of how to find Icont in Section 2.2.5.
We used the  grating with the central wavelength of 9000 Å, which delivers a continuous wavelength coverage from 8000 to 10000 Å on 4096 detector pixels.
grating with the central wavelength of 9000 Å, which delivers a continuous wavelength coverage from 8000 to 10000 Å on 4096 detector pixels.
2.2. Data Reduction
We made use of our own data reduction pipeline by Harrington et al. (2015). It follows the standard reduction procedure for spectroscopic data described by Horne (1986) and includes additional reduction steps specific for LRISp. Below, we will outline the instrument-specific data reduction steps and will introduce the major sources of instrument errors. These could be mitigated to a large extent, allowing for spectropolarimetric precision of about 0.1% in our brown dwarf data.
2.2.1. Wavelength Calibration
A wavelength calibration of the CCD spectral pixels has been done with the help of Gaussian fits to several arc lamp calibration exposures. These fits were also used to derive the resolving power of the instrument  , which is R = 2500 at 8000 Å raising to R = 3500 at 10000 Å (see Figure 1 in Harrington et al. 2015). The full widths at half maximum of the Gaussian fits have typically 5–6 pixels.
, which is R = 2500 at 8000 Å raising to R = 3500 at 10000 Å (see Figure 1 in Harrington et al. 2015). The full widths at half maximum of the Gaussian fits have typically 5–6 pixels.
The arc line calibration exposures were also used to correct for wavelength drifts due to beam wobble (imperfect alignment of the ordinary and extraordinary beams at different retarder angles). Rotating retarder causes drifts of roughly 0.15 pixels between two different modulation states.
Instrument flexure due to gravity introduces an additional wavelength drift. This drift can be as big as 0.15 px for a single Stokes measurement that lasts 20 minutes (see Figure 8 in Harrington et al. 2015). We used the sky glow lines and run a cross-correlation analysis to suppress the flexure errors down to 0.05 px.
2.2.2. Signal-to-noise
The S/Ns are derived with the help of the low-pass filter. The low-pass filtered data are subtracted from the observed ones, and a standard deviation of the residual is computed. It gives a measure for the statistical error of the data. The low-pass filter is implemented with the help of the IDL routine SMOOTH, whereby the width of the boxcar average is set the full width at half maximum of the Gaussian fit to the calibration arc lines exposures. Table 2 gives the S/Ns for all individual Stokes profiles.
2.2.3. Cosmic-ray Removal
During single exposures of 10 minutes on our brown-dwarf target, the detector captured a large number of cosmic-ray hits. Cosmic rays typically damage the data over tens of pixels, providing the major source of random errors. We applied an iterative filtering procedure to locate and repair the damaged data points using the information on the averaged spatial profile.
This filtering procedure works as follows. First, all spatial profiles are averaged to obtain a median spatial profile. Next, the special profiles with the analog counts exceeding a certain threshold are identified. The damaged pixels typically have one order of magnitude more analog counts than flawless ones. The most offending data point is then replaced by the corresponding one from the median profile, which is shifted and scaled to match the spatial profile. The iterative filtering continues until all data points in all spatial profiles lie below the predefined threshold. An illustrative explanation of this filtering procedure is given in Harrington et al. (2015, Figure 4).
The above filtering procedure works well for small damages, i.e., those damages that affect no more than 30% of the spatial profile and are no more than 10–20 Å wide. Figure 10 (Stokes q) demonstrates an example of severe data damage that extends over 50 Å. In such cases, the data points were omitted from the analysis.
2.2.4. Spectral Fringe
Multiple reflections within the achromatic retarder can introduce another instrumental error, called spectral fringe. Thus, the incoming signal is modulated by a periodic noise, leaving behind a fringe pattern on the detector. Spectral fringes have been found and characterized on a number of night-time spectropolarimeters (Harries & Howarth 1996; Donati et al. 1999; Aitken & Hough 2001).
The amplitude and the phase of the spectral fringe can vary with the retarder orientation and telescope pointing, but its frequency remains generally constant. Because the LRISp uses different retarders to measure the QU and V polarization, their fringe patterns differ noticeably in both frequency and amplitude.
Spectral fringes can be eliminated from the data by either subtracting a signal of an unpolarized standard star or suppressing the disturbing frequencies in the Fourier space. We applied the latter method, and we made use of the HD 20630 data to identify the fringe frequencies.
HD 20630 is a G5V variable star of BY Dra type, which is listed in the UKIRT IRPOL list of the unpolarized standards4 (Gehrels 1974). It was later found by Marcy (1984) that this star possesses a variable magnetic field. We did not find any polarized signatures of magnetic fields in the HD 20630 spectra used to identify the fringe frequencies.
Figure 1 shows the Stokes v signal of our scientific target LSR J1835 and that of the unpolarized standard HD 20630, both modulated by a spectral fringe. For HD 20630, its power spectrum of the Stokes v signal shows several strong peaks that stand out above the noise. These peaks, which we attribute to a spectral fringe and are clearly present in the LSR J1835 power spectrum, were removed from the data.
Figure 1. Top: observed Stokes v signals of the M8.5 dwarf LSR J1835 (black) and the G5V star HD 20630 (blue). The best-fit Stokes v model (red) to the last measurement on August 23 is plotted over the LSR J1835 fringe-subtracted data. For display purposes, the HD 20630 and LSR J1835 raw signals are shifted upward. Bottom: power spectra of the above Stokes v signals. At high frequencies, the LSR J1835 power spectrum shows peaks that coalign with the strong peaks in the HD 20630 power spectrum. These are attributed to a spectral fringe. The strong low-frequency peak in both LSR J1835 data and model is related to the Paschen–Back signature of the CrH 0–0 band (8600–8700 Å).
Download figure:
Standard image High-resolution image2.2.5. Continuum Normalization
To model the intensity spectra in molecular bands, the instrument sensitivity must be calibrated. To normalize the continuum of the data, we remove the spectrograph and telescope throughput with the help of a polynomial fit to selected continuum wavelengths.
Such a throughput curve is well reproduced by a polynomial fit of the order of four or five to the intensity spectrum. Since the spectra of LSR J1835 are chopped by the absorption in molecular bands, a finding of a polynomial that resembles the continuum level becomes difficult. In addition, the telluric absorption contaminates the spectrum and complicates the fitting procedure. For polarimetric stability at high precision, the telescope was defocused and the atmospheric dispersion compensator was not rotated during a data set. This adds some mild time dependence to the instrument throughput.
Because the spectra of stars as hot as G5 spectral type are not subject to strong molecular absorption, we used the spectrum of our unpolarized standard HD 20630 ( K) to derive the instrument throughput.
K) to derive the instrument throughput.
Figure 2 shows an HD 20630 spectrum as it was observed with LRISp. We found that a polynomial of the fifth order reproduces well the throughput curve of the instrument. By dividing the observed spectrum by this polynomial, a normalized spectrum is obtained. Telluric absorption is the main reason for deviation of the polynomial from the spectrum. At the edges of the spectrum, where the instrument sensitivity drops significantly, a deviation from the polynomial can occur as well.
Figure 2. Top: observed and normalized spectrum of the G5V star HD 20630. The dashed line is a polynomial fit to the continuum wavelengths of HD 20630. Bottom: observed and normalized spectrum of M8.5 dwarf LSR J1835. The dashed line is the same polynomial used for the HD 20630 spectrum in the top panel but corrected for the Planck irradiance at  K.
K.
Download figure:
Standard image High-resolution imageAn example LSR J1835 spectrum is shown in Figure 2 as well. When scaled and corrected for the Planck irradiance, the instrument throughput, which we derived with the help of the HD 20630 spectrum, can be used to normalize the intensity spectrum of our scientific target.
2.3. Spurious and Residual Signals
Prior to the scientific analysis, the data have been processed with the help of our data reduction pipeline, which mitigates the instrument errors at the level of 0.1% (Harrington et al. 2015). To double-check the absence of spurious signals, one can inspect the so-called null spectra or possible non-magnetic spectral regions. As will be shown below, these two techniques are, however, inhibited when applied to rapidly rotating faint targets with evolving surface magnetic fields.
Dual-beam spectropolarimetry combined with the beam swapping technique (see Section 2.1) allows for null spectra, which can be calculated similarly to the Equations (1)–(3) but combining spectra with the same polarization state. Null spectra are widely used by the stellar magnetism community to check for spurious signals in the Stokes v data (Donati et al. 1997).
Figure 3 shows the null spectra of our last data set on August 22. The fringe-subtracted null spectra can show regions with more than a 0.1% deviation from the null. These contain data points damaged by cosmic rays or showing the spectral fringe artifacts. In addition, an ostensible change in the magnetic field configuration due to dwarf's fast rotation or evolving magnetic field can leave behind residual signals in the null spectra exceeding the 0.1% level as well.
Figure 3. Observed (gray) and predicted (black) null spectra for the last data set on August 22. Black dots show the fringe-subtracted binned (10:1) null spectra; the error bars give the standard deviation within the bin. For display purposes, the signals are shifted along the vertical axis. The predicted null spectra have been calculated using the best-fit models to the data set. A change in magnetic field strength from 3 to 5 kG and in azimuth χ of the field vector from 45° to 70° is assumed. Not only the cosmic-ray and spectral fringe artifacts, but also the ostensible change in the magnetic field configuration due to the dwarf's fast rotation, can leave behind residual signals in the null spectra above 0.1%.
Download figure:
Standard image High-resolution imageThe modeled wavelength region is dominated by the absorption in the molecules TiO, CrH, and FeH. As has been shown in the example of CaH and TiO in sunspots, in the presence of a magnetic field, the diatomic molecules are generally expected to show magnetic signatures in their polarized spectra (Berdyugina et al. 2006). There is no wavelength region in the near-infrared spectra of cool dwarfs that is not expected to show magnetic signatures in the presence of a magnetic field.
2.4. Signal Detection
We now want to quantitatively assess the magnetic signal detection in the data without taking the model into account. By means of the hypothesis testing (e.g., Lehmann & Romano 2005), we will compare the null spectra with the measured Stokes signals by treating them as statistical data sets. In doing so, we assume that the scatter in the null spectra data set is given solely by the statistical variation of the data points (this assumption, however, is limited for reasons given in Section 2.3).
Two hypotheses, H0 and H1, are constructed. The former hypothesis assumes that the variances of both data sets, the null spectra and the measured signals, are similar, and hence the scatter of the data points in the measured Stokes signals is given by the statistical variation as well. The latter hypothesis assumes that the measured signals have larger variance, e.g., due to the presence of magnetic signatures.
We compare the variances of the binned data points in the null spectra given in Figure 3 with that in the measured signals, and we find that the probability for the H0 hypothesis is between 0.05 and 0.5 for most of our measurements. In our three measurements with the detected magnetic signature, the hypothesis H0 cannot be rejected confidently because of its moderate probability of 0.1 (see Section 4.4).
The test performed cannot, however, provide compelling evidence for the detection when the amplitude of the detected magnetic signatures is no more than a factor of two larger than the noise level in the data, as is the case in most of our measurements (see Figures 8–10). Moreover, the test does not take into account the spectral information contained in the data sets since it only compares the variances of the data sets.
Section 4.4 assesses the significance of our detections by taking the spectral information in the data sets into account. Hence, all three measurements with the detected magnetic signal strongly correlate with the best-fit model due to a broadband magnetic signature in the CrH 0–0 band (Figure 11).
3. Models
We calculate a full-Stokes synthetic spectrum with the help of the code STOPRO (Solanki 1987; Berdyugina et al. 2003). The code is able to calculate the radiative transfer in the presence of a magnetic field, which is assumed to act on a spectral line through the Zeeman and the Paschen–Back effects. The polarized radiative transfer calculations were performed on the BT-Settl solar-metallicity model atmospheres by Allard & Freytag (2010). Polarization due to scattering in the atmosphere has not been taken into account, since it affects the continuum polarization only. We refer to the Stokes profiles calculated by the code STOPRO as isto, qsto, usto, and vsto (see Figures 5–6). These are normalized to the continuum intensity.
Following the Stokes formalism derived by means of the absorption matrix (e.g., Stenflo 1994), the Stokes profiles isto, qsto, usto, and vsto are expressed in terms of the absorption matrix elements,
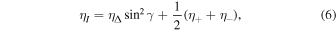
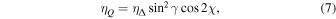
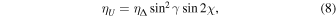
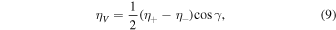
where
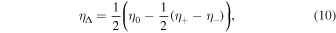
and  ,
,  , and
, and  refer to the total line profiles summed over π (linear polarization),
refer to the total line profiles summed over π (linear polarization),  , and
, and  (circular polarization) Zeeman components, respectively.
(circular polarization) Zeeman components, respectively.
The synthetic spectra are calculated for the wavelength region 8550–8800 Å and comprise nearly 2500 spectral lines, which split into more than 150,000 magnetic components. These lines belong to the vibrational bands of TiO  , 0–0 band of CrH
, 0–0 band of CrH  , 1–0 band of FeH
, 1–0 band of FeH  , and to a number of atomic species. The molecular number densities in the BT-Settl model atmospheres used are shown in Figure 4.
, and to a number of atomic species. The molecular number densities in the BT-Settl model atmospheres used are shown in Figure 4.
Figure 4. Number densities for the molecules TiO, CrH, and FeH in the BT-Settl model atmospheres with Teff = 2200 and 2600 K. Opacity is calculated for the wavelength of 8650 Å.
Download figure:
Standard image High-resolution imageBecause the opacity table in the BT-Settl model atmospheres is calculated for the standard wavelength of 1.25 μm, we recalculated it for the wavelength of 8650 Å. By doing so, we included the following continuous opacity sources:
- 1.bound–free and free–free transitions in H,
 ,
,  ,
,  , He, He−, and metals;
, He, He−, and metals; - 2.
- 3.scattering off free electrons, H, He, and H2.
Dust formation may provide an additional continuous opacity source in the atmospheres of brown dwarfs (Allard et al. 2012), but it is not included in our calculations.
We pre-calculated a grid of synthetic Stokes profiles isto, qsto, usto, and vsto for a range of temperatures, surface gravities, and magnetic field strengths (Figures 5–6). The instrumental broadening, which is derived from the data itself, is fixed to 3 Å (Harrington et al. 2015). Furthermore, we adopt the  of 50 km s−1 from Berger et al. (2008). An overview of the parameters of the synthetic spectra and their ranges can be found in Table 3.
of 50 km s−1 from Berger et al. (2008). An overview of the parameters of the synthetic spectra and their ranges can be found in Table 3.
Figure 5. Modeled full-Stokes spectra of late-M and early-L dwarfs for different surface gravities (top panel) and effective temperatures (bottom panel). In all spectra,  kG,
kG,  ,
,  , the instrumental broadening is 3 Å, and
, the instrumental broadening is 3 Å, and  is 50 km s−1.
is 50 km s−1.
Download figure:
Standard image High-resolution imageFigure 6. Same as Figure 5, but for different magnetic field strengths. Assumed:  ,
,  K (top panel),
K (top panel),  K (bottom panel).
K (bottom panel).
Download figure:
Standard image High-resolution imageTable 3. Parameters of the Synthetic Spectra and Their Ranges
| Parameter | Unit | Range | Step |
|---|---|---|---|
| T | K | 2000–3000 | 100 |
| log g | g in cm s−2 | 2.5–5.5 | 0.5 |
| B | kG | 0–9.5 | 0.5 |

|
km s−1 | 50 | ⋯ |
| instr | Å | 3–6 | 3 |
Note. The instrumental broadening of 6 Å corresponds to the binned (10:1) data.
Download table as: ASCIITypeset image
In order to compare the observed Stokes profiles, which are given by the expressions (1)–(3), with the synthetic spectra, the models imod, qmod, umod, and vmod are constructed,
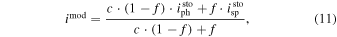
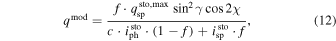
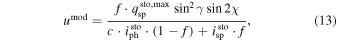
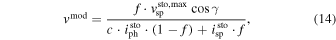
where the subscripts "ph" and "sp" refer to the photosphere and the magnetic spot, respectively; f is the magnetic filling factor, which is the ratio of the area of the spot to the total area of the stellar disk; c is the ratio of the continuum intensity emerging from the photosphere to that emerging from the spot; γ and χ are the inclination and the azimuth of the magnetic field vector, respectively, with respect to the observer.
In order to decrease the computational time for synthetic models, we calculated qsto at γ = 0° and χ = 0°, which we denote  and vsto at γ = 90° and χ = 45°, which is referred to as
and vsto at γ = 90° and χ = 45°, which is referred to as  The Stokes profiles qsto, usto, and vsto at any other magnetic field orientation are then obtained as follows.
The Stokes profiles qsto, usto, and vsto at any other magnetic field orientation are then obtained as follows.
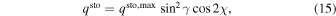
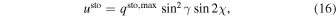
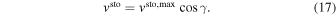
The underlying presumption of models (11)–(14) is that the dwarf LSR J1835 hosts a magnetic region (or regions), which covers the fraction f of the stellar disk and where the observed net magnetic flux is concentrated. When the intensity I, which is formed at the bottom of the photosphere and is assumed to be unpolarized, is absorbed by the molecular and atomic species, the Zeeman and the Paschen–Back effects give rise to the emergent polarization Q, U, and V. The pristine photosphere, which fills up the fraction  of the stellar disk, is assumed to be free from magnetic fields, and hence does not give rise to polarization. Robinson (1980) pointed out the necessity of combining the magnetic and non-magnetic photospheres when modeling a stellar spectrum. This idea has been widely used by the stellar magnetism community since then.
of the stellar disk, is assumed to be free from magnetic fields, and hence does not give rise to polarization. Robinson (1980) pointed out the necessity of combining the magnetic and non-magnetic photospheres when modeling a stellar spectrum. This idea has been widely used by the stellar magnetism community since then.
Our model implies that after cancellation of magnetic fields of opposite polarities the net surface magnetic field can be described by a single vector, which is defined by two angles, azimuth χ and inclination γ, both with respect to the observer. This is a reasonable assumption for a disk-integrated measurement. A more complicated model assuming a distribution of fields of different strengths (e.g., Johns-Krull et al. 1999) will introduce additional free parameters and is therefore not pursued.
By now, the same magnetic filling factor f is assumed for all four Stokes parameters. In fact, the polarimetric profiles q, u, and v yield generally smaller filling factors than the intensity i because of cancellation of magnetic fields of different polarities (e.g., Linsky & Schöller 2015).
The models imod, qmod, umod, and vmod, which are given by expressions (11)–(14), can now be directly compared to the observed signals i, q, u, and v, which are given by the expressions (1)–(5).
4. Data Analysis
Having reduced the data and having built the appropriate models from the pre-calculated synthetic spectra, we can now proceed with the data analysis.
First, imod models are fitted to the data by varying the parameters surface gravity,  , and effective temperature,
, and effective temperature,  (or
(or  and
and  ). Combining the magnetic and the non-magnetic photospheres of different temperatures takes into account the stellar flux dimness as a result of the impediment to stellar convection caused by the surface magnetic field (Vogt 1983). Next, by fixing these parameters at their best-fit values, we fit the polarimetric signals q, u, and v to obtain the strength of the net magnetic field, B. This procedure is given by the fact that the intensity (Stokes i) and the polarimetric signals (Stokes q, u, and v) are differently sensitive to different model parameters. For example, while the shape of the low-resolution intensity signal strongly depends on temperature and surface gravity, it hardly depends on the magnetic field strength (see Figures 5–6). The opposite is true for the polarimetric signals.
). Combining the magnetic and the non-magnetic photospheres of different temperatures takes into account the stellar flux dimness as a result of the impediment to stellar convection caused by the surface magnetic field (Vogt 1983). Next, by fixing these parameters at their best-fit values, we fit the polarimetric signals q, u, and v to obtain the strength of the net magnetic field, B. This procedure is given by the fact that the intensity (Stokes i) and the polarimetric signals (Stokes q, u, and v) are differently sensitive to different model parameters. For example, while the shape of the low-resolution intensity signal strongly depends on temperature and surface gravity, it hardly depends on the magnetic field strength (see Figures 5–6). The opposite is true for the polarimetric signals.
A  -minimization is performed to find the best-fit model, and we presume that its parameters lie the closest to the true stellar parameters of the dwarf. All
-minimization is performed to find the best-fit model, and we presume that its parameters lie the closest to the true stellar parameters of the dwarf. All  values presented in this study are normalized by the number of the fitted data points. Every data point is weighted with its uncertainty derived from the pixel-to-pixel variation of the data, which are over-sampled at 5 pixels per full width at half maximum of the instrument profile in the wavelength region modeled (Section 2.2.1).
values presented in this study are normalized by the number of the fitted data points. Every data point is weighted with its uncertainty derived from the pixel-to-pixel variation of the data, which are over-sampled at 5 pixels per full width at half maximum of the instrument profile in the wavelength region modeled (Section 2.2.1).
In order to increase the S/N of the signals q, u, and v, they are binned in ratio 10 to 1. The uncertainties of the binned data points are derived from their statistical variation within the bin. These are roughly a factor of three smaller than the uncertainties of the original data points.
We refer to the full-Stokes measurements on August 22 and 23 as measurements 1, 2, 3, and 4, 5, 6, respectively.
4.1. Stokes i
When modeling the Stokes i signal, which is an average of 12 intensity spectra obtained during one full-Stokes measurement, the continuum level in the model should be accounted for correctly. For cool dwarfs, this becomes a challenging task because the continuum level in their spectra is chopped by the absorption in molecular bands (Section 2.2.5). Hence, only by taking into account the myriads of the molecular lines—which is both a computationally and theoretically challenging task—the continuum level can be accounted for precisely. Instead, we introduce ad hoc an additive parameter that is constant over the modeled wavelength range. It compensates the underestimated absorption in the models due to missing lines and thus makes the model continuum match the continuum level of the data.
We now fit the models imod to the observed intensity i by varying the parameters  , Tph, Tsp, and f. We note that the common effect of the parameters
, Tph, Tsp, and f. We note that the common effect of the parameters  , Tph, Tsp, and B is to make the spectral lines broader; however, this effect of B is much smaller than that of the other parameters. The best-fit parameters and the corresponding fit statistic are collected in Tables 4 and 5, respectively.
, Tph, Tsp, and B is to make the spectral lines broader; however, this effect of B is much smaller than that of the other parameters. The best-fit parameters and the corresponding fit statistic are collected in Tables 4 and 5, respectively.
Table 4. Stokes i Best-fit Parameters
| Parameter | Best-fit Values | Error | |
|---|---|---|---|
 kG kG |
 kG kG |
||
| log g | 5.0 | 5.0 |

|

|
2600 | − | ±300 |

|
3000 | 2900 |

|

|
2000 | 2200 |

|

|
0.8 | 0.6 | ⋯ |
Note. g has units of cm s−2, and T is given in K. The corresponding fit statistic for B = 5 kG is given in Table 5.
Download table as: ASCIITypeset image
Figure 7 shows a  distribution that results from the above fitting procedure, assuming
distribution that results from the above fitting procedure, assuming  and
and  kG. Hence, the obtained
kG. Hence, the obtained  distribution depends only on two parameters,
distribution depends only on two parameters,  and
and  , with a minimum at
, with a minimum at  K. Both values
K. Both values  and 5.0 fit the data well, whereby the
and 5.0 fit the data well, whereby the  confidence interval is confined to log g = 4.0–5.5. We use the atmospheric models for
confidence interval is confined to log g = 4.0–5.5. We use the atmospheric models for  when fitting the data (see Table 3). The parameter f does not exist in this case.
when fitting the data (see Table 3). The parameter f does not exist in this case.
Figure 7. Two-dimensional  distribution that results from fitting the intensity signal i by varying two model parameters,
distribution that results from fitting the intensity signal i by varying two model parameters,  and
and  (assumed:
(assumed:  ,
,  kG).
kG).
Download figure:
Standard image High-resolution imageTable 5.
Stokes i Fit Statistic ( kG)
kG)
| Measurement | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |

|
2.75 | 2.74 | 2.61 | 2.70 | 2.59 | 2.71 |
Note. The corresponding best-fit models imod are shown in Figures 8–10 (upper-left panels). The best-fit parameters are given in Table 4.
Download table as: ASCIITypeset image
4.2. Stokes q, u, and v
Before we proceed with fitting the spectropolarimetric signals, we normalize the models qmod, umod, and vmod by the observed intensity i, i.e., by the data itself. The reason for this is the remaining discrepancy between the best-fit model I and the signal i (see Figures 8–10, upper-left panel), which will worsen the fit statistic. Moreover, we decouple the Equations (12)–(14), which are coupled via the parameters f, γ, and χ, by introducing the individual scaling factors,
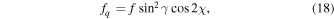
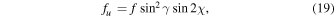
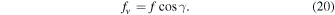
Figure 8. Full-Stokes data i, q, u, and v of LSR J1835 (small circles) and the best-fit models (red curves) to the binned data (big circles). Error bars of the binned data reflect the statistical variation of the data points within the bin. Error bars of the original data are given outside the plot panel, on the right. Lower-left panels show the  distributions, which result from fitting the models to the data by varying B.
distributions, which result from fitting the models to the data by varying B.
Download figure:
Standard image High-resolution imageFigure 9. Same as Figure 8, but for the measurements 3 and 4.
Download figure:
Standard image High-resolution imageFigure 10. Same as Figure 8, but for the measurements 5 and 6. The hatched area marks the part of the spectrum damaged by cosmic rays.
Download figure:
Standard image High-resolution imageConsequently, the models qmod, umod, and vmod read now as follows,
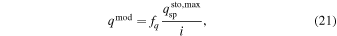
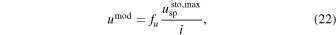

The above models are fitted to the signals q, u, and v by varying the parameter B as well as the scaling factors fq, fu, and fv. Other model parameters are fixed to their best-fit values listed in Tables 3 and 4 ( kG). We emphasize that the shape of the models Q, U, and V depends now on the parameter B, only. This dependence, which is provided by the fact that most of the spectroscopic transitions of CrH approach the Paschen–Back regime at kG fields, allows us to uniquely identify the photospheric magnetic field strength of LSR J1835 (Kuzmychov & Berdyugina 2013).
kG). We emphasize that the shape of the models Q, U, and V depends now on the parameter B, only. This dependence, which is provided by the fact that most of the spectroscopic transitions of CrH approach the Paschen–Back regime at kG fields, allows us to uniquely identify the photospheric magnetic field strength of LSR J1835 (Kuzmychov & Berdyugina 2013).
Table 6 provides the best-fit parameters to the binned signals q, u, and v along with the fit statistic.
Table 6. Best-fit Magnetic Field Strengths and Fit Statistic
| Measurement | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Bq |

|
− |

|

|

|
− |
| Bu |

|
− | − |

|

|
− |
| Bv |

|
− |

|
− | − |

|
| fq (=fu) | 0.04 | − | 0.02 | 0.04 | 0.03 | − |
| fv | 0.01 | − | 0.01 | − | − | 0.03 |

|
3.23 | 2.83 | 4.19 | 2.46 | 4.29 | 4.23 |

|
2.31 | 4.20 | 2.85 | 2.12 | 4.61 | 1.81 |

|
1.60 | 2.22 | 4.53 | 2.09 | 3.65 | 3.56 |

|

|
0.18 | 2.43 | 2.69 | 1.93 | 0.81 |

|
1.49 | 0.17 | 0.22 | 1.93 | 1.23 | 0.38 |

|
1.85 | 0.08 | 3.55 | 0.92 | 0.00 | 3.89 |
| pq | 0.02 | 0.67 | 0.12 | 0.10 | 0.16 | 0.37 |
| pu | 0.22 | 0.68 | 0.64 | 0.16 | 0.27 | 0.54 |
| pv | 0.17 | 0.78 | 0.06 | 0.33 | 1.00 | 0.05 |
Note. For all individual Stokes measurements, the table gives the best-fit magnetic field strengths B with the 1σ uncertainty, and the scaling factors fq, fu, and fv. The fit statistic is given by the values  ,
,  , and the probability p for the absence of a magnetic field (H0 hypothesis). Magnetic field detections at the level of 3σ to 5σ (
, and the probability p for the absence of a magnetic field (H0 hypothesis). Magnetic field detections at the level of 3σ to 5σ ( ) are considered to be tentative, and the detection at the level of >5σ (
) are considered to be tentative, and the detection at the level of >5σ ( ) is considered to be unambiguous and is highlighted in bold. Measurements that conform to the absence of the magnetic field (
) is considered to be unambiguous and is highlighted in bold. Measurements that conform to the absence of the magnetic field ( ) are indicated by "−."
) are indicated by "−."
Download table as: ASCIITypeset image
Figures 8–10 show the best-fit models imod, qmod, umod, and vmod to all six full-Stokes measurements of LSR J1835 obtained on 2012 August 22 and 23. In addition, these figures provide the one-dimensional  distributions that result from fitting the binned signals q, u, and v by varying the parameter B.
distributions that result from fitting the binned signals q, u, and v by varying the parameter B.
4.3. Discrepancy Between Data and Model
Stokes I—Although we included most of the important absorbing species in the modeled wavelength region, our line list is not complete. For instance, we did not consider the VO ( ) vibrational bands 0–1 and 0–0, appearing at 7330 and 7900 Å, respectively (Bernath 2009). When fitting the bands of the molecules TiO, CrH, and FeH separately, similar but different best-fit parameters Teff and
) vibrational bands 0–1 and 0–0, appearing at 7330 and 7900 Å, respectively (Bernath 2009). When fitting the bands of the molecules TiO, CrH, and FeH separately, similar but different best-fit parameters Teff and  are obtained. Numerical simulations by Robinson & Marley (2014) show that temperature fluctuations in the atmosphere of brown dwarfs due to cool spots or clouds might be common. These issues are reflected in the uncertainties of the best-fit parameters given in Table 4.
are obtained. Numerical simulations by Robinson & Marley (2014) show that temperature fluctuations in the atmosphere of brown dwarfs due to cool spots or clouds might be common. These issues are reflected in the uncertainties of the best-fit parameters given in Table 4.
Stokes Q, U, and V—The main reason for the discrepancy between the data and model are random and systematic errors caused by cosmic rays and fringe artifacts as well as a possible (ostensible) change in magnetic field configuration between the rotational phases (see Sections 2.2.3, 2.2.4, and 2.3). These errors are reflected in the uncertainties of the derived magnetic field strengths (Table 6).
4.4. Significance of the Inferred Magnetic Field
We now want to quantify the significance of the determined net magnetic field strength for each Stokes measurement by taking the spectral information in the data sets into account (see Section 2.4). Again, two hypotheses, which we refer to as H0 and HB, are constructed. The hypothesis H0 assumes that LSR J1835 does not possess a magnetic field. Consequently, any deviation of the observational data from the non-magnetic model is solely given by a statistical variation of the data points. In contrast, the hypothesis HB assumes that LSR J1835 does possess a magnetic field. In this case, the observational data can be described by a model that assumes the presence of a magnetic field.
Based on the  distributions obtained as a result of fitting the Stokes signals q, u, and v by varying the parameter B, we calculate the probability p for the hypothesis H0 for each Stokes measurement. Based on the standard convention in statistics, which states that H0 can be considered as likely if its probability is greater than 0.08, we will reject H0 for
distributions obtained as a result of fitting the Stokes signals q, u, and v by varying the parameter B, we calculate the probability p for the hypothesis H0 for each Stokes measurement. Based on the standard convention in statistics, which states that H0 can be considered as likely if its probability is greater than 0.08, we will reject H0 for  and will thus consider the magnetic field detected. The detection will be considered as tentative for
and will thus consider the magnetic field detected. The detection will be considered as tentative for  (3σ to 5σ level) and as unambiguous for
(3σ to 5σ level) and as unambiguous for  (5σ level). The measurement will be judged as being consistent with the absence of a magnetic field for values
(5σ level). The measurement will be judged as being consistent with the absence of a magnetic field for values  . For all measurements, we collect the probabilities p for the H0 hypothesis in Table 6.
. For all measurements, we collect the probabilities p for the H0 hypothesis in Table 6.
Figure 11 shows a scatterplot of data versus best-fit model for our three detections at the >3σ level. These measurements show a strong correlation with the best-fit model in the wavelength region of 8600–8700 Å, where the prominent magnetic signature of the CrH 0–0 band appears (the correlation coefficients are 0.72, 0.86, and 0.89). The correlation becomes less significant if all data points in the wavelength region modeled (8550–8700 Å) are taken into account. This is because the scatter of the data due to random errors increases with the number of the data points (see Sections 2.2.3 and 2.2.4). Furthermore, the magnetic signature of the molecules TiO and FeH is less pronounced than that of CrH at the kG fields.
Figure 11. Scatterplot of data vs. best-fit model for magnetic field detections. Open circles show all data points; filled circles show the data points in the CrH 0–0 band (8600–8700 Å), which indicate strong linear correlation between the data and the best-fit model (the correlation coefficient is 0.72, 0.86, and 0.89, respectively, for black, red, and blue data points). The lines of best fit to the data points in the CrH 0–0 band are shown as well.
Download figure:
Standard image High-resolution imageBoth statistical tests performed (this section and Section 2.4) show that the spectral information in the data sets is important when assessing the significance of the detected signal that is close to the noise level of the data.
5. Low-mass Star or Brown Dwarf?
We use the photometric data from the all-sky survey to independently estimate the effective temperature of our target. Our search in the VizieR database (Ochsenbein et al. 2000) retrieved seven data points for the dwarf LSR J1835, from 2MASS (Skrutskie et al. 2006) and WISE (Wright et al. 2010) surveys. These data points correspond to the J, H, K, W1, W2, W3, and W4 bands at 12,350, 16,620, 21,590, 33,526, 46,028, 115,608, and 220,883 Å, respectively.
We analyze the photometric data and find the best-fit atmospheric model with the help of the Virtual Observatory SED Analyzer tool by Bayo et al. (2008). We have found that fitting the spectral energy distribution (SED) with the model atmospheres from the BT-Settl grid (Allard & Freytag 2010; dust settlement in the atmosphere taken into account) and the NextGen grid (Allard et al. 2012; dust formation in the atmosphere not taken into account) results in different best-fit Teff. The former grid yields  K, and the latter grid gives
K, and the latter grid gives  K (Figure 12, see also Table 4). Dust formation is believed to play an important role in the atmospheres with
K (Figure 12, see also Table 4). Dust formation is believed to play an important role in the atmospheres with  K, giving rise to the greenhouse effect and veiling of the optical SED due to Rayleigh scattering off fine dust and making the SED appear redder (Allard et al. 2012).
K, giving rise to the greenhouse effect and veiling of the optical SED due to Rayleigh scattering off fine dust and making the SED appear redder (Allard et al. 2012).
Figure 12. Top: spectral energy distribution of LSR J1835 scanned by the 2MASS (red) and WISE (blue) surveys. The errors of the data points are smaller than the symbol size, and thus not shown. The best-fit BT-Settl ( K, dust/cloud formation included) and NextGen (
K, dust/cloud formation included) and NextGen ( K, dust/cloud formation not included) models are indicated by the solid and dashed lines, respectively (they almost coincide). Bottom: fit statistic resulting from fitting the spectral energy distribution with the BT-Settl and NextGen model atmospheres (Allard et al. 2012). Solar metallicity and
K, dust/cloud formation not included) models are indicated by the solid and dashed lines, respectively (they almost coincide). Bottom: fit statistic resulting from fitting the spectral energy distribution with the BT-Settl and NextGen model atmospheres (Allard et al. 2012). Solar metallicity and  are assumed.
are assumed.
Download figure:
Standard image High-resolution imageOur  estimate derived from fitting the molecular bands (Section 4.1) conforms with the non-dusty model. Indeed, dust formation in the atmosphere, which can give rise to additional opacity, is not included in the modeled spectra (see Section 3). The modeled wavelength region is too short to be sensitive to the possible reddening of the SED due to dust or clouds.
estimate derived from fitting the molecular bands (Section 4.1) conforms with the non-dusty model. Indeed, dust formation in the atmosphere, which can give rise to additional opacity, is not included in the modeled spectra (see Section 3). The modeled wavelength region is too short to be sensitive to the possible reddening of the SED due to dust or clouds.
Figure 12 shows the best-fit BT-Settl and NextGen models along with the  statistic. In contrast to Teff, the parameter
statistic. In contrast to Teff, the parameter  has almost no effect on the fit statistic.
has almost no effect on the fit statistic.
We estimate the mass and the radius of LSR J1835 with the help of the evolutionary models for the solar-metallicity substellar objects by Burrows et al. (2001). These predict the following scaling relations,
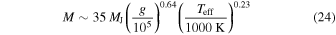
and
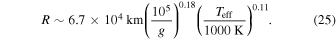
Evaluating the above expressions with  K (assuming dust formation in the atmosphere) and
K (assuming dust formation in the atmosphere) and  , as derived from fitting the molecular bands (Section 4.1), we obtain
, as derived from fitting the molecular bands (Section 4.1), we obtain
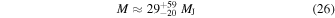
and
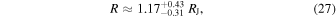
where  and
and  are the mass and the radius of Jupiter. Evaluating the above expressions with
are the mass and the radius of Jupiter. Evaluating the above expressions with  K (without taking dust formation in the atmosphere into account) yields similar results,
K (without taking dust formation in the atmosphere into account) yields similar results,  and
and  . (The effective temperature
. (The effective temperature  K, which is derived from fitting the molecular bands, gives approximately the same values for the mass and radius.) Based on the period of rotation of 2.84 hr and a
K, which is derived from fitting the molecular bands, gives approximately the same values for the mass and radius.) Based on the period of rotation of 2.84 hr and a  of 50 kms−1, Hallinan et al. (2008) estimated the radius of LSR J1835 to
of 50 kms−1, Hallinan et al. (2008) estimated the radius of LSR J1835 to  .
.
Based on their radius estimate and the bolometric luminosity given by Reid et al. (2003), Hallinan et al. (2008) concluded that LSR J1835 is most likely a brown dwarf. Our estimates of the dwarf's effective temperature, mass, and radius substantiate the substellar origin of the dwarf. Berdyugina et al. (2017) have obtained more accurate constraints on its mass and age, and concluded that LSR J1835 is a young brown dwarf in a T Tau-like evolutionary stage.
6. Discussion
Most of our 18 Stokes measurements obtained at different aspect angles indicate the presence of a strong magnetic field on the surface of LSR J1835, while two of them provide a compelling evidence at the level of 3σ and one—at the level of 5σ (see Table 6). This observational fact suggests that the surface of the dwarf might be covered with strong (∼5 kG) small-scale magnetic fields.
A few of our measurements comply with the absence of a magnetic field. This can have several reasons. First, in some cases, the data are strongly afflicted by random errors making finding of the best-fit model difficult. Second, for the highly inclined field ( ), the Stokes v signal will be consistent with the H0 hypothesis (assumes
), the Stokes v signal will be consistent with the H0 hypothesis (assumes  kG), because the factor
kG), because the factor  in the expression (20) vanishes. In this case, either the signal q or u or both are expected to be strong (see Figure 10: measurement five might illustrate this case). Third, cancellation of fields of different polarities can result in non-magnetic Stokes profiles.
in the expression (20) vanishes. In this case, either the signal q or u or both are expected to be strong (see Figure 10: measurement five might illustrate this case). Third, cancellation of fields of different polarities can result in non-magnetic Stokes profiles.
Filling factors derived from the intensity and those derived from the polarimetry differ by roughly one order of magnitude (see Tables 4 and 6). The intensity i is more sensitive to Teff (and  ) than to B, and thus the factor fi balances the temperatures of the magnetic and non-magnetic photospheres rather than accounting for the presence of a magnetic field. Because of low resolution and high
) than to B, and thus the factor fi balances the temperatures of the magnetic and non-magnetic photospheres rather than accounting for the presence of a magnetic field. Because of low resolution and high  , our intensity data alone are not able to provide a constraint on the surface magnetic field of the dwarf.
, our intensity data alone are not able to provide a constraint on the surface magnetic field of the dwarf.
The factors fq, fu, and fv scale the polarized flux and provide a lower limit on the magnetic filling factor f (see expressions (18)–(20)). Because magnetic fields give rise to polarization, the presence of a polarization signal confirmed by the CrH radiative model in the data of LSR J1835 provides strong evidence for its surface magnetic field.
We now want to put our work in the broader context of the observational studies on magnetism of fully convective dwarfs. Apart from the studies making use of indirect techniques (see Section 1 for references), we found only a few works that infer magnetic field properties of fully convective dwarfs from their spectra. Reiners & Basri (2010) have analyzed a dozen Zeeman-broadened FeH lines in the high-resolution intensity spectra of a sample of 63 late-M dwarfs. The authors have found that the magnetic fluxes Bf in their sample vary between 0.5 and 4 kG. With the help of the Zeeman Doppler Imaging (ZDI) technique by Donati & Brown (1997), Morin et al. (2008) have inferred a ∼0.5 kG magnetic field in a sample of 5 ∼ M4 dwarfs from their Stokes V data. We found only a few linear polarization measurements of ultra-cool dwarfs (Goldman et al. 2009; Miles-Páez et al. 2013, 2015). These are interpreted in the framework of scattering off dust or clouds.
Given the observed frequency of 8.46 GHz and a brightness temperature of  K, Berger et al. (2008) concluded that it is a non-thermal gyrosynchrotron plasma emission that is responsible for radio pulses from LSR J1835. Based on further assumptions, namely the size of the emitting region, the density of the emitting electrons, and the angle between the line of sight and the magnetic field, the authors estimated the strength of the uniform and over several rotational periods stable magnetosphere to
K, Berger et al. (2008) concluded that it is a non-thermal gyrosynchrotron plasma emission that is responsible for radio pulses from LSR J1835. Based on further assumptions, namely the size of the emitting region, the density of the emitting electrons, and the angle between the line of sight and the magnetic field, the authors estimated the strength of the uniform and over several rotational periods stable magnetosphere to  G. Hallinan et al. (2008) observed the dwarf at the same frequency and measured nearly 100% circular polarization of its radio emission, suggesting the electron-cyclotron maser instability mechanism at work in a magnetosphere of ∼3 kG. Recently, Hallinan et al. (2015) found that these radio pulses are also associated with the variability in Hα due to the optically thick region of temperature
G. Hallinan et al. (2008) observed the dwarf at the same frequency and measured nearly 100% circular polarization of its radio emission, suggesting the electron-cyclotron maser instability mechanism at work in a magnetosphere of ∼3 kG. Recently, Hallinan et al. (2015) found that these radio pulses are also associated with the variability in Hα due to the optically thick region of temperature  K with the surface coverage of
K with the surface coverage of  % in the low atmosphere of the dwarf.
% in the low atmosphere of the dwarf.
Berdyugina et al. (2017) have analyzed the Na I doublet at 8190 Å and Balmer emission lines in the same data set presented in this work. Under the assumption of a homogeneous longitudinal and inclined field, the authors infer  kG from the sodium Stokes v signal in the measurements one and three. It has been found that emission in Balmer lines is associated with the photospheric magnetic region seen in the Na I doublet. The authors derive the magnetic filling factor
kG from the sodium Stokes v signal in the measurements one and three. It has been found that emission in Balmer lines is associated with the photospheric magnetic region seen in the Na I doublet. The authors derive the magnetic filling factor  from the emission maps obtained with the help of a spectroscopic inversion technique. It has been suggested that the dwarf's magnetic activity may be driven by its entangled and rapidly evolving magnetic field, similar to young dMe stars (e.g., Johns-Krull & Valenti 2000).
from the emission maps obtained with the help of a spectroscopic inversion technique. It has been suggested that the dwarf's magnetic activity may be driven by its entangled and rapidly evolving magnetic field, similar to young dMe stars (e.g., Johns-Krull & Valenti 2000).
We conclude this study with two pictures reflecting the magnetic properties of LSR J1835. Its surface is covered with strong small-scale rapidly evolving magnetic fields of ∼5 kG, which give rise to a flaring emission from the lower atmosphere. It also has a large-scale stable (over at least several rotational periods) magnetosphere of ∼3 kG giving rise to radio emission. The questions of how the both magnetospheres are related to each other and whether they have the same origin in the interior of the dwarf remain to be answered.
7. Conclusions
This work presents the first measurements of the net magnetic field strength at the surface of a brown dwarf in molecular lines. Our measurements at different rotational phases yield one 5σ and two 3σ magnetic field detections on the surface of the M8.5 dwarf LSR J1835. Our approach, which makes use of the Paschen–Back effect in the CrH lines, provides the strength B (not flux Bf) of the net surface magnetic field. Our data analysis in both molecular (this work) and atomic (Berdyugina et al. 2017) lines suggests that the surface of LSR J1835 is most likely covered by strong (∼5 kG) small-scale and rapidly evolving magnetic fields. This field geometry can give rise to frequent reconnection events, and thus flaring activity.
This study demonstrates that the magnetism of brown dwarfs can be successfully assessed with spectropolarimetry, provided the magnetic signatures in molecular bands are understood and modeled correctly. Furthermore, this work leads the way toward studying the surface magnetism of M- and T-type dwarfs and hot exoplanets.
We substantiate the substellar origin of LSR J1835 with the help of our data as well as the photometric data from the all-sky surveys 2MASS and WISE.
This work was supported by the European Research Council Advanced Grant HotMol (ERC-2011-AdG 291659). We thank the Keck staff, support astronomers, and particularly Dr. Bob Goodrich and Dr. Hien Tran for their support. Dr. Harrington and Dr. Berdyugina acknowledge support from the InnoPol grant: SAW-2011-KIS-7 from Leibniz Association, Germany. Dr. Berdyugina acknowledges the support from the NASA Astrobiology Institute and the Institute for Astronomy, University of Hawaii, for the hospitality and allocation of observing time at the Keck telescope. Dr. Kuzmychov is grateful to Dr. France Allard for providing the BT-Settl model atmospheres. The authors are grateful to Dr. Jeff Linsky for his valuable comments on the manuscript. The authors also thank the anonymous referee for a number of suggestions that helped to improve the manuscript. This program was partially supported by the Air Force Research Labs (AFRL) through salary support for Dr. Harrington. This work made use of the Dave Fanning and Markwardt IDL libraries as well as of the online VOSA tool, developed under the Spanish Virtual Observatory project supported from the Spanish MICINN through grant AyA2011-24052.
Facility: Keck:I (LRIS) - .

















