Abstract
The zero offset of the fluxgate magnetometer (FGM) on board the spacecraft varies slowly with time, therefore the FGM needs regular in-flight calibration. There are abundant physical phenomena in the solar wind, such as waves, mirror mode structures, and current sheets. Several in-flight calibration methods have been developed based on the properties of Alfvén waves or mirror mode structures instead of current sheets. Here, we develop a method to determine the zero offset O using current sheets in the solar wind, which is based on an assumption that the magnetic field in the normal direction of the current sheet is zero. The nonzero magnetic field in the normal direction is the projection of O, therefore we can obtain the component of O in the normal direction. In the offset cube, the zero offset is expected to be in a plane, which is referred to as the optimal offset plane (OOP). Each current sheet can obtain an OOP in the offset cube. At least three nonparallel OOPs must be used to determine the zero offset. We test our method by using data from the Magnetospheric Multiscale mission and find that our method is able to determine the zero offset. Our method can simultaneously use Alfvén waves, mirror mode structures, and current sheets to determine the zero offset, thus it might be a useful tool to perform the in-flight calibration of the FGM for solar wind monitors.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The space plasma environment is a natural large-scale laboratory, in which abundant plasma physical processes take place (Zhang et al. 2012; Paschmann et al. 2013; Milan et al. 2017). In-depth study of these physical phenomena is of great significance to understand the solar-terrestrial space environment and the evolution of the planetary atmosphere (Zhang et al. 2016; Milan et al. 2017; Ohtani et al. 2020; Smith et al. 2020). Observations of the physical processes in the space plasma environment rely on satellite measurement of fields and charged particles, of which the magnetic field is an important measurement parameter (Russell et al. 2016; Liu et al. 2020).
The fluxgate magnetometer (FGM) is a kind of magnetometer commonly used on spacecraft (Acuña 2002; Auster et al. 2008; Balogh 2010; Pope et al. 2011; Liu et al. 2020). FGMs have the advantage of small size and light weight and also can adapt to various complicated plasma environments (Acuña 2002). The magnetic field measured by the FGM on board the spacecraft consists of the natural magnetic field, the magnetic field induced by the spacecraft, and the instrumental offset (Leinweber et al. 2008; Russell et al. 2016). The instrumental offset is the measurement value of the FGM when the ambient magnetic field is zero (Acuña 2002; Wallis et al. 2015). It is difficult to distinguish the instrumental offset from the residual magnetic field of the spacecraft as both vary slowly with time (Leinweber et al. 2008). Thus, both magnetic fields are considered as the zero offset of the FGM (Pudney et al. 2012).
In the solar wind, there are abundant magnetic field fluctuations and structures, such as linear magnetic holes (Wang et al. 2020a, 2020b, 2020c, 2021a), magnetic peaks (Burlaga et al. 2006; Wang et al. 2021b), and discontinuities (Artemyev et al. 2019; Neukirch et al. 2020). Alfvén waves are a kind of magnetohydrodynamic wave, and the magnetic field strength BT has no variations during Alfvén waves (Keiling 2008; Wang et al. 2015). The interplanetary magnetic field (IMF) fluctuations have a highly Alfvénic nature, i.e., the magnetic field in a certain component has a large variation while there is no significant variation in BT (Leinweber et al. 2008). Based on the characteristics of Alfvén waves, Davis & Smith (1968), Belcher (1973), and Hedgecock (1975) developed different methods to calculate the zero offset. Because there are no pure Alfvén waves in the solar wind, the accuracy of the estimated zero offset relies on the selection of the magnetic field fluctuations (Leinweber et al. 2008; Meng et al. 2018; Pan et al. 2019). The Davis–Smith method can deal with IMF fluctuations over a much shorter time interval, thus it is the optimal method among these three methods (Leinweber et al. 2008).
Mirror mode structures, generated by the mirror instability, widely exist in the solar wind as well as in the planetary magnetospheres and magnetosheaths (Zhang et al. 2008a; Balikhin et al. 2009; Tsurutani et al. 2011; Wang et al. 2016; Karlsson et al. 2021; Volwerk et al. 2021). By assuming that the maximum variance direction of the mirror mode structure is parallel to the ambient magnetic field, one-dimensional (Plaschke & Narita 2016) and three-dimensional (Plaschke et al. 2017) mirror mode methods have been developed to determine the zero offset of the FGM on board the spinning spacecraft and the three-axis stabilized spacecraft, respectively. More solar wind data can achieve a higher accuracy of the zero offset determined by the mirror mode method, for example, ∼40 hr of the solar wind data can achieve an accuracy of 0.2 nT (Plaschke 2019; Schmid et al. 2020).
Recently, Wang & Pan (2021a, 2021b) developed a new method of determining the zero offset. This new method is referred to as the Wang–Pan method for the convenience of description. The authors first set an offset cube, in which each point is a possible value of the zero offset O . For an Alfvén wave, Wang & Pan (2021a) found that O is on a straight line parallel to the ambient magnetic field in the offset cube, which is referred to as the optimal offset line (OOL). The intersection of at least two nonparallel OOLs is the zero offset (Wang & Pan 2021a). Coincidentally, a mirror mode structure also has an OOL in the offset cube, which is parallel to the maximum variance direction of the structure (Wang & Pan 2021b). Thus, the Wang–Pan method can simultaneously use Alfvén waves and mirror mode structures (or linear magnetic holes).
Besides mirror mode structures, the current sheet is also a common phenomenon in the solar wind (Zhang et al. 2008b). In this study, we further develop the Wang–Pan method to enable it to determine the zero offset using the current sheet in the solar wind. We find that the zero offset is in an optimal offset plane (OOP) in the offset cube for a current sheet, which can be used to determine the zero offset.
2. Optimal Offset Planes for Current Sheets
We use the observation of the Magnetospheric Multiscale (MMS) mission, launched on 2015 March 13 (Burch et al. 2016), to investigate the properties of the current sheet in the solar wind. The MMS spacecraft consists of four identical probes with an interspacecraft distance of 10–400 km. In the present study, the magnetic field data at 16 Hz resolution measured by the FGM (Russell et al. 2016) on board MMS1 are used.
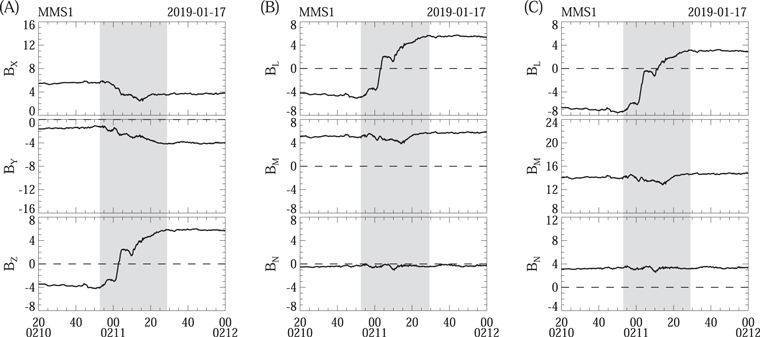
Figure 1(A) shows the magnetic field in Geocentric Solar Magnetospheric (GSM) coordinates observed by the MMS1 spacecraft between 02:10:20 and 02:12 UT on 2019 January 17. Before 02:10:50 UT and after 02:11:30 UT, the magnetic field direction has no significant change. However, the magnetic field direction gradually changes in the interval as shown in the gray region, indicating that there is a current sheet (Zhang et al. 2008b). Figure 1(B) shows the magnetic field in the LMN coordinate system, which is determined by minimum variance analysis (MVA; Sonnerup & Scheible 1998) using the magnetic field data from MMS1 between 02:10:53 and 02:11:29 UT. The maximum variance direction L = (−0.25, −0.24, 0.94), the intermediate variance direction M = (0.9, −0.42, 0.13), and the minimum variance direction N = (0.37, 0.87, 0.32) in GSM. The eigenvalues λ1, λ2, and λ3 are ∼12.18, 0.27, and 0.035, respectively. The N direction can be regarded as the normal direction of the current sheet (see Wang et al. 2021c). The ratio of λ2/λ3 is ∼7.7, indicating that the normal direction of the current sheet is reliable (Sonnerup & Scheible 1998; Wang et al. 2014). One can find that the magnetic field in the normal direction of this current sheet is approximately zero.
Figure 1. Three components of the magnetic field in the GSM (A) and LMN (B and C) coordinate systems observed by MMS1 between 02:10:20 and 02:12 UT on 2019 January 17. The gray region indicates a current sheet. In panel C, a zero offset O = (10, 0, 0) nT has been added to the magnetic field data as shown in panel A before performing the minimum variance analysis.
Download figure:
Standard image High-resolution imageWe arbitrarily set a zero offset O = (10, 0, 0) nT and add it to the magnetic field data B in Figure 1(A). Then, we transform the modified magnetic field data (= B + O ) into the LMN coordinate system based on MVA using the data between 02:10:53 and 02:11:29 UT. The profiles of each component of the magnetic field in Figure 1(C) are the same as those in Figure 1(B) except for the difference in a constant, which is equal to the projection of O in the corresponding direction.
We assume that the magnetic field in the normal direction of the current sheet is zero, i.e., BN
is 0 for a current sheet. For the uncalibrated magnetic field data, the nonzero BN
is expected to result from the projection of
O
(=(OL
, OM
, ON
)) in the
N
direction. Thus, we can obtain the value of ON
, while OL
and OM
cannot be determined. We set an offset cube
O
' in LMN as shown in Figure 2(A); a known parameter ON
and two unknown parameters OL
and OM
indicate that
O
is in the plane parallel to the 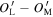 plane with
plane with 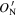 = ON
. Thus, we mark this plane as the OOP. Figure 2(A) shows an example of the OOP with
= ON
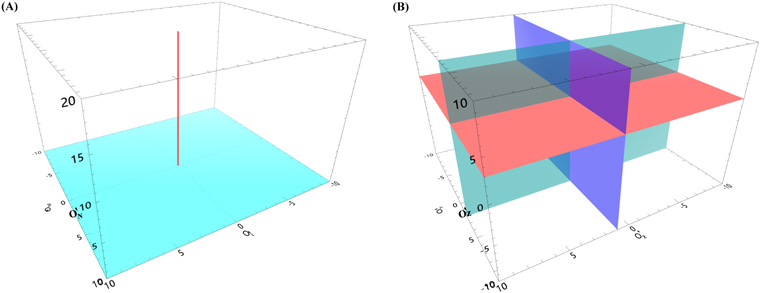
. Thus, we mark this plane as the OOP. Figure 2(A) shows an example of the OOP with 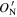 = 0. The OOP means that the most likely value of the real zero offset is reduced to this plane from the whole offset cube by using the properties of one current sheet. If only two current sheets are used, the most likely value of the zero offset is reduced to be on a straight line, which is the intersection of the two nonparallel OOPs determined by the current sheets. Similarly, the zero offset is expected to be the intersection of at least three nonparallel OOPs determined by different current-sheet events as shown in Figure 2(B). Therefore, we can determine the zero offset by using the nonparallel OOPs of at least three current-sheet events.
= 0. The OOP means that the most likely value of the real zero offset is reduced to this plane from the whole offset cube by using the properties of one current sheet. If only two current sheets are used, the most likely value of the zero offset is reduced to be on a straight line, which is the intersection of the two nonparallel OOPs determined by the current sheets. Similarly, the zero offset is expected to be the intersection of at least three nonparallel OOPs determined by different current-sheet events as shown in Figure 2(B). Therefore, we can determine the zero offset by using the nonparallel OOPs of at least three current-sheet events.
Figure 2. (A) A diagram of the optimal offset plane (OOP) in the LMN coordinate system for a current-sheet event. The cyan plane is the OOP, and the red line is the 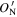 axis. (B) A diagram of the determination of the zero offset using three nonparallel OOPs in the offset cube as shown in red, blue, and cyan.
axis. (B) A diagram of the determination of the zero offset using three nonparallel OOPs in the offset cube as shown in red, blue, and cyan.
Download figure:
Standard image High-resolution imageNext, we try to find out the OOP for the current sheet as shown in Figure 1(A). First, we set an offset cube in GSM, and the magnetic field data are modified by  at the point
O
' in this cube, where
B
is the magnetic field data in Figure 1(A). Here, we use the calibrated MMS data to mimic the natural magnetic field in the solar wind, therefore the parameter
O
is expected to be 0. Then, we perform MVA using the magnetic field data
at the point
O
' in this cube, where
B
is the magnetic field data in Figure 1(A). Here, we use the calibrated MMS data to mimic the natural magnetic field in the solar wind, therefore the parameter
O
is expected to be 0. Then, we perform MVA using the magnetic field data 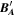 .
. 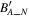 , the N component of
, the N component of 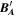 in LMN, is regarded as an indicator for finding the most likely value of the zero offset in the offset cube. Figure 3(A) shows the distribution of
in LMN, is regarded as an indicator for finding the most likely value of the zero offset in the offset cube. Figure 3(A) shows the distribution of 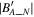 in the
in the  plane at different values of
plane at different values of  . In each panel of Figure 3(A), there is a minimum
. In each panel of Figure 3(A), there is a minimum 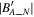 if we look at the values of
if we look at the values of 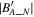 in the
in the  direction at a certain
direction at a certain  . These minima of
. These minima of 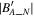 form a straight line in the
form a straight line in the  plane. Such straight lines in the
plane. Such straight lines in the  planes with different values of
planes with different values of 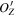 are parallel to the vector
V
1
= (1, −0.42, 0) in GSM. Figure 3(B) shows the distributions of
are parallel to the vector
V
1
= (1, −0.42, 0) in GSM. Figure 3(B) shows the distributions of  in the
in the  plane at different values of
plane at different values of 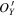 . The local minima of
. The local minima of 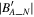 in the
in the 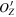 direction at different values of
direction at different values of 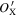 also form a straight line, which is parallel to the vector
V
2
= (1, 0, −1.09) in GSM. One can find that each local minimum of
also form a straight line, which is parallel to the vector
V
2
= (1, 0, −1.09) in GSM. One can find that each local minimum of 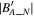 in the offset cube is in a plane perpendicular to
V
1
×
V
2
. We find that the angle between the N direction and
V
1
×
V
2
is ∼0
in the offset cube is in a plane perpendicular to
V
1
×
V
2
. We find that the angle between the N direction and
V
1
×
V
2
is ∼0 9, i.e., the plane formed by the minimum
9, i.e., the plane formed by the minimum 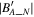 can be regarded as the OOP for this current sheet.
can be regarded as the OOP for this current sheet.
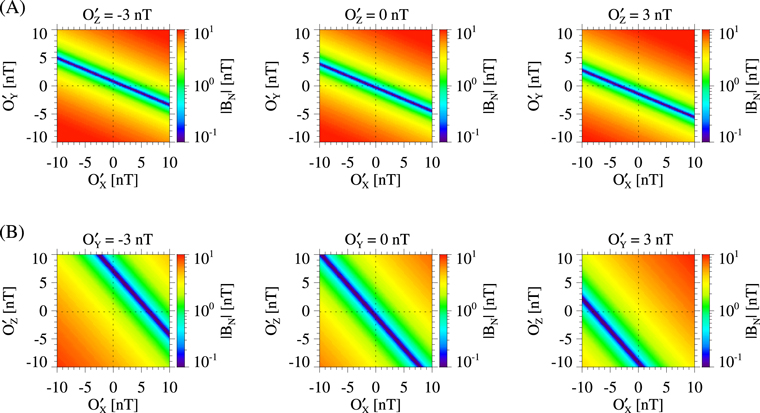
Figure 3. (A) The distributions of 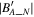 in the
in the 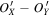 plane at
plane at  , 0, and 3 nT for the current sheet in Figure 1(A). (B) The distributions of
, 0, and 3 nT for the current sheet in Figure 1(A). (B) The distributions of 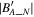 in the
in the  plane at
plane at 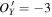 , 0, and 3 nT for the current sheet in Figure 1(A).
, 0, and 3 nT for the current sheet in Figure 1(A).
Download figure:
Standard image High-resolution image3. Application to MMS
The magnetic field data from the MMS spacecraft are well calibrated by performing the Davis–Smith method, cross-calibration with the electron drift instrument, and interspacecraft calibration (Leinweber et al. 2012; Russell et al. 2016). We use the calibrated magnetic field data in GSM to mimic the natural magnetic field in the solar wind measured by a three-axis stabilized spacecraft, i.e., we use the calibrated MMS data to test whether our method can determine the zero offset using current sheets in the solar wind. The zero offset of the FGM changes slowly with time (Leinweber et al. 2008; Russell et al. 2016). To simplify the analysis, we assume that the zero offset is a constant in the interval we used (see Figure 4(A)).
Figure 4. (A) The magnetic field in GSM and the magnetic field strength observed by MMS1 in the solar wind between 20:00 UT on 2019 January 16 and 16:00 UT on 2019 January 18. The vertical red, green, and blue dashed lines denote the selected current-sheet events, wave events, and mirror mode events, respectively. (B—D) The magnetic field in GSM and BT for the selected current-sheet events (B), wave events (C), and mirror mode events (D).
Download figure:
Standard image High-resolution imageFigure 4(A) shows the magnetic field in GSM between 20:00 UT on 2019 January 16 and 16:00 UT on 2019 January 18. This time interval is almost the same as that used by Wang & Pan (2021a, 2021b). The eight red vertical dashed lines denote the times of the current-sheet events we select. The green and blue vertical dashed lines denote the four wave events and four mirror mode events used by Wang & Pan (2021a, 2021b)). Figures 4(B), (C), and (D) display the magnetic field in GSM and BT during the eight current-sheet events, four wave events, and four mirror mode events, respectively. The time interval of each event is marked in gray.
The calibrated MMS magnetic field data in GSM are marked as
B
, and the magnetic field data are modified to be  at the point
O
' in an offset cube in GSM, where
O
is set to be [100, 50, 20] nT. The range of each side of the offset cube is (−10, 10) nT plus the corresponding component of
O
, and the step length is 0.1 nT. Then, we perform MVA using the data of
at the point
O
' in an offset cube in GSM, where
O
is set to be [100, 50, 20] nT. The range of each side of the offset cube is (−10, 10) nT plus the corresponding component of
O
, and the step length is 0.1 nT. Then, we perform MVA using the data of 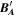 . We find the direction
V
1
of the straight line formed by the minima of
. We find the direction
V
1
of the straight line formed by the minima of 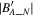 in the
in the  plane at
plane at 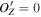 using the same process shown in Figure 3(A). Similarly, we find the direction
V
2
of the straight line formed by the minima of
using the same process shown in Figure 3(A). Similarly, we find the direction
V
2
of the straight line formed by the minima of 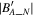 in the
in the  plane at
plane at 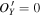 . Based on
V
1
,
V
2
, and the location of one minimum
. Based on
V
1
,
V
2
, and the location of one minimum 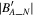 in the offset cube, we can obtain the OOP of the corresponding current sheet.
in the offset cube, we can obtain the OOP of the corresponding current sheet.
Due to the effect of the magnetic field noise and the calculation error of the MVA, the nonparallel OOPs might have no common intersection. Therefore, we define the point in the offset cube to be the zero offset so that the sum of the distances from this point to all the OOPs is the smallest. If the distance Ls from this point to an OOP is much larger than those to the other OOPs, it can cause a big calculation error in the zero offset. To avoid such a big error, we introduce a weight to the parameter Ls , which is
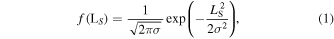
where σ is the standard deviation. The parameter σ can be determined by the degree of dispersion of the parameter Ls . Here, we set σ = 3. Now, we define the point in the offset cube to be the zero offset so that the sum of the probabilities f(Ls ) for this point is the maximum value.
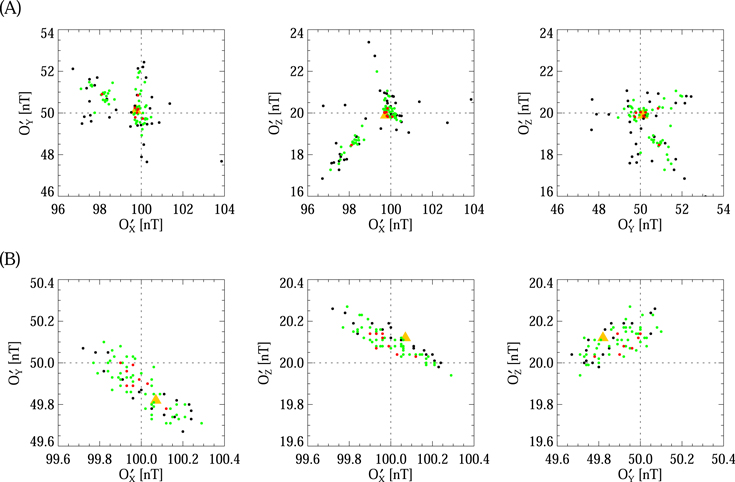
We use any three, five, and seven out of eight current-sheet events to determine the zero offset based on our method, and the results are shown in Figure 5(A). The zero offset we set is [100, 50, 20] nT, thus we can compare the error distribution of the estimated zero offset determined by a different number of current-sheet events. The calculation errors can be up to ∼4 nT when we use three current-sheet events. We can find that the calculation error when using seven events is significantly smaller than that when using three or five events. The orange triangle in Figure 5(A) shows the zero offset with a value of [99.75, 50.12, 19.89] nT determined by all eight current-sheet events, which is very close to the O we set.
Figure 5. (A) The zero offsets determined by any three (black), five (green) and seven (red) of the eight current-sheet events in the 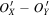 ,
,  , and
, and  planes. The orange triangle denotes the zero offset determined by the eight current-sheet events. (B) The zero offsets determined by the selected four wave events, four mirror mode events, and any two (black), five (green), or seven (red) of the eight current-sheet events. The orange triangle denotes the zero offset determined by the four wave events and four mirror mode events.
planes. The orange triangle denotes the zero offset determined by the eight current-sheet events. (B) The zero offsets determined by the selected four wave events, four mirror mode events, and any two (black), five (green), or seven (red) of the eight current-sheet events. The orange triangle denotes the zero offset determined by the four wave events and four mirror mode events.
Download figure:
Standard image High-resolution imageWe develop the Wang–Pan method so that it can use the current-sheet event. Now, we test whether our method can determine the zero offset using the IMF fluctuation events, mirror mode events, and current-sheet events at the same time. Figures 4(C) and (D) show the four wave events with a highly Alfvénic nature and four mirror mode events. We use all these wave events and mirror mode events to determine the zero offset based on the Wang–Pan method, and the result is [100.07, 49.82, 20.12] nT as shown by the orange triangle in Figure 5(B). We use any two, five, and seven out of the eight current-sheet events as well as the four wave events and four mirror mode events to determine the zero offset, and the results are shown in Figure 5(B). One can find that the estimated zero offset is very close to the O we set, and the red dots (seven out of eight current-sheet events) are closer to O than the black (two out of eight) and green (five out of eight) dots as a whole. This suggests that our method can use the IMF fluctuations, mirror mode structures, and current sheets at the same time, which enables our method to achieve a higher accuracy of the zero offset.
4. Conclusion and Discussion
We have developed the Wang–Pan method to enable it to determine the zero offset using current sheets in the solar wind based on the assumption that the magnetic field strength is zero in the normal direction of the current sheet. The nonzero value of the uncalibrated magnetic field in the normal direction is the projection of the zero offset O . We find that the zero offset is in a plane in the offset cube, which is defined as the OOP. The intersection of at least three nonparallel OOPs can be regarded as the zero offset. Due to the effect of the calculation errors of MVA as well as the magnetic field noise, BN is typically not zero, resulting in no common intersection for the OOPs. To improve the calculation accuracy of the zero offset, we convert the distance Ls from a certain point in the offset cube to the OOP into probability. The smaller the parameter Ls , the greater the probability. We define the zero offset as the point in the offset cube such that the sum of the probabilities associated with the distances from that point to all the OOPs is the largest.
Wang & Pan (2021a, 2021b) found that both Alfvén waves and mirror mode structures have OOLs in the offset cube, and the OOLs of the Alfvén wave and mirror mode structure are determined in different ways. After obtaining the OOLs, the zero offset is determined by finding the point so that the sum of the distances from the point to all the OOLs is the smallest (Wang & Pan 2021a, 2021b). It means that Alfvén waves and mirror mode structures can be simultaneously used by the Wang–Pan method. In this study, we find that there is an OOP in the offset cube for a current-sheet event. The calculation of the zero offset using the OOPs is very similar to that using the OOLs determined by Alfvén waves or mirror mode structures (Wang & Pan 2021a, 2021b). Therefore, our method is actually an extended application of the Wang–Pan method. Our results further expand the application objects of the Wang–Pan method, which can simultaneously use Alfvén waves, mirror mode structures, and current sheets. Making full use of these physical phenomena in the solar wind may help to further improve the accuracy of the zero offset.
As far as we know, this is the first time that it has been shown that the current sheet in the solar wind is able to be used to determine the zero offset of the spaceborne FGM. We use eight current-sheet events to test our method and find that the difference between the zero offsets determined by our method and the FGM team is ∼0.3 nT. Such a small difference indicates that our method is able to obtain a high accuracy of the zero offset. One must note that the current sheet cannot replace IMF fluctuations with a highly Alfvénic nature as the main phenomenon used for in-flight calibration, because IMF fluctuations with a highly Alfvénic nature are more abundant. However, using the current sheet has at least three advantages for in-flight calibration as follows. (1) Using current sheets, mirror mode structures, and IMF fluctuations at the same time enable the Wang–Pan method to achieve a higher accuracy of the zero offset. (2) Using the IMF fluctuations alone might lead to no results over certain periods of time, during which there are fewer IMF fluctuations with a highly Alfvénic nature. Nevertheless, we can still determine the zero offset if there are some current sheets during these intervals. (3) There are current sheets in the planetary magnetosphere (Zhang et al. 2002; Wang et al. 2014, 2019), i.e., our method can be applied in the planetary magnetosphere.
This work in China was supported by the Strategic Priority Research Program of Chinese Academy of Sciences grant XDB 41000000, Shenzhen Science and Technology Research Program (JCYJ20210324121412034), and NSFC grants 41804157, 41774171, 41774167, 41974205 and 41904156. The authors also acknowledge the financial support from the pre-research Project on Civil Aerospace Technologies (No. D020103) funded by CNSA, the 111 project [B18017], CAS Center for Excellence in Comparative Planetology, and the Fundamental Research Funds for the Central Universities. We appreciate the NASA MMS mission and the FGM team of the MMS project.
Data Availability
The data of the MMS spacecraft are publicly available at https://lasp.colorado.edu/mms/sdc/public/.