A Census of Outflow to Magnetic Field Orientations in Nearby Molecular Clouds

In this analysis, we consider the protostellar outflows identified by casi-3d in the four molecular clouds, Ophiuchus, Taurus, Perseus, and Orion. Xu et al. (2022) employed casi-3d to systematically identify protostellar outflows in ¹²CO (1 − 0) and ¹³CO (1 − 0) data cubes. The ¹²CO and ¹³CO data of Ophiuchus, Taurus, and Perseus were observed with the 13.7 m Five College Radio Astronomy Observatory (FCRAO) Telescope (Ridge et al. 2006; Narayanan et al. 2008). The main beam of the antenna pattern has a FWHM of 45'' for ¹²CO and 47'' for ¹³CO. The data are obtained on the fly (OTF), but they are resampled onto a uniform 23'' grid (Ridge et al. 2006). The observations of Orion A were carried out with the Nobeyama Radio Observatory 45 m telescope (NRO 45 m) (Shimajiri et al. 2015a, 2015b; Nakamura et al. 2019; Ishii et al. 2019). The data has a pixel scale of 75 and has an effective angular resolution of 22''. There is a span of distance estimates for the four clouds. We adopt fiducial distance estimates for the four clouds of 120 pc for Ophiuchus (Nakamura et al. 2011), 140 pc for Taurus (Narayanan et al. 2012), 300 for Perseus (Arce et al. 2010), and 420 for Orion (Kong et al. 2018). The physical resolutions for the four clouds are 0.013 pc per pixel for Ophiuchus, 0.016 pc per pixel for Taurus, 0.033 pc per pixel for Perseus, and 0.015 pc per pixel for Orion.

casi-3d is an encoder–decoder-based 3D convolutional neural network, which identifies outflow structures coherently across velocity channels. This indicates that casi-3d identifies outflows using both morphology and velocity information from molecular line data cubes. We train casi-3d on the same training set as that in Xu et al. (2020a), which includes different magnetohydrodynamic model properties, different ¹²CO abundances, and different cloud kinetic temperatures. casi-3d takes ¹²CO data cubes as input and predicts the position of outflows on the voxel level. We separate the outflow prediction into two components: blueshifted lobes and redshifted lobes for each cloud. We exclude the emission near the central velocity where ∣v_cen∣ < 1 km s⁻¹. We adopt the integrated blue- and redshifted outflow components predicted by model MF, a model that is trained to exclude the contamination by emission that is not associated with feedback (e.g., Xu et al. 2020a, 2020b).

casi-3d identifies all the voxels associated with feedback, but does not segment them into individual outflows. Therefore, after applying casi-3d, we carry out a dendrogram analysis ⁵ on the outflow prediction to isolate individual outflow lobes. We vary several different parameters to verify that the results do not strongly depend on the assumed values used to construct the dendrogram tree. For example, in analyzing Perseus, we vary the min_value parameter between 7 and 10σ, min_delta between 1 and 2σ, and min_npix between 10 and 20 pixels. The parameter min_value is the minimum value to consider in constructing the tree, and our values are similar to the detection level of the observations. The parameter min_delta indicates how significant a leaf has to be in order to be considered an independent entity. For observational data, this is usually set to 1σ, which means that any leaf that is locally less than 1σ tall is combined with its neighboring leaf or branch and is no longer considered a separate entity. The parameter min_npix is the minimum number of pixels needed for a leaf to be considered an independent entity. The leaf will be joined to its parent branch or another leaf if the leaf has fewer than this number of pixels. The number of identified blueshifted lobes ranges between 102 and 111, and the number of identified redshifted lobes is between 58 and 62. The relatively bright lobes are universally identified regardless of the tested parameter.

Many of the outflow features are identified in clustered regions where it is difficult to define the outflow direction. To address this, we pair blue- and redshifted lobes if their distance is within 0.1 pc, and then we derive a single outflow orientation using both lobes. We limit our analysis to this set of candidates and exclude all one-lobe outflows, which only have either a blue- or redshifted lobe. We note that it is common for only one lobe of the outflow to appear cleanly in CO data (e.g., Arce et al. 2010); however, at the data resolution, one outflow lobe alone may not have a clear orientation. The outflows tend to be more isolated. We apply principal component analysis (PCA) to the outflow pairs to determine the orientations. Figures 1–4 show the outflow pairs in the four regions. Hereafter, we use the term outflow to refer to identified pairs of blue- and redshifted lobes. Altogether, we identify 43 outflows in Ophiuchus, 41 in Taurus, 23 in Perseus, and 93 in Orion, for a total of 200 outflows in the four regions. We further examine the position–velocity diagram of all 200 outflow candidates. Of these, 136 outflow candidates have significant coherent high-velocity features across at least 1 km s⁻¹, with a characteristic "Hubble wedge" shape in the position–velocity diagram (Arce & Goodman 2001, see supplementary images). We consider these 136 outflow candidates as a subset of the highest-confidence outflows. We retain the rest as likely outflow candidates, which have distinct blue- and redshifted lobes but do not show significantly coherent velocity structure across at least 1 km s⁻¹. However, these outflow candidates are likely real outflows, because many enclose an infrared source. Li et al. (2015) found a significant number of outflows in Taurus that do not have over 1 km s⁻¹ coherent velocity structure in the position–velocity diagram, but they are clear across several channels. Consequently, we adopt all 200 outflow candidates that have both blue- and redshifted lobes as the primary sample in our following work.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We adopt the data from the Planck Third Public Data Release (Planck Collaboration et al. 2020). We infer the magnetic field orientation from the dust polarization angle:

$\begin{eqnarray}&&{\phi }_{B}=\displaystyle \frac{1}{2}\arctan 2(-U,Q)+\displaystyle \frac{\pi }{2},\end{eqnarray} \tag{ 1 }$

where Q and U are the Stokes parameters of polarized dust emission. The maps of Q and U are initially at 4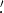8 resolution in HEALPix format with an effective pixel size of 1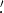07. We calculate the magnetic field orientation of each outflow by taking the mass-weighted magnetic field orientation at the corresponding position. We show the magnetic field orientation of the four clouds in Figures 1–4.

Zoom In Zoom Out Reset image size

In this section, we introduce a new casi-3d model to predict the inclination angle of each protostellar outflow. We define f_v as the ratio between the actual 3D momentum to the line-of-sight (LOS) momentum in each voxel:

$\begin{eqnarray}&&{f}_{v}=\displaystyle \frac{{P}_{3{\rm{D}}}}{{P}_{\mathrm{LOS}}}.\end{eqnarray} \tag{ 2 }$

We adopt the same casi-3d architecture and training set as that in Xu et al. (2020a). We only replace the target from outflow mass to f_v during training. The new model is able to predict the 3D momentum of the outflows in each voxel. We calculate both the 1D line of sight (LOS) and full 3D momentum of each outflow and define the effective outflow inclination angle, i, as

$\begin{eqnarray}&&\cos \,i=\displaystyle \frac{\sum {P}_{\mathrm{LOS}}}{\sum {P}_{3{\rm{D}}}}.\end{eqnarray} \tag{ 3 }$

It is worth noting that this angle is not exactly equal to the geometric inclination angle of the outflow. Considering that most outflows are not pencil-beam jets in ¹²CO emission, the mass/momentum injection occurs over a wide-angle cone structure. This indicates that even if the outflow is launched perpendicularly to our LOS, we are still able to estimate the LOS momentum of the outflow cone, which implies $\cos \,i$ cannot be zero. Consequently, the effective inclination angle is an approximation of the geometric inclination angle of an outflow.

Figure 5 demonstrates the performance of casi-3d for inferring the inclination angle of the synthetic outflows. The error bars indicate the uncertainty of the inferred inclination angle for synthetic outflows with different physical and chemical conditions, including different kinetic temperatures, 10 and 14 K, and different ¹²CO abundances, 10⁻⁴, 5 × 10⁻⁵, and 10⁻⁵ (Xu et al. 2020a). We discuss the performance of casi-3d in more detail in the Appendix.

Zoom In Zoom Out Reset image size

We next apply the casi-3d model to four high-confidence outflows identified in Perseus, Taurus, Ophiuchus, and Orion in order to show the performance for typical sources. The inclination angle is calculated from the LOS momentum in each pixel and the corresponding 3D momentum predicted by casi-3d. For example, the inclination angle of the Ophiuchus outflow in the upper left panel of Figure 6 is generally small compared with that of the other three outflows. This Ophiuchus outflow is likely launching toward us rather than in the plane of sky. The blue- and redshifted lobes significantly overlap, which is consistent with an outflow that has a small inclination angle with respect to the line of sight.

Zoom In Zoom Out Reset image size

For each outflow identified in Section 2.1, we adopt the total LOS momentum of the outflow and total casi-3d predicted 3D momentum to derive the inclination angle. We present the distribution of outflow inclination angles for the four regions in Figure 7.

Zoom In Zoom Out Reset image size

With the exception of Perseus, the distributions are not consistent with a random distribution of inclinations. The outflows in Perseus have larger average inclination angles and a narrower distribution of angles than those in the other regions, i.e., they appear more randomly oriented. One possible explanation is that the plane-of-sky magnetic field might be weaker in Perseus than that in the other regions. When the magnetic field is strong, outflows likely launch along with the large-scale magnetic field direction rather than randomly. Bastien (2020) summarized the recent results in the BISTRO (B-fields In STar-forming Regions Observations) polarimetric survey of several nearby molecular clouds with JCMT and found that the plane-of-sky magnetic field strength in Perseus B1 region is the weakest among the nearby molecular clouds. However, B1 is a small subregion of Perseus and may not be representative of the conditions in the entire cloud. Another caveat is that these measurements are of the plane-of-sky magnetic field strength rather than the line-of-sight magnetic field strength. We note that the strength of the line-of-sight magnetic field at relatively large scales is poorly constrained for these four clouds.

Figure 7 shows the average outflow inclination angle in Ophiuchus, Taurus, and Orion is around 30°–40°, which is smaller than the typical random value of 60^◦. Besides differences in the magnetic field or other cloud properties, a possible explanation is that the casi-3d model has some bias toward identifying outflows with significant coherent high-velocity features. This implies that the identified outflow likely launches toward the line of sight rather than on the plane of sky, where the outflow gas blends with the cloud emission. Such an effect could introduce a bias that leads to a global signature of alignment in 3D, which we discuss further in the following sections.

In this section, we examine the relative position angle of orientation between magnetic fields and outflows on the plane of sky, θ_B−out, for the four regions. We compute the angle between the flux-weighted mean orientation of the magnetic field at the outflow position with the outflow orientation. The angle θ_B−out takes values between 0^◦ and 90^◦. The left panel of Figure 8 shows the cumulative distribution function (CDF) of θ_B−out for the four regions. All four regions have a distribution that is above the distribution expected for a random, i.e., uncorrelated, orientation of outflow axis with orientation of magnetic field direction. Note that this random distribution, after accounting for projection effects on the plane of sky, predicts a uniform distribution in θ_B−out, such that the CDF rises linearly with θ_B−out.

Zoom In Zoom Out Reset image size

To evaluate the significance of this result, we conduct a Kolmogorov–Smirnov (K-S) test to examine the difference between the distribution of θ_B−out for all outflows and the uniform distribution that is expected from random relative orientations. The p-value of the K-S test is 2.7 × 10⁻⁴, which indicates that θ_B−out is not likely to be drawn from a uniform distribution. We then carry out a random sampling test, i.e., we randomly pick 200 numbers from a uniform distribution between 0 and 90, and repeat this process 10⁵ times. The sample size, 200, is given by the number of identified outflows in our study. We show the probability distribution of these samples in the right panel of Figure 8. The observed θ_B−out distribution is unlikely, with a probability of ∼10⁻⁴ that it is drawn from a random distribution. This value is consistent with the p-value found in the K-S test.

The right panel of Figure 8 also displays the measured θ_B−out distribution from Yen et al. (2021), who selected 62 low-mass protostellar outflows in nearby star-forming regions identified in CO 2–1 and compared their orientations with the magnetic fields measured using JCMT POL-2 data. A two-sample K-S test between the Yen et al. (2021) distribution and our distribution returns a p-value of 0.776, which indicates the two distributions are likely drawn from the same distribution. We also present the θ_B−out distribution of only the highest-confidence outflow candidates, i.e., those that have significant coherent high-velocity structure in the position–velocity diagram over a range of at least 1 km s⁻¹. A two-sample K-S test between the Yen et al. (2021) distribution and the highest-confidence outflow distribution returns a p-value of 0.615, which indicates the two distributions are also likely drawn from the same distribution. The similarity of the distributions derived from two different data sets and approaches provides further confidence that the distribution of θ_B−out is not uniform as would result from random relative orientations. Both distributions peak around 30^◦, i.e., where the CDF is rising most steeply, and thus they have a preference toward alignment rather than misalignment.

It is worth noting that the magnetic field direction might vary across different physical scales at the same position (Hull & Zhang 2019). Yen et al. (2021) adopt the magnetic field traced by JCMT 850 μm, which has a much better spatial resolution (a factor of 10) than that of Planck. Meanwhile, the outflow sample in Yen et al. (2021) is different from that in this work. Of our 200 outflow candidates, only 22 outflows have high-confidence matches with those of Yen et al. (2021), which is 35% of the sample in Yen et al. (2021) and 11% of our sample (see Section 3.4). On the other hand, the beam size of the Planck data is 4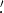8, which corresponds to a physical scale of 0.2 pc for Ophiuchus and Taurus, 0.4 pc for Perseus, and 0.6 pc for Orion. The effective pixel size of the Planck data is 1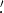07, which is four times higher. The typical outflow width is around 0.5 pc (Xu et al. 2022). This indicates that even for the furthest region, Orion, there are at least 16 (4 × 4) pixels in one outflow. Consequently, the averaged magnetic field direction inside the identified outflow regions will not be significantly affected by the local fluctuation of the magnetic field directions on small scales. Here, we aim to study how large-scale magnetic fields correlate with the launching direction of outflows and leave the examination of smaller scales to future work.

Next, we explore several possibilities for the origin of the distribution we find in the four regions. We first evaluate how uncertainty in the angle measurement affects the distribution. Here, measurement uncertainties include the ability of the Planck dust polarization image to measure the true local plane-of-sky B-field at the 3D position of source (e.g., it could be affected by other material along the line of sight contributing to the overall polarization direction). Measurement uncertainties also include some error in outflow orientations via our method of defining outflow axes, which could also include a contribution from misidentified outflows. To test the impact of measurement uncertainty, we assume the outflow is perfectly aligned with the magnetic field but the measurement of the angles has a Gaussian-distributed uncertainty. We randomly pick 200 numbers from this mock sample, repeating the process 10³ times. The left panel of Figure 9 illustrates the distribution of θ_B−out of the mock samples for four different measurement uncertainties. If either the outflow orientation or the magnetic field direction measurement has about 50^◦ uncertainty, or alternatively both the outflow orientation and the magnetic field direction measurements have about 35^◦ uncertainty, the resulting distribution reproduces the observed misalignment distribution.

Zoom In Zoom Out Reset image size

We next examine how the distribution of the 3D angle between magnetic field and outflow axis influences the distribution of θ_B−out, which is the projected angle. We assume both the outflow orientation and the magnetic field direction are randomly distributed, but we exclude the sample that has a 3D angle over a certain threshold δ_3D . This provides a hint about the degree of alignment between the outflow and the magnetic field direction, e.g., tightly aligned (0^◦–20^◦) or somewhat aligned (0^◦–45^◦). These mock samples have a random 3D angle distribution between 0 and δ_3D . We then project the 3D angle to 2D from a random viewing angle. The middle panel of Figure 9 shows the distribution of θ_B−out of the mock samples with different 3D angle distributions. A random distribution with 3D angles between 0° and 70° also replicates the distribution of θ_B−out we find in this work.

Finally, we combine both the measurement uncertainty and the 3D angle distribution to investigate how together they can affect the distribution of θ_B−out. The right panel of Figure 9 shows the distribution of θ_B−out with different measurement uncertainties and different 3D angle distributions. Several combinations can lead to the distribution we measure. With a moderate angular measurement uncertainty, the magnetic field and outflow could be somewhat aligned. Realistically, we expect at least a 10% uncertainty both in the field direction and the outflow orientation (σ ∼ 15°) (Stephens et al. 2017; Yen et al. 2021).

Uncertainty in the outflow orientation comes from several factors. First, the blue- and redshifted lobes of the outflow may not align with each other. It is not uncommon for two lobes apparently associated with the same source to have different orientations or even appear perpendicular to each other (e.g., some outflows in Arce et al. 2010; Li et al. 2015). Meanwhile, the morphology for each individual outflow lobe is not necessarily oval or jet-like; distortion may be due to inhomogeneous surroundings, e.g., some outflows in Figures 1–4. Outflow directions may also change over time, leading to asymmetric morphologies (Bally 2016; Lee et al. 2017). Consequently, it is difficult to fit one high-confidence line to the direction of the outflow lobe. To mitigate this, we adopt PCA to determine the orientation of the outflow lobes (see Section 2.1). For some outflow lobes, the variances of the two orthogonal components are similar, which indicates a large uncertainty in the outflow orientation estimation. Likewise, the magnetic field direction inferred from the dust polarization contains several systematic uncertainties, including smoothing, contamination by CMB polarization, and leakage correction as discussed in Planck Collaboration et al. (2015). Consequently, it is reasonable to expect σ ∼ 15° uncertainty at minimum in both the field direction and the outflow orientation. In this case, the curve with δ_3D ∈ [0°, 55°] provides a good match to the observed distribution. It is likely that the total measurement uncertainty is larger.

Consequently, we conclude that large-scale magnetic fields play some role in regulating the launching direction of outflows and governing the eventual extent of the CO-traced entrained gas. However, the magnitude of their importance is somewhat degenerate with the accuracy at which the outflow and magnetic field directions can be determined.

In this section, we investigate how the orientations of outflow pairs are correlated with the projected separation distance of the sources. We calculate the plane-of-sky orientation angle difference between all outflows with all other outflows. For each bin of projected separation distance, we calculate the mean relative orientation angle and the standard deviation. The left panel of Figure 10 illustrates how the relative orientation angle between outflow pairs changes with separation for the four regions. At small separations, ≲0.5 pc, the average relative orientation angles are <45°, indicating a modest degree of alignment but with significant dispersion about the perfectly aligned orientation. At larger separations, the average relative orientation angle is close to 45^◦, implying that the relative orientation angles have become decorrelated on these scales.

Zoom In Zoom Out Reset image size

Prior work examining the alignment of protostellar outflow pairs with projected separations of ∼1000–9000 au found that the angle distribution is more consistent with an antialigned distribution (Lee et al. 2016). Similarly, the angle difference of binaries measured in star formation simulations is statistically consistent with a random distribution (Offner et al. 2016; Lee et al. 2019). Synthetic CO observations demonstrate that the apparent antialignment may be produced by a selection affect, whereby aligned outflows are more difficult to identify and separate (Offner et al. 2016; Lee et al. 2019). Likewise, this effect would make the distribution of relative angles more aligned at close separations than we report here. We note the size scale investigated by these studies is slightly below our present resolution. On these scales, it is also likely that the alignment is influenced by dynamical interactions, which erase the initial outflow orientations (e.g., Lee et al. 2017). Because the closest pairs in our study have separations larger than the typical core size, they are not wide-separation companions. This means our results may be less influenced by dynamical evolution and instead better reflect the initial configuration.

As shown in Figures 1–4, magnetic fields are more ordered on smaller scales (<5 pc) and tend to have a similar orientation, such that the relative position angle between the magnetic field at two positions is smaller for closer distances. The middle panel of Figure 10 shows how the relative angle of the magnetic field direction at the corresponding outflow positions changes with separation for the four regions. At small separations, ≲2 pc for Ophiuchus and ≲5 pc for the other three regions, the relative orientation angles increase with the separation, indicating self-correlated magnetic field directions. However, this trend vanishes at larger separations, implying that the relative angles between magnetic field directions become decorrelated on these scales. It is worth noting that the beam size of the Planck data corresponds to a physical scale of 0.2 pc for Ophiuchus and Taurus, 0.4 pc for Perseus, and 0.6 pc for Orion.

We note that, for Perseus, the relative angle between polarization vectors, noted as θ_B−B, behaves differently than the others. It first increases within 4 pc, but decreases and maintains low values between 5 and 15 pc, then significantly increases above 45° after 15 pc. This unusual behavior might be caused by feedback or due to some particular magnetic field morphology on these scales. However, Orion, which is the most active star-forming region, does not show a similar trend. As we discussed in Section 3.1, the plane-of-sky magnetic field strength in Perseus is likely the weakest among the four regions, while Orion seems to have a strong magnetic field (e.g., Hwang et al. 2021). When the magnetic field is strong, θ_B−B is likely small across all separations. Due to turbulence perturbations, θ_B−B likely increases with distance and becomes "random" (∼45°) at larger scales. Perseus exhibits an irregular change in θ_B−B with distance. At smaller distances, the θ_B−B of Perseus is small, as expected, possibly indicating low turbulence or stronger magnetic fields. However, at larger distances, its unusual behavior cannot be explained by strong magnetic fields. Consequently, whether Perseus has weaker magnetic field relative to the other regions is still not clear.

Comparing the left and middle panels of Figure 10 indicates that the angle differences between outflow pairs are correlated less well at small scales than those of the magnetic field directions at the same locations. This may be because outflow orientations change on shorter timescales due to dynamics, or it may be due to small-scale turbulence, which is not reflected in the mean magnetic field direction. We conclude that these results are consistent with the magnetic field influencing the direction of outflow launching and/or propagation (as found in Section 3.2), but with a high dispersion around aligned orientations. This large dispersion means that the outflow to outflow alignment signal decorrelates more rapidly with distance than the B-field to B-field alignment signal and is soon indistinguishable from a random distribution.

Next, we adopt the inclination angles with respect to the line of sight inferred with a casi-3d in Section 2.3. We calculate the 3D launching direction of each outflow by combining both the position angle and the inclination angle. We calculate the 3D outflow angle difference for all outflow pairs in the clouds and bin by separation. The right panel of Figure 10 illustrates how the 3D relative angle between outflow pairs changes with separation for the four regions. We find this angle shows a behavior similar to that of the projected relative angle versus separation relation shown in the left panel of Figure 10, i.e., there is enhanced correlation within ∼0.5 pc but then a relatively constant distribution of the average relative angle with projected separation distance. We also note that this constant value of average angle is significantly smaller than the value expected for a random distribution in 3D space, which is 60°. We attribute this to a detection bias in the inclination angle distribution that selects against certain angles that are either close to the plane of the sky or along the line of sight (see Figure 7). The existence of such a bias implies that results for the correlation of 3D orientations need to be treated with caution.

There have been several prior studies investigating how outflows are oriented with respect to filamentary structures. Assuming that the magnetic field direction correlates with the filament morphology, the filament orientation provides some ancillary insight into the local field behavior. Planck Collaboration et al. (2016) showed that, at low column densities (N(H) ∼ 10²⁰ cm⁻²), structures are preferentially aligned with the magnetic field inferred from the polarization angle. However, at high column densities (N(H) ∼ 10²² cm⁻²), e.g., in molecular clouds, gas structures are preferentially perpendicular with the magnetic field. Therefore, in the regime we study, it is likely that the magnetic fields are perpendicular to the filamentary structures. This would suggest that the outflows we identify are more likely to be oriented perpendicular to the local filament direction.

Indeed, Kong et al. (2019) found that most outflows are preferentially perpendicular to the filaments in IRDC G28.37 + 0.07, rejecting the random distribution at high confidence, which is similar to our work. Feddersen et al. (2020) found a similar trend for the highest-confidence outflows in Orion, which are associated with driving sources and correlated with H₂ 2.122 μm outflow emission. They exhibit a moderately perpendicular outflow-filament alignment. However, when considering all outflow samples in Orion, Feddersen et al. (2020) found random outflow-filament alignment, which is similar to the findings in Perseus (Stephens et al. 2017). One possible explanation is that stronger feedback or turbulence leads to more random alignment, while stronger magnetic fields tend to produce more alignment. Given that Perseus may have a relatively weak magnetic field as discussed in Sections 2.3 and 3.3, this might explain why Stephens et al. (2017) found a random outflow-filament alignment in Perseus. In this section, we also report a one-to-one comparison with the outflow position angles and the magnetic field directions reported in Yen et al. (2021). Yen et al. (2021) adopted 62 outflows previously identified in either ¹²CO (2-1) or ¹²CO (3-2) observations by JCMT and SMA and compared the outflow orientation with the mean magnetic field direction measured from JCMT POL-2 data. To identify sources contained in both catalogs, we conduct a close companion search using the outflow coordinates. We define matches as those with separations within 5'. This identifies 22 outflow matches. We find that 54% of the outflow position angle measurements between the two samples have orientations within 20°. However, 18% of the outflow position angle measurements have discrepancies greater than 70°. The magnetic field direction measurements between the two samples exhibit similar behavior, with 45% of magnetic field orientations within 20° and 18% with over 70° discrepancy. We expect that most of this discrepancy arises from the different data sets used to identify the outflows: the morphologies of the outflows are simply different and the magnetic field directions are measured on different scales. While we expect that the higher-resolution data of Yen et al. (2021) allow a more exact determination of the outflow position angle, we nonetheless find a statistically similar distribution and reach the same conclusion.