In order to model the pressure-pulse-driven solar jets in the quiet-Sun, we consider and implement a gravitationally stratified and magnetized solar atmosphere. This atmosphere is approximated by the ideal MHD equations in their conservative form as outlined below (e.g. Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial t}}& \left(\begin{array}{c}\mathit{\rho }\\ \mathit{\rho }\mathit{v}\\ E\\ \mathit{B}\end{array}\right)+\mathrm{\nabla }\cdot \left(\begin{array}{c}\mathit{\rho }\mathit{v}\\ \mathit{\rho }\mathit{v}\mathit{v}-\frac{\mathit{B}\mathit{B}}{\mathit{\mu }}+\mathbf{I}{p}_{\mathrm{t}}\\ (E+p_{\mathrm{t}})\mathbf{\text{v}}-\frac{\mathit{B}}{\mathit{\mu }}(\mathit{v}\cdot \mathit{B})\\ \mathit{v}\mathit{B}-\mathit{B}\mathit{v}\end{array}\right)\\ & =\left(\begin{array}{c}\mathrm{0}\\ \mathit{\rho }\mathit{g}\\ \mathit{\rho }\mathit{v}\cdot \mathit{g}\\ \mathrm{0}\end{array}\right)\end{array}\end{array}$$

In the above representation of the set of ideal MHD equations, the symbol ρ depicts mass density in the solar atmosphere, v denotes the velocity, B is the magnetic field satisfying $\mathrm{\nabla }\cdot \mathit{B}=\mathrm{0}$ divergence free condition, and μ depicts the magnetic permeability. The parameter $p_{\mathrm{t}}=p+{\mathit{B}}^{\mathrm{2}}/\left(\mathrm{2}\mathit{\mu }\right)$ defines the total pressure, which is an addition of thermal (p) and magnetic (B²∕2μ) pressure. I is a 3×3 unit matrix. The quantity E describes the total energy, which is given as follows in Eq. (2) (e.g. Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014):

$$\begin{array}{}\text{(2)}& E={\displaystyle \frac{p}{\mathit{\gamma }-\mathrm{1}}}+{\displaystyle \frac{\mathit{\rho }{\mathit{v}}^{\mathrm{2}}}{\mathrm{2}}}+{\displaystyle \frac{{\mathit{B}}^{\mathrm{2}}}{\mathrm{2}\mathit{\mu }}}\end{array}$$

In this equation, γ is the specific heat ratio. PLUTO code also satisfies an ideal gas equation under the MHD approximation.

$$\begin{array}{}\text{(3)}& p={\displaystyle \frac{k_{\mathrm{B}}}{m}}\mathit{\rho }T\end{array}$$

In Eq. (3), T symbolizes temperature, and k_B is the Boltzmann constant. The symbol m denotes the mean particle mass. We take a typical value of m for the model atmosphere that is equal to 1.24. We do not consider non-ideal conditions such as the velocity of the background plasma flows, dissipative effects like viscosity and resistivity, magnetic diffusivity, cooling and/or heating of the plasma, because we are interested in understanding the kinematics and evolutionary properties of these pressure-driven jets. We consider ∇⋅B to be equal to zero or a very negligible values of it in the numerical domain.

2.1 Equilibrium model of the solar atmosphere

We consider the numerical simulation box mimicking a realistic solar atmosphere covering the region from the photosphere to the inner corona. In the case of the initial solar atmosphere subjected to the hydrostatic equilibrium, the realistic temperature profile T_e(y) is shown in Fig. 2, which is inferred from the observed line profiles by Avrett and Loeser (2008) and also depicted in Konkol et al. (2012) and Wołoszkiewicz et al. (2014).

Figure 1Equilibrium open and expanding magnetic field lines in the model quiet-Sun solar atmosphere. The x axis and the y axis are given in megametres (Mm).

Download

Figure 2Temperature variation with height in the initial static solar atmosphere.

Download

Figure 3Magnetic field profile (a) and plasma beta profile (b) vs. height (y) in the model quiet solar atmosphere.

Download

In the case of the static equilibrium of the solar atmosphere, i.e. when there is no background initial flows (V_e=0), it is approximated as a force-free as well as a current-free magnetic field. Therefore, we can abbreviate the initial magnetic field condition as

$$\begin{array}{}\text{(4)}& \mathrm{\nabla }\times {\mathit{B}}_{\mathrm{e}}=\mathrm{0},(\mathrm{\nabla }\times {\mathit{B}}_{\mathrm{e}})\times {\mathit{B}}_{\mathrm{e}}=\mathrm{0}\end{array}$$

In the given expression, the subscript “e” represents the equilibrium quantities. The vector magnetic potential can be estimated with the magnetic flux function given as (Konkol et al., 2012; Wołoszkiewicz et al., 2014)

$$\begin{array}{}\text{(5)}& {\mathit{B}}_{\mathrm{e}}(x,y)=[{\mathit{B}}_{\mathrm{e}x},{\mathit{B}}_{\mathrm{e}y},\mathrm{0}]=\mathrm{\nabla }\times \left(A_{\mathrm{e}}\widehat{z}\right),\end{array}$$

where the magnetic flux function is given as follows:

$$\begin{array}{}\text{(6)}& A_{\mathrm{e}}(x,y)={\displaystyle \frac{(x-a)B_{\mathrm{ref}}}{(x-a{)}^{\mathrm{2}}+(y-b{)}^{\mathrm{2}}}}\end{array}$$

Here B_ref is the strength of the pole, and a and b collectively determine its position. In the above-mentioned expression, we fix the vertical coordinate of magnetic pole at $b=-\mathrm{5}$ Mm in the convection zone. The jet is triggering from the chromosphere (1.8 Mm) along the open magnetic field lines and the pulse is initially lunched there. Thus, there is no dynamics occurring in the convection zone related to the evolution of these isolated chromospheric jets. Our realistic temperature model (Fig. 2) smoothly extends from the convection zone to the photosphere; thereafter, it couples to the chromosphere, the transition region (TR), and corona. In order to save on computing time, we do set the lower boundary of the simulation box at the photosphere. For the sake of visualization, we have already given the magnetic field variations in the plot (see Fig. 1 for B=112 gauss pole strength) starting from the photosphere to the corona. It clearly shows that the magnetic pole is set somewhere deeper in the convection zone, and that the magnetic field is smoothly extended into the solar atmosphere at higher heights with an exponential decay. Putting the pole deep below in the convection zone is a requirement of the numerical simulation, as we keep the magnetic singularity away from the simulation box in order to set an appropriate initial force- and current-free magnetic atmosphere. The quiet-Sun cool chromospheric jets are simulated in our model. We set the source magnetic field of a typical order in the quiet Sun. Moreover, the chosen magnetic fields smoothly extend to the inner corona and appropriately set reasonable values of plasma beta and the Alfvén speed (Figs. 3, 5). This helps with the evolution of the perturbations and the launch of the collimated jets. In this model, we chose two different magnetic field strength configurations, i.e. B=56 gauss and B=112 gauss. The reference level is taken in the overlying corona at y_ref=10 Mm. The magnetic field lines exhibit open and expanding field behaviour, as shown in Fig. 1. We take the magnetic field strength typical of the regions of the Sun where chromospheric jets are formed in the quiet Sun.

In the hydrostatic equilibrium of the solar atmosphere set in the simulation box, the gravity force balances the pressure gradient force. This can be written as follows:

$$\begin{array}{}\text{(7)}& -\mathrm{\nabla }p+\mathit{\rho }\mathit{g}=\mathrm{0}\end{array}$$

Here we keep the value of g fixed at 27 400.0 cm s⁻². Using the vertical component of the hydrostatic equilibrium in the model solar atmosphere and the ideal gas law, we determine the equilibrium plasma gas pressure and mass density as follows (Konkol et al., 2012; Wołoszkiewicz et al., 2014):

$$\begin{array}{}\text{(8)}& p_{\mathrm{e}}\left(y\right)=p_{\mathrm{ref}}\exp \left(-\underset{y\mathrm{ref}}{\overset{y}{\int }}{\displaystyle \frac{\mathrm{d}{y}^{\prime }}{\mathrm{\Lambda }\left(y^{\prime }\right)}}\right),{\mathit{\rho }}_{\mathrm{e}}\left(y\right)={\displaystyle \frac{p_{\mathrm{e}}\left(y\right)}{g\mathrm{\Lambda }\left(y\right)}},\end{array}$$

where

$$\begin{array}{}\text{(9)}& \mathrm{\Lambda }\left(y\right)={\displaystyle \frac{k_{\mathrm{B}}{T}_{\mathrm{e}}\left(y\right)}{\widehat{m}g}}\end{array}$$

In these expressions, P_ref is the gas pressure at reference level y_ref, which is attributed as the pressure scale height.

Figure 4Equilibrium profiles of mass density (a) and gas pressure (b) vs. height in the model quiet solar atmosphere.

Download

Figure 5Sound speed (a) and Alfvén speed (b) vs. height (y) in the model quiet solar atmosphere.

Download

For considering the gravitationally stratified and longitudinally structured solar atmosphere, we obtain the plasma temperature profile T_e(y) which is derived by Avrett and Loeser (2008) and displayed in Fig. 2. It should be noted that the typical value of the temperature T_e(y) at the top of the photosphere is about 5700 K. This temperature corresponds to y=0.5 Mm at the photosphere, and it falls gradually and attains its minimum of about 4350 K at higher altitudes of approximately y=0.95 Mm which represents a temperature minimum. As we move higher up in the solar atmosphere, T_e(y) increases gradually with height up to the transition region which is located at y≃2.7 Mm. T_e(y) sharply increases up to the corona and finally attains a constant value of mega-Kelvin at the coronal heights, as shown in Fig. 2.

The magnetic field and plasma beta at y=2.7 Mm (at the transition region) are 6.884 gauss and 0.0005 respectively; they grow with the depth and attain 7.646 gauss and 0.219 respectively at y=1.5 Mm, which is located within the chromosphere (Fig. 3).

Using Eq. (8), we obtain the equilibrium mass density and gas pressure profiles with respect to height (Fig. 4). We found that the equilibrium mass density and gas pressure at 2.7 Mm (at the transition region) are $\mathrm{4.595}\times {\mathrm{10}}^{-\mathrm{12}}$ kg m⁻³ and $\mathrm{1.26}\times {\mathrm{10}}^{-\mathrm{3}}$ Pa respectively. They grow with depth and attain $\mathrm{1.537}\times {\mathrm{10}}^{-\mathrm{7}}$ kg m⁻³ and $\mathrm{6.411}\times {\mathrm{10}}^{-\mathrm{1}}$ Pa respectively at y=1.5 Mm, which is located within the chromosphere. Figure 5 shows the trend of the Alfvén speed and sound speed with respect to height in the solar atmosphere. The Alfvén speed is calculated by $V_{\mathrm{A}}=\sqrt{\frac{B^{\mathrm{2}}}{\mathit{\mu }\mathit{\rho }}}$, which is 1015.583 km s⁻¹ at y=2.7 Mm (i.e. transition region), whereas it decrease with the depth and attains 6.167 km s⁻¹ at y=1.5 Mm located within the chromosphere. The sound speed calculated by $V_{\mathrm{s}}=\sqrt{\frac{\mathit{\gamma }p}{\mathit{\rho }}}$ at the transition region, i.e. 2.7 Mm, is 21.392 km s⁻¹, whereas it decreases with depth and attains 2.638 km s⁻¹ within the chromosphere at y=1.5 Mm.

These background physical quantities (i.e. density, pressure, magnetic field plasma beta, Alfvén speed and sound speed) for the model gravitationally stratified and magnetized solar atmosphere are appropriately set in the model solar atmosphere. We show these profiles for the atmosphere that have source magnetic field value of 112 gauss. The various physical quantities, their values, and variations with the height (y) in the structured solar atmosphere clearly indicate their smooth extension into the inner corona. Their reasonable values are set for the model atmosphere, and are appropriate for launching the perturbations and associated jets.

Perturbations

We consider the initial solar atmosphere to be in hydrostatic equilibrium and to be gravitationally stratified. We perturb the equilibrium atmosphere by the initial pulse in the vertical direction in equilibrium gas pressure. The Gaussian form of the pressure pulse in the vertical direction is given as follows:

$$\begin{array}{}\text{(10)}& P=P_{\mathrm{0}}\left[\mathrm{1}+A_p\times \exp \left(-{\displaystyle \frac{(x-x_{\mathrm{0}}{)}^{\mathrm{2}}+(y-y_{\mathrm{0}}{)}^{\mathrm{2}}}{w^{\mathrm{2}}}}\right)\right]\end{array}$$

Here (x₀,y₀) is the initial position of the pressure pulse, w is the width of the pulse, and A_p denotes the pressure amplitude. We fix the values of x₀ and y₀ at 0 and 1.8 Mm respectively, thereby launching the pressure perturbations in the chromosphere. We set w equal to 0.2 Mm. We imply different pressure pulse strengths of A_p = 4–22, which account for the generation of the variety of solar jets.

Observations reveal that these types of chromospheric jets are found to be associated with an impulsive origin in the chromosphere, and their footpoints are usually associated with brightening. The chosen pressure pulses in this modelling mimic the after-effect of the heating scenario at their footpoints before evolution. This is not a direct implementation of heating, as we use the ideal set of MHD equations in the numerical simulation. However, the Gaussian pressure pulse implies the disturbance that represents the response in the form of the pressure perturbations once the underlying heating episode is completed. This perturbation locally alters the equilibrium and generates the propagating disturbances. The pressure pulse is chosen with varying amplitude A_p = 4–22 in order to understand the evolutionary and propagation properties of the cool chromospheric jets. We perform the numerical simulation at two magnetic fields strengths (i.e. B=56 and 112 gauss), typical of quiet-Sun atmosphere.

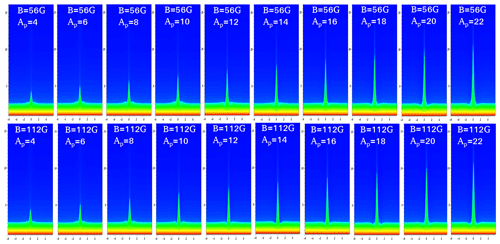
Figure 6Evolution of the plasma jets at different pressure pulses at two different magnetic field strengths, B=56 gauss and B=112 gauss. The mosaic diagram shows the maximum height of the evolved jets at different pressure pulses, e.g. A_p = 4–22. The horizontal (x) and vertical (y) axes are shown in megametres (Mm).

Download

Figure 7Automated detection of the plasma jet in the numerical simulation data to establish its time–distance profile and termination point.

Download

2.2 Numerical methods

PLUTO code is a Godunov-type, non-linear, finite-volume/finite-difference code which takes ideal and non-ideal sets of governing equations into account (Mignone et al., 2007, 2012; Wołoszkiewicz et al., 2014). It is constructed to numerically integrate a system of conservation laws, which can be shown as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\partial \mathit{U}}{\partial t}}+\mathrm{\nabla }\cdot \mathbf{F}\left(\mathit{U}\right)=\mathbf{S}\left(\mathit{U}\right)\end{array}$$

In this equation, U denotes a set of conservative physical fields (e.g. magnetic field, density, velocity, pressure, and so on.); F(U) is the flux tensor and S(U) is the source term.

PLUTO code utilizes a second-order unsplit Godunov solver and adaptive mesh refinement (AMR) of the system of conservation laws as shown in Eq. (11). In order to numerically solve the set of ideal MHD equations (Eq. 1), we set the simulation box as (−6, 6) Mm × (1, 21) Mm. This represents a realistic localized solar atmosphere with a span of 12 and 20 Mm in the horizontal and vertical directions respectively. This solar atmosphere is constructed within the simulation box and all four boundary conditions by fixing the simulation region to their equilibrium values. Numerical simulation is carried out with double-precision arithmetic using multiple passage interface (MPI) (Mignone et al., 2007). The eight processors are used in the parallel calculations. It took approximately 12 h of CPU time for each set of calculations. We adopted a static uniform grid which was divided into 384 equal cells in the x direction. We also adopted a static uniform and stretched grid which were divided into 128 equal cells and 256 equal cells respectively in the y direction. The resolution of the simulation domain was 31 km per numerical cell. We obtained the numerical simulation data every 10 s.

In our modelling, we set the Courant–Friedrichs–Lewy (CFL) number equal to 0.25. We used the Roe solver for the flux computation, which is a linearized Riemann solver based on the characteristic decomposition of the Roe matrix (cf. Mignone et al., 2007, 2012).

Figure 8Height of the jets and their evolution with respect to time.

Download

Figure 9Maximum height of the model jets vs. pressure pulse strength.

Download

The pressure perturbations in the solar chromosphere launch the thin and localized plasma jets (Fig. 6). These jets carry the mass from the chromosphere to the outer corona along the expanding open field lines. The pressure perturbations mimic the impulsive origin of these jets due to the localized heating episodes that might occur at some time epoch in the solar chromosphere and that cause the direct pressure disturbance in the equilibrium atmosphere. As the pressure pulse is launched, the plasma gets essential velocity perturbations guided along the vertical and expanding field lines. These perturbations are converted into magneto-acoustic shocks in the stratified atmosphere which are followed by the motion of cool plasma. Shock leaves the domain quickly, and the resulting after-effect is the formation of the jet. The pressure-pulse-driven cool jets depend on the amplitude of the initial pulse (A_p) as well as the height that it is triggered at. This further converts into the acoustic shocks that trigger plasma in the upward direction. A low-pressure region is created behind the slow magneto-acoustic shock, which drives the cool plasma from the chromosphere upward mimicking cool jet. Therefore, the amplitude of the pressure pulse as well as its triggering site are important factors upon which the evolution of the jets depend. In this model, we studied chromospheric cool jets in order to be able to take a certain amplitude of the pressure pulse at the chromospheric height below the TR to generate these plasma ejecta.

Figure 10(a, b, c) The example spatial profiles of various jets when they reach their respective maximum height. Panels (a), (b), and (c) show spatial profiles of the jet at B=56 gauss and A_p=16, B=56 gauss and A_p=6, and B=112 gauss and A_p=18 respectively. As the base of these jets exhibits a complex shape, the triple or single Gaussian profiles are fitted and the respective full width half maximums (FWHMs) are estimated after determining the Gaussian width. (d) The width of the jets vs. the pressure pulse strength (A_p) in the solar atmosphere for the B=56 gauss (blue diamonds) and B=112 gauss (red circles) magnetic fields. The FWHMs of various jets lie between 0.42 and 0.48 Mm. They show a mild increasing trend for both of the magnetic fields.

Download

Figure 11Lifetime of the model jets vs. pressure pulse strength.

Download

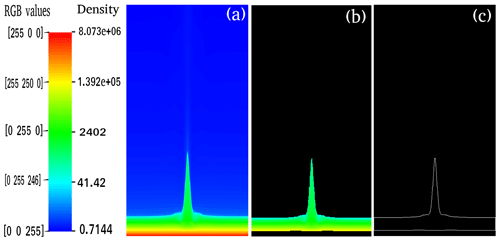
We analysed the kinematical and evolutionary properties of these pressure-pulse-driven solar jets by their detection (Fig. 7). Figure 8 displays the height–time profile of various jets at two different magnetic field configurations (B=56 gauss and B=112 gauss). It shows that the jets exhibit asymmetric parabolic paths, which are different from the normal parabolic path of any ejecta in the gravitational field. We develop a code in MATLAB to find the height of the single isolated jet with time and its termination point. To calculate the height of the jet, we took the time series of the numerical simulation data (Fig. 7a). In this density map, we estimate the assigned RGB values corresponding to the density variations over the colour scales. The highest density corresponds to a fixed value of green, G=255, and the value decreases towards blue (B), moving towards the tip of the jet with decreasing density. Ultimately the value becomes 245 as the jet ends. The value fades away slowly and there is no sharp boundary, so we take B=245 as the approximate boundary value for the jet. We used this observation to calculate the required parameters by fixing G=255 and B≥245; we then generated a masked image with only G=255 and B≤245, and the rest of the portion was left as black (Fig. 7b). Next, we generated the contour of the masked image to generate Fig. 7c; thereafter, we found the height variations automatically with respect to time. We used the snapshots of the density map for the calculation of height when the jet had reached above the transition region, and the snapshots of the pressure map for the calculation of the height of the jet when it was below the transition region. Also, at time t=0 s, we took the value of the height as 1.8 Mm, as was set in the simulation. The lifetime of the isolated jet is estimated in the masked time series where only the jet's motion is visible. We calculate the time when the height of the jet again starts increasing after the fall, and this point is considered to be the termination point of the first isolated jet. For A_p=14 (time = 190 s and corresponding density map), we demonstrated the above-mentioned procedure, in Fig. 7, to detect the jet.

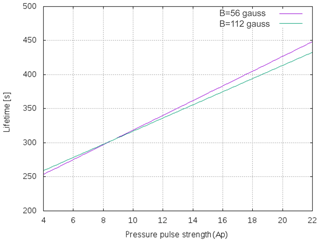
We investigate the evolution of the pulses and associated jets at two different magnetic field strengths (B=56, 112 gauss). The automatically detected height–time profiles for the jets, generated by imposing different pressure pulses, clearly exhibit the asymmetric near-parabolic profiles (Fig. 8). This infers that the upward motion of the jet under the influence of pressure perturbations does occur, however, its downward motion is not singly governed by the gravitational free fall. The downward-propagating counterpart of the perturbation, when reflecting from the photosphere, goes up and causes interaction with the falling jet plasma. This creates the complex scenario near the base of the jet, where we observe the complex plasma motion and evolution of the multiple jets one by one (e.g. Murawski et al., 2011; Kayshap et al., 2018; Li et al., 2019). We aim to study the evolution of the first isolated jet that is generated due to the forward-propagating component of the disturbance. The down-draughting disturbance is usually weak when moving towards the denser lower solar atmosphere; therefore, it is not seen well in the form of significant density perturbations below in the density maps. However, its effect can be visible once it rebounds back a certain later time and helps in the formation of the secondary jets and interaction with the falling material of the first jet. We study the propagation and evolutionary properties of the first upward-propagating isolated jet (at different pressure pulse strengths and different magnetic field strengths); therefore, we do not consider other secondary jets and their evolution. Figure 9 displays an interesting correlation between the maximum height of the jets and strength of the pressure pulse, which shows a linearly increasing trend. This directly infers that if the extent of the heating and, thus, the pressure perturbations is higher then more longer jets can be generated from the same location in the chromosphere. For the strong magnetic field, the height of the jet will be longer at a particular pressure pulse strength compared with the same for the weaker magnetic field strength. The width of the jets may be determined by the conservation of mass in the cross section of the flowing jet spire, although many other factors, i.e. the configuration of the magnetic field, the interaction of counter-propagating disturbances near the base of the jet, and so on, can affect its value. The width of the jets is measured using a Gaussian fit to the spatial profile of the jets when they attain maximum height. The example spatial profiles of various jets when they reach at their respective maximum heights are shown in Fig. 10a–c. As the base of these jets exhibits complex shape and motions, the triple or single Gaussian profiles are fitted on their spatial profiles and the respective FWHMs are estimated after determining the fitted Gaussian width. The width of the jets vs. the pressure pulse strength (A_p) in the solar atmosphere for the B=56 gauss (blue diamonds) and B=112 gauss (red circles) magnetic fields are shown in Fig. 10d. The FWHMs of various jets lie between 0.42 and 0.48 Mm, although, they exhibit a mild increasing trend on average for both the magnetic fields. The lifetime of the jets shows linear variation and a positive slope with respect to the pressure pulse strength (Fig. 11). This scenario depicts that more localized energy released into the chromosphere results in more larger perturbations that, in turn, lead to longer jets with long lifetimes. Moreover, the lifetime of the jet for a particularly larger pressure pulse strength will be smaller in the presence of a strong magnetic field and vice-versa (A_p≥10). However, in our simulation under the given initial condition, the lifetime is almost same for the two magnetic field strengths, particularly at low amplitude pressure perturbations (A_p≤10).

The numerical simulation data are available from the lead author.

All authors have contributed in a equal manner.

The authors declare that they have no conflict of interest.

This article is part of the special issue “Solar magnetism from interior to corona and beyond”. It is a result of the Dynamic Sun II: Solar Magnetism from Interior to Corona, Siem Reap, Angkor Wat, Cambodia, 12–16 February 2018.

This paper was edited by Sergiy Shelyag and reviewed by two anonymous referees.