pert网络时间的模型和算法实现

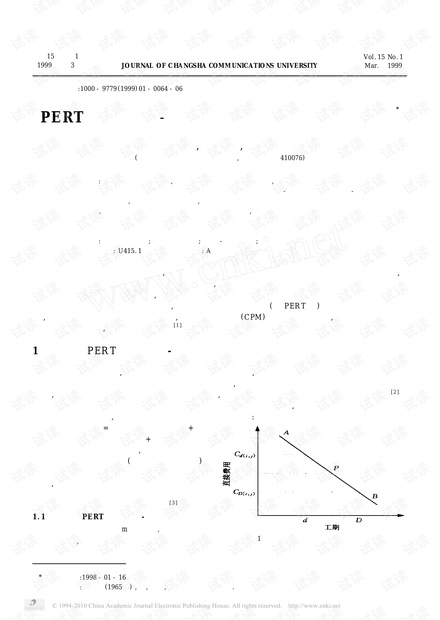
### PERT网络时间-费用优化数学模型及其算法实现 #### 概述 在公路工程建设项目中，合理规划项目进度和费用对于确保项目按时完成并控制成本至关重要。为此，本研究提出了一个结合计划评审技术（Program Evaluation and Review Technique，简称PERT）与关键路径法（Critical Path Method，简称CPM）的时间-费用优化模型。该模型旨在帮助决策者在面对复杂项目时做出更有效的决策，并通过计算机程序处理得到最优的日程安排和成本控制方案。 #### PERT网络时间-费用优化模型的构建 PERT是一种统计工具，用于项目管理中估计在一定时间内完成项目活动的概率。它主要关注的是不确定性下的活动持续时间估计。本研究将PERT与公路工程项目的特定需求相结合，建立了一个能够反映不同工序间时间-费用关系的数学模型。 ##### 工程项目分解 将整个公路工程项目分解为一系列工序，并使用网络计划图将这些工序连接起来形成一个完整的项目流程。每个工序都具有自己的时间参数和费用参数。 ##### 时间-费用关系建模 假设每个工序都具有非增线性的时间-费用关系，即随着工序时间的缩短，所需的成本会呈非线性增长。这种情况下，可以通过调整关键路径上的工序时间来实现时间和费用的优化。 ##### 数学模型 - **直接费用**：直接费用是指直接与工序时间相关的费用，可以表示为`Ci,j = Ki,j - δi,j * t(i,j)`，其中`Ki,j`是固定部分的直接费用，`δi,j`是费用斜率，`t(i,j)`是工序时间。 - **间接费用**：间接费用是不直接与工序时间相关的费用，例如管理费用等，可以用`C′ = a - q(S - S′)`表示，其中`a`是固定间接费用，`q`是每天增加的间接费用，`S`是原始计划的总工期，`S′`是调整后的总工期。 #### 关键路线的确定与优化 在确定了每个工序的时间-费用关系后，接下来的任务就是找到关键路径。关键路径是所有可能路径中最长的路径，决定了项目的总工期。 - **单关键路径的情况**：如果网络中只有一条关键路径，则选择直接费用斜率最小的关键工序进行压缩，即选取`d1cmin = min{d1j}`作为压缩对象。 - **多关键路径的情况**：当存在多条关键路径时，需要在每条路径上选取直接费用斜率最小的工序进行同步压缩。 #### 最低成本日程求解 通过对关键路径上的工序进行压缩，可以得到不同工期下的最低成本。为了求解最低成本日程，可以采用迭代的方法逐步缩短关键路径上的工序时间，并计算相应的成本变化。具体步骤如下： 1. **初始化**：设定初始工期为正常工期，计算此时的总成本。 2. **压缩工序**：选择关键路径上的关键工序进行压缩，计算压缩后的总成本。 3. **迭代优化**：重复上述过程，直到找到最低成本的工期为止。 #### 结论 通过上述模型和算法，可以有效地解决公路工程项目中的时间-费用优化问题。该方法不仅能够帮助决策者快速做出决策，还能确保项目的高效执行。未来的研究可以进一步探索如何将更多的不确定性因素纳入模型之中，使得优化结果更加贴近实际情况。