4-polytope: Difference between revisions
9900634102 Tags: Visual edit Mobile edit Mobile web edit |
→Classes: can one identify an unknown example? |
||
| (32 intermediate revisions by 21 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Four-dimensional geometric object with flat sides}} |
|||
| ⚫ | In [[geometry]], a '''4-polytope''' (sometimes also called a '''polychoron'''<ref>[[Norman Johnson (mathematician)|N.W. Johnson]]: ''Geometries and Transformations'', (2018) {{ISBN|978-1-107-10340-5}} Chapter 11: ''Finite Symmetry Groups'', 11.1 ''Polytopes and Honeycombs'', p.224</ref> |
||
{| align=right class=wikitable |
|||
| ⚫ | |||
|+ Graphs of the six [[convex regular 4-polytope]]s |
|||
|- |
|||
!{3,3,3} |
|||
!{3,3,4} |
|||
!{4,3,3} |
|||
|- valign=top align=center |
|||
|[[Image:4-simplex t0.svg|120px]]<BR>[[5-cell]]<BR>Pentatope<BR>4-[[simplex]] |
|||
|[[Image:4-cube t3.svg|121px]]<BR>[[16-cell]]<BR>Orthoplex<BR>4-[[orthoplex]] |
|||
|[[Image:4-cube t0.svg|120px]]<BR>[[8-cell]]<BR>[[Tesseract]]<BR>4-[[hypercube|cube]] |
|||
|- |
|||
!{3,4,3} |
|||
!{3,3,5} |
|||
!{5,3,3} |
|||
|- valign=top align=center |
|||
|[[Image:24-cell t0 F4.svg|120px]]<BR>[[24-cell]]<BR>Octaplex |
|||
|[[Image:600-cell graph H4.svg|120px]]<BR>[[600-cell]]<BR>Tetraplex |
|||
|[[Image:120-cell graph H4.svg|120px]]<BR>[[120-cell]]<BR>Dodecaplex |
|||
|} |
|||
| ⚫ | In [[geometry]], a '''4-polytope''' (sometimes also called a '''polychoron''',<ref>[[Norman Johnson (mathematician)|N.W. Johnson]]: ''Geometries and Transformations'', (2018) {{ISBN|978-1-107-10340-5}} Chapter 11: ''Finite Symmetry Groups'', 11.1 ''Polytopes and Honeycombs'', p.224</ref> '''polycell''', or '''polyhedroid''') is a [[four-dimensional]] [[polytope]].<ref>{{Cite book | last = Vialar | first = T. | title = Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance | publisher = Springer | year = 2009 | page = 674 |
||
| ⚫ | |||
| last = Capecchi | first = V. |author2=Contucci, P. |author3=Buscema, M. |author4=D'Amore, B. | title = Applications of Mathematics in Models, Artificial Neural Networks and Arts |
| last = Capecchi | first = V. |author2=Contucci, P. |author3=Buscema, M. |author4=D'Amore, B. | title = Applications of Mathematics in Models, Artificial Neural Networks and Arts |
||
| publisher = Springer | year = 2010 | page = 598 | url = https://books.google.com/books?id=oNy5MxGXLEwC |
| publisher = Springer | year = 2010 | page = 598 | url = https://books.google.com/books?id=oNy5MxGXLEwC&q=polychoron&pg=PA598 | doi = 10.1007/978-90-481-8581-8 |
||
| isbn = 978-90-481-8580-1}}</ref> It is a connected and closed figure, composed of lower-dimensional polytopal elements: [[Vertex (geometry)|vertices]], [[Edge (geometry)|edges]], [[Face (geometry)|faces]] ([[polygon]]s), and [[Cell (mathematics)|cells]] ([[Polyhedron|polyhedra]]). Each face is shared by exactly two cells. |
| isbn = 978-90-481-8580-1}}</ref> It is a connected and closed figure, composed of lower-dimensional polytopal elements: [[Vertex (geometry)|vertices]], [[Edge (geometry)|edges]], [[Face (geometry)|faces]] ([[polygon]]s), and [[Cell (mathematics)|cells]] ([[Polyhedron|polyhedra]]). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician [[Ludwig Schläfli]] before 1853.{{Sfn|Coxeter|1973|p=141|loc=§7-x. Historical remarks}} |
||
The two-dimensional analogue of a 4-polytope is a [[polygon]], and the three-dimensional analogue is a [[polyhedron]]. |
The two-dimensional analogue of a 4-polytope is a [[polygon]], and the three-dimensional analogue is a [[polyhedron]]. |
||
| Line 12: | Line 33: | ||
A 4-polytope is a closed [[Four-dimensional space|four-dimension]]al figure. It comprises [[vertex (geometry)|vertices]] (corner points), [[edge (geometry)|edges]], [[face (geometry)|faces]] and [[cell (mathematics)|cells]]. A cell is the three-dimensional analogue of a face, and is therefore a [[polyhedron]]. Each face must join exactly two cells, analogous to the way in which each edge of a polyhedron joins just two faces. Like any polytope, the elements of a 4-polytope cannot be subdivided into two or more sets which are also 4-polytopes, i.e. it is not a compound. |
A 4-polytope is a closed [[Four-dimensional space|four-dimension]]al figure. It comprises [[vertex (geometry)|vertices]] (corner points), [[edge (geometry)|edges]], [[face (geometry)|faces]] and [[cell (mathematics)|cells]]. A cell is the three-dimensional analogue of a face, and is therefore a [[polyhedron]]. Each face must join exactly two cells, analogous to the way in which each edge of a polyhedron joins just two faces. Like any polytope, the elements of a 4-polytope cannot be subdivided into two or more sets which are also 4-polytopes, i.e. it is not a compound. |
||
==Geometry== |
|||
The most familiar 4-polytope is the [[tesseract]] or hypercube, the 4D analogue of the cube. |
The convex [[regular 4-polytopes]] are the four-dimensional analogues of the [[Platonic solids]]. The most familiar 4-polytope is the [[tesseract]] or hypercube, the 4D analogue of the cube. |
||
{{-}} |
|||
The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is ''rounder'' than its predecessor, enclosing more content{{Sfn|Coxeter|1973|pp=292-293|loc=Table I(ii): The sixteen regular polytopes {''p,q,r''} in four dimensions|ps=: [An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.]}} within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing [[Regular 4-polytope#As configurations|configuration matrices]] or simply the number of vertices) follows the same ordering. |
|||
{{Regular convex 4-polytopes}} |
|||
==Visualisation== |
==Visualisation== |
||
| Line 86: | Line 111: | ||
** 10 (regular) [[Schläfli-Hess polytope]]s |
** 10 (regular) [[Schläfli-Hess polytope]]s |
||
** 57 hyperprisms built on [[Nonconvex uniform polyhedron|nonconvex uniform polyhedra]] |
** 57 hyperprisms built on [[Nonconvex uniform polyhedron|nonconvex uniform polyhedra]] |
||
** Unknown total number of nonconvex uniform 4-polytopes: [[Norman Johnson (mathematician)|Norman Johnson]] and other collaborators have identified |
** Unknown total number of nonconvex uniform 4-polytopes: [[Norman Johnson (mathematician)|Norman Johnson]] and other collaborators have identified 2191 forms (convex and star, excluding the infinite families), all constructed by [[vertex figures]] by [[Stella (software)|Stella4D software]].<ref>[https://www.mit.edu/~hlb/Associahedron/program.pdf Uniform Polychora], Norman W. Johnson (Wheaton College), 1845 cases in 2005</ref> |
||
'''Other convex 4-polytopes''': |
'''Other convex 4-polytopes''': |
||
* [[Polyhedral pyramid]] |
* [[Polyhedral pyramid]] |
||
* [[Polyhedral bipyramid]] |
|||
* [[Polyhedral prism]] |
* [[Polyhedral prism]] |
||
<!--* [[Polyhedral antiprism]]--> |
<!--* [[Polyhedral antiprism]]--> |
||
| Line 121: | Line 147: | ||
*[[Regular 4-polytope]] |
*[[Regular 4-polytope]] |
||
* |
*[[3-sphere]] – analogue of a sphere in 4-dimensional space. This is not a 4-polytope, since it is not bounded by polyhedral cells. |
||
*The [[duocylinder]] is a figure in 4-dimensional space related to the [[duoprism]]s. It is also not a 4-polytope because its bounding volumes are not polyhedral. |
*The [[duocylinder]] is a figure in 4-dimensional space related to the [[duoprism]]s. It is also not a 4-polytope because its bounding volumes are not polyhedral. |
||
| Line 128: | Line 154: | ||
=== Notes === |
=== Notes === |
||
{{Reflist}} |
{{Reflist}} |
||
{{notelist}} |
|||
=== Bibliography === |
=== Bibliography === |
||
* [[Harold Scott MacDonald Coxeter|H.S.M. Coxeter]]: |
* [[Harold Scott MacDonald Coxeter|H.S.M. Coxeter]]: |
||
** {{Cite book | last=Coxeter | first=H.S.M. | author-link=Harold Scott MacDonald Coxeter | year=1973 | orig-year=1948 | title=Regular Polytopes | publisher=Dover | place=New York | edition=3rd | title-link=Regular Polytopes (book) }} |
|||
** H. |
** H.S.M. Coxeter, M.S. Longuet-Higgins and [[J.C.P. Miller]]: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 1954 |
||
** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 |
|||
* '''Kaleidoscopes: Selected Writings of H.S.M. Coxeter''', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, {{ISBN|978-0-471-01003-6}} [http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html] |
** '''Kaleidoscopes: Selected Writings of H.S.M. Coxeter''', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, {{ISBN|978-0-471-01003-6}} [http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html] |
||
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380–407, MR 2,10] |
*** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380–407, MR 2,10] |
||
** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', [Math. Zeit. 188 (1985) 559–591] |
*** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', [Math. Zeit. 188 (1985) 559–591] |
||
** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3–45] |
*** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3–45] |
||
* [[John Horton Conway|J.H. Conway]] and [[Michael Guy (computer scientist)|M.J.T. Guy]]: ''Four-Dimensional Archimedean Polytopes'', Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965 |
* [[John Horton Conway|J.H. Conway]] and [[Michael Guy (computer scientist)|M.J.T. Guy]]: ''Four-Dimensional Archimedean Polytopes'', Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965 |
||
* [[Norman Johnson (mathematician)|N.W. Johnson]]: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 |
* [[Norman Johnson (mathematician)|N.W. Johnson]]: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 |
||
*[http://www.polytope.de Four-dimensional Archimedean Polytopes] (German), Marco Möller, 2004 PhD dissertation [http://www.sub.uni-hamburg.de/opus/volltexte/2004/2196/pdf/Dissertation.pdf] |
*[http://www.polytope.de Four-dimensional Archimedean Polytopes] (German), Marco Möller, 2004 PhD dissertation [http://www.sub.uni-hamburg.de/opus/volltexte/2004/2196/pdf/Dissertation.pdf] {{Webarchive|url=https://web.archive.org/web/20050322235615/http://www.sub.uni-hamburg.de/opus/volltexte/2004/2196/pdf/Dissertation.pdf |date=2005-03-22 }} |
||
==External links== |
==External links== |
||
{{Commons category |
{{Commons category}} |
||
*{{Mathworld | urlname=Polychoron | title=Polychoron }} |
*{{Mathworld | urlname=Polychoron | title=Polychoron }} |
||
*{{Mathworld | urlname=PolyhedralFormula | title=Polyhedral formula }} |
*{{Mathworld | urlname=PolyhedralFormula | title=Polyhedral formula }} |
||
*{{Mathworld | urlname=RegularPolychoron | title=Regular polychoron Euler characteristics}} |
*{{Mathworld | urlname=RegularPolychoron | title=Regular polychoron Euler characteristics}} |
||
*{{PolyCell | urlname = uniform.html| title = Four dimensional figures page}} |
|||
*{{GlossaryForHyperspace | anchor=Polychoron | title=Polychoron}} |
|||
*[http://www.polytope.net/hedrondude/polychora.htm Uniform Polychora], Jonathan Bowers |
*[http://www.polytope.net/hedrondude/polychora.htm Uniform Polychora], Jonathan Bowers |
||
*[http://public.beuth-hochschule.de/~meiko/pentatope.html Uniform polychoron Viewer - Java3D Applet with sources] |
*[https://web.archive.org/web/20110718202453/http://public.beuth-hochschule.de/~meiko/pentatope.html Uniform polychoron Viewer - Java3D Applet with sources] |
||
* |
* R. Klitzing, [http://www.bendwavy.org/klitzing/dimensions/polychora-neu.htm polychora] |
||
{{Polytopes}} |
{{Polytopes}} |
||
| Line 156: | Line 181: | ||
[[Category:Four-dimensional geometry]] |
[[Category:Four-dimensional geometry]] |
||
[[Category:Algebraic topology]] |
[[Category:Algebraic topology]] |
||
[[Category: |
[[Category:4-polytopes| ]] |
||
Latest revision as of 00:57, 17 October 2024
| {3,3,3} | {3,3,4} | {4,3,3} |
|---|---|---|
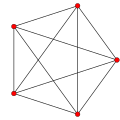 5-cell Pentatope 4-simplex |
 16-cell Orthoplex 4-orthoplex |
 8-cell Tesseract 4-cube |
| {3,4,3} | {3,3,5} | {5,3,3} |
 24-cell Octaplex |
 600-cell Tetraplex |
 120-cell Dodecaplex |
In geometry, a 4-polytope (sometimes also called a polychoron,[1] polycell, or polyhedroid) is a four-dimensional polytope.[2][3] It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.[4]
The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron.
Topologically 4-polytopes are closely related to the uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be cut and unfolded as nets in 3-space.
Definition
[edit]A 4-polytope is a closed four-dimensional figure. It comprises vertices (corner points), edges, faces and cells. A cell is the three-dimensional analogue of a face, and is therefore a polyhedron. Each face must join exactly two cells, analogous to the way in which each edge of a polyhedron joins just two faces. Like any polytope, the elements of a 4-polytope cannot be subdivided into two or more sets which are also 4-polytopes, i.e. it is not a compound.
Geometry
[edit]The convex regular 4-polytopes are the four-dimensional analogues of the Platonic solids. The most familiar 4-polytope is the tesseract or hypercube, the 4D analogue of the cube.
The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content[5] within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering.
| Regular convex 4-polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | |||
| Name | 5-cell Hyper-tetrahedron |
16-cell Hyper-octahedron |
8-cell Hyper-cube |
24-cell
|
600-cell Hyper-icosahedron |
120-cell Hyper-dodecahedron | |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Coxeter mirrors | |||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | |
| Graph | 
|

|

|

|

|

| |
| Vertices | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral | |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular | |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons | |
| Cells | 5 tetrahedra | 16 tetrahedra | 8 cubes | 24 octahedra | 600 tetrahedra | 120 dodecahedra | |
| Tori | 1 5-tetrahedron | 2 8-tetrahedron | 2 4-cube | 4 6-octahedron | 20 30-tetrahedron | 12 10-dodecahedron | |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells | |
| Great polygons | 2 squares x 3 | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | ||
| Petrie polygons | 1 pentagon x 2 | 1 octagon x 3 | 2 octagons x 4 | 2 dodecagons x 4 | 4 30-gons x 6 | 20 30-gons x 4 | |
| Long radius | |||||||
| Edge length | |||||||
| Short radius | |||||||
| Area | |||||||
| Volume | |||||||
| 4-Content | |||||||
Visualisation
[edit]| Sectioning | Net | |
|---|---|---|

|

| |
| Projections | ||
| Schlegel | 2D orthogonal | 3D orthogonal |

|

|

|
4-polytopes cannot be seen in three-dimensional space due to their extra dimension. Several techniques are used to help visualise them.
- Orthogonal projection
Orthogonal projections can be used to show various symmetry orientations of a 4-polytope. They can be drawn in 2D as vertex-edge graphs, and can be shown in 3D with solid faces as visible projective envelopes.
- Perspective projection
Just as a 3D shape can be projected onto a flat sheet, so a 4-D shape can be projected onto 3-space or even onto a flat sheet. One common projection is a Schlegel diagram which uses stereographic projection of points on the surface of a 3-sphere into three dimensions, connected by straight edges, faces, and cells drawn in 3-space.
- Sectioning
Just as a slice through a polyhedron reveals a cut surface, so a slice through a 4-polytope reveals a cut "hypersurface" in three dimensions. A sequence of such sections can be used to build up an understanding of the overall shape. The extra dimension can be equated with time to produce a smooth animation of these cross sections.
- Nets
A net of a 4-polytope is composed of polyhedral cells that are connected by their faces and all occupy the same three-dimensional space, just as the polygon faces of a net of a polyhedron are connected by their edges and all occupy the same plane.
Topological characteristics
[edit]
The topology of any given 4-polytope is defined by its Betti numbers and torsion coefficients.[6]
The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, and is zero for all 4-polytopes, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.[6]
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal 4-polytopes, and this led to the use of torsion coefficients.[6]
Classification
[edit]Criteria
[edit]Like all polytopes, 4-polytopes may be classified based on properties like "convexity" and "symmetry".
- A 4-polytope is convex if its boundary (including its cells, faces and edges) does not intersect itself and the line segment joining any two points of the 4-polytope is contained in the 4-polytope or its interior; otherwise, it is non-convex. Self-intersecting 4-polytopes are also known as star 4-polytopes, from analogy with the star-like shapes of the non-convex star polygons and Kepler–Poinsot polyhedra.
- A 4-polytope is regular if it is transitive on its flags. This means that its cells are all congruent regular polyhedra, and similarly its vertex figures are congruent and of another kind of regular polyhedron.
- A convex 4-polytope is semi-regular if it has a symmetry group under which all vertices are equivalent (vertex-transitive) and its cells are regular polyhedra. The cells may be of two or more kinds, provided that they have the same kind of face. There are only 3 cases identified by Thorold Gosset in 1900: the rectified 5-cell, rectified 600-cell, and snub 24-cell.
- A 4-polytope is uniform if it has a symmetry group under which all vertices are equivalent, and its cells are uniform polyhedra. The faces of a uniform 4-polytope must be regular.
- A 4-polytope is scaliform if it is vertex-transitive, and has all equal length edges. This allows cells which are not uniform, such as the regular-faced convex Johnson solids.
- A regular 4-polytope which is also convex is said to be a convex regular 4-polytope.
- A 4-polytope is prismatic if it is the Cartesian product of two or more lower-dimensional polytopes. A prismatic 4-polytope is uniform if its factors are uniform. The hypercube is prismatic (product of two squares, or of a cube and line segment), but is considered separately because it has symmetries other than those inherited from its factors.
- A tiling or honeycomb of 3-space is the division of three-dimensional Euclidean space into a repetitive grid of polyhedral cells. Such tilings or tessellations are infinite and do not bound a "4D" volume, and are examples of infinite 4-polytopes. A uniform tiling of 3-space is one whose vertices are congruent and related by a space group and whose cells are uniform polyhedra.
Classes
[edit]The following lists the various categories of 4-polytopes classified according to the criteria above:

Uniform 4-polytope (vertex-transitive):
- Convex uniform 4-polytopes (64, plus two infinite families)
- 47 non-prismatic convex uniform 4-polytope including:
- Prismatic uniform 4-polytopes:
- {} × {p,q} : 18 polyhedral hyperprisms (including cubic hyperprism, the regular hypercube)
- Prisms built on antiprisms (infinite family)
- {p} × {q} : duoprisms (infinite family)
- Non-convex uniform 4-polytopes (10 + unknown)

The great grand stellated 120-cell is the largest of 10 regular star 4-polytopes, having 600 vertices. - 10 (regular) Schläfli-Hess polytopes
- 57 hyperprisms built on nonconvex uniform polyhedra
- Unknown total number of nonconvex uniform 4-polytopes: Norman Johnson and other collaborators have identified 2191 forms (convex and star, excluding the infinite families), all constructed by vertex figures by Stella4D software.[7]
Other convex 4-polytopes:

Infinite uniform 4-polytopes of Euclidean 3-space (uniform tessellations of convex uniform cells)
- 28 convex uniform honeycombs: uniform convex polyhedral tessellations, including:
- 1 regular tessellation, cubic honeycomb: {4,3,4}
Infinite uniform 4-polytopes of hyperbolic 3-space (uniform tessellations of convex uniform cells)
- 76 Wythoffian convex uniform honeycombs in hyperbolic space, including:
- 4 regular tessellation of compact hyperbolic 3-space: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
Dual uniform 4-polytope (cell-transitive):
- 41 unique dual convex uniform 4-polytopes
- 17 unique dual convex uniform polyhedral prisms
- infinite family of dual convex uniform duoprisms (irregular tetrahedral cells)
- 27 unique convex dual uniform honeycombs, including:
Others:
- Weaire–Phelan structure periodic space-filling honeycomb with irregular cells

These categories include only the 4-polytopes that exhibit a high degree of symmetry. Many other 4-polytopes are possible, but they have not been studied as extensively as the ones included in these categories.
See also
[edit]- Regular 4-polytope
- 3-sphere – analogue of a sphere in 4-dimensional space. This is not a 4-polytope, since it is not bounded by polyhedral cells.
- The duocylinder is a figure in 4-dimensional space related to the duoprisms. It is also not a 4-polytope because its bounding volumes are not polyhedral.
References
[edit]Notes
[edit]- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.1 Polytopes and Honeycombs, p.224
- ^ Vialar, T. (2009). Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance. Springer. p. 674. ISBN 978-3-540-85977-2.
- ^ Capecchi, V.; Contucci, P.; Buscema, M.; D'Amore, B. (2010). Applications of Mathematics in Models, Artificial Neural Networks and Arts. Springer. p. 598. doi:10.1007/978-90-481-8581-8. ISBN 978-90-481-8580-1.
- ^ Coxeter 1973, p. 141, §7-x. Historical remarks.
- ^ Coxeter 1973, pp. 292–293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions: [An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.]
- ^ a b c Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.
- ^ Uniform Polychora, Norman W. Johnson (Wheaton College), 1845 cases in 2005
Bibliography
[edit]- H.S.M. Coxeter:
- Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
- H.S.M. Coxeter, M.S. Longuet-Higgins and J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2] Archived 2005-03-22 at the Wayback Machine
External links
[edit]- Weisstein, Eric W. "Polychoron". MathWorld.
- Weisstein, Eric W. "Polyhedral formula". MathWorld.
- Weisstein, Eric W. "Regular polychoron Euler characteristics". MathWorld.
- Uniform Polychora, Jonathan Bowers
- Uniform polychoron Viewer - Java3D Applet with sources
- R. Klitzing, polychora


























