diff --git a/.gitignore b/.gitignore
new file mode 100644
index 0000000000..4bd29f751f
--- /dev/null
+++ b/.gitignore
@@ -0,0 +1,7 @@
+.idea/
+.DS_Store
+.vscode
+.temp
+.cache
+*.iml
+__pycache__
diff --git a/README.md b/README.md
index 148f49d885..993d7c6df8 100644
--- a/README.md
+++ b/README.md
@@ -2,35 +2,23 @@
👉 推荐 [在线阅读](http://programmercarl.com/) (Github在国内访问经常不稳定)
👉 推荐 [Gitee同步](https://gitee.com/programmercarl/leetcode-master)
-> 1. **介绍**:本项目是一套完整的刷题计划,旨在帮助大家少走弯路,循序渐进学算法,[关注作者](#关于作者)
-> 2. **PDF版本** : [「代码随想录」算法精讲 PDF 版本](https://programmercarl.com/other/algo_pdf.html) 。
-> 3. **最强八股文:**:[代码随想录知识星球精华PDF](https://www.programmercarl.com/other/kstar_baguwen.html)
-> 4. **刷题顺序** : README已经将刷题顺序排好了,按照顺序一道一道刷就可以。
-> 5. **学习社区** : 一起学习打卡/面试技巧/如何选择offer/大厂内推/职场规则/简历修改/技术分享/程序人生。欢迎加入[「代码随想录」知识星球](https://programmercarl.com/other/kstar.html) 。
-> 6. **提交代码**:本项目统一使用C++语言进行讲解,但已经有Java、Python、Go、JavaScript等等多语言版本,感谢[这里的每一位贡献者](https://github.com/youngyangyang04/leetcode-master/graphs/contributors),如果你也想贡献代码点亮你的头像,[点击这里](https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A)了解提交代码的方式。
-> 7. **转载须知** :以下所有文章皆为我([程序员Carl](https://github.com/youngyangyang04))的原创。引用本项目文章请注明出处,发现恶意抄袭或搬运,会动用法律武器维护自己的权益。让我们一起维护一个良好的技术创作环境!
+> 1. **介绍** :本项目是一套完整的刷题计划,旨在帮助大家少走弯路,循序渐进学算法,[关注作者](#关于作者)
+> 2. **正式出版** :[《代码随想录》](https://programmercarl.com/qita/publish.html) 。
+> 3. **PDF版本** :[「代码随想录」算法精讲 PDF 版本](https://programmercarl.com/qita/algo_pdf.html) 。
+> 4. **算法公开课** :[《代码随想录》算法视频公开课](https://www.bilibili.com/video/BV1fA4y1o715) 。
+> 5. **最强八股文** :[代码随想录知识星球精华PDF](https://www.programmercarl.com/other/kstar_baguwen.html) 。
+> 6. **刷题顺序** :README已经将刷题顺序排好了,按照顺序一道一道刷就可以。
+> 7. **学习社区** :一起学习打卡/面试技巧/如何选择offer/大厂内推/职场规则/简历修改/技术分享/程序人生。欢迎加入[「代码随想录」知识星球](https://programmercarl.com/other/kstar.html) 。
+> 8. **提交代码** :本项目统一使用C++语言进行讲解,但已经有Java、Python、Go、JavaScript等等多语言版本,感谢[这里的每一位贡献者](https://github.com/youngyangyang04/leetcode-master/graphs/contributors),如果你也想贡献代码点亮你的头像,[点击这里](https://www.programmercarl.com/qita/join.html)了解提交代码的方式。
+> 9. **转载须知** :以下所有文章皆为我([程序员Carl](https://github.com/youngyangyang04))的原创。引用本项目文章请注明出处,发现恶意抄袭或搬运,会动用法律武器维护自己的权益。让我们一起维护一个良好的技术创作环境!
-
-
-  -
-
-  -
-  -
-  -
-  -
-
-
-《代码随想录》正式出版啦!!录友专属福利,点击下方可以享五折优惠!详细可以点击这里
-
-
-
-  +
+
+
+ 
-
# LeetCode 刷题攻略
## 刷题攻略的背景
@@ -63,24 +51,17 @@
## 如何使用该刷题攻略
-电脑端还看不到留言,大家可以在公众号[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png),左下角有「刷题攻略」,这是手机版刷题攻略,看完就会发现有很多录友(代码随想录的朋友们)在文章下留言打卡,这份刷题顺序和题解已经陪伴了上万录友了,同时也说明文章的质量是经过上万人的考验!
-
-欢迎每一位学习算法的小伙伴加入到这个学习阵营来!
-
-**目前已经更新了,数组-> 链表-> 哈希表->字符串->栈与队列->树->回溯->贪心,八个专题了,正在讲解动态规划!**
+按照先面的排列顺序,从数组开始刷起就可以了,顺序都安排好了,按顺序刷就好。
在刷题攻略中,每个专题开始都有理论基础篇,并不像是教科书般的理论介绍,而是从实战中归纳需要的基础知识。每个专题结束都有总结篇,最这个专题的归纳总结。
如果你是算法老手,这篇攻略也是复习的最佳资料,如果把每个系列对应的总结篇,快速过一遍,整个算法知识体系以及各种解法就重现脑海了。
-
-目前「代码随想录」刷题攻略更新了:**200多篇文章,精讲了200道经典算法题目,共60w字的详细图解,部分难点题目还搭配了20分钟左右的视频讲解**。
-
**这里每一篇题解,都是精品,值得仔细琢磨**。
-我在题目讲解中统一使用C++,但你会发现下面几乎每篇题解都配有其他语言版本,Java、Python、Go、JavaScript等等,正是这些[热心小伙们](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)的贡献的代码,当然我也会严格把控代码质量。
+我在题目讲解中统一使用C++,但你会发现下面几乎每篇题解都配有其他语言版本,Java、Python、Go、JavaScript等等,正是这些[热心小伙们](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)贡献的代码,当然我也会严格把控代码质量。
-**所以也欢迎大家参与进来,完善题解的各个语言版本,拥抱开源,让更多小伙伴们收益**。
+**所以也欢迎大家参与进来,完善题解的各个语言版本,拥抱开源,让更多小伙伴们受益**。
准备好了么,刷题攻略开始咯,go go go!
@@ -88,22 +69,14 @@
## 前序
-* [「代码随想录」学习社区](https://programmercarl.com/other/kstar.html)
+* [做项目(多个C++、Java、Go、前端、测开项目)](https://programmercarl.com/other/kstar.html)
* 编程语言
* [C++面试&C++学习指南知识点整理](https://github.com/youngyangyang04/TechCPP)
-
-* 项目
- * [基于跳表的轻量级KV存储引擎](https://github.com/youngyangyang04/Skiplist-CPP)
- * [Nosql数据库注入攻击系统](https://github.com/youngyangyang04/NoSQLAttack)
-
-* 编程素养
- * [看了这么多代码,谈一谈代码风格!](./problems/前序/代码风格.md)
- * [力扣上的代码想在本地编译运行?](./problems/前序/力扣上的代码想在本地编译运行?.md)
- * [什么是核心代码模式,什么又是ACM模式?](./problems/前序/什么是核心代码模式,什么又是ACM模式?.md)
- * [ACM模式如何构造二叉树](./problems/前序/ACM模式如何构建二叉树.md)
- * [解密互联网大厂研发流程](./problems/前序/互联网大厂研发流程.md)
+ * [编程语言基础课](https://kamacoder.com/courseshop.php)
+ * [23种设计模式](https://github.com/youngyangyang04/kama-DesignPattern)
+ * [大厂算法笔试题](https://kamacoder.com/company.php)
* 工具
* [一站式vim配置](https://github.com/youngyangyang04/PowerVim)
@@ -111,357 +84,331 @@
* [程序员应该用什么用具来写文档?](./problems/前序/程序员写文档工具.md)
* 求职
+ * [ACM模式练习网站,卡码网](https://kamacoder.com/)
* [程序员的简历应该这么写!!(附简历模板)](./problems/前序/程序员简历.md)
+ * [【专业技能】应该这样写!](https://programmercarl.com/other/jianlizhuanye.html)
+ * [【项目经历】应该这样写!](https://programmercarl.com/other/jianlixiangmu.html)
* [BAT级别技术面试流程和注意事项都在这里了](./problems/前序/BAT级别技术面试流程和注意事项都在这里了.md)
- * [北京有这些互联网公司,你都知道么?](./problems/前序/北京互联网公司总结.md)
- * [上海有这些互联网公司,你都知道么?](./problems/前序/上海互联网公司总结.md)
- * [深圳有这些互联网公司,你都知道么?](./problems/前序/深圳互联网公司总结.md)
- * [广州有这些互联网公司,你都知道么?](./problems/前序/广州互联网公司总结.md)
- * [成都有这些互联网公司,你都知道么?](./problems/前序/成都互联网公司总结.md)
- * [杭州有这些互联网公司,你都知道么?](./problems/前序/杭州互联网公司总结.md)
* 算法性能分析
- * [关于时间复杂度,你不知道的都在这里!](./problems/前序/关于时间复杂度,你不知道的都在这里!.md)
- * [O(n)的算法居然超时了,此时的n究竟是多大?](./problems/前序/On的算法居然超时了,此时的n究竟是多大?.md)
- * [通过一道面试题目,讲一讲递归算法的时间复杂度!](./problems/前序/通过一道面试题目,讲一讲递归算法的时间复杂度!.md)
- * [本周小结!(算法性能分析系列一)](./problems/周总结/20201210复杂度分析周末总结.md)
- * [关于空间复杂度,可能有几个疑问?](./problems/前序/关于空间复杂度,可能有几个疑问?.md)
+ * [关于时间复杂度,你不知道的都在这里!](./problems/前序/时间复杂度.md)
+ * [O(n)的算法居然超时了,此时的n究竟是多大?](./problems/前序/算法超时.md)
+ * [通过一道面试题目,讲一讲递归算法的时间复杂度!](./problems/前序/递归算法的时间复杂度.md)
+ * [关于空间复杂度,可能有几个疑问?](./problems/前序/空间复杂度.md)
* [递归算法的时间与空间复杂度分析!](./problems/前序/递归算法的时间与空间复杂度分析.md)
- * [刷了这么多题,你了解自己代码的内存消耗么?](./problems/前序/刷了这么多题,你了解自己代码的内存消耗么?.md)
-
-## 知识星球精选
-
-* [秋招面试,心态很重要!](./problems/知识星球精选/秋招总结3.md)
-* [秋招倒霉透顶,触底反弹!](./problems/知识星球精选/秋招总结2.md)
-* [无竞赛,无实习,如何秋招?](./problems/知识星球精选/秋招总结1.md)
-* [offer总决赛,何去何从!](./problems/知识星球精选/offer总决赛,何去何从.md)
-* [入职后担心代码能力跟不上!](./problems/知识星球精选/入职后担心代码能力跟不上.md)
-* [秋招进入offer决赛圈!](./problems/知识星球精选/offer对比-决赛圈.md)
-* [非科班的困扰](./problems/知识星球精选/非科班的困扰.md)
-* [offer的选择-开奖](./problems/知识星球精选/秋招开奖.md)
-* [看到代码就抵触!怎么办?](./problems/知识星球精选/不喜欢写代码怎么办.md)
-* [遭遇逼签,怎么办?](./problems/知识星球精选/逼签.md)
-* [HR特意刁难非科班!](./problems/知识星球精选/HR特意刁难非科班.md)
-* [offer的选择](./problems/知识星球精选/offer的选择.md)
-* [天下乌鸦一般黑,哪家没有PUA?](./problems/知识星球精选/天下乌鸦一般黑.md)
-* [初入大三,考研VS工作](./problems/知识星球精选/初入大三选择考研VS工作.md)
-* [非科班2021秋招总结](./problems/知识星球精选/非科班2021秋招总结.md)
-* [秋招下半场依然没offer,怎么办?](./problems/知识星球精选/秋招下半场依然没offer.md)
-* [合适自己的就是最好的](./problems/知识星球精选/合适自己的就是最好的.md)
-* [为什么都说客户端会消失](./problems/知识星球精选/客三消.md)
-* [博士转计算机如何找工作](./problems/知识星球精选/博士转行计算机.md)
-* [不一样的七夕](./problems/知识星球精选/不一样的七夕.md)
-* [HR面注意事项](./problems/知识星球精选/HR面注意事项.md)
-* [刷题攻略要刷两遍!](./problems/知识星球精选/刷题攻略要刷两遍.md)
-* [秋招进行中的迷茫与焦虑......](./problems/知识星球精选/秋招进行中的迷茫与焦虑.md)
-* [大厂新人培养体系应该是什么样的?](./problems/知识星球精选/大厂新人培养体系.md)
-* [你的简历里「专业技能」写的够专业么?](./problems/知识星球精选/专业技能可以这么写.md)
-* [Carl看了上百份简历,总结了这些!](./problems/知识星球精选/写简历的一些问题.md)
-* [备战2022届秋招](./problems/知识星球精选/备战2022届秋招.md)
-* [技术不太好,如果选择方向](./problems/知识星球精选/技术不好如何选择技术方向.md)
-* [刷题要不要使用库函数](./problems/知识星球精选/刷力扣用不用库函数.md)
-* [关于实习的几点问题](./problems/知识星球精选/关于实习大家的疑问.md)
-* [面试中遇到了发散性问题,怎么办?](./problems/知识星球精选/面试中发散性问题.md)
-* [英语到底重不重要!](./problems/知识星球精选/英语到底重不重要.md)
-* [计算机专业要不要读研!](./problems/知识星球精选/要不要考研.md)
-* [关于提前批的一些建议](./problems/知识星球精选/关于提前批的一些建议.md)
-* [已经在实习的录友要如何准备秋招](./problems/知识星球精选/如何权衡实习与秋招复习.md)
-* [华为提前批已经开始了](./problems/知识星球精选/提前批已经开始了.md)
-
-## 杂谈
-
-* [「代码随想录」刷题网站上线](https://mp.weixin.qq.com/s/-6rd_g7LrVD1fuKBYk2tXQ)。
-* [LeetCode-Master上榜了](https://mp.weixin.qq.com/s/wZRTrA9Rbvgq1yEkSw4vfQ)
-* [上榜之后,都有哪些变化?](https://mp.weixin.qq.com/s/VJBV0qSBthjnbbmW-lctLA)
-* [大半年过去了......](https://mp.weixin.qq.com/s/lubfeistPxBLSQIe5XYg5g)
-* [一万录友在B站学算法!](https://mp.weixin.qq.com/s/Vzq4zkMZY7erKeu0fqGLgw)
+ * [刷了这么多题,你了解自己代码的内存消耗么?](./problems/前序/内存消耗.md)
+
## 数组
1. [数组过于简单,但你该了解这些!](./problems/数组理论基础.md)
-2. [数组:每次遇到二分法,都是一看就会,一写就废](./problems/0704.二分查找.md)
-3. [数组:就移除个元素很难么?](./problems/0027.移除元素.md)
-4. [数组:有序数组的平方,还有序么?](./problems/0977.有序数组的平方.md)
-5. [数组:滑动窗口拯救了你](./problems/0209.长度最小的子数组.md)
-6. [数组:这个循环可以转懵很多人!](./problems/0059.螺旋矩阵II.md)
-7. [数组:总结篇](./problems/数组总结篇.md)
+2. [数组:704.二分查找](./problems/0704.二分查找.md)
+3. [数组:27.移除元素](./problems/0027.移除元素.md)
+4. [数组:977.有序数组的平方](./problems/0977.有序数组的平方.md)
+5. [数组:209.长度最小的子数组](./problems/0209.长度最小的子数组.md)
+6. [数组:区间和](./problems/kamacoder/0058.区间和.md)
+7. [数组:开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
+8. [数组:59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
+9. [数组:总结篇](./problems/数组总结篇.md)
## 链表
1. [关于链表,你该了解这些!](./problems/链表理论基础.md)
-2. [链表:听说用虚拟头节点会方便很多?](./problems/0203.移除链表元素.md)
-3. [链表:一道题目考察了常见的五个操作!](./problems/0707.设计链表.md)
-4. [链表:听说过两天反转链表又写不出来了?](./problems/0206.翻转链表.md)
-5. [链表:两两交换链表中的节点](./problems/0024.两两交换链表中的节点.md)
-6. [链表:删除链表的倒数第 N 个结点](./problems/0019.删除链表的倒数第N个节点.md)
+2. [链表:203.移除链表元素](./problems/0203.移除链表元素.md)
+3. [链表:707.设计链表](./problems/0707.设计链表.md)
+4. [链表:206.翻转链表](./problems/0206.翻转链表.md)
+5. [链表:24.两两交换链表中的节点](./problems/0024.两两交换链表中的节点.md)
+6. [链表:19.删除链表的倒数第 N 个结点](./problems/0019.删除链表的倒数第N个节点.md)
7. [链表:链表相交](./problems/面试题02.07.链表相交.md)
-8. [链表:环找到了,那入口呢?](./problems/0142.环形链表II.md)
+8. [链表:142.环形链表](./problems/0142.环形链表II.md)
9. [链表:总结篇!](./problems/链表总结篇.md)
## 哈希表
1. [关于哈希表,你该了解这些!](./problems/哈希表理论基础.md)
-2. [哈希表:可以拿数组当哈希表来用,但哈希值不要太大](./problems/0242.有效的字母异位词.md)
-3. [哈希表:查找常用字符](./problems/1002.查找常用字符.md)
-4. [哈希表:哈希值太大了,还是得用set](./problems/0349.两个数组的交集.md)
-5. [哈希表:用set来判断快乐数](./problems/0202.快乐数.md)
-6. [哈希表:map等候多时了](./problems/0001.两数之和.md)
-7. [哈希表:其实需要哈希的地方都能找到map的身影](./problems/0454.四数相加II.md)
-8. [哈希表:这道题目我做过?](./problems/0383.赎金信.md)
-9. [哈希表:解决了两数之和,那么能解决三数之和么?](./problems/0015.三数之和.md)
-10. [双指针法:一样的道理,能解决四数之和](./problems/0018.四数之和.md)
-11. [哈希表:总结篇!(每逢总结必经典)](./problems/哈希表总结.md)
+2. [哈希表:242.有效的字母异位词](./problems/0242.有效的字母异位词.md)
+3. [哈希表:1002.查找常用字符](./problems/1002.查找常用字符.md)
+4. [哈希表:349.两个数组的交集](./problems/0349.两个数组的交集.md)
+5. [哈希表:202.快乐数](./problems/0202.快乐数.md)
+6. [哈希表:1.两数之和](./problems/0001.两数之和.md)
+7. [哈希表:454.四数相加II](./problems/0454.四数相加II.md)
+8. [哈希表:383.赎金信](./problems/0383.赎金信.md)
+9. [哈希表:15.三数之和](./problems/0015.三数之和.md)
+10. [双指针法:18.四数之和](./problems/0018.四数之和.md)
+11. [哈希表:总结篇!](./problems/哈希表总结.md)
## 字符串
-1. [字符串:这道题目,使用库函数一行代码搞定](./problems/0344.反转字符串.md)
-2. [字符串:简单的反转还不够!](./problems/0541.反转字符串II.md)
-3. [字符串:替换空格](./problems/剑指Offer05.替换空格.md)
-4. [字符串:花式反转还不够!](./problems/0151.翻转字符串里的单词.md)
-5. [字符串:反转个字符串还有这个用处?](./problems/剑指Offer58-II.左旋转字符串.md)
+1. [字符串:344.反转字符串](./problems/0344.反转字符串.md)
+2. [字符串:541.反转字符串II](./problems/0541.反转字符串II.md)
+3. [字符串:替换数字](./problems/kamacoder/0054.替换数字.md)
+4. [字符串:151.翻转字符串里的单词](./problems/0151.翻转字符串里的单词.md)
+5. [字符串:右旋字符串](./problems/kamacoder/0055.右旋字符串.md)
6. [帮你把KMP算法学个通透](./problems/0028.实现strStr.md)
-8. [字符串:KMP算法还能干这个!](./problems/0459.重复的子字符串.md)
+8. [字符串:459.重复的子字符串](./problems/0459.重复的子字符串.md)
9. [字符串:总结篇!](./problems/字符串总结.md)
## 双指针法
双指针法基本都是应用在数组,字符串与链表的题目上
-1. [数组:就移除个元素很难么?](./problems/0027.移除元素.md)
-2. [字符串:这道题目,使用库函数一行代码搞定](./problems/0344.反转字符串.md)
-3. [字符串:替换空格](./problems/剑指Offer05.替换空格.md)
-4. [字符串:花式反转还不够!](./problems/0151.翻转字符串里的单词.md)
-5. [链表:听说过两天反转链表又写不出来了?](./problems/0206.翻转链表.md)
-6. [链表:删除链表的倒数第 N 个结点](./problems/0019.删除链表的倒数第N个节点.md)
+1. [数组:27.移除元素](./problems/0027.移除元素.md)
+2. [字符串:344.反转字符串](./problems/0344.反转字符串.md)
+3. [字符串:替换数字](./problems/kamacoder/0054.替换数字.md)
+4. [字符串:151.翻转字符串里的单词](./problems/0151.翻转字符串里的单词.md)
+5. [链表:206.翻转链表](./problems/0206.翻转链表.md)
+6. [链表:19.删除链表的倒数第 N 个结点](./problems/0019.删除链表的倒数第N个节点.md)
7. [链表:链表相交](./problems/面试题02.07.链表相交.md)
-8. [链表:环找到了,那入口呢?](./problems/0142.环形链表II.md)
-9. [哈希表:解决了两数之和,那么能解决三数之和么?](./problems/0015.三数之和.md)
-10. [双指针法:一样的道理,能解决四数之和](./problems/0018.四数之和.md)
-11. [双指针法:总结篇!](./problems/双指针总结.md)
+8. [链表:142.环形链表](./problems/0142.环形链表II.md)
+9. [双指针:15.三数之和](./problems/0015.三数之和.md)
+10. [双指针:18.四数之和](./problems/0018.四数之和.md)
+11. [双指针:总结篇!](./problems/双指针总结.md)
## 栈与队列
-1. [栈与队列:来看看栈和队列不为人知的一面](./problems/栈与队列理论基础.md)
-2. [栈与队列:我用栈来实现队列怎么样?](./problems/0232.用栈实现队列.md)
-3. [栈与队列:用队列实现栈还有点别扭](./problems/0225.用队列实现栈.md)
-4. [栈与队列:系统中处处都是栈的应用](./problems/0020.有效的括号.md)
-5. [栈与队列:匹配问题都是栈的强项](./problems/1047.删除字符串中的所有相邻重复项.md)
-6. [栈与队列:有没有想过计算机是如何处理表达式的?](./problems/0150.逆波兰表达式求值.md)
-7. [栈与队列:滑动窗口里求最大值引出一个重要数据结构](./problems/0239.滑动窗口最大值.md)
-8. [栈与队列:求前 K 个高频元素和队列有啥关系?](./problems/0347.前K个高频元素.md)
+1. [栈与队列:理论基础](./problems/栈与队列理论基础.md)
+2. [栈与队列:232.用栈实现队列](./problems/0232.用栈实现队列.md)
+3. [栈与队列:225.用队列实现栈](./problems/0225.用队列实现栈.md)
+4. [栈与队列:20.有效的括号](./problems/0020.有效的括号.md)
+5. [栈与队列:1047.删除字符串中的所有相邻重复项](./problems/1047.删除字符串中的所有相邻重复项.md)
+6. [栈与队列:150.逆波兰表达式求值](./problems/0150.逆波兰表达式求值.md)
+7. [栈与队列:239.滑动窗口最大值](./problems/0239.滑动窗口最大值.md)
+8. [栈与队列:347.前K个高频元素](./problems/0347.前K个高频元素.md)
9. [栈与队列:总结篇!](./problems/栈与队列总结.md)
## 二叉树
+
题目分类大纲如下:
-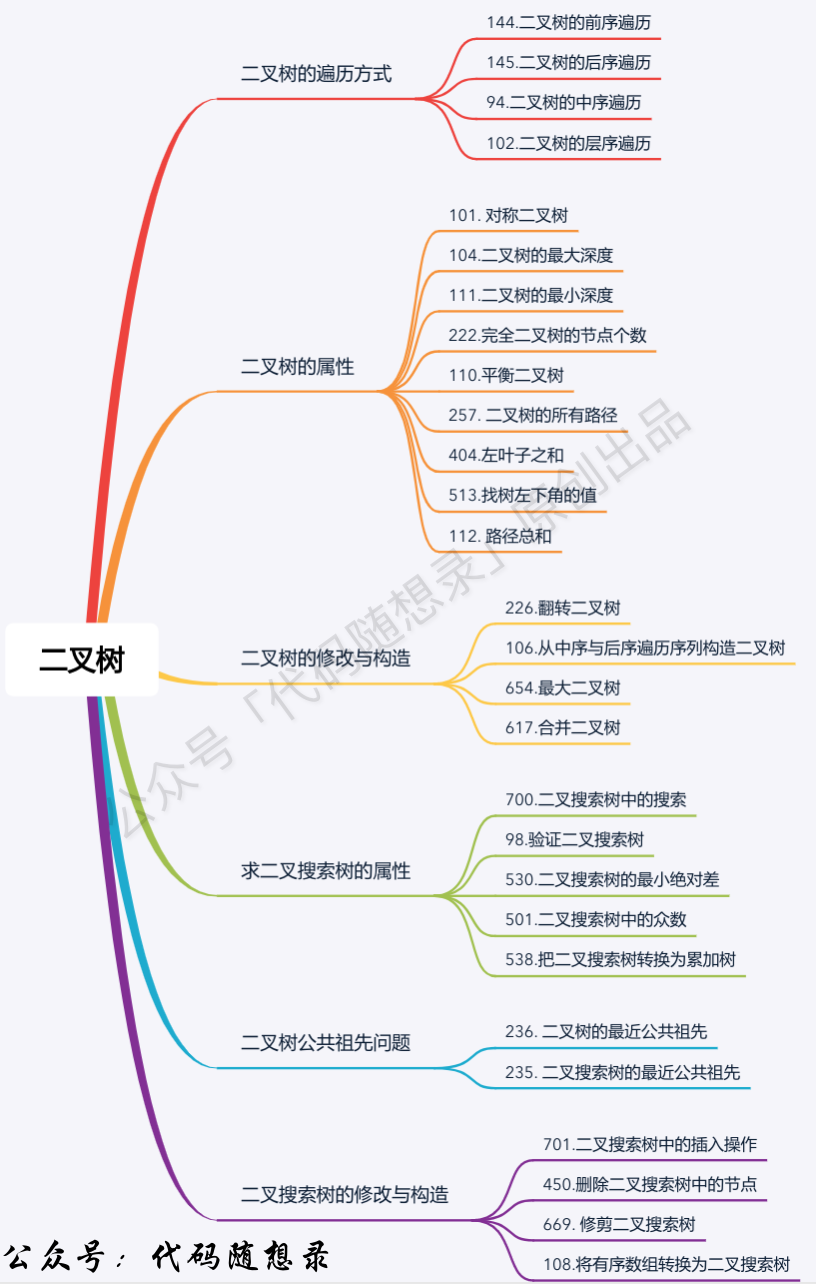 +
+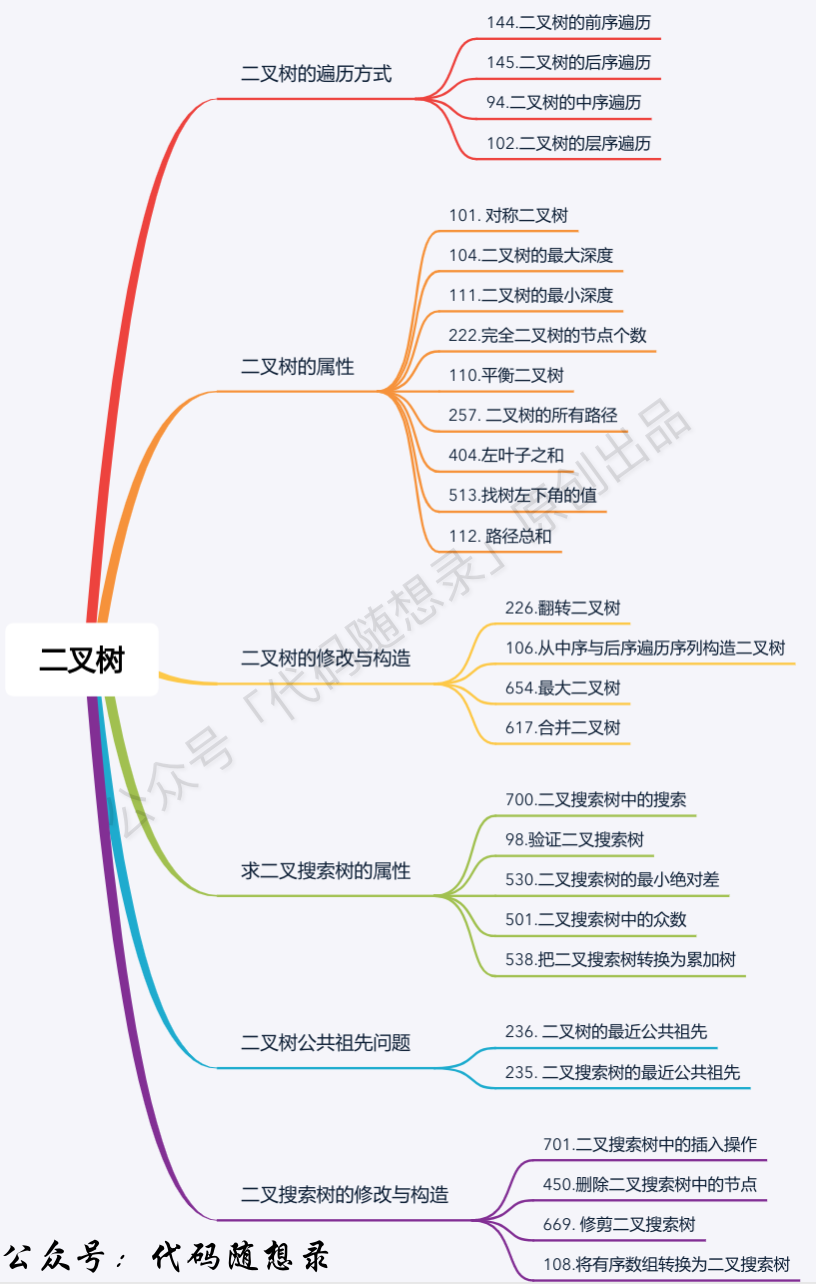 1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
-2. [二叉树:一入递归深似海,从此offer是路人](./problems/二叉树的递归遍历.md)
-3. [二叉树:听说递归能做的,栈也能做!](./problems/二叉树的迭代遍历.md)
-4. [二叉树:前中后序迭代方式的写法就不能统一一下么?](./problems/二叉树的统一迭代法.md)
-5. [二叉树:层序遍历登场!](./problems/0102.二叉树的层序遍历.md)
-6. [二叉树:你真的会翻转二叉树么?](./problems/0226.翻转二叉树.md)
+2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
+3. [二叉树:二叉树的迭代遍历](./problems/二叉树的迭代遍历.md)
+4. [二叉树:二叉树的统一迭代法](./problems/二叉树的统一迭代法.md)
+5. [二叉树:二叉树的层序遍历](./problems/0102.二叉树的层序遍历.md)
+6. [二叉树:226.翻转二叉树](./problems/0226.翻转二叉树.md)
7. [本周小结!(二叉树)](./problems/周总结/20200927二叉树周末总结.md)
-8. [二叉树:我对称么?](./problems/0101.对称二叉树.md)
-9. [二叉树:看看这些树的最大深度](./problems/0104.二叉树的最大深度.md)
-10. [二叉树:看看这些树的最小深度](./problems/0111.二叉树的最小深度.md)
-11. [二叉树:我有多少个节点?](./problems/0222.完全二叉树的节点个数.md)
-12. [二叉树:我平衡么?](./problems/0110.平衡二叉树.md)
-13. [二叉树:找我的所有路径?](./problems/0257.二叉树的所有路径.md)
-14. [本周总结!二叉树系列二](./problems/周总结/20201003二叉树周末总结.md)
-15. [二叉树:以为使用了递归,其实还隐藏着回溯](./problems/二叉树中递归带着回溯.md)
-16. [二叉树:做了这么多题目了,我的左叶子之和是多少?](./problems/0404.左叶子之和.md)
-17. [二叉树:我的左下角的值是多少?](./problems/0513.找树左下角的值.md)
-18. [二叉树:路径总和](./problems/0112.路径总和.md)
-19. [二叉树:构造二叉树登场!](./problems/0106.从中序与后序遍历序列构造二叉树.md)
-20. [二叉树:构造一棵最大的二叉树](./problems/0654.最大二叉树.md)
-21. [本周小结!(二叉树系列三)](./problems/周总结/20201010二叉树周末总结.md)
-22. [二叉树:合并两个二叉树](./problems/0617.合并二叉树.md)
-23. [二叉树:二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
-24. [二叉树:我是不是一棵二叉搜索树](./problems/0098.验证二叉搜索树.md)
-25. [二叉树:搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
-26. [二叉树:我的众数是多少?](./problems/0501.二叉搜索树中的众数.md)
-27. [二叉树:公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
-28. [本周小结!(二叉树系列四)](./problems/周总结/20201017二叉树周末总结.md)
-29. [二叉树:搜索树的公共祖先问题](./problems/0235.二叉搜索树的最近公共祖先.md)
-30. [二叉树:搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
-31. [二叉树:搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
-32. [二叉树:修剪一棵搜索树](./problems/0669.修剪二叉搜索树.md)
-33. [二叉树:构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
-34. [二叉树:搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
+8. [二叉树:101.对称二叉树](./problems/0101.对称二叉树.md)
+9. [二叉树:104.二叉树的最大深度](./problems/0104.二叉树的最大深度.md)
+10. [二叉树:111.二叉树的最小深度](./problems/0111.二叉树的最小深度.md)
+11. [二叉树:222.完全二叉树的节点个数](./problems/0222.完全二叉树的节点个数.md)
+12. [二叉树:110.平衡二叉树](./problems/0110.平衡二叉树.md)
+13. [二叉树:257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
+14. [本周总结!(二叉树)](./problems/周总结/20201003二叉树周末总结.md)
+16. [二叉树:404.左叶子之和](./problems/0404.左叶子之和.md)
+17. [二叉树:513.找树左下角的值](./problems/0513.找树左下角的值.md)
+18. [二叉树:112.路径总和](./problems/0112.路径总和.md)
+19. [二叉树:106.构造二叉树](./problems/0106.从中序与后序遍历序列构造二叉树.md)
+20. [二叉树:654.最大二叉树](./problems/0654.最大二叉树.md)
+21. [本周小结!(二叉树)](./problems/周总结/20201010二叉树周末总结.md)
+22. [二叉树:617.合并两个二叉树](./problems/0617.合并二叉树.md)
+23. [二叉树:700.二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
+24. [二叉树:98.验证二叉搜索树](./problems/0098.验证二叉搜索树.md)
+25. [二叉树:530.搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
+26. [二叉树:501.二叉搜索树中的众数](./problems/0501.二叉搜索树中的众数.md)
+27. [二叉树:236.公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
+28. [本周小结!(二叉树)](./problems/周总结/20201017二叉树周末总结.md)
+29. [二叉树:235.搜索树的最近公共祖先](./problems/0235.二叉搜索树的最近公共祖先.md)
+30. [二叉树:701.搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
+31. [二叉树:450.搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
+32. [二叉树:669.修剪二叉搜索树](./problems/0669.修剪二叉搜索树.md)
+33. [二叉树:108.将有序数组转换为二叉搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
+34. [二叉树:538.把二叉搜索树转换为累加树](./problems/0538.把二叉搜索树转换为累加树.md)
35. [二叉树:总结篇!(需要掌握的二叉树技能都在这里了)](./problems/二叉树总结篇.md)
-
+
## 回溯算法
题目分类大纲如下:
-
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
-2. [二叉树:一入递归深似海,从此offer是路人](./problems/二叉树的递归遍历.md)
-3. [二叉树:听说递归能做的,栈也能做!](./problems/二叉树的迭代遍历.md)
-4. [二叉树:前中后序迭代方式的写法就不能统一一下么?](./problems/二叉树的统一迭代法.md)
-5. [二叉树:层序遍历登场!](./problems/0102.二叉树的层序遍历.md)
-6. [二叉树:你真的会翻转二叉树么?](./problems/0226.翻转二叉树.md)
+2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
+3. [二叉树:二叉树的迭代遍历](./problems/二叉树的迭代遍历.md)
+4. [二叉树:二叉树的统一迭代法](./problems/二叉树的统一迭代法.md)
+5. [二叉树:二叉树的层序遍历](./problems/0102.二叉树的层序遍历.md)
+6. [二叉树:226.翻转二叉树](./problems/0226.翻转二叉树.md)
7. [本周小结!(二叉树)](./problems/周总结/20200927二叉树周末总结.md)
-8. [二叉树:我对称么?](./problems/0101.对称二叉树.md)
-9. [二叉树:看看这些树的最大深度](./problems/0104.二叉树的最大深度.md)
-10. [二叉树:看看这些树的最小深度](./problems/0111.二叉树的最小深度.md)
-11. [二叉树:我有多少个节点?](./problems/0222.完全二叉树的节点个数.md)
-12. [二叉树:我平衡么?](./problems/0110.平衡二叉树.md)
-13. [二叉树:找我的所有路径?](./problems/0257.二叉树的所有路径.md)
-14. [本周总结!二叉树系列二](./problems/周总结/20201003二叉树周末总结.md)
-15. [二叉树:以为使用了递归,其实还隐藏着回溯](./problems/二叉树中递归带着回溯.md)
-16. [二叉树:做了这么多题目了,我的左叶子之和是多少?](./problems/0404.左叶子之和.md)
-17. [二叉树:我的左下角的值是多少?](./problems/0513.找树左下角的值.md)
-18. [二叉树:路径总和](./problems/0112.路径总和.md)
-19. [二叉树:构造二叉树登场!](./problems/0106.从中序与后序遍历序列构造二叉树.md)
-20. [二叉树:构造一棵最大的二叉树](./problems/0654.最大二叉树.md)
-21. [本周小结!(二叉树系列三)](./problems/周总结/20201010二叉树周末总结.md)
-22. [二叉树:合并两个二叉树](./problems/0617.合并二叉树.md)
-23. [二叉树:二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
-24. [二叉树:我是不是一棵二叉搜索树](./problems/0098.验证二叉搜索树.md)
-25. [二叉树:搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
-26. [二叉树:我的众数是多少?](./problems/0501.二叉搜索树中的众数.md)
-27. [二叉树:公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
-28. [本周小结!(二叉树系列四)](./problems/周总结/20201017二叉树周末总结.md)
-29. [二叉树:搜索树的公共祖先问题](./problems/0235.二叉搜索树的最近公共祖先.md)
-30. [二叉树:搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
-31. [二叉树:搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
-32. [二叉树:修剪一棵搜索树](./problems/0669.修剪二叉搜索树.md)
-33. [二叉树:构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
-34. [二叉树:搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
+8. [二叉树:101.对称二叉树](./problems/0101.对称二叉树.md)
+9. [二叉树:104.二叉树的最大深度](./problems/0104.二叉树的最大深度.md)
+10. [二叉树:111.二叉树的最小深度](./problems/0111.二叉树的最小深度.md)
+11. [二叉树:222.完全二叉树的节点个数](./problems/0222.完全二叉树的节点个数.md)
+12. [二叉树:110.平衡二叉树](./problems/0110.平衡二叉树.md)
+13. [二叉树:257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
+14. [本周总结!(二叉树)](./problems/周总结/20201003二叉树周末总结.md)
+16. [二叉树:404.左叶子之和](./problems/0404.左叶子之和.md)
+17. [二叉树:513.找树左下角的值](./problems/0513.找树左下角的值.md)
+18. [二叉树:112.路径总和](./problems/0112.路径总和.md)
+19. [二叉树:106.构造二叉树](./problems/0106.从中序与后序遍历序列构造二叉树.md)
+20. [二叉树:654.最大二叉树](./problems/0654.最大二叉树.md)
+21. [本周小结!(二叉树)](./problems/周总结/20201010二叉树周末总结.md)
+22. [二叉树:617.合并两个二叉树](./problems/0617.合并二叉树.md)
+23. [二叉树:700.二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
+24. [二叉树:98.验证二叉搜索树](./problems/0098.验证二叉搜索树.md)
+25. [二叉树:530.搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
+26. [二叉树:501.二叉搜索树中的众数](./problems/0501.二叉搜索树中的众数.md)
+27. [二叉树:236.公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
+28. [本周小结!(二叉树)](./problems/周总结/20201017二叉树周末总结.md)
+29. [二叉树:235.搜索树的最近公共祖先](./problems/0235.二叉搜索树的最近公共祖先.md)
+30. [二叉树:701.搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
+31. [二叉树:450.搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
+32. [二叉树:669.修剪二叉搜索树](./problems/0669.修剪二叉搜索树.md)
+33. [二叉树:108.将有序数组转换为二叉搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
+34. [二叉树:538.把二叉搜索树转换为累加树](./problems/0538.把二叉搜索树转换为累加树.md)
35. [二叉树:总结篇!(需要掌握的二叉树技能都在这里了)](./problems/二叉树总结篇.md)
-
+
## 回溯算法
题目分类大纲如下:
- +
+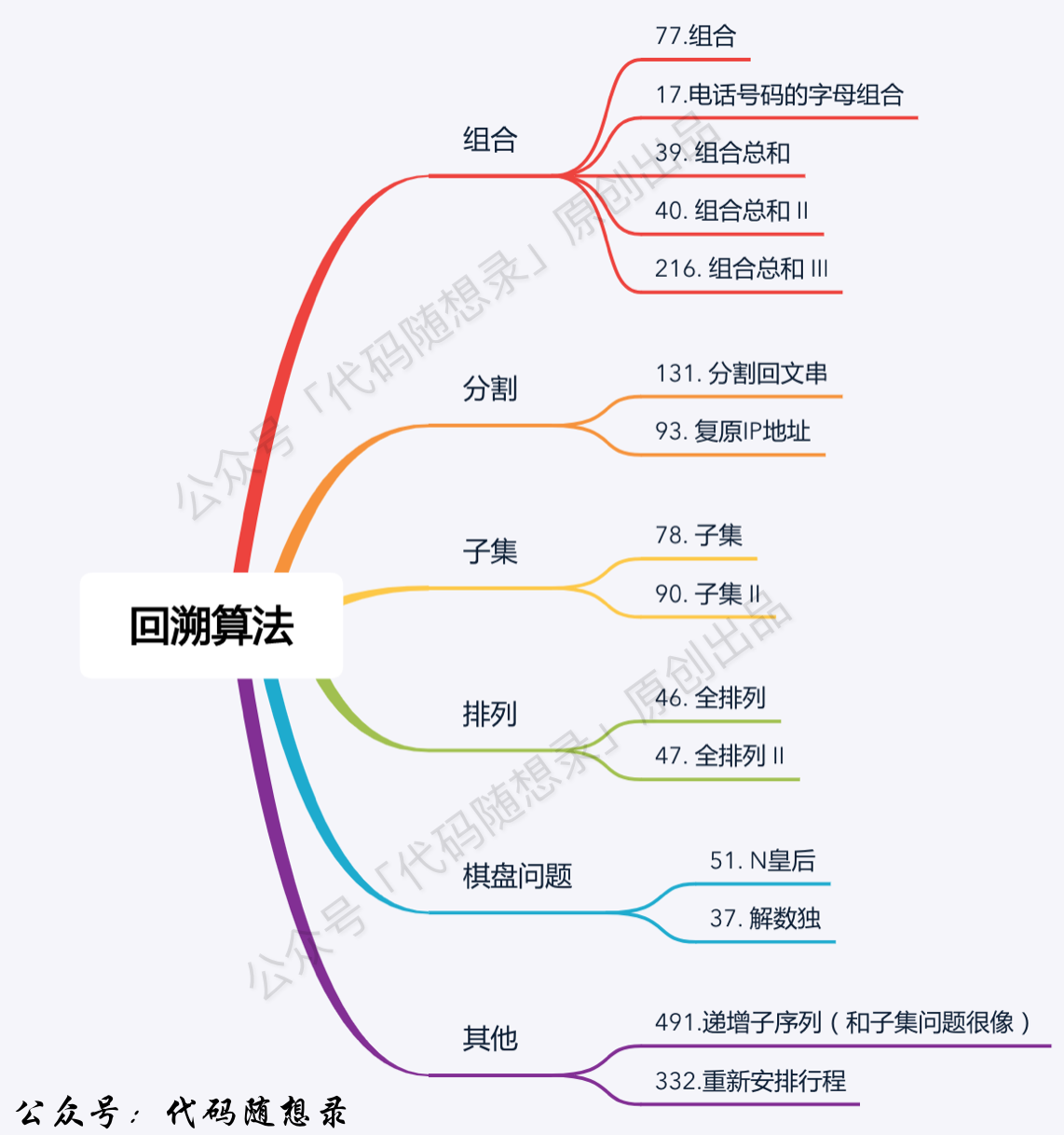 1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
-2. [回溯算法:组合问题](./problems/0077.组合.md)
-3. [回溯算法:组合问题再剪剪枝](./problems/0077.组合优化.md)
-4. [回溯算法:求组合总和!](./problems/0216.组合总和III.md)
-5. [回溯算法:电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+2. [回溯算法:77.组合](./problems/0077.组合.md)
+3. [回溯算法:77.组合优化](./problems/0077.组合优化.md)
+4. [回溯算法:216.组合总和III](./problems/0216.组合总和III.md)
+5. [回溯算法:17.电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
6. [本周小结!(回溯算法系列一)](./problems/周总结/20201030回溯周末总结.md)
-7. [回溯算法:求组合总和(二)](./problems/0039.组合总和.md)
-8. [回溯算法:求组合总和(三)](./problems/0040.组合总和II.md)
-9. [回溯算法:分割回文串](./problems/0131.分割回文串.md)
-10. [回溯算法:复原IP地址](./problems/0093.复原IP地址.md)
-11. [回溯算法:求子集问题!](./problems/0078.子集.md)
+7. [回溯算法:39.组合总和](./problems/0039.组合总和.md)
+8. [回溯算法:40.组合总和II](./problems/0040.组合总和II.md)
+9. [回溯算法:131.分割回文串](./problems/0131.分割回文串.md)
+10. [回溯算法:93.复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法:78.子集](./problems/0078.子集.md)
12. [本周小结!(回溯算法系列二)](./problems/周总结/20201107回溯周末总结.md)
-13. [回溯算法:求子集问题(二)](./problems/0090.子集II.md)
-14. [回溯算法:递增子序列](./problems/0491.递增子序列.md)
-15. [回溯算法:排列问题!](./problems/0046.全排列.md)
-16. [回溯算法:排列问题(二)](./problems/0047.全排列II.md)
+13. [回溯算法:90.子集II](./problems/0090.子集II.md)
+14. [回溯算法:491.递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法:46.全排列](./problems/0046.全排列.md)
+16. [回溯算法:47.全排列II](./problems/0047.全排列II.md)
17. [本周小结!(回溯算法系列三)](./problems/周总结/20201112回溯周末总结.md)
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
-19. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
-20. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
-21. [回溯算法:解数独](./problems/0037.解数独.md)
-22. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
+19. [回溯算法:332.重新安排行程](./problems/0332.重新安排行程.md)
+20. [回溯算法:51.N皇后](./problems/0051.N皇后.md)
+21. [回溯算法:37.解数独](./problems/0037.解数独.md)
+22. [回溯算法总结篇](./problems/回溯总结.md)
## 贪心算法
题目分类大纲如下:
-
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
-2. [回溯算法:组合问题](./problems/0077.组合.md)
-3. [回溯算法:组合问题再剪剪枝](./problems/0077.组合优化.md)
-4. [回溯算法:求组合总和!](./problems/0216.组合总和III.md)
-5. [回溯算法:电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+2. [回溯算法:77.组合](./problems/0077.组合.md)
+3. [回溯算法:77.组合优化](./problems/0077.组合优化.md)
+4. [回溯算法:216.组合总和III](./problems/0216.组合总和III.md)
+5. [回溯算法:17.电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
6. [本周小结!(回溯算法系列一)](./problems/周总结/20201030回溯周末总结.md)
-7. [回溯算法:求组合总和(二)](./problems/0039.组合总和.md)
-8. [回溯算法:求组合总和(三)](./problems/0040.组合总和II.md)
-9. [回溯算法:分割回文串](./problems/0131.分割回文串.md)
-10. [回溯算法:复原IP地址](./problems/0093.复原IP地址.md)
-11. [回溯算法:求子集问题!](./problems/0078.子集.md)
+7. [回溯算法:39.组合总和](./problems/0039.组合总和.md)
+8. [回溯算法:40.组合总和II](./problems/0040.组合总和II.md)
+9. [回溯算法:131.分割回文串](./problems/0131.分割回文串.md)
+10. [回溯算法:93.复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法:78.子集](./problems/0078.子集.md)
12. [本周小结!(回溯算法系列二)](./problems/周总结/20201107回溯周末总结.md)
-13. [回溯算法:求子集问题(二)](./problems/0090.子集II.md)
-14. [回溯算法:递增子序列](./problems/0491.递增子序列.md)
-15. [回溯算法:排列问题!](./problems/0046.全排列.md)
-16. [回溯算法:排列问题(二)](./problems/0047.全排列II.md)
+13. [回溯算法:90.子集II](./problems/0090.子集II.md)
+14. [回溯算法:491.递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法:46.全排列](./problems/0046.全排列.md)
+16. [回溯算法:47.全排列II](./problems/0047.全排列II.md)
17. [本周小结!(回溯算法系列三)](./problems/周总结/20201112回溯周末总结.md)
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
-19. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
-20. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
-21. [回溯算法:解数独](./problems/0037.解数独.md)
-22. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
+19. [回溯算法:332.重新安排行程](./problems/0332.重新安排行程.md)
+20. [回溯算法:51.N皇后](./problems/0051.N皇后.md)
+21. [回溯算法:37.解数独](./problems/0037.解数独.md)
+22. [回溯算法总结篇](./problems/回溯总结.md)
## 贪心算法
题目分类大纲如下:
-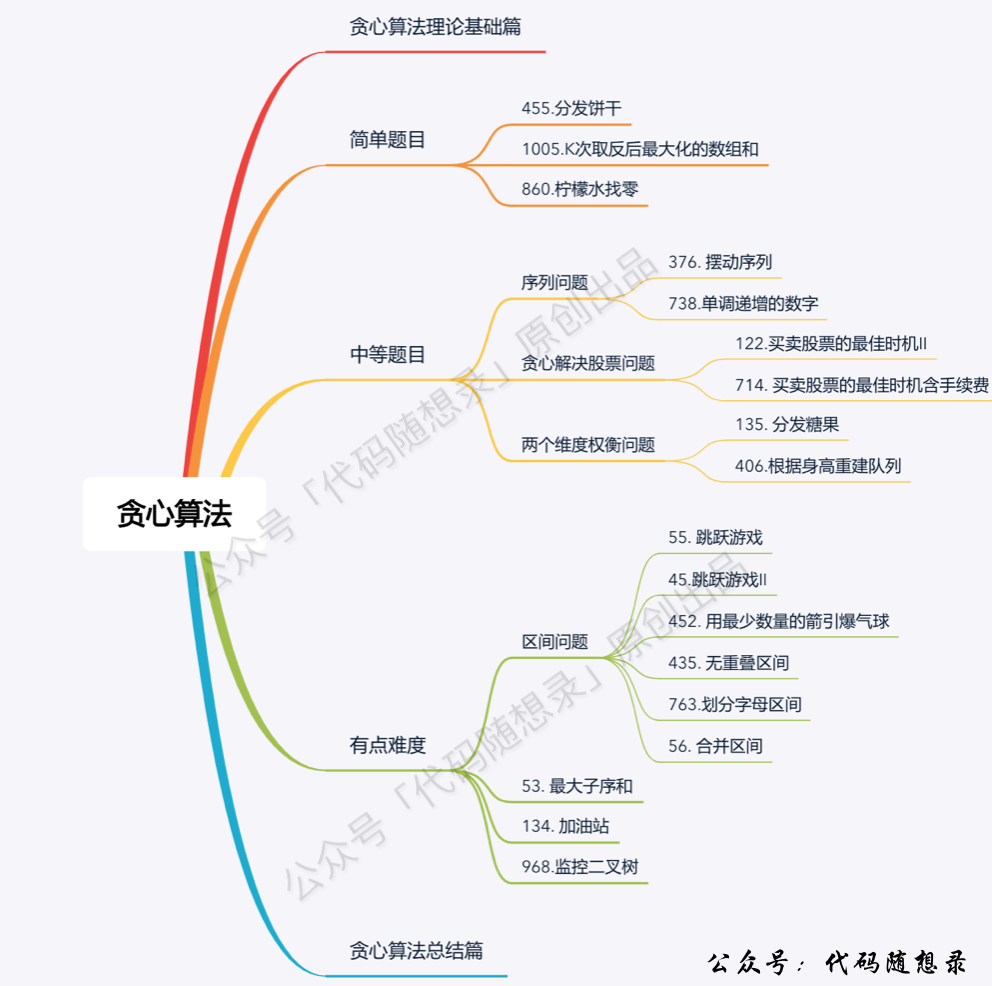 +
+ 1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
-2. [贪心算法:分发饼干](./problems/0455.分发饼干.md)
-3. [贪心算法:摆动序列](./problems/0376.摆动序列.md)
-4. [贪心算法:最大子序和](./problems/0053.最大子序和.md)
+2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
+3. [贪心算法:376.摆动序列](./problems/0376.摆动序列.md)
+4. [贪心算法:53.最大子序和](./problems/0053.最大子序和.md)
5. [本周小结!(贪心算法系列一)](./problems/周总结/20201126贪心周末总结.md)
-6. [贪心算法:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
-7. [贪心算法:跳跃游戏](./problems/0055.跳跃游戏.md)
-8. [贪心算法:跳跃游戏II](./problems/0045.跳跃游戏II.md)
-9. [贪心算法:K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
+6. [贪心算法:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
+7. [贪心算法:55.跳跃游戏](./problems/0055.跳跃游戏.md)
+8. [贪心算法:45.跳跃游戏II](./problems/0045.跳跃游戏II.md)
+9. [贪心算法:1005.K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
10. [本周小结!(贪心算法系列二)](./problems/周总结/20201203贪心周末总结.md)
-11. [贪心算法:加油站](./problems/0134.加油站.md)
-12. [贪心算法:分发糖果](./problems/0135.分发糖果.md)
-13. [贪心算法:柠檬水找零](./problems/0860.柠檬水找零.md)
-14. [贪心算法:根据身高重建队列](./problems/0406.根据身高重建队列.md)
+11. [贪心算法:134.加油站](./problems/0134.加油站.md)
+12. [贪心算法:135.分发糖果](./problems/0135.分发糖果.md)
+13. [贪心算法:860.柠檬水找零](./problems/0860.柠檬水找零.md)
+14. [贪心算法:406.根据身高重建队列](./problems/0406.根据身高重建队列.md)
15. [本周小结!(贪心算法系列三)](./problems/周总结/20201217贪心周末总结.md)
-16. [贪心算法:根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
-17. [贪心算法:用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
-18. [贪心算法:无重叠区间](./problems/0435.无重叠区间.md)
-19. [贪心算法:划分字母区间](./problems/0763.划分字母区间.md)
-20. [贪心算法:合并区间](./problems/0056.合并区间.md)
+16. [贪心算法:406.根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
+17. [贪心算法:452.用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
+18. [贪心算法:435.无重叠区间](./problems/0435.无重叠区间.md)
+19. [贪心算法:763.划分字母区间](./problems/0763.划分字母区间.md)
+20. [贪心算法:56.合并区间](./problems/0056.合并区间.md)
21. [本周小结!(贪心算法系列四)](./problems/周总结/20201224贪心周末总结.md)
-22. [贪心算法:单调递增的数字](./problems/0738.单调递增的数字.md)
-23. [贪心算法:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
-24. [贪心算法:我要监控二叉树!](./problems/0968.监控二叉树.md)
-25. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
+22. [贪心算法:738.单调递增的数字](./problems/0738.单调递增的数字.md)
+23. [贪心算法:968.监控二叉树](./problems/0968.监控二叉树.md)
+24. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
## 动态规划
动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
-
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
-2. [贪心算法:分发饼干](./problems/0455.分发饼干.md)
-3. [贪心算法:摆动序列](./problems/0376.摆动序列.md)
-4. [贪心算法:最大子序和](./problems/0053.最大子序和.md)
+2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
+3. [贪心算法:376.摆动序列](./problems/0376.摆动序列.md)
+4. [贪心算法:53.最大子序和](./problems/0053.最大子序和.md)
5. [本周小结!(贪心算法系列一)](./problems/周总结/20201126贪心周末总结.md)
-6. [贪心算法:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
-7. [贪心算法:跳跃游戏](./problems/0055.跳跃游戏.md)
-8. [贪心算法:跳跃游戏II](./problems/0045.跳跃游戏II.md)
-9. [贪心算法:K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
+6. [贪心算法:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
+7. [贪心算法:55.跳跃游戏](./problems/0055.跳跃游戏.md)
+8. [贪心算法:45.跳跃游戏II](./problems/0045.跳跃游戏II.md)
+9. [贪心算法:1005.K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
10. [本周小结!(贪心算法系列二)](./problems/周总结/20201203贪心周末总结.md)
-11. [贪心算法:加油站](./problems/0134.加油站.md)
-12. [贪心算法:分发糖果](./problems/0135.分发糖果.md)
-13. [贪心算法:柠檬水找零](./problems/0860.柠檬水找零.md)
-14. [贪心算法:根据身高重建队列](./problems/0406.根据身高重建队列.md)
+11. [贪心算法:134.加油站](./problems/0134.加油站.md)
+12. [贪心算法:135.分发糖果](./problems/0135.分发糖果.md)
+13. [贪心算法:860.柠檬水找零](./problems/0860.柠檬水找零.md)
+14. [贪心算法:406.根据身高重建队列](./problems/0406.根据身高重建队列.md)
15. [本周小结!(贪心算法系列三)](./problems/周总结/20201217贪心周末总结.md)
-16. [贪心算法:根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
-17. [贪心算法:用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
-18. [贪心算法:无重叠区间](./problems/0435.无重叠区间.md)
-19. [贪心算法:划分字母区间](./problems/0763.划分字母区间.md)
-20. [贪心算法:合并区间](./problems/0056.合并区间.md)
+16. [贪心算法:406.根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
+17. [贪心算法:452.用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
+18. [贪心算法:435.无重叠区间](./problems/0435.无重叠区间.md)
+19. [贪心算法:763.划分字母区间](./problems/0763.划分字母区间.md)
+20. [贪心算法:56.合并区间](./problems/0056.合并区间.md)
21. [本周小结!(贪心算法系列四)](./problems/周总结/20201224贪心周末总结.md)
-22. [贪心算法:单调递增的数字](./problems/0738.单调递增的数字.md)
-23. [贪心算法:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
-24. [贪心算法:我要监控二叉树!](./problems/0968.监控二叉树.md)
-25. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
+22. [贪心算法:738.单调递增的数字](./problems/0738.单调递增的数字.md)
+23. [贪心算法:968.监控二叉树](./problems/0968.监控二叉树.md)
+24. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
## 动态规划
动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
- +
+ 1. [关于动态规划,你该了解这些!](./problems/动态规划理论基础.md)
-2. [动态规划:斐波那契数](./problems/0509.斐波那契数.md)
-3. [动态规划:爬楼梯](./problems/0070.爬楼梯.md)
-4. [动态规划:使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+2. [动态规划:509.斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划:70.爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划:746.使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
5. [本周小结!(动态规划系列一)](./problems/周总结/20210107动规周末总结.md)
-6. [动态规划:不同路径](./problems/0062.不同路径.md)
-7. [动态规划:不同路径还不够,要有障碍!](./problems/0063.不同路径II.md)
-8. [动态规划:整数拆分,你要怎么拆?](./problems/0343.整数拆分.md)
-9. [动态规划:不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+6. [动态规划:62.不同路径](./problems/0062.不同路径.md)
+7. [动态规划:63.不同路径II](./problems/0063.不同路径II.md)
+8. [动态规划:343.整数拆分](./problems/0343.整数拆分.md)
+9. [动态规划:96.不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
10. [本周小结!(动态规划系列二)](./problems/周总结/20210114动规周末总结.md)
背包问题系列:
-
1. [关于动态规划,你该了解这些!](./problems/动态规划理论基础.md)
-2. [动态规划:斐波那契数](./problems/0509.斐波那契数.md)
-3. [动态规划:爬楼梯](./problems/0070.爬楼梯.md)
-4. [动态规划:使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+2. [动态规划:509.斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划:70.爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划:746.使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
5. [本周小结!(动态规划系列一)](./problems/周总结/20210107动规周末总结.md)
-6. [动态规划:不同路径](./problems/0062.不同路径.md)
-7. [动态规划:不同路径还不够,要有障碍!](./problems/0063.不同路径II.md)
-8. [动态规划:整数拆分,你要怎么拆?](./problems/0343.整数拆分.md)
-9. [动态规划:不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+6. [动态规划:62.不同路径](./problems/0062.不同路径.md)
+7. [动态规划:63.不同路径II](./problems/0063.不同路径II.md)
+8. [动态规划:343.整数拆分](./problems/0343.整数拆分.md)
+9. [动态规划:96.不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
10. [本周小结!(动态规划系列二)](./problems/周总结/20210114动规周末总结.md)
背包问题系列:
- +
+ -11. [动态规划:关于01背包问题,你该了解这些!](./problems/背包理论基础01背包-1.md)
-12. [动态规划:关于01背包问题,你该了解这些!(滚动数组)](./problems/背包理论基础01背包-2.md)
-13. [动态规划:分割等和子集可以用01背包!](./problems/0416.分割等和子集.md)
-14. [动态规划:最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+11. [动态规划:01背包理论基础(二维dp数组)](./problems/背包理论基础01背包-1.md)
+12. [动态规划:01背包理论基础(一维dp数组)](./problems/背包理论基础01背包-2.md)
+13. [动态规划:416.分割等和子集](./problems/0416.分割等和子集.md)
+14. [动态规划:1049.最后一块石头的重量II](./problems/1049.最后一块石头的重量II.md)
15. [本周小结!(动态规划系列三)](./problems/周总结/20210121动规周末总结.md)
-16. [动态规划:目标和!](./problems/0494.目标和.md)
-17. [动态规划:一和零!](./problems/0474.一和零.md)
-18. [动态规划:关于完全背包,你该了解这些!](./problems/背包问题理论基础完全背包.md)
-19. [动态规划:给你一些零钱,你要怎么凑?](./problems/0518.零钱兑换II.md)
-20. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
-21. [动态规划:Carl称它为排列总和!](./problems/0377.组合总和Ⅳ.md)
-22. [动态规划:以前我没得选,现在我选择再爬一次!](./problems/0070.爬楼梯完全背包版本.md)
-23. [动态规划: 给我个机会,我再兑换一次零钱](./problems/0322.零钱兑换.md)
-24. [动态规划:一样的套路,再求一次完全平方数](./problems/0279.完全平方数.md)
-25. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
-26. [动态规划:单词拆分](./problems/0139.单词拆分.md)
-27. [动态规划:关于多重背包,你该了解这些!](./problems/背包问题理论基础多重背包.md)
-28. [听说背包问题很难? 这篇总结篇来拯救你了](./problems/背包总结篇.md)
+16. [动态规划:494.目标和](./problems/0494.目标和.md)
+17. [动态规划:474.一和零](./problems/0474.一和零.md)
+18. [动态规划:完全背包理论基础(二维dp数组)](./problems/背包问题理论基础完全背包.md)
+19. [动态规划:完全背包理论基础(一维dp数组)](./problems/背包问题完全背包一维.md)
+20. [动态规划:518.零钱兑换II](./problems/0518.零钱兑换II.md)
+21. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
+22. [动态规划:377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md)
+23. [动态规划:70.爬楼梯(完全背包版本)](./problems/0070.爬楼梯完全背包版本.md)
+24. [动态规划:322.零钱兑换](./problems/0322.零钱兑换.md)
+25. [动态规划:279.完全平方数](./problems/0279.完全平方数.md)
+26. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
+27. [动态规划:139.单词拆分](./problems/0139.单词拆分.md)
+28. [动态规划:多重背包理论基础](./problems/背包问题理论基础多重背包.md)
+29. [背包问题总结篇](./problems/背包总结篇.md)
打家劫舍系列:
-29. [动态规划:开始打家劫舍!](./problems/0198.打家劫舍.md)
-30. [动态规划:继续打家劫舍!](./problems/0213.打家劫舍II.md)
-31. [动态规划:还要打家劫舍!](./problems/0337.打家劫舍III.md)
+29. [动态规划:198.打家劫舍](./problems/0198.打家劫舍.md)
+30. [动态规划:213.打家劫舍II](./problems/0213.打家劫舍II.md)
+31. [动态规划:337.打家劫舍III](./problems/0337.打家劫舍III.md)
股票系列:
-
-11. [动态规划:关于01背包问题,你该了解这些!](./problems/背包理论基础01背包-1.md)
-12. [动态规划:关于01背包问题,你该了解这些!(滚动数组)](./problems/背包理论基础01背包-2.md)
-13. [动态规划:分割等和子集可以用01背包!](./problems/0416.分割等和子集.md)
-14. [动态规划:最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+11. [动态规划:01背包理论基础(二维dp数组)](./problems/背包理论基础01背包-1.md)
+12. [动态规划:01背包理论基础(一维dp数组)](./problems/背包理论基础01背包-2.md)
+13. [动态规划:416.分割等和子集](./problems/0416.分割等和子集.md)
+14. [动态规划:1049.最后一块石头的重量II](./problems/1049.最后一块石头的重量II.md)
15. [本周小结!(动态规划系列三)](./problems/周总结/20210121动规周末总结.md)
-16. [动态规划:目标和!](./problems/0494.目标和.md)
-17. [动态规划:一和零!](./problems/0474.一和零.md)
-18. [动态规划:关于完全背包,你该了解这些!](./problems/背包问题理论基础完全背包.md)
-19. [动态规划:给你一些零钱,你要怎么凑?](./problems/0518.零钱兑换II.md)
-20. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
-21. [动态规划:Carl称它为排列总和!](./problems/0377.组合总和Ⅳ.md)
-22. [动态规划:以前我没得选,现在我选择再爬一次!](./problems/0070.爬楼梯完全背包版本.md)
-23. [动态规划: 给我个机会,我再兑换一次零钱](./problems/0322.零钱兑换.md)
-24. [动态规划:一样的套路,再求一次完全平方数](./problems/0279.完全平方数.md)
-25. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
-26. [动态规划:单词拆分](./problems/0139.单词拆分.md)
-27. [动态规划:关于多重背包,你该了解这些!](./problems/背包问题理论基础多重背包.md)
-28. [听说背包问题很难? 这篇总结篇来拯救你了](./problems/背包总结篇.md)
+16. [动态规划:494.目标和](./problems/0494.目标和.md)
+17. [动态规划:474.一和零](./problems/0474.一和零.md)
+18. [动态规划:完全背包理论基础(二维dp数组)](./problems/背包问题理论基础完全背包.md)
+19. [动态规划:完全背包理论基础(一维dp数组)](./problems/背包问题完全背包一维.md)
+20. [动态规划:518.零钱兑换II](./problems/0518.零钱兑换II.md)
+21. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
+22. [动态规划:377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md)
+23. [动态规划:70.爬楼梯(完全背包版本)](./problems/0070.爬楼梯完全背包版本.md)
+24. [动态规划:322.零钱兑换](./problems/0322.零钱兑换.md)
+25. [动态规划:279.完全平方数](./problems/0279.完全平方数.md)
+26. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
+27. [动态规划:139.单词拆分](./problems/0139.单词拆分.md)
+28. [动态规划:多重背包理论基础](./problems/背包问题理论基础多重背包.md)
+29. [背包问题总结篇](./problems/背包总结篇.md)
打家劫舍系列:
-29. [动态规划:开始打家劫舍!](./problems/0198.打家劫舍.md)
-30. [动态规划:继续打家劫舍!](./problems/0213.打家劫舍II.md)
-31. [动态规划:还要打家劫舍!](./problems/0337.打家劫舍III.md)
+29. [动态规划:198.打家劫舍](./problems/0198.打家劫舍.md)
+30. [动态规划:213.打家劫舍II](./problems/0213.打家劫舍II.md)
+31. [动态规划:337.打家劫舍III](./problems/0337.打家劫舍III.md)
股票系列:
- +
+ -32. [动态规划:买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
-33. [动态规划:本周我们都讲了这些(系列六)](./problems/周总结/20210225动规周末总结.md)
-34. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
-35. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
-36. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
-37. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
-38. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
-39. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
+32. [动态规划:121.买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划:本周小结(系列六)](./problems/周总结/20210225动规周末总结.md)
+34. [动态规划:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
+35. [动态规划:123.买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+36. [动态规划:188.买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+37. [动态规划:309.最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+38. [动态规划:本周小结(系列七)](./problems/周总结/20210304动规周末总结.md)
+39. [动态规划:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
40. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列:
-
-32. [动态规划:买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
-33. [动态规划:本周我们都讲了这些(系列六)](./problems/周总结/20210225动规周末总结.md)
-34. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
-35. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
-36. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
-37. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
-38. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
-39. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
+32. [动态规划:121.买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划:本周小结(系列六)](./problems/周总结/20210225动规周末总结.md)
+34. [动态规划:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
+35. [动态规划:123.买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+36. [动态规划:188.买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+37. [动态规划:309.最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+38. [动态规划:本周小结(系列七)](./problems/周总结/20210304动规周末总结.md)
+39. [动态规划:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
40. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列:
- -
-
-41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
-45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
-46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
-47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
-48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
-49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-52. [动态规划:回文子串](./problems/0647.回文子串.md)
-53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+
-
-
-41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
-45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
-46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
-47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
-48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
-49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-52. [动态规划:回文子串](./problems/0647.回文子串.md)
-53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+ +
+
+41. [动态规划:300.最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:674.最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:718.最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:1143.最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划:1035.不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划:53.最大子序和](./problems/0053.最大子序和(动态规划).md)
+47. [动态规划:392.判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划:115.不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划:583.两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+50. [动态规划:72.编辑距离](./problems/0072.编辑距离.md)
+51. [编辑距离总结篇](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:647.回文子串](./problems/0647.回文子串.md)
+53. [动态规划:516.最长回文子序列](./problems/0516.最长回文子序列.md)
54. [动态规划总结篇](./problems/动态规划总结篇.md)
## 单调栈
-1. [单调栈:每日温度](./problems/0739.每日温度.md)
-2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
-3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
-4. [单调栈:接雨水](./problems/0042.接雨水.md)
-5. [单调栈:柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
+1. [单调栈:739.每日温度](./problems/0739.每日温度.md)
+2. [单调栈:496.下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:503.下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:42.接雨水](./problems/0042.接雨水.md)
+5. [单调栈:84.柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
-(持续更新中....)
## 图论
-## 十大排序
+**[图论正式发布](./problems/qita/tulunfabu.md)**
+
+1. [图论:理论基础](./problems/kamacoder/图论理论基础.md)
+2. [图论:深度优先搜索理论基础](./problems/kamacoder/图论深搜理论基础.md)
+3. [图论:所有可达路径](./problems/kamacoder/0098.所有可达路径.md)
+4. [图论:广度优先搜索理论基础](./problems/kamacoder/图论广搜理论基础.md)
+5. [图论:岛屿数量.深搜版](./problems/kamacoder/0099.岛屿的数量深搜.md)
+6. [图论:岛屿数量.广搜版](./problems/kamacoder/0099.岛屿的数量广搜.md)
+7. [图论:岛屿的最大面积](./problems/kamacoder/0100.岛屿的最大面积.md)
+8. [图论:孤岛的总面积](./problems/kamacoder/0101.孤岛的总面积.md)
+9. [图论:沉没孤岛](./problems/kamacoder/0102.沉没孤岛.md)
+10. [图论:水流问题](./problems/kamacoder/0103.水流问题.md)
+11. [图论:建造最大岛屿](./problems/kamacoder/0104.建造最大岛屿.md)
+12. [图论:岛屿的周长](./problems/kamacoder/0106.岛屿的周长.md)
+13. [图论:字符串接龙](./problems/kamacoder/0110.字符串接龙.md)
+14. [图论:有向图的完全可达性](./problems/kamacoder/0105.有向图的完全可达性.md)
+15. [图论:并查集理论基础](./problems/kamacoder/图论并查集理论基础.md)
+16. [图论:寻找存在的路径](./problems/kamacoder/0107.寻找存在的路径.md)
+17. [图论:冗余连接](./problems/kamacoder/0108.冗余连接.md)
+18. [图论:冗余连接II](./problems/kamacoder/0109.冗余连接II.md)
+19. [图论:最小生成树之prim](./problems/kamacoder/0053.寻宝-prim.md)
+20. [图论:最小生成树之kruskal](./problems/kamacoder/0053.寻宝-Kruskal.md)
+21. [图论:拓扑排序](./problems/kamacoder/0117.软件构建.md)
+22. [图论:dijkstra(朴素版)](./problems/kamacoder/0047.参会dijkstra朴素.md)
+23. [图论:dijkstra(堆优化版)](./problems/kamacoder/0047.参会dijkstra堆.md)
+24. [图论:Bellman_ford 算法](./problems/kamacoder/0094.城市间货物运输I.md)
+25. [图论:Bellman_ford 队列优化算法(又名SPFA)](./problems/kamacoder/0094.城市间货物运输I-SPFA.md)
+26. [图论:Bellman_ford之判断负权回路](./problems/kamacoder/0095.城市间货物运输II.md)
+27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0096.城市间货物运输III.md)
+28. [图论:Floyd 算法](./problems/kamacoder/0097.小明逛公园.md)
+29. [图论:A * 算法](./problems/kamacoder/0126.骑士的攻击astar.md)
+30. [图论:最短路算法总结篇](./problems/kamacoder/最短路问题总结篇.md)
+31. [图论:图论总结篇](./problems/kamacoder/图论总结篇.md)
-## 数论
-## 高级数据结构经典题目
-
-* 并查集
-* 最小生成树
-* 线段树
-* 树状数组
-* 字典树
-
-## 海量数据处理
+(持续更新中....)
# 补充题目
@@ -538,49 +485,23 @@
[各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
-
-
-# B站算法视频讲解
-
-以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频:
-
-* [KMP算法(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd)
-* [KMP算法(代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
-* [回溯算法理论基础](https://www.bilibili.com/video/BV1cy4y167mM)
-* [回溯算法之组合问题(力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv)
-* [组合问题的剪枝操作(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1wi4y157er)
-* [组合总和(对应力扣题目:39.组合总和)](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-* [分割回文串(对应力扣题目:131.分割回文串)](https://www.bilibili.com/video/BV1c54y1e7k6)
-* [二叉树理论基础](https://www.bilibili.com/video/BV1Hy4y1t7ij)
-* [二叉树的递归遍历](https://www.bilibili.com/video/BV1Wh411S7xt)
-* [二叉树的非递归遍历(一)](https://www.bilibili.com/video/BV15f4y1W7i2)
-
-(持续更新中....)
-
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
-
-# 关于作者
-
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发,CSDN博客专家。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
-
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码加我微信。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
-
-
+# Star 趋势
+[](https://star-history.com/#youngyangyang04/leetcode-master&Date)
+# 关于作者
-# 公众号
+大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术底层技术研发。
-更多精彩文章持续更新,微信搜索:「代码随想录」第一时间围观,关注后回复:666,可以获得我的所有算法专题原创PDF。
+# PDF下载
-**「代码随想录」每天准时为你推送一篇经典面试题目,帮你梳理算法知识体系,轻松学习算法!**,并且公众号里有大量学习资源,也有我自己的学习心得和方法总结,更有上万录友们在这里打卡学习。
+添加如下企业微信,会自动发送给大家PDF版本,顺便可以选择是否加入刷题群。
-**来看看就知道了,你会发现相见恨晚!**
+添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-
-
+
diff --git "a/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg" "b/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg"
new file mode 100644
index 0000000000..547d570418
Binary files /dev/null and "b/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg" differ
diff --git "a/pics/\350\256\255\347\273\203\350\220\245.png" "b/pics/\350\256\255\347\273\203\350\220\245.png"
new file mode 100644
index 0000000000..34433d7b37
Binary files /dev/null and "b/pics/\350\256\255\347\273\203\350\220\245.png" differ
diff --git "a/pics/\351\230\277\351\207\214\344\272\221.png" "b/pics/\351\230\277\351\207\214\344\272\221.png"
deleted file mode 100644
index 79f41d6beb..0000000000
Binary files "a/pics/\351\230\277\351\207\214\344\272\221.png" and /dev/null differ
diff --git "a/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md" "b/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
old mode 100644
new mode 100755
index 9571a7737b..a11527961d
--- "a/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
+++ "b/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
@@ -1,13 +1,11 @@
-
+
+
+41. [动态规划:300.最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:674.最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:718.最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:1143.最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划:1035.不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划:53.最大子序和](./problems/0053.最大子序和(动态规划).md)
+47. [动态规划:392.判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划:115.不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划:583.两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+50. [动态规划:72.编辑距离](./problems/0072.编辑距离.md)
+51. [编辑距离总结篇](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:647.回文子串](./problems/0647.回文子串.md)
+53. [动态规划:516.最长回文子序列](./problems/0516.最长回文子序列.md)
54. [动态规划总结篇](./problems/动态规划总结篇.md)
## 单调栈
-1. [单调栈:每日温度](./problems/0739.每日温度.md)
-2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
-3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
-4. [单调栈:接雨水](./problems/0042.接雨水.md)
-5. [单调栈:柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
+1. [单调栈:739.每日温度](./problems/0739.每日温度.md)
+2. [单调栈:496.下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:503.下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:42.接雨水](./problems/0042.接雨水.md)
+5. [单调栈:84.柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
-(持续更新中....)
## 图论
-## 十大排序
+**[图论正式发布](./problems/qita/tulunfabu.md)**
+
+1. [图论:理论基础](./problems/kamacoder/图论理论基础.md)
+2. [图论:深度优先搜索理论基础](./problems/kamacoder/图论深搜理论基础.md)
+3. [图论:所有可达路径](./problems/kamacoder/0098.所有可达路径.md)
+4. [图论:广度优先搜索理论基础](./problems/kamacoder/图论广搜理论基础.md)
+5. [图论:岛屿数量.深搜版](./problems/kamacoder/0099.岛屿的数量深搜.md)
+6. [图论:岛屿数量.广搜版](./problems/kamacoder/0099.岛屿的数量广搜.md)
+7. [图论:岛屿的最大面积](./problems/kamacoder/0100.岛屿的最大面积.md)
+8. [图论:孤岛的总面积](./problems/kamacoder/0101.孤岛的总面积.md)
+9. [图论:沉没孤岛](./problems/kamacoder/0102.沉没孤岛.md)
+10. [图论:水流问题](./problems/kamacoder/0103.水流问题.md)
+11. [图论:建造最大岛屿](./problems/kamacoder/0104.建造最大岛屿.md)
+12. [图论:岛屿的周长](./problems/kamacoder/0106.岛屿的周长.md)
+13. [图论:字符串接龙](./problems/kamacoder/0110.字符串接龙.md)
+14. [图论:有向图的完全可达性](./problems/kamacoder/0105.有向图的完全可达性.md)
+15. [图论:并查集理论基础](./problems/kamacoder/图论并查集理论基础.md)
+16. [图论:寻找存在的路径](./problems/kamacoder/0107.寻找存在的路径.md)
+17. [图论:冗余连接](./problems/kamacoder/0108.冗余连接.md)
+18. [图论:冗余连接II](./problems/kamacoder/0109.冗余连接II.md)
+19. [图论:最小生成树之prim](./problems/kamacoder/0053.寻宝-prim.md)
+20. [图论:最小生成树之kruskal](./problems/kamacoder/0053.寻宝-Kruskal.md)
+21. [图论:拓扑排序](./problems/kamacoder/0117.软件构建.md)
+22. [图论:dijkstra(朴素版)](./problems/kamacoder/0047.参会dijkstra朴素.md)
+23. [图论:dijkstra(堆优化版)](./problems/kamacoder/0047.参会dijkstra堆.md)
+24. [图论:Bellman_ford 算法](./problems/kamacoder/0094.城市间货物运输I.md)
+25. [图论:Bellman_ford 队列优化算法(又名SPFA)](./problems/kamacoder/0094.城市间货物运输I-SPFA.md)
+26. [图论:Bellman_ford之判断负权回路](./problems/kamacoder/0095.城市间货物运输II.md)
+27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0096.城市间货物运输III.md)
+28. [图论:Floyd 算法](./problems/kamacoder/0097.小明逛公园.md)
+29. [图论:A * 算法](./problems/kamacoder/0126.骑士的攻击astar.md)
+30. [图论:最短路算法总结篇](./problems/kamacoder/最短路问题总结篇.md)
+31. [图论:图论总结篇](./problems/kamacoder/图论总结篇.md)
-## 数论
-## 高级数据结构经典题目
-
-* 并查集
-* 最小生成树
-* 线段树
-* 树状数组
-* 字典树
-
-## 海量数据处理
+(持续更新中....)
# 补充题目
@@ -538,49 +485,23 @@
[各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
-
-
-# B站算法视频讲解
-
-以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频:
-
-* [KMP算法(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd)
-* [KMP算法(代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
-* [回溯算法理论基础](https://www.bilibili.com/video/BV1cy4y167mM)
-* [回溯算法之组合问题(力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv)
-* [组合问题的剪枝操作(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1wi4y157er)
-* [组合总和(对应力扣题目:39.组合总和)](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-* [分割回文串(对应力扣题目:131.分割回文串)](https://www.bilibili.com/video/BV1c54y1e7k6)
-* [二叉树理论基础](https://www.bilibili.com/video/BV1Hy4y1t7ij)
-* [二叉树的递归遍历](https://www.bilibili.com/video/BV1Wh411S7xt)
-* [二叉树的非递归遍历(一)](https://www.bilibili.com/video/BV15f4y1W7i2)
-
-(持续更新中....)
-
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
-
-# 关于作者
-
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发,CSDN博客专家。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
-
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码加我微信。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
-
-
+# Star 趋势
+[](https://star-history.com/#youngyangyang04/leetcode-master&Date)
+# 关于作者
-# 公众号
+大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术底层技术研发。
-更多精彩文章持续更新,微信搜索:「代码随想录」第一时间围观,关注后回复:666,可以获得我的所有算法专题原创PDF。
+# PDF下载
-**「代码随想录」每天准时为你推送一篇经典面试题目,帮你梳理算法知识体系,轻松学习算法!**,并且公众号里有大量学习资源,也有我自己的学习心得和方法总结,更有上万录友们在这里打卡学习。
+添加如下企业微信,会自动发送给大家PDF版本,顺便可以选择是否加入刷题群。
-**来看看就知道了,你会发现相见恨晚!**
+添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-
-
+
diff --git "a/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg" "b/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg"
new file mode 100644
index 0000000000..547d570418
Binary files /dev/null and "b/pics/\347\275\221\347\253\231\346\230\237\347\220\203\345\256\243\344\274\240\346\265\267\346\212\245.jpg" differ
diff --git "a/pics/\350\256\255\347\273\203\350\220\245.png" "b/pics/\350\256\255\347\273\203\350\220\245.png"
new file mode 100644
index 0000000000..34433d7b37
Binary files /dev/null and "b/pics/\350\256\255\347\273\203\350\220\245.png" differ
diff --git "a/pics/\351\230\277\351\207\214\344\272\221.png" "b/pics/\351\230\277\351\207\214\344\272\221.png"
deleted file mode 100644
index 79f41d6beb..0000000000
Binary files "a/pics/\351\230\277\351\207\214\344\272\221.png" and /dev/null differ
diff --git "a/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md" "b/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
old mode 100644
new mode 100755
index 9571a7737b..a11527961d
--- "a/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
+++ "b/problems/0001.\344\270\244\346\225\260\344\271\213\345\222\214.md"
@@ -1,13 +1,11 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 1. 两数之和
+# 1. 两数之和
-[力扣题目链接](https://leetcode-cn.com/problems/two-sum/)
+[力扣题目链接](https://leetcode.cn/problems/two-sum/)
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
@@ -21,10 +19,14 @@
所以返回 [0, 1]
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[梦开始的地方,Leetcode:1.两数之和](https://www.bilibili.com/video/BV1aT41177mK),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
-很明显暴力的解法是两层for循环查找,时间复杂度是$O(n^2)$。
+很明显暴力的解法是两层for循环查找,时间复杂度是O(n^2)。
建议大家做这道题目之前,先做一下这两道
* [242. 有效的字母异位词](https://www.programmercarl.com/0242.有效的字母异位词.html)
@@ -32,31 +34,59 @@
[242. 有效的字母异位词](https://www.programmercarl.com/0242.有效的字母异位词.html) 这道题目是用数组作为哈希表来解决哈希问题,[349. 两个数组的交集](https://www.programmercarl.com/0349.两个数组的交集.html)这道题目是通过set作为哈希表来解决哈希问题。
-本题呢,则要使用map,那么来看一下使用数组和set来做哈希法的局限。
+
+首先我再强调一下 **什么时候使用哈希法**,当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
+
+本题呢,我就需要一个集合来存放我们遍历过的元素,然后在遍历数组的时候去询问这个集合,某元素是否遍历过,也就是 是否出现在这个集合。
+
+那么我们就应该想到使用哈希法了。
+
+因为本题,我们不仅要知道元素有没有遍历过,还要知道这个元素对应的下标,**需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适**。
+
+再来看一下使用数组和set来做哈希法的局限。
* 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
* set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
-此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value在保存数值所在的下标。
+此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value再保存数值所在的下标。
C++中map,有三种类型:
|映射 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率|
|---|---| --- |---| --- | --- | ---|
-|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | $O(\log n)$|$O(\log n)$ |
-|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|$O(\log n)$ |$O(\log n)$ |
-|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |$O(1)$ | $O(1)$|
+|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | O(log n)|O(log n) |
+|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|O(log n) |O(log n) |
+|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |O(1) | O(1)|
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。
同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。 更多哈希表的理论知识请看[关于哈希表,你该了解这些!](https://www.programmercarl.com/哈希表理论基础.html)。
-**这道题目中并不需要key有序,选择std::unordered_map 效率更高!**
+**这道题目中并不需要key有序,选择std::unordered_map 效率更高!** 使用其他语言的录友注意了解一下自己所用语言的数据结构就行。
+
+接下来需要明确两点:
+
+* **map用来做什么**
+* **map中key和value分别表示什么**
+
+map目的用来存放我们访问过的元素,因为遍历数组的时候,需要记录我们之前遍历过哪些元素和对应的下标,这样才能找到与当前元素相匹配的(也就是相加等于target)
+
+接下来是map中key和value分别表示什么。
-解题思路动画如下:
+这道题 我们需要 给出一个元素,判断这个元素是否出现过,如果出现过,返回这个元素的下标。
-
+那么判断元素是否出现,这个元素就要作为key,所以数组中的元素作为key,有key对应的就是value,value用来存下标。
+所以 map中的存储结构为 {key:数据元素,value:数组元素对应的下标}。
+
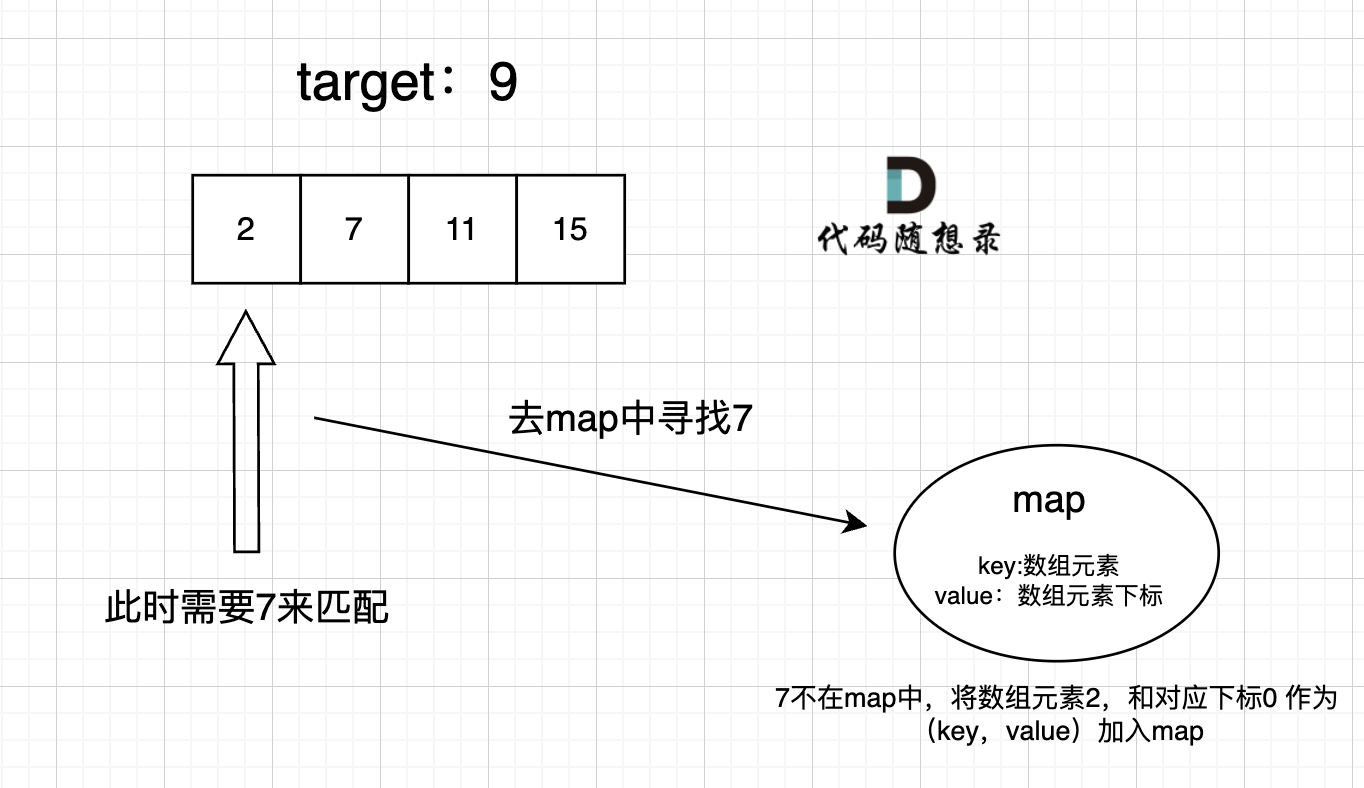
+在遍历数组的时候,只需要向map去查询是否有和目前遍历元素匹配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
+
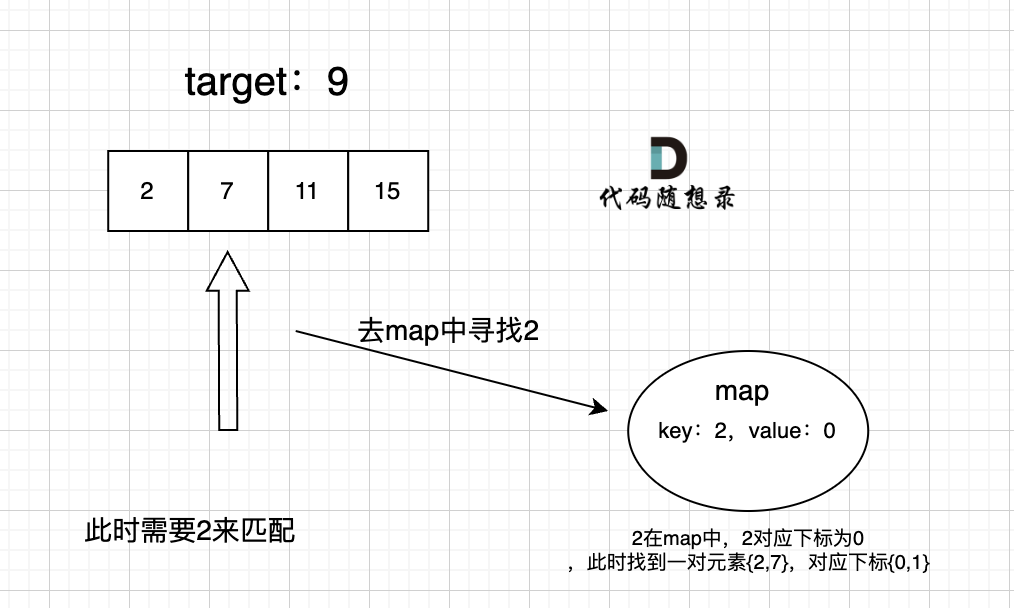
+过程如下:
+
+
+
+
+
C++代码:
@@ -66,25 +96,42 @@ public:
vector twoSum(vector& nums, int target) {
std::unordered_map map;
for(int i = 0; i < nums.size(); i++) {
- auto iter = map.find(target - nums[i]);
+ // 遍历当前元素,并在map中寻找是否有匹配的key
+ auto iter = map.find(target - nums[i]);
if(iter != map.end()) {
return {iter->second, i};
}
- map.insert(pair(nums[i], i));
+ // 如果没找到匹配对,就把访问过的元素和下标加入到map中
+ map.insert(pair(nums[i], i));
}
return {};
}
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(n)
+
+## 总结
+本题其实有四个重点:
+
+* 为什么会想到用哈希表
+* 哈希表为什么用map
+* 本题map是用来存什么的
+* map中的key和value用来存什么的
+
+把这四点想清楚了,本题才算是理解透彻了。
+
+很多录友把这道题目 通过了,但都没想清楚map是用来做什么的,以至于对代码的理解其实是 一知半解的。
## 其他语言版本
+### Java:
-Java:
```java
+//使用哈希表
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
if(nums == null || nums.length == 0){
@@ -92,48 +139,139 @@ public int[] twoSum(int[] nums, int target) {
}
Map map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
- int temp = target - nums[i];
+ int temp = target - nums[i]; // 遍历当前元素,并在map中寻找是否有匹配的key
if(map.containsKey(temp)){
res[1] = i;
res[0] = map.get(temp);
+ break;
+ }
+ map.put(nums[i], i); // 如果没找到匹配对,就把访问过的元素和下标加入到map中
+ }
+ return res;
+}
+```
+
+```java
+//使用哈希表方法2
+public int[] twoSum(int[] nums, int target) {
+ Map indexMap = new HashMap<>();
+
+ for(int i = 0; i < nums.length; i++){
+ int balance = target - nums[i]; // 记录当前的目标值的余数
+ if(indexMap.containsKey(balance)){ // 查找当前的map中是否有满足要求的值
+ return new int []{i, indexMap.get(balance)}; // 如果有,返回目标值
+ } else{
+ indexMap.put(nums[i], i); // 如果没有,把访问过的元素和下标加入map中
+ }
+ }
+ return null;
+}
+```
+
+```java
+//使用双指针
+public int[] twoSum(int[] nums, int target) {
+ int m=0,n=0,k,board=0;
+ int[] res=new int[2];
+ int[] tmp1=new int[nums.length];
+ //备份原本下标的nums数组
+ System.arraycopy(nums,0,tmp1,0,nums.length);
+ //将nums排序
+ Arrays.sort(nums);
+ //双指针
+ for(int i=0,j=nums.length-1;itarget)
+ j--;
+ else if(nums[i]+nums[j]==target){
+ m=i;
+ n=j;
+ break;
}
- map.put(nums[i], i);
+ }
+ //找到nums[m]在tmp1数组中的下标
+ for(k=0;k List[int]:
records = dict()
- # 用枚举更方便,就不需要通过索引再去取当前位置的值
- for idx, val in enumerate(nums):
- if target - val not in records:
- records[val] = idx
+ for index, value in enumerate(nums):
+ if target - value in records: # 遍历当前元素,并在map中寻找是否有匹配的key
+ return [records[target- value], index]
+ records[value] = index # 如果没找到匹配对,就把访问过的元素和下标加入到map中
+ return []
+```
+(版本二)使用集合
+```python
+class Solution:
+ def twoSum(self, nums: List[int], target: int) -> List[int]:
+ #创建一个集合来存储我们目前看到的数字
+ seen = set()
+ for i, num in enumerate(nums):
+ complement = target - num
+ if complement in seen:
+ return [nums.index(complement), i]
+ seen.add(num)
+```
+(版本三)使用双指针
+```python
+class Solution:
+ def twoSum(self, nums: List[int], target: int) -> List[int]:
+ # 对输入列表进行排序
+ nums_sorted = sorted(nums)
+
+ # 使用双指针
+ left = 0
+ right = len(nums_sorted) - 1
+ while left < right:
+ current_sum = nums_sorted[left] + nums_sorted[right]
+ if current_sum == target:
+ # 如果和等于目标数,则返回两个数的下标
+ left_index = nums.index(nums_sorted[left])
+ right_index = nums.index(nums_sorted[right])
+ if left_index == right_index:
+ right_index = nums[left_index+1:].index(nums_sorted[right]) + left_index + 1
+ return [left_index, right_index]
+ elif current_sum < target:
+ # 如果总和小于目标,则将左侧指针向右移动
+ left += 1
else:
- return [records[target - val], idx] # 如果存在就返回字典记录索引和当前索引
+ # 如果总和大于目标值,则将右指针向左移动
+ right -= 1
```
-
-Python (v2):
-
+(版本四)暴力法
```python
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
- rec = {}
for i in range(len(nums)):
- rest = target - nums[i]
- # Use get to get the index of the data, making use of one of the dictionary properties.
- if rec.get(rest, None) is not None: return [rec[rest], i]
- rec[nums[i]] = i
+ for j in range(i+1, len(nums)):
+ if nums[i] + nums[j] == target:
+ return [i,j]
```
-Go:
+### Go:
```go
+// 暴力解法
func twoSum(nums []int, target int) []int {
for k1, _ := range nums {
for k2 := k1 + 1; k2 < len(nums); k2++ {
@@ -161,7 +299,7 @@ func twoSum(nums []int, target int) []int {
}
```
-Rust
+### Rust:
```rust
use std::collections::HashMap;
@@ -182,23 +320,41 @@ impl Solution {
}
}
```
+```rust
+use std::collections::HashMap;
+
+impl Solution {
+ pub fn two_sum(nums: Vec, target: i32) -> Vec {
+ let mut hm: HashMap = HashMap::new();
+ for i in 0..nums.len() {
+ let j = target - nums[i];
+ if hm.contains_key(&j) {
+ return vec![*hm.get(&j).unwrap(), i as i32]
+ } else {
+ hm.insert(nums[i], i as i32);
+ }
+ }
+ vec![-1, -1]
+ }
+}
+```
-Javascript
+### JavaScript:
```javascript
var twoSum = function (nums, target) {
let hash = {};
- for (let i = 0; i < nums.length; i++) {
+ for (let i = 0; i < nums.length; i++) { // 遍历当前元素,并在map中寻找是否有匹配的key
if (hash[target - nums[i]] !== undefined) {
return [i, hash[target - nums[i]]];
}
- hash[nums[i]] = i;
+ hash[nums[i]] = i; // 如果没找到匹配对,就把访问过的元素和下标加入到map中
}
return [];
};
```
-TypeScript:
+### TypeScript:
```typescript
function twoSum(nums: number[], target: number): number[] {
@@ -209,6 +365,7 @@ function twoSum(nums: number[], target: number): number[] {
index = helperMap.get(target - nums[i]);
if (index !== undefined) {
resArr = [i, index];
+ break;
}
helperMap.set(nums[i], i);
}
@@ -216,25 +373,28 @@ function twoSum(nums: number[], target: number): number[] {
};
```
-php
+### PhP:
```php
function twoSum(array $nums, int $target): array
{
- for ($i = 0; $i < count($nums);$i++) {
- // 计算剩下的数
- $residue = $target - $nums[$i];
- // 匹配的index,有则返回index, 无则返回false
- $match_index = array_search($residue, $nums);
- if ($match_index !== false && $match_index != $i) {
- return array($i, $match_index);
+ $map = [];
+ foreach($nums as $i => $num) {
+ if (isset($map[$target - $num])) {
+ return [
+ $i,
+ $map[$target - $num]
+ ];
+ } else {
+ $map[$num] = $i;
}
}
return [];
}
```
-Swift:
+### Swift:
+
```swift
func twoSum(_ nums: [Int], _ target: Int) -> [Int] {
// 值: 下标
@@ -250,30 +410,148 @@ func twoSum(_ nums: [Int], _ target: Int) -> [Int] {
}
```
-PHP:
-```php
-class Solution {
- /**
- * @param Integer[] $nums
- * @param Integer $target
- * @return Integer[]
- */
- function twoSum($nums, $target) {
- if (count($nums) == 0) {
- return [];
- }
- $table = [];
- for ($i = 0; $i < count($nums); $i++) {
- $temp = $target - $nums[$i];
- if (isset($table[$temp])) {
- return [$table[$temp], $i];
+### Scala:
+
+```scala
+object Solution {
+ // 导入包
+ import scala.collection.mutable
+ def twoSum(nums: Array[Int], target: Int): Array[Int] = {
+ // key存储值,value存储下标
+ val map = new mutable.HashMap[Int, Int]()
+ for (i <- nums.indices) {
+ val tmp = target - nums(i) // 计算差值
+ // 如果这个差值存在于map,则说明找到了结果
+ if (map.contains(tmp)) {
+ return Array(map.get(tmp).get, i)
+ }
+ // 如果不包含把当前值与其下标放到map
+ map.put(nums(i), i)
+ }
+ // 如果没有找到直接返回一个空的数组,return关键字可以省略
+ new Array[Int](2)
+ }
+}
+```
+
+### C#:
+
+```csharp
+public class Solution {
+ public int[] TwoSum(int[] nums, int target) {
+ Dictionary dic= new Dictionary();
+ for(int i=0;i twoSum(List nums, int target) {
+ HashMap hashMap = HashMap();
+ for (int i = 0; i < nums.length; i++) {
+ int rest = target - nums[i];
+ if (hashMap.containsKey(rest)) {
+ return [hashMap[rest]!, i];
+ }
+ hashMap.addEntries({nums[i]: i}.entries);
+ }
+ return [];
+}
+```
+
+### C:
+
+```c
+
+
+/**
+ * Note: The returned array must be malloced, assume caller calls free().
+ */
+
+// leetcode 支持 ut_hash 函式庫
+
+ typedef struct {
+ int key;
+ int value;
+ UT_hash_handle hh; // make this structure hashable
+ } map;
+
+map* hashMap = NULL;
+
+ void hashMapAdd(int key, int value){
+ map* s;
+ // key already in the hash?
+ HASH_FIND_INT(hashMap, &key, s);
+ if(s == NULL){
+ s = (map*)malloc(sizeof(map));
+ s -> key = key;
+ HASH_ADD_INT(hashMap, key, s);
+ }
+ s -> value = value;
+ }
+
+map* hashMapFind(int key){
+ map* s;
+ // *s: output pointer
+ HASH_FIND_INT(hashMap, &key, s);
+ return s;
+ }
+
+ void hashMapCleanup(){
+ map* cur, *tmp;
+ HASH_ITER(hh, hashMap, cur, tmp){
+ HASH_DEL(hashMap, cur);
+ free(cur);
+ }
+ }
+
+ void hashPrint(){
+ map* s;
+ for(s = hashMap; s != NULL; s=(map*)(s -> hh.next)){
+ printf("key %d, value %d\n", s -> key, s -> value);
+ }
+ }
+
+
+int* twoSum(int* nums, int numsSize, int target, int* returnSize){
+ int i, *ans;
+ // hash find result
+ map* hashMapRes;
+ hashMap = NULL;
+ ans = malloc(sizeof(int) * 2);
+
+ for(i = 0; i < numsSize; i++){
+ // key 代表 nums[i] 的值,value 代表所在 index;
+ hashMapAdd(nums[i], i);
+ }
+
+ hashPrint();
+
+ for(i = 0; i < numsSize; i++){
+ hashMapRes = hashMapFind(target - nums[i]);
+ if(hashMapRes && hashMapRes -> value != i){
+ ans[0] = i;
+ ans[1] = hashMapRes -> value ;
+ *returnSize = 2;
+ return ans;
+ }
}
+
+ hashMapCleanup();
+ return NULL;
}
```
------------------------
-
diff --git "a/problems/0005.\346\234\200\351\225\277\345\233\236\346\226\207\345\255\220\344\270\262.md" "b/problems/0005.\346\234\200\351\225\277\345\233\236\346\226\207\345\255\220\344\270\262.md"
old mode 100644
new mode 100755
index eaebb5ab4d..05dd610a72
--- "a/problems/0005.\346\234\200\351\225\277\345\233\236\346\226\207\345\255\220\344\270\262.md"
+++ "b/problems/0005.\346\234\200\351\225\277\345\233\236\346\226\207\345\255\220\344\270\262.md"
@@ -1,14 +1,12 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 5.最长回文子串
-[力扣题目链接](https://leetcode-cn.com/problems/longest-palindromic-substring/)
+[力扣题目链接](https://leetcode.cn/problems/longest-palindromic-substring/)
给你一个字符串 s,找到 s 中最长的回文子串。
@@ -30,17 +28,17 @@
* 输出:"a"
-# 思路
+## 思路
本题和[647.回文子串](https://programmercarl.com/0647.回文子串.html) 差不多是一样的,但647.回文子串更基本一点,建议可以先做647.回文子串
-## 暴力解法
+### 暴力解法
两层for循环,遍历区间起始位置和终止位置,然后判断这个区间是不是回文。
时间复杂度:O(n^3)
-## 动态规划
+### 动态规划
动规五部曲:
@@ -108,7 +106,7 @@ dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹
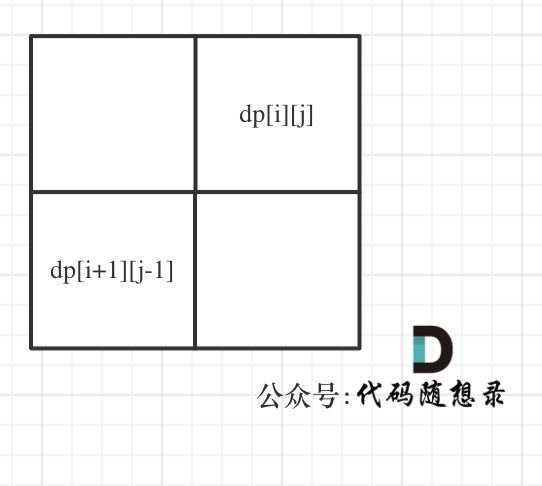
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
-
+
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
@@ -142,7 +140,7 @@ for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
举例,输入:"aaa",dp[i][j]状态如下:
-
+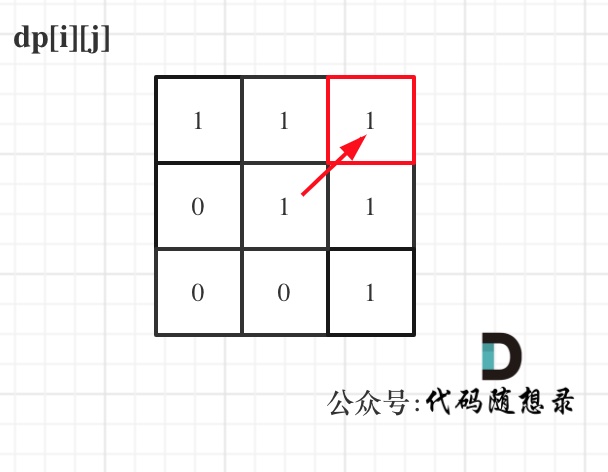
**注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分**。
@@ -208,7 +206,7 @@ public:
* 时间复杂度:O(n^2)
* 空间复杂度:O(n^2)
-## 双指针
+### 双指针
动态规划的空间复杂度是偏高的,我们再看一下双指针法。
@@ -256,28 +254,98 @@ public:
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
+### Manacher 算法
+Manacher 算法的关键在于高效利用回文的对称性,通过插入分隔符和维护中心、边界等信息,在线性时间内找到最长回文子串。这种方法避免了重复计算,是处理回文问题的最优解。
-# 其他语言版本
+```c++
+//Manacher 算法
+class Solution {
+public:
+ string longestPalindrome(string s) {
+ // 预处理字符串,在每个字符之间插入 '#'
+ string t = "#";
+ for (char c : s) {
+ t += c; // 添加字符
+ t += '#';// 添加分隔符
+ }
+ int n = t.size();// 新字符串的长度
+ vector p(n, 0);// p[i] 表示以 t[i] 为中心的回文半径
+ int center = 0, right = 0;// 当前回文的中心和右边界
+
+
+ // 遍历预处理后的字符串
+ for (int i = 0; i < n; i++) {
+ // 如果当前索引在右边界内,利用对称性初始化 p[i]
+ if (i < right) {
+ p[i] = min(right - i, p[2 * center - i]);
+ }
+ // 尝试扩展回文
+ while (i - p[i] - 1 >= 0 && i + p[i] + 1 < n && t[i - p[i] - 1] == t[i + p[i] + 1]) {
+ p[i]++;// 增加回文半径
+ }
+ // 如果当前回文扩展超出右边界,更新中心和右边界
+ if (i + p[i] > right) {
+ center = i;// 更新中心
+ right = i + p[i];// 更新右边界
+ }
+ }
+ // 找到最大回文半径和对应的中心
+ int maxLen = 0, centerIndex = 0;
+ for (int i = 0; i < n; i++) {
+ if (p[i] > maxLen) {
+ maxLen = p[i];// 更新最大回文长度
+ centerIndex = i;// 更新中心索引
+ }
+ }
+ // 计算原字符串中回文子串的起始位置并返回
+ return s.substr((centerIndex - maxLen) / 2, maxLen);
+ }
+};
+```
+
+
+
+* 时间复杂度:O(n)
+* 空间复杂度:O(n)
+
+## 其他语言版本
-Java:
+### Java:
```java
-public int[] twoSum(int[] nums, int target) {
- int[] res = new int[2];
- if(nums == null || nums.length == 0){
- return res;
- }
- Map map = new HashMap<>();
- for(int i = 0; i < nums.length; i++){
- int temp = target - nums[i];
- if(map.containsKey(temp)){
- res[1] = i;
- res[0] = map.get(temp);
+// 双指针 动态规划
+class Solution {
+ public String longestPalindrome(String s) {
+ if (s.length() == 0 || s.length() == 1) return s;
+ int length = 1;
+ int index = 0;
+ boolean[][] palindrome = new boolean[s.length()][s.length()];
+ for (int i = 0; i < s.length(); i++) {
+ palindrome[i][i] = true;
}
- map.put(nums[i], i);
+
+ for (int L = 2; L <= s.length(); L++) {
+ for (int i = 0; i < s.length(); i++) {
+ int j = i + L - 1;
+ if (j >= s.length()) break;
+ if (s.charAt(i) != s.charAt(j)) {
+ palindrome[i][j] = false;
+ } else {
+ if (j - i < 3) {
+ palindrome[i][j] = true;
+ } else {
+ palindrome[i][j] = palindrome[i + 1][j - 1];
+ }
+ }
+ if (palindrome[i][j] && j - i + 1 > length) {
+ length = j - i + 1;
+ index = i;
+ }
+ }
+ }
+ return s.substring(index, index + length);
}
- return res;
}
```
@@ -310,7 +378,7 @@ class Solution {
}
```
-Python:
+### Python:
```python
class Solution:
@@ -360,13 +428,41 @@ class Solution:
return s[start:end]
```
-Go:
+### Go:
```go
+func longestPalindrome(s string) string {
+ maxLen := 0
+ left := 0
+ length := 0
+ dp := make([][]bool, len(s))
+ for i := 0; i < len(s); i++ {
+ dp[i] = make([]bool,len(s))
+ }
+ for i := len(s)-1; i >= 0; i-- {
+ for j := i; j < len(s); j++ {
+ if s[i] == s[j]{
+ if j-i <= 1{ // 情况一和情况二
+ length = j-i
+ dp[i][j]=true
+ }else if dp[i+1][j-1]{ // 情况三
+ length = j-i
+ dp[i][j] = true
+ }
+ }
+ }
+ if length > maxLen {
+ maxLen = length
+ left = i
+ }
+ }
+ return s[left: left+maxLen+1]
+}
+
```
-JavaScript:
+### JavaScript:
```js
//动态规划解法
@@ -482,7 +578,7 @@ var longestPalindrome = function(s) {
};
```
-C:
+### C:
动态规划:
```c
@@ -570,5 +666,67 @@ char * longestPalindrome(char * s){
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-> 用哈希表解决了[两数之和](https://programmercarl.com/0001.两数之和.html),那么三数之和呢?
-
# 第15题. 三数之和
-[力扣题目链接](https://leetcode-cn.com/problems/3sum/)
+[力扣题目链接](https://leetcode.cn/problems/3sum/)
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
@@ -26,20 +22,23 @@
[-1, -1, 2]
]
+## 算法公开课
-# 思路
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[梦破碎的地方!| LeetCode:15.三数之和](https://www.bilibili.com/video/BV1GW4y127qo),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
**注意[0, 0, 0, 0] 这组数据**
-## 哈希解法
+## 思路
+
+### 哈希解法
-两层for循环就可以确定 a 和b 的数值了,可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
+两层for循环就可以确定 两个数值,可以使用哈希法来确定 第三个数 0-(a+b) 或者 0 - (a + c) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
把符合条件的三元组放进vector中,然后再去重,这样是非常费时的,很容易超时,也是这道题目通过率如此之低的根源所在。
去重的过程不好处理,有很多小细节,如果在面试中很难想到位。
-时间复杂度可以做到$O(n^2)$,但还是比较费时的,因为不好做剪枝操作。
+时间复杂度可以做到O(n^2),但还是比较费时的,因为不好做剪枝操作。
大家可以尝试使用哈希法写一写,就知道其困难的程度了。
@@ -47,61 +46,71 @@
```CPP
class Solution {
public:
+ // 在一个数组中找到3个数形成的三元组,它们的和为0,不能重复使用(三数下标互不相同),且三元组不能重复。
+ // b(存储)== 0-(a+c)(检索)
vector> threeSum(vector& nums) {
vector> result;
sort(nums.begin(), nums.end());
- // 找出a + b + c = 0
- // a = nums[i], b = nums[j], c = -(a + b)
+
for (int i = 0; i < nums.size(); i++) {
- // 排序之后如果第一个元素已经大于零,那么不可能凑成三元组
- if (nums[i] > 0) {
+ // 如果a是正数,a 0)
break;
- }
- if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重
+
+ // [a, a, ...] 如果本轮a和上轮a相同,那么找到的b,c也是相同的,所以去重a
+ if (i > 0 && nums[i] == nums[i - 1])
continue;
- }
+
+ // 这个set的作用是存储b
unordered_set set;
- for (int j = i + 1; j < nums.size(); j++) {
- if (j > i + 2
- && nums[j] == nums[j-1]
- && nums[j-1] == nums[j-2]) { // 三元组元素b去重
+
+ for (int k = i + 1; k < nums.size(); k++) {
+ // 去重b=c时的b和c
+ if (k > i + 2 && nums[k] == nums[k - 1] && nums[k - 1] == nums[k - 2])
continue;
+
+ // a+b+c=0 <=> b=0-(a+c)
+ int target = 0 - (nums[i] + nums[k]);
+ if (set.find(target) != set.end()) {
+ result.push_back({nums[i], target, nums[k]}); // nums[k]成为c
+ set.erase(target);
}
- int c = 0 - (nums[i] + nums[j]);
- if (set.find(c) != set.end()) {
- result.push_back({nums[i], nums[j], c});
- set.erase(c);// 三元组元素c去重
- } else {
- set.insert(nums[j]);
+ else {
+ set.insert(nums[k]); // nums[k]成为b
}
}
}
+
return result;
}
};
```
-## 双指针
+* 时间复杂度: O(n^2)
+* 空间复杂度: O(n),额外的 set 开销
+
+
+### 双指针
**其实这道题目使用哈希法并不十分合适**,因为在去重的操作中有很多细节需要注意,在面试中很难直接写出没有bug的代码。
-而且使用哈希法 在使用两层for循环的时候,能做的剪枝操作很有限,虽然时间复杂度是$O(n^2)$,也是可以在leetcode上通过,但是程序的执行时间依然比较长 。
+而且使用哈希法 在使用两层for循环的时候,能做的剪枝操作很有限,虽然时间复杂度是O(n^2),也是可以在leetcode上通过,但是程序的执行时间依然比较长 。
接下来我来介绍另一个解法:双指针法,**这道题目使用双指针法 要比哈希法高效一些**,那么来讲解一下具体实现的思路。
动画效果如下:
-
+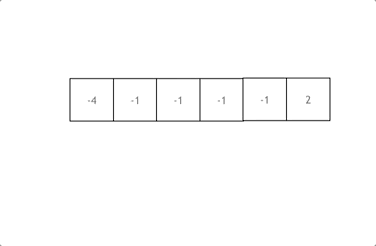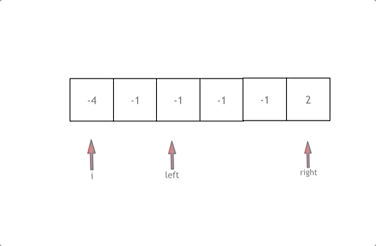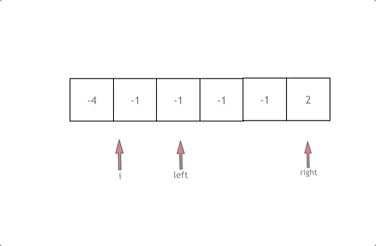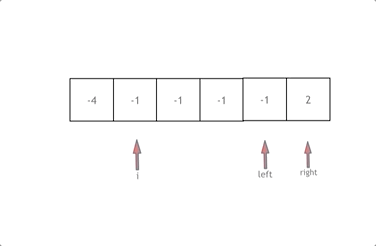
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
-依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。
+依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
-时间复杂度:$O(n^2)$。
+时间复杂度:O(n^2)。
C++代码代码如下:
@@ -118,13 +127,13 @@ public:
if (nums[i] > 0) {
return result;
}
- // 错误去重方法,将会漏掉-1,-1,2 这种情况
+ // 错误去重a方法,将会漏掉-1,-1,2 这种情况
/*
if (nums[i] == nums[i + 1]) {
continue;
}
*/
- // 正确去重方法
+ // 正确去重a方法
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
@@ -136,17 +145,11 @@ public:
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
*/
- if (nums[i] + nums[left] + nums[right] > 0) {
- right--;
- // 当前元素不合适了,可以去重
- while (left < right && nums[right] == nums[right + 1]) right--;
- } else if (nums[i] + nums[left] + nums[right] < 0) {
- left++;
- // 不合适,去重
- while (left < right && nums[left] == nums[left - 1]) left++;
- } else {
+ if (nums[i] + nums[left] + nums[right] > 0) right--;
+ else if (nums[i] + nums[left] + nums[right] < 0) left++;
+ else {
result.push_back(vector{nums[i], nums[left], nums[right]});
- // 去重逻辑应该放在找到一个三元组之后
+ // 去重逻辑应该放在找到一个三元组之后,对b 和 c去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
@@ -162,7 +165,83 @@ public:
};
```
-# 思考题
+* 时间复杂度: O(n^2)
+* 空间复杂度: O(1)
+
+
+### 去重逻辑的思考
+
+#### a的去重
+
+说到去重,其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i],nums[left],nums[right]
+
+a 如果重复了怎么办,a是nums里遍历的元素,那么应该直接跳过去。
+
+但这里有一个问题,是判断 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同。
+
+有同学可能想,这不都一样吗。
+
+其实不一样!
+
+都是和 nums[i]进行比较,是比较它的前一个,还是比较它的后一个。
+
+如果我们的写法是 这样:
+
+```C++
+if (nums[i] == nums[i + 1]) { // 去重操作
+ continue;
+}
+```
+
+那我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了。
+
+**我们要做的是 不能有重复的三元组,但三元组内的元素是可以重复的!**
+
+所以这里是有两个重复的维度。
+
+那么应该这么写:
+
+```C++
+if (i > 0 && nums[i] == nums[i - 1]) {
+ continue;
+}
+```
+
+这么写就是当前使用 nums[i],我们判断前一位是不是一样的元素,在看 {-1, -1 ,2} 这组数据,当遍历到 第一个 -1 的时候,只要前一位没有-1,那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。
+
+这是一个非常细节的思考过程。
+
+#### b与c的去重
+
+很多同学写本题的时候,去重的逻辑多加了 对right 和left 的去重:(代码中注释部分)
+
+```C++
+while (right > left) {
+ if (nums[i] + nums[left] + nums[right] > 0) {
+ right--;
+ // 去重 right
+ while (left < right && nums[right] == nums[right + 1]) right--;
+ } else if (nums[i] + nums[left] + nums[right] < 0) {
+ left++;
+ // 去重 left
+ while (left < right && nums[left] == nums[left - 1]) left++;
+ } else {
+ }
+}
+```
+
+但细想一下,这种去重其实对提升程序运行效率是没有帮助的。
+
+拿right去重为例,即使不加这个去重逻辑,依然根据 `while (right > left) ` 和 `if (nums[i] + nums[left] + nums[right] > 0)` 去完成right-- 的操作。
+
+多加了 ` while (left < right && nums[right] == nums[right + 1]) right--;` 这一行代码,其实就是把 需要执行的逻辑提前执行了,但并没有减少 判断的逻辑。
+
+最直白的思考过程,就是right还是一个数一个数的减下去的,所以在哪里减的都是一样的。
+
+所以这种去重 是可以不加的。 仅仅是 把去重的逻辑提前了而已。
+
+
+## 思考题
既然三数之和可以使用双指针法,我们之前讲过的[1.两数之和](https://programmercarl.com/0001.两数之和.html),可不可以使用双指针法呢?
@@ -178,20 +257,22 @@ public:
## 其他语言版本
-
-Java:
+### Java:
+(版本一) 双指针
```Java
class Solution {
public List> threeSum(int[] nums) {
List> result = new ArrayList<>();
Arrays.sort(nums);
-
+ // 找出a + b + c = 0
+ // a = nums[i], b = nums[left], c = nums[right]
for (int i = 0; i < nums.length; i++) {
- if (nums[i] > 0) {
+ // 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了
+ if (nums[i] > 0) {
return result;
}
- if (i > 0 && nums[i] == nums[i - 1]) {
+ if (i > 0 && nums[i] == nums[i - 1]) { // 去重a
continue;
}
@@ -205,7 +286,7 @@ class Solution {
left++;
} else {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
-
+ // 去重逻辑应该放在找到一个三元组之后,对b 和 c去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
@@ -218,90 +299,147 @@ class Solution {
}
}
```
+(版本二) 使用哈希集合
+```Java
+class Solution {
+ public List> threeSum(int[] nums) {
+ List> result = new ArrayList<>();
+ Arrays.sort(nums);
+
+ for (int i = 0; i < nums.length; i++) {
+ // 如果第一个元素大于零,不可能凑成三元组
+ if (nums[i] > 0) {
+ return result;
+ }
+ // 三元组元素a去重
+ if (i > 0 && nums[i] == nums[i - 1]) {
+ continue;
+ }
+
+ HashSet set = new HashSet<>();
+ for (int j = i + 1; j < nums.length; j++) {
+ // 三元组元素b去重
+ if (j > i + 2 && nums[j] == nums[j - 1] && nums[j - 1] == nums[j - 2]) {
+ continue;
+ }
+
+ int c = -nums[i] - nums[j];
+ if (set.contains(c)) {
+ result.add(Arrays.asList(nums[i], nums[j], c));
+ set.remove(c); // 三元组元素c去重
+ } else {
+ set.add(nums[j]);
+ }
+ }
+ }
+ return result;
+ }
+}
+```
+### Python:
+(版本一) 双指针
-Python:
```Python
class Solution:
- def threeSum(self, nums):
- ans = []
- n = len(nums)
+ def threeSum(self, nums: List[int]) -> List[List[int]]:
+ result = []
nums.sort()
- for i in range(n):
- left = i + 1
- right = n - 1
+
+ for i in range(len(nums)):
+ # 如果第一个元素已经大于0,不需要进一步检查
if nums[i] > 0:
- break
- if i >= 1 and nums[i] == nums[i - 1]:
+ return result
+
+ # 跳过相同的元素以避免重复
+ if i > 0 and nums[i] == nums[i - 1]:
continue
- while left < right:
- total = nums[i] + nums[left] + nums[right]
- if total > 0:
- right -= 1
- elif total < 0:
+
+ left = i + 1
+ right = len(nums) - 1
+
+ while right > left:
+ sum_ = nums[i] + nums[left] + nums[right]
+
+ if sum_ < 0:
left += 1
+ elif sum_ > 0:
+ right -= 1
else:
- ans.append([nums[i], nums[left], nums[right]])
- while left != right and nums[left] == nums[left + 1]: left += 1
- while left != right and nums[right] == nums[right - 1]: right -= 1
- left += 1
+ result.append([nums[i], nums[left], nums[right]])
+
+ # 跳过相同的元素以避免重复
+ while right > left and nums[right] == nums[right - 1]:
+ right -= 1
+ while right > left and nums[left] == nums[left + 1]:
+ left += 1
+
right -= 1
- return ans
+ left += 1
+
+ return result
```
-Python (v2):
+(版本二) 使用字典
```python
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
- if len(nums) < 3: return []
- nums, res = sorted(nums), []
- for i in range(len(nums) - 2):
- cur, l, r = nums[i], i + 1, len(nums) - 1
- if res != [] and res[-1][0] == cur: continue # Drop duplicates for the first time.
-
- while l < r:
- if cur + nums[l] + nums[r] == 0:
- res.append([cur, nums[l], nums[r]])
- # Drop duplicates for the second time in interation of l & r. Only used when target situation occurs, because that is the reason for dropping duplicates.
- while l < r - 1 and nums[l] == nums[l + 1]:
- l += 1
- while r > l + 1 and nums[r] == nums[r - 1]:
- r -= 1
- if cur + nums[l] + nums[r] > 0:
- r -= 1
+ result = []
+ nums.sort()
+ # 找出a + b + c = 0
+ # a = nums[i], b = nums[j], c = -(a + b)
+ for i in range(len(nums)):
+ # 排序之后如果第一个元素已经大于零,那么不可能凑成三元组
+ if nums[i] > 0:
+ break
+ if i > 0 and nums[i] == nums[i - 1]: #三元组元素a去重
+ continue
+ d = {}
+ for j in range(i + 1, len(nums)):
+ if j > i + 2 and nums[j] == nums[j-1] == nums[j-2]: # 三元组元素b去重
+ continue
+ c = 0 - (nums[i] + nums[j])
+ if c in d:
+ result.append([nums[i], nums[j], c])
+ d.pop(c) # 三元组元素c去重
else:
- l += 1
- return res
+ d[nums[j]] = j
+ return result
```
-Go:
+### Go:
+(版本一) 双指针
```Go
-func threeSum(nums []int)[][]int{
+func threeSum(nums []int) [][]int {
sort.Ints(nums)
- res:=[][]int{}
-
- for i:=0;i0{
+ res := [][]int{}
+ // 找出a + b + c = 0
+ // a = nums[i], b = nums[left], c = nums[right]
+ for i := 0; i < len(nums)-2; i++ {
+ // 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了
+ n1 := nums[i]
+ if n1 > 0 {
break
}
- if i>0&&n1==nums[i-1]{
+ // 去重a
+ if i > 0 && n1 == nums[i-1] {
continue
}
- l,r:=i+1,len(nums)-1
- for l 0 {
+ break
+ }
+ // 三元组元素a去重
+ if i > 0 && nums[i] == nums[i-1] {
+ continue
+ }
+ set := make(map[int]struct{})
+ for j := i + 1; j < len(nums); j++ {
+ // 三元组元素b去重
+ if j > i + 2 && nums[j] == nums[j-1] && nums[j-1] == nums[j-2] {
+ continue
+ }
+ c := -nums[i] - nums[j]
+ if _, ok := set[c]; ok {
+ res = append(res, []int{nums[i], nums[j], c})
+ // 三元组元素c去重
+ delete(set, c)
+ } else {
+ set[nums[j]] = struct{}{}
+ }
+ }
+ }
+ return res
+}
+```
-javaScript:
+### JavaScript:
+
+```js
+var threeSum = function(nums) {
+ const res = [], len = nums.length
+ // 将数组排序
+ nums.sort((a, b) => a - b)
+ for (let i = 0; i < len; i++) {
+ let l = i + 1, r = len - 1, iNum = nums[i]
+ // 数组排过序,如果第一个数大于0直接返回res
+ if (iNum > 0) return res
+ // 去重
+ if (iNum == nums[i - 1]) continue
+ while(l < r) {
+ let lNum = nums[l], rNum = nums[r], threeSum = iNum + lNum + rNum
+ // 三数之和小于0,则左指针向右移动
+ if (threeSum < 0) l++
+ else if (threeSum > 0) r--
+ else {
+ res.push([iNum, lNum, rNum])
+ // 去重
+ while(l < r && nums[l] == nums[l + 1]){
+ l++
+ }
+ while(l < r && nums[r] == nums[r - 1]) {
+ r--
+ }
+ l++
+ r--
+ }
+ }
+ }
+ return res
+};
+```
+
+解法二:nSum通用解法。递归
```js
/**
+ * nsum通用解法,支持2sum,3sum,4sum...等等
+ * 时间复杂度分析:
+ * 1. n = 2时,时间复杂度O(NlogN),排序所消耗的时间。、
+ * 2. n > 2时,时间复杂度为O(N^n-1),即N的n-1次方,至少是2次方,此时可省略排序所消耗的时间。举例:3sum为O(n^2),4sum为O(n^3)
* @param {number[]} nums
* @return {number[][]}
*/
-
-// 循环内不考虑去重
-var threeSum = function(nums) {
- const len = nums.length;
- if(len < 3) return [];
- nums.sort((a, b) => a - b);
- const resSet = new Set();
- for(let i = 0; i < len - 2; i++) {
- if(nums[i] > 0) break;
- let l = i + 1, r = len - 1;
- while(l < r) {
- const sum = nums[i] + nums[l] + nums[r];
- if(sum < 0) { l++; continue };
- if(sum > 0) { r--; continue };
- resSet.add(`${nums[i]},${nums[l]},${nums[r]}`);
- l++;
- r--;
+var threeSum = function (nums) {
+ // nsum通用解法核心方法
+ function nSumTarget(nums, n, start, target) {
+ // 前提:nums要先排序好
+ let res = [];
+ if (n === 2) {
+ res = towSumTarget(nums, start, target);
+ } else {
+ for (let i = start; i < nums.length; i++) {
+ // 递归求(n - 1)sum
+ let subRes = nSumTarget(
+ nums,
+ n - 1,
+ i + 1,
+ target - nums[i]
+ );
+ for (let j = 0; j < subRes.length; j++) {
+ res.push([nums[i], ...subRes[j]]);
+ }
+ // 跳过相同元素
+ while (nums[i] === nums[i + 1]) i++;
+ }
}
+ return res;
}
- return Array.from(resSet).map(i => i.split(","));
-};
-// 去重优化
-var threeSum = function(nums) {
- const len = nums.length;
- if(len < 3) return [];
- nums.sort((a, b) => a - b);
- const res = [];
- for(let i = 0; i < len - 2; i++) {
- if(nums[i] > 0) break;
- // a去重
- if(i > 0 && nums[i] === nums[i - 1]) continue;
- let l = i + 1, r = len - 1;
- while(l < r) {
- const sum = nums[i] + nums[l] + nums[r];
- if(sum < 0) { l++; continue };
- if(sum > 0) { r--; continue };
- res.push([nums[i], nums[l], nums[r]])
- // b c 去重
- while(l < r && nums[l] === nums[++l]);
- while(l < r && nums[r] === nums[--r]);
+ function towSumTarget(nums, start, target) {
+ // 前提:nums要先排序好
+ let res = [];
+ let len = nums.length;
+ let left = start;
+ let right = len - 1;
+ while (left < right) {
+ let sum = nums[left] + nums[right];
+ if (sum < target) {
+ while (nums[left] === nums[left + 1]) left++;
+ left++;
+ } else if (sum > target) {
+ while (nums[right] === nums[right - 1]) right--;
+ right--;
+ } else {
+ // 相等
+ res.push([nums[left], nums[right]]);
+ // 跳过相同元素
+ while (nums[left] === nums[left + 1]) left++;
+ while (nums[right] === nums[right - 1]) right--;
+ left++;
+ right--;
+ }
}
+ return res;
}
- return res;
+ nums.sort((a, b) => a - b);
+ // n = 3,此时求3sum之和
+ return nSumTarget(nums, 3, 0, 0);
};
```
-TypeScript:
+
+### TypeScript:
```typescript
function threeSum(nums: number[]): number[][] {
@@ -373,6 +599,9 @@ function threeSum(nums: number[]): number[][] {
right: number = length - 1;
let resArr: number[][] = [];
for (let i = 0; i < length; i++) {
+ if (nums[i]>0) {
+ return resArr; //nums经过排序后,只要nums[i]>0, 此后的nums[i] + nums[left] + nums[right]均大于0,可以提前终止循环。
+ }
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
}
@@ -401,7 +630,8 @@ function threeSum(nums: number[]): number[][] {
};
```
-ruby:
+### Ruby:
+
```ruby
def is_valid(strs)
symbol_map = {')' => '(', '}' => '{', ']' => '['}
@@ -419,8 +649,8 @@ def is_valid(strs)
end
```
+### PHP:
-PHP:
```php
class Solution {
/**
@@ -461,7 +691,8 @@ class Solution {
}
```
-Swift:
+### Swift:
+
```swift
// 双指针法
func threeSum(_ nums: [Int]) -> [[Int]] {
@@ -502,7 +733,73 @@ func threeSum(_ nums: [Int]) -> [[Int]] {
}
```
-C:
+### Rust:
+
+```Rust
+// 哈希解法
+use std::collections::HashSet;
+impl Solution {
+ pub fn three_sum(nums: Vec) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut nums = nums;
+ nums.sort();
+ let len = nums.len();
+ for i in 0..len {
+ if nums[i] > 0 { break; }
+ if i > 0 && nums[i] == nums[i - 1] { continue; }
+ let mut set = HashSet::new();
+ for j in (i + 1)..len {
+ if j > i + 2 && nums[j] == nums[j - 1] && nums[j] == nums[j - 2] { continue; }
+ let c = 0 - (nums[i] + nums[j]);
+ if set.contains(&c) {
+ result.push(vec![nums[i], nums[j], c]);
+ set.remove(&c);
+ } else { set.insert(nums[j]); }
+ }
+ }
+ result
+ }
+}
+```
+
+```Rust
+// 双指针法
+use std::cmp::Ordering;
+impl Solution {
+ pub fn three_sum(nums: Vec) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut nums = nums;
+ nums.sort();
+ let len = nums.len();
+ for i in 0..len {
+ if nums[i] > 0 { return result; }
+ if i > 0 && nums[i] == nums[i - 1] { continue; }
+ let (mut left, mut right) = (i + 1, len - 1);
+ while left < right {
+ match (nums[i] + nums[left] + nums[right]).cmp(&0){
+ Ordering::Equal =>{
+ result.push(vec![nums[i], nums[left], nums[right]]);
+ left +=1;
+ right -=1;
+ while left < right && nums[left] == nums[left - 1]{
+ left += 1;
+ }
+ while left < right && nums[right] == nums[right+1]{
+ right -= 1;
+ }
+ }
+ Ordering::Greater => right -= 1,
+ Ordering::Less => left += 1,
+ }
+ }
+ }
+ result
+ }
+}
+```
+
+### C:
+
```C
//qsort辅助cmp函数
int cmp(const void* ptr1, const void* ptr2) {
@@ -576,7 +873,8 @@ int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes
}
```
-C#:
+### C#:
+
```csharp
public class Solution
{
@@ -634,6 +932,49 @@ public class Solution
}
}
```
+### Scala:
+
+```scala
+object Solution {
+ // 导包
+ import scala.collection.mutable.ListBuffer
+ import scala.util.control.Breaks.{break, breakable}
+
+ def threeSum(nums: Array[Int]): List[List[Int]] = {
+ // 定义结果集,最后需要转换为List
+ val res = ListBuffer[List[Int]]()
+ val nums_tmp = nums.sorted // 对nums进行排序
+ for (i <- nums_tmp.indices) {
+ // 如果要排的第一个数字大于0,直接返回结果
+ if (nums_tmp(i) > 0) {
+ return res.toList
+ }
+ // 如果i大于0并且和前一个数字重复,则跳过本次循环,相当于continue
+ breakable {
+ if (i > 0 && nums_tmp(i) == nums_tmp(i - 1)) {
+ break
+ } else {
+ var left = i + 1
+ var right = nums_tmp.length - 1
+ while (left < right) {
+ var sum = nums_tmp(i) + nums_tmp(left) + nums_tmp(right) // 求三数之和
+ if (sum < 0) left += 1
+ else if (sum > 0) right -= 1
+ else {
+ res += List(nums_tmp(i), nums_tmp(left), nums_tmp(right)) // 如果等于0 添加进结果集
+ // 为了避免重复,对left和right进行移动
+ while (left < right && nums_tmp(left) == nums_tmp(left + 1)) left += 1
+ while (left < right && nums_tmp(right) == nums_tmp(right - 1)) right -= 1
+ left += 1
+ right -= 1
+ }
+ }
+ }
+ }
+ }
+ // 最终返回需要转换为List,return关键字可以省略
+ res.toList
+ }
+}
+```
------------------------
-
diff --git "a/problems/0017.\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md" "b/problems/0017.\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
old mode 100644
new mode 100755
index 7040182f3b..6dcf9ee690
--- "a/problems/0017.\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
+++ "b/problems/0017.\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
@@ -1,27 +1,30 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 17.电话号码的字母组合
-[力扣题目链接](https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/)
+[力扣题目链接](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
-
+
示例:
-输入:"23"
-输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
+* 输入:"23"
+* 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
-# 思路
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)::[还得用回溯算法!| LeetCode:17.电话号码的字母组合](https://www.bilibili.com/video/BV1yV4y1V7Ug),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+
+## 思路
从示例上来说,输入"23",最直接的想法就是两层for循环遍历了吧,正好把组合的情况都输出了。
@@ -35,7 +38,7 @@
2. 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
3. 输入1 * #按键等等异常情况
-## 数字和字母如何映射
+### 数字和字母如何映射
可以使用map或者定义一个二维数组,例如:string letterMap[10],来做映射,我这里定义一个二维数组,代码如下:
@@ -54,14 +57,14 @@ const string letterMap[10] = {
};
```
-## 回溯法来解决n个for循环的问题
+### 回溯法来解决n个for循环的问题
对于回溯法还不了解的同学看这篇:[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)
例如:输入:"23",抽象为树形结构,如图所示:
-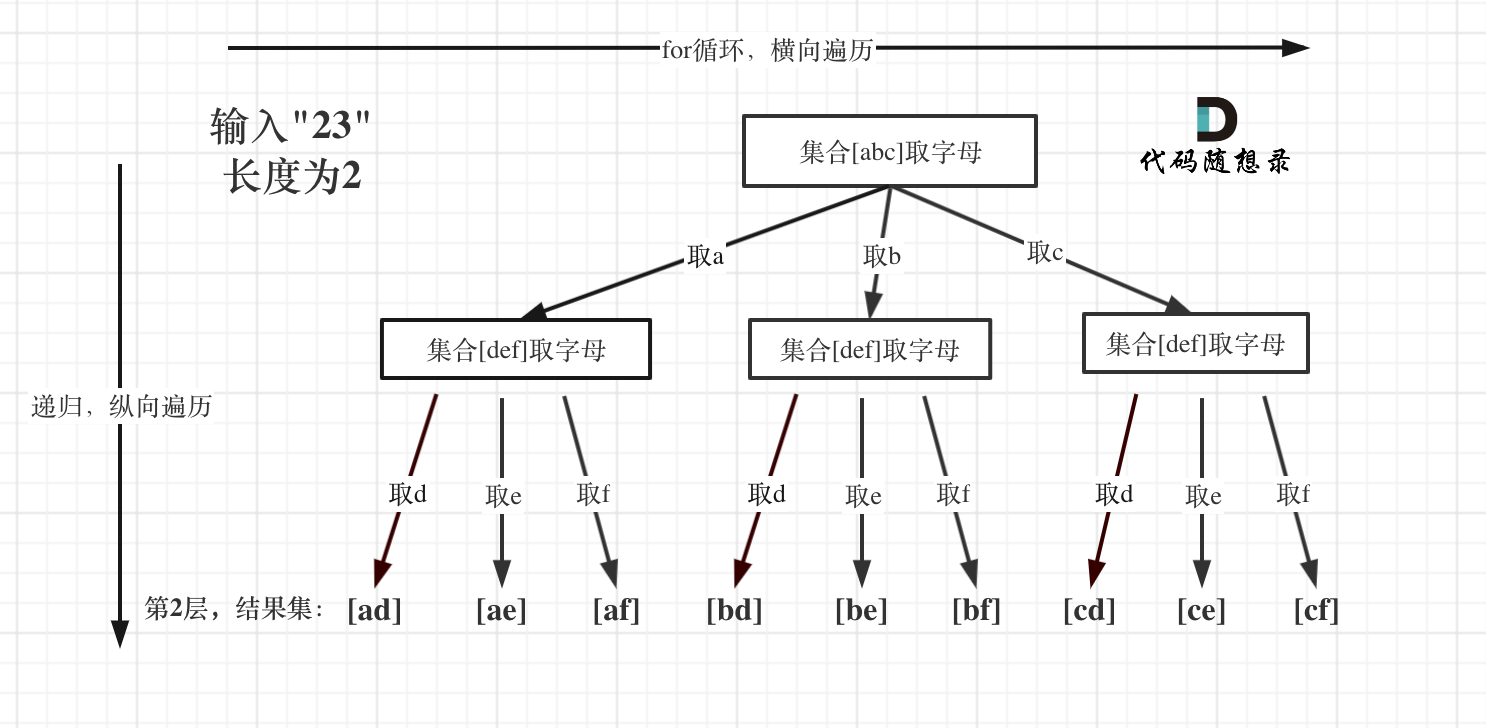
+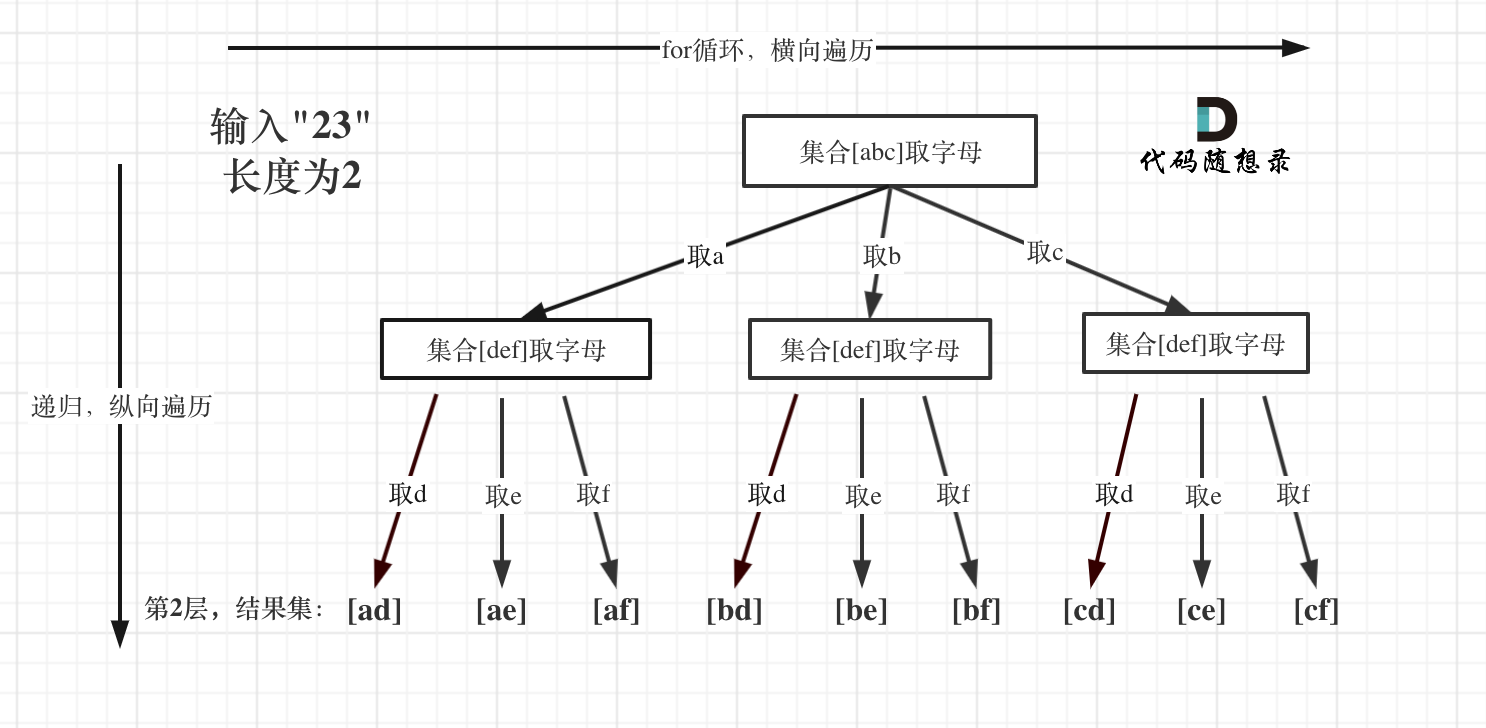
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
@@ -120,7 +123,7 @@ for (int i = 0; i < letters.size(); i++) {
**注意这里for循环,可不像是在[回溯算法:求组合问题!](https://programmercarl.com/0077.组合.html)和[回溯算法:求组合总和!](https://programmercarl.com/0216.组合总和III.html)中从startIndex开始遍历的**。
-**因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是是求同一个集合中的组合!**
+**因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是求同一个集合中的组合!**
注意:输入1 * #按键等等异常情况
@@ -129,9 +132,6 @@ for (int i = 0; i < letters.size(); i++) {
**但是要知道会有这些异常,如果是现场面试中,一定要考虑到!**
-
-## C++代码
-
关键地方都讲完了,按照[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中的回溯法模板,不难写出如下C++代码:
@@ -178,6 +178,8 @@ public:
}
};
```
+* 时间复杂度: O(3^m * 4^n),其中 m 是对应三个字母的数字个数,n 是对应四个字母的数字个数
+* 空间复杂度: O(3^m * 4^n)
一些写法,是把回溯的过程放在递归函数里了,例如如下代码,我可以写成这样:(注意注释中不一样的地方)
@@ -226,7 +228,7 @@ public:
所以大家可以按照版本一来写就可以了。
-# 总结
+## 总结
本篇将题目的三个要点一一列出,并重点强调了和前面讲解过的[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)的区别,本题是多个集合求组合,所以在回溯的搜索过程中,都有一些细节需要注意的。
@@ -234,10 +236,10 @@ public:
-# 其他语言版本
+## 其他语言版本
-## Java
+### Java
```Java
class Solution {
@@ -256,7 +258,7 @@ class Solution {
}
- //每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuild
+ //每次迭代获取一个字符串,所以会涉及大量的字符串拼接,所以这里选择更为高效的 StringBuilder
StringBuilder temp = new StringBuilder();
//比如digits如果为"23",num 为0,则str表示2对应的 abc
@@ -270,7 +272,7 @@ class Solution {
String str = numString[digits.charAt(num) - '0'];
for (int i = 0; i < str.length(); i++) {
temp.append(str.charAt(i));
- //c
+ //递归,处理下一层
backTracking(digits, numString, num + 1);
//剔除末尾的继续尝试
temp.deleteCharAt(temp.length() - 1);
@@ -279,120 +281,191 @@ class Solution {
}
```
-## Python
-**回溯**
+### Python
+回溯
```python
class Solution:
def __init__(self):
- self.answers: List[str] = []
- self.answer: str = ''
- self.letter_map = {
- '2': 'abc',
- '3': 'def',
- '4': 'ghi',
- '5': 'jkl',
- '6': 'mno',
- '7': 'pqrs',
- '8': 'tuv',
- '9': 'wxyz'
- }
-
- def letterCombinations(self, digits: str) -> List[str]:
- self.answers.clear()
- if not digits: return []
+ self.letterMap = [
+ "", # 0
+ "", # 1
+ "abc", # 2
+ "def", # 3
+ "ghi", # 4
+ "jkl", # 5
+ "mno", # 6
+ "pqrs", # 7
+ "tuv", # 8
+ "wxyz" # 9
+ ]
+ self.result = []
+ self.s = ""
+
+ def backtracking(self, digits, index):
+ if index == len(digits):
+ self.result.append(self.s)
+ return
+ digit = int(digits[index]) # 将索引处的数字转换为整数
+ letters = self.letterMap[digit] # 获取对应的字符集
+ for i in range(len(letters)):
+ self.s += letters[i] # 处理字符
+ self.backtracking(digits, index + 1) # 递归调用,注意索引加1,处理下一个数字
+ self.s = self.s[:-1] # 回溯,删除最后添加的字符
+
+ def letterCombinations(self, digits):
+ if len(digits) == 0:
+ return self.result
self.backtracking(digits, 0)
- return self.answers
+ return self.result
+
+```
+回溯精简(版本一)
+```python
+class Solution:
+ def __init__(self):
+ self.letterMap = [
+ "", # 0
+ "", # 1
+ "abc", # 2
+ "def", # 3
+ "ghi", # 4
+ "jkl", # 5
+ "mno", # 6
+ "pqrs", # 7
+ "tuv", # 8
+ "wxyz" # 9
+ ]
+ self.result = []
- def backtracking(self, digits: str, index: int) -> None:
- # 回溯函数没有返回值
- # Base Case
- if index == len(digits): # 当遍历穷尽后的下一层时
- self.answers.append(self.answer)
- return
- # 单层递归逻辑
- letters: str = self.letter_map[digits[index]]
+ def getCombinations(self, digits, index, s):
+ if index == len(digits):
+ self.result.append(s)
+ return
+ digit = int(digits[index])
+ letters = self.letterMap[digit]
for letter in letters:
- self.answer += letter # 处理
- self.backtracking(digits, index + 1) # 递归至下一层
- self.answer = self.answer[:-1] # 回溯
+ self.getCombinations(digits, index + 1, s + letter)
+
+ def letterCombinations(self, digits):
+ if len(digits) == 0:
+ return self.result
+ self.getCombinations(digits, 0, "")
+ return self.result
+
```
-**回溯简化**
+回溯精简(版本二)
```python
class Solution:
def __init__(self):
- self.answers: List[str] = []
- self.letter_map = {
- '2': 'abc',
- '3': 'def',
- '4': 'ghi',
- '5': 'jkl',
- '6': 'mno',
- '7': 'pqrs',
- '8': 'tuv',
- '9': 'wxyz'
- }
+ self.letterMap = [
+ "", # 0
+ "", # 1
+ "abc", # 2
+ "def", # 3
+ "ghi", # 4
+ "jkl", # 5
+ "mno", # 6
+ "pqrs", # 7
+ "tuv", # 8
+ "wxyz" # 9
+ ]
+
+ def getCombinations(self, digits, index, s, result):
+ if index == len(digits):
+ result.append(s)
+ return
+ digit = int(digits[index])
+ letters = self.letterMap[digit]
+ for letter in letters:
+ self.getCombinations(digits, index + 1, s + letter, result)
+
+ def letterCombinations(self, digits):
+ result = []
+ if len(digits) == 0:
+ return result
+ self.getCombinations(digits, 0, "", result)
+ return result
+
- def letterCombinations(self, digits: str) -> List[str]:
- self.answers.clear()
- if not digits: return []
- self.backtracking(digits, 0, '')
- return self.answers
+```
+
+回溯优化使用列表
+```python
+class Solution:
+ def __init__(self):
+ self.letterMap = [
+ "", # 0
+ "", # 1
+ "abc", # 2
+ "def", # 3
+ "ghi", # 4
+ "jkl", # 5
+ "mno", # 6
+ "pqrs", # 7
+ "tuv", # 8
+ "wxyz" # 9
+ ]
- def backtracking(self, digits: str, index: int, answer: str) -> None:
- # 回溯函数没有返回值
- # Base Case
- if index == len(digits): # 当遍历穷尽后的下一层时
- self.answers.append(answer)
- return
- # 单层递归逻辑
- letters: str = self.letter_map[digits[index]]
+ def getCombinations(self, digits, index, path, result):
+ if index == len(digits):
+ result.append(''.join(path))
+ return
+ digit = int(digits[index])
+ letters = self.letterMap[digit]
for letter in letters:
- self.backtracking(digits, index + 1, answer + letter) # 递归至下一层 + 回溯
+ path.append(letter)
+ self.getCombinations(digits, index + 1, path, result)
+ path.pop()
+
+ def letterCombinations(self, digits):
+ result = []
+ if len(digits) == 0:
+ return result
+ self.getCombinations(digits, 0, [], result)
+ return result
+
+
+
```
-## Go
+
+### Go
主要在于递归中传递下一个数字
```go
+var (
+ m []string
+ path []byte
+ res []string
+)
func letterCombinations(digits string) []string {
- lenth:=len(digits)
- if lenth==0 ||lenth>4{
- return nil
+ m = []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
+ path, res = make([]byte, 0), make([]string, 0)
+ if digits == "" {
+ return res
}
- digitsMap:= [10]string{
- "", // 0
- "", // 1
- "abc", // 2
- "def", // 3
- "ghi", // 4
- "jkl", // 5
- "mno", // 6
- "pqrs", // 7
- "tuv", // 8
- "wxyz", // 9
- }
- res:=make([]string,0)
- recursion("",digits,0,digitsMap,&res)
- return res
+ dfs(digits, 0)
+ return res
}
-func recursion(tempString ,digits string, Index int,digitsMap [10]string, res *[]string) {//index表示第几个数字
- if len(tempString)==len(digits){//终止条件,字符串长度等于digits的长度
- *res=append(*res,tempString)
+func dfs(digits string, start int) {
+ if len(path) == len(digits) { //终止条件,字符串长度等于digits的长度
+ tmp := string(path)
+ res = append(res, tmp)
return
}
- tmpK:=digits[Index]-'0' // 将index指向的数字转为int(确定下一个数字)
- letter:=digitsMap[tmpK]// 取数字对应的字符集
- for i:=0;i, s: &mut String, digits: &String, index: usize) {
+ let len = digits.len();
+ if len == index {
+ result.push(s.to_string());
+ return;
+ }
+ let digit = (digits.as_bytes()[index] - b'0') as usize;
+ for i in map[digit].chars() {
+ s.push(i);
+ Self::back_trace(result, s, digits, index + 1);
+ s.pop();
+ }
+ }
+ pub fn letter_combinations(digits: String) -> Vec {
+ if digits.is_empty() {
+ return vec![];
+ }
+ let mut res = vec![];
+ let mut s = String::new();
+ Self::back_trace(&mut res, &mut s, &digits, 0);
+ res
+ }
+}
+```
+
+### C
```c
char* path;
@@ -482,7 +620,7 @@ char ** letterCombinations(char * digits, int* returnSize){
}
```
-## Swift
+### Swift
```swift
func letterCombinations(_ digits: String) -> [String] {
@@ -523,6 +661,106 @@ func letterCombinations(_ digits: String) -> [String] {
}
```
+### Scala
+
+```scala
+object Solution {
+ import scala.collection.mutable
+ def letterCombinations(digits: String): List[String] = {
+ var result = mutable.ListBuffer[String]()
+ if(digits == "") return result.toList // 如果参数为空,返回空结果集的List形式
+ var path = mutable.ListBuffer[Char]()
+ // 数字和字符的映射关系
+ val map = Array[String]("", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz")
+
+ def backtracking(index: Int): Unit = {
+ if (index == digits.size) {
+ result.append(path.mkString) // mkString语法:将数组类型直接转换为字符串
+ return
+ }
+ var digit = digits(index) - '0' // 这里使用toInt会报错!必须 -'0'
+ for (i <- 0 until map(digit).size) {
+ path.append(map(digit)(i))
+ backtracking(index + 1)
+ path = path.take(path.size - 1)
+ }
+ }
+
+ backtracking(0)
+ result.toList
+ }
+}
+```
+
+### Ruby
+```ruby
+def letter_combinations(digits)
+ letter_map = {
+ 2 => ['a','b','c'],
+ 3 => ['d','e','f'],
+ 4 => ['g','h','i'],
+ 5 => ['j','k','l'],
+ 6 => ['m','n','o'],
+ 7 => ['p','q','r','s'],
+ 8 => ['t','u','v'],
+ 9 => ['w','x','y','z']
+ }
+
+ result = []
+ path = []
+
+ return result if digits.size == 0
+
+ backtracking(result, letter_map, digits.split(''), path, 0)
+ result
+end
+
+def backtracking(result, letter_map, digits, path, index)
+ if path.size == digits.size
+ result << path.join('')
+ return
+ end
+
+ hash[digits[index].to_i].each do |chr|
+ path << chr
+ #index + 1代表处理下一个数字
+ backtracking(result, letter_map, digits, path, index + 1)
+ #回溯,撤销处理过的数字
+ path.pop
+ end
+end
+```
+### C#
+```csharp
+public class Solution
+{
+ public IList res = new List();
+ public string s;
+ public string[] letterMap = new string[10] { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
+ public IList LetterCombinations(string digits)
+ {
+ if (digits.Length == 0)
+ return res;
+ BackTracking(digits, 0);
+ return res;
+ }
+ public void BackTracking(string digits, int index)
+ {
+ if (index == digits.Length)
+ {
+ res.Add(s);
+ return;
+ }
+ int digit = digits[index] - '0';
+ string letters = letterMap[digit];
+ for (int i = 0; i < letters.Length; i++)
+ {
+ s += letters[i];
+ BackTracking(digits, index + 1);
+ s = s.Substring(0, s.Length - 1);
+ }
+ }
+}
+```
+
------------------------
-
diff --git "a/problems/0018.\345\233\233\346\225\260\344\271\213\345\222\214.md" "b/problems/0018.\345\233\233\346\225\260\344\271\213\345\222\214.md"
old mode 100644
new mode 100755
index 7304254e54..bf7d3bd4ee
--- "a/problems/0018.\345\233\233\346\225\260\344\271\213\345\222\214.md"
+++ "b/problems/0018.\345\233\233\346\225\260\344\271\213\345\222\214.md"
@@ -1,8 +1,6 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
> 一样的道理,能解决四数之和
@@ -10,7 +8,7 @@
# 第18题. 四数之和
-[力扣题目链接](https://leetcode-cn.com/problems/4sum/)
+[力扣题目链接](https://leetcode.cn/problems/4sum/)
题意:给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
@@ -27,19 +25,23 @@
[-2, 0, 0, 2]
]
-# 思路
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[难在去重和剪枝!| LeetCode:18. 四数之和](https://www.bilibili.com/video/BV1DS4y147US),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+## 思路
四数之和,和[15.三数之和](https://programmercarl.com/0015.三数之和.html)是一个思路,都是使用双指针法, 基本解法就是在[15.三数之和](https://programmercarl.com/0015.三数之和.html) 的基础上再套一层for循环。
-但是有一些细节需要注意,例如: 不要判断`nums[k] > target` 就返回了,三数之和 可以通过 `nums[i] > 0` 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。(大家亲自写代码就能感受出来)
+但是有一些细节需要注意,例如: 不要判断`nums[k] > target` 就返回了,三数之和 可以通过 `nums[i] > 0` 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。比如:数组是`[-4, -3, -2, -1]`,`target`是`-10`,不能因为`-4 > -10`而跳过。但是我们依旧可以去做剪枝,逻辑变成`nums[k] > target && (nums[k] >=0 || target >= 0)`就可以了。
[15.三数之和](https://programmercarl.com/0015.三数之和.html)的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
-四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是$O(n^2)$,四数之和的时间复杂度是$O(n^3)$ 。
+四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2),四数之和的时间复杂度是O(n^3) 。
那么一样的道理,五数之和、六数之和等等都采用这种解法。
-对于[15.三数之和](https://programmercarl.com/0015.三数之和.html)双指针法就是将原本暴力$O(n^3)$的解法,降为$O(n^2)$的解法,四数之和的双指针解法就是将原本暴力$O(n^4)$的解法,降为$O(n^3)$的解法。
+对于[15.三数之和](https://programmercarl.com/0015.三数之和.html)双指针法就是将原本暴力O(n^3)的解法,降为O(n^2)的解法,四数之和的双指针解法就是将原本暴力O(n^4)的解法,降为O(n^3)的解法。
之前我们讲过哈希表的经典题目:[454.四数相加II](https://programmercarl.com/0454.四数相加II.html),相对于本题简单很多,因为本题是要求在一个集合中找出四个数相加等于target,同时四元组不能重复。
@@ -47,14 +49,13 @@
我们来回顾一下,几道题目使用了双指针法。
-双指针法将时间复杂度:$O(n^2)$的解法优化为 $O(n)$的解法。也就是降一个数量级,题目如下:
+双指针法将时间复杂度:O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,题目如下:
* [27.移除元素](https://programmercarl.com/0027.移除元素.html)
* [15.三数之和](https://programmercarl.com/0015.三数之和.html)
* [18.四数之和](https://programmercarl.com/0018.四数之和.html)
-
-操作链表:
+链表相关双指针题目:
* [206.反转链表](https://programmercarl.com/0206.翻转链表.html)
* [19.删除链表的倒数第N个节点](https://programmercarl.com/0019.删除链表的倒数第N个节点.html)
@@ -72,16 +73,21 @@ public:
vector> result;
sort(nums.begin(), nums.end());
for (int k = 0; k < nums.size(); k++) {
- // 这种剪枝是错误的,这道题目target 是任意值
- // if (nums[k] > target) {
- // return result;
- // }
- // 去重
+ // 剪枝处理
+ if (nums[k] > target && nums[k] >= 0) {
+ break; // 这里使用break,统一通过最后的return返回
+ }
+ // 对nums[k]去重
if (k > 0 && nums[k] == nums[k - 1]) {
continue;
}
for (int i = k + 1; i < nums.size(); i++) {
- // 正确去重方法
+ // 2级剪枝处理
+ if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {
+ break;
+ }
+
+ // 对nums[i]去重
if (i > k + 1 && nums[i] == nums[i - 1]) {
continue;
}
@@ -89,18 +95,14 @@ public:
int right = nums.size() - 1;
while (right > left) {
// nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
- if (nums[k] + nums[i] > target - (nums[left] + nums[right])) {
+ if ((long) nums[k] + nums[i] + nums[left] + nums[right] > target) {
right--;
- // 当前元素不合适了,可以去重
- while (left < right && nums[right] == nums[right + 1]) right--;
// nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出
- } else if (nums[k] + nums[i] < target - (nums[left] + nums[right])) {
+ } else if ((long) nums[k] + nums[i] + nums[left] + nums[right] < target) {
left++;
- // 不合适,去重
- while (left < right && nums[left] == nums[left - 1]) left++;
} else {
result.push_back(vector{nums[k], nums[i], nums[left], nums[right]});
- // 去重逻辑应该放在找到一个四元组之后
+ // 对nums[left]和nums[right]去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
@@ -119,86 +121,225 @@ public:
```
+* 时间复杂度: O(n^3)
+* 空间复杂度: O(1)
+
+
+## 补充
+
+二级剪枝的部分:
+
+```C++
+if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {
+ break;
+}
+```
+
+可以优化为:
+```C++
+if (nums[k] + nums[i] > target && nums[i] >= 0) {
+ break;
+}
+```
+因为只要 nums[k] + nums[i] > target,那么 nums[i] 后面的数都是正数的话,就一定 不符合条件了。
+不过这种剪枝 其实有点 小绕,大家能够理解 文章给的完整代码的剪枝 就够了。
## 其他语言版本
+### C:
-Java:
-```Java
-class Solution {
- public List> fourSum(int[] nums, int target) {
- List> result = new ArrayList<>();
- Arrays.sort(nums);
-
- for (int i = 0; i < nums.length; i++) {
+```C
+/* qsort */
+static int cmp(const void* arg1, const void* arg2) {
+ int a = *(int *)arg1;
+ int b = *(int *)arg2;
+ return (a > b);
+}
- if (i > 0 && nums[i - 1] == nums[i]) {
+int** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {
+
+ /* 对nums数组进行排序 */
+ qsort(nums, numsSize, sizeof(int), cmp);
+
+ int **res = (int **)malloc(sizeof(int *) * 40000);
+ int index = 0;
+
+ /* k */
+ for (int k = 0; k < numsSize - 3; k++) { /* 第一级 */
+
+ /* k剪枝 */
+ if ((nums[k] > target) && (nums[k] >= 0)) {
+ break;
+ }
+ /* k去重 */
+ if ((k > 0) && (nums[k] == nums[k - 1])) {
+ continue;
+ }
+
+ /* i */
+ for (int i = k + 1; i < numsSize - 2; i++) { /* 第二级 */
+
+ /* i剪枝 */
+ if ((nums[k] + nums[i] > target) && (nums[i] >= 0)) {
+ break;
+ }
+ /* i去重 */
+ if ((i > (k + 1)) && (nums[i] == nums[i - 1])) {
continue;
}
-
- for (int j = i + 1; j < nums.length; j++) {
- if (j > i + 1 && nums[j - 1] == nums[j]) {
- continue;
+ /* left and right */
+ int left = i + 1;
+ int right = numsSize - 1;
+
+ while (left < right) {
+
+ /* 防止大数溢出 */
+ long long val = (long long)nums[k] + nums[i] + nums[left] + nums[right];
+ if (val > target) {
+ right--;
+ } else if (val < target) {
+ left++;
+ } else {
+ int *res_tmp = (int *)malloc(sizeof(int) * 4);
+ res_tmp[0] = nums[k];
+ res_tmp[1] = nums[i];
+ res_tmp[2] = nums[left];
+ res_tmp[3] = nums[right];
+ res[index++] = res_tmp;
+
+ /* right去重 */
+ while ((right > left) && (nums[right] == nums[right - 1])) {
+ right--;
+ }
+ /* left去重 */
+ while ((left < right) && (nums[left] == nums[left + 1])) {
+ left++;
+ }
+
+ /* 更新right与left */
+ left++, right--;
}
+ }
+ }
+ }
- int left = j + 1;
+ /* 返回值处理 */
+ *returnSize = index;
+
+ int *column = (int *)malloc(sizeof(int) * index);
+ for (int i = 0; i < index; i++) {
+ column[i] = 4;
+ }
+ *returnColumnSizes = column;
+ return res;
+}
+```
+
+### Java:
+
+```Java
+import java.util.*;
+
+public class Solution {
+ public List> fourSum(int[] nums, int target) {
+ Arrays.sort(nums); // 排序数组
+ List> result = new ArrayList<>(); // 结果集
+ for (int k = 0; k < nums.length; k++) {
+ // 剪枝处理
+ if (nums[k] > target && nums[k] >= 0) {
+ break; // 此处的break可以等价于return result;
+ }
+ // 对nums[k]去重
+ if (k > 0 && nums[k] == nums[k - 1]) {
+ continue;
+ }
+ for (int i = k + 1; i < nums.length; i++) {
+ // 第二级剪枝
+ if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {
+ break; // 注意是break到上一级for循环,如果直接return result;会有遗漏
+ }
+ // 对nums[i]去重
+ if (i > k + 1 && nums[i] == nums[i - 1]) {
+ continue;
+ }
+ int left = i + 1;
int right = nums.length - 1;
while (right > left) {
- int sum = nums[i] + nums[j] + nums[left] + nums[right];
+ long sum = (long) nums[k] + nums[i] + nums[left] + nums[right];
if (sum > target) {
right--;
} else if (sum < target) {
left++;
} else {
- result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
-
+ result.add(Arrays.asList(nums[k], nums[i], nums[left], nums[right]));
+ // 对nums[left]和nums[right]去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
-
- left++;
right--;
+ left++;
}
}
}
}
return result;
}
+
+ public static void main(String[] args) {
+ Solution solution = new Solution();
+ int[] nums = {1, 0, -1, 0, -2, 2};
+ int target = 0;
+ List> results = solution.fourSum(nums, target);
+ for (List result : results) {
+ System.out.println(result);
+ }
+ }
}
```
-Python:
+### Python:
+(版本一) 双指针
+
```python
-# 双指针法
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
-
nums.sort()
n = len(nums)
- res = []
+ result = []
for i in range(n):
- if i > 0 and nums[i] == nums[i - 1]: continue
- for k in range(i+1, n):
- if k > i + 1 and nums[k] == nums[k-1]: continue
- p = k + 1
- q = n - 1
-
- while p < q:
- if nums[i] + nums[k] + nums[p] + nums[q] > target: q -= 1
- elif nums[i] + nums[k] + nums[p] + nums[q] < target: p += 1
+ if nums[i] > target and nums[i] > 0 and target > 0:# 剪枝(可省)
+ break
+ if i > 0 and nums[i] == nums[i-1]:# 去重
+ continue
+ for j in range(i+1, n):
+ if nums[i] + nums[j] > target and target > 0: #剪枝(可省)
+ break
+ if j > i+1 and nums[j] == nums[j-1]: # 去重
+ continue
+ left, right = j+1, n-1
+ while left < right:
+ s = nums[i] + nums[j] + nums[left] + nums[right]
+ if s == target:
+ result.append([nums[i], nums[j], nums[left], nums[right]])
+ while left < right and nums[left] == nums[left+1]:
+ left += 1
+ while left < right and nums[right] == nums[right-1]:
+ right -= 1
+ left += 1
+ right -= 1
+ elif s < target:
+ left += 1
else:
- res.append([nums[i], nums[k], nums[p], nums[q]])
- while p < q and nums[p] == nums[p + 1]: p += 1
- while p < q and nums[q] == nums[q - 1]: q -= 1
- p += 1
- q -= 1
- return res
+ right -= 1
+ return result
+
```
+(版本二) 使用字典
+
```python
-# 哈希表法
class Solution(object):
def fourSum(self, nums, target):
"""
@@ -206,39 +347,29 @@ class Solution(object):
:type target: int
:rtype: List[List[int]]
"""
- # use a dict to store value:showtimes
- hashmap = dict()
- for n in nums:
- if n in hashmap:
- hashmap[n] += 1
- else:
- hashmap[n] = 1
+ # 创建一个字典来存储输入列表中每个数字的频率
+ freq = {}
+ for num in nums:
+ freq[num] = freq.get(num, 0) + 1
- # good thing about using python is you can use set to drop duplicates.
+ # 创建一个集合来存储最终答案,并遍历4个数字的所有唯一组合
ans = set()
- # ans = [] # save results by list()
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
for k in range(j + 1, len(nums)):
val = target - (nums[i] + nums[j] + nums[k])
- if val in hashmap:
- # make sure no duplicates.
+ if val in freq:
+ # 确保没有重复
count = (nums[i] == val) + (nums[j] == val) + (nums[k] == val)
- if hashmap[val] > count:
- ans_tmp = tuple(sorted([nums[i], nums[j], nums[k], val]))
- ans.add(ans_tmp)
- # Avoiding duplication in list manner but it cause time complexity increases
- # if ans_tmp not in ans:
- # ans.append(ans_tmp)
- else:
- continue
- return list(ans)
- # if used list() to save results, just
- # return ans
+ if freq[val] > count:
+ ans.add(tuple(sorted([nums[i], nums[j], nums[k], val])))
+ return [list(x) for x in ans]
+
```
-Go:
+### Go:
+
```go
func fourSum(nums []int, target int) [][]int {
if len(nums) < 4 {
@@ -251,12 +382,12 @@ func fourSum(nums []int, target int) [][]int {
// if n1 > target { // 不能这样写,因为可能是负数
// break
// }
- if i > 0 && n1 == nums[i-1] {
+ if i > 0 && n1 == nums[i-1] { // 对nums[i]去重
continue
}
for j := i + 1; j < len(nums)-2; j++ {
n2 := nums[j]
- if j > i+1 && n2 == nums[j-1] {
+ if j > i+1 && n2 == nums[j-1] { // 对nums[j]去重
continue
}
l := j + 1
@@ -288,7 +419,7 @@ func fourSum(nums []int, target int) [][]int {
}
```
-javaScript:
+### JavaScript:
```js
/**
@@ -313,6 +444,8 @@ var fourSum = function(nums, target) {
if(sum < target) { l++; continue}
if(sum > target) { r--; continue}
res.push([nums[i], nums[j], nums[l], nums[r]]);
+
+ // 对nums[left]和nums[right]去重
while(l < r && nums[l] === nums[++l]);
while(l < r && nums[r] === nums[--r]);
}
@@ -322,7 +455,7 @@ var fourSum = function(nums, target) {
};
```
-TypeScript:
+### TypeScript:
```typescript
function fourSum(nums: number[], target: number): number[][] {
@@ -363,7 +496,7 @@ function fourSum(nums: number[], target: number): number[][] {
};
```
-PHP:
+### PHP:
```php
class Solution {
@@ -408,7 +541,8 @@ class Solution {
}
```
-Swift:
+### Swift:
+
```swift
func fourSum(_ nums: [Int], _ target: Int) -> [[Int]] {
var res = [[Int]]()
@@ -456,7 +590,8 @@ func fourSum(_ nums: [Int], _ target: Int) -> [[Int]] {
}
```
-C#:
+### C#:
+
```csharp
public class Solution
{
@@ -518,5 +653,147 @@ public class Solution
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 19.删除链表的倒数第N个节点
+# 19.删除链表的倒数第N个节点
-[力扣题目链接](https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/)
+[力扣题目链接](https://leetcode.cn/problems/remove-nth-node-from-end-of-list/)
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
@@ -17,42 +15,50 @@
示例 1:
-
+
+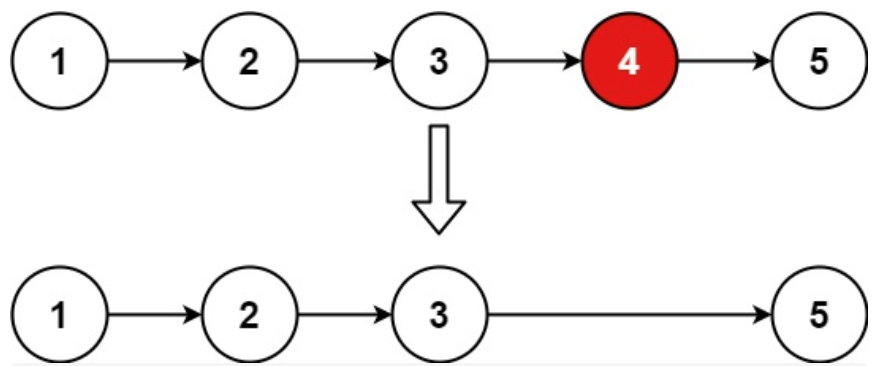
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
+
示例 2:
输入:head = [1], n = 1
输出:[]
+
示例 3:
输入:head = [1,2], n = 1
输出:[1]
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)::[链表遍历学清楚! | LeetCode:19.删除链表倒数第N个节点](https://www.bilibili.com/video/BV1vW4y1U7Gf),相信结合视频再看本篇题解,更有助于大家对链表的理解。**
+
## 思路
+
双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
思路是这样的,但要注意一些细节。
分为如下几步:
-* 首先这里我推荐大家使用虚拟头结点,这样方面处理删除实际头结点的逻辑,如果虚拟头结点不清楚,可以看这篇: [链表:听说用虚拟头节点会方便很多?](https://programmercarl.com/0203.移除链表元素.html)
+* 首先这里我推荐大家使用虚拟头结点,这样方便处理删除实际头结点的逻辑,如果虚拟头结点不清楚,可以看这篇: [链表:听说用虚拟头节点会方便很多?](https://programmercarl.com/0203.移除链表元素.html)
* 定义fast指针和slow指针,初始值为虚拟头结点,如图:
- +
+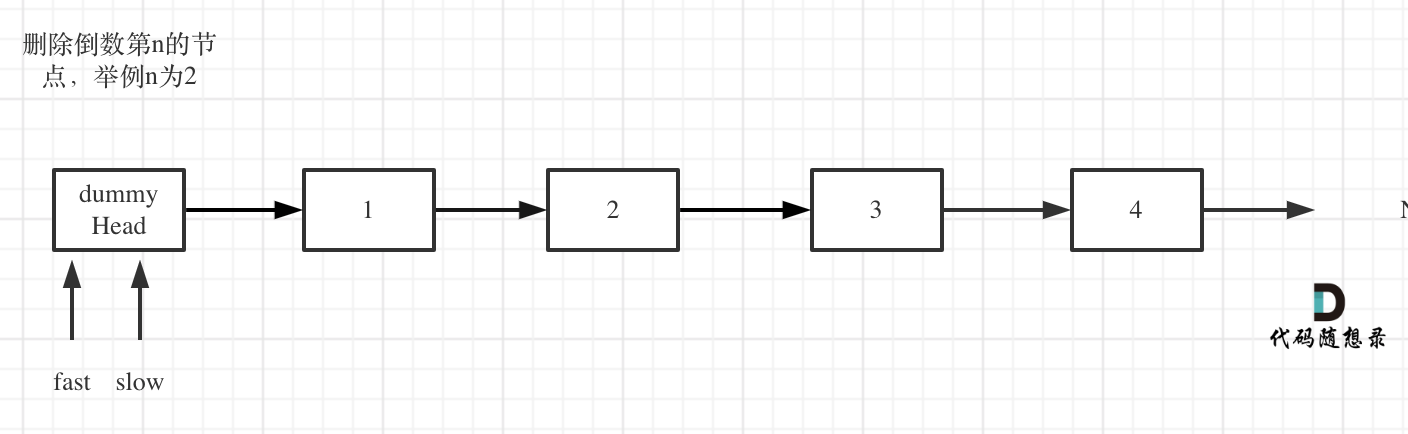 * fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
-
* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
- +
+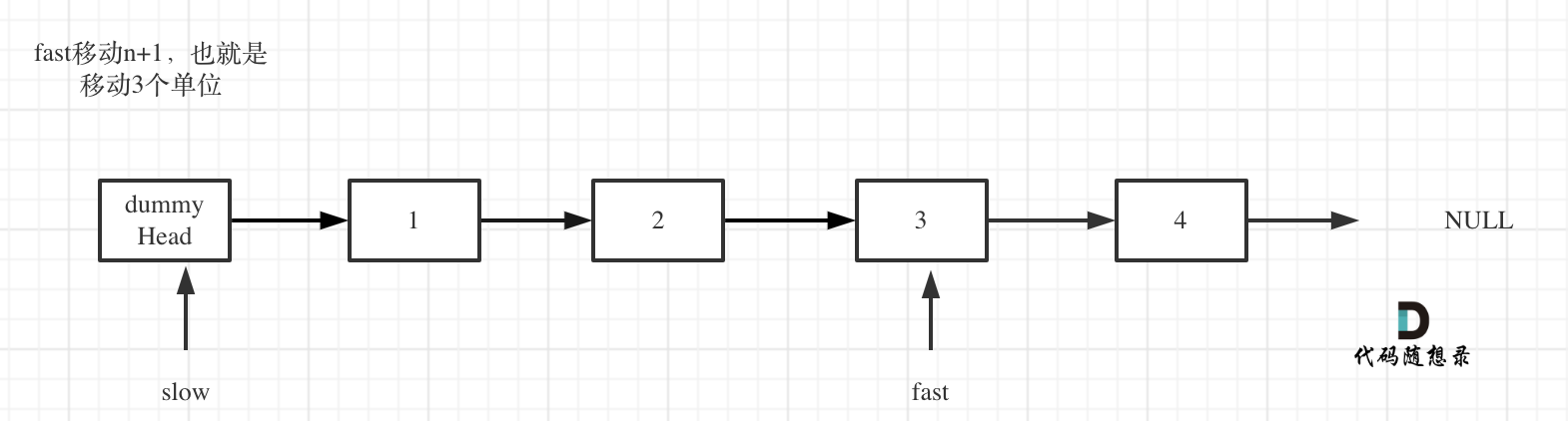 * fast和slow同时移动,直到fast指向末尾,如题:
-
* fast和slow同时移动,直到fast指向末尾,如题:
- -
+
-
+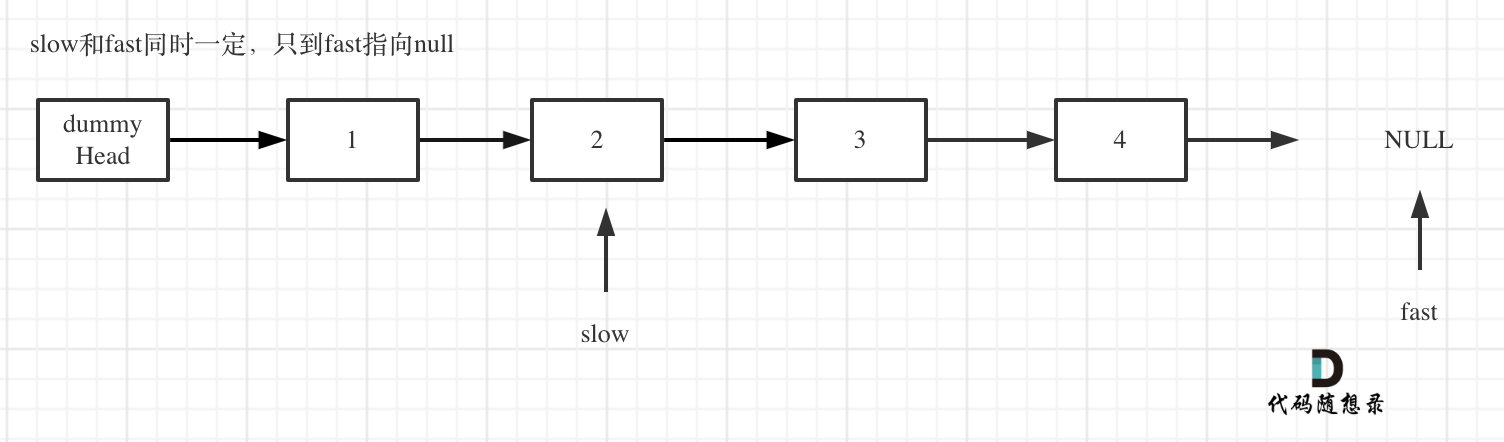 +//图片中有错别词:应该将“只到”改为“直到”
* 删除slow指向的下一个节点,如图:
-
+//图片中有错别词:应该将“只到”改为“直到”
* 删除slow指向的下一个节点,如图:
- +
+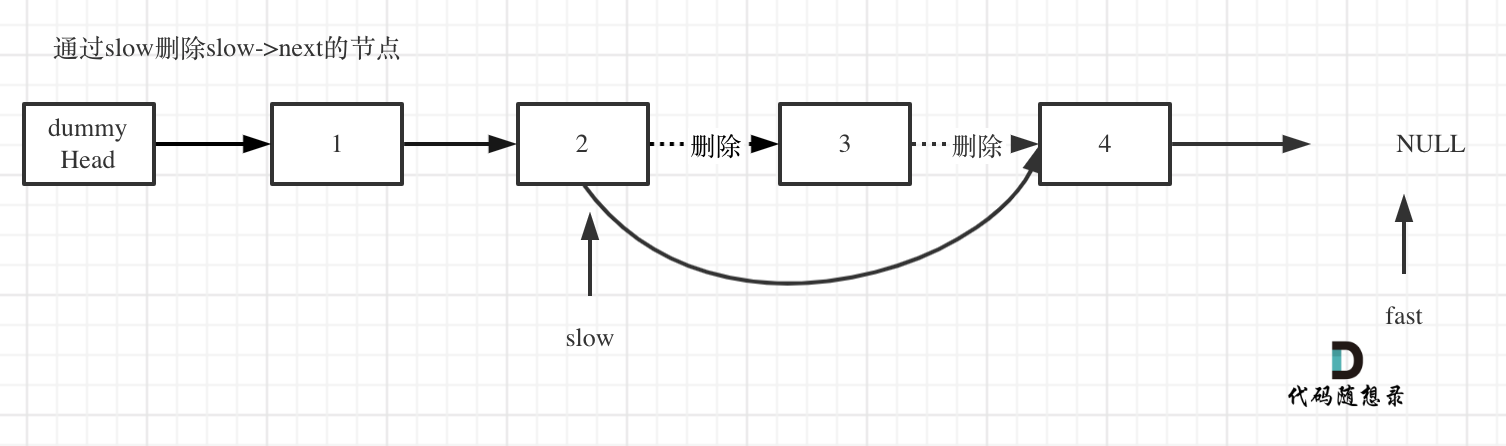 此时不难写出如下C++代码:
@@ -72,69 +78,119 @@ public:
fast = fast->next;
slow = slow->next;
}
- slow->next = slow->next->next;
+ slow->next = slow->next->next;
+
+ // ListNode *tmp = slow->next; C++释放内存的逻辑
+ // slow->next = tmp->next;
+ // delete tmp;
+
return dummyHead->next;
}
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
## 其他语言版本
-java:
+### Java:
```java
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
- ListNode dummy = new ListNode(-1);
- dummy.next = head;
-
- ListNode slow = dummy;
- ListNode fast = dummy;
- while (n-- > 0) {
- fast = fast.next;
+ //新建一个虚拟头节点指向head
+ ListNode dummyNode = new ListNode(0);
+ dummyNode.next = head;
+ //快慢指针指向虚拟头节点
+ ListNode fastIndex = dummyNode;
+ ListNode slowIndex = dummyNode;
+
+ // 只要快慢指针相差 n 个结点即可
+ for (int i = 0; i <= n; i++) {
+ fastIndex = fastIndex.next;
}
- // 记住 待删除节点slow 的上一节点
- ListNode prev = null;
- while (fast != null) {
- prev = slow;
- slow = slow.next;
- fast = fast.next;
+ while (fastIndex != null) {
+ fastIndex = fastIndex.next;
+ slowIndex = slowIndex.next;
}
- // 上一节点的next指针绕过 待删除节点slow 直接指向slow的下一节点
- prev.next = slow.next;
- // 释放 待删除节点slow 的next指针, 这句删掉也能AC
- slow.next = null;
- return dummy.next;
+ // 此时 slowIndex 的位置就是待删除元素的前一个位置。
+ // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
+ // 检查 slowIndex.next 是否为 null,以避免空指针异常
+ if (slowIndex.next != null) {
+ slowIndex.next = slowIndex.next.next;
+ }
+ return dummyNode.next;
}
}
```
-Python:
+
+```java
+class Solution {
+ public ListNode removeNthFromEnd(ListNode head, int n) {
+ // 创建一个新的哑节点,指向原链表头
+ ListNode s = new ListNode(-1, head);
+ // 递归调用remove方法,从哑节点开始进行删除操作
+ remove(s, n);
+ // 返回新链表的头(去掉可能的哑节点)
+ return s.next;
+ }
+
+ public int remove(ListNode p, int n) {
+ // 递归结束条件:如果当前节点为空,返回0
+ if (p == null) {
+ return 0;
+ }
+ // 递归深入到下一个节点
+ int net = remove(p.next, n);
+ // 如果当前节点是倒数第n个节点,进行删除操作
+ if (net == n) {
+ p.next = p.next.next;
+ }
+ // 返回当前节点的总深度
+ return net + 1;
+ }
+}
+```
+
+
+### Python:
+
```python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
+
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
- head_dummy = ListNode()
- head_dummy.next = head
-
- slow, fast = head_dummy, head_dummy
- while(n!=0): #fast先往前走n步
+ # 创建一个虚拟节点,并将其下一个指针设置为链表的头部
+ dummy_head = ListNode(0, head)
+
+ # 创建两个指针,慢指针和快指针,并将它们初始化为虚拟节点
+ slow = fast = dummy_head
+
+ # 快指针比慢指针快 n+1 步
+ for i in range(n+1):
fast = fast.next
- n -= 1
- while(fast.next!=None):
+
+ # 移动两个指针,直到快速指针到达链表的末尾
+ while fast:
slow = slow.next
fast = fast.next
- #fast 走到结尾后,slow的下一个节点为倒数第N个节点
- slow.next = slow.next.next #删除
- return head_dummy.next
+
+ # 通过更新第 (n-1) 个节点的 next 指针删除第 n 个节点
+ slow.next = slow.next.next
+
+ return dummy_head.next
+
```
-Go:
+### Go:
+
```Go
/**
* Definition for singly-linked list.
@@ -144,24 +200,21 @@ Go:
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
- dummyHead := &ListNode{}
- dummyHead.Next = head
- cur := head
- prev := dummyHead
- i := 1
- for cur != nil {
- cur = cur.Next
- if i > n {
- prev = prev.Next
- }
- i++
- }
- prev.Next = prev.Next.Next
- return dummyHead.Next
+ dummyNode := &ListNode{0, head}
+ fast, slow := dummyNode, dummyNode
+ for i := 0; i <= n; i++ { // 注意<=,否则快指针为空时,慢指针正好在倒数第n个上面
+ fast = fast.Next
+ }
+ for fast != nil {
+ fast = fast.Next
+ slow = slow.Next
+ }
+ slow.Next = slow.Next.Next
+ return dummyNode.Next
}
```
-JavaScript:
+### JavaScript:
```js
/**
@@ -169,37 +222,41 @@ JavaScript:
* @param {number} n
* @return {ListNode}
*/
-var removeNthFromEnd = function(head, n) {
- let ret = new ListNode(0, head),
- slow = fast = ret;
- while(n--) fast = fast.next;
- while (fast.next !== null) {
- fast = fast.next;
- slow = slow.next
- };
- slow.next = slow.next.next;
- return ret.next;
+var removeNthFromEnd = function (head, n) {
+ // 创建哨兵节点,简化解题逻辑
+ let dummyHead = new ListNode(0, head);
+ let fast = dummyHead;
+ let slow = dummyHead;
+ while (n--) fast = fast.next;
+ while (fast.next !== null) {
+ slow = slow.next;
+ fast = fast.next;
+ }
+ slow.next = slow.next.next;
+ return dummyHead.next;
};
```
-TypeScript:
+### TypeScript:
版本一(快慢指针法):
```typescript
function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
let newHead: ListNode | null = new ListNode(0, head);
- let slowNode: ListNode | null = newHead,
- fastNode: ListNode | null = newHead;
- for (let i = 0; i < n; i++) {
- fastNode = fastNode.next;
+ //根据leetcode题目的定义可推断这里快慢指针均不需要定义为ListNode | null。
+ let slowNode: ListNode = newHead;
+ let fastNode: ListNode = newHead;
+
+ while(n--) {
+ fastNode = fastNode.next!; //由虚拟头节点前进n个节点时,fastNode.next可推断不为null。
}
- while (fastNode.next) {
+ while(fastNode.next) { //遍历直至fastNode.next = null, 即尾部节点。 此时slowNode指向倒数第n个节点。
fastNode = fastNode.next;
- slowNode = slowNode.next;
+ slowNode = slowNode.next!;
}
- slowNode.next = slowNode.next.next;
- return newHead.next;
-};
+ slowNode.next = slowNode.next!.next; //倒数第n个节点可推断其next节点不为空。
+ return newHead.next;
+}
```
版本二(计算节点总数法):
@@ -244,7 +301,7 @@ function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
};
```
-Kotlin:
+### Kotlin:
```Kotlin
fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
@@ -265,7 +322,8 @@ fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
if head == nil {
@@ -290,5 +348,132 @@ func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
}
```
------------------------
-
此时不难写出如下C++代码:
@@ -72,69 +78,119 @@ public:
fast = fast->next;
slow = slow->next;
}
- slow->next = slow->next->next;
+ slow->next = slow->next->next;
+
+ // ListNode *tmp = slow->next; C++释放内存的逻辑
+ // slow->next = tmp->next;
+ // delete tmp;
+
return dummyHead->next;
}
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
## 其他语言版本
-java:
+### Java:
```java
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
- ListNode dummy = new ListNode(-1);
- dummy.next = head;
-
- ListNode slow = dummy;
- ListNode fast = dummy;
- while (n-- > 0) {
- fast = fast.next;
+ //新建一个虚拟头节点指向head
+ ListNode dummyNode = new ListNode(0);
+ dummyNode.next = head;
+ //快慢指针指向虚拟头节点
+ ListNode fastIndex = dummyNode;
+ ListNode slowIndex = dummyNode;
+
+ // 只要快慢指针相差 n 个结点即可
+ for (int i = 0; i <= n; i++) {
+ fastIndex = fastIndex.next;
}
- // 记住 待删除节点slow 的上一节点
- ListNode prev = null;
- while (fast != null) {
- prev = slow;
- slow = slow.next;
- fast = fast.next;
+ while (fastIndex != null) {
+ fastIndex = fastIndex.next;
+ slowIndex = slowIndex.next;
}
- // 上一节点的next指针绕过 待删除节点slow 直接指向slow的下一节点
- prev.next = slow.next;
- // 释放 待删除节点slow 的next指针, 这句删掉也能AC
- slow.next = null;
- return dummy.next;
+ // 此时 slowIndex 的位置就是待删除元素的前一个位置。
+ // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
+ // 检查 slowIndex.next 是否为 null,以避免空指针异常
+ if (slowIndex.next != null) {
+ slowIndex.next = slowIndex.next.next;
+ }
+ return dummyNode.next;
}
}
```
-Python:
+
+```java
+class Solution {
+ public ListNode removeNthFromEnd(ListNode head, int n) {
+ // 创建一个新的哑节点,指向原链表头
+ ListNode s = new ListNode(-1, head);
+ // 递归调用remove方法,从哑节点开始进行删除操作
+ remove(s, n);
+ // 返回新链表的头(去掉可能的哑节点)
+ return s.next;
+ }
+
+ public int remove(ListNode p, int n) {
+ // 递归结束条件:如果当前节点为空,返回0
+ if (p == null) {
+ return 0;
+ }
+ // 递归深入到下一个节点
+ int net = remove(p.next, n);
+ // 如果当前节点是倒数第n个节点,进行删除操作
+ if (net == n) {
+ p.next = p.next.next;
+ }
+ // 返回当前节点的总深度
+ return net + 1;
+ }
+}
+```
+
+
+### Python:
+
```python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
+
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
- head_dummy = ListNode()
- head_dummy.next = head
-
- slow, fast = head_dummy, head_dummy
- while(n!=0): #fast先往前走n步
+ # 创建一个虚拟节点,并将其下一个指针设置为链表的头部
+ dummy_head = ListNode(0, head)
+
+ # 创建两个指针,慢指针和快指针,并将它们初始化为虚拟节点
+ slow = fast = dummy_head
+
+ # 快指针比慢指针快 n+1 步
+ for i in range(n+1):
fast = fast.next
- n -= 1
- while(fast.next!=None):
+
+ # 移动两个指针,直到快速指针到达链表的末尾
+ while fast:
slow = slow.next
fast = fast.next
- #fast 走到结尾后,slow的下一个节点为倒数第N个节点
- slow.next = slow.next.next #删除
- return head_dummy.next
+
+ # 通过更新第 (n-1) 个节点的 next 指针删除第 n 个节点
+ slow.next = slow.next.next
+
+ return dummy_head.next
+
```
-Go:
+### Go:
+
```Go
/**
* Definition for singly-linked list.
@@ -144,24 +200,21 @@ Go:
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
- dummyHead := &ListNode{}
- dummyHead.Next = head
- cur := head
- prev := dummyHead
- i := 1
- for cur != nil {
- cur = cur.Next
- if i > n {
- prev = prev.Next
- }
- i++
- }
- prev.Next = prev.Next.Next
- return dummyHead.Next
+ dummyNode := &ListNode{0, head}
+ fast, slow := dummyNode, dummyNode
+ for i := 0; i <= n; i++ { // 注意<=,否则快指针为空时,慢指针正好在倒数第n个上面
+ fast = fast.Next
+ }
+ for fast != nil {
+ fast = fast.Next
+ slow = slow.Next
+ }
+ slow.Next = slow.Next.Next
+ return dummyNode.Next
}
```
-JavaScript:
+### JavaScript:
```js
/**
@@ -169,37 +222,41 @@ JavaScript:
* @param {number} n
* @return {ListNode}
*/
-var removeNthFromEnd = function(head, n) {
- let ret = new ListNode(0, head),
- slow = fast = ret;
- while(n--) fast = fast.next;
- while (fast.next !== null) {
- fast = fast.next;
- slow = slow.next
- };
- slow.next = slow.next.next;
- return ret.next;
+var removeNthFromEnd = function (head, n) {
+ // 创建哨兵节点,简化解题逻辑
+ let dummyHead = new ListNode(0, head);
+ let fast = dummyHead;
+ let slow = dummyHead;
+ while (n--) fast = fast.next;
+ while (fast.next !== null) {
+ slow = slow.next;
+ fast = fast.next;
+ }
+ slow.next = slow.next.next;
+ return dummyHead.next;
};
```
-TypeScript:
+### TypeScript:
版本一(快慢指针法):
```typescript
function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
let newHead: ListNode | null = new ListNode(0, head);
- let slowNode: ListNode | null = newHead,
- fastNode: ListNode | null = newHead;
- for (let i = 0; i < n; i++) {
- fastNode = fastNode.next;
+ //根据leetcode题目的定义可推断这里快慢指针均不需要定义为ListNode | null。
+ let slowNode: ListNode = newHead;
+ let fastNode: ListNode = newHead;
+
+ while(n--) {
+ fastNode = fastNode.next!; //由虚拟头节点前进n个节点时,fastNode.next可推断不为null。
}
- while (fastNode.next) {
+ while(fastNode.next) { //遍历直至fastNode.next = null, 即尾部节点。 此时slowNode指向倒数第n个节点。
fastNode = fastNode.next;
- slowNode = slowNode.next;
+ slowNode = slowNode.next!;
}
- slowNode.next = slowNode.next.next;
- return newHead.next;
-};
+ slowNode.next = slowNode.next!.next; //倒数第n个节点可推断其next节点不为空。
+ return newHead.next;
+}
```
版本二(计算节点总数法):
@@ -244,7 +301,7 @@ function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
};
```
-Kotlin:
+### Kotlin:
```Kotlin
fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
@@ -265,7 +322,8 @@ fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
if head == nil {
@@ -290,5 +348,132 @@ func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
@@ -10,7 +8,7 @@
# 20. 有效的括号
-[力扣题目链接](https://leetcode-cn.com/problems/valid-parentheses/)
+[力扣题目链接](https://leetcode.cn/problems/valid-parentheses/)
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
@@ -39,9 +37,13 @@
* 输入: "{[]}"
* 输出: true
-# 思路
+## 算法公开课
-## 题外话
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[栈的拿手好戏!| LeetCode:20. 有效的括号](https://www.bilibili.com/video/BV1AF411w78g),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+## 思路
+
+### 题外话
**括号匹配是使用栈解决的经典问题。**
@@ -65,7 +67,7 @@ cd a/b/c/../../
这里我就不过多展开了,先来看题。
-## 进入正题
+### 进入正题
由于栈结构的特殊性,非常适合做对称匹配类的题目。
@@ -73,22 +75,27 @@ cd a/b/c/../../
**一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越乱。**
-建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
+建议在写代码之前要分析好有哪几种不匹配的情况,如果不在动手之前分析好,写出的代码也会有很多问题。
先来分析一下 这里有三种不匹配的情况,
+
1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
-
+
+
2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
-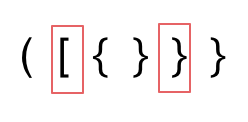
+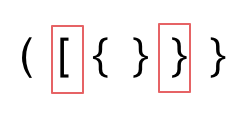
+
3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
-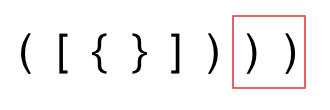
+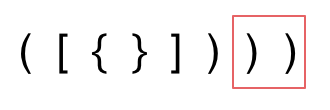
+
+
我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
动画如下:
-
+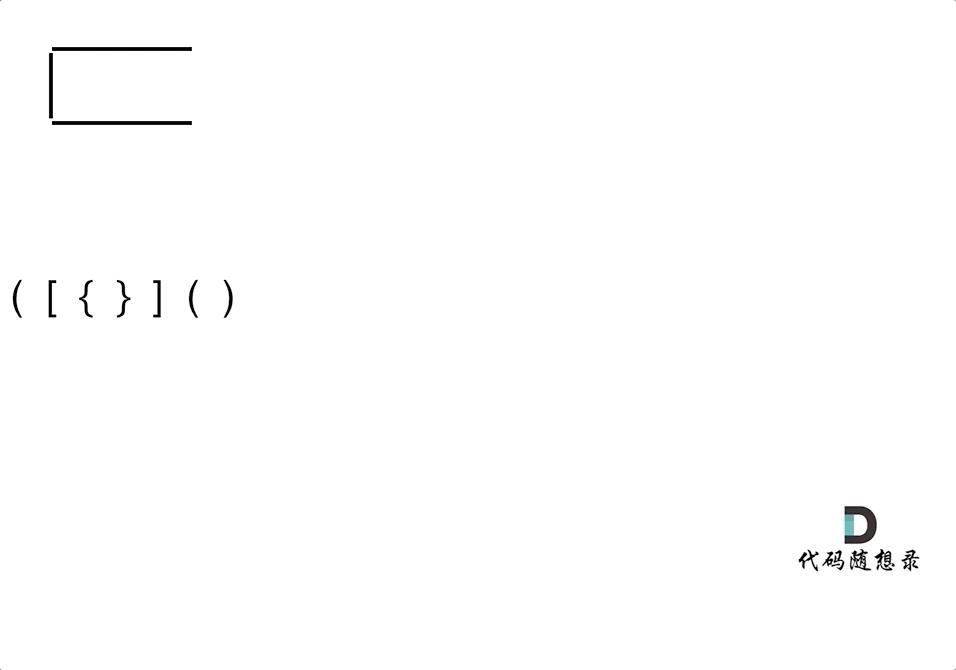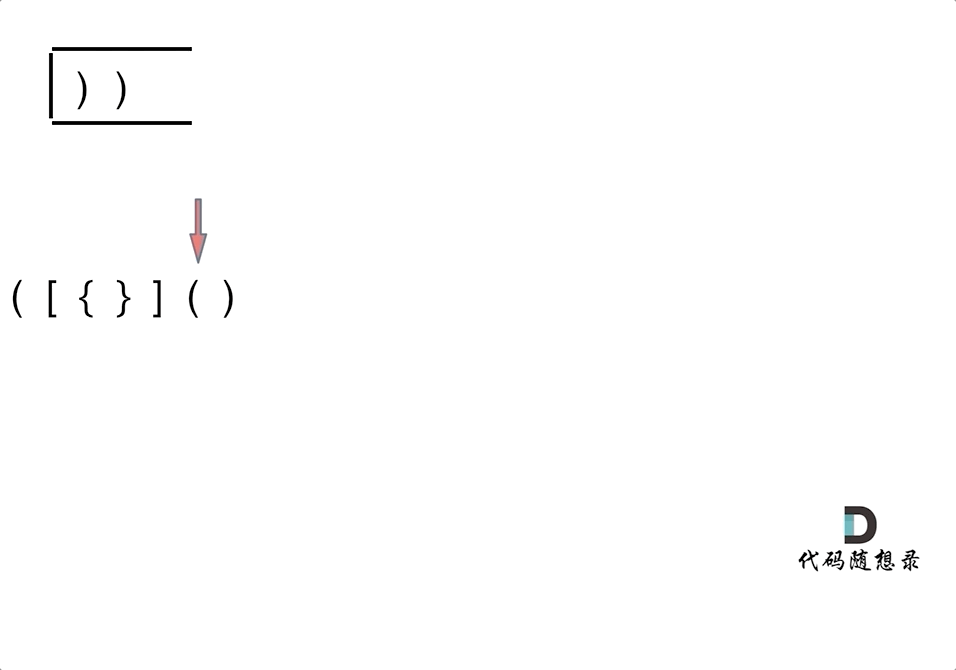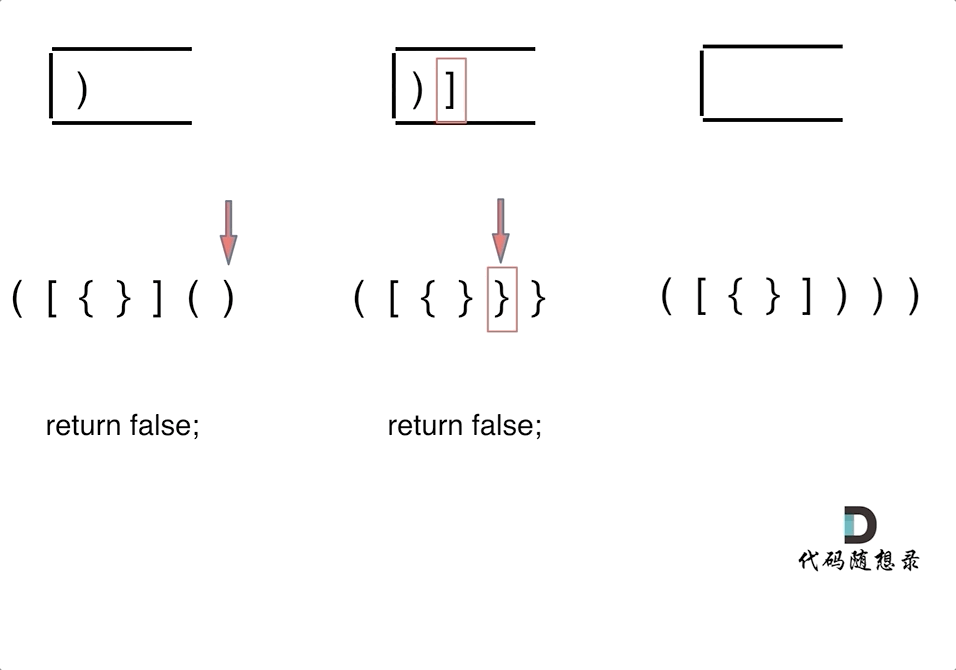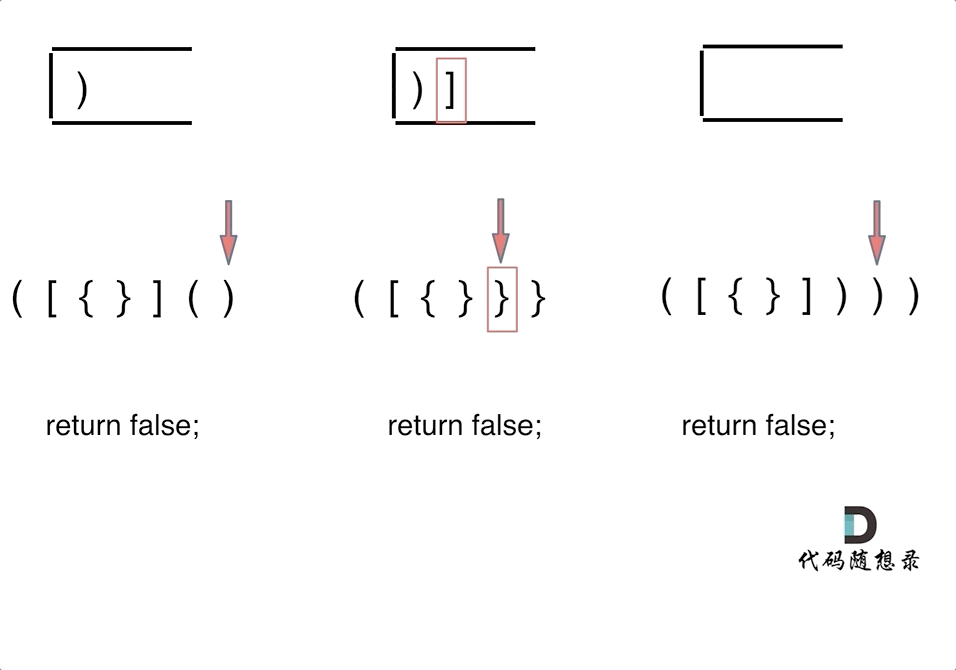
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
@@ -110,7 +117,8 @@ cd a/b/c/../../
class Solution {
public:
bool isValid(string s) {
- stack st;
+ if (s.size() % 2 != 0) return false; // 如果s的长度为奇数,一定不符合要求
+ stack st;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') st.push(')');
else if (s[i] == '{') st.push('}');
@@ -124,14 +132,18 @@ public:
return st.empty();
}
};
+
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(n)
+
技巧性的东西没有固定的学习方法,还是要多看多练,自己灵活运用了。
## 其他语言版本
+### Java:
-Java:
```Java
class Solution {
public boolean isValid(String s) {
@@ -152,13 +164,37 @@ class Solution {
deque.pop();
}
}
- //最后判断栈中元素是否匹配
+ //遍历结束,如果栈为空,则括号全部匹配
return deque.isEmpty();
}
}
```
-Python:
+```java
+// 解法二
+// 对应的另一半一定在栈顶
+class Solution {
+ public boolean isValid(String s) {
+ Stack stack = new Stack<>();
+ for(char c : s.toCharArray()){
+ // 有对应的另一半就直接消消乐
+ if(c == ')' && !stack.isEmpty() && stack.peek() == '(')
+ stack.pop();
+ else if(c == '}' && !stack.isEmpty() && stack.peek() == '{')
+ stack.pop();
+ else if(c == ']' && !stack.isEmpty() && stack.peek() == '[')
+ stack.pop();
+ else
+ stack.push(c);// 没有匹配的就放进去
+ }
+
+ return stack.isEmpty();
+ }
+}
+```
+
+### Python:
+
```python
# 方法一,仅使用栈,更省空间
class Solution:
@@ -200,29 +236,49 @@ class Solution:
return True if not stack else False
```
-Go:
+### Go:
+
```Go
+// 思路: 使用栈来进行括号的匹配
+// 时间复杂度 O(n)
+// 空间复杂度 O(n)
func isValid(s string) bool {
- hash := map[byte]byte{')':'(', ']':'[', '}':'{'}
- stack := make([]byte, 0)
- if s == "" {
- return true
- }
-
- for i := 0; i < len(s); i++ {
- if s[i] == '(' || s[i] == '[' || s[i] == '{' {
- stack = append(stack, s[i])
- } else if len(stack) > 0 && stack[len(stack)-1] == hash[s[i]] {
- stack = stack[:len(stack)-1]
- } else {
- return false
- }
- }
- return len(stack) == 0
+ // 使用切片模拟栈的行为
+ stack := make([]rune, 0)
+
+ // m 用于记录某个右括号对应的左括号
+ m := make(map[rune]rune)
+ m[')'] = '('
+ m[']'] = '['
+ m['}'] = '{'
+
+ // 遍历字符串中的 rune
+ for _, c := range s {
+ // 左括号直接入栈
+ if c == '(' || c == '[' || c == '{' {
+ stack = append(stack, c)
+ } else {
+ // 如果是右括号,先判断栈内是否还有元素
+ if len(stack) == 0 {
+ return false
+ }
+ // 再判断栈顶元素是否能够匹配
+ peek := stack[len(stack)-1]
+ if peek != m[c] {
+ return false
+ }
+ // 模拟栈顶弹出
+ stack = stack[:len(stack)-1]
+ }
+ }
+
+ // 若栈中不再包含元素,则能完全匹配
+ return len(stack) == 0
}
```
-Ruby:
+### Ruby:
+
```ruby
def is_valid(strs)
symbol_map = {')' => '(', '}' => '{', ']' => '['}
@@ -240,7 +296,8 @@ def is_valid(strs)
end
```
-Javascript:
+### JavaScript:
+
```javascript
var isValid = function (s) {
const stack = [];
@@ -283,7 +340,7 @@ var isValid = function(s) {
};
```
-TypeScript:
+### TypeScript:
版本一:普通版
@@ -335,7 +392,7 @@ function isValid(s: string): boolean {
};
```
-Swift
+### Swift:
```swift
func isValid(_ s: String) -> Bool {
@@ -360,7 +417,8 @@ func isValid(_ s: String) -> Bool {
}
```
-C:
+### C:
+
```C
//辅助函数:判断栈顶元素与输入的括号是否为一对。若不是,则返回False
int notMatch(char par, char* stack, int stackTop) {
@@ -401,5 +459,117 @@ bool isValid(char * s){
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 24. 两两交换链表中的节点
+# 24. 两两交换链表中的节点
-[力扣题目链接](https://leetcode-cn.com/problems/swap-nodes-in-pairs/)
+[力扣题目链接](https://leetcode.cn/problems/swap-nodes-in-pairs/)
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
- +
+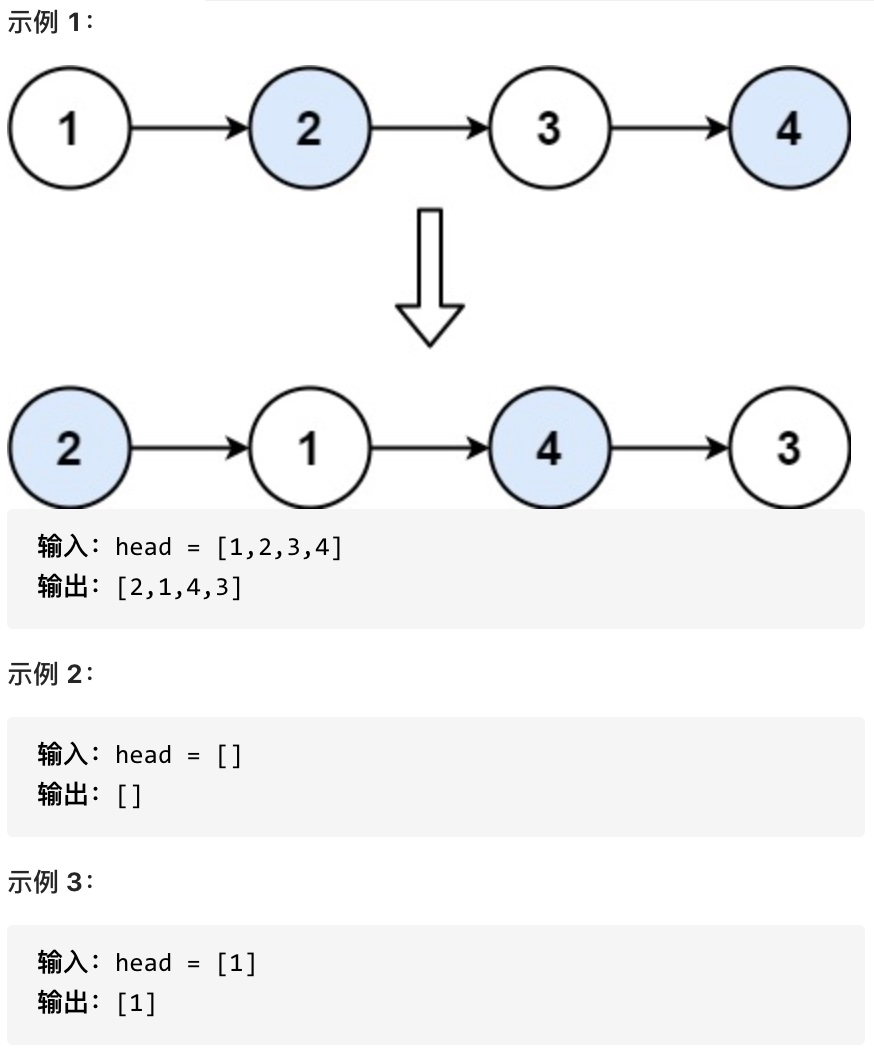 +
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[帮你把链表细节学清楚! | LeetCode:24. 两两交换链表中的节点](https://www.bilibili.com/video/BV1YT411g7br),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
+
这道题目正常模拟就可以了。
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
@@ -28,16 +31,16 @@
初始时,cur指向虚拟头结点,然后进行如下三步:
-
+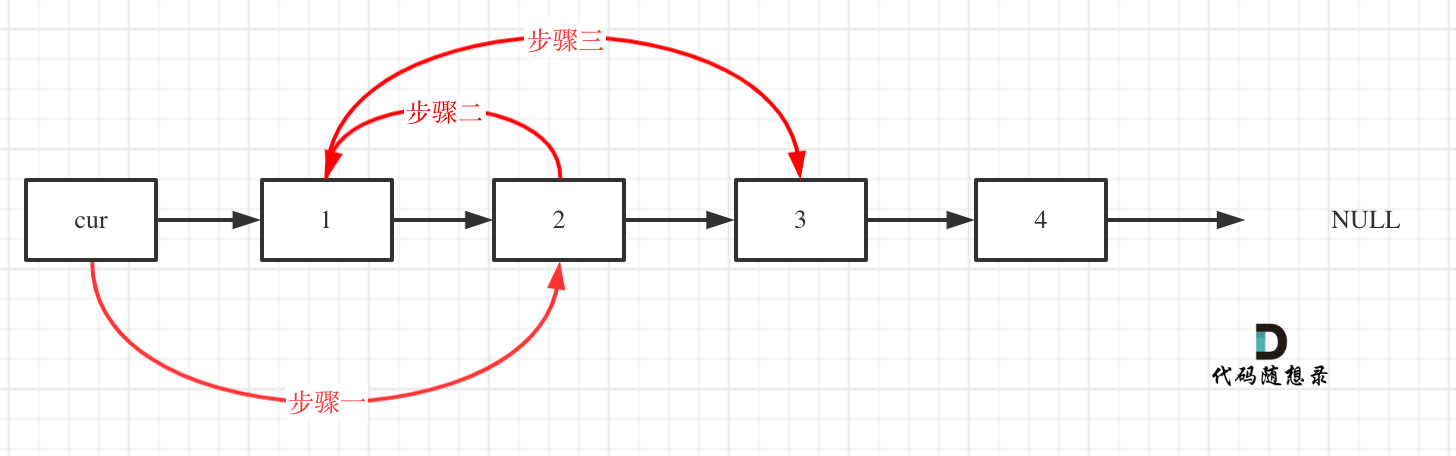
操作之后,链表如下:
-
+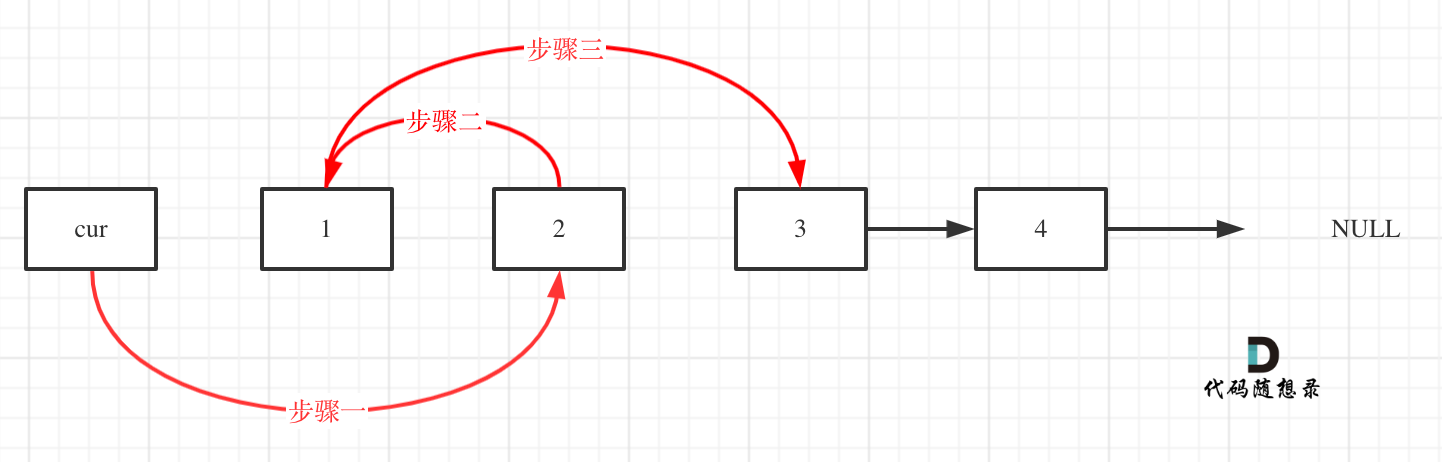
看这个可能就更直观一些了:
-
+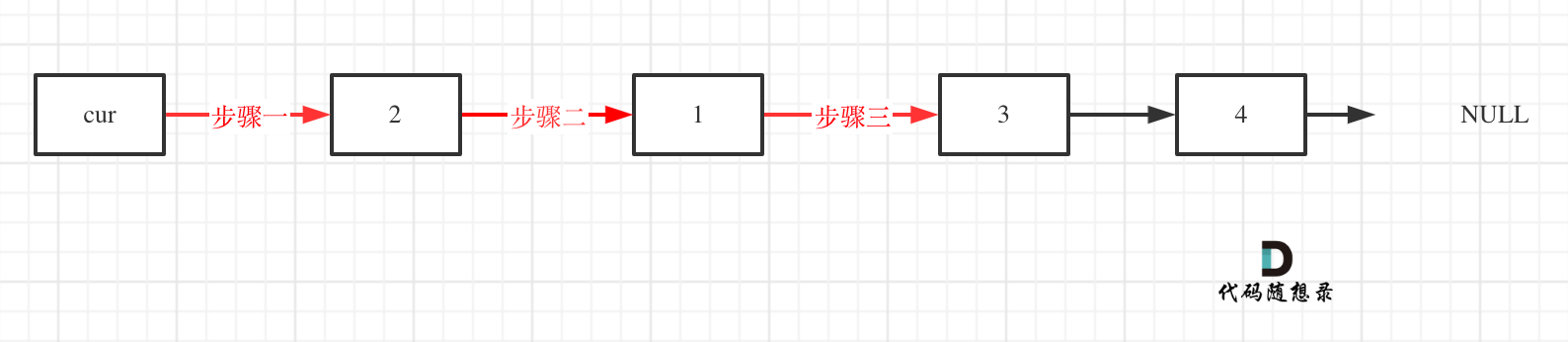
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
@@ -46,7 +49,7 @@ class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
+ dummyHead->next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
@@ -58,13 +61,15 @@ public:
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
- return dummyHead->next;
+ ListNode* result = dummyHead->next;
+ delete dummyHead;
+ return result;
}
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
## 拓展
@@ -74,9 +79,9 @@ public:
上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-心想应该没有更好的方法了吧,也就$O(n)$的时间复杂度,重复提交几次,这样了:
+心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:
-
+
力扣上的统计如果两份代码是 100ms 和 300ms的耗时,其实是需要注意的。
@@ -85,7 +90,8 @@ public:
## 其他语言版本
-C:
+### C:
+
```c
/**
* Definition for singly-linked list.
@@ -129,7 +135,7 @@ struct ListNode* swapPairs(struct ListNode* head){
}
```
-Java:
+### Java:
```Java
// 递归版本
@@ -151,28 +157,71 @@ class Solution {
```
```java
-// 虚拟头结点
class Solution {
public ListNode swapPairs(ListNode head) {
+ ListNode dumyhead = new ListNode(-1); // 设置一个虚拟头结点
+ dumyhead.next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
+ ListNode cur = dumyhead;
+ ListNode temp; // 临时节点,保存两个节点后面的节点
+ ListNode firstnode; // 临时节点,保存两个节点之中的第一个节点
+ ListNode secondnode; // 临时节点,保存两个节点之中的第二个节点
+ while (cur.next != null && cur.next.next != null) {
+ temp = cur.next.next.next;
+ firstnode = cur.next;
+ secondnode = cur.next.next;
+ cur.next = secondnode; // 步骤一
+ secondnode.next = firstnode; // 步骤二
+ firstnode.next = temp; // 步骤三
+ cur = firstnode; // cur移动,准备下一轮交换
+ }
+ return dumyhead.next;
+ }
+}
+```
- ListNode dummyNode = new ListNode(0);
- dummyNode.next = head;
- ListNode prev = dummyNode;
-
- while (prev.next != null && prev.next.next != null) {
- ListNode temp = head.next.next; // 缓存 next
- prev.next = head.next; // 将 prev 的 next 改为 head 的 next
- head.next.next = head; // 将 head.next(prev.next) 的next,指向 head
- head.next = temp; // 将head 的 next 接上缓存的temp
- prev = head; // 步进1位
- head = head.next; // 步进1位
+```java
+// 将步骤 2,3 交换顺序,这样不用定义 temp 节点
+public ListNode swapPairs(ListNode head) {
+ ListNode dummy = new ListNode(0, head);
+ ListNode cur = dummy;
+ while (cur.next != null && cur.next.next != null) {
+ ListNode node1 = cur.next;// 第 1 个节点
+ ListNode node2 = cur.next.next;// 第 2 个节点
+ cur.next = node2; // 步骤 1
+ node1.next = node2.next;// 步骤 3
+ node2.next = node1;// 步骤 2
+ cur = cur.next.next;
}
- return dummyNode.next;
- }
+ return dummy.next;
}
```
-Python:
+### Python:
+
+```python
+# 递归版本
+# Definition for singly-linked list.
+# class ListNode:
+# def __init__(self, val=0, next=None):
+# self.val = val
+# self.next = next
+
+class Solution:
+ def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
+ if head is None or head.next is None:
+ return head
+
+ # 待翻转的两个node分别是pre和cur
+ pre = head
+ cur = head.next
+ next = head.next.next
+
+ cur.next = pre # 交换
+ pre.next = self.swapPairs(next) # 将以next为head的后续链表两两交换
+
+ return cur
+```
+
```python
# Definition for singly-linked list.
# class ListNode:
@@ -182,24 +231,24 @@ Python:
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
- res = ListNode(next=head)
- pre = res
+ dummy_head = ListNode(next=head)
+ current = dummy_head
- # 必须有pre的下一个和下下个才能交换,否则说明已经交换结束了
- while pre.next and pre.next.next:
- cur = pre.next
- post = pre.next.next
+ # 必须有cur的下一个和下下个才能交换,否则说明已经交换结束了
+ while current.next and current.next.next:
+ temp = current.next # 防止节点修改
+ temp1 = current.next.next.next
- # pre,cur,post对应最左,中间的,最右边的节点
- cur.next = post.next
- post.next = cur
- pre.next = post
+ current.next = current.next.next
+ current.next.next = temp
+ temp.next = temp1
+ current = current.next.next
+ return dummy_head.next
- pre = pre.next.next
- return res.next
```
-Go:
+### Go:
+
```go
func swapPairs(head *ListNode) *ListNode {
dummy := &ListNode{
@@ -235,7 +284,8 @@ func swapPairs(head *ListNode) *ListNode {
}
```
-Javascript:
+### JavaScript:
+
```javascript
var swapPairs = function (head) {
let ret = new ListNode(0, head), temp = ret;
@@ -250,27 +300,41 @@ var swapPairs = function (head) {
};
```
-TypeScript:
+```javascript
+// 递归版本
+var swapPairs = function (head) {
+ if (head == null || head.next == null) {
+ return head;
+ }
+
+ let after = head.next;
+ head.next = swapPairs(after.next);
+ after.next = head;
+
+ return after;
+};
+```
+
+### TypeScript:
```typescript
function swapPairs(head: ListNode | null): ListNode | null {
- const dummyHead: ListNode = new ListNode(0, head);
- let cur: ListNode = dummyHead;
- while(cur.next !== null && cur.next.next !== null) {
- const tem: ListNode = cur.next;
- const tem1: ListNode = cur.next.next.next;
-
- cur.next = cur.next.next; // step 1
- cur.next.next = tem; // step 2
- cur.next.next.next = tem1; // step 3
-
- cur = cur.next.next;
- }
- return dummyHead.next;
-}
+ const dummyNode: ListNode = new ListNode(0, head);
+ let curNode: ListNode | null = dummyNode;
+ while (curNode && curNode.next && curNode.next.next) {
+ let firstNode: ListNode = curNode.next,
+ secNode: ListNode = curNode.next.next,
+ thirdNode: ListNode | null = curNode.next.next.next;
+ curNode.next = secNode;
+ secNode.next = firstNode;
+ firstNode.next = thirdNode;
+ curNode = firstNode;
+ }
+ return dummyNode.next;
+};
```
-Kotlin:
+### Kotlin:
```kotlin
fun swapPairs(head: ListNode?): ListNode? {
@@ -290,7 +354,8 @@ fun swapPairs(head: ListNode?): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func swapPairs(_ head: ListNode?) -> ListNode? {
if head == nil || head?.next == nil {
@@ -311,7 +376,152 @@ func swapPairs(_ head: ListNode?) -> ListNode? {
return dummyHead.next
}
```
+### Scala:
+
+```scala
+// 虚拟头节点
+object Solution {
+ def swapPairs(head: ListNode): ListNode = {
+ var dummy = new ListNode(0, head) // 虚拟头节点
+ var pre = dummy
+ var cur = head
+ // 当pre的下一个和下下个都不为空,才进行两两转换
+ while (pre.next != null && pre.next.next != null) {
+ var tmp: ListNode = cur.next.next // 缓存下一次要进行转换的第一个节点
+ pre.next = cur.next // 步骤一
+ cur.next.next = cur // 步骤二
+ cur.next = tmp // 步骤三
+ // 下面是准备下一轮的交换
+ pre = cur
+ cur = tmp
+ }
+ // 最终返回dummy虚拟头节点的下一个,return可以省略
+ dummy.next
+ }
+}
+```
+
+### PHP:
+
+```php
+//虚拟头结点
+function swapPairs($head) {
+ if ($head == null || $head->next == null) {
+ return $head;
+ }
+
+ $dummyNode = new ListNode(0, $head);
+ $preNode = $dummyNode; //虚拟头结点
+ $curNode = $head;
+ $nextNode = $head->next;
+ while($curNode && $nextNode) {
+ $nextNextNode = $nextNode->next; //存下一个节点
+ $nextNode->next = $curNode; //交换curHead 和 nextHead
+ $curNode->next = $nextNextNode;
+ $preNode->next = $nextNode; //上一个节点的下一个指向指向nextHead
+
+ //更新当前的几个指针
+ $preNode = $preNode->next->next;
+ $curNode = $nextNextNode;
+ $nextNode = $nextNextNode->next;
+ }
+
+ return $dummyNode->next;
+}
+
+//递归版本
+function swapPairs($head)
+{
+ // 终止条件
+ if ($head === null || $head->next === null) {
+ return $head;
+ }
+
+ //结果要返回的头结点
+ $next = $head->next;
+ $head->next = $this->swapPairs($next->next); //当前头结点->next指向更新
+ $next->next = $head; //当前第二个节点的->next指向更新
+ return $next; //返回翻转后的头结点
+}
+```
+### Rust:
+
+```rust
+// 虚拟头节点
+impl Solution {
+ pub fn swap_pairs(head: Option>) -> Option> {
+ let mut dummy_head = Box::new(ListNode::new(0));
+ dummy_head.next = head;
+ let mut cur = dummy_head.as_mut();
+ while let Some(mut node) = cur.next.take() {
+ if let Some(mut next) = node.next.take() {
+ node.next = next.next.take();
+ next.next = Some(node);
+ cur.next = Some(next);
+ cur = cur.next.as_mut().unwrap().next.as_mut().unwrap();
+ } else {
+ cur.next = Some(node);
+ cur = cur.next.as_mut().unwrap();
+ }
+ }
+ dummy_head.next
+ }
+}
+```
+
+```rust
+// 递归
+impl Solution {
+ pub fn swap_pairs(head: Option>) -> Option> {
+ if head.is_none() || head.as_ref().unwrap().next.is_none() {
+ return head;
+ }
+
+ let mut node = head.unwrap();
+
+ if let Some(mut next) = node.next.take() {
+ node.next = Solution::swap_pairs(next.next);
+ next.next = Some(node);
+ Some(next)
+ } else {
+ Some(node)
+ }
+ }
+}
+```
+
+### C#
+```csharp
+// 虚拟头结点
+public ListNode SwapPairs(ListNode head)
+{
+ var dummyHead = new ListNode();
+ dummyHead.next = head;
+ ListNode cur = dummyHead;
+ while (cur.next != null && cur.next.next != null)
+ {
+ ListNode tmp1 = cur.next;
+ ListNode tmp2 = cur.next.next.next;
+
+ cur.next = cur.next.next;
+ cur.next.next = tmp1;
+ cur.next.next.next = tmp2;
+
+ cur = cur.next.next;
+ }
+ return dummyHead.next;
+}
+```
+``` C#
+// 递归
+public ListNode SwapPairs(ListNode head)
+{
+ if (head == null || head.next == null) return head;
+ var cur = head.next;
+ head.next = SwapPairs(head.next.next);
+ cur.next = head;
+ return cur;
+}
+```
------------------------
-
diff --git "a/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md" "b/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
old mode 100644
new mode 100755
index 8d6ca5022d..47e05eec6a
--- "a/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
+++ "b/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
@@ -1,13 +1,11 @@
-
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[帮你把链表细节学清楚! | LeetCode:24. 两两交换链表中的节点](https://www.bilibili.com/video/BV1YT411g7br),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
+
这道题目正常模拟就可以了。
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
@@ -28,16 +31,16 @@
初始时,cur指向虚拟头结点,然后进行如下三步:
-
+
操作之后,链表如下:
-
+
看这个可能就更直观一些了:
-
+
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
@@ -46,7 +49,7 @@ class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
+ dummyHead->next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
@@ -58,13 +61,15 @@ public:
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
- return dummyHead->next;
+ ListNode* result = dummyHead->next;
+ delete dummyHead;
+ return result;
}
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
## 拓展
@@ -74,9 +79,9 @@ public:
上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-心想应该没有更好的方法了吧,也就$O(n)$的时间复杂度,重复提交几次,这样了:
+心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:
-
+
力扣上的统计如果两份代码是 100ms 和 300ms的耗时,其实是需要注意的。
@@ -85,7 +90,8 @@ public:
## 其他语言版本
-C:
+### C:
+
```c
/**
* Definition for singly-linked list.
@@ -129,7 +135,7 @@ struct ListNode* swapPairs(struct ListNode* head){
}
```
-Java:
+### Java:
```Java
// 递归版本
@@ -151,28 +157,71 @@ class Solution {
```
```java
-// 虚拟头结点
class Solution {
public ListNode swapPairs(ListNode head) {
+ ListNode dumyhead = new ListNode(-1); // 设置一个虚拟头结点
+ dumyhead.next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
+ ListNode cur = dumyhead;
+ ListNode temp; // 临时节点,保存两个节点后面的节点
+ ListNode firstnode; // 临时节点,保存两个节点之中的第一个节点
+ ListNode secondnode; // 临时节点,保存两个节点之中的第二个节点
+ while (cur.next != null && cur.next.next != null) {
+ temp = cur.next.next.next;
+ firstnode = cur.next;
+ secondnode = cur.next.next;
+ cur.next = secondnode; // 步骤一
+ secondnode.next = firstnode; // 步骤二
+ firstnode.next = temp; // 步骤三
+ cur = firstnode; // cur移动,准备下一轮交换
+ }
+ return dumyhead.next;
+ }
+}
+```
- ListNode dummyNode = new ListNode(0);
- dummyNode.next = head;
- ListNode prev = dummyNode;
-
- while (prev.next != null && prev.next.next != null) {
- ListNode temp = head.next.next; // 缓存 next
- prev.next = head.next; // 将 prev 的 next 改为 head 的 next
- head.next.next = head; // 将 head.next(prev.next) 的next,指向 head
- head.next = temp; // 将head 的 next 接上缓存的temp
- prev = head; // 步进1位
- head = head.next; // 步进1位
+```java
+// 将步骤 2,3 交换顺序,这样不用定义 temp 节点
+public ListNode swapPairs(ListNode head) {
+ ListNode dummy = new ListNode(0, head);
+ ListNode cur = dummy;
+ while (cur.next != null && cur.next.next != null) {
+ ListNode node1 = cur.next;// 第 1 个节点
+ ListNode node2 = cur.next.next;// 第 2 个节点
+ cur.next = node2; // 步骤 1
+ node1.next = node2.next;// 步骤 3
+ node2.next = node1;// 步骤 2
+ cur = cur.next.next;
}
- return dummyNode.next;
- }
+ return dummy.next;
}
```
-Python:
+### Python:
+
+```python
+# 递归版本
+# Definition for singly-linked list.
+# class ListNode:
+# def __init__(self, val=0, next=None):
+# self.val = val
+# self.next = next
+
+class Solution:
+ def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
+ if head is None or head.next is None:
+ return head
+
+ # 待翻转的两个node分别是pre和cur
+ pre = head
+ cur = head.next
+ next = head.next.next
+
+ cur.next = pre # 交换
+ pre.next = self.swapPairs(next) # 将以next为head的后续链表两两交换
+
+ return cur
+```
+
```python
# Definition for singly-linked list.
# class ListNode:
@@ -182,24 +231,24 @@ Python:
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
- res = ListNode(next=head)
- pre = res
+ dummy_head = ListNode(next=head)
+ current = dummy_head
- # 必须有pre的下一个和下下个才能交换,否则说明已经交换结束了
- while pre.next and pre.next.next:
- cur = pre.next
- post = pre.next.next
+ # 必须有cur的下一个和下下个才能交换,否则说明已经交换结束了
+ while current.next and current.next.next:
+ temp = current.next # 防止节点修改
+ temp1 = current.next.next.next
- # pre,cur,post对应最左,中间的,最右边的节点
- cur.next = post.next
- post.next = cur
- pre.next = post
+ current.next = current.next.next
+ current.next.next = temp
+ temp.next = temp1
+ current = current.next.next
+ return dummy_head.next
- pre = pre.next.next
- return res.next
```
-Go:
+### Go:
+
```go
func swapPairs(head *ListNode) *ListNode {
dummy := &ListNode{
@@ -235,7 +284,8 @@ func swapPairs(head *ListNode) *ListNode {
}
```
-Javascript:
+### JavaScript:
+
```javascript
var swapPairs = function (head) {
let ret = new ListNode(0, head), temp = ret;
@@ -250,27 +300,41 @@ var swapPairs = function (head) {
};
```
-TypeScript:
+```javascript
+// 递归版本
+var swapPairs = function (head) {
+ if (head == null || head.next == null) {
+ return head;
+ }
+
+ let after = head.next;
+ head.next = swapPairs(after.next);
+ after.next = head;
+
+ return after;
+};
+```
+
+### TypeScript:
```typescript
function swapPairs(head: ListNode | null): ListNode | null {
- const dummyHead: ListNode = new ListNode(0, head);
- let cur: ListNode = dummyHead;
- while(cur.next !== null && cur.next.next !== null) {
- const tem: ListNode = cur.next;
- const tem1: ListNode = cur.next.next.next;
-
- cur.next = cur.next.next; // step 1
- cur.next.next = tem; // step 2
- cur.next.next.next = tem1; // step 3
-
- cur = cur.next.next;
- }
- return dummyHead.next;
-}
+ const dummyNode: ListNode = new ListNode(0, head);
+ let curNode: ListNode | null = dummyNode;
+ while (curNode && curNode.next && curNode.next.next) {
+ let firstNode: ListNode = curNode.next,
+ secNode: ListNode = curNode.next.next,
+ thirdNode: ListNode | null = curNode.next.next.next;
+ curNode.next = secNode;
+ secNode.next = firstNode;
+ firstNode.next = thirdNode;
+ curNode = firstNode;
+ }
+ return dummyNode.next;
+};
```
-Kotlin:
+### Kotlin:
```kotlin
fun swapPairs(head: ListNode?): ListNode? {
@@ -290,7 +354,8 @@ fun swapPairs(head: ListNode?): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func swapPairs(_ head: ListNode?) -> ListNode? {
if head == nil || head?.next == nil {
@@ -311,7 +376,152 @@ func swapPairs(_ head: ListNode?) -> ListNode? {
return dummyHead.next
}
```
+### Scala:
+
+```scala
+// 虚拟头节点
+object Solution {
+ def swapPairs(head: ListNode): ListNode = {
+ var dummy = new ListNode(0, head) // 虚拟头节点
+ var pre = dummy
+ var cur = head
+ // 当pre的下一个和下下个都不为空,才进行两两转换
+ while (pre.next != null && pre.next.next != null) {
+ var tmp: ListNode = cur.next.next // 缓存下一次要进行转换的第一个节点
+ pre.next = cur.next // 步骤一
+ cur.next.next = cur // 步骤二
+ cur.next = tmp // 步骤三
+ // 下面是准备下一轮的交换
+ pre = cur
+ cur = tmp
+ }
+ // 最终返回dummy虚拟头节点的下一个,return可以省略
+ dummy.next
+ }
+}
+```
+
+### PHP:
+
+```php
+//虚拟头结点
+function swapPairs($head) {
+ if ($head == null || $head->next == null) {
+ return $head;
+ }
+
+ $dummyNode = new ListNode(0, $head);
+ $preNode = $dummyNode; //虚拟头结点
+ $curNode = $head;
+ $nextNode = $head->next;
+ while($curNode && $nextNode) {
+ $nextNextNode = $nextNode->next; //存下一个节点
+ $nextNode->next = $curNode; //交换curHead 和 nextHead
+ $curNode->next = $nextNextNode;
+ $preNode->next = $nextNode; //上一个节点的下一个指向指向nextHead
+
+ //更新当前的几个指针
+ $preNode = $preNode->next->next;
+ $curNode = $nextNextNode;
+ $nextNode = $nextNextNode->next;
+ }
+
+ return $dummyNode->next;
+}
+
+//递归版本
+function swapPairs($head)
+{
+ // 终止条件
+ if ($head === null || $head->next === null) {
+ return $head;
+ }
+
+ //结果要返回的头结点
+ $next = $head->next;
+ $head->next = $this->swapPairs($next->next); //当前头结点->next指向更新
+ $next->next = $head; //当前第二个节点的->next指向更新
+ return $next; //返回翻转后的头结点
+}
+```
+### Rust:
+
+```rust
+// 虚拟头节点
+impl Solution {
+ pub fn swap_pairs(head: Option>) -> Option> {
+ let mut dummy_head = Box::new(ListNode::new(0));
+ dummy_head.next = head;
+ let mut cur = dummy_head.as_mut();
+ while let Some(mut node) = cur.next.take() {
+ if let Some(mut next) = node.next.take() {
+ node.next = next.next.take();
+ next.next = Some(node);
+ cur.next = Some(next);
+ cur = cur.next.as_mut().unwrap().next.as_mut().unwrap();
+ } else {
+ cur.next = Some(node);
+ cur = cur.next.as_mut().unwrap();
+ }
+ }
+ dummy_head.next
+ }
+}
+```
+
+```rust
+// 递归
+impl Solution {
+ pub fn swap_pairs(head: Option>) -> Option> {
+ if head.is_none() || head.as_ref().unwrap().next.is_none() {
+ return head;
+ }
+
+ let mut node = head.unwrap();
+
+ if let Some(mut next) = node.next.take() {
+ node.next = Solution::swap_pairs(next.next);
+ next.next = Some(node);
+ Some(next)
+ } else {
+ Some(node)
+ }
+ }
+}
+```
+
+### C#
+```csharp
+// 虚拟头结点
+public ListNode SwapPairs(ListNode head)
+{
+ var dummyHead = new ListNode();
+ dummyHead.next = head;
+ ListNode cur = dummyHead;
+ while (cur.next != null && cur.next.next != null)
+ {
+ ListNode tmp1 = cur.next;
+ ListNode tmp2 = cur.next.next.next;
+
+ cur.next = cur.next.next;
+ cur.next.next = tmp1;
+ cur.next.next.next = tmp2;
+
+ cur = cur.next.next;
+ }
+ return dummyHead.next;
+}
+```
+``` C#
+// 递归
+public ListNode SwapPairs(ListNode head)
+{
+ if (head == null || head.next == null) return head;
+ var cur = head.next;
+ head.next = SwapPairs(head.next.next);
+ cur.next = head;
+ return cur;
+}
+```
------------------------
-
diff --git "a/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md" "b/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
old mode 100644
new mode 100755
index 8d6ca5022d..47e05eec6a
--- "a/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
+++ "b/problems/0027.\347\247\273\351\231\244\345\205\203\347\264\240.md"
@@ -1,13 +1,11 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 27. 移除元素
+# 27. 移除元素
-[力扣题目链接](https://leetcode-cn.com/problems/remove-element/)
+[力扣题目链接](https://leetcode.cn/problems/remove-element/)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
@@ -26,6 +24,11 @@
**你不需要考虑数组中超出新长度后面的元素。**
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[数组中移除元素并不容易!LeetCode:27. 移除元素](https://www.bilibili.com/video/BV12A4y1Z7LP),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
有的同学可能说了,多余的元素,删掉不就得了。
@@ -40,7 +43,7 @@
删除过程如下:
-
+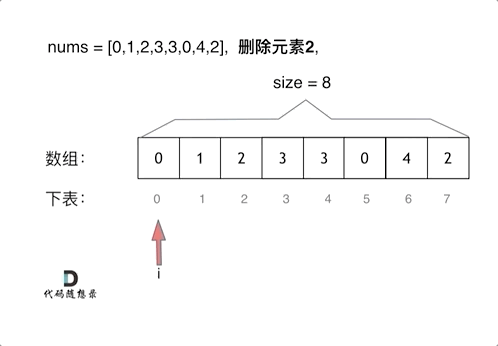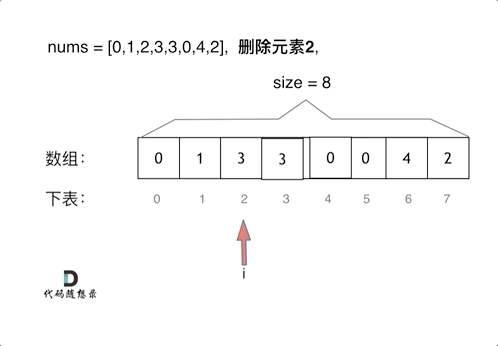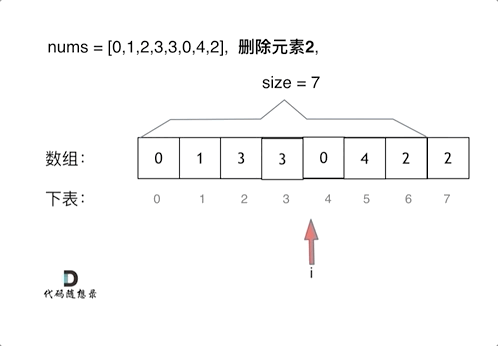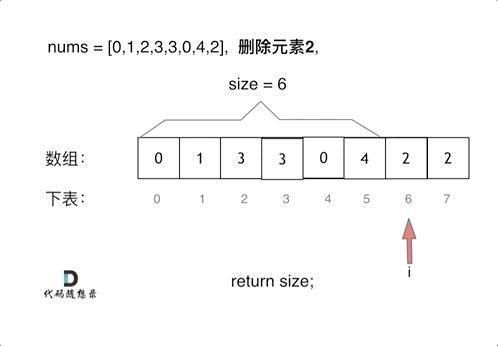
很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
@@ -75,13 +78,23 @@ public:
双指针法(快慢指针法): **通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。**
+定义快慢指针
+
+* 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
+* 慢指针:指向更新 新数组下标的位置
+
+很多同学这道题目做的很懵,就是不理解 快慢指针究竟都是什么含义,所以一定要明确含义,后面的思路就更容易理解了。
+
删除过程如下:
-
+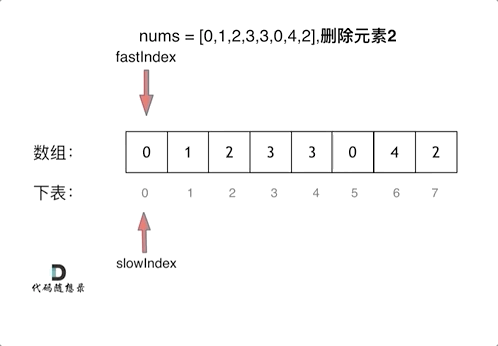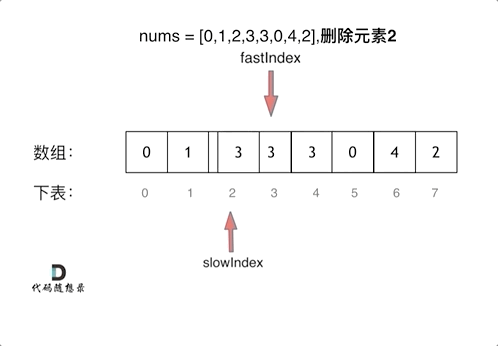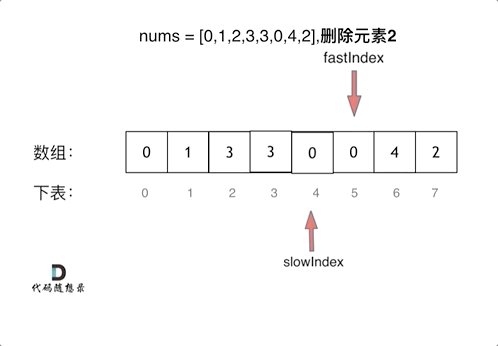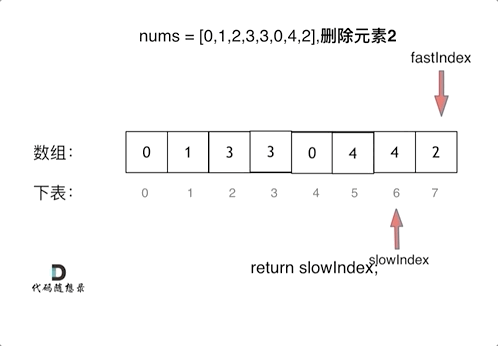
+
+很多同学不了解
+
**双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组、链表、字符串等操作的面试题,都使用双指针法。**
-后序都会一一介绍到,本题代码如下:
+后续都会一一介绍到,本题代码如下:
```CPP
// 时间复杂度:O(n)
@@ -104,116 +117,217 @@ public:
* 时间复杂度:O(n)
* 空间复杂度:O(1)
-旧文链接:[数组:就移除个元素很难么?](https://programmercarl.com/0027.移除元素.html)
-```CPP
-/**
-* 相向双指针方法,基于元素顺序可以改变的题目描述改变了元素相对位置,确保了移动最少元素
-* 时间复杂度:O(n)
-* 空间复杂度:O(1)
-*/
-class Solution {
-public:
- int removeElement(vector& nums, int val) {
- int leftIndex = 0;
- int rightIndex = nums.size() - 1;
- while (leftIndex <= rightIndex) {
- // 找左边等于val的元素
- while (leftIndex <= rightIndex && nums[leftIndex] != val){
- ++leftIndex;
- }
- // 找右边不等于val的元素
- while (leftIndex <= rightIndex && nums[rightIndex] == val) {
- -- rightIndex;
- }
- // 将右边不等于val的元素覆盖左边等于val的元素
- if (leftIndex < rightIndex) {
- nums[leftIndex++] = nums[rightIndex--];
- }
- }
- return leftIndex; // leftIndex一定指向了最终数组末尾的下一个元素
- }
-};
-```
-
## 相关题目推荐
-* 26.删除排序数组中的重复项
-* 283.移动零
-* 844.比较含退格的字符串
-* 977.有序数组的平方
-
-
-
-
+* [26.删除排序数组中的重复项](https://leetcode.cn/problems/remove-duplicates-from-sorted-array/)
+* [283.移动零](https://leetcode.cn/problems/move-zeroes/)
+* [844.比较含退格的字符串](https://leetcode.cn/problems/backspace-string-compare/)
+* [977.有序数组的平方](https://leetcode.cn/problems/squares-of-a-sorted-array/)
## 其他语言版本
-
-Java:
+### Java:
+```java
+class Solution {
+ public int removeElement(int[] nums, int val) {
+ // 暴力法
+ int n = nums.length;
+ for (int i = 0; i < n; i++) {
+ if (nums[i] == val) {
+ for (int j = i + 1; j < n; j++) {
+ nums[j - 1] = nums[j];
+ }
+ i--;
+ n--;
+ }
+ }
+ return n;
+ }
+}
+```
```java
class Solution {
public int removeElement(int[] nums, int val) {
-
// 快慢指针
- int fastIndex = 0;
- int slowIndex;
- for (slowIndex = 0; fastIndex < nums.length; fastIndex++) {
+ int slowIndex = 0;
+ for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
if (nums[fastIndex] != val) {
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
return slowIndex;
-
+ }
+}
+```
+```java
+//相向双指针法
+class Solution {
+ public int removeElement(int[] nums, int val) {
+ int left = 0;
+ int right = nums.length - 1;
+ while(right >= 0 && nums[right] == val) right--; //将right移到从右数第一个值不为val的位置
+ while(left <= right) {
+ if(nums[left] == val) { //left位置的元素需要移除
+ //将right位置的元素移到left(覆盖),right位置移除
+ nums[left] = nums[right];
+ right--;
+ }
+ left++;
+ while(right >= 0 && nums[right] == val) right--;
+ }
+ return left;
}
}
```
-Python:
-
-```python
-class Solution:
- """双指针法
- 时间复杂度:O(n)
- 空间复杂度:O(1)
- """
+```java
+// 相向双指针法(版本二)
+class Solution {
+ public int removeElement(int[] nums, int val) {
+ int left = 0;
+ int right = nums.length - 1;
+ while(left <= right){
+ if(nums[left] == val){
+ nums[left] = nums[right];
+ right--;
+ }else {
+ // 这里兼容了right指针指向的值与val相等的情况
+ left++;
+ }
+ }
+ return left;
+ }
+}
+```
- @classmethod
- def removeElement(cls, nums: List[int], val: int) -> int:
- fast = slow = 0
+### Python:
- while fast < len(nums):
+``` python 3
+(版本一)快慢指针法
+class Solution:
+ def removeElement(self, nums: List[int], val: int) -> int:
+ # 快慢指针
+ fast = 0 # 快指针
+ slow = 0 # 慢指针
+ size = len(nums)
+ while fast < size: # 不加等于是因为,a = size 时,nums[a] 会越界
+ # slow 用来收集不等于 val 的值,如果 fast 对应值不等于 val,则把它与 slow 替换
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
-
- # 当 fast 指针遇到要删除的元素时停止赋值
- # slow 指针停止移动, fast 指针继续前进
fast += 1
-
return slow
```
+``` python 3
+(版本二)暴力法
+class Solution:
+ def removeElement(self, nums: List[int], val: int) -> int:
+ i, l = 0, len(nums)
+ while i < l:
+ if nums[i] == val: # 找到等于目标值的节点
+ for j in range(i+1, l): # 移除该元素,并将后面元素向前平移
+ nums[j - 1] = nums[j]
+ l -= 1
+ i -= 1
+ i += 1
+ return l
+
+```
+
+``` python 3
+# 相向双指针法
+# 时间复杂度 O(n)
+# 空间复杂度 O(1)
+class Solution:
+ def removeElement(self, nums: List[int], val: int) -> int:
+ n = len(nums)
+ left, right = 0, n - 1
+ while left <= right:
+ while left <= right and nums[left] != val:
+ left += 1
+ while left <= right and nums[right] == val:
+ right -= 1
+ if left < right:
+ nums[left] = nums[right]
+ left += 1
+ right -= 1
+ return left
+
+```
+
+### Go:
-Go:
```go
+// 暴力法
+// 时间复杂度 O(n^2)
+// 空间复杂度 O(1)
func removeElement(nums []int, val int) int {
- length:=len(nums)
- res:=0
- for i:=0;i {
};
```
-TypeScript:
+### TypeScript:
```typescript
function removeElement(nums: number[], val: number): number {
@@ -243,12 +357,12 @@ function removeElement(nums: number[], val: number): number {
};
```
-Ruby:
+### Ruby:
```ruby
def remove_element(nums, val)
i = 0
- nums.each_index do |j|
+ nums.each_index do |j|
if nums[j] != val
nums[i] = nums[j]
i+=1
@@ -257,7 +371,8 @@ def remove_element(nums, val)
i
end
```
-Rust:
+### Rust:
+
```rust
impl Solution {
pub fn remove_element(nums: &mut Vec, val: i32) -> i32 {
@@ -273,7 +388,7 @@ impl Solution {
}
```
-Swift:
+### Swift:
```swift
func removeElement(_ nums: inout [Int], _ val: Int) -> Int {
@@ -281,17 +396,16 @@ func removeElement(_ nums: inout [Int], _ val: Int) -> Int {
for fastIndex in 0.. +### Kotlin:
+
+```kotlin
+fun removeElement(nums: IntArray, `val`: Int): Int {
+ var slowIndex = 0 // 初始化慢指针
+ for (fastIndex in nums.indices) {
+ if (nums[fastIndex] != `val`) nums[slowIndex++] = nums[fastIndex] // 在慢指针所在位置存储未被删除的元素
+ }
+ return slowIndex
+ }
+```
+
+### Scala:
+
+```scala
+object Solution {
+ def removeElement(nums: Array[Int], `val`: Int): Int = {
+ var slow = 0
+ for (fast <- 0 until nums.length) {
+ if (`val` != nums(fast)) {
+ nums(slow) = nums(fast)
+ slow += 1
+ }
+ }
+ slow
+ }
+}
+```
+
+### C#:
+
+```csharp
+public class Solution {
+ public int RemoveElement(int[] nums, int val) {
+ int slow = 0;
+ for (int fast = 0; fast < nums.Length; fast++) {
+ if (val != nums[fast]) {
+ nums[slow++] = nums[fast];
+ }
+ }
+ return slow;
+ }
+}
+```
+
+###Dart:
+```dart
+int removeElement(List nums, int val) {
+ //相向双指针法
+ var left = 0;
+ var right = nums.length - 1;
+ while (left <= right) {
+ //寻找左侧的val,将其被右侧非val覆盖
+ if (nums[left] == val) {
+ while (nums[right] == val&&left<=right) {
+ right--;
+ if (right < 0) {
+ return 0;
+ }
+ }
+ nums[left] = nums[right--];
+ } else {
+ left++;
+ }
+ }
+ //覆盖后可以将0至left部分视为所需部分
+ return left;
+}
+
+```
+
diff --git "a/problems/0028.\345\256\236\347\216\260strStr.md" "b/problems/0028.\345\256\236\347\216\260strStr.md"
old mode 100644
new mode 100755
index 634d8535a2..ef8a6c58e6
--- "a/problems/0028.\345\256\236\347\216\260strStr.md"
+++ "b/problems/0028.\345\256\236\347\216\260strStr.md"
@@ -1,15 +1,13 @@
-
+### Kotlin:
+
+```kotlin
+fun removeElement(nums: IntArray, `val`: Int): Int {
+ var slowIndex = 0 // 初始化慢指针
+ for (fastIndex in nums.indices) {
+ if (nums[fastIndex] != `val`) nums[slowIndex++] = nums[fastIndex] // 在慢指针所在位置存储未被删除的元素
+ }
+ return slowIndex
+ }
+```
+
+### Scala:
+
+```scala
+object Solution {
+ def removeElement(nums: Array[Int], `val`: Int): Int = {
+ var slow = 0
+ for (fast <- 0 until nums.length) {
+ if (`val` != nums(fast)) {
+ nums(slow) = nums(fast)
+ slow += 1
+ }
+ }
+ slow
+ }
+}
+```
+
+### C#:
+
+```csharp
+public class Solution {
+ public int RemoveElement(int[] nums, int val) {
+ int slow = 0;
+ for (int fast = 0; fast < nums.Length; fast++) {
+ if (val != nums[fast]) {
+ nums[slow++] = nums[fast];
+ }
+ }
+ return slow;
+ }
+}
+```
+
+###Dart:
+```dart
+int removeElement(List nums, int val) {
+ //相向双指针法
+ var left = 0;
+ var right = nums.length - 1;
+ while (left <= right) {
+ //寻找左侧的val,将其被右侧非val覆盖
+ if (nums[left] == val) {
+ while (nums[right] == val&&left<=right) {
+ right--;
+ if (right < 0) {
+ return 0;
+ }
+ }
+ nums[left] = nums[right--];
+ } else {
+ left++;
+ }
+ }
+ //覆盖后可以将0至left部分视为所需部分
+ return left;
+}
+
+```
+
diff --git "a/problems/0028.\345\256\236\347\216\260strStr.md" "b/problems/0028.\345\256\236\347\216\260strStr.md"
old mode 100644
new mode 100755
index 634d8535a2..ef8a6c58e6
--- "a/problems/0028.\345\256\236\347\216\260strStr.md"
+++ "b/problems/0028.\345\256\236\347\216\260strStr.md"
@@ -1,15 +1,13 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
> 在一个串中查找是否出现过另一个串,这是KMP的看家本领。
# 28. 实现 strStr()
-[力扣题目链接](https://leetcode-cn.com/problems/implement-strstr/)
+[力扣题目链接](https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/)
实现 strStr() 函数。
@@ -27,16 +25,16 @@
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
+## 算法公开课
-# 思路
-
-本题是KMP 经典题目。
-
-以下文字如果看不进去,可以看我的B站视频:
+本题是KMP 经典题目。以下文字如果看不进去,可以看[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html),相信结合视频再看本篇题解,更有助于大家对本题的理解。
* [帮你把KMP算法学个通透!B站(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd/)
* [帮你把KMP算法学个通透!(求next数组代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
+
+## 思路
+
KMP的经典思想就是:**当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。**
本篇将以如下顺序来讲解KMP,
@@ -60,13 +58,13 @@ KMP的经典思想就是:**当出现字符串不匹配时,可以记录一部
读完本篇可以顺便把leetcode上28.实现strStr()题目做了。
-# 什么是KMP
+### 什么是KMP
说到KMP,先说一下KMP这个名字是怎么来的,为什么叫做KMP呢。
因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP
-# KMP有什么用
+### KMP有什么用
KMP主要应用在字符串匹配上。
@@ -84,7 +82,7 @@ KMP的主要思想是**当出现字符串不匹配时,可以知道一部分之
下面Carl就带大家把KMP的精髓,next数组弄清楚。
-# 什么是前缀表
+### 什么是前缀表
写过KMP的同学,一定都写过next数组,那么这个next数组究竟是个啥呢?
@@ -94,7 +92,7 @@ next数组就是一个前缀表(prefix table)。
**前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。**
-为了清楚的了解前缀表的来历,我们来举一个例子:
+为了清楚地了解前缀表的来历,我们来举一个例子:
要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
@@ -108,11 +106,11 @@ next数组就是一个前缀表(prefix table)。
如动画所示:
-
+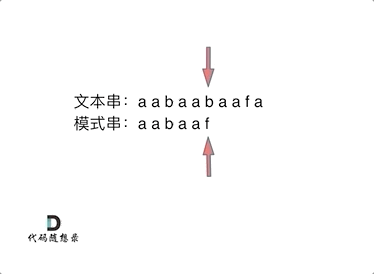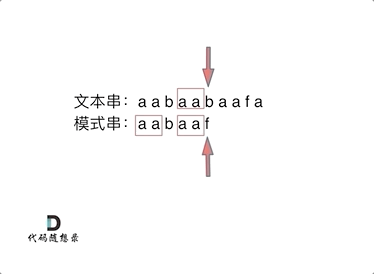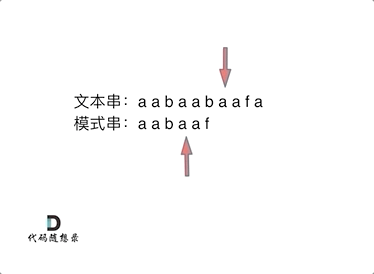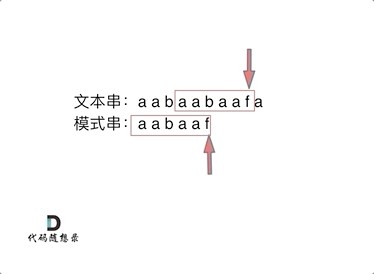
-动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说道。
+动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说到。
-可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
+可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
@@ -122,7 +120,7 @@ next数组就是一个前缀表(prefix table)。
那么什么是前缀表:**记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
-# 最长公共前后缀?
+### 最长公共前后缀
文章中字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**。
@@ -144,39 +142,41 @@ next数组就是一个前缀表(prefix table)。
等等.....。
-# 为什么一定要用前缀表
+### 为什么一定要用前缀表
这就是前缀表,那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
回顾一下,刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图:
- +
+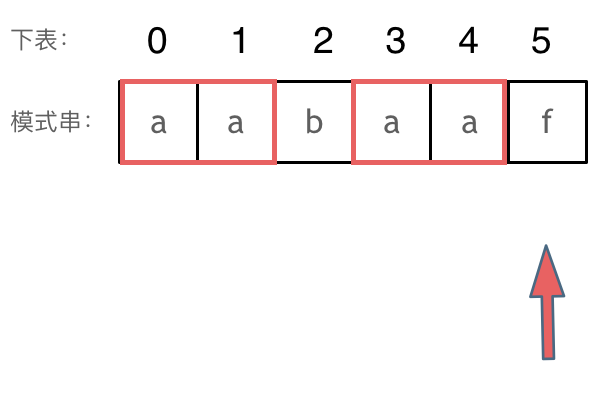 然后就找到了下标2,指向b,继续匹配:如图:
-
然后就找到了下标2,指向b,继续匹配:如图:
- +
+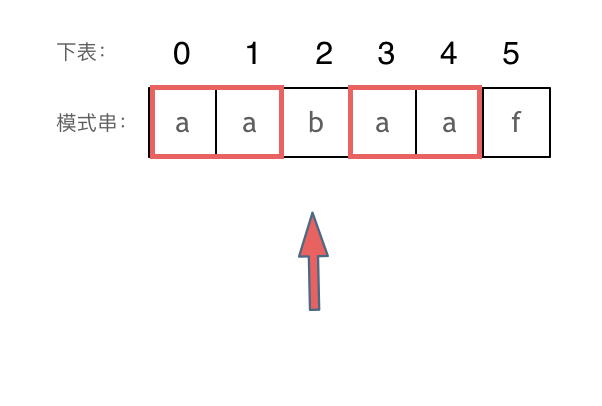 以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
+**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。**
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-# 如何计算前缀表
+### 如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图:
-
以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
+**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。**
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-# 如何计算前缀表
+### 如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图:
- +
+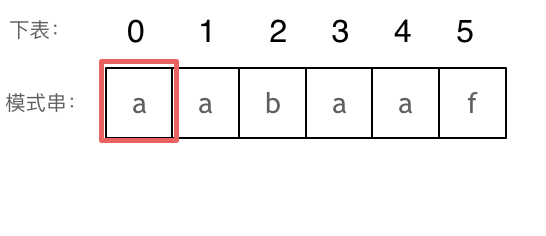 长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
- +
+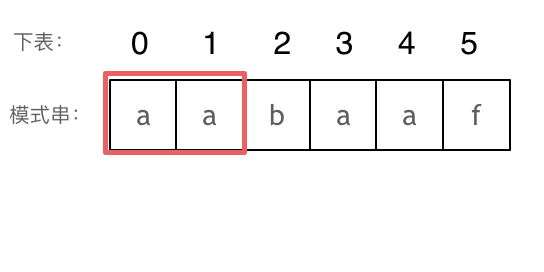 +
长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
+
长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
- +
+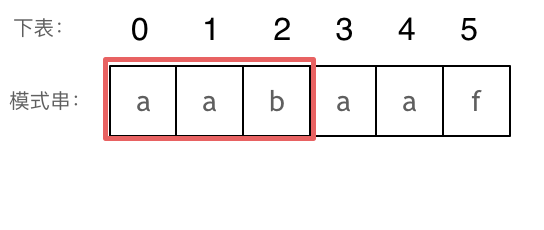 +
长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
以此类推:
@@ -185,13 +185,13 @@ next数组就是一个前缀表(prefix table)。
长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
-
+
长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
以此类推:
@@ -185,13 +185,13 @@ next数组就是一个前缀表(prefix table)。
长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
- +
+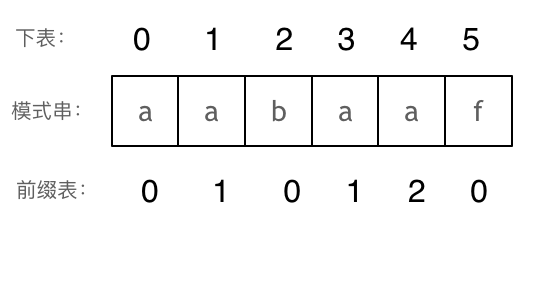 可以看出模式串与前缀表对应位置的数字表示的就是:**下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
+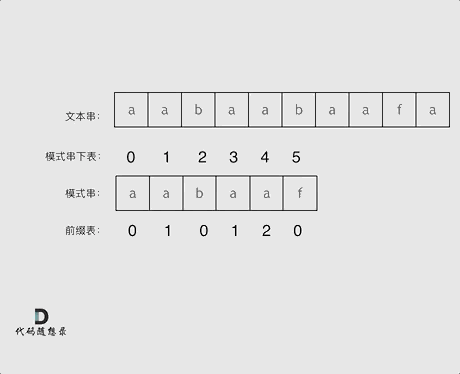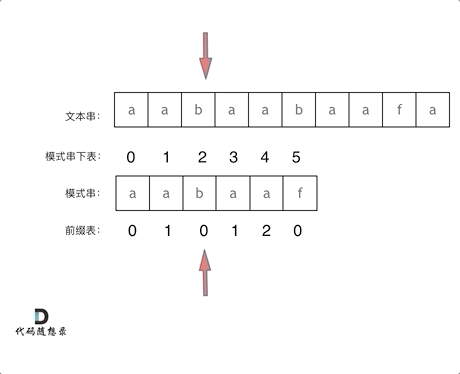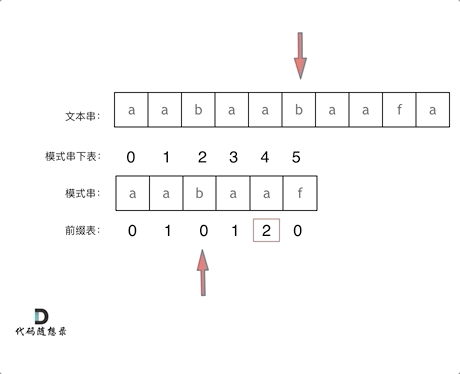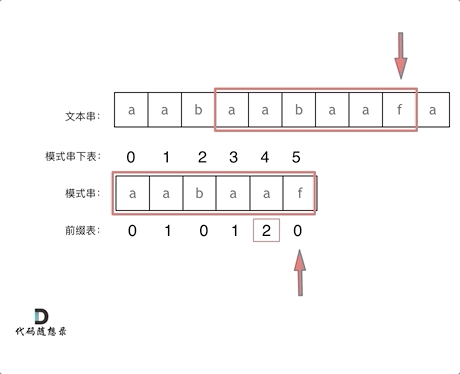
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
@@ -199,23 +199,23 @@ next数组就是一个前缀表(prefix table)。
所以要看前一位的 前缀表的数值。
-前一个字符的前缀表的数值是2, 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
+前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
-# 前缀表与next数组
+### 前缀表与next数组
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
+很多KMP算法的实现都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
+其实**这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
后面我会提供两种不同的实现代码,大家就明白了。
-# 使用next数组来匹配
+### 使用next数组来匹配
**以下我们以前缀表统一减一之后的next数组来做演示**。
@@ -225,19 +225,19 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
匹配过程动画如下:
-
+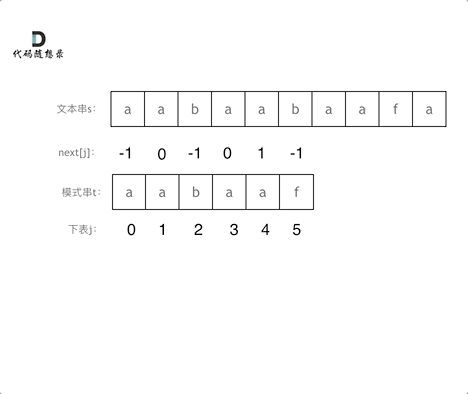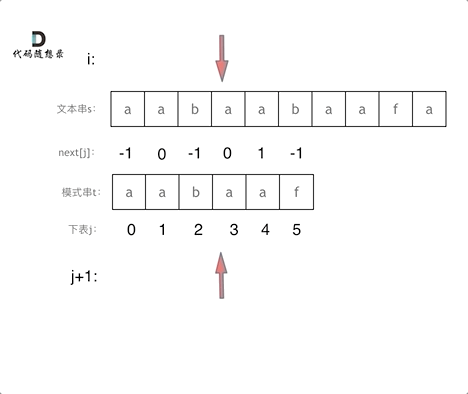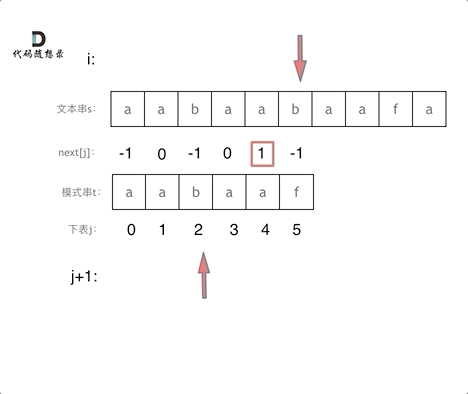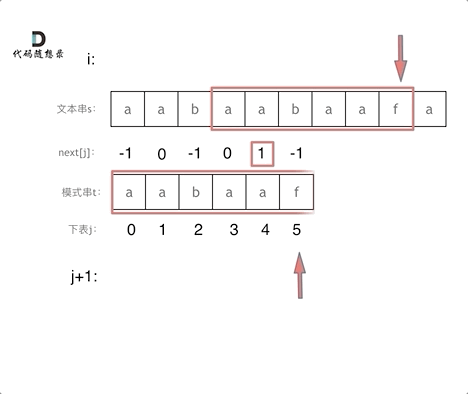
-# 时间复杂度分析
+### 时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
+暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大地提高了搜索的效率。**
为了和力扣题目28.实现strStr保持一致,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法,一定要构造next数组。
-# 构造next数组
+### 构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
@@ -251,7 +251,7 @@ void getNext(int* next, const string& s)
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况
-接下来我们详解详解一下。
+接下来我们详解一下。
1. 初始化:
@@ -332,11 +332,11 @@ void getNext(int* next, const string& s){
代码构造next数组的逻辑流程动画如下:
-
+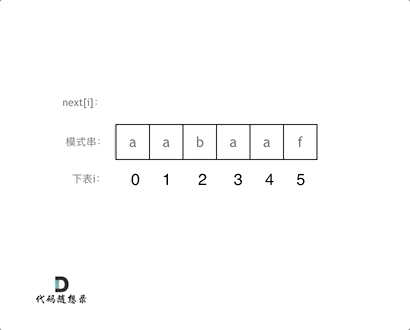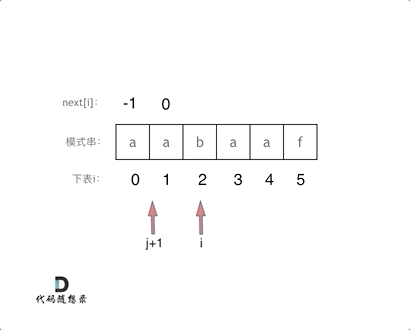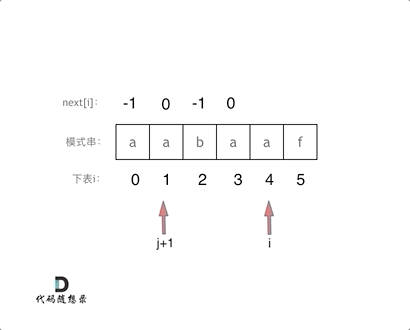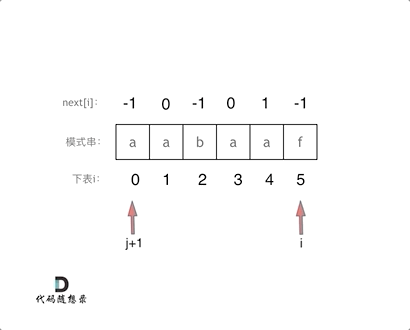
得到了next数组之后,就要用这个来做匹配了。
-# 使用next数组来做匹配
+### 使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
@@ -401,7 +401,7 @@ for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
此时所有逻辑的代码都已经写出来了,力扣 28.实现strStr 题目的整体代码如下:
-# 前缀表统一减一 C++代码实现
+### 前缀表统一减一 C++代码实现
```CPP
class Solution {
@@ -423,8 +423,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector next(needle.size());
+ getNext(&next[0], needle);
int j = -1; // // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
@@ -442,8 +442,10 @@ public:
};
```
+* 时间复杂度: O(n + m)
+* 空间复杂度: O(m), 只需要保存字符串needle的前缀表
-# 前缀表(不减一)C++实现
+### 前缀表(不减一)C++实现
那么前缀表就不减一了,也不右移的,到底行不行呢?
@@ -520,8 +522,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector next(needle.size());
+ getNext(&next[0], needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
@@ -538,8 +540,11 @@ public:
}
};
```
+* 时间复杂度: O(n + m)
+* 空间复杂度: O(m)
+
-# 总结
+## 总结
我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
@@ -556,8 +561,39 @@ public:
## 其他语言版本
+### Java:
+```Java
+class Solution {
+ /**
+ 牺牲空间,换取最直白的暴力法
+ 时间复杂度 O(n * m)
+ 空间 O(n + m)
+ */
+ public int strStr(String haystack, String needle) {
+ // 获取 haystack 和 needle 的长度
+ int n = haystack.length(), m = needle.length();
+ // 将字符串转换为字符数组,方便索引操作
+ char[] s = haystack.toCharArray(), p = needle.toCharArray();
+
+ // 遍历 haystack 字符串
+ for (int i = 0; i < n - m + 1; i++) {
+ // 初始化匹配的指针
+ int a = i, b = 0;
+ // 循环检查 needle 是否在当前位置开始匹配
+ while (b < m && s[a] == p[b]) {
+ // 如果当前字符匹配,则移动指针
+ a++;
+ b++;
+ }
+ // 如果 b 等于 m,说明 needle 已经完全匹配,返回当前位置 i
+ if (b == m) return i;
+ }
-Java:
+ // 如果遍历完毕仍未找到匹配的子串,则返回 -1
+ return -1;
+ }
+}
+```
```Java
class Solution {
@@ -613,12 +649,12 @@ class Solution {
public void getNext(int[] next, String s){
int j = -1;
next[0] = j;
- for (int i = 1; i=0 && s.charAt(i) != s.charAt(j+1)){
+ for (int i = 1; i < s.length(); i++){
+ while(j >= 0 && s.charAt(i) != s.charAt(j+1)){
j=next[j];
}
- if(s.charAt(i)==s.charAt(j+1)){
+ if(s.charAt(i) == s.charAt(j+1)){
j++;
}
next[i] = j;
@@ -632,14 +668,14 @@ class Solution {
int[] next = new int[needle.length()];
getNext(next, needle);
int j = -1;
- for(int i = 0; i=0 && haystack.charAt(i) != needle.charAt(j+1)){
j = next[j];
}
- if(haystack.charAt(i)==needle.charAt(j+1)){
+ if(haystack.charAt(i) == needle.charAt(j+1)){
j++;
}
- if(j==needle.length()-1){
+ if(j == needle.length()-1){
return (i-needle.length()+1);
}
}
@@ -684,76 +720,100 @@ class Solution {
}
```
-Python3:
+### Python3:
+(版本一)前缀表(减一)
```python
-// 方法一
class Solution:
+ def getNext(self, next, s):
+ j = -1
+ next[0] = j
+ for i in range(1, len(s)):
+ while j >= 0 and s[i] != s[j+1]:
+ j = next[j]
+ if s[i] == s[j+1]:
+ j += 1
+ next[i] = j
+
def strStr(self, haystack: str, needle: str) -> int:
- a=len(needle)
- b=len(haystack)
- if a==0:
+ if not needle:
return 0
- next=self.getnext(a,needle)
- p=-1
- for j in range(b):
- while p>=0 and needle[p+1]!=haystack[j]:
- p=next[p]
- if needle[p+1]==haystack[j]:
- p+=1
- if p==a-1:
- return j-a+1
+ next = [0] * len(needle)
+ self.getNext(next, needle)
+ j = -1
+ for i in range(len(haystack)):
+ while j >= 0 and haystack[i] != needle[j+1]:
+ j = next[j]
+ if haystack[i] == needle[j+1]:
+ j += 1
+ if j == len(needle) - 1:
+ return i - len(needle) + 1
return -1
-
- def getnext(self,a,needle):
- next=['' for i in range(a)]
- k=-1
- next[0]=k
- for i in range(1,len(needle)):
- while (k>-1 and needle[k+1]!=needle[i]):
- k=next[k]
- if needle[k+1]==needle[i]:
- k+=1
- next[i]=k
- return next
```
+(版本二)前缀表(不减一)
```python
-// 方法二
class Solution:
+ def getNext(self, next: List[int], s: str) -> None:
+ j = 0
+ next[0] = 0
+ for i in range(1, len(s)):
+ while j > 0 and s[i] != s[j]:
+ j = next[j - 1]
+ if s[i] == s[j]:
+ j += 1
+ next[i] = j
+
def strStr(self, haystack: str, needle: str) -> int:
- a=len(needle)
- b=len(haystack)
- if a==0:
+ if len(needle) == 0:
return 0
- i=j=0
- next=self.getnext(a,needle)
- while(i 0 and haystack[i] != needle[j]:
+ j = next[j - 1]
+ if haystack[i] == needle[j]:
+ j += 1
+ if j == len(needle):
+ return i - len(needle) + 1
+ return -1
+```
+
- def getnext(self,a,needle):
- next=['' for i in range(a)]
- j,k=0,-1
- next[0]=k
- while(j int:
+ try:
+ return haystack.index(needle)
+ except ValueError:
+ return -1
+```
+(版本五)使用 find
+```python
+class Solution:
+ def strStr(self, haystack: str, needle: str) -> int:
+ return haystack.find(needle)
+
```
-Go:
+### Go:
```go
// 方法一:前缀表使用减1实现
@@ -763,17 +823,17 @@ Go:
// next 前缀表数组
// s 模式串
func getNext(next []int, s string) {
- j := -1 // j表示 最长相等前后缀长度
+ j := -1 // j表示 最长相等前后缀长度
next[0] = j
for i := 1; i < len(s); i++ {
for j >= 0 && s[i] != s[j+1] {
- j = next[j] // 回退前一位
+ j = next[j] // 回退前一位
}
if s[i] == s[j+1] {
j++
}
- next[i] = j // next[i]是i(包括i)之前的最长相等前后缀长度
+ next[i] = j // next[i]是i(包括i)之前的最长相等前后缀长度
}
}
func strStr(haystack string, needle string) int {
@@ -782,15 +842,15 @@ func strStr(haystack string, needle string) int {
}
next := make([]int, len(needle))
getNext(next, needle)
- j := -1 // 模式串的起始位置 next为-1 因此也为-1
+ j := -1 // 模式串的起始位置 next为-1 因此也为-1
for i := 0; i < len(haystack); i++ {
for j >= 0 && haystack[i] != needle[j+1] {
- j = next[j] // 寻找下一个匹配点
+ j = next[j] // 寻找下一个匹配点
}
if haystack[i] == needle[j+1] {
j++
}
- if j == len(needle)-1 { // j指向了模式串的末尾
+ if j == len(needle)-1 { // j指向了模式串的末尾
return i - len(needle) + 1
}
}
@@ -828,7 +888,7 @@ func strStr(haystack string, needle string) int {
getNext(next, needle)
for i := 0; i < len(haystack); i++ {
for j > 0 && haystack[i] != needle[j] {
- j = next[j-1] // 回退到j的前一位
+ j = next[j-1] // 回退到j的前一位
}
if haystack[i] == needle[j] {
j++
@@ -841,7 +901,7 @@ func strStr(haystack string, needle string) int {
}
```
-JavaScript版本
+### JavaScript:
> 前缀表统一减一
@@ -929,7 +989,7 @@ var strStr = function (haystack, needle) {
};
```
-TypeScript版本:
+### TypeScript:
> 前缀表统一减一
@@ -1006,7 +1066,7 @@ function strStr(haystack: string, needle: string): number {
}
```
-Swift 版本
+### Swift:
> 前缀表统一减一
@@ -1059,5 +1119,402 @@ func getNext(_ next: inout [Int], needle: [Character]) {
```
------------------------
-
可以看出模式串与前缀表对应位置的数字表示的就是:**下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
+
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
@@ -199,23 +199,23 @@ next数组就是一个前缀表(prefix table)。
所以要看前一位的 前缀表的数值。
-前一个字符的前缀表的数值是2, 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
+前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
-# 前缀表与next数组
+### 前缀表与next数组
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
+很多KMP算法的实现都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
+其实**这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
后面我会提供两种不同的实现代码,大家就明白了。
-# 使用next数组来匹配
+### 使用next数组来匹配
**以下我们以前缀表统一减一之后的next数组来做演示**。
@@ -225,19 +225,19 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
匹配过程动画如下:
-
+
-# 时间复杂度分析
+### 时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
+暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大地提高了搜索的效率。**
为了和力扣题目28.实现strStr保持一致,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法,一定要构造next数组。
-# 构造next数组
+### 构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
@@ -251,7 +251,7 @@ void getNext(int* next, const string& s)
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况
-接下来我们详解详解一下。
+接下来我们详解一下。
1. 初始化:
@@ -332,11 +332,11 @@ void getNext(int* next, const string& s){
代码构造next数组的逻辑流程动画如下:
-
+
得到了next数组之后,就要用这个来做匹配了。
-# 使用next数组来做匹配
+### 使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
@@ -401,7 +401,7 @@ for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
此时所有逻辑的代码都已经写出来了,力扣 28.实现strStr 题目的整体代码如下:
-# 前缀表统一减一 C++代码实现
+### 前缀表统一减一 C++代码实现
```CPP
class Solution {
@@ -423,8 +423,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector next(needle.size());
+ getNext(&next[0], needle);
int j = -1; // // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
@@ -442,8 +442,10 @@ public:
};
```
+* 时间复杂度: O(n + m)
+* 空间复杂度: O(m), 只需要保存字符串needle的前缀表
-# 前缀表(不减一)C++实现
+### 前缀表(不减一)C++实现
那么前缀表就不减一了,也不右移的,到底行不行呢?
@@ -520,8 +522,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector next(needle.size());
+ getNext(&next[0], needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
@@ -538,8 +540,11 @@ public:
}
};
```
+* 时间复杂度: O(n + m)
+* 空间复杂度: O(m)
+
-# 总结
+## 总结
我们介绍了什么是KMP,KMP可以解决什么问题,然后分析KMP算法里的next数组,知道了next数组就是前缀表,再分析为什么要是前缀表而不是什么其他表。
@@ -556,8 +561,39 @@ public:
## 其他语言版本
+### Java:
+```Java
+class Solution {
+ /**
+ 牺牲空间,换取最直白的暴力法
+ 时间复杂度 O(n * m)
+ 空间 O(n + m)
+ */
+ public int strStr(String haystack, String needle) {
+ // 获取 haystack 和 needle 的长度
+ int n = haystack.length(), m = needle.length();
+ // 将字符串转换为字符数组,方便索引操作
+ char[] s = haystack.toCharArray(), p = needle.toCharArray();
+
+ // 遍历 haystack 字符串
+ for (int i = 0; i < n - m + 1; i++) {
+ // 初始化匹配的指针
+ int a = i, b = 0;
+ // 循环检查 needle 是否在当前位置开始匹配
+ while (b < m && s[a] == p[b]) {
+ // 如果当前字符匹配,则移动指针
+ a++;
+ b++;
+ }
+ // 如果 b 等于 m,说明 needle 已经完全匹配,返回当前位置 i
+ if (b == m) return i;
+ }
-Java:
+ // 如果遍历完毕仍未找到匹配的子串,则返回 -1
+ return -1;
+ }
+}
+```
```Java
class Solution {
@@ -613,12 +649,12 @@ class Solution {
public void getNext(int[] next, String s){
int j = -1;
next[0] = j;
- for (int i = 1; i=0 && s.charAt(i) != s.charAt(j+1)){
+ for (int i = 1; i < s.length(); i++){
+ while(j >= 0 && s.charAt(i) != s.charAt(j+1)){
j=next[j];
}
- if(s.charAt(i)==s.charAt(j+1)){
+ if(s.charAt(i) == s.charAt(j+1)){
j++;
}
next[i] = j;
@@ -632,14 +668,14 @@ class Solution {
int[] next = new int[needle.length()];
getNext(next, needle);
int j = -1;
- for(int i = 0; i=0 && haystack.charAt(i) != needle.charAt(j+1)){
j = next[j];
}
- if(haystack.charAt(i)==needle.charAt(j+1)){
+ if(haystack.charAt(i) == needle.charAt(j+1)){
j++;
}
- if(j==needle.length()-1){
+ if(j == needle.length()-1){
return (i-needle.length()+1);
}
}
@@ -684,76 +720,100 @@ class Solution {
}
```
-Python3:
+### Python3:
+(版本一)前缀表(减一)
```python
-// 方法一
class Solution:
+ def getNext(self, next, s):
+ j = -1
+ next[0] = j
+ for i in range(1, len(s)):
+ while j >= 0 and s[i] != s[j+1]:
+ j = next[j]
+ if s[i] == s[j+1]:
+ j += 1
+ next[i] = j
+
def strStr(self, haystack: str, needle: str) -> int:
- a=len(needle)
- b=len(haystack)
- if a==0:
+ if not needle:
return 0
- next=self.getnext(a,needle)
- p=-1
- for j in range(b):
- while p>=0 and needle[p+1]!=haystack[j]:
- p=next[p]
- if needle[p+1]==haystack[j]:
- p+=1
- if p==a-1:
- return j-a+1
+ next = [0] * len(needle)
+ self.getNext(next, needle)
+ j = -1
+ for i in range(len(haystack)):
+ while j >= 0 and haystack[i] != needle[j+1]:
+ j = next[j]
+ if haystack[i] == needle[j+1]:
+ j += 1
+ if j == len(needle) - 1:
+ return i - len(needle) + 1
return -1
-
- def getnext(self,a,needle):
- next=['' for i in range(a)]
- k=-1
- next[0]=k
- for i in range(1,len(needle)):
- while (k>-1 and needle[k+1]!=needle[i]):
- k=next[k]
- if needle[k+1]==needle[i]:
- k+=1
- next[i]=k
- return next
```
+(版本二)前缀表(不减一)
```python
-// 方法二
class Solution:
+ def getNext(self, next: List[int], s: str) -> None:
+ j = 0
+ next[0] = 0
+ for i in range(1, len(s)):
+ while j > 0 and s[i] != s[j]:
+ j = next[j - 1]
+ if s[i] == s[j]:
+ j += 1
+ next[i] = j
+
def strStr(self, haystack: str, needle: str) -> int:
- a=len(needle)
- b=len(haystack)
- if a==0:
+ if len(needle) == 0:
return 0
- i=j=0
- next=self.getnext(a,needle)
- while(i 0 and haystack[i] != needle[j]:
+ j = next[j - 1]
+ if haystack[i] == needle[j]:
+ j += 1
+ if j == len(needle):
+ return i - len(needle) + 1
+ return -1
+```
+
- def getnext(self,a,needle):
- next=['' for i in range(a)]
- j,k=0,-1
- next[0]=k
- while(j int:
+ try:
+ return haystack.index(needle)
+ except ValueError:
+ return -1
+```
+(版本五)使用 find
+```python
+class Solution:
+ def strStr(self, haystack: str, needle: str) -> int:
+ return haystack.find(needle)
+
```
-Go:
+### Go:
```go
// 方法一:前缀表使用减1实现
@@ -763,17 +823,17 @@ Go:
// next 前缀表数组
// s 模式串
func getNext(next []int, s string) {
- j := -1 // j表示 最长相等前后缀长度
+ j := -1 // j表示 最长相等前后缀长度
next[0] = j
for i := 1; i < len(s); i++ {
for j >= 0 && s[i] != s[j+1] {
- j = next[j] // 回退前一位
+ j = next[j] // 回退前一位
}
if s[i] == s[j+1] {
j++
}
- next[i] = j // next[i]是i(包括i)之前的最长相等前后缀长度
+ next[i] = j // next[i]是i(包括i)之前的最长相等前后缀长度
}
}
func strStr(haystack string, needle string) int {
@@ -782,15 +842,15 @@ func strStr(haystack string, needle string) int {
}
next := make([]int, len(needle))
getNext(next, needle)
- j := -1 // 模式串的起始位置 next为-1 因此也为-1
+ j := -1 // 模式串的起始位置 next为-1 因此也为-1
for i := 0; i < len(haystack); i++ {
for j >= 0 && haystack[i] != needle[j+1] {
- j = next[j] // 寻找下一个匹配点
+ j = next[j] // 寻找下一个匹配点
}
if haystack[i] == needle[j+1] {
j++
}
- if j == len(needle)-1 { // j指向了模式串的末尾
+ if j == len(needle)-1 { // j指向了模式串的末尾
return i - len(needle) + 1
}
}
@@ -828,7 +888,7 @@ func strStr(haystack string, needle string) int {
getNext(next, needle)
for i := 0; i < len(haystack); i++ {
for j > 0 && haystack[i] != needle[j] {
- j = next[j-1] // 回退到j的前一位
+ j = next[j-1] // 回退到j的前一位
}
if haystack[i] == needle[j] {
j++
@@ -841,7 +901,7 @@ func strStr(haystack string, needle string) int {
}
```
-JavaScript版本
+### JavaScript:
> 前缀表统一减一
@@ -929,7 +989,7 @@ var strStr = function (haystack, needle) {
};
```
-TypeScript版本:
+### TypeScript:
> 前缀表统一减一
@@ -1006,7 +1066,7 @@ function strStr(haystack: string, needle: string): number {
}
```
-Swift 版本
+### Swift:
> 前缀表统一减一
@@ -1059,5 +1119,402 @@ func getNext(_ next: inout [Int], needle: [Character]) {
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 31.下一个排列
-[力扣题目链接](https://leetcode-cn.com/problems/next-permutation/)
+[力扣题目链接](https://leetcode.cn/problems/next-permutation/)
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
@@ -34,7 +32,7 @@
* 输出:[1]
-# 思路
+## 思路
一些同学可能手动写排列的顺序,都没有写对,那么写程序的话思路一定是有问题的了,我这里以1234为例子,把全排列都列出来。可以参考一下规律所在:
@@ -69,7 +67,7 @@
以求1243为例,流程如图:
- +
+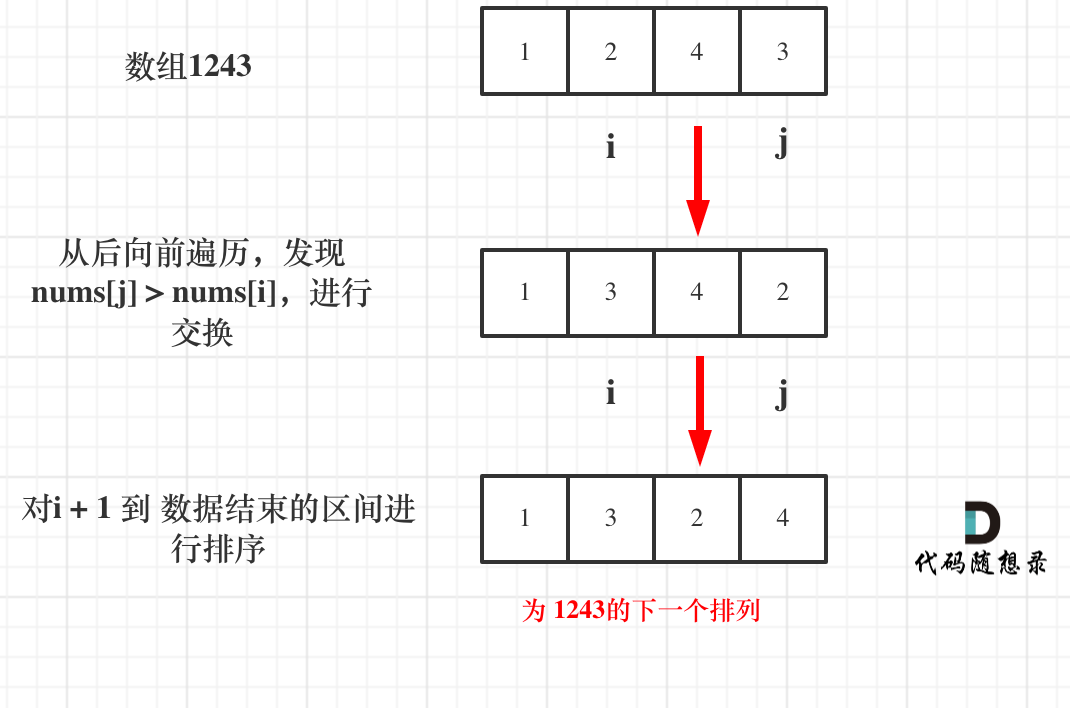 对应的C++代码如下:
@@ -92,9 +90,9 @@ public:
};
```
-# 其他语言版本
+## 其他语言版本
-## Java
+### Java
```java
class Solution {
@@ -116,83 +114,107 @@ class Solution {
}
}
```
+> 优化时间复杂度为O(N),空间复杂度为O(1)
+```Java
+class Solution {
+ public void nextPermutation(int[] nums) {
+ // 1.从后向前获取逆序区域的前一位
+ int index = findIndex(nums);
+ // 判断数组是否处于最小组合状态
+ if(index != 0){
+ // 2.交换逆序区域刚好大于它的最小数字
+ exchange(nums,index);
+ }
+ // 3.把原来的逆序区转为顺序
+ reverse(nums,index);
+ }
+
+ public static int findIndex(int [] nums){
+ for(int i = nums.length-1;i>0;i--){
+ if(nums[i]>nums[i-1]){
+ return i;
+ }
+ }
+ return 0;
+ }
+ public static void exchange(int [] nums, int index){
+ int head = nums[index-1];
+ for(int i = nums.length-1;i>0;i--){
+ if(head < nums[i]){
+ nums[index-1] = nums[i];
+ nums[i] = head;
+ break;
+ }
+ }
+ }
+ public static void reverse(int [] nums, int index){
+ for(int i = index,j = nums.length-1;i直接使用sorted()不符合题意
+### Python
+>直接使用sorted()会开辟新的空间并返回一个新的list,故补充一个原地反转函数
```python
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
- for i in range(len(nums)-1, -1, -1):
- for j in range(len(nums)-1, i, -1):
+ length = len(nums)
+ for i in range(length - 2, -1, -1): # 从倒数第二个开始
+ if nums[i]>=nums[i+1]: continue # 剪枝去重
+ for j in range(length - 1, i, -1):
if nums[j] > nums[i]:
nums[j], nums[i] = nums[i], nums[j]
- nums[i+1:len(nums)] = sorted(nums[i+1:len(nums)])
- return
- nums.sort()
+ self.reverse(nums, i + 1, length - 1)
+ return
+ self.reverse(nums, 0, length - 1)
+
+ def reverse(self, nums: List[int], left: int, right: int) -> None:
+ while left < right:
+ nums[left], nums[right] = nums[right], nums[left]
+ left += 1
+ right -= 1
+
+"""
+265 / 265 个通过测试用例
+状态:通过
+执行用时: 36 ms
+内存消耗: 14.9 MB
+"""
```
->另一种思路
-```python
-class Solution:
- '''
- 抛砖引玉:因题目要求“必须原地修改,只允许使用额外常数空间”,python内置sorted函数以及数组切片+sort()无法使用。
- 故选择另一种算法暂且提供一种python思路
- '''
- def nextPermutation(self, nums: List[int]) -> None:
- """
- Do not return anything, modify nums in-place instead.
- """
- length = len(nums)
- for i in range(length-1, 0, -1):
- if nums[i-1] < nums[i]:
- for j in range(length-1, 0, -1):
- if nums[j] > nums[i-1]:
- nums[i-1], nums[j] = nums[j], nums[i-1]
- break
- self.reverse(nums, i, length-1)
- break
- else:
- # 若正常结束循环,则对原数组直接翻转
- self.reverse(nums, 0, length-1)
-
- def reverse(self, nums: List[int], low: int, high: int) -> None:
- while low < high:
- nums[low], nums[high] = nums[high], nums[low]
- low += 1
- high -= 1
-```
->上一版本简化版
-'''python
-class Solution(object):
- def nextPermutation(self, nums: List[int]) -> None:
- n = len(nums)
- i = n-2
- while i >= 0 and nums[i] >= nums[i+1]:
- i -= 1
-
- if i > -1: // i==-1,不存在下一个更大的排列
- j = n-1
- while j >= 0 and nums[j] <= nums[i]:
- j -= 1
- nums[i], nums[j] = nums[j], nums[i]
-
- start, end = i+1, n-1
- while start < end:
- nums[start], nums[end] = nums[end], nums[start]
- start += 1
- end -= 1
-
- return nums
-'''
-
-## Go
+
+### Go
```go
+//卡尔的解法
+func nextPermutation(nums []int) {
+ for i:=len(nums)-1;i>=0;i--{
+ for j:=len(nums)-1;j>i;j--{
+ if nums[j]>nums[i]{
+ //交换
+ nums[j],nums[i]=nums[i],nums[j]
+ reverse(nums,0+i+1,len(nums)-1)
+ return
+ }
+ }
+ }
+ reverse(nums,0,len(nums)-1)
+}
+//对目标切片指定区间的反转方法
+func reverse(a []int,begin,end int){
+ for i,j:=begin,end;i
对应的C++代码如下:
@@ -92,9 +90,9 @@ public:
};
```
-# 其他语言版本
+## 其他语言版本
-## Java
+### Java
```java
class Solution {
@@ -116,83 +114,107 @@ class Solution {
}
}
```
+> 优化时间复杂度为O(N),空间复杂度为O(1)
+```Java
+class Solution {
+ public void nextPermutation(int[] nums) {
+ // 1.从后向前获取逆序区域的前一位
+ int index = findIndex(nums);
+ // 判断数组是否处于最小组合状态
+ if(index != 0){
+ // 2.交换逆序区域刚好大于它的最小数字
+ exchange(nums,index);
+ }
+ // 3.把原来的逆序区转为顺序
+ reverse(nums,index);
+ }
+
+ public static int findIndex(int [] nums){
+ for(int i = nums.length-1;i>0;i--){
+ if(nums[i]>nums[i-1]){
+ return i;
+ }
+ }
+ return 0;
+ }
+ public static void exchange(int [] nums, int index){
+ int head = nums[index-1];
+ for(int i = nums.length-1;i>0;i--){
+ if(head < nums[i]){
+ nums[index-1] = nums[i];
+ nums[i] = head;
+ break;
+ }
+ }
+ }
+ public static void reverse(int [] nums, int index){
+ for(int i = index,j = nums.length-1;i直接使用sorted()不符合题意
+### Python
+>直接使用sorted()会开辟新的空间并返回一个新的list,故补充一个原地反转函数
```python
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
- for i in range(len(nums)-1, -1, -1):
- for j in range(len(nums)-1, i, -1):
+ length = len(nums)
+ for i in range(length - 2, -1, -1): # 从倒数第二个开始
+ if nums[i]>=nums[i+1]: continue # 剪枝去重
+ for j in range(length - 1, i, -1):
if nums[j] > nums[i]:
nums[j], nums[i] = nums[i], nums[j]
- nums[i+1:len(nums)] = sorted(nums[i+1:len(nums)])
- return
- nums.sort()
+ self.reverse(nums, i + 1, length - 1)
+ return
+ self.reverse(nums, 0, length - 1)
+
+ def reverse(self, nums: List[int], left: int, right: int) -> None:
+ while left < right:
+ nums[left], nums[right] = nums[right], nums[left]
+ left += 1
+ right -= 1
+
+"""
+265 / 265 个通过测试用例
+状态:通过
+执行用时: 36 ms
+内存消耗: 14.9 MB
+"""
```
->另一种思路
-```python
-class Solution:
- '''
- 抛砖引玉:因题目要求“必须原地修改,只允许使用额外常数空间”,python内置sorted函数以及数组切片+sort()无法使用。
- 故选择另一种算法暂且提供一种python思路
- '''
- def nextPermutation(self, nums: List[int]) -> None:
- """
- Do not return anything, modify nums in-place instead.
- """
- length = len(nums)
- for i in range(length-1, 0, -1):
- if nums[i-1] < nums[i]:
- for j in range(length-1, 0, -1):
- if nums[j] > nums[i-1]:
- nums[i-1], nums[j] = nums[j], nums[i-1]
- break
- self.reverse(nums, i, length-1)
- break
- else:
- # 若正常结束循环,则对原数组直接翻转
- self.reverse(nums, 0, length-1)
-
- def reverse(self, nums: List[int], low: int, high: int) -> None:
- while low < high:
- nums[low], nums[high] = nums[high], nums[low]
- low += 1
- high -= 1
-```
->上一版本简化版
-'''python
-class Solution(object):
- def nextPermutation(self, nums: List[int]) -> None:
- n = len(nums)
- i = n-2
- while i >= 0 and nums[i] >= nums[i+1]:
- i -= 1
-
- if i > -1: // i==-1,不存在下一个更大的排列
- j = n-1
- while j >= 0 and nums[j] <= nums[i]:
- j -= 1
- nums[i], nums[j] = nums[j], nums[i]
-
- start, end = i+1, n-1
- while start < end:
- nums[start], nums[end] = nums[end], nums[start]
- start += 1
- end -= 1
-
- return nums
-'''
-
-## Go
+
+### Go
```go
+//卡尔的解法
+func nextPermutation(nums []int) {
+ for i:=len(nums)-1;i>=0;i--{
+ for j:=len(nums)-1;j>i;j--{
+ if nums[j]>nums[i]{
+ //交换
+ nums[j],nums[i]=nums[i],nums[j]
+ reverse(nums,0+i+1,len(nums)-1)
+ return
+ }
+ }
+ }
+ reverse(nums,0,len(nums)-1)
+}
+//对目标切片指定区间的反转方法
+func reverse(a []int,begin,end int){
+ for i,j:=begin,end;i +
diff --git "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
old mode 100644
new mode 100755
index dfd90b8280..37248e4819
--- "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
@@ -1,12 +1,13 @@
-
+
diff --git "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
old mode 100644
new mode 100755
index dfd90b8280..37248e4819
--- "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
@@ -1,12 +1,13 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 34. 在排序数组中查找元素的第一个和最后一个位置
+[力扣链接](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)
+
+
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
@@ -230,14 +231,14 @@ class Solution {
if (index == -1) { // nums 中不存在 target,直接返回 {-1, -1}
return new int[] {-1, -1}; // 匿名数组
}
- // nums 中存在 targe,则左右滑动指针,来找到符合题意的区间
+ // nums 中存在 target,则左右滑动指针,来找到符合题意的区间
int left = index;
int right = index;
// 向左滑动,找左边界
while (left - 1 >= 0 && nums[left - 1] == nums[index]) { // 防止数组越界。逻辑短路,两个条件顺序不能换
left--;
}
- // 向左滑动,找右边界
+ // 向右滑动,找右边界
while (right + 1 < nums.length && nums[right + 1] == nums[index]) { // 防止数组越界。
right++;
}
@@ -268,6 +269,125 @@ class Solution {
}
```
+```java
+// 解法三
+class Solution {
+ public int[] searchRange(int[] nums, int target) {
+ int left = searchLeft(nums,target);
+ int right = searchRight(nums,target);
+ return new int[]{left,right};
+ }
+ public int searchLeft(int[] nums,int target){
+ // 寻找元素第一次出现的地方
+ int left = 0;
+ int right = nums.length-1;
+ while(left<=right){
+ int mid = left+(right-left)/2;
+ // >= 的都要缩小 因为要找第一个元素
+ if(nums[mid]>=target){
+ right = mid - 1;
+ }else{
+ left = mid + 1;
+ }
+ }
+ // right = left - 1
+ // 如果存在答案 right是首选
+ if(right>=0&&right=0&&left=0&&left=0&&right<=nums.length&&nums[right]==target){
+ return right;
+ }
+ return -1;
+ }
+}
+```
+
+### C#
+
+```csharp
+public int[] SearchRange(int[] nums, int target) {
+
+ var leftBorder = GetLeftBorder(nums, target);
+ var rightBorder = GetRightBorder(nums, target);
+
+ if (leftBorder == -2 || rightBorder == -2) {
+ return new int[] {-1, -1};
+ }
+
+ if (rightBorder - leftBorder >=2) {
+ return new int[] {leftBorder + 1, rightBorder - 1};
+ }
+
+ return new int[] {-1, -1};
+
+}
+
+public int GetLeftBorder(int[] nums, int target){
+ var left = 0;
+ var right = nums.Length - 1;
+ var leftBorder = -2;
+
+ while (left <= right) {
+ var mid = (left + right) / 2;
+
+ if (target <= nums[mid]) {
+ right = mid - 1;
+ leftBorder = right;
+ }
+ else {
+ left = mid + 1;
+ }
+ }
+
+ return leftBorder;
+}
+
+public int GetRightBorder(int[] nums, int target){
+ var left = 0;
+ var right = nums.Length - 1;
+ var rightBorder = -2;
+
+ while (left <= right) {
+ var mid = (left + right) / 2;
+
+ if (target >= nums[mid]) {
+ left = mid + 1;
+ rightBorder = left;
+ }
+ else {
+ right = mid - 1;
+ }
+ }
+
+ return rightBorder;
+}
+```
+
### Python
@@ -294,8 +414,8 @@ class Solution:
while left <= right:
middle = left + (right-left) // 2
if nums[middle] >= target: # 寻找左边界,nums[middle] == target的时候更新right
- right = middle - 1;
- leftBoder = right;
+ right = middle - 1
+ leftBoder = right
else:
left = middle + 1
return leftBoder
@@ -328,7 +448,7 @@ class Solution:
return -1
index = binarySearch(nums, target)
if index == -1:return [-1, -1] # nums 中不存在 target,直接返回 {-1, -1}
- # nums 中存在 targe,则左右滑动指针,来找到符合题意的区间
+ # nums 中存在 target,则左右滑动指针,来找到符合题意的区间
left, right = index, index
# 向左滑动,找左边界
while left -1 >=0 and nums[left - 1] == target: left -=1
@@ -386,6 +506,57 @@ class Solution:
return [leftBorder, rightBorder]
```
+### Rust
+
+```rust
+
+impl Solution {
+ pub fn search_range(nums: Vec, target: i32) -> Vec {
+ let right_border = Solution::get_right_border(&nums, target);
+ let left_border = Solution::get_left_border(&nums, target);
+ if right_border == -2 || left_border == -2 {
+ return vec![-1, -1];
+ }
+ if right_border - left_border > 0 {
+ return vec![left_border, right_border - 1];
+ }
+ vec![-1, -1]
+ }
+
+ pub fn get_right_border(nums: &Vec, target: i32) -> i32 {
+ let mut left = 0;
+ let mut right = nums.len();
+ let mut right_border: i32 = -2;
+ while left < right {
+ let mid = (left + right) / 2;
+ if nums[mid] > target {
+ right = mid;
+ } else {
+ left = mid + 1;
+ right_border = left as i32;
+ }
+ }
+ right_border as i32
+ }
+
+ pub fn get_left_border(nums: &Vec, target: i32) -> i32 {
+ let mut left = 0;
+ let mut right = nums.len();
+ let mut left_border: i32 = -2;
+ while left < right {
+ let mid = (left + right) / 2;
+ if nums[mid] >= target {
+ right = mid;
+ left_border = right as i32;
+ } else {
+ left = mid + 1;
+ }
+ }
+ left_border as i32
+ }
+}
+```
+
### Go
```go
@@ -482,5 +653,203 @@ var searchRange = function(nums, target) {
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+
+
# 35.搜索插入位置
-[力扣题目链接](https://leetcode-cn.com/problems/search-insert-position/)
+[力扣题目链接](https://leetcode.cn/problems/search-insert-position/)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
+
* 输入: [1,3,5,6], 5
* 输出: 2
-示例 2:
+示例 2:
+
* 输入: [1,3,5,6], 2
* 输出: 1
示例 3:
+
* 输入: [1,3,5,6], 7
* 输出: 4
示例 4:
+
* 输入: [1,3,5,6], 0
* 输出: 0
@@ -37,7 +41,7 @@
这道题目,要在数组中插入目标值,无非是这四种情况。
-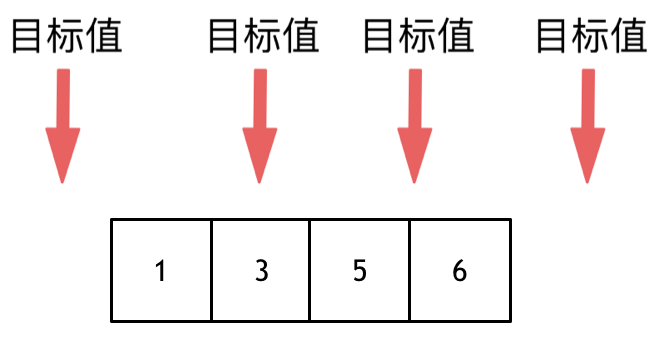
+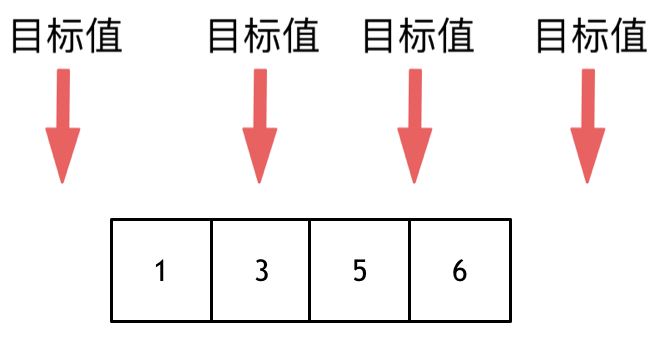
* 目标值在数组所有元素之前
* 目标值等于数组中某一个元素
@@ -73,18 +77,19 @@ public:
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
效率如下:
-
+
### 二分法
-既然暴力解法的时间复杂度是$O(n)$,就要尝试一下使用二分查找法。
+既然暴力解法的时间复杂度是O(n),就要尝试一下使用二分查找法。
+
-
+
大家注意这道题目的前提是数组是有序数组,这也是使用二分查找的基础条件。
@@ -94,7 +99,7 @@ public:
大体讲解一下二分法的思路,这里来举一个例子,例如在这个数组中,使用二分法寻找元素为5的位置,并返回其下标。
-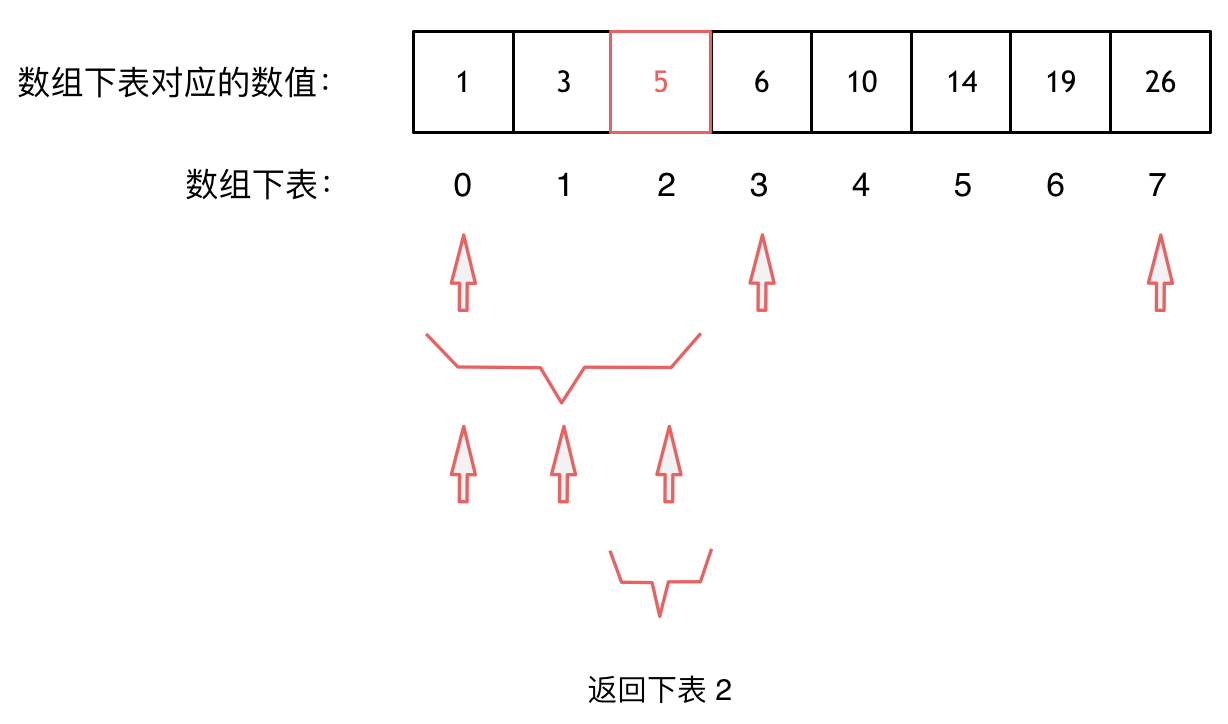
+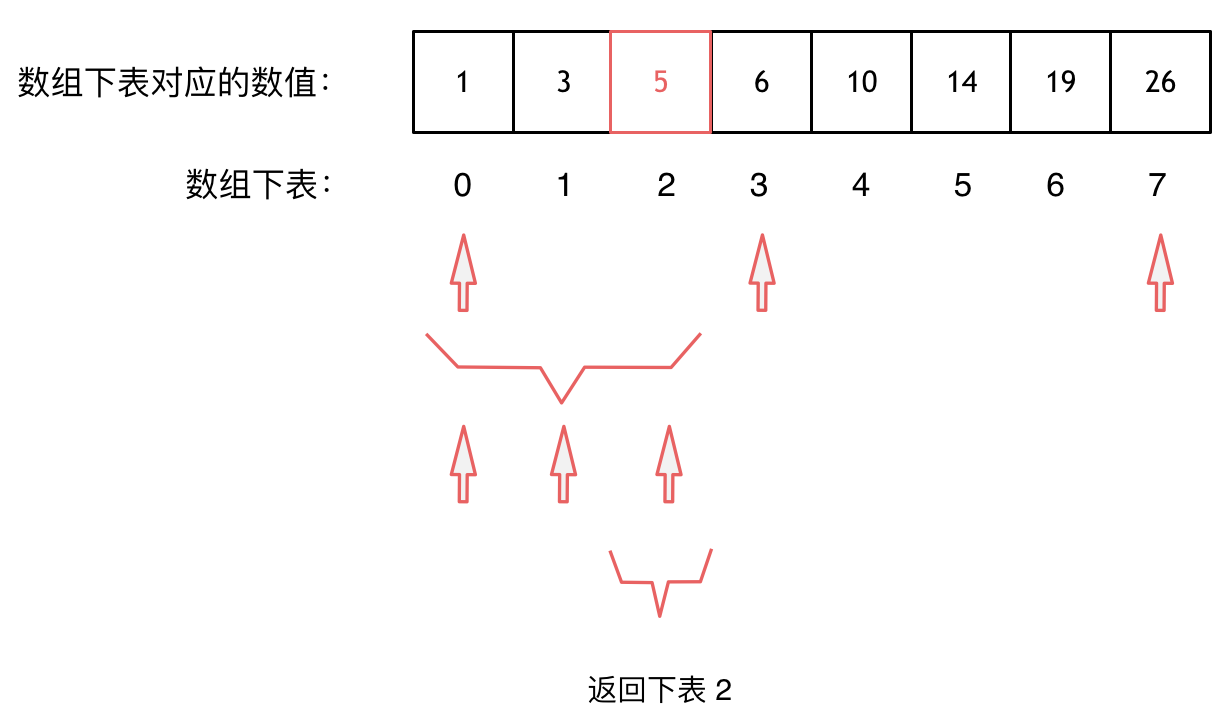
二分查找涉及的很多的边界条件,逻辑比较简单,就是写不好。
@@ -135,17 +140,17 @@ public:
// 目标值在数组所有元素之前 [0, -1]
// 目标值等于数组中某一个元素 return middle;
// 目标值插入数组中的位置 [left, right],return right + 1
- // 目标值在数组所有元素之后的情况 [left, right], return right + 1
+ // 目标值在数组所有元素之后的情况 [left, right], 因为是右闭区间,所以 return right + 1
return right + 1;
}
};
```
-* 时间复杂度:$O(\log n)$
-* 时间复杂度:$O(1)$
+* 时间复杂度:O(log n)
+* 空间复杂度:O(1)
效率如下:
-
+
### 二分法第二种写法
@@ -178,14 +183,14 @@ public:
// 目标值在数组所有元素之前 [0,0)
// 目标值等于数组中某一个元素 return middle
// 目标值插入数组中的位置 [left, right) ,return right 即可
- // 目标值在数组所有元素之后的情况 [left, right),return right 即可
+ // 目标值在数组所有元素之后的情况 [left, right),因为是右开区间,所以 return right
return right;
}
};
```
-* 时间复杂度:$O(\log n)$
-* 时间复杂度:$O(1)$
+* 时间复杂度:O(log n)
+* 空间复杂度:O(1)
## 总结
@@ -199,7 +204,7 @@ public:
## 其他语言版本
-### Java
+### Java
```java
class Solution {
@@ -226,27 +231,106 @@ class Solution {
}
}
```
-Golang:
-```golang
+
+```java
+//第二种二分法:左闭右开
+public int searchInsert(int[] nums, int target) {
+ int left = 0;
+ int right = nums.length;
+ while (left < right) { //左闭右开 [left, right)
+ int middle = left + ((right - left) >> 1);
+ if (nums[middle] > target) {
+ right = middle; // target 在左区间,在[left, middle)中
+ } else if (nums[middle] < target) {
+ left = middle + 1; // target 在右区间,在 [middle+1, right)中
+ } else { // nums[middle] == target
+ return middle; // 数组中找到目标值的情况,直接返回下标
+ }
+ }
+ // 目标值在数组所有元素之前 [0,0)
+ // 目标值插入数组中的位置 [left, right) ,return right 即可
+ // 目标值在数组所有元素之后的情况 [left, right),因为是右开区间,所以 return right
+ return right;
+}
+```
+
+
+
+### C#
+
+```go
+public int SearchInsert(int[] nums, int target) {
+
+ var left = 0;
+ var right = nums.Length - 1;
+
+ while (left <= right) {
+
+ var curr = (left + right) / 2;
+
+ if (nums[curr] == target)
+ {
+ return curr;
+ }
+
+ if (target > nums[curr]) {
+ left = curr + 1;
+ }
+ else {
+ right = curr - 1;
+ }
+ }
+
+ return left;
+}
+```
+
+
+
+### Golang
+
+```go
// 第一种二分法
func searchInsert(nums []int, target int) int {
- l, r := 0, len(nums) - 1
- for l <= r{
- m := l + (r - l)/2
- if nums[m] == target{
- return m
- }else if nums[m] > target{
- r = m - 1
- }else{
- l = m + 1
+ left, right := 0, len(nums)-1
+ for left <= right {
+ mid := left + (right-left)/2
+ if nums[mid] == target {
+ return mid
+ } else if nums[mid] > target {
+ right = mid - 1
+ } else {
+ left = mid + 1
+ }
+ }
+ return right+1
+}
+```
+
+### Rust
+
+```rust
+impl Solution {
+ pub fn search_insert(nums: Vec, target: i32) -> i32 {
+ use std::cmp::Ordering::{Equal, Greater, Less};
+ let (mut left, mut right) = (0, nums.len() as i32 - 1);
+ while left <= right {
+ let mid = (left + right) / 2;
+ match nums[mid as usize].cmp(&target) {
+ Less => left = mid + 1,
+ Equal => return mid,
+ Greater => right = mid - 1,
+ }
}
+ right + 1
}
- return r + 1
}
```
-### Python
+### Python
+
```python
+# 第一种二分法: [left, right]左闭右闭区间
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
@@ -263,7 +347,28 @@ class Solution:
return right + 1
```
-### JavaScript
+```python
+# 第二种二分法: [left, right)左闭右开区间
+class Solution:
+ def searchInsert(self, nums: List[int], target: int) -> int:
+ left = 0
+ right = len(nums)
+
+ while (left < right):
+ middle = (left + right) // 2
+
+ if nums[middle] > target:
+ right = middle
+ elif nums[middle] < target:
+ left = middle + 1
+ else:
+ return middle
+
+ return right
+```
+
+### JavaScript
+
```js
var searchInsert = function (nums, target) {
let l = 0, r = nums.length - 1, ans = nums.length;
@@ -283,7 +388,29 @@ var searchInsert = function (nums, target) {
};
```
-### Swift
+### TypeScript
+
+```typescript
+// 第一种二分法
+function searchInsert(nums: number[], target: number): number {
+ const length: number = nums.length;
+ let left: number = 0,
+ right: number = length - 1;
+ while (left <= right) {
+ const mid: number = Math.floor((left + right) / 2);
+ if (nums[mid] < target) {
+ left = mid + 1;
+ } else if (nums[mid] === target) {
+ return mid;
+ } else {
+ right = mid - 1;
+ }
+ }
+ return right + 1;
+};
+```
+
+### Swift
```swift
// 暴力法
@@ -317,8 +444,106 @@ func searchInsert(_ nums: [Int], _ target: Int) -> Int {
}
```
+### Scala
+
+```scala
+object Solution {
+ def searchInsert(nums: Array[Int], target: Int): Int = {
+ var left = 0
+ var right = nums.length - 1
+ while (left <= right) {
+ var mid = left + (right - left) / 2
+ if (target == nums(mid)) {
+ return mid
+ } else if (target > nums(mid)) {
+ left = mid + 1
+ } else {
+ right = mid - 1
+ }
+ }
+ right + 1
+ }
+}
+```
+### PHP
+
+```php
+// 二分法(1):[左闭右闭]
+function searchInsert($nums, $target)
+{
+ $n = count($nums);
+ $l = 0;
+ $r = $n - 1;
+ while ($l <= $r) {
+ $mid = floor(($l + $r) / 2);
+ if ($nums[$mid] > $target) {
+ // 下次搜索在左区间:[$l,$mid-1]
+ $r = $mid - 1;
+ } else if ($nums[$mid] < $target) {
+ // 下次搜索在右区间:[$mid+1,$r]
+ $l = $mid + 1;
+ } else {
+ // 命中返回
+ return $mid;
+ }
+ }
+ return $r + 1;
+}
+```
+
+### C
+
+```c
+//版本一 [left, right]左闭右闭区间
+int searchInsert(int* nums, int numsSize, int target){
+ //左闭右开区间 [0 , numsSize-1]
+ int left =0;
+ int mid =0;
+ int right = numsSize - 1;
+ while(left <= right){//左闭右闭区间 所以可以 left == right
+ mid = left + (right - left) / 2;
+ if(target < nums[mid]){
+ //target 在左区间 [left, mid - 1]中,原区间包含mid,右区间边界可以向左内缩
+ right = mid -1;
+ }else if( target > nums[mid]){
+ //target 在右区间 [mid + 1, right]中,原区间包含mid,左区间边界可以向右内缩
+ left = mid + 1;
+ }else {
+ // nums[mid] == target ,顺利找到target,直接返回mid
+ return mid;
+ }
+ }
+ //数组中未找到target元素
+ //target在数组所有元素之后,[left, right]是右闭区间,需要返回 right +1
+ return right + 1;
+}
+```
+
+```c
+//版本二 [left, right]左闭右开区间
+int searchInsert(int* nums, int numsSize, int target){
+ //左闭右开区间 [0 , numsSize)
+ int left =0;
+ int mid =0;
+ int right = numsSize;
+ while(left < right){//左闭右闭区间 所以 left < right
+ mid = left + (right - left) / 2;
+ if(target < nums[mid]){
+ //target 在左区间 [left, mid)中,原区间没有包含mid,右区间边界不能内缩
+ right = mid ;
+ }else if( target > nums[mid]){
+ // target 在右区间 [mid+1, right)中,原区间包含mid,左区间边界可以向右内缩
+ left = mid + 1;
+ }else {
+ // nums[mid] == target ,顺利找到target,直接返回mid
+ return mid;
+ }
+ }
+ //数组中未找到target元素
+ //target在数组所有元素之后,[left, right)是右开区间, return right即可
+ return right;
+}
+```
------------------------
-
diff --git "a/problems/0037.\350\247\243\346\225\260\347\213\254.md" "b/problems/0037.\350\247\243\346\225\260\347\213\254.md"
old mode 100644
new mode 100755
index 53b9bb67e0..204f0cc092
--- "a/problems/0037.\350\247\243\346\225\260\347\213\254.md"
+++ "b/problems/0037.\350\247\243\346\225\260\347\213\254.md"
@@ -1,37 +1,41 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
+
+> 如果对回溯法理论还不清楚的同学,可以先看这个视频[视频来了!!带你学透回溯算法(理论篇)](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
# 37. 解数独
-[力扣题目链接](https://leetcode-cn.com/problems/sudoku-solver/)
+[力扣题目链接](https://leetcode.cn/problems/sudoku-solver/)
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则:
-数字 1-9 在每一行只能出现一次。
-数字 1-9 在每一列只能出现一次。
-数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
-空白格用 '.' 表示。
+数字 1-9 在每一行只能出现一次。
+数字 1-9 在每一列只能出现一次。
+数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
+空白格用 '.' 表示。
-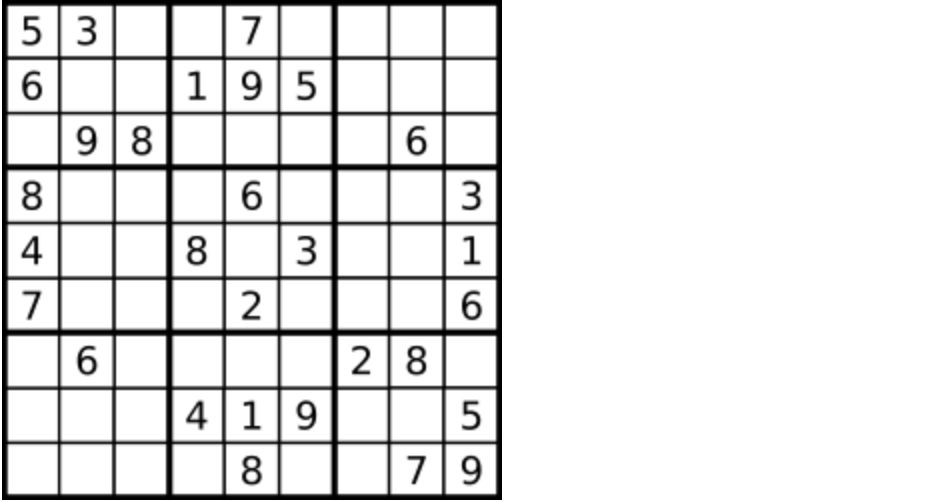
+
一个数独。
-
+
答案被标成红色。
提示:
+
* 给定的数独序列只包含数字 1-9 和字符 '.' 。
* 你可以假设给定的数独只有唯一解。
* 给定数独永远是 9x9 形式的。
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[回溯算法二维递归?解数独不过如此!| LeetCode:37. 解数独](https://www.bilibili.com/video/BV1TW4y1471V/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是**二维递归**。
@@ -42,13 +46,13 @@
**如果以上这几道题目没有做过的话,不建议上来就做这道题哈!**
-[N皇后问题](https://programmercarl.com/0051.N皇后.html)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
+[N皇后问题](https://programmercarl.com/0051.N皇后.html)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
-本题就不一样了,**本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
+本题就不一样了,**本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深**。
因为这个树形结构太大了,我抽取一部分,如图所示:
-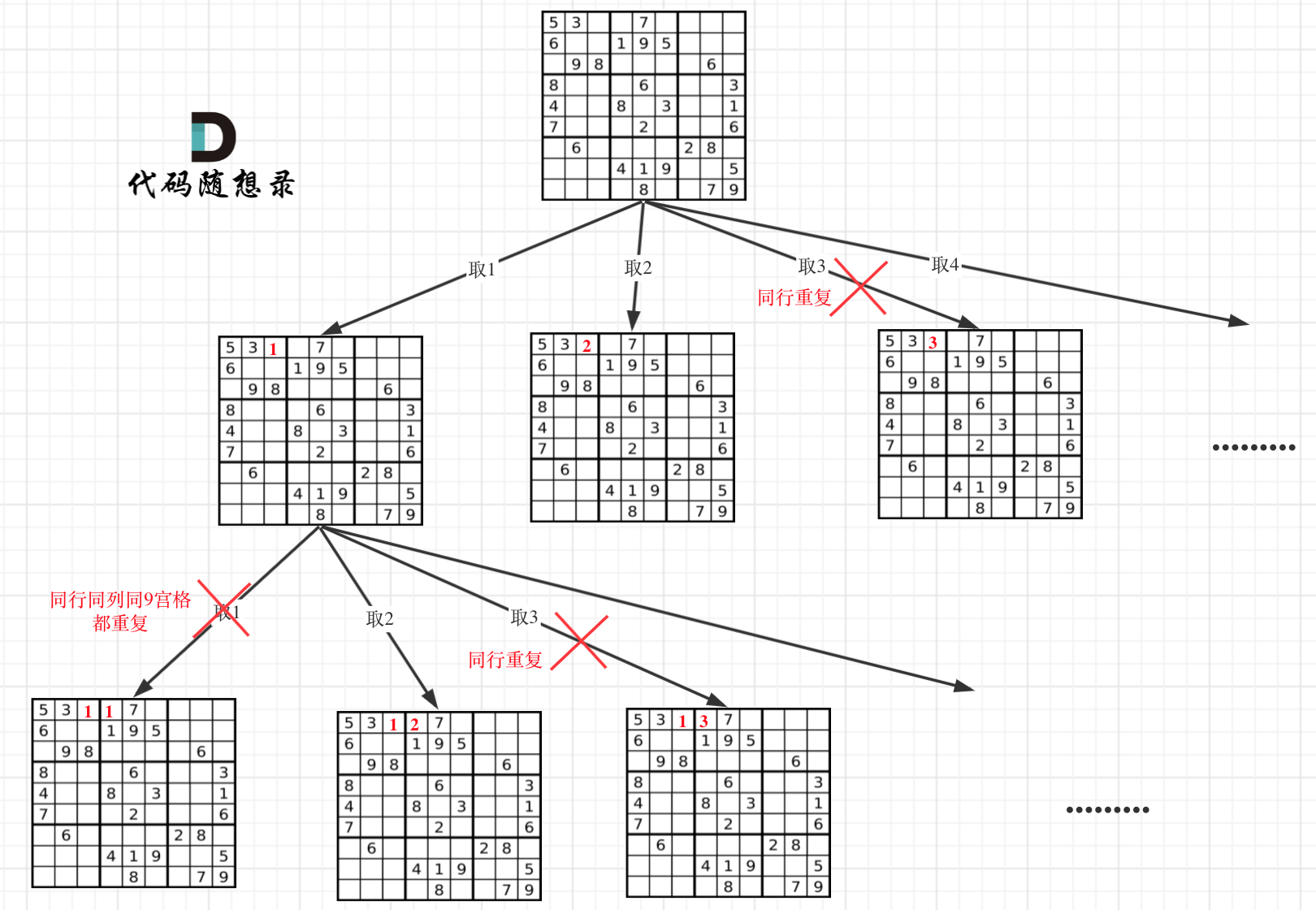
+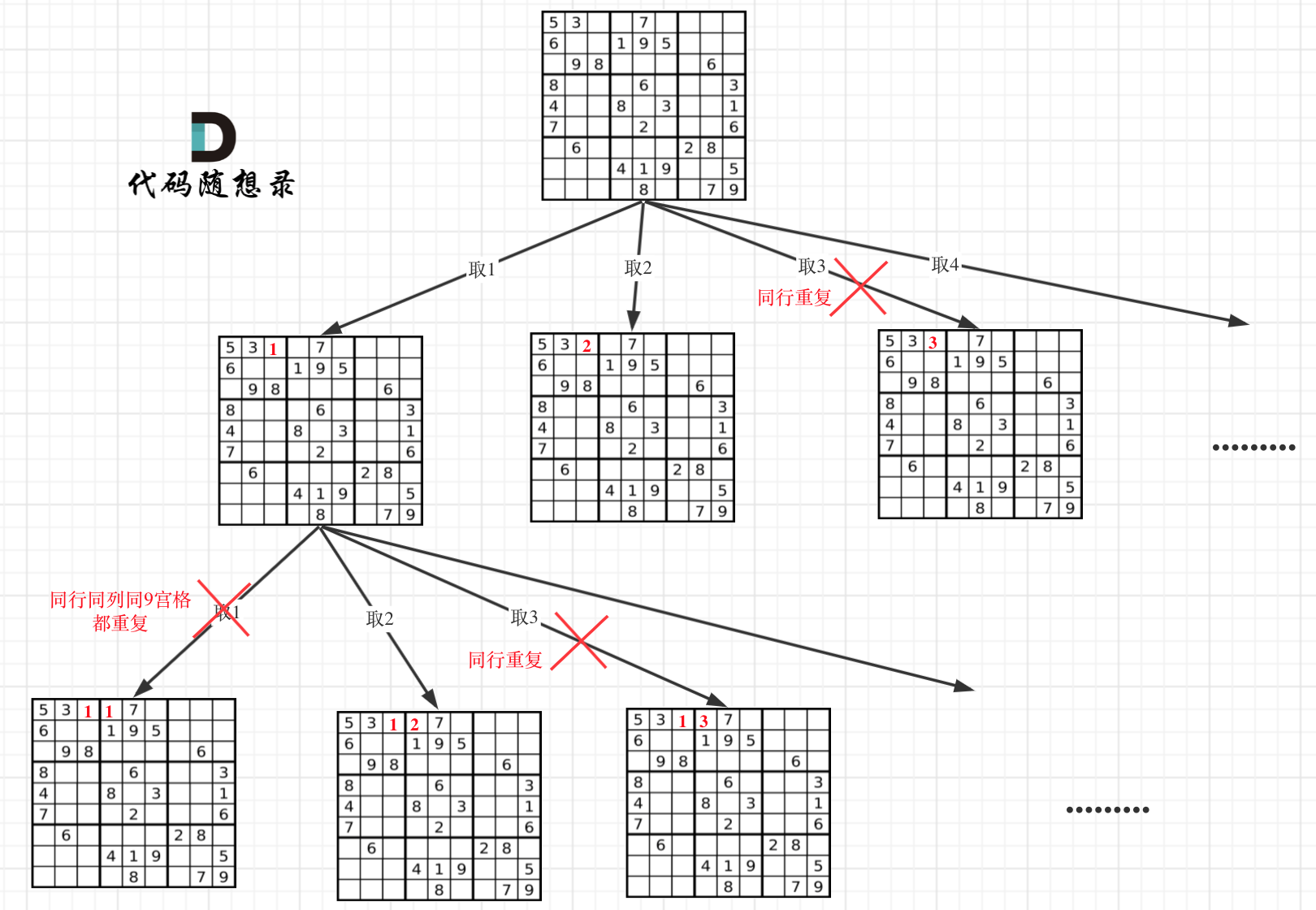
### 回溯三部曲
@@ -57,7 +61,7 @@
**递归函数的返回值需要是bool类型,为什么呢?**
-因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值,这一点在[回溯算法:N皇后问题](https://programmercarl.com/0051.N皇后.html)中已经介绍过了,一样的道理。
+因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
代码如下:
@@ -75,13 +79,13 @@ bool backtracking(vector>& board)
**那么有没有永远填不满的情况呢?**
-这个问题我在递归单层搜索逻辑里在来讲!
+这个问题我在递归单层搜索逻辑里再来讲!
* 递归单层搜索逻辑
-
+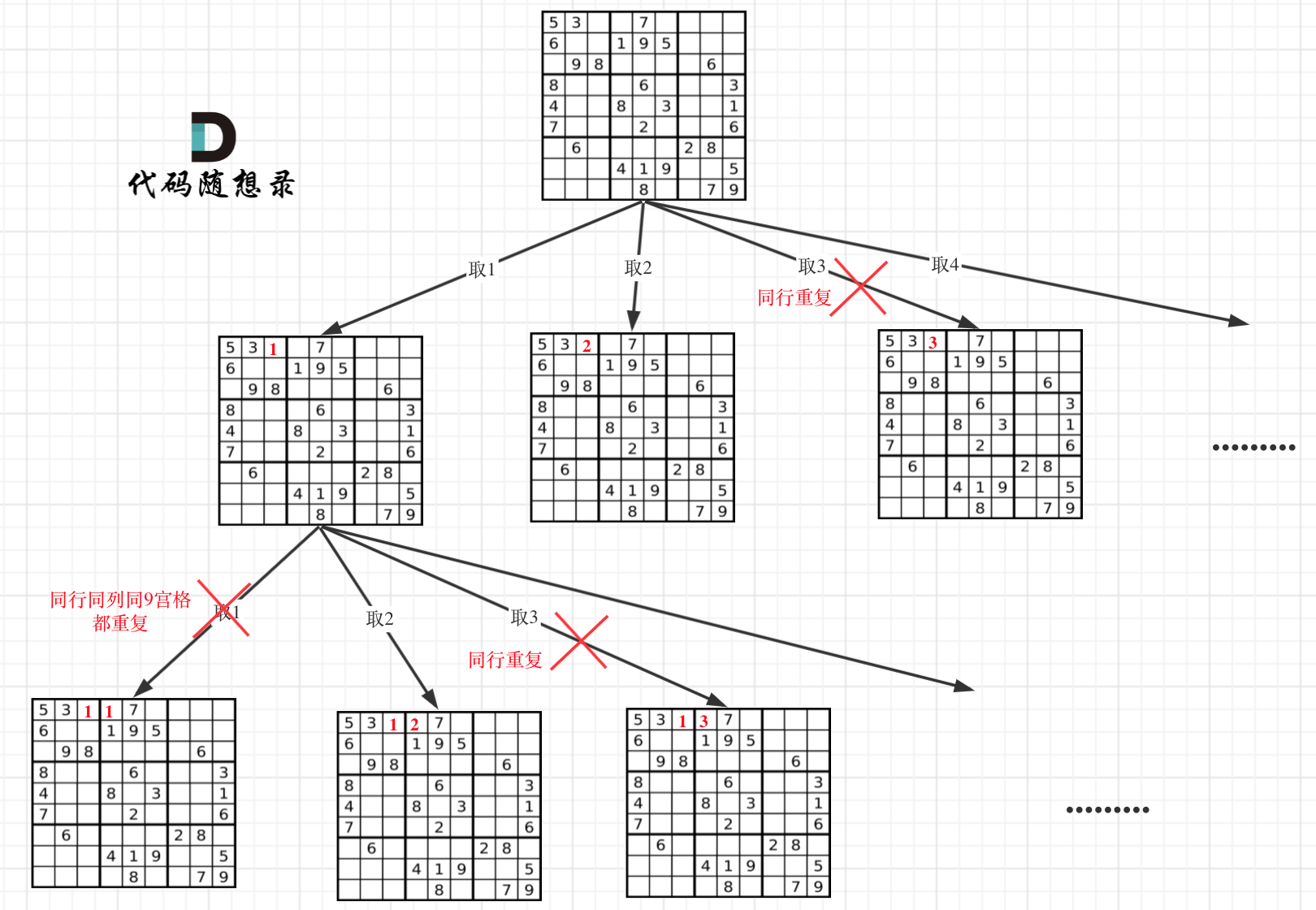
-在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
+在树形图中可以看出我们需要的是一个二维的递归 (一行一列)
**一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!**
@@ -157,15 +161,16 @@ private:
bool backtracking(vector>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
- if (board[i][j] != '.') continue;
- for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
- if (isValid(i, j, k, board)) {
- board[i][j] = k; // 放置k
- if (backtracking(board)) return true; // 如果找到合适一组立刻返回
- board[i][j] = '.'; // 回溯,撤销k
+ if (board[i][j] == '.') {
+ for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
+ if (isValid(i, j, k, board)) {
+ board[i][j] = k; // 放置k
+ if (backtracking(board)) return true; // 如果找到合适一组立刻返回
+ board[i][j] = '.'; // 回溯,撤销k
+ }
}
+ return false; // 9个数都试完了,都不行,那么就返回false
}
- return false; // 9个数都试完了,都不行,那么就返回false
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
@@ -197,6 +202,7 @@ public:
backtracking(board);
}
};
+
```
## 总结
@@ -205,7 +211,7 @@ public:
所以我在开篇就提到了**二维递归**,这也是我自创词汇,希望可以帮助大家理解解数独的搜索过程。
-一波分析之后,在看代码会发现其实也不难,唯一难点就是理解**二维递归**的思维逻辑。
+一波分析之后,再看代码会发现其实也不难,唯一难点就是理解**二维递归**的思维逻辑。
**这样,解数独这么难的问题,也被我们攻克了**。
@@ -215,7 +221,8 @@ public:
## 其他语言版本
-### Java
+### Java
+解法一:
```java
class Solution {
public void solveSudoku(char[][] board) {
@@ -282,108 +289,193 @@ class Solution {
}
}
```
+解法二(bitmap标记)
+```
+class Solution{
+ int[] rowBit = new int[9];
+ int[] colBit = new int[9];
+ int[] square9Bit = new int[9];
+
+ public void solveSudoku(char[][] board) {
+ // 1 10 11
+ for (int y = 0; y < board.length; y++) {
+ for (int x = 0; x < board[y].length; x++) {
+ int numBit = 1 << (board[y][x] - '1');
+ rowBit[y] ^= numBit;
+ colBit[x] ^= numBit;
+ square9Bit[(y / 3) * 3 + x / 3] ^= numBit;
+ }
+ }
+ backtrack(board, 0);
+ }
+
+ public boolean backtrack(char[][] board, int n) {
+ if (n >= 81) {
+ return true;
+ }
+
+ // 快速算出行列编号 n/9 n%9
+ int row = n / 9;
+ int col = n % 9;
+
+ if (board[row][col] != '.') {
+ return backtrack(board, n + 1);
+ }
+
+ for (char c = '1'; c <= '9'; c++) {
+ int numBit = 1 << (c - '1');
+ if (!isValid(numBit, row, col)) continue;
+ {
+ board[row][col] = c; // 当前的数字放入到数组之中,
+ rowBit[row] ^= numBit; // 第一行rowBit[0],第一个元素eg: 1 , 0^1=1,第一个元素:4, 100^1=101,...
+ colBit[col] ^= numBit;
+ square9Bit[(row / 3) * 3 + col / 3] ^= numBit;
+ }
+ if (backtrack(board, n + 1)) return true;
+ {
+ board[row][col] = '.'; // 不满足条件,回退成'.'
+ rowBit[row] &= ~numBit; // 第一行rowBit[0],第一个元素eg: 1 , 101&=~1==>101&111111110==>100
+ colBit[col] &= ~numBit;
+ square9Bit[(row / 3) * 3 + col / 3] &= ~numBit;
+ }
+ }
+ return false;
+ }
+
+
+ boolean isValid(int numBit, int row, int col) {
+ // 左右
+ if ((rowBit[row] & numBit) > 0) return false;
+ // 上下
+ if ((colBit[col] & numBit) > 0) return false;
+ // 9宫格: 快速算出第n个九宫格,编号[0,8] , 编号=(row / 3) * 3 + col / 3
+ if ((square9Bit[(row / 3) * 3 + col / 3] & numBit) > 0) return false;
+ return true;
+ }
+
+}
+
+```
+### Python
-### Python
```python
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
- self.backtracking(board)
-
- def backtracking(self, board: List[List[str]]) -> bool:
- # 若有解,返回True;若无解,返回False
- for i in range(len(board)): # 遍历行
- for j in range(len(board[0])): # 遍历列
- # 若空格内已有数字,跳过
- if board[i][j] != '.': continue
- for k in range(1, 10):
- if self.is_valid(i, j, k, board):
- board[i][j] = str(k)
- if self.backtracking(board): return True
- board[i][j] = '.'
- # 若数字1-9都不能成功填入空格,返回False无解
- return False
- return True # 有解
-
- def is_valid(self, row: int, col: int, val: int, board: List[List[str]]) -> bool:
- # 判断同一行是否冲突
- for i in range(9):
- if board[row][i] == str(val):
- return False
- # 判断同一列是否冲突
- for j in range(9):
- if board[j][col] == str(val):
- return False
- # 判断同一九宫格是否有冲突
- start_row = (row // 3) * 3
- start_col = (col // 3) * 3
- for i in range(start_row, start_row + 3):
- for j in range(start_col, start_col + 3):
- if board[i][j] == str(val):
- return False
- return True
+ row_used = [set() for _ in range(9)]
+ col_used = [set() for _ in range(9)]
+ box_used = [set() for _ in range(9)]
+ for row in range(9):
+ for col in range(9):
+ num = board[row][col]
+ if num == ".":
+ continue
+ row_used[row].add(num)
+ col_used[col].add(num)
+ box_used[(row // 3) * 3 + col // 3].add(num)
+ self.backtracking(0, 0, board, row_used, col_used, box_used)
+
+ def backtracking(
+ self,
+ row: int,
+ col: int,
+ board: List[List[str]],
+ row_used: List[List[int]],
+ col_used: List[List[int]],
+ box_used: List[List[int]],
+ ) -> bool:
+ if row == 9:
+ return True
+
+ next_row, next_col = (row, col + 1) if col < 8 else (row + 1, 0)
+ if board[row][col] != ".":
+ return self.backtracking(
+ next_row, next_col, board, row_used, col_used, box_used
+ )
+
+ for num in map(str, range(1, 10)):
+ if (
+ num not in row_used[row]
+ and num not in col_used[col]
+ and num not in box_used[(row // 3) * 3 + col // 3]
+ ):
+ board[row][col] = num
+ row_used[row].add(num)
+ col_used[col].add(num)
+ box_used[(row // 3) * 3 + col // 3].add(num)
+ if self.backtracking(
+ next_row, next_col, board, row_used, col_used, box_used
+ ):
+ return True
+ board[row][col] = "."
+ row_used[row].remove(num)
+ col_used[col].remove(num)
+ box_used[(row // 3) * 3 + col // 3].remove(num)
+ return False
```
-### Go
+### Go
```go
-func solveSudoku(board [][]byte) {
- var backtracking func(board [][]byte) bool
- backtracking=func(board [][]byte) bool{
- for i:=0;i<9;i++{
- for j:=0;j<9;j++{
- //判断此位置是否适合填数字
- if board[i][j]!='.'{
- continue
- }
- //尝试填1-9
- for k:='1';k<='9';k++{
- if isvalid(i,j,byte(k),board)==true{//如果满足要求就填
- board[i][j]=byte(k)
- if backtracking(board)==true{
- return true
- }
- board[i][j]='.'
- }
- }
- return false
- }
- }
- return true
- }
- backtracking(board)
+func solveSudoku(board [][]byte) {
+ var backtracking func(board [][]byte) bool
+ backtracking = func(board [][]byte) bool {
+ for i := 0; i < 9; i++ {
+ for j := 0; j < 9; j++ {
+ //判断此位置是否适合填数字
+ if board[i][j] != '.' {
+ continue
+ }
+ //尝试填1-9
+ for k := '1'; k <= '9'; k++ {
+ if isvalid(i, j, byte(k), board) == true { //如果满足要求就填
+ board[i][j] = byte(k)
+ if backtracking(board) == true {
+ return true
+ }
+ board[i][j] = '.'
+ }
+ }
+ return false
+ }
+ }
+ return true
+ }
+ backtracking(board)
}
+
//判断填入数字是否满足要求
-func isvalid(row,col int,k byte,board [][]byte)bool{
- for i:=0;i<9;i++{//行
- if board[row][i]==k{
- return false
- }
- }
- for i:=0;i<9;i++{//列
- if board[i][col]==k{
- return false
- }
- }
- //方格
- startrow:=(row/3)*3
- startcol:=(col/3)*3
- for i:=startrow;i>) -> bool{
+ for i in 0..9 {
+ if board[row][i] == val { return false; }
+ }
+ for j in 0..9 {
+ if board[j][col] == val {
+ return false;
+ }
+ }
+ let start_row = (row / 3) * 3;
+ let start_col = (col / 3) * 3;
+ for i in start_row..(start_row + 3) {
+ for j in start_col..(start_col + 3) {
+ if board[i][j] == val { return false; }
+ }
+ }
+ return true;
+ }
+
+ fn backtracking(board: &mut Vec>) -> bool{
+ for i in 0..board.len() {
+ for j in 0..board[0].len() {
+ if board[i][j] != '.' { continue; }
+ for k in '1'..='9' {
+ if Self::is_valid(i, j, k, board) {
+ board[i][j] = k;
+ if Self::backtracking(board) { return true; }
+ board[i][j] = '.';
+ }
+ }
+ return false;
+ }
+ }
+ return true;
+ }
+
+ pub fn solve_sudoku(board: &mut Vec>) {
+ Self::backtracking(board);
+ }
+}
+```
+
+### C
```C
bool isValid(char** board, int row, int col, int k) {
@@ -553,5 +740,154 @@ func solveSudoku(_ board: inout [[Character]]) {
}
```
------------------------
-
+### Scala
+
+详细写法:
+
+```scala
+object Solution {
+
+ def solveSudoku(board: Array[Array[Char]]): Unit = {
+ backtracking(board)
+ }
+
+ def backtracking(board: Array[Array[Char]]): Boolean = {
+ for (i <- 0 until 9) {
+ for (j <- 0 until 9) {
+ if (board(i)(j) == '.') { // 必须是为 . 的数字才放数字
+ for (k <- '1' to '9') { // 这个位置放k是否合适
+ if (isVaild(i, j, k, board)) {
+ board(i)(j) = k
+ if (backtracking(board)) return true // 找到了立刻返回
+ board(i)(j) = '.' // 回溯
+ }
+ }
+ return false // 9个数都试完了,都不行就返回false
+ }
+ }
+ }
+ true // 遍历完所有的都没返回false,说明找到了
+ }
+
+ def isVaild(x: Int, y: Int, value: Char, board: Array[Array[Char]]): Boolean = {
+ // 行
+ for (i <- 0 until 9 ) {
+ if (board(i)(y) == value) {
+ return false
+ }
+ }
+
+ // 列
+ for (j <- 0 until 9) {
+ if (board(x)(j) == value) {
+ return false
+ }
+ }
+
+ // 宫
+ var row = (x / 3) * 3
+ var col = (y / 3) * 3
+ for (i <- row until row + 3) {
+ for (j <- col until col + 3) {
+ if (board(i)(j) == value) {
+ return false
+ }
+ }
+ }
+
+ true
+ }
+}
+```
+
+遵循Scala至简原则写法:
+
+```scala
+object Solution {
+
+ def solveSudoku(board: Array[Array[Char]]): Unit = {
+ backtracking(board)
+ }
+
+ def backtracking(board: Array[Array[Char]]): Boolean = {
+ // 双重for循环 + 循环守卫
+ for (i <- 0 until 9; j <- 0 until 9 if board(i)(j) == '.') {
+ // 必须是为 . 的数字才放数字,使用循环守卫判断该位置是否可以放置当前循环的数字
+ for (k <- '1' to '9' if isVaild(i, j, k, board)) { // 这个位置放k是否合适
+ board(i)(j) = k
+ if (backtracking(board)) return true // 找到了立刻返回
+ board(i)(j) = '.' // 回溯
+ }
+ return false // 9个数都试完了,都不行就返回false
+ }
+ true // 遍历完所有的都没返回false,说明找到了
+ }
+
+ def isVaild(x: Int, y: Int, value: Char, board: Array[Array[Char]]): Boolean = {
+ // 行,循环守卫进行判断
+ for (i <- 0 until 9 if board(i)(y) == value) return false
+ // 列,循环守卫进行判断
+ for (j <- 0 until 9 if board(x)(j) == value) return false
+ // 宫,循环守卫进行判断
+ var row = (x / 3) * 3
+ var col = (y / 3) * 3
+ for (i <- row until row + 3; j <- col until col + 3 if board(i)(j) == value) return false
+ true // 最终没有返回false,就说明该位置可以填写true
+ }
+}
+```
+### C#
+```csharp
+public class Solution
+{
+ public void SolveSudoku(char[][] board)
+ {
+ BackTracking(board);
+ }
+ public bool BackTracking(char[][] board)
+ {
+ for (int i = 0; i < board.Length; i++)
+ {
+ for (int j = 0; j < board[0].Length; j++)
+ {
+ if (board[i][j] != '.') continue;
+ for (char k = '1'; k <= '9'; k++)
+ {
+ if (IsValid(board, i, j, k))
+ {
+ board[i][j] = k;
+ if (BackTracking(board)) return true;
+ board[i][j] = '.';
+ }
+ }
+ return false;
+ }
+
+ }
+ return true;
+ }
+ public bool IsValid(char[][] board, int row, int col, char val)
+ {
+ for (int i = 0; i < 9; i++)
+ {
+ if (board[i][col] == val) return false;
+ }
+ for (int i = 0; i < 9; i++)
+ {
+ if (board[row][i] == val) return false;
+ }
+ int startRow = (row / 3) * 3;
+ int startCol = (col / 3) * 3;
+ for (int i = startRow; i < startRow + 3; i++)
+ {
+ for (int j = startCol; j < startCol + 3; j++)
+ {
+ if (board[i][j] == val) return false;
+ }
+ }
+ return true;
+ }
+}
+```
+
+
diff --git "a/problems/0039.\347\273\204\345\220\210\346\200\273\345\222\214.md" "b/problems/0039.\347\273\204\345\220\210\346\200\273\345\222\214.md"
old mode 100644
new mode 100755
index 7a2084dd19..d8dac0b45b
--- "a/problems/0039.\347\273\204\345\220\210\346\200\273\345\222\214.md"
+++ "b/problems/0039.\347\273\204\345\220\210\346\200\273\345\222\214.md"
@@ -1,57 +1,61 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+
+
# 39. 组合总和
-[力扣题目链接](https://leetcode-cn.com/problems/combination-sum/)
+[力扣题目链接](https://leetcode.cn/problems/combination-sum/)
-给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
+给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
-candidates 中的数字可以无限制重复被选取。
+candidates 中的数字可以无限制重复被选取。
说明:
-* 所有数字(包括 target)都是正整数。
-* 解集不能包含重复的组合。
+* 所有数字(包括 target)都是正整数。
+* 解集不能包含重复的组合。
示例 1:
-输入:candidates = [2,3,6,7], target = 7,
-所求解集为:
-[
+
+* 输入:candidates = [2,3,6,7], target = 7,
+* 所求解集为:
+ [
[7],
[2,2,3]
-]
+ ]
-示例 2:
-输入:candidates = [2,3,5], target = 8,
-所求解集为:
-[
- [2,2,2,2],
- [2,3,3],
- [3,5]
-]
+示例 2:
-# 思路
+* 输入:candidates = [2,3,5], target = 8,
+* 所求解集为:
+ [
+ [2,2,2,2],
+ [2,3,3],
+ [3,5]
+ ]
-[B站视频讲解-组合总和](https://www.bilibili.com/video/BV1KT4y1M7HJ)
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[Leetcode:39. 组合总和讲解](https://www.bilibili.com/video/BV1KT4y1M7HJ),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+## 思路
题目中的**无限制重复被选取,吓得我赶紧想想 出现0 可咋办**,然后看到下面提示:1 <= candidates[i] <= 200,我就放心了。
-本题和[77.组合](https://programmercarl.com/0077.组合.html),[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)和区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
+本题和[77.组合](https://programmercarl.com/0077.组合.html),[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)的区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
本题搜索的过程抽象成树形结构如下:
-
+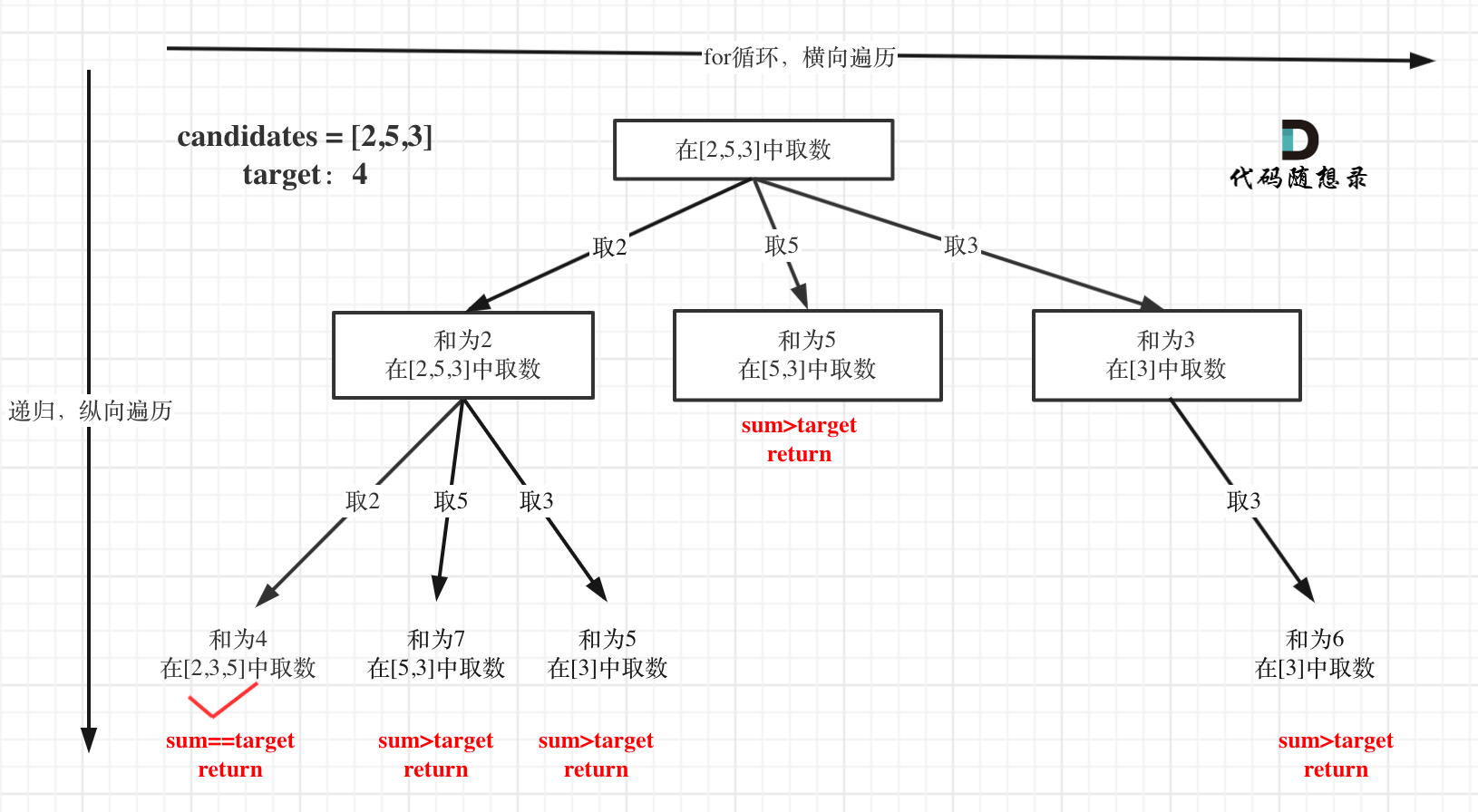
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
而在[77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html) 中都可以知道要递归K层,因为要取k个元素的组合。
-## 回溯三部曲
+### 回溯三部曲
* 递归函数参数
@@ -67,7 +71,7 @@ candidates 中的数字可以无限制重复被选取。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:[17.电话号码的字母组合](https://programmercarl.com/0017.电话号码的字母组合.html)
-**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我再讲解排列的时候就重点介绍**。
+**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我在讲解排列的时候会重点介绍**。
代码如下:
@@ -81,7 +85,7 @@ void backtracking(vector& candidates, int target, int sum, int startIndex)
在如下树形结构中:
-
+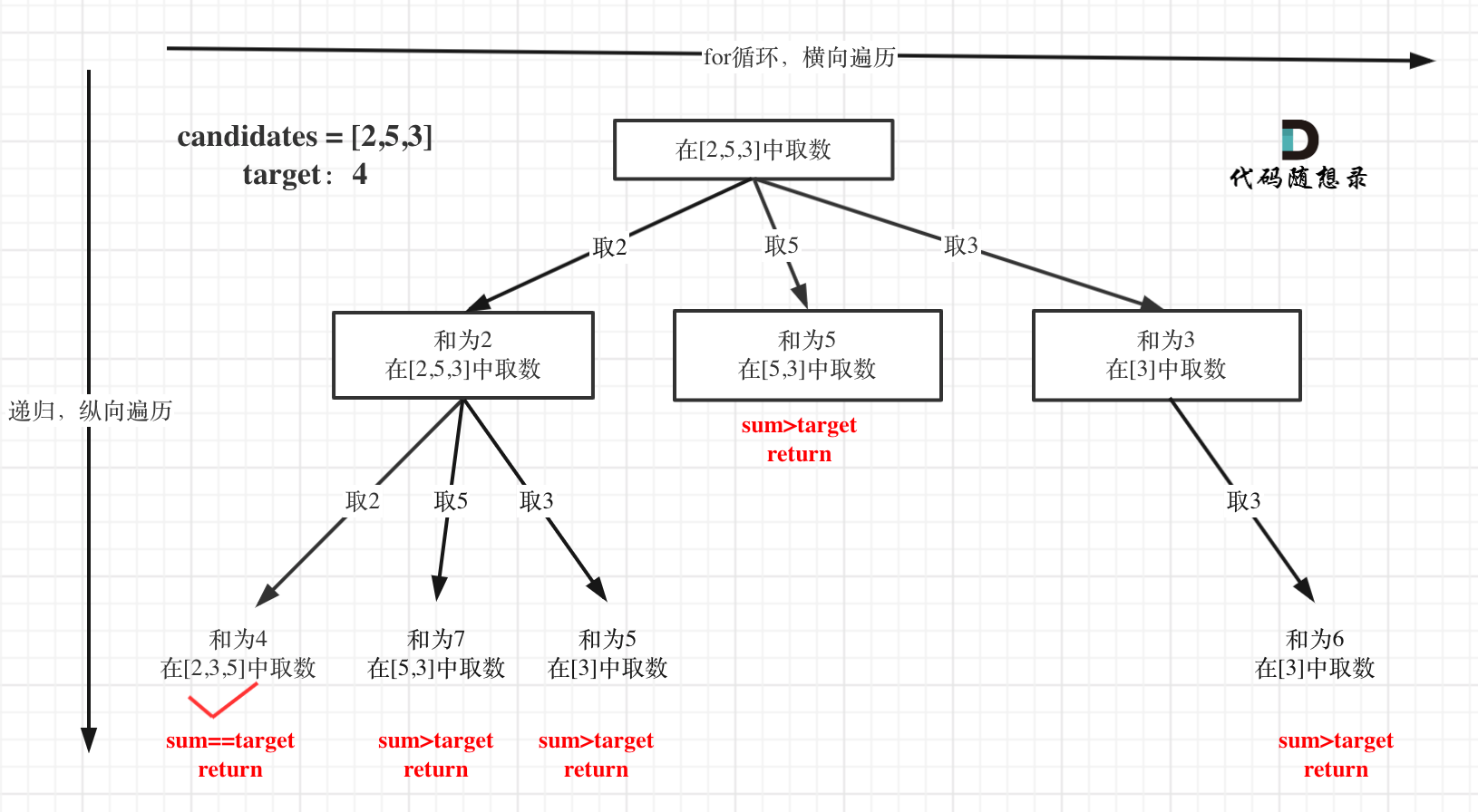
从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
@@ -150,11 +154,11 @@ public:
};
```
-## 剪枝优化
+### 剪枝优化
在这个树形结构中:
-
+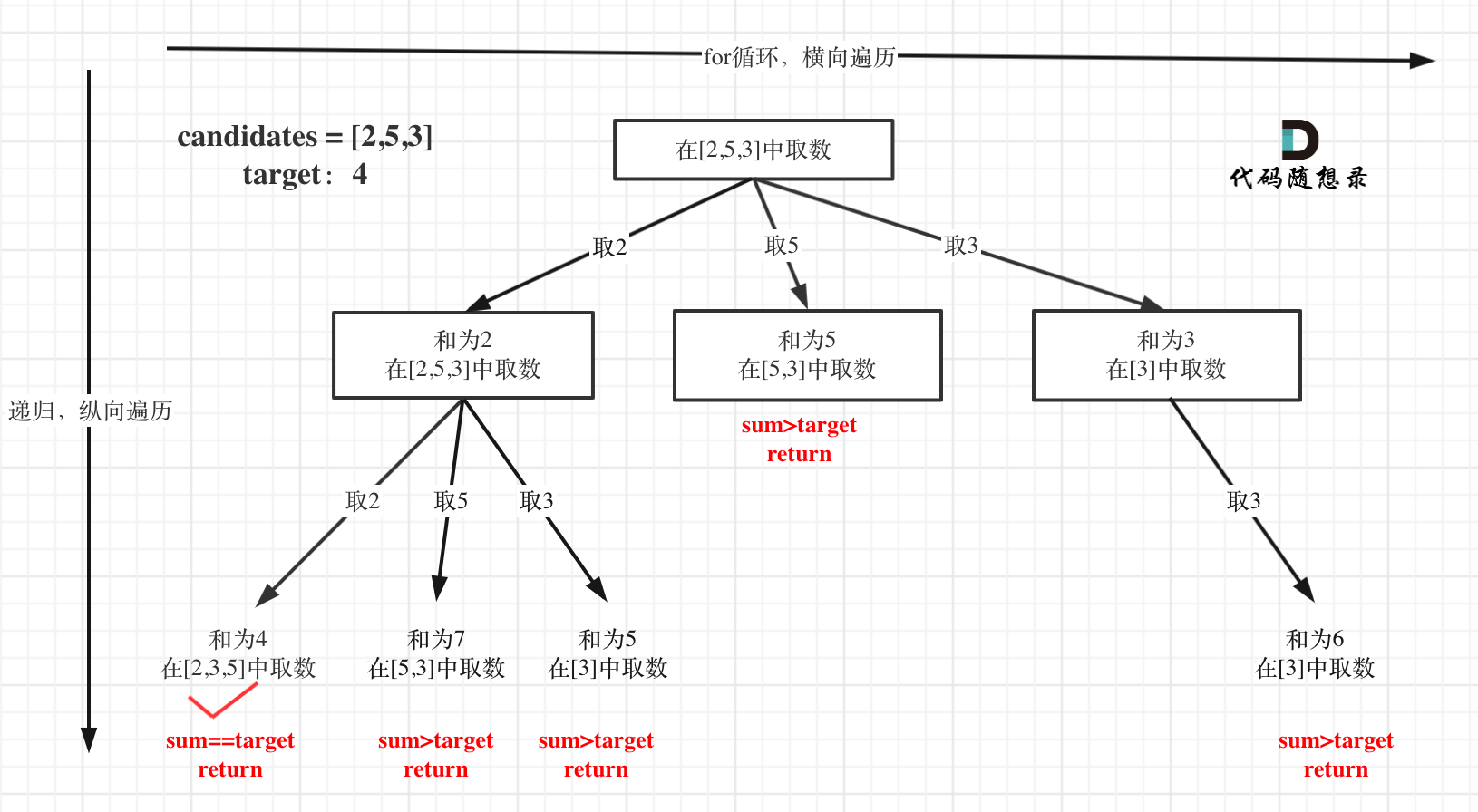
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
@@ -167,7 +171,7 @@ public:
如图:
-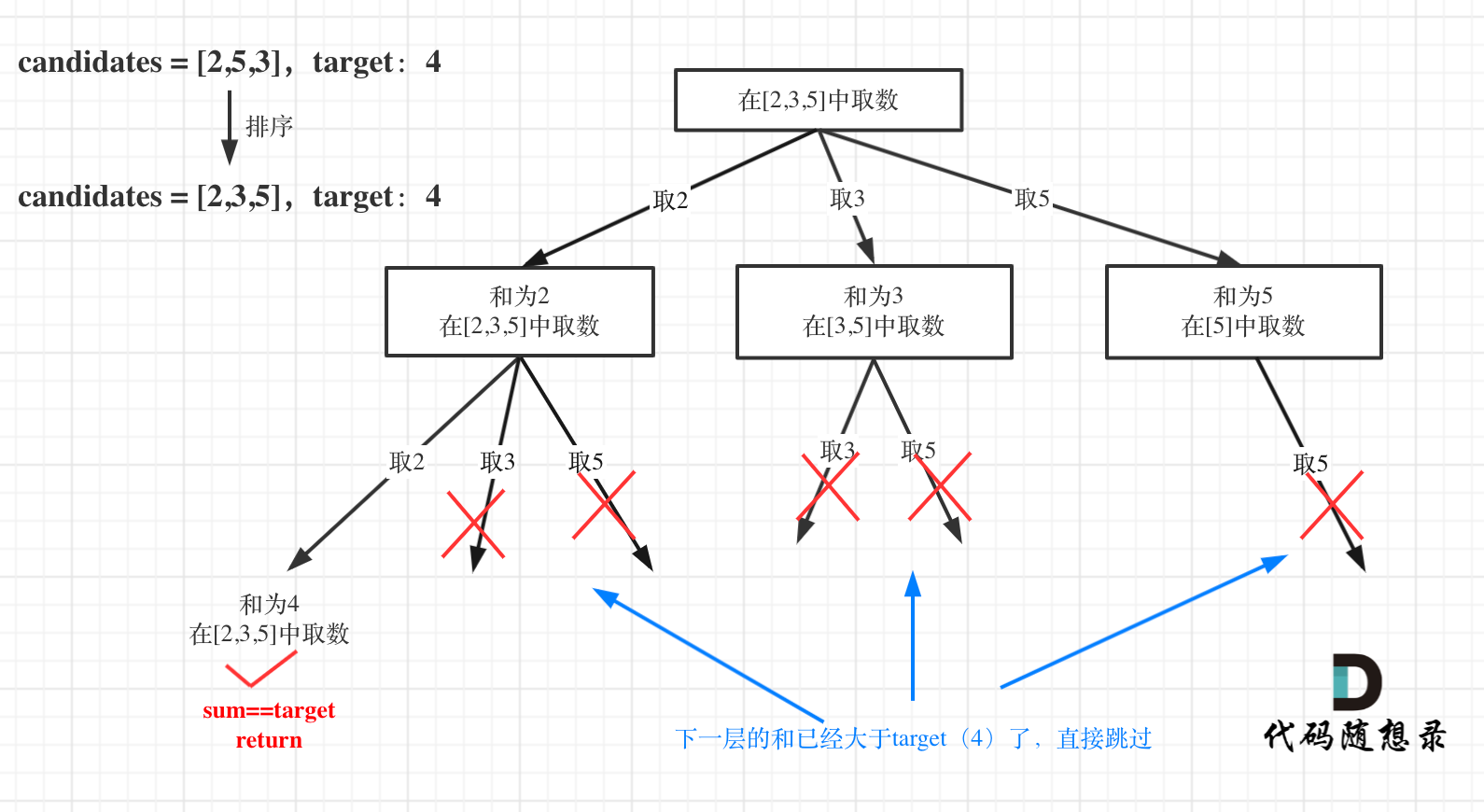
+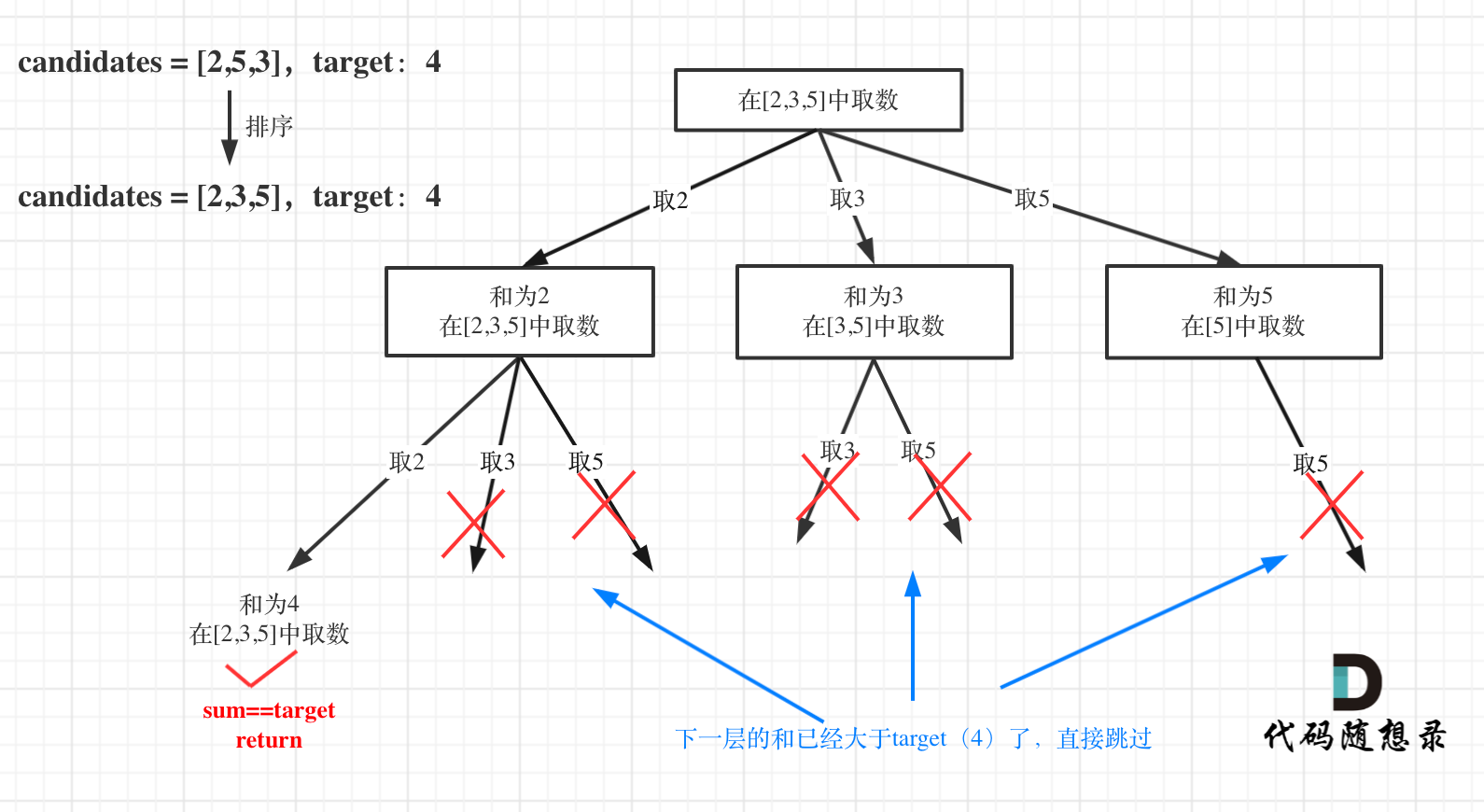
for循环剪枝代码如下:
@@ -208,8 +212,10 @@ public:
}
};
```
+* 时间复杂度: O(n * 2^n),注意这只是复杂度的上界,因为剪枝的存在,真实的时间复杂度远小于此
+* 空间复杂度: O(target)
-# 总结
+## 总结
本题和我们之前讲过的[77.组合](https://programmercarl.com/0077.组合.html)、[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)有两点不同:
@@ -230,10 +236,11 @@ public:
-# 其他语言版本
+## 其他语言版本
+
+### Java
-## Java
```Java
// 剪枝优化
class Solution {
@@ -262,126 +269,155 @@ class Solution {
}
```
-## Python
-**回溯**
+### Python
+
+回溯(版本一)
+
```python
class Solution:
- def __init__(self):
- self.path = []
- self.paths = []
- def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
- '''
- 因为本题没有组合数量限制,所以只要元素总和大于target就算结束
- '''
- self.path.clear()
- self.paths.clear()
- self.backtracking(candidates, target, 0, 0)
- return self.paths
-
- def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
- # Base Case
- if sum_ == target:
- self.paths.append(self.path[:]) # 因为是shallow copy,所以不能直接传入self.path
+ def backtracking(self, candidates, target, total, startIndex, path, result):
+ if total > target:
return
- if sum_ > target:
- return
-
- # 单层递归逻辑
- for i in range(start_index, len(candidates)):
- sum_ += candidates[i]
- self.path.append(candidates[i])
- self.backtracking(candidates, target, sum_, i) # 因为无限制重复选取,所以不是i-1
- sum_ -= candidates[i] # 回溯
- self.path.pop() # 回溯
+ if total == target:
+ result.append(path[:])
+ return
+
+ for i in range(startIndex, len(candidates)):
+ total += candidates[i]
+ path.append(candidates[i])
+ self.backtracking(candidates, target, total, i, path, result) # 不用i+1了,表示可以重复读取当前的数
+ total -= candidates[i]
+ path.pop()
+
+ def combinationSum(self, candidates, target):
+ result = []
+ self.backtracking(candidates, target, 0, 0, [], result)
+ return result
+
```
-**剪枝回溯**
+
+回溯剪枝(版本一)
+
```python
class Solution:
- def __init__(self):
- self.path = []
- self.paths = []
+ def backtracking(self, candidates, target, total, startIndex, path, result):
+ if total == target:
+ result.append(path[:])
+ return
+
+ for i in range(startIndex, len(candidates)):
+ if total + candidates[i] > target:
+ break
+ total += candidates[i]
+ path.append(candidates[i])
+ self.backtracking(candidates, target, total, i, path, result)
+ total -= candidates[i]
+ path.pop()
+
+ def combinationSum(self, candidates, target):
+ result = []
+ candidates.sort() # 需要排序
+ self.backtracking(candidates, target, 0, 0, [], result)
+ return result
+
+```
+
+回溯(版本二)
+
+```python
+class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
- '''
- 因为本题没有组合数量限制,所以只要元素总和大于target就算结束
- '''
- self.path.clear()
- self.paths.clear()
+ result =[]
+ self.backtracking(candidates, target, 0, [], result)
+ return result
+ def backtracking(self, candidates, target, startIndex, path, result):
+ if target == 0:
+ result.append(path[:])
+ return
+ if target < 0:
+ return
+ for i in range(startIndex, len(candidates)):
+ path.append(candidates[i])
+ self.backtracking(candidates, target - candidates[i], i, path, result)
+ path.pop()
- # 为了剪枝需要提前进行排序
- candidates.sort()
- self.backtracking(candidates, target, 0, 0)
- return self.paths
+```
+
+回溯剪枝(版本二)
- def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
- # Base Case
- if sum_ == target:
- self.paths.append(self.path[:]) # 因为是shallow copy,所以不能直接传入self.path
+```python
+class Solution:
+ def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
+ result =[]
+ candidates.sort()
+ self.backtracking(candidates, target, 0, [], result)
+ return result
+ def backtracking(self, candidates, target, startIndex, path, result):
+ if target == 0:
+ result.append(path[:])
return
- # 单层递归逻辑
- # 如果本层 sum + condidates[i] > target,就提前结束遍历,剪枝
- for i in range(start_index, len(candidates)):
- if sum_ + candidates[i] > target:
- return
- sum_ += candidates[i]
- self.path.append(candidates[i])
- self.backtracking(candidates, target, sum_, i) # 因为无限制重复选取,所以不是i-1
- sum_ -= candidates[i] # 回溯
- self.path.pop() # 回溯
+
+ for i in range(startIndex, len(candidates)):
+ if target - candidates[i] < 0:
+ break
+ path.append(candidates[i])
+ self.backtracking(candidates, target - candidates[i], i, path, result)
+ path.pop()
+
```
-## Go
+### Go
+
主要在于递归中传递下一个数字
```go
+var (
+ res [][]int
+ path []int
+)
func combinationSum(candidates []int, target int) [][]int {
- var trcak []int
- var res [][]int
- backtracking(0,0,target,candidates,trcak,&res)
+ res, path = make([][]int, 0), make([]int, 0, len(candidates))
+ sort.Ints(candidates) // 排序,为剪枝做准备
+ dfs(candidates, 0, target)
return res
}
-func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int){
- //终止条件
- if sum==target{
- tmp:=make([]int,len(trcak))
- copy(tmp,trcak)//拷贝
- *res=append(*res,tmp)//放入结果集
+
+func dfs(candidates []int, start int, target int) {
+ if target == 0 { // target 不断减小,如果为0说明达到了目标值
+ tmp := make([]int, len(path))
+ copy(tmp, path)
+ res = append(res, tmp)
return
}
- if sum>target{return}
- //回溯
- for i:=startIndex;i target { // 剪枝,提前返回
+ break
+ }
+ path = append(path, candidates[i])
+ dfs(candidates, i, target - candidates[i])
+ path = path[:len(path) - 1]
}
-
}
```
-## JavaScript
+### JavaScript
```js
var combinationSum = function(candidates, target) {
const res = [], path = [];
- candidates.sort(); // 排序
+ candidates.sort((a,b)=>a-b); // 排序
backtracking(0, 0);
return res;
function backtracking(j, sum) {
- if (sum > target) return;
if (sum === target) {
res.push(Array.from(path));
return;
}
for(let i = j; i < candidates.length; i++ ) {
const n = candidates[i];
- if(n > target - sum) continue;
+ if(n > target - sum) break;
path.push(n);
sum += n;
backtracking(i, sum);
@@ -392,7 +428,63 @@ var combinationSum = function(candidates, target) {
};
```
-## C
+### TypeScript
+
+```typescript
+function combinationSum(candidates: number[], target: number): number[][] {
+ const resArr: number[][] = [];
+ function backTracking(
+ candidates: number[], target: number,
+ startIndex: number, route: number[], curSum: number
+ ): void {
+ if (curSum > target) return;
+ if (curSum === target) {
+ resArr.push(route.slice());
+ return
+ }
+ for (let i = startIndex, length = candidates.length; i < length; i++) {
+ let tempVal: number = candidates[i];
+ route.push(tempVal);
+ backTracking(candidates, target, i, route, curSum + tempVal);
+ route.pop();
+ }
+ }
+ backTracking(candidates, target, 0, [], 0);
+ return resArr;
+};
+```
+
+### Rust
+
+```Rust
+impl Solution {
+ pub fn backtracking(result: &mut Vec>, path: &mut Vec, candidates: &Vec, target: i32, mut sum: i32, start_index: usize) {
+ if sum == target {
+ result.push(path.to_vec());
+ return;
+ }
+ for i in start_index..candidates.len() {
+ if sum + candidates[i] <= target {
+ sum += candidates[i];
+ path.push(candidates[i]);
+ Self::backtracking(result, path, candidates, target, sum, i);
+ sum -= candidates[i];
+ path.pop();
+ }
+ }
+ }
+
+ pub fn combination_sum(candidates: Vec, target: i32) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut path: Vec = Vec::new();
+ Self::backtracking(&mut result, &mut path, &candidates, target, 0, 0);
+ result
+ }
+}
+```
+
+### C
+
```c
int* path;
int pathTop;
@@ -447,7 +539,7 @@ int** combinationSum(int* candidates, int candidatesSize, int target, int* retur
}
```
-## Swift
+### Swift
```swift
func combinationSum(_ candidates: [Int], _ target: Int) -> [[Int]] {
@@ -476,5 +568,94 @@ func combinationSum(_ candidates: [Int], _ target: Int) -> [[Int]] {
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-> 这篇可以说是全网把组合问题如何去重,讲的最清晰的了!
-
# 40.组合总和II
-[力扣题目链接](https://leetcode-cn.com/problems/combination-sum-ii/)
+[力扣题目链接](https://leetcode.cn/problems/combination-sum-ii/)
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
-所有数字(包括目标数)都是正整数。
-解集不能包含重复的组合。
+所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
-示例 1:
-输入: candidates = [10,1,2,7,6,1,5], target = 8,
-所求解集为:
+* 示例 1:
+* 输入: candidates = [10,1,2,7,6,1,5], target = 8,
+* 所求解集为:
+```
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
+```
+
+* 示例 2:
+* 输入: candidates = [2,5,2,1,2], target = 5,
+* 所求解集为:
-示例 2:
-输入: candidates = [2,5,2,1,2], target = 5,
-所求解集为:
+```
[
[1,2,2],
[5]
]
+```
-# 思路
+## 算法公开课
-**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[回溯算法中的去重,树层去重树枝去重,你弄清楚了没?| LeetCode:40.组合总和II](https://www.bilibili.com/video/BV12V4y1V73A),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+## 思路
这道题目和[39.组合总和](https://programmercarl.com/0039.组合总和.html)如下区别:
@@ -74,11 +76,11 @@ candidates 中的每个数字在每个组合中只能使用一次。
选择过程树形结构如图所示:
-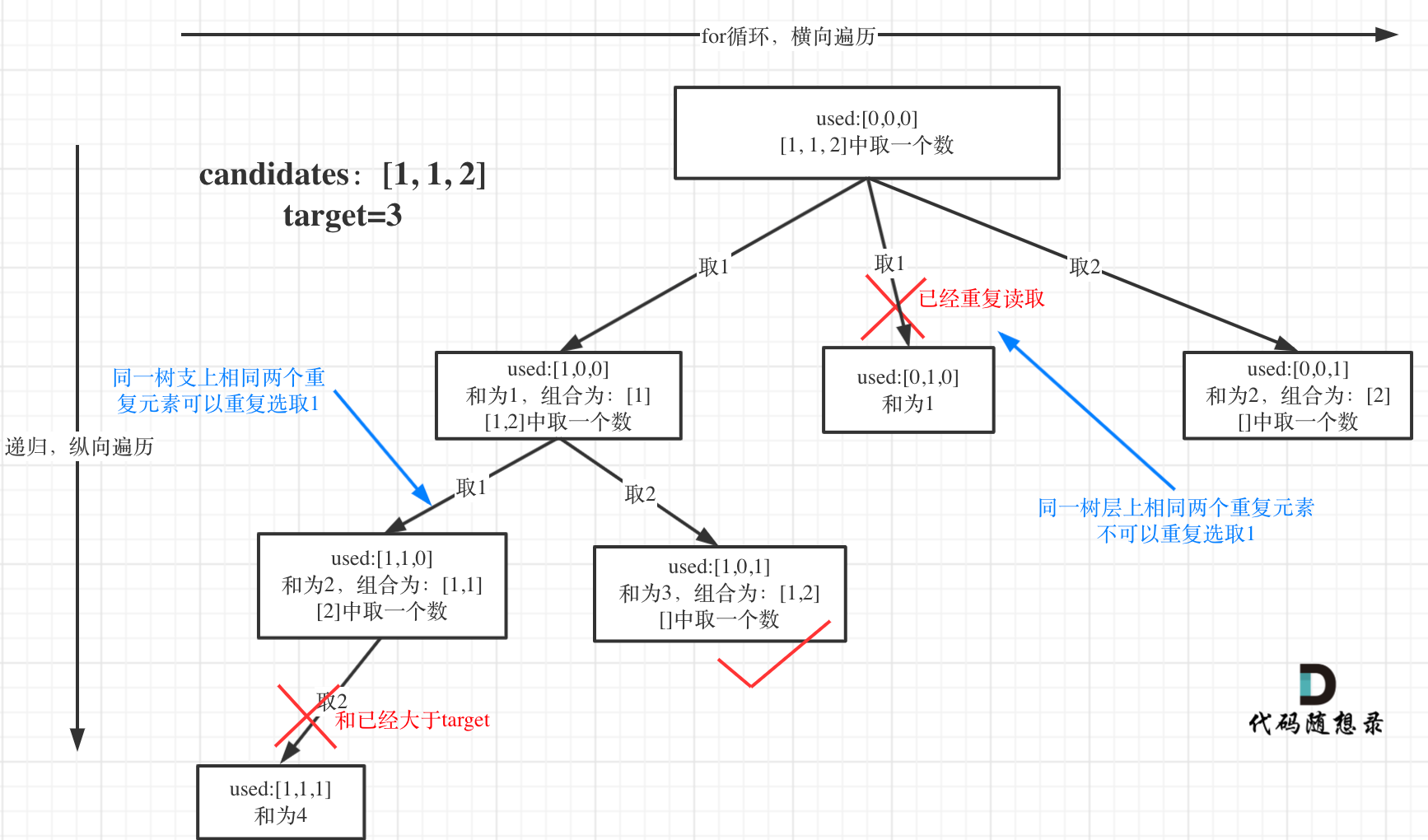
+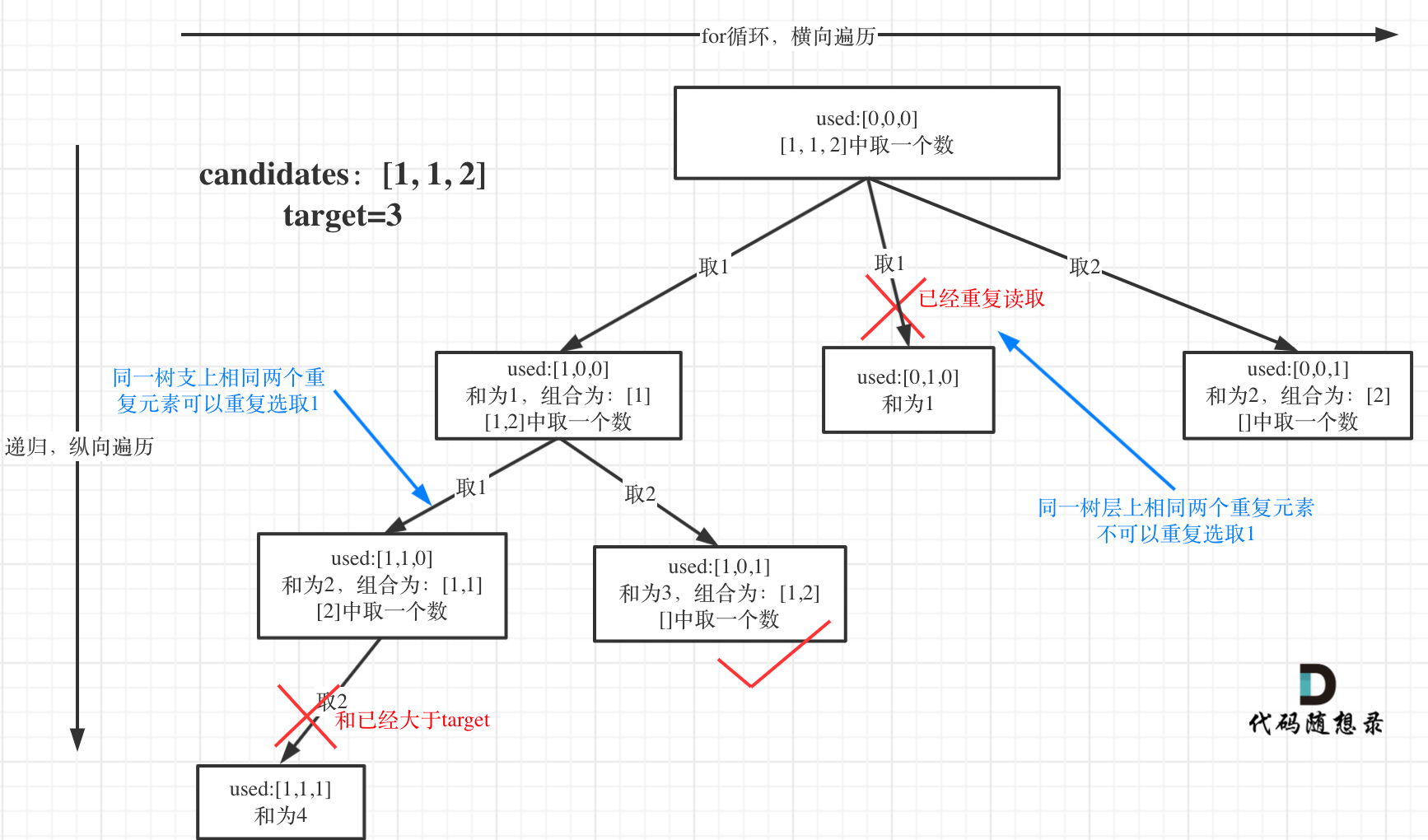
可以看到图中,每个节点相对于 [39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)我多加了used数组,这个used数组下面会重点介绍。
-## 回溯三部曲
+### 回溯三部曲
* **递归函数参数**
@@ -110,13 +112,13 @@ if (sum == target) {
}
```
-`sum > target` 这个条件其实可以省略,因为和在递归单层遍历的时候,会有剪枝的操作,下面会介绍到。
+`sum > target` 这个条件其实可以省略,因为在递归单层遍历的时候,会有剪枝的操作,下面会介绍到。
* **单层搜索的逻辑**
这里与[39.组合总和](https://programmercarl.com/0039.组合总和.html)最大的不同就是要去重了。
-前面我们提到:要去重的是“同一树层上的使用过”,如果判断同一树层上元素(相同的元素)是否使用过了呢。
+前面我们提到:要去重的是“同一树层上的使用过”,如何判断同一树层上元素(相同的元素)是否使用过了呢。
**如果`candidates[i] == candidates[i - 1]` 并且 `used[i - 1] == false`,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]**。
@@ -124,15 +126,23 @@ if (sum == target) {
这块比较抽象,如图:
-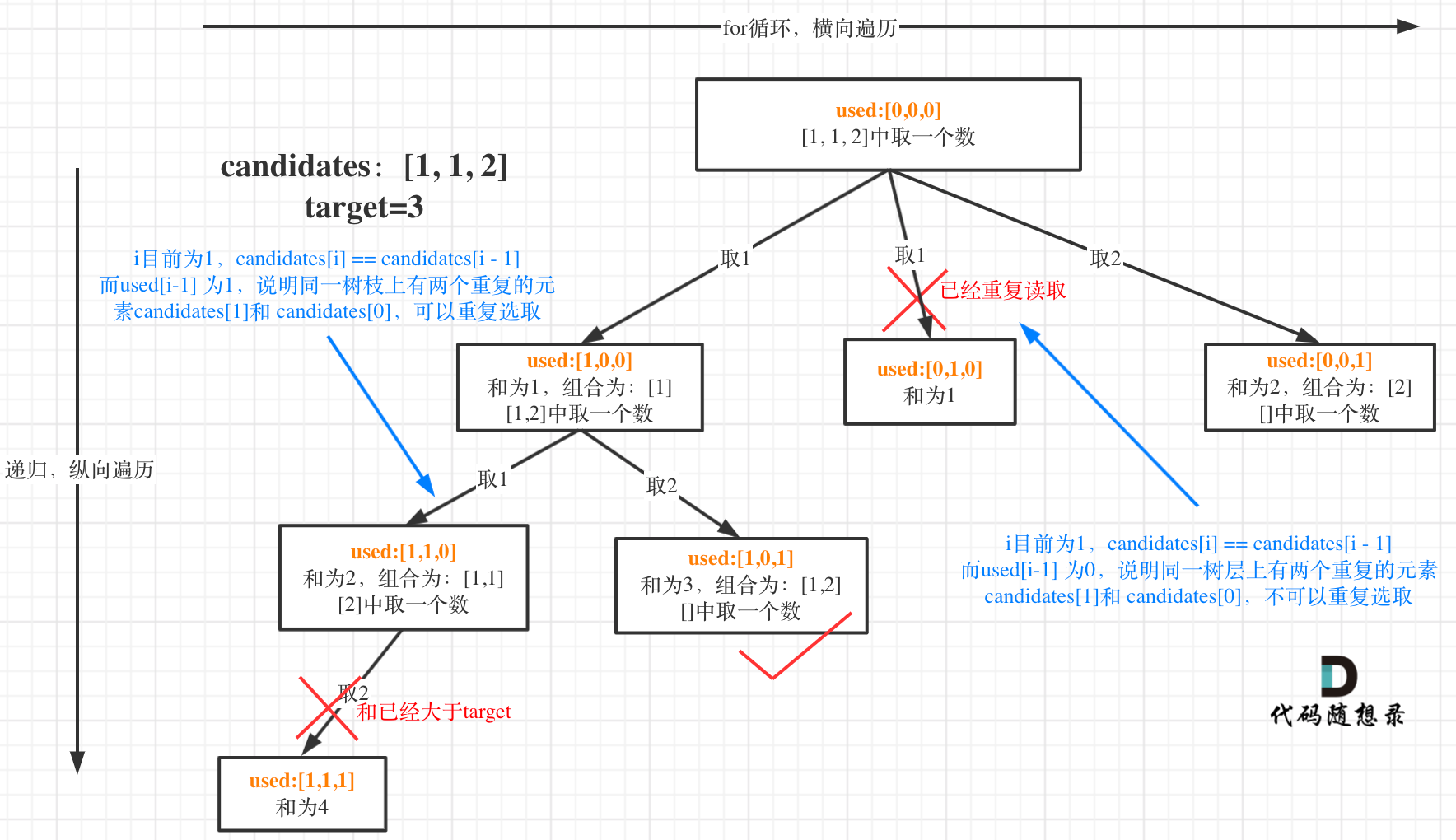
+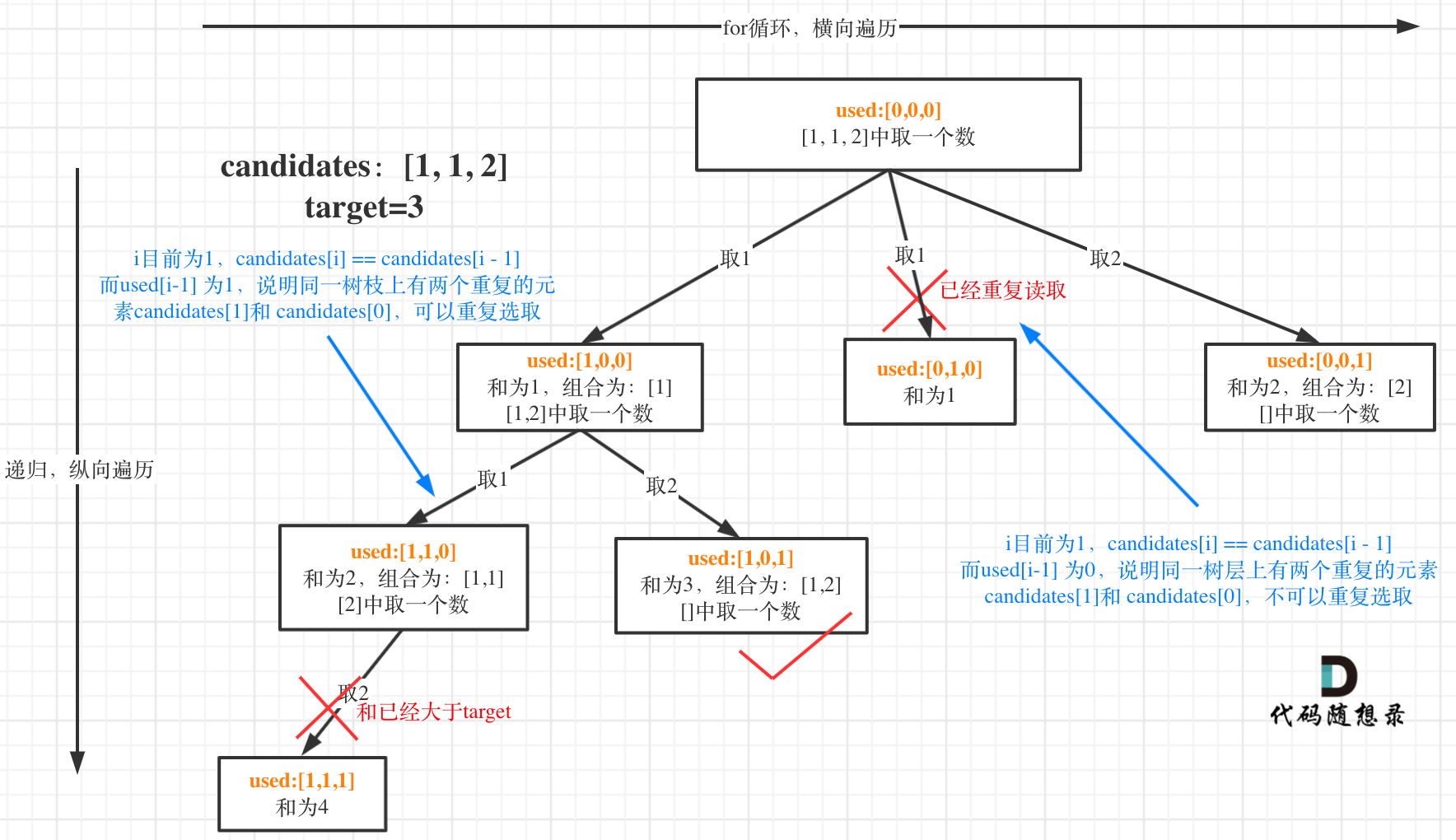
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
* used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
* used[i - 1] == false,说明同一树层candidates[i - 1]使用过
+可能有的录友想,为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
+
+而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
+
+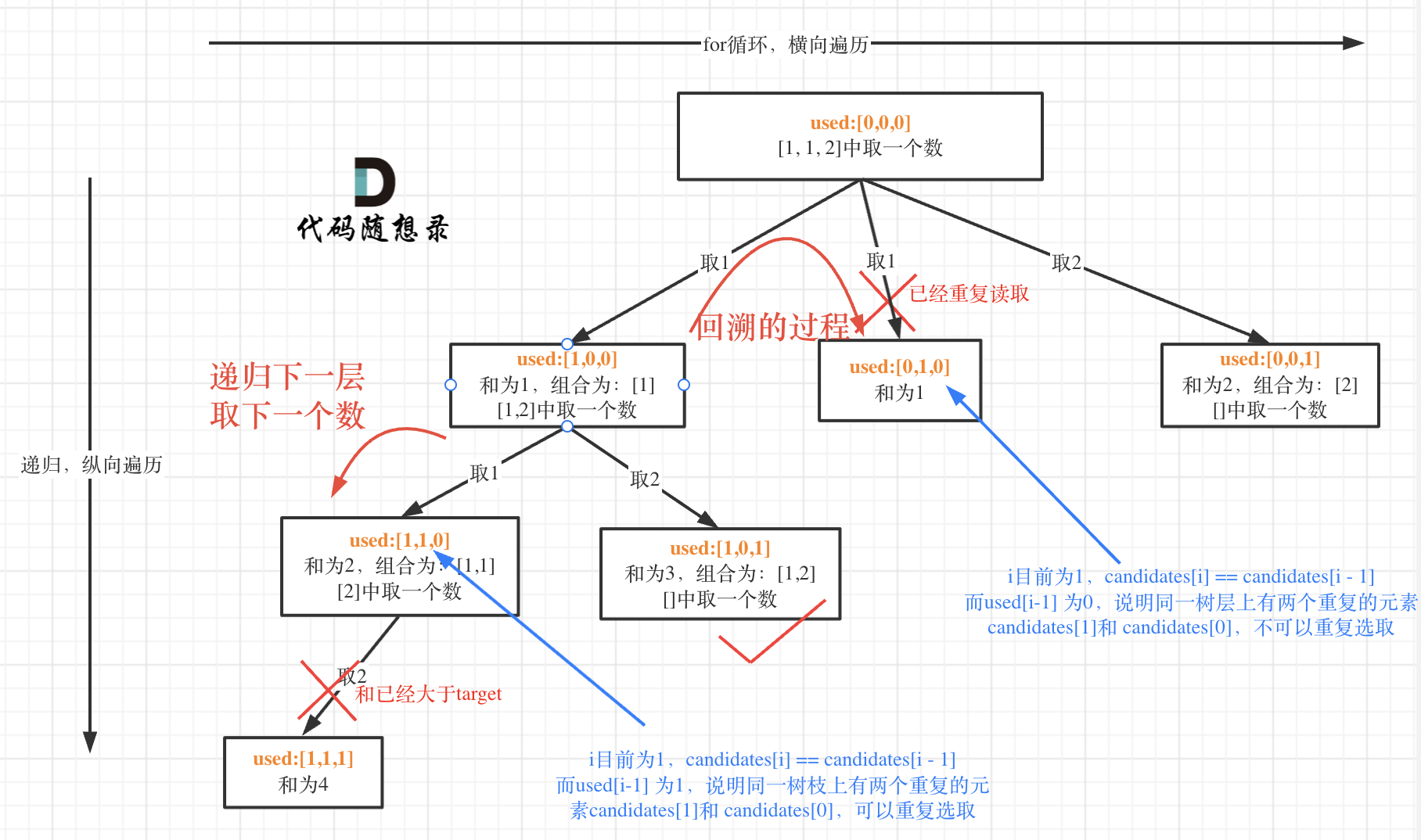
+
+
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
+
那么单层搜索的逻辑代码如下:
```CPP
@@ -198,8 +208,10 @@ public:
};
```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
-## 补充
+### 补充
这里直接用startIndex来去重也是可以的, 就不用used数组了。
@@ -239,7 +251,7 @@ public:
```
-# 总结
+## 总结
本题同样是求组合总和,但就是因为其数组candidates有重复元素,而要求不能有重复的组合,所以相对于[39.组合总和](https://programmercarl.com/0039.组合总和.html)难度提升了不少。
@@ -247,51 +259,52 @@ public:
所以Carl有必要把去重的这块彻彻底底的给大家讲清楚,**就连“树层去重”和“树枝去重”都是我自创的词汇,希望对大家理解有帮助!**
+## 其他语言版本
-
-
-# 其他语言版本
-
-
-## Java
+### Java
**使用标记数组**
```Java
class Solution {
- List> lists = new ArrayList<>();
- Deque deque = new LinkedList<>();
- int sum = 0;
-
- public List> combinationSum2(int[] candidates, int target) {
- //为了将重复的数字都放到一起,所以先进行排序
- Arrays.sort(candidates);
- //加标志数组,用来辅助判断同层节点是否已经遍历
- boolean[] flag = new boolean[candidates.length];
- backTracking(candidates, target, 0, flag);
- return lists;
- }
+ LinkedList path = new LinkedList<>();
+ List> ans = new ArrayList<>();
+ boolean[] used;
+ int sum = 0;
- public void backTracking(int[] arr, int target, int index, boolean[] flag) {
- if (sum == target) {
- lists.add(new ArrayList(deque));
- return;
- }
- for (int i = index; i < arr.length && arr[i] + sum <= target; i++) {
- //出现重复节点,同层的第一个节点已经被访问过,所以直接跳过
- if (i > 0 && arr[i] == arr[i - 1] && !flag[i - 1]) {
- continue;
- }
- flag[i] = true;
- sum += arr[i];
- deque.push(arr[i]);
- //每个节点仅能选择一次,所以从下一位开始
- backTracking(arr, target, i + 1, flag);
- int temp = deque.pop();
- flag[i] = false;
- sum -= temp;
- }
+ public List> combinationSum2(int[] candidates, int target) {
+ used = new boolean[candidates.length];
+ // 加标志数组,用来辅助判断同层节点是否已经遍历
+ Arrays.fill(used, false);
+ // 为了将重复的数字都放到一起,所以先进行排序
+ Arrays.sort(candidates);
+ backTracking(candidates, target, 0);
+ return ans;
+ }
+
+ private void backTracking(int[] candidates, int target, int startIndex) {
+ if (sum == target) {
+ ans.add(new ArrayList(path));
}
+ for (int i = startIndex; i < candidates.length; i++) {
+ if (sum + candidates[i] > target) {
+ break;
+ }
+ // 出现重复节点,同层的第一个节点已经被访问过,所以直接跳过
+ if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
+ continue;
+ }
+ used[i] = true;
+ sum += candidates[i];
+ path.add(candidates[i]);
+ // 每个节点仅能选择一次,所以从下一位开始
+ backTracking(candidates, target, i + 1);
+ used[i] = false;
+ sum -= candidates[i];
+ path.removeLast();
+ }
+ }
}
+
```
**不使用标记数组**
```Java
@@ -332,173 +345,170 @@ class Solution {
}
```
-## Python
-**回溯+巧妙去重(省去使用used**
+### Python
+回溯
```python
class Solution:
- def __init__(self):
- self.paths = []
- self.path = []
- def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
- '''
- 类似于求三数之和,求四数之和,为了避免重复组合,需要提前进行数组排序
- '''
- self.paths.clear()
- self.path.clear()
- # 必须提前进行数组排序,避免重复
- candidates.sort()
- self.backtracking(candidates, target, 0, 0)
- return self.paths
- def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
- # Base Case
- if sum_ == target:
- self.paths.append(self.path[:])
+ def backtracking(self, candidates, target, total, startIndex, path, result):
+ if total == target:
+ result.append(path[:])
return
-
- # 单层递归逻辑
- for i in range(start_index, len(candidates)):
- # 剪枝,同39.组合总和
- if sum_ + candidates[i] > target:
- return
-
- # 跳过同一树层使用过的元素
- if i > start_index and candidates[i] == candidates[i-1]:
+
+ for i in range(startIndex, len(candidates)):
+ if i > startIndex and candidates[i] == candidates[i - 1]:
continue
-
- sum_ += candidates[i]
- self.path.append(candidates[i])
- self.backtracking(candidates, target, sum_, i+1)
- self.path.pop() # 回溯,为了下一轮for loop
- sum_ -= candidates[i] # 回溯,为了下一轮for loop
+
+ if total + candidates[i] > target:
+ break
+
+ total += candidates[i]
+ path.append(candidates[i])
+ self.backtracking(candidates, target, total, i + 1, path, result)
+ total -= candidates[i]
+ path.pop()
+
+ def combinationSum2(self, candidates, target):
+ result = []
+ candidates.sort()
+ self.backtracking(candidates, target, 0, 0, [], result)
+ return result
+
```
-**回溯+去重(使用used)**
+回溯 使用used
```python
class Solution:
- def __init__(self):
- self.paths = []
- self.path = []
- self.used = []
- def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
- '''
- 类似于求三数之和,求四数之和,为了避免重复组合,需要提前进行数组排序
- 本题需要使用used,用来标记区别同一树层的元素使用重复情况:注意区分递归纵向遍历遇到的重复元素,和for循环遇到的重复元素,这两者的区别
- '''
- self.paths.clear()
- self.path.clear()
- self.usage_list = [False] * len(candidates)
- # 必须提前进行数组排序,避免重复
- candidates.sort()
- self.backtracking(candidates, target, 0, 0)
- return self.paths
- def backtracking(self, candidates: List[int], target: int, sum_: int, start_index: int) -> None:
- # Base Case
- if sum_ == target:
- self.paths.append(self.path[:])
+ def backtracking(self, candidates, target, total, startIndex, used, path, result):
+ if total == target:
+ result.append(path[:])
return
-
- # 单层递归逻辑
- for i in range(start_index, len(candidates)):
- # 剪枝,同39.组合总和
- if sum_ + candidates[i] > target:
- return
-
- # 检查同一树层是否出现曾经使用过的相同元素
- # 若数组中前后元素值相同,但前者却未被使用(used == False),说明是for loop中的同一树层的相同元素情况
- if i > 0 and candidates[i] == candidates[i-1] and self.usage_list[i-1] == False:
+
+ for i in range(startIndex, len(candidates)):
+ # 对于相同的数字,只选择第一个未被使用的数字,跳过其他相同数字
+ if i > startIndex and candidates[i] == candidates[i - 1] and not used[i - 1]:
continue
- sum_ += candidates[i]
- self.path.append(candidates[i])
- self.usage_list[i] = True
- self.backtracking(candidates, target, sum_, i+1)
- self.usage_list[i] = False # 回溯,为了下一轮for loop
- self.path.pop() # 回溯,为了下一轮for loop
- sum_ -= candidates[i] # 回溯,为了下一轮for loop
+ if total + candidates[i] > target:
+ break
+
+ total += candidates[i]
+ path.append(candidates[i])
+ used[i] = True
+ self.backtracking(candidates, target, total, i + 1, used, path, result)
+ used[i] = False
+ total -= candidates[i]
+ path.pop()
+
+ def combinationSum2(self, candidates, target):
+ used = [False] * len(candidates)
+ result = []
+ candidates.sort()
+ self.backtracking(candidates, target, 0, 0, used, [], result)
+ return result
+
```
+回溯优化
+```python
+class Solution:
+ def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
+ candidates.sort()
+ results = []
+ self.combinationSumHelper(candidates, target, 0, [], results)
+ return results
-## Go
+ def combinationSumHelper(self, candidates, target, index, path, results):
+ if target == 0:
+ results.append(path[:])
+ return
+ for i in range(index, len(candidates)):
+ if i > index and candidates[i] == candidates[i - 1]:
+ continue
+ if candidates[i] > target:
+ break
+ path.append(candidates[i])
+ self.combinationSumHelper(candidates, target - candidates[i], i + 1, path, results)
+ path.pop()
+```
+### Go
主要在于如何在回溯中去重
**使用used数组**
```go
+var (
+ res [][]int
+ path []int
+ used []bool
+)
func combinationSum2(candidates []int, target int) [][]int {
- var trcak []int
- var res [][]int
- var history map[int]bool
- history=make(map[int]bool)
- sort.Ints(candidates)
- backtracking(0,0,target,candidates,trcak,&res,history)
+ res, path = make([][]int, 0), make([]int, 0, len(candidates))
+ used = make([]bool, len(candidates))
+ sort.Ints(candidates) // 排序,为剪枝做准备
+ dfs(candidates, 0, target)
return res
}
-func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int,history map[int]bool){
- //终止条件
- if sum==target{
- tmp:=make([]int,len(trcak))
- copy(tmp,trcak)//拷贝
- *res=append(*res,tmp)//放入结果集
+
+func dfs(candidates []int, start int, target int) {
+ if target == 0 { // target 不断减小,如果为0说明达到了目标值
+ tmp := make([]int, len(path))
+ copy(tmp, path)
+ res = append(res, tmp)
return
}
- if sum>target{return}
- //回溯
- // used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
- for i:=startIndex;i0&&candidates[i]==candidates[i-1]&&history[i-1]==false{
- continue
+ for i := start; i < len(candidates); i++ {
+ if candidates[i] > target { // 剪枝,提前返回
+ break
}
- //更新路径集合和sum
- trcak=append(trcak,candidates[i])
- sum+=candidates[i]
- history[i]=true
- //递归
- backtracking(i+1,sum,target,candidates,trcak,res,history)
- //回溯
- trcak=trcak[:len(trcak)-1]
- sum-=candidates[i]
- history[i]=false
+ // used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
+ // used[i - 1] == false,说明同一树层candidates[i - 1]使用过
+ if i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false {
+ continue
+ }
+ path = append(path, candidates[i])
+ used[i] = true
+ dfs(candidates, i+1, target - candidates[i])
+ used[i] = false
+ path = path[:len(path) - 1]
}
}
```
**不使用used数组**
```go
+var (
+ res [][]int
+ path []int
+)
func combinationSum2(candidates []int, target int) [][]int {
- var trcak []int
- var res [][]int
- sort.Ints(candidates)
- backtracking(0,0,target,candidates,trcak,&res)
+ res, path = make([][]int, 0), make([]int, 0, len(candidates))
+ sort.Ints(candidates) // 排序,为剪枝做准备
+ dfs(candidates, 0, target)
return res
}
-func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int){
- //终止条件
- if sum==target{
- tmp:=make([]int,len(trcak))
- //拷贝
- copy(tmp,trcak)
- //放入结果集
- *res=append(*res,tmp)
+
+func dfs(candidates []int, start int, target int) {
+ if target == 0 { // target 不断减小,如果为0说明达到了目标值
+ tmp := make([]int, len(path))
+ copy(tmp, path)
+ res = append(res, tmp)
return
}
- //回溯
- for i:=startIndex;istartIndex&&candidates[i]==candidates[i-1]{
- continue
+ for i := start; i < len(candidates); i++ {
+ if candidates[i] > target { // 剪枝,提前返回
+ break
}
- //更新路径集合和sum
- trcak=append(trcak,candidates[i])
- sum+=candidates[i]
- backtracking(i+1,sum,target,candidates,trcak,res)
- //回溯
- trcak=trcak[:len(trcak)-1]
- sum-=candidates[i]
+ // i != start 限制了这不对深度遍历到达的此值去重
+ if i != start && candidates[i] == candidates[i-1] { // 去重
+ continue
+ }
+ path = append(path, candidates[i])
+ dfs(candidates, i+1, target - candidates[i])
+ path = path[:len(path) - 1]
}
}
```
-## javaScript
+### JavaScript
```js
/**
@@ -508,22 +518,27 @@ func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int)
*/
var combinationSum2 = function(candidates, target) {
const res = []; path = [], len = candidates.length;
- candidates.sort();
+ candidates.sort((a,b)=>a-b);
backtracking(0, 0);
return res;
function backtracking(sum, i) {
- if (sum > target) return;
if (sum === target) {
res.push(Array.from(path));
return;
}
- let f = -1;
for(let j = i; j < len; j++) {
const n = candidates[j];
- if(n > target - sum || n === f) continue;
+ if(j > i && candidates[j] === candidates[j-1]){
+ //若当前元素和前一个元素相等
+ //则本次循环结束,防止出现重复组合
+ continue;
+ }
+ //如果当前元素值大于目标值-总和的值
+ //由于数组已排序,那么该元素之后的元素必定不满足条件
+ //直接终止当前层的递归
+ if(n > target - sum) break;
path.push(n);
sum += n;
- f = n;
backtracking(sum, j + 1);
path.pop();
sum -= n;
@@ -532,6 +547,7 @@ var combinationSum2 = function(candidates, target) {
};
```
**使用used去重**
+
```js
var combinationSum2 = function(candidates, target) {
let res = [];
@@ -562,7 +578,73 @@ var combinationSum2 = function(candidates, target) {
};
```
-## C
+### TypeScript
+
+```typescript
+function combinationSum2(candidates: number[], target: number): number[][] {
+ candidates.sort((a, b) => a - b);
+ const resArr: number[][] = [];
+ function backTracking(
+ candidates: number[], target: number,
+ curSum: number, startIndex: number, route: number[]
+ ) {
+ if (curSum > target) return;
+ if (curSum === target) {
+ resArr.push(route.slice());
+ return;
+ }
+ for (let i = startIndex, length = candidates.length; i < length; i++) {
+ if (i > startIndex && candidates[i] === candidates[i - 1]) {
+ continue;
+ }
+ let tempVal: number = candidates[i];
+ route.push(tempVal);
+ backTracking(candidates, target, curSum + tempVal, i + 1, route);
+ route.pop();
+
+ }
+ }
+ backTracking(candidates, target, 0, 0, []);
+ return resArr;
+};
+```
+
+### Rust
+
+```Rust
+impl Solution {
+ pub fn backtracking(result: &mut Vec>, path: &mut Vec, candidates: &Vec, target: i32, mut sum: i32, start_index: usize, used: &mut Vec) {
+ if sum == target {
+ result.push(path.to_vec());
+ return;
+ }
+ for i in start_index..candidates.len() {
+ if sum + candidates[i] <= target {
+ if i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false { continue; }
+ sum += candidates[i];
+ path.push(candidates[i]);
+ used[i] = true;
+ Self::backtracking(result, path, candidates, target, sum, i + 1, used);
+ used[i] = false;
+ sum -= candidates[i];
+ path.pop();
+ }
+ }
+ }
+
+ pub fn combination_sum2(candidates: Vec, target: i32) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut path: Vec = Vec::new();
+ let mut used: Vec = vec![false; candidates.len()];
+ let mut candidates = candidates;
+ candidates.sort();
+ Self::backtracking(&mut result, &mut path, &candidates, target, 0, 0, &mut used);
+ result
+ }
+}
+```
+
+### C
```c
int* path;
@@ -624,7 +706,7 @@ int** combinationSum2(int* candidates, int candidatesSize, int target, int* retu
}
```
-## Swift
+### Swift
```swift
func combinationSum2(_ candidates: [Int], _ target: Int) -> [[Int]] {
@@ -656,5 +738,68 @@ func combinationSum2(_ candidates: [Int], _ target: Int) -> [[Int]] {
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-> 这个图就是大厂面试经典题目,接雨水! 最常青藤的一道题,面试官百出不厌!
-# 42. 接雨水
-[力扣题目链接](https://leetcode-cn.com/problems/trapping-rain-water/)
+
+# 42. 接雨水
+
+[力扣题目链接](https://leetcode.cn/problems/trapping-rain-water/)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
-
+
* 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
* 输出:6
@@ -26,27 +25,32 @@
* 输入:height = [4,2,0,3,2,5]
* 输出:9
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[单调栈,经典来袭!LeetCode:42.接雨水](https://www.bilibili.com/video/BV1uD4y1u75P/),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
+
-# 思路
+## 思路
接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
本文深度讲解如下三种方法:
-* 双指针法
-* 动态规划
+
+* 暴力解法
+* 双指针优化
* 单调栈
-## 双指针解法
+### 暴力解法
-这道题目使用双指针法并不简单,我们来看一下思路。
+本题暴力解法也是也是使用双指针。
首先要明确,要按照行来计算,还是按照列来计算。
按照行来计算如图:
-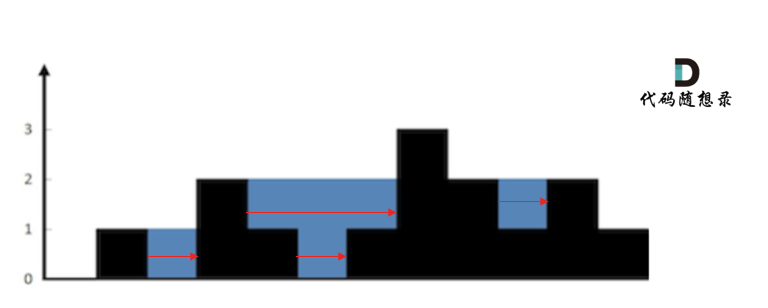
+
按照列来计算如图:
-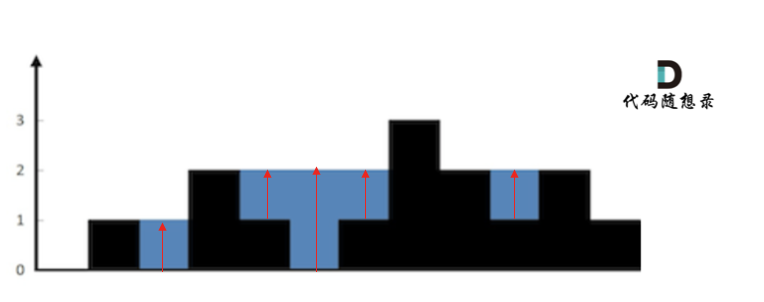
+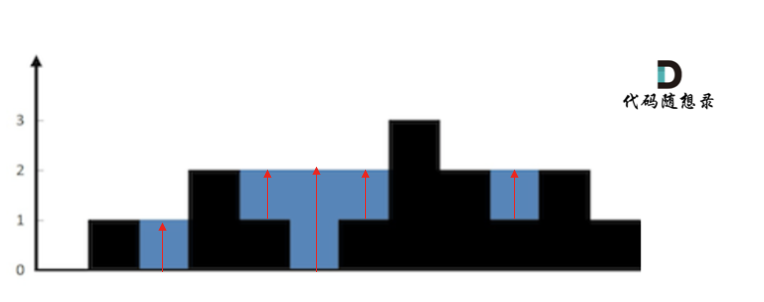
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
@@ -58,7 +62,7 @@
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
-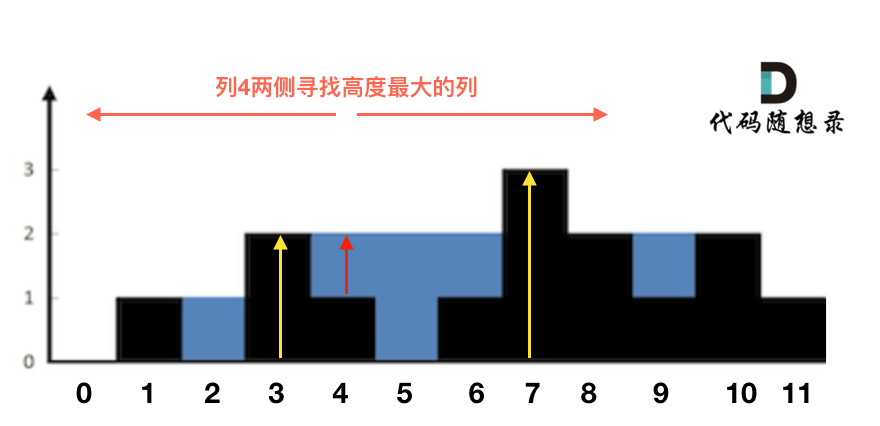
+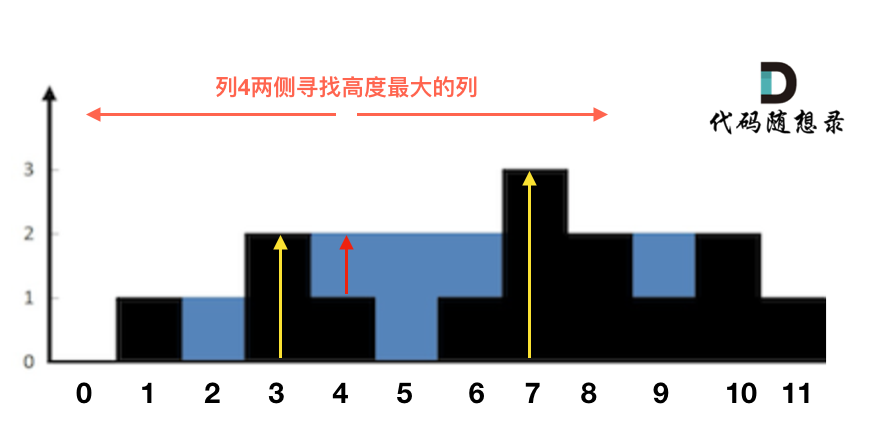
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
@@ -72,9 +76,10 @@
此时求出了列4的雨水体积。
-一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
+一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
+
```CPP
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
@@ -129,19 +134,18 @@ public:
};
```
-因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2)。
-空间复杂度为O(1)。
-
+因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2),空间复杂度为O(1)。
+力扣后面修改了后台测试数据,所以以上暴力解法超时了。
+### 双指针优化
-## 动态规划解法
-在上一节的双指针解法中,我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度,就可以计算当前位置的雨水面积,这就是通过列来计算。
+在暴力解法中,我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度,就可以计算当前位置的雨水面积,这就是通过列来计算。
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
-为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。这样就避免了重复计算,这就用到了动态规划。
+为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
@@ -149,8 +153,6 @@ public:
从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
-这样就找到递推公式。
-
代码如下:
```CPP
@@ -183,20 +185,23 @@ public:
};
```
-## 单调栈解法
+### 单调栈解法
-这个解法可以说是最不好理解的了,所以下面我花了大量的篇幅来介绍这种方法。
+关于单调栈的理论基础,单调栈适合解决什么问题,单调栈的工作过程,大家可以先看这题讲解 [739. 每日温度](https://programmercarl.com/0739.每日温度.html)。
单调栈就是保持栈内元素有序。和[栈与队列:单调队列](https://programmercarl.com/0239.滑动窗口最大值.html)一样,需要我们自己维持顺序,没有现成的容器可以用。
+通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
+
+而接雨水这道题目,我们正需要寻找一个元素,右边最大元素以及左边最大元素,来计算雨水面积。
-### 准备工作
+#### 准备工作
那么本题使用单调栈有如下几个问题:
1. 首先单调栈是按照行方向来计算雨水,如图:
-
+
知道这一点,后面的就可以理解了。
@@ -210,10 +215,11 @@ public:
如图:
-
+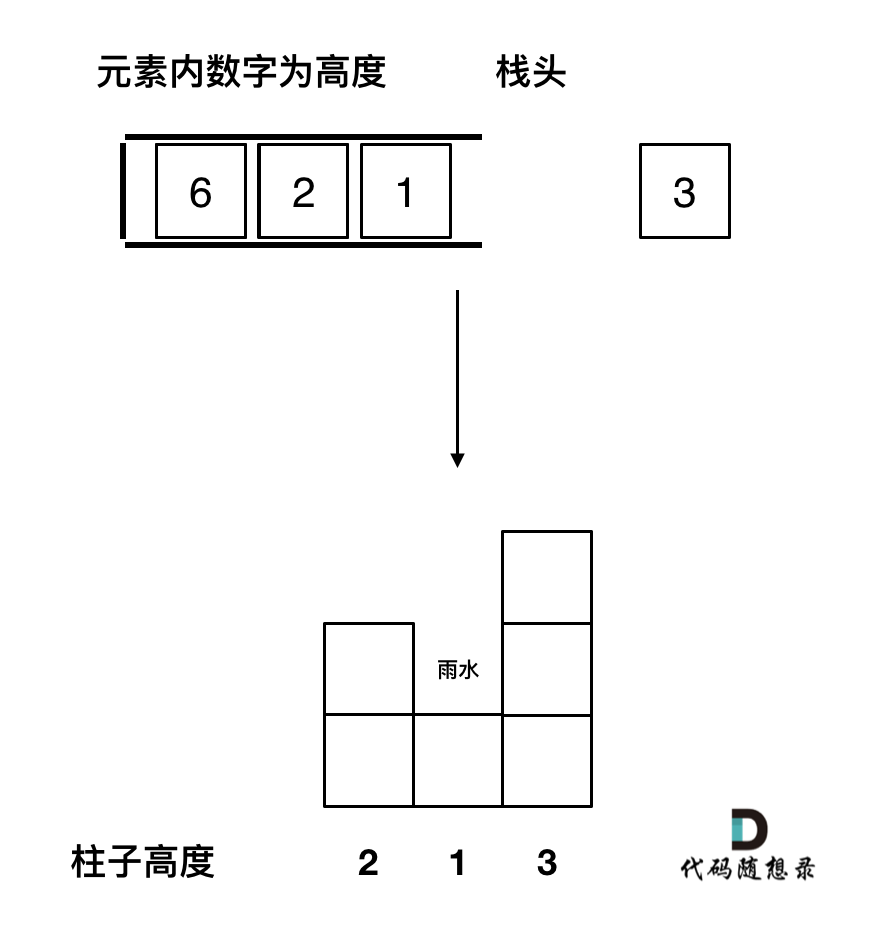
+关于单调栈的顺序给大家一个总结: [739. 每日温度](https://programmercarl.com/0739.每日温度.html) 中求一个元素右边第一个更大元素,单调栈就是递增的,[84.柱状图中最大的矩形](https://programmercarl.com/0084.柱状图中最大的矩形.html)求一个元素右边第一个更小元素,单调栈就是递减的。
-3. 遇到相同高度的柱子怎么办。
+3. 遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
@@ -223,17 +229,17 @@ public:
如图所示:
-
+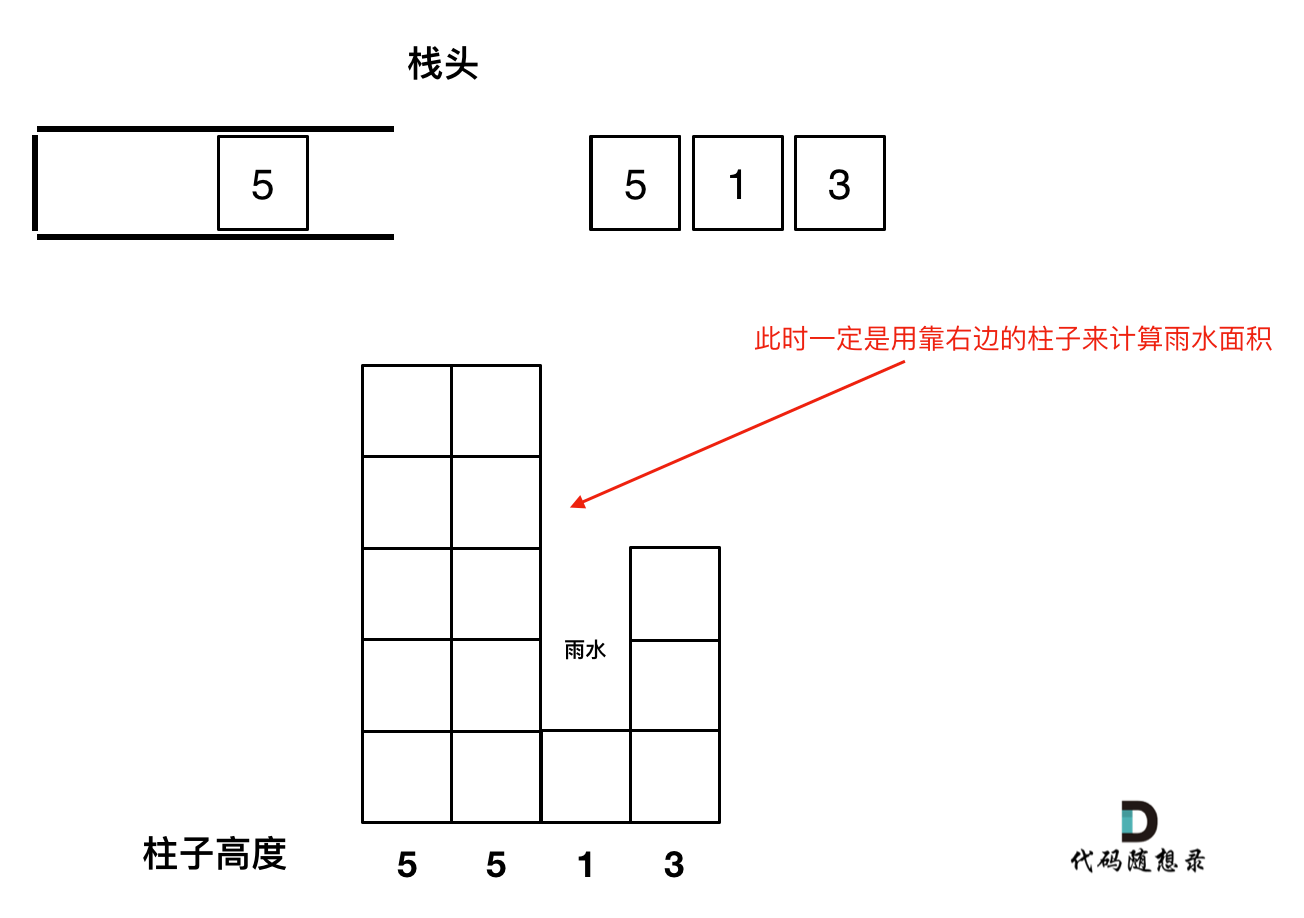
4. 栈里要保存什么数值
-是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
+使用单调栈,也是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
-那么栈里有没有必要存一个pair类型的元素,保存柱子的高度和下标呢。
+那么栈里有没有必要存一个pair类型的元素,保存柱子的高度和下标呢。
-其实不用,栈里就存放int类型的元素就行了,表示下标,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
+其实不用,栈里就存放下标就行,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
@@ -243,9 +249,17 @@ stack st; // 存着下标,计算的时候用下标对应的柱子高度
明确了如上几点,我们再来看处理逻辑。
-### 单调栈处理逻辑
+#### 单调栈处理逻辑
+
+以下操作过程其实和 [739. 每日温度](https://programmercarl.com/0739.每日温度.html) 也是一样的,建议先做 [739. 每日温度](https://programmercarl.com/0739.每日温度.html)。
+
+以下逻辑主要就是三种情况
-先将下标0的柱子加入到栈中,`st.push(0);`。
+* 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
+* 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
+* 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
+
+先将下标0的柱子加入到栈中,`st.push(0);`。 栈中存放我们遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,`for (int i = 1; i < height.size(); i++)`。
@@ -268,9 +282,9 @@ if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
}
```
-如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
+如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
-
+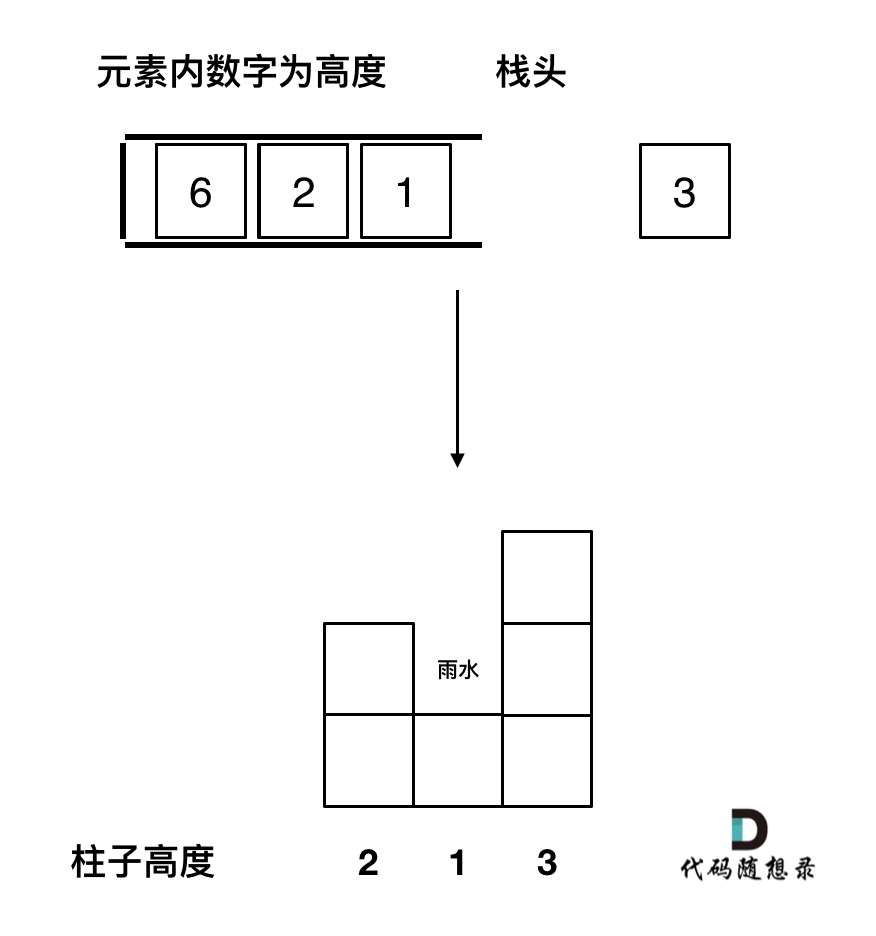
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
@@ -278,9 +292,9 @@ if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
-此时大家应该可以发现其实就是**栈顶和栈顶的下一个元素以及要入栈的三个元素来接水!**
+此时大家应该可以发现其实就是**栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!**
-那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
+那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
@@ -363,11 +377,12 @@ public:
精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
-## 其他语言版本
+## 其他语言版本
+
+### Java:
-### Java:
+暴力解法:
-双指针法
```java
class Solution {
public int trap(int[] height) {
@@ -375,7 +390,7 @@ class Solution {
for (int i = 0; i < height.length; i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i==0 || i== height.length - 1) continue;
-
+
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i+1; r < height.length; r++) {
@@ -393,7 +408,8 @@ class Solution {
}
```
-动态规划法
+双指针:
+
```java
class Solution {
public int trap(int[] height) {
@@ -401,15 +417,15 @@ class Solution {
if (length <= 2) return 0;
int[] maxLeft = new int[length];
int[] maxRight = new int[length];
-
+
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
-
+
// 记录每个柱子右边柱子最大高度
maxRight[length - 1] = height[length - 1];
for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);
-
+
// 求和
int sum = 0;
for (int i = 0; i < length; i++) {
@@ -421,14 +437,42 @@ class Solution {
}
```
+双指针优化
+```java
+class Solution {
+ public int trap(int[] height) {
+ if (height.length <= 2) {
+ return 0;
+ }
+ // 从两边向中间寻找最值
+ int maxLeft = height[0], maxRight = height[height.length - 1];
+ int l = 1, r = height.length - 2;
+ int res = 0;
+ while (l <= r) {
+ // 不确定上一轮是左边移动还是右边移动,所以两边都需更新最值
+ maxLeft = Math.max(maxLeft, height[l]);
+ maxRight = Math.max(maxRight, height[r]);
+ // 最值较小的一边所能装的水量已定,所以移动较小的一边。
+ if (maxLeft < maxRight) {
+ res += maxLeft - height[l ++];
+ } else {
+ res += maxRight - height[r --];
+ }
+ }
+ return res;
+ }
+}
+```
+
单调栈法
+
```java
class Solution {
public int trap(int[] height){
int size = height.length;
if (size <= 2) return 0;
-
+
// in the stack, we push the index of array
// using height[] to access the real height
Stack stack = new Stack();
@@ -448,7 +492,7 @@ class Solution {
int heightAtIdx = height[index];
while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
int mid = stack.pop();
-
+
if (!stack.isEmpty()){
int left = stack.peek();
@@ -462,7 +506,7 @@ class Solution {
stack.push(index);
}
}
-
+
return sum;
}
}
@@ -470,8 +514,9 @@ class Solution {
### Python:
-双指针法
-```python3
+暴力解法:
+
+```Python
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
@@ -485,32 +530,36 @@ class Solution:
for k in range(i+2,len(height)):
if height[k] > rHight:
rHight = height[k]
- res1 = min(lHight,rHight) - height[i]
+ res1 = min(lHight,rHight) - height[i]
if res1 > 0:
res += res1
return res
```
-动态规划
+
+双指针:
+
```python
class Solution:
def trap(self, height: List[int]) -> int:
leftheight, rightheight = [0]*len(height), [0]*len(height)
-
+
leftheight[0]=height[0]
for i in range(1,len(height)):
leftheight[i]=max(leftheight[i-1],height[i])
rightheight[-1]=height[-1]
for i in range(len(height)-2,-1,-1):
rightheight[i]=max(rightheight[i+1],height[i])
-
+
result = 0
for i in range(0,len(height)):
summ = min(leftheight[i],rightheight[i])-height[i]
result += summ
return result
```
+
单调栈
-```python3
+
+```Python
class Solution:
def trap(self, height: List[int]) -> int:
# 单调栈
@@ -554,8 +603,8 @@ class Solution:
result += h * w
stack.append(i)
return result
-
-# 单调栈压缩版
+
+# 单调栈压缩版
class Solution:
def trap(self, height: List[int]) -> int:
stack = [0]
@@ -575,7 +624,7 @@ class Solution:
```
-### Go
+### Go:
```go
func trap(height []int) int {
@@ -590,7 +639,7 @@ func trap(height []int) int {
}
left++
} else {
- if height[right] > rightMax {
+ if height[right] > rightMax {
rightMax = height[right] // //设置右边最高柱子
} else {
res += rightMax - height[right] // //左边必定有柱子挡水,所以,遇到所有值小于等于rightMax的,全部加入水池
@@ -602,7 +651,7 @@ func trap(height []int) int {
}
```
-动态规划解法:
+双指针解法:
```go
func trap(height []int) int {
@@ -640,12 +689,88 @@ func min(a,b int)int{
}
```
+单调栈解法
+```go
+func trap(height []int) int {
+ if len(height) <= 2 {
+ return 0
+ }
+ st := make([]int, 1, len(height)) // 切片模拟单调栈,st存储的是高度数组下标
+ var res int
+ for i := 1; i < len(height); i++ {
+ if height[i] < height[st[len(st)-1]] {
+ st = append(st, i)
+ } else if height[i] == height[st[len(st)-1]] {
+ st = st[:len(st)-1] // 比较的新元素和栈顶的元素相等,去掉栈中的,入栈新元素下标
+ st = append(st, i)
+ } else {
+ for len(st) != 0 && height[i] > height[st[len(st)-1]] {
+ top := st[len(st)-1]
+ st = st[:len(st)-1]
+ if len(st) != 0 {
+ tmp := (min(height[i], height[st[len(st)-1]]) - height[top]) * (i - st[len(st)-1] - 1)
+ res += tmp
+ }
+ }
+ st = append(st, i)
+ }
+ }
+ return res
+}
+
+
+func min(x, y int) int {
+ if x >= y {
+ return y
+ }
+ return x
+}
+```
+
+单调栈压缩版:
+
+```go
+func trap(height []int) int {
+ stack := make([]int, 0)
+ res := 0
+
+ // 无需事先将第一个柱子的坐标入栈,因为它会在该for循环的最后入栈
+ for i := 0; i < len(height); i ++ {
+ // 满足栈不为空并且当前柱子高度大于栈顶对应的柱子高度的情况时
+ for len(stack) > 0 && height[stack[len(stack) - 1]] < height[i] {
+ // 获得凹槽高度
+ mid := height[stack[len(stack) - 1]]
+ // 凹槽坐标出栈
+ stack = stack[: len(stack) - 1]
+
+ // 如果栈不为空则此时栈顶元素为左侧柱子坐标
+ if len(stack) > 0 {
+ // 求得雨水高度
+ h := min(height[i], height[stack[len(stack) - 1]]) - mid
+ // 求得雨水宽度
+ w := i - stack[len(stack) - 1] - 1
+ res += h * w
+ }
+ }
+ // 如果栈为空或者当前柱子高度小于等于栈顶对应的柱子高度时入栈
+ stack = append(stack, i)
+ }
+ return res
+}
+
+func min(x, y int) int {
+ if x < y {
+ return x
+ }
+ return y
+}
+```
### JavaScript:
```javascript
-//双指针
+//暴力解法
var trap = function(height) {
const len = height.length;
let sum = 0;
@@ -666,7 +791,7 @@ var trap = function(height) {
return sum;
};
-//动态规划
+//双指针
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
@@ -744,6 +869,91 @@ var trap = function(height) {
};
```
+### TypeScript:
+
+暴力解法:
+
+```typescript
+function trap(height: number[]): number {
+ const length: number = height.length;
+ let resVal: number = 0;
+ for (let i = 0; i < length; i++) {
+ let leftMaxHeight: number = height[i],
+ rightMaxHeight: number = height[i];
+ let leftIndex: number = i - 1,
+ rightIndex: number = i + 1;
+ while (leftIndex >= 0) {
+ if (height[leftIndex] > leftMaxHeight)
+ leftMaxHeight = height[leftIndex];
+ leftIndex--;
+ }
+ while (rightIndex < length) {
+ if (height[rightIndex] > rightMaxHeight)
+ rightMaxHeight = height[rightIndex];
+ rightIndex++;
+ }
+ resVal += Math.min(leftMaxHeight, rightMaxHeight) - height[i];
+ }
+ return resVal;
+};
+```
+
+双指针:
+
+```typescript
+function trap(height: number[]): number {
+ const length: number = height.length;
+ const leftMaxHeightDp: number[] = [],
+ rightMaxHeightDp: number[] = [];
+ leftMaxHeightDp[0] = height[0];
+ rightMaxHeightDp[length - 1] = height[length - 1];
+ for (let i = 1; i < length; i++) {
+ leftMaxHeightDp[i] = Math.max(height[i], leftMaxHeightDp[i - 1]);
+ }
+ for (let i = length - 2; i >= 0; i--) {
+ rightMaxHeightDp[i] = Math.max(height[i], rightMaxHeightDp[i + 1]);
+ }
+ let resVal: number = 0;
+ for (let i = 0; i < length; i++) {
+ resVal += Math.min(leftMaxHeightDp[i], rightMaxHeightDp[i]) - height[i];
+ }
+ return resVal;
+};
+```
+
+单调栈:
+
+```typescript
+function trap(height: number[]): number {
+ const length: number = height.length;
+ const stack: number[] = [];
+ stack.push(0);
+ let resVal: number = 0;
+ for (let i = 1; i < length; i++) {
+ let top = stack[stack.length - 1];
+ if (height[top] > height[i]) {
+ stack.push(i);
+ } else if (height[top] === height[i]) {
+ stack.pop();
+ stack.push(i);
+ } else {
+ while (stack.length > 0 && height[top] < height[i]) {
+ let mid = stack.pop();
+ if (stack.length > 0) {
+ let left = stack[stack.length - 1];
+ let h = Math.min(height[left], height[i]) - height[mid];
+ let w = i - left - 1;
+ resVal += h * w;
+ top = stack[stack.length - 1];
+ }
+ }
+ stack.push(i);
+ }
+ }
+ return resVal;
+};
+```
+
### C:
一种更简便的双指针方法:
@@ -764,12 +974,12 @@ int trap(int* height, int heightSize) {
while (left < right) { //两个指针重合就结束
leftMax = fmax(leftMax, height[left]);
rightMax = fmax(rightMax, height[right]);
- if (leftMax < rightMax) {
+ if (leftMax < rightMax) {
ans += leftMax - height[left]; //这里考虑的是下标为left的“底”能装多少水
++left;//指针的移动次序是这个方法的关键
//这里左指针右移是因为左“墙”较矮,左边这一片实际情况下的盛水量是受制于这个矮的左“墙”的
//而较高的右边在实际情况下的限制条件可能不是当前的左“墙”,比如限制条件可能是右“墙”,就能装更高的水,
- }
+ }
else {
ans += rightMax - height[right]; //同理,考虑下标为right的元素
--right;
@@ -782,6 +992,103 @@ int trap(int* height, int heightSize) {
* 时间复杂度 O(n)
* 空间复杂度 O(1)
+### Rust:
+
+双指针
+
+```rust
+impl Solution {
+ pub fn trap(height: Vec) -> i32 {
+ let n = height.len();
+ let mut max_left = vec![0; height.len()];
+ let mut max_right = vec![0; height.len()];
+ max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
+ let lmax = lm.max(height[idx]);
+ let rmax = rm.max(height[n - 1 - idx]);
+ *x = lmax; *y = rmax;
+ (lmax, rmax)
+ });
+ height.iter().enumerate().fold(0, |acc, (idx, x)| {
+ let h = max_left[idx].min(max_right[idx]);
+ if h > 0 { h - x + acc } else { acc }
+ })
+ }
+}
+```
+
+单调栈
+
+```rust
+impl Solution {
+ pub fn trap(height: Vec) -> i32 {
+ let mut stack = vec![];
+ let mut ans = 0;
+ for (right_pos, &right_h) in height.iter().enumerate() {
+ while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
+ let mid_pos = stack.pop().unwrap();
+ if !stack.is_empty() {
+ let left_pos = *stack.last().unwrap();
+ let left_h = height[left_pos];
+ let top = std::cmp::min(left_h, right_h);
+ if top > height[mid_pos] {
+ ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
+ }
+ }
+ }
+ stack.push(right_pos);
+ }
+ ans
+ }
+}
+```
+
+Rust
+
+双指针
+
+```rust
+impl Solution {
+ pub fn trap(height: Vec) -> i32 {
+ let n = height.len();
+ let mut max_left = vec![0; height.len()];
+ let mut max_right = vec![0; height.len()];
+ max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
+ let lmax = lm.max(height[idx]);
+ let rmax = rm.max(height[n - 1 - idx]);
+ *x = lmax; *y = rmax;
+ (lmax, rmax)
+ });
+ height.iter().enumerate().fold(0, |acc, (idx, x)| {
+ let h = max_left[idx].min(max_right[idx]);
+ if h > 0 { h - x + acc } else { acc }
+ })
+ }
+}
+```
+
+单调栈
+
+```rust
+impl Solution {
+ pub fn trap(height: Vec) -> i32 {
+ let mut stack = vec![];
+ let mut ans = 0;
+ for (right_pos, &right_h) in height.iter().enumerate() {
+ while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
+ let mid_pos = stack.pop().unwrap();
+ if !stack.is_empty() {
+ let left_pos = *stack.last().unwrap();
+ let left_h = height[left_pos];
+ let top = std::cmp::min(left_h, right_h);
+ if top > height[mid_pos] {
+ ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
+ }
+ }
+ }
+ stack.push(right_pos);
+ }
+ ans
+ }
+}
+```
------------------------
-
diff --git "a/problems/0045.\350\267\263\350\267\203\346\270\270\346\210\217II.md" "b/problems/0045.\350\267\263\350\267\203\346\270\270\346\210\217II.md"
old mode 100644
new mode 100755
index 7a3f048c60..c20cdc65e6
--- "a/problems/0045.\350\267\263\350\267\203\346\270\270\346\210\217II.md"
+++ "b/problems/0045.\350\267\263\350\267\203\346\270\270\346\210\217II.md"
@@ -1,15 +1,12 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心理准备!
-> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
+# 45.跳跃游戏 II
-# 45.跳跃游戏II
-
-[力扣题目链接](https://leetcode-cn.com/problems/jump-game-ii/)
+[力扣题目链接](https://leetcode.cn/problems/jump-game-ii/)
给定一个非负整数数组,你最初位于数组的第一个位置。
@@ -18,13 +15,17 @@
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
-* 输入: [2,3,1,1,4]
-* 输出: 2
-* 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
+
+- 输入: [2,3,1,1,4]
+- 输出: 2
+- 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法,最少跳几步还得看覆盖范围 | LeetCode: 45.跳跃游戏 II](https://www.bilibili.com/video/BV1Y24y1r7XZ),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
## 思路
@@ -32,13 +33,13 @@
但思路是相似的,还是要看最大覆盖范围。
-本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
+本题要计算最少步数,那么就要想清楚什么时候步数才一定要加一呢?
-贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
+贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最少步数。
-思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
+思路虽然是这样,但在写代码的时候还不能真的能跳多远就跳多远,那样就不知道下一步最远能跳到哪里了。
-**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
+**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!**
**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
@@ -46,18 +47,18 @@
如图:
-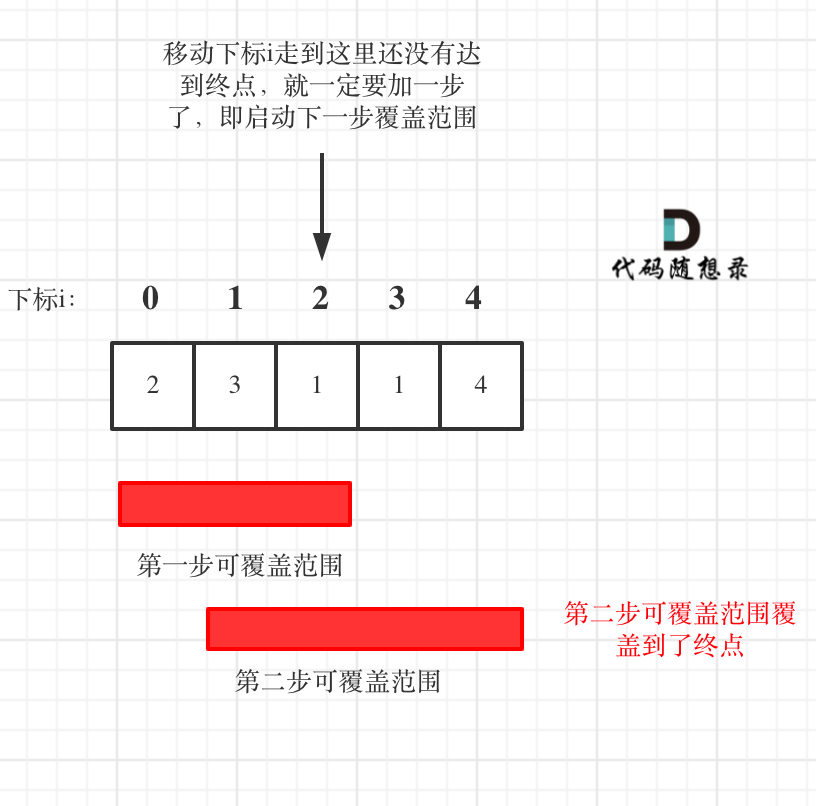
+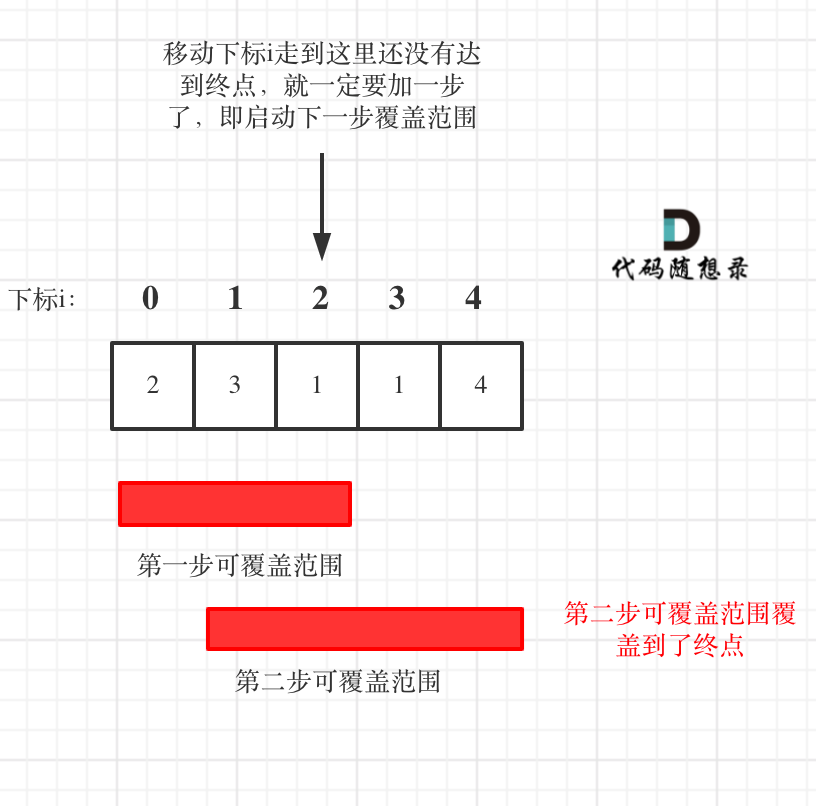
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
-## 方法一
+### 方法一
从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
-* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
-* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
+- 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
+- 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
C++代码如下:(详细注释)
@@ -73,11 +74,9 @@ public:
for (int i = 0; i < nums.size(); i++) {
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
if (i == curDistance) { // 遇到当前覆盖最远距离下标
- if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
- ans++; // 需要走下一步
- curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
- if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
- } else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
+ ans++; // 需要走下一步
+ curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
+ if (nextDistance >= nums.size() - 1) break; // 当前覆盖最远距到达集合终点,不用做ans++操作了,直接结束
}
}
return ans;
@@ -85,22 +84,26 @@ public:
};
```
-## 方法二
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
+
+### 方法二
依然是贪心,思路和方法一差不多,代码可以简洁一些。
**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
-想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
+想要达到这样的效果,只要让移动下标,最大只能移动到 nums.size - 2 的地方就可以了。
-因为当移动下标指向nums.size - 2时:
+因为当移动下标指向 nums.size - 2 时:
-* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
-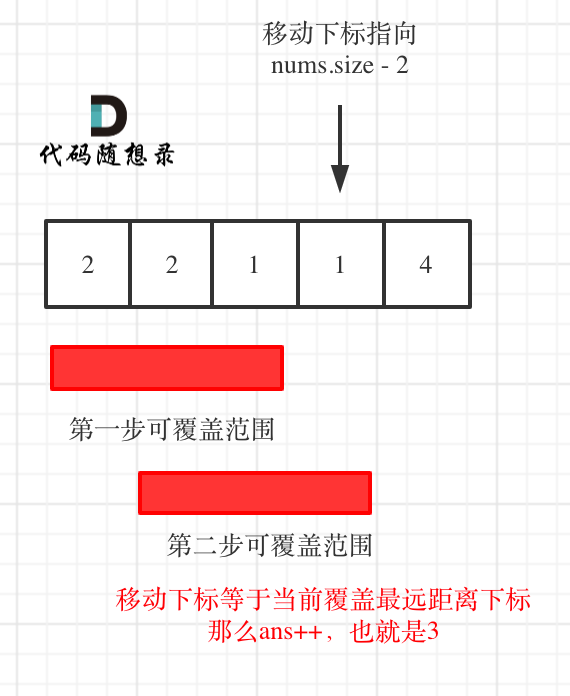
+- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
+ 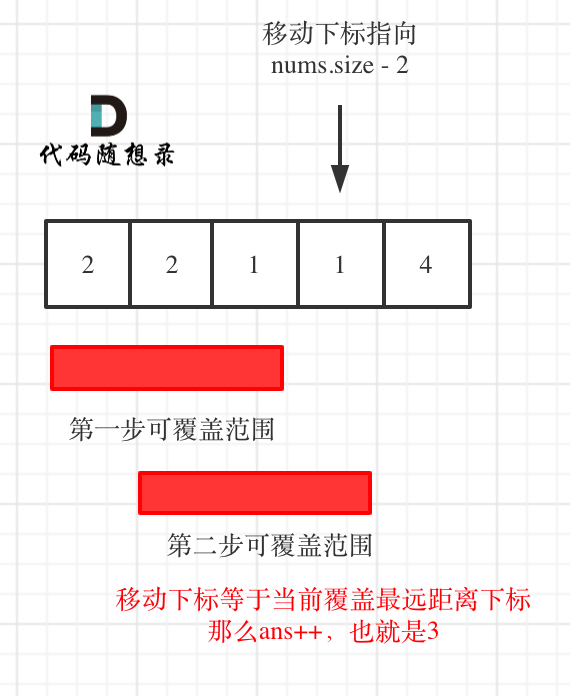
-* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
+- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
-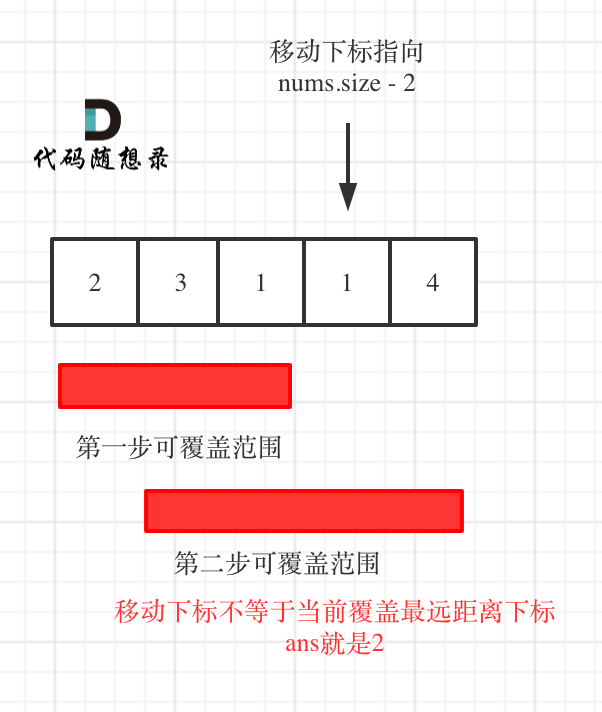
+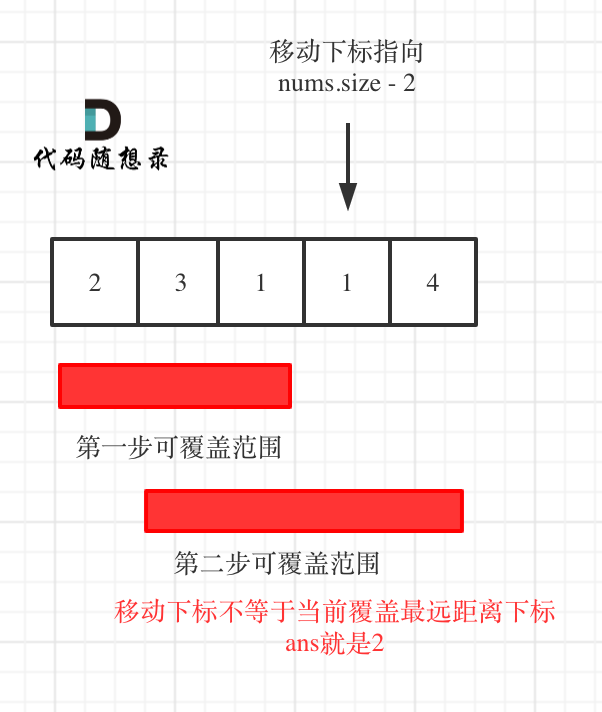
代码如下:
@@ -124,9 +127,14 @@ public:
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
+
+
可以看出版本二的代码相对于版本一简化了不少!
-其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
+**其精髓在于控制移动下标 i 只移动到 nums.size() - 2 的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
## 总结
@@ -134,13 +142,12 @@ public:
但代码又十分简单,贪心就是这么巧妙。
-理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
-
+理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最少步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
## 其他语言版本
+### Java
-### Java
```Java
// 版本一
class Solution {
@@ -196,43 +203,177 @@ class Solution {
```
### Python
-
+贪心(版本一)
```python
class Solution:
- def jump(self, nums: List[int]) -> int:
- if len(nums) == 1: return 0
- ans = 0
- curDistance = 0
- nextDistance = 0
+ def jump(self, nums):
+ if len(nums) == 1:
+ return 0
+
+ cur_distance = 0 # 当前覆盖最远距离下标
+ ans = 0 # 记录走的最大步数
+ next_distance = 0 # 下一步覆盖最远距离下标
+
for i in range(len(nums)):
- nextDistance = max(i + nums[i], nextDistance)
- if i == curDistance:
- if curDistance != len(nums) - 1:
- ans += 1
- curDistance = nextDistance
- if nextDistance >= len(nums) - 1: break
+ next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖最远距离下标
+ if i == cur_distance: # 遇到当前覆盖最远距离下标
+ ans += 1 # 需要走下一步
+ cur_distance = next_distance # 更新当前覆盖最远距离下标(相当于加油了)
+ if next_distance >= len(nums) - 1: # 当前覆盖最远距离达到数组末尾,不用再做ans++操作,直接结束
+ break
+
+ return ans
+
+```
+贪心(版本二)
+
+```python
+class Solution:
+ def jump(self, nums):
+ cur_distance = 0 # 当前覆盖的最远距离下标
+ ans = 0 # 记录走的最大步数
+ next_distance = 0 # 下一步覆盖的最远距离下标
+
+ for i in range(len(nums) - 1): # 注意这里是小于len(nums) - 1,这是关键所在
+ next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖的最远距离下标
+ if i == cur_distance: # 遇到当前覆盖的最远距离下标
+ cur_distance = next_distance # 更新当前覆盖的最远距离下标
+ ans += 1
+
return ans
+
+```
+贪心(版本三) 类似‘55-跳跃游戏’写法
+
+```python
+class Solution:
+ def jump(self, nums) -> int:
+ if len(nums)==1: # 如果数组只有一个元素,不需要跳跃,步数为0
+ return 0
+
+ i = 0 # 当前位置
+ count = 0 # 步数计数器
+ cover = 0 # 当前能够覆盖的最远距离
+
+ while i <= cover: # 当前位置小于等于当前能够覆盖的最远距离时循环
+ for i in range(i, cover+1): # 遍历从当前位置到当前能够覆盖的最远距离之间的所有位置
+ cover = max(nums[i]+i, cover) # 更新当前能够覆盖的最远距离
+ if cover >= len(nums)-1: # 如果当前能够覆盖的最远距离达到或超过数组的最后一个位置,直接返回步数+1
+ return count+1
+ count += 1 # 每一轮遍历结束后,步数+1
+
+
+```
+动态规划
+```python
+class Solution:
+ def jump(self, nums: List[int]) -> int:
+ result = [10**4+1] * len(nums) # 初始化结果数组,初始值为一个较大的数
+ result[0] = 0 # 起始位置的步数为0
+
+ for i in range(len(nums)): # 遍历数组
+ for j in range(nums[i] + 1): # 在当前位置能够跳跃的范围内遍历
+ if i + j < len(nums): # 确保下一跳的位置不超过数组范围
+ result[i + j] = min(result[i + j], result[i] + 1) # 更新到达下一跳位置的最少步数
+
+ return result[-1] # 返回到达最后一个位置的最少步数
+
+
```
### Go
-```Go
+
+
+```go
+/**
+ * @date: 2024 Jan 06
+ * @time: 13:44
+ * @author: Chris
+**/
+// 贪心算法优化版
+
+// 记录步骤规则:每超过上一次可达最大范围,需要跳跃一次,次数+1
+// 记录位置:i == lastDistance + 1
func jump(nums []int) int {
- dp:=make([]int ,len(nums))
- dp[0]=0
-
- for i:=1;ii{
- dp[i]=min(dp[j]+1,dp[i])
- }
+ // 根据题目规则,初始位置为nums[0]
+ lastDistance := 0 // 上一次覆盖范围
+ curDistance := 0 // 当前覆盖范围(可达最大范围)
+ minStep := 0 // 记录最少跳跃次数
+
+ for i := 0; i < len(nums); i++ {
+ if i == lastDistance+1 { // 在上一次可达范围+1的位置,记录步骤
+ minStep++ // 跳跃次数+1
+ lastDistance = curDistance // 记录时才可以更新
}
+ curDistance = max(nums[i]+i, curDistance) // 更新当前可达的最大范围
}
- return dp[len(nums)-1]
+ return minStep
}
```
-### Javascript
+```go
+// 贪心版本一
+func jump(nums []int) int {
+ n := len(nums)
+ if n == 1 {
+ return 0
+ }
+ cur, next := 0, 0
+ step := 0
+ for i := 0; i < n; i++ {
+ next = max(nums[i]+i, next)
+ if i == cur {
+ if cur != n-1 {
+ step++
+ cur = next
+ if cur >= n-1 {
+ return step
+ }
+ } else {
+ return step
+ }
+ }
+ }
+ return step
+}
+
+func max(a, b int) int {
+ if a > b {
+ return a
+ }
+ return b
+}
+```
+
+```go
+// 贪心版本二
+func jump(nums []int) int {
+ n := len(nums)
+ if n == 1 {
+ return 0
+ }
+ cur, next := 0, 0
+ step := 0
+ for i := 0; i < n-1; i++ {
+ next = max(nums[i]+i, next)
+ if i == cur {
+ cur = next
+ step++
+ }
+ }
+ return step
+}
+
+func max(a, b int) int {
+ if a > b {
+ return a
+ }
+ return b
+}
+```
+
+### JavaScript
+
```Javascript
var jump = function(nums) {
let curIndex = 0
@@ -250,9 +391,152 @@ var jump = function(nums) {
};
```
+### TypeScript
+
+```typescript
+function jump(nums: number[]): number {
+ const length: number = nums.length;
+ let curFarthestIndex: number = 0,
+ nextFarthestIndex: number = 0;
+ let curIndex: number = 0;
+ let stepNum: number = 0;
+ while (curIndex < length - 1) {
+ nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
+ if (curIndex === curFarthestIndex) {
+ curFarthestIndex = nextFarthestIndex;
+ stepNum++;
+ }
+ curIndex++;
+ }
+ return stepNum;
+}
+```
+
+### Scala
+
+```scala
+object Solution {
+ def jump(nums: Array[Int]): Int = {
+ if (nums.length == 0) return 0
+ var result = 0 // 记录走的最大步数
+ var curDistance = 0 // 当前覆盖最远距离下标
+ var nextDistance = 0 // 下一步覆盖最远距离下标
+ for (i <- nums.indices) {
+ nextDistance = math.max(nums(i) + i, nextDistance) // 更新下一步覆盖最远距离下标
+ if (i == curDistance) {
+ if (curDistance != nums.length - 1) {
+ result += 1
+ curDistance = nextDistance
+ if (nextDistance >= nums.length - 1) return result
+ } else {
+ return result
+ }
+ }
+ }
+ result
+ }
+}
+```
+
+### Rust
+
+```Rust
+//版本一
+impl Solution {
+ pub fn jump(nums: Vec) -> i32 {
+ if nums.len() == 1 {
+ return 0;
+ }
+ let mut cur_distance = 0;
+ let mut ans = 0;
+ let mut next_distance = 0;
+ for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
+ next_distance = (n as usize + i).max(next_distance);
+ if i == cur_distance {
+ if cur_distance < nums.len() - 1 {
+ ans += 1;
+ cur_distance = next_distance;
+ if next_distance >= nums.len() - 1 {
+ break;
+ };
+ } else {
+ break;
+ }
+ }
+ }
+ ans
+ }
+}
+```
+
+```Rust
+//版本二
+impl Solution {
+ pub fn jump(nums: Vec) -> i32 {
+ if nums.len() == 1 {
+ return 0;
+ }
+ let mut cur_distance = 0;
+ let mut ans = 0;
+ let mut next_distance = 0;
+ for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
+ next_distance = (n as usize + i).max(next_distance);
+ if i == cur_distance {
+ cur_distance = next_distance;
+ ans += 1;
+ }
+ }
+ ans
+ }
+}
+```
+### C
+```c
+#define max(a, b) ((a) > (b) ? (a) : (b))
+int jump(int* nums, int numsSize) {
+ if(numsSize == 1){
+ return 0;
+ }
+ int count = 0;
+ // 记录当前能走的最远距离
+ int curDistance = 0;
+ // 记录下一步能走的最远距离
+ int nextDistance = 0;
+ for(int i = 0; i < numsSize; i++){
+ nextDistance = max(i + nums[i], nextDistance);
+ // 下标到了当前的最大距离
+ if(i == nextDistance){
+ count++;
+ curDistance = nextDistance;
+ }
+ }
+ return count;
+}
+```
+
+### C#
+
+```csharp
+// 版本二
+public class Solution
+{
+ public int Jump(int[] nums)
+ {
+ int cur = 0, next = 0, step = 0;
+ for (int i = 0; i < nums.Length - 1; i++)
+ {
+ next = Math.Max(next, i + nums[i]);
+ if (i == cur)
+ {
+ cur = next;
+ step++;
+ }
+ }
+ return step;
+ }
+}
+```
------------------------
-
diff --git "a/problems/0046.\345\205\250\346\216\222\345\210\227.md" "b/problems/0046.\345\205\250\346\216\222\345\210\227.md"
old mode 100644
new mode 100755
index c5369ddd1b..356f51b5a8
--- "a/problems/0046.\345\205\250\346\216\222\345\210\227.md"
+++ "b/problems/0046.\345\205\250\346\216\222\345\210\227.md"
@@ -1,13 +1,11 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 46.全排列
-[力扣题目链接](https://leetcode-cn.com/problems/permutations/)
+[力扣题目链接](https://leetcode.cn/problems/permutations/)
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
@@ -23,9 +21,13 @@
[3,2,1]
]
-## 思路
-**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[组合与排列的区别,回溯算法求解的时候,有何不同?| LeetCode:46.全排列](https://www.bilibili.com/video/BV19v4y1S79W/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
+
+## 思路
此时我们已经学习了[77.组合问题](https://programmercarl.com/0077.组合.html)、 [131.分割回文串](https://programmercarl.com/0131.分割回文串.html)和[78.子集问题](https://programmercarl.com/0078.子集.html),接下来看一看排列问题。
@@ -38,7 +40,8 @@
我以[1,2,3]为例,抽象成树形结构如下:
-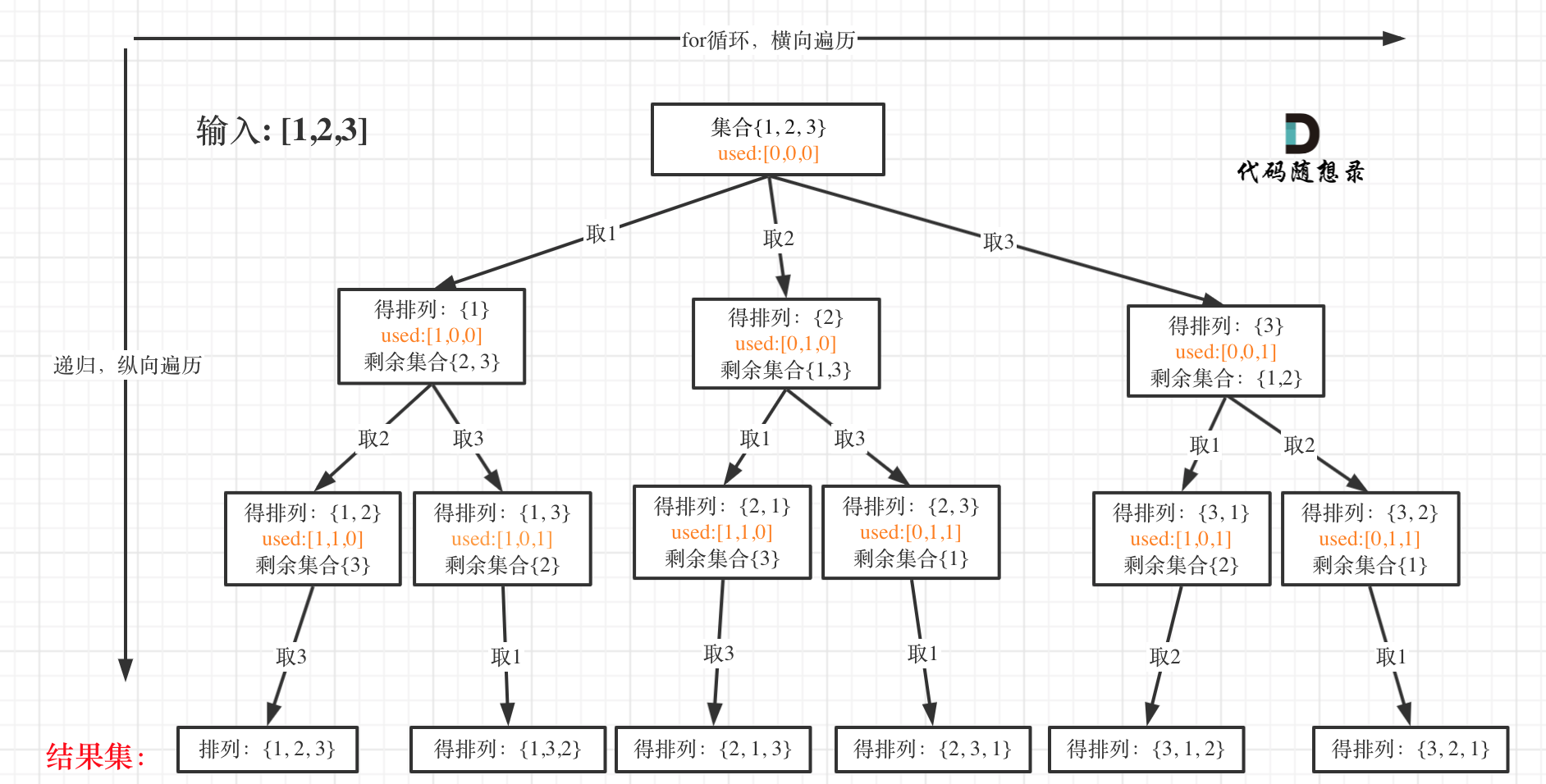
+
+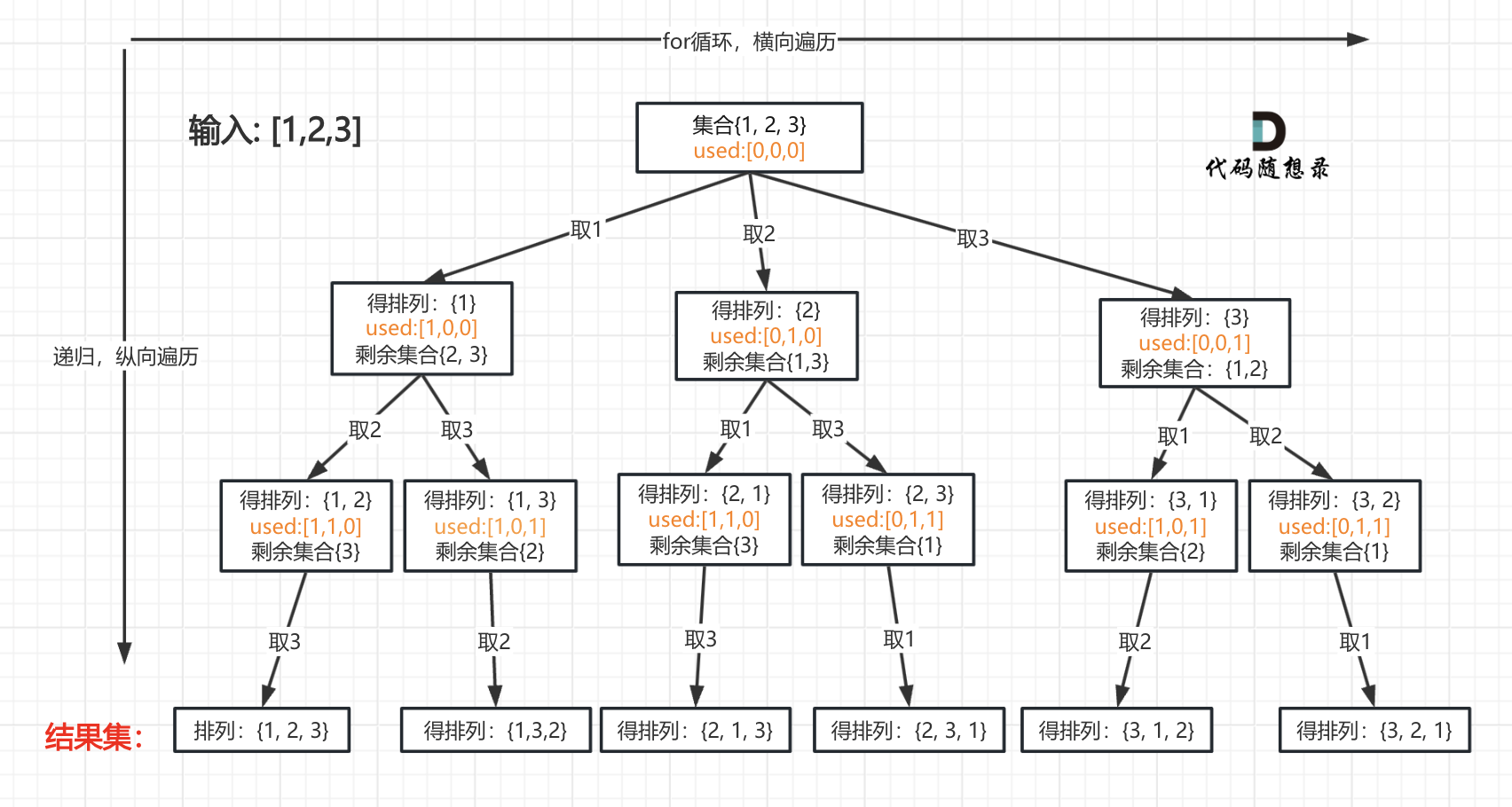
### 回溯三部曲
@@ -50,7 +53,7 @@
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
-
+
代码如下:
@@ -62,7 +65,7 @@ void backtracking (vector& nums, vector& used)
* 递归终止条件
-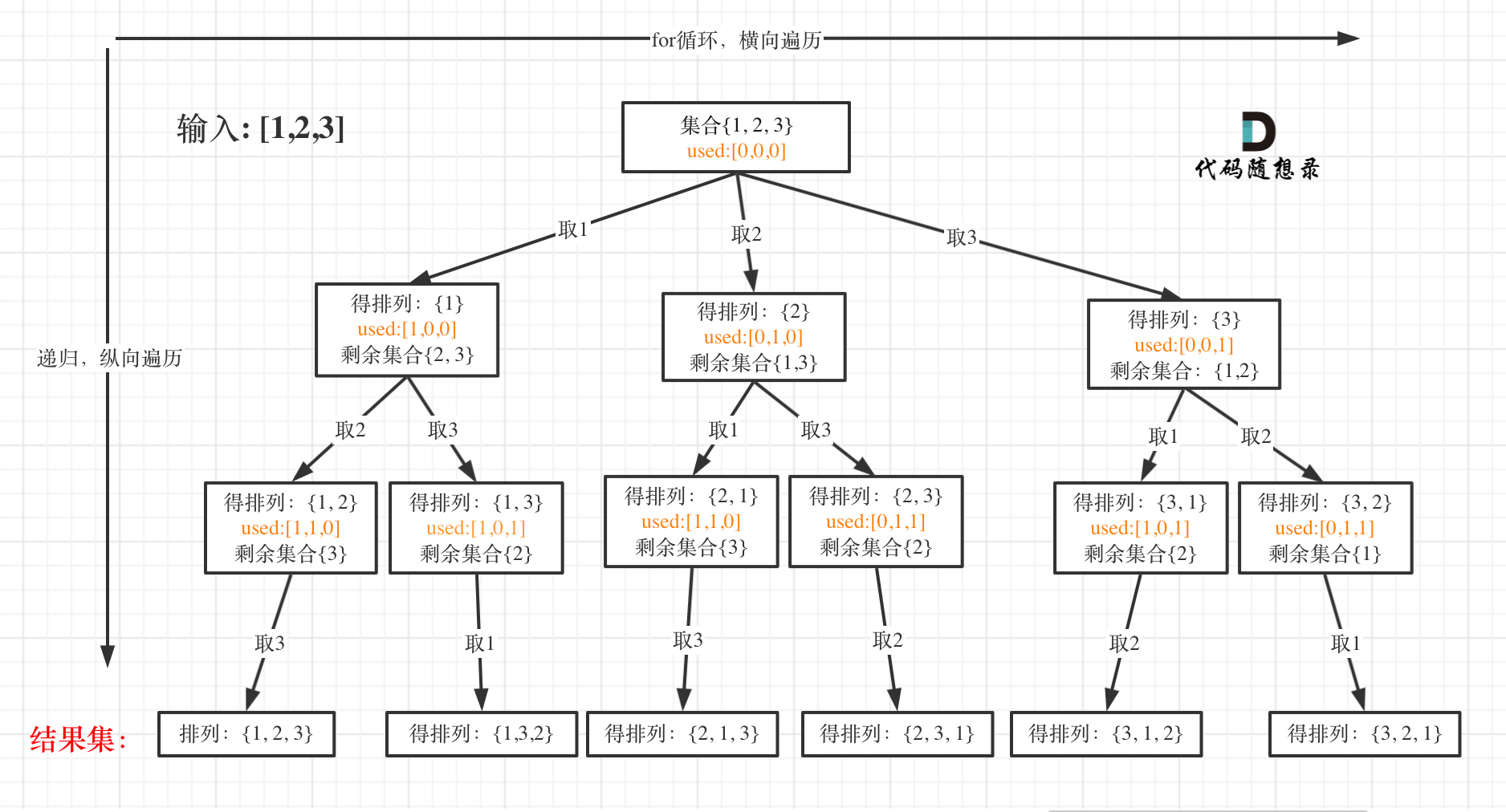
+
可以看出叶子节点,就是收割结果的地方。
@@ -132,6 +135,8 @@ public:
}
};
```
+* 时间复杂度: O(n!)
+* 空间复杂度: O(n)
## 总结
@@ -194,6 +199,7 @@ class Solution {
public void backtrack(int[] nums, LinkedList path) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
+ return;
}
for (int i =0; i < nums.length; i++) {
// 如果path中已有,则跳过
@@ -209,98 +215,62 @@ class Solution {
```
### Python
-**回溯**
+回溯 使用used
```python
class Solution:
- def __init__(self):
- self.path = []
- self.paths = []
-
- def permute(self, nums: List[int]) -> List[List[int]]:
- '''
- 因为本题排列是有序的,这意味着同一层的元素可以重复使用,但同一树枝上不能重复使用(usage_list)
- 所以处理排列问题每层都需要从头搜索,故不再使用start_index
- '''
- usage_list = [False] * len(nums)
- self.backtracking(nums, usage_list)
- return self.paths
-
- def backtracking(self, nums: List[int], usage_list: List[bool]) -> None:
- # Base Case本题求叶子节点
- if len(self.path) == len(nums):
- self.paths.append(self.path[:])
+ def permute(self, nums):
+ result = []
+ self.backtracking(nums, [], [False] * len(nums), result)
+ return result
+
+ def backtracking(self, nums, path, used, result):
+ if len(path) == len(nums):
+ result.append(path[:])
return
-
- # 单层递归逻辑
- for i in range(0, len(nums)): # 从头开始搜索
- # 若遇到self.path里已收录的元素,跳过
- if usage_list[i] == True:
+ for i in range(len(nums)):
+ if used[i]:
continue
- usage_list[i] = True
- self.path.append(nums[i])
- self.backtracking(nums, usage_list) # 纵向传递使用信息,去重
- self.path.pop()
- usage_list[i] = False
-```
-**回溯+丢掉usage_list**
-```python
-class Solution:
- def __init__(self):
- self.path = []
- self.paths = []
-
- def permute(self, nums: List[int]) -> List[List[int]]:
- '''
- 因为本题排列是有序的,这意味着同一层的元素可以重复使用,但同一树枝上不能重复使用
- 所以处理排列问题每层都需要从头搜索,故不再使用start_index
- '''
- self.backtracking(nums)
- return self.paths
-
- def backtracking(self, nums: List[int]) -> None:
- # Base Case本题求叶子节点
- if len(self.path) == len(nums):
- self.paths.append(self.path[:])
- return
+ used[i] = True
+ path.append(nums[i])
+ self.backtracking(nums, path, used, result)
+ path.pop()
+ used[i] = False
- # 单层递归逻辑
- for i in range(0, len(nums)): # 从头开始搜索
- # 若遇到self.path里已收录的元素,跳过
- if nums[i] in self.path:
- continue
- self.path.append(nums[i])
- self.backtracking(nums)
- self.path.pop()
```
### Go
```Go
-var res [][]int
+var (
+ res [][]int
+ path []int
+ st []bool // state的缩写
+)
func permute(nums []int) [][]int {
- res = [][]int{}
- backTrack(nums,len(nums),[]int{})
- return res
-}
-func backTrack(nums []int,numsLen int,path []int) {
- if len(nums)==0{
- p:=make([]int,len(path))
- copy(p,path)
- res = append(res,p)
- }
- for i:=0;i = new Set();
+ backTracking(nums, []);
+ return resArr;
+ function backTracking(nums: number[], route: number[]): void {
+ if (route.length === nums.length) {
+ resArr.push([...route]);
+ return;
+ }
+ let tempVal: number;
+ for (let i = 0, length = nums.length; i < length; i++) {
+ tempVal = nums[i];
+ if (!helperSet.has(tempVal)) {
+ route.push(tempVal);
+ helperSet.add(tempVal);
+ backTracking(nums, route);
+ route.pop();
+ helperSet.delete(tempVal);
+ }
+ }
+ }
+};
+```
+
+### Rust
+
+```Rust
+impl Solution {
+ fn backtracking(result: &mut Vec>, path: &mut Vec, nums: &Vec, used: &mut Vec) {
+ let len = nums.len();
+ if path.len() == len {
+ result.push(path.clone());
+ return;
+ }
+ for i in 0..len {
+ if used[i] == true { continue; }
+ used[i] = true;
+ path.push(nums[i]);
+ Self::backtracking(result, path, nums, used);
+ path.pop();
+ used[i] = false;
+ }
+ }
+
+ pub fn permute(nums: Vec) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut path: Vec = Vec::new();
+ let mut used = vec![false; nums.len()];
+ Self::backtracking(&mut result, &mut path, &nums, &mut used);
+ result
+ }
+}
+```
+
### C
```c
@@ -428,6 +456,67 @@ func permute(_ nums: [Int]) -> [[Int]] {
}
```
+### Scala
+
+```scala
+object Solution {
+ import scala.collection.mutable
+ def permute(nums: Array[Int]): List[List[Int]] = {
+ var result = mutable.ListBuffer[List[Int]]()
+ var path = mutable.ListBuffer[Int]()
+
+ def backtracking(used: Array[Boolean]): Unit = {
+ if (path.size == nums.size) {
+ // 如果path的长度和nums相等,那么可以添加到结果集
+ result.append(path.toList)
+ return
+ }
+ // 添加循环守卫,只有当当前数字没有用过的情况下才进入回溯
+ for (i <- nums.indices if used(i) == false) {
+ used(i) = true
+ path.append(nums(i))
+ backtracking(used) // 回溯
+ path.remove(path.size - 1)
+ used(i) = false
+ }
+ }
+
+ backtracking(new Array[Boolean](nums.size)) // 调用方法
+ result.toList // 最终返回结果集的List形式
+ }
+}
+```
+### C#
+```csharp
+public class Solution
+{
+ public IList> res = new List>();
+ public IList path = new List();
+ public IList> Permute(int[] nums)
+ {
+ var used = new bool[nums.Length];
+ BackTracking(nums, used);
+ return res;
+ }
+ public void BackTracking(int[] nums, bool[] used)
+ {
+ if (path.Count == nums.Length)
+ {
+ res.Add(new List(path));
+ return;
+ }
+ for (int i = 0; i < nums.Length; i++)
+ {
+ if (used[i]) continue;
+ used[i] = true;
+ path.Add(nums[i]);
+ BackTracking(nums, used);
+ used[i] = false;
+ path.RemoveAt(path.Count - 1);
+ }
+ }
+}
+```
+
+
------------------------
-
diff --git "a/problems/0047.\345\205\250\346\216\222\345\210\227II.md" "b/problems/0047.\345\205\250\346\216\222\345\210\227II.md"
old mode 100644
new mode 100755
index 0cecac5058..5330997a66
--- "a/problems/0047.\345\205\250\346\216\222\345\210\227II.md"
+++ "b/problems/0047.\345\205\250\346\216\222\345\210\227II.md"
@@ -1,36 +1,41 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-# 排列问题(二)
-## 47.全排列 II
-[力扣题目链接](https://leetcode-cn.com/problems/permutations-ii/)
+
+# 47.全排列 II
+
+[力扣题目链接](https://leetcode.cn/problems/permutations-ii/)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
+
* 输入:nums = [1,1,2]
* 输出:
-[[1,1,2],
- [1,2,1],
- [2,1,1]]
+ [[1,1,2],
+ [1,2,1],
+ [2,1,1]]
示例 2:
+
* 输入:nums = [1,2,3]
* 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
+
* 1 <= nums.length <= 8
* -10 <= nums[i] <= 10
-## 思路
-**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II](https://www.bilibili.com/video/BV1R84y1i7Tm/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+## 思路
+
这道题目和[46.全排列](https://programmercarl.com/0046.全排列.html)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
这里又涉及到去重了。
@@ -43,15 +48,15 @@
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
-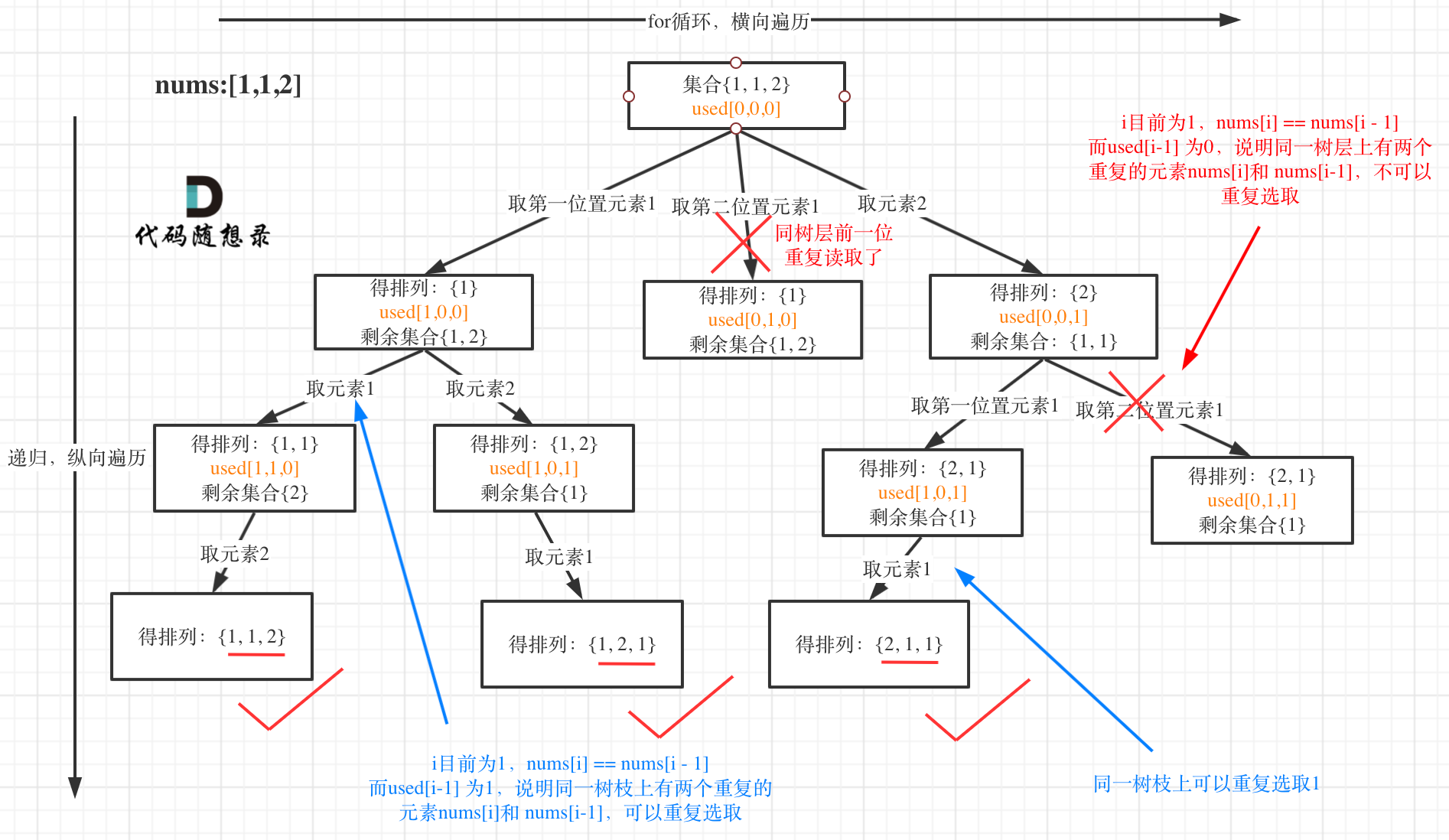
+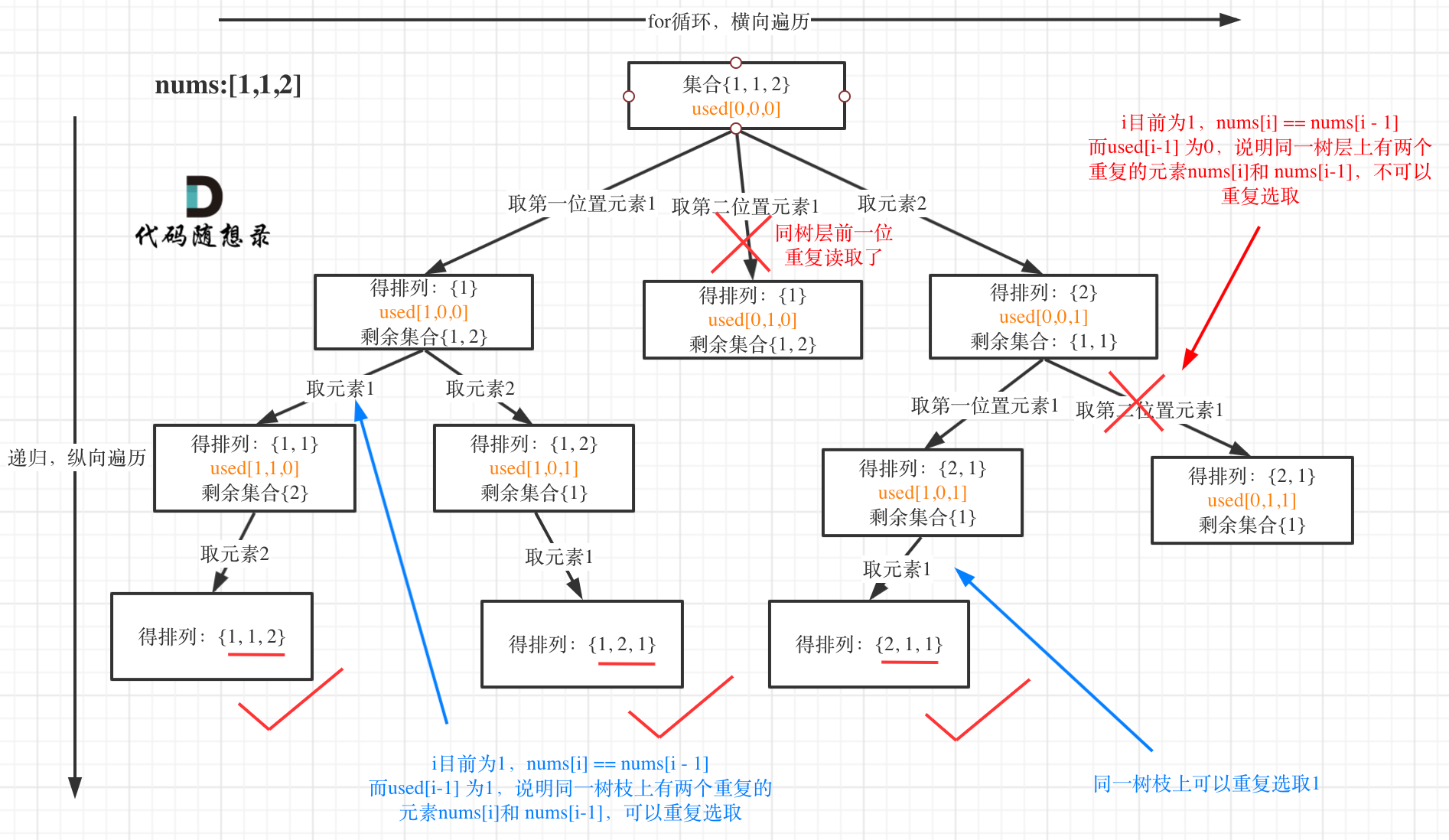
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
**一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果**。
-在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详解讲解了排列问题的写法,在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解的去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
+在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详细讲解了排列问题的写法,在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解了去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
+
-## C++代码
```CPP
class Solution {
@@ -91,7 +96,11 @@ public:
}
};
+// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案,我们需要 O(n) 去复制最终放到 result 数组
+// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素
```
+* 时间复杂度: O(n! * n)
+* 空间复杂度: O(n)
## 拓展
@@ -121,23 +130,26 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
树层上去重(used[i - 1] == false),的树形结构如下:
-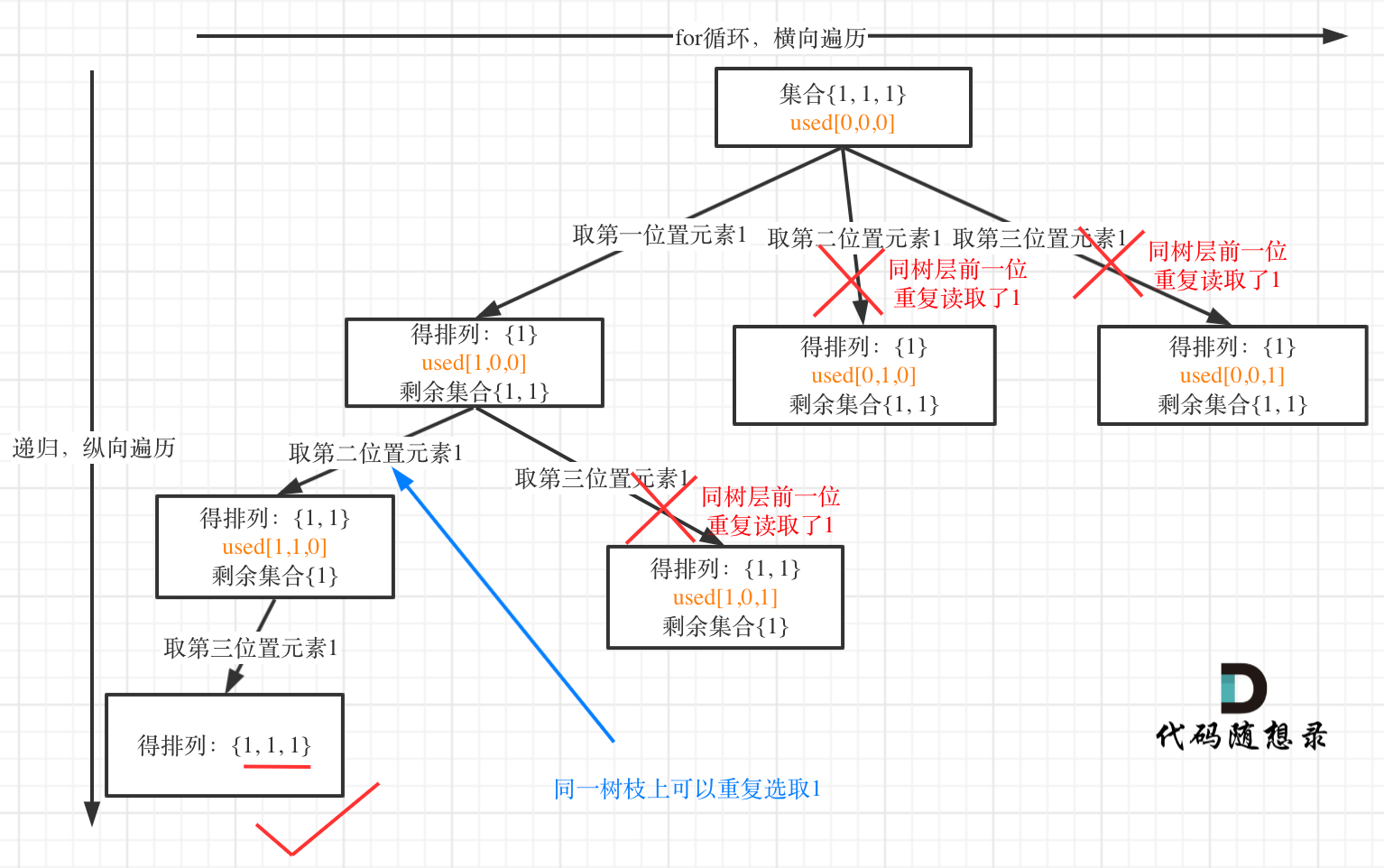
+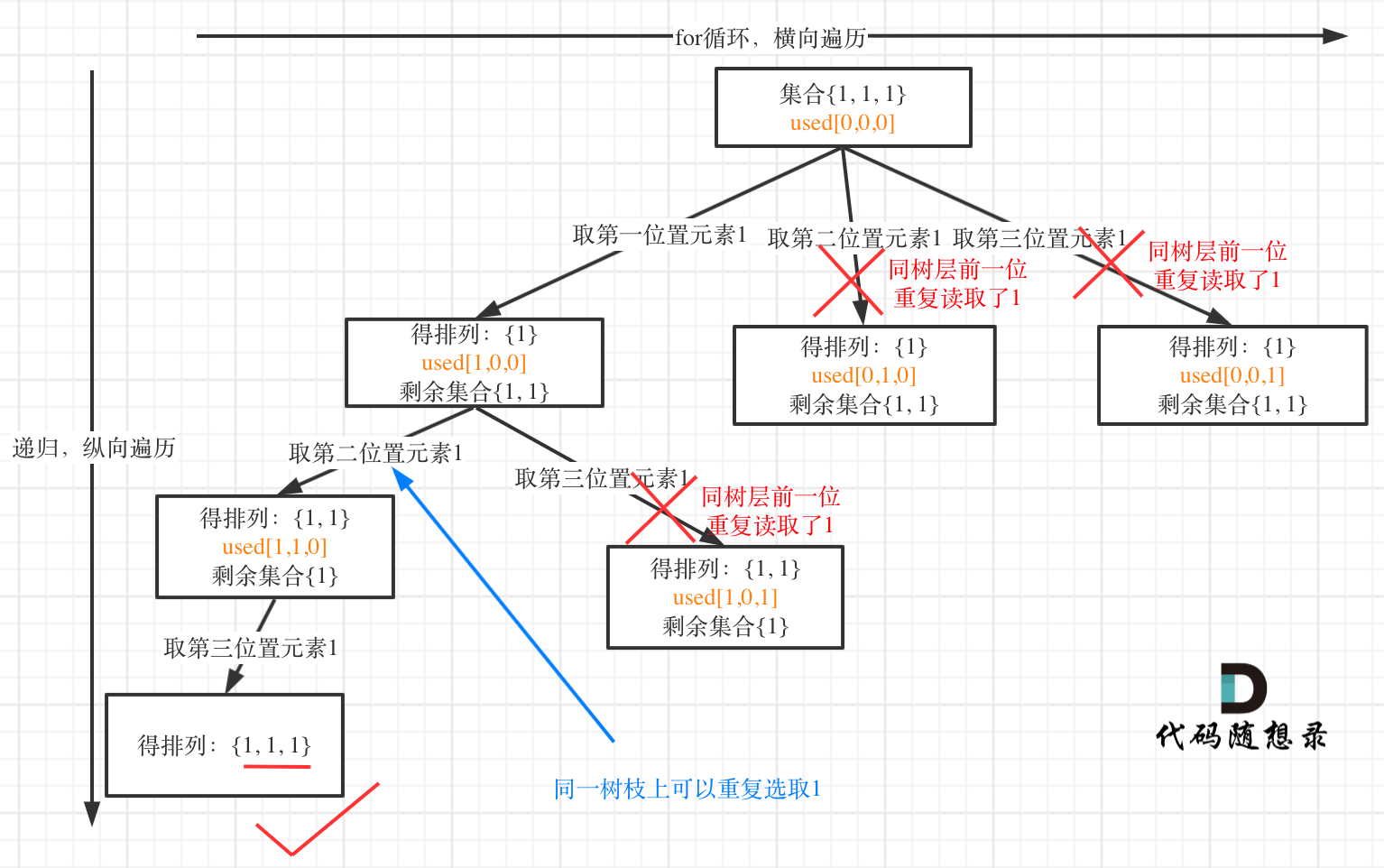
树枝上去重(used[i - 1] == true)的树型结构如下:
-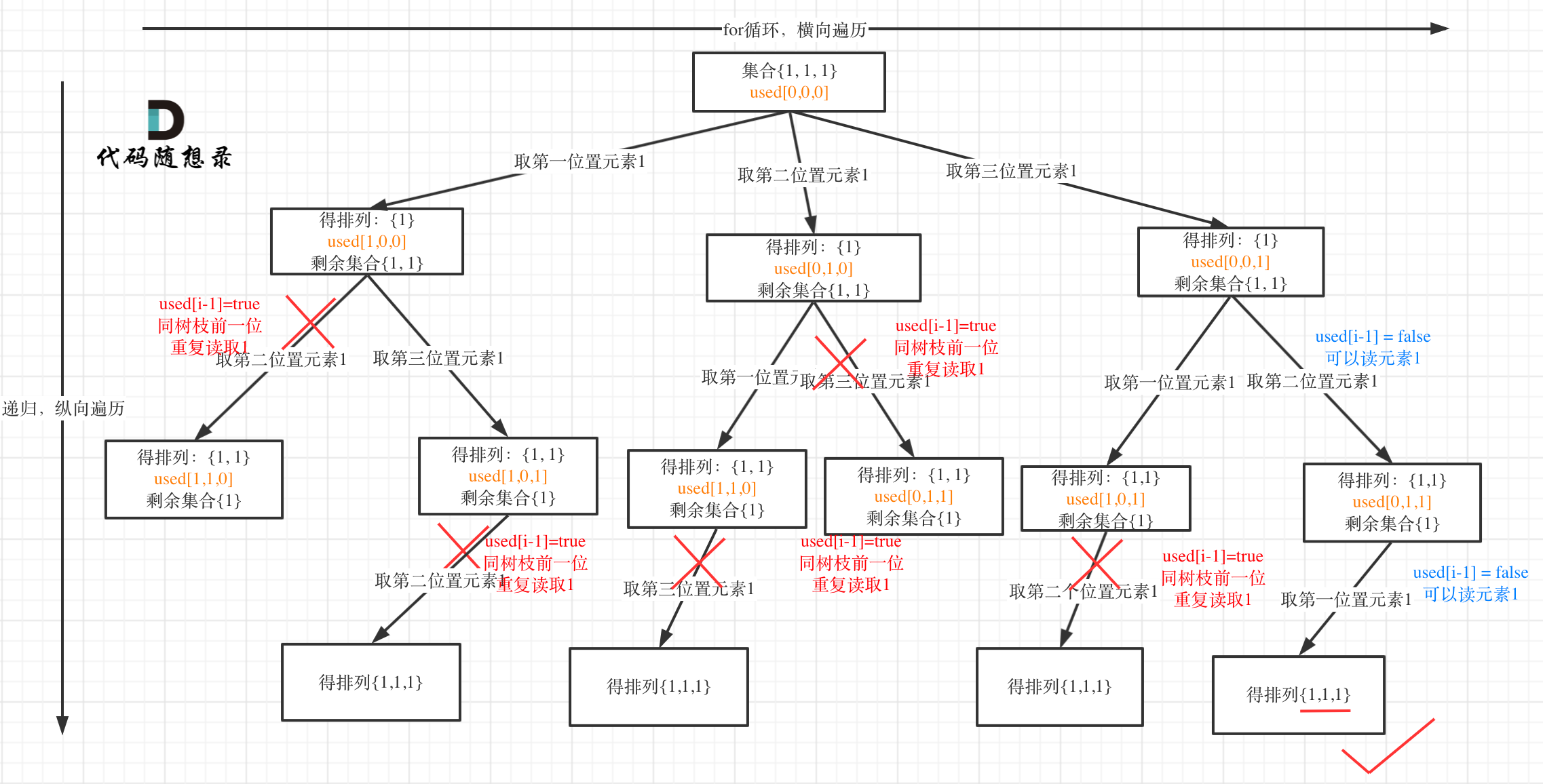
+
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
## 总结
这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
+
```cpp
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
```
+
和这么写:
+
```cpp
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
continue;
@@ -148,11 +160,24 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
+这里可能大家又有疑惑,既然 `used[i - 1] == false`也行而`used[i - 1] == true`也行,那为什么还要写这个条件呢?
+
+直接这样写 不就完事了?
+
+```cpp
+if (i > 0 && nums[i] == nums[i - 1]) {
+ continue;
+}
+```
+
+其实并不行,一定要加上 `used[i - 1] == false`或者`used[i - 1] == true`,因为 used[i - 1] 要一直是 true 或者一直是false 才可以,而不是 一会是true 一会又是false。 所以这个条件要写上。
+
+
是不是豁然开朗了!!
## 其他语言版本
-### java
+### Java
```java
class Solution {
@@ -194,71 +219,71 @@ class Solution {
}
```
-### python
+Python
```python
class Solution:
- def permuteUnique(self, nums: List[int]) -> List[List[int]]:
- # res用来存放结果
- if not nums: return []
- res = []
- used = [0] * len(nums)
- def backtracking(nums, used, path):
- # 终止条件
- if len(path) == len(nums):
- res.append(path.copy())
- return
- for i in range(len(nums)):
- if not used[i]:
- if i>0 and nums[i] == nums[i-1] and not used[i-1]:
- continue
- used[i] = 1
- path.append(nums[i])
- backtracking(nums, used, path)
- path.pop()
- used[i] = 0
- # 记得给nums排序
- backtracking(sorted(nums),used,[])
- return res
+ def permuteUnique(self, nums):
+ nums.sort() # 排序
+ result = []
+ self.backtracking(nums, [], [False] * len(nums), result)
+ return result
+
+ def backtracking(self, nums, path, used, result):
+ if len(path) == len(nums):
+ result.append(path[:])
+ return
+ for i in range(len(nums)):
+ if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
+ continue
+ used[i] = True
+ path.append(nums[i])
+ self.backtracking(nums, path, used, result)
+ path.pop()
+ used[i] = False
+
```
-### Go
+### Go
```go
-var res [][]int
-func permute(nums []int) [][]int {
- res = [][]int{}
- backTrack(nums,len(nums),[]int{})
- return res
+var (
+ res [][]int
+ path []int
+ st []bool // state的缩写
+)
+func permuteUnique(nums []int) [][]int {
+ res, path = make([][]int, 0), make([]int, 0, len(nums))
+ st = make([]bool, len(nums))
+ sort.Ints(nums)
+ dfs(nums, 0)
+ return res
}
-func backTrack(nums []int,numsLen int,path []int) {
- if len(nums)==0{
- p:=make([]int,len(path))
- copy(p,path)
- res = append(res,p)
- }
- used := [21]int{}//跟前一题唯一的区别,同一层不使用重复的数。关于used的思想carl在递增子序列那一题中提到过
- for i:=0;i {
return a - b
@@ -268,7 +293,7 @@ var permuteUnique = function (nums) {
function backtracing( used) {
if (path.length === nums.length) {
- result.push(path.slice())
+ result.push([...path])
return
}
for (let i = 0; i < nums.length; i++) {
@@ -292,6 +317,34 @@ var permuteUnique = function (nums) {
```
+### TypeScript
+
+```typescript
+function permuteUnique(nums: number[]): number[][] {
+ nums.sort((a, b) => a - b);
+ const resArr: number[][] = [];
+ const usedArr: boolean[] = new Array(nums.length).fill(false);
+ backTracking(nums, []);
+ return resArr;
+ function backTracking(nums: number[], route: number[]): void {
+ if (route.length === nums.length) {
+ resArr.push([...route]);
+ return;
+ }
+ for (let i = 0, length = nums.length; i < length; i++) {
+ if (i > 0 && nums[i] === nums[i - 1] && usedArr[i - 1] === false) continue;
+ if (usedArr[i] === false) {
+ route.push(nums[i]);
+ usedArr[i] = true;
+ backTracking(nums, route);
+ usedArr[i] = false;
+ route.pop();
+ }
+ }
+ }
+};
+```
+
### Swift
```swift
@@ -323,7 +376,42 @@ func permuteUnique(_ nums: [Int]) -> [[Int]] {
}
```
+### Rust
+
+```Rust
+impl Solution {
+ fn backtracking(result: &mut Vec>, path: &mut Vec, nums: &Vec, used: &mut Vec) {
+ let len = nums.len();
+ if path.len() == len {
+ result.push(path.clone());
+ return;
+ }
+ for i in 0..len {
+ if i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false { continue; }
+ if used[i] == false {
+ used[i] = true;
+ path.push(nums[i]);
+ Self::backtracking(result, path, nums, used);
+ path.pop();
+ used[i] = false;
+ }
+ }
+ }
+
+ pub fn permute_unique(nums: Vec) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut path: Vec = Vec::new();
+ let mut used = vec![false; nums.len()];
+ let mut nums= nums;
+ nums.sort();
+ Self::backtracking(&mut result, &mut path, &nums, &mut used);
+ result
+ }
+}
+```
+
### C
+
```c
//临时数组
int *path;
@@ -394,5 +482,74 @@ int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumn
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-# 第51题. N皇后
+# 51. N皇后
-[力扣题目链接](https://leetcode-cn.com/problems/n-queens/)
+[力扣题目链接](https://leetcode.cn/problems/n-queens/)
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
@@ -17,7 +15,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
示例 1:
-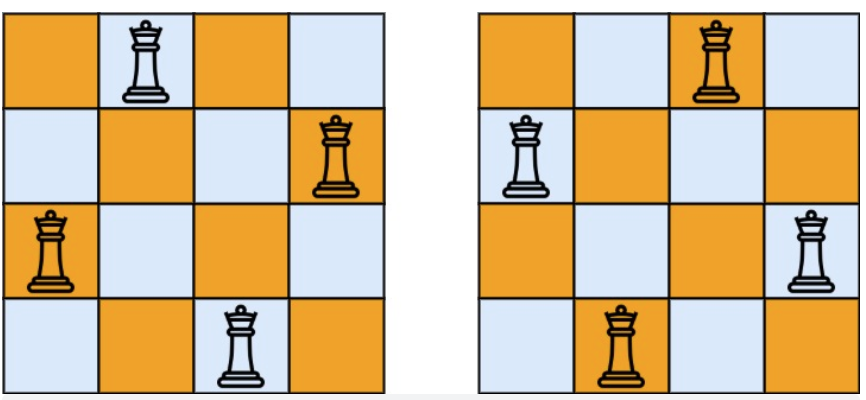
+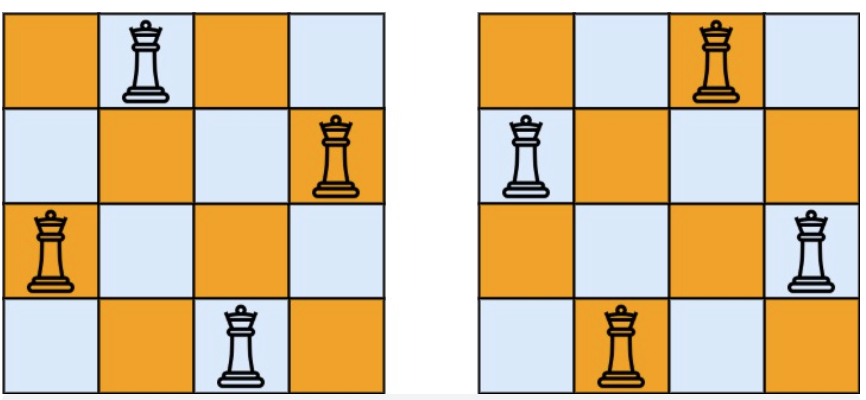
* 输入:n = 4
* 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
@@ -28,10 +26,12 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
* 输入:n = 1
* 输出:[["Q"]]
-## 思路
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[这就是传说中的N皇后? 回溯算法安排!| LeetCode:51.N皇后](https://www.bilibili.com/video/BV1Rd4y1c7Bq/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
-**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
+## 思路
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
@@ -45,7 +45,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
-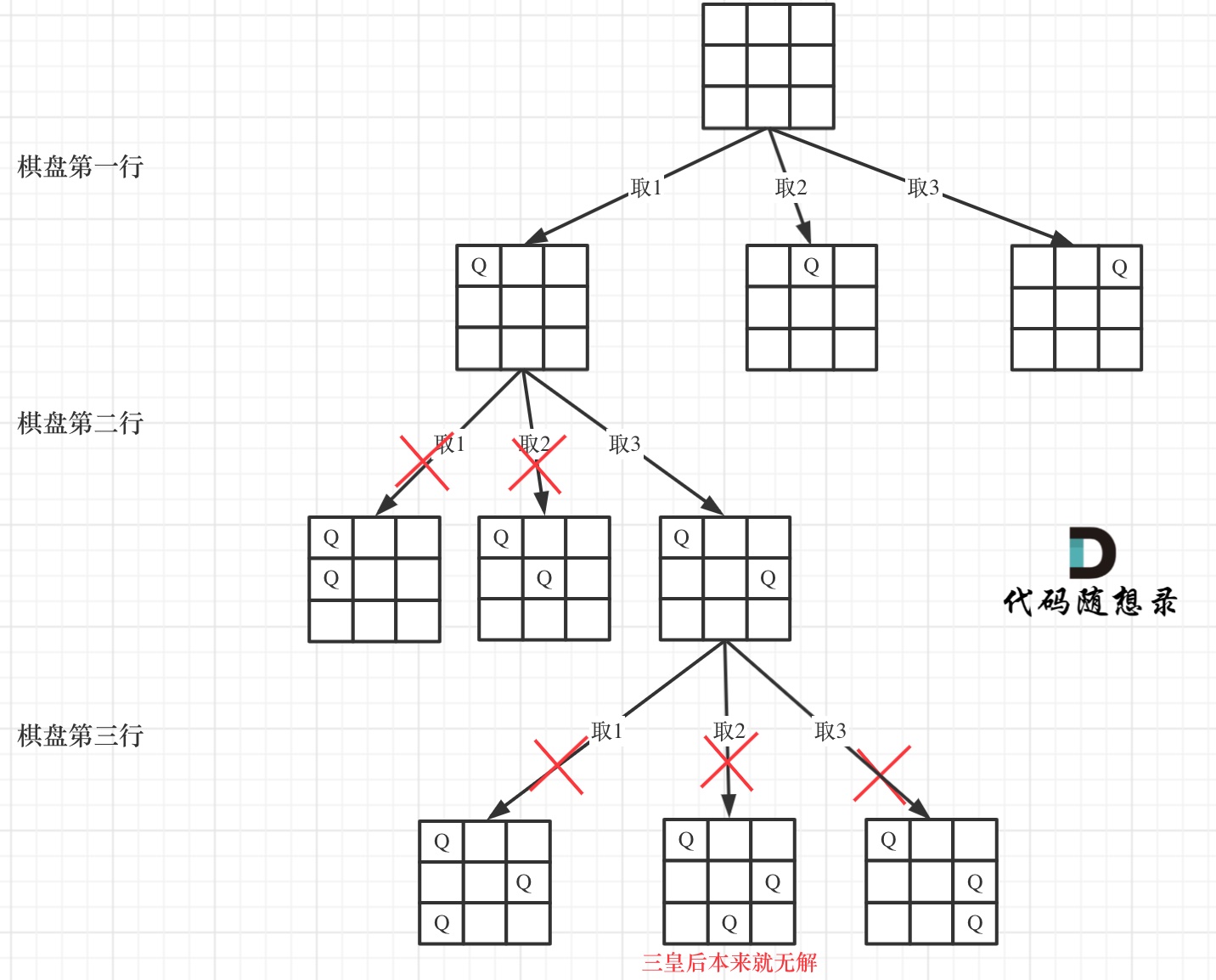
+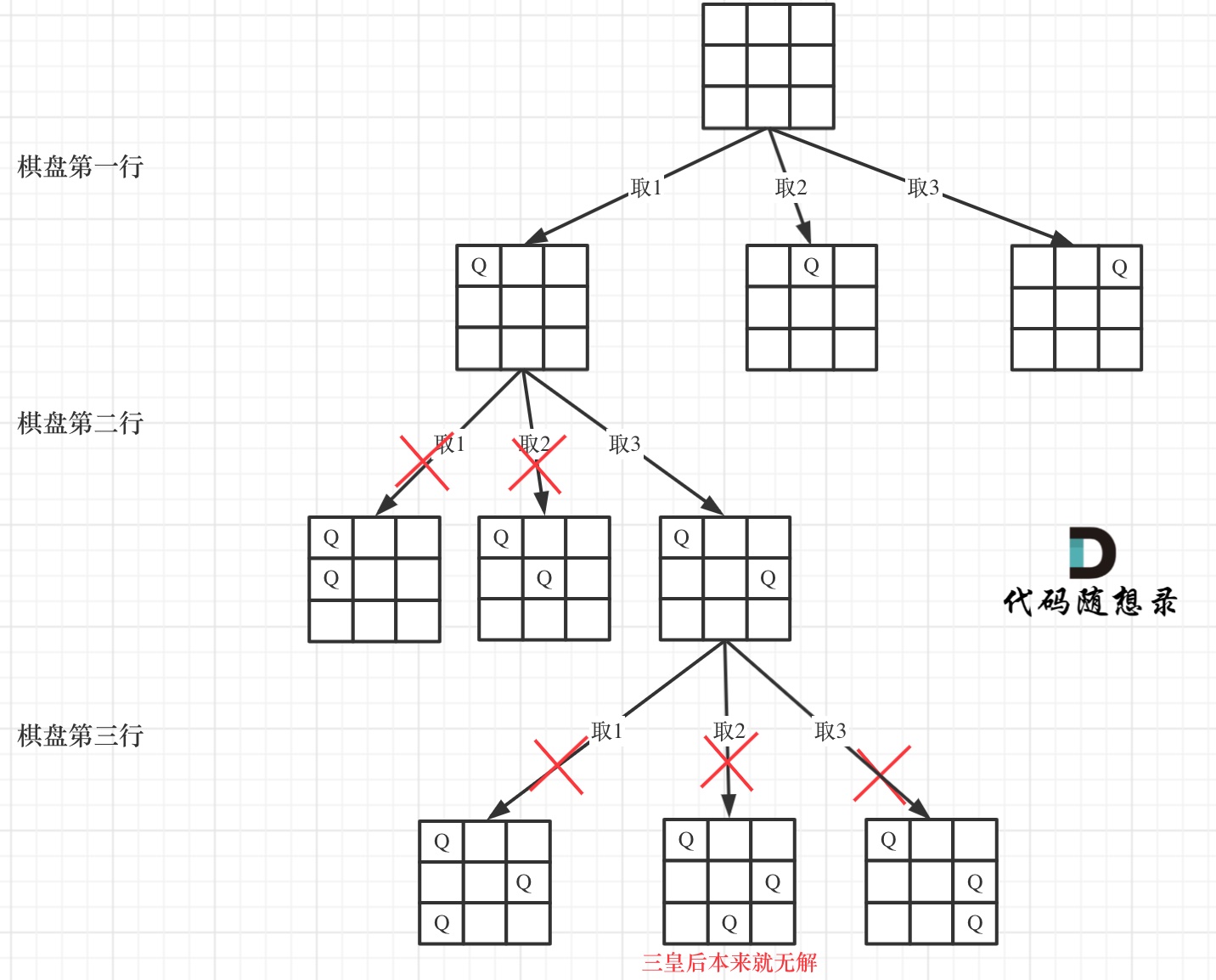
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
@@ -85,7 +85,7 @@ void backtracking(int n, int row, vector& chessboard) {
* 递归终止条件
在如下树形结构中:
-
+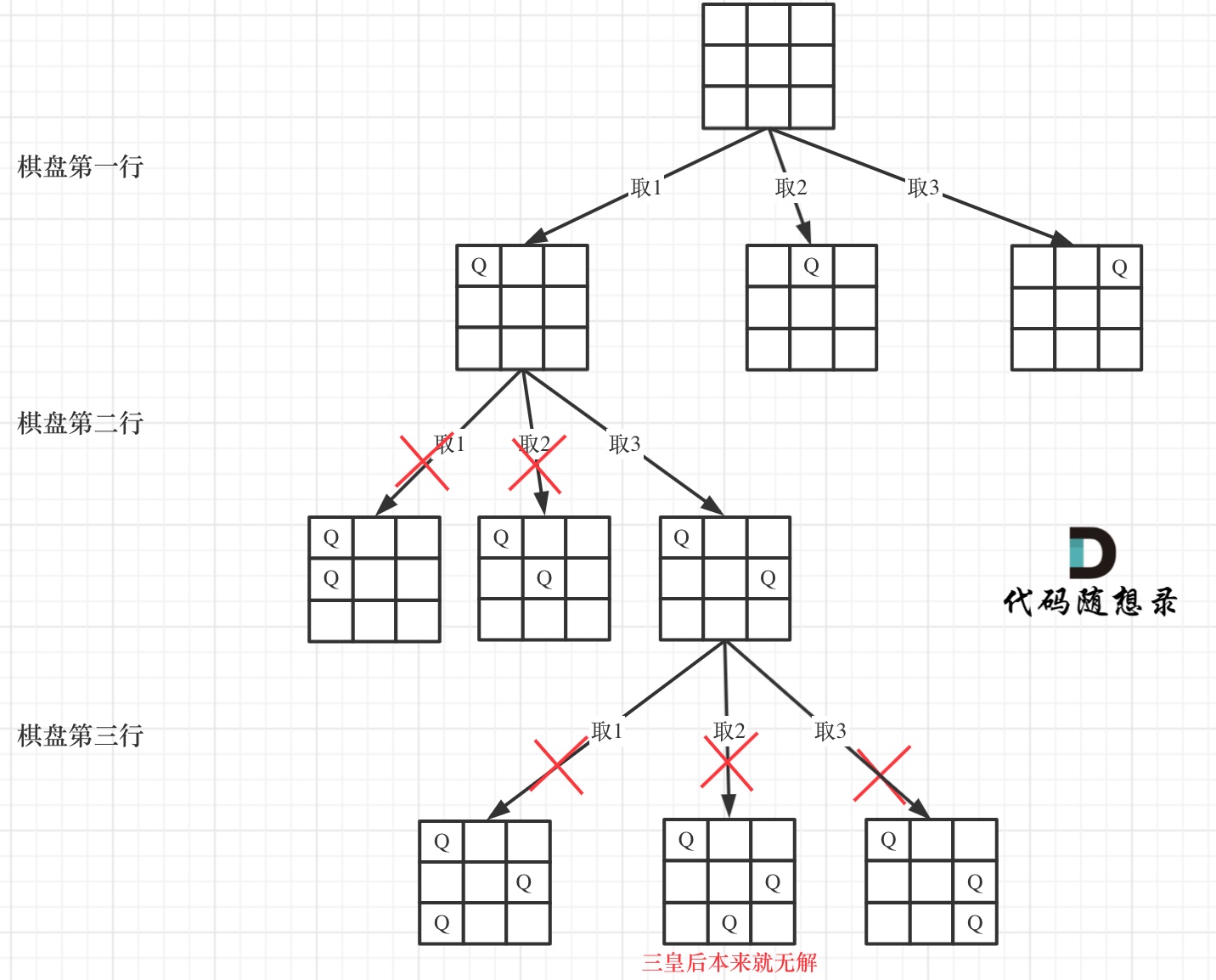
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
@@ -129,7 +129,6 @@ for (int col = 0; col < n; col++) {
```CPP
bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
@@ -178,7 +177,6 @@ void backtracking(int n, int row, vector& chessboard) {
}
}
bool isValid(int row, int col, vector& chessboard, int n) {
- int count = 0;
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
@@ -208,6 +206,9 @@ public:
}
};
```
+* 时间复杂度: O(n!)
+* 空间复杂度: O(n)
+
可以看出,除了验证棋盘合法性的代码,省下来部分就是按照回溯法模板来的。
@@ -224,56 +225,6 @@ public:
## 其他语言补充
-
-### Python
-
-```python
-class Solution:
- def solveNQueens(self, n: int) -> List[List[str]]:
- if not n: return []
- board = [['.'] * n for _ in range(n)]
- res = []
- def isVaild(board,row, col):
- #判断同一列是否冲突
- for i in range(len(board)):
- if board[i][col] == 'Q':
- return False
- # 判断左上角是否冲突
- i = row -1
- j = col -1
- while i>=0 and j>=0:
- if board[i][j] == 'Q':
- return False
- i -= 1
- j -= 1
- # 判断右上角是否冲突
- i = row - 1
- j = col + 1
- while i>=0 and j < len(board):
- if board[i][j] == 'Q':
- return False
- i -= 1
- j += 1
- return True
-
- def backtracking(board, row, n):
- # 如果走到最后一行,说明已经找到一个解
- if row == n:
- temp_res = []
- for temp in board:
- temp_str = "".join(temp)
- temp_res.append(temp_str)
- res.append(temp_res)
- for col in range(n):
- if not isVaild(board, row, col):
- continue
- board[row][col] = 'Q'
- backtracking(board, row+1, n)
- board[row][col] = '.'
- backtracking(board, 0, n)
- return res
-```
-
### Java
```java
@@ -343,6 +294,104 @@ class Solution {
}
```
+```java
+// 方法2:使用boolean数组表示已经占用的直(斜)线
+class Solution {
+ List> res = new ArrayList<>();
+ boolean[] usedCol, usedDiag45, usedDiag135; // boolean数组中的每个元素代表一条直(斜)线
+ public List> solveNQueens(int n) {
+ usedCol = new boolean[n]; // 列方向的直线条数为 n
+ usedDiag45 = new boolean[2 * n - 1]; // 45°方向的斜线条数为 2 * n - 1
+ usedDiag135 = new boolean[2 * n - 1]; // 135°方向的斜线条数为 2 * n - 1
+ //用于收集结果, 元素的index表示棋盘的row,元素的value代表棋盘的column
+ int[] board = new int[n];
+ backTracking(board, n, 0);
+ return res;
+ }
+ private void backTracking(int[] board, int n, int row) {
+ if (row == n) {
+ //收集结果
+ List temp = new ArrayList<>();
+ for (int i : board) {
+ char[] str = new char[n];
+ Arrays.fill(str, '.');
+ str[i] = 'Q';
+ temp.add(new String(str));
+ }
+ res.add(temp);
+ return;
+ }
+
+ for (int col = 0; col < n; col++) {
+ if (usedCol[col] | usedDiag45[row + col] | usedDiag135[row - col + n - 1]) {
+ continue;
+ }
+ board[row] = col;
+ // 标记该列出现过
+ usedCol[col] = true;
+ // 同一45°斜线上元素的row + col为定值, 且各不相同
+ usedDiag45[row + col] = true;
+ // 同一135°斜线上元素row - col为定值, 且各不相同
+ // row - col 值有正有负, 加 n - 1 是为了对齐零点
+ usedDiag135[row - col + n - 1] = true;
+ // 递归
+ backTracking(board, n, row + 1);
+ usedCol[col] = false;
+ usedDiag45[row + col] = false;
+ usedDiag135[row - col + n - 1] = false;
+ }
+ }
+}
+```
+
+### Python
+
+```python
+class Solution:
+ def solveNQueens(self, n: int) -> List[List[str]]:
+ result = [] # 存储最终结果的二维字符串数组
+
+ chessboard = ['.' * n for _ in range(n)] # 初始化棋盘
+ self.backtracking(n, 0, chessboard, result) # 回溯求解
+ return [[''.join(row) for row in solution] for solution in result] # 返回结果集
+
+ def backtracking(self, n: int, row: int, chessboard: List[str], result: List[List[str]]) -> None:
+ if row == n:
+ result.append(chessboard[:]) # 棋盘填满,将当前解加入结果集
+ return
+
+ for col in range(n):
+ if self.isValid(row, col, chessboard):
+ chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col+1:] # 放置皇后
+ self.backtracking(n, row + 1, chessboard, result) # 递归到下一行
+ chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col+1:] # 回溯,撤销当前位置的皇后
+
+ def isValid(self, row: int, col: int, chessboard: List[str]) -> bool:
+ # 检查列
+ for i in range(row):
+ if chessboard[i][col] == 'Q':
+ return False # 当前列已经存在皇后,不合法
+
+ # 检查 45 度角是否有皇后
+ i, j = row - 1, col - 1
+ while i >= 0 and j >= 0:
+ if chessboard[i][j] == 'Q':
+ return False # 左上方向已经存在皇后,不合法
+ i -= 1
+ j -= 1
+
+ # 检查 135 度角是否有皇后
+ i, j = row - 1, col + 1
+ while i >= 0 and j < len(chessboard):
+ if chessboard[i][j] == 'Q':
+ return False # 右上方向已经存在皇后,不合法
+ i -= 1
+ j += 1
+
+ return True # 当前位置合法
+
+```
+
### Go
```Go
@@ -398,63 +447,123 @@ func isValid(n, row, col int, chessboard [][]string) bool {
return true
}
```
-### Javascript
-```Javascript
-var solveNQueens = function(n) {
- function isValid(row, col, chessBoard, n) {
-
- for(let i = 0; i < row; i++) {
- if(chessBoard[i][col] === 'Q') {
- return false
- }
- }
-
- for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
- if(chessBoard[i][j] === 'Q') {
- return false
- }
- }
-
- for(let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
- if(chessBoard[i][j] === 'Q') {
- return false
- }
- }
- return true
- }
- function transformChessBoard(chessBoard) {
- let chessBoardBack = []
- chessBoard.forEach(row => {
- let rowStr = ''
- row.forEach(value => {
- rowStr += value
- })
- chessBoardBack.push(rowStr)
- })
- return chessBoardBack
- }
+### JavaScript
+```Javascript
+/**
+ * @param {number} n
+ * @return {string[][]}
+ */
+var solveNQueens = function (n) {
+ const ans = [];
+ const path = [];
+ const matrix = new Array(n).fill(0).map(() => new Array(n).fill("."));
+ // 判断是否能相互攻击
+ const canAttack = (matrix, row, col) => {
+ let i;
+ let j;
+ // 判断正上方和正下方是否有皇后
+ for (i = 0, j = col; i < n; i++) {
+ if (matrix[i][j] === "Q") {
+ return true;
+ }
+ }
+ // 判断正左边和正右边是否有皇后
+ for (i = row, j = 0; j < n; j++) {
+ if (matrix[i][j] === "Q") {
+ return true;
+ }
+ }
+ // 判断左上方是否有皇后
+ for (i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
+ if (matrix[i][j] === "Q") {
+ return true;
+ }
+ }
+ // 判断右上方是否有皇后
+ for (i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
+ if (matrix[i][j] === "Q") {
+ return true;
+ }
+ }
+ return false;
+ };
+ const backtrack = (matrix, row, col) => {
+ if (path.length === matrix.length) {
+ ans.push(path.slice());
+ return;
+ }
+ for (let i = row; i < matrix.length; i++) {
+ for (let j = col; j < matrix.length; j++) {
+ // 当前位置会导致互相攻击 继续下一轮搜索
+ if (canAttack(matrix, i, j)) {
+ continue;
+ }
+ matrix[i][j] = "Q";
+ path.push(matrix[i].join(""));
+ // 另起一行搜索 同一行只能有一个皇后
+ backtrack(matrix, i + 1, 0);
+ matrix[i][j] = ".";
+ path.pop();
+ }
+ }
+ };
+ backtrack(matrix, 0, 0);
+ return ans;
+};
+```
- let result = []
- function backtracing(row,chessBoard) {
- if(row === n) {
- result.push(transformChessBoard(chessBoard))
- return
+### TypeScript
+
+```typescript
+function solveNQueens(n: number): string[][] {
+ const board: string[][] = new Array(n).fill(0).map(_ => new Array(n).fill('.'));
+ const resArr: string[][] = [];
+ backTracking(n, 0, board);
+ return resArr;
+ function backTracking(n: number, rowNum: number, board: string[][]): void {
+ if (rowNum === n) {
+ resArr.push(transformBoard(board));
+ return;
}
- for(let col = 0; col < n; col++) {
- if(isValid(row, col, chessBoard, n)) {
- chessBoard[row][col] = 'Q'
- backtracing(row + 1,chessBoard)
- chessBoard[row][col] = '.'
+ for (let i = 0; i < n; i++) {
+ if (isValid(i, rowNum, board) === true) {
+ board[rowNum][i] = 'Q';
+ backTracking(n, rowNum + 1, board);
+ board[rowNum][i] = '.';
}
}
}
- let chessBoard = new Array(n).fill([]).map(() => new Array(n).fill('.'))
- backtracing(0,chessBoard)
- return result
-
};
+function isValid(col: number, row: number, board: string[][]): boolean {
+ const n: number = board.length;
+ if (col < 0 || col >= n || row < 0 || row >= n) return false;
+ // 检查列
+ for (let row of board) {
+ if (row[col] === 'Q') return false;
+ }
+ // 检查45度方向
+ let x: number = col,
+ y: number = row;
+ while (y >= 0 && x < n) {
+ if (board[y--][x++] === 'Q') return false;
+ }
+ // 检查135度方向
+ x = col;
+ y = row;
+ while (x >= 0 && y >= 0) {
+ if (board[y--][x--] === 'Q') return false;
+ }
+ return true;
+}
+function transformBoard(board: string[][]): string[] {
+ const resArr = [];
+ for (let row of board) {
+ resArr.push(row.join(''));
+ }
+ return resArr;
+}
```
### Swift
@@ -508,6 +617,56 @@ func solveNQueens(_ n: Int) -> [[String]] {
}
```
+### Rust
+
+```Rust
+impl Solution {
+ fn is_valid(row: usize, col: usize, chessboard: &mut Vec>, n: usize) -> bool {
+ let mut i = 0 as usize;
+ while i < row {
+ if chessboard[i][col] == 'Q' { return false; }
+ i += 1;
+ }
+ let (mut i, mut j) = (row as i32 - 1, col as i32 - 1);
+ while i >= 0 && j >= 0 {
+ if chessboard[i as usize][j as usize] == 'Q' { return false; }
+ i -= 1;
+ j -= 1;
+ }
+ let (mut i, mut j) = (row as i32 - 1, col as i32 + 1);
+ while i >= 0 && j < n as i32 {
+ if chessboard[i as usize][j as usize] == 'Q' { return false; }
+ i -= 1;
+ j += 1;
+ }
+ return true;
+ }
+ fn backtracking(result: &mut Vec>, n: usize, row: usize, chessboard: &mut Vec>) {
+ if row == n {
+ let mut chessboard_clone: Vec = Vec::new();
+ for i in chessboard {
+ chessboard_clone.push(i.iter().collect::());
+ }
+ result.push(chessboard_clone);
+ return;
+ }
+ for col in 0..n {
+ if Self::is_valid(row, col, chessboard, n) {
+ chessboard[row][col] = 'Q';
+ Self::backtracking(result, n, row + 1, chessboard);
+ chessboard[row][col] = '.';
+ }
+ }
+ }
+ pub fn solve_n_queens(n: i32) -> Vec> {
+ let mut result: Vec> = Vec::new();
+ let mut chessboard: Vec> = vec![vec!['.'; n as usize]; n as usize];
+ Self::backtracking(&mut result, n as usize, 0, &mut chessboard);
+ result
+ }
+}
+```
+
### C
```c
char ***ans;
@@ -633,5 +792,130 @@ char *** solveNQueens(int n, int* returnSize, int** returnColumnSizes){
}
```
------------------------
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 52. N皇后II
-题目链接:https://leetcode-cn.com/problems/n-queens-ii/
+题目链接:[https://leetcode.cn/problems/n-queens-ii/](https://leetcode.cn/problems/n-queens-ii/)
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
-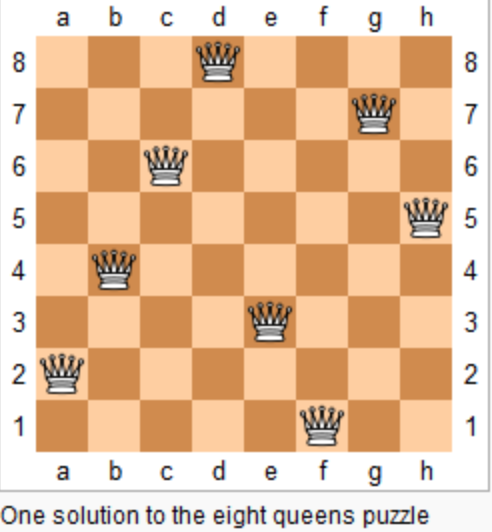
+
+
+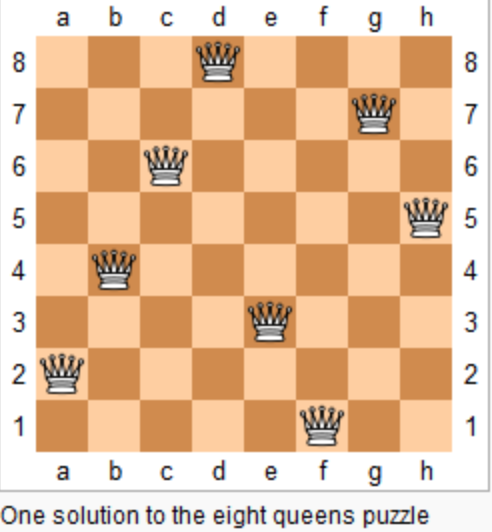
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
@@ -41,12 +41,10 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并
".Q.."]
]
-# 思路
-
+## 思路
-想看:[51.N皇后](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg) ,基本没有区别
-# C++代码
+详看:[51.N皇后](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg) ,基本没有区别
```CPP
class Solution {
@@ -98,8 +96,9 @@ public:
};
```
-# 其他语言补充
-JavaScript
+## 其他语言补充
+### JavaScript
+
```javascript
var totalNQueens = function(n) {
let count = 0;
@@ -144,7 +143,61 @@ var totalNQueens = function(n) {
};
```
-C
+### TypeScript
+
+```typescript
+// 0-该格为空,1-该格有皇后
+type GridStatus = 0 | 1;
+function totalNQueens(n: number): number {
+ let resCount: number = 0;
+ const chess: GridStatus[][] = new Array(n).fill(0)
+ .map(_ => new Array(n).fill(0));
+ backTracking(chess, n, 0);
+ return resCount;
+ function backTracking(chess: GridStatus[][], n: number, startRowIndex: number): void {
+ if (startRowIndex === n) {
+ resCount++;
+ return;
+ }
+ for (let j = 0; j < n; j++) {
+ if (checkValid(chess, startRowIndex, j, n) === true) {
+ chess[startRowIndex][j] = 1;
+ backTracking(chess, n, startRowIndex + 1);
+ chess[startRowIndex][j] = 0;
+ }
+ }
+ }
+};
+function checkValid(chess: GridStatus[][], i: number, j: number, n: number): boolean {
+ // 向上纵向检查
+ let tempI: number = i - 1,
+ tempJ: number = j;
+ while (tempI >= 0) {
+ if (chess[tempI][tempJ] === 1) return false;
+ tempI--;
+ }
+ // 斜向左上检查
+ tempI = i - 1;
+ tempJ = j - 1;
+ while (tempI >= 0 && tempJ >= 0) {
+ if (chess[tempI][tempJ] === 1) return false;
+ tempI--;
+ tempJ--;
+ }
+ // 斜向右上检查
+ tempI = i - 1;
+ tempJ = j + 1;
+ while (tempI >= 0 && tempJ < n) {
+ if (chess[tempI][tempJ] === 1) return false;
+ tempI--;
+ tempJ++;
+ }
+ return true;
+}
+```
+
+### C
+
```c
//path[i]为在i行,path[i]列上存在皇后
int *path;
@@ -202,6 +255,53 @@ int totalNQueens(int n){
return answer;
}
```
+### Java
+
+```java
+class Solution {
+ int count = 0;
+ public int totalNQueens(int n) {
+ char[][] board = new char[n][n];
+ for (char[] chars : board) {
+ Arrays.fill(chars, '.');
+ }
+ backTrack(n, 0, board);
+ return count;
+ }
+ private void backTrack(int n, int row, char[][] board) {
+ if (row == n) {
+ count++;
+ return;
+ }
+ for (int col = 0; col < n; col++) {
+ if (isValid(row, col, n, board)) {
+ board[row][col] = 'Q';
+ backTrack(n, row + 1, board);
+ board[row][col] = '.';
+ }
+ }
+ }
+ private boolean isValid(int row, int col, int n, char[][] board) {
+ // 检查列
+ for (int i = 0; i < row; ++i) {
+ if (board[i][col] == 'Q') {
+ return false;
+ }
+ }
+ // 检查45度对角线
+ for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
+ if (board[i][j] == 'Q') {
+ return false;
+ }
+ }
+ // 检查135度对角线
+ for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) {
+ if (board[i][j] == 'Q') {
+ return false;
+ }
+ }
+ return true;
+ }
+}
+```
------------------------
-
diff --git "a/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214.md" "b/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214.md"
old mode 100644
new mode 100755
index 3d11c91efb..84bb5f6663
--- "a/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214.md"
+++ "b/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214.md"
@@ -1,28 +1,29 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
-
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 53. 最大子序和
-[力扣题目链接](https://leetcode-cn.com/problems/maximum-subarray/)
+[力扣题目链接](https://leetcode.cn/problems/maximum-subarray/)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
+- 输入: [-2,1,-3,4,-1,2,1,-5,4]
+- 输出: 6
+- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
-## 暴力解法
+## 算法公开课
-暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法的巧妙需要慢慢体会!LeetCode:53. 最大子序和](https://www.bilibili.com/video/BV1aY4y1Z7ya),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
+
+## 思路
+
+### 暴力解法
+
+暴力解法的思路,第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值
-* 时间复杂度:O(n^2)
-* 空间复杂度:O(1)
```CPP
class Solution {
@@ -41,14 +42,17 @@ public:
}
};
```
+* 时间复杂度:O(n^2)
+* 空间复杂度:O(1)
+
-以上暴力的解法C++勉强可以过,其他语言就不确定了。
+以上暴力的解法 C++勉强可以过,其他语言就不确定了。
-## 贪心解法
+### 贪心解法
**贪心贪的是哪里呢?**
-如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
+如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
@@ -56,29 +60,27 @@ public:
**局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。
-
-从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
+从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
**这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。
-
**那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?**
-区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
+区间的终止位置,其实就是如果 count 取到最大值了,及时记录下来了。例如如下代码:
```
if (count > result) result = count;
```
-**这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。
+**这样相当于是用 result 记录最大子序和区间和(变相的算是调整了终止位置)**。
如动画所示:
-
+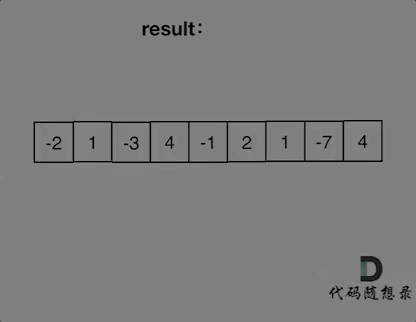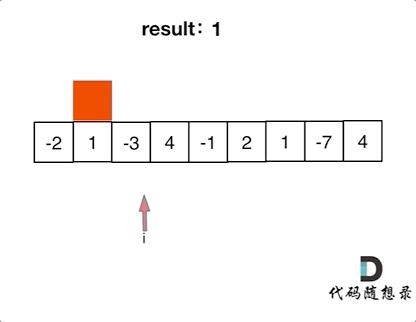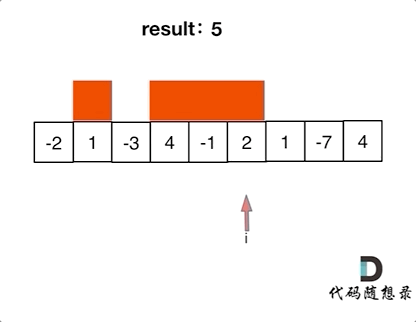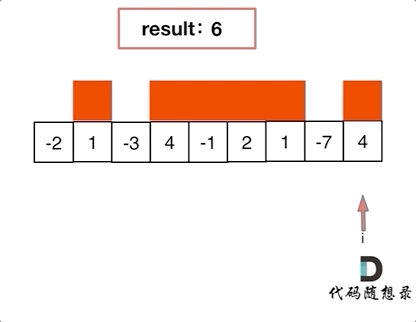
-红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
+红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计。
-那么不难写出如下C++代码(关键地方已经注释)
+那么不难写出如下 C++代码(关键地方已经注释)
```CPP
class Solution {
@@ -97,19 +99,34 @@ public:
}
};
```
-
-* 时间复杂度:O(n)
-* 空间复杂度:O(1)
+- 时间复杂度:O(n)
+- 空间复杂度:O(1)
当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
-不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
+### 常见误区
-## 动态规划
+误区一:
-当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。
+不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是 0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
-那么先给出我的dp代码如下,有时间的录友可以提前做一做:
+误区二:
+
+大家在使用贪心算法求解本题,经常陷入的误区,就是分不清,是遇到 负数就选择起始位置,还是连续和为负选择起始位置。
+
+在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
+
+因为和为 3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
+
+这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
+
+其实并不会,因为还有一个变量 result 一直在更新 最大的连续和,只要有更大的连续和出现,result 就更新了,那么 result 已经把 4 更新了,后面 连续和变成 3,也不会对最后结果有影响。
+
+### 动态规划
+
+当然本题还可以用动态规划来做,在代码随想录动态规划章节我会详细介绍,如果大家想在想看,可以直接跳转:[动态规划版本详解](https://programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html#%E6%80%9D%E8%B7%AF)
+
+那么先给出我的 dp 代码如下,有时间的录友可以提前做一做:
```CPP
class Solution {
@@ -128,19 +145,19 @@ public:
};
```
-* 时间复杂度:O(n)
-* 空间复杂度:O(n)
+- 时间复杂度:O(n)
+- 空间复杂度:O(n)
## 总结
本题的贪心思路其实并不好想,这也进一步验证了,别看贪心理论很直白,有时候看似是常识,但贪心的题目一点都不简单!
-后续将介绍的贪心题目都挺难的,哈哈,所以贪心很有意思,别小看贪心!
+后续将介绍的贪心题目都挺难的,所以贪心很有意思,别小看贪心!
## 其他语言版本
+### Java
-### Java
```java
class Solution {
public int maxSubArray(int[] nums) {
@@ -180,23 +197,103 @@ class Solution {
}
```
-### Python
+### Python
+暴力法
```python
class Solution:
- def maxSubArray(self, nums: List[int]) -> int:
- result = -float('inf')
+ def maxSubArray(self, nums):
+ result = float('-inf') # 初始化结果为负无穷大
+ count = 0
+ for i in range(len(nums)): # 设置起始位置
+ count = 0
+ for j in range(i, len(nums)): # 从起始位置i开始遍历寻找最大值
+ count += nums[j]
+ result = max(count, result) # 更新最大值
+ return result
+
+```
+贪心法
+```python
+class Solution:
+ def maxSubArray(self, nums):
+ result = float('-inf') # 初始化结果为负无穷大
count = 0
for i in range(len(nums)):
count += nums[i]
- if count > result:
+ if count > result: # 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count
- if count <= 0:
+ if count <= 0: # 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
count = 0
return result
```
+动态规划
+```python
+class Solution:
+ def maxSubArray(self, nums: List[int]) -> int:
+ dp = [0] * len(nums)
+ dp[0] = nums[0]
+ res = nums[0]
+ for i in range(1, len(nums)):
+ dp[i] = max(dp[i-1] + nums[i], nums[i])
+ res = max(res, dp[i])
+ return res
+```
+
+动态规划
-### Go
+```python
+class Solution:
+ def maxSubArray(self, nums):
+ if not nums:
+ return 0
+ dp = [0] * len(nums) # dp[i]表示包括i之前的最大连续子序列和
+ dp[0] = nums[0]
+ result = dp[0]
+ for i in range(1, len(nums)):
+ dp[i] = max(dp[i-1]+nums[i], nums[i]) # 状态转移公式
+ if dp[i] > result:
+ result = dp[i] # result 保存dp[i]的最大值
+ return result
+```
+动态规划优化
+
+```python
+class Solution:
+ def maxSubArray(self, nums: List[int]) -> int:
+ max_sum = float("-inf") # 初始化结果为负无穷大,方便比较取最大值
+ current_sum = 0 # 初始化当前连续和
+
+ for num in nums:
+
+ # 更新当前连续和
+ # 如果原本的连续和加上当前数字之后没有当前数字大,说明原本的连续和是负数,那么就直接从当前数字开始重新计算连续和
+ current_sum = max(current_sum+num, num)
+ max_sum = max(max_sum, current_sum) # 更新结果
+
+ return max_sum
+```
+
+### Go
+贪心法
+```go
+func maxSubArray(nums []int) int {
+ max := nums[0]
+ count := 0
+
+ for i := 0; i < len(nums); i++{
+ count += nums[i]
+ if count > max{
+ max = count
+ }
+ if count < 0 {
+ count = 0
+ }
+ }
+ return max
+}
+```
+动态规划
```go
func maxSubArray(nums []int) int {
maxSum := nums[0]
@@ -211,8 +308,24 @@ func maxSubArray(nums []int) int {
return maxSum
}
```
-
-### Javascript:
+
+### Rust
+
+```rust
+pub fn max_sub_array(nums: Vec) -> i32 {
+ let mut max_sum = i32::MIN;
+ let mut curr = 0;
+ for n in nums.iter() {
+ curr += n;
+ max_sum = max_sum.max(curr);
+ curr = curr.max(0);
+ }
+ max_sum
+}
+```
+
+### JavaScript:
+
```Javascript
var maxSubArray = function(nums) {
let result = -Infinity
@@ -230,7 +343,150 @@ var maxSubArray = function(nums) {
};
```
+### C:
+
+贪心:
+
+```c
+int maxSubArray(int* nums, int numsSize){
+ int maxVal = INT_MIN;
+ int subArrSum = 0;
+
+ int i;
+ for(i = 0; i < numsSize; ++i) {
+ subArrSum += nums[i];
+ // 若当前局部和大于之前的最大结果,对结果进行更新
+ maxVal = subArrSum > maxVal ? subArrSum : maxVal;
+ // 若当前局部和为负,对结果无益。则从nums[i+1]开始应重新计算。
+ subArrSum = subArrSum < 0 ? 0 : subArrSum;
+ }
+
+ return maxVal;
+}
+```
+
+动态规划:
+
+```c
+/**
+ * 解题思路:动态规划:
+ * 1. dp数组:dp[i]表示从0到i的子序列中最大序列和的值
+ * 2. 递推公式:dp[i] = max(dp[i-1] + nums[i], nums[i])
+ 若dp[i-1]<0,对最后结果无益。dp[i]则为nums[i]。
+ * 3. dp数组初始化:dp[0]的最大子数组和为nums[0]
+ * 4. 推导顺序:从前往后遍历
+ */
+
+#define max(a, b) (((a) > (b)) ? (a) : (b))
+
+int maxSubArray(int* nums, int numsSize){
+ int dp[numsSize];
+ // dp[0]最大子数组和为nums[0]
+ dp[0] = nums[0];
+ // 若numsSize为1,应直接返回nums[0]
+ int subArrSum = nums[0];
+
+ int i;
+ for(i = 1; i < numsSize; ++i) {
+ dp[i] = max(dp[i - 1] + nums[i], nums[i]);
+
+ // 若dp[i]大于之前记录的最大值,进行更新
+ if(dp[i] > subArrSum)
+ subArrSum = dp[i];
+ }
+
+ return subArrSum;
+}
+```
+
+### TypeScript
+
+**贪心**
+
+```typescript
+function maxSubArray(nums: number[]): number {
+ let curSum: number = 0;
+ let resMax: number = -Infinity;
+ for (let i = 0, length = nums.length; i < length; i++) {
+ curSum += nums[i];
+ resMax = Math.max(curSum, resMax);
+ if (curSum < 0) curSum = 0;
+ }
+ return resMax;
+}
+```
+
+**动态规划**
+
+```typescript
+// 动态规划
+function maxSubArray(nums: number[]): number {
+ const length = nums.length;
+ if (length === 0) return 0;
+ const dp: number[] = [];
+ dp[0] = nums[0];
+ let resMax: number = nums[0];
+ for (let i = 1; i < length; i++) {
+ dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
+ resMax = Math.max(resMax, dp[i]);
+ }
+ return resMax;
+}
+```
+
+### Scala
+
+**贪心**
+
+```scala
+object Solution {
+ def maxSubArray(nums: Array[Int]): Int = {
+ var result = Int.MinValue
+ var count = 0
+ for (i <- nums.indices) {
+ count += nums(i) // count累加
+ if (count > result) result = count // 记录最大值
+ if (count <= 0) count = 0 // 一旦count为负,则count归0
+ }
+ result
+ }
+}
+```
+
+**动态规划**
+
+```scala
+object Solution {
+ def maxSubArray(nums: Array[Int]): Int = {
+ var dp = new Array[Int](nums.length)
+ var result = nums(0)
+ dp(0) = nums(0)
+ for (i <- 1 until nums.length) {
+ dp(i) = math.max(nums(i), dp(i - 1) + nums(i))
+ result = math.max(result, dp(i)) // 更新最大值
+ }
+ result
+ }
+}
+```
+### C#
+**贪心**
+```csharp
+public class Solution
+{
+ public int MaxSubArray(int[] nums)
+ {
+ int res = Int32.MinValue;
+ int count = 0;
+ for (int i = 0; i < nums.Length; i++)
+ {
+ count += nums[i];
+ res = Math.Max(res, count);
+ if (count < 0) count = 0;
+ }
+ return res;
+ }
+}
+```
------------------------
-
diff --git "a/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214\357\274\210\345\212\250\346\200\201\350\247\204\345\210\222\357\274\211.md" "b/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214\357\274\210\345\212\250\346\200\201\350\247\204\345\210\222\357\274\211.md"
old mode 100644
new mode 100755
index 4c883cb66c..ba44a36104
--- "a/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214\357\274\210\345\212\250\346\200\201\350\247\204\345\210\222\357\274\211.md"
+++ "b/problems/0053.\346\234\200\345\244\247\345\255\220\345\272\217\345\222\214\357\274\210\345\212\250\346\200\201\350\247\204\345\210\222\357\274\211.md"
@@ -1,19 +1,22 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 53. 最大子序和
+# 53. 最大子序和
-[力扣题目链接](https://leetcode-cn.com/problems/maximum-subarray/)
+[力扣题目链接](https://leetcode.cn/problems/maximum-subarray/)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
+* 输入: [-2,1,-3,4,-1,2,1,-5,4]
+* 输出: 6
+* 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[看起来复杂,其实是简单动态规划 | LeetCode:53.最大子序和](https://www.bilibili.com/video/BV19V4y1F7b5),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
@@ -25,7 +28,7 @@
1. 确定dp数组(dp table)以及下标的含义
-**dp[i]:包括下标i之前的最大连续子序列和为dp[i]**。
+**dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]**。
2. 确定递推公式
@@ -51,7 +54,7 @@ dp[0]应该是多少呢?
5. 举例推导dp数组
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
-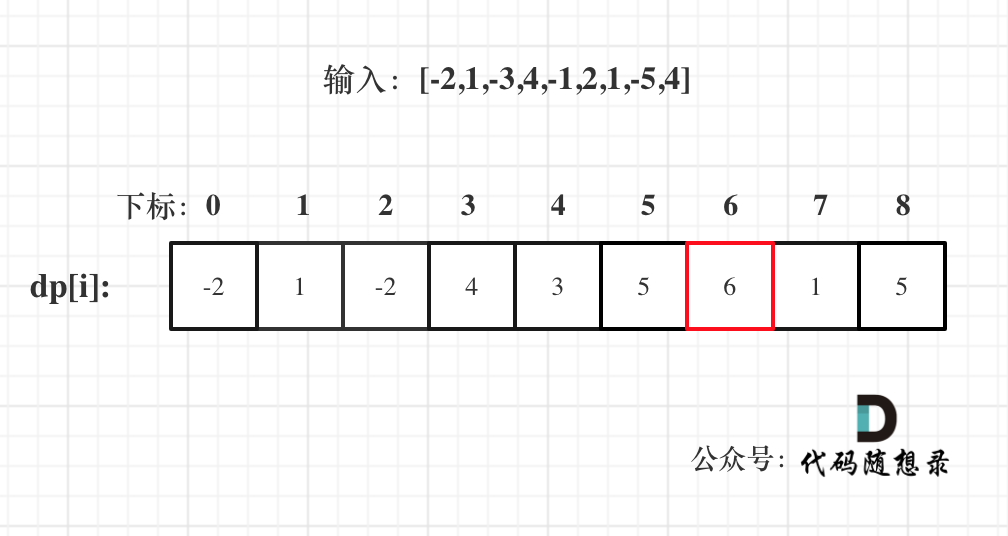
+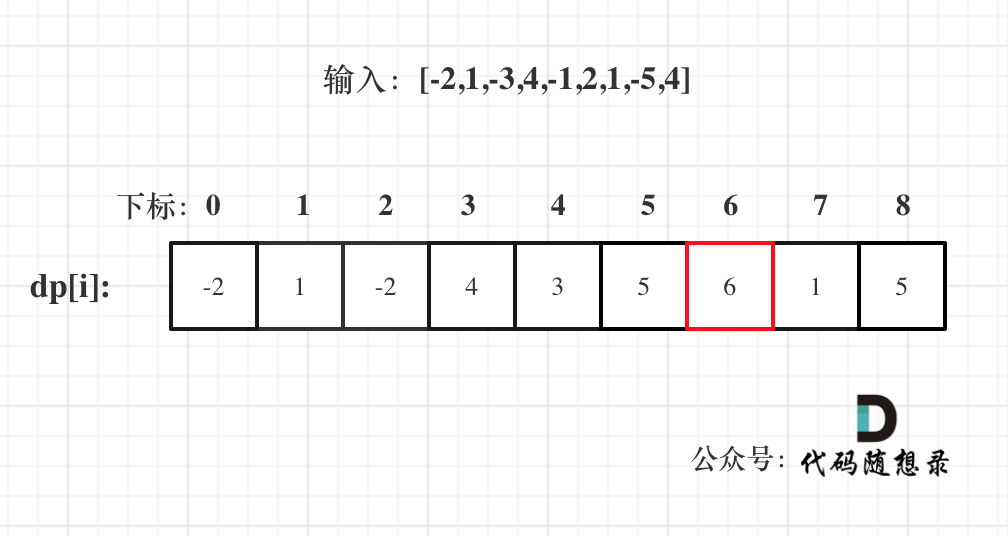
**注意最后的结果可不是dp[nums.size() - 1]!** ,而是dp[6]。
@@ -92,8 +95,8 @@ public:
## 其他语言版本
+### Java:
-Java:
```java
/**
* 1.dp[i]代表当前下标对应的最大值
@@ -120,13 +123,26 @@ Java:
return res;
}
```
+```Java
+//因为dp[i]的递推公式只与前一个值有关,所以可以用一个变量代替dp数组,空间复杂度为O(1)
+class Solution {
+ public int maxSubArray(int[] nums) {
+ int res = nums[0];
+ int pre = nums[0];
+ for(int i = 1; i < nums.length; i++) {
+ pre = Math.max(pre + nums[i], nums[i]);
+ res = Math.max(res, pre);
+ }
+ return res;
+ }
+}
+```
+
+### Python:
-Python:
```python
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
- if len(nums) == 0:
- return 0
dp = [0] * len(nums)
dp[0] = nums[0]
result = dp[0]
@@ -136,7 +152,8 @@ class Solution:
return result
```
-Go:
+### Go:
+
```Go
// solution
// 1, dp
@@ -167,7 +184,7 @@ func max(a,b int) int{
}
```
-JavaScript:
+### JavaScript:
```javascript
const maxSubArray = nums => {
@@ -186,7 +203,42 @@ const maxSubArray = nums => {
};
```
+### Scala:
+
+```scala
+object Solution {
+ def maxSubArray(nums: Array[Int]): Int = {
+ var dp = new Array[Int](nums.length)
+ var result = nums(0)
+ dp(0) = nums(0)
+ for (i <- 1 until nums.length) {
+ dp(i) = math.max(nums(i), dp(i - 1) + nums(i))
+ result = math.max(result, dp(i)) // 更新最大值
+ }
+ result
+ }
+}
+```
+
+### TypeScript:
+
+```typescript
+function maxSubArray(nums: number[]): number {
+ const len = nums.length
+ if (len === 1) return nums[0]
+
+ const dp: number[] = new Array(len)
+ let resMax: number = dp[0] = nums[0]
+
+ for (let i = 1; i < len; i++) {
+ dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])
+ // 注意值为负数的情况
+ if (dp[i] > resMax) resMax = dp[i]
+ }
+
+ return resMax
+}
+```
+
------------------------
-
diff --git "a/problems/0054.\350\236\272\346\227\213\347\237\251\351\230\265.md" "b/problems/0054.\350\236\272\346\227\213\347\237\251\351\230\265.md"
old mode 100644
new mode 100755
index ccf6f47161..8b700c1fe8
--- "a/problems/0054.\350\236\272\346\227\213\347\237\251\351\230\265.md"
+++ "b/problems/0054.\350\236\272\346\227\213\347\237\251\351\230\265.md"
@@ -1,14 +1,12 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 54.螺旋矩阵
+# 54.螺旋矩阵
-[力扣题目链接](https://leetcode-cn.com/problems/spiral-matrix/)
+[力扣题目链接](https://leetcode.cn/problems/spiral-matrix/)
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
@@ -37,7 +35,8 @@
由外向内一圈一圈这么画下去,如下所示:
-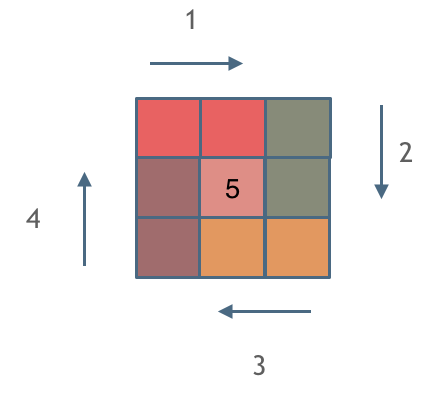
+
+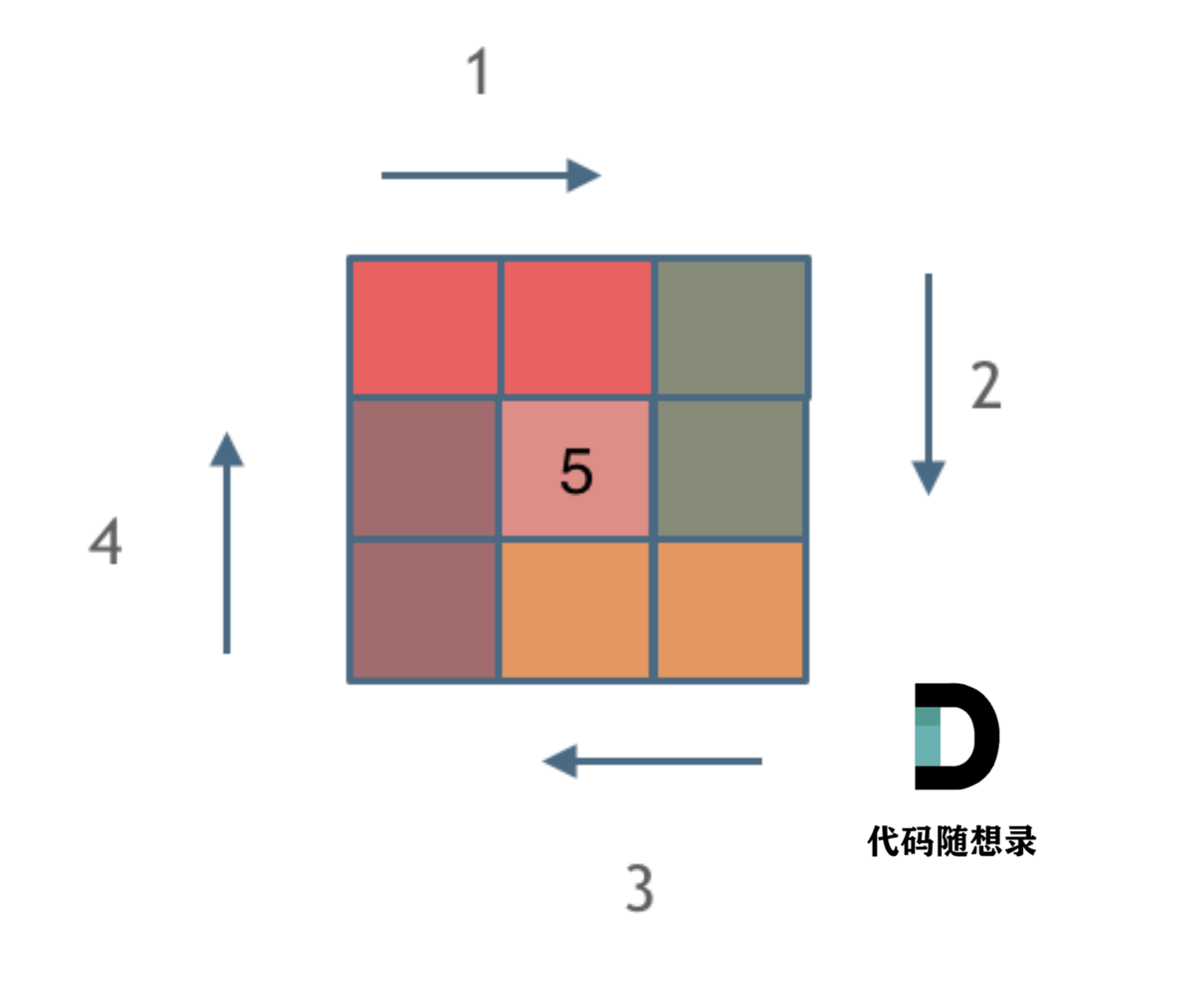
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
@@ -128,49 +127,359 @@ public:
## 类似题目
-* [59.螺旋矩阵II](https://leetcode-cn.com/problems/spiral-matrix-ii/)
-* [剑指Offer 29.顺时针打印矩阵](https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/)
+* [59.螺旋矩阵II](https://leetcode.cn/problems/spiral-matrix-ii/)
+* [剑指Offer 29.顺时针打印矩阵](https://leetcode.cn/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/)
## 其他语言版本
-Python:
-```python
-class Solution:
- def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
- m, n = len(matrix), len(matrix[0])
- left, right, up, down = 0, n - 1, 0, m - 1 # 定位四个方向的边界,闭区间
- res = []
-
- while True:
- for i in range(left, right + 1): # 上边,从左到右
- res.append(matrix[up][i])
- up += 1 # 上边界下移
- if len(res) >= m * n: # 判断是否已经遍历完
- break
-
- for i in range(up, down + 1): # 右边,从上到下
- res.append(matrix[i][right])
- right -= 1 # 右边界左移
+### Java
- if len(res) >= m * n:
- break
+```java
+class Solution {
+ public List spiralOrder(int[][] matrix) {
+ //存放数组的数
+ List ans = new ArrayList<>();
+ //列数
+ int columns = matrix[0].length;
+ //行数
+ int rows = matrix.length;
+ //遍历起点
+ int start = 0;
+ //循环的次数 行数和列数中的最小值除以二
+ int loop = Math.min(rows,columns) / 2;
+ //未遍历的中间列(行)的列(行)下标
+ int mid = loop;
+ //终止条件
+ int offSet = 1;
+ int i,j;
+ while(loop-- > 0) {
+ //初始化起点
+ i = j = start;
- for i in range(right, left - 1, -1): # 下边,从右到左
- res.append(matrix[down][i])
- down -= 1 # 下边界上移
+ //从左往右
+ for(; j < columns - offSet; j++)
+ ans.add(matrix[i][j]);
- if len(res) >= m * n:
- break
+ //从上往下
+ for(; i < rows - offSet; i++)
+ ans.add(matrix[i][j]);
- for i in range(down, up - 1, -1): # 左边,从下到上
- res.append(matrix[i][left])
- left += 1 # 左边界右移
+ //从右往左
+ for(; j > start; j--)
+ ans.add(matrix[i][j]);
- if len(res) >= m * n:
- break
+ //从下往上
+ for(; i > start; i--)
+ ans.add(matrix[i][j]);
+
+ //每循环一次 改变起点位置
+ start++;
+ //终止条件改变
+ offSet++;
+ }
+
+ //如果行和列中的最小值是奇数 则会产生中间行或者中间列没有遍历
+ if(Math.min(rows,columns) % 2 != 0) {
+ //行大于列则产生中间列
+ if(rows > columns) {
+ //中间列的行的最大下标的下一位的下标为mid + rows - columns + 1
+ for(int k = mid; k < mid + rows - columns + 1; k++) {
+ ans.add(matrix[k][mid]);
+ }
+ }else {//列大于等于行则产生中间行
+ //中间行的列的最大下标的下一位的下标为mid + columns - rows + 1
+ for(int k = mid; k < mid + columns - rows + 1; k++) {
+ ans.add(matrix[mid][k]);
+ }
+ }
+ }
+ return ans;
+ }
+}
+```
+
+```java
+class Solution {
+ public List spiralOrder(int[][] matrix) {
+ List res = new ArrayList<>(); // 存放结果
+ if (matrix.length == 0 || matrix[0].length == 0)
+ return res;
+ int rows = matrix.length, columns = matrix[0].length;
+ int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
+ int loop = 0; // 循环次数
+ int offset = 1; // 每一圈循环,需要控制每一条边遍历的长度
+ while (loop < Math.min(rows, columns) / 2) {
+ int i = startx;
+ int j = starty;
+ // 模拟填充上行从左到右(左闭右开)
+ for (; j < columns - offset; j++) {
+ res.add(matrix[i][j]);
+ }
+ // 模拟填充右列从上到下(左闭右开)
+ for (; i < rows - offset; i++) {
+ res.add(matrix[i][j]);
+ }
+ // 模拟填充下行从右到左(左闭右开)
+ for (; j > starty; j--) {
+ res.add(matrix[i][j]);
+ }
+ // 模拟填充左列从下到上(左闭右开)
+ for (; i > startx; i--) {
+ res.add(matrix[i][j]);
+ }
+
+ // 起始位置加1 循环次数加1 并控制每条边遍历的长度
+ startx++;
+ starty++;
+ offset++;
+ loop++;
+ }
+
+ // 如果列或行中的最小值为奇数 则一定有未遍历的部分
+ // 可以自行画图理解
+ if (Math.min(rows, columns) % 2 == 1) {
+ // 当行大于列时 未遍历的部分是列
+ // (startx, starty)即下一个要遍历位置 从该位置出发 遍历完未遍历的列
+ // 遍历次数为rows - columns + 1
+ if (rows > columns) {
+ for (int i = 0; i < rows - columns + 1; i++) {
+ res.add(matrix[startx++][starty]);
+ }
+ } else {
+ // 此处与上面同理 遍历完未遍历的行
+ for (int i = 0; i < columns - rows + 1; i++) {
+ res.add(matrix[startx][starty++]);
+ }
+ }
+ }
+
+ return res;
+ }
+}
+```
+
+### JavaScript
+```
+/**
+ * @param {number[][]} matrix
+ * @return {number[]}
+ */
+var spiralOrder = function(matrix) {
+ let m = matrix.length
+ let n = matrix[0].length
+
+ let startX = startY = 0
+ let i = 0
+ let arr = new Array(m*n).fill(0)
+ let offset = 1
+ let loop = mid = Math.floor(Math.min(m,n) / 2)
+ while (loop--) {
+ let row = startX
+ let col = startY
+ // -->
+ for (; col < n + startY - offset; col++) {
+ arr[i++] = matrix[row][col]
+ }
+ // down
+ for (; row < m + startX - offset; row++) {
+ arr[i++] = matrix[row][col]
+ }
+ // <--
+ for (; col > startY; col--) {
+ arr[i++] = matrix[row][col]
+ }
+ for (; row > startX; row--) {
+ arr[i++] = matrix[row][col]
+ }
+ startX++
+ startY++
+ offset += 2
+ }
+ if (Math.min(m, n) % 2 === 1) {
+ if (n > m) {
+ for (let j = mid; j < mid + n - m + 1; j++) {
+ arr[i++] = matrix[mid][j]
+ }
+ } else {
+ for (let j = mid; j < mid + m - n + 1; j++) {
+ arr[i++] = matrix[j][mid]
+ }
+ }
+ }
+ return arr
+};
+```
+### Python
+
+```python
+class Solution(object):
+ def spiralOrder(self, matrix):
+ """
+ :type matrix: List[List[int]]
+ :rtype: List[int]
+ """
+ if len(matrix) == 0 or len(matrix[0]) == 0 : # 判定List是否为空
+ return []
+ row, col = len(matrix), len(matrix[0]) # 行数,列数
+ loop = min(row, col) // 2 # 循环轮数
+ stx, sty = 0, 0 # 起始x,y坐标
+ i, j =0, 0
+ count = 0 # 计数
+ offset = 1 # 每轮减少的格子数
+ result = [0] * (row * col)
+ while loop>0 :# 左闭右开
+ i, j = stx, sty
+ while j < col - offset : # 从左到右
+ result[count] = matrix[i][j]
+ count += 1
+ j += 1
+ while i < row - offset : # 从上到下
+ result[count] = matrix[i][j]
+ count += 1
+ i += 1
+ while j>sty : # 从右到左
+ result[count] = matrix[i][j]
+ count += 1
+ j -= 1
+ while i>stx : # 从下到上
+ result[count] = matrix[i][j]
+ count += 1
+ i -= 1
+ stx += 1
+ sty += 1
+ offset += 1
+ loop -= 1
+ if min(row, col) % 2 == 1 : # 判定是否需要填充多出来的一行
+ i = stx
+ if row < col :
+ while i < stx + col - row + 1 :
+ result[count] = matrix[stx][i]
+ count += 1
+ i += 1
+ else :
+ while i < stx + row - col + 1 :
+ result[count] = matrix[i][stx]
+ count += 1
+ i += 1
+ return result
+```
+
+版本二:定义四个边界
+```python
+class Solution(object):
+ def spiralOrder(self, matrix):
+ """
+ :type matrix: List[List[int]]
+ :rtype: List[int]
+ """
+ if not matrix:
+ return []
+
+ rows = len(matrix)
+ cols = len(matrix[0])
+ top, bottom, left, right = 0, rows - 1, 0, cols - 1
+ print_list = []
+
+ while top <= bottom and left <= right:
+ # 从左到右
+ for i in range(left, right + 1):
+ print_list.append(matrix[top][i])
+ top += 1
+
+ # 从上到下
+ for i in range(top, bottom + 1):
+ print_list.append(matrix[i][right])
+ right -= 1
+
+ # 从右到左
+ if top <= bottom:
+ for i in range(right, left - 1, -1):
+ print_list.append(matrix[bottom][i])
+ bottom -= 1
+
+ # 从下到上
+ if left <= right:
+ for i in range(bottom, top - 1, -1):
+ print_list.append(matrix[i][left])
+ left += 1
+
+ return print_list
+```
+
+### Go
- return res
+```go
+func spiralOrder(matrix [][]int) []int {
+ rows := len(matrix)
+ if rows == 0 {
+ return []int{}
+ }
+ columns := len(matrix[0])
+ if columns == 0 {
+ return []int{}
+ }
+ res := make([]int, rows * columns)
+ startx, starty := 0, 0 // 定义每循环一个圈的起始位置
+ loop := min(rows, columns) / 2
+ mid := min(rows, columns) / 2
+ count := 0 // 用来给矩阵中每一个空格赋值
+ offset := 1 // 每一圈循环,需要控制每一条边遍历的长度
+ for loop > 0 {
+ i, j := startx, starty
+
+ // 模拟填充上行从左到右(左闭右开)
+ for ; j < starty + columns - offset; j++ {
+ res[count] = matrix[startx][j]
+ count++
+ }
+ // 模拟填充右列从上到下(左闭右开)
+ for ; i < startx + rows - offset; i++ {
+ res[count] = matrix[i][j]
+ count++
+ }
+ // 模拟填充下行从右到左(左闭右开)
+ for ; j > starty; j-- {
+ res[count] = matrix[i][j]
+ count++
+ }
+ // 模拟填充左列从下到上(左闭右开)
+ for ; i > startx; i-- {
+ res[count] = matrix[i][starty]
+ count++
+ }
+
+ // 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
+ startx++
+ starty++
+
+ // offset 控制每一圈里每一条边遍历的长度
+ offset += 2
+ loop--
+ }
+
+ // 如果min(rows, columns)为奇数的话,需要单独给矩阵最中间的位置赋值
+ if min(rows, columns) % 2 == 1 {
+ if rows > columns {
+ for i := mid; i < mid + rows - columns + 1; i++ {
+ res[count] = matrix[i][mid]
+ count++
+ }
+ } else {
+ for i := mid; i < mid + columns - rows + 1; i++ {
+ res[count] = matrix[mid][i]
+ count++
+ }
+ }
+ }
+ return res
+}
+
+func min(x, y int) int {
+ if x < y {
+ return x
+ }
+ return y
+}
```
------------------------
-
+
diff --git "a/problems/0055.\350\267\263\350\267\203\346\270\270\346\210\217.md" "b/problems/0055.\350\267\263\350\267\203\346\270\270\346\210\217.md"
old mode 100644
new mode 100755
index c0890f75f3..513fc2e340
--- "a/problems/0055.\350\267\263\350\267\203\346\270\270\346\210\217.md"
+++ "b/problems/0055.\350\267\263\350\267\203\346\270\270\346\210\217.md"
@@ -1,13 +1,10 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
-
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 55. 跳跃游戏
-[力扣题目链接](https://leetcode-cn.com/problems/jump-game/)
+[力扣题目链接](https://leetcode.cn/problems/jump-game/)
给定一个非负整数数组,你最初位于数组的第一个位置。
@@ -15,20 +12,25 @@
判断你是否能够到达最后一个位置。
-示例 1:
-* 输入: [2,3,1,1,4]
-* 输出: true
-* 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
+示例 1:
+
+- 输入: [2,3,1,1,4]
+- 输出: true
+- 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
+
+示例 2:
+
+- 输入: [3,2,1,0,4]
+- 输出: false
+- 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
-示例 2:
-* 输入: [3,2,1,0,4]
-* 输出: false
-* 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
+## 算法公开课
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法,怎么跳跃不重要,关键在覆盖范围 | LeetCode:55.跳跃游戏](https://www.bilibili.com/video/BV1VG4y1X7kB),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
## 思路
-刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
+刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
其实跳几步无所谓,关键在于可跳的覆盖范围!
@@ -46,13 +48,14 @@
如图:
-
+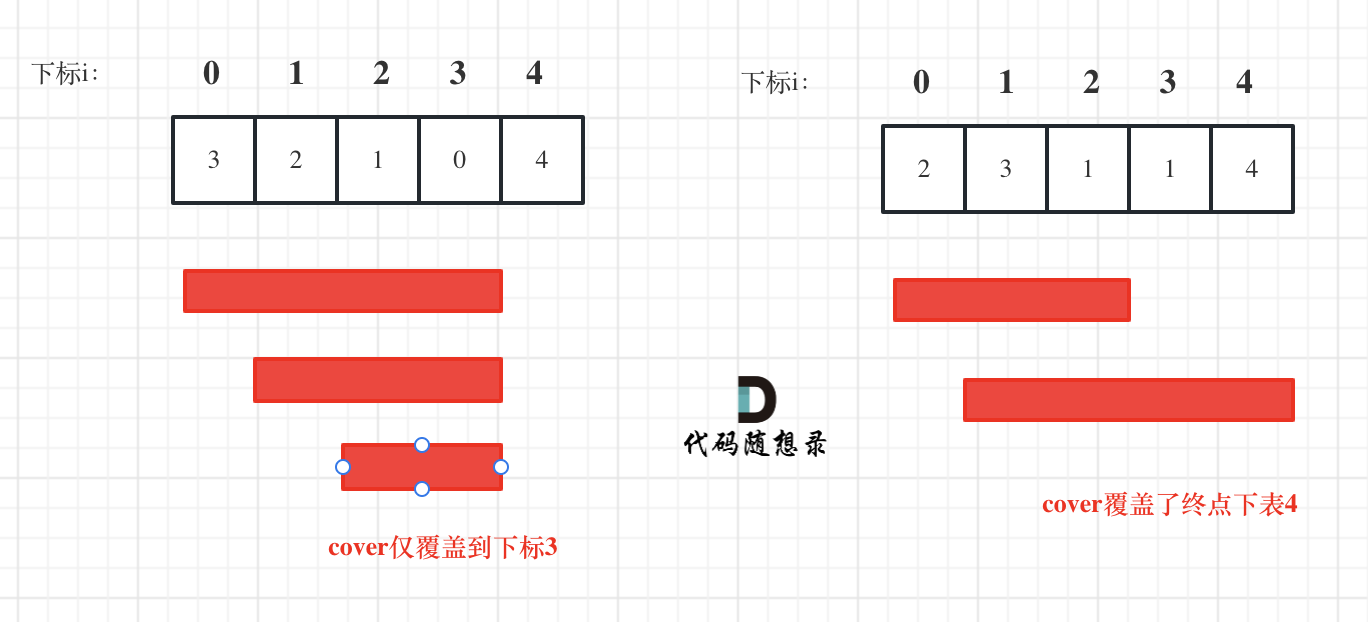
-i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去。
-而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。
+i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
-如果cover大于等于了终点下标,直接return true就可以了。
+而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
+
+如果 cover 大于等于了终点下标,直接 return true 就可以了。
C++代码如下:
@@ -70,20 +73,25 @@ public:
}
};
```
+
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
+
## 总结
-这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
+这道题目关键点在于:不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
大家可以看出思路想出来了,代码还是非常简单的。
一些同学可能感觉,我在讲贪心系列的时候,题目和题目之间貌似没有什么联系?
-**是真的就是没什么联系,因为贪心无套路!**没有个整体的贪心框架解决一些列问题,只能是接触各种类型的题目锻炼自己的贪心思维!
+**是真的就是没什么联系,因为贪心无套路**!没有个整体的贪心框架解决一系列问题,只能是接触各种类型的题目锻炼自己的贪心思维!
## 其他语言版本
+### Java
-### Java
```Java
class Solution {
public boolean canJump(int[] nums) {
@@ -105,6 +113,7 @@ class Solution {
```
### Python
+
```python
class Solution:
def canJump(self, nums: List[int]) -> bool:
@@ -119,27 +128,61 @@ class Solution:
return False
```
+```python
+## for循环
+class Solution:
+ def canJump(self, nums: List[int]) -> bool:
+ cover = 0
+ if len(nums) == 1: return True
+ for i in range(len(nums)):
+ if i <= cover:
+ cover = max(i + nums[i], cover)
+ if cover >= len(nums) - 1: return True
+ return False
+```
+
+```python
+## 基于当前最远可到达位置判断
+class Solution:
+ def canJump(self, nums: List[int]) -> bool:
+ far = nums[0]
+ for i in range(len(nums)):
+ # 要考虑两个情况
+ # 1. i <= far - 表示 当前位置i 可以到达
+ # 2. i > far - 表示 当前位置i 无法到达
+ if i > far:
+ return False
+ far = max(far, nums[i]+i)
+ # 如果循环正常结束,表示最后一个位置也可以到达,否则会在中途直接退出
+ # 关键点在于,要想明白其实列表中的每个位置都是需要验证能否到达的
+ return True
+```
+
### Go
-```Go
-func canJUmp(nums []int) bool {
- if len(nums)<=1{
- return true
- }
- dp:=make([]bool,len(nums))
- dp[0]=true
- for i:=1;i=0;j--{
- if dp[j]&&nums[j]+j>=i{
- dp[i]=true
- break
- }
- }
- }
- return dp[len(nums)-1]
+
+```go
+// 贪心
+func canJump(nums []int) bool {
+ cover := 0
+ n := len(nums)-1
+ for i := 0; i <= cover; i++ { // 每次与覆盖值比较
+ cover = max(i+nums[i], cover) //每走一步都将 cover 更新为最大值
+ if cover >= n {
+ return true
+ }
+ }
+ return false
+}
+func max(a, b int ) int {
+ if a > b {
+ return a
+ }
+ return b
}
```
-### Javascript
+### JavaScript
+
```Javascript
var canJump = function(nums) {
if(nums.length === 1) return true
@@ -154,6 +197,97 @@ var canJump = function(nums) {
};
```
+### Rust
+
+```Rust
+impl Solution {
+ pub fn can_jump(nums: Vec) -> bool {
+ if nums.len() == 1 {
+ return true;
+ }
+ let (mut i, mut cover) = (0, 0);
+ while i <= cover {
+ cover = (i + nums[i] as usize).max(cover);
+ if cover >= nums.len() - 1 {
+ return true;
+ }
+ i += 1;
+ }
+ false
+ }
+}
+```
+
+### C
+
+```c
+#define max(a, b) (((a) > (b)) ? (a) : (b))
+
+bool canJump(int* nums, int numsSize){
+ int cover = 0;
+
+ int i;
+ // 只可能获取cover范围中的步数,所以i<=cover
+ for(i = 0; i <= cover; ++i) {
+ // 更新cover为从i出发能到达的最大值/cover的值中较大值
+ cover = max(i + nums[i], cover);
+
+ // 若更新后cover可以到达最后的元素,返回true
+ if(cover >= numsSize - 1)
+ return true;
+ }
+
+ return false;
+}
+```
+
+### TypeScript
+
+```typescript
+function canJump(nums: number[]): boolean {
+ let farthestIndex: number = 0;
+ let cur: number = 0;
+ while (cur <= farthestIndex) {
+ farthestIndex = Math.max(farthestIndex, cur + nums[cur]);
+ if (farthestIndex >= nums.length - 1) return true;
+ cur++;
+ }
+ return false;
+}
+```
+
+### Scala
+
+```scala
+object Solution {
+ def canJump(nums: Array[Int]): Boolean = {
+ var cover = 0
+ if (nums.length == 1) return true // 如果只有一个元素,那么必定到达
+ var i = 0
+ while (i <= cover) { // i表示下标,当前只能够走cover步
+ cover = math.max(i + nums(i), cover)
+ if (cover >= nums.length - 1) return true // 说明可以覆盖到终点,直接返回
+ i += 1
+ }
+ false // 如果上面没有返回就是跳不到
+ }
+}
+```
+### C#
+```csharp
+public class Solution
+{
+ public bool CanJump(int[] nums)
+ {
+ int cover = 0;
+ if (nums.Length == 1) return true;
+ for (int i = 0; i <= cover; i++)
+ {
+ cover = Math.Max(i + nums[i], cover);
+ if (cover >= nums.Length - 1) return true;
+ }
+ return false;
+ }
+}
+```
------------------------
-
diff --git "a/problems/0056.\345\220\210\345\271\266\345\214\272\351\227\264.md" "b/problems/0056.\345\220\210\345\271\266\345\214\272\351\227\264.md"
old mode 100644
new mode 100755
index a9caeaf057..24a97f6c5a
--- "a/problems/0056.\345\220\210\345\271\266\345\214\272\351\227\264.md"
+++ "b/problems/0056.\345\220\210\345\271\266\345\214\272\351\227\264.md"
@@ -1,13 +1,11 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 56. 合并区间
-[力扣题目链接](https://leetcode-cn.com/problems/merge-intervals/)
+[力扣题目链接](https://leetcode.cn/problems/merge-intervals/)
给出一个区间的集合,请合并所有重叠的区间。
@@ -22,31 +20,25 @@
* 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
* 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
-提示:
+## 算法公开课
-* intervals[i][0] <= intervals[i][1]
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法,合并区间有细节!LeetCode:56.合并区间](https://www.bilibili.com/video/BV1wx4y157nD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
## 思路
-大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
+本题的本质其实还是判断重叠区间问题。
-都可以!
+大家如果认真做题的话,话发现和我们刚刚讲过的[452. 用最少数量的箭引爆气球](https://programmercarl.com/0452.用最少数量的箭引爆气球.html) 和 [435. 无重叠区间](https://programmercarl.com/0435.无重叠区间.html) 都是一个套路。
-那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
+这几道题都是判断区间重叠,区别就是判断区间重叠后的逻辑,本题是判断区间重贴后要进行区间合并。
-局部最优可以推出全局最优,找不出反例,试试贪心。
+所以一样的套路,先排序,让所有的相邻区间尽可能的重叠在一起,按左边界,或者右边界排序都可以,处理逻辑稍有不同。
-那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
-
-有时候贪心就是常识!哈哈
-
-按照左边界从小到大排序之后,如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
-
-即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
+按照左边界从小到大排序之后,如果 `intervals[i][0] <= intervals[i - 1][1]` 即intervals[i]的左边界 <= intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴,所以是<=)
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
-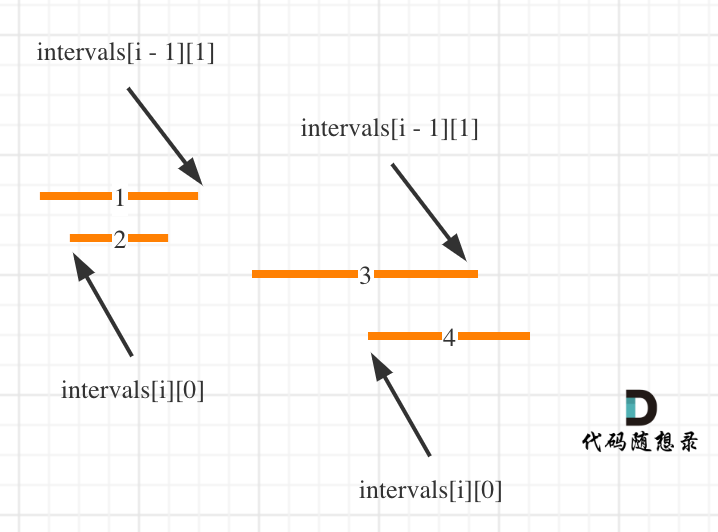
+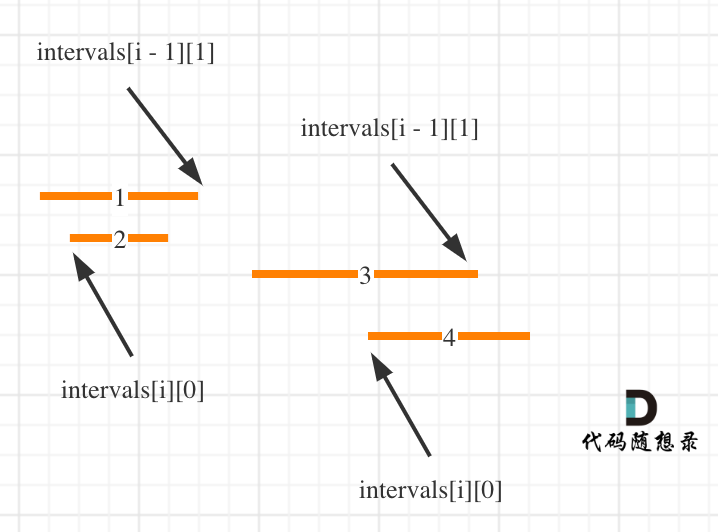
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
@@ -54,57 +46,24 @@
C++代码如下:
-```CPP
-class Solution {
-public:
- // 按照区间左边界从小到大排序
- static bool cmp (const vector& a, const vector& b) {
- return a[0] < b[0];
- }
- vector> merge(vector>& intervals) {
- vector> result;
- if (intervals.size() == 0) return result;
- sort(intervals.begin(), intervals.end(), cmp);
- bool flag = false; // 标记最后一个区间有没有合并
- int length = intervals.size();
-
- for (int i = 1; i < length; i++) {
- int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
- int end = intervals[i - 1][1]; // 初始i-1区间的右边界
- while (i < length && intervals[i][0] <= end) { // 合并区间
- end = max(end, intervals[i][1]); // 不断更新右区间
- if (i == length - 1) flag = true; // 最后一个区间也合并了
- i++; // 继续合并下一个区间
- }
- // start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
- result.push_back({start, end});
- }
- // 如果最后一个区间没有合并,将其加入result
- if (flag == false) {
- result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
- }
- return result;
- }
-};
-```
-
-当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
-
```CPP
class Solution {
public:
vector> merge(vector>& intervals) {
vector> result;
- if (intervals.size() == 0) return result;
- // 排序的参数使用了lamda表达式
+ if (intervals.size() == 0) return result; // 区间集合为空直接返回
+ // 排序的参数使用了lambda表达式
sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){return a[0] < b[0];});
- result.push_back(intervals[0]);
+ // 第一个区间就可以放进结果集里,后面如果重叠,在result上直接合并
+ result.push_back(intervals[0]);
+
for (int i = 1; i < intervals.size(); i++) {
- if (result.back()[1] >= intervals[i][0]) { // 合并区间
- result.back()[1] = max(result.back()[1], intervals[i][1]);
+ if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
+ // 合并区间,只更新右边界就好,因为result.back()的左边界一定是最小值,因为我们按照左边界排序的
+ result.back()[1] = max(result.back()[1], intervals[i][1]);
} else {
- result.push_back(intervals[i]);
+ result.push_back(intervals[i]); // 区间不重叠
}
}
return result;
@@ -112,23 +71,8 @@ public:
};
```
-* 时间复杂度:$O(n\log n)$ ,有一个快排
-* 空间复杂度:$O(1)$,我没有算result数组(返回值所需容器占的空间)
-
-
-## 总结
-
-对于贪心算法,很多同学都是:**如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
-
-跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
-
-那应该怎么办呢?
-
-正如我贪心系列开篇词[关于贪心算法,你该了解这些!](https://programmercarl.com/贪心算法理论基础.html)中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
-
-「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
-
-
+* 时间复杂度: O(nlogn)
+* 空间复杂度: O(logn),排序需要的空间开销
## 其他语言版本
@@ -136,24 +80,37 @@ public:
### Java
```java
+
+/**
+时间复杂度 : O(NlogN) 排序需要O(NlogN)
+空间复杂度 : O(logN) java 的内置排序是快速排序 需要 O(logN)空间
+
+*/
class Solution {
public int[][] merge(int[][] intervals) {
List res = new LinkedList<>();
- Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
-
+ //按照左边界排序
+ Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
+ //initial start 是最小左边界
int start = intervals[0][0];
+ int rightmostRightBound = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
- if (intervals[i][0] > intervals[i - 1][1]) {
- res.add(new int[]{start, intervals[i - 1][1]});
+ //如果左边界大于最大右边界
+ if (intervals[i][0] > rightmostRightBound) {
+ //加入区间 并且更新start
+ res.add(new int[]{start, rightmostRightBound});
start = intervals[i][0];
+ rightmostRightBound = intervals[i][1];
} else {
- intervals[i][1] = Math.max(intervals[i][1], intervals[i - 1][1]);
+ //更新最大右边界
+ rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
}
}
- res.add(new int[]{start, intervals[intervals.length - 1][1]});
+ res.add(new int[]{start, rightmostRightBound});
return res.toArray(new int[res.size()][]);
}
}
+
```
```java
// 版本2
@@ -181,46 +138,82 @@ class Solution {
### Python
```python
class Solution:
- def merge(self, intervals: List[List[int]]) -> List[List[int]]:
- if len(intervals) == 0: return intervals
- intervals.sort(key=lambda x: x[0])
+ def merge(self, intervals):
result = []
- result.append(intervals[0])
+ if len(intervals) == 0:
+ return result # 区间集合为空直接返回
+
+ intervals.sort(key=lambda x: x[0]) # 按照区间的左边界进行排序
+
+ result.append(intervals[0]) # 第一个区间可以直接放入结果集中
+
for i in range(1, len(intervals)):
- last = result[-1]
- if last[1] >= intervals[i][0]:
- result[-1] = [last[0], max(last[1], intervals[i][1])]
+ if result[-1][1] >= intervals[i][0]: # 发现重叠区间
+ # 合并区间,只需要更新结果集最后一个区间的右边界,因为根据排序,左边界已经是最小的
+ result[-1][1] = max(result[-1][1], intervals[i][1])
else:
- result.append(intervals[i])
+ result.append(intervals[i]) # 区间不重叠
+
return result
+
```
### Go
-```golang
+```go
func merge(intervals [][]int) [][]int {
- //先从小到大排序
- sort.Slice(intervals,func(i,j int)bool{
- return intervals[i][0]=intervals[i+1][0]{
- intervals[i][1]=max(intervals[i][1],intervals[i+1][1])//赋值最大值
- intervals=append(intervals[:i+1],intervals[i+2:]...)
- i--
+ res := make([][]int, 0, len(intervals))
+ left, right := intervals[0][0], intervals[0][1]
+ for i := 1; i < len(intervals); i++ {
+ if right < intervals[i][0] {
+ res = append(res, []int{left, right})
+ left, right = intervals[i][0], intervals[i][1]
+ } else {
+ right = max(right, intervals[i][1])
}
}
- return intervals
+ res = append(res, []int{left, right}) // 将最后一个区间放入
+ return res
}
-func max(a,b int)int{
- if a>b{
+func max(a, b int) int {
+ if a > b {
return a
}
return b
}
```
+```go
+// 版本2
+func merge(intervals [][]int) [][]int {
+ if len(intervals) == 1 {
+ return intervals
+ }
+ sort.Slice(intervals, func(i, j int) bool {
+ return intervals[i][0] < intervals[j][0]
+ })
+ res := make([][]int, 0)
+ res = append(res, intervals[0])
+ for i := 1; i < len(intervals); i++ {
+ if intervals[i][0] <= res[len(res)-1][1]{
+ res[len(res)-1][1] = max56(res[len(res)-1][1],intervals[i][1])
+ } else {
+ res = append(res, intervals[i])
+ }
+ }
+ return res
+}
+func max56(a, b int) int {
+ if a > b {
+ return a
+ }
+ return b
+}
+```
+
-### Javascript
+### JavaScript
```javascript
var merge = function (intervals) {
intervals.sort((a, b) => a[0] - b[0]);
@@ -266,7 +259,147 @@ var merge = function(intervals) {
};
```
+### TypeScript
+
+```typescript
+function merge(intervals: number[][]): number[][] {
+ const resArr: number[][] = [];
+ intervals.sort((a, b) => a[0] - b[0]);
+ resArr[0] = [...intervals[0]]; // 避免修改原intervals
+ for (let i = 1, length = intervals.length; i < length; i++) {
+ let interval: number[] = intervals[i];
+ let last: number[] = resArr[resArr.length - 1];
+ if (interval[0] <= last[1]) {
+ last[1] = Math.max(interval[1], last[1]);
+ } else {
+ resArr.push([...intervals[i]]);
+ }
+ }
+ return resArr;
+};
+```
+
+### Scala
+
+```scala
+object Solution {
+ import scala.collection.mutable
+ def merge(intervals: Array[Array[Int]]): Array[Array[Int]] = {
+ var res = mutable.ArrayBuffer[Array[Int]]()
+
+ // 排序
+ var interval = intervals.sortWith((a, b) => {
+ a(0) < b(0)
+ })
+
+ var left = interval(0)(0)
+ var right = interval(0)(1)
+
+ for (i <- 1 until interval.length) {
+ if (interval(i)(0) <= right) {
+ left = math.min(left, interval(i)(0))
+ right = math.max(right, interval(i)(1))
+ } else {
+ res.append(Array[Int](left, right))
+ left = interval(i)(0)
+ right = interval(i)(1)
+ }
+ }
+ res.append(Array[Int](left, right))
+ res.toArray // 返回res的Array形式
+ }
+}
+```
+
+### Rust
+```Rust
+impl Solution {
+ pub fn merge(mut intervals: Vec>) -> Vec> {
+ let mut res = vec![];
+ if intervals.is_empty() {
+ return res;
+ }
+ intervals.sort_by_key(|a| a[0]);
+ res.push(intervals[0].clone());
+ for interval in intervals.into_iter().skip(1) {
+ let res_last_ele = res.last_mut().unwrap();
+ if res_last_ele[1] >= interval[0] {
+ res_last_ele[1] = interval[1].max(res_last_ele[1]);
+ } else {
+ res.push(interval);
+ }
+ }
+ res
+ }
+}
+```
+### C
+
+```c
+#define max(a, b) ((a) > (b) ? (a) : (b))
+
+// 根据左边界进行排序
+int cmp(const void * var1, const void * var2){
+ int *v1 = *(int **) var1;
+ int *v2 = *(int **) var2;
+ return v1[0] - v2[0];
+}
+
+int** merge(int** intervals, int intervalsSize, int* intervalsColSize, int* returnSize, int** returnColumnSizes) {
+ int ** result = malloc(sizeof (int *) * intervalsSize);
+ * returnColumnSizes = malloc(sizeof (int ) * intervalsSize);
+ for(int i = 0; i < intervalsSize; i++){
+ result[i] = malloc(sizeof (int ) * 2);
+ }
+ qsort(intervals, intervalsSize, sizeof (int *), cmp);
+ int count = 0;
+ for(int i = 0; i < intervalsSize; i++){
+ // 记录区间的左右边界
+ int L = intervals[i][0], R = intervals[i][1];
+ // 如果count为0或者前一区间的右区间小于此时的左边,加入结果中
+ if (count == 0 || result[count - 1][1] < L) {
+ returnColumnSizes[0][count] = 2;
+ result[count][0] = L;
+ result[count][1] = R;
+ count++;
+ }
+ else{ // 更新右边界的值
+ result[count - 1][1] = max(R, result[count - 1][1]);
+ }
+ }
+ *returnSize = count;
+ return result;
+}
+```
+
+
+
+### C#
+
+```csharp
+public class Solution
+{
+ public int[][] Merge(int[][] intervals)
+ {
+ if (intervals.Length == 0)
+ return intervals;
+ Array.Sort(intervals, (a, b) => a[0] - b[0]);
+ List> res = new List>();
+ res.Add(intervals[0].ToList());
+ for (int i = 1; i < intervals.Length; i++)
+ {
+ if (res[res.Count - 1][1] >= intervals[i][0])
+ {
+ res[res.Count - 1][1] = Math.Max(res[res.Count - 1][1], intervals[i][1]);
+ }
+ else
+ {
+ res.Add(intervals[i].ToList());
+ }
+ }
+ return res.Select(x => x.ToArray()).ToArray();
+ }
+}
+```
------------------------
-
diff --git "a/problems/0059.\350\236\272\346\227\213\347\237\251\351\230\265II.md" "b/problems/0059.\350\236\272\346\227\213\347\237\251\351\230\265II.md"
old mode 100644
new mode 100755
index 5c679982ce..927df1c6c1
--- "a/problems/0059.\350\236\272\346\227\213\347\237\251\351\230\265II.md"
+++ "b/problems/0059.\350\236\272\346\227\213\347\237\251\351\230\265II.md"
@@ -1,14 +1,12 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 59.螺旋矩阵II
+# 59.螺旋矩阵II
-[力扣题目链接](https://leetcode-cn.com/problems/spiral-matrix-ii/)
+[力扣题目链接](https://leetcode.cn/problems/spiral-matrix-ii/)
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
@@ -22,6 +20,11 @@
[ 7, 6, 5 ]
]
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[拿下螺旋矩阵!LeetCode:59.螺旋矩阵II](https://www.bilibili.com/video/BV1SL4y1N7mV),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
这道题目可以说在面试中出现频率较高的题目,**本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。**
@@ -30,7 +33,7 @@
相信很多同学刚开始做这种题目的时候,上来就是一波判断猛如虎。
-结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里哪里有问题,改了那里这里又跑不起来了。
+结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里那里有问题,改了那里这里又跑不起来了。
大家还记得我们在这篇文章[数组:每次遇到二分法,都是一看就会,一写就废](https://programmercarl.com/0704.二分查找.html)中讲解了二分法,提到如果要写出正确的二分法一定要坚持**循环不变量原则**。
@@ -47,11 +50,11 @@
可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是**一进循环深似海,从此offer是路人**。
-这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开又闭的原则,这样这一圈才能按照统一的规则画下来。
+这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
那么我按照左闭右开的原则,来画一圈,大家看一下:
-
+
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
@@ -59,7 +62,7 @@
一些同学做这道题目之所以一直写不好,代码越写越乱。
-就是因为在画每一条边的时候,一会左开又闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
+就是因为在画每一条边的时候,一会左开右闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
@@ -74,7 +77,7 @@ public:
int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
int count = 1; // 用来给矩阵中每一个空格赋值
- int offset = 1; // 每一圈循环,需要控制每一条边遍历的长度
+ int offset = 1; // 需要控制每一条边遍历的长度,每次循环右边界收缩一位
int i,j;
while (loop --) {
i = startx;
@@ -82,11 +85,11 @@ public:
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
- for (j = starty; j < starty + n - offset; j++) {
- res[startx][j] = count++;
+ for (j; j < n - offset; j++) {
+ res[i][j] = count++;
}
// 模拟填充右列从上到下(左闭右开)
- for (i = startx; i < startx + n - offset; i++) {
+ for (i; i < n - offset; i++) {
res[i][j] = count++;
}
// 模拟填充下行从右到左(左闭右开)
@@ -103,7 +106,7 @@ public:
starty++;
// offset 控制每一圈里每一条边遍历的长度
- offset += 2;
+ offset += 1;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
@@ -115,80 +118,72 @@ public:
};
```
+* 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
+* 空间复杂度 O(1)
+
## 类似题目
-* 54.螺旋矩阵
-* 剑指Offer 29.顺时针打印矩阵
+* [54.螺旋矩阵](https://leetcode.cn/problems/spiral-matrix/)
+* [剑指Offer 29.顺时针打印矩阵](https://leetcode.cn/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/)
## 其他语言版本
-Java:
+### Java:
```Java
class Solution {
public int[][] generateMatrix(int n) {
- int[][] res = new int[n][n];
-
- // 循环次数
- int loop = n / 2;
-
- // 定义每次循环起始位置
- int startX = 0;
- int startY = 0;
-
- // 定义偏移量
+ int[][] nums = new int[n][n];
+ int startX = 0, startY = 0; // 每一圈的起始点
int offset = 1;
+ int count = 1; // 矩阵中需要填写的数字
+ int loop = 1; // 记录当前的圈数
+ int i, j; // j 代表列, i 代表行;
- // 定义填充数字
- int count = 1;
-
- // 定义中间位置
- int mid = n / 2;
- while (loop > 0) {
- int i = startX;
- int j = startY;
+ while (loop <= n / 2) {
- // 模拟上侧从左到右
- for (; j startY; j--) {
- res[i][j] = count++;
+ nums[i][j] = count++;
}
- // 模拟左侧从下到上
+ // 左列
+ // 左闭右开,所以判断循环结束时, i != startX
for (; i > startX; i--) {
- res[i][j] = count++;
+ nums[i][j] = count++;
}
-
- loop--;
-
- startX += 1;
- startY += 1;
-
- offset += 2;
+ startX++;
+ startY++;
+ offset++;
+ loop++;
}
-
- if (n % 2 == 1) {
- res[mid][mid] = count;
+ if (n % 2 == 1) { // n 为奇数时,单独处理矩阵中心的值
+ nums[startX][startY] = count;
}
-
- return res;
+ return nums;
}
}
+
+
```
-python3:
+### python3:
```python
class Solution:
@@ -219,14 +214,54 @@ class Solution:
return nums
```
-javaScript
+版本二:定义四个边界
+```python
+class Solution(object):
+ def generateMatrix(self, n):
+ if n <= 0:
+ return []
+
+ # 初始化 n x n 矩阵
+ matrix = [[0]*n for _ in range(n)]
+
+ # 初始化边界和起始值
+ top, bottom, left, right = 0, n-1, 0, n-1
+ num = 1
+
+ while top <= bottom and left <= right:
+ # 从左到右填充上边界
+ for i in range(left, right + 1):
+ matrix[top][i] = num
+ num += 1
+ top += 1
+
+ # 从上到下填充右边界
+ for i in range(top, bottom + 1):
+ matrix[i][right] = num
+ num += 1
+ right -= 1
+
+ # 从右到左填充下边界
+
+ for i in range(right, left - 1, -1):
+ matrix[bottom][i] = num
+ num += 1
+ bottom -= 1
+
+ # 从下到上填充左边界
+
+ for i in range(bottom, top - 1, -1):
+ matrix[i][left] = num
+ num += 1
+ left += 1
+
+ return matrix
+```
+
+### JavaScript:
```javascript
-/**
- * @param {number} n
- * @return {number[][]}
- */
var generateMatrix = function(n) {
let startX = startY = 0; // 起始位置
let loop = Math.floor(n/2); // 旋转圈数
@@ -238,19 +273,19 @@ var generateMatrix = function(n) {
while (loop--) {
let row = startX, col = startY;
// 上行从左到右(左闭右开)
- for (; col < startY + n - offset; col++) {
+ for (; col < n - offset; col++) {
res[row][col] = count++;
}
// 右列从上到下(左闭右开)
- for (; row < startX + n - offset; row++) {
+ for (; row < n - offset; row++) {
res[row][col] = count++;
}
// 下行从右到左(左闭右开)
- for (; col > startX; col--) {
+ for (; col > startY; col--) {
res[row][col] = count++;
}
// 左列做下到上(左闭右开)
- for (; row > startY; row--) {
+ for (; row > startX; row--) {
res[row][col] = count++;
}
@@ -259,7 +294,7 @@ var generateMatrix = function(n) {
startY++;
// 更新offset
- offset += 2;
+ offset += 1;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2 === 1) {
@@ -267,11 +302,12 @@ var generateMatrix = function(n) {
}
return res;
};
+
```
-TypeScript:
+### TypeScript:
```typescript
function generateMatrix(n: number): number[][] {
@@ -316,7 +352,62 @@ function generateMatrix(n: number): number[][] {
};
```
-Go:
+### Go:
+
+```go
+package main
+
+import "fmt"
+
+func main() {
+ n := 3
+ fmt.Println(generateMatrix(n))
+}
+
+func generateMatrix(n int) [][]int {
+ startx, starty := 0, 0
+ var loop int = n / 2
+ var center int = n / 2
+ count := 1
+ offset := 1
+ res := make([][]int, n)
+ for i := 0; i < n; i++ {
+ res[i] = make([]int, n)
+ }
+ for loop > 0 {
+ i, j := startx, starty
+
+ //行数不变 列数在变
+ for j = starty; j < n-offset; j++ {
+ res[startx][j] = count
+ count++
+ }
+ //列数不变是j 行数变
+ for i = startx; i < n-offset; i++ {
+ res[i][j] = count
+ count++
+ }
+ //行数不变 i 列数变 j--
+ for ; j > starty; j-- {
+ res[i][j] = count
+ count++
+ }
+ //列不变 行变
+ for ; i > startx; i-- {
+ res[i][j] = count
+ count++
+ }
+ startx++
+ starty++
+ offset++
+ loop--
+ }
+ if n%2 == 1 {
+ res[center][center] = n * n
+ }
+ return res
+}
+```
```go
func generateMatrix(n int) [][]int {
@@ -354,7 +445,7 @@ func generateMatrix(n int) [][]int {
}
```
-Swift:
+### Swift:
```swift
func generateMatrix(_ n: Int) -> [[Int]] {
@@ -410,7 +501,7 @@ func generateMatrix(_ n: Int) -> [[Int]] {
}
```
-Rust:
+### Rust:
```rust
impl Solution {
@@ -463,7 +554,8 @@ impl Solution {
}
```
-PHP:
+### PHP:
+
```php
class Solution {
/**
@@ -505,7 +597,8 @@ class Solution {
}
```
-C:
+### C:
+
```c
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
//初始化返回的结果数组的大小
@@ -564,6 +657,173 @@ int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
return ans;
}
```
+### Scala:
+
+```scala
+object Solution {
+ def generateMatrix(n: Int): Array[Array[Int]] = {
+ var res = Array.ofDim[Int](n, n) // 定义一个n*n的二维矩阵
+ var num = 1 // 标志当前到了哪个数字
+ var i = 0 // 横坐标
+ var j = 0 // 竖坐标
+
+ while (num <= n * n) {
+ // 向右:当j不越界,并且下一个要填的数字是空白时
+ while (j < n && res(i)(j) == 0) {
+ res(i)(j) = num // 当前坐标等于num
+ num += 1 // num++
+ j += 1 // 竖坐标+1
+ }
+ i += 1 // 下移一行
+ j -= 1 // 左移一列
+
+ // 剩下的都同上
+
+ // 向下
+ while (i < n && res(i)(j) == 0) {
+ res(i)(j) = num
+ num += 1
+ i += 1
+ }
+ i -= 1
+ j -= 1
+
+ // 向左
+ while (j >= 0 && res(i)(j) == 0) {
+ res(i)(j) = num
+ num += 1
+ j -= 1
+ }
+ i -= 1
+ j += 1
+
+ // 向上
+ while (i >= 0 && res(i)(j) == 0) {
+ res(i)(j) = num
+ num += 1
+ i -= 1
+ }
+ i += 1
+ j += 1
+ }
+ res
+ }
+}
+```
+### C#:
+
+```csharp
+public int[][] GenerateMatrix(int n)
+{
+ // 参考Carl的代码随想录里面C++的思路
+ // https://www.programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html#%E6%80%9D%E8%B7%AF
+ int startX = 0, startY = 0; // 定义每循环一个圈的起始位置
+ int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
+ int count = 1; // 用来给矩阵每个空格赋值
+ int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
+ int offset = 1;// 需要控制每一条边遍历的长度,每次循环右边界收缩一位
+
+ // 构建result二维数组
+ int[][] result = new int[n][];
+ for (int k = 0; k < n; k++)
+ {
+ result[k] = new int[n];
+ }
+
+ int i = 0, j = 0; // [i,j]
+ while (loop > 0)
+ {
+ i = startX;
+ j = startY;
+ // 四个For循环模拟转一圈
+ // 第一排,从左往右遍历,不取最右侧的值(左闭右开)
+ for (; j < n - offset; j++)
+ {
+ result[i][j] = count++;
+ }
+ // 右侧的第一列,从上往下遍历,不取最下面的值(左闭右开)
+ for (; i < n - offset; i++)
+ {
+ result[i][j] = count++;
+ }
+
+ // 最下面的第一行,从右往左遍历,不取最左侧的值(左闭右开)
+ for (; j > startY; j--)
+ {
+ result[i][j] = count++;
+ }
+
+ // 左侧第一列,从下往上遍历,不取最左侧的值(左闭右开)
+ for (; i > startX; i--)
+ {
+ result[i][j] = count++;
+ }
+ // 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
+ startX++;
+ startY++;
+
+ // offset 控制每一圈里每一条边遍历的长度
+ offset++;
+ loop--;
+ }
+ if (n % 2 == 1)
+ {
+ // n 为奇数
+ result[mid][mid] = count;
+ }
+ return result;
+}
+```
+
+### Ruby:
+```ruby
+def generate_matrix(n)
+ result = Array.new(n) { Array.new(n, 0) }
+ #循环次数
+ loop_times = 0
+ #步长
+ step = n - 1
+ val = 1
+
+
+ while loop_times < n / 2
+ #模拟从左向右
+ for i in 0..step - 1
+ #行数不变,列数变
+ result[loop_times][i+loop_times] = val
+ val += 1
+ end
+
+ #模拟从上到下
+ for i in 0..step - 1
+ #列数不变,行数变
+ result[i+loop_times][n-loop_times-1] = val
+ val += 1
+ end
+
+ #模拟从右到左
+ for i in 0..step - 1
+ #行数不变,列数变
+ result[n-loop_times-1][n-loop_times-i-1] = val
+ val += 1
+ end
+
+ #模拟从下到上
+ for i in 0..step - 1
+ #列数不变,行数变
+ result[n-loop_times-i-1][loop_times] = val
+ val += 1
+ end
+
+ loop_times += 1
+ step -= 2
+ end
+
+ #如果是奇数,则填充最后一个元素
+ result[n/2][n/2] = n**2 if n % 2
+
+ return result
+
+end
+```
------------------------
-
diff --git "a/problems/0062.\344\270\215\345\220\214\350\267\257\345\276\204.md" "b/problems/0062.\344\270\215\345\220\214\350\267\257\345\276\204.md"
old mode 100644
new mode 100755
index 4a9af12965..ac60767dce
--- "a/problems/0062.\344\270\215\345\220\214\350\267\257\345\276\204.md"
+++ "b/problems/0062.\344\270\215\345\220\214\350\267\257\345\276\204.md"
@@ -1,14 +1,14 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+
+
# 62.不同路径
-[力扣题目链接](https://leetcode-cn.com/problems/unique-paths/)
+[力扣题目链接](https://leetcode.cn/problems/unique-paths/)
-一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
+一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
@@ -16,33 +16,42 @@
示例 1:
-
+
* 输入:m = 3, n = 7
* 输出:28
示例 2:
+
* 输入:m = 2, n = 3
* 输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
+
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 3:
+
* 输入:m = 7, n = 3
* 输出:28
示例 4:
+
* 输入:m = 3, n = 3
* 输出:6
提示:
+
* 1 <= m, n <= 100
* 题目数据保证答案小于等于 2 * 10^9
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划中如何初始化很重要!| LeetCode:62.不同路径](https://www.bilibili.com/video/BV1ve4y1x7Eu/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
### 深搜
@@ -53,7 +62,7 @@
如图举例:
-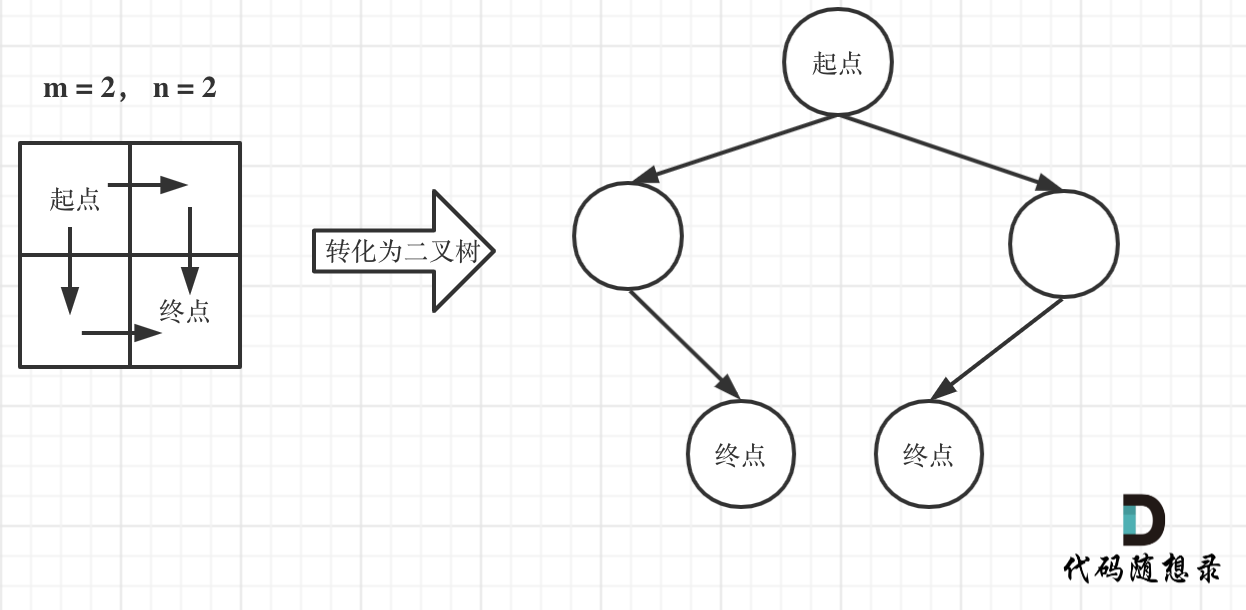
+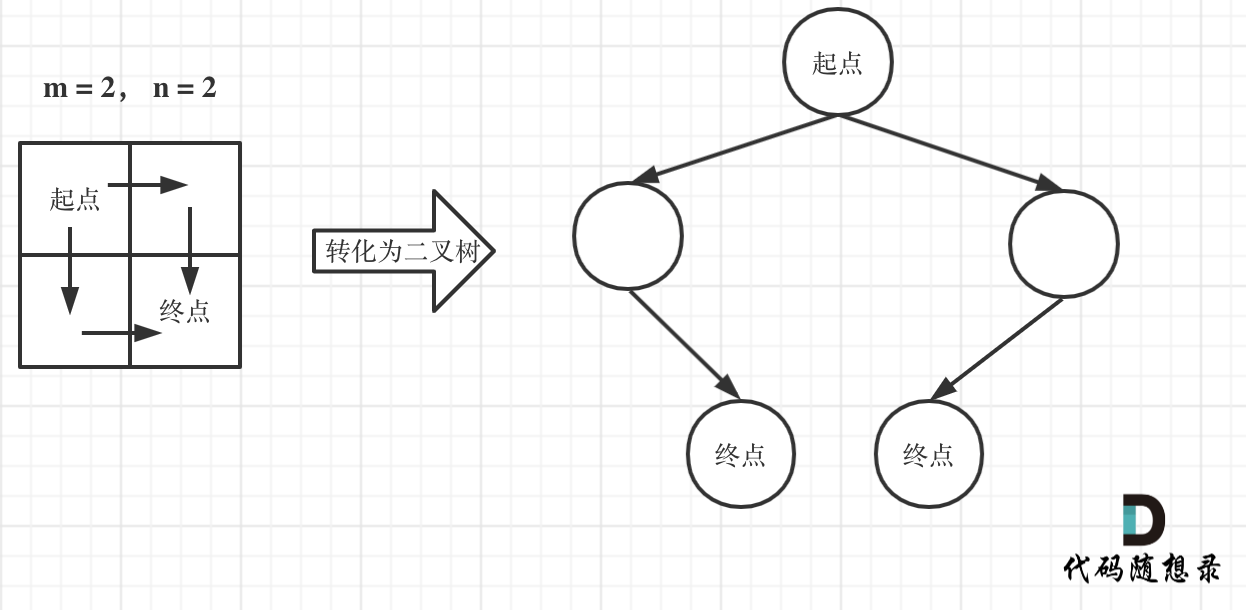
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
@@ -114,7 +123,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
4. 确定遍历顺序
-这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
+这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
@@ -122,7 +131,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
如图所示:
-
+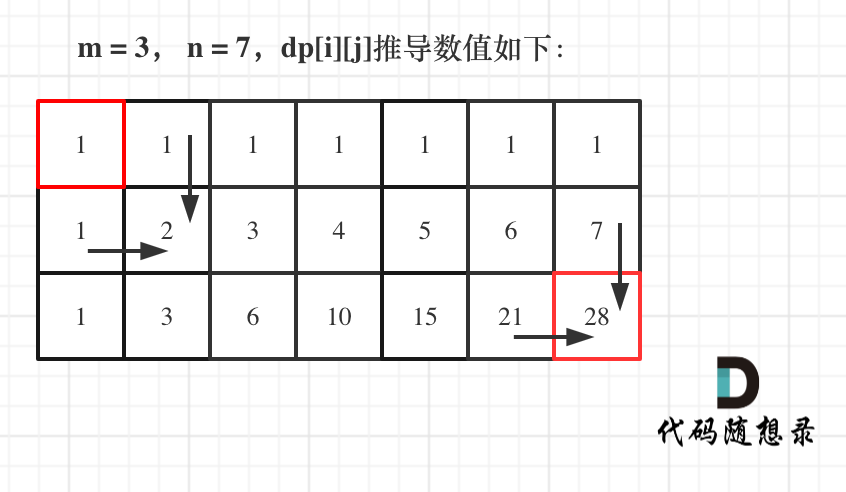
以上动规五部曲分析完毕,C++代码如下:
@@ -171,7 +180,7 @@ public:
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
-
+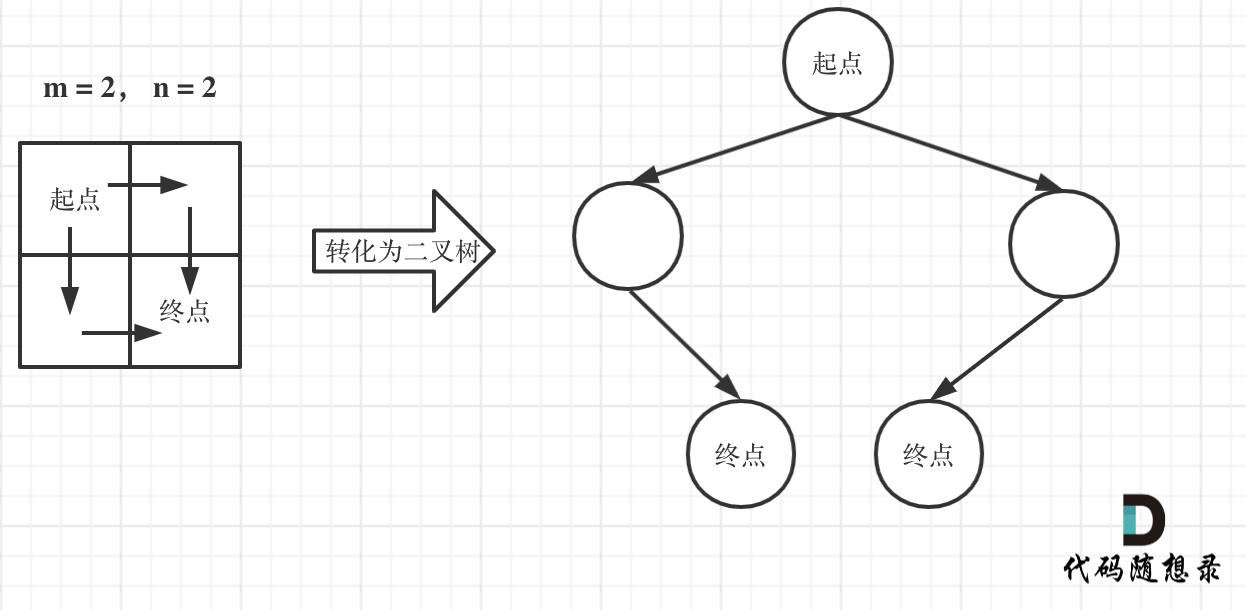
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
@@ -181,7 +190,7 @@ public:
那么答案,如图所示:
-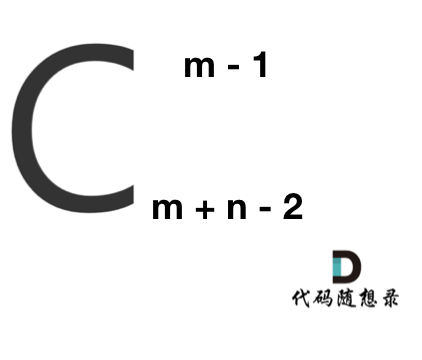
+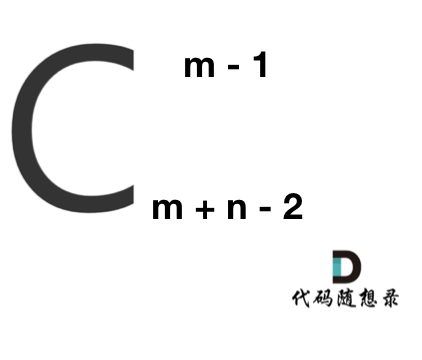
**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。
@@ -237,12 +246,12 @@ public:
然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!
-就酱,循序渐进学算法,认准「代码随想录」!
## 其他语言版本
-### Java
+### Java
+
```java
/**
* 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
@@ -273,20 +282,94 @@ public:
return dp[m-1][n-1];
}
-```
+```
+状态压缩
+```java
+class Solution {
+ public int uniquePaths(int m, int n) {
+ // 在二维dp数组中,当前值的计算只依赖正上方和正左方,因此可以压缩成一维数组。
+ int[] dp = new int[n];
+ // 初始化,第一行只能从正左方跳过来,所以只有一条路径。
+ Arrays.fill(dp, 1);
+ for (int i = 1; i < m; i ++) {
+ // 第一列也只有一条路,不用迭代,所以从第二列开始
+ for (int j = 1; j < n; j ++) {
+ dp[j] += dp[j - 1]; // dp[j] = dp[j] (正上方)+ dp[j - 1] (正左方)
+ }
+ }
+ return dp[n - 1];
+ }
+}
+```
+
+### Python
+递归
+```python
+class Solution:
+ def uniquePaths(self, m: int, n: int) -> int:
+ if m == 1 or n == 1:
+ return 1
+ return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)
-### Python
+```
+动态规划(版本一)
```python
-class Solution: # 动态规划
+class Solution:
def uniquePaths(self, m: int, n: int) -> int:
- dp = [[1 for i in range(n)] for j in range(m)]
+ # 创建一个二维列表用于存储唯一路径数
+ dp = [[0] * n for _ in range(m)]
+
+ # 设置第一行和第一列的基本情况
+ for i in range(m):
+ dp[i][0] = 1
+ for j in range(n):
+ dp[0][j] = 1
+
+ # 计算每个单元格的唯一路径数
for i in range(1, m):
for j in range(1, n):
- dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
+
+ # 返回右下角单元格的唯一路径数
return dp[m - 1][n - 1]
+
```
+动态规划(版本二)
+```python
+class Solution:
+ def uniquePaths(self, m: int, n: int) -> int:
+ # 创建一个一维列表用于存储每列的唯一路径数
+ dp = [1] * n
+
+ # 计算每个单元格的唯一路径数
+ for j in range(1, m):
+ for i in range(1, n):
+ dp[i] += dp[i - 1]
+
+ # 返回右下角单元格的唯一路径数
+ return dp[n - 1]
+```
+数论
+```python
+class Solution:
+ def uniquePaths(self, m: int, n: int) -> int:
+ numerator = 1 # 分子
+ denominator = m - 1 # 分母
+ count = m - 1 # 计数器,表示剩余需要计算的乘积项个数
+ t = m + n - 2 # 初始乘积项
+ while count > 0:
+ numerator *= t # 计算乘积项的分子部分
+ t -= 1 # 递减乘积项
+ while denominator != 0 and numerator % denominator == 0:
+ numerator //= denominator # 约简分子
+ denominator -= 1 # 递减分母
+ count -= 1 # 计数器减1,继续下一项的计算
+ return numerator # 返回最终的唯一路径数
+
+```
+### Go
-### Go
+动态规划
```Go
func uniquePaths(m int, n int) int {
dp := make([][]int, m)
@@ -306,19 +389,40 @@ func uniquePaths(m int, n int) int {
}
```
-### Javascript
+数论方法
+```Go
+func uniquePaths(m int, n int) int {
+ numerator := 1
+ denominator := m - 1
+ count := m - 1
+ t := m + n - 2
+ for count > 0 {
+ numerator *= t
+ t--
+ for denominator != 0 && numerator % denominator == 0 {
+ numerator /= denominator
+ denominator--
+ }
+ count--
+ }
+ return numerator
+}
+```
+
+### JavaScript
+
```Javascript
var uniquePaths = function(m, n) {
const dp = Array(m).fill().map(item => Array(n))
-
+
for (let i = 0; i < m; ++i) {
dp[i][0] = 1
}
-
+
for (let i = 0; i < n; ++i) {
dp[0][i] = 1
}
-
+
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
@@ -327,7 +431,9 @@ var uniquePaths = function(m, n) {
return dp[m - 1][n - 1]
};
```
+
>版本二:直接将dp数值值初始化为1
+
```javascript
/**
* @param {number} m
@@ -347,7 +453,52 @@ var uniquePaths = function(m, n) {
};
```
+### TypeScript
+
+```typescript
+function uniquePaths(m: number, n: number): number {
+ /**
+ dp[i][j]: 到达(i, j)的路径数
+ dp[0][*]: 1;
+ dp[*][0]: 1;
+ ...
+ dp[i][j]: dp[i - 1][j] + dp[i][j - 1];
+ */
+ const dp: number[][] = new Array(m).fill(0).map(_ => []);
+ for (let i = 0; i < m; i++) {
+ dp[i][0] = 1;
+ }
+ for (let i = 0; i < n; i++) {
+ dp[0][i] = 1;
+ }
+ for (let i = 1; i < m; i++) {
+ for (let j = 1; j < n; j++) {
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ }
+ }
+ return dp[m - 1][n - 1];
+};
+```
+
+### Rust
+
+```Rust
+impl Solution {
+ pub fn unique_paths(m: i32, n: i32) -> i32 {
+ let (m, n) = (m as usize, n as usize);
+ let mut dp = vec![vec![1; n]; m];
+ for i in 1..m {
+ for j in 1..n {
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ }
+ }
+ dp[m - 1][n - 1]
+ }
+}
+```
+
### C
+
```c
//初始化dp数组
int **initDP(int m, int n) {
@@ -359,9 +510,9 @@ int **initDP(int m, int n) {
}
//从0,0到i,0只有一种走法,所以dp[i][0]都是1,同理dp[0][j]也是1
- for(i = 0; i < m; ++i)
+ for(i = 0; i < m; ++i)
dp[i][0] = 1;
- for(j = 0; j < n; ++j)
+ for(j = 0; j < n; ++j)
dp[0][j] = 1;
return dp;
}
@@ -384,5 +535,82 @@ int uniquePaths(int m, int n){
}
```
------------------------
-
+滚动数组解法:
+
+```c
+int uniquePaths(int m, int n){
+ int i, j;
+
+ // 初始化dp数组
+ int *dp = (int*)malloc(sizeof(int) * n);
+ for (i = 0; i < n; ++i)
+ dp[i] = 1;
+
+ for (j = 1; j < m; ++j) {
+ for (i = 1; i < n; ++i) {
+ // dp[i]为二维数组解法中dp[i-1][j]。dp[i-1]为二维数组解法中dp[i][j-1]
+ dp[i] += dp[i - 1];
+ }
+ }
+ return dp[n - 1];
+}
+```
+
+### Scala
+
+```scala
+object Solution {
+ def uniquePaths(m: Int, n: Int): Int = {
+ var dp = Array.ofDim[Int](m, n)
+ for (i <- 0 until m) dp(i)(0) = 1
+ for (j <- 1 until n) dp(0)(j) = 1
+ for (i <- 1 until m; j <- 1 until n) {
+ dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1)
+ }
+ dp(m - 1)(n - 1)
+ }
+}
+```
+
+### c#
+```csharp
+// 二维数组
+public class Solution
+{
+ public int UniquePaths(int m, int n)
+ {
+ int[,] dp = new int[m, n];
+ for (int i = 0; i < m; i++) dp[i, 0] = 1;
+ for (int j = 0; j < n; j++) dp[0, j] = 1;
+ for (int i = 1; i < m; i++)
+ {
+ for (int j = 1; j < n; j++)
+ {
+ dp[i, j] = dp[i - 1, j] + dp[i, j - 1];
+ }
+ }
+ return dp[m - 1, n - 1];
+ }
+}
+```
+
+```csharp
+// 一维数组
+public class Solution
+{
+ public int UniquePaths(int m, int n)
+ {
+ int[] dp = new int[n];
+ for (int i = 0; i < n; i++)
+ dp[i] = 1;
+ for (int i = 1; i < m; i++)
+ for (int j = 1; j < n; j++)
+ dp[j] += dp[j - 1];
+ return dp[n - 1];
+ }
+}
+```
+
+
+
+
diff --git "a/problems/0063.\344\270\215\345\220\214\350\267\257\345\276\204II.md" "b/problems/0063.\344\270\215\345\220\214\350\267\257\345\276\204II.md"
old mode 100644
new mode 100755
index c71cf79649..f39afe8455
--- "a/problems/0063.\344\270\215\345\220\214\350\267\257\345\276\204II.md"
+++ "b/problems/0063.\344\270\215\345\220\214\350\267\257\345\276\204II.md"
@@ -1,12 +1,12 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+
+
# 63. 不同路径 II
-[力扣题目链接](https://leetcode-cn.com/problems/unique-paths-ii/)
+[力扣题目链接](https://leetcode.cn/problems/unique-paths-ii/)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
@@ -14,35 +14,40 @@
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
-
+
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
-
+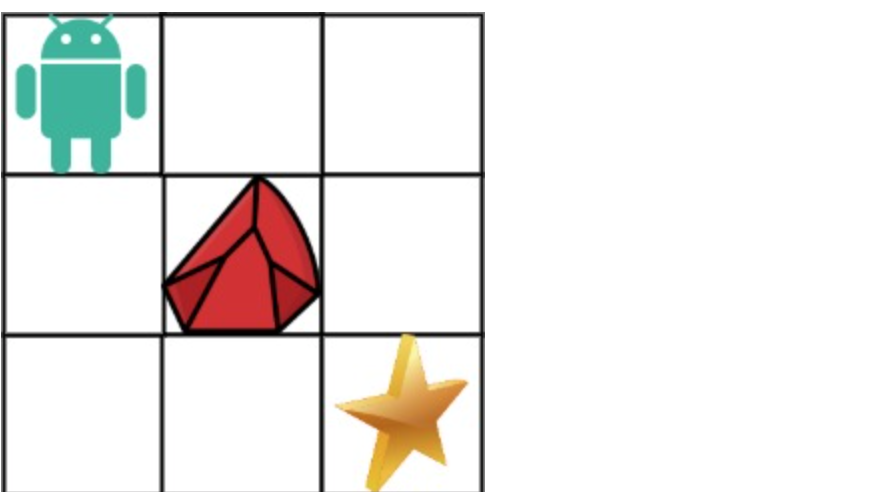
* 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
* 输出:2
-解释:
+ 解释:
* 3x3 网格的正中间有一个障碍物。
* 从左上角到右下角一共有 2 条不同的路径:
- 1. 向右 -> 向右 -> 向下 -> 向下
- 2. 向下 -> 向下 -> 向右 -> 向右
+ 1. 向右 -> 向右 -> 向下 -> 向下
+ 2. 向下 -> 向下 -> 向右 -> 向右
示例 2:
-
+
* 输入:obstacleGrid = [[0,1],[0,0]]
* 输出:1
提示:
-* m == obstacleGrid.length
-* n == obstacleGrid[i].length
+
+* m == obstacleGrid.length
+* n == obstacleGrid[i].length
* 1 <= m, n <= 100
* obstacleGrid[i][j] 为 0 或 1
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划,这次遇到障碍了| LeetCode:63. 不同路径 II](https://www.bilibili.com/video/BV1Ld4y1k7c6/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
+
## 思路
@@ -66,7 +71,7 @@ dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路
所以代码为:
-```
+```cpp
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
@@ -76,7 +81,7 @@ if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i
在[62.不同路径](https://programmercarl.com/0062.不同路径.html)不同路径中我们给出如下的初始化:
-```
+```cpp
vector> dp(m, vector(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
@@ -88,7 +93,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
如图:
-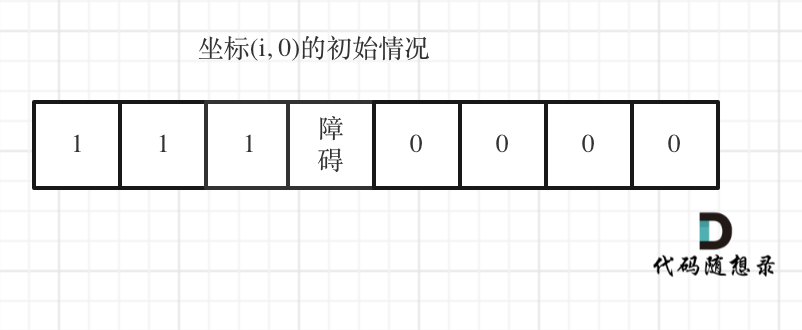
+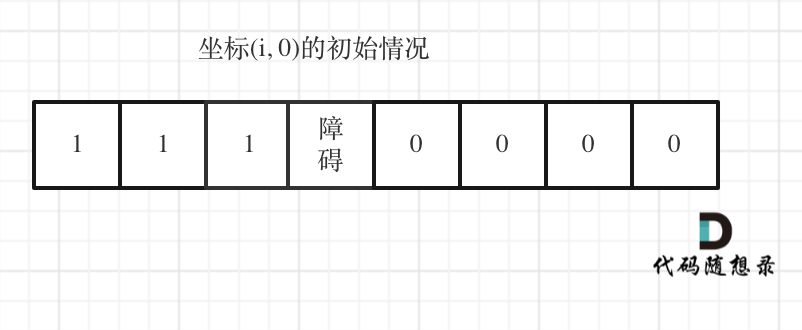
下标(0, j)的初始化情况同理。
@@ -122,13 +127,13 @@ for (int i = 1; i < m; i++) {
拿示例1来举例如题:
-
+
对应的dp table 如图:
-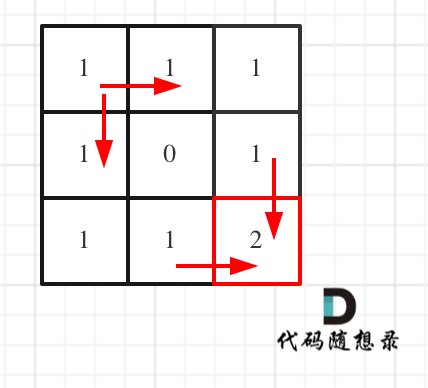
+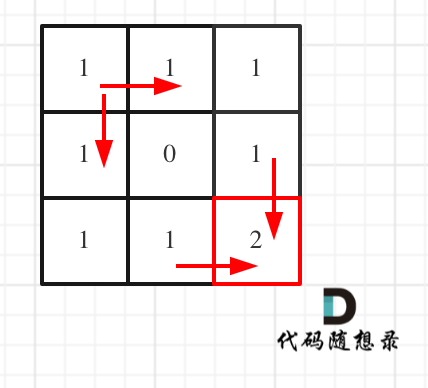
-如果这个图看不同,建议在理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
+如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应C++代码如下:
@@ -138,6 +143,8 @@ public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
+ if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0
+ return 0;
vector> dp(m, vector(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
@@ -157,6 +164,7 @@ public:
同样我们给出空间优化版本:
+
```CPP
class Solution {
public:
@@ -184,8 +192,8 @@ public:
};
```
-* 时间复杂度:$O(n × m)$,n、m 分别为obstacleGrid 长度和宽度
-* 空间复杂度:$O(m)$
+* 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
+* 空间复杂度:O(m)
## 总结
@@ -198,107 +206,237 @@ public:
也有一些小细节,例如:初始化的部分,很容易忽略了障碍之后应该都是0的情况。
-就酱,「代码随想录」值得推荐给身边学算法的同学朋友们,关注后都会发现相见恨晚!
## 其他语言版本
-### Java
+### Java
```java
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
- int n = obstacleGrid.length, m = obstacleGrid[0].length;
- int[][] dp = new int[n][m];
-
- for (int i = 0; i < m; i++) {
- if (obstacleGrid[0][i] == 1) break; //一旦遇到障碍,后续都到不了
- dp[0][i] = 1;
+ int m = obstacleGrid.length;
+ int n = obstacleGrid[0].length;
+ int[][] dp = new int[m][n];
+
+ //如果在起点或终点出现了障碍,直接返回0
+ if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
+ return 0;
}
- for (int i = 0; i < n; i++) {
- if (obstacleGrid[i][0] == 1) break; ////一旦遇到障碍,后续都到不了
- dp[i][0] = 1;
+
+ for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
+ dp[i][0] = 1;
}
- for (int i = 1; i < n; i++) {
- for (int j = 1; j < m; j++) {
- if (obstacleGrid[i][j] == 1) continue;
- dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
+ dp[0][j] = 1;
+ }
+
+ for (int i = 1; i < m; i++) {
+ for (int j = 1; j < n; j++) {
+ dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
- return dp[n - 1][m - 1];
+ return dp[m - 1][n - 1];
+ }
+}
+```
+
+```java
+// 空间优化版本
+class Solution {
+ public int uniquePathsWithObstacles(int[][] obstacleGrid) {
+ int m = obstacleGrid.length;
+ int n = obstacleGrid[0].length;
+ int[] dp = new int[n];
+
+ for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
+ dp[j] = 1;
+ }
+
+ for (int i = 1; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ if (obstacleGrid[i][j] == 1) {
+ dp[j] = 0;
+ } else if (j != 0) {
+ dp[j] += dp[j - 1];
+ }
+ }
+ }
+ return dp[n - 1];
}
}
```
### Python
+动态规划(版本一)
+```python
+class Solution:
+ def uniquePathsWithObstacles(self, obstacleGrid):
+ m = len(obstacleGrid)
+ n = len(obstacleGrid[0])
+ if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
+ return 0
+ dp = [[0] * n for _ in range(m)]
+ for i in range(m):
+ if obstacleGrid[i][0] == 0: # 遇到障碍物时,直接退出循环,后面默认都是0
+ dp[i][0] = 1
+ else:
+ break
+ for j in range(n):
+ if obstacleGrid[0][j] == 0:
+ dp[0][j] = 1
+ else:
+ break
+ for i in range(1, m):
+ for j in range(1, n):
+ if obstacleGrid[i][j] == 1:
+ continue
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
+ return dp[m - 1][n - 1]
+```
+动态规划(版本二)
```python
class Solution:
- def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
- # 构造一个DP table
- row = len(obstacleGrid)
- col = len(obstacleGrid[0])
- dp = [[0 for _ in range(col)] for _ in range(row)]
-
- dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
- if dp[0][0] == 0: return 0 # 如果第一个格子就是障碍,return 0
- # 第一行
- for i in range(1, col):
- if obstacleGrid[0][i] != 1:
- dp[0][i] = dp[0][i-1]
-
- # 第一列
- for i in range(1, row):
- if obstacleGrid[i][0] != 1:
- dp[i][0] = dp[i-1][0]
- print(dp)
-
- for i in range(1, row):
- for j in range(1, col):
- if obstacleGrid[i][j] != 1:
- dp[i][j] = dp[i-1][j] + dp[i][j-1]
- return dp[-1][-1]
+ def uniquePathsWithObstacles(self, obstacleGrid):
+ m = len(obstacleGrid) # 网格的行数
+ n = len(obstacleGrid[0]) # 网格的列数
+
+ if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
+ # 如果起点或终点有障碍物,直接返回0
+ return 0
+
+ dp = [[0] * n for _ in range(m)] # 创建一个二维列表用于存储路径数
+
+ # 设置起点的路径数为1
+ dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0
+
+ # 计算第一列的路径数
+ for i in range(1, m):
+ if obstacleGrid[i][0] == 0:
+ dp[i][0] = dp[i - 1][0]
+
+ # 计算第一行的路径数
+ for j in range(1, n):
+ if obstacleGrid[0][j] == 0:
+ dp[0][j] = dp[0][j - 1]
+
+ # 计算其他位置的路径数
+ for i in range(1, m):
+ for j in range(1, n):
+ if obstacleGrid[i][j] == 1:
+ continue
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
+
+ return dp[m - 1][n - 1] # 返回终点的路径数
+
+
```
+动态规划(版本三)
```python
class Solution:
- """
- 使用一维dp数组
- """
+ def uniquePathsWithObstacles(self, obstacleGrid):
+ if obstacleGrid[0][0] == 1:
+ return 0
+
+ dp = [0] * len(obstacleGrid[0]) # 创建一个一维列表用于存储路径数
+
+ # 初始化第一行的路径数
+ for j in range(len(dp)):
+ if obstacleGrid[0][j] == 1:
+ dp[j] = 0
+ elif j == 0:
+ dp[j] = 1
+ else:
+ dp[j] = dp[j - 1]
+
+ # 计算其他行的路径数
+ for i in range(1, len(obstacleGrid)):
+ for j in range(len(dp)):
+ if obstacleGrid[i][j] == 1:
+ dp[j] = 0
+ elif j != 0:
+ dp[j] = dp[j] + dp[j - 1]
+
+ return dp[-1] # 返回最后一个元素,即终点的路径数
- def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
- m, n = len(obstacleGrid), len(obstacleGrid[0])
+```
+动态规划(版本四)
- # 初始化dp数组
- # 该数组缓存当前行
- curr = [0] * n
+```python
+class Solution:
+ def uniquePathsWithObstacles(self, obstacleGrid):
+ if obstacleGrid[0][0] == 1:
+ return 0
+
+ m, n = len(obstacleGrid), len(obstacleGrid[0])
+
+ dp = [0] * n # 创建一个一维列表用于存储路径数
+
+ # 初始化第一行的路径数
for j in range(n):
if obstacleGrid[0][j] == 1:
break
- curr[j] = 1
-
- for i in range(1, m): # 从第二行开始
- for j in range(n): # 从第一列开始,因为第一列可能有障碍物
- # 有障碍物处无法通行,状态就设成0
+ dp[j] = 1
+
+ # 计算其他行的路径数
+ for i in range(1, m):
+ if obstacleGrid[i][0] == 1:
+ dp[0] = 0
+ for j in range(1, n):
if obstacleGrid[i][j] == 1:
- curr[j] = 0
- elif j > 0:
- # 等价于
- # dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
- curr[j] = curr[j] + curr[j - 1]
- # 隐含的状态更新
- # dp[i][0] = dp[i - 1][0]
+ dp[j] = 0
+ else:
+ dp[j] += dp[j - 1]
- return curr[n - 1]
+ return dp[-1] # 返回最后一个元素,即终点的路径数
+
```
+动态规划(版本五)
+
+```python
+class Solution:
+ def uniquePathsWithObstacles(self, obstacleGrid):
+ if obstacleGrid[0][0] == 1:
+ return 0
+
+ m, n = len(obstacleGrid), len(obstacleGrid[0])
+
+ dp = [0] * n # 创建一个一维列表用于存储路径数
+
+ # 初始化第一行的路径数
+ for j in range(n):
+ if obstacleGrid[0][j] == 1:
+ break
+ dp[j] = 1
+
+ # 计算其他行的路径数
+ for i in range(1, m):
+ if obstacleGrid[i][0] == 1:
+ dp[0] = 0
+ for j in range(1, n):
+ if obstacleGrid[i][j] == 1:
+ dp[j] = 0
+ continue
+
+ dp[j] += dp[j - 1]
+
+ return dp[-1] # 返回最后一个元素,即终点的路径数
+
+```
### Go
```go
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
m, n := len(obstacleGrid), len(obstacleGrid[0])
+ //如果在起点或终点出现了障碍,直接返回0
+ if obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1 {
+ return 0
+ }
// 定义一个dp数组
dp := make([][]int, m)
for i, _ := range dp {
@@ -323,36 +461,179 @@ func uniquePathsWithObstacles(obstacleGrid [][]int) int {
}
return dp[m-1][n-1]
}
-
-
```
-### Javascript
+### JavaScript
+
```Javascript
var uniquePathsWithObstacles = function(obstacleGrid) {
const m = obstacleGrid.length
const n = obstacleGrid[0].length
const dp = Array(m).fill().map(item => Array(n).fill(0))
-
+
for (let i = 0; i < m && obstacleGrid[i][0] === 0; ++i) {
dp[i][0] = 1
}
-
+
for (let i = 0; i < n && obstacleGrid[0][i] === 0; ++i) {
dp[0][i] = 1
}
-
+
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = obstacleGrid[i][j] === 1 ? 0 : dp[i - 1][j] + dp[i][j - 1]
}
}
-
+
return dp[m - 1][n - 1]
};
+
+// 版本二:内存优化,直接以原数组为dp数组
+var uniquePathsWithObstacles = function(obstacleGrid) {
+ const m = obstacleGrid.length;
+ const n = obstacleGrid[0].length;
+ for (let i = 0; i < m; i++) {
+ for (let j = 0; j < n; j++) {
+ if (obstacleGrid[i][j] === 0) {
+ // 不是障碍物
+ if (i === 0) {
+ // 取左边的值
+ obstacleGrid[i][j] = obstacleGrid[i][j - 1] ?? 1;
+ } else if (j === 0) {
+ // 取上边的值
+ obstacleGrid[i][j] = obstacleGrid[i - 1]?.[j] ?? 1;
+ } else {
+ // 取左边和上边的和
+ obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
+ }
+ } else {
+ // 如果是障碍物,则路径为0
+ obstacleGrid[i][j] = 0;
+ }
+ }
+ }
+ return obstacleGrid[m - 1][n - 1];
+};
```
-C
+
+
+### TypeScript
+
+```typescript
+function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
+ /**
+ dp[i][j]: 到达(i, j)的路径数
+ dp[0][*]: 用u表示第一个障碍物下标,则u之前为1,u之后(含u)为0
+ dp[*][0]: 同上
+ ...
+ dp[i][j]: obstacleGrid[i][j] === 1 ? 0 : dp[i-1][j] + dp[i][j-1];
+ */
+ const m: number = obstacleGrid.length;
+ const n: number = obstacleGrid[0].length;
+ const dp: number[][] = new Array(m).fill(0).map(_ => new Array(n).fill(0));
+ for (let i = 0; i < m && obstacleGrid[i][0] === 0; i++) {
+ dp[i][0] = 1;
+ }
+ for (let i = 0; i < n && obstacleGrid[0][i] === 0; i++) {
+ dp[0][i] = 1;
+ }
+ for (let i = 1; i < m; i++) {
+ for (let j = 1; j < n; j++) {
+ if (obstacleGrid[i][j] === 1) continue;
+ dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
+ }
+ }
+ return dp[m - 1][n - 1];
+};
+```
+
+// 版本二: dp改為使用一維陣列,從終點開始遍歷
+```typescript
+function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
+ const m = obstacleGrid.length;
+ const n = obstacleGrid[0].length;
+
+ const dp: number[] = new Array(n).fill(0);
+ dp[n - 1] = 1;
+
+ // 由下而上,右而左進行遍歷
+ for (let i = m - 1; i >= 0; i--) {
+ for (let j = n - 1; j >= 0; j--) {
+ if (obstacleGrid[i][j] === 1) dp[j] = 0;
+ else dp[j] = dp[j] + (dp[j + 1] || 0);
+ }
+ }
+
+ return dp[0];
+};
+```
+
+### Rust
+
+```Rust
+impl Solution {
+ pub fn unique_paths_with_obstacles(obstacle_grid: Vec>) -> i32 {
+ let m: usize = obstacle_grid.len();
+ let n: usize = obstacle_grid[0].len();
+ if obstacle_grid[0][0] == 1 || obstacle_grid[m-1][n-1] == 1 {
+ return 0;
+ }
+ let mut dp = vec![vec![0; n]; m];
+ for i in 0..m {
+ if obstacle_grid[i][0] == 1 {
+ break;
+ }
+ else { dp[i][0] = 1; }
+ }
+ for j in 0..n {
+ if obstacle_grid[0][j] == 1 {
+ break;
+ }
+ else { dp[0][j] = 1; }
+ }
+ for i in 1..m {
+ for j in 1..n {
+ if obstacle_grid[i][j] == 1 {
+ continue;
+ }
+ dp[i][j] = dp[i-1][j] + dp[i][j-1];
+ }
+ }
+ dp[m-1][n-1]
+ }
+}
+```
+
+空间优化:
+
+```rust
+impl Solution {
+ pub fn unique_paths_with_obstacles(obstacle_grid: Vec>) -> i32 {
+ let mut dp = vec![0; obstacle_grid[0].len()];
+ for (i, &v) in obstacle_grid[0].iter().enumerate() {
+ if v == 0 {
+ dp[i] = 1;
+ } else {
+ break;
+ }
+ }
+ for rows in obstacle_grid.iter().skip(1) {
+ for j in 0..rows.len() {
+ if rows[j] == 1 {
+ dp[j] = 0;
+ } else if j != 0 {
+ dp[j] += dp[j - 1];
+ }
+ }
+ }
+ dp.pop().unwrap()
+ }
+}
+```
+
+### C
+
```c
//初始化dp数组
int **initDP(int m, int n, int** obstacleGrid) {
@@ -407,5 +688,94 @@ int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obst
}
```
------------------------
-
+空间优化版本:
+
+```c
+int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize){
+ int m = obstacleGridSize;
+ int n = obstacleGridColSize[0];
+ int *dp = (int*)malloc(sizeof(int) * n);
+ int i, j;
+
+ // 初始化dp为第一行起始状态。
+ for (j = 0; j < n; ++j) {
+ if (obstacleGrid[0][j] == 1)
+ dp[j] = 0;
+ else if (j == 0)
+ dp[j] = 1;
+ else
+ dp[j] = dp[j - 1];
+ }
+
+ for (i = 1; i < m; ++i) {
+ for (j = 0; j < n; ++j) {
+ if (obstacleGrid[i][j] == 1)
+ dp[j] = 0;
+ // 若j为0,dp[j]表示最左边一列,无需改动
+ // 此处dp[j],dp[j-1]等同于二维dp中的dp[i-1][j]和dp[i][j-1]
+ else if (j != 0)
+ dp[j] += dp[j - 1];
+ }
+ }
+
+ return dp[n - 1];
+}
+```
+
+### Scala
+
+```scala
+object Solution {
+ import scala.util.control.Breaks._
+ def uniquePathsWithObstacles(obstacleGrid: Array[Array[Int]]): Int = {
+ var (m, n) = (obstacleGrid.length, obstacleGrid(0).length)
+ var dp = Array.ofDim[Int](m, n)
+
+ // 比如break、continue这些流程控制需要使用breakable
+ breakable(
+ for (i <- 0 until m) {
+ if (obstacleGrid(i)(0) != 1) dp(i)(0) = 1
+ else break()
+ }
+ )
+ breakable(
+ for (j <- 0 until n) {
+ if (obstacleGrid(0)(j) != 1) dp(0)(j) = 1
+ else break()
+ }
+ )
+
+ for (i <- 1 until m; j <- 1 until n; if obstacleGrid(i)(j) != 1) {
+ dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1)
+ }
+
+ dp(m - 1)(n - 1)
+ }
+}
+```
+### C#
+```csharp
+public class Solution
+{
+ public int UniquePathsWithObstacles(int[][] obstacleGrid)
+ {
+ int m = obstacleGrid.Length;
+ int n = obstacleGrid[0].Length;
+ int[,] dp = new int[m, n];
+ if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
+ for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i, 0] = 1;
+ for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0, j] = 1;
+ for (int i = 1; i < m; i++)
+ {
+ for (int j = 1; j < n; j++)
+ {
+ if (obstacleGrid[i][j] == 1) continue;
+ dp[i, j] = dp[i - 1, j] + dp[i, j - 1];
+ }
+ }
+ return dp[m - 1, n - 1];
+ }
+}
+```
+
+
diff --git "a/problems/0070.\347\210\254\346\245\274\346\242\257.md" "b/problems/0070.\347\210\254\346\245\274\346\242\257.md"
old mode 100644
new mode 100755
index da19ea0ec1..316fbd4f39
--- "a/problems/0070.\347\210\254\346\245\274\346\242\257.md"
+++ "b/problems/0070.\347\210\254\346\245\274\346\242\257.md"
@@ -1,11 +1,10 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
# 70. 爬楼梯
-[力扣题目链接](https://leetcode-cn.com/problems/climbing-stairs/)
+
+[力扣题目链接](https://leetcode.cn/problems/climbing-stairs/)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
@@ -28,6 +27,10 @@
* 1 阶 + 2 阶
* 2 阶 + 1 阶
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透动态规划-爬楼梯|LeetCode:70.爬楼梯)](https://www.bilibili.com/video/BV17h411h7UH),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
+
## 思路
@@ -49,7 +52,7 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
2. 确定递推公式
-如果可以推出dp[i]呢?
+如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
@@ -67,9 +70,9 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
3. dp数组如何初始化
-在回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]中方法。
+再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
-那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但都基本是直接奔着答案去解释的。
+那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层,也有一种方法,什么都不做也就是一种方法即:dp[0] = 1,相当于直接站在楼顶。
@@ -87,7 +90,7 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
-所以我的原则是:不考虑dp[0]如果初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
+所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4. 确定遍历顺序
@@ -97,7 +100,8 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
举例当n为5的时候,dp table(dp数组)应该是这样的
-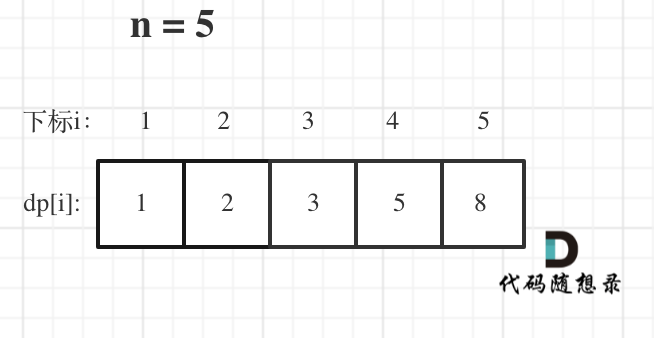
+
+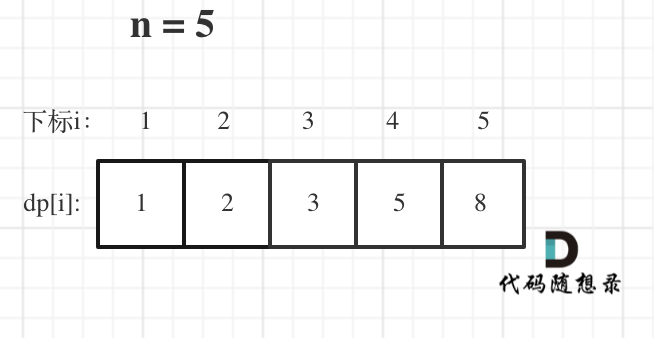
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
@@ -124,8 +128,8 @@ public:
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(n)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(n)
当然依然也可以,优化一下空间复杂度,代码如下:
@@ -148,8 +152,8 @@ public:
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,**但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化**。
@@ -159,9 +163,12 @@ public:
这道题目还可以继续深化,就是一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。
-这又有难度了,这其实是一个完全背包问题,但力扣上没有这种题目,所以后续我在讲解背包问题的时候,今天这道题还会拿从背包问题的角度上来再讲一遍。
+这又有难度了,这其实是一个完全背包问题,但力扣上没有这种题目,大家可以去卡码网去做一下 [57. 爬楼梯](https://kamacoder.com/problempage.php?pid=1067)
-这里我先给出我的实现代码:
+
+所以后续我在讲解背包问题的时候,今天这道题还会从背包问题的角度上来再讲一遍。 如果想提前看一下,可以看这篇:[70.爬楼梯完全背包版本](https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html)
+
+这里我先给出本题的代码:
```CPP
class Solution {
@@ -181,7 +188,7 @@ public:
代码中m表示最多可以爬m个台阶。
-**以上代码不能运行哈,我主要是为了体现只要把m换成2,粘过去,就可以AC爬楼梯这道题,不信你就粘一下试试,哈哈**。
+**以上代码不能运行哈,我主要是为了体现只要把m换成2,粘过去,就可以AC爬楼梯这道题,不信你就粘一下试试**。
**此时我就发现一个绝佳的大厂面试题**,第一道题就是单纯的爬楼梯,然后看候选人的代码实现,如果把dp[0]的定义成1了,就可以发难了,为什么dp[0]一定要初始化为1,此时可能候选人就要强行给dp[0]应该是1找各种理由。那这就是一个考察点了,对dp[i]的定义理解的不深入。
@@ -190,7 +197,7 @@ public:
这一连套问下来,候选人算法能力如何,面试官心里就有数了。
-**其实大厂面试最喜欢问题的就是这种简单题,然后慢慢变化,在小细节上考察候选人**。
+**其实大厂面试最喜欢的问题就是这种简单题,然后慢慢变化,在小细节上考察候选人**。
@@ -206,29 +213,11 @@ public:
所以不要轻视简单题,那种凭感觉就刷过去了,其实和没掌握区别不大,只有掌握方法论并说清一二三,才能触类旁通,举一反三哈!
-就酱,循序渐进学算法,认准「代码随想录」!
-
## 其他语言版本
-### Java
-```Java
-class Solution {
- public int climbStairs(int n) {
- // 跟斐波那契数列一样
- if(n <= 2) return n;
- int a = 1, b = 2, sum = 0;
-
- for(int i = 3; i <= n; i++){
- sum = a + b;
- a = b;
- b = sum;
- }
- return b;
- }
-}
-```
+### Java
```java
// 常规方式
@@ -241,61 +230,102 @@ public int climbStairs(int n) {
}
return dp[n];
}
+```
+
+```Java
// 用变量记录代替数组
-public int climbStairs(int n) {
- int a = 0, b = 1, c = 0; // 默认需要1次
- for (int i = 1; i <= n; i++) {
- c = a + b; // f(i - 1) + f(n - 2)
- a = b; // 记录上一轮的值
- b = c; // 向后步进1个数
+class Solution {
+ public int climbStairs(int n) {
+ if(n <= 2) return n;
+ int a = 1, b = 2, sum = 0;
+
+ for(int i = 3; i <= n; i++){
+ sum = a + b; // f(i - 1) + f(i - 2)
+ a = b; // 记录f(i - 1),即下一轮的f(i - 2)
+ b = sum; // 记录f(i),即下一轮的f(i - 1)
+ }
+ return b;
}
- return c;
}
```
### Python
-
+动态规划(版本一)
```python
# 空间复杂度为O(n)版本
class Solution:
def climbStairs(self, n: int) -> int:
- # dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
- dp=[0]*(n+1)
- dp[0]=1
- dp[1]=1
- for i in range(2,n+1):
- dp[i]=dp[i-1]+dp[i-2]
+ if n <= 1:
+ return n
+
+ dp = [0] * (n + 1)
+ dp[1] = 1
+ dp[2] = 2
+
+ for i in range(3, n + 1):
+ dp[i] = dp[i - 1] + dp[i - 2]
+
return dp[n]
+
+```
+动态规划(版本二)
+```python
+
+# 空间复杂度为O(3)版本
+class Solution:
+ def climbStairs(self, n: int) -> int:
+ if n <= 1:
+ return n
+ dp = [0] * 3
+ dp[1] = 1
+ dp[2] = 2
+
+ for i in range(3, n + 1):
+ total = dp[1] + dp[2]
+ dp[1] = dp[2]
+ dp[2] = total
+
+ return dp[2]
+
+```
+动态规划(版本三)
+```python
+
# 空间复杂度为O(1)版本
class Solution:
def climbStairs(self, n: int) -> int:
- dp=[0]*(n+1)
- dp[0]=1
- dp[1]=1
- for i in range(2,n+1):
- tmp=dp[0]+dp[1]
- dp[0]=dp[1]
- dp[1]=tmp
- return dp[1]
-```
+ if n <= 1:
+ return n
+
+ prev1 = 1
+ prev2 = 2
+
+ for i in range(3, n + 1):
+ total = prev1 + prev2
+ prev1 = prev2
+ prev2 = total
+
+ return prev2
+
-### Go
+```
+### Go
```Go
func climbStairs(n int) int {
- if n==1{
+ if n == 1 {
return 1
}
- dp:=make([]int,n+1)
- dp[1]=1
- dp[2]=2
- for i:=3;i<=n;i++{
- dp[i]=dp[i-1]+dp[i-2]
+ dp := make([]int, n+1)
+ dp[1] = 1
+ dp[2] = 2
+ for i := 3; i <= n; i++ {
+ dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
```
-### Javascript
+### JavaScript
```Javascript
var climbStairs = function(n) {
// dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
@@ -308,7 +338,58 @@ var climbStairs = function(n) {
};
```
+### TypeScript
+
+> 爬2阶
+
+```typescript
+function climbStairs(n: number): number {
+ /**
+ dp[i]: i阶楼梯的方法种数
+ dp[1]: 1;
+ dp[2]: 2;
+ ...
+ dp[i]: dp[i - 1] + dp[i - 2];
+ */
+ const dp: number[] = [];
+ dp[1] = 1;
+ dp[2] = 2;
+ for (let i = 3; i <= n; i++) {
+ dp[i] = dp[i - 1] + dp[i - 2];
+ }
+ return dp[n];
+};
+```
+
+> 爬m阶
+
+```typescript
+function climbStairs(n: number): number {
+ /**
+ 一次可以爬m阶
+ dp[i]: i阶楼梯的方法种数
+ dp[1]: 1;
+ dp[2]: 2;
+ dp[3]: dp[2] + dp[1];
+ ...
+ dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; 从i-1加到max(i-m, 1)
+ */
+ const m: number = 2; // 本题m为2
+ const dp: number[] = new Array(n + 1).fill(0);
+ dp[1] = 1;
+ dp[2] = 2;
+ for (let i = 3; i <= n; i++) {
+ const end: number = Math.max(i - m, 1);
+ for (let j = i - 1; j >= end; j--) {
+ dp[i] += dp[j];
+ }
+ }
+ return dp[n];
+};
+```
+
### C
+
```c
int climbStairs(int n){
//若n<=2,返回n
@@ -350,6 +431,91 @@ int climbStairs(int n){
}
```
+### Scala
+
+```scala
+object Solution {
+ def climbStairs(n: Int): Int = {
+ if (n <= 2) return n
+ var dp = new Array[Int](n + 1)
+ dp(1) = 1
+ dp(2) = 2
+ for (i <- 3 to n) {
+ dp(i) = dp(i - 1) + dp(i - 2)
+ }
+ dp(n)
+ }
+}
+```
+
+优化空间复杂度:
+```scala
+object Solution {
+ def climbStairs(n: Int): Int = {
+ if (n <= 2) return n
+ var (a, b) = (1, 2)
+ for (i <- 3 to n) {
+ var tmp = a + b
+ a = b
+ b = tmp
+ }
+ b // 最终返回b
+ }
+}
+```
+
+### C#
+
+```csharp
+public class Solution {
+ public int ClimbStairs(int n) {
+ if(n<=2) return n;
+ int[] dp = new int[2] { 1, 2 };
+ for (int i = 3; i <= n; i++)
+ {
+ int temp = dp[0] + dp[1];
+ dp[0] = dp[1];
+ dp[1] = temp;
+ }
+ return dp[1];
+ }
+}
+```
+
+### Rust
+
+```rust
+impl Solution {
+ pub fn climb_stairs(n: i32) -> i32 {
+ if n <= 1 {
+ return n;
+ }
+ let (mut a, mut b, mut f) = (1, 1, 0);
+ for _ in 2..=n {
+ f = a + b;
+ a = b;
+ b = f;
+ }
+ f
+}
+```
+
+dp 数组
+
+```rust
+impl Solution {
+ pub fn climb_stairs(n: i32) -> i32 {
+ let n = n as usize;
+ let mut dp = vec![0; n + 1];
+ dp[0] = 1;
+ dp[1] = 1;
+ for i in 2..=n {
+ dp[i] = dp[i - 1] + dp[i - 2];
+ }
+ dp[n]
+ }
+}
+```
+
+
------------------------
-
diff --git "a/problems/0070.\347\210\254\346\245\274\346\242\257\345\256\214\345\205\250\350\203\214\345\214\205\347\211\210\346\234\254.md" "b/problems/0070.\347\210\254\346\245\274\346\242\257\345\256\214\345\205\250\350\203\214\345\214\205\347\211\210\346\234\254.md"
old mode 100644
new mode 100755
index 2286de2d1f..a5435ddd71
--- "a/problems/0070.\347\210\254\346\245\274\346\242\257\345\256\214\345\205\250\350\203\214\345\214\205\347\211\210\346\234\254.md"
+++ "b/problems/0070.\347\210\254\346\245\274\346\242\257\345\256\214\345\205\250\350\203\214\345\214\205\347\211\210\346\234\254.md"
@@ -1,46 +1,49 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
-# 动态规划:以前我没得选,现在我选择再爬一次!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。
+# 70. 爬楼梯(进阶版)
-**这次终于讲到了背包问题,我选择带录友们再爬一次楼梯!**
+[卡码网:57. 爬楼梯](https://kamacoder.com/problempage.php?pid=1067)
+
+假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
+
+每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
-## 70. 爬楼梯
+注意:给定 n 是一个正整数。
-[力扣题目链接](https://leetcode-cn.com/problems/climbing-stairs/)
+输入描述:输入共一行,包含两个正整数,分别表示n, m
-假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
+输出描述:输出一个整数,表示爬到楼顶的方法数。
-每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
+输入示例:3 2
-注意:给定 n 是一个正整数。
+输出示例:3
-示例 1:
-输入: 2
-输出: 2
-解释: 有两种方法可以爬到楼顶。
-1. 1 阶 + 1 阶
-2. 2 阶
+提示:
+
+当 m = 2,n = 3 时,n = 3 这表示一共有三个台阶,m = 2 代表你每次可以爬一个台阶或者两个台阶。
+
+此时你有三种方法可以爬到楼顶。
+
+* 1 阶 + 1 阶 + 1 阶段
+* 1 阶 + 2 阶
+* 2 阶 + 1 阶
-示例 2:
-输入: 3
-输出: 3
-解释: 有三种方法可以爬到楼顶。
-1. 1 阶 + 1 阶 + 1 阶
-2. 1 阶 + 2 阶
-3. 2 阶 + 1 阶
## 思路
-这道题目 我们在[动态规划:爬楼梯](https://programmercarl.com/0070.爬楼梯.html) 中已经讲过一次了,原题其实是一道简单动规的题目。
+之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。
-既然这么简单为什么还要讲呢,其实本题稍加改动就是一道面试好题。
+**这次终于讲到了背包问题,我选择带录友们再爬一次楼梯!**
+
+这道题目 我们在[动态规划:爬楼梯](https://programmercarl.com/0070.爬楼梯.html) 中已经讲过一次了,这次我又给本题加点料,力扣上没有原题,所以可以在卡码网[57. 爬楼梯](https://kamacoder.com/problempage.php?pid=1067)上来刷这道题目。
+
+我们之前做的 爬楼梯 是只能至多爬两个台阶。
+
+这次**改为:一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?**
-**改为:一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?**
+这又有难度了,这其实是一个完全背包问题。
1阶,2阶,.... m阶就是物品,楼顶就是背包。
@@ -87,9 +90,12 @@
以上分析完毕,C++代码如下:
```CPP
-class Solution {
-public:
- int climbStairs(int n) {
+#include
+#include
+using namespace std;
+int main() {
+ int n, m;
+ while (cin >> n >> m) {
vector dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) { // 遍历背包
@@ -97,12 +103,18 @@ public:
if (i - j >= 0) dp[i] += dp[i - j];
}
}
- return dp[n];
+ cout << dp[n] << endl;
}
-};
+}
```
-代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯可以AC的代码了。
+* 时间复杂度: O(n * m)
+* 空间复杂度: O(n)
+
+代码中m表示最多可以爬m个台阶,代码中把m改成2就是 力扣:70.爬楼梯的解题思路。
+
+**当然注意 力扣是 核心代码模式,卡码网是ACM模式**
+
## 总结
@@ -123,82 +135,118 @@ public:
## 其他语言版本
-
-Java:
-```java
-class Solution {
- public int climbStairs(int n) {
- int[] dp = new int[n + 1];
- int[] weight = {1,2};
- dp[0] = 1;
-
- for (int i = 0; i <= n; i++) {
- for (int j = 0; j < weight.length; j++) {
- if (i >= weight[j]) dp[i] += dp[i - weight[j]];
+### Java:
+
+```Java
+import java.util.Scanner;
+class climbStairs{
+ public static void main(String [] args){
+ Scanner sc = new Scanner(System.in);
+ int m, n;
+ while (sc.hasNextInt()) {
+ // 从键盘输入参数,中间用空格隔开
+ n = sc.nextInt();
+ m = sc.nextInt();
+
+ // 求排列问题,先遍历背包再遍历物品
+ int[] dp = new int[n + 1];
+ dp[0] = 1;
+ for (int j = 1; j <= n; j++) {
+ for (int i = 1; i <= m; i++) {
+ if (j - i >= 0) dp[j] += dp[j - i];
+ }
}
+ System.out.println(dp[n]);
}
-
- return dp[n];
}
}
```
-Python3:
-
-
-```python
-class Solution:
- def climbStairs(self, n: int) -> int:
- dp = [0]*(n + 1)
- dp[0] = 1
- m = 2
- # 遍历背包
- for j in range(n + 1):
- # 遍历物品
- for step in range(1, m + 1):
- if j >= step:
- dp[j] += dp[j - step]
- return dp[n]
+### Python3:
+```python3
+def climbing_stairs(n,m):
+ dp = [0]*(n+1) # 背包总容量
+ dp[0] = 1
+ # 排列题,注意循环顺序,背包在外物品在内
+ for j in range(1,n+1):
+ for i in range(1,m+1):
+ if j>=i:
+ dp[j] += dp[j-i] # 这里i就是重量而非index
+ return dp[n]
+
+if __name__ == '__main__':
+ n,m = list(map(int,input().split(' ')))
+ print(climbing_stairs(n,m))
```
-Go:
+### Go:
```go
-func climbStairs(n int) int {
- //定义
- dp := make([]int, n+1)
- //初始化
- dp[0] = 1
- // 本题物品只有两个1,2
- m := 2
- // 遍历顺序
- for j := 1; j <= n; j++ { //先遍历背包
- for i := 1; i <= m; i++ { //再遍历物品
- if j >= i {
- dp[j] += dp[j-i]
- }
- //fmt.Println(dp)
- }
- }
- return dp[n]
+package main
+
+import (
+ "bufio"
+ "fmt"
+ "os"
+ "strconv"
+ "strings"
+)
+
+func climbStairs(n int, m int) int {
+ dp := make([]int, n+1)
+ dp[0] = 1
+ for i := 1; i <= n; i++ {
+ for j := 1; j <= m; j++ {
+ if i-j >= 0 {
+ dp[i] += dp[i-j]
+ }
+ }
+ }
+ return dp[n]
+}
+
+func main() {
+ // 读取输入n,m
+ reader := bufio.NewReader(os.Stdin)
+ input, _ := reader.ReadString('\n')
+ input = strings.TrimSpace(input)
+ nv := strings.Split(input, " ")
+ n, _ := strconv.Atoi(nv[0])
+ m, _ := strconv.Atoi(nv[1])
+ result := climbStairs(n, m)
+ fmt.Println(result)
}
```
-JavaScript:
-```javascript
-var climbStairs = function(n) {
- const dp = new Array(n+1).fill(0);
- const weight = [1,2];
+### JavaScript:
+```javaScript
+var climbStairs = function (n) {
+ let dp = new Array(n + 1).fill(0);
+ dp[0] = 1;
+ // 排列题,注意循环顺序,背包在外物品在内
+ for (let j = 1; j <= n; j++) {//遍历背包
+ for (let i = 1; i <= 2; i++) {//遍历物品
+ if (j - i >= 0) dp[j] = dp[j] + dp[j - i];
+ }
+ }
+ return dp[n];
+}
+```
+
+### TypeScript:
+```typescript
+var climbStairs = function (n: number): number {
+ let dp: number[] = new Array(n + 1).fill(0);
dp[0] = 1;
- for(let i = 0; i <= n; i++){ //先遍历背包
- for(let j = 0; j < weight.length; j++){ // 再遍历物品
- if(i >= weight[j]) dp[i] += dp[i-weight[j]];
+ for (let j = 1; j <= n; j++) {//遍历背包
+ for (let i = 1; i <= 2; i++) {//遍历物品
+ if (j - i >= 0) dp[j] = dp[j] + dp[j - i];
}
}
return dp[n];
-};
+}
```
+### Rust:
+
------------------------
-
diff --git "a/problems/0072.\347\274\226\350\276\221\350\267\235\347\246\273.md" "b/problems/0072.\347\274\226\350\276\221\350\267\235\347\246\273.md"
old mode 100644
new mode 100755
index 3802c228d6..c4bcbb4338
--- "a/problems/0072.\347\274\226\350\276\221\350\267\235\347\246\273.md"
+++ "b/problems/0072.\347\274\226\350\276\221\350\267\235\347\246\273.md"
@@ -1,12 +1,10 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
-## 72. 编辑距离
+# 72. 编辑距离
-[力扣题目链接](https://leetcode-cn.com/problems/edit-distance/)
+[力扣题目链接](https://leetcode.cn/problems/edit-distance/)
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
@@ -16,30 +14,33 @@
* 删除一个字符
* 替换一个字符
-示例 1:
-输入:word1 = "horse", word2 = "ros"
-输出:3
-解释:
+* 示例 1:
+* 输入:word1 = "horse", word2 = "ros"
+* 输出:3
+* 解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
-示例 2:
-输入:word1 = "intention", word2 = "execution"
-输出:5
-解释:
+
+* 示例 2:
+* 输入:word1 = "intention", word2 = "execution"
+* 输出:5
+* 解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
-
提示:
* 0 <= word1.length, word2.length <= 500
* word1 和 word2 由小写英文字母组成
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划终极绝杀! LeetCode:72.编辑距离](https://www.bilibili.com/video/BV1qv4y1q78f/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
@@ -54,10 +55,11 @@ exection -> execution (插入 'u')
**dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]**。
-这里在强调一下:为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
+有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
-用i来表示也可以! 但我统一以下标i-1为结尾的字符串,在下面的递归公式中会容易理解一点。
+为什么这么定义我在 [718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html) 中做了详细的讲解。
+其实用i来表示也可以! 用i-1就是为了方便后面dp数组初始化的。
### 2. 确定递推公式
@@ -111,9 +113,13 @@ if (word1[i - 1] != word2[j - 1])
+-----+-----+
```
-操作三:替换元素,`word1`替换`word1[i - 1]`,使其与`word2[j - 1]`相同,此时不用增加元素,那么以下标`i-2`为结尾的`word1` 与 `j-2`为结尾的`word2`的最近编辑距离 加上一个替换元素的操作。
+操作三:替换元素,`word1`替换`word1[i - 1]`,使其与`word2[j - 1]`相同,此时不用增删加元素。
+
+可以回顾一下,`if (word1[i - 1] == word2[j - 1])`的时候我们的操作 是 `dp[i][j] = dp[i - 1][j - 1]` 对吧。
-即 `dp[i][j] = dp[i - 1][j - 1] + 1;`
+那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
+
+所以 `dp[i][j] = dp[i - 1][j - 1] + 1;`
综上,当 `if (word1[i - 1] != word2[j - 1])` 时取最小的,即:`dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;`
@@ -164,7 +170,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
-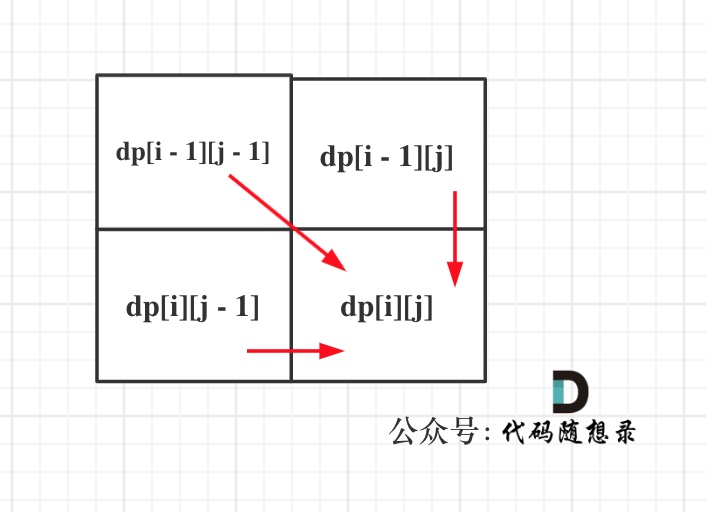
+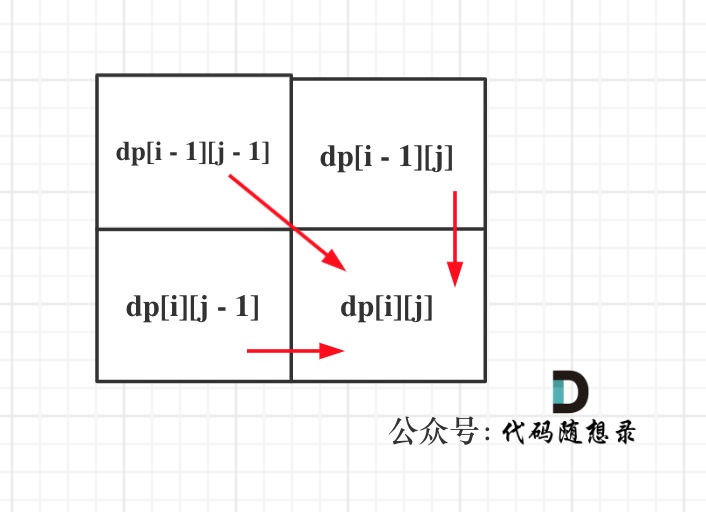
所以在dp矩阵中一定是从左到右从上到下去遍历。
@@ -188,7 +194,7 @@ for (int i = 1; i <= word1.size(); i++) {
以示例1为例,输入:`word1 = "horse", word2 = "ros"`为例,dp矩阵状态图如下:
-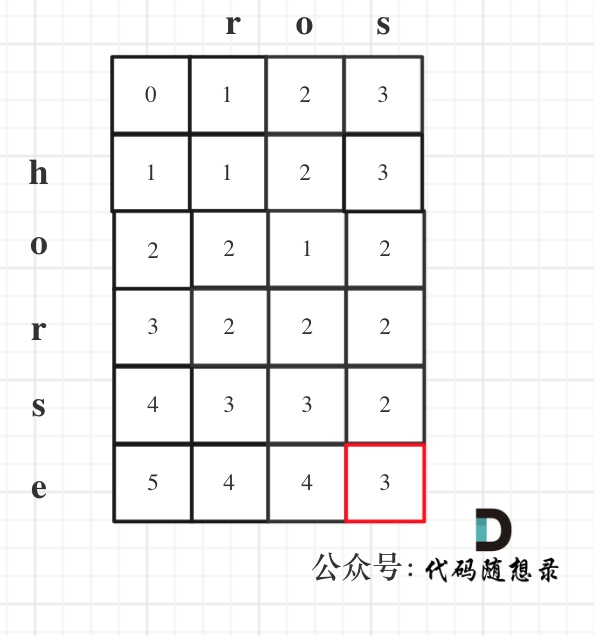
+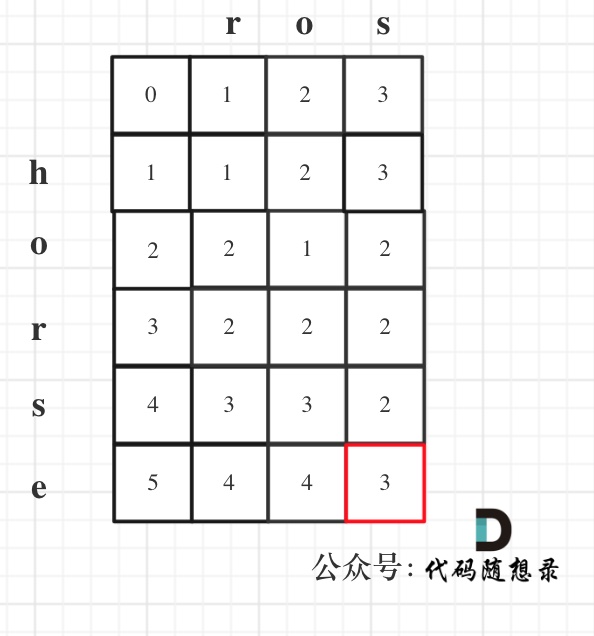
以上动规五部分析完毕,C++代码如下:
@@ -213,11 +219,15 @@ public:
}
};
```
+* 时间复杂度: O(n * m)
+* 空间复杂度: O(n * m)
+
+
## 其他语言版本
+### Java:
-Java:
```java
public int minDistance(String word1, String word2) {
int m = word1.length();
@@ -245,7 +255,8 @@ public int minDistance(String word1, String word2) {
}
```
-Python:
+### Python:
+
```python
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
@@ -263,7 +274,8 @@ class Solution:
return dp[-1][-1]
```
-Go:
+### Go:
+
```Go
func minDistance(word1 string, word2 string) int {
m, n := len(word1), len(word2)
@@ -299,8 +311,8 @@ func Min(args ...int) int {
}
```
+### JavaScript:
-Javascript:
```javascript
const minDistance = (word1, word2) => {
let dp = Array.from(Array(word1.length + 1), () => Array(word2.length+1).fill(0));
@@ -327,5 +339,124 @@ const minDistance = (word1, word2) => {
};
```
------------------------
-
+### TypeScript:
+
+```typescript
+function minDistance(word1: string, word2: string): number {
+ /**
+ dp[i][j]: word1前i个字符,word2前j个字符,最少操作数
+ dp[0][0]=0:表示word1前0个字符为'', word2前0个字符为''
+ */
+ const length1: number = word1.length,
+ length2: number = word2.length;
+ const dp: number[][] = new Array(length1 + 1).fill(0)
+ .map(_ => new Array(length2 + 1).fill(0));
+ for (let i = 0; i <= length1; i++) {
+ dp[i][0] = i;
+ }
+ for (let i = 0; i <= length2; i++) {
+ dp[0][i] = i;
+ }
+ for (let i = 1; i <= length1; i++) {
+ for (let j = 1; j <= length2; j++) {
+ if (word1[i - 1] === word2[j - 1]) {
+ dp[i][j] = dp[i - 1][j - 1];
+ } else {
+ dp[i][j] = Math.min(
+ dp[i - 1][j],
+ dp[i][j - 1],
+ dp[i - 1][j - 1]
+ ) + 1;
+ }
+ }
+ }
+ return dp[length1][length2];
+};
+```
+
+### C:
+
+
+```c
+int min(int num1, int num2, int num3) {
+ return num1 > num2 ? (num2 > num3 ? num3 : num2) : (num1 > num3 ? num3 : num1);
+}
+
+int minDistance(char * word1, char * word2){
+ int dp[strlen(word1)+1][strlen(word2)+1];
+ dp[0][0] = 0;
+ for (int i = 1; i <= strlen(word1); i++) dp[i][0] = i;
+ for (int i = 1; i <= strlen(word2); i++) dp[0][i] = i;
+
+ for (int i = 1; i <= strlen(word1); i++) {
+ for (int j = 1; j <= strlen(word2); j++) {
+ if (word1[i-1] == word2[j-1]) {
+ dp[i][j] = dp[i-1][j-1];
+ }
+ else {
+ dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1;
+ }
+ }
+ }
+ return dp[strlen(word1)][strlen(word2)];
+}
+```
+
+Rust:
+
+```rust
+impl Solution {
+ pub fn min_distance(word1: String, word2: String) -> i32 {
+ let mut dp = vec![vec![0; word2.len() + 1]; word1.len() + 1];
+ for i in 1..=word2.len() {
+ dp[0][i] = i;
+ }
+
+ for (j, v) in dp.iter_mut().enumerate().skip(1) {
+ v[0] = j;
+ }
+ for (i, char1) in word1.chars().enumerate() {
+ for (j, char2) in word2.chars().enumerate() {
+ if char1 == char2 {
+ dp[i + 1][j + 1] = dp[i][j];
+ continue;
+ }
+ dp[i + 1][j + 1] = dp[i][j + 1].min(dp[i + 1][j]).min(dp[i][j]) + 1;
+ }
+ }
+
+ dp[word1.len()][word2.len()] as i32
+ }
+}
+```
+
+> 一维 dp
+
+```rust
+impl Solution {
+ pub fn min_distance(word1: String, word2: String) -> i32 {
+ let mut dp = vec![0; word1.len() + 1];
+ for (i, v) in dp.iter_mut().enumerate().skip(1) {
+ *v = i;
+ }
+
+ for char2 in word2.chars() {
+ // 相当于 dp[i][0] 的初始化
+ let mut pre = dp[0];
+ dp[0] += 1; // j = 0, 将前 i 个字符变成空串的个数
+ for (j, char1) in word1.chars().enumerate() {
+ let temp = dp[j + 1];
+ if char1 == char2 {
+ dp[j + 1] = pre;
+ } else {
+ dp[j + 1] = dp[j + 1].min(dp[j]).min(pre) + 1;
+ }
+ pre = temp;
+ }
+ }
+
+ dp[word1.len()] as i32
+ }
+}
+```
+
diff --git "a/problems/0077.\347\273\204\345\220\210.md" "b/problems/0077.\347\273\204\345\220\210.md"
old mode 100644
new mode 100755
index 4560c5b7eb..4c9e97fd47
--- "a/problems/0077.\347\273\204\345\220\210.md"
+++ "b/problems/0077.\347\273\204\345\220\210.md"
@@ -1,40 +1,40 @@
-
-
-  -
-
-
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
+* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
+* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
+# 第77题. 组合
+[力扣题目链接](https://leetcode.cn/problems/combinations/ )
-# 第77题. 组合
+给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
-[力扣题目链接](https://leetcode-cn.com/problems/combinations/ )
+示例:
+输入: n = 4, k = 2
+输出:
+[
+ [2,4],
+ [3,4],
+ [2,3],
+ [1,2],
+ [1,3],
+ [1,4],
+]
-给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
+## 算法公开课
-示例:
-输入: n = 4, k = 2
-输出:
-[
- [2,4],
- [3,4],
- [2,3],
- [1,2],
- [1,3],
- [1,4],
-]
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透回溯算法-组合问题(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv),[组合问题的剪枝操作](https://www.bilibili.com/video/BV1wi4y157er),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
-也可以直接看我的B站视频:[带你学透回溯算法-组合问题(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv#reply3733925949)
-# 思路
+## 思路
-本题这是回溯法的经典题目。
+本题是回溯法的经典题目。
直接的解法当然是使用for循环,例如示例中k为2,很容易想到 用两个for循环,这样就可以输出 和示例中一样的结果。
代码如下:
+
```CPP
int n = 4;
for (int i = 1; i <= n; i++) {
@@ -62,7 +62,7 @@ for (int i = 1; i <= n; i++) {
**此时就会发现虽然想暴力搜索,但是用for循环嵌套连暴力都写不出来!**
-咋整?
+咋整?
回溯搜索法来了,虽然回溯法也是暴力,但至少能写出来,不像for循环嵌套k层让人绝望。
@@ -78,19 +78,19 @@ for (int i = 1; i <= n; i++) {
如果脑洞模拟回溯搜索的过程,绝对可以让人窒息,所以需要抽象图形结构来进一步理解。
-**我们在[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中说道回溯法解决的问题都可以抽象为树形结构(N叉树),用树形结构来理解回溯就容易多了**。
+**我们在[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中说到回溯法解决的问题都可以抽象为树形结构(N叉树),用树形结构来理解回溯就容易多了**。
那么我把组合问题抽象为如下树形结构:
-
+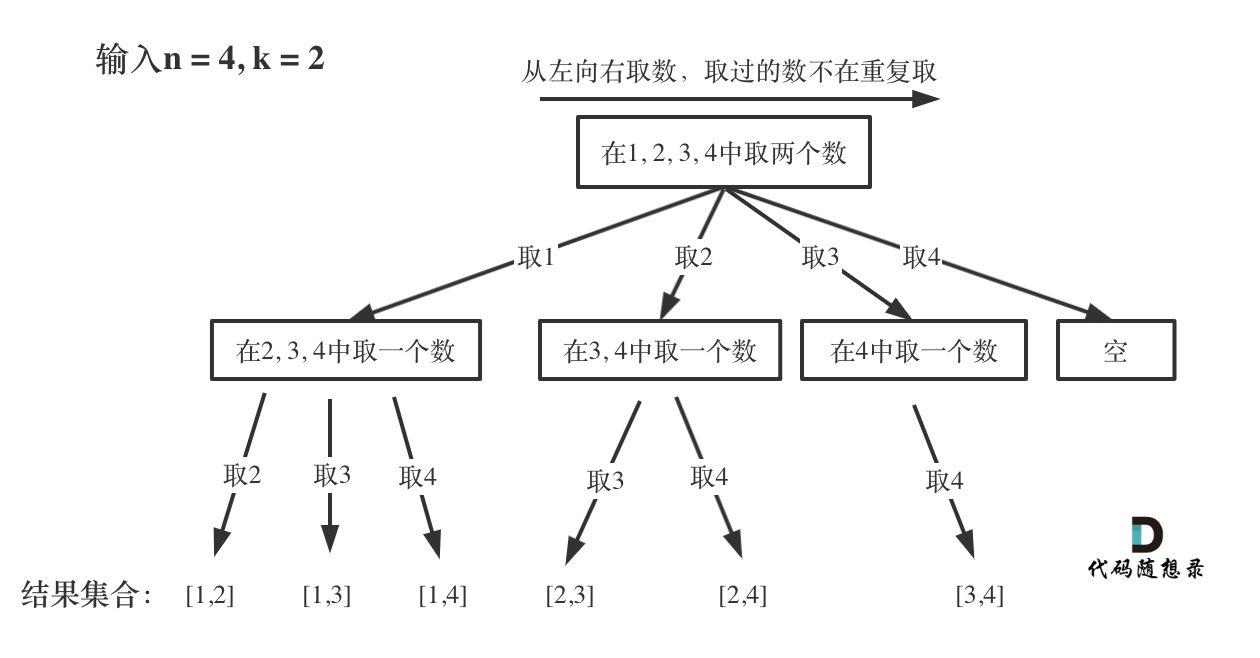
-可以看出这个棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不在重复取。
+可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
**每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围**。
-**图中可以发现n相当于树的宽度,k相当于树的深度**。
+**图中可以发现n相当于树的宽度,k相当于树的深度**。
那么如何在这个树上遍历,然后收集到我们要的结果集呢?
@@ -101,9 +101,9 @@ for (int i = 1; i <= n; i++) {
在[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中我们提到了回溯法三部曲,那么我们按照回溯法三部曲开始正式讲解代码了。
-## 回溯法三部曲
+### 回溯法三部曲
-* 递归函数的返回值以及参数
+* 递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
@@ -114,31 +114,31 @@ vector> result; // 存放符合条件结果的集合
vector path; // 用来存放符合条件结果
```
-其实不定义这两个全局遍历也是可以的,把这两个变量放进递归函数的参数里,但函数里参数太多影响可读性,所以我定义全局变量了。
+其实不定义这两个全局变量也是可以的,把这两个变量放进递归函数的参数里,但函数里参数太多影响可读性,所以我定义全局变量了。
-函数里一定有两个参数,既然是集合n里面取k的数,那么n和k是两个int型的参数。
+函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
-为什么要有这个startIndex呢?
+为什么要有这个startIndex呢?
-**每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex**。
+**建议在[77.组合视频讲解](https://www.bilibili.com/video/BV1ti4y1L7cv)中,07:36的时候开始听,startIndex 就是防止出现重复的组合**。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
-
+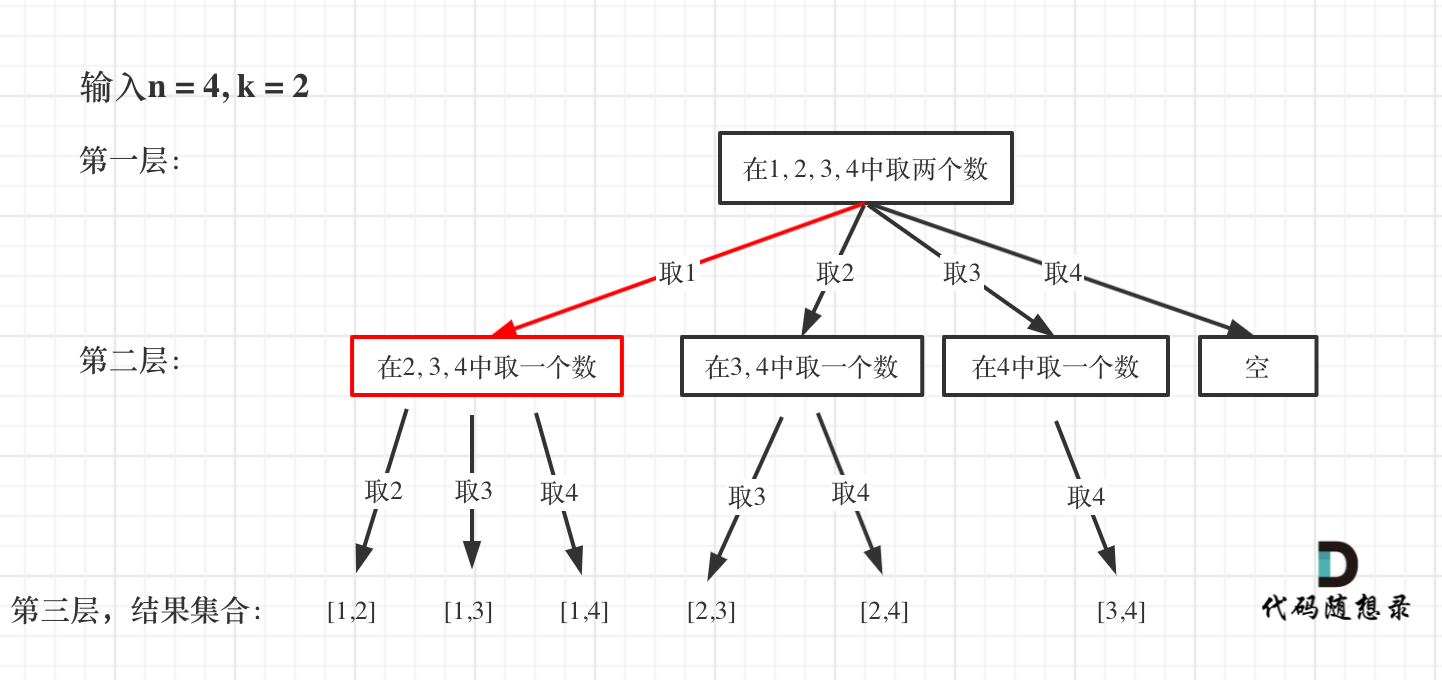
-所以需要startIndex来记录下一层递归,搜索的起始位置。
+所以需要startIndex来记录下一层递归,搜索的起始位置。
那么整体代码如下:
```cpp
vector> result; // 存放符合条件结果的集合
vector path; // 用来存放符合条件单一结果
-void backtracking(int n, int k, int startIndex)
+void backtracking(int n, int k, int startIndex)
```
-* 回溯函数终止条件
+* 回溯函数终止条件
什么时候到达所谓的叶子节点了呢?
@@ -146,7 +146,7 @@ path这个数组的大小如果达到k,说明我们找到了一个子集大小
如图红色部分:
-
+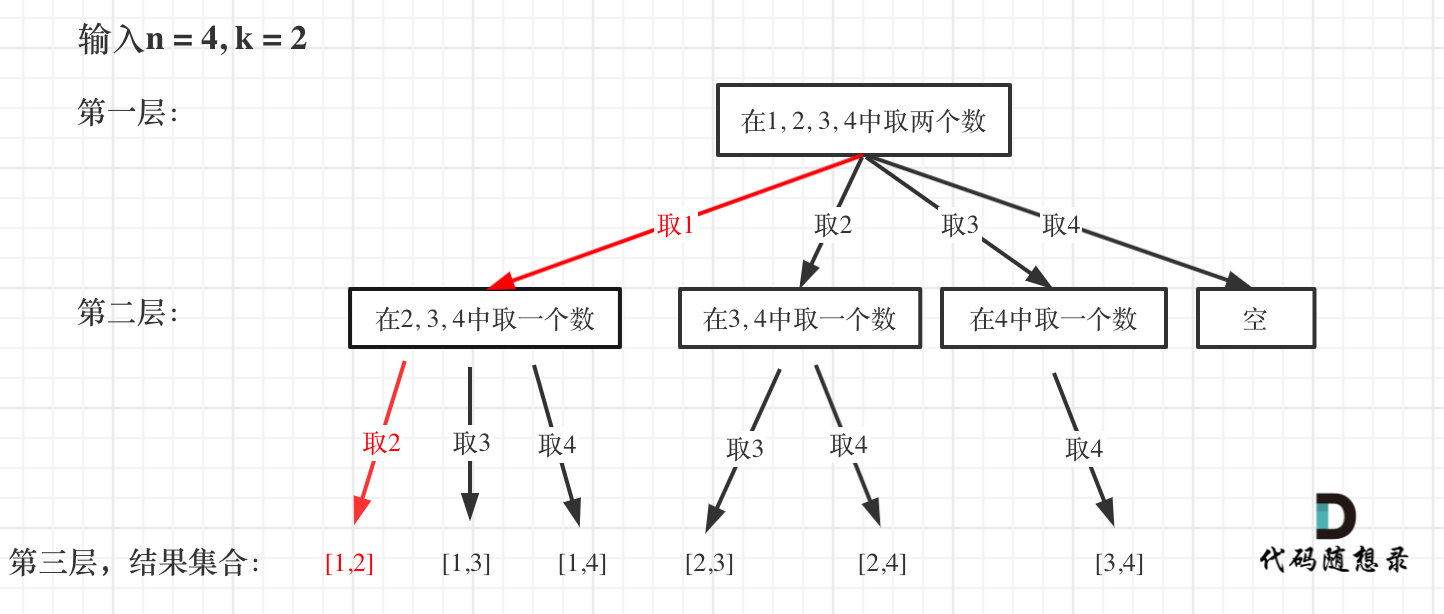
此时用result二维数组,把path保存起来,并终止本层递归。
@@ -159,21 +159,21 @@ if (path.size() == k) {
}
```
-* 单层搜索的过程
+* 单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
-
+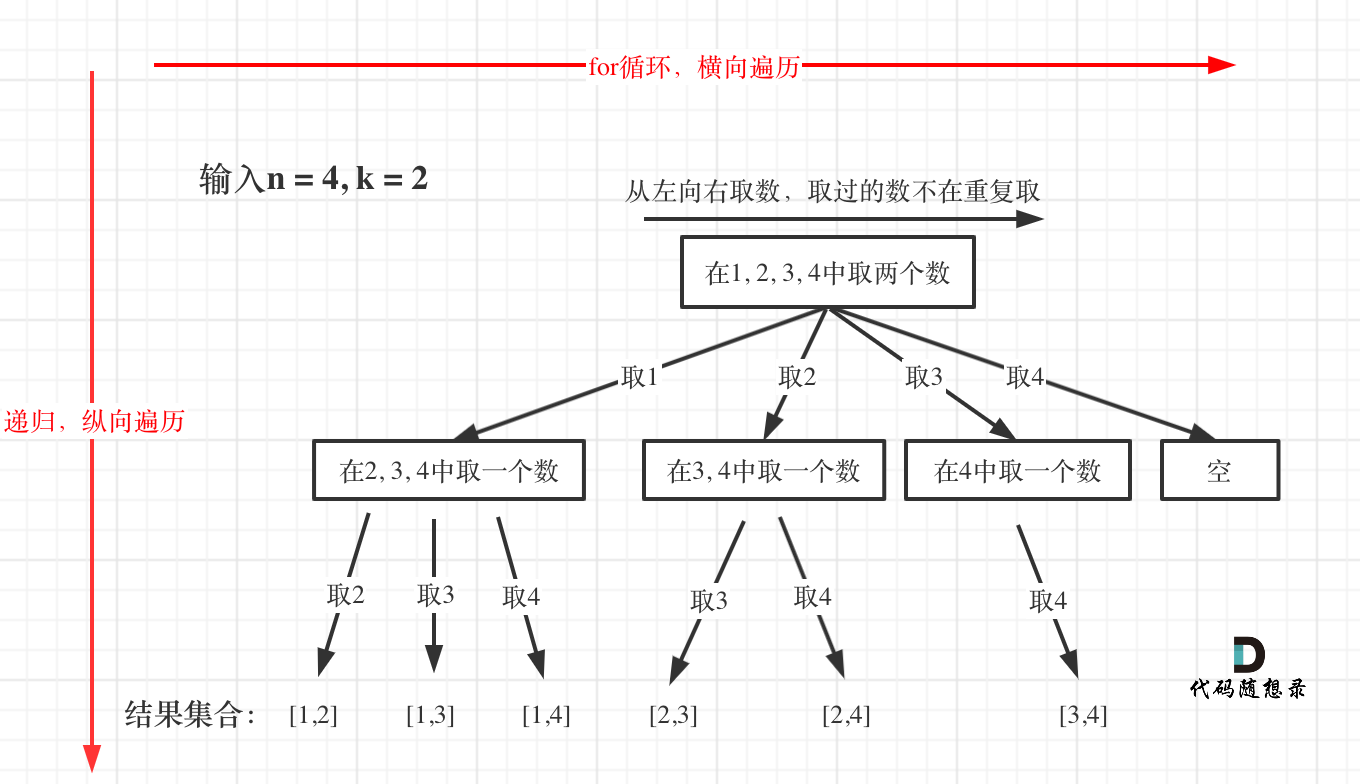
如此我们才遍历完图中的这棵树。
-for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
+for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
代码如下:
```CPP
for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
- path.push_back(i); // 处理节点
+ path.push_back(i); // 处理节点
backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始
path.pop_back(); // 回溯,撤销处理的节点
}
@@ -197,7 +197,7 @@ private:
return;
}
for (int i = startIndex; i <= n; i++) {
- path.push_back(i); // 处理节点
+ path.push_back(i); // 处理节点
backtracking(n, k, i + 1); // 递归
path.pop_back(); // 回溯,撤销处理的节点
}
@@ -211,10 +211,15 @@ public:
}
};
```
+* 时间复杂度: O(n * 2^n)
+* 空间复杂度: O(n)
-还记得我们在[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中给出的回溯法模板么?
+
+
+还记得我们在[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中给出的回溯法模板么?
如下:
+
```
void backtracking(参数) {
if (终止条件) {
@@ -230,19 +235,19 @@ void backtracking(参数) {
}
```
-**对比一下本题的代码,是不是发现有点像!** 所以有了这个模板,就有解题的大体方向,不至于毫无头绪。
+**对比一下本题的代码,是不是发现有点像!** 所以有了这个模板,就有解题的大体方向,不至于毫无头绪。
-# 总结
+## 总结
组合问题是回溯法解决的经典问题,我们开始的时候给大家列举一个很形象的例子,就是n为100,k为50的话,直接想法就需要50层for循环。
从而引出了回溯法就是解决这种k层for循环嵌套的问题。
-然后进一步把回溯法的搜索过程抽象为树形结构,可以直观的看出搜索的过程。
+然后进一步把回溯法的搜索过程抽象为树形结构,可以直观的看出搜索的过程。
接着用回溯法三部曲,逐步分析了函数参数、终止条件和单层搜索的过程。
-# 剪枝优化
+## 剪枝优化
我们说过,回溯法虽然是暴力搜索,但也有时候可以有点剪枝优化一下的。
@@ -262,7 +267,7 @@ for (int i = startIndex; i <= n; i++) {
这么说有点抽象,如图所示:
-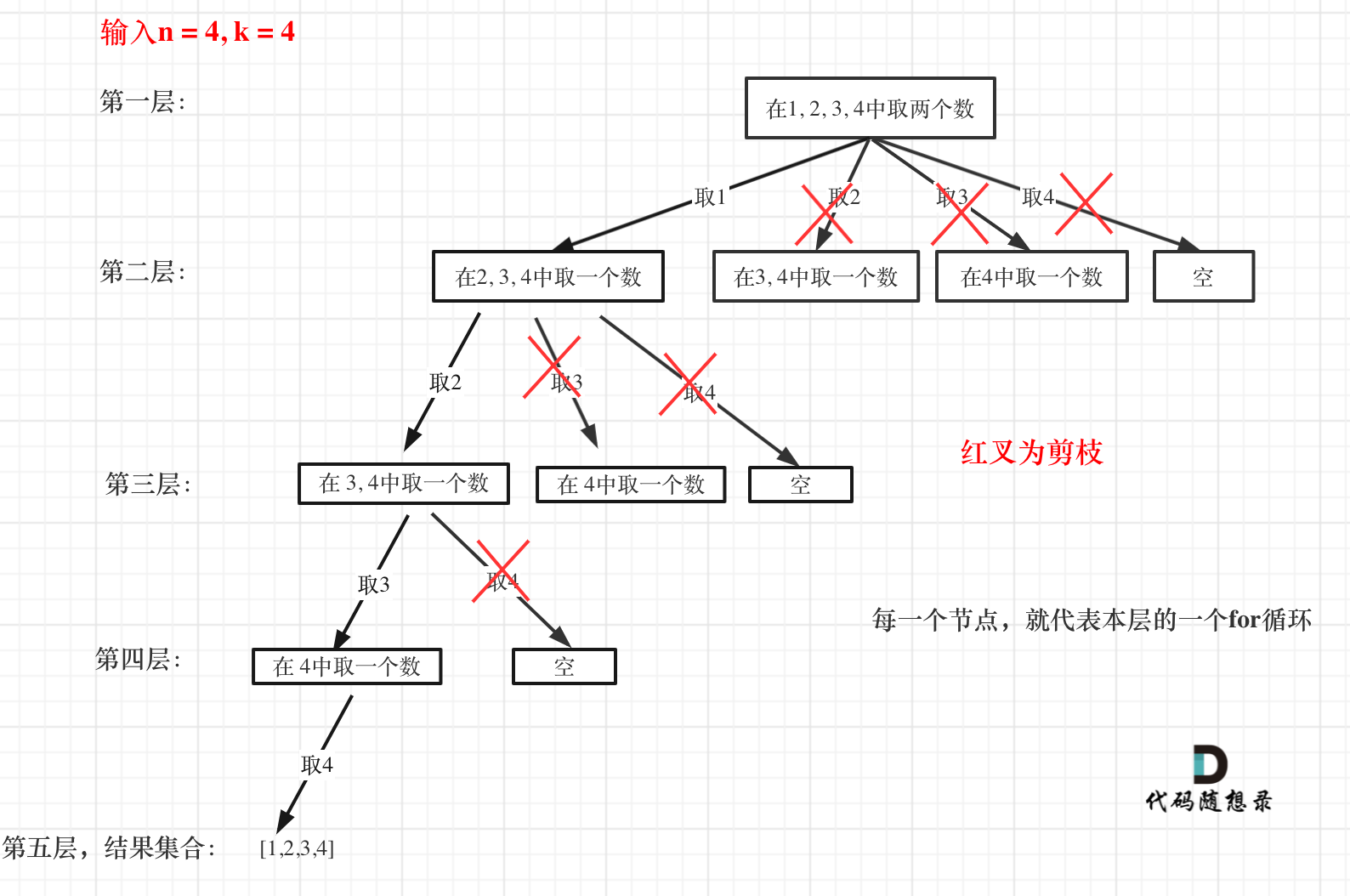
+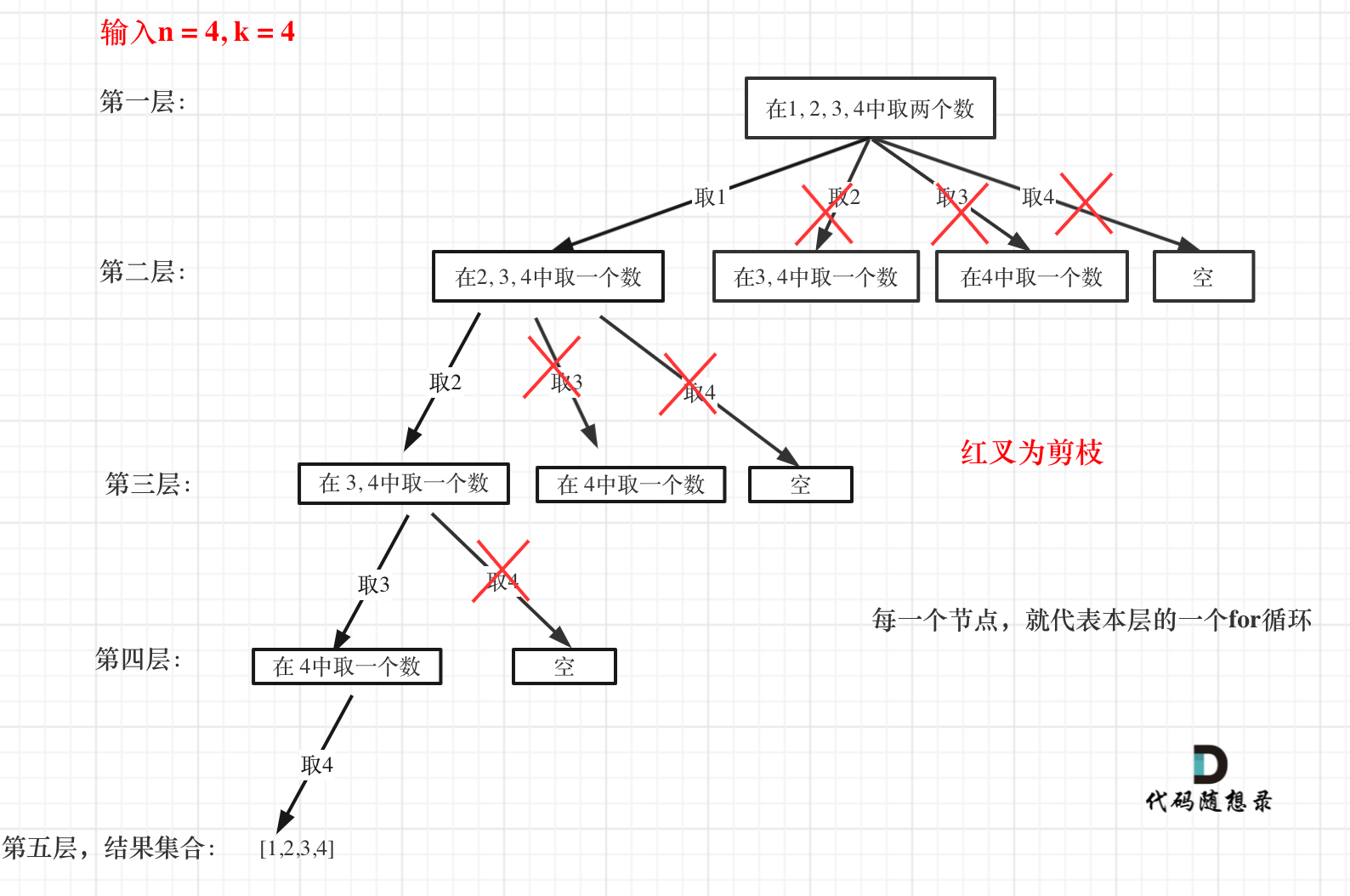
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
@@ -271,6 +276,7 @@ for (int i = startIndex; i <= n; i++) {
**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
注意代码中i,就是for循环里选择的起始位置。
+
```
for (int i = startIndex; i <= n; i++) {
```
@@ -324,7 +330,7 @@ public:
};
```
-# 剪枝总结
+## 剪枝总结
本篇我们准对求组合问题的回溯法代码做了剪枝优化,这个优化如果不画图的话,其实不好理解,也不好讲清楚。
@@ -332,12 +338,35 @@ public:
+## 其他语言版本
-# 其他语言版本
+### Java:
+未剪枝优化
+```java
+class Solution {
+ List> result= new ArrayList<>();
+ LinkedList path = new LinkedList<>();
+ public List> combine(int n, int k) {
+ backtracking(n,k,1);
+ return result;
+ }
-## Java:
+ public void backtracking(int n,int k,int startIndex){
+ if (path.size() == k){
+ result.add(new ArrayList<>(path));
+ return;
+ }
+ for (int i =startIndex;i<=n;i++){
+ path.add(i);
+ backtracking(n,k,i+1);
+ path.removeLast();
+ }
+ }
+}
+```
+剪枝优化:
```java
class Solution {
List> result = new ArrayList<>();
@@ -366,97 +395,133 @@ class Solution {
}
```
-Python2:
-```python
-class Solution(object):
- def combine(self, n, k):
- """
- :type n: int
- :type k: int
- :rtype: List[List[int]]
- """
- result = []
- path = []
- def backtracking(n, k, startidx):
- if len(path) == k:
- result.append(path[:])
- return
-
- # 剪枝, 最后k - len(path)个节点直接构造结果,无需递归
- last_startidx = n - (k - len(path)) + 1
- result.append(path + [idx for idx in range(last_startidx, n + 1)])
-
- for x in range(startidx, last_startidx):
- path.append(x)
- backtracking(n, k, x + 1) # 递归
- path.pop() # 回溯
-
- backtracking(n, k, 1)
- return result
-```
-
-## Python
+### Python
+未剪枝优化
```python
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
- res = []
- path = []
- def backtrack(n, k, StartIndex):
- if len(path) == k:
- res.append(path[:])
- return
- for i in range(StartIndex, n + 1):
- path.append(i)
- backtrack(n, k, i+1)
- path.pop()
- backtrack(n, k, 1)
- return res
+ result = [] # 存放结果集
+ self.backtracking(n, k, 1, [], result)
+ return result
+ def backtracking(self, n, k, startIndex, path, result):
+ if len(path) == k:
+ result.append(path[:])
+ return
+ for i in range(startIndex, n + 1): # 需要优化的地方
+ path.append(i) # 处理节点
+ self.backtracking(n, k, i + 1, path, result)
+ path.pop() # 回溯,撤销处理的节点
+
```
-剪枝:
+
+剪枝优化:
+
```python
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
- res=[] #存放符合条件结果的集合
- path=[] #用来存放符合条件结果
- def backtrack(n,k,startIndex):
- if len(path) == k:
- res.append(path[:])
- return
- for i in range(startIndex,n-(k-len(path))+2): #优化的地方
- path.append(i) #处理节点
- backtrack(n,k,i+1) #递归
- path.pop() #回溯,撤销处理的节点
- backtrack(n,k,1)
- return res
+ result = [] # 存放结果集
+ self.backtracking(n, k, 1, [], result)
+ return result
+ def backtracking(self, n, k, startIndex, path, result):
+ if len(path) == k:
+ result.append(path[:])
+ return
+ for i in range(startIndex, n - (k - len(path)) + 2): # 优化的地方
+ path.append(i) # 处理节点
+ self.backtracking(n, k, i + 1, path, result)
+ path.pop() # 回溯,撤销处理的节点
+
```
+### Go
-## javascript
+```Go
+var (
+ path []int
+ res [][]int
+)
+
+func combine(n int, k int) [][]int {
+ path, res = make([]int, 0, k), make([][]int, 0)
+ dfs(n, k, 1)
+ return res
+}
+
+func dfs(n int, k int, start int) {
+ if len(path) == k { // 说明已经满足了k个数的要求
+ tmp := make([]int, k)
+ copy(tmp, path)
+ res = append(res, tmp)
+ return
+ }
+ for i := start; i <= n; i++ { // 从start开始,不往回走,避免出现重复组合
+ if n - i + 1 < k - len(path) { // 剪枝
+ break
+ }
+ path = append(path, i)
+ dfs(n, k, i+1)
+ path = path[:len(path)-1]
+ }
+}
+```
+
+### JavaScript
+未剪枝:
+
+```js
+var combine = function (n, k) {
+ // 回溯法
+ let result = [],
+ path = [];
+ let backtracking = (_n, _k, startIndex) => {
+ // 终止条件
+ if (path.length === _k) {
+ result.push(path.slice());
+ return;
+ }
+ // 循环本层集合元素
+ for (let i = startIndex; i <= _n; i++) {
+ path.push(i);
+ // 递归
+ backtracking(_n, _k, i + 1);
+ // 回溯操作
+ path.pop();
+ }
+ };
+ backtracking(n, k, 1);
+ return result;
+};
+```
剪枝:
+
```javascript
-let result = []
-let path = []
-var combine = function(n, k) {
- result = []
- combineHelper(n, k, 1)
- return result
+var combine = function (n, k) {
+ // 回溯法
+ let result = [],
+ path = [];
+ let backtracking = (_n, _k, startIndex) => {
+ // 终止条件
+ if (path.length === _k) {
+ result.push(path.slice());
+ return;
+ }
+ // 循环本层集合元素
+ for (let i = startIndex; i <= _n - (_k - path.length) + 1; i++) {
+ path.push(i);
+ // 递归
+ backtracking(_n, _k, i + 1);
+ // 回溯操作
+ path.pop();
+ }
+ };
+ backtracking(n, k, 1);
+ return result;
};
-const combineHelper = (n, k, startIndex) => {
- if (path.length === k) {
- result.push([...path])
- return
- }
- for (let i = startIndex; i <= n - (k - path.length) + 1; ++i) {
- path.push(i)
- combineHelper(n, k, i + 1)
- path.pop()
- }
-}
```
-## TypeScript
+### TypeScript
```typescript
function combine(n: number, k: number): number[][] {
@@ -477,64 +542,59 @@ function combine(n: number, k: number): number[][] {
};
```
+### Rust
-
-## Go
-```Go
-var res [][]int
-func combine(n int, k int) [][]int {
- res=[][]int{}
- if n <= 0 || k <= 0 || k > n {
- return res
- }
- backtrack(n, k, 1, []int{})
- return res
-}
-func backtrack(n,k,start int,track []int){
- if len(track)==k{
- temp:=make([]int,k)
- copy(temp,track)
- res=append(res,temp)
- }
- if len(track)+n-start+1 < k {
- return
- }
- for i:=start;i<=n;i++{
- track=append(track,i)
- backtrack(n,k,i+1,track)
- track=track[:len(track)-1]
+```Rust
+impl Solution {
+ fn backtracking(result: &mut Vec>, path: &mut Vec, n: i32, k: i32, start_index: i32) {
+ let len= path.len() as i32;
+ if len == k{
+ result.push(path.to_vec());
+ return;
+ }
+ for i in start_index..= n {
+ path.push(i);
+ Self::backtracking(result, path, n, k, i+1);
+ path.pop();
+ }
+ }
+ pub fn combine(n: i32, k: i32) -> Vec  -
-
 -
-
 +
+ 1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
-2. [二叉树:一入递归深似海,从此offer是路人](./problems/二叉树的递归遍历.md)
-3. [二叉树:听说递归能做的,栈也能做!](./problems/二叉树的迭代遍历.md)
-4. [二叉树:前中后序迭代方式的写法就不能统一一下么?](./problems/二叉树的统一迭代法.md)
-5. [二叉树:层序遍历登场!](./problems/0102.二叉树的层序遍历.md)
-6. [二叉树:你真的会翻转二叉树么?](./problems/0226.翻转二叉树.md)
+2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
+3. [二叉树:二叉树的迭代遍历](./problems/二叉树的迭代遍历.md)
+4. [二叉树:二叉树的统一迭代法](./problems/二叉树的统一迭代法.md)
+5. [二叉树:二叉树的层序遍历](./problems/0102.二叉树的层序遍历.md)
+6. [二叉树:226.翻转二叉树](./problems/0226.翻转二叉树.md)
7. [本周小结!(二叉树)](./problems/周总结/20200927二叉树周末总结.md)
-8. [二叉树:我对称么?](./problems/0101.对称二叉树.md)
-9. [二叉树:看看这些树的最大深度](./problems/0104.二叉树的最大深度.md)
-10. [二叉树:看看这些树的最小深度](./problems/0111.二叉树的最小深度.md)
-11. [二叉树:我有多少个节点?](./problems/0222.完全二叉树的节点个数.md)
-12. [二叉树:我平衡么?](./problems/0110.平衡二叉树.md)
-13. [二叉树:找我的所有路径?](./problems/0257.二叉树的所有路径.md)
-14. [本周总结!二叉树系列二](./problems/周总结/20201003二叉树周末总结.md)
-15. [二叉树:以为使用了递归,其实还隐藏着回溯](./problems/二叉树中递归带着回溯.md)
-16. [二叉树:做了这么多题目了,我的左叶子之和是多少?](./problems/0404.左叶子之和.md)
-17. [二叉树:我的左下角的值是多少?](./problems/0513.找树左下角的值.md)
-18. [二叉树:路径总和](./problems/0112.路径总和.md)
-19. [二叉树:构造二叉树登场!](./problems/0106.从中序与后序遍历序列构造二叉树.md)
-20. [二叉树:构造一棵最大的二叉树](./problems/0654.最大二叉树.md)
-21. [本周小结!(二叉树系列三)](./problems/周总结/20201010二叉树周末总结.md)
-22. [二叉树:合并两个二叉树](./problems/0617.合并二叉树.md)
-23. [二叉树:二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
-24. [二叉树:我是不是一棵二叉搜索树](./problems/0098.验证二叉搜索树.md)
-25. [二叉树:搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
-26. [二叉树:我的众数是多少?](./problems/0501.二叉搜索树中的众数.md)
-27. [二叉树:公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
-28. [本周小结!(二叉树系列四)](./problems/周总结/20201017二叉树周末总结.md)
-29. [二叉树:搜索树的公共祖先问题](./problems/0235.二叉搜索树的最近公共祖先.md)
-30. [二叉树:搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
-31. [二叉树:搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
-32. [二叉树:修剪一棵搜索树](./problems/0669.修剪二叉搜索树.md)
-33. [二叉树:构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
-34. [二叉树:搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
+8. [二叉树:101.对称二叉树](./problems/0101.对称二叉树.md)
+9. [二叉树:104.二叉树的最大深度](./problems/0104.二叉树的最大深度.md)
+10. [二叉树:111.二叉树的最小深度](./problems/0111.二叉树的最小深度.md)
+11. [二叉树:222.完全二叉树的节点个数](./problems/0222.完全二叉树的节点个数.md)
+12. [二叉树:110.平衡二叉树](./problems/0110.平衡二叉树.md)
+13. [二叉树:257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
+14. [本周总结!(二叉树)](./problems/周总结/20201003二叉树周末总结.md)
+16. [二叉树:404.左叶子之和](./problems/0404.左叶子之和.md)
+17. [二叉树:513.找树左下角的值](./problems/0513.找树左下角的值.md)
+18. [二叉树:112.路径总和](./problems/0112.路径总和.md)
+19. [二叉树:106.构造二叉树](./problems/0106.从中序与后序遍历序列构造二叉树.md)
+20. [二叉树:654.最大二叉树](./problems/0654.最大二叉树.md)
+21. [本周小结!(二叉树)](./problems/周总结/20201010二叉树周末总结.md)
+22. [二叉树:617.合并两个二叉树](./problems/0617.合并二叉树.md)
+23. [二叉树:700.二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
+24. [二叉树:98.验证二叉搜索树](./problems/0098.验证二叉搜索树.md)
+25. [二叉树:530.搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
+26. [二叉树:501.二叉搜索树中的众数](./problems/0501.二叉搜索树中的众数.md)
+27. [二叉树:236.公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
+28. [本周小结!(二叉树)](./problems/周总结/20201017二叉树周末总结.md)
+29. [二叉树:235.搜索树的最近公共祖先](./problems/0235.二叉搜索树的最近公共祖先.md)
+30. [二叉树:701.搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
+31. [二叉树:450.搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
+32. [二叉树:669.修剪二叉搜索树](./problems/0669.修剪二叉搜索树.md)
+33. [二叉树:108.将有序数组转换为二叉搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
+34. [二叉树:538.把二叉搜索树转换为累加树](./problems/0538.把二叉搜索树转换为累加树.md)
35. [二叉树:总结篇!(需要掌握的二叉树技能都在这里了)](./problems/二叉树总结篇.md)
-
+
## 回溯算法
题目分类大纲如下:
-
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
-2. [二叉树:一入递归深似海,从此offer是路人](./problems/二叉树的递归遍历.md)
-3. [二叉树:听说递归能做的,栈也能做!](./problems/二叉树的迭代遍历.md)
-4. [二叉树:前中后序迭代方式的写法就不能统一一下么?](./problems/二叉树的统一迭代法.md)
-5. [二叉树:层序遍历登场!](./problems/0102.二叉树的层序遍历.md)
-6. [二叉树:你真的会翻转二叉树么?](./problems/0226.翻转二叉树.md)
+2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
+3. [二叉树:二叉树的迭代遍历](./problems/二叉树的迭代遍历.md)
+4. [二叉树:二叉树的统一迭代法](./problems/二叉树的统一迭代法.md)
+5. [二叉树:二叉树的层序遍历](./problems/0102.二叉树的层序遍历.md)
+6. [二叉树:226.翻转二叉树](./problems/0226.翻转二叉树.md)
7. [本周小结!(二叉树)](./problems/周总结/20200927二叉树周末总结.md)
-8. [二叉树:我对称么?](./problems/0101.对称二叉树.md)
-9. [二叉树:看看这些树的最大深度](./problems/0104.二叉树的最大深度.md)
-10. [二叉树:看看这些树的最小深度](./problems/0111.二叉树的最小深度.md)
-11. [二叉树:我有多少个节点?](./problems/0222.完全二叉树的节点个数.md)
-12. [二叉树:我平衡么?](./problems/0110.平衡二叉树.md)
-13. [二叉树:找我的所有路径?](./problems/0257.二叉树的所有路径.md)
-14. [本周总结!二叉树系列二](./problems/周总结/20201003二叉树周末总结.md)
-15. [二叉树:以为使用了递归,其实还隐藏着回溯](./problems/二叉树中递归带着回溯.md)
-16. [二叉树:做了这么多题目了,我的左叶子之和是多少?](./problems/0404.左叶子之和.md)
-17. [二叉树:我的左下角的值是多少?](./problems/0513.找树左下角的值.md)
-18. [二叉树:路径总和](./problems/0112.路径总和.md)
-19. [二叉树:构造二叉树登场!](./problems/0106.从中序与后序遍历序列构造二叉树.md)
-20. [二叉树:构造一棵最大的二叉树](./problems/0654.最大二叉树.md)
-21. [本周小结!(二叉树系列三)](./problems/周总结/20201010二叉树周末总结.md)
-22. [二叉树:合并两个二叉树](./problems/0617.合并二叉树.md)
-23. [二叉树:二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
-24. [二叉树:我是不是一棵二叉搜索树](./problems/0098.验证二叉搜索树.md)
-25. [二叉树:搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
-26. [二叉树:我的众数是多少?](./problems/0501.二叉搜索树中的众数.md)
-27. [二叉树:公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
-28. [本周小结!(二叉树系列四)](./problems/周总结/20201017二叉树周末总结.md)
-29. [二叉树:搜索树的公共祖先问题](./problems/0235.二叉搜索树的最近公共祖先.md)
-30. [二叉树:搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
-31. [二叉树:搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
-32. [二叉树:修剪一棵搜索树](./problems/0669.修剪二叉搜索树.md)
-33. [二叉树:构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
-34. [二叉树:搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
+8. [二叉树:101.对称二叉树](./problems/0101.对称二叉树.md)
+9. [二叉树:104.二叉树的最大深度](./problems/0104.二叉树的最大深度.md)
+10. [二叉树:111.二叉树的最小深度](./problems/0111.二叉树的最小深度.md)
+11. [二叉树:222.完全二叉树的节点个数](./problems/0222.完全二叉树的节点个数.md)
+12. [二叉树:110.平衡二叉树](./problems/0110.平衡二叉树.md)
+13. [二叉树:257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
+14. [本周总结!(二叉树)](./problems/周总结/20201003二叉树周末总结.md)
+16. [二叉树:404.左叶子之和](./problems/0404.左叶子之和.md)
+17. [二叉树:513.找树左下角的值](./problems/0513.找树左下角的值.md)
+18. [二叉树:112.路径总和](./problems/0112.路径总和.md)
+19. [二叉树:106.构造二叉树](./problems/0106.从中序与后序遍历序列构造二叉树.md)
+20. [二叉树:654.最大二叉树](./problems/0654.最大二叉树.md)
+21. [本周小结!(二叉树)](./problems/周总结/20201010二叉树周末总结.md)
+22. [二叉树:617.合并两个二叉树](./problems/0617.合并二叉树.md)
+23. [二叉树:700.二叉搜索树登场!](./problems/0700.二叉搜索树中的搜索.md)
+24. [二叉树:98.验证二叉搜索树](./problems/0098.验证二叉搜索树.md)
+25. [二叉树:530.搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
+26. [二叉树:501.二叉搜索树中的众数](./problems/0501.二叉搜索树中的众数.md)
+27. [二叉树:236.公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
+28. [本周小结!(二叉树)](./problems/周总结/20201017二叉树周末总结.md)
+29. [二叉树:235.搜索树的最近公共祖先](./problems/0235.二叉搜索树的最近公共祖先.md)
+30. [二叉树:701.搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
+31. [二叉树:450.搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
+32. [二叉树:669.修剪二叉搜索树](./problems/0669.修剪二叉搜索树.md)
+33. [二叉树:108.将有序数组转换为二叉搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
+34. [二叉树:538.把二叉搜索树转换为累加树](./problems/0538.把二叉搜索树转换为累加树.md)
35. [二叉树:总结篇!(需要掌握的二叉树技能都在这里了)](./problems/二叉树总结篇.md)
-
+
## 回溯算法
题目分类大纲如下:
- +
+ 1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
-2. [回溯算法:组合问题](./problems/0077.组合.md)
-3. [回溯算法:组合问题再剪剪枝](./problems/0077.组合优化.md)
-4. [回溯算法:求组合总和!](./problems/0216.组合总和III.md)
-5. [回溯算法:电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+2. [回溯算法:77.组合](./problems/0077.组合.md)
+3. [回溯算法:77.组合优化](./problems/0077.组合优化.md)
+4. [回溯算法:216.组合总和III](./problems/0216.组合总和III.md)
+5. [回溯算法:17.电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
6. [本周小结!(回溯算法系列一)](./problems/周总结/20201030回溯周末总结.md)
-7. [回溯算法:求组合总和(二)](./problems/0039.组合总和.md)
-8. [回溯算法:求组合总和(三)](./problems/0040.组合总和II.md)
-9. [回溯算法:分割回文串](./problems/0131.分割回文串.md)
-10. [回溯算法:复原IP地址](./problems/0093.复原IP地址.md)
-11. [回溯算法:求子集问题!](./problems/0078.子集.md)
+7. [回溯算法:39.组合总和](./problems/0039.组合总和.md)
+8. [回溯算法:40.组合总和II](./problems/0040.组合总和II.md)
+9. [回溯算法:131.分割回文串](./problems/0131.分割回文串.md)
+10. [回溯算法:93.复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法:78.子集](./problems/0078.子集.md)
12. [本周小结!(回溯算法系列二)](./problems/周总结/20201107回溯周末总结.md)
-13. [回溯算法:求子集问题(二)](./problems/0090.子集II.md)
-14. [回溯算法:递增子序列](./problems/0491.递增子序列.md)
-15. [回溯算法:排列问题!](./problems/0046.全排列.md)
-16. [回溯算法:排列问题(二)](./problems/0047.全排列II.md)
+13. [回溯算法:90.子集II](./problems/0090.子集II.md)
+14. [回溯算法:491.递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法:46.全排列](./problems/0046.全排列.md)
+16. [回溯算法:47.全排列II](./problems/0047.全排列II.md)
17. [本周小结!(回溯算法系列三)](./problems/周总结/20201112回溯周末总结.md)
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
-19. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
-20. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
-21. [回溯算法:解数独](./problems/0037.解数独.md)
-22. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
+19. [回溯算法:332.重新安排行程](./problems/0332.重新安排行程.md)
+20. [回溯算法:51.N皇后](./problems/0051.N皇后.md)
+21. [回溯算法:37.解数独](./problems/0037.解数独.md)
+22. [回溯算法总结篇](./problems/回溯总结.md)
## 贪心算法
题目分类大纲如下:
-
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
-2. [回溯算法:组合问题](./problems/0077.组合.md)
-3. [回溯算法:组合问题再剪剪枝](./problems/0077.组合优化.md)
-4. [回溯算法:求组合总和!](./problems/0216.组合总和III.md)
-5. [回溯算法:电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+2. [回溯算法:77.组合](./problems/0077.组合.md)
+3. [回溯算法:77.组合优化](./problems/0077.组合优化.md)
+4. [回溯算法:216.组合总和III](./problems/0216.组合总和III.md)
+5. [回溯算法:17.电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
6. [本周小结!(回溯算法系列一)](./problems/周总结/20201030回溯周末总结.md)
-7. [回溯算法:求组合总和(二)](./problems/0039.组合总和.md)
-8. [回溯算法:求组合总和(三)](./problems/0040.组合总和II.md)
-9. [回溯算法:分割回文串](./problems/0131.分割回文串.md)
-10. [回溯算法:复原IP地址](./problems/0093.复原IP地址.md)
-11. [回溯算法:求子集问题!](./problems/0078.子集.md)
+7. [回溯算法:39.组合总和](./problems/0039.组合总和.md)
+8. [回溯算法:40.组合总和II](./problems/0040.组合总和II.md)
+9. [回溯算法:131.分割回文串](./problems/0131.分割回文串.md)
+10. [回溯算法:93.复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法:78.子集](./problems/0078.子集.md)
12. [本周小结!(回溯算法系列二)](./problems/周总结/20201107回溯周末总结.md)
-13. [回溯算法:求子集问题(二)](./problems/0090.子集II.md)
-14. [回溯算法:递增子序列](./problems/0491.递增子序列.md)
-15. [回溯算法:排列问题!](./problems/0046.全排列.md)
-16. [回溯算法:排列问题(二)](./problems/0047.全排列II.md)
+13. [回溯算法:90.子集II](./problems/0090.子集II.md)
+14. [回溯算法:491.递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法:46.全排列](./problems/0046.全排列.md)
+16. [回溯算法:47.全排列II](./problems/0047.全排列II.md)
17. [本周小结!(回溯算法系列三)](./problems/周总结/20201112回溯周末总结.md)
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
-19. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
-20. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
-21. [回溯算法:解数独](./problems/0037.解数独.md)
-22. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
+19. [回溯算法:332.重新安排行程](./problems/0332.重新安排行程.md)
+20. [回溯算法:51.N皇后](./problems/0051.N皇后.md)
+21. [回溯算法:37.解数独](./problems/0037.解数独.md)
+22. [回溯算法总结篇](./problems/回溯总结.md)
## 贪心算法
题目分类大纲如下:
- +
+ 1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
-2. [贪心算法:分发饼干](./problems/0455.分发饼干.md)
-3. [贪心算法:摆动序列](./problems/0376.摆动序列.md)
-4. [贪心算法:最大子序和](./problems/0053.最大子序和.md)
+2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
+3. [贪心算法:376.摆动序列](./problems/0376.摆动序列.md)
+4. [贪心算法:53.最大子序和](./problems/0053.最大子序和.md)
5. [本周小结!(贪心算法系列一)](./problems/周总结/20201126贪心周末总结.md)
-6. [贪心算法:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
-7. [贪心算法:跳跃游戏](./problems/0055.跳跃游戏.md)
-8. [贪心算法:跳跃游戏II](./problems/0045.跳跃游戏II.md)
-9. [贪心算法:K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
+6. [贪心算法:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
+7. [贪心算法:55.跳跃游戏](./problems/0055.跳跃游戏.md)
+8. [贪心算法:45.跳跃游戏II](./problems/0045.跳跃游戏II.md)
+9. [贪心算法:1005.K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
10. [本周小结!(贪心算法系列二)](./problems/周总结/20201203贪心周末总结.md)
-11. [贪心算法:加油站](./problems/0134.加油站.md)
-12. [贪心算法:分发糖果](./problems/0135.分发糖果.md)
-13. [贪心算法:柠檬水找零](./problems/0860.柠檬水找零.md)
-14. [贪心算法:根据身高重建队列](./problems/0406.根据身高重建队列.md)
+11. [贪心算法:134.加油站](./problems/0134.加油站.md)
+12. [贪心算法:135.分发糖果](./problems/0135.分发糖果.md)
+13. [贪心算法:860.柠檬水找零](./problems/0860.柠檬水找零.md)
+14. [贪心算法:406.根据身高重建队列](./problems/0406.根据身高重建队列.md)
15. [本周小结!(贪心算法系列三)](./problems/周总结/20201217贪心周末总结.md)
-16. [贪心算法:根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
-17. [贪心算法:用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
-18. [贪心算法:无重叠区间](./problems/0435.无重叠区间.md)
-19. [贪心算法:划分字母区间](./problems/0763.划分字母区间.md)
-20. [贪心算法:合并区间](./problems/0056.合并区间.md)
+16. [贪心算法:406.根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
+17. [贪心算法:452.用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
+18. [贪心算法:435.无重叠区间](./problems/0435.无重叠区间.md)
+19. [贪心算法:763.划分字母区间](./problems/0763.划分字母区间.md)
+20. [贪心算法:56.合并区间](./problems/0056.合并区间.md)
21. [本周小结!(贪心算法系列四)](./problems/周总结/20201224贪心周末总结.md)
-22. [贪心算法:单调递增的数字](./problems/0738.单调递增的数字.md)
-23. [贪心算法:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
-24. [贪心算法:我要监控二叉树!](./problems/0968.监控二叉树.md)
-25. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
+22. [贪心算法:738.单调递增的数字](./problems/0738.单调递增的数字.md)
+23. [贪心算法:968.监控二叉树](./problems/0968.监控二叉树.md)
+24. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
## 动态规划
动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
-
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
-2. [贪心算法:分发饼干](./problems/0455.分发饼干.md)
-3. [贪心算法:摆动序列](./problems/0376.摆动序列.md)
-4. [贪心算法:最大子序和](./problems/0053.最大子序和.md)
+2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
+3. [贪心算法:376.摆动序列](./problems/0376.摆动序列.md)
+4. [贪心算法:53.最大子序和](./problems/0053.最大子序和.md)
5. [本周小结!(贪心算法系列一)](./problems/周总结/20201126贪心周末总结.md)
-6. [贪心算法:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
-7. [贪心算法:跳跃游戏](./problems/0055.跳跃游戏.md)
-8. [贪心算法:跳跃游戏II](./problems/0045.跳跃游戏II.md)
-9. [贪心算法:K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
+6. [贪心算法:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
+7. [贪心算法:55.跳跃游戏](./problems/0055.跳跃游戏.md)
+8. [贪心算法:45.跳跃游戏II](./problems/0045.跳跃游戏II.md)
+9. [贪心算法:1005.K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
10. [本周小结!(贪心算法系列二)](./problems/周总结/20201203贪心周末总结.md)
-11. [贪心算法:加油站](./problems/0134.加油站.md)
-12. [贪心算法:分发糖果](./problems/0135.分发糖果.md)
-13. [贪心算法:柠檬水找零](./problems/0860.柠檬水找零.md)
-14. [贪心算法:根据身高重建队列](./problems/0406.根据身高重建队列.md)
+11. [贪心算法:134.加油站](./problems/0134.加油站.md)
+12. [贪心算法:135.分发糖果](./problems/0135.分发糖果.md)
+13. [贪心算法:860.柠檬水找零](./problems/0860.柠檬水找零.md)
+14. [贪心算法:406.根据身高重建队列](./problems/0406.根据身高重建队列.md)
15. [本周小结!(贪心算法系列三)](./problems/周总结/20201217贪心周末总结.md)
-16. [贪心算法:根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
-17. [贪心算法:用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
-18. [贪心算法:无重叠区间](./problems/0435.无重叠区间.md)
-19. [贪心算法:划分字母区间](./problems/0763.划分字母区间.md)
-20. [贪心算法:合并区间](./problems/0056.合并区间.md)
+16. [贪心算法:406.根据身高重建队列(续集)](./problems/根据身高重建队列(vector原理讲解).md)
+17. [贪心算法:452.用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
+18. [贪心算法:435.无重叠区间](./problems/0435.无重叠区间.md)
+19. [贪心算法:763.划分字母区间](./problems/0763.划分字母区间.md)
+20. [贪心算法:56.合并区间](./problems/0056.合并区间.md)
21. [本周小结!(贪心算法系列四)](./problems/周总结/20201224贪心周末总结.md)
-22. [贪心算法:单调递增的数字](./problems/0738.单调递增的数字.md)
-23. [贪心算法:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
-24. [贪心算法:我要监控二叉树!](./problems/0968.监控二叉树.md)
-25. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
+22. [贪心算法:738.单调递增的数字](./problems/0738.单调递增的数字.md)
+23. [贪心算法:968.监控二叉树](./problems/0968.监控二叉树.md)
+24. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
## 动态规划
动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
- +
+ 1. [关于动态规划,你该了解这些!](./problems/动态规划理论基础.md)
-2. [动态规划:斐波那契数](./problems/0509.斐波那契数.md)
-3. [动态规划:爬楼梯](./problems/0070.爬楼梯.md)
-4. [动态规划:使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+2. [动态规划:509.斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划:70.爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划:746.使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
5. [本周小结!(动态规划系列一)](./problems/周总结/20210107动规周末总结.md)
-6. [动态规划:不同路径](./problems/0062.不同路径.md)
-7. [动态规划:不同路径还不够,要有障碍!](./problems/0063.不同路径II.md)
-8. [动态规划:整数拆分,你要怎么拆?](./problems/0343.整数拆分.md)
-9. [动态规划:不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+6. [动态规划:62.不同路径](./problems/0062.不同路径.md)
+7. [动态规划:63.不同路径II](./problems/0063.不同路径II.md)
+8. [动态规划:343.整数拆分](./problems/0343.整数拆分.md)
+9. [动态规划:96.不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
10. [本周小结!(动态规划系列二)](./problems/周总结/20210114动规周末总结.md)
背包问题系列:
-
1. [关于动态规划,你该了解这些!](./problems/动态规划理论基础.md)
-2. [动态规划:斐波那契数](./problems/0509.斐波那契数.md)
-3. [动态规划:爬楼梯](./problems/0070.爬楼梯.md)
-4. [动态规划:使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+2. [动态规划:509.斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划:70.爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划:746.使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
5. [本周小结!(动态规划系列一)](./problems/周总结/20210107动规周末总结.md)
-6. [动态规划:不同路径](./problems/0062.不同路径.md)
-7. [动态规划:不同路径还不够,要有障碍!](./problems/0063.不同路径II.md)
-8. [动态规划:整数拆分,你要怎么拆?](./problems/0343.整数拆分.md)
-9. [动态规划:不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+6. [动态规划:62.不同路径](./problems/0062.不同路径.md)
+7. [动态规划:63.不同路径II](./problems/0063.不同路径II.md)
+8. [动态规划:343.整数拆分](./problems/0343.整数拆分.md)
+9. [动态规划:96.不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
10. [本周小结!(动态规划系列二)](./problems/周总结/20210114动规周末总结.md)
背包问题系列:
- +
+ -11. [动态规划:关于01背包问题,你该了解这些!](./problems/背包理论基础01背包-1.md)
-12. [动态规划:关于01背包问题,你该了解这些!(滚动数组)](./problems/背包理论基础01背包-2.md)
-13. [动态规划:分割等和子集可以用01背包!](./problems/0416.分割等和子集.md)
-14. [动态规划:最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+11. [动态规划:01背包理论基础(二维dp数组)](./problems/背包理论基础01背包-1.md)
+12. [动态规划:01背包理论基础(一维dp数组)](./problems/背包理论基础01背包-2.md)
+13. [动态规划:416.分割等和子集](./problems/0416.分割等和子集.md)
+14. [动态规划:1049.最后一块石头的重量II](./problems/1049.最后一块石头的重量II.md)
15. [本周小结!(动态规划系列三)](./problems/周总结/20210121动规周末总结.md)
-16. [动态规划:目标和!](./problems/0494.目标和.md)
-17. [动态规划:一和零!](./problems/0474.一和零.md)
-18. [动态规划:关于完全背包,你该了解这些!](./problems/背包问题理论基础完全背包.md)
-19. [动态规划:给你一些零钱,你要怎么凑?](./problems/0518.零钱兑换II.md)
-20. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
-21. [动态规划:Carl称它为排列总和!](./problems/0377.组合总和Ⅳ.md)
-22. [动态规划:以前我没得选,现在我选择再爬一次!](./problems/0070.爬楼梯完全背包版本.md)
-23. [动态规划: 给我个机会,我再兑换一次零钱](./problems/0322.零钱兑换.md)
-24. [动态规划:一样的套路,再求一次完全平方数](./problems/0279.完全平方数.md)
-25. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
-26. [动态规划:单词拆分](./problems/0139.单词拆分.md)
-27. [动态规划:关于多重背包,你该了解这些!](./problems/背包问题理论基础多重背包.md)
-28. [听说背包问题很难? 这篇总结篇来拯救你了](./problems/背包总结篇.md)
+16. [动态规划:494.目标和](./problems/0494.目标和.md)
+17. [动态规划:474.一和零](./problems/0474.一和零.md)
+18. [动态规划:完全背包理论基础(二维dp数组)](./problems/背包问题理论基础完全背包.md)
+19. [动态规划:完全背包理论基础(一维dp数组)](./problems/背包问题完全背包一维.md)
+20. [动态规划:518.零钱兑换II](./problems/0518.零钱兑换II.md)
+21. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
+22. [动态规划:377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md)
+23. [动态规划:70.爬楼梯(完全背包版本)](./problems/0070.爬楼梯完全背包版本.md)
+24. [动态规划:322.零钱兑换](./problems/0322.零钱兑换.md)
+25. [动态规划:279.完全平方数](./problems/0279.完全平方数.md)
+26. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
+27. [动态规划:139.单词拆分](./problems/0139.单词拆分.md)
+28. [动态规划:多重背包理论基础](./problems/背包问题理论基础多重背包.md)
+29. [背包问题总结篇](./problems/背包总结篇.md)
打家劫舍系列:
-29. [动态规划:开始打家劫舍!](./problems/0198.打家劫舍.md)
-30. [动态规划:继续打家劫舍!](./problems/0213.打家劫舍II.md)
-31. [动态规划:还要打家劫舍!](./problems/0337.打家劫舍III.md)
+29. [动态规划:198.打家劫舍](./problems/0198.打家劫舍.md)
+30. [动态规划:213.打家劫舍II](./problems/0213.打家劫舍II.md)
+31. [动态规划:337.打家劫舍III](./problems/0337.打家劫舍III.md)
股票系列:
-
-11. [动态规划:关于01背包问题,你该了解这些!](./problems/背包理论基础01背包-1.md)
-12. [动态规划:关于01背包问题,你该了解这些!(滚动数组)](./problems/背包理论基础01背包-2.md)
-13. [动态规划:分割等和子集可以用01背包!](./problems/0416.分割等和子集.md)
-14. [动态规划:最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+11. [动态规划:01背包理论基础(二维dp数组)](./problems/背包理论基础01背包-1.md)
+12. [动态规划:01背包理论基础(一维dp数组)](./problems/背包理论基础01背包-2.md)
+13. [动态规划:416.分割等和子集](./problems/0416.分割等和子集.md)
+14. [动态规划:1049.最后一块石头的重量II](./problems/1049.最后一块石头的重量II.md)
15. [本周小结!(动态规划系列三)](./problems/周总结/20210121动规周末总结.md)
-16. [动态规划:目标和!](./problems/0494.目标和.md)
-17. [动态规划:一和零!](./problems/0474.一和零.md)
-18. [动态规划:关于完全背包,你该了解这些!](./problems/背包问题理论基础完全背包.md)
-19. [动态规划:给你一些零钱,你要怎么凑?](./problems/0518.零钱兑换II.md)
-20. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
-21. [动态规划:Carl称它为排列总和!](./problems/0377.组合总和Ⅳ.md)
-22. [动态规划:以前我没得选,现在我选择再爬一次!](./problems/0070.爬楼梯完全背包版本.md)
-23. [动态规划: 给我个机会,我再兑换一次零钱](./problems/0322.零钱兑换.md)
-24. [动态规划:一样的套路,再求一次完全平方数](./problems/0279.完全平方数.md)
-25. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
-26. [动态规划:单词拆分](./problems/0139.单词拆分.md)
-27. [动态规划:关于多重背包,你该了解这些!](./problems/背包问题理论基础多重背包.md)
-28. [听说背包问题很难? 这篇总结篇来拯救你了](./problems/背包总结篇.md)
+16. [动态规划:494.目标和](./problems/0494.目标和.md)
+17. [动态规划:474.一和零](./problems/0474.一和零.md)
+18. [动态规划:完全背包理论基础(二维dp数组)](./problems/背包问题理论基础完全背包.md)
+19. [动态规划:完全背包理论基础(一维dp数组)](./problems/背包问题完全背包一维.md)
+20. [动态规划:518.零钱兑换II](./problems/0518.零钱兑换II.md)
+21. [本周小结!(动态规划系列四)](./problems/周总结/20210128动规周末总结.md)
+22. [动态规划:377.组合总和Ⅳ](./problems/0377.组合总和Ⅳ.md)
+23. [动态规划:70.爬楼梯(完全背包版本)](./problems/0070.爬楼梯完全背包版本.md)
+24. [动态规划:322.零钱兑换](./problems/0322.零钱兑换.md)
+25. [动态规划:279.完全平方数](./problems/0279.完全平方数.md)
+26. [本周小结!(动态规划系列五)](./problems/周总结/20210204动规周末总结.md)
+27. [动态规划:139.单词拆分](./problems/0139.单词拆分.md)
+28. [动态规划:多重背包理论基础](./problems/背包问题理论基础多重背包.md)
+29. [背包问题总结篇](./problems/背包总结篇.md)
打家劫舍系列:
-29. [动态规划:开始打家劫舍!](./problems/0198.打家劫舍.md)
-30. [动态规划:继续打家劫舍!](./problems/0213.打家劫舍II.md)
-31. [动态规划:还要打家劫舍!](./problems/0337.打家劫舍III.md)
+29. [动态规划:198.打家劫舍](./problems/0198.打家劫舍.md)
+30. [动态规划:213.打家劫舍II](./problems/0213.打家劫舍II.md)
+31. [动态规划:337.打家劫舍III](./problems/0337.打家劫舍III.md)
股票系列:
- +
+ -32. [动态规划:买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
-33. [动态规划:本周我们都讲了这些(系列六)](./problems/周总结/20210225动规周末总结.md)
-34. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
-35. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
-36. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
-37. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
-38. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
-39. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
+32. [动态规划:121.买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划:本周小结(系列六)](./problems/周总结/20210225动规周末总结.md)
+34. [动态规划:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
+35. [动态规划:123.买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+36. [动态规划:188.买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+37. [动态规划:309.最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+38. [动态规划:本周小结(系列七)](./problems/周总结/20210304动规周末总结.md)
+39. [动态规划:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
40. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列:
-
-32. [动态规划:买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
-33. [动态规划:本周我们都讲了这些(系列六)](./problems/周总结/20210225动规周末总结.md)
-34. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
-35. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
-36. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
-37. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
-38. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
-39. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
+32. [动态规划:121.买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划:本周小结(系列六)](./problems/周总结/20210225动规周末总结.md)
+34. [动态规划:122.买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
+35. [动态规划:123.买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+36. [动态规划:188.买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+37. [动态规划:309.最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+38. [动态规划:本周小结(系列七)](./problems/周总结/20210304动规周末总结.md)
+39. [动态规划:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
40. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列:
- -
-
-41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
-45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
-46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
-47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
-48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
-49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-52. [动态规划:回文子串](./problems/0647.回文子串.md)
-53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+
-
-
-41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
-45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
-46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
-47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
-48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
-49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-52. [动态规划:回文子串](./problems/0647.回文子串.md)
-53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+ +
+
+41. [动态规划:300.最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:674.最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:718.最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:1143.最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划:1035.不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划:53.最大子序和](./problems/0053.最大子序和(动态规划).md)
+47. [动态规划:392.判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划:115.不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划:583.两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+50. [动态规划:72.编辑距离](./problems/0072.编辑距离.md)
+51. [编辑距离总结篇](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:647.回文子串](./problems/0647.回文子串.md)
+53. [动态规划:516.最长回文子序列](./problems/0516.最长回文子序列.md)
54. [动态规划总结篇](./problems/动态规划总结篇.md)
## 单调栈
-1. [单调栈:每日温度](./problems/0739.每日温度.md)
-2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
-3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
-4. [单调栈:接雨水](./problems/0042.接雨水.md)
-5. [单调栈:柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
+1. [单调栈:739.每日温度](./problems/0739.每日温度.md)
+2. [单调栈:496.下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:503.下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:42.接雨水](./problems/0042.接雨水.md)
+5. [单调栈:84.柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
-(持续更新中....)
## 图论
-## 十大排序
+**[图论正式发布](./problems/qita/tulunfabu.md)**
+
+1. [图论:理论基础](./problems/kamacoder/图论理论基础.md)
+2. [图论:深度优先搜索理论基础](./problems/kamacoder/图论深搜理论基础.md)
+3. [图论:所有可达路径](./problems/kamacoder/0098.所有可达路径.md)
+4. [图论:广度优先搜索理论基础](./problems/kamacoder/图论广搜理论基础.md)
+5. [图论:岛屿数量.深搜版](./problems/kamacoder/0099.岛屿的数量深搜.md)
+6. [图论:岛屿数量.广搜版](./problems/kamacoder/0099.岛屿的数量广搜.md)
+7. [图论:岛屿的最大面积](./problems/kamacoder/0100.岛屿的最大面积.md)
+8. [图论:孤岛的总面积](./problems/kamacoder/0101.孤岛的总面积.md)
+9. [图论:沉没孤岛](./problems/kamacoder/0102.沉没孤岛.md)
+10. [图论:水流问题](./problems/kamacoder/0103.水流问题.md)
+11. [图论:建造最大岛屿](./problems/kamacoder/0104.建造最大岛屿.md)
+12. [图论:岛屿的周长](./problems/kamacoder/0106.岛屿的周长.md)
+13. [图论:字符串接龙](./problems/kamacoder/0110.字符串接龙.md)
+14. [图论:有向图的完全可达性](./problems/kamacoder/0105.有向图的完全可达性.md)
+15. [图论:并查集理论基础](./problems/kamacoder/图论并查集理论基础.md)
+16. [图论:寻找存在的路径](./problems/kamacoder/0107.寻找存在的路径.md)
+17. [图论:冗余连接](./problems/kamacoder/0108.冗余连接.md)
+18. [图论:冗余连接II](./problems/kamacoder/0109.冗余连接II.md)
+19. [图论:最小生成树之prim](./problems/kamacoder/0053.寻宝-prim.md)
+20. [图论:最小生成树之kruskal](./problems/kamacoder/0053.寻宝-Kruskal.md)
+21. [图论:拓扑排序](./problems/kamacoder/0117.软件构建.md)
+22. [图论:dijkstra(朴素版)](./problems/kamacoder/0047.参会dijkstra朴素.md)
+23. [图论:dijkstra(堆优化版)](./problems/kamacoder/0047.参会dijkstra堆.md)
+24. [图论:Bellman_ford 算法](./problems/kamacoder/0094.城市间货物运输I.md)
+25. [图论:Bellman_ford 队列优化算法(又名SPFA)](./problems/kamacoder/0094.城市间货物运输I-SPFA.md)
+26. [图论:Bellman_ford之判断负权回路](./problems/kamacoder/0095.城市间货物运输II.md)
+27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0096.城市间货物运输III.md)
+28. [图论:Floyd 算法](./problems/kamacoder/0097.小明逛公园.md)
+29. [图论:A * 算法](./problems/kamacoder/0126.骑士的攻击astar.md)
+30. [图论:最短路算法总结篇](./problems/kamacoder/最短路问题总结篇.md)
+31. [图论:图论总结篇](./problems/kamacoder/图论总结篇.md)
-## 数论
-## 高级数据结构经典题目
-
-* 并查集
-* 最小生成树
-* 线段树
-* 树状数组
-* 字典树
-
-## 海量数据处理
+(持续更新中....)
# 补充题目
@@ -538,49 +485,23 @@
[各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
-
-
-# B站算法视频讲解
-
-以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频:
-
-* [KMP算法(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd)
-* [KMP算法(代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
-* [回溯算法理论基础](https://www.bilibili.com/video/BV1cy4y167mM)
-* [回溯算法之组合问题(力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv)
-* [组合问题的剪枝操作(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1wi4y157er)
-* [组合总和(对应力扣题目:39.组合总和)](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-* [分割回文串(对应力扣题目:131.分割回文串)](https://www.bilibili.com/video/BV1c54y1e7k6)
-* [二叉树理论基础](https://www.bilibili.com/video/BV1Hy4y1t7ij)
-* [二叉树的递归遍历](https://www.bilibili.com/video/BV1Wh411S7xt)
-* [二叉树的非递归遍历(一)](https://www.bilibili.com/video/BV15f4y1W7i2)
-
-(持续更新中....)
-
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
-
-# 关于作者
-
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发,CSDN博客专家。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
-
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码加我微信。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
-
-
+
+
+41. [动态规划:300.最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:674.最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:718.最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:1143.最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划:1035.不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划:53.最大子序和](./problems/0053.最大子序和(动态规划).md)
+47. [动态规划:392.判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划:115.不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划:583.两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+50. [动态规划:72.编辑距离](./problems/0072.编辑距离.md)
+51. [编辑距离总结篇](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:647.回文子串](./problems/0647.回文子串.md)
+53. [动态规划:516.最长回文子序列](./problems/0516.最长回文子序列.md)
54. [动态规划总结篇](./problems/动态规划总结篇.md)
## 单调栈
-1. [单调栈:每日温度](./problems/0739.每日温度.md)
-2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
-3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
-4. [单调栈:接雨水](./problems/0042.接雨水.md)
-5. [单调栈:柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
+1. [单调栈:739.每日温度](./problems/0739.每日温度.md)
+2. [单调栈:496.下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:503.下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:42.接雨水](./problems/0042.接雨水.md)
+5. [单调栈:84.柱状图中最大的矩形](./problems/0084.柱状图中最大的矩形.md)
-(持续更新中....)
## 图论
-## 十大排序
+**[图论正式发布](./problems/qita/tulunfabu.md)**
+
+1. [图论:理论基础](./problems/kamacoder/图论理论基础.md)
+2. [图论:深度优先搜索理论基础](./problems/kamacoder/图论深搜理论基础.md)
+3. [图论:所有可达路径](./problems/kamacoder/0098.所有可达路径.md)
+4. [图论:广度优先搜索理论基础](./problems/kamacoder/图论广搜理论基础.md)
+5. [图论:岛屿数量.深搜版](./problems/kamacoder/0099.岛屿的数量深搜.md)
+6. [图论:岛屿数量.广搜版](./problems/kamacoder/0099.岛屿的数量广搜.md)
+7. [图论:岛屿的最大面积](./problems/kamacoder/0100.岛屿的最大面积.md)
+8. [图论:孤岛的总面积](./problems/kamacoder/0101.孤岛的总面积.md)
+9. [图论:沉没孤岛](./problems/kamacoder/0102.沉没孤岛.md)
+10. [图论:水流问题](./problems/kamacoder/0103.水流问题.md)
+11. [图论:建造最大岛屿](./problems/kamacoder/0104.建造最大岛屿.md)
+12. [图论:岛屿的周长](./problems/kamacoder/0106.岛屿的周长.md)
+13. [图论:字符串接龙](./problems/kamacoder/0110.字符串接龙.md)
+14. [图论:有向图的完全可达性](./problems/kamacoder/0105.有向图的完全可达性.md)
+15. [图论:并查集理论基础](./problems/kamacoder/图论并查集理论基础.md)
+16. [图论:寻找存在的路径](./problems/kamacoder/0107.寻找存在的路径.md)
+17. [图论:冗余连接](./problems/kamacoder/0108.冗余连接.md)
+18. [图论:冗余连接II](./problems/kamacoder/0109.冗余连接II.md)
+19. [图论:最小生成树之prim](./problems/kamacoder/0053.寻宝-prim.md)
+20. [图论:最小生成树之kruskal](./problems/kamacoder/0053.寻宝-Kruskal.md)
+21. [图论:拓扑排序](./problems/kamacoder/0117.软件构建.md)
+22. [图论:dijkstra(朴素版)](./problems/kamacoder/0047.参会dijkstra朴素.md)
+23. [图论:dijkstra(堆优化版)](./problems/kamacoder/0047.参会dijkstra堆.md)
+24. [图论:Bellman_ford 算法](./problems/kamacoder/0094.城市间货物运输I.md)
+25. [图论:Bellman_ford 队列优化算法(又名SPFA)](./problems/kamacoder/0094.城市间货物运输I-SPFA.md)
+26. [图论:Bellman_ford之判断负权回路](./problems/kamacoder/0095.城市间货物运输II.md)
+27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0096.城市间货物运输III.md)
+28. [图论:Floyd 算法](./problems/kamacoder/0097.小明逛公园.md)
+29. [图论:A * 算法](./problems/kamacoder/0126.骑士的攻击astar.md)
+30. [图论:最短路算法总结篇](./problems/kamacoder/最短路问题总结篇.md)
+31. [图论:图论总结篇](./problems/kamacoder/图论总结篇.md)
-## 数论
-## 高级数据结构经典题目
-
-* 并查集
-* 最小生成树
-* 线段树
-* 树状数组
-* 字典树
-
-## 海量数据处理
+(持续更新中....)
# 补充题目
@@ -538,49 +485,23 @@
[各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
-
-
-# B站算法视频讲解
-
-以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频:
-
-* [KMP算法(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd)
-* [KMP算法(代码篇)](https://www.bilibili.com/video/BV1M5411j7Xx)
-* [回溯算法理论基础](https://www.bilibili.com/video/BV1cy4y167mM)
-* [回溯算法之组合问题(力扣题目:77.组合)](https://www.bilibili.com/video/BV1ti4y1L7cv)
-* [组合问题的剪枝操作(对应力扣题目:77.组合)](https://www.bilibili.com/video/BV1wi4y157er)
-* [组合总和(对应力扣题目:39.组合总和)](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-* [分割回文串(对应力扣题目:131.分割回文串)](https://www.bilibili.com/video/BV1c54y1e7k6)
-* [二叉树理论基础](https://www.bilibili.com/video/BV1Hy4y1t7ij)
-* [二叉树的递归遍历](https://www.bilibili.com/video/BV1Wh411S7xt)
-* [二叉树的非递归遍历(一)](https://www.bilibili.com/video/BV15f4y1W7i2)
-
-(持续更新中....)
-
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
-
-# 关于作者
-
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发,CSDN博客专家。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
-
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码加我微信。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
-
-


 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
- +
+ * fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
-
* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
- +
+ * fast和slow同时移动,直到fast指向末尾,如题:
-
* fast和slow同时移动,直到fast指向末尾,如题:
- -
+
-
+ +//图片中有错别词:应该将“只到”改为“直到”
* 删除slow指向的下一个节点,如图:
-
+//图片中有错别词:应该将“只到”改为“直到”
* 删除slow指向的下一个节点,如图:
- +
+ 此时不难写出如下C++代码:
@@ -72,69 +78,119 @@ public:
fast = fast->next;
slow = slow->next;
}
- slow->next = slow->next->next;
+ slow->next = slow->next->next;
+
+ // ListNode *tmp = slow->next; C++释放内存的逻辑
+ // slow->next = tmp->next;
+ // delete tmp;
+
return dummyHead->next;
}
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
## 其他语言版本
-java:
+### Java:
```java
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
- ListNode dummy = new ListNode(-1);
- dummy.next = head;
-
- ListNode slow = dummy;
- ListNode fast = dummy;
- while (n-- > 0) {
- fast = fast.next;
+ //新建一个虚拟头节点指向head
+ ListNode dummyNode = new ListNode(0);
+ dummyNode.next = head;
+ //快慢指针指向虚拟头节点
+ ListNode fastIndex = dummyNode;
+ ListNode slowIndex = dummyNode;
+
+ // 只要快慢指针相差 n 个结点即可
+ for (int i = 0; i <= n; i++) {
+ fastIndex = fastIndex.next;
}
- // 记住 待删除节点slow 的上一节点
- ListNode prev = null;
- while (fast != null) {
- prev = slow;
- slow = slow.next;
- fast = fast.next;
+ while (fastIndex != null) {
+ fastIndex = fastIndex.next;
+ slowIndex = slowIndex.next;
}
- // 上一节点的next指针绕过 待删除节点slow 直接指向slow的下一节点
- prev.next = slow.next;
- // 释放 待删除节点slow 的next指针, 这句删掉也能AC
- slow.next = null;
- return dummy.next;
+ // 此时 slowIndex 的位置就是待删除元素的前一个位置。
+ // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
+ // 检查 slowIndex.next 是否为 null,以避免空指针异常
+ if (slowIndex.next != null) {
+ slowIndex.next = slowIndex.next.next;
+ }
+ return dummyNode.next;
}
}
```
-Python:
+
+```java
+class Solution {
+ public ListNode removeNthFromEnd(ListNode head, int n) {
+ // 创建一个新的哑节点,指向原链表头
+ ListNode s = new ListNode(-1, head);
+ // 递归调用remove方法,从哑节点开始进行删除操作
+ remove(s, n);
+ // 返回新链表的头(去掉可能的哑节点)
+ return s.next;
+ }
+
+ public int remove(ListNode p, int n) {
+ // 递归结束条件:如果当前节点为空,返回0
+ if (p == null) {
+ return 0;
+ }
+ // 递归深入到下一个节点
+ int net = remove(p.next, n);
+ // 如果当前节点是倒数第n个节点,进行删除操作
+ if (net == n) {
+ p.next = p.next.next;
+ }
+ // 返回当前节点的总深度
+ return net + 1;
+ }
+}
+```
+
+
+### Python:
+
```python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
+
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
- head_dummy = ListNode()
- head_dummy.next = head
-
- slow, fast = head_dummy, head_dummy
- while(n!=0): #fast先往前走n步
+ # 创建一个虚拟节点,并将其下一个指针设置为链表的头部
+ dummy_head = ListNode(0, head)
+
+ # 创建两个指针,慢指针和快指针,并将它们初始化为虚拟节点
+ slow = fast = dummy_head
+
+ # 快指针比慢指针快 n+1 步
+ for i in range(n+1):
fast = fast.next
- n -= 1
- while(fast.next!=None):
+
+ # 移动两个指针,直到快速指针到达链表的末尾
+ while fast:
slow = slow.next
fast = fast.next
- #fast 走到结尾后,slow的下一个节点为倒数第N个节点
- slow.next = slow.next.next #删除
- return head_dummy.next
+
+ # 通过更新第 (n-1) 个节点的 next 指针删除第 n 个节点
+ slow.next = slow.next.next
+
+ return dummy_head.next
+
```
-Go:
+### Go:
+
```Go
/**
* Definition for singly-linked list.
@@ -144,24 +200,21 @@ Go:
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
- dummyHead := &ListNode{}
- dummyHead.Next = head
- cur := head
- prev := dummyHead
- i := 1
- for cur != nil {
- cur = cur.Next
- if i > n {
- prev = prev.Next
- }
- i++
- }
- prev.Next = prev.Next.Next
- return dummyHead.Next
+ dummyNode := &ListNode{0, head}
+ fast, slow := dummyNode, dummyNode
+ for i := 0; i <= n; i++ { // 注意<=,否则快指针为空时,慢指针正好在倒数第n个上面
+ fast = fast.Next
+ }
+ for fast != nil {
+ fast = fast.Next
+ slow = slow.Next
+ }
+ slow.Next = slow.Next.Next
+ return dummyNode.Next
}
```
-JavaScript:
+### JavaScript:
```js
/**
@@ -169,37 +222,41 @@ JavaScript:
* @param {number} n
* @return {ListNode}
*/
-var removeNthFromEnd = function(head, n) {
- let ret = new ListNode(0, head),
- slow = fast = ret;
- while(n--) fast = fast.next;
- while (fast.next !== null) {
- fast = fast.next;
- slow = slow.next
- };
- slow.next = slow.next.next;
- return ret.next;
+var removeNthFromEnd = function (head, n) {
+ // 创建哨兵节点,简化解题逻辑
+ let dummyHead = new ListNode(0, head);
+ let fast = dummyHead;
+ let slow = dummyHead;
+ while (n--) fast = fast.next;
+ while (fast.next !== null) {
+ slow = slow.next;
+ fast = fast.next;
+ }
+ slow.next = slow.next.next;
+ return dummyHead.next;
};
```
-TypeScript:
+### TypeScript:
版本一(快慢指针法):
```typescript
function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
let newHead: ListNode | null = new ListNode(0, head);
- let slowNode: ListNode | null = newHead,
- fastNode: ListNode | null = newHead;
- for (let i = 0; i < n; i++) {
- fastNode = fastNode.next;
+ //根据leetcode题目的定义可推断这里快慢指针均不需要定义为ListNode | null。
+ let slowNode: ListNode = newHead;
+ let fastNode: ListNode = newHead;
+
+ while(n--) {
+ fastNode = fastNode.next!; //由虚拟头节点前进n个节点时,fastNode.next可推断不为null。
}
- while (fastNode.next) {
+ while(fastNode.next) { //遍历直至fastNode.next = null, 即尾部节点。 此时slowNode指向倒数第n个节点。
fastNode = fastNode.next;
- slowNode = slowNode.next;
+ slowNode = slowNode.next!;
}
- slowNode.next = slowNode.next.next;
- return newHead.next;
-};
+ slowNode.next = slowNode.next!.next; //倒数第n个节点可推断其next节点不为空。
+ return newHead.next;
+}
```
版本二(计算节点总数法):
@@ -244,7 +301,7 @@ function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
};
```
-Kotlin:
+### Kotlin:
```Kotlin
fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
@@ -265,7 +322,8 @@ fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
if head == nil {
@@ -290,5 +348,132 @@ func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
}
```
------------------------
-
此时不难写出如下C++代码:
@@ -72,69 +78,119 @@ public:
fast = fast->next;
slow = slow->next;
}
- slow->next = slow->next->next;
+ slow->next = slow->next->next;
+
+ // ListNode *tmp = slow->next; C++释放内存的逻辑
+ // slow->next = tmp->next;
+ // delete tmp;
+
return dummyHead->next;
}
};
```
+* 时间复杂度: O(n)
+* 空间复杂度: O(1)
+
## 其他语言版本
-java:
+### Java:
```java
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
- ListNode dummy = new ListNode(-1);
- dummy.next = head;
-
- ListNode slow = dummy;
- ListNode fast = dummy;
- while (n-- > 0) {
- fast = fast.next;
+ //新建一个虚拟头节点指向head
+ ListNode dummyNode = new ListNode(0);
+ dummyNode.next = head;
+ //快慢指针指向虚拟头节点
+ ListNode fastIndex = dummyNode;
+ ListNode slowIndex = dummyNode;
+
+ // 只要快慢指针相差 n 个结点即可
+ for (int i = 0; i <= n; i++) {
+ fastIndex = fastIndex.next;
}
- // 记住 待删除节点slow 的上一节点
- ListNode prev = null;
- while (fast != null) {
- prev = slow;
- slow = slow.next;
- fast = fast.next;
+ while (fastIndex != null) {
+ fastIndex = fastIndex.next;
+ slowIndex = slowIndex.next;
}
- // 上一节点的next指针绕过 待删除节点slow 直接指向slow的下一节点
- prev.next = slow.next;
- // 释放 待删除节点slow 的next指针, 这句删掉也能AC
- slow.next = null;
- return dummy.next;
+ // 此时 slowIndex 的位置就是待删除元素的前一个位置。
+ // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
+ // 检查 slowIndex.next 是否为 null,以避免空指针异常
+ if (slowIndex.next != null) {
+ slowIndex.next = slowIndex.next.next;
+ }
+ return dummyNode.next;
}
}
```
-Python:
+
+```java
+class Solution {
+ public ListNode removeNthFromEnd(ListNode head, int n) {
+ // 创建一个新的哑节点,指向原链表头
+ ListNode s = new ListNode(-1, head);
+ // 递归调用remove方法,从哑节点开始进行删除操作
+ remove(s, n);
+ // 返回新链表的头(去掉可能的哑节点)
+ return s.next;
+ }
+
+ public int remove(ListNode p, int n) {
+ // 递归结束条件:如果当前节点为空,返回0
+ if (p == null) {
+ return 0;
+ }
+ // 递归深入到下一个节点
+ int net = remove(p.next, n);
+ // 如果当前节点是倒数第n个节点,进行删除操作
+ if (net == n) {
+ p.next = p.next.next;
+ }
+ // 返回当前节点的总深度
+ return net + 1;
+ }
+}
+```
+
+
+### Python:
+
```python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
+
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
- head_dummy = ListNode()
- head_dummy.next = head
-
- slow, fast = head_dummy, head_dummy
- while(n!=0): #fast先往前走n步
+ # 创建一个虚拟节点,并将其下一个指针设置为链表的头部
+ dummy_head = ListNode(0, head)
+
+ # 创建两个指针,慢指针和快指针,并将它们初始化为虚拟节点
+ slow = fast = dummy_head
+
+ # 快指针比慢指针快 n+1 步
+ for i in range(n+1):
fast = fast.next
- n -= 1
- while(fast.next!=None):
+
+ # 移动两个指针,直到快速指针到达链表的末尾
+ while fast:
slow = slow.next
fast = fast.next
- #fast 走到结尾后,slow的下一个节点为倒数第N个节点
- slow.next = slow.next.next #删除
- return head_dummy.next
+
+ # 通过更新第 (n-1) 个节点的 next 指针删除第 n 个节点
+ slow.next = slow.next.next
+
+ return dummy_head.next
+
```
-Go:
+### Go:
+
```Go
/**
* Definition for singly-linked list.
@@ -144,24 +200,21 @@ Go:
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
- dummyHead := &ListNode{}
- dummyHead.Next = head
- cur := head
- prev := dummyHead
- i := 1
- for cur != nil {
- cur = cur.Next
- if i > n {
- prev = prev.Next
- }
- i++
- }
- prev.Next = prev.Next.Next
- return dummyHead.Next
+ dummyNode := &ListNode{0, head}
+ fast, slow := dummyNode, dummyNode
+ for i := 0; i <= n; i++ { // 注意<=,否则快指针为空时,慢指针正好在倒数第n个上面
+ fast = fast.Next
+ }
+ for fast != nil {
+ fast = fast.Next
+ slow = slow.Next
+ }
+ slow.Next = slow.Next.Next
+ return dummyNode.Next
}
```
-JavaScript:
+### JavaScript:
```js
/**
@@ -169,37 +222,41 @@ JavaScript:
* @param {number} n
* @return {ListNode}
*/
-var removeNthFromEnd = function(head, n) {
- let ret = new ListNode(0, head),
- slow = fast = ret;
- while(n--) fast = fast.next;
- while (fast.next !== null) {
- fast = fast.next;
- slow = slow.next
- };
- slow.next = slow.next.next;
- return ret.next;
+var removeNthFromEnd = function (head, n) {
+ // 创建哨兵节点,简化解题逻辑
+ let dummyHead = new ListNode(0, head);
+ let fast = dummyHead;
+ let slow = dummyHead;
+ while (n--) fast = fast.next;
+ while (fast.next !== null) {
+ slow = slow.next;
+ fast = fast.next;
+ }
+ slow.next = slow.next.next;
+ return dummyHead.next;
};
```
-TypeScript:
+### TypeScript:
版本一(快慢指针法):
```typescript
function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
let newHead: ListNode | null = new ListNode(0, head);
- let slowNode: ListNode | null = newHead,
- fastNode: ListNode | null = newHead;
- for (let i = 0; i < n; i++) {
- fastNode = fastNode.next;
+ //根据leetcode题目的定义可推断这里快慢指针均不需要定义为ListNode | null。
+ let slowNode: ListNode = newHead;
+ let fastNode: ListNode = newHead;
+
+ while(n--) {
+ fastNode = fastNode.next!; //由虚拟头节点前进n个节点时,fastNode.next可推断不为null。
}
- while (fastNode.next) {
+ while(fastNode.next) { //遍历直至fastNode.next = null, 即尾部节点。 此时slowNode指向倒数第n个节点。
fastNode = fastNode.next;
- slowNode = slowNode.next;
+ slowNode = slowNode.next!;
}
- slowNode.next = slowNode.next.next;
- return newHead.next;
-};
+ slowNode.next = slowNode.next!.next; //倒数第n个节点可推断其next节点不为空。
+ return newHead.next;
+}
```
版本二(计算节点总数法):
@@ -244,7 +301,7 @@ function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
};
```
-Kotlin:
+### Kotlin:
```Kotlin
fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
@@ -265,7 +322,8 @@ fun removeNthFromEnd(head: ListNode?, n: Int): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
if head == nil {
@@ -290,5 +348,132 @@ func removeNthFromEnd(_ head: ListNode?, _ n: Int) -> ListNode? {
}
```
------------------------
-
 -
-
-
-
 -
-
-
- +
+ +
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[帮你把链表细节学清楚! | LeetCode:24. 两两交换链表中的节点](https://www.bilibili.com/video/BV1YT411g7br),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
+
这道题目正常模拟就可以了。
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
@@ -28,16 +31,16 @@
初始时,cur指向虚拟头结点,然后进行如下三步:
-
+
操作之后,链表如下:
-
+
看这个可能就更直观一些了:
-
+
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
@@ -46,7 +49,7 @@ class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
+ dummyHead->next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
@@ -58,13 +61,15 @@ public:
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
- return dummyHead->next;
+ ListNode* result = dummyHead->next;
+ delete dummyHead;
+ return result;
}
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
## 拓展
@@ -74,9 +79,9 @@ public:
上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-心想应该没有更好的方法了吧,也就$O(n)$的时间复杂度,重复提交几次,这样了:
+心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:
-
+
力扣上的统计如果两份代码是 100ms 和 300ms的耗时,其实是需要注意的。
@@ -85,7 +90,8 @@ public:
## 其他语言版本
-C:
+### C:
+
```c
/**
* Definition for singly-linked list.
@@ -129,7 +135,7 @@ struct ListNode* swapPairs(struct ListNode* head){
}
```
-Java:
+### Java:
```Java
// 递归版本
@@ -151,28 +157,71 @@ class Solution {
```
```java
-// 虚拟头结点
class Solution {
public ListNode swapPairs(ListNode head) {
+ ListNode dumyhead = new ListNode(-1); // 设置一个虚拟头结点
+ dumyhead.next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
+ ListNode cur = dumyhead;
+ ListNode temp; // 临时节点,保存两个节点后面的节点
+ ListNode firstnode; // 临时节点,保存两个节点之中的第一个节点
+ ListNode secondnode; // 临时节点,保存两个节点之中的第二个节点
+ while (cur.next != null && cur.next.next != null) {
+ temp = cur.next.next.next;
+ firstnode = cur.next;
+ secondnode = cur.next.next;
+ cur.next = secondnode; // 步骤一
+ secondnode.next = firstnode; // 步骤二
+ firstnode.next = temp; // 步骤三
+ cur = firstnode; // cur移动,准备下一轮交换
+ }
+ return dumyhead.next;
+ }
+}
+```
- ListNode dummyNode = new ListNode(0);
- dummyNode.next = head;
- ListNode prev = dummyNode;
-
- while (prev.next != null && prev.next.next != null) {
- ListNode temp = head.next.next; // 缓存 next
- prev.next = head.next; // 将 prev 的 next 改为 head 的 next
- head.next.next = head; // 将 head.next(prev.next) 的next,指向 head
- head.next = temp; // 将head 的 next 接上缓存的temp
- prev = head; // 步进1位
- head = head.next; // 步进1位
+```java
+// 将步骤 2,3 交换顺序,这样不用定义 temp 节点
+public ListNode swapPairs(ListNode head) {
+ ListNode dummy = new ListNode(0, head);
+ ListNode cur = dummy;
+ while (cur.next != null && cur.next.next != null) {
+ ListNode node1 = cur.next;// 第 1 个节点
+ ListNode node2 = cur.next.next;// 第 2 个节点
+ cur.next = node2; // 步骤 1
+ node1.next = node2.next;// 步骤 3
+ node2.next = node1;// 步骤 2
+ cur = cur.next.next;
}
- return dummyNode.next;
- }
+ return dummy.next;
}
```
-Python:
+### Python:
+
+```python
+# 递归版本
+# Definition for singly-linked list.
+# class ListNode:
+# def __init__(self, val=0, next=None):
+# self.val = val
+# self.next = next
+
+class Solution:
+ def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
+ if head is None or head.next is None:
+ return head
+
+ # 待翻转的两个node分别是pre和cur
+ pre = head
+ cur = head.next
+ next = head.next.next
+
+ cur.next = pre # 交换
+ pre.next = self.swapPairs(next) # 将以next为head的后续链表两两交换
+
+ return cur
+```
+
```python
# Definition for singly-linked list.
# class ListNode:
@@ -182,24 +231,24 @@ Python:
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
- res = ListNode(next=head)
- pre = res
+ dummy_head = ListNode(next=head)
+ current = dummy_head
- # 必须有pre的下一个和下下个才能交换,否则说明已经交换结束了
- while pre.next and pre.next.next:
- cur = pre.next
- post = pre.next.next
+ # 必须有cur的下一个和下下个才能交换,否则说明已经交换结束了
+ while current.next and current.next.next:
+ temp = current.next # 防止节点修改
+ temp1 = current.next.next.next
- # pre,cur,post对应最左,中间的,最右边的节点
- cur.next = post.next
- post.next = cur
- pre.next = post
+ current.next = current.next.next
+ current.next.next = temp
+ temp.next = temp1
+ current = current.next.next
+ return dummy_head.next
- pre = pre.next.next
- return res.next
```
-Go:
+### Go:
+
```go
func swapPairs(head *ListNode) *ListNode {
dummy := &ListNode{
@@ -235,7 +284,8 @@ func swapPairs(head *ListNode) *ListNode {
}
```
-Javascript:
+### JavaScript:
+
```javascript
var swapPairs = function (head) {
let ret = new ListNode(0, head), temp = ret;
@@ -250,27 +300,41 @@ var swapPairs = function (head) {
};
```
-TypeScript:
+```javascript
+// 递归版本
+var swapPairs = function (head) {
+ if (head == null || head.next == null) {
+ return head;
+ }
+
+ let after = head.next;
+ head.next = swapPairs(after.next);
+ after.next = head;
+
+ return after;
+};
+```
+
+### TypeScript:
```typescript
function swapPairs(head: ListNode | null): ListNode | null {
- const dummyHead: ListNode = new ListNode(0, head);
- let cur: ListNode = dummyHead;
- while(cur.next !== null && cur.next.next !== null) {
- const tem: ListNode = cur.next;
- const tem1: ListNode = cur.next.next.next;
-
- cur.next = cur.next.next; // step 1
- cur.next.next = tem; // step 2
- cur.next.next.next = tem1; // step 3
-
- cur = cur.next.next;
- }
- return dummyHead.next;
-}
+ const dummyNode: ListNode = new ListNode(0, head);
+ let curNode: ListNode | null = dummyNode;
+ while (curNode && curNode.next && curNode.next.next) {
+ let firstNode: ListNode = curNode.next,
+ secNode: ListNode = curNode.next.next,
+ thirdNode: ListNode | null = curNode.next.next.next;
+ curNode.next = secNode;
+ secNode.next = firstNode;
+ firstNode.next = thirdNode;
+ curNode = firstNode;
+ }
+ return dummyNode.next;
+};
```
-Kotlin:
+### Kotlin:
```kotlin
fun swapPairs(head: ListNode?): ListNode? {
@@ -290,7 +354,8 @@ fun swapPairs(head: ListNode?): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func swapPairs(_ head: ListNode?) -> ListNode? {
if head == nil || head?.next == nil {
@@ -311,7 +376,152 @@ func swapPairs(_ head: ListNode?) -> ListNode? {
return dummyHead.next
}
```
+### Scala:
+
+```scala
+// 虚拟头节点
+object Solution {
+ def swapPairs(head: ListNode): ListNode = {
+ var dummy = new ListNode(0, head) // 虚拟头节点
+ var pre = dummy
+ var cur = head
+ // 当pre的下一个和下下个都不为空,才进行两两转换
+ while (pre.next != null && pre.next.next != null) {
+ var tmp: ListNode = cur.next.next // 缓存下一次要进行转换的第一个节点
+ pre.next = cur.next // 步骤一
+ cur.next.next = cur // 步骤二
+ cur.next = tmp // 步骤三
+ // 下面是准备下一轮的交换
+ pre = cur
+ cur = tmp
+ }
+ // 最终返回dummy虚拟头节点的下一个,return可以省略
+ dummy.next
+ }
+}
+```
+
+### PHP:
+
+```php
+//虚拟头结点
+function swapPairs($head) {
+ if ($head == null || $head->next == null) {
+ return $head;
+ }
+
+ $dummyNode = new ListNode(0, $head);
+ $preNode = $dummyNode; //虚拟头结点
+ $curNode = $head;
+ $nextNode = $head->next;
+ while($curNode && $nextNode) {
+ $nextNextNode = $nextNode->next; //存下一个节点
+ $nextNode->next = $curNode; //交换curHead 和 nextHead
+ $curNode->next = $nextNextNode;
+ $preNode->next = $nextNode; //上一个节点的下一个指向指向nextHead
+
+ //更新当前的几个指针
+ $preNode = $preNode->next->next;
+ $curNode = $nextNextNode;
+ $nextNode = $nextNextNode->next;
+ }
+
+ return $dummyNode->next;
+}
+
+//递归版本
+function swapPairs($head)
+{
+ // 终止条件
+ if ($head === null || $head->next === null) {
+ return $head;
+ }
+
+ //结果要返回的头结点
+ $next = $head->next;
+ $head->next = $this->swapPairs($next->next); //当前头结点->next指向更新
+ $next->next = $head; //当前第二个节点的->next指向更新
+ return $next; //返回翻转后的头结点
+}
+```
+### Rust:
+
+```rust
+// 虚拟头节点
+impl Solution {
+ pub fn swap_pairs(head: Option
+
+## 算法公开课
+
+**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[帮你把链表细节学清楚! | LeetCode:24. 两两交换链表中的节点](https://www.bilibili.com/video/BV1YT411g7br),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
+
这道题目正常模拟就可以了。
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
@@ -28,16 +31,16 @@
初始时,cur指向虚拟头结点,然后进行如下三步:
-
+
操作之后,链表如下:
-
+
看这个可能就更直观一些了:
-
+
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
@@ -46,7 +49,7 @@ class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
- dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
+ dummyHead->next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
@@ -58,13 +61,15 @@ public:
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
- return dummyHead->next;
+ ListNode* result = dummyHead->next;
+ delete dummyHead;
+ return result;
}
};
```
-* 时间复杂度:$O(n)$
-* 空间复杂度:$O(1)$
+* 时间复杂度:O(n)
+* 空间复杂度:O(1)
## 拓展
@@ -74,9 +79,9 @@ public:
上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。
-心想应该没有更好的方法了吧,也就$O(n)$的时间复杂度,重复提交几次,这样了:
+心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:
-
+
力扣上的统计如果两份代码是 100ms 和 300ms的耗时,其实是需要注意的。
@@ -85,7 +90,8 @@ public:
## 其他语言版本
-C:
+### C:
+
```c
/**
* Definition for singly-linked list.
@@ -129,7 +135,7 @@ struct ListNode* swapPairs(struct ListNode* head){
}
```
-Java:
+### Java:
```Java
// 递归版本
@@ -151,28 +157,71 @@ class Solution {
```
```java
-// 虚拟头结点
class Solution {
public ListNode swapPairs(ListNode head) {
+ ListNode dumyhead = new ListNode(-1); // 设置一个虚拟头结点
+ dumyhead.next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
+ ListNode cur = dumyhead;
+ ListNode temp; // 临时节点,保存两个节点后面的节点
+ ListNode firstnode; // 临时节点,保存两个节点之中的第一个节点
+ ListNode secondnode; // 临时节点,保存两个节点之中的第二个节点
+ while (cur.next != null && cur.next.next != null) {
+ temp = cur.next.next.next;
+ firstnode = cur.next;
+ secondnode = cur.next.next;
+ cur.next = secondnode; // 步骤一
+ secondnode.next = firstnode; // 步骤二
+ firstnode.next = temp; // 步骤三
+ cur = firstnode; // cur移动,准备下一轮交换
+ }
+ return dumyhead.next;
+ }
+}
+```
- ListNode dummyNode = new ListNode(0);
- dummyNode.next = head;
- ListNode prev = dummyNode;
-
- while (prev.next != null && prev.next.next != null) {
- ListNode temp = head.next.next; // 缓存 next
- prev.next = head.next; // 将 prev 的 next 改为 head 的 next
- head.next.next = head; // 将 head.next(prev.next) 的next,指向 head
- head.next = temp; // 将head 的 next 接上缓存的temp
- prev = head; // 步进1位
- head = head.next; // 步进1位
+```java
+// 将步骤 2,3 交换顺序,这样不用定义 temp 节点
+public ListNode swapPairs(ListNode head) {
+ ListNode dummy = new ListNode(0, head);
+ ListNode cur = dummy;
+ while (cur.next != null && cur.next.next != null) {
+ ListNode node1 = cur.next;// 第 1 个节点
+ ListNode node2 = cur.next.next;// 第 2 个节点
+ cur.next = node2; // 步骤 1
+ node1.next = node2.next;// 步骤 3
+ node2.next = node1;// 步骤 2
+ cur = cur.next.next;
}
- return dummyNode.next;
- }
+ return dummy.next;
}
```
-Python:
+### Python:
+
+```python
+# 递归版本
+# Definition for singly-linked list.
+# class ListNode:
+# def __init__(self, val=0, next=None):
+# self.val = val
+# self.next = next
+
+class Solution:
+ def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
+ if head is None or head.next is None:
+ return head
+
+ # 待翻转的两个node分别是pre和cur
+ pre = head
+ cur = head.next
+ next = head.next.next
+
+ cur.next = pre # 交换
+ pre.next = self.swapPairs(next) # 将以next为head的后续链表两两交换
+
+ return cur
+```
+
```python
# Definition for singly-linked list.
# class ListNode:
@@ -182,24 +231,24 @@ Python:
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
- res = ListNode(next=head)
- pre = res
+ dummy_head = ListNode(next=head)
+ current = dummy_head
- # 必须有pre的下一个和下下个才能交换,否则说明已经交换结束了
- while pre.next and pre.next.next:
- cur = pre.next
- post = pre.next.next
+ # 必须有cur的下一个和下下个才能交换,否则说明已经交换结束了
+ while current.next and current.next.next:
+ temp = current.next # 防止节点修改
+ temp1 = current.next.next.next
- # pre,cur,post对应最左,中间的,最右边的节点
- cur.next = post.next
- post.next = cur
- pre.next = post
+ current.next = current.next.next
+ current.next.next = temp
+ temp.next = temp1
+ current = current.next.next
+ return dummy_head.next
- pre = pre.next.next
- return res.next
```
-Go:
+### Go:
+
```go
func swapPairs(head *ListNode) *ListNode {
dummy := &ListNode{
@@ -235,7 +284,8 @@ func swapPairs(head *ListNode) *ListNode {
}
```
-Javascript:
+### JavaScript:
+
```javascript
var swapPairs = function (head) {
let ret = new ListNode(0, head), temp = ret;
@@ -250,27 +300,41 @@ var swapPairs = function (head) {
};
```
-TypeScript:
+```javascript
+// 递归版本
+var swapPairs = function (head) {
+ if (head == null || head.next == null) {
+ return head;
+ }
+
+ let after = head.next;
+ head.next = swapPairs(after.next);
+ after.next = head;
+
+ return after;
+};
+```
+
+### TypeScript:
```typescript
function swapPairs(head: ListNode | null): ListNode | null {
- const dummyHead: ListNode = new ListNode(0, head);
- let cur: ListNode = dummyHead;
- while(cur.next !== null && cur.next.next !== null) {
- const tem: ListNode = cur.next;
- const tem1: ListNode = cur.next.next.next;
-
- cur.next = cur.next.next; // step 1
- cur.next.next = tem; // step 2
- cur.next.next.next = tem1; // step 3
-
- cur = cur.next.next;
- }
- return dummyHead.next;
-}
+ const dummyNode: ListNode = new ListNode(0, head);
+ let curNode: ListNode | null = dummyNode;
+ while (curNode && curNode.next && curNode.next.next) {
+ let firstNode: ListNode = curNode.next,
+ secNode: ListNode = curNode.next.next,
+ thirdNode: ListNode | null = curNode.next.next.next;
+ curNode.next = secNode;
+ secNode.next = firstNode;
+ firstNode.next = thirdNode;
+ curNode = firstNode;
+ }
+ return dummyNode.next;
+};
```
-Kotlin:
+### Kotlin:
```kotlin
fun swapPairs(head: ListNode?): ListNode? {
@@ -290,7 +354,8 @@ fun swapPairs(head: ListNode?): ListNode? {
}
```
-Swift:
+### Swift:
+
```swift
func swapPairs(_ head: ListNode?) -> ListNode? {
if head == nil || head?.next == nil {
@@ -311,7 +376,152 @@ func swapPairs(_ head: ListNode?) -> ListNode? {
return dummyHead.next
}
```
+### Scala:
+
+```scala
+// 虚拟头节点
+object Solution {
+ def swapPairs(head: ListNode): ListNode = {
+ var dummy = new ListNode(0, head) // 虚拟头节点
+ var pre = dummy
+ var cur = head
+ // 当pre的下一个和下下个都不为空,才进行两两转换
+ while (pre.next != null && pre.next.next != null) {
+ var tmp: ListNode = cur.next.next // 缓存下一次要进行转换的第一个节点
+ pre.next = cur.next // 步骤一
+ cur.next.next = cur // 步骤二
+ cur.next = tmp // 步骤三
+ // 下面是准备下一轮的交换
+ pre = cur
+ cur = tmp
+ }
+ // 最终返回dummy虚拟头节点的下一个,return可以省略
+ dummy.next
+ }
+}
+```
+
+### PHP:
+
+```php
+//虚拟头结点
+function swapPairs($head) {
+ if ($head == null || $head->next == null) {
+ return $head;
+ }
+
+ $dummyNode = new ListNode(0, $head);
+ $preNode = $dummyNode; //虚拟头结点
+ $curNode = $head;
+ $nextNode = $head->next;
+ while($curNode && $nextNode) {
+ $nextNextNode = $nextNode->next; //存下一个节点
+ $nextNode->next = $curNode; //交换curHead 和 nextHead
+ $curNode->next = $nextNextNode;
+ $preNode->next = $nextNode; //上一个节点的下一个指向指向nextHead
+
+ //更新当前的几个指针
+ $preNode = $preNode->next->next;
+ $curNode = $nextNextNode;
+ $nextNode = $nextNextNode->next;
+ }
+
+ return $dummyNode->next;
+}
+
+//递归版本
+function swapPairs($head)
+{
+ // 终止条件
+ if ($head === null || $head->next === null) {
+ return $head;
+ }
+
+ //结果要返回的头结点
+ $next = $head->next;
+ $head->next = $this->swapPairs($next->next); //当前头结点->next指向更新
+ $next->next = $head; //当前第二个节点的->next指向更新
+ return $next; //返回翻转后的头结点
+}
+```
+### Rust:
+
+```rust
+// 虚拟头节点
+impl Solution {
+ pub fn swap_pairs(head: Option
 -
-
-
- +### Kotlin:
+
+```kotlin
+fun removeElement(nums: IntArray, `val`: Int): Int {
+ var slowIndex = 0 // 初始化慢指针
+ for (fastIndex in nums.indices) {
+ if (nums[fastIndex] != `val`) nums[slowIndex++] = nums[fastIndex] // 在慢指针所在位置存储未被删除的元素
+ }
+ return slowIndex
+ }
+```
+
+### Scala:
+
+```scala
+object Solution {
+ def removeElement(nums: Array[Int], `val`: Int): Int = {
+ var slow = 0
+ for (fast <- 0 until nums.length) {
+ if (`val` != nums(fast)) {
+ nums(slow) = nums(fast)
+ slow += 1
+ }
+ }
+ slow
+ }
+}
+```
+
+### C#:
+
+```csharp
+public class Solution {
+ public int RemoveElement(int[] nums, int val) {
+ int slow = 0;
+ for (int fast = 0; fast < nums.Length; fast++) {
+ if (val != nums[fast]) {
+ nums[slow++] = nums[fast];
+ }
+ }
+ return slow;
+ }
+}
+```
+
+###Dart:
+```dart
+int removeElement(List
+### Kotlin:
+
+```kotlin
+fun removeElement(nums: IntArray, `val`: Int): Int {
+ var slowIndex = 0 // 初始化慢指针
+ for (fastIndex in nums.indices) {
+ if (nums[fastIndex] != `val`) nums[slowIndex++] = nums[fastIndex] // 在慢指针所在位置存储未被删除的元素
+ }
+ return slowIndex
+ }
+```
+
+### Scala:
+
+```scala
+object Solution {
+ def removeElement(nums: Array[Int], `val`: Int): Int = {
+ var slow = 0
+ for (fast <- 0 until nums.length) {
+ if (`val` != nums(fast)) {
+ nums(slow) = nums(fast)
+ slow += 1
+ }
+ }
+ slow
+ }
+}
+```
+
+### C#:
+
+```csharp
+public class Solution {
+ public int RemoveElement(int[] nums, int val) {
+ int slow = 0;
+ for (int fast = 0; fast < nums.Length; fast++) {
+ if (val != nums[fast]) {
+ nums[slow++] = nums[fast];
+ }
+ }
+ return slow;
+ }
+}
+```
+
+###Dart:
+```dart
+int removeElement(List -
-
-
- +
+ 然后就找到了下标2,指向b,继续匹配:如图:
-
然后就找到了下标2,指向b,继续匹配:如图:
- +
+ 以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
+**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。**
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-# 如何计算前缀表
+### 如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图:
-
以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
-**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。**
+**下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。**
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
**很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。**
-# 如何计算前缀表
+### 如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图:
- +
+ 长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
-
长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
- +
+ +
长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
-
+
长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
- +
+ +
长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
以此类推:
@@ -185,13 +185,13 @@ next数组就是一个前缀表(prefix table)。
长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
-
+
长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
以此类推:
@@ -185,13 +185,13 @@ next数组就是一个前缀表(prefix table)。
长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
- +
+ 可以看出模式串与前缀表对应位置的数字表示的就是:**下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
+
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
@@ -199,23 +199,23 @@ next数组就是一个前缀表(prefix table)。
所以要看前一位的 前缀表的数值。
-前一个字符的前缀表的数值是2, 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
+前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
-# 前缀表与next数组
+### 前缀表与next数组
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
+很多KMP算法的实现都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
+其实**这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
后面我会提供两种不同的实现代码,大家就明白了。
-# 使用next数组来匹配
+### 使用next数组来匹配
**以下我们以前缀表统一减一之后的next数组来做演示**。
@@ -225,19 +225,19 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
匹配过程动画如下:
-
+
-# 时间复杂度分析
+### 时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
+暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大地提高了搜索的效率。**
为了和力扣题目28.实现strStr保持一致,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法,一定要构造next数组。
-# 构造next数组
+### 构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
@@ -251,7 +251,7 @@ void getNext(int* next, const string& s)
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况
-接下来我们详解详解一下。
+接下来我们详解一下。
1. 初始化:
@@ -332,11 +332,11 @@ void getNext(int* next, const string& s){
代码构造next数组的逻辑流程动画如下:
-
+
得到了next数组之后,就要用这个来做匹配了。
-# 使用next数组来做匹配
+### 使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
@@ -401,7 +401,7 @@ for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
此时所有逻辑的代码都已经写出来了,力扣 28.实现strStr 题目的整体代码如下:
-# 前缀表统一减一 C++代码实现
+### 前缀表统一减一 C++代码实现
```CPP
class Solution {
@@ -423,8 +423,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector
可以看出模式串与前缀表对应位置的数字表示的就是:**下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
-
+
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
@@ -199,23 +199,23 @@ next数组就是一个前缀表(prefix table)。
所以要看前一位的 前缀表的数值。
-前一个字符的前缀表的数值是2, 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
+前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
-# 前缀表与next数组
+### 前缀表与next数组
-很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
+很多KMP算法的实现都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
-其实**这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
+其实**这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。**
后面我会提供两种不同的实现代码,大家就明白了。
-# 使用next数组来匹配
+### 使用next数组来匹配
**以下我们以前缀表统一减一之后的next数组来做演示**。
@@ -225,19 +225,19 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
匹配过程动画如下:
-
+
-# 时间复杂度分析
+### 时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
-暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大的提高的搜索的效率。**
+暴力的解法显而易见是O(n × m),所以**KMP在字符串匹配中极大地提高了搜索的效率。**
为了和力扣题目28.实现strStr保持一致,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法,一定要构造next数组。
-# 构造next数组
+### 构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
@@ -251,7 +251,7 @@ void getNext(int* next, const string& s)
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况
-接下来我们详解详解一下。
+接下来我们详解一下。
1. 初始化:
@@ -332,11 +332,11 @@ void getNext(int* next, const string& s){
代码构造next数组的逻辑流程动画如下:
-
+
得到了next数组之后,就要用这个来做匹配了。
-# 使用next数组来做匹配
+### 使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
@@ -401,7 +401,7 @@ for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
此时所有逻辑的代码都已经写出来了,力扣 28.实现strStr 题目的整体代码如下:
-# 前缀表统一减一 C++代码实现
+### 前缀表统一减一 C++代码实现
```CPP
class Solution {
@@ -423,8 +423,8 @@ public:
if (needle.size() == 0) {
return 0;
}
- int next[needle.size()];
- getNext(next, needle);
+ vector
 -
-
-
- +
+ 对应的C++代码如下:
@@ -92,9 +90,9 @@ public:
};
```
-# 其他语言版本
+## 其他语言版本
-## Java
+### Java
```java
class Solution {
@@ -116,83 +114,107 @@ class Solution {
}
}
```
+> 优化时间复杂度为O(N),空间复杂度为O(1)
+```Java
+class Solution {
+ public void nextPermutation(int[] nums) {
+ // 1.从后向前获取逆序区域的前一位
+ int index = findIndex(nums);
+ // 判断数组是否处于最小组合状态
+ if(index != 0){
+ // 2.交换逆序区域刚好大于它的最小数字
+ exchange(nums,index);
+ }
+ // 3.把原来的逆序区转为顺序
+ reverse(nums,index);
+ }
+
+ public static int findIndex(int [] nums){
+ for(int i = nums.length-1;i>0;i--){
+ if(nums[i]>nums[i-1]){
+ return i;
+ }
+ }
+ return 0;
+ }
+ public static void exchange(int [] nums, int index){
+ int head = nums[index-1];
+ for(int i = nums.length-1;i>0;i--){
+ if(head < nums[i]){
+ nums[index-1] = nums[i];
+ nums[i] = head;
+ break;
+ }
+ }
+ }
+ public static void reverse(int [] nums, int index){
+ for(int i = index,j = nums.length-1;i
对应的C++代码如下:
@@ -92,9 +90,9 @@ public:
};
```
-# 其他语言版本
+## 其他语言版本
-## Java
+### Java
```java
class Solution {
@@ -116,83 +114,107 @@ class Solution {
}
}
```
+> 优化时间复杂度为O(N),空间复杂度为O(1)
+```Java
+class Solution {
+ public void nextPermutation(int[] nums) {
+ // 1.从后向前获取逆序区域的前一位
+ int index = findIndex(nums);
+ // 判断数组是否处于最小组合状态
+ if(index != 0){
+ // 2.交换逆序区域刚好大于它的最小数字
+ exchange(nums,index);
+ }
+ // 3.把原来的逆序区转为顺序
+ reverse(nums,index);
+ }
+
+ public static int findIndex(int [] nums){
+ for(int i = nums.length-1;i>0;i--){
+ if(nums[i]>nums[i-1]){
+ return i;
+ }
+ }
+ return 0;
+ }
+ public static void exchange(int [] nums, int index){
+ int head = nums[index-1];
+ for(int i = nums.length-1;i>0;i--){
+ if(head < nums[i]){
+ nums[index-1] = nums[i];
+ nums[i] = head;
+ break;
+ }
+ }
+ }
+ public static void reverse(int [] nums, int index){
+ for(int i = index,j = nums.length-1;i +
diff --git "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
old mode 100644
new mode 100755
index dfd90b8280..37248e4819
--- "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
@@ -1,12 +1,13 @@
-
+
diff --git "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
old mode 100644
new mode 100755
index dfd90b8280..37248e4819
--- "a/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ "b/problems/0034.\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
@@ -1,12 +1,13 @@
- -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-
 -
-
-
-