|
| 1 | + |
| 2 | +# 思路 |
| 3 | + |
| 4 | +## 深搜 |
| 5 | + |
| 6 | +这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。 |
| 7 | + |
| 8 | +注意题目中说机器人每次只能向下或者向右移动一步,那么其实**机器人走过的路径可以抽象为一颗二叉树,而叶子节点就是终点!** |
| 9 | + |
| 10 | +如图举例: |
| 11 | + |
| 12 | +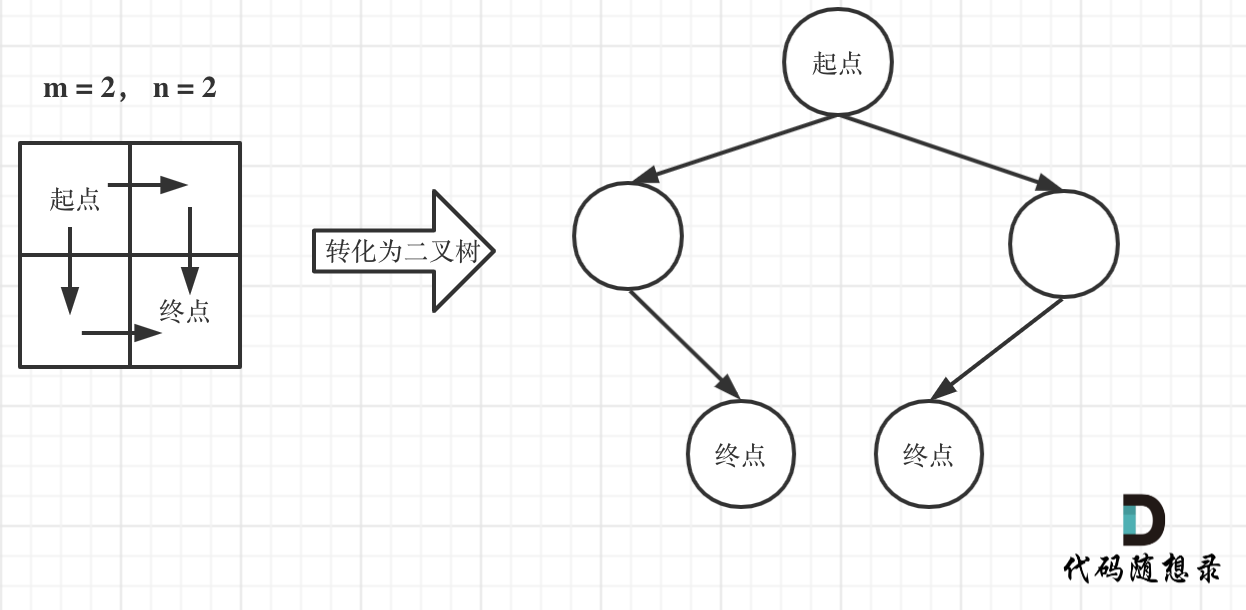 |
| 13 | + |
| 14 | +此时问题就可以转化为求二叉树叶子节点的个数,代码如下: |
| 15 | + |
| 16 | +```C++ |
| 17 | +class Solution { |
| 18 | +private: |
| 19 | + int dfs(int i, int j, int m, int n) { |
| 20 | + if (i > m || j > n) return 0; // 越界了 |
| 21 | + if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点 |
| 22 | + return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n); |
| 23 | + } |
| 24 | +public: |
| 25 | + int uniquePaths(int m, int n) { |
| 26 | + return dfs(1, 1, m, n); |
| 27 | + } |
| 28 | +}; |
| 29 | +``` |
| 30 | +
|
| 31 | +大家如果提交了代码就会发现超时了! |
| 32 | +
|
| 33 | +来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。 |
| 34 | +
|
| 35 | +这颗树的深度其实就是m+n-1(深度按从1开始计算)。 |
| 36 | +
|
| 37 | +那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有把搜索节点都遍历到,只是近似而已) |
| 38 | +
|
| 39 | +所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。 |
| 40 | +
|
| 41 | +## 动态规划 |
| 42 | +
|
| 43 | +机器人从(0 , 0) 位置触发,到(m - 1, n - 1)终点。 |
| 44 | +
|
| 45 | +按照动规三部曲来分析: |
| 46 | +
|
| 47 | +* dp数组表述啥 |
| 48 | +
|
| 49 | +这里设计一个dp二维数组,dp[i][j] 表示从(0 ,0)出发,到(i, j) 有几条不同的路径。 |
| 50 | +
|
| 51 | +* dp数组的初始化 |
| 52 | +
|
| 53 | +如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。 |
| 54 | +
|
| 55 | +所以初始化代码为: |
| 56 | +
|
| 57 | +``` |
| 58 | +for (int i = 0; i < m; i++) dp[i][0] = 1; |
| 59 | +for (int j = 0; j < n; j++) dp[0][j] = 1; |
| 60 | +``` |
| 61 | +
|
| 62 | +* 递推公式 |
| 63 | +
|
| 64 | +想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。 |
| 65 | +
|
| 66 | +此时在回顾一下 dp[i-1][j] 表示啥,是从(0, 0)的位置到(i-1, j)有几条路径,dp[i][j - 1]同理。 |
| 67 | +
|
| 68 | +那么很自然,dp[i][j] = dp[i-1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。 |
| 69 | +
|
| 70 | +如图所示: |
| 71 | +
|
| 72 | + |
| 73 | +
|
| 74 | +C++代码如下: |
| 75 | +
|
| 76 | +```C++ |
| 77 | +class Solution { |
| 78 | +public: |
| 79 | + int uniquePaths(int m, int n) { |
| 80 | + vector<vector<int>> dp(m, vector<int>(n, 0)); |
| 81 | + for (int i = 0; i < m; i++) dp[i][0] = 1; |
| 82 | + for (int j = 0; j < n; j++) dp[0][j] = 1; |
| 83 | + for (int i = 1; i < m; i++) { |
| 84 | + for (int j = 1; j < n; j++) { |
| 85 | + dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; |
| 86 | + } |
| 87 | + } |
| 88 | + return dp[m - 1][n - 1]; |
| 89 | + } |
| 90 | +}; |
| 91 | +``` |
| 92 | +* 时间复杂度:O(m * n) |
| 93 | +* 空间复杂度:O(m * n) |
| 94 | + |
| 95 | +其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下: |
| 96 | + |
| 97 | +```C++ |
| 98 | +class Solution { |
| 99 | +public: |
| 100 | + int uniquePaths(int m, int n) { |
| 101 | + vector<int> dp(n); |
| 102 | + for (int i = 0; i < n; i++) dp[i] = 1; |
| 103 | + for (int j = 1; j < m; j++) { |
| 104 | + for (int i = 1; i < n; i++) { |
| 105 | + dp[i] += dp[i - 1]; |
| 106 | + } |
| 107 | + } |
| 108 | + return dp[n - 1]; |
| 109 | + } |
| 110 | +}; |
| 111 | +``` |
| 112 | +* 时间复杂度:O(m * n) |
| 113 | +* 空间复杂度:O(n) |
| 114 | +
|
| 115 | +# 数论方法 |
| 116 | +
|
| 117 | +在这个图中,可以看出一共 m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。 |
| 118 | +
|
| 119 | + |
| 120 | +
|
| 121 | +在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。 |
| 122 | +
|
| 123 | +那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。 |
| 124 | +
|
| 125 | +那么这就是一个组合问题了。 |
| 126 | +
|
| 127 | +那么答案,如图所示: |
| 128 | +
|
| 129 | +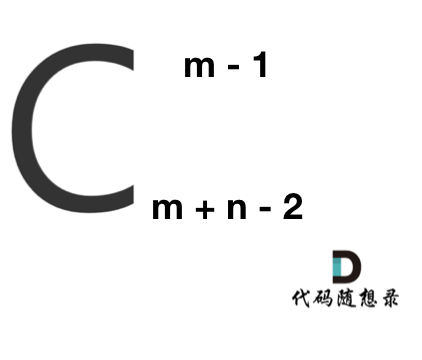 |
| 130 | +
|
| 131 | +**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。 |
| 132 | +
|
| 133 | +``` |
| 134 | +class Solution { |
| 135 | +public: |
| 136 | + int uniquePaths(int m, int n) { |
| 137 | + int numerator = 1, denominator = 1; |
| 138 | + int count = m - 1; |
| 139 | + int t = m + n - 2; |
| 140 | + while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出 |
| 141 | + for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母 |
| 142 | + return numerator / denominator; |
| 143 | + } |
| 144 | +}; |
| 145 | + |
| 146 | +``` |
| 147 | +
|
| 148 | +需要在计算分子的时候,不算除以分母,代码如下: |
| 149 | +
|
| 150 | +``` |
| 151 | +class Solution { |
| 152 | +public: |
| 153 | + int uniquePaths(int m, int n) { |
| 154 | + long long numerator = 1; // 分子 |
| 155 | + int denominator = m - 1; // 分母 |
| 156 | + int count = m - 1; |
| 157 | + int t = m + n - 2; |
| 158 | + while (count--) { |
| 159 | + numerator *= (t--); |
| 160 | + while (denominator != 0 && numerator % denominator == 0) { |
| 161 | + numerator /= denominator; |
| 162 | + denominator--; |
| 163 | + } |
| 164 | + } |
| 165 | + return numerator; |
| 166 | + } |
| 167 | +}; |
| 168 | +``` |
| 169 | +
|
| 170 | +计算组合问题的代码还是有难度的,特别是处理溢出的情况! |
| 171 | +
|
| 172 | +最后这个代码还有点复杂了,还是可以优化,我就不继续优化了,有空在整理一下,哈哈,就酱! |
| 173 | +
|
| 174 | +
|
| 175 | +
|
| 176 | +
|
0 commit comments