diff --git a/01_array/215.md b/01_array/215.md
deleted file mode 100644
index 5072f6e..0000000
--- a/01_array/215.md
+++ /dev/null
@@ -1,60 +0,0 @@
-## 215 数组中第K大的元素-中等
-
-题目要求:返回数组中第K大元素
-
-题目链接:https://leetcode-cn.com/problems/sort-an-array/
-
-算法分析:利用小顶堆保存K的元素,则堆顶就是想要的结果。
-
-
-
-首先将前k个元素保存,然后初始化小顶堆;继续遍历,如果元素大于堆顶元素,则与堆顶元素交换,重新调整小顶堆。
-
-```go
-// date 2022/09/24
-func findKthLargest(nums []int, k int) int {
- res := make([]int, 0, k)
- for i := 0; i < len(nums); i++ {
- if i < k {
- res = append(res, nums[i])
- if len(res) == k {
- makeMinHeap(res)
- }
- } else if nums[i] > res[0] {
- res[0] = nums[i]
- minHeapify(res, 0)
- }
- }
- return res[0]
-}
-
-// 采用自底向上的建堆方法
-func makeMinHeap(nums []int) {
- for i := len(nums) >> 1 - 1; i >= 0; i-- {
- minHeapify(nums, i)
- }
-}
-
-//
-func minHeapify(nums []int, k int) {
- if k > len(nums) {
- return
- }
- temp, n := nums[k], len(nums)
- l, r := k<<1+1, k<<1+2
- for l < n {
- r = l+1
- if r < n && nums[r] < nums[l] {
- l++
- }
- if nums[k] < nums[l] {
- break
- }
- nums[k] = nums[l]
- nums[l] = temp
- k = l
- l = k<<1+1
- }
-}
-```
-
diff --git a/01_array/220.md b/01_array/220.md
deleted file mode 100644
index e51771b..0000000
--- a/01_array/220.md
+++ /dev/null
@@ -1,40 +0,0 @@
-## 220 存在重复元素3-困难
-
-题目:
-
-给定一个数组nums和两个整数k,t。判断是否存在两个不同的下标,使得`nums[i]-nums[j] <= t`,同时`abs(i-j) <= k`,如果存在返回true,否则返回false。
-
-
-
-分析:
-
-滑动窗口,使用双指针控制窗口大小。该算法可行,但是某些测试用例会超时,所以需要寻找其他解法。
-
-```go
-// 该算法会超时
-func containsNearbyAlmostDuplicate(nums []int, indexDiff int, valueDiff int) bool {
- n := len(nums)
- left, right := 0, 0
- for left < n {
- right = left+1
- for right - left <= indexDiff && right < n {
- if abs(nums[left], nums[right]) <= valueDiff {
- return true
- }
- right++
- }
- left++
- }
- return false
-}
-
-func abs(x, y int) int {
- if x < y {
- return y-x
- }
- return x-y
-}
-```
-
-
-
diff --git "a/01_array/No.001_\344\270\244\346\225\260\344\271\213\345\222\214.md" "b/01_array/No.001_\344\270\244\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index 150b86b..0000000
--- "a/01_array/No.001_\344\270\244\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 1 两数之和-简单
-
-题目:
-
-给定一个整数数组 `nums` 和一个整数目标值 `target`,请你在该数组中找出 **和为目标值** *`target`* 的那 **两个** 整数,并返回它们的数组下标。
-
-你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
-
-你可以按任意顺序返回答案。
-
-
-
-**解题思路**
-
-题目中已经说明每种输入只会对应一种输出,所以可以有多种解法。
-
-- 两层循环。第一层遍历当前 x,然后从元素的 x 的下一个元素 y 开始遍历,如果 x + y 等于目标值,则返回两者的坐标,详见解法1。
-
-- 哈希表。利用map存储已经遍历过的元素和下标,达到O(1)查找,详见解法2。时间和空间复杂度都是`O(N)`。
-
-```go
-// date 2020/09/14
-// 解法1
-// 两层循环
-// 时间复杂度O(N^2)
-func twoSum(nums []int, target int) []int {
- res := make([]int, 0, 2)
- n := len(nums)
-
- for i := 0; i < n; i++ {
- for j := i+1; j < n; j++ {
- if nums[i] + nums[j] == target {
- res = append(res, i, j)
- return res
- }
- }
- }
-
- return res
-}
-// 解法2
-// map 查找
-func twoSum(nums []int, target int) []int {
- set := make(map[int]int, len(nums))
- res := []int{}
- for j, v := range nums {
- d := target - v
- if i, ok := set[d]; ok && i != j {
- res = append(res, i, j)
- break
- } else {
- set[v] = j
- }
- }
- return res
-}
-```
-
-扩展题目:两数之和
-
-**问题延伸:给定一个无序且元素可重复的数组a[],以及一个数sum,求a[]中是否存在两个元素的和等于sum,并输出这两个元素的下标。答案可能不止一种,请输出所有可能的答案结果集。**
-
-这是VMware面试中的一道题,以下是个人的解法。这个算法的时间复杂度为O(n),但是需要辅助空间。
-
-```go
-// data 2021/02/21
-// 解法一:两层循环
-func twoSum(nums []int, target int) [][]int {
- res := make([][]int, 0, 16)
- idx := make(map[int][]int, 16)
- for i, v := range nums {
- d := target - v
- if oldIdx, ok := idx[d]; ok && len(oldIdx) != 0 {
- for _, j := range oldIdx {
- res = append(res, []int{j, i})
- }
- }
- _, ok := idx[v]
- if !ok {
- idx[v] = []int{}
- }
- idx[v] = append(idx[v], i)
- }
- return res
-}
-```
-
diff --git "a/01_array/No.004_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\344\270\255\344\275\215\346\225\260.md" "b/01_array/No.004_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\344\270\255\344\275\215\346\225\260.md"
deleted file mode 100644
index 00b3744..0000000
--- "a/01_array/No.004_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\344\270\255\344\275\215\346\225\260.md"
+++ /dev/null
@@ -1,84 +0,0 @@
-## 004 寻找两个正序数组中的中位数-困难
-
-题目:
-
-给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
-
-算法的时间复杂度应该为 O(log (m+n)) 。
-
-
-分析:
-
-
-```go
-// date 2023/11/01
-func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
- s1, s2 := len(nums1), len(nums2)
- total := s1+s2
- if total == 0 {
- return 0
- }
- targetIdx := total/2
- onlyOne := total % 2 == 1
- if s1 == 0 {
- if onlyOne {
- return float64(nums2[targetIdx])
- } else {
- return (float64(nums2[targetIdx-1]) + float64(nums2[targetIdx]))/2
- }
- }
- if s2 == 0 {
- if onlyOne {
- return float64(nums1[targetIdx])
- } else {
- return (float64(nums1[targetIdx-1]) + float64(nums1[targetIdx]))/2
- }
- }
-
- pre, cur := 0, 0
- i, j, nIdx := 0, 0, 0
- for i < s1 && j < s2 {
- if nums1[i] < nums2[j] {
- pre, cur = cur, nums1[i]
- i++
- } else {
- pre, cur = cur, nums2[j]
- j++
- }
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
- for i < s1 {
- pre, cur = cur, nums1[i]
- i++
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
- for j < s2 {
- pre, cur = cur, nums2[j]
- j++
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
-
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
-}
-```
diff --git "a/01_array/No.011_\347\233\233\346\234\200\345\244\232\346\260\264\347\232\204\345\256\271\345\231\250.md" "b/01_array/No.011_\347\233\233\346\234\200\345\244\232\346\260\264\347\232\204\345\256\271\345\231\250.md"
deleted file mode 100644
index 2e96cb7..0000000
--- "a/01_array/No.011_\347\233\233\346\234\200\345\244\232\346\260\264\347\232\204\345\256\271\345\231\250.md"
+++ /dev/null
@@ -1,41 +0,0 @@
-## 11 盛最多水的容器-中等
-
-题目:
-
-给定一个长度为 `n` 的整数数组 `height` 。有 `n` 条垂线,第 `i` 条线的两个端点是 `(i, 0)` 和 `(i, height[i])` 。
-
-找出其中的两条线,使得它们与 `x` 轴共同构成的容器可以容纳最多的水。
-
-返回容器可以储存的最大水量。
-
-**说明:**你不能倾斜容器。
-
-
-
-分析:
-
-利用双指针从两头向中间逼近,计算中间结果,并保存最大结果。
-
-```go
-// date: 2022-09-14
-func maxArea(height []int) int {
- left, right := 0, len(height)-1
- res, temp := 0, 0
- width := 0
- for left < right {
- width = right - left
- if height[left] < height[right] {
- temp = height[left] * width
- left++
- } else {
- temp = height[right] * width
- right--
- }
- if temp > res {
- res = temp
- }
- }
- return res
-}
-```
-
diff --git "a/01_array/No.015_\344\270\211\346\225\260\344\271\213\345\222\214.md" "b/01_array/No.015_\344\270\211\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index cc835de..0000000
--- "a/01_array/No.015_\344\270\211\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,101 +0,0 @@
-## 15 三数之和-中等
-
-题目:
-
-给你一个整数数组 `nums` ,判断是否存在三元组 `[nums[i], nums[j], nums[k]]` 满足 `i != j`、`i != k` 且 `j != k` ,同时还满足 `nums[i] + nums[j] + nums[k] == 0` 。请
-
-你返回所有和为 `0` 且不重复的三元组。
-
-**注意:**答案中不可以包含重复的三元组。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [-1,0,1,2,-1,-4]
-> 输出:[[-1,-1,2],[-1,0,1]]
-> 解释:
-> nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
-> nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
-> nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
-> 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
-> 注意,输出的顺序和三元组的顺序并不重要。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0,1,1]
-> 输出:[]
-> 解释:唯一可能的三元组和不为 0 。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:nums = [0,0,0]
-> 输出:[[0,0,0]]
-> 解释:唯一可能的三元组和为 0 。
-> ```
-
-
-
-**解题思路**
-
-算法:时间复杂度O(n2)
-
-1-对数组进行升序排序,然后逐一遍历,固定当前元素nums[i],使用左右指针遍历当前元素后面的所有元素,nums[l]和nums[r],如果三数之和=0,则添加进结果集
-
-2-当nums[i] > 0 结束循环 // 升序排序,三数之和必然大于零
-
-3-当nums[i] == nums[i-1] 表明用重复元素,跳过
-
-4-sum = 0零时,如果nums[l] == nums[l+1] 重复元素,跳过
-
-5-sum = 0, nums[r] == nums[r-1] 重复元素,跳过
-
-```go
-// date 2022/09/14
-func threeSum(nums []int) [][]int {
- ans := make([][]int, 0, 16)
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- n := len(nums)
- for i := 0; i < n; i++ {
- // case 0
- if nums[i] > 0 {
- break
- }
- // case 1
- if i > 0 && nums[i] == nums[i-1] {
- continue
- }
- left := i+1
- right := n-1
- for left < right {
- sum := nums[i] + nums[left] + nums[right]
- if sum < 0 {
- left++
- } else if sum > 0 {
- right--
- } else if sum == 0 {
- ans = append(ans, []int{nums[i], nums[left], nums[right]})
- for left < right && nums[left] == nums[left+1] {
- left++
- }
- for left < right && nums[right] == nums[right-1] {
- right--
- }
- left++
- right--
- }
- }
- }
-
- return ans
-}
-```
-
diff --git "a/01_array/No.016_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md" "b/01_array/No.016_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index 0c7a89a..0000000
--- "a/01_array/No.016_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,77 +0,0 @@
-## 16 最接近的三数之和-中等
-
-题目:
-
-给你一个长度为 `n` 的整数数组 `nums` 和 一个目标值 `target`。请你从 `nums` 中选出三个整数,使它们的和与 `target` 最接近。
-
-返回这三个数的和。
-
-假定每组输入只存在恰好一个解。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [-1,2,1,-4], target = 1
-> 输出:2
-> 解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0,0,0], target = 1
-> 输出:0
-> ```
-
-
-
-**解题思路**
-
-这道题可用双指针解决。思路是先排序,然后对撞指针找最接近的答案。
-
-```go
-// date 2024/01/15
-func threeSumClosest(nums []int, target int) int {
- // sort and left, right
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- ans := math.MaxInt32
- n := len(nums)
- for i := 0; i < n; i++ {
- if i > 0 && nums[i] == nums[i-1] {
- continue
- }
- l, r := i+1, n-1
- for l < r {
- sum := nums[i] + nums[l] + nums[r]
- if sum == target {
- return sum
- }
- // update the ans
- if abs(ans, target) > abs(sum, target) {
- ans = sum
- }
- if sum > target {
- r--
- } else {
- l++
- }
- }
- }
-
-
- return ans
-}
-
-func abs(x, y int) int {
- if x > y {
- return x-y
- }
- return y-x
-}
-```
-
diff --git "a/01_array/No.018_\345\233\233\346\225\260\344\271\213\345\222\214.md" "b/01_array/No.018_\345\233\233\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index 0aeac7c..0000000
--- "a/01_array/No.018_\345\233\233\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,108 +0,0 @@
-## 18 四数之和-中等
-
-题目:
-
-给你一个由 `n` 个整数组成的数组 `nums` ,和一个目标值 `target` 。请你找出并返回满足下述全部条件且**不重复**的四元组 `[nums[a], nums[b], nums[c], nums[d]]` (若两个四元组元素一一对应,则认为两个四元组重复):
-
-- `0 <= a, b, c, d < n`
-- `a`、`b`、`c` 和 `d` **互不相同**
-- `nums[a] + nums[b] + nums[c] + nums[d] == target`
-
-你可以按 **任意顺序** 返回答案 。
-
-
-
-分析:
-
-这道题属于简单的复杂度。思路比较简单,但要注意各种条件进行剪枝,检查不必要的计算。
-
-去重是指如果当前值和前一个值一样,跳过检查。
-
-1. 整体思路是,先排序,然后两层循环,两个指针
-
-2. 第一层循环:
-
- 剪枝1:连续的四个值已经超过目标值,直接退出
-
- 剪枝2:去重
-
- 剪枝3:如果第一层循环的当前值加上尾部的三个值,小于目标值,那么直接 continue 掉
-
-3. 第二层循环:
-
- 剪枝1:第一层的当前值 加上 第二层循环连续的三个值,如果超过目标值,直接 break 掉
-
- 剪枝2:第二层去重
-
- 剪枝3:第一层的当前值 加上 第二层的当前值,加上最后的两个值,如果小于目标值,continue 掉
-
-4. 双指针
-
- left = j + 1, right := n-1
-
- 剪枝1:去重
-
-```go
-// date 2023/12/11
-func fourSum(nums []int, target int) [][]int {
- // sort
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- ans := make([][]int, 0, 4)
- n := len(nums)
-
- for i := 0; i < n-3; i++ {
- // 连续四个已经超过目标值,不会再有解,break
- if nums[i] + nums[i+1] + nums[i+2] + nums[i+3] > target {
- break
- }
- // 加上最大的三个 小于 目标值,继续检查下一个
- if nums[i] + nums[n-3] + nums[n-2] + nums[n-1] < target {
- continue
- }
- // 去重
- if i > 0 && nums[i] == nums[i-1] {
- continue
- }
- // 注意这里的 for 循环条件也可以这样
- // for j := i+1; j < n-2 && nums[i] + nums[j] + nums[j+1] + nums[j+2] <= target; j++ {
- for j := i+1; j < n-2; j++ {
- if nums[i] + nums[j] + nums[j+1] + nums[j+2] > target {
- break
- }
- if nums[i] + nums[j] + nums[n-2] + nums[n-1] < target {
- continue
- }
- // 去重
- if j > i+1 && nums[j] == nums[j-1] {
- continue
- }
- left, right := j+1, n-1
- for left < right {
- sum := nums[i] + nums[j] + nums[left] + nums[right]
- if sum == target {
- // add to res
- ans = append(ans, []int{nums[i], nums[j], nums[left], nums[right]})
- left++
- for left < right && nums[left] == nums[left-1] {
- left++
- }
- right--
- for left < right && nums[right] == nums[right+1] {
- right--
- }
- } else if sum < target {
- left++
- } else {
- right--
- }
- }
- }
- }
-
- return ans
-}
-```
-
diff --git "a/01_array/No.026_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\351\241\271.md" "b/01_array/No.026_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\351\241\271.md"
deleted file mode 100644
index d770c1f..0000000
--- "a/01_array/No.026_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\351\241\271.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 26 删除有序数组中的重复项-简单
-
-题目:
-
-给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
-
-考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
-
-更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
-返回 k 。
-判题标准:
-
-系统会用下面的代码来测试你的题解:
-
-int[] nums = [...]; // 输入数组
-int[] expectedNums = [...]; // 长度正确的期望答案
-
-int k = removeDuplicates(nums); // 调用
-
-assert k == expectedNums.length;
-for (int i = 0; i < k; i++) {
- assert nums[i] == expectedNums[i];
-}
-如果所有断言都通过,那么您的题解将被 通过。
-
-
-分析:
-
-前后指针,一个用来遍历,一个用来维护最终数据。
-
-```go
-// date 2023/11/02
-func removeDuplicates(nums []int) int {
- idx := 0
- for i := 0; i < len(nums); i++ {
- if i > 0 && nums[i] == nums[i-1] {
- continue
- }
- nums[idx] = nums[i]
- idx++
- }
- return idx
-}
-```
diff --git "a/01_array/No.027_\347\247\273\351\231\244\345\205\203\347\264\240.md" "b/01_array/No.027_\347\247\273\351\231\244\345\205\203\347\264\240.md"
deleted file mode 100644
index 25ed22f..0000000
--- "a/01_array/No.027_\347\247\273\351\231\244\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,48 +0,0 @@
-## 27 移除元素-简单
-
-题目:
-
-给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
-
-不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
-
-元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
-
-
-分析:
-
-前后指针,前面的指针负责记录符合条件的元素,后面的指针遍历整个数组
-
-```go
-// date 2022-09-15
-func removeElement(nums []int, val int) int {
- idx := 0
- for i := 0; i < len(nums); i++ {
- if nums[i] != val {
- nums[idx] = nums[i]
- idx++
- }
- }
- return idx
-}
-```
-
-算法2:交换的思想,将每个等于val的元素,交换至数组的尾部,维护尾部索引,返回新的尾部索引。时间复杂度O(n) 空间复杂度O(n)
-
-```go
-// date 2021-03-13
-func removeElements(nums []int, val int) int {
- i, tail := 0, len(nums)
- for i < tail; {
- if nums[i] == val {
- tail--
- nums[i] = nums[tail]
- nums[tail] = val
- } else {
- i++
- }
- }
- return tail
-}
-```
-
diff --git "a/01_array/No.033_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204.md" "b/01_array/No.033_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204.md"
deleted file mode 100644
index 523da30..0000000
--- "a/01_array/No.033_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,55 +0,0 @@
-## 33 搜索旋转排序数组-中等
-
-题目:
-
-整数数组 nums 按升序排列,数组中的值 互不相同 。
-
-在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
-
-给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
-
-你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
-
-
-
-分析:
-
-通过第一个元素来判断从前半段查找,还是从后半段查找;并且在查找过程中注意翻转的点,一旦到达直接终止查找。
-
-```go
-// date 2023/11/02
-func search(nums []int, target int) int {
- res := -1
- s := len(nums)
- if s == 0 {
- return res
- }
- if nums[0] <= target {
- i := 0
- for i < s {
- if nums[i] == target {
- res = i
- break
- }
- if i + 1 < s && nums[i+1] < nums[i] {
- break
- }
- i++
- }
- } else {
- i := s-1
- for i >= 0 {
- if nums[i] == target {
- res = i
- break
- }
- if i > 0 && nums[i-1] > nums[i] {
- break
- }
- i--
- }
- }
-
- return res
-}
-```
diff --git "a/01_array/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md" "b/01_array/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md"
deleted file mode 100644
index 1b7320d..0000000
--- "a/01_array/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md"
+++ /dev/null
@@ -1,24 +0,0 @@
-## 35 搜索插入位置-简单
-
-题目:
-
-给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
-
-请必须使用时间复杂度为 O(log n) 的算法。
-
-
-分析:
-
-```go
-// date 2023/11/02
-func searchInsert(nums []int, target int) int {
- i, s := 0, len(nums)
- for i < s {
- if nums[i] >= target {
- return i
- }
- i++
- }
- return i
-}
-```
diff --git "a/01_array/No.041_\347\274\272\345\244\261\347\232\204\347\254\254\344\270\200\344\270\252\346\255\243\346\225\260.md" "b/01_array/No.041_\347\274\272\345\244\261\347\232\204\347\254\254\344\270\200\344\270\252\346\255\243\346\225\260.md"
deleted file mode 100644
index 6f34c7b..0000000
--- "a/01_array/No.041_\347\274\272\345\244\261\347\232\204\347\254\254\344\270\200\344\270\252\346\255\243\346\225\260.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 41 缺失的第一个正数-困难
-
-题目:
-
-给你一个未排序的整数数组 `nums` ,请你找出其中没有出现的最小的正整数。
-
-请你实现时间复杂度为 `O(n)` 并且只使用常数级别额外空间的解决方案。
-
-
-
-**解题思路**
-
-- 排序,详见解法1。要求最小的正数,可以先讲数组排序,然后从头开始遍历;遍历的时候注意1)跳过小于等于零的元素;2)跳过重复的元素。假定结果 ans 为1,遍历的时候如果元素等于 ans,那么 ans+1,如果不等于那么 ans 就是答案。
-
-- 哈希表,详见解法2。
-
- 最朴素的做法就是遍历原数组把大于等于零的元素都存入哈希表;然后从 1 开始枚举正整数从哈希表里查找,第一个不在哈希表里的正整数就是答案。
-
- 这样的设计需要额外的空间,题目要求常数级的空间,所以需要考虑把数组设计成哈希表的替代品。
-
- 一个事实。
-
- 对于一个长度为 N 的数组,其中没有出现的最小正整数只能在区间`[1, N+1]`中。如果区间`[1, N]`中所有元素都在数组中出现了,那么答案就是 N+1,否则答案就在`[1,N]`中。
-
- 基于这样的事实,我们可以这样设计:
-
- 1)第一次遍历,把小于等于零的元素都修改为 N+1
-
- 2)第二次遍历,对元素求绝对值x,如果绝对值x在区间`[1,N]`中,那么把数组`x-1`位置的元素变成其值的负数。
-
- 3)第三次遍历,**经过第二次遍历数组中出现过的元素,已经把元素映射成索引所对应位置上的元素变成负数**,所以此时再出现的正数,其索引+1就是答案。
-
-```go
-// date 2024/01/24
-// 解法1 排序
-func firstMissingPositive(nums []int) int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- ans := 1
- for i, v := range nums {
- if v <= 0 {
- continue
- }
- if i > 0 && v == nums[i-1] {
- continue
- }
- if v == ans {
- ans++
- } else {
- break
- }
- }
- return ans
-}
-
-// 解法2
-// 设计哈希表
-func firstMissingPositive(nums []int) int {
- n := len(nums)
- for i := 0; i < n; i++ {
- if nums[i] <= 0 {
- nums[i] = n+1
- }
- }
- for i := 0; i < n; i++ {
- v := abs(nums[i])
- if v <= n {
- nums[v-1] = -abs(nums[v-1])
- }
- }
- for i := 0; i < n; i++ {
- if nums[i] > 0 {
- return i+1
- }
- }
- return n+1
-}
-
-func abs(x int) int {
- if x < 0 {
- return -x
- }
- return x
-}
-```
-
diff --git "a/01_array/No.046_\345\205\250\346\216\222\345\210\227.md" "b/01_array/No.046_\345\205\250\346\216\222\345\210\227.md"
deleted file mode 100644
index 2dfd785..0000000
--- "a/01_array/No.046_\345\205\250\346\216\222\345\210\227.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 全排列-中等
-
-题目:
-
-给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
-
-
-分析:
-
-回溯算法
-
-```go
-// date 2023/11/06
-func permute(nums []int) [][]int {
- // res 存放所有的结果
- res := make([][]int, 0, 1024)
-
- // nums 表示待添加的元素
- // temp 表示临时结果
- var backtrack func(nums []int, temp []int)
- backtrack = func(nums []int, temp []int) {
- // 说明都已经添加过了,那么 temp 就是其中的一个结果,直接追加到结果集中
- if len(nums) == 0 {
- res = append(res, temp)
- return
- }
- for i := range nums {
- // 依次添加到 temp 中,形成新的切片
- // 并对未使用的元素,回溯添加
- newtemp := append(temp, nums[i])
- unused := make([]int, 0, len(nums)-1)
- unused = append(unused, nums[:i]...)
- unused = append(unused, nums[i+1:]...)
- backtrack(unused, newtemp)
- }
- }
-
- backtrack(nums, make([]int, 0))
-
- return res
-}
-```
diff --git "a/01_array/No.047_\345\205\250\346\216\222\345\210\2272.md" "b/01_array/No.047_\345\205\250\346\216\222\345\210\2272.md"
deleted file mode 100644
index 245d1ad..0000000
--- "a/01_array/No.047_\345\205\250\346\216\222\345\210\2272.md"
+++ /dev/null
@@ -1,50 +0,0 @@
-## 47 全排列2-中等
-
-题目:
-
-给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
-
-
-分析:
-
-剪枝,回溯
-
-```go
-// date 2023/11/07
-func permuteUnique(nums []int) [][]int {
- res := make([][]int, 0, 1024)
- vis := make(map[int]bool)
- n := len(nums)
-
- temp := make([]int, 0, 16)
-
- var backtrack func(idx int)
- backtrack = func(idx int) {
- if idx == n {
- res = append(res, append([]int{}, temp...))
- return
- }
- for i, v := range nums {
- // vis[i] 已经填充过的,不再填充
- // i > 0 && nums[i-1] == && !vis[i-1]
- // 相同元素,及时没填充过,也不需要填充
- if i > 0 && nums[i-1] == v && !vis[i-1] || vis[i] {
- continue
- }
- temp = append(temp, v)
- vis[i] = true
- backtrack(idx+1)
- vis[i] = false
- temp = temp[:len(temp)-1]
- }
- }
-
- sort.Slice(nums, func(i,j int) bool {
- return nums[i] < nums[j]
- })
-
- backtrack(0)
-
- return res
-}
-```
diff --git "a/01_array/No.048_\346\227\213\350\275\254\345\233\276\345\203\217.md" "b/01_array/No.048_\346\227\213\350\275\254\345\233\276\345\203\217.md"
deleted file mode 100644
index 7192f34..0000000
--- "a/01_array/No.048_\346\227\213\350\275\254\345\233\276\345\203\217.md"
+++ /dev/null
@@ -1,80 +0,0 @@
-## 48 旋转图像-中等
-
-题目:
-
-给定一个 *n* × *n* 的二维矩阵 `matrix` 表示一个图像。请你将图像顺时针旋转 90 度。
-
-你必须在**[ 原地](https://baike.baidu.com/item/原地算法)** 旋转图像,这意味着你需要直接修改输入的二维矩阵。**请不要** 使用另一个矩阵来旋转图像。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
-> 输出:[[7,4,1],[8,5,2],[9,6,3]]
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
-> 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
-> ```
-
-
-
-**解题思路**
-
-没啥好说的,细节题,模拟旋转。
-
-```go
-// date 2024/01/30
-// 解法1 模拟
-func rotate(matrix [][]int) {
- n := len(matrix)
- left, right := 0, n-1
- up, down := 0, n-1
- for left < right && up < down {
- data := make([]int, 0, 16)
- // save data
- for j := left; j <= right; j++ {
- data = append(data, matrix[up][j])
- }
- // loop 1,4,7
- idx := right
- for i := up; i <= down; i++ {
- matrix[up][idx] = matrix[i][left]
- idx--
- }
- // loop 7,8,9
- idx = up
- for j := left; j <= right; j++ {
- matrix[idx][left] = matrix[down][j]
- idx++
- }
- // loop 9,6,3
- idx = left
- for i := down; i >= up; i-- {
- matrix[down][idx] = matrix[i][right]
- idx++
- }
- // restore data
- // 1,2,3
- idx = up
- for _, v := range data {
- matrix[idx][right] = v
- idx++
- }
- left++
- right--
- up++
- down--
- }
-}
-```
-
diff --git "a/01_array/No.053_\346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md" "b/01_array/No.053_\346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md"
deleted file mode 100644
index 8ca7371..0000000
--- "a/01_array/No.053_\346\234\200\345\244\247\345\255\220\346\225\260\347\273\204\345\222\214.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 53 最大子数组和-中等
-
-题目:
-
-给你一个整数数组 `nums` ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
-
-**子数组** 是数组中的一个连续部分。
-
-
-
-分析:
-
-典型的动态规划题。
-
-子问题:
-
-- 以 -2 结尾的连续子数组的最大和是多少
-- 以 1 结尾的连续子数组的最大和是多少
-- 以 -3 结尾的连续子数组的最大和是多少
-- 以 4 结尾的连续子数组的最大和是多少
-- 以 -1 结尾的连续子数组的最大和是多少
-- 以 2 结尾的连续子数组的最大和是多少
-- 以 1 结尾的连续子数组的最大和是多少
-- 以 -5 结尾的连续子数组的最大和是多少
-- 以 4 结尾的连续子数组的最大和是多少
-
-我们可以发现以 1 结尾的连续子数组有`[-2, 1]` 和 `[1]` ,`[-2, 1]` 就是在子问题1的后面加上1得到的。
-
-`-2 + 1 = -1 < 1` 因此子问题的答案就是1
-
-由此我们可以得出:
-
-当遍历到v时,如果之前的结果 `curMax` 小于零;那么不如另起炉灶,重新计算 `curMax`;如果大于等于零,才考虑增加当前元素。
-
-```go
-// date 2023/11/04
-func maxSubArray(nums []int) int {
- ans := nums[0]
- curMax := 0
- for _, v := range nums {
- if curMax < 0 {
- curMax = v
- } else {
- curMax += v
- }
- if curMax > ans {
- ans = curMax
- }
- }
- return ans
-}
-```
diff --git "a/01_array/No.054_\350\236\272\346\227\213\347\237\251\351\230\265.md" "b/01_array/No.054_\350\236\272\346\227\213\347\237\251\351\230\265.md"
deleted file mode 100644
index a8bbf1b..0000000
--- "a/01_array/No.054_\350\236\272\346\227\213\347\237\251\351\230\265.md"
+++ /dev/null
@@ -1,66 +0,0 @@
-## 54 螺旋矩阵-中等
-
-题目:
-
-给你一个 `m` 行 `n` 列的矩阵 `matrix` ,请按照 **顺时针螺旋顺序** ,返回矩阵中的所有元素。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
-> 输出:[1,2,3,6,9,8,7,4,5]
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
-> 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
-> ```
-
-
-
-**解题思路**
-
-
-
-```go
-// date 2024/01/30
-// 解法1 模拟输出
-func spiralOrder(matrix [][]int) []int {
- ans := make([]int, 0, 16)
- m := len(matrix)
- n := len(matrix[0])
- left, right := 0, n-1
- up, down := 0, m-1
- for left <= right && up <= down {
- for j := left; j <= right; j++ {
- ans = append(ans, matrix[up][j])
- }
- up++
- for i := up; i <= down; i++ {
- ans = append(ans, matrix[i][right])
- }
- right--
- // up, right 已经发生变化,需要重新判断
- if left <= right && up <= down {
- for j := right; j >= left; j-- {
- ans = append(ans, matrix[down][j])
- }
- down--
- for i := down; i >= up; i-- {
- ans = append(ans, matrix[i][left])
- }
- left++
- }
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.056_\345\220\210\345\271\266\345\214\272\351\227\264.md" "b/01_array/No.056_\345\220\210\345\271\266\345\214\272\351\227\264.md"
deleted file mode 100644
index a7a2f37..0000000
--- "a/01_array/No.056_\345\220\210\345\271\266\345\214\272\351\227\264.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 56 合并区间-中等
-
-题目:
-
-以数组 `intervals` 表示若干个区间的集合,其中单个区间为 `intervals[i] = [starti, endi]` 。请你合并所有重叠的区间,并返回 *一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间* 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
-> 输出:[[1,6],[8,10],[15,18]]
-> 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:intervals = [[1,4],[4,5]]
-> 输出:[[1,5]]
-> 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
-> ```
-
-
-
-**解题思路**
-
-这道题最朴素的做法就是按照题意依次合并。具体为,先对集合按每个区间的 start 大小排序,排序后每个区间是依次展开的;然后把第一个区间保存为 one,从第二个开始进行合并,合并规则如下:
-
-1. 如果当前区间的 start 和 end,均在上一个区间内部,即跳过该区间
-2. 如果当前区间的 start 小于等于上一个区间(one) 的 end,那么上个区间(one)可修改为`[start, end2]`
-3. 如果 1和 2 都不满足,则表示得到一个新的区间,加入结果集即可;同时将当前区间保存为 one,合并
-
-```go
-// date 2024/01/16
-func merge(intervals [][]int) [][]int {
- n := len(intervals)
- if n < 2 {
- return intervals
- }
- sort.Slice(intervals, func(i, j int) bool {
- return intervals[i][0] < intervals[j][0]
- })
-
- ans := make([][]int, 0, 16)
- one := intervals[0]
- for i := 1; i < n; i++ {
- if intervals[i][0] >= one[0] && intervals[i][1] <= one[1] {
- continue
- }
- if intervals[i][0] <= one[1] {
- one[1] = intervals[i][1]
- } else {
- ans = append(ans, one)
- one = intervals[i]
- }
- }
- ans = append(ans, one)
- return ans
-}
-```
-
diff --git "a/01_array/No.066_\345\212\240\344\270\200.md" "b/01_array/No.066_\345\212\240\344\270\200.md"
deleted file mode 100644
index 96a900a..0000000
--- "a/01_array/No.066_\345\212\240\344\270\200.md"
+++ /dev/null
@@ -1,32 +0,0 @@
-## 66 加一-简单
-
-题目:
-
-给定一个由 **整数** 组成的 **非空** 数组所表示的非负整数,在该数的基础上加一。
-
-最高位数字存放在数组的首位, 数组中每个元素只存储**单个**数字。
-
-你可以假设除了整数 0 之外,这个整数不会以零开头。
-
-
-
-分析:
-
-细节题,注意进位
-
-```go
-//date 2022/09/20
-func plusOne(digits []int) []int {
- carry, temp := 1, 0
- for i := len(digits)-1; i >= 0; i-- {
- temp = digits[i]+carry
- carry = temp / 10
- digits[i] = temp % 10
- }
- if carry == 1 {
- digits = append([]int{1}, digits...)
- }
- return digits
-}
-```
-
diff --git "a/01_array/No.073_\347\237\251\351\230\265\347\275\256\346\215\242.md" "b/01_array/No.073_\347\237\251\351\230\265\347\275\256\346\215\242.md"
deleted file mode 100644
index 2cf46eb..0000000
--- "a/01_array/No.073_\347\237\251\351\230\265\347\275\256\346\215\242.md"
+++ /dev/null
@@ -1,127 +0,0 @@
-
-
-## 73 矩阵置换-中等
-
-题目:
-
-给定一个 `*m* x *n*` 的矩阵,如果一个元素为 **0** ,则将其所在行和列的所有元素都设为 **0** 。请使用 **[原地](http://baike.baidu.com/item/原地算法)** 算法。
-
-- 一个直观的解决方案是使用 `O(*m**n*)` 的额外空间,但这并不是一个好的解决方案。
-- 一个简单的改进方案是使用 `O(*m* + *n*)` 的额外空间,但这仍然不是最好的解决方案。
-- 你能想出一个仅使用常量空间的解决方案吗?
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
-> 输出:[[1,0,1],[0,0,0],[1,0,1]]
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
-> 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
-> ```
-
-
-
-**解题思路**
-
-- 最朴素的算法,详见解法1。因为一行或一列中的零有可能重复,所以可以先进行一次遍历,把为零的行列信息保存在哈希表中,然后遍历哈希表,就地置换。该算法使用`O(M+N)`的额外空间。
-
-- 第0行,第0列,特殊处理,详见解法2。具体为,先遍历第0行和第0列,用两个变量标记是否有零;然后整个遍历矩阵,把行列为零的信息保存到第0行和第0列;然后根据第0行第0列的信息置零;最后,在根据两个变量把第0行第0列置零。
-
-
-
-
-
-```go
-// date 2024/01/30
-// 解法1 哈希表
-func setZeroes(matrix [][]int) {
- m := len(matrix)
- if m == 0 {
- return
- }
- n := len(matrix[0])
- rset := make(map[int]int, 16)
- cset := make(map[int]int, 16)
- for i := 0; i < m; i++ {
- for j := 0; j < n; j++ {
- if matrix[i][j] == 0 {
- rset[i] = i
- cset[j] = j
- }
- }
- }
- for row := range rset {
- for j := 0; j < n; j++ {
- matrix[row][j] = 0
- }
- }
- for col := range cset {
- for i := 0; i < m; i++ {
- matrix[i][col] = 0
- }
- }
-}
-
-// 解法2
-// 两个变量,0行0列特殊处理
-// 时间复杂度 O(MN)
-// 空间复杂度 O(1)
-func setZeroes(matrix [][]int) {
- m := len(matrix)
- if m == 0 {
- return
- }
- n := len(matrix[0])
- row0, col0 := false, false
- for j := 0; j < n; j++ {
- if matrix[0][j] == 0 {
- row0 = true
- }
- }
- for i := 0; i < m; i++ {
- if matrix[i][0] == 0 {
- col0 = true
- }
- }
-
- for i := 1; i < m; i++ {
- for j := 1; j < n; j++ {
- if matrix[i][j] == 0 {
- matrix[i][0] = 0
- matrix[0][j] = 0
- }
- }
- }
- for i := 1; i < m; i++ {
- for j := 1; j < n; j++ {
- if matrix[i][0] == 0 || matrix[0][j] == 0 {
- matrix[i][j] = 0
- }
- }
- }
-
-
- if row0 {
- for j := 0; j < n; j++ {
- matrix[0][j] = 0
- }
- }
- if col0 {
- for i := 0; i < m; i++ {
- matrix[i][0] = 0
- }
- }
-}
-```
-
diff --git "a/01_array/No.075_\351\242\234\350\211\262\345\210\206\347\261\273.md" "b/01_array/No.075_\351\242\234\350\211\262\345\210\206\347\261\273.md"
deleted file mode 100644
index b39bec8..0000000
--- "a/01_array/No.075_\351\242\234\350\211\262\345\210\206\347\261\273.md"
+++ /dev/null
@@ -1,37 +0,0 @@
-## 75 颜色分类-中等
-
-题目:
-
-给定一个包含红色、白色和蓝色、共 `n` 个元素的数组 `nums` ,**[原地](https://baike.baidu.com/item/原地算法)**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
-
-我们使用整数 `0`、 `1` 和 `2` 分别表示红色、白色和蓝色。
-
-必须在不使用库内置的 sort 函数的情况下解决这个问题。
-
-
-
-分析:
-
-双指针,加上交换的思想;k指针负责遍历,遇到蓝色`2`则将其交换到尾部,由`j`指针从尾部开始维护蓝色`2`的下标;遇到红色`0`则交换到头部,由`i`指针从头部开始维护红色`0`下标。
-
-```go
-// date 2023/11/04
-func sortColors(nums []int) {
- k, ri, bj := 0, 0, len(nums)-1
- for k <= bj {
- if nums[k] == 2 {
- nums[k] = nums[bj]
- nums[bj] = 2
- bj--
- } else if nums[k] == 0 {
- nums[k] = nums[ri]
- nums[ri] = 0
- k++ // 此时 nums[k] 只可能为 1,所以跳过检查
- ri++
- } else {
- k++
- }
- }
-}
-```
-
diff --git "a/01_array/No.078_\345\255\220\351\233\206.md" "b/01_array/No.078_\345\255\220\351\233\206.md"
deleted file mode 100644
index bb7d3e8..0000000
--- "a/01_array/No.078_\345\255\220\351\233\206.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 78 子集-中等
-
-题目:
-
-给你一个整数数组 `nums` ,数组中的元素 **互不相同** 。返回该数组所有可能的子集(幂集)。
-
-解集 **不能** 包含重复的子集。你可以按 **任意顺序** 返回解集。
-
-
-
-分析:因为其子集需要遍历所有可能,需要保留中间结果集。
-
-算法:外层遍历当前元素;内层遍历结果集,取结果集+当前元素组成新的结果集,并追加到最终的结果集中。
-
-```go
-// date 2022/09/20
-func subsets(nums []int) [][]int {
- // res表示结果集合
- res := make([][]int, 0, 1024)
- // 空集合也是一种结果,先追加进去
- res = append(res, []int{})
- for _, v := range nums {
- // 遍历当前的元素,取出之前的所有结果集,追加当前元素
- s := len(res)
- for i := 0; i < s; i++ {
- t := make([]int, 0)
- t = append(t, res[i]...)
- t = append(t, v)
- res = append(res, t)
- }
- }
- return res
-}
-```
-
-
-
-算法图解:
-
-
\ No newline at end of file
diff --git "a/01_array/No.080_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md" "b/01_array/No.080_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md"
deleted file mode 100644
index a80829c..0000000
--- "a/01_array/No.080_\345\210\240\351\231\244\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 80 删除有序数组中的重复元素2-中等
-
-题目:
-
-给你一个有序数组 `nums` ,请你**[ 原地](http://baike.baidu.com/item/原地算法)** 删除重复出现的元素,使得出现次数超过两次的元素**只出现两次** ,返回删除后数组的新长度。
-
-不要使用额外的数组空间,你必须在 **[原地 ](https://baike.baidu.com/item/原地算法)修改输入数组** 并在使用 O(1) 额外空间的条件下完成。
-
-
-
-分析:
-
-算法:双指针,idx指针负责维护目标结果的下标;cur指针负责遍历元素;另外需要额外保留一个指针pre,用于判断当前元素是否与前面第二个元素是否相等
-
-```go
-// date 2022/09/20
-// cur 维护当前要检查的下标
-// last 维护新数组的下标
-// pre 维护新数组中 last 前一个的下标
-func removeDuplicates(nums []int) int {
- size := len(nums)
- if size <= 2 {
- return size
- }
- cur, last, pre := 2, 1, 0
- for cur < size {
- if nums[cur] != nums[last] || nums[cur] != nums[pre] {
- pre = last
- last++
- nums[last] = nums[cur]
- }
- cur++
- }
- return last+1
-}
-```
-
-
-
-算法图解:
-
-
\ No newline at end of file
diff --git "a/01_array/No.088_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\346\225\260\347\273\204.md" "b/01_array/No.088_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\346\225\260\347\273\204.md"
deleted file mode 100644
index d7dbbff..0000000
--- "a/01_array/No.088_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 88 合并两个有序数组-简单
-
-题目:
-
-将两个非递减数组nums1和nums2,按非递减顺序合并到nums1
-
-
-
-分析:
-
-从后往前充填,可以节省nums1中元素的挪动
-
-```go
-// date 2022/09/24
-func merge(nums1 []int, m int, nums2 []int, n int) {
- i, j, cur := m-1, n-1, m+n-1
- for i >= 0 && j >= 0 {
- if nums1[i] > nums2[j] {
- nums1[cur] = nums1[i]
- i--
- } else {
- nums1[cur] = nums2[j]
- j--
- }
- cur--
- }
- for i >= 0 {
- nums1[cur] = nums1[i]
- cur--
- i--
- }
- for j >= 0 {
- nums1[cur] = nums2[j]
- cur--
- j--
- }
-}
-```
-
diff --git "a/01_array/No.1089_\345\244\215\345\206\231\351\233\266.md" "b/01_array/No.1089_\345\244\215\345\206\231\351\233\266.md"
deleted file mode 100644
index 15b53ec..0000000
--- "a/01_array/No.1089_\345\244\215\345\206\231\351\233\266.md"
+++ /dev/null
@@ -1,35 +0,0 @@
-## 1089 复写零-简单
-
-题目:
-
-给你一个长度固定的整数数组 `arr` ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
-
-注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 **就地** 进行上述修改,不要从函数返回任何东西。
-
-
-
-分析:
-
-直接遍历,遇到 零 时,将后续的元素向右移动一格。
-
-```go
-// date 2020/04/19
-func duplicateZeros(arr []int) {
- n := len(arr)
- j := 0
-
- for i := 0; i < n; i++ {
- if arr[i] == 0 {
- // copy and remove the last one
- j = n-2
- for j > i {
- arr[j+1] = arr[j]
- j--
- }
- arr[j+1] = 0
- i++
- }
- }
-}
-```
-
diff --git "a/01_array/No.1109_\350\210\252\347\217\255\351\242\204\350\256\242\347\273\237\350\256\241.md" "b/01_array/No.1109_\350\210\252\347\217\255\351\242\204\350\256\242\347\273\237\350\256\241.md"
deleted file mode 100644
index a84d109..0000000
--- "a/01_array/No.1109_\350\210\252\347\217\255\351\242\204\350\256\242\347\273\237\350\256\241.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 1109 航班预订统计-中等
-
-题目:
-
-这里有 `n` 个航班,它们分别从 `1` 到 `n` 进行编号。
-
-有一份航班预订表 `bookings` ,表中第 `i` 条预订记录 `bookings[i] = [firsti, lasti, seatsi]` 意味着在从 `firsti` 到 `lasti` (**包含** `firsti` 和 `lasti` )的 **每个航班** 上预订了 `seatsi` 个座位。
-
-请你返回一个长度为 `n` 的数组 `answer`,里面的元素是每个航班预定的座位总数。
-
-
-
-分析:
-
-差分数组。
-
-```go
-// date 2023/12/12
-func corpFlightBookings(bookings [][]int, n int) []int {
- // diff nums
- ans := make([]int, n)
- for _, num := range bookings {
- if num[0] <= n {
- ans[num[0]-1] += num[2]
- }
- if num[1] < n {
- ans[num[1]] -= num[2]
- }
- }
-
- // 复原差分数组
- for i := 1; i < n; i++ {
- ans[i] += ans[i-1]
- }
-
- return ans
-}
-```
-
diff --git "a/01_array/No.1295_\347\273\237\350\256\241\344\275\215\346\225\260\344\270\272\345\201\266\346\225\260\347\232\204\346\225\260\345\255\227.md" "b/01_array/No.1295_\347\273\237\350\256\241\344\275\215\346\225\260\344\270\272\345\201\266\346\225\260\347\232\204\346\225\260\345\255\227.md"
deleted file mode 100644
index b9696f2..0000000
--- "a/01_array/No.1295_\347\273\237\350\256\241\344\275\215\346\225\260\344\270\272\345\201\266\346\225\260\347\232\204\346\225\260\345\255\227.md"
+++ /dev/null
@@ -1,36 +0,0 @@
-## 1295 统计位数为偶数的数字-简单
-
-题目:
-
-给你一个整数数组 `nums`,请你返回其中位数为 **偶数** 的数字的个数。
-
-
-
-分析:
-
-注意,题目中的位数是指十进制的位数。
-
-```go
-// date 2020/04/19
-func findNumbers(nums []int) int {
- res := 0
-
- for _, v := range nums {
- if isEvenDigits(v) {
- res++
- }
- }
-
- return res
-}
-
-func isEvenDigits(num int) bool {
- dig := 0
- for num > 0 {
- dig++
- num /= 10
- }
- return dig & 0x1 == 0
-}
-```
-
diff --git "a/01_array/No.1299_\345\260\206\346\257\217\344\270\252\345\205\203\347\264\240\346\233\277\346\215\242\344\270\272\345\217\263\344\276\247\346\234\200\345\244\247\345\205\203\347\264\240.md" "b/01_array/No.1299_\345\260\206\346\257\217\344\270\252\345\205\203\347\264\240\346\233\277\346\215\242\344\270\272\345\217\263\344\276\247\346\234\200\345\244\247\345\205\203\347\264\240.md"
deleted file mode 100644
index 40ab6df..0000000
--- "a/01_array/No.1299_\345\260\206\346\257\217\344\270\252\345\205\203\347\264\240\346\233\277\346\215\242\344\270\272\345\217\263\344\276\247\346\234\200\345\244\247\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,30 +0,0 @@
-## 1299 将每个元素替换为右侧最大元素-简单
-
-题目:
-
-给你一个数组 `arr` ,请你将每个元素用它右边最大的元素替换,如果是最后一个元素,用 `-1` 替换。
-
-完成所有替换操作后,请你返回这个数组。
-
-
-
-算法:
-
-```go
-// date 2022/10/01
-func replaceElements(arr []int) []int {
- cur, right_max := -1, -1
- for i := len(arr)-1; i >= 0; i-- {
- // 保存当前值
- cur = arr[i]
- // 将当前值赋值为右侧最大值
- arr[i] = right_max
- // 更新右侧最大值
- if cur > right_max {
- right_max = cur
- }
- }
- return arr
-}
-```
-
diff --git "a/01_array/No.167_\344\270\244\346\225\260\344\271\213\345\222\214_\350\276\223\345\205\245\346\234\211\345\272\217\346\225\260\347\273\204.md" "b/01_array/No.167_\344\270\244\346\225\260\344\271\213\345\222\214_\350\276\223\345\205\245\346\234\211\345\272\217\346\225\260\347\273\204.md"
deleted file mode 100644
index 9a687f8..0000000
--- "a/01_array/No.167_\344\270\244\346\225\260\344\271\213\345\222\214_\350\276\223\345\205\245\346\234\211\345\272\217\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,41 +0,0 @@
-## 167 两数之和2-输入有序数组-中等
-
-题目:
-
-给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
-
-以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
-
-你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
-
-你所设计的解决方案必须只使用常量级的额外空间。
-
-
-
-分析:
-
-对撞指针,因为数组是有序的,所以可以使用对撞指针,逼近结果。
-
-```go
-// date 2022/10/01
-func twoSum(numbers []int, target int) []int {
- ans := make([]int, 2, 2)
-
- left, right := 0, len(numbers)-1
- for left < right {
- tg := numbers[left] + numbers[right]
- if tg == target {
- ans[0] = left+1
- ans[1] = right+1
- break
- } else if tg < target {
- left++
- } else if tg > target {
- right--
- }
- }
-
- return ans
-}
-```
-
diff --git "a/01_array/No.169_\345\244\232\346\225\260\345\205\203\347\264\240.md" "b/01_array/No.169_\345\244\232\346\225\260\345\205\203\347\264\240.md"
deleted file mode 100644
index 1eea048..0000000
--- "a/01_array/No.169_\345\244\232\346\225\260\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,91 +0,0 @@
-## 169 多数元素-中等
-
-题目:
-
-给定一个大小为 `n` 的数组 `nums` ,返回其中的多数元素。多数元素是指在数组中出现次数 **大于** `⌊ n/2 ⌋` 的元素。
-
-你可以假设数组是非空的,并且给定的数组总是存在多数元素。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [3,2,3]
-> 输出:3
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [2,2,1,1,1,2,2]
-> 输出:2
-> ```
-
-
-**解题思路**
-
-这道题是求数组中的众数,可有多种解法。
-
-- 排序,详见解法1。因为众数的个数大于 n/2,所以排序以后,中间位置的元素肯定是众数。
-- map 去重,详见解法2。具体是,遍历数组,存入 map,统计出现的次数;然后遍历 map 找到出现次数最多的 key。
-- Boyer-Moore 投票算法,详见解法3。如果我们把众数记为 +1,其他数记为 -1,全部加起来,那么和必然大于0。从结果本身也能看出众数比其他数多,这就是 Boyer-Moore 算法。具体步骤就是:
- 1. 维护一个候选众数 ans,和它出现的次数 cnt,初始值 ans = nums[0], cnt = 1
- 2. 遍历数组,如果元素 x 等于 ans,那么 cnt 递增;不相等,则 cnt 递减;如果 cnt 小于等于 0,则把当前元素 x 选为 ans,cnt = 1,重复1,2
- 3. 最后得到的 ans 就是众数
-
-
-
-```go
-// date 2024/01/16
-// 解法1
-// 排序
-func majorityElement(nums []int) int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- return nums[len(nums)>>1]
-}
-
-// 解法2
-// map 统计出现的次数
-func majorityElement(nums []int) int {
- set := make(map[int]int, 16)
- for _, v := range nums {
- set[v]++
- }
- ans, cnt := 0, 0
- for k, v := range set {
- if v > cnt {
- cnt = v
- ans = k
- }
- }
-
- return ans
-}
-
-// 解法3
-// Boyer-Moore 投票算法
-func majorityElement(nums []int) int {
- n := len(nums)
- if n == 1 {
- return nums[0]
- }
- ans := nums[0]
- cnt := 1
- for i := 1; i < n; i++ {
- if ans == nums[i] {
- cnt++
- } else {
- cnt--
- if cnt <= 0 {
- ans = nums[i]
- cnt = 1
- }
- }
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.189_\350\275\256\350\275\254\346\225\260\347\273\204.md" "b/01_array/No.189_\350\275\256\350\275\254\346\225\260\347\273\204.md"
deleted file mode 100644
index 358b201..0000000
--- "a/01_array/No.189_\350\275\256\350\275\254\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 189 轮转数组-中等
-
-题目:
-
-给定一个数组,将数组中的元素向右移动K个位置,K是非负整数。
-
-
-
-分析:【推荐该算法】
-
-向右轮转 K 个位置,就是将数组的后 K 个元素放到数组的头部。那么,可以通过下面的方式得到:
-
-1. 先整体反转数组
-2. 再反转前 K-1 个元素,最后反转 后面的 n-k 个元素。
-
-```go
-// date 2022/09/22
-func rotate(nums []int, k int) {
- n := len(nums)
- k %= n
- reverse(nums, 0, n-1)
- reverse(nums, 0, k-1)
- reverse(nums, k, n-1)
-}
-
-func reverse(nums []int, left, right int) {
- for left < right {
- nums[left], nums[right] = nums[right], nums[left]
- left++
- right--
- }
-}
-```
-
-算法图解:
-
-
-
-
-
-其他算法:
-
-暴力解法。时间复杂度O(n*k),空间复杂度O(1)
-
-先移动1步,再移动k步
-
-```go
-// date 2022/09/24
-func rotate(nums []int, k int) {
- n := len(nums)
- k %= n
- for k > 0 {
- moveOneStep(nums)
- k--
- }
-}
-
-func moveOneStep(nums []int) {
- if len(nums) < 2 {
- return
- }
- n := len(nums)
- tail := nums[n-1]
- copy(nums[1:], nums[0:n-1])
- nums[0] = tail
-}
-```
-
-算法图解:
-
-
diff --git "a/01_array/No.1968_\346\236\204\351\200\240\345\205\203\347\264\240\344\270\215\347\255\211\344\272\216\344\270\244\347\233\270\351\202\273\345\205\203\347\264\240\345\271\263\345\235\207\345\200\274\347\232\204\346\225\260\347\273\204.md" "b/01_array/No.1968_\346\236\204\351\200\240\345\205\203\347\264\240\344\270\215\347\255\211\344\272\216\344\270\244\347\233\270\351\202\273\345\205\203\347\264\240\345\271\263\345\235\207\345\200\274\347\232\204\346\225\260\347\273\204.md"
deleted file mode 100644
index 5408d10..0000000
--- "a/01_array/No.1968_\346\236\204\351\200\240\345\205\203\347\264\240\344\270\215\347\255\211\344\272\216\344\270\244\347\233\270\351\202\273\345\205\203\347\264\240\345\271\263\345\235\207\345\200\274\347\232\204\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,37 +0,0 @@
-## 1968 构造元素不等于两相邻元素平均值的数组-中等
-
-题目:
-
-给你一个 下标从 0 开始 的数组 nums ,数组由若干 互不相同的 整数组成。你打算重新排列数组中的元素以满足:重排后,数组中的每个元素都 不等于 其两侧相邻元素的 平均值 。
-
-更公式化的说法是,重新排列的数组应当满足这一属性:对于范围 1 <= i < nums.length - 1 中的每个 i ,(nums[i-1] + nums[i+1]) / 2 不等于 nums[i] 均成立 。
-
-返回满足题意的任一重排结果。
-
-
-分析:
-
-因为元素各不相同,直接升序排序。那么排序后的数组,前半部分的任意两个元素的平均值肯定不等于后半部分任意两个元素的平均值。
-
-所以,再将前半部分和后半部分交叉存放即可。
-
-
-```go
-// date 2023/11/09
-func rearrangeArray(nums []int) []int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- mid := (len(nums) + 1)/2
- res := make([]int, 0, len(nums))
-
- for i := 0; i < mid; i++ {
- res = append(res, nums[i])
- if i + mid < len(nums) {
- res = append(res, nums[i+mid])
- }
- }
-
- return res
-}
-```
diff --git "a/01_array/No.238_\351\231\244\350\207\252\350\272\253\344\273\245\345\244\226\346\225\260\347\273\204\347\232\204\344\271\230\347\247\257.md" "b/01_array/No.238_\351\231\244\350\207\252\350\272\253\344\273\245\345\244\226\346\225\260\347\273\204\347\232\204\344\271\230\347\247\257.md"
deleted file mode 100644
index 47e22ea..0000000
--- "a/01_array/No.238_\351\231\244\350\207\252\350\272\253\344\273\245\345\244\226\346\225\260\347\273\204\347\232\204\344\271\230\347\247\257.md"
+++ /dev/null
@@ -1,62 +0,0 @@
-## 238 除自身以外数组的乘积-中等
-
-题目:
-
-给你一个整数数组 `nums`,返回 *数组 `answer` ,其中 `answer[i]` 等于 `nums` 中除 `nums[i]` 之外其余各元素的乘积* 。
-
-题目数据 **保证** 数组 `nums`之中任意元素的全部前缀元素和后缀的乘积都在 **32 位** 整数范围内。
-
-请 **不要使用除法,**且在 `O(*n*)` 时间复杂度内完成此题。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: nums = [1,2,3,4]
-> 输出: [24,12,8,6]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: nums = [-1,1,0,-3,3]
-> 输出: [0,0,9,0,0]
-> ```
-
-
-
-**解题思路**
-
-这道题可用前缀乘积和后缀乘积解决,详见解法1。具体为,初始化两个变量 left 和 right,分别表示前缀乘积和后缀乘积,初始值为1。
-
-先从前向后遍历,left 负责记录前缀乘积,并更新 ans;在从后向前遍历,right 记录后缀乘积,并更新 ans。
-
-```go
-// date 2024/01/16
-// 解法1
-// 前缀乘积 * 后缀乘积
-func productExceptSelf(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
-
- ans := make([]int, n)
- left := 1
- // fill left
- for i := 0; i < n; i++ {
- ans[i] = left
- left *= nums[i]
- }
-
- // fill right
- right := 1
- for i := n-1; i >= 0; i-- {
- ans[i] = ans[i] * right
- right *= nums[i]
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.2740_\346\211\276\345\207\272\345\210\206\345\214\272\345\200\274.md" "b/01_array/No.2740_\346\211\276\345\207\272\345\210\206\345\214\272\345\200\274.md"
deleted file mode 100644
index a7f8ec2..0000000
--- "a/01_array/No.2740_\346\211\276\345\207\272\345\210\206\345\214\272\345\200\274.md"
+++ /dev/null
@@ -1,68 +0,0 @@
-## 2740 找出分区值-中等
-
-题目:
-
-给你一个 **正** 整数数组 `nums` 。
-
-将 `nums` 分成两个数组:`nums1` 和 `nums2` ,并满足下述条件:
-
-- 数组 `nums` 中的每个元素都属于数组 `nums1` 或数组 `nums2` 。
-- 两个数组都 **非空** 。
-- 分区值 **最小** 。
-
-分区值的计算方法是 `|max(nums1) - min(nums2)|` 。
-
-其中,`max(nums1)` 表示数组 `nums1` 中的最大元素,`min(nums2)` 表示数组 `nums2` 中的最小元素。
-
-返回表示分区值的整数。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,3,2,4]
-> 输出:1
-> 解释:可以将数组 nums 分成 nums1 = [1,2] 和 nums2 = [3,4] 。
-> - 数组 nums1 的最大值等于 2 。
-> - 数组 nums2 的最小值等于 3 。
-> 分区值等于 |2 - 3| = 1 。
-> 可以证明 1 是所有分区方案的最小值。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [100,1,10]
-> 输出:9
-> 解释:可以将数组 nums 分成 nums1 = [10] 和 nums2 = [100,1] 。
-> - 数组 nums1 的最大值等于 10 。
-> - 数组 nums2 的最小值等于 1 。
-> 分区值等于 |10 - 1| = 9 。
-> 可以证明 9 是所有分区方案的最小值。
-> ```
-
-
-
-分析:
-
-这道题就是求两个元素的最小值,解题思路是先排序,然后求相邻元素的最小值。
-
-```go
-// date 2024/01/04
-func findValueOfPartition(nums []int) int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- n := len(nums)
- ans := nums[1] - nums[0]
- for i := 2; i < n; i++ {
- if nums[i] - nums[i-1] < ans {
- ans = nums[i] - nums[i-1]
- }
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.283_\347\247\273\345\212\250\351\233\266.md" "b/01_array/No.283_\347\247\273\345\212\250\351\233\266.md"
deleted file mode 100644
index 8aa0542..0000000
--- "a/01_array/No.283_\347\247\273\345\212\250\351\233\266.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 283 移动零-简单
-
-> 给定一个数组 `nums`,编写一个函数将所有 `0` 移动到数组的末尾,同时保持非零元素的相对顺序。
->
-> **请注意** ,必须在不复制数组的情况下原地对数组进行操作。
-
-
-
-算法:
-
-维护好非零元素应该使用的索引,遍历数组,将非零元素放在其索引。
-
-```go
-// date 2023/11/21
-func moveZeroes(nums []int) {
- idx := 0
- i, n := 0, len(nums)
- for i < n {
- if nums[i] != 0 {
- // 有可能整个数组全是非零元素,所以要判断
- // 因为只要有零存在,idx 比小于 i
- if idx < i {
- nums[idx] = nums[i]
- nums[i] = 0
- }
- idx++
- }
- i++
- }
-}
-```
-
-推荐下面的写法,简洁粗暴。
-
-先直接复制非零元素,然后尾部全部置零。
-
-```go
-func moveZeroes(nums []int) {
- idx := 0
- i, n := 0, len(nums)
- for i < n {
- if nums[i] != 0 {
- nums[idx] = nums[i]
- idx++
- }
- i++
- }
- for idx < n {
- nums[idx] = 0
- idx++
- }
-}
-```
-
diff --git "a/01_array/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md" "b/01_array/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md"
deleted file mode 100644
index 1ad6cbb..0000000
--- "a/01_array/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 303 区域和检索-数组不可变-简单
-
-题目:
-
-给定一个整数数组 `nums`,处理以下类型的多个查询:
-
-1. 计算索引 `left` 和 `right` (包含 `left` 和 `right`)之间的 `nums` 元素的 **和** ,其中 `left <= right`
-
-实现 `NumArray` 类:
-
-- `NumArray(int[] nums)` 使用数组 `nums` 初始化对象
-- `int sumRange(int i, int j)` 返回数组 `nums` 中索引 `left` 和 `right` 之间的元素的 **总和** ,包含 `left` 和 `right` 两点(也就是 `nums[left] + nums[left + 1] + ... + nums[right]` )
-
-
-
-分析:
-
-简单的前缀和。
-
-```go
-// date 2023/12/11
-type NumArray struct {
- data []int
-}
-
-
-func Constructor(nums []int) NumArray {
- sums := make([]int, len(nums))
- sum := 0
- for i, v := range nums {
- sum += v
- sums[i] = sum
- }
- return NumArray{data: sums}
-}
-
-
-func (this *NumArray) SumRange(left int, right int) int {
- v1 := 0
- if left > 0 {
- v1 = this.data[left-1]
- }
- v2 := this.data[right]
- return v2-v1
-}
-
-
-/**
- * Your NumArray object will be instantiated and called as such:
- * obj := Constructor(nums);
- * param_1 := obj.SumRange(left,right);
- */
-```
-
diff --git "a/01_array/No.304_\344\272\214\347\273\264\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\347\237\251\351\230\265\344\270\215\345\217\257\345\217\230.md" "b/01_array/No.304_\344\272\214\347\273\264\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\347\237\251\351\230\265\344\270\215\345\217\257\345\217\230.md"
deleted file mode 100644
index c94ac03..0000000
--- "a/01_array/No.304_\344\272\214\347\273\264\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\347\237\251\351\230\265\344\270\215\345\217\257\345\217\230.md"
+++ /dev/null
@@ -1,55 +0,0 @@
-## 304 二维区域和检索-矩阵不可变-中等
-
-题目:
-
-给定一个二维矩阵 `matrix`,以下类型的多个请求:
-
-- 计算其子矩形范围内元素的总和,该子矩阵的 **左上角** 为 `(row1, col1)` ,**右下角** 为 `(row2, col2)` 。
-
-实现 `NumMatrix` 类:
-
-- `NumMatrix(int[][] matrix)` 给定整数矩阵 `matrix` 进行初始化
-- `int sumRegion(int row1, int col1, int row2, int col2)` 返回 **左上角** `(row1, col1)` 、**右下角** `(row2, col2)` 所描述的子矩阵的元素 **总和** 。
-
-
-
-分析:
-
-
-
-```go
-// date 2023/12/12
-type NumMatrix struct {
- preSum [][]int
-}
-
-
-func Constructor(matrix [][]int) NumMatrix {
- m := len(matrix)
- n := len(matrix[0])
- data := make([][]int, m+1)
- for i := 0; i <= m; i++ {
- data[i] = make([]int, n+1)
- }
-
- for i := 1; i <= m; i++ {
- for j := 1; j <= n; j++ {
- data[i][j] = data[i-1][j] + data[i][j-1] + matrix[i-1][j-1] - data[i-1][j-1]
- }
- }
- return NumMatrix{preSum: data}
-}
-
-
-func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
- return this.preSum[row2+1][col2+1] - this.preSum[row1][col2+1] - this.preSum[row2+1][col1] + this.preSum[row1][col1]
-}
-
-
-/**
- * Your NumMatrix object will be instantiated and called as such:
- * obj := Constructor(matrix);
- * param_1 := obj.SumRegion(row1,col1,row2,col2);
- */
-```
-
diff --git "a/01_array/No.485_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\260.md" "b/01_array/No.485_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\260.md"
deleted file mode 100644
index 7b4e61e..0000000
--- "a/01_array/No.485_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\260.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 495 最大连续1的个数-简单
-
-题目:
-
-给定一个二进制数组 `nums` , 计算其中最大连续 `1` 的个数。
-
-数组中只包含1和0。
-
-
-
-分析:
-
-前后指针
-
-```go
-// date 2022/10/07
-func findMaxConsecutiveOnes(nums []int) int {
- res, n := 0, len(nums)
- start, end := 0, 0
- for start < n && nums[start] == 0 {
- start++
- }
-
- end = start
-
- for end < n {
- // find the first 0
- if nums[end] == 0 {
- if res < (end - start) {
- res = end - start
- }
- for end < n && nums[end] == 0 {
- end++
- }
- start = end
- }
- end++
- }
- if res < end - start {
- res = end - start
- }
- return res
-}
-```
-
diff --git "a/01_array/No.498_\345\257\271\350\247\222\347\272\277\351\201\215\345\216\206.md" "b/01_array/No.498_\345\257\271\350\247\222\347\272\277\351\201\215\345\216\206.md"
deleted file mode 100644
index 7756383..0000000
--- "a/01_array/No.498_\345\257\271\350\247\222\347\272\277\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,66 +0,0 @@
-## 498 对角线遍历-中等
-
-题目:
-
-给定一个二维数组,返回其对角线遍历序列。
-
-
-
-分析:
-
-这种题目是细节题,通过寻找遍历的规律求解。
-
-观察对角线遍历,有以下几个规律:
-
-1. 总的遍历次数等于行数加上列数,减一;即`totalTravel = m+n-1`
-2. 每次对角线遍历,横坐标和纵坐标的和是固定值,且等于当前的遍历次数。如果设横坐标为 x,纵坐标为 y,那么 x + y = travel。
-3. 对角线遍历分为两种,自上而下,和自下而上;如果是自下而上,那么x--,y++;如果是自上而下,那么x++,y--。
-4. 每次对角线遍历,x 如何确定。如果不超过边界,x 等于当前遍历次数,如果超过边界,取边界上限。
-5. y 直接通过 i - x 得到。
-
-```go
-// date 2020/02/21
-func findDiagonalOrder(mat [][]int) []int {
- res := make([]int, 0, 16)
- m := len(mat)
- n := len(mat[0])
-
- totalTravel := m+n-1
- // xtravel: bottom to up, x--, y++
- // ytravel: up to bottom, x++, y--
- xTravel := true
- xLimit, yLimit := 0, 0
- x, y := 0, 0
-
- for i := 0; i < totalTravel; i++ {
- if xTravel {
- xLimit = m
- yLimit = n
- } else {
- xLimit = n
- yLimit = m
- }
-
- if i < xLimit {
- x = i
- } else {
- x = xLimit-1
- }
- y = i - x //
- for x >= 0 && y < yLimit {
- if xTravel {
- res = append(res, mat[x][y])
- } else {
- res = append(res, mat[y][x])
- }
- x--
- y++
- }
-
- xTravel = !xTravel
- }
- return res
-}
-```
-
-
diff --git "a/01_array/No.560_\345\222\214\344\270\272k\347\232\204\345\255\220\346\225\260\347\273\204.md" "b/01_array/No.560_\345\222\214\344\270\272k\347\232\204\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index 85eb04a..0000000
--- "a/01_array/No.560_\345\222\214\344\270\272k\347\232\204\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,74 +0,0 @@
-## 560 和为k的子数组-中等
-
-题目:
-
-给你一个整数数组 `nums` 和一个整数 `k` ,请你统计并返回 *该数组中和为 `k` 的子数组的个数* 。
-
-子数组是数组中元素的连续非空序列。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,1,1], k = 2
-> 输出:2
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [1,2,3], k = 3
-> 输出:2
-> ```
-
-
-
-**解题思路**
-
-子数组是指连续的非空序列。
-
-- 暴力求解,详见解法1。既然是连续的子数组,那么就可以两层遍历,第一层遍历每个元素,第二层从该元素开始往前遍历求和,只要等于目标指,结果加一。目标值可能为零,元素也可能为零,所以第二层遍历不能够匹配到目标值后就跳出,所以遍历所有情况。
-- 前缀和,详见解法2。子序和为k,也可以看成是前缀和之间的差为 k,所以我们可以这样做:声明变量 preSum,然后从前往后遍历,计算前缀和,并保存在 map 中,从 map 中查找 pre-k的个数。
-
-
-
-```go
-// date 2024/01/16
-// 解法1
-// 暴力求解
-func subarraySum(nums []int, k int) int {
- n := len(nums)
- ans := 0
- for i := 0; i < n; i++{
- sum := 0
- for j := i; j >= 0; j-- {
- sum += nums[j]
- if sum == k {
- ans++
- }
- }
- }
- return ans
-}
-// 解法2
-// 前缀和 + 哈希查找
-func subarraySum(nums []int, k int) int {
- n := len(nums)
- ans := 0
- preSum := 0
- m := make(map[int]int)
- m[0] = 1
- for i := 0; i < n; i++{
- preSum += nums[i]
-
- if ct, ok := m[preSum-k]; ok {
- ans += ct
- }
-
- m[preSum]++
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.674_\346\234\200\351\225\277\350\277\236\347\273\255\351\200\222\345\242\236\345\272\217\345\210\227.md" "b/01_array/No.674_\346\234\200\351\225\277\350\277\236\347\273\255\351\200\222\345\242\236\345\272\217\345\210\227.md"
deleted file mode 100644
index 6a8c7c7..0000000
--- "a/01_array/No.674_\346\234\200\351\225\277\350\277\236\347\273\255\351\200\222\345\242\236\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,36 +0,0 @@
-## 674 最长连续递增序列-简单
-
-题目:
-
-给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
-
-连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
-
-
-
-
-分析:
-
-直接遍历,统计即可。
-
-```go
-// date 2022/10/01
-func findLengthOfLCIS(nums []int) int {
- if len(nums) < 1 {
- return 0
- }
- ans, curMax := 1, 1
- for i := 1; i < len(nums); i++ {
- if nums[i] > nums[i-1] {
- curMax++
- } else {
- curMax = 1
- }
- if ans < curMax {
- ans = curMax
- }
- }
- return ans
-}
-```
-
diff --git "a/01_array/No.724_\345\257\273\346\211\276\346\225\260\347\273\204\347\232\204\344\270\255\345\277\203\344\270\213\346\240\207.md" "b/01_array/No.724_\345\257\273\346\211\276\346\225\260\347\273\204\347\232\204\344\270\255\345\277\203\344\270\213\346\240\207.md"
deleted file mode 100644
index 9fb641d..0000000
--- "a/01_array/No.724_\345\257\273\346\211\276\346\225\260\347\273\204\347\232\204\344\270\255\345\277\203\344\270\213\346\240\207.md"
+++ /dev/null
@@ -1,35 +0,0 @@
-## 724 寻找数组的中心下标-简单
-
-给你一个整数数组 nums ,请计算数组的 中心下标 。
-
-数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
-
-如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
-
-如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
-
-
-
-分析:
-
-两次遍历,先求总和,二次遍历的时候判断左右和是否相等。
-
-```go
-// date 2022/10/07
-func pivotIndex(nums []int) int {
- leftSum, rightSum := 0, 0
- for _, v := range nums {
- rightSum += v
- }
-
- for i, v := range nums {
- rightSum -= v
- if leftSum == rightSum {
- return i
- }
- leftSum += v
- }
- return -1
-}
-```
-
diff --git "a/01_array/No.746_\344\275\277\347\224\250\346\234\200\345\260\217\350\212\261\350\264\271\347\210\254\346\245\274\346\242\257.md" "b/01_array/No.746_\344\275\277\347\224\250\346\234\200\345\260\217\350\212\261\350\264\271\347\210\254\346\245\274\346\242\257.md"
deleted file mode 100644
index 7ce35ad..0000000
--- "a/01_array/No.746_\344\275\277\347\224\250\346\234\200\345\260\217\350\212\261\350\264\271\347\210\254\346\245\274\346\242\257.md"
+++ /dev/null
@@ -1,49 +0,0 @@
-## 746 使用最小花费爬楼梯-简单
-
-题目:
-
-给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
-
-你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
-
-请你计算并返回达到楼梯顶部的最低花费。
-
-分析
-
-还是动态规划,对于到达 step 台阶,有如下递推公式:
-
-```
-total_cost[step] = min(total_cost[step-1], total_cost[step-2]) + cost[step]
-```
-
-```go
-// date 2023/11/09
-func minCostClimbingStairs(cost []int) int {
- // total cost for step
- // total_cost[step] = min(total_cost[step-1], total_cost[step-2]) + cost[step]
-
- n := len(cost)
- if n == 0 {
- return 0
- }
- if n == 1 {
- return cost[0]
- }
- step1, step2 := cost[1], cost[0]
- var tempCost int
- for i := 2; i < len(cost); i++ {
- tempCost = min(step1, step2) + cost[i]
- step2 = step1
- step1 = tempCost
- }
-
- return min(step1, step2)
-}
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
diff --git "a/01_array/No.747_\350\207\263\345\260\221\346\230\257\345\205\266\344\273\226\346\225\260\345\255\227\344\270\244\345\200\215\347\232\204\346\234\200\345\244\247\346\225\260.md" "b/01_array/No.747_\350\207\263\345\260\221\346\230\257\345\205\266\344\273\226\346\225\260\345\255\227\344\270\244\345\200\215\347\232\204\346\234\200\345\244\247\346\225\260.md"
deleted file mode 100644
index 0deb440..0000000
--- "a/01_array/No.747_\350\207\263\345\260\221\346\230\257\345\205\266\344\273\226\346\225\260\345\255\227\344\270\244\345\200\215\347\232\204\346\234\200\345\244\247\346\225\260.md"
+++ /dev/null
@@ -1,36 +0,0 @@
-## 747 至少是其他数字两倍的最大数-简单
-
-给你一个整数数组 nums ,其中总是存在 唯一的 一个最大整数 。
-
-请你找出数组中的最大元素并检查它是否 至少是数组中每个其他数字的两倍 。如果是,则返回 最大元素的下标 ,否则返回 -1 。
-
-
-
-分析:
-
-题目要求最大元素至少是数组中每个其他数字的两倍,因此只需要检查最大数和次大数即可,只要最大数是次大数的两倍,则返回结果,否则返回-1。
-
-```go
-// date 2022/10/07
-func dominantIndex(nums []int) int {
- if len(nums) <= 1 {
- return len(nums)-1
- }
- max1, max2 := 0, 0
- res := -1
- for i, v := range nums {
- if v > max1 {
- max2 = max1
- max1 = v
- res = i
- } else if v > max2 {
- max2 = v
- }
- }
- if max1 >= 2 * max2 {
- return res
- }
- return -1
-}
-```
-
diff --git "a/01_array/No.905_\346\214\211\345\245\207\345\201\266\346\216\222\345\272\217\346\225\260\347\273\204.md" "b/01_array/No.905_\346\214\211\345\245\207\345\201\266\346\216\222\345\272\217\346\225\260\347\273\204.md"
deleted file mode 100644
index f2e6145..0000000
--- "a/01_array/No.905_\346\214\211\345\245\207\345\201\266\346\216\222\345\272\217\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,30 +0,0 @@
-## 905 按奇偶排序数组-简单
-
-题目:
-
-给定一个数组,通过就地修改使所有偶数位于所有基数的前面。你可以返回满足此条件的任何数组作为答案。
-
-
-
-分析:
-
-对撞指针,然后交换。
-
-```go
-// date 2022/10/7
-func sortArrayByParity(nums []int) []int {
- left, right := 0, len(nums)-1
- for left < right {
- for left < right && nums[left] & 0x1 == 0x0 {
- left++
- }
- for left < right && nums[right] & 0x1 == 0x1 {
- right--
- }
- nums[left], nums[right] = nums[right], nums[left]
- left++
- right--
- }
- return nums
-}
-```
\ No newline at end of file
diff --git "a/01_array/No.941_\346\234\211\346\225\210\347\232\204\345\261\261\350\204\211\346\225\260\347\273\204.md" "b/01_array/No.941_\346\234\211\346\225\210\347\232\204\345\261\261\350\204\211\346\225\260\347\273\204.md"
deleted file mode 100644
index 8518ee1..0000000
--- "a/01_array/No.941_\346\234\211\346\225\210\347\232\204\345\261\261\350\204\211\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,49 +0,0 @@
-## 941 有效的山脉数组-简单
-
-给定一个整数数组 arr,如果它是有效的山脉数组就返回 true,否则返回 false。
-
-让我们回顾一下,如果 arr 满足下述条件,那么它是一个山脉数组:
-
-arr.length >= 3
-在 0 < i < arr.length - 1 条件下,存在 i 使得:
-arr[0] < arr[1] < ... arr[i-1] < arr[i]
-arr[i] > arr[i+1] > ... > arr[arr.length - 1]
-
-
-
-算法分析:
-
-```go
-// date 2020/05/20
-func validMountainArray(arr []int) bool {
- n := len(arr)
- if n < 3 { return false }
- top, index := arr[0], 0
- // 找到最高峰
- for i := 1; i < n; i++ {
- if arr[i] == arr[i-1] { return false } // 不能有平的
- if arr[i] > top {
- top = arr[i]
- index = i
- }
- }
- // 判断是否是斜坡
- if index == 0 || index == n-1 {
- return false
- }
- // 判断上坡
- for i := 1; i < index; i++ {
- if arr[i-1] >= arr[i] {
- return false
- }
- }
- // 判断下坡
- for i := index+1; i < n; i++ {
- if arr[i-1] <= arr[i] {
- return false
- }
- }
- return true
-}
-```
-
diff --git "a/01_array/No.977_\346\234\211\345\272\217\346\225\260\347\273\204\347\232\204\345\271\263\346\226\271.md" "b/01_array/No.977_\346\234\211\345\272\217\346\225\260\347\273\204\347\232\204\345\271\263\346\226\271.md"
deleted file mode 100644
index d28c426..0000000
--- "a/01_array/No.977_\346\234\211\345\272\217\346\225\260\347\273\204\347\232\204\345\271\263\346\226\271.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 977 有序数组的平方-简单
-
-题目:
-
-给你一个按 **非递减顺序** 排序的整数数组 `nums`,返回 **每个数字的平方** 组成的新数组,要求也按 **非递减顺序** 排序。
-
-
-
-分析:
-
-对撞指针,因为可能存在负数,所以两头的平方比较大
-
-```go
-// date 2021/03/13
-func sortedSquares(nums []int) []int {
- n := len(nums)
- res := make([]int, n, n)
- left, right := 0, n-1
- idx := n-1
-
- for left <= right {
- if left == right {
- res[idx] = sqar(nums[left])
- break
- }
- sl, sr := sqar(nums[left]), sqar(nums[right])
- if sr > sl {
- res[idx] = sr
- right--
- } else {
- res[idx] = sl
- left++
- }
- idx--
- }
-
- return res
-}
-
-func sqar(x int) int {
- return x*x
-}
-```
-
diff --git "a/01_array/No.997_\346\211\276\345\210\260\345\260\217\351\225\207\347\232\204\346\263\225\345\256\230.md" "b/01_array/No.997_\346\211\276\345\210\260\345\260\217\351\225\207\347\232\204\346\263\225\345\256\230.md"
deleted file mode 100644
index 1a43730..0000000
--- "a/01_array/No.997_\346\211\276\345\210\260\345\260\217\351\225\207\347\232\204\346\263\225\345\256\230.md"
+++ /dev/null
@@ -1,50 +0,0 @@
-## 997 找到小镇的法官-简单
-
-题目:
-
-小镇里有 n 个人,按从 1 到 n 的顺序编号。传言称,这些人中有一个暗地里是小镇法官。
-
-如果小镇法官真的存在,那么:
-
-小镇法官不会信任任何人。
-每个人(除了小镇法官)都信任这位小镇法官。
-只有一个人同时满足属性 1 和属性 2 。
-给你一个数组 trust ,其中 trust[i] = [ai, bi] 表示编号为 ai 的人信任编号为 bi 的人。
-
-如果小镇法官存在并且可以确定他的身份,请返回该法官的编号;否则,返回 -1 。
-
-
-分享:
-
-直接遍历,信任别人的人直接赋值 -1,被信任的人,如果没有信任别人,直接递增,并保留结果。
-
-最后,判断被信任的人是否得到了所有人的信任。
-
-
-```go
-// date 2023/11/09
-func findJudge(n int, trust [][]int) int {
- if len(trust) == 0 {
- if n == 1 {
- return n
- }
- return -1
- }
- dp := make([]int , n+1)
- dp[0] = -1
- res := -1
- for _, v := range trust {
- dp[v[0]] = -1
- if dp[v[1]] != -1 {
- dp[v[1]] += 1
- res = v[1]
- }
- }
-
- if dp[res] == n-1 {
- return res
- }
-
- return -1
-}
-```
diff --git a/01_array/images/img304.png b/01_array/images/img304.png
deleted file mode 100644
index 8af88b6..0000000
Binary files a/01_array/images/img304.png and /dev/null differ
diff --git a/01_array/images/img498.png b/01_array/images/img498.png
deleted file mode 100644
index 734c8b3..0000000
Binary files a/01_array/images/img498.png and /dev/null differ
diff --git a/01_array/largest_sum_contiguous_subarray.md b/01_array/largest_sum_contiguous_subarray.md
deleted file mode 100644
index d912725..0000000
--- a/01_array/largest_sum_contiguous_subarray.md
+++ /dev/null
@@ -1,139 +0,0 @@
-## 连续最大子序列和
-
-[TOC]
-
-
-### 问题定义
-
-给定一个数组,输出其最大连续子序列和的大小。
-
-例如:数组为{-2, -3, 4, -1, -2, 1, 5, -3},输出为7(即4,-1,-2,1,5}。
-
-### 算法分析
-
-```cpp
-Initialize:
- max_so_far = 0
- max_ending_here = 0
-
-Loop for each element of the array
- (a) max_ending_here = max_ending_here + a[i]
- (b) if(max_ending_here < 0)
- max_ending_here = 0
- (c) if(max_so_far < max_ending_here)
- max_so_far = max_ending_here
-return max_so_far
-```
-
-### 算法实现
-
-```cpp
-int MaxSubArraySum(int a[], int n) {
- int max_so_far = 0, max_ending_here = 0;
- int first = 0, last = 0; // 起始点坐标
- for(int i = 0; i < n; i++) {
- max_ending_here = max_ending_here + a[i];
- if(max_ending_here < 0) {
- max_ending_here = 0;
- first = i + 1;
- } else if(max_ending_here > max_so_far) {
- max_so_far = max_ending_here;
- last = i;
- }
- }
- cout << "From " << first << " to " << last << endl;
- return max_so_far;
-}
-```
-
-### 二维空间问题
-
-Maximum sum rectangle in a 2D matrix,即二维矩阵中的最大和矩形
-
-
-
-如图所示,图中蓝色矩形框内就是最大的矩阵和。
-
-### 算法分析
-
-借助上面的算法原理,我们可以找到一行或者一列中的最大连续子序列和,以及子序列的起点和终点。
-
-```cpp
-Initialize:
- start = -1
- finish = -1
- sum = 0
-
-for i = 0; i < n; i++
- 1) sum += a[i]
- 2) if(sum < 0) {
- sum = 0;start = i + 1;
- } else if(sum > maxsum) {
- maxsum = sum; finish = i;
- }
- 3) if(finish != -1)
- return maxsum;
-```
-
-同样,对二维矩阵而言,子矩阵的和需要从 **左上角** 开始,计算到 **右下角** 元素,因此,子矩阵的和的累计过程即向下延伸,也向右延伸。所以,用temp[i]计算每列中自顶行至尾行的和,同时将列作为基本的移动单元。
-
-时间复杂度为O(n^3)
-
-### 算法实现
-
-```
-// 找到一列中的最大连续子序列的和,并返回起点和终点
-int FindOne(int a[], int &start, int &finish, int n) {
- int sum = 0, res = 0;
- int stemp = -1;
- start = -1;
- finish = -1;
- for(int i = 0; i < n; i++) {
- sum += a[i];
- if(sum < 0) {
- sum = 0;
- stemp = i + 1;
- } else if(sum > res) {
- res = sum;
- start = stemp;
- finish = i;
- }
- }
- if(finish != -1)
- return res;
- // 特殊情况,即所有元素均小于零
- res = a[0];
- start = 0;
- finish = 0;
- for(int i = 0; i < n; i++) {
- if(a[i] > res) {
- res = a[i];
- start = finish = i;
- }
- }
- return res;
-}
-//
-int FindTow(int a[R][C]) {
- int res, finalleft, finalright, finaltop, finaldown;
- int left, right, i;
- int temp[R], sum, start, finish;
- for(left = 0; left < C; left++) {
- for(right = left; right < C; right++) {
- for(i = 0; i < R; i++)
- temp[i] += a[i][right];
- sum = FindOne(temp, start, finish, R);
- if(sum > res) {
- res = sum;
- finalleft = left;
- finalright = right;
- finaltop = start;
- finaldown = finish;
- }
- }
- }
- printf("(Top, Left) (%d, %d)n", finalTop, finalLeft);
- printf("(Bottom, Right) (%d, %d)n", finalBottom, finalRight);
- printf("Max sum is: %dn", res);
-}
-```
diff --git a/01_array/readme.md b/01_array/readme.md
deleted file mode 100644
index 218403f..0000000
--- a/01_array/readme.md
+++ /dev/null
@@ -1,244 +0,0 @@
-# Array
-
-Array[数组]是用于在相邻位置存储均匀元素的数据结构。 必须在存储数据之前提供数组的大小。
-
-[TOC]
-
-## 1、基本操作
-
-数组的性质决定了其基本操作的复杂度;
-
-* 无序数组
-
- + 查找:O(n)
- + 插入:O(1)
- + 删除:O(n)
-
-* 有序数组
-
- + 查找:O(Logn)【使用二分查找】
- + 插入:O(n)【最坏的情况下需要移动所有元素】
- + 删除:O(n)【最坏的情况下需要移动所有元素】
-
-## 2、常用技巧
-
-### 2.1 双指针算法
-
-双指针,是指在遍历对象的过程中,不在普通地使用单个指针进行访问,而是两个相同方向(快慢指针)或相反方向(对撞指针)的指针进行遍历,从而达到相应的目的。
-
-**快慢指针**:一个指针负责维护目标索引(因为符合条件的元素较少,所以这个指针移动较慢,也称为慢指针),一个指针负责遍历数组(也称为快指针)。
-
-相关题目:
-
-- [026删除排序数组中的重复项](026.md)
-- [027移除元素](027.md)
-- [209长度最小的子数组](209.md)
-
-
-
-**对撞指针**:两个指针分别从最左侧(left指针)和最右侧(right指针)向数组中间进行遍历。
-
-相关题目:
-
-- [011盛最多水的容器](011.md)
-- [015三数之和](015.md)
-- [034在排序数组中查找元素的第一个和最后一个位置](034.md)
-
-
-
-
-
-#### 从尾部到头部
-
-如果知道的数组的长度,可从尾部按照某种规则依次插入元素,例如[88 合并两个有序数组](088.md)
-
-#### 就地替换
-
-in-place操作是指在不申请额外空间的情况下,通过索引找到目标值并进行就地替换的操作,该操作可以极大地减少时间和空间复杂度。
-
-
-
-### 2.2 前缀和技巧
-
-
-
-### 2.3 差分数组技巧
-
-
-
-
-
----
-
-相关题目
-
-#### 46 全排列
-
-题目要求:给定一个**没有重复**数字的序列,返回其所有可能的全排列。
-
-算法:回溯法
-
-```go
-func permute(nums []int) [][]int {
- res := make([][]int, 0, total(len(nums)))
- func bt(nums, temp []int) {
- if len(nums) == 0 {
- res = append(res, temp)
- return
- }
- for i := range nums {
- temp = append(temp, nums[i])
- n := make([]int, 0, len(nums)-1)
- n = append(n, nums[:i]...)
- n = append(n, nums[i+1:]...)
- bt(n, temp)
- }
- }(nums, make([]int, 0))
- return res
-}
-
-func total(n int) int {
- if n <= 0 {return 0}
- res := 1
- for n >= 1 {
- res *= n
- n--
- }
- return res
-}
-```
-
-
-
-#### 54 螺旋矩阵
-
-题目要求:给定一个m * n的二维矩阵,顺时针打印。
-
-算法1:for循环,用x,y坐标加以限制
-
-```go
-func spiralOrder(matrix [][]int) []int {
- if len(matrix) < 1 { return []int{} }
- startX, endX := 0, len(matrix[0])-1
- startY, endY := 0, len(matrix)-1
- res := make([]int, 0, (endX+1)*(endY+1))
- for {
- for i := startX, i <= endX; i++ {
- res = append(res, matrix[startY][i]) // left -> right
- }
- startY++
- if stratY > endY { break }
- for i := startY; i <= endY; i++ {
- res = append(res, matrix[i][endX]) // top -> bottom
- }
- endX--
- if startX > endX { break }
- for i := endX; i >= startX; i-- {
- res = append(res, matrix[endY][i]) // right -> left
- }
- endY--
- if startY > endY { break }
- for i := endY; i >= startY; i-- {
- res = append(res, matrix[i][startX]) // bottom -> top
- }
- startX++
- if startX > endX { break }
- }
- return res
-}
-```
-
-算法2: 每次打印一轮
-
-```go
-func spiralOrder(matrix [][]int) []int {
- if len(matrix) < 1 { return []int{}}
- m, n := len(matrix)-1, len(matrix[0]) - 1
- res := make([]int, 0, (m+1)*(n+1))
- k := 0
- for k <= len(matrix)/2 {
- for i := k; i <= n-k; i++ {
- res = append(res, matrix[k][i]) // left -> right
- }
- for i := k+1; i <= m-k; i++ {
- res = append(res, matrix[i][n-k]) // top -> bottom
- }
- for i := n-k-1; i >= k; i-- {
- res = append(res, matrix[m-k][i]) // right -> left
- }
- for i := m-k-1; i >= k+1; i-- {
- res = append(res, matrix[i][k]) // bottom -> top
- }
- k++
- }
- return res
-}
-```
-
-#### 118 杨辉三角
-
-题目要求:给定一个非负整数,返回其杨辉三角二维数组。
-
-算法:下一行由上一行生成,生成规则如下:
-
-```go
-1)rows[i][0] = rows[i-1][0]
-2)rows[i][j] = rows[i-1][j] + rows[i-1][j-1]
-3)rows[i][end] = 1
-```
-
-```go
-// date 2020/02/02
-func generate(numRows int) [][]int {
- if numRows <= 0 { return [][]int{} }
- res := make([][]int, numRows)
- for i := 0; i < numRows; i++ {
- t := make([]int, 0)
- if i == 0 {
- t = append(t, 1)
- }
- res[i] = t
- }
- for i := 1; i < numRows; i++ {
- n := len(res[i-1])
- for j := 0; j < n; j++ {
- if j == 0 {
- res[i][j] = res[i-1][j]
- } else {
- res[i][j] = res[i-1][j] + res[i-1][j-1]
- }
- }
- res[i] = append(res[i], 1)
- }
- return res
-}
-```
-
-#### 447 回旋镖的数量【中等】
-
-思路分析
-
-算法1:以每个点当做第一个点,计算该点与其他点的距离,如果这个距离出现过那么必定有两个答案(j,k顺序交换)
-
-两层循环,外层循环用map记录距离
-
-```go
-// date 2020/01/01
-func numberOfBoomerangs(points [][]int) int {
- res, d, n := 0, 0, len(points)
- for i := 0; i < n; i++ {
- m := make(map[int]int)
- for j := 0; j < n; j++ {
- if j == i {continue}
- d = (points[i][0] - points[j][0]) * (points[i][0] - points[j][0]) + (points[i][1] - points[j][1]) * (points[i][1] - points[j][1])
- if _, ok := m[d]; ok {
- res += m[d] * 2
- m[d]++
- } else {
- m[d] = 1
- }
- }
- }
- return res
-}
-```
diff --git "a/02_linkedlist/No.002_\344\270\244\346\225\260\346\261\202\345\222\214.md" "b/02_linkedlist/No.002_\344\270\244\346\225\260\346\261\202\345\222\214.md"
deleted file mode 100644
index 97f99b7..0000000
--- "a/02_linkedlist/No.002_\344\270\244\346\225\260\346\261\202\345\222\214.md"
+++ /dev/null
@@ -1,48 +0,0 @@
-## 002 两数相加-中等
-
-题目:
-
-给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
-
-请你将两个数相加,并以相同形式返回一个表示和的链表。
-
-你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
-
-
-
-分析:
-
-哑结点,开辟空间计算
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
- dumy := &ListNode{}
- pre := dumy
- tempRes, n1, n2, carrry := 0, 0, 0, 0
- for l1 != nil || l2 != nil || carrry != 0 {
- n1, n2 = 0, 0
- if l1 != nil {
- n1 = l1.Val
- l1 = l1.Next
- }
- if l2 != nil {
- n2 = l2.Val
- l2 = l2.Next
- }
- tempRes = n1 + n2 + carrry
- carrry = tempRes / 10
-
- pre.Next = &ListNode{Val: tempRes % 10}
- pre = pre.Next
- }
- return dumy.Next
-}
-```
diff --git "a/02_linkedlist/No.019_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\345\200\222\346\225\260\347\254\254N\344\270\252\350\212\202\347\202\271.md" "b/02_linkedlist/No.019_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\345\200\222\346\225\260\347\254\254N\344\270\252\350\212\202\347\202\271.md"
deleted file mode 100644
index 7d6352e..0000000
--- "a/02_linkedlist/No.019_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\345\200\222\346\225\260\347\254\254N\344\270\252\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,74 +0,0 @@
-## 19 删除链表的倒数第N个结点-中等
-
-题目:
-
-给你一个链表,删除链表的**倒数**第 `n` 个结点,并且返回链表的头结点。
-
-
-
-**解题思路**
-
-- 双指针,快慢指针。具体为,双指针slow和fast,fast快指针先走n步(n有效,所以最坏的情况是快指针走到表尾,即是删除表头元素);然后slow指针和fast指针同走,当fast指针走到最后一个元素时,因为slow与fast慢指针差n步,slow刚好为欲删除节点的前驱节点,详见解法1。时间复杂度`O(N)`,空间复杂度`O(1)`
-- 栈。栈具有先入后出的特点,我们可以将所有的节点依次入栈,然后在栈中操作指针,注意检查 n 的合法性,详见解法2。时间复杂度`O(N)`,空间复杂度`O(N)`
-
-```go
-// date 2023/10/11
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// 解法1
-// 双指针
-func removeNthFromEnd(head *ListNode, n int) *ListNode {
- if head == nil {
- return head
- }
- slow, fast := head, head
- for n > 0 && fast != nil {
- fast = fast.Next
- n--
- }
- // 到这里,我们期望 n 为零,表示链表中存在要删除的点
- // 如果 n > 0 表示已经超出要删除的点了,直接返回 head
- if n > 0 {
- return head
- }
- // n 为零,如果 fast 为空 表示要删除 头节点
- if fast == nil {
- // delete the head
- return head.Next
- }
-
- for fast.Next != nil {
- slow, fast = slow.Next, fast.Next
- }
- slow.Next = slow.Next.Next
- return head
-}
-
-// 解法2
-// 栈
-func removeNthFromEnd(head *ListNode, n int) *ListNode {
- stack := make([]*ListNode, 0, 16)
- cur := head
- for cur != nil {
- stack = append(stack, cur)
- cur = cur.Next
- }
- size := len(stack)
- if n > size {
- return head
- }
- if n == size {
- return head.Next
- }
- prev := stack[size-n-1]
- prev.Next = prev.Next.Next
- return head
-}
-```
-
-
diff --git "a/02_linkedlist/No.021_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\351\223\276\350\241\250.md" "b/02_linkedlist/No.021_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\351\223\276\350\241\250.md"
deleted file mode 100644
index 1785d54..0000000
--- "a/02_linkedlist/No.021_\345\220\210\345\271\266\344\270\244\344\270\252\346\234\211\345\272\217\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,67 +0,0 @@
-## 021 合并两个有序链表-简单
-
-题目:
-
-将两个升序链表合并为一个新的 **升序** 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
-
-
-
-分析:
-
-算法1:利用哑结点
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
- l1, l2 := list1, list2
- dumy := &ListNode{}
- pre := dumy
- for l1 != nil && l2 != nil {
- if l1.Val < l2.Val {
- pre.Next = l1
- l1 = l1.Next
- } else {
- pre.Next = l2
- l2 = l2.Next
- }
- pre = pre.Next
- }
- if l1 != nil {
- pre.Next = l1
- }
- if l2 != nil {
- pre.Next = l2
- }
- return dumy.Next
-}
-```
-
-
-
-算法2:递归版
-
-每个节点只会访问一次,因此时间复杂度为O(n+m);只有到达l1或l2的底部,递归才会返回,所以空间复杂度为O(n+m)
-
-```go
-// 递归版
-func mergeTwoLists(l1, l2 *ListNode) *ListNode {
- if l1 == nil {return l2}
- if l2 == nil {return l1}
- var newHead *ListNode
- if l1.Val < l2.Val {
- newHead = l1
- newHead.Next = mergeTwoLists(l1.Next, l2)
- } else {
- newHead = l2
- newHead.Next = mergeTwoLists(l1, l2.Next)
- }
- return newHead
-}
-```
diff --git "a/02_linkedlist/No.023_\345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md" "b/02_linkedlist/No.023_\345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md"
deleted file mode 100644
index 0126347..0000000
--- "a/02_linkedlist/No.023_\345\220\210\345\271\266K\344\270\252\345\215\207\345\272\217\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,113 +0,0 @@
-## 023 合并K个升序链表-困难
-
-题目:
-
-给你一个链表数组,每个链表都已经按升序排列。
-
-请你将所有链表合并到一个升序链表中,返回合并后的链表。
-
-
-
-**解题思路**
-
-复习递归算法,掌握自底向上和自上向下的递归方法。
-
-- 最朴素的算法,顺次两两合并,详见解法1。递归算法,自底向上的两两合并。每个链表遍历一遍,所示时间复杂度O(n*k),空间复杂度O(1)。
-- 分治算法,类似归并排序,详见解法2。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// 解法1
-// 最朴素的顺序两两合并
-func mergeKLists(lists []*ListNode) *ListNode {
- if len(lists) == 0 {
- return nil
- }
- if len(lists) == 1 {
- return lists[0]
- }
- k := len(lists)
- l1, l2 := mergeKLists(lists[:k-1]), lists[k-1]
- dumy := &ListNode{}
- pre := dumy
- for l1 != nil && l2 != nil {
- if l1.Val < l2.Val {
- pre.Next = l1
- l1 = l1.Next
- } else {
- pre.Next = l2
- l2 = l2.Next
- }
- pre = pre.Next
- }
- if l1 != nil {
- pre.Next = l1
- }
- if l2 != nil {
- pre.Next = l2
- }
- return dumy.Next
-}
-
-// 解法2
-// 分治思想,归并排序思想的合并
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func mergeKLists(lists []*ListNode) *ListNode {
-
- var merge func(lists []*ListNode, left, right int) *ListNode
- merge = func(lists []*ListNode, left, right int) *ListNode {
- if left == right {
- return lists[left]
- }
- if left > right {
- return nil
- }
- mid := left + (right- left)/2
- return mergeTwoList(merge(lists, left, mid), merge(lists, mid+1, right))
- }
-
- return merge(lists, 0, len(lists)-1)
-}
-
-func mergeTwoList(l1, l2 *ListNode) *ListNode {
- if l1 == nil {
- return l2
- }
- if l2 == nil {
- return l1
- }
- dummy := &ListNode{}
- cur := dummy
- for l1 != nil && l2 != nil {
- if l1.Val < l2.Val {
- cur.Next = l1
- l1 = l1.Next
- } else {
- cur.Next = l2
- l2 = l2.Next
- }
- cur = cur.Next
- }
- if l1 != nil {
- cur.Next = l1
- }
- if l2 != nil {
- cur.Next = l2
- }
- return dummy.Next
-}
-```
-
diff --git "a/02_linkedlist/No.024_\344\270\244\344\270\244\344\272\244\346\215\242\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md" "b/02_linkedlist/No.024_\344\270\244\344\270\244\344\272\244\346\215\242\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md"
deleted file mode 100644
index 6fbd950..0000000
--- "a/02_linkedlist/No.024_\344\270\244\344\270\244\344\272\244\346\215\242\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,73 +0,0 @@
-## 24 两两交换链表中的节点-中等
-
-题目:
-
-给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
-
-
-
-**解题思路**
-
-这道题有2种解法。一种是先交换前两个,然后递归交换后面的,详见解法1。
-
-第二种解法是迭代版本,思路一样。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// 解法1
-func swapPairs(head *ListNode) *ListNode {
- // basic case
- if head == nil || head.Next == nil {
- return head
- }
- var newHead *ListNode
- unSwap := head.Next.Next // save un-swap node
- newHead = head.Next // find the new head
- newHead.Next = head // update next pointer of new head
- head.Next = swapPairs(unSwap) // swap others
- return newHead
-}
-```
-
-
-
-先找出新的头节点,并保存两两交换后的第二个节点,用于更新其Next指针。
-
-```go
-// date 2022/10/09
-// 解法2
-func swapPairs(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- var nHead *ListNode
- // 1. 找到新的头节点
- nHead = head.Next
- // save unswap list
- after := nHead.Next
- p1, p2 := head, head.Next
- p1.Next = after
- p2.Next = p1
- // 2. 继续交换
- pre := p1
- p1 = after
- for p1 != nil && p1.Next != nil {
- p2 = p1.Next
- after = p2.Next
- p1.Next = after
- p2.Next = p1
- pre.Next = p2
- pre = p1
- p1 = after
- }
- return nHead
-}
-```
-
diff --git "a/02_linkedlist/No.025_K\344\270\252\344\270\200\347\273\204\347\277\273\350\275\254\351\223\276\350\241\250.md" "b/02_linkedlist/No.025_K\344\270\252\344\270\200\347\273\204\347\277\273\350\275\254\351\223\276\350\241\250.md"
deleted file mode 100644
index fc73eea..0000000
--- "a/02_linkedlist/No.025_K\344\270\252\344\270\200\347\273\204\347\277\273\350\275\254\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,76 +0,0 @@
-## 25 K个一组翻转链表-困难
-
-题目:
-
-给你链表的头节点 `head` ,每 `k` 个节点一组进行翻转,请你返回修改后的链表。
-
-`k` 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 `k` 的整数倍,那么请将最后剩余的节点保持原有顺序。
-
-你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
-
-
-
-> **示例 1:**
->
-> 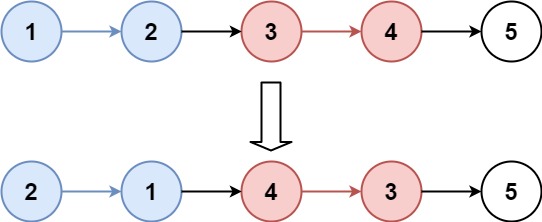
->
-> ```
-> 输入:head = [1,2,3,4,5], k = 2
-> 输出:[2,1,4,3,5]
-> ```
->
-> **示例 2:**
->
-> 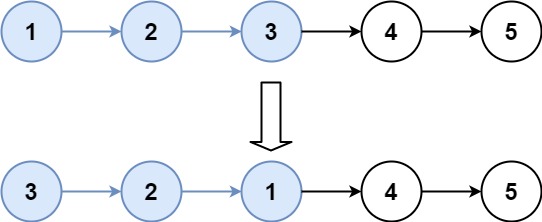
->
-> ```
-> 输入:head = [1,2,3,4,5], k = 3
-> 输出:[3,2,1,4,5]
-> ```
-
-
-
-**解题思路**
-
-这道题可以递归翻转,具体为:
-
-1. 先实现一个区间翻转的函数,满足K个直接进入区间翻转
-2. 不足 k 个直接返回
-
-```go
-// date 2024/01/11
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func reverseKGroup(head *ListNode, k int) *ListNode {
- node := head
- for i := 0; i < k; i++ {
- if node == nil {
- return head
- }
- node = node.Next
- }
- newHead := reverse(head, node) // reverse 之后 head.Next = node
- head.Next = reverseKGroup(node, k)
- return newHead
-}
-
-// reverse [first, last) then return new head
-// not contains the last node
-func reverseBetween(first, last *ListNode) *ListNode {
- prev := last
- for first != last {
- tmp := first.Next
- first.Next = prev
- prev = first
- first = tmp
- }
- return prev
-}
-```
-
-
diff --git "a/02_linkedlist/No.061_\346\227\213\350\275\254\351\223\276\350\241\250.md" "b/02_linkedlist/No.061_\346\227\213\350\275\254\351\223\276\350\241\250.md"
deleted file mode 100644
index c446815..0000000
--- "a/02_linkedlist/No.061_\346\227\213\350\275\254\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-#### No.61 旋转链表【中等】
-
-题目:
-
-给你一个链表的头节点 head,旋转链表,将链表的每个节点向右移动 k 个位置。
-
-
-
-分析:【推荐使用该算法】
-
-把链表每个节点向右移动 k 个位置,相当于把倒数 k 个节点形成新链表的前半部分,原来前面的 l - k 个形成新链表的后半部分。那么,l - k - 1 位置(从0计算索引)的节点就是新链表的最后一个节点,其Next就是新头节点。
-
-具体这样做:
-
-1. 求链表求长度 l,并将其形成环
-2. 对 k 取模,k = k % l
-3. 重新从 head 开始走 l - k - 1 步,找到新链表的尾巴,断开即可。
-
-```go
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// date 2023/10/11
-func rotateRight(head *ListNode, k int) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- pre := head
- l := 1
- for pre.Next != nil {
- l++
- pre = pre.Next
- }
- pre.Next = head
-
- k = k % l
- step := l - k - 1
- pre = head
- for step > 0 {
- pre = pre.Next
- step -= 1
- }
- head = pre.Next
- pre.Next = nil
- return head
-}
-```
-
diff --git "a/02_linkedlist/No.082_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md" "b/02_linkedlist/No.082_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md"
deleted file mode 100644
index 1fb3933..0000000
--- "a/02_linkedlist/No.082_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\2402.md"
+++ /dev/null
@@ -1,57 +0,0 @@
-## 82 删除排序链表中的重复元素2-中等
-
-题目:
-
-给定一个已排序的链表的头 `head` , *删除原始链表中所有重复数字的节点,只留下不同的数字* 。返回 *已排序的链表* 。
-
-这一题跟83题的区别在于,83题是要求删除重复节点,保证所有节点只出现一次。
-
-而82题则要求删除所有重复出现的元素,只保留出现过一次的节点。
-
-
-
-分析:
-
-哑结点 和 快慢指针
-
-其中,慢指针slow 从哑结点开始,并且 slow.next 指向 head,即未检查的数据(潜在的结果)。slow 指针保存最终的结果集。
-
-快指针 fast 从 head 开始。
-
-当 fast 与 fast.next 值不相等时,fast 是一个可能的结果,然后在通过 fast 与 slow 的距离来判断,fast 是否满足条件。
-
-slow.next 与 fast 之间的数据就是重复元素。
-
-```go
-// date 2022/10/08
-// 83升级版,所有重复元素都不要,只保留出现过一次的元素
-func deleteDuplicates(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- dummy := &ListNode{Val: -1}
- dummy.Next = head
- slow := dummy
- fast := head
- for fast.Next != nil {
- // 可能需要更新
- if fast.Val != fast.Next.Val {
- if slow.Next == fast {
- // 说明slow和fast之间没有重复元素,更新slow节点
- slow = fast
- } else {
- // 说明slow和fast之间有重复元素,更新slow的next节点
- slow.Next = fast.Next
- }
- }
- fast = fast.Next
- }
- // 查看尾部是否有重复
- // slow.Next != nil && slow.Next == fast 表示尾部没有重复,已经在17行进行更新了
- if slow.Next != nil && slow.Next != fast && slow.Next.Val == fast.Val {
- // 表示fast为重复元素,需要舍弃
- slow.Next = nil
- }
- return dummy.Next
-}
-```
diff --git "a/02_linkedlist/No.083_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\240.md" "b/02_linkedlist/No.083_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\240.md"
deleted file mode 100644
index 6240b2c..0000000
--- "a/02_linkedlist/No.083_\345\210\240\351\231\244\346\216\222\345\272\217\351\223\276\350\241\250\344\270\255\347\232\204\351\207\215\345\244\215\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 83 删除排序链表中的重复元素-简单
-
-题目:
-
-给定一个已排序的链表的头 `head` , *删除所有重复的元素,使每个元素只出现一次* 。返回 *已排序的链表* 。
-
-
-
-**解题思路**
-
-这道题有2种解法。一种是利用哑结点,遍历链表,只连接值不同的节点,详见解法1。
-
-另一个解法是直接判断当前指针 cur 与当前指针的Next值是否一致,如果是,直接删掉后一个,详见解法2。
-
-解法2更优雅一些。
-
-```go
-// date 2022/10/08
-// 解法1
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func deleteDuplicates(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- dumy := &ListNode{}
- pre := dumy
- // add head
- pre.Next = head
- pre = head
-
- lastVal := head.Val
-
- cur := head.Next
- for cur != nil {
- if cur.Val != lastVal { // find a new node
- pre.Next = cur
- pre = pre.Next
- lastVal = cur.Val // update last value
- }
- cur = cur.Next
- }
- pre.Next = nil
- return dumy.Next
-}
-// 解法2
-func deleteDuplicates(head *ListNode) *ListNode {
- cur := head
- for cur != nil && cur.Next != nil {
- if cur.Val == cur.Next.Val {
- cur.Next = cur.Next.Next
- continue
- }
- cur = cur.Next
- }
- return head
-}
-```
-
diff --git "a/02_linkedlist/No.086_\345\210\206\345\211\262\351\223\276\350\241\250.md" "b/02_linkedlist/No.086_\345\210\206\345\211\262\351\223\276\350\241\250.md"
deleted file mode 100644
index 1664216..0000000
--- "a/02_linkedlist/No.086_\345\210\206\345\211\262\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 86 分割链表-中等
-
-题目:
-
-给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
-
-你应当 保留 两个分区中每个节点的初始相对位置。
-
-
-
-分析:
-
-两个哑结点分别保存两个分区的数据。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func partition(head *ListNode, x int) *ListNode {
- dumy1 := &ListNode{}
- dumy2 := &ListNode{}
- d1, d2 := dumy1, dumy2
- pre := head
- for pre != nil {
- if pre.Val < x {
- d1.Next = pre
- d1 = d1.Next
- } else {
- d2.Next = pre
- d2 = d2.Next
- }
- pre = pre.Next
- }
- d2.Next = nil
- d1.Next = dumy2.Next
-
- return dumy1.Next
-}
-```
-
diff --git "a/02_linkedlist/No.092_\345\217\215\350\275\254\351\223\276\350\241\2502.md" "b/02_linkedlist/No.092_\345\217\215\350\275\254\351\223\276\350\241\2502.md"
deleted file mode 100644
index 1375581..0000000
--- "a/02_linkedlist/No.092_\345\217\215\350\275\254\351\223\276\350\241\2502.md"
+++ /dev/null
@@ -1,78 +0,0 @@
-## No.092 反转链表2
-
-题目:
-
-给你单链表的头指针 head 和两个整数 left, right,其中 left <= right。请你反转从位置 left 到 位置 right 的链表节点,返回反转后的链表。
-
-
-
-分析:
-
-使用一趟扫描,在扫描过程中:
-
-1. 先找到 left 及其前驱节点 leftpre,并保存
-2. 同时将 left 节点保存为 lefttail,继续遍历,并反转 [left, right] 中的节点
-3. 找到 right 节点之后,更新 left, right 节点的Next值
-4. 确定新的 head
-
-```go
-// date 2023/10/11
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func reverseBetween(head *ListNode, left int, right int) *ListNode {
- // leftpre, left, right, rightpost
- // leftpre.Next = right
- // left.Next = rightpost
- if head == nil || head.Next == nil {
- return head
- }
- // 区间内没有节点,不需要反转
- if left == right {
- return head
- }
-
- var leftPre, tail, cur *ListNode
- cur = head
- for left > 1 {
- leftPre = cur
- cur = cur.Next
- left--
- right--
- }
- // now cur is the left node
- // save it
- l := cur
- for right > 1 {
- after := cur.Next
- cur.Next = tail
- tail = cur
- cur = after
- right--
- }
- // now cur is the right node
- l.Next = cur.Next
- cur.Next = tail
- // when left > 1, the head is newHead
- if leftPre != nil {
- leftPre.Next = cur
- return head
- }
- // when left = 1, the right is new head
- return cur
-}
-```
-
-
-
diff --git "a/02_linkedlist/No.138_\351\232\217\346\234\272\351\223\276\350\241\250\347\232\204\345\244\215\345\210\266.md" "b/02_linkedlist/No.138_\351\232\217\346\234\272\351\223\276\350\241\250\347\232\204\345\244\215\345\210\266.md"
deleted file mode 100644
index c2ff4fb..0000000
--- "a/02_linkedlist/No.138_\351\232\217\346\234\272\351\223\276\350\241\250\347\232\204\345\244\215\345\210\266.md"
+++ /dev/null
@@ -1,128 +0,0 @@
-## 138 随机链表的复制-中等
-
-题目:
-
-给你一个长度为 `n` 的链表,每个节点包含一个额外增加的随机指针 `random` ,该指针可以指向链表中的任何节点或空节点。
-
-构造这个链表的 **[深拷贝](https://baike.baidu.com/item/深拷贝/22785317?fr=aladdin)**。 深拷贝应该正好由 `n` 个 **全新** 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 `next` 指针和 `random` 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。**复制链表中的指针都不应指向原链表中的节点** 。
-
-例如,如果原链表中有 `X` 和 `Y` 两个节点,其中 `X.random --> Y` 。那么在复制链表中对应的两个节点 `x` 和 `y` ,同样有 `x.random --> y` 。
-
-返回复制链表的头节点。
-
-用一个由 `n` 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 `[val, random_index]` 表示:
-
-- `val`:一个表示 `Node.val` 的整数。
-- `random_index`:随机指针指向的节点索引(范围从 `0` 到 `n-1`);如果不指向任何节点,则为 `null` 。
-
-你的代码 **只** 接受原链表的头节点 `head` 作为传入参数
-
-
-
-分析:
-
-算法1:【推荐该算法】
-
-哈希表+回溯
-
-哈希表的 key 和 value 分别是原链表中的节点 和 结果集中的节点,用于表示那些原来的节点已经被创建,
-
-```go
-// date 2023/10/18
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Next *Node
- * Random *Node
- * }
- */
-
-func copyRandomList(head *Node) *Node {
- if head == nil {
- return head
- }
- cache := make(map[*Node]*Node, 1024)
- var deepcopy func(h *Node) *Node
- deepcopy = func(h *Node) *Node {
- if h == nil {
- return h
- }
- old, ok := cache[h]
- if ok {
- return old
- }
- node := &Node{Val: h.Val}
- cache[h] = node
- node.Next = deepcopy(h.Next)
- node.Random = deepcopy(h.Random)
- return node
- }
-
- return deepcopy(head)
-}
-```
-
-
-
-
-
-算法2:
-
-原链表遍历两次:
-
-第一次:根据 next 节点,创建结果集,并将原链表中的节点和索引存入 map。新创建的节点,存到数组。
-
-第二次,遍历原链表,根据 random 修改结果集中的 random 指针。
-
-```go
-// date 2023/10/18
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Next *Node
- * Random *Node
- * }
- */
-
-func copyRandomList(head *Node) *Node {
- if head == nil {
- return head
- }
-
- dumy := &Node{}
- dpre := dumy
- resA := make([]*Node, 0, 1024)
- pre := head
- cache := make(map[*Node]int, 1024)
- index := int(0)
- for pre != nil {
- cache[pre] = index
- nd := &Node{Val: pre.Val}
- dpre.Next = nd
- dpre = dpre.Next
- pre = pre.Next
-
- resA = append(resA, nd)
- index++
- }
-
- pre = head
- index = 0
- for pre != nil {
- if pre.Random != nil {
- if idx, ok := cache[pre.Random]; ok {
- resA[index].Random = resA[idx]
- }
- }
- pre = pre.Next
- index++
- }
-
- return dumy.Next
-}
-```
-
-
-
diff --git "a/02_linkedlist/No.141_\347\216\257\345\275\242\351\223\276\350\241\250.md" "b/02_linkedlist/No.141_\347\216\257\345\275\242\351\223\276\350\241\250.md"
deleted file mode 100644
index d2c11a2..0000000
--- "a/02_linkedlist/No.141_\347\216\257\345\275\242\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,35 +0,0 @@
-## 141 环形链表-简单
-
-题目:
-
-给你一个链表的头节点 head ,判断链表中是否有环。
-
-如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
-
-如果链表中存在环 ,则返回 true 。 否则,返回 false 。
-
-
-
-**解题思路**
-
-通过快慢指针是否相遇来判断链表中是否存在环。
-
-```go
-// date 2023/10/11
-// 算法1:快慢指针
-// 时间复杂度分析
-// 如果链表中不存在环,则fast指针最多移动N/2次;如果链表中存在环,则fast指针需要移动M次才能与slow指针相遇,M为环的元素个数。
-// 总体来讲,时间复杂度为O(N)
-func hasCycle(head *ListNode) bool {
- slow, fast := head, head
- for fast != nil && fast.Next != nil {
- slow = slow.Next
- fast = fast.Next.Next
- if slow == fast {
- return true
- }
- }
- return false
-}
-```
-
diff --git "a/02_linkedlist/No.142_\347\216\257\345\275\242\351\223\276\350\241\2502_\346\261\202\347\216\257\345\205\245\345\217\243.md" "b/02_linkedlist/No.142_\347\216\257\345\275\242\351\223\276\350\241\2502_\346\261\202\347\216\257\345\205\245\345\217\243.md"
deleted file mode 100644
index f46313b..0000000
--- "a/02_linkedlist/No.142_\347\216\257\345\275\242\351\223\276\350\241\2502_\346\261\202\347\216\257\345\205\245\345\217\243.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 142 环形链表2
-
-题目:
-
-> 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
->
-> 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
->
-> 不允许修改 链表。
->
-> 来源:力扣(LeetCode)
-> 链接:https://leetcode.cn/problems/linked-list-cycle-ii
-> 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-
-
-
-分析:
-
-推荐算法2。
-
-```go
-// 算法1:利用额外空间,时间复杂度和空间复杂度均为O(n)
-func detectCycle(head *ListNode) *ListNode {
- visited := make(map[*ListNode]struct{})
- for head != nil {
- if _, ok := visited[head]; ok {
- return head
- }
- visited[head] = struct{}{}
- head = head.Next
- }
- return nil
-}
-// date 2023/10/11
-// 算法2:Floyd算法
-/*
-假设:环外有F个元素,环上C个元素
-快慢指针判断是否有相遇,相遇(h节点)时,快指多走一个环【F+a+b+a】;慢指针走了【F+a】;因为2(F+a) = F+a+b+a,所以f=b
-因此,相遇节点和头节点同时走f步,即是环的入口
-*/
-func detectCycle(head *ListNode) *ListNode {
- slow, fast := head, head
- for fast != nil && fast.Next != nil {
- slow, fast = slow.Next, fast.Next.Next
- if slow == fast {
- break
- }
- }
- if fast == nil || fast.Next == nil {return nil}
- fast = head
- for fast != slow {
- slow, fast = slow.Next, fast.Next
- }
- return fast
-}
-```
-
-
diff --git "a/02_linkedlist/No.143_\351\207\215\346\216\222\351\223\276\350\241\250.md" "b/02_linkedlist/No.143_\351\207\215\346\216\222\351\223\276\350\241\250.md"
deleted file mode 100644
index 73ae1e0..0000000
--- "a/02_linkedlist/No.143_\351\207\215\346\216\222\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,81 +0,0 @@
-## 143 重排链表-中等
-
-题目:
-
-给定一个单链表 L 的头节点 head ,单链表 L 表示为:
-
-L0 → L1 → … → Ln - 1 → Ln
-请将其重新排列后变为:
-
-L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
-不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
-
-
-
-分析:
-
-快慢指针,找出链表的中间节点;slow 指针继续走,同时反转后半段链表。
-
-然后将前半段和后半段链表合并。
-
-
-
-要对每一段代码很熟悉,要精确的知道每段代码的结果是什么样子;然后大问题拆成小问题去解决。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func reorderList(head *ListNode) {
- var tail *ListNode
- slow, fast := head, head
- spre := head
- for fast != nil && fast.Next != nil {
- spre = slow
- slow = slow.Next
- fast = fast.Next.Next
- }
- if fast != nil {
- spre = slow
- slow = slow.Next
- }
- // make part one, [head, spre]
- spre.Next = nil
- part1 := head
-
- for slow != nil {
- sn := slow.Next
- slow.Next = tail
- tail = slow
- slow = sn
- }
-
- head = merge(part1, tail)
-}
-
-func merge(l1, l2 *ListNode) *ListNode{
- dumy := &ListNode{}
- pre := dumy
- for l1 != nil && l2 != nil {
- l1f := l1.Next
- l2f := l2.Next
-
- l1.Next = l2
- pre.Next = l1
- pre = l2
-
- l1 = l1f
- l2 = l2f
- }
- if l1 != nil {
- pre.Next = l1
- }
- return dumy.Next
-}
-```
-
diff --git "a/02_linkedlist/No.1472_\350\256\276\350\256\241\346\265\217\350\247\210\345\231\250\345\216\206\345\217\262\350\256\260\345\275\225.md" "b/02_linkedlist/No.1472_\350\256\276\350\256\241\346\265\217\350\247\210\345\231\250\345\216\206\345\217\262\350\256\260\345\275\225.md"
deleted file mode 100644
index aff44cf..0000000
--- "a/02_linkedlist/No.1472_\350\256\276\350\256\241\346\265\217\350\247\210\345\231\250\345\216\206\345\217\262\350\256\260\345\275\225.md"
+++ /dev/null
@@ -1,105 +0,0 @@
-## 1472 设计浏览器历史记录-中等
-
-题目:
-
-你有一个只支持单个标签页的 **浏览器** ,最开始你浏览的网页是 `homepage` ,你可以访问其他的网站 `url` ,也可以在浏览历史中后退 `steps` 步或前进 `steps` 步。
-
-请你实现 `BrowserHistory` 类:
-
-- `BrowserHistory(string homepage)` ,用 `homepage` 初始化浏览器类。
-- `void visit(string url)` 从当前页跳转访问 `url` 对应的页面 。执行此操作会把浏览历史前进的记录全部删除。
-- `string back(int steps)` 在浏览历史中后退 `steps` 步。如果你只能在浏览历史中后退至多 `x` 步且 `steps > x` ,那么你只后退 `x` 步。请返回后退 **至多** `steps` 步以后的 `url` 。
-- `string forward(int steps)` 在浏览历史中前进 `steps` 步。如果你只能在浏览历史中前进至多 `x` 步且 `steps > x` ,那么你只前进 `x` 步。请返回前进 **至多** `steps`步以后的 `url` 。
-
-
-
-分析:
-
-这个问题重点在于理解 visit 操作,只要发生 visit 操作,**浏览历史中的前进记录全部删除**。
-
-所以,需要一个当前指针 cur 指向当前浏览的页面。
-
-然后,用 head, tail 辅助做头尾的哑结点。
-
-设计 双向链表,方便从当前页面 cur 根据 steps 步数前进或后退。
-
-前进、后退遍历的时候,要校验当前指针是否为头尾指针,以免越界。
-
-```go
-// date 2023/10/17
-type BrowserHistory struct {
- cur *MyNode
- head, tail *MyNode
-}
-
-type MyNode struct {
- key string
- prev, next *MyNode
-}
-
-
-func Constructor(homepage string) BrowserHistory {
- ss := BrowserHistory{
- head: &MyNode{},
- tail: &MyNode{},
- }
- node := &MyNode{key: homepage}
- node.next = ss.tail
- node.prev = ss.head
- ss.tail.prev = node
- ss.head.next = node
-
- ss.cur = node
- return ss
-}
-
-
-func (this *BrowserHistory) Visit(url string) {
- node := &MyNode{key: url}
- this.cur.next = node
- node.prev = this.cur
-
- node.next = this.tail
- this.tail.prev = node
-
- this.cur = node
-}
-
-
-func (this *BrowserHistory) Back(steps int) string {
- pre := this.cur
- for steps > 0 {
- if pre.prev == this.head {
- break
- }
- pre = pre.prev
- steps--
- }
- this.cur = pre
- return this.cur.key
-}
-
-
-func (this *BrowserHistory) Forward(steps int) string {
- pre := this.cur
- for steps > 0 {
- if pre.next == this.tail {
- break
- }
- pre = pre.next
- steps--
- }
- this.cur = pre
- return this.cur.key
-}
-
-
-/**
- * Your BrowserHistory object will be instantiated and called as such:
- * obj := Constructor(homepage);
- * obj.Visit(url);
- * param_2 := obj.Back(steps);
- * param_3 := obj.Forward(steps);
- */
-```
-
diff --git "a/02_linkedlist/No.147_\345\257\271\351\223\276\350\241\250\350\277\233\350\241\214\346\217\222\345\205\245\346\216\222\345\272\217.md" "b/02_linkedlist/No.147_\345\257\271\351\223\276\350\241\250\350\277\233\350\241\214\346\217\222\345\205\245\346\216\222\345\272\217.md"
deleted file mode 100644
index 3eeaa6d..0000000
--- "a/02_linkedlist/No.147_\345\257\271\351\223\276\350\241\250\350\277\233\350\241\214\346\217\222\345\205\245\346\216\222\345\272\217.md"
+++ /dev/null
@@ -1,65 +0,0 @@
-## 147 对链表进行插入排序-中等
-
-题目:
-
-给定单链表的头 head,使用 **插入排序** 对链表进行排序,并返回 排序后的链表的头。
-
-
-
-分析:
-
-为了代码简洁我们写一个已排序的链表中插入单个节点的辅助函数。
-
-```go
-// date 2023/10/16
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func insertionSortList(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
-
- cur := head.Next
-
- newHead := head
- newHead.Next = nil
-
- for cur != nil {
- after := cur.Next
- cur.Next = nil
- newHead = insertOneNode(newHead, cur)
- cur = after
- }
- return newHead
-}
-
-func insertOneNode(head, node *ListNode) *ListNode {
- if node.Val < head.Val {
- node.Next = head
- head = node
- return head
- }
- pre := head
- cur := head.Next
- for cur != nil && cur.Val <= node.Val {
- pre = cur
- cur = cur.Next
- }
- node.Next = cur
- pre.Next = node
- return head
-}
-```
-
diff --git "a/02_linkedlist/No.148_\346\216\222\345\272\217\351\223\276\350\241\250.md" "b/02_linkedlist/No.148_\346\216\222\345\272\217\351\223\276\350\241\250.md"
deleted file mode 100644
index b40b47e..0000000
--- "a/02_linkedlist/No.148_\346\216\222\345\272\217\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,79 +0,0 @@
-## 148 排序链表-中等
-
-题目:
-
-给你链表的头节点 head,请你将其按升序排列并返回排序后的链表。
-
-你可以在`o(NlogN)`时间复杂度和常数级空间复杂度下,对链表进行排序吗?
-
-
-
-**解题思路**
-
-要想实现 `O(nlogn)`的时间复杂度,可以考虑归并排序。具体为,自顶向下的归并排序:
-
-1. 找到链表的中点,以中点为界分成两个子链。
-2. 对子链分别进行排序。
-3. 对排序的子链,进行合并。
-
-这里依赖基本 case,即子链中只有一个元素时,就是递归的返回原点。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func sortList(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- spre, slow, fast := head, head, head
- for fast != nil && fast.Next != nil {
- spre = slow
- slow = slow.Next
- fast = fast.Next.Next
- }
- if fast != nil {
- spre = slow
- slow = slow.Next
- }
- spre.Next = nil
- left, right := sortList(head), sortList(slow)
- return mergeTwoList(left, right)
-}
-
-func mergeTwoList(l1, l2 *ListNode) *ListNode {
- if l1 == nil {
- return l2
- }
- if l2 == nil {
- return l1
- }
- dummy := &ListNode{}
- prev := dummy
- for l1 != nil && l2 != nil {
- if l1.Val < l2.Val {
- prev.Next = l1
- l1 = l1.Next
- } else {
- prev.Next = l2
- l2 = l2.Next
- }
- prev = prev.Next
- }
- if l1 != nil {
- prev.Next = l1
- }
- if l2 != nil {
- prev.Next = l2
- }
- return dummy.Next
-}
-```
-
-
-
diff --git "a/02_linkedlist/No.160_\347\233\270\344\272\244\351\223\276\350\241\250.md" "b/02_linkedlist/No.160_\347\233\270\344\272\244\351\223\276\350\241\250.md"
deleted file mode 100644
index a85a444..0000000
--- "a/02_linkedlist/No.160_\347\233\270\344\272\244\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 160 相交链表-简单
-
-题目:
-
-给你两个链表的头节点 headA 和 headB,请你找出并返回两个链表相交的节点。如果不存在相交节点,则返回 nil。
-
-
-
-分析:
-
-一句话,我曾走过你曾走过的路。
-
-一开始 a,b 指针分别从各自头指针开始走,等走到尾部的时候,a 指针在从 headB 开始走,b 指针则从 headA 开始走,a,b 指针相等的时候就是 相交的起点。
-
-```go
-// date 2023/10/11
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func getIntersectionNode(headA, headB *ListNode) *ListNode {
- if headA == nil || headB == nil { return nil }
- pa, pb := headA, headB
-
- for pa != pb {
- pa, pb = pa.Next, pb.Next
- if pa == nil && pb == nil {
- return nil
- }
- if pa == nil {
- pa = headB
- }
- if pb == nil {
- pb = headA
- }
- }
- return pa
-}
-```
-
-
\ No newline at end of file
diff --git "a/02_linkedlist/No.1669_\345\220\210\345\271\266\344\270\244\344\270\252\351\223\276\350\241\250.md" "b/02_linkedlist/No.1669_\345\220\210\345\271\266\344\270\244\344\270\252\351\223\276\350\241\250.md"
deleted file mode 100644
index 7690065..0000000
--- "a/02_linkedlist/No.1669_\345\220\210\345\271\266\344\270\244\344\270\252\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,61 +0,0 @@
-## 1669 合并两个链表-中等
-
-题目:
-
-给你两个链表 `list1` 和 `list2` ,它们包含的元素分别为 `n` 个和 `m` 个。
-
-请你将 `list1` 中下标从 `a` 到 `b` 的全部节点都删除,并将`list2` 接在被删除节点的位置。
-
-下图中蓝色边和节点展示了操作后的结果:
-
-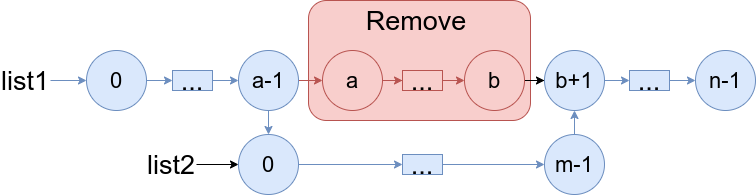
-
-请你返回结果链表的头指针。
-
-
-
-**提示:**
-
-- `3 <= list1.length <= 104`
-- `1 <= a <= b < list1.length - 1`
-- `1 <= list2.length <= 104`
-
-
-
-**解题思路**:
-
-因为题目中已经说明 a、b的范围,a 比大于1,所以新链表的表头一定是 list1。
-
-只需要考虑链表的区间删除即可。思路是遍历 list1 找到 a 的前驱,然后遍历 list2 找到最后一个节点,然后继续遍历 list1 找到 b,最后把 a 的前驱下一跳指向 list2,list2 的表尾节点指向 b 的后驱节点即可。
-
-```go
-// date 2024/01/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func mergeInBetween(list1 *ListNode, a int, b int, list2 *ListNode) *ListNode {
- apre, cur := list1, list1
- for a > 0 {
- apre = cur
- cur = cur.Next
- a--
- b--
- }
- apre.Next = list2
- l2Last := list2
- for l2Last.Next != nil {
- l2Last = l2Last.Next
- }
- for b > 0 {
- cur = cur.Next
- b--
- }
- l2Last.Next = cur.Next
- return list1
-}
-```
-
diff --git "a/02_linkedlist/No.1836_\344\273\216\346\234\252\346\216\222\345\272\217\347\232\204\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\351\207\215\345\244\215\345\205\203\347\264\240.md" "b/02_linkedlist/No.1836_\344\273\216\346\234\252\346\216\222\345\272\217\347\232\204\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\351\207\215\345\244\215\345\205\203\347\264\240.md"
deleted file mode 100644
index 411701e..0000000
--- "a/02_linkedlist/No.1836_\344\273\216\346\234\252\346\216\222\345\272\217\347\232\204\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\351\207\215\345\244\215\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,67 +0,0 @@
-## 1836 从未排序的链表中移除重复元素-中等
-
-题目:
-
-给定一个链表的第一个节点 `head` ,找到链表中所有出现**多于一次**的元素,并删除这些元素所在的节点。
-
-返回删除后的链表。
-
-
-
-> ```
-> 输入: head = [1,2,3,2]
-> 输出: [1,3]
-> 解释: 2 在链表中出现了两次,所以所有的 2 都需要被删除。删除了所有的 2 之后,我们还剩下 [1,3] 。
-> ```
-
-
-
-**解题思路**
-
-这道题的要求是把出现次数大于1次的节点都去掉,并保持原节点的相对位置不变。
-
-一种思路是借助 map 记录节点出现的次数,详见解法1。
-
-具体是第一次遍历,把节点的值存入 map,记录次数;第二次遍历,借助哑结点把出现次数为1的节点加入哑结点所在的链表,最后返回哑结点的链表。这个解法有个优化点,就是第一次遍历的时候,后面重复的节点可以先删除,以便第二次连接的时候少操作一部分。
-
-
-
-```go
-// date 2024/01/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// 解法1
-func deleteDuplicatesUnsorted(head *ListNode) *ListNode {
- cnt := make(map[int]int, 4)
- cur := head
- prev := head
- for cur != nil {
- cnt[cur.Val]++
- // 优化1: 遍历的同时直接去掉后面出现的 重复的
- if cnt[cur.Val] > 1 && cur.Next != nil {
- prev.Next = cur.Next
- }
- prev = cur
- cur = cur.Next
- }
-
- dummy := &ListNode{}
- pre := dummy
- cur = head
- for cur != nil {
- if cnt[cur.Val] == 1 {
- pre.Next = cur
- pre = cur
- }
- cur = cur.Next
- }
- pre.Next = nil
- return dummy.Next
-}
-```
-
diff --git "a/02_linkedlist/No.203_\347\247\273\351\231\244\351\223\276\350\241\250\345\205\203\347\264\240.md" "b/02_linkedlist/No.203_\347\247\273\351\231\244\351\223\276\350\241\250\345\205\203\347\264\240.md"
deleted file mode 100644
index 70d4ce3..0000000
--- "a/02_linkedlist/No.203_\347\247\273\351\231\244\351\223\276\350\241\250\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,37 +0,0 @@
-## 203 移除链表元素-简单
-
-题目:
-
-给你一个链表的头节点 head 和一个整数 val,请你删除链表中所有满足 `node.val == val` 的节点,并返回新的头节点。
-
-
-
-分析:
-
-```go
-// date 2023/10/16
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func removeElements(head *ListNode, val int) *ListNode {
- if head == nil {
- return head
- }
- dumy := &ListNode{}
- pre := dumy
- for head != nil {
- if head.Val != val {
- pre.Next = head
- pre = pre.Next
- }
- head = head.Next
- }
- pre.Next = nil
- return dumy.Next
-}
-```
-
diff --git "a/02_linkedlist/No.206_\345\217\215\350\275\254\351\223\276\350\241\250.md" "b/02_linkedlist/No.206_\345\217\215\350\275\254\351\223\276\350\241\250.md"
deleted file mode 100644
index 5b5fb45..0000000
--- "a/02_linkedlist/No.206_\345\217\215\350\275\254\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,43 +0,0 @@
-## 206 反转链表-简单
-
-题目:
-
-给你单链表的头节点 `head` ,请你反转链表,并返回反转后的链表。
-
-
-
-**解题思路**
-
-直接迭代,时间复杂度O(n),空间复杂度O(1)。
-
-```go
-// 算法1:迭代
-func reverseList(head *ListNode) *ListNode {
- var pre, after *ListNode
- for head != nil {
- after = head.Next
- head.Next = pre
- pre, head = head, after
- }
- return pre
-}
-```
-
-算法2:假设链表为n1->n2->...->nk-1->nk->nk+1->...nm;如果从节点nk+1到结点nm均已经反转,即
-
-n1->n2->...->nk-1->nk->nk+1<-...<-nm那么nk的操作则需要nk.Next.Next = nk
-
-时间复杂度O(n),空间复杂度O(n),因为递归会达到n层。
-
-```go
-// 算法2:递归
-func reverseList(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {return head}
- pre := reverseList(head.Next)
- head.Next.Next = head
- head.Next = nil
- return pre
-}
-```
-
-####
\ No newline at end of file
diff --git "a/02_linkedlist/No.2095_\345\210\240\351\231\244\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md" "b/02_linkedlist/No.2095_\345\210\240\351\231\244\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md"
deleted file mode 100644
index 351cd34..0000000
--- "a/02_linkedlist/No.2095_\345\210\240\351\231\244\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,73 +0,0 @@
-## 2095 删除链表的中间节点-中等
-
-题目:
-
-给你一个链表的头节点 `head` 。**删除** 链表的 **中间节点** ,并返回修改后的链表的头节点 `head` 。
-
-长度为 `n` 链表的中间节点是从头数起第 `⌊n / 2⌋` 个节点(下标从 **0** 开始),其中 `⌊x⌋` 表示小于或等于 `x` 的最大整数。
-
-- 对于 `n` = `1`、`2`、`3`、`4` 和 `5` 的情况,中间节点的下标分别是 `0`、`1`、`1`、`2` 和 `2` 。
-
-
-
-**解题思路**
-
-这道题有2种解法。一种是先遍历求链表长度,计算出中间节点,再次遍历,到达中间节点的时候删除之。详见解法1。
-
-另一个种,快慢指针。快指针走到表尾时,慢指针刚好走到中间节点,删除之。详见解法2。
-
-
-
-```go
-// date 2024/10/12
-// 解法1
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func deleteMiddle(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return nil
- }
- cur := head
- cnt, mid := 0, 0
- for cur != nil {
- mid++
- cur = cur.Next
- }
- mid = mid >> 1
-
- prev := head
- cur = head
- cnt = 0
- for cur != nil {
- if cnt == mid {
- prev.Next = cur.Next
- break
- }
- cnt++
- prev = cur
- cur = cur.Next
- }
- return head
-}
-
-// 解法2
-func deleteMiddle(head *ListNode) *ListNode {
- if head == nil || head.Next == nil {
- return nil
- }
- prev, slow, fast := head, head, head
- for fast != nil && fast.Next != nil {
- prev = slow
- slow = slow.Next
- fast = fast.Next.Next
- }
- prev.Next = slow.Next
- return head
-}
-```
-
diff --git "a/02_linkedlist/No.234_\345\233\236\346\226\207\351\223\276\350\241\250.md" "b/02_linkedlist/No.234_\345\233\236\346\226\207\351\223\276\350\241\250.md"
deleted file mode 100644
index d657f35..0000000
--- "a/02_linkedlist/No.234_\345\233\236\346\226\207\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,73 +0,0 @@
-## 234 回文链表-简单
-
-题目:
-
-给你一个单链表的头节点 head,请你判断该链表是否为回文链表。如果是,返回 true,否则,返回 false。
-
-
-
-**解题思路**
-
-- 数组,双指针,详见解法1。遍历链表,将元素存入数组,然后判断数组是否回文。时间复杂度`O(N)`,空间复杂度`O(N)`。
-- 双指针,快慢指针,详见解法2。利用快慢指针找到链表的中点,同时反转前半段,然后比较快慢指针的元素。时间复杂度`O(N)`,空间复杂度`O(1)`。
-
-快慢指针,找到中间节点,反转前半段。
-
-```go
-// date 2023/10/16
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// 解法1
-// 数组
-func isPalindrome(head *ListNode) bool {
- nums := make([]int, 0, 16)
- cur := head
- for cur != nil {
- nums = append(nums, cur.Val)
- cur = cur.Next
- }
- left, right := 0, len(nums)-1
- for left < right {
- if nums[left] != nums[right] {
- return false
- }
- left++
- right--
- }
- return true
-}
-
-// 解法2
-// 快慢指针
-func isPalindrome(head *ListNode) bool {
- var leftTail *ListNode
- slow, fast := head, head
- for fast != nil && fast.Next != nil {
- fast = fast.Next.Next
-
- slowNext := slow.Next
- slow.Next = leftTail
- leftTail = slow
- slow = slowNext
- }
- // 奇数个节点
- if fast != nil {
- slow = slow.Next
- }
- // now slow is the right part
- for slow != nil && leftTail != nil {
- if slow.Val != leftTail.Val {
- return false
- }
- slow = slow.Next
- leftTail = leftTail.Next
- }
- return true
-}
-```
-
diff --git "a/02_linkedlist/No.237_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md" "b/02_linkedlist/No.237_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md"
deleted file mode 100644
index d0cdf65..0000000
--- "a/02_linkedlist/No.237_\345\210\240\351\231\244\351\223\276\350\241\250\344\270\255\347\232\204\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,46 +0,0 @@
-## 237 删除链表中的点-中等
-
-题目:
-
-有一个单链表 head,我们想删除链表中的一个节点 node。
-
-已知给你一个需要删除的节点 node,你无法访问第一个节点 head。
-
-链表的所有值都是唯一的,并且保证给定的节点 node 不是链表中的最后一个节点。
-
-注意,删除节点并不是指从内存中删除它。这里的意思是:
-
-- 给定节点的值不应该存在于链表中。
-- 链表节点的数量应该减少1。
-- `node`前面的所有值顺序相同。
-- `node`后面的所有值顺序相同。
-
-
-
-分析:
-
-采用 后者赋值 的方法,让后面的值依次覆盖 node 开始的值就可以;然后把最后一个节点删除。
-
-```go
-// date 2023/10/13
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func deleteNode(node *ListNode) {
- if node == nil {
- return
- }
- pre := node
- for node.Next != nil {
- pre = node
- node.Val = node.Next.Val
- node = node.Next
- }
- pre.Next = nil
-}
-```
-
diff --git "a/02_linkedlist/No.2487_\344\273\216\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\350\212\202\347\202\271.md" "b/02_linkedlist/No.2487_\344\273\216\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\350\212\202\347\202\271.md"
deleted file mode 100644
index e527473..0000000
--- "a/02_linkedlist/No.2487_\344\273\216\351\223\276\350\241\250\344\270\255\347\247\273\351\231\244\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,77 +0,0 @@
-## 2487 从链表中移除节点-中等
-
-题目:
-
-给你一个链表的头节点 `head` 。
-
-移除每个右侧有一个更大数值的节点。
-
-返回修改后链表的头节点 `head` 。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:head = [5,2,13,3,8]
-> 输出:[13,8]
-> 解释:需要移除的节点是 5 ,2 和 3 。
-> - 节点 13 在节点 5 右侧。
-> - 节点 13 在节点 2 右侧。
-> - 节点 8 在节点 3 右侧。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:head = [1,1,1,1]
-> 输出:[1,1,1,1]
-> 解释:每个节点的值都是 1 ,所以没有需要移除的节点。
-> ```
-
-
-
-**解题思路**:
-
-这道题的要求是,如果右侧有值更大的节点,那么当前节点就应该移除,使得最终的链表是单调递减的。
-
-这道题可以这样解,新的表头不容易确定,所以可以先反转链表,然后移除每个节点后面小于当前节点的节点。最后在反转链表即可。
-
-```go
-// date 2024/01/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func removeNodes(head *ListNode) *ListNode {
- lr := reverse(head)
- cur := lr
- for cur != nil {
- if cur.Next != nil && cur.Next.Val < cur.Val {
- cur.Next = cur.Next.Next
- continue
- }
- cur = cur.Next
- }
- res := reverse(lr)
- return res
-}
-
-func reverse(head *ListNode) *ListNode {
- var tail *ListNode
- cur := head
- for cur != nil {
- after := cur.Next
- cur.Next = tail
- tail = cur
- cur = after
- }
- return tail
-}
-```
-
diff --git "a/02_linkedlist/No.328_\345\245\207\345\201\266\351\223\276\350\241\250.md" "b/02_linkedlist/No.328_\345\245\207\345\201\266\351\223\276\350\241\250.md"
deleted file mode 100644
index 8c8d95e..0000000
--- "a/02_linkedlist/No.328_\345\245\207\345\201\266\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,60 +0,0 @@
-## 328 奇偶链表-中等
-
-题目:
-
-给定单链表的头节点 head,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排列的链表。
-
-第一个节点的索引被认为是奇数,第二个节点的索引被认为是偶数。
-
-请注意,偶数组和奇数组内部的相对位置应该与输入时保持一致。
-
-你必须在 O(1) 的额外空间复杂度和 O(N) 的时间复杂度下解决这个问题。
-
-
-
-分析:
-
-这个问题过于简单了,就是按索引重新分组。
-
-利用两个【哑结点】,分别保存索引为奇数和偶数的节点,然后重新拼接。
-
-```go
-// date 2023/10/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func oddEvenList(head *ListNode) *ListNode {
- if head == nil || head.Next == nil || head.Next.Next == nil {
- return head
- }
- d1, d2 := &ListNode{}, &ListNode{}
- p1, p2 := d1, d2
- idx := 0
- for head != nil {
- if idx % 2 == 0 {
- p1.Next = head
- p1 = p1.Next
- } else {
- p2.Next = head
- p2 = p2.Next
- }
- idx++
- head = head.Next
- }
- p2.Next = nil
- p1.Next = d2.Next
- return d1.Next
-}
-```
-
-
-
-## 延展一下
-
-不以索引的奇偶作为分组标准,而是以链表中结点值的奇偶性作为分组的标准。
-
-请注意,以第一个节点值的奇偶性作为起始。即如果第一个节点值为奇数,那么所有的奇数在前。
\ No newline at end of file
diff --git "a/02_linkedlist/No.369_\347\273\231\345\215\225\351\223\276\350\241\250\345\212\2401.md" "b/02_linkedlist/No.369_\347\273\231\345\215\225\351\223\276\350\241\250\345\212\2401.md"
deleted file mode 100644
index 08afdba..0000000
--- "a/02_linkedlist/No.369_\347\273\231\345\215\225\351\223\276\350\241\250\345\212\2401.md"
+++ /dev/null
@@ -1,78 +0,0 @@
-## 369 给单链表加1-中等
-
-题目:
-
-给定一个用**链表**表示的非负整数, 然后将这个整数 *再加上 1* 。
-
-这些数字的存储是这样的:最高位有效的数字位于链表的首位 `head` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: head = [1,2,3]
-> 输出: [1,2,4]
-> ```
->
->
->
-> **示例** **2:**
->
-> ```
-> 输入: head = [0]
-> 输出: [1]
-> ```
-
-
-
-**解题思路**
-
-因为低位在单链表的尾部,对低位加1不是很方便,所以需要先将链表反转,加1计算后,在反转一次即可。
-
-```go
-// date 2024/01/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func plusOne(head *ListNode) *ListNode {
- if head == nil {
- return head
- }
- l2 := reverseList(head)
- carry := 1
- cur := l2
- prev := l2
- for cur != nil {
- after := cur.Next
- temp := cur.Val + carry
- cur.Val = temp % 10
- carry = temp / 10
-
- prev = cur
- cur = after
- }
- if carry == 1 {
- prev.Next = &ListNode{Val: 1}
- }
- l3 := reverseList(l2)
- return l3
-}
-
-func reverseList(head *ListNode) *ListNode {
- var tail *ListNode
- cur := head
- for cur != nil {
- after := cur.Next
- cur.Next = tail
- tail = cur
- cur = after
- }
- return tail
-}
-```
-
diff --git "a/02_linkedlist/No.426_\345\260\206\344\272\214\345\217\211\346\220\234\347\264\242\346\225\260\350\275\254\346\215\242\344\270\272\346\216\222\345\272\217\345\220\216\347\232\204\345\217\214\345\220\221\351\223\276\350\241\250.md" "b/02_linkedlist/No.426_\345\260\206\344\272\214\345\217\211\346\220\234\347\264\242\346\225\260\350\275\254\346\215\242\344\270\272\346\216\222\345\272\217\345\220\216\347\232\204\345\217\214\345\220\221\351\223\276\350\241\250.md"
deleted file mode 100644
index 667323f..0000000
--- "a/02_linkedlist/No.426_\345\260\206\344\272\214\345\217\211\346\220\234\347\264\242\346\225\260\350\275\254\346\215\242\344\270\272\346\216\222\345\272\217\345\220\216\347\232\204\345\217\214\345\220\221\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,99 +0,0 @@
-## 426 将二叉搜索树转化为排序后的双向链表-中等
-
-题目:
-
-将一个 **二叉搜索树** 就地转化为一个 **已排序的双向循环链表** 。
-
-对于双向循环列表,你可以将左右孩子指针作为双向循环链表的前驱和后继指针,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
-
-特别地,我们希望可以 **就地** 完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:root = [4,2,5,1,3]
->
->
-> 输出:[1,2,3,4,5]
->
-> 解释:下图显示了转化后的二叉搜索树,实线表示后继关系,虚线表示前驱关系。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:root = [2,1,3]
-> 输出:[1,2,3]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:root = []
-> 输出:[]
-> 解释:输入是空树,所以输出也是空链表。
-> ```
->
-> **示例 4:**
->
-> ```
-> 输入:root = [1]
-> 输出:[1]
-> ```
-
-
-
-**解题思路**
-
-根据访问根节点的顺序不同,树有三种遍历方式,前序、中序和后序。这道题给出的是二叉搜索树,而且要求给出排序的双向链表,那么递归版中序更合适。
-
-因为递归中序遍历的时候,可以最先达到值最小的那个节点,把它保存为 first。
-
-同时,第一个点也是 last 节点。然后递归遍历,将节点依次追加到 last 即可。
-
-最后,再把 last 的后继指向 first,first 的前驱指向 last。
-
-```go
-// date 2024/01/11
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Left *Node
- * Right *Node
- * }
- */
-
-func treeToDoublyList(root *Node) *Node {
- if root == nil {
- return root
- }
- var first, last *Node
-
- var inorder func(root *Node)
- inorder = func(root *Node) {
- if root == nil {
- return
- }
- inorder(root.Left)
- if last != nil {
- last.Right = root
- root.Left = last
- } else {
- // last == nil
- // this is first
- first = root
- }
- // save root
- last = root
- inorder(root.Right)
- }
- inorder(root)
- last.Right = first
- first.Left = last
- return first
-}
-```
-
diff --git "a/02_linkedlist/No.430_\346\211\201\345\271\263\345\214\226\345\244\232\347\272\247\345\217\214\345\220\221\351\223\276\350\241\250.md" "b/02_linkedlist/No.430_\346\211\201\345\271\263\345\214\226\345\244\232\347\272\247\345\217\214\345\220\221\351\223\276\350\241\250.md"
deleted file mode 100644
index d4012f0..0000000
--- "a/02_linkedlist/No.430_\346\211\201\345\271\263\345\214\226\345\244\232\347\272\247\345\217\214\345\220\221\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 430 扁平化多级双向链表-中等
-
-题目:
-
-你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 **子指针** 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一个或多个自己的子列表,以此类推,以生成如下面的示例所示的 **多层数据结构** 。
-
-给定链表的头节点 head ,将链表 **扁平化** ,以便所有节点都出现在单层双链表中。让 `curr` 是一个带有子列表的节点。子列表中的节点应该出现在**扁平化列表**中的 `curr` **之后** 和 `curr.next` **之前** 。
-
-返回 *扁平列表的 `head` 。列表中的节点必须将其 **所有** 子指针设置为 `null` 。*
-
-
-
-分析:
-
-深度优先搜索
-
-```go
-// date 2023/10/17
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Prev *Node
- * Next *Node
- * Child *Node
- * }
- */
-
-func flatten(root *Node) *Node {
- dfs(root)
- return root
-}
-
-func dfs(root *Node) (last *Node) {
- cur := root
- for cur != nil {
- next := cur.Next
- if cur.Child != nil {
- chdRes := dfs(cur.Child)
-
- next = cur.Next // save next
-
- // change cur Next to Child
- cur.Next = cur.Child
- cur.Child.Prev = cur
-
- if next != nil {
- chdRes.Next = next
- next.Prev = chdRes
- }
-
- cur.Child = nil
- last = chdRes
- } else {
- last = cur
- }
-
- // 遍历 next
- cur = next
- }
- return
-}
-```
-
diff --git "a/02_linkedlist/No.445_\344\270\244\346\225\260\347\233\270\345\212\2402.md" "b/02_linkedlist/No.445_\344\270\244\346\225\260\347\233\270\345\212\2402.md"
deleted file mode 100644
index e73617b..0000000
--- "a/02_linkedlist/No.445_\344\270\244\346\225\260\347\233\270\345\212\2402.md"
+++ /dev/null
@@ -1,95 +0,0 @@
-## 445 两数相加-中等
-
-题目:
-
-给你两个 **非空** 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
-
-你可以假设除了数字 0 之外,这两个数字都不会以零开头。
-
-
-
-> **示例1:**
->
-> 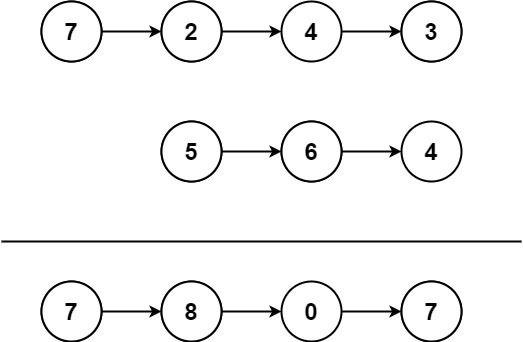
->
-> ```
-> 输入:l1 = [7,2,4,3], l2 = [5,6,4]
-> 输出:[7,8,0,7]
-> ```
->
-> **示例2:**
->
-> ```
-> 输入:l1 = [2,4,3], l2 = [5,6,4]
-> 输出:[8,0,7]
-> ```
->
-> **示例3:**
->
-> ```
-> 输入:l1 = [0], l2 = [0]
-> 输出:[0]
-> ```
-
-
-
-分析:
-
-先讲原始链表反转,然后顺次相加。
-
-```go
-// date 2023/12/18
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
- if l1 == nil { return l2 }
- if l2 == nil { return l1 }
-
- l1 = reverseList(l1)
- l2 = reverseList(l2)
-
- v1, v2, carry := 0, 0, 0
- var res *ListNode
-
- for l1 != nil || l2 != nil || carry > 0 {
- v1, v2 = 0, 0
- if l1 != nil {
- v1 = l1.Val
- l1 = l1.Next
- }
- if l2 != nil {
- v2 = l2.Val
- l2 = l2.Next
- }
- temp := v1 + v2 + carry
- carry = temp / 10
-
- head := &ListNode{Val: temp%10}
- head.Next = res
- res = head
- }
-
- return res
-}
-
-func reverseList(l *ListNode) *ListNode {
- if l == nil || l.Next == nil {
- return l
- }
- var tail *ListNode
- pre := l
- for pre != nil {
- pn := pre.Next
- pre.Next = tail
- tail = pre
- pre = pn
- }
- return tail
-}
-```
-
diff --git "a/02_linkedlist/No.707_\350\256\276\350\256\241\351\223\276\350\241\250.md" "b/02_linkedlist/No.707_\350\256\276\350\256\241\351\223\276\350\241\250.md"
deleted file mode 100644
index fcf41cf..0000000
--- "a/02_linkedlist/No.707_\350\256\276\350\256\241\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,143 +0,0 @@
-## 707 设计链表-中等
-
-题目:
-
-你可以选择使用单链表或者双链表,设计并实现自己的链表。
-
-单链表中的节点应该具备两个属性:`val` 和 `next` 。`val` 是当前节点的值,`next` 是指向下一个节点的指针/引用。
-
-如果是双向链表,则还需要属性 `prev` 以指示链表中的上一个节点。假设链表中的所有节点下标从 **0** 开始。
-
-实现 `MyLinkedList` 类:
-
-- `MyLinkedList()` 初始化 `MyLinkedList` 对象。
-- `int get(int index)` 获取链表中下标为 `index` 的节点的值。如果下标无效,则返回 `-1` 。
-- `void addAtHead(int val)` 将一个值为 `val` 的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。
-- `void addAtTail(int val)` 将一个值为 `val` 的节点追加到链表中作为链表的最后一个元素。
-- `void addAtIndex(int index, int val)` 将一个值为 `val` 的节点插入到链表中下标为 `index` 的节点之前。如果 `index` 等于链表的长度,那么该节点会被追加到链表的末尾。如果 `index` 比长度更大,该节点将 **不会插入** 到链表中。
-- `void deleteAtIndex(int index)` 如果下标有效,则删除链表中下标为 `index` 的节点。
-
-
-
-分析:
-
-使用 双链表 方便在尾部增加,同时把双向链表的 head 和 tail 用哑结点 表示,这样可以减少不必要的判断。
-
-size 表示链表中的元素个数,对 index 进行校验。
-
-```go
-// date 2023/10/17
-type MyLinkedList struct {
- size int
- head, tail *MyNode
-}
-
-type MyNode struct {
- val int
- prev, next *MyNode
-}
-
-
-func Constructor() MyLinkedList {
- ll := MyLinkedList{
- size: -1,
- head: &MyNode{},
- tail: &MyNode{},
- }
- ll.head.next = ll.tail
- ll.tail.prev = ll.head
- return ll
-}
-
-
-func (this *MyLinkedList) Get(index int) int {
- if index < 0 || index > this.size {
- return -1
- }
- pre := this.head
- for index >= 0 {
- pre = pre.next
- index--
- }
- return pre.val
-}
-
-
-func (this *MyLinkedList) AddAtHead(val int) {
- node := &MyNode{val, nil, nil}
- node.next = this.head.next
- this.head.next.prev = node
-
- this.head.next = node
- node.prev = this.head
- this.size++
-}
-
-
-func (this *MyLinkedList) AddAtTail(val int) {
- node := &MyNode{val, nil, nil}
- this.tail.prev.next = node
- node.prev = this.tail.prev
-
- node.next = this.tail
- this.tail.prev = node
- this.size++
-}
-
-
-func (this *MyLinkedList) AddAtIndex(index int, val int) {
- if index < 0 || index > this.size + 1 {
- return
- }
- if index == 0 {
- this.AddAtHead(val)
- return
- }
- if index == this.size+1 {
- this.AddAtTail(val)
- return
- }
- node := &MyNode{val, nil, nil}
- pre := this.head
- for index > 0 {
- pre = pre.next
- index--
- }
- after := pre.next
-
- pre.next = node
- after.prev = node
-
- node.prev = pre
- node.next = after
- this.size++
-}
-
-
-func (this *MyLinkedList) DeleteAtIndex(index int) {
- if index < 0 || index > this.size {
- return
- }
- pre := this.head
- for index > 0 {
- index--
- pre = pre.next
- }
- after := pre.next.next
- pre.next = after
- after.prev = pre
- this.size--
-}
-
-
-/**
- * Your MyLinkedList object will be instantiated and called as such:
- * obj := Constructor();
- * param_1 := obj.Get(index);
- * obj.AddAtHead(val);
- * obj.AddAtTail(val);
- * obj.AddAtIndex(index,val);
- * obj.DeleteAtIndex(index);
- */
-```
-
diff --git "a/02_linkedlist/No.725_\345\210\206\351\232\224\351\223\276\350\241\250.md" "b/02_linkedlist/No.725_\345\210\206\351\232\224\351\223\276\350\241\250.md"
deleted file mode 100644
index dbd310d..0000000
--- "a/02_linkedlist/No.725_\345\210\206\351\232\224\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 725 分隔链表-中等
-
-题目:
-
-给你一个头节点为 head 的单链表和一个整数 k,请你设计一个算法将链表分隔为 k 个连续的部分。
-
-每部分的长度尽可能的相等:任意两部分的长度差距不能超过 1。这可能导致有些部分为 null。【也就是不够分的时候,用空链表填充。】
-
-这 k 个部分应该按照在链表中出现的顺序排列,并且排列在前面的部分的长度应该大于或等于排在后面的长度。
-
-请返回一个由上述 k 部分组成的数组。
-
-
-
-分析:
-
-如果把链表的长度记为 x,那么该问题可以转化为 如何尽可能把 x 等分 k 份。这个问题容易解决,直接对 x 进行 k 求余和整除
-
-```go
-base := x / k
-rmd := x % k // remainder
-```
-
-然后构造有 k 个元素的数组,其中前 rmd 个 元素大小为 base + 1,其他元素为 base。
-
-那么该数组表示的就是最终结果集各个链表的元素个数。根据该数组就可以的链表分隔了。
-
-
-
-```go
-// date 2023/10/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func splitListToParts(head *ListNode, k int) []*ListNode {
- res := make([]*ListNode, k, k)
- if head == nil {
- return res
- }
- pre := head
- total := 0
- for pre != nil {
- total++
- pre = pre.Next
- }
-
- sglen := getSingleLenRes(total, k)
- pre = head
- for i, x := range sglen {
- dy := &ListNode{}
- dpre := dy
- for x > 0 {
- dpre.Next = pre
- pre = pre.Next
- dpre = dpre.Next
- x--
- }
- dpre.Next = nil
- res[i] = dy.Next
- }
- return res
-}
-
-func getSingleLenRes(total, k int) []int {
- res := make([]int, k, k)
- idx := k
-
- base := total / k
- rmd := total % k
- for k > 0 {
- if rmd > 0 {
- res[idx-k] = base + 1
- rmd--
- } else {
- res[idx-k] = base
- }
- k--
- }
- return res
-}
-```
-
diff --git "a/02_linkedlist/No.817_\351\223\276\350\241\250\347\273\204\344\273\266.md" "b/02_linkedlist/No.817_\351\223\276\350\241\250\347\273\204\344\273\266.md"
deleted file mode 100644
index 367df27..0000000
--- "a/02_linkedlist/No.817_\351\223\276\350\241\250\347\273\204\344\273\266.md"
+++ /dev/null
@@ -1,162 +0,0 @@
-## 817 链表组件-中等
-
-题目:
-
-给定链表的头节点 head,该链表上的每个结点都有一个唯一的整型值。同时给定列表 nums,该列表是上述链表中整型值的一个子集。
-
-返回列表 nums 中组件的个数。组件的定义为:链表中一段最长连续结点的值(该值必须在列表 nums 中)构成的集合。
-
-
-
-分析:
-
-这个题目主要在于理解题意,理解以后就会发现跟「求最长连续子序列的个数」类似。所以解法就是中规中矩的 快慢指针 或者 滑动窗口。
-
-1. 找到第一个 start 点,如果找不到,直接返回 0
-2. 有了 start,遍历链表,开始寻找 end(即第一个不在列表中的点),这样区间 [start, end) 就形成了一个解,结果集+1
-3. 然后重复 1,2
-
-```go
-// date 2023/10/12
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func numComponents(head *ListNode, nums []int) int {
- set := make(map[int]struct{}, 1024)
- for _, v := range nums {
- set[v] = struct{}{}
- }
-
- var start, end *ListNode
- var res int
- // find the start
- for head != nil {
- _, ok := set[head.Val]
- if !ok {
- head = head.Next
- } else {
- start = head
- break
- }
- }
- // 说明没有找到,直接返回
- if start == nil {
- return 0
- }
- // 开始寻找可能的解
- // [start, end)
- end = start
- for end != nil {
- for end != nil && end.Next != nil {
- _, ok := set[end.Val]
- if ok {
- end = end.Next
- } else {
- // 找到了,此时区间[start, end) 就是一个解
- break
- }
- }
- // 判断是否为 尾节点
- if end.Next == nil { // the tail
- res++
- break
- }
- res++
- start = end
- // 重新寻找 start
- for start != nil {
- _, ok := set[start.Val]
- if !ok {
- start = start.Next
- } else {
- end = start
- break
- }
- }
- if start == nil {
- break
- }
- }
- return res
-}
-```
-
-
-
-
-
-====
-
-下面的代码是一样的思路,只是在一个循环中搞定,需要考虑的边界的条件更多,可读性反而不如上面的写法,不推荐。
-
-```go
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func numComponents(head *ListNode, nums []int) int {
- set := make(map[int]struct{}, 1024)
- for _, v := range nums {
- set[v] = struct{}{}
- }
-
- var start, end *ListNode
- var res int
-
- end = head
- for end != nil {
- // find the start
- for end != nil && end.Next != nil {
- _, ok := set[end.Val]
- if ok {
- start = end
- break
- } else {
- end = end.Next
- }
- }
- // 这说明走到的最后一个节点
- // 如果 start 为空,且 最后一个节点在列表中,那么这是一个解 res++
- // 如果 start 不为空,这时候只要 start != end,那么就是一个解 res++
- if end.Next == nil {
- // the tail node
- _, ok := set[end.Val]
- if start == nil && ok {
- res++
- } else if start != nil && start != end {
- res++
- }
- break
- }
- // 更新 start 节点
- start = end
- // find the end
- end = end.Next
- for end != nil {
- _, ok := set[end.Val]
- if ok {
- end = end.Next
- } else {
- // [start, end) is one of result
- res++
- start = nil
- break
- }
- }
- // the tail node
- if end == nil {
- res++
- }
- }
-
- return res
-}
-```
-
diff --git "a/02_linkedlist/No.876_\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md" "b/02_linkedlist/No.876_\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md"
deleted file mode 100644
index 8409416..0000000
--- "a/02_linkedlist/No.876_\351\223\276\350\241\250\347\232\204\344\270\255\351\227\264\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,33 +0,0 @@
-## 876 链表的中间节点-简单
-
-题目:
-
-给你单链表的头节点 head,请你找出并返回链表的中间节点。
-
-如果有两个中间节点,则返回第二个节点。
-
-
-
-分析:
-
-快慢指针。
-
-```go
-// date 2023/10/17
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func middleNode(head *ListNode) *ListNode {
- slow, fast := head, head
- for fast != nil && fast.Next != nil {
- slow = slow.Next
- fast = fast.Next.Next
- }
- return slow
-}
-```
-
diff --git a/02_linkedlist/double_linkedlist.md b/02_linkedlist/double_linkedlist.md
deleted file mode 100644
index 4d88ced..0000000
--- a/02_linkedlist/double_linkedlist.md
+++ /dev/null
@@ -1,14 +0,0 @@
-## 双向链表
-
-### 1、结构定义
-
-
-
-### 2、在表头插入
-
-
-
-```go
-// code
-```
-
diff --git a/02_linkedlist/images/double_list_add_front.png b/02_linkedlist/images/double_list_add_front.png
deleted file mode 100644
index e5dd54f..0000000
Binary files a/02_linkedlist/images/double_list_add_front.png and /dev/null differ
diff --git a/02_linkedlist/images/image019.png b/02_linkedlist/images/image019.png
deleted file mode 100644
index 8a96abe..0000000
Binary files a/02_linkedlist/images/image019.png and /dev/null differ
diff --git a/02_linkedlist/images/image092.png b/02_linkedlist/images/image092.png
deleted file mode 100644
index 78cf18a..0000000
Binary files a/02_linkedlist/images/image092.png and /dev/null differ
diff --git a/02_linkedlist/images/image142.png b/02_linkedlist/images/image142.png
deleted file mode 100644
index de48f58..0000000
Binary files a/02_linkedlist/images/image142.png and /dev/null differ
diff --git a/02_linkedlist/images/image160.png b/02_linkedlist/images/image160.png
deleted file mode 100644
index 083fc47..0000000
Binary files a/02_linkedlist/images/image160.png and /dev/null differ
diff --git a/02_linkedlist/images/image817.png b/02_linkedlist/images/image817.png
deleted file mode 100644
index a5d7a27..0000000
Binary files a/02_linkedlist/images/image817.png and /dev/null differ
diff --git a/02_linkedlist/images/img025.svg b/02_linkedlist/images/img025.svg
deleted file mode 100644
index 5468e5e..0000000
--- a/02_linkedlist/images/img025.svg
+++ /dev/null
@@ -1,4 +0,0 @@
-
-
-
-
\ No newline at end of file
diff --git a/02_linkedlist/linkedlist_others.md b/02_linkedlist/linkedlist_others.md
deleted file mode 100644
index 7ea1055..0000000
--- a/02_linkedlist/linkedlist_others.md
+++ /dev/null
@@ -1,250 +0,0 @@
-## 关于单链表的其他问题 | set 1
-
-[TOC]
-
-单链表节点的定义
-
-```go
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-```
-
-
-
-### 1、判断一个链表是否存在环
-
-解法:利用 **快慢指针** 遍历链表,当快慢两个指针在某一时刻指向同一个节点时,则存在环,否则不存在环。
-
-```go
-func hasCycle(head *ListNode) bool {
- slow, fast := head, head
- for fast != nil && fast.Next != nil {
- slow = slow.Next
- fast = fast.Next.Next
- if slow == fast {
- return true
- }
- }
- return false
-}
-```
-
-### 2、合并两个有序链表
-
-注意保存新链表的头节点。
-
-```go
-func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
- l1, l2 := list1, list2
- dumy := &ListNode{}
- pre := dumy
- for l1 != nil && l2 != nil {
- if l1.Val < l2.Val {
- pre.Next = l1
- l1 = l1.Next
- } else {
- pre.Next = l2
- l2 = l2.Next
- }
- pre = pre.Next
- }
- if l1 != nil {
- pre.Next = l1
- }
- if l2 != nil {
- pre.Next = l2
- }
- return dumy.Next
-}
-```
-
-### 3、在不给出链表的头指针条件下,删除链表中的某个节点
-
-解法:将准备删除的节点的下一个节点的值拷贝至将要删除的节点,后删除下一个节点。需要考虑,这个节点是否为尾节点。
-
-```go
-func deleteNode(node *ListNode) {
- if node == nil {
- return
- }
- pre := node
- for node.Next != nil {
- pre = node
- node.Val = node.Next.Val
- node = node.Next
- }
- pre.Next = nil
-}
-```
-
-### 4、删除一个已排序链表中的重复元素
-
-两种思路,详见 83 题。
-
-
-
-### 5、删除一个未排序链表中重复元素
-
-这类题的要求是只保留链表中元素值出现1次的节点。详见 1836 题。
-
-需要借助 map 统计出现次数。
-
-```go
-func deleteDuplicatesUnsorted(head *ListNode) *ListNode {
- cnt := make(map[int]int, 4)
- cur := head
- prev := head
- for cur != nil {
- cnt[cur.Val]++
- // 优化1: 遍历的同时直接去掉后面出现的 重复的
- if cnt[cur.Val] > 1 && cur.Next != nil {
- prev.Next = cur.Next
- }
- prev = cur
- cur = cur.Next
- }
-
- dummy := &ListNode{}
- pre := dummy
- cur = head
- for cur != nil {
- if cnt[cur.Val] == 1 {
- pre.Next = cur
- pre = cur
- }
- cur = cur.Next
- }
- pre.Next = nil
- return dummy.Next
-}
-```
-
-### 6、将链表中的最后一个元素移动至链表的最前面
-
-直接遍历,记录前驱节点和当前节点,当当前节点是最后一个节点时,直接指向 head,从其前驱节点断开即可。
-
-```go
-func MoveTheLastToFront(head *ListNode) *ListNode {
- if head == nil || head.next == nil {
- return head
- }
- prev, cur := head, head
- for cur != nil {
- if cur.next == nil {
- cur.next = head
- prev.next = nil
- break
- }
- prev = cur
- cur = cur.next
- }
- return cur
-}
-```
-
-
-
-### 7、删除偶数位置上的节点
-
-```go
-func DeleteEven(head *ListNode) *ListNode {
- cur := head
- for cur != nil && cur.Next != nil {
- cur.Next = cur.Next.Next
- cur = cur.Next
- }
- return head
-}
-```
-
-### 8、反转固定个数的节点
-
-例如:1->2->3->4->5->6->7->8->NULL;当k=3时,反转后为3->2->1->6->5->4->8->7->NULL。
-
-```
-Node* Reverse(Node *phead, int k) {
- Node *p = phead;
- Node *pnext = NULL;
- Node *pre = NULL;
- int count = 0;
- while(p != NULL && count < k) {
- pnext = p->next;
- p->next = pre;
- pre = p;
- p = pnext;
- count++;
- }
- if(pnext != NULL)
- phead->next = Reverse(next, k);
- return pre;
-}
-```
-
-### 9、交替反转链表中固定个数的节点
-
-输入:1->2->3->4->5->6->7->8 k=3
-输出:3->2->1->4->5->6->8->7
-
-```
-Node *KReverse(Node *phead, int k) {
- Node *p = phead;
- Node *pnext = NULL;
- Node *pre = NULL;
- count = 0;
- while(p != NULL && count < k) {
- pnext = p->next;
- p->next = pre;
- pre = p;
- p = pnext;
- count++;
- }
- if(phead != NULL)
- phead->next = p;
- count = 0;
- while(count < (k - 1) && p != NULL) {
- p = p->next;
- count++;
- }
- if(p != NULL)
- p->next = KReverse(p->next, k);
- return pre;
-}
-```
-
-### 10、单调递减链表
-
-解释:Delete nodes which have a greater value on right side
-
-保证原有链表节点相对位置不变的情况下,使之变为单调递减链表。
-
-输入:12->15->10->11->5->6->2->3
-输出:15->11->6->3
-
-如果当前节点的值比其下一个节点的值小,则删除当前节点,保留其下一个节点。
-
-解法:先将链表反转,这样程序的逻辑就变为如果后一个节点小于前一个节点,则删除后一个节点。这样做的目的是 **确定新链表的头部**。原来的程序逻辑不太容易确定链表的头部,但是尾部相对容易确定,
-
-这就是第 2487 题。
-
-```go
-func (l *LinkedList) DeleteSmallerRight() {
- if l.size > 1 {
- l.Reverse()
- cur := l.head.next
- for cur != nil && cur.next != nil {
- if cur.val > cur.next.val {
- cur.next = cur.next.next
- l.size--
- continue
- }
- cur = cur.next
- }
- l.Reverse()
- }
-}
-```
diff --git a/02_linkedlist/linkedlist_sort.md b/02_linkedlist/linkedlist_sort.md
deleted file mode 100644
index 48fdbc3..0000000
--- a/02_linkedlist/linkedlist_sort.md
+++ /dev/null
@@ -1,157 +0,0 @@
-## 单链表的排序算法
-
-### 1、插入排序
-
-插入排序可以通过直接交换节点得到。
-
-```go
-/*
-功能:插入排序
-参数:传入链表头指针作为参数,返回排序后的头指针
-说明:时间复杂度O(n^2),空间复杂度O(1)
-第一步:选择插入的位置;
-第二步:如果在已排序的链表的尾部,则直接加入到尾部,否则,插入到选好的位置。注意:需要保存前驱节点。
- */
-
-func InsertSort(head *ListNode) *ListNode {
- if head == nil || head.Next == nil { return head }
- var pre, p, start, end *ListNode
-
- p, start, end, pre = head.Next, head, head, head
- var next *ListNode
-
- for p != nil {
- next, pre = p.Next, start
- for next != p && p.Val >= next.Val {
- next = next.Next
- pre = pre.Next
- }
- // 追加到已经排序的队尾
- if next == p {
- pend = p
- } else {
- pend.Next = p.Next
- p.Next = next
- pre.Next = p
- }
- p = pend.Next
- }
- return head
-}
-```
-
-### 2、选择排序
-
-```
-/*
-功能:选择排序(选择未排序序列中的最值,然后放到已排序的最前面或最后面,只交换节点的值)
-参数:输入链表的头指针,返回排序后的头指针
-说明:时间复杂度O(n^2),空间复杂度O(1)
- */
-Node *SelectSort(Node *phead) {
- if(phead == NULL || phead->next == NULL) return phead;
- Node *pend = phead;
- while(pend->next != NULL) {
- Node *minNode = pend->next;
- Node *p = minNode->next;
- while(p != NULL) {
- if(p->val < minNode->val)
- minNode = p;
- p = p->next;
- }
- swap(minNode->val, pend->val);
- pend = pend->next;
- }
- return phead;
-}
-```
-
-### 3、快速排序
-
-```
-/*
-功能:快速排序,链表指向下一个元素的特性,partition是选择左闭合区间
-第一步,partiton,因为链表不支持随机访问元素,因此partiton中选取第一个节点值作为基准
-第二步,排序
-参数:输入链表头指针,输出排序后的头指针
-说明:平均时间复杂度O(nlogn),空间复杂度O(1)
- */
-Node *Partition(Node *low, Node *high) {
- //左闭合区间[low, high)
- int base = low->val;
- Node *location = low;
- for(Node *i = low->next; i != high; i = i->next) {
- if(i->val > base) {
- location = location->next;
- swap(location->val, i->val);
- }
- }
- swap(low->val, location->val);
- return location;
-}
-void QuickList(Node *phead, Node *tail) {
- //左闭合区间[phead, tail)
- if(phead != tail && phead->next != tail) {
- Node *mid = Partition(phead, tail);
- QuickList(phead, mid);
- QuickList(mid->next, tail);
- }
-}
-Node *QuickSort(Node *phead) {
- if(phead == NULL || phead->next == NULL) return phead;
- QuickList(phead, NULL);
- return phead;
-}
-```
-
-### 4、归并排序
-
-```
-/*
-功能:归并排序,交换链表节点
-第一步:先写归并函数;第二步:利用快慢指针找到链表中点,然后递归对子链进行排序
-参数:输出链表的头指针,输出排序后的头指针
-说明:时间复杂度O(nlogn),空间复杂度O(1)。归并排序应该算是链表排序中最佳的选择,保证最好和最坏的时间复杂度都是O(nlogn),而且在将空间复杂度由数组中O(n),降到链表中的O(1)
- */
-Node *merge(Node *phead1, Node *phead2) {
- if(phead1 == NULL) return phead2;
- if(phead2 == NULL) return phead1;
- Node *res, *p;
- if(phead1->val < phead2->val) {
- res = phead1;
- phead1 = phead1->next;
- } else {
- res = phead2;
- phead2 = phead2->next;
- }
- p = res;
- while(phead1 != NULL && phead2 != NULL) {
- if(phead1->val < phead2->val) {
- p->next = phead1;
- phead1 = phead1->next;
- } else {
- p->next = phead2;
- phead2 = phead2->next;
- }
- p = p->next;
- }
- if(phead1 != NULL) p->next = phead1;
- else if(phead2 != NULL) p->next = phead2;
- return res;
-}
-Node *MergeSort(Node *phead) {
- if(phead == NULL || phead->next == NULL) return phead;
- Node *fast = phead;
- Node *slow = phead;
- while(fast->next != NULL && fast->next->next != NULL) {
- fast = fast->next->next;
- slow = slow->next;
- }
- fast = slow;
- slow = slow->next;
- fast->next = NULL;
- fast = MergeSort(phead);
- slow = MergeSort(slow);
- return merge(fast, slow);
-}
-```
diff --git a/02_linkedlist/readme.md b/02_linkedlist/readme.md
deleted file mode 100644
index 32c3bcc..0000000
--- a/02_linkedlist/readme.md
+++ /dev/null
@@ -1,67 +0,0 @@
-# 链表LinkedList
-
-[TOC]
-
-## 1、快慢指针
-
-在数组章节我们学习的双指针技巧,通常是两个指针从前后一起遍历,向中间逼近;或者读写指针维护不同的数据元素;而在链表的运用中,由于单向链表只能单向遍历,通过调整两个指针的遍历速度完成某种特定任务,因此也称为”快慢指针“技巧。
-
-快慢指针有几个常见的用法:
-
-**用法1:找单链表的中点**
-
-快指针走2步,慢指针走1步,当快指针走完的时候,慢指针刚好在一半的位置。
-
-这类题目有:
-
-- 143—重排链表,快慢的同时反转一部分链表
-- 876—链表的中间节点
-- 234—回文链表,快慢的同时反转一部分链表
-
-
-
-**用法2:判断是否相交,或者是否有环****
-
-如果存在相交或者有环,那么两个指针一定会走到一起。
-
-这类题目有 第 141 题,第 142 题,第 160 题。
-
-- 141—判断链表是否有环
-- 142—判断链表是否有环,如果有,返回环入口
-- 160—相交链表,求两个链表的交点
-
-
-
-**用法3:寻找倒数第 N 个节点**
-
-快指针先行 N 步,慢指针再从头节点开始走,那么当快指针走到结束的时候,慢指针刚好走到第 N 个节点。
-
-这类题目有:
-
-- 19—删除链表中的倒数第N个节点
-
-
-
-**用法4:快慢指针形成一个窗口**
-
-对于要求链表中节点连续,并满足一定条件的题目,可使用 start/end 指针形成的窗口进行判断。
-
-这类题目有:
-
-- 82—删除链表中的重复元素2
-- 817—链表的组件,类似求最长连续子序列和
-
-
-
-## 2、哑结点
-
-哑结点,也称为哨兵结点。常见的场景有:
-
-**用法1:保存结果集**
-
-遍历原链表,将最终的结果保存在哑结点起始的链表中。
-
-这类题目有:
-
-- 002—两数相加(开辟新空间保存结果)
-- 021—合并两个有序链表(不需要开辟空间,直接将结果链接到哑结点上)
diff --git "a/02_linkedlist/\351\235\242\350\257\225\351\242\2300204.md" "b/02_linkedlist/\351\235\242\350\257\225\351\242\2300204.md"
deleted file mode 100644
index 16c3da0..0000000
--- "a/02_linkedlist/\351\235\242\350\257\225\351\242\2300204.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 程序员面试金典02.04 分割链表-中等
-
-题目:
-
-给你一个链表的头节点 head 和一个特定值 x,请你对链表进行分割,使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。
-
-你不需要保留每个分区中各节点的初始相对位置。
-
-
-
-**解题思路**
-
-利用两个哑结点 left 和 right,遍历整个链表,其中 left 保存小于 x 的节点,right 保存大于或等于x的节点。
-
-遍历结束,将两个链表在拼接起来。
-
-注意,拼接前把 right 尾部置空。
-
-```go
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-// date 2023/10/09
-func partition(head *ListNode, x int) *ListNode {
- if head == nil || head.Next == nil {
- return head
- }
- left, right := &ListNode{}, &ListNode{}
- p1, p2 := left, right
-
- for head != nil {
- if head.Val < x {
- p1.Next = head
- p1 = head
- } else {
- p2.Next = head
- p2 = head
- }
- head = head.Next
- }
-
- // 将 right 尾部封住
- if p2 != nil {
- p2.Next = nil
- }
- p1.Next = right.Next
- return left.Next
-}
-```
-
diff --git "a/03_queue/No.225_\347\224\250\351\230\237\345\210\227\345\256\236\347\216\260\346\240\210.md" "b/03_queue/No.225_\347\224\250\351\230\237\345\210\227\345\256\236\347\216\260\346\240\210.md"
deleted file mode 100644
index a126c36..0000000
--- "a/03_queue/No.225_\347\224\250\351\230\237\345\210\227\345\256\236\347\216\260\346\240\210.md"
+++ /dev/null
@@ -1,72 +0,0 @@
-## 225 用队列实现栈-简单
-
-题目:
-
-请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(`push`、`top`、`pop` 和 `empty`)。
-
-实现 `MyStack` 类:
-
-- `void push(int x)` 将元素 x 压入栈顶。
-- `int pop()` 移除并返回栈顶元素。
-- `int top()` 返回栈顶元素。
-- `boolean empty()` 如果栈是空的,返回 `true` ;否则,返回 `false` 。
-
-
-
-分析:
-
-每次压栈的时候,都把已有的元素先出队,再入队。这样,队头元素永远都是最后压栈的这个。
-
-```go
-// date 2023/11/30
-type MyStack struct {
- queue []int
-}
-
-
-func Constructor() MyStack {
- return MyStack{
- queue: make([]int, 0, 16),
- }
-}
-
-
-func (this *MyStack) Push(x int) {
- n := len(this.queue)
- this.queue = append(this.queue, x)
- i := 0
- for i < n {
- this.queue = append(this.queue, this.queue[i])
- i++
- }
- this.queue = this.queue[n:]
-}
-
-
-func (this *MyStack) Pop() int {
- res := this.queue[0]
- this.queue = this.queue[1:]
- return res
-}
-
-
-func (this *MyStack) Top() int {
- return this.queue[0]
-}
-
-
-func (this *MyStack) Empty() bool {
- return len(this.queue) == 0
-}
-
-
-/**
- * Your MyStack object will be instantiated and called as such:
- * obj := Constructor();
- * obj.Push(x);
- * param_2 := obj.Pop();
- * param_3 := obj.Top();
- * param_4 := obj.Empty();
- */
-```
-
diff --git "a/03_queue/No.232_\347\224\250\346\240\210\345\256\236\347\216\260\351\230\237\345\210\227.md" "b/03_queue/No.232_\347\224\250\346\240\210\345\256\236\347\216\260\351\230\237\345\210\227.md"
deleted file mode 100644
index 77da488..0000000
--- "a/03_queue/No.232_\347\224\250\346\240\210\345\256\236\347\216\260\351\230\237\345\210\227.md"
+++ /dev/null
@@ -1,95 +0,0 @@
-## 232 用栈实现队列-简单
-
-题目:
-
-请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(`push`、`pop`、`peek`、`empty`):
-
-实现 `MyQueue` 类:
-
-- `void push(int x)` 将元素 x 推到队列的末尾
-- `int pop()` 从队列的开头移除并返回元素
-- `int peek()` 返回队列开头的元素
-- `boolean empty()` 如果队列为空,返回 `true` ;否则,返回 `false`
-
-**说明:**
-
-- 你 **只能** 使用标准的栈操作 —— 也就是只有 `push to top`, `peek/pop from top`, `size`, 和 `is empty` 操作是合法的。
-- 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
-
-
-
-分析:
-
-栈是先入后出的结构,队列是先入先出的结构。
-
-如果要用栈实现队列,需要2个栈:
-
-`stack_push`负责 push 存储入队的元素;另一个`stack_pop`负责 pop 出队,当`stack_pop` 为空时,从 `stack_push` 中倒一次手。
-
-```go
-// date 2023/11/29
-type MyQueue struct {
- stackPush []int
- stackPop []int
-}
-
-
-func Constructor() MyQueue {
- return MyQueue{
- stackPush: make([]int, 0, 16),
- stackPop: make([]int, 0, 16),
- }
-}
-
-
-func (this *MyQueue) Push(x int) {
- this.stackPush = append(this.stackPush, x)
-}
-
-
-func (this *MyQueue) Pop() int {
- if len(this.stackPop) == 0 {
- n := len(this.stackPush)-1
- for n >= 0 {
- this.stackPop = append(this.stackPop, this.stackPush[n])
- n--
- }
- this.stackPush = this.stackPush[:0]
- }
- n := len(this.stackPop)
- v := this.stackPop[n-1]
- this.stackPop = this.stackPop[:n-1]
- return v
-}
-
-
-func (this *MyQueue) Peek() int {
- n := len(this.stackPop)
- if n > 0 {
- return this.stackPop[n-1]
- }
- m := len(this.stackPush)-1
- for m >= 0 {
- this.stackPop = append(this.stackPop, this.stackPush[m])
- m--
- }
- this.stackPush = this.stackPush[:0]
- return this.stackPop[len(this.stackPop)-1]
-}
-
-
-func (this *MyQueue) Empty() bool {
- return len(this.stackPush) == 0 && len(this.stackPop) == 0
-}
-
-
-/**
- * Your MyQueue object will be instantiated and called as such:
- * obj := Constructor();
- * obj.Push(x);
- * param_2 := obj.Pop();
- * param_3 := obj.Peek();
- * param_4 := obj.Empty();
- */
-```
-
diff --git "a/03_queue/No.341_\346\211\201\345\271\263\345\214\226\345\265\214\345\245\227\345\210\227\350\241\250\350\277\255\344\273\243\345\231\250.md" "b/03_queue/No.341_\346\211\201\345\271\263\345\214\226\345\265\214\345\245\227\345\210\227\350\241\250\350\277\255\344\273\243\345\231\250.md"
deleted file mode 100644
index 20c8ca1..0000000
--- "a/03_queue/No.341_\346\211\201\345\271\263\345\214\226\345\265\214\345\245\227\345\210\227\350\241\250\350\277\255\344\273\243\345\231\250.md"
+++ /dev/null
@@ -1,98 +0,0 @@
-## 341 扁平化嵌套列表迭代器-中等
-
-题目:
-
-给你一个嵌套的整数列表 `nestedList` 。每个元素要么是一个整数,要么是一个列表;该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化,使之能够遍历这个列表中的所有整数。
-
-实现扁平迭代器类 `NestedIterator` :
-
-- `NestedIterator(List nestedList)` 用嵌套列表 `nestedList` 初始化迭代器。
-- `int next()` 返回嵌套列表的下一个整数。
-- `boolean hasNext()` 如果仍然存在待迭代的整数,返回 `true` ;否则,返回 `false` 。
-
-你的代码将会用下述伪代码检测:
-
-```
-initialize iterator with nestedList
-res = []
-while iterator.hasNext()
- append iterator.next() to the end of res
-return res
-```
-
-如果 `res` 与预期的扁平化列表匹配,那么你的代码将会被判为正确。
-
-
-
-分析:
-
-深度优先搜索。
-
-嵌套的整数列表实际上是一个树形结构,树上的叶子节点对应一个整数,非叶子节点对应一个列表。
-
-所以直接对嵌套结构进行深度优先搜索,得到的就是迭代器的遍历顺序。
-
-把遍历到的元素存入数组即可。
-
-
-
-```go
-// date 2023/11/30
-/**
- * // This is the interface that allows for creating nested lists.
- * // You should not implement it, or speculate about its implementation
- * type NestedInteger struct {
- * }
- *
- * // Return true if this NestedInteger holds a single integer, rather than a nested list.
- * func (this NestedInteger) IsInteger() bool {}
- *
- * // Return the single integer that this NestedInteger holds, if it holds a single integer
- * // The result is undefined if this NestedInteger holds a nested list
- * // So before calling this method, you should have a check
- * func (this NestedInteger) GetInteger() int {}
- *
- * // Set this NestedInteger to hold a single integer.
- * func (n *NestedInteger) SetInteger(value int) {}
- *
- * // Set this NestedInteger to hold a nested list and adds a nested integer to it.
- * func (this *NestedInteger) Add(elem NestedInteger) {}
- *
- * // Return the nested list that this NestedInteger holds, if it holds a nested list
- * // The list length is zero if this NestedInteger holds a single integer
- * // You can access NestedInteger's List element directly if you want to modify it
- * func (this NestedInteger) GetList() []*NestedInteger {}
- */
-
-type NestedIterator struct {
- vals []int
-}
-
-func Constructor(nestedList []*NestedInteger) *NestedIterator {
- nums := make([]int, 0, 32)
- var dfs func([]*NestedInteger)
- dfs = func(nestedList []*NestedInteger) {
- for _, nest := range nestedList {
- if nest.IsInteger() {
- nums = append(nums, nest.GetInteger())
- } else {
- dfs(nest.GetList())
- }
- }
- }
-
- dfs(nestedList)
- return &NestedIterator{vals: nums}
-}
-
-func (this *NestedIterator) Next() int {
- res := this.vals[0]
- this.vals = this.vals[1:]
- return res
-}
-
-func (this *NestedIterator) HasNext() bool {
- return len(this.vals) != 0
-}
-```
-
diff --git "a/03_queue/No.387_\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\347\254\254\344\270\200\344\270\252\345\224\257\344\270\200\345\255\227\347\254\246.md" "b/03_queue/No.387_\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\347\254\254\344\270\200\344\270\252\345\224\257\344\270\200\345\255\227\347\254\246.md"
deleted file mode 100644
index 582560e..0000000
--- "a/03_queue/No.387_\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\347\254\254\344\270\200\344\270\252\345\224\257\344\270\200\345\255\227\347\254\246.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 387 字符串中的第一个唯一字符
-
-题目:
-
-给定一个字符串 `s` ,找到 *它的第一个不重复的字符,并返回它的索引* 。如果不存在,则返回 `-1` 。
-
-
-
-分析:
-
-利用 map 存储字符出现的次数,如果首次出现,map 值为下标索引,否则为 -1。
-
-然后,对 map 进行遍历找最小值。
-
-```go
-// date 2023/11/30
-func firstUniqChar(s string) int {
- chSet := make(map[rune]int, 32)
- for i, c := range s {
- _, ok := chSet[c]
- if ok {
- chSet[c] = -1
- } else {
- chSet[c] = i
- }
- }
- ans := len(s)
- for _, v:= range chSet {
- if v != -1 && v < ans {
- ans = v
- }
- }
- if ans == len(s) {
- return -1
- }
- return ans
-}
-```
-
diff --git "a/03_queue/No.622_\350\256\276\350\256\241\345\276\252\347\216\257\351\230\237\345\210\227.md" "b/03_queue/No.622_\350\256\276\350\256\241\345\276\252\347\216\257\351\230\237\345\210\227.md"
deleted file mode 100644
index af9befe..0000000
--- "a/03_queue/No.622_\350\256\276\350\256\241\345\276\252\347\216\257\351\230\237\345\210\227.md"
+++ /dev/null
@@ -1,123 +0,0 @@
-## 622 设计循环队列-中等
-
-题目:
-
-设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
-
-循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
-
-你的实现应该支持如下操作:
-
-- `MyCircularQueue(k)`: 构造器,设置队列长度为 k 。
-- `Front`: 从队首获取元素。如果队列为空,返回 -1 。
-- `Rear`: 获取队尾元素。如果队列为空,返回 -1 。
-- `enQueue(value)`: 向循环队列插入一个元素。如果成功插入则返回真。
-- `deQueue()`: 从循环队列中删除一个元素。如果成功删除则返回真。
-- `isEmpty()`: 检查循环队列是否为空。
-- `isFull()`: 检查循环队列是否已满。
-
-
-
-分析:
-
-循环队列可以用数组实现,用 front, rear 分别指向队列的队头元素和队尾元素。
-
-初始化,front, rear 都指向 -1,这也是队列为空的判断标准。
-
-为空判断:front, rear 是否指向 -1。
-
-队满判断:队尾 rear 再走一步就到队头 front 了,则循环队列满了。
-
-入队:如果为空,front++, rear++;满了则直接返回,否则 rear++
-
-出队:如果为空,直接返回;如果 front == rear,那么只有一个元素,直接清空;否则 front++。
-
-
-
-```go
-// date 2023/11/30
-type MyCircularQueue struct {
- queue []int
- front, rear int
- size int
-}
-
-
-func Constructor(k int) MyCircularQueue {
- return MyCircularQueue{
- queue: make([]int, k, k),
- front: -1,
- rear: -1,
- size: k,
- }
-}
-
-
-func (this *MyCircularQueue) EnQueue(value int) bool {
- if this.IsEmpty() {
- this.front++
- this.rear++
- this.queue[this.rear] = value
- return true
- }
- if this.IsFull() {
- return false
- }
- this.rear = (this.rear+1) % this.size
- this.queue[this.rear] = value
- return true
-}
-
-
-func (this *MyCircularQueue) DeQueue() bool {
- if this.IsEmpty() {
- return false
- }
- if this.front == this.rear {
- this.front = -1
- this.rear = -1
- return true
- }
- this.front = (this.front+1) % this.size
- return true
-}
-
-
-func (this *MyCircularQueue) Front() int {
- if this.IsEmpty() {
- return -1
- }
- return this.queue[this.front]
-}
-
-
-func (this *MyCircularQueue) Rear() int {
- if this.IsEmpty() {
- return -1
- }
- return this.queue[this.rear]
-}
-
-
-func (this *MyCircularQueue) IsEmpty() bool {
- return this.front == -1
-}
-
-
-func (this *MyCircularQueue) IsFull() bool {
- return (this.rear + 1) % this.size == this.front
-}
-
-
-/**
- * Your MyCircularQueue object will be instantiated and called as such:
- * obj := Constructor(k);
- * param_1 := obj.EnQueue(value);
- * param_2 := obj.DeQueue();
- * param_3 := obj.Front();
- * param_4 := obj.Rear();
- * param_5 := obj.IsEmpty();
- * param_6 := obj.IsFull();
- */
-```
-
diff --git "a/03_queue/No.641_\350\256\276\350\256\241\345\276\252\347\216\257\345\217\214\347\253\257\351\230\237\345\210\227.md" "b/03_queue/No.641_\350\256\276\350\256\241\345\276\252\347\216\257\345\217\214\347\253\257\351\230\237\345\210\227.md"
deleted file mode 100644
index 955a9a4..0000000
--- "a/03_queue/No.641_\350\256\276\350\256\241\345\276\252\347\216\257\345\217\214\347\253\257\351\230\237\345\210\227.md"
+++ /dev/null
@@ -1,149 +0,0 @@
-## 641 设计循环双端队列-中等
-
-题目:
-
-设计实现双端队列。
-
-实现 `MyCircularDeque` 类:
-
-- `MyCircularDeque(int k)` :构造函数,双端队列最大为 `k` 。
-- `boolean insertFront()`:将一个元素添加到双端队列头部。 如果操作成功返回 `true` ,否则返回 `false` 。
-- `boolean insertLast()` :将一个元素添加到双端队列尾部。如果操作成功返回 `true` ,否则返回 `false` 。
-- `boolean deleteFront()` :从双端队列头部删除一个元素。 如果操作成功返回 `true` ,否则返回 `false` 。
-- `boolean deleteLast()` :从双端队列尾部删除一个元素。如果操作成功返回 `true` ,否则返回 `false` 。
-- `int getFront()` ):从双端队列头部获得一个元素。如果双端队列为空,返回 `-1` 。
-- `int getRear()` :获得双端队列的最后一个元素。 如果双端队列为空,返回 `-1` 。
-- `boolean isEmpty()` :若双端队列为空,则返回 `true` ,否则返回 `false` 。
-- `boolean isFull()` :若双端队列满了,则返回 `true` ,否则返回 `false` 。
-
-
-
-分析:
-
-跟单端队列类似,处理好 front, rear 即可。
-
-```go
-// date 2023/11/30
-type MyCircularDeque struct {
- queue []int
- front, rear int
- size int
-}
-
-
-func Constructor(k int) MyCircularDeque {
- return MyCircularDeque{
- queue: make([]int, k, k),
- front: -1,
- rear: -1,
- size: k,
- }
-}
-
-
-func (this *MyCircularDeque) InsertFront(value int) bool {
- if this.IsEmpty() {
- this.front++
- this.rear++
- this.queue[this.front] = value
- return true
- }
- if this.IsFull() {
- return false
- }
- if this.front == 0 {
- this.front = this.size
- }
- this.front--
- this.queue[this.front] = value
- return true
-}
-
-
-func (this *MyCircularDeque) InsertLast(value int) bool {
- if this.IsEmpty() {
- this.front++
- this.rear++
- this.queue[this.rear] = value
- return true
- }
- if this.IsFull() {
- return false
- }
- this.rear = (this.rear+1) % this.size
- this.queue[this.rear] = value
- return true
-}
-
-
-func (this *MyCircularDeque) DeleteFront() bool {
- if this.IsEmpty() {
- return false
- }
- if this.front == this.rear {
- this.front = -1
- this.rear = -1
- return true
- }
- this.front = (this.front+1) % this.size
- return true
-}
-
-
-func (this *MyCircularDeque) DeleteLast() bool {
- if this.IsEmpty() {
- return false
- }
- if this.front == this.rear {
- this.front = -1
- this.rear = -1
- return true
- }
- if this.rear == 0 {
- this.rear = this.size
- }
- this.rear--
- return true
-}
-
-
-func (this *MyCircularDeque) GetFront() int {
- if this.IsEmpty() {
- return -1
- }
- return this.queue[this.front]
-}
-
-
-func (this *MyCircularDeque) GetRear() int {
- if this.IsEmpty() {
- return -1
- }
- return this.queue[this.rear]
-}
-
-
-func (this *MyCircularDeque) IsEmpty() bool {
- return this.front == -1
-}
-
-
-func (this *MyCircularDeque) IsFull() bool {
- return (this.rear + 1) % this.size == this.front
-}
-
-
-/**
- * Your MyCircularDeque object will be instantiated and called as such:
- * obj := Constructor(k);
- * param_1 := obj.InsertFront(value);
- * param_2 := obj.InsertLast(value);
- * param_3 := obj.DeleteFront();
- * param_4 := obj.DeleteLast();
- * param_5 := obj.GetFront();
- * param_6 := obj.GetRear();
- * param_7 := obj.IsEmpty();
- * param_8 := obj.IsFull();
- */
-```
-
diff --git "a/03_queue/No.918_\347\216\257\345\275\242\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\222\214.md" "b/03_queue/No.918_\347\216\257\345\275\242\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\222\214.md"
deleted file mode 100644
index d0cebc8..0000000
--- "a/03_queue/No.918_\347\216\257\345\275\242\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\222\214.md"
+++ /dev/null
@@ -1,70 +0,0 @@
-## 918 环形子数组的最大和-中等
-
-题目:
-
-给定一个长度为 `n` 的**环形整数数组** `nums` ,返回 *`nums` 的非空 **子数组** 的最大可能和* 。
-
-**环形数组** 意味着数组的末端将会与开头相连呈环状。形式上, `nums[i]` 的下一个元素是 `nums[(i + 1) % n]` , `nums[i]` 的前一个元素是 `nums[(i - 1 + n) % n]` 。
-
-**子数组** 最多只能包含固定缓冲区 `nums` 中的每个元素一次。形式上,对于子数组 `nums[i], nums[i + 1], ..., nums[j]` ,不存在 `i <= k1, k2 <= j` 其中 `k1 % n == k2 % n` 。
-
-
-
-分析:
-
-单调队列。
-
-既然可以环形,那么我们将数组延长一倍,对于 i >= n 的元素,nums[i] = nums[i-n]。
-
-问题就变成了:在长度为 2n 的数组上,求长度不超过 n 的最大子数组和。
-
-思路:前缀和作差。
-
-令 Si 表示前缀和,那么在不规定子数组的长度时,求最大的子数组和,就等于求 Si - Sj 的最大值,其中 j < i。
-
-现在规定了,子数组的长度不能超过 n,那我们用单调队列维护该集合。
-
-1. 遍历到 i 时,如果队头元素的坐标小于 i - n(即子数组长度超过 n),就需要出队,一直重复,知道队列为空或者队头元素的坐标大于或等于 i - n
-2. 取 队头元素的值,计算 Si - Sj,并更新结果
-3. 维护队列的单调性。Si 加入队列的时候,任何大于等于 Si 的元素都需要出队,然后 Si 在入队。
-
-```go
-// date 2023/11/30
-func maxSubarraySumCircular(nums []int) int {
- type pair struct {
- idx int
- val int
- }
- n := len(nums)
- preSum := nums[0]
- res := nums[0]
- queue := make([]pair, 0, 32)
- queue = append(queue, pair{idx:0, val: preSum})
-
- for i := 1; i < 2*n; i++ {
- for len(queue) > 0 && queue[0].idx < i - n {
- queue = queue[1:]
- }
-
- preSum += nums[i%n]
-
- res = max(res, preSum - queue[0].val)
-
- for len(queue) > 0 && queue[len(queue)-1].val >= preSum {
- queue = queue[:len(queue)-1]
- }
-
- queue = append(queue, pair{idx:i, val: preSum})
- }
-
- return res
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/03_queue/No.933_\346\234\200\350\277\221\347\232\204\350\257\267\346\261\202\346\254\241\346\225\260.md" "b/03_queue/No.933_\346\234\200\350\277\221\347\232\204\350\257\267\346\261\202\346\254\241\346\225\260.md"
deleted file mode 100644
index fb673ed..0000000
--- "a/03_queue/No.933_\346\234\200\350\277\221\347\232\204\350\257\267\346\261\202\346\254\241\346\225\260.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 933 最近的请求次数-简单
-
-题目:
-
-写一个 `RecentCounter` 类来计算特定时间范围内最近的请求。
-
-请你实现 `RecentCounter` 类:
-
-- `RecentCounter()` 初始化计数器,请求数为 0 。
-- `int ping(int t)` 在时间 `t` 添加一个新请求,其中 `t` 表示以毫秒为单位的某个时间,并返回过去 `3000` 毫秒内发生的所有请求数(包括新请求)。确切地说,返回在 `[t-3000, t]` 内发生的请求数。
-
-**保证** 每次对 `ping` 的调用都使用比之前更大的 `t` 值。
-
-
-
-分析:
-
-先直接入队,入队后,把历史上超过时间的出队即可。
-
-```go
-// date 2023/11/30
-type RecentCounter struct {
- ct []int
-}
-
-
-func Constructor() RecentCounter {
- return RecentCounter{
- ct: make([]int, 0, 16),
- }
-}
-
-
-func (this *RecentCounter) Ping(t int) int {
- this.ct = append(this.ct, t)
- start := t - 3000
- for i := 0; i < len(this.ct); i++ {
- if this.ct[i] >= start {
- this.ct = this.ct[i:]
- break
- }
- }
- return len(this.ct)
-}
-```
\ No newline at end of file
diff --git a/03_queue/queue.md b/03_queue/queue.md
deleted file mode 100644
index 1d4cacc..0000000
--- a/03_queue/queue.md
+++ /dev/null
@@ -1,269 +0,0 @@
-## Queue
-
-[TOC]
-
-### 基本定义
-
-队列实现的是一种先进先出(FIFO)策略的线性表。
-
-队列有队头(head)和队尾(tail),当有一个元素入队时,放入队尾;出队时,即删除队头元素。
-
-### 队列的基本操作
-
- + push(x):将元素x加入到队列的尾部
- + pop():弹出队列的第一个元素,但是,**不会返回被弹元素的值**
- + front():返回队首元素
- + back():返回队尾元素
- + empty():判断队列是否为空,当队列为空时,返回true
- + size():返回队列中的元素个数
-
-注意:以上操作均基于c++模板类,位于头文件和中。以下是两个数据结构互相转换算法和程序。
-
-### 队列的实现
-
-从时间复杂度角度而言,push(), pop(), front(),back(), empty()操作只需要O(1)的时间。从实现角度而言,队列的实现方式有两种,**数组和线性表**。
-
-```cpp
-class MyQueue
-{
-private:
- int front, rear, size;
- unsigned capacity;
- int *array;
-public:
- MyQueue(unsigned num);
- bool Push(int x);
- bool Pop();
- int Front();
- int Back();
- bool Empty();
- bool Full();
-};
-// 初始化
-MyQueue::MyQueue(unsigned num) {
- capacity = num;
- array = new int[capacity];
- front = 0;
- rear = capacity - 1;
- size = 0;
-}
-bool MyQueue::Full() {
- if(size == capacity)
- return true;
- else
- return false;
-}
-bool MyQueue::Empty() {
- if(size == 0)
- return true;
- else
- return false;
-}
-// 入队
-bool MyQueue::Push(int x) {
- if(size == capacity) {
- cout << "Queue is Overflow" << endl;
- return false;
- }
- rear = (rear + 1) % capacity;
- array[rear] = x;
- size += 1;
- return true;
-}
-// 出队
-bool MyQueue::Pop() {
- if(size == 0) {
- cout << "Queue is Underflow" << endl;
- return false;
- }
- int x = array[front];
- front = (front + 1) % capacity;
- size -= 1;
- return x;
-}
-// 取队头元素
-int MyQueue::Front() {
- if(size == 0) {
- cout << "Queue is Underflow" << endl;
- return -1;
- }
- return array[front];
-}
-// 取队尾元素
-int MyQueue::Back() {
- if(size == 0) {
- cout << "Queue is Underflow" << endl;
- return -1;
- }
- return array[rear];
-}
-```
-
-### 由栈实现队列
-
-```cpp
-#include
-#include
-using namespace std;
-class MyQueue {
-private:
- stack s; // 用于入队
- stack s2; // 用于出队
-public:
- void Push(int x);
- void Pop();
- int Front();
- int Back();
- bool Empty();
- int Size();
-};
-// 入队
-void MyQueue::Push(int x) {
- s.push(x);
-}
-// 出队
-void MyQueue::Pop() {
- if(s2.empty()) {
- if(s.empty()) {
- // s2为空,s为空,表示整个队列为空
- cout << "The Queue is Empty" << endl;
- return;
- } else {
- // s2为空,s不为空,则将s中的元素依次压入s2中
- while(!s.empty()) {
- s2.push(s.top());
- s.pop();
- }
- }
- }
- if(!s2.empty()) {
- // s2不为空,其栈顶元素就是最先进入的元素,即队首元素
- s2.pop();
- }
-}
-// 获取队首元素
-int MyQueue::Front() {
- // 与出队原理一样,只是将pop()变为top()
- if(s2.empty()) {
- if(s.empty()) {
- cout << "The Queue is Empty" << endl;
- return -1;
- } else {
- while(!s.empty()) {
- s2.push(s.top());
- s.pop();
- }
- }
- }
- if(!s2.empty()) {
- return s2.top();
- }
-}
-// 获取队尾元素
-int MyQueue::Back() {
- // 因为每次入队均将元素压入s中,因此s的栈顶元素即为队尾元素
- // 同样的道理,当s为空使,s2不为空时,s2中的栈顶->栈底 对应 队首->队尾
- // 因此,需要将s2中的元素依次压入s中
- if(s.empty()) {
- if(s2.empty()) {
- // s为空,s2为空,即整个队列为空
- cout << "The Queue is Empty" << endl;
- return -1;
- } else {
- // s为空,s2不为空,则将s2中的元素依次压入s中
- while(!s2.empty()) {
- s.push(s2.top());
- s2.pop();
- }
- }
- }
- if(!s.empty()) {
- // s不为空,其栈顶元素就是队列的队尾元素
- return s.top();
- }
-}
-// 判断队列是否为空
-bool MyQueue::Empty() {
- return (s.empty() && s2.empty());
-}
-// 获取栈中元素的个数
-int MyQueue::Size() {
- return (s.size() + s2.size());
-}
-```
-
-### 相关题目
-
-[TOC]
-
-#### 621 Task Scheduler【任务调度器】
-
-题目描述:
-
-给定一个用字符数组表示的 CPU 需要执行的任务列表。其中包含使用大写的 A - Z 字母表示的26 种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。CPU 在任何一个单位时间内都可以执行一个任务,或者在待命状态。
-
-然而,两个相同种类的任务之间必须有长度为 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
-
-你需要计算完成所有任务所需要的最短时间。
-
-示例1:
-
-```
-输入: tasks = ["A","A","A","B","B","B"], n = 2
-输出: 8
-执行顺序: A -> B -> (待命) -> A -> B -> (待命) -> A -> B.
-```
-
-```go
-// 算法1:优先安排出现次数最多的任务
-func leastInterval(tasks []byte, n int) int {
- m := make([]int, 26)
- for _, t := range tasks {
- m[t - 'A']++
- }
- sort.Slice(m, func(i, j int) bool {
- return m[i] < m[j]
- })
- var res int
- for m[25] > 0 {
- i := 0
- for i <= n {
- if m[25] == 0 {
- break
- }
- if i < 16 && m[25-i] > 0 {
- m[25-i]--
- }
- res++
- i++
- }
- sort.Slice(m, func(i, j int) bool {
- return m[i] < m[j]
- })
- }
- return res
-}
-// 算法二:设计,利用空闲时间[leetcode-cn]
-func leastInterval(tasks []byte, n int) int {
- m := make([]int, 26)
- for _, t := range tasks {
- m[t - 'A']++
- }
- sort.Slice(m, func(i, j int) bool {
- return m[i] < m[j]
- })
- max_val := m[25] - 1
- idle := n * max_val
- for i := 24; i >= 0 && m[i] > 0; i-- {
- if m[i] <= max_val {
- idle -= m[i]
- } else {
- idle -= max_val
- }
- }
- if idle > 0 {
- return idle + len(tasks)
- }
- return len(tasks)
-}
-```
diff --git "a/04_stack/No.071_\347\256\200\345\214\226\350\267\257\345\276\204.md" "b/04_stack/No.071_\347\256\200\345\214\226\350\267\257\345\276\204.md"
deleted file mode 100644
index 03bd031..0000000
--- "a/04_stack/No.071_\347\256\200\345\214\226\350\267\257\345\276\204.md"
+++ /dev/null
@@ -1,91 +0,0 @@
-## 71 简化路径-中等
-
-题目:
-
-给你一个字符串 `path` ,表示指向某一文件或目录的 Unix 风格 **绝对路径** (以 `'/'` 开头),请你将其转化为更加简洁的规范路径。
-
-在 Unix 风格的文件系统中,一个点(`.`)表示当前目录本身;此外,两个点 (`..`) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,`'//'`)都被视为单个斜杠 `'/'` 。 对于此问题,任何其他格式的点(例如,`'...'`)均被视为文件/目录名称。
-
-请注意,返回的 **规范路径** 必须遵循下述格式:
-
-- 始终以斜杠 `'/'` 开头。
-- 两个目录名之间必须只有一个斜杠 `'/'` 。
-- 最后一个目录名(如果存在)**不能** 以 `'/'` 结尾。
-- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 `'.'` 或 `'..'`)。
-
-返回简化后得到的 **规范路径** 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:path = "/home/"
-> 输出:"/home"
-> 解释:注意,最后一个目录名后面没有斜杠。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:path = "/../"
-> 输出:"/"
-> 解释:从根目录向上一级是不可行的,因为根目录是你可以到达的最高级。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:path = "/home//foo/"
-> 输出:"/home/foo"
-> 解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
-> ```
->
-> **示例 4:**
->
-> ```
-> 输入:path = "/a/./b/../../c/"
-> 输出:"/c"
-> ```
-
-
-
-分析:
-
-还是入栈、出栈的思想。
-
-先通过 strings 库函数,将字符串切分。
-
-对每一部分进行判断,如果遇到 `..` 出栈;如果不为空且不等于`.`,表示当前是一个有效的目录,入栈。
-
-最后,判断栈的大小,并将 stack 内容组成字符串。
-
-```go
-// date 2023/12/18
-func simplifyPath(path string) string {
- arr := strings.Split(path, "/")
- stack := make([]string, 0, 16)
- for i := 0; i < len(arr); i++ {
- v := arr[i]
- // 有可能存在多个 ///
- // 切分以后,每个元素就是空,直接跳过
- if len(v) == 0 {
- continue
- }
- // 上一级目录,直接出栈
- if v == ".." {
- if len(stack) > 0 {
- stack = stack[:len(stack)-1]
- }
- } else if v != "." { // . 表示当前目录,没有必要添加,去掉
- stack = append(stack, v)
- }
- }
-
- if len(stack) == 0 {
- return "/"
- }
- return "/" + strings.Join(stack, "/")
-}
-```
-
diff --git "a/04_stack/No.1019_\351\223\276\350\241\250\344\270\255\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\350\212\202\347\202\271.md" "b/04_stack/No.1019_\351\223\276\350\241\250\344\270\255\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\350\212\202\347\202\271.md"
deleted file mode 100644
index e2fe276..0000000
--- "a/04_stack/No.1019_\351\223\276\350\241\250\344\270\255\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,113 +0,0 @@
-## 1019 链表中的下一个更大的节点-中等
-
-题目:
-
-给定一个长度为 `n` 的链表 `head`
-
-对于列表中的每个节点,查找下一个 **更大节点** 的值。也就是说,对于每个节点,找到它旁边的第一个节点的值,这个节点的值 **严格大于** 它的值。
-
-返回一个整数数组 `answer` ,其中 `answer[i]` 是第 `i` 个节点( **从1开始** )的下一个更大的节点的值。如果第 `i` 个节点没有下一个更大的节点,设置 `answer[i] = 0` 。
-
-
-
-> **示例 1:**
->
-> 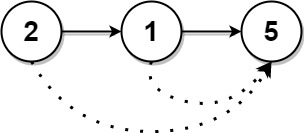
->
-> ```
-> 输入:head = [2,1,5]
-> 输出:[5,5,0]
-> ```
->
-> **示例 2:**
->
-> 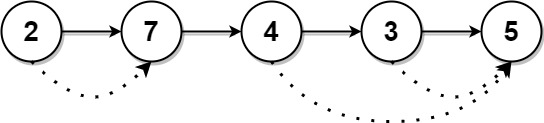
->
-> ```
-> 输入:head = [2,7,4,3,5]
-> 输出:[7,0,5,5,0]
-> ```
-
-
-
-分析:
-
-解法1:最朴素的解法就是两层循环,依次查找,找到就退出
-
-```go
-// date 2023/12/21
-// 两层查找
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func nextLargerNodes(head *ListNode) []int {
- ans := make([]int, 0, 16)
-
- pre := head
-
- for pre != nil {
- res := 0
- next := pre.Next
- for next != nil {
- if next.Val > pre.Val {
- res = next.Val
- break
- }
- next = next.Next
- }
- ans = append(ans, res)
- pre = pre.Next
- }
-
- return ans
-}
-```
-
-
-
-解法2:单调栈
-
-跟数组的题目类似,只不过链表的要自己保存索引。
-
-```go
-// date 2023/12/21
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func nextLargerNodes(head *ListNode) []int {
- type node struct {
- idx, val int
- }
- ans := make([]int, 0, 16)
- stack := make([]node, 0, 16)
-
- pre := head
- i := 0
-
- for pre != nil {
- v := pre.Val
-
- for len(stack) > 0 && v > stack[len(stack)-1].val {
- ans[stack[len(stack)-1].idx] = v
- stack = stack[:len(stack)-1]
- }
-
-
- stack = append(stack, node{idx: i, val: v})
- ans = append(ans, 0)
- pre = pre.Next
- i++
- }
-
- return ans
-}
-```
-
diff --git "a/04_stack/No.1021_\345\210\240\351\231\244\346\234\200\345\244\226\345\261\202\347\232\204\346\213\254\345\217\267.md" "b/04_stack/No.1021_\345\210\240\351\231\244\346\234\200\345\244\226\345\261\202\347\232\204\346\213\254\345\217\267.md"
deleted file mode 100644
index 0167b5e..0000000
--- "a/04_stack/No.1021_\345\210\240\351\231\244\346\234\200\345\244\226\345\261\202\347\232\204\346\213\254\345\217\267.md"
+++ /dev/null
@@ -1,79 +0,0 @@
-## 1021 删除最外层的括号-简单
-
-题目:
-
-有效括号字符串为空 `""`、`"(" + A + ")"` 或 `A + B` ,其中 `A` 和 `B` 都是有效的括号字符串,`+` 代表字符串的连接。
-
-- 例如,`""`,`"()"`,`"(())()"` 和 `"(()(()))"` 都是有效的括号字符串。
-
-如果有效字符串 `s` 非空,且不存在将其拆分为 `s = A + B` 的方法,我们称其为**原语(primitive)**,其中 `A` 和 `B` 都是非空有效括号字符串。
-
-给出一个非空有效字符串 `s`,考虑将其进行原语化分解,使得:`s = P_1 + P_2 + ... + P_k`,其中 `P_i` 是有效括号字符串原语。
-
-对 `s` 进行原语化分解,删除分解中每个原语字符串的最外层括号,返回 `s` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "(()())(())"
-> 输出:"()()()"
-> 解释:
-> 输入字符串为 "(()())(())",原语化分解得到 "(()())" + "(())",
-> 删除每个部分中的最外层括号后得到 "()()" + "()" = "()()()"。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = "(()())(())(()(()))"
-> 输出:"()()()()(())"
-> 解释:
-> 输入字符串为 "(()())(())(()(()))",原语化分解得到 "(()())" + "(())" + "(()(()))",
-> 删除每个部分中的最外层括号后得到 "()()" + "()" + "()(())" = "()()()()(())"。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:s = "()()"
-> 输出:""
-> 解释:
-> 输入字符串为 "()()",原语化分解得到 "()" + "()",
-> 删除每个部分中的最外层括号后得到 "" + "" = ""。
-> ```
-
-
-
-分析:
-
-利用栈的思维进行模拟,正序遍历,遇到 `(` 计数增加1,遇到 `)`计数减少1,同时保存在临时结果中。
-
-当计数 cnt 为零时,表示找到一个原语,去掉最外层的括号,存入结果。
-
-```go
-// date 2023/12/18
-func removeOuterParentheses(s string) string {
- // 统计一个原语
- cnt := 0
- stack := ""
- res := ""
- for i := 0; i < len(s); i++ {
- char := s[i]
- if char == '(' {
- cnt++
- } else if char == ')' {
- cnt--
- }
- stack += string(char)
- if cnt == 0 {
- res += stack[1:len(stack)-1]
- stack = ""
- }
- }
-
- return res
-}
-```
-
diff --git "a/04_stack/No.1047_\345\210\240\351\231\244\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\347\233\270\351\202\273\351\207\215\345\244\215\351\241\271.md" "b/04_stack/No.1047_\345\210\240\351\231\244\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\347\233\270\351\202\273\351\207\215\345\244\215\351\241\271.md"
deleted file mode 100644
index f0174a3..0000000
--- "a/04_stack/No.1047_\345\210\240\351\231\244\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\347\233\270\351\202\273\351\207\215\345\244\215\351\241\271.md"
+++ /dev/null
@@ -1,46 +0,0 @@
-## 1047 删除字符串中的所有相邻重复项-简单
-
-题目:
-
-给出由小写字母组成的字符串 `S`,**重复项删除操作**会选择两个相邻且相同的字母,并删除它们。
-
-在 S 上反复执行重复项删除操作,直到无法继续删除。
-
-在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
-
-
-
-> **示例:**
->
-> ```
-> 输入:"abbaca"
-> 输出:"ca"
-> 解释:
-> 例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
-> ```
-
-
-
-分析:
-
-入栈出栈思维。
-
-如果栈不为空,且栈顶元素等于当前元素,直接出栈;否则入栈。
-
-最终栈里面的元素就是唯一的。
-
-```go
-// date 2023/12/18
-func removeDuplicates(s string) string {
- res := make([]rune, 0, 16)
- for _, v := range s {
- if len(res) > 0 && res[len(res)-1] == v {
- res = res[:len(res)-1]
- } else {
- res = append(res, v)
- }
- }
- return string(res)
-}
-```
-
diff --git "a/04_stack/No.150_\351\200\206\346\263\242\345\205\260\350\241\250\350\276\276\345\274\217\346\261\202\345\200\274.md" "b/04_stack/No.150_\351\200\206\346\263\242\345\205\260\350\241\250\350\276\276\345\274\217\346\261\202\345\200\274.md"
deleted file mode 100644
index 7849700..0000000
--- "a/04_stack/No.150_\351\200\206\346\263\242\345\205\260\350\241\250\350\276\276\345\274\217\346\261\202\345\200\274.md"
+++ /dev/null
@@ -1,99 +0,0 @@
-## 150 逆波兰表达式求值-中等
-
-题目:
-
-给你一个字符串数组 `tokens` ,表示一个根据 [逆波兰表示法](https://baike.baidu.com/item/逆波兰式/128437) 表示的算术表达式。
-
-请你计算该表达式。返回一个表示表达式值的整数。
-
-**注意:**
-
-- 有效的算符为 `'+'`、`'-'`、`'*'` 和 `'/'` 。
-- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
-- 两个整数之间的除法总是 **向零截断** 。
-- 表达式中不含除零运算。
-- 输入是一个根据逆波兰表示法表示的算术表达式。
-- 答案及所有中间计算结果可以用 **32 位** 整数表示。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:tokens = ["2","1","+","3","*"]
-> 输出:9
-> 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:tokens = ["4","13","5","/","+"]
-> 输出:6
-> 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
-> 输出:22
-> 解释:该算式转化为常见的中缀算术表达式为:
-> ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
-> = ((10 * (6 / (12 * -11))) + 17) + 5
-> = ((10 * (6 / -132)) + 17) + 5
-> = ((10 * 0) + 17) + 5
-> = (0 + 17) + 5
-> = 17 + 5
-> = 22
-> ```
-
-
-
-分析:
-
-栈的基本操作。
-
-遇到运算符,出栈计算,并把新结果入栈;
-
-遇到数字,直接入栈。
-
-```go
-// date 2023/12/18
-func evalRPN(tokens []string) int {
- stack := make([]string, 0, 16)
- n := len(tokens)
- for i := 0; i < n; i++ {
- char := tokens[i]
- if char == "+" || char == "-" || char == "*" || char == "/" {
- res := calc(stack[len(stack)-2], stack[len(stack)-1], char)
- stack = stack[:len(stack)-2]
- stack = append(stack, fmt.Sprintf("%d", res))
- } else {
- stack = append(stack, char)
- }
- }
- if len(stack) > 0 {
- v, _ := strconv.Atoi(stack[len(stack)-1])
- return v
- }
- return 0
-}
-
-func calc(x, y string, k string) int {
- v1, _ := strconv.Atoi(x)
- v2, _ := strconv.Atoi(y)
- switch k {
- case "+":
- return v1 + v2
- case "-":
- return v1 - v2
- case "*":
- return v1 * v2
- case "/":
- return v1 / v2
- }
- return 0
-}
-```
-
diff --git "a/04_stack/No.155_\346\234\200\345\260\217\346\240\210.md" "b/04_stack/No.155_\346\234\200\345\260\217\346\240\210.md"
deleted file mode 100644
index 039891a..0000000
--- "a/04_stack/No.155_\346\234\200\345\260\217\346\240\210.md"
+++ /dev/null
@@ -1,139 +0,0 @@
-## 155 最小栈-中等
-
-题目:
-
-设计一个支持 `push` ,`pop` ,`top` 操作,并能在常数时间内检索到最小元素的栈。
-
-实现 `MinStack` 类:
-
-- `MinStack()` 初始化堆栈对象。
-- `void push(int val)` 将元素val推入堆栈。
-- `void pop()` 删除堆栈顶部的元素。
-- `int top()` 获取堆栈顶部的元素。
-- `int getMin()` 获取堆栈中的最小元素。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:
-> ["MinStack","push","push","push","getMin","pop","top","getMin"]
-> [[],[-2],[0],[-3],[],[],[],[]]
->
-> 输出:
-> [null,null,null,null,-3,null,0,-2]
->
-> 解释:
-> MinStack minStack = new MinStack();
-> minStack.push(-2);
-> minStack.push(0);
-> minStack.push(-3);
-> minStack.getMin(); --> 返回 -3.
-> minStack.pop();
-> minStack.top(); --> 返回 0.
-> minStack.getMin(); --> 返回 -2.
-> ```
-
-
-
-分析:
-
-因为要求在常数时间内检索到最小元素,所以考虑使用辅助栈。
-
-数据栈 dataStack 保存所有的元素。
-
-小元素栈 minStack 保存当前的最小元素。
-
-入栈的时候,如果 minStack 的栈顶元素 大于等于入栈元素,那么把入栈元素 val 也放入 minStack 中。
-
-出栈的时候,如果 minStack 的栈顶元素 等于 dataStack 的栈顶元素,那么 minStack 也要出栈。
-
-```go
-// date 2020/03/23
-// 第一种方案:辅助栈stackMin只保留当前栈中的最小值,即辅助栈和数据栈stackData长度不相等
-type MinStack struct {
- stackData []int
- stackMin []int
-}
-
-
-/** initialize your data structure here. */
-func Constructor() MinStack {
- return MinStack{
- stackData: make([]int, 0),
- stackMin: make([]int, 0),
- }
-}
-
-
-func (this *MinStack) Push(x int) {
- if len(this.stackMin) == 0 || this.stackMin[len(this.stackMin)-1] >= x {
- this.stackMin = append(this.stackMin, x)
- }
- this.stackData = append(this.stackData, x)
-}
-
-
-func (this *MinStack) Pop() {
- if len(this.stackData) <= 0 {return}
- if len(this.stackMin) > 0 && this.stackMin[len(this.stackMin)-1] == this.stackData[len(this.stackData)-1] {
- this.stackMin = this.stackMin[:len(this.stackMin)-1]
- }
- this.stackData = this.stackData[:len(this.stackData)-1]
-}
-
-
-func (this *MinStack) Top() int {
- return this.stackData[len(this.stackData)-1]
-}
-
-
-func (this *MinStack) GetMin() int {
- if len(this.stackMin) <= 0 { return 0 }
- return this.stackMin[len(this.stackMin)-1]
-}
-// 第二种方案:辅助栈stackMin随时保留当前栈的最小值,保持和数据栈stackData长度相等
-type MinStack struct {
- stackData []int
- stackMin []int
-}
-
-
-/** initialize your data structure here. */
-func Constructor() MinStack {
- return MinStack{
- stackData: make([]int, 0),
- stackMin: make([]int, 0),
- }
-}
-
-
-func (this *MinStack) Push(x int) {
- if len(this.stackMin) == 0 || this.stackMin[len(this.stackMin)-1] >= x {
- this.stackMin = append(this.stackMin, x)
- } else {
- this.stackMin = append(this.stackMin, this.stackMin[len(this.stackMin)-1])
- }
- this.stackData = append(this.stackData, x)
-}
-
-
-func (this *MinStack) Pop() {
- if len(this.stackData) <= 0 {return}
- this.stackData = this.stackData[:len(this.stackData)-1]
- this.stackMin = this.stackMin[:len(this.stackMin)-1]
-}
-
-
-func (this *MinStack) Top() int {
- return this.stackData[len(this.stackData)-1]
-}
-
-
-func (this *MinStack) GetMin() int {
- if len(this.stackMin) <= 0 { return 0 }
- return this.stackMin[len(this.stackMin)-1]
-}
-```
-
diff --git "a/04_stack/No.224_\345\237\272\346\234\254\350\256\241\347\256\227\345\231\250.md" "b/04_stack/No.224_\345\237\272\346\234\254\350\256\241\347\256\227\345\231\250.md"
deleted file mode 100644
index 5389a69..0000000
--- "a/04_stack/No.224_\345\237\272\346\234\254\350\256\241\347\256\227\345\231\250.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 224 基本计算器-困难
-
-题目:
-
-给你一个字符串表达式 `s` ,请你实现一个基本计算器来计算并返回它的值。
-
-注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 `eval()` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "1 + 1"
-> 输出:2
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = " 2-1 + 2 "
-> 输出:3
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:s = "(1+(4+5+2)-3)+(6+8)"
-> 输出:23
-> ```
-
-
-
-分析:
-
-还是入栈、出栈的思路,有几个点需要注意。
-
-- 可能存在空格,需要跳过
-- `-`是有效的,所以可能出现负负得正的情况,所以记录每次计算出来的结果
-- 遇到左括号,需要重新计算,主要保存之前的结果和符号
-- 遇到右括号,取出保存的结果和符号,更新当前结果
-
-```go
-// date 2023/12/18
-func calculate(s string) int {
- i := 0
- res := 0
- sign := 1 // 保存加减状态
- stack := make([]int, 0, 16) // 保存括号外的中间结果和加减符号
-
- n := len(s)
- for i < n {
- if s[i] == ' ' {
- i++
- } else if s[i] <= '9' && s[i] >= '0' {
- // find a num
- base, v := 10, int(s[i] - '0')
- for i+1 < n && s[i+1] <= '9' && s[i+1] >= '0' {
- v = v * base + int(s[i+1] - '0')
- i++
- }
- res += v * sign
- i++
- } else if s[i] == '+' {
- sign = 1
- i++
- } else if s[i] == '-' {
- sign = -1
- i++
- } else if s[i] == '(' { // 遇到左括号,保存之前的结果,重新计算
- stack = append(stack, res, sign)
- res = 0
- sign = 1
- i++
- } else if s[i] == ')' { // 取出之前的结果和符号,计算
- if len(stack) > 1 {
- res = res * stack[len(stack)-1] + stack[len(stack)-2]
- stack = stack[:len(stack)-2]
- }
- //res = res
- i++
- }
- }
- return res
-}
-```
-
diff --git "a/04_stack/No.394_\345\255\227\347\254\246\344\270\262\347\274\226\347\240\201.md" "b/04_stack/No.394_\345\255\227\347\254\246\344\270\262\347\274\226\347\240\201.md"
deleted file mode 100644
index 2bf99b4..0000000
--- "a/04_stack/No.394_\345\255\227\347\254\246\344\270\262\347\274\226\347\240\201.md"
+++ /dev/null
@@ -1,103 +0,0 @@
-## 394 字符串编码-中等
-
-题目:
-
-给定一个经过编码的字符串,返回它解码后的字符串。
-
-编码规则为: `k[encoded_string]`,表示其中方括号内部的 `encoded_string` 正好重复 `k` 次。注意 `k` 保证为正整数。
-
-你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
-
-此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 `k` ,例如不会出现像 `3a` 或 `2[4]` 的输入。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "3[a]2[bc]"
-> 输出:"aaabcbc"
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = "3[a2[c]]"
-> 输出:"accaccacc"
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:s = "2[abc]3[cd]ef"
-> 输出:"abcabccdcdcdef"
-> ```
->
-> **示例 4:**
->
-> ```
-> 输入:s = "abc3[cd]xyz"
-> 输出:"abccdcdcdxyz"
-> ```
-
-
-
-分析:
-
-这道题跟 224 类似,关键是遇到什么字符的时候,需要入栈;以及遇到什么字符开始出栈。
-
-出栈的时候,要把内容一次性处理。
-
-```go
-// date 2023/12/19
-func decodeString(s string) string {
- strStack := make([]string, 0, 16)
-
- for _, str := range s {
- if len(strStack) == 0 || len(strStack) > 0 && str != ']' {
- strStack = append(strStack, string(str))
- } else {
- // 遇到 ']'
- // 说明前面有可以处理的字符和数字
- // 开始出栈,先出栈 字符串
- tmp := ""
- for strStack[len(strStack)-1] != "[" {
- tmp = strStack[len(strStack)-1] + tmp // 连接字符
- strStack = strStack[:len(strStack)-1]
- }
- // 出栈 '['
- strStack = strStack[:len(strStack)-1]
-
- // 出栈 数字
- idx, repeat := 0, ""
- for idx = len(strStack)-1; idx >= 0; idx-- {
- if strStack[idx] >= "0" && strStack[idx] <= "9" {
- repeat = strStack[idx] + repeat
- } else {
- break
- }
- }
- // 去掉数字
- strStack = strStack[:len(strStack)-len(repeat)]
-
- repeatVal, _ := strconv.Atoi(repeat)
- copyTmp := tmp
- for repeatVal > 1 {
- tmp += copyTmp
- repeatVal--
- }
-
- // 将重复完成的字符串在入栈
- strStack = append(strStack, tmp)
- }
- }
-
- res := ""
- for _, v := range strStack {
- res += v
- }
-
- return res
-}
-```
-
diff --git "a/04_stack/No.456_132\346\250\241\345\274\217.md" "b/04_stack/No.456_132\346\250\241\345\274\217.md"
deleted file mode 100644
index 11e3029..0000000
--- "a/04_stack/No.456_132\346\250\241\345\274\217.md"
+++ /dev/null
@@ -1,90 +0,0 @@
-## 456 132模式-中等
-
-题目:
-
-给你一个整数数组 `nums` ,数组中共有 `n` 个整数。**132 模式的子序列** 由三个整数 `nums[i]`、`nums[j]` 和 `nums[k]` 组成,并同时满足:`i < j < k` 和 `nums[i] < nums[k] < nums[j]` 。
-
-如果 `nums` 中存在 **132 模式的子序列** ,返回 `true` ;否则,返回 `false` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,2,3,4]
-> 输出:false
-> 解释:序列中不存在 132 模式的子序列。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [3,1,4,2]
-> 输出:true
-> 解释:序列中有 1 个 132 模式的子序列: [1, 4, 2] 。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:nums = [-1,3,2,0]
-> 输出:true
-> 解释:序列中有 3 个 132 模式的的子序列:[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。
-> ```
-
-
-
-分析:
-
-这道题可以这样想,先说 123 模式。什么是 123 模式呢?就是简单的单调递增数组。
-
-判断一个数组是不是单调递增有两种方式:
-
-方式1,从前向后遍历,检查每个元素是不是比前一个元素更大。
-
-方式2,从后往前遍历,检查每个元素是不是比后一个元素更小。
-
-在方式2的基础上,把遍历元素依次入栈,那么就是单调递减栈。
-
-单调递减栈,即栈顶小于栈底。
-
-```sh
-// 栈底 -- 栈顶
-// 4,3,2,1
-```
-
-其次,还要叠加从后往前遍历数组,如果 stack 的顺序是我们期望的`4,3,2,1`,那么说明我们已经遍历过的部分数组是单调递增的。
-
-此时,如果有元素打破了这里的单调递减栈,则说明更靠近数组头部的元素出现了较大的值,即我们要找的 `j`出现了,索引在中间,但值更大。
-
-此时,把栈中较小的值依次出栈,保存在 num3 中, 即我们要找的 k,而且,ak 是小于aj里面最大的那个。
-
-那么,再接着往前遍历,只要出现比 ak 还小的元素,那么 132 就成立了。
-
-```go
-// date 2023/12/20
-func find132pattern(nums []int) bool {
- if len(nums) < 3 {
- return false
- }
- // i < j < k
- // ai < ak < aj
- num3 := math.MinInt64
- stack := make([]int, 0, 16)
- for i := len(nums)-1; i >= 0; i-- {
- v := nums[i]
- if v < num3 {
- return true
- }
- // if v > stack[len(stack)-1], so v is aj
- for len(stack) > 0 && v > stack[len(stack)-1] {
- // save the smmal to num3, num3 is ak
- num3 = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- }
- stack = append(stack, v)
- }
- return false
-}
-```
-
diff --git "a/04_stack/No.496_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2401.md" "b/04_stack/No.496_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2401.md"
deleted file mode 100644
index 07e6320..0000000
--- "a/04_stack/No.496_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2401.md"
+++ /dev/null
@@ -1,83 +0,0 @@
-## 496 下一个更大元素1-简单
-
-题目:
-
-`nums1` 中数字 `x` 的 **下一个更大元素** 是指 `x` 在 `nums2` 中对应位置 **右侧** 的 **第一个** 比 `x` 大的元素。
-
-给你两个 **没有重复元素** 的数组 `nums1` 和 `nums2` ,下标从 **0** 开始计数,其中`nums1` 是 `nums2` 的子集。
-
-对于每个 `0 <= i < nums1.length` ,找出满足 `nums1[i] == nums2[j]` 的下标 `j` ,并且在 `nums2` 确定 `nums2[j]` 的 **下一个更大元素** 。如果不存在下一个更大元素,那么本次查询的答案是 `-1` 。
-
-返回一个长度为 `nums1.length` 的数组 `ans` 作为答案,满足 `ans[i]` 是如上所述的 **下一个更大元素** 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
-> 输出:[-1,3,-1]
-> 解释:nums1 中每个值的下一个更大元素如下所述:
-> - 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
-> - 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
-> - 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums1 = [2,4], nums2 = [1,2,3,4].
-> 输出:[3,-1]
-> 解释:nums1 中每个值的下一个更大元素如下所述:
-> - 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
-> - 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
-> ```
-
-
-
-
-
-分析:
-
-下一个更大的元素是指右侧第一个比 x 大的元素,所以可以逆序遍历,使用单调栈保存下一个更大的元素。
-
-遍历的时候,如果单调栈不为空,依次弹出栈顶元素。
-
-此后,如果栈不为空,那么栈顶元素就是下一个更大的元素,否则就是 -1。
-
-因为题目中表明数组的中的元素互不相同,可用 map 存储结果,方便 num1 检索。
-
-```go
-// date 2023/12/18
-func nextGreaterElement(nums1 []int, nums2 []int) []int {
- set := make(map[int]int, 16)
-
- // 寻找右侧 第一个 比 x 大的元素
- // 逆序遍历,单调栈保存右侧第一个比x大的元素
- stack := make([]int, 0, 16)
- for i := len(nums2)-1; i >= 0; i-- {
- v := nums2[i]
- for len(stack) > 0 && v >= stack[len(stack)-1] {
- stack = stack[:len(stack)-1]
- }
- if len(stack) == 0 {
- set[v] = -1
- } else {
- set[v] = stack[len(stack)-1]
- }
- stack = append(stack, v)
- }
- ans := make([]int, len(nums1))
- for i, v1 := range nums1 {
- res, ok := set[v1]
- if ok {
- ans[i] = res
- } else {
- ans[i] = -1
- }
- }
-
- return ans
-}
-```
-
diff --git "a/04_stack/No.503_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2402.md" "b/04_stack/No.503_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2402.md"
deleted file mode 100644
index 50e48a5..0000000
--- "a/04_stack/No.503_\344\270\213\344\270\200\344\270\252\346\233\264\345\244\247\347\232\204\345\205\203\347\264\2402.md"
+++ /dev/null
@@ -1,62 +0,0 @@
-## 503 下一个更大的元素2-中等
-
-题目:
-
-给定一个循环数组 `nums` ( `nums[nums.length - 1]` 的下一个元素是 `nums[0]` ),返回 *`nums` 中每个元素的 **下一个更大元素*** 。
-
-数字 `x` 的 **下一个更大的元素** 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 `-1` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: nums = [1,2,1]
-> 输出: [2,-1,2]
-> 解释: 第一个 1 的下一个更大的数是 2;
-> 数字 2 找不到下一个更大的数;
-> 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: nums = [1,2,3,4,3]
-> 输出: [2,3,4,-1,4]
-> ```
-
-
-
-分析:
-
-输入为循环数组,所以考虑把数组膨胀1倍,然后逆序遍历,求新数组的下一个更大元素。然后只返回结果集的前一半。
-
-```go
-// date 2023/12/18
-func nextGreaterElements(nums []int) []int {
- n := len(nums)
- nums2 := make([]int, 2*n, 2*n)
- for i, v := range nums {
- nums2[i] = v
- nums2[n+i] = v
- }
- stack := make([]int, 0, 16)
- ans := make([]int, 2*n)
- for i := len(nums2)-1; i >= 0; i-- {
- v := nums2[i]
- for len(stack) > 0 && v >= stack[len(stack)-1] {
- stack = stack[:len(stack)-1]
- }
- if len(stack) > 0 {
- ans[i] = stack[len(stack)-1]
- } else {
- ans[i] = -1
- }
- stack = append(stack, v)
- }
-
- ans = ans[:n]
- return ans
-}
-```
-
diff --git "a/04_stack/No.682_\346\243\222\347\220\203\346\257\224\350\265\233.md" "b/04_stack/No.682_\346\243\222\347\220\203\346\257\224\350\265\233.md"
deleted file mode 100644
index 38483a1..0000000
--- "a/04_stack/No.682_\346\243\222\347\220\203\346\257\224\350\265\233.md"
+++ /dev/null
@@ -1,92 +0,0 @@
-## 682 棒球比赛-简单
-
-题目:
-
-你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。
-
-比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 `ops`,其中 `ops[i]` 是你需要记录的第 `i` 项操作,`ops` 遵循下述规则:
-
-1. 整数 `x` - 表示本回合新获得分数 `x`
-2. `"+"` - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
-3. `"D"` - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
-4. `"C"` - 表示前一次得分无效,将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
-
-请你返回记录中所有得分的总和。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:ops = ["5","2","C","D","+"]
-> 输出:30
-> 解释:
-> "5" - 记录加 5 ,记录现在是 [5]
-> "2" - 记录加 2 ,记录现在是 [5, 2]
-> "C" - 使前一次得分的记录无效并将其移除,记录现在是 [5].
-> "D" - 记录加 2 * 5 = 10 ,记录现在是 [5, 10].
-> "+" - 记录加 5 + 10 = 15 ,记录现在是 [5, 10, 15].
-> 所有得分的总和 5 + 10 + 15 = 30
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:ops = ["5","-2","4","C","D","9","+","+"]
-> 输出:27
-> 解释:
-> "5" - 记录加 5 ,记录现在是 [5]
-> "-2" - 记录加 -2 ,记录现在是 [5, -2]
-> "4" - 记录加 4 ,记录现在是 [5, -2, 4]
-> "C" - 使前一次得分的记录无效并将其移除,记录现在是 [5, -2]
-> "D" - 记录加 2 * -2 = -4 ,记录现在是 [5, -2, -4]
-> "9" - 记录加 9 ,记录现在是 [5, -2, -4, 9]
-> "+" - 记录加 -4 + 9 = 5 ,记录现在是 [5, -2, -4, 9, 5]
-> "+" - 记录加 9 + 5 = 14 ,记录现在是 [5, -2, -4, 9, 5, 14]
-> 所有得分的总和 5 + -2 + -4 + 9 + 5 + 14 = 27
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:ops = ["1"]
-> 输出:1
-> ```
-
-
-
-分析:
-
-按每个字符的含义去处理即可,用栈记录所有的得分,最后汇总得分。
-
-```go
-func calPoints(operations []string) int {
- numStack := make([]int, 0, 16)
- for _, str := range operations {
- if str == "+" {
- n := len(numStack)
- v := numStack[n-1] + numStack[n-2]
-
- numStack = append(numStack, v)
- } else if str == "D" {
- v := 2 * numStack[len(numStack)-1]
-
- numStack = append(numStack, v)
- } else if str == "C" {
- numStack = numStack[:len(numStack)-1]
- } else {
- v, _ := strconv.Atoi(str)
-
- numStack = append(numStack, v)
- }
- }
- sum := int(0)
-
- for _, num := range numStack {
- sum += num
- }
-
- return sum
-}
-```
-
diff --git "a/04_stack/No.739_\346\257\217\346\227\245\346\270\251\345\272\246.md" "b/04_stack/No.739_\346\257\217\346\227\245\346\270\251\345\272\246.md"
deleted file mode 100644
index 467a995..0000000
--- "a/04_stack/No.739_\346\257\217\346\227\245\346\270\251\345\272\246.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 739 每日温度-中等
-
-题目:
-
-给定一个整数数组 `temperatures` ,表示每天的温度,返回一个数组 `answer` ,其中 `answer[i]` 是指对于第 `i` 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 `0` 来代替。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: temperatures = [73,74,75,71,69,72,76,73]
-> 输出: [1,1,4,2,1,1,0,0]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: temperatures = [30,40,50,60]
-> 输出: [1,1,1,0]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入: temperatures = [30,60,90]
-> 输出: [1,1,0]
-> ```
-
-
-
-分析:
-
-正序遍历,维护一个单调递减栈,当出现大于栈顶元素的时候,在出栈更新。
-
-栈里面放的数组索引,比较出栈的时候是取温度。
-
-```go
-// date 2023/12/21
-func dailyTemperatures(temperatures []int) []int {
- stack := make([]int, 0, 16)
- n := len(temperatures)
- ans := make([]int, n, n)
-
- for i := 0; i < n; i++ {
- v := temperatures[i]
-
- for len(stack) > 0 && v > temperatures[stack[len(stack)-1]] {
- preIdx := stack[len(stack)-1]
- ans[preIdx] = i - preIdx
- stack = stack[:len(stack)-1]
- }
- stack = append(stack, i)
- // 没有出栈之前,一直入栈,那么则说明 v 一直小于栈顶元素
- // 栈是单调递减的,对应的数组也是单调递减的
- // 栈维护的是温度单调递减
- // 只要出现一个v比栈顶大的,那么栈里面比 v 小的都可以更新掉
- }
-
- return ans
-}
-```
-
diff --git "a/04_stack/No.856_\346\213\254\345\217\267\347\232\204\345\210\206\346\225\260.md" "b/04_stack/No.856_\346\213\254\345\217\267\347\232\204\345\210\206\346\225\260.md"
deleted file mode 100644
index 10c3da2..0000000
--- "a/04_stack/No.856_\346\213\254\345\217\267\347\232\204\345\210\206\346\225\260.md"
+++ /dev/null
@@ -1,88 +0,0 @@
-## 856 括号的分数-中等
-
-题目:
-
-给定一个平衡括号字符串 `S`,按下述规则计算该字符串的分数:
-
-- `()` 得 1 分。
-- `AB` 得 `A + B` 分,其中 A 和 B 是平衡括号字符串。
-- `(A)` 得 `2 * A` 分,其中 A 是平衡括号字符串。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: "()"
-> 输出: 1
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: "(())"
-> 输出: 2
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入: "()()"
-> 输出: 2
-> ```
->
-> **示例 4:**
->
-> ```
-> 输入: "(()(()))"
-> 输出: 6
-> ```
-
-
-
-分析:
-
-还是入栈,出栈的思路。
-
-遇到`)`开始出栈,通过栈中已有的元素来判断,题目中所说的三种情况:
-
-- 如果前一个为-1,即temp == 0,表示得1分
-- 如果前一个不为-1,即 stack 中的得分是 A+B 形式,需要累计;并且需要扩大1倍
-
-```go
-// date 2023/12/19
-func scoreOfParentheses(s string) int {
- res := 0
- stack := make([]int, 0, 16) // score stack
-
- for _, str := range s {
- if str == '(' {
- stack = append(stack, -1)
- } else { // ')'
- // 取出之前的数据
- // 如果紧挨着 -1,得分为1
- // 否则就是 A+B 形式, 求和
- temp := 0
- for stack[len(stack)-1] != -1 {
- temp += stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- }
-
- // 去掉 -1
- stack = stack[:len(stack)-1]
-
- if temp == 0 {
- stack = append(stack, 1)
- } else {
- stack = append(stack, 2*temp)
- }
- }
- }
- for _, v := range stack {
- res += v
- }
-
- return res
-}
-```
-
diff --git "a/04_stack/No.921_\344\275\277\346\213\254\345\217\267\346\234\211\346\225\210\347\232\204\346\234\200\345\260\221\346\267\273\345\212\240.md" "b/04_stack/No.921_\344\275\277\346\213\254\345\217\267\346\234\211\346\225\210\347\232\204\346\234\200\345\260\221\346\267\273\345\212\240.md"
deleted file mode 100644
index 80726dc..0000000
--- "a/04_stack/No.921_\344\275\277\346\213\254\345\217\267\346\234\211\346\225\210\347\232\204\346\234\200\345\260\221\346\267\273\345\212\240.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 921 使括号有效的最少添加-简单
-
-题目:
-
-只有满足下面几点之一,括号字符串才是有效的:
-
-- 它是一个空字符串,或者
-- 它可以被写成 `AB` (`A` 与 `B` 连接), 其中 `A` 和 `B` 都是有效字符串,或者
-- 它可以被写作 `(A)`,其中 `A` 是有效字符串。
-
-给定一个括号字符串 `s` ,在每一次操作中,你都可以在字符串的任何位置插入一个括号
-
-- 例如,如果 `s = "()))"` ,你可以插入一个开始括号为 `"(()))"` 或结束括号为 `"())))"` 。
-
-返回 *为使结果字符串 `s` 有效而必须添加的最少括号数*。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "())"
-> 输出:1
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = "((("
-> 输出:3
-> ```
-
-
-
-分析:
-
-这个问题跟第 20 题(有效括号)类似,第 20 题是判断一个字符串是否是有效的括号,通过对左括号入栈,右括号出栈的操作,判断最后栈是否为空来判断括号是否有效。
-
-这个题目也是类似,能出栈的时候就出栈,不能出栈了,表示需要添加一个,直接计数返回即可。
-
-```go
-// date 2023/12/18
-func minAddToMakeValid(s string) int {
- res := 0
- stack := make([]rune, 0, 16)
-
- for _, v := range s {
- if v == '(' {
- stack = append(stack, v)
- } else if v == ')' {
- if len(stack) > 0 {
- stack = stack[:len(stack)-1]
- } else {
- res++
- }
- }
- }
- if len(stack) > 0 {
- res += len(stack)
- }
- return res
-}
-```
-
diff --git "a/04_stack/No.946_\351\252\214\350\257\201\346\240\210\345\272\217\345\210\227.md" "b/04_stack/No.946_\351\252\214\350\257\201\346\240\210\345\272\217\345\210\227.md"
deleted file mode 100644
index b2d30ca..0000000
--- "a/04_stack/No.946_\351\252\214\350\257\201\346\240\210\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,53 +0,0 @@
-## 946 验证栈序列-中等
-
-题目:
-
-给定 `pushed` 和 `popped` 两个序列,每个序列中的 **值都不重复**,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 `true`;否则,返回 `false` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
-> 输出:true
-> 解释:我们可以按以下顺序执行:
-> push(1), push(2), push(3), push(4), pop() -> 4,
-> push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
-> 输出:false
-> 解释:1 不能在 2 之前弹出。
-> ```
-
-
-
-分析:
-
-思路就是按照入栈队列依次入栈,取栈顶元素看看是不是在出栈序列中,如果在出栈。
-
-如果入栈序列和出栈序列能够契合,那么出栈的指针就会走到最后,否则不会。
-
-```go
-// date 2023/12/18
-func validateStackSequences(pushed []int, popped []int) bool {
- stack := make([]int, 0, 16)
- j := 0
- n := len(pushed)
-
- for _, v := range pushed {
- stack = append(stack, v)
-
- for len(stack) > 0 && j < n && stack[len(stack)-1] == popped[j] {
- stack = stack[:len(stack)-1]
- j++
- }
- }
- return j == n
-}
-```
-
diff --git a/04_stack/README.md b/04_stack/README.md
deleted file mode 100644
index a3ffd1d..0000000
--- a/04_stack/README.md
+++ /dev/null
@@ -1,43 +0,0 @@
-## stack
-
-
-
-## 题目介绍
-
-第一类:括号匹配,及其类似的问题
-
-比如:
-
-- 第 20 题:有效括号
-- 第 921 题:使括号有效的最少添加
-- 第 1021 题:删除最外层的括号
-
-
-
-第二类:常规的 push、pop 操作
-
-- 第 71 题:简化路径
-- 第 150 题:逆波兰表达式计算
-- 第 155 题:最小栈
-- 第 224 题:基本计算器【重点看】
-- 第 225 题:用队列实现栈
-- 第 232 题:用栈实现队列
-- 第 946 题:验证栈序列
-- 第 1047 题:删除字符串中的所有相邻重复项
-
-
-
-第三类:利用栈进行编码问题
-
-- 第 394 题:字符串编码【重点看,注意细节】
-- 第 682 题:棒球比赛
-- 第 856 题:括号的分数【重点看,看思路】
-
-
-
-第四类:单调栈。利用栈维护一个单调递增或单调递减的下标数组。
-
-- 第 456 题:132 模式【重点看】
-- 第 496 题:下一个更大的元素1
-- 第 503 题:下一个更大的元素2
-- 第 739 题:每日温度【单调栈思路,重点思路】
diff --git a/04_stack/stack.md b/04_stack/stack.md
deleted file mode 100644
index 816ab4b..0000000
--- a/04_stack/stack.md
+++ /dev/null
@@ -1,814 +0,0 @@
-## 栈
-
-[TOC]
-
-### 栈的基本操作
-
- + push(x):将元素x加入到栈中
- + pop():弹出栈顶元素,但是,**不会返回弹出元素的值**
- + top():取出栈顶元素,但是,**不会弹出栈顶元素**
- + empty():判断栈是否为空,当栈为空时,返回true
- + size():返回栈中的元素个数
-
-### 栈的实现
-
-从时间复杂度角度而言,push(), pop(), top(),empty()操作只需要O(1)的时间。从实现角度而言,栈的的实现方式有两种,**数组和线性表**。
-
-### C++
-
-```cpp
-#define MAX 1000
-class Stack
-{
-private:
- int top;
-public:
- int a[MAX];
- Stack() {top = -1;}
- bool push(int x);
- int pop();
- bool empty();
-};
-// 入栈
-bool Stack::push(int x) {
- if(top >= MAX) {
- cout << "Stack Overflow";
- return false;
- } else {
- a[++top] = x;
- return true;
- }
-}
-// 出栈,一般情况下不带返回,直接删除元素;而自己写的函数可以允许删除的时候返回元素的值
-int Stack::pop() {
- if(top < 0) {
- cout << "Stack Underflow";
- return 0;
- } else {
- int x = a[top--];
- return x;
- }
-}
-// 空判断
-bool Stack::empty() {
- return (top < 0)
-}
-```
-
-### Python
-
-```python
-class Stack:
- """模拟栈的基本操作"""
- # 初始化
- def __init__(self):
- self.item = []
- # 判空
- def isEmpty(self):
- return len(self.item) == 0
- # 压栈
- def push(self, data):
- self.item.append(data)
- # 出栈
- def pop(self):
- if not self.isEmpty():
- return self.item.pop()
- # 去栈顶元素
- def top(self):
- if not self.isEmpty():
- return self.item[len(self.item)-1]
- # 栈的大小
- def size(self):
- return len(self.item)
-```
-
-### 栈的应用
-
-栈的主要应用包括:运算符的优先级,字符串反转。
-
-### 由队列实现栈
-
-```cpp
-#include
-#include
-using namespace std;
-class MyStack {
-private:
- queue q;
-public:
- void Push(int x);
- void Pop();
- int Top();
- bool Empty();
- int Size();
-};
-// 压栈
-void MyStack::Push(int x) {
- q.push(x);
-}
-// 出栈
-void MyStack::Pop() {
- if(q.size() == 0) {
- cout << "The Stack is Empty" << endl;
- return;
- }
- if(q.size() == 1)
- q.pop();
- else {
- int n = q.size();
- while(n > 1) {
- q.push(q.front());
- q.pop();
- n--;
- }
- q.pop();
- }
-}
-// 获取栈顶元素
-int MyStack::Top() {
- if(q.size() == 0) {
- cout << "The Stack is Empty" << endl;
- return -1;
- }
- if(q.size() == 1)
- return q.front();
- else {
- int n = q.size();
- while(n > 1) {
- q.push(q.front());
- q.pop();
- n--;
- }
- return q.front();
- }
-}
-// 判断栈是否为空
-bool MyStack::Empty() {
- return q.empty();
-}
-// 获取栈中元素的个数
-int MyStack::Size() {
- return q.size();
-}
-```
-
-### 栈的反转
-
-利用迭代思想,实现栈的反转,只能使用push(),pop(),empty(),size()操作。
-
-```
-栈: 栈:
-4 -> top 1 -> top
-3 反转后 2
-2 3
-1 4
-```
-
-分析:栈的标准push()是向栈顶压入新元素,如果将push()改为向栈底压入新元素,那么就可以利用empty(),pop()来递归实现栈的反转。
-
-```cpp
-stack st;
-void push_bottom(int x) {
- if(st.size() == 0)
- st.push(x);
- else {
- int temp = st.top();
- st.pop();
- push_bottom(x);
- st.push(temp);
- }
-}
-void Reverse() {
- if(st.size() > 0) {
- int x = st.top();
- st.pop();
- Reverse();
- push_bottom(x);
- }
-}
-```
-
-* Python
-
-```Python
-def insertAtBottom(stack, item):
- if isEmpty(stack):
- push(stack, item)
- else:
- temp = pop(stack)
- insertAtBottom(stack, item)
- push(stack, temp)
-
-# Below is the function that reverses the given stack
-# using insertAtBottom()
-def reverse(stack):
- if not isEmpty(stack):
- temp = pop(stack)
- reverse(stack)
- insertAtBottom(stack, temp)
-```
-
-### 栈的排序
-
-注意:利用递归思想,只能使用栈的基本操作。
-
-### 算法分析
-
-```
-// 排序
-sortStack(stack S)
- if stack is not empty:
- temp = pop(S);
- sortStack(S);
- sortedInsert(S, temp);
-// 向已排序的栈中插入元素
-sortedInsert(Stack S, element)
- if stack is empty OR element > top element
- push(S, elem)
- else
- temp = pop(S)
- sortedInsert(S, element)
- push(S, temp)
-```
-
-### 算法实现
-
-* C++
-
-```cpp
-// 递归实现向已排序栈中插入元素
-void SortedInsert(stack &s, int x)
-{
- if(s.empty() || x > s.top()) {
- s.push(x);
- return;
- }
- int temp = s.top();
- s.pop();
- SortedInsert(s, x);
- s.push(temp);
-}
-// 排序
-void StackSort(stack &s) {
- if(!s.empty()) {
- int temp = s.top();
- s.pop();
- StackSort(s);
- SortedInsert(s, temp);
- }
-}
-```
-
-* Python
-
-```Python
-def SortedInsert(s, x):
- if s.isEmpty() or x > s.top():
- s.push(x)
- return;
- else:
- temp = s.top()
- s.pop()
- SortedInsert(s, x)
- s.push(temp)
-
-def StackSort(s):
- if not s.isEmpty():
- temp = s.top()
- s.pop()
- StackSort(s)
- SortedInsert(s, temp)
-```
-
-### SpecialStack
-
-实现一种特殊的栈结构,让其push(),pop(),empty(),getmin()的四种操作的时间复杂度为O(1)。
-
-```
-// 继承上面栈的实现部分,Stack类
-class SpecialStack: public Stack
-{
-private:
- Stack min;
-public:
- int pop();
- void push(int x);
- int getmin();
-};
-// 入栈
-void SpecialStack::push(int x) {
- if(empty()) {
- Stack::push(x);
- min.push(x);
- } else {
- Stack::push(x);
- int y = min.pop();
- min.push(y);
- if(x < y)
- min.push(x);
- else
- min.push(y);
- }
-}
-// 出栈
-int SpecialStack::pop() {
- int x = Stack::pop();
- min.pop();
- return x;
-}
-// getmin
-int SpecialStack::getmin() {
- int x = min.pop();
- min.push(x);
- return x;
-}
-```
-
-### 相关题目
-
-#### 二叉搜索树的前序序列判断
-
-问题描述
-
-给定一个数组,判断其是否为一个二叉搜索树的前序遍历,并且要求时间复杂度为O(n)。
-
-提示:左节点的值 小于 根节点的值 小于或等于 右节点的值,满足二叉搜索树的特征。
-
-算法分析
-
-这个问题与NGE问题类似,可以采用栈进行求解。算法如下:
-
-```
-1. 创建一个空栈
-2. 初始化root = INT_MIN
-3. 遍历每一个节点pre[i]
- a) If pre[i] is smaller than current root, return false.
- b) Keep removing elements from stack while pre[i] is greater than stack top.
- Make the last removed item as new root.
- At this point, pre[i] is greater than the removed root.
- c) push pre[i] to stack (All elements in stack are in decreasing order.
-```
-
-算法实现
-
-```cpp
-bool BSTCheck(int pre[], int n) {
- stack s;
- int root = INT_MIN;
- for(int i = 0; i < n; i++) {
- if(pre[i] < root)
- return false;
- while(!s.empty() && s.top() < pre[i]) {
- // 进入到while(),则说明存在右子树
- root = s.top();
- s.pop();
- }
- // 压入左子树的根节点
- s.push(pre[i]);
- }
- return true;
-}
-```
-
-#### Next Greater Element
-
-问题定义
-
-给定一个整型数组array[n],输出数组中每个元素对应的下一个比其大元素(NGE)。其规则如下:
-
-+ 对于最后一个元素,其NGE = -1;
-+ 对于一个非递增数组,所有元素的NGE均为-1
-
-例如,数组{4, 5, 2, 25}对应的NGE数组为{5, 25, 25, -1}。
-
-算法分析
-
-方法一:两层循环,外层循环负责检查每个元素,内层循环负责选取后面元素中第一个比其大的元素。
-
-方法二:利用stack。
-
-1) 创建两个栈s和s2,s,s2均存储存储当前元素至末尾元素的的元素序列,s用于判决比较,s2用于覆盖s。
-2)当s不为空时,若s栈顶元素大于当前元素,则NGE = s.top(),否则,s.pop()后继续判断。
-3)若s为空时,仍没有找到大于当前元素的值,则NGE = -1。
-
-算法实现
-
-```cpp
-void NextGreaterElement(int arr[], int n) {
- if(n < 1)
- return;
- int nge[n];
- stack s, s2;
- nge[n - 1] = -1;
- s.push(arr[n - 1]);
- s2.push(arr[n - 1]);
- int i, j;
- for(i = n - 2; i >= 0; i--) {
- s2.push(arr[i]);
- while(!s.empty()) {
- int x = s.top();
- if(arr[i] < x) {
- nge[i] = x;
- break;
- } else {
- s.pop();
- }
- }
- if(s.empty()) {
- nge[i] = -1;
- }
- s = s2;
- }
- for(i = 0; i < n; i++)
- cout << arr[i] << "--" << nge[i] << endl;;
-}
-```
-
-#### Middle Stack
-
-问题定义
-
-设计并实现一种特殊栈结构,具有以下四种操作,且四种操作的时间复杂度均为O(1)。
-
-1) push() which adds an element to the top of stack.
-2) pop() which removes an element from top of stack.
-3) findMiddle() which will return middle element of the stack.
-4) deleteMiddle() which will delete the middle element.
-其中push()和pop()操作属于栈的标准操作。
-
-算法分析
-
-栈的底层实现是利用数组或线性表来进行构建的。对于push(),pop()和findMiddle()操作,数组可满足O(1)时间复杂度,但是deleteMiddle()设计元素的移动,数组无法满足。同样,单链表也无法满足两个方向(即,push()和pop())上的中间元素的移动。
-
-因此,我们利用双向链表来实现这一特殊的栈结构。
-
-算法实现
-
-```cpp
-// 双链表
-struct Node {
- struct Node *pre, *next;
- int val;
-};
-// 栈结构
-struct MyStack {
- struct Node *head;
- struct Node *mid;
- int count;
-};
-// 初始化
-struct MyStack *CreateStack() {
- MyStack *ms = (MyStack*)malloc(sizeof(struct MyStack));
- ms->count = 0;
- return ms;
-}
-// 入栈
-void Push(struct MyStack *ms, int x) {
- struct Node *data = (struct Node*)malloc(sizeof(struct Node));
- data->val = x;
- data->pre = NULL;
- data->next = ms->head;
- ms->count += 1;
- // 第一个元素
- if(ms->count == 1) {
- ms->mid = data;
- } else {
- // 让栈顶的元素指向新元素
- ms->head->pre = data;
- // 当有奇数个元素时,mid指针才发生一次移动
- if(ms->count & 1)
- ms->mid = ms->mid->pre;
- }
- ms->head = data;
-}
-// 出栈
-int Pop(struct MyStack *ms) {
- if(ms->count == 0) {
- cout << "Stack is Empty" << endl;
- return -1;
- }
- struct Node *temp = ms->head;
- int x = temp->val;
- ms->head = temp->next;
- if(ms->head != NULL)
- ms->head->pre = NULL;
- ms->count -= 1;
- // 元素个数由奇数变为偶数时,mid指针需要移动
- if(!(ms->count & 1))
- ms->mid = ms->mid->next;
- free(temp);
- return x;
-}
-// 取”栈中“元素
-int FindMiddle(struct MyStack *ms) {
- if(ms->count == 0) {
- cout << "Stack is Empty" << endl;
- return -1;
- } else {
- return ms->mid->val;
- }
-}
-// 删除”栈中“元素
-int DeleteMiddle(struct MyStack *ms) {
- if(ms->count == 0) {
- cout << "Stack is Empty" << endl;
- return -1;
- }
- struct Node *temp = ms->mid;
- int x = temp->val;
- ms->count -= 1;
- // 元素个数由偶数变为奇数,mid指针向pre方向移动
- if((ms->count) & 1) {
- ms->mid = temp->pre;
- if(ms->count == 1) {
- ms->mid->next = NULL;
- } else {
- temp->next->pre = ms->mid;
- ms->mid->next = temp->next;
- }
- } else {
- // 元素个数由奇数变为偶数,mid指针向next方向移动
- if(ms->count == 0) {
- ms->head = NULL;
- ms->mid = NULL;
- } else {
- ms->mid = temp->next;
- temp->pre->next = ms->mid;
- ms->mid->pre = temp->pre;
- }
- }
- free(temp);
- return x;
-}
-```
-
-#### 队列与栈的有限操作间的转换
-
-题目一:已知Stack类及其3个方法Push()、Pop()和 Count(),请用2个Stack实现Queue类的入队(Enqueue)、出队(Dequeue)方法以及判空(Empty)操作。*注意,这里假定Pop()操作可以获得元素的值*。
-
-题目主要考察对基本数据结构的理解,以及操作的转换。
-
-面试公司:VMware
-
-**提示**:
-
-两个栈A和B,栈A提供入队操作,栈B提供出队操作,算法如下:
-
-1)如果栈B不为空,直接弹出栈B的元素;
-2)如果栈B为空,则依次弹出栈A的元素,放入栈B中,再弹出栈B的元素.
-
-```cpp
-// Using Stack implement the Queue's Operations
-// Stack's Operations: s.push(x) s.pop() s.size()
-// Queue's Operations: q.enqueue(x) q.dequeue() q.empty()
-class MyQueue {
-private:
- stack s; // 用于入队
- stack s2; // 用于出队
-public:
- void enqueue(int x);
- void dequeue(int &x);
- bool empty();
-};
-// 入队
-void MyQueue::enqueue(int x) {
- s.push(x);
-}
-// 出队
-void MyQueue::dequeue(int &x) {
- int temp;
- if(s2.size() == 0) {
- if(s.size() == 0) {
- cout << "The Queue is Empty" << endl;
- } else {
- while(s.size() > 0) {
- s.pop(&temp);
- s2.push(temp);
- }
- }
- }
- if(s2.size() != 0)
- s2.pop(&x);
-}
-// 判断队列是否为空
-bool MyQueue::empty() {
- return ((s.size() == 0) && (s2.size() == 0));
-}
-```
-
-#### 由队列实现栈
-
-Queue的操作包括enqueue(),dequeue(),Stack的操作包括push(),pop()。
-
-方法一
-
-使用两个queue,即q1,q2。每个新加入的元素,均位于q1的队头,因此,pop()操作,直接dequeue即可。q2用于保存新加入的元素。这个情况下,push()操作具有较高的复杂度。
-
-算法分析
-
-```
-push(s, x) // x is the element to be pushed and s is stack
- 1) Enqueue x to q2
- 2) One by one dequeue everything from q1 and enqueue to q2.
- 3) Swap the names of q1 and q2
-
-pop(s)
- 1) Dequeue an item from q1 and return it.
-```
-
-方法二
-
-这个方法与方法一类似,只是pop()操作的复杂度相对高。
-
-算法分析
-
-```
-push(s, x)
- 1) Enqueue x to q1 (assuming size of q1 is unlimited).
-
-pop(s)
- 1) One by one dequeue everything except the last element from q1 and enqueue to q2.
- 2) Dequeue the last item of q1, the dequeued item is result, store it.
- 3) Swap the names of q1 and q2
- 4) Return the item stored in step 2.
-```
-
-方法三
-
-只使用一个Queue,即每次push()的时候将元素放在队列的队头。
-
-算法实现
-
-```cpp
-class MyStack
-{
- queue q;
-public:
- void push(int x);
- void pop();
- int top();
- bool empty();
-};
-// 压栈
-void MyStack::push(int x) {
- int s = q.size();
- q.push(x);
- // 将之前的元素依次加入到队列的尾部
- for(int i = 0; i < s; i++) {
- q.push(q.front());
- q.pop();
- }
-}
-// 出栈
-void MyStack::pop() {
- if(q.empty())
- cout << "Stack is Underflow";
- else
- q.pop();
-}
-// 栈顶元素
-int MyStack::top() {
- if(q.empty()) {
- cout << "Stack is Underflow";
- return -1;
- } else {
- return q.front();
- }
-}
-// 判空
-bool MyStack::empty() {
- return q.empty();
-}
-```
-
-#### twoStack
-
-利用数组Array实现一种双栈数据结构twoStack,towStack满足以下功能:
-
-+ push1(int x):向栈1压入元素x
-+ push2(int x):向栈2压入元素x
-+ pop1():删除栈1中的栈顶元素,并返回删除的元素值
-+ pop2():删除栈2中的栈顶元素,并返回删除的元素值
-
-注意:实现twoStack的过程中尽量保证空间效率。
-
-分析:
-
-第一种方法,将数组分为两部分,array[0]~array[n/2]用于栈1,array[n/2+1]~array[n-1]用于栈2。但是这个情况下存在的问题是,当其中的一个栈满时,而另一个栈可能还有可用空间,造成空间上的浪费。
-
-第二种方法,分别将数组array[0]和array[n-1]作为两个栈的栈底,从数组两端向中间开始存储数据,当index1(栈1)和index2(栈2)相等时,栈满。
-
-下面基本第二种方法进行实现:
-
-* C++
-
-```cpp
-class twoStack()
-{
-private:
- int *arr;
- int size;
- int top1, top2;
-public:
- twoStack(int n);
- bool push1(int x);
- bool push2(int x);
- int pop1();
- int pop2();
-}
-// 初始化
-void twoStack::twoStack(int n) {
- size = n;
- arr = new int[n];
- top1 = -1;
- top2 = size;
-}
-// 栈1-入栈
-bool twoStack::push1(int x) {
- if(top1 < top2 - 1) {
- arr[++top1] = x;
- return true;
- } else {
- cout << "Stack is Overflow";
- exit(1);
- }
-}
-// 栈2-入栈
-bool twoStack::push2(int x) {
- if(top1 < top2 - 1) {
- arr[--top2] = x;
- return true;
- } else {
- cout << "Stack is Overflow";
- exit(1);
- }
-}
-// 栈1-出栈
-int twoStack::pop1() {
- if(top1 >= 0) {
- int x = arr[top1];
- top1--;
- return x;
- } else {
- cout << "Stack1 is Empty";
- exit(1);
- }
-}
-// 栈2-出栈
-int twoStack::pop2() {
- if(top2 <= size) {
- int x = arr[top2];
- top2++;
- return x;
- } else {
- cout << "Stack2 is Empty";
- exit(1);
- }
-}
-```
-
-* Python
-
-```Python
-class twoStack:
-
- def __init__(self, n):
- self.size = n;
- self.arr = [None] * n;
- self.top1 = -1;
- self.top2 = self.size
-
- def push1(self, x):
- if self.top1 < self.top2 - 1:
- self.top1 = self.top1 + 1
- self.arr[self.top1] = x
- else:
- print("Stack is Overflow")
- exit(1)
-
- def push2(self, x):
- if self.top1 < self.top2 - 1:
- self.top2 = self.top2 - 1
- self.arr[self.top2] = x
- else:
- print("Stack is Overflow")
- exit(1)
-
- def pop1(self):
- if self.top1 >= 0:
- x = self.arr[self.top1]
- self.top1 = self.top1 - 1
- return x
- else:
- print("Stack is Underflow")
- exit(1)
-
- def pop2(self):
- if self.top2 <= self.size:
- x = self.arr[self.top2]
- self.top2 = self.top2 - 1
- return x
- else:
- print("Stack is Underflow")
- exit(1)
-```
diff --git "a/05_string/No.003_\346\227\240\351\207\215\345\244\215\345\255\227\347\254\246\347\232\204\346\234\200\351\225\277\345\255\220\344\270\262.md" "b/05_string/No.003_\346\227\240\351\207\215\345\244\215\345\255\227\347\254\246\347\232\204\346\234\200\351\225\277\345\255\220\344\270\262.md"
deleted file mode 100644
index 8319f21..0000000
--- "a/05_string/No.003_\346\227\240\351\207\215\345\244\215\345\255\227\347\254\246\347\232\204\346\234\200\351\225\277\345\255\220\344\270\262.md"
+++ /dev/null
@@ -1,46 +0,0 @@
-## 3 无重复字符的最长子串
-
-题目:
-
-给定一个字符串 `s` ,请你找出其中不含有重复字符的 **最长子串** 的长度。
-
-
-
-**解题思路**
-
-- 滑动窗口,详见解法1。具体是初始化一个数组 list,保存遍历过的元素;以及 left,right 两个指针,移动 right 并将元素加入 list;前置判断,如果 list 不为空,且包含当前元素,则移除最早加入的元素,Left 指针递增;左右指针的差就是不含重复字符的子串,求其最大长度即可。
-
-```go
-// date 2022/09/29
-func lengthOfLongestSubstring(s string) int {
- left, right := 0, 0
- ans, n := 0, len(s)
- list := make([]uint8, 0, 64) // 需要判断是否重复,list存在窗口的元素
- // 构造窗口
- for right < n {
- // 当窗口不在满足条件,即当前元素s[right]已经出现重复
- // 增加left指针,使窗口缩写
- for len(list) != 0 && isContains(s[right], list) {
- list = list[1:]
- left++
- }
- // 增加right
- list = append(list, s[right])
- right++
- if right - left > ans {
- ans = right - left
- }
- }
- return ans
-}
-
-func isContains(c uint8, list []uint8) bool {
- for _, v := range list {
- if v == c {
- return true
- }
- }
- return false
-}
-```
-
diff --git "a/05_string/No.005_\346\234\200\351\225\277\345\233\236\346\226\207\345\255\227\347\254\246\344\270\262.md" "b/05_string/No.005_\346\234\200\351\225\277\345\233\236\346\226\207\345\255\227\347\254\246\344\270\262.md"
deleted file mode 100644
index 4bb4638..0000000
--- "a/05_string/No.005_\346\234\200\351\225\277\345\233\236\346\226\207\345\255\227\347\254\246\344\270\262.md"
+++ /dev/null
@@ -1,41 +0,0 @@
-## 5 最长回文字符串-中等
-
-题目:
-
-给你一个字符串 `s`,找到 `s` 中最长的回文子串。
-
-如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
-
-
-
-分析:
-
-从中心到两边的双指针。
-
-```go
-// date 2023/12/09
-func longestPalindrome(s string) string {
- n := len(s)
- res := ""
- for i:= 0; i < n; i++ {
- s1 := palindrome(s, i, i)
- s2 := palindrome(s, i, i+1)
- if len(s1) > len(res) {
- res = s1
- }
- if len(s2) > len(res) {
- res = s2
- }
- }
- return res
-}
-
-func palindrome(s string, l, r int) string {
- for l >= 0 && r < len(s) && s[l] == s[r] {
- l--
- r++
- }
- return string(s[l+1:r])
-}
-```
-
diff --git "a/05_string/No.020_\346\234\211\346\225\210\346\213\254\345\217\267.md" "b/05_string/No.020_\346\234\211\346\225\210\346\213\254\345\217\267.md"
deleted file mode 100644
index 2f3e776..0000000
--- "a/05_string/No.020_\346\234\211\346\225\210\346\213\254\345\217\267.md"
+++ /dev/null
@@ -1,49 +0,0 @@
-## 20 有效的括号
-
-题目要求:
-
-给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
-
-有效字符串需满足:
-
-左括号必须用相同类型的右括号闭合。
-左括号必须以正确的顺序闭合。
-每个右括号都有一个对应的相同类型的左括号。
-
-题目链接:https://leetcode.cn/problems/valid-parentheses
-
-
-思路分析:stack数据结构,压栈及出栈
-
-算法如下:时间复杂度O(n) 空间复杂度O(1)
-
-```go
-// date 2020/01/06
-/* 算法:
- 0. 如果字符串长度为单数,直接返回false.
- 1. 遇到左括号,入栈
- 2. 遇到右括号,判断栈是否为空,如果为空,返回false
- 3. 如果不为空,出栈
- 4. 遍历结束后,判断栈是否为空。
-*/
-func isValid(s string) bool {
- if len(s) & 0x1 == 1 {return false}
- stack := make([]rune, 0)
- var c rune
- for _, v := range s {
- if v == '(' || v == '{' || v == '[' {
- stack = append(stack, v)
- } else {
- if len(stack) == 0 {return false}
- c = stack[len(stack)-1]
- if v == ')' && c == '(' || v == '}' && c == '{' || v == ']' && c == '[' {
- stack = stack[:len(stack)-1]
- } else {
- return false
- }
- }
- }
- return len(stack) == 0
-}
-```
-
diff --git "a/05_string/No.028_\346\211\276\345\207\272\345\255\227\347\254\246\344\270\262\344\270\255\347\254\254\344\270\200\344\270\252\345\214\271\351\205\215\351\241\271\347\232\204\344\270\213\346\240\207.md" "b/05_string/No.028_\346\211\276\345\207\272\345\255\227\347\254\246\344\270\262\344\270\255\347\254\254\344\270\200\344\270\252\345\214\271\351\205\215\351\241\271\347\232\204\344\270\213\346\240\207.md"
deleted file mode 100644
index 2ac87a1..0000000
--- "a/05_string/No.028_\346\211\276\345\207\272\345\255\227\347\254\246\344\270\262\344\270\255\347\254\254\344\270\200\344\270\252\345\214\271\351\205\215\351\241\271\347\232\204\344\270\213\346\240\207.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 28 找出字符串中第一个匹配项的下标-简单
-
-题目:
-
-给你两个字符串 `haystack` 和 `needle` ,请你在 `haystack` 字符串中找出 `needle` 字符串的第一个匹配项的下标(下标从 0 开始)。如果 `needle` 不是 `haystack` 的一部分,则返回 `-1` 。
-
-
-
-分析:
-
-单指针,逐位匹配。
-
-超过匹配长度时,注意剪枝。
-
-```go
-// date 2023/12/10
-func strStr(haystack string, needle string) int {
- s1, s2 := len(haystack), len(needle)
- if s1 < s2 {
- return -1
- }
- for i := 0; i < s1; i++ {
- if i + s2 > s1 {
- return -1
- }
- left := i
- j := 0
- for j < s2 && haystack[left] == needle[j] {
- left++
- j++
- }
- if j == s2 {
- return i
- }
- }
- return -1
-}
-```
-
diff --git "a/05_string/No.031_\344\270\213\344\270\200\344\270\252\346\216\222\345\210\227.md" "b/05_string/No.031_\344\270\213\344\270\200\344\270\252\346\216\222\345\210\227.md"
deleted file mode 100644
index 42de895..0000000
--- "a/05_string/No.031_\344\270\213\344\270\200\344\270\252\346\216\222\345\210\227.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 31 下一个排列-中等
-
-题目:
-
-整数数组的一个 **排列** 就是将其所有成员以序列或线性顺序排列。
-
-- 例如,`arr = [1,2,3]` ,以下这些都可以视作 `arr` 的排列:`[1,2,3]`、`[1,3,2]`、`[3,1,2]`、`[2,3,1]` 。
-
-整数数组的 **下一个排列** 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 **下一个排列** 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
-
-- 例如,`arr = [1,2,3]` 的下一个排列是 `[1,3,2]` 。
-- 类似地,`arr = [2,3,1]` 的下一个排列是 `[3,1,2]` 。
-- 而 `arr = [3,2,1]` 的下一个排列是 `[1,2,3]` ,因为 `[3,2,1]` 不存在一个字典序更大的排列。
-
-给你一个整数数组 `nums` ,找出 `nums` 的下一个排列。
-
-必须**[ 原地 ](https://baike.baidu.com/item/原地算法)**修改,只允许使用额外常数空间。
-
-
-
-分析:
-
-1. 从后往前,查找第一个相邻升序的元素A,假设索引为 i,那么 [i+1, n-1] 必然是降序
-
-2. 然后以此为基础,从后往前查找第一个大于A的元素,假设为B
-3. 交换 A 和 B,此时 [i+1, n-1] 依然是降序,将其反转,得到下一个排列
-
-```go
-// date 2023/12/10
-func nextPermutation(nums []int) {
- n := len(nums)
- // find the first small from right
- i := n-2
- for i >= 0 && nums[i] >= nums[i+1] {
- i--
- }
-
- if i >= 0 {
- // find the first elem bigger than nums[i]
- j := n-1
- for j >= 0 && nums[i] >= nums[j] {
- j--
- }
- nums[i], nums[j] = nums[j], nums[i]
- }
- reverse(nums[i+1:])
-}
-
-func reverse(nums []int) {
- i, j := 0, len(nums)-1
- for i < j {
- nums[i], nums[j] = nums[j], nums[i]
- i++
- j--
- }
-}
-```
-
diff --git "a/05_string/No.043_\345\255\227\347\254\246\344\270\262\347\233\270\344\271\230.md" "b/05_string/No.043_\345\255\227\347\254\246\344\270\262\347\233\270\344\271\230.md"
deleted file mode 100644
index 1eb3534..0000000
--- "a/05_string/No.043_\345\255\227\347\254\246\344\270\262\347\233\270\344\271\230.md"
+++ /dev/null
@@ -1,70 +0,0 @@
-## 43 字符串相乘-中等
-
-给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
-
-注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
-
-
-
-分析:任务拆解,把大任务拆解成一个一个的小任务。
-
-```go
-// date 2020/03/28
-/*
-1. 先实现两个字符串相加;2.实现单个数字的相乘,3.实现零的追加。
-*/
-func multiply(num1 string, num2 string) string {
- if len(num1) == 0 { return num2 }
- if len(num2) == 0 { return num1 }
- if len(num1) == 1 && num1[0] == '0' { return "0" }
- if len(num2) == 1 && num2[0] == '0' { return "0" }
- var res string
- for i := len(num2)-1; i >= 0; i-- {
- t := product(num1, num2[i])
- t = appendZeros(t, len(num2)-1-i)
- res = addString(res, t)
- }
- return res
-}
-
-func appendZeros(s string, c int) string {
- if c <= 0 { return s }
- for c > 0 {
- s += fmt.Sprintf("%d", 0)
- c--
- }
- return s
-}
-
-func product(s1 string, s2 byte) string {
- var res string
- var carry, n1, t int
- i, n2 := len(s1)-1, int(s2 - '0')
- for i >= 0 || carry > 0 {
- n1 = 0
- if i >= 0 { n1 = int(s1[i]-'0') }
- t = n1 * n2 + carry
- carry = t / 10
- res = fmt.Sprintf("%d", t%10) + res
- i--
- }
- return res
-}
-
-func addString(s1, s2 string) string {
- var res string
- var carry, n1, n2, t int
- i, j := len(s1)-1, len(s2)-1
- for i >= 0 || j >= 0 || carry > 0 {
- n1, n2 = 0, 0
- if i >= 0 { n1 = int(s1[i] - '0') }
- if j >= 0 { n2 = int(s2[j] - '0') }
- t = n1 + n2 + carry
- carry = t / 10
- res = fmt.Sprintf("%d", t%10) + res
- i--
- j--
- }
- return res
-}
-```
diff --git "a/05_string/No.049_\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215\345\210\206\347\273\204.md" "b/05_string/No.049_\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215\345\210\206\347\273\204.md"
deleted file mode 100644
index c1af7a9..0000000
--- "a/05_string/No.049_\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215\345\210\206\347\273\204.md"
+++ /dev/null
@@ -1,50 +0,0 @@
-## 49 字母异位词分组-中等
-
-题目:
-
-给你一个字符串数组,请你将 **字母异位词** 组合在一起。可以按任意顺序返回结果列表。
-
-**字母异位词** 是由重新排列源单词的所有字母得到的一个新单词。
-
-
-
-**解题思路**
-
-所谓字母异位词,就是字母字符个数一样,且出现的次数也一样。
-
-所以我们可以对每个字符串进行计数,统计每个字母出现的次数,并保存在数组中。
-
-进而以数组为 key,进行查找合并。
-
-```go
-// date 2024/01/24
-// 解法1
-// 字符计数
-func groupAnagrams(strs []string) [][]string {
- // key = [26]int
- // value = []string
- checkMap := map[[26]int][]string{} // key = [26]int
-
- ans := make([][]string, 0, 16)
-
- for _, str := range strs {
- one := toCheck(str)
- checkMap[one] = append(checkMap[one], str)
- }
-
- for _, v := range checkMap {
- ans = append(ans, v)
- }
-
- return ans
-}
-
-func toCheck(str string) [26]int {
- res := [26]int{}
- for _, v := range str {
- res[v-'a']++
- }
- return res
-}
-```
-
diff --git "a/05_string/No.058_\346\234\200\345\220\216\344\270\200\344\270\252\345\215\225\350\257\215\347\232\204\351\225\277\345\272\246.md" "b/05_string/No.058_\346\234\200\345\220\216\344\270\200\344\270\252\345\215\225\350\257\215\347\232\204\351\225\277\345\272\246.md"
deleted file mode 100644
index 6282d03..0000000
--- "a/05_string/No.058_\346\234\200\345\220\216\344\270\200\344\270\252\345\215\225\350\257\215\347\232\204\351\225\277\345\272\246.md"
+++ /dev/null
@@ -1,28 +0,0 @@
-## 58 最后一个单词的长度-简单
-
-给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
-
-单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
-
-
-
-分析:
-
-简单的指针技巧。
-
-给定一个字符串,返回其最后一个单词的长度。注意字符串末尾的空字符串。
-
-```go
-// date 2020/01/19
-func lengthOfLastWord(s string) int {
- var res int
- for i := len(s) - 1; i >= 0; i-- {
- if res == 0 && s[i] == ' ' {continue}
- if s[i] == ' ' {return res}
- res++
- }
- return res
-}
-```
-
-####
diff --git "a/05_string/No.067_\344\272\214\350\277\233\345\210\266\346\261\202\345\222\214.md" "b/05_string/No.067_\344\272\214\350\277\233\345\210\266\346\261\202\345\222\214.md"
deleted file mode 100644
index 7cd8744..0000000
--- "a/05_string/No.067_\344\272\214\350\277\233\345\210\266\346\261\202\345\222\214.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 67 二进制求和-简单
-
-题目:
-
-给你两个二进制字符串 `a` 和 `b` ,以二进制字符串的形式返回它们的和。
-
-
-
-分析:
-
-这道题跟 415 题没有区别,直接从尾部开始相加即可。
-
-```go
-// date 2022/10/17
-func addBinary(a string, b string) string {
- ans := ""
-
- v1, v2, carry := 0, 0, 0
- i, j := len(a)-1, len(b)-1
- temp := 0
-
- for i >= 0 || j >= 0 || carry > 0 {
- v1, v2 = 0, 0
- if i >= 0 {
- v1 = int(a[i] - '0')
- }
- if j >= 0 {
- v2 = int(b[j] - '0')
- }
- temp = v1 + v2 + carry
- carry = temp / 2
- ans = fmt.Sprintf("%d", temp % 2) + ans
- i--
- j--
- }
-
- return ans
-}
-```
-
diff --git "a/05_string/No.1208_\345\260\275\345\217\257\350\203\275\344\275\277\345\255\227\347\254\246\344\270\262\347\233\270\347\255\211.md" "b/05_string/No.1208_\345\260\275\345\217\257\350\203\275\344\275\277\345\255\227\347\254\246\344\270\262\347\233\270\347\255\211.md"
deleted file mode 100644
index 026ba30..0000000
--- "a/05_string/No.1208_\345\260\275\345\217\257\350\203\275\344\275\277\345\255\227\347\254\246\344\270\262\347\233\270\347\255\211.md"
+++ /dev/null
@@ -1,75 +0,0 @@
-## 1208 尽可能使字符串相等
-
-题目:
-
-给你两个长度相同的字符串,s 和 t。
-
-将 s 中的第 i 个字符变到 t 中的第 i 个字符需要 |s[i] - t[i]| 的开销(开销可能为 0),也就是两个字符的 ASCII 码值的差的绝对值。
-
-用于变更字符串的最大预算是 maxCost。在转化字符串时,总开销应当小于等于该预算,这也意味着字符串的转化可能是不完全的。
-
-如果你可以将 s 的子字符串转化为它在 t 中对应的子字符串,则返回可以转化的最大长度。
-
-如果 s 中没有子字符串可以转化成 t 中对应的子字符串,则返回 0。
-
-> **示例 1:**
->
-> ```
-> 输入:s = "abcd", t = "bcdf", maxCost = 3
-> 输出:3
-> 解释:s 中的 "abc" 可以变为 "bcd"。开销为 3,所以最大长度为 3。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = "abcd", t = "cdef", maxCost = 3
-> 输出:1
-> 解释:s 中的任一字符要想变成 t 中对应的字符,其开销都是 2。因此,最大长度为 1。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:s = "abcd", t = "acde", maxCost = 0
-> 输出:1
-> 解释:a -> a, cost = 0,字符串未发生变化,所以最大长度为 1。
-> ```
-
-
-
-算法:
-
-因为题目中并没有要求一定要从 s 字符串的第一个字符开始替换,所以只要能够有可以替换的就算。
-
-所以选择滑动窗口,窗口大小不固定。
-
-```go
-func equalSubstring(s, t string, maxCost int) int {
- left, right := 0, 0
- n := len(s)
- sumCost, ans := 0, 0
- // 构造窗口
- for right < n {
- sumCost += abs(s[right], t[right]) // 计算每一点的费用
- right++ // 增加right指针,扩大窗口
- for sumCost > maxCost { // 因为求最大值,所以不满足条件时需要增加left指针,缩小窗口
- sumCost -= abs(s[left], t[left])
- left++
- }
- // 此时窗口已经形成,检查是否需要更新结果
- if right - left > ans {
- ans = right - left
- }
- }
- return ans
-}
-
-func abs(x, y uint8) int {
- if x > y {
- return int(x-y)
- }
- return int(y-x)
-}
-```
-
diff --git "a/05_string/No.125_\351\252\214\350\257\201\345\233\236\346\226\207\344\270\262.md" "b/05_string/No.125_\351\252\214\350\257\201\345\233\236\346\226\207\344\270\262.md"
deleted file mode 100644
index 5829cfb..0000000
--- "a/05_string/No.125_\351\252\214\350\257\201\345\233\236\346\226\207\344\270\262.md"
+++ /dev/null
@@ -1,69 +0,0 @@
-## 125 验证回文串-简单
-
-题目:
-
-如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
-
-字母和数字都属于字母数字字符。
-
-给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
-
-
-
-**解题思路**
-
-去除不需要比较的字符,然后双指针首尾对撞。
-
-```go
-// date 2022/10/17
-func isPalindrome(s string) bool {
- s = strings.ToLower(s)
- var res string
- for i := 0; i < len(s); i++ {
- if 'a' <= s[i] && s[i] <= 'z' || '0' <= s[i] && s[i] <= '9' {
- res += string(s[i])
- }
- }
- i, j := 0, len(res)-1
- for i < j {
- if res[i] != res[j] {
- return false
- }
- i++
- j--
- }
- return true
-}
-// 写法2
-// 双指针,直接在原字符串上操作,只判断字母和数字字符
-func isPalindrome(s string) bool {
- s = strings.ToLower(s)
- left, right := 0, len(s)-1
-
- for left < right {
- if !isCharNum(s[left]) {
- left++
- continue
- }
- if !isCharNum(s[right]) {
- right--
- continue
- }
- if s[left] != s[right] {
- return false
- }
- left++
- right--
- }
-
- return true
-}
-
-func isCharNum(x uint8) bool {
- if x >= 'a' && x <= 'z' || x >= '0' && x <= '9' {
- return true
- }
- return false
-}
-```
-
diff --git "a/05_string/No.151_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\345\215\225\350\257\215.md" "b/05_string/No.151_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\345\215\225\350\257\215.md"
deleted file mode 100644
index fe3618a..0000000
--- "a/05_string/No.151_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262\344\270\255\347\232\204\345\215\225\350\257\215.md"
+++ /dev/null
@@ -1,55 +0,0 @@
-## 151 反转字符串中的单词-中等
-
-题目:
-
-给你一个字符串 `s` ,请你反转字符串中 **单词** 的顺序。
-
-**单词** 是由非空格字符组成的字符串。`s` 中使用至少一个空格将字符串中的 **单词** 分隔开。
-
-返回 **单词** 顺序颠倒且 **单词** 之间用单个空格连接的结果字符串。
-
-**注意:**输入字符串 `s`中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
-
-
-
-分析:
-
-1. 先去除头尾的空格无效字符
-2. 从尾部开始遍历,每找到一个单词就追加到结果中
-
-
-
-```go
-// date 2023/12/10
-func reverseWords(s string) string {
- res := ""
- i, j := 0, len(s)-1
- for j >= 0 && s[j] == ' ' {
- j--
- }
- for i >= 0 && s[i] == ' ' {
- i++
- }
- start := i
- end := j
-
- for j >= start {
- for j >= start && s[j] != ' ' {
- j--
- }
- // now, the [j+1:end+1] is a word
- if res == "" {
- res = string(s[j+1:end+1])
- } else {
- res += " "
- res += string(s[j+1:end+1])
- }
- for j >= start && s[j] == ' ' {
- j--
- }
- end = j
- }
- return res
-}
-```
-
diff --git "a/05_string/No.165_\346\257\224\350\276\203\347\211\210\346\234\254\345\217\267.md" "b/05_string/No.165_\346\257\224\350\276\203\347\211\210\346\234\254\345\217\267.md"
deleted file mode 100644
index 111176f..0000000
--- "a/05_string/No.165_\346\257\224\350\276\203\347\211\210\346\234\254\345\217\267.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 165 比较版本好-中等
-
-题目:
-
-给你两个版本号 `version1` 和 `version2` ,请你比较它们。
-
-版本号由一个或多个修订号组成,各修订号由一个 `'.'` 连接。每个修订号由 **多位数字** 组成,可能包含 **前导零** 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,`2.5.33` 和 `0.1` 都是有效的版本号。
-
-比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 **忽略任何前导零后的整数值** 。也就是说,修订号 `1` 和修订号 `001` **相等** 。如果版本号没有指定某个下标处的修订号,则该修订号视为 `0` 。例如,版本 `1.0` 小于版本 `1.1` ,因为它们下标为 `0` 的修订号相同,而下标为 `1` 的修订号分别为 `0` 和 `1` ,`0 < 1` 。
-
-返回规则如下:
-
-- 如果 `*version1* > *version2*` 返回 `1`,
-- 如果 `*version1* < *version2*` 返回 `-1`,
-- 除此之外返回 `0`。
-
-
-
-分析:
-
-双指针,通过将版本号转成数字的方式进行比较。
-
-这样做的好处就是变相地把前导零去掉了。
-
-```go
-// date 2023/12/10
-func compareVersion(version1 string, version2 string) int {
- n1, n2 := len(version1), len(version2)
- i, j := 0, 0
- for i < n1 || j < n2 {
- v1 := 0
- for i < n1 && version1[i] != '.' {
- v1 = v1 * 10 + int(version1[i] - '0')
- i++
- }
- i++
- v2 := 0
- for j < n2 && version2[j] != '.' {
- v2 = v2 * 10 + int(version2[j] - '0')
- j++
- }
- j++
- if v1 > v2 {
- return 1
- } else if v1 < v2 {
- return -1
- }
- }
- return 0
-}
-```
-
diff --git "a/05_string/No.242_\346\234\211\346\225\210\347\232\204\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md" "b/05_string/No.242_\346\234\211\346\225\210\347\232\204\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md"
deleted file mode 100644
index a0baad2..0000000
--- "a/05_string/No.242_\346\234\211\346\225\210\347\232\204\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md"
+++ /dev/null
@@ -1,25 +0,0 @@
-## 242 有效的字母异位词
-
-给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
-
-注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
-
-
-
-分析
-
-算法1:题目中说明了只包含小写字母,因此可以用数组判断。
-
-```go
-func isAnagram(s string, t string) bool {
- if len(s) != len(t) {return false}
- ms, mt := [26]int{}, [26]int{}
- for i := 0; i < len(s); i++ {
- ms[s[i] - 'a']++
- mt[t[i] - 'a']++
- }
- return ms == mt
-}
-```
-
-####
\ No newline at end of file
diff --git "a/05_string/No.344_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262.md" "b/05_string/No.344_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262.md"
deleted file mode 100644
index f2cc18f..0000000
--- "a/05_string/No.344_\345\217\215\350\275\254\345\255\227\347\254\246\344\270\262.md"
+++ /dev/null
@@ -1,26 +0,0 @@
-## 344 反转字符串-简单
-
-题目:
-
-编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
-
-不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
-
-
-
-分析:
-
-双指针
-
-```go
-// date 2020/03/18
-func reverseString(s []byte) {
- left, right := 0, len(s)-1
- for left < right {
- s[left], s[right] = s[right], s[left]
- left++
- right--
- }
-}
-```
-
diff --git "a/05_string/No.392_\345\210\244\346\226\255\345\255\220\345\272\217\345\210\227.md" "b/05_string/No.392_\345\210\244\346\226\255\345\255\220\345\272\217\345\210\227.md"
deleted file mode 100644
index b8280da..0000000
--- "a/05_string/No.392_\345\210\244\346\226\255\345\255\220\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,41 +0,0 @@
-## 392 判断子序列-简单
-
-题目:
-
-给定字符串 **s** 和 **t** ,判断 **s** 是否为 **t** 的子序列。
-
-字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,`"ace"`是`"abcde"`的一个子序列,而`"aec"`不是)。
-
-**进阶:**
-
-如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
-
-**致谢:**
-
-特别感谢 [@pbrother ](https://leetcode.com/pbrother/)添加此问题并且创建所有测试用例。
-
-
-
-分析:
-
-双指针,逐位判断。如果相同,继续匹配下一位,否则指向 t 的指针右移下一位。
-
-这就是贪心算法。
-
-```go
-// date 2023/12/11
-func isSubsequence(s string, t string) bool {
- n1, n2 := len(s), len(t)
- i, j := 0, 0
- for i < n1 && j < n2 {
- if s[i] == t[j] {
- i++
- }
- j++
- }
- return i == n1
-}
-```
-
-
-
diff --git "a/05_string/No.415_\345\255\227\347\254\246\344\270\262\347\233\270\345\212\240.md" "b/05_string/No.415_\345\255\227\347\254\246\344\270\262\347\233\270\345\212\240.md"
deleted file mode 100644
index e950d7c..0000000
--- "a/05_string/No.415_\345\255\227\347\254\246\344\270\262\347\233\270\345\212\240.md"
+++ /dev/null
@@ -1,38 +0,0 @@
-## 415 字符串相加-简单
-
-题目:
-
-给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
-
-你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
-
-
-
-算法分析:
-
-从尾部到头部依次计算。
-
-```go
-// date 2020/03/28
-func addStrings(num1 string, num2 string) string {
- ans := ""
- carry, v1, v2 := 0, 0, 0
- i, j := len(num1)-1, len(num2)-1
- for i >= 0 || j >= 0 || carry != 0 {
- v1, v2 = 0, 0
- if i >= 0 {
- v1 = int(num1[i] - '0')
- }
- if j >= 0 {
- v2 = int(num2[j] - '0')
- }
- t := carry + v1 + v2
- carry = t / 10
- ans = fmt.Sprintf("%d", t % 10) + ans
- i--
- j--
- }
- return ans
-}
-```
-
diff --git "a/05_string/No.438_\346\211\276\345\210\260\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md" "b/05_string/No.438_\346\211\276\345\210\260\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md"
deleted file mode 100644
index 9de0266..0000000
--- "a/05_string/No.438_\346\211\276\345\210\260\345\255\227\347\254\246\344\270\262\344\270\255\346\211\200\346\234\211\345\255\227\346\257\215\345\274\202\344\275\215\350\257\215.md"
+++ /dev/null
@@ -1,68 +0,0 @@
-## 438 找到字符串中所有字母异位词-中等
-
-题目:
-
-给定两个字符串 `s` 和 `p`,找到 `s` 中所有 `p` 的 **异位词** 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
-
-**异位词** 指由相同字母重排列形成的字符串(包括相同的字符串)。
-
-
-
-**解题思路**
-
-- 滑动窗口,详见解法1。具体为,先处理 p 字符串,将其每个元素存入 map,记为 mp;滑动窗口遍历字符串s,并将元素存入 map,记为 ms,当滑动窗口区间等于字符串p的长度时,比较 ms, mp 是否相等,如果相等那么 left 就是答案之一。
-
-
-
-
-
-```go
-// date 2024/01/23
-// 解法1 滑动窗口
-func findAnagrams(s string, p string) []int {
- s1 := len(p)
- mp := make(map[uint8]int)
- for i := 0; i < len(p); i++ {
- mp[p[i]]++
- }
-
- ans := []int{}
- left, right := 0, 0
- ms := make(map[uint8]int)
- for right < len(s) {
- if right - left >= s1 {
- if isSame(ms, mp) {
- ans = append(ans, left)
- }
- ms[s[left]]--
- if ms[s[left]] == 0 {
- delete(ms, s[left])
- }
- left++
- }
- ms[s[right]]++
- right++
- }
- if right - left >= s1 {
- if isSame(ms, mp) {
- ans = append(ans, left)
- }
- }
-
- return ans
-}
-
-func isSame(ms, mp map[uint8]int) bool {
- if len(ms) != len(mp) {
- return false
- }
- for k, v := range mp {
- ov, ok := ms[k]
- if !ok || v != ov {
- return false
- }
- }
- return true
-}
-```
-
diff --git a/05_string/string.md b/05_string/string.md
deleted file mode 100644
index 12835f1..0000000
--- a/05_string/string.md
+++ /dev/null
@@ -1,448 +0,0 @@
-## String
-
-[TOC]
-
-### Golang中的字符串
-
-golang语言中字符串中所包含的类型
-
-```go
- str := "su"
- for i, s := range str {
- fmt.Printf("i %T, v %T, s[i] %T\n", i, s, str[i]) // int, int32, uint8
- }
- for _, v := range str {
- fmt.Printf("%T \n", v) // int32
- }
- for i := range str {
- fmt.Printf("%T \n", i) // int
- }
-byte是uint8的别名, rune是int32的别名。
-```
-
-### 相关题目
-
-#### 14 Longest Common Prefix【最长公共前缀】
-
-思路分析:
-
-算法1:最长公共前缀一定存在最短的那个字符串中,因此先求出最短的字符串的长度minLen,然后依次比较每个字符串中的第i个字符(0 <= i < minLen),如果相同则追加到结果中,否则退出,返回之前的结果。【垂直扫描】
-
-算法2:水平扫描法,n个字符串的最长公共前缀,一定是前n-1个字符串的最长公共前缀与第n个字符串的公共前缀,即公式LCP(S1...Sn) = LCP(LCP(LCP(S1, S2) S3)...Sn)
-
-```go
-// 算法1:直接比较,也称为垂直扫描
-func longestCommonPrefix(strs []string) string {
- if len(strs) == 0 {return ""}
- if len(strs) == 1 {return strs[0]}
- // find the minLen
- minLen := 1 << 31 -1
- for _, str := range strs {
- if len(str) < minLen {
- minLen = len(str)
- }
- }
- var res string
- for i:= 0; i < minLen; i++ {
- r := strs[0][i]
- ok := true
- for j := 1; j < len(strs); j++ {
- if r != strs[j][i] {
- ok = false
- break
- }
- }
- if !ok {
- break
- }
- res = res + string(r)
- }
- return res
-}
-
-// 算法2: 水平扫描,利用公式LCP(S1...Sn) = LCP(LCP(LCP(S1,S2), S3)...Sn)
-func longestCommonPrefix(strs []string) string {
- if len(strs) == 0 { return "" }
- prefix := strs[0]
- for i := 1; i < len(strs); i++ {
- prefix = findPrefix(prefix, strs[i])
- if len(prefix) == 0 {return ""}
- }
- return prefix
-}
-
-func findPrefix(s1, s2 string) string {
- minLen := len(s1)
- if len(s2) < minLen {
- minLen = len(s2)
- }
- var res string
- for i := 0; i < minLen; i++ {
- if s1[i] != s2[i] {break}
- res += string(s1[i])
- }
- return res
-}
-```
-
-
-
-#### 实现strStr()
-
-思路分析
-
-算法1:找到起始点,并判断是否相同。
-
-```go
-func strStr(haystack, needle string) int {
- if len(needle) <= 0 {return 0}
- n1, n2 := len(haystack), len(needle)
- for i := 0; i < n1; i++ {
- if haystack[i] != needle[0] {
- continue
- }
- if i + n2 > n1 {
- return -1
- }
- if string(haystack[i:i+n]) == needle {return i}
- }
- return -1
-}
-```
-
-#### 151 翻转字符串里的单词
-
-题目要求:
-
-思路分析:
-
-```go
-// date 2020/03/29
-/*
-1. 从字符串尾部开始遍历,依次翻转每个单词
-2. 遍历字符串的时候主要去掉多余空格,最后的结果也需要去掉多余的空格
-*/
-func reverseWords(s string) string {
- res, word_res := make([]byte, 0), make([]byte, 0)
- end := len(s)-1
- // 去掉尾部多余的空格
- for end >= 0 && s[end] == ' ' { end-- }
- for i := end; i >= 0; i-- {
- if s[i] != ' ' {
- word_res = append(word_res, s[i])
- } else {
- // 找到一个单词
- res = append(res, reverseWord(word_res)...)
- res = append(res, ' ')
- // 去掉中间多余的空格
- for i >= 0 && s[i] == ' ' { i-- }
- i++
- word_res = word_res[:0]
- }
- }
- if len(word_res) > 0 {
- res = append(res, reverseWord(word_res)...)
- }
- if len(res) > 0 && res[len(res)-1] == ' ' {
- res = res[:len(res)-1]
- }
- return string(res)
-}
-
-func reverseWord(word []byte) []byte {
- i, j := 0, len(word)-1
- var c byte
- for i < j {
- c = word[i]
- word[i] = word[j]
- word[j] = c
- i++
- j--
- }
- return word
-}
-```
-
-
-
-#### 246 中心对称数
-
-题目要求:https://leetcode-cn.com/problems/strobogrammatic-number/
-
-```go
-// date 2020/03/21
-func isStrobogrammatic(num string) bool {
- m := map[byte]byte{
- '6': '9',
- '9': '6',
- '8': '8',
- '0': '0',
- '1': '1',
- }
- l, r, n := 0, len(num)-1, len(num)
- for l < r {
- if m[num[l]] == num[r] {
- l++
- r--
- } else {
- return false
- }
- }
- // 如果是奇数个元素
- if n & 0x1 == 1 && m[num[n/2]] != num[n/2] { return false }
- return true
-}
-```
-
-#### 345 反转字符串中的元音字母
-
-```go
-// date 2019/12/28
-// 双指针
-func reverseVowels(s string) {
- vs := make([byte]int)
- vs['a'] = 1
- vs['e'] = 1
- vs['i'] = 1
- vs['o'] = 1
- vs['u'] = 1
- vs['A'] = 1
- vs['E'] = 1
- vs['I'] = 1
- vs['O'] = 1
- vs['U'] = 1
- i, j := 0, len(s) - 1
- var temp byte
- for i < j {
- _, ok := vs[s[i]]
- if ok {
- _, ok2 := vs[s[j]]
- if ok2 {
- temp = s[j]
- s[j] = s[i]
- s[i] = temp
- i++
- j--
- } else {
- j--
- }
- } else {
- i++
- }
- }
-}
-```
-
-#### 521 最长特殊序列I
-
-题目要求:https://leetcode-cn.com/problems/longest-uncommon-subsequence-i/
-
-思路分析:题意难以理解
-
-```go
-// date 2020/03/08
-func findLUSlength(a, b string) int {
- if a == b { return len(a) }
- if len(a) == len(b) || len(a) > len(b) { return len(a) }
- return len(b)
-}
-```
-
-#### 576 字符串的排列
-
-题目要求:https://leetcode-cn.com/problems/permutation-in-string/
-
-思路分析:
-
-```go
-// date 2020/03/28
-/*
-1. 注意题目要求,字符串问题很多都可以使用数组,好处就是golang中数组可以直接比较的
-2. 第一个字符串的排列之一是第二个字符串的子串,所以字符出现的顺序很重要
-*/
-func checkInclusion(s1 string, s2 string) bool {
- if len(s1) > len(s2) { return false }
- // 题目中只包含小写字母,所以使用数组更方便[26]int
- var s1map [26]int
- for _, c := range s1 { s1map[c - 'a']++ }
- for i := 0; i <= len(s2)-len(s1); i++ {
- var s2map [26]int
- for j := 0; j < len(s1); j++ {
- s2map[s2[i+j] - 'a']++
- }
- if s1map == s2map { return true }
- }
- return false
-}
-```
-
-
-
-#### 594 最长和谐子序列
-
-题目要求:https://leetcode-cn.com/problems/longest-harmonious-subsequence/
-
-算法分析
-
-```go
-// date 2020/03/08
-// 算法一:两层循环,超时
-// 算法二:利用map,时间复杂度O(N),空间复杂度O(N)
-func findLHS(nums []int) int {
- m := make(map[int]int, 0)
- for _, v := range nums {
- if _, ok := m[v]; ok {
- m[v]++
- } else {
- m[v] = 1
- }
- }
- res := 0
- for k, v1 := range m {
- if v2, ok := m[k+1]; ok && v1+v2 > res { res = v1+v2 }
- }
- return res
-}
-// 算法三,算法二的优化版
-func findLHS(nums []int) int{
- res, m := 0, make(map[int]int, 0)
- for _, v := range nums {
- if _, ok := m[v]; ok {
- m[v]++
- } else {
- m[v] = 1
- }
- // cal
- if v1, ok := m[v-1]; ok && m[v]+v1 > res { res = v1+m[v] }
- if v1, ok := m[v+1]; ok && m[v]+v1 > res { res = v1+m[v] }
- }
- return res
-}
-```
-
-
-
-#### 674 最长连续递增序列
-
-题目要求:https://leetcode-cn.com/problems/longest-continuous-increasing-subsequence/
-
-算法分析:
-
-```go
-// date 2020/03/08
-func findLengthOfLCIS(nums []int) int {
- if len(nums) == 0 { return 0 }
- res, temp := 1, 1
- for i := 0; i < len(nums)-1; i++ {
- if nums[i+1] > nums[i] {
- temp++
- } else {
- temp = 1
- }
- if temp > res { res = temp }
- }
- return res
-}
-```
-
-#### 字符串中第一个唯一的字符
-
-```go
-func firstUniqChar(s string) int {
- m := make(map[uint8]int, len(s))
- for i := 0; i < len(s); i++ {
- if _, ok := m[s[i]]; ok {
- m[s[i]] = -1
- } else {
- m[s[i]] = i
- }
- }
- for i := 0; i < len(s); i++ {
- if v, ok := m[s[i]]; ok && v != -1 {
- return v
- }
- }
- return -1
-}
-```
-
-#### 翻转字符串里的单词
-
-题目要求:给定一个字符串,返回其按单词翻转,并去除多余空格的结果。
-
-算法:从字符串的尾部遍历,找到单个单词,并翻转放入其结果,注意空格。
-
-```go
-// date 2020/02/02
-func reverseWords(s string) string {
- res, temp := make([]byte, 0), make([]byte, 0) // 存放结果和单个单词
- end := len(s)-1
- for end >= 0 && s[end] == ' ' { end-- }
- for i := end; i >= 0; i-- {
- if s[i] != ' ' {
- temp = append(temp, s[i])
- } else {
- // find the word
- res = append(res, reverseWord(temp)...)
- res = append(res, ' ')
- for i >= 0 && s[i] == ' ' { i-- }
- i++
- temp = make([]byte, 0)
- }
- }
- if 0 != len(temp) {
- res = append(res, reverseWord(temp)...)
- }
- if len(res) > 0 && res[len(res)-1] == ' ' {
- res = res[:len(res)-1]
- }
- return string(res[:len(res)])
-}
-func reverseWord(word []byte) []byte {
- s, e := 0, len(word)-1
- var t byte
- for s < e {
- t = word[s]
- word[s] = word[e]
- word[e] = t
- s++
- e--
- }
- return word
-}
-```
-
-#### 820 单词的压缩编码
-
-题目要求:https://leetcode-cn.com/problems/short-encoding-of-words/
-
-思路分析:考察知识点,字典树
-
-如果一个单词是另一个单词的后缀,则该单词不需要重新编码。
-
-```go
-// date 2020/03/28
-func minimumLengthEncoding(words []string) int {
- // 将单词存入哈希表,方便删除
- set := make(map[string]string, len(words))
- for _, w := range words {
- set[w] = w
- }
- // 查找可能存在的单词后缀,并删除它,注意单词的索引从1开始
- for _, word := range words {
- for i := 1; i < len(word); i++ {
- key := string(word[i:])
- if _, ok := set[key]; ok {
- delete(set, key)
- }
- }
- }
- // 统计并返回结果
- var res int
- for word := range set {
- res += len(word)+1
- }
- return res
-}
-```
-
diff --git a/06_hash/hashTable.md b/06_hash/hashTable.md
deleted file mode 100644
index ee5a3ee..0000000
--- a/06_hash/hashTable.md
+++ /dev/null
@@ -1,722 +0,0 @@
-### HashTable
-
-哈希表是一种数据结构,使用哈希函数组织数据,支持快速插入和搜索。
-
-
-
-#### 哈希表原理
-
-哈希表的关键思想是使用**哈希函数**将**键映射到存储桶**。具体来说就是:
-
-1.当我们插入一个新的键时,哈希函数将决定该键应该分配到哪个桶中,并将该键存储在相应的桶中;
-
-2.当我们想要搜索一个键时,哈希表将使用同样的哈希函数来查找相应的桶,并只在特定的桶中进行搜索。
-
-#### 哈希集合的设计
-
-```go
-const MAX_LEN = 10000
-type MyHashSet struct {
- set [MAX_LEN][]int
-}
-/** Initialize your data structure here. */
-func Constructor() MyHashSet {
- return MyHashSet{
- set: [MAX_LEN][]int{},
- }
-}
-func (this *MyHashSet) getIndex(key int) int {
- return key % MAX_LEN // 这就是关键的哈希函数
-}
-func (this *MyHashSet) getPos(key, index int) int {
- for i := 0; i < len(this.set[index]); i++ {
- if this.set[index][i] == key {
- return i
- }
- }
- return -1
-}
-
-func (this *MyHashSet) Add(key int) {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- if pos < 0 {
- this.set[index] = append(this.set[index], key)
- }
-}
-
-func (this *MyHashSet) Remove(key int) {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- if pos >= 0 {
- for i := 0; i < len(this.set[index]); i++ {
- if this.set[index][i] == key {
- // 优化,利用交换的思想
- ns := this.set[index][:i]
- ns = append(ns, this.set[index][i+1:]...)
- this.set[index] = ns
- return
- }
- }
- }
-}
-
-/** Returns true if this set contains the specified element */
-func (this *MyHashSet) Contains(key int) bool {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- return pos >= 0
-}
-```
-
-remove元素中可以使用交换的思想,代码如下
-
-```go
-for i := 0; i < len(this.set[index]); i++ {
- if this.set[index][i] == key {
- this.set[index][i] = this.set[index][len(this.set[index]) - 1]
- break
- }
-}
-this.set[index] = this.set[index][:n-1]
-```
-
-
-
-#### 哈希映射的设计
-
-```go
-const MAX_LEN = 1000000
-type MyHashMap struct {
- hashmap [MAX_LEN]map[int]int
-}
-
-
-/** Initialize your data structure here. */
-func Constructor() MyHashMap {
- return MyHashMap{
- hashmap: [MAX_LEN]map[int]int{},
- }
-}
-
-func (this *MyHashMap) getIndex(key int) int {
- return key % MAX_LEN // 关键哈希函数
-}
-func (this *MyHashMap) getPos(key, index int) int {
- for k := range this.hashmap[index] {
- if k == key {
- return k
- }
- }
- return -1
-}
-
-
-/** value will always be non-negative. */
-func (this *MyHashMap) Put(key int, value int) {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- if pos < 0 {
- if len(this.hashmap[index]) == 0 {
- this.hashmap[index] = make(map[int]int)
- }
- this.hashmap[index][key] = value
- } else {
- this.hashmap[index][pos] = value
- }
-}
-
-
-/** Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key */
-func (this *MyHashMap) Get(key int) int {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- if pos >= 0 {
- return this.hashmap[index][pos]
- }
- return -1
-}
-
-
-/** Removes the mapping of the specified value key if this map contains a mapping for the key */
-func (this *MyHashMap) Remove(key int) {
- index := this.getIndex(key)
- pos := this.getPos(key, index)
- if pos >= 0 {
- nm := make(map[int]int, len(this.hashmap[index]) - 1)
- for k, v := range this.hashmap[index] {
- if k != key {
- nm[k] = v
- }
- }
- this.hashmap[index] = nm
- }
-}
-```
-
-### 相关题目
-
-- 1 两数之和
-- 202 快乐数
-- 36 有效的数独
-- 170 两数之和III - 数据结构设计
-- 349 两个数组的交集
-- 652 寻找重复的树【中等】
-- 49 字母异位词分组【M】
-- 四数相加II
-- 常数时间插入,删除和获取
-- 146 LRU缓存机制【M】
-
-#### 1 两数之和
-
-思路分析:
-
-利用哈希映射原理。先将数组中所有的元素存入map中(相同的元素值,取index较大的一个,后序判断需要),然后遍历数组,并判断target-value是否在map中。如果map存在,并且index不一样则找到结果。
-
-```go
-// date
-func twoSum(nums []int, target int) []int {
- res := make([]int, 2)
- m := make(m[int]int, len(nums))
- for index, v := range nums {
- m[v] = index
- }
- for i, v := range nums {
- if j, ok := m[target-v]; ok && i != j {
- res[0], res[1] = i, j
- break
- }
- }
- return res
-}
-// date 2019/12/30
-// 上一版的优化,上一版中需要遍历数组两次,而实际上可以只遍历一次,如下
-func twoSum(nums []int, target int) []int {
- res := make([]int, 2)
- m := make(map[int]int)
- for i, v := range nums {
- if j, ok := m[target-v]; ok {
- res[0], res[1] = j, i
- break
- }
- m[v] = i
- }
- return res
-}
-```
-
-#### 202 快乐数
-
-思路分析
-
-算法1:利用快慢指针的思想判断是否有循环。
-
-```go
-func isHappy(n int) bool {
- slow := bitSquareSum(n)
- fast := bitSquareSum(bitSquareSum(n))
- for slow != fast {
- slow = bitSquareSum(slow)
- fast = bitSquareSum(bitSquareSum(fast))
- }
- return slow == 1
-}
-func bitSquareSum(n int) int {
- sum := 0
- for n > 0 {
- bit := n % 10
- sum += bit * bit
- n /= 10
- }
- return sum
-}
-```
-
-算法2:利用set,判断之前出现的数是否会再次出现,如果出现,则不是快乐数
-
-```go
-// date 2019/12/30
-// 算法:set检查是否重复
-func isHappy(n int) bool {
- sum, m := 0, make(map[int]struct{})
- for n != 1 {
- for n > 0 {
- sum += (n%10) * (n%10)
- n /= 10
- }
- if _, ok := m[sum]; ok {
- return sum == 1
- }
- m[sum] = struct{}{}
- n, sum = sum,
- }
- return true
-}
-```
-
-
-
-
-
-#### 36 有效的数据 【M】
-
-思路分析
-
-如何获得3x3的子数独,boxes = (rows / 3) * 3 + (columns / 3)。然后保证行,列,子数独每个元素只能出现一次。
-
-```go
-func isValidSudoku(board [][]byte) bool {
- rows := [9]map[byte]int{}
- cols := [9]map[byte]int{}
- boxes := [9]map[byte]int{}
- for i := 0; i < 9; i++ {
- rows[i] = make(map[byte]int)
- cols[i] = make(map[byte]int)
- boxes[i] = make(map[byte]int)
- }
- for i := 0; i < 9; i++ {
- for j := 0; j < 9; j++ {
- k := board[i][j]
- if k == byte('.') {continue}
- if _, ok := rows[i][k]; ok {
- return false
- } else {rows[i][k] = 1}
-
- if _, ok := cols[j][k]; ok {
- return false
- } else {cols[j][k] = 1}
-
- b := (i/3)*3 + j/3
- if _, ok := boxes[b][k]; ok {
- return false
- } else {boxes[b][k] = 1}
- }
- }
- return true
-}
-```
-
-
-
-#### 170 两数之和III - 数据结构设计
-
-思路分析:
-
-
-
-```go
-type TwoSum struct {
- set map[int]int
-}
-
-func Constructor() TwoSum {
- return TwoSum{
- set: make(map[int]int),
- }
-}
-
-func (this *TwoSum) Add(number int) {
- if _, ok := this.set[number]; ok {
- this.set[number]++
- } else {
- this.set[number] = 1
- }
-}
-
-func (this *TwoSum) Find(value int) bool {
- for k, _ := range this.set {
- if c, ok := this.set[value - k]; ok && (k == value - k && c > 1 || k != value - k) {
- return true
- }
- }
- return false
-}
-```
-
-
-
-#### 349 两个数组的交集
-
-思路分析:两个数组中均可能存在重复元素,所以在第二个数组中找到后需要删除key。
-
-```go
-func intersection(nums1, nums2 []int) []int {
- res := make([]int, 0)
- m := make(map[int]struct{})
- for _, v := range nums1 {
- if _, ok := m[v]; !ok {
- m[v] = struct{}{}
- }
- }
- for _, v := range nums2 {
- if _, ok := m[v]; ok {
- res = append(res, v)
- delete(m, v)
- }
- }
- return res
-}
-```
-
-#### 350 两个数组的交集 II
-
-题目:
-
-
-
-```go
-func intersect(nums1, nums2 []int) []int {
- res := make([]int, 0)
- m := make(map[int]int)
- for _, v := range nums1 {
- if _, ok := m[v]; ok {
- m[v]++
- } else {
- m[v] = 1
- }
- }
- for _, v := range nums2 {
- if c, ok := m[v]; ok && c >= 1 {
- res = append(res, v)
- m[v]--
- }
- }
- return res
-}
-```
-
-#### 存在重复元素II
-
-```go
-func containsNearByDuplicate(nums []int, k int) bool {
- m := make(map[int]int)
- for index, v := range nums {
- if j, ok := m[v]; ok && index - j <= k {
- return true
- }
- m[v] = index
- }
- return false
-}
-```
-
-#### 652 寻找重复的树
-
-思路分析:
-
-将树的节点进行先序遍历,并存储。【即序列化】,然后判断是否出现过。
-
-```go
-func
-```
-
-
-
-#### 49 字母异位词分组【M】
-
-思路分析:
-
-将每个单词中,每个字符出现的频率映射到一个map中,然后比较每个单词的map是否一致。
-
-```go
-func groupAnagrams(strs []string) [][]string {
- n := len(strs)
- grouped := make(map[string]int, n)
- res := make([][]string, 0)
- strM := make(map[string]map[rune]int)
- for i, str := range strs {
- // 已经归属于某个组,直接跳过
- if _, ok := grouped[str]; ok {continue}
- grouped[str] = i
- gstr := make([]string, 0)
- gstr = append(gstr, str)
- im := strMap(str)
- strM[str] = im
- for j := i + 1; j < n; j++ {
- // 长度不一样,肯定不在一组,跳过
- if len(strs[j]) != len(str) {continue}
- // 两个单词一样,直接加入当前组
- if strs[j] == str {
- grouped[strs[j]] = j
- gstr = append(gstr, strs[j])
- continue
- }
- // 如果被分组过,且是当前元素,跳过
- if v, ok := grouped[strs[j]]; ok && v == j {continue}
- // 如果被分过组,且不是当前元素,可能是重复元素
- jm := strMap(strs[j])
- strM[strs[j]] = jm
- if isSame(im, jm) {
- grouped[strs[j]] = j
- gstr = append(gstr, strs[j])
- }
- }
- res = append(res, gstr)
- }
- return res
-}
-
-func isSame(m1, m2 map[rune]int) bool {
- if len(m1) != len(m2) {return false}
- for k, v := range m1 {
- if v2, ok := m2[k]; !ok || v2 != v {
- return false
- }
- }
- return true
-}
-
-func strMap(s string) map[rune]int {
- res := make(map[rune]int)
- for _, v := range s {
- if _, ok := res[v]; ok {
- res[v]++
- } else {
- res[v] = 1
- }
- }
- return res
-}
-```
-
-思路分析
-
-算法优化:将每个单词按字符出现的次数形成key,作为映射的基础,同一个key,可以对应多个单词,即分组。【golang数组是可比较类型,可以用作map的key】
-
-例如aab, aba, baa, 这三个单词的key都是a2b1。
-
-```go
-func groupAnagrams(strs []string) [][]string {
- m := make(map[[26]int][]string)
- for _, str := range strs {
- k := strArray(str)
- s, ok := m[k]
- if !ok {
- s = make([]string, 0)
- }
- s = append(s, str)
- m[k] = s
- }
- res := make([][]string, 0, len(m))
- for _, v := range m {
- res = append(res, v)
- }
- return res
-}
-
-func strArray(s string) [26]int {
- res := [26]int{}
- for _, v := range s {
- res[v - 'a']++
- }
- return res
-}
-```
-
-#### 249 移位字符串分组
-
-思路分析
-
-异位字符串分组中对字符出现的次数作为key,移位字符串的key可以视为在一个具有26个槽位的哈希环上,每个字符的相对位置是一样的。
-
-```go
-func groupStrings(strs []string) [][]string {
- m := make(map[[26]int][]string)
- for _, str := range strs {
- k := strArray(str)
- s, ok := m[k]
- if !ok {
- s = make([]string, 0)
- }
- s = append(s, str)
- m[k] = s
- }
- res := make([][]string, 0, len(m))
- for _, v := range m {
- res = append(res, v)
- }
- return res
-}
-
-func strArray(s string) [26]int {
- res := [26]int{}
- if len(s) == 0 {return res}
- for _, v := range s {
- res[(v - s[0] + 26) % 26]++
- }
- return res
-}
-```
-
-#### 四数相加II
-
-思路分析
-
-正常情况下需要四层循环,比较耗时;可以通过map优化,即先将两个数组合并,记录其出现的值及可能的组合次数;然后用map查看结果,并将组合数相乘。
-
-```go
-func fourSumCount(A []int, B []int, C []int, D []int) int {
- res := 0
- abm, cdm := make(map[int]int, len(A)*2), make(map[int]int, len(A)*2)
- for _, a := range A {
- for _, b := range B {
- if _, ok := abm[a+b]; ok {
- abm[a+b]++
- } else {
- abm[a+b] = 1
- }
- }
- }
- for _, c := range C {
- for _, d := range D {
- if _, ok := cdm[c+d]; ok {
- cdm[c+d]++
- } else {
- cdm[c+d] = 1
- }
- }
- }
- for k, v1 := range abm {
- if v2, ok := cdm[0-k]; ok {
- res += v1 * v2
- }
- }
- return res
-}
-```
-
-#### 常数时间插入、删除和获取
-
-```go
-type RandomizedSet struct {
- set map[int]int // 存放元素及其对应的下标
- data []int // 存放元素
-}
-
-func Constructor() RandomizedSet {
- return RandomizedSet{
- set: make(map[int]int),
- data: make([]int, 0),
- }
-}
-func (this *RandomizedSet) Insert(val int) bool {
- if _, ok := this.set[val]; ok {
- return false
- }
- this.set[val] = len(this.data)
- this.data = append(this.data, val)
- return true
-}
-
-func (this *RandomizedSet) Remove(val int) bool {
- if _, ok := this.set[val]; !ok {
- return false
- }
- // 将欲删除的元素从data中删除,利用和最后一个元素交换的方式删除
- // 将set中data中最后一个元素的下标更新为想要删除元素的下标
- this.set[this.data[len(this.data) - 1]] = this.set[val]
- // data中要删除的元素的位置上放上最后一个元素
- this.data[this.set[val]] = this.data[len(this.data) - 1]
- // 删除set
- delete(this.set, val)
- // 删除data最后一个元素
- this.data = this.data[:len(this.data) - 1]
- return true
-}
-
-func (this *RandomizedSet) GetRandom() int {
- return this.data[rand.Intn(len(this.data))]
-}
-```
-
-#### 146 LRU缓存机制
-
-题目解析:
-
-LRU是Least Recently Used,即最近最少使用。
-
-算法:哈希表+双向链表
-
-```go
-// data 2020/01/29
-// 算法 哈希表+双向链表,用头节点保存最近操作过的节点,尾巴节点即是最近最少使用的节点。
-type LRUCache struct {
- cache map[int]*DLinkNode
- size int
- head, tail *DLinkNode
-}
-type (
- DLinkNode struct {
- key, value int
- pre, next *DLinkNode
- }
-)
-func newLinkNode(k, v int) *DLinkNode {
- return &DLinkNode{
- key: k,
- value: v,
- }
-}
-// alway add node next to head
-func (this *LRUCache) addNode(n *DLinkNode) {
- n.pre = this.head
- n.next = this.head.next
- this.head.next.pre = n
- this.head.next = n
-}
-// delete node from the link list
-func (this *LRUCache) removeNode(n *DLinkNode) {
- p1, p2 := n.pre, n.next
- p1.next = p2
- p2.pre = p1
-}
-// move certain node to the head
-func (this *LRUCache) move2Head(n *DLinkNode) {
- this.removeNode(n)
- this.addNode(n)
-}
-// delete tail node
-func (this *LRUCache) removeTail() int {
- t := this.tail.pre
- this.removeNode(t)
- return t.key
-}
-
-func Constructor(capacity int) LRUCache {
- l := LRUCache{
- cache: make(map[int]*DLinkNode),
- size: capacity,
- head: newLinkNode(0,0),
- tail: newLinkNode(0,0),
- }
- l.head.next = l.tail
- l.tail.pre = l.head
- return l
-}
-
-
-func (this *LRUCache) Get(key int) int {
- v, ok := this.cache[key]
- if !ok { return -1 }
- this.move2Head(v) // head总是保存最新的记录
- return v.value
-}
-
-
-func (this *LRUCache) Put(key int, value int) {
- v, ok := this.cache[key]
- if ok {
- v.value = value
- this.move2Head(v) // head总是保存最新的记录
- return
- }
- v = newLinkNode(key, value)
- this.cache[key] = v
- this.addNode(v)
- if len(this.cache) > this.size {
- tkey := this.removeTail()
- delete(this.cache, tkey)
- }
-}
-```
-
diff --git "a/07_heap/No.215_\346\225\260\347\273\204\344\270\255\347\232\204\347\254\254K\344\270\252\346\234\200\345\244\247\345\205\203\347\264\240.md" "b/07_heap/No.215_\346\225\260\347\273\204\344\270\255\347\232\204\347\254\254K\344\270\252\346\234\200\345\244\247\345\205\203\347\264\240.md"
deleted file mode 100644
index a197306..0000000
--- "a/07_heap/No.215_\346\225\260\347\273\204\344\270\255\347\232\204\347\254\254K\344\270\252\346\234\200\345\244\247\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,92 +0,0 @@
-## 215 数组中的第K个最大元素-中等
-
-题目:
-
-给定整数数组 `nums` 和整数 `k`,请返回数组中第 `**k**` 个最大的元素。
-
-请注意,你需要找的是数组排序后的第 `k` 个最大的元素,而不是第 `k` 个不同的元素。
-
-你必须设计并实现时间复杂度为 `O(n)` 的算法解决此问题。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: [3,2,1,5,6,4], k = 2
-> 输出: 5
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: [3,2,3,1,2,4,5,5,6], k = 4
-> 输出: 4
-> ```
-
-
-
-分析:
-
-算法1:直接排序,返回第k个
-
-算法2:小顶堆
-
-```go
-// date 2024/01/03
-func findKthLargest(nums []int, k int) int {
- res := make([]int, k)
- idx := 0
- for _, v := range nums {
- if idx < k {
- res[idx] = v
- idx++
- if idx == k {
- makeMinHeap(res)
- }
- } else if v > res[0] {
- res[0] = v
- minHeapify(res, 0)
- }
- }
- return res[0]
-}
-
-// 把 arr 数组变成最小堆
-func makeMinHeap(arr []int) {
- for i := len(arr)/2 - 1; i >= 0; i-- {
- minHeapify(arr, i)
- }
-}
-
-// sink
-// 把较小值浮到上面
-func minHeapify(arr []int, i int) {
- n := len(arr)
- if i > n {
- return
- }
- temp := arr[i]
-
- // left = 2*i + 1
- // right = left + 1
- l := i << 1 + 1
- for l < n {
- // 取左右节点中的较小值
- if l+1 < n && arr[l+1] < arr[l] {
- l++
- }
- // 如果 父结点小于左右节点,那么最小堆已成立,直接跳出
- if arr[i] < arr[l] {
- break
- }
- // swap
- arr[i] = arr[l]
- arr[l] = temp
-
- i = l
- l = i << 1 + 1
- }
-}
-```
-
diff --git "a/07_heap/No.347_\345\211\215K\344\270\252\351\253\230\351\242\221\345\205\203\347\264\240.md" "b/07_heap/No.347_\345\211\215K\344\270\252\351\253\230\351\242\221\345\205\203\347\264\240.md"
deleted file mode 100644
index 160bb15..0000000
--- "a/07_heap/No.347_\345\211\215K\344\270\252\351\253\230\351\242\221\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,96 +0,0 @@
-## 347 前K个高频元素-中等
-
-题目:
-
-给你一个整数数组 `nums` 和一个整数 `k` ,请你返回其中出现频率前 `k` 高的元素。你可以按 **任意顺序** 返回答案。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: nums = [1,1,1,2,2,3], k = 2
-> 输出: [1,2]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: nums = [1], k = 1
-> 输出: [1]
-> ```
-
-
-
-分析:
-
-这道题依然是小顶堆的解题思路。
-
-自己构造一个结构体,保存元素值和元素出现的次数。
-
-先遍历数组,统计元素的出现次数,保存在 map 中,然后对 map 遍历,构造小顶堆。
-
-```go
-// date 2024/01/03
-func topKFrequent(nums []int, k int) []int {
- set := make(map[int]int, 16)
- arr := make([]*MyNode, 0, 16)
- for _, v := range nums {
- set[v]++
- }
- idx := 0
- for num, count := range set {
- re := &MyNode{val: num, time: count}
- if idx < k {
- arr = append(arr, re)
- idx++
- if idx == k {
- makeMinHeap(arr)
- }
- } else if count > arr[0].time {
- arr[0] = re
- minHeapify(arr, 0)
- }
- }
- ans := make([]int, 0, k)
- for _, v := range arr {
- ans = append(ans, v.val)
- }
- return ans
-}
-
-type MyNode struct {
- val int
- time int
-}
-
-func makeMinHeap(arr []*MyNode) {
- for i := len(arr)/2 - 1; i >= 0; i-- {
- minHeapify(arr, i)
- }
-}
-
-func minHeapify(arr []*MyNode, start int) {
- n := len(arr)
- if start > n {
- return
- }
- temp := arr[start]
- left := start * 2 + 1
- for left < n {
- right := left + 1
- if right < n && arr[right].time < arr[left].time {
- left++
- }
- if arr[start].time < arr[left].time {
- break
- }
- arr[start] = arr[left]
- arr[left] = temp
-
- start = left
- left = 2*start + 1
- }
-}
-```
-
diff --git a/07_heap/heap.md b/07_heap/heap.md
deleted file mode 100644
index 2dd357e..0000000
--- a/07_heap/heap.md
+++ /dev/null
@@ -1,265 +0,0 @@
-## 堆
-
-### 堆的定义
-
-
-
-(二叉)堆是一个数组,每个元素都保证 **大于等于** 或者 **小于等于** 另两个特定位置的元素。
-
-数据结构二叉堆能够很好地实现有线队列的基本操作。
-
-> 当一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。
-
-二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级存储。
-
-对于任意结点i,那么`i`对应的左右子结点分别为`2i+1`和`2i+2`,结点`i`对应的父结点为`i/2 -1`。
-
-最大堆:即父结点>=子结点
-
-最小堆:即父结点<=子结点
-
-堆排序的时间复杂度为O(nlogn)
-
-### 堆的特点
-
-1. 可以在O(nlogn)时间复杂度内,向堆插入元素
-2. 可以在O(nlogn)时间复杂度内,向堆删除元素
-3. 可以在O(1)时间复杂度内,取得最值
-
-### 堆的算法
-
-堆的操作会首先进行一些简单的改动,打破堆的状态,然后再遍历堆并按照要求将堆的状态恢复,这个过程称为堆的有序化(reheapifying)。
-
-堆的有序化有两种策略,分别是自下而上的堆有序化(上浮,swim)和自上而下的堆有序化(下沉,sink),其伪代码分别如下:
-
-```go
-// date 2020/03/01
-// 自下而上swim
-func swim(k int) {
- for k > 1 && less(k/2, i) {
- swap(k/2, k)
- k = k / 2
- }
-}
-// 自上而下sink
-func sink(k int) {
- l := 2 * k // 左节点
- r := l + 1 // 右节点
- for l < n {
- r = l + 1
- if r < n && less(l, r) { l++ }
- if !less(k, l) { break }
- swap(k, l)
- k = l
- l = 2 * k
- }
-}
-```
-
-**插入元素**
-
-将新元素插入到数组的末尾,并使用自下而上的堆有序化将新元素上浮到合适的位置。时间复杂度O(logN)
-
-**删除元素**
-
-将数组顶端的元素删除,将数组最后一个元素放到顶端,并使用自上而下的堆有序化将这个元素下沉到合适的位置。时间复杂度O(logN)
-
-### 堆排序
-
-基本思路:先构造堆,然后将堆顶元素与数组的最后一个元素交换,然后对N-1的堆重新堆有序化。伪代码如下:
-
-```go
-// date 2020/03/01
-func heapSort(nums []int) []int {
- makeMaxHeap(nums)
- n := len(nums)
- for n > 0 {
- swap(nums, 0, n-1)
- n--
- sink(nums, 0, n)
- }
-}
-
-// 构造堆
-func makeMaxHeap(nums []int) {
- for i := len(nums) >> 1 - 1; i >= 0; i-- { sink(nums, 0, len(nums)) }
-}
-
-func sink(nums []int, start, end int) {
- if start > end { return }
- l := start >> 1 + 1
- temp := nums[start]
- for l < end {
- r := l + 1
- if r < end && nums[r] > nums[l] { l++ }
- if nums[start] > nums[l] { break }
- nums[start] = nums[l]
- nums[l] = temp
- start = l
- l = start >> 1 + 1
- }
-}
-```
-
-### 相关题目
-
-- 912 排序数组【M】
-- 1046 最后一块石头的重量
-- 215 数组中第K个最大元素
-- 面试题40 最小的K个数
-- 面试题17.09 第K个数
-
-#### 912 排序数组
-
-题目要求:https://leetcode-cn.com/problems/sort-an-array/
-
-思路分析:
-
-算法一:堆排序。时间复杂度O(NlogN)。
-
-> 将N个元素排序,堆排序只需少于(2NlgN+2N)次比较,以及一半次数的交换。
-
-```go
-// date 2020/03/01
-func sortArray(nums []int) []int {
- makeMaxHeap(nums)
- n := len(nums)
- for n > 0 {
- swap(nums, 0, n-1)
- n--
- maxHeapify(nums, 0, n)
- }
- return nums
-}
-// 堆排序
-// 构建大顶堆
-func makeMaxHeap(nums []int) {
- for i := len(nums) >> 1 - 1; i >= 0; i-- {
- maxHeapify(nums, i, len(nums))
- }
-}
-// 自上而下的堆有序化
-func maxHeapify(nums []int, start, end int) {
- if start > end { return }
- temp, l, r := nums[start], start << 1 + 1, start << 1 + 2
- for l < end {
- r = l + 1
- if r < end && nums[r] > nums[l] { l++ }
- if nums[start] > nums[l] { break }
- nums[start] = nums[l]
- nums[l] = temp
- start = l
- l = start << 1 + 1
- }
-}
-// swap
-func swap(nums []int, i, j int) {
- t := nums[i]
- nums[i] = nums[j]
- nums[j] = t
-}
-```
-
-
-
-#### 1046 最后一块石头的重量
-
-题目要求:https://leetcode-cn.com/problems/last-stone-weight/
-
-思路分析:
-
-```go
-// date 2020/02/29
-func lastStoneWeight(stones []int) int {
- if len(stones) == 1 { return stones[0] }
- sort.Ints(stones)
- n := len(stones)
- for stones[n-2] != 0 {
- stones[n-1] -= stones[n-2]
- stones[n-2] = 0
- sort.Ints(stones)
- }
- return stones[n-1]
-}
-```
-
-#### 面试题40 最小的k个数
-
-题目要求:https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/
-
-思路分析:
-
-1)注意边界条件k等于零
-
-2)建立大顶堆的结果集
-
-3)遍历数组,如果小于堆顶元素,则替换,并调整堆
-
-```go
-// date 2020/02/29
-func getLeastNumbers(arr []int, k int) []int {
- if k == 0 { return []int{} }
- res, size := make([]int, k), 0
- for _, v := range arr {
- if size < k {
- res[size] = v
- size++
- if size == k {
- makeMaxHeap(res)
- }
- } else if v < res[0] {
- res[0] = v
- maxHeapify(res, 0)
- }
- }
- return res
-}
-// 实现大顶堆的两个函数
-func makeMaxHeap(nums []int) {
- for i := len(nums) >> 1 - 1; i >= 0; i-- {
- maxHeapify(nums, i)
- }
-}
-func maxHeapify(nums []int, i int) {
- if i > len(nums) { return }
- temp, n := nums[i], len(nums)
- l, r := i << 1 + 1, i << 1 + 2
- for l < n {
- r = l+1
- if r < n && nums[r] > nums[l] { l++ }
- if nums[i] > nums[l] { break }
- nums[i] = nums[l]
- nums[l] = temp
- i = l
- l = i << 1 + 1
- }
-}
-```
-
-#### 面试题17.09 第k个数
-
-题目要求:https://leetcode-cn.com/problems/get-kth-magic-number-lcci/
-
-思路分析:动态规划
-
-```go
-// date 2020/02/29
-func getKthMagicNumber(k int) int {
- l1, l2, l3 := 0, 0, 0
- res := make([]int, k)
- res[0] = 1
- for i := 1; i < k; i++ {
- res[i] = min(res[l1] * 3, min(res[l2] * 5, res[l3] * 7))
- if res[i] == res[l1] * 3 { l1++ }
- if res[i] == res[l2] * 5 { l2++ }
- if res[i] == res[l3] * 7 { l3++ }
- }
- return res[k-1]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
-
diff --git a/08_binaryTree/589.md b/08_binaryTree/589.md
deleted file mode 100644
index e792728..0000000
--- a/08_binaryTree/589.md
+++ /dev/null
@@ -1,59 +0,0 @@
-## 589 N叉树的前序遍历-简单
-
-> 给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
->
-> n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
->
-> 来源:力扣(LeetCode)
-> 链接:https://leetcode.cn/problems/n-ary-tree-preorder-traversal
-> 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-
-
-
-算法分析:
-
-算法1:递归
-
-```go
-// date 2022/10/21
-func preorder(root *Node) []int {
- res := make([]int, 0, 16)
- if root == nil {
- return res
- }
- res = append(res, root.Val)
- for i := 0; i < len(root.Children); i++ {
- res = append(res, preorder(root.Children[i])...)
- }
- return res
-}
-```
-
-
-
-算法2:迭代
-
-```go
-// date 2022/10/19
-func preorder(root *Node) []int {
- res := make([]int, 0, 16)
- if root == nil {
- return res
- }
- stack := make([]*Node, 0, 16)
- stack = append(stack, root)
-
- for len(stack) != 0 {
- cur := stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- res = append(res, cur.Val)
- for i := len(cur.Children)-1; i >= 0; i-- { // 直接逆序存放,出栈时就是最左边的那个
- if cur.Children[i] != nil {
- stack = append(stack, cur.Children[i])
- }
- }
- }
- return res
-}
-```
-
diff --git a/08_binaryTree/655.md b/08_binaryTree/655.md
deleted file mode 100644
index 3c1dfd9..0000000
--- a/08_binaryTree/655.md
+++ /dev/null
@@ -1,55 +0,0 @@
-## 655 输出二叉树-中等
-
-> 给你一棵二叉树的根节点 root ,请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ,用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则:
->
-> 树的 高度 为 height ,矩阵的行数 m 应该等于 height + 1 。
-> 矩阵的列数 n 应该等于 2height+1 - 1 。
-> 根节点 需要放置在 顶行 的 正中间 ,对应位置为 res[0][(n-1)/2] 。
-> 对于放置在矩阵中的每个节点,设对应位置为 res[r][c] ,将其左子节点放置在 res[r+1][c-2height-r-1] ,右子节点放置在 res[r+1][c+2height-r-1] 。
-> 继续这一过程,直到树中的所有节点都妥善放置。
-> 任意空单元格都应该包含空字符串 "" 。
-> 返回构造得到的矩阵 res 。
->
-> 来源:力扣(LeetCode)
-> 链接:https://leetcode.cn/problems/print-binary-tree
-> 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-
-算法分析:
-
-先构造结果集,然后逐层填充。
-
-```go
-// date 2020/02/25
-func printTree(root *TreeNode) [][]string {
- depth := findDepth(root) // 行数
- // 列数
- length := 1 << depth - 1
- res := make([][]string, depth)
- for i := 0; i < depth; i++ {
- res[i] = make([]string, length)
- }
- fill(res, root, 0, 0, length)
- return res
-}
-
-func fill(res [][]string, t *TreeNode, i, l, r int) {
- if t == nil {
- return
- }
- res[i][(l+r)/2] = fmt.Sprintf("%d", t.Val)
- fill(res, t.Left, i+1, l, (l+r)/2)
- fill(res, t.Right, i+1, (l+r+1)/2, r)
-}
-
-func findDepth(root *TreeNode) int {
- if root == nil {
- return 0
- }
- l, r := findDepth(root.Left), findDepth(root.Right)
- if l > r {
- return l+1
- }
- return r+1
-}
-```
-
diff --git "a/08_binaryTree/No.094_\344\272\214\345\217\211\346\240\221\347\232\204\344\270\255\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.094_\344\272\214\345\217\211\346\240\221\347\232\204\344\270\255\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index 30a47c2..0000000
--- "a/08_binaryTree/No.094_\344\272\214\345\217\211\346\240\221\347\232\204\344\270\255\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,68 +0,0 @@
-## 94 二叉树的中序遍历-简单
-
-题目:
-
-给定一个二叉树的根节点 `root` ,返回 *它的 **中序** 遍历* 。
-
-
-
-分析:
-
-算法1:递归版
-
-```go
-func inorderTraversal(root *TreeNode) []int {
- res := make([]int, 0)
- if root == nil { return res }
- // 先访问左子树
- if root.Left != nil {
- res = append(res, inorderTraversal(root.Left)...)
- }
- // 后访问根结点
- res = append(res, root.Val)
- // 最后访问右子树
- if root.Right != nil {
- res = append(res, inorderTraversal(root.Right)...)
- }
- return res
-}
-```
-
-
-
-算法2:迭代
-
-这里跟前序遍历类似,只是取根节点值加入结果集的时机略有区别。
-
-其主要思路为:
-
-1. 持续检查其左子树,重复1,直到左子树为空【此时栈中保留的是一系列的左子树节点】
-2. 出栈一次,并取根节点值加入结果集,然后检查最后一个左子树的右子树,重复1,2
-
-```go
-// date 2023/10/18
-// 迭代版
-// 需要stack结构
-// left->root->right
-func inorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- stack := make([]*TreeNode, 0, 16)
- res := make([]int, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- if len(stack) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- res = append(res, root.Val)
- root = root.Right
- }
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.095_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\225\2602.md" "b/08_binaryTree/No.095_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\225\2602.md"
deleted file mode 100644
index 2bb9c10..0000000
--- "a/08_binaryTree/No.095_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\225\2602.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 95 不同的二叉搜索树-中等
-
-题目:
-
-给你一个整数 `n` ,请你生成并返回所有由 `n` 个节点组成且节点值从 `1` 到 `n` 互不相同的不同 **二叉搜索树** 。可以按 **任意顺序** 返回答案。
-
-
-
-分析:
-
-题目看着很难,实际利用递归思想没有那么难。
-
-从序列`1..n`取出数字`1` 作为当前树的根节点,那么就有i-1个元素用来构造左子树,二另外的i+1..n个元素用来构造右子树。最后我们将得到G(i-1)棵不同的左子树,G(n-i)棵不同的右子树,其中G为卡特兰数。
-
-这样就可以以i为根节点,和两个可能的左右子树序列,遍历一遍左右子树序列,将左右子树和根节点链接起来。
-
-```go
-// date 2022/10/01
-func generateTrees(n int) []*TreeNode {
- var genWithNode func(start, end int) []*TreeNode
- genWithNode = func(start, end int) []*TreeNode {
- res := make([]*TreeNode, 0, 16)
- if start > end {
- // 空树
- res = append(res, nil)
- return res
- }
- for i := start; i <= end; i++ {
- left := genWithNode(start, i-1)
- right := genWithNode(i+1, end)
- for _, l := range left {
- for _, r := range right {
- res = append(res, &TreeNode{Val: i, Left: l, Right: r})
- }
- }
- }
- return res
- }
- return genWithNode(1, n)
-}
-```
-
diff --git "a/08_binaryTree/No.096_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.096_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index 6d8023d..0000000
--- "a/08_binaryTree/No.096_\344\270\215\345\220\214\347\232\204\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,35 +0,0 @@
-## 096 不同的二叉搜索树-中等
-
-题目:
-
-给你一个整数 `n` ,求恰由 `n` 个节点组成且节点值从 `1` 到 `n` 互不相同的 **二叉搜索树** 有多少种?返回满足题意的二叉搜索树的种数。
-
-
-
-分析:
-
-由于二叉搜索树的特殊性,我们可以知道:对于`[1, n]` 序列,如果选取 `i` 作为根节点,那么总的二叉搜索树的数目就是由 `[1,i]`组成的左子树 乘以 由 `[i+1,n]` 组成的右子树。
-
-所以可以用动态规划来解决这个问题,其初值为:
-
-```bash
-g[0], g[1] = 1, 1
-```
-
-
-
-```go
-//
-func numTrees(n int) int {
- g := make([]int, n+1, n+1)
- g[0], g[1] = 1, 1
- for i := 2; i <=n; i++ {
- // 根节点为i,有多少种可能
- for j := 1; j <= i; j++ {
- g[i] += g[j-1] * g[i-j]
- }
- }
- return g[n]
-}
-```
-
diff --git "a/08_binaryTree/No.098_\351\252\214\350\257\201\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.098_\351\252\214\350\257\201\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index aaa9179..0000000
--- "a/08_binaryTree/No.098_\351\252\214\350\257\201\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 98 验证二叉搜索树-中等
-
-题目:
-
-给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
-
-有效 二叉搜索树定义如下:
-
-节点的左子树只包含 小于 当前节点的数。
-节点的右子树只包含 大于 当前节点的数。
-所有左子树和右子树自身必须也是二叉搜索树。
-
-
-
-**解题思路**
-
-- 迭代版本的中序遍历,详见解法1。二叉搜索树的中序遍历为递增序列。
-- 递归得到中序遍历数组,然后判断数组,详见解法2。
-- 带区间值的DFS,详见解法3。
-
-```go
-// date 2023/10/22
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-// 解法1
-// 迭代 中序遍历
-func isValidBST(root *TreeNode) bool {
- stack := make([]*TreeNode, 0, 16)
- preVal := math.Inf(-1)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- cur := stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- if float64(cur.Val) <= preVal {
- return false
- }
- preVal = float64(cur.Val)
- root = cur.Right
- }
- return true
-}
-
-// date 2020/03/21
-// 解法2
-// 遍历其中序遍历序列,并判断其序列是否为递增
-func isValidBST(root *TreeNode) bool {
- nums := inOrder(root)
- for i := 0; i < len(nums)-1; i++ {
- if nums[i] >= nums[i+1] { return false }
- }
- return true
-}
-
-func inOrder(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- if root.Left != nil { res = append(res, inOrder(root.Left)...) }
- res = append(res, root.Val)
- if root.Right != nil { res = append(res, inOrder(root.Right)...) }
- return res
-}
-
-// 解法3:递归
-// 递归判断当前结点的值是否位于上下边界之中
-// 时间复杂度O(N)
-func isValidBST(root *TreeNode) bool {
- if root == nil { return true }
- var isValid func(root *TreeNode, min, max float64) bool
- isValid = func(root *TreeNode, min, max float64) bool {
- if root == nil { return true }
- if float64(root.Val) <= min || float64(root.Val) >= max { return false }
- return isValid(root.Left, min, float64(root.Val)) && isValid(root.Right, float64(root.Val), max)
- }
- return isValid(root, math.Inf(-1), math.Inf(0))
-}
-```
-
diff --git "a/08_binaryTree/No.099_\346\201\242\345\244\215\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.099_\346\201\242\345\244\215\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 9b8257a..0000000
--- "a/08_binaryTree/No.099_\346\201\242\345\244\215\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 99 恢复二叉树-中等
-
-题目:
-
-给你二叉搜索树的根节点 `root` ,该树中的 **恰好** 两个节点的值被错误地交换。*请在不改变其结构的情况下,恢复这棵树* 。
-
-
-
-分析:
-
-二叉树的中序遍历肯定为递增序列,所以迭代的方式遍历,根据当前节点与前继节点的大小关系来判断是否被交换过,并记录。
-
-在递增序列中交换两个值,那么第一次打破递增关系时,一定是前驱节点大于当前节点,前驱节点为被换过的。
-
-第二次打破递增关系时,同样前驱节点大于当前节点,但是当前节点是被换过的。
-
-```sh
-原始序列:1, 2, 3, 4, 5, 6, 7
-交换后的序列:1, 2, 6, 4, 5, 3, 7
-第一次为[6,4], 6为置换过的
-第二次为[5,3], 3为置换过的
-```
-
-下面看具体算法:
-
-```go
-// date 2023/10/22
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func recoverTree(root *TreeNode) {
- stack := make([]*TreeNode, 0, 16)
- // x, y 记录被交换的两个节点
- // pre 记录前驱节点,通过判断当前节点与前驱节点的关系
- // 找到两个被错误交换的节点,然后进行交换
- var x, y, pre *TreeNode
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- cur := stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- if pre != nil && cur.Val < pre.Val {
- y = cur
- if x == nil {
- x = pre
- } else {
- break
- }
- }
- pre = cur
- root = cur.Right
- }
- x.Val, y.Val = y.Val, x.Val
-}
-```
-
diff --git "a/08_binaryTree/No.1008_\345\211\215\345\272\217\351\201\215\345\216\206\346\236\204\351\200\240\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.1008_\345\211\215\345\272\217\351\201\215\345\216\206\346\236\204\351\200\240\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index febaf8f..0000000
--- "a/08_binaryTree/No.1008_\345\211\215\345\272\217\351\201\215\345\216\206\346\236\204\351\200\240\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 1008 前序遍历构造二叉搜索树-中等
-
-题目:
-
-给定一个整数数组,它表示BST(即 二叉搜索树 )的 先序遍历 ,构造树并返回其根。
-
-保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
-
-二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。
-
-二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
-
-
-
-分析:
-
-根据二叉搜索树特性,从前序序列中找到右子树节点,递归构造。
-
-需要注意的是,要考虑左子树可能为空。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func bstFromPreorder(preorder []int) *TreeNode {
- if len(preorder) == 0 {
- return nil
- }
- if len(preorder) == 1 {
- return &TreeNode{Val: preorder[0]}
- }
-
- root := &TreeNode{Val: preorder[0]}
-
- // find right index
- idx := 0
- for i, v := range preorder{
- if v > preorder[idx] {
- idx = i
- break
- }
- }
- // left
- if idx == 0 {
- // all val is left
- root.Left = bstFromPreorder(preorder[1:])
- } else {
- root.Left = bstFromPreorder(preorder[1:idx])
- }
-
- // find the right
- if idx != 0 {
- root.Right = bstFromPreorder(preorder[idx:])
- }
-
- return root
-}
-```
diff --git "a/08_binaryTree/No.100_\347\233\270\345\220\214\347\232\204\346\240\221.md" "b/08_binaryTree/No.100_\347\233\270\345\220\214\347\232\204\346\240\221.md"
deleted file mode 100644
index 995a1be..0000000
--- "a/08_binaryTree/No.100_\347\233\270\345\220\214\347\232\204\346\240\221.md"
+++ /dev/null
@@ -1,30 +0,0 @@
-## 100 相同的树-简单
-
-题目:
-
-给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
-
-
-
-分析:
-
-直接递归判断就可以。
-
-从递归可以看到,这是一种**自底向上**的方式,需要结合左右子树的情况以及当前节点本身,确定最终结果。
-
-```go
-// date 2022/10/10
-func isSameTree(p *TreeNode, q *TreeNode) bool {
- if p == nil && q == nil {
- return true
- }
- if p == nil || q == nil {
- return false
- }
- if p.Val != q.Val {
- return false
- }
- return isSameTree(p.Left, q.Left) && isSameTree(p.Right, q.Right)
-}
-```
-
diff --git "a/08_binaryTree/No.101_\345\257\271\347\247\260\344\272\214\345\217\211\346\225\260.md" "b/08_binaryTree/No.101_\345\257\271\347\247\260\344\272\214\345\217\211\346\225\260.md"
deleted file mode 100644
index 029f6e1..0000000
--- "a/08_binaryTree/No.101_\345\257\271\347\247\260\344\272\214\345\217\211\346\225\260.md"
+++ /dev/null
@@ -1,89 +0,0 @@
-## 101 对称二叉树-简单
-
-题目:
-
-给你一个二叉树的根节点 `root` , 检查它是否轴对称。
-
-轴对称的意思是节点关于整棵树的根节点 root 对称。
-
-
-
-**解题思路**
-
-解法1:子树互为镜像
-
-如果一个树的左右子树关于根节点对称,那么这个树就是轴对称的。
-
-很直观看就是左右子树互为镜像,那么两个树在什么情况下互为镜像呢?
-
-> 如果两个树同时满足两个条件,则互为镜像。
->
-> 1.它们的根节点具有相同的值;
->
-> 2.一个树的右子树和另一个树的左子树对称;一个树的左子树与另一个树的右子树对称
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isSymmetric(root *TreeNode) bool {
- var isMirror func(r1, r2 *TreeNode) bool
- isMirror = func(r1, r2 *TreeNode) bool {
- if r1 == nil && r2 == nil {
- return true
- }
- if r1 == nil || r2 == nil {
- return false
- }
- return r1.Val == r2.Val && isMirror(r1.Left, r2.Right) && isMirror(r1.Right, r2.Left)
- }
-
- return isMirror(root, root)
-}
-```
-
-
-
-解法2:【推荐该算法】
-
-类似层序遍历,将子树的左右结点依次放入队列,通过判断队列中的连续的两个值是否相同来确认是否对称。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isSymmetric(root *TreeNode) bool {
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root, root)
- for len(queue) != 0 {
- n := len(queue)
- for i := 0; i < n; i += 2 {
- r1, r2 := queue[i], queue[i+1]
- if r1 == nil && r2 == nil {
- continue
- }
- if r1 == nil || r2 == nil {
- return false
- }
- if r1.Val != r2.Val {
- return false
- }
- queue = append(queue, r1.Left, r2.Right, r1.Right, r2.Left)
- }
- queue = queue[n:]
- }
- return true
-}
-```
diff --git "a/08_binaryTree/No.102_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.102_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index b9eecb9..0000000
--- "a/08_binaryTree/No.102_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,74 +0,0 @@
-## 102 二叉树的层序遍历-中等
-
-题目:
-
-给你二叉树的根节点 `root` ,返回其节点值的 **层序遍历** 。 (即逐层地,从左到右访问所有节点)。
-
-
-
-
-分析:
-
-算法1:bfs广度优先搜索
-
-借助队列数据结构,先入先出,实现层序遍历。
-
-```go
-// date 2020/03/21
-// 层序遍历
-// bfs广度优先搜索
-// 算法一:使用队列,逐层遍历
-func levelOrder(root *TreeNode) [][]int {
- if root == nil {
- return [][]int{}
- }
- res := make([][]int, 0, 16)
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- for len(queue) != 0 {
- n := len(queue)
- curRes := make([]int, 0, 16)
- for i := 0; i < n; i++ {
- cur := queue[i]
- curRes = append(curRes, cur.Val)
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- res = append(res, curRes)
- queue = queue[n:]
- }
- return res
-}
-```
-
-算法2:dfs深度优先搜索
-
-这里的思路类似求二叉树的最大深度,借助dfs搜索,在每一层追加结果。
-
-```go
-// date 2020/03/21
-func levelOrder(root *TreeNode) [][]int {
- res := make([][]int, 0, 16)
- var dfs func(root *TreeNode, level int)
- dfs = func(root *TreeNode, level int) {
- if root == nil {
- return
- }
- if len(res) == level {
- res = append(res, make([]int, 0, 4))
- }
- res[level] = append(res[level], root.Val)
- level++
- dfs(root.Left, level)
- dfs(root.Right, level)
- }
- dfs(root, 0)
- return res
-}
-```
-
-**注意**,从上面两种实现的方式来看,层序遍历既可以使用广度优先搜索,也可以使用深度优先搜索。
diff --git "a/08_binaryTree/No.1038_\344\273\216\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\345\210\260\346\233\264\345\244\247\345\222\214\346\240\221.md" "b/08_binaryTree/No.1038_\344\273\216\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\345\210\260\346\233\264\345\244\247\345\222\214\346\240\221.md"
deleted file mode 100644
index f1030cf..0000000
--- "a/08_binaryTree/No.1038_\344\273\216\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\345\210\260\346\233\264\345\244\247\345\222\214\346\240\221.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 1038 从二叉搜索树到更大的和树-中等
-
-题目:
-
-给定一个二叉搜索树 root (BST),请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
-
-提醒一下, 二叉搜索树 满足下列约束条件:
-
-节点的左子树仅包含键 小于 节点键的节点。
-节点的右子树仅包含键 大于 节点键的节点。
-左右子树也必须是二叉搜索树。
-
-
-分析:
-
-递归后续遍历,直接更新。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func bstToGst(root *TreeNode) *TreeNode {
- var sum int
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Right)
- sum += root.Val
- root.Val = sum
- dfs(root.Left)
- }
-
- dfs(root)
-
- return root
-}
-```
diff --git "a/08_binaryTree/No.103_\344\272\214\345\217\211\346\240\221\347\232\204\351\224\257\351\275\277\345\275\242\345\261\202\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.103_\344\272\214\345\217\211\346\240\221\347\232\204\351\224\257\351\275\277\345\275\242\345\261\202\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index 29e44cc..0000000
--- "a/08_binaryTree/No.103_\344\272\214\345\217\211\346\240\221\347\232\204\351\224\257\351\275\277\345\275\242\345\261\202\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 103 二叉树的锯齿形层序遍历-中等
-
-题目:
-
-给你二叉树的根节点 `root` ,返回其节点值的 **锯齿形层序遍历** 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
-
-
-
-分析:
-
-正常层序遍历,每层存储结果的时候,先正向再反向。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func zigzagLevelOrder(root *TreeNode) [][]int {
- res := make([][]int, 0, 16)
- if root == nil {
- return res
- }
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- isLeftFirst := true
-
- for len(queue) != 0 {
- n := len(queue)
- lRes := make([]int, n)
- for i := 0; i < n; i++ {
- cur := queue[i]
-
- if isLeftFirst {
- lRes[i] = cur.Val
- } else {
- lRes[n-1-i] = cur.Val
- }
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- queue = queue[n:]
- res = append(res, lRes)
- isLeftFirst = !isLeftFirst
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.104_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\346\267\261\345\272\246.md" "b/08_binaryTree/No.104_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\346\267\261\345\272\246.md"
deleted file mode 100644
index 811052b..0000000
--- "a/08_binaryTree/No.104_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\346\267\261\345\272\246.md"
+++ /dev/null
@@ -1,99 +0,0 @@
-## 104二叉树的最大深度-简单
-
-题目:
-
-给定一个二叉树,找出其最大深度。
-
-二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
-
-**说明:** 叶子节点是指没有子节点的节点。
-
-
-
-分析:
-
-算法1:递归
-
-```go
-// 算法一: 递归,采用自底向上的递归思想
-// 时间复杂度O(N),空间复杂度O(NlogN)
-// 自底向上的递归
-func maxDepth(root *TreeNode) int {
- if root == nil {
- return 0
- }
- l, r := maxDepth(root.Left), maxDepth(root.Right)
- if l > r {
- return l+1
- }
- return r+1
-}
-```
-
-
-
-算法2:dfs深度优先搜索
-
-这里跟递归算法其实是一样的,只不过中间过程记录一个深度值 depth, 初始为零。
-
-- 当遇到空节点,直接返回 depth;否则递增
-- 如果当前节点为叶子节点,返回depth
-- 否则分别搜索左子树和右子树,返回其中的最大值
-
-```go
-
-// 算法2 dfs深度优先搜索
-// 时间复杂度O(N),空间复杂度O(NlogN)
-// 自顶向下的递归
-func maxDepth(root *TreeNode) int {
- var dfs func(root *TreeNode, depth int) int
- dfs = func(root *TreeNode, depth int) int {
- if root == nil {
- return depth
- }
- depth++
- l, r := dfs(root.Left, depth), dfs(root.Right, depth)
- if l > r {
- return l
- }
- return r
- }
-
- return dfs(root, 0)
-}
-```
-
-
-
-算法3:bfs广度优先搜索
-
-所谓广度优先搜索,其实就是层序遍历的思路,当遍历到最后一层时,即为最大深度。
-
-```go
-// 算法3
-// bfs广度优先搜索
-// 时间复杂度O(N),空间复杂度O(N)
-func maxDepth(root *TreeNode) int {
- if root == nil {return 0}
- queue := make([]*TreeNode, 0)
- queue = append(queue, root)
- depth, n := 0, 0
- // 判断是否还有新的一层
- for len(queue) != 0 {
- n = len(queue)
- // 从上一层中取节点,并查看其左右子树
- for i := 0; i < n; i++ {
- if queue[i].Left != nil {
- queue = append(queue, queue[i].Left)
- }
- if queue[i].Right != nil {
- queue = append(queue, queue[i].Right)
- }
- }
- queue = queue[n:]
- depth++
- }
- return depth
-}
-```
-
diff --git "a/08_binaryTree/No.105_\344\273\216\345\211\215\345\272\217\345\222\214\344\270\255\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.105_\344\273\216\345\211\215\345\272\217\345\222\214\344\270\255\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 708881b..0000000
--- "a/08_binaryTree/No.105_\344\273\216\345\211\215\345\272\217\345\222\214\344\270\255\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 105 从前序与中序遍历序列构造二叉树-中等
-
-题目:
-
-给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
-
-
-
-分析:
-
-前序序列是按照「根左右」的顺序遍历,而中序序列是按照「左根右」的顺序遍历,所以根节点肯定是前序序列中的第一个元素,然后再中序序列中找到该根节点的位置,将其分为左右子树,递归构建。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func buildTree(preorder []int, inorder []int) *TreeNode {
- if len(preorder) == 0 {
- return nil
- }
- root := &TreeNode{Val: preorder[0]}
- index := 0
- for i := 0; i < len(inorder); i++ {
- if inorder[i] == preorder[0] {
- index = i
- break
- }
- }
- root.Left = buildTree(preorder[1:index+1], inorder[0:index])
- root.Right = buildTree(preorder[index+1:], inorder[index+1:])
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.106_\344\273\216\344\270\255\345\272\217\345\222\214\345\220\216\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.106_\344\273\216\344\270\255\345\272\217\345\222\214\345\220\216\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 56b1aab..0000000
--- "a/08_binaryTree/No.106_\344\273\216\344\270\255\345\272\217\345\222\214\345\220\216\345\272\217\345\272\217\345\210\227\346\236\204\351\200\240\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 106从中序与后序遍历序列构造二叉树-中等
-
-题目:
-
-给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
-
-
-
-分析:
-
-后序序列中的最后一个元素为根节点,然后再中序序列中找到根节点的位置,依次递归构造左右子树。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func buildTree(inorder []int, postorder []int) *TreeNode {
- if len(inorder) == 0 {
- return nil
- }
- n := len(postorder)
- index := 0
- root := &TreeNode{Val: postorder[n-1]}
-
- for i := 0; i < n; i++ {
- if inorder[i] == postorder[n-1] {
- index = i
- break
- }
- }
- // inorder 左右根
- // postorder 左右根
- root.Left = buildTree(inorder[0:index], postorder[0:index]) // 一样长
- root.Right = buildTree(inorder[index+1:], postorder[index:n-1]) // 一样的起点
-
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.107_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\2062.md" "b/08_binaryTree/No.107_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\2062.md"
deleted file mode 100644
index 0fa6fb4..0000000
--- "a/08_binaryTree/No.107_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\2062.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 107 二叉树的层序遍历2-中等
-
-题目:
-
-给你二叉树的根节点 `root` ,返回其节点值 **自底向上的层序遍历** 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
-
-
-
-分析:
-
-这里先正常层序遍历,然后再将结果集反转一下。【推荐该算法】
-
-想了下,暂时没有比这更好的算法,因为向数组的头部插入数据,涉及拷贝,所以并不能够将每一层的结果一次性放入指定位置。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func levelOrderBottom(root *TreeNode) [][]int {
- res := make([][]int, 0, 16)
- if root == nil {
- return res
- }
-
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
-
- lRes := make([]int, 0, 16)
- for i := 0; i < n; i++ {
- cur := queue[i]
- lRes = append(lRes, cur.Val)
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- res = append(res, lRes)
- queue = queue[n:]
- }
-
- i, j := 0, len(res)-1
- for i < j {
- res[i], res[j] = res[j], res[i]
- i++
- j--
- }
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.108_\345\260\206\346\234\211\345\272\217\346\225\260\347\273\204\350\275\254\346\215\242\346\210\220\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.108_\345\260\206\346\234\211\345\272\217\346\225\260\347\273\204\350\275\254\346\215\242\346\210\220\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index d11d10a..0000000
--- "a/08_binaryTree/No.108_\345\260\206\346\234\211\345\272\217\346\225\260\347\273\204\350\275\254\346\215\242\346\210\220\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,38 +0,0 @@
-## 108 将有序数组转换为二叉搜索树-简单
-
-题目:
-
-给你一个整数数组 nums,其中元素已经按升序排列,请你将其转换为一个 高度平衡 的二叉搜索树。
-
-高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1」的二叉树。
-
-
-
-分析:
-
-跟【从中序和后序序列构造二叉树】类似,为了保持高度平衡,从有序数组中去中间值作为根,依次递归生成左右子树。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func sortedArrayToBST(nums []int) *TreeNode {
- if len(nums) == 0 {
- return nil
- }
- mid := len(nums)/2
-
- root := &TreeNode{Val: nums[mid]}
- root.Left = sortedArrayToBST(nums[0:mid])
- root.Right = sortedArrayToBST(nums[mid+1:])
-
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.109_\346\234\211\345\272\217\351\223\276\350\241\250\350\275\254\346\215\242\344\270\272\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.109_\346\234\211\345\272\217\351\223\276\350\241\250\350\275\254\346\215\242\344\270\272\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index e2f7c96..0000000
--- "a/08_binaryTree/No.109_\346\234\211\345\272\217\351\223\276\350\241\250\350\275\254\346\215\242\344\270\272\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 109 有序链表转换为二叉搜索树-中等
-
-题目:
-
-给定一个单链表的头节点 head,其中的元素按升序排列,将其转换为高度平衡的二叉搜索树。
-
-一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差不超过 1。
-
-
-
-分析:
-
-这个题目跟 108 题目类似,只不过从【有序数组】换成了【有序链表】。但思路是一样的,找到中间节点,递归构造。
-
-```go
-// date 2023/10/23
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func sortedListToBST(head *ListNode) *TreeNode {
- if head == nil {
- return nil
- }
- if head.Next == nil {
- return &TreeNode{Val: head.Val}
- }
-
- var pre, slow, fast *ListNode
- slow = head
- fast = head
- for fast != nil && fast.Next != nil {
- pre = slow
- slow = slow.Next
- fast = fast.Next.Next
-
- }
-
- pre.Next = nil
- root := &TreeNode{Val: slow.Val}
- root.Left = sortedListToBST(head)
-
- slow = slow.Next
- if slow == nil {
- return root
- }
- root.Right = sortedListToBST(slow)
-
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.110_\345\271\263\350\241\241\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.110_\345\271\263\350\241\241\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index b311662..0000000
--- "a/08_binaryTree/No.110_\345\271\263\350\241\241\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,59 +0,0 @@
-## 110 平衡二叉树-简单
-
-题目:
-
-给定一个二叉树,判断它是否是高度平衡的二叉树。
-
-本题中,一棵高度平衡二叉树定义为:
-
-一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
-
-
-
-分析:
-
-因为每个节点都需要保证平衡,所以采用自底向上的深度优先搜索,
-
-因为需要每个节点都保证是平衡,所以可以采用自底向上的递归。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isBalanced(root *TreeNode) bool {
- res := true
- var dfs func(root *TreeNode, depth int) int
- dfs = func(root *TreeNode, depth int) int {
- if root == nil {
- return depth
- }
- l := dfs(root.Left, depth)
- r := dfs(root.Right, depth)
- if abs(l, r) > 1 {
- res = false
- }
- if l > r {
- return l+1
- }
- return r+1
- }
-
- dfs(root, 0)
-
- return res
-}
-
-func abs(x, y int) int{
- if x > y {
- return x-y
- }
- return y-x
-}
-```
-
diff --git "a/08_binaryTree/No.111_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\260\217\346\267\261\345\272\246.md" "b/08_binaryTree/No.111_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\260\217\346\267\261\345\272\246.md"
deleted file mode 100644
index 65d8322..0000000
--- "a/08_binaryTree/No.111_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\260\217\346\267\261\345\272\246.md"
+++ /dev/null
@@ -1,106 +0,0 @@
-## 111 二叉树的最小深度-简单
-
-给定一个二叉树,找出其最小深度。
-
-最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
-
-**说明:**叶子节点是指没有子节点的节点。
-
-
-
-算法1:递归
-
-这里还是递归的思想,只不过返回左右子树其中的最小值。需要注意的是,如果不存在左子树,则返回右子树的最小深度并加1,同理右子树也是如此。
-
-```go
-// date 2020/03/21
-func minDepth(root *TreeNode) int {
- if root == nil {
- return 0
- }
- if root.Left == nil {
- return 1+minDepth(root.Right)
- }
- if root.Right == nil {
- return 1+minDepth(root.Left)
- }
- l, r := minDepth(root.Left), minDepth(root.Right)
- if l > r {
- return r+1
- }
- return l+1
-}
-```
-
-
-
-算法2:bfs【推荐该算法】
-
-该算法与层序遍历类似,依次入队,判断当前节点是否同时没有左右子树,从而找到最近的一层,即为最小深度。
-
-```go
-// date 2022/10/19
-func minDepth(root *TreeNode) int {
- if root == nil {
- return 0
- }
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- n := len(queue)
- var depth int
- for len(queue) != 0 {
- depth++
- n = len(queue)
- for i := 0; i < n; i++ {
- cur := queue[i]
- // 已经找到了最近的一层
- if cur.Left == nil && cur.Right == nil {
- return depth
- }
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- queue = queue[n:]
- }
- return depth
-}
-```
-
-
-
-算法3:dfs深度优先搜索
-
-这里跟递归类似,只是写法不一样。
-
-```go
-func minDepth(root *TreeNode) int {
- var dfs func(root *TreeNode, depth int) int
- dfs = func(root *TreeNode, depth int) int {
- if root == nil {
- return depth
- }
- depth++
- if root.Left == nil && root.Right == nil {
- return depth
- }
- if root.Left == nil {
- return dfs(root.Right, depth)
- }
- if root.Right == nil {
- return dfs(root.Left, depth)
- }
- l, r := dfs(root.Left, depth), dfs(root.Right, depth)
- if l < r {
- return l
- }
- return r
- }
-
- return dfs(root, 0)
-}
-```
-
diff --git "a/08_binaryTree/No.112_\350\267\257\345\276\204\346\200\273\345\222\214.md" "b/08_binaryTree/No.112_\350\267\257\345\276\204\346\200\273\345\222\214.md"
deleted file mode 100644
index 865ce9e..0000000
--- "a/08_binaryTree/No.112_\350\267\257\345\276\204\346\200\273\345\222\214.md"
+++ /dev/null
@@ -1,81 +0,0 @@
-## 112 路径总和-简单
-
-题目:
-
-给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
-
-叶子节点 是指没有子节点的节点。
-
-
-
-
-
-分析:
-
-算法1:递归
-
-这种递归是**自顶向下**的方式,通过结合当前节点值,向下一层级传递新的目标值,以判断到达叶子节点时是否满足条件。
-
-```go
-// date 2022/10/19
-func hasPathSum(root *TreeNode, targetSum int) bool {
- if root == nil {
- return false
- }
- targetSum -= root.Val
- if root.Left == nil && root.Right == nil {
- return targetSum == 0
- }
- return hasPathSum(root.Left, targetSum) || hasPathSum(root.Right, targetSum)
-}
-```
-
-
-
-算法2:【推荐该算法】
-
-迭代,类似层序遍历,当遍历到叶子节点时,判断值是否为零
-
-```go
-// date 2023/10/18
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func hasPathSum(root *TreeNode, targetSum int) bool {
- if root == nil {
- return false
- }
- queue := make([]*TreeNode, 0, 16)
- csum := make([]int, 0, 16)
- queue = append(queue, root)
- csum = append(csum, targetSum-root.Val)
- n := len(queue)
- for len(queue) != 0 {
- n = len(queue)
- for i := 0; i < n; i++ {
- cur := queue[i]
- // 找到叶子节点
- if cur.Left == nil && cur.Right == nil && csum[i] == 0 {
- return true
- }
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- csum = append(csum, csum[i] - cur.Left.Val)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- csum = append(csum, csum[i] - cur.Right.Val)
- }
- }
- queue = queue[n:]
- csum = csum[n:]
- }
- return false
-}
-```
-
diff --git "a/08_binaryTree/No.113_\350\267\257\345\276\204\346\200\273\345\222\2142.md" "b/08_binaryTree/No.113_\350\267\257\345\276\204\346\200\273\345\222\2142.md"
deleted file mode 100644
index ce0cd55..0000000
--- "a/08_binaryTree/No.113_\350\267\257\345\276\204\346\200\273\345\222\2142.md"
+++ /dev/null
@@ -1,100 +0,0 @@
-## 113 路径总和2-中等
-
-题目:
-
-给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
-
-叶子节点 是指没有子节点的节点。
-
-
-
-分析:
-
-算法1:
-
-这里采用深度优先搜索,当遍历到叶子节点且节点的值等于剩下的值,那么就直接追加结果,并返回。如果不是,递归遍历左右子树。
-
-但是这里的写法相对麻烦一些,因为是自底向上的递推;其实可以采用自顶向下的递推,利用path记录已经遍历过的节点。详见算法2。
-
-```go
-// date 2022/10/24
-func pathSum(root *TreeNode, targetSum int) [][]int {
- var dfs func(root *TreeNode, v int) ([][]int, bool)
- dfs = func(root *TreeNode, v int) ([][]int, bool) {
- if root == nil {
- return nil, false
- }
- res := make([][]int, 0, 16)
- if root.Left == nil && root.Right == nil && root.Val == v {
- t := []int{root.Val}
- res = append(res, t)
- return res, true
- }
- v -= root.Val
- l, ok1 := dfs(root.Left, v)
- r, ok2 := dfs(root.Right, v)
- if ok1 {
- for i := 0; i < len(l); i++ {
- t := make([]int, 0, 16)
- t = append(t, root.Val)
- t = append(t, l[i]...)
- res = append(res, t)
- }
- }
- if ok2 {
- for i := 0; i < len(r); i++ {
- t := make([]int, 0, 16)
- t = append(t, root.Val)
- t = append(t, r[i]...)
- res = append(res, t)
- }
- }
- if ok1 || ok2 {
- return res, true
- }
- return nil, false
- }
-
- asn, _ := dfs(root, targetSum)
- return asn
-}
-```
-
-
-
-算法2:【推荐该算法】
-
-同样采用深度优先搜索,`path` 记录已经遍历过的节点值。
-
-1. 当遍历到节点时,直接追加值到path中
-2. 如果遇到叶子节点且满足条件,直接将path追加到最终结果,
-3. 因为每次遍历,整个路径会变化,因为需要返回前将1中增加的值去掉。
-
-```go
-// date 2022/10/24
-func pathSum(root *TreeNode, targetSum int) [][]int {
- ans := make([][]int, 0, 16)
- path := make([]int, 0, 16)
-
- var dfs func(root *TreeNode, leftVal int)
- dfs = func(root *TreeNode, leftVal int) {
- if root == nil {
- return
- }
- path = append(path, root.Val)
- defer func() {
- path = path[:len(path)-1]
- }()
- leftVal -= root.Val
- if root.Left == nil && root.Right == nil && leftVal == 0 {
- ans = append(ans, append([]int{}, path...))
- return
- }
- dfs(root.Left, leftVal)
- dfs(root.Right, leftVal)
- }
- dfs(root, targetSum)
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.114_\344\272\214\345\217\211\346\240\221\345\261\225\345\274\200\344\270\272\351\223\276\350\241\250.md" "b/08_binaryTree/No.114_\344\272\214\345\217\211\346\240\221\345\261\225\345\274\200\344\270\272\351\223\276\350\241\250.md"
deleted file mode 100644
index 8d97482..0000000
--- "a/08_binaryTree/No.114_\344\272\214\345\217\211\346\240\221\345\261\225\345\274\200\344\270\272\351\223\276\350\241\250.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 114 二叉树展开为链表-中等
-
-题目:
-
-给你二叉树的根结点 `root` ,请你将它展开为一个单链表:
-
-- 展开后的单链表应该同样使用 `TreeNode` ,其中 `right` 子指针指向链表中下一个结点,而左子指针始终为 `null` 。
-- 展开后的单链表应该与二叉树 [**先序遍历**](https://baike.baidu.com/item/先序遍历/6442839?fr=aladdin) 顺序相同。
-
-
-
-分析:
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func flatten(root *TreeNode) {
- cur := root
-
- for cur != nil {
- if cur.Left != nil {
- next := cur.Left
- pre := next
- for pre.Right != nil {
- pre = pre.Right
- }
- pre.Right = cur.Right
-
- cur.Left = nil
- cur.Right = next
- }
-
- cur = cur.Right
- }
-}
-```
-
diff --git "a/08_binaryTree/No.1161_\346\234\200\345\244\247\345\261\202\345\206\205\345\205\203\347\264\240\345\222\214.md" "b/08_binaryTree/No.1161_\346\234\200\345\244\247\345\261\202\345\206\205\345\205\203\347\264\240\345\222\214.md"
deleted file mode 100644
index e94ddf6..0000000
--- "a/08_binaryTree/No.1161_\346\234\200\345\244\247\345\261\202\345\206\205\345\205\203\347\264\240\345\222\214.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 1161 最大层内元素和-中等
-
-题目:
-
-给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
-
-请返回层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
-
-
-
-分析:
-
-这里就是层序遍历,根据每层的结果更新最终的结果即可。
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func maxLevelSum(root *TreeNode) int {
- if root == nil {
- return 0
- }
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- n := len(queue)
- ls := 0 // level sum
- lsMax := math.Inf(-1)
- level, res := 1, 1
- for len(queue) != 0 {
- n = len(queue)
- ls = 0
- for i := 0; i < n; i++ {
- cur := queue[i]
- ls += cur.Val
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- if float64(ls) > lsMax {
- lsMax = float64(ls)
- res = level
- }
- queue = queue[n:]
- level++
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.116_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md" "b/08_binaryTree/No.116_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md"
deleted file mode 100644
index 4eaf30e..0000000
--- "a/08_binaryTree/No.116_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md"
+++ /dev/null
@@ -1,62 +0,0 @@
-## 116 填充每个节点的下一个右侧节点-中等
-
-题目:
-
-给定一个 **完美二叉树** ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
-
-```
-struct Node {
- int val;
- Node *left;
- Node *right;
- Node *next;
-}
-```
-
-填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 `NULL`。
-
-初始状态下,所有 next 指针都被设置为 `NULL`。
-
-
-
-分析:
-
-
-```go
-// date 2023/10/23
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Left *Node
- * Right *Node
- * Next *Node
- * }
- */
-
-func connect(root *Node) *Node {
- if root == nil {
- return nil
- }
- queue := make([]*Node, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
- for i := 0; i < n; i++ {
- cur := queue[i]
- if i + 1 < n {
- cur.Next = queue[i+1]
- }
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- queue = queue[n:]
- }
- return root
-}
-```
diff --git "a/08_binaryTree/No.117_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md" "b/08_binaryTree/No.117_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md"
deleted file mode 100644
index 6eee8f0..0000000
--- "a/08_binaryTree/No.117_\345\241\253\345\205\205\346\257\217\344\270\252\350\212\202\347\202\271\347\232\204\344\270\213\344\270\200\344\270\252\345\217\263\344\276\247\350\212\202\347\202\271\346\214\207\351\222\210.md"
+++ /dev/null
@@ -1,115 +0,0 @@
-## 117 填充每个节点的下一个右侧节点指针2-中等
-
-题目:
-
-给定一个二叉树:
-
-```
-struct Node {
- int val;
- Node *left;
- Node *right;
- Node *next;
-}
-```
-
-填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 `NULL` 。
-
-初始状态下,所有 next 指针都被设置为 `NULL` 。
-
-
-
-分析:
-
-
-```go
-// date 2023/10/23
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Left *Node
- * Right *Node
- * Next *Node
- * }
- */
-
-func connect(root *Node) *Node {
- if root == nil {
- return root
- }
-
- queue := make([]*Node, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
-
- for i := 0; i < n; i++ {
- cur := queue[i]
-
- if i+1 < n {
- cur.Next = queue[i+1]
- }
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
-
- queue = queue[n:]
- }
-
- return root
-}
-```
-
-
-算法2:【推荐该算法,很巧妙】
-
-像链表一样的处理。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Left *Node
- * Right *Node
- * Next *Node
- * }
- */
-
-func connect(root *Node) *Node {
- if root == nil {
- return root
- }
-
- cur := root
-
- for cur != nil {
- dumy := &Node{}
- pre := dumy
-
- for cur != nil {
- if cur.Left != nil {
- pre.Next = cur.Left
- pre = pre.Next
- }
- if cur.Right != nil {
- pre.Next = cur.Right
- pre = pre.Next
- }
- cur = cur.Next
- }
-
- cur = dumy.Next
- }
-
- return root
-}
-```
diff --git "a/08_binaryTree/No.124_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\350\267\257\345\276\204\345\222\214.md" "b/08_binaryTree/No.124_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\350\267\257\345\276\204\345\222\214.md"
deleted file mode 100644
index 037d705..0000000
--- "a/08_binaryTree/No.124_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\350\267\257\345\276\204\345\222\214.md"
+++ /dev/null
@@ -1,82 +0,0 @@
-## 124 二叉树的最大路径和-中等
-
-题目:
-
-二叉树中的 **路径** 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 **至多出现一次** 。该路径 **至少包含一个** 节点,且不一定经过根节点。
-
-**路径和** 是路径中各节点值的总和。
-
-给你一个二叉树的根节点 `root` ,返回其 **最大路径和** 。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:root = [1,2,3]
-> 输出:6
-> 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:root = [-10,9,20,null,null,15,7]
-> 输出:42
-> 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
-> ```
-
-
-
-**解题思路**
-
-这道题可用 BFS 解。
-
-所谓路径,就是树中节点可以连接起来,且有起点和终点。所以对于某个节点而言,最大路径和就是其节点值加上左右子树的最大路径和。
-
-需要注意的是,BFS 返回的时候,选取左右子树其中最大的即可,因为要有起点或者终点。
-
-```go
-// date 2024/01/16
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func maxPathSum(root *TreeNode) int {
- ans := math.MinInt32
-
- var bfs func(root *TreeNode) int
- bfs = func(root *TreeNode) int {
- if root == nil {
- return 0
- }
- left := max(bfs(root.Left), 0)
- right := max(bfs(root.Right), 0)
-
- sum := root.Val + left + right
- ans = max(ans, sum)
-
- return root.Val + max(left, right)
- }
-
- bfs(root)
-
- return ans
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/08_binaryTree/No.129_\346\261\202\346\240\271\350\212\202\347\202\271\345\210\260\345\217\266\345\255\220\350\212\202\347\202\271\346\225\260\345\255\227\344\271\213\345\222\214.md" "b/08_binaryTree/No.129_\346\261\202\346\240\271\350\212\202\347\202\271\345\210\260\345\217\266\345\255\220\350\212\202\347\202\271\346\225\260\345\255\227\344\271\213\345\222\214.md"
deleted file mode 100644
index d9e01ae..0000000
--- "a/08_binaryTree/No.129_\346\261\202\346\240\271\350\212\202\347\202\271\345\210\260\345\217\266\345\255\220\350\212\202\347\202\271\346\225\260\345\255\227\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 129 求从根节点到叶子节点数字之和-中等
-
-给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
-每条从根节点到叶节点的路径都代表一个数字:
-
-例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
-计算从根节点到叶节点生成的 所有数字之和 。
-
-叶节点 是指没有子节点的节点。
-
-
-
-分析:
-
-自顶向下递归,并且携带已知的值;当遇到叶子节点时计算到结果中。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func sumNumbers(root *TreeNode) int {
- var ans int
- var dfs func(root *TreeNode, has int)
- dfs = func(root *TreeNode, has int) {
- if root == nil {
- return
- }
- if root.Left == nil && root.Right == nil {
- ans += has + root.Val
- return
- }
- has = (has + root.Val) * 10
- if root.Left != nil {
- dfs(root.Left, has)
- }
- if root.Right != nil {
- dfs(root.Right, has)
- }
- }
-
- dfs(root, 0)
-
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.1302_\345\261\202\346\225\260\346\234\200\346\267\261\345\217\266\345\255\220\350\212\202\347\202\271\347\232\204\345\222\214.md" "b/08_binaryTree/No.1302_\345\261\202\346\225\260\346\234\200\346\267\261\345\217\266\345\255\220\350\212\202\347\202\271\347\232\204\345\222\214.md"
deleted file mode 100644
index 5de854b..0000000
--- "a/08_binaryTree/No.1302_\345\261\202\346\225\260\346\234\200\346\267\261\345\217\266\345\255\220\350\212\202\347\202\271\347\232\204\345\222\214.md"
+++ /dev/null
@@ -1,51 +0,0 @@
-## 1302 层数最深叶子节点的和-中等
-
-题目:
-
-给你一棵二叉树的根节点 `root` ,请你返回 **层数最深的叶子节点的和** 。
-
-
-
-分析:
-
-就是层序遍历,只存储当前层结果,那么最后一次结果就是答案。
-
-```go
-// date 2023/20/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func deepestLeavesSum(root *TreeNode) int {
- var res int
- if root == nil {
- return res
- }
-
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
- res = 0
- for i := 0; i < n; i++ {
- cur := queue[i]
- res += cur.Val
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- queue = queue[n:]
- }
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.1305_\344\270\244\346\243\265\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\211\200\346\234\211\345\205\203\347\264\240.md" "b/08_binaryTree/No.1305_\344\270\244\346\243\265\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\211\200\346\234\211\345\205\203\347\264\240.md"
deleted file mode 100644
index 2a06a6b..0000000
--- "a/08_binaryTree/No.1305_\344\270\244\346\243\265\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\211\200\346\234\211\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,72 +0,0 @@
-## 1305 两棵二叉搜索树的所有元素-中等
-
-题目:
-
-给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含 两棵树 中的所有整数并按 升序 排序。.
-
-
-
-分析:
-
-前序遍历,变成两个有序数组,然后归并。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func getAllElements(root1 *TreeNode, root2 *TreeNode) []int {
- s1 := bst2array(root1)
- s2 := bst2array(root2)
- ans := make([]int, 0, 16)
- i, j := 0, 0
- k1, k2 := len(s1), len(s2)
- for i < k1 || j < k2 {
- if i >= k1 {
- break
- }
- if j >= k2 {
- break
- }
- if s1[i] < s2[j] {
- ans = append(ans, s1[i])
- i++
- } else {
- ans = append(ans, s2[j])
- j++
- }
- }
-
- if i < k1 {
- ans = append(ans, s1[i:]...)
- }
- if j < k2 {
- ans = append(ans, s2[j:]...)
- }
-
- return ans
-}
-
-func bst2array(r1 *TreeNode) []int {
- ans := make([]int, 0, 16)
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Left)
- ans = append(ans, root.Val)
- dfs(root.Right)
- }
-
- dfs(r1)
-
- return ans
-}
-```
diff --git "a/08_binaryTree/No.144_\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.144_\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index 0bae439..0000000
--- "a/08_binaryTree/No.144_\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,70 +0,0 @@
-## 144 二叉树的前序遍历-简单
-
-题目:
-
-给你二叉树的根节点 `root` ,返回它节点值的 **前序** 遍历。
-
-
-
-分析:
-
-算法1:递归
-
-```go
-// root -> left -> right
-func preorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- res = append(res, root.Val)
- if root.Left != nil {
- res = append(res, preorderTraversal(root.Left)...)
- }
- if root.Right != nil {
- res = append(res, preorderTraversal(root.Right)...)
- }
- return res
-}
-```
-
-
-
-算法2:迭代
-
-迭代的思想就是利用节点仅有左右指针,不断的搜索,同时借助 stack 数据结构,保存已经遍历过的节点。
-
-其主要思路为:
-
-1. 先取根节点值加入结果集,并将根节点入栈;持续检查其左子树,重复1,直到左子树为空【此时栈中保留的是一系列的左子树节点】
-2. 出栈一次,检查最后一个左子树的右子树,重复1,2
-
-```go
-// date 2023/10/18
-func preorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- stack := make([]*TreeNode, 0, 16)
- res := make([]int, 0, 16)
- for root != nil || len(stack) != 0 {
- // 不断地查找左子树
- for root != nil {
- // 先将根节点加入结果集
- res = append(res, root.Val)
- // 根节点已经遍历过,入栈,后续出栈检查其右子树
- stack = append(stack, root)
- root = root.Left
- }
- // 此时栈中最后一个元素就是没有左子树节点
- // 取出并检查其右子树
- if len(stack) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- root = root.Right
- }
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.145_\344\272\214\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.145_\344\272\214\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index c5407d3..0000000
--- "a/08_binaryTree/No.145_\344\272\214\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,78 +0,0 @@
-## 145 二叉树的后序遍历-简单
-
-题目:
-
-给你一棵二叉树的根节点 `root` ,返回其节点值的 **后序遍历** 。
-
-
-
-分析:
-
-算法1:递归
-
-```go
-// 递归
-func postorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- if root.Left != nil {
- res = append(res, postorderTraversal(root.Left)...)
- }
- if root.Right != nil {
- res = append(res, postorderTraversal(root.Right)...)
- }
- res = append(res, root.Val)
- return res
-}
-```
-
-
-
-算法2:迭代【推荐该算法】
-
-迭代遍历的时候依然需要 stack 结构来保存已经遍历过的节点;同时借助 pre 指针保存上次出栈的节点,用于判断当前节点是否同时具有左右子树,还是只有单个子树。
-
-1. 先将根节点入栈,循环遍历栈是否为空
-2. 出栈,取出当前节点
- 1. 如果当前节点没有左右子树,则为叶子节点,直接加入结果集
- 2. 其次判断上次出栈的节点是否是当前节点的左右子树,如果是,表明当前节点的子树已经处理完毕,也需要加入结果集【这里依赖的是左右子树的入栈,因为在栈中左右子树不具备前继关系,至于根节点具备】
- 3. 依次检查当前节点的右子树,左子树,重复1,2
-
-```go
-// 迭代版
-// date 2023/10/18
-// left->right-root
-func postorderTraversal(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- var pre, cur *TreeNode // 记录前驱节点和当前节点
- for len(stack) != 0 {
- // 出栈 当前结点
- cur = stack[len(stack)-1]
- // 如果当前结点为叶子结点,则直接加入结果集
- // 如果当前结点不是叶子结点,但是上次遍历结点为当前结点的左右子树时(说明当前结点只有单个子树,且子树已经处理完毕),也加入结果集
- if cur.Left == nil && cur.Right == nil || pre != nil && (pre == cur.Left || pre == cur.Right) {
- res = append(res, cur.Val)
- // 出栈,继续检查
- stack = stack[:len(stack)-1]
- pre = cur
- } else {
- // 因为在出栈的时候检查结点,并追加到结果中
- // 所以,先入栈右子树,后入栈左子树
- if cur.Right != nil {
- stack = append(stack, cur.Right)
- }
- if cur.Left != nil {
- stack = append(stack, cur.Left)
- }
- }
- }
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.1609_\345\245\207\345\201\266\346\240\221.md" "b/08_binaryTree/No.1609_\345\245\207\345\201\266\346\240\221.md"
deleted file mode 100644
index 52b1f0a..0000000
--- "a/08_binaryTree/No.1609_\345\245\207\345\201\266\346\240\221.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 1609 奇偶树-中等
-
-题目:
-
-如果一棵二叉树满足下述几个条件,则可以称为 **奇偶树** :
-
-- 二叉树根节点所在层下标为 `0` ,根的子节点所在层下标为 `1` ,根的孙节点所在层下标为 `2` ,依此类推。
-- **偶数下标** 层上的所有节点的值都是 **奇** 整数,从左到右按顺序 **严格递增**
-- **奇数下标** 层上的所有节点的值都是 **偶** 整数,从左到右按顺序 **严格递减**
-
-给你二叉树的根节点,如果二叉树为 **奇偶树** ,则返回 `true` ,否则返回 `false` 。
-
-
-
-分析:
-
-没啥好说的,就是基本的层序遍历。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isEvenOddTree(root *TreeNode) bool {
- if root == nil {
- return false
- }
-
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
-
- var preVal int
- isEvenIdx := false
-
- for len(queue) != 0 {
- n := len(queue)
-
- for i := 0; i < n; i++ {
- cur := queue[i]
-
- if isEvenIdx {
- if cur.Val % 2 == 1 {
- return false
- }
- } else {
- if cur.Val % 2 == 0 {
- return false
- }
- }
-
- if i == 0 {
- preVal = cur.Val
- } else {
- if isEvenIdx {
- // 严格递减
- if cur.Val >= preVal {
- return false
- }
- } else {
- if cur.Val <= preVal {
- return false
- }
- }
- preVal = cur.Val
- }
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
-
- queue = queue[n:]
- isEvenIdx = !isEvenIdx
- }
-
- return true
-}
-```
-
diff --git "a/08_binaryTree/No.173_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\277\255\344\273\243\345\231\250.md" "b/08_binaryTree/No.173_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\277\255\344\273\243\345\231\250.md"
deleted file mode 100644
index f1695e9..0000000
--- "a/08_binaryTree/No.173_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\277\255\344\273\243\345\231\250.md"
+++ /dev/null
@@ -1,76 +0,0 @@
-## 173 二叉搜索树迭代器-中等
-
-题目:
-
-实现一个二叉搜索树迭代器类`BSTIterator` ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
-
-- `BSTIterator(TreeNode root)` 初始化 `BSTIterator` 类的一个对象。BST 的根节点 `root` 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。
-- `boolean hasNext()` 如果向指针右侧遍历存在数字,则返回 `true` ;否则返回 `false` 。
-- `int next()`将指针向右移动,然后返回指针处的数字。
-
-注意,指针初始化为一个不存在于 BST 中的数字,所以对 `next()` 的首次调用将返回 BST 中的最小元素。
-
-你可以假设 `next()` 调用总是有效的,也就是说,当调用 `next()` 时,BST 的中序遍历中至少存在一个下一个数字。
-
-
-
-分析:
-
-中序遍历,变成数组。
-
-```go
-// date 2023/10/23
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-type BSTIterator struct {
- index int
- values []int
-}
-
-
-func Constructor(root *TreeNode) BSTIterator {
- res := make([]int, 0, 16)
- stack := make([]*TreeNode, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- res = append(res, root.Val)
- root = root.Right
- }
-
- return BSTIterator{index: -1, values: res}
-}
-
-
-func (this *BSTIterator) Next() int {
- this.index++
- if this.index >= len(this.values) {
- return 0
- }
- return this.values[this.index]
-}
-
-
-func (this *BSTIterator) HasNext() bool {
- return this.index < len(this.values)-1
-}
-
-
-/**
- * Your BSTIterator object will be instantiated and called as such:
- * obj := Constructor(root);
- * param_1 := obj.Next();
- * param_2 := obj.HasNext();
- */
-```
-
diff --git "a/08_binaryTree/No.199_\344\272\214\345\217\211\346\240\221\347\232\204\345\217\263\350\247\206\345\233\276.md" "b/08_binaryTree/No.199_\344\272\214\345\217\211\346\240\221\347\232\204\345\217\263\350\247\206\345\233\276.md"
deleted file mode 100644
index 4fd3d51..0000000
--- "a/08_binaryTree/No.199_\344\272\214\345\217\211\346\240\221\347\232\204\345\217\263\350\247\206\345\233\276.md"
+++ /dev/null
@@ -1,31 +0,0 @@
-## 199 二叉树的右视图-中等
-
-题目:
-
-给定一个二叉树的根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
-
-
-
-**解题思路**
-
-层序遍历的最后一个节点值。
-
-```go
-// date 2023/10/23
-func rightSideView(root *TreeNode) []int {
- res := make([]int, 0)
- if root == nil { return res }
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- for len(stack) != 0 {
- n := len(stack)
- res = append(res, stack[0].Val)
- for i := 0; i < n; i++ {
- if stack[i].Right != nil { stack = append(stack, stack[i].Right) }
- if stack[i].Left != nil { stack = append(stack, stack[i].Left) }
- }
- stack = stack[n:]
- }
- return res
-}
-```
diff --git "a/08_binaryTree/No.230_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\254\254K\345\260\217\347\232\204\345\205\203\347\264\240.md" "b/08_binaryTree/No.230_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\254\254K\345\260\217\347\232\204\345\205\203\347\264\240.md"
deleted file mode 100644
index 4ba002e..0000000
--- "a/08_binaryTree/No.230_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\254\254K\345\260\217\347\232\204\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,46 +0,0 @@
-## 230 二叉搜索树中第K小的元素
-
-题目:
-
-给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
-
-
-
-分析:
-
-利用二叉搜索树的特点,其左根右(前序遍历)序列为非递减序列。
-
-所以,直接递归遍历,数数即可。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func kthSmallest(root *TreeNode, k int) int {
- var res int
- var count int
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Left)
- count++
- if count == k {
- res = root.Val
- return
- }
- dfs(root.Right)
- }
-
- dfs(root)
-
- return res
-}
-```
diff --git "a/08_binaryTree/No.235_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md" "b/08_binaryTree/No.235_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md"
deleted file mode 100644
index 4846c5b..0000000
--- "a/08_binaryTree/No.235_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 235 二叉搜索数的最近公共祖先-中等
-
-题目:
-
-给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
-
-[百度百科](https://baike.baidu.com/item/最近公共祖先/8918834?fr=aladdin)中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(**一个节点也可以是它自己的祖先**)。”
-
-
-
-分析:
-
-与 236 不同的是,二叉搜索数的节点值是有规律的,可以借助这个规律进行递归。
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-
-func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q {
- return root
- }
- if p == q {
- return p
- }
- if root.Val > q.Val && root.Val > p.Val {
- return lowestCommonAncestor(root.Left, p, q)
- }
- if root.Val < q.Val && root.Val < p.Val {
- return lowestCommonAncestor(root.Right, p, q)
- }
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.236_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md" "b/08_binaryTree/No.236_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md"
deleted file mode 100644
index 368a3d0..0000000
--- "a/08_binaryTree/No.236_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\350\277\221\345\205\254\345\205\261\347\245\226\345\205\210.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 236 二叉树的最近公共祖先-中等
-
-题目:
-
-给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
-
-百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
-
-
-
-分析:
-
-这里主要是把思路转变一下,通过寻找 p, q 在二叉树的位置来判断。
-
-如果 p, q 分别位于二叉树的左右子树中,那么 root 就是最近的公共祖先。
-
-否则,在左右子树中分别递归查找。
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
- func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q {
- return root
- }
- left := lowestCommonAncestor(root.Left, p, q)
- right := lowestCommonAncestor(root.Right, p, q)
- if left != nil && right != nil {
- return root
- }
- if left == nil {
- return right
- }
- return left
-}
-```
-
diff --git "a/08_binaryTree/No.257_\344\272\214\345\217\211\346\240\221\347\232\204\346\211\200\346\234\211\350\267\257\345\276\204.md" "b/08_binaryTree/No.257_\344\272\214\345\217\211\346\240\221\347\232\204\346\211\200\346\234\211\350\267\257\345\276\204.md"
deleted file mode 100644
index a2e8f48..0000000
--- "a/08_binaryTree/No.257_\344\272\214\345\217\211\346\240\221\347\232\204\346\211\200\346\234\211\350\267\257\345\276\204.md"
+++ /dev/null
@@ -1,69 +0,0 @@
-## 257 二叉树的所有路径-简单
-
-题目:
-
-给你一个二叉树的根节点 `root` ,按 **任意顺序** ,返回所有从根节点到叶子节点的路径。
-
-**叶子节点** 是指没有子节点的节点。
-
-
-
-分析:
-
-深搜,记录了访问每个节点的路径,如果到达叶子结点,直接追加结果,并且返回时去掉当前结果;
-
-如果不是叶子结点,继续深搜。
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func binaryTreePaths(root *TreeNode) []string {
- res := make([]string, 0, 16)
- path := make([]int, 0, 16)
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- path = append(path, root.Val)
- defer func() {
- path = path[:len(path)-1]
- }()
- if root.Left == nil && root.Right == nil {
- res = append(res, path2Str(path))
- return
- }
- if root.Left != nil {
- dfs(root.Left)
- }
- if root.Right != nil {
- dfs(root.Right)
- }
- }
-
- dfs(root)
-
- return res
-}
-
-func path2Str(nums []int) string {
- var res string
- for i, v := range nums {
- if i == 0 {
- res = fmt.Sprintf("%d", v)
- } else {
- res += fmt.Sprintf("->%d", v)
- }
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.331_\351\252\214\350\257\201\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\345\272\217\345\210\227\345\214\226.md" "b/08_binaryTree/No.331_\351\252\214\350\257\201\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\345\272\217\345\210\227\345\214\226.md"
deleted file mode 100644
index bec9531..0000000
--- "a/08_binaryTree/No.331_\351\252\214\350\257\201\344\272\214\345\217\211\346\240\221\347\232\204\345\211\215\345\272\217\345\272\217\345\210\227\345\214\226.md"
+++ /dev/null
@@ -1,82 +0,0 @@
-## 331 验证二叉树的前序序列化-中等
-
-题目:
-
-序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
-
-例如,上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#",其中 # 代表一个空节点。
-
-给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
-
-保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
-
-你可以认为输入格式总是有效的
-
-例如它永远不会包含两个连续的逗号,比如 "1,,3" 。
-
-注意:不允许重建树。
-
-
-
-分析:
-
-算法1:
-
-还是用递归的思想,只要满足 `数字,#,#`这样的模式,那么就是合法的二叉树。那么是从底部向上分析还是从顶向下分析呢?很显然需要从底向上,因为只要叶子节点满足 `数字,#,#` 的模式,进而将其替换为 `#` ,继续判断其父结点。
-
-所以这里需要用到栈结构,从左到右依次入栈,当栈顶的三个元素满足 `数字,#,#` 模式时,继续判断。最后栈中应该只剩下一个 `#`,那么就是一个合法的二叉树。
-
-```go
-// date 2022/10/24
-func isValidSerialization(preorder string) bool {
- stack := make([]string, 0, 16)
- parts := strings.Split(preorder, ",")
- for _, v := range parts {
- stack = append(stack, v)
- for len(stack) >= 3 && stack[len(stack)-1] == "#" && stack[len(stack)-2] == "#" && stack[len(stack)-3] != "#" {
- stack = stack[:len(stack)-3]
- stack = append(stack, "#")
- }
- }
- return len(stack) == 1 && stack[0] == "#"
-}
-```
-
-
-
-算法2:【推荐该算法】
-
-从出度和入度的角度重新理解树。
-
-我们知道对于一个二叉树,所有节点的入度之和等于其出度之和。那么我们就可以根据这个条件进行有效判断。
-
-对于二叉树,我们将空节点也是为叶子节点(即题目中的 `#`),那么则有:
-
-1. 所有的非空节点,提供2个出度,1个入度(根节点除外)
-2. 所有的空节点,提供0个出度,1个入度
-
-我们在遍历的时候,可以计算出度与入度之差`diff = outdegree - indegree`。我们从根开始遍历,当一个节点出现的时候 `diff-1`,因为它提供一个入度;当节点不是空节点的时候 `diff+2`,因为非空节点提供2个出度。
-
-如果序列式是合法的,那么整个遍历过程中 `diff >= 0`,并且最后的结果为零。
-
-这里解释为为什么 `diff` 初始化为1,因为根节点没有父结点,所以根节点提供2个出度,0个入度。在整个遍历过程中都是先减一,如果是非空节点再加二。所以初始化为1,保证了根节点先减去1个入度,再加上2个出度,正好为2,类似链表中 `伪头节点` 的做法。
-
-```go
-// date 2022/10/24
-func isValidSerialization(preorder string) bool {
- // diff = outdegree - indegree
- diff := 1
- parts := strings.Split(preorder, ",")
- for _, v := range parts {
- diff -= 1
- if diff < 0 {
- return false
- }
- if v != "#" {
- diff += 2
- }
- }
- return diff == 0
-}
-```
-
diff --git "a/08_binaryTree/No.404_\345\267\246\345\217\266\345\255\220\344\271\213\345\222\214.md" "b/08_binaryTree/No.404_\345\267\246\345\217\266\345\255\220\344\271\213\345\222\214.md"
deleted file mode 100644
index 67bab06..0000000
--- "a/08_binaryTree/No.404_\345\267\246\345\217\266\345\255\220\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,46 +0,0 @@
-## 404 左叶子之和-简单
-
-题目:
-
-给定二叉树的根节点 `root` ,返回所有左叶子之和。
-
-
-
-分析:
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func sumOfLeftLeaves(root *TreeNode) int {
- var res int
-
- var dfs func(root *TreeNode, isLeft bool)
- dfs = func(root *TreeNode, isLeft bool) {
- if root == nil {
- return
- }
- if root.Left == nil && root.Right == nil && isLeft {
- res += root.Val
- return
- }
- if root.Left != nil {
- dfs(root.Left, true)
- }
- if root.Right != nil {
- dfs(root.Right, false)
- }
- }
-
- dfs(root, false)
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.429_N\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.429_N\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index 46b74ab..0000000
--- "a/08_binaryTree/No.429_N\345\217\211\346\240\221\347\232\204\345\261\202\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 429 N叉树的层序遍历-中等
-
-题目:
-
-给定一个 N 叉树,返回其节点值的*层序遍历*。(即从左到右,逐层遍历)。
-
-树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
-
-
-
-
-
-分析:bfs
-
-换汤不换药,还是老规矩,一层层的搜索。
-
-```go
-// date 2022/10/21
-func levelOrder(root *Node) [][]int {
- res := make([][]int, 0, 16)
- if root == nil {
- return res
- }
- queue := make([]*Node, 0, 16)
- queue = append(queue, root)
- for len(queue) != 0 {
- n := len(queue)
- lRes := make([]int, 0, 16)
- for i := 0; i < n; i++ {
- cur := queue[i]
- lRes = append(lRes, cur.Val)
- for j := 0; j < len(cur.Children); j++ {
- if cur.Children[j] != nil {
- queue = append(queue, cur.Children[j])
- }
- }
- }
- queue = queue[n:]
- res = append(res, lRes)
- }
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.437_\350\267\257\345\276\204\346\200\273\345\222\2143.md" "b/08_binaryTree/No.437_\350\267\257\345\276\204\346\200\273\345\222\2143.md"
deleted file mode 100644
index b60875a..0000000
--- "a/08_binaryTree/No.437_\350\267\257\345\276\204\346\200\273\345\222\2143.md"
+++ /dev/null
@@ -1,104 +0,0 @@
-## 437 路径总和3-中等
-
-题目:
-
-给定一个二叉树的根节点 `root` ,和一个整数 `targetSum` ,求该二叉树里节点值之和等于 `targetSum` 的 **路径** 的数目。
-
-**路径** 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
-
-
-
-分析:
-
-算法1:前缀和【推荐该算法】
-
-因为题目中的路径并不需要从根节点开始,也不需要从叶子节点结束。只要路径上任意连续的值求和等于目标就是其中一个解。
-
-所以可以在深度优先搜索的时候,将从根节点到当前节点(包含当前节点)的路径总和(定义为 cur )保存起来(保存到map preSum中)。保存起来有两个用处:
-
-1)如果 cur - targetSum == 0,那么这就是一个解。
-
-2)如果 cur - targetSum 作为 key,在 preSum 中存在,那么表示在这条路径存在一个解。
-
-需要注意的是,当结束当前节点的遍历时,需要将前缀和从保存路径和的 map 中去掉。因为当前节点的所有可能已经查看过了,如果还在 map 中存在,会影响其他节点的判断。
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func pathSum(root *TreeNode, targetSum int) int {
- var ans int
- preSum := map[int64]int{0:1}
-
- var dfs func(root *TreeNode, cur int64)
- dfs = func(root *TreeNode, cur int64) {
- if root == nil {
- return
- }
- cur += int64(root.Val)
- ans += preSum[cur - int64(targetSum)]
-
- preSum[cur]++
- dfs(root.Left, cur)
- dfs(root.Right, cur)
- preSum[cur]--
- }
-
- dfs(root, 0)
-
- return ans
-}
-```
-
-
-
-算法2:
-
-深度优先搜索。
-
-定义`rootSum()`
-
-```go
-// date 2023/10/24
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func pathSum(root *TreeNode, targetSum int) int {
- res := 0
- if root == nil {
- return res
- }
-
- res = rootSum(root, targetSum)
- res += pathSum(root.Left, targetSum)
- res += pathSum(root.Right, targetSum)
-
- return res
-}
-
-// 以 root 为起点满足条件的路径总和
-func rootSum(root *TreeNode, tg int) int {
- res := 0
- if root == nil {
- return res
- }
- if root.Val == tg {
- res++
- }
- res += rootSum(root.Left, tg - root.Val)
- res += rootSum(root.Right, tg - root.Val)
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.501_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\344\274\227\346\225\260.md" "b/08_binaryTree/No.501_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\344\274\227\346\225\260.md"
deleted file mode 100644
index d387cb9..0000000
--- "a/08_binaryTree/No.501_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\344\274\227\346\225\260.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 501 二叉搜索树中的众数-中等
-
-题目:
-
-给你一个含重复值的二叉搜索树(BST)的根节点 `root` ,找出并返回 BST 中的所有 [众数](https://baike.baidu.com/item/众数/44796)(即,出现频率最高的元素)。
-
-如果树中有不止一个众数,可以按 **任意顺序** 返回。
-
-假定 BST 满足如下定义:
-
-- 结点左子树中所含节点的值 **小于等于** 当前节点的值
-- 结点右子树中所含节点的值 **大于等于** 当前节点的值
-- 左子树和右子树都是二叉搜索树
-
-
-
-分析:
-
-充分利用二叉搜索数的特点,其中序遍历序列为非递减序列。
-
-所以,递归中序遍历,统计每个元素出现的次数,一旦形成结果,就更新结果。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func findMode(root *TreeNode) []int {
- ans := make([]int, 0, 16)
-
- var base, count, maxCount int
-
- var updateNodeVal func(x int)
- updateNodeVal = func(x int) {
- if x == base {
- count++
- } else {
- base, count = x, 1
- }
- // check count and maxcount
- if count == maxCount {
- // find a answer
- ans = append(ans, x)
- } else if count > maxCount {
- // find new answer
- maxCount = count
- ans = []int{x} // 重新定义结果集
- }
- }
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Left)
- updateNodeVal(root.Val)
- dfs(root.Right)
- }
-
- dfs(root)
-
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.530_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\345\260\217\347\273\235\345\257\271\345\267\256.md" "b/08_binaryTree/No.530_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\345\260\217\347\273\235\345\257\271\345\267\256.md"
deleted file mode 100644
index 6778ead..0000000
--- "a/08_binaryTree/No.530_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\234\200\345\260\217\347\273\235\345\257\271\345\267\256.md"
+++ /dev/null
@@ -1,47 +0,0 @@
-## 530 二叉搜索树的最小绝对差-中等
-
-题目:
-
-给你一个二叉搜索树的根节点 `root` ,返回 **树中任意两不同节点值之间的最小差值** 。
-
-差值是一个正数,其数值等于两值之差的绝对值。
-
-
-
-分析:
-
-递归中序遍历,求相邻元素的最小值。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func getMinimumDifference(root *TreeNode) int {
- res := 1 << 32 - 1
- preVal := -1
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Left)
-
- if preVal != -1 && root.Val - preVal < res {
- res = root.Val - preVal
- }
- preVal = root.Val
- dfs(root.Right)
- }
-
- dfs(root)
-
- return res
-}
-```
diff --git "a/08_binaryTree/No.538_\346\212\212\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\275\254\346\215\242\344\270\272\347\264\257\345\212\240\346\240\221.md" "b/08_binaryTree/No.538_\346\212\212\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\275\254\346\215\242\344\270\272\347\264\257\345\212\240\346\240\221.md"
deleted file mode 100644
index f3ce943..0000000
--- "a/08_binaryTree/No.538_\346\212\212\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\350\275\254\346\215\242\344\270\272\347\264\257\345\212\240\346\240\221.md"
+++ /dev/null
@@ -1,47 +0,0 @@
-## 538 把二叉搜索树转换为累加树-中等
-
-题目:
-
-给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
-
-提醒一下,二叉搜索树满足下列约束条件:
-
-节点的左子树仅包含键 小于 节点键的节点。
-节点的右子树仅包含键 大于 节点键的节点。
-左右子树也必须是二叉搜索树。
-
-
-
-分析:
-
-对于二叉搜索树其中序遍历序列肯定是递增序列,而要转换为 大于或等于 节点值之和,那么可以采用 中序 的逆序遍历,然后再遍历过程中直接求和。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func convertBST(root *TreeNode) *TreeNode {
- var sum int
- var deorder func(root *TreeNode)
- deorder = func(root *TreeNode) {
- if root == nil {
- return
- }
- deorder(root.Right)
- sum += root.Val
- root.Val = sum
- deorder(root.Left)
- }
-
- deorder(root)
-
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.543_\344\272\214\345\217\211\346\240\221\347\232\204\347\233\264\345\276\204.md" "b/08_binaryTree/No.543_\344\272\214\345\217\211\346\240\221\347\232\204\347\233\264\345\276\204.md"
deleted file mode 100644
index 5453013..0000000
--- "a/08_binaryTree/No.543_\344\272\214\345\217\211\346\240\221\347\232\204\347\233\264\345\276\204.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 543 二叉树的直径
-
-题目:
-
-给你一棵二叉树的根节点,返回该树的 **直径** 。
-
-二叉树的 **直径** 是指树中任意两个节点之间最长路径的 **长度** 。这条路径可能经过也可能不经过根节点 `root` 。
-
-两节点之间路径的 **长度** 由它们之间边数表示。
-
-
-
-分析:
-
-所谓直径就是每个节点的左右子树深度之和的全局最大值。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func diameterOfBinaryTree(root *TreeNode) int {
- var ans int
-
- var depth func(root *TreeNode) int
- depth = func(root *TreeNode) int {
- if root == nil {
- return 0
- }
- l, r := depth(root.Left), depth(root.Right)
- // update ans
- if l + r > ans {
- ans = l + r
- }
-
- if l > r {
- return l+1
- }
- return r+1
- }
-
- depth(root)
-
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.545_\344\272\214\345\217\211\346\240\221\347\232\204\350\276\271\347\225\214.md" "b/08_binaryTree/No.545_\344\272\214\345\217\211\346\240\221\347\232\204\350\276\271\347\225\214.md"
deleted file mode 100644
index ac82a76..0000000
--- "a/08_binaryTree/No.545_\344\272\214\345\217\211\346\240\221\347\232\204\350\276\271\347\225\214.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 545 二叉树的边界-中等
-
-题目:
-
-给定一个二叉树,按逆时针返回其边界。
-
-
-
-分析:
-
-分别求其左边界,右边界,和所有的叶子节点,用visited辅助去重,算法如下:
-
-```go
-// date 2020/02/23
-func boundaryOfBinaryTree(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- left, right := make([]*TreeNode, 0), make([]*TreeNode, 0)
- visited := make(map[*TreeNode]int, 0)
- res = append(res, root.Val)
- visited[root] = 1
- // find left node
- pre := root.Left
- for pre != nil {
- left = append(left, pre)
- visited[pre] = 1
- if pre.Left != nil {
- pre = pre.Left
- } else {
- pre = pre.Right
- }
- }
- // find right node
- pre = root.Right
- for pre != nil {
- right = append(right, pre)
- visited[pre] = 1
- if pre.Right != nil {
- pre = pre.Right
- } else {
- pre = pre.Left
- }
- }
- leafs := findLeafs(root)
- // make res
- for i := 0; i < len(left); i++ {
- res = append(res, left[i].Val)
- }
- for i := 0; i < len(leafs); i++ {
- if _, ok := visited[leafs[i]]; ok { continue }
- res = append(res, ,leafs[i].Val)
- }
- for i := len(right) - 1; i >= 0; i-- {
- res = append(res, right[i].Val)
- }
- return res
-}
-
-func findLeafs(root *TreeNode) []*TreeNode {
- res := make([]*TreeNode, 0)
- if root == nil { return res }
- if root.Left == nil && root.Right == nil {
- res = append(res, root)
- return res
- }
- res = append(res, findLeafs(root.Left)...)
- res = append(res, findLeafs(root.Right)...)
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.563_\344\272\214\345\217\211\346\240\221\347\232\204\345\235\241\345\272\246.md" "b/08_binaryTree/No.563_\344\272\214\345\217\211\346\240\221\347\232\204\345\235\241\345\272\246.md"
deleted file mode 100644
index bd95b7f..0000000
--- "a/08_binaryTree/No.563_\344\272\214\345\217\211\346\240\221\347\232\204\345\235\241\345\272\246.md"
+++ /dev/null
@@ -1,53 +0,0 @@
-## 563 二叉树的坡度-中等
-
-题目:
-
-给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
-
-一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
-
-整个树 的坡度就是其所有节点的坡度之和。
-
-
-
-分析:深度优先搜索
-
-递归的思路,求每个节点的左右子树和,并在求和过程中更新坡度值。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func findTilt(root *TreeNode) int {
- var ans int
- var sum func(root *TreeNode) int
- sum = func(root *TreeNode) int {
- if root == nil {
- return 0
- }
- ls, rs := sum(root.Left), sum(root.Right)
-
- ans += abs(ls, rs)
-
- return ls + rs + root.Val
- }
-
- sum(root)
-
- return ans
-}
-
-func abs(x, y int) int {
- if x > y {
- return x-y
- }
- return y-x
-}
-```
-
diff --git "a/08_binaryTree/No.572_\345\217\246\344\270\200\346\243\265\346\240\221\347\232\204\345\255\220\346\240\221.md" "b/08_binaryTree/No.572_\345\217\246\344\270\200\346\243\265\346\240\221\347\232\204\345\255\220\346\240\221.md"
deleted file mode 100644
index b855aef..0000000
--- "a/08_binaryTree/No.572_\345\217\246\344\270\200\346\243\265\346\240\221\347\232\204\345\255\220\346\240\221.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 572 另一棵树的子树-中等
-
-题目:
-
-给你两棵二叉树 `root` 和 `subRoot` 。检验 `root` 中是否包含和 `subRoot` 具有相同结构和节点值的子树。如果存在,返回 `true` ;否则,返回 `false` 。
-
-二叉树 `tree` 的一棵子树包括 `tree` 的某个节点和这个节点的所有后代节点。`tree` 也可以看做它自身的一棵子树。
-
-
-
-分析:【推荐该算法】
-
-这道题跟相同的树很类似,判断是不是子树,就等于判断树的子树是否与另一个树相同。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isSubtree(root *TreeNode, subRoot *TreeNode) bool {
- if root == nil {
- return false
- }
- return checkIsSame(root, subRoot) || isSubtree(root.Left, subRoot) || isSubtree(root.Right, subRoot)
-}
-
-func checkIsSame(r1, r2 *TreeNode) bool {
- if r1 == nil && r2 == nil {
- return true
- }
- if r1 == nil || r2 == nil {
- return false
- }
- if r1.Val == r2.Val {
- return checkIsSame(r1.Left, r2.Left) && checkIsSame(r1.Right, r2.Right)
- }
- return false
-}
-```
-
-
-
-算法2:
-
-这个算法是通过将二叉树的延展成先序序列,并且延展的时候把空节点也当成字符充填进去。
-
-那么,是不是子树,就等价于判断一个字符串中是否存在子串。
\ No newline at end of file
diff --git "a/08_binaryTree/No.590_N\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.590_N\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index f8f94c1..0000000
--- "a/08_binaryTree/No.590_N\345\217\211\346\240\221\347\232\204\345\220\216\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,69 +0,0 @@
-## 590 N叉树的后序遍历-简单
-
-给定一个 n 叉树的根节点 root ,返回 其节点值的 后序遍历 。
-
-n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
-
-
-
-分析:
-
-算法1:递归
-
-```go
-// date 2022/10/12
-func postorder(root *Node) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- for i := 0; i < len(root.Children); i++ {
- res = append(res, postorder(root.Children[i])...)
- }
- res = append(res, root.Val)
- return res
-}
-```
-
-
-
-算法2:迭代【推荐该算法】
-
-```go
-// date 2023/10/31
-/**
- * Definition for a Node.
- * type Node struct {
- * Val int
- * Children []*Node
- * }
- */
-func postorder(root *Node) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- stack := make([]*Node, 0, 16)
- stack = append(stack, root)
- visited := make(map[*Node]bool, 16)
- for len(stack) != 0 {
- cur := stack[len(stack)-1]
- // 如果当前节点为叶子节点,或者所有子结点已经遍历过,直接追加结果并更新栈
- if len(cur.Children) == 0 || visited[cur] {
- res = append(res, cur.Val)
- stack = stack[:len(stack)-1]
- continue
- }
- // 入栈当前节点的所有子结点
- for i := len(cur.Children)-1; i >= 0; i-- {
- if cur.Children[i] != nil {
- stack = append(stack, cur.Children[i])
- }
- }
- // 标记当前结点的所有子结点已经入栈
- visited[cur] = true
- }
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.617_\345\220\210\345\271\266\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.617_\345\220\210\345\271\266\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 0429e1b..0000000
--- "a/08_binaryTree/No.617_\345\220\210\345\271\266\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,41 +0,0 @@
-## 617 合并二叉树-简单
-
-给你两棵二叉树: root1 和 root2 。
-
-想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
-返回合并后的二叉树。
-注意: 合并过程必须从两个树的根节点开始。
-
-
-
-分析:
-
-递归覆盖计算。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
- if root1 == nil {
- return root2
- }
- if root2 == nil {
- return root1
- }
-
- root1.Val += root2.Val
-
- root1.Left = mergeTrees(root1.Left, root2.Left)
- root1.Right = mergeTrees(root1.Right, root2.Right)
-
- return root1
-}
-```
-
diff --git "a/08_binaryTree/No.623_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\242\236\345\212\240\344\270\200\350\241\214.md" "b/08_binaryTree/No.623_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\242\236\345\212\240\344\270\200\350\241\214.md"
deleted file mode 100644
index 2455316..0000000
--- "a/08_binaryTree/No.623_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\242\236\345\212\240\344\270\200\350\241\214.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 623 在二叉树中增加一行-中等
-
-题目:
-
-给定一个二叉树的根 `root` 和两个整数 `val` 和 `depth` ,在给定的深度 `depth` 处添加一个值为 `val` 的节点行。
-
-注意,根节点 `root` 位于深度 `1` 。
-
-加法规则如下:
-
-- 给定整数 `depth`,对于深度为 `depth - 1` 的每个非空树节点 `cur` ,创建两个值为 `val` 的树节点作为 `cur` 的左子树根和右子树根。
-- `cur` 原来的左子树应该是新的左子树根的左子树。
-- `cur` 原来的右子树应该是新的右子树根的右子树。
-- 如果 `depth == 1 `意味着 `depth - 1` 根本没有深度,那么创建一个树节点,值 `val `作为整个原始树的新根,而原始树就是新根的左子树。
-
-
-
-分析:
-
-层序遍历。找到目标层的上一次,然后插入。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func addOneRow(root *TreeNode, val int, depth int) *TreeNode {
- if depth == 1 {
- r2 := &TreeNode{Val: val}
- r2.Left = root
- return r2
- }
- curs := make([]*TreeNode, 0, 16)
- curs = append(curs, root)
- depth--
- for depth > 1 {
- n := len(curs)
- for i := 0; i < n; i++ {
- cur := curs[i]
- if cur.Left != nil {
- curs = append(curs, cur.Left)
- }
- if cur.Right != nil {
- curs = append(curs, cur.Right)
- }
- }
- curs = curs[n:]
- depth--
- }
- if len(curs) != 0 {
- n := len(curs)
- for i := 0; i < n; i++ {
- cur := curs[i]
- r1, r2 := &TreeNode{Val: val}, &TreeNode{Val: val}
- // save origin left and right
- rl, rr := cur.Left, cur.Right
- cur.Left = r1
- cur.Right = r2
- r1.Left = rl
- r2.Right = rr
- }
- }
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.637_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\271\263\345\235\207\345\200\274.md" "b/08_binaryTree/No.637_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\271\263\345\235\207\345\200\274.md"
deleted file mode 100644
index b533f3a..0000000
--- "a/08_binaryTree/No.637_\344\272\214\345\217\211\346\240\221\347\232\204\345\261\202\345\271\263\345\235\207\345\200\274.md"
+++ /dev/null
@@ -1,55 +0,0 @@
-## 637 二叉树的层平均值-简单
-
-题目:
-
-给定一个非空二叉树的根节点 `root` , 以数组的形式返回每一层节点的平均值。与实际答案相差 `10-5` 以内的答案可以被接受。
-
-
-
-分析:
-
-没啥好说的,就是算它。
-
-```go
-// date 2023/10/25
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func averageOfLevels(root *TreeNode) []float64 {
- res := make([]float64, 0, 16)
- if root == nil {
- return res
- }
-
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
- levelSum := 0
- for i := 0; i < n; i++ {
- cur := queue[i]
-
- levelSum += cur.Val
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- res = append(res, float64(levelSum) / float64(n))
-
- queue = queue[n:]
- }
-
- return res
-}
-```
-
diff --git "a/08_binaryTree/No.653_\344\270\244\346\225\260\344\271\213\345\222\2144_\350\276\223\345\205\245\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.653_\344\270\244\346\225\260\344\271\213\345\222\2144_\350\276\223\345\205\245\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index f701c65..0000000
--- "a/08_binaryTree/No.653_\344\270\244\346\225\260\344\271\213\345\222\2144_\350\276\223\345\205\245\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,95 +0,0 @@
-## 653 两数之和4-输入二叉搜索树-简单
-
-题目:
-
-给定一个二叉搜索树 `root` 和一个目标结果 `k`,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 `true`。
-
-
-
-分析:【推荐该算法】
-
-深度搜索,记录已经遍历过的节点。
-
-```go
-// date 2023/10/26
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func findTarget(root *TreeNode, k int) bool {
- var res bool
- has := make(map[int]struct{}, 16)
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- if _, ok := has[k-root.Val]; ok {
- res = true
- return
- }
- has[root.Val] = struct{}{}
- dfs(root.Left)
- dfs(root.Right)
- }
-
- dfs(root)
-
- return res
-}
-```
-
-算法2:
-
-因为二叉搜索树的前序遍历序列为递增序列,所以可以先将二叉搜索树转换为递增数组,然后从排序数组中求两数之和。
-
-```go
-// date 2023/10/26
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func findTarget(root *TreeNode, k int) bool {
- nums := preOrder(root)
- i, j := 0, len(nums)-1
- for i < j {
- tg := nums[i] + nums[j]
- if tg == k {
- return true
- }
- if tg < k {
- i++
- }
- if tg > k {
- j--
- }
- }
- return false
-}
-
-func preOrder(root *TreeNode) []int {
- nums := make([]int, 0, 16)
- stack := make([]*TreeNode, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
-
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- nums = append(nums, root.Val)
- root = root.Right
- }
- return nums
-}
-```
-
diff --git "a/08_binaryTree/No.654_\346\234\200\345\244\247\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.654_\346\234\200\345\244\247\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 4729fa2..0000000
--- "a/08_binaryTree/No.654_\346\234\200\345\244\247\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,48 +0,0 @@
-## 654 最大二叉树-中等
-
-题目:
-
-给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
-
-创建一个根节点,其值为 nums 中的最大值。
-递归地在最大值 左边 的 子数组前缀上 构建左子树。
-递归地在最大值 右边 的 子数组后缀上 构建右子树。
-返回 nums 构建的 最大二叉树 。
-
-
-
-分析:
-
-找到数组中的最大值,然后递归构造。
-
-```go
-// date 2023/10/26
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func constructMaximumBinaryTree(nums []int) *TreeNode {
- if len(nums) == 0 {
- return nil
- }
- if len(nums) == 1 {
- return &TreeNode{Val: nums[0]}
- }
- // find the max
- idx := 0
- for i, v := range nums {
- if v > nums[idx] {
- idx = i
- }
- }
- root := &TreeNode{Val: nums[idx]}
- root.Left = constructMaximumBinaryTree(nums[:idx])
- root.Right = constructMaximumBinaryTree(nums[idx+1:])
- return root
-}
-```
-
diff --git "a/08_binaryTree/No.655_\350\276\223\345\207\272\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.655_\350\276\223\345\207\272\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index f1b9c49..0000000
--- "a/08_binaryTree/No.655_\350\276\223\345\207\272\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,67 +0,0 @@
-## 655 输出二叉树-中等
-
-题目:
-
-给你一棵二叉树的根节点 root ,请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ,用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则:
-
-树的 高度 为 height ,矩阵的行数 m 应该等于 height + 1 。
-
-矩阵的列数 n 应该等于 2height+1 - 1 。
-
-根节点 需要放置在 顶行 的 正中间 ,对应位置为 res[0][(n-1)/2] 。
-
-对于放置在矩阵中的每个节点,设对应位置为 res[r][c] ,将其左子节点放置在 res[r+1][c-2height-r-1] ,右子节点放置在 res[r+1][c+2height-r-1] 。
-
-继续这一过程,直到树中的所有节点都妥善放置。
-
-任意空单元格都应该包含空字符串 "" 。
-
-
-分析:
-
-先构建 res,然后逐层填充。
-
-```go
-// date 2023/11/01
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func printTree(root *TreeNode) [][]string {
- depth := findDepth(root)
- length := 1 << depth - 1
- res := make([][]string, depth)
-
- for i := 0; i < depth; i++ {
- res[i] = make([]string, length)
- }
-
- fillRes(res, root, 0, 0, length)
-
- return res
-}
-
-func fillRes(res [][]string, node *TreeNode, row, left, right int) {
- if node == nil {
- return
- }
- res[row][(left+right)/2] = fmt.Sprintf("%d", node.Val)
- fillRes(res, node.Left, row+1, left, (left+right)/2)
- fillRes(res, node.Right, row+1, (left+right+1)/2, right)
-}
-
-func findDepth(root *TreeNode) int {
- if root == nil {
- return 0
- }
- l, r := findDepth(root.Left), findDepth(root.Right)
- if l > r {
- return l+1
- }
- return r+1
-}
-```
diff --git "a/08_binaryTree/No.662_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\345\256\275\345\272\246.md" "b/08_binaryTree/No.662_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\345\256\275\345\272\246.md"
deleted file mode 100644
index 0c8a8c4..0000000
--- "a/08_binaryTree/No.662_\344\272\214\345\217\211\346\240\221\347\232\204\346\234\200\345\244\247\345\256\275\345\272\246.md"
+++ /dev/null
@@ -1,59 +0,0 @@
-## 662 二叉树的最大宽度-中等
-
-题目:
-
-给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
-
-树的 最大宽度 是所有层中最大的 宽度 。
-
-每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
-
-题目数据保证答案将会在 32 位 带符号整数范围内。
-
-
-
-分析:
-
-因为空节点也算数,所以可通过对节点进行编号进行计算,设父结点编号为 `i`,其左右子节点分别为`2i`和`2i+1`,那么每层的最大跨度就是最大的编号,减去最小的编号。
-
-这里使用深度优先搜索,进行编号,先遍历左子树,再遍历右子树。这样最小的编号就会先被填充。
-
-在遍历到每个节点时,求当前节点与同层最左侧的节点跨度,如果大于结果集,就更新结果。
-
-这样的代码可读性更高。
-
-```go
-// date 2023/10/26
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func widthOfBinaryTree(root *TreeNode) int {
- ans := 0
- levelMinIdx := map[int]int{}
- var dfs func(root *TreeNode, depth, idx int)
- dfs = func(root *TreeNode, depth, idx int) {
- if root == nil {
- return
- }
- if _, ok := levelMinIdx[depth]; !ok {
- levelMinIdx[depth] = idx
- }
- curNodeWidth := idx - levelMinIdx[depth] + 1
- if curNodeWidth > ans {
- ans = curNodeWidth
- }
- dfs(root.Left, depth+1, idx*2)
- dfs(root.Right, depth+1, idx*2+1)
- }
-
- dfs(root, 1, 1)
-
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.669_\344\277\256\345\211\252\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md" "b/08_binaryTree/No.669_\344\277\256\345\211\252\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
deleted file mode 100644
index 9c463d1..0000000
--- "a/08_binaryTree/No.669_\344\277\256\345\211\252\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 669 修剪二叉搜索树-中等
-
-题目:
-
-给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
-
-所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
-
-
-分析:
-
-
-根据二叉搜索树特征,直接修剪。
-
-```go
-// date 2023/11/01
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func trimBST(root *TreeNode, low int, high int) *TreeNode {
- if root == nil {
- return nil
- }
- if root.Val < low {
- // 说明左子树完全不需要,直接舍弃
- // 直接修剪右子树
- return trimBST(root.Right, low, high)
- }
- if root.Val > high {
- // 同理,舍弃右子树,直接修剪左子树
- return trimBST(root.Left, low, high)
- }
- root.Left = trimBST(root.Left, low, high)
- root.Right = trimBST(root.Right, low, high)
- return root
-}
-```
diff --git "a/08_binaryTree/No.700_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\346\220\234\347\264\242.md" "b/08_binaryTree/No.700_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\346\220\234\347\264\242.md"
deleted file mode 100644
index 53ccd09..0000000
--- "a/08_binaryTree/No.700_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\344\270\255\347\232\204\346\220\234\347\264\242.md"
+++ /dev/null
@@ -1,38 +0,0 @@
-## 700 二叉搜索树中的搜索-简单
-
-题目:
-
-给定二叉搜索树(BST)的根节点 `root` 和一个整数值 `val`。
-
-你需要在 BST 中找到节点值等于 `val` 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 `null` 。
-
-
-
-分析:
-
-根据二叉搜索树的特性,直接递归搜索即可。
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func searchBST(root *TreeNode, val int) *TreeNode {
- if root == nil {
- return nil
- }
- if root.Val == val {
- return root
- }
- if root.Val < val {
- return searchBST(root.Right, val)
- }
- return searchBST(root.Left, val)
-}
-```
-
diff --git "a/08_binaryTree/No.701_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\217\222\345\205\245\346\223\215\344\275\234.md" "b/08_binaryTree/No.701_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\217\222\345\205\245\346\223\215\344\275\234.md"
deleted file mode 100644
index 4cca966..0000000
--- "a/08_binaryTree/No.701_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\346\217\222\345\205\245\346\223\215\344\275\234.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 701 二叉搜索树的插入操作-中等
-
-题目:
-
-给定二叉搜索树(BST)的根节点 `root` 和要插入树中的值 `value` ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 **保证** ,新值和原始二叉搜索树中的任意节点值都不同。
-
-**注意**,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 **任意有效的结果** 。
-
-
-
-分析:
-
-
-```go
-// date 2023/10/30
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func insertIntoBST(root *TreeNode, val int) *TreeNode {
- if root == nil {
- return &TreeNode{Val: val}
- }
- if root.Val > val {
- if root.Left == nil {
- root.Left = &TreeNode{Val: val}
- } else {
- insertIntoBST(root.Left, val)
- }
- }
- if root.Val < val {
- if root.Right == nil {
- root.Right = &TreeNode{Val: val}
- } else {
- insertIntoBST(root.Right, val)
- }
- }
-
- return root
-}
-```
diff --git "a/08_binaryTree/No.783_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\212\202\347\202\271\346\234\200\345\260\217\350\267\235\347\246\273.md" "b/08_binaryTree/No.783_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\212\202\347\202\271\346\234\200\345\260\217\350\267\235\347\246\273.md"
deleted file mode 100644
index e6581be..0000000
--- "a/08_binaryTree/No.783_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\212\202\347\202\271\346\234\200\345\260\217\350\267\235\347\246\273.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 783 二叉搜索树节点最小距离-简单
-
-题目:
-
-给你一个二叉搜索树的根节点 `root` ,返回 **树中任意两不同节点值之间的最小差值** 。
-
-差值是一个正数,其数值等于两值之差的绝对值。
-
-
-
-分析:
-
-中序遍历,相邻的两个差值最小。
-
-```go
-// date 2023/10/27
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func minDiffInBST(root *TreeNode) int {
- var ans, pre int
- ans = math.MaxInt64 - 1
- pre = -1
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- dfs(root.Left)
- if pre != -1 && root.Val - pre < ans {
- ans = root.Val - pre
- }
- pre = root.Val
- dfs(root.Right)
- }
-
- dfs(root)
-
- return ans
-}
-```
-
-迭代版
-
-```go
-// date 2023/10/27
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func minDiffInBST(root *TreeNode) int {
- var ans, pre int
- ans = math.MaxInt64 - 1
- pre = -1
-
- stack := make([]*TreeNode, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- if len(stack) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- if pre != -1 && root.Val - pre < ans {
- ans = root.Val - pre
- }
- // update pre
- pre = root.Val
- root = root.Right
- }
- }
-
- return ans
-}
-```
-
diff --git "a/08_binaryTree/No.814_\344\272\214\345\217\211\346\240\221\345\211\252\346\236\235.md" "b/08_binaryTree/No.814_\344\272\214\345\217\211\346\240\221\345\211\252\346\236\235.md"
deleted file mode 100644
index 1f2ce9c..0000000
--- "a/08_binaryTree/No.814_\344\272\214\345\217\211\346\240\221\345\211\252\346\236\235.md"
+++ /dev/null
@@ -1,78 +0,0 @@
-## 814 二叉树剪枝-中等
-题目:
-
-给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
-返回移除了所有不包含 1 的子树的原二叉树。
-节点 node 的子树为 node 本身加上所有 node 的后代。
-
-
-
-分析:
-
-算法1【推荐该算法】
-
-先递归左右子树,然后判断子树是否为空,以及当前节点是否为零,如果是直接剪枝。
-
-```go
-// date 2023/10/27
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func pruneTree(root *TreeNode) *TreeNode {
- if root == nil {
- return root
- }
- root.Left = pruneTree(root.Left)
- root.Right = pruneTree(root.Right)
- if root.Left == nil && root.Right == nil && root.Val == 0 {
- return nil
- }
- return root
-}
-```
-
-
-
-
-
-算法2
-
-使用 `containsOne()` 递归判断节点以及节点的左右子树是否包含1,如果不包含,直接剪枝。
-
-```go
-// date 2023/10/27
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func pruneTree(root *TreeNode) *TreeNode {
- if containsOne(root) {
- return root
- }
- return nil
-}
-
-func containsOne(root *TreeNode) bool {
- if root == nil {
- return false
- }
- l, r := containsOne(root.Left), containsOne(root.Right)
- if !l {
- root.Left = nil
- }
- if !r {
- root.Right = nil
- }
- return root.Val == 1 || l || r
-}
-```
-
diff --git "a/08_binaryTree/No.865_\345\205\267\346\234\211\346\211\200\346\234\211\346\234\200\346\267\261\350\212\202\347\202\271\347\232\204\346\234\200\345\260\217\345\255\220\346\240\221.md" "b/08_binaryTree/No.865_\345\205\267\346\234\211\346\211\200\346\234\211\346\234\200\346\267\261\350\212\202\347\202\271\347\232\204\346\234\200\345\260\217\345\255\220\346\240\221.md"
deleted file mode 100644
index 4877460..0000000
--- "a/08_binaryTree/No.865_\345\205\267\346\234\211\346\211\200\346\234\211\346\234\200\346\267\261\350\212\202\347\202\271\347\232\204\346\234\200\345\260\217\345\255\220\346\240\221.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 865 具有所有最深节点的最小子树
-
-题目:
-
-给定一个根为 root 的二叉树,每个节点的深度是 该节点到根的最短距离 。
-
-返回包含原始树中所有 最深节点 的 最小子树 。
-
-如果一个节点在 整个树 的任意节点之间具有最大的深度,则该节点是 最深的 。
-
-一个节点的 子树 是该节点加上它的所有后代的集合。
-
-
-
-分析:
-
-该问题就是求所有叶子节点的最近公共祖先。
-
-定义函数 find 寻找每个节点的深度和最近公共祖先。如果深度相等,说明左右子树中都有最深的叶子节点,那么当前节点就是所有叶子节点的最近公共祖先。
-
-如果左子树深度大,那么返回左子树结果。
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func subtreeWithAllDeepest(root *TreeNode) *TreeNode {
- // 问题就是 求所有叶子节点的最近公共祖先
- _, res := find(root)
- return res
-}
-
-// 求 子树的深度 和 子树叶子节点的最近公共祖先
-func find(root *TreeNode) (int, *TreeNode) {
- if root == nil {
- return 0, nil
- }
- ld, ln := find(root.Left)
- rd, rn := find(root.Right)
- if ld > rd {
- return ld+1, ln
- }
- if ld < rd {
- return rd+1, rn
- }
- return ld+1, root
-}
-```
diff --git "a/08_binaryTree/No.938_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\214\203\345\233\264\345\222\214.md" "b/08_binaryTree/No.938_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\214\203\345\233\264\345\222\214.md"
deleted file mode 100644
index 0ce5ce6..0000000
--- "a/08_binaryTree/No.938_\344\272\214\345\217\211\346\220\234\347\264\242\346\240\221\347\232\204\350\214\203\345\233\264\345\222\214.md"
+++ /dev/null
@@ -1,70 +0,0 @@
-## 938 二叉搜索树的范围和-简单
-
-题目:
-
-给定二叉搜索树的根结点 `root`,返回值位于范围 *`[low, high]`* 之间的所有结点的值的和。
-
-
-
-分析:
-
-算法1:深度优先搜索
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func rangeSumBST(root *TreeNode, low int, high int) int {
- var sum int
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- if low <= root.Val && root.Val <= high {
- sum += root.Val
- }
- dfs(root.Left)
- dfs(root.Right)
- }
-
- dfs(root)
-
- return sum
-}
-```
-
-算法2:
-
-递归
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func rangeSumBST(root *TreeNode, low int, high int) int {
- if root == nil {
- return 0
- }
- var sum int
- sum += rangeSumBST(root.Left, low, high)
- sum += rangeSumBST(root.Right, low, high)
- if root.Val <= high && root.Val >= low {
- sum += root.Val
- }
- return sum
-}
-```
diff --git "a/08_binaryTree/No.951_\347\277\273\350\275\254\347\255\211\344\273\267\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.951_\347\277\273\350\275\254\347\255\211\344\273\267\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index f77c0db..0000000
--- "a/08_binaryTree/No.951_\347\277\273\350\275\254\347\255\211\344\273\267\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,43 +0,0 @@
-## 951 翻转等价二叉树-中等
-
-题目:
-
-我们可以为二叉树 **T** 定义一个 **翻转操作** ,如下所示:选择任意节点,然后交换它的左子树和右子树。
-
-只要经过一定次数的翻转操作后,能使 **X** 等于 **Y**,我们就称二叉树 **X** *翻转 等价* 于二叉树 **Y**。
-
-这些树由根节点 `root1` 和 `root2` 给出。如果两个二叉树是否是*翻转 等价* 的函数,则返回 `true` ,否则返回 `false` 。
-
-
-
-分析:【推荐该算法】
-
-递归判断,左右互搏。
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func flipEquiv(root1 *TreeNode, root2 *TreeNode) bool {
- if root1 == nil && root2 == nil {
- return true
- }
- if root1 == nil || root2 == nil {
- return false
- }
- if root1.Val != root2.Val {
- return false
- }
- return flipEquiv(root1.Left, root2.Left) && flipEquiv(root1.Right, root2.Right) || flipEquiv(root1.Left, root2.Right) && flipEquiv(root1.Right, root2.Left)
-}
-```
-
-
-
-还有一种思路,因为树中每个节点值都是唯一的,可以通过翻转操作将左子树的值永远小于右子树的值,然后比较两棵树是不是一样即可。
diff --git "a/08_binaryTree/No.965_\345\215\225\345\200\274\344\272\214\345\217\211\346\240\221.md" "b/08_binaryTree/No.965_\345\215\225\345\200\274\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 21c12d8..0000000
--- "a/08_binaryTree/No.965_\345\215\225\345\200\274\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 965 单值二叉树-中等
-
-题目:
-
-如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
-
-只有给定的树是单值二叉树时,才返回 true,否则返回 false。
-
-
-分析:
-
-递归比较即可。
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isUnivalTree(root *TreeNode) bool {
- if root == nil {
- return false
- }
-
-
- var isSame func(root *TreeNode, target int) bool
- isSame = func(root *TreeNode, target int) bool {
- if root == nil {
- return true
- }
- return root.Val == target && isSame(root.Left, target) && isSame(root.Right, target)
- }
-
- return isSame(root, root.Val)
-}
-```
diff --git "a/08_binaryTree/No.979_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\210\206\351\205\215\347\241\254\345\270\201.md" "b/08_binaryTree/No.979_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\210\206\351\205\215\347\241\254\345\270\201.md"
deleted file mode 100644
index 6c7eefd..0000000
--- "a/08_binaryTree/No.979_\345\234\250\344\272\214\345\217\211\346\240\221\344\270\255\345\210\206\351\205\215\347\241\254\345\270\201.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 979 在二叉树中分配硬币-中等
-
-题目:
-
-给你一个有 `n` 个结点的二叉树的根结点 `root` ,其中树中每个结点 `node` 都对应有 `node.val` 枚硬币。整棵树上一共有 `n` 枚硬币。
-
-在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点,或者从子结点移动到父结点。
-
-返回使每个结点上 **只有** 一枚硬币所需的 **最少** 移动次数。
-
-
-
-分析:
-
-从流通的角度计算。
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func distributeCoins(root *TreeNode) int {
- var ans int
-
- // 以每个节点目标为1开始计算,
- // 计算该节点所在的子树每个节点都满足1,所需要或者贡献出去的金币数
- var dfs func(root *TreeNode) int
- dfs = func(root *TreeNode) int {
- if root == nil {
- return 0
- }
- // 每个节点最终都要有 1 个
- // 1 表示需要 1 个, 0 表示不需要, 负数表示需要贡献出去的
- need := 1 - root.Val
- l := dfs(root.Left) // left 贡献或者需要
- r := dfs(root.Right) // right 贡献或者需要的
-
- // 在当前节点的视角看来,左右之间的不平衡就是需要 流桶 的次数
- ans += abs(l) + abs(r)
-
- // 跳出当前节点的视角,从外部看该节点
- // 左右相加,加上节点本身,就是该节点整体对外需要或者贡献的
- return l + r + need
- }
-
- dfs(root)
-
- return ans
-}
-
-func abs(x int) int {
- if x > 0 {
- return x
- }
- return -x
-}
-```
-
diff --git "a/08_binaryTree/No.987_\344\272\214\345\217\211\346\240\221\347\232\204\345\236\202\345\272\217\351\201\215\345\216\206.md" "b/08_binaryTree/No.987_\344\272\214\345\217\211\346\240\221\347\232\204\345\236\202\345\272\217\351\201\215\345\216\206.md"
deleted file mode 100644
index 1b00b54..0000000
--- "a/08_binaryTree/No.987_\344\272\214\345\217\211\346\240\221\347\232\204\345\236\202\345\272\217\351\201\215\345\216\206.md"
+++ /dev/null
@@ -1,109 +0,0 @@
-## 987 二叉树的垂序遍历-困难
-
-题目:
-
-给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
-
-对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
-
-二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。返回二叉树的 垂序遍历 序列。
-
-
-
-算法分析:
-
-从题目垂直遍历的要求中获取到三个信息,也称为三个目标:
-
-1. 要按照从左到右的顺利存放最终结果
-2. 每一列按照从上到下的顺序遍历,其实隐含的就是层序遍历的思想,要一层一层处理
-3. 同一层的时候,如果同一列上存在多个值,要升序排列一下
-
-
-
-因此大框架上我们还是选择层序遍历。
-
-1. 用一个队列 `queue` 保存每一层的节点,同时在辅助一个队列 `colIdx` 保存 `queue`中每个节点的列信息。其次初始化两个变量 `lv` 和 `rv` 分别表示整棵树最左和最右边界,用于最后整理总结果集。
-
-2. 每次出队的时候,更新 `lv` 和 `rv`,完成1目标。
-
-3. 在层序遍历中,当遍历完当前层,取得当前层结果,因为当前层的结果是个中间状态,需要进行升序排序后,才能放入总结果集中。完成3目标
-4. 当所有层都遍历后,再根据左右边界,重新整理一次结果。
-
-
-
-```go
-// date 2022/10/22
-func verticalTraversal(root *TreeNode) [][]int {
- if root == nil {
- return [][]int{}
- }
- colRes := make(map[int][]int, 16) // 存储每一列的所有结果,key为列值
- lv, rv := int(0), int(0) // 整棵树的左右边界
- queue := make([]*TreeNode, 0, 16)
- colIdx := make([]int, 0, 16)
- queue = append(queue, root)
- colIdx = append(colIdx, 0)
-
- for len(queue) != 0 {
- n := len(queue)
- cr := make(map[int][]int, 16) // 记录当前层结果
- // 遍历当前层
- for i := 0; i < n; i++ {
- // 出队
- cur := queue[i]
- idx := colIdx[i]
- // 更新左右边界
- if idx > rv {
- rv = idx
- }
- if idx < lv {
- lv = idx
- }
- // 更新当前层结果
- ov, ok := cr[idx]
- if !ok {
- ov = make([]int, 0, 16)
- }
- ov = append(ov, cur.Val)
- cr[idx] = ov
- // 继续检查左右结点
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- colIdx = append(colIdx, idx-1)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- colIdx = append(colIdx, idx+1)
- }
- }
- // 排序当前层结果,并加入总结果集
- for k, v := range cr {
- if len(v) > 1 {
- sort.Slice(v, func(i, j int) bool {
- return v[i] < v[j]
- })
- }
- if len(v) != 0 {
- if old, ok := colRes[k]; ok {
- old = append(old, v...)
- colRes[k] = old
- } else {
- colRes[k] = v
- }
- }
- }
- // 检查下一层
- queue = queue[n:]
- colIdx = colIdx[n:]
- }
-
- // 按左右边界整理总结果
- ans := make([][]int, 0, 16)
- for i := lv; i <= rv; i++ {
- if v, ok := colRes[i]; ok && len(v) != 0 {
- ans = append(ans, v)
- }
- }
- return ans
-}
-```
\ No newline at end of file
diff --git "a/08_binaryTree/No.993_\344\272\214\345\217\211\346\240\221\347\232\204\345\240\202\345\205\204\345\274\237\350\212\202\347\202\271.md" "b/08_binaryTree/No.993_\344\272\214\345\217\211\346\240\221\347\232\204\345\240\202\345\205\204\345\274\237\350\212\202\347\202\271.md"
deleted file mode 100644
index 09efe52..0000000
--- "a/08_binaryTree/No.993_\344\272\214\345\217\211\346\240\221\347\232\204\345\240\202\345\205\204\345\274\237\350\212\202\347\202\271.md"
+++ /dev/null
@@ -1,139 +0,0 @@
-## 993 二叉树的堂兄弟节点-简单
-题目:
-
-在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
-如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
-我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
-只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
-
-
-
-分析:
-
-算法1:
-
-通过查找 x,y 的父结点以及深度来进行判断。这里的算法需要遍历树两次。
-
-
-```go
-func isCousins(root *TreeNode, x int, y int) bool {
- xf, xd := findFatherAndDepth(root, x)
- yf, yd := findFatherAndDepth(root, y)
- return xd == yd && xf != yf
-}
-
-func findFatherAndDepth(root *TreeNode, v int) (*TreeNode, int) {
- if root == nil || root.Val == v {
- return nil, 0
- }
- if root.Left != nil && root.Left.Val == v {
- return root, 1
- }
- if root.Right != nil && root.Right.Val == v {
- return root, 1
- }
- l, lv := findFatherAndDepth(root.Left, v)
- r, rv := findFatherAndDepth(root.Right, v)
- if l != nil {
- return l, lv+1
- }
- return r, rv+1
-}
-```
-
-
-
-算法2:【推荐该算法】
-
-这里用深度优先搜索只遍历一次,搜索过程中记录x,y的深度和父结点。
-
-```go
-// date 2022/10/02
-func isCousins(root *TreeNode, x int, y int) bool {
- if root == nil {return false}
- xd, yd := 0, 0 // 存储x,y的深度
- f := make(map[int]*TreeNode, 2) // 存储x,y父结点
- path := make([]*TreeNode, 0, 16)
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- path = append(path, root)
- defer func() {
- path = path[:len(path)-1]
- }()
- if root.Val == x {
- xd = len(path)
- if len(path) > 1 {
- f[x] = path[len(path)-2]
- }
- } else if root.Val == y {
- yd = len(path)
- if len(path) > 1 {
- f[y] = path[len(path)-2]
- }
- }
- dfs(root.Left)
- dfs(root.Right)
- }
- dfs(root)
- xf, ok1 := f[x]
- yf, ok2 := f[y]
- return ok1 && ok2 && xf != yf && xd == yd
-}
-```
-
-另一个写法
-
-```go
-// date 2023/10/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-func isCousins(root *TreeNode, x int, y int) bool {
- // 深度一样,且父结点不同
-
- xd, yd := 0, 0
- var xf, yf *TreeNode
-
- var dfs func(root *TreeNode, depth int)
- dfs = func(root *TreeNode, depth int) {
- if root == nil {
- return
- }
- if root.Left != nil {
- if root.Left.Val == x {
- xd = depth+1
- xf = root
- }
- if root.Left.Val == y {
- yd = depth+1
- yf = root
- }
- }
- if root.Right != nil {
- if root.Right.Val == x {
- xd = depth+1
- xf = root
- }
- if root.Right.Val == y {
- yd = depth+1
- yf = root
- }
- }
- dfs(root.Left, depth+1)
- dfs(root.Right, depth+1)
- }
-
- dfs(root, 0)
-
- return xd == yd && xf != nil && yf != nil && xf != yf
-}
-```
-
diff --git a/08_binaryTree/bst.md b/08_binaryTree/bst.md
deleted file mode 100644
index d0dfaa9..0000000
--- a/08_binaryTree/bst.md
+++ /dev/null
@@ -1,503 +0,0 @@
-# 二叉搜索树
-
-### 什么是二叉搜索树
-
-顾名思义,二叉搜索树是以一棵二叉树来组织的,其满足一下条件:x为二叉树的一个节点,如果y是x左子树的一个节点,那么`y.Val <= x.Val`;如果y是x右子树的一个节点,则`y.Val >= x.Val`
-
-根据二叉树的性质可得知,二叉搜索树的中序遍历为升序序列,相反如果交换左右子树的遍历顺序亦可得到降序序列。
-
-```go
-// inorder伪代码
-func inOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, inOrder(root.Left)...)
- res = append(res, root.Val)
- res = append(res, inOrder(root.Right)...)
- }
- return res
-}
-
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-### 二叉搜索树的基本操作
-
-二叉搜索树的基本操作包括查询,最小关键字元素,最大关键字元素,前继节点,后继节点,插入和删除,这些基本操作所花费的时间与二叉搜索树的高度成正比。
-
-**查询**
-
-如果二叉搜索树的高度为h,则查询的时间复杂度为O(h)。
-
-```go
-// 查询伪代码
-// 递归版
-func searchBST(root *TreeNode, key int) *TreeNode {
- if root == nil || root.Val == key { return root }
- if root.Val < key {
- return searchBST(root.Right, key)
- }
- return searchBST(root.Left, key)
-}
-// 迭代版
-func searchBST(root *TreeNode, key int) *TreeNode {
- for root != nil && root.Val != key {
- if root.Val < key {
- root = root.Right
- } else {
- root = root.Left
- }
- }
- return root
-}
-```
-
-**最大关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最大关键字元素的伪代码
-func maximumBST(root *TreeNode) *TreeNode {
- for root.Right != nil { root = root.Right }
- return root
-}
-// 递归版
-func maximumBST(root *TeeNode) *TreeNode {
- if root.Right != nil {
- return maximumBST(root.Right)
- }
- return root
-}
-```
-
-**最小关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最小关键字元素的伪代码
-func minimumBST(root *TreeNode) *TreeNode {
- for root.Left != nil { root = root.Left }
- return root
-}
-// 递归版
-func minimumBST(root *TreeNode) *TreeNode {
- if root.Left != nil {
- return minimum(root.Left)
- }
- return root
-}
-```
-
-**前继节点**
-
-前继节点是指给定一个节点x,如果存在x的前继节点则返回前继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找前继节点的操作时间复杂度为O(h)。
-
-```go
-func predecessorBST(x *TreeNode) *TreeNode {
- // x节点存在左子树,则返回左子树中最大的节点
- if x.Left != nil {
- return maximum(root.Left)
- }
- // 如果x节点没有左子树,则找到其父节点,且父节点的右子树包含x
- y := x.Present
- for y != nil && x == y.Left {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**后继节点**
-
-后继节点是指给定一个节点x,如果存在x的后继节点则返回后继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找后继节点的操作时间复杂度为O(h)。
-
-```go
-// 后继节点的伪代码
-func successorBST(x *TreeNode) *TreeNode {
- // x节点存在右子树,则返回右子树中最小的节点
- if x.Right != nil {
- return minimum(root.Right)
- }
- // 如果x节点没有右子树,则找到其父节点,且父节点的左子树包含x
- y := x.Present
- for y != nil && x == y.Right {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**插入**
-
-插入和删除会引起二叉搜索树所表示的动态集合的变化。一定要修改数据结构来反映这种变化,单修改要保持二叉搜索树的性质不变。
-
-```go
-// x.Val = val, x.Right = x.Left = x.Present = nil
-// 插入的伪代码
-func insertBST(root, x *TreeNode) {
- var y *TreeNode
- for root != nil {
- y = root
- if x.Val < root.Val {
- root = root.Left
- } else {
- root = root.Right
- }
- }
- x.Present = y
- if y == nil { // empty tree
- root = x
- } else if x.Val < y.Val {
- y.Left = x
- } else {
- y.Right = x
- }
-}
-// 没有父指针
-// 递归版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root = x
- return root
- }
- if root.Val < x.Val {
- return insertBST(root.Right)
- }
- return insertBST(root.Left)
-}
-// 迭代版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root == x
- return root
- }
- pre, head := root, root
- for head != nil {
- pre = head
- if root.Val < x.Val {
- head = head.Right
- } else {
- head = head.Left
- }
- }
- if y.Val < x.Val {
- y.Right = x
- } else {
- y.Left = x
- }
- return root
-}
-```
-
-**删除**
-
-从一棵二叉搜索树中删除一个节点x的整个策略分为三个情况,分别是:
-
-1)如果x没有孩子节点,那么直接删除即可;
-
-2)如果x只有一个孩子节点,那么将该孩子节点提升到x即可;
-
-3)如果x有两个孩子,那么需要找到x的后继节点y(一定存在x的右子树中),让y占据x的位置,那么x原来的右子树部分称为y的右子树,x的左子树称为y的新的左子树。
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-### 相关题目
-
-- 108 将有序数组转换为二叉搜索树【M】
-- 235 二叉搜素树的最近公共祖先
-- 230 二叉搜索树中第K小的元素
-- 450 删除二叉搜索树中的节点
-- 1038 从二叉搜索树到更大和树【M】
-- 1214 查找两棵二叉搜索树之和【M】
-- 面试题 17.12 BiNode【E】
-- 面试题54 二叉搜索树的第K大节点
-
-#### 108 将有序数组转换为二叉搜索树
-
-题目要求:给定一个升序数据,返回一棵高度平衡二叉树。
-
-思路分析:
-
-二叉搜索树的定义:
-
-1)若任意节点的左子树不为空,则左子树上所有的节点值均小于它的根节点值;
-
-2)若任意节点的右子树不为空,则右子树上所有的节点值均大于它的根节点值;
-
-3)任意节点的左,右子树均为二叉搜索树;
-
-4)没有键值相等的点。
-
-如何构造一棵树,可拆分成无数个这样的子问题:构造树的每个节点,以及节点之间的关系。对于每个节点来说,都需要:
-
-1)选取节点;
-
-2)构造该节点的左子树;
-
-3)构造该节点的右子树。
-
-算法一:对于升序序列,可以选择中间的节点作为根节点,然后递归调用。因为每个节点只遍历一遍,所以时间复杂度为O(n);因为递归调用,空间复杂度为O(log(n))。
-
-```go
-//date 2020/02/20
-// 算法一:递归版
-func sortedArrayToBST(nums []int) *TreeNode {
- if len(nums) == 0 { return nil }
- // 选择根节点
- mid := len(nums) >> 1
- // 构造左子树和右子树
- left := nums[:mid]
- right := nums[mid+1:]
-
- return &TreeNode{
- Val: nums[mid],
- Left: sortedArrayToBST(left),
- Right: sortedArrayToBST(right),
- }
-}
-```
-
-#### 230 二叉搜索树中第K小的元素
-
-题目要求:给定一个二叉搜索树,返回其第K小的元素,你可以假设K总是有效的,即1<=k<=n。
-
-算法:因为是二叉搜索树,先得到其中序遍历结果,然后直接返回k-1所在的元素。
-
-```go
-// date 2020/01/11
-func kthSmallest(root *TreeNode) int {
- data := inOrder(root)
- if len(data) < k {return 0}
- return data[k-1]
-}
-
-func inOrder(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- if root.Left != nil { res = append(res, inOrder(root.Left)...) }
- res = append(res, root.Val)
- if root.Right != nil { res = append(res, inOrder(root.Right)...) }
-}
-```
-
-
-#### 235 二叉搜索树的最近公共祖先
-
-题目要求:给定一个二叉搜素树和两个节点,返回其最近公共祖先。
-
-算法:递归,并充分利用二叉搜索树的性质`left.Val < root.Val < right.Val`。
-
-```go
-// date 2020/02/18
-func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q {return root }
- if p == nil { return q }
- if q == nil { return p }
- if root.Val > q.Val && root.Val > p.Val { return lowestCommonAncestor(root.Left) }
- if root.Val < q.Val && root.Val < p.Val { return lowestCommonAncestor(root.Right) }
- return root
-}
-```
-
-
-
-#### 450 删除二叉搜索树中的节点
-
-题目要求:给定一个二叉搜索树和key,删除key节点,并返回树的根节点
-
-算法一:二叉搜索树的中序遍历序列是个升序序列,则欲要删除的节点需要用其前驱节点或后驱节点来代替。
-
-1)如果为叶子节点,则直接删除;
-
-2)如果不是叶子节点且有右子树,则用后驱节点代替。后驱节点为右子树中的较低位置;
-
-3)如果不是叶子节点且有左子树,则用前驱节点代替。前驱节点为左子树中的较高位置;
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-#### 1038 从二叉搜索树到更大和树
-
-题目要求:给出二叉**搜索**树的根节点,该二叉树的节点值各不相同,修改二叉树,使每个节点 `node` 的新值等于原树中大于或等于 `node.val` 的值之和
-
-思路分析:
-
-`root.Val = root.Val + root.Right.Val`
-
-`root.Left.Val = root.Left.Val + root.Val`
-
-首先得到二叉搜索树的中序遍历序列的逆序列,然后从序列的第一个开始,将累加值记录到当前树的节点上。
-
-```go
-// date 2020/02/23
-func bsttoGST(root *TreeNode) *TreeNode{
- array := decOrder(root)
- val := 0
- for i := 0; i < len(array); i++ {
- val += array[i]
- setNewVal(root, array[i], val)
- }
-}
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-
-func setNewVal(root *TreeNode, key, val int) {
- if root != nil {
- if root.Val == key {
- root.Val = val
- } else if root.Val > key {
- setNewVal(root.Left, key, val)
- } else {
- setNewVal(root.Right, key, val)
- }
- }
-}
-```
-
-#### 面试题 BiNode
-
-题目要求:将一颗二叉搜索树转换成单链表,Right指针指向下一个节点。
-
-思路分析:
-
-要求返回头节点,所以先转换left。
-
-```go
-// date 2020/02/19
-func convertBiNode(root *TreeNode) *TreeNode {
- if root == nil { return nil }
- // 左子树不为空,需要转换
- if root.Left != nil {
- // 得到左子树序列,并找到最后一个节点
- left := convertBiNode(root.Left)
- pre := left
- for pre.Right != nil { pre = pre.Right }
- // 将最后一个节点right指向root
- pre.Right = root
- root.Left = nil
- // 得到右子树序列
- root.Right = convertBiNode(root.Right)
- return left
- }
- root.Right = convertBiNode(root.Right)
- return root
-}
-```
-
-#### 面试题54 二叉搜索树的第K大节点
-
-题目要求:给定一个二叉搜索树,找出其中第k大节点。
-
-算法一:二叉搜索树的中序遍历为升序序列,按照Right->root->Left的顺序遍历可得到降序序列,然后返回第k节点。
-
-```go
-// date 2020/02/18
-func kthLargest(root *TreeNode, k int) int {
- if root == nil || k < 0 { return -1 }
- nums := decOrder(root)
- if len(nums) < k {return -1}
- return nums[k-1]
-}
-
-// right->root->left
-func decOrder(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- if root.Right != nil {
- res = append(res, decOrder(root.Right)...)
- }
- res = append(res, root.Val)
- if root.Left != nil {
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-####
\ No newline at end of file
diff --git a/08_binaryTree/images/image145.png b/08_binaryTree/images/image145.png
deleted file mode 100644
index 333c655..0000000
Binary files a/08_binaryTree/images/image145.png and /dev/null differ
diff --git a/08_binaryTree/leetcode_bt.md b/08_binaryTree/leetcode_bt.md
deleted file mode 100644
index 938a5a7..0000000
--- a/08_binaryTree/leetcode_bt.md
+++ /dev/null
@@ -1,184 +0,0 @@
-### 二叉树的相关题目
-
-[TOC]
-
-#### 156 上下翻转二叉树【中等】
-
-题目要求:给定一个二叉树,其中所有的右节点要么是具有兄弟节点(拥有相同父节点的左节点)的叶节点,要么为空,将此二叉树上下翻转并将它变成一棵树, 原来的右节点将转换成左叶节点。返回新的根。
-
-算法分析:
-
-```go
-// date 2020/02/25
-func upsideDownBinaryTree(root *TreeNode) *TreeNode {
- var parent, parent_right *TreeNode
- for root != nil {
- // 0.保存当前left, right
- root_left := root.Left
- root.Left = parent_right // 重新构建root,其left为上一论的right
- parent_right := root.Right // 保存right
- root.Right = parent // 重新构建root,其right为上一论的root
- parent = root
- root = root_left
- }
- return parent
-}
-```
-
-#### 270 最接近的二叉搜索树值【简单】
-
-题目要求:给定一个不为空的二叉搜索树和一个目标值 target,请在该二叉搜索树中找到最接近目标值 target 的数值。
-
-算法分析:使用层序遍历,广度优先搜索。
-
-```go
-// date 2020/02/23
-func closestValue(root *TreeNode, target float64) int {
- if root == nil { return 0 }
- var res int
- cur := math.Inf(1)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- for len(stack) != 0 {
- n := len(stack)
- for i := 0; i < n; i++ {
- if math.Abs(float64(stack[i].Val) - target) < cur {
- cur = math.Abs(float64(stack[i].Val) - target)
- res = stack[i].Val
- }
- if stack[i].Left != nil { stack = append(stack, stack[i].Left) }
- if stack[i].Right != nil { stack = append(stack, stack[i].Right) }
- }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 703 数据流中第K大元素【简单】
-
-解题思路:
-
-0。使用数据构建一个容量为k的小顶堆。
-
-1。如果小顶堆堆满后,向其增加元素,若大于堆顶元素,则重新建堆,否则掉弃。
-
-2。堆顶元素即为第k大元素。
-
-```go
-// date 2020/02/19
-type KthLargest struct {
- minHeap []int
- size
-}
-
-func Constructor(k int, nums []int) KthLargest {
- res := KthLargest{
- minHeap: make([]int, k),
- }
- for _, v := range nums {
- res.Add(v)
- }
-}
-
-func (this *KthLargest) Add(val int) int {
- if this.size < len(this.minHeap) {
- this.size++
- this.minHeap[this.size-1] = val
- if this.size == len(this.minHeap) {
- this.makeMinHeap()
- }
- } else if this.minHeap[0] < val {
- this.minHeap[0] = val
- this.minHeapify(0)
- }
- return this.minHeap[0]
-}
-
-func (this *KthLargest) makeMinHeap() {
- // 为什么最后一个根节点是n >> 1 - 1
- // 长度为n,最后一个叶子节点的索引是n-1; left = i >> 1 + 1; right = i >> 1 + 2
- // 父节点是 n >> 1 - 1
- for i := len(this.minHeap) >> 1 - 1; i >= 0; i-- {
- this.minHeapify(i)
- }
-}
-
-func (this *KthLargest) minHeapify(i int) {
- if i > len(this.minHeap) {return}
- temp, n := this.minHeap[i], len(this.minHeap)
- left := i << 1 + 1
- right := i << 1 + 2
- for left < n {
- right = left + 1
- // 找到left, right中较小的那个
- if right < n && this.minHeap[left] > this.minHeap[right] { left++ }
- // left, right 均小于root否和小顶堆,跳出
- if this.minHeap[left] >= this.minHeap[i] { break }
- this.minHeap[i] = this.minHeap[left]
- this.minHeap[left] = temp
- // left发生变化,继续调整
- i = left
- left = i << 1 + 1
- }
-}
-```
-
-#### 1104 二叉树寻路【中等】
-
-题目要求:https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree/
-
-算法分析:
-
-```go
-// date 2020/02/25
-func pathInZigZagTree(label int) []int {
- res := make([]int, 0)
- for label != 1 {
- res = append(res, label)
- label >>= 1
- y := highBit(label)
- lable = ^(label-y)+y
- }
- res = append(res, 1)
- i, j := 0, len(res)-1
- for i < j {
- t := res[i]
- res[i] = res[j]
- res[j] = t
- i++
- j--
- }
- return res
-}label = label ^(1 << (label.bit_length() - 1)) - 1
-
-func bitLen(x int) int {
- res := 0
- for x > 0 {
- x >>= 1
- res++
- }
- return res
-}
-```
-
-#### 面试题27 二叉树的镜像【简单】
-
-题目链接:https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/
-
-题目要求:给定一棵二叉树,返回其镜像二叉树。
-
-```go
-// date 2020/02/23
-// 递归算法
-func mirrorTree(root *TreeNode) *TreeNode {
- if root == nil { return root }
- left := root.Left
- root.Left = root.Right
- root.Right = left
- root.Left = mirrorTree(root.Left)
- root.Right = mirrorTree(root.Right)
- return root
-}
-```
-
diff --git a/08_binaryTree/readme.md b/08_binaryTree/readme.md
deleted file mode 100644
index 10d6b73..0000000
--- a/08_binaryTree/readme.md
+++ /dev/null
@@ -1,1393 +0,0 @@
-## 二叉树
-
-[TOC]
-
-### 1.什么是二叉树
-
- 树是一种数据结构,树中的每个节点都包含一个键值和所有子节点的列表,对于二叉树来说,每个节点最多有两个子树结构,分别称为左子树和右子树。
-
-#### 二叉树的深度
-
- 二叉树的深度是指二叉树的根结点到叶子结点的距离。
-
- 最大深度 = 根结点到叶子结点的最大距离
-
- 最小深度 = 根结点到叶子结点的最小距离。
-
- 常见的问题包括求取二叉树的最大/最大深度,一般可以使用递归算法或者DFS。
-
-参见题目:
-
-- [二叉树的最大深度](104.md)
-- [二叉树的最小深度](111.md)
-
-
-
-### 2.二叉树的遍历
-
-按照 root 节点的访问顺序,可分为前序遍历,中序遍历和后序遍历。其顺序如下:
-
-- 前序遍历:按「根-左-右」依次访问各节点
-- 中序遍历:按「左-根-右」依次访问各节点
-- 后序遍历:按「左-右-根」依次访问各节点
-
-中序遍历的题目参见
-
-- 098 验证二叉搜索树,迭代中序遍历
-- 099 恢复二叉搜索树,迭代中序遍历
-
-
-
-递归版本的遍历,只要理解其思想就很好写;而对于非递归版本的遍历,需要深入理解其结点的遍历顺序,并记录下来之前经过的结点,所以一定会用到栈。
-
-
-
-层序遍历是一种特殊的遍历,从二叉树的深度来理解就是,将同一深度的结果按照从左到右的顺序形成一个数组,不同深度的结果再放到另一个数组里面,最终形成一个二维数组。
-
-
-
-从广度搜索和深度搜索的角度来讲,层序遍历属于广度优先搜索,而前序,中序,后序遍历均为深度优先搜索。
-
-参见题目
-
-- No.094—二叉树的中序遍历
-- No.102—二叉树的层序遍历
-- No.144—二叉树的前序遍历
-- No.145—二叉树的后序遍历
-
-
-
-#### 2.1 前序遍历
-
-前序遍历是指先访问root节点,然后左子树,最后是右子树。
-
-```go
-// date 2020/10/19
-// 递归版
-func preorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- res = append(res, root.Val)
- if root.Left != nil {
- res = append(res, preorderTraversal(root.Left)...)
- }
- if root.Right != nil {
- res = append(res, preorderTraversal(root.Right)...)
- }
- return res
-}
-
-// 迭代版
-// 前序遍历:root->left->right
-func preorderTraversal(root *TreeNode) []int {
- res := make([]int, 0)
- if root == nil { return res }
- stack := make([]*TreeNode, 0)
- for root != nil || len(stack) != 0 {
- // find root and left
- for root != nil {
- res = append(res, root.Val) // 先将根节点加入结果集
- stack = append(stack, root) // 将遍历过的结点加入栈,后序出栈依次访问结点的右子树
- root = root.Left // 遍历当前结点的左子树
- }
- // find the right
- if len(queue) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- root = root.Right
- }
- }
- return res
-}
-```
-
-参见题目:
-
-- 105—从前序和中序遍历序列构造二叉树
-
-
-
-#### 2.2 中序遍历
-
-中序遍历是指访问左子树,然后root节点,最后是右子树。
-
-```go
-// 递归版
-func inOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root == nil { return res }
- // 先访问左子树
- if root.Left != nil {
- res = append(res, inOrder(root.Left)...)
- }
- // 后访问根结点
- res = append(res, root.Val)
- // 最后访问右子树
- if root.Right != nil {
- res = append(res, inOrder(root.Right)...)
- }
- return res
-}
-```
-
-这里跟前序遍历类似,只是取根节点值加入结果集的时机略有区别。
-
-其主要思路为:
-
-1. 持续检查其左子树,重复1,直到左子树为空【此时栈中保留的是一系列的左子树节点】
-2. 出栈一次,并取根节点值加入结果集,然后检查最后一个左子树的右子树,重复1,2
-
-```go
-// 迭代版
-// 需要stack结构
-// left->root->right
-func inorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- stack := make([]*TreeNode, 0, 16)
- res := make([]int, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- if len(stack) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- res = append(res, root.Val)
- root = root.Right
- }
- }
- return res
-}
-```
-
-参见题目:
-
-- 106—从中序和后序遍历序列构造二叉树
-- 538—把二叉搜索树转换为累加树,递归中序遍历解法
-- 783—二叉搜索树节点最小距离,递归中序遍历
-
-
-
-#### 2.3 后序遍历
-
-后序遍历是指先访问左子树,然后右子树,最后是root节点。
-
-递归算法:
-
-```go
-// date 2020/10/19
-// 递归
-func postorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- res := make([]int, 0, 16)
- if root.Left != nil {
- res = append(res, postorderTraversal(root.Left)...)
- }
- if root.Right != nil {
- res = append(res, postorderTraversal(root.Right)...)
- }
- res = append(res, root.Val)
- return res
-}
-
-```
-
-迭代算法:
-
-迭代遍历的时候依然需要 stack 结构来保存已经遍历过的节点;同时借助 pre 指针保存上次出栈的节点,用于判断当前节点是否同时具有左右子树,还是只有单个子树。
-
-1. 先将根节点入栈,循环遍历栈是否为空
-2. 出栈,取出当前节点
- 1. 如果当前节点没有左右子树,则为叶子节点,直接加入结果集
- 2. 其次判断上次出栈的节点是否是当前节点的左右子树,如果是,表明当前节点的子树已经处理完毕,也需要加入结果集【这里依赖的是左右子树的入栈,因为在栈中左右子树不具备前继关系,至于根节点具备】
- 3. 依次检查当前节点的右子树,左子树,重复1,2
-
-```go
-// 迭代版
-// left->right-root
-func postorderTraversal(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- var pre, cur *TreeNode // 记录前驱节点和当前节点
- for len(stack) != 0 {
- // 出栈 当前结点
- cur = stack[len(stack)-1]
- // 如果当前结点为叶子结点,则直接加入结果集
- // 如果当前结点不是叶子结点,但是上次遍历结点为当前结点的左右子树时(说明当前结点只有单个子树,且子树已经处理完毕),也加入结果集
- if cur.Left == nil && cur.Right == nil || pre != nil && (pre == cur.Left || pre == cur.Right) {
- res = append(res, cur.Val)
- // 出栈,继续检查
- stack = stack[:len(stack)-1]
- pre = cur
- } else {
- // 因为在出栈的时候检查结点,并追加到结果中
- // 所以,先入栈右子树,后入栈左子树
- if cur.Right != nil {
- stack = append(stack, cur.Right)
- }
- if cur.Left != nil {
- stack = append(stack, cur.Left)
- }
- }
- }
-
- return res
-}
-```
-
-
-
-
-
-参见题目:
-
-- 106—从中序和后序遍历序列构造二叉树
-
-
-
-#### 2.4 层序遍历
-
-层序遍历是指逐层遍历树的结构,也称为广度优先搜索,算法从一个根节点开始,先访问根节点,然后遍历其相邻的节点,其次遍历它的二级、三级节点。
-
-借助队列数据结构,先入先出的顺序,实现层序遍历。
-
-```go
-// date 2020/03/21
-// 层序遍历
-// bfs广度优先搜索
-// 算法一:使用队列,逐层遍历
-func levelOrder(root *TreeNode) [][]int {
- if root == nil {
- return [][]int{}
- }
- res := make([][]int, 0, 16)
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- for len(queue) != 0 {
- n := len(queue)
- curRes := make([]int, 0, 16)
- for i := 0; i < n; i++ {
- cur := queue[i]
- curRes = append(curRes, cur.Val)
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- res = append(res, curRes)
- queue = queue[n:]
- }
- return res
-}
-```
-
-算法2:dfs深度优先搜索
-
-这里的思路类似求二叉树的最大深度,借助dfs搜索,在每一层追加结果。
-
-```go
-// date 2020/03/21
-func levelOrder(root *TreeNode) [][]int {
- res := make([][]int, 0, 16)
- var dfs func(root *TreeNode, level int)
- dfs = func(root *TreeNode, level int) {
- if root == nil {
- return
- }
- if len(res) == level {
- res = append(res, make([]int, 0, 4))
- }
- res[level] = append(res[level], root.Val)
- level++
- dfs(root.Left, level)
- dfs(root.Right, level)
- }
- dfs(root, 0)
- return res
-}
-```
-
-**注意**,从上面两种实现的方式来看,层序遍历既可以使用广度优先搜索,也可以使用深度优先搜索。
-
-参见题目
-
-- 102—二叉树的层序遍历
-- 103—二叉树的锯齿形层序遍历
-- 107—二叉树的层序遍历2,将底部结果放到开头,没有新意
-- 199—二叉树的右视图,取层序遍历最后一个节点
-- 404—左叶子之和
-- 987—二叉树的垂序遍历,层序遍历,每个节点标注坐标,根据坐标排序
-
-
-
-
-
-#### 2.5 垂序遍历
-
-> 给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
->
-> 对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
->
-> 二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
->
-> 返回二叉树的 垂序遍历 序列。
->
-> 来源:力扣(LeetCode)
-> 链接:https://leetcode.cn/problems/vertical-order-traversal-of-a-binary-tree
-> 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-
-详见题目[987二叉树的垂序遍历](987.md)
-
-
-
-#### 2.6 相关题目
-
-- [094二叉树的中序遍历](094.md)
-
-- [102二叉树的层序遍历](102.md)
-
-- [102二叉树的锯齿形层序遍历](103.md)
-
-- [105从前序与中序遍历序列构造二叉树](105.md)
-- [106从后续与中序遍历序列构造二叉树](106.md)
-- [107二叉树的层序遍历2](107.md)
-- [144二叉树的前序遍历](144.md)
-- [145二叉树的后序遍历](145.md)
-- [331验证二叉树的前序序列化](331.md)
-- [429N叉树的层序遍历](429.md)
-- [637二叉树的层平均值](637.md)
-- [1161最大层内元素和](1161.md)
-
-
-
-
-
-### 3.递归解决树的问题
-
-递归通常是解决树的相关问题最有效和最常用的方法之一,分为**自顶向下**和**自底向上**两种。
-
-**自顶向下**的解决方案
-
-自顶向下意味着在每个递归层级,需要先计算一些值,然后递归调用并将这些值传递给子节点,视为**前序遍历**。参见题目【二叉树的最大深度】
-
-```go
-// 通用的框架,自顶向下
-1. return specific value for null node
-2. update the answer if needed // answer <-- params
-3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
-4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
-5. return the answer if needed // answer <-- left_ans, right_ans
-```
-
-参见题目
-
-- No.95—不同的二叉搜索数2,生成所有的二叉搜索数
-- No.113—路径总和2,求满足条件的所有路径
-- No.129—求根节点到叶子节点数字之和,携带已知内容递归到叶子节点
-- No.257—二叉树的所有路径
-
-
-
-**自底向上**的解决方案
-
-自底向上意味着在每个递归层级,需要先对子节点递归调用函数,然后根据返回值和根节点本身得到答案,视为**后序遍历**。
-
-```go
-// 通用的框架,自底向上
-1. return specific value for null node
-2. left_ans = bottom_up(root.left) // call function recursively for left child
-3. right_ans = bottom_up(root.right) // call function recursively for right child
-4. return answers // answer <-- left_ans, right_ans, root.val
-```
-
-参见题目:
-
-- 543—二叉树的直径,求左右深度之和。
-- 865—具有所有最深节点的最小子树
-
-
-
-
-
-**总结**:
-
-当遇到树的问题时,先思考一下两个问题:
-
-> 1.你能确定一些参数,从该节点自身解决出发寻找答案吗?
->
-> 2.你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗?
-
-如果答案是肯定的,那么可以尝试使用自顶向下的递归来解决问题。
-
-当然也可以这样思考:
-
-> 对于树中的任意一个节点,如果你知道它子节点的结果,你能计算出该节点的答案吗?
-
-如果答案是肯定的,可以尝试使用自底向上的递归来解决问题。
-
-
-
-### 深度优先搜索
-
-深度优先搜索的过程,过程中计算最终的结果集,和深搜本身的返回值不一致。这并不矛盾。反而,有些题目更好使。参见题目979-在二叉树中分配硬币。
-
-参见题目:
-
-
-
-
-
-### 广度优先搜索
-
-
-
-
-
-### 4 平衡二叉树
-
-一棵高度平衡二叉树的定义为:
-
-> 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
-
-参见题目:
-
-- 108—将有序数组转换为二叉搜索树,递归实现
-
-
-
-### 5 对称二叉树
-
-如果一棵二叉树关于根结点左右对称,则称为对称二叉树,也称为镜像二叉树。
-
-参见题目:
-
-- 101—对称二叉树,递归,或者迭代两个树
-
-
-
----
-
-### 6 Binary Indexed Tree \[二叉索引树\]
-
- * 1.[结构介绍](#结构介绍)
- * 2.[问题定义](#问题定义)
- * 3.[表面形式](#表现形式)
- * 3.1[更新操作](#更新操作)
- * 3.2[求和操作](#求和操作)
- * 4.[工作原理](#BIT工作原理)
- * 5.[代码实现](#代码实现)
-
-#### 结构介绍
-
-二叉索引树,Binary Indexed Tree,又名树状数组,或者Fenwick Tree,因为本算法由Fenwick创造。
-
-#### 问题定义
-
-给定一个数组array[0....n-1],实现两个函数:1)求取前i项和;2)更新第i项值。
-
-分析:
-
-其中一个比较简单的解法就是通过循环累计(0-i-1)求和(需要O(n)时间),根据下标更新值(需要O(1)时间)。另一种解法是创建一个前n项和数组(即,第i项存储前i项的和),这样求和需要O(1)时间,更新需要O(n)时间。
-
-而使用BIT数据结构,可以在O(Logn)时间内进行求和操作和更新操作。下面具体介绍一下。
-
-#### 表现形式
-
-BIT这种数据结构使用一般数组进行存储,每个节点存储 **部分** 输入数组的元素之和。BIT数组的元素个数与输入数组的元素个数一致,均为n。BIT数组的初始值均为0,通过更新操作获取输入数组部分元素之和,并存储在相应的位置上。
-
-#### 更新操作
-
-更新操作是指根据输入数组的元素来更新BIT数组的元素,进而根据BIT数组求前i项和。
-
-```
-update(index, val): Updates BIT for operation arr[index] += val
-// Note that arr[] is not changed here. It changes
-// only BI Tree for the already made change in arr[].
-1) Initialize index as index+1.
-2) Do following while index is smaller than or equal to n.
-...a) Add value to BITree[index]
-...b) Go to parent of BITree[index]. Parent can be obtained by removing
- the last set bit from index, i.e., index = index + (index & (-index))
-```
-
-令BIT数组为:BIT[i] = Input[i-lowbit(i)+1] + Input[i-lowbit(i)+2] + ... + Input[i];
-
-即从最左边的孩子,到自身的和,如BIT[12]= A9+A10+A11+A12
-
-#### 求和操作
-
-求和操作是指利用BIT数组求原来输入数组的前i项和。
-
-```
-getSum(index): Returns sum of arr[0..index]
-// Returns sum of arr[0..index] using BITree[0..n]. It assumes that
-// BITree[] is constructed for given array arr[0..n-1]
-1) Initialize sum as 0 and index as index+1.
-2) Do following while index is greater than 0.
-...a) Add BITree[index] to sum
-...b) Go to parent of BITree[index]. Parent can be obtained by removing
- the last set bit from index, i.e., index = index - (index & (-index))
-3) Return sum.
-```
-
-
-说明:
-
-1. 如果节点y是节点x的父节点,那么节点y可以由节点x通过移除Lowbit(x)获得。**Lowbit(natural)为自然数(即1,2,3…n)的二进制形式中最右边出现1的值**。即通过以下公式获得 $parent(i) = i - i & (-i)$。
-
-2. 节点y的子节点x(对BIT数组而言)存储从y(不包括y)到x(包括x)(对输入数组而言)的的元素之和。即BIT数组的值由输入数组两者之间下标的节点对应关系获得。
-
-
-计算前缀和Sum(i)的计算:顺着节点i往左走,边走边“往上爬”,把经过的BIT[i]累加起来即可。
-
-
-
-#### BIT工作原理
-
-BIT工作原理得益于所有的正整数,均可以表示为多个2的幂次方之和。例如,19 = 16 + 2 + 1。BIT的每个节点都存储n个元素的总和,其中n是2的幂。例如,在上面的getSum()的第一个图中,前12个元素的和可以通过最后4个元素(从9到12) )加上8个元素的总和(从1到8)。 数字n的二进制表示中的设置位数为O(Logn)。 因此,我们遍历getSum()和update()操作中最多的O(Logn)节点。 构造的时间复杂度为O(nLogn),因为它为所有n个元素调用update()。
-
-#### 代码实现
-
-```
-void updateBIT(int BITree[], int n, int index, int val) {
- index = index + 1;
- while(index <= n) {
- BITree[index] += val;
- index += index & (-index);
- }
-}
-
-int getSum(int BITree[], int index) {
- int sum = 0;
- index = index + 1;
- while(index > 0) {
- sum += BITree[index];
- index -= index & (-index);
- }
- return sum;
-}
-
-int *conBIT(int arr[], int n) {
- int *BITree = new int[n + 1];
- for(int i = 0; i <= n; i++)
- BITree[i] = 0;
- for(int i = 0; i < n; i++)
- updateBIT(BITree, n, i, arr[i]);
- return BITree;
-}
-```
-
-
-
-
-
----
-
-### 二叉搜索树
-
-顾名思义,二叉搜索树是以一棵二叉树来组织的,其满足一下条件:x为二叉树的一个节点,如果y是x左子树的一个节点,那么`y.Val <= x.Val`;如果y是x右子树的一个节点,则`y.Val >= x.Val`
-
-根据二叉树的性质可得知,二叉搜索树的中序遍历为升序序列,相反如果交换左右子树的遍历顺序亦可得到降序序列。
-
-```go
-// inorder伪代码
-func inOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, inOrder(root.Left)...)
- res = append(res, root.Val)
- res = append(res, inOrder(root.Right)...)
- }
- return res
-}
-
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-#### 二叉搜索树的基本操作
-
-二叉搜索树的基本操作包括查询,最小关键字元素,最大关键字元素,前继节点,后继节点,插入和删除,这些基本操作所花费的时间与二叉搜索树的高度成正比。
-
-**查询**
-
-如果二叉搜索树的高度为h,则查询的时间复杂度为O(h)。
-
-```go
-// 查询伪代码
-// 递归版
-func searchBST(root *TreeNode, key int) *TreeNode {
- if root == nil || root.Val == key { return root }
- if root.Val < key {
- return searchBST(root.Right, key)
- }
- return searchBST(root.Left, key)
-}
-// 迭代版
-func searchBST(root *TreeNode, key int) *TreeNode {
- for root != nil && root.Val != key {
- if root.Val < key {
- root = root.Right
- } else {
- root = root.Left
- }
- }
- return root
-}
-```
-
-**最大关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最大关键字元素的伪代码
-func maximumBST(root *TreeNode) *TreeNode {
- for root.Right != nil { root = root.Right }
- return root
-}
-// 递归版
-func maximumBST(root *TeeNode) *TreeNode {
- if root.Right != nil {
- return maximumBST(root.Right)
- }
- return root
-}
-```
-
-**最小关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最小关键字元素的伪代码
-func minimumBST(root *TreeNode) *TreeNode {
- for root.Left != nil { root = root.Left }
- return root
-}
-// 递归版
-func minimumBST(root *TreeNode) *TreeNode {
- if root.Left != nil {
- return minimum(root.Left)
- }
- return root
-}
-```
-
-**前继节点**
-
-前继节点是指给定一个节点x,如果存在x的前继节点则返回前继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找前继节点的操作时间复杂度为O(h)。
-
-```go
-func predecessorBST(x *TreeNode) *TreeNode {
- // x节点存在左子树,则返回左子树中最大的节点
- if x.Left != nil {
- return maximum(root.Left)
- }
- // 如果x节点没有左子树,则找到其父节点,且父节点的右子树包含x
- y := x.Present
- for y != nil && x == y.Left {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**后继节点**
-
-后继节点是指给定一个节点x,如果存在x的后继节点则返回后继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找后继节点的操作时间复杂度为O(h)。
-
-```go
-// 后继节点的伪代码
-func successorBST(x *TreeNode) *TreeNode {
- // x节点存在右子树,则返回右子树中最小的节点
- if x.Right != nil {
- return minimum(root.Right)
- }
- // 如果x节点没有右子树,则找到其父节点,且父节点的左子树包含x
- y := x.Present
- for y != nil && x == y.Right {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**插入**
-
-插入和删除会引起二叉搜索树所表示的动态集合的变化。一定要修改数据结构来反映这种变化,单修改要保持二叉搜索树的性质不变。
-
-```go
-// x.Val = val, x.Right = x.Left = x.Present = nil
-// 插入的伪代码
-func insertBST(root, x *TreeNode) {
- var y *TreeNode
- for root != nil {
- y = root
- if x.Val < root.Val {
- root = root.Left
- } else {
- root = root.Right
- }
- }
- x.Present = y
- if y == nil { // empty tree
- root = x
- } else if x.Val < y.Val {
- y.Left = x
- } else {
- y.Right = x
- }
-}
-// 没有父指针
-// 递归版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root = x
- return root
- }
- if root.Val < x.Val {
- return insertBST(root.Right)
- }
- return insertBST(root.Left)
-}
-// 迭代版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root == x
- return root
- }
- pre, head := root, root
- for head != nil {
- pre = head
- if root.Val < x.Val {
- head = head.Right
- } else {
- head = head.Left
- }
- }
- if y.Val < x.Val {
- y.Right = x
- } else {
- y.Left = x
- }
- return root
-}
-```
-
-**删除**
-
-从一棵二叉搜索树中删除一个节点x的整个策略分为三个情况,分别是:
-
-1)如果x没有孩子节点,那么直接删除即可;
-
-2)如果x只有一个孩子节点,那么将该孩子节点提升到x即可;
-
-3)如果x有两个孩子,那么需要找到x的后继节点y(一定存在x的右子树中),让y占据x的位置,那么x原来的右子树部分称为y的右子树,x的左子树称为y的新的左子树。
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-### 二叉搜索树相关题目
-
-- 108 将有序数组转换为二叉搜索树【M】
-- 109—将有序链表转换为二叉搜索树
-- 235 二叉搜素树的最近公共祖先
-- 230 二叉搜索树中第K小的元素
-- 450 删除二叉搜索树中的节点
-- 1038 从二叉搜索树到更大和树【M】
-- 1214 查找两棵二叉搜索树之和【M】
-- 面试题 17.12 BiNode【E】
-- 面试题54 二叉搜索树的第K大节点
-
-#### 108 将有序数组转换为二叉搜索树
-
-题目要求:给定一个升序数据,返回一棵高度平衡二叉树。
-
-思路分析:
-
-二叉搜索树的定义:
-
-1)若任意节点的左子树不为空,则左子树上所有的节点值均小于它的根节点值;
-
-2)若任意节点的右子树不为空,则右子树上所有的节点值均大于它的根节点值;
-
-3)任意节点的左,右子树均为二叉搜索树;
-
-4)没有键值相等的点。
-
-如何构造一棵树,可拆分成无数个这样的子问题:构造树的每个节点,以及节点之间的关系。对于每个节点来说,都需要:
-
-1)选取节点;
-
-2)构造该节点的左子树;
-
-3)构造该节点的右子树。
-
-算法一:对于升序序列,可以选择中间的节点作为根节点,然后递归调用。因为每个节点只遍历一遍,所以时间复杂度为O(n);因为递归调用,空间复杂度为O(log(n))。
-
-```go
-//date 2020/02/20
-// 算法一:递归版
-func sortedArrayToBST(nums []int) *TreeNode {
- if len(nums) == 0 { return nil }
- // 选择根节点
- mid := len(nums) >> 1
- // 构造左子树和右子树
- left := nums[:mid]
- right := nums[mid+1:]
-
- return &TreeNode{
- Val: nums[mid],
- Left: sortedArrayToBST(left),
- Right: sortedArrayToBST(right),
- }
-}
-```
-
-#### 230 二叉搜索树中第K小的元素
-
-题目要求:给定一个二叉搜索树,返回其第K小的元素,你可以假设K总是有效的,即1<=k<=n。
-
-算法:因为是二叉搜索树,先得到其中序遍历结果,然后直接返回k-1所在的元素。
-
-```go
-// date 2020/01/11
-func kthSmallest(root *TreeNode) int {
- data := inOrder(root)
- if len(data) < k {return 0}
- return data[k-1]
-}
-
-func inOrder(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- if root.Left != nil { res = append(res, inOrder(root.Left)...) }
- res = append(res, root.Val)
- if root.Right != nil { res = append(res, inOrder(root.Right)...) }
-}
-```
-
-
-#### 235 二叉搜索树的最近公共祖先
-
-题目要求:给定一个二叉搜素树和两个节点,返回其最近公共祖先。
-
-算法:递归,并充分利用二叉搜索树的性质`left.Val < root.Val < right.Val`。
-
-```go
-// date 2020/02/18
-func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q {return root }
- if p == nil { return q }
- if q == nil { return p }
- if root.Val > q.Val && root.Val > p.Val { return lowestCommonAncestor(root.Left) }
- if root.Val < q.Val && root.Val < p.Val { return lowestCommonAncestor(root.Right) }
- return root
-}
-```
-
-
-
-#### 450 删除二叉搜索树中的节点
-
-题目要求:给定一个二叉搜索树和key,删除key节点,并返回树的根节点
-
-算法一:二叉搜索树的中序遍历序列是个升序序列,则欲要删除的节点需要用其前驱节点或后驱节点来代替。
-
-1)如果为叶子节点,则直接删除;
-
-2)如果不是叶子节点且有右子树,则用后驱节点代替。后驱节点为右子树中的较低位置;
-
-3)如果不是叶子节点且有左子树,则用前驱节点代替。前驱节点为左子树中的较高位置;
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-#### 1038 从二叉搜索树到更大和树
-
-题目要求:给出二叉**搜索**树的根节点,该二叉树的节点值各不相同,修改二叉树,使每个节点 `node` 的新值等于原树中大于或等于 `node.val` 的值之和
-
-思路分析:
-
-`root.Val = root.Val + root.Right.Val`
-
-`root.Left.Val = root.Left.Val + root.Val`
-
-首先得到二叉搜索树的中序遍历序列的逆序列,然后从序列的第一个开始,将累加值记录到当前树的节点上。
-
-```go
-// date 2020/02/23
-func bsttoGST(root *TreeNode) *TreeNode{
- array := decOrder(root)
- val := 0
- for i := 0; i < len(array); i++ {
- val += array[i]
- setNewVal(root, array[i], val)
- }
-}
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-
-func setNewVal(root *TreeNode, key, val int) {
- if root != nil {
- if root.Val == key {
- root.Val = val
- } else if root.Val > key {
- setNewVal(root.Left, key, val)
- } else {
- setNewVal(root.Right, key, val)
- }
- }
-}
-```
-
-#### 面试题 BiNode
-
-题目要求:将一颗二叉搜索树转换成单链表,Right指针指向下一个节点。
-
-思路分析:
-
-要求返回头节点,所以先转换left。
-
-```go
-// date 2020/02/19
-func convertBiNode(root *TreeNode) *TreeNode {
- if root == nil { return nil }
- // 左子树不为空,需要转换
- if root.Left != nil {
- // 得到左子树序列,并找到最后一个节点
- left := convertBiNode(root.Left)
- pre := left
- for pre.Right != nil { pre = pre.Right }
- // 将最后一个节点right指向root
- pre.Right = root
- root.Left = nil
- // 得到右子树序列
- root.Right = convertBiNode(root.Right)
- return left
- }
- root.Right = convertBiNode(root.Right)
- return root
-}
-```
-
-#### 面试题54 二叉搜索树的第K大节点
-
-题目要求:给定一个二叉搜索树,找出其中第k大节点。
-
-算法一:二叉搜索树的中序遍历为升序序列,按照Right->root->Left的顺序遍历可得到降序序列,然后返回第k节点。
-
-```go
-// date 2020/02/18
-func kthLargest(root *TreeNode, k int) int {
- if root == nil || k < 0 { return -1 }
- nums := decOrder(root)
- if len(nums) < k {return -1}
- return nums[k-1]
-}
-
-// right->root->left
-func decOrder(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- if root.Right != nil {
- res = append(res, decOrder(root.Right)...)
- }
- res = append(res, root.Val)
- if root.Left != nil {
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-
-
-### [相关题目](leetcode_bt.md)
-
-#### 156 上下翻转二叉树【中等】
-
-题目要求:给定一个二叉树,其中所有的右节点要么是具有兄弟节点(拥有相同父节点的左节点)的叶节点,要么为空,将此二叉树上下翻转并将它变成一棵树, 原来的右节点将转换成左叶节点。返回新的根。
-
-算法分析:
-
-```go
-// date 2020/02/25
-func upsideDownBinaryTree(root *TreeNode) *TreeNode {
- var parent, parent_right *TreeNode
- for root != nil {
- // 0.保存当前left, right
- root_left := root.Left
- root.Left = parent_right // 重新构建root,其left为上一论的right
- parent_right := root.Right // 保存right
- root.Right = parent // 重新构建root,其right为上一论的root
- parent = root
- root = root_left
- }
- return parent
-}
-```
-
-#### 270 最接近的二叉搜索树值【简单】
-
-题目要求:给定一个不为空的二叉搜索树和一个目标值 target,请在该二叉搜索树中找到最接近目标值 target 的数值。
-
-算法分析:使用层序遍历,广度优先搜索。
-
-```go
-// date 2020/02/23
-func closestValue(root *TreeNode, target float64) int {
- if root == nil { return 0 }
- var res int
- cur := math.Inf(1)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- for len(stack) != 0 {
- n := len(stack)
- for i := 0; i < n; i++ {
- if math.Abs(float64(stack[i].Val) - target) < cur {
- cur = math.Abs(float64(stack[i].Val) - target)
- res = stack[i].Val
- }
- if stack[i].Left != nil { stack = append(stack, stack[i].Left) }
- if stack[i].Right != nil { stack = append(stack, stack[i].Right) }
- }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 543 二叉树的直径【简单】
-
-题目要求:给定一棵二叉树,返回其直径。
-
-算法分析:左右子树深度和的最大值。
-
-```go
-// date 2020/02/23
-func diameterOfBinaryTree(root *TreeNode) int {
- v1, _ := findDepth(root)
- return v1
-}
-
-func findDepth(root *TreeNode) (int, int) {
- if root == nil { return 0, 0 }
- var v int
- v1, l := findDepth(root.Left)
- v2, r := findDepth(root.Right)
- if v1 > v2 {
- v = v1
- } else {
- v = v2
- }
- if l+r > v { v = l+r }
- if l > r { return v, l+1}
- return v, r+1
-}
-```
-
-#### 662 二叉树的最大宽度【中等】
-
-题目要求:给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
-
-每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
- 链接:https://leetcode-cn.com/problems/maximum-width-of-binary-tree
-
-算法分析:使用栈stack逐层遍历,计算每一层的宽度,注意全空节点的时候要返回。时间复杂度O(n),空间复杂度O(logn)。
-
-```go
-// date 2020/02/26
-func widthOfBinaryTree(root *TreeNode) int {
- res := 0
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- var n, i, j int
- var isAllNil bool
- for 0 != len(stack) {
- i, j, n = 0, len(stack)-1, len(stack)
- // 去掉每一层两头的空节点
- for i < j && stack[i] == nil { i++ }
- for i < j && stack[j] == nil { j-- }
- // 计算结果
- if j-i+1 > res { res = j-i+1 }
- // 添加下一层
- isAllNil = true
- for ; i <= j; i++ {
- if stack[i] != nil {
- stack = append(stack, stack[i].Left, stack[i].Right)
- isAllNil = false
- } else {
- stack = append(stack, nil, nil)
- }
- }
- if isAllNil { break }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 669 修剪二叉搜索树【简单】
-
-题目要求:给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
-
-算法分析:
-
-```go
-// date 2020/02/25
-func trimBST(root *TreeNode, L, R int) *TreeNode {
- if root == nil { return nil }
- if root.Val < L { return trimBST(root.Right, L, R) }
- if root.Val > R { return trimBST(root.Left, L, R) }
- root.Left = trimBST(root.Left, L, R)
- root.Right = trimBST(root.Right, L, R)
- return root
-}
-```
-
-#### 703 数据流中第K大元素【简单】
-
-解题思路:
-
-0。使用数据构建一个容量为k的小顶堆。
-
-1。如果小顶堆堆满后,向其增加元素,若大于堆顶元素,则重新建堆,否则掉弃。
-
-2。堆顶元素即为第k大元素。
-
-```go
-// date 2020/02/19
-type KthLargest struct {
- minHeap []int
- size
-}
-
-func Constructor(k int, nums []int) KthLargest {
- res := KthLargest{
- minHeap: make([]int, k),
- }
- for _, v := range nums {
- res.Add(v)
- }
-}
-
-func (this *KthLargest) Add(val int) int {
- if this.size < len(this.minHeap) {
- this.size++
- this.minHeap[this.size-1] = val
- if this.size == len(this.minHeap) {
- this.makeMinHeap()
- }
- } else if this.minHeap[0] < val {
- this.minHeap[0] = val
- this.minHeapify(0)
- }
- return this.minHeap[0]
-}
-
-func (this *KthLargest) makeMinHeap() {
- // 为什么最后一个根节点是n >> 1 - 1
- // 长度为n,最后一个叶子节点的索引是n-1; left = i >> 1 + 1; right = i >> 1 + 2
- // 父节点是 n >> 1 - 1
- for i := len(this.minHeap) >> 1 - 1; i >= 0; i-- {
- this.minHeapify(i)
- }
-}
-
-func (this *KthLargest) minHeapify(i int) {
- if i > len(this.minHeap) {return}
- temp, n := this.minHeap[i], len(this.minHeap)
- left := i << 1 + 1
- right := i << 1 + 2
- for left < n {
- right = left + 1
- // 找到left, right中较小的那个
- if right < n && this.minHeap[left] > this.minHeap[right] { left++ }
- // left, right 均小于root否和小顶堆,跳出
- if this.minHeap[left] >= this.minHeap[i] { break }
- this.minHeap[i] = this.minHeap[left]
- this.minHeap[left] = temp
- // left发生变化,继续调整
- i = left
- left = i << 1 + 1
- }
-}
-```
-
-#### 814 二叉树剪枝【中等】
-
-题目要求:给定一个二叉树,每个节点的值要么是0,要么是1。返回移除了所有不包括1的子树的原二叉树。
-
-算法分析:
-
-使用containOne()函数判断节点以及节点的左右子树是否包含1。
-
-```go
-// date 2020/02/25
-func pruneTree(root *TreeNode) *TreeNode {
- if containsOne(root) { return root }
- return nil
-}
-
-func containsOne(root *TreeNode) bool {
- if root == nil { return false }
- l, r := containsOne(root.Left), containsOne(root.Right)
- if !l { root.Left = nil }
- if !r { root.Right = nil }
- return root.Val == 1 || l || r
-}
-```
-
-#### 1104 二叉树寻路【中等】
-
-题目要求:https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree/
-
-算法分析:
-
-```go
-// date 2020/02/25
-func pathInZigZagTree(label int) []int {
- res := make([]int, 0)
- for label != 1 {
- res = append(res, label)
- label >>= 1
- y := highBit(label)
- lable = ^(label-y)+y
- }
- res = append(res, 1)
- i, j := 0, len(res)-1
- for i < j {
- t := res[i]
- res[i] = res[j]
- res[j] = t
- i++
- j--
- }
- return res
-}label = label ^(1 << (label.bit_length() - 1)) - 1
-
-func bitLen(x int) int {
- res := 0
- for x > 0 {
- x >>= 1
- res++
- }
- return res
-}
-```
-
-#### 面试题27 二叉树的镜像【简单】
-
-题目链接:https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/
-
-题目要求:给定一棵二叉树,返回其镜像二叉树。
-
-```go
-// date 2020/02/23
-// 递归算法
-func mirrorTree(root *TreeNode) *TreeNode {
- if root == nil { return root }
- left := root.Left
- root.Left = root.Right
- root.Right = left
- root.Left = mirrorTree(root.Left)
- root.Right = mirrorTree(root.Right)
- return root
-}
-```
-
diff --git a/08_binaryTree/readme_new.md b/08_binaryTree/readme_new.md
deleted file mode 100644
index ad2f1f5..0000000
--- a/08_binaryTree/readme_new.md
+++ /dev/null
@@ -1,380 +0,0 @@
-## 二叉树
-
-[TOC]
-
-### 1.什么是二叉树
-
- 树是一种数据结构,树中的每个节点都包含一个键值和所有子节点的列表,对于二叉树来说,每个节点最多有两个子树结构,分别称为左子树和右子树。
-
-#### 二叉树的深度
-
- 二叉树的深度是指二叉树的根结点到叶子结点的距离。
-
- 最大深度 = 根结点到叶子结点的最大距离
-
- 最小深度 = 根结点到叶子结点的最小距离。
-
- 常见的问题包括求二叉树的最大/最小深度,一般可以使用递归算法,或者自顶向下的 DFS。
-
-参见题目:
-
-- 104—二叉树的最大深度
-- 110—平衡二叉树,自底向上的 DFS
-- 111—二叉树的最小深度
-
-
-
-### 2.二叉树的遍历
-
-按照 root 节点的访问顺序,可分为前序遍历,中序遍历和后序遍历。其顺序如下:
-
-- 前序遍历:按「根-左-右」依次访问各节点
-- 中序遍历:按「左-根-右」依次访问各节点
-- 后序遍历:按「左-右-根」依次访问各节点
-
-
-
-递归版本的遍历,只要理解其思想就很好写;而对于非递归版本的遍历,需要深入理解其结点的遍历顺序,并记录下来之前经过的结点,所以一定会用到栈。
-
-层序遍历是一种特殊的遍历,从二叉树的深度来理解就是,将同一深度的结果按照从左到右的顺序形成一个数组,不同深度的结果再放到另一个数组里面,最终形成一个二维数组。
-
-从广度搜索和深度搜索的角度来讲,层序遍历属于广度优先搜索,而前序,中序,后序遍历均为深度优先搜索。
-
-
-
-除了以上遍历顺序,在实际解题过程中,根据访问「根左右」的前后顺序,可以灵活使用。比如题目【1038 从二叉搜索树到更大和树】就用到了「右-根-左」的遍历顺序。
-
-
-
-#### 2.1 前序遍历
-
-参见题目:
-
-- 144—二叉树的前序遍历
-- 105—从前序和中序遍历序列构造二叉树
-- 530—二叉搜索树的最小绝对值差,前序遍历DFS,求相邻元素的最小值
-- 1305—两棵二叉搜索树的所有元素,前序遍历形成数组,然后归并排序
-
-
-
-#### 2.2 中序遍历
-
-这里跟前序遍历类似,只是取根节点值加入结果集的时机略有区别。
-
-其主要思路为:
-
-1. 持续检查其左子树,重复1,直到左子树为空【此时栈中保留的是一系列的左子树节点】
-2. 出栈一次,并取根节点值加入结果集,然后检查最后一个左子树的右子树,重复1,2
-
-```go
-// 迭代版
-// 需要stack结构
-// left->root->right
-func inorderTraversal(root *TreeNode) []int {
- if root == nil {
- return []int{}
- }
- stack := make([]*TreeNode, 0, 16)
- res := make([]int, 0, 16)
- for root != nil || len(stack) != 0 {
- for root != nil {
- stack = append(stack, root)
- root = root.Left
- }
- if len(stack) != 0 {
- root = stack[len(stack)-1]
- stack = stack[:len(stack)-1]
- res = append(res, root.Val)
- root = root.Right
- }
- }
- return res
-}
-```
-
-参见题目:
-
-- 106—从中序和后序遍历序列构造二叉树
-- 173—二叉搜索树迭代器,迭代中序遍历变成数组
-- 538—把二叉搜索树转换为累加树,递归中序遍历解法
-- 783—二叉搜索树节点最小距离,递归中序遍历
-
-
-
-#### 2.3 后序遍历
-
-后序遍历的迭代算法依然需要 stack 结构来保存已经遍历过的节点;同时借助 pre 指针保存上次出栈的节点,用于判断当前节点是否同时具有左右子树,还是只有单个子树。
-
-1. 先将根节点入栈,循环遍历栈是否为空
-2. 出栈,取出当前节点
- 1. 如果当前节点没有左右子树,则为叶子节点,直接加入结果集
- 2. 其次判断上次出栈的节点是否是当前节点的左右子树,如果是,表明当前节点的子树已经处理完毕,也需要加入结果集【这里依赖的是左右子树的入栈,因为在栈中左右子树不具备前继关系,只有根节点具备】
- 3. 依次检查当前节点的右子树,左子树,重复1,2
-
-```go
-// 迭代版
-// left->right-root
-func postorderTraversal(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- var pre, cur *TreeNode // 记录前驱节点和当前节点
- for len(stack) != 0 {
- // 出栈 当前结点
- cur = stack[len(stack)-1]
- // 如果当前结点为叶子结点,则直接加入结果集
- // 如果当前结点不是叶子结点,但是上次遍历结点为当前结点的左右子树时(说明当前结点只有单个子树,且子树已经处理完毕),也加入结果集
- if cur.Left == nil && cur.Right == nil || pre != nil && (pre == cur.Left || pre == cur.Right) {
- res = append(res, cur.Val)
- // 出栈,继续检查
- stack = stack[:len(stack)-1]
- pre = cur
- } else {
- // 因为在出栈的时候检查结点,并追加到结果中
- // 所以,先入栈右子树,后入栈左子树
- if cur.Right != nil {
- stack = append(stack, cur.Right)
- }
- if cur.Left != nil {
- stack = append(stack, cur.Left)
- }
- }
- }
-
- return res
-}
-```
-
-
-
-
-
-参见题目:
-
-- 145—二叉树的后续遍历
-- 106—从中序和后序遍历序列构造二叉树
-
-
-
-#### 2.4 层序遍历
-
-层序遍历是指逐层遍历树的结构,也称为广度优先搜索,算法从一个根节点开始,先访问根节点,然后遍历其相邻的节点,其次遍历它的二级、三级节点。
-
-借助队列数据结构,先入先出的顺序,实现层序遍历。
-
-```go
-// date 2020/03/21
-// 层序遍历
-// bfs广度优先搜索
-// 算法一:使用队列,逐层遍历
-func levelOrder(root *TreeNode) [][]int {
- if root == nil {
- return [][]int{}
- }
- res := make([][]int, 0, 16)
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
- for len(queue) != 0 {
- n := len(queue)
- curRes := make([]int, 0, 16)
- for i := 0; i < n; i++ {
- cur := queue[i]
- curRes = append(curRes, cur.Val)
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
- res = append(res, curRes)
- queue = queue[n:]
- }
- return res
-}
-```
-
-算法2:DFS 深度优先搜索
-
-这里的思路类似求二叉树的最大深度,借助dfs搜索,在每一层追加结果。
-
-```go
-// date 2020/03/21
-func levelOrder(root *TreeNode) [][]int {
- res := make([][]int, 0, 16)
- var dfs func(root *TreeNode, level int)
- dfs = func(root *TreeNode, level int) {
- if root == nil {
- return
- }
- if len(res) == level {
- res = append(res, make([]int, 0, 4))
- }
- res[level] = append(res[level], root.Val)
- level++
- dfs(root.Left, level)
- dfs(root.Right, level)
- }
- dfs(root, 0)
- return res
-}
-```
-
-**注意**,从上面两种实现的方式来看,层序遍历既可以使用广度优先搜索,也可以使用深度优先搜索。
-
-参见题目
-
-- 102—二叉树的层序遍历
-- 103—二叉树的锯齿形层序遍历,奇偶层反转
-- 107—二叉树的层序遍历2,将底部结果放到开头,没有新意
-- 116—填充每个节点的下一个右侧节点指针,就是层序遍历
-- 117—填充每个节点的下一个右侧节点指针,巧妙地层序遍历
-- 199—二叉树的右视图,取层序遍历最后一个节点
-- 404—左叶子之和
-- 429—N 叉树的层序遍历
-- 590—N 叉树的后序遍历,迭代的层序遍历解法
-- 623—在二叉树中增加一行,层序遍历
-- 637—二叉树的层平均值,就是层序遍历,求每层平均值
-- 951—翻转等价二叉树,递归判断
-- 987—二叉树的垂序遍历,层序遍历,每个节点标注坐标,根据坐标排序
-- 1161—最大层内元素和,层序遍历,求和
-- 1302—层数最深叶子节点的和,层序遍历,只保留最后一次的和
-- 1609—奇偶树,基本的层序遍历
-
-
-
-
-
-### 3.递归解决树的问题
-
-递归通常是解决树的相关问题最有效和最常用的方法之一,分为**自顶向下**和**自底向上**两种。
-
-**自顶向下**的解决方案
-
-自顶向下意味着在每个递归层级,需要先计算一些值,然后递归调用并将这些值传递给子节点,视为**前序遍历**。参见题目【二叉树的最大深度】
-
-```go
-// 通用的框架,自顶向下
-1. return specific value for null node
-2. update the answer if needed // answer <-- params
-3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
-4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
-5. return the answer if needed // answer <-- left_ans, right_ans
-```
-
-参见题目
-
-- 95—不同的二叉搜索数2,生成所有的二叉搜索数
-- 112—路径总和,判断是否存在一个路径
-- 113—路径总和2,求满足条件的所有路径,DFS
-- 129—求根节点到叶子节点数字之和,携带已知内容递归到叶子节点
-- 235—二叉搜索树的最近公共祖先,利用二叉搜索树的规律
-- 236—二叉树的最近公共祖先
-- 257—二叉树的所有路径,与求路径和2一样的解法
-- 572—另一棵树的子树,递归判断
-- 617—合并二叉树,递归覆盖
-- 654—最大二叉树,递归构造即可
-- 700—二叉搜索树的搜索,递归判断并查找
-- 701—二叉搜索树的插入操作,递归判断并插入
-- 814—二叉树剪枝
-- 1161 最大层内元素和,层序遍历,求和,求最大,无新意
-
-
-
-**自底向上**的解决方案
-
-自底向上意味着在每个递归层级,需要先对子节点递归调用函数,然后根据返回值和根节点本身得到答案,视为**后序遍历**。
-
-```go
-// 通用的框架,自底向上
-1. return specific value for null node
-2. left_ans = bottom_up(root.left) // call function recursively for left child
-3. right_ans = bottom_up(root.right) // call function recursively for right child
-4. return answers // answer <-- left_ans, right_ans, root.val
-```
-
-参见题目:
-
-- 543—二叉树的直径,求左右深度之和。
-- 865—具有所有最深节点的最小子树
-- 1038—从二叉搜索树到更大和树,递归后序遍历,并更新
-
-
-
-**小结**:
-
-当遇到树的问题时,先思考一下两个问题:
-
-> 1.你能确定一些参数,从该节点自身解决出发寻找答案吗?
->
-> 2.你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗?
-
-如果答案是肯定的,那么可以尝试使用自顶向下的递归来解决问题。
-
-当然也可以这样思考:
-
-> 对于树中的任意一个节点,如果你知道它子节点的结果,你能计算出该节点的答案吗?
-
-如果答案是肯定的,可以尝试使用自底向上的递归来解决问题。
-
-
-
-### 深度优先搜索
-
-深度优先搜索的过程,过程中计算最终的结果集,和深搜本身的返回值不一致。这并不矛盾。反而,有些题目更好使。参见题目979-在二叉树中分配硬币。
-
-参见题目:
-
-- 114—二叉树展开为链表
-- 230—二叉搜索树中第K小的元素,递归中序深搜,求第K个
-- 257—二叉树的所有路径,深搜,记录路径,并更新结果
-- 404—左叶子之和,深搜,求和
-- 437—路径总和3,深搜,并记录前缀和
-- 501—二叉搜索树中的众数,DFS,中序遍历,求连续最多的值
-- 543—二叉树的直径,DFS,并返回子树深度,并求和
-- 545—二叉树的边界,深搜,最后去重,主要考虑边界去重,细节题
-- 563—二叉树的坡度,DFS 并返回子树节点和,过程中求左右子树的和差值
-- 653—两数之和,输入为二叉搜索树,DFS 并保持已经遍历过的节点
-- 662—二叉树的最大宽度,有技巧的DFS
-- 865—具有所有最深节点的最小子树,DFS或递归,并返回叶子节点的最近公共祖先
-- 938—二叉搜索树的范围和
-- 965—单值二叉树,直接 DFS
-- 979—在二叉树中分配硬币,DFS 并返回左右子树的需要硬币的差值
-- 993—二叉树的堂兄弟节点,DFS 记录各自的父节点和深度
-
-
-
-### 广度优先搜索
-
-也就是层序遍历,在每一层寻找结果。
-
-参见题目:
-
-- 111—二叉树的最小深度
-
-
-
-
-
-### 4 平衡二叉树
-
-一棵高度平衡二叉树的定义为:
-
-> 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
-
-参见题目:
-
-- 108—将有序数组转换为二叉搜索树,递归实现
-- 110—平衡二叉树,DFS 求每个子树的深度,并比较
-
-
-
-### 5 对称二叉树
-
-如果一棵二叉树关于根结点左右对称,则称为对称二叉树,也称为镜像二叉树。
-
-参见题目:
-
-- 101—对称二叉树,递归,或者迭代两个树
-
diff --git a/08_binaryTree/recursion.md b/08_binaryTree/recursion.md
deleted file mode 100644
index d04c37b..0000000
--- a/08_binaryTree/recursion.md
+++ /dev/null
@@ -1,47 +0,0 @@
-### 递归Recursion
-
-#### 相关题目
-
-- 爬楼梯
-- Pow(x, n)
-
-#### 爬楼梯
-
-思路分析
-
-基本情况:n = 1, res = 1, n = 2, res = 2; f(n) = f(n-1) + f(n2)
-
-```go
-// 斐波那契数列 时间复杂度O(n) 空间复杂度O(1)
-func climbStairs(n int) int {
- if n <= 2 {return n}
- c, p1, p2 := 0, 2, 1
- for i := 3; i <= n; i++ {
- c = p1 + p2
- p1, p2 = c, p1
- }
- return c
-}
-```
-
-#### Pow(x,n)
-
-```go
-// 迭代快速幂等法
-func myPow(x float64, n int) float64 {
- if n < 0 {
- x = float64(1) / x
- n = -n
- }
- res := float64(1)
- c := x
- for i := n; i >= 0; i >>= 1 {
- if i & 0x1 == 1 {
- res *= c
- }
- c = c * c
- }
- return res
-}
-```
-
diff --git "a/09_binary_search/No.034_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/09_binary_search/No.034_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
deleted file mode 100644
index bfea6d5..0000000
--- "a/09_binary_search/No.034_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ /dev/null
@@ -1,65 +0,0 @@
-## 34 在排序数组中查找元素的第一个和最后一个位置-中等
-
-题目:
-
-给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
-
-如果数组中不存在目标值 target,返回 [-1, -1]。
-
-你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
-
-
-
-分析:
-
-复习二分查找,[详见](../binary_search.md)
-
-```go
-// date 2022/09/15
-func searchRange(nums []int, target int) []int {
- res := make([]int, 2, 2)
-
- l := searchFirstEqual(nums, target)
- r := searchLastEqual(nums, target)
-
- res[0] = l
- res[1] = r
-
- return res
-}
-
-func searchFirstEqual(nums []int, target int) int {
- left, right := 0, len(nums)-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= target {
- right = mid - 1
- } else if nums[mid] < target {
- left = mid + 1
- }
- }
- if left < len(nums) && nums[left] == target {
- return left
- }
- return -1
-}
-
-// 从 right 找边界
-func searchLastEqual(nums []int, target int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > target {
- right = mid - 1
- } else if nums[mid] <= target { // 从右侧找边界,left 不断地向 right 靠近
- left = mid + 1
- }
- }
- if right >= 0 && nums[right] == target {
- return right
- }
- return -1
-}
-```
-
diff --git "a/09_binary_search/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md" "b/09_binary_search/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md"
deleted file mode 100644
index add9f3b..0000000
--- "a/09_binary_search/No.035_\346\220\234\347\264\242\346\217\222\345\205\245\344\275\215\347\275\256.md"
+++ /dev/null
@@ -1,33 +0,0 @@
-## 35 搜索插入位置-中等
-
-题目:
-
-给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
-
-请必须使用时间复杂度为 `O(log n)` 的算法。
-
-
-
-分析:
-
-查找第一个等于或大于 key 的元素。
-
-```go
-// date 2023/12/04
-func searchInsert(nums []int, target int) int {
- n := len(nums)
- left, right := 0, n-1
-
- // first equal or larger
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] < target {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return left
-}
-```
-
diff --git "a/09_binary_search/No.069_x\347\232\204\345\271\263\346\226\271\346\240\271.md" "b/09_binary_search/No.069_x\347\232\204\345\271\263\346\226\271\346\240\271.md"
deleted file mode 100644
index a2b879c..0000000
--- "a/09_binary_search/No.069_x\347\232\204\345\271\263\346\226\271\346\240\271.md"
+++ /dev/null
@@ -1,33 +0,0 @@
-## 69 x的平方根-简单
-
-题目:
-
-给你一个非负整数 `x` ,计算并返回 `x` 的 **算术平方根** 。
-
-由于返回类型是整数,结果只保留 **整数部分** ,小数部分将被 **舍去 。**
-
-**注意:**不允许使用任何内置指数函数和算符,例如 `pow(x, 0.5)` 或者 `x ** 0.5` 。
-
-
-
-分析:
-
-二分查找,求最后一个等于或小于 x 的值。
-
-```go
-// data 2023/12/06
-func mySqrt(x int) int {
- left, right := 0, x
- for left <= right {
- mid := left + (right - left) / 2
- v := mid * mid
- if v > x {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- return right
-}
-```
-
diff --git "a/09_binary_search/No.074_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\265.md" "b/09_binary_search/No.074_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\265.md"
deleted file mode 100644
index dbb41f2..0000000
--- "a/09_binary_search/No.074_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\265.md"
+++ /dev/null
@@ -1,51 +0,0 @@
-## 74 搜索二维矩阵-中等
-
-题目:
-
-给你一个满足下述两条属性的 `m x n` 整数矩阵:
-
-- 每行中的整数从左到右按非严格递增顺序排列。
-- 每行的第一个整数大于前一行的最后一个整数。
-
-给你一个整数 `target` ,如果 `target` 在矩阵中,返回 `true` ;否则,返回 `false` 。
-
-
-
-分析:
-
-先对每一行的第一个元素进行 LastEqualOrSmaller 二分查找,找到相应的行,然后在进行 FirstEqual 查找。
-
-```go
-// date 2023/12/04
-func searchMatrix(matrix [][]int, target int) bool {
- m := len(matrix)
- up, down := 0, m-1
- // find the last equal or smaller
- for up <= down {
- mid := (up + down) / 2
- if matrix[mid][0] > target {
- down = mid - 1
- } else {
- up = mid + 1
- }
- }
- // find
- if down >= 0 && down < m {
- // find col
- n := len(matrix[down])
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if matrix[down][mid] == target {
- return true
- } else if matrix[down][mid] < target {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- }
- return false
-}
-```
-
diff --git "a/09_binary_search/No.081_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\2042.md" "b/09_binary_search/No.081_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\2042.md"
deleted file mode 100644
index fa3b760..0000000
--- "a/09_binary_search/No.081_\346\220\234\347\264\242\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\2042.md"
+++ /dev/null
@@ -1,61 +0,0 @@
-## 81 搜索旋转排序数组2-中等
-
-题目:
-
-已知存在一个按非降序排列的整数数组 `nums` ,数组中的值不必互不相同。
-
-在传递给函数之前,`nums` 在预先未知的某个下标 `k`(`0 <= k < nums.length`)上进行了 **旋转** ,使数组变为 `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]`(下标 **从 0 开始** 计数)。例如, `[0,1,2,4,4,4,5,6,6,7]` 在下标 `5` 处经旋转后可能变为 `[4,5,6,6,7,0,1,2,4,4]` 。
-
-给你 **旋转后** 的数组 `nums` 和一个整数 `target` ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 `nums` 中存在这个目标值 `target` ,则返回 `true` ,否则返回 `false` 。
-
-你必须尽可能减少整个操作步骤。
-
-
-
-分析:
-
-先根据第一个元素与目标值的大小关系,去掉不可能的部分,然后二分查找。
-
-```go
-// date 2023/12/04
-func search(nums []int, target int) bool {
- n := len(nums)
- if target == nums[0] {
- return true
- } else if target > nums[0] {
- left, right := 1, n-1
- for right >= left && nums[right] <= nums[0] {
- right--
- }
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] == target {
- return true
- } else if nums[mid] < target {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return false
- } else if target < nums[0] {
- left, right := 0, n-1
- for left <= right && nums[left] >= nums[0] {
- left++
- }
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] == target {
- return true
- } else if nums[mid] < target {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return false
- }
- return false
-}
-```
-
diff --git "a/09_binary_search/No.153_\345\257\273\346\211\276\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\346\234\200\345\260\217\345\200\274.md" "b/09_binary_search/No.153_\345\257\273\346\211\276\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\346\234\200\345\260\217\345\200\274.md"
deleted file mode 100644
index 152176e..0000000
--- "a/09_binary_search/No.153_\345\257\273\346\211\276\346\227\213\350\275\254\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\346\234\200\345\260\217\345\200\274.md"
+++ /dev/null
@@ -1,48 +0,0 @@
-## 153 寻找旋转排序数组中的最小值-中等
-
-题目:
-
-已知一个长度为 `n` 的数组,预先按照升序排列,经由 `1` 到 `n` 次 **旋转** 后,得到输入数组。例如,原数组 `nums = [0,1,2,4,5,6,7]` 在变化后可能得到:
-
-- 若旋转 `4` 次,则可以得到 `[4,5,6,7,0,1,2]`
-- 若旋转 `7` 次,则可以得到 `[0,1,2,4,5,6,7]`
-
-注意,数组 `[a[0], a[1], a[2], ..., a[n-1]]` **旋转一次** 的结果为数组 `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]` 。
-
-给你一个元素值 **互不相同** 的数组 `nums` ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 **最小元素** 。
-
-你必须设计一个时间复杂度为 `O(log n)` 的算法解决此问题。
-
-
-
-分析:
-
-先根据首尾元素判断数组是否有序,如果有序直接返回第一个元素。
-
-否则,从下标 1 开始,二分查找数组中第一个小于 nums[0] 的元素。
-
-```go
-// date 2023/12/04
-func findMin(nums []int) int {
- n := len(nums)
- if n == 1 {
- return nums[0]
- }
- if nums[0] < nums[n-1] {
- return nums[0]
- }
- // find the first small than key
- left, right := 1, n-1
- key := nums[0]
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- left = mid + 1
- } else if nums[mid] <= key {
- right = mid - 1
- }
- }
- return nums[left]
-}
-```
-
diff --git "a/09_binary_search/No.240_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\2652.md" "b/09_binary_search/No.240_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\2652.md"
deleted file mode 100644
index 899e27e..0000000
--- "a/09_binary_search/No.240_\346\220\234\347\264\242\344\272\214\347\273\264\347\237\251\351\230\2652.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 240 搜索二维矩阵-中等
-
-题目:
-
-编写一个高效的算法来搜索 `*m* x *n*` 矩阵 `matrix` 中的一个目标值 `target` 。该矩阵具有以下特性:
-
-- 每行的元素从左到右升序排列。
-- 每列的元素从上到下升序排列。
-
-
-
-分析:
-
-因为矩阵是每行升序,每列升序,所以可以以右上角的元素为基准。
-
-如果右上角元素大于目标值,那么这一列不会有答案;
-
-如果右上角元素小于目标值,那么这一行不会有答案;
-
-```go
-// date 2023/12/05
-func searchMatrix(matrix [][]int, target int) bool {
- m := len(matrix)
- n := len(matrix[0])
- // Z 字查找
- x, y := 0, n-1
- for x < m && y >= 0 {
- if matrix[x][y] == target {
- return true
- } else if matrix[x][y] > target { // 说明这一列不可能有
- y--
- } else { // 说明这一行不可能存在答案
- x++
- }
- }
- return false
-}
-```
-
diff --git "a/09_binary_search/No.268_\344\270\242\345\244\261\347\232\204\346\225\260\345\255\227.md" "b/09_binary_search/No.268_\344\270\242\345\244\261\347\232\204\346\225\260\345\255\227.md"
deleted file mode 100644
index 94348c7..0000000
--- "a/09_binary_search/No.268_\344\270\242\345\244\261\347\232\204\346\225\260\345\255\227.md"
+++ /dev/null
@@ -1,34 +0,0 @@
-## 268 丢失的数字
-
-题目:
-
-给定一个包含 `[0, n]` 中 `n` 个数的数组 `nums` ,找出 `[0, n]` 这个范围内没有出现在数组中的那个数。
-
-
-
-分析:
-
-直接异或计算。
-
-一个值和他本身异或,结果为零。
-
-直接把 0-n 之间所有的数字和 nums 中的数字,异或一次。
-
-没出现的数字,只会出现一次,其他数字出现两次。所以最终的结果就是丢失的数字。
-
-```go
-// date 2023/12/05
-func missingNumber(nums []int) int {
- ans := int(0)
- n := len(nums)
- for i := 0; i < n; i++ {
- ans ^= nums[i]
- ans ^= i
- }
-
- ans ^= n
-
- return ans
-}
-```
-
diff --git "a/09_binary_search/No.275_H\346\214\207\346\225\2602.md" "b/09_binary_search/No.275_H\346\214\207\346\225\2602.md"
deleted file mode 100644
index 8d5ea0f..0000000
--- "a/09_binary_search/No.275_H\346\214\207\346\225\2602.md"
+++ /dev/null
@@ -1,37 +0,0 @@
-## 275 H指数2-中等
-
-题目:
-
-给你一个整数数组 `citations` ,其中 `citations[i]` 表示研究者的第 `i` 篇论文被引用的次数,`citations` 已经按照 **升序排列** 。计算并返回该研究者的 h 指数。
-
-[h 指数的定义](https://baike.baidu.com/item/h-index/3991452?fr=aladdin):h 代表“高引用次数”(high citations),一名科研人员的 `h` 指数是指他(她)的 (`n` 篇论文中)**至少** 有 `h` 篇论文分别被引用了**至少** `h` 次。
-
-请你设计并实现对数时间复杂度的算法解决此问题。
-
-
-
-分析:
-
-假设数组长度为 n,其实就是求 nums[i] >= n - i 的最右边界。
-
-变相地等价于求数组中第一个小于 n - i 的元素。
-
-```go
-// date 2023/12/05
-func hIndex(citations []int) int {
- n := len(citations)
- left, right := 0, n-1
- // find the first small key(key = n - mid)
- // the result is n - left
- for left <= right {
- mid := (left + right) / 2
- if citations[mid] >= n - mid {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- return n - left
-}
-```
-
diff --git "a/09_binary_search/No.278_\347\254\254\344\270\200\344\270\252\351\224\231\350\257\257\347\211\210\346\234\254.md" "b/09_binary_search/No.278_\347\254\254\344\270\200\344\270\252\351\224\231\350\257\257\347\211\210\346\234\254.md"
deleted file mode 100644
index de84edc..0000000
--- "a/09_binary_search/No.278_\347\254\254\344\270\200\344\270\252\351\224\231\350\257\257\347\211\210\346\234\254.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 278 第一个错误的版本-中等
-
-题目:
-
-你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
-
-假设你有 `n` 个版本 `[1, 2, ..., n]`,你想找出导致之后所有版本出错的第一个错误的版本。
-
-你可以通过调用 `bool isBadVersion(version)` 接口来判断版本号 `version` 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
-
-
-
-分析:
-
-查找第一个错误的版本。
-
-```go
-// date 2023/12/05
-/**
- * Forward declaration of isBadVersion API.
- * @param version your guess about first bad version
- * @return true if current version is bad
- * false if current version is good
- * func isBadVersion(version int) bool;
- */
-
-func firstBadVersion(n int) int {
- left, right := 0, n
- for left <= right {
- mid := (left + right) / 2
- if isBadVersion(mid) {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- return left
-}
-```
-
diff --git "a/09_binary_search/No.287_\345\257\273\346\211\276\351\207\215\345\244\215\346\225\260.md" "b/09_binary_search/No.287_\345\257\273\346\211\276\351\207\215\345\244\215\346\225\260.md"
deleted file mode 100644
index 6c67e60..0000000
--- "a/09_binary_search/No.287_\345\257\273\346\211\276\351\207\215\345\244\215\346\225\260.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 287 寻找重复数-中等
-
-题目:
-
-给定一个包含 `n + 1` 个整数的数组 `nums` ,其数字都在 `[1, n]` 范围内(包括 `1` 和 `n`),可知至少存在一个重复的整数。
-
-假设 `nums` 只有 **一个重复的整数** ,返回 **这个重复的数** 。
-
-你设计的解决方案必须 **不修改** 数组 `nums` 且只用常量级 `O(1)` 的额外空间。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,3,4,2,2]
-> 输出:2
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [3,1,3,4,2]
-> 输出:3
-> ```
-
-
-
-**解题思路**
-
-这道题可用二分查找。
-
-题目中说,所有的数字都在区间`[1,n]`之间,且只有一个数出现2次,其他数字只出现1次。那我们可以对数组的数字计数,对计数进行二分查找。
-
-以示例1为例,在区间`[1,5]`上,区间`[1,1]`满足 cnt[i] < i;而区间`[2,4]`上,cnt[i] > [i]。
-
-```go
-// date 2024/01/15
-func findDuplicate(nums []int) int {
- // [1, n]
- n := len(nums)
- left, right := 0, n-1
-
- ans := -1
- for left <= right {
- mid := left +(right-left)>>1
- cnt := 0
- for i := 0; i < n; i++ {
- if nums[i] <= mid {
- cnt++
- }
- }
- if cnt <= mid {
- left = mid+1
- } else {
- right = mid-1
- ans = mid
- }
- }
-
- return ans
-}
-```
-
diff --git "a/09_binary_search/No.349_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\206.md" "b/09_binary_search/No.349_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\206.md"
deleted file mode 100644
index a4356fa..0000000
--- "a/09_binary_search/No.349_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\206.md"
+++ /dev/null
@@ -1,89 +0,0 @@
-## 349 两个数组的交集-中等
-
-题目:
-
-给定两个数组 `nums1` 和 `nums2` ,返回 *它们的交集* 。输出结果中的每个元素一定是 **唯一** 的。我们可以 **不考虑输出结果的顺序** 。
-
-
-
-分析:
-
-哈希表存储,如果存在第一个数组中,值为1,如果存在第二个数组,值为2。
-
-最后遍历哈希表即可。
-
-```go
-// date 2023/12/05
-func intersection(nums1 []int, nums2 []int) []int {
- set := make(map[int]int, 32)
- for _, v := range nums1 {
- _, ok := set[v]
- if !ok {
- set[v] = 1
- }
- }
- for _, v := range nums2 {
- _, ok := set[v]
- if ok {
- set[v] = 2
- }
- }
- res := make([]int, 0, 4)
- for k, v := range set {
- if v == 2 {
- res = append(res, k)
- }
- }
- return res
-}
-```
-
-思考:如果是已经排序的数组,如何求交集。
-
-如果是有序数组,直接在另一个数组中二分查找。算法如下:
-
-```go
-// date 2023/12/05
-func intersection(nums1 []int, nums2 []int) []int {
- res := make([]int, 0, 16)
- sort.Slice(nums1, func(i, j int) bool {
- return nums1[i] < nums1[j]
- })
- sort.Slice(nums2, func(i, j int) bool {
- return nums2[i] < nums2[j]
- })
-
- for i := 0; i < len(nums1); i++ {
- if i > 0 && nums1[i] == nums1[i-1] {
- continue
- }
- if findEqual(nums2, nums1[i]) {
- res = append(res, nums1[i])
- }
- }
-
- return res
-}
-
-func findEqual(nums []int, key int) bool {
- n := len(nums)
-
- if nums[0] > key || nums[n-1] < key {
- return false
- }
-
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] == key {
- return true
- } else if nums[mid] < key {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return false
-}
-```
-
diff --git "a/09_binary_search/No.350_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\2062.md" "b/09_binary_search/No.350_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\2062.md"
deleted file mode 100644
index e532b1a..0000000
--- "a/09_binary_search/No.350_\344\270\244\344\270\252\346\225\260\347\273\204\347\232\204\344\272\244\351\233\2062.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 350 两个数组的交集2-中等
-
-题目:
-
-给你两个整数数组 `nums1` 和 `nums2` ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
-
-
-
-分析:
-
-两个哈希表分别记录两个数组中各元素出现的次数,然后对哈希表进行遍历查找,取重复元素在数组中出现的最小次数,追加到结果中。
-
-```go
-// date 2023/12/05
-func intersect(nums1 []int, nums2 []int) []int {
- n1, n2 := len(nums1), len(nums2)
- set1 := make(map[int]int, n1)
- set2 := make(map[int]int, n2)
- for _, v := range nums1 {
- set1[v]++
- }
- for _, v := range nums2 {
- set2[v]++
- }
-
- res := make([]int, 0, 16)
- for k, v := range set1 {
- v2, ok := set2[k]
- if ok {
- ct := min(v, v2)
- for ct > 0 {
- res = append(res, k)
- ct--
- }
- }
- }
- return res
-}
-
-func min(x, y int) int {
- if x <= y {
- return x
- }
- return y
-}
-```
-
-进阶思考:
-
-1. 如果给定的数组已经排好序呢?你将如何优化你的算法?
-
-【可用二分查找,返回第一个和最后一个等于 key 的下标】
-
-2. 如果 `nums1` 的大小比 `nums2` 小,哪种方法更优?
-
-
-
-3. 如果 `nums2` 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
\ No newline at end of file
diff --git "a/09_binary_search/No.367_\346\234\211\346\225\210\347\232\204\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md" "b/09_binary_search/No.367_\346\234\211\346\225\210\347\232\204\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md"
deleted file mode 100644
index c079e10..0000000
--- "a/09_binary_search/No.367_\346\234\211\346\225\210\347\232\204\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md"
+++ /dev/null
@@ -1,38 +0,0 @@
-## 367 有效的完全平方数-简单
-
-题目:
-
-给你一个正整数 `num` 。如果 `num` 是一个完全平方数,则返回 `true` ,否则返回 `false` 。
-
-**完全平方数** 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
-
-不能使用任何内置的库函数,如 `sqrt` 。
-
-
-
-分析:
-
-如果存在一个数 x 的平方等于 num,那么这个数一定是`1<=x <= num`。
-
-所以我们直接对[1, num]区间中的数进行二分查找。
-
-```go
-// date 2023/12/05
-func isPerfectSquare(num int) bool {
- left, right := 0, num
-
- for left <= right {
- mid := (left + right) / 2
- v := mid * mid
- if v == num {
- return true
- } else if v < num {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return false
-}
-```
-
diff --git "a/09_binary_search/No.374_\347\214\234\346\225\260\345\255\227\345\244\247\345\260\217.md" "b/09_binary_search/No.374_\347\214\234\346\225\260\345\255\227\345\244\247\345\260\217.md"
deleted file mode 100644
index 5f28d5d..0000000
--- "a/09_binary_search/No.374_\347\214\234\346\225\260\345\255\227\345\244\247\345\260\217.md"
+++ /dev/null
@@ -1,51 +0,0 @@
-## 374 猜数字大小-简单
-
-题目:
-
-猜数字游戏的规则如下:
-
-- 每轮游戏,我都会从 **1** 到 ***n*** 随机选择一个数字。 请你猜选出的是哪个数字。
-- 如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
-
-你可以通过调用一个预先定义好的接口 `int guess(int num)` 来获取猜测结果,返回值一共有 3 种可能的情况(`-1`,`1` 或 `0`):
-
-- -1:我选出的数字比你猜的数字小 `pick < num`
-- 1:我选出的数字比你猜的数字大 `pick > num`
-- 0:我选出的数字和你猜的数字一样。恭喜!你猜对了!`pick == num`
-
-返回我选出的数字。
-
-
-
-分析:
-
-没啥好说的,直接二分查找。
-
-```go
-// date 2023/12/05
-/**
- * Forward declaration of guess API.
- * @param num your guess
- * @return -1 if num is higher than the picked number
- * 1 if num is lower than the picked number
- * otherwise return 0
- * func guess(num int) int;
- */
-
-func guessNumber(n int) int {
- left, right := 1, n
- for left <= right {
- mid := (left + right) / 2
- v := guess(mid)
- if v == 0 {
- return mid
- } else if v > 0 {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- return -1
-}
-```
-
diff --git "a/09_binary_search/No.441_\346\216\222\345\210\227\347\241\254\345\270\201.md" "b/09_binary_search/No.441_\346\216\222\345\210\227\347\241\254\345\270\201.md"
deleted file mode 100644
index 9e2c210..0000000
--- "a/09_binary_search/No.441_\346\216\222\345\210\227\347\241\254\345\270\201.md"
+++ /dev/null
@@ -1,29 +0,0 @@
-## 441 排列硬币-简单
-
-题目:
-
-你总共有 `n` 枚硬币,并计划将它们按阶梯状排列。对于一个由 `k` 行组成的阶梯,其第 `i` 行必须正好有 `i` 枚硬币。阶梯的最后一行 **可能** 是不完整的。
-
-给你一个数字 `n` ,计算并返回可形成 **完整阶梯行** 的总行数。
-
-
-
-分析:
-
-直接计算。
-
-```go
-// date 2023/12/06
-func arrangeCoins(n int) int {
- ans := 0
- sum := 0
-
- for sum <= n {
- ans++
- sum += ans
- }
-
- return ans-1
-}
-```
-
diff --git "a/09_binary_search/No.540_\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\345\215\225\344\270\200\345\205\203\347\264\240.md" "b/09_binary_search/No.540_\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\345\215\225\344\270\200\345\205\203\347\264\240.md"
deleted file mode 100644
index aaf7b86..0000000
--- "a/09_binary_search/No.540_\346\234\211\345\272\217\346\225\260\347\273\204\344\270\255\347\232\204\345\215\225\344\270\200\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,35 +0,0 @@
-## 540 有序数组中的单一元素-中等
-
-题目:
-
-给你一个仅由整数组成的有序数组,其中每个元素都会出现两次,唯有一个数只会出现一次。
-
-请你找出并返回只出现一次的那个数。
-
-你设计的解决方案必须满足 `O(log n)` 时间复杂度和 `O(1)` 空间复杂度。
-
-
-
-分析:
-
-```go
-// date 2023/12/05
-func singleNonDuplicate(nums []int) int {
- n := len(nums)
-
- // find the first index x that nums[x] != nums[x^1]
- left, right := 0, n-1
- for left < right {
- mid := (right - left) / 2 + left
- // 只要和相邻的元素相等,那么 x 一定在右边
- // left = mid + 1
- if nums[mid] == nums[mid^1] {
- left = mid+1
- } else {
- right = mid
- }
- }
- return nums[left]
-}
-```
-
diff --git a/09_binary_search/binarySearch.md b/09_binary_search/binarySearch.md
deleted file mode 100644
index 38d55b9..0000000
--- a/09_binary_search/binarySearch.md
+++ /dev/null
@@ -1,97 +0,0 @@
-## Binary Search \[二分查找\]
-
- * 1.[问题定义](#问题定义)
- * 2.[复杂度分析](#复杂度分析)
- * 3.[算法流程](#算法流程)
- * 4.[代码实现](#代码实现)
- * 4.1[递归实现](#二分查找的递归实现)
- * 4.2[迭代实现](#二分查找的迭代实现)
-
-### 问题定义
-
-给定一个具有n个元素的有序序列,实现一个能够查找元素x的函数。
-
-### 复杂度分析
-
-最简单的方法是**线性搜索**,即依次比较每个元素,其时间复杂度为O(n)。而二分查找利用序列有序的特性,将时间复杂度降为O(Logn)。
-
-### 算法流程
-
-二分查找是指在已排序的序列中查看数据,每次查找均将排序序列分为一半的有序序列。查找的初始为整个序列,如果搜索的关键字小于或等于序列的中间值,则对前半序列继续搜索;否则对后半序列继续搜索。
-
-在每一次的比较中,几乎可以筛选出一半的元素是否符合预期值。
-
-1. 比较x与序列中间值
-2. 如果x等于中间值,则返回中间值的索引
-3. 如果x大于中间值,则x落在中间值的右半个子序列,进而对右半子序列进行查找
-4. 如果x小于中间值,则x落在中间值的左半个子序列,进而对左半子序列进行查找
-
-### 代码实现
-
-#### 二分查找的递归实现
-
-* C++
-
-```cpp
-int BinarySearch(int arry[], int l, int r, int x) {
- if(l <= r) {
- int mid = l + (r - 1) / 2;
- if(x == arry[mid])
- return mid;
- if(x < arry[mid])
- return BinarySearch(arry, l, mid - 1, x);
- else
- return BinarySearch(arry, mid + 1, r, x);
- }
- return -1;
-}
-```
-
-* Python
-
-```python
-def BinarySearch(arry, l, r, x)
- if l <= r:
- mid = l + (r - 1)/2
- if x == arry[mid]:
- return mid
- if x < arry[mid]:
- return BinarySearch(arry, l, mid - 1, x)
- else:
- return BinayrSearch(arry, mid + 1, r, x)
- else:
- return -1
-```
-
-### 二分查找的迭代实现
-
-* C++
-
-```cpp
-int BinarySearch(int arry[], int l, int r, int x) {
- while(l <= r) {
- if(x == arry[mid])
- return mid;
- if(x < arry[mid])
- r = mid - 1;
- else
- l = mid + 1;
- }
- return -1;
-}
-```
-
-* Python
-
-```python
-def BinarySearch(arry, l, r, x)
- while l <= r:
- mid = l + (r - 1)/2
- if x== arry[mid]:
- return mid
- elif x < arry[mid]:
- r = mid - 1
- else:
- l = mid + 1
- return -1
-```
diff --git a/09_binary_search/readme.md b/09_binary_search/readme.md
deleted file mode 100644
index 1fcf2ba..0000000
--- a/09_binary_search/readme.md
+++ /dev/null
@@ -1,359 +0,0 @@
-## 二分查找
-
-二分查找,是指在已排序的数组中查找目标值。
-
-感觉很简单,其实二分查找并不简单,尤其二分法的各种变种。
-
-首先,我们从最简单的开始:
-
-问题1:从已经排序好的数组中找出与 key 相等的元素,如果找到,请返回元素下标,否则返回 -1。
-
-如果存在答案,你可以假设只有唯一的答案。
-
-
-
-### 1.找出与 key 相等的元素
-
-请在已排序的数组中找出与 key 相等的元素,且数组中的元素不重复。如果能够找到,请返回元素下标,否则返回 -1。
-
-因为答案唯一,所以判断 `nums[mid] == key`,只要相等直接返回结果。
-
-```go
-func search(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] == key {
- return mid
- } else if nums[mid] > key {
- right = mid -1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- return -1
-}
-```
-
-程序不复杂,但是也要注意一点,每次移动 left 和 right 指针的时候,要在 mid 的基础上 +1 或者 -1。
-
-
-
-### 2.找出第一个与 key 相等的元素
-
-已知排序数组中的元素有重复,请找到第一个。
-
-```go
-func searchFirstEqual(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- if left < n && nums[left] == key {
- return left
- }
- return -1
-}
-```
-
-注意,只要是查找第一个的,一定是返回 left 指针。
-
-另外,在二分查找的循环体中,left 指针的判断条件是`nums[mid] < key`,所以有可能不存在第一个与 key 相等的元素,所以二分查找结束后,要校验 left 的 合法性,以及 nums[left] == key。
-
-
-
-### 3.找出最后一个与 key 相等的元素
-
-已知排序数组中的元素有重复,请找出最后一个。
-
-```go
-func searchLastEqual(nums []int, n int, key int) int {
- left, right := 0, n-1
- // left <= right,
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else if nums[mid] <= key {
- left = mid + 1
- }
- }
- if right >= 0 && nums[right] == key {
- return right
- }
- return -1
-}
-```
-
-注意:只要是查找最后一个,一定是返回 right 指针。
-
-
-
-### 4.找出第一个等于或大于 key 的元素
-
-这个变种,不在要求一定是等于,而是等于或者大于都可以,且第一个。
-
-那么,返回 left 指针,且去掉最后 left 合法性的校验。
-
-```go
-func searchFirstEqualOrLarger(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- if left > n-1 {
- return -1
- }
- return left
-}
-```
-
-
-
-### 5.找出第一个大于 key 的元素
-
-这个变种,去掉了相当,寻找第一个大于的。
-
-```go
-func searchFirstLarger(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else if nums[mid] <= key { // 不满足条件的
- left = mid + 1
- }
- }
- if left > n-1 {
- return -1
- }
- return left
-}
-```
-
-
-
-### 6.找出最后一个等于或小于 key 的元素
-
-返回右侧。
-
-```go
-func searchLastEqualOrSmaller(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else if nums[mid] <= key {
- left = mid + 1
- }
- }
- return right
-}
-```
-
-
-
-### 7.找出最后一个小于 key 的元素
-
-
-
-```go
-func searchLastSmaller(nums []int, n int, key int) int {
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key { // 这些是不要的
- right = mid - 1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- return right
-}
-```
-
-
-
-## 小结
-
-总结下,这类问题的要点是:
-
-- 根据返回元素的位置(第一个还是最后一个),决定返回 left 指针,还是 right 指针
-- 在二分查找判断的过程中,根据要求排除不符合的元素,缩小 left 或者 right 的范围。
-
-
-
-以下是测试用例。
-
-```go
-// date 2023/12/04
-package main
-
-import "fmt"
-
-func main() {
- nums := []int{1, 2, 2, 3, 3, 3, 5, 5, 7, 7}
-
- fmt.Printf("nums = %d\n", nums)
- fmt.Printf("expect = 6, First Equal 5: %d\n", searchFirstEqual(nums, 5))
- fmt.Printf("expect = 7, Last Equal 5: %d\n", searchLastEqual(nums, 5))
- fmt.Printf("expect = 6, First Equal Or Larger 4: %d\n", searchFirstEqualOrLarger(nums, 4))
- fmt.Printf("expect = 6, First Equal Or Larger 5: %d\n", searchFirstEqualOrLarger(nums, 5))
- fmt.Printf("expect = 3, First Larger 2: %d\n", searchFirstLarger(nums, 2))
- fmt.Printf("expect = 6, First Larger 4: %d\n", searchFirstLarger(nums, 4))
- fmt.Printf("expect = 5, Last Equal or Smaller 3: %d\n", searchLastEqualOrSmaller(nums, 3))
- fmt.Printf("expect = 5, Last Equal or Smaller 4: %d\n", searchLastEqualOrSmaller(nums, 4))
- fmt.Printf("expect = 7, Last Smaller 6: %d\n", searchLastSmaller(nums, 6))
-}
-
-// 1. 查找第一个与 key 相等的元素
-func searchFirstEqual(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- if left < n && nums[left] == key {
- return left
- }
- return -1
-}
-
-// 2. 查找最后一个与 key 相等的元素
-func searchLastEqual(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else if nums[mid] <= key {
- left = mid + 1
- }
- }
- if right >= 0 && nums[right] == key {
- return right
- }
- return -1
-}
-
-// 3. 查找第一个等于或大于 key 的元素
-func searchFirstEqualOrLarger(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] < key {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- if left >= n {
- return -1
- }
- return left
-}
-
-// 4. 查找第一个大于 key 的元素
-func searchFirstLarger(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] <= key {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- if left >= n {
- return -1
- }
- return left
-}
-
-// 5. 查找最后一个等于或小于 key 的元素
-func searchLastEqualOrSmaller(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- if right >= 0 {
- return right
- }
- return -1
-}
-
-// 6. 查找最后一个小于 key 的元素
-func searchLastSmaller(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- if right >= 0 {
- return right
- }
- return -1
-}
-```
-
-
-
-## 二分查找的模板
-
-**模板1**
-
-1. 查找等于目标值 key 的索引
-
-```go
-func searchEqual(nums []int, key int) int {
- n := len(nums)
- if n == 0 {
- return -1
- }
- left, right := 0, n-1
- for left <= right {
- // 为了避免 left + right 溢出,使用 left + (right - left) / 2 的方式求中心点
- mid := left + (right - left) / 2
- if nums[mid] == key {
- return mid
- } else if nums[mid] < key {
- left = mid +1
- } else {
- right = mid - 1
- }
- }
- return -1
-}
-```
-
diff --git a/09_binary_search/srcgo/binary_search.go b/09_binary_search/srcgo/binary_search.go
deleted file mode 100644
index b1c7648..0000000
--- a/09_binary_search/srcgo/binary_search.go
+++ /dev/null
@@ -1,126 +0,0 @@
-package main
-
-import "fmt"
-
-func main() {
- nums := []int{1, 2, 2, 3, 3, 3, 5, 5, 7, 7}
-
- fmt.Printf("nums = %d\n", nums)
- fmt.Printf("expect = 6, First Equal 5: %d\n", searchFirstEqual(nums, 5))
- fmt.Printf("expect = 7, Last Equal 5: %d\n", searchLastEqual(nums, 5))
- fmt.Printf("expect = 6, First Equal Or Larger 4: %d\n", searchFirstEqualOrLarger(nums, 4))
- fmt.Printf("expect = 6, First Equal Or Larger 5: %d\n", searchFirstEqualOrLarger(nums, 5))
- fmt.Printf("expect = 3, First Larger 2: %d\n", searchFirstLarger(nums, 2))
- fmt.Printf("expect = 6, First Larger 4: %d\n", searchFirstLarger(nums, 4))
- fmt.Printf("expect = 5, Last Equal or Smaller 3: %d\n", searchLastEqualOrSmaller(nums, 3))
- fmt.Printf("expect = 5, Last Equal or Smaller 4: %d\n", searchLastEqualOrSmaller(nums, 4))
- fmt.Printf("expect = 7, Last Smaller 6: %d\n", searchLastSmaller(nums, 6))
-}
-
-// 1. 查找第一个与 key 相等的元素
-func searchFirstEqual(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else if nums[mid] < key {
- left = mid + 1
- }
- }
- if left < n && nums[left] == key {
- return left
- }
- return -1
-}
-
-// 2. 查找最后一个与 key 相等的元素
-func searchLastEqual(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else if nums[mid] <= key {
- left = mid + 1
- }
- }
- if right >= 0 && nums[right] == key {
- return right
- }
- return -1
-}
-
-// 3. 查找第一个等于或大于 key 的元素
-func searchFirstEqualOrLarger(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] < key {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- if left >= n {
- return -1
- }
- return left
-}
-
-// 4. 查找第一个大于 key 的元素
-func searchFirstLarger(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] <= key {
- left = mid + 1
- } else {
- right = mid - 1
- }
- }
- if left >= n {
- return -1
- }
- return left
-}
-
-// 5. 查找最后一个等于或小于 key 的元素
-func searchLastEqualOrSmaller(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] > key {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- if right >= 0 {
- return right
- }
- return -1
-}
-
-// 6. 查找最后一个小于 key 的元素
-func searchLastSmaller(nums []int, key int) int {
- n := len(nums)
- left, right := 0, n-1
- for left <= right {
- mid := (left + right) / 2
- if nums[mid] >= key {
- right = mid - 1
- } else {
- left = mid + 1
- }
- }
- if right >= 0 {
- return right
- }
- return -1
-}
diff --git "a/10_sliding_window/424_\344\270\255\347\255\211_\346\233\277\346\215\242\345\220\216\347\232\204\346\234\200\351\225\277\351\207\215\345\244\215\345\255\227\347\254\246.md" "b/10_sliding_window/424_\344\270\255\347\255\211_\346\233\277\346\215\242\345\220\216\347\232\204\346\234\200\351\225\277\351\207\215\345\244\215\345\255\227\347\254\246.md"
deleted file mode 100644
index 516fb06..0000000
--- "a/10_sliding_window/424_\344\270\255\347\255\211_\346\233\277\346\215\242\345\220\216\347\232\204\346\234\200\351\225\277\351\207\215\345\244\215\345\255\227\347\254\246.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 424 替换后的最长重复字符
-
-题目要求:
-
-给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
-
-在执行上述操作后,返回包含相同字母的最长子字符串的长度。
-题目链接:https://leetcode.cn/problems/longest-repeating-character-replacement
-
-
-
-算法分析:
-
-这道题也是滑动窗口的算法,关键是滑动窗口内我们关心什么样的数据?
-
-在一个连续的区间内,如果我们能够统计出每个字符出现的次数ct,并找出现次数最多的字符次数maxCt,那么剩下的就是其他字符出现的次数`right - left - maxCt`,如果这个值小于等于k,那就是一个可行解。
-
-当窗口不满足条件(即`right - left - maxCt > k`)时,将最左端元素移除,统计次数减一即可。
-
-
-
-1. 假设闭区间 `[left, right]`表示一个窗口;
-2. ct统计窗口内各个字符出现的次数,并不断更新
-
-```go
-// date 2022/09/30
-func characterReplacement(s string, k int) int {
- left, right := 0, 0
- maxCt, ans, n := 0, 0, len(s)
- ct := [26]int{}
- var idx uint8
- // 构造窗口
- for right < n {
- idx = s[right] - 'A'
- ct[idx]++
- // 窗口长度只能增大或者维持不变, left指针增加0/1位
- // maxCt 一直维护最大值,因为我们求的是最长,如果找不到更长,不影响结果
- right++
- if maxCt < ct[idx] {
- maxCt = ct[idx]
- }
- // 窗口构造完成
- if right - left - maxCt <= k {
- ans = max(ans, right-left)
- } else {
- // 超过可替换次数k,开始增加left
- // 因为求最大值,left移动1位即可
- idx = s[left] - 'A'
- ct[idx]--
- left++
- }
- }
- return ans
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/10_sliding_window/480_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\344\270\255\344\275\215\346\225\260.md" "b/10_sliding_window/480_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\344\270\255\344\275\215\346\225\260.md"
deleted file mode 100644
index 0159258..0000000
--- "a/10_sliding_window/480_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\344\270\255\344\275\215\346\225\260.md"
+++ /dev/null
@@ -1,91 +0,0 @@
-## 480 滑动窗口中位数-困难
-
-题目:
-
-中位数是有序序列中最中间的那个数。如果序列长度为偶数,那么则是最中间两个数的平均数。
-
-给定一个数组 `nums` 和 整数 `k`,`k` 表示滑动窗口大小,从最左边滑动到最右边,每次窗口向右移动1位,请你找出滑动窗口中的中位数。
-
-
-
-分析:
-
-因为原始数组是无序的,所以形成的窗口也是无序的。需要借助辅助数组,对窗口内的元素进行排序。
-
-另外,如果形成窗口之后进行排序,会超时,所以构造窗口时就要保证辅助数组的有序性。
-
-为此,对辅助数组实现三个函数:
-
-```
-1. add(x int) 插入排序,保证插入元素后辅助数组有序
-2. del(x int) 在有序数组中删除一个元素
-3. mid() 返回辅助数组的中位数
-```
-
-因为 k 可能为奇数或偶数,所以分别设计。
-
-```go
-func medianSlidingWindow(nums []int, k int) []float64 {
- left, right := 0, 0
- ans := make([]float64, 0, 64)
- f := k & 0x1 == 0x1
- s := k >> 1
-
- lt := &winList{one: f, step: s, data: make([]int, 0, 16)}
-
- for right < len(nums) {
- lt.add(nums[right])
- right++
- if right - left >= k {
- ans = append(ans, lt.mid())
- lt.del(nums[left])
- left++
- }
- }
-
- return ans
-}
-
-type winList struct {
- one bool
- step int
- data []int
-}
-
-func (w *winList) add(x int) {
- n := len(w.data)
- w.data = append(w.data, 0)
- i := n-1
- for i >= 0 {
- if x > w.data[i] {
- break
- } else {
- w.data[i+1] = w.data[i]
- }
- i--
- }
- w.data[i+1] = x
-}
-
-func (w *winList) del(x int) {
- i := 0
- n := len(w.data)
- s1 := n-1
- for i < n {
- if w.data[i] == x {
- copy(w.data[i:], w.data[i+1:])
- break
- } else {
- i++
- }
- }
- w.data = w.data[:s1]
-}
-
-func (w *winList) mid() float64 {
- if w.one {
- return float64(w.data[w.step])
- }
- return (float64(w.data[w.step-1]) + float64(w.data[w.step])) / 2.0
-}
-```
diff --git "a/10_sliding_window/No.030_\344\270\262\350\201\224\346\211\200\346\234\211\345\215\225\350\257\215\347\232\204\345\255\220\344\270\262.md" "b/10_sliding_window/No.030_\344\270\262\350\201\224\346\211\200\346\234\211\345\215\225\350\257\215\347\232\204\345\255\220\344\270\262.md"
deleted file mode 100644
index ee53e22..0000000
--- "a/10_sliding_window/No.030_\344\270\262\350\201\224\346\211\200\346\234\211\345\215\225\350\257\215\347\232\204\345\255\220\344\270\262.md"
+++ /dev/null
@@ -1,64 +0,0 @@
-## 30 串联所有单词的子串
-
-题目:
-
-给定一个字符串 `s` 和一个字符串数组 `words`**。** `words` 中所有字符串 **长度相同**。
-
- `s` 中的 **串联子串** 是指一个包含 `words` 中所有字符串以任意顺序排列连接起来的子串。
-
-- 例如,如果 `words = ["ab","cd","ef"]`, 那么 `"abcdef"`, `"abefcd"`,`"cdabef"`, `"cdefab"`,`"efabcd"`, 和 `"efcdab"` 都是串联子串。 `"acdbef"` 不是串联子串,因为他不是任何 `words` 排列的连接。
-
-返回所有串联子串在 `s` 中的开始索引。你可以以 **任意顺序** 返回答案。
-
-
-
-分析:
-
-滑动窗口。
-
-注意判断子串是否在 words 中,要求单词的数量。
-
-```go
-// date 2023/11/20
-func findSubstring(s string, words []string) []int {
- ans := make([]int, 0, 64)
- s1 := len(words)
- s2 := len(words[0])
- total := s1 * s2
-
- idx := 0
- for idx + total <= len(s) {
- s3 := string(s[idx:idx+total])
- if isInWords(s3, words) {
- ans = append(ans, idx)
- }
- idx++
- }
-
- return ans
-}
-
-func isInWords(s string, words []string) bool {
- set := make(map[string]int, 64)
- for i := 0; i < len(words); i++ {
- set[words[i]]++
- }
-
- size := len(words[0])
- base := 0
- for base + size <= len(s) {
- s1 := string(s[base:base+size])
- _, ok := set[s1]
- if !ok {
- return false
- }
- set[s1]--
- if set[s1] == 0 {
- delete(set, s1)
- }
- base += size
- }
- return len(set) == 0
-}
-```
-
diff --git "a/10_sliding_window/No.076_\346\234\200\345\260\217\350\246\206\347\233\226\345\255\220\344\270\262.md" "b/10_sliding_window/No.076_\346\234\200\345\260\217\350\246\206\347\233\226\345\255\220\344\270\262.md"
deleted file mode 100644
index abeeab0..0000000
--- "a/10_sliding_window/No.076_\346\234\200\345\260\217\350\246\206\347\233\226\345\255\220\344\270\262.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 76 最小覆盖子串-困难
-
-题目:
-
-给你一个字符串 `s` 、一个字符串 `t` 。返回 `s` 中涵盖 `t` 所有字符的最小子串。如果 `s` 中不存在涵盖 `t` 所有字符的子串,则返回空字符串 `""` 。
-
-
-
-分析:
-
-详见 readme
-
-```go
-// date 2023/11/28
-func minWindow(s string, t string) string {
- tset := make(map[byte]int, 32)
- for i := 0; i < len(t); i++ {
- tset[t[i]]++
- }
- scnt := make(map[byte]int, 32)
- isContainT := func() bool {
- for k, v := range tset {
- if scnt[k] < v {
- return false
- }
- }
- return true
- }
- ans := -1
- al, ar := 0, 0
- left, right := 0, 0
- n := len(s)
- for right < n {
- scnt[s[right]]++
- right++
-
- for isContainT() {
- if ans == -1 {
- ans = right - left
- al, ar = left, right
- } else if right - left < ans {
- ans = right - left
- al, ar = left, right
- }
- scnt[s[left]]--
- if scnt[s[left]] == 0 {
- delete(scnt, s[left])
- }
- left++
- }
- }
- if ans == -1 {
- return ""
- }
- return string(s[al:ar])
-}
-```
-
diff --git "a/10_sliding_window/No.1004_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\2603.md" "b/10_sliding_window/No.1004_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\2603.md"
deleted file mode 100644
index 5d3aca3..0000000
--- "a/10_sliding_window/No.1004_\346\234\200\345\244\247\350\277\236\347\273\2551\347\232\204\344\270\252\346\225\2603.md"
+++ /dev/null
@@ -1,53 +0,0 @@
-## 1004 最大连续1的个数3-中等
-
-题目:
-
-给定一个二进制数组 `nums` 和一个整数 `k`,如果可以翻转最多 `k` 个 `0` ,则返回 *数组中连续 `1` 的最大个数* 。
-
-
-
-分析:
-
-对于数组区间 [left, right] 而言,只要区间内不超过 k 个 0,那么该区间就可以满足条件,其长度为 right-left+1。
-
-由此,这个问题可以转化成:
-
-> 对于任意的右端点 right,希望找到最小的左端点 left,使得 [left, right] 包含不超过 k 个 0
-
-想要快速判断一个区间内 0 的个数,我们可以把数组中的 1 变成 0,0 变成 1,对数组求前缀和。
-
-只要 left 的前缀和 lsum,与 右端点 right 的前缀和 rsum,满足 lsum < rsum - k,那么符合条件的区间就形成了。
-
-
-
-```go
-// date 2023/11/22
-func longestOnes(nums []int, k int) int {
- var ans int
- left, lsum, rsum := 0, 0, 0
-
- // 问题变成求:索引 right 前 0 的个数不能超 k 个 的最长元素个数
- for right, v := range nums {
- // 求 0 的个数,即前缀和
- rsum += 1 - v
-
- // 当 lsum < rsum - k,说明已经超过了 k 个
- // left++
- for lsum < rsum - k {
- lsum += 1 - nums[left]
- left++
- }
- ans = max(ans, right-left+1)
- }
-
- return ans
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/10_sliding_window/No.1052_\347\210\261\347\224\237\346\260\224\347\232\204\344\271\246\345\272\227\350\200\201\346\235\277.md" "b/10_sliding_window/No.1052_\347\210\261\347\224\237\346\260\224\347\232\204\344\271\246\345\272\227\350\200\201\346\235\277.md"
deleted file mode 100644
index c61fec7..0000000
--- "a/10_sliding_window/No.1052_\347\210\261\347\224\237\346\260\224\347\232\204\344\271\246\345\272\227\350\200\201\346\235\277.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 1052 爱生气的书店老板-中等
-
-题目:
-
-有一个书店老板,他的书店开了 `n` 分钟。每分钟都有一些顾客进入这家商店。给定一个长度为 `n` 的整数数组 `customers` ,其中 `customers[i]` 是在第 `i` 分钟开始时进入商店的顾客数量,所有这些顾客在第 `i` 分钟结束后离开。
-
-在某些时候,书店老板会生气。 如果书店老板在第 `i` 分钟生气,那么 `grumpy[i] = 1`,否则 `grumpy[i] = 0`。
-
-当书店老板生气时,那一分钟的顾客就会不满意,若老板不生气则顾客是满意的。
-
-书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续 `minutes` 分钟不生气,但却只能使用一次。
-
-请你返回 *这一天营业下来,最多有多少客户能够感到满意* 。
-
-
-
-分析:
-
-有些顾客是确定满意的,有些是确定不满意的,那么想求满意顾客的最大数量,其实就是求 minutes 窗口内不满意的顾客最大数量 extra,把这些变成满意的,那么总数量就是:
-
-确定满意的 total + 【minutes窗口内的 extra】
-
-```go
-// date 2023/11/22
-func maxSatisfied(customers []int, grumpy []int, minutes int) int {
- var total, extra, temp int
- n := len(customers)
- left, right := 0, 0
- for right < n {
- // 确定满意的顾客
- total += (1 - grumpy[right]) * customers[right]
-
- //
- temp += grumpy[right] * customers[right] // 不满意的顾客
- right++
- extra = max(extra, temp)
- for right - left >= minutes {
- temp -= grumpy[left] * customers[left]
- left++
- }
- }
- return total + extra
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/10_sliding_window/No.1343_\345\244\247\345\260\217\344\270\272K\344\270\224\345\271\263\345\235\207\345\200\274\345\244\247\344\272\216\347\255\211\344\272\216\351\230\210\345\200\274\347\232\204\345\255\220\346\225\260\347\273\204\346\225\260\347\233\256.md" "b/10_sliding_window/No.1343_\345\244\247\345\260\217\344\270\272K\344\270\224\345\271\263\345\235\207\345\200\274\345\244\247\344\272\216\347\255\211\344\272\216\351\230\210\345\200\274\347\232\204\345\255\220\346\225\260\347\273\204\346\225\260\347\233\256.md"
deleted file mode 100644
index 2edb4a6..0000000
--- "a/10_sliding_window/No.1343_\345\244\247\345\260\217\344\270\272K\344\270\224\345\271\263\345\235\207\345\200\274\345\244\247\344\272\216\347\255\211\344\272\216\351\230\210\345\200\274\347\232\204\345\255\220\346\225\260\347\273\204\346\225\260\347\233\256.md"
+++ /dev/null
@@ -1,39 +0,0 @@
-## 1343 大小为K且平均值大于等于阈值的子数组数目-中等
-
-题目:
-
-给你一个整数数组 `arr` 和两个整数 `k` 和 `threshold` 。
-
-请你返回长度为 `k` 且平均值大于等于 `threshold` 的子数组数目。
-
-
-
-分析:
-
-最基本的滑动窗口。
-
-```go
-// date 2023/11/22
-func numOfSubarrays(arr []int, k int, threshold int) int {
- var ans int
- left, right := 0, 0
- n := len(arr)
- sum := 0
-
- for right < n {
- sum += arr[right]
- right++
- if right - left == k {
- fm := float64(sum) / float64(k)
- if fm >= float64(threshold) {
- ans++
- }
- sum -= arr[left]
- left++
- }
- }
-
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.1477_\346\211\276\344\270\244\344\270\252\345\222\214\344\270\272\347\233\256\346\240\207\345\200\274\344\270\224\344\270\215\351\207\215\345\217\240\347\232\204\345\255\220\346\225\260\347\273\204.md" "b/10_sliding_window/No.1477_\346\211\276\344\270\244\344\270\252\345\222\214\344\270\272\347\233\256\346\240\207\345\200\274\344\270\224\344\270\215\351\207\215\345\217\240\347\232\204\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index abe3b3d..0000000
--- "a/10_sliding_window/No.1477_\346\211\276\344\270\244\344\270\252\345\222\214\344\270\272\347\233\256\346\240\207\345\200\274\344\270\224\344\270\215\351\207\215\345\217\240\347\232\204\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,89 +0,0 @@
-## 1477 找两个和为目标值且不重叠的子数组-中等
-
-题目:
-
-给你一个整数数组 `arr` 和一个整数值 `target` 。
-
-请你在 `arr` 中找 **两个互不重叠的子数组** 且它们的和都等于 `target` 。可能会有多种方案,请你返回满足要求的两个子数组长度和的 **最小值** 。
-
-请返回满足要求的最小长度和,如果无法找到这样的两个子数组,请返回 **-1** 。
-
-
-
-分析:
-
-
-
-1. 利用滑动窗口,找出所有满足条件的子数组【这些子数组可能重叠,也可能不重叠,需要剪枝操作】
-2. 对所有的子数组按 长度 排序,以便找到第一个答案后即可退出循环
-3. 剪枝1:判断子数组的长度,如果超过原数组的长度的一半,那么肯定无解,直接退出。
-4. 剪枝2:对有包含关系的子数组直接跳过
-
-```go
-// date 2023/11/24
-type resNum struct {
- start int
- length int
-}
-
-func minSumOfLengths(arr []int, target int) int {
- ans := len(arr) * 2
- res := make([]*resNum, 0, 16)
- left, right := 0, 0
- sum := 0
- n := len(arr)
-
- for right < n {
- sum += arr[right]
- right++
-
- for sum >= target {
- if sum == target {
- // one result
- // res = append(res, right-left)
- res = append(res, &resNum{start: left, length: right - left})
- }
- sum -= arr[left]
- left++
- }
- }
-
- // 防止超时
- // 按子数组长度排序,后面剪枝之后,只要找到答案,即可 break
- sort.Slice(res, func(i, j int) bool {
- return res[i].length < res[j].length
- })
-
- m := len(res)
- for i := 0; i < m; i++ {
- // 防止超时
- // 如果单个子数组的长度已经超过一半,那么肯定无解,直接跳出
- if res[i].length * 2 > n {
- break
- }
- for j := i+1; j < m; j++ {
- if res[i].start < res[j].start && res[j].start < res[i].start + res[i].length {
- continue
- }
- if res[j].start < res[i].start && res[i].start < res[j].start + res[j].length {
- continue
- }
- ans = min(ans, res[i].length + res[j].length)
- break
- }
- }
-
- if ans == len(arr) * 2 {
- return -1
- }
- return ans
-}
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
-
diff --git "a/10_sliding_window/No.1493_\345\210\240\346\216\211\344\270\200\344\270\252\345\205\203\347\264\240\344\273\245\345\220\216\345\205\250\344\270\2721\347\232\204\346\234\200\351\225\277\345\255\220\346\225\260\347\273\204.md" "b/10_sliding_window/No.1493_\345\210\240\346\216\211\344\270\200\344\270\252\345\205\203\347\264\240\344\273\245\345\220\216\345\205\250\344\270\2721\347\232\204\346\234\200\351\225\277\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index 32c9bec..0000000
--- "a/10_sliding_window/No.1493_\345\210\240\346\216\211\344\270\200\344\270\252\345\205\203\347\264\240\344\273\245\345\220\216\345\205\250\344\270\2721\347\232\204\346\234\200\351\225\277\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 1493 删除一个元素以后全为1的最长子数组-中等
-
-题目:
-
-给你一个二进制数组 `nums` ,你需要从中删掉一个元素。
-
-请你在删掉元素的结果数组中,返回最长的且只包含 1 的非空子数组的长度。
-
-如果不存在这样的子数组,请返回 0 。
-
-
-
-分析:
-
-声明两个变量,分别记录连续 1 的个数,因为允许删除一个元素,那么如果该元素为0,那么此时连续 1 的长度可以复用前一个值。
-
-```go
-// date 2023/11/28
-func longestSubarray(nums []int) int {
- var ans int
- p1, p0 := 0, 0
-
- for _, v := range nums {
- if v == 1 {
- p1++
- p0++
- } else {
- // 遇到第一个零,连续 1 的个数沿用前值
- p1 = p0
- p0 = 0
- }
- if ans < p1 {
- ans = p1
- }
- }
-
-
- if ans == len(nums) {
- ans--
- }
-
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.180_\351\207\215\345\244\215\347\232\204DNA\345\272\217\345\210\227.md" "b/10_sliding_window/No.180_\351\207\215\345\244\215\347\232\204DNA\345\272\217\345\210\227.md"
deleted file mode 100644
index 4d700fa..0000000
--- "a/10_sliding_window/No.180_\351\207\215\345\244\215\347\232\204DNA\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,47 +0,0 @@
-## 180 重复的DNA序列
-
-题目:
-
-**DNA序列** 由一系列核苷酸组成,缩写为 `'A'`, `'C'`, `'G'` 和 `'T'`.。
-
-- 例如,`"ACGAATTCCG"` 是一个 **DNA序列** 。
-
-在研究 **DNA** 时,识别 DNA 中的重复序列非常有用。
-
-给定一个表示 **DNA序列** 的字符串 `s` ,返回所有在 DNA 分子中出现不止一次的 **长度为 `10`** 的序列(子字符串)。你可以按 **任意顺序** 返回答案。
-
-
-
-分析:
-
-滑动窗口。
-
-通过 map 记录出现过的子字符串的次数,最终在梳理结果。
-
-```go
-// date 2023/11/20
-func findRepeatedDnaSequences(s string) []string {
- left, right := 0, 0
- ans := make([]string, 0, 64)
- set := make(map[string]int, 64)
-
- for right < len(s) {
-
- right++
- if right - left >= 10 {
- ss := string(s[left:right])
- set[ss]++
- left++
- }
- }
-
- for k, v := range set {
- if v > 1 {
- ans = append(ans, k)
- }
- }
-
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.209_\351\225\277\345\272\246\346\234\200\345\260\217\347\232\204\345\255\220\346\225\260\347\273\204.md" "b/10_sliding_window/No.209_\351\225\277\345\272\246\346\234\200\345\260\217\347\232\204\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index b2ef1e5..0000000
--- "a/10_sliding_window/No.209_\351\225\277\345\272\246\346\234\200\345\260\217\347\232\204\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,53 +0,0 @@
-## 209 长度最小的子数组-中等
-
-题目要求:给定一个含有n个正整数的数组和一个正整数target。找出数组中满足其和大小等于目标数的长度最小的连续子数组,并返回起长度,否则返回0。
-
-题目链接:https://leetcode.cn/problems/minimum-size-subarray-sum/
-
-
-
-算法分析:滑动窗口,左右指针
-
-定义left, right表示左右指针,即滑动窗口的边界;sum为滑动窗口元素的总和;`sum=nums[left, right]`
-
-初始状态:left, right为0, sum也为0;
-
-每一次迭代将nums[right]计入总和,如果`sum>=target`,则更新子数组的长度,此时长度为`right-left+1`;
-
-然后将`nums[left]`从sum中减去;并将left右移,如果`sum >= target`更新子数组长度,直到`sum < target`。
-
-
-
-```go
-// date 2022/09/24
-func minSubArrayLen(target int, nums []int) int {
- left, right := 0, 0
- sum := 0
- size := len(nums)
- ans := size+1
- for right < len(nums) {
- sum += nums[right]
- right++
- for sum >= target {
- if ans > right - left {
- ans = right - left
- }
-
- sum -= nums[left]
- left++
- }
- }
-
- if ans == size + 1 {
- return 0
- }
-
- return ans
-}
-```
-
-
-
-算法图解
-
-
diff --git "a/10_sliding_window/No.219_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md" "b/10_sliding_window/No.219_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md"
deleted file mode 100644
index 1e8deb8..0000000
--- "a/10_sliding_window/No.219_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 219 存在重复元素2-简单
-
-题目:
-
-给定一个数组nums和整数k,判断是否存在两个不同的下标,使得`nums[i] == nums[j]`,同时`abs(i-j) <= k`,如果存在返回true,否则返回false。
-
-
-
-分析:
-
-推荐该算法,滑动窗口。
-
-这里滑动窗口的技巧在与题目中所要求的`abs(i-j) <= k`,所以只判断连续的k个元素即可。
-
-```go
-// date 2022/09/27
-func containsNearbyDuplicate(nums []int, k int) bool {
- size := len(nums)
-
- start, end := 0, 0
-
- for start < size {
- end = start+1
- for end - start <= k && end < size {
- if nums[start] == nums[end] {
- return true
- }
- end++
- }
- start++
- }
-
- return false
-}
-```
-
-
-
-算法2:利用map,保存遍历过的元素
-
-```go
-// date 2022/09/27
-func containsNearbyDuplicate(nums []int, k int) bool {
- m := make(map[int]int)
- for index, v := range nums {
- if j, ok := m[v]; ok && index - j <= k {
- return true
- }
- m[v] = index
- }
- return false
-}
-```
-
diff --git "a/10_sliding_window/No.239_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md" "b/10_sliding_window/No.239_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md"
deleted file mode 100644
index 26ac7a3..0000000
--- "a/10_sliding_window/No.239_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md"
+++ /dev/null
@@ -1,47 +0,0 @@
-## 239 滑动窗口最大值-困难
-
-题目:
-
-给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
-
-返回 滑动窗口中的最大值 。
-
-
-
-**解题思路**
-
-这道题可用滑动窗口解,且辅助优先队列。优先队列用于求窗口内的最大值。
-
-这个问题是固定窗口大小,所以形成窗口不难,难在如何对窗口内的元素求最大值。
-
-可以使用辅助数组,维护窗口内的递增子序列。每次新增元素的时候,用插入排序保证序列中比当前值小的元素都剔除。
-
-一旦窗口形成,需要移除序列队头元素的时候,与窗口第一个元素进行判断。
-
-
-```go
-// date 2023/11/20
-func maxSlidingWindow(nums []int, k int) []int {
- left, right := 0, 0
- n := len(nums)
- ans := make([]int, 0, 64)
- priQueue := make([]int, 0, 16)
-
- for right < n {
- for len(priQueue) != 0 && nums[right] > priQueue[len(priQueue)-1] {
- priQueue = priQueue[:len(priQueue)-1]
- }
- priQueue = append(priQueue, nums[right])
- right++
- if right - left >= k {
- ans = append(ans, priQueue[0])
- if priQueue[0] == nums[left] {
- priQueue = priQueue[1:]
- }
- left++
- }
- }
-
- return ans
-}
-```
diff --git "a/10_sliding_window/No.567_\345\255\227\347\254\246\344\270\262\347\232\204\346\216\222\345\210\227.md" "b/10_sliding_window/No.567_\345\255\227\347\254\246\344\270\262\347\232\204\346\216\222\345\210\227.md"
deleted file mode 100644
index 1148c80..0000000
--- "a/10_sliding_window/No.567_\345\255\227\347\254\246\344\270\262\347\232\204\346\216\222\345\210\227.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 567 字符串的排列-中等
-
-题目:
-
-给你两个字符串 `s1` 和 `s2` ,写一个函数来判断 `s2` 是否包含 `s1` 的排列。如果是,返回 `true` ;否则,返回 `false` 。
-
-换句话说,`s1` 的排列之一是 `s2` 的 **子串** 。
-
-
-
-分析:
-
-排列是说两个字符串中每个字符出现的次数一样。
-
-初始化两个数组,分别记录s1和s2固定窗口中每个字符的出现次数,如果一致,则返回 true。
-
-```go
-// date 2023/11/20
-func checkInclusion(s1 string, s2 string) bool {
- n, m := len(s1), len(s2)
- if n > m {
- return false
- }
- var ct1, ct2 [26]int
- for i := range s1 {
- ct1[s1[i]-'a']++
- ct2[s2[i]-'a']++
- }
- if ct1 == ct2 {
- return true
- }
-
- for i := n; i < m; i++ {
- // update ct2
- ct2[s2[i]-'a']++
- ct2[s2[i-n]-'a']--
- if ct1 == ct2 {
- return true
- }
- }
-
- return false
-}
-```
-
diff --git "a/10_sliding_window/No.643_\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\271\263\345\235\207\346\225\2601.md" "b/10_sliding_window/No.643_\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\271\263\345\235\207\346\225\2601.md"
deleted file mode 100644
index 598bc37..0000000
--- "a/10_sliding_window/No.643_\345\255\220\346\225\260\347\273\204\347\232\204\346\234\200\345\244\247\345\271\263\345\235\207\346\225\2601.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 643 子数组的最大平均数-简单
-
-题目:
-
-给你一个由 `n` 个元素组成的整数数组 `nums` 和一个整数 `k` 。
-
-请你找出平均数最大且 **长度为 `k`** 的连续子数组,并输出该最大平均数。
-
-任何误差小于 `10-5` 的答案都将被视为正确答案。
-
-
-
-分析:
-
-滑动窗口,直接计算。
-
-注意元素只有一个,且 k 等于1的时候,平均数有可能小于零。
-
-```go
-// date 2023/11/21
-func findMaxAverage(nums []int, k int) float64 {
- var ans float64
- ansSet := false
- left, right := 0, 0
- n := len(nums)
- ksum := 0
- for right < n {
- ksum += nums[right]
- right++
- if right - left >= k {
- res := float64(ksum) / float64(k)
- if !ansSet {
- ans = res
- ansSet = true
- } else if res > ans {
- ans = res
- }
- ksum -= nums[left]
- left++
- }
- }
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.658_\346\211\276\345\210\260K\344\270\252\346\234\200\346\216\245\350\277\221\347\232\204\345\205\203\347\264\240.md" "b/10_sliding_window/No.658_\346\211\276\345\210\260K\344\270\252\346\234\200\346\216\245\350\277\221\347\232\204\345\205\203\347\264\240.md"
deleted file mode 100644
index 6f6a43e..0000000
--- "a/10_sliding_window/No.658_\346\211\276\345\210\260K\344\270\252\346\234\200\346\216\245\350\277\221\347\232\204\345\205\203\347\264\240.md"
+++ /dev/null
@@ -1,76 +0,0 @@
-## 658 找到K个最接近的元素-中等
-
-题目:
-
-给定一个 **排序好** 的数组 `arr` ,两个整数 `k` 和 `x` ,从数组中找到最靠近 `x`(两数之差最小)的 `k` 个数。返回的结果必须要是按升序排好的。
-
-整数 `a` 比整数 `b` 更接近 `x` 需要满足:
-
-- `|a - x| < |b - x|` 或者
-- `|a - x| == |b - x|` 且 `a < b`
-
-
-
-分析:
-
-分情况讨论:
-
-1. 如果 k 大于等于数组长度,那么整个数组就是答案
-2. 如果 x 小于等于第一个元素,那么数组的前 K 个就是答案
-3. 如果 x 大于等于数组的最后一个元素,那么数组的后 K 个就是答案
-4. 其他情况,找到第一个大于等于 x 的元素,然后双向指针向两头查找;
-5. 一旦一端指针达到临界后,且不满 K 个,那么从另一端开始凑
-
-
-
-优化部分:第 4 步骤查找 x 可以使用二分查找。
-
-```go
-// date 2023/11/21
-func findClosestElements(arr []int, k int, x int) []int {
- n := len(arr)
- if n == 0 || k >= n {
- return arr
- }
-
- if x <= arr[0] {
- return arr[0:k]
- } else if x >= arr[n-1] {
- return arr[n-k:n]
- }
- left, right := 0, 0
- for i := 0; i < n; i++ {
- if arr[i] >= x {
- right = i
- break
- }
- }
- left = right-1
- for k > 0 {
- if left >= 0 && right < n {
- r1 := abs(arr[right], x)
- l1 := abs(arr[left], x)
- if r1 < l1 {
- right++
- } else if l1 <= r1 {
- left--
- }
- } else if right < n {
- right++
- } else if left >= 0 {
- left--
- }
- k--
- }
-
- return arr[left+1:right]
-}
-
-func abs(x, y int) int {
- if x > y {
- return x-y
- }
- return y-x
-}
-```
-
diff --git "a/10_sliding_window/No.713_\344\271\230\347\247\257\345\260\217\344\272\216K\347\232\204\345\255\220\346\225\260\347\273\204.md" "b/10_sliding_window/No.713_\344\271\230\347\247\257\345\260\217\344\272\216K\347\232\204\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index 499e981..0000000
--- "a/10_sliding_window/No.713_\344\271\230\347\247\257\345\260\217\344\272\216K\347\232\204\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 713 乘积小于K的子数组
-
-题目:
-
-给你一个整数数组 `nums` 和一个整数 `k` ,请你返回子数组内所有元素的乘积严格小于 `k` 的连续子数组的数目。
-
-
-
-分析:
-
-两层循环直接计算。
-
-注意,单个元素小于 K 也要计算在内。
-
-```go
-// date 2023/11/21
-func numSubarrayProductLessThanK(nums []int, k int) int {
- var ans int
-
- sum := 1
- n := len(nums)
- for i := 0; i < n; i++ {
- if nums[i] < k {
- ans++
- }
- sum = nums[i]
- for j := i+1; j < n; j++ {
- sum *= nums[j]
- if sum >= k {
- break
- } else {
- ans++
- }
- }
- }
-
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.904_\346\260\264\346\236\234\346\210\220\347\257\256.md" "b/10_sliding_window/No.904_\346\260\264\346\236\234\346\210\220\347\257\256.md"
deleted file mode 100644
index a10b269..0000000
--- "a/10_sliding_window/No.904_\346\260\264\346\236\234\346\210\220\347\257\256.md"
+++ /dev/null
@@ -1,57 +0,0 @@
-## 904 水果成篮-中等
-
-题目:
-
-你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 `fruits` 表示,其中 `fruits[i]` 是第 `i` 棵树上的水果 **种类** 。
-
-你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
-
-- 你只有 **两个** 篮子,并且每个篮子只能装 **单一类型** 的水果。每个篮子能够装的水果总量没有限制。
-- 你可以选择任意一棵树开始采摘,你必须从 **每棵** 树(包括开始采摘的树)上 **恰好摘一个水果** 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
-- 一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
-
-给你一个整数数组 `fruits` ,返回你可以收集的水果的 **最大** 数目。
-
-
-
-分析:
-
-该题目重在理解题目。
-
-1. Fruits 数组中的元素,代表水果的种类编号,即同一个编号表示同一种水果
-2. 你只可采摘两种类型的水果,即子数组中不同的元素个数不能超过两个
-
-所以,这道题就变成了求子数组中连续元素种类不超过2的最大长度。
-
-
-
-滑动窗口算法。
-
-1. 通过 map 维护元素的种类,一旦种类超过两种,那么左指针就要移动,直到元素移除,map 不超过两种为止
-2. 那么,此时左右指针的距离就是子数组的长度,求最大子数组长度
-
-```go
-// date 2023/11/21
-func totalFruit(fruits []int) int {
- var ans int
- set := make(map[int]int, 16)
- left := 0
- for right, v := range fruits {
- set[v]++
- // 一旦超过两种,则缩小
- for len(set) > 2 {
- y := fruits[left]
- set[y]--
- if set[y] == 0 {
- delete(set, y)
- }
- left++
- }
- if right - left + 1 > ans {
- ans = right - left + 1
- }
- }
- return ans
-}
-```
-
diff --git "a/10_sliding_window/No.930_\345\222\214\347\233\270\345\220\214\347\232\204\344\272\214\345\205\203\345\255\220\346\225\260\347\273\204.md" "b/10_sliding_window/No.930_\345\222\214\347\233\270\345\220\214\347\232\204\344\272\214\345\205\203\345\255\220\346\225\260\347\273\204.md"
deleted file mode 100644
index d30df33..0000000
--- "a/10_sliding_window/No.930_\345\222\214\347\233\270\345\220\214\347\232\204\344\272\214\345\205\203\345\255\220\346\225\260\347\273\204.md"
+++ /dev/null
@@ -1,49 +0,0 @@
-## 930 和相同的二元子数组-中等
-
-题目:
-
-给你一个二元数组 `nums` ,和一个整数 `goal` ,请你统计并返回有多少个和为 `goal` 的 **非空** 子数组。
-
-**子数组** 是数组的一段连续部分。
-
-
-
-分析:
-
-整体思路是求数组的前缀和,假设有两个坐标 i 和 j,且 i < j。
-
-前 i 个元素的和为 sum_i,前 j 个元素的和为 sum_j,如果 sum_j - sum_i = goal;
-
-那么区间[i, j] 就是一种解。
-
-考虑到数组中只有 0 和 1,那么当元素为 0 的时候,前缀和的大小不变,但前缀和的个数增加了。这个个数是要计算到总结果中的,因为不包含该元素 0 和包含该元素 0 都是非空子数组。
-
-假设,sum_i 等于 3 出现了4次,sum_j 等于 5 出现了 3 次,在 goal 为 2 的情况下。
-
-sum_j 等于 5 连续出现 3 次,对最终的结果增加了 4+4+4, 总共 12 次。【这是11-13行代码】
-
-
-
-```go
-// date 2023/11/21
-func numSubarraysWithSum(nums []int, goal int) int {
- var ans int
- // 因为后面判断使用的时候是 sum-goal, 所以 sum 初始化为 0
- sum := 0
- cnt := make(map[int]int, 16) // 记录 前缀和 出现的次数
-
- for _, v := range nums {
- cnt[sum]++ // 前缀和 次数递增
- sum += v // 前缀求和
- // 每次都要计算
- // 如果存在,表示 当前元素 和 之前的前缀和 能够构成一个解,
- // 之前的前缀和 出现过几次,就是几个不同的非空子数组
- if ct, ok := cnt[sum-goal]; ok {
- ans += ct
- }
- }
-
- return ans
-}
-```
-
diff --git a/10_sliding_window/images/209.png b/10_sliding_window/images/209.png
deleted file mode 100644
index 79d0cb7..0000000
Binary files a/10_sliding_window/images/209.png and /dev/null differ
diff --git a/10_sliding_window/images/image_slidingwindow.png b/10_sliding_window/images/image_slidingwindow.png
deleted file mode 100644
index f76a0aa..0000000
Binary files a/10_sliding_window/images/image_slidingwindow.png and /dev/null differ
diff --git a/10_sliding_window/readme.md b/10_sliding_window/readme.md
deleted file mode 100644
index 3bb5664..0000000
--- a/10_sliding_window/readme.md
+++ /dev/null
@@ -1,71 +0,0 @@
-## 滑动窗口算法
-
-当我们说滑动窗口时,其实有两层含义:
-
-1. **滑动**:表示说这个窗口是移动的,按照一定的方向来移动
-2. **窗口**:窗口的大小并不是固定的,可以不断地扩大窗口直到满足一定的条件;也可以不断地缩小,直到找到一个满足条件的最小值;也可以是固定大小
-
-
-
-### 解题思路
-
-滑动窗口算法的基本思路是这样的:
-
-我们以这样的题目为例:给定两个字符串 `S` 和 `T`,求字符串 `S` 中包含 `T` 所有字符串的最小子字符串长度。
-
-1. 首先我们使用双指针技巧,初始化 `left = right = 0`,将索引闭区间`[left, right]`成为一个 「窗口」
-2. 不断地增加 `right` 指针,扩大窗口,直到窗口中元素全部满足条件,即包含所有 `T` 中元素
-3. 此时停止增加 `right` ,而要开始增加 `left` 指针,缩小窗口,直到窗口不满足条件,即不包含 `T` 中的字符串
-4. 重复第 2 和 第 3 步,直到 `right` 到达数组或者字符串的边界。
-
-
-
-
-
-综合上面的介绍,对于非固定大小的窗口,伪代码可以这样写:
-
-```go
-func foo() {
- left, right := 0, 0
- n := len(nums)
- // 构造窗口
- for right < n {
- window.add(nums[right])
- right++
- for (window 不满足条件) {
- // 现在已经是一个窗口了,可以做一些事情
- // 一般用于求最小值
- left++
- }
- }
-}
-```
-
-而对于固定大小的窗口,可以这样写:
-
-```go
-// 假设窗口固定大小为k
-func windowWithSize() {
- left, right := 0, 0
- n := len(nums)
- for right < n {
- window.add(nums[right])
- right++
- if right - left >= k {
- // 现在已经是一个窗口了
- // 递增left, 移除最左边的元素
- // 移除时 需要做一些判断
- left++
- }
- }
-}
-```
-
-
-
-### 相关题目:
-
-1. No.239 滑动窗口最大值
- 1. 固定窗口大小,维护最大值列表
-2. No.003 无重复字符的最长子串
-3. No.1298 尽可能的使字符串相等,这题跟编辑距离很像
diff --git a/11_dynamic_programming/Edit_Distance.md b/11_dynamic_programming/Edit_Distance.md
deleted file mode 100644
index da34c5d..0000000
--- a/11_dynamic_programming/Edit_Distance.md
+++ /dev/null
@@ -1,47 +0,0 @@
-## 最小编辑距离
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析](#算法分析)
- * 3.[代码实现](#代码实现)
-
-### 问题定义
-
-给定两个字符串str1和str2,以及三种操作 *插入、删除和替换*, 问str1变为str2所需的最小操作次数。
-
-例如,str1 = sunday, str2 = saturday, 最小操作次数为3,即插入a和t,并将n替换为r。
-
-### 算法分析
-
-对于这种问题,首先应该想到如何将大问题化解为小问题,即如果一两个字母该如何处理。然后运用递归思想不断地进行求解。
-
-```
-令L(s1, s2, n, m)表示字符串s1变成s2所需要的最少操作数,n和m为两个字符串的长度,那么则有以下公式:
-
-当s1[n-1] = s2[m-1],L(s1, s2, n, m) = L(s1, s2, n-1, m-1);
-当s1[n-1] != s2[m-1],三种操作均可以将其变成相等的情况,取三个操作的最小值即可
- L(s1, s2, n, m) = 1 + min(L(s1, s2, n, m - 1), //插入
- L(s1, s2, n - 1, m), //删除
- L(s1, s2, n - 1, m - 1)); //替换
-递归结束条件,即基本条件
-当m=0时,需要全部删除,return n;
-当n=0时,需要全部插入,return m;
-```
-
-### 代码实现
-
-```cpp
-int MinFuc(int x, int y, int z) {
- return z < (x < y ? x : y) ? z : (x < y ? x : y);
-}
-int EditDistance(string s1, string s2, int n, int m) {
- if(n == 0)
- return m;
- if(m == 0)
- return n;
- if(s1[n - 1] == s2[m - 1])
- return EditDistance(s1, s2, n - 1, m - 1);
- else
- // 插入、删除,替换
- return 1 + MinFuc(EditDistance(s1, s2, n, m - 1), EditDistance(s1, s2, n - 1, m), EditDistance(s1, s2, n - 1, m - 1));
-}
-```
diff --git a/11_dynamic_programming/Min_Cost_Path.md b/11_dynamic_programming/Min_Cost_Path.md
deleted file mode 100644
index f3ff650..0000000
--- a/11_dynamic_programming/Min_Cost_Path.md
+++ /dev/null
@@ -1,55 +0,0 @@
-## Min Cost Path \[最小成本路径\]
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析](#算法分析)
- * 3.[算法实现](#算法实现)
-
-### 问题定义
-
-给定一个包含m*n的整型矩阵,每个节点上的值代表路径成本,求从(0,0)节点出发到(x,y)节点(0<=x **示例 1:**
->
-> 
->
-> ```
-> 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
-> 输出:6
-> 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:height = [4,2,0,3,2,5]
-> 输出:9
-> ```
-
-
-
-**解题思路**
-
-这道题有多个思路可解。
-
-- 动态规划,详见解法1
-- 双指针,详见解法2
-
-对于每根柱子 i 来说,该位置上能够接多少雨水,取决于该柱子左右其他柱子高度的较小值,减去该柱子高度,就是该处的雨水量。
-
-那么我们可以维护两个数组 leftMax 和 rightMax,`leftMax[i]`表示区间[0, i-1]的最大高度,递推公式如下:
-
-```sh
-i = 0, leftMax[i] = height[i]
-0 < i < n, leftMax[i] = max(leftMax[i-1], height[i])
-```
-
-同理,对于 rightMax,表示右侧的最大值,有如下公式:
-
-```sh
-i = n-1, rightMax[i] = height[i]
-0 <= i < n-1, rightMax[i] = max(right[i+1], height[i])
-```
-
-有了这两个数组,我们就可以求每根柱子处的雨水,等于`min(leftMax[i], rightMax[i]) - height[i]`。
-
-代码详见解法1。
-
-
-
-解法1中,需要维护两个 max 数组,是不是可以用双指针代替呢?可以。
-
-因为两个 max 数组的作用是为了求左右的较小值,那么我们可用左右指针来维护这个这两个变量。
-
-只要有`height[left] < height[right]`,那么必有`leftMax < rightMax`;则此处雨水量为`leftMax - height[left]`
-
-只有有`height[left] >= height[right]`,那么必有`leftMax > rightMax`,此处雨水量为`rightMax - height[right]`。
-
-详见解法2。
-
-
-
-
-
-```go
-// date 2024/01/16
-// 解法1
-func trap(height []int) int {
- n := len(height)
- leftMax, rightMax := make([]int, n), make([]int, n)
- // fill left Max
- for i := 0; i < n; i++ {
- if i == 0 {
- leftMax[i] = height[i]
- } else {
- leftMax[i] = max(leftMax[i-1], height[i])
- }
- }
-
- // fill right Max
- for i := n-1; i >= 0; i-- {
- if i == n-1 {
- rightMax[i] = height[i]
- } else {
- rightMax[i] = max(rightMax[i+1], height[i])
- }
- }
- ans := 0
-
- for i := 0; i < n; i++ {
- ans += min(leftMax[i], rightMax[i]) - height[i]
- }
-
- return ans
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-
-// 解法2
-// 双指针
-func trap(height []int) int {
- n := len(height)
- left, right := 0, n-1
- leftMax, rightMax := 0, 0
-
- ans := 0
- for left < right {
- leftMax = max(leftMax, height[left])
- rightMax = max(rightMax, height[right])
- if height[left] < height[right] {
- ans += leftMax - height[left]
- left++
- } else {
- ans += rightMax - height[right]
- right--
- }
- }
-
- return ans
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
diff --git "a/11_dynamic_programming/No.062_\344\270\215\345\220\214\350\267\257\345\276\204.md" "b/11_dynamic_programming/No.062_\344\270\215\345\220\214\350\267\257\345\276\204.md"
deleted file mode 100644
index 83b3f61..0000000
--- "a/11_dynamic_programming/No.062_\344\270\215\345\220\214\350\267\257\345\276\204.md"
+++ /dev/null
@@ -1,43 +0,0 @@
-## 62 不同路径-中等
-
-题目:
-
-一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
-
-机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
-
-问总共有多少条不同的路径?
-
-
-
-分析:
-
-动归,直接计算 `dp[i][j] = dp[i-1][j] + dp[i][j-1]`
-
-注意边界条件。
-
-
-```go
-// date 2023/11/07
-func uniquePaths(m int, n int) int {
- dp := make([][]int, m)
- for i := 0; i < m; i++ {
- dp[i] = make([]int, n)
- }
- // 第 0 行,只能一直向右走,所以均为1
- for i := 0; i < m; i++ {
- dp[i][0] = 1
- }
- // 第 0 列,只能一直向下走,所以均为1
- for j := 0; j < n; j++ {
- dp[0][j] = 1
- }
- for i := 1; i < m; i++ {
- for j := 1; j < n; j++ {
- dp[i][j] = dp[i-1][j] + dp[i][j-1]
- }
- }
-
- return dp[m-1][n-1]
-}
-```
diff --git "a/11_dynamic_programming/No.063_\344\270\215\345\220\214\350\267\257\345\276\2042.md" "b/11_dynamic_programming/No.063_\344\270\215\345\220\214\350\267\257\345\276\2042.md"
deleted file mode 100644
index 684b18e..0000000
--- "a/11_dynamic_programming/No.063_\344\270\215\345\220\214\350\267\257\345\276\2042.md"
+++ /dev/null
@@ -1,82 +0,0 @@
-## 63 不同路径2-中等
-
-题目:
-
-一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
-
-机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
-
-现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
-
-网格中的障碍物和空位置分别用 1 和 0 来表示。
-
-
-分析:
-
-直接递推。遇到障碍物,直接复用上一个值,或者变成零。
-
-注意,初始化的时候,遇到障碍物也要变成零。
-
-
-```go
-// date 2023/11/11
-func uniquePathsWithObstacles(obstacleGrid [][]int) int {
- m := len(obstacleGrid)
- if m == 0 {
- return 0
- }
- n := len(obstacleGrid[0])
- dp := make([][]int, m)
- for i := 0; i < m; i++ {
- dp[i] = make([]int, n)
- if i == 0 {
- for j := 0; j < n; j++ {
- if obstacleGrid[i][j] == 1 {
- dp[i][j] = 0
- } else {
- dp[i][j] = 1
- }
- }
- }
- }
- for i := 0; i < m; i++ {
- if obstacleGrid[i][0] == 1 {
- dp[i][0] = 0
- } else {
- dp[i][0] = 1
- }
- }
-
- for i := 0; i < m; i++ {
- for j := 0; j < n; j++ {
- if obstacleGrid[i][j] == 1 {
- continue
- }
- if i > 0 && j > 0 {
- if obstacleGrid[i-1][j] == 1 {
- dp[i][j] = dp[i][j-1]
- } else if obstacleGrid[i][j-1] == 1 {
- dp[i][j] = dp[i-1][j]
- } else if obstacleGrid[i-1][j] == 1 && obstacleGrid[i][j-1] == 1 {
- dp[i][j] = 0
- } else {
- dp[i][j] = dp[i-1][j] + dp[i][j-1]
- }
- } else if i > 0 {
- if obstacleGrid[i-1][j] == 1 {
- dp[i][j] = 0
- } else {
- dp[i][j] = dp[i-1][j]
- }
- } else if j > 0 {
- if obstacleGrid[i][j-1] == 1 {
- dp[i][j] = 0
- } else {
- dp[i][j] = dp[i][j-1]
- }
- }
- }
- }
- return dp[m-1][n-1]
-}
-```
diff --git "a/11_dynamic_programming/No.064_\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md" "b/11_dynamic_programming/No.064_\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md"
deleted file mode 100644
index dfe94de..0000000
--- "a/11_dynamic_programming/No.064_\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md"
+++ /dev/null
@@ -1,40 +0,0 @@
-## 64 最小路径和-中等
-
-题目:
-
-给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
-
-说明:每次只能向下或者向右移动一步。
-
-
-分析:
-
-```go
-// date 2020/03/08
-// 时间复杂度O(M*N),空间复杂度O(1)
-func minPathSum(grid [][]int) int {
- m := len(grid)
- if m == 0 { return 0 }
- n := len(grid[0])
- for i := m-1; i >= 0; i-- {
- for j := n-1; j >= 0; j-- {
- // 如果存在右节点和下节点,选择其中最小的那个
- if i + 1 < m && j + 1 < n {
- grid[i][j] += min(grid[i+1][j], grid[i][j+1])
- // 如果只有右节点,则选择右节点
- } else if j + 1 < n {
- grid[i][j] += grid[i][j+1]
- // 如果只有下节点,则选择下节点
- } else if i + 1 < m {
- grid[i][j] += grid[i+1][j]
- }
- }
- }
- return grid[0][0]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
diff --git "a/11_dynamic_programming/No.070_\347\210\254\346\245\274\346\242\257.md" "b/11_dynamic_programming/No.070_\347\210\254\346\245\274\346\242\257.md"
deleted file mode 100644
index 7bbafa0..0000000
--- "a/11_dynamic_programming/No.070_\347\210\254\346\245\274\346\242\257.md"
+++ /dev/null
@@ -1,58 +0,0 @@
-## 70 爬楼梯-简单
-
-题目:
-
-假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
-
-每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
-
-
-
-**解题思路**
-
-直接递推。c[i] = c[i-1] + c[i-2]
-
-```go
-// date 2023/11/07
-func climbStairs(n int) int {
- if n < 3 {
- return n
- }
- p1, p2 := 1, 2
- var res int
- for i := 3; i <= n; i++ {
- res = p1 + p2
- p1, p2 = p2, res
- }
-
- return res
-}
-```
-
-
-
-## 动归的泛化写法
-
-```go
-// 递推公式 dp[i] 表示第 i 个台阶有多少种走法
-// dp[i] = dp[i-1] + dp[i-2],即两种情况
-// 第一种:到达 i-1 的总解数,再走 1 步就到达 i
-// 第二种:到达 i-2 的总解数,再走 2 步就到达 i
-func climbStairs(n int) int {
- dp := make([]int, n+1)
- steps := []int{1, 2}
- dp[0] = 1
-
- for i := 1; i <= n; i++ {
- for _, step := range steps {
- if i < step {
- continue
- }
- dp[i] += dp[i-step]
- }
- }
-
- return dp[n]
-}
-```
-
diff --git "a/11_dynamic_programming/No.072_\347\274\226\350\276\221\350\267\235\347\246\273.md" "b/11_dynamic_programming/No.072_\347\274\226\350\276\221\350\267\235\347\246\273.md"
deleted file mode 100644
index 4e00a26..0000000
--- "a/11_dynamic_programming/No.072_\347\274\226\350\276\221\350\267\235\347\246\273.md"
+++ /dev/null
@@ -1,59 +0,0 @@
-## 72 编辑距离-中等
-
-题目:
-
-给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
-
-你可以对一个单词进行如下三种操作:
-
-插入一个字符
-删除一个字符
-替换一个字符
-
-
-分析:
-
-```go
-// date 2023/11/07
-func minDistance(word1 string, word2 string) int {
- m, n := len(word1), len(word2)
- dp := make([][]int, m+1)
- // dp[i][j] 表示将 word1[0...i-1] 变成 word2[0...j-1] 所需要的最小编辑数
- for i := 0; i <= m; i++ {
- dp[i] = make([]int, n+1)
- dp[i][0] = i // j = 0, word2 is empty, delete all word1 elem
- }
- for j := 0; j <= n; j++ {
- dp[0][j] = j // i = 0, word1 is empty, insert all elem to word1
- }
-
- for i := 1; i <= m; i++ {
- for j := 1; j <= n; j++ {
- if word1[i-1] == word2[j-1] {
- dp[i][j] = dp[i-1][j-1]
- } else {
- dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1
- // dp[i-1][j] delete 1 elem in word1
- // dp[i][j-1] insert 1 elem to word2 等价于从 word1 删除 1 个
- // dp[i-1][j-1] replace 1 elem of word1
- }
- }
- }
-
- return dp[m][n]
-}
-
-// word1[0...i-1] -> word2[0....j] = dp[i-1][j]
-// word1[0.....i] -> word2[0....j] = dp[i][j]
-// 在 dp[i-1][j] 已知的情况下,word1 中 删除 word1[i] 即可
-// dp[i][j] = dp[i-1][j], delete 1 elem of word1
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
-
-
diff --git "a/11_dynamic_programming/No.1137_\347\254\254N\344\270\252\346\263\260\346\263\242\351\202\243\345\245\221\346\225\260.md" "b/11_dynamic_programming/No.1137_\347\254\254N\344\270\252\346\263\260\346\263\242\351\202\243\345\245\221\346\225\260.md"
deleted file mode 100644
index 406c558..0000000
--- "a/11_dynamic_programming/No.1137_\347\254\254N\344\270\252\346\263\260\346\263\242\351\202\243\345\245\221\346\225\260.md"
+++ /dev/null
@@ -1,33 +0,0 @@
-## 1137 第N个泰波那契数-简单
-
-题目:
-
-泰波那契序列 Tn 定义如下:
-
-T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
-
-给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
-
-
-分析:
-
-递推。
-
-```go
-// date 2023/11/11
-func tribonacci(n int) int {
- if n == 0 {
- return 0
- }
- if n < 3 {
- return 1
- }
- t0, t1, t2 := 0, 1, 1
- t := 0
- for i := 3; i <= n; i++ {
- t = t0+t1+t2
- t0, t1, t2 = t1, t2, t
- }
- return t
-}
-```
diff --git "a/11_dynamic_programming/No.1143_\346\234\200\351\225\277\345\205\254\345\205\261\345\255\220\345\272\217\345\210\227.md" "b/11_dynamic_programming/No.1143_\346\234\200\351\225\277\345\205\254\345\205\261\345\255\220\345\272\217\345\210\227.md"
deleted file mode 100644
index 021b40d..0000000
--- "a/11_dynamic_programming/No.1143_\346\234\200\351\225\277\345\205\254\345\205\261\345\255\220\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,56 +0,0 @@
-## 1143 最长公共子序列-中等
-
-题目:
-
-
-给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
-
-一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
-
-例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
-两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
-
-
-
-**解题思路**
-
-动规,这题跟 No.72 编辑距离很像,思路是一样的。
-
-定义 `lcs[i][j]` 表示两个字符串s1,s2中前 `i`,`j`个字符的最长公共子序列长度,那么有以下转移方程。
-
-```
-1. s1[i] == s2[j]
- lcs[i][j] = lcs[i-1][j-1] + 1
-
-2. s1[i] != s2[j]
- lcs[i][j] = max(lcs[i-1][j], lcs[i][j-1]
-```
-
-
-```go
-// date 2023/11/13
-func longestCommonSubsequence(text1 string, text2 string) int {
- s1, s2 := len(text1), len(text2)
- lcs := make([][]int, s1+1)
- for i := 0; i <= s1; i++ {
- lcs[i] = make([]int, s2+1)
- }
- for i := 0; i < s1; i++ {
- for j := 0; j < s2; j++ {
- if text1[i] == text2[j] {
- lcs[i+1][j+1] = lcs[i][j] + 1
- } else {
- lcs[i+1][j+1] = max(lcs[i][j+1], lcs[i+1][j])
- }
- }
- }
- return lcs[s1][s2]
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
diff --git "a/11_dynamic_programming/No.118_\346\235\250\350\276\211\344\270\211\350\247\222.md" "b/11_dynamic_programming/No.118_\346\235\250\350\276\211\344\270\211\350\247\222.md"
deleted file mode 100644
index ebd1a92..0000000
--- "a/11_dynamic_programming/No.118_\346\235\250\350\276\211\344\270\211\350\247\222.md"
+++ /dev/null
@@ -1,38 +0,0 @@
-## 118 杨辉三角-中等
-
-题目:
-
-给定一个非负整数 *`numRows`,*生成「杨辉三角」的前 *`numRows`* 行。
-
-在「杨辉三角」中,每个数是它左上方和右上方的数的和。
-
-
-
-**解题思路**
-
-这道题也是动态规划的一种,直接模拟杨辉三角的计算过程即可。
-
-```go
-// date 2024/10/30
-func generate(numRows int) [][]int {
- ans := make([][]int, numRows)
- for i := 0; i < numRows; i++ {
- ans[i] = make([]int, 0, 16)
- }
-
- for i := 0; i < numRows; i++ {
- if i == 0 {
- ans[i] = append(ans[i], 1)
- } else {
- ans[i] = append(ans[i], 1)
- for j := 1; j < i; j++ {
- ans[i] = append(ans[i], ans[i-1][j]+ans[i-1][j-1])
- }
- ans[i] = append(ans[i], 1)
- }
- }
-
- return ans
-}
-```
-
diff --git "a/11_dynamic_programming/No.120_\344\270\211\350\247\222\345\275\242\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md" "b/11_dynamic_programming/No.120_\344\270\211\350\247\222\345\275\242\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md"
deleted file mode 100644
index c042027..0000000
--- "a/11_dynamic_programming/No.120_\344\270\211\350\247\222\345\275\242\346\234\200\345\260\217\350\267\257\345\276\204\345\222\214.md"
+++ /dev/null
@@ -1,44 +0,0 @@
-## 120 三角形最小路径和-中等
-
-题目:
-
-给定一个三角形 triangle ,找出自顶向下的最小路径和。
-
-每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
-
-
-分析:
-
-不能正向求,因为正向只能看到局部最优解,而不是全局最优解。
-
-所以,从底往上递归,并更新节点值。更新到顶部就是最小路径。
-
-
-```go
-// date 2023/11/13
-func minimumTotal(triangle [][]int) int {
- m := len(triangle)
- if m == 0 {
- return 0
- }
-
- for i := m-2; i >= 0; i-- {
- // update this line
- th := len(triangle[i])
- for j := th-1; j >= 0; j-- {
- if j + 1 < len(triangle[i+1]) {
- triangle[i][j] += min(triangle[i+1][j], triangle[i+1][j+1])
- }
- }
- }
-
- return triangle[0][0]
-}
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
diff --git "a/11_dynamic_programming/No.121_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\272.md" "b/11_dynamic_programming/No.121_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\272.md"
deleted file mode 100644
index 40f7818..0000000
--- "a/11_dynamic_programming/No.121_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\272.md"
+++ /dev/null
@@ -1,37 +0,0 @@
-## 121 买卖股票的最佳时机
-
-题目:
-
-给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
-
-你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
-
-返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
-
-分析:
-
-因为只能交易一次,所以遍历的时候,记录前面出现的最小值,并用当前值计算出利润,并更新结果。
-
-```go
-// date 2023/11/08
-func maxProfit(prices []int) int {
- var profit int
- if len(prices) < 2 {
- return 0
- }
-
- cur_min := prices[0]
-
- for _, v := range prices {
- if cur_min < v && profit < v - cur_min {
- profit = v - cur_min
- }
- if v < cur_min {
- cur_min = v
- }
- }
-
- return profit
-}
-```
diff --git "a/11_dynamic_programming/No.122_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\2722.md" "b/11_dynamic_programming/No.122_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\2722.md"
deleted file mode 100644
index 1d28b4f..0000000
--- "a/11_dynamic_programming/No.122_\344\271\260\345\215\226\350\202\241\347\245\250\347\232\204\346\234\200\344\275\263\346\227\266\346\234\2722.md"
+++ /dev/null
@@ -1,30 +0,0 @@
-## 122 买卖股票的最佳时机2
-
-题目:
-
-给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
-
-在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
-
-返回 你能获得的 最大 利润 。
-
-
-分析:
-
-因为最多只能持有一只股票,但是可以在同一天买卖。所以总利润就是前后两个价格的差求和。
-
-
-```go
-// date 2023/11/08
-func maxProfit(prices []int) int {
- var res int
-
- for i := 1; i < len(prices); i++ {
- if prices[i] > prices[i-1] {
- res += prices[i] - prices[i-1]
- }
- }
-
- return res
-}
-```
diff --git "a/11_dynamic_programming/No.139_\345\215\225\350\257\215\346\213\206\345\210\206.md" "b/11_dynamic_programming/No.139_\345\215\225\350\257\215\346\213\206\345\210\206.md"
deleted file mode 100644
index b6fe7ff..0000000
--- "a/11_dynamic_programming/No.139_\345\215\225\350\257\215\346\213\206\345\210\206.md"
+++ /dev/null
@@ -1,105 +0,0 @@
-## 139 单次拆分-中等
-
-题目:
-
-给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
-
-注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
-
-
-分析:
-
-以下代码可AC。
-
-我们定义 dp[i] 表示字符串 s[0...i] 可以拆分成若干个字典中存在的单词,那么对于s[0...i]来说,任意分割点j,满足0 <= j < i,那么有如下递推公式:
-
-```
-dp[i] = dp[j] && s[j:i] in wordset
-```
-
-```go
-// date 2023/11/13
-func wordBreak(s string, wordDict []string) bool {
- wordSet := make(map[string]bool, len(wordDict))
- for _, v := range wordDict {
- wordSet[v] = true
- }
-
- dp := make([]bool, len(s)+1)
- dp[0] = true
-
- for i := 0; i <= len(s); i++ {
- for j := 0; j < i; j++ {
- if dp[j] && wordSet[s[j:i]] {
- dp[i] = true
- break
- }
- }
- }
- return dp[len(s)]
-}
-```
-
-
-以下代码不可AC。
-
-这段代码的逻辑是依次匹配单词,如果成功继续匹配。
-
-无法通过这类 case:
-
-```
-s = "cars"
-
-words = ["car", "ca", "rs"]
-```
-
-```go
-// date 2023/11/13
-func wordBreak(s string, wordDict []string) bool {
- start := 0
- end := 0
- total := len(s)
- i := 0
-
- for i < total {
- old := i
- start = i
- end = 0
- for _, word := range wordDict {
- size := len(word)
- end = start + size
-
- if end > total {
- continue
- }
- tgt := s[start:end]
- //if isSame(word, tgt) && end == total {
- // return true
- //}
- if isSame(word, tgt) {
- i = end
- break
- }
- }
- if i == old {
- return false
- }
- }
- if i == total {
- return true
- }
- return false
-}
-
-func isSame(s1, s2 string) bool {
- if len(s1) != len(s2) {
- return false
- }
- for i := 0; i < len(s1); i++ {
- if s1[i] != s2[i] {
- return false
- }
- }
- return true
-}
-```
diff --git "a/11_dynamic_programming/No.198_\346\211\223\345\256\266\345\212\253\350\210\215.md" "b/11_dynamic_programming/No.198_\346\211\223\345\256\266\345\212\253\350\210\215.md"
deleted file mode 100644
index ce31d78..0000000
--- "a/11_dynamic_programming/No.198_\346\211\223\345\256\266\345\212\253\350\210\215.md"
+++ /dev/null
@@ -1,45 +0,0 @@
-## 198 打家劫舍-中等
-
-题目:
-
-你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
-
-给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
-
-
-分析:
-
-动归,递推。每天晚上你都可以选择偷或者不偷,定义dp[i] 表示第i天的偷窃的总金额,那么有如下递推公式:
-
-```
-dp[i] = max(dp[i-1], dp[i-2]+nums[i])
-```
-
-```go
-// date 2023/11/11
-func rob(nums []int) int {
- if len(nums) == 1 {
- return nums[0]
- }
- if len(nums) == 2 {
- return max(nums[0], nums[1])
- }
- n := len(nums)
- dp := make([]int, n)
- // dp[i] = 当晚偷窃的最大值
- dp[0] = nums[0]
- dp[1] = max(nums[0], nums[1])
- for i := 2; i < n; i++ {
- dp[i] = max(dp[i-1], dp[i-2] + nums[i])
- }
-
- return dp[n-1]
-}
-
-func max(x, y int) int {
- if x < y {
- return y
- }
- return x
-}
-```
diff --git "a/11_dynamic_programming/No.264_\344\270\221\346\225\2602.md" "b/11_dynamic_programming/No.264_\344\270\221\346\225\2602.md"
deleted file mode 100644
index f8398bf..0000000
--- "a/11_dynamic_programming/No.264_\344\270\221\346\225\2602.md"
+++ /dev/null
@@ -1,53 +0,0 @@
-## 264 丑数2-中等
-
-题目:
-
-给你一个整数 n ,请你找出并返回第 n 个 丑数 。
-
-丑数 就是质因子只包含 2、3 和 5 的正整数。
-
-
-分析:
-
-所谓丑数,就是说该数字只能是 2,3,5 的倍数。
-
-一个丑数乘以 2 或者 3 或者 5 ,结果还是丑数,要选最小的那个。
-
-所以,需要维护三个指针,p1,p2,p3, 分别表示下一个丑数是当前指针所指向的丑数乘以不同的质因子得来。
-
-一旦被使用,说明该指针所指向的丑数 乘以 指针所代表的质因子,就是当前下一个(最小的)的丑数。
-
-该指针递增,从以往的丑数序列中选最小的丑数作为该质因子新的基数。
-
-所以指针加一。
-
-===
-
-这里可以这样理解:p1,p2,p3 分别表示质因子2,3,5所选以往丑数作为基数的索引。该索引保证该质子下,选最小的那个。
-
-起初,p1,p2,p3 都是从 1(丑数) 作为基数开始。
-
-随着丑数的产生,丑数序列中肯定越靠前的越小。一旦被使用,只能选下一个较小的。
-
-
-```go
-// date 2023/11/09
-func nthUglyNumber(n int) int {
- if n < 1 { return 1 }
- dp := make([]int, n)
- dp[0] = 1
- p1, p2, p3 := 0, 0, 0
- for i := 1; i < n; i++ {
- dp[i] = min(2 * dp[p1], min(3 * dp[p2], 5 * dp[p3]))
- if dp[i] == 2 * dp[p1] { p1++ }
- if dp[i] == 3 * dp[p2] { p2++ }
- if dp[i] == 5 * dp[p3] { p3++ }
- }
- return dp[n-1]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
diff --git "a/11_dynamic_programming/No.279_\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md" "b/11_dynamic_programming/No.279_\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md"
deleted file mode 100644
index 4295f2c..0000000
--- "a/11_dynamic_programming/No.279_\345\256\214\345\205\250\345\271\263\346\226\271\346\225\260.md"
+++ /dev/null
@@ -1,54 +0,0 @@
-## 279 完全平方数-中等
-
-题目:
-
-给你一个整数 `n` ,返回 *和为 `n` 的完全平方数的最少数量* 。
-
-**完全平方数** 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,`1`、`4`、`9` 和 `16` 都是完全平方数,而 `3` 和 `11` 不是。
-
-**提示:**
-
-- `1 <= n <= 104`
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:n = 12
-> 输出:3
-> 解释:12 = 4 + 4 + 4
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:n = 13
-> 输出:2
-> 解释:13 = 4 + 9
-> ```
-
-
-
-**解题思路**
-
-
-
-```go
-// date 2024/01/30
-func numSquares(n int) int {
- dp := make([]int, n+1)
-
- for i := 1; i <= n; i++ {
- // 最多有 i 个
- minn := i
- for j := 1; j*j <= i; j++ {
- minn = min(minn, dp[i-j*j])
- }
- dp[i] = minn + 1
- }
-
- return dp[n]
-}
-```
-
diff --git "a/11_dynamic_programming/No.300_\346\234\200\351\225\277\344\270\212\345\215\207\345\255\220\345\272\217\345\210\227.md" "b/11_dynamic_programming/No.300_\346\234\200\351\225\277\344\270\212\345\215\207\345\255\220\345\272\217\345\210\227.md"
deleted file mode 100644
index a5720fd..0000000
--- "a/11_dynamic_programming/No.300_\346\234\200\351\225\277\344\270\212\345\215\207\345\255\220\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,89 +0,0 @@
-## 300 最长上升子序列
-
-题目:
-
-给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
-
-子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
-
-
-分析:
-
-题目中并没有求最长**连续**上升子序列,所以子序列只是保持相对位置的元素集合。
-
-那么定义 dp[i] 表示包含元素nums[i]的最长上升序列的长度,那么两层遍历即可得到下面的递推公式:
-
-```
-当 0 <= j < i && nums[i] > nums[j] 时
-dp[i] = max(dp[j]) + 1
-```
-
-初始状态为 dp[0] = 1,即一个元素组成的上升序列。
-
-
-```go
-// date 2023/11/09
-func lengthOfLIS(nums []int) int {
- if len(nums) == 0 {
- return 0
- }
- res := 1
- n := len(nums)
-
- dp := make([]int, n)
- dp[0] = 1
-
- for i := 1; i < n; i++ {
- dpj_max := 0
- for j := 0; j < i; j++ {
- if nums[i] > nums[j] {
- dpj_max = max(dpj_max, dp[j])
- }
- }
- dp[i] = dpj_max + 1
-
- res = max(res, dp[i])
- }
-
- return res
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
-算法2:
-
-```go
-// date 2020/03/16
-func lengthOfLIS(nums []int) int {
- if len(nums) == 0 { return 0}
- n := len(nums)
- lis := make([]int, 0, n)
- lis = append(lis, nums[0])
- for i := 1; i < n; i++ {
- // 在lis数组找到第一个比nums[i]大的元素,并替换它,否则进行追加
- m := len(lis)
- // nums[i] > lis[m-1]
- // nums[i] 直接参与最长上升序列
- if nums[i] > lis[m-1] {
- lis = append(lis, nums[i])
- continue
- }
- // 替换的必要性
- // 1. 保证 nums[i] 有机会参与最长上升序列,为后面更大的值剔除障碍
- // 2. 因为不要求连续性,lis 中的大值没有意义,替换相对于变相删除
- for j := 0; j < m; j++ {
- if nums[i] <= lis[j] {
- lis[j] = nums[i]
- break
- }
- }
- }
- return len(lis)
-}
-```
diff --git a/11_dynamic_programming/No.322_coin_change.md b/11_dynamic_programming/No.322_coin_change.md
deleted file mode 100644
index 6f119c5..0000000
--- a/11_dynamic_programming/No.322_coin_change.md
+++ /dev/null
@@ -1,71 +0,0 @@
-## 322 Coin Change \[零钱兑换\]
-
- * 1.[问题定义](#问题定义)
- * 2.[最优子结构解法](#最优子结构解法)
- * 3.[重叠子问题解法](#重叠子问题解法)
-
-### 问题定义
-
-给定一个值M,和一组硬币面值的集合,问将硬币组合值为M的情况一共有几种,不考虑硬币的顺序问题。
-
-例如,值为4,硬币面值为{1,2,3}。那么,一共有四种情况。{1,1,1,1}、{1,1,2}、{1,3}和{2,2}。
-
-变相问题:
-
-给定一个int数组A,数组中元素互不重复,给定一个数x,求所有求和能得到x的数字组合,组合中的元素来自A,可重复使用
-
-### 最优子结构解法
-
-```
-L(set, n, sum)表示(值为sum,硬币面值集合为set, n为硬币面值的个数)硬币的组合情况数量
-L(set, n, sum) = L(set, n - 1, sum) // 不包含面值为set[n]的硬币
- + L(set, n, sum - set[n - 1]); //至少包含一个面值为set[n-1]的硬币
-
-边界条件,即递归结束条件
-if(sum == 0)
- return 1
-if(sum < 0)
- return 0;
-if(n <= 0 && sum >= 1)
- return 0;
-```
-
-```cpp
-// 简易版
-int CoinChange(int coin[], int n, int sum) {
- if(sum == 0)
- return 1;
- if(sum < 0)
- return 0;
- if(n <= 0 && sum > 0)
- return 0;
- return CoinChange(coin, n - 1, sum) + CoinChange(coin, n, sum - coin[n - 1]);
-}
-```
-
-
-
-上面的分析中,我们可以看到在递归地过程中有些值被重复计算了多次,因此,硬币兑换问题同时具有 **最优子结构** 和 **重叠子问题** 两种属性,据此,可对算法进行优化。
-
-### 重叠子问题解法
-
-对于set={3, 4, 7}和sum = 16的情况而言,sum=13/12/9的情况一样,无非是16-set[i]。因此,为了避免重复计算,将每一次计算的结果存储在table[sum+1][n]中,横坐标视为满足当前sum值的子问题结果,而纵坐标体现了集合中元素的包含关系。
-
-```cpp
-int CoinChange(int s[], int n, int sum) {
- int i, j, x, y;
- int table[sum][n];
- for(j = 0; j < n; j++)
- table[0][j] = 1;
- for(i = 1; i <= sum; i++) {
- for(j = 0; j < n; j++) {
- // 包含至少一个s[j]面值的硬币
- x = (i - s[j]) >= 0 ? table[i - s[j]][j] : 0;
- // 不包含s[j]面值的硬币
- y = (y >= 1) ? table[i][j - 1] : 0;
- table[i][j] = x + y;
- }
- }
- return table[sum][n - 1];
-}
-```
diff --git "a/11_dynamic_programming/No.322_\351\233\266\351\222\261\345\205\221\346\215\242.md" "b/11_dynamic_programming/No.322_\351\233\266\351\222\261\345\205\221\346\215\242.md"
deleted file mode 100644
index 09e5d32..0000000
--- "a/11_dynamic_programming/No.322_\351\233\266\351\222\261\345\205\221\346\215\242.md"
+++ /dev/null
@@ -1,42 +0,0 @@
-## 322 零钱兑换-中等
-
-题目:
-
-给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
-
-计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
-
-你可以认为每种硬币的数量是无限的。
-
-
-分析:
-
-该问题具有最优子结构,设目标值为 target,目标值对应的最优解为 opt[target],那么在所有的硬币里面可以得到下面的递推公式:
-
-```
-opt[target] = min(opt[target], 1+opt[target-coin])
-```
-
-
-```go
-// date 2023/11/08
-func coinChange(coins []int, amount int) int {
- opt := make([]int, amount+1)
- for i := 0; i <= amount; i++ {
- opt[i] = amount+1
- }
- opt[0] = 0
- for v := 1; v <= amount; v++ {
- for _, coin := range coins {
- if v < coin {
- continue
- }
- opt[v] = min(opt[v], 1+opt[v-coin])
- }
- }
- if opt[amount] == amount + 1 {
- return -1
- }
- return opt[amount]
-}
-```
diff --git "a/11_dynamic_programming/No.509_\346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md" "b/11_dynamic_programming/No.509_\346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md"
deleted file mode 100644
index 02cb676..0000000
--- "a/11_dynamic_programming/No.509_\346\226\220\346\263\242\351\202\243\345\245\221\346\225\260.md"
+++ /dev/null
@@ -1,30 +0,0 @@
-## 509 斐波那契数
-
-题目:
-
-斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
-
-F(0) = 0,F(1) = 1
-F(n) = F(n - 1) + F(n - 2),其中 n > 1
-给定 n ,请计算 F(n) 。
-
-
-分析:
-
-动归,自底向上,也就是递推。
-
-```go
-// date 2023/11/11
-func fib(n int) int {
- if n < 2 {
- return n
- }
- f1, f2 := 0, 1
- fn := 0
- for i := 2; i <= n; i++ {
- fn = f1 + f2
- f1, f2 = f2, fn
- }
- return fn
-}
-```
diff --git "a/11_dynamic_programming/No.518_\351\233\266\351\222\261\345\205\221\346\215\2422.md" "b/11_dynamic_programming/No.518_\351\233\266\351\222\261\345\205\221\346\215\2422.md"
deleted file mode 100644
index a96b7b2..0000000
--- "a/11_dynamic_programming/No.518_\351\233\266\351\222\261\345\205\221\346\215\2422.md"
+++ /dev/null
@@ -1,90 +0,0 @@
-## 518 零钱兑换2-中等
-
-题目:
-
-给你一个整数数组 `coins` 表示不同面额的硬币,另给一个整数 `amount` 表示总金额。
-
-请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 `0` 。
-
-假设每一种面额的硬币有无限个。
-
-题目数据保证结果符合 32 位带符号整数。
-
-
-
-分析:
-
-典型的动态规划题目。我们设 dp[i] 表示总金额为 i 所对应的组合数,那么对于每一种 coin,有如下递推公式:
-
-```
-dp[i] = dp[i] + dp[i-coin]
-```
-
-该公式表示,当 coin 固定时,dp[i] 和 dp[i-coin] 有同等个数的解。
-
-以下面的图为例,coin = 3,i = 6 为例,coin 提供一个解,再加上 coin = 2 所提供的 i = 6 的一个解,所以 dp[6] = 2。
-
-
-
-所以,整个解法的代码里,外层循环是 coins,对特定coin,求所有 amount 下的解,包含两部分:
-
-1. `amount` 是当前 `coin` 整数倍的,肯定提供一个解
-2. 在之前解的基础上,amount-coin 又提供一种解
-
-所以递推公式:
-
-```
-dp[i] = dp[i] + dp[i-coin]
-等号左边的 dp[i] 是 当前 coin 下总组合数
-等号右边的 dp[i] 是 历史上其他 coin 所提供的组合数
-等号右边的 dp[i-coin] 是 以当前 coin 为步长所形成的解
-```
-
-
-
-```go
-// date 2023/11/09
-func change(amount int, coins []int) int {
- dp := make([]int, amount+1)
- dp[0] = 1
- for _, coin := range coins {
- for i := 1; i <= amount; i++ {
- if i < coin {
- continue
- }
- dp[i] += dp[i-coin]
- }
- }
- return dp[amount]
-}
-```
-
-
-
-
-
----
-
-## 扩展
-
-该问题跟爬楼梯类似,但是有本质区别。
-
-爬楼梯是求**排列数**,该问题是求**组合数**。
-
-**排列数** 是指序列中元素的顺序不同,即为1种解。
-
-但是**组合数**是说序列中元素的种类和数量一样,视为1种解。
-
-举个例子,还是以 coins = {2, 3} 为例,目标是 5。
-
-如果当做爬楼梯来解,那么表示你可以迈2个或3个台阶,求到达第 5 个台阶有多少总走法。
-
-很显然有两种,分别是(2,3)和(3,2),因为先走 2 步,后走 3 步,和先走 3 步,后走 2 步,是看做 2 个解。
-
-
-
-但在零钱兑换里面,就不是这样。2和3,各取一个组合 5,被视为 1 种解。
-
-再看两个问题的解法,就会发现两层循环的区别:
-
-排列数的解法中,总目标在外层循环体;组合数的解法中,总目标在内层循环。
\ No newline at end of file
diff --git "a/11_dynamic_programming/No.673_\346\234\200\351\225\277\351\200\222\345\242\236\345\255\220\345\272\217\345\210\227\347\232\204\344\270\252\346\225\260.md" "b/11_dynamic_programming/No.673_\346\234\200\351\225\277\351\200\222\345\242\236\345\255\220\345\272\217\345\210\227\347\232\204\344\270\252\346\225\260.md"
deleted file mode 100644
index b8004bd..0000000
--- "a/11_dynamic_programming/No.673_\346\234\200\351\225\277\351\200\222\345\242\236\345\255\220\345\272\217\345\210\227\347\232\204\344\270\252\346\225\260.md"
+++ /dev/null
@@ -1,50 +0,0 @@
-## 673 最长递增子序列的个数-中等
-
-题目:
-
-给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
-
-注意 这个数列必须是 严格 递增的。
-
-
-分析:
-
-dp 表示递增子序列的长度。
-
-cnt 表示以 nums[i] 结尾的长度为dp[i]的个数。
-
-```go
-// date 2023/11/13
-func findNumberOfLIS(nums []int) int {
- n := len(nums)
- dp := make([]int, n)
- cnt := make([]int, n)
- maxLen := 0
-
- ans := 0
-
- for i := 0; i < n; i++ {
- dp[i] = 1
- cnt[i] = 1
- for j := 0; j < i; j++ {
- if nums[i] > nums[j] {
- if dp[j] + 1 > dp[i] {
- dp[i] = dp[j] + 1
- cnt[i] = cnt[j] // dp[i] 在更新,所以重置cnt[i]个数
- } else if dp[j] + 1 == dp[i] {
- cnt[i] += cnt[j] // 说明存在多个,累加
- }
-
- }
- }
- // 最终结果集,更新或累加
- if dp[i] > maxLen {
- maxLen = dp[i]
- ans = cnt[i]
- } else if dp[i] == maxLen {
- ans += cnt[i]
- }
- }
- return ans
-}
-```
diff --git "a/11_dynamic_programming/No.740_\345\210\240\351\231\244\345\271\266\350\216\267\345\276\227\347\202\271\346\225\260.md" "b/11_dynamic_programming/No.740_\345\210\240\351\231\244\345\271\266\350\216\267\345\276\227\347\202\271\346\225\260.md"
deleted file mode 100644
index 2f2cc6a..0000000
--- "a/11_dynamic_programming/No.740_\345\210\240\351\231\244\345\271\266\350\216\267\345\276\227\347\202\271\346\225\260.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-## 740 删除并获得点数
-
-题目:
-
-给你一个整数数组 nums ,你可以对它进行一些操作。
-
-每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
-
-开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
-
-
-分析:
-
-进阶版的打家劫舍。
-
-先统计数组中每个元素出现的总点数,然后再做打家劫舍。
-
-```go
-// date 2023/11/11
-func deleteAndEarn(nums []int) int {
- maxVal := 0
- for _, v := range nums {
- maxVal = max(maxVal, v)
- }
- sum := make([]int, maxVal+1)
- for _, v := range nums {
- sum[v] += v
- }
-
- // 对 sum 打家劫舍
- if len(sum) == 1 {
- return sum[0]
- }
- if len(sum) == 2 {
- return max(sum[0], sum[1])
- }
- f1, f2 := sum[0], sum[1]
- f := 0
- for i := 2; i < len(sum); i++ {
- f = max(f2, f1 + sum[i])
- f1, f2 = f2, f
- }
- return f
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
diff --git "a/11_dynamic_programming/No.860_\346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md" "b/11_dynamic_programming/No.860_\346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md"
deleted file mode 100644
index 1486573..0000000
--- "a/11_dynamic_programming/No.860_\346\237\240\346\252\254\346\260\264\346\211\276\351\233\266.md"
+++ /dev/null
@@ -1,47 +0,0 @@
-## 860 柠檬水找零-简单
-
-题目:
-
-在柠檬水摊上,每一杯柠檬水的售价为 `5` 美元。顾客排队购买你的产品,(按账单 `bills` 支付的顺序)一次购买一杯。
-
-每位顾客只买一杯柠檬水,然后向你付 `5` 美元、`10` 美元或 `20` 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 `5` 美元。
-
-注意,一开始你手头没有任何零钱。
-
-给你一个整数数组 `bills` ,其中 `bills[i]` 是第 `i` 位顾客付的账。如果你能给每位顾客正确找零,返回 `true` ,否则返回 `false` 。
-
-
-
-分析:
-
-直接遍历,记录手里 5 块和 10 块的张数;找零优先支出 10 块,不足再找 5 块;如果找不开直接返回 false。
-
-```go
-func lemonadeChange(bills []int) bool {
- a, b := 0, 0
-
- for _, v := range bills {
- if v == 5 {
- a++
- } else if v == 10 {
- if a == 0 {
- return false
- }
- a--
- b++
- } else if v == 20 {
- if a > 0 && b > 0 {
- a--
- b--
- } else if a >= 3 {
- a -= 3
- } else {
- return false
- }
- }
- }
-
- return true
-}
-```
-
diff --git "a/11_dynamic_programming/No.931_\344\270\213\351\231\215\350\267\257\345\276\204\346\234\200\345\260\217\345\222\214.md" "b/11_dynamic_programming/No.931_\344\270\213\351\231\215\350\267\257\345\276\204\346\234\200\345\260\217\345\222\214.md"
deleted file mode 100644
index bf4ba9f..0000000
--- "a/11_dynamic_programming/No.931_\344\270\213\351\231\215\350\267\257\345\276\204\346\234\200\345\260\217\345\222\214.md"
+++ /dev/null
@@ -1,78 +0,0 @@
-## 931 下降路径最小和-中等
-
-题目:
-
-给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
-
-下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
-
-
-分析:
-
-自底向上递推,注意求边界条件。
-
-只有一列时,求所有行的和;只有一行时,求行内最小值。
-
-
-```go
-// date 2023/11/13
-func minFallingPathSum(matrix [][]int) int {
- m := len(matrix)
- if m == 0 {
- return 0
- }
- res := 0
- if m == 1 {
- for j := 0; j < len(matrix[0]); j++ {
- if j == 0 {
- res = matrix[0][0]
- } else {
- res = xy(res, matrix[0][j])
- }
- }
- return res
- }
-
- n := len(matrix[0])
- if n == 1 {
- res = 0
- for i := 0; i < m; i++ {
- res += matrix[i][0]
- }
- return res
- }
-
- for i := m-2; i >= 0; i-- {
- for j := 0; j < n; j++ {
- if j > 0 && j+1 < n {
- matrix[i][j] += min(matrix[i+1][j-1], matrix[i+1][j], matrix[i+1][j+1])
- } else if j > 0 {
- matrix[i][j] += xy(matrix[i+1][j-1], matrix[i+1][j])
- } else if j + 1 < n {
- matrix[i][j] += xy(matrix[i+1][j], matrix[i+1][j+1])
- }
- if i == 0 {
- if j == 0 {
- res = matrix[0][0]
- continue
- } else if j > 0 {
- res = xy(res, matrix[i][j])
- }
- }
- }
- }
-
- return res
-}
-
-func min(x, y, z int) int {
- return xy(xy(x, y), z)
-}
-
-func xy(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
diff --git a/11_dynamic_programming/dp.md b/11_dynamic_programming/dp.md
deleted file mode 100644
index 567bf12..0000000
--- a/11_dynamic_programming/dp.md
+++ /dev/null
@@ -1,554 +0,0 @@
-## Dynamic Programming [动态编程]
-
-[TOC]
-
-动态编程是一种算法范例,其思想是通过将其分解为子问题来解决给定的复杂问题,并存储子问题的结果,以避免再次计算相同的结果。 那么,如何使用动态规划来解决问题?答案是有的。如果一个问题满足以下两个属性之一,那么表明该问题可以使用动态编程来解决。
-
-* 1)重叠子问题
-* 2)最优子结构
-
-### 重叠子问题
-
-类似分治思想,动态规划可以将解决方案与子问题结合。动态规划主要适用于一次又一次地需要子问题的答案来进行求解的问题。因此,在动态规划中将子问题的答案存在表中,以避免重复计算。
-
-例如,二分查找就没有共同的子问题,无法使用动态规划求解。但是,求解斐波那契数列就可以使用动态规划。
-
-一个简单的计算斐波那契数列的递归函数如下:
-
-```cpp
-int fib(int n) {
- if(n <= 1)
- return n;
- return fib(n - 1) + fin(n - 2);
-}
-```
-
-假设求取fib(5)。
-
-
-
-我们可以看到,fib(3)被调用了两次,fib(2)、fib(1)和fib(0)调用的次数就更多了。为了避免重复计算,可以将已经计算出来的值存储到数组中,这样下次计算直接调用数组中存储的值即可。这就是重叠子问题。有两种方式可以实现:
-
-1)记忆(自上而下)
-
-问题的记忆式程序与递归版本相似,在计算解决方案之前,它会对查询表进行小修改。 我们初始化一个所有初始值为NIL的查找数组。 每当我们需要解决一个子问题时,我们首先查看查找表。 如果预先计算的值在那里,那么我们返回该值,否则我们计算该值并将结果放在查找表中,以便稍后重新使用。
-
-```cpp
-// lookup[n]初始化为-1
-int fib(int n) {
- if(lookup[n] == -1) {
- if(n <= 1)
- lookup[n] = 1;
- else
- lookup[n] = fib(n - 1) + fib(n - 2);
- }
- return lookup[n];
-}
-```
-2) 制表(自下而上)
-
-制表(从上到下):给定问题的列表程序以自下而上的方式构建表,并从表返回最后一个条目。 例如,对于相同的斐波那契数,我们首先计算fib(0),然后计算fib(1)然后fib(2)然后fib(3)等等。 从字面上看,我们正在建立自下而上的子问题的解决方案。
-
-```cpp
-int fib(int n) {
- int f[n+1];
- f[0] = 1, f[1] = 1;
- for(int i = 2; i <= n; i++)
- f[n] = f[n - 1] + f[n - 2];
- return f[n];
-}
-```
-
-### 最优子结构
-
-**如果一个问题的最优解可以通过其子问题的最优解获得,那么称这个问题具有最优子结构属性**。例如,最短路径问题就具有最优子结构属性:
-
-假设节点 x 位于起始节点 u 与目的节点 v 之间的最短路径上,那么u-v之间的最短路径就包含了u-x间的最短路径和x-v间的最短路径。
-
-所有的两点之间的最短路径算法,像 Floyd–Warshall 和 Bellman–Ford (贝尔曼-福特算法) 都是典型的动态规划。
-
-相反,最长路径问题就没有最优子结构。这里的最长路径是指两点之间最长的简单路径(不包含环)。
-
-
-
-如图所示,q-t之间的最长路径为q->r->t或q->s->t。但是q-s之间的最长路径确实q->r->t->s。
-
-### 基本思想和解题步骤
-
-动态规划解决的关键是状态定义,状态的转移,初始化和边界条件。
-
-**状态定义**:
-
-**状态的转移**:
-
-**初始化**:
-
-**边界条件:**
-
-**边界条件**:
-
-**边界条件**:
-
-### 相关题目
-
-#### 62 [不同路径](https://leetcode-cn.com/problems/unique-paths/)【中等】
-
-题目要求:给定一个二维数组m x n,返回机器人从二维数组的左上角->右下角的所有不同路径。
-
-算法1:排列组合 res = f(m+n-2)/f(m-1)/f(n-1) f为阶乘
-
-算法2:该问题具有**重复子问题**和**最优子结构**,问题的解可以由子问题的解构成,所以可以用动态规划解决
-
-```go
-// date 2020/01/11
-/* 算法2:递归方程为dp[i][j] = dp[i-1][j] + dp[i][j-1]
- 边界条件:当i == 0 || j == 0; dp[i][j] = 1
-*/
-func uniquePaths(m, n int) int {
- dp := make([][]int, m)
- for i := 0; i < m; i++ {
- dp[i] = make([]int, n)
- }
- for i := 0; i < n; i++ {dp[0][i] = 1} // 第0行,只能一直向右走,所以均为1
- for i := 0; i < m; i++ {dp[i][0] = 1} // 第0列,只能一直向下走,所以均为1
- for i := 1; i < m; i++ {
- for j := 1; j < n; j++ {
- dp[i][j] = dp[i-1][j] + dp[i][j-1]
- }
- }
- return dp[m-1][n-1]
-}
-```
-
-#### 64 [最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)【中等】
-
-题目要求:https://leetcode-cn.com/problems/minimum-path-sum/
-
-给定一个包含非负整数的 `m x n` 网格 `grid` ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
-
-**说明:**每次只能向下或者向右移动一步。
-
-思路分析:自底向上递推
-
-递推公式:`opt[i, j] = grid[i][j] + min(opt[i+1][j], opt[i][j+1])`,注意边界情况
-
-```go
-// date 2020/03/08
-// 时间复杂度O(M*N),空间复杂度O(1)
-func minPathSum(grid [][]int) int {
- m := len(grid)
- if m == 0 { return 0 }
- n := len(grid[0])
- for i := m-1; i >= 0; i-- {
- for j := n-1; j >= 0; j-- {
- // 如果存在右节点和下节点,选择其中最小的那个
- if i + 1 < m && j + 1 < n {
- grid[i][j] += min(grid[i+1][j], grid[i][j+1])
- // 如果只有右节点,则选择右节点
- } else if j + 1 < n {
- grid[i][j] += grid[i][j+1]
- // 如果只有下节点,则选择下节点
- } else if i + 1 < m {
- grid[i][j] += grid[i+1][j]
- }
- }
- }
- return grid[0][0]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
-
-#### 70 [ 爬楼梯](https://leetcode-cn.com/problems/climbing-stairs/)【简单】
-
-题目要求:https://leetcode-cn.com/problems/climbing-stairs/
-
-*假设你正在爬楼梯。需要 n 阶你才能到达楼顶。*
-
-*每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?*
-
-*注意:给定 n 是一个正整数。*
-
-思路分析:这个问题和斐波那契数列很像,可以有三种解法,一个比一个更优。
-
-递推公式等于c[n] = c[n-1] + c[n-2],基本情况n=1, c[n]=1;n=2,c[n]=2
-
-算法一:直接递推
-
-```go
-// date 2020/03/08
-// 算法一:自顶向下直接递推,超时。
-// 时间复杂度O(2^N),空间复杂度O(1)
-func climbStairs(n int) int {
- if n < 3 { return n}
- return climbStairs(n-1) + climbStairs(n-2)
-}
-// 算法二:自底向上递推,并且记录中间结果。
-// 时间复杂度O(N),空间复杂度O(N)
-func climbStairs(n int) int {
- if n < 3 { return n }
- opt := make([]int, n+1)
- opt[1], opt[2] = 1, 2
- for i := 3; i <= n; i++ {
- opt[i] = opt[i-1] + opt[i-2]
- }
- return opt[n]
-}
-// 算法三:自底向上的递推,只保留有用的结果
-// 时间复杂度O(N),空间复杂度O(1)
-func climbStairs(n int) int {
- if n < 3 { return n }
- first, second := 1, 2
- res := 0
- for i := 3; i <= n; i++ {
- res = first + second
- first, second = second, res
- }
- return res
-}
-```
-
-#### 72 编辑距离
-
-题目要求:https://leetcode-cn.com/problems/edit-distance/
-
-思路分析:
-
-```go
-// date 2020/03/16
-func minDistance(word1 string, word2 string) int {
- m, n := len(word1), len(word2)
- dp := make([][]int, m+1)
- // dp[i][j] 表示将 word[0...i] 变成 word2[0...j] 所需要的最小编辑数
- for i := 0; i <= m; i++ {
- dp[i] = make([]int, n+1)
- dp[i][0] = i // j = 0, word2 is empty, delete all word1 elem
- }
- for j := 0; j <= n; j++ {
- dp[0][j] = j // i = 0, word1 is empty, insert all elem to word1
- }
-
- for i := 1; i <= m; i++ {
- for j := 1; j <= n; j++ {
- if word1[i-1] == word2[j-1] {
- dp[i][j] = dp[i-1][j-1]
- } else {
- dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1
- // dp[i-1][j] delete 1 elem in word1
- // dp[i][j-1] insert 1 elem to word2 等价于从 word1 删除 1 个
- // dp[i-1][j-1] replace 1 elem of word1
- }
- }
- }
-
- return dp[m][n]
-}
-
-// word1[0...i-1] -> word2[0....j] = dp[i-1][j]
-// word1[0.....i] -> word2[0....j] = dp[i][j]
-// 在 dp[i-1][j] 已知的情况下,word1 中 删除 word1[i] 即可
-// dp[i][j] = dp[i-1][j], delete 1 elem of word1
-
-func min(x, y int) int {
- if x < y {
- return x
- }
- return y
-}
-```
-
-
-
-#### 121 [买卖股票的最佳时机](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/)【简单】
-
-题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
-
-思路分析:只能交易一次。
-
-遍历一遍,记录之前的最小值。如果当前值大于当前最小值,则计算利润;如果当前值小于当前最小值,则更新当前最小值,具体算法如下
-
-```go
-// date 2020/03/14
-// 时间复杂度O(N),空间复杂度O(1)
-// 非动态规划题解
-func maxProfit(prices []int) int {
- if 0 == len(prices) { return 0 }
- res, cur_min := 0, prices[0]
- for _, v := range prices {
- if v > cur_min && res < v - cur_min { res = v - cur_min }
- if v < cur_min { cur_min = v }
- }
- return res
-}
-```
-
-#### 122 [买卖股票的最佳时机 II](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/)【简单】
-
-题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
-
-思路分析:可以买卖无数次
-
-遍历一遍,只要后面的值大于前面的值,即算作利润。
-
-```go
-// date 2020/03/14
-// 时间复杂度O(N),空间复杂度O(1)
-func maxProfit(prices []int) int {
- profit := 0
- for i := 0; i < len(prices)-1; i++ {
- if prices[i] < prices[i+1] {
- profit =+ prices[i+1] - prices[i]
- }
- }
- return profit
-}
-```
-
-#### 123 [买卖股票的最佳时机 III](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/)【困难】
-
-题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/
-
-思路分析:最多可以交易两笔
-
-遍历一遍,分别从数组[0...i]和[i+1...N]中获取最大利润
-
-```go
-// date 2020/03/14
-// 时间复杂度O(N^2),空间复杂度O(1)
-func maxProfit(prices []int) int {
- res, v1, v2 := 0, 0, 0
- for i := 0; i < len(prices); i++ {
- v1 = maxProfitOnce(prices[:i])
- v2 = maxProfitOnce(prices[i+1:])
- if v1 + v2 > res { res = v1 + v2 }
- }
- return res
-}
-
-func maxProfitOnce(prices []int) int {
- if 0 == len(prices) { return 0 }
- res, cur_min := 0, prices[0]
- for _, v := range prices {
- if v > cur_min && res < v - cur_min { res = v - cur_min }
- if v < cur_min { cur_min = v }
- }
- return res
-}
-// 官方题解
-// 思路2
-func maxProfit(prices []int) int {
- if 0 == len(prices) { return 0 }
- // 代表当前所拥有的钱数
- // buy1 第一次买入, sell1 第一次卖出, buy2 第二次买入, sell2 第二次卖出
- buy1, sell1 := -prices[0], 0
- buy2, sell2 := -prices[0], 0
- for i := 1; i < len(prices); i++ {
- buy1 = max(buy1, -prices[i]) // 保持不变,或者买入
- sell1 = max(sell1, buy1+prices[i]) // 保持不变,或者卖出
- buy2 = max(buy2, sell1-prices[i]) // 保持不变,或者在第一次卖出的情况下买入
- sell2 = max(sell2, buy2+prices[i]) // 保持不变,或者在第二次买入的情况卖出
- }
- return sell2
-}
-
-func max(x, y int) int {
- if x > y { return x }
- return y
-}
-```
-
-#### 188 买卖股票的最佳时机IV
-
-题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/
-
-思路分析:
-
-#### 322 [零钱兑换](https://leetcode-cn.com/problems/coin-change/)【中等】
-
-给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
-
-你可以认为每种硬币的数量是无限的。
-
-题目分析:
-
-问题关键是如果用最少个数的硬币凑成目标值,所以该问题具有最优子结构,设目标值值target,目标值对应的最优解为opt[target],则其递推公式为`opt[target] = min(opt[target], 1+opt[target-coin])`
-
-同时,需要边界条件,当无法找到解时,需要返回-1。
-
-```golang
-// date 2021/03/16
-func coinChange(coins []int, amount int) int {
- // opt[i]表示金额i的最优解,也就是凑成i金额的最少硬币个数
- opt := make([]int, amount+1)
- for i := 0; i <= amount; i++ { opt[i] = amount+1 }
- // 金额0的最优解是0
- opt[0] = 0
- for target := 1; target <= amount; target++ {
- for _, coin := range coins {
- if target < coin { continue }
- opt[target] = min(opt[target], 1+opt[target-coin])
- }
- }
- // 判断是否有解
- if opt[amount] == amount+1 { return -1 }
- return opt[amount]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
-
-
-
-#### 264 丑树
-
-
-
-题目要求:https://leetcode-cn.com/problems/ugly-number-ii/
-
-算法分析:
-
-```go
-// date 2020/03/01
-// 动态规划
-func nthUglyNumber(n int) int {
- if n < 1 { return 1 }
- dp := make([]int, n)
- dp[0] = 1
- p1, p2, p3 := 0, 0, 0
- for i := 1; i < n; i++ {
- dp[i] = min(2 * dp[p1], min(3 * dp[p2], 5 * dp[p3]))
- if dp[i] == 2 * dp[p1] { p1++ }
- if dp[i] == 3 * dp[p2] { p2++ }
- if dp[i] == 5 * dp[p3] { p3++ }
- }
- return dp[n-1]
-}
-
-func min(x, y int) int {
- if x < y { return x }
- return y
-}
-```
-
-#### 300 最长上升子序列
-
-给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
-
-子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
-链接:https://leetcode-cn.com/problems/longest-increasing-subsequence
-
-```
-算法一:动态规划,
-定义dp方程,dp[i]表示包含nums[i]元素的最长上升子序列
-dp[i] = max(dp[j]) + 1; 0 <= j < i && nums[j] < nums[i]
-具体算法如下:
-```
-
-```go
-// date 2020/03/14
-// 时间复杂度O(N^2),空间复杂度O(N)
-func lengthOfLIS(nums []int) int {
- if len(nums) == 0 { return 0 }
- res, cur_max, n := 1, 0, len(nums)
- dp := make([]int, n)
- dp[0] = 1
- for i := 1; i < len(nums); i++ {
- // 找到[0,i]之间最大的最长上升子序列
- cur_max = 0
- for j := 0; j < i; j++ {
- if nums[i] > nums[j] {
- cur_max = max(cur_max, dp[j])
- }
- }
- dp[i] = cur_max + 1 // 如果cur_max为0,+1表示只包含nums[i]自己
- // 否则即为[0,i]的结果集
- res = max(res, dp[i])
- }
- return res
-}
-
-func max(x, y int) int {
- if x > y { return x }
- return y
-}
-```
-
-```
-算法二:
-思路分析:维护一个最长上升子序列数组lis,然后每次更新它,最后数组lis的长度就是结果。
-更新有序数组可以用二分查找,时间复杂度为O(logN)。
-需要知道的是最后的lis结果并不一定是真正的结果,但其长度是所要的结果。
-```
-
-```go
-// date 2020/03/16
-func lengthOfLIS(nums []int) int {
- if len(nums) == 0 { return 0}
- n := len(nums)
- lis := make([]int, 0, n)
- lis = append(lis, nums[0])
- for i := 1; i < n; i++ {
- // 在lis数组找到第一个比nums[i]大的元素,并替换它,否则进行追加
- m := len(lis)
- // nums[i] > lis[m-1]
- // nums[i] 直接参与最长上升序列
- if nums[i] > lis[m-1] {
- lis = append(lis, nums[i])
- continue
- }
- // 替换的必要性
- // 1. 保证 nums[i] 有机会参与最长上升序列,为后面更大的值剔除障碍
- // 2. 因为不要求连续性,lis 中的大值没有意义,替换相对于变相删除
- for j := 0; j < m; j++ {
- if nums[i] <= lis[j] {
- lis[j] = nums[i]
- break
- }
- }
- }
- return len(lis)
-}
-```
-
-#### 面试题17.16 按摩师
-
-题目要求:https://leetcode-cn.com/problems/the-masseuse-lcci/
-
-思路分析:动态规划,动态递推方程`opt[i] = max(opt[i-1], num[i]+max(opt[0...i-2]))`
-
-```go
-// date 2020/03/24
-func massage(nums []int) int {
- if len(nums) == 0 { return 0 }
- if len(nums) == 1 { return nums[0] }
- res, cur_res, n := 0, 0, len(nums)
- opt := make([]int, n)
- opt[0], opt[1] = nums[0], nums[1]
- res = max(opt[0], opt[1])
- for i := 2; i < n; i++ {
- // 找到0...i-2中最大值
- cur_res = 0
- for j := i-2; j >= 0; j-- {
- if nums[i] + opt[j] > cur_res {
- cur_res = nums[i] + opt[j]
- }
- }
- // 更新opt[i]
- opt[i] = max(opt[i-1], cur_res)
- if opt[i] > res { res = opt[i] }
- }
- return res
-}
-
-func max(x, y int) int {
- if x > y { return x }
- return y
-}
-```
-
diff --git a/11_dynamic_programming/find_max_path.md b/11_dynamic_programming/find_max_path.md
deleted file mode 100644
index 249a912..0000000
--- a/11_dynamic_programming/find_max_path.md
+++ /dev/null
@@ -1,84 +0,0 @@
-## 二维空间中的最长递增子序列
-
- * 1.[问题定义](#问题定义)
- * 2.[解题思路](#解题思路)
- * 3.[算法实现](#算法实现)
- * 4.[问题延伸](#问题延伸)
-
-### 问题定义
-
-给定一个N * N的二维整型矩阵,每个元素可以访问前后左右四个元素,找出其中包含严格递增序列的最大节点个数。
-
-
-
-例如,如图所示,符合严格递增序列的最大节点个数分别为16,12,10,相应的路径由红色实线给出。
-
-### 解题思路
-
-1. 对比最短路径问题中保证边的权值最小的问题,利用二维矩阵的坐标保存对应元素的可获得的(满足严格递增序列的)最大节点个数。
-
-2. 利用动态规划思想不断通过遍历节点,并更新每个节点的值,并进行边界条件的设定。
-
-3. 边界条件的设定。当每次遍历后可获得全局的最大值不在发生变化后,即达到收敛条件。
-
-### 算法实现
-
-```cpp
-int FindMaxPath(int data[][4], int n) {
- int num[n][n];
- fill(num[0], num[0] + n * n, 1);
- int maxnum = -1, temp = -1;
- int tempnum = 0;
- while(1) {
- // 遍历所有节点,并更新每个节点num[i][j]值
- for(int i = 0; i < n; i++) {
- // 只进行前后比较即可
- if(i == n-1) {
- for(int j = 0; j < n - 1; j++) {
- if(data[i][j] > data[i][j+1] && num[i][j] <= num[i][j+1])
- num[i][j] = num[i][j+1] + 1;
- if(data[i][j] < data[i][j+1] && num[i][j] >= num[i][j+1])
- num[i][j+1] = num[i][j] + 1;
- tempnum = num[i][j] > num[i][j+1] ? num[i][j] : num[i][j+1];
- temp = tempnum >= temp ? tempnum : temp;
- }
- } else {
- // 进行前后和上下比较
- for(int j = 0; j < n; j++) {
- if(j == n-1) {
- if(data[i][j] > data[i+1][j] && num[i][j] <= num[i+1][j])
- num[i][j] = num[i+1][j] + 1;
- if(data[i][j] < data[i+1][j] && num[i][j] >= num[i+1][j])
- num[i+1][j] = num[i][j] + 1;
- tempnum = num[i][j] > num[i+1][j] ? num[i][j] : num[i+1][j];
- temp = tempnum >= temp ? tempnum : temp;
- } else {
- if(data[i][j] > data[i+1][j] && num[i][j] <= num[i+1][j])
- num[i][j] = num[i+1][j] + 1;
- if(data[i][j] < data[i+1][j] && num[i][j] >= num[i+1][j])
- num[i+1][j] = num[i][j] + 1;
- if(data[i][j] > data[i][j+1] && num[i][j] <= num[i][j+1])
- num[i][j] = num[i][j+1] + 1;
- if(data[i][j] < data[i][j+1] && num[i][j] >= num[i][j+1])
- num[i][j+1] = num[i][j] + 1;
- tempnum = find(num[i][j], num[i+1][j], num[i][j+1]);
- temp = tempnum >= temp ? tempnum : temp;
- }
- }
- }
- }
- // 边界条件的判断
- if(temp == maxnum) {
- return maxnum;
- break;
- }
- // 更新全局最大值
- if(temp > maxnum)
- maxnum = temp;
-}
-}
-```
-
-### 问题延伸
-
-其实,这个问题是对[最长递增子序列](longestincreasingsub.md)的延伸,要深刻理解其算法思想。同样,这个算法的思想可以拓展到三维数组,只不过每个节点需要比较的节点个数变为最少三个,最多六个,但是其思路都一样。
diff --git a/11_dynamic_programming/images/image518.png b/11_dynamic_programming/images/image518.png
deleted file mode 100644
index c9203c8..0000000
Binary files a/11_dynamic_programming/images/image518.png and /dev/null differ
diff --git a/11_dynamic_programming/images/image72.png b/11_dynamic_programming/images/image72.png
deleted file mode 100644
index ee285ee..0000000
Binary files a/11_dynamic_programming/images/image72.png and /dev/null differ
diff --git a/11_dynamic_programming/longestcommonsub.md b/11_dynamic_programming/longestcommonsub.md
deleted file mode 100644
index 500e427..0000000
--- a/11_dynamic_programming/longestcommonsub.md
+++ /dev/null
@@ -1,68 +0,0 @@
-## Longest Common Subsequence \[最长公共子序列\]
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析](#算法分析)
- * 3.[代码实现](#代码实现)
-
-### 问题定义
-
-Given two sequences, find the length of longest subsequence present in both of them.A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.
-
-即,给定两个序列,找出两个序列均包含的子序列的最大长度。**子序列是指以相同的相对顺序出现但不一定相邻的序列**。
-
-例如,"ABCDGH"和"AEDFHR"两个序列的子序列"ADH"的长度为3;"AGGTAB"和"GXTXAYB"两个序列的子序列"GTAB"的长度是4。
-
-计算机科学中,`diff`指令就是一种最长公共子序列的应用。
-
-### 算法分析
-
-1)**最优子结构**
-
-假定用 $X[0...m-1]$ 和 $Y[0...n-1]$ 分别表示长度为m和n的两个序列。$L(X[0...m-1], Y[0...n-1])$ 表示X,Y两个序列的最长公共子序列长度值。
-
-首先考虑两个序列最后一位元素,若相匹配( $X[m-1] == Y[n-1]$ ),则具有如下公式:
-
-$L(X[0...m-1], Y[0...n-1]) = 1 + L(X[0...m-2], Y[0...n-2])$
-
-如果不匹配( $X[m-1] != Y[n-1]$ ),则具有如下公式:
-
-$L(X[0...m-1], Y[0...n-1]) = MAX(L(X[0...m-1], Y[0...n-2]), L(X[0...m-2], Y[0...n-1]))$
-
-举个例子:
-
-对于"AGGTAB"和"GXTXAYB"而言,$L("AGGTAB","GXTXAYB") = 1 + L("AGGTA", "GXTXAY")$
-
-对于"ABCDGH"和"AEDFHR"而言,$L("ABCDGH", "AEDFHR") = MAX(L("ABCDGH", "AEDFH"), L("ABCDG", "AEDFHR"))$
-
-
-
-2) **重叠子问题**
-
-通过上面的分析可以得出这样的结论,通过不断的求解子问题可以获得最终的解。因此,可以通过递归实现该算法。
-
-### 代码实现
-
-* C++
-
-```
-int lcs(char* x, char* y, int m, int n) {
- if(m == 0 | n == 0)
- return 0;
- if(x[m-1] == y[n-1])
- return 1 + lcs(x, y, m - 1, n - 1);
- else
- return max(lcs(x, y, m, n - 1), LCS(x, y, m - 1, n));
-}
-```
-
-* Python
-
-```python
-def lcs(x, y, m, n):
- if m == 0 or n == 0:
- return 0;
- elif x[m-1] == y[n-1]:
- return 1 + lcs(x, y, m - 1, n - 1);
- else
- return max(lcs(x, y, m, n - 1), lcs(x, y, m - 1, n));
-```
diff --git a/11_dynamic_programming/longestincreasingsub.md b/11_dynamic_programming/longestincreasingsub.md
deleted file mode 100644
index b65ab72..0000000
--- a/11_dynamic_programming/longestincreasingsub.md
+++ /dev/null
@@ -1,103 +0,0 @@
-## Longest Increasing Subsequence \[最长递增子序列\]
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析与实现](#算法分析与实现)
- * 3.[问题延伸](#问题延伸)
-
-### 问题定义
-
-The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order.
-
-即,给定一个序列,输出其所有子序列中满足递增关系的最长子序列的长度。**元素不一定要连续**。
-
-### 算法分析与实现
-
-1) **最优子结构**
-
-令 $L(i)$ 表示以索引i所在位置的元素arr[i]为结尾元素的LIS的长度,其中arr[i]为输入序列。则具有如下公式:
-
-$L(i) = 1 + max(L(j))$, 当 $0 < j < i$ , 并且 $arr[j] < arr[i]$ ;
-
-$L(i) = 1$ , 当满足上述条件的 $j$ 不在时。
-
-```cpp
-// 复杂度为O(n^2)
-int LIS(vector data) {
- vector num(data.size());
- int res = 1;;
- fill(num.begin(), num.end(), 1);
- for(int i = 1; i < data.size(); i++) {
- for(int j = 0; j < i; j++) {
- if(data[i] > data[j] && num[i] < num[j] + 1) {
- num[i] = num[j] + 1;
- if(num[i] > res)
- res = num[i];
- }
- }
- }
- return res;
-}
-// 复杂度为O(nLogn)
-#include
-#include
-
-// Binary search (note boundaries in the caller)
-int CeilIndex(std::vector &v, int l, int r, int key) {
- while (r-l > 1) {
- int m = l + (r-l)/2;
- if (v[m] >= key)
- r = m;
- else
- l = m;
- }
- return r;
-}
-
-int LongestIncreasingSubsequenceLength(std::vector &v) {
- if (v.size() == 0)
- return 0;
- std::vector tail(v.size(), 0);
- int length = 1; // always points empty slot in tail
- tail[0] = v[0];
- for (size_t i = 1; i < v.size(); i++) {
- if (v[i] < tail[0])
- tail[0] = v[i];
- else if (v[i] > tail[length-1])
- tail[length++] = v[i];
- else
- tail[CeilIndex(tail, -1, length-1, v[i])] = v[i];
- }
- return length;
-}
-```
-
-其实现过程,可以通过一个例子说明。
-
-
-
-
-
-
-值得注意的是,根据LIS衍生出来的最长非递减序列,最长严格递减序列,其道理是一样的。
-
-### 问题延伸
-
-**最长连续递增子序列**
-
-* C++
-
-```cpp
-int lis(vector data) {
- int result = -1, temp = 1;
- for(int i = 1; i < data.size(); i++) {
- if(data[i-1] < data[i]) {
- temp++;
- if(temp > result)
- result = temp;
- } else {
- temp = 1;
- }
- }
- return result;
-}
-```
diff --git a/11_dynamic_programming/subset_sum.md b/11_dynamic_programming/subset_sum.md
deleted file mode 100644
index c6bf829..0000000
--- a/11_dynamic_programming/subset_sum.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 子集和问题
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析](#算法分析)
- * 3.[算法实现](#算法实现)
- * 4.[问题扩展](#问题扩展)
- * 4.1 [分区和相等](#分区和相等)
- * 4.2 [分区和差值最小](#分区和差值最小)
-
-### 问题定义
-
-给定一个非负整型数值集合set,和一个值sum。如果集合的某个子集的和等于这个值,则返回true,否则返回false。
-
-例如:集合为set = {12, 13, 4, 8, 5, 10}和sum = 9,那么SUM{4, 5} = 9,因此返回true。
-
-### 算法分析
-
-```
-SubSetSum(set, n, sum) = SubSetSum(set, n - 1, sum) || SubSetSum(set, n - 1, sum - set[n - 1])
-// 初始条件
-SubSetSum(set, n, sum) = true, if sum = 0;
-SubSetSum(set, n, sum) = false, if sum > 0 && n = 0;
-```
-
-### 算法实现
-
-* C++
-
-```cpp
-// 递归版
-bool SubSetSum(vector data, int n, int sum) {
- if(sum == 0)
- return true;
- if(sum != 0 && n == 0)
- return false;
- if(data[n-1] > sum)
- return SubSetSum(data, n - 1, sum);
- return SubSetSum(data, n - 1, sum) || SubSetSum(data, n - 1, sum - data[n - 1]);
-}
-```
-
-### 问题拓展
-
-### 分区和相等
-
-问题1:将一个集合分成两个和相等的子集
-
-给定一个非负整型集合,若能将其分为两个和相等的子集,则返回true,否则返回false。
-
-### 解法分析
-
-**问题1**
-
-第一步,首先计算集合中元素的总和,如果和为奇数则返回false;如果和为偶数,进行第二步判断。
-
-第二步,将上述算法中的sum,替换成sum/2即可。
-
-```
-bool SubSetSum(vector data, int n, int sum) {
- if(sum == 0)
- return true;
- if(sum != 0 && n == 0)
- return fasle;
- if(data[n - 1] > sum)
- return SubSetSum(data, n - 1, sum);
- return SubSetEqual(data, n - 1, sum) || SubSetEqual(data, n - 1, (sum - data[n - 1]));
-}
-bool SubSetEqual(vector data) {
- int sum = 0;
- for(int i = 0; i < data.size(); i++) {
- sum += data[i];
- }
- if((sum % 2) == 1)
- return false;
- else
- return SubSetSum(data, data.size(), sum / 2);
-}
-```
-
-### 分区和差值最小
-
-问题2:将一个集合分成两个和的差值最小的子集
-
-给定一个非负整型集合,将其分成两个和的差值最小的子集,并返回差值。
-
-**问题2**
diff --git a/12_sort/01_bubble_sort.md b/12_sort/01_bubble_sort.md
deleted file mode 100644
index 18e151c..0000000
--- a/12_sort/01_bubble_sort.md
+++ /dev/null
@@ -1,27 +0,0 @@
-## 冒泡排序
-
-冒泡排序(Bubble Sort)的思想是:
-
-每次比较两个相邻的两个元素,按照大小顺序进行交换,这样在一次的遍历中,可以将最大或最小的值交换值序列的最后一个。
-
-时间复杂度:O(n x n)
-
-空间复杂度:O(1)
-
-```go
-// 冒泡排序
-// 比较相邻的两个元素,把较大的交换至后面
-func bubbleSort(nums []int) []int {
- n := len(nums)
- for i := 0; i < n-1; i++ {
- for j := 0; j < n-1-i; j++ {
- if nums[j] > nums[j+1] {
- // swap
- nums[j], nums[j+1] = nums[j+1], nums[j]
- }
- }
- }
- return nums
-}
-```
-
diff --git a/12_sort/02_select_sort.md b/12_sort/02_select_sort.md
deleted file mode 100644
index 99daa6c..0000000
--- a/12_sort/02_select_sort.md
+++ /dev/null
@@ -1,32 +0,0 @@
-## 选择排序
-
-选择排序的思想是:
-
-每次选择未排序中的最值,将其放到已排序的尾部。
-
-优势:可就地替换,不占用额外空间
-
-时间复杂度:O(n x n)
-
-空间复杂度:O(1)
-
-```go
-// 选择排序
-func selectSort(nums []int) []int {
- n := len(nums)
-
- for i := 0; i < n; i++ {
- minIdx := i
- for j := i + 1; j < n; j++ {
- if nums[j] < nums[minIdx] {
- minIdx = j
- }
- }
- // swap
- nums[i], nums[minIdx] = nums[minIdx], nums[i]
- }
-
- return nums
-}
-```
-
diff --git a/12_sort/03_insert_sort.md b/12_sort/03_insert_sort.md
deleted file mode 100644
index 65da2ec..0000000
--- a/12_sort/03_insert_sort.md
+++ /dev/null
@@ -1,34 +0,0 @@
-## 插入排序
-
-插入排序的思想是:
-
-依次选择未排序的元素,将其插入到已排序的合适位置。
-
-```sh
-Loop from i = 1 to n-1.
- a) Pick element arr[i] and insert it into sorted sequence arr[0…i-1]
-```
-
-
-
-```go
-// 插入排序
-// 每次选择未排序的元素,将其插入到已排序的合适位置。
-func insertSort(nums []int) []int {
- n := len(nums)
-
- for i := 1; i < n; i++ {
- v := nums[i] // the unsort elem
- j := i - 1
- // find the last euqal or small than v
- for j >= 0 && nums[j] > v {
- nums[j+1] = nums[j]
- j--
- }
- nums[j+1] = v
- }
-
- return nums
-}
-```
-
diff --git a/12_sort/04_quick_sort.md b/12_sort/04_quick_sort.md
deleted file mode 100644
index 70211c1..0000000
--- a/12_sort/04_quick_sort.md
+++ /dev/null
@@ -1,124 +0,0 @@
-## Quick Sort \[快速排序\]
-
-### 算法介绍
-
-快速排序与归并排序均属于分治思想算法(Divide and Conquer algorithm),即选取一个基准值(pivot),然后将其他给定值置于基准值的左右,从而实现排序过程。基准值的选取可以有多种方式:
-
-1. 选取第一个元素作为基准值
-2. 选取最后一个元素作为基准值
-3. 随机选取一个元素作为基准值
-4. 选取中间值作为基准值
-
-快速排序算法的关键是partition()函数,其实现的目标是在给定的序列和基准值x的情况下,将基准值x放在正确的位置上,所有小于x的元素放在x的左边,所有大于等于x的元素放在x的右边。
-
-### 复杂度分析
-
-通常情况下,快速排序的时间复杂度可用如下公式表示:
-
-$T(n) = T(k) + T(n-k-1) + \theta(n)$
-
-其中,前两项表示递归调用,第三项表示分区过程(即,partition)。k代表序列中小于等于基准的元素个数。因此,快速排序的时间复杂度与 **待排序列** 和 **基准值的选取** 有关。下面分三种情况分别讨论:
-
-* 最差的情况
-
- 当分区过程总是选取最大或最小的元素作为基准值时,则发生最差的情况。此时,待排序列实际上已经是有序序列(递增,或递减)。因此,上述时间复杂度公式变为:
-
- $T(n) = T(0) + T(n-1) + \theta(n)$,即时间复杂度为$\theta(n^2)$
-
-* 最好的情况
-
- 当分区过程每次都能选出中间值作为基准值时,则发生最好的情况,此时,时间复杂度公式为:
-
- $T(n) = 2T(n/2) + \theta(n)$,即时间复杂度为 $\theta(nLogn)$
-
-* 一般情况
-
- 其时间复杂度为 $\theta(nLogn)$
-
-### 算法流程
-
-递归形式的快速排序的伪代码如下:
-
-```go
-// low-起始索引;high-结束索引
-quicksort(arry[], low, high) {
- if(low < high) {
- // pi是partition()产生的基准值的索引
- pi = partition(arry, low, high);
- quicksort(arry, low, pi - 1);
- quicksort(arry, pi + 1, high);
- }
-}
-```
-
-
-
-partition()函数实现序列的划分,其逻辑是:
-
-总是选取最左边的元素作为基准值x(也可以选取其他元素最为基准值),然后追踪小于基准值x的索引i;遍历整个序列,若当前元素小于基准值x,则交换当前值值与i所在的值,否则忽略当前值。其伪代码如下:
-
-```golang
-// 函数选取最后一个值作为基准值
-// 将所有小于等于基准值的元素放在基准值的左边,将所有大于基准值的元素放在基准值的右边
-// idx表示元素应该被放在的位置,for循环之后:区间[left, idx-1]均小于等于基准值,
-// 区间[idx, right-1]均大于基准值,再交换一次swap(idx, right)
-// 那么,区间[left, idx] 小于等于base,区间[idx+1, right] 大于base
-func quickSort2(nums []int, left, right int) []int {
- if left >= right {
- return nums
- }
- p := partition(nums, left, right)
- quickSort(nums, left, p-1)
- quickSort(nums, p+1, right)
- return nums
-}
-
-func partition(nums []int, left, right int) int {
- // select the right elem for base
- base := nums[right]
- idx := left // the idx for save equal or smaller than base
- for left < right {
- // loop,
- if nums[left] <= base {
- nums[idx], nums[left] = nums[left], nums[idx]
- idx++
- }
- left++
- }
- // now, the idx elem is large then base, so swap once
- nums[idx], nums[right] = nums[right], nums[idx]
- return idx
-}
-```
-
-```golang
-// 另一种实现方式
-func quickSort(nums []int, left, right int) {
- p := division(nums, left, right)
- quickSort(nums, left, p-1)
- quickSort(nums, p+1, right)
-}
-
-// partition 的另一种实现方式
-// 选取 left 作为基准base, 将数组分成小于和大于基准的两部分
-// 并返回 base 的新下标
-func division(nums []int, left, right int) int {
- base := nums[left]
- for left < right {
- // find the last small than base, and put is to left
- for left < right && nums[right] >= base {
- right--
- }
- nums[left] = nums[right]
- // find the first larger than base, and put it to right
- for left < right && nums[left] <= base {
- left++
- }
- nums[right] = nums[left]
-
- // save base to left
- nums[left] = base
- }
- return left
-}
-```
diff --git a/12_sort/05_merge_sort.md b/12_sort/05_merge_sort.md
deleted file mode 100644
index 25454b0..0000000
--- a/12_sort/05_merge_sort.md
+++ /dev/null
@@ -1,74 +0,0 @@
-## Merge Sort \[归并排序\]
-
- * 1.[算法介绍](#算法介绍)
- * 2.[代码实现](#代码实现)
- * 3.[复杂度分析](#复杂度分析)
- * 4.[归并算法的应用](#归并算法的应用)
-
-
-### 算法介绍
-
-与快速排序一样,归并排序也是采用分治思想。将待排序列分成两个子序列(直到不可再分),然后对两个子序列进行有序合并。merge()函数是归并排序的关键。
-
-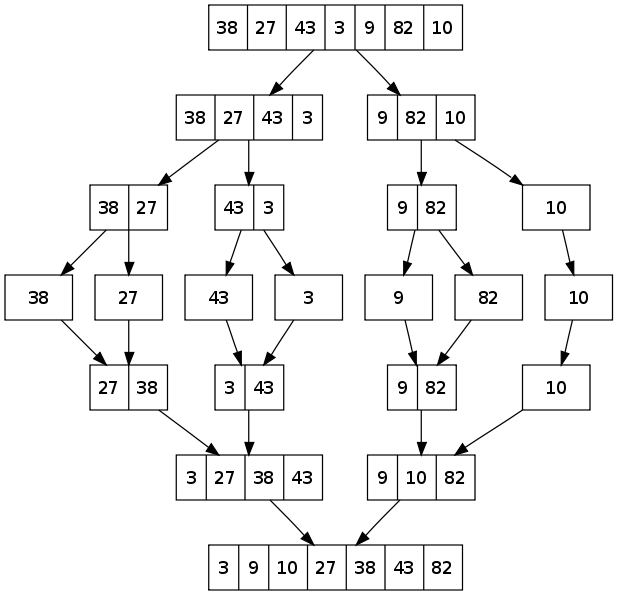
-
-### 代码实现
-
-根据归并算法的原理,很容易想到利用递归的方式进行实现,如下所示:
-
-```go
-// merge sort
-// 递归
-// 不断地对半拆分,直到子序列长度小于2(即有序)
-func mergeSort(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- mid := n / 2
- left := nums[0:mid]
- right := nums[mid:n]
- return merge(mergeSort(left), mergeSort(right))
-}
-
-// 将两个有序的数组合并成一个有序数组
-func merge(nums1, nums2 []int) []int {
- n1, n2 := len(nums1), len(nums2)
- ans := make([]int, 0, n1+n2)
- i, j := 0, 0
- for i < n1 && j < n2 {
- if nums1[i] <= nums2[j] {
- ans = append(ans, nums1[i])
- i++
- } else {
- ans = append(ans, nums2[j])
- j++
- }
- }
- if i < n1 {
- ans = append(ans, nums1[i:]...)
- }
- if j < n2 {
- ans = append(ans, nums2[j:]...)
- }
- return ans
-}
-```
-
-### 复杂度分析
-
-归并排序属于递归算法,其时间复杂度可用如下公式表示:
-
-$T(n) = 2T(n/2) + \theta(n)$
-
-因为归并排序总是将序列分成两个子序列,直到不可分解,然后在 **线性时间** 内进行合并。所以三种情况(最好,最坏,一般)的时间复杂度均是 $\theta(nLogn)$ 。
-
-从稳定性而言,归并排序比快速排序稳定。
-
-辅助空间需要O(n)。
-
-### 归并算法的应用
-
-* 线性表的归并排序
-
- 对于线性表而言,其与数组的主要区别在于并不需要申请内存空间,可以在O(1)的时间内和O(1)的空间内实现元素的插入。因此,对线性表进行归并排序,合并数据的过程不需要额外的辅助空间。
diff --git a/12_sort/06_counting_sort.md b/12_sort/06_counting_sort.md
deleted file mode 100644
index 24ffe73..0000000
--- a/12_sort/06_counting_sort.md
+++ /dev/null
@@ -1,50 +0,0 @@
-## 计数排序
-
-计数排序的思想是:
-
-将待排序数组的值转换为键存储在额外的数组空间。因为键是有序的,通过计数键出现的次数,将待排序的数组在复原出来。
-
-这是一种线性时间复杂度的排序,而且要求输入的数组必须是有确定范围的整数。
-
-
-
-时间复杂度为:O(n)
-
-空间复杂度为:O(n)
-
-如果输入数组的范围未知,需要先求一次最大值,找到数组的范围,这种情况下,其时间复杂度为:O(2N)
-
-
-
-```go
-// counting sort
-func countSort(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- // find the maxValue
- maxV := nums[0]
- for i := 1; i < n; i++ {
- if nums[i] > maxV {
- maxV = nums[i]
- }
- }
- cnt := make([]int, maxV+1, maxV+1)
- // counting the elem
- for _, v := range nums {
- cnt[v]++
- }
-
- idx := 0
- for i, ct := range cnt {
- for ct > 0 {
- nums[idx] = i
- idx++
- ct--
- }
- }
- return nums
-}
-```
-
diff --git a/12_sort/07_bucket_sort.md b/12_sort/07_bucket_sort.md
deleted file mode 100644
index 905a6d0..0000000
--- a/12_sort/07_bucket_sort.md
+++ /dev/null
@@ -1,89 +0,0 @@
-## 桶排序(bucket sort)
-
-桶排序是计数排序的升级版。
-
-其思想是通过映射函数将输入的 N 个数据均匀地分配到 K 个桶中,如果桶内有冲突,再对桶内元素进行排序。
-
-
-
-为了使桶排序更加高效,我们需要做到两点:
-
-1)在额外空间充足的情况下,尽可能增大桶的数量
-
-2)映射函数要能够将 N 个数据均匀地分配到 K 个桶中
-
-
-
-什么时候最快?
-
-当输入的数据可以均匀地分配到每一个桶中。
-
-什么时候最慢?
-
-当输入的数据哈希到同一个桶中。
-
-
-
-```go
-// 07 bucket sort
-func bucketSort(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- // find the min/max value
- minV, maxV := nums[0], nums[0]
- for _, v := range nums {
- if v < minV {
- minV = v
- }
- if v > maxV {
- maxV = v
- }
- }
-
- // bucket init
- bucketSize := 2
- bucket := make([][]int, (maxV-minV)/bucketSize+1)
- for i := 0; i < len(bucket); i++ {
- bucket[i] = make([]int, 0, 4)
- }
-
- // put elem to bucket
- // hash function = (nums[i] - minV) / bucketSize
- for _, v := range nums {
- bIdx := (v - minV) / bucketSize
- bucket[bIdx] = append(bucket[bIdx], v)
- }
-
- // sort bucket and put elem to nums
- idx := 0
- for _, buck := range bucket {
- if len(buck) != 0 {
- insertSort(buck)
- for _, v := range buck {
- nums[idx] = v
- idx++
- }
- }
- }
- return nums
-}
-
-func insertSortForBucket(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- for i := 1; i < n; i++ {
- v := nums[i]
- j := i - 1
- for j >= 0 && nums[j] > v {
- j--
- }
- nums[j+1] = v
- }
- return nums
-}
-```
-
diff --git "a/12_sort/No.16_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md" "b/12_sort/No.16_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index 90b4c93..0000000
--- "a/12_sort/No.16_\346\234\200\346\216\245\350\277\221\347\232\204\344\270\211\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,66 +0,0 @@
-## 16 最接近的三数之和-中等
-
-题目:
-
-给你一个长度为 `n` 的整数数组 `nums` 和 一个目标值 `target`。请你从 `nums` 中选出三个整数,使它们的和与 `target` 最接近。
-
-返回这三个数的和。
-
-假定每组输入只存在恰好一个解。
-
-
-
-分析:
-
-先排序,然后双指针。
-
-```go
-// date 2023/12/08
-func threeSumClosest(nums []int, target int) int {
- // sort and left, right
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- ans := math.MaxInt32
- n := len(nums)
- for i := 0; i < n; i++ {
- if i > 0 && nums[i] == nums[i-1] {
- continue
- }
- l, r := i+1, n-1
- for l < r {
- sum := nums[i] + nums[l] + nums[r]
- if sum == target {
- return sum
- }
- // update the ans
- if abs(ans, target) > abs(sum, target) {
- ans = sum
- }
- if sum > target {
- r--
- for l < r && nums[r] == nums[r-1] {
- r--
- }
- } else {
- l++
- for l < r && nums[l] == nums[l+1] {
- l++
- }
- }
- }
- }
-
-
- return ans
-}
-
-func abs(x, y int) int {
- if x > y {
- return x-y
- }
- return y-x
-}
-```
-
diff --git "a/12_sort/No.969_\347\205\216\351\245\274\346\216\222\345\272\217.md" "b/12_sort/No.969_\347\205\216\351\245\274\346\216\222\345\272\217.md"
deleted file mode 100644
index 0c383c2..0000000
--- "a/12_sort/No.969_\347\205\216\351\245\274\346\216\222\345\272\217.md"
+++ /dev/null
@@ -1,73 +0,0 @@
-## 969 煎饼排序-中等
-
-题目:
-
-给你一个整数数组 `arr` ,请使用 **煎饼翻转** 完成对数组的排序。
-
-一次煎饼翻转的执行过程如下:
-
-- 选择一个整数 `k` ,`1 <= k <= arr.length`
-- 反转子数组 `arr[0...k-1]`(**下标从 0 开始**)
-
-例如,`arr = [3,2,1,4]` ,选择 `k = 3` 进行一次煎饼翻转,反转子数组 `[3,2,1]` ,得到 `arr = [**1**,**2**,**3**,4]` 。
-
-以数组形式返回能使 `arr` 有序的煎饼翻转操作所对应的 `k` 值序列。任何将数组排序且翻转次数在 `10 * arr.length` 范围内的有效答案都将被判断为正确。
-
-
-
-分析:
-
-其核心就是寻找前 N 个中的最大值,通过两次反转,把最大值放到最后面。
-
-```go
-// date 2023/12/08
-func pancakeSort(arr []int) []int {
- n := len(arr)
- if n == 1 {
- return arr
- }
-
- ans := make([]int, 0, 16)
-
- var sort func(nums []int, total int)
-
- sort = func(nums []int, total int) {
- // find the maxV idx
- if total < 2 {
- return
- }
- maxIdx := 0
- maxV := nums[0]
- for i := 0; i < total; i++ {
- if nums[i] > maxV {
- maxIdx = i
- maxV = nums[i]
- }
- }
- // 如果 max 是最后一个,说明不需要反转,直接往前递归
- if maxIdx == total-1 {
- sort(nums, total-1)
- return
- }
- // 两次反转,然后递归
- ans = append(ans, maxIdx+1)
- ans = append(ans, total)
- reverse(nums, 0, maxIdx)
- reverse(nums, 0, total-1)
- sort(nums, total-1)
- }
-
- sort(arr, n)
-
- return ans
-}
-
-func reverse(nums []int, left, right int) {
- for left < right {
- nums[left], nums[right] = nums[right], nums[left]
- left++
- right--
- }
-}
-```
-
diff --git a/12_sort/README.md b/12_sort/README.md
deleted file mode 100644
index 1efb9f6..0000000
--- a/12_sort/README.md
+++ /dev/null
@@ -1,182 +0,0 @@
-## 排序算法
-
-### 1 冒泡排序
-
-冒泡排序(Bubble Sort)的思想是:
-
-每次比较两个相邻的两个元素,按照大小顺序进行交换,这样在一次的遍历中,可以将最大或最小的值交换值序列的最后一个。
-
-时间复杂度:O(n x n)
-
-空间复杂度:O(1)
-
-```go
-// 冒泡排序
-// 比较相邻的两个元素,把较大的交换至后面
-func bubbleSort(nums []int) []int {
- n := len(nums)
- for i := 0; i < n-1; i++ {
- for j := 0; j < n-1-i; j++ {
- if nums[j] > nums[j+1] {
- // swap
- nums[j], nums[j+1] = nums[j+1], nums[j]
- }
- }
- }
- return nums
-}
-```
-
-
-
-### 2 插入排序
-
-插入排序的思想是:
-
-依次选择未排序的元素,将其插入到已排序的合适位置。
-
-```go
-// 插入排序
-// 每次选择未排序的元素,将其插入到已排序的合适位置。
-func insertSort(nums []int) []int {
- n := len(nums)
-
- for i := 1; i < n; i++ {
- v := nums[i] // the unsort elem
- j := i - 1
- // find the last euqal or small than v
- for j >= 0 && nums[j] > v {
- nums[j+1] = nums[j]
- j--
- }
- nums[j+1] = v
- }
-
- return nums
-}
-```
-
-
-
-### 3 选择排序
-
-选择排序的思想是:
-
-每次选择未排序中的最值,将其放到已排序的尾部。
-
-优势:可就地替换,不占用额外空间
-
-时间复杂度:O(n x n)
-
-空间复杂度:O(1)
-
-```go
-// 选择排序
-func selectSort(nums []int) []int {
- n := len(nums)
-
- for i := 0; i < n; i++ {
- minIdx := i
- for j := i + 1; j < n; j++ {
- if nums[j] < nums[minIdx] {
- minIdx = j
- }
- }
- // swap
- nums[i], nums[minIdx] = nums[minIdx], nums[i]
- }
-
- return nums
-}
-```
-
-
-
-### 4 归并排序
-
-归并排序(merge sort)是建立在归并操作上的一种有效的排序算法。该算法是分治思想的一个典型应用。
-
-其思想是:
-
-1. 将待排序数组不断地进行折半分开,直到不能再分(即每一小段是有序的)
-
-2. 将 1 中每个有序的小段合并起来
-
-因为折半拆分,其时间复杂度是O(nlogn)。代价是需要额外的空间保存结果。
-
-```go
-// merge sort
-func mergeSort(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- mid := n / 2
- left := nums[0:mid]
- right := nums[mid:n]
- return merge(mergeSort(left), mergeSort(right))
-}
-
-func merge(nums1, nums2 []int) []int {
- n1, n2 := len(nums1), len(nums2)
- ans := make([]int, 0, n1+n2)
- i, j := 0, 0
- for i < n1 && j < n2 {
- if nums1[i] <= nums2[j] {
- ans = append(ans, nums1[i])
- i++
- } else {
- ans = append(ans, nums2[j])
- j++
- }
- }
- if i < n1 {
- ans = append(ans, nums1[i:]...)
- }
- if j < n2 {
- ans = append(ans, nums2[j:]...)
- }
- return ans
-}
-```
-
-
-
-### 快速排序
-
-
-
-```go
-func quickSort(nums []int, left, right int) []int {
- if left >= right {
- return nums
- }
- p := division(nums, left, right)
- quickSort(nums, left, p-1)
- quickSort(nums, p+1, right)
- return nums
-}
-
-// 选取 left 作为基准base, 将数组分成小于和大于基准的两部分
-// 并返回 base 的新下标
-func division(nums []int, left, right int) int {
- base := nums[left]
- for left < right {
- // find the last small than base, and put is to left
- for left < right && nums[right] >= base {
- right--
- }
- nums[left] = nums[right]
- // find the first larger than base, and put it to right
- for left < right && nums[left] <= base {
- left++
- }
- nums[right] = nums[left]
-
- // save base to left
- nums[left] = base
- }
- return left
-}
-```
-
diff --git a/12_sort/images/bucket_sort.png b/12_sort/images/bucket_sort.png
deleted file mode 100644
index 42d8ec0..0000000
Binary files a/12_sort/images/bucket_sort.png and /dev/null differ
diff --git a/12_sort/mergesort_linkedlist.md b/12_sort/mergesort_linkedlist.md
deleted file mode 100644
index f1f0a9f..0000000
--- a/12_sort/mergesort_linkedlist.md
+++ /dev/null
@@ -1,87 +0,0 @@
-## 对线性表进行归并排序
-
- * 1.[算法流程](#算法流程)
- * 2.[代码实现](#代码实现)
-
-### 算法流程
-
-归并排序通常是线性表(即,链表)排序的优先选择算法。链表的慢随机访问特性使得某些排序算法(比如,快速排序)的执行效率偏低,也使得某些算法(比如,堆排序)难以实现。
-
-链表的归并排序伪代码如下:
-
-```
-// Head is the head node of a linked list
-MergeSort(Head)
-1. 如果头节点为空或只有一个节点,则返回
-2. 其次,将链表分成两个子链表
- Split(Head, &a, &b); // a, b分别为两个子链表
-3. 对两个子链表进行归并排序
- MergeSort(a);
- MergeSort(b);
-4. 合并已经排序的a, b两个子链表,并更新头节点
- *Head = Merge(a, b);
-```
-
-时间复杂度为:O(nLogn)
-
-### 代码实现
-
-* C++
-
-```
-struct Node{
- int val;
- struct Node* next;
-}
-struct Node* Merge(struct Node* a, struct Node* b);
-void Split(struct Node* head, struct Node** front, struct Node** back);
-void MergeSort(struct Node** head) {
- struct Node* phead = *head;
- struct Node* a;
- struct Node* b;
- if(phead == NULL | phead->next == NULL)
- return;
- Split(head, &a, &b);
- MergeSort(&a);
- MergeSort(&b);
- *head = Merge(a, b);
-}
-
-struct Node* Merge(struct Node* a, struct Node* b) {
- struct Node* result = NULL;
- if(a == NULL)
- return b;
- else if (b == NULL)
- return a;
- if(a->val <= b->val) {
- result = a;
- result->next = Merge(a->next, b);
- } else {
- result = b;
- result->next = Merge(a, b->next);
- }
- return result;
-}
-
-void Split(struct Node* head, struct Node** front, struct Node** back) {
- struct Node* fast;
- struct Node* slow;
- if(head == NULL | head->next == NULL) {
- *front = head;
- *back = NULL;
- } else {
- slow = head;
- fast = head->next;
- while(fast != NULL) {
- fast = fast->next;
- if(fast != NULL) {
- slow = slow->next;
- fast = fast->next;
- }
- }
- *front = head;
- *back = slow->next;
- slow->next = NULL;
- }
-}
-```
diff --git a/12_sort/orderstatistic.md b/12_sort/orderstatistic.md
deleted file mode 100644
index 1620053..0000000
--- a/12_sort/orderstatistic.md
+++ /dev/null
@@ -1,68 +0,0 @@
-## Order Statistc [顺序统计]
-
- * 1.[问题定义](#问题定义)
- * 2.[算法分析](#算法分析)
- * 2.1[一般解法](#一般解法)
- * 2.2[随机快速排序](#随机快速排序)
- * 2.3[最优解法](#最优解法)
-
-### 问题定义
-
-```
-K’th Smallest/Largest Element in Unsorted Array.
-即,给定一组未排序序列,输出其中第K个最大(最小)元素。
-```
-该问题是对排序算法的延伸和扩展。
-
-### 算法分析
-
-对于这个问题,其一般思路就是先对数据进行排序,然后输出对应的Kth最大(最小)值。因此,排序算法是这个问题的关键。
-
-### 一般解法
-
-一个比较简单的解法,就是选取一个复杂度为O(nLogn)的排序算法(比如快速排序,归并排序,堆排序等)对数据进行排序,然后输出第k个元素。
-
-时间复杂度为:O(nLogn)
-
-### 随机快速排序
-
-快速排序中基准值的选取有三种方式,即首元素,尾元素,和随机元素。因此,我们选择随机选取基准的方式,实现快速排序中的分区部分,具体实现如下:
-
-* C++
-
-```
-int randpartitioin(vector &data, int low, int high) {
- int n = high - low + 1;
- int pivot = rand() % n;
- int temp = data[pivot];
- while(low < high) {
- while(low < high && data[high] >= temp) high--;
- data[pivot] = data[high];
- while(low < high && data[low] <= temp) low++;
- data[high] = data[low];
- data[low] = temp;
- }
- return low;
-}
-int KthSmallest(vector &data, int low, int high, int k) {
- if(k > 0 && k <= high - low + 1) {
- int pos = randpartitioin(data, low, high);
- if(pos - low == k - 1)
- return data[pos];
- if(pos - low > k - 1)
- return KthSmallest(data, low, pos - 1, k);
- else
- return KthSmallest(data, pos, high, k - pos + low -1);
- } else {
- return -1;
- }
-}
-```
-
-最坏的情况下,时间复杂度为O(nLogn),即每次随机选取的基准值刚好是序列中的最值。一般情况下,其 **预期时间复杂度为O(n)**。
-
-### 最优解法
-
-在解法二的基础上,考虑基准值选取的平衡性,即每次选出的基准值尽量保证左右两个子序列元素个数的相差不多。
-
-这样的解法,即是最坏的情况下,时间复杂度也是O(n)。
diff --git a/12_sort/sort.md b/12_sort/sort.md
deleted file mode 100644
index 86c3eaa..0000000
--- a/12_sort/sort.md
+++ /dev/null
@@ -1,588 +0,0 @@
-## 排序算法
-
-### Quick Sort \[快速排序\]
-
- * 1.[算法介绍](#算法介绍)
- * 2.[复杂度分析](#复杂度分析)
- * 3.[算法流程](#算法流程)
-
-### 算法介绍
-
-快速排序与归并排序均属于分治思想算法(Divide and Conquer algorithm),即选取一个基准值(pivot),然后将其他给定值置于基准值的左右,从而实现排序过程。基准值的选取可以有多种方式:
-
-1. 选取第一个元素作为基准值
-2. 选取最后一个元素作为基准值
-3. 随机选取一个元素作为基准值
-4. 选取中间值作为基准值
-
-快速排序算法的关键是partition()函数,其实现的目标是在给定的序列和基准值x的情况下,将基准值x放在正确的位置上,所有小于x的元素放在x的左边,所有大于等于x的元素放在x的右边。
-
-### 复杂度分析
-
-通常情况下,快速排序的时间复杂度可用如下公式表示:
-
-$T(n) = T(k) + T(n-k-1) + \theta(n)$
-
-其中,前两项表示递归调用,第三项表示分区过程(即,partition)。k代表序列中小于等于基准的元素个数。因此,快速排序的时间复杂度与 **待排序列** 和 **基准值的选取** 有关。下面分三种情况分别讨论:
-
-* 最差的情况
-
- 当分区过程总是选取最大或最小的元素作为基准值时,则发生最差的情况。此时,待排序列实际上已经是有序序列(递增,或递减)。因此,上述时间复杂度公式变为:
-
- $T(n) = T(0) + T(n-1) + \theta(n)$,即时间复杂度为$\theta(n^2)$
-
-* 最好的情况
-
- 当分区过程每次都能选出中间值作为基准值时,则发生最好的情况,此时,时间复杂度公式为:
-
- $T(n) = 2T(n/2) + \theta(n)$,即时间复杂度为 $\theta(nLogn)$
-
-* 一般情况
-
- 其时间复杂度为 $\theta(nLogn)$
-
-### 算法流程
-
-递归形式的快速排序的伪代码如下:
-
-```golang
-// low-起始索引;high-结束索引
-quicksort(arry[], low, high) {
- if(low < high) {
- // pi是partition()产生的基准值的索引
- pi = partition(arry, low, high);
- quicksort(arry, low, pi - 1);
- quicksort(arry, pi + 1, high);
- }
-}
-```
-
-partition()函数实现序列的划分,其逻辑是总是选取最左边的元素作为基准值x(也可以选取其他元素最为基准值),然后追踪小于基准值x的索引i;遍历整个序列,若当前元素小于基准值x,则交换当前值值与i所在的值,否则忽略当前值。其伪代码如下:
-
-```golang
-// 函数选取最后一个值作为基准值
-// 将所有小于等于基准值的元素放在基准值的左边,将所有大于基准值的元素放在基准值的右边
-// index表示元素应该被放在的位置,for循环之后区间[left, index]均小于基准值,区间[index+1, right]均大于基准值,再交换一次swap(index+1, right)
-// 则index+1为基准值,区间[index+2, right]为大于等于基准值
-// 最后返回基准值的位置index+1
-partition(nums []int, left, right int) {
- p := nums[right]
- index := left - 1
- for left <= right-1 {
- if nums[left] <= p {
- index++
- swap(nums, index, left)
- }
- left++
- }
- swap(nums, index+1, rigth)
- return index+1
-}
-```
-
-```golang
-// 另一种实现方式
-func quickSort(nums []int, left, right int) {
- p := division(nums, left, right)
- quickSort(nums, left, p-1)
- quickSort(nums, p+1, right)
-}
-
-func division(nums []int, left, right int) int {
- base := nums[left]
- for left < right {
- for left < right && nums[right] >= base { right-- }
- nums[left] = nums[right]
- for left < right && nums[left] <= base { left++ }
- nums[right] = nums[left]
- nums[left] = base
- }
- return left
-}
-```
-
-### Merge Sort \[归并排序\]
-
- * 1.[算法介绍](#算法介绍)
- * 2.[代码实现](#代码实现)
- * 3.[复杂度分析](#复杂度分析)
- * 4.[归并算法的应用](#归并算法的应用)
-
-### 算法介绍
-
-与快速排序一样,归并排序也是采用分治思想。将待排序列分成两个子序列(直到不可再分),然后对两个子序列进行有序合并。merge()函数是归并排序的关键。
-
-
-
-### 代码实现
-
-根据归并算法的原理,很容易想到利用递归的方式进行实现,如下所示:
-
-* C++
-
-```cpp
-// 将两个有序序列合并成一个序列
-// 需要使用辅助空间
-void merge(vector &data, int first, int mid, int last) {
- int i = first, j = mid + 1;
- vector temp;
- while(i <= mid && j <= last) {
- if(data[i] <= data[j])
- temp.push_back(data[i++]);
- else
- temp.push_back(data[j++]);
- }
- while(i <= mid)
- temp.push_back(data[i++]);
- while(j <= last)
- temp.push_back(data[j++]);
- for(int k = 0; k < temp.size(); k++)
- data[first + k] = temp[k];
- return;
-}
-void mergesort(vector &data, int first, int last) {
- if(first < last) {
- int mid = first + (last - first) / 2;
- mergesort(data, first, mid);
- mergesort(data, mid + 1, last);
- mergedata(data, first, mid, last);
- }
- return;
-}
-```
-
-* python
-
-```python
-def merge(left,right):
- result=[]
- i,j=0,0
- while i intervals[i+1][0] {
- return false
- }
- }
- return true
-}
-```
-
-#### 280 摆动排序
-
-题目要求:给定数组,要求使其奇数位上的元素都大于其两边的元素值。
-
-思路分析:遍历一遍,逐个纠正。
-
-```go
-// date 2020/02/28
-func wiggleSort(nums []int) {
- var t int
- for i := 0; i < len(nums)-1; i++ {
- if (i & 0x1 == 0) == (nums[i] > nums[i+1]) {
- t = nums[i+1]
- nums[i+1] = nums[i]
- nums[i] = t
- }
- }
-}
-```
-
-
-
-#### 56 合并区间
-
-思路分析
-
-算法:先对区间进行排序;维护start, end值,注意处理最后一个
-
-```go
-func merge(intervals [][]int) [][]int {
- if len(intervals) <= 1 {return intervals}
- sort.Slice(intervals, func(i, j int) bool {
- return intervals[i][0] < intervals[j][0]
- })
- res, i, n := make([][]int, 0), 0, len(intervals) // i保存当前start索引
- // init start, end
- start, end := intervals[0][0], intervals[0][1]
- for i < n {
- i++
- // 查找以start开始的最大区间,并更新end值
- for i < n {
- if intervals[i][1] <= end || intervals[i][0] <= end {
- if intervals[i][1] > end { end = intervals[i][1] }
- i++
- } else { break }
- }
- t := make([]int, 2)
- t[0], t[1] = start, end
- res = append(res, t)
- // i >= n 说明处理完毕,直接退出
- if i >= n {break}
- // update start, end
- start, end = intervals[i][0], intervals[i][1]
- }
-}
-```
-
-#### 912 排序数组
-
-##### 快速排序
-
-快速排序的思想是分治算法,partition将数组分成两个子数组,如果两个子数组有序,则这个数组有序。
-
-```go
-// date 2020/03/01
-func sortArray(nums []int) []int {
- if len(nums) == 1 { return nums }
- QuickSort(nums, 0, len(nums)-1)
- return nums
-}
-
-// 快速排序
-// 返回值为index
-func partition(nums []int, l, r int) int {
- p := nums[l]
- index := l
- for i := l; i <= r; i++ {
- if nums[i] <= p {
- swap(nums, index, i)
- index++
- }
- }
- swap(nums, l, index-1)
- return index-1
-}
-
-func QuickSort(nums []int, l, r int) {
- if l >= r { return }
- p := partition(nums, l, r)
- QuickSort(nums, l, p-1)
- QuickSort(nums, p+1, r)
-}
-func swap(nums []int, i, j int) {
- t := nums[i]
- nums[i] = nums[j]
- nums[j] = t
-}
-// 第二种写法
-// partition选最右边的值作为基准值
-func partition(nums []int, left, right int) int {
- // index维护小于基准值的下标
- index, p := left-1, nums[right]
- for left < right {
- if nums[left] < p {
- index++
- swap(nums, index, left)
- }
- left++
- }
- // 将基准值放在index+1上
- swap(nums, index+1, right)
- return index+1
-}
-```
-
-
-
-##### 选择排序
-
-思路分析:选择未排序数组中最小的一个,然后交换值应该所在的位置。时间复杂度O(n^2) 空间复杂度O(1)
-
-```go
-func selectSort(nums []int) {
- n := len(nums)
- for i := 0; i < n; i++ {
- for j := i+1; j < n; j++ {
- if nums[i] > nums[j] {
- swap(nums, i, j)
- }
- }
- }
-}
-func swap(nums []int, i, j int) {
- nums[i], nums[j] = nums[j], nums[i]
-}
-```
-
-##### 插入排序
-
-算法逻辑:一个元素肯定是有序的,然后依次遍历剩下的元素,将其插入到前面已排序的数组的中。
-
-时间复杂度O(n^2) 空间复杂度O(1)
-
-```go
-func insertSort(nums []int) {
- temp, k := 0, 0
- for i := 1; i < len(nums); i++ {
- temp, k = nums[i], i-1
- for k > 0 && nums[k] > temp {
- nums[k+1] = nums[k]
- k--
- }
- nums[k+1] = temp
- }
-}
-```
-
-##### 希尔排序
-
-算法思想
-
-插入排序的思想是使数组相邻的两个元素有序,而希尔排序是使数组中任意间隔为h的元素有序,然后h不断减小,又称为插入排序的快速排序。
-
-```go
-func sortArray(nums []int) []int {
- n, h := len(nums), 1
- for h < n/3 { h = 3*h + 1}
- for h >= 1 {
- for i := h; i < n; i++ {
- for j := i; j >= h && nums[j] < nums[j-h]; j -= h {
- nums[j], nums[j-h] = nums[j-h], nums[j]
- }
- }
- h /= 3
- }
-}
-```
-
-##### 归并排序
-
-算法思想
-
-如果两个数组有序,可以通过归并的方式将其合并成一个有序的数组。
-
-```go
-// date 2020/01/05
-// 自顶向下的归并排序,递归
-// 时间复杂度O(nlgn)
-func sortArray(nums []int) []int {
- if len(nums) < 2 { return nums }
- mid := len(nums) >> 1
- l := sortArray(nums[:mid])
- r := sortArray(nums[mid:])
- return merge(l, r)
-}
-
-// 归并排序
-// 归并排序的merge算法
-func merge(a1, a2 []int) []int {
- if len(a1) == 0 { return a2 }
- if len(a2) == 0 { return a1 }
- n1, n2 := len(a1), len(a2)
- n := n1 + n2
- res := make([]int, n)
- i, j := 0, 0
- for k := 0; k < n; k++ {
- if i >= n1 {
- res[k] = a2[j]
- j++
- } else if j >= n2 {
- res[k] = a1[i]
- i++
- } else if a1[i] < a2[j] {
- res[k] = a1[i]
- i++
- } else {
- res[k] = a2[j]
- j++
- }
- }
- return res
-}
-```
-
-##### 堆排序
-
-算法思想:使用大顶堆
-
-```golang
-func sortArray(nums []int) []int {
- makeMaxHeap(nums)
- n := len(nums)
- for n > 0 {
- swap(nums, 0, n-1)
- n--
- maxHeapify(nums, 0, n)
- }
- return nums
-}
-
-// 堆排序
-// 构建大顶堆
-func makeMaxHeap(nums []int) {
- for i := len(nums) >> 1 - 1; i >= 0; i-- {
- maxHeapify(nums, i, len(nums))
- }
-}
-// 自上而下的堆有序化
-func maxHeapify(nums []int, start, end int) {
- if start > end { return }
- temp, l, r := nums[start], start << 1 + 1, start << 1 + 2
- for l < end {
- // 找到左右结点的最大值,并记录在l中
- r = l + 1
- if r < end && nums[r] > nums[l] { l++ }
- // 如果父节点大于左右中的最大节点,则跳出
- if nums[start] > nums[l] { break }
- // 否则将最大值更新到父节点
- nums[start] = nums[l]
- nums[l] = temp
- // 接着往下调整
- start = l
- l = start << 1 + 1
- }
-}
-// swap
-func swap(nums []int, i, j int) {
- t := nums[i]
- nums[i] = nums[j]
- nums[j] = t
-}
-```
-
-#### 922 按奇偶排序数组II【E】
-
-思路分析:记录每个不"在位"的索引,然后统一调整。注意不能两两依次调整,因为前后两个”不在位“的原因可以一样。
-
-```go
-// date 2020/02/28
-func sortArrayByParityII(A []int) []int {
- p1, p2 := make([]int, 0), make([]int, 0)
- for i := 0; i < len(A); i++ {
- if i & 0x1 == 0 && A[i] & 0x1 != 0 { p1 = append(p1, i) }
- if i & 0x1 == 1 && A[i] & 0x1 != 1 { p2 = append(p2, i) }
- }
- i, n := 0, len(p1)
- var t int
- for i < n {
- t = A[p1[i]]
- A[p1[i]] = A[p2[i]]
- A[p2[i]] = t
- i++
- }
- return A
-}
-```
-
-
-
-#### 1086 前五科的均分
-
-思路分析:先对id排序,再对成绩排序。
-
-```go
-// date 2020/02/28
-func highFive(items [][]int) [][]int {
- sort.Slice(items, func(i, j int) bool {
- if items[i][0] == items[j][0] {
- return items[i][1] > items[j][1] // 对成绩降序排序
- }
- return items[i][0] < items[j][0] // 对id升序排序
- })
- res, id, temp, c := make([][]int, 0), items[0][0], 0, 0
- for _, it := range items {
- if it[0] == id && c < 5 {
- temp += it[1]
- k++
- if k == 5 {
- r := make([]int, 2)
- r[0], r[1] = id, temp/5
- res = append(res, r)
- }
- } else if it[0] != id {
- id = it[0]
- temp = it[1]
- k = 1
- }
- }
- return res
-}
-```
-
-
-
-#### 1356 根据数字二进制下1的数目排序
-
-算法分析:求一个数字的二进制下2的个数。
-
-```go
-// date 2020/02/28
-// 暴力解法
-func sortByBits(arr []int) []int {
- sort.Slice(arr, func(i, j int) bool {
- if bits(arr[i]) == bits(arr[j]) {
- return arr[i] < arr[j]
- }
- return bits(arr[i]) < bits(arr[j])
- })
- return arr
-}
-func bits(x int) int {
- res := 0
- for x > 0 {
- res += x & 0x1
- x >>= 1
- }
- return res
-}
-```
-
-
-
diff --git "a/13_backtrack/No.017_\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md" "b/13_backtrack/No.017_\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
deleted file mode 100644
index 92ddb66..0000000
--- "a/13_backtrack/No.017_\347\224\265\350\257\235\345\217\267\347\240\201\347\232\204\345\255\227\346\257\215\347\273\204\345\220\210.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 17 电话号码的字母组合-中等
-
-题目:
-
-给定一个仅包含数字 `2-9` 的字符串,返回所有它能表示的字母组合。答案可以按 **任意顺序** 返回。
-
-给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
-
-
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:digits = "23"
-> 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:digits = ""
-> 输出:[]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:digits = "2"
-> 输出:["a","b","c"]
-> ```
-
-
-
-分析:
-
-这个题目并不算严格意义上的回溯,一般的 DFS 即可。
-
-把每个数字代表的字母形成不同的数组,存放在 map 里。
-
-正序遍历数字组合,然后深度优先搜索;当数字组合为空时,即找到一个答案,追加到结果集。
-
-
-
-```go
-// date 2023/12/25
-func letterCombinations(digits string) []string {
- res := make([]string, 0, 16)
-
- if len(digits) == 0 {
- return res
- }
-
- chars := map[string][]string{
- "2": []string{"a", "b", "c"},
- "3": []string{"d", "e", "f"},
- "4": []string{"g", "h", "i"},
- "5": []string{"j", "k", "l"},
- "6": []string{"m", "n", "o"},
- "7": []string{"p", "q", "r", "s"},
- "8": []string{"t", "u", "v"},
- "9": []string{"w", "x", "y", "z"},
- }
-
- var backtrack func(digs string, temp string)
- backtrack = func(digs string, temp string) {
- if len(digs) == 0 {
- res = append(res, temp)
- return
- }
- v := string(digs[0])
- all, ok := chars[v]
- if ok {
- for _, s := range all {
- backtrack(string(digs[1:]), temp + s)
- }
- }
- }
-
- backtrack(digits, "")
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.022_\346\213\254\345\217\267\347\224\237\346\210\220.md" "b/13_backtrack/No.022_\346\213\254\345\217\267\347\224\237\346\210\220.md"
deleted file mode 100644
index 9725c35..0000000
--- "a/13_backtrack/No.022_\346\213\254\345\217\267\347\224\237\346\210\220.md"
+++ /dev/null
@@ -1,63 +0,0 @@
-## 22 括号生成-中等
-
-题目:
-
-数字 `n` 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 **有效的** 括号组合。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:n = 3
-> 输出:["((()))","(()())","(())()","()(())","()()()"]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:n = 1
-> 输出:["()"]
-> ```
-
-
-
-分析:
-
-这道题并不需要判断括号的匹配问题,因为在 DFS 回溯的过程中,我们可以控制让`(`和`)`成对的匹配上。
-
-具体怎么做呢?
-
-1. 函数的执行顺序,先左后右,即先添加左括号,后添加右括号
-2. 添加右括号的时候,左括号的添加个数一定要大于右括号
-
-
-
-```go
-// date 2023/12/26
-func generateParenthesis(n int) []string {
- res := make([]string, 0, 16)
-
- var backtrack func(left, right int, temp string)
- backtrack = func(left, right int, temp string) {
- if left == 0 && right == 0 {
- res = append(res, temp)
- return
- }
-
- if left > 0 {
- backtrack(left-1, right, temp+"(")
- }
- // left < right 保证左括号个数大于右括号个数
- if right > 0 && left < right {
- backtrack(left, right-1, temp+")")
- }
- }
-
- backtrack(n, n, "")
-
- return res
-}
-```
-
-
\ No newline at end of file
diff --git "a/13_backtrack/No.039_\347\273\204\345\220\210\346\200\273\345\222\214.md" "b/13_backtrack/No.039_\347\273\204\345\220\210\346\200\273\345\222\214.md"
deleted file mode 100644
index 806119d..0000000
--- "a/13_backtrack/No.039_\347\273\204\345\220\210\346\200\273\345\222\214.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 39 组合总和-中等
-
-题目:
-
-给你一个 **无重复元素** 的整数数组 `candidates` 和一个目标整数 `target` ,找出 `candidates` 中可以使数字和为目标数 `target` 的 所有 **不同组合** ,并以列表形式返回。你可以按 **任意顺序** 返回这些组合。
-
-`candidates` 中的 **同一个** 数字可以 **无限制重复被选取** 。如果至少一个数字的被选数量不同,则两种组合是不同的。
-
-对于给定的输入,保证和为 `target` 的不同组合数少于 `150` 个。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:candidates = [2,3,6,7], target = 7
-> 输出:[[2,2,3],[7]]
-> 解释:
-> 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
-> 7 也是一个候选, 7 = 7 。
-> 仅有这两种组合。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: candidates = [2,3,5], target = 8
-> 输出: [[2,2,2,2],[2,3,3],[3,5]]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入: candidates = [2], target = 1
-> 输出: []
-> ```
-
-
-
-分析:
-
-这道题可以说是很经典的回溯算法,其代码框架是标准的模板。
-
-理解回溯的三大要素:
-
-1)结束条件
-
-2)候选列表
-
-3)已经选择的路径
-
-```go
-// date 2023/12/26
-func combinationSum(candidates []int, target int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(nums []int, idx, target int, temp []int)
- backtrack = func(nums []int, idx, target int, temp []int) {
- if target <= 0 {
- if target == 0 {
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
- }
- return
- }
- for i := idx; i < len(nums); i++ {
- if nums[i] > target {
- break
- }
- temp = append(temp, nums[i]) // nums[i] 加入候选
- backtrack(nums, i, target-nums[i], temp) // 因为元素可以重复选取,所以传递的是i,而不是i+1
- temp = temp[:len(temp)-1] // 取消 nums[i] 的候选
- }
- }
-
- sort.Slice(candidates, func(i, j int) bool {
- return candidates[i] < candidates[j]
- })
-
- backtrack(candidates, 0, target, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.040_\347\273\204\345\220\210\346\200\273\345\222\2142.md" "b/13_backtrack/No.040_\347\273\204\345\220\210\346\200\273\345\222\2142.md"
deleted file mode 100644
index 16e12ab..0000000
--- "a/13_backtrack/No.040_\347\273\204\345\220\210\346\200\273\345\222\2142.md"
+++ /dev/null
@@ -1,93 +0,0 @@
-## 40 组合总和2-中等
-
-题目:
-
-给定一个候选人编号的集合 `candidates` 和一个目标数 `target` ,找出 `candidates` 中所有可以使数字和为 `target` 的组合。
-
-`candidates` 中的每个数字在每个组合中只能使用 **一次** 。
-
-**注意:**解集不能包含重复的组合。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: candidates = [10,1,2,7,6,1,5], target = 8,
-> 输出:
-> [
-> [1,1,6],
-> [1,2,5],
-> [1,7],
-> [2,6]
-> ]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: candidates = [2,5,2,1,2], target = 5,
-> 输出:
-> [
-> [1,2,2],
-> [5]
-> ]
-> ```
-
-
-
-分析:
-
-这道题是 39 题的强化版,其强化条件是 每个数字在组合中只能使用一次。
-
-这意味,如果原数组中的数字不重复,那么回溯递归的时候要往下一个元素去找。
-
-如果原数组的数字有重复,那么重复的数字只能使用有限次。
-
-所以去重的逻辑很关键,在什么时候去重。
-
-```go
-// date 2023/12/26
-func combinationSum2(candidates []int, target int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(nums []int, target, idx int, temp []int)
- backtrack = func(nums []int, target, idx int, temp []int) {
- if target <= 0 {
- if target == 0 {
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
- }
- return
- }
- for i := idx; i < len(nums); i++ {
- // 这里还没有进入递归回溯的函数
- // 所以,也就是说,nums[i] 已经搜索以后
- // 如果存在重复,则跳过
- // 即对于重复的3个元素,取第一个元素的回溯结果,
- // 剩下的两个直接跳过,避免结果集中重复
- if i > idx && nums[i] == nums[i-1] {
- continue
- }
- // 剪枝
- if nums[i] > target {
- break
- }
- temp = append(temp, nums[i])
- // 元素只能使用一次,从 i+1 开始搜索
- backtrack(nums, target-nums[i], i+1, temp)
- temp = temp[:len(temp)-1]
- }
- }
-
- sort.Slice(candidates, func(i, j int) bool {
- return candidates[i] < candidates[j]
- })
-
- backtrack(candidates, target, 0, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.046_\345\205\250\346\216\222\345\210\227.md" "b/13_backtrack/No.046_\345\205\250\346\216\222\345\210\227.md"
deleted file mode 100644
index a83ebd4..0000000
--- "a/13_backtrack/No.046_\345\205\250\346\216\222\345\210\227.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 46 全排列-中等
-
-题目:
-
-给定一个不含重复数字的数组 `nums` ,返回其 *所有可能的全排列* 。你可以 **按任意顺序** 返回答案。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,2,3]
-> 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0,1]
-> 输出:[[0,1],[1,0]]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:nums = [1]
-> 输出:[[1]]
-> ```
-
-
-
-分析:
-
-经典的回溯算法。
-
-这一版的回溯算法条件是:
-
-1. 结束条件:选择列表为空
-2. 遍历的时候,把已经遍历过的元素,不在添加到选择列表中
-
-
-
-```go
-// date 2023/12/25
-func permute(nums []int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(nums []int, temp []int)
-
- backtrack = func(nums []int, temp []int) {
- if len(nums) == 0 {
- res = append(res, temp)
- return
- }
- for i, v := range nums {
- newTemp := append(temp, v)
- unUsed := make([]int, 0, 16)
- unUsed = append(unUsed, nums[:i]...)
- unUsed = append(unUsed, nums[i+1:]...)
- backtrack(unUsed, newTemp)
- }
- }
-
- backtrack(nums, []int{})
-
- return res
-}
-```
-
-
-
diff --git "a/13_backtrack/No.077_\347\273\204\345\220\210.md" "b/13_backtrack/No.077_\347\273\204\345\220\210.md"
deleted file mode 100644
index 9798cfd..0000000
--- "a/13_backtrack/No.077_\347\273\204\345\220\210.md"
+++ /dev/null
@@ -1,66 +0,0 @@
-## 77 组合-中等
-
-题目:
-
-给定两个整数 `n` 和 `k`,返回范围 `[1, n]` 中所有可能的 `k` 个数的组合。
-
-你可以按 **任何顺序** 返回答案。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:n = 4, k = 2
-> 输出:
-> [
-> [2,4],
-> [3,4],
-> [2,3],
-> [1,2],
-> [1,3],
-> [1,4],
-> ]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:n = 1, k = 1
-> 输出:[[1]]
-> ```
-
-
-
-分析:
-
-这道题也是经典的回溯模板。注意,元素不可重复。
-
-```go
-// date 2023/12/26
-func combine(n int, k int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(n, k int, temp []int)
- backtrack = func(idx, k int, temp []int) {
- if k == 0 {
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
- return
- }
- // [1, n] 都是候选
- for i := idx; i <= n; i++ {
- temp = append(temp, i)
- // 不可重复,所以从 i+1 开始
- backtrack(i+1, k-1, temp)
- temp = temp[:len(temp)-1]
- }
- }
-
- backtrack(1, k, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.078_\345\255\220\351\233\206.md" "b/13_backtrack/No.078_\345\255\220\351\233\206.md"
deleted file mode 100644
index 4e47fce..0000000
--- "a/13_backtrack/No.078_\345\255\220\351\233\206.md"
+++ /dev/null
@@ -1,62 +0,0 @@
-## 78 子集-中等
-
-题目:
-
-给你一个整数数组 `nums` ,数组中的元素 **互不相同** 。返回该数组所有可能的子集(幂集)。
-
-解集 **不能** 包含重复的子集。你可以按 **任意顺序** 返回解集。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,2,3]
-> 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0]
-> 输出:[[],[0]]
-> ```
-
-
-
-分析:
-
-迭代算法版本详见数组章节。以下是回溯算法。
-
-这道题要求返回所有的子集,所以空集合也算一个。
-
-因为要找出所以的子集,所以回溯的时候,没有明显的结束条件,查到数组的最后结束即可。
-
-其次,注意拷贝结果的时候,注意深度拷贝。
-
-```go
-// date 2023/12/26
-func subsets(nums []int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(start int, temp []int)
- backtrack = func(start int, temp []int) {
- // 任何大小的子集都算,所以上来就追加结果
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
-
- // 开始遍历
- for i := start; i < len(nums); i++ {
- temp = append(temp, nums[i])
- backtrack(i+1, temp) // 向下一个元素回溯遍历
- temp = temp[:len(temp)-1] // 取消候选
- }
- }
-
- backtrack(0, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.079_\345\215\225\350\257\215\346\220\234\347\264\242.md" "b/13_backtrack/No.079_\345\215\225\350\257\215\346\220\234\347\264\242.md"
deleted file mode 100644
index d85707f..0000000
--- "a/13_backtrack/No.079_\345\215\225\350\257\215\346\220\234\347\264\242.md"
+++ /dev/null
@@ -1,101 +0,0 @@
-## 79 单词搜索-中等
-
-题目:
-
-给定一个 `m x n` 二维字符网格 `board` 和一个字符串单词 `word` 。如果 `word` 存在于网格中,返回 `true` ;否则,返回 `false` 。
-
-单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
-> 输出:true
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
-> 输出:true
-> ```
->
-> **示例 3:**
->
-> 
->
-> ```
-> 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
-> 输出:false
-> ```
-
-
-
-分析:
-
-这道题目可用DFS解决。
-
-在地图上的任意一点,向四个方向 DFS 搜索,直到所有的单词字母都找到了就输出 ture,否则输出 false。
-
-注意,辅助变量 visited,遍历过的元素不可再次遍历。
-
-```go
-// date 2023/12/26
-var dir = [][]int{
- []int{-1, 0}, // x = x-1, y = y
- []int{0, -1}, // x = x, y = y-1
- []int{1, 0}, // x = x+1, y = y
- []int{0, 1}, // x = x, y = y+1
-}
-
-func exist(board [][]byte, word string) bool {
- n := len(board)
- m := len(board[0])
- visited := make([][]bool, n)
- for i := 0; i < n; i++ {
- visited[i] = make([]bool, m)
- }
-
- // 从每个点开始四个方向搜索
- for i := 0; i < n; i++ {
- for j := 0; j < m; j++ {
- if searchWord(board, visited, word, 0, i, j) {
- return true
- }
- }
- }
-
- return false
-}
-
-func isInBoard(board [][]byte, x, y int) bool {
- return x >= 0 && x < len(board) && y >= 0 && y < len(board[0])
-}
-
-func searchWord(board [][]byte, visited [][]bool, word string, idx, x, y int) bool {
- if idx == len(word)-1 {
- return board[x][y] == word[idx]
- }
- if board[x][y] == word[idx] {
- visited[x][y] = true
- // search the next
- for i := 0; i < 4; i++ {
- nx := x + dir[i][0]
- ny := y + dir[i][1]
- if isInBoard(board, nx, ny) && !visited[nx][ny] && searchWord(board, visited, word, idx+1, nx, ny) {
- return true
- }
- }
-
- visited[x][y] = false
- }
- return false
-}
-```
-
diff --git "a/13_backtrack/No.090_\345\255\220\351\233\2062.md" "b/13_backtrack/No.090_\345\255\220\351\233\2062.md"
deleted file mode 100644
index 6615889..0000000
--- "a/13_backtrack/No.090_\345\255\220\351\233\2062.md"
+++ /dev/null
@@ -1,80 +0,0 @@
-## 90 子集2-中等
-
-题目:
-
-给你一个整数数组 `nums` ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
-
-解集 **不能** 包含重复的子集。返回的解集中,子集可以按 **任意顺序** 排列。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,2,2]
-> 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0]
-> 输出:[[],[0]]
-> ```
-
-
-
-分析:
-
-这道题跟 78 题类似,两者的区别是:
-
-78 题,给定的数组中元素不重复,返回所有的子集
-
-这道题,给定的数组中元素有重复,返回所有子集,要求子集去重。
-
-核心思路还是回溯,增加两个辅助条件:
-
-1. 回溯前,对数组进行排序,方便回溯的时候跳过重复元素
-2. 回溯过程中,剪枝优化。剪枝的关键是初次遍历不剪枝,下一次的时候,如果元素跟前一个元素相同,直接跳过回溯。
-
-
-
-```go
-// date 2023/12/26
-func subsetsWithDup(nums []int) [][]int {
- res := make([][]int, 0, 16)
-
- var backtrack func(start int, temp []int)
- backtrack = func(start int, temp []int) {
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
-
- for i := start; i < len(nums); i++ {
- // 去重的关键,本次不去重,下一次去重
- for i < len(nums) && i > start && nums[i] == nums[i-1] {
- i++
- continue
- }
- // 注意判断,去重后是否越界
- if i >= len(nums) {
- break
- }
-
-
- temp = append(temp, nums[i])
- backtrack(i+1, temp)
- temp = temp[:len(temp)-1]
- }
- }
-
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
-
- backtrack(0, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.093_\345\244\215\345\216\237IP\345\234\260\345\235\200.md" "b/13_backtrack/No.093_\345\244\215\345\216\237IP\345\234\260\345\235\200.md"
deleted file mode 100644
index 89d17cd..0000000
--- "a/13_backtrack/No.093_\345\244\215\345\216\237IP\345\234\260\345\235\200.md"
+++ /dev/null
@@ -1,98 +0,0 @@
-## 93 复原IP地址-中等
-
-题目:
-
-**有效 IP 地址** 正好由四个整数(每个整数位于 `0` 到 `255` 之间组成,且不能含有前导 `0`),整数之间用 `'.'` 分隔。
-
-- 例如:`"0.1.2.201"` 和` "192.168.1.1"` 是 **有效** IP 地址,但是 `"0.011.255.245"`、`"192.168.1.312"` 和 `"192.168@1.1"` 是 **无效** IP 地址。
-
-给定一个只包含数字的字符串 `s` ,用以表示一个 IP 地址,返回所有可能的**有效 IP 地址**,这些地址可以通过在 `s` 中插入 `'.'` 来形成。你 **不能** 重新排序或删除 `s` 中的任何数字。你可以按 **任何** 顺序返回答案。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "25525511135"
-> 输出:["255.255.11.135","255.255.111.35"]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:s = "0000"
-> 输出:["0.0.0.0"]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:s = "101023"
-> 输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
-> ```
-
-
-
-分析:
-
-这道题可以选用 DFS。递归深搜的时候需要注意两种情况:
-
-第一种,多个值可以合并,只要不超过 255,且不为零
-
-第二种,单个值,正常递归
-
-中间值不可有前导零,通过判断 idx 来实现。
-
-```go
-// date 2023/12/26
-func restoreIpAddresses(s string) []string {
- res := make([]string, 0, 16)
-
- var dfs func(s string, idx int, ip []int)
- dfs = func(s string, idx int, ip []int) {
- if idx == len(s) {
- if len(ip) == 4 {
- res = append(res, toString(ip))
- }
- return
- }
- if idx == 0 {
- // IP 地址的第一个值可以为零
- // 所以这里不需要判断 num == 0
- num, _ := strconv.Atoi(string(s[0]))
- ip = append(ip, num)
- dfs(s, idx+1, ip)
- } else {
- // 非 IP 地址的第一个值,都需要判断不为零
- num, _ := strconv.Atoi(string(s[idx]))
- next := ip[len(ip)-1]*10 + num
- // 如果多个可以当做一个
- if next <= 255 && ip[len(ip)-1] != 0 {
- ip[len(ip)-1] = next
- dfs(s, idx+1, ip)
- ip[len(ip)-1] /= 10 // 撤销 num 选择
- }
- if len(ip) < 4 {
- ip = append(ip, num)
- dfs(s, idx+1, ip)
- ip = ip[:len(ip)-1]
- }
- }
- }
-
- dfs(s, 0, []int{})
-
- return res
-}
-
-func toString(nums []int) string {
- res := strconv.Itoa(nums[0])
-
- for i := 1; i < len(nums); i++ {
- res += "." + strconv.Itoa(nums[i])
- }
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.216_\347\273\204\345\220\210\346\200\273\345\222\2143.md" "b/13_backtrack/No.216_\347\273\204\345\220\210\346\200\273\345\222\2143.md"
deleted file mode 100644
index 975cf98..0000000
--- "a/13_backtrack/No.216_\347\273\204\345\220\210\346\200\273\345\222\2143.md"
+++ /dev/null
@@ -1,86 +0,0 @@
-## 216 组合总和3-中等
-
-题目:
-
-找出所有相加之和为 `n` 的 `k` 个数的组合,且满足下列条件:
-
-- 只使用数字1到9
-- 每个数字 **最多使用一次**
-
-返回 *所有可能的有效组合的列表* 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: k = 3, n = 7
-> 输出: [[1,2,4]]
-> 解释:
-> 1 + 2 + 4 = 7
-> 没有其他符合的组合了。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: k = 3, n = 9
-> 输出: [[1,2,6], [1,3,5], [2,3,4]]
-> 解释:
-> 1 + 2 + 6 = 9
-> 1 + 3 + 5 = 9
-> 2 + 3 + 4 = 9
-> 没有其他符合的组合了。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入: k = 4, n = 1
-> 输出: []
-> 解释: 不存在有效的组合。
-> 在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
-> ```
-
-
-
-分析:
-
-这道题也是经典的回溯算法。需要注意的是:
-
-1. 结束条件:既要判断剩余空位为零,也要判断等于目标和
-2. 如果空位不足,直接返回
-3. 剪枝:如果候选列表中的元素大于目标和,直接退出
-
-```go
-// date 2023/12/26
-func combinationSum3(k int, n int) [][]int {
- res := make([][]int, 0, 16)
-
- // k 表示还剩余的空位
- var backtrack func(start, k int, target int, temp []int)
- backtrack = func(start, k int, target int, temp []int) {
- if k == 0 && target == 0 {
- one := make([]int, len(temp))
- copy(one, temp)
- res = append(res, one)
- }
- if k <= 0 {
- return
- }
- for i := start; i <= 9; i++ {
- if i > target {
- break
- }
- temp = append(temp, i)
- backtrack(i+1, k-1, target-i, temp)
- temp = temp[:len(temp)-1]
- }
- }
-
- backtrack(1, k, n, []int{})
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.306_\347\264\257\345\212\240\346\225\260.md" "b/13_backtrack/No.306_\347\264\257\345\212\240\346\225\260.md"
deleted file mode 100644
index 049f4c2..0000000
--- "a/13_backtrack/No.306_\347\264\257\345\212\240\346\225\260.md"
+++ /dev/null
@@ -1,92 +0,0 @@
-## 306 累加数-中等
-
-题目:
-
-**累加数** 是一个字符串,组成它的数字可以形成累加序列。
-
-一个有效的 **累加序列** 必须 **至少** 包含 3 个数。除了最开始的两个数以外,序列中的每个后续数字必须是它之前两个数字之和。
-
-给你一个只包含数字 `'0'-'9'` 的字符串,编写一个算法来判断给定输入是否是 **累加数** 。如果是,返回 `true` ;否则,返回 `false` 。
-
-**说明:**累加序列里的数,除数字 0 之外,**不会** 以 0 开头,所以不会出现 `1, 2, 03` 或者 `1, 02, 3` 的情况。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:"112358"
-> 输出:true
-> 解释:累加序列为: 1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:"199100199"
-> 输出:true
-> 解释:累加序列为: 1, 99, 100, 199。1 + 99 = 100, 99 + 100 = 199
-> ```
-
-
-
-分析:
-
-这道题的解题思路是判断字符串是否符合斐波那契形式。
-
-- 每次判断需要维护两个数字,所以在 DFS 遍历的时候维护两个数的边界索引`firstEnd`和`secondEnd`。
-
-- 每次移动`firstEnd`,`secondEnd`的时候,需要判断后面的字符串是否以两个数的和开头。
-
-- ```
- strings.HasPrefix(nums[secondEnd+1:], strconv.Itoa(x1+x2))
- ```
-
-- 其次,无论第一个数和第二个数,只要起始数字出现`0`,都算非法情况,直接返回 false。
-
-
-
-```go
-// date 2023/12/27
-func isAdditiveNumber(num string) bool {
- if len(num) < 3 {
- return false
- }
- for firstEnd := 0; firstEnd < len(num)/2; firstEnd++ {
- if num[0] == '0' && firstEnd > 0 {
- break
- }
- first, _ := strconv.Atoi(num[:firstEnd+1])
-
- // find the second
- for secondEnd := firstEnd+1; max(firstEnd, secondEnd-firstEnd) <= len(num)-secondEnd; secondEnd++ {
- if num[firstEnd+1] == '0' && secondEnd - firstEnd > 1 {
- break
- }
- second, _ := strconv.Atoi(num[firstEnd+1:secondEnd+1])
- if recursiveCheck(num, first, second, secondEnd+1) {
- return true
- }
- }
- }
- return false
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-
-func recursiveCheck(num string, x1, x2 int, left int) bool {
- if left == len(num) {
- return true
- }
- if strings.HasPrefix(num[left:], strconv.Itoa(x1+x2)) {
- return recursiveCheck(num, x2, x1+x2, left + len(strconv.Itoa(x1+x2)))
- }
- return false
-}
-```
-
diff --git "a/13_backtrack/No.494_\347\233\256\346\240\207\345\222\214.md" "b/13_backtrack/No.494_\347\233\256\346\240\207\345\222\214.md"
deleted file mode 100644
index 73dc356..0000000
--- "a/13_backtrack/No.494_\347\233\256\346\240\207\345\222\214.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 494 目标和-中等
-
-题目:
-
-给你一个非负整数数组 `nums` 和一个整数 `target` 。
-
-向数组中的每个整数前添加 `'+'` 或 `'-'` ,然后串联起所有整数,可以构造一个 **表达式** :
-
-- 例如,`nums = [2, 1]` ,可以在 `2` 之前添加 `'+'` ,在 `1` 之前添加 `'-'` ,然后串联起来得到表达式 `"+2-1"` 。
-
-返回可以通过上述方法构造的、运算结果等于 `target` 的不同 **表达式** 的数目。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [1,1,1,1,1], target = 3
-> 输出:5
-> 解释:一共有 5 种方法让最终目标和为 3 。
-> -1 + 1 + 1 + 1 + 1 = 3
-> +1 - 1 + 1 + 1 + 1 = 3
-> +1 + 1 - 1 + 1 + 1 = 3
-> +1 + 1 + 1 - 1 + 1 = 3
-> +1 + 1 + 1 + 1 - 1 = 3
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [1], target = 1
-> 输出:1
-> ```
-
-
-
-分析:
-
-这道题目可以用 DFS 解决。既然可以在每个数字的前面添加`+`或者`-`,那么就有如下的搜索公式:
-
-```sh
-// 定义 dfs(0, target) 表示从下标0开始搜索,目标和为 target 的解的个数,那么
-dfs(0, target) = dfs(1, target-nums[0]) + dfs(1, target+nums[0])
-```
-
-
-
-```go
-// date 2023/12/27
-func findTargetSumWays(nums []int, target int) int {
- res := 0
- n := len(nums)
-
- var backtrack func(idx, target int)
- backtrack = func(idx, target int) {
- if idx == n {
- if target == 0 {
- res += 1
- }
- return
- }
- backtrack(idx+1, target-nums[idx]) // +nums[i]
- backtrack(idx+1, target+nums[idx]) // -nums[i]
- }
-
- backtrack(0, target)
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.698_\345\210\222\345\210\206\344\270\272k\344\270\252\347\233\270\347\255\211\347\232\204\345\255\220\351\233\206.md" "b/13_backtrack/No.698_\345\210\222\345\210\206\344\270\272k\344\270\252\347\233\270\347\255\211\347\232\204\345\255\220\351\233\206.md"
deleted file mode 100644
index b473951..0000000
--- "a/13_backtrack/No.698_\345\210\222\345\210\206\344\270\272k\344\270\252\347\233\270\347\255\211\347\232\204\345\255\220\351\233\206.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 698 划分为k个相等的子集-中等
-
-题目:
-
-给定一个整数数组 `nums` 和一个正整数 `k`,找出是否有可能把这个数组分成 `k` 个非空子集,其总和都相等。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
-> 输出: True
-> 说明: 有可能将其分成 4 个子集(5),(1,4),(2,3),(2,3)等于总和。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: nums = [1,2,3,4], k = 3
-> 输出: false
-> ```
-
-
-
-分析:
-
-这道题的解题思路比较复杂。
-
-既有回溯,又要考虑剪枝,否则会超时。
-
-```go
-// date 2023/12/27
-func canPartitionKSubsets(nums []int, k int) bool {
- sum, theMax := calcSumAndMax(nums)
- if sum % k != 0 {
- return false
- }
- target := sum / k
- if theMax > target {
- return false
- }
- // 剩下的问题就是 求子数组和为 target
- // 也就是把所有的元素放入 K 个桶
- backet := make([]int, k)
- n := len(nums)
- var backtrack func(idx int, buck []int) bool
- backtrack = func(idx int, buck []int) bool {
- if idx == n {
- return true
- }
- for i := 0; i < k; i++ {
- // 剪枝1
- // 如果当前桶和上一个桶一样,当前值已经在上一个桶计算过了,可以跳过
- if i > 0 && buck[i] == buck[i-1] {
- continue
- }
- // 剪枝2
- // 如果桶超过容量,直接跳过
- if buck[i] + nums[idx] > target {
- continue
- }
- buck[i] += nums[idx]
- if backtrack(idx+1, buck) { // 如果有解,直接返回
- return true
- }
- buck[i] -= nums[idx]
- }
- return false
- }
-
- return backtrack(0, backet)
-}
-
-func calcSumAndMax(nums []int) (sum int, max int) {
- sum = 0
- max = nums[0]
- for _, v := range nums {
- sum += v
- if v > max {
- max = v
- }
- }
- return
-}
-```
-
diff --git "a/13_backtrack/No.784_\345\255\227\346\257\215\345\244\247\345\260\217\345\206\231\345\205\250\346\216\222\345\210\227.md" "b/13_backtrack/No.784_\345\255\227\346\257\215\345\244\247\345\260\217\345\206\231\345\205\250\346\216\222\345\210\227.md"
deleted file mode 100644
index e2a586a..0000000
--- "a/13_backtrack/No.784_\345\255\227\346\257\215\345\244\247\345\260\217\345\206\231\345\205\250\346\216\222\345\210\227.md"
+++ /dev/null
@@ -1,70 +0,0 @@
-## 784 字母大小写全排列-中等
-
-题目:
-
-给定一个字符串 `s` ,通过将字符串 `s` 中的每个字母转变大小写,我们可以获得一个新的字符串。
-
-返回 *所有可能得到的字符串集合* 。以 **任意顺序** 返回输出。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:s = "a1b2"
-> 输出:["a1b2", "a1B2", "A1b2", "A1B2"]
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: s = "3z4"
-> 输出: ["3z4","3Z4"]
-> ```
-
-
-
-分析:
-
-这道题的解题思路是 DFS。
-
-- 遇到数字不变,继续深搜
-- 遇到小写字母,变成大写,对大写和小写分别继续搜索
-- 遇到大写字母,变成小写,对大写和小写分别继续搜索
-
-
-
-```go
-// date 2023/12/27
-func letterCasePermutation(s string) []string {
- res := make([]string, 0, 16)
-
- n := len(s)
-
- var backtrack func(idx int, temp string)
- backtrack = func(idx int, temp string) {
- if idx == n {
- res = append(res, temp)
- return
- }
- char := string(s[idx])
- if char >= "0" && char <= "9" {
- backtrack(idx+1, temp + char)
- } else if char >= "a" && char <= "z" {
- char2 := strings.ToUpper(char)
- backtrack(idx+1, temp+char)
- backtrack(idx+1, temp+char2)
- } else if char >= "A" && char <= "Z" {
- char2 := strings.ToLower(char)
- backtrack(idx+1, temp+char)
- backtrack(idx+1, temp+char2)
- }
- }
-
- backtrack(0, "")
-
-
- return res
-}
-```
-
diff --git "a/13_backtrack/No.797_\346\211\200\346\234\211\345\217\257\350\203\275\347\232\204\350\267\257\345\276\204.md" "b/13_backtrack/No.797_\346\211\200\346\234\211\345\217\257\350\203\275\347\232\204\350\267\257\345\276\204.md"
deleted file mode 100644
index e765ec2..0000000
--- "a/13_backtrack/No.797_\346\211\200\346\234\211\345\217\257\350\203\275\347\232\204\350\267\257\345\276\204.md"
+++ /dev/null
@@ -1,71 +0,0 @@
-## 797 所有可能的路径-中等
-
-题目:
-
-给你一个有 `n` 个节点的 **有向无环图(DAG)**,请你找出所有从节点 `0` 到节点 `n-1` 的路径并输出(**不要求按特定顺序**)
-
- `graph[i]` 是一个从节点 `i` 可以访问的所有节点的列表(即从节点 `i` 到节点 `graph[i][j]`存在一条有向边)。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:graph = [[1,2],[3],[3],[]]
-> 输出:[[0,1,3],[0,2,3]]
-> 解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
-> 输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
-> ```
-
-
-
-分析:
-
-这道题的解题思路是 DFS。每次从遍历可选的节点,有两种情况:
-
-- 如果节点值等于`n-1`,那么表示找到一条路径,直接添加结果
-- 如果节点值不等于 `n-1`,那么找出节点的候选列表中继续搜索
-
-无论找到还未找到,在回溯后,都要取消候选。
-
-
-
-```go
-// date 2023/12/27
-func allPathsSourceTarget(graph [][]int) [][]int {
- res := make([][]int, 0, 16)
-
- n := len(graph)
- var backtrack func(nums []int, path []int)
- backtrack = func(nums []int, path []int) {
- for _, v := range nums {
- if v == n-1 {
- path = append(path, v)
- one := make([]int, len(path))
- copy(one, path)
- res = append(res, one)
- path = path[:len(path)-1]
- } else {
- path = append(path, v)
- backtrack(graph[v], path)
- path = path[:len(path)-1]
- }
- }
- }
-
- backtrack(graph[0], []int{0})
-
- return res
-}
-```
-
diff --git a/13_backtrack/README.md b/13_backtrack/README.md
deleted file mode 100644
index d62d76a..0000000
--- a/13_backtrack/README.md
+++ /dev/null
@@ -1,60 +0,0 @@
-## 回溯算法
-
-回溯算法和二叉树的 DFS 类似,本质上是一种暴力穷举算法。
-
-抽象地说,解决一个回溯问题,实际上就是遍历一颗决策树的过程,树的每个叶子节点存放着一个合法答案。
-
-我们把整棵树遍历一遍,把叶子节点上的答案全部收集起来,就能得到所有的合法答案。
-
-
-
-站在回溯决策树的一个节点上,你只需要思考三个问题:
-
-1. 路径:那些已经做出的选择
-2. 选择列表:就是你当前可以做的选择
-3. 结束条件:到达决策树的底层,无法再做选择的条件
-
-
-
-代码方面,回溯算法的基本框架是:
-
-```go
-result = make([][]int, 0, 16)
-
-func backtrace(选择列表, 路径) {
- if 满足结束条件 {
- result = append(result, path)
- return
- }
- for 选择 := range 选择列表 {
- 做出选择
- backtrace(路径, 选择列表) // 或者叫 待选择列表
- }
-}
-```
-
-
-
-## 相关题目
-
-第一类:很经典的回溯算法
-
-- 第 39 题,组合总和,【重点看,很经典】
-- 第 40 题,组合总和,不可重复使用【重点看,很经典】
-- 第 46 题,全排列,【重点看,很经典】
-- 第 77 题,组合
-- 第 78 题,子集
-- 第 90 题,子集2,结果去重
-- 第 216 题,组合总和3,不可重复,和为目标值【很经典】
-
-
-
-第二类:重在理解 DFS
-
-- 第 17 题,电话号码的的字母组合
-- 第 22 题,括号生产
-- 第 79 题,单词搜索
-- 第 93 题,复原IP地址
-- 第 494 题,目标和,顺序递归回溯
-- 第 784 字母大小写全排列,顺序递归回溯
-- 第 797 题,所有可能的路径,图算法【很基本,看看】
diff --git a/13_backtrack/images/img022.png b/13_backtrack/images/img022.png
deleted file mode 100644
index 9cab70c..0000000
Binary files a/13_backtrack/images/img022.png and /dev/null differ
diff --git "a/14_bfs/No.1462_\350\257\276\347\250\213\350\241\2504.md" "b/14_bfs/No.1462_\350\257\276\347\250\213\350\241\2504.md"
deleted file mode 100644
index f34bcd7..0000000
--- "a/14_bfs/No.1462_\350\257\276\347\250\213\350\241\2504.md"
+++ /dev/null
@@ -1,123 +0,0 @@
-## 1462 课程表4-中等
-
-题目:
-
-你总共需要上 `numCourses` 门课,课程编号依次为 `0` 到 `numCourses-1` 。你会得到一个数组 `prerequisite` ,其中 `prerequisites[i] = [ai, bi]` 表示如果你想选 `bi` 课程,你 **必须** 先选 `ai` 课程。
-
-- 有的课会有直接的先修课程,比如如果想上课程 `1` ,你必须先上课程 `0` ,那么会以 `[0,1]` 数对的形式给出先修课程数对。
-
-先决条件也可以是 **间接** 的。如果课程 `a` 是课程 `b` 的先决条件,课程 `b` 是课程 `c` 的先决条件,那么课程 `a` 就是课程 `c` 的先决条件。
-
-你也得到一个数组 `queries` ,其中 `queries[j] = [uj, vj]`。对于第 `j` 个查询,您应该回答课程 `uj` 是否是课程 `vj` 的先决条件。
-
-返回一个布尔数组 `answer` ,其中 `answer[j]` 是第 `j` 个查询的答案。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
-> 输出:[false,true]
-> 解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
-> 输出:[false,false]
-> 解释:没有先修课程对,所以每门课程之间是独立的。
-> ```
->
-> **示例 3:**
->
-> 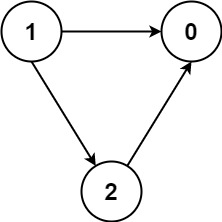
->
-> ```
-> 输入:numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
-> 输出:[true,true]
-> ```
-
-
-
-分析:
-
-这道题也是 AOV 网拓扑排序的思路,需要注意两点:
-
-1)通过拓扑排序,从已排序的数组中查找相对位置关系不可行。因为 aov 网的拓扑排序中对入度为零的节点是依次添加的的,入度为零的节点没有依赖关系,但是依次添加形成了顺序,所以不可行。
-
-2)通过构造 aov 网,对全网进行 BFS 搜索会超时。
-
-3)通过构造 aov 网,进而构造前置依赖 map 列表,会超时内存限制。
-
-
-
-综合来看,这道题的解法是拓扑排序和 BFS。具体这些步骤来完成:
-
-1)根据依赖关系,构建每个节点的入度和出度节点关系
-
-2)构建二维数组 `isPre[i][j]`,表示课程`i`是课程`j`的前置依赖
-
-3)开始拓扑排序,排序过程中根据出度节点更新`isPre二维数组`。需要注意的是,如果课程`cur`是课程`v`的前置依赖,那么所有的课程中,`cur`的前置依赖也是`v`的前置依赖。
-
-```go
-// date 2024/01/02
-func checkIfPrerequisite(numCourses int, prerequisites [][]int, queries [][]int) []bool {
- in := make([]int, numCourses)
- out := make(map[int][]int)
- for _, v := range prerequisites {
- in[v[1]]++
- _, ok := out[v[0]]
- if !ok {
- out[v[0]] = []int{}
- }
- out[v[0]] = append(out[v[0]], v[1])
- }
- queue := make([]int, 0, 16)
- for i, v := range in {
- if v == 0 {
- queue = append(queue, i)
- }
- }
- isPre := make([][]bool, numCourses)
- for i := 0; i < numCourses; i++ {
- isPre[i] = make([]bool, numCourses)
- }
-
- for len(queue) > 0 {
- n := len(queue)
-
- for i := 0; i < n; i++ {
- cur := queue[i]
- if ov, ok := out[cur]; ok && len(ov) != 0 {
- for _, v := range ov {
- isPre[cur][v] = true
-
- // cur 是 v 的前置依赖
- // 那么,所有的课程中 cur 的前置依赖也是 v 的前置依赖
- for j := 0; j < numCourses; j++ {
- isPre[j][v] = isPre[j][v] || isPre[j][cur]
- }
- in[v]--
- if in[v] == 0 {
- queue = append(queue, v)
- }
- }
- }
- }
-
- queue = queue[n:]
- }
-
- ans := make([]bool, 0, 16)
- for _, v := range queries {
- ans = append(ans, isPre[v[0]][v[1]])
- }
-
- return ans
-}
-```
-
diff --git "a/14_bfs/No.200_\345\262\233\345\261\277\347\232\204\346\225\260\351\207\217.md" "b/14_bfs/No.200_\345\262\233\345\261\277\347\232\204\346\225\260\351\207\217.md"
deleted file mode 100644
index 3b21eb7..0000000
--- "a/14_bfs/No.200_\345\262\233\345\261\277\347\232\204\346\225\260\351\207\217.md"
+++ /dev/null
@@ -1,103 +0,0 @@
-## 200 岛屿的数量-中等
-
-**题目**:
-
-给你一个由 `'1'`(陆地)和 `'0'`(水)组成的的二维网格,请你计算网格中岛屿的数量。
-
-岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
-
-此外,你可以假设该网格的四条边均被水包围。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:grid = [
-> ["1","1","1","1","0"],
-> ["1","1","0","1","0"],
-> ["1","1","0","0","0"],
-> ["0","0","0","0","0"]
-> ]
-> 输出:1
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:grid = [
-> ["1","1","0","0","0"],
-> ["1","1","0","0","0"],
-> ["0","0","1","0","0"],
-> ["0","0","0","1","1"]
-> ]
-> 输出:3
-> ```
-
-
-
-**分析:**
-
-这道题是图的 BFS 算法,基本思路是:
-
-1. 通过 visited 标记已经访问过的点
-2. 二层遍历,一旦找到没有访问过,且为`1`的点,结果递增;并且以此点为起点开始四个方向的 BFS
-
-```go
-// date 2023/12/28
-func numIslands(grid [][]byte) int {
- n := len(grid)
- if n == 0 {
- return 0
- }
- m := len(grid[0])
- if m == 0 {
- return 0
- }
-
- dir := [][]int{
- []int{1,0}, // x = x+1, y = y
- []int{-1,0}, // x = x-1, y = y
- []int{0,1}, // x = x, y = y-1
- []int{0,-1}, // x = x, y = y+1
- }
- visited := make([][]bool, n)
- for i := 0; i < n; i++ {
- visited[i] = make([]bool, m)
- }
-
- var isInBoard func(x, y int) bool
- isInBoard = func(x, y int) bool {
- return x >= 0 && x < n && y >= 0 && y < m
- }
-
- // search land
- var bfs func(x, y int)
- bfs = func(x, y int) {
- visited[x][y] = true
- for i := 0; i < 4; i++ {
- nx := x + dir[i][0]
- ny := y + dir[i][1]
- // 继续搜索联通的 1
- if isInBoard(nx, ny) && !visited[nx][ny] && grid[nx][ny] == '1' {
- bfs(nx, ny)
- }
- }
- }
-
- res := 0
- // 依次遍历查找, 如果为 1 且没有被访问过,那么就是新大陆
- // 在新大陆开启四个方向的 BFS 搜索
- for i := 0; i < n; i++ {
- for j := 0; j < m; j++ {
- if grid[i][j] == '1' && !visited[i][j] {
- bfs(i, j)
- res++
- }
- }
- }
-
- return res
-}
-```
-
diff --git "a/14_bfs/No.207_\350\257\276\347\250\213\350\241\250.md" "b/14_bfs/No.207_\350\257\276\347\250\213\350\241\250.md"
deleted file mode 100644
index 89072fc..0000000
--- "a/14_bfs/No.207_\350\257\276\347\250\213\350\241\250.md"
+++ /dev/null
@@ -1,93 +0,0 @@
-## 207 课程表-中等
-
-题目:
-
-你这个学期必须选修 `numCourses` 门课程,记为 `0` 到 `numCourses - 1` 。
-
-在选修某些课程之前需要一些先修课程。 先修课程按数组 `prerequisites` 给出,其中 `prerequisites[i] = [ai, bi]` ,表示如果要学习课程 `ai` 则 **必须** 先学习课程 `bi` 。
-
-- 例如,先修课程对 `[0, 1]` 表示:想要学习课程 `0` ,你需要先完成课程 `1` 。
-
-请你判断是否可能完成所有课程的学习?如果可以,返回 `true` ;否则,返回 `false` 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:numCourses = 2, prerequisites = [[1,0]]
-> 输出:true
-> 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
-> 输出:false
-> 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
-> ```
-
-
-
-**分析**
-
-这道题就是一个标准的 AOV 网的拓扑排序问题,关于 AOV 网详见 README。
-
-拓扑排序问题的解决思路主要是循环执行以下两步,直到不存在入度为零的顶点为止。
-
-- 选择一个入度为零的顶点并将其加入列表
-- 从网中删除该顶点和其所有边(即将其出度指向的节点的入度减一)
-
-循环结束,如果拓扑排序中的节点数小于网中的节点数,那么该 AOV 网中有回路;否则没有。
-
-
-
-```go
-// date 2023/12/28
-func canFinish(numCourses int, prerequisites [][]int) bool {
- n := len(prerequisites)
- if n == 0 {
- return true
- }
- // in dress
- in := make([]int, numCourses)
- // out node list
- out := make([][]int, numCourses)
- // next is the sort list of aov
- next := make([]int, 0, numCourses)
-
- // 计算每个节点的入度和出度列表
- for _, v := range prerequisites {
- // [0, 1] 1->0
- in[v[0]]++
- out[v[1]] = append(out[v[1]], v[0])
- }
-
- // 1. 先把所有入度为零的完成
- for i := 0; i < numCourses; i++ {
- if in[i] == 0 {
- next = append(next, i)
- }
- }
-
- // 2. 遍历 next 列表,更新其他节点
- for i := 0; i != len(next); i++ {
- cur := next[i]
- // the free list of cur
- v := out[cur]
- if len(v) != 0 {
- for _, vv := range v {
- // cur 课程已经完成, 那么对它依赖的课程入度减一
- in[vv]--
- if in[vv] == 0 {
- next = append(next, vv)
- }
- }
- }
- }
- // 如果不存在回环,那么其拓扑排序中的节点数等于总数
- return len(next) == numCourses
-}
-```
-
diff --git "a/14_bfs/No.210_\350\257\276\347\250\213\350\241\2502.md" "b/14_bfs/No.210_\350\257\276\347\250\213\350\241\2502.md"
deleted file mode 100644
index ae704b5..0000000
--- "a/14_bfs/No.210_\350\257\276\347\250\213\350\241\2502.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 210 课程表2-中等
-
-题目:
-
-现在你总共有 `numCourses` 门课需要选,记为 `0` 到 `numCourses - 1`。给你一个数组 `prerequisites` ,其中 `prerequisites[i] = [ai, bi]` ,表示在选修课程 `ai` 前 **必须** 先选修 `bi` 。
-
-- 例如,想要学习课程 `0` ,你需要先完成课程 `1` ,我们用一个匹配来表示:`[0,1]` 。
-
-返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 **任意一种** 就可以了。如果不可能完成所有课程,返回 **一个空数组** 。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:numCourses = 2, prerequisites = [[1,0]]
-> 输出:[0,1]
-> 解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
-> 输出:[0,2,1,3]
-> 解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
-> 因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:numCourses = 1, prerequisites = []
-> 输出:[0]
-> ```
-
-
-
-**分析:**
-
-这道题跟 207 题相同,都是 AOV 网的拓扑排序问题。
-
-```go
-// date 2023/12/28
-func findOrder(numCourses int, prerequisites [][]int) []int {
- res := make([]int, 0, numCourses)
- if len(prerequisites) == 0 {
- for i := 0; i < numCourses; i++ {
- res = append(res, i)
- }
- return res
- }
-
- // 同 207 题目
- in := make([]int, numCourses)
- out := make([][]int, numCourses)
-
- for _, v := range prerequisites {
- in[v[0]]++
- out[v[1]] = append(out[v[1]], v[0])
- }
-
- for i := 0; i < numCourses; i++ {
- if in[i] == 0 {
- res = append(res, i)
- }
- }
-
- for i := 0; i != len(res); i++ {
- cur := res[i]
- v := out[cur]
- for _, vv := range v {
- in[vv]--
- if in[vv] == 0 {
- res = append(res, vv)
- }
- }
- }
-
- if len(res) == numCourses {
- return res
- }
-
- return []int{}
-}
-```
-
diff --git "a/14_bfs/No.226_\347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md" "b/14_bfs/No.226_\347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md"
deleted file mode 100644
index 0530d31..0000000
--- "a/14_bfs/No.226_\347\277\273\350\275\254\344\272\214\345\217\211\346\240\221.md"
+++ /dev/null
@@ -1,79 +0,0 @@
-## 226 翻转二叉树-中等
-
-题目:
-
-给你一棵二叉树的根节点 `root` ,翻转这棵二叉树,并返回其根节点。
-
-
-
-**解题思路**
-
-- DFS,详见解法1。具体是直接深度优先搜索,修改每个节点的左右指针。
-- BFS,详见解法2。将节点加入队列,依次翻转队列中每个节点的左右指针。
-
-```go
-// date 2023/12/28
-/**
- * Definition for a binary tree node.
- * type TreeNode struct {
- * Val int
- * Left *TreeNode
- * Right *TreeNode
- * }
- */
-// 解法1 dfs
-func invertTree(root *TreeNode) *TreeNode {
-
- var dfs func(root *TreeNode)
- dfs = func(root *TreeNode) {
- if root == nil {
- return
- }
- or := root.Right
- root.Right = root.Left
- root.Left = or
-
- dfs(root.Right)
- dfs(root.Left)
- }
-
- dfs(root)
-
- return root
-}
-
-// 解法2
-// BFS
-func invertTree(root *TreeNode) *TreeNode {
- if root == nil {
- return root
- }
- if root.Left == nil && root.Right == nil {
- return root
- }
-
- queue := make([]*TreeNode, 0, 16)
- queue = append(queue, root)
-
- for len(queue) != 0 {
- n := len(queue)
- for i := 0; i < n; i++ {
- cur := queue[i]
- or := cur.Right
- cur.Right = cur.Left
- cur.Left = or
-
- if cur.Left != nil {
- queue = append(queue, cur.Left)
- }
- if cur.Right != nil {
- queue = append(queue, cur.Right)
- }
- }
-
- queue = queue[n:]
- }
-
- return root
-}
-```
diff --git "a/14_bfs/No.310_\346\234\200\345\260\217\351\253\230\345\272\246\346\240\221.md" "b/14_bfs/No.310_\346\234\200\345\260\217\351\253\230\345\272\246\346\240\221.md"
deleted file mode 100644
index 7647dcb..0000000
--- "a/14_bfs/No.310_\346\234\200\345\260\217\351\253\230\345\272\246\346\240\221.md"
+++ /dev/null
@@ -1,97 +0,0 @@
-## 310 最小高度树-中等
-
-题目:
-
-树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
-
-给你一棵包含 `n` 个节点的树,标记为 `0` 到 `n - 1` 。给定数字 `n` 和一个有 `n - 1` 条无向边的 `edges` 列表(每一个边都是一对标签),其中 `edges[i] = [ai, bi]` 表示树中节点 `ai` 和 `bi` 之间存在一条无向边。
-
-可选择树中任何一个节点作为根。当选择节点 `x` 作为根节点时,设结果树的高度为 `h` 。在所有可能的树中,具有最小高度的树(即,`min(h)`)被称为 **最小高度树** 。
-
-请你找到所有的 **最小高度树** 并按 **任意顺序** 返回它们的根节点标签列表。
-
-树的 **高度** 是指根节点和叶子节点之间最长向下路径上边的数量。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:n = 4, edges = [[1,0],[1,2],[1,3]]
-> 输出:[1]
-> 解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
-> 输出:[3,4]
-> ```
-
-
-
-分析:
-
-这道题中所有的节点构成了一个无向图,那么想要求得最小高度树,其实就是求整个图中最长的那条路径上中间的一个或两个点。
-
-如果最长路径的节点树为偶数,那么就是最中间的2个点。
-
-如果最长路径的节点数为奇数,那么就是最中间的1个点。
-
-怎么求最长路径呢?
-
-可以这样考虑,整个图,所有最外层节点的度为1,把度为1的节点去掉,同时将其连接的节点的度减一,不断第重复这个过程,直到度为1的序列中节点数不超过2个。
-
-这个过程其实就是拓扑排序的变形,从外向里搜索,也是 DFS。
-
-```go
-// date 2024/01/02
-func findMinHeightTrees(n int, edges [][]int) []int {
- if n == 1 {
- return []int{0}
- }
- // 计算每个节点的度
- deg := make([]int, n)
- out := make([][]int, n)
- for _, v := range edges {
- out[v[0]] = append(out[v[0]], v[1])
- out[v[1]] = append(out[v[1]], v[0])
- deg[v[0]]++
- deg[v[1]]++
- }
-
- // 所有度为 1 的都在最外层
- // 拓扑排序,直到序列中的节点不超过两个,即最中心的两个
- queue := make([]int, 0, 16)
- for i, v := range deg {
- if v == 1 {
- queue = append(queue, i)
- }
- }
-
- remainNode := n
- for remainNode > 2 {
- x1 := len(queue)
- remainNode -= x1
-
- for _, cur := range queue {
- for _, v := range out[cur] {
- deg[v]--
- if deg[v] == 1 {
- queue = append(queue, v)
- }
- }
- }
-
- queue = queue[x1:]
- }
-
- return queue
-}
-```
-
diff --git "a/14_bfs/No.851_\345\226\247\351\227\271\345\222\214\345\257\214\346\234\211.md" "b/14_bfs/No.851_\345\226\247\351\227\271\345\222\214\345\257\214\346\234\211.md"
deleted file mode 100644
index 3b7acf2..0000000
--- "a/14_bfs/No.851_\345\226\247\351\227\271\345\222\214\345\257\214\346\234\211.md"
+++ /dev/null
@@ -1,76 +0,0 @@
-## 851 喧闹和富有-中等
-
-题目:
-
-有一组 `n` 个人作为实验对象,从 `0` 到 `n - 1` 编号,其中每个人都有不同数目的钱,以及不同程度的安静值(quietness)。为了方便起见,我们将编号为 `x` 的人简称为 "person `x` "。
-
-给你一个数组 `richer` ,其中 `richer[i] = [ai, bi]` 表示 person `ai` 比 person `bi` 更有钱。另给你一个整数数组 `quiet` ,其中 `quiet[i]` 是 person `i` 的安静值。`richer` 中所给出的数据 **逻辑自洽**(也就是说,在 person `x` 比 person `y` 更有钱的同时,不会出现 person `y` 比 person `x` 更有钱的情况 )。
-
-现在,返回一个整数数组 `answer` 作为答案,其中 `answer[x] = y` 的前提是,在所有拥有的钱肯定不少于 person `x` 的人中,person `y` 是最安静的人(也就是安静值 `quiet[y]` 最小的人)。
-
-
-
-分析:
-
-这道题的整体思路是 AOV 网的拓扑排序。
-
-由题意可知,`richer`关系构成了一张有向无环图,则据此构建图的关系,记录每个节点的入度和出度节点。
-
-利用 AOV 网的拓扑排序,从入度为零的节点开始广度优先遍历;不断地使用更富有的人,但安静值更小的人。
-
-当所有入度为零的序列为零时,则终止搜索。
-
-初始化`ans[i] = i`,拓扑排序时,如果`quiet[ans[i]] > quiet[ans[j]]`,那么`ans[i] = ans[j]`。
-
-```go
-// date 2024/01/01
-func loudAndRich(richer [][]int, quiet []int) []int {
- n := len(quiet)
- ans := make([]int, n)
- for i := 0; i < n; i++ {
- ans[i] = i
- }
-
- in := make([]int, n)
- out := make(map[int][]int, 4)
- for _, v := range richer {
- in[v[1]]++
- _, ok := out[v[0]]
- if !ok {
- out[v[0]] = make([]int, 0, 16)
- }
- out[v[0]] = append(out[v[0]], v[1])
- }
-
- // aov 网 拓扑排序
- queue := make([]int, 0, 16)
- for i, v := range in {
- if v == 0 {
- queue = append(queue, i)
- }
- }
-
- for len(queue) != 0 {
- n := len(queue)
- for i := 0; i < n; i++ {
- u := queue[i]
- if ov, ok := out[u]; ok && len(ov) != 0 {
- for _, v := range ov {
- in[v]--
- if quiet[ans[v]] > quiet[ans[u]] {
- ans[v] = ans[u]
- }
- if in[v] == 0 {
- queue = append(queue, v)
- }
- }
- }
- }
-
- queue = queue[n:]
- }
-
- return ans
-}
-```
-
diff --git a/14_bfs/README.md b/14_bfs/README.md
deleted file mode 100644
index 3aea31e..0000000
--- a/14_bfs/README.md
+++ /dev/null
@@ -1,63 +0,0 @@
-## BFS
-
-
-
-第一类:AOV 网的拓扑排序
-
-- 第 207 题,课程表
-- 第 210 题,课程表2
-- 第 1462 题,课程表4【拓扑排序,BFS】
-
-
-
-第二类:BFS
-
-- 第 200 题,岛屿的数量
-
-
-
-第三类:
-
-第 310 题:最小高度树,拓扑排序的变形
-
-
-
-
-
-## AOV 网络
-
-在图的数据结构中,有向无环图(Directed Acycline Graph,DAG)是一类特殊的有向图。
-
-其中,AOV 网络是 DAG 的典型应用。
-
-在有向图中,用顶点表示活动,用有向边表示活动 a 是活动 b 的前置条件,这种有向图称为用顶点表示活动的网络(Active on Vertices),简称 AOV 网络,如下图所示。
-
-
-
-举例例子,上图中的活动 1 就是活动 3 的前置条件,也就是说活动 1 必须完成,活动 3 才可以进行。
-
-对应到现实中,可以类比课程。比如活动 1 表示 C 语言课程,活动 3 表示数据结构。
-
-
-
-一个 AOV 网络应该是一个有向无环图,即不应该带有回路,因为如果存在回路,某些活动就会形成相互依赖,无法进行。
-
-
-
-**拓扑排序**
-
-一个 AOV 网络中,如果不存在回路,那么所有的活动可以排成一个线性列表,使得每个活动的前驱活动都排在该活动的前面,我们把这种排序称为拓扑排序。
-
-AOV 网的拓扑排序不是唯一的,只要满足上述定义的任一线性序列都称作它的拓扑排序。
-
-例如,序列`[1,2,3,4,5,6,7,8]`和序列`[2,1,4,3,5,7,6,8]`都是上图 AOV 网络的拓扑排序。
-
-
-
-那么,如何得到 AOV 网络的拓扑排序呢?可以从每个节点的入度和出度出发。
-
-如果一个节点没有入度,则说明它没有前置依赖,该节点就可以先进入队列。(即,该课程已经完成)
-
-与此同时,将该节点出度所指向的节点的入度减一。(因为,前置依赖已经完成一个)
-
-通过不断地遍历搜索,指导 AOV 网络中不存在入度为零的节点,所形成的队列就是它的拓扑排序。
\ No newline at end of file
diff --git a/14_bfs/images/img_aov.png b/14_bfs/images/img_aov.png
deleted file mode 100644
index 52df3d5..0000000
Binary files a/14_bfs/images/img_aov.png and /dev/null differ
diff --git "a/15_union_find/No.128_\346\234\200\351\225\277\350\277\236\347\273\255\345\272\217\345\210\227.md" "b/15_union_find/No.128_\346\234\200\351\225\277\350\277\236\347\273\255\345\272\217\345\210\227.md"
deleted file mode 100644
index 1d8b82e..0000000
--- "a/15_union_find/No.128_\346\234\200\351\225\277\350\277\236\347\273\255\345\272\217\345\210\227.md"
+++ /dev/null
@@ -1,239 +0,0 @@
-## 128 最长连续序列-中等
-
-题目:
-
-给定一个未排序的整数数组 `nums` ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
-
-请你设计并实现时间复杂度为 `O(n)` 的算法解决此问题。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [100,4,200,1,3,2]
-> 输出:4
-> 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [0,3,7,2,5,8,4,6,0,1]
-> 输出:9
-> ```
-
-
-
-**解题思路**:
-
-这道题就是求数组中连续元素的最大个数,要求时间复杂度`O(n)`。
-
-- 可以先暴力求解,代码见解法一。思路是先把每个数存入map,然后对 map 进行清洗。
-
- - 遍历 map,把既没有前驱元素也没有后驱元素的节点全部删除。
- - 再次遍历 map,此时 map 中的元素肯定有连续的元素,但不确定连续有多少,那么依次往后查找并删除,在依次往前查找,并删除;过程中统计元素的个数,并更新最终的结果集。
- - 得到就是最长连续序列的个数
-
- 需要注意 corner case 的处理。
-
-- 解法二最优,思路是遍历数组,存入 map,存入的过程中做2件事情。第一件事,先查看`v-1`和`v+1`是否都存在 map 中,如果存在,表示存在连续序列,那么更新`left`和`right`边界,当前元素`v`对应的最小连续序列长度就是`sum = left + right + 1`。第二件事,更新左右边界对应元素的长度。
-
-- 解法三,并查集思路。这个解法不是很好想,不过确实可以这样做,锻炼并查集思维,具体做法是:
- - 先把每个元素的下标当做一个集合。
- - 然后遍历数组,存入 map。如果元素的前一个值`v-1`在 map 中,或者后一个元素`v+1`在 map 中,则将它们的下标进行 `union()`。
- - 然后在`uf`中依次查询每个下标,找到元素最多的集合。
-
-
-
-解法一:
-
-```go
-// date 2024/01/04
-// 解法一
-func longestConsecutive(nums []int) int {
- res := 0
- set := make(map[int]int, len(nums))
- for _, v := range nums {
- set[v] = 1
- }
- // case1 重复元素
- if len(set) < 2 {
- return len(set)
- }
-
- for k := range set {
- k0 := k-1
- k1 := k+1
- _, ok1 := set[k0]
- _, ok2 := set[k1]
- if !ok1 && !ok2 {
- delete(set, k)
- }
- }
- // case2 全部离散,没有连续的
- if len(set) == 0 {
- return 1
- }
-
- for k := range set {
- ans := 1
- kk := k+1
- _, ok := set[kk]
- for ok {
- delete(set, kk)
- kk++
- ans++
- _, ok = set[kk]
- }
- kk = k-1
- _, ok = set[kk]
- for ok {
- kk--
- ans++
- _, ok = set[kk]
- }
- res = max(res, ans)
- }
-
- return res
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
-
-
-
-
-解法二:
-
-```go
-// date 2024/01/04
-// 解法二
-func longestConsecutive(nums []int) int {
- res := 0
- // seqCt 存储包含num连续序列的长度
- seqCt := make(map[int]int)
- for _, num := range nums {
- if seqCt[num] == 0 {
- // left 表示 num 左边连续元素的个数
- // right 表示 num 右边连续元素的个数
- left, right := 0, 0
- if seqCt[num-1] > 0 {
- left = seqCt[num-1]
- }
- if seqCt[num+1] > 0 {
- right = seqCt[num+1]
- }
-
- // 左右加一起,再加上 num 本身,就是 num 所构成连续序列的个数
- sum := left + right + 1
- seqCt[num] = sum
-
- res = max(res, sum)
-
- // 因为序列是连续的,所以可以更新最左边和最右边的个数
- // 如果 left, right 为零,不影响结果
- seqCt[num-left] = sum
- seqCt[num+right] = sum
- }
- }
-
- return res
-}
-
-func max(x, y int) int {
- if x > y {
- return x
- }
- return y
-}
-```
-
-
-
-解法三:
-
-```go
-// date 2024/01/04
-// 解法三
-func longestConsecutive(nums []int) int {
- n := len(nums)
- idxMap := make(map[int]int, len(nums))
- // 初始化,每个idx都是一个集合
- for i, _ := range nums {
- idxMap[i] = 1
- }
-
- uf := newMyUnionFind(n)
- numMap := make(map[int]int, n)
- for i, v := range nums {
- // 跳过重复元素
- if _, ok := numMap[v]; ok {
- continue
- }
- // save idx to num map
- numMap[v] = i
- if idx2, ok1 := numMap[v-1]; ok1 {
- uf.union(i, idx2)
- }
- if idx3, ok2 := numMap[v+1]; ok2 {
- uf.union(i, idx3)
- }
- }
-
- res := 0
- for idx := range idxMap {
- p := uf.find(idx)
- if p != idx {
- idxMap[p]++
- }
- if idxMap[p] > res {
- res = idxMap[p]
- }
- }
- return res
-}
-
-type (
- MyUnionFind struct {
- parent []int // 存储每个节点的父结点
- }
-)
-
-// n 表示图中一共有多少个节点
-func newMyUnionFind(n int) *MyUnionFind {
- u := &MyUnionFind{
- parent: make([]int, n),
- }
- // 初始化时, 每个节点的父结点都是自己
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-// 将两个节点x y 合并
-func (u *MyUnionFind) union(x, y int) {
- xp, yp := u.find(x), u.find(y)
- if xp == yp {
- return
- }
- u.parent[yp] = xp
-}
-
-// 查找 x 的父结点
-func (u *MyUnionFind) find(x int) int {
- if u.parent[x] != x {
- u.parent[x] = u.find(u.parent[x])
- }
- return u.parent[x]
-}
-```
-
diff --git "a/15_union_find/No.130_\350\242\253\345\233\264\347\273\225\347\232\204\345\214\272\345\237\237.md" "b/15_union_find/No.130_\350\242\253\345\233\264\347\273\225\347\232\204\345\214\272\345\237\237.md"
deleted file mode 100644
index 3e887f0..0000000
--- "a/15_union_find/No.130_\350\242\253\345\233\264\347\273\225\347\232\204\345\214\272\345\237\237.md"
+++ /dev/null
@@ -1,116 +0,0 @@
-## 130 被围绕的区域-中等
-
-题目:
-
-给你一个 `m x n` 的矩阵 `board` ,由若干字符 `'X'` 和 `'O'` ,找到所有被 `'X'` 围绕的区域,并将这些区域里所有的 `'O'` 用 `'X'` 填充。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
-> 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
-> 解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:board = [["X"]]
-> 输出:[["X"]]
-> ```
-
-
-
-**解题思路**
-
-这道题可以用并查集解决,但思路并不好想。可以这样思考,矩阵中所有的`O`,肯定是一片一片的存在矩阵中。
-
-既然边缘上的`O`不可能被修改,那么跟边缘形成一片的`O`都不可以修改。
-
-如此一来,我们对`O`的坐标进行并查集操作,具体是:
-
-- 先把边缘的`O`都合作到一个特殊集合里
-- 然后内部的`O`如果在四个方向有相邻,也合并起来【这一步主要是为了把跟边缘搭界的内部`O`合并到一起】
-
-
-
-```go
-// date 2024/01/04
-func solve(board [][]byte) {
- n := len(board)
- m := len(board[0])
- uf := newMyUnionFind(n*m+1)
- spec := n*m
-
- for i := 0; i < n; i++ {
- for j := 0; j < m; j++ {
- if (i == 0 || i == n-1 || j == 0 || j == m-1) && board[i][j] == 'O' {
- // 边缘上的 O 跟 n*m(特殊点) 合并
- uf.union(i*m+j, spec)
- } else if board[i][j] == 'O' {
- // 内部 O
- // 如果四个方向上有 O 直接合并
- if board[i-1][j] == 'O' {
- uf.union(i*m+j, (i-1)*m+j)
- }
- if board[i+1][j] == 'O' {
- uf.union(i*n+j, (i+1)*m+j)
- }
- if board[i][j-1] == 'O' {
- uf.union(i*m+j, i*m+j-1)
- }
- if board[i][j+1] == 'O' {
- uf.union(i*m+j, i*m+j+1)
- }
- }
- }
- }
- // 经过上面的合并,只要内部的O和边缘的O有相邻,那么内部的O一定会合并到边缘O的特殊集合里面
- // 剩下的不在特殊集合里面的,都可以被标记为 'X'
- specP := uf.find(spec)
- for i := 0; i < n; i++ {
- for j := 0; j < m; j++ {
- if uf.find(i*m+j) != specP {
- board[i][j] = 'X'
- }
- }
- }
-}
-
-type (
- MyUnionFind struct {
- parent []int // 存储每个节点的父结点
- }
-)
-
-// n 表示图中一共有多少个节点
-func newMyUnionFind(n int) *MyUnionFind {
- u := &MyUnionFind{
- parent: make([]int, n),
- }
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-func (u *MyUnionFind) union(x, y int) {
- xp, yp := u.find(x), u.find(y)
- if xp == yp {
- return
- }
- u.parent[yp] = xp
-}
-
-func (u *MyUnionFind) find(x int) int {
- if u.parent[x] != x {
- u.parent[x] = u.find(u.parent[x])
- }
- return u.parent[x]
-}
-```
-
diff --git "a/15_union_find/No.323_\346\227\240\345\220\221\345\233\276\344\270\255\350\277\236\351\200\232\345\210\206\351\207\217\347\232\204\344\270\252\346\225\260.md" "b/15_union_find/No.323_\346\227\240\345\220\221\345\233\276\344\270\255\350\277\236\351\200\232\345\210\206\351\207\217\347\232\204\344\270\252\346\225\260.md"
deleted file mode 100644
index 9660171..0000000
--- "a/15_union_find/No.323_\346\227\240\345\220\221\345\233\276\344\270\255\350\277\236\351\200\232\345\210\206\351\207\217\347\232\204\344\270\252\346\225\260.md"
+++ /dev/null
@@ -1,143 +0,0 @@
-## 323 无向图中连通分量的个数-中等
-
-题目:
-
-你有一个包含 `n` 个节点的图。给定一个整数 `n` 和一个数组 `edges` ,其中 `edges[i] = [ai, bi]` 表示图中 `ai` 和 `bi` 之间有一条边。
-
-返回 *图中已连接分量的数目* 。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入: n = 5, edges = [[0, 1], [1, 2], [3, 4]]
-> 输出: 2
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入: n = 5, edges = [[0,1], [1,2], [2,3], [3,4]]
-> 输出: 1
-> ```
-
-
-
-分析:
-
-算法1:
-
-这道题跟第 200 题【岛屿的数量】类似,可以用 DFS 搜索,具体为:
-
-- 先讲边的关系构造成有出向节点的图
-- 开始遍历,通过 visited 标记已经遍历过的,一旦发现没有遍历过的节点,计数增加1
-
-```go
-// date 2024/01/04
-func countComponents(n int, edges [][]int) int {
- // out
- out := make(map[int][]int, 4)
- visited := make(map[int]bool, n)
- for _, v := range edges {
- v0, v1 := v[0], v[1]
- _, ok := out[v0]
- if !ok {
- out[v0] = []int{}
- }
- out[v0] = append(out[v0], v1)
- _, ok = out[v1]
- if !ok {
- out[v1] = []int{}
- }
- out[v1] = append(out[v1], v0)
- }
- count := 0
-
- var dfs func(start int)
- dfs = func(start int) {
- if visited[start] {
- return
- }
- visited[start] = true
- if ov, ok := out[start]; ok && len(ov) != 0 {
- for _, v := range ov {
- dfs(v)
- }
- }
- }
-
- for i := 0; i < n; i++ {
- if !visited[i] {
- count++
- dfs(i)
- }
- }
-
- return count
-}
-```
-
-
-
-算法2:
-
-这道题也是基本的并查集算法。
-
-```go
-// date 2024/01/04
-func countComponents(n int, edges [][]int) int {
- uf := newMyUnionFind(n)
- for _, v := range edges {
- uf.union(v[0], v[1])
- }
- return uf.getCount()
-}
-
-type (
- MyUnionFind struct {
- parent []int // 存储每个节点的父结点
- count int // 存储连通分量
- }
-)
-
-// n 表示图中一共有多少个节点
-func newMyUnionFind(n int) *MyUnionFind {
- u := &MyUnionFind{
- count: n,
- parent: make([]int, n),
- }
- // 初始化时, 每个节点的父结点都是自己
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-// 将两个节点x y 合并
-func (u *MyUnionFind) union(x, y int) {
- xp, yp := u.find(x), u.find(y)
- if xp == yp {
- return
- }
- u.parent[yp] = xp
- u.count--
-}
-
-// 查找 x 的父结点
-func (u *MyUnionFind) find(x int) int {
- if u.parent[x] != x {
- u.parent[x] = u.find(u.parent[x])
- }
- return u.parent[x]
-}
-
-func (u *MyUnionFind) getCount() int {
- return u.count
-}
-```
-
diff --git "a/15_union_find/No.547_\347\234\201\344\273\275\347\232\204\346\225\260\351\207\217.md" "b/15_union_find/No.547_\347\234\201\344\273\275\347\232\204\346\225\260\351\207\217.md"
deleted file mode 100644
index 8558da4..0000000
--- "a/15_union_find/No.547_\347\234\201\344\273\275\347\232\204\346\225\260\351\207\217.md"
+++ /dev/null
@@ -1,137 +0,0 @@
-## 547 省份数量-中等
-
-题目:
-
-有 `n` 个城市,其中一些彼此相连,另一些没有相连。如果城市 `a` 与城市 `b` 直接相连,且城市 `b` 与城市 `c` 直接相连,那么城市 `a` 与城市 `c` 间接相连。
-
-**省份** 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
-
-给你一个 `n x n` 的矩阵 `isConnected` ,其中 `isConnected[i][j] = 1` 表示第 `i` 个城市和第 `j` 个城市直接相连,而 `isConnected[i][j] = 0` 表示二者不直接相连。
-
-返回矩阵中 **省份** 的数量。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
-> 输出:2
-> ```
->
-> **示例 2:**
->
-> 
->
-> ```
-> 输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
-> 输出:3
-> ```
-
-
-
-**解题思路:**
-
-这道题可以有多种解法。
-
-- 并查集思想,详见解法一。思路是求连通分量的并查集,把有连通的城市合并,返回连通分量即可。
-- DFS 或者 BFS,详见解法二。思路是利用 FloodFill 思想染色,采用逐行扫描的方式。每一行都是一个城市,如果它和其他城市联通,那么继续去扫描其他城市,直到扫描完成;这样和该城市所有的连通就是一个省份。
-
-
-
-```go
-// date 2024/01/04
-// 解法一
-func findCircleNum(isConnected [][]int) int {
- n := len(isConnected)
- uf := NewUnionFind(n)
-
- for i := 0; i < n; i++ {
- for j := 0; j < n; j++ {
- if i != j && isConnected[i][j] == 1 {
- uf.Union(i, j)
- }
- }
- }
-
- return uf.GetCount()
-}
-
-// 并查集,求联通分量
-type UnionFind struct {
- parent []int
- count int
-}
-
-func NewUnionFind(n int) *UnionFind {
- u := &UnionFind{
- parent: make([]int, n),
- count: n,
- }
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-func (u *UnionFind) Union(x, y int) {
- xp, yp := u.Find(x), u.Find(y)
- if xp == yp {
- return
- }
- u.parent[yp] = xp
- u.count--
-}
-
-func (u *UnionFind) Find(x int) int {
- root := x
- for root != u.parent[root] {
- root = u.parent[root]
- }
- // 路径压缩
- for x != u.parent[x] {
- ox := u.parent[x]
- u.parent[x] = root
- x = ox
- }
- return root
-}
-
-func (u *UnionFind) GetCount() int {
- return u.count
-}
-```
-
-
-
-```go
-// date 2024/01/05
-// 解法二
-func findCircleNum(isConnected [][]int) int {
- n := len(isConnected)
- visited := make(map[int]bool, n)
-
- var dfs func(isConnected [][]int, cur int, vit map[int]bool)
- dfs = func(isConnected [][]int, cur int, vit map[int]bool) {
- vit[cur] = true
- for j := 0; j < len(isConnected[cur]); j++ {
- if !visited[j] && isConnected[cur][j] == 1 {
- dfs(isConnected, j, vit)
- }
- }
- }
-
- count := 0
- for i := 0; i < n; i++ {
- if !visited[i] {
- dfs(isConnected, i, visited)
- count++
- }
- }
-
- return count
-}
-```
-
diff --git "a/15_union_find/No.684_\345\206\227\344\275\231\350\277\236\346\216\245.md" "b/15_union_find/No.684_\345\206\227\344\275\231\350\277\236\346\216\245.md"
deleted file mode 100644
index 2f92c35..0000000
--- "a/15_union_find/No.684_\345\206\227\344\275\231\350\277\236\346\216\245.md"
+++ /dev/null
@@ -1,97 +0,0 @@
-## 684 冗余连接-中等
-
-题目:
-
-树可以看成是一个连通且 **无环** 的 **无向** 图。
-
-给定往一棵 `n` 个节点 (节点值 `1~n`) 的树中添加一条边后的图。添加的边的两个顶点包含在 `1` 到 `n` 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 `n` 的二维数组 `edges` ,`edges[i] = [ai, bi]` 表示图中在 `ai` 和 `bi` 之间存在一条边。
-
-请找出一条可以删去的边,删除后可使得剩余部分是一个有着 `n` 个节点的树。如果有多个答案,则返回数组 `edges` 中最后出现的那个。
-
-
-
-> **示例 1:**
->
-> 
->
-> ```
-> 输入: edges = [[1,2], [1,3], [2,3]]
-> 输出: [2,3]
-> ```
->
-> **示例 2:**
->
-> 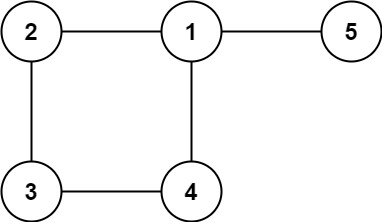
->
-> ```
-> 输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
-> 输出: [1,4]
-> ```
-
-
-
-**解题思路**
-
-从题意可知,冗余的连接是指本来已经连通的节点,再加一条连接是意义的。
-
-所以,这道题也用并查集解决。思路是把有边的节点合并,并且合并的时候做判断,如果合并失败(即两个节点的父结点相同,表示这两个节点已经通过其他边连通了),则说明这条边是冗余的。
-
-```go
-// date 2024/01/05
-func findRedundantConnection(edges [][]int) []int {
- n := len(edges)
- uf := NewUnionFind(n+1)
-
- res := []int{}
- for _, v := range edges {
- if !uf.Union(v[0], v[1]) {
- res = []int{v[0], v[1]}
- return res
- }
- }
-
- return res
-}
-
-// 并查集,判断是否能够进行合并
-type UnionFind struct {
- parent []int
- count int
-}
-
-func NewUnionFind(n int) *UnionFind {
- u := &UnionFind{
- parent: make([]int, n),
- count: n,
- }
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-func (u *UnionFind) Union(x, y int) bool {
- xp, yp := u.Find(x), u.Find(y)
- if xp == yp {
- return false
- }
- u.parent[yp] = xp
- u.count--
- return true
-}
-
-func (u *UnionFind) Find(x int) int {
- root := x
- for root != u.parent[root] {
- root = u.parent[root]
- }
- // 路径压缩
- for x != u.parent[x] {
- ox := u.parent[x]
- u.parent[x] = root
- x = ox
- }
- return root
-}
-```
-
diff --git a/15_union_find/README.md b/15_union_find/README.md
deleted file mode 100644
index c86830e..0000000
--- a/15_union_find/README.md
+++ /dev/null
@@ -1,180 +0,0 @@
-## 并查集Union-Find
-
-### 1、基本概念
-
-并查集被认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组问题。
-
-它管理一系列不相交的集合,并支持两种操作:
-
-- 合并(Union):把两个不相交的集合合并成一个集合
-- 查询(Find):查询两个元素是否在同一个集合中
-
-
-
-并查集的应用场景很多,其中最直接的一个场景是:亲戚问题。
-
-> 题目:
->
-> 如果某个家族人员过于庞大,要判断两个人是否有亲戚关系,不是很容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
->
-> 规定,如果x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。
->
-> 规定,如果x和y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
-
-
-
-### 2、代码设计
-
-通常并查集的数据结构中有两个变量,parent和count。
-
-Parent 表示节点的关系;count 表示连通分量。
-
-初始化时,每个节点指向自己,连通分量就等于节点总数。
-
-合并操作,先判断两个节点的父结点是否相同,如果相同表示已经在同一个集合了,直接返回;否则将其中一个节点的父结点更新为另一个的父结点。
-
-查询操作,如果节点的父结点不是自己,那么一定要继续查找直到找到根节点。
-
-```go
-type (
- UnionFind struct {
- parent []int // 存储每个节点的父结点
- count int // 存储连通分量
- }
-)
-
-// NewUnionFind define
-func NewUnionFind(n int) *UnionFind {
- u := &UnionFind{
- count: n,
- parent: make([]int, n),
- }
- // 初始化时, 每个节点的根节点都是自身
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-// Union define
-// merge x, y to the single set
-func (u *UnionFind) Union(x, y int) {
- xp, yp := u.Find(x), u.Find(y)
- if xp == yp {
- return
- }
- u.parent[yp] = xp
- u.count--
-}
-
-// Find define
-// search the root of x
-func (u *UnionFind) Find(x int) int {
- // 包含了路径压缩
- // 递归写法
- if u.parent[x] != x {
- u.parent[x] = u.Find(u.parent[x])
- }
- return u.parent[x]
-}
-
-// GetCount define
-// the total counts
-func (u *UnionFind) GetCount() int {
- return u.count
-}
-```
-
-### 3、路径压缩
-
-从上面的代码可以看到,`find`函数很重要,即查找集合里的祖宗节点。但实际上,**我们并不关心集合里这棵树的结构长什么样子,只在乎根节点**。
-
-因为无论树长什么样子,树上每个节点的根节点都是相同的,所以有没有进一步压缩每棵树的高度,使其高度始终保持为常数?
-
-可以的,我们只需要在`find()`函数中增加如下代码,即在查找根节点的时候,顺便把整条链路上的节点的根节点都更新到根节点下面。
-
-```go
-func (u *UnionFind) Find(x int) int {
- root := x
- for root != u.parent[root] {
- root = u.parent[root]
- }
- //compress path
- // 迭代写法
- for x != u.parent[x] {
- temp := u.parent[x]
- u.parent[x] = root
- x = temp
- }
- return root
-}
-```
-
-
-
-### 4、按秩合并
-
-有了路径压缩,有些人可能会有一个误解,以为路径压缩优化以后,并查集始终都是一个菊花图(只有两层的树,俗称菊花图)。
-
-但实际上,路径压缩只发生在查询时,而且也只压缩一条路径,所以并查集树的结构仍然可能比较复杂。
-
-比如,现在我们有一棵较复杂的树和一个单元素的集合进行合并。
-
-图片
-
-如果我们可以选择的话,是把7的父结点设置为8好呢?还是把8的父结点设置为7好呢?
-
-当然是后者。因为如果把7的父结点设置为8,那么整棵树的深度会增加,相应地每个元素都根节点的距离都变长了,查找操作也会变长。尽管有路径压缩,也会消耗时间。
-
-而如果把8的父结点设置为7,则不会有这样的问题,因为这种操作方式并没有影响其他节点。
-
-这就启发我们:**应该把简单的树往复杂的树上合并,而不是相反。**
-
-
-
-我们用数组`rank`记录每棵树根节点对应的树深度(如果不是根节点,那么 rank 就是以它为根节点子树的深度)。
-
-一开始,我们把`rank`(秩)设置为0,合并的时候比较两个根节点的秩,把秩更小的树往秩更大的树上面合并。
-
-
-
-**合并的代码(按秩合并)**
-
-```go
-// Union define
-// merge x, y to the single set
-func (u *UnionFind) Union(x, y int) {
- xp, yp := u.Find(x), u.Find(y)
- if xp == yp {
- return
- }
- // depth of tree_x < depth of tree_y
- if u.rank[xp] < u.rank[yp] {
- u.parent[xp] = yp
- } else {
- u.parent[yp] = xp
- // 如果深度相同,那么新的根节点秩加1
- if u.rank[xp] == u.rank[yp] {
- u.rank[xp]++
- }
- }
- u.count--
-}
-```
-
-为什么深度相同,新的根节点深度要加1?
-
-因为,本来都是根节点`root_x`和`root_y`,现在`root_x`变成了`root_y`的一个子节点,那么新的根节点`root_y`的深度当然要加1了。
-
-
-
-## 题目赏析
-
-第一类:并查集,求连通分量
-
-这类并查集,可有路径压缩和秩序优化的版本,便于快速查找。
-
-- 第 128 题:最长连续序列(也是求最大集合元素个数,思路不好想)
-- 第 130 题:被围绕的区域(连通分量,特殊的连通)
-- 第 323 题:无向图中连通分量的个数
-- 第 547 题:省份的数量(就是求连通分量的个数)
diff --git "a/16_segment_tree/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md" "b/16_segment_tree/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md"
deleted file mode 100644
index c262944..0000000
--- "a/16_segment_tree/No.303_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\344\270\215\345\217\257\345\217\230.md"
+++ /dev/null
@@ -1,87 +0,0 @@
-## 303 区域和检索-数组不可变-中等
-
-题目:
-
-给定一个整数数组 `nums`,处理以下类型的多个查询:
-
-1. 计算索引 `left` 和 `right` (包含 `left` 和 `right`)之间的 `nums` 元素的 **和** ,其中 `left <= right`
-
-实现 `NumArray` 类:
-
-- `NumArray(int[] nums)` 使用数组 `nums` 初始化对象
-- `int sumRange(int i, int j)` 返回数组 `nums` 中索引 `left` 和 `right` 之间的元素的 **总和** ,包含 `left` 和 `right` 两点(也就是 `nums[left] + nums[left + 1] + ... + nums[right]` )
-
-
-
-**解题思路**
-
-这道题可有两个思路。第一个,既然题目中已经说明元素不可变,那么**前缀和**可以实现。具体为遍历数组,计算前缀和,并将前缀和存储另一个数组。查找的时候直接在前缀和数组中做减法即可。
-
-第二个思路是线段树,只要实现 Query 方法即可,详见下面代码。
-
-```go
-// date 2024/01/09
-type NumArray struct {
- data []int
- tree []int
-}
-
-
-func Constructor(nums []int) NumArray {
- n := len(nums)
- res := NumArray{
- data: make([]int, n),
- tree: make([]int, 4*n),
- }
- for i := 0; i < n; i++ {
- res.data[i] = nums[i]
- }
- res.buildSegmentTree(0, 0, n-1)
- return res
-}
-
-
-func (this *NumArray) SumRange(left int, right int) int {
- if left >= 0 && right < len(this.data) {
- return this.queryInTree(0, 0, len(this.data)-1, left, right)
- }
- return 0
-}
-
-func (this *NumArray) buildSegmentTree(root, left, right int) {
- if left == right {
- this.tree[root] = this.data[left]
- return
- }
- mid := left + (right-left)/2
- tl := root*2+1
- tr := root*2+2
- this.buildSegmentTree(tl, left, mid)
- this.buildSegmentTree(tr, mid+1, right)
- this.tree[root] = this.tree[tl] + this.tree[tr]
-}
-
-func (this *NumArray) queryInTree(root, tl, tr, left, right int) int {
- if left == tl && right == tr {
- return this.tree[root]
- }
- mid := tl + (tr - tl)/2
- if left > mid {
- return this.queryInTree(root*2+2, mid+1, tr, left, right)
- }
- if right <= mid {
- return this.queryInTree(root*2+1, tl, mid, left, right)
- }
- lsum := this.queryInTree(root*2+1, tl, mid, left, mid)
- rsum := this.queryInTree(root*2+2, mid+1, tr, mid+1, right)
- return lsum+rsum
-}
-
-
-/**
- * Your NumArray object will be instantiated and called as such:
- * obj := Constructor(nums);
- * param_1 := obj.SumRange(left,right);
- */
-```
-
diff --git "a/16_segment_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md" "b/16_segment_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md"
deleted file mode 100644
index e5c565b..0000000
--- "a/16_segment_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md"
+++ /dev/null
@@ -1,116 +0,0 @@
-## 307 区域和检索-数组可修改-中等
-
-题目:
-
-给你一个数组 `nums` ,请你完成两类查询。
-
-1. 其中一类查询要求 **更新** 数组 `nums` 下标对应的值
-2. 另一类查询要求返回数组 `nums` 中索引 `left` 和索引 `right` 之间( **包含** )的nums元素的 **和** ,其中 `left <= right`
-
-实现 `NumArray` 类:
-
-- `NumArray(int[] nums)` 用整数数组 `nums` 初始化对象
-- `void update(int index, int val)` 将 `nums[index]` 的值 **更新** 为 `val`
-- `int sumRange(int left, int right)` 返回数组 `nums` 中索引 `left` 和索引 `right` 之间( **包含** )的nums元素的 **和** (即,`nums[left] + nums[left + 1], ..., nums[right]`)
-
-
-
-**解题思路**
-
-这道题就是标准的线段树解法,有几个注意点:
-
-- 查询的时候,如果查询区间在某个子树里面,直接查询子树,且查询区间直接透传不变。如果查询区间跨根节点,那么需要左右一起查,并合并结果,这时查询区间要跟线段树的区间边界保持一致。
-- 更新的时候。无论更新左子树还是右子树,最后都要记得更新根节点。
-
-```go
-// date 2024/01/09
-type NumArray struct {
- data []int
- tree []int
-}
-
-
-func Constructor(nums []int) NumArray {
- n := len(nums)
- res := NumArray{
- data: make([]int, n),
- tree: make([]int, 4*n),
- }
- for i := 0; i < n; i++ {
- res.data[i] = nums[i]
- }
- res.buildSegmentTree(0, 0, n-1)
- return res
-}
-
-
-func (this *NumArray) Update(index int, val int) {
- if len(this.data) > 0 {
- this.updateInTree(0, 0, len(this.data)-1, index, val)
- }
-}
-
-
-func (this *NumArray) SumRange(left int, right int) int {
- if len(this.data) > 0 {
- return this.queryInTree(0, 0, len(this.data)-1, left, right)
- }
- return 0
-}
-
-func (this *NumArray) buildSegmentTree(root, left, right int) {
- if left == right {
- this.tree[root] = this.data[left]
- return
- }
- mid := left + (right-left)/2
- ltree := 2*root+1
- rtree := 2*root+2
- this.buildSegmentTree(ltree, left, mid)
- this.buildSegmentTree(rtree, mid+1, right)
- this.tree[root] = this.tree[ltree] + this.tree[rtree]
-}
-
-func (this *NumArray) queryInTree(root, tl, tr, left, right int) int {
- if left == tl && right == tr {
- return this.tree[root]
- }
- mid := tl + (tr-tl)/2
- ltree := root*2+1
- rtree := root*2+2
- if left > mid {
- return this.queryInTree(rtree, mid+1, tr, left, right)
- } else if right <= mid {
- return this.queryInTree(ltree, tl, mid, left, right)
- }
- lsum := this.queryInTree(ltree, tl, mid, left, mid)
- rsum := this.queryInTree(rtree, mid+1, tr, mid+1, right)
- return lsum + rsum
-}
-
-func (this *NumArray) updateInTree(root, tl, tr int, index, val int) {
- if tl == tr {
- this.tree[root] = val
- this.data[index] = val
- return
- }
- mid := tl + (tr-tl)/2
- ltree := 2*root+1
- rtree := 2*root+2
- if index > mid {
- this.updateInTree(rtree, mid+1, tr, index, val)
- } else {
- this.updateInTree(ltree, tl, mid, index, val)
- }
- this.tree[root] = this.tree[ltree]+this.tree[rtree]
-}
-
-
-/**
- * Your NumArray object will be instantiated and called as such:
- * obj := Constructor(nums);
- * obj.Update(index,val);
- * param_2 := obj.SumRange(left,right);
- */
-```
-
diff --git a/16_segment_tree/README.md b/16_segment_tree/README.md
deleted file mode 100644
index b58fa5b..0000000
--- a/16_segment_tree/README.md
+++ /dev/null
@@ -1,269 +0,0 @@
-# 线段树
-
-## 1、什么是线段树
-
-线段树 SegmentTree 是一种二叉树形数据结构,1977 年由 Jon Louis Bentley 发明,用来存储区间或线段,并且允许快速查询结构内包含某一点的所有区间。
-
-一个包含 n 个区间的线段树,空间复杂度为`O(n)`,查询的时间复杂度为`O(logn + k)`,其中 k 是符合条件的区间数量。
-
-
-
-线段树的结构是一个二叉树,**每个节点都代表一个区间**,节点 N 所代表的区间即为 Int(N),其需要这些条件:
-
-- 其每个叶子节点,从左到右代表每个单位区间
-- 其内部节点(即非叶子节点)是其两个孩子节点的并集
-- 每个节点(包含叶子节点)中有一个存储线段的数据结构。
-
-
-
-以原始数据 data 为例,构造区间和的线段树如上所示。
-
-```sh
-// date 为原始数据,tree 为线段树各节点值
-data = [0 1 3 5 -2 3]
-tree = [10 4 6 1 3 3 3 0 1 0 0 5 -2 0 0 0 0 0 0 0 0 0 0 0]
-```
-
-线段树的结构是二叉树,采用数组的方式进行存储,如果索引 root 为根节点,那么其左节点为`2*root+1`,右节点为`2*root+2`。
-
-线段树的节点有三个信息,其中`[x,y]` 表示区间,即该节点包含这个区间的信息(本例为区间和),红色数值就是区间和,蓝色数值为节点的树坐标。
-
-图中蓝色节点为叶子节点,即只包含单位区间的值;黄色节点为内部节点,即包含其子节点的并集。
-
-
-
-通常,一个节点存储一个或多个合并区间的数据,这样的存储方式便于查询。
-
-
-
-## 2、线段树可以做那些事情
-
-许多问题要求我们基于对**可用数据范围或者区间**进行查询,给出结果。这可能是一个繁琐而缓慢的过程,尤其是在查询数量众多且重复的情况下。线段树,作为一个特殊的二叉树,能够让我们以对数时间复杂度有效地处理此类查询。
-
-线段树可用于计算几何和地理信息系统领域。例如,距中心参考点或原点一定距离的空间中可能存在大量的点。假设我们要查找距离原点一定距离范围内的点。一个普通的查找表将需要对所有可能的点或所有可能的距离进行线性扫描;但线段树使我们能够以对数时间实现这一需求,而所需空间也少。
-
-
-
-## 3、构造线段树
-
-我们以线段树解决 Range Sum Query 为例,看看如何构造线段树。
-
-假设数据存在大小为 `n` 的 `arr[]` 数组中。
-
-1. 线段树的根通常代表整个数据区间,即 `arr[0: n-1]`。
-2. 线段树的叶子节点代表一个范围,仅包含一个元素。因此,叶子节点代表`arr[0], arr[1]...`等等,直到`arr[n-1]`。
-3. 线段树的内部节点代表其子节点的合并或者并集结果。
-4. 每个子节点可以代表其父结点所表示范围的大约一半。(二分的思想)
-
-从这个过程可以看到,线段树适合递归构造。
-
-
-
-我们使用数组 tree 来存储线段树的节点(初始化全零),下标从 0 开始。
-
-- 树的节点下标从 0 开始。`tree[0]` 就是树根。
-- `tree[i]`的左右子树,分别存在`tree[2*i+1]`和`tree[2*i+2]`中。
-- 用额外的 0 填充 tree
-
-
-
-一般使用大小为`4*n` 的数组就可以轻松表示 n 个元素范围的线段树。(Stack Overflow 上分析,详见[这里](https://stackoverflow.com/questions/28470692/how-is-the-memory-of-the-array-of-segment-tree-2-2-ceillogn-1)。
-
-
-
-**线段树的构造代码**
-
-```go
-type (
- // SegmentTree define
- SegmentTree struct {
- data []int // 存储原始数据
- tree []int // 存储线段树数据
- }
-)
-
-func NewSegmentTree() *SegmentTree {
- return &SegmentTree{}
-}
-
-func (s *SegmentTree) Init(nums []int) {
- n := len(nums)
- s.data = make([]int, n)
- s.tree = make([]int, 4*n)
- for i := 0; i < n; i++ {
- s.data[i] = nums[i]
- }
- // build segment tree from nums
- left, right := 0, n-1
- s.buildSegmentTree(0, left, right)
-}
-
-func (s *SegmentTree) buildSegmentTree(treeIdx int, left, right int) {
- if left == right {
- // the leaf node
- s.tree[treeIdx] = s.data[left]
- return
- }
- mid := left + (right-left)/2
- leftTreeIdx := leftChild(treeIdx)
- rightTreeIdx := rightChild(treeIdx)
- // build left tree with data [left, mid] elem
- s.buildSegmentTree(leftTreeIdx, left, mid)
- // build right tree with data [mid+1, right] elem
- s.buildSegmentTree(rightTreeIdx, mid+1, right)
- s.tree[treeIdx] = s.tree[leftTreeIdx] + s.tree[rightTreeIdx]
-}
-```
-
-
-
-我们以数组`arr = [0, 1, 3, 5, -2, 3]`为例,构造区间和线段树:
-
-
-
-线段树构造好以后,tree 里面的数据是:
-
-```go
-tree = [10 4 6 1 3 3 3 0 1 0 0 5 -2 0 0 0 0 0 0 0 0 0 0 0]
-```
-
-
-
-
-
-## 4、线段树的查询
-
-线段树的查询方法有两种,一种是直接查询,另一种是懒查询。
-
-### 4.1 直接查询
-
-当查询范围与当前节点表示的范围一致时,直接返回节点值即可。否则,继续深入遍历线段树,找到与节点的一部分完全匹配的节点。
-
-```go
-// Query define
-// 查询 [left, right] 区间和
-func (s *SegmentTree) Query(left, right int) int {
- if len(s.data) > 0 {
- return s.queryInTree(0, 0, len(s.data)-1, left, right)
- }
- return 0
-}
-
-// 在以 root 为根的线段树中,[tl, tr] 范围内, 搜索 [left, right] 区间值
-// 如果线段树的区间和查询区间一致,那么直接返回线段树的节点
-// 否则分左子树,右子树,左右子树三个情况,分别查询
-func (s *SegmentTree) queryInTree(root, tl, tr int, left, right int) int {
- // 如果区间一样,直接返回根节点数据
- if left == tl && right == tr {
- return s.tree[root]
- }
- mid := tl + (tr-tl)/2
- leftTree, rightTree := leftChild(root), rightChild(root)
- // query in the right tree
- if left > mid {
- return s.queryInTree(rightTree, mid+1, tr, left, right)
- } else if right <= mid {
- // query in the left tree
- return s.queryInTree(leftTree, tl, mid, left, right)
- }
- lSum := s.queryInTree(leftTree, tl, mid, left, mid)
- rSum := s.queryInTree(rightTree, mid+1, tr, mid+1, right)
- return lSum + rSum
-}
-```
-
-
-
-
-
-在上面的示例中,查询`[0,4]`区间的元素和。线段树中没有任何节点完全代表`[2,4]`的范围,但是可以看到,节点1所代表的区间`[0,2]`,节点5所代表的区间`[3,4]`,这两个节点的并集正好构成区间`[0,4]`,那么区间`[0,4]`的元素和,就是节点1和节点5的值之和。
-
-验证一下,原始数组中区间`[0, 4]`的元素之和是:
-
-```sh
-0 + 1 + 3 + 5 + (-2) = 7
-```
-
-线段树中节点1和节点5的值和为:
-
-```sh
-4 + 3 = 7
-```
-
-答案正确。
-
-
-
-## 5、线段树的更新
-
-### 5.1 单点全量更新
-
-单点更新的过程类似线段树的构建。先更新叶子节点的值,该值与更新后的元素相对应;然后这些更新通过上层节点把影响传递到根节点。
-
-注意:这里的更新是把指定索引的值直接替换掉。
-
-```go
-// Update define
-// 数值全量更新,即原始数组中下标为 index 的值更新为 val
-func (s *SegmentTree) Update(index, val int) {
- if len(s.data) > 0 {
- s.updateInTree(0, 0, len(s.data)-1, index, val)
- }
-}
-
-func (s *SegmentTree) updateInTree(root, tl, tr int, index, val int) {
- // find the leaf node, so update its value
- if tl == tr {
- s.tree[root] = val
- s.data[tl] = val
- return
- }
-
- mid := tl + (tr-tl)/2
- leftTree := leftChild(root)
- rightTree := rightChild(root)
- // if value index is at the right part, then update the right tree
- // otherwise update the left tree
- if index > mid {
- s.updateInTree(rightTree, mid+1, tr, index, val)
- } else if index <= mid {
- s.updateInTree(leftTree, tl, mid, index, val)
- }
- // update the parent's value
- s.tree[root] = s.tree[leftTree] + s.tree[rightTree]
-}
-```
-
-
-
-
-
-在这个示例中,我们原始数组中 index 为 3 的值更新为 12,那么整个线段树的更新如图所示,可以看到节点11,节点5,节点2,节点0依次被修改,传到到树根。
-
-
-
-## 6、线段树的时间复杂度分析
-
-让我们回顾下线段树的构建过程。
-
-构建过程中我们访问了线段树的每个叶子节点(即原数组中的每个元素)。因此,我们处理大约`2 * n`个节点,这使得构建过程的时间复杂度为`O(n)`。
-
-对于每一次递归更新的过程都丢弃一半的区间范围,以到达树的叶子节点,类似二分搜索,只需要对数时间。
-
-叶子更新后,开始返回更新其父节点,这个时间与线段树的高度成线性关系。
-
-
-
-`4*n`个节点可以确保将线段树构建为完整的二叉树,从而树的高度为**以2为底,4n+1**的对数。
-
-线段树查询和更新,时间复杂度都为`O(logN)`。
-
-
-
-## 7、常见题型
-
-第一类:区间和,经典的线段树解法
-
-第 303 题:区域和检索,数组不可变,【直接构造线段树,查询方法即可】
-
-第 307 题:区域和检索,数组可修改
\ No newline at end of file
diff --git a/16_segment_tree/images/segment_tree.png b/16_segment_tree/images/segment_tree.png
deleted file mode 100644
index 9979d19..0000000
Binary files a/16_segment_tree/images/segment_tree.png and /dev/null differ
diff --git a/16_segment_tree/images/segment_tree_logn.png b/16_segment_tree/images/segment_tree_logn.png
deleted file mode 100644
index 4be1c72..0000000
Binary files a/16_segment_tree/images/segment_tree_logn.png and /dev/null differ
diff --git a/16_segment_tree/images/segment_tree_query.png b/16_segment_tree/images/segment_tree_query.png
deleted file mode 100644
index e919ebb..0000000
Binary files a/16_segment_tree/images/segment_tree_query.png and /dev/null differ
diff --git a/16_segment_tree/images/segment_tree_update.png b/16_segment_tree/images/segment_tree_update.png
deleted file mode 100644
index 9317c46..0000000
Binary files a/16_segment_tree/images/segment_tree_update.png and /dev/null differ
diff --git "a/17_lru_cache/No.146_LRU\347\274\223\345\255\230.md" "b/17_lru_cache/No.146_LRU\347\274\223\345\255\230.md"
deleted file mode 100644
index 9b2dd0e..0000000
--- "a/17_lru_cache/No.146_LRU\347\274\223\345\255\230.md"
+++ /dev/null
@@ -1,144 +0,0 @@
-## 146 LRU 缓存-中等
-
-题目:
-
-请你设计并实现一个满足 LRU(最少最近使用)缓存约束的数据结构。
-
-实现 LRUCache 类:
-
-- `LRUCache(int capacity)` 以正整数作为容量 capacity 初始化 LRU 缓存
-- `int get(int key)` 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1
-- `void put(int key, int value)` 如果关键字 key 已经存在,则变更其数据值 value;如果不存在,则向缓存中插入该组`key-value`。如果插入操作导致关键字数量超过 capacity,则应该逐出最久未使用的关键字。
-
-函数 get 和 put 必须在 O(1) 的平均时间复杂度运行。
-
-
-
-分析:
-
-这里重点理解 LRU 的机制。LRU(Least Recently Used)即,最近最少使用,其核心是:
-
-1. 最近。最近访问的要保留在缓存中。
-2. 最少。并不是值访问次数最少,而是很久没有访问,且超过缓存容量的时候,可以删除。比如容量为 2 的缓存。A 访问次数为100,最近一次访问是 B 数据,从访问次数为2,那么 新插入的数据会取代 A,而不是 B。因为最近访问的 B 数据位于队头,而 A 位于队尾。
-
-所谓,热数据也是这个道理,按访问时间,越是最近访问的,越是位于链表的头部。
-
-
-
-要求 get 和 put 函数在 O(1) 时间内完成,那么考虑双向链表来实现。同时,用 head, tail 做头和尾的伪节点。这样在头部插入、去除尾部会很方便。
-
-辅助 map 结构实现 O(1)查找。
-
-`get`函数:
-
-如果不存在,直接返回 -1;如果存在,把缓存 node 移到 头部。
-
-`put`函数:
-
-如果不存在,直接在头部插入,插入后超过容量的,直接删除尾部。
-
-如果存在,直接更新数据,并移到头部。
-
-```go
-// 辅助函数
-addToHead(node)
-removeNode(node)
-moveToHead(node)
-removeTail()
-```
-
-
-
-
-
-```go
-// date 2023/10/16
-type MyNode struct {
- key, val int
- pre, next *MyNode
-}
-
-type LRUCache struct {
- size, capacity int
- cache map[int]*MyNode
- head, tail *MyNode
-}
-
-
-func Constructor(capacity int) LRUCache {
- lr := LRUCache{
- capacity: capacity,
- cache: map[int]*MyNode{},
- head: &MyNode{0,0,nil,nil},
- tail: &MyNode{0,0,nil,nil},
- }
- lr.head.next = lr.tail
- lr.tail.pre = lr.head
- return lr
-}
-
-
-func (this *LRUCache) Get(key int) int {
- node, ok := this.cache[key]
- if !ok {
- return -1
- }
- this.moveToHead(node)
- return node.val
-}
-
-
-func (this *LRUCache) Put(key int, value int) {
- node, ok := this.cache[key]
- if !ok {
- // add
- node := &MyNode{key, value, nil, nil}
- this.cache[key] = node
- this.addToHead(node)
- this.size++
- if this.size > this.capacity {
- // remove tail
- rmd := this.removeTail()
- delete(this.cache, rmd.key)
- this.size--
- }
- } else {
- node.val = value
- this.moveToHead(node)
- }
-}
-
-func (this *LRUCache) addToHead(node *MyNode) {
- node.pre = this.head
- node.next = this.head.next
-
- this.head.next.pre = node
- this.head.next = node
-}
-
-func (this *LRUCache) removeNode(node *MyNode) {
- node.pre.next = node.next
- node.next.pre = node.pre
-}
-
-func(this *LRUCache) moveToHead(node *MyNode) {
- this.removeNode(node)
- this.addToHead(node)
-}
-
-func (this *LRUCache) removeTail() *MyNode {
- node := this.tail.pre
- this.removeNode(node)
- return node
-}
-
-
-
-/**
- * Your LRUCache object will be instantiated and called as such:
- * obj := Constructor(capacity);
- * param_1 := obj.Get(key);
- * obj.Put(key,value);
- */
-```
-
diff --git a/17_lru_cache/README.md b/17_lru_cache/README.md
deleted file mode 100644
index 7e027d4..0000000
--- a/17_lru_cache/README.md
+++ /dev/null
@@ -1,142 +0,0 @@
-## LRU缓存
-
-LRU 是 Least Recently Used 的缩写,即最近最少使用,是数据缓冲淘汰的一种常见机制,重点在于理解**最近**和**最少**两个关键词。
-
-- 最近。即最近访问过的数据要留在缓冲区内。
-- 最少。这里的最少并不是值总的访问次数最少,而是很久没有访问,如果超出缓冲容量,那么可以删除。
-
-比如容量为 2 的一个缓冲序列,历史上数据 A 被访问了 100 次,数据 B 被访问了 2 次,但最后一次访问是访问数据 B,那么当新的数据 C 需要缓存的时候,新插入的数据 C 会踢掉数据 A,而不是数据 B。
-
-
-
-所以,从数据结构来讲,LRU 应该是一个链表,按访问时间,越是最近访问的,越靠近链表的头部。
-
-
-
-LRU 主要有两个方法`Get`和`Put`,要求`O(1)`的时间复杂度,那么考虑双向链表来实现。具体为:
-
-- 用 head 和 tail 做头、尾的伪节点,便于做头部插入,尾部删除
-- 利用 map 辅助存储
-
-链表的节点既要存储 key,也要储存 value。这是因为当超过缓存容量时,要从双向链表中删除数据。在双向链表中删除淘汰的 value,在 map 中删除淘汰出去的 value 对应的 key。
-
-
-
-### 1、结构定义
-
-```go
-type (
- // CacheNode define
- // key, val 存储缓存的键值对
- // pre, next 指向双向链表的前驱和后驱节点
- CacheNode struct {
- key, val int
- pre, next *CacheNode
- }
-
- // LRUCache define
- LRUCache struct {
- size, capacity int
- head, tail *CacheNode
- cache map[int]*CacheNode
- }
-)
-```
-
-
-
-### 2、初始化
-
-```go
-// NewLRUCache define
-func NewLRUCache(cap int) *LRUCache {
- ca := &LRUCache{
- size: 0,
- capacity: cap,
- head: &CacheNode{0, 0, nil, nil},
- tail: &CacheNode{0, 0, nil, nil},
- cache: make(map[int]*CacheNode, cap),
- }
- ca.head.next = ca.tail
- ca.tail.pre = ca.head
- return ca
-}
-```
-
-初始化的时候,创建两个伪节点 head 和 tail,便于在头部插入和尾部删除。
-
-```go
-// add node to head
-func (l *LRUCache) addToHead(node *CacheNode) {
- node.pre = l.head
- node.next = l.head.next
-
- l.head.next.pre = node
- l.head.next = node
-}
-
-// remove and return the tail node
-func (l *LRUCache) removeTail() *CacheNode {
- node := l.tail.pre
- l.removeNode(node)
- return node
-}
-```
-
-
-
-### 3、查询
-
-```go
-// Get define
-func (l *LRUCache) Get(key int) int {
- node, ok := l.cache[key]
- if !ok {
- return -1
- }
- l.moveToHead(node)
- return node.val
-}
-```
-
-
-
-
-
-### 4、创建和更新
-
-```go
-// Put define
-func (l *LRUCache) Put(key, value int) {
- if node, ok := l.cache[key]; ok {
- // update node and move to head
- node.val = value
- l.moveToHead(node)
- return
- }
-
- // add node
- node := &CacheNode{key: key, val: value}
- l.cache[key] = node
- l.addToHead(node)
- l.size++
- if l.size > l.capacity {
- // remote tail
- rmd := l.removeTail()
- delete(l.cache, rmd.key)
- l.size--
- }
-}
-```
-
-LRUCache 的创建和更新,都是`Put`函数。先从 map 中查,如果存在直接更新,并把该节点移到双向链表的头部。
-
-如果不存在,直接创建,然后在移到双向链表的头部。
-
-再判断已经缓存的数据量是否超过容量,如果超过,直接从尾部开始删除,并删除 map 中的数据。
-
-
-
-总结下,LRU 是一个由 map 和 双向链表组成的数据结构。map 中 key 对应的 value 是双向链表的节点。双向链表中存储具体的 key-value 信息。双向链表表头用于更新缓存,表尾用于淘汰缓存。
-
-
diff --git a/17_lru_cache/images/lru_cache.png b/17_lru_cache/images/lru_cache.png
deleted file mode 100644
index 788b4f5..0000000
Binary files a/17_lru_cache/images/lru_cache.png and /dev/null differ
diff --git "a/18_lfu_cache/No.460_LFU\347\274\223\345\255\230.md" "b/18_lfu_cache/No.460_LFU\347\274\223\345\255\230.md"
deleted file mode 100644
index bc532c4..0000000
--- "a/18_lfu_cache/No.460_LFU\347\274\223\345\255\230.md"
+++ /dev/null
@@ -1,147 +0,0 @@
-## 460 LFU缓存-困难
-
-题目:
-
-请你为 [最不经常使用(LFU)](https://baike.baidu.com/item/缓存算法)缓存算法设计并实现数据结构。
-
-实现 `LFUCache` 类:
-
-- `LFUCache(int capacity)` - 用数据结构的容量 `capacity` 初始化对象
-- `int get(int key)` - 如果键 `key` 存在于缓存中,则获取键的值,否则返回 `-1` 。
-- `void put(int key, int value)` - 如果键 `key` 已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量 `capacity` 时,则应该在插入新项之前,移除最不经常使用的项。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 **最久未使用** 的键。
-
-为了确定最不常使用的键,可以为缓存中的每个键维护一个 **使用计数器** 。使用计数最小的键是最久未使用的键。
-
-当一个键首次插入到缓存中时,它的使用计数器被设置为 `1` (由于 put 操作)。对缓存中的键执行 `get` 或 `put` 操作,使用计数器的值将会递增。
-
-函数 `get` 和 `put` 必须以 `O(1)` 的平均时间复杂度运行。
-
-
-
-**解题思路**
-
-```go
-// date 2024/01/09
-type LFUNode struct {
- key, val int
- frequency int
- pre, next *LFUNode
-}
-
-type LFUList struct {
- size int
- head, tail *LFUNode
-}
-
-type LFUCache struct {
- cache map[int]*LFUNode
- list map[int]*LFUList
- min int
- cap int
-}
-
-func Constructor(capacity int) LFUCache {
- return LFUCache{
- cap: capacity,
- min: 0,
- cache: make(map[int]*LFUNode),
- list: make(map[int]*LFUList),
- }
-}
-
-
-func (this *LFUCache) Get(key int) int {
- node, ok := this.cache[key]
- if !ok {
- return -1
- }
- this.list[node.frequency].removeNode(node)
- node.frequency++
- if _, ok = this.list[node.frequency]; !ok {
- this.list[node.frequency] = NewLFUList()
- }
- oldList := this.list[node.frequency]
- oldList.addToFront(node)
-
- if node.frequency-1 == this.min {
- if minList, ok := this.list[this.min]; !ok || minList.isEmpty() {
- this.min = node.frequency
- }
- }
- return node.val
-}
-
-
-func (this *LFUCache) Put(key int, value int) {
- if this.cap == 0 {
- return
- }
- if node, ok := this.cache[key]; ok {
- node.val = value
- this.Get(key)
- return
- }
- if this.cap == len(this.cache) {
- minList := this.list[this.min]
- rmd := minList.removeFromRear()
- delete(this.cache, rmd.key)
- }
- node := &LFUNode{key: key, val: value, frequency: 1}
- this.min = 1
- if _, ok := this.list[this.min]; !ok {
- this.list[this.min] = NewLFUList()
- }
- minList := this.list[this.min]
- minList.addToFront(node)
- this.cache[key] = node
-}
-
-func NewLFUList() *LFUList {
- res := &LFUList{
- size: 0,
- head: &LFUNode{0, 0, 0, nil, nil},
- tail: &LFUNode{0, 0, 0, nil, nil},
- }
- res.head.next = res.tail
- res.tail.pre = res.head
- return res
-}
-
-// addToHead define
-// node is update or new, so insert to front
-// 新节点肯定是被访问或者新插入的
-func (l *LFUList) addToFront(node *LFUNode) {
- node.pre = l.head
- node.next = l.head.next
-
- l.head.next.pre = node
- l.head.next = node
- l.size++
-}
-
-func (l *LFUList) removeFromRear() *LFUNode {
- node := l.tail.pre
- l.removeNode(node)
- return node
-}
-
-func (l *LFUList) removeNode(node *LFUNode) {
- node.pre.next = node.next
- node.next.pre = node.pre
- l.size--
-}
-
-func (l *LFUList) isEmpty() bool {
- return l.size == 0
-}
-
-
-
-/**
- * Your LFUCache object will be instantiated and called as such:
- * obj := Constructor(capacity);
- * param_1 := obj.Get(key);
- * obj.Put(key,value);
- */
-```
-
diff --git a/18_lfu_cache/README.md b/18_lfu_cache/README.md
deleted file mode 100644
index b9219f0..0000000
--- a/18_lfu_cache/README.md
+++ /dev/null
@@ -1,194 +0,0 @@
-## LFU缓存
-
-### 1、什么是LFU
-
-LFU 是 Least Frequently Used 的缩写,即最不经常、最少使用,也是一种常见缓存淘汰机制,选择访问计数器最小的页面进行淘汰。
-
-所以,对每个缓存数据都带有一个访问计数器。
-
-
-
-根据 LFU 的策略,每访问一次都需要更新该数据的访问计数器,并把数据移到访问计数器从大到小的位置。
-
-举个例子,一个容量为 3 个缓存器,当前缓存器中的数据及其计数器分别是:
-
-```sh
-数据 A 计数器为23
-数据 B 计数器为12
-数据 C 计数器为12
-```
-
-插入数据 B,发现缓存中有 B,那么 B 的计数器加1,并移到按数据计数器排序的位置;
-
-插入数据 D,发现缓存中没有 B,插入 D 将导致容量超过,那么计数器为12的数据 C,会被淘汰;数据 D 放在数据 B 的后面,计数器为1。
-
-此时,缓存器中的数据及其计数器分别是:
-
-```sh
-数据 A 计数器为23
-数据 B 计数器为13
-数据 D 计数器为1
-```
-
-
-
-### 2、LFU的淘汰机制
-
-这里有一个 LRU 特别的地方。如果淘汰的数据有多个相同的计数器,那么选择最靠近尾部的数据,即从尾部删除。
-
-
-
-比如上图中数据 A、B、C的访问次数相同,都是 1,新插入的数据 F 不在缓存中,那么要淘汰 A,并把 F 放到数据 C 的前面。也就是说**相同访问次数,按照新旧顺序排列,淘汰最旧的数据。**
-
-所以,可见**LFU 更新和插入可以发生在链表的任意位置,删除都发生在表尾。**
-
-
-
-同样的,LFU 同样要求查询尽量高效,`O(1)`查询。那么,我们可以选择 map 辅助查询,选用双向链表存储 key-value。因为,LFU 需要记录访问次数,所以每个节点除了存储key, value,还要存储 frequency 访问次数。
-
-
-
-### 3、按频次排序?
-
-前面讲到过,相同频次的数据按先后时间排序。那么不同频次的数据,如何排序呢?
-
-如果你开始考虑排序算法,那么你的思考方向就偏离了最佳答案。排序至少`O(logN)`。
-
-回过头来看 LFU 的原理,你会发现它**只关心最小频次,其他频次之间的顺序不需要排序。**
-
-因为,数据存在的时候,直接更新频次就好;只有数据不存在,新插入数据导致旧数据删除的时候,才会看数据的频次,且只看最小频次的数据。
-
-
-
-我们可以选择 min 变量保存最小频次,淘汰时读取这个值找到要删除的数据。
-
-相同频次的数据,按先后顺序排序,这个特点双向表插入动作已经体现了。
-
-如何把相同频次的数据组织在一起呢?还是用 map,map 的 key 为访问频次,value 为该频次下双向链表。
-
-当超过缓存容量时,需要删除,先找到最小频次 min,再从 map 中找到 min 对应的双向链表,从该链表的表尾删除一个数据即可,这就解决了 LFU 的删除操作。
-
-
-
-### 4、LFU 的实现
-
-有了上面的介绍,我们就可以定义 LFU 的数据结构:
-
-```go
-type (
- // LFUNode define
- LFUNode struct {
- key, val int
- frequency int
- pre, next *LFUNode
- }
- // LFUList define
- LFUList struct {
- size int
- head, tail *LFUNode
- }
- // LFUCache define
- LFUCache struct {
- cache map[int]*LFUNode // key is node key
- list map[int]*LFUList // key is frequency
- capacity int
- min int
- }
-)
-```
-
-`LFUNode`存储具体的 key-value 信息,同时 frequency 记录访问频次。
-
-`LFUList`是一个双向链表,相同频次的 `LFUNode`会组织到同一个双向链表中。
-
-`LFUCache`是主结构,包含两个 map,分别记录节点和双向链表,capacity 和 min 两个变量。
-
-
-
-LFUCache 的 Get 操作,涉及 frequency 的更新和 map 的调整。具体为:先在 cache map 中通过 key 查到节点信息,根据节点的 frequency 在 list map 中找到该 frequency 的双向链表,删除该节点。删除后,frequency 递增,再次从 list map 中查找新的 frequency 所在的双向链表,如果不存在,直接创建一个,然后在双向链表的表头插入该节点。
-
-最后记得更新 min 值。如果老的 frequency 等于 min,那么就需要进一步判断 list map 中是否存在 min(即最小的frequency)对应的双向链表。如果不存在,或者存在,但双向链表为空,那么都需要更新 min 值。
-
-这是因为 Get 操作会把节点从 frequency 对应的双向链表,移到 frequency+1 对应的双向链表。如果移到导致老的 frequency 双向链表为空,那么 min 就需要更新为 frequency。
-
-```go
-func (l *LFUCache) Get(key int) int {
- node, ok := l.cache[key]
- if !ok {
- return -1
- }
- // first remote from the old frequency, then move to the new double list
- l.list[node.frequency].removeNode(node)
- node.frequency++
- if _, ok = l.list[node.frequency]; !ok {
- l.list[node.frequency] = NewLFUList()
- }
- oldList := l.list[node.frequency]
- oldList.addToFront(node)
-
- // if l.min is empty update
- if node.frequency-1 == l.min {
- if minList, ok := l.list[l.min]; !ok || minList.isEmpty() {
- l.min = node.frequency
- }
- }
- return node.val
-}
-```
-
-
-
-LFUCache 的 Put 操作会稍微复杂一些。
-
-先在 cache map 中查询 key 是否存在,如果存在,直接更新 value 和 frequency 值即可,更新 frequency 值与Get中的逻辑一样,直接复用。
-
-如果不存在,就需要进行插入。插入前,先判断是否满了,如果装满,根据 min 找到双向链表,表尾删除节点,同时在 cache map 也要删除该节点。
-
-因为新插入的数据访问次数为1,所以 min 也要更新为1。新建节点,插入两个 map 即可。
-
-```go
-func (l *LFUCache) Put(key, value int) {
- if l.capacity == 0 {
- return
- }
- // update node's frequency if exist
- if node, ok := l.cache[key]; ok {
- node.val = value
- // 处理过程与 get 一样,直接复用
- l.Get(key)
- return
- }
-
- // not exist
- // 如果不存在且缓冲满了,需要删除
- if l.capacity == len(l.cache) {
- minList := l.list[l.min]
- rmd := minList.removeFromRear()
- delete(l.cache, rmd.key)
- }
-
- // new node, insert to map
- node := &LFUNode{key: key, val: value, frequency: 1}
- // the min change to 1, once create a new node
- l.min = 1
- if _, ok := l.list[l.min]; !ok {
- l.list[l.min] = NewLFUList()
- }
- oldList := l.list[l.min]
- oldList.addToFront(node)
- // insert node to all cache
- l.cache[key] = node
-}
-```
-
-
-
-总结下,LFU 是由两个 map 和一个 min 变量组成的数据结构。
-
-一个 map 的 key 存储的是访问次数,对应的 value 是一个个双向链表,双向链表的作用是在相同频次的情况下,淘汰删除表尾的数据;而数据更新(或者新建)则从表头插入。
-
-另一个 map 中 key 对应的 value 就是双向链表的节点,即实际存储的缓存数据。这里的双向链表节点比 LRU 多储存了一个访问次数的值,即 key-value-frequency 元组。
-
-这里的双向链表的作用与 LRU 类似,既可以根据 map 中 key 更新双向链表节点的 value 和 frequency,也可以根据双向链表节点中的 key 和 frequency 反向更新 map 中的对应关系。
-
-
diff --git a/18_lfu_cache/images/lfu_cache.png b/18_lfu_cache/images/lfu_cache.png
deleted file mode 100644
index 8247426..0000000
Binary files a/18_lfu_cache/images/lfu_cache.png and /dev/null differ
diff --git a/18_lfu_cache/images/lfu_cache_struct.png b/18_lfu_cache/images/lfu_cache_struct.png
deleted file mode 100644
index fe4ac4a..0000000
Binary files a/18_lfu_cache/images/lfu_cache_struct.png and /dev/null differ
diff --git "a/19_binary_index_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md" "b/19_binary_index_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md"
deleted file mode 100644
index f1f5f3c..0000000
--- "a/19_binary_index_tree/No.307_\345\214\272\345\237\237\345\222\214\346\243\200\347\264\242_\346\225\260\347\273\204\345\217\257\346\233\264\346\226\260.md"
+++ /dev/null
@@ -1,98 +0,0 @@
-## 307 区域和检索-数组可修改-中等
-
-题目:
-
-给你一个数组 `nums` ,请你完成两类查询。
-
-1. 其中一类查询要求 **更新** 数组 `nums` 下标对应的值
-2. 另一类查询要求返回数组 `nums` 中索引 `left` 和索引 `right` 之间( **包含** )的nums元素的 **和** ,其中 `left <= right`
-
-实现 `NumArray` 类:
-
-- `NumArray(int[] nums)` 用整数数组 `nums` 初始化对象
-- `void update(int index, int val)` 将 `nums[index]` 的值 **更新** 为 `val`
-- `int sumRange(int left, int right)` 返回数组 `nums` 中索引 `left` 和索引 `right` 之间( **包含** )的nums元素的 **和** (即,`nums[left] + nums[left + 1], ..., nums[right]`)
-
-
-
-**解题思路**
-
-这道题既可以用标准的线段数解法,也可以用树形数组(即二叉索引树)解决。线段树解法详见线段树部分,下面给出树形数组的解法。
-
-注意,这里的树形数组更新使用的是增量更新,所以维护原始数组的数据。
-
-```go
-// 2024/01/10
-// binary indexed tree
-type NumArray struct {
- data []int
- tree []int
-}
-
-func Constructor(nums []int) NumArray {
- n := len(nums)
- res := NumArray{
- data: make([]int, n+1),
- tree: make([]int, n+1),
- }
- // B[i] = sum(j, i) of A
- // j = i - 2^k - 1
- for i := 1; i <= n; i++ {
- res.data[i] = nums[i-1]
- res.tree[i] = nums[i-1]
- for j := i-2; j >= i-lowbit(i); j-- {
- res.tree[i] += nums[j]
- }
- }
- return res
-}
-
-
-func (this *NumArray) Update(index int, val int) {
- // convert to bit index
- index++
- dt := val - this.data[index]
- this.data[index] = val
- this.update(index, dt)
-}
-
-
-func (this *NumArray) SumRange(left int, right int) int {
- s1 := this.query(left-1)
- s2 := this.query(right)
- return s2-s1
-}
-
-// 增量更新
-func (this *NumArray) update(index, val int) {
- // son to parent
- for index < len(this.tree) {
- this.tree[index] += val
- index += lowbit(index)
- }
-}
-
-func (this *NumArray) query(index int) int {
- // sum is [1, index]
- sum := 0
- index += 1
- for index >= 1 {
- sum += this.tree[index]
- index -= lowbit(index)
- }
- return sum
-}
-
-func lowbit(x int) int {
- return x & -x
-}
-
-
-/**
- * Your NumArray object will be instantiated and called as such:
- * obj := Constructor(nums);
- * obj.Update(index,val);
- * param_2 := obj.SumRange(left,right);
- */
-```
-
diff --git "a/19_binary_index_tree/No.315_\350\256\241\347\256\227\345\217\263\344\276\247\345\260\217\344\272\216\345\275\223\345\211\215\345\205\203\347\264\240\347\232\204\344\270\252\346\225\260.md" "b/19_binary_index_tree/No.315_\350\256\241\347\256\227\345\217\263\344\276\247\345\260\217\344\272\216\345\275\223\345\211\215\345\205\203\347\264\240\347\232\204\344\270\252\346\225\260.md"
deleted file mode 100644
index 121b440..0000000
--- "a/19_binary_index_tree/No.315_\350\256\241\347\256\227\345\217\263\344\276\247\345\260\217\344\272\216\345\275\223\345\211\215\345\205\203\347\264\240\347\232\204\344\270\252\346\225\260.md"
+++ /dev/null
@@ -1,125 +0,0 @@
-## 315 计算右侧小于当前元素的个数-困难
-
-题目:
-
-给你一个整数数组 `nums` ,按要求返回一个新数组 `counts` 。数组 `counts` 有该性质: `counts[i]` 的值是 `nums[i]` 右侧小于 `nums[i]` 的元素的数量。
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [5,2,6,1]
-> 输出:[2,1,1,0]
-> 解释:
-> 5 的右侧有 2 个更小的元素 (2 和 1)
-> 2 的右侧仅有 1 个更小的元素 (1)
-> 6 的右侧有 1 个更小的元素 (1)
-> 1 的右侧有 0 个更小的元素
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [-1]
-> 输出:[0]
-> ```
->
-> **示例 3:**
->
-> ```
-> 输入:nums = [-1,-1]
-> 输出:[0,0]
-> ```
-
-
-
-**解题思路**
-
-这道题可用树形数组来解决。
-
-前提是先讲原始数组排序去重,并离散化到一段连续的区域。然后对这段连续的区域进行树形数组。
-
-树形数组可求前缀和,在本题中树形数组初始为 0;增量更新每个位置,值为1,那么得到的前缀和就是小于当前元素的个数。
-
-具体过程如下:
-
-
-
-
-
-```go
-// date 2024/01/11
-type MyBit struct {
- tree []int
-}
-
-func NewMyBit(cap int) *MyBit {
- // 原数组中的值都为零,所以直接初始化tree就可以
- return &MyBit{tree: make([]int, cap+1)}
-}
-
-func (this *MyBit) Query(idx int) int {
- sum := 0
- for idx >= 1 {
- sum += this.tree[idx]
- idx -= lowbit(idx)
- }
- return sum
-}
-
-func (this *MyBit) Add(idx int, val int) {
- for idx < len(this.tree) {
- this.tree[idx] += val
- idx += lowbit(idx)
- }
-}
-
-func countSmaller(nums []int) []int {
- n := len(nums)
- // c
- one := make([]int, n)
- copy(one, nums)
-
- // 先排序,然后去重,并离散化
- // 这样做的目的是1)升序排序,这样树形数组查询的时候,前缀和就是小于当前元素的个数
- // 2)把原数组中的值映射到一个连续的区域,便于做树形数组
- sort.Slice(one, func(i, j int) bool {
- return one[i] < one[j]
- })
- k := 1
- kth := map[int]int{one[0]: 1}
- for i := 1; i < n; i++ {
- if one[i] != one[i-1] {
- k++
- kth[one[i]] = k
- }
- }
-
- bit := NewMyBit(k)
- res := make([]int, 0, n)
- for i := n-1; i >= 0; i-- {
- v := kth[nums[i]]
- // 求小于v的个数,就是求 v-1 前缀和
- res = append(res, bit.Query(v-1))
- bit.Add(v, 1)
- }
- reverseArr(res)
- return res
-}
-
-func reverseArr(arr []int) []int {
- left, right := 0, len(arr)-1
- for left < right {
- arr[left], arr[right] = arr[right], arr[left]
- left++
- right--
- }
- return arr
-}
-
-func lowbit(x int) int {
- return x & -x
-}
-```
-
diff --git a/19_binary_index_tree/README.md b/19_binary_index_tree/README.md
deleted file mode 100644
index 7961ac3..0000000
--- a/19_binary_index_tree/README.md
+++ /dev/null
@@ -1,255 +0,0 @@
-# Binary Indexed Tree \[二叉索引树\]
-
-[TOC]
-
-## 1、结构介绍
-
-二叉索引树,Binary Indexed Tree,又名树状数组,或者Fenwick Tree,因为本算法由Fenwick创造。
-
-
-
-## 2、问题定义
-
-给定一个数组array[0....n-1],实现两个函数:1)求取前i项和;2)更新第i项值。
-
-分析:
-
-一个比较简单的解法就是通过循环累计求和(需要`O(N)`时间复杂度),根据下标更新值(需要`O(1)`时间复杂度)。
-
-另一种解法是前缀和,创建一个前 n 项和数组,这样求和需要O(1)时间,更新需要O(n)时间。
-
-而使用BIT数据结构,可以在O(Logn)时间内进行求和操作和更新操作。下面具体介绍一下。
-
-
-
-## 3、树形数组概念
-
-
-
-说明:图中实线表示数组 B 中节点之间的关系;虚线表示两个数组下标对齐。
-
-图中数组 A 为原始数组,B 为树形数组。树形数组的底层结构是数组,但每个节点有树的关系。如图所示,树形数组中父子节点具有这样的关系:
-
-```sh
-// parent, son 均为下标,k 为 son 下标对应二进制末尾0的个数
-parent = son + 2^k
-```
-
-在 B 数组中,B4,B6,B7 都是 B8 的子节点。因为
-
-```sh
-# 4 的二进制是 0b100
-4 + 2^2 = 8
-# 6 的二进制是 0b110
-6 + 2^1 = 8
-# 7 的二进制是 0b111
-7 + 2^0 = 8
-```
-
-所以,B4,B6,B7 的父结点都是 B8。
-
-从另一个角度看,`2^k`也是 son 下标的二进制表示形式中从尾部数第一个 1 所代表的数值。
-
-```go
-// 4 = 0b100
-4 + 4 = 8
-// 6 = 0b110
-6 + 2 = 8
-// 7 = 0b111
-7 + 1 = 8
-```
-
-
-
-## 4、节点的意义
-
-树形数组可用于求区间和,下面以求区间和为例。
-
-在树形数组中,所有奇数下标的节点都叶子节点,即单点,没有子节点,那么它存储的就是原始数组中的值。比如,图中的 B1,B3,B5,B7,B9 都是叶子节点,分别存储 A1,A3,A5,A7,A9 的值。
-
-所有的偶数下标的节点都是父节点。父节点存储的是区间和。比如,B4 存储的就是 B2,B3,A4 的和,开展之后就是:
-
-```sh
-B4 = B2 + B3 + A4 = A1 + A2 + A3 + A4
-```
-
-这个区间的左边界是该父节点最左边的叶子节点,右边界就是自己的下标。对 B 数组下标按个计算如下:
-
-```sh
-B1 = A1
-B2 = B1 + A2 = A1 + A2
-B3 = A3
-B4 = B2 + B3 + A4 = A1 + A2 + A3 + A4
-B5 = A5
-B6 = B5 + A6 = A5 + A6
-B7 = A7
-B8 = B4 + B6 + B7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7
-```
-
-通过数学归纳法可以得出,左边界的下标一定是 `i - 2^k + 1`,其中 i 为父结点的下标,k 为 i 对应二进制中末尾0 的个数。
-
-所以 B 数组每个节点的值可以表示为:
-
-```go
-// j = i - 2^k + 1
-// k 为 i 二进制表现形式中末尾0的个数
-B[i] = sum(j, i) of A
-```
-
-所以,可知,**数组B每个节点的值是数组A部分节点的和**。
-
-
-
-### 5、树形数组初始化
-
-有了上面的介绍,我们就从原始数组 A 初始化树形数组B,代码如下:
-
-```go
-type (
- // BinaryIndexedTree define
- BinaryIndexedTree struct {
- capacity int
- tree []int
- }
-)
-
-// NewBinaryIndexedTree define
-func NewBinaryIndexedTree(arr []int) *BinaryIndexedTree {
- n := len(arr)
- b := &BinaryIndexedTree{
- capacity: n + 1,
- tree: make([]int, n+1), // 为了计算方便,初始化为n+1
- }
- for i := 1; i <= n; i++ {
- b.tree[i] = arr[i-1]
- for j := i - 2; j >= i-lowbit(i); j-- {
- b.tree[i] += arr[j]
- }
- }
- return b
-}
-
-// 返回 x 二进制形式中,末尾最后一个1所代表的数值,即 2^k
-// k 为 x 二进制中末尾零的的个数
-func lowbit(x int) int {
- return x & -x
-}
-```
-
-初始化以后,原始数组 A 和树形数组 B 的对应关系如下:
-
-
-
-
-
-### 5、查询操作
-
-**树形数组 B 可以查询原数组 A 区间`[1, i]`的和**。
-
-按照数组B中节点的定义,以及与A数组的关系,可以得知:
-
-```go
-Query(i) = A1 + A2 + ... + Ai
-= A1 + A2 + ... + A(i-2^k) + A(i-2^k+1) + ... + Ai
-= Query(i-2^k) + Bi
-= Query(i-lowbit(i)) + Bi
-```
-
-所以,对数组A的区间和查询,等价于对数组B中某些节点求和。
-
-对数组B求和的时候,`i-lowbit(i)` 不断地将 i 二进制中末尾的 1 去掉,进行递归求和。
-
-对于任意的数值 i,其最多有`log(i)`个1,所以原本对数组A求区间和所需要的时间复杂度为`O(N)`,可以转变为对树形数组B求和,其时间复杂度为`O(logN)`。
-
-这就是树形数组在解决区间和问题上的优势。
-
-具体查询代码如下:
-
-```go
-// Query define
-// 求区间和,返回原始数组中[0, index] 的区间和
-func (b *BinaryIndexedTree) Query(index int) int {
- sum := 0
- for index > 1 {
- sum += b.tree[index]
- index -= lowbit(index)
- }
- return sum
-}
-```
-
-
-
-既然能够高效地查询从数组头开始的区间和,那么任意区间的和也可求解。
-
-```go
-// RangeSum define
-// 对任意区间求和,返回A[start, end]区间和
-func (b *BinaryIndexedTree) RangeSum(start, end int) int {
- s1 := b.Query(start - 1)
- s2 := b.Query(end)
- return s2 - s1
-}
-```
-
-
-
-查询操作如此高效,也得益于这样一个事实:**任意正整数都可以表示为多个2的幂次方之和**。
-
-比如,12 = 8 + 4,要想得到原始数组A中前 12 项的和,那么只需要将 B12 + B8 即可。B8 存储了前8项的和,B12 存储了后4项的和。
-
-
-
-
-
-### 6、更新操作(增量更新)
-
-树形数组 B 中父子节点的关系是`parnet = son + 2^k`,那么可以通过这个公式,从叶子节点不断向上递推,知直到最大的父结点为止。
-
-祖先节点最多`logN`个,所以更新操作的时间复杂度为`O(logN)`。
-
-**注意,这里指的是增量更新,即某个节点增加或减少某个值**
-
-```go
-// Add define
-// 增量更新,即对原始数组A index下标的值 增加 val
-func (b *BinaryIndexedTree) Add(index, val int) {
- // parent = son + 2^k
- for index <= b.capacity {
- b.tree[index] += val
- index += lowbit(index)
- }
-}
-```
-
-
-
-
-
-### 7、不同场景下树形数组的功能
-
-根据节点维护数据的含义不同,树形数组可以提供不同的功能来满足各种区间和问题。
-
-
-
-**第一类:单点更新+区间求和**
-
-这是树形数组最典型的场景。单点更新,一般是增量更新,直接 `add(index, val)`即可,如果是全量更新,树形数组结构中多维护一个原始数据,全量更新可以转化为增量更新。
-
-区间求和,直接两次查询即可。求`[left, right]`区间和,等于:
-
-```go
-query(right) - query(left-1)
-```
-
-这类题目有:
-
-- 第 307 题:区域和检索,数组可修改。
-
-
-
-**第二类:区间增减+单点查询**
-
-这类情况可用差分数组,区间更新,只修改区间两头的值即可;
-
-单点查询,就变成了对差分数组的前缀和。
diff --git a/19_binary_index_tree/binaryIndexTree.md b/19_binary_index_tree/binaryIndexTree.md
deleted file mode 100644
index d6247ee..0000000
--- a/19_binary_index_tree/binaryIndexTree.md
+++ /dev/null
@@ -1,1378 +0,0 @@
-## 二叉树索引树
-
-[TOC]
-
----
-
-### 1. 结构介绍
-
-二叉索引树,Binary Indexed Tree,又名树状数组,或者Fenwick Tree,因为本算法由Fenwick创造。
-
-
-
-### 2. 问题定义
-
-假设有这样一个问题:
-
-> 给定一个数组array[0....n-1],实现两个函数:1)求取前i项和;2)更新第i项值。
-
-
-
-其中一个比较简单的思路就是通过循环累计 `[0, i-1]` 求和(需要O(n)时间),根据下标更新值(需要O(1)时间)。
-
-另一种解法是创建一个前n项和数组(即,第 `i` 项存储前 `i` 项的和),这样求和需要O(1)时间,更新需要O(n)时间。
-
-而使用BIT数据结构,可以在O(Logn)时间内进行求和操作和更新操作。下面具体介绍一下。
-
-
-
-### 3. 表现形式
-
-BIT这种数据结构使用一般数组进行存储,每个节点存储 **部分** 输入数组的元素之和。BIT数组的元素个数与输入数组的元素个数一致,均为n。BIT数组的初始值均为0,通过更新操作获取输入数组部分元素之和,并存储在相应的位置上。
-
-
-
-### 4. 更新操作
-
-更新操作是指根据输入数组的元素来更新BIT数组的元素,进而根据BIT数组求前i项和。
-
-```
-update(index, val): Updates BIT for operation arr[index] += val
-// Note that arr[] is not changed here. It changes
-// only BI Tree for the already made change in arr[].
-1) Initialize index as index+1.
-2) Do following while index is smaller than or equal to n.
-...a) Add value to BITree[index]
-...b) Go to parent of BITree[index]. Parent can be obtained by removing
- the last set bit from index, i.e., index = index + (index & (-index))
-```
-
-令BIT数组为:BIT[i] = Input[i-lowbit(i)+1] + Input[i-lowbit(i)+2] + ... + Input[i];
-
-即从最左边的孩子,到自身的和,如BIT[12]= A9+A10+A11+A12
-
-### 5. 求和操作
-
-求和操作是指利用BIT数组求原来输入数组的前i项和。
-
-```
-getSum(index): Returns sum of arr[0..index]
-// Returns sum of arr[0..index] using BITree[0..n]. It assumes that
-// BITree[] is constructed for given array arr[0..n-1]
-1) Initialize sum as 0 and index as index+1.
-2) Do following while index is greater than 0.
-...a) Add BITree[index] to sum
-...b) Go to parent of BITree[index]. Parent can be obtained by removing
- the last set bit from index, i.e., index = index - (index & (-index))
-3) Return sum.
-```
-
-
-说明:
-
-1. 如果节点y是节点x的父节点,那么节点y可以由节点x通过移除Lowbit(x)获得。**Lowbit(natural)为自然数(即1,2,3…n)的二进制形式中最右边出现1的值**。即通过以下公式获得 $parent(i) = i - i & (-i)$。
-
-2. 节点y的子节点x(对BIT数组而言)存储从y(不包括y)到x(包括x)(对输入数组而言)的的元素之和。即BIT数组的值由输入数组两者之间下标的节点对应关系获得。
-
-
-计算前缀和Sum(i)的计算:顺着节点i往左走,边走边“往上爬”,把经过的BIT[i]累加起来即可。
-
-
-
-#### BIT工作原理
-
-BIT工作原理得益于所有的正整数,均可以表示为多个2的幂次方之和。例如,19 = 16 + 2 + 1。BIT的每个节点都存储n个元素的总和,其中n是2的幂。例如,在上面的getSum()的第一个图中,前12个元素的和可以通过最后4个元素(从9到12) )加上8个元素的总和(从1到8)。 数字n的二进制表示中的设置位数为O(Logn)。 因此,我们遍历getSum()和update()操作中最多的O(Logn)节点。 构造的时间复杂度为O(nLogn),因为它为所有n个元素调用update()。
-
-#### 代码实现
-
-```
-void updateBIT(int BITree[], int n, int index, int val) {
- index = index + 1;
- while(index <= n) {
- BITree[index] += val;
- index += index & (-index);
- }
-}
-
-int getSum(int BITree[], int index) {
- int sum = 0;
- index = index + 1;
- while(index > 0) {
- sum += BITree[index];
- index -= index & (-index);
- }
- return sum;
-}
-
-int *conBIT(int arr[], int n) {
- int *BITree = new int[n + 1];
- for(int i = 0; i <= n; i++)
- BITree[i] = 0;
- for(int i = 0; i < n; i++)
- updateBIT(BITree, n, i, arr[i]);
- return BITree;
-}
-```
-
-
-
-
-
----
-
-### 二叉搜索树
-
-顾名思义,二叉搜索树是以一棵二叉树来组织的,其满足一下条件:x为二叉树的一个节点,如果y是x左子树的一个节点,那么`y.Val <= x.Val`;如果y是x右子树的一个节点,则`y.Val >= x.Val`
-
-根据二叉树的性质可得知,二叉搜索树的中序遍历为升序序列,相反如果交换左右子树的遍历顺序亦可得到降序序列。
-
-```go
-// inorder伪代码
-func inOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, inOrder(root.Left)...)
- res = append(res, root.Val)
- res = append(res, inOrder(root.Right)...)
- }
- return res
-}
-
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-#### 二叉搜索树的基本操作
-
-二叉搜索树的基本操作包括查询,最小关键字元素,最大关键字元素,前继节点,后继节点,插入和删除,这些基本操作所花费的时间与二叉搜索树的高度成正比。
-
-**查询**
-
-如果二叉搜索树的高度为h,则查询的时间复杂度为O(h)。
-
-```go
-// 查询伪代码
-// 递归版
-func searchBST(root *TreeNode, key int) *TreeNode {
- if root == nil || root.Val == key { return root }
- if root.Val < key {
- return searchBST(root.Right, key)
- }
- return searchBST(root.Left, key)
-}
-// 迭代版
-func searchBST(root *TreeNode, key int) *TreeNode {
- for root != nil && root.Val != key {
- if root.Val < key {
- root = root.Right
- } else {
- root = root.Left
- }
- }
- return root
-}
-```
-
-**最大关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最大关键字元素的伪代码
-func maximumBST(root *TreeNode) *TreeNode {
- for root.Right != nil { root = root.Right }
- return root
-}
-// 递归版
-func maximumBST(root *TeeNode) *TreeNode {
- if root.Right != nil {
- return maximumBST(root.Right)
- }
- return root
-}
-```
-
-**最小关键字元素**
-
-如果二叉搜素树的高度为h,则最大关键字元素的操作时间复杂度为O(h)。
-
-```go
-// 最小关键字元素的伪代码
-func minimumBST(root *TreeNode) *TreeNode {
- for root.Left != nil { root = root.Left }
- return root
-}
-// 递归版
-func minimumBST(root *TreeNode) *TreeNode {
- if root.Left != nil {
- return minimum(root.Left)
- }
- return root
-}
-```
-
-**前继节点**
-
-前继节点是指给定一个节点x,如果存在x的前继节点则返回前继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找前继节点的操作时间复杂度为O(h)。
-
-```go
-func predecessorBST(x *TreeNode) *TreeNode {
- // x节点存在左子树,则返回左子树中最大的节点
- if x.Left != nil {
- return maximum(root.Left)
- }
- // 如果x节点没有左子树,则找到其父节点,且父节点的右子树包含x
- y := x.Present
- for y != nil && x == y.Left {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**后继节点**
-
-后继节点是指给定一个节点x,如果存在x的后继节点则返回后继节点,否则返回nil。
-
-如果二叉搜素树的高度为h,则查找后继节点的操作时间复杂度为O(h)。
-
-```go
-// 后继节点的伪代码
-func successorBST(x *TreeNode) *TreeNode {
- // x节点存在右子树,则返回右子树中最小的节点
- if x.Right != nil {
- return minimum(root.Right)
- }
- // 如果x节点没有右子树,则找到其父节点,且父节点的左子树包含x
- y := x.Present
- for y != nil && x == y.Right {
- x = y
- y = y.Present
- }
- return y
-}
-```
-
-**插入**
-
-插入和删除会引起二叉搜索树所表示的动态集合的变化。一定要修改数据结构来反映这种变化,单修改要保持二叉搜索树的性质不变。
-
-```go
-// x.Val = val, x.Right = x.Left = x.Present = nil
-// 插入的伪代码
-func insertBST(root, x *TreeNode) {
- var y *TreeNode
- for root != nil {
- y = root
- if x.Val < root.Val {
- root = root.Left
- } else {
- root = root.Right
- }
- }
- x.Present = y
- if y == nil { // empty tree
- root = x
- } else if x.Val < y.Val {
- y.Left = x
- } else {
- y.Right = x
- }
-}
-// 没有父指针
-// 递归版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root = x
- return root
- }
- if root.Val < x.Val {
- return insertBST(root.Right)
- }
- return insertBST(root.Left)
-}
-// 迭代版
-func insertBST(root, x *TreeNode) *TreeNode {
- if root == nil {
- root == x
- return root
- }
- pre, head := root, root
- for head != nil {
- pre = head
- if root.Val < x.Val {
- head = head.Right
- } else {
- head = head.Left
- }
- }
- if y.Val < x.Val {
- y.Right = x
- } else {
- y.Left = x
- }
- return root
-}
-```
-
-**删除**
-
-从一棵二叉搜索树中删除一个节点x的整个策略分为三个情况,分别是:
-
-1)如果x没有孩子节点,那么直接删除即可;
-
-2)如果x只有一个孩子节点,那么将该孩子节点提升到x即可;
-
-3)如果x有两个孩子,那么需要找到x的后继节点y(一定存在x的右子树中),让y占据x的位置,那么x原来的右子树部分称为y的右子树,x的左子树称为y的新的左子树。
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-### 二叉搜索树相关题目
-
-- 108 将有序数组转换为二叉搜索树【M】
-- 235 二叉搜素树的最近公共祖先
-- 230 二叉搜索树中第K小的元素
-- 450 删除二叉搜索树中的节点
-- 1038 从二叉搜索树到更大和树【M】
-- 1214 查找两棵二叉搜索树之和【M】
-- 面试题 17.12 BiNode【E】
-- 面试题54 二叉搜索树的第K大节点
-
-#### 108 将有序数组转换为二叉搜索树
-
-题目要求:给定一个升序数据,返回一棵高度平衡二叉树。
-
-思路分析:
-
-二叉搜索树的定义:
-
-1)若任意节点的左子树不为空,则左子树上所有的节点值均小于它的根节点值;
-
-2)若任意节点的右子树不为空,则右子树上所有的节点值均大于它的根节点值;
-
-3)任意节点的左,右子树均为二叉搜索树;
-
-4)没有键值相等的点。
-
-如何构造一棵树,可拆分成无数个这样的子问题:构造树的每个节点,以及节点之间的关系。对于每个节点来说,都需要:
-
-1)选取节点;
-
-2)构造该节点的左子树;
-
-3)构造该节点的右子树。
-
-算法一:对于升序序列,可以选择中间的节点作为根节点,然后递归调用。因为每个节点只遍历一遍,所以时间复杂度为O(n);因为递归调用,空间复杂度为O(log(n))。
-
-```go
-//date 2020/02/20
-// 算法一:递归版
-func sortedArrayToBST(nums []int) *TreeNode {
- if len(nums) == 0 { return nil }
- // 选择根节点
- mid := len(nums) >> 1
- // 构造左子树和右子树
- left := nums[:mid]
- right := nums[mid+1:]
-
- return &TreeNode{
- Val: nums[mid],
- Left: sortedArrayToBST(left),
- Right: sortedArrayToBST(right),
- }
-}
-```
-
-#### 230 二叉搜索树中第K小的元素
-
-题目要求:给定一个二叉搜索树,返回其第K小的元素,你可以假设K总是有效的,即1<=k<=n。
-
-算法:因为是二叉搜索树,先得到其中序遍历结果,然后直接返回k-1所在的元素。
-
-```go
-// date 2020/01/11
-func kthSmallest(root *TreeNode) int {
- data := inOrder(root)
- if len(data) < k {return 0}
- return data[k-1]
-}
-
-func inOrder(root *TreeNode) []int {
- if root == nil {return nil}
- res := make([]int, 0)
- if root.Left != nil { res = append(res, inOrder(root.Left)...) }
- res = append(res, root.Val)
- if root.Right != nil { res = append(res, inOrder(root.Right)...) }
-}
-```
-
-
-#### 235 二叉搜索树的最近公共祖先
-
-题目要求:给定一个二叉搜素树和两个节点,返回其最近公共祖先。
-
-算法:递归,并充分利用二叉搜索树的性质`left.Val < root.Val < right.Val`。
-
-```go
-// date 2020/02/18
-func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q {return root }
- if p == nil { return q }
- if q == nil { return p }
- if root.Val > q.Val && root.Val > p.Val { return lowestCommonAncestor(root.Left) }
- if root.Val < q.Val && root.Val < p.Val { return lowestCommonAncestor(root.Right) }
- return root
-}
-```
-
-
-
-#### 450 删除二叉搜索树中的节点
-
-题目要求:给定一个二叉搜索树和key,删除key节点,并返回树的根节点
-
-算法一:二叉搜索树的中序遍历序列是个升序序列,则欲要删除的节点需要用其前驱节点或后驱节点来代替。
-
-1)如果为叶子节点,则直接删除;
-
-2)如果不是叶子节点且有右子树,则用后驱节点代替。后驱节点为右子树中的较低位置;
-
-3)如果不是叶子节点且有左子树,则用前驱节点代替。前驱节点为左子树中的较高位置;
-
-```go
-func deleteBST(root *TreeNode, key int) *TreeNode{
- if root == nil { return root }
- if root.Val < key {
- return deleteBST(root.Right, key)
- } else if root.Val > key {
- return deleteBST(root.Left, key)
- } else {
- // no child node
- if root.Left == nil && root.Right == nil {
- root = nil
- } else if root.Right != nil {
- root.Val = postNodeVal(root.Right)
- root.Right = deleteBST(root.Right, root.Val)
- } else {
- root.Val = preNodeVal(root.Left)
- root.Left = deleteBST(root.Left, root.Val)
- }
- }
- return root
-}
-
-// find post node val in right
-func postNodeVal(root *TreeNode) int {
- for root.Left != nil { root = root.Left }
- return root.Val
-}
-// find pre node val in left
-func preNodeVal(root *TreeNode) int {
- for root.Right != nil { root = root.Right }
- return root.Val
-}
-```
-
-#### 1038 从二叉搜索树到更大和树
-
-题目要求:给出二叉**搜索**树的根节点,该二叉树的节点值各不相同,修改二叉树,使每个节点 `node` 的新值等于原树中大于或等于 `node.val` 的值之和
-
-思路分析:
-
-`root.Val = root.Val + root.Right.Val`
-
-`root.Left.Val = root.Left.Val + root.Val`
-
-首先得到二叉搜索树的中序遍历序列的逆序列,然后从序列的第一个开始,将累加值记录到当前树的节点上。
-
-```go
-// date 2020/02/23
-func bsttoGST(root *TreeNode) *TreeNode{
- array := decOrder(root)
- val := 0
- for i := 0; i < len(array); i++ {
- val += array[i]
- setNewVal(root, array[i], val)
- }
-}
-func decOrder(root *TreeNode) []int {
- res := make([]int, 0)
- if root != nil {
- res = append(res, decOrder(root.Right)...)
- res = append(res, root.Val)
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-
-func setNewVal(root *TreeNode, key, val int) {
- if root != nil {
- if root.Val == key {
- root.Val = val
- } else if root.Val > key {
- setNewVal(root.Left, key, val)
- } else {
- setNewVal(root.Right, key, val)
- }
- }
-}
-```
-
-#### 面试题 BiNode
-
-题目要求:将一颗二叉搜索树转换成单链表,Right指针指向下一个节点。
-
-思路分析:
-
-要求返回头节点,所以先转换left。
-
-```go
-// date 2020/02/19
-func convertBiNode(root *TreeNode) *TreeNode {
- if root == nil { return nil }
- // 左子树不为空,需要转换
- if root.Left != nil {
- // 得到左子树序列,并找到最后一个节点
- left := convertBiNode(root.Left)
- pre := left
- for pre.Right != nil { pre = pre.Right }
- // 将最后一个节点right指向root
- pre.Right = root
- root.Left = nil
- // 得到右子树序列
- root.Right = convertBiNode(root.Right)
- return left
- }
- root.Right = convertBiNode(root.Right)
- return root
-}
-```
-
-#### 面试题54 二叉搜索树的第K大节点
-
-题目要求:给定一个二叉搜索树,找出其中第k大节点。
-
-算法一:二叉搜索树的中序遍历为升序序列,按照Right->root->Left的顺序遍历可得到降序序列,然后返回第k节点。
-
-```go
-// date 2020/02/18
-func kthLargest(root *TreeNode, k int) int {
- if root == nil || k < 0 { return -1 }
- nums := decOrder(root)
- if len(nums) < k {return -1}
- return nums[k-1]
-}
-
-// right->root->left
-func decOrder(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- if root.Right != nil {
- res = append(res, decOrder(root.Right)...)
- }
- res = append(res, root.Val)
- if root.Left != nil {
- res = append(res, decOrder(root.Left)...)
- }
- return res
-}
-```
-
-
-
-### [相关题目](leetcode_bt.md)
-
-#### 95 不同的二叉搜索树 II【中等】
-
-题目要求:给定一个整数n,生成所有由1...n为节点所组成的二叉搜索树。
-
-思路分析
-
-题目看着很难,实际利用递归思想没有那么难。
-
-从序列`1..n`取出数字`1` 作为当前树的根节点,那么就有i-1个元素用来构造左子树,二另外的i+1..n个元素用来构造右子树。最后我们将得到G(i-1)棵不同的左子树,G(n-i)棵不同的右子树,其中G为卡特兰数。
-
-这样就可以以i为根节点,和两个可能的左右子树序列,遍历一遍左右子树序列,将左右子树和根节点链接起来。
-
-```go
-func generateTrees(n int) []*TreeNode {
- if n == 0 { return nil }
- return generateTreesWithNode(1, n)
-}
-
-func generateTreesWithNode(start, end int) []*TreeNode {
- res := make([]*TreeNode, 0)
- if start > end {
- // 表示空树
- res = append(res, nil)
- return res
- }
- for i := start; i <= end; i++ {
- left := generateTreesWithNode(start, i-1)
- right := generateTreesWithNode(i+1, end)
- for _, l := range left {
- for _, r := range right {
- res = append(res, &TreeNode{
- Val: i,
- Left: l,
- Right: r,
- })
- }
- }
- }
- return res
- }
-```
-
-
-
-#### 106 从中序和后序遍历序列构造二叉树【中等】
-
-思路分析
-
-利用根节点在中序遍历的位置
-
-```go
-// 递归, 中序和后序
-func buildTree(inorder, postorder []int) *TreeNode {
- if len(postorder) == 0 {return nil}
- n := len(postorder)
- root = &TreeNode{
- Val: postorder[n-1],
- }
- index := -1
- for i := 0; i < len(inorder); i++ {
- if inorder[i] == root.Val {
- index = i
- break
- }
- }
- if index >= 0 && index < n {
- root.Left = buildTree(inorder[:index], postorder[:index])
- root.Right = buildTree(inorder[index+1:], postorder[index:n-1]))
- }
- return root
-}
-// 递归,前序和中序
-func buildTree(preorder, inorder []int) *TreeNode {
- if 0 == len(preorder) {return nil}
- n := len(preorder)
- root := &TreeNode{
- Val: preorder[0],
- }
- index := -1
- for i := 0; i < len(inorder); i++ {
- if inorder[i] == root.Val{
- index = i
- break
- }
- }
- if index >= 0 && index < n {
- root.Left = buildTree(preorder[1:index+1], inorder[:index])
- root.Right = buildTree(preorder[index+1:], inorder[index+1:])
- }
- return root
-}
-```
-
-#### 110 平衡二叉树【简单】
-
-题目要求:给定一个二叉树,判断其是否为高度平衡二叉树。【一个二叉树的每个节点的左右两个子树的高度差的绝对值不超过1,视为高度平衡二叉树】
-
-算法一:递归
-
-```go
-// date 2020/02/18
-func isBalanced(root *TreeNode) bool {
- if root == nil { return true }
- if !isBalanced(root.Left) || !isBalanced(root.Right) { return false }
- if Math.Abs(float64(getHeight(root.Left)-getHeight(root.Right))) > float64(1) { return false }
- return true
-}
-func getHeight(root *TreeNode) int {
- if root == nil { return 0 }
- if root.Left == nil && root.Right == nil { return 1 }
- l, r := getHeight(root.Left), getHeight(root.Right)
- if l > r { return l+1 }
- return r+1
-}
-```
-
-
-
-#### 156 上下翻转二叉树【中等】
-
-题目要求:给定一个二叉树,其中所有的右节点要么是具有兄弟节点(拥有相同父节点的左节点)的叶节点,要么为空,将此二叉树上下翻转并将它变成一棵树, 原来的右节点将转换成左叶节点。返回新的根。
-
-算法分析:
-
-```go
-// date 2020/02/25
-func upsideDownBinaryTree(root *TreeNode) *TreeNode {
- var parent, parent_right *TreeNode
- for root != nil {
- // 0.保存当前left, right
- root_left := root.Left
- root.Left = parent_right // 重新构建root,其left为上一论的right
- parent_right := root.Right // 保存right
- root.Right = parent // 重新构建root,其right为上一论的root
- parent = root
- root = root_left
- }
- return parent
-}
-```
-
-#### 199 二叉树的右视图【中等】
-
-算法分析:层序遍历的最后一个节点值。
-
-```go
-// date 2020/02/26
-func rightSideView(root *TreeNode) []int {
- res := make([]int, 0)
- if root == nil { return res }
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- for len(stack) != 0 {
- n := len(stack)
- res = append(res, stack[0].Val)
- for i := 0; i < n; i++ {
- if stack[i].Right != nil { stack = append(stack, stack[i].Right) }
- if stack[i].Left != nil { stack = append(stack, stack[i].Left) }
- }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 236 二叉树的最近公共祖先【中等】
-
-题目要求:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
-
-思路分析:
-
-```go
-// date 2020/03/29
-// 递归
-// 在左右子树中分别查找p,q结点
-func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
- if root == nil || root == p || root == q { return root }
- if p == q { return p }
- left := lowestCommonAncestor(root.Left, p, q)
- right := lowestCommonAncestor(root.Right, p, q)
- // 左右均不为空,表示p,q分别位于左右子树中
- if left != nil && right != nil { return root }
- // 左为空,表示p,q位于右子树,否则位于左子树
- if left == nil { return right }
- return left
-}
-```
-
-#### 257 二叉树的所有路径【简单】
-
-题目要求:给定一个二叉树,返回所有从根节点到叶子节点的路径。
-
-算法分析:
-
-```go
-// date 2020/02/23
-func binaryTreePaths(root *TreeNode) []string {
- res := make([]string, 0)
- if root == nil { return res }
- if root.Left == nil && root.Right == nil {
- res = append(res, fmt.Sprintf("%d", root.Val))
- return res
- } else if root.Left != nil {
- for _, v := range binaryTreePaths(root.Left) {
- res = append(res, fmt.Sprintf("%d->%s", root.Val, v))
- }
- } else if root.Right != nil {
- for _, v := range binaryTreePaths(root.Right) {
- res = append(res, fmt.Sprintf("%d->%s", root.Val, v))
- }
- }
- return res
-}
-```
-
-```go
-class MinStack {
-public:
- /** initialize your data structure here. */
- stack _stack;
- int _min = INT_MAX;
- MinStack() {
-
- }
-
- void push(int x) {
- if(_min >= x){
- if(!_stack.empty()){
- _stack.push(_min);
- }
- _min = x;
- }
- _stack.push(x);
- }
-
- void pop() {
- if(_stack.empty())
- return;
- if(_stack.size() == 1)
- _min = INT_MAX;
- else if(_min == _stack.top()){//下一个元素是下一个最小值
- _stack.pop();
- _min = _stack.top();
- }
- _stack.pop();
- }
-
- int top() {
- return _stack.top();
- }
-
- int getMin() {
- return _min;
- }
-};
-```
-
-#### 270 最接近的二叉搜索树值【简单】
-
-题目要求:给定一个不为空的二叉搜索树和一个目标值 target,请在该二叉搜索树中找到最接近目标值 target 的数值。
-
-算法分析:使用层序遍历,广度优先搜索。
-
-```go
-// date 2020/02/23
-func closestValue(root *TreeNode, target float64) int {
- if root == nil { return 0 }
- var res int
- cur := math.Inf(1)
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- for len(stack) != 0 {
- n := len(stack)
- for i := 0; i < n; i++ {
- if math.Abs(float64(stack[i].Val) - target) < cur {
- cur = math.Abs(float64(stack[i].Val) - target)
- res = stack[i].Val
- }
- if stack[i].Left != nil { stack = append(stack, stack[i].Left) }
- if stack[i].Right != nil { stack = append(stack, stack[i].Right) }
- }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 538 把二叉树转换成累加树【简单】
-
-算法:逆序的中序遍历,查找。
-
-```go
-// date 2020/02/26
-func convertBST(root *TreeNode) *TreeNode {
- var sum int
- decOrder(root, &sum)
- return root
-}
-
-func decOrder(root *TreeNode, sum *int) {
- if root == nil { return }
- decOrder(root.Right, sum)
- *sum += root.Val
- root.Val = *sum
- decOrder(root.Left, sum)
-}
-```
-
-#### 543 二叉树的直径【简单】
-
-题目要求:给定一棵二叉树,返回其直径。
-
-算法分析:左右子树深度和的最大值。
-
-```go
-// date 2020/02/23
-func diameterOfBinaryTree(root *TreeNode) int {
- v1, _ := findDepth(root)
- return v1
-}
-
-func findDepth(root *TreeNode) (int, int) {
- if root == nil { return 0, 0 }
- var v int
- v1, l := findDepth(root.Left)
- v2, r := findDepth(root.Right)
- if v1 > v2 {
- v = v1
- } else {
- v = v2
- }
- if l+r > v { v = l+r }
- if l > r { return v, l+1}
- return v, r+1
-}
-```
-
-#### 545 二叉树的边界【中等】
-
-题目要求:给定一个二叉树,按逆时针返回其边界。
-
-思路分析:分别求其左边界,右边界,和所有的叶子节点,用visited辅助去重,算法如下:
-
-```go
-// date 2020/02/23
-func boundaryOfBinaryTree(root *TreeNode) []int {
- if root == nil { return []int{} }
- res := make([]int, 0)
- left, right := make([]*TreeNode, 0), make([]*TreeNode, 0)
- visited := make(map[*TreeNode]int, 0)
- res = append(res, root.Val)
- visited[root] = 1
- // find left node
- pre := root.Left
- for pre != nil {
- left = append(left, pre)
- visited[pre] = 1
- if pre.Left != nil {
- pre = pre.Left
- } else {
- pre = pre.Right
- }
- }
- // find right node
- pre = root.Right
- for pre != nil {
- right = append(right, pre)
- visited[pre] = 1
- if pre.Right != nil {
- pre = pre.Right
- } else {
- pre = pre.Left
- }
- }
- leafs := findLeafs(root)
- // make res
- for i := 0; i < len(left); i++ {
- res = append(res, left[i].Val)
- }
- for i := 0; i < len(leafs); i++ {
- if _, ok := visited[leafs[i]]; ok { continue }
- res = append(res, ,leafs[i].Val)
- }
- for i := len(right) - 1; i >= 0; i-- {
- res = append(res, right[i].Val)
- }
- return res
-}
-
-func findLeafs(root *TreeNode) []*TreeNode {
- res := make([]*TreeNode, 0)
- if root == nil { return res }
- if root.Left == nil && root.Right == nil {
- res = append(res, root)
- return res
- }
- res = append(res, findLeafs(root.Left)...)
- res = append(res, findLeafs(root.Right)...)
- return res
-}
-```
-
-#### 563 二叉树的坡度【简单】
-
-题目要求:给定一棵二叉树,返回其坡度。
-
-算法一:根据定义,递归计算。
-
-```go
-func findTilt(root *TreeNode) int {
- if root == nil || root.Left == nil && root.Right == nil { return 0 }
- left := sum(root.Left)
- right := sum(root.Right)
- var res int
- if left > right {
- res = left - right
- } else {
- res = right - left
- }
- return res + findTilt(root.Left) + findTilt(root.Right)
-}
-
-func sum(root *TreeNode) int {
- if root == nil { return 0 }
- return sum(root.Left) + sum(root.Right) + root.Val
-}
-```
-
-#### 617 合并二叉树【简单】
-
-给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
-
-你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
-
-```go
-// date 2020/02/23
-// 递归
-func mergeTrees(t1, t2 *TreeNode) *TreeNode {
- if t1 == nil { return t2 }
- if t2 == nil { return t1 }
- t1.Val += t2.Val
- t1.Left = mergeTrees(t1.Left, t2.Left)
- t1.Right = mergeTrees(t1.Right, t2.Right)
- return t1
-}
-```
-
-#### 654 最大二叉树【中等】
-
-题目要求:
-
-给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
-
-二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。
- 通过给定的数组构建最大二叉树,并且输出这个树的根节点。
-
-算法分析:
-
-找到数组中的最大值,构建根节点,然后递归调用。
-
-```go
-// date 2020/02/25
-// 递归版
-func constructMaximumBinaryTree(nums []int) *TreeNode {
- if len(nums) == 0 { return nil }
- if len(nums) == 1 { return &TreeNode{Val: nums[0]} }
- p := 0
- for i, v := range nums {
- if v > nums[p] { p = i }
- }
- root := &TreeNode{Val: nums[p]}
- root.Left = constructMaximumBinaryTree(nums[:p])
- root.Right = constructMaximumBinaryTree(nums[p+1:])
- return root
-}
-```
-
-#### 655 输出二叉树【中等】
-
-题目要求:将二叉树输出到m*n的二维字符串数组中。
-
-算法思路:先构建好res,然后逐层填充。
-
-```go
-// date 2020/02/25
-func printTree(root *TreeNode) [][]string {
- depth := findDepth(root)
- length := 1 << depth - 1
- res := make([][]string, depth)
- for i := 0; i < depth; i++ {
- res[i] = make([]string, length)
- }
- fill(res, root, 0, 0, length)
-}
-
-func fill(res [][]string, t *TreeNode, i, l, r int) {
- if t == nil { return }
- res[i][(l+r)/2] = fmt.Sprintf("%d", root.Val)
- fill(res, t.Left, i+1, l, (l+r)/2)
- fill(res, t.Right, i+1, (l+r+1)/2, r)
-}
-
-func findDepth(root *TreeNode) int {
- if root == nil { return 0 }
- l, r := findDepth(root.Left), findDepth(root.Right)
- if l > r { return l+1 }
- return r+1
-}
-```
-
-#### 662 二叉树的最大宽度【中等】
-
-题目要求:给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
-
-每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
- 链接:https://leetcode-cn.com/problems/maximum-width-of-binary-tree
-
-算法分析:使用栈stack逐层遍历,计算每一层的宽度,注意全空节点的时候要返回。时间复杂度O(n),空间复杂度O(logn)。
-
-```go
-// date 2020/02/26
-func widthOfBinaryTree(root *TreeNode) int {
- res := 0
- stack := make([]*TreeNode, 0)
- stack = append(stack, root)
- var n, i, j int
- var isAllNil bool
- for 0 != len(stack) {
- i, j, n = 0, len(stack)-1, len(stack)
- // 去掉每一层两头的空节点
- for i < j && stack[i] == nil { i++ }
- for i < j && stack[j] == nil { j-- }
- // 计算结果
- if j-i+1 > res { res = j-i+1 }
- // 添加下一层
- isAllNil = true
- for ; i <= j; i++ {
- if stack[i] != nil {
- stack = append(stack, stack[i].Left, stack[i].Right)
- isAllNil = false
- } else {
- stack = append(stack, nil, nil)
- }
- }
- if isAllNil { break }
- stack = stack[n:]
- }
- return res
-}
-```
-
-#### 669 修剪二叉搜索树【简单】
-
-题目要求:给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
-
-算法分析:
-
-```go
-// date 2020/02/25
-func trimBST(root *TreeNode, L, R int) *TreeNode {
- if root == nil { return nil }
- if root.Val < L { return trimBST(root.Right, L, R) }
- if root.Val > R { return trimBST(root.Left, L, R) }
- root.Left = trimBST(root.Left, L, R)
- root.Right = trimBST(root.Right, L, R)
- return root
-}
-```
-
-#### 703 数据流中第K大元素【简单】
-
-解题思路:
-
-0。使用数据构建一个容量为k的小顶堆。
-
-1。如果小顶堆堆满后,向其增加元素,若大于堆顶元素,则重新建堆,否则掉弃。
-
-2。堆顶元素即为第k大元素。
-
-```go
-// date 2020/02/19
-type KthLargest struct {
- minHeap []int
- size
-}
-
-func Constructor(k int, nums []int) KthLargest {
- res := KthLargest{
- minHeap: make([]int, k),
- }
- for _, v := range nums {
- res.Add(v)
- }
-}
-
-func (this *KthLargest) Add(val int) int {
- if this.size < len(this.minHeap) {
- this.size++
- this.minHeap[this.size-1] = val
- if this.size == len(this.minHeap) {
- this.makeMinHeap()
- }
- } else if this.minHeap[0] < val {
- this.minHeap[0] = val
- this.minHeapify(0)
- }
- return this.minHeap[0]
-}
-
-func (this *KthLargest) makeMinHeap() {
- // 为什么最后一个根节点是n >> 1 - 1
- // 长度为n,最后一个叶子节点的索引是n-1; left = i >> 1 + 1; right = i >> 1 + 2
- // 父节点是 n >> 1 - 1
- for i := len(this.minHeap) >> 1 - 1; i >= 0; i-- {
- this.minHeapify(i)
- }
-}
-
-func (this *KthLargest) minHeapify(i int) {
- if i > len(this.minHeap) {return}
- temp, n := this.minHeap[i], len(this.minHeap)
- left := i << 1 + 1
- right := i << 1 + 2
- for left < n {
- right = left + 1
- // 找到left, right中较小的那个
- if right < n && this.minHeap[left] > this.minHeap[right] { left++ }
- // left, right 均小于root否和小顶堆,跳出
- if this.minHeap[left] >= this.minHeap[i] { break }
- this.minHeap[i] = this.minHeap[left]
- this.minHeap[left] = temp
- // left发生变化,继续调整
- i = left
- left = i << 1 + 1
- }
-}
-```
-
-#### 814 二叉树剪枝【中等】
-
-题目要求:给定一个二叉树,每个节点的值要么是0,要么是1。返回移除了所有不包括1的子树的原二叉树。
-
-算法分析:
-
-使用containOne()函数判断节点以及节点的左右子树是否包含1。
-
-```go
-// date 2020/02/25
-func pruneTree(root *TreeNode) *TreeNode {
- if containsOne(root) { return root }
- return nil
-}
-
-func containsOne(root *TreeNode) bool {
- if root == nil { return false }
- l, r := containsOne(root.Left), containsOne(root.Right)
- if !l { root.Left = nil }
- if !r { root.Right = nil }
- return root.Val == 1 || l || r
-}
-```
-
-#### 993 二叉树的堂兄弟节点【简单】
-
-题目链接:https://leetcode-cn.com/problems/cousins-in-binary-tree/
-
-题目要求:给定一个二叉树和两个节点元素值,判断两个节点值是否是堂兄弟节点。
-
-堂兄弟节点的定义:两个节点的深度一样,但父节点不一样。
-
-算法分析:
-
-使用findFatherAndDepth函数递归找到每个节点的父节点和深度,并进行比较。
-
-```go
-// date 2020/02/25
-func isCousins(root *TreeNode, x, y int) bool {
- xf, xd := findFatherAndDepth(root, x)
- yf, yd := findFatherAndDepth(root, y)
- return xd == yd && xf != yf
-}
-func findFatherAndDepth(root *TreeNode, x int) (*TreeNode, int) {
- if root == nil || root.Val == x { return nil, 0 }
- if root.Left != nil && root.Left.Val == x { return root, 1 }
- if root.Right != nil && root.Right.Val == y { return root, 1 }
- l, lv := findFatherAndDepth(root.Left, x)
- r, rv := findFatherAndDepth(root.Right, x)
- if l != nil { return l, lv+1 }
- return r, rv+1
-}
-```
-
-#### 1104 二叉树寻路【中等】
-
-题目要求:https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree/
-
-算法分析:
-
-```go
-// date 2020/02/25
-func pathInZigZagTree(label int) []int {
- res := make([]int, 0)
- for label != 1 {
- res = append(res, label)
- label >>= 1
- y := highBit(label)
- lable = ^(label-y)+y
- }
- res = append(res, 1)
- i, j := 0, len(res)-1
- for i < j {
- t := res[i]
- res[i] = res[j]
- res[j] = t
- i++
- j--
- }
- return res
-}label = label ^(1 << (label.bit_length() - 1)) - 1
-
-func bitLen(x int) int {
- res := 0
- for x > 0 {
- x >>= 1
- res++
- }
- return res
-}
-```
-
-#### 面试题27 二叉树的镜像【简单】
-
-题目链接:https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/
-
-题目要求:给定一棵二叉树,返回其镜像二叉树。
-
-```go
-// date 2020/02/23
-// 递归算法
-func mirrorTree(root *TreeNode) *TreeNode {
- if root == nil { return root }
- left := root.Left
- root.Left = root.Right
- root.Right = left
- root.Left = mirrorTree(root.Left)
- root.Right = mirrorTree(root.Right)
- return root
-}
-```
-
diff --git a/19_binary_index_tree/images/bit.png b/19_binary_index_tree/images/bit.png
deleted file mode 100644
index d6dd02b..0000000
Binary files a/19_binary_index_tree/images/bit.png and /dev/null differ
diff --git a/19_binary_index_tree/images/bit_init.png b/19_binary_index_tree/images/bit_init.png
deleted file mode 100644
index 8d4f48f..0000000
Binary files a/19_binary_index_tree/images/bit_init.png and /dev/null differ
diff --git a/19_binary_index_tree/images/bit_query.png b/19_binary_index_tree/images/bit_query.png
deleted file mode 100644
index 6c1a420..0000000
Binary files a/19_binary_index_tree/images/bit_query.png and /dev/null differ
diff --git a/19_binary_index_tree/images/bit_update.png b/19_binary_index_tree/images/bit_update.png
deleted file mode 100644
index 202897f..0000000
Binary files a/19_binary_index_tree/images/bit_update.png and /dev/null differ
diff --git a/19_binary_index_tree/images/image315.png b/19_binary_index_tree/images/image315.png
deleted file mode 100644
index b71965e..0000000
Binary files a/19_binary_index_tree/images/image315.png and /dev/null differ
diff --git a/19_binary_index_tree/images/image315.svg b/19_binary_index_tree/images/image315.svg
deleted file mode 100644
index ab13341..0000000
--- a/19_binary_index_tree/images/image315.svg
+++ /dev/null
@@ -1,4 +0,0 @@
-
-
-
-
\ No newline at end of file
diff --git "a/20_bit_manipulation/No.029_\344\270\244\346\225\260\347\233\270\351\231\244.md" "b/20_bit_manipulation/No.029_\344\270\244\346\225\260\347\233\270\351\231\244.md"
deleted file mode 100644
index e2bac9f..0000000
--- "a/20_bit_manipulation/No.029_\344\270\244\346\225\260\347\233\270\351\231\244.md"
+++ /dev/null
@@ -1,84 +0,0 @@
-## 29 两数相除-中等
-
-题目:
-
-给你两个整数,被除数 `dividend` 和除数 `divisor`。将两数相除,要求 **不使用** 乘法、除法和取余运算。
-
-整数除法应该向零截断,也就是截去(`truncate`)其小数部分。例如,`8.345` 将被截断为 `8` ,`-2.7335` 将被截断至 `-2` 。
-
-返回被除数 `dividend` 除以除数 `divisor` 得到的 **商** 。
-
-**注意:**假设我们的环境只能存储 **32 位** 有符号整数,其数值范围是 `[−231, 231 − 1]` 。本题中,如果商 **严格大于** `231 − 1` ,则返回 `231 − 1` ;如果商 **严格小于** `-231` ,则返回 `-231` 。
-
-
-
-**解题思路**
-
-这道题可用二分查找。把商作为搜索的目标,商的取值范围是[0, 被除数],所以从区间 0 到 被除数 搜索。
-
-```go
-// 当 (商+1)* 除数 > 被除数 并且 商 * 除数 <= 被除数
-// 或者 商+1)* 除数 >= 被除数 并且 商 * 除数 < 被除数
-// 就算找到商了
-```
-
-注意,二分查找容易写错的点:
-
-1. `low <= high`,这是循环的条件
-2. `mid = low + (right-low)/2`,防止溢出
-3. `low = mid-1, high = mid+1`,边界的更新要减1
-
-
-
-```go
-// date 2024/01/11
-func divide(dividend int, divisor int) int {
- res, sign := 1, -1
- if dividend == 0 {
- return 0
- }
- if divisor == 1 {
- return dividend
- }
-
- if dividend < 0 && divisor < 0 || dividend > 0 && divisor > 0 {
- sign = 1
- }
-
- res = binarySearch(0, abs(dividend), abs(dividend), abs(divisor))
- if res > math.MaxInt32 {
- res = math.MaxInt32
- }
- if res < math.MinInt32 {
- res = math.MinInt32
- }
- return res * sign
-}
-
-// x/y
-func binarySearch(left, right int, x, y int) int {
- mid := left + (right-left)>>1
- if (mid+1) * y > x && mid * y <= x || (mid+1) * y >= x && mid * y < x {
- if (mid+1) * y == x {
- return mid+1
- }
- return mid
- }
- if (mid+1) * y > x && mid * y > x {
- return binarySearch(left, mid-1, x, y)
- }
- if (mid+1) * y < x && mid * y < x {
- return binarySearch(mid+1, right, x, y)
- }
-
- return 0
-}
-
-func abs(x int) int {
- if x < 0 {
- return -x
- }
- return x
-}
-```
-
diff --git "a/20_bit_manipulation/No.136_\345\217\252\345\207\272\347\216\260\344\270\200\346\254\241\347\232\204\346\225\260\345\255\227.md" "b/20_bit_manipulation/No.136_\345\217\252\345\207\272\347\216\260\344\270\200\346\254\241\347\232\204\346\225\260\345\255\227.md"
deleted file mode 100644
index f9bad49..0000000
--- "a/20_bit_manipulation/No.136_\345\217\252\345\207\272\347\216\260\344\270\200\346\254\241\347\232\204\346\225\260\345\255\227.md"
+++ /dev/null
@@ -1,50 +0,0 @@
-## 136 只出现一次的数字-简单
-
-题目:
-
-给你一个 **非空** 整数数组 `nums` ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
-
-你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
-
-
-
-> **示例 1 :**
->
-> ```
-> 输入:nums = [2,2,1]
-> 输出:1
-> ```
->
-> **示例 2 :**
->
-> ```
-> 输入:nums = [4,1,2,1,2]
-> 输出:4
-> ```
->
-> **示例 3 :**
->
-> ```
-> 输入:nums = [1]
-> 输出:1
-> ```
-
-
-
-**解题思路**
-
-- 一个数和其本身异或,结果为0,详见解法1。
-
-
-
-```go
-// date 2024/01/16
-func singleNumber(nums []int) int {
- ans := 0
- for _, v := range nums {
- ans ^= v
- }
- return ans
-}
-```
-
diff --git a/20_bit_manipulation/README.md b/20_bit_manipulation/README.md
deleted file mode 100644
index 61c2303..0000000
--- a/20_bit_manipulation/README.md
+++ /dev/null
@@ -1,26 +0,0 @@
-## 位运算
-
-
-
-
-
-### 异或
-
-异或,是指按二进制位进行,相同为零,不同为1。
-
-因此,异或运算有以下三个性质:
-
-1. 任何数和 0 进行异或运算,仍然是这个数本身。
-2. 任何数和其自身异或,结果为 0。
-3. 异或运算满足交换律和结合律。
-
-```go
-// rule 1
-x ^ 0 = x
-// rule 2
-x ^ x = 0
-// rule 4
-a ^ b = b ^ a
-a ^ b ^ c = (a ^ b) ^ c = a ^ (b ^ c)
-```
-
diff --git "a/21_trie/No.014_\346\234\200\351\225\277\345\205\254\345\205\261\345\211\215\347\274\200.md" "b/21_trie/No.014_\346\234\200\351\225\277\345\205\254\345\205\261\345\211\215\347\274\200.md"
deleted file mode 100644
index 79e9870..0000000
--- "a/21_trie/No.014_\346\234\200\351\225\277\345\205\254\345\205\261\345\211\215\347\274\200.md"
+++ /dev/null
@@ -1,80 +0,0 @@
-## 14 最长公共前缀-简单
-
-题目:
-
-编写一个函数来查找字符串数组中的最长公共前缀。
-
-如果不存在公共前缀,返回空字符串 `""`。
-
-
-
-**解题思路**
-
-字典树的词频应用。
-
-具体为,先用输入构造字典树,然后在字典树中查找出现次数等于字符串总数的字符。
-
-```go
-// date 2024/01/25
-type Trie struct {
- child [26]*Trie
- cnt int
-}
-
-
-func NewTrie() *Trie {
- return &Trie{
- child: [26]*Trie{},
- cnt: 0,
- }
-}
-
-
-func (this *Trie) Insert(word string) {
- n := len(word)
- cur := this
- for i := 0; i < n; i++ {
- idx := word[i] - 'a'
- if cur.child[idx] == nil {
- cur.child[idx] = &Trie{child: [26]*Trie{}, cnt: 0}
- }
- cur.child[idx].cnt++
- cur = cur.child[idx]
- }
-}
-
-func (this *Trie) findLongestCommonPrefix(totalTime int) string {
- ans := ""
- idx := -1
- cur := this
- for cur != nil {
- idx = -1
- for i := 0; i < 26; i++ {
- node := cur.child[i]
- if node != nil && node.cnt == totalTime {
- idx = i
- }
- }
- if idx == -1 {
- break
- }
- ans += string(idx+'a')
- cur = cur.child[idx]
- }
- return ans
-}
-
-func longestCommonPrefix(strs []string) string {
- n := len(strs)
- if n == 0 {
- return ""
- }
- tie := NewTrie()
- for _, v := range strs {
- tie.Insert(v)
- }
- res := tie.findLongestCommonPrefix(n)
- return res
-}
-```
-
diff --git "a/21_trie/No.208_\345\256\236\347\216\260Trie.md" "b/21_trie/No.208_\345\256\236\347\216\260Trie.md"
deleted file mode 100644
index 4607ba0..0000000
--- "a/21_trie/No.208_\345\256\236\347\216\260Trie.md"
+++ /dev/null
@@ -1,116 +0,0 @@
-## 208 实现Trie-中等
-
-题目:
-
-**[Trie](https://baike.baidu.com/item/字典树/9825209?fr=aladdin)**(发音类似 "try")或者说 **前缀树** 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
-
-请你实现 Trie 类:
-
-- `Trie()` 初始化前缀树对象。
-- `void insert(String word)` 向前缀树中插入字符串 `word` 。
-- `boolean search(String word)` 如果字符串 `word` 在前缀树中,返回 `true`(即,在检索之前已经插入);否则,返回 `false` 。
-- `boolean startsWith(String prefix)` 如果之前已经插入的字符串 `word` 的前缀之一为 `prefix` ,返回 `true` ;否则,返回 `false` 。
-
-
-
-> **示例:**
->
-> ```
-> 输入
-> ["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
-> [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
-> 输出
-> [null, null, true, false, true, null, true]
->
-> 解释
-> Trie trie = new Trie();
-> trie.insert("apple");
-> trie.search("apple"); // 返回 True
-> trie.search("app"); // 返回 False
-> trie.startsWith("app"); // 返回 True
-> trie.insert("app");
-> trie.search("app"); // 返回 True
-> ```
->
->
->
-> **提示:**
->
-> - `1 <= word.length, prefix.length <= 2000`
-> - `word` 和 `prefix` 仅由小写英文字母组成
-> - `insert`、`search` 和 `startsWith` 调用次数 **总计** 不超过 `3 * 104` 次
-
-
-
-**解题思路**
-
-基本的前缀树构造,详见 readme。
-
-```go
-// date 2024/01/25
-type Trie struct {
- child [26]*Trie
- isEndOfWord bool
-}
-
-
-func Constructor() Trie {
- return Trie{
- child: [26]*Trie{},
- isEndOfWord: false,
- }
-}
-
-
-func (this *Trie) Insert(word string) {
- n := len(word)
- cur := this
- for i := 0; i < n; i++ {
- idx := word[i] - 'a'
- if cur.child[idx] == nil {
- cur.child[idx] = &Trie{child: [26]*Trie{}, isEndOfWord: false}
- }
- cur = cur.child[idx]
- }
- cur.isEndOfWord = true
-}
-
-
-func (this *Trie) Search(word string) bool {
- n := len(word)
- cur := this
- for i := 0; i < n; i++ {
- idx := word[i] - 'a'
- if cur.child[idx] == nil {
- return false
- }
- cur = cur.child[idx]
- }
- return cur.isEndOfWord
-}
-
-
-func (this *Trie) StartsWith(prefix string) bool {
- n := len(prefix)
- cur := this
-
- for i := 0; i < n; i++ {
- idx := prefix[i] - 'a'
- if cur.child[idx] == nil {
- return false
- }
- cur = cur.child[idx]
- }
- return true
-}
-
-
-/**
- * Your Trie object will be instantiated and called as such:
- * obj := Constructor();
- * obj.Insert(word);
- * param_2 := obj.Search(word);
- * param_3 := obj.StartsWith(prefix);
- */
-```
-
diff --git "a/21_trie/No.211_\346\267\273\345\212\240\345\222\214\346\220\234\347\264\242\345\215\225\350\257\215_\346\225\260\346\215\256\347\273\223\346\236\204\350\256\276\350\256\241.md" "b/21_trie/No.211_\346\267\273\345\212\240\345\222\214\346\220\234\347\264\242\345\215\225\350\257\215_\346\225\260\346\215\256\347\273\223\346\236\204\350\256\276\350\256\241.md"
deleted file mode 100644
index a54dae2..0000000
--- "a/21_trie/No.211_\346\267\273\345\212\240\345\222\214\346\220\234\347\264\242\345\215\225\350\257\215_\346\225\260\346\215\256\347\273\223\346\236\204\350\256\276\350\256\241.md"
+++ /dev/null
@@ -1,117 +0,0 @@
-## 211 添加与搜索单词-数据结构设计-中等
-
-题目:
-
-请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
-
-实现词典类 `WordDictionary` :
-
-- `WordDictionary()` 初始化词典对象
-- `void addWord(word)` 将 `word` 添加到数据结构中,之后可以对它进行匹配
-- `bool search(word)` 如果数据结构中存在字符串与 `word` 匹配,则返回 `true` ;否则,返回 `false` 。`word` 中可能包含一些 `'.'` ,每个 `.` 都可以表示任何一个字母。
-
-
-
-> **示例:**
->
-> ```
-> 输入:
-> ["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
-> [[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
-> 输出:
-> [null,null,null,null,false,true,true,true]
->
-> 解释:
-> WordDictionary wordDictionary = new WordDictionary();
-> wordDictionary.addWord("bad");
-> wordDictionary.addWord("dad");
-> wordDictionary.addWord("mad");
-> wordDictionary.search("pad"); // 返回 False
-> wordDictionary.search("bad"); // 返回 True
-> wordDictionary.search(".ad"); // 返回 True
-> wordDictionary.search("b.."); // 返回 True
-> wordDictionary.search("b."); // 返回 false, 因为存在 b. 前缀,但不存在长度为2的单词
-> ```
-
-
-
-**解题思路**
-
-这道题也是标准的字典树。需要注意的是:
-
-- 尽管查找的时候,可用`'.'`进行模糊匹配,但是也要判断当前节点是不是单词节点,如果查找的 key 只是某个单词的前缀,需要返回 false。
-
-```go
-// date 2024/01/25
-type WordDictionary struct {
- child [26]*WordDictionary
- isEndOfWord bool
-}
-
-func NewWordDictionary() *WordDictionary {
- return &WordDictionary{child: [26]*WordDictionary{}}
-}
-
-func Constructor() WordDictionary {
- return WordDictionary{child: [26]*WordDictionary{}}
-}
-
-
-func (this *WordDictionary) AddWord(word string) {
- n := len(word)
- cur := this
- for i := 0; i < n; i++ {
- idx := word[i] - 'a'
- if cur.child[idx] == nil {
- cur.child[idx] = NewWordDictionary()
- }
- cur = cur.child[idx]
- }
- cur.isEndOfWord = true
-}
-
-
-func (this *WordDictionary) Search(word string) bool {
- var searchNode func(root *WordDictionary, word string, depth int) bool
- searchNode = func(root *WordDictionary, word string, depth int) bool {
- if root == nil {
- return false
- }
- // check the last character of word
- if depth == len(word) {
- return root.isEndOfWord
- }
- if word[depth] != '.' {
- idx := word[depth] - 'a'
- if root.child[idx] == nil {
- return false
- }
- return searchNode(root.child[idx], word, depth+1)
- } else {
- // '.'
- // 依次 dfs 搜索,并合并结果
- temp := false
- for i := 0; i < 26; i++ {
- if root.child[i] != nil {
- r1 := searchNode(root.child[i], word, depth+1)
- temp = temp || r1
- }
- }
- return temp
- }
- return false
- }
-
-
- return searchNode(this, word, 0)
-}
-
-
-/**
- * Your WordDictionary object will be instantiated and called as such:
- * obj := Constructor();
- * obj.AddWord(word);
- * param_2 := obj.Search(word);
- */
-```
-
diff --git "a/21_trie/No.421_\346\225\260\347\273\204\344\270\255\344\270\244\344\270\252\346\225\260\347\232\204\346\234\200\345\244\247\345\274\202\346\210\226\345\200\274.md" "b/21_trie/No.421_\346\225\260\347\273\204\344\270\255\344\270\244\344\270\252\346\225\260\347\232\204\346\234\200\345\244\247\345\274\202\346\210\226\345\200\274.md"
deleted file mode 100644
index 596e196..0000000
--- "a/21_trie/No.421_\346\225\260\347\273\204\344\270\255\344\270\244\344\270\252\346\225\260\347\232\204\346\234\200\345\244\247\345\274\202\346\210\226\345\200\274.md"
+++ /dev/null
@@ -1,135 +0,0 @@
-## 421 数组中两个数的最大异或值
-
-题目:
-
-给你一个整数数组 `nums` ,返回 `nums[i] XOR nums[j]` 的最大运算结果,其中 `0 ≤ i ≤ j < n` 。
-
- **提示:**
-
-- `1 <= nums.length <= 2 * 105`
-- `0 <= nums[i] <= 231 - 1`
-
-
-
-> **示例 1:**
->
-> ```
-> 输入:nums = [3,10,5,25,2,8]
-> 输出:28
-> 解释:最大运算结果是 5 XOR 25 = 28.
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入:nums = [14,70,53,83,49,91,36,80,92,51,66,70]
-> 输出:127
-> ```
-
-
-
-**解题思路**
-
-异或,就是二进制位中不同为 1,相同为 0。要求两个数的异或值最大,那么这两个数的二进制位应该尽可能的不一样。
-
-最朴素的解法是两层循环,依次计算。
-
-更快的方法是字典树。
-
-题目中已经说明数组中的值在区间`[0, 2^31-1]`之间,所以我们可以按位处理每个值,存储在字典树中。
-
-考虑到二进制中每位只可能是0或者1,所以字典树的节点可以用左右表示:
-
-```go
-type Trie struct {
- left, right *Trie // left for 0, right for 1
-}
-```
-
-具体为:
-
-- 把数组第一个元素加入字典树
-- 从第二个元素x开始,先从字典树中查找与 x 异或的最大值,然后再把 x 也加入到字典树中。
-- 遍历的时候,顺便保留最大的异或值即可。
-
-如何从字典树中查找最大的异或值呢?
-
-从字典树的根节点开始,如果元素 x 的当前位为 0,那么就往字典树的 right(即该位 为1)继续查找;否则,往字典树的 left 中查找。
-
-
-
-```go
-// date 2024/01/26
-type Trie struct {
- left, right *Trie // left 0, right 1
-}
-
-func (t *Trie) Add(num int) {
- cur := t
- for i := 30; i >= 0; i-- {
- bit := num >> i & 0x1
- if bit == 0 {
- // left 0
- if cur.left == nil {
- cur.left = &Trie{}
- }
- cur = cur.left
- } else {
- if cur.right == nil {
- cur.right = &Trie{}
- }
- cur = cur.right
- }
- }
-}
-
-func (t *Trie) findMaxXORForNum(num int) int {
- cur := t
- ans := 0
- for i := 30; i >= 0; i-- {
- bit := num >> i & 0x1
- ans = ans << 1
- if bit == 0 {
- // use the right of exist num
- if cur.right != nil {
- cur = cur.right
- ans += 1
- } else {
- cur = cur.left
- }
- } else {
- // use the left
- if cur.left != nil {
- cur = cur.left
- ans += 1
- } else {
- cur = cur.right
- }
- }
- }
- return ans
-}
-
-func findMaximumXOR(nums []int) int {
- ans := 0
- tie := &Trie{}
- for i, v := range nums {
- if i == 0 {
- tie.Add(v)
- continue
- }
- res := tie.findMaxXORForNum(nums[i])
- if res > ans {
- ans = res
- }
- tie.Add(nums[i])
- }
- return ans
-}
-```
-
-
-
-为什么一次遍历就可以?
-
-因为异或满足交换律。
\ No newline at end of file
diff --git "a/21_trie/No.440_\345\255\227\345\205\270\345\272\217\347\232\204\347\254\254K\344\270\252\345\260\217\346\225\260\345\255\227.md" "b/21_trie/No.440_\345\255\227\345\205\270\345\272\217\347\232\204\347\254\254K\344\270\252\345\260\217\346\225\260\345\255\227.md"
deleted file mode 100644
index 579d098..0000000
--- "a/21_trie/No.440_\345\255\227\345\205\270\345\272\217\347\232\204\347\254\254K\344\270\252\345\260\217\346\225\260\345\255\227.md"
+++ /dev/null
@@ -1,34 +0,0 @@
-## 440 字典序的第K个小数字-困难
-
-题目:
-
-给定整数 `n` 和 `k`,返回 `[1, n]` 中字典序第 `k` 小的数字。
-
-**提示:**
-
-- `1 <= k <= n <= 109`
-
-
-
-> **示例 1:**
->
-> ```
-> 输入: n = 13, k = 2
-> 输出: 10
-> 解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。
-> ```
->
-> **示例 2:**
->
-> ```
-> 输入: n = 1, k = 1
-> 输出: 1
-> ```
-
-
-
-**解题思路**
-
-字典树,但是巧妙的字典树。
-
-其他代码,见 template。
\ No newline at end of file
diff --git a/21_trie/README.md b/21_trie/README.md
deleted file mode 100644
index 68aef99..0000000
--- a/21_trie/README.md
+++ /dev/null
@@ -1,196 +0,0 @@
-# 字典树 Trie
-
-## 定义
-
-Trie,字典树(digital tree),也叫前缀树(prefix tree),顾名思义,就是像字典一样的树,像字典一样可以快速查找一个单词是不是在字典中。
-
-字典树是一种多路树数据结构,用于在字母表上存储字符串。它可以存储大量的字符串,并且可以有效地完成模式匹配。
-
-
-
-我们以单词为例,介绍下字典树。
-
-如下图所示,字典树有一个根节点,从根节点出发,依次存储单词的一个字符;如果某个节点正好是单词的结尾,那么标记为单词节点,否则为普通节点。
-
-
-
-一个简单的字典树节点可如下表示:
-
-```go
-const ALPHABET_SIZE = 26
-
-// TrieNode define
-type TrieNode struct {
- child [ALPHABET_SIZE]*TrieNode
- // isEndOfWord is true if the node represents
- // end of a word
- isEndOfWord bool
-}
-```
-
-以单词为例,每个字符的下一个字符都有 26 中可能,所以 child 用一个大小为 26 的数组,`isEndOfWord`表当前节点是否是单词。
-
-
-
-## 插入操作
-
-向字典树中插入一个单词 key,可使用下面这种方法:
-
-1. 把 key 的每个字符充当 child 的索引,如果字符不存在或者是已有字符的延伸,那么构建新的节点,并把最后一个节点标记为单词
-2. 如果字符已经在字典中存在,找到最后一个节点,标记为单词即可
-
-```go
-// InsertKey define
-// If not present, inserts key into trie
-// If the key is prefix of trie node, just
-// marks leaf node
-func (t *TrieNode) InsertKey(key string) {
- n := len(key)
- if n <= 0 {
- return
- }
- cur := t
- for i := 0; i < n; i++ {
- idx := key[i] - 'a'
- if cur.child[idx] == nil {
- cur.child[idx] = NewTrieNode()
- }
- cur = cur.child[idx]
- }
- cur.isEndOfWord = true
-}
-```
-
-从插入操作可以看出,**key 越长,字典树的深度越大**。
-
-
-
-## 查询操作
-
-查询一个单词 key 是否在字典树中,可以这样做:
-
-从根节点开始,**顺次**查找 child,如果 child 为空,表示不存在;不为空,就继续查找。
-
-直到最后一个节点,返回该节点是否为单词的标记位即可。
-
-```go
-// SearchKey define
-// Returns true if key presents in trie, else
-// false
-func (t *TrieNode) SearchKey(key string) bool {
- n := len(key)
- if n == 0 {
- return false
- }
- cur := t
- for i := 0; i < n; i++ {
- idx := key[i] - 'a'
- if cur.child[idx] == nil {
- return false
- }
- cur = cur.child[idx]
- }
- return cur.isEndOfWord
-}
-```
-
-
-
-## 删除操作
-
-从字典树中删除 key,我们可以使用递归的方式进行删除,需要考虑一下几种情况:
-
-- 如果 key 不在字典树中,那么字典树不应该被修改。
-- 如果 key 在字典树中唯一,或者说这个 key 也不是其他更长 key 的前缀,那么应该删除所有的节点。
-- 如果 key 是另一个更长 key 的前缀,那么需要修改单词节点的标记。
-- 如果 key 中包含另一个 key 的前缀,那么只需要删除非公共前缀的部分。
-
-```go
-// DeleteKey define
-func (t *TrieNode) DeleteKey(key string) {
- n := len(key)
- if n == 0 {
- return
- }
- // dfs
- var dfs func(root *TrieNode, key string, depth int) *TrieNode
- dfs = func(root *TrieNode, key string, depth int) *TrieNode {
- // if tree is empty
- if root == nil {
- return root
- }
- // process the last character of key
- if depth == len(key) {
- // unmark
- // this node is no more end of word after delete of given key
- if root.isEndOfWord {
- root.isEndOfWord = false
- }
- // if the given key is not prefix of any other word
- if root.isEmpty() {
- root = nil
- }
- return root
- }
- // if not last character, recur for the child
- idx := key[depth] - 'a'
- // if not find key, just return
- if root.child[idx] == nil {
- return root
- }
- // recur the child
- root.child[idx] = dfs(root.child[idx], key, depth+1)
- // if current node is not the prefix of given key, remote it
- if root.isEmpty() && !root.isEndOfWord {
- root = nil
- }
- return root
- }
- dfs(t, key, 0)
-}
-```
-
-
-
-
-
-## 字典树可做那些事情
-
-字典树可以用来做很多事请。
-
-第一个:**词频统计**。
-
-如果有大量的单词,想要统计每个单词出现的次数。当然哈希表可以做,但是如果内存有限呢?
-
-用字典树来做可以压缩空间,因为公共前缀都是一个节点来表示。
-
-
-
-第二个:**前缀匹配**
-
-
-
-
-
-## 字典树的优势
-
-通过上面的介绍,可以发现字典树具有以下优势:
-
-- 因为字典树使用了公共的,相同的前缀,所以查找更快。查找速度取决于字典树的高度。
-- 如果存在大量的,短的字符串,字典树所使用的内存空间更少。因为 key 之间的前缀可复用。
-- 前缀匹配模式,可查找。
-
-
-
-如何拿字典树和哈希表相比的话?
-
-1. 与不完美的哈希表相比,在最坏的情况下,字典树的查找更快。
-2. 字典树中,不同的 key 不存在哈希冲突。
-3. 字典树中,如果单个 key 可以跟多个值关联,那么它就类似哈希表中的桶。
-4. 字典树中,没有哈希函数。
-5. 有时,从字典树中查找比哈希慢很多。
-6. 以字符串作为 key,有时候很复杂。比如当浮点数变成字符串在字典树中插入和查找,会很复杂。
-7. 通常情况下,字典树比哈希表占用的内存空间更多。
-
-
-
diff --git a/21_trie/images/trie.svg b/21_trie/images/trie.svg
deleted file mode 100644
index 9a28b7b..0000000
--- a/21_trie/images/trie.svg
+++ /dev/null
@@ -1,3 +0,0 @@
-
-
-
\ No newline at end of file
diff --git a/Greedy.md b/Greedy.md
new file mode 100644
index 0000000..71983d8
--- /dev/null
+++ b/Greedy.md
@@ -0,0 +1,31 @@
+### 贪心算法
+
+
+
+### 相关题目
+
+- 122 买卖股票的最佳时机II
+
+
+
+#### 122 买卖股票的最佳时机
+
+题目要求:https://leetcode-cn.com/problems/strobogrammatic-number/
+
+算法分析:
+
+因为题目要求只能持有一种股票,同时可以操作无数次,所以可以采用贪心算法,计算每天的利润。
+
+```go
+// date 2020/03/21
+func maxProfit(prices []int) int {
+ profit := 0
+ for i := 0; i < len(prices) - 1; i++ {
+ if prices[i] < prices[i+1] {
+ profit += prices[i+1] - prices[i]
+ }
+ }
+ return profit
+}
+```
+
diff --git a/README.md b/README.md
index 343e3fb..fb92a34 100644
--- a/README.md
+++ b/README.md
@@ -1,173 +1,22 @@
-# 数据结构与算法
+# subond
+LeetCode_golang题解,每周日更新
-数据结构和算法是一个程序员的基石,本仓库用于个人学习基本数据结构和算法。
+## 动态规划
-*题目指数*:表征题目中设计技巧的程度, 1 到 5 颗⭐️, ⭐️越多表示题目设计的越好,值得学习
+[动态规划](dp.md)
----
+[贪心算法](Greedy.md)
-## 时间复杂度
- - [时间复杂度分析](complexity.md)
+## 二叉树
-## leetcode
+[二叉树](binarytree.md)
-| 序号 | 题目名称 | 难易程度 | 归类 | 题目指数 | 技巧 |
-| ---- | ------------------------------------------ | -------- | ---------- | -------- | :------------------------------- |
-| 1 | 两数之和 | 简单 | 数组 | | |
-| 2 | 两数相加 | 中等 | 链表 | | 哑结点 |
-| 3 | 无重复字符的最长子串 | 中等 | string | | 滑动窗口 |
-| 4 | 寻找两个正序数字的中位数 | 困难 | 数组 | | 类似双指针,记录当前值和前一个值 |
-| 7 | 整数反转 | | 数组 | | |
-| 8 | 字符串转整型 | | string | | |
-| 9 | Palindrome Number | | | | |
-| 11 | 盛最多水的容器 | 中等 | 数组 | | 左右指针 |
-| 14 | 最长公共前缀 | | | | |
-| 15 | 三数之和 | 中等 | 数组 | | 排序,左右指针 |
-| 19 | 删除链表的倒数第N个结点 | 中等 | 链表 | | 快慢指针 |
-| 20 | 有效的括号 | 简单 | string | | |
-| 21 | 合并两个有序链表 | 简单 | 链表 | | 哑结点 |
-| 23 | 合并K个排序链表 | 困难 | 链表 | | 递归 |
-| 24 | 两两交换链表中的节点 | 中等 | 链表 | | |
-| 26 | 从排序数组中删除重复项 | 简单 | 数组 | | 双指针,前后指针 |
-| 27 | 移除元素 | 简单 | 数组 | | 双指针,前后指针 |
-| 34 | 在排序数组中查找元素的第一个和最后一个位置 | 中等 | 数组 | | 双指针,左右指针 |
-| 43 | 字符串相乘 | 中等 | 字符串 | ⭐️⭐️ | 细节题 |
-| 45 | 跳跃游戏 II | | | | |
-| 46 | 全排列 | | 数组 | | |
-| 53 | 最大子数组和 | 中等 | 数组 | ⭐️⭐️⭐️ | 动态规划 |
-| 54 | 螺旋矩阵 | | 数组 | | |
-| 55 | 跳跃游戏 | | | | |
-| 58 | 最后一个单词的长度 | 简单 | 字符串 | | |
-| 61 | 旋转链表 | 中等 | 链表 | | |
-| 62 | 不同路径 | 中等 | 动态规划 | | |
-| 64 | 最小路径和 | 中等 | 动态规划 | | |
-| 66 | 加一 | 简单 | 数组 | | |
-| 67 | 二进制求和 | 简单 | 字符串 | | 细节题 |
-| 70 | 爬楼梯 | 简单 | 动态规划 | | |
-| 75 | 颜色分类 | 中等 | 数组 | | |
-| 78 | 子集 | | 数组 | | |
-| 80 | 从排序数组中删除重复项II | | 数组 | ⭐️⭐️ | 快慢指针 |
-| 82 | 从排序链表中移除重复元素 II | 中等 | 链表 | ⭐️⭐️⭐️ | 哑结点,快慢指针 |
-| 83 | 从排序链表中移除重复元素 | 简单 | 链表 | | |
-| 86 | 分割链表 | 中等 | 链表 | | 哑结点 |
-| 88 | 合并两个有序数组 | 简单 | 数组 | | |
-| 89 | 格雷编码 | | | | |
-| 92 | 反转链表 II | | 链表 | | |
-| 94 | 二叉树的中序遍历 | 简单 | 二叉树 | | 栈 |
-| 95 | 不同的二叉搜索树 | 中等 | 二叉树 | | |
-| 96 | 不同的二叉搜索树 | 中等 | 二叉树 | ⭐️⭐️ | 动态规划 |
-| 98 | 验证二叉搜索树 | 中等 | 二叉搜索树 | ⭐️⭐️ | 三种算法 |
-| 99 | 恢复二叉树 | 中等 | | | |
-| 100 | 相同的树 | 简单 | 二叉树 | | |
-| 101 | 对称二叉树 | 简单 | 二叉树 | | |
-| 102 | 二叉树的层序遍历 | 中等 | 二叉树 | ⭐⭐️⭐️ | BFS, DFS |
-| 104 | 二叉树的最大深度 | 简单 | 二叉树 | ⭐️⭐️ | 递归,层序遍历,dfs |
-| 105 | 从前序与中序遍历序列构造二叉树 | 中等 | 二叉树 | | |
-| 106 | 从中序和后序遍历序列构造二叉树 | 中等 | 二叉树 | | |
-| 107 | 二叉树的层序遍历2 | 中等 | 二叉树 | | |
-| 110 | 平衡二叉树 | 简单 | 二叉树 | | |
-| 111 | 二叉树的最小深度 | 简单 | 二叉树 | | |
-| 112 | 路径总和 | 简单 | 二叉树 | | |
-| 113 | 路径总和2 | 中等 | 二叉树 | ⭐️⭐️⭐️ | DFS |
-| 118 | 杨辉三角 | | 数组 | | |
-| 121 | 买卖股票的最佳时机 | 简单 | | | |
-| 122 | 买卖股票的最佳时机 II | | | | |
-| 123 | 买卖股票 | | | | |
-| 125 | 验证回文串 | 简单 | 字符串 | | 双指针 |
-| 129 | 求根节点到叶子节点数字之和 | 中等 | 二叉树 | ⭐️⭐️ | DFS |
-| 141 | 环形链表 | 简单 | 链表 | ⭐️⭐️ | 快慢指针 |
-| 142 | 环形链表2 | 中等 | | ⭐️⭐️⭐️ | 快慢指针 |
-| 143 | 重排链表 | 中等 | 链表 | ⭐️⭐️⭐️ | |
-| 144 | 二叉树的前序遍历 | 简单 | 二叉树 | | |
-| 145 | 二叉树的后序遍历 | 简单 | 二叉树 | ⭐️⭐️ | 栈 |
-| 147 | 对链表进行插入排序 | 中等 | 链表 | | |
-| 149 | 直线上最多的点数 | | | | |
-| 148 | 排序链表 | | 链表 | | |
-| 151 | 翻转字符串里的单词 | | | | |
-| 155 | 最小栈 | | 栈 | | |
-| 156 | 上下翻转二叉树 | 中等 | 二叉树 | | |
-| 160 | 两个链表的交点 | 简单 | 链表 | | |
-| 167 | 两数之和II | 简单 | 数组 | | |
-| 189 | 旋转数组 | 中等 | 数组 | ⭐️⭐️ | |
-| 191 | 位1的个数 | 简单 | 数学 | | |
-| 199 | 二叉树的右视图 | 中等 | 二叉树 | | 层序遍历 |
-| 203 | 移除链表元素 | 简单 | 链表 | | |
-| 206 | 反转链表 | 简单 | 链表 | | |
-| 209 | 长度最小的子数组 | 中等 | 数组 | ⭐️⭐️⭐️ | |
-| 215 | 数组中的第K个最大元素 | | 数组 | | 栈 |
-| 219 | 存在重复元素II | 简单 | 数组 | | |
-| 220 | 存在重复元素III | 困难 | 数组 | ⭐️⭐️⭐️ | 滑动窗口 |
-| 231 | 2的幂 | 简单 | | | |
-| 234 | 回文链表 | 简单 | 链表 | | |
-| 236 | 二叉树的最近公共祖先 | 中等 | 二叉树 | | |
-| 239 | 滑动窗口最大值 | 困难 | 单调队列 | | |
-| 246 | 中心对称数 | | | | |
-| 257 | 二叉树的所有路径 | 简单 | 二叉树 | | DFS |
-| 264 | 丑数 | | | | |
-| 270 | 最接近的二叉搜索树 | 简单 | 二叉树 | | |
-| | 零钱兑换 | 中等 | 动态规划 | | |
-| 283 | 移动零 | 简单 | 数组 | | 就地替换 |
-| 292 | Nim游戏 | | | | |
-| 300 | 最长上升子序列 | 中等 | 动态规划 | | |
-| 322 | 零钱兑换 | 中等 | 动态规划 | | |
-| 328 | 奇偶链表 | 中等 | 链表 | | |
-| 331 | 验证二叉树的前序序列化 | 中等 | 二叉树 | ⭐️⭐️⭐️ | 栈;出度,入度 |
-| 338 | 比特位计数 | | | | |
-| 344 | 反转字符串 | 简单 | 字符串 | | 双指针 |
-| 345 | 反转字符串中的元音字母 | | | | |
-| 404 | 左叶子之和 | 简单 | 二叉树 | | |
-| 415 | 字符串相加 | 简单 | 字符串 | | |
-| 424 | 替换后的最长重复字符 | 中等 | string | ⭐️⭐️ | 滑动窗口 |
-| 429 | N叉树的层序遍历 | 中等 | N叉树 | | |
-| 447 | 回旋镖的数量 | 中等 | 数组 | | |
-| 461 | 汉明距离 | 简单 | 数学 | | |
-| 476 | 汉明距离 | 简单 | | | |
-| 480 | 滑动窗口中位数 | 困难 | 滑动窗口 | ⭐️⭐️⭐️⭐️ | |
-| 485 | 最大连续1的个数 | 简单 | 数组 | | 前后指针 |
-| 498 | 对角线遍历 | | 数组 | | |
-| 509 | 斐波那契数 | 简单 | 动态规划 | | |
-| 538 | 把二叉树转换成累加树 | 简单 | 二叉树 | | |
-| 521 | 最长特殊序列 I | | | | |
-| 543 | 二叉树的直径 | 简单 | 二叉树 | | |
-| 545 | 二叉树的边界 | 中等 | 二叉树 | | |
-| 563 | 二叉树的坡度 | 简单 | 二叉树 | | |
-| 576 | 字符串的排列 | | | | |
-| 589 | N叉树的前序遍历 | 简单 | N叉树 | ⭐️⭐️ | 迭代,栈 |
-| 590 | N叉树的后序遍历 | 简单 | N叉树 | ⭐️⭐️ | 迭代,栈 |
-| 594 | 最长和谐子序列 | | | | |
-| 617 | 合并二叉树 | 简单 | 二叉树 | | |
-| 621 | 任务调度器 | | | | |
-| 622 | 设计循环队列 | 中等 | | | |
-| 637 | 二叉树的层平均值 | 中等 | 二叉树 | | |
-| 641 | 设计循环双端队列 | 中等 | | | |
-| 654 | 最大二叉树 | 中等 | 二叉树 | | |
-| 655 | 输出二叉树 | 中等 | 二叉树 | | |
-| 662 | 二叉树的最大宽度 | 中等 | 二叉树 | | |
-| 669 | 修剪二叉搜索树 | 简单 | 二叉搜索树 | | |
-| 674 | 最长连续递增序列 | 简单 | 数组 | | |
-| 695 | 岛屿的最大面积 | | | | 广度优先搜索 |
-| 703 | 数据流中第K大元素 | 简单 | | | |
-| 707 | 设计链表 | | 链表 | | |
-| 724 | 寻找数组的中心索引 | 简单 | 数组 | | |
-| 747 | 至少是其他数字两倍的最大数 | 简单 | 数组 | | |
-| 814 | 二叉树剪枝 | 中等 | 二叉树 | | |
-| 820 | 单词的压缩编码 | | | | |
-| 876 | Middle of The Linked List | | | | |
-| 905 | 按奇偶排序数组 | 简单 | 数组 | | 对撞指针 |
-| 914 | 卡牌分组 | | | | |
-| 977 | 有序数组的平方 | 简单 | 数组 | | 对撞指针 |
-| 933 | Number of Recent Calls | | | | |
-| 941 | 有效的山型数组 | 简单 | 数组 | | |
-| 987 | 二叉树的垂序遍历 | 困难 | 二叉树 | ⭐️⭐️⭐️ | 复杂的层序遍历 |
-| 993 | 二叉树的堂兄弟节点 | 简单 | 二叉树 | | |
-| 1089 | 重复零 | 简单 | 数组 | | |
-| 1104 | 二叉树寻路 | 中等 | 二叉树 | | |
-| 1161 | 最大层内元素和 | 中等 | 二叉树 | | 层序遍历 |
-| 1162 | 地图分析 | | | | |
-| 1208 | 尽可能使字符串相等 | 中等 | string | ⭐️⭐️⭐️ | 滑动窗口 |
-| 1295 | 找出具有偶数位数字的个数 | 简单 | 数组 | | |
-| 1299 | 将每个元素替换为右侧最大元素 | 简单 | 数组 | | 就地替换 |
-| 1302 | 层数最深叶子节点的和 | 中等 | 二叉树 | | |
+
+
+
+#### 日常题集
+
+- [169多数元素](notebook/169.md)【Easy】
\ No newline at end of file
diff --git a/SUMMARY.md b/SUMMARY.md
deleted file mode 100644
index 08dcd21..0000000
--- a/SUMMARY.md
+++ /dev/null
@@ -1,136 +0,0 @@
-# SUMMARY
-
-## [封面](README.md)
-
-
-
-## 数组部分
-
-* [数组](01su/readme.md)
- 1. [001两数之和](01su/001.md)
- 2. [011盛最多水的容器](01su/011.md)
- 3. [026删除有序数组中的重复项](01su/026.md)
- 4. [027移除元素](01su/027.md)
- 5. [034在排序数组中查找元素的第一个和最后一个位置](01su/034.md)
- 6. [053最大子数组和](01su/053.md)
- 7. [066加1](01su/066.md)
- 8. [075颜色分类](01su/075.md)
- 9. [078子集](01su/078.md)
- 10. [080删除有序数组中的重复项2](01su/080.md)
- 11. [088合并两个有序数组](01su/088.md)
- 12. [167两数之和2-输入有序数组](01su/167.md)
- 13. [189轮转数组](01su/189.md)
- 14. [209长度最小的子数组](01su/209.md)
- 15. [215数组中第K大的元素](01su/215.md)
- 16. [219存在重复元素2](01su/219.md)
- 17. [220存在重复元素3](01su/220.md)
- 18. [283移动零](01su/283.md)
- 19. [485最大连续1的个数](01su/485.md)
- 20. [498对角线遍历](01su/498.md)
- 21. [674最长连续递增序列](01su/674.md)
- 22. [724寻找数组的中心下标](01su/724.md)
- 23. [747至少是其他数组两倍的最大数](01su/747.md)
- 24. [905按奇偶排序数组](01su/905.md)
- 25. [941有效的山脉数组](01su/941.md)
- 26. [977有序数组的平方](01su/977.md)
- 27. [1089复写零](01su/1089.md)
- 28. [1295统计位数为偶数的数字](01su/1295.md)
- 29. [1299将每个元素替换为右侧最大元素](1299.md)
- 30. [连续最大子序和问题](01su/largest_sum_contiguous_subarray.md)
-
-
-
-## 链表部分
-* [链表](02linkedlist/readme.md)
- 1. [002两数之和](02linkedlist/002.md)
- 2. [019删除链表的倒数第N个结点](02linkedlist/019.md)
- 3. [021合并两个有序链表](02linkedlist/021.md)
- 4. [023合并K个排序链表](02linkedlist/023.md)
- 5. [024两两交换链表中的节点](02linkedlist/024.md)
- 6. [082从排序链表中删除重复元素2](02linkedlist/082.md)
- 7. [083从排序链表中删除重复元素](02linkedlist/083.md)
- 8. [086分割链表](02linkedlist/086.md)
- 9. [141环形链表](02linkedlist/141.md)
- 10. [142环形链表2](02linkedlist/142.md)
- 11. [143重排链表](02linkedlist/143.md)
- 12. [206反转链表](02linkedlist/206.md)
-
-
-
-## 字符串部分
-
-* [字符串](05string/string.md)
- 1. [003无重复字符的最长子串](05string/003.md)
- 2. [020有效的括号](05string/020.md)
- 3. [043字符串相乘](05string/043.md)
- 4. [058最后一个单词的长度](05string/058.md)
- 5. [067无重复字符的最长子串](05string/067.md)
- 6. [125验证回文串](05string/125.md)
- 7. [242有效的字符异位词](05string/242.md)
- 8. [344反转字符串](05string/344.md)
- 9. [415字符串相加](05string/415.md)
- 10. [1208尽可能使字符串相等](05string/1208.md)
-
-
-
-## 树
-
-- [树的介绍](08binaryTree/readme.md)
- 1. [094二叉树的中序遍历](08binaryTree/094.md)
- 1. [095不同的二叉搜索树2](08binaryTree/095.md)
- 1. [096不同的二叉搜索树](08binaryTree/096.md)
- 1. [098验证二叉树搜索树](08binaryTree/098.md)
- 1. [099恢复二叉树](08binaryTree/099.md)
- 1. [100相同的树](08binaryTree/100.md)
- 1. [101对称二叉树](08binaryTree/101.md)
- 1. [102二叉树的层序遍历](08binaryTree/102.md)
- 1. [103二叉树的锯齿形层序遍历](08binaryTree/103.md)
- 1. [104二叉树的最大深度](08binaryTree/104.md)
- 1. [105从前序与中序遍历序列构造二叉树](08binaryTree/105.md)
- 1. [106从中序与后序遍历序列构造二叉树](08binaryTree/106.md)
- 1. [107二叉树的层序遍历2](107.md)
- 1. [110平衡二叉树](08binaryTree/110.md)
- 1. [111二叉树的最小深度](08binaryTree/111.md)
- 1. [112路径总和](08binaryTree/112.md)
- 1. [113路径总和2](08binaryTree/113.md)
- 1. [129求从根节点到叶子节点数字之和](08binaryTree/129.md)
- 1. [144二叉树的前序遍历](08binaryTree/144.md)
- 1. [145二叉树的后序遍历](08binaryTree/145.md)
- 1. [199二叉树的右视图](08binaryTree/199.md)
- 1. [236二叉树的最近公共祖先](08binaryTree/236.md)
- 1. [257二叉树的所有路径](08binaryTree/257.md)
- 1. [331验证二叉树的前序序列化](08binaryTree/331.md)
- 1. [404左叶子之和](08binaryTree/404.md)
- 1. [429N叉树的层序遍历](08binaryTree/429.md)
- 1. [538把二叉搜索树转换为累加树](08binaryTree/538.md)
- 1. [545二叉树的边界](08binaryTree/545.md)
- 1. [563N叉树的坡度](08binaryTree/563.md)
- 1. [589N叉树的前序遍历](08binaryTree/589.md)
- 1. [590N叉树的后序遍历](08binaryTree/590.md)
- 1. [617合并二叉树](08binaryTree/617.md)
- 1. [637二叉树的层平均值](08binaryTree/637.md)
- 1. [654最大二叉树](08binaryTree/654.md)
- 1. [655输出二叉树](08binaryTree/655.md)
- 1. [662二叉树的最大宽度](08binaryTree/662.md)
- 1. [814二叉树的剪枝](08binaryTree/814.md)
- 1. [987二叉树的垂序遍历](08binaryTree/987.md)
- 1. [993二叉树的堂兄弟节点](08binaryTree/993.md)
- 1. [1302层数最深叶子节点的和](08binaryTree/1302.md)
- 1. [1161最大层内元素和](08binaryTree/1161.md)
-
-
-
-- [二叉索引树](08binaryTree/binaryIndexTree.md)
- -
-
-
-
-## 堆算法
-
-* [堆算法](07heap/heap.md)
-
-
-
-## 滑动窗口算法
-
-* [滑动窗口](10SlidingWindow/sliding_window.md)
diff --git a/algorithm/bfs/bfs.md b/algorithm/bfs/bfs.md
deleted file mode 100644
index 02bbe55..0000000
--- a/algorithm/bfs/bfs.md
+++ /dev/null
@@ -1,117 +0,0 @@
-## 广度优先搜索
-
-[TOC]
-
-
-
-### 知识点回顾
-
-
-
-### 相关题目
-
-#### 695 岛屿的最大面积
-
-题目要求:
-
-思路分析:
-
-```go
-// date 2020/03/29
-// 广度优先搜索,注意使用visited变量,可以快速搜索
-func maxAreaOfIsland(grid [][]int) int {
- n := len(grid)
- if n < 1 { return 0 }
- m := len(grid[0])
- res := 0
- var visited [50][50]int
- // 广度优先搜索,找到岛屿的最大值
- var findLandArea func(x, y int) int
- findLandArea = func(x, y int) int {
- area := 1
- dx, dy := [4]int{-1, 0, 1, 0}, [4]int{0, -1, 0, 1}
- queue := make([][2]int, 0)
- queue = append(queue, [2]int{x, y})
- visited[x][y] = 1
- for len(queue) != 0 {
- l := len(queue)
- for i := 0; i < l; i++ {
- for j := 0; j < 4; j++ {
- nx, ny := queue[i][0]+dx[j], queue[i][1]+dy[j]
- if nx < 0 || nx >=n || ny < 0 || ny >= m { continue }
- if grid[nx][ny] == 1 && visited[nx][ny] != 1 {
- queue = append(queue, [2]int{nx, ny})
- visited[nx][ny] = 1
- }
- }
- }
- queue = queue[l:]
- area += len(queue)
- }
- return area
- }
-
- for i := 0; i < n; i++ {
- for j := 0; j < m; j++ {
- if grid[i][j] == 1 && visited[i][j] != 1 {
- area := findLandArea(i, j)
- if res < area { res = area }
- }
- }
- }
- return res
-}
-```
-
-#### 1162 地图分析
-
-题目要求:https://leetcode-cn.com/problems/as-far-from-land-as-possible/
-
-思路分析:
-
-```go
-// date 2020/03/29
-func maxDistance(grid [][]int) int {
- // 第一步,找到某个海洋距离最近的陆地
- dx, dy := [4]int{-1, 0, 1, 0}, [4]int{0, -1, 0, 1}
- var findNearestLand func(x, y int) int
- findNearestLand = func(x, y int) int {
- queue := make([][3]int, 0) // 0, 1, 2分别是横坐标,纵坐标,和距离
- vis := [100][100]int{} // 每一次搜索都需要初始化
- queue = append(queue, [3]int{x, y, 0})
- vis[x][y] = 1
- nx, ny := 0, 0
- for len(queue) != 0 {
- l := len(queue)
- for i := 0; i < l; i++ {
- for j := 0; j < 4; j++ {
- nx, ny = queue[i][0] + dx[j], queue[i][1] + dy[j]
- if nx < 0 || nx >= n || ny < 0 || ny >= n { continue }
- if vis[nx][ny] == 1 { continue }
- queue = append(queue, [3]int{nx, ny, queue[i][2]+1})
- vis[nx][ny] = 1
- if grid[nx][ny] == 1 { return queue[i][2]+1 }
- }
- }
- queue = queue[l:]
- }
- return -1
- }
-
- res, n := -1, len(grid)
- for i := 0; i < n; i++ {
- for j := 0; j < n; j++ {
- if grid[i][j] == 0 {
- res = max(res, findNearestLand(i, j))
- }
- }
- }
- return res
-}
-
-func max(x, y int) int {
- if x > y { return x }
- return y
-}
-```
-
diff --git a/algorithm/greedy/greedy_algorithm.md b/algorithm/greedy/greedy_algorithm.md
deleted file mode 100644
index 163d14d..0000000
--- a/algorithm/greedy/greedy_algorithm.md
+++ /dev/null
@@ -1,90 +0,0 @@
-### 贪心算法
-
-贪心算法一般用来解决需要"找到要做某事的最小数量"或”找到在某些情况下适合的最大物品数量的问题”,且提供无序的输入。
-
-贪心算法的思想是每一步都选择最佳解决方案,最终获得全局最佳的解决方案。
-
-### 相关题目
-
-- 55 跳跃游戏
-- 45 跳远游戏II
-
-
-
-#### 55 跳跃游戏
-
-思路分析
-
-第一种:正向,检查当前的每一个值,看是否可能跳跃到更远的地方。
-
-第二种:反向检查,看是否能够从最远处到达起点。
-
-```go
-// 正向检查
-func canJump(nums []int) bool {
- if len(nums) <= 1 {return true}
- reach := nums[0]
- for i := 0; i <= reach && i < len(nums); i++ {
- if reach < i + nums[i] {
- reach = i + nums[i]
- }
- }
- return reach >= len(nums) - 1
-}
-// 反向检查
-func canJump(nums []int) bool {
- if len(nums) <= 1 {return true}
- left := len(nums)-1
- for i := len(nums) - 2; i >= 0; i-- {
- if i + nums[i] >= left {
- left = i
- }
- }
- return left == 0
-}
-```
-
-#### 45 跳跃游戏II
-
-
-
-```go
-func jump(nums[] int) int {
- if len(nums) <= 1 {return 0}
- reach := nums[0]
- for i := 0; i < len(nums) - 1; i++ {
- for j := i; j < reach; j++ {
- if j + nums[j] > reach {
- reach = j + nums[j]
- }
- }
- }
-}
-```
-
-#### 452 用最少数量的箭引爆气球
-
-思路分析
-
-1 先对气球的结束end坐标进行排序
-
-2 凡是气球的起始坐标大于当前能够引爆的气球的end坐标的均需要增加一支箭,并更新end坐标
-
-```go
-func findMinArrowsShots(points [][]int) int {
- if len(points) == 0 {return 0}
- sort.Slice(points, func(i, j int) bool {
- return s[i][1] < s[j][1]
- })
- res := 1
- end := points[0][1]
- for _, p := range points {
- if end < p[0] {
- res++
- end = p[1]
- }
- }
- return res
-}
-```
-
diff --git a/algorithm/math/math.md b/algorithm/math/math.md
deleted file mode 100644
index f52a00d..0000000
--- a/algorithm/math/math.md
+++ /dev/null
@@ -1,512 +0,0 @@
-## Math
-
-[TOC]
-
-### 1、相关题目
-
-#### 7 整数反转
-
-给你一个 32 位的有符号整数 `x` ,返回将 `x` 中的数字部分反转后的结果。
-
-```go
-// date 2022-09-15
-func reverse(x int) int {
- mMax, mMin := 1 << 31 - 1, -1 << 31
- res, flag := 0, 1
- if x < 0 {
- flag, x = -1, -x
- }
- for x > 0 {
- res = res * 10 + x % 10
- x /= 10
- }
- res *= flag
- if res > 0 && res > mMax || res < 0 && res <= mMin {
- res = 0
- }
- return res
-}
-```
-
-
-
-#### 8 String to Integer
-
-https://leetcode.com/problems/string-to-integer-atoi/
-
-```go
-/* 细节题: 需要各种异常场景
-1. 忽略开头的空白字符
-2. 数字的符号
-3. 溢出
-4. 无效输入
-*/
-func myAtoi(str string) int {
- myMAX := 1 << 31 - 1
- myMIN := -1 << 31
- sign := 1
- var res int
- i := 0
- n := len(str)
- for i < n && str[i] == ' ' {i++}
- if i == n {return res}
- if str[i] == '+' {
- i++
- } else if str[i] == '-' {
- i++
- sign = -1
- }
- for ; i < n; i++ {
- if str[i] - '0' < 0 || str[i] - '0' > 9 {break}
- t := int(str[i] - '0')
- if res > myMAX / 10 || res == myMAX / 10 && t > myMAX % 10 {
- if sign == 1 {
- return myMAX
- } else if sign == -1 {
- return myMIN
- }
- }
- res = res * 10 + t
- }
- return res * sign
-}
-```
-
-
-
-#### 9 Palindrome Number
-
-```go
-// 算法1:直接比较数字的每一位,更通用的算法
-func isPalindrome(x int) bool {
- if x < 0 || (x != 0 && x % 10 == 0) {return false}
- d := 1
- for x / d >= 10 {
- d *= 10
- }
- for x > 0 {
- // 最高位
- q := x / d
- // 最低位
- p := x % 10
- if q != p { return false }
- // 移动至次高位,同时去掉最后一位
- x = x % d / 10
- d /= 100
- }
- return true
-}
-// 算法2:将数字从中间分开,判断左边和右边的数字是否相等
-func isPalindrome(x int) bool {
- if x < 0 || (x != 0 && x % 10 == 0) {return false}
- left := 0
- for x > left {
- left = left * 10 + x % 10
- x /= 10
- }
- return x == left || x == left/10
-}
-```
-
-思路学习:算法2对于判断链表同样适用。参考题目234https://leetcode.com/problems/palindrome-linked-list/
-
-#### 15 三数之和【M】
-
-题目要求:给你一个包含 *n* 个整数的数组 `nums`,判断 `nums` 中是否存在三个元素 *a,b,c ,*使得 *a + b + c =* 0 ?请你找出所有满足条件且不重复的三元组。
-
-**注意:**答案中不可以包含重复的三元组。
-
-思路分析
-
-
-
-```go
-// date 2020/03/29
-func threeSum(nums []int) [][]int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- res, n, sum := make([][]int, 0), len(nums), -1
- left, right := 0, n-1
- for i := 0; i < n; i++ {
- // 升序排列,大于零则退出
- if nums[i] > 0 { break }
- // 去重
- if i > 0 && nums[i] == nums[i-1] { continue }
- left, right = i+1, n-1
- for left < right {
- sum = nums[i] + nums[left] + nums[right]
- if sum < 0 {
- left++
- } else if sum > 0 {
- right--
- } else if sum == 0 {
- res = append(res, []int{nums[i], nums[left], nums[right]})
- // 去重
- for left < right && nums[left] == nums[left+1] { left++ }
- for left < right && nums[right] == nums[right-1] { right-- }
- left++
- right--
- }
- }
- }
- return res
-}
-```
-
-#### 89 格雷编码
-
-题目要求:给定一个格雷编码的总位数n,输出器格雷编码序列(格雷编码序列:相邻的两个数字只有一位不同)。
-
-算法:镜像反射法
-
-```go
-// date 2020/01/11
-/* 算法:G(n) = G(n-1) + R(n-1) // R(n-1)为G(n-1)反序+head
-0 0 00
- 1 01
- 11
- 10
-*/
-func grayCode(n int) []int {
- res, head := make([]int, 0), 1
- res = append(res, 0)
- for i := 0; i < n; i++ {
- n := len(res) - 1
- for j = n; j >= 0; j-- {
- res = append(res, head + res[j])
- }
- head <<= 1
- }
- return res
-}
-```
-
-#### 四数求和
-
-思路分析
-
-算法:原理同三数求和
-
-```go
-func fourSum(nums []int, target int) [][]int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- res, n, sum := make([][]int, 0), len(nums), 0
- l, r := 0, n-1
- for i := 0; i < n; i++ {
- // nums[i]可以是负数 if nums[i] > target {break}
- if i > 0 && nums[i] == nums[i-1] {continue}
- for j := i+1; j < n; j++ {
- if j > i+1 && nums[j] == nums[j-1] {continue}
- l, r = j+1, n-1
- for l < r {
- sum = nums[i] + nums[j] + nums[l] + nums[r]
- if sum == target {
- t := make([]int, 0)
- t = append(t, nums[i], nums[j], nums[l], nums[r])
- res = append(res, t)
- for l < r && nums[l] == nums[l+1] {l++}
- for l < r && nums[r] == nums[r-1] {r--}
- l++
- r--
- } else if sum < target {
- l++
- } else {
- r--
- }
- }
- }
- }
- return res
-}
-```
-
-#### 191 位1的个数【简单】
-
-题目链接:https://leetcode-cn.com/problems/number-of-1-bits/
-
-编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为[汉明重量](https://baike.baidu.com/item/汉明重量))。
-
-思路分析:
-
-```golang
-func hammingWeight(num uint32) int {
- var c int
- for num > 0 {
- c += int(num & 0x1)
- num >>= 1
- }
- return c
-}
-```
-
-#### 149 直线上最多的点数【H】
-
-题目要求:给定二维平面上的n个点,求最多有多少个点在同一条直线上。
-
-算法:哈希表,欧几里得最大公约数算法
-
-```go
-// data 2020/02/01
-func maxPoints(points [][]int) int {
- if len(points) < 3 { return len(points) }
- n, count := len(points), make([]int, len(points))
- size, same := 1, 0
- for i := 0; i < n; i++ {
- m := make(map[[2]int]int, 0)
- count[i] = 1
- size, same = 1, 0
- for j := 0; j < n; j++ {
- if i == j { continue }
- // x坐标一样
- if points[i][0] == points[j][0] {
- if points[i][1] == points[j][1] {
- same++
- }
- size++
- } else {
- // x坐标不一样 求斜率
- dy := points[j][1] - points[i][1]
- dx := points[j][0] - points[i][0]
- g := gcd(dy, dx)
- if g != 0 {
- dy, dx = dy/g, dx/g
- }
- k := [2]int
- k[0], k[1] = dy, dx
- find := false
- for mk, mv := range m {
- if mk[0] == k[0] && mk[1] == k[1] {
- find = true
- m[mk]++
- }
- }
- if !find {
- m[k] = 1
- }
- }
- }
- for _, v := range m {
- if v + 1 > count[i] {
- count[i] = v + 1
- }
- }
- count[i] += same
- if count[i] < size {
- count[i] = size
- }
- }
- maxIndex := 0
- for i := 0; i < n; i++ {
- if count[i] > count[maxIndex] {
- maxIndex = i
- }
- }
- return count[maxIndex]
-}
-
-func gcd(x, y int) int {
- if y == 0 { return x }
- return gcd(y, x % y)
-}
-```
-
-#### 231 2的幂【E】
-
-题目要求:给定一个整数,判断其是否是2的幂次方。
-
-思路分析:判断这个数是否不断的被2整数,直接结果等于1。如果某一次结果为奇数,直接返回false。
-
-```golang
-// date 2020/01/11
-func isPowerOfTwo(n int) bool {
- for n > 1 {
- if n &0x1 == 1 {return false}
- n >>= 1
- }
- return n == 1
-}
-```
-
-#### 292 Nim游戏
-
-算法思路:只要是4的倍数,你一定输。
-
-```go
-// date 2020/01/09
-func canWinNim(n int) bool {
- if n % 4 == 0 {
- return false
- }
- return true
-}
-```
-
-#### 338 比特位计数
-
-题目要求:https://leetcode-cn.com/problems/counting-bits/
-
-思路分析:
-
-```go
-// date 2020/03/30
-/*
-递推,二进制的表示
-如果当前为奇数,则在上一个偶数的基础上加一;如果当前为偶数,则和上一个偶数保持一致
-*/
-func countBits(num int) []int {
- res := make([]int, num+1)
- res[0] = 0
- for i := 1; i <= num; i++ {
- if i & 0x1 == 1 {
- res[i] = res[i-1]+1
- } else {
- res[i] = res[i>>1]
- }
- }
- return res
-}
-```
-
-#### 461 汉明距离【简单】
-
-题目链接:https://leetcode-cn.com/problems/hamming-distance/
-
-两个整数之间的[汉明距离](https://baike.baidu.com/item/汉明距离)指的是这两个数字对应二进制位不同的位置的数目。
-
-给出两个整数 `x` 和 `y`,计算它们之间的汉明距离。
-
-思路分析:
-
-```golang
-func hammingDistance(x int, y int) int {
- return hammingWeight(x^y)
-}
-
-func hammingWeight(num int) int {
- var c int
- for num > 0 {
- c += num & 0x1
- num >>= 1
- }
- return c
-}
-```
-
-#### 476 数字的补数
-
-题目链接:https://leetcode-cn.com/problems/number-complement/
-
-题目要求:给定一个正整数,输出它的补数。补数是对该数的二进制表示取反。
-
-思路分析:
-
-```go
-// date 2020/05/04
-// 找到第一个比这个数大的二进制整数,进而求得全F,然后减去这个数即可
-func findComplement(num int) int {
- x := 1
- for x <= num {
- x <<= 1
- }
- return x - 1 - num
-}
-```
-
-#### 斐波那契数列
-
-思路分析
-
-记忆化递归
-
-```go
-func fib(N int) int {
- if N < 2 {return N}
- c, p1, p2 := 1, 1, 0
- for i := 2; i <= N; i++ {
- c = p1+p2
- p1, p2 = c, p1
- }
- return c
-}
-```
-
-#### 914 卡牌分组
-
-题目要求:https://leetcode-cn.com/problems/x-of-a-kind-in-a-deck-of-cards/
-
-思路分析:
-
-第一种:暴力求解,先统计每个元素出现的次数C,然后对可能的X值进行两个判断,X必须是N的约数,也是C的约数。
-
-```go
-// date 2020/03/27
-func hasGroupsSizeX(deck []int) bool {
- count := make([]int, 10000)
- // 统计每个数出现的次数
- for _, v := range deck {
- count[v]++
- }
- value := make([]int, 0)
- // 将出现的次数放入数组
- for _, c := range count {
- if c > 0 { value = append(value, c) }
- }
- // 暴露求解
- n := len(deck)
- for x := 2; x <= n; x++ {
- // x需要是n的约数
- if n % x == 0 {
- ok := true
- // 每个数字出现的次数也需要是x的倍数
- for _, v := range value {
- if v % x != 0 {
- ok = false
- break
- }
- }
- if ok { return true }
- }
- }
- return false
-}
-```
-
-第二种:统计每个元素出现的次数C,能够分组的前提就是所有C的最大公约数。
-
-```go
-// data 2020/03/27
-func hasGroupsSizeX(deck []int) bool {
- count := make(map[int]int)
- // 统计每个数出现的次数
- for _, v := range deck {
- if _, ok := count[v]; ok {
- count[v]++
- } else {
- count[v] = 1
- }
- }
- value := make([]int, 0)
- // 将出现的次数放入数组
- for _, c := range count {
- if c > 0 { value = append(value, c) }
- }
- g := -1
- for _, v := range value {
- if g == -1 {
- g = v
- } else {
- g = gcd(g, v)
- }
- }
- return g >= 2
-}
-
-func gcd(x, y int) int {
- if x == 0 { return y }
- return gcd(y%x, x)
-}
-```
-
diff --git a/binarytree.md b/binarytree.md
new file mode 100644
index 0000000..1e56ce8
--- /dev/null
+++ b/binarytree.md
@@ -0,0 +1,55 @@
+### 二叉树
+
+
+
+#### 相关题目
+
+- 102 二叉树的层次遍历【M】
+
+
+
+#### 102 二叉树的层次遍历
+
+题目要求:https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
+
+算法分析:bfs广度优先搜索和dfs深度优先搜索
+
+```go
+// date 2020/03/21
+// bfs广度优先搜索
+func levelOrder(root *TreeNode) [][]int {
+ res := make([][]int, 0)
+ if root == nil { return res }
+ queue := make([]*TreeNode, 0)
+ queue = append(queue, root)
+ for len(queue) != 0 {
+ n := len(queue)
+ temp_res := make([]int, 0)
+ for i := 0; i < n; i++ {
+ temp_res = append(temp_res, queue[i].Val)
+ if queue[i].Left != nil { queue = append(queue, queue[i].Left) }
+ if queue[i].Right != nil { queue = append(queue, queue[i].Right) }
+ }
+ res = append(res, temp_res)
+ queue = queue[n:]
+ }
+ return res
+}
+// dfs深度优先搜索
+func levelOrder(root *TreeNode) [][]int {
+ res := make([][]int, 0)
+ var dfs_ func(root *TreeNode, level int)
+ dfs_ = func(root *TreeNode, level int) {
+ if root == nil { return }
+ if level == len(res) {
+ res = append(res, make([]int, 0))
+ }
+ res[level] = append(res[level], root.Val)
+ dfs_(root.Left, level+1)
+ dfs_(root.Right,level+1)
+ }
+ dfs_(root, 0)
+ return res
+}
+```
+
diff --git a/book.json b/book.json
deleted file mode 100644
index d0c3e63..0000000
--- a/book.json
+++ /dev/null
@@ -1,36 +0,0 @@
-{
- "author": "subond",
- "description": "This is a sample book created by gitbook",
- "extension": null,
- "generator": "site",
- "isbn": null,
- "links": {
- "sharing": {
- "all": null,
- "facebook": null,
- "google": null,
- "twitter": null,
- "weibo": null
- },
- "sidebar": {
- "Chengwei's Blog": "http://www.subond.com"
- }
- },
- "output": null,
- "pdf": {
- "fontSize": 12,
- "footerTemplate": null,
- "headerTemplate": null,
- "margin": {
- "bottom": 36,
- "left": 62,
- "right": 62,
- "top": 36
- },
- "pageNumbers": false,
- "paperSize": "a4"
- },
- "plugins": [],
- "title": "LeetCode With Go",
- "variables": {}
-}
diff --git a/complexity.md b/complexity.md
deleted file mode 100644
index 8681874..0000000
--- a/complexity.md
+++ /dev/null
@@ -1,19 +0,0 @@
-# 复杂度
-
-常见数据结构的时间复杂度比较
-
-| | | 数组 | 单向链表 | 双向链表 | 队列 | 栈 |
-| :--- | -------------- | ---- | -------- | -------- | ---- | ---- |
-| 访问 | 通过索引 | O(1) | O(1) | O(1) | O(N) | O(N) |
-| 增加 | 第一个结点前 | O(N) | O(1) | O(1) | O(N) | O(N) |
-| 增加 | 特定结点后 | O(N) | O(1) | O(1) | O(N) | O(N) |
-| 增加 | 最后一个节点后 | O(1) | O(1) | O(1) | O(1) | O(1) |
-| 删除 | 第一个结点 | O(N) | O(1) | O(1) | O(1) | O(N) |
-| 删除 | 指定结点 | O(1) | O(1) | O(1) | O(N) | O(N) |
-| 删除 | 最后一个结点 | O(1) | O(N) | O(1) | O(N) | O(1) |
-| 查找 | 指定结点 | O(N) | O(N) | O(N) | O(N) | O(N) |
-
-
-
-## 附录
-原文地址: https://www.bigocheatsheet.com/
diff --git a/context.md b/context.md
deleted file mode 100644
index 358a57e..0000000
--- a/context.md
+++ /dev/null
@@ -1,312 +0,0 @@
-# leetcode
-
-数据结构和算法是一个程序员的基石,本仓库用于个人学习基本数据结构和算法。
-
-题目完成度:[263/500]
-
-[TOC]
-
----
-
-# 一、基本数据结构
-
-**[线性表](linear_list.md)**(Linear List)是由N(N>=0)个数据元素组成的有限序列,一般记为`a[0], a[1], ..., a[n-1]`。
-
-其中,表中的数据元素个数N定义为表的长度,当N=0称为空表。
-
-## [数组Array](array/array.md)
-
-数组属于线性表的一种,底层使用连续的空间进行存储,因此在声明数组的时候需要指定数组的大小,即需要申请多大的内存空间。
-
-根据数组长度是否可以调整,还有动态数组的概念,即数组的长度是可调节的。golang语言中动态数组即为切片,Slice。
-
-
-## [链表Linked List](linkedlist/linkedlist.md)
-
-链表也属于线性表的一种,底层使用非连续的空间进行存储,因此在声明链表的时候不需要指定链表大小。
-
-由于链表不必按照顺序存储,链表的插入操作可以达到O(1)的时间复杂度,而数组相应的操作平均需要O(logN)时间复杂度;但是,链表的查找和访问平均需要O(N)的时间复杂度,而数组相应的操作需要O(1)时间复杂度。
-
-链表有很多不同的类型:单向链表,双向链表,以及循环链表。
-
-### 相关题目
-
-- 2 两数相加【M】
-- 19 Remove Nth Node From End of List【M】
-- 21 合并两个有序链表
-- 23 合并K个排序链表
-- 24 两两交换链表中的节点
-- 61 Rotate List【旋转链表】
-- 82 Remove Duplicates From Sorted List II
-- 83 Remove Duplicates From Sorted List
-- 86 Partition List
-- 92 反转链表II
-- 141 Linked List Cycle【E】
-- 142 Linked List Cycle II【M】
-- 143 Reorder List
-- 147 Insertion Sort List【对链表进行插入排序】【M】
-- 148 排序链表
-- 160 Intersection of Two Linked List【E】
-- 203 移除链表元素【E】
-- 206 反转链表【E】
-- 234 回文链表【E】
-- 328 奇偶链表【M】
-- 707 设计链表【M】
-- 876 Middle of the Linked List
-
-### 单向链表的排序
-
-[单向链表的排序](linkedlist/linkedlist_sort.md)
-
-## [队列Queue](queue/queue.md)
-
-### 基本定义
-
-### 相关题目
-
-- 621 Task Scheduler【任务调度器】
-- 622 Design Circular Queue
-- 641 Design Circular Deque【M】
-- 933 Number of Recent Calls
-
-## [栈Stack](stack/stack.md)
-
-
-
-## [字符串String](string/string.md)
-
-golang语言中byte是uint8的别名,rune是int32的别名,字符串中的单个字符有byte表示。
-
-### 相关题目
-
-- 14 Longest Common Prefix
-- 有效的字母异位词
-- 反转字符串
-- 246 中心对称数【E】
-- 58 最后一个单词的长度
-- 521 最长特殊序列I【E】
-
-## [哈希表HashTable](hashTable/hashTable.md)
-
-### 哈希表的原理
-
-### 哈希集合的设计
-
-### 哈希映射的设计
-
-### 相关题目
-
-- 1 两数之和
-- 202 快乐数
-- 36 有效的数独
-- 170 两数之和III - 数据结构设计
-- 349 两个数组的交集
-- 652 寻找重复的树【中等】
-- 49 字母异位词分组【M】
-- 四数相加II
-- 常数时间插入,删除和获取
-- 146 LRU缓存机制【M】
-
-## [数学题目](math/math.md)
-
-### 相关题目
-
-- 8 String to Integer
-- 9 Palindrome Number
-- 15 三数之和
-
----
-
-# 二、抽象数据结构
-
-优先队列是一种抽象的数据结构,可以使用堆实现。
-
-## [堆Heap](heap/heap.md)
-
-[堆](heap/heap.md)
-
-### 堆的定义
-### 堆的算法
-### 堆的排序
-### 相关题目
-
-- 912 排序数组【M】
-- 1046 最后一块石头的重量
-- 215 数组中第K个最大元素
-- 面试题40 最小的K个数
-- 面试题17.09 第K个数
-
-## [二叉树Binary Tree](binaryTree/binaryTree.md)
-
-二叉树属于非线性表的一种,与链表不同的是,二叉树有两个后继节点。
-
-### 什么是二叉树
-
-### 二叉树的遍历
-
-- 前序遍历(递归和迭代)
-- 中序遍历(递归和迭代)
-- 后序遍历(递归和迭代)
-- 层序遍历(广度优先搜索和深度优先搜索)
-
-前中后三种遍历算法的迭代版本一定会使用**栈**数据结构,通过出栈检查每个结点来完成遍历;
-
-层序遍历的广度优先搜索一定会使用**队列**,通过入队与出队检查每一层的结果。
-
-### 递归解决二叉树问题
-
-递归通常是解决树的相关问题最有效和最常用的方法之一,分为**自顶向下**和**自底向上**两种。
-
-**自顶向下**的解决方案
-
-自顶向下意味着在每个递归层级,需要先计算一些值,然后递归调用并将这些值传递给子节点,视为前序遍历。参见题目【二叉树的最大深度】
-
-**自底向上**的解决方案
-
-自底向上意味着在每个递归层级,需要先对子节点递归调用函数,然后根据返回值和根节点本身得到答案。
-
-**总结**:
-
-当遇到树的问题时,先思考一下两个问题:
-
-> 1.你能确定一些参数,从该节点自身解决出发寻找答案吗?
->
-> 2.你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗?
-
-如果答案是肯定的,那么可以尝试使用自顶向下的递归来解决问题。
-
-当然也可以这样思考:对于树中的任意一个节点,如果你知道它子节点的结果,你能计算出该节点的答案吗?如果答案是肯定的,可以尝试使用自底向上的递归来解决问题。
-
-### 相关题目
-
-- 95 不同的二叉搜索树 II【中等】
-- 98 验证二叉搜索树【中等】
-- 101 对称二叉树【简单】
-- 104 二叉树的最大深度【简单】
-- 105 从前序与中序遍历序列构造二叉树【中等】
-- 106 从中序和后序遍历序列构造二叉树【中等】
-- 110 平衡二叉树【简单】
-- 111 二叉树的最小深度【简单】
-- 112 路径总和【简单】
-- 156 上下翻转二叉树【中等】
-- 199 二叉树的右视图【中等】
-- 236 二叉树的最近公共祖先【中等】
-- 257 二叉树的所有路径【简单】
-- 270 最接近的二叉搜索树值【简单】
-- 538 把二叉树转换成累加树【简单】
-- 543 二叉树的直径【简单】
-- 545 二叉树的边界【中等】
-- 563 二叉树的坡度【简单】
-- 617 合并二叉树【简单】
-- 654 最大二叉树【中等】
-- 655 输出二叉树【中等】
-- 662 二叉树的最大宽度【中等】
-- 669 修剪二叉搜索树【简单】
-- 703 数据流中第K大元素【简单】
-- 814 二叉树剪枝【中等】
-- 993 二叉树的堂兄弟节点【简单】
-- 1104 二叉树寻路【中等】
-- 面试题27 二叉树的镜像【简单】
-
-## [二叉搜索树Binary Search Tree](binaryTree/bst.md)
-
-[二叉搜索树](binaryTree/bst.md)
-
-### 什么是二叉搜索树
-
-### 二叉搜索树的基本操作
-
-- 查询
-- 最小关键字元素
-- 最大关键字元素
-- 前继节点
-- 后继节点
-- 插入
-- 删除
-
-### 相关题目
-
-- 98 验证二叉搜索树【M】
-- 108 将有序数组转换为二叉搜索树【M】
-- 235 二叉搜素树的最近公共祖先
-- 450 删除二叉搜索树中的节点
-- 1038 从二叉搜索树到更大和树【M】
-- 1214 查找两棵二叉搜索树之和【M】
-- 面试题 17.12 BiNode【E】
-- 面试题54 二叉搜索树的第K大节点
-
-## [二叉索引树Binary Index Tree](binaryTree/bit.md)
-
- - 1.结构介绍
- - 2.问题定义
- - 3.表面形式
- - 3.1更新操作
- - 3.2求和操作
- - 4.工作原理
- - 5.代码实现
-
-# 三、基本算法理论
-
-算法不仅仅是一种解决问题的思路,更是一种思想。
-
-## 排序算法
-
-## [二分查找](binarySearch/binarySearch.md)
-
-### 相关题目
-
-- 704 二分查找
-- 162 寻找峰值
-- 658 找到K个最接近的元素
-
-## [贪心算法](greedy/greed_algorithm.md)
-
-### 算法介绍
-
-### 相关题目
-
-- 55 跳跃游戏
-- 45 跳远游戏II
-
-## 递归思想
-
-
-
-## [广度优先搜索](bfs/bfs.md)
-
-
-
-## [深度优先搜索](dfs/dfs.md)
-
-
-
-## [动态规划](dynamicProgramming/dp.md)
-
-### 算法介绍
-
-### 解题思路
-
-### 相关题目
-
-- 64 最小路径和【M】
-- 70 爬楼梯
-- 72 编辑距离【H】
-- 121 买卖股票的最佳时机
-- 122 买卖股票的最佳时机II
-- 123 买卖股票的最佳时机III
-- 188 买卖股票的最佳时机IV
-- 746 使用最少花费爬楼梯
-- 264 丑数【M】
-- 300 最长上升子序列【M】
-
-## 剪枝思想
-
-剪枝是搜索算法的优化手段,目的是为了去掉不必要的搜索。
-
-# [其他题目](others.md)
-
-- 位1的个数
-- 汉明距离
-- 292 Nim游戏
-- 89 格雷编码
-
diff --git a/dp.md b/dp.md
new file mode 100644
index 0000000..114164c
--- /dev/null
+++ b/dp.md
@@ -0,0 +1,386 @@
+#### 动态规划
+
+
+
+
+
+### 相关题目
+
+- 64 最小路径和【M】
+- 70 爬楼梯
+- 72 编辑距离【H】
+- 121 买卖股票的最佳时机
+- 122 买卖股票的最佳时机II
+- 123 买卖股票的最佳时机III
+- 188 买卖股票的最佳时机IV
+- 746 使用最少花费爬楼梯
+- 264 丑数【M】
+- 300 最长上升子序列【M】
+
+
+
+#### 64 最小路径和
+
+题目要求:https://leetcode-cn.com/problems/minimum-path-sum/
+
+思路分析:自底向上递推
+
+递推公式:`opt[i, j] += min(opt[i+1][j], opt[i][j+1])`,注意边界情况
+
+```go
+// date 2020/03/08
+// 时间复杂度O(M*N),空间复杂度O(1)
+func minPathSum(grid [][]int) int {
+ m := len(grid)
+ if m == 0 { return 0 }
+ n := len(grid[0])
+ for i := m-1; i >= 0; i-- {
+ for j := n-1; j >= 0; j-- {
+ // 如果存在右节点和下节点,选择其中最小的那个
+ if i + 1 < m && j + 1 < n {
+ if grid[i+1][j] < grid[i][j+1] {
+ grid[i][j] += grid[i+1][j]
+ } else {
+ grid[i][j] += grid[i][j+1]
+ }
+ // 如果只有右节点,则选择右节点
+ } else if j + 1 < n {
+ grid[i][j] += grid[i][j+1]
+ // 如果只有下节点,则选择下节点
+ } else if i + 1 < m {
+ grid[i][j] += grid[i+1][j]
+ }
+ }
+ }
+ return grid[0][0]
+}
+```
+
+
+
+#### 70 爬楼梯
+
+题目要求:https://leetcode-cn.com/problems/climbing-stairs/
+
+思路分析:这个问题和斐波那契数列很像,可以有三种解法,一个比一个更优。
+
+递推公式等于c[n] = c[n-1] + c[n-2],基本情况n=1, c[n]=1;n=2,c[n]=2
+
+算法一:直接递推
+
+```go
+// date 2020/03/08
+// 算法一:自顶向下直接递推,超时。
+// 时间复杂度O(2^N),空间复杂度O(1)
+func climbStairs(n int) int {
+ if n < 3 { return n}
+ return climbStairs(n-1) + climbStairs(n-2)
+}
+// 算法二:自底向上递推,并且记录中间结果。
+// 时间复杂度O(N),空间复杂度O(N)
+func climbStairs(n int) int {
+ if n < 3 { return n }
+ opt := make([]int, n+1)
+ opt[1], opt[2] = 1, 2
+ for i := 3; i <= n; i++ {
+ opt[i] = opt[i-1] + opt[i-2]
+ }
+ return opt[n]
+}
+// 算法三:自底向上的递推,只保留有用的结果
+// 时间复杂度O(N),空间复杂度O(1)
+func climbStairs(n int) int {
+ if n < 3 { return n }
+ first, second := 1, 2
+ res := 0
+ for i := 3; i <= n; i++ {
+ res = first + second
+ first = second
+ second = res
+ }
+ return res
+}
+```
+
+#### 72 编辑距离
+
+题目要求:https://leetcode-cn.com/problems/edit-distance/
+
+思路分析:
+
+```go
+// date 2020/03/16
+func minDistance(word1 string, word2 string) int {
+ m, n := len(word1), len(word2)
+ dp := make([][]int, m+1)
+ for i := 0; i <= m; i++ {
+ // base case
+ dp[i] = make([]int, n+1)
+ dp[i][0] = i
+ }
+ // base case
+ for j := 0; j <= n; j++ {
+ dp[0][j] = j
+ }
+ for i := 1; i <= m; i++ {
+ for j := 1; j <= n; j++ {
+ if word1[i-1] == word2[j-1] {
+ dp[i][j] = dp[i-1][j-1]
+ } else {
+ dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1
+ }
+ }
+ }
+ return dp[m][n]
+}
+func min(x, y int) int {
+ if x < y { return x }
+ return y
+}
+
+// 动态规划
+// dp[i][j] 将word1[0...i]变成word2[0...j]所需要的最小步数
+// if word1[i] == word2[j]; dp[i][j] = dp[i-1][j-1]
+// else dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
+// dp[i-1][j] insert word1
+// dp[i][j-1] delete word1
+// dp[i-1][j-1] replace
+```
+
+
+
+#### 121 买卖股票的最佳时机
+
+题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
+
+思路分析:只能交易一次。
+
+遍历一遍,记录之前的最小值。如果当前值大于当前最小值,则计算利润;如果当前值小于当前最小值,则更新当前最小值,具体算法如下
+
+```go
+// date 2020/03/14
+// 时间复杂度O(N),空间复杂度O(1)
+func maxProfit(prices []int) int {
+ if 0 == len(prices) { return 0 }
+ res, cur_min := 0, prices[0]
+ for _, v := range prices {
+ if v > cur_min && res < v - cur_min { res = v - cur_min }
+ if v < cur_min { cur_min = v }
+ }
+ return res
+}
+```
+
+#### 122 买卖股票的最佳时机II
+
+题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
+
+思路分析:可以买卖无数次
+
+遍历一遍,只要后面的值大于前面的值,即算作利润。
+
+```go
+// date 2020/03/14
+// 时间复杂度O(N),空间复杂度O(1)
+func maxProfit(prices []int) int {
+ profit := 0
+ for i := 0; i < len(prices)-1; i++ {
+ if prices[i] < prices[i+1] {
+ profit =+ prices[i+1] - prices[i]
+ }
+ }
+ return profit
+}
+```
+
+#### 123 买卖股票的最佳时机III
+
+题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/
+
+思路分析:最多可以交易两笔
+
+遍历一遍,分别从数组[0...i]和[i+1...N]中获取最大利润
+
+```go
+// date 2020/03/14
+// 时间复杂度O(N^2),空间复杂度O(1)
+func maxProfix(prices []int) int {
+ res, v1, v2 := 0, 0, 0
+ for i := 0; i < len(prices); i++ {
+ v1 = maxProfitOnce(prices[:i])
+ v2 = maxProfitOnce(prices[i+1:])
+ if v1 + v2 > res { res = v1 + v2 }
+ }
+ return res
+}
+
+func maxProfitOnce(prices []int) int {
+ if 0 == len(prices) { return 0 }
+ res, cur_min := 0, prices[0]
+ for _, v := range prices {
+ if v > cur_min && res < v - cur_min { res = v - cur_min }
+ if v < cur_min { cur_min = v }
+ }
+ return res
+}
+```
+
+#### 188 买卖股票的最佳时机IV
+
+题目要求:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/
+
+思路分析:
+
+#### 746 使用最小花费爬楼梯
+
+题目要求:
+
+考察知识:动态规划
+
+算法分析
+
+```go
+// date 2020/03/08
+// 算法一:自顶向下递推
+func minCostClimbingStairs(cost []int) int {
+ n := len(cost)
+ if n == 0 { return 0 }
+ if n == 1 { return cost[0] }
+ if n == 2 { return min(cost[0], cost[1]) }
+ return min(minCostClimbingStairs(cost[:n-1]) + cost[n-1], minCostClimbingStairs(cost[:n-2]) + cost[n-2])
+}
+func min(x, y int) int {
+ if x < y { return x }
+ return y
+}
+// 算法二:自底向上递推
+func minCostClimbingStairs(cost []int) int {
+ n := len(cost)
+ if n == 0 { return 0 }
+ if n == 1 { return cost[0] }
+ if n == 2 { return min(cost[0], cost[1]) }
+ opt := make([]int, n)
+ opt[0], opt[1] = cost[0], cost[1]
+ for i := 2; i < n; i++ {
+ opt[i] = min(opt[i-2], opt[i-1]) + cost[i]
+ }
+ return min(opt[n-1], opt[n-2])
+}
+// 算法三:算法二的优化版
+func minCostClimbingStairs(cost []int) int {
+ n := len(cost)
+ if n == 0 { return 0 }
+ if n == 1 { return cost[0] }
+ first, second := cost[0], cost[1]
+ res := min(first, second)
+ for i := 2; i < n; i++ {
+ res = min(first, second) + cost[i]
+ first = second
+ second = res
+ }
+ return min(first, second)
+}
+```
+
+
+
+
+
+#### 264 丑树
+
+
+
+题目要求:https://leetcode-cn.com/problems/ugly-number-ii/
+
+算法分析:
+
+```go
+// date 2020/03/01
+// 动态规划
+func nthUglyNumber(n int) int {
+ if n < 1 { return 1 }
+ dp := make([]int, n)
+ dp[0] = 1
+ p1, p2, p3 := 0, 0, 0
+ for i := 1; i < n; i++ {
+ dp[i] = min(2 * dp[p1], min(3 * dp[p2], 5 * dp[p3]))
+ if dp[i] == 2 * dp[p1] { p1++ }
+ if dp[i] == 3 * dp[p2] { p2++ }
+ if dp[i] == 5 * dp[p3] { p3++ }
+ }
+ return dp[n-1]
+}
+
+func min(x, y int) int {
+ if x < y { return x }
+ return y
+}
+```
+
+#### 300 最长上升子序列
+
+题目要求:https://leetcode-cn.com/problems/longest-increasing-subsequence/
+
+思路分析:
+
+```
+定义dp方程,dp[i]表示包含nums[i]元素的最长上升子序列
+dp[i] = maxvalue + 1
+maxvalue = 0 <= j < i && nums[i] > nums[j]; max(maxvalue, dp[j])
+具体算法如下:
+```
+
+```go
+// date 2020/03/14
+// 时间复杂度O(N^2),空间复杂度O(N)
+func lengthOfLIS(nums []int) int {
+ if len(nums) == 0 { return 0 }
+ n, res, maxvalue := len(nums), 1, 1
+ dp := make([]int, n)
+ dp[0] = 1
+ for i := 1; i < n; i++ {
+ // 找到nums[i]所满足的最长上升子序列
+ maxvalue = 0 // 初值为0
+ for j := 0; j < i; j++ {
+ if nums[i] > nums[j] { maxvalue = max(maxvalue, dp[j]) }
+ }
+ // 更新dp[i]
+ dp[i] = maxvalue + 1
+ res = max(res, dp[i])
+ }
+ return res
+}
+
+func max(x, y int) int {
+ if x > y { return x }
+ return y
+}
+```
+
+思路分析:维护一个最长上升子序列数组lis,然后每次更新它,最后数组lis的长度就是结果。
+
+更新有序数组可以用二分查找,时间复杂度为O(logN)。
+
+```go
+// date 2020/03/16
+func lengthOfLIS(nums []int) int {
+ if len(nums) == 0 { return 0}
+ lis := make([]int, 0)
+ lis = append(lis, nums[0])
+ for i := 1; i < len(nums); i++ {
+ // 在lis数组找到第一个比nums[i]大的元素,并替换它,否则进行追加
+ if nums[i] > lis[len(lis)-1] {
+ lis = append(lis, nums[i])
+ continue
+ }
+ for j := 0; j < len(lis); j++ {
+ if nums[i] <= lis[j] {
+ lis[j] = nums[i]
+ break
+ }
+ }
+ }
+ return len(lis)
+}
+```
+
diff --git "a/golangset/13_\344\270\255\347\255\211_\344\270\211\346\225\260\344\271\213\345\222\214.md" "b/golangset/13_\344\270\255\347\255\211_\344\270\211\346\225\260\344\271\213\345\222\214.md"
deleted file mode 100644
index 0dbe66f..0000000
--- "a/golangset/13_\344\270\255\347\255\211_\344\270\211\346\225\260\344\271\213\345\222\214.md"
+++ /dev/null
@@ -1,52 +0,0 @@
-13 三数之和
-
-https://leetcode.cn/problems/3sum/
-
-
-
-算法:时间复杂度O(n2)
-
-1-先对数组进行升序排序,然后逐一遍历,固定当前元素nums[i],使用左右指针遍历当前元素后面的所有元素,nums[l]和nums[r],如果三数之和=0,则添加进结果集
-
-2-当nums[i] > 0 结束循环 // 升序排序,三数之和必然大于零
-
-3-当nums[i] == nums[i-1] 表明用重复元素,跳过
-
-4-sum = 0时, 如果nums[l] == nums[l+1] 重复元素,跳过
-
-5-sum = 0时, nums[r] == nums[r-1] 重复元素,跳过
-
-```go
-// date 2020/03/29
-func threeSum(nums []int) [][]int {
- sort.Slice(nums, func(i, j int) bool {
- return nums[i] < nums[j]
- })
- res, n, sum := make([][]int, 0), len(nums), -1
- left, right := 0, n-1
- for i := 0; i < n; i++ {
- // 升序排列,大于零则退出
- if nums[i] > 0 { break }
- // 去重
- if i > 0 && nums[i] == nums[i-1] { continue }
- left, right = i+1, n-1
- for left < right {
- sum = nums[i] + nums[left] + nums[right]
- if sum < 0 {
- left++
- } else if sum > 0 {
- right--
- } else if sum == 0 {
- res = append(res, []int{nums[i], nums[left], nums[right]})
- // 去重
- for left < right && nums[left] == nums[left+1] { left++ }
- for left < right && nums[right] == nums[right-1] { right-- }
- left++
- right--
- }
- }
- }
- return res
-}
-```
-
diff --git "a/golangset/1456_\344\270\255\347\255\211_\345\256\232\351\225\277\345\255\220\344\270\262\344\270\255\345\205\203\351\237\263\347\232\204\346\234\200\345\244\247\346\225\260\347\233\256.md" "b/golangset/1456_\344\270\255\347\255\211_\345\256\232\351\225\277\345\255\220\344\270\262\344\270\255\345\205\203\351\237\263\347\232\204\346\234\200\345\244\247\346\225\260\347\233\256.md"
deleted file mode 100644
index fe00db9..0000000
--- "a/golangset/1456_\344\270\255\347\255\211_\345\256\232\351\225\277\345\255\220\344\270\262\344\270\255\345\205\203\351\237\263\347\232\204\346\234\200\345\244\247\346\225\260\347\233\256.md"
+++ /dev/null
@@ -1,51 +0,0 @@
-## 1456 定长子串中元音的最大数目
-
-题目要求:给定字符串`s`和整数`k`,返回字符串`s`中长度为`k`的单个子字符串中可能包含的最大元音字母数。
-
-题目链接:https://leetcode.cn/problems/maximum-number-of-vowels-in-a-substring-of-given-length/
-
-
-
-算法分析:滑动窗口的思想
-
-1. 构造窗口;初始化中间变量 `sum` ,统计窗口中元音的个数
-2. 不断地增加 `right` ,如果是元音,`sum++`
-3. 当窗口超过指定大小k时,不断地增加 `left` ,如果移除的 `left` 是元音,`sum--`
-
-```go
-// date 2022/09/29
-func maxVowels(s string, k int) int {
- left, right := 0, 0
- sum, ans := 0, 0
- // 构造窗口
- for right < len(s) {
- // 不断地增加right
- if isY(s[right]) {
- sum += 1
- }
- right++
- // 当窗口超过k大小时,增加left
- for right - left > k {
- if isY(s[left]) {
- sum -= 1
- }
- left++
- }
- if sum > ans {
- ans = sum
- }
- }
- return ans
-}
-
-func isY(a uint8) bool {
- s := []uint8{'a', 'e', 'i', 'o', 'u'}
- for _, v := range s {
- if a == v {
- return true
- }
- }
- return false
-}
-```
-
diff --git "a/golangset/219_\347\256\200\345\215\225_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md" "b/golangset/219_\347\256\200\345\215\225_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md"
deleted file mode 100644
index a44b77b..0000000
--- "a/golangset/219_\347\256\200\345\215\225_\345\255\230\345\234\250\351\207\215\345\244\215\345\205\203\347\264\2402.md"
+++ /dev/null
@@ -1,81 +0,0 @@
-219 存在重复元素II 简单
-
-https://leetcode.cn/problems/contains-duplicate-ii/
-
-算法1:利用map保存索引
-
-```go
-// data 2020/01/01
-// map
-func containsNearbyDuplicate(nums []int, k int) bool {
- m := make(map[int]int)
- for index, v := range nums {
- if j, ok := m[v]; ok && index - j <= k {
- return true
- }
- m[v] = index
- }
- return false
-}
-// date 2022/09/07
-// 优化版本:只保留需要个数的索引
-func containsNearbyDuplicate(nums []int, k int) bool {
- set := make(map[int]int, k)
- for idx, v := range nums {
- if o, ok := set[v]; ok && idx - o <= k {
- return true
- }
- set[v] = idx
- if idx >= k {
- delete(set, nums[idx-k])
- }
- }
- return false
-}
-```
-
-算法2:双指针
-
-```go
-// data 2020/02/02
-// two points
-func containNearbyDuplicate(nums []int, k int) bool {
- i, j, n := 0, 0, len(nums)
- for i < n {
- j = i + 1
- for j - i <= k && j < n{
- if nums[i] == nums[j] {return true}
- j++
- }
- i++
- }
- return false
-}
-```
-
-算法3:滑动窗口
-
-```go
-func containsNearbyDuplicate(nums []int, k int) bool {
- queue := make([]int, 0, k)
- for _, v := range nums {
- if checkQueue(queue, v) {
- return true
- }
- queue = append(queue, v)
- if len(queue) > k {
- queue = queue[1:]
- }
- }
- return false
-}
-
-func checkQueue(nums []int, n int) bool {
- for _, v := range nums {
- if v == n {
- return true
- }
- }
- return false
-}
-```
\ No newline at end of file
diff --git "a/golangset/239_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md" "b/golangset/239_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md"
deleted file mode 100644
index 744f584..0000000
--- "a/golangset/239_\345\233\260\351\232\276_\346\273\221\345\212\250\347\252\227\345\217\243\346\234\200\345\244\247\345\200\274.md"
+++ /dev/null
@@ -1,93 +0,0 @@
-239 滑动窗口最大值
-
-https://leetcode.cn/problems/sliding-window-maximum/
-
-算法1:单调递减队列
-
-```go
-// date 2022-09-08
-func maxSlidingWindow(nums []int, k int) []int {
- size := len(nums)
- que := NewDeque()
- res := make([]int, 0, 1024)
- for i := 0; i < k; i++ {
- que.Push(nums[i])
- }
- res = append(res, que.Max())
- for i := k; i < size; i++ {
- que.Pop(nums[i-k])
- que.Push(nums[i])
- res = append(res, que.Max())
- }
- return res
-}
-
-type Deque struct {
- queue []int
-}
-
-func NewDeque() *Deque {
- return &Deque{
- queue: make([]int, 0, 1024),
- }
-}
-
-func (s *Deque) Push(x int) {
- for len(s.queue) != 0 && x > s.queue[len(s.queue)-1] {
- s.queue = s.queue[:len(s.queue)-1]
- }
- s.queue = append(s.queue, x)
-}
-
-func (s *Deque) Max() int {
- return s.queue[0]
-}
-
-func (s *Deque) Pop(x int) {
- if len(s.queue) != 0 && x == s.queue[0] {
- s.queue = s.queue[1:]
- }
-}
-
-```
-
-
-
-算法2:滑动窗口
-
-其实这种解法跟上面的单调递减队列是一个原理,只不过借滑动窗口的思想,由 `list` 充当单调递减队列。
-
-1. 初始化`left = right = 0`,闭区间`[left, right]` 表示一个固定窗口,即k个大小
-2. 初始化`list`充当单调递减队列,当队列不为空且 `nums[right]` 大于队列尾部元素时,不断地移除队尾元素
-3. 增加right,扩大窗口
-4. 当窗口构造完成后,取队头元素加入结果集;增加left
-
-```go
-// date 2022/09/29
-func maxSlidingWindow(nums []int, k int) []int {
- left, right := 0, 0
- ans := make([]int, 0, 64)
- list := make([]int, 0, 64)
- // 开始构造窗口
- for right < len(nums) {
- // 特殊处理:因为需要保证list为单调递减队列,需要判断窗口最右边的元素
- for len(list) != 0 && nums[right] > list[len(list)-1] {
- list = list[:len(list)-1]
- }
- // 不断地增加right
- list = append(list, nums[right])
- right++
- // 窗口构造完成,当不满足条件时,需要增加left
- if right >= k {
- ans = append(ans, list[0])
- // 特殊处理:增加left意味着移除窗口最左边的元素,如果等于队头元素,需要从单调递减队列中移除
- if list[0] == nums[left] {
- list = list[1:]
- }
- left++
- }
- }
- return ans
-}
-```
-
diff --git "a/golangset/2_\344\270\255\347\255\211_\344\270\244\346\225\260\347\233\270\345\212\240.md" "b/golangset/2_\344\270\255\347\255\211_\344\270\244\346\225\260\347\233\270\345\212\240.md"
deleted file mode 100644
index 9eda4bf..0000000
--- "a/golangset/2_\344\270\255\347\255\211_\344\270\244\346\225\260\347\233\270\345\212\240.md"
+++ /dev/null
@@ -1,51 +0,0 @@
-2 两数相加
-
-https://leetcode.cn/problems/add-two-numbers/submissions/
-
-
-
-算法1:利用伪头节点,开辟空间直接计算。
-
-```go
-// date 2022-09-09
-/**
- * Definition for singly-linked list.
- * type ListNode struct {
- * Val int
- * Next *ListNode
- * }
- */
-func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
- if l1 == nil {
- return l2
- }
- if l2 == nil {
- return l1
- }
- dummy := &ListNode{Val: -1}
- pre := dummy
- temp, carry := 0, 0
- n1, n2 := 0, 0
- for l1 != nil || l2 != nil || carry != 0 {
- n1, n2 = 0, 0
- if l1 != nil {
- n1 = l1.Val
- l1 = l1.Next
- }
- if l2 != nil {
- n2 = l2.Val
- l2 = l2.Next
- }
- temp = n1 + n2 + carry
- carry = temp / 10
- pre.Next = &ListNode{Val: temp%10}
- pre = pre.Next
- }
- return dummy.Next
-}
-```
-
-
-
-算法2:
-
diff --git "a/golangset/34_\344\270\255\347\255\211_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md" "b/golangset/34_\344\270\255\347\255\211_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
deleted file mode 100644
index 9068f32..0000000
--- "a/golangset/34_\344\270\255\347\255\211_\345\234\250\346\216\222\345\272\217\346\225\260\347\273\204\344\270\255\346\237\245\346\211\276\345\205\203\347\264\240\347\232\204\347\254\254\344\270\200\344\270\252\345\222\214\346\234\200\345\220\216\344\270\200\344\270\252\344\275\215\347\275\256.md"
+++ /dev/null
@@ -1,33 +0,0 @@
-34 在排序数组中查找元素的第一个和最后一个位置
-
-https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/
-
-题目要求:给你一个按照非递减顺序排列的整数数组 `nums`,和一个目标值 `target`。请你找出给定目标值在数组中的开始位置和结束位置。
-
-算法:
-
-1- 先寻找左边界,再查找右边界,需要注意左右指针需要小于等于,因为可能数组中只存在一个元素与目标值相等
-
-```go
-// date 2022-09-15
-func searchRange(nums []int, target int) []int {
- res := []int{-1, -1}
- left, right := 0, len(nums)-1
- for left <= right {
- if nums[left] == target {
- res[0] = left
- break
- }
- left++
- }
- for left <= right {
- if nums[right] == target {
- res[1] = right
- break
- }
- right--
- }
- return res
-}
-```
-
diff --git "a/golangset/4_\345\233\260\351\232\276_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\347\232\204\344\270\255\344\275\215\346\225\260.md" "b/golangset/4_\345\233\260\351\232\276_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\347\232\204\344\270\255\344\275\215\346\225\260.md"
deleted file mode 100644
index 77ad677..0000000
--- "a/golangset/4_\345\233\260\351\232\276_\345\257\273\346\211\276\344\270\244\344\270\252\346\255\243\345\272\217\346\225\260\347\273\204\347\232\204\344\270\255\344\275\215\346\225\260.md"
+++ /dev/null
@@ -1,85 +0,0 @@
-4:寻找两个正序数组的中位数
-
-https://leetcode.cn/problems/median-of-two-sorted-arrays/
-
-
-
-算法:
-
-```go
-// date 2022-09-09
-func findMedianSortedArrays(nums1, nums2 []int) float64 {
- s1, s2 := len(nums1), len(nums2)
- total := s1+s2
- if total == 0 {
- return 0
- }
- targetIdx := total/2
- onlyOne := total % 2 == 1
- // 如果nums1为空,在nums2中查找中位数
- if s1 == 0 {
- if onlyOne {
- return float64(nums2[targetIdx])
- } else {
- return (float64(nums2[targetIdx-1]) + float64(nums2[targetIdx]))/2
- }
- }
- // 如果nums2为空,在nums1中查找中位数
- if s2 == 0 {
- if onlyOne {
- return float64(nums1[targetIdx])
- } else {
- return (float64(nums1[targetIdx-1]) + float64(nums1[targetIdx]))/2
- }
- }
-
- pre, cur := 0, 0 // 记录合成数组的两个值
- i, j, nIdx := 0, 0, 0
- // 开始遍历并记录pre,cur
- // nidx为合成数组的索引
- for i < s1 && j < s2 {
- if nums1[i] < nums2[j] {
- pre, cur = cur, nums1[i]
- i++
- } else {
- pre, cur = cur, nums2[j]
- j++
- }
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
- for i < s1 {
- pre, cur = cur, nums1[i]
- i++
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
- for j < s2 {
- pre, cur = cur, nums2[j]
- j++
- if nIdx == targetIdx {
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
- }
- nIdx++
- }
-
- if onlyOne {
- return float64(cur)
- }
- return (float64(pre)+float64(cur))/2
-}
-```
-
diff --git a/images/078.png b/images/078.png
deleted file mode 100644
index 717a3fe..0000000
Binary files a/images/078.png and /dev/null differ
diff --git a/images/80.png b/images/80.png
deleted file mode 100644
index 2041260..0000000
Binary files a/images/80.png and /dev/null differ
diff --git a/images/image_189.png b/images/image_189.png
deleted file mode 100644
index 90ef5da..0000000
Binary files a/images/image_189.png and /dev/null differ
diff --git a/images/image_heap.png b/images/image_heap.png
deleted file mode 100644
index 4aa1dc6..0000000
Binary files a/images/image_heap.png and /dev/null differ
diff --git a/images/subond.drawio b/images/subond.drawio
deleted file mode 100644
index 5673a8a..0000000
--- a/images/subond.drawio
+++ /dev/null
@@ -1,2505 +0,0 @@
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
diff --git a/linear_list.md b/linear_list.md
deleted file mode 100644
index 813959d..0000000
--- a/linear_list.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 线性表 Linear List
-
-1. [线性表的存储结构](#线性表的存储结构)
- 1.1 [顺序存储](#顺序存储)
- 1.2 [链式存储](#链式存储)
-
-**线性表**:零个或多个数据元素的有限序列
-
-**抽象的数据结构**
-
-```
-定义
- 线性表
-数据
- 线性表的数据对象集合为{a1, a2, ..., an},每个数据元素类型均为DataType
- 其中,除第一个元素a1外,每个元素都有且只有一个直接前驱元素
- 除最后一个元素an外,每个元素都有且只有一个直接后驱元素
- 数据元素之间的关系是一对一的关系
-操作
- 初始化
- 增,删,改,除
- 空判断
- 获取元素
- 清空元素
-```
-
-### 线性表的存储结构
-
-* 顺序存储
-* 链式存储
-
-### 顺序存储
-
-1. 线性表顺序存储的三个基本属性
-
- * 存储空间的起始位置
- * 线性表的最大存储容量
- * 线性表的当前长度
-
-2. 顺序存储的优点及缺点
- * 优点:
- * 不需要为表示表中元素之间的逻辑关系而增加额外的存储空间
- * 可以快速存取表中的任意一个位置的元素
- * 缺点:
- * 插入和删除操作,需要移动大量的元素
- * 当线性表长度变化较大时,难以确定存储空间的容量
- * 造成存储空间的“碎片化”
-
-数组就是最常见的顺序存储的线性表。
-
-### 链式存储
-
-1. 线性表链式存储的属性
- * 头指针,头节点
- * 指针域,数据域
-
- 头指针与头节点的区别:
- * 头指针
- * 头指针是指向链表第一个节点的指针,若链表有头节点,则是指向头节点的指针
- * 头指针具有标识作用,常用于标识链表的名字
- * 无论链表是否为空,头指针都不为空。**头指针是链表的必要元素**。
- * 头节点
- * 头节点是为了操作的统一和方便设计的,放在第一个元素的节点之前,其数据一般无意义(可以存放链表的长度信息)。
- * 头节点不是链表的必要元素。
-
-2. 链式存储的优点和缺点
- * 优点:
- * 采用链式存储单元存放线性表数据元素
- * 不需要预先分配固定大小的存储空间
- * 缺点:
- * 查找时间复杂度O(n)
- * 找到元素后,插入和删除操作的时间复杂度为O(1)
-
-链式存储的线性表根据指针域的不同,可分为单向链表,循环链表和双向链表等。
-
-### 单向链表
-
-单向链表中每个节点有两个域,一个数据域和一个指针域。数据域用于表示单链表中的数据,指针域用于指向当前节点后驱节点的指针,简称为单链表。
-
-### 循环链表
-
-将单链表中的最后一个节点的指针指向该单链表的头节点,使得整个链表形成一个环。这种首尾相连的单链表称为单循环链表,简称循环链表。
-
-### 双向链表
-
-若在单链表中增加一个指向当前节点前驱节点的指针域,则构成双向链表。双向链表中包含三个域,一个数据域和两个指针域(一个指向后驱节点,一个指向前驱节点)。
diff --git a/notebook/169.md b/notebook/169.md
new file mode 100644
index 0000000..9fa80e1
--- /dev/null
+++ b/notebook/169.md
@@ -0,0 +1,49 @@
+#### 169 多数元素【Easy】
+
+题目要求:https://leetcode-cn.com/problems/majority-element/
+
+思路分析:
+
+```go
+// date 2020/03/18
+// 算法1,两层循环
+// 时间复杂度O(N^2),空间复杂度O(1)
+func majorityElement(nums []int) int {
+ n, c := len(nums), 1
+ for i := 0; i < n; i++ {
+ c = 1
+ for j := i+1; j < n; j++ {
+ if nums[i] == nums[j] {
+ c++
+ }
+ }
+ if n & 0x1 == 0 && c >= n >> 1 { return nums[i] }
+ if n & 0x1 == 1 && c >= n >> 1 + 1 { return nums[i] }
+ }
+ return 0
+}
+// 算法2:利用map,空间换时间
+// 时间复杂度O(N), 空间复杂度O(N); 题目中说明答案一定存在,所以空间复杂度可以是O(N/2)
+func majorityElement(nums []int) int {
+ set := make(map[int]int, len(nums) >> 1)
+ for _, v := range nums {
+ if _, ok := set[v]; ok {
+ set[v]++
+ } else {
+ set[v] = 1
+ }
+ if len(nums) & 0x1 == 1 && set[v] > len(nums) >> 1 { return v }
+ if len(nums) & 0x1 == 0 && set[v] >= len(nums) >> 1 { return v }
+ }
+ return -1
+}
+// 算法3:对数组排序,返回中间元素
+// 时间复杂度O(NlogN)
+func majorityElement(nums []int) int {
+ sort.Slice(nums, func(i, j int) bool {
+ return nums[i] < nums[j]
+ })
+ return nums[len(nums)>>1]
+}
+```
+
diff --git a/practice.md b/practice.md
deleted file mode 100644
index 8136f11..0000000
--- a/practice.md
+++ /dev/null
@@ -1,46 +0,0 @@
-## 题目练习
-
-题目1:
-
-把一张 100 元面值的纸币,换成1,2,5,10,20,50元面值的纸币,共有多少种换法?
-
-如果限制换来的纸币数量不超过 N 张,有多少中换法?
-
-
-
-分析:
-
-求组合数,详见第 518 题。
-
-```go
-func change(coins []int, total int) int {
- //coins := []int{1, 2, 5, 10, 20, 50}
- //total := 100
- dp := make([]int, total+1)
- dp[0] = 1
- for _, coin := range coins {
- for i := 1; i <= total; i++ {
- if i < coin {
- continue
- }
- dp[i] = dp[i] + dp[i-coin]
- }
- }
- return dp[total]
-}
-```
-
-
-
-
-
-
-
-
-题目2:
-
-要求构造一个函数,实现以下功能:
-
-输入一个列表 list,返回一个计数列表 count,count[i] 表示 list 中第 i 个元素右边有多少个数小于list[i]。
-
-要求算法复杂度度尽可能低。
diff --git a/show_total.sh b/show_total.sh
deleted file mode 100755
index 1aee028..0000000
--- a/show_total.sh
+++ /dev/null
@@ -1,2 +0,0 @@
-#!/bin/zsh
-tree . | grep "No" | wc -l
diff --git a/subond2024.drawio b/subond2024.drawio
deleted file mode 100644
index dc9a33f..0000000
--- a/subond2024.drawio
+++ /dev/null
@@ -1,3450 +0,0 @@
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
diff --git a/template/binary_indexed_tree.go b/template/binary_indexed_tree.go
deleted file mode 100644
index f53524e..0000000
--- a/template/binary_indexed_tree.go
+++ /dev/null
@@ -1,86 +0,0 @@
-package template
-
-import "fmt"
-
-type (
- // BinaryIndexedTree define
- BinaryIndexedTree struct {
- capacity int
- data []int // array A
- tree []int // array B
- }
-)
-
-// NewBinaryIndexedTree define
-func NewBinaryIndexedTree(arr []int) *BinaryIndexedTree {
- n := len(arr)
- b := &BinaryIndexedTree{
- capacity: n + 1,
- data: make([]int, n+1),
- tree: make([]int, n+1), // 为了计算方便,初始化为n+1
- }
- for i := 1; i <= n; i++ {
- b.data[i] = arr[i-1]
- b.tree[i] = arr[i-1]
- for j := i - 2; j >= i-lowbit(i); j-- {
- b.tree[i] += arr[j]
- }
- }
- return b
-}
-
-// Query define
-// 求区间和,返回原始数组中[0, index] 的区间和
-// 输入index 为原始数组的下标,需要+1
-func (b *BinaryIndexedTree) Query(i int) int {
- return b.queryWithBIT(i + 1)
-}
-
-// SumRange define
-// 对任意区间求和,返回原始数组 A [start, end]区间和
-func (b *BinaryIndexedTree) SumRange(left, right int) int {
- s1 := b.Query(left - 1)
- s2 := b.Query(right)
- return s2 - s1
-}
-
-// Add define
-// 增量更新,即对原始数组A index下标的值 增加 val
-func (b *BinaryIndexedTree) Add(i, val int) {
- b.addWithBit(i+1, val)
-}
-
-// Set define
-func (b *BinaryIndexedTree) Set(i, val int) {
- // old := b.data[i+1]
- // dt := val - old
- b.Add(i, val-b.data[i+1])
-}
-
-func (b *BinaryIndexedTree) queryWithBIT(index int) int {
- sum := 0
- for index >= 1 {
- sum += b.tree[index]
- index -= lowbit(index)
- }
- return sum
-}
-
-func (b *BinaryIndexedTree) addWithBit(idx int, val int) {
- b.data[idx] += val
- for idx <= b.capacity {
- b.tree[idx] += val
- idx += lowbit(idx)
- }
-}
-
-func (b *BinaryIndexedTree) Show() {
- fmt.Printf("data = %d\n", b.data)
- fmt.Printf("tree = %d\n", b.tree)
-}
-
-// 返回 x 二进制形式中,末尾最后一个1所代表的数值,即 2^k
-// k 为 x 二进制中末尾零的的个数
-func lowbit(x int) int {
- return x & -x
-}
diff --git a/template/binary_indexed_tree_test.go b/template/binary_indexed_tree_test.go
deleted file mode 100644
index b02bcc9..0000000
--- a/template/binary_indexed_tree_test.go
+++ /dev/null
@@ -1,62 +0,0 @@
-package template
-
-import (
- "testing"
-)
-
-func TestNewBinaryIndexedTree(t *testing.T) {
- arr := []int{2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9}
- preSum := getPreSum(arr)
-
- bit := NewBinaryIndexedTree(arr)
- bit.Show()
-
- // define test query func
- testQuery := func(arr []int) {
- n := len(arr)
- sum := 0
- for i := 0; i < n; i++ {
- sum += arr[i]
- res := bit.Query(i)
- if res != sum {
- t.Fatalf("fail, query [0, %d] = %d, expect %d\n", i, res, sum)
- }
- }
- }
-
- // test query
- testQuery(arr)
-
- // test sum range
- left, right := 2, 6
- res := bit.SumRange(left, right)
- expect := preSum[right] - preSum[left-1]
- if res != expect {
- t.Fatalf("SumRange fail, get sum range of [%d, %d] = %d, expect %d\n", left, right, res, expect)
- }
-
- // test add
- arr[3] += 3
- preSum = getPreSum(arr)
-
- bit.Add(3, 3)
- bit.Show()
-
- testQuery(arr)
- res = bit.SumRange(left, right)
- expect = preSum[right] - preSum[left-1]
- if res != expect {
- t.Fatalf("SumRange fail, get sum range of [%d, %d] = %d, expect %d\n", left, right, res, expect)
- }
-}
-
-func getPreSum(arr []int) []int {
- n := len(arr)
- preSum := make([]int, n)
- sum := 0
- for i := 0; i < n; i++ {
- sum += arr[i]
- preSum[i] = sum
- }
- return preSum
-}
diff --git a/template/double_linkedlist.go b/template/double_linkedlist.go
deleted file mode 100644
index e504911..0000000
--- a/template/double_linkedlist.go
+++ /dev/null
@@ -1,89 +0,0 @@
-package template
-
-import (
- "fmt"
- "strings"
-)
-
-type (
- DoubleListNode struct {
- val int
- pre, next *DoubleListNode
- }
- DoubleLinkedList struct {
- size int
- head, tail *DoubleListNode
- }
-)
-
-func NewDoubleLinkedList() *DoubleLinkedList {
- list := &DoubleLinkedList{
- size: 0,
- head: &DoubleListNode{},
- tail: &DoubleListNode{},
- }
- list.head.next = list.tail
- list.tail.pre = list.head
- return list
-}
-
-func (l *DoubleLinkedList) AddFront(node *DoubleListNode) {
- node.pre = l.head
- node.next = l.head.next
- l.head.next.pre = node
- l.head.next = node
- l.size++
-}
-
-func (l *DoubleLinkedList) AddRear(node *DoubleListNode) {
- node.pre = l.tail.pre
- node.next = l.tail
- l.tail.pre.next = node
- l.tail.pre = node
- l.size++
-}
-
-func (l *DoubleLinkedList) RemoteFront() *DoubleListNode {
- if l.size > 0 {
- node := l.head.next
- l.removeNode(node)
- return node
- }
- return nil
-}
-
-func (l *DoubleLinkedList) RemoveRear() *DoubleListNode {
- if l.size > 0 {
- node := l.tail.pre
- l.removeNode(node)
- return node
- }
- return nil
-}
-
-func (l *DoubleLinkedList) removeNode(node *DoubleListNode) {
- node.pre.next = node.next
- node.next.pre = node.pre
- l.size--
-}
-
-func (l *DoubleLinkedList) Len() int {
- return l.size
-}
-
-func (l *DoubleLinkedList) Show() {
- k := l.size
- str := make([]string, 0, k)
- if k > 0 {
- fmt.Printf("total node: %d\n", k)
- }
- pre := l.head.next
- for k > 0 {
- str = append(str, fmt.Sprintf("%d", pre.val))
- pre = pre.next
- k--
- }
- if len(str) != 0 {
- fmt.Printf("list: %s\n", strings.Join(str, "<->"))
- }
-}
diff --git a/template/double_linkedlist_test.go b/template/double_linkedlist_test.go
deleted file mode 100644
index 0d5743f..0000000
--- a/template/double_linkedlist_test.go
+++ /dev/null
@@ -1,33 +0,0 @@
-package template
-
-import "testing"
-
-func TestNewDoubleLinkedList(t *testing.T) {
- list := NewDoubleLinkedList()
- list.Show()
-
- n1 := &DoubleListNode{val: 1}
- n2 := &DoubleListNode{val: 2}
- n3 := &DoubleListNode{val: 3}
- n4 := &DoubleListNode{val: 4}
- n5 := &DoubleListNode{val: 5}
- list.AddRear(n1)
- list.AddRear(n2)
- list.AddRear(n3)
- list.Show()
- list.AddFront(n4)
- list.AddFront(n5)
- list.Show()
- if 5 != list.Len() {
- t.Fatalf("fail")
- }
-
- list.RemoveRear()
- list.Show()
-
- list.RemoteFront()
- list.Show()
- if 3 != list.Len() {
- t.Fatalf("fail")
- }
-}
diff --git a/template/lfu_cache.go b/template/lfu_cache.go
deleted file mode 100644
index 0fdee35..0000000
--- a/template/lfu_cache.go
+++ /dev/null
@@ -1,135 +0,0 @@
-package template
-
-import "fmt"
-
-type (
- // LFUNode define
- LFUNode struct {
- key, val int
- frequency int
- pre, next *LFUNode
- }
- // LFUList define
- LFUList struct {
- size int // the total nodes in lfu list
- head, tail *LFUNode
- }
- // LFUCache define
- LFUCache struct {
- cache map[int]*LFUNode // key is node key
- list map[int]*LFUList // key is frequency
- capacity int
- min int
- }
-)
-
-// NewLFUList new a double linked list
-func NewLFUList() *LFUList {
- list := &LFUList{
- size: 0,
- head: &LFUNode{0, 0, 0, nil, nil},
- tail: &LFUNode{0, 0, 0, nil, nil},
- }
- list.head.next = list.tail
- list.tail.pre = list.head
- return list
-}
-
-// addToHead define
-// node is update or new, so insert to front
-// 新节点肯定是被访问或者新插入的
-func (l *LFUList) addToFront(node *LFUNode) {
- node.pre = l.head
- node.next = l.head.next
-
- l.head.next.pre = node
- l.head.next = node
- l.size++
-}
-
-func (l *LFUList) removeFromRear() *LFUNode {
- node := l.tail.pre
- l.removeNode(node)
- return node
-}
-
-func (l *LFUList) removeNode(node *LFUNode) {
- node.pre.next = node.next
- node.next.pre = node.pre
- l.size--
-}
-
-func (l *LFUList) isEmpty() bool {
- return l.size == 0
-}
-
-func NewLFUCache(cap int) *LFUCache {
- return &LFUCache{
- capacity: cap,
- min: 0,
- cache: make(map[int]*LFUNode),
- list: make(map[int]*LFUList),
- }
-}
-
-func (l *LFUCache) Put(key, value int) {
- if l.capacity == 0 {
- return
- }
- // update node's frequency if exist
- if node, ok := l.cache[key]; ok {
- node.val = value
- // 处理过程与 get 一样,直接复用
- l.Get(key)
- return
- }
-
- // not exist
- // 如果不存在且缓冲满了,需要删除
- if l.capacity == len(l.cache) {
- minList := l.list[l.min]
- rmd := minList.removeFromRear()
- delete(l.cache, rmd.key)
- }
-
- // new node, insert to map
- node := &LFUNode{key: key, val: value, frequency: 1}
- // the min change to 1, once create a new node
- l.min = 1
- if _, ok := l.list[l.min]; !ok {
- l.list[l.min] = NewLFUList()
- }
- oldList := l.list[l.min]
- oldList.addToFront(node)
- // insert node to all cache
- l.cache[key] = node
-}
-
-func (l *LFUCache) Get(key int) int {
- node, ok := l.cache[key]
- if !ok {
- return -1
- }
- // first remote from the old frequency, then move to the new double list
- l.list[node.frequency].removeNode(node)
- node.frequency++
- if _, ok = l.list[node.frequency]; !ok {
- l.list[node.frequency] = NewLFUList()
- }
- oldList := l.list[node.frequency]
- oldList.addToFront(node)
-
- // if l.min is empty update
- if node.frequency-1 == l.min {
- if minList, ok := l.list[l.min]; !ok || minList.isEmpty() {
- l.min = node.frequency
- }
- }
- return node.val
-}
-
-func (l *LFUCache) ShowLFUNode() {
- for k, v := range l.cache {
- fmt.Printf("node key %d, value = %+v\n", k, v)
- }
-}
diff --git a/template/lfu_cache_test.go b/template/lfu_cache_test.go
deleted file mode 100644
index d13e2f5..0000000
--- a/template/lfu_cache_test.go
+++ /dev/null
@@ -1,59 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-func TestLFUCache(t *testing.T) {
- lfu := NewLFUCache(2)
- fmt.Printf("put node 1, 1\n")
- lfu.Put(1, 1) // cnt(1) = 1
- fmt.Printf("put node 2, 2\n")
- lfu.Put(2, 2) // cnt(2) = 1
- lfu.ShowLFUNode()
-
- fmt.Printf("get node 1\n")
- res := lfu.Get(1) // cnt(1) = 2
- if res != 1 {
- t.Fatalf("fail")
- }
- lfu.ShowLFUNode()
-
- // push 3, delete 2
- fmt.Printf("put node 3, 3\n")
- lfu.Put(3, 3) // cnt(3) = 1
- res = lfu.Get(2)
- if res != -1 {
- t.Fatalf("fail")
- }
- lfu.ShowLFUNode()
-
- fmt.Printf("get node 3\n")
- res = lfu.Get(3) // cnt(3) = 2
- if res != 3 {
- t.Fatalf("fail")
- }
- lfu.ShowLFUNode()
-
- // push 4, delete 1
- fmt.Printf("put node 4, 4\n")
- lfu.Put(4, 4) // cnt(4) = 1
- res = lfu.Get(1)
- if res != -1 {
- t.Fatalf("fail")
- }
- lfu.ShowLFUNode()
-
- fmt.Printf("get node 3\n")
- res = lfu.Get(3)
- if res != 3 {
- t.Fatalf("fail")
- }
- fmt.Printf("get node 4\n")
- res = lfu.Get(4)
- if res != 4 {
- t.Fatalf("fail")
- }
- lfu.ShowLFUNode()
-}
diff --git a/template/linkedlist.go b/template/linkedlist.go
deleted file mode 100644
index 10aa9ba..0000000
--- a/template/linkedlist.go
+++ /dev/null
@@ -1,235 +0,0 @@
-package template
-
-import (
- "fmt"
- "strings"
-)
-
-type (
- Node struct {
- val int
- next *Node
- }
- LinkedList struct {
- size int
- head *Node
- }
-)
-
-func NewLinkedList() *LinkedList {
- return &LinkedList{
- size: 0,
- head: &Node{},
- }
-}
-
-func (l *LinkedList) AddFront(node *Node) {
- node.next = l.head.next
- l.head.next = node
- l.size++
-}
-
-func (l *LinkedList) AddRear(node *Node) {
- pre := l.head
- for pre.next != nil {
- pre = pre.next
- }
- pre.next = node
- l.size++
-}
-
-func (l *LinkedList) Size() int {
- return l.size
-}
-
-// Reverse define
-// 翻转链表
-func (l *LinkedList) Reverse() {
- if l.size > 0 {
- var tail *Node
- pre := l.head.next
- for pre != nil {
- after := pre.next
- pre.next = tail
- tail = pre
- pre = after
- }
- l.head.next = tail
- }
-}
-
-// InsertSort define
-// 对链表进行插入排序
-func (l *LinkedList) InsertSort() {
- if l.size < 2 {
- return
- }
- dummy := &Node{}
- first := true
- pre := l.head.next
- for pre != nil {
- after := pre.next
- // insert pre to dummy
- pre.next = nil
- if first {
- first = false
- dummy.next = pre
- } else {
- cur := dummy.next
- curP := dummy
- for cur != nil && cur.val < pre.val {
- curP = cur
- cur = cur.next
- }
- curP.next = pre
- pre.next = cur
- }
-
- pre = after
- }
-
- l.head.next = dummy.next
-}
-
-// MoveTheLastToFront define
-// 把链表中最后一个元素移到表头
-func (l *LinkedList) MoveTheLastToFront() {
- if l.size > 0 {
- prev, cur := l.head.next, l.head.next
- for cur != nil {
- if cur.next == nil {
- cur.next = l.head.next
- prev.next = nil
- l.head.next = cur
- break
- }
- prev = cur
- cur = cur.next
- }
- }
-}
-
-// DeleteEvenNode define
-// 删除偶数位置上的节点
-func (l *LinkedList) DeleteEvenNode() {
- if l.size > 1 {
- cur := l.head.next
- for cur != nil && cur.next != nil {
- cur.next = cur.next.next
- cur = cur.next
- l.size--
- }
- }
-}
-
-// DeleteSmallerRight define
-/*
-保证原有链表节点相对位置不变的情况下,使之变为单调递减链表。
-输入:12->15->10->11->5->6->2->3
-输出:15->11->6->3
-*/
-/*
-思路:先反转链表,然后遍历,如果后一个节点小于当前节点,则删除后一个节点。这与题意一致。
-先反转的目的是更容易确定新的表头
-*/
-func (l *LinkedList) DeleteSmallerRight() {
- if l.size > 1 {
- l.Reverse()
- cur := l.head.next
- for cur != nil && cur.next != nil {
- if cur.val > cur.next.val {
- cur.next = cur.next.next
- l.size--
- continue
- }
- cur = cur.next
- }
- l.Reverse()
- }
-}
-
-// ReverseBetween define
-// 92. 区间反转
-// 单链表一个共有 n 的节点,反转闭区间[left, right]中的节点,其中
-// 1 <= left <= right <= n
-func (l *LinkedList) ReverseBetween(left, right int) {
- // 只有一个节点的时候,不存在反转
- for l.size > 2 {
- // 必须区间只有一个节点,反转之后,原链表不变,直接返回即可
- if left == right {
- return
- }
- // 参数校验
- if left < 1 || left > l.size {
- return
- }
- if right < 1 || right > l.size {
- return
- }
- if left > right {
- return
- }
- // leftpre, left, right, post
- // leftpre.Next = right, if leftpre is nil, right is the new head
- // left.Next = post
- var leftPre *Node
- cur := l.head.next
- for left > 1 {
- leftPre = cur
- cur = cur.next
- left--
- right--
- }
- // now the cur is left node
- leftNode := cur
- tail := leftNode
- for right > 1 {
- after := cur.next
- cur.next = tail
- tail = cur
- cur = after
- right--
- }
- // now cur is the right node
- rightNode := cur
- leftNode.next = rightNode.next
- rightNode.next = tail
- if leftPre != nil {
- leftPre.next = rightNode
- return
- }
- l.head.next = rightNode
- }
-}
-
-func (l *LinkedList) Show() {
- if l.size > 0 {
- str := make([]string, 0, l.size)
- pre := l.head.next
- for pre != nil {
- str = append(str, fmt.Sprintf("%d", pre.val))
- pre = pre.next
- }
-
- fmt.Printf("total node: %d\n", l.size)
- fmt.Printf("linkedlist = %s\n", strings.Join(str, "<-"))
- fmt.Println()
- }
-}
-
-func MoveTheLastToFront(head *Node) *Node {
- if head == nil || head.next == nil {
- return head
- }
- prev, cur := head, head
- for cur != nil {
- if cur.next == nil {
- cur.next = head
- prev.next = nil
- break
- }
- prev = cur
- cur = cur.next
- }
- return cur
-}
diff --git a/template/linkedlist_test.go b/template/linkedlist_test.go
deleted file mode 100644
index 14bc564..0000000
--- a/template/linkedlist_test.go
+++ /dev/null
@@ -1,167 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-func TestNewLinkedList(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
-
- list := NewLinkedList()
- list.AddRear(n1)
- list.AddRear(n2)
- list.AddRear(n3)
- list.AddRear(n4)
- list.AddRear(n5)
- list.Show()
-
- if 5 != list.Size() {
- t.Fatalf("fail")
- }
- list.Reverse()
- list.Show()
-}
-
-func TestLinkedList_InsertSort(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
-
- list := NewLinkedList()
- list.AddRear(n5)
- list.AddRear(n4)
- list.AddRear(n3)
- list.AddRear(n2)
- list.AddRear(n1)
- list.Show()
-
- if 5 != list.Size() {
- t.Fatalf("fail")
- }
- list.InsertSort()
- list.Show()
-}
-
-func TestLinkedList_MoveTheLastToFront(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
-
- list := NewLinkedList()
- list.AddRear(n1)
- list.Show()
- fmt.Printf("move the last to front\n")
- list.MoveTheLastToFront()
- list.Show()
-
- list.AddRear(n2)
- list.Show()
- fmt.Printf("move the last to front\n")
- list.MoveTheLastToFront()
- list.Show()
-
- list.AddRear(n3)
- list.AddRear(n4)
- list.AddRear(n5)
- list.Show()
-
- if 5 != list.Size() {
- t.Fatalf("fail")
- }
- fmt.Printf("move the last to front\n")
- list.MoveTheLastToFront()
- list.Show()
-
- res2 := MoveTheLastToFront(list.head.next)
- pre := res2
- for pre != nil {
- t.Logf("%d\n", pre.val)
- pre = pre.next
- }
-}
-
-func TestLinkedList_DeleteEven(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
-
- list := NewLinkedList()
- list.AddRear(n1)
- list.AddRear(n2)
- list.AddRear(n3)
- list.AddRear(n4)
- list.AddRear(n5)
- list.Show()
-
- if 5 != list.Size() {
- t.Fatalf("fail")
- }
- list.DeleteEvenNode()
- list.Show()
-}
-
-func TestLinkedList_DeleteSmallerRight(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
- n6 := &Node{6, nil}
-
- list := NewLinkedList()
- list.AddRear(n1)
- list.AddRear(n2)
- list.AddRear(n6)
- list.AddRear(n3)
- list.AddRear(n4)
- list.AddRear(n5)
- list.Show()
-
- list.DeleteSmallerRight()
- list.Show()
- if 2 != list.Size() {
- t.Fatalf("fail")
- }
-}
-
-func TestLinkedList_ReverseBetween(t *testing.T) {
- n1 := &Node{1, nil}
- n2 := &Node{2, nil}
- n3 := &Node{3, nil}
- n4 := &Node{4, nil}
- n5 := &Node{5, nil}
-
- list := NewLinkedList()
- list.AddRear(n1)
- list.AddRear(n2)
- list.AddRear(n3)
- list.AddRear(n4)
- list.AddRear(n5)
- list.Show() // 1,2,3,4,5
-
- list.ReverseBetween(1, 5)
- list.Show() // 5,4,3,2,1
-
- list.ReverseBetween(3, 3)
- list.Show() // 5,4,3,2,1
-
- list.ReverseBetween(1, 3)
- list.Show() // 3,4,5,2,1
-
- list.ReverseBetween(4, 5)
- list.Show() // 3,4,5,1,2
-
- list.ReverseBetween(2, 4)
- list.Show() // 3,1,5,4,2
-}
diff --git a/template/lru_cache.go b/template/lru_cache.go
deleted file mode 100644
index 1aae52a..0000000
--- a/template/lru_cache.go
+++ /dev/null
@@ -1,92 +0,0 @@
-package template
-
-type (
- // CacheNode define
- // key, val 存储缓存的键值对
- // pre, next 指向双向链表的前驱和后驱节点
- CacheNode struct {
- key, val int
- pre, next *CacheNode
- }
-
- // LRUCache define
- LRUCache struct {
- size, capacity int
- head, tail *CacheNode
- cache map[int]*CacheNode
- }
-)
-
-// NewLRUCache define
-func NewLRUCache(cap int) *LRUCache {
- ca := &LRUCache{
- size: 0,
- capacity: cap,
- head: &CacheNode{0, 0, nil, nil},
- tail: &CacheNode{0, 0, nil, nil},
- cache: make(map[int]*CacheNode, cap),
- }
- ca.head.next = ca.tail
- ca.tail.pre = ca.head
- return ca
-}
-
-// Get define
-func (l *LRUCache) Get(key int) int {
- node, ok := l.cache[key]
- if !ok {
- return -1
- }
- l.moveToHead(node)
- return node.val
-}
-
-// Put define
-func (l *LRUCache) Put(key, value int) {
- if node, ok := l.cache[key]; ok {
- // update node and move to head
- node.val = value
- l.moveToHead(node)
- return
- }
-
- // add node
- node := &CacheNode{key: key, val: value}
- l.cache[key] = node
- l.addToHead(node)
- l.size++
- if l.size > l.capacity {
- // remote tail
- rmd := l.removeTail()
- delete(l.cache, rmd.key)
- l.size--
- }
-}
-
-// add node to head
-func (l *LRUCache) addToHead(node *CacheNode) {
- node.pre = l.head
- node.next = l.head.next
-
- l.head.next.pre = node
- l.head.next = node
-}
-
-// remove the node from linklist
-func (l *LRUCache) removeNode(node *CacheNode) {
- node.pre.next = node.next
- node.next.pre = node.pre
-}
-
-// move the node to head
-func (l *LRUCache) moveToHead(node *CacheNode) {
- l.removeNode(node)
- l.addToHead(node)
-}
-
-// remove and return the tail node
-func (l *LRUCache) removeTail() *CacheNode {
- node := l.tail.pre
- l.removeNode(node)
- return node
-}
diff --git a/template/segment_tree.go b/template/segment_tree.go
deleted file mode 100644
index faea636..0000000
--- a/template/segment_tree.go
+++ /dev/null
@@ -1,124 +0,0 @@
-package template
-
-import (
- "fmt"
-)
-
-type (
- // SegmentTree define
- SegmentTree struct {
- data []int // 存储原始数据
- tree []int // 存储线段树数据
- }
-)
-
-func NewSegmentTree() *SegmentTree {
- return &SegmentTree{}
-}
-
-func (s *SegmentTree) Init(nums []int) {
- n := len(nums)
- s.data = make([]int, n)
- s.tree = make([]int, 4*n)
- for i := 0; i < n; i++ {
- s.data[i] = nums[i]
- }
- // build segment tree from nums
- left, right := 0, n-1
- s.buildSegmentTree(0, left, right)
-}
-
-func (s *SegmentTree) buildSegmentTree(treeIdx int, left, right int) {
- if left == right {
- // the leaf node
- s.tree[treeIdx] = s.data[left]
- return
- }
- mid := left + (right-left)/2
- leftTreeIdx := leftChild(treeIdx)
- rightTreeIdx := rightChild(treeIdx)
- // build left tree with data [left, mid] elem
- s.buildSegmentTree(leftTreeIdx, left, mid)
- // build right tree with data [mid+1, right] elem
- s.buildSegmentTree(rightTreeIdx, mid+1, right)
- // 注意,递归构建左右子树,别忘了最后求和
- s.tree[treeIdx] = s.tree[leftTreeIdx] + s.tree[rightTreeIdx]
-}
-
-// Query define
-// 查询 [left, right] 区间和
-func (s *SegmentTree) Query(left, right int) int {
- if len(s.data) > 0 {
- return s.queryInTree(0, 0, len(s.data)-1, left, right)
- }
- return 0
-}
-
-// 在以 root 为根的线段树中,[tl, tr] 范围内, 搜索 [left, right] 区间值
-// 如果线段树的区间和查询区间一致,那么直接返回线段树的节点
-// 否则分左子树,右子树,左右子树三个情况,分别查询
-func (s *SegmentTree) queryInTree(root, tl, tr int, left, right int) int {
- // 如果区间一样,直接返回根节点数据
- if left == tl && right == tr {
- return s.tree[root]
- }
- mid := tl + (tr-tl)/2
- leftTree, rightTree := leftChild(root), rightChild(root)
- // query in the right tree
- // 注意,如果查询区间在某个子树里,直接返回查询子树的结构
- // 此时,查询子树,left, right 不能变,因为,区间[tl, tr] 包含 [left, right]
- if left > mid {
- return s.queryInTree(rightTree, mid+1, tr, left, right)
- } else if right <= mid {
- // query in the left tree
- return s.queryInTree(leftTree, tl, mid, left, right)
- }
- // 区间跨两个子树,那么分开查询
- // 此时,left, right 要跟线段树的左右区间边界重合
- lSum := s.queryInTree(leftTree, tl, mid, left, mid)
- rSum := s.queryInTree(rightTree, mid+1, tr, mid+1, right)
- return lSum + rSum
-}
-
-// Update define
-// 数值全量更新,即原始数组中下标为 index 的值更新为 val
-func (s *SegmentTree) Update(index, val int) {
- if len(s.data) > 0 {
- s.updateInTree(0, 0, len(s.data)-1, index, val)
- }
-}
-
-func (s *SegmentTree) updateInTree(root, tl, tr int, index, val int) {
- // find the leaf node, so update its value
- if tl == tr {
- s.tree[root] = val
- s.data[tl] = val
- return
- }
-
- mid := tl + (tr-tl)/2
- leftTree := leftChild(root)
- rightTree := rightChild(root)
- // if value index is at the right part, then update the right tree
- // otherwise update the left tree
- if index > mid {
- s.updateInTree(rightTree, mid+1, tr, index, val)
- } else if index <= mid {
- s.updateInTree(leftTree, tl, mid, index, val)
- }
- // update the parent's value
- s.tree[root] = s.tree[leftTree] + s.tree[rightTree]
-}
-
-func (s *SegmentTree) Show() {
- fmt.Printf("data = %d\n", s.data)
- fmt.Printf("tree = %d\n", s.tree)
-}
-
-func leftChild(treeIdx int) int {
- return treeIdx*2 + 1
-}
-
-func rightChild(treeIdx int) int {
- return treeIdx*2 + 2
-}
diff --git a/template/segment_tree_test.go b/template/segment_tree_test.go
deleted file mode 100644
index 3c4fb60..0000000
--- a/template/segment_tree_test.go
+++ /dev/null
@@ -1,24 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-func TestSegmentTree_Init(t *testing.T) {
- arr := []int{0, 1, 3, 5, -2, 3}
- sg := NewSegmentTree()
- sg.Init(arr)
- sg.Show()
- res := sg.Query(0, 4)
- fmt.Printf("sum [0, 4] = %d\n", res)
-
- res2 := sg.Query(3, 4)
- fmt.Printf("sum [3, 4] = %d\n", res2)
-
- sg.Update(3, 12)
- fmt.Printf("update index 3 to 12\n")
- sg.Show()
- res2 = sg.Query(3, 4)
- fmt.Printf("sum [3, 4] = %d\n", res2)
-}
diff --git a/template/sort.go b/template/sort.go
deleted file mode 100644
index 8cdb357..0000000
--- a/template/sort.go
+++ /dev/null
@@ -1,125 +0,0 @@
-package template
-
-// BubbleSort define
-// 冒泡排序的思路
-// 通过交换不断地把最大值移动到数组的后面
-func BubbleSort(nums []int) []int {
- n := len(nums)
- for i := 0; i < n; i++ {
- for j := 0; j < n-1-i; j++ {
- if nums[j] > nums[j+1] {
- // swap
- nums[j], nums[j+1] = nums[j+1], nums[j]
- }
- }
- }
- return nums
-}
-
-// SelectSort define
-// 选择排序的思路是
-// 从未排序的列表中选择最值,交换到数组的前面
-func SelectSort(nums []int) []int {
- n := len(nums)
- for i := 0; i < n; i++ {
- minIdx := i
- for j := i + 1; j < n; j++ {
- if nums[j] < nums[minIdx] {
- minIdx = j
- }
- }
- // swap the smallest to idx
- nums[i], nums[minIdx] = nums[minIdx], nums[i]
- }
-
- return nums
-}
-
-// InsertSort define
-// 插入排序的思路是
-// 依次选择未排序的元素,插入到已排序(前面)的序列中
-func InsertSort(nums []int) []int {
- n := len(nums)
- for i := 1; i < n; i++ {
- v := nums[i] // the unsort elem
-
- // find the last equal or smaller than v
- // from end to start
- j := i - 1
- for j >= 0 && nums[j] > v {
- nums[j+1] = nums[j]
- j--
- }
- nums[j+1] = v
- }
- return nums
-}
-
-// QuickSort define
-func QuickSort(nums []int) []int {
- left, right := 0, len(nums)-1
- quickSortArr(nums, left, right)
- return nums
-}
-
-// 选择 left 作为基准base,把数组分成小于等于和大于base的两部分
-// 并返回两部分的分界线下标
-func quickDivision(nums []int, left, right int) int {
- base := nums[left]
- for left < right {
- for left < right && nums[right] > base {
- right--
- }
- nums[left] = nums[right]
- for left < right && nums[left] <= base {
- left++
- }
- nums[right] = nums[left]
- nums[left] = base
- }
- return left
-}
-
-func quickSortArr(nums []int, left, right int) {
- if left >= right {
- return
- }
- p := quickDivision(nums, left, right)
- quickSortArr(nums, left, p-1)
- quickSortArr(nums, p+1, right)
-}
-
-// MergeSort define
-func MergeSort(nums []int) []int {
- n := len(nums)
- if n < 2 {
- return nums
- }
- mid := n / 2
- left := nums[0:mid]
- right := nums[mid:n]
- return mergeArr(MergeSort(left), MergeSort(right))
-}
-
-// merge the sorted arrays
-func mergeArr(nums1, nums2 []int) []int {
- n1, n2 := len(nums1), len(nums2)
- ans := make([]int, 0, n1+n2)
- i, j := 0, 0
- for i < n1 && j < n2 {
- if nums1[i] <= nums2[j] {
- ans = append(ans, nums1[i])
- i++
- } else {
- ans = append(ans, nums2[j])
- j++
- }
- }
- if i < n1 {
- ans = append(ans, nums1[i:]...)
- }
- if j < n2 {
- ans = append(ans, nums2[j:]...)
- }
- return ans
-}
diff --git a/template/sort_test.go b/template/sort_test.go
deleted file mode 100644
index a47aa83..0000000
--- a/template/sort_test.go
+++ /dev/null
@@ -1,82 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-var (
- unSortArr = []int{5, 4, 3, 3, 2, 2, 1}
-)
-
-func TestBubbleSort(t *testing.T) {
- // deep copy from un sort array
- n := len(unSortArr)
- one := make([]int, n)
- copy(one, unSortArr)
-
- fmt.Printf("unSortArr = %d\n", one)
- res := BubbleSort(one)
- checkSortArr(t, res)
- fmt.Printf("sort res = %d\n", res)
-}
-
-func TestSelectSort(t *testing.T) {
- // deep copy from un sort array
- n := len(unSortArr)
- one := make([]int, n)
- copy(one, unSortArr)
-
- fmt.Printf("unSortArr = %d\n", one)
- res := SelectSort(one)
- checkSortArr(t, res)
- fmt.Printf("sort res = %d\n", res)
-}
-
-func TestInsertSort(t *testing.T) {
- // deep copy from un sort array
- n := len(unSortArr)
- one := make([]int, n)
- copy(one, unSortArr)
-
- fmt.Printf("unSortArr = %d\n", one)
- res := InsertSort(one)
- checkSortArr(t, res)
- fmt.Printf("sort res = %d\n", res)
-}
-
-func TestQuickSort(t *testing.T) {
- // deep copy from un sort array
- n := len(unSortArr)
- one := make([]int, n)
- copy(one, unSortArr)
-
- fmt.Printf("unSortArr = %d\n", one)
- res := QuickSort(one)
- checkSortArr(t, res)
- fmt.Printf("sort res = %d\n", res)
-}
-
-func TestMergeSort(t *testing.T) {
- // deep copy from un sort array
- n := len(unSortArr)
- one := make([]int, n)
- copy(one, unSortArr)
-
- fmt.Printf("unSortArr = %d\n", one)
- res := MergeSort(one)
- checkSortArr(t, res)
- fmt.Printf("sort res = %d\n", res)
-}
-
-func checkSortArr(t *testing.T, sortArr []int) {
- expectLen := len(unSortArr)
- if len(sortArr) != expectLen {
- t.Fatalf("expect arr len %d\n", expectLen)
- }
- for i := 1; i < expectLen; i++ {
- if sortArr[i-1] > sortArr[i] {
- t.Fatalf("sort fail res = %d\n", sortArr)
- }
- }
-}
diff --git a/template/trie.go b/template/trie.go
deleted file mode 100644
index eff7ee1..0000000
--- a/template/trie.go
+++ /dev/null
@@ -1,111 +0,0 @@
-package template
-
-const ALPHABET_SIZE = 26
-
-// TrieNode define
-type TrieNode struct {
- child [ALPHABET_SIZE]*TrieNode
- // isEndOfWord is true if the node represents
- // end of a word
- isEndOfWord bool
-}
-
-// NewTrieNode define
-func NewTrieNode() *TrieNode {
- node := &TrieNode{
- child: [26]*TrieNode{},
- isEndOfWord: false,
- }
- return node
-}
-
-// InsertKey define
-// If not present, inserts key into trie
-// If the key is prefix of trie node, just
-// marks leaf node
-func (t *TrieNode) InsertKey(key string) {
- n := len(key)
- if n <= 0 {
- return
- }
- cur := t
- for i := 0; i < n; i++ {
- idx := key[i] - 'a'
- if cur.child[idx] == nil {
- cur.child[idx] = NewTrieNode()
- }
- cur = cur.child[idx]
- }
- cur.isEndOfWord = true
-}
-
-// SearchKey define
-// Returns true if key presents in trie, else
-// false
-func (t *TrieNode) SearchKey(key string) bool {
- n := len(key)
- if n == 0 {
- return false
- }
- cur := t
- for i := 0; i < n; i++ {
- idx := key[i] - 'a'
- if cur.child[idx] == nil {
- return false
- }
- cur = cur.child[idx]
- }
- return cur.isEndOfWord
-}
-
-// DeleteKey define
-func (t *TrieNode) DeleteKey(key string) {
- n := len(key)
- if n == 0 {
- return
- }
- // dfs
- var dfs func(root *TrieNode, key string, depth int) *TrieNode
- dfs = func(root *TrieNode, key string, depth int) *TrieNode {
- // if tree is empty
- if root == nil {
- return root
- }
- // process the last character of key
- if depth == len(key) {
- // unmark
- // this node is no more end of word after delete of given key
- if root.isEndOfWord {
- root.isEndOfWord = false
- }
- // if the given key is not prefix of any other word
- if root.isEmpty() {
- root = nil
- }
- return root
- }
- // if not last character, recur for the child
- idx := key[depth] - 'a'
- // if not find key, just return
- if root.child[idx] == nil {
- return root
- }
- // recur the child
- root.child[idx] = dfs(root.child[idx], key, depth+1)
- // if current node is not the prefix of given key, remote it
- if root.isEmpty() && !root.isEndOfWord {
- root = nil
- }
- return root
- }
- dfs(t, key, 0)
-}
-
-func (t *TrieNode) isEmpty() bool {
- for _, v := range t.child {
- if v != nil {
- return false
- }
- }
- return true
-}
diff --git a/template/trie_kth.go b/template/trie_kth.go
deleted file mode 100644
index ce96c24..0000000
--- a/template/trie_kth.go
+++ /dev/null
@@ -1,72 +0,0 @@
-package template
-
-const MaxBit = 10
-
-type TrieKth struct {
- child [MaxBit]*TrieKth
- cnt int
- isNum bool
-}
-
-func NewTrieKth() *TrieKth {
- return &TrieKth{
- child: [MaxBit]*TrieKth{},
- isNum: false,
- }
-}
-
-func (t *TrieKth) Add(num string) {
- cur := t
- for i := 0; i < len(num); i++ {
- idx := num[i] - '0'
- if cur.child[idx] == nil {
- cur.child[idx] = NewTrieKth()
- }
- cur.child[idx].cnt++
- cur = cur.child[idx]
- }
- cur.isNum = true
-}
-
-func (t *TrieKth) FindTrieKth(k int) int {
- ans := 0
- path := make([]int, 0, 16)
- isFind := false
- var dfsNode func(root *TrieKth, target int)
- dfsNode = func(root *TrieKth, target int) {
- if root == nil {
- return
- }
- if target == 0 {
- // fmt.Printf("path = %d\n", path)
- isFind = true
- for _, v := range path {
- ans = ans*10 + v
- }
- return
- }
- for i := 0; i < MaxBit; i++ {
- if isFind {
- break
- }
- chd := root.child[i]
- if chd != nil {
- // fmt.Printf("child cnt %d, target %d\n", chd.cnt, target)
- if chd.cnt < target {
- target -= chd.cnt
- } else {
- path = append(path, i)
- if chd.isNum {
- target -= 1
- }
- dfsNode(chd, target)
- path = path[:len(path)-1]
- }
- }
- }
- }
-
- target := k
- dfsNode(t, target)
- return ans
-}
diff --git a/template/trie_kth_test.go b/template/trie_kth_test.go
deleted file mode 100644
index 3ccd1d7..0000000
--- a/template/trie_kth_test.go
+++ /dev/null
@@ -1,35 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-func TestTrieKth_FindTrieKth(t *testing.T) {
- n := 13
- k := 2
-
- tie := NewTrieKth()
- for i := 1; i <= n; i++ {
- str := fmt.Sprintf("%d", i)
- tie.Add(str)
- }
- ans := tie.FindTrieKth(k)
- if ans != 10 {
- t.Fatalf("fail")
- }
-}
-
-func TestTrieKth_FindTrieKthBig(t *testing.T) {
- // this test case timeout on leetcode
- n := 7747794
- k := 5857460
-
- tie := NewTrieKth()
- for i := 1; i <= n; i++ {
- str := fmt.Sprintf("%d", i)
- tie.Add(str)
- }
- ans := tie.FindTrieKth(k)
- fmt.Printf("ans = %d\n", ans)
-}
diff --git a/template/trie_test.go b/template/trie_test.go
deleted file mode 100644
index 2676945..0000000
--- a/template/trie_test.go
+++ /dev/null
@@ -1,54 +0,0 @@
-package template
-
-import (
- "fmt"
- "testing"
-)
-
-func TestNewTrieNode(t *testing.T) {
- keys := []string{"the", "this", "these", "answer", "any", "by", "bye", "pl", "plane"}
- tie := NewTrieNode()
- for _, v := range keys {
- tie.InsertKey(v)
- }
- s1 := "there"
- r1 := tie.SearchKey(s1)
- fmt.Printf("search %s in trie, res = %t\n", s1, r1)
- if r1 {
- t.Fatalf("fail")
- }
-
- s1 = "the"
- r1 = tie.SearchKey(s1)
- fmt.Printf("search %s in trie, res = %t\n", s1, r1)
- if !r1 {
- t.Fatalf("fail")
- }
-
- s1 = "any"
- r1 = tie.SearchKey(s1)
- fmt.Printf("search %s in trie, res = %t\n", s1, r1)
- if !r1 {
- t.Fatalf("fail")
- }
-
- s1 = "and"
- r1 = tie.SearchKey(s1)
- fmt.Printf("search %s in trie, res = %t\n", s1, r1)
- if r1 {
- t.Fatalf("fail")
- }
-
- // test delete
- s1 = "plane"
- r1 = tie.SearchKey(s1)
- if !r1 {
- t.Fatalf("fail search %s\n", s1)
- }
- tie.DeleteKey("plane")
- s1 = "pl"
- r1 = tie.SearchKey(s1)
- if !r1 {
- t.Fatalf("fail delete")
- }
-}
diff --git a/template/union_find.go b/template/union_find.go
deleted file mode 100644
index 0c5dcd4..0000000
--- a/template/union_find.go
+++ /dev/null
@@ -1,137 +0,0 @@
-package template
-
-type (
- // UnionFind define
- // 路径压缩 + 秩优化
- UnionFind struct {
- parent []int // 存储每个节点的父结点
- rank []int //
- count int // 存储连通分量
- }
-)
-
-// NewUnionFind define
-func NewUnionFind(n int) *UnionFind {
- u := &UnionFind{
- count: n,
- parent: make([]int, n),
- rank: make([]int, n),
- }
- // 初始化时, 每个节点的根节点都是自身
- for i := 0; i < n; i++ {
- u.parent[i] = i
- }
- return u
-}
-
-// Union define
-// merge x, y to the single set
-func (u *UnionFind) Union(x, y int) {
- xp, yp := u.Find(x), u.Find(y)
- if xp == yp {
- return
- }
- // depth of tree_x < depth of tree_y
- if u.rank[xp] < u.rank[yp] {
- u.parent[xp] = yp
- } else {
- u.parent[yp] = xp
- // 如果深度相同,那么新的根节点秩加1
- if u.rank[xp] == u.rank[yp] {
- u.rank[xp]++
- }
- }
- u.count--
-}
-
-// Find define
-// search the root of x
-func (u *UnionFind) Find(x int) int {
- root := x
- for root != u.parent[root] {
- root = u.parent[root]
- }
- //compress path
- for x != u.parent[x] {
- temp := u.parent[x]
- u.parent[x] = root
- x = temp
- }
- return root
-}
-
-// GetCount define
-// the total counts
-func (u *UnionFind) GetCount() int {
- return u.count
-}
-
-type (
- // UnionFindCount define
- // 计算每个集合中的元素个数,以及最大元素集合个数
- UnionFindCount struct {
- parent []int
- count []int
- maxCount int
- }
-)
-
-// NewUnionFindCount define
-func NewUnionFindCount(n int) *UnionFindCount {
- c := &UnionFindCount{
- parent: make([]int, n),
- count: make([]int, n),
- maxCount: 1,
- }
- // init
- // 每个元素都是一个集合,根节点指向自身
- // 每个根节点的集合元素个数都是1
- for i := 0; i < n; i++ {
- c.parent[i] = i
- c.count[i] = 1
- }
- return c
-}
-
-// Union define
-func (c *UnionFindCount) Union(x, y int) {
- xp, yp := c.Find(x), c.Find(y)
- if xp == yp {
- return
- }
- // always merge to n-1
- root := len(c.parent) - 1
- if xp == root {
- // xp is root
- } else if yp == root {
- xp, yp = yp, xp
- } else if c.count[xp] > c.count[yp] {
- xp, yp = yp, xp
- }
- // merge tree_y to tree_x
- c.parent[yp] = xp
- c.count[xp] += c.count[yp]
- if c.count[xp] > c.maxCount {
- c.maxCount = c.count[xp]
- }
-}
-
-// Find define
-func (c *UnionFindCount) Find(x int) int {
- root := x
- for root != c.parent[root] {
- root = c.parent[root]
- }
- // compress path
- for x != c.parent[x] {
- ox := c.parent[x]
- c.parent[x] = root
- x = ox
- }
- return root
-}
-
-// MaxCount define
-func (c *UnionFindCount) MaxCount() int {
- return c.maxCount
-}