Abstract
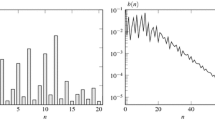
In this work we look at the delay analysis of a customer in a discrete-time queueing system with one permanent server and one occasional extra server. The arrival process is assumed to be general independent, the buffer size infinite and the service times deterministically equal to one slot. The system resides in one of two different states defined by the number of available servers. In the UP-state 2 servers are available and in the DOWN-state 1 server is available. State changes can only occur at slot boundaries. When the extra server becomes available, an UP-period starts (DOWN-period ends) and when the extra server becomes unavailable a DOWN-period starts (UP-period ends). The lengths of these periods, expressed in their number of slots, are assumed to follow a geometric distribution, with different parameter for UP-periods and DOWN-periods. Also, the extension is made to DOWN-periods according to a mixture of M geometric distributions. Using the technique of the dominant singularity, we provide a method to evaluate the tail characteristics of the delay of an arbitrary customer. The method is illustrated with a numerical example.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bruneel, H., Kim, B.G.: Discrete-Time Models for Communication Systems Including ATM. Kluwer Academic Publishers Group, Boston (1993)
Bruneel, H., Steyaert, B., Desmet, E., Petit, G.: Analytic derivation of tail probabilities for queue lengths and waiting times in atm multiserver queues. Eur. J. Oper. Res. 76(3), 563–572 (1994)
Bruneel, H., Wittevrongel, S.: Analysis of a discrete-time single-server queue with an occasional extra server. Perform. Eval. 116, 119–142 (2017)
Krishnamoorthy, A., Pramod, P., Chakravarthy, S.: Queues with interruptions: a survey. TOP 22, 290–320 (2014)
Laevens, K., Bruneel, H.: Delay analysis for discrete-time queueing systems with multiple randomly interrupted servers. Eur. J. Oper. Res. 85, 161–177 (1995)
Núñez-Queija, R.: Sojourn times in a processor sharing queue with service interruptions. Queueing Syst. 34, 351–386 (2000)
Takine, T., Sengupta, B.: A single server queue with service interruptions. Queueing Syst. 26(3–4), 285–300 (1997)
Vinck, B., Bruneel, H.: System delay versus system content for discrete-time queueing systems subject to server interruptions. Eur. J. Oper. Res. 175(1), 362–375 (2006)
Woodside, C., Ho, E.: Engineering calculation of overflow probabilities in buffers with Markov-interrupted service. IEEE Trans. Commun. 35(12), 1272–1277 (1987)
Yajima, M., Phung-Duc, T.: Batch arrival single server queue with variable service speed and setup time. Queueing Syst. 86(3–4), 241–260 (2017)
Yue, D., Qin, Y.: A production inventory system with service time and production vacations. J. Syst. Sci. Syst. Eng. 28, 168–180 (2019)
Zhou, Y., Anderson, R., Vakilzadian, H., Moeller, D., Deutschmann, A.: Developing a dynamic queueing model for the airport check-in process. In: 2018 IEEE International Conference on Electro/Information Technology (EIT), pp. 871–876 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Verdonck, F., Bruneel, H., Wittevrongel, S. (2019). Delay Analysis of a Two-Server Discrete-Time Queue Where One Server Is Only Intermittently Available. In: Phung-Duc, T., Kasahara, S., Wittevrongel, S. (eds) Queueing Theory and Network Applications. QTNA 2019. Lecture Notes in Computer Science(), vol 11688. Springer, Cham. https://doi.org/10.1007/978-3-030-27181-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-27181-7_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-27180-0
Online ISBN: 978-3-030-27181-7
eBook Packages: Computer ScienceComputer Science (R0)