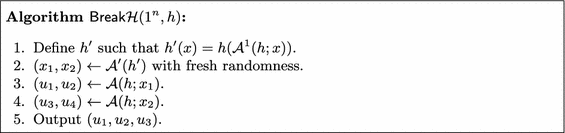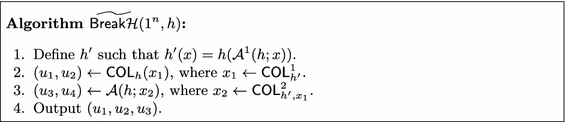On Distributional Collision Resistant Hashing

Abstract

Collision resistant hashing is a fundamental concept that is the basis for many of the important cryptographic primitives and protocols. Collision resistant hashing is a family of compressing functions such that no efficient adversary can find any collision given a random function in the family.

In this work we study a relaxation of collision resistance called distributional collision resistance, introduced by Dubrov and Ishai (STOC ’06). This relaxation of collision resistance only guarantees that no efficient adversary, given a random function in the family, can sample a pair (x, y) where x is uniformly random and y is uniformly random conditioned on colliding with x.

Our first result shows that distributional collision resistance can be based on the existence of multi-collision resistance hash (with no additional assumptions). Multi-collision resistance is another relaxation of collision resistance which guarantees that an efficient adversary cannot find any tuple of $k>2$ inputs that collide relative to a random function in the family. The construction is non-explicit, non-black-box, and yields an infinitely-often secure family. This partially resolves a question of Berman et al. (EUROCRYPT ’18). We further observe that in a black-box model such an implication (from multi-collision resistance to distributional collision resistance) does not exist.

Our second result is a construction of a distributional collision resistant hash from the average-case hardness of SZK. Previously, this assumption was not known to imply any form of collision resistance (other than the ones implied by one-way functions).

I. Komargodski—Supported in part by a Packard Foundation Fellowship and by an AFOSR grant FA9550-15-1-0262.

E. Yogev—Supported in part by a grant from the Israel Science Foundation (no. 950/16).

1 Introduction

Collision resistant hashing (CRH) is one of the most fundamental building blocks in any cryptographic protocol. Collision resistance is associated with a family of compressing functions $\mathcal H = \{h :\{0,1\}^{2n}\rightarrow \{0,1\}^n\}$ and it assures us that while it is easy to compute h(x) for any $h\in \mathcal H$ and $x\in \{0,1\}^{2n}$, for any polynomial time algorithm it is hard to find $x_1\ne x_2$ such that $h(x_1)=h(x_2)$ for a random $h\leftarrow \mathcal H$. Families of functions with the above presumed hardness exist based on a variety of assumptions such as the hardness of factoring integers, finding discrete logs in finite groups, learning with errors (LWE), and more. On the other hand there is no known construction of CRHs based solely on the existence of one-way functions or even one-way permutations and, furthermore, such a construction does not exist in a black-box model [34].

Recently, [22] introduced a relaxation of collision resistance called multi-collision resistance (MCRH). In multi-collision resistance, the family of compressing functions $\mathcal H$ is associated with a parameter $k=k(n)$ and the security requirement is that for any polynomial-time algorithm and a random $h\leftarrow \mathcal H$ it is hard to find distinct $x_1,\ldots ,x_k$ such that $h(x_1) = \ldots = h(x_k)$. In follow-up works [5, 7, 23], multi-collision resistance was studied as an independent primitive and shown to have many applications.

CRH trivially implies MCRH for any $k\ge 2$ and the latter implies one-way functions. Furthermore, in a black-box model, MCRH for any $k>2$ cannot be used to get a CRH, yet MCRH cannot be constructed from one-way permutations [5, 23]. In terms of constructions, [5] gave a construction of an MCRH from the (average-case) min-max entropy approximation assumption first studied in [13]. This is a strengthening of the entropy approximation assumption that is known to be complete for (average-case) non-interactive statistical zero-knowledge (NISZK) [17]. The applications of MCRH in [5, 7, 23] are broad, showing that not only it is a natural relaxation of CRH, but it is also a useful replacement in several key applications such as constant-round statistically-hiding succinct commitments and various zero-knowledge protocols.

In this work we study yet another relaxation of CRH, called distributional collision resistance ($\mathsf {d}\text {CRH}$), introduced by Dubrov and Ishai [12] (see more on their work below). The security notion of this primitive says that it may be possible to find some specific collision, but it is computationally hard to sample a random collision. More precisely, given a random hash function $h\leftarrow \mathcal H$, it is computationally hard to sample a pair $(x_1,x_2)$ such that $x_1$ is uniform and $x_2$ is uniform in the set $h^{-1}(x_1)=\{x :h(x_1) = h(x)\}$. This definition is reminiscent of the distributional version of one-way function, where we require hardness of coming up with a uniform preimage of a random image. In the world of one-way functions, by a result of Impagliazzo and Luby [20], the distributional version is known to be existentially equivalent to plain one-way functions (by an explicit and black-box transformation).

Very little is known about $\mathsf {d}\text {CRH}$ function families. Intuitively, this is a very weak notion of collision resistance since an adversary may be able to actually find all collisions (but with a skewed distribution). Nevertheless, as observed by Dubrov and Ishai [12], in a black-box model, $\mathsf {d}\text {CRH}$ cannot be constructed from one-way permutations. (The oracle of Simon [34] that finds a random collision is actually an oracle that breaks $\mathsf {d}\text {CRH}$.) The main question we are interested in is the power of $\mathsf {d}\text {CRH}$ and its relation to MCRH and CRH. Can CRH be constructed from $\mathsf {d}\text {CRH}$? Can $\mathsf {d}\text {CRH}$ be constructed from weak assumptions that are not known to imply CRH or MCRH? In what scenarios does the notion of $\mathsf {d}\text {CRH}$ suffice? What is the relation between MCRH and $\mathsf {d}\text {CRH}$? (The latter question was explicitly asked by Berman et al. [5]).

Fig. 1.

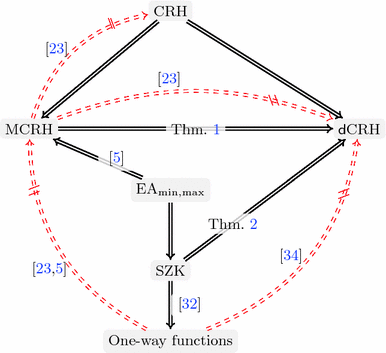
An illustration of the known results and our new implications. Solid lines mean positive implications, namely, a solid arrow from A to B means that the existence of A implies the existence of B. Crossed out dashed red lines mean black-box separations, namely, such a line from A to B means that there is an impossibility for a black-box construction of B from A. (Color figure online)

1.1 Our Results

We begin by observing that the separation of [23] of CRH from MCRH uses the same oracle of Simon [34] that finds a random collision. Thus, the separation actually applies to $\mathsf {d}\text {CRH}$, thereby implying that there is no black-box construction of a $\mathsf {d}\text {CRH}$ from an MCRH.

MCRH $\Rightarrow$ DCRH. Our first result is that the existence of MCRH for any constant $k\in {\mathbb {N}}$ implies the existence of $\mathsf {d}\text {CRH}$ (and no further assumptions). Our proof is non-constructive and uses an adversary in a non-black-box way. Actually, our proof results in an infinitely-often $\mathsf {d}\text {CRH}$, and should merely serve as evidence that multi-collision resistance is a stronger assumption than distributional collision resistance. This partially resolves the question of Berman et al. [5] mentioned above.

SZK $\Rightarrow$ DCRH. Our second result is an explicit construction of a $\mathsf {d}\text {CRH}$ from the average-case hardness of the class of problems that posses a statistical zero-knowledge (SZK) proof. More concretely, our construction is based on the average-case hardness of the statistical difference problem, that is known to be complete for SZK, by a result of Sahai and Vadhan [33]. This assumption is known to imply one-way functions by a result of Ostrovsky [32], but is not known to imply multi-collision resistance (let alone plain collision resistance). It is also weaker than the assumption used by Berman et al. [5] to construct an MCRH.

As an application, we obtain that indistinguishability obfuscation and one-way permutations (and thus their many derivatives) do not imply hardness in SZK via black-box reductions. We use the result of Asharov and Segev [1] that shows that indistinguishability obfuscation and one-way permutations do not imply (in a black-box model) collision resistance. We observe that their separation applies to distributional collision resistance as well (again, because they use the oracle of Simon [34] that finds a random collision) which immediately implies our result. Previously, a direct proof of this result (i.e., not going through [1]) was shown by Bitansky et al. [6].

A summary of the known results together with ours appears in Fig. 1.

1.2 Related Work

The work of Dubrov and Ishai. Dubrov and Ishai [12] studied the question of whether every efficiently samplable distribution can be efficiently sampled, up to a small statistical distance, using roughly as much randomness as the length of its output. They gave a positive answer to this question under various assumptions. They further showed that a negative answer to their question gives rise to a construction of a distributional collision resistant hash from any one-way permutation, thus bypassing the separation of Simon [34].

Overcoming black-box barriers. The framework of black-box constructions was introduced by Impagliazzo and Rudich [21] in order to capture “natural” constructions of one primitive from another. This framework has been extensively used to capture the limits of cryptographic primitives under this sort of constructions. Black-box constructions are not only the most natural ones, but often they result with more efficient and scalable construction since each building block is treated independently as a “black-box”.

A black-box separation does not mean that one primitive cannot be constructed from another, but rather that specific or natural types of constructions cannot work. Due to the nature of these constructions, in many cases it is hard to imagine a construction that circumvents the separation. Indeed, we have only a few examples where a black-box barrier was circumvented.

A well known tool that enables to bypass such limitations is using garbled circuits on circuits with embedded cryptography (e.g., a one-way function). This technique was used by Beaver [4] to construct round-efficient OT extension protocols (see also the recent work of Garg et al. [15]). They have also been recently used by Döttling and Garg [11] to construct an IBE scheme from the computational Diffie-Hellman assumption.

Another technique, introduced by Barak et al. [3], is via derandomization. Mahmoody and Pass [31] showed a black-box separation for constructions of non-interactive commitments from a stronger notion of one-way functions, which they called hitting one-way functions. Then, using the derandomization technique, they showed that there exists a non-black-box construction of non-interactive commitments from hitting one-way functions. Note that the notion of a hitting one-way function was introduced especially for this purpose.

Another technique inspired by complexity theory is due to Harnik and Naor [19] who introduced the task of compressibility of NP instances. Here, the task is to come up with a compression scheme that preserves the solution to an instance of a problem rather than preserving the instance itself. One of their results is a construction of a collision resistant hash function from any one-way function, assuming a compression algorithm for SAT. (Recall that there is no black-box construction of collision resistant hash functions from one-way functions [34].) Fortnow and Santhanam [14] showed that such a compression algorithm cannot exist unless ${\textsf {NP}}\subseteq {\textsf {coNP}}/\mathsf {poly}$. The result of Dubrov and Ishai [12] discussed above can be viewed as complementary to the one of Harnik and Naor [19], as they show consequences of the non-existence of (strong forms of) such algorithms.

A more recent technique comes from the area of program obfuscation. There, it was first shown by Asharov and Segev [1] that a private-key functional encryption scheme cannot be used to construct a public-key encryption scheme in a black-box way. Here, the definition of black-box is more delicate as we do not want to limit the obfuscation to circuits that have no cryptography in them. So, the actual separation is from an even stronger primitive called private-key functional encryption for oracle-aided circuits which are allowed to have one-way function gates. This separation was bypassed by Bitansky et al. [8] using a non-black-box component of Brakerski et al. [10] (see also [24]), where they generate a functional key for a function that calls the encryption/key-generation procedure of the same scheme. In the same line of works and the same high-level non-black-box use, indistinguishability obfuscation was constructed from a primitive called constant-degree multilinear maps in works by Lin, Vaikuntanathan, and Tessaro [25,26,27,28], while such constructions were proven impossible in a black-box model by Mahmoody et al. [30].

Lastly, we mention that there is a rich line of work, starting with Barak [2], on non-black-box simulation. Here, the construction is black-box but only the simulator (which is constructed to prove the security of the scheme) is allowed to be non-black-box (usually in a potential adversary).

Statistical zero-knowledge. The notion of statistical zero-knowledge (SZK) proofs was introduced in the seminal work of Goldwasser, Micali and Rackoff [18]. It is known that homomorphic encryption schemes and non-interactive computational private-information retrieval schemes imply hard problems in SZK [9, 29]. Concrete assumptions such as Discrete Log, QR, lattices, and more, are also known to imply SZK hardness.

The class of (promise problems) with SZK proofs is characterized by the problems statistical difference (SD) and entropy difference (ED) by results of Sahai and Vadhan [33] and Goldreich and Vadhan [17]. Statistical difference is the problem of deciding whether two distributions (specified by circuits that sample from them) are close or far in statistical distance. Entropy difference is the problem of deciding which of two given distributions (specified by circuits that sample from them) has noticeably higher Shannon entropy than the other.

There are closely related problems that are known to be complete for the class NISZK – the class that contains all (promise) problems for which there is a non-interactive statistical zero-knowledge proof. The complete problems, presented by Goldreich et al. [16], are statistical difference from uniform (SDU) and entropy approximation (EA). The former is the SD problem but where one of the distributions is the uniform one. The latter is the ED problem but where one of the distributions has known entropy k (so the goal is to decide whether the other distribution has entropy bigger than $k+1$ or smaller than $k-1$).

The assumption of Berman et al. [5] (leading to a construction of MCRH) is the average-case hardness of the promise problem to distinguish between distributions (specified by circuits) whose min-entropy is at least k from ones with max-entropy at most $k-1$. It is a strengthening of the (average-case) EA assumption which is in turn stronger than (average-case) ED and (average-case) SD.

1.3 Our Techniques

We give an overview of our proof of existence of a $\mathsf {d}\text {CRH}$ family based on MCRH. It is instructive to give the idea of the construction and proof first in an idealized world where we have an (imaginary) oracle $\textsc {Magic}$. This oracle $\textsc {Magic}$, given any efficiently samplabe distribution D over pairs $(x_1,x_2)$ and any particular value $x_1^*$, samples $x_2$ from the marginal of D conditioned on $x_1^*$ being the first output. Using this oracle, we show how to transform an MCRH family to a $\mathsf {d}\text {CRH}$ family. Then, we show how to replace the oracle with an efficient procedure; this is the non-black-box part in our construction. Notice that in general this oracle cannot be implemented in polynomial time (unless P = NP). Our implementation will not exactly be of the oracle $\textsc {Magic}$, but of a much weaker one which is still enough to carry out the proof.

To simplify the argument even further let us start with a 3-MCRH function family ${\mathcal H}$ where each function maps 2n bits to n bits. By definition, no polynomial-time algorithm, given $h\leftarrow {\mathcal H}$, can find a triple of values that are mapped to the same image. We assume towards contradiction that $\mathsf {d}\text {CRH}$ families do not exist. In particular, ${\mathcal H}$ is not a $\mathsf {d}\text {CRH}$ and thus there exists an adversary ${\mathcal A}$ that can break its security. Namely, ${\mathcal A}$ can sample random pairs of collisions relative to $h \leftarrow {\mathcal H}$. We show that given ${\mathcal A}$ and the oracle $\textsc {Magic}$ we can find a 3-collision relative to a given h.

Given h, we run ${\mathcal A}$ to get a collision $(x_1,x_2)$, i.e., $h(x_1)=h(x_2)$. We treat ${\mathcal A}$ as describing a distribution over pairs of inputs that collide and run the oracle $\textsc {Magic}$ on ${\mathcal A}$ with $x_1^*=x_1$ to sample another pair of collision $(x_1,x_3)$, i.e., $h(x_1)=h(x_2)$. This results with three values $x_1,x_2,x_3$ that collide relative to h, that is, $h(x_1)=h(x_2)=h(x_3)$. Are they all distinct? We argue that indeed this is the case.

The first pair $(x_1,x_2)$ was sampled uniformly at random, namely, $x_1$ is uniformly random and $x_2$ is uniformly random conditioned on colliding with $x_1$. Since our hash function is compressing enough, with high probability we have that the set of preimages $h^{(-1)}(x_1)$ is exponentially large and thus the probability that $x_1 = x_2$ is negligible. What about $x_3$? Recall that $x_3$ is also sampled uniformly at random conditioned on colliding with $x_1$, that is, uniformly at random from all the preimages of h(x). Thus, the probability that $x_3$ is either $x_1$ or $x_2$ is negligible, which completes the argument that $x_1,x_2$ and $x_3$ are a 3-way collision.

We have shown that if ${\mathcal H}$ is not a $\mathsf {d}\text {CRH}$ family, then the adversary together with the oracle $\textsc {Magic}$ can be used to find a 3-way collision. It remains to explain how we implement this oracle. Our key observation is that in the (false) world where $\mathsf {d}\text {CRH}$ do not exist and MCRH does exist, we can actually implement an efficient yet limited version of this oracle (where $x^*$ is uniform rather than arbitrary) which suffices for the purposes of our proof. This is the non-constructive (and non-black-box) part of the proof and is our main new insight.

We define a new hash family ${\mathcal H}'$ that depends not only on ${\mathcal H}$ but also on the adversary ${\mathcal A}$. Each $h'\in {\mathcal H}'$ uses the input x as random coins to run the adversary ${\mathcal A}$. If the adversary needs $\ell$ random coins then our hash function $h'$ will map $\ell$ bits to n bits (w.l.o.g. $\ell > 2n$). First, let ${\mathcal A}^1$ be the adversary ${\mathcal A}$ that outputs only the first element of the collision that ${\mathcal A}$ finds. That is, ${\mathcal A}^1(h;r)$ on input a hash function $h\leftarrow {\mathcal H}$ and random coins r, runs ${\mathcal A}(h;r)$ on h with coins r to get a collision (x, y) and it outputs only x. Using ${\mathcal A}^1$ and a key $h \in {\mathcal H}$ we define a key $h' \in {\mathcal H}'$ as follows:

$$\begin{aligned} h'(x) = h({\mathcal A}^1(h;x)). \end{aligned}$$

This is why our construction is non-explicit: we do not know who the adversary ${\mathcal A}$ is, but we only know it exists.

Since ${\mathcal H}'$ is also not a $\mathsf {d}\text {CRH}$ function family, there exists an adversary ${\mathcal A}'$ that can sample a random collision relative to $h'\leftarrow {\mathcal H}'$. We use ${\mathcal A}'$ in order to implement (some version of) the oracle $\textsc {Magic}$. First, we run ${\mathcal A}'$ on $h'$ to get a collision $(x_1,x_2)$. Since $x_1$ is uniform, we have that ${\mathcal A}^1$ gets random bits and will output $u_1$ which is part of a pair $(u_1,u_2)$ that collides relative to h. Moreover, $x_2$ is chosen such that it collides with $x_1$. Thus, if we let $(u_3,u_4) \leftarrow {\mathcal A}(h;x_2)$, then it must be that $h(u_1)=h(u_3)$, and therefore $h(u_1)=h(u_2)=h(u_3)$. Can we show that $u_1,u_2$, and $u_3$ are all distinct?

Let $U_{y}$ be the set of all u’s that h maps to $y=h(u_1)$. Since h is compressing enough, the set $U_y$ is exponentially large. Moreover, since $x_1$ is uniformly random, then $(u_1,u_2)$ is a random collision (under the right distribution) which implies that $u_1 \ne u_2$ with high probability. Arguing distinctness of $u_3$ is slightly more involved. Our goal is to show that indeed $u_3$ is sampled uniformly from the set $U_{y}$ and thus will be distinct from $u_1,u_2$ with high probability.

Recall that $x_2$ is sampled uniformly at random conditioned on $h'(x_2) \in U_{y}$. Thus, the distribution of the element $u_3$ depends on the adversary ${\mathcal A}$, and how he uses his random coins to output a pair $(u_3,u_4)$ that collide relative to h and where $h(u_3)=y$. Since ${\mathcal A}$ is an adversary for ${\mathcal H}$, we know that ${\mathcal A}^1$ “maps” randomnesses x to elements u. For a string u, denote by $X_u$ the set of all x’s such that ${\mathcal A}^1(h;x)= u$. By the guarantee on the output distribution of ${\mathcal A}$, this mapping is regular in the sense that for each $u,u'\in U_y$, it holds that $|X_u| = |X_{u'}|$. Thus, the probability that $u_3=u_1$ (and similarly $u_3=u_2$) is bounded by the probability that $x_2$ comes from $X_{u_1}$. By the above, $x_2$ comes (uniformly) from one of the $X_u$’s where $u\in U_y$. But, $U_y$ is exponentially large and all the $X_u$’s are of the same size, implying that the probability that $u_3=u_1$ is exponentially small. Altogether, indeed $u_1,u_2$, and $u_3$ form a 3-way collision.

The above argument is slightly over-simplified since it does not take into account errors that ${\mathcal A}$ or ${\mathcal A}'$ can make. In addition, we assumed that ${\mathcal A}$ and ${\mathcal A}'$ above output uniformly random collisions in the corresponding families, while in reality they can only be used to sample a collision which is statistically close to a random one. In the formal proof we handle these issues.

Finding larger collisions. In the proof above we used an adversary ${\mathcal A}$ that can find random pairs of collisions to construct a new hash function family, for which there is an adversary ${\mathcal A}'$ with which we designed an algorithm that finds 3-way collisions in the alleged 3-MCRH function family ${\mathcal H}$. Let us call this algorithm by $\mathsf {BreakMCRH}$. We first observe that $\mathsf {BreakMCRH}$ actually finds an (almost) random 3-way collision, namely, breaking the security of ${\mathcal H}$ as a distributional 3-MCRH. The distribution of our 3-way collision $(x_1,x_2,x_3)$ is such that $x_1$ is uniformly random and $x_2$ and $x_3$ are independent uniformly random conditioned on colliding with $x_1$.

We thus use $\mathsf {BreakMCRH}$ in a recursive manner to replace the adversary ${\mathcal A}$ (that finds pairs) and define a new hash function family. Finally, we modify the final algorithm $\mathsf {BreakMCRH}$ to find a 4-way collision. To this end, we define a new hash function family ${\mathcal H}'$ such that each $h'\in {\mathcal H}'$ is defined as

$$\begin{aligned} h'(x)=h(\mathsf {BreakMCRH}^1(h;x)), \end{aligned}$$

where $\mathsf {BreakMCRH}^1(h;x)$ is the algorithm $\mathsf {BreakMCRH}$ but outputs only the first element from the triple. Since (distributional) 3-MCRH do not exist, there is an adversary that can find a triple of collisions in a random $h'$. Similarly to the proof above, we use the first two elements to get a 3-way collision. Then, since the extra third element in the collision is sampled uniformly from a large set of pre-images it can be used to find the fourth colliding input.

This process can be generalized and continued for several iterations. The cost of each iteration is a polynomial blow-up in the running time of the hash function and the reduction (and also the success probability). Thus, we can apply this iteratively for k times where $k\in \mathbb N$ is any fixed constant, resulting with the statement that k-MCRH implies a $\mathsf {d}\text {CRH}$.

A construction from statistical difference. To present the idea behind the construction let us assume first that we have circuits $C_0,C_1:\{0,1\}^n\rightarrow \{0,1\}^n$ such that it is computationally hard to distinguish whether they describe distributions that are identical or disjoint. This corresponds to the statistical difference problem with parameters 0 and 1. We will overload $C_0$ and $C_1$ and let them denote (also) the corresponding distributions.

Our hash function $h:\{0,1\}^{n+1}\rightarrow \{0,1\}^n$ is indexed by both circuits $C_0$ and $C_1$, and it operates as follows

$$\begin{aligned} h_{C_0,C_1}(x,b) = C_b(x). \end{aligned}$$

Let us assume that it is not a $\mathsf {d}\text {CRH}$. Namely, there is an efficient adversary ${\mathcal A}$ that gets $C_0$ and $C_1$, and finds $(x,b),(x',b')$ that collide relative to $h_{C_0,C_1}$, as defined above. We claim that if the collision is such that $b\ne b'$ then the circuits $C_0$ and $C_1$ must be identically distributed. Indeed, if $b\ne b'$, this means that we have $x,x'$ such that, say, $C_0(x)=C_1(x')$ which means that the induced distributions are not disjoint (and hence must be identical). The other case, if $b= b'$, can occur in both cases that the distributions are identical or disjoint, but each will happen only with probability 1/2. Thus, to distinguish the two cases we run the adversary ${\mathcal A}$ and check whether $b\ne b'$. If the distributions are identical, it will always be that $b=b'$, while if they are disjoint this will happen only with probability 1/2. This is enough to distinguish between whether $C_0$ and $C_1$ are disjoint or identical with noticeable probability.

The case where the statistical distance is not 0 or 1 but is $\epsilon$ vs. $(1-\epsilon )$ for a small constant $\epsilon >0$ follows the same high-level idea but requires a slightly more involved analysis. The goal is to relate the probability that $b=b'$ to the statistical distance between $C_0$ and $C_1$ and show that these values are correlated. We choose to use a specific f-divergence called the triangular discrimination¹ measure which is defined by

$$\begin{aligned} \varDelta _{\mathsf {TD}}(C_0,C_1) = \sum _{y} \frac{(\Pr [C_0=y] - \Pr [C_1=y])^2}{\Pr [C_0=y] + \Pr [C_1=y]}. \end{aligned}$$

We first related the probability that $b' = b$ to the triangular discrimination between $C_0$ and $C_1$ by (simple) algebraic manipulations. Concretely, we show that

$$\begin{aligned} \Pr [b' = b] = \frac{1}{2} + \frac{\varDelta _{\mathsf {TD}}(C_0,C_1)}{4}. \end{aligned}$$

Then, we use the fact that the triangular discrimination can be bounded both from above and from below by a function that depends on the statistical distance.² More precisely, it holds that

$$\begin{aligned} 2\varDelta (C_0, C_1)^2 \le \varDelta _{\mathsf {TD}}(C_0, C_1) \le 2\varDelta (C_0, C_1). \end{aligned}$$

We use this to get our separation between the value of $\Pr [b' = b]$ in the case that $C_0$ and $C_1$ are close and in the case that they are far.

2 Preliminaries

Unless stated otherwise, the logarithms in this paper are base 2. For an integer $n \in \mathbb {N}$ we denote by [n] the set $\{1,\ldots , n\}$. For a distribution X we denote by $x \leftarrow X$ an element chosen from X uniformly at random. We denote by $\circ$ the string concatenation operation. A function $\mathsf{negl}:{\mathbb {N}}\rightarrow {\mathbb {R}}^+$ is negligible if for every constant $c > 0$, there exists an integer $N_c$ such that $\mathsf{negl}(n) < n^{-c}$ for all $n > N_c$. Throughout the paper, we denote by n the security parameter.

2.1 Distance Measures

Definition 1 (Statistical distance)

The statistical distance between two random variables X, Y over a finite domain $\varOmega$, is defined by

$$\begin{aligned} \varDelta (X,Y) \triangleq \frac{1}{2}\cdot \sum _{x\in \varOmega }^{} \left| {\Pr [X=x] - \Pr [Y=x]}\right| . \end{aligned}$$

We say that X and Y are $\delta$-close (resp. -far) if $\varDelta (X,Y)\le \delta$ (resp. $\varDelta (X,Y)\ge \delta$).

We will use another (less well-known) distance measure called the triangular discrimination (a.k.a Le Cam Divergence).

Definition 2 (Triangular discrimination)

The triangular discrimination between two random variables X, Y over a finite domain $\varOmega$, is defined by

$$\begin{aligned} \varDelta _{\mathsf {TD}}(X,Y) = \sum _{x\in \varOmega } \frac{(\Pr [X=x] - \Pr [Y=x])^2}{\Pr [X=x] + \Pr [Y=x]} \end{aligned}$$

It is known that the triangular discrimination is bounded from above by the statistical distance and from below by the statistical distance squared (see, for example, [35, Eq. (2.11)]).

Proposition 1

For any two random variables X, Y over the same finite domain, it holds that

$$\begin{aligned} 2\cdot \varDelta (X, Y)^2 \le \varDelta _{\mathsf {TD}}(X,Y) \le 2\cdot \varDelta (X, Y). \end{aligned}$$

2.2 Efficient Function Families

A function f, with input length $m_1(n)$ and outputs length $m_2(n)$, specifies for every $n\in {\mathbb {N}}$ a function $f_n:\{0,1\}^{m_1(n)}\rightarrow \{0,1\}^{m_2(n)}$. We only consider functions with polynomial input lengths (in n) and occasionally abuse notation and write f(x) rather than $f_n(x)$ for simplicity. The function f is computable in polynomial time (efficiently computable) if there exists an algorithm that for any $x \in \{0,1\}^ {m_1(n)}$ outputs $f_n(x)$ and runs in time polynomial in n.

A function family ensemble is an infinite set of function families, whose elements (families) are indexed by the set of integers. Let $\mathcal {F}= \{\mathcal {F}_n:\mathcal D_n\rightarrow \mathcal R_n\}_{n\in {\mathbb {N}}}$ stand for an ensemble of function families, where each $f\in \mathcal {F}_n$ has domain $\mathcal D_n$ and range $\mathcal R_n$. An efficient function family ensemble is one that has an efficient sampling and evaluation algorithms.

Definition 3 (Efficient function family ensemble)

A function family ensemble $\mathcal {F}= \{\mathcal {F}_n:\mathcal D_n\rightarrow \mathcal R_n\}_{n\in {\mathbb {N}}}$ is efficient if:

• $\mathcal {F}$ is samplable in polynomial time: there exists a probabilistic polynomial-time machine that given $1^n$, outputs (the description of) a uniform element in $\mathcal {F}_n$.

• There exists a deterministic algorithm that given $x \in \mathcal D_n$ and (a description of) $f \in \mathcal F_n$, runs in time $\mathsf {poly}(n, |x|)$ and outputs f(x).

2.3 Distributional Collision Resistant Hash Functions

A distributional collision resistant hash function is a hash function with the security guarantee that no efficient adversary can sample a uniform collision. This relaxation of classical collision resistance was introduced by Dubrov and Ishai [12].

For $h:\{0,1\}^{m}\rightarrow \{0,1\}^n$, we associate a random variable $\mathsf {COL}_h \subseteq \{0,1\}^{m}\times \{0,1\}^{m}$ over pairs of inputs $(x_1,x_2)$ to h sampled by the following process: $x_1$ is chosen uniformly at random from $\{0,1\}^{m}$ and then $x_2$ is chosen uniformly at random from the set $\{x \in \{0,1\}^{m} :h(x)=h(x_1)\}$. Note that it is possible that $x_1=x_2$.

Definition 4 (Distributional collision resistant hashing)

Let ${\mathcal H}= \{ {\mathcal H}_n:\{0,1\}^{m(n)} \rightarrow \{0,1\}^{n} \}_{n\in {\mathbb {N}}}$ be an efficient function family ensemble, where $m(n)<n$. We say that ${\mathcal H}$ is a secure distributional collision resistant hash ($\mathsf {d}\text {CRH}$) function family if for any probabilistic polynomial-time algorithm ${\mathcal A}$ and any two negligible functions $\delta (\cdot )$ and $\epsilon (\cdot )$, it holds that

$$\begin{aligned} \mathop {\Pr }\limits _{h\leftarrow {\mathcal H}}\left[ \varDelta \left( {\mathcal A}(1^n,h),\mathsf {COL}_h\right) \le \delta (n) \right] \le 1-\epsilon (n) \end{aligned}$$

for all sufficiently large $n\in {\mathbb {N}}$. Note that the probability above is only over the choice of $h\leftarrow {\mathcal H}$.

We say that a $\mathsf {d}\text {CRH}$ as above is infinitely-often secure if the above security only holds for infinitely many n’s rather than for all large enough n’s.

2.4 Multi-collision Resistant Hash Functions

A multi-collision resistant hash function is a relaxation of standard notion of collision resistant hash function in which it is hard to find multiple distinct values that all collide on the same value. This primitive has been recently studied in several works [5, 7, 22, 23].

Definition 5 (Multi-collision resistant hashing)

Let $k = k(n)$ be a polynomial function. An efficient function family ensemble ${\mathcal H}= \{ {\mathcal H}_n:\{0,1\}^{2n} \rightarrow \{0,1\}^{n} \}_{n\in {\mathbb {N}}}$ is a secure k-multi-collision resistant hash (MCRH) function family if for any probabilistic polynomial-time algorithm ${\mathcal A}$ there exists a negligible function $\mathsf{negl}(\cdot )$ such that for all $n\in {\mathbb {N}}$, it holds that

$$\begin{aligned} \Pr \left[ \genfrac{}{}{0.0pt}{}{x_1, \dots , x_k \text{ are } \text{ distinct } \text{ and }}{h(x_1) = \dots = h(x_k)} \left| \genfrac{}{}{0.0pt}{}{h \leftarrow {\mathcal H}_n}{(x_1,\dots ,x_k) \leftarrow \mathcal {A}(h)} \right. \right] \le \mathsf{negl}(n). \end{aligned}$$

We call such $x_1, \dots , x_k$ that map to the same value under h a k-way collision.

3 Constructing $\mathsf {d}\text {CRH}$ from MCRH

In this section we present our main result. The theorem states that the existence of any MCRH implies the existence of a $\mathsf {d}\text {CRH}$. Our construction is non-black-box.

Theorem 1

Assuming the existence of a secure 3-MCRH function family that compresses 2n bits to n bits, then there exists an (infinitely often) secure $\mathsf {d}\text {CRH}$ function family.

Proof

Let ${\mathcal H}= \{h:\{0,1\}^{2n}\rightarrow \{0,1\}^{n}\}$ be a secure 3-MCRH function family. Assume towards contradiction that infinitely-often $\mathsf {d}\text {CRH}$ function families do not exist, and we will show that 3-MCRH families do not exist as well (which is a contradiction). Since there are no $\mathsf {d}\text {CRH}$ function families, in particular, ${\mathcal H}$ is not a $\mathsf {d}\text {CRH}$ and there exists an adversary ${\mathcal A}$ and two negligible functions $\delta (\cdot )$ and $\epsilon$ such that for all large enough n’s it holds that

$$\begin{aligned} \mathop {\Pr }\limits _{h\leftarrow {\mathcal H}}\left[ \varDelta \left( {\mathcal A}(1^n,h),\mathsf {COL}_h\right) \le \delta (n)\right] > 1-\epsilon (n) \end{aligned}$$

That is, ${\mathcal A}$ gets $h \in {\mathcal H}$ as input, and randomness r and outputs a collision $(x_1,x_2)$ that is distributed as a random collision from $\mathsf {COL}_h$. We denote this process by $(x_1,x_2) \leftarrow {\mathcal A}(h;r)$ (notice that we omit the $1^n$ argument to simplify notation). Denote by ${\mathcal A}^1$ the same adversary that outputs only $x_1$. That is, $x_1 \leftarrow A^1(h;r)$.

Our key observation is that we can use $A^1$ to define a new family ${\mathcal H}'$ of hash functions which will be an infinitely-often secure $\mathsf {d}\text {CRH}$ function family. The keys in this family are denoted by $h'$ and have the same representation as $h \in {\mathcal H}$ but perform a different operation. Let $\ell = \ell (n)$ be an upper bound on the number of random bits that ${\mathcal A}$ uses, and assume that $\ell > 2n$ without loss of generality. We define a new hash family where the input x is used as random coins to run the adversary ${\mathcal A}^1$. Formally, we define each function in the family ${\mathcal H}' = \{h':\{0,1\}^{\ell } \rightarrow \{0,1\}^n\}$ by

$$\begin{aligned} h'(x)=h(A^1(h;x)). \end{aligned}$$

Again, since there are no infinitely-often $\mathsf {d}\text {CRH}$ function families, then in particular, ${\mathcal H}'$ is not a $\mathsf {d}\text {CRH}$. Thus, again again there is an adversary ${\mathcal A}'$ and two negligible functions $\delta '(\cdot )$ and $\epsilon '(\cdot )$ such that

$$\begin{aligned} \mathop {\Pr }\limits _{h'\leftarrow {\mathcal H}'}\left[ \varDelta \left( {\mathcal A}'(1^n,h'),\mathsf {COL}_{h'}\right) \le \delta (n) \right] > 1-\epsilon (n)~. \end{aligned}$$

We show how to construct an adversary $\mathsf {Break}{\mathcal H}$ that uses both ${\mathcal A}$ and ${\mathcal A}'$ to break the security of the given MCRH. The full description of $\mathsf {Break}{\mathcal H}(1^n,h)$ is given in Fig. 2.

Fig. 2.

The description of the adversary $\mathsf {Break}{\mathcal H}$ that uses ${\mathcal A}$ and ${\mathcal A}'$ to break the security of the MCRH function family ${\mathcal H}$.

To simplify the analysis we will analyze a different adversary called $\widetilde{\mathsf {Break}{\mathcal H}}$. This adversary is inefficient but its output distribution is negligibly close (in statistical distance) to the output distribution of $\mathsf {Break}{\mathcal H}$. So, once we show that $\widetilde{\mathsf {Break}{\mathcal H}}$ breaks ${\mathcal H}$, we will get that $\mathsf {Break}{\mathcal H}$ breaks ${\mathcal H}$ with almost the same probability which is a contradiction.

Let us set-up some notation first. Recall that $\mathsf {COL}_h$ is a distribution over pairs of inputs $(x_1,x_2)$ to h such that $x_1$ is chosen uniformly at random and $x_2$ is chosen uniformly at random conditioned on $h(x_1)=h(x_2)$. Let $\mathsf {COL}_h^1$ be a distribution that outputs the first element in the collision, namely $x_1$. Let $\mathsf {COL}_{h,x_1}^2$ be the distribution that outputs the second elements conditioned on colliding with the first, namely, a random $x_2$ conditioned on $h(x_1)=h(x_2)$. We also denote by $\mathsf {COL}_{h}(r)$ a sample from $\mathsf {COL}_h$ using randomness r.

Fig. 3.

The description of the adversary $\widetilde{\mathsf {Break}{\mathcal H}}$ that uses ${\mathcal A}$ and ${\mathcal A}'$ to break the security of the MCRH function family ${\mathcal H}$.

Claim 1

If $\widetilde{\mathsf {Break}{\mathcal H}}$ breaks the security of ${\mathcal H}$, then so does $\mathsf {Break}{\mathcal H}$.

Proof

We prove the claim by defining a hybrid adversaries $\mathsf {Break}{\mathcal H}^*$ and show the following sequence of implications:

• 1. If $\widetilde{\mathsf {Break}{\mathcal H}}$ breaks the security of ${\mathcal H}$, then so does $\mathsf {Break}{\mathcal H}^*$.

• 2. If $\mathsf {Break}{\mathcal H}^*$ breaks the security of ${\mathcal H}$, then so does $\mathsf {Break}{\mathcal H}$.

The adversary $\mathsf {Break}{\mathcal H}^*$ is the same as $\widetilde{\mathsf {Break}{\mathcal H}}$ except that we change Item 3 to the following:

• 2. $(u_1,u_2) \leftarrow {\mathcal A}(h;x_1)$, where $x_1 \leftarrow \mathsf {COL}^1_{h'}$.

First, we argue that if $\widetilde{\mathsf {Break}{\mathcal H}}$ breaks the security of ${\mathcal H}$, then so does $\mathsf {Break}{\mathcal H}^*$. Denote by $\widetilde{\mu }(n)$ the success probability of $\widetilde{\mathsf {Break}{\mathcal H}}$ in breaking the security of ${\mathcal H}$. With probability $1-\epsilon (n)$ over the choice of $h\leftarrow {\mathcal H}$ we sample a “good” h, that is, a h for which the adversary ${\mathcal A}$ outputs a collision that is $\delta (n)$-close to one from $\mathsf {COL}_{h}$. Then, for any such “good” h, the success probability of $\mathsf {Break}{\mathcal H}^*$ is $\widetilde{\mu }(n) - \delta (n)$. So, overall, the success probability of $\mathsf {Break}{\mathcal H}^*$ is $\mu ^*(n) = \widetilde{\mu }(n) - \delta (n) - \epsilon (n)$. To simplify the analysis we will analyze a different adversary called $\widetilde{\mathsf {Break}{\mathcal H}}$, described in Fig. 3.

Second, we argue that if $\mathsf {Break}{\mathcal H}^*$ breaks the security of ${\mathcal H}$, then so does $\mathsf {Break}{\mathcal H}$. Denote by $\mu ^*(n)$ the success probability of $\mathsf {Break}{\mathcal H}^*$ in breaking the security of ${\mathcal H}$. With probability $1-\epsilon '(n)$ (over the choice of $h'\leftarrow {\mathcal H}'$) the adversary ${\mathcal A}'$ outputs a collision that is $\delta '(n)$-close to one from $\mathsf {COL}_{h'}$. Then, for any such “good” h, the success probability of $\mathsf {Break}{\mathcal H}$ is ${\mu }^*(n) - \delta '(n)$. So, overall, the success probability of $\mathsf {Break}{\mathcal H}$ is $\mu (n) = {\mu }^*(n) - \delta '(n) - \epsilon '(n)$.

Combining both of the above, we have that if $\widetilde{\mathsf {Break}{\mathcal H}}$ breaks the security of ${\mathcal H}$ with probability $\widetilde{\mu }(n)$, then $\mathsf {Break}{\mathcal H}$ breaks it with probability

$$\begin{aligned} \mu (n) = \widetilde{\mu }(n) - \delta (n) - \epsilon (n) - \delta '(n) - \epsilon '(n). \end{aligned}$$

   $\blacksquare$

By the definition of $x_1\leftarrow \mathsf {COL}_h^1$ and $x_2\leftarrow \mathsf {COL}_{h,x_1}^2$, we have that $x_1$ is uniformly random in the domain of $h'$ (namely, $\{0,1\}^\ell$) and $x_2$ is a uniform element in $\{0,1\}^\ell$ conditioned on satisfying $h(x_1) = h(x_2)$.

Lemma 1

With all but negligible probability we have that $h(u_1)=h(u_2)=h(u_3)$.

Proof

By the union bound

$$\begin{aligned} \Pr [h(u_1) = h(u_2) = h(u_3)]&\ge 1- \Pr [h(u_1) \ne h(u_2) \text { or } h(u_1) \ne h(u_3)] \\&\ge 1- \Pr [h(u_1) \ne h(u_2)] - \Pr [h(u_1) \ne h(u_3)]. \end{aligned}$$

If $(x_1,x_2)$ is a collision under $h'$, by definition of $h'$, then it holds that

$$\begin{aligned} h(u_1) = h({\mathcal A}^1(h;x_1)) = h({\mathcal A}^1(h;x_2)) = h(u_3). \end{aligned}$$

Thus, since by the definition of $\mathsf {COL}_{h'}$, the inputs $x_1$ and $x_2$ are a collision relative to $h'$, then $u_1$ and $u_3$ are a collision relative to h. That is,

$$\begin{aligned} \Pr [h(u_1) \ne h(u_3)] = 0. \end{aligned}$$

Additionally, recall that the pair $(x_1,x_2)$ is a random collision sampled via $\mathsf {COL}_h$. Namely, $x_1$ is uniformly random in $\{0,1\}^{\ell }$. Since ${\mathcal A}$ outputs a collision relative to h for all but a $\delta (n)$-fraction of possible randomnesses, it must be that $h(u_1)=h(u_2)$, except with probability $\delta (n)$. That is,

$$\begin{aligned} \Pr [h(u_1) \ne h(u_2)] \le \delta (n). \end{aligned}$$

   $\blacksquare$

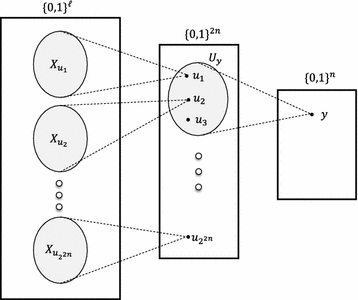
What is left to show, and is the most technical part of the proof, is that all three elements $u_1,u_2,u_3$ are distinct. An illustration of the main ideas and the notations used in the proof is given in Fig. 4.

Fig. 4.

An illustration of the ideas and notations used in the proof of the proof.

Lemma 2

With all but negligible probability we have that $u_1,u_2,u_3$ are distinct.

Proof

To argue distinctness, we first show that set of inverses of $h(u_1)$ is large with high probability. We use the following claim.

Claim 2

For any $h\in {\mathcal H}$, it holds that

$$\begin{aligned} \mathop {\Pr }\limits _{x\leftarrow \{0,1\}^{2n}}[|h^{-1}(h(x))| > 2^{n/2}] \ge 1-2^{-n/2}. \end{aligned}$$

Proof

We count how many x’s might there be that satisfy $|\{h^{-1}(h(x))\}| \le 2^{n/2}$. Let us denote by $U_1,\ldots ,U_k$ a partition of $\{0,1\}^{2n}$ into sets according to the output of h. That is, $\forall i \;\forall x,y\in U_i:h(x)=h(y)$ and for all $i \ne j$ and $x \in U_i,y \in U_j$ it holds that $h(x) \ne h(y)$. Each set $U_i$ that is larger than $2^{n/2}$ is called “good” and others are called “bad”. The total number of sets k is bounded by $2^n$ and thus, there can be at most $2^{n}$ bad sets $U_i$. Namely, the total number of elements in the bad sets is bounded by $2^{n}\cdot 2^{n/2} = 2^{3n/2}$. Thus, the number of elements in good sets is $2^{2n} - 2^{3n/2} = (1-2^{-n/2})\cdot 2^{2n}$ and each such good element x satisfies $|\{h^{-1}(h(x))\}| > 2^{n/2}$.    $\blacksquare$

Let $y=h(u_1)$ and let us denote all the values u that are mapped to y by:

$$\begin{aligned} U_y = \{ u \mid h(u) = y\}. \end{aligned}$$

Note that, by Claim 2, with very high probability over the choice of $x_1$, it holds that

$$\begin{aligned} |U_y| \ge 2^{n/2}. \end{aligned}$$

(1)

The elements $u_1$ and $u_2$ are a sample of $\mathsf {COL}_h$ using fresh randomness $x_1$. Since $x_2$ is sampled from the set of all preimages of $x_1$, we have that

$$\begin{aligned} \Pr [u_1\ne u_2]&\ge \Pr \left[ u_1 \ne u_2 \mid |U|> 2^{n/2}\right] \cdot \Pr \left[ |U| > 2^{n/2}\right] \\&\ge 1-\mathsf{negl}(n). \end{aligned}$$

We continue to show that $u_3$ is distinct from $u_1,u_2$. From now on, let us condition on $x_1$ being such that Eq. (1) holds. We also condition on $h\in {\mathcal H}$ being such that $\varDelta ({\mathcal A}(1^n,h),\mathsf {COL}_h)\le \delta (n)$. The former happens with probability $1-2^{-\varOmega (n)}$ and the latter happens with probability $1-\epsilon (n)$. Overall, by the conditioning we will lose an additive $\mathsf{negl}(n)$ term in the overall success probability of $\widetilde{\mathsf {Break}{\mathcal H}}$.

The algorithm ${\mathcal A}^1$ (i.e., ${\mathcal A}$ when restricted to output only the first element) gives us a mapping between x’s and u’s. Namely, for every $x\in \{0,1\}^\ell$, there is a $u\in \{0,1\}^{2n}$ such that $(u,\cdot )={\mathcal A}(h;x)$. For $u\in \{0,1\}^{2n}$, denote

$$\begin{aligned} X_u = \{ x \mid {\mathcal A}^1(h; x) = u\}. \end{aligned}$$

We claim that for any two $u,u'$, the sizes of $X_u$ and $X_{u'}$ are roughly the same.

Claim 3

For any $u,u'\in U_y$,

$$\begin{aligned} \mathop {\Pr }\limits _{(x_1,x_2)\leftarrow \mathsf {COL}_{h'}}[x_2 \in X_u] \in \mathop {\Pr }\limits _{(x_1,x_2)\leftarrow \mathsf {COL}_{h'}}[x_2 \in X_{u'}] \pm \delta (n). \end{aligned}$$

Proof

Since ${\mathcal A}(h;\cdot )$ outputs a pair that is distributed statistically close to a pair coming from $\mathsf {COL}_h$ and in the latter the first element is uniformly random in $\{0,1\}^{2n}$, it must be that ${\mathcal A}^1(h;\cdot )$ is distributed almost uniformly at random. Hence, the mapping between x’s and u’s is regular, except with probability $\delta (n)$. Namely,

$$\begin{aligned} \frac{|X_u|}{2^{\ell }} \in \frac{|X_{u'}|}{2^{\ell }} \pm \delta (n). \end{aligned}$$

The claim now follows since $x_2$ is chosen uniformly at random from the set of all values that go to y.    $\blacksquare$

By the definition of $X_u$, by Claim 3, and by Eq. (1), we have that

$$\begin{aligned} \Pr [u_3 = u_1] \le \Pr [ x_2 \in X_{u_1} ] \le \frac{1}{|U_y|} + \delta (n) \le \mathsf{negl}(n). \end{aligned}$$

By a similar reasoning, it holds that

$$\begin{aligned} \Pr [u_3 = u_2] \le \Pr [ x_2 \in X_{u_2} ] \le \frac{1}{|U_y|} + \delta (n) \le \mathsf{negl}(n). \end{aligned}$$

Therefore, we get that $u_3 \notin \{u_1,u_2\}$ with all but negligible probability.    $\blacksquare$

Combining Lemmas 1 and 2 we get that we will find a 3-way collision with high probability which concludes the proof.    $\blacksquare$

Distributional MCRH. One can also defined a distribution notion for a k-MCRH. Here, the task of the adversary is to find, given a hash function $h\leftarrow {\mathcal H}$, not an arbitrary k-way collision, but one that is statistically close to a random one. By a random k-way collision we mean the following distribution. First, sample $x_1$ uniformly at random and then sample $x_2,\ldots ,x_k$ independently uniformly at random conditioned on $h(x_i) = h(x_1)$ for every $2 \le i \le k$. We call this distribution $\mathsf {COL}_h^k$.

We observe that in the proof above we get an algorithm that finds a 3-way collision that is statistically close to a random one from $\mathsf {COL}_h^3$. That is, the proof above shows that existence of $\mathsf {d}\text {CRH}$ can be based on the existence of the seemingly weaker notion of distributional 3-MCRH.

3.1 Going Beyond 3-MCRH

In the previous section we have shown how to construct a $\mathsf {d}\text {CRH}$ from a 3-MCRH family. Our construction and proof inherently relied on the fact that an adversary cannot find a 3-way collision. In this part, we show how to extend the ideas from the above proof to give a recursive construction that shows the existence of a $\mathsf {d}\text {CRH}$ from the existence of a k-MCRH for any constant k. We will exemplify the idea for $k=4$ next and explain the general afterwards.

Suppose that we are given a 4-MCRH family ${\mathcal H}$ and assume towards contradiction that $\mathsf {d}\text {CRH}$ function families do not exist. As in the proof above, there is an adversary ${\mathcal A}$ that breaks ${\mathcal H}$ as a $\mathsf {d}\text {CRH}$ and finds a random collision from $\mathsf {COL}_h$, where $h\leftarrow {\mathcal H}$. We define ${\mathcal H}' = \{h':\{0,1\}^\ell \rightarrow \{0,1\}^n\}$ as in the proof above

$$\begin{aligned} h'(x) = h({\mathcal A}^1(h;x)). \end{aligned}$$

Since ${\mathcal H}'$ do not exist, the adversary $\mathsf {Break}{\mathcal H}_3\triangleq \mathsf {Break}{\mathcal H}$ from Fig. 2 can be used to find a random 3-way collision $(u_1,u_2,u_3)$ for a random key $h\leftarrow {\mathcal H}$. Denote by $\ell '=\ell '(n)$ an upper bound on the number of bits of randomness used by $\mathsf {Break}{\mathcal H}_3$.

The key observation is that we can use $\mathsf {Break}{\mathcal H}_3$ recursively to get an algorithm $\mathsf {Break}{\mathcal H}_4$ that find a 4-way collision. We define an new hash function family ${\mathcal H}''=\{h'':\{0,1\}^{\ell '}\rightarrow \{0,1\}^n\}$ by

$$\begin{aligned} h''(x)=h(\mathsf {Break}{\mathcal H}_3^1(h;x)), \end{aligned}$$

where $\mathsf {Break}{\mathcal H}_3^1$ is a modified version of the algorithm $\mathsf {Break}{\mathcal H}_3$ that outputs only the first element from its output triple. Since the function family ${\mathcal H}''$ is not a $\mathsf {d}\text {CRH}$, there is an algorithm ${\mathcal A}''$ that can find a collision in $h''\leftarrow {\mathcal H}''$ that is statistically close to one from $\mathsf {COL}_{h''}$. We construct an algorithm $\mathsf {Break}{\mathcal H}_4(1^n, h)$ that is similar to $\mathsf {Break}{\mathcal H}_3(1^n, h)$, except that it uses $\mathsf {Break}{\mathcal H}_3(1^n, h)$ instead of the adversary ${\mathcal A}$ to find a 4-way collision.

That is, $\mathsf {Break}{\mathcal H}_4$ runs ${\mathcal A}''$ to get a random collision $(x_1,x_2)$. Then, $x_1$ is used as randomness to $\mathsf {Break}{\mathcal H}_3(1^n, h)$ to get a 3-way collision $(u_1,u_2,u_3)$, and $x_2$ is used to get $(u_4,u_5,u_6)$. Similarly to the arguments in the original proof, here we claim that $u_4$ will also hash to the same value as $u_1$, $u_2$, and $u_3$, and since it is random in the set of all elements that collide with $u_1$, the probability that it is distinct from $u_1,u_2$, and $u_3$ is very high. Thus, $u_1,u_2,u_3,u_4$ is a 4-way collision with high probability. (Not only that, it is actually negligibly-close to a random 4-way collision.)

The general case. The above idea extends to starting with a k-MCRH for higher values of k. Namely, our transformation allows one to go from k-MCRH to $\mathsf {d}\text {CRH}$. But, there is a cost in parameters since in each step, the algorithm we construct and the construction itself incur a polynomial blowup in the running time (and also a decrease in the success probability). Thus, we can apply this iteratively k times for any constant $k\in \mathbb N$. This results with the statement that the existence of k-MCRH for any constant k implies the existence of $\mathsf {d}\text {CRH}$. The resulting algorithm is denoted $\mathsf {Break}{\mathcal H}_{k+1}(1^n, h)$ and is given in Fig. 5.

Fig. 5.

The description of the adversary $\mathsf {Break}{\mathcal H}_{k+1}$.

Remark 1 (A note on non-uniformity)

Notice that the first step in the above argument from 3-MCRH to $\mathsf {d}\text {CRH}$ results with an infinitely-often $\mathsf {d}\text {CRH}$. This can be circumvented by having a non-uniform construction. In particular, instead of having a single adversary ${\mathcal A}$ that works for infinitely many input length, we can hardwire an adversary that works for each input length. The result is a standard $\mathsf {d}\text {CRH}$ (as opposed to an infinitely-often one) that is computed by circuits instead of Turing machines. This is important for our recursive argument, as otherwise each step of the reduction might work on a different sequence of input lengths.

Remark 2 (Distributional multi-collision resistance)

The above idea can be summarized as a transformation from k-$\mathsf {d}\text {MCRH}$ to a $(k-1)$-$\mathsf {d}\text {MCRH}$. A k-$\mathsf {d}\text {MCRH}$ is the distributional analog of MCRH, where the goal of the adversary is to come up with a random k-way collision $(x_1,\ldots ,x_k)$. The distribution of such a collision relative to a hash function h is that $x_1$ is chosen uniformly at random and $x_2,\ldots ,x_k$ are all chosen independently and uniformly at random conditioned on colliding with $x_1$ on h.

4 Constructing $\mathsf {d}\text {CRH}$ from SZK

In this section we show how to construct a $\mathsf {d}\text {CRH}$ from the average-case hardness of SZK. The statistical difference problem, which is complete for SZK [33], is a promise problem where one is given two distributions, described by circuits that sample from them, and the goal is to decide whether the distributions are close or far in statistical distance. The hardness of SZK implies the hardness of SD. For our application we will need the average-case hardness of this problem, where there is an underlying efficient sampler that samples the two aforementioned circuits.

Definition 6 (Distributions encoded by circuits)

Let $C:\{0,1\}^n\rightarrow \{0,1\}^n$ be a Boolean circuit. The distribution encoded by C is the distribution induced on $\{0,1\}^n$ by evaluating the circuit C on a uniformly sampled string of length n. We abuse notation and sometimes write C for the distribution defined by C.

Definition 7 (The statistical difference problem)

Statistical Difference is the promise problem $\mathsf {SD}^{\epsilon ,1-\epsilon }=(\mathsf {SD}_{Y},\mathsf {SD}_{N})$ over all pairs of circuits $C_0,C_1:\{0,1\}^n\rightarrow \{0,1\}^n$, where the “Yes” instances are those that encode statistically far distributions

$$\begin{aligned} \mathsf {SD}_{Y} = \{(C_0,C_1) : \varDelta (C_0,C_1) \ge 1-\epsilon \} \end{aligned}$$

and the “No” instances are those that encode statistically close distributions

$$\begin{aligned} \mathsf {SD}_{N} = \{(C_0,C_1) : \varDelta (C_0,C_1) \le \epsilon \}. \end{aligned}$$

Definition 8 (Average-case hardness)

We say that the $\mathsf {SD}^{\epsilon ,1-\epsilon }$ problem is hard-on-the-average if there exists a probabilistic polynomial-time sampler S that outputs pairs of circuits $C_0,C_1:\{0,1\}^n\rightarrow \{0,1\}^n$ such that for any (non-uniform) probabilistic polynomial-time decider D that outputs “Y” or “N”, there exists a negligible function $\mathsf{negl}(\cdot )$ such that for all $n\in {\mathbb {N}}$ it holds that

$$\begin{aligned} \mathop {\Pr }\limits _{(C_0,C_1) \leftarrow S(1^n)}[x \leftarrow D(C_0,C_1) \text { and } (C_0,C_1) \in \mathsf {SD}_x] \le \frac{1}{2} + \mathsf{negl}(n). \end{aligned}$$

The beautiful result of Sahai and Vadhan [33] shows that (average-case) $\mathsf {SD}^{\frac{1}{3},\frac{2}{3}}$ is complete for (average-case) SZK. Not only that, they showed that the constants 1/3 and 2/3 in the Statistical Difference problem are somewhat arbitrary and the gap can be amplified. In more detail, they showed that given two distributions $D_0,D_1$, and a number k, then in polynomial time (in k) one can sample from distributions $D_0'$ and $D_1'$ such that if $\varDelta (D_0,D_1)\le 1/3$, then $\varDelta (D'_0,D'_1)\le 2^{-k}$, and if $\varDelta (D_0,D_1)\ge 2/3$, then $\varDelta (D'_0,D'_1)\le 1-2^{-k}$.

Our main result in this section is a construction of a $\mathsf {d}\text {CRH}$ that compresses by 1 bit from the average-case hardness of SZK.

Theorem 2

There exists an explicit $\mathsf {d}\text {CRH}$ mapping n bit to $(n-1)$ bits assuming the average-case hardness of SZK.

Proof

Since SZK is hard-on-the-average, $\mathsf {SD}^{\frac{1}{3},\frac{2}{3}}$ is hard-on-the-average. Also, $\mathsf {SD}^{\epsilon ,1-\epsilon }$ for $\epsilon =0.01$ is average-case hard [33]. Let S be the sampler for $\mathsf {SD}^{\epsilon ,1-\epsilon }$.

We define our $\mathsf {d}\text {CRH}$ family ${\mathcal H}$ next. The key sampler for ${\mathcal H}$ runs the simulator S and outputs the two circuits (that describe distributions). Given a key $(C_0,C_1)$ we define the hash function $h_{(C_0,C_1)}:\{0,1\}^n \rightarrow \{0,1\}^{n-1}$ in by

$$\begin{aligned} h_{C_0,C_1}(x,b) = C_b(x). \end{aligned}$$

(2)

In the rest of the proof we shall prove that this function family is a $\mathsf {d}\text {CRH}$. We will do so by contradiction, showing that if it were insecure, then we would get a statistical-distance distinguisher for circuits that are output by S. This is a contradiction to the average-case hardness of $\mathsf {SD}^{\epsilon ,1-\epsilon }$.

Suppose (towards contradiction) that ${\mathcal H}$ is not a $\mathsf {d}\text {CRH}$. This means that there is a probabilistic polynomial-time adversary ${\mathcal A}$ and two negligible functions $\delta (\cdot )$ and $\epsilon (\cdot )$ such that ${\mathcal A}$ with probability at least $1-\epsilon (n)$ over the choice of $h\leftarrow {\mathcal H}$ can generate a collision which is $\delta$-close to a uniform one from $\mathsf {COL}_h$. That is,

$$\begin{aligned} \mathop {\Pr }\limits _{h\leftarrow {\mathcal H}}\left[ \varDelta \left( {\mathcal A}(1^n,h),\mathsf {COL}_h\right) \le \delta (n) \right] > 1-\epsilon (n). \end{aligned}$$

We design an algorithm $\mathsf {BreakSD}$ that uses ${\mathcal A}$ and solves SD on circuits given by $S(1^n;\cdot )$. The idea is pretty simple: we run ${\mathcal A}$ to get a collision pair $\left( (x,b), (x',b')\right)$. If $b= b'$, then we output “Y” (i.e., far) and otherwise, we output “N” (i.e., close). This algorithm is described in Fig. 6.

Fig. 6.

The description of the adversary $\mathsf {BreakSD}$.

We next prove that when the statistical distance between $C_0$ and $C_1$ is large, then with high probability the collision will be such that $b=b'$. On the other hand, when the distributions are far, the collision will be with $b=b'$ only with bounded probability. If the gap between the events is noticeable, then our algorithm is able to decide whether $C_0$ and $C_1$ are close or far with noticeable probability which violates the average-case hardness of SD.

Before we formalize this intuition, let us set up some notation. We say that $h \in {\mathcal H}$ is “good” if the adversary ${\mathcal A}$ acts well on this h, namely,

$$\begin{aligned} \varDelta \left( {\mathcal A}(1^n,h),\mathsf {COL}_h\right) \le \delta (n). \end{aligned}$$

Since ${\mathcal A}$ succeeds to come up with a uniform collision for all but a negligible fraction of the h’s, we have that

From now on, we condition on the case that h is “good” and lose a factor of $n^{-1}$ in the success probability. Moreover, we know that for good functions h it holds that ${\mathcal A}$ outputs a collision that is negligibly-close to $\mathsf {COL}_h$. Thus, we can analyze the success probability of $\mathsf {BreakSD}$ with $\mathsf {COL}_h$ instead of ${\mathcal A}$, and at the end lose another factor of $\delta (n)$. Together, these two lost factors will not be significant since our distinguishing gap will be $\varOmega (1)$.

In the following lemma we show that the probability that the adversary outputs a collision in which $b=b'$ is related to the triangular discrimination between $C_0$ and $C_1$ (see Definition 2).

Lemma 3

It holds that

$$\begin{aligned} \Pr [b' = b] = \frac{1}{2} + \frac{\varDelta _{\mathsf {TD}}(C_0,C_1)}{4}. \end{aligned}$$

By this lemma together with Proposition 1 (that says that the triangular discrimination is bounded from above by the statistical distance and from below by the square of the statistical distance), we get that when the statistical distance between $C_0$ and $C_1$ is at least $1-\epsilon =0.99$, then $\Pr [b' = b] > 0.6$, while when the statistical distance between $C_0$ and $C_1$ is at most $\epsilon =0.01$, then $\Pr [b' = b] < 0.55$. Overall, our adversary has a noticeable distinguishing gap, as required. We prove Lemma 3 next.

Proof of Lemma 3. Let $P_y = \mathop {\Pr }\nolimits _{x\leftarrow \{0,1\}^n}[C_0(x)=y]$ be the probability that $C_0$ outputs y and similarly define $Q_y = \mathop {\Pr }\nolimits _{x\leftarrow \{0,1\}^n}[C_1(x)=y]$.

It happens that $b'=b$ if $b=b'=0$ or if $b=b'=1$. So, by the rule of total probability

$$\begin{aligned} \Pr [b' = b]&= \Pr [b=0]\cdot \Pr [b'=0\mid b=0] + \Pr [b=1]\cdot \Pr [b'=1\mid b=1]. \end{aligned}$$

Expanding the LHS (the RHS is expanded analogously):

$$\begin{aligned} \Pr [b=0]\cdot&\Pr [b'=0\mid b=0] \\&= \frac{1}{2}\cdot \sum _{y\in \{0,1\}^n} \Pr [b'=0\wedge y'=y\mid b=0] \\&= \frac{1}{2}\cdot \sum _{y\in \{0,1\}^n} \Pr [b'=0\mid b=0 \wedge y'=y] \cdot \Pr [ y'=y \mid b=0] \\&=\frac{1}{2}\cdot \sum _{y\in \{0,1\}^n}{P_y\cdot \frac{P_y}{P_y + Q_y}}. \end{aligned}$$

Thus,

$$\begin{aligned} \Pr [b' = b]&= \frac{1}{2}\cdot \sum _{y\in \{0,1\}^n}{ \frac{P_y^2}{P_y + Q_y}} + \frac{1}{2}\cdot \sum _{y\in \{0,1\}^n}{ \frac{Q_y^2}{P_y + Q_y}}. \end{aligned}$$

(3)

Let us expand the LHS (again, the RHS is expanded analogously):

$$\begin{aligned} \sum _{y\in \{0,1\}^n}{ \frac{P_y^2}{P_y + Q_y}}&= \sum _{y\in \{0,1\}^n}{ \frac{P_y^2 - Q_y^2+ Q_y^2}{P_y + Q_y}} \\&= \sum _{y\in \{0,1\}^n}{(P_y - Q_y) + \sum _{y\in \{0,1\}^n} \frac{Q_y^2 }{P_y + Q_y}} \\&= \sum _{y\in \{0,1\}^n} \frac{Q_y^2 }{P_y + Q_y}. \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{y\in \{0,1\}^n}{ \frac{P_y^2}{P_y + Q_y}}&= \frac{1}{2}\cdot \sum _{y\in \{0,1\}^n} \frac{P_y^2+Q_y^2}{P_y+Q_y} \\&= \frac{1}{4}\cdot \sum _{y\in \{0,1\}^n} \frac{(P_y+Q_y)^2}{P_y+Q_y} + \frac{1}{4}\cdot \sum _{y\in \{0,1\}^n} \frac{(P_y - Q_y)^2}{P_y + Q_y} \\&= \frac{1}{2} + \frac{1}{4}\cdot \sum _{y\in \{0,1\}^n} \frac{(P_y - Q_y)^2}{P_y + Q_y}. \end{aligned}$$

   $\blacksquare$

By plugging this into Eq. (3), we finish the proof.    $\blacksquare$

5 Open Questions and Further Research

In this work, we presented two constructions of DCRH from different assumptions. The first construction is from the existence of an MCRH. This construction is non-black-box which is necessary due to a black-box separation between the two. The other construction is from the average-case hardness of SZK. This construction is fully black-box. There are many questions still left open regarding the power of DCRH and its relation to other notions of collision resistance.

We do not know how to construct an MCRH from a $\mathsf {d}\text {CRH}$. We also do not know how to separate MCRH from $\mathsf {d}\text {CRH}$ or even CRH from $\mathsf {d}\text {CRH}$. The latter questions require coming up with a new oracle that can only be used to find collision that are far from random ones.

Another question we did not address in this work is the applicability of $\mathsf {d}\text {CRH}$. Does it (existentially) imply any useful cryptographic primitive that is not implied by one-way functions?