LSWAVE: a MATLAB software for the least-squares wavelet and cross-wavelet analyses

Abstract

The least-squares wavelet analysis (LSWA) is a robust method of analyzing any type of time/data series without the need for editing and preprocessing of the original series. The LSWA can rigorously analyze any non-stationary and equally/unequally spaced series with an associated covariance matrix that may have trends and/or datum shifts. The least-squares cross-wavelet analysis complements the LSWA in the study of the coherency and phase differences of two series of any type. A MATLAB software package including a graphical user interface is developed for these methods to aid researchers in analyzing pairs of series. The package also includes the least-squares spectral analysis, the antileakage least-squares spectral analysis, and the least-squares cross-spectral analysis to further help researchers study the components of interest in a series. We demonstrate the steps that users need to take for a successful analysis using three examples: two synthetic time series, and a Global Positioning System time series.

Appendix A: Error estimation of the least-squares coefficients

We show how one may calculate the unbiased covariance matrix of simultaneously estimated coefficients in the LSSA or ALLSSA. Then we show how the GUI calculates the amplitudes and phases of sine waves with their errors.

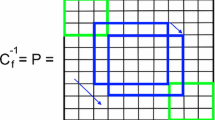
Let ${\mathbf{f}}~=~\left[ {f\left( t \right)} \right]$ be a time series of size $n$ with associated covariance matrix ${{\mathbf{C}}_{\mathbf{f}}}$ and ${\mathbf{P}}~=~{\mathbf{C}}_{{\mathbf{f}}}^{{ - 1}}$. Assume that ${\mathbf{f}}$ has d significant datum shifts, and so column vectors ${\mathbf{\Phi} _1}~=\left[ {\mathbf{1}_1} \right]$, ${\mathbf{\Phi} _2}~=\left[ {\mathbf{1}_2} \right]$, …, ${\mathbf{\Phi} _d}~=\left[ {\mathbf{1}_d} \right]$, of size n whose elements are zeros and ones will estimate the total shifts of data. The elements of each vector are ones if their locations align with a datum shift segment and zeros elsewhere. Assume that ${{\mathbf{\Phi }}_{d+1}}~=[{\mathbf{t}}]$, ${{\mathbf{\Phi }}_{d+2}}~=[{{\mathbf{t}}^2}]$, and ${{\mathbf{\Phi }}_{d+3}}~=[{{\mathbf{t}}^3}]$ to estimate a consistent trend for all datum shifts.

Let ${{\mathbf{\Phi }}_{d+4}}~=~~{\text{cos}}\left( {2\pi {\omega _1}{\mathbf{t}}} \right)$, ${{\mathbf{\Phi }}_{d+5}}~=~~{\text{sin}}\left( {2\pi {\omega _1}{\mathbf{t}}} \right)$, ..., ${{\mathbf{\Phi }}_{q - 1}}~=~~{\text{cos}}\left( {2\pi {\omega _k}{\mathbf{t}}} \right)$, and ${{\mathbf{\Phi }}_q}~=~~{\text{sin}}\left( {2\pi {\omega _k}{\mathbf{t}}} \right)$ be the constituents of known forms whose frequencies (${\omega _k}$’s) are either entered by users in the LSSA or estimated by the ALLSSA. Therefore, $\underline {{\mathbf{\Phi }}} =\left[ {{{\mathbf{\Phi }}_1},~ \ldots ,{{\mathbf{\Phi }}_d}, \ldots ,{{\mathbf{\Phi }}_q}} \right]$ is the $n~ \times ~q$ matrix of the constituents of known forms. In the LSSA or ALLSSA, the coefficients of constituents of known forms are estimated as follows:

$$\underline {{{\mathbf{\hat {c}}}}} ={\left( {{{\underline {{\mathbf{\Phi }}} }^{\text{T}}}{\mathbf{P}}~\underline {{\mathbf{\Phi }}} } \right)^{ - 1}}{\underline {{\mathbf{\Phi }}} ^{\text{T}}}{\mathbf{P}}~{\mathbf{f}}$$

(3)

that is a column vector of size $q$. Therefore, the residual series is ${\mathbf{\hat {g}}}=~{\mathbf{f}}~ - ~\underline {{\mathbf{\Phi }}} ~\underline {{{\mathbf{\hat {c}}}}}$. From the covariance law, the covariance matrix of $\underline {{{\mathbf{\hat {c}}}}}$ is estimated as

$${{\mathbf{C}}_{\underline {{{\mathbf{\hat {c}}}}} }}~=~\hat {\sigma }_{0}^{2}~{\left( {{{\underline {{\mathbf{\Phi }}} }^{\text{T}}}{\mathbf{P}}~\underline {{\mathbf{\Phi }}} } \right)^{ - 1}}$$

(4)

where $\hat {\sigma }_{0}^{2}=\left( {{{{\mathbf{\hat {g}}}}^{\text{T}}}{\mathbf{P}}~{\mathbf{\hat {g}}}} \right)/\left( {n - q} \right)$ is unbiased estimator (Wells and Krakiwsky 1971, Chap. 7).

Now from (3), suppose that ${\hat {c}_1}$ and ${\hat {c}_2}$ are the estimated coefficients of ${\text{cos}}\left( {2\pi {\omega _1}{\mathbf{t}}} \right)$ and ${\text{sin}}\left( {2\pi {\omega _1}{\mathbf{t}}} \right)$ whose variances $\hat {\sigma }_{1}^{2}$ and $\hat {\sigma }_{2}^{2}$ and covariance ${\hat {\sigma }_{12}}$ are obtained from the elements of ${{\mathbf{C}}_{\underline {{{\mathbf{\hat {c}}}}} }}$ in (4), respectively. To find the estimated amplitude $\hat {a}$ and phase $\hat {\theta }$, we use the following equations:

$$a~{\text{sin}}\left( {2\pi {\omega _1}t~+~\theta } \right)=~a~{\text{sin}}\left( \theta \right)~{\text{cos}}\left( {2\pi {\omega _1}t} \right)+~a~{\text{cos}}\left( \theta \right)~{\text{sin}}\left( {2\pi {\omega _1}t} \right)$$

(5)

$${\cos ^2}\left( \theta \right)~+{\sin ^2}\left( \theta \right)~=~1$$

(6)

Thus, we have ${\hat {c}_1}~=~\hat {a}~\sin \left( {\hat {\theta }} \right)$ and ${\hat {c}_2}~=~\hat {a}~\cos \left( {\hat {\theta }} \right)$, so $\hat {a}=\sqrt {\hat {c}_{1}^{2}+\hat {c}_{2}^{2}} ~$, $\hat {\theta }=2{\tan ^{ - 1}}\left( {\hat {a} - ~{{\hat {c}}_2}} \right)/{\hat {c}_1}$, where $- \pi ~<~\hat {\theta }~<~\pi$. If $F~=~F\left( {X,Y} \right)$ is a function of variables $X$ and $Y$, then the uncertainty or error in $F$ may be obtained after approximation to a first-order Taylor series:

$${\hat {\sigma }_F}=\sqrt {{{\left( {\frac{{\partial F}}{{\partial X}}} \right)}^2}\hat {\sigma }_{X}^{2}+{{\left( {\frac{{\partial F}}{{\partial Y}}} \right)}^2}\hat {\sigma }_{Y}^{2}+2\left( {\frac{{\partial F}}{{\partial X}}} \right)\left( {\frac{{\partial F}}{{\partial Y}}} \right){{\hat {\sigma }}_{XY}}~}$$

(7)

where $\partial F/\partial X$ is the partial derivative of $F$ with respect to $X$, $\hat {\sigma }_{X}^{2}$ is the variance of $X$, and ${\hat {\sigma }_{XY}}$ is the covariance between X and Y (Ku 1966). Using (7), we obtain

$${\hat {\sigma }_{\hat {a}}}=\left( {1/\hat {a}} \right)~\sqrt {\hat {c}_{1}^{2}\hat {\sigma }_{1}^{2}+\hat {c}_{2}^{2}\hat {\sigma }_{2}^{2}+2{{\hat {c}}_1}{{\hat {c}}_2}~{{\hat {\sigma }}_{12}}~}$$

(8)

$${\hat {\sigma }_{\hat {\theta }}}=\frac{{2\sqrt {\left( {({{\hat {c}}_2}/{{\hat {c}}_1}} )( {\hat {a} - ~{{\hat {c}}_2}} )\right){^2}~\hat {\sigma }_{1}^{2}+{{( {\hat {a} - ~{{\hat {c}}_2}} )}^2}\hat {\sigma }_{2}^{2} - 2({{\hat {c}}_2}/{{\hat {c}}_1}){{( {\hat {a} - ~{{\hat {c}}_2}} )}^2}~{{\hat {\sigma }}_{12}}} }}{{\left| {\hat {a}~{{\hat {c}}_1}} \right|\left( {1+{{\left( {\hat {a} - ~{{\hat {c}}_2}} \right)}^2}/\hat {c}_{1}^{2}} \right)~}}~$$

(9)

that are the errors of $\hat {a}$ and $\hat {\theta }$, respectively.