Influence of the sensitivity of plastic deformation to the third invariant on the stress state achievable during stretch forming of isotropic materials

Abstract

For isotropic materials, the von Mises yield criterion is generally used to interpret bulge test data and assess formability. In this paper, we investigate the role played by the ${J}_{3}$ dependence of the plastic response on the behavior during stretch forming under pressure. To this end, we consider the isotropic yield criterion of Drucker, which involves a unique parameter c expressible solely in terms of the ratio between the yield stresses in shear and uniaxial tension, ${\tau }_{Y}/{\sigma }_{T}$. In the case when ${\tau }_{Y}/{\sigma }_{T}=\sqrt{3}$, the parameter c = 0 and the von Mises yield criterion is recovered, otherwise Drucker’s criterion accounts for dependence on both ${J}_{2}$ and ${J}_{3}$. First, an analytical estimate of the ratio of the principal stresses at the apex of the dome is deduced. It is demonstrated that the stress ratio depends on the parameter c, the deviation from an equibiaxial stress state induced by changing the die aspect ratio is more pronounced for materials with higher ${\tau }_{Y}/{\sigma }_{Y}$ ratio. Finite element predictions using the yield criterion and isotropic hardening confirm the trends put into evidence theoretically. Moreover, the F.E. simulations show that there is a correlation between the value of the parameter c that describes the dependence on ${J}_{3}$ in the model and the strain paths that can be achieved in any given test, the level of plastic strains that develop in the dome, and the thickness reduction. Specifically, for a material characterized by c > 0 (${\tau }_{Y}/{\sigma }_{T}<1/\sqrt{3}$) under elliptical bulging, at the apex the plastic strain ratio is greater than in the case of a von Mises material, while the stress ratio is less. On the other hand, for a material characterized by c < 0 (${\tau }_{Y}/{\sigma }_{T}>1/\sqrt{3}$), the reverse holds true. The FE results also suggest that for certain isotropic materials neglecting the dependence of their plastic behavior on ${J}_{3}$ would lead to an underestimation of the thickness reduction.

Appendix : Proof of the unicity of the solution for the stress ratio Ω∞ in the interval (1,+∞)

Proof of the unicity of the solution for the stress ratio ${\varvec{\Omega}}$ in the interval $\left(1,+\mathbf{\infty }\right)$.

The stress ratio $\Omega$, with $\Omega \ge$ 1, is the solution of the algebraic equation $g\left(\Omega \right)={p}_{5}{\Omega }^{5}+{p}_{4}{\Omega }^{4}+{p}_{3}{\Omega }^{3}+{p}_{2}{\Omega }^{2}+{p}_{1}\Omega +{p}_{0}$=0,

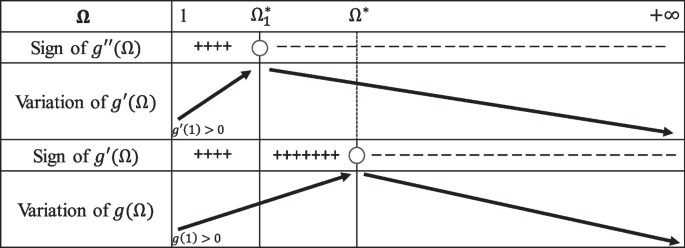
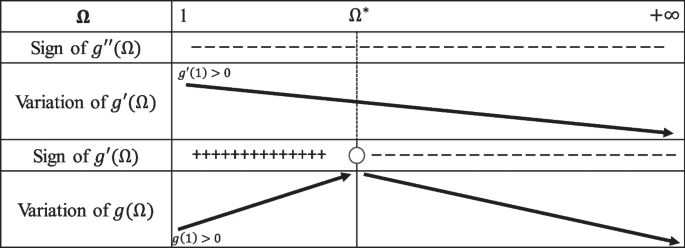
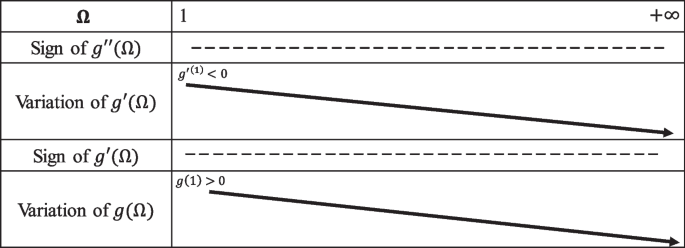
the coefficients ${p}_{k}$ $(k=0...5)$ depending on the die ratio b and the material parameter c, their expressions being given by Eq. (12). The parameter c in Drucker’s yield criterion belongs to: $-3.375\le c\le 2.25$. Irrespective of the value of the parameter c in this range, the equation $g\left(\Omega \right)$=0 admits a unique solution in the interval $\left(1,+\infty \right)$. The key arguments of the proof are shown in Figures 12, 13 and 14 which provide the variation of $g\left(\Omega \right)$ and its derivatives. Detailed explanations are given in the following.

The first derivative of $g\left(\Omega \right)$ is a 4th order polynomial, which is expressed as

$${g}^{\mathrm{^{\prime}}}\left(\Omega \right)=5{p}_{5}{\Omega }^{4}+4{p}_{4}{\Omega }^{3}+3{p}_{3}{\Omega }^{2}+2{p}_{2}\Omega +{p}_{1}$$

(A1)

Since $\beta \ge 1$ and the parameter c in Drucker’s yield criterion belongs to: $-3.375\le c\le 2.25$, we have ${p}_{1}\le 0$ and ${p}_{5}\le 0$, so $g{\prime}\left(0\right)<0$ and $\underset{\Omega \to \infty }{{\text{lim}}}{g}{\prime}\left(\Omega \right)=-\infty$.

The second derivative of $g\left(\Omega \right)$ is the 3rd order polynomial given by

$${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)=20{p}_{5}{\Omega }^{3}+12{p}_{4}{\Omega }^{2}+6{p}_{3}\Omega +2{p}_{2}$$

(A2)

while the 3rd order derivative of $g\left(\Omega \right)$ is the 2nd order polynomial

$${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)=6\left(10{p}_{5}{\Omega }^{2}+4{p}_{4}\Omega +{p}_{3}\right)$$

(A3)

It can be easily shown that ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)\le 0$ for any $\Omega \ge 1$.

Indeed, in order to determine the sign of ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)$, we need to calculate the discriminant of the equation ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)=0$, which is:

$$\Delta =16{p}_{4}^{2}-40{p}_{5}{p}_{3}$$

(A4)

By substituting Eq. (12) for the coefficients ${p}_{k}$ in Eq. (A4) and straightforward calculations we obtain that the sign of the discriminant $\Delta$ is the sign of

$$\left(8c+27\right)\left(\begin{array}{c}2c\left(11{\beta }^{2}+20\beta +20\right)\\ -27\left({\beta }^{2}+10\beta +10\right)\end{array}\right)$$

Therefore, $\Delta =0$ has the roots

$$\begin{array}{c}{c}_{1}=\frac{27\left({\beta }^{2}+10\beta +10\right)}{2\left(11{\beta }^{2}+20\beta +20\right)}\\ {c}_{2}=-\frac{27}{8}\end{array}$$

(A5)

Note that ${c}_{1}>2.25$ for any $\beta \in \left[\mathrm{1,2}\right].$

Given that$-27/8\le c\le 2.25$, it follows that for any value of the material parameter$c$, we have$\Delta \le 0$. This means that the sign of ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)$ is the sign of ${p}_{5}$ (see Eq. (A3)). Since ${p}_{5}\le 0$, it follows that ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)\le 0$.

Therefore, ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\left(\Omega \right)}$ is monotonically decreasing for any $\Omega \ge 1$.

Next, we determine the sign of ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\left(\Omega \right)}$.

Given that

$${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(1\right)=-\frac{4c}{243}\left(11\beta +13\right)-\frac{14}{9}+\frac{2\beta }{9}$$

(A6)

we have:

$$\begin{array}{c}{g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(1\right)\le 0\ \ \ \mathrm{ if } \ \ \ c \ge \frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)}\\ {g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(1\right)>0 \ \ \ \mathrm{ if } \ \ \ c<\frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)}\end{array}$$

(A7)

Therefore we need to consider the following cases.

• Case 1:$-27/8 \le c<\frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)}$,

Since for this range of variation of the parameter c, ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(1\right)>0$ and ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}$ is monotonically decreasing for any $\Omega \ge 1$, it follows that the equation ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)=0$ has a unique real solution, ${\Omega }_{1}^{*}$, in the interval ($1,+\infty$). Moreover, ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)\le 0$ for any $\Omega \ge {\Omega }_{1}^{*}$. Therefore,

• –for $\Omega \in \left[1,{\Omega }_{1}^{*}\right]$:$g{\mathrm{^{\prime}}}\left(\Omega \right)$ is monotonically increasing

and

• –for $\Omega >{\Omega }_{1}^{*}:$ $g{\mathrm{^{\prime}}}\left(\Omega \right)$ is monotonically decreasing (see also Fig. 12).

Next, let us examine the sign of $g{\mathrm{^{\prime}}}\left(\Omega \right)$.

Since

$${g}^{\mathrm{^{\prime}}}\left(1\right)=-\frac{2c}{243}\left(11\beta +1\right)+\frac{\beta }{9}-\frac{4}{9}$$

(A9)

it follows that:

$${g}^{\mathrm{^{\prime}}}\left(1\right)>0 \ \ \ \mathrm{if } \ \ \ c<\frac{27\left(\beta -4\right)}{2\left(11\beta +1\right)}$$

(A10)

Given that for $\beta \ge 1$,

$$\frac{\beta -4}{11\beta +1}\ge \frac{\beta -7}{11\beta +13}$$

(A11)

it follows that for $-27/8 \le c<\frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)}$, we have ${g}^{\mathrm{^{\prime}}}\left(1\right) >0$. Therefore, the equation ${g}^{\mathrm{^{\prime}}}\left(\Omega \right)=0$ admits a unique real solution ${\Omega }^{*}$ in the interval $\left(1,+\infty \right)$. This means that the function $g\left(\Omega \right)$ is monotonically increasing for $\Omega \in \left[1,{\Omega }^{*}\right]$ and monotonically decreasing for any $\Omega \ge {\Omega }^{*}$. Since $g\left(1\right)>0$, it follows that the equation $g\left(\Omega \right)=0$ has a unique solution in the interval $\left(1,+\infty \right)$ (see also Fig. 12, which shows the variation of $g\left(\Omega \right)$ and its derivatives for the given range of the parameter c).

• Case 2: For $\frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)}\le c\le \frac{27\left(\beta -4\right)}{2\left(11\beta +1\right)}$, we have ${g}{\mathrm{^{\prime}}}\left(1\right) \ge 0$ (see Eq. (A9)) and $g\mathrm{^{\prime}}\mathrm{^{\prime}}\left(1\right) <0$ (see Eq.(A7). Therefore, ${g}^{\mathrm{^{\prime}}}\left(\Omega \right)=0$ admit a unique real solution, ${\Omega }^{*}$, for any $\Omega \ge 1$. Thus, the function $g\left(\Omega \right)$ is monotonically increasing for $\Omega \in \left[1,{\Omega }^{*}\right]$ and monotonically decreasing for $\Omega \ge {\Omega }^{*}$. Since $g\left(1\right)>0$, it follows that the equation $g\left(\Omega \right)=0$ has a unique solution in the interval $\left(1,+\infty \right)$ (see also Fig. 13).

• Case 3: For$\frac{27\left(\beta -7\right)}{2\left(11\beta +13\right)} \le c \le 2.25$, we have ${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\Omega \right)\le 0$ for any $\Omega \ge 1$. Therefore, ${g}^{\mathrm{^{\prime}}}\left(\Omega \right)$ is monotonically decreasing. Also For $c>\frac{27\left(\beta -4\right)}{2\left(11\beta +1\right)},{g}{\mathrm{^{\prime}}}\left(1\right)<0$ (See Eq. (A9)), therefore the function $g\left(\Omega \right)$ is monotonic decreasing for any $\Omega \ge 1$ and since $g\left(1\right)\ge 0$, there is a unique solution to the equation $g\left(\Omega \right)=0$ in the interval $\left(1,+\infty \right)$ (see also Fig. 14).

See Fig. 12, 13 and 14.

Fig. 12

Table of variation for the function ${\text{g}}\left(\Omega \right)$ in the interval $\left(1,+\infty \right)$ for the case:$-27/8 \le {\text{c}}<\frac{27\left(\upbeta -7\right)}{2\left(11\upbeta +13\right)}$

Fig. 13

Table of variation for the function ${\text{g}}\left(\Omega \right)$ in the interval $\left(1,+\infty \right)$ for the case: $\frac{27\left(\upbeta -7\right)}{2\left(11\upbeta +13\right)}\le {\text{c}}\le \frac{27\left(\upbeta -4\right)}{2\left(11\upbeta +1\right)}$

Fig. 14

Table of variation for the function ${\text{g}}\left(\Omega \right)$ in the interval $\left(1,+\infty \right)$ for the case: $\frac{27\left(\upbeta -7\right)}{2\left(11\upbeta +13\right)} \le \mathrm{c }\le 2.25$