1 Introduction

A wide range of theoretical and practical problems arise in various fields of mathematical, economical, physical, and engineering sciences which can be formulated as a polynomial equation of degree n with arbitrary real or complex coefficient:

$$\begin{aligned} f(x)=x^{n}+a_{n-1}x^{n-1}+\cdots+a_{0}= \prod_{j=1}^{{n}}(x-\zeta _{j})=(x-\zeta _{i}) \mathop{\prod _{j=1}}_{j\neq i}^{n}(x-\zeta _{j}), \end{aligned}$$
(1)

where \(\zeta _{1}\cdots \zeta _{n}\) denote all the simple or complex roots of (1). Approximating all roots of the nonlinear polynomial equation using simultaneous methods has a lot of applications in sciences and engineering because simultaneous iterative methods are less time consuming since they can be implemented for parallel processing as well. Further details about their convergence properties, computational efficiency, and parallel processing may be found in [1–25] and the references cited there in. The main objective of this paper is to develop simultaneous methods which have a higher convergence order and are more efficient as compared to the existing methods. A very high computational efficiency is achieved by using two suitable corrections [26, 27] with convergence orders equal to ten and twelve with a minimal number of function evaluations in each step.

1.1 Construction of simultaneous methods for multiple roots

Consider two-step fourth-order Newton’s method [26] for finding multiple roots of nonlinear equation (1)

$$\begin{aligned} \textstyle\begin{cases} y_{i}=x_{i}-\sigma \frac{f(x_{i})}{f^{{\prime }}(x_{i})}, \\ z_{{i}}=y_{i}-\sigma \frac{f(y_{i})}{f^{{\prime }}(y_{i})},\end{cases}\displaystyle \end{aligned}$$
(2)

where σ is the multiplicity of exact root, say ζ, of (1). We would like to convert (2) into a simultaneous method for extracting all the distinct as well as multiple roots of (1). We use the third-order Dong et al. method [26] as a correction to increase the efficiency and convergence order requiring no additional evaluation of the function:

$$\begin{aligned} \textstyle\begin{cases} v_{i}=x_{i}-\sqrt{\sigma }\frac{f(x_{i})}{f^{{\prime }}(x_{i})}, \\ u_{{i}}=v_{i}-\sigma (1-\frac{1}{\sqrt{\sigma }})^{1-\sigma } \frac{f(v_{i})}{f^{{\prime }}(x_{i})}.\end{cases}\displaystyle \end{aligned}$$
(3)

Suppose that the nonlinear polynomial equation (1) has n roots. Then

$$\begin{aligned} f(x)=\prod_{i=1}^{n} ( x-x_{i} ) \quad\text{and}\quad f^{{ \prime }}(x)=\sum_{j=1}^{n} \mathop{\prod_{j=1}}_{j\neq i}^{{n}} ( x-x_{i} ). \end{aligned}$$
(4)

This implies

$$\begin{aligned} \frac{f(x_{i})}{f^{{\prime }}(x_{i})}=\sum_{\overset{j=1}{j\neq i}}^{n}\frac{1}{(x-x_{i})}= \frac{1}{\frac{1}{x-x_{i}}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{1}{(x-x_{j})}}. \end{aligned}$$

This gives

$$\begin{aligned} x-x_{i}= \frac{1}{\frac{1}{N_{i}(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{1}{(x-x_{j})}}, \end{aligned}$$

where \(\frac{1}{N_{i}(x_{i})}=\frac{f^{{\prime }}(x_{i})}{f(x_{i})}\) or

$$\begin{aligned} \frac{f(x_{i})}{f^{{\prime }}(x_{i})}= \frac{1}{\frac{1}{N_{i}(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{1}{(x-x_{j})}}. \end{aligned}$$
(5)

The multiple root equation (5) can be written as

$$\begin{aligned} \sigma _{i}\frac{f(x_{i})}{f^{{\prime }}(x_{i})}= \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x-x_{j})}}. \end{aligned}$$
(6)

Replacing \(x_{j}\) by \(x_{j}^{\ast }\) in (6), we have

$$\begin{aligned} \sigma _{i}\frac{f(x_{i})}{f^{{\prime }}(x_{i})}= \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x-x_{j}^{\ast })}}, \end{aligned}$$
(7)

where

$$\begin{aligned} x_{j}^{\ast }=u_{j} \quad\bigl(\text{using } \text{(3)}\bigr). \end{aligned}$$

Using (7) in the first step of (2), we have

$$\begin{aligned} \textstyle\begin{cases} y_{i}^{(k)}=x_{i}^{(k)}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(x_{i}^{(k)})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}^{(k)}-x_{j}^{{*(k)} })}}, \quad k=0,1,\ldots, \\ z_{{i}}^{(k)}=y_{i}^{(k)}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(y_{i}^{(k)})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}^{(k)}-y_{j}^{(k)})}}.\end{cases}\displaystyle \end{aligned}$$
(8)

Thus we have constructed a new simultaneous method (8) abbreviated as MNS10M for extracting all distinct as well as multiple roots of polynomial equation (1).

1.2 Convergence analysis

In this section, the convergence analysis of a family of two-step simultaneous methods (8) given in a form of the following theorem is presented.

Theorem 1

Let \(\zeta _{{1}},\ldots,\zeta _{n}\) be simple roots of (1). If \(x_{1}^{(0)},\ldots, x_{n}^{(0)}\) are the initial approximations of the roots respectively and sufficiently close to the actual roots, then the order of convergence of method (8) equals ten.

Proof

Let \(\epsilon _{i}=x_{i}-\zeta _{i},\epsilon _{i}^{\prime }=y_{i}-\zeta _{i} \), and \(\epsilon _{i}^{{\prime \prime }}=z_{i}-\zeta _{i}\) be the errors in \(x_{i}\), \(y_{i}\), and \(z_{i}\) approximations respectively. Consider the first step of (8), which is

$$\begin{aligned} y_{i}=x_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-x_{j}^{\ast })}}, \end{aligned}$$

where \(N(x_{i})=\frac{f(x_{i})}{f^{\prime }(x_{i})}\). Then, obviously, for distinct roots, we have

$$\begin{aligned} \frac{1}{N(x_{i})}=\frac{f^{\prime }(x_{i})}{f(x_{i})}=\sum_{j=1}^{n} \frac{1}{(x_{i}-\zeta _{j})}=\frac{1}{(x_{i}-\zeta _{i})}+\sum_{ \overset{j=1}{j\neq i}}^{n} \frac{1}{(x_{i}-\zeta _{j})}. \end{aligned}$$

Thus, for multiple roots, we have from (8)

$$\begin{aligned} &y_{i}=x_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{(x_{i}-\zeta _{i})}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-x_{{j}}^{\ast })}}, \\ &y_{i}-\zeta _{i}=x_{i}-\zeta _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{(x_{i}-\zeta _{i})}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}(x_{i}-x_{j}^{\ast }-x_{i}+\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-x_{{j}}^{\ast })}}, \\ &\epsilon _{i}^{\prime }=\epsilon _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{\epsilon _{i}}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{j}(x_{j}^{\ast }-\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-x_{j}^{\ast })}} =\epsilon _{i}- \frac{\sigma _{i}\epsilon _{i}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{j}(x_{j}^{\ast }-\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-x_{j}^{\ast })}} =\epsilon _{i}- \frac{\sigma _{i}.\epsilon _{i}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}E_{i}\epsilon _{j}^{3}}, \end{aligned}$$

where \(x_{j}^{\ast }-\zeta _{j}=\epsilon _{j}^{3}\) [26] and \(E_{i}= \frac{-\sigma _{j}}{(x_{i}-\zeta _{j})(x_{i}-x_{j}^{\ast })}\).

Thus

$$\begin{aligned} \epsilon _{i}^{{\prime }}= \frac{\epsilon _{i}^{2}\sum_{\overset{j=1}{j\neq i}}^{n}E_{i}\epsilon _{j}^{3}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}E_{i}\epsilon _{j}^{3}}. \end{aligned}$$
(9)

If it is assumed that absolute values of all errors \(\epsilon _{j}\ (j=1,2,3,\ldots)\) are of the same order as, say, \(\vert \epsilon _{j} \vert =O \vert \epsilon \vert \), then from (9) we have

$$\begin{aligned} \epsilon _{i}^{{\prime }}=O(\epsilon )^{5}. \end{aligned}$$
(10)

From the second equation of (8), we get

$$\begin{aligned} &z_{i}=y_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N(y_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{j})}}, \\ &z_{i}-\zeta _{i}=y_{i}-\zeta _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{y_{i}-\zeta _{i}}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{{j}})}}, \\ &\epsilon _{i}^{{\prime \prime }}=\epsilon _{i}^{\prime }- \frac{\sigma _{i}}{\frac{\sigma _{i}}{\epsilon _{i}^{\prime }}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{{j}})}} =\epsilon _{i}^{ \prime }- \frac{\sigma _{i}.\epsilon _{i}^{\prime }}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}.(y_{i}-y_{j}-y_{i}+\zeta _{j})}{(y_{i}-\zeta _{j})(y_{i}-y_{j})} ) } \\ &\phantom{\epsilon _{i}^{{\prime \prime }}} = \epsilon _{i}^{\prime }- \frac{\sigma _{i}.\epsilon _{i}^{\prime }}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{{j}}.(y_{{j}}-\zeta _{j})}{(y_{i}-\zeta _{j})(y_{i}-y_{j})} ) -\epsilon _{i}^{{\prime }}\alpha } =\epsilon _{i}^{\prime }- \frac{\sigma _{i}\epsilon _{i}^{{\prime }}}{\sigma _{i}+\epsilon _{i}^{{\prime }}\sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}F_{i}-\epsilon _{i}^{{\prime }}\alpha }, \end{aligned}$$

where \(F_{i}=\frac{-\sigma _{j}}{(y_{i}-\zeta _{j})(y_{i}-y_{j})}\). This implies

$$\begin{aligned} \epsilon _{i}^{{\prime \prime }}=\epsilon _{i}^{{\prime }}- \frac{\sigma _{i}.\epsilon _{i}^{{\prime }}}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}F_{i}-\alpha \epsilon _{i}^{{\prime }} ) } =\bigl(\epsilon _{i}^{{\prime }} \bigr)^{2} \biggl( \frac{\sum_{\overset{j=1}{ j\neq i}}^{n}F_{i}-\alpha }{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}F_{i}-\alpha ) } \biggr) =\bigl(\epsilon _{i}^{{\prime }}\bigr)^{2}C_{i}, \end{aligned}$$

where \(C_{i}= \frac{\sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}F_{i}-\alpha }{\sigma _{i}+\epsilon _{i}^{{\prime }}\sum_{\overset{j=1}{j\neq i}}^{n}(\epsilon _{j}^{{\prime }}F_{i}-\epsilon _{i}^{{\prime }}\alpha )}\). By (10), \(\epsilon _{i}^{{\prime }}=O(\epsilon )^{5}\) and thus

$$\begin{aligned} \epsilon _{i}^{{\prime \prime }} =O\bigl((\epsilon )^{5} \bigr)^{2}=O(\epsilon )^{10}, \end{aligned}$$

which shows that the convergence order of method (8) is ten. Hence we have proved the theorem. □

1.3 Improvement of efficiency and convergence order

To improve the convergence order of method (8) from 10 to 12, using same function evaluation, we use

$$\begin{aligned} Z_{j}^{\ast }=v_{j}-\sigma _{j} \frac{f(v_{j})}{f^{{\prime }}(v_{j})}\quad\text{and}\quad v_{j}=x_{j}-\sqrt{ \sigma _{j}} \frac{f(x_{j})}{f^{{\prime }}(x_{j})} \end{aligned}$$

instead of \(x_{j }^{\ast }=\) \(Z_{j}^{\ast }\) in (7), i.e.,

$$\begin{aligned} \sigma _{i}\frac{f(x_{i})}{f^{{\prime }}(x_{i})}= \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-Z_{j}^{\ast })}}, \end{aligned}$$
(11)

where \(Z_{j}^{\ast }\) is a fourth-order method [27]. Using (11) in the first step of (2), we have

$$\begin{aligned} \textstyle\begin{cases} y_{i}^{(k)}=x_{i}^{(k)}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(x_{i}^{(k)})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}^{(k)}-Z_{j}^{{*(k)} })}}, \\ z_{{i}}^{(k)}=y_{i}^{(k)}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N_{i}(y_{i}^{(k)})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}^{(k)}-y_{j}^{(k)})}}.\end{cases}\displaystyle \end{aligned}$$
(12)

Thus we have constructed a new simultaneous method (12), abbreviated as MNS12M for extracting all multiple roots of polynomial equation (1). For multiplicity unity, we used method (12) for determing all the distinct roots of (1), abbreviated as MNS12D.

1.4 Convergence analysis

In this section, the convergence analysis of a family of two-step simultaneous methods (12) is given in a form of the following theorem.

Theorem 2

Let \(\zeta _{{1}},\zeta _{{2}},\ldots,\zeta _{n}\) be simple roots of (1). If \(x_{1}^{(0)}\), \(x_{2}^{(0)}\), \(x_{3}^{(0)},\ldots, x_{n}^{(0)}\) are the initial approximations of the roots respectively and sufficiently close to the actual roots, then the order of convergence of method (12) equals twelve.

Proof

Let \(\epsilon _{i}=x_{i}-\zeta _{i},\epsilon _{i}^{\prime }=y_{i}-\zeta _{i} \), and \(\epsilon _{i}^{{\prime \prime }}=z_{i}-\zeta _{i}\) be the errors in \(x_{i}\), \(y_{i}\), and \(z_{i}\) approximations respectively. Consider the first step of (12), which is

$$\begin{aligned} y_{i}=x_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N(x_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-Z_{j}^{\ast })}}, \end{aligned}$$

where \(N(x_{i})=\frac{f(x_{i})}{f^{\prime }(x_{i})}\). Then, obviously, for distinct roots, we have

$$\begin{aligned} \frac{1}{N(x_{i})}=\frac{f^{\prime }(x_{i})}{f(x_{i})}=\sum_{j=1}^{n} \frac{1}{(x_{i}-\zeta _{j})}=\frac{1}{(x_{i}-\zeta _{i})}+\sum_{ \overset{j=1}{j\neq i}}^{n} \frac{1}{(x_{i}-\zeta _{j})}. \end{aligned}$$

Thus, for multiple roots, we have from (6)

$$\begin{aligned} &y_{i}=x_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{(x_{i}-\zeta _{i})}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(x_{i}-Z_{j}^{\ast })}}, \\ &y_{i}-\zeta _{i}=x_{i}-\zeta _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{(x_{i}-\zeta _{i})}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}(x_{i}-Z_{j}^{\ast }-x_{i}+\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-Z_{j}^{\ast })}}, \\ &\epsilon _{i}^{\prime }=\epsilon _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{\epsilon _{i}}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{j}(Z_{j}^{\ast }-\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-Z_{j}^{\ast })}} =\epsilon _{i}- \frac{\sigma _{i}\epsilon _{i}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{j}(Z_{j}^{\ast }-\zeta _{j})}{(x_{i}-\zeta _{j})(x_{i}-Z_{j}^{\ast })}} =\epsilon _{i}- \frac{\sigma _{i}.\epsilon _{i}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}G_{i}\epsilon _{j}^{4}}, \end{aligned}$$

where \(Z_{j}^{\ast }-\zeta _{j}=\epsilon _{j}^{4}\) [27] and \(G_{i}=\frac{-\sigma _{j}}{(x_{i}-\zeta _{j})(x_{i}-Z_{j}^{\ast })}\). Thus

$$\begin{aligned} \epsilon _{i}^{{\prime }}= \frac{\epsilon _{i}^{2}\sum_{\overset{j=1}{j\neq i}}^{n}G_{i}\epsilon _{j}^{4}}{\sigma _{i}+\epsilon _{i}\sum_{\overset{j=1}{j\neq i}}^{n}G_{i}\epsilon _{j}^{4}}. \end{aligned}$$
(13)

If it is assumed that absolute values of all errors \(\epsilon _{j}\ (j=1,2,3,\ldots)\) are of the same order as, say, \(\vert \epsilon _{j} \vert =O \vert \epsilon \vert \), then from (13) we have

$$\begin{aligned} \epsilon _{i}^{{\prime }}=O(\epsilon )^{6}. \end{aligned}$$
(14)

From the second equation of (12), we have

$$\begin{aligned} &z_{i}=y_{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{N(y_{i})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{j})}}, \\ &z_{i}-\zeta _{i}=y_{i}-\zeta _{i}- \frac{\sigma _{i}}{\frac{\sigma _{i}}{y_{i}-\zeta _{i}}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{{j}})}}, \\ &\epsilon _{i}^{{\prime \prime }} = \epsilon _{i}^{\prime }- \frac{\sigma _{i}}{\frac{\sigma _{i}}{\epsilon _{i}^{\prime }}+\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-\zeta _{j})}-\sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}}{(y_{i}-y_{{j}})}} =\epsilon _{i}^{ \prime }- \frac{\sigma _{i}\epsilon _{i}^{\prime }}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\frac{\sigma _{j}(y_{i}-y_{j}-y_{i}+\zeta _{j})}{(y_{i}-\zeta _{j})(y_{i}-y_{j})} ) }, \\ &\phantom{\epsilon _{i}^{{\prime \prime }}} = \epsilon _{i}^{\prime }- \frac{\sigma _{i}\epsilon _{i}^{\prime }}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\frac{-\sigma _{{j}}(y_{{j}}-\zeta _{j})}{(y_{i}-\zeta _{j})(y_{i}-y_{j})} ) } =\epsilon _{i}^{\prime }- \frac{\sigma _{i}\epsilon _{i}^{{\prime }}}{\sigma _{i}+\epsilon _{i}^{{\prime }}\sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}H_{i}}, \end{aligned}$$

where \(H_{i}=\frac{-\sigma _{j}}{ (y_{i}-\zeta _{j})(y_{i}-y_{j})}\). This implies

$$\begin{aligned} \epsilon _{i}^{{\prime \prime }}=\epsilon _{i}^{{\prime }}- \frac{\sigma _{i}\epsilon _{i}^{{\prime }}}{\sigma _{i}+\epsilon _{i}^{{\prime }} ( \sum_{\overset{j=1}{j\neq i}}^{n}\epsilon _{j}^{{\prime }}H_{i} ) }. \end{aligned}$$

If it is assumed that absolute values of all errors \(\epsilon _{j}\ (j=1,2,3,\ldots)\) are of the same order as, say, \(\vert \epsilon _{j} \vert =O \vert \epsilon \vert \), then we have

$$\begin{aligned} =\bigl(\epsilon _{i}^{{\prime }}\bigr)^{2} \biggl( \frac{\sum_{\overset{j=1}{j\neq i}}^{n}H_{i}}{\sigma _{i}+(\epsilon _{i}^{{\prime }})^{2} ( \sum_{\overset{j=1}{j\neq i}}^{n}H_{i} ) } \biggr) =\bigl(\epsilon _{i}^{{\prime }} \bigr)^{2}D_{i}, \end{aligned}$$

where \(D_{i}= \frac{\sum_{\overset{j=1}{j\neq i}}^{n}H_{i}}{\sigma _{i}+(\epsilon _{i}^{{\prime }})^{2}\sum_{\overset{j=1}{j\neq i}}^{n}H_{i}}\). By (14), \(\epsilon _{i}^{{\prime }}=O(\epsilon )^{6}\) and thus

$$\begin{aligned} \epsilon _{i}^{{\prime \prime }} =O\bigl((\epsilon )^{6} \bigr)^{2}=O(\epsilon )^{12}, \end{aligned}$$

which shows that the convergence order of method (12) is twelve. Hence we have proved the theorem. □

2 Computational analysis

Here we compare the computational efficiency and convergence behavior of the Petkovic et al. [28] method (abbreviated as PJM10D) and the new simultaneous iterative methods (8) and (12). As presented in [28], the efficiency of an iterative method can be estimated using the efficiency index given by

$$\begin{aligned} EF(n)=\frac{\log r}{D}, \end{aligned}$$
(15)

where D is the computational cost and r is the order of convergence of the iterative method. The number of addition and subtraction, multiplications, and divisions per iteration for all n roots of a given polynomial of degree m is denoted by \(AS_{m}\), \(M_{m}\), and \(D_{m}\). The computational cost can be approximated as

$$\begin{aligned} D=D(m)=w_{as}AS_{m}+w_{m}M_{m}+w_{d}D_{m}, \end{aligned}$$
(16)

and thus (15) becomes

$$\begin{aligned} EF(m)=\frac{\log r}{w_{as}AS_{m}+w_{m}M_{m}+w_{d}D_{m}}. \end{aligned}$$
(17)

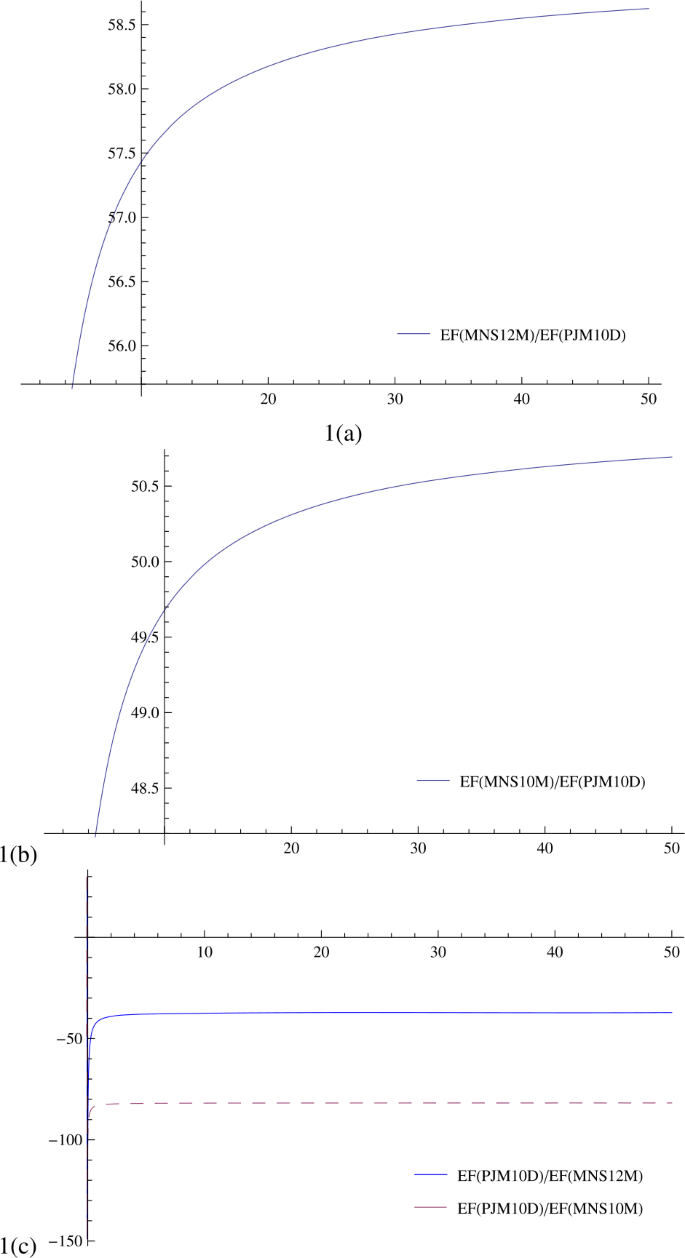
Applying (17) and by data given in Table 1, we calculate the percentage ratio \(\rho (\text{(8)},(X))\) and \(\rho (\text{(12)},(X))\) [28] given by

$$\begin{aligned} &\rho \bigl(\text{(8)},(X)\bigr) = \biggl( \frac{EF\text{(8)}}{EF(X)}-1 \biggr) \times 100\quad\text{(in percent),} \end{aligned}$$
(18)
$$\begin{aligned} &\rho \bigl(\text{(12)},(X)\bigr) = \biggl( \frac{EF\text{(12)}}{EF(X)}-1 \biggr) \times 100\quad \text{(in percent),} \end{aligned}$$
(19)

where X is the Petkovic method PJM10D. These ratios are graphically displayed in Fig. 1(a), (b), (c). It is evident from Fig. 1(a), (b), (c) that the new methods (8) and (12) are more efficient as compared to the Petkovic method PJM10D.

Figure 1
figure 1

(a)–(c) show percentage computational efficiency of simultaneous methods MNS10M, MNS12M, and PJ10D, respectively

Full size image
Table 1 Number of operations (real arithmetic)
Full size table

We also calculate the CPU execution time, as all the calculations are done using Maple 18 on (Processor Intel(R) Core(TM) i3-3110m CPU@2.4 GHz with 64-bit operating system. We observe that CPU times of the methods MMS10M and MNS12M are less than those of PJM10D, showing the dominant efficiency of our methods (8) and (12) as compared to them.

3 Numerical results

Here some numerical examples are considered in order to demonstrate the performance of our family of two-step tenth-order simultaneous methods, namely \(MNS10M\) (8) and \(MNS12M\) (12). We compare our family of methods with the Petkovic et al. [28] method of convergence of order ten for finding all distinct roots of (1) (abbreviated as PJM10D). All the computations are performed using Maple 15 with 64 digits floating point arithmetic. We take \(\in =10^{-30}\) as a tolerance and use the following stopping criteria for estimating the roots:

$$\begin{aligned} \mathrm{(i)}\quad e_{i}= \bigl\vert f \bigl( x_{i}^{ ( k+1 ) } \bigr) \bigr\vert < \in, \end{aligned}$$

where \(e_{i}\) represents the absolute error of function values in \((i)\)

Numerical test examples from [10, 28, 29] are provided in Tables 2, 3, and 4. In all tables, CO represents the convergence order, n represents the number of iterations, and CPU represents execution time in seconds. All calculations are done using Maple 15 on (Processor Intel(R) Core(TM) i3-3110m CPU@2.4 GHz with 4 GB (3.89 GB USABLE)) with 64-bit operating system. For multiplicity unity in MNS10M and MNS12M, we get the numerical results for distinct roots, i.e., MNS10D and MNS12D respectively. We observed that numerical results of the methods MNS10D, MNS10M, MNS12D, and MNS12M are comparable with those of the PJM10D method but have a lower number of iterations.

Table 2 Residual errors of simultaneous methods PJM10D, MNS10D and MNS12D for finding all the distinct roots of polynomial equation used in Example 1
Full size table
Table 3 Residual errors of simultaneous methods PJM10D, MNS10D, MNS10M, MNS12D and MNS12M for finding all the distinct as well as multiple roots of polynomial equation used in Example 2
Full size table
Table 4 Residual errors of simultaneous methods PJM10D, MNS10D, MNS10M, MNS12D and MNS12M for finding all the distinct as well as multiple roots of nonlinear equation used in Example 3
Full size table

Example 1

Consider

$$\begin{aligned} f(x) ={}&x^{12}-(2+5i)x^{11}-(1-10i)x^{10}+(12-25i)x^{9}-30x^{8}-x^{4}+(2+5i)x^{3}\\ &{}+(1-10i)x^{2} -(12-25i)x+30, \end{aligned}$$

with exact roots

$$\begin{aligned} &\zeta _{1,2} =\pm 1,\qquad \zeta _{3,4}=\pm i,\qquad \zeta _{5,6}= \frac{\sqrt{2}}{2}\pm \frac{\sqrt{2}i}{2},\qquad \zeta _{7,8}=- \frac{\sqrt{2}}{2}\pm \frac{\sqrt{2}i}{2},\qquad \zeta _{9}=2i, \\ &\zeta _{10} =3i,\qquad \zeta _{11,12}=1\pm 2i. \end{aligned}$$

The initial approximations have been taken as

$$\begin{aligned} &\overset{(0)}{x_{1}} =1.3+0.2i,\qquad \overset{(0)}{x_{2}}=-1.3+0.2i,\qquad \overset{(0)}{x}_{3}=-0.3-1.2i, \qquad\overset{(0)}{x}_{4}=-0.3+1.2i,\\ & \overset{(0)}{x}_{5}=0.5+0.5i,\qquad \overset{(0)}{x}_{6} =0.5-0.5i, \qquad\overset{(0)}{x}_{7}=-0.5+0.5i,\qquad \overset{(0)}{x_{8}}=-0.5-0.5i, \\ &\overset{(0)}{x_{9}}=-0.2+2.2i,\qquad \overset{(0)}{x}_{10}=0.2+2.3i, \qquad \overset{(0)}{x}_{11} =1.3+2.2i,\qquad \overset{(0)}{x}_{12}=1.3-2.2i. \end{aligned}$$

Example 2

Consider

$$\begin{aligned} f(x)=(x+1)^{2}(x+2)^{3}\bigl(x^{2}-2x+2 \bigr)^{2}\bigl(x^{2}+1\bigr)^{2}(x-2)^{3}(x+2-i)^{2}, \end{aligned}$$

with exact roots

$$\begin{aligned} \zeta _{1}=-1,\qquad \zeta _{2}=-2,\qquad \zeta _{3,4}=1\pm i,\qquad \zeta _{5,6}=\pm i,\qquad \zeta _{7}=2,\qquad \zeta _{8}=-2+i. \end{aligned}$$

The initial approximations have been taken as

$$\begin{aligned} &\overset{(0)}{x_{1}} =-1.3+0.2i,\qquad \overset{(0)}{x_{2}}=-2.2-0.3i,\qquad \overset{(0)}{x}_{3}=1.3+1.2i, \qquad\overset{(0)}{x}_{4}=0.7-1.2i,\\ & \overset{(0)}{x}_{5}=-0.2+0.8i,\qquad \overset{(0)}{x}_{6} =0.2-1.3i,\qquad \overset{(0)}{x}_{7}=2.2-0.3i,\qquad \overset{(0)}{x}_{8}=-2.2+0.7i. \end{aligned}$$

Example 3

Consider

$$\begin{aligned} f(x)=\bigl(e^{x(x-1)(x-2)(x-3)}-1\bigr)^{4}, \end{aligned}$$

with exact roots

$$\begin{aligned} \zeta _{1}=0, \qquad\zeta _{2}=1,\qquad \zeta _{3}=2, \qquad\zeta _{4}=3. \end{aligned}$$

The initial approximations have been taken as

$$\begin{aligned} \overset{(0)}{x_{1}}=0.1,\qquad \overset{(0)}{x_{2}}=0.9,\qquad \overset{(0)}{x}_{3}=1.8,\qquad \overset{(0)}{x}_{4}=2.9, \end{aligned}$$

3.1 Results and discussion

From Tables 2–4 and from Fig. 1(a)–(c), we conclude that

  • Our methods MNS10D and MNS12D are more efficient as compared to PJM10D in terms of the number of iterations and CPU time.

  • Our methods MNS10M and MNS12M are applicable for multiple as well as distinct roots, whereas PJM10D is applicable for distinct roots only.

4 Conclusion

We have developed here two simultaneous two-step methods of order ten and twelve, namely MNS10D, MNS10M, MNS12D, and MNS12M for determination of all the distinct as well as multiple roots of nonlinear polynomial equation (1). From Tables 1–4, we observed that our methods are very effective and more efficient as compared to the existing method PJM10D [28].